Category: Class 9

MP Board Class 9th Sanskrit Solutions Durva Chapter 2 अलसस्य स्वप्नः (कथा)

MP Board Class 9th Sanskrit Chapter 2 पाठ्य पुस्तक के प्रश्न

संस्कृत कक्षा 9 पाठ 2 प्रश्न उत्तर MP Board प्रश्न 1.
एकपदेन उत्तरं लिखत (एक शब्द में उत्तर लिखो)।
(क) विप्रपुत्रस्य नाम किम् आसीत्? (विप्र पुत्र का नाम क्या था?)
उत्तर:
विप्रपुत्रस्य नाम सोम शर्मा आसीत्। (विप्र पुत्र का नाम सोम शर्मा था।)

(ख) सक्तुभिः कति रुप्यकाणि उत्पत्स्यन्ते? (सत्तू से कितने रुपये हुये?)
उत्तर:
सक्तुभिः शतम् रुप्यकाणि उत्पस्यन्ते (सत्तू से सौ रुपये हुए।)

(ग) विप्रः कं सततम् अवलोकयति? (विप्र किसे एकटक देख रहा था?)
उत्तर:
विप्रः सक्तुम सततम् अवलोकयति। (विप्र सत्तू को एकटक देख रहा था।)

(घ) अश्वानां विक्रयात् किं भविष्यति? (घोड़ों को बेचने से क्या होगा?)
उत्तर:
अश्वानां विक्रयात् सुवर्णम् भविष्यति। (घोड़ों को बेचने से स्वर्ण मुद्रा आयेगी।)

(ङ) विप्रस्य प्रहारेण कः भग्नः? (विप्र के प्रहार से क्या टूट गया?)
उत्तर:
विप्रस्य प्रहारेण घटः भग्नः। (विप्र के प्रहार से घड़ा टूट गया।)

संस्कृत कक्षा 9 पाठ 2 Question Answer MP Board प्रश्न 2.
एक वाक्येन उत्तर लिखत् (एक वाक्य में उत्तर लिखो)
(क) विप्रः स्वपत्नी किम् अभिधारयति? (ब्राह्मण अपनी पत्नी से क्या बोलेगा?)
उत्तर:
गृहाण तावद् बालकम्। (अपने बच्चे को पकड़ो।)

(ख) घट कैः सम्पूरितः? (घड़े में क्या भरा था?)
उत्तर:
सक्तुभिः। (सत्तू)।

(ग) सुवर्णेन किं सम्मत्स्यत्? (स्वर्ण मुद्रा से क्या बनेगा?)
उत्तर:
चतुः शालम् गृहम्। (चौकोर घर)।

(घ) सोम शर्मा कुतः विप्रसमीपम् आगच्छति? (सोम शर्मा ब्राह्मण के पास कहां आयेगा?)
उत्तर:
अश्वखुरासन्नवर्ती। (घुड़साल में मेरे समीप)।।

(ङ) विप्रः पुत्रम् कुतः अवधारयिष्यति? (ब्राह्मण पुत्र को कहां ग्रहण करेगा?)
उत्तर:
अश्वशालयः पृष्ठदेशे। (घुड़साल के पीछे)।

संस्कृत कक्षा 9 पाठ 2 सवाल जवाब MP Board प्रश्न 3.
अधोलिखित प्रश्नानाम् उत्तराणि लिखत् (नीचे लिखे प्रश्नों के उत्तर लिखो)
(क) सोम शर्मा पितरं दृष्ट्वा किं करिष्यति? (सोम शर्मा पिता को देखकर क्या करेगा?)
उत्तर:
ितु समीपम् आगमिष्यति। (पिता को देखकर उसके पास जायेगा।)

(ख) विप्रः रात्रो सुप्तः किं चिन्तयामास? (ब्राह्मण रात में सोते हुए क्या विचार किया?)
उत्तर:
अयं घटः सक्तुभि परिपूर्णः वर्तते। (इस घेड़े में सत्तू भरा हुआ है।)

(ग) विप्रः कं कदा कुतश्च अवधारिष्यति? (ब्राह्मण किसको कहा और कब धारण करेगा?)
उत्तर:
पुत्रम् अश्वशालायाः पृष्ठ देशे। (पुत्र को अश्वशाला के पीछे के भाग में ब्राह्मण ग्रहण करेगा।)

(घ) यदा दुर्भिक्षं भविष्यति तदा सक्तुभिः किंकिंभविष्यति? (जब अकाल होगा तब सत्तू के द्वारा क्या-क्या होगा?)
उत्तर:
स्वकणाम् सतम्। (अकाल के समय सैकड़ों रुपये सत्तू से प्राप्त होंगे)

(ङ) अस्याः कथायाः आशयः कः? (इस कथा का सार क्या है?)
उत्तर:
अविचार्यं न कर्तव्यम्। (बिना विचारे कोई कार्य नहीं करना चाहिए।) यही इस कथा का सार है।)

संस्कृत कक्षा 9 पाठ 2 MP Board प्रश्न 4.
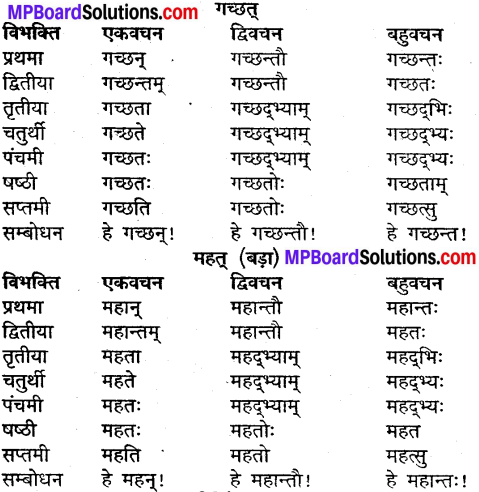
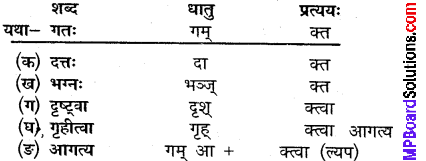
उदाहरणानुसारं शब्दानां धातु प्रत्यय च पृथक कुरुत

स्वर्णकाकः प्रश्न उत्तर MP Board प्रश्न 5.
अव्ययः वाक्यनिर्माणं कुरुत
यथा- सः अत्र अस्ति।
(क) च – रमेश सुरेशश्च आपणं गच्छति।
(ख) अपि – अहं अपि भोपालम् गमिष्यामि।
(ग) तावत् – तावत् वर्षा वभूव।
(घ) न – अहं न गमिष्यामि।
(ङ) ततः – ततः पुत्रः आगतः।

संस्कृत कक्षा 9 पाठ 2 Answer MP Board प्रश्न 6.
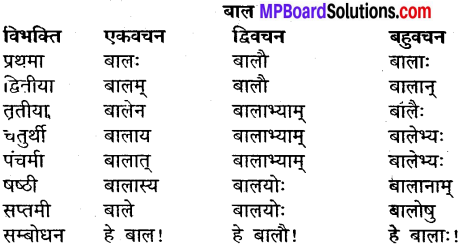
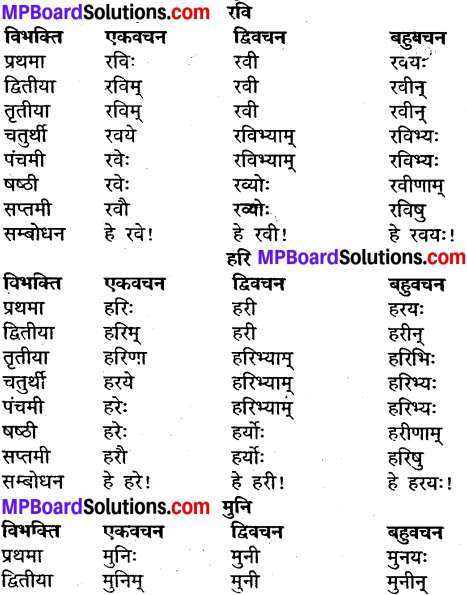
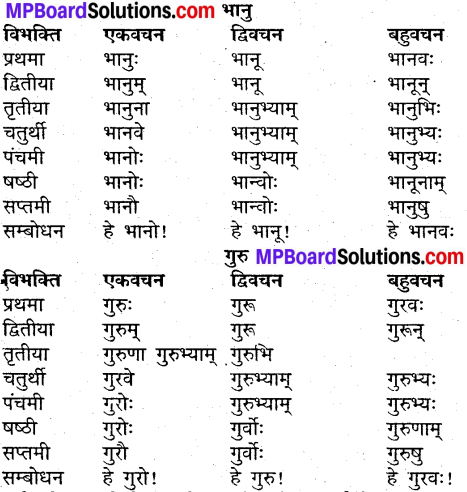
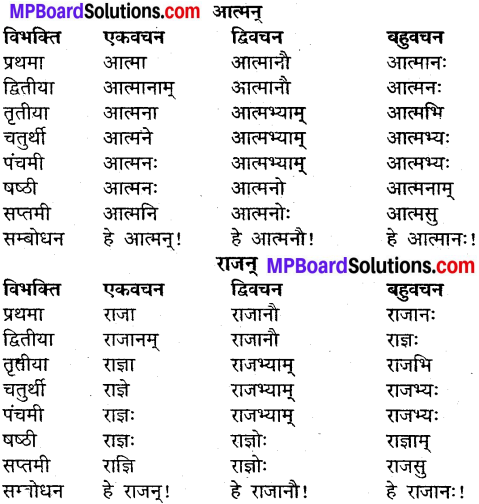
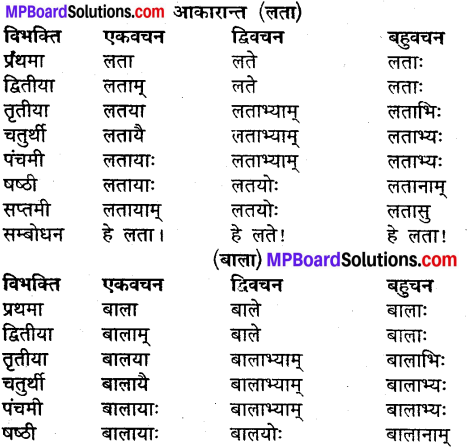
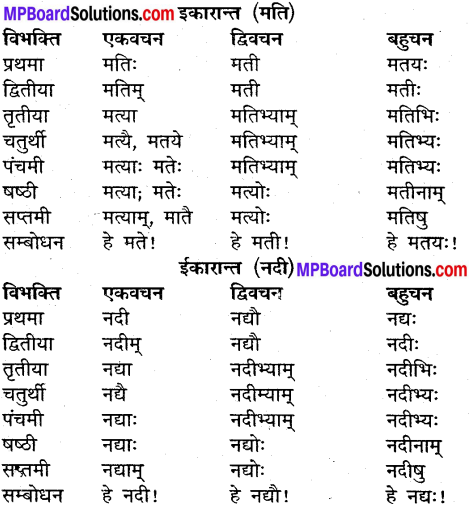
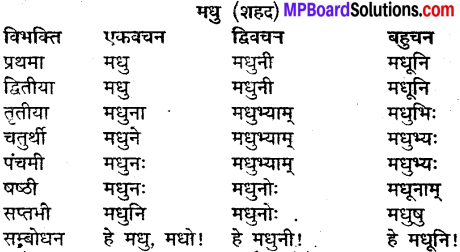
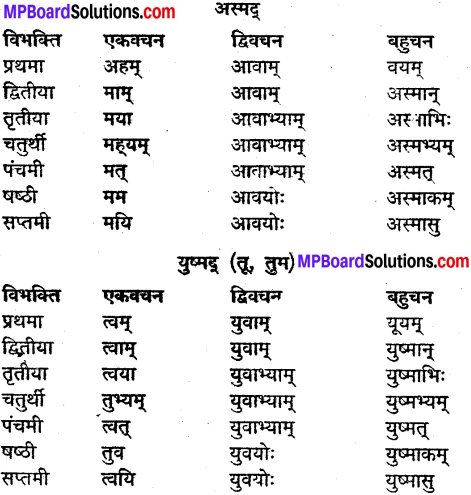
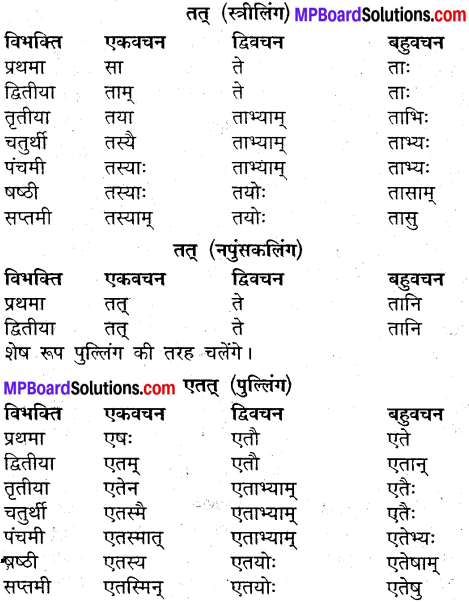
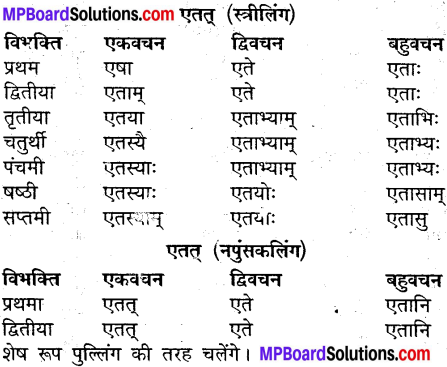
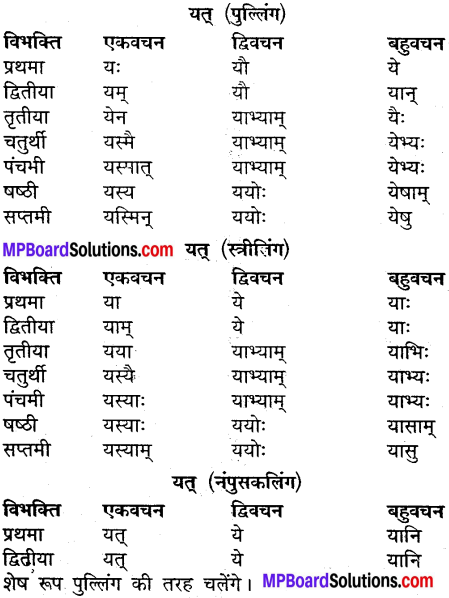
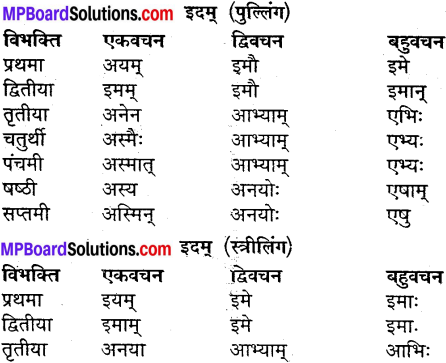
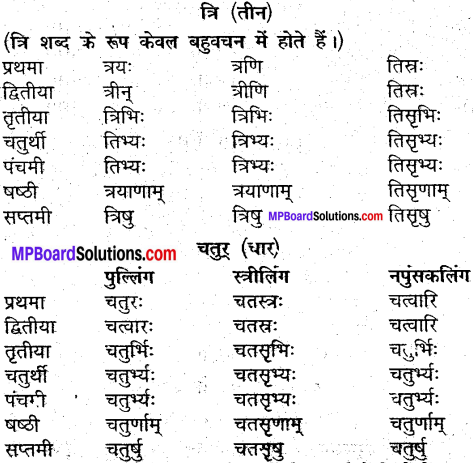
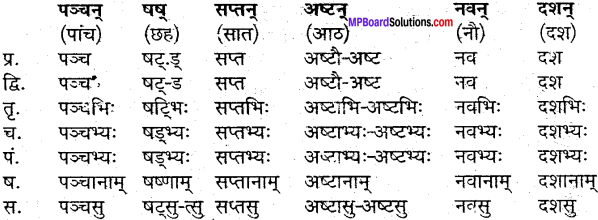
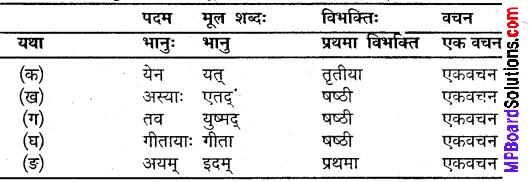
उदाहरणानुसारं शब्दानां विभक्तिं, वचनं च लिखत्

Mp Board Class 9th Sanskrit Solution प्रश्न 7.
संधिविच्छेदं कृत्वा संधिः नाम लिखत्
(क) तद्यदि
उत्तर:
तत् + यदि = व्यंजन

(ख) कदाचिद्रात्रो
उत्तर:
कदाचित् + रात्रो = व्यंजन

(ग) तदनेन
उत्तर:
तत + अनेन = व्यंजन

(घ) कश्चित
उत्तर:
कः + चित = विसर्ग

(ङ) तथैव
उत्तर:
तथा + ऐव = वृद्धि स्वर

कक्षा 9 वीं संस्कृत अध्याय 2 MP Board प्रश्न 8.
क्रियापदानां धातु लकारम्, पुरुषं च लिखत्क्रियापदम्

संस्कृत कक्षा 9 पाठ 2 Solution MP Board प्रश्न 9.
शुद्धवाक्यानां समक्षम् “आम्” अशुद्ध वाक्यानां समक्षं “न” इति लिखत्

उत्तर:
(क) न
(ख) आम्
(ग) आम्
(घ) आम्
(ङ) आम्

Class 9th Sanskrit Solution Mp Board प्रश्न 10.
रिक्तस्थानानि पूरयत् (खाली स्थान भरो)
(क) स एव पाण्डुरः शेते सोम शर्मा पिता यथा।
(ख) सुवर्णेन चतुः शालम् गृहं सम्पत्स्ये।
(ग) अजाभिः प्रभूता गा गृहीष्यामि।
(घ) तस्य अहम सोम शर्मा इति नाम करिष्यामि।
(ङ) वऽवा प्रसवतः प्रभूता अस्वाः भविष्यति

Mp Board Class 9 Sanskrit Chapter 2 प्रश्न 11.
यथायोग्यं योजयत् (सही जोड़ी बनाओ)

अलसस्य स्वप्नः पाठ-सन्दर्भ प्रतिपाद्य

यह कथा विष्णु शर्मा द्वारा रचित सुप्रसिद्ध कथा ग्रंथ ‘पंचतंत्र’ के ‘अपरीक्षित कारक’ नामक कृति से बालकों के ज्ञान-वृद्धि के उद्देश्य से ली गई है।

अलसस्य स्वप्नः पाठ का हिन्दी अर्थ

1. कस्मिंश्चिन्नगरे कश्चित् स्वभाव कृपणः विप्रः प्रतिवसति स्म। तेन भिक्षार्जितैः
भुक्तशेषैः सक्तुभिः कलशः सम्पूरितः। तं च घटं नागदन्ते अवलम्ब्य तस्याधस्तात् खट्वां निधाय सततम् एकदृष्ट्या तम् अवलोकयति।

शब्दार्थ :
कस्मिं-किसी-any; स्वभावकृपणा-स्वभाव से कँजूस-miser by nature; विप्रः-ब्राह्मण-Pandit, Wiseman; प्रतिवाति-रहता-Lives; भिक्षार्जितः-भिाक्षा के द्वारा अर्जित-Collection begging: भुक्तशेषैः-खाने से बचे हुए-Remaining food; सक्तुभिः-सत्तू-Power of Gram; तं-उसे-Complet, full, finish; च-और-him/ her/its; अवलम्ब्य-अवलंबित-Support; खटवां-खूटी-Nails; अवलोकयति-देखता था-Looks.

हिन्दी अर्थ :
किसी नगर में स्वभाव से कंजूस (कृपण) एक ब्राह्मण रहता था। वह भिक्षा से प्राप्त भोजन के बाद बचे हुए सत्तू को एक घड़े में भरता जाता। तब उस घड़े को एक खूटी से लटका कर उसके नीचे चारपाई पर बैठ घड़े को निरंतर देखता जाता।

2. अथ कदाचिद्रात्रौ सुप्तश्चिन्तयामास-यत् अयं घटः सक्तुभि परिपूर्णः वर्तते। तद्यदि दुर्भिक्षं भवति, तदनेन रुप्यकाणां शतमुत्पत्स्यते। ततस्तेन मया अजाद्वयं ग्रहीतव्यम्। ततः षाण्मासिकात् आप्रसववशात् ताभ्यां यूथंभविष्यति। ततोऽजाभिः प्रभूता गा गृहीष्यामि। गोभिर्महिषीः। महिषीभिर्वडवा। वडवाप्रसवतः प्रभूता अश्वा भविष्यन्ति। तेषां विक्रयात् प्रभूतां सुवर्णं भविष्यति। सुवर्णेन चतुः शालं गृहे सम्पत्स्यते।

शब्दार्थ :
अथ-इस प्रकार-This type; कदाचित-किसी-Anybody; सुप्त-सोते हुए-With sleeping; अयं-इस-This; सक्तुभि-सत्तू-Powder of gram; परिपूर्णः-परिपूर्ण-fulfill, over; शतमुत्पत्स्यते-सौहो जायेंगे-Hundred will be; तेन-उससे-Its; अजदूयं-दो बकरी-Two she goat; गृहीत्यम्-खरीदी जायेगी-Will have purchased; दुर्भिक्षम-अकाल-Starving; षाण्मासिकात्-छः महीने में होने वाली-Six monthly/Half yearly; ताभ्याम्-उससे-His; यूथम्-झुण्ड (समूह)-Group; गृहीष्यामि-ग्रहण करना-Will recieve; तेषां-उनके-Them; विक्रयात्-विक्रय से-From sell; प्रभूतं-बहुत अधिक-Very much; सुवर्ण-सोना-Gold; चतुःशालं-चौकोर-Square; गृहम्-घर-Home, House, Residence; सम्पत्स्यते-निर्मित करूँगा-Will build;

हिन्दी अर्थ :
तत्पश्चात् रात्रि में शयन करते समय मन में यह विचार करता कि सत्तू से यह कलश पूरी तरह भरा हुआ है। यदि अकाल पड़ जाता तो इसके द्वारा सैकड़ों रुपये प्राप्त हो जाएँगे। फिर उन रुपयों से वह दो बकरियाँ खरीदेगा। पुनः उन बकरियों से छः माह बाद पैदा होने वाले बच्चों का एक बहुत बड़ा समूह ही जाएगा। फिर वह इन बकरियों के बेचने से होने वाली आय से गायें, भैसें, भैसों से होने वाली आय से थोड़ी, उस घोड़ी से (अच्छे) किस्म के घोड़े होंगे। उन घोड़ों के बेचने से बहुत अधिक स्वर्ण प्राप्त होगा। उन स्वर्ण मुद्राओं से एक अच्छा घर निर्मित करूँगा।

3. ततः कश्चिद विप्रः मम गृहम् आगत्य रूपाढ्यां कन्यां मह्यं दास्यति। तत्सकाशात् पुत्रो मे भविष्यति। तस्य अहं “सोमशा” इति नाम करिष्यामि। ततः तस्मिञ्जानुचलन-योग्ये सजाते अहं पुस्तकंगृहीत्वा अश्वशालायाः पृष्ठदेशे उपविष्टस्तदवधारयिष्यामि। अत्रान्तरे सोमशर्मा मां दृष्ट्वा जनन्युत्सङ्गात् जानुचलनपरः अश्वखुरासन्नवर्ती मत्समीपमा गमिष्यति। ततोऽहं स्वपत्नी कोपाविष्टोऽभिधास्यामि ‘गृहाण तावद बालकम्। सा अपि गृहकर्म व्यग्रतयाऽस्मद्वचनं न श्रोष्यति। ततोऽहं समुत्थाय तं ताडयिष्यामि।

शब्दार्थ :
कश्चिद-कोई-Anybody; आगत्य-आकर-After coming; रूपाढ्यां रूपमति-Beautiful; दास्यति-देगा-Will give; तस्य-उससे-Her/Him; भविष्यति-होगा-Will/Shall; करिष्यामि-करूंगा-Will do/shall do; गृहीत्वा-ग्रहण करके-Except; जानुचलनयोग्ये-घुटने से चलने योग्य होने पर-Walking with knee, With fulfill of qualification; उत्सङ्गात्-गोद से-by lap; भग्नः-टूट गया-broke; षाण्डुरताम्-पीले रंग का-The colour of yellow; असम्भव्याम-असम्भव-Impossible; पृष्ठदेशे-पृष्ठ देश में-Behind of the stable; धारयिष्यामि-धारण करूँगा-Keep,except; तावद् बालकम-तुम्हारे बालक का-To your son; श्रोष्यति-सुना जाता है-Is listen; ताडयिस्यामि-पिटाई करूँगा-Will beating;

हिन्दी अर्थ :
तत्पश्चात् कोई ब्राह्मण मेरे घर आकर अपनी रूपवती कन्या मुझे देगा। उससे मेरा पुत्र होगा। उसका नाम मैं सोम शर्मा रलूँगा। तत्पश्चात् बालक के चलने योग्य हो जाने पर मैं पुस्तक लेकर घुड़साल के पीछे बैठकर अध्ययन करूँगा और बालक सोम शर्मा मुझे देखकर घुटने के बल घोड़े के खुरों के पास से होता हुआ घुड़साल में मेरे पास आ जाएगा। तब मैं अपनी पत्नी को गुस्से में डाँटते हुए पकड़ने को कहूँगा। वह भी गृहकार्य में व्यस्त होने के कारण मेरे वचन नहीं सुनेगी तो मैं उसकी पिटाई करूँगा।

4. एवं तेन ध्यानस्थितेन प्रहारो दत्तो यथा स घटो भग्नः स्वयं च पाण्डुरतां गतः अतोऽहं ब्रवीमि –
अनागतवती चिंताम असम्भाव्यां करोति यः।
स एव पाण्डुरः शेते सोमशर्मपिता यथा ॥

शब्दार्थ :
अनागतवतीम्-न आयी हुई को-Unreachable/miss call; ध्यानस्थितेन-ध्यान करते हुए-With meditate; ततैव-इसी प्रकार-This type; प्रहारो-प्रहार किया-Stroke.
हिन्दी अर्थ-इस प्रकार वह ब्राह्मण मन में ध्यान करते हुए उसी प्रकार प्रहार किया जिससे वह घड़ा फूट गया और ब्राह्मण (सत्तू के गिरने से) पीला पड़ गया। अतः मैं कहता हूँ –

“न आई हुई की चिंता करते हुए असंभावित कार्य की जो कल्पना करता है वह सोम शर्मा के पिता की तरह पीले रंग का हो जाता है।

MP Board Class 9th Sanskrit Solutions

MP Board Class 9th Sanskrit व्याकरण शब्द रूप

संस्कृत में तीन लिंग होते हैं-पुल्लिंग, स्त्रीलिंग और नपुंसकलिंग। ये लिंग सदा अर्थ के अनुसार नहीं होते अपितु पहले से ही निश्चिय हैं।

उदाहरणार्थ-
पत्नी, अर्थ में ‘भार्या’ शब्द स्त्रीलिंग है तो उसी अर्थ में ‘दार’ शब्द पुल्लिंग और ‘कलत्र’ शब्द नपुंसकलिंग है। यद्यपि तीनों का अर्थ एक ही है तो भी उनके लिंग भिन्न हैं। ऐसे ही ‘काय’ और ‘देह’ शब्द पुल्लिंग हैं किन्तु ‘शरीर’ शब्द नपुंसकलिंग है।

संस्कृत में सात विभक्तियां होती हैं। (प्रथमा से सप्तमी तक)। प्रत्येक विभक्ति में तीन वचन होने के कारण प्रत्येक शब्द के इक्कीस रूप बनते हैं। इसके अतिरिक्त एक वचन में सम्बोधन के रूप भिन्न होते हैं। तीनों वचनों में मूल शब्द से चिह्न जोड़े जाते हैं। विभक्ति चिह्रों को सुप् भी कहते हैं। जिस शब्द के आगे कोई विभक्ति चिह्न लगा रहता है उसे सुबन्त या पद कहते हैं। नीचे कुछ महत्त्वपूर्ण शब्दों के रूप दिए जाते हैं।

अकारान्त पुल्लिंग शब्द

टिप्पणी-जिन शब्दों का उच्चारण करने पर अन्त में ‘अ’ की ध्वनि आती है। वे आकारान्त शब्द कहलाते हैं।

अकारान्त पुल्लिंग शब्दों जैसे देव, नर, नृप, बालक, विद्यालय आदि के रूप राम शब्द की तरह चलते हैं।

इकारान्त पुल्लिंग शब्द

टिप्पणी-जिन शब्दों का उच्चारण करने पर अन्त में ‘इ’ की ध्वनि आती है, उन्हें इकारान्त शब्द कहते हैं। इकारान्त पुल्लिंग शब्दों, जैसे-कवि, कपि, गिरि, आदि के रूप रवि शब्द की तरह चलेंगे।

उकारान्त पुल्लिंग शब्द

टिप्पणी-जिन शब्दों के अन्त में ‘उ’ की ध्वनि आती है वे उकारान्त शब्द कहलाते हैं। उकारान्त पुल्लिंग शब्दों जैसे-साधु, शिशु आदि के रूप भानु शब्द की तरह चलते हैं।

ऋकारान्त पुल्लिंग शब्द

नकारान्त पुल्लिंग शब्द

स्त्रीलिंग शब्द

टिप्पणी-इसी प्रकार रमा, बालिका, प्रभा आदि आकारान्त स्त्रीलिंग शब्दों के रूप चलेंगे।

इलन्त स्त्रीलिंग वाच = वाणी

दिश = दिशा

ऋकारान्त मातृ (माता)

नपुंसकलिंग शब्द

इकारान्त नपुंसकलिंग

उकारान्त नपुंसकलिंग

सकारान्त नपुंसकलिंग

तकारान्त नपुंसकलिंग

सर्वनाम शब्द रूप

संख्यावाचक शब्दों के रूप
‘एक’ (केवल एकवचन में)

द्वि (दो) (द्वि शब्दों के रूप केवल द्विवचन में तीनों लिंगों में होते हैं। नंपुसकलिंग तथा स्त्रीलिंग के रूप एक से ही होते हैं।)

पञ्चन शब्द के आगे के संख्यावाचक शब्दों के रूप तीनों लिंगों में समान होते हैं।

संख्यावाचक शब्द

इनमें एक केवल एकवचन में वि द्विचन में तथा शेष अष्टादशन तक बहुवचन में होते हैं। उसके बाद की संख्याएं में आती हैं। यदि द्विवचन में आई तो उनके दूने का बोध होगा और बहुवचन में कई गुने का।
यथा-शते = दो सौ। शतानि = कई सौ।

MP Board Class 9th Sanskrit Solutions

MP Board Solutions for Class 9 Textbook General English Writing Skills Essay Writing Questions and Answers aids you to prepare all topics in it effectively. You need not worry about accuracy of Madhya Pradesh State Board Solutions for Class 9 English Composition: Visual Stimulus as they are given adhering to latest exam pattern and syllabus guidelines. You Can Download MP Board Class 9 English Solutions Questions and Answers, Notes, Summary, Guide pdf on is page. Enhance your subject knowledge by preparing from Chapterwise MP Board Solutions for Class 9 English and clarify your doubts on corresponding topics.

MP Board Class 9th General English Essay Writing

Kick start your preparation by using our online resource Madhya Pradesh State Board Solutions for Class 9 Textbook General English Writing Skills Essay Writing. You can even download MP Board Solutions for Class 9 English free of cost rough direct links available on our page. Clear your queries and understand concept behind in a simple manner. Simply tap on concept you wish to prepare chapterwise and go rough it.

1. My Hobby

My Hobby Essay For Class 9 MP Board Introduction :
Hobby means some work done in free time. When a man gets time after doing his r routine work, he wants to enjoy. At this time if he does some different work, it is called his hobby. Hobbies are many such as painting, playing on some instruments, photography, stamp-collecting, gardening etc.

My Hobby—My hobby is gardening. I think it is the best hobby. Plants and trees are very useful for our life. They not only provide us food to eat, but also serve us in many ways. They make the air fresh and cool for us. They check the air pollution also. Plants give us flowers. Trees give-us fruits to eat and wood to bum. So I like trees and plants very much.

My Garden—There is no ground around our house. So I have planted several kinds of flowers in flower pots. I love flowers very much. I water the plants and care for them. I bring small plants from the nursery. I prepare the flower pots and then cultivate the plants. I give fertilizer to them. When buds appear, it gives me great pleasure. I wait for their blossoming into beautiful flowers. Sometimes when I get up in the morning and see the flowers my joy knows no bounds. My parents and other family members too become very happy to see them. Guests coming to our home appreciate my hobby.

Conclusion—Sometimes we sit in our small garden and do our home work or take tea and breakfast. It gives us great joy. My mind becomes sharp and my memory is increased in the company of flowers. Sometimes I see flowers in my dream and my
heart is filled with pleasure.

2. An Indian Festival
Or
Diwali

My Hobby Essay In English For 9th Class MP Board

Introduction—Diwali is an important festival of the Hindus. It often comes in the month of October or November every year. It is celebrated in the memory of Lord Ram’s return to Ayodhya after 14 years of exile. The people of Ayodhya welcomed Lord Ram graciously. They decorated their homes with flowers and lighted earthen lamps before their houses. Diwali is a remembrance of that day.

Preparations—Several days before people start preparing for this festival. They clean their houses and whitewash them. The merchants paint their shops and set them. The market gets a new look.

How Celebrated—People buy new clothes and new dresses. They buy many things for this festival. Children buy crackers. Ladies buy sarees and material for preparing sweets. People give presents to friends and relatives. Main days of celebration of Diwali are three—‘Dhan Teras’, ‘Roop Chaudas’ and ‘Diwali’ on Amavasya day. In the evening ladies and children bum candle and lamps. Many electric bulbs of several colours are also lighted.

Worship of Goddess Laxmi—On Diwali day people worship goddess Laxmi. They pray her for health, wealth and happiness for the whole year. The rich and the poor enjoy Diwali. Diwali also marks the end of the year.

Importance—Diwali is an all India festival. People of all parts of India and all communities celebrate’it. It is a festival of national importance. It promotes national unity also.

For AH People—All age groups of people enjoy celebration of Diwali. The rich and the poor all celebrate it as per their capacity.

Conclusion—Some people gamble and drink wine. Some are injured at the time of bursting crackers due to carelessness. However, Diwali brings happiness to every home in India.

3. Importance of Newspapers
Newspapers are the world’s mirrors.

My Hobby Paragraph For Class 9 MP Board

—James Ellis

Introduction—The word News is made up of four letters N, E, W and S. Each letter symbolises one direction. N stands for North, E for East; W for West and S for South. Hence, a newspaper is a paper that contains news of all directions—North, South, East and West.

A newspaper collects information about happenings in the world through news agencies and prints them on a paper.

Contents of a Newspaper—A newspaper contains political, social, economical, religious and several other kinds of news. Everybody finds something of his/her interest in it. Children, young persons as well as old persons find newspaper interesting. There is a column for market report exhibiting wholesale prices of a lot of articles of daily use and quoting market value of shares and stocks of leading concerns. So a man of business is also interested in it. Art, music, entertainment, games, general knowledge and all such things are there in a newspaper.

There are advertisements of various kinds in the newspapers. They inform us about new and useful inventions. They are a source of income for the newspaper. Advertisements concerning matrimonial alliance provide immense relief to parents in choosing consorts for their sons or daughters. Assorted advertisements provide an unfathomable relief to people of different sorts. Only because of these advertisements we get a newspaper within our reach price.

Importance of Newspapers—Newspapers guide and teach us. They try to educate and shape public opinion. They are necessary for a democratic society. They express the views of the public in a free and fearless manner. Most of us are too busy to think of the great problems of our country, so we rely upon- the newspaper and accept the view they present to us. We can also express our views under the column ‘Letters to the Editor’.

Conclusion—Newspaper is a powerful weapon. It is a measuring rod to determine the length of democracy in a country. And as such it should be handled carefully. Rumours and sensational news create a nasty atmosphere. Newspapers must present constructive and objective matter before their readers. They should not misuse freedom given to the press. Their criticism should not be biased. They should be impartial in their news and views.

4. Wonders of Science Or
Science is a Good Servant but a Bad Master

My Hobby Essay Class 9th MP Board

Introduction—It is the age of science. Science plays an important role in our life. It has made our life easier and comfortable. Science is a systematic way of knowledge and living.

Scientific Wonders—Science has given us many wonderful gifts. The various inventions of science are its wonders. We cannot imagine our life without them.

Various Inventions—Electricity is the most useful gift of science. It gives us light. Heaters, fans, coolers, refrigerators, computers etc., all work by electricity. It also runs machines and trains.

Medicine and Surgery—Science has given wonderful medicines. Vaccination helps us in preventing diseases like polio, cholera, small pox etc. It has brought down the death rate. Modem surgical equipment have made operations less painful.

Means of Communication—Today we amuse ourselves by watching television and listening to music on radio and tape recorder. Television has become a powerful medium of education and knowledge. U.G.C. and IGNOU lessons on television are very useful. Fast means of transport and communication help us to reach distant places in a short time.

Computers—Scientists have invented computers. These are wonderful inventions. Computers can do complex calculations and work quickly. They have solved a lot of problems of man.

Disadvantages of Science—-Everything has two sides. Science too has a dark side. The invention and production of atom bombs and other dangerous weapons are a great threat to the existence of humanity. They can destroy the world in seconds. Secondly, big factories, mills and other machines have polluted the atmosphere.

Conclusion—Science is a great help to modem man. If properly used it can make the life of man healthier and happier.

5. My Best Friend

Essay On My Hobby For Class 9 MP Board

Introduction— ‘No man is an island entire of itself’. We need someone to share our sorrows and joys. I have several friends but Pinki is my best friend. She studies in my class and is my neighbor.

Details—Pinki’s father is a businessman. He is a simple man. Her mother is a teacher. She is a virtuous lady. Qualities of her parents are present in Pinki also.

Her qualities—Pinki is an intelligent girl. She always stands first in class. But she is not proud. She is kind and cooperative. She helps her classmates. She is a ‘friend in need’ and thus ‘a friend indeed’. We go to school together and come home together.

Her love for games—She is good at sports and games too. Last year she won the badminton championship.

Why I like her—I like her because she has a very good nature. She is cheerful, kind, honest and truthful. She faces problems boldly. She always helps me. Everybody praises her. She bears a good moral character. She believes in simple living and high thinking.

Conclusion—A good person inspires others to be good. There is a saying that a person is known by the company he keeps. Thus her company inspires me to be good and become like her. I am proud of my friend.

6. My Mother

Essay My Hobby Class 9th MP Board

Introduction—‘A hand that rocks the cradle rules the world1. The above saying holds true as a child is only a mother’s reflection. ‘Mother, or mama’ the first word spoken by a child holds in itself the essence of love and care.

We can’t compare the relation of a mother with any other relation. Mother not only gives us birth but she brings us up as well, looks after us and gives all her attention to our well-being. She does many sacrifices for us.

My mother—My mother Mrs. Pramila Devi is an ideal mother. She is a symbol of love and sacrifice. She gets up early in the morning and works late till night. She keeps the home neat and clean. When I get up she gives me warm water to wash my mouth. She gives me hot tea to drink. She prepares food with keen interest. The food is tasty to eat. She pays attention to all my needs.

Education and other qualities—My mother is B.A. She has a good knowledge of several subjects especially of Hindi and English. She possesses a great experience of many arts. She knows knitting and sewing well. She instructs us in other fields too. My mother is religious minded. She worships God daily without fail.

Social side of my mother—My mother has good relations with our neighbours. She helps them at the time of their troubles. My mother helps the poor and the needy. She takes part in various social activities. She is a member of the Woman Organisation for helping the weaker sections of the society.

7. An Ideal Teacher

My Hobby Essay 9th Class MP Board

Introduction—I study in Modem Public School, Bhopal. It is a very good school. It has forty teachers. All the teachers are good but Mr. S. K. Gupta is my favorite teacher.

His personality and qualities—He is about thirty-five years old. He teaches us English. He is our class teacher too. He is smart and handsome.

He believes in ‘simple living and high thinking’. He works hard with his students. He takes extra classes on his student’s demand. He helps weak students. Mr. Gupta loves us as his younger brothers. We also respect him as our elder brother.

His method of teaching—He is very punctual. His teaching method is very good. He uses simple language in teaching, so we easily understand his lessons. His examination results are always very good. He’is both strict and kind. We obey him.

His love for sports—He is good at games. He plays cricket well. He is a good sportsman. He has created an interest for cricket among the boys.

Conclusion—Mr. Gupta, therefore, possesses all the qualities of an ideal teacher. I have great respect for him in my heart. I like him a lot.

8. The Books I Like Most

My Hobby Essay Class 9 MP Board

Introduction—Books are our best friends. They are treasures of knowledge. No one can feel lonely in their company. They also act as our guide and teacher.

My favorite book—My favorite book is the Ramayana written by the great poet Tulsidas. The book is full of conceptions of Indian philosophy. The greatest secrets of divine knowledge are explained in simple verse. Doubts shatter, pride melts away, evil thoughts escape and greed gallops away after its study.

About the theme—The story is too well-known to be narrated in details. The deep knowledge of Hindu culture over the book is quite clear. Ram represents all that is good. Ravan stands for the evil. Ram’s victory over Ravan means the victory of truth over falsehood, or good over evil.

Conclusion—The biggest number of commentaries have been written over it. It has been translated in more than 100 languages of the world and foreigners know India through it. When they read Ramayana, they know about India’s glory. They bow their heads in honor to India.

We believe information shared regarding MP Board Solutions for Class 9 Textbook General English Writing Skills Essay Writing Questions and Answers as far as our knowledge is concerned is true and reliable. In case of any queries or suggestions do leave us your feedback and our team will guide you at soonest possibility. Bookmark our site to avail latest updates on several state board Solutions at your fingertips.

MP Board Class 9th Hindi Vasanti Solutions Chapter 4 बूढ़ी काकी (प्रेमचन्द)

बूढ़ी काकी अभ्यास प्रश्न

बूढ़ी काकी लघूत्तरीय प्रश्नोत्तर

Budhi Kaki Question Answer In Hindi MP Board Class 9th प्रश्न 1.
बूढ़ी काकी बुद्धिराम के पास क्यों रहती थी?
उत्तर
बूढ़ी काकी का बुद्धिराम के सिवा और कोई नहीं था। इसलिए वह बुद्धिराम के पास रहती थी।

Budhi Kaki Question Answer MP Board Class 9th प्रश्न 2.
सुखराम के तिलक पर घर का वातावरण कैसा था?
उत्तर
सुखराम के तिलक पर घर का वातावरण बड़ा ही आनंददायक था। लोगों की भारी भीड़ थी। तरह-तरह के खान-पान तैयार हो रहे थे। मेहमानों का खूब आदर-सत्कार हो रहा था। बुद्धिराम और रूपा कार्यभार संभालने में बहुत व्यस्त थे।

Budhi Kaki Question Answer In Hindi Class 9 प्रश्न 3.
लाडली और बूढ़ी काकी में परस्पर सहानुभूति क्यों थी?
उत्तर
लाडली को अपने दोनों भाइयों के डर से अपने हिस्से की मिठाई-चबैना खाने के लिए बढ़ी काकी के सिवा और कोई सरक्षित जगह नहीं थी। उससे बढ़ी काकी को कुछ खाने के लिए मिल जाता था। इस तरह दोनों में परस्पर सहानुभूति थी।

Budhi Kaki Saransh MP Board Class 9th प्रश्न 4.
रूपा का व्यवहार काकी के प्रति किस प्रकार का था?
उत्तर
रूपा का व्यवहार बूढ़ी काकी के प्रति बड़ा ही अन्यायपूर्ण और कठोर था।

Budhi Kaki Ke Prashn Uttar MP Board Class 9th प्रश्न 5.
बूढ़ी काकी को भोजन न देने पर लाडली का मन क्यों अधीर हो रहा था?
उत्तर
बूढ़ी काकी को भोजन न देने पर लाडली का मन अधीर हो रहा था। यह इसलिए कि वह अपने माता-पिता द्वारा बूढ़ी काकी के प्रति किए गए दुर्व्यवहार से दुखी
और चिंतित थी।

बूढ़ी काकी दीर्घ उत्तरीय प्रश्नोत्तर

Budhi Kaki Question Answer In Hindi Class 9 प्रश्न 1.
“बुढ़ापा बहुधा बचपन का पुनरागमन हुआ करता है।” पाठ के आधार पर स्पष्ट कीजिए।
उत्तर
बुढ़ापा आने पर किसी प्रकार की जिम्मेदारी और उत्तरदायित्व निभाने की न कोई क्षमता होती है और न कोई सोच-समझ। बुढ़ापा में बच्चों के समान स्वतंत्रता आ जाती है। स्वार्थपरता के कारण अच्छा-बुरा का कुष्ठ भी ख्याल न बुढ़ापा में होता है और न बचपन में। इस प्रकार की और भी कई बातें होती हैं, जो बचपन और बढ़ापा में होती हैं। इस आधार पर यह कहा जा सकता है कि, “बुढ़ापा बहुधा बचपन का पुनरागमन हुआ करता है।”

Boodhi Kaki Question Answer MP Board Class 9th प्रश्न 2.
भोजन की वाली अपने सम्मुख देख बूढ़ी काकी की मनोदशा का वर्णन कीजिए।
उत्तर
भोजन की थाली अपने सामने देखकर बूढ़ी काकी खिल उठी। उसके रोम-रोम में ताजगी आ गई। उस समय वह अपने ऊपर हुए अत्याचार और तिरस्कार को बिल्कुल भूल गई। वह भोजन की थाली पर टूट पड़ी। धड़ाधड़ पूड़ियों को खाने के लिए वह आतुर हो उठी। उसके एक-एक रोएँ रूपा को आशीर्वाद दे रहे थे।

प्रश्न 3.
रूपा का हृदय परिवर्तन कैसे हुआ?
उत्तर
बूढ़ी काकी को जूठे पत्तलों पर से पूड़ियों के टुकड़े उठा-उठाकर खाते हुए देखकर रूपा का हृदय सन्न हो गया। उसे बूढ़ी काकी के प्रति किए गए अन्याय और अत्याचार का भारी पश्चाताप हुआ। इस प्रकार रूपा का हृदय परिवर्तन हुआ।

प्रश्न 4.
इस पाठ से आपको क्या शिक्षा मिलती है?
उत्तर
इस पाठ से हमें निम्नलिखित शिक्षा मिलती है

1. हमें बुजुर्गों की भावनाओं को समझना चाहिए।
2. हमें बुजुर्गों का मान-सम्मान करना चाहिए।
3. हमें बुजुर्गों की सेवा सच्ची भावना से करनी चाहिए।
4. हम भी किसी समय बुजुर्ग होंगे। यह समझकर हमें बुजुर्गों पर होने वाले अत्याचार-अन्याय का विरोध करना चाहिए।

प्रश्न 5.
रूपा की जगह यदि आप होते तो बूढ़ी काकी के प्रति आपका व्यवहार कैसा होता?
उत्तर
रूपा की जगह हम होते तो बूढ़ी काकी के प्रति सहानुभूति रखते। उनकी भावनाओं को समझते। उनकी इच्छाओं को पूरी करने की कोशिश करते। अगर वे कोई अनुचित या अशोभनीय कदम उठातीं, तो हम उन पर क्रोध नहीं करते। उन्हें बड़े प्यार और आदर के साथ समझाते। उनकी कठिन जिद्द को नम्रतापूर्वक दूर करने का प्रयास करते।

प्रश्न 6.
स्पष्ट कीजिए।
(क) नदी में जब कगार का कोई वृहद खंड कटकर गिरता है तो आस पास का जल-समूह चारों ओर से उसी स्थान को पूरा करने के लिए दौड़ता है।
(ख) संतोष का सेतु जब टूट जाता है तब इच्छा का बहाव अपरिमित हो जाता है।
उत्तर
(क) उपर्युक्त वाक्य के कथन का आशय यह है कि जब कहीं कोई अवांछित और अनचाही घटना किसी के जीवन में घटित होती है तो हदय और मस्तिष्क की सारी शक्तियाँ, सारे विचार और सभी भार उसी ओर केंद्रित हो जाते हैं।
(ख) उपर्युक्त वाक्य के कथन का आशय यह है कि संतोष से इच्छाओं का प्रवाह रुक जाता है। इसके विपरीत असंतोष से इच्छाओं का प्रवाह किसी प्रकार की सीमा को तोड़ने में तनिक भी देर नहीं लगाता है।

बूढ़ी काकी भाषा-अध्ययन

1. जिह्वा, कृपाण आदि तत्सम शब्द हैं। पाठ में आए ऐसे ही तत्सम शब्दों की सूची बनाइए।
2. दिए हुए शब्दों में से उपसर्ग-प्रत्या छाँटकर अलग कीजिए
स्वाभाविक, प्रतिकूल, मसालेदार, सुगन्धित, अविश्वास, विनष्ट, लोलुपता, असहाय, निर्दयी।
3. ‘दिन-रात खाती न होती तो न जाने किसकी हाँडी में मुँह डालती।’
उपर्युक्त वाक्य में दिन का विलोम शब्द रात आया है। पाठ में आए ऐसे ही अन्य वाक्य छाँटिए जिनमें विलोम शब्दों का एक साथ प्रयोग हुआ हो।
उत्तर
1. चेष्टा, नेत्र, प्रतिकूल, पूर्ण, परिणाम, कालान्तर, तरुण, आय, वार्षिक, ईश्वर, तीव्र, व्यय, संताप, आर्तनाद, अनुराग, क्षुधावर्द्धक, सम्मुख, उद्विग्न, कार्य, क्रोध, वृहद, दीर्घाहार, व्यर्थ, मिथ्या, वाटिका, वर्षा, क्षुधा, प्रबल, प्रत्यक्ष, वृद्धा, आकाश, निमग्न आदि।

3. (i) फिर जब माता-पिता का यह रंग देखते, तो बूढ़ी काकी को और भी सताया करते।
(ii) यद्यपि उपद्रव-शांति का यह उपाय रोने से कहीं अधिक उपयुक्त था।
(iii) लाडली अपने दोनों भाइयों के भय से अपने हिस्से की मिठाई-चबैना बूढ़ी काकी के पास बैठकर खाया करती थी।
(iv) आघात ऐसा कठोर था कि हृदय और मस्तिष्क की संपूर्ण शक्तियाँ, संपूर्ण । विचार और संपूर्ण भार उसी ओर आकर्षित हो गए।
(v) अवश्य ही लोग खा-पीकर चले गए।

बूढ़ी काकी योग्यता-विस्तार

1. “वृद्धजन का सम्मान ही परिवार का सम्मान है।” इस विषय पर कक्षा में परिचर्चा कीजिए।
2. आप अपनी दादी या नानी से कितना प्यार करते हैं। अपने शब्दों में लिखिए।
उत्तर
उपर्युक्त प्रश्नों को छात्र छात्रा अपने अध्यापक/अध्यापिका की सहायता से हल करें।

बूढ़ी काकी परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्नोत्तर

लघूत्तरीय प्रश्नोत्तर

प्रश्न 1.
बूढ़ी काकी कब-कब रोती थीं?
उत्तर
जब घरवाले कोई बात उनकी इच्छा के विपरीत करते, भोजन का समय टल जाता या उसका परिणाम पूरा न होता अथवा बाजार से कोई वस्तु आई और उन्हें न मिलती, तो वे रोने लगती थीं।

प्रश्न 2.
बूढ़ी काकी को रोना आया लेकिन वे रो न सकीं। क्यों?
उत्तर
बूढ़ी काकी को रोना आया, लेकिन वे रो न सकीं क्योंकि उन्हें अपशकुन का भय हो गया था।

प्रश्न 3.
बूढ़ी काकी अपनी कोठरी में क्या पश्चाताप कर रही थी?
उत्तर
बूढ़ी काकी अपनी कोठरी में यह पश्चाताप कर रही थीं कि उन्होंने बड़ी जल्दीबाजी की। मेहमानों के खाने तक तो इंतजार करना ही चाहिए था। मेहमानों से पहले घर के लोग कैसे खाएँगे?

प्रश्न 4.
लाडली ही बूढ़ी काकी के लिए क्यों कुढ़ रही थी?
उत्तर
लाडली ही बूढ़ी काकी के लिए कुढ़ रही थी, क्योंकि उसे ही उनसे अत्यधिक प्रेम था।

प्रश्न 5.
रूपा ने रुद्ध कंठ से क्या कहा?
उत्तर
रूपा ने रुद्ध कंठ से कहा, “काकी उठो, भोजन कर लो। मुझसे आज बड़ी भूल हुई। उसका बुरा न मानना। परमात्मा से प्रार्थना कर दो कि वह मेरा अपराध क्षमा कर दें।”

बूढ़ी काकी दीर्य उत्तरीय प्रश्नोत्तर

प्रश्न 1.
बूढ़ी काकी को भरपेट भोजन बड़ी कठिनाई से क्यों मिलता था?
उत्तर
बूढ़ी काकी ने अपनी सारी सम्पत्ति अपने भतीजे बुद्धिराम को लिख दी। थी। सम्पत्ति लिखाते समय बुद्धिराम ने खूब लंबे-चौड़े वादे किए थे, लेकिन वे खोखले साबित हुए। बुद्धिराम की कृपणता ही इसके मूल में रही। उसी के फलस्वरूप वे बूढ़ी काकी के भोजन में कमी रखने का प्रयास करना नहीं भूलते थे।

प्रश्न 2.
बूढ़ी काकी प्रतीक्षा की घड़ी कैसे बिता रही थीं?
उत्तर
बूढ़ी काकी को एक-एक पल एक-एक युग के समान मालूम होता था। अब पत्तल बिछ गई होंगी। अब मेहमान आ गए होंगे। लोग हाथ-पैर धो रहे हैं. नाई पानी दे रहा है। मालूम होता है लोग खाने बैठ गए। जेवनार गाया जा रहा है, यह विचार कर वह मन को बहलाने के लिए लेट गई। धीरे-धीरे एक गीत गुनगुनाने लगी। उन्हें मालूम हुआ कि मुझे गाते देर हो गई। क्या इतनी देर तक लोग भोजन कर ही रहे होंगे? किसी की आवाज नहीं सुनाई देती। अवश्य ही लोग खा-पीकर चले गए। मुझे कोई बुलाने नहीं आया। रूपा चिढ़ गई। क्या जाने न बुलाए, सोचती हो कि आप ही आवेगी। वह कोई मेहमान तो नहीं जो उन्हें बुलाऊँ। बूढ़ी काकी चलने के लिए तैयार हुई।

प्रश्न 3.
बुद्धिराम ने बूढ़ी काकी के प्रति क्या कठोरता दिखाई?
उत्तर
बुद्धिराम ने जब बूढ़ी काकी को मेहमानों के बीच में देखा तो उनको क्रोध आ गया। वे इससे अपने को संभाल न सके। हाथ में लिए हए पूड़ियों के थाल को उन्होंने जमीन पर पटक दिया। फिर जिस तरह कोई निर्दय महाजन अपने किसी बेईमान और भगोड़े आसामी को देखते ही लपककर उसका टेंटुआ पकड़ लेता है। उसी तरह से उन्होंने भी बुढ़ी काकी के दोनों हाथों को कसकर पकड़ लिया। फिर उन्हें घसीटते हुए उनकी उसी अँधेरी कोठरी में लाकर पटक दिया।

प्रश्न 4.
रूपा ने अपनी गलती का पञ्चाताप किस प्रकार किया?
उत्तर
रूपा ने अपनी गलती का पश्चाताप इस प्रकार किया
“हाय कितनी निर्दयी हूँ! जिसकी सम्पत्ति से मुझे दो सौ रुपया वार्षिक आय हो रही है। उसकी यह दुर्गति! और मेरे कारण! हे दयामय भगवान! मुझसे बड़ी भारी चूक हुई है। मुझे क्षमा करो। आज मेरे बेटे का तिलक था। सैकड़ों मनुष्यों ने भोजन किया। मैं उनके इशारों की दासी बनी रही। अपने नाम के लिए सैकड़ों रुपए व्यय कर दिए, परंतु जिनकी बदौलत हजारों रुपए खाए, उसे इस उत्सव में भरपेट भोजन न दे सकी। केवल इसी कारण कि वह वृद्धा है, असहाय है।”

प्रश्न 5.
रूपा ने बूढ़ी काकी से अपने अपराध के क्षमा के लिए क्या किया?
उत्तर
आधी रात जा चुकी थी। आकाश पर तारों के थाल सजे हुए थे। और उन पर बैठे हुए देवगण स्वर्गीय पदार्थ सजा रहे थे। परंतु उनमें किसी को वह परमानंद प्राप्त न हो सकता था, जो बूढ़ी काकी को अपने सम्मुख थाल देखकर प्राप्त हुआ। रूपा ने कंठावरुद्ध स्वर में कहा, “काकी उठो, भोजन कर लो। मुझसे आज बड़ी भूल हुई, उसका बुरा न मानना। परमात्मा से प्रार्थना कर दो कि वह मेरा अपराध क्षमा कर दें।” भोले-भोले बच्चों की भाँति जो मिठाइयाँ पाकर मार और तिरस्कार सब भूल जाता है, बूढ़ी काकी वैसे सब भुलाकर बैठी हुई खाना खा रही थीं। उनके एक-एक रोएँ से सच्ची सदिच्छाएँ निकल रही थीं और रूपा बैठी इस स्वर्गीय दृश्य का आनंद लूटने में निमग्न थी।

बूढ़ी काकी लेखक-परिचय

प्रश्न
प्रेमचंद का संक्षिप्त जीवन-परिचय देते हुए उनके साहित्य के महत्त्व पर प्रकाश डालिए।
उत्तर
जीवन-परिचय-प्रेमचंद का जन्म उत्तर प्रदेश राज्य के वाराणसी जिले के लमही गाँव में सन् 1880 ई. में हुआ था। उनका वास्तविक नाम धनपतराय था, परन्तु आप साहित्य के क्षेत्र में प्रेमचंद नाम से प्रसिद्ध हुए। छोटी आयु में पिता की मृत्यु हो जाने से उनका जीवन गरीबी में बीता था। मैट्रिक पास करने के पश्चात् आपने स्कूल में अध्यापन कार्य किया। उसके बाद स्वाध्याय से बी.ए. की परीक्षा पास की और शिक्षा विभाग में सब-इंस्पेक्टर पद पर कार्य किया। कुछ समय के बाद वहाँ से भी त्याग-पत्र दे दिया और आजीवन साहित्य-सेवा में लगे रहे। बीमारी के कारण 56 वर्ष की आय में सन् 1936 में आपका देहान्त हो गया।
साहित्यिक सेवा-प्रेमचंद ने सर्वप्रथम नवाबराय के नाम से उर्दू में लिखना आरंभ किया था।

उनका ‘सोजेवतन’ नामक कहानी-संग्रह तत्कालीन अंग्रेजी सरकार ने जब्त कर लिया और नवाबराय पर अनेक प्रतिबंध लगा दिए। इसके बाद आपने हिंदी में प्रेमचंद के नाम से लिखना आरंभ किया। आपके साहित्य का मुख्य स्वर समाज-सुधार है। आपने समाज-सुधार और राष्ट्रीय भावना से ओत-प्रोत कई उपन्यास और लगभग तीन सौ कहानियाँ लिखी हैं। उन्होंने अपने साहित्य में किसानों की दशा, सामाजिक बंधनों में तड़पती नारियों की वेदना और वर्ण-व्यवस्था की कठोरता के भीतर संत्रस्त हरिजनों की पीड़ा का मार्मिक चित्रण किया है।

भाषा-शैली-प्रेमचंद की भाषा साधारण बोल-चाल की भाषा है। इसमें उर्द, फारसी. अंग्रेजी तथा तत्सम, तदभव शब्दों के साथ-साथ देशज शब्दों का प्रयोग भी मिलता है। इनकी भाषा मुहावरे-लोकोक्तियों और सूक्तियों से युक्त है। हास्य-व्यंग्य के छींटे भाषा को जीवंत बनाए रखते हैं। उन्होंने वर्णनात्मक, आत्मकथात्मक आदि शैलियों का प्रयोग किया है।

रचनाएँ-उपन्यास-सेवासदन, निर्मला, रंगभूमि, कर्मभूमि, गबन और गोदान आदि प्रसिद्ध उपन्यास हैं।

नाटक-कर्बला, संग्राम और प्रेम की बेदी।

निबंध-संग्रह-कुछ विचार संग्रह। सामाजिक और राजनीतिक निबंधों का संग्रह ‘विविध-प्रसंग’ नाम से तीन भागों में प्रकाशित है।

उन्होंने हंस, मर्यादा और जागरण पत्रिकाओं का संपादन किया।कहानी-प्रेमचंद ने अनेक प्रसिद्ध कहानियों की रचना की। उन्होंने लगभग तीन सौ कहानियाँ लिखीं। उनकी कहानियाँ ‘मानसरोवर’ नाम से आठ भागों में संग्रहीत हैं। संक्षेप में यह कहा जा सकता है कि प्रेमचंद का साहित्यिक महत्त्व बहुत अधिक है। फलस्वरूप वे युग-युग तक आने वाली साहित्यिक पीढ़ी को प्रेरित करते रहेंगे।

बूढ़ी काकी कहानी का सारांश

प्रश्न
प्रेमचंद-लिखित कहानी ‘बूढ़ी काकी’ का सारांश अपने शब्दों में लिखिए।
उत्तर
प्रेमचंद-लिखित कहानी ‘बूढ़ी काकी’ एक सामाजिक-पारिवारिक कहानी है। इसमें वृद्धों की मानसिक स्थितियों को सामने लाने का प्रयास किया गया है। इस कहानी का सारांश इस प्रकार है बूढ़ी काकी जीभ का स्वाद न पूरा होने पर गला फाड़-फाड़कर रोने लगती थी। उनके पतिदेव और जवान बेटे की मौत के बाद उनका भतीजा बुद्धिराम ही उनका अपना था। उसी के नाम उन्होंने अपनी सारी सम्पत्ति लिख दी। सम्पत्ति लिखाते समय बुद्धिराम ने उनकी देखभाल के लम्बे-चौड़े वादे किए थे, लेकिन बाद में वे वादे खोखले साबित होने लगे। बुद्धिराम इतने सज्जन थे कि उनके कोष पर कोई आंच न आए।

उनकी पत्नी रूप-स्वभाव से तीव्र होने पर भी ईश्वर से डरती थी। बढी काकी अपनी जीभ के स्वाद या अपनी भूख मिटाने के लिए किसी की परवाह किए बिना रोती-चिल्लाती थीं। बच्चों के चिढ़ाने पर वह उन्हें गालियाँ देने लगती थीं। रूपा के आते ही वह शान्त हो जाती थीं। पूरे परिवार में बूढ़ी काकी से बुद्धिराम की छोटी लड़की लाडली ही प्रेम संबंध रखती थी। वह अपने खाने-पीने की चीजों में से कुछ चीजें निकालकर चुपके से बूढ़ी काकी को खिला दिया करती थी।

एक दिन बुद्धिराम के लड़के सुखराम का तिलक आया तो मेहमानों के खाने-पीने के लिए तरह-तरह के पकवान-मिठाइयाँ बनाए गए। उनकी सगन्ध से बढ़ी काकी अपनी कोठरी में बैठी हुई बेचैन हो रही थीं। वह एक-एक घड़ी का अंदाजा लगा रही थीं कि इतने देर बाद उन्हें भी वह भोजन मिलेगा। काफी देर बाद जब उनके लिए भोजन लेकर कोई उनके पास नहीं आया, तब उनके धैर्य का बाँध टूट गया। वह उक. बैठकर हाथों के बल सरकती हुई बड़ी कठिनाई से कड़ाह के पास जा बैठीं। उन्हें इस तरह कड़ाह के पास बैठी हुई देखकर रूपा के क्रोध की सीमा न रही। उसने सबके सामने बूढ़ी काकी को खूब खरी-खोटी सुनाई। उसे सुनकर बूढ़ी काकी चुपचाप रेंगती-सरकती हुई अपनी कोठरी में चली गई। किसी के बुलाने की प्रतीक्षा करने लगीं।

बूढ़ी काकी ने बहुत इंतजार किया, लेकिन उन्हें कोई बुलाने नहीं आया। उन्होंने शांत वातावरण से यह अनुमान लगा लिया कि मेहमान खा-पीकर चले गए हैं। मुझे कोई बुलाने नहीं आया तो क्या हुआ। वह मेहमान तो नहीं हैं कि उन्हें कोई बुलाने आएगा। इन्हीं बातों को सोच-समझकर वह पहले की तरह सरकती हुई आँगन में खा रहे मेहमानों के बीच में पहुंच गई। उन्हें देखते ही बुद्धिराम क्रोध से उबल पड़े। उन्होंने बूढ़ी काकी को घसीटते हुए अँधेरी कोठरी में लाकर धम्म से पटक दिया। यह देखकर लाडली को क्रोध तो आया, लेकिन डर से वह कुछ कह न सकी। वह अपने हिस्से की पूड़ियों को सबके सोने के बाद बूढ़ी काकी को खिलाने के लिए उस अँधेरी कोठरी में गई। उसने बूढ़ी काकी को उन पूड़ियों को खाने के लिए सामने रख दिया। उन पूड़ियों को उन्होंने पाँच मिनट में खा लिया। इसके बाद उन्होंने उससे और पूड़ियाँ अपनी माँ रूपा से माँगकर लाने के लिए कहा।

लाडली ने जब अपनी अम्मा से अपने डर की बात कही तब उन्होंने उससे कहा, “मेरा हाथ पकड़कर वहाँ ले चलो, जहाँ मेहमानों ने बैठकर भोजन किया है।” लाडली जब उन्हें वहाँ ले गई, तब उन्होंने पूड़ियों के टुकड़े चुन-चुनकर खाना शुरू किया। नींद खुलने पर रूपा लाडली को खोजती हुई वहाँ पहुँच गई, जहाँ बूढ़ी काकी पूड़ियों के टुकड़े उठा-उठाकर खा रही थीं। उन्हें इस तरह देखकर रूपा काँप उठी। उसे ऐसा लगा, मानो आसमान चक्कर खा रहा है। संसार पर कोई नई विपत्ति आने वाली है। करुणा और भय के आँसुओं से उसने हृदय खोलकर आकाश की ओर हाथ उठाते हुए कहा, “परमात्मा, मेरे बच्चों पर दया करो। इस अधर्म का दंड मुझे मत दो, नहीं तो मेरा सत्यानाश हो जाएगा। मुझे क्षमा करो। आज मेरे बेटे का तिलक था। सैकड़ों मनुष्यों ने भोजन किया। मैं उनके इशारों की दासी बनी रही। अपने नाम के लिए सैकड़ों रुपए खर्च कर दिए। परन्तु जिनकी बदौलत हजारों रुपए खाए, उसे इस उत्सव में भरपेट भोजन न दे सकी। केवल इसी कारण कि वह वृद्धा है, असहाय है।”

रूपा दिया जलाकर भंडार से थाली में सारी सामग्रियाँ सजाकर काकी के पास गई। उसने रुंधे हुए स्वर में कहा, “काकी उठो, भोजन कर लो। मुझसे आज बड़ी भूल हुई, उसका बुरा न मानना। परमात्मा से प्रार्थना कर दो कि वह मेरा अपराध क्षमा कर दे।”
मिठाइयाँ पाकर मार और तिरस्कार भूल जाने वाले भोले-भाले बच्चों की तरह बूढ़ी काकी सब कुछ भुलाकर वह खाना.खा रही थी। उनके रोम-रोम से सदिच्छाएँ निकल रही थीं। रूपा वहाँ बैठी उस स्वगीय आनंद को लूट रही थी।

बूढ़ी काकी संदर्भ-प्रसंग सहित व्याख्या

गद्यांशों की सप्रसंग व्याख्या, अर्थग्रहण एवं विषय-वस्तु पर आधारित प्रश्नोत्तर

1. संपूर्ण परिवार में यदि काकी से किसी को अनुराग था, तो वह बुद्धिराम की छोटी लड़की लाडली थी। लाडली अपने दोनों भाइयों के भय से अपने हिस्से की -मिठाई-चबेना बूढ़ी काकी के पास बैठकर खाया करती थी। वह उसका रक्षागार था और यद्यपि काकी की शरण उनकी लोलुपता के कारण बहुत महँगी पड़ती थी, तथापि भाइयों के अन्याय से वहीं सुलभ थी। इसी स्वार्थानुकूलता ने उन दोनों में प्रेम और सहानुभूति का आरोपण कर दिया था।

शब्दार्थ-अनुराग-प्रेम । लोलुपता-लालच । स्वार्थानुकूलता- स्वार्थ के अनुसार। आरोपण-आरोप लगाना।

प्रसंग-प्रस्तुत गद्यांश हमारी पाठ्य-पुस्तक ‘वासंती-हिंदी सामान्य’ में संकलित तथा मुंशी प्रेमचंद-लिखित कहानी ‘बूढ़ी काकी’ से है। इसमें लेखक ने बूढ़ी काकी और लाडली के विषय में बतलाने का प्रयास किया है।

व्याख्या-लेखक का कहना है कि बूढ़ी काकी के प्रति परिवार में किसी को कोई लगाव नहीं था। बूढ़ी काकी का भतीजा बुद्धिराम, उसकी पत्नी रूपा और उसके बच्चे बूढ़ी काकी के प्रति सहानुभूति नहीं रखते थे। अगर उनके प्रति लगाव या सहानुभूति रखने वाला घर का कोई सदस्य था, तो वह थी बुद्धिराम की छोटी लड़की लाडली। वह अपनी सहानुभूति उनके प्रति बराबर दिखाती थी। वह अपना अधिकांश समय उनके पास ही बिताया करती थी। अपने भाइयों से डरी हुई वह अपने हिस्से की मिठाई-चबैना उनके पास बैठकर खाया करती थी। उन्हें देखकर उनको लालच होने लगता था। उनकी लपलपाती हुई जीभ को शांत करने के लिए उसे अपने हिस्से की मिठाई-चबैना के कुछ भाग को दे देना पड़ता है। इससे उसकी उनके प्रति प्रकट की जाने वाली सहानुभूति दुखद साबित होती थी, फिर भी उसे यह अपने भाइयों के बेईमानी से अच्छी लगती थी। इस प्रकार दोनों की स्वार्थपरता ने उन दोनों में प्रेम और सहानुभूति को पैदा कर दिया था।

विशेष-

1. भाषा तत्सम और तद्भव शब्दों की है।
2. बाल-स्वभाव और वृद्ध-स्वभाव की समानता का संकेत है।
3. शैली वर्णनात्मक है।

1. गद्यांश पर आधारित अर्थग्रहण संबंधी प्रश्नोत्तर

प्रश्न
(i) बूढ़ी काकी से लाडली को क्यों अनुराग था?
(ii) बूढ़ी काकी लाडली को क्यों चाहती थी?
उत्तर
(i) बूढ़ी काकी से लाडली को अनुराग था। यह इसलिए कि वह अपने भाइयों के भय से अपने हिस्से की मिठाई-चबैना बूढ़ी काकी के पास बैठकर निडर हो खाया करती थी।
(ii) बूढ़ी काकी लाडली को चाहती थी। यह इसलिए कि लाडली ही कुछ खिलाकर उनकी लपलपाती हुई जीभ को शांत करती थी।

2. गद्यांश पर आधारित विषय-वस्त से संबंधित प्रश्नोत्तर

प्रश्न
(i) बूढ़ी काकी और लाडली में परस्पर प्रेम क्यों हो गया था?
(ii) उपर्युक्त गयांश का मुख्य भाव क्या है?
उत्तर
(i) बूढ़ी काकी और लाडली में परस्पर सहानुभूति और प्रेम उन दोनों के परस्पर स्वार्थपूर्ति के फलस्वरूप हो गया था।
(ii) उपर्युक्त गद्यांश का मुख्य भाव है-बाल-स्वभाव और वृद्ध-स्वभाव की समानता को दर्शाना।

2. जिस प्रकार मेढक कॅचए पर झपटता है, उसी प्रकार वह बड़ी काकी पर झपटी और उन्हें दोनों हाथों से झिंझोड़कर बोली, “ऐसे पेट में आग लगे, पेट है या भाड़? कोठरी में बैठते क्या दम घुटता था? अभी मेहमानों ने नहीं खाया, भगवान का भोग नहीं लगा, तब तक धैर्य न हो सका? आकर छाती पर सवार हो गई। जल जाय ऐसी जीभ । दिन-रात खाती न होती, तो न जाने किसकी हाड़ी में मुँह डालती? गाँव देखेगा तो कहेगा, बुढ़िया भरपेट खाने को नहीं पाती, तभी तो इस तरह मुंह बाये फिरती है। डायन, न मरे न माँचा छोड़े। नाम बेचने पर लगी है। नाक कटवाकर दम लेगी। इतना ढूँसती है, न जाने कहाँ भस्म हो जाता है। लो! भला चाहती हो तो जाकर कोठरी में बैठो, जब घर के लोग खाने लगेंगे तब तुम्हें भी मिलेगा। तुम कोई देवी नहीं हो कि चाहे किसी के मुँह में पानी न जाए, परंतु तुम्हारी पूजा पहले हो ही जाए।”

शब्दार्थ-झिंझोड़-झिड़ककर । डायन-राक्षसी।

प्रसंग-पूर्ववत् इसमें लेखक ने उस समय का उल्लेख किया है, जब बढ़ी काकी खाने के लिए अपने धैर्य की सीमा को तोड़ती हुई सबके सामने कड़ाह के पास जा बैठी। उन्हें इस तरह देखकर रूपा ने बहुत तेज फटकार लगाई। उसे बतलाते हुए लेखक ने कहा है।

व्याख्या-बूढ़ी काकी को कड़ाह के सामने बैठी हुई देखकर रूपा के क्रोध की सीमा न रही। उसने सबके सामने ही बूढ़ी काकी पर वैसे ही झपट पड़ी, जैसे मेढक केंचुए पर झपट पड़ता है। उसने उनके दोनों हाथों को कसकर पकड़कर झकझोर दिया। फिर उसने आगबबूला होकर उन्हें फटकारना शुरू कर दिया, “तुम्हें पेट में आग लगी है। तुम्हारा पेट है या भाड़? चुपचाप कोठरी में बैठी रहती तो क्या मरने लगती। तुम्हें इतनी भी समझ नहीं है कि मेहमानों के लिए अभी तो खाना बन रहा है। न पूरा खाना बना और न भगवान को उसे चढ़ाया ही गया, इससे पहले ही छाती पर आकर सवार हो गई। धिक्कार है, तुम्हारी ऐसी जीभ पर। भरपेट भोजन न पाती तो न जाने कहाँ-कहाँ इस लपलपाती जीभ को लिए फिरती। लोग तुम्हें इस तरह देखकर यह अवश्य मान जाएँगे, तुम्हें हम भरपेट नहीं खिलाते हैं। सच ही कहा है-‘डायन, न मरे, न माँचा छोड़े।

3. अब समझ में आ गया कि हम लोगों को बदनाम करने के लिए ऐसा कर रही हो। इसलिए हम लोगों की नाक जब तक नहीं कटवा लेगी, तब तक चुप नहीं बैठेगी। बड़ा अचरज होता है कि लूंस-ठूसकर खाने पर भी खाने के लिए मरती है। अब कान खोलकर सुनो अपनी भलाई चाहती है तो चुपचाप अपनी कोठरी में जाकर बैठ जाओ। घर के लोगों के खाने के समय तुम्हें खिलाया जाएगा। यह अच्छी तरह समझ वह उसका रेंटुआ पकड़कर उससे अपना बकाया वसूल लेने की कोशिश करता है। कुछ इसी प्रकार का कठोर दुर्व्यवहार बुद्धिराम ने बूढ़ी काकी के प्रति किया। उसने बढ़ी काकी के दोनों हाथों को कसकर पकड़ लिया। फिर उन्हें वह घसीटते हुए उनकी उसी अँधेरी कोठरी में लाकर पटक दिया। उसके इस प्रकार के कठोर दुर्व्यवहार से बूढ़ी काकी की आशामयी वाटिका वैसे ही सूख गई, जैसे लू से हरियाली समाप्त हो जाती है।

विशेष-

1. बुद्धिराम की मनोदशा का स्वाभाविक चित्रण है।
2. संपूर्ण उल्लेख विश्वसनीय है।
3. ‘आशा रूपी वाटिका’ में रूपक अलंकार है तो बुद्धिराम की तुलना निर्दय महाजन से किए जाने से उपमा अलंकार है।
4. शैली दृष्टांत है।
5. करुण रस का संचार है।

1. गद्यांश पर आधारित अर्थग्रहण संबंधी प्रश्नोत्तर

प्रश्न-
(i) बुद्धिराम काकी को देखते ही क्रोध से क्यों तिलमिला गए?
(ii) बुद्धिराम ने पूड़ियों के चाल को क्यों पटक दिया?
उत्तर-
(i) बुद्धिराम बूढ़ी काकी को देखते ही क्रोध से तिलमिला गए। यह इसलिए कि उन्हें उस समय खाना खा रहे मेहमानों के बीच बूढ़ी काकी का आना एकदम सहन नहीं हुआ।
(ii) बुद्धिराम ने पूड़ियों के.थाल को पटक दिया। यह इसलिए कि उनका अपने क्रोध पर नियंत्रण न रहा। उन्हें उचित-अनुचित का ध्यान बिल्कुल नहीं रहा।

2. गद्यांश पर आधारित विषय-वस्त से संबंधित प्रश्नोत्तर

प्रश्न-
(i) बुद्धिराम ने बूढ़ी काकी के प्रति किस प्रकार का व्यवहार किया?
(ii) बुद्धिराम की जगह आप होते तो क्या करते?
उत्तर
(i) बुद्धिराम ने बूढ़ी काकी के प्रति बड़ा ही कठोर और बेगानापन का व्यवहार किया। उसके द्वारा किया गया व्यवहार वैसे ही कठोर था जैसे किसी निर्दय महाजन का अपने बेईमान और भगोड़े आसामी के प्रति होता है।
(ii) बुद्धिराम की जगह अगर हम होते तो बूढ़ी काकी के प्रति शिष्ट और उदार व्यवहार करते। उन्हें समझा-बुझाकर उन्हें उनकी कोठरी में वापस ले जाते।

4. रूपा का हृदय सन्न हो गया। किसी गाय के गर्दन पर छुरी चलते देखकर जो अवस्था उसकी होती वही उस समय हुई। एक ब्राह्मणी दूसरों की जूठी पत्तल टटोले, इससे अधिक शोकमय दृश्य असंभव था। पूड़ियों के कुछ ग्रासों के लिए उनकी चचेरी सासं ऐसा पतित और निकृष्ट कर्म कर रही है। यह वह दृश्य था जिसे देखकर देखने वालों के हृदय काँप उठते हैं। ऐसा प्रतीत होता था मानो जमीन रुक गई, आसमान चक्कर खा रहा है, संसार पर कोई नई विपत्ति आने वाली है। रूपा को क्रोध न आया। शोक के सम्मुख क्रोध कहाँ? करुणा और भय से उसकी आँखें भर आईं। इस अधर्म के पाप का भागी कौन है? उसने सच्चे हृदय से गगनमंडल की ओर हाथ उठाकर कहा-“परमात्मा, मेरे बच्चों पर दया करो। इस अधर्म का दंड मुझे मत दो, नहीं तो हमारा सत्यानाश हो जावेगा।”

शब्दार्च-ग्रास-टुकड़ा। पतित-पापपूर्ण। निकृष्ट-अधम, तुच्छ । प्रतीत होना-जानना ज्ञात होना। सम्मुख-सामने।

प्रसंग-पूर्ववत् । इसमें लेखक ने रूपा की शोकमय दशा का उल्लेख करते हुए कहा है कि

व्याख्या-बूढ़ी काकी को जूठे पत्तलों पर से पूड़ियों के टुकड़ों को उठा-उठाकर खाते हुए देखकर रूपा का कलेजा धक् से रह गया। उसकी उस समय ऐसी अवस्था हो गई थी। जैसे मानों किसी गाय के गर्दन पर कोई छुरी चला रहा है और वह उसे देखकर बिल्कुल हकबक हो रही है। एक ऐसी असहाय और दुखी वृद्धा को जूठी पत्तलों से पूड़ियों के टुकड़ों को टटोल-टटोलकर अपनी भूख मिटाने के लिए ऐसा नीच कर्म करे, इस प्रकार का दृश्य उसके लिए शोकमय और हार्दिक दुखद होने के अतिरिक्त और क्या हो सकता है। उसे स्वयं पर इस बात की ग्लानि हुई कि उसकी चचेरी सास उसकी संपन्नता के बावजूद जूठी पत्तलों के पूड़ियों के कुछ टुकड़ों के लिए इतना नीच और अधम काम कर रही है।

इस प्रकार का दृश्य उसके लिए ही नहीं, अपितु किसी के लिए भी ग्लानिपूर्ण हो सकता है। किसी के लिए दुखद और शोकमय हो सकता है। उस समय रूपा को ऐसा लग रहा था, मानो उसके नीचे की जमीन रुक गई है। आसमान चकरा रहा है। यही नहीं शायद अब कोई नई मुसीबत आने वाली है। इससे उसे क्रोध नहीं आया। उसे तो उस समय शोक ही नहीं अपितु भय और करुणा ने घेर लिया। इससे उसकी आँखें छलछला उठीं। उसे यह नहीं समझ में आ रहा था कि इस अधम पाप का कौन दोषी है? फलस्वरूप उसने बड़ी असहाय होकर आकाश की ओर हाथ उठाकर सच्चे हदय से कहा, “हे प्रभु! आप इस अधम पाप के लिए मुझे क्षमा कर देना। मेरे परिवार पर दया करना। मुझे अगर आप क्षमा नहीं करोगे तो मेरा सारा परिवार बर्बाद हो जाएगा।”

विशेष-

1. भाषा सरल शब्दों की है।
2. शैली चित्रमयी है।
3. मुहावरों के सटीक प्रयोग हैं।
4. यह अंश मार्मिक है।

1. गद्यांश पर आधारित अर्थग्रहण संबंधी प्रश्नोत्तर

प्रश्न
(i) रूपा का हृदय सन्न क्यों हो गया?
(ii)-बूढ़ी काकी जूठे पत्तलों पर से पूड़ियों के टुकड़े उठाकर क्यों खा रही थी?
उत्तर
0रूपा का हृदय सन्न हो गया। यह इसलिए कि उसने बूढ़ी काकी को जूठे पत्तलों पर से पूड़ियों के टुकड़े उठाकर खाते हुए देखा। इससे उसे भारी ग्लानि और शोक हुआ कि उसकी ही चचेरी सास इतना अधम काम कर रही है।
(i) बूढ़ी काकी जूठे पत्तलों पर से पूड़ियों के टुकड़े उठाकर खा रही थी। यह इसलिए कि उसका भोजन के लिए बुलाए जाने के लिए और इंतजार करने का धैर्य नहीं रहा। फलस्वरूप उसे इसके सिवा और कोई चारा नहीं दिखाई पड़ा था।

2. गद्यांश पर आधारित विषय-वस्त से संबंधित प्रश्नोत्तर

प्रश्न
(i) रूपा को क्रोध क्यों नहीं आया?
(ii) रूपा ने परमात्मा से क्यों प्रार्थना की?
उत्तर
(i) रूपा को क्रोध नहीं आया। यह इसलिए कि बूढ़ी काकी का जूठे पत्तलों पर से पूड़ियों के टुकड़ों को उठा-उठाकर खाने का दृश्य उसके लिए ग्लानिपूर्ण और शोकजनक दृश्य था।
(ii) रूपा ने परमात्मा से प्रार्थना की। यह इसलिए कि उसे यह पूरा भरोसा हो गया था कि उसे परमात्मा ही क्षमा कर सकता है और कोई नहीं।

5. रूपा को अपनी स्वार्थपरता और अन्याय इस प्रकार प्रत्यक्ष रूप से कभी न देख पड़े थे। वह सोचने लगी, हाय! कितनी निर्दयी हूँ! जिसकी संपत्ति से मुझे दो सौ रुपया वार्षिक आय हो रही है उसकी यह दुर्गति! और मेरे कारण! हे दयामय भगवान! मुझसे बड़ी भारी चूक हुई है, मुझे क्षमा करो। आज मेरे बेटे का तिलक था। सैकड़ों मनुष्यों ने भोजन पाया। मैं उनके इशारों की दासी बनी रही, अपने नाम के लिए सैकड़ों रुपए व्यय कर दिए, परंतु जिनकी बदौलत हजारों रुपए खाए उसे इस उत्सव में भरपेट भोजन न दे सकी। केवल इसी कारण तो कि वह वृद्धा है, असहाय है।

शब्दार्थ-निर्दयी-कठोर । दुर्गति-दुर्दशा। चूक-भूल । व्यय-खर्च । बदौलत-कारण।

प्रसंग-पूर्ववत्। इसमें लेखक ने रूपा को किस प्रकार अपनी स्वार्थपरता और अन्याय का बोध हुआ, उस पर प्रकाश डालते हुए कहा है कि

व्याख्या-बूढ़ी काकी को जूठे पत्तलों पर से पूड़ियों के टुकड़े उठाकर खाते हुए देखकर रूपा ने अपना अन्याय और अपना स्वार्थ ही माना। उसने इस प्रकार कभी नहीं देखा था। इसका अनुमान भी उसे नहीं था। उसने इसे गंभीरतापूर्वक सोचा-समझा तो यह पाया कि इस अन्याय और स्वार्थ के लिए वही दोषी है। उसकी ही कठोरता से यह हुआ है। उसने हदय से यह स्वीकार किया कि बूढ़ी काकी की ही दी हुई संपत्ति से उसे जो दो सौ रुपए की सालाना आमदनी हो रही है, उसी की इस प्रकार की दुर्दशा हो रही है। उसके लिए वही अपराधी है। इस प्रकार दुखी होकर उसने ईश्वर से अपनी इस कठोरता और अन्याय के लिए क्षमा माँगी। उसने यह पश्चाताप कि उसके बेटे के तिलक के सुअवसर पर अनेक लोगों ने तरह-तरह के भोजन किए। सैकड़ों रुपए उसने अनेक लिए खर्च भी किए। लेकिन यह बड़ी अफसोस की बात है कि जिसके कारण उसने खर्च किए और जिसके दिए-किए से आज वह सुखी-संपन्न है, उसी को इस दुर्दशा में डाल रही है। क्या इसलिए कि वह एक ऐसी वृद्धा है, जिसका कोई सहारा नहीं है।

विशेष

1. संपूर्ण कथन मार्मिक है।
2. करुण रस का संचार है।
3. भाव यथार्थपूर्ण और विश्वसनीय है।
4. भावात्मक शैली है।

1. गद्यांश पर आधारित अर्थग्रहण संबंधी प्रश्नोत्तर

प्रश्न
(i) रूपा की स्वापरता और अन्याय क्या वा?
(ii) रूपा से बड़ी भारी चूक क्या हुई?
उत्तर
(i) रूपा की स्वार्थपरता और अन्याय यही था कि वह बूढ़ी काकी की संपत्ति से पल-बढ़ रही थी, फिर भी वह बूढ़ी काकी को जूठे पत्तलों से पूड़ियों के टुकड़े खाने के लिए मजबूर दुर्दशा में डाल रही थी।
(ii) रूपा से बड़ी भारी यह चूक हुई कि बूढ़ी काकी की संपत्ति से दो सौ रुपए की सालाना आमदनी पाकर भी उन्हें दाने-दाने के लिए लाचार बना रही थी।

2. गद्यांश पर आधारित विषय-वस्तु से संबंधित प्रश्नोत्तर

प्रश्न
(i) रूपा ने भगवान से क्या क्षमा माँगी?
(ii) रूपा को किस बात का सबसे अधिक अफसोस हुआ?
उत्तर
(i) रूपा ने भगवान से यह कहा कि बूढ़ी काकी की दुर्गति कर उससे बड़ी भारी चूक हुई। वह इसके लिए उसे क्षमा कर दे।
(ii) रूपा को इस बात का सबसे अधिक अफसोस हुआ कि जिनकी बदौलत हजारों रुपए खाये, उसे ही वह इस उत्सव में भरपेट भोजन न दे सकी। केवल इसलिए कि वह वृद्धा है और बेसहारा है।

MP Board Class 9th Hindi Solutions

MP Board Class 9th Hindi Navneet Solutions एकांकी Chapter 1 दीपदान (एकांकी, डॉ. रामकुमार वर्मा)

दीपदान अभ्यास

बोध प्रश्न

दीपदान अति लघु उत्तरीय प्रश्न

दीपदान एकांकी के प्रश्न उत्तर Class 9th प्रश्न 1.
पन्ना कौन थी?
उत्तर:
पन्ना चित्तौड़ के राजसिंहासन के उत्तराधिकारी महाराणा साँगा के पुत्र कुँवर उदयसिंह की धाय थी।

दीपदान एकांकी का प्रश्न उत्तर MP Board Class 9th प्रश्न 2.
चित्तौड़ में ‘दीपदान’ का उत्सव क्यों मनाया जा रहा था?
उत्तर:
चित्तौड़ में ‘दीपदान’ का उत्सव बनवीर के षड्यंत्र द्वारा मनाया जा रहा था।

MP Board Solution Class 9 Hindi Ekanki प्रश्न 3.
पन्ना किसका बलिदान करती है?
उत्तर:
इस एकांकी में पन्ना अपने एकमात्र पुत्र चन्दन का बलिदान करती है।

Deepdan Question Answers MP Board Class 9th प्रश्न 4.
चित्तौड़ का कुलदीपक कौन था?
उत्तर:
चित्तौड़ का कुलदीपक सज परिवार का एकमात्र पुत्र कुँवर उदयसिंह था।

Deepdan Ekanki Workbook Answers MP Board Class 9th प्रश्न 5.
बनवीर कौन था? और वह कुँवरजी को क्यों मारना चाहता था?
उत्तर:
बनवीर महाराणा साँगा के छोटे भाई पृथ्वीसिंह की दासी का एक पुत्र था। वह महत्वाकांक्षी था। राज्य प्राप्त करने के षड्यंत्र द्वारा वह उदयसिंह की हत्या कर स्वयं राजा बनना चाहता था।

दीपदान लघु उत्तरीय प्रश्न

Deepdan Ekanki Questions And Answers MP Board Class 9th प्रश्न 1.
कीरतबारी ने उदयसिंह की सहायता किस प्रकार की?
उत्तर:
कीरतबारी नाई जाति का है। उसका काम राज्य परिवार में होने वाली दावतों की झूठी पत्तल उठाना था। वह एक राजभक्त सेवक था। पन्ना धाय को उसकी राजभक्ति पर पूरा भरोसा था। जब पन्ना धाय को बनवीर के षड्यंत्र का पता लग जाता है तो वह उदयसिंह को झूठी पत्तलों के टोकरे में छिपाकर राजमहल से बाहर बनास नदी के किनारे स्थित श्मशान भूमि पर ले जाने का आदेश देती है। कीरतबारी यदि उदयसिंह को टोकरी में छिपाकर नहीं ले जाता तो उदयसिंह के प्राणों की रक्षा नहीं हो सकती थी। इस प्रकार कीरतबारी ने उदयसिंह के प्राणों की रक्षा करके अपनी राजभक्ति का परिचय दिया है।

Deepdan Question And Answers MP Board Class 9th प्रश्न 2.
पन्ना धाय कुँवर उदयसिंह की रक्षा क्यों करना चाहती थी?
उत्तर:
पन्ना धाय कुँवर उदयसिंह का पालन-पोषण करने वाली धाय माँ थी। वह कुँवर उदयसिंह को अत्यधिक स्नेह करती थी। दासी पुत्र बनवीर चित्तौड़ राज्य सिंहासन के एकमात्र उत्तराधिकारी कुँवर उदयसिंह की हत्या कर चित्तौड़ का राजा बनना चाहता था। उसने इसी मकसद को प्राप्त करने के लिए उस समय दीपदान का उत्सव मनाया। पन्ना ने बनतीर के षड्यंत्र को जान लिया। अतः उसने कुँवर उदयसिंह को उस उत्सव में जाने से रोक लिया। अपने भावी शासक के प्राणों की रक्षा के लिए वह दुष्ट बनवीर के सामने अपने एकमात्र पुत्र चन्दन का बलिदान चढ़ा देती है। इस प्रकार अपने पुत्र का बलिदान करके उसने उदयसिंह के प्राणों की रक्षा की है।

Deepdan Questions And Answers MP Board Class 9th प्रश्न 3.
उदयसिंह पन्ना धाय से रूठकर क्यों सो गया था?
उत्तर:
बनवीर राजमहल में दीपदान का उत्सव मनाने की आज्ञा देता है। इस उत्सव में तुलजा भवानी के सामने सुन्दर-सुन्दर लड़कियाँ नृत्य करती हैं। कुँवर उदयसिंह उत्सव में जाकर नृत्य देखने की इच्छा पन्ना धाय के समक्ष करता है। पर पन्ना को इस उत्सव की आड़ में बनवीर द्वारा रचे गये षड्यंत्र की गंध लग जाती है। अतः वह कुँवर को वहाँ नहीं जाने देती है। बस इसी बात से। कुँवर रूठकर बिना भोजन किये ही अपने शयनकक्ष में चले गये।

Class 9 Hindi Deepdan MP Board  प्रश्न 4.
धाय माँ का उदयसिंह के प्रति वात्सल्य स्पष्ट कीजिए।
उत्तर:
धाय माँ ममता की साक्षात् मूर्ति है। वह कुँवर को अपने प्राणों से भी अधिक प्यार करती है। उदयसिंह की धाय होने के साथ-ही-साथ उसकी सुरक्षा का भी वह विशेष ध्यान रखती है। अतः जैसे ही उसे उदयसिंह की हत्या के षड्यंत्र के विषय में जानकारी होती है तो तुरन्त ही राज्यभक्त एवं झूठी पत्तल उठाने वाले कीरतबारी को विश्वास में लेकर झूठी पत्तलों के बीच में कुंवर उदयसिंह को छिपाकर सुरक्षित स्थान पर पहुँचा देती है। बनवीर के आने पर वह अपने सोये हुए पुत्र चन्दन का बलिदान करके अपनी अद्भुत स्वामिभक्ति का परिचय देती है।

Deepdan Ekanki Class 9 MP Board प्रश्न 5.
उदयसिंह के विरुद्ध रचे जाने वाले षड्यंत्र का आभास पन्ना को कैसे होता है?
उत्तर:
उदयसिंह के विरुद्ध रचे जाने वाले षड्यंत्र का आभास पन्ना को दासी साँवली की उस सूचना से मिलता है जिसमें साँवली बताती है कि कुछ सैनिकों को अपनी ओर मिलाकर बनवीर ने विक्रमादित्य की हत्या कर दी है और उसका अगला लक्ष्य उदयसिंह है।

दीपदान दीर्घ उत्तरीय प्रश्न

Deepdan Ekanki Ke Prashn Uttar MP Board Class 9th  प्रश्न 1.
निम्नलिखित पंक्तियों का आशय स्पष्ट कीजिए
(अ) चारो तरफ जहरीले सर्प घूम रहे हैं।
उत्तर:
आशय-जब उदयसिंह दीपदान उत्सव में जाने की जिद्द करने लगता है तो पन्ना धाय भावी अनिष्ट की आशंका से उसे उसमें भाग लेने से रोकती है। जब उदयसिंह कहता है कि मैं अकेला ही वहाँ चला जाऊँगा तब पन्ना धाय उसे समझाते हुए कहती है कि तुम रात में अकेले कहीं नहीं जाओगे क्योंकि यहाँ चारों तरफ दुश्मन रूपी जहरीले सर्प घूम रहे हैं और वे किसी भी समय तुम्हें डस सकते हैं अर्थात् तुम्हारा वध कर सकते हैं।

(ब) दिन में तुम चित्तौड़ के सूरज हो कुँवर और रात में तुम राजवंश के दीपक हो।
उत्तर:
आशय-पन्ना धाय कुँवर उदयसिंह को समझाते हुए कहती है कि तुम चित्तौड़ के सूरज हो। सूरज की तरह तुम्हारा उदय हुआ है तभी तुम्हारा नाम उदयसिंह रखा गया है। अत: दिन में तो तुम चित्तौड़ के सूरज हो और रात में तुम राजवंश के दीपक हो।

Deepdan Ekanki Answers MP Board Class 9th प्रश्न 2.
“लाल तुम्हारी माला मैं नहीं गूंथ सकी। तुम्हारा जीवन अधूरा होने जा रहा है तो माला कैसे पूरी होगी” इस वाक्य में छिपी करुणा को स्पष्ट कीजिए।
उत्तर:
पन्ना धाय को जब यह पूरा विश्वास हो जाता है कि बनवीर विक्रमादित्य की हत्या के पश्चात् अगला निशाना उदयसिंह को ही बनायेगा तो वह अपनी चतुराई से कीरतबारी के सहयोग से उदयसिंह को तो सुरक्षित स्थान पर पहुँचा देती है पर इस रहस्य को छिपाये रखने के लिए कुँवर उदयसिंह की शैया पर अपने इकलौते पुत्र चन्दन को सुला देती है। चन्दन सोने से पूर्व अपनी टूटी हुई माला को गूंथने की बात कहता है तो धाय माँ उसे कल गूंथने का आश्वासन देकर सुला देती है। लेकिन अब उसके हृदय में चन्दन की होने वाली हत्या की आशंका से अनेकानेक भाव उत्पन्न होते हैं और उन्हीं विचारों में खोकर वह कहने लग जाती है कि हे लाल ! तुम्हारी माला मैं नहीं गूंथ सकी। अत्याचारी बनवीर के हाथों तुम्हारा जीवन अधूरा होने जा रहा है तो फिर तुम्हारी माला गूंथकर मैं किसे पहनाऊँगी। यह कहकर उसके हृदय में करूणा का ज्वार उठने लगता है।

Deepdan Ki Kahani MP Board Class 9th प्रश्न 3.
इस एकांकी में निहित पन्ना धाय के त्याग व एकनिष्ठा के भाव का वर्णन कीजिए।
उत्तर:
‘दीपदान’ एकांकी की प्रधान पात्र पन्ना धाय है। पन्ना धाय में अपूर्व बलिदान एवं त्याग की भावना है। उसके मन मानस में स्वामिभक्ति की भावना कूट-कूट कर भरी हुई है। इसी भावना के वशीभूत होकर वह राजवंश के अन्तिम दीपक उदयसिंह की प्राण रक्षा के लिए अपना सब कुछ बलिदान कर देती है। उसके जीवन में कर्त्तव्यपालन सर्वोपरि है।

उसका त्याग अभूतपूर्व है। उसके त्याग में स्वार्थ की गन्ध नहीं है। राजवंश के उत्तराधिकारी उदयसिंह की प्राणरक्षा के लिए वह अपने इकलौते पुत्र चन्दन की बलि दे देती है। चन्दन को मौत की शैया पर सुलाते समय वह कहती है-“दीपदान! अपने जीवन का दीप मैंने रक्त की धारा में तैरा दिया है। ऐसा दीपदान भी किसी ने किया है?” निश्चय ही ऐसा दीपदान कोई भी नहीं कर सका। यह उसका अपूर्व त्याग था। इस प्रकार हम कह सकते हैं कि पन्ना धाय में एकनिष्ठ स्वामिभक्ति की भावना एवं अपूर्व त्याग था।

दीपदान भाषा अध्ययन

प्रश्न 1.
निम्नलिखित शब्दों में से कुछ शब्दों की वर्तनी अशुद्ध है, उन्हें शुद्ध कीजिए
चित्तौड़, प्रस्थान, इर्ष्या, विक्रमादीत्य, कुंवरजी, अन्नदाता, शैया, अट्ठास, राजपुतानी, शीर्षक, छत्राणी।
उत्तर:

प्रश्न 2.
निम्नलिखित शब्दों के विलोम शब्द लिखिएउदय, जीवन, इच्छा, ईर्ष्या, रात।
उत्तर:

प्रश्न 3.
एकांकी में आए शब्द सोना, जाल आदि अनेकार्थी शब्द हैं। पाठ में आए ऐसे ही अनेकार्थी शब्द छाँटकर उनके दो-दो अर्थ लिखिए।
उत्तर:
शब्द            अर्थ
सोना       – निद्रा, धातु का नाम
लाल       – पुत्र, रंग का नाम
ताल        – तालाब, पग चाल
काल       – समय, मृत्यु
जाल       – धोखा, पाश
जवान     – नवयुवक-युवती, वाणी
पहाड़     – पर्वत, रुकावट
सूरज      – सूर्य, कुल के सूरज या देश के सूरज
बारी       – क्रम, नाई, जाति का कर्मी
दीपक     – दीया, कुल के दीपक
उजाला    – प्रकाश, वंश को चलाने वाला
तिनका    – छोटा व्यक्ति, घास।

प्रश्न 4.
निम्नलिखित शब्दों में से तत्सम और तद्भव अलग-अलग करके लिखिए।
उत्तर:
तत्सम शब्द – शैय्या, कक्ष, उदय, दासी, दीपक, प्रस्थान, पुत्र, लता।
तद्भव शब्द – सूरज, रात, भोजन, नाच, पैर, पत्थर, सिर।

दीपदान पाठ का सारांश

चित्तौड़ के महाराणा साँगा की मृत्यु के पश्चात् उनका पुत्र ‘उदयसिंह’ राज्य का उत्तराधिकारी था पर उसकी अवस्था छोटी होने के कारण राज्य का उत्तरदायित्व विक्रमादित्य को दिया गया। पर जनता, सरदार एवं सामन्त उनके व्यवहार से दुःखी थे। बनवीर महाराणा साँगा के छोटे भाई पृथ्वीसिंह की दासी का पुत्र था। विक्रमादित्य के कुशासन से जब सब लोग परेशान थे तो बनवीर ने एक षड्यंत्र रचकर चित्तौड़ में ‘दीपदान’ उत्सव का आयोजन किया।

पन्नाधाय कुँवर उदयसिंह की संरक्षिका है। कुँवर उदयसिंह को जब दीपदान उत्सव के आयोजन की खबर लगती है तो वह पन्नाधाय से उत्सव में जाने की जिद्द करता है। पन्ना दूरदर्शी थी अत: किसी अनिष्ट की आशंका के कारण वह उदयसिंह को उत्सव में शामिल होने के आज्ञा नहीं देती है। इस पर उदयसिंह क्रोधित होकर अपने शयन कक्ष में चला जाता है।

इसी समय रावल रूपसिंह की परम सुन्दरी बेटी बनवीर के इशारे पर उदयसिंह को उत्सव में ले जाने का प्रयास करती है पर पन्नाधाय उसको भी फटकार कर भगा देती है।

इसी समय पन्नाधाय के तेरह वर्षीय पुत्र चन्दन का आगमन होता है। पन्ना उससे भोजन का आग्रह करती है पर चन्दन उदयसिंह के बिना भोजन नहीं करना चाहता है। उसी क्षण चीखते हुए तथा बेचैन दशा में दासी साँवली आती है और वह पन्नाधाय को यह बताती है कि बनवीर ने कुछ सैनिकों को अपने साथ मिलाकर राजा विक्रमादित्य की हत्या कर दी है और अब उसका अगला लक्ष्य उदयसिंह है। अतः उसे उदयसिंह की रक्षा करनी चाहिए। पन्ना उदयसिंह की रक्षा के लिए प्राणपण से तैयार हो जाती है। इसी समय कीरतबारी नामक नाई कुँवर उदयसिंह की झूठी पतल उठाने के लिए पन्ना धाय के कक्ष में प्रवेश करता है। कीरतबारी देशभक्त था अतः पन्ना उसे विश्वास में लेकर घटित घटनाक्रम को समझा देती है। साथ ही वह उदयसिंह की रक्षा हेतु उदयसिंह को झूठी पतलों की टोकरी में लिटाकर तथा ऊपर से झूठे पत्तलों से ढककर उदयसिंह को राजमहल से निकाल ले जाने की योजना बनाती है।

कीरतबारी टोकरी में उदयसिंह को सुलाकर तथा झूठी पत्तलों से ढककर महल से बाहर ले जाता है। कुँवर उदयसिंह के बिछौने पर वह अपने पुत्र चन्दन को सुला देती है। चन्दन को कुँवर उदयसिंह के बिछौने पर सुला देने के पश्चात् पन्ना धाय का मातृहृदय भावी अनिष्ट की आशंका से व्याकुल होकर रुदन करने लगता है। इसी समय मदिरा के नशे में चूर होकर बनवीर अपने हाथ में विक्रमादित्य के खून से सनी हुई तलवार लेकर आता है और उदयसिंह के बारे में पूछता है। पन्ना को जब उसका इरादा पता चल गया तो वह बनवीर से उदयसिंह के प्राणों की भिक्षा माँगती है।

क्रूर बनवीर से उदयसिंह के बदले पन्ना को जागीर देने की बात कहता है लेकिन पन्ना इस प्रस्ताव को ठुकरा देती है और उस पर अपने कटार से प्रहार करती है। बनवीर कटार छीन लेता है और आगे बढ़कर शैय्या पर सोये हुए चन्दनसिंह को उदयसिंह समझकर तलवार से प्रहार करता है। पन्ना चीखकर बेहोश हो जाती है। इस प्रकार पन्नाधाय अपने अभूतपूर्व, त्याग, कर्त्तव्यपालन एवं बलिदान द्वारा अपने राजा के पुत्र के प्राणों की रक्षा करती है। यहीं एकांकी समाप्त हो जाती है।

MP Board Class 9th Hindi Solutions

In this article, we will share MP Board Class 8th Hindi Book Solutions Chapter 4 सबके चेहरे खिल उठे Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 8th Hindi Sugam Bharti Solutions Chapter 4 सबके चेहरे खिल उठे

प्रश्न अभ्यास

अनुभव विस्तार

Mp Board Class 8 Hindi Chapter 4 प्रश्न 1.
वस्तुनिष्ठ प्रश्न
(क) सही जोड़ी बनाइए
(अ) मानवाधिकार – 1. सद्भाव
(ब) सांप्रदायिक – 2. संरक्षण
(स) राष्ट्रीय – 3. आयोग
(द) कानूनी – 4. हित
उत्तर-
(अ) – 3
(ब) – 1
(स) – 4
(द) – 2

Mp Board Class 8th Hindi Solution Chapter 4 प्रश्न 2.
दिए गए विकल्पों से रिक्त स्थानों की पूर्ति कीजिए
(अ) रामू के काका को पुलिस …………………. के लिए पकड़कर ले जा रही थी। (गिरफ्तार करने, पूछताछ करने)
(ब) पुलिस की मुख्य जिम्मेदारी ………………….. (जनता को सताना, नागरिकों की सुरक्षा)
(स) पुलिस अपराधी को …………………… घंटे के भीतर मजिस्ट्रेट के सामने ले जाती है। (चौबीस, बत्तीस)
उत्तर-
(अ) पूछताछ,
(ब) नागरिकों की सुरक्षा,
(स) चौबीस।

Class 8 Hindi Chapter 4 Mp Board प्रश्न 2.
अति लघु उत्तरीय प्रश्न
(अ) पुलिस से क्यों नहीं डरना चाहिए?
(ब) पुलिस लोगों से पूछताछ क्यों करती है?
(स) पुलिस विभाग के उच्चाधिकारी कौन-कौन से हैं?
(द) हम पुलिस का सहयोग किस प्रकार कर सकते हैं?
उत्तर-
(अ) पुलिस हमारी रक्षा के लिए है। इसलिए हमें पुलिस से नहीं डरना चाहिए।
(ब) जब कोई अप्रिय घटना या अपराध हो जाता है, तब पुलिस लोगों से पूछताछ करती है।
(स) जिला पुलिस अधीक्षक, डी.आई.जी., रेंज एवं राज्य के पुलिस महानिदेशक पुलिस विभाग के उच्चाधिकारी हैं।
(द) कानून व्यवस्था को बनाए रख करके, सूचना का आदान-प्रदान करके, कानून एवं नियमों का स्वेच्छा से पालन करके और कानून व संविधान में आस्था रख करके हम पुलिस का सहयोग कर सकते हैं।

Class 8 Hindi Chapter 4 प्रश्न 3.
लघु उत्तरीय प्रश्न-
(अ) पुलिस किस-किस स्थिति में हथकड़ी लगा सकतीहै?
उत्तर-
यदि पुलिस को विश्वास हो कि अपराधी भाग जाएगा, तो वह उसे हथकड़ी लगा सकती है। यह भी कि यदि कोई खतरनाक आरोपी है, तो न्यायालय की अनुमति मिलने पर भी पुलिस उसे हथकड़ी लगा सकती है।

(ब) पुलिस को सहयोग करना क्यों आवश्यक है?
उत्तर-
पुलिस असामाजिक और आपराधिक तत्त्वों के विरुद्ध कार्यवाही करके अपराध को रोकती है। इसके लिए वह हमारा सहयोग चाहती है। इसलिए पुलिस को सहयोग करना आवश्यक है।

(स) महिलाओं से पूछताछ के लिए क्या-क्या सावधानियाँ जरूरी हैं?
उत्तर-
महिलाओं से पूछताछ के लिए निम्नलिखित सावधानियाँ जरूरी हैं

1. पुलिस हिरासत में उनके साथ कोई दुर्व्यवहार न हो।
2. कोई अपमानजनक बात न हो।
3. उनके साथ कोई अपराध घटित होने पर या महिला उत्पीड़न से संबंधित कोई भी रिपोर्ट थाने पर प्राप्त होने पर उसे तत्काल खोजकर उनको उचित संरक्षण और कानूनी सहायता प्रदान हो।

(द) नागरिकों के पुलिस के प्रति क्या कर्त्तव्य हैं?
उत्तर-
नागरिकों के पुलिस के प्रति निम्नलिखित कर्त्तव्य हैं

1. प्रत्येक नागरिक का यह कर्त्तव्य है कि वह सामाजिक शांति, सांप्रदायिक सद्भावना एवं राष्ट्रीय हित को प्रभावित करने वाली कोई भी महत्त्वपूर्ण सूचना पुलिस को दे।
2. प्रत्येक नागरिक का यह कर्तव्य है कि दुर्घटनाग्रस्त लोगों को निकट के अस्पताल में पहुँचाकर पुलिस को सूचना दे।
3. प्रत्येक नागरिक का यह भी कर्तव्य है कि राष्ट्रीय एवं सार्वजनिक संपत्ति, राष्ट्रीय ध्वज आदि की सुरक्षा और सम्मान करना एवं उनकी खोज संबंधी सही गवाही पुलिस को दे।

भाषा की बात

Sugam Bharti Class 4 Hindi Solutions प्रश्न 1.
बोलिए और लिखिए-
दृष्ट्या, अधीक्षक, मजिस्ट्रेट, गिरफ्तार, उत्पीड़न, विशेष, अनुसंधान, संरक्षण।
उत्तर-
दृष्ट्या, अधीक्षक, मजिस्ट्रेट, गिरफ्तार, उत्पीड़न, विशेष, अनुसंधान, संरक्षण।

Class 8 Hindi Chapter 4 Question Answer प्रश्न 2.
रेखांकित शब्दों के विरुद्धार्थी शब्द लिखकर वाक्य बनाइए
(अ) दोषी व्यक्ति को दण्ड मिलता है।
(ब) सज्जनों का सभी सम्मान करते हैं।
(स) अपराधी जितने दूर हों उतना अच्छा।
(द) मैं आज कक्षा में उपस्थित रहूँगा।
उत्तर-
(अ) निर्दोषी व्यक्ति को सम्मान मिलता है।
(ब) दुर्जनों का सभी अपमान करते हैं।
(स) अपराधी जितने पास हों, उतना बुरा।
(द) मैं कल कक्षा में अनुपस्थित रहूँगा।

Mp Board Class 8 Hindi Book Solution प्रश्न 3.
उदाहरण के अनुसार ई प्रत्यय लगाकर नए शब्द लिखिए
उत्तर-
‘ई’ प्रत्यय लगाकर नए शब्द

♦ प्रमुख गद्यांशों की संदर्भ-प्रसंग सहित व्याख्याएँ

1. गिरफ्तारी का मतलब पुलिस अपने रिकॉर्ड में लिखते हुए उसे अपनी हिरासत में रखेगी, गिरफ्तार करने के बाद उसे 24 घंटे के भीतर ही मजिस्ट्रेट के सामने प्रस्तुत करेगी। पूछताछ की और जरूरत होने पर मजिस्ट्रेट उसे पुलिस को अपने पास रखने की अनुमति देंगे या फिर जेल भेज देंगे। हो सकता है किसी की जमानत पर उसे छोड़ भी दे।

शब्दार्थ-रिकॉर्ड-लिखित विवरण। हिरासत-निगरानी। मजिस्ट्रेट-दंडाधिकारी। अनुमति-आदेश, आज्ञा।।

संदर्भ-प्रस्तुत पंक्तियाँ हमारी पाठ्य-पुस्तक ‘सुगम्र भारती’ (हिंदी सामान्य) भाग-8 के पाठ-4 ‘सबके चेहरे खिल उठे’ से ली गई हैं।

प्रसंग-प्रस्तुत पंक्तियों में लेखक ने पुलिस द्वारा गिरफ्तार किए जाने के विषय में जानकारी देते हुए कहा है कि

व्याख्या-जब पुलिस किसी को गिरफ्तार करती है तो उसका खास मतलब होता है। वह यह कि इससे वह अपने लिखित विवरण में जरूरी बातों को दर्ज कर लेती है। इसके बाद वह अपनी निगरानी में रख लेती है। फिर वह उसे दंडाधिकारी के सामने अपना अगला कदम उठाने के लिए पेश करती है। यह कदम वह किसी को गिरफ्तार करने के 24 घंटे के अंतर्गत ही उठाती है। दंडाधिकारी पर यह निर्भर करता है कि वह क्या कदम उठाता है। वह उसे पुलिस के पास रखने का आदेश देता है अथवा उसे जेल की सजा सुनाता है। यह भी वह कदम उठा सकता है कि वह उसे जमानत पर भी रिहा कर दे।

विशेष-

• पुलिस की कार्यविधि को स्पष्ट किया गया है।
• भाषा मिली-जुली है।

2. पुलिस विभाग अपराध पर नियंत्रण रखने के लिए हमसे असामाजिक एवं आपराधिक तत्त्वों के विरुद्ध कार्यवाही में सकारात्मक सहयोग चाहता है। कानून व्यवस्था बनाए रखना, सूचना का आदान-प्रदान करना, कानून एवं नियमों का स्वेच्छा से पालन करना, कानून व संविधान में आस्था बनाए रखना भी पुलिस विभाग को सहयोग करना ही है।

शब्दार्थ-नियंत्रण-वश। असामाजिक-समाज विरोधी। आपराधिक-अपराध करने वाले। स्वेच्छा-अपने-आप। आस्था-विश्वास। सहयोग-सहायता।

संदर्भ-पूर्ववत्।

प्रसंग-इन ,पंक्तियों में लेखक ने पुलिस द्वारा अपराध रोकने के लिए उठाए जाने वाले कदम के विषय में बतलाते हुए कहा है कि

व्याख्या-पुलिस विभाग हमेशा किसी प्रकार के सामाजिक-असामाजिक तत्त्वों द्वारा किए जा रहे अपराधों पर रोक लगाने की पूरी कोशिश करती है। इसके लिए वह अपराधियों के विरुद्ध कदम उठाती है। इस दिशा में वह अधिक-से-अधिक हम सभी की सहायता-सहयोग चाहती है। यह तभी संभव है जब हम अपने देश के नियम-कानून का पालन करें। परस्पर सूचना और संपर्क बनाए रखें । स्वतंत्र रूप से कानून-नियम का न केवल पालन करें, अपितु आस्था और विश्वास भी रखें। ऐसा करके भी हम पुलिस विभाग को सहायता-सहयोग प्रदान कर सकते हैं।

विशेष-

• किसी प्रकार के अपराध पर नियंत्रण रखने के लिए पुलिस विभाग का सहयोग करने की आवश्यकता बतलायी है।
• यह अंश ज्ञानवर्द्धक है।

MP Board Class 9th Sanskrit Solutions Durva Chapter 4 पितृसेवा परं ज्ञानम् (कथा)

MP Board Class 9th Sanskrit Chapter 4 पाठ्य पुस्तक के प्रश्न

संस्कृत कक्षा 9 पाठ 4 Question Answer MP Board प्रश्न 1.
एकपदेन उत्तरं लिख-(एक शब्द में उत्तर दीजिए)
(क) मदन विनोदः कस्य पुत्रः आसीत्? (मदन, विनोद किसके पुत्र थे?)
उत्तर:
हरिदत्तस्य। (हरिदत्त के)

(ख) मदनं विनोदेन स्वर्णपञ्जरस्थः शुकः कुत्र स्थापितः? (मदन विनोद ने सोने के पिंजरे में स्थित शुक को कहाँ रखा?)
उत्तर:
शयनेन कक्षे। (सोने वाले कमरे)

(ग) त्रिविक्रमनामा द्विजः कस्य सखा आसीत्? (विक्रम नाम का ब्राह्मण किसका मित्र था?)
उत्तर:
हरिदत्तस्य (हरिदत्त का)।

(घ) देवशर्मा कुत्र तपः अकरोत्? (देवशर्मा ने कहाँ तपस्या किया?)
उत्तर:
गंगातीरे (गंगा के किनारे)।

(ङ) देवशर्मोपरि केन पुरीषोत्सर्ग कृतः? (देवशर्मा के ऊपर किसने टट्टी किया?)
उत्तर:
बलाकि (बगुली)।

कक्षा 9 संस्कृत पाठ 4 के प्रश्न उत्तर MP Board प्रश्न 2.
अधोलिखित प्रश्नां एकवाक्येन उत्तरं लिखत (नीचे लिखे प्रश्नों का एक वाक्य में उत्तर लिखो)
(क) मदनविनोद पितुः शिक्षा केन कारणेन न शृणोति? (मदनविनोद पिता की शिक्षा किस कारण से नहीं सुनता था?)
उत्तर:
मदन विनोद पितुः शिक्षा दुखश्यनेनो कारणेन न शृणोति। (मदन विनोद पिता की शिक्षा दुख के कारण नहीं सुनता था।)

(ख) मदन विनोदस्य आसक्तिः केषु आसीत्? (मदन विनोद का लगाव किसमें था?)
उत्तर:
मदनविनोदस्य आसक्तिः द्यूतमृगयवेश्यामद्यादिषु आसीत्। (मदन विनोद का लगाव जुआ खेलने, वेश्यावृत्ति और मदिरापान आदि में था।)

(ग) द्विजपत्नी देवशर्माणं किम उक्तवती? (ब्राह्मण की पत्नी ने देवशर्मा से क्या बोली?)
उत्तर:
द्विजपत्नी देवशर्माणं नाहं बलाकेव त्वत्कोपस्थानम् उक्तवती। (ब्राह्मण की पत्नी देव शर्मा से बोली, मैं तुम्हारे बालक को स्थापित नहीं की हूँ।)

(घ) देवशर्मा विस्मितः कथं सजातः? (देवशर्मा किस तरह से विस्मित हो गए?)
उत्तर:
देवशर्मा विस्मितः प्रच्छन्नपातकज्ञानादीत सञ्जातः। (देव शर्मा छुपे हुए पापी ज्ञान के कारण विस्मित हो गए।)

(ङ) देवशर्मा व्याधं कीदृशम् अपश्यत्? (देवशर्मा ने बहेलिया को किस तरह से देखा?)
उत्तर:
देवशर्मा व्याधं रक्ताक्तहस्तं यम प्रतिमं मांसविक्रयं विद्धानं अपश्यत्। (देवशर्मा ने बहेलिए को रक्तरंजित हाथ तथा मांस बेचते हुए देखा।)

संस्कृत कक्षा 9 पाठ 4 Solution MP Board प्रश्न 3.
अधोलिखित प्रश्नां उत्तराणि लिखत (निम्नलिखित प्रश्नों के उत्तर लिखो)
(क) शुको देवशर्मणः पतनाय किं कारणमवोचत्? (तोते ने देवशर्मा के पतन के लिए क्या कारण बताया?)
उत्तर:
शुको देवशर्मणः पतनाय पित्रोस्ते दुःखिनोर्दुः खात्पतत्यश्रुचयो भूवि कारणमवोचत्। (तोते ने देव शर्मा के पतन का कारण बताया कि तुम्हारे पिता दुख से दुखी थे और उनके अश्रु भूमि पर गिर रहे थे।)

(ख) बलाका कथं भस्मीभूता जाता? (बगुला किस तरह से भस्म हुआ?)
उत्तर:
बलाका तपस्वी क्रोधाग्निना भष्मीभूता जाता। (बगुला तपस्वी के क्रोध के कारण भस्म हुआ।)

(ग) के जनाः निन्द्यमानाः जीवन्ति? (कौन लोग निन्दनीय जीवन जीते हैं?)
उत्तर:
स गृही मुनिः साधु स योगी स च धार्मिकः पितृशुश्रूषको नित्यं जन्तुः साधारणश्च य। (वही व्यक्ति गृहस्थ है, वही मुनि साधु योगी है, जो पिता की सेवा में नित्य लगा हुआ है, ऐसे व्यक्ति साधारण होते हुए भी श्रेष्ठ हैं।)

(घ) व्याधः स्वज्ञानस्य कारणम् किम् उत्कवान? बहेलिया ने अपने ज्ञान का क्या कारण बताया?
उत्तर:
न पूजयन्ति ये पूज्यान्मान्यान्न मानयन्ति ये। जीवन्ति निन्द्यमानास्ते मताः स्वर्ग न यान्ति च। (जो पूजा योग्य की पूजा नहीं करते, मानने योग्य को नहीं मानते, निन्द्य होकर वह इस जीवन में जीते तथा मरने पर उन्हें स्वर्ग नहीं मिलता ऐसे लोग निन्दनीय जीवन जीते हैं।)

(ङ) अस्य पाठस्य आशयः कः? (इस पाठ का क्या आशय है?)
उत्तर:
अस्य पाठस्य आशयः-पितरौ सेवा। (इस पाठ का आशय है-माता-पिता की सेवा करना)

संस्कृत कक्षा 9 पाठ 4 प्रश्न उत्तर MP Board प्रश्न 4.
अधोलिखत वाक्येषु पदपूर्ति कुरुत
(क) हरिदत्तः कुपुत्रं दृष्ट्वा दुखितः सञ्जातः।
(ख) शुकं सपत्नीकं पुत्रवत्वं परिपालय।
(ग) तपस्वी गङ्गातीरे जपार्थमुपविष्टः।
(घ) ब्राह्मण ज्ञानकारणं व्याध प्रप्रच्छ।
(ङ) नाहं बलाकेय त्वत्कोपस्थानम्
(च) क्रोधाग्निना भस्भीभूतां बलाकां भूमौ पतिताम्।

Class 9 Sanskrit Chapter 4 Question Answer MP Board प्रश्न 5.
‘अ’ ‘ब’ स्तम्भयों यथायोग्यं मेलनम् कुरुत-

उत्तर:
क. 5
ख. 3
ग. 1
घ. 2
ड. 4

Class 9th Sanskrit Chapter 4 Question Answer MP Board प्रश्न 6.
अधोलिखित संधीनां विच्छेदं कुरुत

संस्कृत कक्षा 9 पाठ 4 के प्रश्न उत्तर MP Board प्रश्न 7.
अधोलिखित समासानां विग्रहं कुरुत

Class 9th Sanskrit Chapter 4 MP Board प्रश्न 8.
अधोलिखिताव्ययाना वाक्येषु प्रयोगं कुरुत
(उपरि, च, तत्र, एवम, न, ऊर्ध्वम, इव, कथम्)
उपरि – वायुयानमः उपरि-उपरि उड्डयति।
च – राम-लक्ष्मणसीताश्च वनं आगच्छत्।
तत्र – तत्र वायु प्रवहति।
एवम् – सः एवम् कथाम् अकथयत्।
न – वृष्टिः न भविष्यति।
ऊर्ध्वम् – खगाः ऊर्ध्वम् उड्डयन्ति।
इव – गीता वाक्देवि इव पठति।
कथम – कथम् सः शीघ्रम संस्कृतं पठति।

Sanskrit Class 9 Solutions Chapter 4 MP Board प्रश्न 9.
अधोलिखित वाक्यानि कः कम् कथयति
(क) एनं शुकं सपत्नीक पुत्रत्व परिपालय।
उत्तर:
त्रिविक्रमाः हरिदत्तं कथयति।

(ख) अस्ति पञ्चपुरं नाम नगरम्।
उतर:
शुकः मदनविनोदम् कथयति।

(ग) नाहं बलाकेव त्वत्कोपस्थानम्।
उत्तर:
नारायणस्य पनि देवशर्माणम् कथयति।

(घ) कथं सती ज्ञानवती, कथं च त्वं ज्ञानवान।
उत्तर:
देवशर्मा व्याधम् कथयति।।

(ङ) ये मान्यान न मानयन्ति ते मृताः स्वर्गं न यान्ति।
उत्तर:
व्याधाः ब्राह्मणं कथयति।

Class 9 Sanskrit Chapter 4 MP Board प्रश्न 10.
अधोलिखित शब्दानां प्रकृति प्रत्ययम् च पृथक कुरुत
(क) गृहीत्वा
उत्तर:
गृह्+क्त्वा

(ख) दत्तम्
उत्तर:
दा+क्त

(ग) ज्ञानवान
उत्तर:
ज्ञान+मतुप

(घ) परित्यज्य
उत्तर:
परि+त्यज क्त्वा (ल्यप)

(ङ) निन्द्यमानाः
उत्तर:
निन्द्य+शानच्।

Class 9 Sanskrit Chapter 4 Solutions MP Board प्रश्न 11.
अधोलिखित शब्दानां मूलशब्दं विभक्ति वचनञ्च लिखत

पितृसेवा परं ज्ञानम् पाठ-सन्दर्भ/प्रतिपाद्य

संस्कृत साहित्य में कथा (आख्यान) साहित्य की दो विधाएँ उपलब्ध हैं। पहली विधा में उपदेशात्मक नीति-कथात्मक साहित्य है जिसमें ‘पंचतंत्र’ पशु-पक्षियों के माध्यम से (प्रेरक एवं ज्ञानवर्द्धक कथाएँ) रोचक ढंग से कही गई हैं। दूसरी विधा में लोककथात्मक मनोरंजक साहित्य आता है। उपदेशात्मक नीति कथा साहित्य में ‘शुक सप्ततिः’ प्रसिद्ध ग्रंथ है। नीति-कथा में उपदेश की प्रवृत्ति तथा लोक-कथा साहित्य में मनोरंजन की वृत्ति प्रमुख रूप से होती है। शुक सप्ततिः उपदेशात्मक कथा का एक उत्तम ग्रंथ है। इस (ग्रंथ के) लेखक के विषय में अथवा इसके रचना काल में निश्चय नहीं है किंतु इस समय शुक नाम से उपलब्ध है। सन् 1400 ई. का मध्य इस कथा-ग्रंथ का रचना काल अनुमानित है। अतः उसी में से एक मातृ-पितृ भक्ति परक कथा शिक्षण के दृष्टिकोण से उपलब्ध है।

पितृसेवा परं ज्ञानम् पाठ का हिन्दी अर्थ

1. चन्द्रपुरनाम्नि नगरे श्रेष्ठिनः हरदत्तस्य पुत्रः मदनविनोदस्तु अतीवविषयासक्तः कुपुत्रः पितुः शिक्षा न शृणोति स्म। तस्य द्यूतमृगयावेश्यामद्यादिषु अतीव आसक्तिः। कुमार्गचारिणं तं कुपुत्रं दृष्ट्वा तत्पिता हरिदत्तः सपत्नीकः अतीव दुःखितः सञ्जातः। तं हरिदत्तं कुपुत्रदुःखेन पीडितं दृष्ट्वा। तस्य सखा त्रिविक्रमनामा द्विजः स्वगृहतो नीतिनिपुणं शुकं सारिकां च गृहीत्वा तद्गृहे गत्वा प्राह-‘सखे हरिदत्त! एनं शुकं पुत्रवत्त्वं सपत्नीकं परिपालय। एतत्संरक्षणेन तव दुःखं दूरीभविष्यति।’ हरिदत्तस्तु शुकंगृहीत्वा पुत्राया समर्पयामास। मदनविनीदेन शयनमन्दिरे स्वर्णपञ्जरस्थः स्थापितः परिपोषितश्च। अथैकदा रहसि शुको मदनं प्राह-हे सखे!

पित्रोस्ते दुःखिनोर्दुःखात्पतत्यश्रुचयो भुवि।
तेन पापेन ते वत्स पतनं देवशर्मवत्॥2॥

Sanskrit Class 9 Chapter 4 Question Answer MP Board शब्दार्थ :
श्रेष्ठिनः-सम्पन्न व्यापारी का-Talented Businessman or Rich Businessman; मदनविनोदस्तु-मदन और विनोद–Madan and Vinod ; विषयासक्तः-विषयों में आसक्त-Strongly attached in bad habit; न शृणोत स्म-नहीं सुनते थे-did not listen; दृष्ट्वा -देखकर-to see , to look; तत्पिता-उसके पिता-his father; हरिदत्तं-हरिदत्त को-to Hari datt; स्वगृहतो-अपने घर में-in his oun house. नीतिनिपुणं-नीति में निपुणं-talented in policy; मद्गृहे-उस घर में-In its house. एतत्संरक्षणेन-इसके संरक्षण से –By his patronage; समर्पयामास-समर्पित किया-dedicated; शयनमन्दिर-शयन मन्दिर में-in sleeping room. स्वर्णपञ्जरथः-सोने के पिंजरे-cage of gold;अथैकदा-इस प्रकार एक दिन-inthis type one day;रहसि-अकेले में-inalone; पित्तोश्ते-तुम्हारे पिता-your father; भुवि-संसार में-inworld; देवशर्मवत्-देव शर्मा के सामन-like Dev Sharma.

संस्कृत कक्षा 9 पाठ 4 कल्पतरु MP Board हिन्दी अर्थ :
चन्द्रपुर नामक नगर में हरिदत्त का पुत्र मदन विनोद अत्यधिक विषयासक्त होने के कारण कुपुत्रों (की भांति) पिता की शिक्षा को नहीं सुनता था। उसमें जुआ, मृगया, वेश्यागमन आदि में विशेष आसक्ति थी। कुपुत्र के कुमार्ग गामी होने को देखकर उसका पिता हरिदत्त पत्नी सहित बहुत दुखी रहता था। उस हरिदत्त को कुपुत्र की कुआदतों से दुखी देखकर उसका मित्र त्रिविक्रम नामक ब्राह्मण अपने घर से नीति निपुण तोता-मैना लेकर हरिदत्त के घर जाकर बोला-‘हे मित्र हरिदत्त! इस तोते का सपत्नीक पुत्रवत पालन करो। इसका संरक्षण करने से तुम्हारा दुःख दूर होगा। हरिदत्त ने तोते को लेकर अपने पुत्र को दे दिया। तोता मदन विनोद के शयनकक्ष में स्वर्ण निर्मित पिंजरे में रहता एवं पोषित होता हुआ तोता एक दिन अकेले में उससे बोला-हे मित्र!

तुम्हारे पिता के कष्ट में होने के कारण उनका आँसू भूमि पर गिर गया। हे वत्स! उस पाप से तुम्हारा भी पतन देवशर्मा के समान होगा।

2. स प्राह-‘कथमेतत?’
शुक आह-अस्ति पञ्चपुरं नाम नगरम्। तत्र सत्यशर्मा ब्राह्मणः। तद्भार्या धर्मशीलानाम्नी। पुत्रस्तु देवशर्मा। स च अधीतविद्यः पितृप्रच्छन्नवृत्या देशान्तरं गत्वा भागीरथीतीरे तपः कृतवान्।

एकदा स तपस्वी गङ्गातीरे जपार्थमुपविष्टः। तस्मिन्काले कयाचित् बलाकया उड्डीयमानया तदङ्गोपरि पुरीषोत्सर्गः कृतः। स च तपस्वी क्रोधाकुलितनेत्रः यावदूर्ध्वं पश्यति तावत्तत्क्रोधग्निना भस्मीभूतां बालकं भूमौ पतितां दृष्ट्वा (बलाकां दग्ध्वा) नारायणद्विजगृहे भिक्षार्थ ययौ। स्वभर्तृशुश्रूषापरया तत्पत्न्या कोपाभिविष्टो निर्भर्त्सतः सत्पक्षिहायमुक्तश्च –

‘नाहं बलाकेव त्वत्कोपस्थानम्।’-
स च प्रच्छन्नपातकज्ञानादीतो विस्मितश्च, प्रेषितश्च तया धर्मव्याधपार्वे वाराणसी नगरी ययौ। तत्र रक्ताक्तहस्तं यमप्रतिभं मांसविक्रयं विद्धानं तं दृष्टवा दृशामन्तः स्थितः। व्याधेन स्वागतप्रश्नपूर्वकं स्वगृहं नीत्वा निजपितरी सभक्तिकं भोजयित्वा पश्चातस्य भोजनं दत्तम्। तदनन्तरं स च व्याधं ज्ञानकारणं पप्रच्छ-‘कथं सती ज्ञानवती, कथं च त्वं ज्ञानवान्।’

शब्दार्थ :
कथमेतत्-यह कैसे-How titis; धर्मशीलानाम्नी-धर्म शीला नाम की-Name of Dharmsheela; पितृपृच्छत्तवृत्या-पिता के द्वारा बताये गए, मार्ग पर-obey by father’s way; देशान्तरं-दूसरे देश को-to other country. भागीरथीतीरे-गंगा के किनारे-Bank ofGanga;जापार्शमुपविष्टः-जप करने के लिए बैठा-reading meettering of prayers; तस्मिन्काले-उसी समय-that time; उड्डीयमानथा-उठते हुए-flies; तदङ्गोपरि-उसके ऊपर-on thepartofhis body;पुरीषोत्सर्गः-उसके ऊपर मल (टट्टी)-onhis body;क्रोधाकुलित-क्रोध पूर,-forcefull; यावदूर्ध्वं-जब ऊपर-when on; पश्यति-देखता है-looks, sees; क्रोधाग्निना-क्रोध की अग्नि में-in the fire of angry.

भस्मीभूतां-जल गया-burnt; सत्पक्षिहायमुक्तश्च-निर्दोष पक्षी को मारने वाला-innocent birdkiller; ज्ञानावदीतो-ज्ञान से डरा हुआ-afraid of knowledge; विस्मित्-आश्चर्य चकित-wonderfull; प्रेषितश्च-भेजा-send; रक्ताक्तहस्तं-जिसके हाथ रक्त से रंगे हुए हों वह-red handed; यमप्रतिभं-यमराज के समान भयंकर-Horrible like Yamraj;ब्याधेन-बेहलिया ने-Hunter; दृशामन्तः स्थितः-गांव के कुछ दूर में स्थिति-few far of village in situated; स्वागतप्रश्नपूर्वक-स्वागत प्रश्न पूर्वक-wellcomed with question/ happyness: स्वगृह-अपने घर को-his own house; सभक्तिक-भक्ति पूर्वक-full of worship; तदनन्तरं-उसके बाद-often that; ज्ञानकारणं-ज्ञान का कारण-reasonof knowledge; पप्रच्छ-पूछा-asked.

हिन्दी अर्थ :
तब वह बोला-वह कैसे?
तोता बोला-पञ्चपुर नामक एक नगर था। वहाँ सत्य शर्मा नामक ब्राह्मण था। धर्मशीला नाम की उसकी पत्नी थी। उसका पुत्र देवशर्मा था। वह सभी विद्याओं में पारंगत होकर पिता के द्वारा निर्दिष्ट मार्ग पर चलते हुए देशान्तर जाकर गंगा के तट पर तप करने लगा।

एक बार वह तपस्वी गंगा के तट पर तप के उद्देश्य से बैठा था। उसी समय कोई बगुली ऊपर से उड़ती हुई उसके ऊपर विष्ठा कर दी। तब वह तपस्वी क्रोध में ज्यों ही ऊपर की ओर देखा, उसकी क्रोधाग्नि से वह बगुली भस्म होकर भूमि पर आ गिरी। बगुली को जला देखकर वह नारायण नामक ब्राह्मण के घर भिक्षा के उद्देश्य से गया। अपने पति की सेवा में परायण नारायण की पत्नी ने निरीह पक्षी के हत्यारे उस ब्राह्मण की भर्त्सना करते हुए कहा-बगुली के समान मैं तुम्हारे कोप का स्थान नहीं हूँ।

और इस पाप कृत्य के परिणाम से भयभीत वह ब्राह्मण उस द्वारा भेजा गया वाराणसी में धर्म व्याध नामक बहेलिए के पास गया। वहाँ उसने रक्त से सने हुए दोनों हाथों से मांस बेचते हुए यम के सदृश भयंकर रूप वाले उस व्याध को देखा और कुछ दूर खड़ा हो गया। व्याध ने स्वागत करते हुए आने का कारण पूछते हुए उसे अपने घर ले जाकर आदरपूर्वक अपने माता-पिता को भोजन कराने के पश्चात् भोजन कराया इसके बाद उसने ब्याध के ज्ञानी होने का कारण पूछा साथ ही उस सती स्त्री ज्ञानवती के विषय में पूछा, और तुम केसे ज्ञानवान हुए? यह भी बताने को कहा।

3. तेन व्याधेनोक्तम्
निजान्वयप्रणीतं यः सम्यग्धर्म निषेवते।
उत्तमाधममध्येषु विकारेषु पराङ्मुखः॥3॥
स गृही स मुनिः साधुः स योगी स च धार्मिकः।।
पितृशुश्रूषको नित्यं जन्तुः साधरणश्च यः॥4॥

अहं सापि च एवं ज्ञानिनौ त्वं च निजपतिरौ परित्यज्य भ्रमन्मादृशां न सम्भाषणार्हः। परमतिथिं मत्वा जल्पितः। एवमुक्तः स ब्राह्मणो विनयपरं व्याधं पप्रच्छ। तेनोक्तम् –

न पूजयन्ति ये पूज्यान्मान्यान्न मानयन्ति ये।
जीवन्ति निन्द्यमानास्ते मृताः स्वर्गं न यान्ति च ॥5॥
व्याधेन बोधितस्तेन स ययौ गृहमात्मनः।
अभवत्कीर्तिमाल्लोके परतः कीर्तिभाजनम ॥6॥

तस्माद्वणिग्धर्मं स्वकुलोद्भवं स्मर पित्रोश्च विनयपरो भव।

एवमुक्ताः स मदनः विनयपरः सदाचारी च, अभवत् पितरौ नमस्कृत्य तदनुज्ञातो भार्याञ्चापृच्छय प्रवहणधिरूढवान् गाते देशान्तरम्।

शब्दार्थ :
निजान्वयप्रणीतम्-कुल द्वारा किया हुआ-it was done by family; पराङ्मुख-विमुख-separate; पितृशुश्रूषक-पिता की सेवा में लीन-serve in father; सम्भाषणहिः- संवादयोग्य-able of conversation; निजपतिरो-अपने माता पिता-his own parents; परित्यज्य-छोड़कर-leave; तेनोक्तम्-उसने कहा-he said; न पूजयन्ति-जो नहीं पूजते-who not worshipped; ये पूज्यान्मान्यान्न-जो पूजे जाने योग्य है-who is able to worshiped; ग्रहमात्मनः-अपने घर में-his won house.

हिन्दी अर्थ :
तब व्याध ने कहा-अपने कुलोचार का श्रद्धापूर्वक पालन करते हुए उत्तम, अधम, मध्यम आदि विकार से रहित होकर कार्य करना चाहिए। (जो ऐसा करता है) वही गृही है, वही मुनि है, वही सच्चा साधु है, वही सच्चा योगी व धार्मिक है जो माता-पिता की सेवा में नित्यप्रति लगा रहता है। वह व्यक्ति साधारण होने पर भी श्रेष्ट
है।

इस प्रकार मैं और वह स्त्री ज्ञानवती ज्ञानी हैं। तुम अपने माता-पिता को त्यागकर भ्रमित होकर कुछ भी कहने के योग्य नहीं हो-इस प्रकार वह परम अतिथि जानकर उस ब्राह्मण से विनयपूर्वक कहा ऐसा कहा.

जो पूजनीय व्यक्ति की पूजा नहीं करते, जो मानने योगय को नहीं मानते, ऐसे लोग निन्द्य होकर जीवन जीते हैं और मरने पर स्वर्गगामी नहीं होते। व्याध द्वारा बोधि पूर्ण शिक्षा पाकर वह देवशर्मा अपने घर गया और इस लोक में कीर्तिमान होकर अपना जीवन-यापन करने लगा। इसलिए तुम बनिए का धर्म अपने कुल के अनुसार स्मरण करके माता-पिता के प्रति विनम्र हो। यह सुनकर मदन विनोद विनय युक्त हो सदाचार का अनुसरण करने लगा। वह माता-पिता को नमस्कर करके उनकी आज्ञा ले, अपनी धर्मपत्नी से पूछ वाहन पर सवार होकर दूसरे देश को गमन किया।

MP Board Class 9th Sanskrit Solutions

MP Board Class 9th Sanskrit अनुवाद पकरण

अनुवाद करने के लिए सर्वप्रथम कारक का उचित प्रयोग जानना महत्त्वपूर्ण है।

कारक प्रकरण

कारक वे शब्द हैं, जिनका क्रिया से प्रत्यक्ष सम्बन्ध रहता है। संस्कृत में कारक अपनी विभक्ति के साथ जुड़े हैं, जबकि हिन्दी में विभक्ति चिह्न को कारक शब्द से अलग लिखते हैं। इनके प्रयोग के कुछ विशेष नियम हैं, जो यहाँ दिए जा रहे हैं।

प्रथमा विभक्ति का प्रयोग

1. कर्तवाच्य (Active Voice) में कर्ता प्रथमा विभक्ति में होता है।
जैसे-
(क) बालाः क्रीडन्ति। (बच्चे खेलते हैं।) .
(ख) अहं धावामि। (मैं दौड़ता हूँ।)

2. किसी वस्तु के नाम या लिंग का ज्ञान कराने हेतु प्रथमा का प्रयोग करते हैं। जैसे
(क) एषा माला अस्ति।
(ख) एतानि फलानि सन्ति।

द्वितीय विभक्ति का प्रयोग
1. कर्म हमेशा कर्मकारक (द्वितीया विभक्ति) में रहता है। जैसे
(क) मैं फल खाता हूँ। (अहं फलं खादामि।)
(ख) मैं जल पीता हूँ। (अहं जलं पिबामि।)

2. जिस स्थान को जाते हैं, वह कर्मकारक (द्वितीया) में रहता है। जैसे
(क) रामः वनम् अगच्छत्। (राम वन गये।)
(ख) वयं विद्यालयं गच्छामः। (हम विद्यालय जाते हैं।)

3. किसी अव्यय के योग में जब कोई विशेष विभक्ति हो, तो उसे उपपद विभक्ति कहते हैं। द्वितीया का उपपद विभक्ति के रूप में निम्न अव्ययों के साथ प्रयोग होता है

धिक् (धिक्कार है), अन्तरेण (के बिना), अन्तरा (बीच में), प्रति (की ओर), उभयतः (दोनों ओर), विना (के बिना), निकषा (निकट), अनु (पीछे), सर्वतः (सब ओर), परितः (चारों ओर), अभितः (सामने), अधोऽथः (नीचे-नीचे), उपर्युपरि (ऊपर-ही-ऊपर), हा (अफसोस)।

(क) धिक् अत्याचारिणम्। (अत्याचारी को धिक्कार है।)
(ख) ग्रामं परितः वनानि सन्ति। (गाँव के चारों ओर वन हैं।)
(ग) राधा नगरं प्रति गच्छति। (राधा नगर की ओर जाती है।)
(घ) जलं विना मत्स्यः न जीवति। (जल के बिना मछली जीवित नहीं रहती है।)
(ङ) गृहं निकषा उद्यानम् अस्ति। (घर के निकट उद्यान है।)

4. दुह्, याच्, भिक्ष्, प्रच्छ्, शास्, चि (चुनना), ब्रू (बोलना) आदि धातुओं के योग में द्वितीय विभक्ति का प्रयोग होता है। जैसे
(क) भिक्षुकः धनं भिक्षते। (भिखारी धन की भिक्षा माँगता है।)
(ख) गोपालः धेनोः दुग्धं दुह्यति। (ग्वाला गाय का दूध दुहता है।)

5. शी (सोना), स्था (बैठना, तथा आस् (बैठना) धातुओं में ‘अधि’ उपसर्ग लगा होने पर द्वितीय विभक्ति का प्रयोग होता है। जैसे
(क) राज्यपालः राजभवनम् अध्यासते। (राज्यपाल राजभवन में बैठते हैं।)
(ख) सीता पर्यकम् अधिशेते। (सीता पलंग पर सोती है।)
(ग) रामः आसनम् अधितिष्ठति। (राम आसन पर बैठता है।)

6. वस् (रहना) धातु में ‘अधि, उप, आ, अनु’ उपसर्ग लगा होने पर द्वितीय विभक्ति का प्रयोग होता है।

तृतीया विभक्ति का प्रयोग

1. जिसके द्वारा कार्य हो, वह कारणकारक (तृतीया) में रहता है।
जैसे-
(क) बालकाः कंदुकेन क्रीडन्ति। (लड़के गेंद से खेलते हैं।)
(ख) बालिका कलमेन लिखति। (लड़की कलम से लिखती है।)
(ग) वयं नेत्राभ्यां पश्यामः। (हम आँखों से देखते हैं।)

2. जिसका साथ बतलाना हो, वह कारणकारक में रहता है। सह, साकम् सार्धम् आदि सहार्थक अव्यय हैं। इसके साथ सदैव तृतीया विभक्ति रहती है।
जैसे-
(क) अहं मित्रेण सह गच्छामि। (मैं मित्र के साथ जाता हूँ।
(ख) छात्राः शिक्षकैः सह गायन्ति। (छात्र शिक्षकों के साथ गाते हैं।)

3. कारण के अर्थ में तथा विकृतांग वाची शब्दों के साथ तृतीया लगती है। जैसे
(क) जनः सभायां विद्यया शोभते। (सभा में व्यक्ति विद्या के कारण शोभित होता है।)
(ख) सः नेत्रेण काणः। (वह आँख से काना है।)
(ग) हरिः पादेन पंगुः अस्ति। (हरि पैर से लँगड़ा है।)

4. तृतीया विभक्ति का निम्न शब्दों के साथ पयोग होता है-
अलम् (बस करो), सह (साथ), साकम् (साथ), सार्धम् (साथ), समान (बराबर), सम (समान), सदृश्य (समान), तुल्य (समान), बिना/विना (के बिना)।
(क) अलम् हसितेन। (हँसो मत।).
(ख) रामेण सह लक्ष्मणः अपि वनम् अगच्छत्। (राम के साथ लक्ष्मण भी वन को गए।)
(ग) सः पित्रा साकम् आपणं गच्छति। (वह पिता के साथ बाजार जाता है।)
(घ) धर्मेण विना जीवनं शून्यम् अस्ति। (धर्म के बिना जीवन मूल्य है।)

5. हेतु या स्वाभाव के अर्थ में तृतीया विभक्ति होती है।
6. पृथक् और हीन के अर्थ में तृतीय विभक्ति होती है।
7. तुलनात्मक शब्दों में तृतीया विभक्ति होती है।

चतुर्थी विभक्ति का प्रयोग
1. सम्प्रदान में चतुर्थी विभक्ति होती है। जिसे कुछ दिया जावे या जिस उद्देश्य से क्रिया की जावे, या जिसके लिए कार्य हो, वह सम्प्रदान होता है।
जैसे-
(क) एतत् फलं रामाय अस्ति। (यह फल राम के लिए है।)
(ख) नद्यः परोपकाराय वहन्ति। (नदियाँ परोपकार के लिए बहती हैं।)

2. नमः, स्वस्ति, स्वाहा और अलम् अव्ययों के साथ चतुर्थी का प्रयोग होता है। अलम् के योग में बढ़कर बताया जावे, या ‘पर्याप्त है’ का अर्थ हो, तब उसमें चतुर्थी का प्रयोग होता है। जैसे
(क) शिवाय नमः ! (शिवजी को नमस्कार है।)
(ख) श्री गणेशाय नमः। (श्री गणेशजी को नमस्कार है।)
(ग) अनुजाय स्वस्ति। (छोटे भाई का कल्याण हो।)
(घ) अग्नये स्वाहा। (यह आहुति अग्नि के लिए है।)
(ङ) रामः रावणाय अलम्। (राम रावण से बढ़कर हैं।)
(च) एतनि फलानि पंच जनेभ्यः अलम् सन्ति। (ये फल पाँच लोगों के लिए पर्याप्त हैं।)

नमः अव्यय और नम् धातु में भ्रमित न होवे। नम् धातु के साथ अन्य विभक्तियाँ भी प्रयुक्त होती हैं।

जैसे-
अहं शिवं नमामि। (मैं शिवजी को नमन करता हूँ।)

3. दा, रुच, क्रुध, कुप, द्रुह (विद्रोह करना), स्पृह् (इच्छा करना) असूय् (द्वेष करना) व स्निह् धातुओं के योग में चतुर्थी प्रयुक्त होती है। जैसे
(क) प्राचार्यः छात्राय पुरस्कारं यच्छति। (प्राचार्य छात्र को पुरस्कार देते हैं।)
(ख) मह्यं दुग्धं रोचते। (मुझे दूध अच्छा लगता है।)
(ग) रामः सुरेशाय कुप्यति। (राम सुरेश पर नाराज होता है)
(घ) बालिकाः पुष्पेभ्यः स्पृहयन्ति। (लड़कियाँ फूलों की इच्छा करती हैं।)
(ङ) सः मोहनाय ईयति। (वह मोहन से ईर्ष्या करता है।)
(च) अध्यापकः शिष्याय क्रुध्यति। (शिक्षक शिष्य पर क्रोधित होते हैं।)

पंचमी विभक्ति का प्रयोग
1. जिससे अलग होना बतलाना हो, वह पंचमी में रहता है।

जैसे-
(क) वृक्षात् पत्रं पतति। (वृक्ष से पत्ता गिरता है।)
(ख) सः ग्रामात् आगच्छति। (वह गाँव से आता है।)

2. भय, रक्षा आदि के योग में पंचमी विभक्ति का प्रयोग किया जाता है।
जैसे-
(क) व्याघ्रात् भयम् अस्ति। (शेर से डर लगता है।)
(ख) रमा बालः दुर्जनात् रक्षति। (रमा बालक की दुष्ट से रक्षा करती है।)

3. जिससे शिक्षा ग्रहण की जाये, या जिससे उत्पत्ति हो, उसके योग में पंचमी का प्रयोग किया जाता है।

जैसे-

(क) छात्राः अध्यापकात् विद्यां पठन्ति। (छात्र अध्यापक से विद्या पढ़ते हैं।)
(ख) हिमालयात गङ्गा प्रभवति। (हिमालय से गंगा निकलती है।)

4. निलीयते (छिपना) के योग में पंचमी का प्रयोग किया जाता है।

जैसे-
(क) सुरेशः अध्यापकात् निलीयते। (सुरेश शिक्षक से छिपता है।)
(ख) चौरः रक्षकात् निलीयते। (चोर सिपाही से छिपता है।)

5. पृथक्, विना और नाना शब्दों के साथ द्वितीया, तृतीया या पंचमी में से कोई भी एक विभक्ति हो सकती है। जैसे
(क) जलं बिना मत्स्यः न जीवति। (जल के बिना मछली नहीं जीती।)
(ख) जलेन विना मत्स्यः न जीवति। (जल के बिना मछली नहीं जीती।)
(ग) जलाद् विना मत्स्यः न जीवति। (जल के बिना मछली नहीं जीती।)

6. पंचर्मी विभक्ति का निम्न शब्दों के साथ प्रयोग होता है ऋते (बिना), प्रभृति (लेकर), आरात् (के पास), अनन्तरम् (के बाद), दूरम् (दूर), बहिः (बाहर), अन्तिकम् (पास), ऊर्ध्वम् (ऊपर)।
(क) ग्रामात् दूरे नद्यः अस्ति। (गाँव से नदी दूर है।)
(ख) उद्यानात् अन्तिकम् देवालयः अस्ति। (उद्यान के पास मंदिर है।)
(ग) ग्रामात् आरात् तडागः अस्ति। (गाँव के पास तालाब है।)
(घ) उद्यानात् बहिः भोजनालयः अस्ति। (उद्यान के बाहर भोजनालय है।)

षष्ठी विभक्ति का प्रयोग

1. वस्तुओं में सम्बन्ध स्थापित करने में षष्ठी विभक्ति का प्रयोग होता है। जैसे
(क) दशरथस्य चत्वारः पुत्राःआसन्। (दशरथ के चार पुत्र थे।)
(ख) इयं तव पुस्तकम् अस्ति। (यह तुम्हारी पुस्तक है।)

2. जंघ खेद पूर्वक याद किया जावे, तो ‘स्मृ’ के योग में षष्ठी प्रयुक्त होती है। जैसे
(क) राधा पितुः स्मरति। (राधा पिता के उपकारों को याद करती है।)

3. षष्ठी विभक्ति का निम्न शब्दों के साथ प्रयोग होता है पुरः (सामने), अधः (नीचे), उपरि (ऊपर), पश्चात् (बाद में), पुरस्तात् (सामने), अन्तिके (पास में), अधस्तात् (नीचे)।
(क) वृक्षस्य अधः पथिकः तिष्ठति। (वृक्ष के नीचे राहगीर बैठा है।)
(ख) उद्यानस्य पुरस्तात् कूपः अस्ति। (बाग के सामने कुआँ है।)
(ग) ग्रामस्य अन्तिके देवालयः अस्ति। (गाँव के पास मंदिर है।)
(घ) वृक्षस्य अधस्तात् जनाः सन्ति (वृक्ष के नीचे लोग हैं।)

4. विशेषण की उत्तमावस्था बताने में षष्ठी या सप्तमी का प्रयोग होता है। जैसे
(क) कवीनां कालिदासः श्रेष्ठः अस्ति। (कालीदास कवियों में श्रेष्ठ हैं।)
(ख) कवीष कालिदासः श्रेष्ठः अस्ति। (कालीदास कवियों में श्रेष्ठ हैं।)

5. तुलना, कुशलता के योग में षष्ठी का प्रयोग होता है।

जैसे-
(क) रामस्य तुल्यः कोऽपि न अस्ति। (राम की तुलना में कोई नहीं है।)
(ख) तस्य मुखम् चन्द्रस्य सदृशं अस्ति। (उसका मुख चन्द्रमा के समान सुंदर है।)

सप्तमी विभक्ति का प्रयोग

1. स्थान या समय सूचक शब्द अधिकारकारक (सप्तमी) में रहते हैं।
जैसे-
(क) तडागे जलम् अस्ति। (तालाब में पानी है।)
(ख) बिले मूषकः तिष्ठति। (बिल में चूहा रहता है।)
(ग) ते मम गृहे न्यवसन्। (वे सब मेरे घर में रहते थे।)
(घ) वृक्षेषु फलानि सन्ति। (वृक्षों पर फल हैं।)
(ङ) जले मत्स्याः निवसन्ति। (जल में मछलियाँ रहती हैं।)

2. स्निह्, अभिलष् आदि के योग में सप्तमी विभक्ति होती है।
जैसे-
(क) माता पुत्रे स्निह्यति। (माता पुत्र से स्नेह करती है।)

3. तत्परता, चतुरता, कुशलता आदि के योग में सप्तमी विभक्ति होती है।

जैसे-
(क) शीला गायने निपुणा अस्ति। (शीला गाने में निपुण है।)
(ख) हरिः कार्ये तत्परः अस्ति। (हरि कार्य में तत्पर है।)
(ग) रामः व्यापारे कुशलः अस्ति। (राम व्यापार में कुशल है।)

4. एक कार्य होने के लिए उपरान्त दूसरा प्रारम्भ होने पर सप्तमी का पयोग होता है।

जैसे-
(क) सूर्ये अस्तं गते रात्रिः आगच्छति। (सूर्य अस्त होने के बाद रात्रि आती है।)
(ख) शिक्षके गते छात्राः कोलाहलं कृतवन्तः। (शिक्षक के जाने पर छात्रों ने शोर मचाया) . . .. .. ……. .

सम्बोधनम् का प्रयोग

1. सम्बोधन हेतु सम्बोधनकारक का प्रयोग होता है।

जैसे-
(क) हे राम, उत्तिष्ठ। (राम, खड़े हो जाओ।)
(ख) हे प्रभु! रक्ष माम्। (हे भगवान! मेरी रक्षा करो।)

अनुवाद के अन्य नियम
नियम 1. विशेषण का पयोग उसी लिंग, वचन और कारक में होगा, जिस लिंग, वचन और कारक में उसका विशेष (अर्थात् जिसकी वह विशेषता बतलाता है) रहेगा।
जैसे-
(क) चह चतुर बालक है। = एषः चतुरः बालकः अस्ति!
(ख) यह चतुर लड़की है। = एषा चतुरा बालिका अस्ति।
(ग) यह सफेद घोड़ा है। = एषः श्वेत अश्वः अस्ति।
(घ) यह सफेद बकरी है। = एषा श्वेता अजा अस्ति।
(ङ) यह सफेद गाय है। = एषा श्वेता धेनुः अस्ति।
(च) सफेद घोड़े को लाओ। = श्वेतम् अश्वम् आनय।
(छ) काले घोड़े पर बैठो। = कृष्णे अश्वे उपविश।

नियम 2. भूतकालिक कृदन्त का प्रयोग विशेषण के समान करेंगे।
जैसे-
(क) यह गिरा हुआ फल है। = एतत् पतितं फलं अस्ति।
नियम 3. पूर्वकालिक कृदन्त, हेतुवाचक कृदन्त तथा अव्ययों के रूप में कोई परिवर्तन नहीं होता है।
नियम 4. मकारांत शब्द के बाद व्यंजन से प्रारम्भ होने वाला शब्द आवें, तो म् के बदले अनुस्वार (-) लिखते हैं। यदि म के बाद स्वर से प्रारम्भ होने वाला शब्द आये, तब म् की उस स्वर में संधि हो जाती है।

जैसे-
(क) अहम् गच्छामि = अहं गच्छामि। (मैं जाता हूँ।) (ख) अहम् अगच्छम् = अहमगच्छम्। (मैं गया था।)
नियम 5. संस्कृत में वाक्य की क्रिया यदि ‘भू’ (भवति) = होना या ‘अस्’ (होना) या कोई उसके समान अर्थ वाली हो, तो वाक्य में प्रायः उसे नहीं लिखा जाता है और उसका अर्थ ऊपर से कर लिया जाता है।

जैसे-
(क) सुरेशः स्वपितुः एकः पुत्रः भवति। – सुरेशः स्वपितुः एकः पुत्र। (सुरेश अपने पिता का एक पुत्र है।)
(ख) एतत् चक्रम् अस्ति। (यह पहिया है।) = एतत् चक्रम।

नियम 6. कुत्रचित् (कहीं), किंचित् (कुछ), कदाचित् (कभी) आदि का प्रयोग-संस्कृत में कहीं, किसी, कोई, कभी, कुछ आदि शब्दों का अव्यय या अनिश्चय वाचक विशेषण या सर्वनाम के रूप प्रयोग करने हेतु “किम्’ सर्वनाम के रूपों में ‘चित्’ जोड़ देते हैं। यह ध्यान में रखना चाहिए कि किम् के लिंग और वचन वही हों, जो उसके विशेष के हैं। किम् के रूपों की चित् के साथ संधि करते समय उचित नियमों का पालन करें। यथा न को अनुस्वार और श् में बदल देते हैं। जैसे-कस्मिन् चित् कस्मिंश्चित् आदि। इसी तरह किम् के रूपों का विसर्ग भी श् में बदल जाता है। कः+ चित -कश्चित् आदि। इसी तरह अन्य नियमों का प्रयोग करें। इसके उदाहरण निम्नानुसार हैं.

(क) किसी वृक्ष पर एक तोता बैठा था।
कस्माच्चित् वृक्षे एकः शुकः अतिष्ठत्।
(ख) प्राचीन काल में मथुरा में कोई सेठ रहता था।
पुरा मथुरा नगर्यां कश्चित् श्रेष्ठी अवसत्।
(सा) किसी गाँव में एक साधु रहता था।
कास्मिंश्चित् ग्रामे एकः साधुः अनिवसत्।

इसी तरह किसी तालाब में = कस्माच्चित् सरोवरे, किसी सुंदरी का = कस्याश्चित सुंदर्याः, कुछ पक्षी = केचित् विहगाः, किसी आदमी ने = कश्चित् जनः आदि का अनुवाद किया जाता है।

परीक्षापयोगी महत्वपूर्ण अनुवाद के वाक्य-

1. 1. वृक्ष से पत्ता गिरता है। – वृक्षात् पत्रं पतति।
2. 2. गुरु शिष्य को पुस्तक देता है। – गुरुः शिष्याय पुस्तकं यच्छति।
3. 3. छात्र पुस्तक पढ़ते हैं। – छात्राः पुस्तकानि पठन्ति।
4. 4. सीता राम के साथ बन गई। – सीताः रामेण सह वनं गता।
5. 5. सूर्य को नमस्कार। – सूर्याय नमः।
6. 6. गंगा हिमालय से निकलती है। – गंगा हिमालयात् प्रभवति।
7. 7. राम शीतल जल पीता है। – रामः शीतलं जलं पिबति।
8. मोहन शीतल जल पीता है। – मोहनः अद्य गृहं गमिष्यति।
9. अति सभी जगह वर्जित है। – अति सर्वत्र वर्जयेत्।
10. विद्या विनय देती है। – विद्या विनयं ददाति।
11. तुम कहाँ जा रहे हो? – त्वं कुत्र गच्छसि?
12. उसे संस्कृत पढ़ी। – सः संस्कृतभाषाम् अपठत्।
13. गणेश जी को नमस्कार है। – श्री गणेशाय नमः।
14. यह हमारा देश है। – एषः अस्माकं देशः अस्ति।
15. आत्मा जल से शुद्ध नहीं होती है। – आत्मा जलेन ने शुद्धयति।
16. उनकी माता पुतली बाई थीं। – तस्य माता पुतलीबाई आसीत्।
17. मुझे लड्डू अच्छे लगते हैं। – मह्यम् मोदकानि रोचन्ते।
18. यह मेरी पुस्तक है। – इदं मम पुस्तकं अस्ति।
19. मैं विद्यालय जाता हूँ! – अहं विद्यालयं गच्छमि।
20. सीमा गेंद से खेलती है। – सीताः कन्दुकेन क्रीडति।

वाक्यों को शुद्ध करके लिखना
          अशुद्ध           –     शुद्ध वाक्य
1. सः पुस्तकं पठामि। – सः पुस्तकं पठति।
2. सः फलं खादामि। – सः फलं खादति।
3. सः रामस्य सह गतः। – सः रामेण सह गतः।
4. सः क्रीडन्ति। – सः क्रीडति।
5. अहं पाठशालाः गच्छामः। – अहम् पाठशालांग छमि।
6. वयं विद्यालये गच्छमि। – वयं विद्यालयं गच्छामः।
7. ह्यः रविवासरः अस्ति। – ह्यः रविवासरः आसीत्।
8. युवां क्रीडसि। – युवां क्रीडथः।
9. त्वम् कदा पठति? – त्वं कदा पठसि?
10. बालकः कुत्र गच्छसि। – बालकः कुत्र गच्छति?
11. अहं पाठशाले गच्छामि ? – अहं पाठशाला गच्छामि।
12. त्वम पठामि। – त्वं पठसि।
13. बालकाः फलाः खादन्ति। – बालकाः फलानि खादन्ति।
14. ते गच्छामि। – ते गच्छन्ति।
15. सर्वाणि बालकाः पठन्ति। – सर्वे बालकाः पठन्ति।
16. रामस्य नमः। – रामाय नमः।
17. पिता पुत्रे क्रुध्यति। – पिता पुत्राय क्रुध्यति।
18. नोहनः सुरेशम् ईष्यति। – मोहनः सुरेशाय ईष्यति।
19. मां दुग्धं न रोचते। – मह्यं दुग्धं न रोचते।
20. ग्रामस्य परितः वनानि सन्ति। – ग्रामं परितः वनानि सन्ति।

अभ्यास

1. निम्नलिखित वाक्यों का संस्कृत में अनुवाद कीजिए-
किसी किसान के चार पुत्र थे। वे चारों मुर्ख थे। निदेय मनुष्य पशुओं पर दया नहीं करते। ईश्वर उन्हें सद्बुद्धि दे। किसी नगर में कोई वैश्य रहता था। वह बहुत अमीर था। एक बार नदी में किसी नारी का हार गिर गया। एक मछुआरे ने उसे निकला। जब तक मैं न आऊँ, तब तक तुम अपना पाठ पढ़ो। राजा के आदेश से सेनापति ने आक्रमण किया। जहाँ परिश्रम है, वहाँ सुख निवास करता है। छात्रों को रात-दिन मेहनत करना चाहिए, तभी सफलता मिलेगी। झूठ मत बोलो। यह अच्छी बात नहीं है। सदैव सच्चे और हितकारी वचन बोलो। गाँव से शाला दूर है, अतः _ वह बैलगाड़ी से शाला जाता है। (बैलगाड़ी से = शकटेन)

MP Board Class 9th Sanskrit Solutions

MP Board Class 9th Sanskrit Solutions Durva Chapter 1 जयतु मे माता (गीतम्)

MP Board Class 9th Sanskrit Chapter 1 पाठ्य पुस्तक के प्रश्न

Class 9 Sanskrit Chapter 1 Mp Board प्रश्न 1.
एकपदेन उत्तरं लिखत-(एक शब्द में उत्तर दीजिए)।
(क) गीतायाः गाता क? (गीता का गाने वाला कौन है?)
उत्तर:
गीतायाः गाता कृष्णः। (गीता का गान करने वाला कृष्ण है।)

(ख) सीमान्तरक्षकः कः अस्ति? (सीमा का रक्षक कौन है?)
उत्तर:
सीमान्तरक्षकः सैनिकः अस्ति। (सीमा का रक्षक सैनिक है।)

(ग) वेदोपनिषज्जनयित्री का? (वेद और उपनिषद् की माता कौन है?)
उत्तर:
वेदोपनिषज्जनयित्री भारतभूमिः। (वेद और उपनिषद् की माता भारतभूमि है)

(घ) निष्कारणविद्वेषकरः कुत्र याति? (बिना कारण के बैर करने वाला कहां जाता है?)
उत्तर:
निष्कारणविद्वेषकर कालमुखिः याति। (बिना कारण के बैर करने वाला काल के मुख अर्थात् मृत्यु के मुख में जाता है)

(ङ) मातुः कष्टकर दुर्दैवं कः शमयतु? (माता के दुखों या कष्टों को कौन दूर करता है)
उत्तर:
मातुः कष्टकरं दुर्दैवं विधाता शमयतु। (माता के दुखों व कष्टों को विधाता दूर करता है।)

You can download MP Board 10th sanskrit solution to help you to revise complete syllabus and score more marks in your examinations.

Mp Board Class 9 Sanskrit Chapter 1 प्रश्न 2.
एकवाक्येन उत्तरं लिखत्-(एक वाक्य में उत्तर लिखें)।
(क) मातर्यशशांगाता कः? (माता की यश महिमा का गान करने वाला कौन है?)
उत्तर:
चतुर्दिगन्तवहः पवनः। (चारों दिशाओं में बहने वाली हवा।)

(ख) भारतमाता कैः वंदिता?। (भारत माता किसके द्वारा वंदित की गई है।)
उत्तर:
हर्ष-भोज-शिवराज वंदिता। (हर्ष-भोज और शिवराज के द्वारा पूजी गई।)

(ग) भारतमाता कैः नंदिता? (भारत माता किसके द्वारा प्रसन्न की गई है?)
उत्तर:
मौर्य-शुङ्ग गुप्ताभिनन्दिता। (मौर्य-शुङ्ग और गुप्त के द्वारा प्रसन्न की गई है।)

(घ) अहिंसाव्रती किमर्थं वाणसंधान करोति? (अहिंसा का व्रत धारण करने वाले वाणों का संधान किसलिए करते हैं?)
उत्तर:
निजरक्षार्थमहिंसाव्रती। (अपनी रक्षा के लिए अहिंसाव्रत धारी भी वाण संधान करता है।)

(ङ) आदौ ज्ञानभानुः कुत्र उदितः? (पहले ज्ञान का सूर्य कहां उदित होता है?)
उत्तर:
ज्ञान भानुरादौ त्वय्युदितः।। (ज्ञान का सूर्य तुम ही से उदित होता है।)

संस्कृत कक्षा 9 पाठ 1 Question Answer MP Board प्रश्न 3.
रिक्त स्थानानिपूरयत-(रिक्त स्थानों की पूर्ति करो)
(क) येन न दस्यति कोऽपि तक्षकः।
(ख) भारत रामायण कवयित्री।
(ग) मौर्य शुंङ्ग गुप्ताभिनन्दिता।
(घ) कच्छ शम रूपान्त वासिनी।
(ङ) निष्कारणविद्वेषकरस्तव कालमुखं प्रतियाता।

Mp Board Class 9 Sanskrit Solution प्रश्न 4.
संधिविच्छेदं कृत्वा सन्धेः नाम लिखत् (संधि विच्छेद कर संधि नाम लिखो)।
(क) त्वय्युदित
उत्तर:
त्वयि + उदिता = यण स्वर संधि।

(ख) शूरस्ते
उत्तर:
शूरः + ते = विसर्ग संधि।

(ग) गणोऽयम्
उत्तर:
गणः + अयम् = पूर्वरूप स्वर संधि।

(घ) कोऽपि
उत्तर:
कः + अपि = पूर्वरूप स्वर संधि।

(ङ) विद्वेषकरस्तव
उत्तर:
विद्वेषकरः + तव = विसर्ग संधि।

कक्षा 9 संस्कृत अध्याय 1 सवाल जवाब MP Board प्रश्न 5.
यथायोग्यं योजयत (सही जोड़ी बनाओ)

कक्षा 9वी संस्कृत के प्रश्न उत्तर MP Board प्रश्न 6.
शुद्धवाक्यानां समक्षम् “आम्” अशुद्धवाक्यानां समक्षं “न” इति लिखत् उदाहरणम्
यथा- पवनः चतुदिर्गन्तवहः अस्ति। – आम्
अस्याः तनः हिंसार्थम् बाण संधाता। –  न
(क) गोपालः गीतायाः गाता।
(ख) भारत माता मौर्य शुङ्ग-गुप्ताभिवन्दिता अस्ति।
(ग) सकल लोकगणः सीमां त्राता अस्ति।
(घ) अस्यां आदौ ज्ञानभानु न उदितः।
उत्तर:
(क) आम्
(ख) आम्
(ग) आम्
(घ) न

संस्कृत कक्षा 9 पाठ 1 सवाल जवाब MP Board प्रश्न 7.
उदाहरणानुसारं पदानां मूल शब्द विभन्ति च लिखत

जयतु मे माता पाठ संदर्भ/प्रतिपाद्य

आधुनिक काल में भी संस्कृत में गद्य-पद्य लेखन की बहुलता है। इस भाषा के मूर्धन्य विद्वान, कवि और लेखकों के बीच आचार्य डॉ. प्रभुदयाल अग्निहोत्री का विशेष स्थान है। इनकी संस्कृत साहित्य में दर्शन, इतिहास, मनोविज्ञान, कथा, काव्य, नाटक आदि विधाओं में अनेक पुस्तकें प्रकाशित हुई हैं। ‘त्रिपथगा’ कविता संग्रह 2005 में प्रकाशित हुई। प्रस्तुत गीत भी ‘त्रिपथगा’ नामक कृति से ही लिया गया है। इस गीत में स्वतंत्रता सेनानी एवं संस्कृत के मूर्धन्य विद्वान अग्निहोत्री दारा सुंदर, मधुर एवं भावपूर्ण शब्दों में भारत माता की वंदना की गई है।

जयतु मे माता पाठ का हिन्दी अर्थ

1. जयतु जयतु मे माता,
अस्याः कष्टकरं दुर्दैवं शमयतु सदा विधाता।।

शब्दार्थ :
जयतु-जय हो-Vicrory; अस्याः -इसकी-Her/Him; कष्टकरंदुखी-Sorrow; दुर्दैवं-दुर्भाग्य को या बाधाओं को-Misfortune/Unfortunately; शमयतु-शांत कराये/ दूर करवाये; विधाता-ब्रह्मा-God Almighty; सदा-हमेशा-Always.

हिन्दी-अर्ध :
मेरी माता (मातृभूमि) की जय हो, जय हो। हे विधाता! तुम इसके कष्टों एवं आपदाओं को सदैव के लिए शान्त करें।

2. त्वं वेदोपनिषज्जनयित्री,
भारत-रामायण कवयित्री
अजनिष्ठाः कृष्णं गोपालं यो गीतायाः गाता॥

शब्दार्थ :
त्वं–तुम्हारा-Your; वेदोपनिषद्-वेद और उपनिषद्-Ved and Upnishad; जनयित्री-पैदा करने वाली-Mother, Originatee; गाता-गान करने वाले-Singer.

हिन्दी अर्थ :
हे भारत भूमि-तुम ही वेद और उपनिषदों की जननी हो। हे माँ! तुम ही महाभारत, रामायण की रचयित्री हो। हे माँ! तुम ही गीता का गान करने वाले मुरली-मनोहर कन्हैया की जननी हो।

3. ज्ञान-भानुरादौ त्वरयुदितः,
शूरस्ते तनयः सम्मुदितः,
केवल-निजरक्षार्थमहिंसाव्रती वाण-सन्धाता।

शब्दार्थ :
ज्ञान-ज्ञान-Knowledge; भानु-सूर्य-Sun; तनयः-पुत्र-Son; शूर-वीर-Brave; निज-स्वयं के-Myself; वाण-सन्धाता-वाण से लक्ष्य भेद करने पाला-Arjun or Bowman.

सरलार्थ :
हे भारत माँ! तुममें ही ज्ञान का सूर्य सर्व प्रथम उदित हुआ (अर्थात् भारतभूमि पर सर्व प्रथम ज्ञान रूपी सूर्य उदित हुआ।)। वीर पुत्र की जननी तुम्ही हो (अर्थात् वीरों का जन्म भारतभूमि पर ही हुआ)। केवल अपनी रक्षा के लिए अहिंसा का व्रत धारण करने वाला भी वाण संधान करता है अर्थात् वाणों से लक्ष्य साधता है।

4. मौर्य-शुङ्ग-गुप्ताभिनन्दिता,
हर्ष-भोज-शिवराज-वंदिता,
संप्रति लोकगणोऽयं सकल स्तव सीम्नां त्राता॥

शब्दार्थ :
नंदिता-प्रसन्न की गई-Toglad; वंदिता-पूजित-Worshipper; सम्प्रति-इस समय-This time; अयमं-इस-It; सकल-सभी-All, every; सीमनां-सीमाओं के-Limit; त्राता-रक्षक-Guard.

सरलार्थ :
हे भारत माँ! तुम मौर्य, शुंग, गुप्त वंशों द्वारा पूजित हो और (राजा) हर्ष, (राजा) भोज एवं शिवाजी द्वारा वंदित हुई हो। हे माँ! (इस पावन भूमि पर पैदा हुए) सभी जन तुम्हारी रक्षा करने वाले हैं।

5. कालिदास-कविता-रस-मग्ना,
सांख्ययोग-साधन-संलग्ना,
नालन्दाजन्ता मातस्ते श्रद्धाञ्जलि-प्रदाता॥

शब्दार्थ :
मग्ना-मग्न-Meditate; सांख्ययोग-सांख्ययोग-Sankhyoga; संलग्ना-संलग्न-Enclouse; नालन्दाजन्ता-नालन्दा और अजंता-Nalanda & Ajanta; प्रदाता-प्रदान करने वाले-Giver, Doner.

सरलार्थ :
हे मातृभूमि! कविता (की मधुर रागिनी) रस में मग्न कालिदास (सदृश कवि), सांख्य (दर्शन) योग में निमग्न अजंता एवं नालंदा के विद्वान जन तुम्हारी चरण वंदना करते हैं।

6. कच्छे-कामरूपान्त-वासिनी,
गङ्गा-कावेरी-सुहासिनी,
चतुर्दिगन्तवहः पवनस्ते मातर्यशसां गाता॥

शब्दार्थ :
वासिनी-निवास करने वाली-Inhahitant; चतुर्दिगन्तवहः-चारों दिशाओं में बहने वाला-Omni; पवनः-पवन-Air; ते-तुम्हारे-Your.

सरलार्थ :
हे भारत माते! तुम कच्छ से कामरूप तक निवास करने वाली (के अंक में) को गंगा-कावेरी (आदि नदियाँ) शोभायमान करती हैं तथा चारों दिशाओं में प्रवाहित होने वाला वायु तुम्हारी महिमा गान करता है।

7. सावहितः सीमान्त-रक्षकः
येन न दंशति कोऽपि तक्षकः
निष्कारण-विद्वेषकरस्तव कालमुखं प्रतियाता॥
जयतु जयतु मे माता। जयतु जयतु मे माता॥

शब्दार्थ :
सावहितः-सावधान-Attention; दंशति-दशता है-Sting; येन-जो-Who, what, which; तक्षकः-लुटेरा-Robber; कोपि-कोई भी-Any one; निष्कारण-बिना कारण के-Without reason; विद्वेष-द्वेष के कारण-Reason of jealous; प्रतिभाता-समाहित होता है-To meet.

सरलार्थ :
हे भारत माता की सीमा को रक्षित करने वाले रखवालो (जवानों)! सावधान रहो जिससे कोई बाहरी दस्यु भारत का नुकसान न कर सके। हे माँ! जो तुमसे (अर्थात् इस भूमि से) वैर भाव रखता है. वह काल रूपी गाल में समा जाता है। हे भारत माता! तुम्हारी जय हो, तुम्हारी जय हो, जय-जय हो माँ।

MP Board Class 9th Sanskrit Solutions