MP Board Class 11th Chemistry Solutions Chapter 1 रसायन विज्ञान की कुछ मूल अवधारणाए
रसायन विज्ञान की कुछ मूल अवधारणाए NCERT अभ्यास प्रश्न
रसायन विज्ञान कक्षा 11 Mp Board प्रश्न 1.
निम्नलिखित के लिए मोलर द्रव्यमान का परिकलन कीजिए –
- H2O
- CO2
- CH4
उत्तर:
- H2O का अणुभार = 2 (1.008 amu) + 16.00 amu = 18.016 amu.
- CO2 का अणुभार = 12.01 amu + 2 x 16.00 amu = 44.01 amu.
- CH4 का अणुभार = 12.01 amu + 4(1.008 amu) = 16.042 amu.
Mulanupati Sutra In Chemistry In Hindi प्रश्न 2.
सोडियम सल्फेट (Na2SO4) में उपस्थित विभिन्न तत्वों के द्रव्यमान प्रतिशत की गणना कीजिए।
हल:

Mp Board Class 11th Chemistry Solution प्रश्न 3.
आयरन के एक ऑक्साइड का मूलानुपाती सूत्र ज्ञात कीजिए जिसमें 69.9% आयरन तथा 30.1% डाइऑक्सीजन भारानुसार हो।
हल:
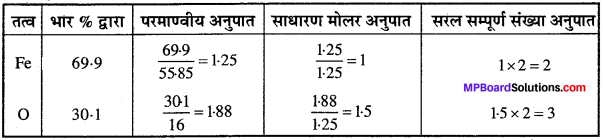
∴ मूलानुपाती सूत्र = Fe2O3.
Mp Board Solution Class 11 Chemistry प्रश्न 4.
बनने वाले कार्बन डाइऑक्साइड की मात्रा की गणना कीजिए जब –
- हवा में 1 मोल कार्बन जलती है।
- 16g डाइऑक्सीजन में 1 मोल कार्बन जलती है।
- 16g डाइऑक्सीजन में 2 मोल कार्बन जलती है।
उत्तर:

- कार्बन का 1 मोल CO2 के 44 ग्राम देता है।
- डाइऑक्सीजन के केवल 16g उपलब्ध है ये कार्बन के केवल 0.5 मोल से संयोग करती है। अतः डाइऑक्सीजन सीमान्त अभिकारक है। अतः बना हुआ CO2 = 22g.
- यहाँ O2 सीमान्त अभिकारक है, O2 के 0.5 मोल CO2 के 22g देता है।
प्रश्न 5.
सोडियम ऐसीटेट (CH3COONa) का 500 ml, 0.375 मोलर जलीय विलयन बनाने के लिए, उसके कितने द्रव्यमान की आवश्यकता होगी? सोडियम ऐसीटेट का मोलर द्रव्यमान 82-0245 g mor’ है।
हल:

जहाँ, WB = विलेय का द्रव्यमान, MB = विलेय का मोलर द्रव्यमान प्रश्नानुसार
विलयन की मोलरता, M = 0.375 M
विलेय का मोलर द्रव्यमान, MB = 82.0245g mol-1
विलयन का आयतन = 500 ml
विलेय का द्रव्यमान, WB = ?
विलेय का द्रव्यमान, WB = \(\frac { MxM_{ B }xV }{ 1000 } \)
= \(\frac{0.375×82.0245×500}{1000}\)
= 15.379g ≅ 15.38g.
प्रश्न 6.
सान्द्र नाइट्रिक अम्ल के उस प्रतिदर्श की मोल प्रति लीटर में सान्द्रता का परिकलन कीजिए, जिसमें उसका द्रव्यमान प्रतिशत 69% हो और घनत्व 1.41gm-1 हो।
हल:
![]()
प्रश्नानुसार d = 1.41 gmL-1, HNO3 का द्रव्यमान प्रतिशत = 69%
69% HNO3 का अर्थ है नाइट्रिक अम्ल के 100g विलयन में 69g HNO3 उपस्थित है,
अत: HNO3 (विलेय) का द्रव्यमान WB = 69g
HNO3 का मोलर द्रव्यमान = 1.0079 + 14.0067 + (3 x 16.00)
= 63.0146 gmol-1

प्रश्न 7.
100 g CuSO4(कॉपर सल्फेट) से कितना कॉपर प्राप्त होता है?
हल:
CuSO 4के 1 मोल में Cu के 1 मोल (1g परमाणु) होते हैं।
CuSO4 अणुभार = 63.5 + 32+4 x 16 = 159.5 g मोल-1
∴ 159.5g CuSO4 से प्राप्त Cu= 63.5g
100g CuSO4 से प्राप्त Cu = \(\frac{63.5}{159.5}\) x 100g = 39.81g.
प्रश्न 8.
आयरन के एक ऑक्साइड के आण्विक सूत्र की गणना कीजिये जिसमें आयरन तथा ऑक्सीजन का भार प्रतिशत क्रमशः 69.9 तथा 30.1 है।
हल:
प्रश्न 3 से मूलानुपाती सूत्र FeO3 है।
FeO3 का मूलानुपाती सूत्र भार = 2 x 55.85 + 3 x 16
= 159.7
![]()
अतः आयरन ऑक्साइड का अणुसूत्र = Fe2O3.
प्रश्न 9.
क्लोरीन के परमाणु भार की गणना नीचे दिये गये आँकड़ों का उपयोग करके कीजिए –

हल:
औसत परमाणु द्रव्यमान \(\overline { A } \), समस्थानिकों की आंशिक बाहुल्यता (Fi) तथा उनके संगत मोलर द्रव्यमान Ai के गुणनफल के योग के बराबर होता है।
औसत परमाणु द्रव्यमान \(\overline { A } \) = Σ Fi.Ai = F1 x A1 + F2 x A2 + ………….
अतः क्लोरीन का औसत द्रव्यमान, \(\overline { A } \) = 0.7577 x 34.9689 + 0. 2423 x 36.9659
= 26.4959 + 8.9568
= 35.4527µ = 35.5µ
प्रश्न 10.
एथेन के तीन मोल में निम्नलिखित की गणना कीजिए –
- कार्बन परमाणु के मोलों की संख्या
- हाइड्रोजन परमाणु के मोलों की संख्या
- एथेन के अणुओं की संख्या।
उत्तर:
C2H6 के 3 मोल में है –
- कार्बन परमाणु के 6 मोल।
- हाइड्रोजन परमाणु के 18 मोल।
- अणुओं की संख्या = 3 x 6.07 x 1023 = 18.21 x 1023.
प्रश्न 11.
शर्करा की सान्द्रता मोल लीटर में क्या होगी यदि इसके 20g को पर्याप्त मात्रा में जल में घोलकर अंतिम आयतन 2L बनाया जाये?
हल:
शर्करा का अणुभार = 12 x 12 + 1 x 22 + 16x 11 = 342
मोलर सांद्रता अर्थात्
M = \(\frac{\mathrm{W}}{\mathrm{M}_{\mathrm{B}} \mathrm{V}_{(\mathrm{L})}}\) = \(\frac{20}{342×2}\) = 0.0292
प्रश्न 12.
यदि मेथेनॉल का घनत्व 0.793 kg L-1 है, तो 0.25M विलयन 2.5 L में बनाने के लिये इसका कितना आयतन आवश्यक होगा?
हल:
M = \(\frac { W_{ B } }{ M_{ B }xV } \)
M= 0.25 g
V = 2.5 L
MB = 32g मोल-1
0.25 = \(\frac { W_{ B } }{ 32×2.5 } \)
या wB = 20g
![]()
(यहाँ घनत्व = 0.793kg L-1 या 0.793 g ml-1)
प्रश्न 13.
दाब को पृष्ठ के बल प्रति इकाई क्षेत्रफल के रूप में ज्ञात कीजिए।दाब की S.I. इकाई पास्कल नीचे दिखाई गई है –
1Pa = 1Nm-2
यदि समुद्र सतह पर हवा का भार 1034 gcm है, तो पास्कल में दाब निकालिये।
हल:

= 1.01 x 105kg m-1s-2
= 1.01 x 105Nm-2 = 1.01 x 105Pa,
(न्यूटन (N) = kg m s-2; Pa = \(\frac { N }{ m^{ 2 } } \) = kg m-1s-2)
प्रश्न 14.
द्रव्यमान की S.I. इकाई क्या है ? इसे किस तरह परिभाषित करते हैं?
उत्तर:
द्रव्यमान की S.I. इकाई किलोग्राम (kg) है, इसका मान अन्तर्राष्ट्रीय मानक किलोग्राम के समान है। किसी पदार्थ का द्रव्यमान उसमें उपस्थित द्रव्य की मात्रा है। किसी वस्तु का द्रव्यमान स्थिर रहता है।
प्रश्न 15.
निम्नलिखित पूर्वलग्न को उनके गुणक से मिलान कीजिए –
पूर्वलग्न(उपसर्ग) गुणक
(i) माइक्रो 106
(ii) डेका 109
(iii) मेगा 10-6
(iv) गीगा 10-15
(v) फेम्टो 10
उत्तर:
माइक्रो = 10-6, डेका = 10, मेगा = 106, गीगा = 109, फेम्टो = 10-15.
प्रश्न 16.
सार्थक अंकों का क्या अर्थ होता है?
उत्तर:
परिभाषा (Definition)-किसी मापन के परिणाम को पूर्ण रूप से दर्शाने के लिए शन्य से नौ तक के अंकों में से न्यूनतम संख्या में जिन अंकों का प्रयोग आवश्यक होता है उन अंकों को सार्थक अंक कहते हैं। अथवा, किसी संख्या के उन अंकों (0 से लेकर 9 तक) को जिनके द्वारा किसी भौतिक राशि के परिमाण को पूर्णतः उसके यथार्थ मान तक व्यक्त करते हैं, सार्थक अंक (Significant figures) कहलाते हैं।
ये वे अंक हैं जो किसी मापन की परिशुद्धता को व्यक्त करने के लिए आवश्यक होते हैं। सार्थक अंकों की संख्या मापन के लिए प्रयुक्त उपकरण की परिशुद्धता पर निर्भर होती है। यदि मापन के लिए प्रयुक्त स्केल/ उपकरण की परिशुद्धता अधिक है तो मापन में अनिश्चितता भी कम होगी। किसी संख्या का अन्तिम अंक अनिश्चित होता है।
यदि किसी संख्यात्मक माप को 125.47 m3 दर्शाते हैं तो उसमें पाँच सार्थक अंक हैं तथा अन्तिम अंक 7 अनिश्चित है।
प्रश्न 17.
पीने के पानी का एक नमूना क्लोरोफॉर्म CHCl3 से दूषित हो गया जो अति कैंसरकारी प्रकृति का होता है। प्रदूषण का स्तर 15ppm (भार द्वारा) है।
- इसे प्रतिशत में दर्शाइये भार द्वारा।
- क्लोरोफॉर्म की मोललता पानी के नमूने में ज्ञात कीजिए।
हल:
15 ppm दूषित अर्थात् 15g क्लोरोफॉर्म 106g विलयन में घुला हुआ है।
अर्थात् , WB = 15g, WA = 106 – 15 ≅ 106g
विलेय का अणुभार (MB) = 119.5

प्रश्न 18.
निम्नलिखित को वैज्ञानिक अंकन में प्रदर्शित कीजिए –
- 0.0048
- 234,000
- 8008
- 500.0
- 6.0012.
उत्तर:
- 48 x 10-3
- 2.34 x 105
- 8.008 x 103
- 5.000 x 102
- 6.0012 x 100
प्रश्न 19.
निम्न में कितने सार्थक अंक उपस्थित हैं –
- 0.0025
- 208
- 5005
- 126,000
- 500.0
- 2.0034.
उत्तर:
- 2
- 3
- 4
- 6
- 4
- 5.
प्रश्न 20.
निम्न को तीन सार्थक अंकों तक व्यवस्थित कीजिए –
- 34.216
- 10.4107
- 0.04597
- 2808
उत्तर:
- 34.2
- 10.4
- 0.0460
- 2.80 x 102.
प्रश्न 21.
डाइनाइट्रोजन तथा डाइऑक्सीजन की क्रिया द्वारा विभिन्न यौगिक बनते हैं तथा निम्नलिखित आँकड़े प्राप्त होते हैं –
डाइनाइट्रोजन डाइऑक्सीजन
का भार का भार
(i) 14g 16g
(ii) 14g 32g
(iii) 28g 32g
(iv) 28g 80g
(a) ऊपर दिये प्रायोगिक आँकड़ों में कौन-सा रासायनिक संयोजन के नियम का पालन होता है इसका विवरण दीजिए।
(b) निम्नलिखित परिवर्तन में खाली स्थान भरिए –
- 1 km = …………… mm = …………… pm
- 1 mg = …………… kg = …………… ng
- 1 ml = ………….. L = …………… dm3.
उत्तर:
(a) यहाँ गुणित अनुपात के नियम का पालन हो रहा है, इसके अनुसार, जब दो तत्त्व संयोग करके दो या दो से अधिक यौगिक बनाते हैं तो एक तत्त्व के भिन्न-भिन्न भार जो कि दूसरे तत्त्व के निश्चित भार से संयोग करते हैं; परस्पर सरल अनुपात में होते हैं। यहाँ आँकड़ों से ज्ञात होता है कि ऑक्सीजन के भिन्न-भिन्न द्रव्यमान 16, 32, 40 जो नाइट्रोजन के एक निश्चित द्रव्यमान 14 से संयुक्त होते हैं, जो 2 : 4 : 5 के सरल अनुपात में हैं।

प्रश्न 22.
यदि प्रकाश की गति 3.0 x 108 ms-1 है, तो प्रकाश द्वारा 2.00 ns में तय की गई दूरी की गणना कीजिए।
हल:
दूरी = गति x समय
= 3 x 108 x 2 x 10-9
= 6 x 10-1 = 0.6m.
प्रश्न 23.
अभिक्रिया में A + B2 → AB2 सीमांत अभिकर्मक की पहचान कीजिये यदि कोई निम्नांकित अभिक्रिया मिश्रण में हो –
- A के 300 परमाणु + B के 200 अणु
- A के 2 मोल + Bके 3 मोल
- A के 100 परमाणु + B के 100 अणु
- 5 मोल A + 2.5 मोल B
- 2.5 मोल A +5 मोल B.
उत्तर:
सीमांत अभिकर्मक अभिक्रिया में सबसे पहले खत्म होता है। अतः इस अभिकर्मक को ज्ञात करने के लिए A और B की मात्रा का तुलना करते हैं।
A + B2 → AB2
1. उपर्युक्त समी. के अनुसार A का 1 परमाणु, B के 1 अणु के साथ क्रिया करता है।
अत: A का 200 परमाणु B के 200 अणु से क्रिया करेंगे।
अत: B सीमांत अभिकर्मक है तथा A अधिकता में होगा।
2. उपर्युक्त समी. के अनुसार A के 1 मोल, B के 1 के साथ क्रिया करते हैं।
अतः A के 2 मोल, B के 2 मोल से क्रिया करेंगे।
इस दशा में A सीमांत अभिकर्मक होगा। B अधिकता में रहेगा।
3. उपर्युक्त समी. के अनुसार A के 1 परमाणु, B के 1 अणु से क्रिया करते हैं।
अतः A के 100 परमाणु, B के 100 अणु से क्रिया करेंगे।
अत: यह एक स्टाइकियोमेट्री मिश्रण है।
अतः कोई सीमान्त अभिकर्मक नहीं है, न A और न B।
4. इस दशा में A के 2.5 मोल, B के 2.5 मोल से क्रिया करेंगे।
अत: B सीमान्त अभिकर्मक है। A अधिकता में रहेगा।
5. इस दशा में A सीमान्त अभिकर्मक होगा। B अधिकता में रहेगा।
प्रश्न 24.
डाइनाइट्रोजन तथा डाइहाइड्रोजन एक-दूसरे के साथ क्रिया करके निम्न रासायनिक क्रिया के अनुसार अमोनिया
बनाती है –
N2(g) + 3H2(g) → 2NH3(g)
- बने अमोनिया के भार की गणना कीजिए यदि 2.00 x 103g डाइनाइट्रोजन 1.00 x 103g डाइहाइड्रोजन के साथ क्रिया करता है।
- क्या कोई दो अभिकारक अक्रियाशील है?
- यदि हाँ तो कौन-सा है तथा उसका भार क्या होगा?
हल:
1.
![]()
28g N2 अमोनिया बनाती है = 34g
2 x 103g N2 अमोनिया बनायेगी
= \(\frac{34 \times 2 \times 10^{3}}{28}\) = 2.43 x 103g
फिर ∴ 6g H2 अमोनिया बनाती है = 34g
∴ 1 x 103g H, अमोनिया बनाती है
= \(\frac{34 \times 1 \times 10^{3}}{6}\) = 5.66 x 103g.
2. N2 से प्राप्त अमोनिया कम है अतः N2 सीमान्त अभिकर्मक है। H2 अप्रभावित रहता है।
3. ∴ 28g N2, H2 से क्रिया करता है = 6g
∴ 2 x 103g N2 क्रिया करता है।
\(\frac{6 \times 2 \times 10^{3}}{28}\)
बची H = 1 x 103 – 4.286 x 102 = 571.4 g.
प्रश्न 25.
0.50 मोल Na2CO3 तथा 0-50 M NaCO3 में क्या अंतर है?
हल:
Na2CO3 का मोलर द्रव्यमान = (2 x 23) + 12 + (3 x 16)
= 106 g mol-1
0.50 मोल Na2CO3, का द्रव्यमान = मोलों की संख्या – मोलर द्रव्यमान
= 0.50 x 106 = 53g Na2CO3
अत: 0.50 M Nayco का तात्पर्य है कि 1 लीटर विलयन में Narco के 53g उपस्थित है।
प्रश्न 26.
डाइहाइड्रोजन के दस आयतन डाइऑक्सीजन के पाँच आयतन से क्रिया करके जलवाष्य के कितने आयतन बनायेंगे?
उत्तर:
H2(g) + \(\frac{1}{2}\)O2(g) → H2O(g)
1 मोल \(\frac{1}{2}\)मोल 1 मोल
1 आयतन \(\frac{1}{2}\)आयतन 1 आयतन
10 आयतन 5 आयतन 10 आयतन
अतः जलवाष्प के 10 आयतन प्राप्त होते हैं।
प्रश्न 27.
निम्नलिखित को आधारभूत इकाई में बदलिये –
- 28.7 pm
- 15.15 µs,
- 25365 mg.
हल:
1. 28.7pm = 28.7pm x \(\frac { 10^{ -12 }m }{ 1pm } \) = 287 x 10-11m.
2. 15.15µs = 15.15µs x \(\frac { 10^{ -6 }m }{ 1µs } \) = 1.515 x 10-5s.
= 2.5365×10-2kg.
3.25365 mg = 25365 mg x \(\frac{1g}{1000mg}\) x \(\frac{1kg}{1000g}\)
प्रश्न 28.
निम्न में से किस एक में अधिकतम परमाणुओं की संख्या होगी –
- 1g Au(s)
- 1g Na(s)
- 1g Li(s)
- 1g Cl2(g)
हल:
1. 1g Au = \(\frac{1}{197}\)mol = \(\frac{1}{197}\) x 6.02 x 1023 परमाणु
2. 1g Na = \(\frac{1}{23}\)mol = \(\frac{1}{27}\) x 6.02 x 1023 परमाणु
3. 1g Li = \(\frac{1}{7}\)mol = \(\frac{1}{7}\) x 6.02 x 1023 परमाणु
4. 1g Cl2 = \(\frac{1}{71}\)mol = 4 x 6.02 x 1023 अणु = \(\frac{2}{71}\) x 6.02 x 1023 परमाणु
अत: 1g Li में परमाणुओं की अधिकतम संख्या होती है।
प्रश्न 29.
एथेनॉल का जल में बने विलयन की मोलरता की गणना कीजिए जिसमें एथेनॉल का मोल प्रभाज 0.040 है।
हल:
1 लीटर विलयन में उपस्थित विलेय (एथेनॉल) के मोलों की संख्या मोलरता होगी।
1L एथेनॉल विलयन (तनु विलयन) = 1L जल
1L जल में H2O की मोलों की संख्या = \(\frac{1000g}{18}\) = 55.55 मोल
द्विअंगी विलयन में दो घटक होते हैं।

प्रश्न 30.
एक C परमाणु का भार (द्रव्यमान) क्या होगा?
हल:
कार्बन के एक परमाणु का भार
= \(\frac { 12 }{ 6.02×10^{ 23 } } \) = 1.9933 x 10-23g.
प्रश्न 31.
निम्नलिखित गणना के उत्तर में उपस्थित सार्थक अंक कितना होगा –
- \(\frac{0.02856×298.15×0.112}{0.5785}\)
- 5 x 5.364
- 0.0125 + 0.7864 + 0.0215.
उत्तर:
- सबसे कम यथार्थ पद 0.112 में 3 सार्थक अंक है। अतः उत्तर 3 है।
- 5 सही संख्या है। दूसरा पद 5.364 में 4 सार्थक अंक है। अतः उत्तर 4 है।
- प्रत्येक पद में 4 सार्थक अंक है। अतः उत्तर 4 है।
प्रश्न 32.
नीचे दिये गये सारणी के आँकड़ों का उपयोग करके प्राकृतिक रूप से प्राप्त (उत्पन्न) आर्गन समस्थानिक के मोलर भार की गणना कीजिए –

हल:
औसत आण्विक भार
![]()
प्रश्न 33.
निम्नलिखित में प्रत्येक में परमाणुओं की संख्या की गणना कीजिए –
- He के 52 मोल
- He के 52 u
- He के 52 g
हल:
1. ∴ He के 1 मोल = 6.02 x 1023 परमाणु
∴ He में 52 मोल = 52 x 6.02 x 1023
= 313.04 x 1023 परमाणु
2. ∴ He के 4u = He का एक परमाणु
∴ He में 52u = \(\frac{1×52}{4}\) = 13 परमाणु
3. He के 1 मोल = 4g = 6.02 x 1023 परमाणु
∴ 52g He = \(\frac { 6.02×10^{ 23 }x52 }{ 4 } \)
प्रश्न 34.
एक वेल्डिंग ईंधन गैस में केवल कार्बन तथा हाइड्रोजन है। इसके छोटे से नमूने के ऑक्सीजन में जलने पर ये 3-38 g कार्बन डाइऑक्साइड, 0.690 g पानी तथा कोई दूसरा उत्पाद नहीं देता। इस वेल्डिंग गैस के 10.0 L आयतन (STP पर मापा गया) का भार 11.6g है, तो गणना कीजिए –
- मूलानुपाती सूत्र
- गैस का अणुभार
- आण्विक सूत्र।
हल:
1. ∴ 44g CO2 = 12g कार्बन
∴ 3.38g CO2 = \(\frac{12}{44}\) x 338g = 0.9218g कार्बन
18g H2O = 2g हाइड्रोजन
∴ 0.690g H2O = \(\frac{2}{18}\) x 0.690g = 0.0767g हाइड्रोजन
यौगिक का द्रव्यमान = 0.9218 + 0.0767 = 0.9985g
(चूँकि यौगिक में केवल कार्बन तथा हाइड्रोजन है)
यौगिक में C की % मात्रा = \(\frac{0.9218}{0.9985}\) x 100 = 92.32%
यौगिक में H की % मात्रा = \(\frac{0.0767}{0.9985}\) x 100 = 7.68%
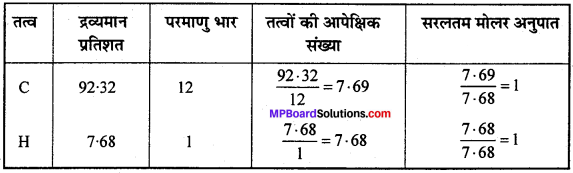
अतः मूलानुपाती सूत्र = CH.
2. गैस के अणु द्रव्यमान की गणना:
∴ STP पर, गैस के 10.0L का भार = 11.6g
∴ STP पर, गैस के 22.4L का भार = \(\frac{116×22.4}{10.0}\) = 25.984g ≅ 26g mol-1.
3. अणुसूत्र की गणना:
मूलानुपाती सूत्रभार (CH) = 12 + 1 =13
![]()
= (मूलानुपाती सूत्र)n [n = 2]
= (CH)2 = C2H2
प्रश्न 35.
कैल्सियम कार्बोनेट जलीय HCl के साथ क्रिया करके CaCl2 तथा CO2 निम्न अभिक्रिया के अनुसार देता है –
CaCO3(s) + 2HCl(aq) → CaCl2(aq) + CO2(g) + H2O(l).
0.75 M HCl के 25 ml के साथ पूर्ण क्रिया के लिये CaCO3 की आवश्यक मात्रा क्या होगी?
हल:
HCl के मोल = मोलरता x V(L)
= 0.75 x 25 x 10-3 = 0.01875
HCl का भार = मोल x HCl का अणुभार (36.5)
= 0.01875 x 36.5 = 0.684g
CaCO3 + 2HCl → CaCl2 +H2O + CO2
100g 2 x 36.5 = 73g
∴ 73g HCl के लिये आवश्यक CaCO3 = 100g
∴ 0.684g HCl के लिये आवश्यक CaCO3 = \(\frac{100×0.684}{73}\) = 0.937g.
प्रश्न 36.
प्रयोगशाला में क्लोरीन को मैंगनीज डाइऑक्साइड की जलीय हाइड्रोक्लोरिक अम्ल के साथ क्रिया द्वारा निम्नांकित अभिक्रिया के अनुसार बनाया जाता है –
4HCl(aq) + MnO2(s) → 2H3O(l) + MnCl2(aq) + Cl2(l).
5.0g मैंगनीज डाइऑक्साइड के साथ HCl के कितने ग्राम क्रिया करेंगे?
हल:
4HCl + MnO2 → MnCl + Cl + 2H2O
146g 87g
87g MnO2 HCl के साथ क्रिया करता है = 146g
5g MnO2 HCl के साथ क्रिया करता है = \(\frac{146×5}{87}\) = 8.39g.
रसायन विज्ञान की कुछ मूल अवधारणाए अन्य महत्वपूर्ण प्रश्न
रसायन विज्ञान की कुछ मूल अवधारणाए वस्तुनिष्ठ प्रश्न
प्रश्न 1.
सही विकल्प चुनकर लिखिए –
प्रश्न 1.
2.0 ग्राम हाइड्रोजन का N.T.P. आयतन होता है –
(a) 224 लिटर
(b) 22.4 लिटर
(c) 2.24 लिटर
(d) 112 लिटर
उत्तर:
(b) 22.4 लिटर
प्रश्न 2.
शुद्ध जल की मोलरता –
(a) 18
(b) 50
(c) 556
(d) 100
उत्तर:
(c) 556
प्रश्न 3.
12 gm CR में परमाणुओं की संख्या –
(a) 6
(b) 12
(c) 6.02 x 1023
(d) 12 x 6.02 x 1023
उत्तर:
(c) 6.02 x 1023
प्रश्न 4.
नाइट्रोजन के पाँच ऑक्साइड N2O NO, N2O3, N2O4 व N2O5 रासायनिक संयोग के किस नियम का पालन करते हैं –
(a) स्थिर अनुपात नियम
(b) तुल्य अनुपात नियम
(c) गे-लुसाक का गैस आयतन संबंधी नियम
(d) गुणित अनुपात नियम।
उत्तर:
(d) गुणित अनुपात नियम।
प्रश्न 5.
एक कार्बनिक यौगिक का मूलानुपाती सूत्र CH2 है। यौगिक के एक मोल का द्रव्यमान 42 ग्राम है। इसका अणुसूत्र होगा –
(a) CH2
(b) C3H6
(c) CH2
(d) C3Hg
उत्तर:
(b) C3H6
प्रश्न 6.
ZnSO4.7H2O में ऑक्सीजन की प्रतिशत मात्रा होगी –
(a) 22.65%
(b) 11.15%
(c) 22.30%
(d) 43.90%.
उत्तर:
(c) 22.30%
प्रश्न 7.
एक मोलल विलयन वह है, जिसमें एक मोल विलेय उपस्थित हो –
(a) 1000 ग्राम विलायक में
(b) 1 लिटर विलयन में
(c) 1 लिटर विलायक में
(d) 224 लिटर विलयन में
उत्तर:
(a) 1000 ग्राम विलायक में
प्रश्न 8.
क्यूप्रिक ऑक्साइड में कॉपर का भार प्रतिशत क्या होगा –
(a) 22.2%
(b) 79.8%
(c) 63.5%
(d) 16%.
उत्तर:
(b) 79.8%
प्रश्न 9.
112 cm3 CH4 का S.T.P. पर द्रव्यमान होगा –
(a) 0.16 ग्राम
(b) 0.8 ग्राम
(c) 0.08 ग्राम
(d) 1.6 ग्राम
उत्तर:
(d) 1.6 ग्राम
प्रश्न 10.
दो पदार्थों को पृथक करने की प्रभाजी क्रिस्टलन विधि इनके अन्तर पर निर्भर करती है –
(a) घनत्व
(b) वाष्पशीलता
(c) विलेयता
(d) क्रिस्टलीय आकार
उत्तर:
(c) विलेयता
प्रश्न 11.
O2 व SO2 के अणु द्रव्यमान क्रमशः 32 व 64 हैं। यदि एक लिटर O2, में 13°C व 750 mm दाब पर N अणु हैं तो दो लिटर SO2 में समान ताप व दाब पर अणुओं की संख्या होगी –
(a) N/2
(b) N
(c) 2N
(d) 4N
उत्तर:
(c) 2N
प्रश्न 12.
यदि सामान्य ताप और दाब पर दो समान आयतन के पात्र में दो गैसें रखी गई हैं तो उनमें –
(a) अणुओं की संख्या समान होगी
(b) परमाणुओं की संख्या समान होगी
(c) उनके द्रव्यमान समान होंगे
(d) उनके घनत्व समान होंगे
उत्तर:
(a) अणुओं की संख्या समान होगी
प्रश्न 13.
3.4 ग्राम H2O2 के विघटन से N.T.P. पर O2 का निम्न आयतन प्राप्त होगा –
(a) 0.56 लिटर
(b) 1.12 लिटर
(c) 2.24 लिटर
(d) 3.36 लिटर
उत्तर:
(b) 1.12 लिटर
प्रश्न 14.
2 मोल C2H5OH को वायु के आधिक्य में जलाने पर CO2 प्राप्त होगा –
(a) 88 ग्राम
(b) 176 ग्राम
(c) 44 ग्राम
(d) 22 ग्राम
उत्तर:
(b) 176 ग्राम
प्रश्न 15.
12 ग्राम Mg (परमाणु द्रव्यमान = 24) अम्ल से पूर्णतया क्रिया करने पर H2 उत्पन्न करता है जिसका आयतन N.T.P. पर होगा –
(a) 22.4 लिटर
(b) 11.2 लिटर
(c) 44.8 लिटर
(d) 6.4 लिटर
उत्तर:
(c) 44.8 लिटर
प्रश्न 2.
रिक्त स्थानों की पूर्ति कीजिए
- बेंजीन का मूलानुपाती सूत्र …………. होगा।
- समान ताप तथा दाब पर समस्त गैसों के समान आयतन में अणुओं की संख्या समान होती है। इसे …………. ने पारित किया था।
- 180 ग्राम जल में मोलों की संख्या …………. होगी।
- किलोग्राम मीटर …………. की मात्रा है।
- 1 मोल CO2 में …………. कार्बन परमाणु हैं।
- यदि सामान्य ताप तथा दाब पर दो समान आयतन के पात्र में दो गैसें रखी गई हैं तो उनमें अणुओं की संख्या …………. होगी।
- 2 मोल C2H5OH को वायु के आधिक्य में जलाने पर …………. CO2 प्राप्त होगी।
- एक रासायनिक अभिक्रिया के अन्त में अभिकारक का कुल द्रव्यमान …………. नहीं होता है।
- बेंजीन अणुसूत्र वाले यौगिक का सरल सूत्र …………. है।
- एक यौगिक में C = 40.6%, H = 6.5%, O = 52.8% का मूलानुपाती सूत्र ………… होगा।
उत्तर:
- CH
- एवोगेड्रो
- 10 मोल
- घनत्व
- 6.023 x 1023
- समान
- 176 ग्राम
- परिवर्तित
- CH
- CH2O.
प्रश्न 3.
उचित संबंध जोडिए –
(A)

उत्तर:
- (c)
- (e)
- (a)
- (b)
- (d).
(B).

उत्तर:
- (d)
- (a)
- (b)
- (e)
- (c).
प्रश्न 4.
एक शब्द/वाक्य में उत्तर दीजिए –
- परमाणु द्रव्यमान की मानक इकाई है।
- O2 का ग्राम अणु द्रव्यमान है।
- विभिन्न स्रोतों से प्राप्त NaCl के तत्व Na तथा Cl के मध्य सभी में भार की दृष्टि से अनुपात 23 : 35.5 प्राप्त हुआ। इस नियम से पुष्टि होती है।
- ऑक्सीजन के क्रमशः 16 और 32 ग्राम भार N2 के 28 ग्राम भार से अलग-अलग संयोग कर दो ऑक्साइड N2O एवं N2O2 बनाते हैं। इससे किस नियम की पुष्टि होती है?
- 6.023 x 1023 किसी भी द्रव्य के एक ग्राम अणुभार में उपस्थित अणुओं की संख्या को कहा जाता है।
उत्तर:
- परमाणु द्रव्यमान इकाई (amu) (1amu = \(\frac{1}{12}\))
- 32 ग्राम
- स्थिर अनुपात
- गुणित अनुपात,
- मोल या एवोगेड्रो संख्या।
रसायन विज्ञान की कुछ मूल अति लघु उत्तरीय प्रश्न
प्रश्न 1.
स्थिर अनुपात का नियम क्या है?
उत्तर:
रासायनिक यौगिकों में उनके अवयवी तत्व भार की दृष्टि से हमेशा एक निश्चित अनुपात में रहते हैं।
उदाहरण:
विभिन्न स्थानों से प्राप्त जल से शुद्ध करने के पश्चात् विश्लेषित करने पर ज्ञात हुआ कि जल के प्रत्येक नमूने में हाइड्रोजन और ऑक्सीजन द्रव्यमान के अनुसार 2 : 16 या 1 : 8 में है।
प्रश्न 2.
गे-लुसाक का गैस आयतन संबंधी नियम लिखिए।
अथवा
N2 और H2 परस्पर संयुक्त होकर NH3 गैस का निर्माण करती है। समान ताप व दाब पर इनके आयतनों में 1 : 3 : 2 का अनुपात है। इससे जिस नियम की पुष्टि होती है, उस नियम को लिखिए।
उत्तर:
गैस आयतन सम्बन्धी नियम या गे-लुसाक का गैस आयतन सम्बन्धी नियम-इसके अनुसार, “जब गैसें आपस में संयोग करती हैं, तो उनके आयतनों में सरल अनुपात होता है और यदि उनके संयोग से बना हुआ पदार्थ भी गैस ही हो तो उसका आयतन भी अभिकारी गैसों के आयतनों के सरल अनुपात में होता है (जब सभी आयतन समान ताप और दाब पर मापे जाएँ)।”
उदाहरण:
N2 + 3H2 → 2NH3
1आयतन 3 आयतन 2 आयतन
इनके आयतनों में 1 : 3 : 2 का सरल अनुपात है।
अत: उपर्युक्त उदाहरणों से गे-लुसाक के गैस आयतन सम्बन्धी नियम की पुष्टि होती है।
प्रश्न 3.
निम्नलिखित की परिभाषा लिखिए –
- ग्राम परमाणु द्रव्यमान
- ग्राम आण्विक द्रव्यमान।
उत्तर:
1. ग्राम परमाणु द्रव्यमान-किसी तत्व का ग्राम परमाणु द्रव्यमान उसका ग्रामों में दर्शाया गया वह द्रव्यमान है जो संख्यात्मक रूप से परमाणु द्रव्यमान के बराबर है, उसे ग्राम परमाणु द्रव्यमान कहते हैं।
2. ग्राम आण्विक द्रव्यमान-ग्रामों में प्रदर्शित वह द्रव्यमान जो संख्यात्मक रूप से आण्विक द्रव्यमान के बराबर हो, ग्राम आण्विक द्रव्यमान कहलाता है।
प्रश्न 4.
मूलानुपाती सूत्र क्या है?
उत्तर:
वह सूत्र जो किसी यौगिक के अणु में विद्यमान विभिन्न तत्वों के परमाणुओं के सरल अनुपात को दर्शाता है मूलानुपाती सूत्र (Empirical formula) कहलाता है। जैसे:
ऐसीटिक अम्ल का मूलानुपाती सूत्र = CH2O
ग्लूकोज का मूलानुपाती सूत्र = CH2O.
प्रश्न 5.
किसी विलयन की मोललता को परिभाषित कीजिए।
उत्तर:
किसी विलयन की मोललता प्रति 1000 ग्राम विलायक में उपस्थित विलेय पदार्थ के मोलों की संख्या है। इसे m द्वारा प्रदर्शित करते हैं।

प्रश्न 6.
मोल क्या है? स्पष्ट कीजिये।
उत्तर:
एक मोल वह संख्या है जिसका मान कार्बन-12 के 0.012 कि.ग्रा. में उपस्थित परमाणु के संख्या के बराबर होता है। इस संख्या का मान 6.023 x 1023 होता है।
प्रश्न 7.
सीमांत अभिकर्मक क्या है?
उत्तर:
संतुलित समीकरण में जो क्रियाकारक कम मात्रा में उपस्थित रहता है, वह पहले समाप्त हो जाता है। ऐसे क्रियाकारक को सीमांत अभिकर्मक कहते हैं क्योंकि वह उत्पाद की मात्रा को सीमित कर देता है।
प्रश्न 8.
सार्थक अंक का निकटन कैसे किया जाता है?
उत्तर:
किसी संख्या को तीन सार्थक अंकों तक निकटित करने के लिए, यदि चौथा अंक 5 से छोटा है तो उसे छोड़ देते हैं परन्तु यदि चौथा अंक 5 या 5 से अधिक है तो तीसरे सार्थक अंक में 1 जोड़ देते हैं।
प्रश्न 9.
द्रव्यमान, लम्बाई, समय, तापक्रम एवं पदार्थ की मात्रा का SI मात्रक क्या है?
उत्तर:
द्रव्यमान का-किलोग्राम (kg), लंबाई का-मीटर (m), समय का-सेकण्ड (s), तापक्रम काकेल्विन (K) एवं पदार्थ की मात्रा का-मोल (mol) है।
रसायन विज्ञान की कुछ मूल लघु उत्तरीय प्रश्न
प्रश्न 1.
यदि डाइ हाइड्रोजन गैस के 10 आयतन डाइऑक्साइड गैस के 5 आयतनों के साथ अभिक्रिया करे तो जल वाष्प के कितने आयतन प्राप्त होंगे?
हल:
![]()
गे-लुसाक के गैसीय आयतन के नियमानुसार,
आयतन अनुपात 2 : 1 : 2
प्रश्नानुसार 10 : 5 : 10
अत: 10 आयतन H2, 5 आयतन O2 से क्रिया करके 10 आयतन जल वाष्प बनाएगा।
प्रश्न 2.
द्रव्यमान संरक्षण का नियम क्या है? इस नियम की आधुनिक स्थिति क्या है?
उत्तर:
द्रव्यमान संरक्षण का नियम-इस नियम को लेवोजियर ने सन् 1744 में प्रतिपादित किया था। इस नियम के अनुसार, “रासायनिक परिवर्तन में भाग लेने वाले पदार्थों का कुल द्रव्यमान परिवर्तन के पश्चात् बने हुए पदार्थों के कुल द्रव्यमान के बराबर होता है अर्थात् रासायनिक परिवर्तन में द्रव्य न तो उत्पन्न होता है और न ही नष्ट होता है, उसके केवल रूप या अवस्था में परिवर्तन हो सकता है।”
उदाहरण:
C + O2 → CO2
12 ग्राम कार्बन 32 ग्राम ऑक्सीजन से संयोग करता है, तो 44 ग्राम कार्बन डाइऑक्साइड प्राप्त होता है।
आधुनिक स्थिति:
आइन्स्टीन के अनुसार द्रव्यमान को ऊर्जा में परिवर्तित किया जा सकता है।
E = mc2
जहाँ E = ऊर्जा, m = द्रव्यमान और c = प्रकाश का वेग।
किन्तु जो रासायनिक क्रियाएँ हम प्रयोगशाला में करते हैं उनमें बहुत कम ऊर्जा उत्पन्न या अवशोषित होती है, इसलिये द्रव्य की मात्रा में बहुत कमी या वृद्धि होती है। अतः साधारण परिस्थितियों में द्रव्यमान संरक्षण नियम को सत्य माना जा सकता है।
प्रश्न 3.
गे-लुसाक का आयतन संबंधी नियम क्या है?
अथवा
N2 और H2 परस्पर संयुक्त होकर NH3 गैस का निर्माण करते हैं। समान ताप व दाब पर इनके आयतनों में 1:3:2 का अनुपात है। इससे जिस नियम की पुष्टि होती है, उस नियम को लिखिये।
उत्तर:
जब गैसें आपस में संयोग करती हैं, तो उनके आयतनों में सरल अनुपात होता है और यदि उनके संयोग से बना हुआ पदार्थ भी गैस ही हो, तो उसका आयतन भी अभिकारी गैसों के आयतनों के सरल अनुपात में होता है, जब सभी समान आयतन समान ताप और दाब पर नापे जायें।
उदाहरण:
एक आयतन N2 तीन आयतन H2 के साथ संयोग करके दो आयतन अमोनिया बनाता है। अभिकारी गैस N2, H2 तथा अमोनिया में परस्पर 1 : 3 : 2 का सरल अनुपात है। इससे इस नियम की पुष्टि होती है।

प्रश्न 4.
तुल्य अनुपात का नियम क्या है ? उदाहरण सहित समझाइये।
उत्तर:
यह नियम सर्वप्रथम रिचर द्वारा सन् 1792 में दिया गया तथा सन् 1810 में बर्जीलियस ने इसकी पुष्टि की। इस नियम के अनुसार, “यदि दो भिन्न-भिन्न तत्व किसी तीसरे तत्व के निश्चित भार से संयोग करते हैं तो पहले दोनों तत्वों के भार या तो उस अनुपात में होंगे जिससे वे दोनों आपस में संयोग करते हैं अथवा यह अनुपात उनके संयोग करने के भारों का सरल गुणांक होगा।
उदाहरण:
दो तत्व कार्बन और ऑक्सीजन अलग-अलग हाइड्रोजन के एक निश्चित भार से संयोग करते हैं।
मेथेन में H : C = 4 : 12
H2O में H : 0 = 2 : 16
या 4:32
हाइड्रोजन के एक निश्चित भार से संयुक्त होने वाले ये तत्व कार्बन और ऑक्सीजन आपस में संयुक्त होकर CO2 बनाते हैं।
CO2 में C : O = 12 : 32
यह अनुपात 12 : 32 वही है जो CH4 और H2O में C और O का अनुपात है, इससे तुल्य अनुपात नियम की पुष्टि होती है।
प्रश्न 5.
किसी पदार्थ का अणुसूत्र उनके मूलानुपाती सूत्र से किस प्रकार संबंधित होता है?
उत्तर:
अणुसूत्र व मूलानुपाती सूत्र में संबंध-अणुसूत्र यह किसी यौगिक में उपस्थित तत्वों के परमाणुओं में उपस्थित वास्तविक संख्या को प्रकट करता है। यह या तो मूलानुपाती सूत्र के समान होती है या इसका एक सरल गुणक होता है।
अणुसूत्र = n x (मूलानुपाती सूत्र)
या
![]()
उदाहरण:
एक यौगिक का जिसका मूलानुपाती सूत्र CH2O है तथा अणुभार 180 है।

अतः अणु सूत्र = n x मूलानुपाती सूत्र = 6(CH2O)
= C6H12O6.
प्रश्न 6.
गुणित अनुपात का नियम क्या है ? एक उदाहरण द्वारा समझाइए।
उत्तर:]
गुणित अनुपात का नियम-“जब दो तत्व परस्पर संयोग करके दो या दो से अधिक यौगिक बनाते हैं, तो एक तत्व के भिन्न-भिन्न भार, जो दूसरे तत्वों के निश्चित भार से संयोग करते हैं, सदैव सरल गुणित अनुपात में होते हैं।”
उदाहरण:
भार अनुसार, CO में 12 भाग C और 16 भाग O तथा CO2 में 12 भाग C और 32 भाग O.
यहाँ पर C के निश्चित भार (12 भाग) से संयुक्त होने वाले O के विभिन्न भार क्रमश: 16 और 32 सरल अनुपात 1 : 2 में हैं।
प्रश्न 7.
स्थिर अनुपात का नियम क्या है ? समस्थानिक की खोज ने इसे किस प्रकार प्रभावित किया?
उत्तर:
स्थिर अनुपात का नियम-प्राऊस्ट के अनुसार, “प्रत्येक रासायनिक यौगिक में चाहे वह कहीं से प्राप्त किया गया हो अथवा किसी भी विधि से बनाया गया हो उसके अवयवी तत्व भार की दृष्टि से सदैव एक निश्चित अनुपात में रहते हैं।”
जैसे:
शुद्ध जल जिसे नदी, वर्षा, कुँआ, समुद्र आदि कहीं से प्राप्त किया जा सकता है अथवा किसी भी रासायनिक विधि से बनाया जा सकता है, परन्तु हाइड्रोजन एवं ऑक्सीजन के भारों का अनुपात सदैव 1 : 8 होता है।
वर्तमान परिवेश में स्थिर अनुपात का नियम:
समस्थानिकों की खोज ने यह सिद्ध कर दिया है कि एक ही तत्व के भिन्न-भिन्न परमाणु भार वाले परमाणु सम्भव हैं। अतः किसी भी यौगिक का संघटन निश्चित नहीं होगा। जैसे-जल का संघटन अग्रलिखित सारणी से स्पष्ट है –
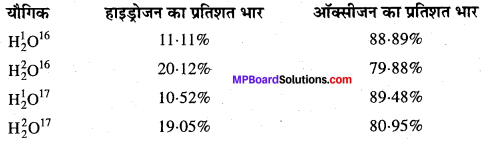
उपर्युक्त आँकड़े इस नियम के विपरीत हैं, परन्तु नियम सर्वमान्य है, क्योंकि प्रकृति में पाये जाने वाले तत्व के प्रत्येक भाग में समस्थानिकों का वितरण समान है।
प्रश्न 8.
प्रकृति में उपलब्ध ऑर्गन के मोलर द्रव्यमान की गणना के लिए निम्नलिखित तालिका में दिए गए आँकड़ों का उपयोग कीजिए –

हल:
Ar का औसत मोलर द्रव्यमान Σ fi x Ai
= (0.00337 x 35.96755) + (0.00063 x 37.96272) + (0.99600 x 39.9624)
= 0.121 + 0.024 + 39.803
= 39.948g mol-1.
प्रश्न 9.
डॉल्टन के परमाणु सिद्धान्त का आधुनिक स्वरूप संक्षिप्त में समझाइये।
उत्तर:
डॉल्टन के परमाणु सिद्धान्त का आधुनिक स्वरूप –
- परमाणु अब अविभाज्य कण नहीं है, परमाणु का विखण्डन संभव है।
- परमाणु रासायनिक अभिक्रिया में भाग लेने वाला सूक्ष्मतम कण है।
- डॉल्टन के अनुसार एक ही तत्व के समस्त परमाणु एक समान होते हैं, किन्तु अब ऐसे परमाणु भी ज्ञात हैं, जिनके रासायनिक गुण समान होते हैं किन्तु भार भिन्न-भिन्न होते हैं।
- डॉल्टन के अनुसार भिन्न-भिन्न तत्वों के परमाणु भार भिन्न-भिन्न होते हैं। परन्तु समभारी की खोज से स्पष्ट है कि भिन्न-भिन्न तत्वों के परमाणुओं के परमाणु भार समान हो सकते हैं।
- आधुनिक अनुसंधानों से स्पष्ट है कि परमाणु के द्रव्यमान को ऊर्जा में परिवर्तित किया जा सकता है।
- अन्य अणुभार वाले कार्बनिक यौगिकों के अणुओं में परमाणुओं की संख्या सरल अनुपात में हो, यह जरूरी नहीं है।
प्रश्न 10.
अणु और परमाणु में अंतर लिखिये।
उत्तर:
अण और परमाण में अंतर:
अणु
- यह द्रव्य का सूक्ष्मतम कण है जो स्वतंत्र अवस्था में रहता है।
- यह रासायनिक अभिक्रिया में भाग नहीं लेता।
- यह रासायनिक अभिक्रिया में प्रायः परमाणु में विभाजित हो जाता है।
- यह एक या एक से अधिक परमाणुओं से मिलकर बना होता है।
परमाणु
- यह किसी तत्व का सूक्ष्मतम कण है जो स्वतंत्र अवस्था में नहीं रह सकता है।
- यह रासायनिक अभिक्रिया में भाग लेता है।
- यह रासायनिक अभिक्रिया में विभाजित नहीं होता है।
- यह रासायनिक क्रिया में भाग लेने वाले तत्व का सूक्ष्मतम कण है।
रसायन विज्ञान की कुछ मूल दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
रासायनिक समीकरण क्या है? उसे संतुलित करने के नियम उदाहरण सहित समझाइये।
उत्तर:
रासायनिक अभिक्रिया में भाग लेने वाले पदार्थों तथा बनने वाले पदार्थों को रासायनिक सूत्रों द्वारा समीकरण के रूप में दर्शाया जाता है। रासायनिक अभिक्रिया को रासायनिक सूत्रों द्वारा समीकरण के रूप में दर्शाने की विधि को रासायनिक समीकरण कहते हैं। रासायनिक समीकरण को सन्तुलित करने के नियम:
- अनुमान विधि (Hit and trial method)
- आंशिक समीकरण विधि (Partial equation method)।
1. अनुमान विधि:
(i) सबसे पहले उस तत्व के परमाणुओं को जो सबसे कम स्थान में आते हैं, उन्हें समीकरण के दोनों ओर बराबर कर लेते हैं।
(ii) जिन समीकरणों में ऑक्सीजन, नाइट्रोजन, हाइड्रोजन आदि तात्विक गैसें बनती हैं, उन्हें पहले परमाण्विक अवस्था में ही रखा जाता है। इस प्रकार प्राप्त समीकरण परमाण्विक समीकरण कहलाता है। परमाण्विक समीकरण को दो से गुणा करके आण्विक समीकरण (Molecular equation) में बदला जाता है।
उदाहरण:
(i) पोटैशियम क्लोरेट को गर्म करने से पोटैशियम क्लोराइड और ऑक्सीजन बनते हैं। अतः
(a) पोटैशियम क्लोरेट → पोटैशियम क्लोराइड + ऑक्सीजन।
KClO3 → KCl + O(ढाँचा)
(b) ऊपर के समीकरण में ऑक्सीजन परमाणु दोनों ओर बराबर नहीं हैं। दायीं ओर के ऑक्सीजन परमाणु को 3 से गुणा करने पर दोनों ओर ऑक्सीजन परमाणुओं की संख्या बराबर हो जाती है।
KClO3 → KCI + 3O
(c) परन्तु ऊपर के समीकरण में ऑक्सीजन परमाणु के रूप में है। उसे अणु के रूप में परिवर्तित करने के लिए समीकरण को दो से गुणा करना पड़ेगा। अतः
2KClO3 → 2KCl + 3O, (संतुलित)
(ii) (a) कॉपर को सान्द्र H2SO के साथ गर्म करने से कॉपर सल्फेट, सल्फर डाइऑक्साइड और जल बनता है। अतः
Cu + H2SO4 → CuSO4 + SO2 + H2O (ढाँचा)
(b) सल्फर परमाणुओं को दोनों ओर बराबर करने के लिएH,SO, को दो से गुणा कर देते हैं।
Cu + 2H2SO4 → CuSO4 + SO2 + H2O
(c) अब हाइड्रोजन के परमाणुओं को दोनों ओर बराबर करने के लिए HO को दो से गुणा कर देते हैं।
Cu + 2H2SO4 → CuSO4 + SO2 + 2H2O (संतुलित)
2. आंशिक समीकरण विधि:
जटिल समीकरणों को प्रायः अनुमान विधि द्वारा सन्तुलित करना कठिन होता है। यह माना जाता है कि जटिल समीकरण दो या दो से अधिक पदों में सम्पन्न होता है। इन समीकरणों को सन्तुलित कर लेते हैं। यदि आवश्यक हुआ तो आंशिक समीकरण को किसी पूर्णांक से गुणा कर देते हैं। इसके पश्चात् सभी आंशिक समीकरणों को इस प्रकार से जोड़ा जाता है कि माध्यमिक उत्पाद जो अन्तिम अभिक्रिया में प्राप्त नहीं होते, कट जायें। इस प्रकार प्राप्त अन्तिम समीकरण सही एवं सन्तुलित होता है।
उदाहरण:
Cu को सान्द्र H2SO4 के साथ गर्म करने पर कॉपर सल्फेट, सल्फर डाइऑक्साइड और जल बनता है। इस समीकरण को निम्नलिखित आंशिक समीकरणों के योग के रूप में दर्शाया जा सकता है –
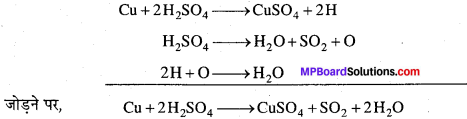
माध्यमिक क्रियाफल 26 और O आंशिक समीकरणों में दोनों ओर स्थित होने के कारण काट दिये गये हैं।
प्रश्न 2.
मोल तथा ऐवोगैड्रो संख्या को समझाइये। मोल संकल्पना के आधार पर परमाणु द्रव्यमान तथा आण्विक द्रव्यमान की परिभाषा लिखिए।
उत्तर:
मोल संकल्पना-परमाणु तथा अणु अत्यन्त सूक्ष्ण कण है। किसी पदार्थ की अति अल्प मात्रा में भी परमाणुओं तथा अणुओं की संख्या बहुत अधिक होती है। उदाहरणार्थ, कार्बन के 1 मिलीग्राम (0.001 ग्राम) में कुल 5-019 x 1019 परमाणु होते हैं। प्रायः रासायनिक अध्ययनों में पदार्थ की काफी मात्राएँ प्रयुक्त होती है, जिनमें परमाणु या अणुओं की अत्यधिक बड़ी संख्या होती है। इन परमाणुओं को गिनना असम्भव है, किन्तु इनकी संख्या का ज्ञान होना आवश्यक है। जिस प्रकार 12
पेन को एक दर्जन पेन तथा 1000 मीटर को एक किलोमीटर कहते हैं उसी प्रकार 6.023 x 1023 कणों के समूह को हम एक मोल कहते हैं। ये कण अणु, परमाणु अथवा आयन हो सकते हैं।
अत: मोल एक इकाई है, जो 6.023 x 1023 कणों (अणु, परमाणु या आयन) को व्यक्त करती है।
एक मोल अणु में अणुओं की संख्या = 6.023 x 1023 होती है।
एक मोल परमाणु में परमाणुओं की संख्या = 6.023 x 1023 होती है। एक मोल आयन में आयनों की संख्या = 6.023 x 1023 होती है। मोल भार को भी दर्शाता है –
एक ग्राम मोल ऑक्सीजन अर्थात् 32 ग्राम ऑक्सीजन में ऑक्सीजन के कुल 6.023 x 1023 अणु होंगे। एक ग्राम मोल सोडियम अर्थात् 23 ग्राम सोडियम में सोडियम के 6.023 x 1023 परमाणु होंगे।
सोडियम क्लोराइड का सूत्र भार 58.5 है। अतः सोडियम क्लोराइड के 58.5 ग्राम में एक मोल सोडियम आयन तथा एक मोल क्लोराइड आयन होंगे।
“समान ताप और समान दाब पर सभी गैसों के समान आयतन में अणुओं की संख्या समान होती है।” इस नियम के अनुसार N.T.P. पर प्रत्येक गैस के एक ग्राम मोल में अणुओं की संख्या 6.023 x 1023 होती है। इस संख्या को ऐवोगैड्रो संख्या (Avogadro Number) कहते हैं तथा इसे N से प्रदर्शित करते हैं।
प्रश्न 3.
स्टॉइकियोमेट्री क्या है? रासायनिक समीकरणों पर आधारित समस्याओं का हल इससे किस प्रकार किया जाता है?
उत्तर:
‘स्टॉइकियोमेट्री’ यूनानी भाषा से (‘स्टॉकियोन’ का अर्थ, तत्व तथा मेट्रोन’ (Metron) का अर्थ मापन) लिया गया है, जिसका शाब्दिक अर्थ है तत्व या यौगिकों की मात्रा का मापन।
एक संतुलित रासायनिक समीकरण में रासायनिक अभिक्रिया में भाग लेने वाले अभिकारकों तथा उत्पादों के मध्य अणुओं, द्रव्यमानों, मोलों और आयतनों के संदर्भ में मात्रात्मक संबंध होता है। इन गणनाओं से सम्बन्धित समस्याएँ तीन प्रकार की होती हैं –
(a) द्रव्यमान-द्रव्यमान संबंधित (Involving mass – mass relationship):
इस प्रकार की समस्याओं में एक उत्पाद या अभिकारक का द्रव्यमान दिया जाता है तथा दूसरे की गणना की जाती है। .
(b) द्रव्यमान-आयतन संबंधित (Involving mass – volume relationship):
इस प्रकार के प्रश्नों में एक अभिकारक अथवा उत्पाद का द्रव्यमान/आयतन दिया जाता है तथा दूसरे की गणना की जाती है।
(c) आयतन-आयतन संबंधित (Involving volume – volume relationship):
इस प्रकार की समस्याओं में एक अभिकारक या उत्पाद का आयतन दिया जाता है तथा दूसरे की गणना की जाती है।
उपर्युक्त प्रकार के प्रश्नों (समस्याओं) को हल करने के लिए निम्न प्रक्रिया अपनाई जाती है –
- संतुलित रासायनिक समीकरण को उसके आण्विक रूप में लिखते हैं।
- उन स्पीशीज (परमाणुओं या अणुओं) के संकेतों एवं सूत्रों को चुनिए जिनके भार/आयतन या तो दिये गये हैं अथवा गणना द्वारा निकाले गये हैं।
- गणना में शामिल अणुओं तथा परमाणुओं का परमाणु द्रव्यमान/आण्विक द्रव्यमान/मोल/मोलर आयतन लिखते हैं।
- सामान्य गणितीय गणनाओं द्वारा इच्छित पदार्थ की मात्रा की गणना करते हैं। निम्न संतुलित समीकरण पर विचार करें –

अणु की संख्या (मोल) ही स्टॉइकियोमेट्रिक गुणांक कहलाता है।
प्रश्न 4.
रासायनिक समीकरण क्या है? उसकी सीमाएँ क्या हैं? उसे और अधिक सूचनाप्रद किस प्रकार बनाया जा सकता है ? रासायनिक समीकरणों को संतुलित करना क्यों आवश्यक है?
उत्तर:
किसी रासायनिक अभिक्रिया में भाग लेने वाले पदार्थों (अभिकारकों तथा बनने वाले पदार्थों (उत्पादकों) को रासायनिक सूत्रों द्वारा समीकरण के रूप में दर्शाने की विधि रासायनिक समीकरण कहलाती है। रासायनिक समीकरण से निम्नलिखित बातों की जानकारी नहीं होती –
- अभिकारकों तथा उत्पादकों की भौतिक अवस्था।
- अभिकारकों तथा उत्पादकों का सान्द्रण।
- यह रासायनिक अभिक्रिया की परिस्थितियाँ जैसे-ताप, दाब, उत्प्रेरक आदि की जानकारी नहीं देता।
- अभिक्रिया के वेग का ज्ञान नहीं होता।
- अभिक्रिया में होने वाले ऊष्मीय परिवर्तन का ज्ञान नहीं होता।
- अभिक्रिया में सावधानियों का ज्ञान नहीं होता।
- अभिक्रिया की क्रिया-विधि का ज्ञान नहीं होता।
- यह ज्ञात नहीं होता कि अभिक्रिया उत्क्रमणीय है या अनुत्क्रमणीय।
- अभिक्रिया के पूर्ण होने का समय नहीं बतलाता।
- रासायनिक समीकरण से अभिक्रिया में प्रकाश का उत्पन्न होना, विस्फोटक पदार्थों का बनना आदि के बारे में मालूम नहीं होता।
रासायनिक समीकरणों को संतुलित करके तथा उचित निर्देश चिन्हों का प्रयोग करके इसे ज्यादा स्पष्ट, जानकारीपूर्ण तथा लाभदायक बनाया जा सकता है। इससे होने वाले फायदे निम्नानुसार हैं –
- अभिक्रिया में भाग लेने वाली अभिकारकों तथा उत्पादकों की संख्या।
- यदि तत्वों के परमाणु द्रव्यमान ज्ञात हो तो अभिकारकों एवं उत्पादकों के आण्विक द्रव्यमान भी ज्ञात किये जा सकते हैं।
- यदि क्रियाकारक व क्रियाफल पदार्थ गैसीय हो, तो उनका आयतन भी ज्ञात किया जा सकता है।
- इससे द्रव्य की अनिश्चिता के नियम की पुष्टि होती है।
- तत्वों की संयोजकता व तुल्यांकी द्रव्यमान के गणना भी की जा सकती है।