Prasanna

MP Board Class 12th Hindi Makrand Solutions Chapter 20 ‘हम कहाँ जा रहे हैं…!’ (कविता, सुदर्शन ‘प्रियदर्शिनी’)

हम कहाँ जा रहे हैं…! पाठ्य-पुस्तक पर आधारित प्रश्न

हम कहाँ जा रहे हैं…! लघु उत्तरीय प्रश्न

प्रश्न 1.
कवि का दोगली-दोहरी सभ्यता से क्या आशय है?
उत्तर:
दोगली-दोहरी सभ्यता से आशय है-पाश्चात्य सभ्यता और भारतीय सभ्यता का सम्मिश्रण।

प्रश्न 2.
हम कैसी दुंदुभी बजा रहे हैं?
उत्तर:
हम विदेशी जीवन-शैली में अपनी संस्कृति की ही वस्तुओं को आयायित समझकर अपना रहे और आधुनिक होने की दुंदुभी बजा रहे हैं।

प्रश्न 3.
हम विदेश क्यों जा रहे हैं?
उत्तर:
अपनी ही संस्कृति के रहस्यों को जानने के लिए हम विदेश जा रहे हैं।

हम कहाँ जा रहे हैं…! दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
‘उल्टे बाँस बरेली को’ कवि ने किस संदर्भ में कहा है? (M.P. 2009)
उत्तर:
विदेशियों द्वारा हमारी परंपराओं और उपलब्धियों को अपना कहकर प्रचारित करने के सौंदर्य में कवि ‘उल्टे बाँस बरेली को’ कहा है।

प्रश्न 2.
हमने दूसरों को क्या सौंप दिया है? (M.P. 2010)
उत्तर:
हमने दूसरों को अपनी सभ्यता और संस्कृति सौंप दी है।

प्रश्न 3.
‘हम कहाँ जा रहे हैं’ से कवि क्या संदेश देना चाहता है?
उत्तर:
‘हम कहाँ जा रहे हैं’ से कवि यह संदेश केता चाहता है कि भारतीय सभ्यता, संस्कृति, उसकी परंपराएँ, व्यवहार, उपलब्धियाँ और जीवन-मूल्य सर्वश्रेष्ठ है। हमें पाश्चात्य जीवन-शैली और वस्तुओं को नहीं अपनाना चाहिए। हमें भारतीय ही बने रहना चाहिए; क्योंकि इसी में हमारा कल्याण है।

हम कहाँ जा रहे हैं…! भाव-विस्तार/पल्लवन

प्रश्न 1.
निम्नलिखित का भाव पल्लवन कीजिए –

1. मान्यताएँ बदल कर हम अपना सर मुड़ा रहे हैं।
2. अपना खालिसे कलश भी हम विदेशी बना रहे हैं।

उत्तर:
1. हम भारतीय पुरातन काल से चली आ रही परंपराओं, जीवन-मूल्यों और आदर्शों को बदलकर, पाश्चात्य जीवन-शैली को अपनाकर, अपनी संस्कृति और अपने व्यवहार को भूलते जा रहे हैं। आज जब विश्व हमारे चिंतन और ज्ञान से नई चेतना प्राप्त कर रहा है, तब हम अपनी विरासत को छोड़कर विदेशी चिंतन और व्यवहार को ग्रहण करें, यह उचित नहीं है।

2. हम विदेशी वस्तुओं के प्रति इतने आकर्षित हो रहे हैं कि हमने शुद्ध भारतीय ‘देन कलश को विदेशी की देन बता दिया है। कवि ने इसके द्वारा भारतीयों पर व्यंग्य किया है कि हम अपनी सांस्कृतिक उपलब्धियों को भी नकार रहे हैं।

हम कहाँ जा रहे हैं…! भाषा-अनुशीलन

प्रश्न 1.
निम्नलिखित मुहावरों का अर्थ लिखकर वाक्य में प्रयोग कीजिए –
(अ) मुलम्में पर मुलम्मा चढ़ाना।
(ब) उल्टे बाँस बरेली को
(स) दुदंभी बजाना
(द) सर मुंडाना।
उत्तर:

प्रश्न 2.
विलोम शब्द लिखिए –

1. कड़वा
2. नीति
3. ज्ञान
4. सभ्यता
5. रहस्य
6. दानवीर।

उत्तर:

हम कहाँ जा रहे हैं…! योग्यता-विस्तार

प्रश्न 1.
किसी प्रवासी भारतीय की कविता खोजिए और उसे कक्षा में सुनाइए।
उत्तर:
छात्र स्वयं करें।

प्रश्न 2.
चाणक्य और अभिमन्यु के संबंध में जानकारी प्राप्त करें।
उत्तर:
चाणक्य चंद्रगुप्त का प्रधानमंत्री था और अर्थशास्त्र का रचयिता था। अभिमन्यु अर्जुन का पुत्र था। महाभारत युद्ध में द्रोणाचार्य के चक्रव्यूह को तोड़ने के लिए वह उसमें प्रवेश कर गया, किंतु वहाँ कई महारथियों ने मिलकर उसका वध कर दिया था।

प्रश्न 3.
पाश्चात्य संस्कृति के अंधानुकरण को आप कैसा मानते हैं? अपने विचार लिखिए।
उत्तर:
छात्र स्वयं करें।

प्रश्न 4.
विश्व में हिन्दी भाषा के प्रचार-प्रसार की स्थिति पर अपने विचार अपने साथियों के साथ बाँटिए।
उत्तर:
छात्र स्वयं करें।

हम कहाँ जा रहे हैं…! परीक्षोपयोगी अन्य महत्वपूर्ण प्रश्न

I. वस्तुनिष्ठ प्रश्न

प्रश्न 1.
‘हम कहाँ जा रहे हैं। कविता के कवि हैं –
(क) मैथिलीशरण गुप्त
(ख) देवेंद्र ‘दर्शिक’
(ग) बालकवि ‘वैरागी’
(घ) सुदर्शन ‘प्रियदर्शिनी’
उत्तर:
(घ) सुदर्शन ‘प्रियदर्शिनी’

प्रश्न 2.
मान्यताएँ बदलकर हम अपना सर……………………..रहे हैं –
(क) कटा
(ख) मुँडा
(ग) झुका
(घ) ऊँचा
उत्तर:
(ख) मुँड़ा।

प्रश्न 3.
चक्रव्यूह में फँसा था –
(क) अभिमन्यु
(ख) अर्जुन
(ग) भीम
(घ) द्रोणाचार्य
उत्तर:
(क) अभिमन्यु।

प्रश्न 4.
हम ‘डॉविंची कोड’ बना रहे हैं, कैसे ………..
(क) दबाव में आकर
(ख) जान-बूझकर
(ग) अनजाने में
(घ) देख-सुनकर
उत्तर:
(ख) जान-बूझकर।

प्रश्न 5.
हम कैसी सभ्यता के रंग में रंगे हैं –
(क) दोहरी-दोगली
(ख) भारतीय पाश्चात्य
(ग) असली-नकली
(घ) अच्छी-बुरी
उत्तर:
(क) दोहरी-दोगली।

प्रश्न 6.
कवि ने हमें संदेश दिया है –
(क) हम भारतीय बने रहें
(ख) हम आधुनिक बनने के लिए पाश्चात्य जीवन-शैली अपनाएँ
(ग) हम अपनी संस्कृति-सभ्यता को भूल जाएँ
(घ) हम अपनी उपलब्धियों को नकार दें
उत्तर:
(क) हम भारतीय बने रहें।

प्रश्न 7.
हमारा कल्याण इसी में है कि –
(क) हम भारतीय बने रहें।
(ख) हम नकली जीवन-शैली को उतार फेंकें।
(ग) हम अपनी सांस्कृतिक चेतना को पहचानें।
(घ) हम अपनी शक्ति को, अपनी उपलब्धियों को और अपनी सांस्कृतिक चेतना पहचानें।
उत्तर:
(घ) हम अपनी शक्ति को, अपनी उपलब्धियों को और अपनी सांस्कृतिक चेतना को पहचानें।

II. निम्नलिखित रिक्त स्थानों की पूर्ति दिए गए विकल्पों के आधार कीजिए –

1. सुदर्शन ‘प्रियदर्शनी’ ………. हैं। (प्रवासी भारतीय/अप्रवासी भारतीय)
2. विश्व में ………. पहले स्थान पर है। (चीनी भाषा/हिंदी भाषा)
3. हिंदी जानने वालों की संख्या ………. करोड़ है। (100/102)
4. पाश्चात्य जीवन-शैली और वस्तुओं को देखकर हम ………. रहे। (भाग/ललचा)
5. ‘हम कहाँ जा रहे हैं…!’ कविता के कवि ……… हैं। (बालकवि वैरागी/सुदर्शन प्रियदर्शिनी)

उत्तर:

1. अप्रवासी भातीय
2. हिंदी भाषा
3. 102
4. ललचा
5. सुदर्शन “प्रियदर्शिनी।

III. निम्नलिखित कथनों में सत्य/असत्य छाँटिए –

1. महाभारत के चक्रव्यूह में अभिमन्यु फँसा था।
2. कविता ‘हम कहाँ जा रहे हैं’…में हैरीपीटर फिल्म का उल्लेख है।
3. हम दोहरी-दोगली सभ्यता के रंग में रंगे हैं।
4. कवि ने संदेश दिया है कि हम भारतीय बने रहें।
5. ‘दोगली-दोहरी’ में उपमा अलंकार है।

उत्तर:

1. सत्य
2. असत्य
3. सत्य
4. सत्य
5. असत्य।

IV. निम्नलिखित के सही जोड़े मिलाइए –

प्रश्न 1.

उत्तर:

(i) (ङ)
(i) (ग)
(iii) (घ)
(iv) (ख)
(v) (क)।

V. निम्नलिखित प्रश्नों के उत्तर एक शब्द या एक वाक्य में दीजिए –

1. हमारे लिए क्या शुभ संकेत नहीं है।
2. विदेशी किसे क्या कहकर प्रचारित कर रहे हैं?
3. हमारा कल्याण किसमें है?
4. चाणक्य-नीति क्या है?
5. ‘सब कुछ गड़मड़ा रहा है?

उत्तर:

1. हमारे लिए यह शुभ संकेत नहीं है कि हम अपनी उपलब्धियों को नकार रहे हैं।
2. विदेशी हमारी देन वास्तुकला, सत्वज्ञान और योग को अपना कहकर प्रचारित कर रहे हैं।
3. हमारा कल्याण इसी में हैं कि हम भारतीय बने रहें।
4. खूब सोच-विचार कर ही कदम उठाना चाणक्य नीति है।
5. ‘सब कुछ गड़मड़ा रहा है’ से कवि का तात्पर्य है-भारतीय और पाश्चात्य जीवन-शैली एक-दूसरे से इतनी मिल गई हैं कि क्या भारतीय है और क्या पाश्चात्य, यह समझ पाना कठिन होता जा रहा है।

हम कहाँ जा रहे हैं…! लघु उत्तरीय प्रश्न

प्रश्न 1.
सुभद्रा कौन-सी कथा सुनते-सुनते सो गई थी?
उत्तर:
सुभद्रा चक्रव्यूह की कथा सुनते-सुनते सो. गई थी?

प्रश्न 2.
‘डॉविंची कोड’ से क्या तात्पर्य है?
उत्तर:
‘डॉविंची कोड’ से तात्पर्य है नकली नियमावली।

प्रश्न 3.
विदेशी क्या कर रहे हैं?
उत्तर:
विदेशी हमारी वास्तुकला, सत्वज्ञान और योग को अपना कहकर प्रचारित कर रहे हैं।

प्रश्न 4.
विदेशी हमारा क्या-क्या ग्रहण कर उन्हें क्या-क्या बना दिया है?
उत्तर:
विदेशी हमारी वास्तुकला को ग्रहण कर उसे फेंगशुई, सत्वज्ञान को रेकी और योग को योगा बना दिया है।

प्रश्न 5.
कवि ने क्या उतार फेंकने के लिए कहा है?
उत्तर”:
कवि ने नकली जीवन-शैली उतार फेंकने के लिए कहा है।

प्रश्न 6.
‘उल्टे बाँस बरेली को’ कवि सुदर्शन ने किस संदर्भ में कहा है? (M.P. 2009)
उत्तर:
‘उल्टे बाँस बरेली को’ कवि सुदर्शन ने उस संदर्भ में कहा है कि विदेशी हमारी ही वस्तुओं को ग्रहण करके उसे अपना अच्छा बताकर हमें लौटा रहे हैं।

हम कहाँ जा रहे हैं…! दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
कवि ने किन प्रसंगों को उजागर किया है?
उत्तर:
कवि ने भारतीय और पाश्चात्य जीवन-बोध के उन प्रसंगों को उजागर किया है जिनमें हम अपनी संस्कृति और अपने परंपरागत व्यवहार को भूल रहे हैं।

प्रश्न 2.
हम पाश्चात्य जीवन-शैली की चकाचौंध में क्या-क्या खोते जा रहे हैं?
उत्तर:
हम पाश्चात्य जीवन-शैली की चकाचौंध में अपनी सांस्कृतिक पहचान, धर्म-कर्म, वेशभूषा, भाषा-ज्ञान, विधि-विधान आदि खोते जा रहे हैं।

प्रश्न 3.
हमारा क्या-क्या विदेशी हो गया है?
उत्तर:
हमारा खालिस कलश, धर्म, कर्म, वेशभूषा, भाषा-विज्ञान, विधि-विधान सभ्यता, संस्कृति, दानवीरता, वास्तुकला, सत्वज्ञान, योग, नीम की निमोली आदि विदेशी हो गए हैं। इन्हें विदेशी अपना मुलम्मा चढ़ाकर अपना बतलाते हुए प्रचारित कर रहे हैं।

प्रश्न 4.
‘हम कहाँ जा रहे हैं….. कविता के उद्देश्य पर प्रकाश डालिए।
उत्तर:
‘हम कहाँ जा रहे हैं…!’ कविता सोद्देश्यपूर्ण कविता है। इसमें कवि सुदर्शन का यह उद्देश्य है कि हमें बाहरी आडम्बरों से दूर रहना चाहिए। तथाकथित सभ्यता और पाश्चात्य जीवन-शैली को बिना सोचे-समझे अपनाना मूर्खता है। हमारी ही विरासत और सांस्कृतिक निष्ठा दुनिया में श्रेष्ठ है। विदेशी वस्तुओं की ओर दौड़ना अच्छी बात नहीं है। अच्छी बात यही है कि हम भारतीय हैं और भारतीय बने रहें।

हम कहाँ जा रहे हैं…! पाठ का सारांश

प्रश्न 1.
“हम कहाँ जा रहे हैं…!” कविता का सार अपने शब्दों में लिखिए।
उत्तर:
‘हम कहाँ जा रहे हैं। कविता में कवि सुदर्शन ‘प्रियदर्शिनी’ ने भारतीय और पाश्चात्य जीवन-बोध के उन प्रसंगों को उजागर किया है। जिन्हें हम भारतीय अपनी भारतीय संस्कृति और परंपरागत व्यवहार में होने पर भी भूलते जा रहे हैं। कविने इस बात पर बल दिया है कि हम अपनी छम प्रवृत्ति को छोड़ दें। बाह्य आडंबर को नष्ट कर दें। कुछ नवीन सभ्यता के नाम पर पाश्चात्य जीवन-शैली का अपनाना बुद्धिमानी नहीं है। सच तो यह है कि हमारी विरासत एवं सांस्कृतिक निष्ठा विश्व में श्रेष्ठ है। पाश्चात्य जीवन-शैली और उनकी वस्तुओं को देखकर हम ललचा रहे हैं। उन्हें स्वीकार कर रहे हैं।

अपनी उपलब्धियों को नकार रहे हैं। हम अपनी संस्कृति को देखने-समझने के लिए विदेश जा रहे हैं। यहाँ तक कि हम अपने स्वयं के कलश (धरोहर) को भी विदेशी बता रहे हैं। मैंनशुई, रेकी और योगा का उल्लेख करते हुए कवि कहता है कि यह सब कुछ हमारी वास्तुकला, सत्वज्ञान और योग हमारी ही देन हैं। विदेशी लोग अपना कहकर प्रचारित कर रहे हैं। कवि हमें सचेत करता है कि हमें अपनी शक्ति को, अपनी उपलब्धियों को अपनी सांस्कृतिक चेतना को पहचानना चाहिए। इसी में हमारा कल्याण है कि हम भारतीय बने रहे। नकली जीवन-शैली को त्याग दें।

काव्यांशों की सप्रसंग व्याख्या

प्रश्न 1.
चिरंतन काल से
लिख-पीढ़ी दर –
पीढ़ियाँ चली
मान्यताएँ बदलकर
अपना सर हम

मुड़ा रहे हैं…!
न जाने हम कहाँ
जा रहे हैं…!

चाणक्य नीतियों
के चक्रव्यूह में फँसे
हम अभिमन्यु के
व्यूह को दुहरा रहे हैं…।

सुनते-सुनते
कथा, सो गई
सुभद्रा-हम जान-बूझकर
डॉविंची कोड बना रहे हैं।
रहस्य पर रहस्य
दबे हैं संस्कृति के
उन्हें देखने-समझने
विदेश आ रहे हैं…!

पगड़ी उतरी –
बार-बार-हमारी
फिर भी कलगी
की-कलफ सहला रहे हैं…… (Page 93)

शब्दार्थ:

• चिरंतन – पुरातन, बहुत पहले से चलते रहने वाला।
• मान्यताएँ – किसी सिद्धांत आदि का मान्य होना, मानने योग्य।
• सर मुड़ाना – अपने पास का धन गँवा देना।
• चाणक्य-नीति – चंद्रगुप्त मौर्य के प्रधानमंत्री की चतुराई भरी चाल।
• व्यूह – सैनिकों को युद्धभूमि में उपयुक्त स्थान पर रखना।
• डॉविची कोड – नकली आचारसंहिता, नकली नियमावली।
• रहस्य – गुप्त भेद।
• पगड़ी उतारना – प्रतिष्ठा समाप्त करना।
• कलगी – पगड़ी। में लगाया जाने वाला फूंदना।
• कलफ़ – माँड़ी।

प्रसंग:
प्रस्तुत काव्यांश.सुदर्शन ‘प्रिंयदिर्शनी’ द्वारा रचित कविता ‘हम कहाँ जा रहे हैं…!’ से उद्धृत है। कवि ने भारतीयों को पुरातन समय से चली आ रही भारतीय संस्कृति की मान्यताओं को छोड़कर पाश्चात्य जीवन-शैली को बिना सोचे-समझे अपनाने और अपनी जीवन-शैली को भूलते जाने को उचित नहीं मानता। इन्हीं भावों को इस काव्यांश में व्यक्त किया गया है।

व्याख्या:
कवि का कहना है कि हम भारतीय पुरातन काल से पीढ़ी-दर-पीढ़ी अपनी संस्कृति की परंपरागत जीवन-शैली को बदलकर, अपने परंपरागत व्यवहार को भूलते जा रहे हैं। हम अपने जीवन-मूल्यों और आदर्श परंपराओं को छोड़कर पाश्चात्य परंपराओं और जीवन-शैली का अंधानुकरण करके कहाँ जा रहे हैं। हम पाश्चात्य संस्कृति की चतुराईभरी नीतियों के चक्रव्यूह में फंसकर अभिमन्यु वध वाले कांड को दुहरा रहे हैं; अर्थात् हम भारतीय पाश्चात्य जीवन-शैली के शिकार होते जा रहे हैं, जिसमें एक बार फँसने के बाद निकलना अभिमन्यु की तरह असंभव है।

जिस प्रकार अभिमन्यु ने सुभद्रा के गर्भ में ही चक्रव्यूह में प्रवेश का मार्ग जान लिया या किंतु कहानी सुनते-सुनते सुभद्रा के सो जाने पर वह उससे निकलने का मार्ग नहीं जान पाया क्योंकि सुभद्रा कथा के बीच में ही सो गई थी। अभिमन्यु चक्रव्यूह में घुस तो गया, लेकिन वापस नहीं लौट सका। वही स्थिति हमारी है। हम पाश्चात्य जीवन-शैली के चक्रव्यूह में फँसते जा रहे हैं। हमारे लिए उससे छुटकारा पाना कठिन है। हम जान-बूझकर इसमें फँस रहे हैं तथा बिना सोचे-समझे इसे अपनाकर, नकली नियमावली बना रहे हैं। हमें यह अपनी छद्म प्रवृत्ति छोड़ देनी चाहिए।

हमारी भारतीय सभ्यता और संस्कृति में अनेक गुप्त भेद दबे पड़े हैं। हम उन गुप्त भेदों को जानने के लिए विदेश आ रहे हैं। आज जब हमारे चिंतन और ज्ञान को अपनाकर विश्व नई चेतना ग्रहण कर रहा है, तब हम अपनी विरासत को छोड़कर विदेशी चिंतन और व्यवहार को अपनाने के लिए आतुर हो रहे हैं। ऐसा करने से बारम्बार हमारी प्रतिष्ठा घटती जा रही, है, फिर भी हम कलगी में लगे कलफ़ को सहला रहे हैं।

विशेष:

1. कवि ने भारतीय संस्कृति को पाश्चात्य संस्कृति से श्रेष्ठ बताया है और पाश्चात्य शैली को बिना विचारे स्वीकार करना उचित नहीं है।
2. सुनते-सुनते, बार-बार मैं पुनरुक्तिप्रकाश अलंकार है।
3. कलगी की कलफ़ में अनुप्रास अलंकार है।
4. मुहावरों का सटीक, सार्थक प्रयोग किया गया है।
5. महाभारत की पौराणिक कथी का प्रयोग हुआ है।
6. भाषा तत्सम प्रधान है जिसमें अंग्रेजी के शब्दों का प्रयोग किया गया है।
7. मुक्त छंद है। तुकांत का अभाव है।

पद्यांश पर आधारित विषय-वस्तु संबंधित प्रश्नोत्तर

प्रश्न (i)
चिरंतन काल से चली आ रही मान्यताओं को बदलेकर हम क्या कर रहे हैं?
उत्तर:
पुरातन काल से चली आ रही अपनी संस्कृति और परंपरागत मान्यताओं को बदलकर हम पाश्चात्य जीवन-शैली का अनुकरण कर अपनी संस्कृति और परंपरागत व्यवहार को भूलते जा रहे हैं।

प्रश्न (ii)
चाणक्य नीतियों से क्या आशय है?
उत्तर:
चाणक्य नीतियों से आशय है चतुराई की चालें। हम पाश्चात्य जीवन-शैली की चतुराईभरी चालों में फँसते जा रहे हैं। आशय यह कि हम बिना सोचे-विचारे उन्हें अपना रहे हैं।

प्रश्न (iii)
हम किन्हें देखने-समझने विदेश जा रहे हैं?
उत्तर:
भारतीय सभ्यता-संस्कृति में अनेक. गुप्त भेद दवे पड़े हैं। हम उन गुप्त भेदों को जानने के लिए विदेश जा रहे हैं।

पयांश पर आधारित सौंदर्य संबंधित प्रश्नोत्तर

प्रश्न (i)
प्रस्तुत पद्यांश के भाव-सौंदर्य पर प्रकाश डालिए।.
उत्तर:
भाव-सौंदर्य:
हम भारतीय अपनी संस्कृति और अपने परंपरागत व्यवहार को भूलते जा रहे हैं। शताब्दियों से पीढ़ी-दर-पीढ़ी चली आ रही मान्यताओं, जीवन आदर्शों और जीवन-शैली को छोड़कर पाश्चात्य जीवन-शैली को बिना सोचे विचारे अपना रहे हैं। अपनी ही संस्कृति के रहस्यों को जानने के लिए हम विदेशों में जा रहे हैं। यह उचित नहीं है।

प्रश्न (ii)
पद्यांश के शिल्प-सौंदर्य को स्पष्ट कीजिए।
उत्तर:
शिल्प-सौंदर्य:
कवि कहता है कि पाश्चात्य जीवन-शैली का बिना सोचे-विचारे स्वीकार करना बुद्धिमानी नहीं है। सुनते-सुनते, बार-बार में पुनरुक्तिप्रकाश अलंकार है। ‘कलगी की कलफ’ में अनुप्रास अलंकार है। मुहावरों को सटीक, सार्थक प्रयोग किया गया है। महाभारत की पौराणिक कथा और चाणक्य का उल्लेख करने से उदाहरण अलंकार है। चाणक्य…सुभद्रा में रूपक अलंकार है। मुक्तक छंद है। तुकांत का अभाव है। भाषा तत्सम प्रधान है, जिसमें अंग्रेजी शब्दों का प्रयोग किया है।

प्रश्न (iii)
पद्यांश का मुख्य भाव बताइए।
उत्तर:
पद्यांश का मुख्य भाव यह है कि हमारी विरासत एवं संस्कृति दुनिया में सर्वश्रेष्ठ है।

प्रश्न 2.
सब कुछ गड़मड़ा
रहा है-क्या है
हमारा-क्या
पाश्चात्य –
जानकर भी
नकारा –
सर हिला रहे हैं…।
दोगली-दोहरी
सभ्यता के रंग
में रंगे हैं –
हम और हमारा
कुछ भी नहीं
यही…
मुलम्में पर
मुलम्मा चढ़ा
रहे हैं…। (Page 94)

शब्दार्थ:

• गड़मड़ा – अस्त-व्यस्त होना।
• मुलम्मे पर मुलम्मा चढ़ाना – दिखावे पर दिखावा करना, सोने या चाँदी का पानी चढ़ाया हुआ।
• नकारा – अस्वीकृत, इनकार, निकम्मा।
• दोगली – वर्णसंकर।
• दोहरी – दो तरह की बात।

प्रसंग:
प्रस्तुत काव्यांश सुदर्शन ‘प्रियदर्शिनी’ द्वारा रचित कविता ‘हम कहाँ जा रहे हैं’ से उद्धृत है। कवि का मानना है कि हम न तो भारतीय रह पाए हैं और न ही पूरी तरह पाश्चात्य जीवन-शैली को अपना सके। हम दो रंगी सभ्यता में रंगे जा रहे हैं।

व्याख्या:
कवि कहता है कि आज सब कुछ अस्त-व्यस्त हो रहा है। कहने का भाव यह है कि भारतीय संस्कृति, परंपराएँ और मान्यताएँ तथा पाश्चात्य जीवन-शैली दोनों ही एक-दूसरे में मिलकर गड़मड़ होकर अस्त-व्यस्त हो रही हैं। इस कारण पता ही नहीं चलता कि क्या हमारा है अर्थात् क्या भारतीय है और क्या पाश्चात्य है। सत्य तो यह है कि हम सब कुछ जानकर भी निकम्मे बने हुए अस्वीकृति में सर हिला रहे हैं। हम वर्णसंकर; अर्थात् दो प्रकार की जीवन-शैली अपनाकर दो तरह की बातें करते हैं।

हम एक ओर भारतीय सभ्यता-संस्कृति की अपनी परंपरागत जीवन-शैली को नहीं छोड़ पा रहे हैं और दूसरी ओर हम पाश्चात्य सभ्यता-संस्कृति की जीवन-पद्धति को बिना विचारे अपनाकर दोहरी जिन्दगी जी रहे हैं। कहने का भाव यह है कि हम आधुनिक होने का दिखावा कर रहे हैं। हम अपनी विरासत को भुलाकर पाश्चात्य जीवन-शैली और वस्तुओं को देखकर ललंचा रहे हैं अपनी उपलब्धियों को नकार रहे हैं। इस प्रकार हम दिखावे पर दिखावा कर रहे हैं। भारतीय जीवन-शैली पर पाश्चात्य जीवन-शैली को चढ़ा रहे हैं।

विशेष:

1. भारतीय जीवन-शैली को छोड़कर पाश्चात्य जीवन-शैली को अपनाने वालों पर व्यंग्य किया है।
2. भारतीय पाश्चात्य होने का दिखावा कर रहे हैं। अपनी उपलब्धियों को नकार रहे हैं।
3. दोगली-दोहरी में अनुप्रास अलंकार है।
4. मुहावरों का सार्थक प्रयोग किया गया है।
5. छंदविहीन रचना में तुक और लय का अभाव है।
6. भाषा सरल और उर्दू शब्दावली से युक्त खड़ी बोली है।

पद्यांश पर आधारित विषय-वस्तु संबंधित प्रश्नोत्तर

प्रश्न (i)
कवि और कविता का नाम लिखिए।
उत्तर:
कवि-सुदर्शन ‘प्रियदर्शनी, कविता-‘हम कहाँ जा रहे हैं…!’

प्रश्न (ii)
‘हम और हमारा’ से कवि का क्या तात्पर्य है?
उत्तर:
‘हम’ से कवि का तात्पर्य है हम भारतीय और ‘हमारा’ से तात्पर्य है-हम भारतीयों की उपलब्धियों से, अपनी विरासत से हे जिसे हम भूलते जा रहे हैं।

प्रश्न (iii)
‘दोगली-दोहरी सभ्यता के रंग में रंगे’ द्वारा कवि क्या कहना चाहता है?
उत्तर:
कवि यह कहना चाहता है कि हा भारतीय अपनी संस्कृति की मान्यताओं और जीवन-शैली के साथ-साथ पाश्चात्य जीवन-शैली और उनकी वस्तुओं के प्रति ललचा रहे हैं। इस तरह हम न तो अपनी जीवन-शैली को छोड़ पा रहे हैं और न ही पाश्चात्य जीवन-शैली को पूरी तरह अपना पा रहे हैं।

पद्यांश पर आधारित सौंदर्य-संबंधित प्रश्नोत्तर

प्रश्न (i)
पद्यांश का भाव-सौदर्य स्पष्ट कीजिए।
उत्तर:
भाव-सौंदर्य:
भारतीय जीवन-शैली और पाश्चात्य जीवन-पद्धति दोनों मिल जाने के कारण सभी कुछ अस्त-व्यस्त हो रहा है। हम अपनी विरासत और उपलब्धियों को भी जानते हुए नकार रहे हैं। हमें लगता है कि हमारा कुछ भी नहीं है। यही कारण है कि हम परत पर परत चढ़ा रहे हैं।

प्रश्न (ii)
पद्यांश का शिल्प-सौंदर्य स्पष्ट कीजिए।
उत्तर:
शिल्प-सौंदर्य:
हम भारतीय पाश्चात्य होने का दिखावा कर रहे हैं और अपनी उपलब्धियों को नकार रहे हैं। दोगली-दोहरी में अनुप्रास अलंकार है। मुहावरों का सार्थक प्रयोग किया गया है। छंदविहीन रचना में तुक और लय का अभाव है। भाषा सरल और उर्दू शब्दावली से युक्त खड़ी बोली है। विशेषणों का प्रयोग अर्थवत्ता में वृद्धि कर रहा है।

प्रश्न 3.
अपना खालिस
कलश भी हम
विदेश बता रहे, हैं…।
न धर्म न कर्म-अपना
न वेश-न भूषा
न भाषा-न विज्ञान
न विधि-न विधान –
सब कुछ दूसरों
के हवाले –
किए जा रहे हैं….।
बड़े त्यागी –
ऋषि-और दानवीर हैं हम –
दूसरे-हमें –
हमारे ही प्याले
से-हमारी सभ्यता
संस्कृति का
घुट पिला रहे हैं… (Page 94)

शब्दार्थ:

• खालिस – शुद्ध।
• कलश – घड़ा।
• विधि – रचना, ढंग।
• विधान – व्यवस्था।

प्रसंग:
प्रस्तुत पद्यांश सुर्दशन ‘प्रियदर्शनी’ द्वारा रचित कविता ‘हम कहाँ जा रहे हैं….!’ से उद्धृत है। कवि भारतीयों पर व्यंग्य करते हुए कहता है कि हम अपनी उपलब्धियों को नकार रहे हैं। यहाँ तक कि इमने स्वयं के कलश (धरोहर) को भी विदेशी दर्शा दिया है।

व्याख्या:
कवि कहता है कि हम अपनी उपलब्धियों को नकार रहे हैं। यहाँ तक अपने शुद्ध देशी कलश (धरोहर) को भी विदेशी बता रहे हैं। दूसरे शब्दों में, मांगलिक कार्यों में रखा जाने वाला कलश भारतीय संस्कृति की देन है। विदेशी वस्तुओं को अपनाने के चक्कर में हमने उसे भी विदेशी संस्कृति की देन बता दिया है। न धर्म – हमारा है, न कर्म अपना है और न ही पहनावा अपना रहा है। यहाँ तक कि विधि-विधान भी अपने नहीं रहे। हम सब कुछ हवाले किए जा रहे हैं। हम बड़े त्यागी बन रहे हैं। कहने का भाव यह है कि हम अपनी उपलब्धियों को विदेशियों को दिए जा रहे हैं।

हम अपने-आपको ऋषि और दानवीर समझ रहे हैं। दूसरी ओर विदेशी हमारी इन्हीं परंपराओं का सत्व ग्रहण करके हमें ही परोस रहे हैं और हम उन्हें विदेशी मानकर ग्रहण कर रहे हैं। दूसरे शब्दों में, पाश्चात्य संस्कृति के लोग हमारी भारतीय संस्कृति की मान्यताओं व हमारी उपलब्धियों को दूसरा नाम देकर हमारी सभ्यता और संस्कृति हमें ही परोस रहे हैं और हम उन्हें अपना रहे हैं। यह हमारे लिए शुभ संकेत नहीं है।

विशेष:

1. हम भारतीय अपनी संस्कृति, अपनी मान्यताएँ और परंपरागत व्यवहार को त्यागकर विदेशी जीवन-शैली अपना रहे हैं जो शुभ संकेत नहीं है।
2. सभ्यता-संस्कृति में अनुप्रास अलंकार है।
3. मुहावरों का सार्थक प्रयोग किया गया है।
4. भाषा सरल खड़ी बोली है जिसमें उर्दू के शब्दों का प्रयोग किया गया है।
5. छंदविहीन रचना में तुक और लय का अभाव है।
6. व्यंग्यात्मकता का प्रयोग, किया गया है।

पद्यांश पर आधारित विषय-वस्तु संबंधित प्रश्नोत्तर

प्रश्न (i)
कवि ने भारतीयों पर क्या व्यंग्य किया है?
उत्तर:
कवि ने भारतीयों पर व्यंग्य किया है कि हम लोग विदेशी वस्तुओं के प्रति ललचा रहे हैं इसलिए हमें अपनी संस्कृति में मांगलिक कार्यों में प्रयोग होने वाले भारतीय देन कलश को भी विदेशी बता दिया है। यह सर्वथा अनुचित है।

प्रश्न (ii)
भारतीय अपनी किन-किन सांस्कृतिक उपलब्धियों को दूसरों को सौंप रहे हैं?
उत्तर:
भारतीय अपना धर्म-कर्म, वेशभूषा, भाषा और ज्ञान एवं विधि-विधान आदि दूसरों को सौंप रहे हैं और उनकी जीवन-शैली को अपना रहे हैं। हमारे पास अपना कुछ नहीं रहा है।

प्रश्न (iii)
विदेशी हमें क्या परोस रहे हैं?
उत्तर:
विदेशी हमारी सभ्यता और संस्कृति को अपने साँचे में ढोलकर हमें ही परोस रहे हैं।

पयांश पर आधारित सौंदर्य-संबंधित प्रश्नोत्तर

प्रश्न (i)
पद्यांश का भाव-सौंदर्य स्पष्ट कीजिए।
उत्तर:
भाव-सौंदर्य:
कवि ने भारतीयों को व्यंग्य का निशाना बनाया है। हम पाश्चात्य जीवन-शैली और वस्तुओं को देखकर ललचा रहे हैं। इसलिए हम अपना सब कुछ उन्हें सौंप रहे हैं। हमारी यह स्थिति हो गई है कि न हमारा धर्म-कर्म, न ही वेशभूषा, भाषा-ज्ञान और न कोई विधि-विधान रहा है। पाश्चात्य सभ्यता और संस्कृति के लोग हमारी उपलब्धियों को अपना बताकर हमें परोस रहे हैं।

प्रश्न (ii)
पद्यांश का शिल्प-सौंदर्य स्पष्ट. कीजिए।
उत्तर:
शिल्प-सौंदर्य:
कवि ने भारतीयों की मनःस्थिति को व्यंग्य का निशाना बनाया है। अतः पद्यांश की भाषा में व्यंग्यात्मकता है। हमें हमारे’ व ‘सभ्यता-संस्कृति’ में अनुप्रास अलंकार है। मुहावरों का सार्थक प्रयोग किया गया है। भाषा सरल खड़ी बोली है इसमें उर्दू शब्दों का प्रयोग हुआ है। छंदविहीन रचना में तुक और लय का अभाव है।

प्रश्न 4.
उल्टे बाँस
बरेली को –
योग-साधना –
धर्म नीति –
सब उल्टे हमें
परोसे
जा रहे हैं…।
वास्तुकला
हुई फेंगशुई
सत्वज्ञान को
रेकी-बना रहे हैं
योग को योगा हुआ देख
कैसी हम
दुंदुभी-बजा
रहे हैं…!
नीम भी
गले नहीं उतरी –
हमें कड़वी लगी –
निमोली की
तरह-तोड़ कर
उन्हें खिला रहे हैं –
हम कहाँ जा रहे हैं…! (Page 94)

शब्दार्थ:

• दुंदुभी – एक तरह का वाद्य-यंत्र।
• उल्टे बाँस बरेली को – जैसा होना चाहिए उसके विपरीत होना।

प्रसंग:
प्रस्तुत काव्यांश सुदर्शन ‘प्रियदर्शिनी’ द्वारा रचित कविता ‘हम कहाँ जा रहे हैं…!’ से उद्धृत है। इसमें कवि कह रहा है कि पाश्चात्य और अन्य देशों केलोग हमारी परंपराओं का सत्व ग्रहण करके हमें ही परोस रहे हैं और हम उन्हें विदेशी मानकर स्वीकार कर रहे हैं। हमें आधुनिक चकाचौंध में अपनी संस्कृति को नहीं भूलना चाहिए।

व्याख्या:
कवि का कहना है कि विदेशी उल्टे बाँस बरेली की कहावत को चरितार्थ करते हुए अर्थात् हमारी उपलब्धियों, परंपराओं और जीवन-पद्धति को हमें लौटा रहे हैं जबकि होना यह चाहिए था कि हमें ही उन्हें सब कुछ अपना बता कर देना चाहिए था, पर हो रहा इसके विपरीत है। हमारी संस्कृति में प्रारंभ से ही योग-साधना पर बल दिया जाता रहा है। धर्म-नीति हमारी परंपरा का अंग रही है। वे इन्हें हमसे लेकर हमें ही परोस रहे हैं। उदाहरणार्थ-हमारी वास्तुकला को ग्रहण कर उसे फेंगशुई नाम दे दिया गया, सत्वज्ञान को ग्रहण कर रेकी बना दिया और योग को योगा बना दिया गया।

इस प्रकार वास्तुकला, सत्वज्ञान और योग हमारी ही देन है। इसे विदेशी लोग अपना कहकर – प्रचारित कर रहे हैं और हम इन्हें विदेशी मानकर और इन्हें अपनाकर कितने प्रसन्न हो रहे हैं। कवि कहता है कि नीम का वृक्ष हमारी संस्कृति की देन है, लेकिन वह भी – हमारे गले नहीं उतरा। वह भी हमें कड़वा लगा। उसके औषधीय गुणों को हमने नहीं जाना। हम उनकी निमोलियों की दवाई बना-बनाकर उन्हें खिला रहे हैं। दूसरे शब्दों में, विदेशियों ने नीम के महत्त्व को पहचानकर उसे पेटेंट कराने का प्रयास किया।

कवि कहता है कि हम लोग कहाँ जा रहे हैं। हम अपनी संस्कृति को भूले जा रहे हैं। सच तो यह है कि हमारी विरासत और सांस्कृतिक निष्ठा दुनिया में श्रेष्ठ है। हमें अपनी संस्कृति को नहीं भूलना चाहिए। उसकी प्रासंगिकता को आधुनिकता के साथ तलाशें और भली-भाँति भारतीय जीवन-मूल्यों के महत्त्व को समझें। हम भारतीय बने रहें और नकली जीवन-शैली को उतार दें।

विशेष:

1. कवि ने हमें अपनी शक्ति को, अपनी उपलब्धियों और अपनी सांस्कृतिक चेतना को पहचानने और भारतीय बने रहने का संदेश दिया है।
2. बाँस बरेली में अनुप्रास अलंकार है।
3. उदाहरण अलंकार भी है।
4. मुहावरों और कहावतों का सुंदर प्रयोग किया गया है।
5. भाषा सरल, तत्सम और विदेशी शब्दों से युक्त खड़ी बोली है।
6. छंदविहीन रचना में लय और तुक का नितांत अभाव है।

पद्यांश पर आधारित विषय-वस्तु संबंधित प्रश्नोत्तर

प्रश्न (i)
हमारी संस्कृति की किन-किन उपलब्धियों को विदेशी किन-किन नामों से हमें परोस रहे हैं?
उत्तर:
हमारी संस्कृति की वास्तुकला, सत्वज्ञान और योग को विदेशी ग्रहण करके हमें ही फेंगशुई, रेकी और योगा के नाम से परोस रहे हैं।

प्रश्न (ii)
‘कैसी हम दुंदुभी बजा रहे हैं…!’ के द्वारा कवि हम पर क्या व्यंग्य कर रहा है?
उत्तर:
इसके द्वारा कवि यह व्यंग्य कर रहा है कि हम अपनी ही वास्तुकला को फेंगशुई, सत्वज्ञान को रेकी और योग को योगा को विदेशी मानकर, अपनाकर स्वयं को आधुनिक समझकर अत्यंत प्रसन्न हो रहे हैं। यह हमारे लिए उचित नहीं है।

प्रश्न (iii)
कवि क्या संदेश देना चाहता है?
उत्तर:
कवि यह संदेश देना चाहता है कि हम अपनी शक्ति, अपनी उपलब्धियों और अपनी सांस्कृतिक चेतना को पहचानें। हमारी विरासत विश्व में सर्वश्रेष्ठ है। आधुनिक जीवन की चकाचौंध में अपनी संस्कृति को न भूलें भारतीय बने रहें तथा नकली पाश्चात्य जीवन-शैली को उतार फेंकें।

काव्यांश पर आधारित सौंदर्य-संबंधित प्रश्नोत्तर

प्रश्न (i)
काव्यांश का भाव-सौंदर्य स्पष्ट कीजिए।
उत्तर:
भाव-सौंदर्य:
इस काव्यांश में कवि ने यह भाव व्यक्त किया है कि हमारी सभ्यता संस्कृति के जीवन-मूल्य विश्व में सर्वश्रेष्ठ है। विदेशी लोग हमारी संस्कृति की उपलब्धियों को ही अपनी उपलब्धियाँ बताकर प्रचारित कर रहे हैं। वे हमारी वास्तुकला को फेंगशुई, सत्वज्ञान को रेकी और योग का योगा बनाकर हमें परोस रहे हैं। आज आवश्यकता इस बात की है कि हम अपनी संस्कृति की उपलब्धियों को पहचानें और भारतीय बने रहें। इस तरह हमें पाश्चात्य जीवन-शैली अपनाने की आवश्यकता नहीं है।

प्रश्न (ii)
काव्यांश का शिल्प-सौंदर्य स्पष्ट कीजिए।
उत्तर:
शिल्प-सौंदर्य:
‘बाँस बरेली, तरह-तोड़’ में अनुप्रास अलंकार है। उदाहरण अलंकार भी है। मुहावरों और कहावतों का सुंदर प्रयोग किया गया है। भाषा सरल, तत्सम और विदेशी शब्दों से युक्त खड़ी बोली है। छंदविहीन रचना में लय और तुक का अभाव है। शब्द चयन भावानुकूल है।

MP Board Class 12th Hindi Solutions

MP Board Class 11th Physics Solutions Chapter 13 अणुगति सिद्धांत

अणुगति सिद्धांत अभ्यास के प्रश्न एवं उनके उत्तर

प्रश्न 13.1.
ऑक्सीजन के अणुओं के आयतन और STP पर इनके द्वारा घेरे गए कुल आयतन का अनुपात ज्ञात कीजिए। ऑक्सीजन के एक अणु का व्यास 3Å लीजिए।
उत्तर:
दिया है:
d = 3 Å
∴ r = \(\frac{1}{2}\) × 3 = 1.5 Å
= 1.5 × 10^-10 मीटर
STP पर 1 मोल गैस का आयतन
V₁ = 22.41 = 22.4 × 10^-3 मीटर ³
तथा 1 मोल गैस में अणुओं की संख्या
= N = 6.02 × 10²³
∴ अणुओं का आयतन, V₂ = एक अणु का आयतन × N
= \(\frac{4}{3}\) π³ × N
= \(\frac{4}{3}\) × 3.14 × (1.5 × 10^-10)³ × 6.02 × ²³
= 8.52 × 10^-6 मीटर ²
∴ \(\frac { V_{ 2 } }{ V_{ 1 } } \) = \(\frac { 8.52\times 10^{ -6 } }{ 22.4\times 10^{ -3 } } \) = 3.8 × 10^-4
अतः अणुओं के आयतन तथा STP पर इनके द्वारा घेरे गए आयतन का अनुपात 3.8 × 10^-4 है।\

प्रश्न 13.2.
मोलर आयतन STP पर किसी गैस (आदर्श) के 1 मोल द्वारा घेरा गया आयतन है। (STP : 1 atm) दाब, 0°C। दर्शाइये कि यह 22.4 लीटर है।
उत्तर:
दिया है: STP पर,
P = 1 atm = 7.6 m of Hg column
= 0.76 × 13.6 × 10 ³ × 9.9
= 1.013 × 105 Nm^-2
T = 0°C = 273 K
R = 8.31 J mol^-1K^-1
n = 1 मोल V = 22.41 सिद्ध करने के लिए,
सूत्र PV = nRT से
V = \(\frac { nRT }{ P } \)
= \(\frac { 1\times 8.31\times 273 }{ 1.013\times 10^{ 5 } } \)
= 22.4 × 10 ^-3 m³
= 22.4 लीटर

प्रश्न 13.3.
चित्र में ऑक्सीजन के 100 x 10-3 kg द्रव्यमान के लिए PV/T एवं P में, दो अलग-अलग तापों पर ग्राफ दर्शाये गए हैं।

(a) बिंदुकित रेखा क्या दर्शाती है?
(b) क्या सत्य है: T₁ >T₂, अथवा T₁ < T₂ ?
(c) y – अक्ष पर जहाँ वक्र मिलते हैं वहाँ PV/T का मान क्या है?
(d) यदि हम ऐसे ही ग्राफ 100 × 10^-3 kg हाइड्रोजन के लिए बनाएँ तो भी क्या उस बिंदु पर जहाँ वक्र y – अक्ष से मिलते हैं PV/T का मान यही होगा? यदि नहीं तो हाइड्रोजन के कितने द्रव्यमान के लिए PV/T का मान कम दाब और उच्च ताप के क्षेत्र के लिए वही होगा? H₂ का अणु द्रव्यमान = 2.02 u, O₂ का अणु द्रव्यमान = 32.0 u, R = 8.31 Jmol^-1K^-1
उत्तर:
(a) बिन्दुकित रेखा यह व्यक्त करती है कि राशि | PV/T स्थिर है। यह तथ्य केवल आदर्श गैस के लिए सत्य है। अर्थात् बिन्दुकित रेखा आदर्श गैस का ग्राफ है।

(b) ताप T, पर ग्राफ की तुलना में ताप T, पर गैस का ग्राफ आदर्श गैस के ग्राफ के अधिक समीप है। हम जानते हैं कि वास्तविक गैसें निम्न ताप पर आदर्श गैस के व्यवहार से अधिक । विचलित होती हैं। अतः T₁ > T₂

(c) जहाँ ग्राफ y – अक्ष पर मिलते हैं ठीक उसी बिन्दु पर आदर्श गैस का ग्राफ भी गुजरता है। अतः इस बिन्दु पर ऑक्सीजन – गैस, आदर्श गैस का पालन करती है।
अतः गैस समीकरण से,
\(\frac { PV }{ T } \) = nR
हम जानते हैं O₂ का 32 × 10^-3 kg = 1 मोल
∴ O₂ का 1.00 × 10^-3 kg
= \(\frac { 1 }{ 32\times 10^{ -3 } } \) × 1 × 10^-3
i.e; n = \(\frac{1}{32}\)
R = 8.31 JK^-1mol^-1
∴ \(\frac{PV}{T}\) = \(\frac{1}{32}\) × 8.31 = 0.26 JK^-1

(d) नहीं, हाइड्रोजन गैस के लिए PV/T का मान समान नहीं रहता है। चूंकि यह द्रव्यमान पर निर्भर करता है तथा H₂ का द्रव्यमान O₂ से कम है।
माना हाइड्रोजन का अभीष्ट द्रव्यमान m किया है जिसमें PV/T का समान मान प्राप्त होता है।
∴ n = \(\frac { m }{ 2.02\times 10^{ -3 } } \)
\(\frac{PV}{T}\) = nR = 0.26 JK^-1 से,
n = \(\frac { 0.26 }{ R } \) = \(\frac { 0.26JK^{ -1 } }{ 8.31JK^{ -1 }mol^{ -1 } } \)
= 0.0313 mol
∴ समी० (i) व (ii) से,
n₁ = 2.02 × 10^-3 × 0.313
= 0.0632 × 10^-3 kg
= 6.32 × 10^-5 kg

प्रश्न 13.4.
एक ऑक्सीजन सिलिंडर जिसका आयतन 30 लीटर है, में ऑक्सीजन का आरंभिक दाब 15 atm एवं ताप 27°C है। इसमें से कुछ गैस निकाल लेने के बाद प्रमापी (गेज)दाब गिर कर 11 atm एवं ताप गिर कर 17°C हो जाता है। ज्ञात कीजिए कि सिलिंडर से ऑक्सीजन की कितनी मात्रा निकाली गई है। (R = 8.31 Jmol^-1K^-1, ऑक्सीजन का अणु द्रव्यमान 0₂ = 32 u)।
उत्तर:
दिया है: ऑक्सीजन सिलिण्डर में प्रारम्भ में
V₁ = 30 litres = 30 × 10^-3 m³
P₁ = 15 atm = 15 × 1.013 × 10⁵ Pa
T₁ = 27 + 273 = 300K
R = 8.31 JK^-1mol^-1
माना सिलिण्डर में ऑक्सीजन गैस के n₂ मोल हैं।
अतः सूत्र PV = nRT से,
n¹ = \(\frac { P_{ 1 }V_{ 1 } }{ RT_{ 1 } } \)
= \(\frac { 15\times 1.013\times 10^{ 5 } }{ 8.31\times 300 } \) = 18.253
ऑक्सीजन का अणु भार
M = 32 = 32 × 10^-3kg
सिलिंडर में ऑक्सीजन का प्रारम्भिक द्रव्यमान
m₁ = n₁M
= 18.253 × 32 × 10^-3kg
माना अन्त में सिलिंडर में O₂ kg के n² kg मोल बचे हैं।
दिया है: V₂ = 30 × 10^-3 m³, P₂ = 11 atm
= 11 × 1.013 × 10⁵ pa
∴ n₂ = \(\frac { P_{ 2 }V_{ 2 } }{ RT_{ 2 } } \)
= \(\frac { (11\times 1.013\times 10^{ 5 })\times (30\times 10^{ -3 }) }{ 8.31\times 290 } \)
= 13.847
∴ सिलिंडर में O₂ गैस का अन्तिम द्रव्यमान
m₂ = 13.847 × 32 × 10^-3
∴ सिलिंडर से O₂ का लिया गया द्रव्यमान
= m₁ – m₂
= (584.1 – 453.1) × 10^-3 kg
= 141 × 10^-3 kg = 0.141 kg

प्रश्न 13.5.
वायु का एक बुलबुला, जिसका आयतन 1.0 cm³ है, 40 m गहरी झील की तली में जहाँ ताप 12°C है, उठकर ऊपर पृष्ठ पर आता है जहाँ ताप 35°C है। अब इसका आयतन क्या होगा?
उत्तर;
जब वायु का बुलबुला 40 मी० गहराई पर है तब
V₁ = 1.0 cm³ = 1.0 × 10^-6m³
T₁ = 12°C = 12 + 273 = 285 K
= 1 atm + 40 m पानी की गहराई
Pc = 1 atm – h₁ρg
= 1.013 × 10c + 40 × 10³ × 9.8
= 493000 Pa = 4.93 × 10⁵ × Pa
जब वायु का बुलबुला झील की सतह पर पहुँचता है तब
V₂ = ?, T₂ = 35°C = 35 + 273 = 308 K
P₂ = 1 atm = 1.013 × 10⁵ Pa
सूत्र \(\frac { P_{ 1 }V_{ 1 } }{ T_{ 1 } } \) = \(\frac { P_{ 2 }V_{ 2 } }{ T_{ 2 } } \) से,
= \(\frac { P_{ 1 }V_{ 1 } }{ T_{ 1 } } \) × \(\frac { T_{ 2 } }{ P_{ 2 } } \)
= \(\frac { 4.95\times 10^{ 5 }\times 1\times 10^{ -6 }\times 308 }{ 285\times 1.013\times 10^{ 5 } } \)
= 5.275 × 10^-6 m
= 5.3 × 10^-6 m

प्रश्न 13.6.
एक कमरे में, जिसकी धारिता 25.0 m³ है, 27°C ताप और 1 atm दाब पर, वायु के कुल अणुओं (जिनमें नाइट्रोजन, ऑक्सीजन, जलवाष्प और अन्य सभी अवयवों के कण सम्मिलित हैं) की संख्या ज्ञात कीजिए।
उत्तर:
दिया है: V = 25.0 m³
T = 27°C = 27 + 273 = 300 K
K = 1.38 × 10^-23 JK^-1
P =1 atm = 1.013 × 10⁵ Pa
गौस समीकरण से, P = \(\frac { nRT }{ V } \)
= \(\frac{n}{V}\) (Nk) T
= (nN) \(\frac{kT}{V}\) = N’\(\frac{kT}{V}\)
जहाँ N’ =nN = दी गई गैस में ऑक्सीजन अणुओं की संख्या
N’ = \(\frac{PV}{KT}\)
= \(\frac { (1.013\times 10^{ 5 })\times 25 }{ 1.38\times 10^{ -23 }\times 300 } \)
= 6.10 × 10²⁶

प्रश्न 13.7.
हीलियम परमाणु की औसत तापीय ऊर्जा का आंकलन कीजिए

1. कमरे के ताप (27°C) पर
2. सूर्य के पृष्ठीय ताप (6000 K) पर
3. 100 लाख केल्विन ताप (तारे के क्रोड का प्रारूपिक ताप) पर।

उत्तर:
गैस के अणुगति सिद्धान्त के अनुसार, ताप T पर गैस की औसत गतिज ऊर्जा (i. e., औसत ऊष्मीय ऊर्जा) निम्नवत् है –
E = \(\frac{3}{2}\) kT
दिया है: k = 1.38 × 10^-23 JK^-1
1. T = 27°C = 273 + 27 = 300 K पर,
E = \(\frac{3}{2}\) × 1.38 × 10^-23 × 300
= 621 × 10 ^-23 J
= 6.21 × 10 ^-21 J

2. T = 6000 K पर
∴ E = \(\frac{3}{2}\) × 0138 × 10^-23 × 6000
= 1.24 × 10^-19 J

3. T = 10 × 10⁶ K = 10⁷ K पर,
∴ E = 3 × 1.38 × 10^-23 × 10⁷
= 2.07 × 10^-16 J
= 2.1 × 10^-16 J

प्रश्न 13.8.
समान धारिता के तीन बर्तनों में एक ही ताप और दाब पर गैसें भरी हैं। पहले बर्तन में नियॉन (एकपरमाणुक) गैस है, दूसरे में क्लोरीन (द्विपरमाणुक) गैस है और तीसरे में यूरेनियम हेक्साफ्लोराइड (बहुपरमाणुक) गैस है। क्या तीनों बर्तनों में गैसों के संगत अणुओं की संख्या समान है? क्या तीनों प्रकरणों में अणुओं की v_rms (वर्ग माध्य मूल चाल) समान है।
उत्तर:
(a) हाँ, चूँकि आवोगाद्रों परिकल्पना से, समान परिस्थितियों में गैसों के समान आयतन में अणुओं की संख्या समान होती है।
(b) नहीं चूँकि V_rms = \(\sqrt { \frac { 3RT }{ m } } \)
∴ V_rms ∝ \(\frac { 1 }{ \sqrt { m } } \)
अतः तीनों गैसों के ग्राम – अणु भार अलग – अलग हैं। अतः अणुओं की वर्ग माध्य – मूल चाल अलग – अलग होगी।

प्रश्न 13.9.
किस ताप पर आर्गन गैस सिलिंडर में अणुओं की V_rms – 20°C पर हीलियम गैस परमाणुओं की V_rms के बराबर होगी। (Ar का परमाणु द्रव्यमान = 39.9 u एवं हीलियम का परमाणु द्रव्यमान = 4.0 u)।
उत्तर:
माना कि T₁ व T₂ K ताप पर आर्गन व हीलियम गैस की वर्ग माध्य मूल वेग क्रमश: C₁ व C₂ हैं।
दिया है:
M₁ = 39.9 × 10^-3 kg,
M₂ = 4.0 × 10^-3 kg, T₁ = ?
T₂ = – 20 + 273 = 253 K
हम जानते हैं कि वर्ग माध्य मूल वेग
C = \(\sqrt { \frac { 3RT }{ M } } \)
C₁ = \(\sqrt { \frac { 3RT_{ 1 } }{ M_{ 1 } } } \)
तथा C₂ = \(\sqrt { \frac { 3RT_{ 1 } }{ M_{ 2 } } } \)
चूँकि C₁ = C₂ (दिया है)
∴ \(\sqrt { \frac { 3RT_{ 1 } }{ M_{ 1 } } } \) = \(\sqrt { \frac { 3RT_{ 1 } }{ M_{ 2 } } } \)
या \(\frac { T_{ 1 } }{ M_{ 1 } } \) = \(\frac { T_{ 1 } }{ M_{ 2 } } \)
= \(\frac { 39.9\times 10^{ -3 } }{ 4.0\times 10^{ -3 } } \) × 253
या T = 2523.7 K = 2524 K
= 2.524 × 10³ K

प्रश्न 13.10.
नाइट्रोजन गैस के एक सिलिंडर में, 2.0 atm दाब एवं 17°C ताप पर नाइट्रोजन अणुओं के माध्य मुक्त पथ एवं संघट्ट आवृत्ति का आंकलन कीजिए। नाइट्रोजन अणु की त्रिज्या लगभग 1.0 Å लीजिए। संघट्ट काल की तुलना अणुओं द्वारा दो संघट्टों के बीच स्वतंत्रतापूर्वक चलने में लगे समय से कीजिए। ( नाइट्रोजन का आण्विक द्रव्यमान = 28.0 u)।
उत्तर:
मैक्सवेल संशोधन ने गैस अणुओं का मध्य मुक्त पद
λ = \(\frac { 1 }{ \sqrt { 2\pi nd^{ 2 } } } \)
जहाँ d = अणु का व्यास
तथा = N = \(\frac{N}{V}\) = image 1
2 atm दाब पर, m द्रव्यमान गैस का आयतन
V = \(\frac{RT}{P}\), T = 273 + 17 = 290 K
∴ n = \(\frac{N}{V}\) = \(\frac{NP}{RT}\)
दिया है: N = 6.023 × 10²³ mole^-1
P = 2 atm = 2 × 1.013 × 10⁵ Nm^-2
R = 8.3 JK^-1mol^-1

= 5.08 × 10² ms^-1
= 5.10 × 10² ms^-1
∴ संघट्ट आवृत्ति,
v = \(\frac { C }{ \lambda } \) = \(\frac { 5.1\times 10^{ 2 } }{ 1.0\times 10^{ -7 } } \)
= 2.0 × 10^-10 s ….. (i)
पुनः माना संघट्ट के लिया गया समय t है।
∴ t = \(\frac { d }{ C } \) = \(\frac { 2\times 10^{ -10 } }{ 5.10\times 10^{ 2 } } \)
= 4 × 10^-13 s
समी० (i) को (ii) से भाग देने पर,
\(\frac { \tau }{ \tau } \) = \(\frac { 2.0\times 10^{ -10 }s }{ 4\times 10^{ -13 }s } \) = 500
या τ = 500t
अतः दो क्रमागत टक्करों के मध्य समय टक्कर में लिये गए समय का 500 गुना है। इससे यह प्रदर्शित होता है कि गैस के अणु लगभग हर समय मुक्त रूप से चलायमान रहते हैं।

अणुगति सिद्धांत अतिरिक्त अभ्यास के प्रश्न एवं उनके उत्तर

प्रश्न 13.11.
1 मीटर लंबी संकरी (और एक सिरे पर बंद) नली क्षैतिज रखी गई है। इसमें 76 cm लंबाई भरा पारद सूत्र, वायु के 15 cm स्तंभ को नली में रोककर रखता है। क्या होगा यदि खुला सिरा नीचे की ओर रखते हुए नली को ऊर्ध्वाधर कर दिया जाए।
उत्तर:
प्रारम्भ में नली क्षैतिज है तब बंद सिरे पर रोकी गई वायु का दाब वायुमण्डलीय दाब के समान होगा।
∴ P₁ = 76 सेमी पारे स्तम्भ का दाब।
माना कि नली का अनुप्रस्थ क्षेत्रफल A सेमी² है।
वायु का आयतन = 15 × A = 15A सेमी³
जब नली का खुला सिरा नीचे की ओर रखते हैं तथा ऊर्ध्वाधर करते हैं जब खुले’ सिरे पर बाहर की ओर से वायुमण्डलीय दाब कार्य करता है जबकि ऊपर की ओर से 76 सेमी पारद सूत्र का दाब व बंद सिरे पर एकत्र वायु का दाब अधिक है। अतः पारद सूत्र असंचुलित रहेगा व नीचे गिरते हुए वायु को बाहर निकाल देता है।
माना कि पारद सूत्र की λ लम्बाई नीचे नली से बाहर निकलती है।
∴ नली में पारद सूत्र की शेष लम्बाई = (76 – h) सेमी तथा बंद सिरे पर वायु स्तम्भ की लम्बाई
= (15 + 9 + h)
= (24 + h) सेमी³
तथा वायु का आयतन V₂ = (24 + h) A सेमी³
माना कि इस वायु का दाब P₂ है।
∴ सन्तुलन में,
P₂ + (76 – h) सेमी पारद सूत्र का दाब = वायुमण्डलीय दाब
∴ P₂= R सेमी पारद सूत्र का दाब
सूत्र P₁V₁ = P₂V₂ से,
76 × 15A = h × (24 + h) A
या 1140 = 24h + h²
या h² + 24h – 1140 = 0
∴ h = – 24 ± \(\sqrt { 24^{ 2 }-4\times 17-1140 } \)
= 28.23 या – 4784 सेमी
परन्तु h ≠ ऋणात्मक
∴ h = 28.23 सेमी।
अतः पारद सूत्र की 28.23 सेमी लम्बाई नली से बाहर निकल जाएगी।

प्रश्न 13.12.
किसी उपकरण से हाइड्रोजन गैस 28.7 cm³s^-1 की दर से विसरित हो रही है। उन्हीं स्थितियों में कोई दूसरी गैस 7.2 cm³ s^-1 की दर से विसरित होती है। इस दूसरी गैस को पहचानिए। [संकेत : ग्राहम के विसरण नियम R₁/R₂ = (M₂/ M₁)^1/21/2 का उपयोग कीजिए, यहाँ R₁, R₂ क्रमशः गैसों की विसरण दर तथा M₁ एवं M₂ उनके आण्विक द्रव्यमान हैं। यह नियम अणुगति सिद्धांत का एक सरल परिणाम है।
उत्तर:
विसरण के ग्राहम के नियम से,
\(\frac { R_{ 1 } }{ R_{ 2 } } \) = \(\sqrt { \frac { M_{ 2 } }{ M_{ 1 } } } \) … (i)
जहाँ R₁ = गैस – 1 की विसरण दर = 28.7 cm³s^-1
R₂ = गैस – 2 की विसरण दर = 7.2 cm²s^-1 … (ii)
माना इनके संगत अणुभार M₁ व M₂ हैं।
∴H₂ के लिए, M₁ = 2
∴समी० (i) तथा (ii) से
\(\frac { 28.7 }{ 7.2 } \) = \(\sqrt { \frac { M_{ 2 } }{ 2 } } \)
या \(\frac { M_{ 2 } }{ 2 } \) = (\(\frac { 28.7 }{ 7.2 } \))²
या M₂ = 2 × 15.89 = 31.77 = 32 u
हम जानते हैं कि O₂ का अणुभार 32 है। अत: अज्ञात गैस O₂ हैं।

प्रश्न 13.13.
साम्यावस्था में किसी गैस का घनत्व और दाब अपने संपूर्ण आयतन में एकसमान है। यह पूर्णतया सत्य केवल तभी है जब कोई भी बाह्य प्रभाव न हो। उदाहरण के लिए, गुरुत्व से प्रभावित किसी गैस स्तंभ का घनत्व (और दाब) एकसमान नहीं होता है। जैसा कि आप आशा करेंगे इसका घनत्व ऊँचाई के साथ घटता है। परिशुद्ध निर्भरता ‘वातावरण के नियम’ n₂ = n₁ exp [\(\frac { – mg }{ k_{ B }T } \) (h₂ – h₁)] से दी जाती है, यहाँ n₂,n₁ क्रमश: h₂ व h₁ ऊँचाइयों पर संख्यात्मक घनत्व को प्रदर्शित करते हैं। इस संबंध का उपयोग द्रव स्तंभ में निलंबित किसी कण के अवसादन साम्य के लिए समीकरण n₂ = n₁exp \(-\frac { mgN_{ A } }{ \rho RT } \)(ρ – ρ’)( h₂ – h₁)] को व्युत्पन्न करने के लिए कीजिए, यहाँ निलंबित कण का घनत्व तथा ρ’ चारों तरफ के माध्यम का घनत्व है। N_A आवोगाद्रो संख्या, तथा सार्वत्रिक गैस नियतांक है। संकेत: निलंबित कण के आभासी भार को जानने के लिए आर्किमिडीज के सिद्धांत का उपयोग कीजिए।
उत्तर:
माना कि कणों तथा अणुओं का आकार गोलाकार है। कणों का भार निम्नवत् है।
w = mg = \(\frac{4}{3}\) π r²ρg … (i)
जहाँ r = कणों की त्रिज्या
तथा ρ = कणों का घनत्व है।
कणों की गति गुरुत्व के अधीन होने पर, ऊपर की ओर उत्क्षेप लगाती है जिसका मान निम्नवत् है –
B = कण का आयतन × प्रतिवेश का घनत्व × g
= \(\frac{4}{3}\) π r³(ρ – ρ’) g … (ii)
मन कण पर नीचे की और लगाने वाला बा F है।
अतः F = W – B
= \(\frac{4}{3}\) π r³(ρ – ρ’) g … (iii)
पुनः n₂ = n₁ exp [\(\frac { – mg }{ k_{ B }T } \) (h₂ – h₁)] … (iv)
जहाँ k_B = बोल्ट्जमैन नियतांक है।
तथा n₁ व n₂ क्रमश: h₁ व h₂ ऊँचाई पर संख्या घनत्व है। समीकरण (iii) में mg के स्थान पर बल F रखने पर, समीकरण (ii) व (iv) से,

जो कि अभीष्ट समीकरण है।
जहाँ \(\frac{4}{3}\) π r³ ρg
= कण का द्रव्यमान × g = mg

प्रश्न 13.14.
नीचे कुछ ठोसों व द्रवों के घनत्व दिए गए हैं। उनके परमाणुओं की आमापों का आंकलन(लगभग)कीजिए।

[संकेत: मान लीजिए कि परमाणु ठोस अथवा द्रव प्रावस्था में दृढ़ता से बंधे हैं तथा आवोगाद्रो संख्या के ज्ञात मान का उपयोग कीजिए। फिर भी आपको विभिन्न परमाण्वीय आकारों के लिए अपने द्वारा प्राप्त वास्तविक संख्याओं का बिल्कुल अक्षरशः प्रयोग नहीं करना चाहिए क्योंकि दृढ़ संवेष्टन सन्निकटन की रुक्षता के परमाणवीय आकार कुछA के परास में हैं।
उत्तर:
1. कार्बन का परमाणु भार
M = 12.01 × 10^-3 kg
N = 6.023 × 10²³
∴ एक कार्बन परमाणु का द्रव्यमान
M = \(\frac{M}{N}\) = \(\frac { 12.01\times 10^{ -3 } }{ 6.023\times 10^{ 23 } } \)
या m = 1.99 × 10^-26kg
= 2 × 10^-26 kg
कार्बन का घनत्व ρ_e = 2.2 × 10⁺³ kg m^-3
∴ प्रत्येक कार्बन परमाणु का आयतन
V = \(\frac { m }{ \rho C } \) = \(\frac { 2\times 10^{ -26 } }{ 2.2\times 10^{ 3 } } \)
= 0.9007 × 10^-29m³
माना r_C = कार्बन परमाणु की त्रिज्या
∴ \(\frac{4}{3}\) πr³_C = 0.9007 × 10^-29
या
r_C = [\(\frac { 0.9007\times 10^{ -29 } }{ 4\pi } \) × 3]^1/3
= [2.16 × 10^-30]^1/3
= 1.29 × 10^-10m = 1.29 Å

2.  दिया है: स्वर्ण परमाणु का परमाणु भार
M = 1.97 × 10^-3 kg
∴ प्रत्येक स्वर्ण परमाणु का द्रव्यमान
= \(\frac{M}{N}\) = \(\frac { 197\times 10^{ 3 } }{ 6.023\times 10^{ 23 } } \)
= 3.721 × 10^-25 kg
ρ_g = 19.32 × 10³kg m^-3
माना r_g = गोल्ड परमाणु की त्रिज्या

= (0.04 × 10^-28)^1/3
= 0.159 × 10^-9m
= 1.59 × 10^-10m = 1.59 Å

3. दिया है: नाइट्रोजन परमाणु का परमाणु भार
M = 14.01 × 10^-3 kg
∴ प्रत्येक परमाणु का द्रव्यमान
M = \(\frac{M}{N}\) = \(\frac { 14.01\times 10^{ -3 }kg }{ 6.023\times 10^{ 23 } } \)
= 2.3261 × 10^-26 kg
माना r_n = इसके प्रत्येक परमाणु की त्रिज्या
ρ_n = 1 × 10³ kg m^-3

= (5.55 × 10^-30 m³)^1/3
= 1.77 × 10^-10m = 1.77 Å

4. दिया है: M_Li = 6.94 × 10^-3 kg
ρ_Li = 0.53 × 10³ kg m^-3
∴ M_Li = mass of Li atom
= \(\frac { M_{ Li } }{ \rho _{ Li } } \) = \(\frac { 6.94\times 10^{ -3 } }{ 6.023\times 10^{ 23 } } \)
= 1.152 × 10^-26 kg
माना r_Li = L_i परमाणु की त्रिज्या

5. दिया है: M_F = 19 × 10^-3 kg
ρ_F = 1.14 × 10³ kg m^-3
∴ प्रत्येक फलुओरीन परमाणु का द्रव्यमान
m_F = \(\frac { M_{ F } }{ \rho _{ F } } \) = \(\frac { 19\times 10^{ -3 } }{ 6.023\times 10^{ 23 } } \)
= 3.155 × 10^-26 kg
माना प्रत्येक फलुओरीन परमाणु की त्रिज्या r_F है। अतः

= 1.88 × 10^-10 m = 1.88 Å

MP Board Class 11 Physics Solutions

MP Board Class 12th Hindi Makrand Solutions Chapter 19 पुस्तक (निबन्ध, देवेन्द्र ‘दीपक’)

पुस्तक पाठ्य-पुस्तक पर अधिारित प्रश्न

पुस्तक लघु उत्तरीय प्रश्न

प्रश्न 1.
बख्तियार खिलजी के आक्रमण से क्या हानि हुई?
उत्तर:
बख्तियार खिलजी के आक्रमण से सबसे बड़ी हानि नालंदा के पुस्तकालयों को जलाने से हुई।

प्रश्न 2.
पुस्तक पढ़ने की आदत कम क्यों होती जा रही है?
उत्तर:
सूचना क्रांति और दूरदर्शन के प्रभाव से पुस्तकें पढ़ने की आदत कम होती जा रही है।

प्रश्न 3.
नालंदा विश्वविद्यालय में कौन-से तीन पुस्तकालय थे?
उत्तर:
नालंदा विश्वविद्यालय में रत्न सागर, रत्नोदधि और रत्नरंजक नाम के तीन विशाल पुस्तकालय थे।

प्रश्न 4.
पुस्तक या यात्रा का क्या संबंध है?
उत्तर:
पुस्तक बाहरी और भीतरी यात्रा का घनिष्ठ संबंध है।

पुस्तक दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
नालंदा विश्वविद्यालय की विशेषताएँ लिखिए।
उत्तर:
नालंदा विश्वविद्यालय में पुस्तकालय का एक विशिष्ट क्षेत्र था। उसे धर्मगंज कहा जाता था। इसमें रत्नसागर, रत्नोदधि और रत्नरंजक नामक तीन विशाल पुस्तकालय थे। रत्नसागर पुस्तकालय का भवन नौमंजिला था। बख्तियार खिलजी ने इन पुस्तकालयों को जला डाला। इस अग्निकांड में अमूल्य ग्रंथ जलकर सदा के लिए भस्म हो गए।

प्रश्न 2.
पुस्तकें किन षड्यंत्रों का शिकार होती हैं?
उत्तर:
पुस्तकें कई षड्यंत्रों का शिकार होती हैं। षड्यंत्रों के शिकार के कारण ही कुछ पुस्तकें तिरस्कृत हो जाती हैं। कुछ प्रतिबंधित कर दी जाती हैं और कुछ विशेष लेखकों की पुस्तकें जला दी हैं। पुस्तकें भी राजनीतिक, साहित्यिक, धार्मिक और भाषाई षड्यंत्रों का शिकार होती हैं।

प्रश्न 3.
लेखक के अनुसार पुस्तक की समीक्षा किस प्रकार की जाती है?
उत्तर:
लेखक के अनुसार पुस्तक की समीक्षा बेबाक होती है और प्रायः प्रायोजित होती है। समीक्षा में अक्सर एक अनावश्यक लंबी भूमिका होती है। इसमें पुस्तक के अंदर जो कुछ है उसकी चर्चा कम होती है और जो नहीं है उसकी चर्चा अधिक होती है। दूसरे शब्दों में, पुस्तक की समीक्षा ठीक प्रकार से नहीं होती है।

प्रश्न 4.
पुस्तकों के जलने से होने वाली क्षति का वर्णन कीजिए।
उत्तर:
पुस्तकों के जलने से देश की सबसे बड़ी क्षति होती है। ज्ञान का अपार भंडार जलकर राख हो जाता है। प्रत्येक, ग्रंथ रचनाकार की साधना और परिश्रम का प्रतिफल होता है। उसका सारा परिश्रम व्यर्थ चला जाता है। कितने लोगों का शोध व्यर्थ चला जाता है। कितने ही विद्वानों का चिंतन-मनन नष्ट हो जाता है, जो पुनः लौटकर नहीं आता। आगामी पीढ़ियों को ज्ञान नहीं मिल पाता। विश्वधरोहर जलकर नष्ट हो जाती है।

पुस्तक भाव-विस्तार/पल्लवन

प्रश्न 1.
निम्नलिखित पंक्ति का भाव-विस्तार कीजिए“यात्रा में पुस्तक, पुस्तक में यात्रा, यों यात्रा में यात्रा।”
उत्तर:
यात्रा में पुस्तकें यात्रा की मित्र होती हैं। उनको पढ़ने से यात्री की यात्रा आराम से कट जातं. है। पुस्तकें पढ़ने से उनका ज्ञान भी बढ़ता है और मनोरंजन भी होता है। यात्री जिन स्थानों की यात्रा करता है, उनका वर्णन वह पुस्तकों में करता है। उन स्थानों के निवासियों के रहन-सहन, खान-पान, रीति-रिवाज, त्योहारों और ऐतिहासिक, सांस्कृतिक धरोहरों का वर्णन करता है। इस प्रकार यात्रा में यात्रा हो जाती है। यात्रा से सभी का ज्ञान बढ़ता है और मनोरंजन होता है।

पुस्तक भाषा-अनुशीलन

प्रश्न 1.
समीक्षा शब्द विशिष्ट अर्थ में प्रयुक्त होने के कारण पारिभाषिक शब्द है। इसी तरह के पाँच पारिभाषिक शब्द लिखिए –
उत्तर:
विदेश नीति, विमोचन, प्राक्कथन, प्रायोजित, समालोचक।

प्रश्न 2.
निम्नलिखित में से विदेशी शब्द और तत्सम शब्द छाँटिए –
वहशत, ग्रंथ, दहशत, दिमाग, सारस्वत, गैरजरूरी, सुटेबिल, जलयात्रा, अलमारी, समवाय, दुर्लभ, समीक्षा।
उत्तर:

प्रश्न 3.
(क) यह आम रास्ता नहीं है।
(ख) आम के फल मीठे होते हैं।
उपर्युक्त वाक्यों में ‘आम’ शब्द दो अर्थों में प्रयुक्त हुआ है। पहले वाक्य में आम का अर्थ ‘जन साधारण’ है, जबकि दूसरे वाक्य में ‘आम’ फल के लिए आया है। इसी प्रकार अंक, अम्बर, अर्थ, उत्तर और मूल शब्दों के उदाहरण के अनुसार वाक्य बनाइए।
उत्तर:

• अंक – विमला को सौ में से पचास अंक मिले हैं।
  माँ ने रोते बच्चे को अंक में उठा लिया।
• अंबर – अंबर में तारे छिटके हैं।
  श्रीकृष्ण पीत अंबर धारण करते हैं।
• अर्थ – ‘गगन’ शब्द का अर्थ आकाश है।
  आजकल हम अर्थ-अभाव से गुजर रहे हैं।
• उत्तर – इस प्रश्न का उत्तर बीस शब्दों में लिखिए।
  भारत के उत्तर में पर्वतराज हिमालय है।
• मूल – मूल कट जाने के कारण यह पौधा सूख गया है।
  मैं मूल रूप से राजस्थान का निवसी हूँ।

प्रश्न 4.
निम्नलिखित वाक्यों को शुद्ध कीजिए –

1. पुस्तक चुराया जाता है।
2. जितना सोचता हूँ उतना खिन्नता बढ़ती है।
3. हर पाठक को पुस्तक मिलना चाहिए।
4. रविवार के दिन की छुट्टी रहती है।

उत्तर:

1. पुस्तक चुराई जाती है।
2. जितना सोचता हूँ, उतनी खिन्नता बढ़ती है।
3. हर पाठक को पुस्तक मिलनी चाहिए।
4. रविवार को छुट्टी रहती है।

पुस्तक योग्यता-विस्तार

प्रश्न 1.
‘पुस्तक मित्र’ पर एक निबंध लिखिए।
उत्तर:
छात्र स्वयं करें।

प्रश्न 2.
आधुनिक विश्वविद्यालयों में नालंदा विश्वविद्यालय से भिन्न जिन नए विषयों का अध्ययन किया जाता है, उन नए विषयों की सूची बनाइए।
उत्तर:
छात्र स्वयं सूची बनाएँ।

प्रश्न 3.
पुस्तकालय जाकर देखिकए कि वहाँ पुस्तकें कैसे व्यवस्थित रखी जाती हैं, ताकि कोई भी पुस्तक एक मिनिट में आप खोज सकें।
उत्तर:
छात्र स्वयं करें।

प्रश्न 4.
अपने विद्यालय के पुस्तकालय से ऐसी पुस्तकें प्राप्त कीजिए, जो बहुत पुरानी हो चुकी हों, तथा जो फट रही हों, उन्हें प्राप्त कर चिपकाइए तथा व्यवस्थित कीजिए ताकित वह लम्बे समय तक सुरक्षित रह सकें।
उत्तर:
छात्र स्वयं करें।

पुस्तक परीक्षोपयोगी अन्य महत्वपूर्ण प्रश्न

I. वस्तुनिष्ठ प्रश्न

प्रश्न 1.
विचारों की जययात्रा का मूर्तरूप है ……..
(क) पुस्तक
(ख) नालंदा
(ग) शिक्षा
(घ) पुस्तकालय
उत्तर:
(क) पुस्तक।

प्रश्न 2.
पुस्तक रची, छापी और ………… की जाती है –
(क) बिक्री
(ख) भेंट
(ग) विमोचित
(घ) चुराई
उत्तर:
(ग) विमोचित।

प्रश्न 3.
पुस्तक समीक्षाओं में होती है ……
(क) एक आवश्यक लंबी भूमिका
(ख) एक गैरज़रूरी लंबी भूमिका
(ग) एक बेकार अर्थहीन भूमिका
(घ) एक सार्थक लंबी भूमिका
उत्तर:
(ख) एक गैरज़रूरी लंबी भूमिका।

प्रश्न 4.
नालंदा विश्वविद्यालय को ………. नामक आक्रमणकारी ने जलाकर राख कर दिया।
(क) अलाउद्दीन खिलजी
(ख) ग्यासुद्दीन खिलजी
(ग) बख्तियार खिलजी
(घ) जलालुद्दीन खिलजी
उत्तर:
(ग) बख्तियार खिलजी।

प्रश्न 5.
नालंदा में पुस्तकालयों के विशिष्ट क्षेत्र को कहते थे ………..।
(क) धर्मगंज
(ख) पुस्तकगंज
(ग) दर्शन गंज
(घ) आचार्य गंज
उत्तर:
(क) धर्मगंज।

प्रश्न 6.
पुस्तकालय वाले कहते हैं, दान में किताबें ही नहीं, उन्हें रखने के लिए ……….. भी दो।
(क) अलमारियाँ
(ख) धन
(ग) स्थान
(घ) आदमी
उत्तर:
(क) अलमारियाँ।

प्रश्न 7.
कमरे को रोशनदान चाहिए, तो याद रखिए दिमाग को भी ………..।
(क) दवाई चाहिए
(ख) पुस्तक चाहिए
(ग) ज्ञान चाहिए
(घ) प्रकाश चाहिए
उत्तर:
(ख) पुस्तक चाहिए।

प्रश्न 8.
हर पुस्तक को उसका मिलना चाहिए ……….. ।
(क) खरीददार
(ख) पाठक
(ग) आलोचक
(घ) समीक्षक
उत्तर:
(ख) पाठक।

प्रश्न 9.
ग्रंथों में प्रक्षेप करते हैं ………..।
(क) कुछ धूर्त लोग
(ख) कुछ धूर्त रचनाकार
(ग) कुछ बेईमान लोग
(घ) कुछ पागल लोग
उत्तर:
(क) कुछ धूर्त लोग।

प्रश्न 10.
सूचना क्रांति और दूरदर्शन के कारण आदत कम होती जा रही है ………….।
(क) पुस्तकें पढ़ने की
(ख) पुस्तकें खरीदने की
(ग) पुस्तकें भेंट करने की
(घ) पुस्तकें एकत्र करने की
उत्तर:
(क) पुस्तकें पढ़ने की।

प्रश्न 11.
एक उम्र होती है कि –
(क) आदमी पुस्तकें लिखता है
(ख) आदमी पुस्तकें सहेजता है
(ग) आदमी पुस्तकें बेचता है
(घ) आदमी पुस्तकें खरीदता है
उत्तर:
(ख) आदमी पुस्तकें सहेजता है।

II. निम्नलिखित रिक्त स्थानों की पूर्ति दिए गए विकल्पों के आधार पर कीजिए –

1. रातों रात कोई पुस्तक ………. हो जाती है। (बहिष्कृत/तिरस्कृत)
2. हर पुस्तक को’ उसका ………. मिलना चाहिए। (लेखक/पाठक)
3. ………. का भवन नौमंजिला था। (रत्नसागर/रत्नरंजक)
4. आज ………. का दौर है। (हरितक्रांति/सूचनाक्रांति)
5. पुस्तक ………. जाती है। (रची/लिखी)

उत्तर:

1. तिरस्कृत
2. पाठक
3. रत्नासागर
4. सूचनाक्रान्ति
5. रची।

III. निम्नलिखित कथनों में सत्य/असत्य छाँटिए –

1. ‘पुस्तक’ एक कहानी है।
2. ‘पुस्तक’ के लेखक देवेन्द्र ‘दीपक’ हैं।
3. नालंदा में पन्द्रह हजार विद्यार्थी थे।
4. पुस्तकें षड्यंत्रों का शिकार होती हैं।
5. कुछ धूर्त लोग कुछ वाक्यों को लुप्त कर देते हैं।

उत्तर:

1. असत्य
2. सत्य
3. असत्य
4. सत्य
5. सत्य।

IV. निम्नलिखित के सही जोड़े मिलाइए –

प्रश्न 1.

उत्तर:

(i) (ङ)
(ii) (ग)
(iii) (घ)
(iv) (ख)
(v) (क)।

V. निम्नलिखित प्रश्नों के उत्तर एक शब्द या एक वाक्य में दीजिए –

प्रश्न 1.
पुस्तक किसका समवाय है?
उत्तर:
पुस्तक बाहरी और भीतरी यात्रा का समवाय है।

प्रश्न 2.
हमारे देश में सबसे बड़ा विद्या का केन्द्र कौन था?
उत्तर:
नालंदा का पुस्तकालय।

प्रश्न 3.
पुस्तक का जलना किसका जलना है?
उत्तर:
पुस्तक का जलना विश्व धरोहर का जलना है।

प्रश्न 4.
नालंदा के पुस्तकालय को किसने जला डाला था?
उत्तर:
बख्तियार खिलजी ने।

प्रश्न 5.
पुस्तक जलाना और उसे नष्ट करना क्या है?
उत्तर:
पुस्तक जलाना और उसे नष्ट करना घोर अपराध जैसा कत्य है।

पुस्तक लघु उत्तरीय प्रश्न

प्रश्न 1.
पुस्तक किसका मूर्तरूप है?
उत्तर:
पुस्तक लेखक के पुरुषार्थ का सारस्वत मूर्तरूप है।

प्रश्न 2.
पुस्तक की भूमिका और प्राक्कथन कैसे लिखवाया जाता है?
उत्तर:
पुस्तक की भूमिका और प्राक्काय लिखवाने के लिए उपयुक्त व्यक्ति खोजे जाते हैं। फिर उनसे प्राक्कथन और भूमिका लिखवाई जाती है।

प्रश्न 3.
पुस्तकों के क्या-क्या प्रयोग किए जाते हैं?
उत्तर:
पुस्तकें भेंट की जाती हैं, माँगी, चुराई, दबाई और पढ़ी जाती हैं।

प्रश्न 4.
पुस्तकालय वाले दान में किताबों के साथ क्या माँगते हैं?
उत्तर:
पुस्तकालय वाले दान में किताबों के लिए अलमारियाँ भी माँगते हैं।

प्रश्न 5.
नालंदा विश्वविद्यालय के साथ कौन-सा काला ध भी लगा है?
उत्तर:
नालंदा विश्वविद्यालय के साथ पुस्तकालय जलाने का काला धब्बा भी लगा है।

प्रश्न 6.
पुस्तकों के संबंध में लेखक की क्या आशा है?
उत्तर:
लेखक की आशा है कि पुस्तक मित्र थीं, मित्र हैं और मित्र रहेंगी।

प्रश्न 7.
‘पुस्तक’ निबंध में लेखक का कौन-सा स्वर है?
उत्तर:
‘पुस्तक’ निबंध में लेखक का आशावादी स्वर है।

प्रश्न 8.
शिक्षा के क्षेत्र में किसका दबदबा रहा?
उत्तर:
शिक्षा के क्षेत्र में नालंदा विश्वविद्यालय का दबदबा रहा।

प्रश्न 9.
‘रत्नसागर’ का भवन कैसा था?
उत्तर:
रत्नसागर’ का भवन नौमंजिला था।

पुस्तक दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
पुस्तकालय को लेकर घर में चिकचिक क्यों होने लगती है?
उत्तर:
जब घर में आदमी के अपने लिए जगह कम पड़ने लगती है, तो निजी पुस्तकालय को लेकर घर में चिकचिक होने लगती है। प्राध्यापकों की संतानों की शिक्षण में रुचि न होना भी एक कारण है।

प्रश्न 2.
नालंदा विश्वविद्यालय की महिमा का वर्णन कीजिए। (M.P. 2012)
उत्तर:
नालंदा प्राचीन भारत का एक सुप्रसिद्ध विश्वविद्यालय था। शिक्षा के क्षेत्र – में इसका बड़ा दबदबा था, जहाँ दस हजार विद्यार्थी शिक्षा ग्रहण करते थे। इन विद्यार्थियों को शिक्षा देने के लिए 1500 आचार्य थे। यहाँ अनेक विषयों की शिक्षा दी जाती थी। नालंदा का पुस्तकालय बहुत विशाल था। आक्रमणकारी बख्तियार खिलजी ने नालंदा के पुस्तकालय को जलाकर राख कर दिया था।

प्रश्न 3.
नालंदा में किन-किन विषयों की शिक्षा दी जाती थी? (M.P. 2012)
उत्तर:
नालंदा में बौद्धदर्शन, दर्शन, इतिहास, निरुक्त, वेद, हेतुविद्या, न्यायशास्त्र, व्याकरण, चिकित्साशास्त्र, ज्योतिष आदि के शिक्षा की व्यवस्था थी।

प्रश्न 4.
नालंदा विश्वविद्यालय में कार्यरत आचार्य कौन-कौन से थे? (M.P. 2010)
उत्तर:
नालंदा विश्वविद्यालय में कार्यरत आचार्य शीलभद्र, नागार्जुन, आचार्य धर्म कीर्ति, आचार्य ज्ञानश्री, आचार्य बुद्ध भंद्र, आचार्य गुणमति, आचार्य स्थिरमति, आचार्य सागरमति आदि विख्यात आचार्य कार्यरत थे।

प्रश्न 5.
‘पुस्तक’ नामक निबंध में देवेन्द्र ‘दीपक’ (लेखक) ने नालंदा विश्वविद्यालय की क्या विशेषताएँ बताई हैं? (M.P. 2009)
उत्तर:
‘पुस्तक’ नामक निबंध में देवेन्द्र ‘दीपक’ (लेखक) नै नालंदा विश्वविद्यालय की निम्नलिखित विशेषताएँ बताई हैं –
नालंदा विश्वविद्यालय का शिक्षा के क्षेत्र में बड़ा दबदबा था। वहाँ दस हजार विद्यार्थी और पन्द्रह सौ आचार्य थे। बौद्ध-दर्शन, इतिहास, निरुक्त, वेद, हेतुविद्या, न्यायशास्त्र, व्याकरण, चिकित्साशास्त्र, ज्योतिष आदि के शिक्षण की व्यवस्था थी। आचार्य शीलभद्र, नागार्जुन, आचार्य धर्मकीर्ति, आचार्य ज्ञानश्री, आचार्य बुद्ध भट्ट,आचार्य गुणमति, आचार्य स्थिरमति, आचार्य सागरमीरा जैसे विश्वविख्यात आचार्य वहाँ थे।

प्रश्न 6.
पुस्तक-समीक्षा की क्या विशेषता है?
उत्तर:
पुस्तक-समीक्षा के लिए सुटेबिल आदमी खोजे जाते हैं। समीक्षा कभी बेबाक होती है। समीक्षा प्रायः प्रायोजित होती है। इस प्रकार की समीक्षाओं में प्रायः एक गैरज़रूरी लम्बी भूमिका होती है। पुस्तक में जो है, उसकी चर्चा कम, जो नहीं है, उसकी चर्चा अधिक होती है।

पुस्तक लेखक-परिचय

प्रश्न 1.
देवेन्द्र ‘दीपक’ का संक्षिप्त जीवन-परिचय देते हुए उनकी साहित्यिक विशेषताओं पर प्रकाश डालिए।
उत्तर:
जीवन-परिचय:
राष्ट्रवादी चिंतक और रचनाकार देवेंद्र ‘दीपक’ का जन्म 31 जुलाई, 1934 ई० को उत्तर प्रदेश के सहारनपुर में हुआ। आपने शालेय शिक्षा के बाद साहित्य रत्न, एम.ए. (हिंदी, अंग्रेजी में) किया। उसके बाद पी-एच.डी. की उपाधि प्राप्त की। आपने वंचित समाज के विकास में शब्द और कर्म द्वारा अपूर्व कार्य कर महत्त्वपूर्ण योगदान किया। मारीशस, लंदन, सूरीनाम तथा न्यूयार्क में आयोजित विश्व हिंदी सम्मेलनों में अपना सक्रिय योगदान दिया है। आप उन चिंतकों में से हैं, जिन्होंने हिंदी की प्रतिष्ठा के लिए स्वयं को समर्पित कर दिया है। आप्रे अनुसूचित जाति से संबद्ध परीक्षा पूर्व प्रशिक्षण केंद्र का प्राचार्य रहे हैं। मध्य प्रदेश हिंदी ग्रंथ अकादमी के निदेशक के रूप में आपने सराहनीय कार्य किया है।

साहित्यिक-परिचय:
वर्तमान में आप साहित्य अकादमी, मध्य प्रदेश संस्कृति परिषद् के निदेशक पद पर कार्य करते हुए साहित्य सेवा में जुटे हैं। ‘साक्षात्कार’ पत्रिका के प्रधान संपादक हैं। ‘दीपक’ जी बहुमुखी प्रतिभा के धनी हैं। आपने काव्य, काव्य नाटक, कठपुतली नाटक और अनेक ग्रंथों का अनुवाद किया है। काव्य-सृजन में उन्होंने अपनी प्रभावशाली उपस्थिति दर्ज कराई है। आपने गद्य-क्षेत्र में भी मानदंड स्थापित किए हैं। आपकी गद्य रचनाओं में जीवन-बोध के सहज और आत्मीय प्रसंग मिलते हैं। आपकी गद्य रचनाओं में सामाजिक चिंताओं और आस्थामूलक दृष्टि का समावेश है।

रचनाएँ:

• काव्य-संग्रह – सूरज बनती किरण, बंद कमरा, दुली कविताएँ (आपत्तकालीन) मास्टर धर्मदास, हम दंने नहीं (अन्त्यज कविता)
• काव्य-नाटक – भूगोल राजा का। खगोल राजा का।
• कठपुतली – नाटक दवाव।
• अन्य रचनाएँ – शिक्षाशास्त्रियों के सिद्धांत, विचारणा विथि का, कुंडली चक्र पर मेरी वार्ता आदि।

भाव-शैली:
‘दीपक’ जी को भाषा-शैली शब्द विपर्यय के चमत्कार आपकी गद्य रचनाओं के भाव-सौन्दर्य में विशेष रूप से वृद्धि करते हैं। वे भाषा के क्षेत्र में अपनी रचनात्मकता के माध्यम से मुहावर जैरे. चते चलते है। उनकी भाषा सहज स्वाभाविक खड़ी बोली है। उसमें यथास्थान तत्सम, उर्दू और अंग्रेजी के शब्दों का समावेश है।

पुस्तक पाठ का सारांश

प्रश्न 1.
‘पुस्तक’ पाठ का सार अपने शब्दों में लिखिए।
उत्तर:
‘पुस्तक’ निबंध में देवेंद्र ‘दीपक’ ने पुस्तक को केंद्र बनाकर अनेक प्रकार के विचारों को प्रस्तुत किया है। लेखक कहता है कि पुस्तक का जीवन में बड़ा महत्त्व है। पुस्तक जीवन की बाहरी और भीतरी,मात्रा का समन्वय है। पुस्तकें लिखी, छापी और विमोचित की जाती हैं। पुस्तकें बेची, खरीदी जाती हैं। बुक डिपो में अलमारी में करीने से सजी होती हैं। ये कभी चौराहे पर भी रेहड़ी में भी बेची जाती हैं। इतना ही नहीं पुस्तकें भेंट की जाती हैं, माँगी, चुराई और दबाई जाती हैं। अंततः पुस्तकें पढ़ी जाती हैं। कुछ पुस्तकें रखी जाती हैं, जबकि कुछ निगली और उनमें से कुछ ही पचाई जाती हैं।

पुस्तकों की भूमिका लिखने के लिए उपयुक्त व्यक्ति खोजे जाते हैं। पुस्तक की समीक्षा की जाती है। व्यक्ति एक आयु में पुस्तकें खरीदता है, पढ़ता है और अंत में पुस्तकालय के कमरे को लेकर परिवार में झगड़ा होता है। पुस्तकालय वाले : भी उन दुर्लभ पुस्तकों को दान में स्वीकार नहीं करते। पुस्तकों को राजनीति के कारण कई उतार-चढ़ाव देखने पड़ते हैं। नालंदा विश्वविद्यालय के पुस्तकालय को बख्तियार खिलजी ने जला डाला था। पुस्तक का जलना विश्व धरोहर का जलना है। पुस्तक जलाना और नष्ट करना घोर अपराध जैसा कार्य है। पुस्तकों को जलाना, जलवाना रचनाकार के कठोर परिश्रम और साधना को बरबाद करने के समान है।

कितनों का शोध और सोचा-समझा व्यर्थ हो जाता, जो पुनः लौट कर नहीं आता। पुस्तकें भी षड्यंत्रों का शिकार होती हैं। कुछ धूर्त लोग ग्रंथों में प्रक्षेप कर देते हैं इसलिए जो ग्रंथ नष्ट होने से बच गए, उनमें भी बहुत बदलाव आ गए। लेखक का आशावादी स्वर भी उभरा है। आधुनिक युग में सूचना क्रांति का दौर होने के कारण पुस्तकों को पढ़ने की आदत अवश्य कम हुई है, लेकिन यह भी पुस्तकों के महत्त्व को कम भी नहीं कर सकता। पुस्तक की उपस्थिति और उपयोगिता बनी ही रहेगी।

पुस्तक संदर्भ-प्रसंगसहित व्याख्या

प्रश्न 1.
पुस्तक बेची जाती हैं-पुस्तक खरीदी जाती हैं-कभी किसी बुक डिपो में करीने से सजी अलमारियों से, तो कभी चौराहे पर खड़े किसी ठेले पर लगे ढेर से। पुस्तक भेंट की जाती है, पुस्तक माँगी जाती है। पुस्तक चुराई जाती है। पुस्तक दबाई जाती है। और यह सब इसलिए कि अंततः पुस्तक पढ़ी जाती है। पढ़ने में कुछ पुस्तकें केवल रखी जाती हैं, कुछ निगली जाती हैं, कुछ ही हैं जो पचाई जाती हैं। पुस्तक की भूमिका और प्राक्कथन के लिए सुटेबिल आदमी खोजे जाते हैं। पुस्तक की समीक्षा की जाती है। कभी यह समीक्षा बेबाक होती है, अक्सर प्रायोजित। इन समीक्षाओं में अक्सर एक गैरज़रूरी लंबी भूमिका होती है। पुस्तक में जो है उसकी चर्चा कम, जो नहीं है उसकी चर्चा अधिक। (Pages 89-90)

शब्दार्थ:

• सुटेबिल – उपयुक्त।
• बेबाक – अचूक, सटीक।
• गैरज़रूरी – अनावश्यक।

प्रसंग:
प्रस्तुत गद्यांश देवेंद्र ‘दीपक’ के द्वारा लिखित निबंध ‘पुस्तक’ से उद्धृत है। लेखक इस गद्यांश में पुस्तकों की उपयोगिता और उनकी समीक्षा पर प्रकाश डाल रहा है।

व्याख्या:
लेखक पुस्तकों की उपयोगिता के संबंध में कहता है कि प्रकाशक पुस्तकों का व्यापार करता है। पुस्तकें प्रकाशन गृहों और बुक डिपों में बेची जाती हैं। बुक डिपो वाले पुस्तकों को अलमारियों में सजाकर रखते हैं और बेचते हैं। कभी-कभी पुस्तकें चौराहे पर खुद को दुकानदारों द्वारा ठेले पर ढेर के रूप में रखकर भी बेची जाती हैं। पाठक पुस्तकों को खरीदते हैं। सुशिक्षित तथा पुस्तकों के सुधी पाठक अपने साहित्यिक मित्रों, सगे-संबंधियों अथवा अन्य लोगों को उपहार के रूप में भी देते हैं। पुस्तकें कुछ लोगों द्वारा माँग कर पढ़ी जाती हैं।

इतना ही नहीं पुस्तकालयों से महत्त्वपूर्ण दुर्लभ पुस्तकों को चुराया भी जाता है और आवश्यक पुस्तकों को इधर-उधर दबाकर भी रख दिया जाता है ताकि जरूरत पड़ने पर उसे प्राप्त किया जा सके। ये सारे काम इसलिए किए जाते हैं कि अंत में पुस्तक पढ़ी जाती है। पुस्तक पढ़ने के बाद कुछ पुस्तकें केवल रखी जाती हैं क्योंकि उन्हें फेंका नहीं जा सकता। कुछ पुस्तकें रोचक अथवा मनोरंजक न होने के कारण जबरदस्ती पढ़ी जाती हैं जबकि कुछ ही पुस्तकें ऐसी होती हैं जिन्हें पाठक पढ़ता है और चिंतन-मनन कर उन्हें आत्मसात् करता है।

लेखक पुस्तक की भूमिका और समीक्षा पर टिप्पणी करते हुए कहता है कि पुस्तक का सर्जन करने वाला अपनी पुस्तक की भूमिका और प्राक्कथन लिखवाने के लिए उपयुक्त आदमी को ढूँढ़कर, उससे भूमिका और प्राक्कथन लिखवाता है। पुस्तक के विषय, उसकी शैली, उसके उद्देश्य और गुण-दोषों की समीक्षा की जाती है। पुस्तक की यह समीक्षा एकदम सटीक होती है। प्रायः यह समीक्षा प्रायोजित होती है। इन समीक्षाओं में प्रायः एक अनावश्यक लंबी भूमिका रहती है, जिसमें जो कुछ पुस्तक के अंदर होता है, उसकी – चर्चा कम होती है और जो उसमें नहीं होता, उसकी चर्चा अधिक की जाती है।

विशेष:

1. पुस्तकों के अच्छी-बुरी होने का वर्णन रखी, निगली और पचाई जाने जैसे शब्दों से किया गया है।
2. समीक्षा के ढंग पर व्यंग्य किया गया है।
3. भाषा तत्सम शब्दों के साथ-साथ विदेशी शब्दों से युक्त खड़ी बोली है।

गद्यांश पर आधारित अर्थग्रहण संबंधित प्रश्नोत्तर

प्रश्न (i)
पुस्तकें चुराई और दबाई क्यों जाती हैं?
उत्तर:
कुछ पुस्तकें महत्त्वपूर्ण होती हैं। बाजार में वे उपलब्ध नहीं होती हैं। ऐसी पुस्तकें दुर्लभ होती हैं। जो केवल पुस्तकालयों में ही होती हैं, पाठक या छात्र अथवा शोधकर्ता ऐसी पुस्तकों को चुरा लेते हैं और अपना काम सरलता से निपटा लेते हैं। कुछ पुस्तकें पुस्तकालय में प्रायः छात्रों द्वारा ही दबाई जाती हैं। वे अपने विषय से संबंधित पुस्तक को इधर-उधर दबाकर रख देते हैं और जरूरत पड़ने पर निकाल लेते हैं।

प्रश्न (ii)
पुस्तकों के निगलने और पचाने से लेखक का क्या आशय है?
उत्तर:
पुस्तकों के निगलने से लेखक का आशय यह है कि पुस्तकें विषय पर शैली की दृष्टि से रोचक, मनोरंजक नहीं होतीं। ऐसी पुस्तकों को पाठक जबरदस्ती पढ़ता है। कुछ पुस्तकें विषय की दृष्टि से, शैली और उद्देश्य की दृष्टि से रोचक, मनोरंजक और जीविनोपयोगी होती हैं। ऐसी पुस्तकों को पाठक पढ़कर चिंतन-मनन करता है और जीवन में उनकी बातों को व्यवहार में लाता है। यही पुस्तकों का पचाना है।

गद्यांश पर आधारित बोधात्मक प्रश्नोत्तर

प्रश्न (i)
पुस्तक की भूमिका और प्राक्कथन लिखवाने के लिए क्या किया जाता है?
उत्तर:
पुस्तक की भूमिका और प्राक्कथन लिखवाने के लिए उपयुक्त व्यक्ति को खोजा जाता है और उससे ही भूमिका और प्राक्कथन लिखवाया जाता है।

प्रश्न (ii)
पुस्तक-समीक्षा पर लेखक ने क्या व्यंग्य किया है?
उत्तर:
पुस्तक-समीक्षा पर लेखक ने व्यंग्य किया है कि पुस्तक प्रायः प्रायोजित है। समीक्षा चर्चा होती है जो पुस्तक में होती ही नहीं है। पुस्तक में होने वाली बातों की चर्चा कम की जाती है।

प्रश्न 2.
पागल कौन है?-वह जो पुस्तक लिखता है या वह जो पुस्तकालय को जलाता है, जलवाता है। क्या होता है किसी पुस्तक का जलना? क्या होता है किसी पुस्तकालय का जलना! जितना सोचता हूँ, उतनी खिन्नता बढ़ती है। हर पुस्तक अपने में लंबी साधना और परिश्रम का प्रतिफल होती है। कितनी आँखों का कितना जागरण व्यर्थ चला गया। कितने लोगों के कितने शोध व्यर्थ हो गए। कितनों का सोचा-समझा था जो अब लौटकर नहीं आएगा। यह तो विश्वधरोहर को नष्ट करना हुआ। शताब्दियों की सारस्वत साधना के साथ छल किया पुस्तकालय जलाने बालों ने। वहत और दहशत की जुगलबंदी के अलावा और क्या था वह! (Page 90) (M.P. 2010)

शब्दार्थ:

• खिन्नता – दुख।
• प्रतिफल – परिणाम।
• वहशत – असभ्यता, जंगलीपन।
• दहशत – आतंक।
• सारस्वत – सरस्वती संबंधी।

प्रसंग:
प्रस्तुत गद्यांश देवेंद्र ‘दीपक’ द्वारा रचित निबंध ‘पुस्तक’ से लिया गया है। लेखक पुस्तकालय जलाने पर अपनी प्रतिक्रिया व्यक्त कर रहा है।

व्याख्या:
लेखक पाठकों से प्रश्न करता है कि पागल कौन है? जो पुस्तक की रचना करता है या वह जो पुस्तकालय को जलाता है, अपने लोगों से जलवाता है। इन दोनों में से पागल व्यक्ति कौन है? इसका उत्तर देने से पूर्व लेखक फिर प्रश्न करता है कि इस संबंध में जितना सोचता हूँ, उतनी ही दुख में वृद्धि होती है। लेखक के मतानुसार प्रत्येक पुस्तक लेखक की लंबी साधना और परिश्रम का परिणाम होती है अर्थात लेखक किसी पुस्तक की रचना लंबी साधना और परिश्रम से करता है। पुस्तक के जलने के कारण लेखक का रातों को जागकर पुस्तक लिखना व्यर्थ हो जाता है।

उसकी कृति नष्ट हो जाती है। कितने ही लोगों के अनुसंधान से संबंधित ग्रंथ पुस्तकालय जलने से नष्ट हो जाते हैं। शोधकर्ताओं द्वारा परिश्रम से खोजे गए नए सिद्धांत और नए फार्मूले बेकार हो जाते हैं। अनेक विद्वानों, चिंतकों, दर्शनशास्त्रियों और चिकित्सकों का चिंतन-मनन जलकर राख हो जाता है जो कभी पुनः प्राप्त नहीं हो सकता। पुस्तकों और पुस्तकालयों को जलाना विश्वधरोहर को नष्ट करना है।

इस तरह विश्वधरोहर को नष्ट करना घोर अपराध जैसा कार्य किया है, पुस्तकालय को जलाने वालों ने। शताब्दियों की विद्या की देवी सरस्वती की साधना के साथ धोखा किया है। यह उनकी असभ्यता और आतंक फैलाने के अतिरिक्त और कुछ नहीं था। उन्होंने पुस्तकालय जलाकर विश्व को ज्ञान के स्रोत से वंचित किया। यह उनके असभ्य होने का ही परिचायक है।

विशेष:

1. लेखक ने पुस्तकालय जलाने को घोर अपराध माना है।
2. पुस्तकालय जलाने वालों को असभ्य कहा है।
3. विचारात्मक और प्रश्नात्मक शैली है।
4. भाषा तत्सम व उर्दू शब्दावली युक्त खड़ी बोली है।

गयांश पर आधारित अर्थग्रहण संबंधित प्रश्नोत्तर

प्रश्न (i)
लेखक ने पुस्तक लेखक और पुस्तकालय जलाने वाले में से किसे पागल माना है?
उत्तर:
लेखक ने पुस्तक लेखक और पुस्तकालय जलाने वाले में से पुस्तकालय जलाने वाले को पागल माना है ऐसा इसलिए कि पुस्तकालय जलाने से पुस्तक लेखकों की लंबी साधना, शोधकर्ताओं का परिश्रम और विद्वानों का चिंतन-मनन नष्ट हो गया।

प्रश्न (ii)
पुस्तकालय को जलाना लेखक की दृष्टि में कैसा कार्य है?
उत्तर:
पुस्तकालय को जलाना लेखक की दृष्टि में घोर आपराधिक कार्य है।

गयांश पर आधारित बोधात्मक प्रश्नोत्तर

प्रश्न (i)
पुस्तकालय जलाने वालों ने किसके साथ छल किया?
उत्तर:
लेखक के अनुसार पुस्तकालय जलाने वालों ने शताब्दियों की विद्या की देवी सरस्वती के साधकों की साधना के साथ छल किया।

प्रश्न (ii)
लेखक पुस्तकालय जलाने वालों को क्या मानता है?
उत्तर:
लेखक पुस्तकालय जलाने वालों को असभ्य और आतंक फैलाने वाले मानता है; क्योंकि पुस्तकालय जलाना असभ्यता और आतंक फैलाने की मनोवृत्ति का ही सूचक है।

MP Board Class 12th Hindi Solutions

MP Board Class 12th Hindi Makrand Solutions Chapter 18 माँ (कविता, बालकवि बैरागी’ एवं संकलित)

माँ पाठ्य-पुस्तक पर आधारित प्रश्न

माँ लघु उत्तरीय प्रश्न

प्रश्न 1.
विश्व की शुभकामना किसे कहा गया है? (M.P. 2010)
उत्तर:
माँ के वात्सल्य भाव को ही विश्व की शुभकामना कहा गया है।

प्रश्न 2.
माँ किस राग के गीत गाने का निर्देश देती है?
उत्तर:
माँ भैरवी राग के गीत गाने का निर्देश देती है।

प्रश्न 3.
मुसीबत में किसका नाम लेना चाहिए? और क्यों?
उत्तर:
मुसीबत में माँ का नाम लेना चाहिए।

प्रश्न 4.
पथ पर चलने के लिए प्रतिफल कैसा कदम चाहिए?
उत्तर:
पथ पर चलने के लिए गतिशील कदम चाहिए।

प्रश्न 5.
गुरुता का ज्ञान क्यों अपेक्षित है?
उत्तर:
गुरुता का ज्ञान जीवन में प्रेरणा के लिए अपेक्षित है।

माँ दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
पंचतत्त्वों के किन गुणों को माँ धारण किए हुए है? (M.P. 2010)
उत्तर:
पृथ्वी, आकाश, अग्नि, जल और वायु पाँच तत्त्व होते हैं। माँ इन सभी गुणों को धारण किए हुए हैं। माँ पृथ्वी का गुण धैर्य, आकाश के गुण चैतन्य अथवा प्रकाश को, अग्नि के गुण तीव्रता, पवन की गतिमयी व्यापकता तथा जल के गुण गंभीरता को धारण किए हुए है।

प्रश्न 2.
माँ किस प्रकार शिक्षा देती है?
उत्तर:
माँ अपनी संतान को जागृत होने की शिक्षा देती है। वह जगाकर संघर्ष का मार्ग दिखताती और जीवन में संघर्ष करने के लिए प्रेरित करती है। इतना ही नहीं वह कर्तव्य निभाने की भी शिक्षा देती है। वह जीवन में होश के साथ कार्य करने की भी शिक्षा देती है।

प्रश्न 3.
कवि माँ से क्या कामना करता है? (M.P.2011)
उत्तर:
कवि माँ से कामना करता है कि वह वरदान स्वरूप ऐसी शक्ति प्रदान करें कि उसके आधार पर जीवन में आने वाली कठिनाइयों पर विजय प्राप्त कर सके। वह हार-जीत को समान भाव से ग्रहण कर सके। यही नहीं वह देश की उन्नति-प्रगति के लिए अपने स्वार्थों को त्यागकर समर्पित हो सके।

प्रश्न 4.
देश की जय के लिए कवि किस भाव का आकांक्षी है?
उत्तर:
देश की जय के लिए कवि अपनी हार, स्वार्थ, त्याग और बलिदान के भाव का आकांक्षी है।

प्रश्न 5.
कवि किस उद्देश्य के लिए जीवन देना चाहता है?
उत्तर:
कवि संसार को खुशहाल जीवन देने के लिए उद्देश्य से अपना जीवन देना चाहता है।

माँ भाव-विस्तार/पल्लवन

प्रश्न 1.
‘मेरी हार देश की जय हो’ का भाव-विस्तार कीजिए।
उत्तर:
कवि चाहता है कि जीवन संघर्ष में बेशक उसकी हार हो जाए, वह जीवन में प्रगति और उन्नति बेशक न कर पाए, किंतु देश सदैव विजयी हो, उसकी संघर्षों में सदैव विजय हो। मेरी व्यक्तिगत समस्याएँ हल हों या न हौं, लेकिन देश अपनी समस्त समस्याओं पर विजय प्राप्त कर, निरंतर उन्नति-प्रगति करता रहे। देश की विजय में ही उसकी स्वतंत्रता, अखंडता और एकता निहित होती है। उसकी विजय से जनता में खुशहाली, सुख और शांति आती है इसलिए व्यक्ति की बेशक हार हो जाए, लेकिन देश की हार नहीं होनी चाहिए।

माँ भाषा-अनुशीलन

प्रश्न 1.
निम्नलिखित समोच्चित शब्दों का वाक्य बनाकर अर्थ स्पष्ट कीजिएअनिल-अनल, फाँस-पाश, ह्रास-हास, नीर-नीड़, पवन-पावन।
उत्तर:

• अनिल – शीतल अनिल शरीर की थकान हर लेता है।
• अनल – यह तुम्हारी स्वार्थ की अनल तुम्हें जलाकर राख कर देगी।
• फाँस – मित्र के असत्य वचन मेरे लिए फाँस बन गए हैं।
• पाश-मोह – माया के पाश में बँधे हो और मुक्ति चाहते हो, कैसे संभव है।
• हास – जीवन में हास और त्रास मिलते रहते हैं।
• हास – जीवन में हास (हास्य) को महत्त्व दिया जाना चाहिए।
• नीर – महादेवी वर्मा ने कहा है, मैं नीर भरी दुख की बदली हूँ।
• नीड़ – इस वृक्ष पर पक्षी नीड़ों में बैठे विश्राम कर रहे हैं।
• पवन – प्रातःकाल का शीतल, मंद और सुगंधित पवन स्वान्मावर्धक होता है।
• पावन – गंगा पावन नदी है।

प्रश्न 2.
निम्नलिखित सामासिक शब्दों का विग्रह सहित नाम लिखिए –
कंटक पथ, दावानल, टालो-संभालो, गिरें-उठे।
उत्तर:

प्रश्न 3.
दिए गए मुहावरों का वाक्यों में प्रयोग कीजिए –
तिल-तिल कर जलना, गिर-गिर कर उठना, कंटक पथ पर चलना, लोरियाँ गाकर सुनाना, भैरवी गीत गाना।
उत्तर:

माँ योग्यता-विस्तार

प्रश्न 1.
माँ की आराधना विषयक अन्य गीतों को याद कर कक्षा में सुनाइए।
उत्तर:
छात्र स्वयं करें।

प्रश्न 2.
‘देश की जय’ के लिए अपने प्राणों की बलि चढ़ाने वाले अमर शहीदों की जानकारी संगृहीत कीजिए।
उत्तर:
छात्र स्वयं करें।

प्रश्न 3.
‘माँ’ विषय पर अपने विचार लिखिए तथा उसे कथा में सुनाइए।
उत्तर:
छात्र स्वयं करें।

माँ परीक्षोपयोगी अन्य महत्वपूर्ण प्रश्न

I. वस्तुनिष्ठ प्रश्न –

प्रश्न 1.
‘माँ’ कविता के कवि हैं –
(क) मनमोहन मदारिया
(ख) बालकवि वैरागी
(ग) मैथिलीशरण गुप्त
(घ) कवि सुदर्शन
उत्तर:
(ख) बालकवि वैरागी।

प्रश्न 2.
कवि किससे वरदान माँग रहा है –
(क) ईश्वर से
(ख) दुर्गा देवी से
(ग) माँ से
(घ) भगवान शिव से
उत्तर:
(ग) माँ से।

प्रश्न 3.
संसार को सुखद और सरल बनाने वाला भाव है –
(क) वात्सल्य भाव
(ख) भक्तिभाव
(ग) स्वार्थ भाव
(घ) अहिंसा भाव
उत्तर:
(क) वात्सल्य भाव।

प्रश्न 4.
माँ से व्यक्तित्व में पवन से…… का गुण निहित है –
(क) गंभीरता
(ख) व्यापकता
(ग) धैर्य
(घ) तीव्रता
उत्तर:
(ख) व्यापकता।

प्रश्न 5.
कवि को जीवन का अभिमान चाहिए ताकि वह –
(क) जीवन-मार्ग पर बढ़ता रहे
(ख) वह निराश न हो
(ग) जीवन-संघर्षों से घबराए
(घ) वह जीवन के संघर्षों पर विजय प्राप्त करे
उत्तर:
(घ) वह जीवन-संघर्षों में विजय प्राप्त करे।

प्रश्न 6.
मुसीबत के समय किसे याद करना चाहिए –
(क) ईश्वर को
(ख) माँ को
(ग) मित्र को
(घ) पिता को
उत्तर:
(ख) माँ को।

प्रश्न 7.
कवि को गुरुता का ज्ञान चाहिए; क्योंकि –
(क) वह जीवन की प्रेरणा बने
(ख) वह जीवन की आशा बने
(ग) वह जीवन का त्याग बने
(घ) वह जीवन की कठिनाई बने
उत्तर:
(क) वह जीवन की प्रेरणा बने।

प्रश्न 8.
जीवन के समस्त स्वार्थ त्यागकर…………के लिए समर्पित होना ही हमारा लक्ष्य है।
(क) मातृ-सेवा
(ख) राष्ट्र-सेवा
(ग) समाज-सेवा
(घ) प्रभु-सेवा
उत्तर:
(ख) राष्ट्र-सेवा।

प्रश्न 9.
कवि किससे वरदान की अपेक्षा करता है? (M.P. 2012)
(क) माँ से
(ख) गुरु से
(ग) प्रभु से
(घ) भाई से
उत्तर:
(क) माँ से।

प्रश्न 10.
‘माँ की भावनाओं में है –
(क) पहाड़ जैसी ऊँचाई
(ख) समुद्र जैसी चौड़ाई
(ग) धरती जैसा विस्तार
(घ) धरती जैसा धैर्य
उत्तर:
(घ) धरती जैसा धैर्य।

II. निम्नलिखित रिक्त स्थानों की पूर्ति दिए गए विकल्पों के आधार पर कीजिए –

1. तिल-तिलकर ………. जले। (मन/तन)
2. माँ ………. की रचना है। (मैथिलीशरण गुप्त/वालकवि ‘वैरागी’)
3. बालकवि ‘वैरागी’ ………. हैं। (आलोचक/कवि)
4. बाल कवि ‘वैरागी’ का जन्म ………. को हुआ था। (1931/1941)
5. कवि माँ से ………. की अपेक्षा करता है। (वरदान प्यार)

उत्तर:

1. तन
2. बालकवि ‘वैरागी’
3. कवि
4. 1931
5. वरदान।

III. निम्नलिखित कथनों में सत्य असत्य छाँटिए –

1. ‘माँ’ एक निबन्ध है।
2. ‘माँ’ संघर्ष का मार्ग दिखाती है।
3. ‘जल-जलकर जीवन’ में अनुप्रास अलंकार है।
4. बालकवि वैरागी का वास्तविक नाम नन्दरामदास वैरागी है।
5. मुसीबत में बस माँ का नाम लेना चाहिए।

उत्तर:

1. असत्य
2. सत्य
3. असत्य
4. सत्य
5. सत्य।

IV. निम्नलिखित के सही जोड़े मिलाइए –

प्रश्न 1.

उत्तर:

(i) (ङ)
(ii) (घ)
(iii) (ख)
(iv) (क)
(v) (ग)।

V. निम्नलिखित प्रश्नों के उत्तर एक शब्द या एक वाक्य में दीजिए –

प्रश्न 1.
माँ से कवि क्या चाहता है?
उत्तर:
वरदान।

प्रश्न 2.
माँ क्या गाकर सुलाती है?
उत्तर:
लोरियाँ।

प्रश्न 3
मुसीबत आने पर क्या करना चाहिए?
उत्तर:
माँ का नाम लेना चाहिए।

प्रश्न 4.
जीवन के संघर्षों में क्या होना चाहिए?
उत्तर:
होठों पर मुस्कान होनी चाहिए।

प्रश्न 5.
जीवन में क्या स्वाभाविक है?
उत्तर:
काँटों के रास्ते पर गिरना-बढ़ना और हार-जीत।

माँ लघु उत्तरीय प्रश्न

प्रश्न 1.
‘माँ’ कविता में किसके व्यक्तित्व को अभिव्यक्ति दी है?
उत्तर:
‘माँ’ कविता में माँ के विराट व्यक्तित्व को अभिव्यक्ति दी है।

प्रश्न 2.
‘माँ’ में पृथ्वी तत्त्व का कौन-सा गुण निहित है? (M.P. 2012)
उत्तर:
‘माँ’ में पृथ्वी तत्त्व का धैर्य गुण निहित है।

प्रश्न 3.
माँ का कौन-सा भाव संसार को सुखद और सरल बनाता है?
उत्तर:
माँ का वात्सल्य-भाव ही संसार को सुखद और सरल बनाता है।

प्रश्न 4.
जीवन-पथ कंटकमय होने पर भी कवि किसकी कामना करता है?
उत्तर:
जीवन-पथ कंटकमय होने पर भी कवि जीवन-मार्ग पर निरंतर गतिशील रहने की कामना करता है।

प्रश्न 5.
कवि किस पर विजय प्राप्त करना चाहता है?
उत्तर:
कवि जीवन में आने वाली कठिनाइयों पर विजय प्राप्त करना चाहता है।

प्रश्न 6.
‘माँ’ संसार की क्या है?
उत्तर:
माँ संसार की शुभकामना है।

प्रश्न 7.
कवि की माँ से एक कामना क्या है?
उत्तर:
कवि की माँ से एक कामना यह है कि उसके पैर हर क्षण गतिमान होने चाहिए।

प्रश्न 8.
उठ-उठकर गिरने और फिर उठने पर कवि को माँ से क्या चाहिए?
उत्तर:
उठ-उठकर गिरने और फिर उठने पर कवि को माँ से गुरुता का ज्ञान होने का वरदान चहिए।

माँ दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
माँ के व्यक्तित्व की विशेषताओं का उल्लेख कीजिए।
उत्तर:
माँ का व्यक्तित्व विराट है। उसके व्यक्तित्व में धैर्य, तीव्रता, व्यापकता और गंभीरता के साथ-साथ ममता, वात्सल्य आदि गुण निहित हैं। उसका व्यक्तित्व केवल स्नेहमयी है, अपितु वह अपनी संतान को जगाती है। संघर्ष करने की प्रेरणा देती है। वह कर्तव्य मार्ग पर चलने के प्रेरित करने वाली शक्ति है।

प्रश्न 2.
कवि कैसी माँ को अपनी स्मृतियों में बसाने की प्रेरणा देता है? (M.P. 2012)
उत्तर:
कवि धैर्यशाली, तीव्र प्रकाशयुक्त, गतिमयी व्यापकता और गंभीरता से युक्त स्नेहमयी, वात्सल्यमयी, संघर्ष का मार्ग दिखाने वाली तथा कर्तव्य के लिए प्रेरित करने वाली माँ को सदैव अपनी स्मृतियों में बसाने की प्रेरणा देता है।

प्रश्न 3.
कवि देश और जगत् के लिए क्या-क्या करने के लिए तैयार है?
उत्तर:
कवि देश के लिए अपनी हार स्वीकार करने के लिए तैयार है। वह अपने स्वार्थों को देश-सेवा के लिए त्यागने को तैयार है। जगत् के लिए वह अपना जीवन भी देने के लिए तैयार है।

प्रश्न 4.
कवि को कौन-सा सम्मान चाहिए?
उत्तर:
कवि को अपना स्वार्थ त्यागकर राष्ट्र सेवा के लिए समर्पित होने का ही सम्मान चाहिए। इस सम्मान के अतिरिक्त उसे कोई अन्य सम्मान नहीं चाहिए। यही सम्मान प्राप्त करना, उसके जीवन का लक्ष्य है। इसी लेंए वह कहता है-‘बस इतना सम्मान चाहिए।’

प्रश्न 5.
माँ का स्वरूप क्या है?
उत्तर:
माँ धरा का धैर्य है। वह आसमान की ज्योति है। वह आग की लपट है। वह हवा तीव्र गति है। वह पानी का गंभीर स्वर है। यही नहीं वह वत्सला है। वह वंदना है, वह जननी है और जन्मदात्री भी है।

प्रश्न 6.
कवि माँ से कब-कब वरदान चास’ है?
उत्तर:
कवि माँ से तब-तब वरदान चाह जब उसका जीवन काँटों से भर जाए, विपदाओं से घिर जाए, उसे हास मिले ना त्रास मिले, विश्वास मिले या फाँस मिले, उसके सामने काल ही आकर क्यों न गरजे, इस प्रकार के संकटमय और दुखमय जीवन में कवि माँ से वरदान चाहता है।

माँ कवि-परिचय

प्रश्न 1.
बालकवि वैरागी का संक्षिप्त जीवन-परिचय देते हुए उनकी साहित्यिक विशेषताओं पर प्रकाश डालिए।
उत्तर:
श्रीबालकवि वैरागी युगचेतना को ओजस्वी स्वर देने वाले आधुनिक युग के कवियों में सुप्रसिद्ध हैं।
जीवन-परिचय:
बालकवि वैरागी का जन्म मध्य प्रदेश के जिला मंदसोर के नीमच नामक स्थान में 10 फरवरी, सन् 1931 ई० को हुआ था। आपकी प्रारंभिक शिक्षा स्थानीय विद्यालयों में हुई। इसके उपरान्त आपने विक्रम विश्वविद्यालय, उज्जैन से एम.ए. हिंदी की परीक्षा प्रथम श्रेणी में उत्तीर्ण की। इस प्रकार आपने एक मेधावी छात्र होने का परिचय दिया। आपने शिक्षा-समाप्ति के उपरांत साहित्य और राजनीति दोनों में ही दखल देना शुरू कर दिया। आप मध्य प्रदेश के एक सम्मानित विधायक और सांसद होने के साथ साथ आप मध्य प्रदेश सरकार में मंत्री भी रह चुके हैं किंतु आपने साहित्य-सृजन को नहीं छोड़ा। आपकी कविताएँ राजनीतिक क्षितिज से उठकर जन-सामान्य के दुख-दर्द और आशा-आकांक्षाओं से जड़ी रही हैं।

रचनाएँ:
बालकवि वैरागी की रचनाएँ मुख्य रूप से काव्य ही हैं। अब तक आपके कई काव्य-संग्रह प्रकाशित हो चुके हैं। आपके निम्नलिखित काव्य-संग्रह हैं –

‘दरद दीवानी’, ‘जूझ रहा है हिन्दुस्तान’, ‘गौरव-गीत’, ‘भावी रक्षक देश के’, ‘दो टूक’, ‘दादी का कर्ज’, ‘रेत के रिश्ते’, ‘कोई तो समझें’, ‘शीलवती आग’, ‘गाओ बच्चों’, ‘पुलिवर’ (पद्यानुवाद), ‘वंशज का वक्तव्य’, ‘ओ अमलतास’ आदि। . इनके अतिरिक्त ‘चटक म्हारा चम्पा’ मालवीय काव्य-संग्रह भी बालकवि ‘वैरागी’ का एक जीवंत और सशक्त प्रकाशित काव्य-संग्रह हैं।

बालकवि वैरागी की कार्यशैली ‘गद्य’ विधा में भी है। कुछ प्रकाशित गद्य रचनाओं के उल्लेख इस प्रकार किए जा सकते हैं-गद्य सरपंच (सहयोगी उपन्यास), ‘कच्छ का पदयात्री’ (यात्रा-संस्मरण), ‘बर्लिन से बच्चू को’ (विदेशी यात्रा के पत्र) आदि।’

भाषा-शैली:
बालकवि वैरागी की भाषा-शैली में एकरूपता है। दूसरे शब्दों में, हम यह कह सकते हैं कि कविवर बालकवि की भाषा और शैली में काव्यात्मकता है। दूसरे शब्दों में, बालकवि वैरागी जी मूलतः कवि हैं, अतएव उनकी भाषा-शैली का काव्यमयी होना स्वाभाविक है। आपकी भाषा-शैली संबंधित निम्नलिखित विशेषताएँ हैं –

1. भाषा:
बालकवि वैरागी की भाषा मध्यस्तरीय काव्यमयी भाषा है। उसमें मुहावरों, कहावतों के प्रयोग आवश्यकतानुसार हुए हैं। इस प्रकार की भाषा में आए शब्द प्रायः तद्भव श्रेणी के हैं। इस प्रकार से यह कहा जा सकता है कि तत्सम शब्द और विदेशी शब्दों की तुलना में प्रयुक्त देशज शब्द बहुत अधिक हैं। इनके बाद ही उर्दू के प्रचलित शब्द प्रयुक्त हुए। इस प्रकार से बने हुए शब्दों से वाच्यार्थ और विषय के प्रतिपादन बहुत अच्छी तरह से हुए हैं।

2. शैली:
बालकवि वैरागी की शैली मुख्य रूप से काव्यमयी है। अतः उसमें अलंकारिता, चमत्कारिता और रसात्मकता जैसे स्वाभाविक और आवश्यक गुण सर्वत्र दिखाई देते हैं। इस प्रकार की शैली में प्रयुक्त हुए अलंकारों में मुख्य रूप से अनुप्रास, रूपक, स्वभावोक्ति और दृष्टांत अलंकार हैं। आपकी रचनाधारा को प्रवाहित करने वाले रस मुख्य रूप से वीररस, करुणरत, रौद्ररस आदि हैं। आपकी कविताओं में संगीतात्मकता और लयात्मकता ये दोनों ही गुण सर्वत्र दिखाई देते हैं।

महत्त्व:
बालकवि वैरागी का आधुनिक हिंदी कविता धारा का राष्ट्रीय तरंगित भावोत्थान में एक विशिष्ट और सुपरिचित स्थान है। राष्ट्र-प्रेम के भावों से भीग-भीगकर राष्ट्र के प्रति अपार प्रेम दिखलाने वाले आप बहुत ऊँचे कवि हैं। कविताओं के अतिरिक्त गद्य-रचना के क्षेत्र में भी आपकी बड़ी शान और मान है। इस प्रकार बालकवि वैरागी आधुनिक हिंदी काव्य-जगत के एक उज्ज्वल और प्रकाशवान रचनाकार हैं। आपका साहित्यिक महत्त्वांकन करके ही आपको राजसभा के मनोनीत सदस्य के रूप में चुना गया। अभी आपसे अनेक साहित्यिक उपलब्धियों की अपेक्षाएँ हैं।

‘माँ’ पाठ का सारांश

प्रश्न 1.
‘माँ’ कविता का सार अपने शब्दों में लिखिए।
उत्तर:
‘माँ’ कविता बालकवि वैरागी द्वारा रचित है। इस कविता में कवि ने माँ के विराट व्यक्तित्व को अनुभूति के स्तर पर अभिव्यक्ति दी है। माँ में धरती के जैसा धैर्य, उसमें आकाश ज्योति की तीव्रता है, पवन की गतिमयी व्यापकता है और जल जैसी गंभीरता है। वह वात्सल्य भाव से भरी हुई पूजनीय है। माँ जन्म देने वाली है और वह संसार को सुखद और सरल बनाने वाली है।

कवि कहता है कि माँ का व्यक्तित्व केवल स्नेह का पर्याय नहीं है। वह लोरियाँ गाकर सुलाती है तो वह जगाती भी है और संघर्ष का मार्ग भी दिखलाती है। माँ पालन-पोषण करने वाली शक्ति भी है तो वह कर्तव्य के लिए प्रेरित करने वाली शक्ति भी है। माँ कहती है कि मुझे बहाने बनाकर टालने का प्रयास मत करो, होश से काम लो और जब कभी मुसीबत आए तो तुम केवल माँ को याद करो। तुम ऐसी माँ को सदैव स्मृतियों में बसाकर रखो।

दूसरी कविता ‘माँ बस यह वरदान चाहिए’ है। इस कविता में कवि माँ से वरदान स्वरूप वह शक्ति माँगता है, जिसके आधार पर जीवन में आने वाली कठिनाइयों पर विजय प्राप्त की जा सके। कवि चाहता है कि उसकी यही इच्छा है कि उसका प्रत्येक पग गतिशील रहे। उसे जीवन में हास मिले या त्रास मिले, विश्वास प्राप्त हो या विश्वासघात प्राप्त हो और चाहे उसके सामने मृत्यु ही क्यों न आ जाए, लेकिन जीवन के इन विरोधों के बीच भी स्वाभिमान जागृत रहे।

कष्टों में भी जीवन की प्रसन्नता बनी रहे। काँटोंभरे रास्तों पर गिरना, चढ़ना और हार-जीत स्वाभाविक हैं, किंतु फिर भी जीवन में बड़प्पन, गंभीरता का भाव बना रहे। हार-जीत को समान भाव से ग्रहण करने का ज्ञान हमारे जीवन की प्रेरणा बने। हम सदा देश की उन्नति के लिए क्रियाशील रहें। इस हेतु जीवन से समस्त स्वार्थ त्यागकर राष्ट्र-सेवा के लिए. समर्पित होना ही हमारा लक्ष्य रहे। यही जीवन का सबसे बड़ा सम्मान है। कवि माँ से ऐसे ही वरदान की अपेक्षा करता है।

माँ संदर्भ-प्रसंगसहित व्याख्या

प्रश्न 1.
मैं धरा का धैर्य हूँ
ज्योति हूँ मैं ही गगन की
अग्नि की मैं ही लपट हूँ
तीव्र गति हूँ मैं पवन की
नीर का गंभीर स्वर हूँ,
वत्सला हूँ-वंदना हूँ ,
मैं जननि हूँ-जन्मदात्री
विश्व की शुभकामना हूँ। (Page 86) (M.P. 2011)

शब्दार्थ:

• धरा – पृथ्वी, जमीन, धरती।
• ज्योति – प्रकाश।
• गगन – आकाश।
• अग्नि – आग।
• तीव्र – तेज।
• गति – चाल।
• पवन – वायु।
• नीर – पानी, जल।
• वत्सला – ममतामयी, स्नेहमयी।
• वंदना – प्रार्थना, पूजन।
• जननि – जन्म देने वाली।
• विश्व – संसार।
• शुभकामना – अच्छी इच्छा।

प्रसंग:
प्रस्तुत काव्यांश बालकवि वैरागी द्वारा रचित कविता ‘माँ’ से उद्धृत है। कवि माँ के विराट व्यक्तित्व को अनुभूति के स्तर पर अभिव्यक्त करते हुए कहता है कि-माँ की भावनाओं में धैर्य, तीव्र गति और गंभीरता है। इन्हीं भावों को इस काव्यांश में व्यक्त किया गया है।

व्याख्या:
कवि कहता है कि माँ के लिए विराट व्यक्तित्व में अनेक भावनाएँ निहित हैं। माँ कहती है कि मेरी भावनाओं में धरती के जैसा धैर्य है; अर्थात् मेरे व्यक्तित्व पृथ्वी के समान धैर्य हैं। मैं अत्यंत धैर्यवान हूँ। मैं ही आकाश की ज्योति हूँ। मैं ही आग की लपट हूँ और मुझ में ही वायु की गति व्यापक है। मुझ में ही जल की गंभीरता है। मैं ममतामयी, स्नेहमयी और पूजनीय हूँ। मैं जन्म देने वाली माता हूँ। मेरा वात्सल्य भाव से ही संसार को सुखद और सरल बनाने वाली हूँ। कहने का भाव यह है कि माँ का व्यक्तित्व विराट है। उसके व्यक्तित्व में धरती के समान धैर्य, तीव्रता, पवन की गतिमयी व्यापकता और गंभीरता है। वह स्नेहमयी, पूजनीय और जन्म देने वाली माँ हैं। वह पूजनीय है। उसमें विश्व का कल्याण को चाहने की कामना है।

विशेष:

1. माँ के विराट व्यक्तित्व का चित्रण किया गया है।
2. माँ के व्यक्तित्व में अनेक गुणों का समावेश है।
3. तत्सम शब्दावली युक्त खड़ी बोली है।
4. तुकांतात्मकता और लयात्मकता है।
5. ‘मैं धरा का धैर्य हूँ’ में उदाहरण अलंकार है।
6. ‘वत्सला हूँ-वंदना हूँ’ में अनुप्रास अलंकार है।
7. रूपक अलंकार है।
8. विशेषणों का सार्थक प्रयोग किया गया है।

पद्य पर आधारित विषय-वस्तु से संबंधित प्रश्नोत्तर

प्रश्न (i)
कवि और कविता का नाम लिखिए।
उत्तर:
कवि-बालकवि वैरागी, कविता-‘माँ’।

प्रश्न (ii)
कविता में किसके व्यक्तित्व का अभिव्यक्ति हुई है?
उत्तर:
कविता में माँ के विराट व्यक्तित्व की अभिव्यक्ति हुई है।

प्रश्न (iii)
माँ के व्यक्तित्व में क्या निहित है?
उत्तर:
माँ के व्यक्तित्व में पृथ्वी जैसा धैर्य, आकाश की तीव्रता, पवन की गतिमयी व्यापकता और जल जैसी गंभीरता और वात्सल्य भाव निहित हैं।

पद्य पर आधारित सौंदर्य संबंधित प्रश्नोत्तर

प्रश्न (i)
प्रस्तुत पद्य के भाव-सौंदर्य पर प्रकाश डालिए।
उत्तर:
भाव-सौंदर्य:
कवि ने इस पद्य में माँ के विराट व्यक्तित्व को अनुभूति के स्तर पर अभिव्यक्ति दी है। उसके व्यक्तित्व में धैर्य, तेजी, व्यापकता, गंभीरता और वात्सल्य भावना निहित है। वह पूजनीय है।

प्रश्न (ii)
प्रस्तुत पद्य के काव्य-सौंदर्य पर प्रकाश डालिए।
उत्तर:
काव्य-सौंदर्य:
पद्य की भाषा तत्सम शब्दावली युक्त खड़ी बोली है। ‘धरा का धैर्य हूँ’ में उदाहरण अलंकार है। ‘वत्सला हूँ-वंदना हूँ’ में अनुप्रास अलंकार है। छंदबद्ध रचना में तुकांतात्मकता और लयात्मकता है। शांतरस है। पद्य में माँ का विराट रूप साकार हो उठा है। शब्द चयन सटीक और भावानुकूल है। विशेषणों का सार्थक प्रयोग हुआ है।

प्रश्न 2.
लोरियाँ गाकर सुलाया
अब जगाती हूँ तुम्हें,
भैरवी गाओ-उठो!
रस्ता दिखाती हूँ तुम्हें
मत मुझे टालो-सम्हालो,
होश से कुछ काम लो,
जब कभी आए मुसीबत
सिर्फ माँ का नाम लो। (Page 86)

शब्दार्थ:

• लोरियाँ – बच्चों को सुलाने के समय गाया जाने वाला गीत।
• भैरवी – एक राग।

प्रसंग:
प्रस्तुत पद्यांश बालकवि ‘वैरागी’ द्वारा रचित कविता ‘माँ’ से उद्धृत है। कवि माँ के विराट स्वरूप को व्यक्त करते हुए कहता है।

व्याख्या:
कवि कहता है कि माँ का व्यक्तित्व केवल स्नेहमयी, ममतामयी ही नहीं है अपितु माँ अपने बच्चों को गीत गाकर सुलाती है, तो वह जगाती भी है। वह भैरवी राग गाकर, दुर्गा की भाँति उठाती भी है और जीवन में संघर्ष का मार्ग भी दिखाती है। वह कहती है कि तुम मुझे विभिन्न प्रकार बहाने करके टालने का प्रयास मत करो। उठो, और संघर्ष करो। कुछ होश से कार्य करो अर्थात् माँ पालित-पोषित करने वाली ममता है, तो वह कर्तव्य के लिए प्रेरित करने वाली शक्ति भी है। कवि कहता है कि जब भी तुम पर कोई मुसीबत आए, तो तुम केवल माँ को याद करो। उसका नाम लो, तुम्हें संकट से छुटकारा मिलेगा। ऐसी माँ को सदा अपनी स्मृतियों में बसाए रखो।

विशेष:

1. कवि ने माँ व्यक्तित्व की विशेषताओं का वर्णन किया है।
2. तत्सम शब्दावली युक्त खड़ी बोली है।
3. तुकांतात्मकता और लयात्मकता है।
4. ‘कुछ काम’ में अनुप्रास अलंकार है।
5. ‘टालो-सम्हालो’ में पद-मैत्री है।
6. माँ को शक्ति के रूप में चित्रण किया गया है।

पद्य पर आधारित विषय-वस्तु से संबंधित प्रश्नोत्तर

प्रश्न (i)
कवि और कविता का नाम लिखिए।
उत्तर:
कवि-बालकवि ‘वैरागी’। कविता-‘माँ’

प्रश्न (ii)
‘माँ’ को किस रूप में चित्रित किया गया है?
उत्तर:
माँ को अपनी संतान का पालन-पोषण करने वाली ममतामयी माता के रूप में तथा कर्तव्य के लिए प्रेरित करने वाली शक्ति के रूप में चित्रित किया है।

प्रश्न (iii)
इस पद्य में कवि ने क्या प्रेरणा दी है?
उत्तर:
इस पद्य में कवि ने माँ को सदा अपनी स्मृतियों में वसाने की प्रेरणा दी है।

पद्यांश पर आधारित काव्य-सौंदर्य संबंधित प्रश्नोत्तर

प्रश्न (i)
प्रस्तुत काव्यांश का भाव-सौंदर्य लिखिए।
उत्तर:
प्रस्तुत काव्यांश में कवि ने माँ के विराट व्यक्तित्व को अभिव्यक्ति दी है। माँ एक ओर अपनी संतान का स्नेहपूर्वक पालन-पोषण करती है। अपनी संतान को लोरी गाकर सुलाती है, तो दूसरी ओर वह उसे जगाती है और संघर्ष का मार्ग भी दिखलाती है। वह ममतामयी भी है तो कर्तव्य के लिए प्रेरित करने वाली शक्ति भी है। हमें ऐसी माँ को सदैव स्मृतियों में बसाए रखना चाहिए।

प्रश्न (ii)
प्रस्तुत काव्यांश का शिल्प-सौंदर्य स्पष्ट कीजिए।
उत्तर:
इस पद्यांश की भाषा तत्सम शब्दावलीयुक्त खड़ी बोली हैं। छंदबद्ध रचना है। तुकांतात्मकता और लयात्मकता है। ‘मत मुझे’ ‘कुछ काम’ में अनुप्रास अलंकार है। शब्द-चयन में मितव्ययता और सटीकता है। ‘टालो-सम्हालो’ में पद-मैत्री है।

प्रश्न 3.
माँ बस यह वरदान चाहिए!
जीवन-पथ जो कंटकमय हो,
विपदाओं का घोर वलय हो,
किंतु कामना एक यही बस,
प्रतिपल पग गतिमान चाहिए। (M.P. 2010)

ह्रास मिले या त्रास मिले,
विश्वास मिले या फाँस मिले,
गरजे क्यों न काल ही सम्मुख
जीवन का अभिमान चाहिए। (Page 86)

शब्दार्थ:

• वरदान – किसी को इष्ट वस्तु देना।
• जीवन-पथ – जीवन रूपी रास्ता।
• कंटकमय – काँटों से भरा।
• विपदाओं – संकटों।
• वलय – घेरा।
• कामना – इच्छा, अभिलाषा।
• हास – हानि।
• त्रास – कष्ट।
• विपत्ति – फाँस।
• काल – मृत्यु।

प्रसंग:
प्रस्तुत काव्यांश बालकवि वैरागी द्वारा रचित ‘संकलित’ कविता से उद्धृत है। इस कविता में कवि द्वारा माँ से वरदानस्वरूप वह शक्ति माँगी गई है, जिसके आधार पर जीवन में आने वाली कठिनाइयों पर विजय प्राप्त की जा सके।

व्याख्या:
कवि माँ से कहता है कि हे माँ! मुझे केवल आपसे यही वरदान चाहिए कि चाहे जीवन रूपी मार्ग काँटों से भरा हो और मेरा जीवन विभिन्न प्रकार के कष्टों और संकटों में क्यों न घिरा हो, फिर भी मेरी यही अभिलाषा है कि मैं समस्त, दुखों, कष्टों और संकटों से संघर्ष करता हुआ हर क्षण नितर आगे बढ़ता रहूँ।

मुझे जीवन रूप मार्ग आगे बढ़ते हुए चाहे हानि प्राप्त हो अथवा कष्टों विपत्तियों का सामना करना पड़े, जीवन में विश्वास प्राप्त हो अथवा मेरी अपघात (विश्वासघात) हो, चाहे मेरे सामने साक्षात् मृत्यु ही क्यों न आ जाए, किंतु ‘सी स्थिति में भी मेरा स्वाभिामान बना रहना चाहिए। कहने का भाव यह कि कवि माँ से ऐसा वरदान चाहता है कि जीवन-मार्ग में आगे बढ़ते हुए आने वाली कठिनाइयों ५ विजय प्राप्त कर ..सके। जीवन के समस्त विरोधों के बावजूद स्वाभिमान जागृत र।

विशेष:

1. कवि ने माँ से ऐसा वरदान देने की कामना की है जिससे जीवन के कष्टों के बीच भी उसका स्वाभिमान बना रहे।
2. ‘जीवन-पथ’ में रूपक अलंकार है।
3. ‘किंतु कामना और प्रतिफल पग’ में अनुप्रास अलंकार है।
4. ह्रास मिले…या फाँस मिले, में संदेह अलंकार है।
5. ह्रास और त्रास क्रमशः हानि और कष्ट के प्रतीक हैं।
6. भाषा तत्सम शब्दावलीयुक्त परिमार्जित खड़ी बोली है।
7. तुकांतात्मकता और लयात्मकता है।
8. विशेषणों का सार्थक प्रयोग किया गया है।

काव्यांश पर आधारित विषय-वस्तु से संबंधित प्रश्नोत्तर

प्रश्न (i)
कविता का नाम लिखिए।
उत्तर:
कविता-‘माँ बस यह वरदान चाहिए’।

प्रश्न (ii)
कवि माँ से क्या चाहता है और क्यों?
उत्तर:
कवि माँ से ऐसा वरदान चाहता है, जिसके द्वारा जीवन में आने वाली समस्त कठिनाइयों पर विजय प्राप्त कर सके।

प्रश्न (iii)
कवि ने माँ से क्या वरदान देने की कामना की है?
उत्तर:
कवि ने माँ से बस ऐसा वरदान देने की कामना की है कि उसे जीवन में चाहे हानि प्राप्त हो या कष्ट, विपत्ति मिले, या फिर विश्वास प्राप्त हो या विश्वासघात प्राप्त हो किंतु जीवन के इन कष्टों के मध्य भी जीवन में स्वाभिमान सदा बना रहे।

काव्यांश पर आधारित सौंदर्य-बोध संबंधित प्रश्नोत्तर

प्रश्न (i)
प्रस्तुत काव्यांश का भाव-सौंदर्य स्पष्ट कीजिए?
उत्तर:
भाव-सौंदर्य-इस कविता में कवि माँ से वरदान प्राप्त करना चाहता है कि जिसके द्वारा वह जीवन में आने वाली कठिनाइयों पर विजय प्राप्त करने में सफल हो। वह यह भी चाहता है कि उसे जीवन के सभी लाभ-हानि, विश्वासघातों, कष्टों, विपत्तियों और विरोधों के बीच स्वाभिमान बना रहे।

प्रश्न (ii)
काव्य-सौंदर्य स्पष्ट कीजिए।
उत्तर:
काव्य-सौंदर्य:
‘जीवन-पथ’ में रूपक अलंकार है। किंतु कामना, प्रतिपल पग में अनुप्रास अलंकार है। ह्रास मिले…फाँस मिले में संदेह अलंकार है। ह्रास और त्रास क्रमशः हानि और कष्ट के प्रतीक हैं। तुकांतात्मकता और लयात्मकता है। विशेषणों का सार्थक प्रयोग है। भाषा तत्सम शब्दावली युक्त परिमार्जित खड़ी बोली है।

प्रश्न (iii)
कवि किससे और क्या माँग रहा है?
उत्तर:
कवि माँ से वरदान स्वरूप ऐसी शक्ति माँग रहा है जिसके बल पर वह जीवन में आने वाली कठिनाइयों पर विजय प्राप्त कर सके।

प्रश्न 4.
जीवन के इन संघर्षों में
दुःख कष्ट के दावानल में
तिल तिलकर तन जले न क्यों पर,
होठों पर मुस्कान चाहिए।

कंटक पथ पर गिरना, चढ़ना,
स्वाभाविक है हार जीतना,
उठ-उठ कर हम गिरें, उठे फिर
पर गुरुता का ज्ञान चाहिए। (Page 87)

शब्दार्थ:

• दावानल – जंगल की आग।
• तन – शरीर।
• मुस्कान – हँसी, प्रसन्नता।
• गुरुता – बड़प्पन, गंभीरता।

प्रसंग:
प्रस्तुत काव्यांश बालकवि वैरागी द्वारा रचित ‘संकलित कविता’ से उद्धृत है। इस काव्यांश में कवि माँ से वरदान स्वरूप ऐसी शक्ति की कामना करता है कि कष्टों में भी जीवन का प्रसन्नता बनी रहे, यह स्पष्ट किया है।

व्याख्या:
कवि माँ से कामना करता है कि वरदान स्वरूप ऐसी शक्ति प्रदान करे कि जीवन मार्ग पर बढ़ते हुए जीवन के संघर्षों में दुख और कष्टों की जंगल की आग में यह शरीर थोड़ा-थोड़ा जलकर क्यों न जले किंतु इन समस्त कष्टों-दुखों में भी जीवन की प्रसन्नता समाप्त न हो। अर्थात् कवि चाहता है कि जीवन में कष्टों और दुखों के कारण यह शरीर धीरे-धीरे नष्ट क्यों न हो जाए किंतु होंठों पर सदा मुस्कान बनी रहनी चाहिए।

मुख पर निराशा या पीड़ा के भाव नहीं आने चाहिए। काँटों और दुखों, विपत्तियों से भरे जीवन मार्ग पर बढ़ते हुए अवनति की ओर जाना और फिर उठकर चढ़ना तथा जीवन में हार-जीत आना तो स्वाभाविक प्रक्रिया है। जीवन-मार्ग पर चलते हुए हम गिरें, उठें और फिर उठें और गिरें। ऐसी स्थिति में भी मन में सदैव गंभीरता बनी रहे। जीवन में हार-जीत तो होती रहती है। किंतु हमें हार-जीत को समान भाव से ग्रहण करने की शक्ति प्रदान करें। हार-जीत को समान भाव से ग्रहण करने का ज्ञान हमारे जीवन की प्रेरणा बने।

विशेष:

1. कवि चाहता है कि माँ वरदान स्वरूप ऐसी शक्ति प्रदान करें कि कष्टमय जीवन व्यतीत करते हुए भी प्रसन्नता का भाव बना रहे।
2. कवि हार-जीत को समान भाव से ग्रहण करने की क्षमता चाहता है।
3. तिल-तिलकर तन में अनुप्रास अलंकार है।
4. ‘तिल-तिलकर जलना’ मुहावरे का सटीक प्रयोग किया है।
5. ‘दुख कष्ट के साथ दावानल’ में रूपक अलंकार है।
6. ‘गिरना’ अवनति का और ‘चढ़ना’ प्रगति, उन्नति का प्रतीक है।
7. ‘उठ-उठ’ में पुनरुक्तिप्रकाश अलंकार है।
8. भाषा तत्सम शब्दावली युक्त खड़ी बोली है।

काव्यांश पर आधारित विषय-वस्तु से संबंधित प्रश्नोत्तर

प्रश्न (i)
कविता का नाम लिखिए।
उत्तर:
संकलित कविता।

प्रश्न (ii)
कंटक पथ पर गिरना, चढ़ना का प्रतिकार्थ स्पष्ट कीजिए।
उत्तर:
‘कंटक पथ’ दुखों और कष्टों से भरे जीवन पथ का प्रतीक है, तो ‘गिरना’.. अवनति का और ‘चढ़ना’ उन्नति प्रगति का प्रतीक। कवि कहना चाहता है कि हम दुखों और कष्टों से भरे जीवन मार्ग पर बढ़ते हुए संघर्ष द्वारा जीवन में उन्नति-प्रगति करें, किंतु हम इन्हें समान भाव से ग्रहण करें और हमारे मुख पर कभी निराशा का भाव न आने पाए।

प्रश्न (iii)
कवि को गुरुता का ज्ञान क्यों चाहिए?
उत्तर:
कवि को गुरुता का ज्ञान इसलिए चाहिए, ताकि वह हार-जीत को समान भाव से ग्रहण कर सके और उसमें जीवन की प्रेरणा बनी रहे।

काव्यांश पर आधारित काव्य-सौंदर्य से संबंधित प्रश्नोत्तर

प्रश्न (i)
काव्यांश के भाव-सौंदर्य पर प्रकाश डालिए।
उत्तर:
भाव-सौंदर्य:
इस काव्यांश में कवि ने जीवन कष्टों में भी प्रसन्नता बनी रहने की कामना व्यक्त की है। इसके साथ ही जीवन में हार-जीत को समान भाव से ग्रहण करने का वरदान माँ से प्राप्त करना चाहता है। उसकी इच्छा है कि उसमें जीवन की प्रेरणा सदैव बनी रहे।

प्रश्न (ii)
काव्यांश का शिल्प-सौंदर्य स्पष्ट कीजिए।
उत्तर:
शिल्प-सौंदर्य:
‘तिल-तिलकर तन’ में अनुप्रास अलंकार है। ‘तिल-तिलकर जलना’ मुहावरे का सटीक प्रयोग किया गया है। ‘दुख-कष्ट के दावानल’ में रूपक अलंकार है। गिरना और चढ़ना क्रमश जीवन में अवनति का और उन्नति प्रगति का प्रतीक है। ‘उठ-उठ’ में पुनरुक्तिप्रकाश अलंकार है। भाषा तत्सम शब्दावली युक्त खड़ी बोली है।

प्रश्न 5.
मेरी हार देश की जय हो,
स्वार्थ-भाव का क्षण-क्षण क्षय हो,
जल-जल कर जीवन दूं जग को,
बस इतना सम्मान चाहिए।
माँ बस यह वरदान चाहिए
माँ बस यह वरदान चाहिए! (Page 87)

शब्दार्थ:

• हार – पराजय।
• जय – विजय।
• क्षय – कम होना, नष्ट होना।
• जग – संसार।

प्रसंग:
प्रस्तुत काव्यांश बालकवि वैरागी द्वारा रचित ‘संकलित कविता’ से उद्धृत है। कवि इस काव्यांश में माँ से वरदानस्वरूप ऐसी शक्ति की कामना करता है जिसके द्वारा वह अपने समस्त स्वार्थ त्याग कर राष्ट्र-सेवा के लिए समर्पित हो सके।

व्याख्या:
कवि कहता है कि हे माँ! तुम हमें वरदानस्वरूप वह शक्ति प्रदान करो, जिससे हम सदैव देश की उन्नति और प्रगति के लिए क्रियाशील रहें। इसमें हमारी बेशक पराजय हो लेकिन देश की विजय हो। अर्थात् हम अपने जीवन में उन्नति और प्रगति करें या न करें लेकिन देश की उन्नति और प्रगति हो। हमारे स्वार्थ मानों का हर क्षण क्षय हो भाव यह कि हम अपने समस्त स्वार्थ त्यागकर राष्ट्र सेवा में लगे रहें। हम जल-जल कर जीवन को जग के लिए समर्पित कर दें। हमारा लक्ष्य यही रहे, यही जीवन का सबसे बड़ा सम्मान है। माँ, हमें वरदान स्वरूप यही शक्ति प्रदान करो। इसके अतिरिक्त हमें और कुछ नहीं चाहिए।

विशेष:

1. देश-सेवा के लिए समर्पित होने का वरदान कवि माँ से चाहता है।
2. कवि अपनी हार में देश की विजय चाहता है।
3. ‘स्वार्थ-भाव’ में रूपक अलंकार है।
4. क्षण-क्षण क्षय, जल-जल में अनुप्रास अलंकार है।
5. क्षण-क्षण, जल-जल में पुनरुक्तिप्रकाश अलंकार है।
6. भाषा तत्सम शब्दावली युक्त खड़ी बोली है।

काव्यांश पर आधारित विषय-वस्तु से संबंधित प्रश्नोत्तर

प्रश्न (i)
इस काव्यांश में कवि माँ से क्या वरदान चाहता है?
उत्तर:
इस काव्यांश में कवि सदैव देश की उन्नति और विकास के लिए क्रियाशील रहने का वरदान चाहता है।

प्रश्न (ii)
कवि ने अपना जीवन-लक्ष्य क्या बताया है?
उत्तर:
कवि ने देश की उन्नति और प्रगति हेतु जीवन के समस्त स्वार्थ त्यागकर राष्ट्र-सेवा के लिए समर्पित होना ही अपने जीवन का लक्ष्य बताया है।

प्रश्न (iii)
जीवन का सबसे बड़ा सम्मान क्या है?
उत्तर:
अपने जीवन से समस्त स्वार्थ त्यागकर देश की उन्नति-प्रगति के समर्पित हो जाना ही जीवन का सबसे बड़ा सम्मान है।

काव्यांश पर आधारित काव्य-सौंदर्य से संबंधित प्रश्नोत्तर

प्रश्न (i)
काव्यांश का भाव-सौंदर्य स्पष्ट कीजिए।
उत्तर:
इस काव्यांश में कवि अपनी जीत की अपेक्षा देश की जीत चाहता है। वह चाहता है कि उसका देश उन्नति और प्रगति करे। इसके लिए वह अपने स्वार्थ त्याग कर राष्ट्र सेवा में जुट जाने का भाव व्यक्त कर रहा है। राष्ट्र सेवा में समर्पित होना ही उसके जीवन का लक्ष्य और सबसे बड़ा सम्मान है। कवि माँ से ऐसे ही वरदान की अपेक्षा करता है।

प्रश्न (ii)
काव्यांश का शिल्प-सौंदर्य स्पष्ट कीजिए।
उत्तर:
कवि की राष्ट्र-सेवा की भावना को अभिव्यक्ति मिली है। ‘स्वार्थ-भाव’ में रूपक अलंकार है। ‘क्षण-क्षण-क्षय’, ‘जल-जल’ में अनुप्रास अलंकार है। ‘क्षण-क्षण, जल-जल’ में पुनरुक्तिप्रकाश है। ‘माँ बस यह वरदान’ पंक्ति की पुनरावृत्ति है। काव्यांश की भाषा तत्सम शब्दावली युक्त खड़ी बोली है।

MP Board Class 12th Hindi Solutions

MP Board Class 8th Science Solutions Chapter 15 Some Natural Phenomena

Select the correct option in questions 1. and 2.

Question 1.
Which of the following cannot be changed easily by friction?
(a) A plastic scale
(b) A copper rod
(c) An inflated balloon
(d) A woolen cloth.
Answer:
(b) A copper rod

Question 2.
When a glass rod is rubbed with a piece of silk cloth the rod
(a) And the cloth both acquire positive charge.
(b) Becomes positively charged while the cloth has a negative charge.
(c) And the cloth both acquire negative charge.
(d) Becomes negatively charged while the cloth has a positive charge.
Answer:
(b) Becomes positively charged while the cloth has a negative charge.

Question 3.
Write ‘T against true and ‘F’ against False in the following statements:

1. Like charges attract each other.
2. A charged glass rod attract a charged plastic straw.
3. Lightning conductor cannot protect a building from lightning.
4. Earthquakes can be predicted in advance.

Answer:

1. False
2. True
3. False
4. False.

Question 4.
Sometimes, a crackling sound is heard while taking off sweater during winters. Explain.
Answer:
This occurs due to electric discharge between sweater and body. Some energy is always released with electric discharge, which in this case is released in the form of a crackling sound.

Question 5.
Explain why a charged body loses its charge if we touch it with our hand.
Answer:
When we touch a charged body, it loses its charge due to the process of earthing. Our body is a good conductor of electricity and transfers the charges to the earth.

Question 6.
Name the scale on which the destructive energy of an earthquake is measured. An earthquake measures 3 on this scale. Would it be recorded by a seismograph? Is it likely to cause much damage?
Answer:
The destructive energy of an earthquake is measured on Richter Scale. The magnitude 3 on this scale can be recorded by a seismograph. Such an earthquake rarely causes damage.

Question 7.
Suggest three measures to protect ourselves from lightning.
Answer:
Three measures to protect from lightning:

1. Find a safe place like a house or a building. If travelling by a bus or by a car, stay inside with windows and doors of the vehicle shut.
2. If outside, take shelter under shorter trees. Stay away from tall trees and poles. Do not lie on the ground but sit placing your hands on your knees, with your head between the hands.
3. If inside, avoid bathing, unplugging electric appliances like TV, computer and switching off air conditioners.

Question 8.
Explain why a charged balloon is repelled by another charged balloon whereas an uncharged balloon is attracted by another charged balloon?
Answer:
A charged balloon is repelled by another charged balloon because both have the same charge. And we know similar charges repel each other. But a charged balloon attracts an uncharged balloon and lose its own charge to the other balloon.

Question 9.
Describe with the help of a diagram an instrument which can be used to detect a charged body.
Answer:
Electroscope is a device used to detect the presence of charge on an object or body. When the metal strips repel each other, that proves that the body is charged. As repulsion is the sure test to detect if a body carries charge or not.

Question 10.
List three states in India where earthquakes are more likely to strike.
Answer:
Kashmir, Gujarat and Rajasthan.

Question 11.
Suppose you are outside your home and an earthquke strikes. What precautions would you take to protect yourself?
Answer:
If we are outside and an earthquake strikes, we should take the following precautions:

1. We should find a clear spot away from buildings, trees and overhead power lines.
2. If we are in a bus or a car, do not come out. Ask the driver to drive slowly to a clear spot.
3. Do not come out of bus or car till the tremors stop.

Question 12.
The weather department has predicted that a thunderstorm is likely to occur on a certain day. Suppose you have to go out on that day. Would you carry an umbrella? Explain.
Answer:
During thunderstorm, we should not carry an umbrella. An umbrella can become electrically charged due to lightning. It can be dangerous to life during thunderstorm. Therefore, carrying an umbrella is not proper during thunderstorm.

MP Board Class 8th Science Some Natural Phenomena NCERT Extended Learning – Activities and Projects

Question 1.
Open a water tap. Adjust the flow so that if forms a thin stream. Charge a refill. Bring it near the water stream. Observe what happens. Write a short report on the activity.
Answer:
Do yourself.

Question 2.
Make your own charge detector. Take a paper strip roughly 10 cm x 3 cm. Give it a shape as shown in Fig 15.2. Balance it on a needle. Bring a charged body near it. Observe what happens. Write a brief report, explaining its working.

Answer:
Do yourself.

Question 3.
This activity should be performed at night. Go to a room where there is a fluorescent tube light. Charge a balloon. Switch off the tube light so that the room is completely dark. Bring the charged balloon near the tube light. You should see a faint glow. Move the balloon along the length of the tube and observe how glow changes.
Caution: Do not touch the metal parts of the tube or the wires connecting the tube with the mains.
Answer:
Do yourself.

Question 4.
Find out if there is an organisation in your area which provides relief to those suffering from natural disaster. Enquire about the type of help they render to the victims of earthquakes. Prepare a brief report on the problems of the earthquake victims.
Answer:
Several NGOs extend help in time of natural disaster. These organisations provide relief to the victims with food packets, blankets, water bottles etc. They help government in their rehabilitation.

MP Board Class 8th Science Some Natural Phenomena NCERT Additional Important Questions

A. Short Answer Type Questions

Question 1.
Name any three natural phenomena.
Answer:
Earthquakes, cyclones and lightning.

Question 2.
What is static electricity?
Answer:
The electrical charge generated by rubbing is called static electricity because these charges do not move.

Question 3.
What happens when a charged eraser is brought close to charged balloon?
Answer:
They would attract each other because there is attraction between opposite charges.

Question 4.
What is earthing?
Answer:
The process of transfer of charges from a charged object to the earth is called earthing.

Question 5.
What is an earthquake?
Answer:
An earthquake is the sudden shaking of the earth which lasts for a very short time.

Question 6.
What happens when earthquake occurs?
Answer:
The earthquake causes immense damage to buildings, bridges, dams and people. There can be great loss of life and property. The earthquake can cause floods, landslides and tsunamis. Thousands of people may lose their lives.

B. Long Answer Type Questions

Question 7.
What did Ancient Greeks know about amber?
Answer:
Ancient Greeks knew as early as 600 BC that a resin names amber, when rubbed with fur, acquired some properties, which attracted objects with lightweight towards it. They knew that if amber is rubbed for longer period, it produced sparks as seen in sky during thunderstorm.

Question 8.
How does electrical discharge take place in clouds?
Answer:
During thunderstorms the negative charges get accumulated near the clouds and positive charges accumulate near the ground. When these negative and positive charges meet, electrical discharge takes place between clouds and grounds. It produces a huge amount of energy which is released in the form of lightning and thunder.

Question 9.
What precautions should we take to secure ourselves from lightning stroke during thunderstorm when we are in our homes?
Answer:
Following precautions should be taken while in house:

• We should not use wired phone.
• Electrical appliances should be plugged off.
• We should not bathe in running water.

Question 10.
How would you protect yourself when an earthquake strikes?
Answer:
In the event that an earthquake does strike, we can take the following steps to protect ourselves:

If we are at home:
Take shelter under a table and stay there till shaking stops.
Stay away from tall and heavy objects that may fall on you.
If we are in bed, do not get up. Protect our head with a pillow.

If we are outdoors:
Find a clear spot, away from buildings, trees and overhead power lines. Drop to the ground.
If we are in a car or a bus, do not come out. Ask the driver to drive slowly to a clear spot. Do not come out until the tremors stop.

MP Board Class 8th Science Solutions

MP Board Class 12th Hindi Makrand Solutions Chapter 17 हंसिनी की भविष्यवाणी (लोककथा, मनमोहन मदारिया)

हंसिनी की भविष्यवाणी पाठ्य-पुस्तक पर आधारित प्रश्न

हंसिनी की भविष्यवाणी लघु उत्तरीय प्रश्न

प्रश्न 1.
मंत्री ने राजा को क्या सलाह दी?
उत्तर:
मंत्री ने निस्संतान राजा को किसी होनहार बालक को गोद लेने की सलाह दी।

प्रश्न 2.
राजा का चुनाव करना क्यों आवश्यक था? (M.P. 2011)
उत्तर:
राजा की मृत्यु हो गई थी। राजकाज चलाने वाला कोई नहीं था। इसलिए राजा का चुनाव करना आवश्यक था।

प्रश्न 3.
मंत्री जी सरोवर किनारे क्यों जाते थे?
उत्तर:
मंत्रीजी को जब कोई गहरी बात सोचनी होती थी तो वे सरोवर के किनारे चले जाते थे।

प्रश्न 4.
हंसिनी ने प्रजा को राज स्थापित करने का कौन-सा उपाय बताया?
उत्तर:
जिसका देश है, उसी प्रजा को राजकाज सौंपने का उपाय हंसिनी ने बताया।

हंसिनी की भविष्यवाणी दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
मंत्री जी क्यों उदास थे?
उत्तर:
देश के राजा निसंतान चल बसे थे। तब राजा किसे चुना जाए, इसी फिक्र में मंत्रीजी उदास थे।

प्रश्न 2.
मंत्री जी ने देश का राजा चुनने की समस्या, किस प्रकार हल की?
उत्तर:
मंत्री ने एक विचारसभा की स्थापना की। उसमें तीन सौ आदमी थे। ये आदमी प्रजा ने चुने थे। एक लाख आबादी में से एक आदमी चुना गया था। इस विचारसभा में जाने-माने व्यक्ति थे। तीन सौ आदमियों ने अपना एक नेता चुना। वह देश का मुखिया हुआ। उसने विचार सभा में से चार आदमी और चुन लिए वे सब मिलकर देश का राजकाज चलाने लगे। इक्त मकार मंत्रीजी ने देश का राजा चुनने की समस्या हल कर ली।

प्रश्न 3.
नए ढंग के राज्य से क्या लाभ हुआ?
उत्तर:
नए ढंग के राज्य से देश का राजकाज ठीक ढंग से चलने लगा। यह प्रजा के लिए बड़ा हितकारी हुआ। प्रजा पहले से भी अधिक सुखी और धनी हो गई। जिसका देश था, उसी को राज्य मिल गया।

प्रश्न 4.
किसने किससे कहा?

1. ‘भगवान नहीं चाहते कि इस देश के सिंहासन पर मेरे वंश का राज रहे।’
2. अरे! तुझे नहीं मालूम? देश के राजा नहीं रहे।
3. हाँ, यही न्याय की बात है। मंत्री जी को चाहिए कि वह प्रजा के हाथ में राज-काज सौंप दें।
4. अरे तूने सुना, अपने देश में प्रजा का ही राज कायम हो गया है?

उत्तर:

1. राजा ने मंत्री से कहा।
2. हंस ने हंसिनी से कहा।
3. हंसिनी ने हंस से कहा।
4. हस ने हंसिनी से कहा।

हंसिनी की भविष्यवाणी भाव-विस्तार पल्लवन

प्रश्न 1.
निम्नलिखित कथनों का भाव-विस्तार कीजिए –

प्रश्न 1.
मैं भगवान की मरजी के खिलाफ काम नहीं करना चाहता।
उत्तर:
देश के राजा के कोई संतान नहीं थी। राजा बूढ़ा हो चला था। मंत्रीजी ने उसे किसी होनहार बालक को गोद लेने की सलाह दी ताकि उनके बाद उसे राजा बनाया जा सके। इस पर राजा ने कहा कि मैं भगवान की इच्छा के विरुद्ध कोई कार्य नहीं करूँगा, क्योंकि यदि भगवान यह चाहता कि उसके वंश का राज कायम रहे तो भगवान उसे संतान अवश्य देते।

किन्तु भावान नहीं चाहते कि देश पर उसका वंश राज करे इसलिए उन्होंने मुझे निस्संतान रखो। भगवान की इच्छा के विरुद्ध कार्य करना सर्वथा अनुचित होता है। उसकी इच्छा के विरुद्ध कार्य करने से मन अशांत रहता है। हानि होने का अंदेशा बना रहता है। ईश्वर की मरजी के विरुद्ध कार्य करना धर्म के विरुद्ध है। अतः ईश्वर की मरजी के बिना कार्य नहीं करना चाहिए।

प्रश्न 2.
‘आखिरी वक्त तो मुझ से एक न्याय का काम हुआ? ईश्वर दूसरे देश बालों को भी ऐसी ही समझ दे।’
उत्तर:
राजा के मंत्री पद पर कार्य करते हुए, राजा की आज्ञा का पालन करते हुए प्रजा के हित अवहेलना करके, प्रजा पर अत्याचार और अन्याय किए। उनके हितों का बिलकुल ध्यान नहीं रखा परंतु जीवन के अंतिम समय में जिस प्रजा का देश है, उसी को उसका राज सौंपकर मैंने एक तो न्याय का काम किया है। जैसे इस देश में प्रजा का राज स्थापित हुआ है, ऐसी समझ भगवान दूसरे देश वालों को भी दे। दूसरे शब्दों में, दूसरे देशों में भी प्रजातंत्र की स्थापना हो।

हंसिनी की भविष्यवाणी भाषा-अनुशीलन

प्रश्न 1.
निम्नलिखित मुहावरों का अर्थ लिखकर वाक्यों में प्रयोग कीजिए – (M.P. 2009)

1. स्वर्ग सिधार जाना।
2. कानों में भनक पड़ना।
3. हँसी खेल न होना।

उत्तर:

प्रश्न 2.
निम्नलिखित शब्दों के विलोम शब्द लिखिए –
साधारण, बूढ़ा, हित, आसान, मालिक, धनी।
उत्तर:

प्रश्न 3.
निम्नलिखित शब्दों का समास-विग्रह कर नाम लिखिए –
राज-सिंहासन, राज-काज, हित-अनहित, हंस-हंसिनी, नील गगन, यथा शक्ति।
उत्तर:

प्रश्न 4.
निम्नलिखित गद्यांश को पढ़कर यथास्थान विराम चिह्नों का प्रयोग कीजिए – (M.P. 2012)
मंत्री को फिक्र हुई अब कौन राज काज संभाले कौन राजा बने ऐसा चतुर आदमी कहाँ मिले कैसे मिले मंत्री को कुछ सूझ नहीं रहा था क्या करें राजा का चुनाव साधारण काम तो नहीं राजभर की जनता के हित-अनहित का सवाल था कहीं किसी गलत आदमी को राजा चुन बैठे तो राज बरबाद हो सकता था मंत्री को यह सवाल नामुमकिन जान पड़ने लगा?
उत्तर:
मंत्री को फिक्र हुई, अब कौन राज काज सँभाले? कौन राजा बने? ऐसा चतुर आदमी कहाँ मिले, कैसे मिले? मंत्री को कुछ सूझ नहीं रहा था। क्या करें? राजा का चुनाव साधारण काम तो नहीं? राजभर की जनता के हित-अनहित का सवाल था। कहीं किसी गलत को राजा चुन बैठे, तो राज बरबाद हो सकता था। मंत्री को यह सवाल नामुमकिन जान पड़ने लगा।

प्रश्न 5.
उदाहरण के अनुसार ‘तंत्र’ शब्द जोड़कर चार नए शब्द बनाइए –
प्रजा + तंत्र = प्रजातंत्र
उत्तर:

1. स्व + तंत्र = स्वतंत्र
2. राज + तंत्र = राजतंत्र
3. पर + तंत्र = परतंत्र
4. लोक + तंत्र = लोकतंत्र

हंसिनी की भविष्यवाणी योग्यता-विस्तार

प्रश्न 1.
हंस और हंसिनी की लोककथा बाल-सभा में सुनाइए।
उत्तर:
छात्र स्वयं करें।

प्रश्न 2.
अपने परिवेश में प्रचलित किसी लोक कथा की जानकारी प्राप्त कीजिए।
उत्तर:
छात्र स्वयं करें।

प्रश्न 3.
पशु-पक्षियों के वार्तालाप से प्राप्त बोल कथाओं का संकलन कीजिए।
उत्तर:
छात्र स्वयं करें।

प्रश्न 4.
हमारे देश में भी प्रजातंत्र है। लोक सभा और विधान सभा के सदस्यों की संख्या पता कीजिए और उनके अधिभारों पर चर्चा कीजिए।
उत्तर:
छात्र स्वयं करें।

हंसिनी की भविष्यवाणी परीक्षोपयोगी अन्य महत्वपूर्ण प्रश्न

I. वस्तुनिष्ठ प्रश्न 

प्रश्न 1.
मंत्री ने राजा को सलाह दी कि –
(क) वह किसी बालक को गोद ले लें।
(ख) वह किसी बालक को अपना उत्तराधिकारी बना दें।
(ग) वह किसी मंत्री को राजकाज सौंप दें।
(घ) वह किसी को भी अपना राजसिंहासन न सौंपें ।
उत्तर:
(क) वह किसी बालक को गोद ले लें।

प्रश्न 2.
मंत्री ने राजा को किसी बालक को गोद लेने की सलाह दी, क्योंकि –
(क) राजा बूढ़े हो गए थे
(ख) राजा निस्संतान थे
(ग) राजा के केवल लड़की थी
(घ) राजा को दूसरे राजा से खतराथा
उत्तर:
(ख) राजा निस्संतान थे।

प्रश्न 3.
राजा का चुनाव साधारण काम नहीं था क्योंकि –
(क) मंत्री को अपना पद जाने का सवाल था
(ख) जनता के हित-अहित का सवाल था
(ग) राज्य की रक्षा का सवाल था
(घ) राजा के परिवार का सवाल था।
उत्तर:
(ख) जनता के हित-अहित का सवाल था।

प्रश्न 4.
बातचीत की आवाज आ रही थी –
(क) महल के पीछे से
(ख) सरोवर के किनारे से
(ग) सरोवर के बीच से
(घ) सरोवर के पेड़ों के पीछे से
उत्तर:
(ग) सरोवर के बीच से।

प्रश्न 5.
वाह! यह छोटी-सी बात कैसे हुई? किसने कहा?
(क) मंत्री ने
(ख) राजा ने
(ग) हंसिनी ने
(घ) हंस ने
उत्तर:
(घ) हंस ने।

प्रश्न 6.
‘अब दूसरे देशों में भी ऐसा ही राज कायम होगा’ में किस राज की बात की गई है?
(क) तानाशाही राज की
(ख) राजा के राज की
(ग) प्रजा के राज की
(घ) स्वतंत्र राज की
उत्तर:
(ग) प्रजा के राज की।

प्रश्न 7.
हंसिनी ने क्या भविष्यवाणी की?
(क) दूसरे देशों में प्रजातंत्र कायम होने की
(ख) दूसरे देशों में राजतंत्र कायम होने की
(ग) दूसरे देशों में परतंत्र कायम होने की
(घ) दूसरे देशों में भीड़तंत्र कायम होने की।
उत्तर:
(क) दूसरे देशों में प्रजातंत्र कायम होने की।

प्रश्न 8.
मंत्री ने इस तरह व्यवस्था बनाई कि –
(क) प्रजातंत्र का प्रारंभ हुआ
(ख) राजा का चुनाव करना आसान हो गया
(ग) राज्य में राजतंत्र पुनःस्थापित हो गया
(घ) मंत्री आसानी से राजा बन गया
उत्तर:
(क) प्रजातंत्र का प्रारंभ हुआ।

प्रश्न 9.
मंत्री को कुछ सूझ नहीं रहा था क्योंकि –
(क) राजा का चुनाव साधारण काम नहीं था
(ख) उसको अपना पद जाने का भय था
(ग) उसे किसी और के पदासीन होने की आशंका थी
(घ) उसे राज्य से निर्वासित होने का डर सता रहा था।
उत्तर:
(क) राजा का चुनाव साधारण काम नहीं था।

II. निम्नलिखित रिक्त स्थानों की पूर्ति दिए गए विकल्पों के आधार पर कीजिए –

1. ‘हंसिनी की भविष्यवाणी’ ………. है। (लोककथा/वेदकथा)
2. ‘हंसिनी की भविष्यवाणी’ के लेखक हैं ……….। (उदयशंकर भट्ट/मनमोहन मदारिया)
3. ………. का मालिक तो प्रजा ही है। (राज/राजा)
4. जिसका यह देश है, उसको ही इसका ………. सँभालने दिया जाए। (शासन/राजकाज)
5. मनमोहन मदारिया का साहित्य ………. है। (समाजोपयोगी बालोपयोगी)

उत्तर:

1. लोककथा
2. मनमोहन मदारिया
3. राज
4. राजकाज
5. समाजोपयोगी।

III. निम्नलिखित कथनों में सत्य/असत्य छाँटिए –

1. राजा ने कहा, “भगवान नहीं चाहते कि इस देश के राजसिंहासन पर दूसरे वंश का राज रहे।”
2. मंत्री ने कहा, “राजन्! आप किसी होनहार बालक को गोद ले लें।”
3. मंत्रीजी राजकाज से छुटकारा नहीं चाहते थे।
4. किसी गलत आदमी के राजा बनने से राज बरबाद हो सकता था।
5. देश में प्रजा के राज को राजतंत्र कहते हैं।

उत्तर:

1. असत्य
2. सत्य
3. असत्य
4. सत्य
5. असत्य।

IV. निम्नलिखित के सही जोड़े मिलाइए –

प्रश्न 1.

उत्तर:

(i) (ङ)
(ii) (ग)
(iii) (घ)
(iv) (ख)
(v) (क)।

V. निम्नलिखित प्रश्नों में प्रत्येक प्रश्न का उत्तर एक शब्द या एक वाक्य में दीजिए –

प्रश्न 1.
मंत्री ने राजा को अपना वारिस चुनने की सलाह क्यों दी?
उत्तर:
मंत्री ने राजा को अपना वारिस चुनने की सलाह इसलिए दी कि वह बुड्ढा हो गया था।

प्रश्न 2.
राजा का चुनाव क्या नहीं था?
उत्तर:
राजा का चुनाव साधारण काम नहीं था।

प्रश्न 3.
मंत्री ने किसकी बात कान लगाकर सुनी?
उत्तर:
मंत्री ने हंस और हंसिनी की वात कान लगाकर सुनी।

प्रश्न 4.
हंस ने न्याय की क्या बात कही?
उत्तर:
हंस ने यह न्याय की बात कही, “देश की असल मालिक तो प्रजा है, देश उसका ही है।”

प्रश्न 5.
मंत्री ने संतोष की साँस क्यों ली?’
उत्तर:
मंत्री ने संतोष की साँस ली; क्योंकि आखिरी वक्त में उससे एक न्याय का काम हुआ था।

हंसिनी की भविष्यवाणी लघु उत्तरीय प्रश्न

प्रश्न 1.
मंत्री ने बूढ़े राजा को किसी बालक को गोद लेने की सलाह क्यों दी?
उत्तर:
बूढ़े राजा निस्संतान थे। मंत्री ने राजा को किसी बालक को गोद लेने की सलाह इसलिए दी, ताकि उनके बाद उस बालक को राजकाज दिया जा सके।

प्रश्न 2.
राजा ने बालक को गोद लेने से इनकार क्यों कर दिया?
उत्तर:
राजा समझता था किसी बालक को गोद लेना भगवान की मरजी के खिलाफ होगा।

प्रश्न 3.
मंत्री राजकाज से छुटकारा क्यों पाना चाहता था?
उत्तर:
मंत्री राजकाज से छुटकारा पाना चाहता था; क्योंकि मंत्री बहुत बूढ़ा हो गया था।

प्रश्न 4.
सरोवर में हंस-हंसिनी किस संबंध में बातें कर रहे थे?
उत्तर:
सरोवर में हंस-हंसिनी मंत्री और देश के राजकाज के संबंध में बातें कर रहे थे।

प्रश्न 5.
हंसिनी ने राजकाज किसे सौंपने का सुझाव दिया?
उत्तर:
हंसिनी ने देश की असल मालिक प्रजा को राजकाज सौंपने का सुझाव दिया।

प्रश्न 6.
मंत्रीजी ने राज की किस पद्धति का आरंभ किया? उसे किस नाम से : जाना जाता है?
उत्तर:
मंत्रीजी द्वारा प्रारंभ की गई राज-पद्धति को प्रजातंत्र के नाम से जाना जाता है।

प्रश्न 7.
राजा क्या था?
उत्तर:
राजा बूढ़ा और निस्संतान था।

प्रश्न 8.
मंत्री की चिंता कैसे दूर हुई?
उत्तर:
मंत्री की चिन्ता हंस-हंसिनी के परस्पर बातचीत को सुनने से दूर हुई।

प्रश्न 9.
दूसरे देशों में भी किस ढंग का राज्य फैला?
उत्तर:
दूसरे देशों में भी प्रजातंत्र का राज्य फैला।

प्रश्न 10.
हंसिनी ने राजकाज किसे सौंपने का सुझाव दिया? (M.P. 2009)
उत्तर:
हंसिनी ने राजकाज प्रजा को सौंपने का सुझाव दिया।

हंसिनी की भविष्यवाणी दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
राजा ने किसी बालक को गोद न लेने के लिए क्या तर्क दिए?
उत्तर:
राजा ने किसी बालक को गोद न लेने के लिए निम्नलिखित तर्क दिए –

1. भगवान नहीं चाहते कि देश के राजसिंहासन पर मेरे वंश का राज रहे।
2. मैं भगवान की मर्जी के खिलाफ कुछ नहीं करूँगा। मैं भगवान की मरजी के खिलाफ कुछ नहीं करना चाहता।

प्रश्न 2.
हंसिनी ने राजा चुनने के प्रश्न को कैसे हल कर दिया?
उत्तर:
हंसिनी ने राजा चुनने के प्रश्न को बड़ी सरलता से हल कर दिया। उसने – हंस से कहा कि जो देश का असली मालिक है, उसे राजकाज सौंप दो। देश की असली मालिक प्रजा है और प्रजा को ही उसका राजकाज सौंप देना चाहिए।

प्रश्न 3.
हंसिनी ने राजकाज प्रजा को सौंपने की क्या योजना बताई? (M.P. 2012)
उत्तर:
हंसिनी ने राजकाज प्रजा को सौंपने की निम्नलिखित योजना बताई-प्रजा अपने में से कुछ व्यक्तियों को चुन ले। वे प्रजा की ओर से राजकाज सँभाले। उन व्यक्तियों में से एक मुखिया चुन लें और वह मुखिया चार-पाँच व्यक्तियों को चुन ले। वे सब मिलकर काम करें। यदि ठीक काम न करें तो प्रजा उन्हें हटाकर दूसरे आदमी चुन लें।

प्रश्न 4.
मंत्री की क्या परेशानी थी?
उत्तर:
मंत्री की यह परेशानी थी कि वह राजा का चुनाव कैसे करे, क्योंकि राजा का चुनाव आसान काम नहीं था। यह पूरे देश की जनता के हित-अनहित का प्रश्न था, इसके लिए उसने कुछ चतुर-सयाने लोगों से सलाह ली। लेकिन किसी ने सही सलाह नहीं दी थी। गलत आदमी को राजा बनाने से पूरा देश बरबाद हो सकता था।

प्रश्न 5.
विचार-सभा बनने से क्या हुआ?
उत्तर:
विचार-सभा बनने से देश में नए ढंग का राज होने लगा। इससे प्रजा को बहुत अधिक लाभ हुआ। प्रजा पहले कभी उतनी सुखी और धनी नहीं रही थी, जितनी इस नए ढंग के राज में सुखी रही।

हंसिनी की भविष्यवाणी लेखक-परिचय

प्रश्न 1.
मनमोहन मदारिया का संक्षिप्त जीवन-परिचय देते हुए उनकी साहित्यिक विशेषताओं का उल्लेख कीजिए।
उत्तर:
जीवन-परिचय:
समाज-कल्याण से निरंतर रूप से जुड़े मनमोहन मदारिया का जन्म मध्य प्रदेश के बोहानी नरसिंहपुर गाँव में 3 सितंबर, 1929 को हुआ। आपने बी.एस.सी., एम.ए. और एल.एल.बी. तक शिक्षा प्राप्त की। उसके उपरान्त आप दैनिक अखबारों में संपादक के कार्य से जुड़े। विज्ञान और साहित्य की समझ और पत्रकारिता की समझ के कारण ही आप साहित्य-सृजन की ओर मुड़ पड़े। साहित्य-सृजन के क्षेत्र में आपने कहानी, उपन्यास, संस्मरण, व्यंग्य और बालोपयोगी साहित्य की रचना की। आपने मध्य प्रदेश शासन के समाज-कल्याण विभाग से अवकाश ग्रहण किया। आज भी आप साहित्य-सृजन के क्षेत्र में सक्रिय हैं।

साहित्यिक विशेषताएँ:
मदनमोहनजी ने अपनी साहित्य रचनाओं में अपने विचार, अनुभव और समकालीन सोच में सामंजस्य को स्थान दिया है। यह सामंजस्य उनकी रचनाओं से स्पष्ट झलकता है। जमीन से जुड़ाव और सामाजिक समस्याओं से साक्षात्कार ने उनकी रचनात्मकता को व्यापक फलक प्रदान किया है। यही कारण है कि उन्होंने विविध विधाओं पर अपनी लेखनी चलाई है।

रचनाएँ:

• कहानी-संकलन – एक वासंती रात, समुद्र के किनारे।
• उपन्यास – चार दीवारी, मिसेज लाल।
• संस्मरण-संग्रह – वे सहचर आत्मा के।
• व्यंग्य-संग्रह – मेरी प्रिय व्यंग्य रचनाएँ।
• एकांकी-संग्रह – सूरज की धूप।
• बालोपयोगी साहित्य – गुदड़ी का लाल (उपन्यास), आज की लोककथाएँ, बाल, कथाएँ आदि।

भाषा-शैली:
मनमोहन मदारिया की भाषा-शैली सहज, सरल, प्रांजल खड़ी बोली है। उनकी भाषा में उर्दू और अंग्रेजी शब्दों का प्रयोग भी हुआ है। उनकी भाषा में व्यंग्य के छींटे भी हैं। बालोपयोगी साहित्य की भाषा सहज और स्वाभाविक है। वे नवसाक्षरों हेतु उपयोगी साहित्य-सृजन में सिद्धहस्त हैं। समाज कल्याण विभाग से संबद्धता और संपादन कार्य ने उन्हें समाजोपयोगी सृजन का विस्तृत क्षेत्र प्रदान किया है।

हंसिनी की भविष्यवाणी पाठ का सारांश

प्रश्न 1.
‘हंसिनी की भविष्यवाणी’ कहानी का सार अपने शब्दों में लिखिए।
उत्तर:
मनमोहन मदारिया ने इस कहानी में लोककथा शैली को अपनाते हुए प्रजातंत्र शासन-पद्धति की प्रारंभिक अवधारणा को एक कल्पना कथा के द्वारा प्रस्तुत किया है। कहानी का सार इस प्रकार है –

एक देश के राजा को कोई संतान नहीं थी। उस बूढ़े राजा को मन्त्री ने किसी योग्य बालक को गोद लेने की सलाह दी परंतु राजा ने इस सलाह को यह कहकर मानने से इनकार कर दिया कि भगवान नहीं चाहते कि इस देश के राजसिंहासन, पर मेरे वंश का राज रहे। मैं भगवान की इच्छा के विपरीत कार्य नहीं करना चाहता। कुछ समय बाद राजा की मृत्यु हो गई। मंत्रीजी बड़े चिंतित हुए कि अब राज-काज कौन चलाये। कौन राजा बने? वह स्वयं भी बहुत वृद्ध थे। वे मरने से पहले किसी चतुर आदमी के हाथ में राज-काज सौंपना चाहते थे।

उन्होंने कई लोगों की सलाह ली, पर कोई ठीक से राय नहीं दे सका। – एक दिन मंत्रीजी महल के पीछे सरोवर के किनारे टहल रहे थे और नया राजा चुनने के संबंध में सोच रहे थे कि वह समस्या अचानक सुलझ गई। सरोवर के किनारे टहलते हुए उन्हें हंस-हंसिनी की बातें सुनाई पड़ीं जो मंत्रीजी और नया राजा चुनने के संबंध में ही बातें कर रहे थे। हंसिनी ने सुझाव दिया कि जिसका राज-काज है, उसे ही सँभालने दिया जाए। हंस ने कहा, देश की असल मालिक तो प्रजा है, देश उसका ही है। हंसिनी ने कहा-न्याय की बात तो यही है कि मंत्रीजी को राजकाज प्रजा को सौंप देना चाहिए। इसके बाद हंसिनी ने प्रजा को राज-काज सौंपने की सारी प्रक्रिया समझाई।

हंसिनी की बातों को सुनकर मंत्रीजी को उपाय सूझ गया। उन्होंने एक विचार-सभा स्थापित की। उसमें तीन सौ आदमी थे। वे देश की तीन करोड़ जनता द्वारा चुने गए थे। उनमें से एक आदमी को नेता चुना गया। वह देश का मुखिया हुआ। उस मुखिया ने विचार-सभा में से चार आदमी और चुन लिए। वे मिलकर राजकाज चलाने लगे। यह बंदोबस्त प्रजा के लिए बड़ा हितकारी हुआ ! प्रजा नए ढंग के राज में पहले से अधिक धनी और सुखी हुई।

पुराने मंत्री अपने महल में आराम से रहने लगे। एक दिन जब मंत्रीजी सरोवर की ओर विहार के लिए गए तो उन्होंने हंस-हंसिनी को बातें करते सुना। हंस हंसिनी से कह रहा था कि अपने देश में प्रजा का ही राज स्थापित हो गया है। हंसिनी ने कहा, इसमें आश्चर्य की क्या बात है? आज नहीं तो कल यह तो डोने वाला ही था। अब दूसरे देशों में भी ऐसा ही राज कायम होगा। हंस ने कहा, भगवान करे, तेरी बात सच हों। मंत्री ने उनकी बातें सुनकर संतोष की साँस ली और मन ही मन कहा, चलो आखिरी वक्त में मुझसे एक न्याय का काम हुआ। आगे चलकर हंसिनी की भविष्यवाणी सच हुई। दूसरे देशों में भी उस ढंग का राज फैला। इस प्रकार के प्रशासन को आज प्रजातंत्र के नाम से जाना जाता है।

हंसिनी की भविष्यवाणी संदर्भ-प्रसंगसहित व्याख्या

प्रश्न 1.
कुछ दिनों बाद राजा चल बसा। मंत्रीजी को फिक्र हुई, अब कौन राज-काज सँभाले? कौन राजा बने? वह खुद बहुत बूढ़े थे। राज-काज से अब वह भी छुटकारा चाहते थे। मगर इसके पहले किसी चतुर आदमी के हाथ में वह राज-काज सौंप देना चाहते थे। ऐसा चतुर आदमी आखिर कहाँ मिले, कैसे मिले? मंत्री इसी सोच में थे। उन्होंने कुछ चतुर-सयाने लोगों से सलाह ली पर कोई ठीक राय न दे सका। मंत्री सब तरफ से निराश हो गए। कुछ सूझ नहीं रहा था, क्या करें? राजा का चुनाव साधारण काम तो था नहीं राज्यभर की जनता के हित-अनहित का सवाल था। कहीं किसी गलत आदमी को राजा चुन बैठे तो राज बरबाद हो सकता था। मंत्री को यह सवाल नामुमकिन जान पड़ने लगा। (Pages 80-81)

शब्दार्थ:

• चल बसा – मृत्यु होना।
• फ्रिक – चिंता।
• चतुर – चालाक, योग्य।
• सयाने – समझदार।
• राय – सलाह।
• बरबाद – समाप्त।

प्रसंग:
प्रस्तुत गद्यांश मनमोहन मदारिया द्वारा रचित कहानी ‘हंसिनी की भविष्यवाणी’ से उद्धृत है। इस गद्यांश में मंत्री नए राजा के चुनाव को लेकर चिंतित है। उसके सामने नए राजा का चुनाव करना एक समस्या बन गया है। इस पर प्रकाश डालते हुए लेखक ने कहा है –

व्याख्या:
कुछ समय के बाद बूढ़े निस्संतान राजा की मृत्यु हो गई। संतानहीन होने के कारण उसका कोई उत्तराधिकारी नहीं था। उसकी मृत्यु के बाद मंत्री को चिंता हुई कि अब राज्य का कार्य कौन सँभालेगा? कौन राजा बने? मंत्री स्वयं भी बहुत बूढ़ा हो गया था। वह राजकार्य चलाने में असमर्थ था। मंत्री तो स्वयं अब राजकार्य से मुक्त होना चाहता था। मंत्री राजकार्य से मुक्ति पाने से पहले किसी योग्य व्यक्ति को राजकाज दे देना चाहता था। उन्हें इस बात की चिंता हो रही थी कि ऐसा योग्य व्यक्ति उन्हें कहाँ मिलेगा। उसे कहाँ खोजा जाए और कैसे खोजा जाए। मंत्रीजी इसी सोच-विचार में लगे हुए थे। उन्होंने राज्य के कुछ योग्य और समझदार लोगों से इस संबंध में विचार-विमर्श किया। किंतु कोई भी उचित सलाह नहीं दे सका।

मंत्री सब ओर से निराश हो गया। उसकी समझ में कुछ नहीं आ रहा था कि क्या करें और कैसे राजा का चुनाव करें। राजा का चुनाव करना कोई साधारण काम नहीं था। राजा के चुनाव के साथ राज्य की समूची जनता की भलाई और बुराई का प्रश्न जुड़ा था। यदि योग्य व्यक्ति राजा बना, तो वह जनता की भलाई, उसके कल्याण के लिए कार्य करेगा और यदि राजा अयोग्य चुना गया, तो जनता पर अन्याय, अत्याचार करेगा। मंत्री को डर था कि यदि उसने राजा के रूप में गलत व्यक्ति का चुनाव कर दिया, तो सारा राज्य नष्ट हो जाएगा। मंत्री को योग्य राजा चुनने के प्रश्न का उत्तर मिलना असंभव लग रहा था। उसे लगने लगा था कि योग्य राजा का चुनाव करना अत्यंत मुश्किल है।

विशेष:

1. मंत्री की चिंता को व्यक्त किया गया है।
2. विचारात्मक शैली है।
3. सरल, सुबोध खड़ी बोली है।

गद्यांश पर आधारित अर्थग्रहण संबंधित प्रश्नोत्तर

प्रश्न (i)
मंत्री को क्यों चिंता सता रही थी?
उत्तर:
राजा की मृत्यु हो चुकी थी। राज्य का मंत्री इसलिए चिंतित था कि राजा निःसंतान था। उसका कोई उत्तराधिकारी नहीं था। मंत्री को चिंता सता रही थी कि वह अब किसे राजा बनाए, जो राज्य का कार्यभार सँभाल सके।

प्रश्न (ii)
मंत्री स्वयं राजा क्यों नहीं बनना चाहता था?
उत्तर:
मंत्री ईमानदार और स्वामिभक्त था। दूसरे वह बहुत बूढ़ा हो चुका था। समस्त राज-काज संलना उसके बस का नहीं था। मंत्री स्वयं राजकाज से छुटकारा चाहता था इसलिए वह स्वयं राजा नहीं बनना चाहता था।

प्रश्न (iii)
मंत्री ने राजा चुनने के लिए क्या प्रयास किया?
उत्तर:
मंत्री ने योग्य व्यक्ति को राजा चुनने के लिए राज्य के योग्य और समझदार व्यक्तियों से विचार-विमर्श किया किन्तु कोई भी उन्हें उचित सलाह नहीं दे सका।

प्रश्न (iv)
राजा का चुनाव साधारण काम क्यों नहीं था?
उत्तर:
राजा का चुनाव साधारण काम नहीं था, क्योंकि इसके साथ राज्य की प्रजा के हित-अहित का प्रश्न जुड़ा था। राज्य की सुरक्षा का भी प्रश्न था । अयोग्य व्यक्ति राजा बन जाए, तो राज्य बरबाद हो सकता था।

गद्य पर आधारित बोधात्मक प्रश्नोत्तर

प्रश्न (i)
मंत्री कैसा राजा ढूँढना चाहता था और क्यों?
उत्तर:
मंत्री राज्य के लिए योग्य व्यक्ति ढूँढना चाहता था, क्योंकि वह चाहता था कि यदि योग्य व्यक्ति राजा बना, तो वह राज्य की प्रजा के हितों का ध्यान रखेगा और राज्य भी सुरक्षित रहेगा।

प्रश्न (ii)
मंत्री सब तरफ से निराश क्यों हो गया?
उत्तर:
मंत्री चतुर व्यक्ति के हाथ में सारा राजकाज सौंप देना चाहते थे। उसने योग्य व्यक्ति की खोज के लिए राज्य के विद्वानों से विचार-विमर्श किया किंतु कोई भी व्यक्ति उचित सलाह नहीं दे सका। इसलिए मंत्री निराश हो गया।

प्रश्न 2.
हंस-हंसिनी की इन बातों से मंत्री को राह सूझ गई। उनकी एक बड़ी फिक्र मिट गई। उन्होंने हंस-हंसिनी की बातों के मुताबिक काम किया। देश में एक विचारसभा कायम की गई। उसमें तीन सौ आदमी थे। ये आदमी प्रजा ने चुने थे। देश की आबादी तीन करोड़ थी। एक लाख आबादी में से एक आदमी चुना गया था। इस तरह विचारसभा में प्रजा के जाने-माने आदमी थे। विचारसभा के तीन सौ आदमियों ने अपना एक नेता चुना।

वह आदमी देश का मुखिया हुआ, उसने ही पुराने राजा का काम सँभाला। अपनी मदद के लिए उसने विचारसभा में से ही चार आदमी और चुन लिए। वे पाँच लोग मिल-जुलकर राज-काज चलाने लगे। उनके कामों पर विचारसभा की निगरानी रहती थी। विचारसभा राज चलाने के कानून भी बनाती थी। इस तरह देश में नएं ढंग से राज होने लगा। यह बंदोबस्त प्रजा के लिए बड़ा हितकारी हुआ। प्रजा पहले कभी उतनी सुखी और धनी नहीं रही थी जितनी इस नए ढंग के राज में सुखी रही। (Page 82)

शब्दार्थ:

• राह सूझना – रास्ता दिखाई देना।
• फ्रिक – चिंता।
• मुताबिक – के अनुसार।
• कायम – स्थापना, स्थापित करना।
• आबादी – जनसंख्या।
• जाने-माने – प्रसिद्ध, योग्य।
• निगरानी – देख-रेख।
• बंदोबस्त – व्यवस्था।
• हितकारी – कल्याणकारी।

प्रसंग:
प्रस्तुत गद्यांश मनमोहन मदारिया द्वारा रचित कहानी ‘हंसिनी की भविष्यवाणी’ से उद्धृत है। इस गद्यांश से प्रजातंत्र पद्धति की प्रारंभिक अवधारणा को प्रस्तुत करने के साथ-साथ उसके सफल होने का भी वर्णन किया गया है।

व्याख्या:
हंस-हंसिनी के पारस्परिक वार्तालाप को सुनकर राजा की खोज के लिए मंत्री को रास्ता समझ में आ गया। उसकी एक बहुत बड़ी चिंता समाप्त हो गई। मंत्री ने हंस-हंसिनी की बातों के अनुसार प्रजा का राज्य प्रजा को सौंपने का कार्य आरंभ कर दिया। उन्होंने देश में एक विचारसभा की स्थापना की। उस विधारसभा में तीन सौ व्यक्ति थे। ये तीन सौ व्यक्ति प्रजा ने स्वयं चुने थे। देश की कुल जनसंख्या तीन करोड़ थी। इस प्रकार एक लाख की जनसंख्या में से एक आदमी चुना गया था। दूसरे शब्दों में, विचारसभा का गठन प्रजा ने अपने चुने हुए प्रतिनिधियों द्वारा किया। विचारसभा के सदस्यों की संख्या जनसंख्या पर आधारित थी।

एक लाख व्यक्तियों का एक प्रतिनिधि था। विचारसभा के तीन सौ आदमियों ने अपना एक नेता चुना। वह नेता देश का मुखिया हुआ। उस मुखिया ने ही पुराने राजा का कार्य सँभाल लिया। उसने अपनी सहायता के लिए विचारसभा से ही चार व्यक्तियों का चुनाव कर लिया। वे पाँच लोग मिल-जुलकर राज्य का राजकाज चलाने लगे। उनके द्वारा किए गए और किए जाने वाले सभी काम पर विचारसभा देख-रेख करती थी।

विचारसभा ही देश का प्रशासन सुचारु रूप से चलाने के नियम-उपनियम बनाती थी। इस प्रकार देश में नई शासन-व्यवस्था से राज होने लगा। यह शासन-व्यवस्था देश की प्रजा के लिए बड़ा कल्याणकारी सिद्ध हुआ। इस शासन-व्यवस्था के कारण प्रजा पहले की अपेक्षा अधिक सुखी और धनी थी। इस नए ढंग की प्रजातांत्रिक व्यवस्था में प्रजा अत्यंत सुखी रही।

विशेष:

1. प्रजातांत्रिक शासन व्यवस्था की प्रारंभिक अवधारणा को प्रस्तुत किया गया है।
2. विचारात्मक शैली है।
3. भाषा सहज, सरल, उर्दू शब्दों से युक्त खड़ी बोली है।

गद्यांश पर आधारित अर्थग्रहण संबंधित प्रश्नोत्तर

प्रश्न (i)
हंस-हंसिनी की बातों से मंत्री को कौन-सी राह सूझ गई?
उत्तर:
मंत्रीजी देश के लिए योग्य राजा चुनने की चिंता से ग्रस्त थे। उसे राजा के योग्य व्यक्ति नहीं मिल रहा था। हंस-हंसिनी की पारस्परिक बातों से मंत्री को रास्ता मिल गया कि देश की असली मालिक प्रजा है और प्रजा को देश का राजकाज सौंप देना चाहिए। यही न्याय है।

प्रश्न (ii)
मंत्री ने देश की प्रजा को राजकाज सौंपने के लिए क्या किया?
उत्तर:
मंत्री ने देश में एक विचारसभा की स्थापना की। उसमें जनसंख्या के आधार पर जनता को एक प्रतिनिधि चुनकर भेजने को कहा। प्रजा ने अपने तीन सौ प्रतिनिधि चुनकर भेजे। ये सभी देश के जाने-माने व्यक्ति थे। विचारसभा के आदमियों ने अपना एक मुखिया चुना। मुखिया ने उन आदमियों में से चार आदमी चुन लिए। मंत्री ने मुखिया को सारा राजकाज सौंप दिया। वे सब मिलकर राजकाज चलाने लगे।

प्रश्न (iii)
नए ढंग की व्यवस्था से क्या फल हुआ?
उत्तर:
नए ढंग की व्यवस्था से राज में प्रजा का बहुत.हित हुआ। राज में सुख और शांति का वातावरण बना। प्रजा पहले राज की तुलना में अधिक धनी और सुखी हुई।

गद्य पर आधारित बोधात्मक प्रश्नोत्तर

प्रश्न (i)
मंत्री ने किसके मुताबिक कार्य किया और क्यों?
उत्तर:
मंत्री ने हंस-हंसिनी की बातों के मुताबिक कार्य किया क्योंकि उसे देश ‘ की असली मालिक प्रजा को राजकाज सौंपने की बात उचित लगी।

प्रश्न (ii)
पुराने राजा का कार्य किसने सँभाला?
उत्तर:
पुराने राजा का काम विचारसभा में तीन सौ आदमियों द्वारा अपना नेता चुने गए व्यक्ति ने सँभाला।

प्रश्न (iii)
विचारसभा क्या-क्या कार्य करती थी?
उत्तर:
विचारसभा मुखिया उसके सहयोगी के कामों पर निगरानी रखती थी। वह राज चलाने के लिए कानून बनाती थी।

MP Board Class 12th Hindi Solutions

MP Board Class 8th Science Solutions Chapter 14 Chemical Effects of Electric Current

Question 1.
Fill in the blanks:
(a) Most liquids that conduct electricity are solutions of ……………, ……………. and ………….
(b) The passage of an electric current through a solution causes ……………. effects.
(c) If you pass current through copper sulphate solution, copper gets deposited on the plate connected to the ………. terminal of the battery.
(d) The process of depositing a layer of any desired metal on another material by means of electricity is called ………..
Answer:
(a) acids, bases, salts
(b) chemical
(c) negative
(d) electroplating.

Question 2.
When the free ends of a tester are
dipped into a solution, the magnetic needle shows deflection. Can you explain the reason?
Answer:
Yes, the solution conducts electricity.

Question 3.
Name three liquids, which when tested in the manner shown in Fig 14.1 may cause the magnetic needle to deflect.

Answer:
Tap water, lime water, vinegar or lemon juice.

Question 4.
The bulb does not glow in the setup shown in Fig. 14.2. List the, possible reasons. Explain your answer.

Answer:
If the bulb does not glow it may be because of some reasons like the bulb may be fused. Replaced with a new bulb, if it still does not glow, it shows that the connection of wires may be loose. After tightening connections if still the bulb does not glow, then it is for sure that the solution does not conduct electric current.

Question 5.
A tester is used to check the conduction of electricity through two liquids, labelled A and B. It is found that the bulb of the tester glows brightly for liquid Awhile it glows very dimly for liquid B. You would conclude that:
(i) Liquid A is a better conductor than liquid B.
(ii) Liquid B is abeHer conductor than liquid A.
(iii) both liquids are equally conducting.
(iv) conducting properties of liquid cannot be compared in this manner.
Answer:
(i) Liquid A is a better conductor than liquid B.

Question 6.
Does pure water conduct electricity? If not, what can we do to make it conducting?
Answer:
Pure water does not conduct electricity. To make it conducting we may add to it a little common salt or acid or a base.

Question 7.
In case of any fire, before the firemen use the water hoses, they shut off the main electrical supply for the area. Explain the reason why they do this?
Answer:
If an electric wire or appliance becomes wet, the risk of electrocution increases. Therefore, to ensure safety, the firemen shut off the main electrical supply for the area to extinguish fire due to electric short circuit.

Question 8.
A child staying in the coastal region tests the drinking water and also the sea-water with his tester. He finds that the compass needle deflects more in case of sea-water. Can you explain the reason?
Answer:
Sea-water is better conductor than the drinking water because sea-water contains mineral salts dissolved in it. It is therefore, the compass needle deflects more in case of seawater.

Question 9.
Is it safe for the wireman to carry out electrical repairs during heavy downpour? Explain.
Answer:
No, During heavy downpour, there is a risk of electrocution because impure water is good conductor of electricity.

Question 10.
Pooja knew that rainwater is as pure as distilled water. So she collected some rainwater in a clean glass tumbler and tested it using a tester. To her surprise she found that the compass needle showed deflection. What could be the reasons?
Answer:
Rainwater is, of course, as good as distilled water but when it passes through atmosphere, it dissolves a lot of dust, dirt and impurities and becomes conducting. So, when Pooja used a tester, its compass showed deflection.

Question 11.
Prepare a list of objects around you that are electroplated.
Answer:
The objects which are electroplated are:

• Handles and rims of a bicycles
• Utensils of kitchen
• Metallic showpieces
• Metallic containers, buckets
• bath tubs
• Artificial jewelery
• kitchen gas burner.

Question 12.
The process that you saw in Activity 14.7 (NCERT Textbook page no. 178) is used for purification of copper. A thin plate of pure copper and a thick rod of impure copper are used as electrodes. Copper from impure rod is sought to be transferred to the thin copper plate. Which electrode should be attached to the positive terminal of battery and why?
Answer:
Impure copper rod should be attached to the positive terminal of the battery in order to make it anode. This will enable the deposition of copper on thin copper plate which acts as a cathode.

MP Board Class 8th Science Chemical Effects of Electric Current NCERT Extended Learning – Activities

Question 1.
Test the conduction of electricity through various fruits and vegetables, Display your result in a tabular form.
Answer:
Do yourself.

Question 2.
Repeat the Activity 14.7 (Textbook page no. 178) with a zinc plate in place of the copperplate connected to the negative terminal of the battery. Now replace zinc plate with some other metallic object and again repeat the activity. Which metal gets deposited over which other metal? Discuss your findings with your friends.
Answer:
Do yourself.

Question 3.
Find out if there is a commercial electroplating unit in your town. What objects are electroplated there and for what purpose? (The process of electroplating in a commercial unit is much more complex than what we did in Activity 14.7 of textbook. Find out how they dispose off the chemicals they discard.
Answer:
Do yourself.

Question 4.
Imagine that you are an ‘entrepreneur’ and have been provided a loan by a bank to set up a small electroplating unit. What object you would like to electroplate and for what purpose? (Look meaning of ‘entrepreneur’ in a dictionary).
Answer:
Entrepreneur is a person who makes money by starting or running business, especially when this involves taking financial risks.

Question 5.
Find out the health concerns associated with chromium electroplating. How are people trying to resolve them?
Answer:
Do yourself.

Question 6.
You can make a fun pen for yourself. Take a conducting metal plate and spread a moist paste of potassium iodide and starch. Connect the plate to a battery as shown in Fig. 14.3. Now using the free end of the wire, write a few letters on the paste. What do you see?

Answer:
Do yourself.

MP Board Class 8th Science Chemical Effects of Electric Current NCERT Additional Important Questions

A. Short Answer Type Questions

Question 1.
What types of forces do electric charges exert on each other?
Answer:
Unlike charges attract each other referred to as an electric circuit, while like charges repel each other.

Question 2.
What is an electric circuit?
Answer:
The path of an electric current is referred to as an electric circuit.

Question 3.
How can we check magnetic effects of electric current?
Answer:
We can check magnetic effects of electric current by using magnetic compass.

Question 4.
What is used in CFLs?
Answer:
Mercury is used in CFLs.

Question 5.
Why is it very dangerous to operate an electrical appliance with wet hands?
Answer:
If someone operates electrical appliances with wet hands, there is a chance of getting electrocuted.

B. Long Answer Type Questions

Question 6.
What effect does the current produce when it flows through a conducting solution?
Answer:
The passage of an electric current through a conducting solution causes chemical reactions. As a result, bubbles of gas are formed, deposits of metal on electrodes may be seen and changes of colour of solution may occur, depending on what solutions and electrodes are used. These are some of the chemical effects of the electric current.

Question 7.
What are the different effects of electricity?
Answer:
The different effect of electricity are:

• Heating effect
• Chemical effect
• Magnetic effect.

Question 8.
What is the application of chemical effects of electricity in our daily life?
Answer:
Carrying chemical reactions by the effect of electricity is called chemical effect of electric current.

MP Board Class 8th Science Solutions

MP Board Class 12th Hindi Makrand Solutions Chapter 16 दक्षिण भारत की एक झलक (निबन्ध, आचार्य विनय मोहन शर्मा)

दक्षिण भारत की एक झलक पाठ्य-पुस्तक पर आधारित प्रश्न

दक्षिण भारत की एक झलक लघु उत्तरीय प्रश्न

प्रश्न 1.
तमिलनाडु के निवासियों की दृष्टि में सर्वोपरि क्या है?
उत्तर:
तमिलनाडु के निवासियों की दृष्टि में अपनी भाषा और संस्कृति सर्वोपरि है।

प्रश्न 2.
‘महाश्वेता’ की छवि कौन धारण करता है? यहाँ महाश्वेता का क्या अर्थ है?
उत्तर:
महाश्वेता की छवि केरल की स्त्रियाँ धारण करती हैं। यहाँ महाश्वेता का अर्थ है-सरस्वती देवी।

प्रश्न 3.
कन्याकुमारी में कौन-कौन से समुद्रों का मिलन होता है? (M.P. 2011)
उत्तर:
कन्याकुमारी में हिंद महासागर, अरब सागर और बंगाल की खाड़ी समुद्रों का मिलन होता है।

प्रश्न 4.
तमिल कवि की तुलना तुलसी काव्य से क्यों की जाती है?
उत्तर:
तमिल कवि ‘कम्बन’ ने भी तुलसी के समान ही ‘कम्बन रामायण’ की रचना की है।

प्रश्न 5.
पार्वती जी का नाम कन्याकुमारी क्यों पड़ा? (M.P. 2010)
उत्तर:
शिव-पार्वती का विवाह होने वाला था। विवाह का मूहूर्त रात में था। पार्वती उनकी खोज में चली गईं। बारात न पहुँचने के कारण वे उदास होकर अपने निवास में लौट आयीं और तभी से उनका नाम कन्याकुमारी पड़ गया।

दक्षिण भारत की एक झलक दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
आंध्रवासियों का रहन-सहन कैसा है?
उत्तर:
आंध्रवासियों का रहन-सहन साधारण है। स्त्रियाँ खुली साड़ी पहनती हैं। उन्हें अपने बालों को फूलों से सजाने का चाव है। पुरुष धोती पहनते हैं। पीछे लाँग का छोर झंडी की तरह लहराता दिखाई देता है। वे कॉफी पीते हैं और इडली का नाश्ता करते हैं। यहाँ रामायण का बड़ा प्रचार है। स्त्री-पुरुषों में भावुकता अधिक पाई जाती है। वे समय के अनुसार स्वयं को ढालने में सक्षम हैं।

प्रश्न 2.
तमिल और आंध्रवासियों की भोजन पद्धति में क्या नवीनता है?
उत्तर:
तमिल और आंध्रवासियों की भोजन पद्धति में विशेष अंतर नहीं है। केले के पत्ते पर भात का ढेर, रसम, दाल, तरकारी, दही, चटनी, मोर (तक्र) परोसा जाता है। खाने वाला भात में सब कुछ मिलाकर लंबे लंबे पिंड बनाकर गटकता जाता है। अय्यर (ब्राह्मण) निरामिष भोजी होता है और ब्राह्मणोत्तर को आमिष भोजन से परहेज नहीं है। भात की इडली ‘छोले’ के समान दोसा और उपमा, चटनी और दही के साथ बड़े प्रेम से खाये जाते हैं। भात में शुद्ध देशी घी का प्रयोग होता है।

प्रश्न 3.
लेखक के अनुसार नारी किस तरह भारतीय एकता का प्रतीक बन रही है?
उत्तर:
हिंदी फिल्मों के प्रभाव के कारण आधुनिक महाराष्ट्र, तमिल और केरल नारी की वेशभूषा समान होती जा रही है। सभी स्त्रियाँ एक जैसी साड़ी पहनती हैं, जिसका एक छोर दक्षिण कंधे से होता हुआ पीछे एड़ी से छूता हुआ झूलता है। उसका सर सदा खुला रहने का रिवाज धीरे-धीरे उत्तर के शिक्षित घरों में भी बढ़ रहा है। इस प्रकार लेखक के अनुसार वेशभूषा में भारतीय नारी एकता की प्रतीक बनती जा रही है।

प्रश्न 4.
केरल के गाँवों की कौन-कौन सी विशेषताएँ हैं?
उत्तर:
केरल के गाँवों में भोजन के अंत में जीरे से उबाला हुआ कुनकुना पानी पीने के काम में लाया जाता है। वहाँ रहन-सहन का स्तर ऊँचा है। गरीबों के नारियल के अवयवों से बने घर भी बिलकुल स्वच्छ होते हैं। प्रत्येक घर के आँगन में दस-पाँच नारियल, दो-चार केले, कटहल के पेड़ अवश्य होते हैं। गाँव की प्रत्येक गली साफ-सुथरी होती है। अधिकांश गाँवों में बिजली है। पोस्ट ऑफिस, छोटा दवाखाना और स्कूल हैं। दो-चार गाँवों के बीच हाई स्कूल और बीस-पच्चीस गाँवों के बीच कॉलेज की व्यवस्था है। गाँव-गाँव में हिंदी बोलने वाले हैं।

प्रश्न 5.
चेन्नई में हिंदी प्रचार-सभा क्या-क्या कार्य कर रही है?
उत्तर:
चेन्नई में हिंदी प्रचार-सभा हिंदी की विद्यापीठ का कार्य कर रही है। यहाँ से हिंदी के कई सौ अध्यापक-अध्यापिकाएँ प्रतिवर्ष शिक्षा ग्रहण कर दक्षिण के अनेक स्कूल और कॉलेजों में हिंदी अध्यापन का कार्य कर रहे हैं। वे दक्षिण भारत में हिंदी के प्रचार-प्रसार का महत्त्वपूर्ण काम कर रही हैं।

दक्षिण भारत की एक झलक भाषा-अनुशीलन

प्रश्न 1.
‘आमिष’ शब्द में निः उपसर्ग लगाकर ‘निरामिष’ विलोम शब्द बनाया गया है। इसी प्रकार उपसर्गों के प्रयोग से निम्नलिखित के विलोम शब्द लिखिए –
प्रशंसनीय, एकता, सजीव, संस्कृति
उत्तर:

प्रश्न 2.
निम्नलिखित सामासिक पदों का विग्रह कर समासों के नाम लिखिए –
तमिलनाडु, अनंत-शयनम्, शताव्दी, चौपाटी, शृंगार-काल।
उत्तर:

प्रश्न 3.
‘कृष्णा नदी के दर्शन होते हैं।’ वाक्य में ‘दर्शन’ शब्द एकवचन होकर भी बहुवचन की तरह प्रयुक्त हुआ है। हिंदी के ऐसे ही पाँच वाक्य जिसमें बहुवचन के रूप में शब्द का प्रयोग हुआ हो लिखिए।
उत्तर:

1. अधिकारी ने चेक पर हस्ताक्षर कर दिए हैं।
2. बीमार वृद्धा के प्राण-पखेरू उड़ गए।
3. इस मंदिर में भगवान विराजमान हैं।
4. दुखभरी बातें सुनते ही महिला की आँखों से आँसू बह निकले।
5. सुमन के बाल लंबे हैं।

दक्षिण भारत की एक झलक भाव विस्तार/पल्लवन

प्रश्न 1.
प्रकृति पर विजय पाकर ही मनुष्य दम लेता है।
उत्तर:
प्रकृति मनुष्य के मार्ग में अनेक बाधाएँ उपस्थित करती है। समुद्र की लहरों पर मछुआरों की नाव बार-बार ऊपर-नीचे होती है। उन्हें देखकर प्रतीत होता है कि उनकी नावें अब डूबी और तब डूबीं। काफ़ी प्रयास के बाद वे नाव को स्थिर कर पाते हैं। मछुआरे शीघ्र ही समुद्र की सतह पर नाव खेते हुए दिखाई देते हैं। इस प्रकार मनुष्य प्रकृति से हार नहीं मानता, उस पर विजय प्राप्त करके ही दम लेता है। समुद्र की लहरों पर नाव खेना उसके द्वारा प्रकृति पर विजय पाने का ही परिणाम है।

दक्षिण भारत की एक झलक योग्यता-विस्तार

प्रश्न 1.
दक्षिण भारतीय छात्रों से सघन मैत्री कर उनके प्रदेशों की विशेषताएँ ज्ञात कीजिए।
उत्तर:
छात्र स्वयं करें।

प्रश्न 2.
दक्षिण के उन लोगों की सूची बनाइए जो राजनीति, फिल्म, साहित्य, नृत्य …….. और संगीत में प्रसिद्ध हुए हैं।
उत्तर:
छात्र स्वयं करें।

प्रश्न 3.
संविधान स्वीकृत कोई अन्य भाषा सीखने का प्रयत्न कीजिए।
उत्तर:
छात्र स्वयं करें।

प्रश्न 4.
दक्षिण भारत दर्शन का कार्यक्रम बनाइए।
उत्तर:
छात्र स्वयं करें।

प्रश्न 5.
हिंदी प्रचार सभा (चेन्नई) की तरह हिंदी के विकास के लिए जो संस्थाएँ पत्रिकाएँ कार्य करती हैं, उनकी सूची बनाइए।
उत्तर:
छात्र स्वयं करें।

दक्षिण भारत की एक झलक परीक्षोपयोगी अन्य महत्वपूर्ण प्रश्न

I. वस्तुनिष्ठ प्रश्न –

प्रश्न 1.
‘दक्षिण भारत की एक झलक’ यात्रा-वृत्तांत के लेखक हैं –
(क) आचार्य रामचन्द्र शुक्ल
(ख) आचार्य हजारी प्रसाद द्विवेदी
(ग) आचार्य विनय मोहन शर्मा
(घ) आचार्य नरेंद्र देव
उत्तर:
(ग) आचार्य विनय मोहन शर्मा।

प्रश्न 2.
कृष्णा नदी स्थित है –
(क) तमिलनाडु में
(ख) केरल में
(ग) आंध्र प्रदेश में
(घ) महाराष्ट्र में
उत्तर:
(ग) आंध्र प्रदेश में।

प्रश्न 3.
अय्यर (ब्राह्मण) ……….. भोजी होता है।
(क) निरामिष
(ख) आमिष
(ग) शाकाहारी
(घ) रंजक
उत्तर:
(क) निरामिष।

प्रश्न 4.
अनंत-शयनम् के मंदिर में ……….. पहनकर जाना निषिद्ध है।
(क) सिला हुआ वस्त्र या जूता
(ख) पगड़ी या खड़ाऊँ।
(ग) पैंट-कमीज अथवा धोती
(घ) घड़ी, बेल्ट अथवा चप्पल
उत्तर:
(क) सिला हुआ वस्त्र या जूता।

प्रश्न 5.
विश्व में वह कौन-सा स्थान है, जहाँ सूर्य समुद्र में डूबता है और समुद्र से ही उगता है?
(क) कन्याकुमारी का समुद्र तट
(ख) गोवा का समुद्र तट
(ग) मुंबई का समुद्र तट
(घ) कोलकाता का गंगा तट
उत्तर:
(क) कन्याकुमारी का समुद्र तट।

प्रश्न 6.
त्रिवेन्द्रम का दूसरा नाम है –
(क) त्रावणकोर
(ख) तिरुअनन्तपुरम
(ग) गोपुरम
(घ) तिरुचिरापल्ली
उत्तर:
(ख) तिरुअनन्तपुरम।

प्रश्न 7.
मीनाक्षी मंदिर स्थित है –
(क) मदुरा में
(ख) मथुरा में
(ग) रामेश्वरम में
(घ) मद्रास में
उत्तर:
(क) मदुरा में।

प्रश्न 8.
काले पत्थर की विशाल हनुमान मूर्ति दक्षिण के किस मंदिर में है?
(क) शुचिन्द्रम मंदिर
(ख) मीनाक्षी मंदिर
(ग) अनन्तशयनम् मंदिर
(घ) कन्याकुमारी मंदिर
उत्तर:
(क) शुचिन्द्रम मंदिर।

प्रश्न 9.
कन्याकुमारी को मंदिर किस देवी का मंदिर है?
(क) सरस्वती
(ख) दुर्गा
(ग) पार्वती
(घ) लक्ष्मी
उत्तर:
(ग) पार्वती।

प्रश्न 10.
तमिल स्त्रियाँ किससे बनी बाल्टी से कुएँ से पानी खींच रही थीं?
(क) लोहे की
(ख) ताड़ के पत्तों की
(ग) नारियल के पत्तों की
(घ) प्लास्टिक की
उत्तर:
(ख) ताड़ के पत्तों की।

प्रश्न 11.
जब पार्वती का विवाह शिव से होने वाला था –
(क) तब शिवजी की बारात वहाँ पहुँच गई।
(ख) कुमारी पार्वती शिवजी से मिल गईं।
(ग) विवाह का मुहूर्त भोर में था।
(घ) शिवजी के न मिलने पर पार्वती अपने निवास स्थान को लौट आईं।
उत्तर:
(घ) शिवजी के न मिलने पर पार्वती अपने निवास स्थान को लौट आईं।

II. निम्नलिखित रिक्त स्थानों की पूर्ति दिए गए विकल्पों के आधार पर कीजिए –

1. त्रिवेन्द्रम का दूसरा नाम ………. है। (तिरुचिरापल्ली/तिरुअनन्तपुरम्)
2. लेखक ने दक्षिण भारत की यात्रा ………. में की थी। (1853/1953)
3. बेजवाड़ा ………. का एक प्रमुख नगर है। (आंध्र-प्रदेश/तमिलनाड्)
4. तेलुगु भाषा में सत्तर प्रतिशब्द ………. के होते हैं। (तमिल संस्कृत)
5. आंध्र में ………. कृत रामायण का बड़ा प्रचार है। (त्यागराज/तुलसी)

उत्तर:

1. तिरुअनन्तपुरम्
2. 1953
3. आन्ध-प्रदेश
4. संस्कृत
5. तुलसी।

III. निम्नलिखित कथनों में सत्य असत्य छाँटिए –

1. त्रिवेन्द्रम से कन्याकुमारी तक लगातार बस्ती है।
2. गोपुरम् मन्दिर के द्वार को कहते हैं।
3. तमिल का व्याकरण ईसा के आठवीं शताब्दी पूर्व लिखा गया था।
4. मद्रास को चेन्नई कहते हैं।
5. श्री रंगम् का मंदिर कावेरी नदी के द्वीप में है।

उत्तर:

1. सत्य
2. सत्य
3. असत्य
4. सत्य
5. सत्य।

IV. निम्नलिखित के सही जोड़े मिलाइए –

प्रश्न 1.

उत्तर:
(i) (ग), (ii) (घ), (iii) (ङ), (iv) (ख), (v) (क)।

V. निम्नलिखित प्रश्नों के उत्तर एक शब्द या एक वाक्य में दीजिए –

प्रश्न 1.
त्रिवांकुर (त्रावणकोर) जाते समय लेखक ने किसकी झलक देखी?
उत्तर:
त्रिवांकुर (त्रावणकोर) जाते समय लेखक ने आंध्र प्रदेश, तमिलनाडु और केरल की झलक देखी।

प्रश्न 2.
आंध्र का प्रमुख नगर कौन-सा है?
उत्तर:
वेजवाड़ा

प्रश्न 3.
भक्त कवि त्यागराज किस शताब्दी के थे?
उत्तर:
18वीं शताब्दी के

प्रश्न 4.
अय्यर ब्राह्मण कैसे होते हैं?
उत्तर:
अय्यर ब्राह्मण निरामिष भोजी होते हैं।

प्रश्न 5.
आन्ध्र में क्या-क्या अधिक पैदा होता है?
उत्तर:
आंध्र में काजू, केला और धान अधिक पैदा होता है।

दक्षिण भारत की एक झलक लघु उत्तरीय प्रश्न

प्रश्न 1.
आंध्र में हिंदी की किस पुस्तक का बड़ा प्रचार है?
उत्तर:
आंध्र में हिंदी की तुलसीकृत रामायण का बड़ा प्रचार है।

प्रश्न 2.
आंध्रप्रदेश के लोग कौन-सी भाषा बोलते हैं?
उत्तर:
आंध्रप्रदेश के लोग तमिल भाषा बोलते हैं।

प्रश्न 3.
केरल के गरीब लोग क्या खाते हैं?
उत्तर:
केरल के गरीब लोग जंगल से कंद को उखाड़कर उसे भूनकर या उबाल के खाते हैं।

प्रश्न 4.
त्रिवेन्द्रम में बाजारों में बहुत-से लोग नंगे पैर क्यों चलते हैं?
उत्तर:
त्रिवेन्द्रम में बारहों महीने वर्षा होती रहती है। अतः कीचड़ से बचने के लिए लोग नंगे पैर चलते हैं।

प्रश्न 5.
श्रीरंगम् का मंदिर कहाँ बना हुआ है?
उत्तर:
श्रीरंगम् का मंदिर तिरुचिरापल्ली के निकट कावेरी नदी के द्वीप में बना हुआ है।

प्रश्न 6.
मद्रास का कौन-सा वृक्ष जग-प्रसिद्ध है और क्यों?
उत्तर:
मद्रास का वट-वृक्ष जग प्रसिद्ध है, क्योंकि इसकी लंबाई उत्तर से दक्षिण की ओर 200 फुट और चौड़ाई में पूरब से पश्चिम की ओर 205 फुट है।

प्रश्न 7.
तमिल और आंध्र का मुख्य भोजन क्या है?
उत्तर:
भात का ढेर, रसम, दाल, तरकारी, दही, चटनी, मोटर (तक्र), भात की इडली, डोसा और उपमा तमिल और आंध्र का मुख्य भोजन है।

प्रश्न 8.
समुद्र दर्शन के बाद लेखक कहाँ गया?
उत्तर:
समुद्र दर्शन के बाद लेखक अजायबघर गया।

प्रश्न 9.
रामेश्वरम् की क्या विशेषता है?
उत्तर:
रामेश्वरम् में विशाल मंदिर है। कई तीर्थ कूप हैं, जिनका पानी मीठा है। यहाँ हिंदी जानने वाले बहुत हैं।

दक्षिण भारत की एक झलक दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
तमिलानाडु के स्त्री-पुरुषों की वेशभूषा का उल्लेख कीजिए।
उत्तर:
तमिलनाडु के पुरुषों की वेशभूषा में लुंगी, कुरता और आधुनिक बुशर्ट शामिल हैं। स्त्रियाँ खुली साड़ी पहनती हैं। उन्हें हरा रंग अच्छा लगता है। स्त्रियाँ हरा परिधान पहनती हैं।

प्रश्न 2.
लेखक किस व्यावसायिक ईमानदारी से प्रभावित हुआ?
उत्तर:
लेखक ने मद्रास, मदुरा, तिरुचिरापल्ली और रामेश्वरम् आदि स्थानों के होटल में भोजन किया। वहाँ के होटलों में भात पर शुद्ध देशी घी ही डाला गया। होटल वालों की यह ईमानदारी प्रशंसनीय है। दूध के संबंध में वहाँ के दुकानदार बड़े स्पष्टवादी हैं। वे स्पष्ट कहते हैं कि हम शुद्ध दूध नहीं बेचते। हम कॉफी का दूध बेचते हैं, जिसमें पानी मिला होता है। लेखक उनकी इस व्यावसायिक ईमानदारी से बड़ा प्रभावित हुआ।

प्रश्न 3.
लेखक कन्याकुमारी में सूर्यास्त का दृश्य क्यों नहीं देख पाया?
उत्तर:
लेखक सूर्यास्त का दृश्य देखने के लिए कन्याकुमारी के समुद्र तट पर पहुँच गया। बहुत-से सैलानी वहाँ सूर्यास्त का दृश्य देखने के लिए उत्सुक थे, पर बादल सूर्य को रह-रहकर ढाँप लेते थे। लेखक सूर्यास्त की दिशा पर नजरें गड़ाये रहा, पर बादलों ने सूर्य को मुक्त नहीं किया। फलस्वरूप वह सूर्यास्त का दृश्य नहीं देख पाया।

प्रश्न 4.
मीनाक्षी मंदिर की विशेषताएँ बताइए।
उत्तर:
मीनाक्षी मंदिर मदुरा में स्थित है। यह बड़ा विशाल मंदिर है। यह कई गोपुरम से घिरा हुआ है। गोपुरम ऊँचा गुंबद के समान द्वार है। इस मंदिर में अनेक मूर्तियों में पौराणिक गाथाएँ अंकित हैं। मंदिर के प्रत्येक खंभे पर हाथी के ऊपर सवार सिंह दिखलाया गया है। मूर्तियाँ बड़ी सजीव हैं। यहाँ एक हजार खंभों वाला हाल है। मंदिर में दक्षिण के 63 संतों की प्रतिमाएँ हैं। मंदिर में इनकी वाणियों का अध्ययन-मनन होता है।

प्रश्न 5.
अनंतशयनम् के मंदिर की क्या विशेषता है?
उत्तर:
अनंतशयनम् मंदिर में सिला हुआ वस्त्र या जूता पहनकर जाना निषिद्ध है। महिलाओं की साड़ी सिला हुआ वस्त्र न होने के कारण मंदिर में प्रवेश पा सकती, हैं। मंदिर में मूर्ति की विशालता दर्शनीय है।

प्रश्न 6.
मद्रास का जग-प्रसिद्ध वट-वृक्ष कैसा है?
उत्तर:
मद्रास का जग-प्रसिद्ध वट-वृक्ष दर्शनीय है। इसकी लम्बाई उत्तर से दक्षिण की ओर 200 फुट और चौड़ाई पूरब से पश्चिम की ओर 205 फुट है। इसके नीचे एनींबेसेन्ट ने थियोसोफिकल सोसाइटी की अनेक महत्त्वपूर्ण सभाएँ की हैं। यह हजारों दर्शकों का विश्राम-स्थल है।

दक्षिण भारत की एक झलक लेखक-परिचय

प्रश्न 1.
आचार्य विनय मोहन शर्मा का संक्षिप्त जीवन-परिचय देते हुए उनकी साहित्यिक विशेषताओं पर प्रकाश डालिए।
उत्तर:
जीवन-परिचय:
आचार्य विनय मोहन शर्मा का जन्म 19 दिसंबर, सन् 1905 में करकबैल मध्य प्रदेश के नरसिंहपुर जिले में हुआ। इनका मूल नाम शुक देव प्रसाद तिवारी ‘वीरात्मा’ था। आपने एम.ए., पी-एचडी., एल.एल.बी., तक शिक्षा प्राप्त की। इन्होंने पत्रकारिता से साहित्य जगत् में प्रवेश किया। ये ‘कर्मवीर’ पत्रिका के सहायक सम्पादक.रहे। सन् 1940 से शिक्षा-जगत् में विभिन्न पदों पर रहकर अध्यापन किया।

ये नागपुर एवं कुरुक्षेत्र विश्वविद्यालय में प्रोफेसर और महाकौशल विश्वविद्यालय, जबलपुर में प्राचार्य रहे। इन्होंने केन्द्रीय हिंदी संस्थान, आगरा के प्रथम निदेशक पद को भी सुशोभित किया। ये सन् 1970 से 1973 तक विश्वविद्यालय अनुदान आयोग के अंतर्गत विश्वविद्यालय से भी संबद्ध रहे। 5 अगस्त, सन् 1993 को इनका निधन हो गया।

साहित्यिक-परिचय:
हिंदी को मराठी संतों की देन’ शोध प्रबंध पर आपको अनेक पुरस्कार प्राप्त हुए। इन्होंने हिंदी, पंजाबी और मराठी संतों का तथा तुलसी काव्यों का तुलनात्मक अध्ययन किया और ‘गीत-गोविंद’ का हिंदी अनुवाद किया। इनकी ‘दृष्टिकोण’, ‘साहित्य कथा पुराना’, शोध प्रविधि-मध्य प्रदेश और उत्तर प्रदेश सरकार द्वारा पुरस्कृत की जा चुकी है। विभिन्न शासकीय एवं अशासकीय साहित्य संस्थानों तथा सभाओं द्वारा आपको सम्मानित एवं पुरस्कृत भी किया गया है। पं. द्वारिका प्रसाद मिश्र द्वारा रचित महाकाव्य ‘कृष्णायक’ की इन्होंने अवधी से खड़ी बोली में रूपान्तरित किया है। हिंदी साहित्य जगत् में निबंधकार, समीक्षक, एवं शोधकर्ता के रूप में इनका विशिष्ट स्थान है।

रचनाएँ:
इनकी हिंदी को मराठी संतों की देन, हिंदी, पंजाबी और मराठी में कृष्ण तथा तुलसी काव्यों का तुलनात्मक अध्ययन, गीत-गोविन्द का हिंदी अनुवाद, दृष्टिकोण, साहित्य कथा पुराना, शोध प्रविधि, कृष्णायन का खड़ी बोली में रूपांतरण आदि रचनाएँ हैं।

भाषा-शैली:
विनय मोहन शर्मा की भाषा प्रौढ़, सशक्त, परिमार्जित खड़ी बोली – है। भाषा में तत्सम शब्दों के अतिरिक्त प्रचलित उर्दू शब्द भी हैं। साधारण विषयों पर इनकी लेखनी सरल और व्यावहारिक भाषा का रूप धारण कर लेती है।

दक्षिण भारत की एक झलक पाठ का सारांश

प्रश्न 1.
‘दक्षिण भारत की एक झलक’ यात्रा-वृत्तांत का सार अपने शब्दों में लिखिए।
उत्तर:
दक्षिण भारत की एक झलक’ यात्रा-वृत्तांत में आचार्य विनय मोहन शर्मा ने दक्षिण भारत के सुरम्य स्थानों, रीति-रिवाजों और दृश्यों का वर्णन करते हुए वहाँ की संस्कृति की सजीव झाँकियाँ प्रस्तुत की हैं। शर्माजी कहते हैं कि मुझे 1953 में पहली बार त्रावणकोर जाते हुए आंध्र प्रदेश, तमिलनाडु और केरल जाने का अवसर मिला। प्रातःकाल जब उनकी गाड़ी आंध्र प्रदेश के बेजबाड़ा पहुँची तो उन्हें ऐसा लगा मानो किसी नई दुनिया में प्रवेश हो रहा है।

वहाँ की समुद्र से आने वाली वायु तन और मन दोनों को शीतलता प्रदान कर रही थी। वहाँ कृष्णा नदी भी देखी। आंध की स्त्रियाँ खुली साड़ी पहनती हैं और पुरुष धोती पहनते हैं, जिनकी लांग की छोर झंडी की तरह लहराता दिखाई देती है। लोग गोरे रंग के होते हैं और लोग तेलुगू बोलते हैं। यहाँ तुलसीकृत रामायण का बड़ा प्रचार है। 18वीं शताब्दी में भक्त कवि त्यागराज ने भी तुलसी का अनुकरण किया है।

आचार्यजी आंध्र के लोगों के खान-पान के संबंध में बताते हुए कहते हैं कि लोग कॉफी अधिक पीते हैं और इडली का नाश्ता करते हैं। स्त्रियाँ फूलों से केश-सज्जा करती हैं। वहाँ काजू और केले के साथ-साथ धान उत्पन्न होता है। स्त्री-पुरुष भावुक होते हैं। वे स्वयं को समय के अनुरूप ढालने में सक्षम हैं। ‘गुडूर’ से गाड़ी तमिलनाडु में प्रवेश करती है। यहाँ तमिल भाषा बोली जाती है। पुरुष लुंगी, कुर्ता और बुशशर्ट पहनते हैं। यहाँ के लोग रंग के साँवले होते हैं। स्त्रियों को हरा रंग अधिक पसन्द है। तमिल और आंध्र के भोजन में विशेष अंतर नहीं है। वहाँ केले के पत्ते पर भात, रसम, दाल, तरकारी और दही, चटनी, मोर परोसा जाता है।

यहाँ इटली, दोसा, उपमा, चटनी और दही के साथ खाया जाता है। – सुदूर दक्षिण में मिठाइयों की दुकानें नहीं हैं। वहाँ होटल वाले ईमानदार हैं। वे भात में शुद्ध घी का प्रयोग करते हैं परन्तु वे शुद्ध दूध नहीं बेचते। केरल की आबादी सघन है। जमीन हरी-भरी है। गरीब लोग कंद खाते हैं। उसके साथ मछली मिल जाने पर पूरा आहार हो जाता है। नारियल बहुतायत से होता है। अतः लोग उसका कई रूपों में प्रयोग करते हैं। उसका पानी बेंचा जाता है।

केरल में स्त्रियों का पहनावा तमिलनाडु की स्त्रियों से अलग है। वे उजले रंग के वस्त्र पहनती हैं। शहरी स्त्रियों का पहनावा हिंदी फिल्मों के प्रभाव के कारण महाराष्ट्र, तमिल और केरल में एक जैसा है। त्रावणकोर-कोचीन में शिक्षा प्रचार-प्रसार अधिक है। लोगों का जीवन-स्तर ऊँचा है। घर साफ-सुथरे होते हैं। अधिकांश गाँवों में बिजली है। पोस्ट-ऑफिस, दवाखाना, और स्कूल प्रत्येक गाँव में हैं। दो-चार गाँवों के मध्य एक हाई स्कूल और बीस-पच्चीस गाँवों के बीच एक कॉलेज भी स्थापित है। हिंदी का यहाँ बहुत प्रचार है। परीक्षा के लिए हिंदी अनिवार्य है।

त्रिवेन्द्रम से कन्याकुमारी की यात्रा बड़ी रोचक थी। स्त्री-पुरुष बाजारों में नंगे पैर चलते हैं; क्योंकि वर्षा होती रहती है। यहाँ का समुद्र-दर्शन अत्यन्त आकर्षक होता है। समुद्र की आती-जाती लहरों में खड़ा होने में आनन्द आता है। समुद्र में अनेक मछुवारे मछलियाँ पकड़ते दिखाई देते हैं। उनकी नावें समुद्र में तैरती दिखाई देती हैं। वहाँ के अजायबघर में समुद्र की मछलियों, सर्पो, केकड़ों आदि को सुरक्षित रखा गया है। यह अजायबघर भारत में अपनी तरह का एक ही है। वहाँ के अनन्त-शयनम् मन्दिर में सिला हुआ वस्त्र या जूता पहनकर जाना मना है। मन्दिर में मूर्ति की विशालता दर्शनीय है।

त्रिवेन्द्रम से कन्याकुमारी तक इतनी सघन आबादी है कि भारत के किसी भाग में इतनी सघन आबादी नहीं है। तमिल स्त्रियाँ ताड़ की बनी बाल्टी से कुएँ से पानी निकालती हैं। दक्षिण भारत में मामूली स्त्रियाँ सोने के और संभ्रांत स्त्रियाँ हीरे, मोती, जवाहरात के आभूषण पहनती हैं। कन्याकुमारी में सूर्यास्त का दृश्य अत्यन्त भव्य होता है। यहाँ तीन समुद्रों का मिलन होता है। अनेक स्त्री-पुरुष सूर्यास्त का दृश्य देखने को उत्सुक थे, लेकिन बादलों के कारण यह सम्भव नहीं हो सका। संसार में यही स्थान है जहाँ सूर्य समुद्र में डूबता है और समुद्र से ही उगता है।

कन्याकुमारी के मंदिर में पार्वती के दर्शन के लिए गए। इस मंदिर में भी नंगे बदन ही जाना पड़ता था। वहाँ पार्वती विवाह का मुहूर्त निकल जाने के कारण अविवाहित रूप में ही आकर विराजमान हो गई थी। अतः इसीलिए यहाँ का नाम कन्याकुमारी पड़ा है। इसके बाद शुचिन्द्रम के भव्य मंदिर के दर्शन किए। वहाँ पर काले पत्थर की विशाल हनुमान की मूर्ति है। वह मुख्य रूप से शिव-मंदिर है। मंदिर के प्रस्तर स्तंभों की विशेषता है कि उसे हाथ से ठोंकने पर धीमी सुरीली आवाज निकलती है।

त्रिवेन्द्रम और कन्याकुमारी के बीच की भूमि में सुपारी, काजू, केला, नारियल और धान आदि से उर्वरा है। आचार्य कहते हैं कि समय की कमी के कारण मलयालय के कई साहित्यकारों से भेंट नहीं हो पाई। इसके बाद मदुरा का मीनाक्षी मंदिर देखा। वह बहुत विस्तीर्ण है। यह कई गोपुरम से घिरा है। गोपुरम ऊँचा गुम्बद के समान द्वार है। यहाँ की मूर्तियाँ बड़ी सजीव हैं। वहाँ एक हजार खम्भों वाला हॉल है, वहाँ हजारों नर-नारी प्रसाद पा सकते हैं। मदुरा से रामेश्वरम धनुष-कोटि भी गए। रामेश्वरम का मंदिर विशाल है। यहाँ तीर्थयात्री समुद्र में स्नान करते हैं।

यहाँ हिंदी जानने वाले बड़ी संख्या में हैं। तिरुचिरापल्ली का कावेरी नदी के द्वीप पर बना श्रीरंगम का मंदिर दर्शनीय है। त्रिचिन्नापल्ली में सहस्रों सीढ़ियाँ चढ़ने के बाद ऊँचाई पर एक विशाल मंदिर है। यहाँ से । नगर और नदी का दृश्य बड़ा सुन्दर दिखायी देता है। तमिल साहित्य बहुत प्राचीन है। तमिल का व्याकरण आज भी ईसा की चार शताब्दी पूर्व ही लिखा गया व्याकरण है। चेन्नई में भी हिंदी साहित्य में गीत का परिचय मिलता है। वहाँ की हिंदी-प्रचार सभा को दक्षिण में हिंदी की प्रमुख विद्यापीठ का रूप प्रदान कर रही है।

वहाँ से कई सौ अध्यापक-अध्यापिकाएँ प्रतिवर्ष शिक्षा ग्रहण कर दक्षिण के अनेक स्कूल-कॉलेजों दक्षिण भारत की एक झलक में हिंदी पढ़ा रहे हैं। मद्रास में अडयार पुस्तकालय काफी संपन्न है। वहाँ का वटवृक्ष विश्वविख्यात है। वहाँ का समुद्रतट भी बहुत सुन्दर है। वहाँ शाम को सैलानियों का मेला-सा लग जाता है। रात के आठ बजे तक सैलानियों को मद्रास रेडियो स्टेशन का भोंपू कार्यक्रम सुनाता रहता है।

दक्षिण भारत की एक झलक संदर्भ-प्रसंगसहित व्याख्या

प्रश्न 1.
सुदूर दक्षिण में उत्तर भारत के समान तरह-तरह की मिठाइयों की दुकानें नहीं हैं। बड़े-बड़े नगरों में उत्तर भारत के एक-दो हलवाई थोड़ी-बहुत मिठाई बनाते हैं। चटपटी, खारी, खट्टी चीजें दक्षिण भारतीयों को बहुत प्रिय हैं। घी की अपेक्षा नारियल के तेल का इस्तेमाल अधिक होता है। परन्तु वहाँ के होटलों में एक बात यह देखी गई है कि जब वे भात पर घी डालते हैं, तो ह शुद्ध घी ही होता है।

होटल वालों की यह ईमानदारी प्रशंसनीय है। मैंने मद्रास, मदुरा, त्रिचिनापल्ली, रामेश्वरम् आदि स्थानों के होटलों में भोजन किया और मुझे हर जगह शुद्ध ताजे घी का स्वाद मिला। दूध के संबंध में भी यहाँ के दुकानदार बड़े स्पष्टवादी हैं। दक्षिण के स्टेशनों पर आपकी आँखों के सामने की पाल (दूध) में वल्लम (पानी) मिलाकर देंगे और कहेंगे शुद्ध दूध हम नहीं बेचते, हम कॉफी का दूध रखते हैं। इस व्यावसायिक ईमानदारी ने मुझे बड़ा प्रभावित किया। (Page 74)

शब्दार्थ:

• सुदूर – बहुत दूर, बहुत दूर का।
• प्रशंसनीय – प्रशंसा करने योग्य।
• स्पष्टवादी – स्पष्ट बोलने वाले।
• व्यावसायिक – व्यापारिक।

प्रसंग:
प्रस्तुत गद्यांश आचार्य विनय मोहन शर्मा द्वारा रचित यात्रा-वृत्तांत ‘दक्षिण भारत की एक झलक’ से उद्धृत है। लेखक दक्षिण भारत के सुरम्य स्थानों, रीति-रिवाजों और दृश्यों का रोचक वर्णन किया है। इस गद्यांश में लेखक दक्षिण भारत के लोगों की व्यावसायिक ईमानदारी का वर्णन कर रहा है।

व्याख्या:
लेखक ने दक्षिण भारत की कवा के दौरान तमिलनाडु, केरल, आंध्र प्रदेश की यात्रा की। उसने देखा कि बहुत दूर स्थित दक्षिण में उत्तर भारत के समान तरह-तरह की मिठाइयों की दुकानें नहीं हैं। दूसरे शब्दों, जैसे उत्तर भारत में तरह-तरह की मिठाई बनाने वाले हलवाइयों की दुकानें होती हैं, वैसे दुकानें दूरस्थ दक्षिण भारत में नहीं मिलतीं। यहाँ केवल बड़े-बड़े नगरों में ही उत्तर भारत के एक-दो हलवाई ही थोड़ी-बहुत मिठाई बनाते हैं। इसका कारण है दक्षिण भारत के लोगों को मिठाई अधिक रुचिकर नहीं होती है।

दक्षिण भारत के लोगों को मिठाइयों की अपेक्षा चटपटी, मसालेदार, खारी और खट्टी चीजें ही अधिक पसन्द हैं। दक्षिण भारत में लोग घी का कम प्रयोग करते हैं। नारियल के तेल का अधिक इस्तेमाल करते हैं। लेखक यहाँ के होटलों की विशेषता की ओर ध्यान आकर्षित करते हुए कहता है कि यहाँ के होटलों में एक बात यह देखने में आई कि वे भात पर घी डालते हैं और वह भी शुद्ध देशी घी। भात पर देशी घी डालने के संबंध में उनकी ईमानदारी प्रशंसा करने के योग्य है। वे देशी घी में किसी तरह की मिलावट नहीं करते। वे ईमानदारी से भात पर शुद्ध देशी घी ही डालते हैं।

लेखक बताता है कि उसने दक्षिण भारत के मद्रास, मदुरा, त्रिचिन्नापल्ली, रामेश्वरम आदि स्थानों के होटलों में खाना खाया और उसे हर स्थान पर शुद्ध देशी घी का ही स्वाद मिला। इतना ही नहीं दूध के संबंध में भी यहाँ के दुकानदार बहुत स्पष्ट बोलने वाले हैं। दक्षिण भारत के स्टेशनों पर वे आपके द्वारा दूध माँगने पर आपकी आँखों के सामने ही दूध में पानी मिलाकर देंगे। वे स्पष्ट रूप से कहते हैं कि हम लोग शुद्ध दूध नहीं बेचते। हम कॉफी का दूध रखते हैं। कॉफी के दूध में पानी मिला होता है। लेखक दक्षिण भारतीयों की इस व्यापारिक ईमानदारी से वड़ा प्रभावित हुआ।

विशेष:

1. दक्षिण भारतीय होटल वालों की ईमानदारी की प्रशंसा की है।
2. वर्णनात्मक शैली है।
3. भाषा सरल, स्पष्ट खड़ी बोली है।

गद्यांश पर आधारित अर्थग्रहण संबंधी प्रश्नोत्तर

प्रश्न (i)
उत्तर भारतीय तथा दक्षिण भारतीय लोगों के स्वाद में क्या अंतर है?
उत्तर:
उत्तर भारतीयों को भिठाइयाँ अधिक पसंद हैं, तो दक्षिण भारतीयों को चटपटी, खारी और खट्टी चीजें अधिक पसंद हैं।

प्रश्न (ii)
लेखक दक्षिण भारतीयों की किस स्पष्टवादिता से प्रभावित हुआ?
उत्तर:
दक्षिण भारत के लोग आपके सामने दूध में पानी मिलाकर आपको देंगे और स्पष्ट कहेंगे कि हम शुद्ध दूध नहीं बेचते, हम कॉफी का दूध रखते हैं। लेखक उनकी इस स्पष्टवादिता से प्रभावित हुआ।

प्रश्न (iii)
दक्षिण भारत के होटलों में भात पर किस तरह का घी डाला जाता है?
उत्तर:
दक्षिण भारत के होटलों में भात पर शुद्ध देशी घी डाला जाता है।

गद्य पर आधारित बोधात्मक प्रश्नोत्तर

प्रश्न (i)
गद्यांश का मुख्य भाव क्या है?
उत्तर:
दक्षिण भारतीयों की पसंद, ईमानदारी और स्पष्टवादिता की प्रशंसा करना।

प्रश्न (ii)
लेखक ने दक्षिण भारत के किन-किन नगरों के होटल में खाना खाया और उसको क्या अनुभव हुआ?
उत्तर:
लेखक ने दक्षिण भारत के मद्रास, मदुरा, त्रिचिन्नापल्ली, रामेश्वरम आदि चारों होटलों में खाना खाया और उसे हर स्थान पर शुद्ध ताजे घी के स्वाद का अच्छा अनुभव हुआ।

प्रश्न 2.
त्रावणकोर (केरल) में प्रवेश करते ही स्त्रियों की पोशाक के रंग में अंतर दिखाई देने लगता है। यहाँ वे ‘महाश्वेता’ की छवि धारण कर लेती हैं। उन्हें तमिलनाडु की स्त्री के समान हरा-लाल रंग पसन्द नहीं-वे उजले रंग के वस्त्र पहनती हैं। यहाँ एक बात स्पष्ट कर दूं। इस लेख में पोशाक आदि की चर्चा नगर और ग्राम के सामूहिक जीवन को लक्ष्य करके की जा रही है। यों आज महाराष्ट्र, तमिल और केरल राज्यों की ही नहीं, समस्त देश की शहरी स्त्रियों की वेशभूषा प्रायः समान ही होती जा रही है। यह हिंदी चित्रपटों का प्रभाव जान पड़ता है।

आधुनिक महाराष्ट्र की नारी स्वच्छ साड़ी पहनना पसन्द करती है, तमिल और केरल की नारी भी उसी तरह साड़ी पहनती है, जिसका एक छोर दक्षिण कन्धे से होता हुआ पीछे एड़ी से छूता हुआ झूलता है। उसका सर सदा खुला रहने का रिवाज धीरे-धीरे उत्तर के शिक्षित घरों में भी बढ़ रहा है। वेशभूषा में नारी भारतीय एकता का प्रतीक बनती जा रही है। त्रावणकोर-कोचीन में शिक्षा का प्रसार अधिक होने से जनता के रहन-सहन का स्तर अपेक्षाकृत ऊँचा है। गरीबों के घर भी, जो अधिकतर नारियल के विभिन्न अवयवों से बनते हैं, बिल्कुल स्वच्छ रहते हैं।

प्रत्येक छोटे से घर के आँगन में दस-पाँच नारियल, दो-चार केले, कटहल के पेड़ अवश्य दिखाई देंगे। उत्तर के गाँव जहाँ चारों ओर पुरीष से घिरे रहते हैं, वहाँ केरल के गाँव गली-गली स्वच्छ झलकते हैं। यहाँ अधिकांश ग्राम विजली से जगमगाते हैं। पोस्ट ऑफिस, छोटा-सा दवाखाना और स्कूल के बिना तो गाँव बसते ही नहीं, दो-चार गाँवों के मध्य एक हाईस्कूल, बीस-पच्चीस गाँवों के बीच एक कॉलेज आवश्यक समझा जाता है। वहाँ हिंदी का इतना अधिक प्रचार है कि गाँव-गाँव में उसे बोलने-समझने वाले स्त्री-पुरुष मिल जाते हैं। (Page 75)

शब्दार्थ:

• महाश्वेता – सरस्वती।
• छवि – सुंदरता, रूप।
• पोशाक – वेशभूषा।
• सामूहिक – सामाजिक।
• चित्रपटों – फिल्मों।
• स्वच्छ – साफसुथरे।
• रिवाज – परंपरा।
• अवयवों – भागों।
• पुरीष – गंदगी
• कूड़ा – करकट।

प्रसंग:
प्रस्तुत गद्यांश आचार्य विनय मोहन शर्मा द्वारा लिखित यात्रा-वृत्तांत दक्षिण भारत की एक झलक’ से उद्धृत है। इस गद्यांश में लेखक केरल की स्त्रियों की वेशभूषा, वहाँ के घरों तथा शिक्षा-व्यवस्था के साथ-साथ हिंदी की स्थिति पर प्रकाश डाल रहा है।

व्याख्या:
लेखक कहता है कि केरल राज्य में प्रवेश (दाखिल) होते ही स्त्रियों के पहनावे की पोशाकों के रंग में अंतर स्पष्ट दिखाई देने लगता है। वेशभूषा के संबंध में केरल की स्त्रियाँ सरस्वती का रूप ग्रहण करती दिखाई पड़ती हैं। यहाँ की स्त्रियों को तमिलनाडु की स्त्री की तरह हरा और लाल रंग पसंद नहीं है। वे सफेद (उज्ज्वल) रंग के कपड़े पहनती हैं। लेखक यहाँ एक बात स्पष्ट कर रहा है कि इस लेख में पहनावे आदि की चर्चा नगर और गाँव के सामूहिक जीवन को लक्ष्य करके ही की जा रही है। वैसे तो आज महाराष्ट्र, जमिल और केरल राज्यों में ही नहीं, अपितु देश के समस्त राज्यों के शहरी क्षेत्रों की स्त्रियों के पहनावे में समानता आती जा रही है।

सारे देश के शहरी क्षेत्रों नारियों की वेशभूषा में समानता आने का कारण हिंदी फिल्मों का प्रभाव दिखाई देता है। हिंदी फिल्मों में अभिनेत्रियाँ जो वस्त्र पहनती हैं, वही आजकल नगरों की स्त्रियाँ पहनने लगी हैं। आधुनिक महाराष्ट्रीय स्त्री साफ-सुथरी साड़ी पहनना पसंद करती है तो तमिलनाडु और केरल की स्त्रियाँ भी उसी प्रकार की साड़ी पहनती हैं। उस तरह की साड़ी का एक किनारा दक्षिण कंधे से होता पीछे एड़ी से छूता हुआ लटकता रहता है। दूसरे शब्दों में, सभी स्त्रियाँ उलटे पल्ले की साड़ी पहनती हैं। उनका सर बिना पल्ले के खुला रहता है। यह रिवाज धीरे-धीरे उत्तर भारत के सुशिक्षित घरों की नारियों में भी निरंतर बढ़ता जा रहा है।

इस तरह के पहनावे से भारतीय नारी राष्ट्रीय एकता की प्रतीक बनती जा रही है। त्रावणकोर और कोचीन में शिक्षा-प्रसार अधिक होने के कारण जनता के रहन-सहन का स्तर तुलनात्मक दृष्टि से ऊँचा है। गरीबों के घर भी जो अधिकतर नारियल के विभिन्न भागों में बने होते हैं, बिलकुल साफ-सुथरे होते हैं। प्रत्येक छोटे-से घर के आँगन में भी नारियल के दस-पाँच पेड़, दो-चार केले के पेड़ और कटहल के पेड़ अवश्य लगे होते हैं। उत्तर भारत के गाँवों में चारों तरफ कूड़े-करकट के ढेर लगे होते हैं, वहीं दक्षिण भारत के गाँव की गली-गली साफ-सुथरी होती है। यहाँ के अधिकांश गाँवों में बिजली की व्यवस्था है, जिसके प्रकाश से गाँव बिजली की रोशनी से जगमगाते रहते हैं।

केरल के प्रत्येक गाँव में पोस्ट ऑफिस (डाकखाना), छोटा दवाखाना और प्राथमिक स्कूल हैं। दो-चार गाँवों के बीच हाई स्कूल है। तो 20-25 गाँवों के मध्य एक कॉलेज भी है। इस प्रकार केरल राज्य में शिक्षा की अच्छी व्यवस्था है। केरल में हिंदी का प्रचार-प्रसार बहुत है। यही कारण है कि यहाँ के गाँव-गाँव में हिंदी बोलने और समझने वाले स्त्री-पुरुष मिल जाते हैं। दूसरे शब्दों में, केरल में हिंदी बोलने और समझने वालों की संख्या पर्याप्त है।

विशेष:

1. लेखक ने केरल की विशेषताओं का वर्णन किया है।
2. वर्णनात्मक शैली है।
3. भाषा परिमार्जित खड़ी बोली है।

गद्यांश पर आधारित अर्थग्रहण संबंधी प्रश्न

प्रश्न (i)
लेखक ने हिंदी चित्रपट के किस प्रभाव का वर्णन किया है?
उत्तर:
लेखक ने हिंदी चित्रपट के वेशभूषा के प्रभाव का वर्णन किया है। हिंदी फिल्मों के प्रभाव के कारण सारे भारत के शहरी क्षेत्रों की स्त्रियों में एक ही ढंय से साड़ी पहने जाने लगी है।

प्रश्न (ii)
उत्तर भारत और केरल के गाँवों में क्या अंतर है?
उत्तर:
उत्तर भारत के गाँव चारों ओर से कूड़े-करकट से घिरे रहते हैं, जबकि केरल के गाँव की गली-गली साफ-सुथरी रहती हैं।

प्रश्न (iii)
तमिलनाडु और केरल की स्त्रियों की पसंद में क्या अंतर है?
उत्तर:
तमिलनाडु की स्त्रियाँ पहनावे में हरा और लाल रंग पसंद करती हैं, तो केरल की स्त्रियाँ उजले वस्त्र पहनना पसन्द करती हैं।

गद्यांश पर आधारित बोधात्मक प्रश्न

प्रश्न (i)
त्रावणकोर-कोचीन में रहन-सहन का स्तर ऊँचा क्यों है?
उत्तर:
त्रावणकोर-कोचीन में शिक्षा का प्रचार-प्रसार अधिक होने के कारण जनता के रहन-सहन का स्तर गाँवों की अपेक्षा अधिक ऊँचा है।

प्रश्न (ii)
केरल के गाँवों की दो विशेषताएँ लिखिए।
उत्तर:

1. केरल के गाँवों में बिजली की व्यवस्था है। गाँव बिजली से जगमगाते रहते हैं।
2. केरल के गाँवों में डाकखाना, दवाखाना और स्कूल हैं।

प्रश्न (iii)
किस राज्य के गाँव-गाँव में हिंदी बोलने और समझने वाले मिल जाते हैं और क्यों?
उत्तर:
केरल राज्य के गाँव-गाँव में हिंदी बोलने वाले और समझने वाले मिल जाते हैं, क्योंकि यहाँ हिंदी का प्रचार-प्रसार बहुत है। यहाँ हिंदी परीक्षा की अनिवार्य भाषा है।

प्रश्न 3.
त्रिवेन्द्रम से कन्याकुमारी तक लगातार बस्ती होने से ऐसा जान पड़ता है, मानो त्रिवेन्द्रम ही पचास मील तक चला गया हो। इतनी घनी आबादी भारत के किसी भाग में नहीं है। मार्ग में गाड़ी पंचर हो जाने से हम एक निकटवर्ती कुएँ पर गए जहाँ तमिल स्त्रियाँ ताड़ की बनी हुई बाल्टी से पानी खींच रही थीं। उन्होंने हमें प्यासा, अनुमान कर स्वयं पानी पिलाया। उन्हें हम अजनबियों को देखकर कुतूहल होता था और हमें उनके नीचे तक लटके फटे कानों से सोने के कर्णफूल देखकर आश्चर्य होता था। ऐसा जान पड़ता था कि कान अब अधिक भार नहीं सह सकेंगे, फट ही पड़ेंगे। दक्षिण में मामूली स्त्रियाँ सोने के आभूषण पहनती हैं। संभ्रान्त परिवार की स्त्रियाँ हीरे, मोती, जवाहरात को काम में लाती हैं। सोना उनके लिए हल्की धातु है। (Page 76)

शब्दार्थ:

• आबादी – जनसंख्या।
• कुतूहल – आश्चर्य।
• आभूषण – जेवर।

प्रसंग:
प्रस्तुत गद्यांश आचार्य विनय मोहन शर्मा द्वारा रचित यात्रा-वृत्तांत ‘दक्षिण भारत की एक झलक’ से उद्धृत है। लेखक केरल की सघन जनसंख्या और तमिल स्त्रियों की आभूषणप्रियता का वर्णन करता हुआ कर रहा है।

व्याख्या:
लेखक कहता है कि त्रिवेन्द्रम से कन्याकुमारी तक लगातार बस्ती ही बस्ती थी। उस बस्ती को देखकर लमता था, मानो त्रिवेन्द्रम ही पचास मील तक फैला हुआ हो। इतनी अधिक सघन आबादी (जनसंख्या) भारत के किसी भाग में नहीं है जितना त्रिवेन्द्रम से कन्याकुमारी के बीच फैले भाग में है। लेखक कहता है कि कन्याकुमारी की ओर जाते हुए उनकी गाड़ी में पंचर हो गया इसलिए गाड़ी में सवार हम सभी उतरकर पास वाले कुएँ पर चले गए। वहाँ हमने देखा कि तमिल स्त्रियाँ ताड़ के पत्तों से बनी हुई बाल्टी से पानी खींच रही थीं। उन्होंने हम लोगों को प्यासा जानकर अंदाजे से स्वयं ही पानी पिलाया।

उन तमिल स्त्रियों को हम अपरिचितों को देखकर आश्चर्य होता था और हम लोगों को उन स्त्रियों के नीचे तक लटके फटे हुए कानों में सोने के कर्णफूल देखकर आश्चर्य होता था। कहने का भाव यह कि वे तमिल स्त्रियाँ हम अपरिचितों को आश्चर्य से देख रही थीं तो हम लोगों को भी उनके कानों में सोने के कर्णफल नामक आभूषण देखकर आश्चर्य हो रहा था। उन स्त्रियों के कान भी कटे-फटे हुए थे।

उनके कानों की स्थिति देखकर लगता था कि उनके नीचे तक लटके-फटे हुए कान अब अधिक वजन नहीं सह सकेंगे। यदि और थोड़ा वजन अधिक डाला, तो कान फट ही जायेंगे। लेखक बताता है कि दक्षिण भारत में साधारण वर्ग की स्त्रियाँ सोने के जेवर धारण करती हैं और उच्च वर्ग या कुल की स्त्रियाँ हीरे, मोती और जवाहरात के आभूषण पहनती हैं। सोना उनके लिए हल्की वस्तु है; अर्थात् उनके लिए मामूली चीज है।

विशेष:

1. लेखक ने दक्षिण भारत की सामाजिक स्थिति का वर्णन किया है।
2. वर्णानात्मक शैली है।
3. भाषा परिमार्जित खड़ी बोली है।

गद्यांश पर आधारित अर्थग्रहण संबंधी प्रश्न

प्रश्न (i)
तमिल स्त्रियों को क्या देखकर आश्चर्य हो रहा था?
उत्तर:
तमिल स्त्रियों को अजनबियों को अपने गाँव में देखकर आश्चर्य हो रहा था।

प्रश्न (ii)
तमिल स्त्रियों के कटे-फटे कान क्या संकेत कर रहे थे?
उत्तर:
तमिल स्त्रियों के कटे-फटे और लटके कान इस बात की ओर संकेत कर रहे थे कि अपने कानों में वज़नदार आभूषण पहनती होंगी, जिनके कारण कान नीचे तक लटककर फट गए हैं। अब उन कानों में अधिक भार सहने की क्षमता नहीं : रह गई है।

प्रश्न (iii)
तमिल स्त्रियों ने लेखक और उसके साथियों को पानी क्यों पिलाया?
उत्तर:
लेखक और उसके साथी गाड़ी में पंचर होने के कारण गाड़ी से उतरकर एक पास के कुएँ पर गए। वहाँ पानी भरने वाली तमिल स्त्रियों ने समझा कि वे लोग प्यासे हैं और पानी पीने के लिए ही कुएँ पर आए हैं। इसलिए तमिल स्त्रियों ने उन्हें पानी पिलाया।

गद्यांश पर आधारित बोधात्मक प्रश्न

प्रश्न (i)
दक्षिण में साधारण स्त्रियों और संभ्रान्त स्त्रियों के आभूषणों में क्या अंतर होता है?
उत्तर:
दक्षिण में साधारण स्त्रियाँ सोने के आभूषण पहनती हैं और संभ्रान्त परिवार की स्त्रियाँ हीरे, मोती और जवाहरात के आभूषण काम में लाती हैं।

प्रश्न (ii)
त्रिवेन्द्रम से कन्याकुमारी की आबादी के सम्बन्ध में लेखक ने क्या कहा है?
उत्तर:
त्रिवेन्द्रम से कन्याकुमारी की आबादी के संबंध में लेखक ने कहा कि इतनी घनी आबादी तो भारत के किसी भी भाग में नहीं है। दूसरे शब्दों में केरल के इस क्षेत्र में बहुत सघन जनसंख्या है।

प्रश्न 4.
यहाँ हिंदी साहित्य में गति का परिचय मिलता है। यहाँ की हिंदी प्रचार सभा को दक्षिण में हिंदी की प्रमुख विद्यापीठ का रूप प्रदान कर रही है। यहाँ से हिंदी के कई सौ अध्यापक-अध्यापिकाएँ प्रतिवर्ष शिक्षा ग्रहण कर दक्षिण की अनेक शालाओं तथा विश्वविद्यालय के कॉलेजों में हिंदी-अध्यापन कार्य कर रहे हैं। महात्माजी ने जब मद्रास में हिंदी-प्रचार की नींव रखी तब हृषीकेशजी के साथ-साथ रघुवरदयालजी जो यहाँ के हिंदी प्रेमी जन हैं वे भी सभा में पहुँचे।

तब से आज तक हिंदी को राष्ट्रभाषा का अंग मानकर ये सभा में कार्य कर रहे हैं। दक्षिण भारत में कई अहिंदी भाषा-भाषी सज्जन हिंदी की बड़ी सेवा कर रहे हैं। रघुवरदयाल मिश्र ने बतलाया कि तंजोर पुस्तकालय में मणि-प्रवाल शैली में लिखित बहुत पुराना हस्तलिखित ग्रन्थ है, जिसमें अन्य भाषाओं के साथ-साथ हिंदी में भी रचनाएँ हैं। (Page 77)

शब्दार्थ:

• गति – प्रगति।
• महात्माजी – महात्मा गाँधी जी।

प्रसंग:
प्रस्तुत गद्यांश आचार्य विनय मोहन शर्मा द्वारा रचित यात्रा-वृत्तांत ‘दक्षिण भारत की एक झलक’ से उद्धृत है। लेखक इस गाद्यांश में चेन्नई की हिंदी प्रचार सभा के कार्यों पर प्रकाश डालते हुए कहता है।

व्याख्या:
लेखक कहता है कि जब वह दक्षिण भारत की यात्रा करते हुए त्रिचिन्नापल्ली से मद्रास पहुँचा, तो उसे यहाँ हिंदी साहित्य की प्रगति की जानकारी प्राप्त हुई। दूसरे शब्दों में, मद्रास में हिंदी साहित्य के प्रचार-प्रसार में पर्याप्त प्रगति देखने को मिली। यहाँ स्थापित हिंदी प्रचार सभा दक्षिण में हिंदी की प्रमुख विद्यापीठ के रूप में कार्य कर रही है। यहाँ से हिंदी प्रचार सभा के कई सौ अध्यापक और अध्यापिकाओं को हर वर्ष प्रशिक्षण प्रदान कर रही है। वे प्रशिक्षण प्राप्त करके दक्षिण भारत के अनेक स्कूलों और विश्वविद्यालय के अनेक कॉलेजों में हिंदी पढ़ा रहे हैं।

महात्मा गाँधीजी ने जब मद्रास में हिंदी प्रचार सभा की स्थापना की तब हृषीकेशजी के साथ-साथ एक हिंदी प्रेमी सज्जन रघुवरदयाल भी सभा में पहुँचे थे। वे तब से लेकर आज तक हिंदी को राष्ट्रभाषा का अंग मानकर सभा में कार्य कर रहे हैं। लेखक कहता है कि दक्षिण भारत में कई अहिंदी भाषा-भाषी व्यक्ति भी हिंदी की बड़ी सेवा कर रहे हैं; अर्थात् अहिंदी भाषा-भाषी भी हिंदी के प्रचार-प्रसार में जुटे हुए हैं। स्वर्गीय रघुवरदयाल मिश्र ने बतलाया कि तंजोर पुस्तकालय में मणि-प्रवाल शैली में लिखित बहुत पुराना हाथ से लिखा ग्रंथ है, जिसमें अन्य भाषाओं के साथ-साथ हिंदी की रचनाएँ भी सम्मिलित हैं।

विशेष:

1. मद्रास की हिंदी प्रचार सभा के कार्यों का वर्णन किया गया है।
2. वर्णानात्मक शैली है।
3. भाषा परिमार्जित खड़ी बोली है।

गद्य पर आधारित अर्थग्रहण संबंधित प्रश्नोत्तर

प्रश्न (i)
‘हिंदी साहित्य में गति का परिचय मिलता है’ से लेखक का क्या आशय
उत्तर:
इससे लेखक का आशय है कि मद्रास की हिंदी प्रचार सभा के प्रयत्नों से दक्षिण भारत में हिंदी प्रचार-प्रसार में पर्याप्त प्रगति देखने को मिलती है।

प्रश्न (ii)
दक्षिण की हिंदी प्रचार सभा विद्यापीठ के रूप में किस प्रकार कार्य कर रही है?
उत्तर:
दक्षिण की हिंदी प्रचार सभाप्रतिवर्ष कई सौ अध्यापक-अध्यापिकाओं को हिंदी अध्यापन का प्रशिक्षण प्रदान करती है। वे अध्यापक-अध्यापिकाएँ दक्षिण भारत के स्कूल और कॉलेजों में हिंदी-अध्यापन का कार्य कर रहे हैं। इस प्रकार यहाँ की प्रचार सभा हिंदी विद्यापीठ के रूप में कार्य कर रही है।

गद्यांश की विषय-वस्त पर आधारित बोधात्मक प्रश्नोत्तर

प्रश्न (i)
रघुवरदयाल अहिंदीभाषी होते हुए भी हिंदी प्रचार सभा में कार्य क्या कर रहे थे?
उत्तर:
रघुवरदयाल को हिंदी से प्रेम था। वे दक्षिण की हिंदी प्रचार सभा में उसकी स्थापना से लेकर आज तक कार्य कर रहे हैं। वे हिंदी को राष्ट्रभाषा का अंग मानकर सभा में कार्य कर रहे थे।

प्रश्न (ii)
रघुवरदयाल मिश्र ने लेखक को क्या जानकारी दी थी?
उत्तर:
रघुवरदयाल मिश्र ने लेखक को जानकारी दी थी कि तंजोर पुस्तकालय में मणि-प्रवाल शैली में रचित एक बहुत पुराना ग्रंथ है, जो हाथ से लिखा हुआ है। उस ग्रंथ में अन्य भाषाओं के साथ-साथ हिंदी में भी रचनाएँ हैं।

MP Board Class 12th Hindi Solutions

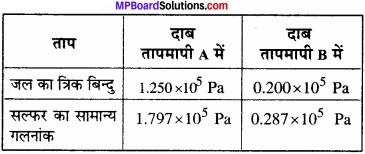
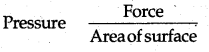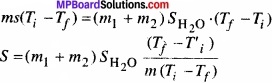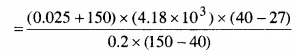MP Board Class 11th Physics Solutions Chapter 12 ऊष्मागतिकी

ऊष्मागतिकी अभ्यास के प्रश्न एवं उनके उत्तर

प्रश्न 12.1.
कोई गीजर 3.0 लीटर प्रति मिनट की दर से बहते हुए जल को 27°C से 77°C तक गर्म करता है। यदि गीजर का परिचालन गैस बर्नर द्वारा किया जाए तो ईंधन के व्यय की क्या दर होगी? बर्नर के ईंधन की दहन-ऊष्मा 4.0 × 10⁴ + Jg^-1 है?
उत्तर:
दिया है: ताप में वृद्धि
∆T = (77 – 27)°C = 50°C
S_H2O = 4.2 × 10³ Jkg^-1 °C^-1
ईंधन की दहन ऊष्मा
H_C = 4 × 10⁴Jg^-1 प्रति मिनट प्रवाहित जल का द्रव्यमान, m = 3 ली
3 किग्रा (∴ 1 ली० = 1kg)
जल द्वारा गर्म होने के लिए ली गई ऊष्मा,
θ = ms ∆T
माना ईंधन के जलने की दर m’ g प्रति मिनट है। … (i)
अतः ईंधन द्वारा 1 मिनट में दी गई ऊष्मा
θ = m’ H_C
ईंधन द्वारा प्रति मिनट दी गई ऊष्मा = प्रति मिनट ली गई ऊष्मा।
∴ m’ Hc = ms ∆T
∴ m’ = \(\frac { ms\Delta t }{ H_{ C } } \)
= \(\frac { 3\times 4.2\times 10^{ 3 }\times 50 }{ 4\times 10^{ 4 } } \)
= 15.75 g = 16 gm
अतः ईंधन 16 gm / मिनट की दर से जलता है।

प्रश्न 12.2.
स्थिर दाब पर 2.0 × 10^-2kg नाइट्रोजन (कमरे के ताप पर) के ताप में 45°C वृद्धि करने के लिए कितनी ऊष्मा की आपूर्ति की जानी चाहिए?
(N₂ का अणुभार 28; R = 8.3 J mol^-1K^-1)।
उत्तर:
दिया है:
N₂ का अणु भार = 28
गैस का द्रव्यमान, m = 2 × 10^-2 किग्रा
ताप वृद्धि T = 45°C
R = 8.3 जूल प्रति मोल प्रति K
आवश्यक ऊष्मा θ = ?
दी गई गैस द्रव्यमान में, ग्राम मोलों की संख्या,
µ = \(\frac { m }{ 28gm } \) = \(\frac{20}{28}\) = 0.714
R = 8.3 mol ^-1 K^-1
माना नियत दाब पर गैस की मोलर विशिष्ट ऊष्मा C_p है।
C_p = \(\frac{7}{2}\) R = \(\frac{7}{2}\) × 8.3 × 45 J
= 933.75 J = 934 J

प्रश्न 12.3.
व्याख्या कीजिए कि ऐसा क्यों होता है?

1. भिन्न-भिन्न तापों T₁ व T₂ के दो पिण्डों को यदि ऊष्मीय संपर्क में लाया जाए तो यह आवश्यक नहीं कि उनका अंतिम ताप (T₁ + T₂)/2 ही हो।
2. रासायनिक या नाभिकीय संयंत्रों में शीतलक (अर्थात् द्रव जो संयंत्र के भिन्न-भिन्न भागों को अधिक गर्म होने से रोकता है) की विशिष्ट ऊष्मा अधिक होनी चाहिए।
3. कार को चलाते – चलाते उसके टायरों में वायुदाब बढ़ जाता है।
4. किसी बंदरगाह के समीप के शहर की जलवायु, समान अक्षांश के किसी रेगिस्तानी शहर की जलवायु से अधिक शीतोष्ण होती है।

उत्तर:

1. इसका कारण यह है कि अन्तिम ताप वस्तुओं को अलग-अलग तापों के अतिरिक्त उनकी. ऊष्मा धारिताओं पर भी निर्भर करता है।
2. चूँकि शीतलक संयन्त्र से अभिक्रिया जनित ऊष्मा को हटाता है अतः शीतलक की विशिष्ट ऊष्मा धारिता अधिक होनी चाहिए ताकि कम ताप-वृद्धि के लिए अधिक ऊष्मा शोषित कर सके।
3. कार को चलाते-चलाते, सड़क के साथ घर्षण के कारण टायर का ताप बढ़ता है। इस कारण टायर में भरी हवा का दाब बढ़ जाता है।
4. बन्दरगाह के समीप के शहरों की आपेक्षिक आर्द्रता समान अक्षांश के रेगिस्तानी शहर की तुलना में अधिक रहती है। इस कारण बन्दरगाह के समीप शहर की जलवायु रेगिस्तानी शहर की अपेक्षा शीतोष्ण बनी रहती है।

प्रश्न 12.4.
गतिशील पिस्टन लगे किसी सिलिंडर में मानक ताप व दाब पर 3 मोल हाइड्रोजन भरी है। सिलिंडर की दीवारें ऊष्मारोधी पदार्थ की बनी हैं तथा पिस्टन को उस पर बालू की परत लगाकर ऊष्मारोधी बनाया गया है। यदि गैस को उसके आरंभिक आयतन के आधे आयतन तक संपीडित किया जाए तो गैस का दाब कितना बढ़ेगा?
उत्तर:
माना V₁ = x
द्विपरमाणुक गैस का हाइड्रोजन के लिए
V₂ = \(\frac { V_{ 1 } }{ 2 } \) = \(\frac{x}{2}\)
γ = \(\frac { C_{ p } }{ C_{ v } } \)
∴dQ = 0 + dw’ or dw’ = dQ
= 9.35 × 4.19 J
दिया है:
dQ = 9.35 cal (1 cal = 4.19J) … (iii)
समी (ii) व (iii) से
dw’ = 9.35 × 4.19 J = 38.97 J
माना निकाय पर कृत कार्य W’ है।
W’ = dw’ – dW = 38.97 – 22.3
= 16.67
= 16.7J

प्रश्न 12.6.
समान धारिता वाले दो सिलिंडर A तथा B एक-दूसरे से स्टॉपकॉक के द्वारा जुड़े हैं। A में मानक ताप व दाब पर गैस भरी है जबकि B पूर्णतः निर्वातित है। स्टॉपकॉक यकायक खोल दी जाती है। निम्नलिखित का उत्तर दीजिए:

1. सिलिंडर A तथा B में अंतिम दाब क्या होगा?
2. गैस की आंतरिक ऊर्जा में कितना परिवर्तन होगा?
3. गैस के ताप में क्या परिवर्तन होगा?
4. क्या निकाय की माध्यमिक अवस्थाएँ ( अंतिम साम्यावस्था प्राप्त करने के पूर्व) इसके P – V – T पृष्ठ पर होंगी?

उत्तर:
1. दिया है: मानक दाब
= P₁ = 1 atm, V₁ = V
P₂ = ? तथा V₂ = 27
चूँकि सिलिंडर B निर्वातित है अतः स्टॉपकॉक खोलने पर गैस का निर्वात में मुक्त प्रसार होगा। अतः गैस न तो कोई कार्य करेगी और न ही ऊष्मा का आदान-प्रदान होगा। अर्थात् गैस की आन्तरिक ऊर्जा व ताप स्थिर रहेंगे।
पुनः बॉयल के नियम से,
P₁V₁ = P₂V₂
∴P₂ = \(\frac { P_{ 1 }V_{ 1 } }{ V_{ 2 } } \) = \(\frac { 1\times V }{ 2v } \) = 0.5 atm

2. चूँकि ω = 0 व θ = 0
∴ ∆V = 0
अर्थात् गैस की आन्तरिक ऊर्जा अपरिवर्तित रहेगी।

3. चूँकि आन्तरिक ऊर्जा अपरिवर्तित रहती है। अतः गैस का ताप भी अपरिवर्तित रहेगा।

4. चूँकि गैस का मुक्त प्रसार हुआ है। इस कारण माध्यमिक अवस्थाएँ साम्य अवस्थाएँ नहीं हैं। अतः ये अवस्थाएँ दाब-आयतन-ताप पृष्ठ पर नहीं होगी।

प्रश्न 12.7.
एक वाष्प इंजन अपने बॉयलर से प्रति मिनट 3.6 × 10⁹ J ऊर्जा प्रदान करता है जो प्रति मिनट 5.4 × 10⁸ J कार्य देता है। इंजन की दक्षता कितनी है? प्रति मिनट कितनी ऊष्मा अपशिष्ट होगी?
उत्तर:
दिया है: प्रति मिनट बॉयलर द्वारा अवशोषित ऊष्मा
Q₁ = 3.6 × 10⁹ J
भाप इंजन द्वारा प्रति मिनट कृत कार्य
= 5.4 × 10⁸ J
प्रति मिनट व्यय/उत्सर्जित ऊष्मा = Q₂ = ?
इंजन की प्रतिशत दक्षता n% = ?
हम जानते हैं कि n% = \(\frac { W }{ Q_{ 1 } } \) × 100
= \(\frac{3}{20}\) × 100 = 15%
सूत्र, Q₁ = W + Q₂ से,
Q₂ = Q₁ – W
= 36 × 10⁸ – 5.4 × 108
= 30.6 × 10⁸ J/min
= 3.06 × 10⁹ J/min
= 3.1 × 10⁹ J/min

प्रश्न 12.8.
एक हीटर किसी निकाय को 100 W की दर से ऊष्मा प्रदान करता है। यदि निकाय 75 Js^-1 की दर से कार्य करता है, तो आंतरिक ऊर्जा की वृद्धि किस दर से होगी? उत्तर:
दिया है: θ = 100
W = 100 Js^-1
∴∆V = θ – W
= 100 – 75 = 25 Js^-1
अत: निकाय की आन्तरिक ऊर्जा वृद्धि दर 25 Js^-1 है।

प्रश्न 12.9.
किसी ऊष्मागतिकीय निकाय को मूल अवस्था से मध्यवर्ती अवस्था तक (चित्र) में दर्शाये अनुसार एक रेखीय प्रक्रम द्वारा ले जाया गया है।एक समदाबी प्रक्रम द्वारा इसके आयतन को E से F तक ले जाकर मूल मान तक कम कर देते हैं। गैस द्वारा D से E तथा वहाँ से F तक कुल किए गये कार्य का आंकलन कीजिए।

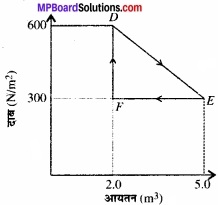
उत्तर:
माना गैस D से E व E से F तक कृत कार्य = W
अतःW = W₁ + W₂ …. (i)
माना W₁ = D से E तक प्रसार में कृत कार्य
= DEHGD का क्षेत्रफल = ∆DEF का क्षे० + आयत EHGF का क्षे०
= \(\frac{1}{2}\) EF × DF + GH × FG … (ii)
दिया है:
EF = 5 – 2 = 3 litre = 3 × 10^-3 m³
DF = 600 – 300 = 300 Nm^-2
FG = 300 – 0 = 300 Nm²
GH = 5 – 2 = 3 × 10^-3 m³
समीकरण (ii) से,
∴W₁ = \(\frac{1}{2}\) × 3 × 10^-3 × 300 + 3 × 10^-3 × 300] J …….. (iii)
माना E से F (संपीडन) तक कृत कार्य = W₂ = EHGF का क्षे०
= – FG × GH
= – (300 – 0) × (5 – 2) × 10^-3
= – 300 × 3 × 10^-3 J …. (iv)
∴समी० (i). (iii) व (iv) से,
w = \(\frac{1}{2}\) × 3 × 10^-3 × 300 + 3 × 10^-3 × 300 + 3 × 10^-3
= 3 × 10³ × 150J = 450 × 10^-3 J
= 0.450 J

प्रश्न 12.10.
खाद्य पदार्थ को एक प्रशीतक के अंदर रखने पर उसे 9°C पर बनाए रखता है। यदि कमरे का ताप 36°C है तो प्रशीतक के निष्पादन गुणांक का आंकलन कीजिए।
उत्तर:
दिया है:
T₁ = 273 + 36 = 309 K
T₂ = 9°C = 282 K
β = ?
सूत्र β = \(\frac { T_{ 2 } }{ T_{ 1 }-T_{ 2 } } \) से
β = \(\frac { 283 }{ 309-282 } \) = \(\frac{282}{27}\) = 10.4

MP Board Class 11 Physics Solutions

MP Board Class 8th Science Solutions Chapter 11 Force and Pressure