MP Board Class 11th Physics Solutions Chapter 10 तरलों के यांत्रिकी गुण
तरलों के यांत्रिकी गुण अभ्यास के प्रश्न एवं उनके उत्तर
प्रश्न 10.1.
स्पष्ट कीजिए क्यों?
(a) मस्तिष्क की अपेक्षा मानव का पैरों पर रक्तचाप अधिक होता है।
(b) 6 km ऊँचाई पर वायुमण्डलीय दाब समुद्र तल पर वायुमण्डलीय दाब का लगभग आधा हो जाता है, यद्यपि वायुमण्डल का विस्तार 100 km से भी अधिक ऊँचाई तक है।
(c) यद्यपि दाब, प्रति एकांक क्षेत्रफल पर लगने वाला बल होता है तथापि द्रवस्थैतिक दाब एक अदिश राशि है।।
उत्तर:
(a) पैरों के ऊपर रक्त स्तम्भ की ऊँचाई मस्तिष्क के ऊपर रक्त स्तम्भ की ऊँचाई से ज्यादा होती है। हम जानते हैं कि द्रव स्तम्भ का दाब गहराई के अनुक्रमानुपाती होता है। इसी कारण पैरों पर रक्त दाब मस्तिष्क की तुलना में अधिक होता है।
(b) पृथ्वी के गुरुत्वीय प्रभाव के कारण वायु के अणु पृथ्वी के नजदीक बने रहते हैं, अधिक ऊँचाई तक नहीं जा पाते हैं। इस प्रकार 6 किमी से अधिक ऊँचाई तक जाने पर वायु बहुत ही विरल हो जाती है तथा घनत्व बहुत कम हो जाता है। चूंकि द्रव – दाब, द्रव के घनत्व के समानुपाती होता है। इस प्रकार 6 किमी से ऊपर की वायु का कुल दाब बहुत कम होता है। अतः पृथ्वी तल से 6 किमी की ऊँचाई पर वायुमण्डलीय दाब समुद्र तल पर वायुमण्डलीय दाब से आधा रह जाता है।
(c) पास्कल के नियमानुसार, किसी बिन्दु पर द्रव दाब समस्त दिशाओं में समान रूप से लगता है। अतः दाब के साथ कोई दिशा नहीं जोड़ी जा सकती है। अतः दाब एक सदिश राशि है।
![]()
प्रश्न 10.2.
स्पष्ट कीजिए क्यों?
(a) पारे का काँच के साथ स्पर्श कोण अधिक कोण होता है जबकि जल का काँच के साथ स्पर्श कोण न्यून कोण होता
(b) काँच के स्वच्छ समतल पृष्ठ पर जल फैलने का प्रयास करता है जबकि पारा उसी पृष्ठ पर बूंदें बनाने का प्रयास करता है। (दूसरे शब्दों में जल काँच को गीला कर देता है जबकि पारा ऐसा नहीं करता है।)
(c) किसी द्रव का पृष्ठ तनाव पृष्ठ के क्षेत्रफल पर निर्भर नहीं करता है।
(d) जल में घुले अपमार्जकों के स्पर्श कोणों का मान कम होना चाहिए।
(e) यदि किसी बाह्य बल का प्रभाव न हो, तो द्रव बँद की आकृति सदैव गोलाकार होती है।
उत्तर:
(a) पारे के अणुओं के मध्य संसजक बल, पारे तथा काँच के अणुओं के मध्य आसंजक बल से अधिक होता है। अतः काँच व पारे का स्पर्श कोण अधिक कोण होता है जबकि जल के अणुओं के मध्य संसजक बल, काँच तथा जल के अणुओं के मध्य आसंजक बल से कम होता है। अत: जल व काँच के मध्य स्पर्श कोण न्यूनकोण होता है।
(b) यहाँ पर उपरोक्त कारण लागू होता है।
(c) किसी द्रव के मुक्त पृष्ठ का क्षेत्रफल बढ़ा देने पर उसके तनाव में कोई परिवर्तन नहीं होता है जबकि रबड़ की झिल्ली को खींचने पर उसमें तनाव बढ़ जाता है। अतः द्रव का पृष्ठ – तनाव उसके मुक्त क्षेत्रफल से निर्भर होता है।
(d) अपमार्जक घुले होने पर जल का पृष्ठ तनाव कम हो जाता है, परिणामस्वरूप स्पर्श कोण भी कम हो जाता है।
(e) बाह्य बल की अनुपस्थिति में बूंद की आकृति सिर्फ पृष्ठ तनाव द्वारा निर्धारित होती है। पृष्ठ तनाव के कारण बूंद न्यूनतम क्षेत्रफल वाली आकृति ले लेती है। चूंकि एक दिए गए आयतन के लिए गोले का युक्त पृष्ठ न्यूनतम होता है। अतः बूंद गोलाकार हो जाती है।
प्रश्न 10.3.
प्रत्येक प्रकथन के साथ संलग्न सूची में से उपयुक्त शब्द छाँटकर उस प्रकथन के रिक्त स्थान की पूर्ति कीजिए –
- व्यापक रूप में द्रवों का पृष्ठ तनाव ताप बढ़ने पर ………………… है। (बढ़ता/घटता)
- गैसों की श्यानता ताप बढ़ने पर ………………………… है, जबकि द्रवों की श्यानता ताप बढ़ने पर ……………………….. है। (बढ़ती/घटती)
- दृढ़ता प्रत्यास्थता गुणांक वाले ठोसों के लिए अपरूपण प्रतिबल ………………………. के अनुक्रमानुपाती होता है, जबकि द्रवों के लिए वह ……………………….. के अनुक्रमानुपाती होता है। (अपरूपण विकृति/अपरूपण विकृति की दर)
- किसी तरल के अपरिवर्ती प्रवाह में आए किसी संकीर्णन पर प्रवाह की चाल में वृद्धि में ………………………… का अनुसरण होता है। (संहति का संरक्षण/बर्नली सिद्धांत)
- किसी वायु सुरंग में किसी वायुयान के मॉडल में प्रक्षोभ की चाल वास्तविक वायुयान के प्रक्षोभ के लिए क्रांतिक चाल की तुलना में ………………………… होती है। (अधिक/कम)
उत्तर:
- घटता
- बढ़ती, घटती
- अपरूपण विकृति, अपरूपण विकृति की दर
- संहति का संरक्षण
- अधिक।
![]()
प्रश्न 10.4.
निम्नलिखित के कारण स्पष्ट कीजिए।
(a) किसी कागज की पट्टी को क्षैतिज रखने के लिए आपको उस कागज पर ऊपर की ओर हवा फूंकनी चाहिए, नीचे की ओर नहीं।
(b) जब हम किसी जल टोंटी को अपनी उँगलियों द्वारा बंद करने का प्रयास करते हैं, तो उँगलियों के बीच की खाली जगह से तीव्र जल धाराएँ फूट निकलती हैं।
(c) इंजेक्शन लगाते समय डॉक्टर के अंगूठे द्वारा आरोपित दाब की अपेक्षा सुई का आकार दवाई की बहिःप्रवाही धारा को अधिक अच्छा नियंत्रित करता है।
(d) किसी पात्र के बारीक छिद्र से निकलने वाला तरल उस पर पीछे की ओर प्रणोद आरोपित करता है।
(e) कोई प्रचक्रमान क्रिकेट की गेंद वायु में परवलीय प्रपथ का अनुसरण नहीं करती।
उत्तर:
(a) कागज पर ऊपर की ओर फूंक मारने से ऊपर की वायु का वेग अधिक हो जाएगा। अत: बर्नूली की प्रमेय से, कागज के ऊपर वायुदाब, नीचे की अपेक्षा कम हो जाएगा। इससे कागज पर उत्थापक बल लगेगा जो कागज को नीचे गिरने से रोकेगा।
(b) जल टोंटी को उँगलियों द्वारा बन्द करने पर उँगलियों के बीच की खाली जगह से तीव्र जल धाराएँ फूट निकलती हैं। यहाँ धारा का अनुप्रस्थ क्षेत्रफल टोंटी के अनुप्रस्थ क्षेत्रफल से कम होता है। अतः अविरतता के नियमानुसार, जल का वेग अधिक हो जाता हैं।
(c) अविरतता के नियम से, समान दाब आरोपित किए जाने पर, सुई बारीक होने पर बहि:प्रवाही धारा का प्रवाह वेग बढ़ जाता है। अत: बहिःप्रवाही वेग सुई के आकार से ज्यादा नियन्त्रित होता
(d) किसी पात्र के बारीक छिद्र से निकलने वाला तत्व उस पर पीछे की ओर प्रणोद आरोपित करता है। इसका कारण यह है कि यहाँ उच्च बहि:स्राव वेग प्राप्त कर लेता है। बाह्य बल के अनुपस्थिति में पात्र तथा तरल का संवेग संरक्षित रहता है। अतः पात्र विपरीत दिशा में संवेग प्राप्त करता है। अर्थात् बाहर निकलता हुआ द्रव पात्र पर विपरीत दिशा में प्रणोद लगाता है।
(e) घूर्णन करती गेंद अपने साथ वायु को खींचती है। अतः गेंद के ऊपर व नीचे वायु के वेग में अन्तर आ जाता है। परिणामस्वरूप दाबों में भी अन्तर आ जाता है। इसी कारण गेंद पर भार के अतिरिक्त एक दूसरा बल भी लगने लगता है तथा गेंद का पथ परवलयाकार नहीं रह पाता है।
प्रश्न 10.5.
ऊँची एड़ी के जूते पहने 50 kg संहति की कोई बालिका अपने शरीर को 1.0 cm व्यास की एक ही वृत्ताकार एड़ी पर संतुलित किए हुए है। क्षैतिज फर्श पर एड़ी द्वारा आरोपित दाब ज्ञात कीजिए।
उत्तर:
दिया है, F = mg = 50 × 9.8 N = 490 N
d = 1.0cm, r = \(\frac{d}{2}\) = 0.5cm
= 0.3 × 10-2m = 5 × 10-3
फर्श का क्षैतिज क्षेत्रफल जहाँ एड़ी लगती है,
A = πr2 = 3.142 (5 × 10-3)2
= 3.142 × 25 × 10-6 m2
माना एड़ी द्वारा क्षैतिज फर्श पर लगाया गया दाब P है।
अतः P = \(\frac{F}{A}\)
या
P = \(\frac { 490 }{ 3.142\times 25\times 10^{ -6 } } \)
= 6.24 × 106 Pascal
P = 6.24 × 106 Pa
![]()
प्रश्न 10.6.
टॉरिसिली के वायुदाब मापी में पारे का उपयोग किया गया था। पास्कल ने ऐसा ही वायुदाब मापी 984kgm -3 Pa घनत्व की फ्रेंच शराब का उपयोग करके बनाया। सामान्य वायुमंडलीय दाब के लिए शराब स्तंभ की ऊँचाई ज्ञात कीजिए।
उत्तर:
माना सामान्य ताप पर संगत फ्रेंच शराब स्तम्भ की ऊँचाई h है।
साधारण वायुमण्डलीय दाब
P = 1.013 × 105 पास्कल
माना शराब स्तम्भ के संगत दाब P’ है।
P’ = Hpwg
जहाँ pw = शराब का घनत्व = 984 kgm-3
प्रश्नानुसार, P’ = P
या hpwg =P
या h = \(\frac { P }{ \rho _{ w }g } \)
= \(\frac { 1.013\times 10^{ 5 } }{ 984\times 9.8 } \) = 10.5 m
प्रश्न 10.7.
समुद्र तट से दूर कोई ऊर्ध्वाधर संरचना 109 Pa के अधिकतम प्रतिबल को सहन करने के लिए बनाई गई है। क्या यह संरचना किसी महासागर के भीतर किसी तेल कप के शिखर पर रखे जाने के लिए उपयुक्त है? महासागर की गहराई लगभग 3 km है। समुद्री धाराओं की उपेक्षा कीजिए।
उत्तर:
दिया है: जल स्तम्भ की गहराई, L = 3 किमी
= 3 × 103 मीटर 3
जल का घनत्व, ρ = 103 किग्रा/मीटर 3
माना जल स्तम्भ द्वारा आरोपित दाब P है।
∴ P = hpg
= 3 × 103 × 103 × 9.8
= 30 × 106 = 3 × 107 पास्कल
चूँकि संरचना को महासागर पर रखा गया है अत: महासागर का जल 3 × 107 पास्कल का दाब लगाता है।
चूंकि ऊर्ध्व संरचना पर अधिकतम भंजक प्रतिबल 109 है।
3 × 107 पास्कल < 10 × 9 पास्कल
अतः यह संरचना महासागर के भीतर तेल कूप के शिखर पर रखी जा सकती है।
प्रश्न 10.8.
किसी द्रवचालित आटोमोबाइल लिफ्ट की संरचना अधिकतम 3000 kg संहति की कारों को उठाने के लिए की गई है। बोझ को उठाने वाले पिस्टन की अनुप्रस्थ काट का क्षेत्रफल 425 cm है। छोटे पिस्टन को कितना अधिकतम दाब सहन करना होगा?
उत्तर:
दिया है: बड़े पिस्टन पर अधिकतम सहनीय बल,
F = 3000 kgf = 3000 × 9.8 N पिस्टन का क्षेत्रफल
A = 425 cm2 = 425 × 10-4m2
माना बड़े पिस्टन पर अधिकतम दाब P है।
अतः P = \(\frac{F}{A}\) = \(\frac { 3000\times 9.8 }{ 425\times 10^{ -4 } } \)
= 6.92 × 105
चूँकि द्रव सभी दिशाओं में समान दाब आरोपित करता है। अतः छोटी पिस्टन 6.92 × 105 पास्कल का अधिकतम दाब सहन करना होगा।
![]()
प्रश्न 10.9.
किसी U – नली की दोनों भुजाओं में भरे जल तथा मेथेलेटिड स्पिरिट को पारा एक – दूसरे से पृथक् करता है। जब जल तथा पारे के स्तंभ क्रमश: 10 cm तथा 12.5 cm ऊँचे हैं, तो दोनों भुजाओं में पारे का स्तर समान है। स्पिरिट का आपेक्षित घनत्व ज्ञात कीजिए।
उत्तर:
दिया है: U नली की एक भुजा में जल की ऊँचाई, h1 = 10 सेमी,
ρ1 = ग्राम/सेमी 3
U नली की एक दूसरी भुजा में स्प्रिट की ऊँचाई, h2 = 12.5 सेमी,
ρ2 = ?
माना जल तथा स्प्रिट द्वारा लगाया गया दाब क्रमश: P1 व P2 है।
∴ P1 = h1ρ1g …………. (i)
व P2 = h2ρ2g ……………. (ii)
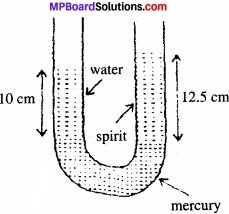
चूँकि दोनों भुजाओं में पारे का स्तम्भ समान है। अतः
P1 = P2
या h1ρ1g = h2ρ2g
या ρ2 = \(\frac { h_{ 1 }\rho _{ 1 } }{ h_{ 2 } } \)
= \(\frac{10 × 1}{12.5}\) = \(\frac{4}{5}\)
= 0.8 cm -3
स्प्रिट का विशिष्ट घनत्व = \(\frac { \rho _{ 1 } }{ \rho _{ 2 } } \)
= \(\frac { 0.8gcm^{ -3 }\quad }{ 1gcm^{ -3 }\quad } \) = 0.800
प्रश्न 10.10.
यदि प्रश्न 10.9 की समस्या में, U – नली की दोनों भुजाओं में इन्हीं दोनों द्रवों को और उड़ेल कर दोनों द्रवों के स्तंभों की ऊँचाई 15 cm और बढ़ा दी जाए, तो दोनों भुजाओं में पारे के स्तरों में क्या अंतर होगा। (पारे का आपेक्षिक घनत्व = 13.6)।
उत्तर:
माना U – नली की दोनों भुजाओं में अन्तर h है।
माना पारे का घनत्व pm है।
माना समान क्षैतिज पर दो बिन्दु A व B हैं।
∴A पर दाब = B पर दाब
या P0 + hwρwg
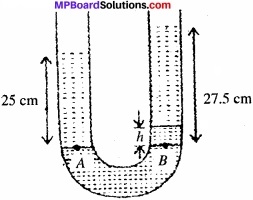
= P0 + hsρsg + hmρmg
जहाँ P0 = वायुमण्डलीय दाब
या hwρw = hsρs + hmρm ………. (i)
या hmρm = hwρw – hsρs
दिया है जल स्तम्भ की ऊँचाई,
hs = 12.5 + 15 = 27.5 cm
ρw = 1 g cm-3
ρs = 0.8 cm-3
ρm = 13.6 g cm-3
समी० (i) व (ii) से
hm × 13.6 = 25 × 1 – 27.5 × 0.8
या hm = \(\frac { 25-22.00 }{ 13.6 } \) = 0.2206 cm
= 0.221 cm
या hm = 0.221 cm
![]()
प्रश्न 10.11.
क्या बली समीकरण का उपयोग किसी नदी की किसी क्षिप्रिका के जल – प्रवाह का विवरण देने के लिए किया जा सकता है? स्पष्ट कीजिए।
उत्तर:
बर्नूली समीकरण केवल धार-रेखी प्रवाह पर लागू होता है। नदी की क्षिप्रिका का जल-प्रवाह धारा रेखी प्रवाह नहीं होता है। इसलिए इसका विवरण देने के लिए बर्नूली समीकरण का प्रयोग नहीं किया जा सकता है।
प्रश्न 10.12.
बर्नूली समीकरण के अनुप्रयोग में यदि निरपेक्ष दाब के स्थान पर प्रमापी दाब (गेज दाब) का प्रयोग करें तो क्या इससे कोई अंतर पड़ेगा? स्पष्ट कीजिए।
उत्तर:
बर्नूली समीकरण से,
P1 + \(\frac{1}{2}\)ρv12 + ρgh1
= P2 + \(\frac{1}{2}\)ρv22 + ρgh2
या P1 – P2 = \(\frac{1}{2}\)ρ (v22 – v12) + ρg(h2 – h1) …….. (i)
माना दो बिन्दुओं पर वायुमण्डलीय व गेज दाब क्रमश:
PaP1a व P1, P12 हैं।
P1 = Pa + P‘2
तथा P2 = P1a + P‘2
P2 – P2 = (Pa – P’a) + (P’1 – P’2) ~ P’1 – P’2 (∴Pa = P’a)
अतः दोनों बिन्दुओं पर वायुमण्डलीय दाबों में बहुत कम अन्तर होने पर परमदाब के स्थान पर गेज दाब का प्रयोग करने से कोई अन्तर नहीं पड़ेगा।
![]()
प्रश्न 10.13.
किसी 1.5 m लंबी 1.0 cm त्रिज्या की क्षैतिज नली से ग्लिसरीन का अपरिवर्ती प्रवाह हो रहा है। यदि नली के एक सिरे पर प्रति सेकंड एकत्र होने वाली ग्लिसरीन का परिणाम 4.0 × 10-3 kgs-1 है, तो नली के दोनों सिरों के बीच दाबांतर ज्ञात कीजिए। (ग्लिसरीन का घनत्व = 1.3 × 103kgm-3 तथा ग्लिसरीन की श्यानता = 0.83 Pas)
[आप यह भी जाँच करना चाहेंगे कि क्या इस नली में स्तरीय प्रवाह की परिकल्पना सही है।]
उत्तर:
दिया है:
r = 1.0 cm = 10-2 cm
l = 1.5 m
ρ = 1.3 × 102kg m-3
प्रति सेकण्ड ग्लिसरीन का प्रवाहित द्रव्यमान,
M = 4 × 10-3 kgs-1
ग्लिसरीन की श्यानता,
η = 0.83 Pas = 0.83 Nm-2s
माना नली के दोनों सिरों पर दाबान्तर P है।
रेनॉल्ड संख्या NR = ?
माना ग्लिसरीन का प्रति सेकण्ड प्रवाहित आयतन V है।
∴V = \(\frac{M}{ρ}\)
= \(\frac { 4\times 10^{ -3 }kgs^{ -1 } }{ 1.3\times 10^{ 3 }kgm^{ -3 } } \)
= \(\frac{4}{1.3}\) × 10-6m3s-1
पासले सूत्र से,

= 9.7537 × 102 Pa
= 9.8 × 102 Pa
धारा रेखीय प्रवाह की अभिग्रहीति जाँचने के लिए हम रेनॉल्ड संख्या का मान निकालते हैं –

= 3.07 × 10-1 = 0.307 = 0.31
अतः प्रवाह स्तरीय (धारा रेखीय) है।
प्रश्न 10.14.
किसी आदर्श वायुयान के परीक्षण प्रयोग में वायु – सुरंग के भीतर पंखों के ऊपर और नीचे के पृष्ठों पर वायु-प्रवाह की गतियाँ क्रमश: 70 ms-1 तथा 63 ms-1 हैं। यदि पंख का क्षेत्रफल 2.5 m2 है, तो उस पर आरोपित उत्थापक बल परिकलित कीजिए। वायु का घनत्व 13 kgm-3 लीजिए।
उत्तर:
माना वायुयान के ऊपरी व निचली पर्तों की चाल क्रमशः v1, व v2, है तथा संगत दाब क्रमशः P1 व P2, है। दिया है –
v1 = 70 मीटर/सेकण्ड
v2 = 63 मीटर/सेकण्ड
ρ = 1.3 किग्रा/मीटर3
माना पंखों की ऊपरी व निचले पर्ते समान ऊँचाई पर हैं।
h1 = h2
पंख का क्षेत्रफल, A = 2.5 मीटर 2
बरनौली प्रमेय से,
P1 + ρgh2 + \(\frac{1}{2}\) ρv12
= P2 + rogh2 + \(\frac{1}{2}\) ρv22
या P2 – P1 = \(\frac{1}{2}\) ρ(v12 – v22)
यह दाबान्तर ही वायुयान को ऊपर उठाता है।
माना, पंखे पर आरोपित बल है। अतः
F = (P2 – P1) × A
= \(\frac{1}{2}\) ρ (v12 – v22) × 2.5
= \(\frac{1}{2}\) × 1.3 × (702 – 632) × 2.5
= \(\frac{1}{2}\) × 1.3 × 931 × 2.5 = 1512.9N
= 1.5129 × 103N = 1.513 × 103N
= 1.5 × 103N
प्रश्न 10.15.
चित्र (a) तथा (b) किसी द्रव (श्यानताहीन) का अपरिवर्ती प्रवाह दर्शाते हैं। इन दोनों चित्रों में से कौन सही नहीं है? कारण स्पष्ट कीजिए।
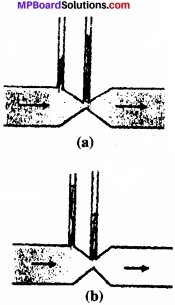
उत्तर:
चित्र (a) सही नहीं है। चूँकि इस चित्र में, नलिका की ग्रीवा में अनुप्रस्थ क्षेत्रफल कम है। अत: अविरतता के सिद्धान्त से, यहाँ वेग अधिक होगा। अर्थात् बर्नूली प्रमेय से यहाँ जल दाब कम होगा जबकि चित्र (a) में ग्रीवा पर जल दाब अधिक दिखाया गया है।
प्रश्न 10.16.
किसी स्प्रे पंप की बेलनाकार नली की अनुप्रस्थ काट का क्षेत्रफल 8.0 cm2 है। इस नली के एक सिरे पर 1.0 mm व्यास के 40 सूक्ष्म छिद्र हैं। यदि इस नली के भीतर द्रव के प्रवाहित होने की दर 1.5 m min-1 है, तो छिद्रों से होकर जाने वाले द्रव की निष्कासन – चाल ज्ञात कीजिए।
उत्तर:
दिया है:
A1 = 8 सेमी 2 = 8 × 10-4 मीटर2
छिद्र की त्रिज्या,
r = 0.5 मिमी = 0.5 × 10 -3 मीटर
छिद्रों का कुल क्षेत्रफल = 40 × π(r2)
= 40 × 3.14 × (0.5 × 10-3)2
= 0.3 × 10-4 मीटर2
v1 = 1.5 मीटर/सेकण्ड
= \(\frac{1.5}{60}\) = \(\frac{1}{40}\) मीटर/सेकण्ड
v2 = ?
सातत्यता समीकरण से,
A2v2 = A1v1
v2 = \(\frac { A_{ 1 } }{ A_{ 2 } } \) v1
= \(\frac { 8\times 10^{ -4 } }{ 0.3\times 10^{ -4 } } \) × 0.025
= 9.64 मीटर/सेकण्ड
![]()
प्रश्न 10.17.
U – आकार के किसी तार को साबुन के विलयन में डुबो कर बाहर निकाला गया जिससे उस पर एक पतली साबुन की फिल्म बन गई। इस तार के दूसरे सिरे पर फिल्म के संपर्क में एक फिसलने वाला हल्का तार लगा है जो 1.5 × 10-2N भार (जिसमें इसका अपना भार भी सम्मिलित है) को सँभालता है। फिसलने वाले तार की लम्बाई 30 cm है। साबुन की फिल्म का पृष्ठ तनाव कितना है?
उत्तर:
दिया है: तार की लंबाई,
l = 30
सेमी = 0.3 मीटर
तार पर लटका भार,
w = 1.5 × 10-2 न्यूटन
माना फिल्म का पृष्ठ तनाव S है।
अतः फिल्म के एक ओर के पृष्ठ के कारण तार पर लगने वाला बल,
F1 = s × 1
दोनों पृष्ठों के कारण तार पर बल,
F = 2F1
= 2sl
यह बल (F) ही भार (W) को सन्तुलित करता है।
2sl = w
पृष्ठ तनाव, s = \(\frac{W}{2l}\)
= \(\frac { 1.5\times 10^{ -2 } }{ 2\times 0.3 } \)
= 2.5 × 10-2 न्यूटन प्रति मीटर
प्रश्न 10.18.
निम्नांकित चित्र (a) में किसी पतली द्रव फिल्म को 4.5 × 10-2 N का छोटा भार सँभाले दर्शाया गया है। चित्र (b) तथा (e) में बनी इसी द्रव की फिल्में इसी ताप पर कितना भार संभाल सकती हैं? अपने उत्तर को प्राकृतिक नियमों के अनुसार स्पष्ट कीजिए।
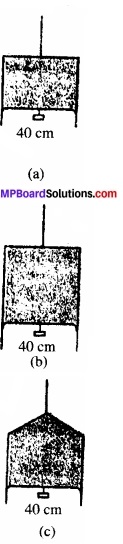
उत्तर:
तीनों चित्रों में, फिल्म के नीचे वाले किनारे की लम्बाई 40 सेमी (समान) है। (F = 25 l)
इस किनारे पर फिल्म के पृष्ठ तनाव (S) के कारण समान बल लगेगा। यह बल लटके हुए भार को साधता है। चूँकि साधने वाला बल प्रत्येक दशा में समान है। इसलिए चित्र (b) तथा (c) में भी वही भार 4.5 × 10 -2 न्यूटन सँभाला जा सकता है।
प्रश्न 10.19.
3.00 mm त्रिज्या की किसी पारे की बूंद के भीतर कमरे के ताप पर दाब क्या है? 20°C ताप पर पारे का पृष्ठ तनाव 4.65 × 10-1 Nm-1 है। यदि वायुमंडलीय दाब 1.01 × 105 Pa है, तो पारे की बूंद के भीतर दाब – आधिक्य भी ज्ञात कीजिए।
उत्तर:
दिया है:
बूंद की त्रिज्या r = 3.0 mm
= 3.0 × 10-3 m
पारे का पृष्ठ तनाव
T = 4.65 × 10-1 Nm-1
बूंद के बाहर दाब, Po = वायुमण्डलीय दाब
= 1.01 × 105 Pa
माना कि बूंद के अन्दर दाब P है तब बूंद के अन्दर आधिक्य दाब निम्नवत् है –
P = Pi – P0 = \(\frac{2T}{r}\)
= \(\frac { 2\times 4.65\times 10^{ -1 } }{ 3\times 10^{ -3 } } \) = 310Pa
Pi = P + P0
= 310 + 1.01 × 105 Pa
= 1.01 × 105 + 0.00310 × 105
= 1.01310 × 105 Pa
![]()
प्रश्न 10.20.
5.00 mm त्रिज्या के किसी साबुन के विलयन के बुलबुले के भीतर दाब – आधिक्य क्या है? 20°C ताप पर साबुन के विलयन का पृष्ठ तनाव 4.65 × 10-1 Nm-1 है। यदि इसी विमा का कोई वायु का बुलबुला 1.20 आपेक्षिक घनत्व के साबुन के विलयन से भरे किसी पात्र में 40.0 cm गहराई पर बनता, तो इस बुलबुले के भीतर क्या दाब होता, ज्ञात कीजिए।
(1 वायुमंडलीय दाब = 1.01 × 105Pa)
उत्तर:
साबुन के घोल का पृष्ठ तनाव,
T = 2.5 × 10-2 Nm-1
साबुन के घोल का घनत्व = ρ
= 1.2 × 103kg m-3
साबुन के बुलबुले की त्रिज्या = r
= 5.0 mm = 5.0 × 10-3m
1 वायुमण्डलीय दाब = 1.01 × 105 Pa
साबुन के बुलबुले के अन्दर आधिक्य दाब निम्नवत् है –
Pi – P0 = \(\frac{4T}{r}\)
= \(\frac { 2\times 2.5\times 10^{ -2 } }{ 5.0\times 10^{ -3 } } \) = 20 Pa
साबुन के घोल में वायु के बुलबुले के अन्दर आधिक्य दाब –
Pi – P0 = \(\frac{2T}{r}\)
= \(\frac { 2\times 2.5\times 10^{ -2 } }{ 5.0\times 10^{ -3 } } \) = 10 Pa
40 सेमी गहराई पर वायु के बुलबुले के बाहर दाब,
P0 = वायुमण्डलीय दाब + 40 सेमी के कारण दाब
= 1.01 × 105 + 0.4 × 1.2 × 103 × 9.8
= 1.05704 × 105 Pa (∴P = hpg)
= 1.06 × 105 Pa
∴ वायु के बुलबुले के अन्दर दाब
Pi = P0 + \(\frac{2T}{r}\)
= (1.06 × 105 + 10)Pa
= 1.06 × 105 + 0.00010 × 105
= 1.06010 × 105Pa
= 1.06 × 105 Pa
तरलों के यांत्रिकी गुणअतिरिक्त अभ्यास के प्रश्न एवं उनके उत्तर
प्रश्न 10.21.
1.0 m2 क्षेत्रफल के वर्गाकार आधार वाले किसी टैंक को बीच में ऊर्ध्वाधर विभाजक दीवार द्वारा दो भागों में बाँटा गया है। विभाजक दीवार में नीचे 20 cm2 क्षेत्रफल का कब्जेदार दरवाजा है। टैंक का एक भाग जल से भरा है तथा दूसरा भाग 1.7 आपेक्षिक घनत्व के अम्ल से भरा है। दोनों भाग 4.0 m ऊँचाई तक भरे गए हैं। दरवाजे को बंद रखने के आवश्यक बल परिकलित कीजिए।
उत्तर:
दिया है: दोनों ओर भरे द्रवों की ऊँचाई
hw = ha = 4 मीटर
जल का घनत्व pw = 103 किग्रा प्रति मीटर 3
अम्ल का आपेक्षिक घनत्व = \(\frac { \rho _{ a } }{ \rho _{ w } } \) = 1.7
दरवाजे का क्षेत्रफल
A = 20 सेमी2 = 2 × 10-3 मीटर 2
जल की साइड से दरवाजे पर दाब
P1 = Pa + hwρwg
= Pa + 4 × 103 × 9.8
= Pa + 3.92 × 10 4 न्यूटन/मीटर 2
अम्ल की साइड से दरवाजे पर दाब
P2 = Pa + haρag
= Pa + ha \(\frac { \rho _{ a } }{ \rho _{ w } } \) × g × ρw
= Pa + 6.66 × 104 न्यूटन/मीटर 2
अतः दाबान्तर P = P2 – P1 = (6.66 – 3.92) × 104
= 2.74 × 104 न्यूटन/मीटर 2
अतः दरवाजा बन्द रखने के लिए आवश्यक बल F = PA
= 2.74 × 104 × 2 × 10-3
= 54.8
= 55 न्यूटन
![]()
प्रश्न 10.22.
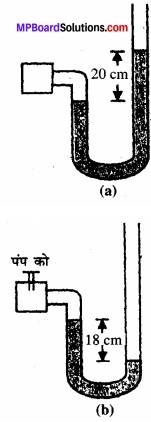
चित्र (a) में दर्शाए अनुसार कोई मैनोमीटर किसी बर्तन में भरी गैस के दाब का पाठ्यांक लेता है। पंप द्वारा कुछ गैस बाहर निकालने के पश्चात् मैनोमीटर चित्र (b) में दर्शाए अनुसार पाठ्यांक लेता है। मैनोमीटर में पारा भरा है तथा वायुमंडलीय दाब का मान 76 cm (Hg) है।
(i) प्रकरणों (a) तथा (b) में बर्तन में भरी गैस के निरपेक्ष दाब तथा प्रमापी दाब cm (Hg) के मात्रक में लिखिए।
(ii) यदि मैनोमीटर की दाहिनी भुजा में 13.6 cm ऊँचाई तक जल (पारे के.साथ अमिश्रणीय) उड़ेल दिया जाए तो प्रकरण (b) में स्तर में क्या परिवर्तन होगा? (गैस के आयतन में हुए थोड़े परिवर्तन की उपेक्षा कीजिए।)
उत्तर:
(i) प्रकरण (a) में
गैस का निरपेक्ष दाब = Pa + h
दिया है: h = 20 सेमी पारा व pa = 76 सेमी पारा (वायुमण्डलीय दाब)
निरपेक्ष दाब = 76 + 20 = 96 सेमी (पारा)
लेकिन प्रमापी दाब (मेज दाब) = 20 सेमी (पारा) प्रकरण (b) में
गैस का निरपेक्ष दाब = Pa + h
= 76 – 18 (h = – 18 सेमी)
= 58 सेमी (पारा)
लेकिन प्रमापी दाब (गेज दाब) = – 18 सेमी (पारा)
(ii) जल स्तम्भ के दाब को सन्तुलित करने के लिए बाईं भुजा में पारा ऊपर चढ़ेगा। माना दोनों ओर के तलों का अन्तर h है।
माना h1 = 13.6 सेमी ऊँचे जल स्तम्भ का दाब h’1, ऊँचाई वाले पारे के स्तम्भ के दाब के समान है।
∴h’1 × ρHg × g = h1.ρw.g
∴h’1 = \(\frac { \rho _{ w } }{ \rho _{ ng } } \) × h1
= \(\frac { 10^{ 3 }\times 13.6 }{ 13.6\times 10^{ 3 } } \) = 1 सेमी।
प्रकरण (c) में गैस का निरपेक्ष दाब,
P = Pa + h’ + h’1
58 = 76 + h + 1
h = 58 – 77 = – 19 सेमी।
अतः प्रथम स्तम्भ में पारे का तल दूसरे स्तम्भ की तुलना में 19 सेमी ऊँचा हो जाएगा।
प्रश्न 10.23.
दो पात्रों के आधारों के क्षेत्रफल समान हैं परंतु आकृतियाँ भिन्न – भिन्न हैं। पहले पात्र में दूसरे पात्र की अपेक्षा किसी ऊँचाई तक भरने पर दो गुना जल आता है। क्या दोनों प्रकरणों में पात्रों के आधारों पर आरोपित बल समान हैं। यदि ऐसा है तो भार मापने की मशीन पर रखे एक ही ऊँचाई तक जल से भरे दोनों पात्रों के पाठ्यांक भिन्न – भिन्न क्यों होते है?
उत्तर:
हाँ, दोनों प्रकरणों में पात्रों के आधारों पर आरोपित बल समान है।
माना प्रत्येक पात्र में जल स्तम्भ की ऊँचाई h व आधार का क्षेत्रफल A है।
अतः आधार पर बल = जल स्तम्भ का दाब × क्षेत्रफल
= hpg × A = Ahpg
अत: दोनों पात्रों के आधारों पर समान बल लगेंगे।
भाप मापने वाली मशीन, पात्रों के आधार पर लगने वाले बल को मापने के स्थान पर पात्र तथा जल का भार मापती है।
चूँकि एक पात्र में दूसरे की तुलना में दो गुना जल है। अतः भार मापने की मशीन के पाठ्यांक अलग – अलग होंगे।
प्रश्न 10.24.
रुधिर – आधान के समय किसी शिरा में, जहाँ दाब 2000 Pa है, एक सुई धुंसाई जाती है। रुधिर के पात्र को किस ऊँचाई पर रखा जाना चाहिए ताकि शिरा में रक्त ठीक – ठीक प्रवेश कर सके।
(सम्पूर्ण रुधिर का घनत्व सारणी 10.1 में दिया गया है।)
उत्तर:
दिया है: शिरा में रक्त दाब,
P = 2000 Pa
रक्त का घनत्व ρ = 1.06 × 103 kg m-3
g = 9.8 ms-2
माना कि रक्त के पात्र की सुई से ऊँचाई = h
सूत्र P = hρg से,
h = \(\frac { P }{ \rho g } \)
= \(\frac { 2000 }{ 1.06\times 10^{ 3 }\times 9.8 } \)
= \(\frac { 1000 }{ 106\times 49 } \)
= 0.193 m
या h = 0.2 m
![]()
प्रश्न 10.25.
बर्नूली समीकरण व्युत्पन्न करने में हमने नली में भरे तरल पर किए गए कार्य को तरल की गतिज तथा स्थितिज ऊर्जाओं में परिवर्तन के बराबर माना था।
(a) यदि क्षयकारी बल उपस्थित है, तब नली के अनुदिश तरल में गति करने पर दाब में परिवर्तन किस प्रकार होता है?
(b) क्या तरल का वेग बढ़ने पर क्षयकारी बल अधिक महत्वपूर्ण हो जाते हैं? गुणात्मक रूप में चर्चा कीजिए।
उत्तर:
(a) क्षयकारी बल की अनुपस्थिति में बहते हुए द्रव के एकांक आयतन की सम्पूर्ण ऊर्जा स्थिर रहती है लेकिन क्षयकारी बल की उपस्थिति में नली में तरल के प्रवाह को बनाए रखने के लिए क्षयकारी बल के विरुद्ध कार्य करना पड़ता है। अतः नली के अनुदिश चलने पर तरल का दाब अधिक तीव्रता से घटता जाता है। इसी कारण शहरों में जल की टंकी से बहुत दूरी पर स्थित मकानों की ऊँचाई टंकी से कम होने पर भी जल उनकी ऊपर वाली मंजिल तक नहीं पहुंच पाता है।
(b) हाँ, तरल का वेग बढ़ने पर तरल की अपरूपण दर बढ़ती है। इस प्रकार क्षयकारी श्यान बल और ज्यादा महत्वपूर्ण हो जाते हैं।
प्रश्न 10.26.
(a) यदि किसी धमनी में रुधिर का प्रवाह पटलीय प्रवाह ही बनाए रखना है तो 2 × 10-3 m त्रिज्या की किसी धमनी में रुधिर-प्रवाह की अधिकतम चाल क्या होनी चाहिए?
(b) तदनुरूपी प्रवाह – दर क्या है? (रुधिर की श्यानता 2.084 × 10-3 Pas लीजिए)।
उत्तर:
दिया है: η = 2.084 × 10-3 Pas,
r = 2 × 10-3 मीटर
(a) माना रुधिर प्रवाह की अधिकतम चाल = vmax
सूत्र रेनाल्ड संख्या, Re = \(\frac { \rho vd }{ \eta } \) = \(\frac { \rho v_{ 2r } }{ \eta } \) से,
vmax = \(\frac { \eta (R_{ e })_{ usb } }{ 2\rho r } \)
= \(\frac { 2.084\times 10^{ -3 }\times 2000 }{ 1.06\times 10^{ 3 }\times 2\times 2\times 10^{ -3 } } \) [∴(Re)max = 2000] = 0.98 मीटर/सेकण्ड
(b) माना तद्नुरूपी प्रवाह दर = प्रति सेकण्ड प्रवाहित रक्त = धमनी का अनुप्रस्थ परिच्छेद × रक्त प्रवाह की दर
= \(\frac { \pi r^{ 2 } }{ 4 } \).v
= \(\frac { \pi }{ 4 } \) × ( 2 × 10-3)2 × 0.98
= 3.08 × 10-6 मीटर 3 प्रति सेकण्ड
प्रश्न 10.27.
कोई वायुयान किसी निश्चित ऊँचाई पर किसी नियत चाल से आकाश में उड़ रहा है तथा इसके दोनों पंखों में प्रत्येक का क्षेत्रफल 25 m2 है। यदि वायु की चाल पंख के निचले पृष्ठ पर 180 kmh-1 तथा ऊपरी पृष्ठ पर 234 kmh-1 है, तो वायुयान की संहति ज्ञात कीजिए। (वायु का घनत्व 1kgm-3 लीजिए)।
उत्तर:
माना पंख के ऊपरी व निचले पृष्ठ पर वायु का वेग क्रमश: v1 व v2 है।
v1 = 234 kmh-1 = 234 × \(\frac{5}{18}\)
= 50 ms-1
प्रत्येक पंख का क्षेत्रफल = 25 m2
पंख का कुल क्षेत्रफल,
A = 25 + 25 = 50 m2
अतः बर्नूली प्रमेय से दोनों पंखों के वायु का घनत्व
ρ = 1 kg m-3
पृष्ठों के बीच दाबान्तर,
∆P = \(\frac{1}{2}\) ρ (v12 – v22)
= \(\frac{1}{2}\) × 1 × (652 – 502)
= \(\frac{1}{2}\) (4225 – 2500)
बल, F = ∆P × A = \(\frac{1725}{2}\) × 50N
![]()
प्रश्न 10.28.
मिलिकन तेल बूंद प्रयोग में, 2.0 × 10-5m त्रिज्या तथा 1.2 × 103 kgm-3 घनत्व की किसी बूंद की सीमांत चाल क्या है? प्रयोग के ताप पर वायु की श्यानता 1.8 × 10-5 Pas लीजिए। इस चाल पर बूंद पर श्यान बल कितना है? (वायु के कारण बूंद पर उत्प्लावन बल की उपेक्षा कीजिए)।
उत्तर:
दिया है:
r = 2.0 × 10-5 m,
ρ = 1.2 × 103kgm-3
η = 1.8 × 10-5 Nsm-2,
vT = ?, F = ?
सीमान्त वेग v = \(\frac{2}{9}\) r2 \(\frac { (\rho -\rho _{ 0 })g }{ \eta } \)
चूँकि वायु के कारण बूंद का घनत्व नगण्य है।
वायु के लिए P0 = 0
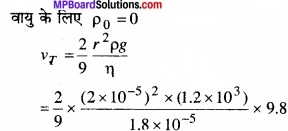
= 5.8 × 10-2 ms-1
= 5.8 cms-1
स्टोक्स के नियम से बिंदु पर सायं बल
F = 6πηrvT
= 6 × 3.142 × (1.8 × 10-5) × ( 2 × 10-5) × (5.8 × 10-2)
= 3.93 × 10-10 N
प्रश्न 10.29.
सोडा काँच के साथ पारे का स्पर्श कोण 140° है। यदि पारे से भरी द्रोणिका में 1.00 mm त्रिज्या की काँच की किसी नली का एक सिरा डुबोया जाता है, तो पारे के बाहरी पृष्ठ के स्तर की तुलना में नली के भीतर पारे का स्तर कितना नीचे चला जाता है? (पारे का घनत्व = 13.6 × 103 kgm-3)
उत्तर:
दिया है: स्पर्श कोण, θ = 140°, r = 1 मिमी = 10-3 मीटर
पृष्ठ तनाव T = 0.465 न्यूटन प्रति मीटर,
पारे का घनत्व ρ = 13.6 × 103 किग्रा प्रति मीटर 3
h = ?
cos θ = cos 140°
= – cos 40°
= – 0.7660
सत्र

यहाँ ऋणात्मक चिन्ह को छोड़ने पर यह प्रदर्शित करता है कि बाहर के पारे के स्तम्भ के सापेक्ष नली के स्तम्भ में अवनमन होता है।
अवनमन = 5.34 मिमी।
प्रश्न 10.30.
3.0 mm तथा 6.0 mm व्यास की दो संकीर्ण नलियों को एक साथ जोड़कर दोनों सिरों से खुली एक U – आकार की नली बनाई जाती है। यदि इस नली में जल भरा है, तो इस नली की दोनों भुजाओं में भरे जल के स्तरों में क्या अंतर है। प्रयोग के ताप पर जल का पृष्ठ तनाव 7.3 × 10-2 Nm-1 है। स्पर्श कोण शून्य लीजिए तथा जल का घनत्व 1.0 × 10 3kgm-3 लीजिए। (g = 9.8 ms-2)
उत्तर:
दिया है:
जल का पृष्ठ घनत्व,
T = 7.3 × 10-2 Nm-1
जल का घनत्व ρ = 1 × 103kg m-3
स्पर्श कोण, θ = 0°, g = 9.8 ms-2
माना दो संकीर्ण नलिकाओं के छिद्रों के व्यास D1 व D2 हैं।
अतः D1 = 3.0 mm तथा D2 = 6.0 mm
∴त्रिज्याएँ, r1 = \(\frac { D_{ 1 } }{ 2 } \) = \(\frac{3}{2}\) = 1.5mm
= 1.5mm = 1.5 × 10-3m
तथा

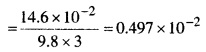
= 4.97 mm
= 5.00 मिमी
![]()
प्रश्न 10.31.
(a) यह ज्ञात है कि वायु का घनत्वp ऊँचाई y(मीटरों में) के साथ इस संबंध के अनुसार घटता है –
ρ = ρ0e-y/y0
यहाँ समुद्र तल पर वायु का घनत्व ρ0 = 1.25 kg m-3 तथा Y0, एक नियतांक है। घनत्व में इस परिवर्तन को वायुमंडल का नियम कहते हैं। यह संकल्पना करते हुए कि वायुमंडल का ताप नियत रहता है (समतापी अवस्था) इस नियम को प्राप्त कीजिए। यह भी मानिए किg का मान नियत रहता है।
(b) 1425 m3 आयतन का हीलियम से भरा कोई बड़ा गुब्बारा 400 kg के किसी पेलोड को उठाने के काम में लाया जाता है। यह मानते हुए कि ऊपर उठते समय गुब्बारे की त्रिज्या नियत रहती है, गुब्बारा कितनी अधिकतम ऊँचाई तक ऊपर उठेगा?
[yo = 8000 m तथा ρHe = 0.18 kg m-3 लीजिए।]
उत्तर:
(a) माना कि एक दूसरे से ऊर्ध्वाधर दूरी dy पर दो बिन्दु A व B हैं।
माना Y = बिन्दु A की समुद्र तल से ऊँचाई
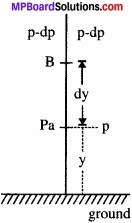
(i) P = A पर दाब
dp = A से B तक दाब में परिवर्तन
जैसे – जैसे हम समुद्र तल से ऊँचाई की ओर चलते हैं, दाब तथा घनत्व दोनों ही ऊँचाई के साथ बढ़ते हैं।
p – dp = B पर दाब
माना A तथा B पर घनत्व क्रमशः ρ व ρ – dρ हैं।
अत: A से B तक दाब में कमी = – dp
बल/क्षेत्रफल = \(\frac{mg}{a}\) = \(\frac{mg}{V.a}\) V
= (\(\frac{m}{V}\)) g . \(\frac{a}{a}\) dy
= pgdy ……… (i)
चूँकि ताप नियत रहता है।
∴ P ∝ρ
(∴ बॉयल के नियम से P ∝\(\frac{1}{v}\) ∝ \(\frac { 1 }{ (\frac { M }{ \rho } ) } \) या \(\frac{P}{M}\) ∝ P)
या p = kp ……. (ii)
जहाँ K नियतांक है।
समी० (i) व (ii) से,
– d(kp) = pgdy
या – kdp = pgdy
या \(\frac { d\rho }{ \rho } \) = \(\frac{g}{k}\) dy
या \(\frac { d\rho }{ \rho } \) + \(\frac{g}{k}\) dy = 0 ………. (iii)
समी (iii) का समाकलन करने पर,
\(\int { \frac { d\rho }{ \rho } } \) + \(\int { \frac { g }{ k } } \) dy = C
या logeρ + \(\int { \frac { g }{ k } } \) y = C ……………. (iv)
जहाँ C समाकलन नियतांक है।
माना Y = 0 पर ρ = ρ0
समी० (iv) से, logeρ0 = C ……….. (v)
समी० (iv) व (v) से
(ii) log eρ + \(\int { \frac { g }{ k } } \) y = logeρ0
या logeρ – logeρ0ρ = \(\int { \frac { -g }{ k } } \) y
या loge \(\frac { \rho }{ \rho _{ 0 } } \) = \(\int { \frac { -g }{ k } } \) y
∴\(\frac { \rho }{ \rho _{ 0 } } \) = e-g/k y = e-y/y0
या ρ = ρ0 e -y/y0
या ρ = ρ0e -y/y0
जो कि अभीष्ट नियम है।
दिया है:
Y0 = \(\frac{k}{g}\) नियतांक है।
(b) माना हीलियम का गुब्बारा Y ऊँचाई तक उड़ता है।
गुब्बारे का आयतन, V = 1425 मीटर3
पेलोड = 400 gN
PHe = 0.18 × 1425 = 256.5 kg
लिफ्ट से अलग कुल लोड
= 400 + 256.5 = 656.5 N
माना h ऊँचाई पर वायु का घनत्व p है। साम्यावस्था में, लिफ्ट से अलग किया लोड = He के गुब्बारे का भार
या 656.5g = V × p × g
या
ρ = \(\frac{656.5}{V}\) = \(\frac{656.5}{1425}\)
= 0.461 kg m-3
सूत्र ρ = ρ0e-y/y0 से
0.461 = 1.25e-y/8
e-y/8 = \(\frac{1.25}{0.461}\) = 2.71
\(\frac{y}{8}\) = ln 2.71 = 0.997
या y = 0.997 × 8 = 7.98 km
~ 8 km
यदि ऊँचाई के साथ 8 में परिवर्तन माना जाए तब ऊँचाई लगभग 8.2 किमी० होगी।