Prasanna

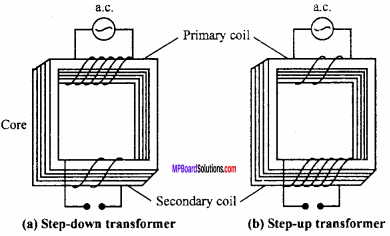
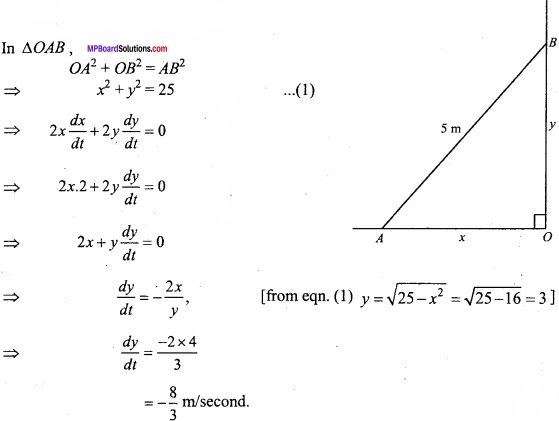
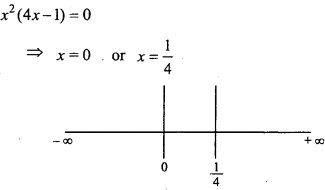
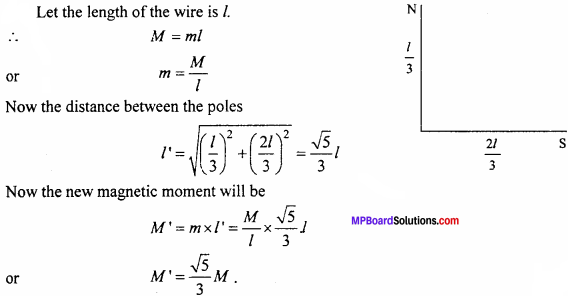
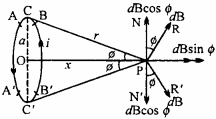
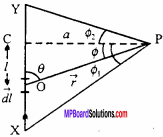
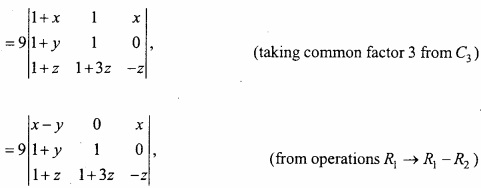
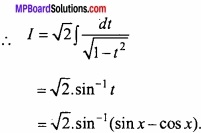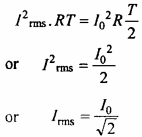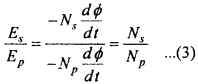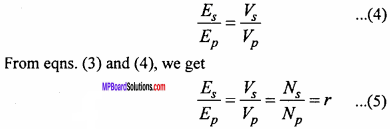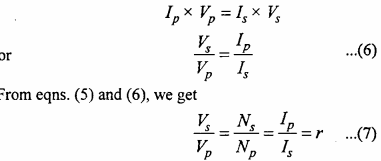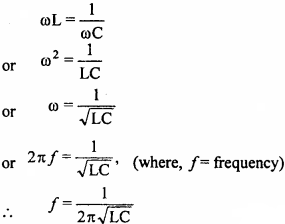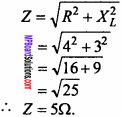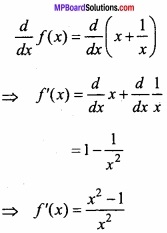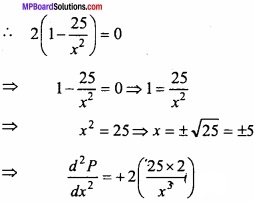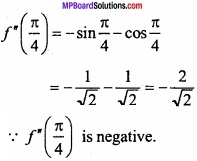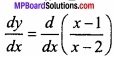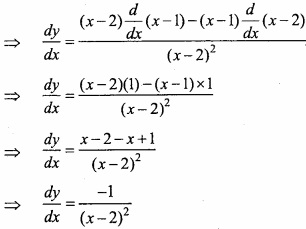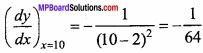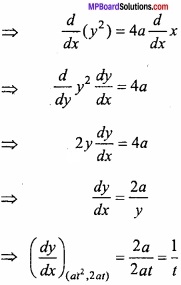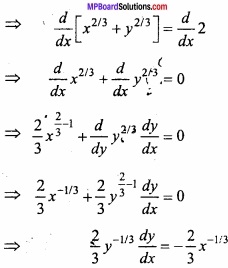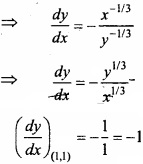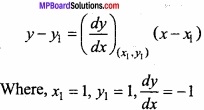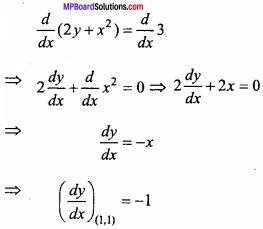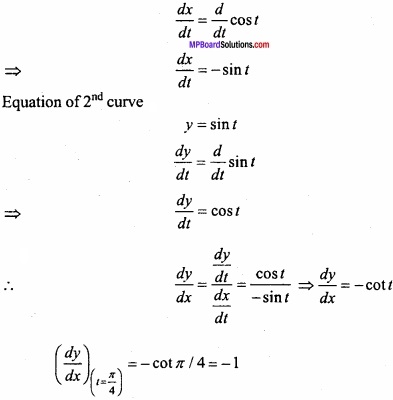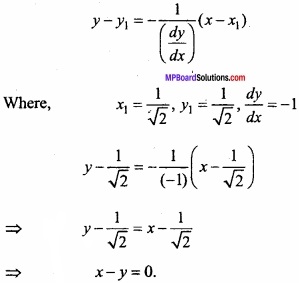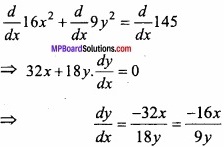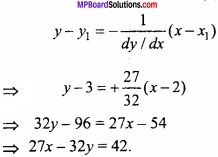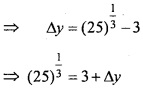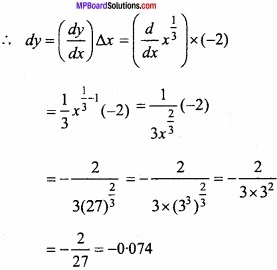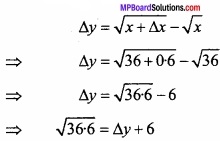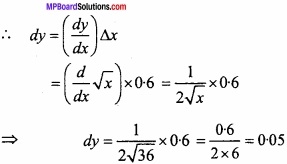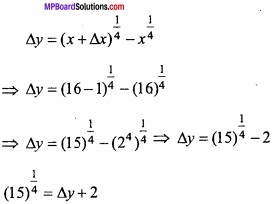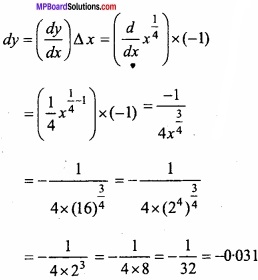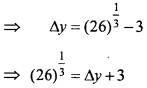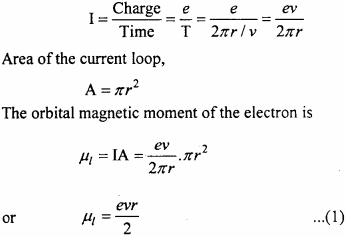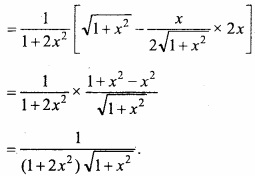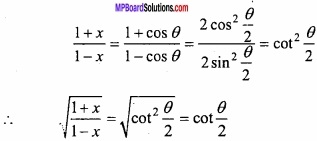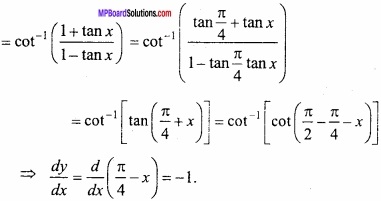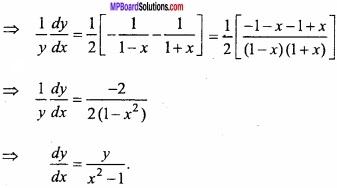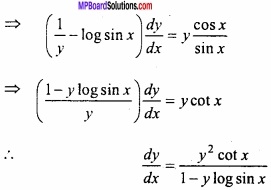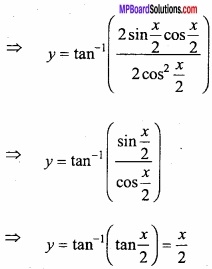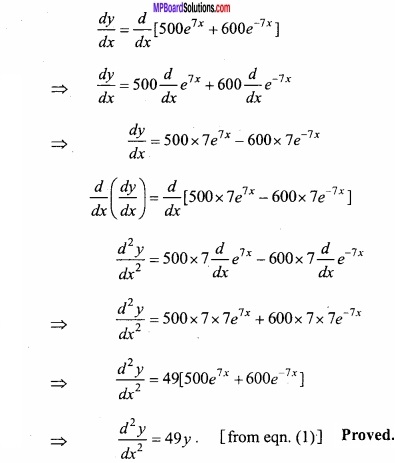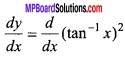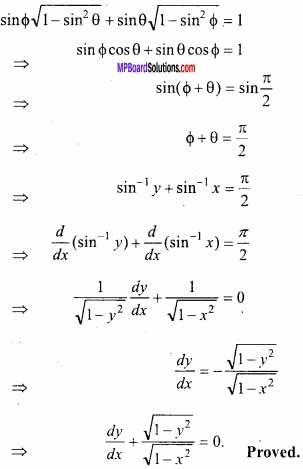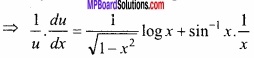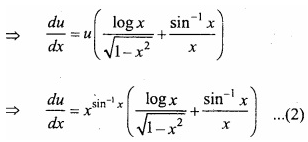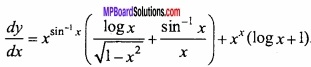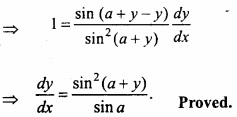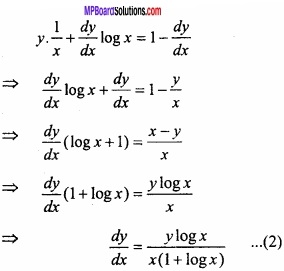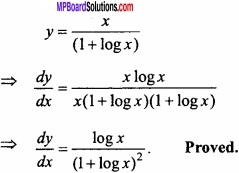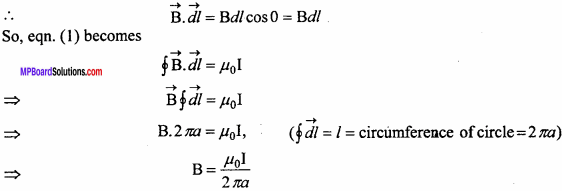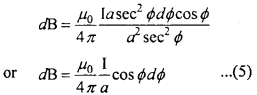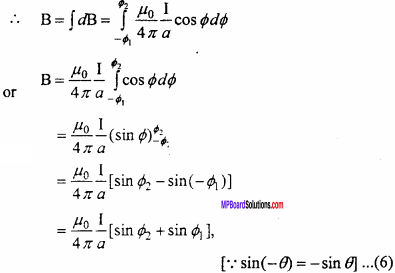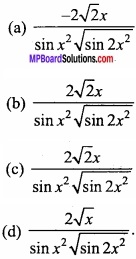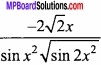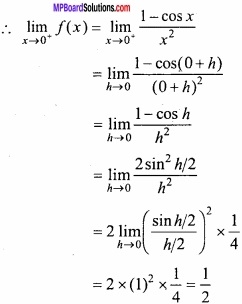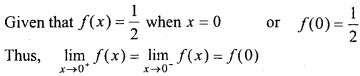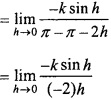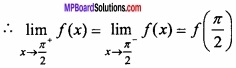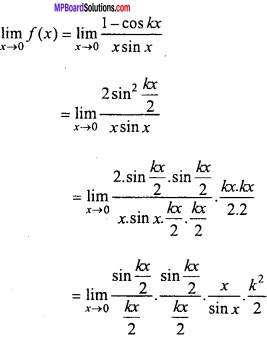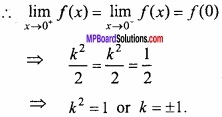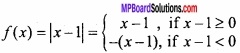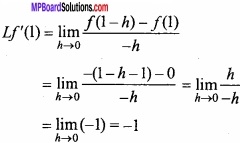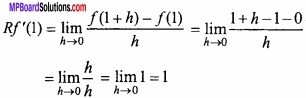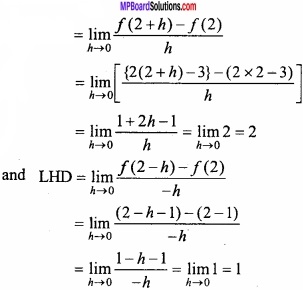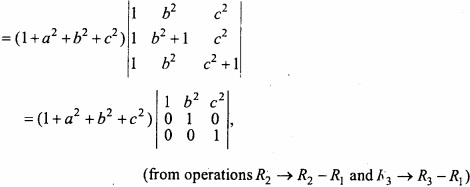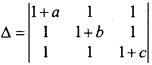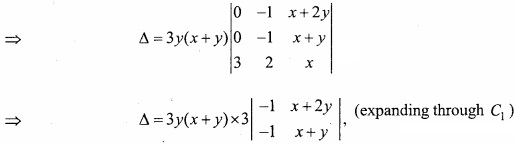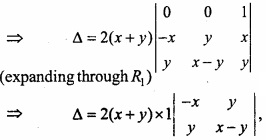MP Board Class 12th Maths Important Questions Chapter 7A Integration

Integration Important Questions

Integration Objective Type Questions:

Question 1.
Choose the correct answer:

Question 1.
The value of \(\int { \frac { sec^{ 2 }x }{ 1+tanx } } \) dx is:
(a) log_e (l + tan x) + c
(b) tan x + c
(c) – cot x + c
(c) – cot x + c
(d) log_e x + c
Answer:
(a) log_e (l + tan x) + c

Question 2.
The value of \(\int { \frac { x }{ 4+x^{ 4 } } } \) dx is:
(a) \(\frac{1}{4}\) x² + c
(b) \(\frac{1}{4}\) tan^-1 \(\frac { x^{ 2 } }{ 2 } \)
(c) \(\frac{1}{2}\) tan^-1 \(\frac { x^{ 2 } }{ 2 } \)
(d) None of these
Answer:
(a) \(\frac{1}{4}\) x² + c

Question 3.
If \(\int \frac{2^{\frac{1}{x}}}{x^{2}}\) dx = k(2)^1/x + c, then find the value of k is:
(a) \(\frac { -1 }{ log_{ e }2 } \)
(b) – log_e 2
(c) -1
(d) \(\frac { 1 }{ 2 } \)
Answer:
(a) \(\frac { -1 }{ log_{ e }2 } \)

Question 4.
The value \(\int \frac{e^{x}(1+x)}{\cos ^{2}\left(x e^{x}\right)}\) dx is:
(a) 2 log_ecos(xe^x) + c
(b) sec(xe^x) + c
(c) tan(xe^x) + c
(d) tan(x + e^x) + c
Answer:
(c) tan(xe^x) + c

Question 5.
If \(\int { xsinxdx } \) = -x cos x + α will be:
(a) sin x + c
(b) cos x + c
(c) c
(d) None of these
Answer:
(a) sin x + c

Question 2.
Fill in the blanks :


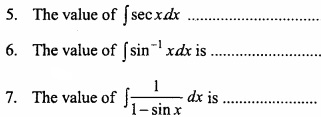
Answer:

1. \(\frac{1}{2}\) tan^-1 ( \(\frac{x}{a}\) ) + c
2. log [x + \(\int { \frac { dx }{ \sqrt { x^{ 2 }-a^{ 2 } } } } \) + c
3. log [x + \(\int { \frac { dx }{ \sqrt { a^{ 2 }-x^{ 2 } } } } \) + c
4. \(\frac{x}{2}\) \(\int { \frac { dx }{ \sqrt { a^{ 2 }-x^{ 2 } } } } \) + \(\frac { a^{ 2 } }{ 2 } \) sin^-1 ( \(\frac{x}{a}\) ) + c
5. log(sec x + tan x) + c
6. sin^-1 x + \(\sqrt { 1-x } \) + c
7. tan x + sec x.

Question 3.
Write True/False:

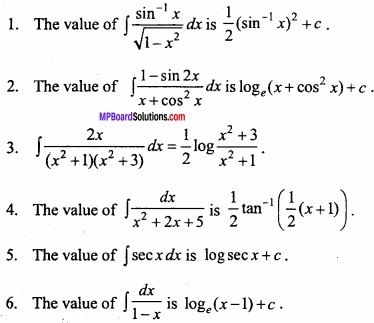
Answer:

1. True
2. True
3. False
4. True
5. False
6. False

Integration Very Short Answer Type Questions

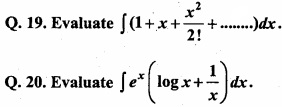
Answer:

1. \(e^{ tan-1x }\) + c
2. – cos x + c
3. sin² x + c
4. \(\frac{1}{2a}\) log \(\frac { a+x }{ a-x } \)
5. \(\frac{1}{2a}\) log \(\frac { x-a }{ x+a } \)
6. \(\frac { e^{ x } }{ x } \) + c
7. x log \(\frac { x }{ e } \) + c
8. 2 tan^-1\(\sqrt{x}\)
9. 1 + log x = t
10. a = – \(\frac { \pi }{ 4 } \), b = 3
11. x = t²
12. – \(\frac{1}{a}\) cos(ax + b)
13. \(\frac{1}{a}\) log (ax + b)
14. tan x – x + c
15. sin^-1 \(\frac{x}{a}\)
16. \(\frac { x^{ 3 } }{ 3 } \) + c
17. \(\frac { x^{ 3 } }{ 2 } \) + c
18. e^xf(x) + c
19. e^x
20. e^x log x + c.

Integration Short Answer Type Questions

Question 1.
Evaluate:
\(\int \frac{\cos 2 x+2 \sin ^{2} x}{\cos ^{2} x} dx\)? (CBSE 2018)
Solution:
Let I = \(\int \frac{\cos 2 x+2 \sin ^{2} x}{\cos ^{2} x} d x\)

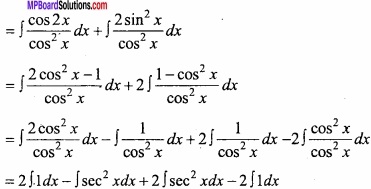
= \(\int { sec^{ 2 }xdx } \)
= tan x + c.

Question 2.
Evaluate \(\int { \frac { 1-sinx }{ cos^{ 2 }x } } \) dx? (NCERT)
Solution:
Let I = \(\int { \frac { 1-sinx }{ cos^{ 2 }x } } \)

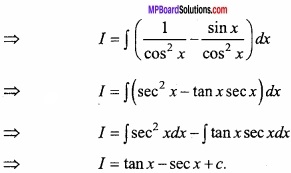
Question 3.
Evaluate \(\int \frac{2-3 \sin x}{\cos ^{2} x} d x\) dx? (NCERT)
Solution:
Let I = \(\int \frac{2-3 \sin x}{\cos ^{2} x} d x\) dx

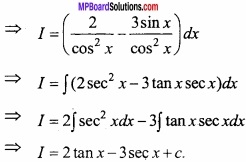
Question 4.
Evaluate \(\int \sin ^{-1}(\cos x) d x\) dx? (NCERT)
Solution:
I = \(\int \sin ^{-1}(\cos x) d x\) dx

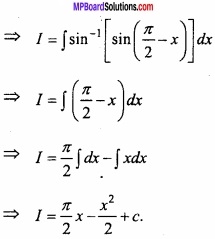
Question 5.
Evaluate \(\int { \frac { dx }{ 1+cos2x } } \)?
Solution:
Let I =

Question 6.
(A) Evaluate \(\int { tan^{ -1 }xdx } \)?
Solution:
Let

(B) Evaluate \(\int { sin^{ -1 }xdx } \) and \(\int { cos^{ -1 }xdx } \)?
(Do it by yourself)

Question 7.
Evaluate \(\int { sin^{ 2 }xdx } \)?
Solution:
Let

Question 8.
Evaluate \(\int { \frac { cosx }{ cos(x-\alpha ) } } \) dx?
Solution:

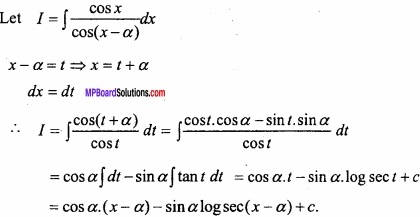
Question 9.
(A) Evaluate \(\int { \frac { 1 }{ \sqrt { 1+cosx } } } \) dx?
Solution:
Let

(B) Evaluate \(\int { \sqrt { 1+cos2xdx } } \)?
Solution:
Solve like Q.No 9 (B)

Question 10.
(A) Evaluate \(\int { \frac { e^{ x }(1+x) }{ cos^{ 2 }(xe^{ x }) } } \) dx?
Solution:
Let

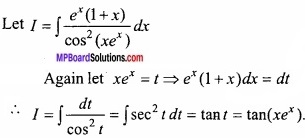
(B) Evaluate \(\int { \frac { e^{ tan-1x } }{ 1+x^{ 2 } } } \) dx?
Solution:
Let

Question 11.
Evaluate \(\int { \frac { dx }{ 1-sinx } } \)?
Solution:
Let

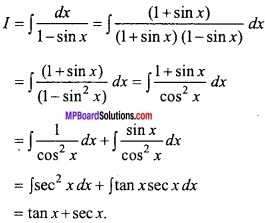
Question 12.
Evaluate \(\int { \frac { logx }{ x } } \) dx?
Solution:
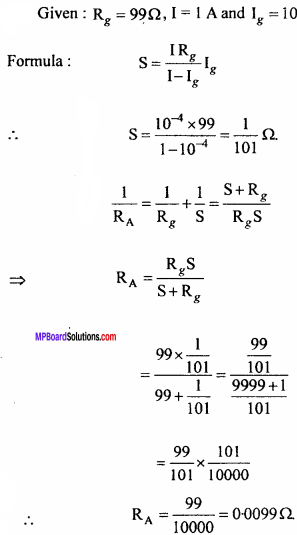
Given:

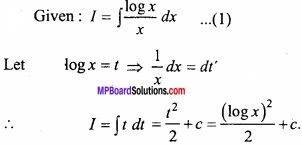
Question 13.
(A) Evaluate \(\int { \frac { dx }{ 1-cosx } } \)?
Solution:
Let

(B) Evaluate \(\int { \frac { logx }{ x } } \) dx?
Solution:
Let

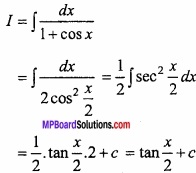
Question 14.
Evaluate \(\int { \frac { dx }{ 1+sinx } } \)?
Solution:
Let

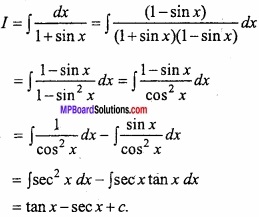
Question 15.
Evaluate \(\int { \frac { cos\sqrt { x } }{ \sqrt { x } } } \) dx?
Solution:
Let

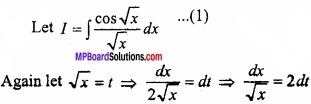
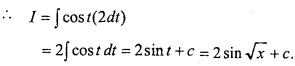
Question 16.
Evaluate \(\int { \frac { 1-cos2x }{ 1+cos2x } } \) dx?
Solution:
Let

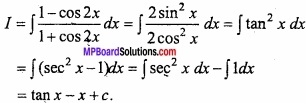
Question 17.
Integrate \(\frac { x^{ 4 } }{ x^{ 2 }+1 } \) with respect to x?
Solution:
Let

Question 18.
Find the value of \(\int { \frac { sec^{ 2 }(logx) }{ x } } \) dx?
Solution:
Let I = \(\int { \frac { sec^{ 2 }(logx) }{ x } } \) dx
Put, log x = t
⇒ \(\frac { 1 }{ x } \) dx = dt
∴ I = ∫sec² t dt
⇒ I = tan x + c
⇒ tan(log x) + c

Question 19.
Find the value of \(\int { \frac { sin(logx) }{ x } } \) dx?
Solution:
Let I = \(\int { \frac { sin(logx) }{ x } } \) dx
Put, log x = t
⇒ \(\frac { 1 }{ x } \) dx = dt
∴ I = ∫sin t dt = -cos t + c
⇒ I = – cos (log x) + c

Question 20.
Find the value of \(\int { \frac { cos(logx) }{ x } } \) dx?
Solution:
Solve like Q.No.19

Question 21.
(A) Find the value of \(\int { tan^{ 2 }xdx } \)?
Solution:
Let I = \(\int { tan^{ 2 }xdx } \) = ∫(sec² x – 1) dx
= ∫sec² x dx – ∫1dx = tan x – x.

(B) Find the value of \(\int { cot^{ 2 }xdx } \)?
Solution:
Let I = \(\int { cot^{ 2 }xdx } \) = ∫(cosec² x – 1) dx
= ∫cosec² x dx – ∫1.dx = – cot x – x.

Question 22.
Find the value of \(\int { \frac { sinx }{ 1+cosx } } \) dx?
Solution:
Let I = \(\int { \frac { sinx }{ 1+cosx } } \) dx
= ∫\(\frac { 1 }{ t } \) dt, (Put 1+cos x = dt ⇒ sin x dx = dt)
= log t
= log (1 + cos x).

Question 23.
Find the value \(\int { \frac { sin^{ -1 }x }{ \sqrt { 1-x^{ 2 } } } } \) dx?
Solution:

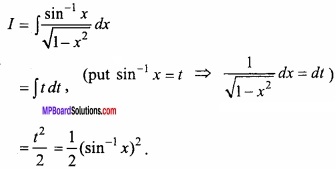
Integration Long Answer Type Questions – I

Question 1.
Find the value of \(\int { \sqrt { \frac { a+x }{ a-x } } } \) dx?
Solution:
Let I = \(\int { \sqrt { \frac { a+x }{ a-x } } } \) dx
Again let x = a cos θ ⇒ dx = – a sin θ dθ

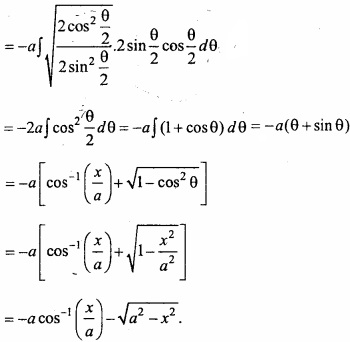
Question 2.
Evaluate \(\int\left[\frac{1}{(\log x)^{2}}-\frac{2}{(\log x)^{3}}\right]\) dx?
Solution:
Let I = \(\int\left[\frac{1}{(\log x)^{2}}-\frac{2}{(\log x)^{3}}\right]\)
Again let log x = t ⇒ x = e^t ⇒ dx = e^tdt

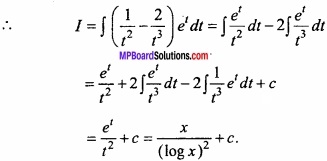
Question 3.
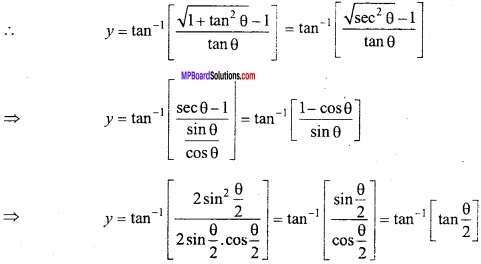
Evaluate \(\int { sin^{ -1 } } \) xdx?
Solution:
Let

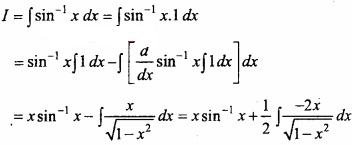
Again let 1 – x² t ⇒ – 2x dx = dt

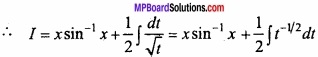
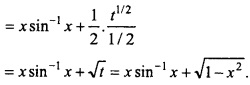
Question 4.
Evaluate \(\int { cos^{ -1 }xdx } \)?
Solution:
Let

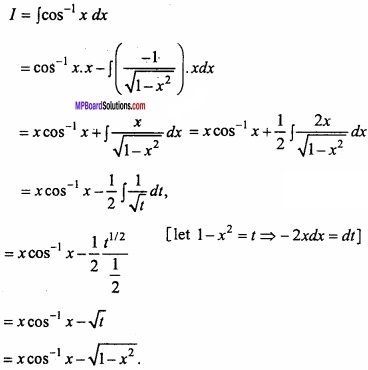
Question 5.
(A) Evaluate \(\int { \frac { x^{ 2 } }{ 1+x } } \) dx?
Solution:
Let

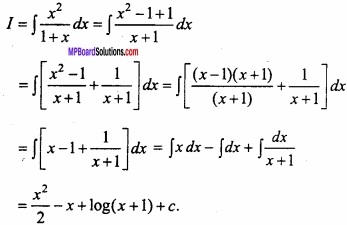
(B) Evaluate \(\int { \frac { x }{ 1+x^{ 4 } } } \) dx?
Solution:
Let

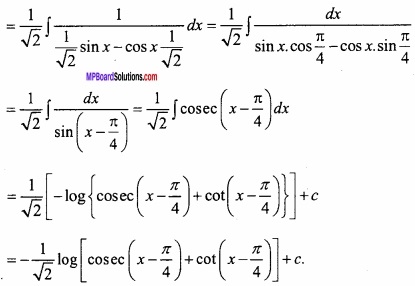
= \(\frac{1}{2}\) tan^-1 t,
= \(\frac{1}{2}\) tan^-1 x²

Question 6.
Evaluate \(\int { \frac { 1 }{ sinx-cosx } } \) dx?
Solution:
Let I = \(\int { \frac { 1 }{ sinx-cosx } } \) dx

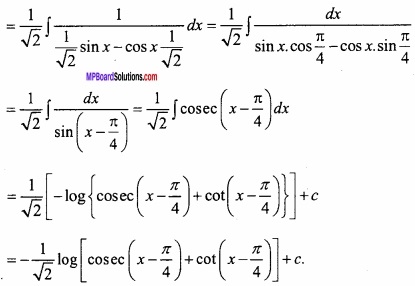
Question 7.
Evaluate \(\int { \frac { dx }{ e^{ x }+1 } } \)?
Solution:
Let

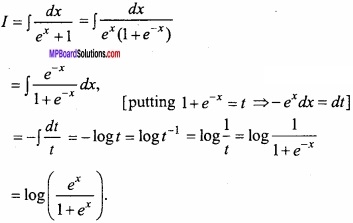
Question 8.
Evaluate \(\int { sec^{ 3 }xdx } \)?
Solution:
Let

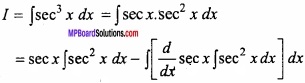
= sec x tan x – ∫sec x tan x tan x dx
= sec x tan x – ∫sec x tan² x dx
= sec x tan x – ∫sec x (sec² x – 1) dx
= sec x tan x – ∫sec³ xdx +∫sec x dx
⇒ I = sec x tan x – I + log(sec x + tan x)
⇒ 2I = sec x tan x + log (sec x + tan x)
⇒ I = \(\frac{1}{2}\) [sec x tan x + log (sec x + tan x)].

Question 9.
Evaluate \(\int { \frac { dx }{ x^{ 2 }-a^{ 2 } } } \)?
Solution:
Let

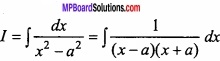
We have to break the term with partial fraction,
img

Question 10.
Evaluate \(\int { \frac { 3x }{ (x-2)(x+1) } } \) dx?
Solution:
Let \(\int { \frac { 3x }{ (x-2)(x+1) } } \) = \(\frac { A }{ (x-2) } \) + \(\frac { B }{ (x+1) } \) ………………… (1)
⇒ \(\frac { 3x }{ (x-2)(x+1) } \) = \(\frac { A(x+1)+B(x-2) }{ (x-2)(x+1) } \)
⇒ 3x = A(x + 1) + B (x – 2)
⇒ 3x = (A + B)x + (A – 2B) …………………… (2)
Comparing the coefficient of x from both sides,
3 = A + B
0 = A – 2B
3 = 3B ⇒ B = 1
and A = 2B = 2
image 40 40 40
= 2 log(x – 2) + log (x + 1) + c.

Question 11.
Evaluate \(\int { \frac { x^{ 2 }+1 }{ x^{ 4 }-x^{ 2 }+1 } } \) dx?
Solution:

Question 12.
Evaluate \(\int { \frac { x^{ 2 }+1 }{ x^{ 4 }+x^{ 2 }+1 } } \) dx?
Solution:
Solve like Q.No.11.
Answer:

Question 13.
Evaluate \(\int { \frac { dx }{ \sqrt { x^{ 2 }+2x+3 } } } \)?
Solution:
Let

Question 14.
Integrate \(\frac { 1 }{ 1+sin^{ 2 }x } \) with respect to x?
Solution:
Let

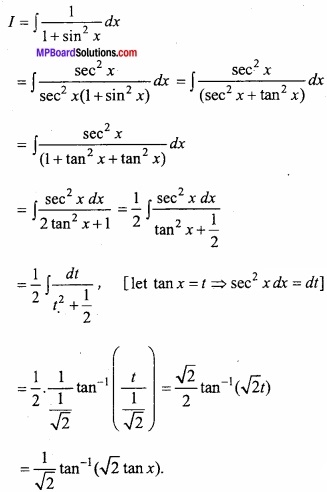
Question 15.
Evaluate \(\int { \frac { cos2x }{ (cosx+sinx)^{ 2 } } } \) dx? (NCERT)
Solution:
Let


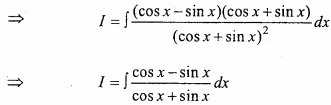
Taking cos x + sin x = t
\(\frac { d }{ dx } \) (cosx + sinx) = \(\frac { dt }{ dx } \)
⇒ (-sinx + cos x) = \(\frac { dt }{ dx } \)
∴ I = ∫ \(\frac { dt }{ t } \)
⇒ I = logt + c
⇒ I = log(cos x + sinx) + c.

Question 16.
Evaluate \(\int { \frac { 1+tanx }{ x+logsecx } } \)dx?
Solution:
Let

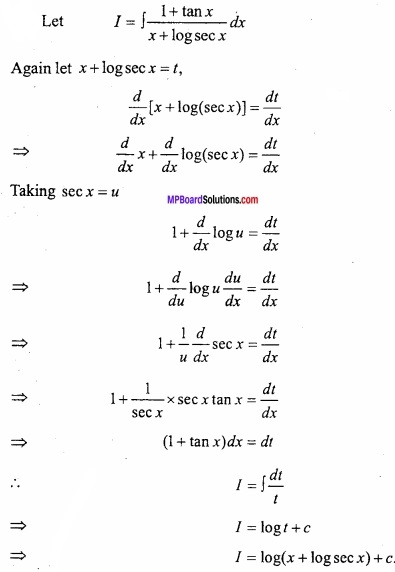
Question 17.
Evaluate \(\int { \frac { cotx }{ log(sinx) } } \) dx?
Solution:
Let I = \(\int { \frac { cotx }{ log(sinx) } } \) dx
Again let log(sin x) = t
\(\frac{d}{dx}\) log (sin x) = \(\frac{dt}{dx}\)
Taking sin x = u,

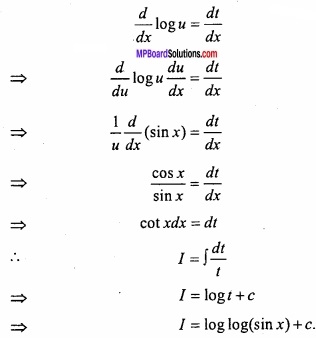
⇒ I = log t + c
⇒ I = log log(sin x) + c.

Question 18.
Evaluate \(\int { \frac { 2cosx-3sinx }{ 6cosx+4sinx } } \) dx? (NCERT)
Solution:
Let I = \(\int { \frac { 2cosx-3sinx }{ 6cosx+4sinx } } \) dx
Again let 6 cosx + 4 sin x = t,

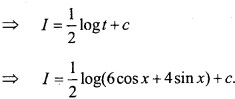
Question 19.
Evaluate \(\int { e^{ 3logx } } (x^{ 4 }+1)^{ -1 }\) dx? (NCERT)
Solution:
Let I = \(\int { e^{ 3logx } } (x^{ 4 }+1)^{ -1 }\) dx

Put x⁴ + 1 = t,

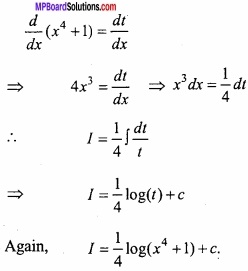
Question 20.
Evaluate \(\int { \frac { dx }{ x-\sqrt { x } } } \)? (NCERT)
Solution:
Let I = \(\int { \frac { dx }{ x-\sqrt { x } } } \)

Put \(\sqrt{x}\) – 1 = t

Question 21.
Evaluate \(\int { \frac { dx }{ 1+3sin^{ 2 }x } } \)?
Solution:
Let I = \(\int { \frac { dx }{ 1+3sin^{ 2 }x } } \)

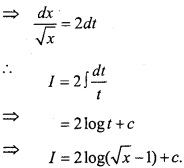
Integration Long Answer Type Questions – II

Question 1.
Evaluate \(\int \sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right) d x\) dx?
Solution:
Let I = \(\int \sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right) d x\) dx
Again let x = tan θ ⇒ dx = sec² θ dθ

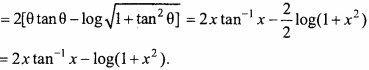
Question 2.
Integrate \(\frac{e^{m \tan ^{-1} x}}{\left(1+x^{2}\right)^{\frac{3}{2}}}\) with respect to x?
Solution:
Let tan^-1 x = t ⇒ x = tan t
dx = sec² t dt

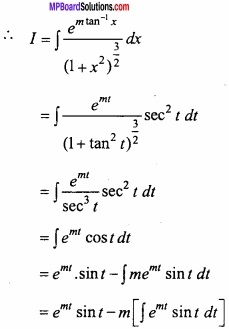
= e^mtsin t – m[e^mt(-cos t) – \(\int { me^{ mt } } \) (-cos t) dt]
= e^mtsin t + me^mtcos t – m² \(\int { e^{ mt } } \) cos t dt
= e^mt (sin t + m cos t) – m² I

Question 3.
Evaluate \(\int { \frac { x^{ 2 }tan^{ -1 }x }{ 1+x^{ 2 } } } \) dx?
Solution:
Let I = \(\int { \frac { x^{ 2 }tan^{ -1 }x }{ 1+x^{ 2 } } } \) dx
Let x = tan θ ⇒ θ = tan^-1 x
⇒ dx = sec² θdθ

Question 4.
Evaluate \(\int { tan^{ -1 }\frac { 2x }{ 1+x^{ 2 } } } \) dx?
Solution:
Let I = \(\int { tan^{ -1 }\frac { 2x }{ 1+x^{ 2 } } } \) dx
Let x = tan θ ⇒ dx = sec² θdθ

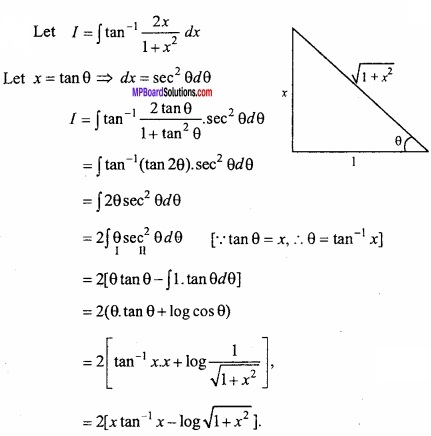
Question 5.
Evaluate \(\int { \frac { xtan^{ -1 }x }{ (1+x^{ 2 })^{ 3/2 } } } \) dx?
Solution:
Let I = \(\int { \frac { xtan^{ -1 }x }{ (1+x^{ 2 })^{ 3/2 } } } \) dx
Let x = tan θ ⇒ dx = sec² θdθ

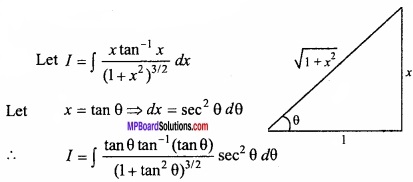
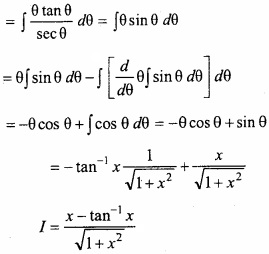
Question 6.
Evaluate \(\int { \frac { dx }{ 3+2cosx } } \)?
Solution:
Let I = \(\int { \frac { dx }{ 3+2cosx } } \)

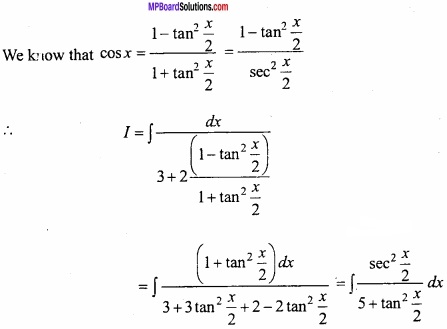
Again let tan \(\frac { x }{ 2 }\) = t,

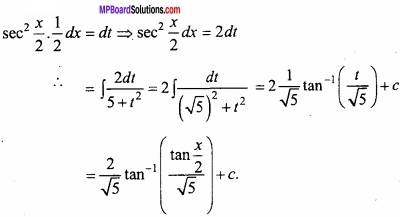
Question 7.
Evaluate \(\int { \frac { dx }{ 4+5cosx } } \)?
Solution:
Solve like Q.No.6.

Question 8.
Evaluate \(\int { \frac { dx }{ 5-3cosx } } \)?
Solution:
Solve like Q.No.6.

Question 9.
Evaluate \(\int { \frac { 1 }{ 4+5sinx } } \) dx?
Solution:

Let tan \(\frac { x }{ 2 }\) = t ⇒ sec² \(\frac { x }{ 2 }\).\(\frac { 1 }{ 2 }\).dx = dt

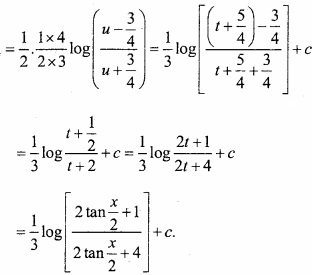
Question 10.
Evaluate \(\int { \frac { e^{ x }(1+sinx) }{ (1+cosx) } } \) dx?
Solution:
Let I = \(\int { \frac { e^{ x }(1+sinx) }{ (1+cosx) } } \) dx

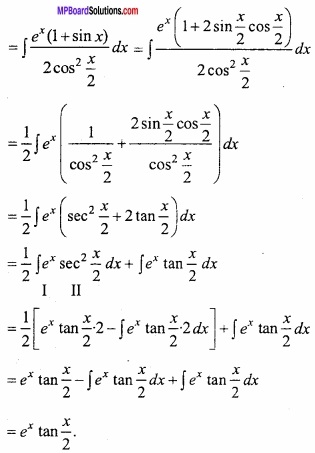
Question 11.
Evaluate \(\int { \frac { xe^{ x } }{ (1+x)^{ 2 } } } \) dx?
Solution:
Let I = \(\int { \frac { xe^{ x } }{ (1+x)^{ 2 } } } \) dx = \(\int { \frac { (1+x-1)e^{ x } }{ (1+x)^{ 2 } } } \)

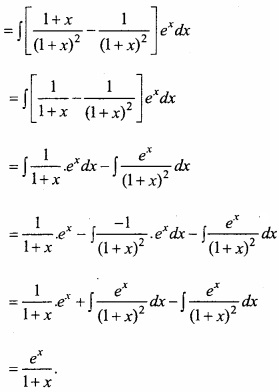
Question 12.
Evaluate \(\int { \frac { 2cosx }{ (1-sinx)(1+sin^{ 2 }x) } } \) dx? (CBSE 2018)
Solution:
Let I = \(\int { \frac { 2cosx }{ (1-sinx)(1+sin^{ 2 }x) } } \) dx
Put sin x = t, cos x dx = dt

⇒ 2 = A(1 + t²) + (1 – t) (Bt + 1)
⇒ 2 = A + At² + Bt – Bt² + 1 – t
⇒ 2 = (A – B)t² + (B – 1) t + (A + 1)
Comparing the cofficient of like terms
∴ A – B = 0
B – 1 = 0
and A + 1 = 2
∴ B = 1, A = 1

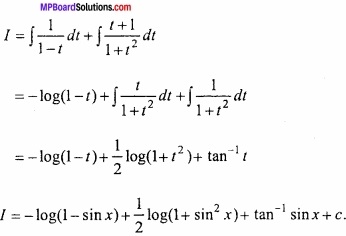
Question 13.
Evaluate \(\int { \frac { dx }{ e^{ x }-1 } } \)? (NCERT)
Solution:
Let I = \(\int { \frac { dx }{ e^{ x }-1 } } \) = \(\int { \frac { e^{ x }dx }{ e^{ x }(e^{ x }-1) } } \)
Again let e^x = t, then e^xdx = dt

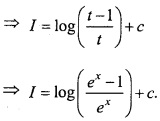
Question 14.
Evaluate \(\int { \frac { dx }{ x(x^{ n }+1) } } \)? (NCERT)
Solution:
Let I = \(\int { \frac { dx }{ x(x^{ n }+1) } } \)

Put xⁿ = t,

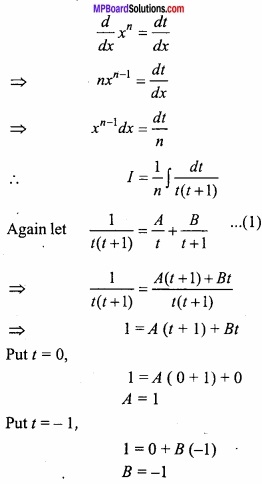
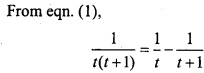
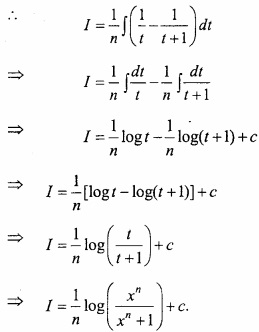
Question 15.
Evaluate \(\int { (\sqrt { tanx } +\sqrt { cotx) } } \) dx? (NCERT)
Solution:
Let

Again let, sin x – cos x = t
(cos x + sin x) dx = dt
(sin x – cos x)² = t²
sin²x + cos²x – 2sinxcos x = t²
⇒ 1 – sin 2x = t²
⇒ sin 2x = 1 – t²

MP Board Class 12 Maths Important Questions

MP Board Class 12th Physics Important Questions Chapter 7 Alternating Current

Alternating Current Important Questions

Alternating Current Objective Type Questions

Question 1.
Choose the correct answer of the following:

Question 1.
The mean value of an A.C. over one complete cycyle is :
(a) \(\frac { { 2I }_{ 0 } }{ \pi }\)
(b) –\(\frac { { 2I }_{ 0 } }{ \pi }\)
(c) Infinite
(d) Zero
Answer:
(d) Zero

Question 2.
The relation between peak value V₀ and rms value Vrms of alternating voltage is:
(a) V₀ = 0.707 V_ms
(b) V_ms = 0.707 V₀
(c) V_ms = 0.637 V₀
(d) V₀= 0.637 V_ms
Answer:
(c) V_ms = 0.637 V₀

Question 3.
A capacitor allows through it:
(a) Only d.c
(b) Only a.c
(c) a.c and d.c both
(d) Neither a.c nor d.c.
Answer:
(b) Only a.c

Question 4.
In a circuit wattless current flows if it contains :
(a) Only R
(b) R – L
(c) R – C
(d) Only L.
Answer:
(d) Only L.

Question 5.
A device which convert mechanical energy into electrical energy is :
(a) d.c moter
(b) a.c generator
(c) Transformer
(d) Choke coil.
Answer:
(b) a.c generator

Question 6.
The relation between peak value on a.c I₀ and virtual value Irms is :
(a) I_{0 =} \(\frac { 1 }{ \sqrt { 3 } }\) = I_ms
(b) I_ms = \(\sqrt { 3{ I }_{ 0 } }\)
(c) I₀ = I_ms
(d) I₀ = \(\sqrt { 3{ I }_{ ms } }\) I_ms
Answer:
(d) I₀ = \(\sqrt { 3{ I }_{ ms } }\) I_ms

Question 2.
Fill in the blanks :

1. The cause of production of induced e.m.f. is change in
2. The dimensional formula of inductance is
3. In an ideal coupling the value of coupling coefficient K is
4. The ohmic resistance of an ideal inductor is
5. Due to eddy currents the decay of electrical energy is in the form of

Answer:

1. Magnetic flux
2. [ML²T^-2A^-2]
3. One
4. Zero
5. Heat energy.

Question 3.
Match the Column :
I.

Answer:

1. (c)
2. (d)
3. (b)
4. (e)
5. (a)

II.

Answer:

1. (e)
2. (c)
3. (b)
4. (d)
5. (a)

Question 4.
Write the answer ¡n one word/sentence:

1. What is the frequency of direct current?
2. Which effect is exhibited by alternating current?
3. What is the magnitude of inductive reactance for direct current?
4. What ¡s the magnitude of capacitive reactance for direct current?
5. What is the unit of \(\sqrt { LC }\)?
6. What ¡s average value of alternating current for one complete cycle?
7. What will be the magnitude of power coefficient for a L – C – R circuit in resonance state?
8. How many times the direction of alternating current charges for one complete cycle?
9. What will be the magnitude of power coefficient for pure inductor or capacitor?
10. What is the phase difference between e.m.f. and a.c. pure resistance, pure inductor and pure capacitor?

Answer:

1. Zero
2. Heating effect
3. Zero
4. Infinity
5. Second
6. Zero
7. One
8. Two times
9. Zero
10. Phase difference ϕ = 0

Alternating Current Very Short Answer Type Questions

Question 1.
In direct current circuit contaning pure inductance, what will be the value of inductive reactance?
Answer:
Since X_L= ωL for d.c. ω = 0, therefore X_L will be zero.

Question 2.
Can battery be charged with alternating current?
Answer:
No, it can’t be charged.

Question 3.
Which is more dangerous a.c. or d.c. at same voltage?
Answer:
Alternating current.

Question 4.
How will you recognize whether the current flowing through the coil of bulb in a.c. or d.c.?
Answer:
If on bringing magnet near the coil, if it vibrate then it will be alternating current.

Alternating Current Short Answer Type Questions

Question 1.
Define rms and peak value of alternating current and state the relation between them.
Answer:
Root mean square value:
Root mean square value of an a.c. is defined as that value of steady current which would generate the same amount of heat in a given resistance in a given time, as is done by the a.c. when passed through the same resistance for the same time. It is also called virtual value.

Peak value:
The maximum value of ax. is called its peak value or amplitude i.e.,
Peak value = \(\sqrt {2}\) x rms value
or I₀ = \(\sqrt {2}\) I_rms

Question 2.
a.c. does not show magnetic and chemical effects, why?
Answer:
a.c. flows in one direction during the first half cycle and in reverse direction in the second half cycle. Therefore, the average value of current for a complete cycle is zero. Thus, it does not show magnetic and chemical effects.

Question 3.
Why a.c. is more dangerous than d.c. of the same voltage?
Answer:
The maximum value of alternating e.m.f. is \(\sqrt {2}\) times of its virtual e.m.f. If virtual value is 220 V, then the peak value of e.m.f. = 220 x \(\sqrt {2}\) = 311.13 V. Hence, the voltage of ax. fluctuates between +311.13 V to – 311.13 V. Therefore, ax. is more dangerous.

Question 4.
a. c. cannot be measured by moving coil galvanometer, why?
Answer:
Moving coil galvanometer works on the principle of magnetic effect of current. a.c. does riot show magnetic effect because when ax. is passed through the coil, the direction and magnitude of current will frequently change and so the deflecting couple produces. But, in each complete cycle, the average deflecting couple is zero. So, there will be no deflection in the coil.

Question 5.
A bulb and a solenoid are connected in series to an a.c. source. If a soft – iron core is inserted inside the solenoid, what will be its effect on the intensity of light coming out of the bulb?
Answer:
The bulb will glow dimmer i.e., intensity decreases. This is because on introducing soft – iron core in the solenoid, the inductance increases. So, inductive reactance increases (by X_L = ωL), hence the current through the bulb decreases.

Question 6.
Write the expression for pure inductive reactance in an a.c. circuit and explain how it depends on the frequency of a.c.? Write its unit.
Answer:
Reactance of pure inductive component,
X_L = ωL = 2 πf L
Where, f= Frequency of a.c and L = Inductance of the coil
Clearly, X_L ∝ f
i.e., the reactance of pure inductive component is proportional to the frequency of a.c. Unit of reactance is ohm.

Question 7.
Write the expression for reactance of capacitor in an a.c. circuit. Explain how does it depend on frequency of a.c.? Write its unit.
Answer:
Capacitive reactance

Where, f = Frequency of a.c. and C = Capacitance of the capacitor. i.e., the capacitive impedance is inversely proportional to the frequency of a.c. Unit of capacitive reactance is ohm.

Question 8.
A capacitor stops d.c., why?
Answer:
In an a.c. circuit, reactance offered by capacitor i.e., capacitive reactance is

Hence, capacitor stops d.c.

Question 9.
What is the resistance of a coil of self – inductance L in a d.c. circuit?
Answer:
Resistance of coil in a.c. circuit i.e., inductive reactance is
X_L = ωL = 2πf L
For d.c., f = 0
Hence, resistance offered by the coil in d.c. circuit
X_L = 2π.0.L = 0.

Question 10.
In order to reduce the current in a.c. circuit, an inductor is more suitable than a resistance. Why?
Answer:
If a resistance is used in an a.c. circuit, a part of electrical energy is lost in the form of heat. Instead, if we use an inductance, there is no energy loss in the form of heat because power factor for inductive component is zero.

Question 11.
An electric heater is operated by direct current and alternating current respectively on the same potential difference. Will the heat liberated, in these two cases be the same? Give reasons for your answer.
Answer:
An electric heater containing a coil has resistance as well as inductance. So, its resistance is large for a.c. than for d.c.
From the formula for produced heat,
H = \(\frac { { V }^{ 2 } }{ R }\)
We conclude, less heat will therefore be produced by a.c.

Question 12.

1. What will be the power loss in a pure inductive or pure capacitive circuit when it is joined to a.c. source?
2. When will voltage and current in an LCR a.c. circuit be in same phase?

Answer:
1. When an inductor is joined to an a.c. source, then voltage is ahead of current by π/2, hence ϕ = π/2.
The power factor is P = V_rmsI_rms cosϕ
= V_rmsI_rms cos\(\frac {π}{2}\) = 0
Hence, there is no consumption of power. When a capacitor is joined, then voltage is lagging behind the current by \(\frac {π}{2}\) . Hence ϕ = \(\frac {π}{2}\) = 0
The power factor is P = V_rmsl_rms cosϕ
= V_rmsl_rms cos(- \(\frac {π}{2}\)) = 0
= 0
Hence, there is no consumption of power.

2. Voltage and current in an LCR a.c. circuit will be in the same phase when frequency is f = \(\frac { 1 }{ 2\pi \sqrt { LC } }\)

Question 13.
What is Wattless current?
Answer:
In a.c. circuit, when the average consumed power is zero, then that current is called wattless current.
If a pure inductance or pure capacitance is used in a.c. circuit, then the phase difference between current and e.m.f. becomes\(\frac {π}{2}\).
P_av = V_rms x I_rms x cosϕ
= V_rms x I_rms x cos\(\frac {π}{2}\)
= V_rms x I_rms x o = 0
Choke coil is made up of thick copper wire. Its ohmic resistance is negligible. Hence, the phase difference between current and e.m.f. is \(\frac {π}{2}\). Thus, the average consumed power becomes zero. Therefore, the current is called wattless.
By using a choke coil in an alternating circuit, we can obtain a wattless current.

Question 14.
For a circuit used for transporting electric power, a low power factor implies large power loss. Why?
Answer:
The power factor is given by cosϕ = \(\frac {R}{Z}\). Therefore, for low power factor, the resistance R will be less. Hence a large current will flow through the secondary coil of the transformer, which will produce more heat as H x I². Thus, a large power will be lost.

Question 15.
A transformer works with a.c. supply but not with d.c. Why?
Answer:
It is because transformer works on the principle of mutual induction. The input a.c. changes the flux (through the soft – iron core) linked with the secondary coil. This produces output current in the secondary coil. This is not possible with d.c. supply input.

Question 16.
In houses, electricity is supplied through a.c. but not through d.c. Why?
Answer:
This is because the strength of current in the form of a.c. can be reduced and supplied from one place to another by using a transformer and thus without power loss. Transformer cannot work with d.c.

Question 17.
Why laminated core is used in transformer?
Answer:
Effect of eddy currents is minimized in a transformer by using laminated core. Lamination causes greater resistance to eddy currents produced. Thus, loss of electrical energy in the form of heat is reduced.

Question 18.
Give difference between resistance and reactance.
Answer:
The obstruction to the flow of alternating current or direct current by the conductor is called resistance. The obstruction to the flow of alternating current offered by inductor or capacity is called reactance.

Question 19.
In series resonance L – C – R circuit what is the value of impendence.
Answer:
Since Z =\(\sqrt { { R }^{ 2 }+({ X }_{ L }-{ X }_{ C })^{ 2 } }\)
But in resonance stage X_L = X_C
∴ Z = R
That is impendence is equal to resistance.

Question 20.
What is the value of peak to peak value of alternating e.m.f.?
Answer:
It will be equal to sum of peak value of e.m.f. in positive half cycle and negative half cycle, i.e., peak to peak value of alternating e.m.f. will be 2E_m = 2\(\sqrt { 2 }\) E_rms.

Question 21.
What are the reasons of energy losses in transformers? How these losses are renuced?
Answer:
Energy losses and their removal:
1.Copper loss:
Some part of the energy is wasted in the form of heat due to the heating effect of current in primary and secondary coil because the coils have some resistance. The amount of heat produced is I² Rt. To reduce it, thick coils are used in the primary coil of step – up transformer and in the secondary coil of a step – down transformer.

2. Iron loss:
Eddy current is produced in the iron core of the transformer, causes heating. This loss is called iron loss. To minimize this loss, the core is laminated.

3. Magnetic flux leakage:
All the magnetic flux produced by primary coil may not be transferred to the secondary coil. Therefore, some energy is wasted. To minimize this loss, soft – iron core is used.

4. Hysteresis loss:
Some amount of energy is wasted because the iron core becomes magnetized during the first half and then gets demagnetized during the other half. This wastes loss of magnetic energy is called hysteresis loss. It is minimized by taking soft- iron core which has thin hysteresis loop.

Question 22.
Give differences between step – up and step – down transformer.
Ans.
Differences between a step – up and step – down transformer :
Step – up transformer

• It increases the voltage.
• It decreases the current strength.
• The number of turns in secondary coil is greater than that of primary coil.
• Its transformation ratio is more than one.

Step – down transformer

• It decreases the voltage.
• It increases the current strength.
• The number of turns in primary coil is greater than that of secondary coil.
• Its transformation ratio is less than one.

Question 23.
What do you mean by root mean square value of a.c. Obtain expression for I_rms.
Answer:
Root mean square value of a.c.:
Root mean square value of an a.c. is defined as that value of steady current which would generate the same amount of heat in a given resistance in a given time, as is done by the a.c. when passed through the same resistance for the same time. It is also called virtual value.

Expression for I_rms:
Let the alternating current is given by the equation
I = I₀sin ωt
This current flows through a resistance R, for a small interval of time dt, then the small amount of heat dH is produced in the resistance R.
Then dH = I² Rdt … (2)
For a complete cycle, the total heat produced will be obtained by integrating equation. (2)

If root mean square value of current is reprsented by Ims then the amount of heat produced in the same resistance R in the same interval of time will be
H = I²_rms RT … (5)
Now from equation (4) and (5), we get

This is required expression.

Question 24.
Prove for an a.c. circuit:
P_av = V_rms x I_rms x cosϕ
Where, the symbols have their usual meaning.
Answer:
Let the potential difference and current of a.c. circuit is given by
V=V₀sm ωt … (1)
and I = I₀sm(ωt – ϕ) … (2)
Where, ϕ is the phase difference between voltage and current.
Here the current lags behind the voltage
Now, instantaneous power, P = V.I
= V₀sin ωt.I₀sin{ωt – ϕ), [from eqns. (1) and (2)]
= V₀I₀sinωt.sin(ωt – ϕ) = \(\frac {1}{2}\)V₀I₀.2sinωt.sin(ωt – ϕ)
= \(\frac {1}{2}\)V₀I₀[cosϕ – cos(2ωt – ϕ)]
= \(\frac {1}{2}\)V₀I₀cosϕ – = \(\frac {1}{2}\)V₀I₀cosϕ(2ωt – ϕ)
But, the value of cos(2ωt – ϕ) for a complete cycle is zero. Therefore, average power for a complete cycle is
P_av = \(\frac {1}{2}\)V₀I₀cosϕ or P_av = \(\frac { { V }_{ 0 } }{ \sqrt { 2 } }\).\(\frac { { I }_{ 0 } }{ \sqrt { 2 } }\).cosϕ
P_av = V_rms x I_rms x c0sϕ
Where, V_rms and I_rmsare average alternating e.m.f. and current and cosϕ is called power factor, its value depends upon the nature of the circuit.

Question 25.
What is meant by wattless current? When the current becomes wattless? Why the current flowing through choke coil is wattless?
Answer:
In a.c. circuit, when the average consumed power is zero, then that current is called wattless current.
If a pure inductance or pure capacitance is used in a.c. circuit, then the phase difference between current and e.m.f. becomes \(\frac {π}{2}\)
P_av = V_rms x I_rms x c0sϕ
= V_rms x I_rms x cos\(\frac {π}{2}\)
= V_rms x I_rms x 0= 0
Choke coil is made up of thick copper wire. Its ohmic resistance is negligible. Hence, the phase difference between current and e.m.f. is \(\frac {π}{2}\). Thus, the average consumed power becomes zero. Therefore, the current is called wattless. By using a choke coil in an alternating circuit, we can obtain a wattless current.

Question 26.
What is the principle of choke coil? Explain its use for controlling current. Why is current flowing in choke coil known as wattless current?
Answer:
Principle of choke coil:
A coil of very low resistance and high inductance is used to control current in an a.c. circuit. This coil is known as choke coil. It causes very little loss of energy. If an a.c. circuit contains zero resistance and a pure inductance, the phase difference between e.m.f. and current is 90°. Under this condition, average power

P_av = V_rms.I_rms cosϕ
= V_rms.I_rms x cos90°
=0, ( ∵ cos90° = 0)
So, there is no loss of energy. But in actual practice, the resistance in the circuit cannot be zero. Therefore, a small part of electrical energy is lost as heat. A choke coil is made up of a thick copper wire wound around a soft – iron core. Due to soft – iron core and so many turns of wire, the inductance is increased and the thick wire reduces its resistance.

Use:
Current in a.c. circuit can be controlled by using a choke coil in the circuit. Since, impedance of the choke coil is XL = caL. So, the current is reduced if inductance is high and is increased if the inductance is low.

Wattless current:
Current in a choke coil is called wattless current because average power consumed is zero (due to 90° phase difference between e.m.f. and current in the coil). The loss of energy due to small resistance of the coil is negligible.

Question 27.
Give differences between a.c. and d.c.
Answer:
Differences between a.c. and d.c. :
a.c.:

• Its direction and magnitude both changes.
• Transformers are used in a.c.
• It cannot be used for electroplating.
• It is generally not used for electro – magnet.
• The measuring instruments are based on its heating effect.
• It is dangerous.

d.c.:

• The magnitude may change but direction does not change.
• Transformers cannot be used.
• It can be used in electroplating.
• It is used for electromagnet.
• Its measuring instruments are based on its magnetic effect.
• It is less dangerous than a.c.

Question 28.
For a circuit used for transporting electric power, a low power factor implies large power loss. Why?
Answer:
The power factor is given by cosϕ =\(\frac {R}{Z}\). Therefore, for low power factor, the resistance R will be less. Hence a large current will flow through the secondary coil of the transformer, which will produce more heat as H x I². Thus, a large power will be lost.

Question 29.
An a.c. circuit contains a pure resistive component. Obtain an expression for current. What is the phase difference between current and voltage? Draw current voltage graph.
Answer:
Let an a.c. source be connected with a resistance R as shown in figure. The alternating e.m.f. is given by the equation.
V = V₀ sinωt … (1)

The corresponding value of current at any instant is
I = \(\frac {V}{R}\) = \(\frac { { V }_{ 0 }sin\omega t }{ R }\)
or I = I₀ sinωt, (∵ I₀ = \(\frac { { V }_{ 0 } }{ R }\) … (2)
Here, V = IR is valid because Ohm’s law is applicable for both a.c. and d.c.

It is. clear from equation (1) and (2) that the phase of both E and I is cot. Hence, current and voltage are in the same phase. Fig. shows variation of current and voltage in an a.c. circuit with respect to time.

Question 30.
An alternating e.m.f. V = V₀ sinωt is applied across a purely inductive a.c. circuit. Calculate the expression for the following :

1. Current flow
2. Inductive reactance and
3. Phase relation between current and voltage and its graph.

Answer:
Suppose an alternating e.m.f. V = V₀ sinωt … (1)
is applied across an a.c. circuit of inductance L. At the instant, when the current is maximum, the rate of change of current is zero. Hence, potential difference is zero, so induced e.m.f. = -L \(\frac {dI}{dt}\)

To maintain the flow of current, the applied voltage must be equal and opposite to the induced e.m.f.

This is the required expression for current flow.

Where, aL is called inductive reactance and is denoted by XL.
Thus, X_L = ωL = 2πfL
Where, f = Frequency of current.
Phase relation between current and voltage:
From eqns. (1) and (3), we find that the phase of voltage is at, whereas that of current is at ωt – \(\frac {π}{2}\). Hence, current lags behind the voltage by \(\frac {π}{2}\). This is shown in the phaser diagram below.

Question 31.
An alternating voltage V = V₀ sinωt is applied across a capacitor C. Obtain an expression for

1. Circuit current
2. Capacitive reactance and
3. Phase relation between current and voltage.

Answer:
1. Suppose the instantaneous voltage at any instant of time t is
V = V₀ sinωt … (1)
If Q is the charge acquired by the capacitor at this instant, c
then
c = \(\frac {Q}{V}\)
or Q = CV or Q = C V₀ sinωt

But the current at any instant is given by

2. From Equation (3), \(\frac { { V }_{ 0 } }{ { I }_{ 0 } }\) =  \(\frac {1}{ωC}\)
Comparing with Ohm’s law, \(\frac {1}{ωC}\)is called capacitive reactance denoted by X_c.
X_c = \(\frac {1}{ωC}\) =\(\frac {1}{2πfC}\)

3. Phase relation between current and voltage:
From eqns. (1) and (2), we find that the phase of voltage is ωt, whereas of current is ωt + \(\frac {π}{2}\) hence current is ahead of voltage by \(\frac {π}{2}\) or we can say that voltage is lagging behind the current by n! 2. This is shown in the figure below:

Question 32.
Explain the behaviour of inductor and capacitor towards a.c. and d.c.
Answer:
The reactance offered by an inductor is given by the equation
X_L = ωL = 2πfL.
Where f is the frequency of the source and L is the inductance of the inductor
For a d.c. f = 0 thus X_L = 0.
For an a.c. f ≠ 0 and X_L ∝L.
Flence, an inductor provides no reactance to the flow of d.c. and provide reactance of the a.c. i.e. an inductor by passes d.c. and blocks a.c.
The reactance offered by a capacitor is given by the equation,
X_c = \(\frac {1}{ωC}\) = \(\frac {1}{2πfC}\)
Where C is the capacitance of the capacitor.
For d.c. f = 0 thus, X_c = ∞
For an a.c. f ≠ 0 and X_c ∝\(\frac {1}{f}\)
Hence, a capacitor provides infinite reactance to d.c. and with increasing frequency of an a.c. the reactance decreases, i.e. a capacitor by passes a.c. and blocks d.c.

Question 33.
What is Q – factor? Write the expression for it.
Answer:
In an L – C – R circuit when a capacitor gets charged, electrical energy is stored in it, and when current flows through the conductor, magnetic energy gets stored in it. During the half cycle of a.c. magnetic energy is maximum and electrical energy is zero and in the next half cycle magnetic energy becomes zero and electrical energy is maximum.

Moreover some amount of energy gets dissipated in the form of heat in the ohmic resistor. Less is the dissipation of energy in the circuit, more sharp will be the resonance. The measurement of the sharpness is done by a dimensionless quantity called ‘Quality factor’ or ‘Q – factor’.

Definition:
In an L – C – R circuit, the ratio of resonant frequency to the difference of its neighbouring frequencies so that their corresponding current is \(\frac { 1 }{ \sqrt { 2 } }\) times of the peak value is called Q factor of the circuit. Its expression is Q factor = \(\frac{1}{R} \sqrt{\frac{L}{C}}\)

Q factor to be maximum :

1. Value of R should be less.
2. Value of \(\frac {L}{C}\) should be more.

Alternating Current Long Answer Type Questions

Question 1.
Describe the transformer on the basis of follow ing points :

1. Principle
2. Types of transformer
3. Any three energy losses.

Or
Explain construction, principle and working method of transformer.
Answer:
Labelled diagram :

Construction:
A transformer consists of laminated core, primary coil and secondary coil. The laminated core is obtained by piling a number of laminated rectangular strips of soft iron. Two insulated copper wires are wound on the opposite arms, in the form of coils. The coil connected to the input of a.c. is called primary coil and the other through which output is taken is called secondary coil.

Method of working and principle:
Let the number of turns in primary and secondary coils are N_P and N_s respectively. If the magnetic flux linked with the primary coil at any instant is ϕ, then the e.m.f. induced in the primary coil will be
E_P = – N_P\(\frac {dϕ}{dt}\) … (1)
If there is no loss of flux, the secondary coil will also be linked with the same flux ϕ. So, the e.m.f. induced in the secondary coil will be
E_s = – N_s\(\frac {dϕ}{dt}\) … (1)
Dividing equation (2) by equation (1), we get

If there is no loss of energy in the primary coil, then the induced e.m.f. produced in the primary coil will be nearly equal to the applied potential difference (V_P) between its ends. Similarly, because the secondary coil is open, hence the potential difference across its ends will be equal to the e.m.f. induced in it i.e., under ideal conditions

Let I_p and I_s be the current through primary and secondary coils respectively. Then under ideal conditions,
Instantaneous input power = Instantaneous output power
i.e., Power in primary coil = Power in secondary coil

The quantity r in equation (5) and (7) is called transformation ratio.
For step – up transformer:

So, a step-up transformer increases the voltage, but decreases the strength of current. Also, the number of turns in the secondary coil is more than that of primary coil.

For step – down transformer:

So, a step – down transformer decreases the voltage but increases the strength of current. The number of turns in secondary coil is less than that of primary coil.

Energy losses:
1.Copper loss:
Some part of the energy is wasted in the form of heat due to the heating effect of current in primary and secondary coil because the coils have some resistance. The amount of heat produced is I²Rt. To reduce it, thick coils are used in the primary coil of step – up transformer and in the secondary coil of a step – down transformer.

2. Iron loss:
Eddy current is produced in the iron core of the transformer, causes heating. This loss is called iron loss. To minimize this loss, the core is laminated.

3. Magnetic flux leakage:
All the magnetic flux produced by primary coil may not be transferred to the secondary coil. Therefore, some energy is wasted. To minimize this loss, soft – iron core is used.

Effect of eddy currents is minimized in a transformer by using laminated core. Lamination cause greater resistance to eddy currents produced. Thus, loss of electrical energy in the form of heat is reduced.

Question 2.
Describe a transformer on the basis of following points :

1. Principle
2. Its types and labelled diagram
3. Energy losses in transformer.

Or

1. Working principle
2. Types and labelled diagram
3. Energy losses
4. Equation of transformation ratio.

Answer:
1. Principle :
Let the number of turns in primary and secondary coils are N_P and N_s respectively. If the magnetic flux linked with the primary coil at any instant is ϕ, then the e.m.f. induced in the primary coil will be
E_P = – N_P\(\frac {dϕ}{dt}\) … (1)
If there is no loss of flux, the secondary coil will also be linked with the same flux ϕ. So, the e.m.f. induced in the secondary coil will be
E_s = – N_s\(\frac {dϕ}{dt}\) … (1)
Dividing equation (2) by equation (1), we get

If there is no loss of energy in the primary coil, then the induced e.m.f. produced in the primary coil will be nearly equal to the applied potential difference (V_P) between its ends. Similarly, because the secondary coil is open, hence the potential difference across its ends will be equal to the e.m.f. induced in it i.e., under ideal conditions

Let I_p and I_s be the current through primary and secondary coils respectively. Then under ideal conditions,
Instantaneous input power = Instantaneous output power
i.e., Power in primary coil = Power in secondary coil

The quantity r in equation (5) and (7) is called transformation ratio.

2. Types and labelled diagram :

3. Energy losses:
(i) Copper loss:
Some part of the energy is wasted in the form of heat due to the heating effect of current in primary and secondary coil because the coils have some resistance. The amount of heat produced is I²Rt. To reduce it, thick coils are used in the primary coil of step – up transformer and in the secondary coil of a step – down transformer.

(ii) Iron loss:
Eddy current is produced in the iron core of the transformer, causes heating. This loss is called iron loss. To minimize this loss, the core is laminated.

(ii) Magnetic flux leakage:
All the magnetic flux produced by primary coil may not be transferred to the secondary coil. Therefore, some energy is wasted. To minimize this loss, soft – iron core is used.

(iv) Hysteresis loss:
Some amount of energy is wasted because the iron core becomes magnetized during the first half and then gets demagnetized during the other half. This wastes loss of magnetic energy is called hysteresis loss. It is minimized by taking soft – iron core which has thin hysteresis loop.

4. Equation of transformation ratio:
Let the number of turns in primary and secondary coils are N_P and N_s respectively. If the magnetic flux linked with the primary coil at any instant is ϕ, then the e.m.f. induced in the primary coil will be
E_P = – N_P\(\frac {dϕ}{dt}\) … (1)
If there is no loss of flux, the secondary coil will also be linked with the same flux ϕ. So, the e.m.f. induced in the secondary coil will be
E_s = – N_s\(\frac {dϕ}{dt}\) … (1)
Dividing equation (2) by equation (1), we get

Question 3.
Obtain an expression for impedance in L – C – R circuit. Under what condition, the current will be maximum?
Or
What is resonant circuit ? Find the resonant frequency of L – C – R circuit.
Or
Obtain the condition of resonant frequency in the L – C – R circuit. Where this circuit is used ?
Or
Explain the resonance of a series L – C – R circuit under the following heads :

1. Resultant voltage
2. Impedance of circuit
3. Frequency of resonance.

Answer:
In L – C circuit or in L – C – R circuit, when the value of impedance is least, the current becomes maximum. This phenomenon is called resonance. In this state, the frequency of the applied e.m.f. is equal to the natural frequency of the L – C circuit called resonant circuit.

Expression for the impedance:
Let inductance L, capacitor C and resistance R are joined in series to an a.c. circuit as shown in the Fig. (a).
Let the instantaneous current is I.
Potential difference across L will be, V_L=I.X_L … (1)
Potential difference across C will be, V_C = I.X_C … (2)
and Potential difference across R will be, V_R= I. R … (3)
Now, V_R and f are in the same phase and V_L leads I by 90° and V_C lags I by 90°. Hence, the angle between V_L and V_C will be 180°.

Now, resultant of V_L and V_C is V_L – V_C, then angle between V_L – V_C and V_R is 90°.
Resultant,
V² = V²_R + (V_L – V_C )²
V² = I²R² + I² (X_L – X_C)²
or R² + (X_L – X_C)²

By comparing equation (4) with Ohm’s law, we get the resultant resistance also

∴ Impedance of the circuit,

This is the equation for impedance from Fig. (a).
If ϕ be the phase difference between V and I, then from Fig. (b). V,

Now, the current flowing through the circuit will be given by
I = I₀ sin(ωt – ϕ)
With respect to voltage, the current is behind ϕ.

Since, impedance is minimum and current is maximum, therefore this state is called resonance.
Again, under resonance condition,

This is the required expression.
This circuit is used for tuning the radio receiver.

Alternating Current Numerical Questions

Question 1.
For a L – R circuit, the reactance of inductor is 3Ω and ohmic resistance is 4Ω . Find out impedance of the circuit.
Solution:

Question 2.
In a transformer, the ratio of number of turns in primary coil to that of secondary coil is 20:1. If it is operated at 200 volt then find out voltage obtained across secondary coil.
Solution:

Question 3.
Alternating current of \(\sqrt { 2A }\) flows through a circuit, what is the maximum value of current ?
Solution:
Maximum value I₀ = \(\sqrt {2}\) × I_rms
I₀ = \(\sqrt {2}\) × \(\sqrt {2}\) = 2A.

Question 4.
The peak value of alternating current is \(\sqrt { 2A }\) . Find out r. m. s. value of the current.
Solution:
Formula:
I_rms = \(\frac { { I }_{ 0 } }{ \sqrt { 2 } }\) = \(\frac { 2\sqrt { 2 } }{ \sqrt { 2 } }\)

Question 5.
In domestic circuit mains voltage is 220 V, find out its maximum value.
Solution:

Question 6.
The r.m.s. value of current in an a.c. circuit is 10A. Find the peak value of current.
Solution:
Given, I_rms = 10A
Formula: I_rms = \(\frac { { I }_{ 0 } }{ \sqrt { 2 } }\) or I₀ = I_rms x \(\sqrt {2}\)
Putting the value in the formula, we get
I₀ = 10 x \(\sqrt {2}\) = 10 x 1.414 = 14.1A.

Question 7.
The equation of a alternating voltage is V = 141 sin50πt. Determine r.m.s. value of voltage.
Solution:
Given, V = 141 sin 50πt.
Comparing with the equation V=V₀ sinωt, we get

Question 8.
An e.m.f. of a.c. source is given by E = 300 sin 314t. Obtain the peak voltage and the frequency of the source.
Solution:
Comparing with E = E₀ sinωt
∴ Peak voltage E₀ = 300 V.
Here, ω = 314
or 2πf = 314
or f = \(\frac {314}{2π}\)
= \(\frac {314}{2×3.14 }\)
= 50 Hz

Question 9.
Self – inductance of a coil is 0.025 henry, calculate the inductive impedance for 50 Hz a.c.
Solution:
Formula: X_L= ωL = 2πfL.
Given: f = 50 Hz and L = 0.025 H.
X_L = 2 x 3.14 x 50 x 0.025
= 78.5Ω

Question 10.
A 1.5µF capacitor is connected to 220 V, 50 Hz source. Find the capacitive reactance and the current in the circuit. (NCERT)
Solution:

Question 11.
The potential drops across a resistor, capacitor and inductor in an a.c. circuit are 80 V, 100 V and 40 V respectively. Calculate the e.m.f. of the source of given a.c. circuit.
Solution:
Formula: V² = V²_R + (V_L – V_C)²
Given : V_R = 80 V, V_L = 40V and V_C = 100V.
Substituting these values in the formula,
V² =80²+(40 – 100)²
= 6400 + 3600 = 10000
∴ V = 100V.

Question 12.
The ratio of number of turns in primary to that of secondary coil of a step up transformer is 1:10. If it is connected to the mains of 220 V, a current of 5 A flows. Calculate the induced e.m.f. and induced current in the secondary coil.
Solution:

Question 13.
A step – down transformer changes 2200 V to 220 V. The number of turns in primary coil is 5000. If its efficiency is 90% and output power is 8 kW, calculate :

1. Number of turns in secondary coil and
2. Input power.

Solution:

MP Board Class 12th Physics Important Questions

MP Board Class 12th Maths Important Questions Chapter 6 Application of Derivatives

Application of Derivatives Important Questions

Application of Derivatives Objective Type Questions:

Question 1.
Choose the correct answer:

Question 1.
The rate of change of the area of a circle with respect to its radius r when r = 5 is:
(a) 10 π
(b) 12 π
(c) 8 π
(d) 11 π.
Answer:
(b) 12 π

Question 2.
Tangent line of a curve y² = 4x at y = x + 1 is:
(a) (1,2)
(b) (2, 1)
(c) (1, -2)
(d) (- 1, 2).
Answer:
(a) (1,2)

Question 3.
Approximate change in the volume of a cube of side x metre caused by increasing the side by 2%:
(a) 0.03 x³
(b) 0.02 x³
(c) 0.06 x³
(d) 0.09 x³
Answer:
(c) 0.06 x³

Question 4.
Point on the curve x² = 2y which lie minimum distance from the point (0,5):
(a) (2\(\sqrt{2}\),4)
(b) (2\(\sqrt{2}\),0)
(c) (0, 0)
(d) (2, 2).
Answer:
(a) (2\(\sqrt{2}\),4)

Question 5.
Minimum value of the function f(x) = x⁴ – x² – 2x + 6:
(a) 6
(b) 4
(c) 8
(d) None of these.
Answer:
(b) 4

Question 2.
Fill in the blanks:

1. The function f(x) = cosx, for 0 ≤ x ≤ π is …………………………..
2. The radius of circular plate is increasing at the rate of 0.2 cm /sec. when r = 10, then the rate of change of the area of the plate is ………………………………
3. The function y = x(5 – x) is maximum at x is equal to ……………………………
4. The minimum value of 2x + 3y is ………………………….. when xy = 6.
5. The maximum value of sin x + cos x is ……………………………
6. If line y = mx+ 1 is a tangent line to the curve y² = 4x. Then value of m will be ……………………………..
7. Slope of the tangent to the curve y = x² at the point (1, 1) is ………………………….
8. Using differential the approximate value of \(\sqrt{0.6}\) is …………………………….

Answer:

1. Decreasing
2. 4πcm²/sec
3. \(\frac{5}{2}\)
4. 12
5. \(\sqrt{2}\)
6. 1,
7. 2,
8. 0.8.

Question 3.
Write True/False:

1. For all real values of x, the function f(x) = e^x – e^-x is increasing function.
2. If the length of equal sides of an isosceles traingle be x then its maximum area will be \(\frac{1}{2}\) x²
3. Function f(x) = 3x² – 4x is increasing in the interval (- ∞, \(\frac{2}{3}\) )
4. Function f(x) = x – cot x is always decreasing.
5. Equation of the normal of the curve y = e^x at point (0, 1) is x + y = l.

Answer:

1. True
2. True
3. False
4. False
5. True.

Application of Derivatives Short Answer Type Questions

Question 1.
The radius of a circle increases at the rate of 2cm/sec. At what rate the area increases when radius is 10cm?
Solution:
Given:
\(\frac { dr }{ dt } \) = 2cm/sec
Let the area of circle be A
Then,

∵ Area of circle A = πr²

= 40π sq.cm/second

Question 2.
The radius of air bubble is increasing at the rate of 1/2 cm per second. At what rate the volume of the air bubble is increasing when the radius is 1 cm?
Solution:
Let the radius of air bubble be r.
∴ Volume V = \(\frac{4}{3}\) πr³

Question 3.
The radius of a balloon is increasing at the rate of 10 cm/sec? At what rate surface area of the balloon is increasing when radius is 15cm?
Solution:
Let r be the radius of balloon at any time t and its surface be x then
A = 4πr²
Differentiating eqn.(1) w.r.t. t,

Hence, when radius of ballon is 15cm, then its area is increasing at rate of 1200π cm/sec.

Question 4.
Find those intervals in which the function f(x) = 2x³ – 15x² + 36x + 1 is increasing or decreasing?
Solution:
f(x) = 2x³ – 15x² + 36x + 1
⇒ f'(x) = 6x² – 30x + 36
= 6(x² – 5x + 6)
= 6(x – 2) (x – 3)
For increasing function of f(x),
f'(x) > 0
or (x – 2) (x – 3) > 0
⇒ x – 2 > 0 and x – 3 > 0
⇒ x > 2 and x < 3 ⇒ x > 3
Clearly the function is increasing in interval (3, ∞)
Again, (x – 2) (x – 3) > 0
or x – 2 < 0 and x – 3 < 0
⇒ x < 2 and x < 3
⇒ x < 2
Clearly the function is increasing in interval (-∞, 2)
Hence, the function is increasing in the interval (-∞, 2) ∪ (3, ∞)
Again for decreasing function of f(x),
f'(x) < 0
⇒ (x – 2) (x – 3) < 0
or x – 2 < 0 and x – 3 > 0
⇒ x < 2 and x > 3, which is impossible
or x – 2 > 0 and x – 3 < 0 ⇒ x > 2 and x < 3
⇒ 2 < x < 3
Hence, f(x) is decreasing function in the interval (2, 3).

Question 5.
(A) If x + y = 8, then find maximum value of xy?
Solution:
Let P = xy
⇒ x + y = 8
⇒ y = 8 – x
∴P = x(8 – x) = 8x – x²
⇒ \(\frac { dP }{ dx } \) = 8 – 2x
⇒ \(\frac { d^{ 2 }P }{ dx^{ 2 } } \) = -2
For maximum or minimum value
8 – 2x = 0
⇒ x = 4
Now, x = 4 then \(\frac { d^{ 2 }P }{ dx^{ 2 } } \) = -2, which is negative
∴ at x = 4, then y = 4
Maximum value of P, when x = 4, y = 4
= 4 × 4 = 16.

(B) If x + y = 10 then find maximum value of xy?
Solution:
Solve like Q.No.5(A).

Question 6.
The radius of a circle increases at the rate of 3cm/sec. At what rate the area increases when the radius is 10cm?
Solution:
Let r be the radius and A be the area of circle then,
A = πr²
\(\frac { dA }{ dt } \) = rate of change of area = ?
⇒ \(\frac { dA }{ dt } \) = 2πr \(\frac { dr }{ dt } \)
⇒ \(\frac { dA }{ dt } \) = 2π.(10).3
= 60π cm²/second.

Question 7.
The volume of a cube is increasing at the rate of 9 cm³/sec? If the edge of cube is 10cm then at what rate the surface area of cube is increasing? (NCERT)
Solution:
Let the edge of cube = a dm
Volufne = V= a³
Surface area of cube = s = 6a²

Surface area of cube

When a = 10cm, then \(\frac { ds }{ dt } \) = \(\frac { 36 }{ 10 } \) = 3.6 cm²/sec.

Question 8.
(A) A man 180 cm high walks away from a lamp post at a rate of 1.2metre per second. If the height of lamp post is 4.5 metre. Find the rate at which the length of his shadow increases?
Solution:
Let AB be the lamp post of the height 4.5 m, PQ be the position of man at time t, CQ = x and BQ = y
drrf

(B) A man of height 2 metre walking away from a lamp post at a rate of 5km/ sec. If the height of the lamp post 6m. Find the rate at which the length of his shadow is increasing? (NCERT)
Solution:
Solve like Q. No.8(A).
[Ans. \(\frac{5}{8}\) km/sec.]

Question 9.
A ladder 5 metre long is leaning against a wall. The bottom of the ladder is pulled along the ground away from the wall, at the rate of 2 metre per second. How just is its height on the wall decreasing when the foot of the ladder is 4 metre away from the wall? (NCERT)
Solution:
Let at any time t, the bottom of the ladder be at a distance x metre from the wall and the height of the wall bey metre.
QA = xm, OB = ym, AB = 5m (given)
\(\frac { dx }{ dt } \) = 2m/sec.
In ∆OAB,

Question 10.
Find the intervals in which f(x) = 5x³ + 7x – 13 is increasing or decreasing?
Solution:
Given:
f(x) = 5x² + 7x – 13 (given)
∴ f'(x) = 10x + 7
If f(x) is increasing,
f'(x) > 0
⇒ 10x + 7 > 0
⇒ x > \(\frac{-7}{10}\)
Hence, f(x) is increasing in interval ( \(\frac{-7}{10}\) , ∞)
If f(x) os decreasing, then,
f'(x) < 0
⇒ 10x + 7 < 0
⇒ x < \(\frac{-7}{10}\)
∴ f(x) is decreasing in (-∞, \(\frac{-7}{10}\) ).

Question 11.
Find the intervals in which the function f(x) = 2x³ – 24x + 5 is increasing or decreasing?
Solution:
f(x) = 2x³ – 24x + 5
Differentiating w.r.t x,
f'(x) = 6x² – 24
⇒ f'(x) = 6(x² – 4)
⇒ f'(x) = 6(x + 2) (x-2) …………………. (2)
(A) If f(x) in is increasing, then
f'(x) > 0
6(x + 2)(x-2) > 0
∴ f(x), x ∈ (-∞,-2) ∪(2, ∞) is increasing.
(B) If f(x) is decreasing,
f'(x) < 0 ⇒ 6(x + 2) (x – 2) < 0
f(x), x ∈ (-2,2) decreasing.

Question 12.
Show that the function f(x) = x – cos x is always increasing?
Solution:
Given function f(x) = x – cos x
∴ f'(x) = 1 – (- sin x)
⇒ f'(x) = 1 + sin x
We know that -1 ≤ x ≤ 1
-1 + 1 ≤ 1 + sin x ≤ 1 + 1
0 ≤ 1 + sin x ≤ 2
Hence f'(x) = 1 + sin x is always positive for all values of x.
∴ f(x) = x – cos x is always increasing.

Question 13.
Find the least value of a such that the function given by f(x) = x² + ax + 1 is strictly increasing on (1, 2)? (NCERT)
Solution:
Given:
f(x) = x² + ax + 1
∴ f'(x) = 2x + a
When, x ∈ (1,2)
∴ 1 < x < 2
⇒ 2 < 2x < 4
⇒ 2 + a < 2x + a < A + a
⇒ 2 + a < f'(x) < 4 + a Since f(x) is increasing function ∴ f'(x) > 0
⇒ 2 + a > 0 ⇒ a > -2
Hence, the least value of a is -2.

Question 14.
Let I be any interval disjoint from [-1, 1] prove that the function f given by f(x) = x + \(\frac{1}{x}\) is strictly increasing on I? (NCERT)
Solution:
f(x) = x + \(\frac{1}{x}\)

x ∈ 1, x ∉ (-1, 1)
x < – 1 0r x > 1
⇒ x² – 1 > 0
⇒ \(\frac { x^{ 2 }-1 }{ x^{ 2 } } \) > 0
⇒ f'(x) > 0, x ∈ 1
∴ f(x) is increasing on I. Proved.

Question 15.
Find the interval in which the given function is increasing or decreasing:
f(x) = x⁴ – \(\frac { x^{ 3 } }{ 3 } \)?
Solution:
f(x) = x⁴ – \(\frac { x^{ 3 } }{ 3 } \)


Hence, the interval 0 and \(\frac{1}{4}\) on X – axis is divided in three intervals
(- ∞, 0), (0, \(\frac{1}{4}\) ), ( \(\frac{1}{4}\), ∞)
In interval (- ∞, 0)
f'(x) = x² (4x – 1),
⇒ f'(x) < 0 [x² = +ve] [4x – 1 > 0]
⇒ f'(x) < 0
∴ In interval (- ∞, 0) the function f(x) decreasing
In interval (0, \(\frac{1}{4}\) ):
f'(x) = x² (4x – 1),
⇒ f'(x) > 0 [∵ x² = positive] [4x – 1 > 0]
∴ In interval (0, \(\frac{1}{4}\) ) f(x) is decreasing
In interval ( \(\frac{1}{4}\), ∞):
f'(x) = x² (4x – 1), [∵ x² = positive] [4x – 1 > 0]
⇒ f'(x) > 0
In interval ( \(\frac{1}{4}\), ∞) in function f(x) increasing.

Question 16.
The perimeter of a rectangle is 100 cm. Find the length of sides of the rectangle for maximum area?
Solution:
Let length of rectangle be x and breadth be y.
∴Perimeter of rectangle = 2(x + y)
⇒ 2x + 2y = 100
⇒ x + y = 50
Let area of rectangle,
A = xy = x(50 – x) = 50x – x², [from eqn.(1)]
\(\frac { dA }{ dx } \) = 50 – 2x
and \(\frac { d^{ 2 }A }{ dx^{ 2 } } \) = -2
For maximum or minimum of A,
\(\frac { dA }{ dx } \) = 0
⇒ 50 – 2x = 0 or or x = 25
For any value of x, \(\frac { d^{ 2 }A }{ dx^{ 2 } } \) is -ve
For x = 25, area of rectangle is maximum
Put in eqn.(1),
y = 50 – x = 50 – 25 = 25.

Question 17.
Area of a rectangle is 25 sq.cm. Find its length and breadth when its perimeter is minimum?
Solution:
Let the length and breadth of rectangle be x and y units and A be the area.
xy = 25 ……………………….. (1)
Perimeter of rectangle,
P = 2(x + y)

For maximum or minimum \(\frac { dP }{ dx } \) = 0

Which is positive for x = 5
∴ For Minimum parimeter x = cm.
y = \(\frac{25}{x}\) = \(\frac{25}{5}\) = 5 cm.

Question 18.
Find the maximum value of sin x + cos x = \(\sqrt{2}\)? (NCERT)
Solution:
Given:
f(x) = sin x + cos x …………………. (1)
∴f'(x) = cos x – sin x …………………… (2)
and f”(x) = – sinx – cos x …………………….. (3)
For maxima or minima
f'(x) = 0
∴ cos x – sin x = 0
⇒ sin x = cos x
⇒ tan x = 1
∴ x = \(\frac { \pi }{ 4 } \), \(\frac { 3\pi }{ 4 } \), \(\frac { 5\pi }{ 4 } \)
Put x = \(\frac { \pi }{ 4 } \) in eqn (3)

Hence, at x = \(\frac { \pi }{ 4 } \) the given function is maximum. In the same way for x = \(\frac { 3\pi }{ 4 } \), \(\frac { 5\pi }{ 4 } \) ………………… the function is maximum.
Put x = \(\frac { \pi }{ 4 } \) in eqn.(1),
Maximum value f ( \(\frac { \pi }{ 4 } \) ) = sin \(\frac { \pi }{ 4 } \) + cos \(\frac { \pi }{ 4 } \)
= \(\frac { 1 }{ \sqrt { 2 } } \) + \(\frac { 1 }{ \sqrt { 2 } } \) = \(\frac { 2 }{ \sqrt { 2 } } \) = \(\sqrt{2}\). Proved.

Question 19.
Two positive numbers are such that x +y = 60 and xy³ is maximum. Prove (NCERT)
Solution:
Given:
x + y = 60 …………………….. (1)
Let p = xy³
⇒ P = (60 – y). y³
⇒ P = 60y³ – y⁴
⇒ \(\frac{dp}{dy}\) = 180 y² – 4y³ …………………….. (2)
Put \(\frac{dp}{dy}\) = 0
180 y² – 4y² = 0
⇒ 4y² (45 – y) = 0
∴ y = 45
Differentiating eqn. (2) w.r.t y,
\(\frac { d^{ 2 }p }{ dy^{ 2 } } \) = 360y – 12y²
= 12 y(30 – y)
Put y = 45,
\(\frac { d^{ 2 }p }{ dy^{ 2 } } \) = 12 × 45 (30 – 45) = – ve
Hence, at y = 45, p is maximum
From eqn.(1),
x + 45 = 60
⇒ x = 15
∴ The two numbers are 15 and 45.

Question 20.
Find the slope of the tangent to curve y = x³ – x + 1 at the point whose x coordinate is 2? (NCERT)
Solution:
The equation of given curve,
y = x³ – x + 1

Slope of tangent at x = 2,

= 3 × 4 – 1 = 11.

Question 21.
Find the slope of the tangent to the curve y = \(\frac { x-1 }{ x-2 } \), x ≠ 2 at x = 10? (NCERT)
Solution:
The equation of given curve:


At x = 10 slope of tangent is:

Question 22.
Find the point at which the tangent to curve y = x³ – 3x² – 9x + 7 is parllel to X – axis? (NCERT)
Solution:
Equation of given curve y = x³ – 3x² – 9x + 7
\(\frac { dy }{ dx } \) = \(\frac { d }{ dx } \) (x³ – 3x² – 9x + 7)
⇒ \(\frac { dy }{ dx } \) = 3x² – 6x – 9
= 3[x² – 2x – 3]
= 3[x² – 3x + x – 3]
= 3[x(x – 3) + 1(x – 3)]
⇒ \(\frac { dy }{ dx } \) = 3(x – 3) (x + 1)
Tangent is parllel to X – axis.
∴\(\frac { dy }{ dx } \) = 0
3 (x – 3) (x + 1) = 0
⇒ x = 3,-1
When x = 3, then y = (3)³ – 3(3)² – 9 × 3 + 7
y = 27 – 27 – 27 + 7
y = – 20
When x = 3, then y = (-1)³ – 3(-1)² – 9(-1) + 7
y = – 1 – 3 + 9 + 7
y = 12
Hence, the point at which the tangent is parllel to X – axis are (3, -20) and (-1, 12).

Question 23.
Find the equation of the tangent to the parabolas y² = 4ax at the point (at², 2at)? (NCERT)
Solution:
Given:
y² = 4ax ……………………. (1)

Equation of tangent is:
y – y₁ = \(\frac { dy }{ dx } \) (x – x₁)
Where x₁ = at², y₁ = 2at, \(\frac { dy }{ dx } \) = \(\frac { 1 }{ t } \)
y – 2at = \(\frac { 1 }{ t } \) (x – at²)
⇒ yt – 2at² = x – at²
⇒ x – ty + at² = 0.

Question 24.
Find the equation of the tangent to the curve x^2/3 + y^2/3 = 2 at point (1, 1)? (NCERT)
Solution:
Equation of curve:
x^2/3 + y^2/3 = 2


Equation of tangent at point (x₁, y₁) is:

y – 1 = – (x – 1)
⇒ y – 1 = – x + 1
⇒ x + y – 2 = 0

Question 25.
Find the equation of tangent to the curve 2y + x² = 3 at point (1, 1)? (NCERT)
Solution:
Equation of given curve:
2y + x² = 3

Equation of tangent at point (x₁, y₁) is:

⇒ y – 1 = x – 1
⇒ x – y = 0.

Question 26.
(A) Find the equation of tangent to the cure x = cos t, y = sin at t = \(\frac { \pi }{ 4 } \)? (NCERT)
Solution:
Equation of 1^st curve:
x = cos t

x = cos t = cos \(\frac { \pi }{ 4 } \) = \(\frac { 1 }{ \sqrt { 2 } } \)
y = sin t = sin \(\frac { \pi }{ 4 } \) = \(\frac { 1 }{ \sqrt { 2 } } \)
Equation of tangent at (x₁, y₁) is:

(B) Find the equation of tangent and normal to the curve 16x² + 9y² = 145 at point (x₁, y₁), where x₁ = 2 and y₁ > 0? (CBSE 2018)
Solution:
Given:
16x² + 9y² = 145 ……………………. (1)

Put x = 2 in eqn.(1), we get
16.(2)² +9y² =145
⇒ 64 + 9y² =145
⇒ 9y² = 145 – 64 = 81
⇒ y² =9, [y ≠ -3 ∵ y₁ > 0]
⇒ y = 3
At point (2, 3)
\(\frac { dy }{ dx } \) = – \(\frac { 16 }{ 9 } \). \(\frac { 2 }{ 3 } \) = – \(\frac { 32 }{ 27 } \)
Equation of tangent of curve (1) at point (2, 3),

and equation of normal of curve (1) at point (2, 3) is,

Question 27.
Use differential to approximate (25)^1/3? (NCERT)
Solution:
Let y = x^1/3
Where, x = 27 and ∆x = -2


∆y is appromimately equal to dy.

Approximately value of (25)^1/3
= 3 + ∆y
= 3 – 0.074 = 2.926.

Question 28.
Use differential to approximate \(\sqrt { 36.6 } \)? (NCERT)
Solution:
Let y = \(\sqrt{x}\), where x = 36 and ∆x = 0.6

∆y is appromimately equal to b,

Approximate value of \(\sqrt { 36.6 } \)
= ∆y + 6
= 0.05 + 6 = 6.05

Question 29.
Use differential to approximate (15)^1/4? (NCERT)
Solution:
Let y = x^1/4
Where, x = 16 and ∆x = -1

∆y is appromimately equal to dy,

Approximately value of (15)^1/4
∆y + 2 = 2 – 0.031 = 1.969.

Question 30.
Use differential to approximate (26)^1/3? (NCERT)
Solution:
Let y = x^1/3
Where, x = 27 and ∆x = -1


∆y is appromimately equal to dy

Approximate value of (26)^1/3
= ∆y + 3
= 3 – 0.037 = 2.963

Question 31.
If the radius of the sphere is measured as 9cm with an error 0.03 cm then find the approximate error in calculating its surface area? (NCERT)
Solution:
Let the radius of circle = r
Given:
r = 9 cm, ∆r = 0.03 cm
Area of sphere

= (8πr) × 0.03
= 8π × 9 × 0.03 = 2.16 π cm²
The approximate error in caluculating the surface area is = 2.16 π cm²

Question 32.
If the radius of a sphere is measured as 7m with an error of 0.02m then find the approximate error in calculating its volume?
Solution:
Let the radius of sphere = r
and ∆r be the error in measuring the radius.
r = 7m, ∆r = 0.02 m (given)
Volume of sphere V = \(\frac{4}{3}\) πr³

The approximate error in calculating the volume is 3.92π m³

Question 33.
Find the approximate change in the volume V of a cube of sides x metre caused by increasing the side by 1%? (NCERT)
Solution:
Let x be the sides of cube.
Volume of cube V = x³, ∆x = 1% of x = \(\frac{x}{100}\)

Change in volume ∆V = ( \(\frac { dV }{ dx } \) ) ∆x

Approximate change in volume = 0.03 x³m³.

Question 34.
Find the approximate change in voume V of a cube of side x metre caused by increasing the side by 2%
Solution:
Let x be the side of cube,
∆x = 2% of x = \(\frac { x\times 2 }{ 100 } \) = 0.02 x
Volume of cube V = x³
\(\frac { dv }{ dx } \) = \(\frac { d }{ dx } \) x³ = 3x²
dV = ( \(\frac { dv }{ dx } \) ) ∆x = 3x² × 0.02 x = 0.06x³ m³
Thus the approximate change in voume = 0.06 x³m³.

MP Board Class 12 Maths Important Questions

MP Board Class 12th Physics Important Questions Chapter 6 Electromagnetic Induction

Electromagnetic Induction Important Questions

Electromagnetic Induction Objective Type Questions

Question 1.
Choose the correct answer of the following:

Question 1.
The SI unit of magnetic flux is :
(a) Weber
(b) Gauss
(c) Oersted
(d) Tesla
Answer:
(a) Weber

Question 2.
The flux linked with a coil can be charged by :
(a) Keeping the coil in a time varying magnetic field
(b) Rotating the coil in a magnetic field
(c) By charging area of coil in the uniform magnetic field
(d) All the above.
Answer:
(d) All the above.

Question 3.
The direction of induced current can be determined by :
(a) Lenz’s law
(b) Flemming’s left hand rule
(c) Right hand palm rule
(d) Ampere’s swimming rule.
Answer:
(a) Lenz’s law

Question 4.
In the phenomenon of elctro magnetic induction :
(a) Electrical energy is transformed into mechanical energy
(b) Mechanical energy is transformed into electrical energy
(c) Electrical energy is transformed into thermal energy
(d) Mechanical energy is transformed into thermal energy.
Answer:
(b) Mechanical energy is transformed into electrical energy

Question 5.
The self inductance of a coil does not depend upon :
(a) Radius of coil
(b) Number of turns in the coil
(c) Lenght of coil
(d) Current through the coil.
Answer:
(d) Current through the coil.

Question 6.
If a core of soft iron is placed between the coil then their mutual inductance :
(a) Decreases
(b) Increases
(c) Remain unchanged
(d) Nothing can be said.
Answer:
(b) Increases

Question 7.
The eddy current are used in :
(a) Electrolysis
(b) Making a galvanometer dead beat
(c) Electroplating
(d) Increasing the sensitivity of galvanometer.
Answer:
(b) Making a galvanometer dead beat

Question 2.
Fill in the blanks :

1. Lenz’s law is used to find out direction of ……………
2. The SI unit of magnetic flux is ……………
3. The core of transformer is made laminated to reduce the loss of energy due to …………… currents.
4. To make the moving coil galvanometer …………… its coil is wound on the aluminium frame.
5. Magnetic flux is a …………… quantity.

Answer:

1. Induced current
2. Weber
3. Eddy
4. Dead beat
5. Scalar.

Question 3.
Match the Column :
I.

Answer:

1. (d)
2. (c)
3. (e)
4. (a)
5. (b)

II.

Answer:

1. (e)
2. (c)
3. (d)
4. (b)
5. (a)

Question 4.
Write the answer in one word/sentence :

1. What is the unit of magnetic flux?
2. What is unit of coefficient of self induction?
3. A straight conductor of length ‘l’ moving with a velocity of ‘V’ in a uniform magnetic field ‘B’ Perpendicular to it. Write the
4. formula for induced e.m.f. in it.
5. Write relation between Henry and Micro Henry.
6. Write the principle of alternating current generator.
7. Induced electric field is conservative field or non conservative field.
8. In which form the energy is stored in a coil?
9. By which law we determine the direction of induced e.m.f.?

Answer:

1. Weber
2. Henry
3. e = Blv
4. 1H = 10⁶pH
5. Electro magnetic induction
6. It is Non conservative field
7. Magnetic energy
8. Lenz’s law.

Electromagnetic Induction Very Short Answer Type Questions

Question 1.
When induced current flow in a closed circuit?
Answer:
When there is change in magnetic flux in a closed circuit, then induced current flow over it.

Question 2.
If a iron core is kept at the centre of a coil, then what will be the effect on coefficient of self induction?
Answer:
Coefficient of self induction will increase.

Question 3.
Lenz’s law is accordance to which law?
Answer:
Law of conservation of energy.

Question 4.
If any metal piece is kept in varying magnetic field, will eddy current generate in it?
Answer:
Yes, eddy current generate in the metallic piece.

Question 5.
Why coil with in the resistance box is double coiled?
Answer:
To avoid self – induction phenomenon.

Question 6.
When the magnitude of magnetic flux become maximum and minimum?
Answer:
When magnetic field is perpendicular to the plane, the magnetic flux is maximum and when it is parallel, its value is minimum.

Electromagnetic Induction Short Answer Type Questions

Question 1.
What is magnetic flux? Write its SI units.
Answer:
The number of magnetic lines of force passing normally through any area in a magnetic field, is called magnetic flux linked with that area. It is denoted by ϕ(phi).

Where, \(\vec { B }\) is the magnetic field, \(\vec { dS }\) is the normal to the surface and θ is the angle between \(\vec { B }\) and normal to surface. SI unit of fluxs weber.

Question 2.
Write Lenz’s law of electromagnetic induction.
Answer:
According to this law, the nature of induced e.m.f. is such that it opposes the cause which produces it. With the help of this law, the direction of induced e.m.f. can be determined.
∴ e = \(\frac {dϕ}{dt}\)
– ve sign is according to Lenz’s law.

Question 3.
A bird sitting on a wire carrying current at high voltage, flies away. Why?
Answer:
As soon as the current flows through the wire, an induced current is produced in the body of the bird, the direction of the current in the wings are opposite. Hence, they are repelled and the bird flies away.

Question 4.
In the given figure, which plate of the capacitor AB is positive and which plate is negative?
Answer:

According to Lenz’s law induced current flows from B to A, therefore plate A is positive and plate B is negative.

Question 5.
A metallic chain touching the ground is attached with the truck carrying explosive matter. Why?
Answer:
During the motion of the truck, the axle cut the magnetic flux of the earth, which causes an induced e.m.f. set up across its axle. This induced charges are earthed by the chain. Which prevent the explosive from the fire.

Question 6.
In metre bridge experiment, the battery’ key is pressed first then galvanometer. Why?
Answer:
If the galvanometer key is pressed first and then battery key, an induced current will be produced in the galvanometer circuit and galvanometer will give deflection even at the position of null point. Thus, the battery key is pressed first.

Question 7.
The resistances in the resistance box are double coiled. Why?
Answer:
In the double coil, the current flows in opposite directions, thus the magnetic fields produced cancel each other and hence induced current is not produced.

Question 8.
When any electric circuit is suddenly cut off, then sparks take place. Why?
Answer:
When the switch is off, the magnetic flux linked with the circuit becomes zero suddenly. Therefore, a strong induced current flows through the circuit in the direction of main current, which causes a high potential difference across the terminal and due to electric discharge, sparks are seen.

Question 9.
What is mutual induction?
Answer:
When the current changes in a coil, then the flux linked with another coil placed near the first changes, hence an induced current is produced in another coil. This phenomenon is known as mutual induction.

Question 10.
A coil in magnetic field is moved

1. Rapidly and
2. Slowly.

Are the e.m.f. and work done in the two cases equal or not?
Answer:
No, the e.m.f. induced in the first case will be larger due to larger rate of change of flux. Obviously, in the second case, the rate of change of flux is slow and hence induced e.m.f will be smaller.

Question 11.
Two coils A and B are kept perpendicular to each other as shown in figure. If flow of current in any one coil is change will induced current will generate in the second.
Answer:
When current is flows in use one coil, the induced flux produce will be parallel to second coil and there will be no change in magnetic flux. Hence no induced current will be produced in second coil.

Question 12.
A ring is hanging in a wall of room. When the north pole of the magnet is brought closer to the ring. Then what will be the direction of induced current if seen from the direction of magnet?
Answer:
The face of the ring which is toward the north pole of the magnet, in.it the direction of induced current will be anti clockwise. Hence this face become magnetic north pole and resist the magnetic pole to come near it.

Question 13.
Three coils are arranged as shown in the figure :

In which coil mutual induction will be maximum?
Answer:
In figure (a), the mutual induction will be maximum before the magnetic lines of force passing in figure (a) is more in comparison to other figure.

Question 14.
What is electromagnetic induction? State Faraday’s laws of electromag neticinduction.
Or
Write down the laws of electromagnetic induction. Find out the expression for the induced electromotive force.
Answer:
When a magnet and a conducting coil are in relative motion, an e.m.f. is induced in the coil. This e.m.f. is called induced e.m.f. If the coil is closed, a current flows in it, then this current is called induced current and the phenomenon is called electromagnetic induction.

Faraday’s laws of electromagnetic induction:
1. Whenever there is a change in magnetic flux linked with an electrical circuit, an e.m.f. is induced in the circuit, therefore an induced current flows in it. The induced current losts so long as there is change in flux.

2. The induced e.m.f. is directly proportional to the rate of change in magnetic flux.

Formula for induced e.m.f.:
Let Φ₁ weber be the flux linked with a closed electrical circuit at any instant of time t₁. After time ∆t i.e., at time t₂ seconds, let the flux be Φ2 weber.

This is the required formula.
Hence, the induced e.m.f. is directly proportional to the rate of change of flux.

Question 15.
Write Lenz’s law and explain how it can be used to determine the direction of induced current?
Answer:
Lenz’s law:
According to this law, the direc¬tion of induced current is such that it opposes the very cause producing it. With the help of this law, the direction of induced current can be determined as follows :

1. When N – pole of a bar magnet is brought closer to a coil, a current is induced to develop N – pole on the adjacent face of the coil to oppose the motion of N – pole towards the coil. This means the induced current must be anticlockwise as seen from the magnet, [see Fig.(a)].

2. When N – pole of the bar magnet is taken away from the coil, an induced current flows in the coil such that the face of the coil near the magnet becomes south pole which attracts the north pole and thus opposes the cause producing it (i.e., opposes the motion of the magnet away from the coil). So, the direction of the induced current in the coil must be clockwise as seen from the magnet, [see Fig. (b)].

Question 16.
Explain that Lenz’s law is in accordance with the law of conservation of eaefgy.
Answer:
When a magnetic north pole is brought near a plane of a coil, the magnetic pole induced in that plane is also north pole causing a repulsive force on the north pole of the magnet. Therefore, work will have to be done against this repulsive force to bring the magnet’s north pole closer to the coil. The work done (mechanical energy) is transformed into electri¬cal energy causing a current induced in the coil.

But, on moving the north pole of the magnet away from the coil, a south pole is developed on the face of the coil and an attractive force is developed on the face of the magnet. So, work has to be done in moving the magnet away from the coil. This results in flow of induced current in reverse direction. Thus, Lenz’s law is in accordance with the law of conservation of energy.

Question 17.
Explain self – induction and demonstrate the phenomenon by an experiment.
Answer:
Self – induction:
During the motion of the truck, the axle cut the magnetic flux of the earth, which causes an induced e.m.f. set up across its axle. This induced charges are earthed by the chain. Which prevent the explosive from the fire.

Experiment:
The circuit of the experiment is shown in the figure. It consists of an insulated copper coil L, wound on soft iron core. Cell E, rheostat Rh and a tapping key K are connected in series. A bulb B is connected in parallel with the coil. Now, the key is closed, the bulb glows slowly, then becomes bright and when it is opened, the bulb flashes bright and then goes off.

As the key is pressed, the flux linked with coil changes and an induced current flows in the opposite direction of main current, because of this the current grows slowly in the circuit.But when the key is opened, the flux suddenly decreases to zero, therefore a strong induced current flows in the same direction of circuit current makes the bulb very bright for a moment.

Question 18.
What is self – induction? What is meant by self-induction of coil? Explain. WritgTts unit.
Answer:
Self – inductance:
When the current flowing through a circuit, an induced e.m.f. is set up in the same circuit, which opposes the main current. This phenomenon is called self – induction.
When the current increases in the circuit, induced current flows in the opposite direc¬tion and when the current decreases in the circuit, the induced current flows in the same direction of circuit current.
Let ϕ be the flux linked with a circuit when a current (l) flows through it. Then,
ϕ ∝I
or ϕ = LI …(1)
Where, L is a constant, called self – inductance of the coil.
Now, if I = 1, then by eqn. (i), we get
ϕ = L
Thus, the self-inductance of a coil is numerically equal to the magnetic flux linked with the coil, produced by unit current.
By Faraday’s law, e = –\(\frac {dϕ}{dt}\)
Putting the value of ϕ from eqn. (i), e = –\(\frac {d(LI)}{dt}\)
or e = -L\(\frac {dI}{dt}\)
If \(\frac {dI}{dt}\) = 1
Then, e = – L
Therefore, the self – inductance of a coil is numerically equal to the opposing e.m.f. produced in the coil due to a unit rate of change of current in the circuit.
Unit : Unit of self-inductance is henry (H).

Question 19.
Explain mutual inductance. Give its unit. On what factors does it depend?
or
Write down the definition, unit and dimensional formula of mutual inductance.
Answer:
Mutual inductance is defined in two ways :
1. Let the flux linked with secondary coil be ϕ due to current l in primary coil.
∴ ϕ ∝ I
or ϕ = MI
Where, M is constant called mutual inductance.
If l = 1, then ϕ = M.
Hence, mutual inductance is defined by numerical value of flux linked with secondary coil, with unit current flows through primary coil.

2. When current changes in primary coil, then flux changes in secondary coil. Thus, by second law of Faraday
Induced e.m.fi, e = –\(\frac {dϕ}{dt}\)
or e = –\(\frac {d(MI)}{dt}\)
or e = ML\(\frac {dI}{dt}\)
If \(\frac {dI}{dt}\) = 1
Then, e = – M
Thus, the mutual inductance of two coils is numerically equal to the induced e.m.f. set up in secondary coil at that moment, when the rate of change of current in primary coil is unity.

Unit : Its unit is Henry in SI system.
Dimensional formula :

It depends upon:

1. Number of turns of both the coils : As the number of turns increases, mutual inductance also increases.
2. Area of cross – section of both the coils : As the area increases, the mutual inductance increases.
3. Material of core : In presence of soft – iron core, the inductance is greater than that of air.

Question 20.
Give differences between self – induction and mutual induction.
Answer:
Difference between self – induction and mutual induction :
Self – induction:

• This phenomenon happens in the same coil when the current flowing through the coil changes.
• One coil is used in this phenomenon.
• Induced current affects the main current.

Mutual induction:

• This phenomenon happens in the another coil placed nearby a coil in which the current is changing.
• Two coils are used in this phenomenon.
• The induced current produced in the second coil, therefore main current is not affected.

Question 21.
What are eddy currents? Show an experiment to demonstrate eddy currents.
Or
What are eddy currents? What are their disadvantages ? Write any two uses of eddy currents.
Answer:
Eddy currents:
When a metallic plate is moved in a magnetic field or placed in a changing magnetic field, then flux linked with the conductor changes, hence an induced current is produced in the plate. This induced current is called eddy current.

Demonstration:
A rectangular copper plate is free to oscillate about a horizontal axis, passing through O. It is placed between the pole pieces of an electromagnet NS. Oscillate the plate, when no current is flowing in the circuit, the plate will oscillate for a long time and due to air resistance finally its amplitude of oscillation decreases.

Now, oscillate and pass the current. It is observed that the oscillations of the plate will be damped soon. Just as eddies are produced on water surface, the change of flux through the metal plate develops induced current known as eddy currents.

Uses : Eddy currents are used in :

1. Making a galvanometer dead beat.
2. Induction furnace.
3. Electric break.
4. Induction motor, etc.

Disadvantages of eddy currents:
Production of eddy currents causes loss of electrical energy in the form of heat. In order to prevent this, soft-iron core is laminated in a transformer. Lamination increases resistance and decreases eddy currents. So, there is very little dissipation of electrical energy in the form of heat.

Question 22.
The self – inductance of two coils P and S are L₁ and L₂ respectively. If the coupling between them is ideal, then prove that the mutual inductance between these coils is M = \(\sqrt { { L }_{ 1 }{ L }_{ 2 } }\)
Answer:
Let coil P is having N₁ total number of turns, length of coil is l and I is the current flowing.

Question 23.
Obtain an expression for the self – inductance of two coils when they are joined in parallel.
Answer:
Consider two inductors of self – inductance L₁ and L₂and joined in parallel.
If I₁ and L₂, be the current flow through L₁and L₂ respectively, then
I = I₁ + I₂

Where 1 is the total current in the circuit differentiating both sides, we get
\(\frac {dI}{dt}\) = \(\frac { { dI }_{ 1 } }{ dt }\) + \(\frac { { dI }_{ 2 } }{ dt }\) … (2)
In parallel combination, the induced e.m.f, across each coil remains the same.

Putting the value of \(\frac {dI}{dt}\) From eqns. (1) and (3), we get

Equation (4) is the required expression

Electromagnetic Induction Long Answer Type Questions

Question 1.
Derive an expression for mutual inductance ¡n between two circular plane coils. Write the factors affecting mutual inductance between circular plane colts.
Answer:
Consider two circular plane coils P and S kept coaxially close to each other. Thenumber of turns in the primary coil P is n₁ and in the secondary coil S is n₂. The radius of primary coil P is r₁ and that of the secondary coil is r₂. Due to flow of current l in the primary coil, the magnetic field produced at its centre is
B = \(\frac { { \mu }_{ 0 } }{ 4\pi } \frac { 2\pi { n }_{ 1 }I }{ { r }_{ 1 } }\) = \(\frac { { \mu }_{ 0 }{ n }_{ 1 }I }{ 2{ r }_{ 1 } }\)
The magnetic flux linked with secondary coil S due to this magnetic field.
ϕ = nBA
=n₁ \(\frac { { \mu }_{ 0 }{ n }_{ 1 }I }{ 2{ r }_{ 1 } }\) πr²₂ … (1)
But, ϕ = MI … (2)
From eqns. (1) and (2),
\(\frac { { \mu }_{ 0 }{ n }_{ 1 }{ n }_{ 2 } }{ 2{ r }_{ 1 } }\).πr²₂
If some other medium is placed inside the coils in place of air or vacuum of perme – ability µ, then
M = µ\(\frac { { n }_{ 1 }{ n }_{ 2 } }{ 2{ r }_{ 1 } }\).πr²₂ … (4)

The mutual inductance between circular plane coils depends on following factors :

1. The mutual inductance increases on increasing the number of trims in primary coil and secondary coil.
2. On increasing the radius of primary coil r¹, the mutual inductance decreases.
3. On increasing the area of secondary coil, mutual inductance increases.
4. If a medium other than air is kept between the coil Mincreases.

Question 2.
Derive an expression for self – inductance of a long solenoid. On what factors does it depend?
Answer:
Expression for self – inductance of a long solenoid:
Let the length and radius of a solenoid be l and r respectively. Also n be the number of turns per unit length.

∴ Area of cross – section, A = πr²
and total number of turns = nl = N.
If current l flows through the solenoid, then the intensity of magnetic field inside the solenoid will be given by
B = µ₀nI, [∵B = \(\frac { { \mu }_{ 0 } }{ 4\pi }\)2πnl(cos0⁰ – cos180⁰)]
(for unit length if l > >r)
Where, µ₀ is the permeability of the medium.
∴ Magnetic flux linked with the total length of solenoid.

If the permeability of soft – iron core inside the solenoid is µ_r, then
L = \(\frac { { \mu }_{ 0 }{ \mu }_{ 1 }{ N }^{ 2 }A }{ l }\) … (3)
Equation (3) is the expression for self – inductance of a long solenoid. From this equation, it is clear that the self – inductance of a solenoid depends upon the following :

1. Area of cross – section of solenoid or radius of the solenoid : The self – inductance of a solenoid increases with radius and hence with the area of cross – section.

2. No. of turns : Self – inductance of a solenoid increases with number of turns.

3. Length of the solenoid : Self – inductance of a solenoid decreases on increasing the length of the solenoid.

4. Relative permeability of the core : The self – inductance of a solenoid increases on placing a core of higher permeability. This is the reason, that self-inductance of a solenoid with soft – iron core is greater than that of air core solenoid.

Equation (3) can be written in terms of radius as follows :
L = \(\frac { { \mu }{ N }^{ 2 }\pi { { r }^{ 2 } } }{ l }\)

Question 3.
Obtain an expression for mutual inductance of two long solenoids. What are the factors on which mutual inductance depends?
Answer:
Let S₁, and S₂ be the two long coaxial solenoids such that S₁, is completely surrounded by S₂. The lengths of both the solenoids are l. n₁ and n₂ are the number of turns per unit length respectively.

Case :
1. Let S₁ be taken as primary and S₂ as secondary solenoid. If I₁ is the current flowing through S₁ then the intensity of field inside S₁ will be
B₁ = μ₀n₁I₁
∴The magnetic field B₁ will superpose on solenoid S₂ and hence, magnetic flux linked with S₂ per turn = B₁A. Where, A is the area of cross – section of S₁.
Hence, net flux associated with S₂ will be
Φ₂₁ = n₂lB₁A
Where, n₂l is the total number of turns in solenoid S₂ and Φ₂₁ is magnetic flux on S₂ due to S₁
Substituting the value of B, from eqn. (1), we get
Φ₂₁ = μ₀n₁I₁n₂A = μ₀n₁n₂lAI₁ … (2)
But, Φ₂₁ = M₂₁I₁ … (3)
From eqns. (2) and (3),
M₂₁ = μ₀n₁n₂Al
This is the equation of mutual inductance of two solenoids. … (4)

2. Let S₂ be taken as primary and S₁ as secondary. If I₂ is the current through S₂, then the intensity of field inside S₂ will be
B₂ = μ₀n₂I₂ … (5)
∴ The magnetic field of S₂ i.e., B₂ will superpose on solenoid S, and hence, magnetic flux linked with each turn of S₁ = B₂A.
Hence, the total flux associated with S₁
Φ₁₂ =n₁lBn₂A … (6)
Where, n₁l is the total number of turns of solenoid S₁, and Φ₁₂ is magnetic flux on S₁, due to S₂.
Putting the value of B₂ from eqn. (5), we get
Φ₁₂ = μ₀n₂I₂An₁l = μ₀n₁n₂lAI₂ … (7)
But, Φ₁₂ = μ₁₂I₂ … (8)
From eqns. (7) and (8), we have
M₁₂ = μ₀n₁n₂Al … (9)
From eqns. (4) and (9), we have
M₂₁ = M₁₂
This is called reciprocity theorem.
It is clear that the mutual inductance of two solenoids remains the same whether cur¬rent flows in one or the other.
Thus, mutual inductance of two long solenoids is given by.
M = μ₀n₁n₂Al .
M = μ₀μ_r\(\frac { { N }_{ 1 } }{ l } \frac { { N }_{ 2 } }{ l }\)Al
μ₀μ_r\(\frac { { N }_{ 1 } }{ l } \frac { { N }_{ 2 } }{ l }\)Al

Mutual inductance depends upon :
1. Number of turns of both the coils : As the number of turns increases, the mutual inductance also increase.

2. Area of cross – section of both the coils : As the area increases, the mutual inductance increases.

3. Material of core : If the permeabilities of the cores in the solenoid are large, then mutual inductance increases. In presence of soft – iron core, the inductance is greater than that of air.

4. Length of the solenoid : For larger solenoids, mutual inductance is less.

Electromagnetic Induction Numerical Questions

Question 1.
The magnetic flux linked with a closed loop is given by the equation ϕ_B = 6t² + 7t +1, where ϕ_B is in milliweber and t is in second. Find the electromotive force induced at time t = 2 second.
Solution:
Formula: e = – \(\frac {dϕ}{dt}\)
Given : ϕ = 6t² + 7t +1
∴ = – latex]\frac {d}{dt}[/latex](6t² + 7t +1) = – 12t – 7
At t = 2 sec,
e = – 12 x 2 – 7
= – 31 milli volt.

Question 2.
An aircraft with a wing span of 40 m flies with a speed of 1080 km hr^-1 towards East where vertical component of Earth’s magnetic field is 1.75 x 10^-5 tesla. Find the e.m.f. developed between the tip of the wings. (NCERT)
Solution:
l = 40m, B_v, B_v = 1.75 x 10^-5T V = 1080\(\frac {Km}{hr}\)
= 1080 x \(\frac {5}{18}\) = 300 m/sec
e = B_vlv = 1.75 x 10^-5 x 40 x300
= 0.21 volt

Question 3.
The flux linked with a coil changes from 1 Wb to 0.1 Wb in 0.1 sec. Calculate the induced e.m.f.
Solution:
Formula : e = – \(\frac {dI}{dt}\)
Given : dl = (0.1 – 1) and dt = 0.1.
e = – \(\frac {(0.1 – 1) }{0.1}\)
or e = \(\frac {(0.9) }{0.1}\)

Question 4.
A current is flowing through a coil having 800 turns. The flux linked with it is 1.5 x 10-s Wb. Find the self-inductance of the coil.
Sol. Formula : = LI
Flux linked with one turn = 1.5 x 10^-5 Wb,
∴ Flux linked with 800 turns = 800 x 1.5 x 10^-5Wb
Substituting the values, we get
800 x 1.5 x 10^-5 = L x 1.5
∴ L = 800×10^-5
= 8.0 x 10^-3H
= 8.0 mH.

Question 5.
An air – core solenoid with length 30 cm area of cross – section 25 cm² and number of turns 500 carries a current of 2.5A. Current is switched off for 1 m sec. Find the average back emf induced across the ends of the open switch in the circuit. (NCERT)
Solution:
l = 30 cm = 0.3 m, A = 25 cm² = 25 x 10^-4m²
N = 500, dt = 10^-3sec., dl = 0 – 2.5 = – 2.5A
Back emf

MP Board Class 12th Physics Important Questions

MP Board Class 12th Physics Important Questions Chapter 5 Magnetism and Matter

Magnetism and Matter Important Questions

Magnetism and Matter Objective Type Questions

Question 1.
Choose the correct answer of the following:

Question 1.
If a bar magnet is placed with its north pole pointing towards geographical north and south pole pointing towards geographical south, then the neutral point will be:
(a) Situated on the axial line
(b) Situated on the equatorial line
(c) Situated at a place where is neither axial line nor equatorial line
(d) Not formed at all.
Answer:
(b) Situated on the equatorial line

Question 2.
Magnetic moment is which type of physical quantity :
(a) Scalar
(b) Vector
(c) Neutral
(d) None of these.
Answer:
(b) Vector

Question 3.
If a bar magnet of magnetic moment M is divided in two equal parts, the magnetic moment of each part will be :
(a) 2M
(b) \(\frac {M}{2}\)
(c) M
(d) Zero
Answer:
(b) \(\frac {M}{2}\)

Question 5.
‘weber’ is the unit of:
(a) Magnetic moment
(b) Magnetic induction
(c) Magnetic field
(d) Magnetic flux
Answer:
(d) Magnetic flux

Question 6.
The two magnetic lines of force :
(a) Meet each other at the poles
(b) Meet at the neutral point
(c) Never meet
(d) All the above statements are correct.
Answer:
(c) Never meet

Question 7.
The intensity of magnetic field is defined as :
(a) Magnetic moment per unit volume
(b) Magnetic induction force acting on unit magnetic pole
(c) Number of magnetic lines of force passing per unit area
(d) Number of lines of force passing through unit volume.
Answer:
(c) Number of magnetic lines of force passing per unit area

Question 8.
A magnetic needle is placed in a non – uniform magnetic field. The needle will experience :
(a) A force without any torque
(b) A torque without any force
(c) A force and a torque
(d) Neither a torque nor a force.
Answer:
(c) A force and a torque

Question 9.
The ratio of magnetic field intensities at equal distance in end on position and broadside on position of a small bar magnet is :
(a) 1 : 4
(b) 1 : 2
(c) 1 : 1
(d) 2 : 1.
Answer:
(d) 2 : 1.

Question 10.
A magnetic dipole of magnetic moment M is placed in a magnetic field of intensity B with its axis along the magnetic field. The work done in rotating it by 180° is :
(a) -MB
(b) MB
(c) Zero
(d) +2 MB
Answer:
(d) +2 MB

Question 11.
If the net magnetic moment of individual atom of a substance is zero, the substance is :
(a) Diamagnetic
(b) Paramagnetic
(c) Ferromagnetic
(d) Non – magnetic.
Answer:
(a) Diamagnetic

Question 12.
Electromagnets are made up of:
(a) Paramagnetic substances
(b) Soft iron
(c) Steel
(d) Diamagnetic substances.
Answer:
(b) Soft iron

Question 13.
At equator the total intensity of earth’s magnetic field is equal to :
(a) V
(b) H
(c) Both
(d) None of these.
Answer:
(b) H

Question 14.
The resultant intensity of earth’s magnetic field at a place is given by :
(a) \(\frac {H}{V}\)
(b) \(\frac {V}{H}\)
(c) \(\sqrt { { H }^{ 2 }+V^{ 2 } }\)
(d) \(\sqrt { { H }^{ 2 }-V^{ 2 } }\)
Answer:
(c) \(\sqrt { { H }^{ 2 }+V^{ 2 } }\)

Question 15.
The value of angle of dip near the magnetic poles is :
(a) 90°
(b) 45°
(c) 30°
(d) Zero.
Answer:
(a) 90°

Question 16.
The south pole of earth’s magnet is :
(a) Near the geographic north pole
(b) Near the geographic south pole
(c) In geographic east
(d) In geographic west.
Answer:
(a) Near the geographic north pole

Question 17.
The angle of dip at equator is :
(a) 90°
(b) 30°
(c) 0°
(d) 45°
Answer:
(c) 0°

Question 18.
In a plane perpendicular to the magnetic meridian, a dip needle :
(a) Will be horizontal
(b) Will be vertical
(c) Will be inclined at angle of dip at that place
(d) Will be inclined at any angle.
Answer:
(b) Will be vertical

Question 2.
Fill in the blanks :

1. The SI unit of pole strength is ……………………….
2. The direction of magnetic moment of a magnet is always from ………………………. to ………………………. pole.
3. The SI unit of magnetic moment is ……………………….
4. The magnetic lines of force are ………………………. curve.
5. The tangent drawn at any point of a magnetic line of force gives ……………………….
6. The magnetic field produced due to a solenoid is same as that produced by a ……………………….
7. A magnet is also called a ……………………….
8. At same distance, magnetic field intensity in broadside on position is ………………………. the intensity in end on position.
9. Nowadays magnetic lines of force are called ……………………….
10. At ………………………. point the resultant intensity of magnetic field is zero.
11. The temperature at which ferromagnetic substance is converted into paramagnetic substance is known as ……………………….
12. The strength of ………………………. magnet can be changed.
13. The vertical component of earth’s magnetic field at a place becomes zero where angle of dip is ……………………….
14. The angle of dip from equator to poles lies between ………………………..
15. ………………………. substances can easily be magnetized.

Answer:

1. ampere x metre
2. south; north
3. ampere x metre²
4. Closed
5. Direction of magnetic field
6. Bar magnet
7. Magnetic dipole
8. Half
9. Magnetic field line
10. Neutral
11. Curie temperature
12. Electro
13. Zero
14. Zero to 90°
15. Ferro – magnetic.

Question 3.
Match the Columns :
I.

Answer:

1. (e)
2. (a)
3. (d)
4. (c)
5. (b).

II.

Answer:

1. (c)
2. (d)
3. (e)
4. (a)
5. (b).

III.

Answer:

1. (d)
2. (a)
3. (b)
4. (e)
5. (c)

Question 4.
Write the answer in one word / sentence :

1. Name the elements or parameters of earth’s magnetic field.
2. What is the value of angle of dip at poles and equator?
3. How is the relative permeability (μ_r) ofthe material related to susceptibility (x_m)?
4. Give two examples of diamagnetic substance.
5. Name any two paramagnetic substances.

Answer:

1.

• Declination
• Angle of dip
• Horizontal component of earth’s magnetic field

2. Angle of dip at poles is 90° and at equator it is 0°

3. μ_r = 1 + x_m

4. Zinc and Bismuth

5. Aluminium and Manganese.

Magnetism and Matter Very Short Answer Type Questions

Question 1.
Define effective length of a magnet?
Answer:
The distance between two poles of magnet is called its effective length.

Question 2.
What do you mean by intensity of magnetic field? Write its SI unit. Is it scalar or vector?
Answer:
Intensity of magnetic field:
The intensity of field at a point is defined by the force experienced by a unit north pole, placed-at that point.
Its SI unit is tesla or weber metre^-2. Magnetic field is a vector.

Question 3.
Define magnetic lines of force.
Answer:
1st definition:
The magnetic lines of force are the curves in the magnetic field, on which if a unit north pole is placed, then it will follow the imaginary curve drawn.

2nd definition:
“A magnetic line of force is a smooth curve in a magnetic field such that the tangent at any point on it gives the direction of the magnetic field at that point.”

Question 4.
Can two magnetic lines of force intersect?
Or
Magnetic lines of force do not intersect each other, why?
Answer:
No. If the two magnetic lines of force intersect, then there will be two tangents and hence two directions of magnetic field at the point of intersection. This is impossible.

Question 5.
Define magnetic moment. Write its SI unit. Is it a scalar or a vector?
Answer:
The product of pole strength (m) and effective length (2l) of the magnet is called magnetic moment (M).
If m be the pole strength and 2l be the effective length, then
M = m x 2l
SI unit of magnetic moment is weber x metre. It is a vector quantity having a direction from south pole to north pole.

Question 6.
What is a diamagnetic substance?
Answer:
A substance which when placed in a magnetizing field develops very weak magnetization in the opposite direction of the applied field is called diamagnetic substance.

Question 7.
What is paramagnetic substance?
Answer:
A substance which when placed in a magnetizing field develops weak magnetism in the direction of the applied field is called paramagnetic substance.

Question 8.
What is paramagnetism?
Answer:
The atoms or molecules of some materials (e.g., Al, CuCl₂) have non – zero magnetic moment. When such a substance is placed in a magnetic field \(\vec { B }\), the individual magnetic dipoles align in the direction of \(\vec { B }\). There is net magnetization in the direction of \(\vec { B }\) and proportional to \(\vec { B }\) This is called paramagnetism.

Question 9.
What are ferromagnetics or ferromagnetic substances?
Answer:
Ferromagnetics are the substances, which when placed in a magnetic field are strongly magnetized in the direction of the magnetizing field. Example Fe. Ni, Co etc.

Question 10.
Write about the number of electrons in diamagnetic and paramagnetic substances.
Answer:
The number of electrons in diamagnetic substances are in even number and in paramagnetic substances electrons are in odd numbers.

Question 11.
Does the magnetism of paramagnetic salts depend upon temperature? Give reason.
Answer:
Yes, with the increase of temperature its magnetism decreases. When a paramagnetic salt is placed in a magnetic field then on each elementary magnet, a torque acts which tends to bring them in the direction of magnetic field. When the temperature is increased the thermal agitation opposes this tendency, hence the paramagnetism is decreased.

Question 12.
Define magnetic intensity. Give its SI unit.
Answer:
Magnetic intensity is the ability of a magnetizing field to magnetize a material and is defined as the number of ampere turns flowing around unit length of solenoid required to produce magnetic induction B0 inside it.
H = \(\frac { { B }_{ 0 } }{ { \mu }_{ 0 } }\)
SI unit of H is Am^-1

Question 13.
Define magnetic permeability. State its SI unit.
Answer:
Magnetic permeability is defined as the ratio of magnetic induction B to the magnetizing field intensity H ie., μ = \(\frac {B}{H}\)
SI unit is TmA^-1.

Question 14.
Why the magnetic property increases in paramagnetic substances with cooling?
Answer:
When a paramagnetic substances is kept in an external magnetic field, then on each elementary magnet a torque acts which tries to bring them parallel to the direction of magnetic field. The thermal vibrations opposes it. If the temperature is decreased, then thermal vibrations decreases, hence the magnetic property increases.

Question 15.
Why is diamagnetism independent of temperature?
Answer:
The induced magnetic moment in diamagnetic sample is always opposite to the magnetizing field, no matter what the internal motion of atom is.

Question 16.
What is Curie point?
Answer:
Curie point is the temperature above which a ferromagnetic substance becomes paramagnetic.

Question 17.
At any point on the surface of earth, horizontal component of earth magnetic field and vertical component of it are equal. What will be the angle of dip at that point?
Solution:
According to question H = V
Or B_H = B_v
But tanθ = \(\frac { { B }_{ v } }{ { B }_{ H } }\)
Or tanθ = \(\frac { { B }_{ v } }{ { B }_{ v } }\)= 1 =tan45°
θ = 45°
Angle of dip will be 45°.

Question 18.
When a bar magnet is cut into two equal pieces perpendicular to its axis, then what will be its charge in magnetic moments.
Answer:
In this position, magnetic moment of each pieces will be M’ = m’ x 2l
But m’= \(\frac {M}{2}\)
∴ M’ = \(\frac {m}{2}\) x 2l
= \(\frac {M}{2}\)
Therefore magnetic moment will become half of its initial value.

Magnetism and Matter Short Answer Type Questions

Question 1.
Write Coulomb’s law of magnetism and define the unit magnetic pole with its help.
Answer:
Coulomb’s law:
The force of attraction or repulsion between two magnetic poles is directly proportional to the product of pole strength and inversely proportional to the square of the distance between them and acts along the line joining the roles.
Let m₁ and m₂ be the pole strengths and d be the distance between them, then

Unit pole:
If F = 10^-7N, d = 1m and m₁=m₂ = m, then putting the values in eqn. (2),
we get
10^-7 = 10^-7\(\frac { { m }^{ 2 } }{ 1 } \) ⇒ m = ±1
Thus, if two similar poles are kept 1m apart in vacuum and repei each other by a force of 10^-7N, then the poles are called unit poles.

Question 2.
What is end – on – position or axial position? Derive an expression for the intensity of field at a point on the axis of a bar magnet. What is the direction of resultant field?
Or
Derive an expression for the intensity of field at a point on the axial position of a bar magnet.
Answer:
End – on – position:
The point where the intensry of the magnetic field is to be found, is on the magnetic axis, then this point is called end – on – position.

Let NS be a bar magnet of pole strength m and effective length 2l. Consider a point P on its axis at a distance d from the centre of the magnet O. Magnetic field at P has to be found out.
Now, the intensity of field at P due to N – pole :
B₁ = \(\frac { { \mu }_{ o } }{ 4\pi } .\frac { m }{ N{ P }^{ 2 } }\),(along\(\vec { NP } \))
NP = OP – ON =d – l
∴ B₁ =\(\frac { { \mu }_{ o } }{ 4\pi } .\frac { m }{ (d-1)^{ 2 } }\) … (1)
Similarly, the intensity of field at P due to S – pole :
B₂ = \(\frac { { \mu }_{ o } }{ 4\pi } .\frac { m }{ S{ P }^{ 2 } } \),(along\(\vec { PS }\))
or ∴ B₁ =\(\frac { { \mu }_{ o } }{ 4\pi } .\frac { m }{ (d+1)^{ 2 } }\) … (2)
Since, B₁ and B₂ are acting in opposite direction and B₁ > B₂
∴Resultant field B = B₁ – B₂ (along \(\vec { NP }\))
Putting the values from eqns. (1) and (2),

This is the required expression for the intensity of field on the axis.
Again, if the magnet is small i.e., I << d
By neglecting l.
\(\frac { { \mu }_{ o } }{ 4\pi } .\frac { 2m }{ ({ d }^{ 2 })^{ 2 } }\)
or \(\frac { { \mu }_{ o } }{ 4\pi } .\frac { 2M }{ ({ d })^{ 3 } }\)
In CGS units, B = \(\frac { 2M }{ ({ d })^{ 3 } }\)
The direction of resultant field is along the magnetic axis from south pole to north pole.

Question 3.
What is broad – side – on position or equatorial position? Derive an expression for the intensity at a point on broad – side – on position of a bar magnet. What will be the direction of resultant field?
Or
Determine the force on a unit north pole, kept on the broad-side-on position of a small bar magnet.
Answer:
Broad – side – on position:
When the point where the intensity of the magnetic field has to be found lies on the perpendicularbisector of magnetic axis, i.e., on the neutral axis, then it is called broad – side – on position.

Magnetic field is the force experienced by unit north pole placed at that point.
Hence, B = \(\frac {F}{m}\)
If m = 1, then B = F.
Let NS be a bar magnet of pole strength m and effective length 2l and magnetic moment M = m2l.
Consider a point P at a distance d from the centre O of a magnet on its neutral axis. Let unit north pole be placed at P.
Now, the intensity of field at P, due to N – pole will be :

Resolving B₁ and B₂ into its components, we have B₁, cosθ along NS and B₂sinθ⊥ to NS along OP. Also B₂ cosθ along NS and B₂ sinθ⊥ to NS along PO.
But B₁ = B₂
⇒ B₁ sinθ= B₂ sinθ
Since, their directions are opposite and their magnitudes are equal, hence they cancel each other.
The resultant field is therefore

Question 4.
What are magnetic lines of force ? Write down its properties.
Answer:
Magnetic lines of force :
1st definition:
The magnetic lines of force are the curves in the magnetic field, on which if a unit north pole is placed, then it will follow the imaginary curve drawn.

2nd definition:
“A magnetic line of force is a smooth curve in a magnetic field such that the tangent at any point on it gives the direction of the magnetic field at that point.”

Properties of lines of force :

1. They are closed and continuous curves.
2. Outside the magnet the direction is from north to south and inside the magnet the direction is from south to north.
3. The tangent drawn at any point on the curve gives the direction of the resultant field at that point.
4. They do not intersect each other. If two lines of force intersect at a point, then there would be two tangents at that point hence, the resultant force would have two directions; which is not possible, therefore the lines of force do not intersect.
5. They are dense near the poles where the magnetic field is strong and get separated where the magnetic field is weak.
6. They repel each other in the direction, perpendicular to it, therefore the like poles repel each other.
7. They experience tension along the lines of force therefore, unlike poles attract each other.
8. They behave just like a stretched elastic string.

Question 5.
Derive an expression for the torque acting on a bar magnet placed in a uniform magnetic field, making angle 0with the field and hence define magnetic moments with its help.
Answer:
Let NS be a bar magnet, placed in a uniform magnetic field of intensity B, making an angle θ with the field. Suppose m be the pole strength and 2l be the effective length, Force acting on each pole will be mB.

On the N – pole this force will be along the direction of field, whereas on S – pole this will be opposite to the direction of field. As two equal and opposite forces are acting on it along different line of action, hence a couple acts on it which tries to bring the magnet along the direction of magnetic field. This couple is called ‘restoring couple’ or ‘restoring torque’.

Restoring torque is defined as the product of magnitude of any one of the forces and the perpendicular distance between them.
∴ τ = Force x Perpendicular distance
or Torque, τ = mB x SP … (1)

Also, in ANPS, we get sinθ = \(\frac {SP}{NS}\)
or SP = NSsinθ = 2lsinθ
Putting the value of SP in eqn. (1),
τ = mB x 2l sinθ
But m x 2l = M (magnetic moment)
∴ τ = mB sinθ
In vector form :
\(\vec { τ }\) = \(\vec { M }\) x \(\vec { B }\)
and the direction of \(\vec { τ }\) will be perpendicular to the plane containing \(\vec { M }\) and \(\vec { B }\).

Definition of magnetic moment :
As τ = MBsinθ
If the magnet is held perpendicular to the field, then 0= 90° or sinθ = 1 then the torque acting on the magnet will be maximum, if the strength of the applied field is 1 i.e., B = 1,then
τ_max = M
Hence, magnetic moment is numerically equal to the maximum torque acting on the bar magnet when it is held perpendicular in a uniform magnetic field of unit intensity.

Question 6.
Compare to a bar magnet and a current – carrying solenoid.
Answer:
Comparison of a bar magnet and a solenoid :
Bar magnet:

• It attracts magnetic substances.
• When it is suspended freely it rests in the direction of N – S.
• It has two poles.
• Like poles of magnet repel and unlike poles attract.

Solenoid:

• It also attracts magnetic substances.
• It also rests in N – S direction if suspended freely.
• It has also two poles.
• Like poles of solenoid also repel and unlike poles attract.

Question 7.
Explain how does an atom behave as a magnetic dipole. Derive an expression for the magnetic dipole moment of the atom. Also define Bohr magneton.
Or
Deduce the expression for the magnetic dipole moment of an electron orbiting around the central nucleus.
Answer:
Magnetic dipole moment of a revolving electron:
In hydrogen – like atoms, an electron revolves around the nucleus. Its motion is equivalent to a current loop which possesses a magnetic dipole moment = IA. As shown in Fig., consider an electron revolving anticlockwise around a nucleus in an orbit of radius r with speed v and time – period T.

Equivalent current,

According to right hand thumb rule, the direction of the magnetic dipole moment of the revolving electron will be perpendicular to the plane of its orbit and it the downward direction, as shown in Fig.
Also, the angular momentum of the electron due to its orbital motion is
I = m_evr  … (2)
The direction of / is normal to the plane of the electron orbit and in the upward direction, as shown in Fig.
Dividing equation. (1) by equation. (2), we get

The above ratio is a constant called gyromagnetic ratio. Its value is 8.8 x 10¹⁰Ckg^-1.
So

The negative sign shows that the direction of \(\vec { l }\) is opposite to that of \(\vec { { \mu }_{ 1 } }\) According to Bohr’s quantization condition, the angular momentum of an electron in any permissible orbit is,
l = \(\frac { nh }{ 2π }\) , where n =1,2 ,3, ………….
∴ µ₁ = n(\(\frac { eh }{ 4\pi { m }_{ e } }\))
This equation gives orbital magnetic moment of an electron revolving in nth orbit.

Bohr magneton:
It is defined as the magnetic moment associated with an electron due to its orbital motion in the first orbit of hydrogen atom. It is the minimum value of µ₁, which can be obtained by putting n = 1 in the above equation. Thus Bohr magneton is given by
µ_B= (µ₁)_min = \(\frac { eh }{ 4\pi { m }_{ e } }\) = 9.27 x 10^-24Am².

Question 8.
Derive an expression for work done in rotating a bar magnet in uniform magnetic field through 8 angle.
Answer:
Let a bar magnet of effective length 2l and of magnetic moment M be kept in uniform magnetic field B. When a bar magnet is rotated through some angle in the magnetic field then some work has to be done against moment of restoring couple.
If magnet is rotated through dQ angle then work done, dW = τ dθ,
(where τ is moment of restoring couple)
or dW = MB sinθ dθ … (1)
When magnet is rotated from θ₁ to θ₂, then work done is given by :

This is the required expression.

Question 9.
Establish the expression for potential energy of a bar magnet placed in a uniform magnetic field.
Answer:
The potential energy of the bar magnet in any orientation is the work done by the external agent to turn the dipole from its zero position (θ = 90°) to that orientation (θ = θ°)
dW = MB sinθ dθ … (1)
Amount of work done to rotate the bar magnet from zero position (θ = π/2) to an arbitrary position (θ = θ) will be obtained by integrating equation  (1) under proper limit.

Question 10.
Define the magnetic elements of earth’s magnetic field at a place.
Or
Establish relation between element of earth’s magnetic field?
Answer:
Elements of earth’s magnetic field:
The earth’s magnetic field at a place can be completely described by three parameters which are called elements of earth’s magnetic field. They are declination, dip and horizontal component of earth’s magnetic field.

1. Magnetic declination:
The angle between the geographical meridian and the magnetic meridian at a place is called the magnetic declination (α) at that place, Or, it is the angle which a compass needle (free to swing in a horizontal planb) makes with the geographic north – south direction.

2. Angle of dip or magnetic inclination:
The angle made by the earth’s total magnetic field \(\vec { B }\) with the horizontal direction in the magnetic meridian is called angle of dip (δ) at any place. Or, it is the angle which a dip needle (free to swing in the plane of the magnetic meridian) makes with the horizontal.

At the magnetic equator, the dip needle rests horizontally so that the angle of dip is zero at the magnetic equator. The dip needle rests vertically at the magnetic poles so that the angle of dip is 90° at the magnetic poles. At all other places, the dip angle lies between 0° and 90°.

3. Horizontal component of earth’s magnetic field:
It is the component of the earth’s total magnetic field \(\vec { B }\) in the horizontal direction in the magnetic meridian. If δ is the angle of dip at any place, then the horizontal component of earth’s field \(\vec { B }\) at that place is given by
B_H = Bcosδ
At the magnetic equator,
δ = 0°,B_H = Bcos0°= B
At the magnetic poles,
δ = 90°,B_H =5cos90°= 0
Thus the value of BH is different at different places on the surface of the earth.

Question 11.
Prove tanδ = \(\frac { { B }_{ v } }{ { B }_{ H } }\) and B = \(\sqrt { { B }_{ H }^{ 2 }+{ B }_{ v }^{ 2 } }\) where symbol have there usual meaning.
Answer:
Relations between elements of earth’s magnetic field:
Fig. shows the three elements of earth’s magnetic field. If 8 is the angle of dip at any place, then the horizontal and vertical components of earth’s magnetic field B at that place will be

B_H = Bcosδ .. (1)
and B_v = Bsinδ
\(\frac { { B }_{ v } }{ { B }_{ H } }\) = \(\frac { Bsinδ }{ Bcosδ}\)
\(\frac { { B }_{ v } }{ { B }_{ H } }\) =tanδ .. (2)
Also
B²_H + B²_v = B²(cos²δ + sin²δ) = B²
or B = \(\sqrt { { B }_{ H }^{ 2 }+{ B }_{ v }^{ 2 } }\) .. (3)
Equations (1), (2) and (3) are the different relations between the elements of earth’s magnetic field.

Question 12.
Compare the magnetic properties of soft iron and steel.
Answer:
Comparison of magnetic properties of soft iron and steel:
Soft iron:

• In soft iron, greater magnetism can be produced, than steel. Its magnetic nature is greater than steel.
• Soft iron does not retain magnetism for longer time. Its retaintivity is less.
• The magnetization and demagnetization of soft iron are easy.
• Temporary magnets are made by soft iron.

Steel:

• In steel, less magnetism can be produced than soft iron, its magnetic nature is less than soft iron.
• Steel retains magnetism for longer time. Its retaintivity is greater than soft iron.
• The magnetization and demagnetization of steel are difficult.
• Permanent magnets are made by soft steels.

Magnetism and Matter Long Answer Type Questions

Question 1.
Answer the following regarding terrestrial magnetism quantities :

1. Three quantities are required to express a vector completely write the name of that there independent quantity.
2. At which place of south India the angle of dip in 18° will you expect more value of angle of dip at britain ?
3. If you draw lines of forces at Melbourne city of Austrilia. This lines of forces will go inside the earth or outside.
4. The magnetic needle which is free to revolve in vertical plane. If it is kept at geographical north or south pole then in which direction it will revolve?

Answer:
1.

• Angle of declination
• Angle of dip
• Horizontal component of Earth magnetic field.

2. Britain is near magnetic pole of earth, therefore angle of dip at Britain is more than the angle of dip at south India (approx. 70°).

3. The magnetic lines of force at Melbourne city of Austrilia will go outside.

4. Geographical North pole or South pole is just situated vertically to the direction of earth magnetic field. Therefore the magnetic needle will be independent to revolve in vertical plane

Question 2.
Compare the magnetic properties of paramagnetic substance and ferromagnetic substance on any three points.
Answer:
Comparison :

Question 3.
What do you mean by magnetic field intensity. Derive an expression for magnetic field due to a bar magnet in general position. How is this formula used to find magnetic field in

1. Axial position
2. Equatorial position.

Answer:
The force experienced by unit north pole at any point in the magnetic field is known as magnetic field intensity. NS is a bar magnet of magnetic moment \(\vec { M }\), we have to find out magnetic field intensity at P, which is situated at θangle from axis of magnet.

Now, we divide M into two components

• Mcosθ
• Msinθ

For Mcosθ point ‘P’ lies in axial position, therefore magnetic field at P due to M cos G component is :
B₁ = \(\frac { { \mu }_{ 0 } }{ 4\pi } \frac { 2Msin\theta }{ { d }^{ 3 } }\) … (1)

For M sinθ point P lies on equatorial position :
B₂ = \(\frac { { \mu }_{ 0 } }{ 4\pi } \frac { Msin\theta }{ { d }^{ 3 } }\) … (2)
∵ B₁is perpendicular to B₂ , the resultant of B₁ and B₂ is given by :

This is the required expression.
(i) For axial position θ = 0° => cos 0°= 1
∴From eqn. (3),
B = \(\frac { { \mu }_{ 0 } }{ 4\pi } \frac { 2M }{ { d }^{ 3 } } \)
From equatorial position θ = 90° ⇒ cos90° = 0
B = \(\frac { { \mu }_{ 0 } }{ 4\pi } \frac { M }{ { d }^{ 3 } } \)

Magnetism and Matter Numerical Questions

Question 1.
Magnetic wire of magnetic moment ‘M’ is bent in the shape of L, at one third of its length. What will be the new magnetic moment.
Solution:

Question 2.
The length of magnetic wire is L and its magnetic moment is M. If it is bent in the form of semi – circle then what will be its new magnetic moment?
Solution:
Initial magnetic moment of magnetic wire M = mL
If it is bent in the form of semi – circle then
L = πr ⇒ r = \(\frac {L}{π}\)
New magnetic moment M’ = m x 2r
M’ = m x \(\frac {2L}{π}\)
or M’ = \(\frac {2M}{π}\)

Question 3.
The distance between two magnetic poles of pole strengths ‘m’ and ‘4m’ is 3m. Find the distance of point in between them at which magnetic field intensity is zero.
Solution:

Question 4.
If the pole strength of each pole of two similar magnetic poles is made two times and distance between them becomes half of its initial value then how will magnetic force acting between them change?
Solution:

Force becomes 16 times its initial value.

Question 5.
Obtain the earth’s magnetization. Assume that the earth’s field can be approximated by a giant bar magnet of magnetic moment 8.0 x 10²²Am². The earth’s radius is 6400 km. [NCERT]
Solution:
Here magnetic moment m = 8.0 x 10²² Am²
Radius of the Earth R = 6400 km = 6.4 x 10⁶m

Question 6.
A solenoid has a core of a material with relative permeability 400. The windings of the solenoid are insulated from the core and carry a current of 2A. If the number of turns is 1000 per metre, calculate (a) H, (b) M, (c) B and (d) the magnetizing current IM. [NCERT]
Solution:
Here n = 1000 tums/m, I = 2A, μ_r = 400
1. H = nI = 1000 x 2 = 2x 10³ Am^-1

2. M = x_mH = (μ_r -1)H
= (400 – 1) x 2 x 10³ ≈ 8 x 10⁵Am^-1

3. B = μH = μ_rμ₀H
= 400 x 4π x 10^-7 x 2 x 10³ T = 1.0T .

4. As M = nI_M
∴ I_M = \(\frac {M}{n}\)
= \(\frac { 8\times { 10 }^{ 5 } }{ 1000 }\)
= 8 x 10² A.

Question 7.
A short bar magnet placed with its axis at 30° experiences a torque of 0.016 Nm in an external field of 800G

1. What is the magnetic moment of the magnet?
2. What is the work done by an external force in moving it from its most stable to most unstable position?
3. What is the work done by the force due to the external magnetic field in the process mentioned in part (b)?
4. The bar magnet is replaced by a solenoid of cross – sectional area 2 x 10^-4 and 1000 turns, but the same magnetic moment Determine the current flowing through the solenoid. [NCERT]

Solution:
1. Here θ = 30°, B = 800G = 800 x 10^-4T, τ = 0.016Nm
Magnetic moment,
m = \(\frac {τ }{B sinθ}\) =\(\frac { 0.016 }{ 800\times { 10 }^{ -4 }\times sin30° }\)
= 0.40 Am².

2. For most stable position θ = 0°and for most unstable position θ = 180°. So the required work done by the external force,
W = mB (cos 180°- cos0°) = 2mB
= 2 x 0.40 x 800 x 10^-4
=0.064J

3. Here the displacement and the torque due to the magnetic field are in opposition. So the work done by the magnetic fied due to the external magnetic field is,
W_B = 0.064J

4. Here A =2 x 10^-4m², N = 1000
Magnetic moment of solenoid,
m_s = m = 0.40 Am²
But m_s = NIA.
∴ current, I = \(\frac { { m }_{ s } }{ NA }\) = \(\frac { 0.40 }{ 1000\times 2\times { 10 }^{ -4 } }\)

Question 8.
In the magnetic meridian of a certain place, the horizontal component of the earth’s magnetic field is 0.26G and the dip angle is 60°. What is the magnetic field of the Earth in this location?
Solution:
Here B_H= 0.26G, δ = 60°
As B_H = Bcosδ
∴ B = \(\frac { { B }_{ H } }{ cos\delta }\)
= \(\frac {0.26}{cos60°}\)
= \(\frac {0.26}{0.5}\)
= 0.52G

Question 9.
What is the magnitude of the equatorial and axial fields due to a bar magnet of length 5 cm at a distance of 50 cm from its mid – point? The magnetic moment of the bar magnet is 0.40 Am². [NCERT]
Sol. Here m = 0.40 Am²
r = 50 cm = 0-50 m, 21 = 5-0 cm
Clearly, the magnet is a short magnet (l<<r)

Question 10.
A planar loop of irregular shape encloses an area of 7.5 x 10^-4 m² and carries a current of 12 A. The sense of flow of current appears to be clockwise to an observer. What is the magnitude and direction of the magnetic moment vector associated with the current loop? [NCERT]
Solution:
Here A = 7.5 x 10^-4m², l = 12A
Magnetic moment associated with the loop is
m = IA = 12 x 7.510^-4 = 9.0 x 10^-3 JT^-1
Applying right hand rule, the direction of magnetic moment is along the normal to the plane of the loop away from the observer.

MP Board Class 12th Physics Important Questions

MP Board Class 12th Maths Important Questions Chapter 5B Differentiation

Differentiation Important Questions

Differentiation Short Answer Type Questions

Question 1.
Differentiate the function sin(cos x²) with respect to x? (NCERT)
Solution:
Let y = sin (cosx²)
\(\frac { dy }{ dx } \) = \(\frac { d }{ dx } \) sin (cos x²)
= \(\frac { d }{ dx } \) sin t, [Putting cos x² = t]
= \(\frac { d }{ dt } \) sin t \(\frac { dt }{ dx } \)
= cos t \(\frac { d }{ dx } \) cos x²
= cos (cos x²) \(\frac { d }{ dx } \) cos u, [Putting x² = u]
= cos (cos x²) \(\frac { d }{ du } \) cos u \(\frac { du }{ dx } \)
= – cos (cos x²) sin u \(\frac { d }{ dx } \) x²
= – 2x cos (cos x²). sin x².

Question 2.
Differentiate the function y = sec [tan \(\sqrt { x } \) ] with respect to x? (NCERT)
Solution:
Given:
y = sec [tan \(\sqrt { x } \) ]
\(\frac { dy }{ dx } \) = \(\frac { d }{ dx } \) sec [tan \(\sqrt { x } \) ]
= \(\frac { d }{ dx } \) sec t, [Putting tan \(\sqrt { x } \) = t]
= \(\frac { d }{ dt } \) sec t \(\frac { dt}{ dx } \)
= sec t tan t \(\frac { d }{ dx } \) tan \(\sqrt { x } \)
= sec (tan \(\sqrt { x } \)) tan (tan \(\sqrt { x } \)) \(\frac { d }{ dx } \) tan u, [Putting \(\sqrt { x } \) = u]
= sec (tan \(\sqrt { x } \)) tan (tan \(\sqrt { x } \)) sec² u \(\frac { d }{ dx } \) \(\sqrt { x } \)
= sec (tan \(\sqrt { x } \)) tan (tan \(\sqrt { x } \)) sec²\(\sqrt { x } \) × \(\frac { 1 }{ 2\sqrt { x } } \)

Question 3.
Differentiate the function y = log [cos e^x] with respect to x? (NCERT)
Solution:
Given:
y = log [cos e^x]
\(\frac { dy }{ dx } \) = \(\frac { d }{ dx } \) [log (cos e^x)]
\(\frac { dy }{ dx } \) = \(\frac { d }{ dx } \) log t, [Putting cos e^x = t]
= \(\frac { d }{ dt } \) log t \(\frac { dt }{ dx } \)
= \(\frac { 1 }{ t } \). \(\frac { d }{ dx } \) cos e^x
= \(\frac { 1 }{ cose^{ x } } \) × \(\frac { d }{ dx } \) cos u, [Putting e^x = u]
= \(\frac { 1 }{ cose^{ x } } \). \(\frac { d }{ du } \) cos u \(\frac { du }{ dx } \)
= \(\frac { -sinu }{ cose^{ x } } \). \(\frac { d }{ dx } \) e^x
= \(\frac { -(sine^{ x })e^{ x } }{ cose^{ x } } \)
= – e^x tan e^x

Question 4.
Differentiate the function y = cos [log x + e^x] with respect to x? (NCERT)
Given:
y = cos [log x + e^x]
\(\frac { dy }{ dx } \) = \(\frac { d }{ dx } \) cos (log x + e^x)
\(\frac { dy }{ dx } \) = \(\frac { d }{ dx } \) cos t, [Putting log x + e^x = t]
= \(\frac { d }{ dt } \) cos t \(\frac { dt }{ dx } \)
= – sin t \(\frac { d }{ dx } \) (log x + e^x)
= – sin (log x + e^x) (\(\frac{1}{x}\) + e^x)
= – \(\frac { (xe^{ x }+1)sin(logx+e^{ x }) }{ x } \)

Question 5.
Differentiate the function y = cos^-1(e^x) with respect to x? (NCERT)
Solution:
Given:
y = cos^-1 (e^x)
∴\(\frac { dy }{ dx } \) = \(\frac { d }{ dx } \) cos^-1 (e^x)
Putting e^x = t,
= \(\frac { d }{ dx } \) cos^-1 t = \(\frac { d }{ dt } \) cos^-1 t \(\frac { dt }{ dx } \)
= \(\frac { 1 }{ \sqrt { 1-t^{ 2 } } } \) \(\frac { d }{ dx } \) e^x
= – \(\frac { e^{ x } }{ \sqrt { 1-e^{ 2x } } } \)

Question 6.
If y + sin y = cos x then find the value of \(\frac { dy }{ dx } \)? (NCERT)
Solution:
Given:
y + sin y = cos x
Differentiating both sides with respect to x,
\(\frac { d }{ dx } \) (y + siny) = \(\frac { d }{ dx } \) cos x
⇒ \(\frac { dy }{ dx } \) + cos y \(\frac { dy }{ dx } \) = – sin x
⇒ \(\frac { dy }{ dx } \) (1 + cos y) = -sin x
⇒ \(\frac { dy }{ dx } \) = \(\frac { -sinx }{ 1+cosy } \)

Question 7.
If 2x + 3y = sin x then find the value of \(\frac { dy }{ dx } \)? (NCERT)
Solution:
Given:
2x + 3y = sin x
Differentiating both sides with respect to x,
\(\frac { d }{ dx } \) (2x + 3y) = \(\frac { d }{ dx } \) sin x
2 \(\frac { d }{ dx } \) x + 3 \(\frac { dy }{ dx } \) = cos x
⇒ 2 + 3 \(\frac { dy }{ dx } \) = cos x – 2
∴ \(\frac { dy }{ dx } \) = \(\frac{cos x – 2}{3}\)

Question 8.
If x = a cos θ, y = a sin θ then find the value of \(\frac { dy }{ dx } \)? (NCERT)
Solution:
Given:
x = a cos θ
y = a sin θ
Differentiating eqn. (1) with respect to θ.
We get, \(\frac { dx }{ d\theta } \) = – a sin θ
Again, \(\frac { dy }{ dx } \) = \(\frac { \frac { dy }{ d\theta } }{ \frac { dx }{ d\theta } } \)
⇒ \(\frac { dy }{ dx } \) = – \(\frac { acos\theta }{ asin\theta } \)
⇒ \(\frac { dy }{ dx } \) = – cot θ.

Question 9.
If x = at² and y = 2at then find the value of \(\frac { dy }{ dx } \)? (NCERT)
Solution:
Given:
x = at²
\(\frac { dx }{ dt } \) = 2at
y = 2at
\(\frac { dy }{ dt } \) = 2a
Again, \(\frac { dy }{ dx } \) = \(\frac { \frac { dy }{ dt } }{ \frac { dx }{ dt } } \) = \(\frac{2a}{2at}\)
⇒ \(\frac { dy }{ dx } \) = \(\frac { 1 }{ t} \).

Question 10.
If y = x² + 3x + 2 then find the value of \(\frac { d^{ 2 }y }{ dx^{ 2 } } \)? (NCERT)
Solution:
Given:
y = x² + 3x + 2
∴ \(\frac { dy }{ dx } \) = 2x + 3.1 + 0
\(\frac { dy }{ dx } \) = 2x + 3
Again differentiating with respect to x,
We get, \(\frac { d }{ dx } \) ( \(\frac { dy }{ dx } \) ) = 2.1 + 0
⇒ \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = 2.

Question 11.
If y = x³ + tan x then find the value of \(\frac { d^{ 2 }y }{ dx^{ 2 } } \)? (NCERT)
Solution:
Given:
y = x³ + tan x
\(\frac { dy }{ dx } \) = \(\frac { d }{ dx } \) [x³ + tan x]
= \(\frac { d }{ dx } \) x³ + \(\frac { d }{ dx } \) tan x
⇒ \(\frac { dy }{ dx } \) = 3x² + sec² x
Again, differentiating with respect to x,
⇒ \(\frac { d }{ dx } \) ( \(\frac { dy }{ dx } \) ) = \(\frac { d }{ dx } \) [3x² + sec²x]
\(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = 3 \(\frac{d}{dx}\) x² + \(\frac{d}{dx}\) sec² x
⇒ \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = 6x + \(\frac{d}{dx}\) t², [Putting sec x = t]
= 6x + \(\frac { d }{ dt } \) t² \(\frac { dt }{ dx } \)
= 6x + 2t \(\frac { d }{ dx } \) sec x
= 6x + 2 sec x.secx tanx
⇒ \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = 6x + 2 sec²x tan x.

Differentiation Long Answer Type Questions – I

Question 1.
If y = tan^-1 \(\frac { x }{ \sqrt { 1+x^{ 2 } } } \) then find the value of \(\frac { dy }{ dx } \)?
Solution:
Given:
y = tan^-1 \(\frac { x }{ \sqrt { 1+x^{ 2 } } } \)
Now putting \(\frac { x }{ \sqrt { 1+x^{ 2 } } } \) = t
\(\frac { dy }{ dx } \) = \(\frac { d }{ dt } \) tan^-1t. \(\frac { dt }{ dx } \)
= \(\frac { 1 }{ 1+t^{ 2 } } \). \(\frac { d }{ dx } \) \(\frac { x }{ \sqrt { 1+x^{ 2 } } } \)

Again Putting 1 + x² = u,

Question 2.
If x = a (t + sin t) and y = a(1 – cost) then find the value of \(\frac { dy }{ dx } \)?
Solution:
Given:
x = a (t + sin t)
∴\(\frac { dx }{ dt } \) = a(1 + cos t)
Again y = a (1 – cos t)
∴\(\frac { dy }{ dt } \) = a (0 + sint) = a sin t
Hence \(\frac { dy }{ dx } \) = \(\frac { \frac { dy }{ dt } }{ \frac { dx }{ dt } } \) = \(\frac { asint }{ a(1+cost) } \)
= \(\frac { sint }{ a(1+cost) } \) = \(\frac { 2sint/2cost/2 }{ 2cos^{ 2 }t/2 } \)
⇒ \(\frac { dy }{ dx } \) = tan \(\frac{t}{2}\).

Question 3.
If x = a(2θ – sin 2θ) and y = a(1 – cos 2θ) then find the value of \(\frac { dy }{ dx } \) where θ = \(\frac { \pi }{ 3 } \)? (CBSE 2018)
Solution:
Given:
x = a (2θ – sin 2θ) ………………… (1)
y = a (1 – cos 2θ) ………………………. (2)
Differentiating eqn. (1) with respect to θ, we get
\(\frac { dx }{ d\theta } \) = a(2.1 – cos 2θ.2)
= 2a (1 – cos 2θ)
= 2a.2 sin²θ
= 4a sin²θ
Differentiating eqn. (2) with respect to θ, ………………… (3)
\(\frac { dy }{ d\theta } \) = a (0 + sin 2θ.2)
= 2a sin 2θ
= 2a.2 sin θ cos θ ……………………….. (4)
= 4a sin θ cos θ
Divinding eqn.(4) by eqn.(3),
\(\frac { dy }{ d\theta } \) + \(\frac { dx }{ d\theta } \) = \(\frac { 4asin\theta cos\theta }{ 4asin^{ 2 }\theta } \)
⇒ \(\frac { dy }{ dx } \) = cot θ
When θ = \(\frac { \pi }{ 3 } \), then
\(\frac { dy }{ dx } \) = cot \(\frac { \pi }{ 3 } \) = \(\frac { 1 }{ \sqrt { 3 } } \).

Question 4.
If y = a sin mx + b cos mx then prove that:
\(\frac { d^{ 2 }y }{ dx^{ 2 } } \) + m²y = 0?
Solution:
Given:
y = a sin mx + b cos mx ……………………. (1)
Differentiating eqn. (2) with respect to x,
\(\frac { dy }{ dx } \) = am cos mx – bm sin mx
Differentiating eqn. (2) with respect to x,
\(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = – am² sin mx – bm² cos mx
⇒ \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = – m² y
∴ \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) + m² y = 0. Proved.

Question 5.
(A) If y = e^msin-1x then prove that (1 – x²) y₂ – xy₁ – m²y = 0?
Solution:
Given:
y = e^msin-1x
\(\frac { dy }{ dx } \) = y₁ = e^msin-1x. \(\frac { d }{ dx } \) (msin^-1x)
⇒ y₁ = y.m. \(\frac { 1 }{ \sqrt { 1-x^{ 2 } } } \)
⇒ \(\sqrt { 1-x^{ 2 } } \) y₁ = my …………………………. (1)
Again, differentiating with respect to x,
\(\sqrt { 1-x^{ 2 } } \). y₂ + y₁. \(\frac{1}{2}\) (1 – x²)^1/2 (- 2x) = my₁
⇒ \(\sqrt { 1-x^{ 2 } } \). y₂ – \(\frac { x }{ \sqrt { 1-x^{ 2 } } } \) y₁ = m\(\frac { my }{ \sqrt { 1-x^{ 2 } } } \). [from eqn.(1)]
⇒ (1 – x²) y₂ – xy₁ = m²y
⇒ (1 – x²) y₂ – xy₁ – m²y = 0. Proved.

Question 5.
(B) If y = e^mtan-1x then prove that (1 + x²) y₂ + (2x – m) y₁ = 0?
Solution:
Solve like Q.5 (A)

Question 5.
(C) If y = e^mcos-1x then prove that (1 – x²) y₂ – xy₁ – m² y = 0?
Solution:
Solve like Q.5 (A)

Question 6.
Differentiate sin^-1 \(\frac { 2x }{ 1+x^{ 2 } } \) with respect to x?
Solution:
Let y = sin^-1 ( \(\frac { 2x }{ 1+x^{ 2 } } \) )
Again let x = tan θ ⇒ θ = tan^-1 x
y = sin^-1 ( \(\frac { 2tan\theta }{ 1+tan^{ 2 }\theta } \) )
= sin^-1 (sin 2θ) = 2θ = 2 tan^-1 x
∴\(\frac { dy }{ dx } \) = 2 \(\frac { d }{ dx } \) (tan^-1 x) = \(\frac { 2 }{ 1+x^{ 2 } } \)

Question 7.
If y = cot^-1 \(\sqrt { \frac { 1+x }{ 1-x } } \) then find \(\frac { dy }{ dx } \)?
Solution:
Given:
y = cot^-1 \(\sqrt { \frac { 1+x }{ 1-x } } \)
Let x = cos θ

Putting in eqn.(1), we get
y = cot^-1 (cot \(\frac{θ}{2}\))
⇒ y = \(\frac{θ}{2}\) = \(\frac{1}{2}\) cos^-1 x, [∵x = cos θ ⇒ ∴θ = cos^-1 x]
Differentiating both sides w.r.t. x,
\(\frac { dy }{ dx } \) = – \(\frac { 1 }{ 2\sqrt { 1-x^{ 2 } } } \)

Question 8.
If y = tan^-1 \(\sqrt { \frac { 1+x }{ 1-x } } \) then find \(\frac { dy }{ dx } \)?
Solution:
Solve like Q.No.7
Answer:
\(\frac { dy }{ dx } \) = \(\frac { 1 }{ 2\sqrt { 1-x^{ 2 } } } \)

Question 9.
If y = cot^-1 ( \(\frac { cosx+sinx }{ cosx-sinx } \) ) then find the value of \(\frac { dy }{ dx } \)?
Solution:
Given:
y = cot^-1 ( \(\frac { cosx+sinx }{ cosx-sinx } \) )

⇒ \(\frac { dy }{ dx } \) = \(\frac { d }{ dx } \) ( \(\frac { \pi }{ 4 } \) – x) = -1.

Question 10.
y = tan^-1 \(\frac { \sqrt { 1+x^{ 2 }-1\quad } }{ x } \) Differentiate with respect to x?
Solution:
Given:
y = tan^-1\(\frac { \sqrt { 1+x^{ 2 }-1\quad } }{ x } \) ……………….. (1)
Put x = tan θ in eqn. (1)
∴ θ = tan^-1 x

⇒ y = \(\frac { \theta }{ 2 } \) = \(\frac{1}{2}\) tan^-1 x
∴\(\frac { dy }{ dx } \) = \(\frac{1}{2}\) tan^-1 x
∴\(\frac { dy }{ dx } \) = \(\frac{1}{2}\) \(\frac { d }{ dx } \) (tan^-1 x ) = \(\frac{1}{2}\) \(\frac { 1 }{ (1+x^{ 2 }) } \)

Question 11.
If y = cot^-1 \(\left[\frac{\sqrt{1+x^{2}}+1}{x}\right]\) then find the value of \(\frac { dy }{ dx } \)?
Solution:
y = cot^-1 \(\left[\frac{\sqrt{1+x^{2}}+1}{x}\right]\)
Put x = tan θ,

⇒ y = \(\frac{1}{2}\) tan^-1x
⇒ \(\frac { dy }{ dx } \) = \(\frac{1}{2}\). \(\frac { 1 }{ 1+x^{ 2 } } \).

Question 12.
If y = x^sinx then find the value of \(\frac { dy }{ dx } \)?
Solution:
Given:
y = x^sinx
Taking log on both sides with respect to x.
\(\frac { 1 }{ y } \) \(\frac { dy }{ dx } \) = sin x × \(\frac{1}{x}\) + logx cos x
∴\(\frac { dy }{ dx } \) = y.[ \(\frac{sinx}{x}\) + log x.cos x]

Question 13.
If y = \(\sqrt { \frac { 1-x }{ 1+x } } \) then prove that \(\frac { dy }{ dx } \) = \(\frac { y }{ x^{ 2 }-1 } \)?
Solution:
Given:
y = \(\sqrt { \frac { 1-x }{ 1+x } } \)^1/2
By taking log , log y = log \(\sqrt { \frac { 1-x }{ 1+x } } \)^1/2
⇒ log y = \(\frac{1}{2}\) [log (1 – x) – log (1 + x)]
Differentiating both sides with respect to x,

Question 14.
If y = (sin x)sinxsinx ………. ∞ then find the value of \(\frac { dy }{ dx } \)?
Solution:
Given:
y = (sin x)sinxsinx ………. ∞
⇒ y = (sin x)^y
⇒ log y = y log sin x
Differentiating both sides with respect to x,
\(\frac{1}{y}\) \(\frac{dy}{dx}\) = y \(\frac{d}{dx}\) (log sin x) + log sin x \(\frac{dy}{dx}\)

Question 15.
(A) If y = \(\sin x+\sqrt{\sin x+\sqrt{\sin x+\ldots+\infty}}\) then prove that:
\(\frac{dy}{dx}\) = \(\frac{cos x}{2y – 1}\)
Solution:

Differentiating both sides with respect to x,
2y \(\frac{dy}{dx}\) = cos x + \(\frac{dy}{dx}\)
⇒ 2y \(\frac{dy}{dx}\) – \(\frac{dy}{dx}\) = cos x
⇒ (2y – 1) \(\frac{dy}{dx}\) = cos x
∴\(\frac{dy}{dx}\) = \(\frac{cos x}{2y – 1}\).

(B) If y = \(\cot x+\sqrt{\cot x+\sqrt{\cot x+\ldots+\infty}}\) then prove that:
\(\frac{dy}{dx}\) = \(\frac { cosec^{ 2 }x }{ 1-2y } \)
Solution:
Solve like Q.No. 15 (A).

(C) If y = \(\begin{aligned}
&x+\sqrt{\tan x+\sqrt{\tan x+\ldots \infty}}\\
\end{aligned}\) then find the value of \(\frac{dy}{dx}\)?
Solution:
Solve like Q.No 15 (A)

Question 16.
If y = e\($x+e^{x+e^{x+e}}-$\) then prove that:
\(\frac{dy}{dx}\) = \(\frac{y}{1-y}\)?
Solution:
Given: y = e\(x+e^{x+e^{x+e}}-x\)
⇒ y = e^x+y
Taking log on both sides,
log y = log e^x+y
log y = x + y
Differentiating both sides with respect to x,
\(\frac{1}{y}\) \(\frac{dy}{dx}\) = 1 + \(\frac{dy}{dx}\)
⇒ \(\frac{dy}{dx}\) ( \(\frac{1}{y}\) – 1) = 1
⇒ \(\frac{dy}{dx}\) ( \(\frac{1-y}{y}\) ) = 1
⇒ \(\frac{dy}{dx}\) = \(\frac{y}{1-y}\) Proved.

Question 17.
Differentiate \(\frac { 1 }{ (x+a)(x+b)(x+c) } \) with respect to x?
Solution:
Let y = \(\frac { 1 }{ (x+a)(x+b)(x+c) } \)
Applying log on both sides,
log y = log 1 – log(x + a) – log (x + b) – log(x + c)
Differentiating both sides with respect to x,
\(\frac{1}{y}\) \(\frac{dy}{dx}\) = 0 – \(\frac{1}{x + a}\) – \(\frac{1}{x + b}\) – \(\frac{1}{x + c}\)
⇒ \(\frac{dy}{dx}\) = – y [ \(\frac{1}{x + a}\) + \(\frac{1}{x + b}\) + \(\frac{1}{x + c}\) ]
⇒ \(\frac{dy}{dx}\) = \(\frac { 1 }{ (x+a)(x+b)(x+c) } \) × { \(\frac { 1 }{ x+a } +\frac { 1 }{ x+b } +\frac { 1 }{ x+c } \) }

Question 18.
Differentiate log ( \(\sqrt{x}\) + \(\frac { 1 }{ \sqrt { x } } \) ) with respect to x?
Solution:
Let y = log ( \(\sqrt{x}\) + \(\frac { 1 }{ \sqrt { x } } \) ) ⇒ y = log ( \(\frac { x+1 }{ \sqrt { x } } \) )
⇒ y = log (x + 1) – log \(\sqrt{x}\)
⇒ y = log (x + 1) – \(\frac{1}{2}\) log x
Differentiating both sides with respect to x,
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) log (x + 1) – \(\frac{1}{2}\). \(\frac{d}{dx}\) log x
⇒ \(\frac{dy}{dx}\) = \(\frac{1}{x + 1}\) – \(\frac{1}{2}\).\(\frac{1}{x}\) = \(\frac{2x-x-1}{2x(x+1)}\)
⇒ \(\frac{dy}{dx}\) = \(\frac{x – 1}{2x(x + 1)}\).

Question 19.
Differentiate y = tan^-1 ( \(\frac { sinx }{ 1+cosx } \) ) with respect to x?
Solution:
y = tan^-1 ( \(\frac { sinx }{ 1+cosx } \) )

⇒ y = tan^-1 (tan \(\frac{x}{2}\) ) = \(\frac{x}{2}\)
Differentiating both sides with respect to x,
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) ( \(\frac{x}{2}\) ) = \(\frac{1}{2}\).

Question 20.
Verify Rolle’s theroem for the function f(x) = x² interval [-1, 1]. (NCERT)
Solution:
Given:
f(x) = x², a = – 1, b = 1.

1. f(x) = x² is a polynomial, hence, f(x) is continous in [-1, 1].
2. f'(x) = 2x exist for every value of x, Hence it is differentiable in (-1, 1).
3. f(-1) = (-1)² = 1, f(1) = (1)² = 1.

∴ f(-1) = f(1)
There exists a value c in (-1, 1) such that:
∴ f'(c) = 0
⇒ 2c = 0, [∵f'(x) = 2x]
⇒ c = 0 ∈ (-1, 1)
Hence, Rolle’s theorem is verified. Proved.

Question 21.
Verify Rolle’s theroem for the function f(x) = x² + 2x – 8, x ∈ [-4, 2]? (NCERT)
Solution:
Given:
f(x) = x² + 2x – 8, a= – 4, b = 2.

1. f(x) = x² + 2x – 8 is a polynomial hence f(x) is continous in [-4, 2].
2. f'(x) = 2x + 2 exist for every value of x, hence it is differentiable in (-4, 2).
3. f(-4) = (-4)² + 2 (-4) – 8

= 16 – 8 – 8 = 0
f(2) = (2)² + 2 × 2 – 8 = 4 + 4 – 8 = 0
∴ f(-4) = f(2).
There exists a value c in (-4, 2),
∴ f'(c) = 0
⇒ 2c + 2 = 0
⇒ c = – 1 ∈ (-4, 2)
Hence, Rolle’s theorem is verified.

Question 22.
Verify Rolle’s theorem for the function f(x) = 2x³ + x² – 4x – 2?
Solution:
Given:
f(x) = 2x³ + x² – 4x – 2 …………………… (1)
We know that polynomial functions are continuous for all real values.
∴ f(x) = o
⇒ 2x³ + x² – 4x – 2 = 0
⇒ x² (2x + 1) – 2(2x + 1) = 0
⇒ (x² – 2) (2x + 1) = 0
⇒ x² = 2, 2x + 1 = 0
⇒ x = ±\(\sqrt { 2 } \), x = – \(\frac{1}{2}\)
⇒ x = – \(\sqrt { 2 } \), \(\sqrt { 2 } \), \(\frac{-1}{2}\)
∴ Interval [-\(\sqrt { 2 } \), \(\sqrt { 2 } \) ].
1. f(x) is continuous in [-\(\sqrt { 2 } \), \(\sqrt { 2 } \) ]
2. f'(x) = 6x² + 2x – 4 is differentiable in [-\(\sqrt { 2 } \), \(\sqrt { 2 } \)].
3. f(-\(\sqrt { 2 } \)) = 2( \(\sqrt { 2 } \) )³ + (-\(\sqrt { 2 } \) ) ² – 4 (- \(\sqrt { 2 } \) ) – 2 = 0
and f ( \(\sqrt { 2 } \) ) = 2( \(\sqrt { 2 } \) )³ + ( \(\sqrt { 2 } \) ) ² – 4( \(\sqrt { 2 } \) ) – 2 = 0
∴ f(- \(\sqrt { 2 } \) ) = f( \(\sqrt { 2 } \) )
There exists a value c in (-\(\sqrt { 2 } \), \(\sqrt { 2 } \) )
∴ f'(c) = 0
⇒ 6c² + 2c – 4 = 0, [∵f'(x) = 6x² + 2x – 4]
∴ c = \(\frac { -2\pm \sqrt { 2^{ 2 }-4\times 6\times (-4) } }{ 2\times 6 } \)
c = \(\frac { -2\pm \sqrt { 4+96 } }{ 12 } \)
⇒ c = \(\frac { -2\pm 10 }{ 12 } \)
⇒ c = \(\frac{-2-10}{12}\) and c = \(\frac{-2+10}{12}\)
⇒ c = -1, \(\frac{2}{3}\) ∈ (- \(\sqrt { 2 } \), \(\sqrt { 2 } \) )
Hence, Rolle’s theroem is verified.

Question 23.
Verify Lagrange’s mean value theorem for the function f(x) = x + \(\frac{1}{x}\) on [1, 3].
Solution:
Given:
f(x) = x + \(\frac{1}{x}\) = \(\frac { x^{ 2 }+1 }{ x } \), x ∈ [1, 3]

1. f(x), x ≠ 0 hence it is a continous function in [1, 3].
2. f'(x) = 1 – \(\frac { 1 }{ x^{ 2 } } \) is differentiable in (1, 3).
3. f(1) = 2 and f(3) = \(\frac{10}{3}\)

Hence, f(1) ≠ f(2)
For mean value theorem,
∴ \(\frac { f(b)-f(a) }{ b-a } \) = f'(c)
⇒ \(\frac { f(3)-f(1) }{ 3-1 } \) = 1 – \(\frac { 1 }{ c^{ 2 } } \)
⇒ \(\frac { \frac { 10 }{ 3 } -2 }{ 2 } \) = 1 – \(\frac { 1 }{ c^{ 2 } } \)
⇒ 1 – \(\frac { 1 }{ c^{ 2 } } \) = \(\frac{2}{3}\)
⇒ \(\frac { 1 }{ c^{ 2 } } \) = \(\frac{3-2}{3}\) = \(\frac{1}{3}\)
⇒ c² = 3
⇒ c = \(\sqrt{3}\) = 1.732 ∈ (1, 3)
Hence, Langrange’s mean value theorem is verified. Proved.

Question 24.
Verify Lagrange’s mean value theorem for the following function f(x) = log x on [1, e]?
Solution:
f(x) = logx, x ∈ [1, e], x > 0.
1. As f(x) = log x, x > 0 is a continuous function, hence f(x) is continuous in [1, e],

2. f'(x) = \(\frac{1}{x}\),
∴ f(x) is differentiable in (1, e).

3. f(1) = log 1 = 0, f(e) = log e = 1.
Now by mean value theorem,
∴ \(\frac{f(e) – f(1)}{e-1}\) = f'(c)
⇒ \(\frac{1-0}{e-1}\) = \(\frac{1}{e}\)
⇒ c = e – 1 ∈ (1, e)
Hence, Langrange’s mean value theorem is verified. Proved.

Question 25.
With the help of Langrange’s value thoerem for the function y = \(\sqrt{x-2}\) in the interval [2, 3]. Find the point where the tangent is parallel to be chord joining the points?
solution:
Given:
f(x) = \(\sqrt{x-2}\), a = 2, b = 3

1. As f(x) = \(\sqrt{x-2}\), x ∈ [2, 3] is defined.
∴ f(x) is continous function for [2, 3].

2. f'(x) = \(\frac { 1 }{ 2\sqrt { x-2 } } \) is defined in interval (2, 3).
∴ f(x) is differentiable in [2, 3]

3. f(2) = 0, f(3) = 1
f(2) ≠ f(3)
Now, by Langrange’s mean value theorem,
∴ \(\frac{f(3)-f(2)}{3-2}\) = f'(c)
⇒ \(\frac{1-0}{1}\) = \(\frac { 1 }{ 2\sqrt { c-2 } } \)
⇒ \(\frac { 1 }{ 2\sqrt { c-2 } } \) = 1
⇒ \(\frac { 1 }{ \sqrt { c-2 } } \) = 2
⇒ \(\sqrt{c-2}\) = \(\frac{1}{2}\)
⇒ c – 2 = \(\frac{1}{4}\)
⇒ c = \(\frac{1}{4}\) + 2 = \(\frac{9}{4}\) = 2.25 ∈ (2,3)
∴ f(c) = \(\sqrt { \frac { 9 }{ 4 } -2 } \) = \(\frac{1}{2}\)
Required points ( \(\frac{9}{4}\), \(\frac{1}{2}\) ).

Differentiation Long Answer Type Questions – II

Question 1.
Differentiate sin^-1 [ \(\frac { 2^{ x+1 } }{ 1+4^{ x } } \) ] with respect to x? (NCERT)
Solution:
y = sin ^-1 [ \(\frac { 2^{ x+1 } }{ 1+4^{ x } } \) ]
⇒ y = sin^-1 [ \(\frac { 2.2^{ x } }{ 1+2^{ 2x } } \) ]
Putting 2^x = tan θ
Then, θ = tan^-1 2^x
⇒ y = sin^-1 [ \(\frac { 2tan\theta }{ 1+tan^{ 2 }\theta } \) ]
⇒ y = sin^-1 [sin 2θ], [∵sin 2θ = \(\frac { 2tan\theta }{ 1+tan^{ 2 }\theta } \) ]
⇒ y = 2θ
⇒ y = 2 tan^-1 (2^x), [θ = tan^-1(2^x)]
∴ \(\frac{dy}{dx}\) = 2 \(\frac{d}{dx}\) tan^-1 (2^x)
Putting 2^x = t
⇒ \(\frac{dy}{dx}\) = 2 \(\frac{d}{dx}\) tan^-1 t
= 2 \(\frac{d}{dt}\) tan^-1 t\(\frac{dt}{dx}\)
⇒ \(\frac{dy}{dx}\) = \(\frac { 2 }{ 1+t^{ 2 } } \) \(\frac{d}{dx}\) (2^x),
= \(\frac { 2 }{ 1+2^{ 2x } } \) × 2^x log 2
⇒ \(\frac{dy}{dx}\) = \(\frac { 2^{ x+1 }log2 }{ 1+4^{ x } } \)

Question 2.
If y = sin^-1 x then prove that: (NCERT)
(1 – x²) \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) – x \(\frac{dy}{dx}\) = 0? (NCERT)
Solution:
Given:
y = sin^-1 x ……………………………. (1)
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) (sin^-1 x)
\(\frac{dy}{dx}\) = \(\frac { 1 }{ \sqrt { 1-x^{ 2 } } } \)
\(\frac{d}{dx}\) ( \(\frac{dy}{dx}\) ) = \(\frac{d}{dx}\) t^-1/2
Putting 1 – x² = t
\(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = \(\frac{d}{dx}\) t^-1/2
= \(\frac{d}{dt}\) t^-1/2 \(\frac{dt}{dx}\)
= – \(\frac{1}{2}\) t^-1/2-1 \(\frac{d}{dx}\) (1 – x²)

Question 3.
If y = tan x + sec x then prove that:
\(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = \(\frac { cosx }{ (1-sinx)^{ 2 } } \)?
Solution:
y = tan x + sec x (given)
\(\frac{dy}{dx}\) = sec² x + sec x tan x
⇒ \(\frac{dy}{dx}\) = sec x(sec x + tan x)
⇒ \(\frac{dy}{dx}\) = \(\frac{1}{cosx}\) [ \(\frac{1}{cosx}\) + \(\frac{sinx}{cosx}\) ]
= \(\frac { 1+sinx }{ cos^{ 2 }x } \) = \(\frac { 1+sinx }{ 1-sin^{ 2 }x } \)
= \(\frac { 1+sinx }{ (1+sinx)(1-sinx) } \)
⇒ \(\frac{dy}{dx}\) = \(\frac{1}{1-sinx}\)
Again differentiating both sides with respect to x,
\(\frac{d}{dx}\) ( \(\frac{dy}{dx}\) ) = \(\frac{d}{dx}\) ( \(\frac{1}{1-sinx}\)
\(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = \(\frac { (1-sinx).0-1.(0-cosx) }{ (1-sinx)^{ 2 } } \)
⇒ \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = \(\frac { cosx }{ (1-sinx)^{ 2 } } \)

Question 4.
If y = sin(sinx) then prove that:
y₂ + y₁ tan x + y cos² x = 0? (CBSE 2018)
Solution:
y = sin(sin x)
Differentiating w.r.t. x,
y₂ = cos (sinx) \(\frac{d}{dx}\) (cos x) + cos x \(\frac{d}{dx}\) {cos (sin x)}
= cos (sin x) (- sinx) + (cos x) [-sin(sin x)] cos x
⇒ y₂ = – sin x cos (sin x) – cos₂ x sin (sin x)
⇒ y₂ = -sin x cos(sin x) – y cos₂ x, [from eqn.(1)]
⇒ y₂ = [ \(-\frac { sinx }{ cosx } \). cos x] cos(sin x) – y cos² x
⇒ y₂ = – tan x {cos (sin x) cos x} – y cos²
⇒ y₂ = -tan x {cos(sin x) cos x} – y cos² x [from eqn.(2)]
⇒ y₂ = (-tan x) y₁ – y cos² x, Proved.
⇒ y₂ + y₁ tan x + y cos² x = 0.

Question 5.
If (x² + y²)² = xy then find \(\frac{dy}{dx}\)? (CBSE 2018)
Solution:
(x² + y²)² = xy
Differentiating with respect to x,
2(x² + y²) (2x + 2y \(\frac{dy}{dx}\) ) = x \(\frac{dy}{dx}\) + y.1
⇒ 2(x² + y²). 2x + 2(x² + y²). 2y \(\frac{dy}{dx}\) = x \(\frac{dy}{dx}\) + y
⇒ [4y(x² + y²) – x] \(\frac{dy}{dx}\) = y – 4x (x² + y²)
⇒ \(\frac{dy}{dx}\) = \(\frac { y-4x(x^{ 2 }+y^{ 2 }) }{ 4(x^{ 2 }+y^{ 2 })y-x } \)

Question 6.
If y = 500e^7x + 600e^-7x then prove that:
\(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = 49 y? (NCERT)
Solution:
Given:
y = 500e^7x + 600e^-7x …………………….. (1)

Question 7.
If y = (tan^-1 x)² then prove that:
(x² + 1)² y₂ + 2x (x² + 1) y₁ = 2? (NCERT)
Solution:
Given:
y = (tan^-1 x)²

Question 8.
Differentiate sec^-1 ( \(\frac { 1 }{ 2x^{ 2 }-1 } \) ) with respect to: \(\sqrt { x^{ 2 }-1 } \)?
Solution:
Let y₁ = sec^-1 ( \(\frac { 1 }{ 2x^{ 2 }-1 } \) )
⇒ y₁ = cos^-1 (2x² – 1)

Question 9.
Differentiate tan^-1 ( \(\frac { 2x }{ 1-x^{ 2 } } \) ) with respect to:
sin^-1 ( \(\frac { 2x }{ 1-x^{ 2 } } \) )
Solution:
Let y₁ = tan^-1 \(\frac { 2x }{ 1+x^{ 2 } } \) and y₂ = sin^-1 \(\frac { 2x }{ 1+x^{ 2 } } \)
Let x = tan θ, then θ = tan^-1 x

⇒ y₁ = tan^-1 (tan 2θ) and y₂ = sin^-1 (sin 2θ)
⇒ y₁ = 2θ and y₂ = 2θ
⇒ y₁ = 2 tan^-1 x and y₂ = 2 tan^-1 x

Question 10.
Differentiate tan^-1 ( \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \) ) with respect to x?
Solution:
Let y₁ = tan^-1 ( \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \) )
Put x = tan θ,

Question 11.
If x \(\sqrt { 1+y } \) + y \(\sqrt { 1+x } \) = 0 then prove that:
\(\frac{dy}{dx}\) = -(1 + x)^-2
Solution:
Given:
x\(\sqrt { 1+y } \) + y \(\sqrt { 1+x } \) = 0
⇒ x \(\sqrt { 1+y } \) = -y\(\sqrt { 1+x } \)
Squaring both sides,
x² (1 + y) = y² (1 + x)
⇒ x² + x²y = xy² + y²
⇒ x² – y² + x²y – xy² = 0
⇒ (x – y) (x + y) + xy (x – y) = 0
⇒ (x – y)(x + y + xy) = 0
⇒ x – y = 0
⇒ x = y
But x ≠ y
∴ x + y + xy = 0
⇒ y (l + x) = – x
∴ y = – \(\frac{x}{1+x}\)
Differentiating both sides with respect to x,

Question 12.
If x^y = e^y-x then prove that:
\(\frac{dy}{dx}\) = \(\frac { 2-log_{ e }x }{ (1-log_{ e }x)^{ 2 } } \)
Solution:
Given: x^y = e^y-x
Applying log on both sides,
∴ log_e x^y = log_e(e^y-x)
⇒ y log_e x = (y – x) log_e e
⇒ y log_e x – y = -x
⇒ y(1 – log_e x) = x
⇒ y = \(\frac { x }{ 1-log_{ e }x } \)
Differentiating with respect to x,
Again,

Question 13.
If y\(\sqrt { 1-x^{ 2 } } \) + x \(\sqrt { 1-y^{ 2 } } \) then prove that:
\(\frac{dy}{dx}\) + \($\sqrt{\frac{1-y^{2}}{1-x^{2}}}$\) = 0?
Solution:
Given:
y\(\sqrt { 1-x^{ 2 } } \) + x \(\sqrt { 1-y^{ 2 } } \) = 1.
Let x = sin θ and y = sin ϕ,

Question 14.
(A) If y = x^sin-1x + x^x then find the value of \(\frac{dy}{dx}\)?
Solution:
Given:
y = x^sin-1x + x^x
y = u + v
∴\(\frac{dy}{dx}\) = \(\frac{du}{dx}\) + \(\frac{dv}{dx}\) ……………………. (1)
Where, u = x^sin-1x
∴ log u = sin^-1 x log x, (taking log both sides)
Differentiating both sides with respect to x,


and v = x^x
∴ log v = x log x
Differentiating both sides with respect to x,
\(\frac{1}{v}\). \(\frac{dv}{dx}\) = 1.log x + x. \(\frac{1}{x}\)
⇒ \(\frac{dv}{dx}\) = v(log x + 1)
⇒ \(\frac{dv}{dx}\) = x^x (log x + 1) ………… (3)∴ From eqn.(1),

(B) If y = x^-1x + x^x, then find the value of \(\frac{dy}{dx}\)?
Solution:
Solve like Q.No. 14(A).

Question 15.
If sin y = x sin (a + y) then prove that:
\(\frac{dy}{dx}\) = \(\frac { sin^{ 2 }(a+y) }{ sina } \)?
Solution:
Given:
sin y = x sin (a + y)
⇒ x = \(\frac { siny }{ sin(a+y) } \)
Differentiating with respect to x,

Question 16.
If x^y = e^x-y then prove that:
\(\frac{dy}{dx}\) = \(\frac { logx }{ (1+logx)^{ 2 } } \)?
Solution:
Given: x^y = e^x-y
Applying log on both sides,
y log x = (x – y) log_ea
⇒ y log x = (x – y).1 = x – y
Differentiating both sides with respect to x,

From eqn.(1),
y log x = x – y
⇒ y log x + y = x
⇒ y(logx + 1) = x
Put the value of y in eqn.(2)

MP Board Class 12 Maths Important Questions

MP Board Class 12th Physics Important Questions Chapter 4 Moving Charges and Magnetism

Moving Charges and Magnetism Important Questions

Moving Charges and Magnetism Objective Type Questions

Question 1.
Choose the correct answer of the following:

Question 1.
The magnetic effect of electric current was discovered by :
(a) Flemming
(b) Faraday
(c) Ampere
(d) Oersted.
Answer:
(d) Oersted.

Question 2.
A moving charge produces :
(a) Only electric field
(b) Only magnetic field
(c) Both electic and magnetic field
(d) Neither electric nor magnetic field.
Answer:
(c) Both electic and magnetic field

Question 3.
The SI unit of magnetic field intensity is :
(a) N/m
(b) Gauss or oersted
(c) N/A – m
(d) weber x metre .
Answer:
(c) N/A – m

Question 4.
Amperes circuital rule is :

Answer:

Question 5.
The magnetic field produced at the centre of a circular coil carrying current is :
(a) In the plane of plane
(b) Perpendicular to the plane of coil
(c) At 45° from the plane of coil
(d) At 60° from the plane of coil.
Answer:
(b) Perpendicular to the plane of coil

Question 6.
The force on a charge moving in a uniform magnetic field is zero if the direction of motion of charge is :
(a) Perpendicular to the magnetic field
(b) At 45° from magnetic field
(c) At 60° from the magnetic field
(d) Parallel to the magnetic field.
Answer:
(d) Parallel to the magnetic field.

Question 7.
The torque on a current carrying loop in a uniform magnetic field is maximum when the plane of loop is :
(a) Parallel to the magnetic field
(b) Perpendicular to the magnetic field
(c) At 45° from the magnetic field
(d) At 60° from the magnetic field.
Answer:
(a) Parallel to the magnetic field

Question 8.
To measure the current in a circuit we use :
(a) Voltmeter
(b) Galvanometer
(c) Ammeter
(d) Voltameter.
Answer:
(c) Ammeter

Question 2.
Fill in the blanks :

1. The SI unit of permeability is ……………..
2. SI unit of magnetic field is ……………..
3. Dimensional formula of magnetic field is ……………..
4. A current carrying solenoid behaves like a ……………..
5. The lorentz force on a charged particle in a uniform magnetic field is given as ……………..
6. The force between two parallel conductors carrying current in same direction is …………….. in nature.
7. The resistance of an ideal ammeter is ……………..

Answer:

1. ampere²
2. newton/ampere
3. [MT^-2 A^-1 ]
4. Bar magnet
5. q\(\vec { (v } ×\vec { B) } \)
6. Attractive
7. Infinite

Question 3.
Match the Column :
I.

Answer:

1. (c)
2. (e)
3. (d)
4. (a)
5. (b)

II.

Answer:

1. (d)
2. (e)
3. (b)
4. (a)
5. (c)

Question 4.
Write the answer in one word/sentence

1. State Ampere’s circuital law.
2. Which material is used for the suspension wire of a moving coil galvanometer and why?
3. What should be the resistance of an ideal voltmeter and ammeter?
4. What happens if a voltmeter is connected in series to the circuit?
5. What is a cyclotron?
6. What do you mean by magnetic effect of current?
7. State Maxwell’s right – hand screw rule.
8. What happens if a voltmeter is connected in series to the circuit?

Answer:
1. Ampere’s circuital law states that the line integral of magnetic field \(\vec { B }\) around any closed path is equal to Mo times the total current I enclosed by the path. Mathematically \(\oint { \vec { B. } } \vec { dl }\) = µ₀I

2. Phosphor bronze alloy is used as suspension wire because it has small restoring torque per unit twist and has a high tensile strength

3. An ideal voltmeter should have infinite resistance and the resistance of an ideal ammeter should be zero

4. The resistance of voltmeter is very high, therefore current will be decreased to almost zero

5. Cyclotron is a device used to accelerate positively charged particles (like protons, a particles). So that they can acquire sufficient energy to carry out nuclear disintegrations

6. When current is passed through any conductor, a magnetic field is produced around it. This phenomenon is called magnetic effect of current.

7. If a cork screw is turned so that it advances in the direction of current along the wire, then the direction in which the thumb rotates gives the direction of magnetic lines of force.

8. The resistance of voltmeter is very high, therefore current will be decreased to almost zero.

Moving Charges and Magnetism Very Short Answer Type Questions

Question 1.
Write practical unit of current and define it.
Answer:
The practical unit of current is ampere. One ampere of current is that current which produces a field of 10^-7 Wb/m², at the centre of the conductor of length 1m, placed in the form of an arc of a circle of radius 1 m.

Question 2.
Write S.I. unit of magnetic field intensity and define it.
Answer:
The S.I. unit of magnetic field intensity is newton / ampere x metre.
The intensity of the magnetic field is 1 newton ampere^-1 metre^-1. If 1 newton force acts on a conductor of length lm carrying a current of 1 ampere and held perpendicular to the magnetic field.

Question 3.
Write an expression for force acting on current – carrying conductor placed in magnetic field. Give the meaning of symbols used.
Answer:
The force on current – carrying conductor kept in magnetic field is given by :
F = IBl sinθ
Where, I = Current, l = Length of conductor, B = Field intensity and θ = Angle between the direction of magnetic field and the conductor.

Question 4.
What is the practical unit of current? Give its definition.
Answer:
If two parallel conductors situated at a perpendicular distance of 1 metre carry equal current in the same direction and exert an attractive force of 2 x 10^-7 newton on each other in air or vacuum, then the current on each conductor is equal to one ampere.

Question 5.
Why a soft iron core is kept in moving coil galvanometer?
Answer:
The magnetic lines of force crossed through the soft iron core. This increases the magnetic field and hence sensitivity of galvanometer. The soft iron core helps to make the magnetic field radial.

Question 6.
The pole pieces of magnet are cut concave in a galvanometer. Why?
Answer:
So that the magnetic field becomes radial, hence the plane of the coil becomes parallel to the magnetic field. Under this condition, the deflecting torque on the coil is maximum.

Question 7.
What happens if an ammeter is connected in parallel to the circuit? What is the resistance of an ideal ammeter?
Answer:
The resistance of an ammeter is very less, hence almost all the current will flow through the ammeter which may damage the ammeter. The resistance of an ideal ammeter is zero.

Question 8.
Why an ammeter is connected in series in an electric field?
Answer:
An ammeter measures the electric current of the circuit, hence all the current should pass through the ammeter. Therefore, it is connected in series.

Question 9.
The resistance of ammeter should be very small. Why?
Or
The resistance of an ideal ammeter is zero. Why?
Answer:
An ammeter measures the current of an electric circuit, therefore it is connected in series. If the resistance of ammeter is large, then it will decrease the current in the circuit. Thus, the resistance of an ammeter should be less or zero.

Question 10.
What will be the resultant magnetic field intensity of point O as shown in the figure?

Answer:
Due to the straight portion of the wire the resultant field will be zero and due to semi circle. The resultant field intensity will be
B = \(\frac { { µ }_{ 0 }I }{ 4R }\)

Moving Charges and Magnetism Short Answer Type Questions

Question 1.
What is second right – hand palm rule? Write its uses.
Answer:
Stretch out the palm of your right – hand such that the fingers are perpendicular to the direction of thumb.

If the thumb points the direction of current and the fingers point the direction of magnetic field, then the force acting on conductor will be in upward direction perpendicular to Direction i the palm.

Uses:
By it’s we can find out intensity of magnetic filed due topufrent carrying conductor.

Question 2.
Write Biot – Savart law for the magnetic field produced due to an element of a current – carrying conductor and explain the term used in it. Define the unit of current with the help of it
Answer:
Let AB be a conductor carrying current I. Consider a small line element dl of the conductor, due to which the magnetic field dB is produced at point P, then the strength of the magnetic field \(\vec { (dB) }\) depends on the following factors :

1. The field is directly proportional to current I.
i.e., dB ∝I

2. The field is directly proportional to the length of element,
i.e., dB ∝ dl

3. The field is directly proportional to the sine of angle between the line joining the point and dl.
i.e., dB ∝ sinθ

4. The field is inversely proportional to the square of the distance between the observation point and line element.
i.e.,
dB ∝ \(\frac { 1 }{ { r }^{ 2 } }\)
Combining all the four points,we get
dB ∝ \(\frac { Idl sinθ }{ { r }^{ 2 } }\)
or dB ∝ K\(\frac { Idl sinθ }{ { r }^{ 2 } }\) … (1)
Where, K is constant of proportionality. Its value depends upon the system of units
In C.G.S system, k = 1
∴ dB ∝ K\(\frac { Idl sinθ }{ { r }^{ 2 } }\) gauss … (2)
In M.K.S. system, K = \(\frac { { μ }_{ 0 } }{ 4π }\)
Where, μ₀ = Permeability of free space.
∴ dB = \(\frac { { μ }_{ 0 } }{ 4π }\) \(\frac { Idl sinθ }{ { r }^{ 2 } }\) Wb/m₂ … (3)
or dB =10^-7 [/latex] \(\frac { Idl sinθ }{ { r }^{ 2 } }\) Wb/m₂ … (4)
The relations given by eqns. (2), (3) and (4) are called Biot – Savart law.
The direction of the magnetic field \(\vec { dB }\) is always perpendicular to the plane containing \(\vec { dl }\) and \(\vec { r }\) and is given by the right – hand screw rule for the cross product of vectors.

Unit of electric current:
1. In C.GS. system : If dl= 1cm, r= 1cm, sinθ = 1 i.e., 9 = 90° and dB = 1 gauss, then from eqn. (2) I = 1 electromagnetic unit (e.m.u.).
For 9= 90°, the conductor should be taken as a part of circle, as the radius is always perpendicular to the circumference. Thus, 1 e.m.u. of current is that current which produces a field of 1 oersted at the centre of the conductor of length 1 cm, kept in the form of an arc of a circle of radius 1 cm.

2. In M.K.S. system: If dl =1m, r = 1m, sinθ = 1 and dB = 10^-7 Wb/m², then from eqn. (4)
I = 1 ampere.
Thus, 1 ampere of current is that current which produces a field of 10^-7 Wb/m², at the centre of tWconductor of length 1m.

Question 3.
Find the expression for magnetic field intensity for a Toroid.
Answer:
A solenoid bent into the form of closed ring is called toroidal solenoid to fig. (a).
In a toroidal solenoid, the magnetic field \(\vec { B }\) has a constant magnitude everywhere inside the toroid while it is zero in the open space interior (point P) and exterior (point Q) to the toroid.

The direction of magnetic field in – side is clockwise as per the right hand thumb rule for circular loops. Three circular Amperian loops are shown by dashed lines.

By symmetry, the magnetic field should be tangential to them and constant in magnitude for each of the loops.

1. For points in the open space interior to the toroid:
Let B₁ be the magnitude of the magnetic field along the Amperian loop 1 of radius r₁
Length of the loop L₁ = 2πr₁
As the loop encloses no current, I = 0
Applying Ampere’s circuital law.
B₁L₁ = μ₀I
or B₁2πr₁ = μ₀ × 0
Thus, the magnetic field at any point P in the open space interior to the toroid is zero.

2. For points inside the toroid:
Let B be the magnitude of the magnetic field along the Amperian loop 2 of radius r.
Length of loop 2, L₂ = 2π r
If N is the total number of turns in the toroid and I the current in the toroid, then total I the current enclosed by the loop 2 = NI.
Applying Ampere’s circuital law.
B × 2πr = μ₀ NI
or B = \(\frac { { μ }_{ 0 }NI }{ 2πr }\)
If r be the average radius of the toroid and n the number of turns per unit length, then
N = 2πrn
∴ B = \(\frac { { μ }_{ 0 }I }{ 2πr }\).2πrn
or B = μ₀I n.

3. For points in the open space exterior to the toroid:
Each turn of the torpid passes twice through the area enclosed by the Amperian loop 3. For each turn, the current coming out of the plane of paper is cancelled by the current going into the plane of paper.
Thus, I = 0 and hence B₃ = 0.

Question 4.
Write four similarities between Biot – savart law and coloumb’s inverse square law.
Answer:
The four similarities between both are :

1. Both laws obey inverse square law.
2. Wide range of field is given by both the law’s.
3. Principle of superpositions held for both the law.
4. Both the law is effected by the medium of surrounding of the conductor.

Question 5.
State and prove Ampere’s circuital law.
Answer:
Ampere’s circuital law:
Ampere’s circuital law states that the line integral of magnetic field B around any closed path is equal to μ₀ times the total current I enclosed by the path.

Mathematically \(\oint { \vec { B. } } \vec { dl }\) = µ₀I
Proof:
Consider an infinitely long straight conductor carrying current I. The magnetic lines of force are produced around the conductor as concentric circles.
The magnetic field due to this current – carrying infinite conductor at a distance a is given by
B = \(\frac { { μ }_{ 0 } }{ 4π }\) \(\frac {2I}{a}\), … (1)
(from Biot – Savart law)

Consider a circle of radius a. Let XY be a small element of length dl. \(\vec { dl }\) and \(\vec { B }\) are in
the same direction because direction of [/latex] and \(\vec { B }\) is along the tangent to the circle.
The line integral for the closed path will be

This proves Ampere’s circuital law.

Question 6.
Obtain an expression for the magnetic field due to a long straight current carrying conductor using Ampere’s circuital law.
Answer:
Consider an infinite long to conductor XY carrying current I as shown in the figure.
Magnetic field at P has to be found out. Distance between P and the wire is ‘a’. Draw an Amperian loop of radius a. Consider a line element RS = \(\vec { dl }\).

Let \(\vec { B}\) be the magnetic field at P; then the line integral of magnetic field along the circular path = \(\oint { Bdl }\) By Ampere’s circuital law,
\(\oint { Bdl }\) = µ₀
Where, I is the total current flowing in the Amperian loop.
Angle between \(\vec { B }\) \(\vec { dl }\) = 0

This is the strength of the magnetic field due to the conductor at a distance a.

Question 7.
Derive on expression for force acting on a current carrying conductor in a magnetic field.
Answer:
We know that a moving charge experiences a magnetic force in a uniform magnetic field. It can be extended for a current conductor placed in a uniform magnetic field, because electric current is the flow of free electrons. Let l be the length of a conductor, A its area of cross – section and n be the number density of free electrons.

Then no. of free electrons in the conductor N=nAl
Let conductor be lying along Y – axis and magnetic field B lying in YY – plane makes angle 6 with Y – axis. Current flows through the coil along the direction of X – axis. Electric current flows through a conductor due to unidirectional flow of free electrons. Therefore, magnetic force acting on each free electron
\(\oint { f }\) = -e\((\vec { { v }_{ d } } \times \vec { B } )\)
Where \(\vec { { v }_{ d } }\) is the drift velocity of electron and e is the charge on an electron. Therefore, total magnetic force acting on the conductor

I \(\vec { l }\) is a current element directed along the direction of current. I \(\vec { l }\) and vd are directed in opposite directions. Therefore, eqn. (2) may be written as

Case I : If θ = 0° , then sinθ = sin 0° = 0
Then from eqn. (4), F = 0
Thus, no magnetic force acts on a current carrying conductor lying parallel to magnetic field.

Case II : If θ = 90° ⇒ sinθ = sin90° = 1
Then p = JlB sin 90° or F = IlB (maximum)
Thus, a current carrying conductor placed perpendicular to a magnetic field experiences maximum magnetic force.

Question 8.
State Fleming’s left – hand rule.
Answer:
Stretch the forefinger, the middle finger and the thumb of your left – hand so that they are mutually perpendicular to each other. If the forefinger points the direction of magnetic field, the middle finger points the direction of current then the thumb indicates the direction of force acting on the conductor.

Question 9.
For circular motion of a charged particle in a uniform magnetic field obtain the expression for radius of path and periodic time of revolution.
Or
Discuss the motion of the charged particle in a uniform magnetic field with the initial velocity perpendicular to magnetic field.
Answer:
Consider a charged particle with charge q which is moving with a velocity v in a magnetic field of intensity B. Then, the maximum Lorentz force acting on the charged particle will be
F = qvB
and the direction of the force is perpendicular to v and B which is according to Fleming’s left – hand rule. So, no work will be done by the force on the charge because d W = Fd cosθ, here 0= 90°, hence d W = 0. It means that kinetic energy or the speed of the charged particle will be constant. So, the charge will move on a circular path.

Now, for circular motion Lorentz force provides the necessary centripetal force.
Let the mass of the charged particle be m and the radius of circular path be r.
Then, Lorentz force = Centripetal force
or qvB = \(\frac { { mv }^{ 2 } }{ r }\)
or r = \(\frac { mv}{ qB }\) … (1)
or r = \(\frac { p}{ qB }\) … (2)
Where, mv = p = Momentum of the particle.
Hence, from eqn. (2), the radius of circular path is directly proportional to the momentum.
Again, angular velocity, w = \(\frac { v}{ r }\) = \(\frac { qB}{ m }\)
Frequency, v = \(\frac { w}{ 2π }\) = \(\frac { qB}{ 2πm }\)
and T = \(\frac { 1}{ v }\)
= \(\frac {2πm}{qB}\)

Question 10.
When the current flows in opposite direction in two parallel wires, both repel each other, why?
Answer:
If direction of current are opposite in the conductor then according to Fleming left hand rule the direction of force acting on the conductor CD will be in the plane of the paper and opposite to conductor AB. The direction of force acting on AB due to CD will be perpendicular to AB and opposite to CD on the plane of paper. Obviously the conductor will be repel each other.

Question 11.
When the current flows in the same direction in two “ parallel wires. Both attract each other, why?
Answer:
In the direction of the current in both the conductors are same, then according to Fleming left hand rule, the direction of force acting on the conductor CD carrying current will be in the plane of paper perpendicular to conductor CD toward the conductor AB on the other hand the direction of force acting in conductor AB will be in the plane of paper perpendicular to conductor AB toward the conductor CD. Obviously the conductor AB and CD will attract each other.

Question 12.
Given two parallel wires carrying currents I₁ and I₂ are kept at a distance d apart. Obtain the expression for force exerted by one on (nt length of another. When will this force be attractive and when will it be repulsive?
Answer:
Let AB and CD be two parallel conductors kept at a distance d apart, current flowing through them is I₁ and I₂ respectively.
A magnetic field due to current I, is produced around AB.
∴ Intensity of magnetic field due to AB at a distance d is
B₁ = \(\frac { { \mu }_{ 0 } }{ 4\pi } .\frac { { 2I }_{ 1 } }{ d }\) Wb/m²
According to right – hand palm rule, the direction of this field is downwards, normal to the plane of the paper.

If another conductor CD carrying current I₂ in the same direction of I₁ is situated in the magnetic field of AB, then force on length l of CD is given by
F = I₂ /B₁ sin 90° = I₂/B₁
or F = I₂l.\(\frac { { \mu }_{ 0 } }{ 4\pi } .\frac { { 2I }_{ 1 } }{ d }\)
or F = \(\frac { { \mu }_{ 0 } }{ 4\pi } .\frac { { 2I }_{ 1 }{ I }_{ 2 }l }{ d } \).
Force acting per unit length on CD will be
\(\frac { F}{ l }\) = \(\frac { { \mu }_{ 0 } }{ 4\pi } .\frac { { 2I }_{ 1 }{ I }_{ 2 }}{ d } \).
This is the required expression.
The direction of magnetic field B, on wire CD is acting inwards. Hence, by Fleming’s left – hand rule, the force F₂ acting on CD will be directed towards AB, hence CD will come near to AB. So, the conductors attract each other, [see Fig. (a)] And when the current flows in opposite direction, they will repel each other, [see Fig. (b)].

Question 13.
Obtain an expression for the torque or the couple acting on a current loop, when it is placed in a magnetic field.
Or
Prove that the torque \(\oint { τ }\) acting bn a rectangular loop is given by \(\oint { τ }\) = \(\oint { m }\) \(\oint { B }\), where \(\oint { m}\) is the magnetic moment of the loop.
Answer:
Consider a rectangular coil ABCD of length ‘l’ and breadth ‘ b’ kept in a magnetic field of strength \(\oint { B }\). Let I be the amount of current flowing through the coil.
Force acting on AB is F₁ = BI/sin90° = BIL. By Fleming’s left hand rule, it comes out of the plane of paper.
Force acting on CD is F₂ = Bl/ sin 90° = Bll. By Fleming’s rule, it goes into the plane of paper.

The forces, F₁ and F₂ are equal in magnitude but act along different line of action, hence they constitute a torque or couple.
At any instant of time, the normal to the coil makes an angle θ w.r.t. magnetic field B. The perpendicular distance between the forces F₁ and F₂ is bsinθ.
Torque acting on the coil is
τ = Magnitude of force × Perpendicular distance between the forces
= BIl x b sinθ
= BI(lb)sinθ
τ = BIAsinθ (∵ lb = A = area of coil)
If the coil consists of N circles, then
τ = NBIAsinθ
This is the expression for the torque acting on a current loop when placed in a magnetic field.
But NIA = m, the magnetic moment of loop.
So τ = mBsinθ
In vector notation, torque r is given by
\(\oint { τ }\) = \(\oint { m }\) \(\oint { B }\), where \(\oint { m}\)
The direction of the torque r is such that it rotates the loop clockwise along the axis of suspension.

Question 14.
Explain the construction of moving coil galvanometer by drawing its diagram; Why is a soft – iron core kept in the moving-coil galvanometer ? Why the pole pieces are made concave?
Answer:
1. A permanent strong horseshoe magnet is taken. Its pole pieces NS are made of cylindrical soft – iron, cut in concave shape. A coil A, is suspended between the pole pieces, by a phosphor bronze wire F. The other end of the coil is connected to a spring Sp. The coil consists of insulated copper wire wound on an aluminium frame and a soft iron cylinder C is fixed within the coil, so that the coil can freely turn around it.

The wire F and spring S_p is connected to the terminals T₁ and T₂. Aconcave mirror M is attached to the wire F, so that the deflection of the coil can be measured with the help of lamp and scale arrangement. All the above arrangement is kept inside a non – magnetic box to protect it by dust, air, etc. The front portion of the box is made of glass and the base is provided by levelling screws.

2. Soft – iron core is used in moving coil galvanometer because :

• The permeability of soft – iron is very high, hence the field intensity increases.
• It makes the field radial.

3. By making pole pieces of magnet concave, the field is made radial, so that the plane of the coil becomes parallel to the magnetic field in all the positions.

Question 15.
Explain the principle of moving – coil galvanometer and find the expression for the current.
Or
What is the principle of moving – coil galvanometer? Prove that the current is proportional to the deflection of the coil.
Answer:
Principle:
Whenever a current is made to pass through a coil placed in a uniform magnetic field, then a torque acts on it which rotates the coil and tries to make it perpendicular to the direction of the field. Let ABCD be a rectangular coil, which is kept in a magnetic field B. such that the sides AB and CD are perpendicular, to field. Let the length of the coil AB be l and breadth BC be b. If I is the current flowing in the coil, then Lorentz force acting on AB and CD will be F = BIl.

The force acting on AB is F₁ which comes out of the plane of paper and on CD is F₂ which goes inside the plane of paper. As the forces are equal in magnitude and opposite in direction along different line of action, hence they produce a couple.

At any instant of time, the axis of coil (i.e., the normal to the coil) makes an angle θ with respect to the magnetic field, then the perpendicular distance between two forces F₁ and F₂ is bsinθ.

Now, torque = Magnitude of force x Perpendicular distance between two forces
= BIl × bsinθ = BIAsinθ
Where, A =lb = Area of the coil.
If N is the number of turns on the coil, then
τ = NBI Asin θ
Initially, when the plane of the coil lies parallel to the magnetic field, then the angle between the magnetic field and normal to the coil is 90°, i.e., θ = 90° therefore sinθ= 1.
∴τ_max =NBIA
This torque is the deflecting torque. Which rotates the coil. As a result, a restoring torque gets developed in the suspension wire which tries to restore the coil back to the initial position.
Let ϕ be the angle of twist and C is the couple for unit twist.
Restoring torque produced = Cϕ
Under equilibrium, deflecting torque = Restoring torque.
∴ NBIA = Cϕ
or I = \(\frac {C}{NBA}\)ϕ
or I = kϕ (where, k = \(\frac {C}{NBA}\)
or I ∝ϕ
This is the principle of moving – coil galvanometer.

Question 16.
What do you understand by the sensitivity of moving – coil galvanometer? Write its expression. On what factors does it depend and how?
Answer:
The current sensitivity of a moving coil galvanometer is defined as the deflection produced by unit current through the coil.
Let ϕ be the deflection produced due to current I, then
I = \(\frac {C}{NBA}\)ϕ
If the current through the galvanometer is I, which produces a deflection ϕ, then
\(\frac {ϕ}{I}\) = \(\frac {NBA}{C}\)
Sensitivity of galvanometer s = \(\frac {ϕ}{I}\)
= \(\frac {NBA}{C}\)

Sensitivity depends on the following factors :

1. N (No. of turns) should be greater. As the nufnber of turns increases, sensitivity increases.
2. For greater sensitivity, magnetic field should be greater. To increase the magnetic field B, a permanent horseshoe magnet must be used. By increasing B, sensitivity increases.
3. Area of the coil : If area increases, sensitivity increases.
4. C (Couple per unit twist) : The value of C should be less for more sensitivity.

Question 17.
What is meant by shunt? If the resistance of a galvanometer is R_g, then calculate the value of the shunt carrying current nth part of total current to pass through the galvanometer.
Answer:
Shunt:
A shunt is a thick copper wire which is joined in parallel with the coil of the galvanometer. It has very low resistance.
Let R_g be the resistance of galvanometer and S be the value of the shunt resistance.

Let I be the total current flow in the circuit. It gets divided as I_g and I_s: where I_g is the current flowing in galvanometer and I, in the shunt resistance (S).
∴ I = I_g + I_s … (1)
Now, potential difference across galvanometer = I_g.R_g
and Potential difference across shunt = I_s.S.
As galvanometer and shunt are in parallel, hence potential difference will be equal
i.e.,

This is the value of shunt resistance.
Adding 1 to both sides of eqn. (2), we get

The above equation gives the value of current flow through the galvanometer in turns of total current.
If the current passing through the galvanometer is nth part of the total current, then
\(\frac { { I }_{ g } }{ I }\) = \(\frac {1}{n}\)
Eqn. (4) becomes
\(\frac {1}{n}\) = \(\frac { s }{ { R }_{ g }+S }\)
or nS = R_g + S
or nS – S = R_g
or S(n -1) = R_g
or S = \(\frac { { R }_{ g } }{ (n-1) }\) … (6)
Hence, for the nth part of total current to pass through the galvanometer, the resistance of the shunt should be (n – l)th of the resistance of galvanometer.

Question 18.
How a galvanometer can be converted to ammeter and voltmeter?
Answer:
Conversion of galvanometer into ammeter:
Since, the coil of the galvanometer has low resistance, so to convert it into ammeter, a low resistance (called shunt) is joined in parallel, so that most of the current passes through the shunt and very less current passes through the coil of galvanometer.

Derive up to eqn. (3) from Short Ans. Type Q. No. 17.
Hence, by joining a shunt resistance of value
S = \(\frac { { I }_{ g }{ R }_{ g } }{ I-{ I }_{ g } }\)
So, the galvanometer gets converted to an ammeter.

Conversion of galvanometer into voltmeter:
The resistance of voltmeter is high, So to convert a galvanometer into a voltmeter, a high resistance wire is connected wire is connected in series to the coil of galvanometer, [see fig.(b)].

Suppose R_g be the resistance of galvanometer and R is the resistance of wire connected A in series. Let I be the current flowing in the galvanometer.
In order to convert a galvanometer into a voltmeter of range (0 – V) volts, we have from adjacent figure
The total potential difference between A and B will be
V = I_g(R_g + R)
or R_g + R = \(\frac { V }{ { I }_{ g } }\)
or R = \(\frac { V }{ { I }_{ g } }\) – R_g.
This is the expression and the value of the resistance required to convert the galvanometer to voltmeter of range 0 to V.

Question 19.
What is a shunt? Write its uses. What are advantages and disadvantages of shunt?
Answer:
Shunt:
It is a wire of low resistance, connected in parallel to the coil of a galvanometer.

Uses:
A galvanometer is converted into an ammeter by using a shunt.

Advantages:

1. It protects the coil of the galvanometer from burning as well as the breaking of the pointer.
2. As the shunt is connected in parallel, the resultant resistance becomes less. So, when the shunted galvanometer (ammeter) is joined in series, then the value of the current does not change.

Disadvantages:
Due to shunt, the sensitivity of galvanometer is reduced. So, it should be removed from the galvanometer when we have to obtain null point.

Moving Charges and Magnetism Long Answer Type Questions

Question 1.
Derive an expression for the intensity of magnetic field at a point on the axis of a circular current loop.
Or
Obtain an expression for the intensity of the magnetic field at a point on the axis of a circular coil.
Answer:
Magnetic field at a point on the axis of a circular current loop:
Let a be the radius of a circular loop and current 1 is flowing through it in the direction shown in the figure. A point P is considered on the axis of the loop, at a distance x from the centre O, at which the intensity of the magnetic field is to be determined.

The plane of the loop is normal to the plane of the paper and its axis OP lies on the plane of the paper. Let the loop be divided into so many small elements, each of length dl, let one of such small part is AB.
∴ The intensity of the magnetic field at P, due to dl, is given by

The direction of dB is along PR, normal to CP. Let ∠CPO = ϕ
Resolving dB in two parts, we get

1. dB sinϕ, along OP and
2. dB cosϕ, along PN, normal to OP.

If another small element dl is considered, diametrically opposite to AB, i.e., A’B’.
∴ Intensity of magnetic field at P, due to A’B’ will be
dB = \(\frac { { \mu }_{ 0 } }{ 4\pi } .\frac { I.dl }{ { r }^{ 2 } }\)
Again, resolving dB, we get

1. dB sin0, along OP and
2. dB cos0, along PN’, normal to OP.

As the directions of PN and PN’, are opposite, hence they will cancel the effect of each other. Similarly, all the resolved parts, perpendicular to OP will be cancelled out. But the components along the direction AP, will be summed up.
∴ Intensity of magnetic field due to the circular loop at point P will be

Question 2.
State Biot – Savart law and with the help of it derive an expression for magnetic field intensity at a point situated at a distance from a current carrying straight wire of infinite length.
Answer:
Biot – Savart law:
Let AB be a conductor carrying current I. Consider a small line element dl of the conductor, due to which the magnetic field dB is produced at point P, then the strength of the magnetic field \(\vec { (dB) }\) depends on the following factors :
(i) The field is directly proportional to current I.
i.e., dB ∝I
(ii) The field is directly proportional to the length of element,
i.e., dB ∝ dl

(iii) The field is directly proportional to the sine of angle between the line joining the point and dl.
i.e., dB ∝ sinθ
(iv) The field is inversely proportional to the square of the distance between the observation point and line element.
i.e.,
dB ∝ \(\frac { 1 }{ { r }^{ 2 } }\)
Combining all the four points,we get
dB ∝ \(\frac { Idl sinθ }{ { r }^{ 2 } }\)
or dB ∝ K\(\frac { Idl sinθ }{ { r }^{ 2 } }\) … (1)
Where, K is constant of proportionality. Its value depends upon the system of units
In C.G.S system, k = 1
∴ dB ∝ K\(\frac { Idl sinθ }{ { r }^{ 2 } }\) gauss … (2)
In M.K.S. system, K = \(\frac { { μ }_{ 0 } }{ 4π }\)
Where, μ₀ = Permeability of free space.
∴ dB = \(\frac { { μ }_{ 0 } }{ 4π }\) \(\frac { Idl sinθ }{ { r }^{ 2 } }\) Wb/m₂ … (3)
or dB =10^-7 [/latex] \(\frac { Idl sinθ }{ { r }^{ 2 } }\) Wb/m₂ … (4)
The relations given by eqns. (2), (3) and (4) are called Biot – Savart law.
The direction of the magnetic field \(\vec { dB }\) is always perpendicular to the plane containing \(\vec { dl }\) and \(\vec { r }\) and is given by the right – hand screw rule for the cross product of vectors.

Unit of electric current:
1. In C.GS. system : If dl= 1cm, r= 1cm, sinθ = 1 i.e., 9 = 90° and dB = 1 gauss, then from eqn. (2) I = 1 electromagnetic unit (e.m.u.).
For 9= 90°, the conductor should be taken as a part of circle, as the radius is always perpendicular to the circumference. Thus, 1 e.m.u. of current is that current which produces a field of 1 oersted at the centre of the conductor of length 1 cm, kept in the form of an arc of a circle of radius 1 cm.

2. In M.K.S. system: If dl =1m, r = 1m, sinθ = 1 and dB = 10^-7 Wb/m², then from eqn. (4)
I = 1 ampere.
Thus, 1 ampere of current is that current which produces a field of 10^-7 Wb/m², at the centre of tWconductor of length 1m.

Consider a long straight conductor XY which is on the plane Y of paper and current flow through it is I, which flows from X to Y. c Then magnetic field has to be found at position P, which is situated t at a distance a (distance measured perpendicularly from the wire) from the wire.
∴PC = a
To find out the total magnetic field at P, we have to first find out the magnetic field due to small line element \(\vec { dl }\), which is situated at a distance l from C. On integrating the magnetic field due to line element \(\vec { dl }\) , we can get the total magnetic field.
Let \(\vec { r }\) be the position vector of P with respect to the line element \(\vec { dl }\) and θ is the angle
between the line element \(\vec { dl }\) and \(\vec { r }\).
By Biot – Savart law,
dB = \(\frac { { \mu }_{ 0 } }{ 4\pi } .\frac { I.dl }{ { r }^{ 2 } }\)
We have to find out the magnetic field due to line element \(\vec { dl }\) at P, which is situated at r from \(\vec { dl }\) . The position of \(\vec { dl }\) can vary, hence θ can change, so we have to find out the value of sinθ and dl. For that, consider right angled triangle POC.

Putting the values of sinθ, r and dl from eqns. (2), (3) and (4) respectively in eqn. (1), we get

Eqn. (5) is the magnetic field due to line element dl. To find out the total magnetic field, integrating both sides under limits from ϕ₁ to ϕ₂ (-ϕ₁ is taken because it is clock wise or below the line joining CP and ϕ₂ is taken because it is anticlockwise or above the line joining CP).

For an infinitely long conductor and if the observation point is very near, then

Question 3.
Describe the cyclotron under the following points :

1. Construction
2. Principle and working process.

Or
What is a cyclotron? Write its principle. Obtain the expression for the cyclotron frequency and the maximum energy of the charged particle when it hits the target.
Answer:
Principle:
It is based on the principle that when a positively charged particle is made to move again and again in a high frequency electric field and using strong magnetic field, then it gets accelerated and acquires sufficiently large amount of energy.

Construction:
It consist of two hollow D – shaped metallic chambers D₁ and D₂ called dees. These dees are separated by a small gap where a source of positively charged particle is placed. Dees are connected to a high frequency oscillator, which provide high frequency electric field across the gap of the dees. This arrangement is placed between two poles of a strong electromagent. The magnetic field due to this electromagnet is perpendicular to the plane of the dees.

Working:
If a positively charged particle (proton) is emitted from O, when D₂ is negatively charged and the dee D₁, is positively charged, it will accelerate towards D₂. As soon as it enters D₂, it is shielded from the electric field by metallic chamber (enclosed space). Inside D₂, it moves at right angles to the magnetic field and hence describes a semi – circle inside it. After completing the semicircle, it enters the gap between the dees at the time when the polarities of the dees have been reversed.

Now, the proton is further accelerated towards D₁. Then it enters D₁ and again describes the semicircle due to the magnetic field which is perpendicular to the motion of the proton. This motion continues till the proton reaches the periphery of the dee system. At this stage, the proton is deflected by the deflecting plate which then comes out through the window and hits the target.

Theory:
When a proton (or any other positively charged particle) moves at right angle to the magnetic field B inside the dees, Lorentz force acts on it.
i. e., F = qvB sin 90° = qvB
Where, q = Charge of particle and v = Velocity of particle.
The force provides the necessary centripetal force \(\frac { m{ v }^{ 2 } }{ r }\) to the charged particle to move in a circular path of radius r.
∴ qvB = { m{ v }^{ 2 } }{ r }[/latex]
or r = \(\frac {mv}{qB}\) … (1)
Time taken to complete one semicircle inside a dee,
t = \(\frac {Distance}{Speed}\) = \(\frac { πr}{v}\)
or t = \(\frac { π}{v}\) × \(\frac { mv}{qB}\) [from eqn.(1)]
t = \(\frac { πm}{qB}\) … (2)
Thus, time taken to complete one semicircle does not depend upon radius of path. If T is the time – period of the alternate electric field, then the polarities of the dees changes in time 772.
i.e., \(\frac {T}{2}\) = t = \(\frac {πm}{qB}\)
or T = \(\frac {2πm}{qB}\) … (3)
So, cyclotron frequency or magnetic resonance frequency,
v = \(\frac {1}{T}\) = \(\frac {qB}{2πm}\) … (4)
Energy gained by a positively charged particle is given by
E = \(\frac {1}{2}\)mv²
From eqn (1), v = \(\frac {qBr}{m}\)
so, E = \(\frac {1}{2}\)m\(\frac { { q }^{ 2 }{ B }^{ 2 }{ r }^{ 2 } }{ { m }^{ 2 } } \)
= \(\frac { { q }^{ 2 }{ B }^{ 2 }{ r }^{ 2 } }{ { 2m } }\)
Maximum energy is gained by the positively charged particle when it is at the periphery of the dees (r is maximum), i.e.,
E_max = \(\frac { { q }^{ 2 }{ B }^{ 2 } }{ { 2m } }\) r²_max

Question 4.
Obtain an expression for magnetic field due to a solenoid using Ampere’s circuital law.
Answer:
Consider a very long solenoid having n turns per unit length carrying current I. The magnetic field inside the solenoid is uniform and directed along the axis of solenoid.

Consider a rectangular Amperian loop abed in a solenoid. Magnetic field B is uniform within the solenoid. Let the length of the Amperian loop be h.
∴Total number of turns in Amperian loop = nh.
The integral \(\oint { \vec { B } .\vec { dl } }\) is basically equal to the sum of four integrals

Comparing eqns.(2) and (3)
Bh = µ₀nhI
⇒ B = µ₀nI.

Question 5.
Explain the experiment to find reduction factor of a tangent galvanometer under following points :

1. Formula
2. Circuit diagram
3. Observation table
4. Any two precautions.

Answer:
1. Formula : i = ktanθ or k = \(\frac {i}{tanθ}\)
Where i = Current flowing through coil, and
θ = Deflection in magnetic needle.

2. Circuit diagram :
TG = Tangent Galvanometer,
K = Reversing key,
B = Cell, Rh = Rheostat,
A = Ammeter.

3. Observation table:

4. Precautions :

There should be no magnet near tangent galvanometer.
After aligning in magnetic meridian, the tangent galvanometer should not be moved.

Moving Charges and Magnetism Numerical Questions

Question 1.
The frequency of a cyclotron oscillator is 10 MHz.What should be the magnetic field required to accelerate a proton (e = 1.6 x 10^-19C, m =1.67 x 10^-27kg)
Solution:
f = \(\frac {qB}{2πm}\)
or B = \(\frac {2πmf}{q}\)
Given : m = 1.67 x 10^-27kg, f = 10 x 10⁶Hz, q = e = 1.6 x 10^-19

Question 2.
A particle having 100 times charge of an electron is revolving in a circle of radius 0-8 metre in each second. Calculate the intensity of magnetic field.
Solution:
Formula: B = \(\frac { { \mu }_{ 0 } }{ 4\pi } .\frac { 2\pi I }{ R }\)
Given : q = 100 x 1.6 x 10^-19
= 1.6 x 10^-17 coulomb, R = 0.8 metre
Putting the value in formula, we get I = \(\frac {q}{t}\)
\(\frac { 1.6\times { 10 }^{ -17 } }{ 1 }\) = 1.6 x 10^-17
B = \(\frac { { \mu }_{ 0 } }{ 4\pi } .\frac { 2\pi \times 1.6\times { 10 }^{ -17 } }{ 0.8 }\) or B = 10^-2µ₀

Question 3.
Calculate the torque on a 20 turns square coil of side 10 cm carrying a current of 12 A, when placed, making an angle of 30° with the magnetic field of 0.8 T.
Solution:
Given : A = 100cm² 100 x 10^-4m² = 10^-2m² n = 20, I = 12A, B = 0.8T, ϕ = 30°
Formula: τ = nIABsinϕ
= 20 x 12 x 10² x 0. 8sin30°
= 20 x 12 x 0.8 x 10² x \(\frac {1}{2}\)
= 96 x 10² = 0.96 N – m.

Question 4.
Resistance of a Galvanometer is 50 ohms, when 0.01 Acurrent flows through it, full scale defections is obtained. How it can be converted into

1. 5 A range ammeter and
2. 5 volts range voltmeter.

Solution:
1. Given : G = 50 ohm, i_g = 0.01 A, I = 5A
Formula : S = \(\frac { { I }_{ g }G }{ I-{ I }_{ g } }\)
Putting the value in the formula are get = \(\frac {0.01 x 50}{5-0.01}\) = \(\frac {0.5}{4.99}\)

2. Given : V = 5 vol
Formula : R = \(\frac { V }{ { I }_{ g } }\) – G
Putting the value in the formula are get
R = \(\frac {5}{0.01}\) – 50 = 500 – 50 = 450 ohms.

Question 5.
Find the magnitude of magnetic field at the centre of a circular coil of radius 10 cm having 100 turns. Current flowing through the coil is 1A. (NCERT Solved Example)
Solution:
Given, R = 10 cm = 10 x 10^-2m; N = 100; I = 1A;
B = \(\frac { { \mu }_{ 0 }NI }{ 2R }\) = \(\frac { 4\pi \times { 10 }^{ -7 }\times 100\times 1 }{ 2\times 10\times { 10 }^{ -2 } }\)
B = 2π x 10^-4
= 6.28 x 10^-4 tesla.

Question 6.
10 A current is flowing through a straight conductor. Determine the intensity of magnetic field at a distance 10 m from it.
Solution:
Formula :B = \(\frac { { \mu }_{ 0 } }{ 4\pi } .\frac { 2I }{ d }\)
Given: I = 10 Aandd = 10m.
Substituting the values in the formula, we get
B = 10^-7 x \(\frac {2×10}{10}\)
∴B = 2 x 10^-7Wb/m².

Question 7.
An ammeter of resistance 99 Ω, gives full – scale deflection with 10^-4A current. What arrangement is required to measure a current of 1A by it? Calculate the resistance of ammeter.
Solution:

Question 8.
A solenoid of length 0.5 m has a radius of 1 cm and is made up of 500 turns. It carries a current of 5A. What is the magnitude of the magnetic field inside the solenoid? (NCERT)
Solution:
Given, l = 0.5 m, r = 1 cm = 1 x 10^-2 m, N = 500; I = 5A Number of turns per unit length
Number of turns per unit length
n = \(\frac {N}{l}\) = \(\frac {500}{0.5}\)
Here l >> r
∴Magnetic field inside the solenoid
B = µ₀nI
= 4π x 10^-7 x \(\frac {500}{0.5}\) x 5
B = 6.28 x 10^-3tesla.

Question 9.
A wire through which a current of 8A is flowing makes an angle of 30° with the direction of magnetic field of 0.15 tesla. Calculate the force acting per unit length of wire.
Solution:
Given : I = 8A, B = 0.15T, θ = 30°, F =?
formula: F = BIlsinθ
⇒ \(\frac {F}{l}\) = BIlsinθ
= 0.15 x 8 x sin30°
= 0.15 x 8 x \(\frac {1}{2}\) = 0.6N/m.

Question 10.
Two parallel wires A and B are carrying currents 10 A and 2 A respectively, in opposite directions. If the length of the wire A is infinite and length of B is 1 metre, calculate the force on B situated at a normal distance of 10 cm from A.
Solution:
Formula : \(\frac { { \mu }_{ 0 } }{ 4\pi } \frac { 2{ I }_{ 1 }{ I }_{ 2 } }{ d } \times l\)
= 10^-7\(\frac { 2{ I }_{ 1 }{ I }_{ 2 } }{ d } \times l\)
Given : I₁ = 10 A, I₂ = 2A , l = 1 m, d = 0.1 m
∴ F = 10^-7 × \(\frac {2×10×2×1}{0.1}\)
= 400 x 10^-7= 4.0 x 10^-5N.

MP Board Class 12th Physics Important Questions

MP Board Class 12th Maths Important Questions Chapter 5A Continuity and Differentiability

Continuity and Differentiability Important Questions

Continuity And Differentiability Objective Type Questions:

Question 1.
Choose the correct answer:

Question 1.
If x = at², y = 2at, then \(\frac{dy}{dx}\) will be:
(a) t
(b) t²
(c) \(\frac{1}{t}\)
(d) \(\frac { 1 }{ t^{ 2 } } \)
Answer:
(c) \(\frac{1}{t}\)

Question 2.
If y = 2\(\sqrt { cot(x^{ 2 }) } \) ,then \(\frac{dy}{dx}\) will be:

Answer:
(a)

Question 3.
The value of \(\frac{d}{dx}\) (x³ + sin x²) is to be:
(a) 3x² + cos x²
(b) 3x² + x sin x²
(c) 3x² + 2x cos x²
(d) 3x² + x cos x²
Answer:
(c) 3x² + 2x cos x²

Question 4.
The value of \(\frac{d}{dx}\) a^x is to be:
(a) a^x
(b) a^x log_a e
(c) a^x log_e a
(d) \(\frac { a^{ x } }{ log_{ e }a } \)
Answer:
(c) a^x log_e a

Question 5.
If y = 500e^7x + 600e^-7x, then the value of \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) will be:
(a) 45 y
(b) 47 y
(c) 49 y
(d) 50 y
Answer:
(c) 49 y

Question 2.
Fill in the blanks:

1. Differential coefficient of cos x⁰ w.r.t x is ……………………………..
2. Differential coefficient of e^log_ea w.r.t x is ……………………………….
3. Differential coefficient of log_e a w.r.t x is ………………………………
4. Differential coefficient of a^x w.r.t x is ……………………………….
5. Differential coefficient of sin 3x w.r.t x is ……………………………….
6. If y = sin^-1 (2x \(\sqrt { (1-x^{ 2 }) } \)), then \(\frac{dy}{dx}\) = ………………………………
7. Differential coefficient of sin x w.r.t. cos x is …………………………………..
8. The value of \(\frac{d}{dx}\) (log tan x) is ………………………………………
9. Differential coefficient of log (log sin x) ………………………………
10. If x = y\(\sqrt { (1-y^{ 2 }) } \), then \(\frac{dy}{dx}\) will be …………………………………
11. n^th differentiation of sin x will be ………………………………………
12. If y = \(\sqrt { x+\sqrt { x+……..\infty } } \), then \(\frac{dy}{dx}\) will be ……………………………….
13. If x = r cos θ, y = r sin θ, then \(\frac{dy}{dx}\) will be ………………………..
14. Differential coefficient of e^x w.r.t \(\sqrt { x } \) will be ………………………….

Answer:

1. – \(\frac { \pi }{ 180 } \) sin x⁰
2. 0
3. 0, 4
4. log_e a.a^x
5. cos 3x
6. \(\frac { 2 }{ \sqrt { 1-x^{ 2 } } } \)
7. – cot x
8. 2 cosec 2x
9. \(\frac { cotx }{ logsinx } \)
10. \(\frac { \sqrt { 1-y^{ 2 } } }{ 1-2y^{ 2 } } \)
11. sin (\(\frac { n\pi }{ 2 } \) + x)
12. \(\frac { 1 }{ 2y-1 } \)
13. – cot θ
14. 2\(\sqrt { x } \)e^x.

Question 3.
Write True/False:

1. Differential coefficient of e^log_ex is \(\frac{1}{x}\)?
2. If f(x) = \(\sqrt { x } \); x>0, then value of f'(2) is \(\frac { 1 }{ 2\sqrt { 2 } } \)?
3. Any function f(x) is said to be differentiatiable at any point x = a when Lf'(a) ≠ Rf'(a)?
4. Differential coefficient of sec^-1a w.r.t x is 0?
5. If y = Ae^mx + Be^-mx, then \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = – m²y?
6. If y = sin^-1( \(\frac { x-1 }{ x+1 } \) ) + cos^-1 ( \(\frac { x-1 }{ x+1 } \) ), then \(\frac{dy}{dx}\) = 0?
7. Every differentiatiable function is continous?
8. Differential coefficient of a^2x is a^2x log_ea?

Answer:

1. Flase
2. True
3. Flase
4. False
5. True
6. True
7. True
8. Flase

Question 4.
Match the Column:

Answer:

1. (d)
2. (e)
3. (a)
4. (f)
5. (h)
6. (g)
7. (c)
8. (b)

Question 5.
Write the answer in one word/sentence:

1. Find differential coefficient of \(\frac { 6^{ x } }{ x^{ 6 } } \) w.r.t. x?
2. Find differential coefficient of y = ^log_etanxw.r.t x?
3. Find n^th derivative of a^x?
4. If y = sin(ax + b), then find the value of \(\frac { d^{ 2 }y }{ dx^{ 2 } } \)?
5. If x² + y² = sin xy, then find the value of \(\frac{dy}{dx}\)?
6. Find differential coefficient of log tan \(\frac{x}{2}\) w.r.t. x?
7. Find differential coefficient of sin^-1 \(\frac { 2x }{ 1+x^{ 2 } } \) w.r.t. x?
8. Find differential coefficient of e^-log_ex w.r.t x?

Answer:

1. \(\frac { 6^{ x } }{ x^{ 6 } } \) [log 6 – \(\frac{6}{x}\) ]
2. sec² x
3. a^x(log_ea)ⁿ
4. -a²y
5. \(\frac { ycosxy-2x }{ 2y-xcosxy } \)
6. cosec x,
7. \(\frac { 2 }{ 1+x^{ 2 } } \)
8. – \(\frac { 1 }{ x^{ 2 } } \)

Continuity And Differentiability Short Answer Type Questions

Question 1.
Find all the points of discontinuity of f, when f is defined as:
f(x) = \(\left\{\begin{array}{lll}
{2 x+3,} & {\text { if }} & {x \leq 2} \\
{2 x-3,} & {\text { if }} & {x>2}
\end{array}\right.\) (NCERT)
Solution:
For x< 2, f(x) = 2x + 3 is polynomial function.
Hence, for x < 2, f(x) is continuous function. For x > 2, f(x) = 2x – 3 is polynomial function.
Hence, x > 2, f(x) is continous.
Now, we shall examine the continuty of f(x) at x = 2 only.
Put x = 2 + h,
When x → 2, then h → 0

= 2(2 + 0) – 3 = 4 – 3 = 1.
Put x = 2 – h,
When x → 2, then h → 0

= 2(2 – 0) + 3 = 7
f(2) = 2(2) + 3 = 7

Hence, f(x) is discontinous at x = 2 only.

Question 2.
Find all the points of discontunity of f, when f is defined as follow:
f(x) = \(\left\{\begin{array}{ccc}
{\frac{|x|}{x},} & {\text { if }} & {x \neq 0} \\
{0} & {\text { if }} & {x=0}
\end{array}\right.\). (NCERT)
Solution:
Hence, we shall examine the continuty of f(x) at x = 0 only,
Put x = 0 + h,
When x → 0, then h → 0

Put x = 0 – h,
When x → 0, then h → 0

= -1
Given: f(0) = 0

Hence, the given function f(x) is discontinous at x = 0.

Question 3.
Examine the continuty of function f(x) at point x = 0?
f(x) = \(\left\{\begin{array}{cc}
{\frac{1-\cos x}{x^{2}},} & {x \neq 0} \\
{\frac{1}{2},} & {x=0}
\end{array}\right.\)
Solution:
f(x) = \(\frac { 1-cosx }{ x^{ 2 } } \), when x ≠ 0.
Put x = 0 + h, when x → 0, then h → 0

Again, put x = 0 – h, when x → 0, then h → 0

Hence, f(x) is continous at x = 0.

Question 4.
Function f is defined as:
f(x) = \(\left\{\begin{aligned}
\frac{|x-4|}{x-4} ; & x \neq 4 \\
0 ; & x = 4
\end{aligned}\right.\)
Then prove that function f is continous function for all points except x = 4?
Solution:

Hence, for x = 4 the function f(x) is dicontinous

When x < 4 then f(x) = -1 which is constant function Hence, it is continous function when x > 4 then f(x) = 1 which is constant function.
Hence, it is continous function
The given functions f is continous at all points except x = 4. Proved.

Question 5.
Find the value of k for which the function
f(x) = \(\left\{\begin{array}{c}
{\frac{k \cos x}{\pi-2 x}, \text { if } x \neq \frac{\pi}{2}} \\
{3, \text { if } x=\frac{\pi}{2}}
\end{array}\right.\)
is contionuous at x = \(\frac { \pi }{ 2 } \). (NCERT)
Solution:
Put x = \(\frac { \pi }{ 2 } \) + h,
When x → \(\frac { \pi }{ 2 } \), then h → 0


\(\frac{k}{2}\) × 1 = \(\frac{k}{2}\)
Put x = \(\frac { \pi }{ 2 } \) – h
When x → \(\frac { \pi }{ 2 } \), then h → 0

\(\frac{k}{2}\) × 1 = \(\frac{k}{2}\)
Given that f ( \(\frac { \pi }{ 2 } \) ) = 3
The given function is continous,

\(\frac{k}{2}\) = \(\frac{k}{2}\) = 3
k = 6.

Question 6.
Find the value of k, if function
f(x) = \(\left\{\begin{array}{lll}
{k x+1,} & {\text { if }} & {x \leq \pi} \\
{\cos x,} & {\text { if }} & {x>\pi}
\end{array}\right.\) is continous at x = π? (NCERT)
Solution:
Put x = π + h,
When x → π, then h → 0

= cos (π + 0)
= -1.
Put x = π – h,
When x → π, then h → 0

= k(π – 0) + 1
= πk + 1
f(π) = kπ + 1
∴ The given function is continous at x = π

-1 = kπ + 1 = kπ + 1
kπ = -2
k =- \(\frac { 2 }{ \pi } \)

Question 7.
Function f is continous at x = 0:
f (x) = \(\left\{\begin{array}{c}
{\frac{1-\cos k x}{x \sin x} ; x \neq 0} \\
{\frac{1}{2} \quad ; x=0}
\end{array}\right.\) Find the value of k?
Solution:
Given:
f(x) = \(\frac { 1-coskx }{ xsinx } \), x ≠ 0


Given: f(0) = \(\frac{1}{2}\)

Question 8.
Find the relationship between a and b so the following function f defined by:
f(x) = \(\left\{\begin{array}{lll}
{a x+1,} & {\text { if }} & {x \leq 3} \\
{b x+3,} & {\text { if }} & {x>3}
\end{array}\right.\) is continous at x = 3. (NCERT; CBSE 2011)
Solution:
Put x = 3 + h,
When x → 3, then h → 0

= b(3 + 0) + 3
= 3b + 3
Put x = 3 – h,
When x → 3, then h → 0

= a(3 – 0) + 1
= 3a + 1
f(3) = 3a + 1
The given function is continous at x = 3.

3b + 3 = 3a + 1 = 3a + 1
3a + 1 = 3b + 3
3a = 3b + 2
a = b + \(\frac{2}{3}\).

Question 9.
Prove that the funcion f(x) = |x – 1|, x ∈ R is not differentiable at x = 1? (NCERT)
Solution:
Given:

f(1) = 1 – 1 = 0
Put x = 1 – h, when x → 1, then h → 0

Put x = 1 + h, when x → 1, then h → 0

Lf'(1) ≠ Rf'(1)

Question 10.
Show that the function:
f(x) = \(\left\{\begin{aligned}
x-1, & \text { if } x<2 \\
2 x-3, & \text { if } x \geq 2
\end{aligned}\right.\), is not differentaible at point x = 2?
Solution:
We know that:
RHD =

From the above, it is clear that,
LHD at x = 2 ≠ RHD at x = 2
∴ f(x) is not differentiable at x = 2. Proved.

Question 11.
Determine the function of defined by
f(x) = \(\left\{\begin{array}{cc}
{x^{2} \sin \frac{1}{x},} & {\text { when } x \neq 0} \\
{0,} & {\text { when } x=0}
\end{array}\right.\) in continous function? (NCERT)
Solution:
Here, f(0) = 0


= 0 × a finite quantiy, [∵ sin \(\frac{1}{h}\) is between -1 and 1]
= 0

Hence, the given function is continous at x = 0.

MP Board Class 12 Maths Important Questions

MP Board Class 12th Maths Important Questions Chapter 4 Determinants

Determinants Structure Important Questions

Determinants Structure Objective Type Questions:

Question 1.
Choose the correct answer:

Question 1.
If A is a square matrix of order 3 × 3, then value of |Adj. A| will be:
(a) |A|
(b) |A|²
(c) |A|³
(d) 3|A|
Answer:
(b) |A|²

Question 2.
If a, b, c are in Arithematic series, then value of determinant \(\left|\begin{array}{ccc}
{x+2} & {x+3} & {x+2 a} \\
{x+3} & {x+4} & {x+2 b} \\
{x+4} & {x+5} & {x+2 c}
\end{array}\right|\) will be:
(a) 0
(b) 1
(c) x
(d) 2x
Answer:
(a) 0

Question 3.
Matrix A = \(\begin{bmatrix} 2 & 3 \\ 1 & 2 \end{bmatrix}\), then A^-1 will be:
(a) A^-1 = \(\begin{bmatrix} 2 & -3 \\ -1 & 2 \end{bmatrix}\)
(b) A^-1 = \(\begin{bmatrix} 2 & -3 \\ 1 & -2 \end{bmatrix}\)
(c) A^-1 = \(\begin{bmatrix} -2 & 3 \\ -1 & 2 \end{bmatrix}\)
(d) A^-1 = \(\begin{bmatrix} -2 & 3 \\ 1 & -2 \end{bmatrix}\)
Answer:
(a) A^-1 = \(\begin{bmatrix} 2 & -3 \\ -1 & 2 \end{bmatrix}\)

Question 4.
If ω is the cube roots of unitary, then \(\left|\begin{array}{ccc}
{\mathbf{1}} & {\omega} & {\omega^{2}} \\
{\omega} & {\omega^{2}} & {1} \\
{\omega^{2}} & {1} & {\omega}
\end{array}\right|\) =
(a) 1
(b) 0
(c) ω
(d) ω²
Answer:
(b) 0

Question 5.
Determinat \(\left|\begin{array}{ccc}
{a+b} & {a+2 b} & {a+3 b} \\
{a+2 b} & {a+3 b} & {a+4 b} \\
{a+4 b} & {a+5 b} & {a+6 b}
\end{array}\right|\) =
(a) a² + b² + c² – 3abc
(b) 0
(c) a³ + b³ + c³
(d) None of these
Answer:
(b) 0

Question 2.
Fill in the blanks:

1. If \(\begin{vmatrix} 3 & m \\ 4 & 5 \end{vmatrix}\) = 3, then m = ………………………..
2. In determinant \(\begin{vmatrix} 2 & -3 \\ 1 & -2 \end{vmatrix}\), the cofactor of element – 3 is ………………………..
3. If A = \(\left|\begin{array}{lll}{1} & {0} & {1} \\ {0} & {1} & {2} \\ {0} & {0} & {4}\end{array}\right|\), then the value of |3A| is …………………………..
4. The value of determinant \(\begin{vmatrix} 1 & log_{ b }a \\ log_{ a }b & 1 \end{vmatrix}\) will be ……………………………
5. The value of determinant \(\begin{vmatrix} cos70^{ \circ }\quad & sin20^{ \circ } \\ sin70^{ \circ } & cos20^{ \circ } \end{vmatrix}\) will be ………………………

Answer:

1. 3
2. -1
3. 27A
4. 0
5. 0

Question 3.
Write True/False

1. The value of determinant \($\left|\begin{array}{ccc}{0} & {a} & {-b} \\ {-a} & {0} & {-c} \\ {b} & {c} & {0}\end{array}\right|$\) is abc?
2. The maximum value of determinant
   \(\left|\begin{array}{ccc}
   {1} & {1} & {1} \\
   {1} & {1+\sin \theta} & {1} \\
   {1} & {1} & {1+\cos \theta}
   \end{array}\right|\) is \(\frac{1}{2}\)?
3. If A is the matrix of order 3 × 3, then find the value of |kA| will be k²|A|²?
4. If \(\begin{vmatrix} x\quad & 2 \\ 18 & x \end{vmatrix}\) = \(\begin{vmatrix} 6\quad & 2 \\ 18 & 6 \end{vmatrix}\), then find the value of x is ± 3?
5. The value of the determinant \(\begin{vmatrix} 1\quad & \omega \\ \omega & -\omega \end{vmatrix}\) is 1?

Answer:

1. True
2. True
3. Flase
4. Flase
5. True

Question 4.
Write the answer in one word/sentence:

1. How many number of value k for which the linear equation 4x+ ky + 2z = 0, kx + 4y + z = 0, 2x + 2y + z = 0 passes a non – zero solution?
2. If α, β are the roots of equation 2x² + 3x + 5 = 0, then find the value of \(\left|\begin{array}{lll}
   {0} & {\beta} & {\beta} \\
   {\alpha} & {0} & {\alpha} \\
   {\beta} & {\alpha} & {0}
   \end{array}\right|\)?
3. If area of the traingle with vertices (2, -6), (5, 4) and (k, 4) be 35 square units, then find the value of k?
4. If x ∈ N and A = \(\begin{vmatrix} x+3\quad & -2 \\ -3x & 2x \end{vmatrix}\) = 8, then find the value of x?
5. Find the value of determinant \(\left|\begin{array}{ccc}
   {1^{2}} & {2^{2}} & {3^{2}} \\
   {2^{2}} & {3^{2}} & {4^{2}} \\
   {3^{2}} & {4^{2}} & {5^{2}}
   \end{array}\right|\)?

Answer:

1. 2
2. \(\frac{-15}{4}\)
3. 12
4. 2
5. -8

Determinants Structure Very Short Answer Type Questions

Question 1.
Find the value of \(\begin{vmatrix} 2\quad & 20 \\ 1 & 6 \end{vmatrix}\)?
Answer:
-8.

Question 2.
Find the value of y if \(\begin{vmatrix} -6\quad & 2 \\ 3 & y \end{vmatrix}\) = 24?
Answer:
-5.

Question 3.
Find x if \(\begin{vmatrix} 2\quad & 4 \\ x & 0 \end{vmatrix}\) = -16?
Answer:
4.

Question 4.
If \(\begin{vmatrix} a\quad & b \\ c & d \end{vmatrix}\) = 5, then find the value of \(\begin{vmatrix} 3a\quad & 3b \\ 3c & 3d \end{vmatrix}\)?
Answer:
45.

Question 5.
If \(\begin{vmatrix} a\quad & ω \\ ω & -ω \end{vmatrix}\) = 1, then value of a will be?
Answer:
1.

Question 6.
If \(\begin{vmatrix} 3\quad & m \\ 4 & 5 \end{vmatrix}\) = 3, then find the value of m?
Answer:
3.

Question 7.
If \(\begin{vmatrix} 2\quad & x \\ 4 & 9 \end{vmatrix}\) = 30, then find the value of x?
Answer:
– 3.

Question 8.
If \(\begin{vmatrix} 4\quad & -3 \\ m & m \end{vmatrix}\) = 21, then find the value of x?
Answer:
3.

Question 9.
If \(\begin{vmatrix} 2\quad & 4 \\ 3 & x \end{vmatrix}\) = 0, then find the value of x?
Answer:
6.

Question 10.
If \(\begin{vmatrix} 4\quad & -3 \\ -m & m \end{vmatrix}\), then find the value of m?
Answer:
21.

Question 11.
If \(\begin{vmatrix} -6\quad & 2 \\ 3 & m \end{vmatrix}\) = 12, then find the value of m?
An.swer:
-3.

Question 12.
If \(\begin{vmatrix} 4\quad & -6 \\ -2 & x \end{vmatrix}\) = 20, then find the value of x?
Answer:
8.

Question 13.
If ω, ω² are the cube root of unity, then find the value of \(\begin{vmatrix} 1\quad & \omega \\ \omega & -\omega \end{vmatrix}\)?
Answer:
1.

Question 14.
Find the value of \(\left|\begin{array}{ccc}
{224} & {777} & {32} \\
{735} & {888} & {105} \\
{812} & {999} & {116}
\end{array}\right|\)?
Answer:
0.

Question 15.
If \(\begin{vmatrix} x\quad & 4 \\ 3 & 3 \end{vmatrix}\) = 0 then find the value of x?
Answer:
4.

Question 16.
If \(\begin{vmatrix} 2+3i\quad & 4 \\ 1 & 2-3i \end{vmatrix}\) find its value?
Answer:
9.

Question 17.
In determinants \(\begin{vmatrix} 2\quad & -3 \\ 1 & -2 \end{vmatrix}\) then find the co – factor of element – 3?
Answer:
1.

Question 18.
If \(\begin{vmatrix} 3\quad & -2 \\ -4 & x \end{vmatrix}\) = 16, then find the value of x?
Answer:
8.

Question 19.
The value of \(\begin{vmatrix} 1\quad & log_{ b }a \\ log_{ a }b & 1 \end{vmatrix}\)?
Answer:
0.

Question 20.
Find the value of 2 from determinant \(\begin{vmatrix} 1\quad & 3 \\ 2 & 4 \end{vmatrix}\)?
Answer:
3.

Question 21.
Find the value of \(\begin{vmatrix} 2+5i\quad & 5 \\ 4 & 2-5i \end{vmatrix}\)?
Answer:
9.

Question 22.
Find the value of \(\begin{vmatrix} cot x\quad & cosec x \\ cosec x & cot x \end{vmatrix}\)?
Answer:
-1.

Question 23.
Find the value of \(\begin{vmatrix} cos70^{ \circ }\quad & sin20^{ \circ } \\ sin70^{ \circ } & cos20^{ \circ } \end{vmatrix}\)?
Answer:
0.

Determinants Long Answer Type Questions – I

Question 1.
Prove that:
\(\left|\begin{array}{ccc}
{a+b+2 c} & {a} & {b} \\
{c} & {b+c+2 a} & {b} \\
{c} & {a} & {c+a+2 b}
\end{array}\right|\) = 2 (a + b + c)³?
Solution:
Let ∆ =

= 2 (a + b + c) . 1. [(a + b + c)² – 0]
= 2 (a + b + c)³. Proved.

Question 2.
Prove that:
\(\left|\begin{array}{ccc}
{a^{2}+1} & {a b} & {a c} \\
{a b} & {b^{2}+1} & {b c} \\
{a c} & {b c} & {c^{2}+1}
\end{array}\right|\) = 1 + a² + b² + c²? (NCERT, CBSE 2016)
Solution:
Let ∆ =


= (1 + a² + b² + c²) . 1 \(\begin{vmatrix} 1\quad & 0 \\ 0 & 1 \end{vmatrix}\)
∆ = (1 + a² + b² + c²). Proved.

Question 3.
Prove that \(\left|\begin{array}{ccc}
{a^{2}} & {b c} & {a c+c^{2}} \\
{a^{2}+a b} & {b^{2}} & {a c} \\
{a b} & {b^{2}+b c} & {c^{2}}
\end{array}\right|\) = 4a² b² c² ?(NCERT, CBSE 2015)
Solution:
Let ∆ =

= abc.2c. \(\begin{vmatrix} a-b\quad & -a \\ a+b & -a \end{vmatrix}\)
= 2abc² [-a(a – b) + a (a + b)]
= 2²bc²[-a + b + a + b]
= 2a²bc².2b = 4a²b²c². Proved.

Question 4.
Solve the following determinant:
\(\left|\begin{array}{ccc}
{x+1} & {3} & {5} \\
{2} & {x+2} & {5} \\
{2} & {3} & {x+4}
\end{array}\right|\) = 0?
Solution:


⇒ (x + 9) × 1 \(\begin{vmatrix} x-1\quad & 0 \\ 0 & x-1 \end{vmatrix}\) = 0
⇒ (x + 9) (x – 1)² = 0
∴ (x + 9) = 0 or (x – 1)² = 0
⇒ x = -9 or x = 1, 1.

Question 5.
Prove that:
\(\left|\begin{array}{ccc}
{\alpha} & {\beta} & {\lambda} \\
{\alpha^{2}} & {\beta^{2}} & {\lambda^{2}} \\
{\beta+\lambda} & {\lambda+\alpha} & {\alpha+\beta}
\end{array}\right|\) = (α – β) (β – λ) (λ – α) (α + β + λ)?
Solution:
Let ∆ =

⇒ ∆ = (α + β + λ) (α – β) (β – λ) (β + λ – α – β)
⇒ ∆ = (α – β) (β – λ) (λ – α) (α + β + λ)
= R.H.S. Proved.

Question 6.
Prove that:
\(\left|\begin{array}{ccc}
{1+a} & {1} & {1} \\
{1} & {1+b} & {1} \\
{1} & {1} & {1+c}
\end{array}\right|\) = (abc) (1 + \(\frac{1}{a}\) + \(\frac{1}{b}\) + \(\frac{1}{c}\) )? (NCERT; CBSE 2012, 14)
Solution:
Let



R.H.S. Proved.

Question 7.
Prove that:
\(\left|\begin{array}{ccc}
{-a^{2}} & {a b} & {a c} \\
{a b} & {-b^{2}} & {b c} \\
{a c} & {b c} & {-c^{2}}
\end{array}\right|\) = 4a²b²
c²?
Solution:

= a²b²c²[2 (1 + 1)]
= a²b²c².4 = 4a²b²c². Proved.

Question 8.
Solve the equation:
\(\left|\begin{array}{ccc}
{3 x-8} & {3} & {3} \\
{3} & {3 x-8} & {3} \\
{3} & {3} & {3 x-8}
\end{array}\right|\) = 0?
Solution:

⇒ (3x – 2) (3x – 11) [1. (1 – 0)] = 0
⇒ (3x – 2) (3x – 11) = 0
∴x = \(\frac{2}{3}\), \(\frac{11}{3}\).

Question 9.
Solve the equation \(\left|\begin{array}{lll}
{a+x} & {a-x} & {a-x} \\
{a-x} & {a+x} & {a-x} \\
{a-x} & {a-x} & {a+x}
\end{array}\right|\) = 0?
Solution:

⇒ (3a – x).1.(4x² – 0) = 0
⇒ 3a – x = 0, 4x² = 0
⇒ x = 3a, 0.

Question 10.
Prove that:
\(\left|\begin{array}{ccc}
{a} & {a+b} & {a+b+c} \\
{2 a} & {3 a+2 b} & {4 a+3 b+2 c} \\
{3 a} & {6 a+3 b} & {10 a+6 b+3 c}
\end{array}\right|\) = 0?
Solution:
Let ∆ =


= a² [7a + 3b – 6a – 3b]
= a²(a)
= a³. Proved.

Question 11.
Prove that:
\(\left|\begin{array}{ccc}
{x} & {x+y} & {x+2 y} \\
{x+2 y} & {x} & {x+y} \\
{x+y} & {x+2 y} & {x}
\end{array}\right|\) = 9y² (x + y)? (CBSE 2017)
Solution:
Let ∆


⇒ ∆ = 9y(x + y) [-x – y + x+ 2y]
⇒ ∆ = 9y² (x + y). Proved.

Question 12.
Prove that:
\(\left|\begin{array}{ccc}
{x+4} & {2 x} & {2 x} \\
{2 x} & {x+4} & {2 x} \\
{2 x} & {2 x} & {x+4}
\end{array}\right|\) = (5x + 4) (4 – x)²? (NCERT)
Solution:
Let



= (5x + 4) (x – 4) (2x – x – 4)
= (5x + 4) (x – 4) (x – 4)
= (5x + 4) (x – 4)². [∵(a – b)² = (b – a)²]
⇒ ∆ = (5x + 4) (4 – x)². Proved.

Question 13.
Prove that:
\(\left|\begin{array}{ccc}
{x} & {y} & {x+y} \\
{y} & {x+y} & {x} \\
{x+y} & {x} & {y}
\end{array}\right|\) = -2(x³ + y³). (NCERT)
Solution:
Let ∆ =


= 2 (x + y) (x² – xy + y²)
⇒ ∆ = – 2(x² + y²). Proved.

Question 14.
Prove that:
\(\left|\begin{array}{ccc}
{a^{2}+2 a} & {2 a+1} & {1} \\
{2 a+1} & {a+2} & {1} \\
{3} & {3} & {1}
\end{array}\right|\) = (a – 1)³? (CBSE 2017)
Solution:
Let ∆ =

⇒ ∆ = (a – 1)² (a + 1 – 2)
⇒ ∆ = (a – 1)² (a – 1)
⇒ ∆ = (a – 1)³. Proved.

Question 15.
Prove that:
\(\left|\begin{array}{ccc}
{1} & {1} & {1+3 x} \\
{1+3 y} & {1} & {1} \\
{1} & {1+3 z} & {1}
\end{array}\right|\) = 9(3 xyz + xy + yz + zx)? (CBSE 2018)
Solution:
Let ∆ =


= 9[x{(1 + y) (1 + 3z) – (1 + z)} – z{(x – y) – 0}]
= 9[x{1 + y + 3z + 3yz – 1 – z} – zx + zy]
= 9 [xy + 3xz + 3xyz – xz – zx + zy]
= 9 [3xyz + xy + yz + zx]. Proved.

MP Board Class 12 Maths Important Questions

MP Board Class 12th Chemistry Important Questions Chapter 16 Chemistry in Everyday Life

Chemistry in Everyday Life Important Questions

Chemistry in Everyday Life Short Answer Type Questions

Question 1.
Why should not medicines be taken without consulting doctors? (NCERT)
Answer:
The drugs or medicines have side effects also. These side effects arise because the drug may bind to more than one type of receptor. Further their wrong choice and over – dose can cause havoc and even may cause death. Therefore, it is must that the medicines should not be given without consulting doctors.

Question 2.
Explain the term, target molecules or drug targets as used in medicinal chemistry. (NCERT)
Answer:
Drugs taken by a patient interact with macromolecules such as proteins, carbo-hydrates, lipids and nucleic acids and these are called drug targets. These macromolecules or drug targets are known to perform several role in the body. The drugs are designed to interact with specific targets so that these have least chances of effecting the other targets. This minimises the side effects and localises the action of the drug.

Question 3.
While antacids and antiallergic drugs interfere with the function of histamines, why do these not interfere with the function of each other? (NCERT)
Answer:
They do not interfere with the functioning of each other because they work on different receptors in the body. Secretion of histamine causes allergy and acidity while ant-acid removes only acidity.

Question 4.
Low level of noradrenaline is the cause of depression. What type of drugs are needed to cure this problem? Name two drugs. (NCERT)
Answer:
Noradrenaline induces a feeling of well being and helps in changing the mood. If the level of noradrenaline is low, then the signal sending activity of the hormone becomes low and the person suffers from depression. In such cases, the patient needs anti – depressant drugs which inhibit the enzymes which catalyses the degradation of noradrenaline. The common drugs used as anti – depressant are iproniazid and phenelzine.

Question 5.
Sleeping pills are recommended by doctors to the patients suffering from sleeplessness but it is not advisable to take its doses without consultation with the doctor. Why? (NCERT)
Answer:
Sleeping pills contain drugs that may be tranquilizers or anti – depressant. They affect the nervous system, relieve anxiety, stress, irritability or excitement. But they should strictly be used under the supervision of a doctor. If not, the uncontrolled and overdose can cause harm to the body and mind because in higher doses, these drugs act as poisons.

Question 6.
With reference to which classification has the statement, “ranitidine is an antacid” been, given? (NCERT)
Answer:
This statement refers to the classification of drugs according to pharmacological effects of the drugs because any drug which is used to neutralise the excess acid present in the stomach will be called an antacid and ranitidine prevents the interaction of histamine with the receptors present in the stomach wall. Histamine stimulates the secretion of pepsin and HCl in the stomach.

Question 7.
What are germicides?
Answer:
Germicides are substances which possess the power Aspirin to destroy germs. Sulphur compounds, mercury compounds (mercuric iodide) and phenolic compounds are used as germicides. Sulphur compounds in soap protect the skin from pimples, dandruff and skin infection. Phenolic compounds are mostly used as germicides. Cresyclic acid which is a mixture of m – cresol and p – cresol is mixed in soap as a germicide.

Question 8.
How are synthetic detergents better than soaps? (NCERT)
Answer:

1. Soaps cannot be used in hard water but detergents can be used.
2. Soaps cannot be used in acidic water but detergents can be used.

Question 9.
Explain the following terms with suitable examples: (NCERT)

1. Cationic detergents
2. Anionic detergents and
3. Non – ionic detergents.

Answer:
1. Cationic detergents are those which have cationic hydrophilic group. These are mostly acetates, chlorides or bromides of quaternary ammonium salts. For example, cetyltrimethyl ammonium chloride.
[CH₃(CH₂)₁₅N(CH₃)₃]⁺+Cl^–

2. Anionic detergents are those which have anionic hydrophilic group. These are of two types:

• Sodium alkyl sulphate example sodium lauiyl sulphate CH₃(CH₂)₁₀CH₃OSO₃^– Na⁺
• Sodium alkyl benzene sulphonate example sodium 4 – (1 – dodecyl) benzene sulphonate (SDS)
  

3. Non – ionic or neutral detergents are esters of high molecular mass alcohols as in fatty acids. For example, polyethylene glycol stearate
CH₃(CH₂)₁₆COO(CH₂CH₂O)_nCH₂CH₂OH
Polyethylene glycol stearate.

Question 10.
What are bio – degradable and non – biodegradable detergents? Give one example of each. (NCERT)
Answer:
1. Bio – degradable detergents are degraded by bacteria. In them, hydrocarbon chain is unbranched. They do not cause water pollution and are bitter.
Example : Sodium lauryl sulphate.

2. Non – biodegradable detergents possess highly branched hydrocarbon chain so bacteria cannot degrade them easily. They cause water pollution.
Example : Sodium 4 – (1, 3, 5, 7 – tetramethyl – actyl) benzene sulphonate.

Question 11.
Why do soaps not work in hard water? (NCERT)
Answer:
Hard water contains calcium and magnesium salts. Therefore, in hard water, soaps get precipitated as insoluble calcium and magnesium soaps which being insoluble stick to the cloth as gummy mass and blocks the ability of soap to move oil or grease from the cloth.

Question 12.
Explain each with an example.

1. Antibiotics
2. Analgesic (Pain Killer).

Answer:
1. Antibiotics:
Chemical substance which are produced by micro – organism and used to destroy micro – organism are called antibiotics.

These are of two types :

• Broad spectrum Antibiotic : Example : Tetracycline, chloramphenicol, Penicillin
• Narrow Spectrum Antibiotic : Example : Niastatin, Penicillin antibiotic medicines are used for the treatment of typhoid, whooping cough, Pneumonia.

2. Analgesic:
Drugs which give relief from pain or reduced pain are called analgesics.
Types and Examples :

• Narcotics : Morphine, Codeine.
• Non – Narcotics : Aspirin, Analgin, Paracetamol.

Question 13.
What is preservative? Give the name and formula of any two preservatives.
Answer:
A preservative is defined as “A substance added to food, capable of retarding the growth of micro – organism which deteriorate the food within no time.
The preservative may be natural compounds such as sugars, salt, acids, etc. as well as they may be synthetic i.e. Sodium benzoate.
Example:

1. Vinegar or acetic acid : CH₃ – COOH
2. Sodium benzoate : C₆H₅COONa.

Question 14.
What are the main differences between soap and detergents?
Answer:
Differences between Soap and Detergents :
Soap:

• Soaps are sodium salts of higher fatty acids.
• These cannot be used with hard water.
• Their aqueous solution is alkaline in nature.
• These contain oil and are not good cleansing agent.
• These cannot be used for soft and delicate cloth.

Detergents:

• Detergents are sodium salt of alkyl benzene sulphonate.
• These can be used with hard water.
• Their aqueous solution is neutral in nature.
• These do not contain oil and are better cleansing agent.
• These can be used for soft and delicate cloth.

Question 15.
What do you understand by antipyretics?
Answer:
These are used to lower down the body temperature in high fever. These drugs are used both as antipyretic and as analgesic, example aspirin (acetylsalicylic acid), paracetamol (4 – acetamido phenol), phenacetin (4 – ethoxy acetanilide), analgin, etc.

Question 16.
What are Antibiotics? Write name of any two antibiotics. (MP 2018)
Answer:
Antibiotics:
are chemical substances which are produced by micro – organisms like bacteria, fungi, actinomycetes and destroy some other micro – organisms are like, virus, ricketsia or obstruct their growth.
Example : Penicillin, Streptomycin etc.

Question 17.
What is Immune system? How does it develop?
Answer:
For the destruction of bacteria or antigen in our body, lymphocytes are developed which are known as Immune. These are a specific type of white blood cells. These prepare and release a special type of protein called globulin to destroy the poison. These proteins destroy the attacking virus, bacteria and poisonous substances. Lymphocyte bind the antigen and themselves divide fast by which immunization increase and effect of antigen is destroyed.

Question 18.
What are antiseptics?
Answer:
Antiseptics:
An antiseptic kills the bacteria or prevents the multiplication of bacteria. These also prevent pus formation. Antiseptics do not harm living tissues. Tincture iodine, phenol (0 – 2%), dettol, chloroxylenol, etc. are applied on skin and bactrim, septran, etc. are taken orally as pills. Bad odour coming out of the wounds due to bacterial decomposition on the body or in the mouth are also reduced by the use of antiseptics. For such purposes, antiseptics are usually incorporated in face powder, breath purifiers, deodorants, etc. to reduce the intensity of bad odour.

Neem soaps containing the extract of neem seeds are also used as antiseptic soaps. Dettol is a mixture of chloroxylenol and terpineol in a suitable solvent is commonly used antiseptic. Bithionol antiseptic is added to soap to provide antiseptic properties to it. Tincture iodine is 2 – 3% solution of iodine in alcohol and water.

Question 19.
What do you mean by Antibiotics? Name the first antibiotic.
Answer:
Chemical substances which are produced by mirco – organism and are used to destroy other micro-organism, are called antibiotics. These chemicals checks the life cycle of bacteria and stop reproduction resulting in release from disease. Antibiotics are almost specific for kinds of illness.

The first antibiotic penicillin was discovered by Alexander Fleming in 1928. He was awarded Nobel prize in 1945 for this important discovery. General formula of penicillin is C₉H₁₁N₂O₄S – R. It is a narrow spectrum drug and used in bronchitis, pneumonia, sore throat and abcesses. Before administration, tolerance has to be tested.

By changing the group R, different penicillin are prepared.

Question 20.
What are artificial sweetening agents? Give two examples. (MP2018)
Answer:
Artificial sweetening agents are the substances produced wholly or partially by chemical synthesis, which are added to food to impart sweet taste.
Example:

1. Sucrose
2. Saccharin.

Question 21.
Give definition of antihistamine drug with name and uses.
Answer:
These are amines which controls the allergy effect produced by histamines. Histamine is found in all body tissue and is also released in allergic conditions due to which allergic responses such as tissue inflammation, asthma, itching etc. are introduced in the body. Drugs which prevent the production of histamine and fight against the allergy effects are called antihistamines.
Example:
1. Entergon : It is used in strong allergic conditions.

2. Benadryl:

Chemistry in Everyday Life Long Answer Type Questions

Question 1.
Write short notes on:

1. Antifertility drugs (MP 2108),
2. Detergents
3. Antacids (MP 2018)
4. Sedatives
5. Sulpha drugs.

Answer:
1. Antifertility drugs:
Drugs which are used to check pregnancy in women are called antifertility drugs. Actually, these drugs control the female menstrual cycle and ovu-lation. The antifertility agent in these drugs are steroids and these drugs are used in the form of oral pills. A mixture of synthetic estrogen and progesterone derivative are used as birth control pill. These are more effective than the natural hormone. Ethynylestradiol and nore- thindrone are the content of common contraceptive pills.

2. Detergents:
Unsaturated hydrocarbon of ethylene type containing 10 to 18 carbon atoms on treatment with sulphuric acid forms organic acid. Sodium salt of organic acid have moisture absorbing and purification property. This compound is called synthetic detergent. Example : Sodium n – dodecyl benzene sulphonate, Sodium n – dodecyl sulphate.

Synthetic detergents have two parts :

• A long chain of hydrocarbon which is hydrophobic (Water repellent).
• Small ionic chain is hydrophilic (Water attracting). Ionic chain is generally of sul- phonate (SO₃Na) or sodium sulphate (SO₄Na).

Detergents are surface active compounds which decreases surface tension of water. When these compounds are dissolved in water they scatter dirt particles leaving the surface clean.

Properties of detergents : Detergents are superior to soap.

• Detergents can be used in hard as well as soft water because they do not form insoluble salt with calcium and magnesium ions of hard water while soap cannot be used in hard water.
• Aqueous solution of detergent is neutral. Therefore, detergents can clean soft fibres without damaging them. Soap solution is alkaline due to hydrolysis and is harmful for washing soft fibres.

Uses of detergents:
Detergensts act as cleansing agent. Like soap it can be used for cleaning cotton, woollen, silky and synthetic fibre cloth and for cleaning other domestic items.

3. Antacids:
Substance which remove the excess acid in the stomach and raise the pH to appropriate level are called antacid Calcium carbonate, Sodium bicarbonate, Magnesium hydroxide or Aluminium hydroxide is used in the form of aqueous suspension or tablets to treats hyperacidity. These substances react with excess hydrochloride acid and neutralizes it partially. Nowadays Omeparazole and Lansoparazole are prescribed as antacids.

4. Sedatives:
These are given to those patients who are violent and mentally agitated.
Example:

1. Equanil
2. Barbituric acid.

5. Sulpha drugs:
Like antibiotics, sulpha drugs are used to kill micro – organism. These are prepared in laboratory. Sulphadiazine, sulphanilamide, sulphathiazole, sulpha guanidine, etc. are important sulpha drugs.

Question 2.
Write notes on the following:

1. Tranquillizers and Hypnotics (MP2018)
2. Antidepressant

Answer:
1. Tranquillizers:
Tranquillizers are the chemical substances which affect higher centres of central nervous systems and reduce anxiety and tension. Tranquillizers are also called psychotherapeutic drugs. These drugs make the patient passive temporarily so that emotional distress or depression is reduced. The patient restores confidence. These drugs if taken for long – time make the person habitual. Luminal, Barbituric acid, seconal, equanil, etc. are the drugs of this class. These are components of sleeping pills.

2. Antidepression:
These are given to patient for boosting their morals in the stage of acute depressions. Some mood elevator drugs are vitellin, methadone, cocaine, etc. These act on the central nervous system. Person becomes healthy by its use and de-velop confidence. These should be taken by the advice of doctor. Tophrenil is one such medicine. The amphetemin group of medicine help to upraise the mental level. Its common example is benzedine.

Question 3.
Write example of the following chemicals :

1. Two Analgesics
2. Two Antiseptic
3. Two Antiseptic chemical
4. Two Antibiotic
5. Two Anaesthetic
6. Two Sulpha drug
7. Two Rocket propellant
8. Two uses of chloramphenicol antibiotic.

Answer:

1. Two Analgesic : (i) Morphine, (ii) Aspirin.
2. Two Antiseptic : (i) Dettol, (ii) Bithional.
3. Two Antiseptic Chemical: (i) Boric acid, (ii) Gention violet.
4. Two Antibiotic : (i) Terramycin, (ii) Streptomycin.
5. Two Anaesthetic : (i) Cyclopropane, (ii) Pelledyne.
6. Two sulpha drug : (i) Sulphonide, (ii) Sulphadyne.
7. Two Rocket Propellant: (i) Polyurethane, (ii) Ammonium perchlorate.
8. Two use of Chloramphenicol Antibiotic : (i) In Typhoid, (ii) High fever and diarrhoea.

Question 4.
Write two differences between Dyes and Pigments.
Answer:
Differences between Dyes and Pigments :
Dyes:

• These are organic substance.
• They colour fibres and food materials also.

Pigments:

• These are inorganic substance.
• Mixed with safeda (white lead) it is used to colour metals and wood.

Question 5.
Give one example of Acidic dye and Basic dye.
Answer:
Acidic dye:
In these, acidic group like phenolic, sulphonic (S03H) are in the form of sodium salts. These colour animal fibre like wool, silk etc. Example : Orange – I and II.

• Acidic dye : Methyl orange , Methyl red.
• Basic dye : Malachite green, Aniline yellow.

Question 6.
What is meant by the term ‘broad spectrum antibiotics’? Explain. (NCERT)
Answer:
The range of bacterias or other micro – organisms that are affected by a certain antibiotic is expressed as its spectrum of action. The term broad spectrum antibiotics means an antibiotic which kills or inhibits a wide range of Gram negative and Gram -positive bacteria.

MP Board Class 12th Chemistry Important Questions