MP Board Class 12th Physics Important Questions Chapter 7 Alternating Current
Alternating Current Important Questions
Alternating Current Objective Type Questions
Question 1.
Choose the correct answer of the following:
Question 1.
The mean value of an A.C. over one complete cycyle is :
(a) \(\frac { { 2I }_{ 0 } }{ \pi }\)
(b) –\(\frac { { 2I }_{ 0 } }{ \pi }\)
(c) Infinite
(d) Zero
Answer:
(d) Zero
Question 2.
The relation between peak value V0 and rms value Vrms of alternating voltage is:
(a) V0 = 0.707 Vms
(b) Vms = 0.707 V0
(c) Vms = 0.637 V0
(d) V0= 0.637 Vms
Answer:
(c) Vms = 0.637 V0
Question 3.
A capacitor allows through it:
(a) Only d.c
(b) Only a.c
(c) a.c and d.c both
(d) Neither a.c nor d.c.
Answer:
(b) Only a.c
Question 4.
In a circuit wattless current flows if it contains :
(a) Only R
(b) R – L
(c) R – C
(d) Only L.
Answer:
(d) Only L.
![]()
Question 5.
A device which convert mechanical energy into electrical energy is :
(a) d.c moter
(b) a.c generator
(c) Transformer
(d) Choke coil.
Answer:
(b) a.c generator
Question 6.
The relation between peak value on a.c I0 and virtual value Irms is :
(a) I0 = \(\frac { 1 }{ \sqrt { 3 } }\) = Ims
(b) Ims = \(\sqrt { 3{ I }_{ 0 } }\)
(c) I0 = Ims
(d) I0 = \(\sqrt { 3{ I }_{ ms } }\) Ims
Answer:
(d) I0 = \(\sqrt { 3{ I }_{ ms } }\) Ims
Question 2.
Fill in the blanks :
- The cause of production of induced e.m.f. is change in
- The dimensional formula of inductance is
- In an ideal coupling the value of coupling coefficient K is
- The ohmic resistance of an ideal inductor is
- Due to eddy currents the decay of electrical energy is in the form of
Answer:
- Magnetic flux
- [ML2T-2A-2]
- One
- Zero
- Heat energy.
Question 3.
Match the Column :
I.

Answer:
- (c)
- (d)
- (b)
- (e)
- (a)
II.

Answer:
- (e)
- (c)
- (b)
- (d)
- (a)
Question 4.
Write the answer ¡n one word/sentence:
- What is the frequency of direct current?
- Which effect is exhibited by alternating current?
- What is the magnitude of inductive reactance for direct current?
- What ¡s the magnitude of capacitive reactance for direct current?
- What is the unit of \(\sqrt { LC }\)?
- What ¡s average value of alternating current for one complete cycle?
- What will be the magnitude of power coefficient for a L – C – R circuit in resonance state?
- How many times the direction of alternating current charges for one complete cycle?
- What will be the magnitude of power coefficient for pure inductor or capacitor?
- What is the phase difference between e.m.f. and a.c. pure resistance, pure inductor and pure capacitor?
Answer:
- Zero
- Heating effect
- Zero
- Infinity
- Second
- Zero
- One
- Two times
- Zero
- Phase difference ϕ = 0
Alternating Current Very Short Answer Type Questions
Question 1.
In direct current circuit contaning pure inductance, what will be the value of inductive reactance?
Answer:
Since XL= ωL for d.c. ω = 0, therefore XL will be zero.
Question 2.
Can battery be charged with alternating current?
Answer:
No, it can’t be charged.
![]()
Question 3.
Which is more dangerous a.c. or d.c. at same voltage?
Answer:
Alternating current.
Question 4.
How will you recognize whether the current flowing through the coil of bulb in a.c. or d.c.?
Answer:
If on bringing magnet near the coil, if it vibrate then it will be alternating current.
Alternating Current Short Answer Type Questions
Question 1.
Define rms and peak value of alternating current and state the relation between them.
Answer:
Root mean square value:
Root mean square value of an a.c. is defined as that value of steady current which would generate the same amount of heat in a given resistance in a given time, as is done by the a.c. when passed through the same resistance for the same time. It is also called virtual value.
Peak value:
The maximum value of ax. is called its peak value or amplitude i.e.,
Peak value = \(\sqrt {2}\) x rms value
or I0 = \(\sqrt {2}\) Irms
Question 2.
a.c. does not show magnetic and chemical effects, why?
Answer:
a.c. flows in one direction during the first half cycle and in reverse direction in the second half cycle. Therefore, the average value of current for a complete cycle is zero. Thus, it does not show magnetic and chemical effects.
Question 3.
Why a.c. is more dangerous than d.c. of the same voltage?
Answer:
The maximum value of alternating e.m.f. is \(\sqrt {2}\) times of its virtual e.m.f. If virtual value is 220 V, then the peak value of e.m.f. = 220 x \(\sqrt {2}\) = 311.13 V. Hence, the voltage of ax. fluctuates between +311.13 V to – 311.13 V. Therefore, ax. is more dangerous.
Question 4.
a. c. cannot be measured by moving coil galvanometer, why?
Answer:
Moving coil galvanometer works on the principle of magnetic effect of current. a.c. does riot show magnetic effect because when ax. is passed through the coil, the direction and magnitude of current will frequently change and so the deflecting couple produces. But, in each complete cycle, the average deflecting couple is zero. So, there will be no deflection in the coil.
![]()
Question 5.
A bulb and a solenoid are connected in series to an a.c. source. If a soft – iron core is inserted inside the solenoid, what will be its effect on the intensity of light coming out of the bulb?
Answer:
The bulb will glow dimmer i.e., intensity decreases. This is because on introducing soft – iron core in the solenoid, the inductance increases. So, inductive reactance increases (by XL = ωL), hence the current through the bulb decreases.
Question 6.
Write the expression for pure inductive reactance in an a.c. circuit and explain how it depends on the frequency of a.c.? Write its unit.
Answer:
Reactance of pure inductive component,
XL = ωL = 2 πf L
Where, f= Frequency of a.c and L = Inductance of the coil
Clearly, XL ∝ f
i.e., the reactance of pure inductive component is proportional to the frequency of a.c. Unit of reactance is ohm.
Question 7.
Write the expression for reactance of capacitor in an a.c. circuit. Explain how does it depend on frequency of a.c.? Write its unit.
Answer:
Capacitive reactance

Where, f = Frequency of a.c. and C = Capacitance of the capacitor. i.e., the capacitive impedance is inversely proportional to the frequency of a.c. Unit of capacitive reactance is ohm.
Question 8.
A capacitor stops d.c., why?
Answer:
In an a.c. circuit, reactance offered by capacitor i.e., capacitive reactance is
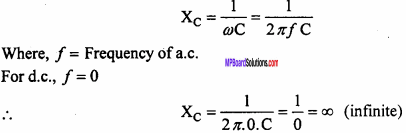
Hence, capacitor stops d.c.
Question 9.
What is the resistance of a coil of self – inductance L in a d.c. circuit?
Answer:
Resistance of coil in a.c. circuit i.e., inductive reactance is
XL = ωL = 2πf L
For d.c., f = 0
Hence, resistance offered by the coil in d.c. circuit
XL = 2π.0.L = 0.
![]()
Question 10.
In order to reduce the current in a.c. circuit, an inductor is more suitable than a resistance. Why?
Answer:
If a resistance is used in an a.c. circuit, a part of electrical energy is lost in the form of heat. Instead, if we use an inductance, there is no energy loss in the form of heat because power factor for inductive component is zero.
Question 11.
An electric heater is operated by direct current and alternating current respectively on the same potential difference. Will the heat liberated, in these two cases be the same? Give reasons for your answer.
Answer:
An electric heater containing a coil has resistance as well as inductance. So, its resistance is large for a.c. than for d.c.
From the formula for produced heat,
H = \(\frac { { V }^{ 2 } }{ R }\)
We conclude, less heat will therefore be produced by a.c.
Question 12.
- What will be the power loss in a pure inductive or pure capacitive circuit when it is joined to a.c. source?
- When will voltage and current in an LCR a.c. circuit be in same phase?
Answer:
1. When an inductor is joined to an a.c. source, then voltage is ahead of current by π/2, hence ϕ = π/2.
The power factor is P = VrmsIrms cosϕ
= VrmsIrms cos\(\frac {π}{2}\) = 0
Hence, there is no consumption of power. When a capacitor is joined, then voltage is lagging behind the current by \(\frac {π}{2}\) . Hence ϕ = \(\frac {π}{2}\) = 0
The power factor is P = Vrmslrms cosϕ
= Vrmslrms cos(- \(\frac {π}{2}\)) = 0
= 0
Hence, there is no consumption of power.
2. Voltage and current in an LCR a.c. circuit will be in the same phase when frequency is f = \(\frac { 1 }{ 2\pi \sqrt { LC } }\)
Question 13.
What is Wattless current?
Answer:
In a.c. circuit, when the average consumed power is zero, then that current is called wattless current.
If a pure inductance or pure capacitance is used in a.c. circuit, then the phase difference between current and e.m.f. becomes\(\frac {π}{2}\).
Pav = Vrms x Irms x cosϕ
= Vrms x Irms x cos\(\frac {π}{2}\)
= Vrms x Irms x o = 0
Choke coil is made up of thick copper wire. Its ohmic resistance is negligible. Hence, the phase difference between current and e.m.f. is \(\frac {π}{2}\). Thus, the average consumed power becomes zero. Therefore, the current is called wattless.
By using a choke coil in an alternating circuit, we can obtain a wattless current.
Question 14.
For a circuit used for transporting electric power, a low power factor implies large power loss. Why?
Answer:
The power factor is given by cosϕ = \(\frac {R}{Z}\). Therefore, for low power factor, the resistance R will be less. Hence a large current will flow through the secondary coil of the transformer, which will produce more heat as H x I2. Thus, a large power will be lost.
Question 15.
A transformer works with a.c. supply but not with d.c. Why?
Answer:
It is because transformer works on the principle of mutual induction. The input a.c. changes the flux (through the soft – iron core) linked with the secondary coil. This produces output current in the secondary coil. This is not possible with d.c. supply input.
Question 16.
In houses, electricity is supplied through a.c. but not through d.c. Why?
Answer:
This is because the strength of current in the form of a.c. can be reduced and supplied from one place to another by using a transformer and thus without power loss. Transformer cannot work with d.c.
Question 17.
Why laminated core is used in transformer?
Answer:
Effect of eddy currents is minimized in a transformer by using laminated core. Lamination causes greater resistance to eddy currents produced. Thus, loss of electrical energy in the form of heat is reduced.
Question 18.
Give difference between resistance and reactance.
Answer:
The obstruction to the flow of alternating current or direct current by the conductor is called resistance. The obstruction to the flow of alternating current offered by inductor or capacity is called reactance.
![]()
Question 19.
In series resonance L – C – R circuit what is the value of impendence.
Answer:
Since Z =\(\sqrt { { R }^{ 2 }+({ X }_{ L }-{ X }_{ C })^{ 2 } }\)
But in resonance stage XL = XC
∴ Z = R
That is impendence is equal to resistance.
Question 20.
What is the value of peak to peak value of alternating e.m.f.?
Answer:
It will be equal to sum of peak value of e.m.f. in positive half cycle and negative half cycle, i.e., peak to peak value of alternating e.m.f. will be 2Em = 2\(\sqrt { 2 }\) Erms.
Question 21.
What are the reasons of energy losses in transformers? How these losses are renuced?
Answer:
Energy losses and their removal:
1.Copper loss:
Some part of the energy is wasted in the form of heat due to the heating effect of current in primary and secondary coil because the coils have some resistance. The amount of heat produced is I2 Rt. To reduce it, thick coils are used in the primary coil of step – up transformer and in the secondary coil of a step – down transformer.
2. Iron loss:
Eddy current is produced in the iron core of the transformer, causes heating. This loss is called iron loss. To minimize this loss, the core is laminated.
3. Magnetic flux leakage:
All the magnetic flux produced by primary coil may not be transferred to the secondary coil. Therefore, some energy is wasted. To minimize this loss, soft – iron core is used.
4. Hysteresis loss:
Some amount of energy is wasted because the iron core becomes magnetized during the first half and then gets demagnetized during the other half. This wastes loss of magnetic energy is called hysteresis loss. It is minimized by taking soft- iron core which has thin hysteresis loop.
Question 22.
Give differences between step – up and step – down transformer.
Ans.
Differences between a step – up and step – down transformer :
Step – up transformer
- It increases the voltage.
- It decreases the current strength.
- The number of turns in secondary coil is greater than that of primary coil.
- Its transformation ratio is more than one.
Step – down transformer
- It decreases the voltage.
- It increases the current strength.
- The number of turns in primary coil is greater than that of secondary coil.
- Its transformation ratio is less than one.
Question 23.
What do you mean by root mean square value of a.c. Obtain expression for Irms.
Answer:
Root mean square value of a.c.:
Root mean square value of an a.c. is defined as that value of steady current which would generate the same amount of heat in a given resistance in a given time, as is done by the a.c. when passed through the same resistance for the same time. It is also called virtual value.
Expression for Irms:
Let the alternating current is given by the equation
I = I0sin ωt
This current flows through a resistance R, for a small interval of time dt, then the small amount of heat dH is produced in the resistance R.
Then dH = I2 Rdt … (2)
For a complete cycle, the total heat produced will be obtained by integrating equation. (2)

If root mean square value of current is reprsented by Ims then the amount of heat produced in the same resistance R in the same interval of time will be
H = I2rms RT … (5)
Now from equation (4) and (5), we get
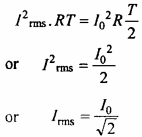
This is required expression.
Question 24.
Prove for an a.c. circuit:
Pav = Vrms x Irms x cosϕ
Where, the symbols have their usual meaning.
Answer:
Let the potential difference and current of a.c. circuit is given by
V=V0sm ωt … (1)
and I = I0sm(ωt – ϕ) … (2)
Where, ϕ is the phase difference between voltage and current.
Here the current lags behind the voltage
Now, instantaneous power, P = V.I
= V0sin ωt.I0sin{ωt – ϕ), [from eqns. (1) and (2)]
= V0I0sinωt.sin(ωt – ϕ) = \(\frac {1}{2}\)V0I0.2sinωt.sin(ωt – ϕ)
= \(\frac {1}{2}\)V0I0[cosϕ – cos(2ωt – ϕ)]
= \(\frac {1}{2}\)V0I0cosϕ – = \(\frac {1}{2}\)V0I0cosϕ(2ωt – ϕ)
But, the value of cos(2ωt – ϕ) for a complete cycle is zero. Therefore, average power for a complete cycle is
Pav = \(\frac {1}{2}\)V0I0cosϕ or Pav = \(\frac { { V }_{ 0 } }{ \sqrt { 2 } }\).\(\frac { { I }_{ 0 } }{ \sqrt { 2 } }\).cosϕ
Pav = Vrms x Irms x c0sϕ
Where, Vrms and Irmsare average alternating e.m.f. and current and cosϕ is called power factor, its value depends upon the nature of the circuit.
![]()
Question 25.
What is meant by wattless current? When the current becomes wattless? Why the current flowing through choke coil is wattless?
Answer:
In a.c. circuit, when the average consumed power is zero, then that current is called wattless current.
If a pure inductance or pure capacitance is used in a.c. circuit, then the phase difference between current and e.m.f. becomes \(\frac {π}{2}\)
Pav = Vrms x Irms x c0sϕ
= Vrms x Irms x cos\(\frac {π}{2}\)
= Vrms x Irms x 0= 0
Choke coil is made up of thick copper wire. Its ohmic resistance is negligible. Hence, the phase difference between current and e.m.f. is \(\frac {π}{2}\). Thus, the average consumed power becomes zero. Therefore, the current is called wattless. By using a choke coil in an alternating circuit, we can obtain a wattless current.
Question 26.
What is the principle of choke coil? Explain its use for controlling current. Why is current flowing in choke coil known as wattless current?
Answer:
Principle of choke coil:
A coil of very low resistance and high inductance is used to control current in an a.c. circuit. This coil is known as choke coil. It causes very little loss of energy. If an a.c. circuit contains zero resistance and a pure inductance, the phase difference between e.m.f. and current is 90°. Under this condition, average power
Pav = Vrms.Irms cosϕ
= Vrms.Irms x cos90°
=0, ( ∵ cos90° = 0)
So, there is no loss of energy. But in actual practice, the resistance in the circuit cannot be zero. Therefore, a small part of electrical energy is lost as heat. A choke coil is made up of a thick copper wire wound around a soft – iron core. Due to soft – iron core and so many turns of wire, the inductance is increased and the thick wire reduces its resistance.
Use:
Current in a.c. circuit can be controlled by using a choke coil in the circuit. Since, impedance of the choke coil is XL = caL. So, the current is reduced if inductance is high and is increased if the inductance is low.
Wattless current:
Current in a choke coil is called wattless current because average power consumed is zero (due to 90° phase difference between e.m.f. and current in the coil). The loss of energy due to small resistance of the coil is negligible.
Question 27.
Give differences between a.c. and d.c.
Answer:
Differences between a.c. and d.c. :
a.c.:
- Its direction and magnitude both changes.
- Transformers are used in a.c.
- It cannot be used for electroplating.
- It is generally not used for electro – magnet.
- The measuring instruments are based on its heating effect.
- It is dangerous.
d.c.:
- The magnitude may change but direction does not change.
- Transformers cannot be used.
- It can be used in electroplating.
- It is used for electromagnet.
- Its measuring instruments are based on its magnetic effect.
- It is less dangerous than a.c.
Question 28.
For a circuit used for transporting electric power, a low power factor implies large power loss. Why?
Answer:
The power factor is given by cosϕ =\(\frac {R}{Z}\). Therefore, for low power factor, the resistance R will be less. Hence a large current will flow through the secondary coil of the transformer, which will produce more heat as H x I2. Thus, a large power will be lost.
Question 29.
An a.c. circuit contains a pure resistive component. Obtain an expression for current. What is the phase difference between current and voltage? Draw current voltage graph.
Answer:
Let an a.c. source be connected with a resistance R as shown in figure. The alternating e.m.f. is given by the equation.
V = V0 sinωt … (1)
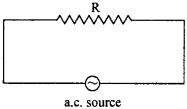
The corresponding value of current at any instant is
I = \(\frac {V}{R}\) = \(\frac { { V }_{ 0 }sin\omega t }{ R }\)
or I = I0 sinωt, (∵ I0 = \(\frac { { V }_{ 0 } }{ R }\) … (2)
Here, V = IR is valid because Ohm’s law is applicable for both a.c. and d.c.
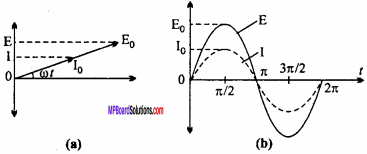
It is. clear from equation (1) and (2) that the phase of both E and I is cot. Hence, current and voltage are in the same phase. Fig. shows variation of current and voltage in an a.c. circuit with respect to time.
Question 30.
An alternating e.m.f. V = V0 sinωt is applied across a purely inductive a.c. circuit. Calculate the expression for the following :
- Current flow
- Inductive reactance and
- Phase relation between current and voltage and its graph.
Answer:
Suppose an alternating e.m.f. V = V0 sinωt … (1)
is applied across an a.c. circuit of inductance L. At the instant, when the current is maximum, the rate of change of current is zero. Hence, potential difference is zero, so induced e.m.f. = -L \(\frac {dI}{dt}\)
To maintain the flow of current, the applied voltage must be equal and opposite to the induced e.m.f.
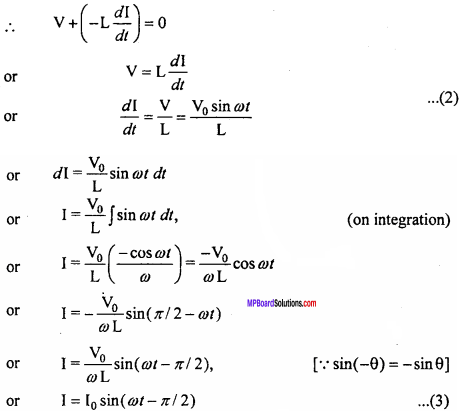
This is the required expression for current flow.
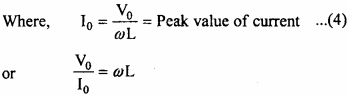
Where, aL is called inductive reactance and is denoted by XL.
Thus, XL = ωL = 2πfL
Where, f = Frequency of current.
Phase relation between current and voltage:
From eqns. (1) and (3), we find that the phase of voltage is at, whereas that of current is at ωt – \(\frac {π}{2}\). Hence, current lags behind the voltage by \(\frac {π}{2}\). This is shown in the phaser diagram below.
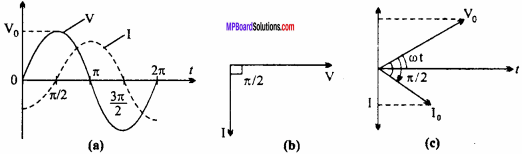
Question 31.
An alternating voltage V = V0 sinωt is applied across a capacitor C. Obtain an expression for
- Circuit current
- Capacitive reactance and
- Phase relation between current and voltage.
Answer:
1. Suppose the instantaneous voltage at any instant of time t is
V = V0 sinωt … (1)
If Q is the charge acquired by the capacitor at this instant, c
then
c = \(\frac {Q}{V}\)
or Q = CV or Q = C V0 sinωt
But the current at any instant is given by

2. From Equation (3), \(\frac { { V }_{ 0 } }{ { I }_{ 0 } }\) = \(\frac {1}{ωC}\)
Comparing with Ohm’s law, \(\frac {1}{ωC}\)is called capacitive reactance denoted by Xc.
Xc = \(\frac {1}{ωC}\) =\(\frac {1}{2πfC}\)
3. Phase relation between current and voltage:
From eqns. (1) and (2), we find that the phase of voltage is ωt, whereas of current is ωt + \(\frac {π}{2}\) hence current is ahead of voltage by \(\frac {π}{2}\) or we can say that voltage is lagging behind the current by n! 2. This is shown in the figure below:
Question 32.
Explain the behaviour of inductor and capacitor towards a.c. and d.c.
Answer:
The reactance offered by an inductor is given by the equation
XL = ωL = 2πfL.
Where f is the frequency of the source and L is the inductance of the inductor
For a d.c. f = 0 thus XL = 0.
For an a.c. f ≠ 0 and XL ∝L.
Flence, an inductor provides no reactance to the flow of d.c. and provide reactance of the a.c. i.e. an inductor by passes d.c. and blocks a.c.
The reactance offered by a capacitor is given by the equation,
Xc = \(\frac {1}{ωC}\) = \(\frac {1}{2πfC}\)
Where C is the capacitance of the capacitor.
For d.c. f = 0 thus, Xc = ∞
For an a.c. f ≠ 0 and Xc ∝\(\frac {1}{f}\)
Hence, a capacitor provides infinite reactance to d.c. and with increasing frequency of an a.c. the reactance decreases, i.e. a capacitor by passes a.c. and blocks d.c.
![]()
Question 33.
What is Q – factor? Write the expression for it.
Answer:
In an L – C – R circuit when a capacitor gets charged, electrical energy is stored in it, and when current flows through the conductor, magnetic energy gets stored in it. During the half cycle of a.c. magnetic energy is maximum and electrical energy is zero and in the next half cycle magnetic energy becomes zero and electrical energy is maximum.
Moreover some amount of energy gets dissipated in the form of heat in the ohmic resistor. Less is the dissipation of energy in the circuit, more sharp will be the resonance. The measurement of the sharpness is done by a dimensionless quantity called ‘Quality factor’ or ‘Q – factor’.
Definition:
In an L – C – R circuit, the ratio of resonant frequency to the difference of its neighbouring frequencies so that their corresponding current is \(\frac { 1 }{ \sqrt { 2 } }\) times of the peak value is called Q factor of the circuit. Its expression is Q factor = \(\frac{1}{R} \sqrt{\frac{L}{C}}\)
Q factor to be maximum :
- Value of R should be less.
- Value of \(\frac {L}{C}\) should be more.
Alternating Current Long Answer Type Questions
Question 1.
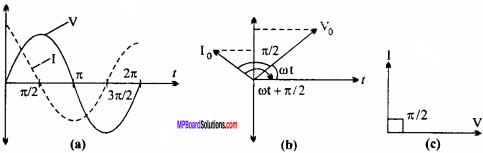
Describe the transformer on the basis of follow ing points :
- Principle
- Types of transformer
- Any three energy losses.
Or
Explain construction, principle and working method of transformer.
Answer:
Labelled diagram :
Construction:
A transformer consists of laminated core, primary coil and secondary coil. The laminated core is obtained by piling a number of laminated rectangular strips of soft iron. Two insulated copper wires are wound on the opposite arms, in the form of coils. The coil connected to the input of a.c. is called primary coil and the other through which output is taken is called secondary coil.
Method of working and principle:
Let the number of turns in primary and secondary coils are NP and Ns respectively. If the magnetic flux linked with the primary coil at any instant is ϕ, then the e.m.f. induced in the primary coil will be
EP = – NP\(\frac {dϕ}{dt}\) … (1)
If there is no loss of flux, the secondary coil will also be linked with the same flux ϕ. So, the e.m.f. induced in the secondary coil will be
Es = – Ns\(\frac {dϕ}{dt}\) … (1)
Dividing equation (2) by equation (1), we get
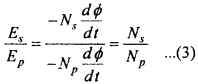
If there is no loss of energy in the primary coil, then the induced e.m.f. produced in the primary coil will be nearly equal to the applied potential difference (VP) between its ends. Similarly, because the secondary coil is open, hence the potential difference across its ends will be equal to the e.m.f. induced in it i.e., under ideal conditions
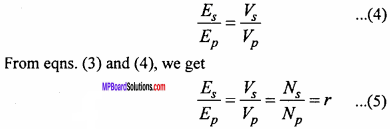
Let Ip and Is be the current through primary and secondary coils respectively. Then under ideal conditions,
Instantaneous input power = Instantaneous output power
i.e., Power in primary coil = Power in secondary coil
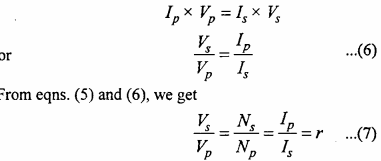
The quantity r in equation (5) and (7) is called transformation ratio.
For step – up transformer:

So, a step-up transformer increases the voltage, but decreases the strength of current. Also, the number of turns in the secondary coil is more than that of primary coil.
For step – down transformer:
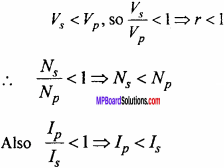
So, a step – down transformer decreases the voltage but increases the strength of current. The number of turns in secondary coil is less than that of primary coil.
Energy losses:
1.Copper loss:
Some part of the energy is wasted in the form of heat due to the heating effect of current in primary and secondary coil because the coils have some resistance. The amount of heat produced is I2Rt. To reduce it, thick coils are used in the primary coil of step – up transformer and in the secondary coil of a step – down transformer.
2. Iron loss:
Eddy current is produced in the iron core of the transformer, causes heating. This loss is called iron loss. To minimize this loss, the core is laminated.
3. Magnetic flux leakage:
All the magnetic flux produced by primary coil may not be transferred to the secondary coil. Therefore, some energy is wasted. To minimize this loss, soft – iron core is used.
Effect of eddy currents is minimized in a transformer by using laminated core. Lamination cause greater resistance to eddy currents produced. Thus, loss of electrical energy in the form of heat is reduced.
![]()
Question 2.
Describe a transformer on the basis of following points :
- Principle
- Its types and labelled diagram
- Energy losses in transformer.
Or
- Working principle
- Types and labelled diagram
- Energy losses
- Equation of transformation ratio.
Answer:
1. Principle :
Let the number of turns in primary and secondary coils are NP and Ns respectively. If the magnetic flux linked with the primary coil at any instant is ϕ, then the e.m.f. induced in the primary coil will be
EP = – NP\(\frac {dϕ}{dt}\) … (1)
If there is no loss of flux, the secondary coil will also be linked with the same flux ϕ. So, the e.m.f. induced in the secondary coil will be
Es = – Ns\(\frac {dϕ}{dt}\) … (1)
Dividing equation (2) by equation (1), we get
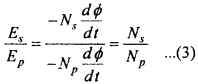
If there is no loss of energy in the primary coil, then the induced e.m.f. produced in the primary coil will be nearly equal to the applied potential difference (VP) between its ends. Similarly, because the secondary coil is open, hence the potential difference across its ends will be equal to the e.m.f. induced in it i.e., under ideal conditions
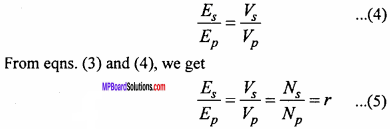
Let Ip and Is be the current through primary and secondary coils respectively. Then under ideal conditions,
Instantaneous input power = Instantaneous output power
i.e., Power in primary coil = Power in secondary coil
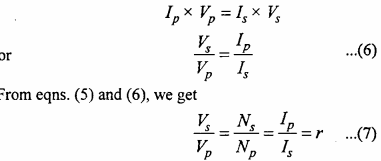
The quantity r in equation (5) and (7) is called transformation ratio.
2. Types and labelled diagram :

3. Energy losses:
(i) Copper loss:
Some part of the energy is wasted in the form of heat due to the heating effect of current in primary and secondary coil because the coils have some resistance. The amount of heat produced is I2Rt. To reduce it, thick coils are used in the primary coil of step – up transformer and in the secondary coil of a step – down transformer.
(ii) Iron loss:
Eddy current is produced in the iron core of the transformer, causes heating. This loss is called iron loss. To minimize this loss, the core is laminated.
(ii) Magnetic flux leakage:
All the magnetic flux produced by primary coil may not be transferred to the secondary coil. Therefore, some energy is wasted. To minimize this loss, soft – iron core is used.
(iv) Hysteresis loss:
Some amount of energy is wasted because the iron core becomes magnetized during the first half and then gets demagnetized during the other half. This wastes loss of magnetic energy is called hysteresis loss. It is minimized by taking soft – iron core which has thin hysteresis loop.
4. Equation of transformation ratio:
Let the number of turns in primary and secondary coils are NP and Ns respectively. If the magnetic flux linked with the primary coil at any instant is ϕ, then the e.m.f. induced in the primary coil will be
EP = – NP\(\frac {dϕ}{dt}\) … (1)
If there is no loss of flux, the secondary coil will also be linked with the same flux ϕ. So, the e.m.f. induced in the secondary coil will be
Es = – Ns\(\frac {dϕ}{dt}\) … (1)
Dividing equation (2) by equation (1), we get
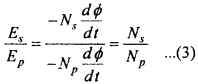
Question 3.
Obtain an expression for impedance in L – C – R circuit. Under what condition, the current will be maximum?
Or
What is resonant circuit ? Find the resonant frequency of L – C – R circuit.
Or
Obtain the condition of resonant frequency in the L – C – R circuit. Where this circuit is used ?
Or
Explain the resonance of a series L – C – R circuit under the following heads :
- Resultant voltage
- Impedance of circuit
- Frequency of resonance.
Answer:
In L – C circuit or in L – C – R circuit, when the value of impedance is least, the current becomes maximum. This phenomenon is called resonance. In this state, the frequency of the applied e.m.f. is equal to the natural frequency of the L – C circuit called resonant circuit.
Expression for the impedance:
Let inductance L, capacitor C and resistance R are joined in series to an a.c. circuit as shown in the Fig. (a).
Let the instantaneous current is I.
Potential difference across L will be, VL=I.XL … (1)
Potential difference across C will be, VC = I.XC … (2)
and Potential difference across R will be, VR= I. R … (3)
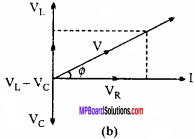
Now, VR and f are in the same phase and VL leads I by 90° and VC lags I by 90°. Hence, the angle between VL and VC will be 180°.
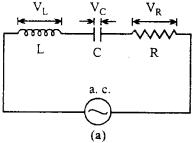
Now, resultant of VL and VC is VL – VC, then angle between VL – VC and VR is 90°.
Resultant,
V2 = V2R + (VL – VC )2
V2 = I2R2 + I2 (XL – XC)2
or R2 + (XL – XC)2
By comparing equation (4) with Ohm’s law, we get the resultant resistance also
![]()
∴ Impedance of the circuit,
![]()
This is the equation for impedance from Fig. (a).
If ϕ be the phase difference between V and I, then from Fig. (b). V,
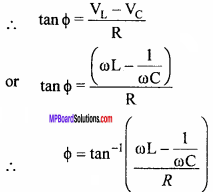
Now, the current flowing through the circuit will be given by
I = I0 sin(ωt – ϕ)
With respect to voltage, the current is behind ϕ.

Since, impedance is minimum and current is maximum, therefore this state is called resonance.
Again, under resonance condition,
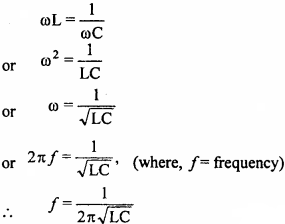
This is the required expression.
This circuit is used for tuning the radio receiver.
Alternating Current Numerical Questions
Question 1.
For a L – R circuit, the reactance of inductor is 3Ω and ohmic resistance is 4Ω . Find out impedance of the circuit.
Solution:
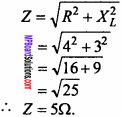
Question 2.
In a transformer, the ratio of number of turns in primary coil to that of secondary coil is 20:1. If it is operated at 200 volt then find out voltage obtained across secondary coil.
Solution:
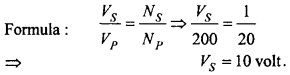
Question 3.
Alternating current of \(\sqrt { 2A }\) flows through a circuit, what is the maximum value of current ?
Solution:
Maximum value I0 = \(\sqrt {2}\) × Irms
I0 = \(\sqrt {2}\) × \(\sqrt {2}\) = 2A.
![]()
Question 4.
The peak value of alternating current is \(\sqrt { 2A }\) . Find out r. m. s. value of the current.
Solution:
Formula:
Irms = \(\frac { { I }_{ 0 } }{ \sqrt { 2 } }\) = \(\frac { 2\sqrt { 2 } }{ \sqrt { 2 } }\)
Question 5.
In domestic circuit mains voltage is 220 V, find out its maximum value.
Solution:
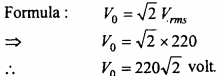
Question 6.
The r.m.s. value of current in an a.c. circuit is 10A. Find the peak value of current.
Solution:
Given, Irms = 10A
Formula: Irms = \(\frac { { I }_{ 0 } }{ \sqrt { 2 } }\) or I0 = Irms x \(\sqrt {2}\)
Putting the value in the formula, we get
I0 = 10 x \(\sqrt {2}\) = 10 x 1.414 = 14.1A.
![]()
Question 7.
The equation of a alternating voltage is V = 141 sin50πt. Determine r.m.s. value of voltage.
Solution:
Given, V = 141 sin 50πt.
Comparing with the equation V=V0 sinωt, we get
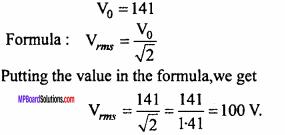
Question 8.
An e.m.f. of a.c. source is given by E = 300 sin 314t. Obtain the peak voltage and the frequency of the source.
Solution:
Comparing with E = E0 sinωt
∴ Peak voltage E0 = 300 V.
Here, ω = 314
or 2πf = 314
or f = \(\frac {314}{2π}\)
= \(\frac {314}{2×3.14 }\)
= 50 Hz
Question 9.
Self – inductance of a coil is 0.025 henry, calculate the inductive impedance for 50 Hz a.c.
Solution:
Formula: XL= ωL = 2πfL.
Given: f = 50 Hz and L = 0.025 H.
XL = 2 x 3.14 x 50 x 0.025
= 78.5Ω
Question 10.
A 1.5µF capacitor is connected to 220 V, 50 Hz source. Find the capacitive reactance and the current in the circuit. (NCERT)
Solution:
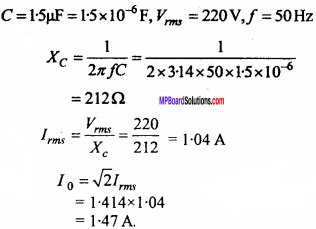
Question 11.
The potential drops across a resistor, capacitor and inductor in an a.c. circuit are 80 V, 100 V and 40 V respectively. Calculate the e.m.f. of the source of given a.c. circuit.
Solution:
Formula: V2 = V2R + (VL – VC)2
Given : VR = 80 V, VL = 40V and VC = 100V.
Substituting these values in the formula,
V2 =802+(40 – 100)2
= 6400 + 3600 = 10000
∴ V = 100V.
![]()
Question 12.
The ratio of number of turns in primary to that of secondary coil of a step up transformer is 1:10. If it is connected to the mains of 220 V, a current of 5 A flows. Calculate the induced e.m.f. and induced current in the secondary coil.
Solution:
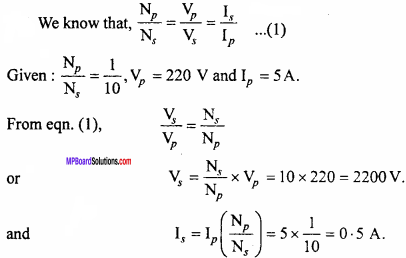
Question 13.
A step – down transformer changes 2200 V to 220 V. The number of turns in primary coil is 5000. If its efficiency is 90% and output power is 8 kW, calculate :
- Number of turns in secondary coil and
- Input power.
Solution:
