MP Board Class 12th Maths Important Questions Chapter 5A Continuity and Differentiability

MP Board Class 12th Maths Important Questions Chapter 5A Continuity and Differentiability

Continuity and Differentiability Important Questions

Continuity And Differentiability Objective Type Questions:

Question 1.
Choose the correct answer:

Question 1.
If x = at², y = 2at, then \(\frac{dy}{dx}\) will be:
(a) t
(b) t²
(c) \(\frac{1}{t}\)
(d) \(\frac { 1 }{ t^{ 2 } } \)
Answer:
(c) \(\frac{1}{t}\)

Question 2.
If y = 2\(\sqrt { cot(x^{ 2 }) } \) ,then \(\frac{dy}{dx}\) will be:

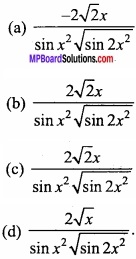
Answer:
(a)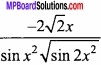

Question 3.
The value of \(\frac{d}{dx}\) (x³ + sin x²) is to be:
(a) 3x² + cos x²
(b) 3x² + x sin x²
(c) 3x² + 2x cos x²
(d) 3x² + x cos x²
Answer:
(c) 3x² + 2x cos x²

Question 4.
The value of \(\frac{d}{dx}\) a^x is to be:
(a) a^x
(b) a^x log_a e
(c) a^x log_e a
(d) \(\frac { a^{ x } }{ log_{ e }a } \)
Answer:
(c) a^x log_e a

Question 5.
If y = 500e^7x + 600e^-7x, then the value of \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) will be:
(a) 45 y
(b) 47 y
(c) 49 y
(d) 50 y
Answer:
(c) 49 y

Question 2.
Fill in the blanks:

1. Differential coefficient of cos x⁰ w.r.t x is ……………………………..
2. Differential coefficient of e^log_ea w.r.t x is ……………………………….
3. Differential coefficient of log_e a w.r.t x is ………………………………
4. Differential coefficient of a^x w.r.t x is ……………………………….
5. Differential coefficient of sin 3x w.r.t x is ……………………………….
6. If y = sin^-1 (2x \(\sqrt { (1-x^{ 2 }) } \)), then \(\frac{dy}{dx}\) = ………………………………
7. Differential coefficient of sin x w.r.t. cos x is …………………………………..
8. The value of \(\frac{d}{dx}\) (log tan x) is ………………………………………
9. Differential coefficient of log (log sin x) ………………………………
10. If x = y\(\sqrt { (1-y^{ 2 }) } \), then \(\frac{dy}{dx}\) will be …………………………………
11. n^th differentiation of sin x will be ………………………………………
12. If y = \(\sqrt { x+\sqrt { x+……..\infty } } \), then \(\frac{dy}{dx}\) will be ……………………………….
13. If x = r cos θ, y = r sin θ, then \(\frac{dy}{dx}\) will be ………………………..
14. Differential coefficient of e^x w.r.t \(\sqrt { x } \) will be ………………………….

Answer:

1. – \(\frac { \pi }{ 180 } \) sin x⁰
2. 0
3. 0, 4
4. log_e a.a^x
5. cos 3x
6. \(\frac { 2 }{ \sqrt { 1-x^{ 2 } } } \)
7. – cot x
8. 2 cosec 2x
9. \(\frac { cotx }{ logsinx } \)
10. \(\frac { \sqrt { 1-y^{ 2 } } }{ 1-2y^{ 2 } } \)
11. sin (\(\frac { n\pi }{ 2 } \) + x)
12. \(\frac { 1 }{ 2y-1 } \)
13. – cot θ
14. 2\(\sqrt { x } \)e^x.

Question 3.
Write True/False:

1. Differential coefficient of e^log_ex is \(\frac{1}{x}\)?
2. If f(x) = \(\sqrt { x } \); x>0, then value of f'(2) is \(\frac { 1 }{ 2\sqrt { 2 } } \)?
3. Any function f(x) is said to be differentiatiable at any point x = a when Lf'(a) ≠ Rf'(a)?
4. Differential coefficient of sec^-1a w.r.t x is 0?
5. If y = Ae^mx + Be^-mx, then \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = – m²y?
6. If y = sin^-1( \(\frac { x-1 }{ x+1 } \) ) + cos^-1 ( \(\frac { x-1 }{ x+1 } \) ), then \(\frac{dy}{dx}\) = 0?
7. Every differentiatiable function is continous?
8. Differential coefficient of a^2x is a^2x log_ea?

Answer:

1. Flase
2. True
3. Flase
4. False
5. True
6. True
7. True
8. Flase

Question 4.
Match the Column:

Answer:

1. (d)
2. (e)
3. (a)
4. (f)
5. (h)
6. (g)
7. (c)
8. (b)

Question 5.
Write the answer in one word/sentence:

1. Find differential coefficient of \(\frac { 6^{ x } }{ x^{ 6 } } \) w.r.t. x?
2. Find differential coefficient of y = ^log_etanxw.r.t x?
3. Find n^th derivative of a^x?
4. If y = sin(ax + b), then find the value of \(\frac { d^{ 2 }y }{ dx^{ 2 } } \)?
5. If x² + y² = sin xy, then find the value of \(\frac{dy}{dx}\)?
6. Find differential coefficient of log tan \(\frac{x}{2}\) w.r.t. x?
7. Find differential coefficient of sin^-1 \(\frac { 2x }{ 1+x^{ 2 } } \) w.r.t. x?
8. Find differential coefficient of e^-log_ex w.r.t x?

Answer:

1. \(\frac { 6^{ x } }{ x^{ 6 } } \) [log 6 – \(\frac{6}{x}\) ]
2. sec² x
3. a^x(log_ea)ⁿ
4. -a²y
5. \(\frac { ycosxy-2x }{ 2y-xcosxy } \)
6. cosec x,
7. \(\frac { 2 }{ 1+x^{ 2 } } \)
8. – \(\frac { 1 }{ x^{ 2 } } \)

Continuity And Differentiability Short Answer Type Questions

Question 1.
Find all the points of discontinuity of f, when f is defined as:
f(x) = \(\left\{\begin{array}{lll}
{2 x+3,} & {\text { if }} & {x \leq 2} \\
{2 x-3,} & {\text { if }} & {x>2}
\end{array}\right.\) (NCERT)
Solution:
For x< 2, f(x) = 2x + 3 is polynomial function.
Hence, for x < 2, f(x) is continuous function. For x > 2, f(x) = 2x – 3 is polynomial function.
Hence, x > 2, f(x) is continous.
Now, we shall examine the continuty of f(x) at x = 2 only.
Put x = 2 + h,
When x → 2, then h → 0

= 2(2 + 0) – 3 = 4 – 3 = 1.
Put x = 2 – h,
When x → 2, then h → 0

= 2(2 – 0) + 3 = 7
f(2) = 2(2) + 3 = 7

Hence, f(x) is discontinous at x = 2 only.

Question 2.
Find all the points of discontunity of f, when f is defined as follow:
f(x) = \(\left\{\begin{array}{ccc}
{\frac{|x|}{x},} & {\text { if }} & {x \neq 0} \\
{0} & {\text { if }} & {x=0}
\end{array}\right.\). (NCERT)
Solution:
Hence, we shall examine the continuty of f(x) at x = 0 only,
Put x = 0 + h,
When x → 0, then h → 0

Put x = 0 – h,
When x → 0, then h → 0

= -1
Given: f(0) = 0

Hence, the given function f(x) is discontinous at x = 0.

Question 3.
Examine the continuty of function f(x) at point x = 0?
f(x) = \(\left\{\begin{array}{cc}
{\frac{1-\cos x}{x^{2}},} & {x \neq 0} \\
{\frac{1}{2},} & {x=0}
\end{array}\right.\)
Solution:
f(x) = \(\frac { 1-cosx }{ x^{ 2 } } \), when x ≠ 0.
Put x = 0 + h, when x → 0, then h → 0

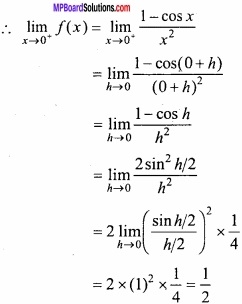
Again, put x = 0 – h, when x → 0, then h → 0

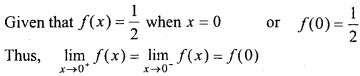
Hence, f(x) is continous at x = 0.

Question 4.
Function f is defined as:
f(x) = \(\left\{\begin{aligned}
\frac{|x-4|}{x-4} ; & x \neq 4 \\
0 ; & x = 4
\end{aligned}\right.\)
Then prove that function f is continous function for all points except x = 4?
Solution:

Hence, for x = 4 the function f(x) is dicontinous

When x < 4 then f(x) = -1 which is constant function Hence, it is continous function when x > 4 then f(x) = 1 which is constant function.
Hence, it is continous function
The given functions f is continous at all points except x = 4. Proved.

Question 5.
Find the value of k for which the function
f(x) = \(\left\{\begin{array}{c}
{\frac{k \cos x}{\pi-2 x}, \text { if } x \neq \frac{\pi}{2}} \\
{3, \text { if } x=\frac{\pi}{2}}
\end{array}\right.\)
is contionuous at x = \(\frac { \pi }{ 2 } \). (NCERT)
Solution:
Put x = \(\frac { \pi }{ 2 } \) + h,
When x → \(\frac { \pi }{ 2 } \), then h → 0


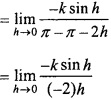
\(\frac{k}{2}\) × 1 = \(\frac{k}{2}\)
Put x = \(\frac { \pi }{ 2 } \) – h
When x → \(\frac { \pi }{ 2 } \), then h → 0

\(\frac{k}{2}\) × 1 = \(\frac{k}{2}\)
Given that f ( \(\frac { \pi }{ 2 } \) ) = 3
The given function is continous,

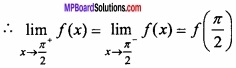
\(\frac{k}{2}\) = \(\frac{k}{2}\) = 3
k = 6.

Question 6.
Find the value of k, if function
f(x) = \(\left\{\begin{array}{lll}
{k x+1,} & {\text { if }} & {x \leq \pi} \\
{\cos x,} & {\text { if }} & {x>\pi}
\end{array}\right.\) is continous at x = π? (NCERT)
Solution:
Put x = π + h,
When x → π, then h → 0

= cos (π + 0)
= -1.
Put x = π – h,
When x → π, then h → 0

= k(π – 0) + 1
= πk + 1
f(π) = kπ + 1
∴ The given function is continous at x = π

-1 = kπ + 1 = kπ + 1
kπ = -2
k =- \(\frac { 2 }{ \pi } \)

Question 7.
Function f is continous at x = 0:
f (x) = \(\left\{\begin{array}{c}
{\frac{1-\cos k x}{x \sin x} ; x \neq 0} \\
{\frac{1}{2} \quad ; x=0}
\end{array}\right.\) Find the value of k?
Solution:
Given:
f(x) = \(\frac { 1-coskx }{ xsinx } \), x ≠ 0


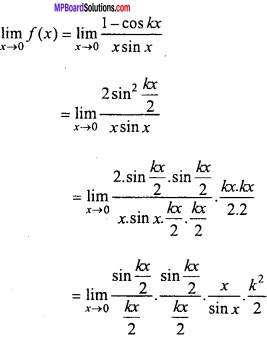
Given: f(0) = \(\frac{1}{2}\)

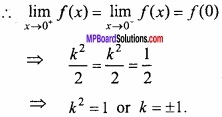
Question 8.
Find the relationship between a and b so the following function f defined by:
f(x) = \(\left\{\begin{array}{lll}
{a x+1,} & {\text { if }} & {x \leq 3} \\
{b x+3,} & {\text { if }} & {x>3}
\end{array}\right.\) is continous at x = 3. (NCERT; CBSE 2011)
Solution:
Put x = 3 + h,
When x → 3, then h → 0

= b(3 + 0) + 3
= 3b + 3
Put x = 3 – h,
When x → 3, then h → 0

= a(3 – 0) + 1
= 3a + 1
f(3) = 3a + 1
The given function is continous at x = 3.

3b + 3 = 3a + 1 = 3a + 1
3a + 1 = 3b + 3
3a = 3b + 2
a = b + \(\frac{2}{3}\).

Question 9.
Prove that the funcion f(x) = |x – 1|, x ∈ R is not differentiable at x = 1? (NCERT)
Solution:
Given:

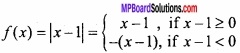
f(1) = 1 – 1 = 0
Put x = 1 – h, when x → 1, then h → 0

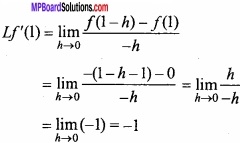
Put x = 1 + h, when x → 1, then h → 0

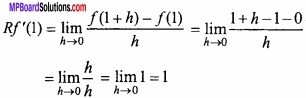
Lf'(1) ≠ Rf'(1)

Question 10.
Show that the function:
f(x) = \(\left\{\begin{aligned}
x-1, & \text { if } x<2 \\
2 x-3, & \text { if } x \geq 2
\end{aligned}\right.\), is not differentaible at point x = 2?
Solution:
We know that:
RHD =

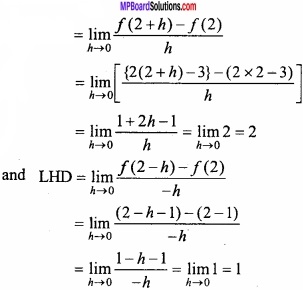
From the above, it is clear that,
LHD at x = 2 ≠ RHD at x = 2
∴ f(x) is not differentiable at x = 2. Proved.

Question 11.
Determine the function of defined by
f(x) = \(\left\{\begin{array}{cc}
{x^{2} \sin \frac{1}{x},} & {\text { when } x \neq 0} \\
{0,} & {\text { when } x=0}
\end{array}\right.\) in continous function? (NCERT)
Solution:
Here, f(0) = 0


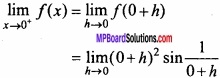
= 0 × a finite quantiy, [∵ sin \(\frac{1}{h}\) is between -1 and 1]
= 0

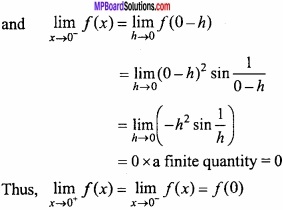
Hence, the given function is continous at x = 0.

MP Board Class 12 Maths Important Questions