MP Board Class 12th Maths Important Questions Chapter 5B Differentiation
Differentiation Important Questions
Differentiation Short Answer Type Questions
Question 1.
Differentiate the function sin(cos x2) with respect to x? (NCERT)
Solution:
Let y = sin (cosx2)
\(\frac { dy }{ dx } \) = \(\frac { d }{ dx } \) sin (cos x2)
= \(\frac { d }{ dx } \) sin t, [Putting cos x2 = t]
= \(\frac { d }{ dt } \) sin t \(\frac { dt }{ dx } \)
= cos t \(\frac { d }{ dx } \) cos x2
= cos (cos x2) \(\frac { d }{ dx } \) cos u, [Putting x2 = u]
= cos (cos x2) \(\frac { d }{ du } \) cos u \(\frac { du }{ dx } \)
= – cos (cos x2) sin u \(\frac { d }{ dx } \) x2
= – 2x cos (cos x2). sin x2.
Question 2.
Differentiate the function y = sec [tan \(\sqrt { x } \) ] with respect to x? (NCERT)
Solution:
Given:
y = sec [tan \(\sqrt { x } \) ]
\(\frac { dy }{ dx } \) = \(\frac { d }{ dx } \) sec [tan \(\sqrt { x } \) ]
= \(\frac { d }{ dx } \) sec t, [Putting tan \(\sqrt { x } \) = t]
= \(\frac { d }{ dt } \) sec t \(\frac { dt}{ dx } \)
= sec t tan t \(\frac { d }{ dx } \) tan \(\sqrt { x } \)
= sec (tan \(\sqrt { x } \)) tan (tan \(\sqrt { x } \)) \(\frac { d }{ dx } \) tan u, [Putting \(\sqrt { x } \) = u]
= sec (tan \(\sqrt { x } \)) tan (tan \(\sqrt { x } \)) sec2 u \(\frac { d }{ dx } \) \(\sqrt { x } \)
= sec (tan \(\sqrt { x } \)) tan (tan \(\sqrt { x } \)) sec2\(\sqrt { x } \) × \(\frac { 1 }{ 2\sqrt { x } } \)
![]()
Question 3.
Differentiate the function y = log [cos ex] with respect to x? (NCERT)
Solution:
Given:
y = log [cos ex]
\(\frac { dy }{ dx } \) = \(\frac { d }{ dx } \) [log (cos ex)]
\(\frac { dy }{ dx } \) = \(\frac { d }{ dx } \) log t, [Putting cos ex = t]
= \(\frac { d }{ dt } \) log t \(\frac { dt }{ dx } \)
= \(\frac { 1 }{ t } \). \(\frac { d }{ dx } \) cos ex
= \(\frac { 1 }{ cose^{ x } } \) × \(\frac { d }{ dx } \) cos u, [Putting ex = u]
= \(\frac { 1 }{ cose^{ x } } \). \(\frac { d }{ du } \) cos u \(\frac { du }{ dx } \)
= \(\frac { -sinu }{ cose^{ x } } \). \(\frac { d }{ dx } \) ex
= \(\frac { -(sine^{ x })e^{ x } }{ cose^{ x } } \)
= – ex tan ex
Question 4.
Differentiate the function y = cos [log x + ex] with respect to x? (NCERT)
Given:
y = cos [log x + ex]
\(\frac { dy }{ dx } \) = \(\frac { d }{ dx } \) cos (log x + ex)
\(\frac { dy }{ dx } \) = \(\frac { d }{ dx } \) cos t, [Putting log x + ex = t]
= \(\frac { d }{ dt } \) cos t \(\frac { dt }{ dx } \)
= – sin t \(\frac { d }{ dx } \) (log x + ex)
= – sin (log x + ex) (\(\frac{1}{x}\) + ex)
= – \(\frac { (xe^{ x }+1)sin(logx+e^{ x }) }{ x } \)
Question 5.
Differentiate the function y = cos-1(ex) with respect to x? (NCERT)
Solution:
Given:
y = cos-1 (ex)
∴\(\frac { dy }{ dx } \) = \(\frac { d }{ dx } \) cos-1 (ex)
Putting ex = t,
= \(\frac { d }{ dx } \) cos-1 t = \(\frac { d }{ dt } \) cos-1 t \(\frac { dt }{ dx } \)
= \(\frac { 1 }{ \sqrt { 1-t^{ 2 } } } \) \(\frac { d }{ dx } \) ex
= – \(\frac { e^{ x } }{ \sqrt { 1-e^{ 2x } } } \)
![]()
Question 6.
If y + sin y = cos x then find the value of \(\frac { dy }{ dx } \)? (NCERT)
Solution:
Given:
y + sin y = cos x
Differentiating both sides with respect to x,
\(\frac { d }{ dx } \) (y + siny) = \(\frac { d }{ dx } \) cos x
⇒ \(\frac { dy }{ dx } \) + cos y \(\frac { dy }{ dx } \) = – sin x
⇒ \(\frac { dy }{ dx } \) (1 + cos y) = -sin x
⇒ \(\frac { dy }{ dx } \) = \(\frac { -sinx }{ 1+cosy } \)
Question 7.
If 2x + 3y = sin x then find the value of \(\frac { dy }{ dx } \)? (NCERT)
Solution:
Given:
2x + 3y = sin x
Differentiating both sides with respect to x,
\(\frac { d }{ dx } \) (2x + 3y) = \(\frac { d }{ dx } \) sin x
2 \(\frac { d }{ dx } \) x + 3 \(\frac { dy }{ dx } \) = cos x
⇒ 2 + 3 \(\frac { dy }{ dx } \) = cos x – 2
∴ \(\frac { dy }{ dx } \) = \(\frac{cos x – 2}{3}\)
![]()
Question 8.
If x = a cos θ, y = a sin θ then find the value of \(\frac { dy }{ dx } \)? (NCERT)
Solution:
Given:
x = a cos θ
y = a sin θ
Differentiating eqn. (1) with respect to θ.
We get, \(\frac { dx }{ d\theta } \) = – a sin θ
Again, \(\frac { dy }{ dx } \) = \(\frac { \frac { dy }{ d\theta } }{ \frac { dx }{ d\theta } } \)
⇒ \(\frac { dy }{ dx } \) = – \(\frac { acos\theta }{ asin\theta } \)
⇒ \(\frac { dy }{ dx } \) = – cot θ.
Question 9.
If x = at2 and y = 2at then find the value of \(\frac { dy }{ dx } \)? (NCERT)
Solution:
Given:
x = at2
\(\frac { dx }{ dt } \) = 2at
y = 2at
\(\frac { dy }{ dt } \) = 2a
Again, \(\frac { dy }{ dx } \) = \(\frac { \frac { dy }{ dt } }{ \frac { dx }{ dt } } \) = \(\frac{2a}{2at}\)
⇒ \(\frac { dy }{ dx } \) = \(\frac { 1 }{ t} \).
Question 10.
If y = x2 + 3x + 2 then find the value of \(\frac { d^{ 2 }y }{ dx^{ 2 } } \)? (NCERT)
Solution:
Given:
y = x2 + 3x + 2
∴ \(\frac { dy }{ dx } \) = 2x + 3.1 + 0
\(\frac { dy }{ dx } \) = 2x + 3
Again differentiating with respect to x,
We get, \(\frac { d }{ dx } \) ( \(\frac { dy }{ dx } \) ) = 2.1 + 0
⇒ \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = 2.
![]()
Question 11.
If y = x3 + tan x then find the value of \(\frac { d^{ 2 }y }{ dx^{ 2 } } \)? (NCERT)
Solution:
Given:
y = x3 + tan x
\(\frac { dy }{ dx } \) = \(\frac { d }{ dx } \) [x3 + tan x]
= \(\frac { d }{ dx } \) x3 + \(\frac { d }{ dx } \) tan x
⇒ \(\frac { dy }{ dx } \) = 3x2 + sec2 x
Again, differentiating with respect to x,
⇒ \(\frac { d }{ dx } \) ( \(\frac { dy }{ dx } \) ) = \(\frac { d }{ dx } \) [3x2 + sec2x]
\(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = 3 \(\frac{d}{dx}\) x2 + \(\frac{d}{dx}\) sec2 x
⇒ \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = 6x + \(\frac{d}{dx}\) t2, [Putting sec x = t]
= 6x + \(\frac { d }{ dt } \) t2 \(\frac { dt }{ dx } \)
= 6x + 2t \(\frac { d }{ dx } \) sec x
= 6x + 2 sec x.secx tanx
⇒ \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = 6x + 2 sec2x tan x.
Differentiation Long Answer Type Questions – I
Question 1.
If y = tan-1 \(\frac { x }{ \sqrt { 1+x^{ 2 } } } \) then find the value of \(\frac { dy }{ dx } \)?
Solution:
Given:
y = tan-1 \(\frac { x }{ \sqrt { 1+x^{ 2 } } } \)
Now putting \(\frac { x }{ \sqrt { 1+x^{ 2 } } } \) = t
\(\frac { dy }{ dx } \) = \(\frac { d }{ dt } \) tan-1t. \(\frac { dt }{ dx } \)
= \(\frac { 1 }{ 1+t^{ 2 } } \). \(\frac { d }{ dx } \) \(\frac { x }{ \sqrt { 1+x^{ 2 } } } \)

Again Putting 1 + x2 = u,

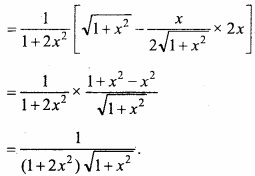
Question 2.
If x = a (t + sin t) and y = a(1 – cost) then find the value of \(\frac { dy }{ dx } \)?
Solution:
Given:
x = a (t + sin t)
∴\(\frac { dx }{ dt } \) = a(1 + cos t)
Again y = a (1 – cos t)
∴\(\frac { dy }{ dt } \) = a (0 + sint) = a sin t
Hence \(\frac { dy }{ dx } \) = \(\frac { \frac { dy }{ dt } }{ \frac { dx }{ dt } } \) = \(\frac { asint }{ a(1+cost) } \)
= \(\frac { sint }{ a(1+cost) } \) = \(\frac { 2sint/2cost/2 }{ 2cos^{ 2 }t/2 } \)
⇒ \(\frac { dy }{ dx } \) = tan \(\frac{t}{2}\).
![]()
Question 3.
If x = a(2θ – sin 2θ) and y = a(1 – cos 2θ) then find the value of \(\frac { dy }{ dx } \) where θ = \(\frac { \pi }{ 3 } \)? (CBSE 2018)
Solution:
Given:
x = a (2θ – sin 2θ) ………………… (1)
y = a (1 – cos 2θ) ………………………. (2)
Differentiating eqn. (1) with respect to θ, we get
\(\frac { dx }{ d\theta } \) = a(2.1 – cos 2θ.2)
= 2a (1 – cos 2θ)
= 2a.2 sin2θ
= 4a sin2θ
Differentiating eqn. (2) with respect to θ, ………………… (3)
\(\frac { dy }{ d\theta } \) = a (0 + sin 2θ.2)
= 2a sin 2θ
= 2a.2 sin θ cos θ ……………………….. (4)
= 4a sin θ cos θ
Divinding eqn.(4) by eqn.(3),
\(\frac { dy }{ d\theta } \) + \(\frac { dx }{ d\theta } \) = \(\frac { 4asin\theta cos\theta }{ 4asin^{ 2 }\theta } \)
⇒ \(\frac { dy }{ dx } \) = cot θ
When θ = \(\frac { \pi }{ 3 } \), then
\(\frac { dy }{ dx } \) = cot \(\frac { \pi }{ 3 } \) = \(\frac { 1 }{ \sqrt { 3 } } \).
Question 4.
If y = a sin mx + b cos mx then prove that:
\(\frac { d^{ 2 }y }{ dx^{ 2 } } \) + m2y = 0?
Solution:
Given:
y = a sin mx + b cos mx ……………………. (1)
Differentiating eqn. (2) with respect to x,
\(\frac { dy }{ dx } \) = am cos mx – bm sin mx
Differentiating eqn. (2) with respect to x,
\(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = – am2 sin mx – bm2 cos mx
⇒ \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = – m2 y
∴ \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) + m2 y = 0. Proved.
![]()
Question 5.
(A) If y = emsin-1x then prove that (1 – x2) y2 – xy1 – m2y = 0?
Solution:
Given:
y = emsin-1x
\(\frac { dy }{ dx } \) = y1 = emsin-1x. \(\frac { d }{ dx } \) (msin-1x)
⇒ y1 = y.m. \(\frac { 1 }{ \sqrt { 1-x^{ 2 } } } \)
⇒ \(\sqrt { 1-x^{ 2 } } \) y1 = my …………………………. (1)
Again, differentiating with respect to x,
\(\sqrt { 1-x^{ 2 } } \). y2 + y1. \(\frac{1}{2}\) (1 – x2)1/2 (- 2x) = my1
⇒ \(\sqrt { 1-x^{ 2 } } \). y2 – \(\frac { x }{ \sqrt { 1-x^{ 2 } } } \) y1 = m\(\frac { my }{ \sqrt { 1-x^{ 2 } } } \). [from eqn.(1)]
⇒ (1 – x2) y2 – xy1 = m2y
⇒ (1 – x2) y2 – xy1 – m2y = 0. Proved.
Question 5.
(B) If y = emtan-1x then prove that (1 + x2) y2 + (2x – m) y1 = 0?
Solution:
Solve like Q.5 (A)
Question 5.
(C) If y = emcos-1x then prove that (1 – x2) y2 – xy1 – m2 y = 0?
Solution:
Solve like Q.5 (A)
![]()
Question 6.
Differentiate sin-1 \(\frac { 2x }{ 1+x^{ 2 } } \) with respect to x?
Solution:
Let y = sin-1 ( \(\frac { 2x }{ 1+x^{ 2 } } \) )
Again let x = tan θ ⇒ θ = tan-1 x
y = sin-1 ( \(\frac { 2tan\theta }{ 1+tan^{ 2 }\theta } \) )
= sin-1 (sin 2θ) = 2θ = 2 tan-1 x
∴\(\frac { dy }{ dx } \) = 2 \(\frac { d }{ dx } \) (tan-1 x) = \(\frac { 2 }{ 1+x^{ 2 } } \)
Question 7.
If y = cot-1 \(\sqrt { \frac { 1+x }{ 1-x } } \) then find \(\frac { dy }{ dx } \)?
Solution:
Given:
y = cot-1 \(\sqrt { \frac { 1+x }{ 1-x } } \)
Let x = cos θ
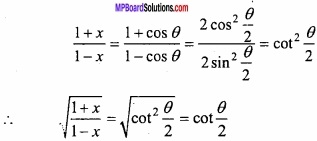
Putting in eqn.(1), we get
y = cot-1 (cot \(\frac{θ}{2}\))
⇒ y = \(\frac{θ}{2}\) = \(\frac{1}{2}\) cos-1 x, [∵x = cos θ ⇒ ∴θ = cos-1 x]
Differentiating both sides w.r.t. x,
\(\frac { dy }{ dx } \) = – \(\frac { 1 }{ 2\sqrt { 1-x^{ 2 } } } \)
Question 8.
If y = tan-1 \(\sqrt { \frac { 1+x }{ 1-x } } \) then find \(\frac { dy }{ dx } \)?
Solution:
Solve like Q.No.7
Answer:
\(\frac { dy }{ dx } \) = \(\frac { 1 }{ 2\sqrt { 1-x^{ 2 } } } \)
Question 9.
If y = cot-1 ( \(\frac { cosx+sinx }{ cosx-sinx } \) ) then find the value of \(\frac { dy }{ dx } \)?
Solution:
Given:
y = cot-1 ( \(\frac { cosx+sinx }{ cosx-sinx } \) )
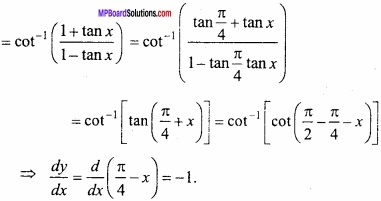
⇒ \(\frac { dy }{ dx } \) = \(\frac { d }{ dx } \) ( \(\frac { \pi }{ 4 } \) – x) = -1.
Question 10.
y = tan-1 \(\frac { \sqrt { 1+x^{ 2 }-1\quad } }{ x } \) Differentiate with respect to x?
Solution:
Given:
y = tan-1\(\frac { \sqrt { 1+x^{ 2 }-1\quad } }{ x } \) ……………….. (1)
Put x = tan θ in eqn. (1)
∴ θ = tan-1 x
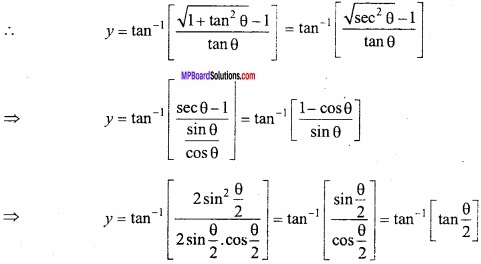
⇒ y = \(\frac { \theta }{ 2 } \) = \(\frac{1}{2}\) tan-1 x
∴\(\frac { dy }{ dx } \) = \(\frac{1}{2}\) tan-1 x
∴\(\frac { dy }{ dx } \) = \(\frac{1}{2}\) \(\frac { d }{ dx } \) (tan-1 x ) = \(\frac{1}{2}\) \(\frac { 1 }{ (1+x^{ 2 }) } \)
Question 11.
If y = cot-1 \(\left[\frac{\sqrt{1+x^{2}}+1}{x}\right]\) then find the value of \(\frac { dy }{ dx } \)?
Solution:
y = cot-1 \(\left[\frac{\sqrt{1+x^{2}}+1}{x}\right]\)
Put x = tan θ,

⇒ y = \(\frac{1}{2}\) tan-1x
⇒ \(\frac { dy }{ dx } \) = \(\frac{1}{2}\). \(\frac { 1 }{ 1+x^{ 2 } } \).
Question 12.
If y = xsinx then find the value of \(\frac { dy }{ dx } \)?
Solution:
Given:
y = xsinx
Taking log on both sides with respect to x.
\(\frac { 1 }{ y } \) \(\frac { dy }{ dx } \) = sin x × \(\frac{1}{x}\) + logx cos x
∴\(\frac { dy }{ dx } \) = y.[ \(\frac{sinx}{x}\) + log x.cos x]
![]()
Question 13.
If y = \(\sqrt { \frac { 1-x }{ 1+x } } \) then prove that \(\frac { dy }{ dx } \) = \(\frac { y }{ x^{ 2 }-1 } \)?
Solution:
Given:
y = \(\sqrt { \frac { 1-x }{ 1+x } } \)1/2
By taking log , log y = log \(\sqrt { \frac { 1-x }{ 1+x } } \)1/2
⇒ log y = \(\frac{1}{2}\) [log (1 – x) – log (1 + x)]
Differentiating both sides with respect to x,
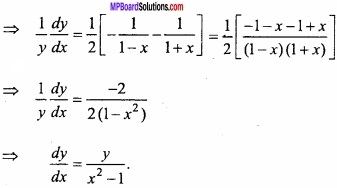
Question 14.
If y = (sin x)sinxsinx ………. ∞ then find the value of \(\frac { dy }{ dx } \)?
Solution:
Given:
y = (sin x)sinxsinx ………. ∞
⇒ y = (sin x)y
⇒ log y = y log sin x
Differentiating both sides with respect to x,
\(\frac{1}{y}\) \(\frac{dy}{dx}\) = y \(\frac{d}{dx}\) (log sin x) + log sin x \(\frac{dy}{dx}\)
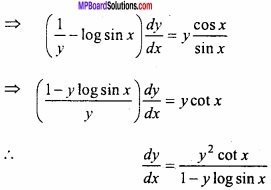
Question 15.
(A) If y = \(\sin x+\sqrt{\sin x+\sqrt{\sin x+\ldots+\infty}}\) then prove that:
\(\frac{dy}{dx}\) = \(\frac{cos x}{2y – 1}\)
Solution:

Differentiating both sides with respect to x,
2y \(\frac{dy}{dx}\) = cos x + \(\frac{dy}{dx}\)
⇒ 2y \(\frac{dy}{dx}\) – \(\frac{dy}{dx}\) = cos x
⇒ (2y – 1) \(\frac{dy}{dx}\) = cos x
∴\(\frac{dy}{dx}\) = \(\frac{cos x}{2y – 1}\).
(B) If y = \(\cot x+\sqrt{\cot x+\sqrt{\cot x+\ldots+\infty}}\) then prove that:
\(\frac{dy}{dx}\) = \(\frac { cosec^{ 2 }x }{ 1-2y } \)
Solution:
Solve like Q.No. 15 (A).
(C) If y = \(\begin{aligned}
&x+\sqrt{\tan x+\sqrt{\tan x+\ldots \infty}}\\
\end{aligned}\) then find the value of \(\frac{dy}{dx}\)?
Solution:
Solve like Q.No 15 (A)
Question 16.
If y = e\($x+e^{x+e^{x+e}}-$\) then prove that:
\(\frac{dy}{dx}\) = \(\frac{y}{1-y}\)?
Solution:
Given: y = e\(x+e^{x+e^{x+e}}-x\)
⇒ y = ex+y
Taking log on both sides,
log y = log ex+y
log y = x + y
Differentiating both sides with respect to x,
\(\frac{1}{y}\) \(\frac{dy}{dx}\) = 1 + \(\frac{dy}{dx}\)
⇒ \(\frac{dy}{dx}\) ( \(\frac{1}{y}\) – 1) = 1
⇒ \(\frac{dy}{dx}\) ( \(\frac{1-y}{y}\) ) = 1
⇒ \(\frac{dy}{dx}\) = \(\frac{y}{1-y}\) Proved.
![]()
Question 17.
Differentiate \(\frac { 1 }{ (x+a)(x+b)(x+c) } \) with respect to x?
Solution:
Let y = \(\frac { 1 }{ (x+a)(x+b)(x+c) } \)
Applying log on both sides,
log y = log 1 – log(x + a) – log (x + b) – log(x + c)
Differentiating both sides with respect to x,
\(\frac{1}{y}\) \(\frac{dy}{dx}\) = 0 – \(\frac{1}{x + a}\) – \(\frac{1}{x + b}\) – \(\frac{1}{x + c}\)
⇒ \(\frac{dy}{dx}\) = – y [ \(\frac{1}{x + a}\) + \(\frac{1}{x + b}\) + \(\frac{1}{x + c}\) ]
⇒ \(\frac{dy}{dx}\) = \(\frac { 1 }{ (x+a)(x+b)(x+c) } \) × { \(\frac { 1 }{ x+a } +\frac { 1 }{ x+b } +\frac { 1 }{ x+c } \) }
Question 18.
Differentiate log ( \(\sqrt{x}\) + \(\frac { 1 }{ \sqrt { x } } \) ) with respect to x?
Solution:
Let y = log ( \(\sqrt{x}\) + \(\frac { 1 }{ \sqrt { x } } \) ) ⇒ y = log ( \(\frac { x+1 }{ \sqrt { x } } \) )
⇒ y = log (x + 1) – log \(\sqrt{x}\)
⇒ y = log (x + 1) – \(\frac{1}{2}\) log x
Differentiating both sides with respect to x,
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) log (x + 1) – \(\frac{1}{2}\). \(\frac{d}{dx}\) log x
⇒ \(\frac{dy}{dx}\) = \(\frac{1}{x + 1}\) – \(\frac{1}{2}\).\(\frac{1}{x}\) = \(\frac{2x-x-1}{2x(x+1)}\)
⇒ \(\frac{dy}{dx}\) = \(\frac{x – 1}{2x(x + 1)}\).
![]()
Question 19.
Differentiate y = tan-1 ( \(\frac { sinx }{ 1+cosx } \) ) with respect to x?
Solution:
y = tan-1 ( \(\frac { sinx }{ 1+cosx } \) )
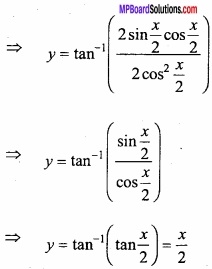
⇒ y = tan-1 (tan \(\frac{x}{2}\) ) = \(\frac{x}{2}\)
Differentiating both sides with respect to x,
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) ( \(\frac{x}{2}\) ) = \(\frac{1}{2}\).
Question 20.
Verify Rolle’s theroem for the function f(x) = x2 interval [-1, 1]. (NCERT)
Solution:
Given:
f(x) = x2, a = – 1, b = 1.
- f(x) = x2 is a polynomial, hence, f(x) is continous in [-1, 1].
- f'(x) = 2x exist for every value of x, Hence it is differentiable in (-1, 1).
- f(-1) = (-1)2 = 1, f(1) = (1)2 = 1.
∴ f(-1) = f(1)
There exists a value c in (-1, 1) such that:
∴ f'(c) = 0
⇒ 2c = 0, [∵f'(x) = 2x]
⇒ c = 0 ∈ (-1, 1)
Hence, Rolle’s theorem is verified. Proved.
![]()
Question 21.
Verify Rolle’s theroem for the function f(x) = x2 + 2x – 8, x ∈ [-4, 2]? (NCERT)
Solution:
Given:
f(x) = x2 + 2x – 8, a= – 4, b = 2.
- f(x) = x2 + 2x – 8 is a polynomial hence f(x) is continous in [-4, 2].
- f'(x) = 2x + 2 exist for every value of x, hence it is differentiable in (-4, 2).
- f(-4) = (-4)2 + 2 (-4) – 8
= 16 – 8 – 8 = 0
f(2) = (2)2 + 2 × 2 – 8 = 4 + 4 – 8 = 0
∴ f(-4) = f(2).
There exists a value c in (-4, 2),
∴ f'(c) = 0
⇒ 2c + 2 = 0
⇒ c = – 1 ∈ (-4, 2)
Hence, Rolle’s theorem is verified.
Question 22.
Verify Rolle’s theorem for the function f(x) = 2x3 + x2 – 4x – 2?
Solution:
Given:
f(x) = 2x3 + x2 – 4x – 2 …………………… (1)
We know that polynomial functions are continuous for all real values.
∴ f(x) = o
⇒ 2x3 + x2 – 4x – 2 = 0
⇒ x2 (2x + 1) – 2(2x + 1) = 0
⇒ (x2 – 2) (2x + 1) = 0
⇒ x2 = 2, 2x + 1 = 0
⇒ x = ±\(\sqrt { 2 } \), x = – \(\frac{1}{2}\)
⇒ x = – \(\sqrt { 2 } \), \(\sqrt { 2 } \), \(\frac{-1}{2}\)
∴ Interval [-\(\sqrt { 2 } \), \(\sqrt { 2 } \) ].
1. f(x) is continuous in [-\(\sqrt { 2 } \), \(\sqrt { 2 } \) ]
2. f'(x) = 6x2 + 2x – 4 is differentiable in [-\(\sqrt { 2 } \), \(\sqrt { 2 } \)].
3. f(-\(\sqrt { 2 } \)) = 2( \(\sqrt { 2 } \) )3 + (-\(\sqrt { 2 } \) ) 2 – 4 (- \(\sqrt { 2 } \) ) – 2 = 0
and f ( \(\sqrt { 2 } \) ) = 2( \(\sqrt { 2 } \) )3 + ( \(\sqrt { 2 } \) ) 2 – 4( \(\sqrt { 2 } \) ) – 2 = 0
∴ f(- \(\sqrt { 2 } \) ) = f( \(\sqrt { 2 } \) )
There exists a value c in (-\(\sqrt { 2 } \), \(\sqrt { 2 } \) )
∴ f'(c) = 0
⇒ 6c2 + 2c – 4 = 0, [∵f'(x) = 6x2 + 2x – 4]
∴ c = \(\frac { -2\pm \sqrt { 2^{ 2 }-4\times 6\times (-4) } }{ 2\times 6 } \)
c = \(\frac { -2\pm \sqrt { 4+96 } }{ 12 } \)
⇒ c = \(\frac { -2\pm 10 }{ 12 } \)
⇒ c = \(\frac{-2-10}{12}\) and c = \(\frac{-2+10}{12}\)
⇒ c = -1, \(\frac{2}{3}\) ∈ (- \(\sqrt { 2 } \), \(\sqrt { 2 } \) )
Hence, Rolle’s theroem is verified.
![]()
Question 23.
Verify Lagrange’s mean value theorem for the function f(x) = x + \(\frac{1}{x}\) on [1, 3].
Solution:
Given:
f(x) = x + \(\frac{1}{x}\) = \(\frac { x^{ 2 }+1 }{ x } \), x ∈ [1, 3]
- f(x), x ≠ 0 hence it is a continous function in [1, 3].
- f'(x) = 1 – \(\frac { 1 }{ x^{ 2 } } \) is differentiable in (1, 3).
- f(1) = 2 and f(3) = \(\frac{10}{3}\)
Hence, f(1) ≠ f(2)
For mean value theorem,
∴ \(\frac { f(b)-f(a) }{ b-a } \) = f'(c)
⇒ \(\frac { f(3)-f(1) }{ 3-1 } \) = 1 – \(\frac { 1 }{ c^{ 2 } } \)
⇒ \(\frac { \frac { 10 }{ 3 } -2 }{ 2 } \) = 1 – \(\frac { 1 }{ c^{ 2 } } \)
⇒ 1 – \(\frac { 1 }{ c^{ 2 } } \) = \(\frac{2}{3}\)
⇒ \(\frac { 1 }{ c^{ 2 } } \) = \(\frac{3-2}{3}\) = \(\frac{1}{3}\)
⇒ c2 = 3
⇒ c = \(\sqrt{3}\) = 1.732 ∈ (1, 3)
Hence, Langrange’s mean value theorem is verified. Proved.
Question 24.
Verify Lagrange’s mean value theorem for the following function f(x) = log x on [1, e]?
Solution:
f(x) = logx, x ∈ [1, e], x > 0.
1. As f(x) = log x, x > 0 is a continuous function, hence f(x) is continuous in [1, e],
2. f'(x) = \(\frac{1}{x}\),
∴ f(x) is differentiable in (1, e).
3. f(1) = log 1 = 0, f(e) = log e = 1.
Now by mean value theorem,
∴ \(\frac{f(e) – f(1)}{e-1}\) = f'(c)
⇒ \(\frac{1-0}{e-1}\) = \(\frac{1}{e}\)
⇒ c = e – 1 ∈ (1, e)
Hence, Langrange’s mean value theorem is verified. Proved.
![]()
Question 25.
With the help of Langrange’s value thoerem for the function y = \(\sqrt{x-2}\) in the interval [2, 3]. Find the point where the tangent is parallel to be chord joining the points?
solution:
Given:
f(x) = \(\sqrt{x-2}\), a = 2, b = 3
1. As f(x) = \(\sqrt{x-2}\), x ∈ [2, 3] is defined.
∴ f(x) is continous function for [2, 3].
2. f'(x) = \(\frac { 1 }{ 2\sqrt { x-2 } } \) is defined in interval (2, 3).
∴ f(x) is differentiable in [2, 3]
3. f(2) = 0, f(3) = 1
f(2) ≠ f(3)
Now, by Langrange’s mean value theorem,
∴ \(\frac{f(3)-f(2)}{3-2}\) = f'(c)
⇒ \(\frac{1-0}{1}\) = \(\frac { 1 }{ 2\sqrt { c-2 } } \)
⇒ \(\frac { 1 }{ 2\sqrt { c-2 } } \) = 1
⇒ \(\frac { 1 }{ \sqrt { c-2 } } \) = 2
⇒ \(\sqrt{c-2}\) = \(\frac{1}{2}\)
⇒ c – 2 = \(\frac{1}{4}\)
⇒ c = \(\frac{1}{4}\) + 2 = \(\frac{9}{4}\) = 2.25 ∈ (2,3)
∴ f(c) = \(\sqrt { \frac { 9 }{ 4 } -2 } \) = \(\frac{1}{2}\)
Required points ( \(\frac{9}{4}\), \(\frac{1}{2}\) ).
Differentiation Long Answer Type Questions – II
Question 1.
Differentiate sin-1 [ \(\frac { 2^{ x+1 } }{ 1+4^{ x } } \) ] with respect to x? (NCERT)
Solution:
y = sin -1 [ \(\frac { 2^{ x+1 } }{ 1+4^{ x } } \) ]
⇒ y = sin-1 [ \(\frac { 2.2^{ x } }{ 1+2^{ 2x } } \) ]
Putting 2x = tan θ
Then, θ = tan-1 2x
⇒ y = sin-1 [ \(\frac { 2tan\theta }{ 1+tan^{ 2 }\theta } \) ]
⇒ y = sin-1 [sin 2θ], [∵sin 2θ = \(\frac { 2tan\theta }{ 1+tan^{ 2 }\theta } \) ]
⇒ y = 2θ
⇒ y = 2 tan-1 (2x), [θ = tan-1(2x)]
∴ \(\frac{dy}{dx}\) = 2 \(\frac{d}{dx}\) tan-1 (2x)
Putting 2x = t
⇒ \(\frac{dy}{dx}\) = 2 \(\frac{d}{dx}\) tan-1 t
= 2 \(\frac{d}{dt}\) tan-1 t\(\frac{dt}{dx}\)
⇒ \(\frac{dy}{dx}\) = \(\frac { 2 }{ 1+t^{ 2 } } \) \(\frac{d}{dx}\) (2x),
= \(\frac { 2 }{ 1+2^{ 2x } } \) × 2x log 2
⇒ \(\frac{dy}{dx}\) = \(\frac { 2^{ x+1 }log2 }{ 1+4^{ x } } \)
![]()
Question 2.
If y = sin-1 x then prove that: (NCERT)
(1 – x2) \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) – x \(\frac{dy}{dx}\) = 0? (NCERT)
Solution:
Given:
y = sin-1 x ……………………………. (1)
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) (sin-1 x)
\(\frac{dy}{dx}\) = \(\frac { 1 }{ \sqrt { 1-x^{ 2 } } } \)
\(\frac{d}{dx}\) ( \(\frac{dy}{dx}\) ) = \(\frac{d}{dx}\) t-1/2
Putting 1 – x2 = t
\(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = \(\frac{d}{dx}\) t-1/2
= \(\frac{d}{dt}\) t-1/2 \(\frac{dt}{dx}\)
= – \(\frac{1}{2}\) t-1/2-1 \(\frac{d}{dx}\) (1 – x2)

Question 3.
If y = tan x + sec x then prove that:
\(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = \(\frac { cosx }{ (1-sinx)^{ 2 } } \)?
Solution:
y = tan x + sec x (given)
\(\frac{dy}{dx}\) = sec2 x + sec x tan x
⇒ \(\frac{dy}{dx}\) = sec x(sec x + tan x)
⇒ \(\frac{dy}{dx}\) = \(\frac{1}{cosx}\) [ \(\frac{1}{cosx}\) + \(\frac{sinx}{cosx}\) ]
= \(\frac { 1+sinx }{ cos^{ 2 }x } \) = \(\frac { 1+sinx }{ 1-sin^{ 2 }x } \)
= \(\frac { 1+sinx }{ (1+sinx)(1-sinx) } \)
⇒ \(\frac{dy}{dx}\) = \(\frac{1}{1-sinx}\)
Again differentiating both sides with respect to x,
\(\frac{d}{dx}\) ( \(\frac{dy}{dx}\) ) = \(\frac{d}{dx}\) ( \(\frac{1}{1-sinx}\)
\(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = \(\frac { (1-sinx).0-1.(0-cosx) }{ (1-sinx)^{ 2 } } \)
⇒ \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = \(\frac { cosx }{ (1-sinx)^{ 2 } } \)
![]()
Question 4.
If y = sin(sinx) then prove that:
y2 + y1 tan x + y cos2 x = 0? (CBSE 2018)
Solution:
y = sin(sin x)
Differentiating w.r.t. x,
y2 = cos (sinx) \(\frac{d}{dx}\) (cos x) + cos x \(\frac{d}{dx}\) {cos (sin x)}
= cos (sin x) (- sinx) + (cos x) [-sin(sin x)] cos x
⇒ y2 = – sin x cos (sin x) – cos2 x sin (sin x)
⇒ y2 = -sin x cos(sin x) – y cos2 x, [from eqn.(1)]
⇒ y2 = [ \(-\frac { sinx }{ cosx } \). cos x] cos(sin x) – y cos2 x
⇒ y2 = – tan x {cos (sin x) cos x} – y cos2
⇒ y2 = -tan x {cos(sin x) cos x} – y cos2 x [from eqn.(2)]
⇒ y2 = (-tan x) y1 – y cos2 x, Proved.
⇒ y2 + y1 tan x + y cos2 x = 0.
Question 5.
If (x2 + y2)2 = xy then find \(\frac{dy}{dx}\)? (CBSE 2018)
Solution:
(x2 + y2)2 = xy
Differentiating with respect to x,
2(x2 + y2) (2x + 2y \(\frac{dy}{dx}\) ) = x \(\frac{dy}{dx}\) + y.1
⇒ 2(x2 + y2). 2x + 2(x2 + y2). 2y \(\frac{dy}{dx}\) = x \(\frac{dy}{dx}\) + y
⇒ [4y(x2 + y2) – x] \(\frac{dy}{dx}\) = y – 4x (x2 + y2)
⇒ \(\frac{dy}{dx}\) = \(\frac { y-4x(x^{ 2 }+y^{ 2 }) }{ 4(x^{ 2 }+y^{ 2 })y-x } \)
![]()
Question 6.
If y = 500e7x + 600e-7x then prove that:
\(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = 49 y? (NCERT)
Solution:
Given:
y = 500e7x + 600e-7x …………………….. (1)
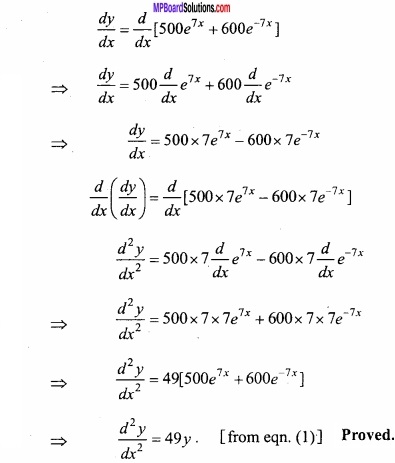
Question 7.
If y = (tan-1 x)2 then prove that:
(x2 + 1)2 y2 + 2x (x2 + 1) y1 = 2? (NCERT)
Solution:
Given:
y = (tan-1 x)2
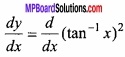
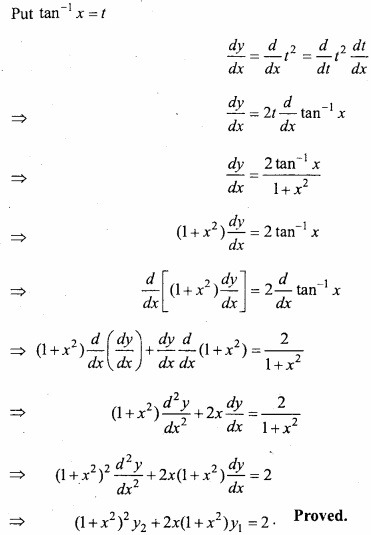
Question 8.
Differentiate sec-1 ( \(\frac { 1 }{ 2x^{ 2 }-1 } \) ) with respect to: \(\sqrt { x^{ 2 }-1 } \)?
Solution:
Let y1 = sec-1 ( \(\frac { 1 }{ 2x^{ 2 }-1 } \) )
⇒ y1 = cos-1 (2x2 – 1)

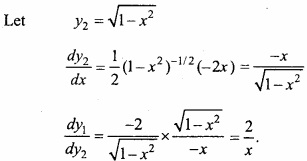
Question 9.
Differentiate tan-1 ( \(\frac { 2x }{ 1-x^{ 2 } } \) ) with respect to:
sin-1 ( \(\frac { 2x }{ 1-x^{ 2 } } \) )
Solution:
Let y1 = tan-1 \(\frac { 2x }{ 1+x^{ 2 } } \) and y2 = sin-1 \(\frac { 2x }{ 1+x^{ 2 } } \)
Let x = tan θ, then θ = tan-1 x
⇒ y1 = tan-1 (tan 2θ) and y2 = sin-1 (sin 2θ)
⇒ y1 = 2θ and y2 = 2θ
⇒ y1 = 2 tan-1 x and y2 = 2 tan-1 x
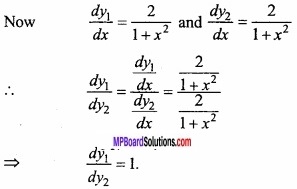
Question 10.
Differentiate tan-1 ( \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \) ) with respect to x?
Solution:
Let y1 = tan-1 ( \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \) )
Put x = tan θ,


Question 11.
If x \(\sqrt { 1+y } \) + y \(\sqrt { 1+x } \) = 0 then prove that:
\(\frac{dy}{dx}\) = -(1 + x)-2
Solution:
Given:
x\(\sqrt { 1+y } \) + y \(\sqrt { 1+x } \) = 0
⇒ x \(\sqrt { 1+y } \) = -y\(\sqrt { 1+x } \)
Squaring both sides,
x2 (1 + y) = y2 (1 + x)
⇒ x2 + x2y = xy2 + y2
⇒ x2 – y2 + x2y – xy2 = 0
⇒ (x – y) (x + y) + xy (x – y) = 0
⇒ (x – y)(x + y + xy) = 0
⇒ x – y = 0
⇒ x = y
But x ≠ y
∴ x + y + xy = 0
⇒ y (l + x) = – x
∴ y = – \(\frac{x}{1+x}\)
Differentiating both sides with respect to x,

Question 12.
If xy = ey-x then prove that:
\(\frac{dy}{dx}\) = \(\frac { 2-log_{ e }x }{ (1-log_{ e }x)^{ 2 } } \)
Solution:
Given: xy = ey-x
Applying log on both sides,
∴ loge xy = loge(ey-x)
⇒ y loge x = (y – x) loge e
⇒ y loge x – y = -x
⇒ y(1 – loge x) = x
⇒ y = \(\frac { x }{ 1-log_{ e }x } \)
Differentiating with respect to x,
Again,
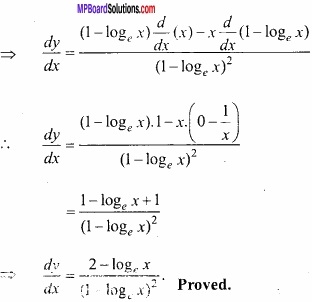
Question 13.
If y\(\sqrt { 1-x^{ 2 } } \) + x \(\sqrt { 1-y^{ 2 } } \) then prove that:
\(\frac{dy}{dx}\) + \($\sqrt{\frac{1-y^{2}}{1-x^{2}}}$\) = 0?
Solution:
Given:
y\(\sqrt { 1-x^{ 2 } } \) + x \(\sqrt { 1-y^{ 2 } } \) = 1.
Let x = sin θ and y = sin ϕ,
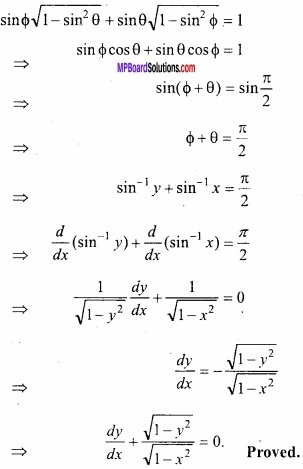
Question 14.
(A) If y = xsin-1x + xx then find the value of \(\frac{dy}{dx}\)?
Solution:
Given:
y = xsin-1x + xx
y = u + v
∴\(\frac{dy}{dx}\) = \(\frac{du}{dx}\) + \(\frac{dv}{dx}\) ……………………. (1)
Where, u = xsin-1x
∴ log u = sin-1 x log x, (taking log both sides)
Differentiating both sides with respect to x,
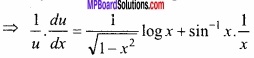
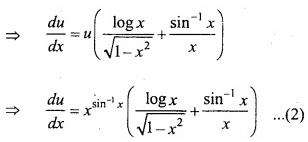
and v = xx
∴ log v = x log x
Differentiating both sides with respect to x,
\(\frac{1}{v}\). \(\frac{dv}{dx}\) = 1.log x + x. \(\frac{1}{x}\)
⇒ \(\frac{dv}{dx}\) = v(log x + 1)
⇒ \(\frac{dv}{dx}\) = xx (log x + 1) ………… (3)∴ From eqn.(1),
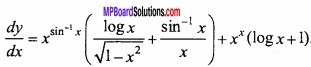
(B) If y = x-1x + xx, then find the value of \(\frac{dy}{dx}\)?
Solution:
Solve like Q.No. 14(A).
Question 15.
If sin y = x sin (a + y) then prove that:
\(\frac{dy}{dx}\) = \(\frac { sin^{ 2 }(a+y) }{ sina } \)?
Solution:
Given:
sin y = x sin (a + y)
⇒ x = \(\frac { siny }{ sin(a+y) } \)
Differentiating with respect to x,

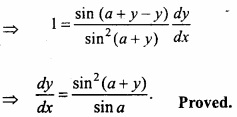
Question 16.
If xy = ex-y then prove that:
\(\frac{dy}{dx}\) = \(\frac { logx }{ (1+logx)^{ 2 } } \)?
Solution:
Given: xy = ex-y
Applying log on both sides,
y log x = (x – y) logea
⇒ y log x = (x – y).1 = x – y
Differentiating both sides with respect to x,
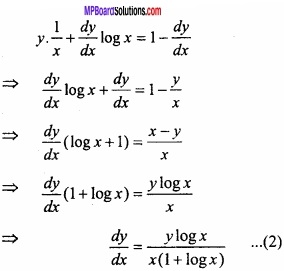
From eqn.(1),
y log x = x – y
⇒ y log x + y = x
⇒ y(logx + 1) = x
Put the value of y in eqn.(2)