Prasanna

MP Board Class 9th Maths Solutions Chapter 7 त्रिभुज Ex 7.1

प्रश्न 1.
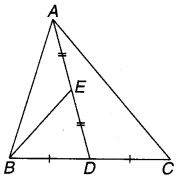
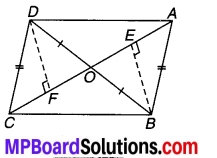
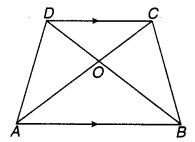
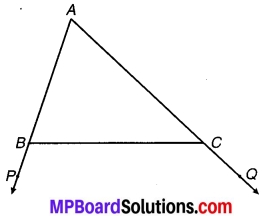
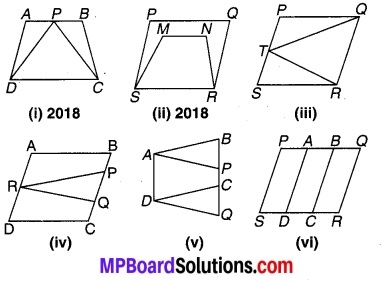
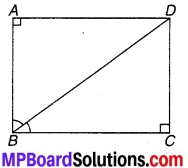
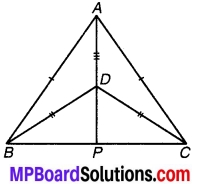
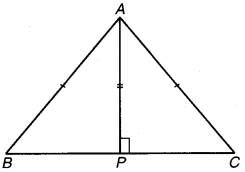
चतुर्भुज ∆CBD में AC=AD और AB कोणA को समद्विभाजित करता है। (देखिए चित्र 7.1) दर्शाइए कि ∆ ABC ≅ ∆ ABD है। BC और BD के बारे में आप क्या कह सकते हैं ?
(2018, 19)

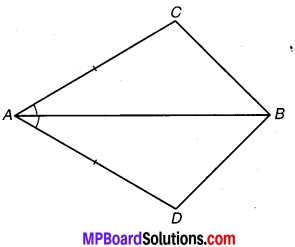
चित्र 7.1
हल:
चित्रानुसार ∆ABC और ∆ABD में,
∵ भुजा AC = भुजा AD
∵ ∠BAC = ∠BAD
∵ भुजा AB = भुजा AB
∵ ∆ABC ≅ ∆ABD (SAS सर्वांगसमता नियम से) इति सिद्धम्
भुजा BC = भुजा BD. (CPCT)

प्रश्न 2.
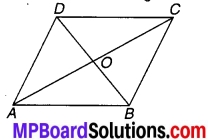
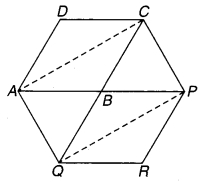
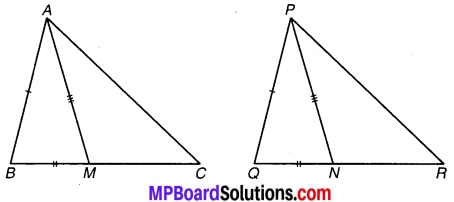
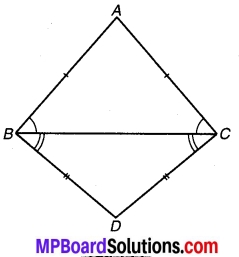
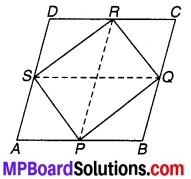
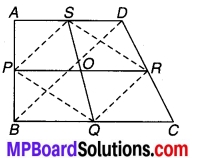
ABCD एक चतुर्भुज है जिसमें AD = BC और । ∠DAB = ∠CBA है। (देखिए चित्र 7.2) सिद्ध कीजिए कि-
(i) ∆ABD ≅ ∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.

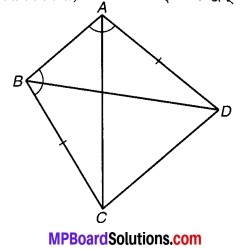
चित्र 7.2
हल:
(i) चित्रानुसार ∆ ABD और ∆BAC में,
∵ भुजा AD = भुजा BC (दिया है)
∵ ∠DAB = ∠CBA (दिया है)
∵ भुजा AB = भुजा AB (उभयनिष्ठ हैं)
∴ ∆ABD = ∆BAC. (SAS सर्वांगसमता नियम से) इति सिद्धम्

(ii) ∵ ∆ABD ≅ ∆BAC (सिद्ध कर चुके हैं)
∴ भुजा BD = भुजा AC. (CPCT) इति सिद्धम्

(iii) ∵∆ABD ≅ ∆BAC (सिद्ध कर चुके हैं)
∴ ∠ABD = ∠BAC. (CPCT) इति सिद्धम्

प्रश्न 3.
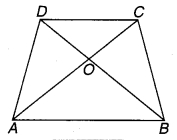
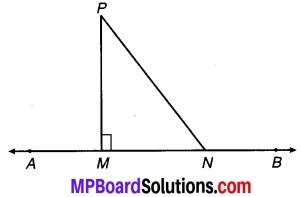
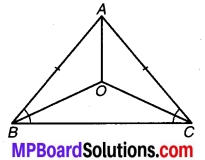
एक रेखाखण्ड AB पर AD और BC दो बराबर लम्ब रेखाखण्ड हैं (देखिए चित्र 7.3)। दर्शाइए कि चित्र CD रेखाखण्ड AB को समद्विभाजित करता है।

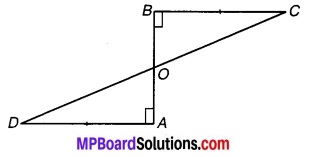
चित्र 7.3
हल:
चित्रानुसार रेखाखण्ड CD, रेखाखण्ड AB को बिन्दु O पर प्रतिच्छेद करता है।
अब ∆OAD और ∆OBC में,
∵ भुजा AD = भुजा BC (दिया है)
∵ ∠OAD = ∠OBC = 90° (दिया है)
∵ ∠AOD = ∠BOC (शीर्षाभिमुख कोण हैं)
∴ ∆OAD ≅ ∆OBC (SAA सर्वांगसमता नियम से)
∴ भुजा OA = भुजा OB (CPCT)
अतः रेखाखण्ड CD रेखाखण्ड AB को समद्विभाजित करता है। इति सिद्धम्

प्रश्न 4.
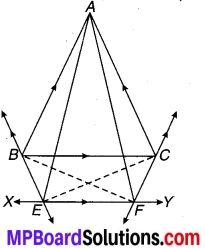
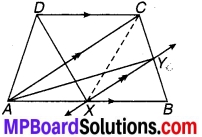
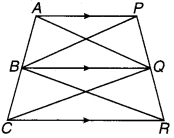
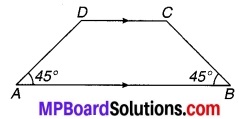
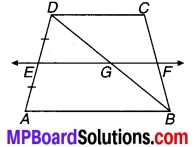
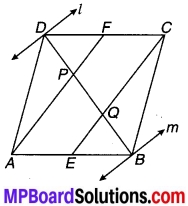
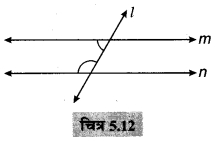
1 और m दो समान्तर रेखाएँ हैं जिन्हें समान्तर रेखाओंp और का एक अन्य युग्म प्रतिच्छेदित करता है। (देखिए चित्र 7.4)। दर्शाइए कि-
∆ABC ≅ ∆CDA है।

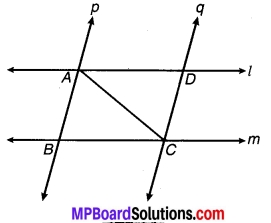
चित्र 7.4
हल:
∵l || m को रेखाखण्ड AC क्रमश: A और C बिन्दुओं पर प्रतिच्छेद करता है।
∴ ∠ACB = ∠CAD …(1) (एकान्तर कोण हैं)
∵ p || q को रेखाखण्ड AC क्रमशः A और C बिन्दुओं पर प्रतिच्छेद करता है।
∴ ∠CAB = ∠ACD (एकान्तर कोण है)…(2)
अब ∆ABC एवं ∆CDA में,
∵ ∠ACB = ∠CAD [सिद्ध कर चुके हैं समीकरण (1) से]
∵ ∠CAB = ∠ACD [सिद्ध कर चुके हैं समीकरण (2) से]
∵ भुजा AC = भुजा AC (उभयनिष्ठ है)
अतः ∆ABC ≅ ∆CDA. (ASA सर्वांगसमता नियम से) इति सिद्धम्

प्रश्न 5.
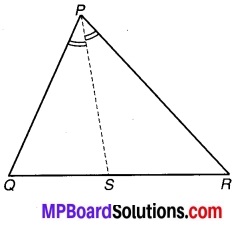
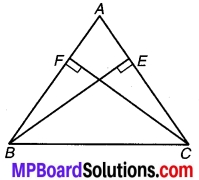
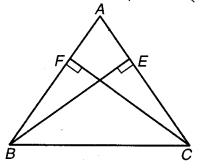
रेखा l कोण A को समद्विभाजित करती है और B रेखा l पर स्थित कोई बिन्दु है। BP और BQ कोण A की भुजाओं पर B से डाले गए लम्ब हैं (देखिए चित्र 7.5)। दर्शाइए कि
(i) ∆APB ≅ ∆AQB.
(ii) BP = BQ अर्थात् बिन्दु B कोणों की भुजाओं से समदूरस्थ है।

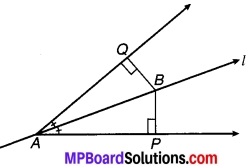
चित्र 7.5
हल:
∵ रेखा l कोण A की समद्विभाजक है। (दिया है)
∴ ∠BAP = ∠BAQ ..(1)
∵ BP L AP एवं BQ LAQ (दिया है)
∵ LAPB = ∠AQB = 90° ….(2)
अब (i) ∆APB और ∆AQB में,
∵ ∠BAP = ∠BAQ [समीकरण (1) से ]
∵ ∠APB = ∠AQB [समीकरण (2) से]
∵ भुजा AB = भुजा AB (उभयनिष्ठ है)
∴ ∆APB ≅ ∆AQB. (SAA सर्वांगसमता नियम से) इति सिद्धम्

एवं (ii) ∵ ΔΡΒΕ ≅ ΔΑΟΒ (सिद्ध कर चुके हैं)
∴ भुजा BP = भुजा BQ (CPCT)
अर्थात् बिन्दु B कोणों की भुजाओं से समदूरस्थ है। इति सिद्धम्

प्रश्न 6.
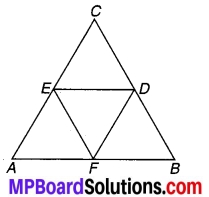
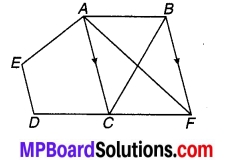
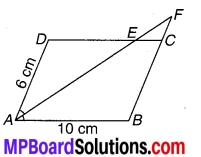
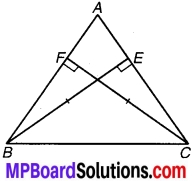
चित्र 7.6 में AC = AE एवं AB = AD और ∠BAD = ∠EAC है। दर्शाइए कि BC = DE है।

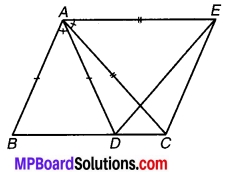
चित्र 7.6
हल:
चित्रानुसार ΔABC एवं ΔADE में,
∵ भुजा AB = भुजा AD. (दिया है)
∵ ∠BAD = ∠EAC (दिया है)
∵ भुजा AC = भुजा AE (दिया है)
ΔABC ≅ ΔADE (SAS सर्वांगसमता नियम)
अतः भुजा BC = भुजा DE (CPCT) इति सिद्धम्

प्रश्न 7.
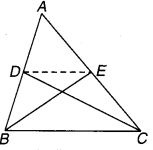
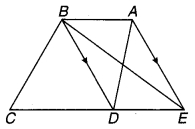
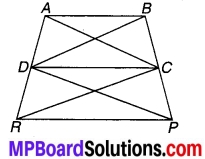
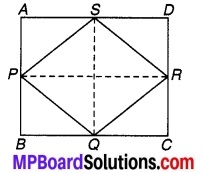
संलग्न चित्र में AB एक रेखाखण्ड है और Pइसका मध्य-बिन्दु है। D और E रेखाखण्ड AB के एक ही ओर स्थित दो बिन्दु इस प्रकार हैं कि ∠BAD = ∠ABE और ∠EPA = ∠DPB. दर्शाइए कि-
(i) ΔDAP ≅ ΔEBP.
(ii) AD = BE.

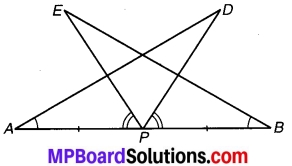
चित्र 7.7
हल:
प्रश्नानुसार, AP = BP (दिया है AB का मध्य-बिन्दु P)…(1)
∵ ∠EPA = ∠DPB (दिया है)
⇒ ∠EPA + ∠EPD = ∠DPB + ∠EPD (यूक्लिड अभिगृहीत-II)
⇒ ∠APD = ∠BPE (चित्रानुसार)…(2)
∵ ∠BAD = ∠ABE (दिया है)
⇒ ∠PAD = ∠PBE (चित्रानुसार) …(3)

(i) अब ΔDAP एवं ΔEBP में,
∵ ∠PAD = ∠PBE [समीकरण (3) से]
∵ AP = BP [समीकरण (1) से]
∵ ∠APD = ∠BPE [समीकरण(2) से]
अतः ΔDAP ≅ ΔEBP (ASA सर्वांगसमता गुण) इति सिद्धम्

(ii) ∵ ΔDAP ≅ ΔEBP [भाग (i) में सिद्ध कर चुके हैं।
अतः AD = BE. (CPCT) इति सिद्धम्

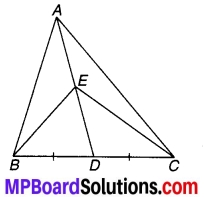
प्रश्न 8.
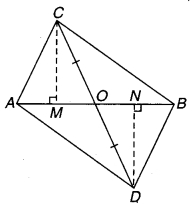
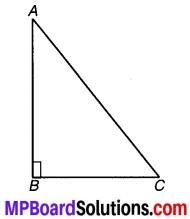
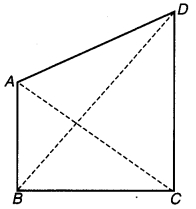
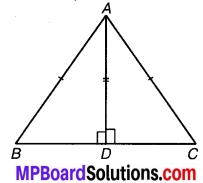
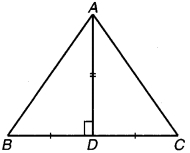
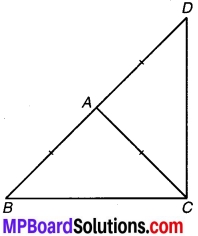
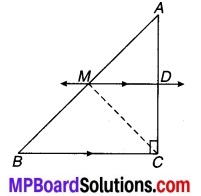
एक समकोण त्रिभुज ABC में जिसमें कोण C समकोण है। M कर्ण AB का मध्य-बिन्दु है। C को M से मिलाकर D तक इस प्रकार बढ़ाया गया है कि DM = CM है। बिन्दु D को बिन्दु B से मिला दिया जाता है (संलग्न चित्र देखिए)। D दर्शाइए कि-
(i) ΔAMC ≅ ΔBMD.
(ii) ∠DBC एक समकोण है।
(iii) ΔBDC ≅ ΔACB.
(iv) CM = \(\frac { 1 }{ 2 }\) AB.

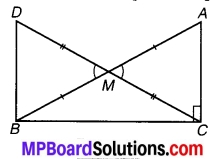
चित्र 7.8
हल:
(i) ΔAMC और ΔBMD में,
∵ AM = BM (दिया है : AB का मध्य-बिन्दु M)
∵ CM = DM (दिया है)
∵∠AMC=∠BMD (शीर्षाभिमुख कोण हैं)
ΔAMC ≅ ΔBMD. (SAS सर्वांगसमता गुण) इति सिद्धम्

(ii) चूँकि ΔAMC ≅ ΔBMD. (सिद्ध कर चुके हैं।)
⇒ ∠ACM= ∠BDM (CPCT)
⇒ DB || AC (एकान्तर कोण बराबर हैं)
⇒ ∠DBC + ∠ACB = 180° (एक ही ओर के अन्तः कोण हैं)
⇒ ∠DBC + 90° = 180° (∠ACB समकोण है।)
⇒ ∠DBC = 180° – 90° = 90°
अत: ∠DBC एक समकोण है। इति सिद्धम्

(iii) चूँकि ΔAMC ≅ ΔBMD. (सिद्ध कर चुके हैं)
⇒ AC = BD (CPCT)
अब ΔDBC और ΔACB में,
चूँकि BD = AC (सिद्ध कर चुके हैं)
∠DBC = ∠ACB = 90° (सिद्ध कर चुके हैं)
एवं BC = BC (उभयनिष्ठ है)
अतः ΔDBC ≅ ΔACB. इति सिद्धम्

(iv) चूँकि ΔDBC ≅ ΔACB (सिद्ध कर चुके हैं)
⇒ DC = AB (CPCT)
अतः CM = 1/2AB. (CPCT) [∵ CM = DM (दिया है)] इति सिद्धम्

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 6 रेखाएँ और कोण Ex 6.3

प्रश्न 1.
संलग्न चित्र में ∆PQR की भुजाओं OP और RO को क्रमशः बिन्दुओं S और T तक बढ़ाया गया है। यदि ∠SPR = 135° है और ∠PQT = 110° है, तो ∠PRQ
ज्ञात कीजिए।

चित्र 6.23
हल:
∵ ∠PQT + ∠PQR = 180° (रैखिक युग्म अभिगृहीत से)
110° + ∠PQR = 180° ∵ ∠PQT = 110° (दिया हुआ है)]
∠PQR = 180° – 110° = 70°
∵ ∠SPR + ∠QPR = 180° (रैखिक युग्म अभिगृहीत)
135° + ∠QPR = 180° [∵ ∠SPR = 135° (दिया हुआ है)]
∠QPR = 180° – 135° = 45° …..(2)
अब ∆PQR में, :: LOPR + ∠PQR + ∠PRQ = 180° (प्रमेय 6.7, त्रिभुज के तीनों अन्त:कोणों का योग है)
⇒ 45° + 70° + ∠PRQ = 180° [समीकरण (1) एवं समीकरण (2) से]
⇒ ∠PRQ = 180° – 45° – 70°
⇒ ∠PRQ = 180° – 115° = 65°
अतः ∠PRO का अभीष्ट मान = 65°.

प्रश्न 2.
संलग्न चित्र में ∠X = 62° और ∠XYZ = 54° है। यदि YO और ∠O क्रमश: ∠XYZ के ∠XYZ और ∠XZY के समद्विभाजक हैं, तो ∠OZY और ∠YOZ ज्ञात कीजिए।

हल:
∆XYZ में,
∵ ∠YXZ + ∠XYZ + ∠XZY = 180° [प्रमेय 6.7, त्रिभुज के तीनों अन्तः कोणों का योग है।]
⇒ 62° + 54° + ∠XZY = 180° [∵ ∠YXZ = 62° एवं ∠XYZ = 54° (दिया है)]
⇒∠XZY = 180° – 62° – 54° = 180° – 116° = 64°
∵∠YO, ∠XZY का समद्विभाजक है।

अब ∆OYZ में,
∵∠OYZ+ ∠OZY + ∠YOZ = 180° (प्रमेय 6.7, त्रिभुज के तीनों अन्तः कोणों का योग है)
⇒ 27° + 32° + ∠YOZ = 180°
[∵ ∠OZY = 32° एवं ∠OYZ = 27° (ज्ञात कर चुके हैं)]
∠YOZ = 180° – 27° – 32° = 180° – 59° = 121°
अतः ∠OZY का अभीष्ट मान = 32° एवं ∠YOZ का अभीष्ट मान = 121.

प्रश्न 3.
संलग्न चित्र में यदि AB || DE, ∠BAC = 35° और LCDE = 53°, तो ∠DCE ज्ञात कीजिए। (2019)

चित्र 6.25
हल:
दिया है: AB ||DE, ∠BAC = 35° एवं ∠CDE = 53°
∵ AB || DE एवं AE तिर्यक रेखा है।
⇒ ∠CED = ∠BAC = 35° [एकान्तर कोण हैं तथा/BAC = 35° (दिया है)]
अब ∆CDE में (प्रमेय 6.7 त्रिभुज के तीनों अन्तः कोणों का योग 180° होता है)
∵ ∠DCE + ∠CDE + ∠CED = 180°
⇒ ∠DCE + 53° + 35° = 180° [∵∠CDE = 53° दिया है तथा
∠CED = 35° ज्ञात कर चुके हैं।
⇒ ∠DCE = 180° – 53° – 35° = 180° – 88° = 92°
अत: ∠DCE का अभीष्ट मान = 92°.

प्रश्न 4.
संलग्न चित्र में यदि रेखाएँ PO और RS बिन्दु T पर इस प्रकार प्रतिच्छेद करती है कि ∠PRT = 40°, ∠RPT = 95° और ∠TSQ = 75°, तो ∠SQT ज्ञात कीजिए।

चित्र 6.26
हल:
∆PRT में,
∵ ∠PTR + CRPT + ∠PRT = 180° (प्रमेय 6.7 त्रिभुज के तीनों अन्तः कोण हैं)
⇒ ∠PTR + 95° + 40° = 180° [∵∠RPT = 95° एवं ∠PRT = 40° (दिया है)]
⇒ ∠PTR = 180° – 950 – 40° = 180° – 135° = 450
∵ PQ एवं RS एक-दूसरे को बिन्दु T पर प्रतिच्छेद करती हैं।
⇒ ∠QTS = ∠PTR = 45° (शीर्षाभिमुख कोण हैं और ∠PTR = 45°)
अब ∆QTS में,
∵ ∠SQT + ∠TSQ + ∠OTS = 180°
∵∠SOT + 75° + 45° = 180°
[∵ ∠TSQ = 75° (दिया है) तथा ∠QTS = 45° ज्ञात कर चुके हैं ]
∠SOT = 180° – 75° – 45° = 180° – 120° = 60°
अतः ∠SOT का अभीष्ट मान = 60°.

प्रश्न 5.
संलग्न चित्र में, यदि PQ ⊥ PS, PQ || SR, ∠SOR = 28° और ∠QRT = 65° है, तो x और y के मान ज्ञात कीजिए।

चित्र 6.27
हल:
∵ PQ ⊥ PS = ∠OPS = 90°
∵ ∠SQR = 28° एवं ∠QRT = 65° (दिए हैं)
∵ PQ || SR को QR तिर्यक रेखा प्रतिच्छेद करती है।
⇒ ∠PQR = ∠QRT (एकान्तर कोण है)
⇒ ∠PQS + ∠SOR = ∠ORT (चित्रानुसार)
⇒ x + 28° = 65° [∵ ∠SOR = 28° एवं ∠QRT = 65° (दिया है)]
⇒ x = 65° – 28° = 37°
अब ∆POS में,
∵ ∠OPS + ∠PQS + ∠PSQ = 180° (प्रमेय 6.7 से A के तीनों अन्तः कोणों का योग है)
⇒ 90° + 37° + y = 180°
⇒ y = 180° – 90° – 37° = 180° – 127° = 53°
[∠QPS = 90° एवं ∠PQS = x = 37° (ज्ञात है)]
अतः x एवं के अभीष्ट मान क्रमशः 37° एवं 53° हैं।

प्रश्न 6.
संलग्न चित्र में, ∆POR की भुजा QR को बिन्दु S तक बढ़ाया गया है। यदि ∠PQR और ∠PRS के समद्विभाजक बिन्दु T पर मिलते हैं तो सिद्ध कीजिए कि
∠QTR = \(\frac { 1 }{ 2 }\)∠QPR.

चित्र 6.28
हल:
∆PQR का बहिष्कोण ∠PRS है।
= ∠PRS = ∠QPR + ∠PQR (प्रमेय 6.8)…(1)
∆TOR का बहिष्कोण ∠TRS है।
⇒ ∠TRS = ∠QTR + ∠TOR (प्रमेय 6.8)…(2)
∵ ∠PQR और ∠PRS के समद्विभाजक क्रमशः OT एवं RT हैं।

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Ex 9.3

प्रश्न 1.
संलग्न चित्र में ∆ABC की एक माध्यिका AD पर स्थित E कोई बिन्दु है। दर्शाइए कि
ar (ABE) = ar (ACE).
हल:

चित्र 9.8
चूँकि A ABC की माध्यिका AD हैं।
⇒ ar (ADB) = ar (ADC)
⇒ ar (ABE) + ar (EDB) = ar (ACE) + ar (EDC) …(1)
चूँकि A EBC की माध्यिका ED है।
⇒ ar (EDB) = ar (EDC) …(2)
अतः ar (ABE) = ar (ACE) [समीकरण (1) और (2) से] इति सिद्धम्

प्रश्न 2.
∆ABC में, E माध्यिका AD का मध्य-बिन्दु है। दर्शाइए कि-
ar (BED) = \(\frac { 1 }{ 4 }\)ar (ABC)
हल:

चित्र 9.9
∆ABC की माध्यिका का मध्य-बिन्दु E है।
चूँकि ∆ABC की माध्यिका AD है
⇒ ar (ADB) = \(\frac { 1 }{ 4 }\) ar (ABC) …(1) ,
चूँकि BE, ∆ADB की माध्यिका है।
⇒ ar (BED) = \(\frac { 1 }{ 2 }\) ar (ADB) …(2)
अतः ar (BED) = \(\frac { 1 }{ 4 }\)ar (ABC). [समीकरण (1) और (2) से] इति सिद्धम्

प्रश्न 3.
दर्शाइए कि समान्तर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफल वाले चार त्रिभुजों में बाँटते हैं।
हल:

चित्र 9.10
दिया है : ABCD एक समान्तर चतुर्भुज है जिसके विकर्ण AC और BD परस्पर बिन्दु O पर प्रतिच्छेद करते हैं।
चूँकि ar (ABC) = ar (ADC) …(1)
(विकर्ण समान्तर चतुर्भुज A को समद्विभाजित करते हैं।)
ar (OAB) = ar (OBC) = \(\frac { 1 }{ 2 }\) ar (ABC) . …(2) (BO,A ABC की माध्यिका है)
ar (ODA) = ar (OCD) = \(\frac { 1 }{ 2 }\)ar (ADC) …(3) (DO,AADC की माध्यिका है)
ar (OAB) = ar (OBC) = ar (ODA) = ar (OCD) [समीकरण (1), (2) एवं (3) से]
अतः समान्तर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफल वाले चार त्रिभुजों में बाँटते हैं इति सिद्धम्

प्रश्न 4.
संलग्न चित्र में ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं। यदि रेखाखण्ड CD, रेखाखण्ड AB से बिन्दु O पर समद्विभाजित होता है तो दर्शाइए कि-
ar (ABC) = ar (ABD) है।

चित्र 9.11
हल:
एक ही आधार AB पर दो त्रिभुज A ABC एवं A ABD दिए हैं जिसमें AB एवं CD परस्पर O बिन्दु पर समद्विभाजित करते हैं।
⇒ ADBC एक समान्तर चतुर्भुज है (विकर्ण AB, CD पर परस्पर समद्विभाजित कर रहे हैं)
CM ⊥ AB एवं DN ⊥ AB खींचिए।
अब ∆AMC और ∆BND में,
चूँकि AC = BD (समान्तर चतुर्भुज की सम्मुख भुजाएँ हैं)
∠CAM = ∠DBN (एकान्तर कोण हैं)
एवं ∠AMC = ∠BND = 90° (CM ⊥ AB एवं DN ⊥ AB)
⇒ ∆AMC = ∆BND , (AAS सर्वांगसमता प्रमेय)
⇒ CM = DN (CPCT)
चूँकि ∆ABC और ∆ABD एक ही आधार AB पर स्थित हैं तथा उनके शीर्षलम्ब CM = DN (सिद्ध कर चुके हैं)
अतः ar (ABC) = ar (ABD). इति सिद्धम्

प्रश्न 5.
D, E और F क्रमशः त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य-बिन्दु हैं। दर्शाइए कि-
(i) BDEF एक समान्तर चतुर्भुज है।
(ii) ar (DEF) = \(\frac { 1 }{ 4 }\) ar (ABC).
(iii) ar (BDEF) = \(\frac { 1 }{ 2 }\)ar (ABC).
हल:

चित्र 9.12
दिया है : AABC की भुजाओं BC, CA और AB के मध्य-बिन्दु
क्रमश: D, E और F हैं। DE, EF एवं FD को मिलाया गया है।
(i) चूँकि D एवं E क्रमशः BC और CA के मध्य-बिन्दु हैं।
⇒ DE = \(\frac { 1 }{ 2 }\)AB एवं DE || AB
⇒ DE = FB एवं DE || FB (AB का मध्य-बिन्दु F है)
अत: BDEF एक समान्तर चतुर्भुज है। (सम्मुख भुजाओं का युग्म बराबर एवं समान्तर है) इति सिद्धम्

(ii) चूँकि BDEF एक समान्तर चतुर्भुज सिद्ध कर चुके हैं।
इसी प्रकार सिद्ध कर सकते हैं कि DCEF एवं EAFD भी समान्तर □ हैं।
चूँकि समान्तर चतुर्भुज BDEF, DCEF एवं EAFD के विकर्ण क्रमश: FD, DE एवं EF हैं, जो उनको समद्विभाजित करते हैं।
⇒ ar (DFB) = ar (DCE) = ar (EAF) = ar (DEF)
लेकिन ar (DFB) + ar (DCE) + ar (EAF) + ar (DEF) = ar (ABC)
अतः ar (DEF) = \(\frac { 1 }{ 4 }\) ar (ABC). इति सिद्धम्

(iii) ar (BDEF) = ar (DFB) + ar (DEF) (चित्रानुसार)
= 2 ar (DEF) [ar (DFB) = ar (DEF)]
= 2 x \(\frac { 1 }{ 4 }\) ar (ABC) ar (DEF) = \(\frac { 1 }{ 4 }\)ar (ABC)
अतः ar (BDEF) = \(\frac { 1 }{ 2 }\) ar (ABC). इति सिद्धम्

प्रश्न 6.
संलग्न चित्र में चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु 0 पर इस प्रकार प्रतिच्छेद करते हैं कि OB = OD है। यदि AB = CD है, तो दर्शाइए कि-
(i) ar (DOC) = ar (AOB).
(ii) ar (DCB) = ar (ACB).
(iii) DA || CB या ABCD एक समान्तर चतुर्भुज है।

चित्र 9.13
हल:
दिया है : ABCD चतुर्भुज के विकर्ण AC एवं BD परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB = OD तथा AB = CD है।
बिन्दु B एवं D से क्रमशः BE I AC एवं DF I AC खींचिए। (i) अब ADOF एवं ABOE में, OD = OB
(दिया है) ∠DOF = ∠BOE
(सम्मुख कोण हैं) ∠DFO = ∠BEO = 90° (DF ⊥ AC एवं BE ⊥AC)
⇒ ∆DOF ≅ ∆BOE (SAA सर्वांगसमता प्रमेय)…(1)
⇒ DF = BE (CPCT)
पुनः समकोण ∆DFC और समकोण ∆BEA में,
चूँकि कर्ण CD = कर्ण AB (दिया है)
DF = BE (सिद्ध कर चुके हैं)
∠DFC =∠BEA = 90° (RHS सर्वांगसमता प्रमेय) …(2)
⇒ ∆DFC ≅ ∆BEA (RHS सर्वांगसमता प्रमेय)…(2)
⇒ ∆DOF + ∆DFC = ∆BOE + ∆BEA [समीकरण (1) और (2) से]
⇒ ∆DOC = ∆AOB (चित्रानुसार)
अतः ar (DOC) = ar (AOB). (सर्वांगसम क्षेत्रों के क्षेत्रफल हैं) इति सिद्धम्

(ii) चूँकि ar (DOC) = ar (AOB) (सिद्ध कर चुके हैं)
⇒ ar (DOC) + ar (OCB) = ar (AOB) + ar (OCB) (बराबर संख्याओं में समान संख्या का योग बराबर होता है)
अतः ar (DCB) = ar (ACB). (चित्रानुसार) इति सिद्धम्

(iii) चूँकि ∆DOC ≅ ∆AOB (सिद्ध कर चुके हैं)
⇒ ∠DCO = ∠BAO (CPCT)
⇒ DC || AB (∠DCO = ∠BAO (एकान्तर कोण है).
अतः DA || CB (DC || AB एवं DC = AB)
या ABCD एक समान्तर चतुर्भुज है। (DA || CB एवं CD || AB). इति सिद्धम्

प्रश्न 7.
बिन्दु D और E क्रमश: ∆ABC की भुजाओं AB और AC पर इस प्रकार स्थित हैं कि ar (DBC) = ar (EBC) है। दर्शाइए कि DE || BC है। (2018)
हल:

चित्र 9.14
दिया है : ∆ABC की भुजाओं AB एवं AC पर दो बिन्दु D और E इस प्रकार हैं कि ar (DBC) = ar (EBC)
DE को मिलाइए। चूँकि ∆DBC एवं ∆EBC एक उभयनिष्ठ आधार BC पर तथा रेखाखण्ड BC एवं DE के मध्य स्थित है तथा ar (DBC) = ar (EBC)
अतः DE || BC. (एक ही आधार पर बराबर क्षेत्रफल वाले ∆ हैं) इति सिद्धम्

प्रश्न 8.
XY त्रिभुज ABC की भुजा BC के समान्तर एक रेखा है। यदि BE|| AC और CF || AB रेखा XYसे क्रमशः E और F पर मिलती हैं, तो दर्शाइए कि-ar (ABE) = ar (ACF).
हल:

चित्र 9.15
ABC एक दिया हुआ त्रिभुज है जिसकी भुजा BC के समान्तर
XY एक रेखा खींची जाती है जो BE || AC और CF || AB को क्रमश: E और F बिन्दुओं पर प्रतिच्छेद करती है।
BF एवं CE को मिलाइए।
चूँकि उभयनिष्ठ आधार BE पर BE || AC के मध्य ∆ABE और ∆CBE स्थित हैं।
⇒ ar (ABE) = ar (CBE) …(1)
चूँकि उभयनिष्ठ आधार CF पर CF || AB के मध्य ∆ACF और ∆BCF स्थित हैं।
⇒ ar (ACF) = ar (BCF) …(2) .
चूँकि उभयनिष्ठ आधार BC पर BC || EF के मध्य ∆CBE और ∆BCF स्थित हैं।
⇒ ar (CBE) = ar (BCF)
अतः ar (ABE) = ar (ACF).
समीकरण (1), (2) एवं (3) से] इति सिद्धम्

प्रश्न 9.
संलग्न चित्र में समान्तर चतुर्भुज ABCD की एक भुजा AB को एक बिन्दु P तक बढ़ाया गया है। A से होकर CP के समान्तर खींची गई रेखा बढ़ाई गई CB को Q पर मिलती है और फिर समान्तर चतुर्भुज PBQR को पूरा किया जाता है। दर्शाइए कि-
ar (ABCD) = ar (PBQR) है।

चित्र 9.16
हल:
चित्र 9.16 में ABCD एक समान्तर चतुर्भुज है। CP|| AQ है तथा PBOR भी एक समान्तर चतुर्भुज है।
AC और QP को मिलाइए।
अब उभयनिष्ठ आधार AQ पर AQ || CP के मध्य दो त्रिभुज ∆CAQ एवं ∆PAQ स्थित हैं।
⇒ ar (CAQ) = ar (PAQ)
⇒ ar (CAB) + ar (BAQ) = ar (BAQ) + ar (BQP)
⇒ ar (CAB) = ar (BQP) [ar (BAQ) उभयनिष्ठ है]
⇒\(\frac { 1 }{ 2 }\)ar (ABCD) = \(\frac { 1 }{ 2 }\)ar (PBOR)
(AC और PQ क्रमशः समान्तर चतुर्भुज ABCD और PBQR के विकर्ण हैं)
अतः ar (ABCD) = ar (PBOR). (बराबर के दोनों बराबर होते हैं) इति सिद्धम्

प्रश्न 10.
एक समलम्ब ABCD, जिसमें AB || DC है, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं। दर्शाइए कि ar (AOD) = ar (BOC) है।
हल:

चित्र 9.17
ABCD एक समलम्ब चतुर्भुज है जिसमें AB || DC तथा उसके विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं।
उभयनिष्ठ आधार AB पर AB || DC के मध्य A DAB एवं ACAB स्थित हैं।
⇒ ar (DAB) = ar (CAB)
⇒ ar (AOD) + ar (OAB) = ar (OAB) + ar (BOC) (चित्रानुसार)
अतः ar (AOD) = ar (BOC). (ar (OAB) उभयनिष्ठ है) इति सिद्धम्

प्रश्न 11.
संलग्न चित्र में ABCDE एक पंचभुज है। B से होकर AC के समान्तर खींची गई रेखा बढ़ाई गई DC को F पर मिलती है। दर्शाइए कि-
(i) ar (ACB) = ar (ACF).
(ii) ar (AEDF) = ar (ABCDE).

चित्र 9.18
हल:
ABCDE एक पंचभुज है जिसकी भुजा DC बढ़ाई गई है।
बिन्दु B से BF || AC खींची गई है जो DC को F पर मिलती है।
(i) चूँकि उभयनिष्ठ आधार AC पर AC || BF के मध्य दो चित्र 9.18 त्रिभुज क्रमशः ∆ACB एवं ∆ACF स्थित हैं
अतः ar (ACB) = ar (ACF). इति सिद्धम्

(ii) ar (ACB) = ar (ACF) (सिद्ध कर चुके हैं)
⇒ ar (BAC) + ar (ACDE) = ar (FAC) + ar (ACDE) (बराबर संख्याओं में एक ही संख्या जोड़ने पर)
⇒ ar (ABCDE) = ar (AEDF)
⇒ ar (AEDF) = ar (ABCDE). इति सिद्धम्

प्रश्न 12.
गाँव के एक निवासी इतवारी के पास एक चतुर्भुजाकार भूखण्ड था। उस गाँव की ग्राम पंचायत ने उसके भूखण्ड के एक कोने से उसका कुछ भाग लेने का निर्णय लिया ताकि वहाँ एक स्वास्थ्य केन्द्र का निर्माण कराया जा सके। इतवारी इस प्रस्ताव को इस प्रतिबन्ध के साथ स्वीकार कर लेता है कि उसे इस भाग के बदले उसी भूखण्ड से संलग्न एक भाग ऐसा दे दिया जाए कि उसका भूखण्ड त्रिभुजाकार हो जाए। स्पष्ट कीजिए कि इस प्रस्ताव को किस प्रकार क्रियान्वित किया जा सकता है ?

चित्र 9.19
हल:
ग्राम निवासी के पास चतुर्भुज ABCD के आकार का भूखण्ड है। प्रतिबन्ध के साथ प्रस्ताव निम्न प्रकार क्रियान्वित किया जा सकता है-
चित्रानुसार CD को आगे बढ़ाइए। विकर्ण BD के समान्तर AE खींचिए जो CD को E पर मिलती है।
ग्रामवासी अपने भूखण्ड से भाग ABD ग्राम पंचायत को देगा तथा बदले में भूखण्ड BDE लेगा। इस प्रकार उसका भूखण्ड BCE हो जायेगा। जो त्रिभुजाकार है तथा क्षेत्रफल में मूल भूखण्ड के बराबर है। चूँकि उभयनिष्ठ आधार BD पर BD || AE के मध्य दो त्रिभुज ∆ABD एवं ∆EBD स्थित हैं।
⇒ ar (ABD) = ar (EBD)
⇒ ar (ABD) + ar (BCD) = ar (EBD) + ar (BCD) (बराबर संख्याओं में एक ही संख्या जोड़ी गई है)
अतः ar (BCE) = ar (ABCD). इति सिद्धम्

प्रश्न 13.
ABCD एक समलम्ब है जिसमें AB || DC है। AC के समान्तर रेखा AB को X पर और BC को Y पर प्रतिच्छेद करती है। सिद्ध कीजिए कि-
ar (ADX) = ar (ACY)
हल:

चित्र 9.20
ABCD एक समलम्ब चतुर्भुज दिया है जिसमें AB || DC एवं विकर्ण AC के समान्तर खींची गई रेखा AB को X पर और BC को Y पर प्रतिच्छेद करती है।
CX को मिलाइए।
उभयनिष्ठ आधार AX पर AX || DC के मध्य ∆ADX एवं ∆ACX स्थित हैं।
⇒ ar (ADX) = ar (ACX) …(1)
उभयनिष्ठ आधार AC पर AC || XY के मध्य ∆ACX और ∆ACY स्थित हैं।
⇒ ar (ACX) = ar (ACY) …(2)
अतः ar (ADX) = ar (AC) है। [समीकरण (1) और (2) से] इति सिद्धम्

प्रश्न 14.
संलग्न चित्र में AP || BQ || CR है। तो, सिद्ध कीजिए कि-
ar (AQC) = ar (PBR) है।
हल:

चित्र 9.21
दिया है : AP || BQ || CR
विकर्ण AQ, BP, CQ, BR को मिलाया गया है।
चूँकि उभयनिष्ठ आधार BQ पर BQ || AP के मध्य ∆ABQ एवं ∆PBQ स्थित हैं।
चूँकि उभयनिष्ठ आधार BQ पर BQ || CR के मध्य ∆BCQ एवं ∆BRQ स्थित हैं।
⇒ ar (BCQ) = ar (BRQ) …(2)
⇒ ar (ABQ) + ar (BCQ) = ar (PBQ) + ar (BRQ) [समीकरण (1) एवं (2) से]
अतः ar (AQC) = ar (PBR). (चित्रानुसार) इति सिद्धम्

प्रश्न 15.
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद करते हैं कि ar (AOD) = ar (BOC) है। सिद्ध कीजिए कि ABCD एक समलम्ब चतुर्भुज है।
हल:

चित्र 9.22
ABCD चतुर्भुज के विकर्ण AC और BD एक-दूसरे को बिन्दु O पर प्रतिच्छेद करते हैं,
जहाँ ar (AOD) = ar (BOC) …(1)
⇒ ar (AOD) + ar (ODC) = ar (BOC) + ar (ODC) (बराबर संख्याओं में समान संख्या का योग है)
⇒ ar (ACD) = ar (BCD)
ये दोनों त्रिभुज उभयनिष्ठ आधार CD पर दो रेखाओं DC एवं AB के मध्य स्थित हैं।
अत: AB || DC अर्थात् ABCD एक समलम्ब चतुर्भुज है। इति सिद्धम्

प्रश्न 16.
संलग्न चित्र में ar (DRC) = ar (DPC) है और ar (BDP) = ar (ARC) है। दर्शाइए कि दोनों चतुर्भुज ABCD और DCPR समलम्ब हैं।

हल:
प्रश्नानुसार,
चूँकि ar (DRC) = ar (DPC) (दिया है)…(1)
ये दोनों त्रिभुज DRC एवं DPC उभयनिष्ठ आधार DC और दो रेखाओं DC एवं RP के मध्य स्थित हैं।
⇒ DC || RP अर्थात् □DCPR एक समलम्ब चतुर्भुज है।
चूँकि ar (BDP) = ar (ARC) (दिया है)
⇒ ar (BDC) + ar (DPC) = ar (DRC) + ar (ADC) (चित्रानुसार)…(1)
⇒ ar (BDC) = ar (ADC) [समीकरण (1) और (2) से]
ये दोनों त्रिभुज BDC एवं ADC उभयनिष्ठ आधार DC एवं दो रेखाओं DC एवं AB के मध्य स्थित हैं।
⇒ DC || AB अर्थात् चतुर्भुज ABCD एक समलम्ब चतुर्भुज है।
अतः दोनों चतुर्भुज ABCD और DCPR समलम्ब चतुर्भुज हैं। इति सिद्धम्

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 7 त्रिभुज Ex 7.4

प्रश्न 1.
दर्शाइए कि समकोण त्रिभुज में कर्ण सबसे लम्बी भुजा होती है। (2018)
हल:
ज्ञात है ∆ABC का कोण B समकोण है।

चित्र 7.20
चूँकि ∠B > ∠C तथा ∠B > ∠A (त्रिभुज में समकोण सबसे बड़ा होता है)
⇒ AC > AB तथा AC > BC (बड़े कोण की सम्मुख भुजा बड़ी होती है)
अतः समकोण त्रिभुज में कर्ण सबसे बड़ा होता है। इति सिद्धम् ।

प्रश्न 2.
संलग्न चित्र में ∆ABC की भुजाएँ AB और AC को क्रमशः बिन्दुओं Pऔर ए तक बढ़ाया गया है। साथ ही ∠PBC < ∠QCB है। दर्शाइए कि AC > AB है।
हल:
चूँकि ∠PBC < ∠QCB (दिया है)

चित्र 7.21
⇒ ABC > ∠ACB (छोटे कोण का सम्पूरक बड़े कोण के सम्पूरक से बड़ा होता है)
अतः AC > AB. (त्रिभुज से बड़े कोण के सामने की भुजा बड़ी होती है) इति सिद्धम्

प्रश्न 3.
संलग्न चित्र में ∠ B < ∠A और ∠C < ∠D BN है। दर्शाइए कि-
AD < BC है।

चित्र 7.22
हल:
चूँकि ∆OAB में, ∠B < ∠A (दिया है)
⇒ AO < BO …(1) AD (∆ में छोटे कोण के सामने की भुजा छोटी होती है)
चूँकि ∆OCD में, ∠C < ∠D (दिया है)
⇒ OD ⇒ AO + OD < BO + OC – [समीकरण (1) और (2) से]
अतः AD < BC. (∵ AO + OD = AD एवं BO + OC = BC) इति सिद्धम् प्रश्न 4. AB और CD क्रमशः एक चतुर्भुज की सबसे छोटी और सबसे बड़ी भुजाएँ हैं (देखिए संलग्न चित्र)। दर्शाइए कि- ∠A >∠C और ∠B >∠D है।

चित्र 7.23
हल:
प्रश्नानुसार, AB < BC, AB < CD एवं AB < AD तथा CD > AB, CD > BC एवं CD > AD.
AC और BD को मिलाइए।
चूँकि ∆ABC में, BC > AB (∵ AB < BC दिया है) ⇒ ∠BAC > ∠BCA, (बड़ी भुजा के सामने का कोण) …(1)
तथा ∆ACD में, CD > AD (दिया है)
⇒ ∠CAD > ∠ACD (बड़ी भुजा के सामने का कोण) …(2)
⇒ ∠BAC + ∠CAD > ∠BCA + ∠ACD [समी. (1) और (2) से]
अतः ∠A > ∠C. इति सिद्धम् चूँकि
चूँकि ∆ABD में, AD > AB (दिया है)
⇒ ∠ABD > ∠ADB . (बड़ी भुजा का सम्मुख कोण) …(1)
तथा ∆BCD में, CD > BC (दिया है)
⇒ ∠DBC > ∠BDC (बड़ी भुजा का सम्मुख कोण) …(2)
⇒ ∠ABD + ∠DBC > ∠ADB+ ∠BDC [समी. (1) और (2) से]
अतः ∠B >∠D. इति सिद्धम्

प्रश्न 5.
संलग्न चित्र में PR> PQ और PS कोण DPR को समद्विभाजित करता है।
सिद्ध कीजिए कि – ∠PSR> ∠PSQ.

चित्र 7.24
हल:
चूँकि ∆POR में, PR > PQ
⇒ ∠Q >∠R (बड़ी भुजा का सम्मुख कोण) …(1)
दिया है : ∠OPS = ∠SPR (PS ∠QPR का समद्विभाजक दिया है) …(2)
अब ∠QPS + ∠Q+ ∠PSQ = ∠SPR + ∠R + ∠PSR = 180°
(त्रिभुज के अन्त:कोणों का योग) ∠Q+ ∠PSQ = ∠R + ∠PSR [∵ ∠QPS = ∠SPR, समी. (2) से]
लेकिन ∠Q > ∠R [समीकरण (1) से]
⇒ ∠PSQ < ∠PSR अतः ∠PSR > ∠PSQ. इति सिद्धम्

प्रश्न 6.
दर्शाइए कि एक रेखा पर एक दिए हुए बिन्दु से, जो उस रेखा पर स्थित नहीं है, जितने रेखाखण्ड खींचे जा सकते हैं, उनमें लम्ब रेखाखण्ड सबसे छोटा होता है।

चित्र 7.25
हल:
ज्ञात है : रेखा AB के बाहर कोई बिन्दु P है। P से PM ⊥ AB खींचा गया है। AB पर एक अन्य कोई बिन्दु N है तथा PN को मिलाया गया है।
अब ∆PMN में, ∠PMN = 90°
⇒ ∠PMN > ∠PNM (समकोण A में समकोण सबसे बड़ा होता है)
⇒ PN > PM (बड़े कोण की सम्मुख भुजा बड़ी होती है)
⇒ PM < PN.
चूँकि रेखा पर N कोई या ऐच्छिक बिन्दु है।
अतः रेखा के बाहर किसी बिन्दु से रेखा पर जितने रेखाखण्ड खींचे जा सकते हैं उनमें लम्ब सबसे छोटा होता है।  इति सिद्धम्

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Ex 9.1

प्रश्न 1.
निम्नलिखित आकृतियों में से कौनसी आकृतियाँ एक ही आधार पर और एक ही समान्तर रेखाओं के बीच स्थित हैं ? ऐसी स्थिति में, उभयनिष्ठ आधार और दोनों समान्तर रेखाएँ लिखिए।

चित्र 9.1
उत्तर:
चित्र : 9.1 (i) उभयनिष्ठ आधार = DC और DC || AB
चित्र : 9.1 (iii) उभयनिष्ठ आधार = QR और QR || PS
चित्र : 9.1 (v) उभयनिष्ठ आधार = AD और AD || BC

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 8 चतुर्भुज Additional Questions

MP Board Class 9th Maths Chapter 8  अतिरिक्त परीक्षोपयोगी प्रश्न

MP Board Class 9th Maths Chapter 8  दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
एक समान्तर चतुर्भुज ABCD में AB = 10 cm और ∠AD = 6 cm है। ∠A का समद्विभाजक DC से E पर मिलता है तथा AE और BC बढ़ाने पर F पर मिलते हैं। CF की लम्बाई ज्ञात कीजिए।

चित्र 8.25
हल:
ABCD एक समानान्तर चतुर्भुज है जिसमें AB = 10 cm AK एवं AD = 6 cm है।
∠A का समद्विभाजक DC को E पर प्रतिच्छेद करता है तथा आगे बढ़ाने पर BC को F पर प्रतिच्छेद करता है।
चूँकि AD || BC को तिर्यक रेखा AB प्रतिच्छेद करती है।
⇒ ∠DAB + ∠ABC = 180° एक ही ओर के अन्त:कोण हैं,
अर्थात् ∠ DAF + ∠ FAB + ∠ABF = 180° ….(1)
एवं ∆ABF में, ∠ FAB + ∠ABF + ∠ BFA = 180° …(2)
⇒ ∠BFA = ∠DAF [समीकरण (1) और (2) से]
अर्थात् ∠BFA = ∠ BAF (∠ DAF = ∠ BAF क्योंकि AF, ∠A का समद्विभाजक है)
⇒ BF = AB (∵ समान कोणों की सम्मुख भुजाएँ हैं)
⇒ BC + CF = AB (चित्रानुसार)
⇒ 6 cm + CF = 10 [AB = 10 cm, BC = AD = 6 cm (दिया है)]
⇒ CF = 10cm – 6 cm = 4 cm
अत: CF का अभीष्ट मान = 4 cm.

प्रश्न 2.
P, Q, R और S क्रमशः चतुर्भुज ABCD की AB, BC, CD R और DA भुजाओं के मध्य-बिन्दु हैं जिसमें AC = BD है। सिद्ध कीजिए कि PQRS एक समचतुर्भुज है।

चित्र 8.26
हल:
ABCD एक चतुर्भुज है जिसकी भुजाओं AB, BC, CD और DA के मध्य-बिन्दु क्रमशः PQR और S हैं।
चतुर्भुज के AC = BD.
चूँकि ∆ABC में AB और BC के मध्य-बिन्दु क्रमशः P और Q हैं।
⇒ PQ = \(\frac { 1 }{ 2 }\) AC …(1)
चूँकि ∆ADC में AD और CD के मध्य-बिन्दु क्रमश: S और R हैं।
SR = \(\frac { 1 }{ 2 }\)AC ….(2)
PQ = SR = \(\frac { 1 }{ 2 }\) AC [समीकरण (1) और (2) से] ..(3)
चूँकि ∆BAD में BA और DA के मध्य-बिन्दु क्रमशः P और S है।
⇒ PS = \(\frac { 1 }{ 2 }\)BD …..(4)
चूँकि ∆BCD में BD एवं CD के मध्य-बिन्दु क्रमशः Q और R है
⇒ QR = \(\frac { 1 }{ 2 }\) = BD …..(5)
⇒ PS = QR = \(\frac { 1 }{ 2 }\)BD
PS = QR = \(\frac { 1 }{ 2 }\)AC (चूँकि AC = BD दिया है) ..(6)
⇒ PQ = SR = PS = QR [समीकरण (3) एवं (6) से]
अत: PQRS एक समचतुर्भुज है। इति सिद्धम्

प्रश्न 3.
P, Q, R और S क्रमशः एक चतुर्भुज ABCD की भुजाओं AB, BC, CD और DA के मध्य-बिन्दु हैं जिसमें AC ⊥ BD है। सिद्ध कीजिए कि PQRS एक आयत है।

चित्र 8.27
हल:
P, Q, R और S क्रमशः एक चतुर्भुज ABCD की भुजाओं AB, BC, CD और DA के मध्य-बिन्दु हैं जिसके विकर्ण AC ⊥ BD
चूँकि ∆ABC की भुजाओं AB और BC के मध्य-बिन्दु क्रमशः P और ए हैं।
PQ = \(\frac { 1 }{ 2 }\) = AC एवं PQ || AC …(1)
चूँकि ∆ADC की भुजाओं CD और AD के मध्य-बिन्दु R और S हैं।
⇒ SR = \(\frac { 1 }{ 2 }\) = AC एवं SR || AC …(2)
⇒ PQ = SR एवं PQ || SR [समीकरण (1) और (2) से]
⇒ PQRS एक समान्तर चतुर्भुज है।
चूँकि ∆BAD की भुजाओं BA और DA के मध्य-बिन्दु क्रमशः P और S हैं।
⇒ PS || BD
⇒ चूँकि PQ || AC और PS || BD तथा AC ⊥ BD
⇒ PQ ⊥ PS ∠SPQ = 90° (दो परस्पर लम्ब रेखाओं के समान्तर रेखाएँ परस्पर लम्ब होती हैं)
अत: PORS एक आयत है। (परिभाषा से) इति सिद्धम्

प्रश्न 4.
ABCD एक आयत है जिसका विकर्ण BD कोण ∠B को समद्विभाजित करता है। दर्शाइए कि ABCD एक वर्ग है।।

चित्र 8.28
हल:
ABCD एक आयत है जिसका विकर्ण BD, ∠B को समद्विभाजित करता है अर्थात्,
∠ABD = ∠CBD = \(\frac { 1 }{ 2 }\)∠B = \(\frac { 1 }{ 2 }\) x 90° = 45° (आयत का कोण = 90°)
अब ∆BCD में, ∠ BCD + ∠CBD + ∠CDB = 180° (∆ के अन्तः कोण हैं)
⇒ 90° + 45° + ∠CDB = 180° (∠BCD = 90° आयत का कोण तथा ∠CBD = 45°)
⇒ ∠CDB = 45° लेकिन ∠CBD = 45° (सिद्ध कर चुके हैं)
⇒ BC = DC (समान कोणों की सम्मुख भुजाएँ हैं)
⇒ AB = BC = CD = DA
अत: ABCD एक वर्ग है। (परिभाषा से) इति सिद्धम्

MP Board Class 9th Maths Chapter 8  लघु उत्तरीय प्रश्न

प्रश्न 1.
एक चतुर्भुज का एक कोण 108° है तथा अन्य तीनों कोण बराबर हैं। तीनों बराबर कोणों में से प्रत्येक का मान ज्ञात कीजिए।
हल:
माना बराबर कोणों में प्रत्येक का मान = x° है।
⇒ 108° + 3x° = 360° (चतुर्भुज के अन्तः कोण हैं)
⇒ 3x = 360° – 108° = 252°
x = 252/3 = 84°
अतः अभीष्ट बराबर कोणों में से प्रत्येक मान = 84°.

प्रश्न 2.
ABCD एक समलम्ब चतुर्भुज है जिसमें AB || DC और ∠A=∠B = 45°। इस समलम्ब के ∠C और ∠D का मान ज्ञात कीजिए।

चित्र 8.29
हल:
समलम्ब चतुर्भुज ABCD में AB || DC एवं ∠A = ∠B = 45°
चूँकि AB || DC को तिर्यक रेखा AD काटती है
⇒ ∠A+∠D = 180° (एक ओर के अन्त:कोण हैं)
⇒ 45° + ∠D = 180° (∵∠A = 45°)
⇒ ∠D = 180° – 45° = 135°
चूँकि AB || DC को तिर्यक रेखा BC प्रतिच्छेद करती है।
⇒ ∠B + ∠C = 180° (एक ही ओर के अन्त: कोण है)
⇒ 45° + ∠C = 180° (∠B = 45° दिया है)
⇒ ∠C = 180° – 45° = 135°
अतः अभीष्ट कोणों ∠C और ∠D का प्रत्येक का मान 135° है।

प्रश्न 3.
ABCD एक समचतुर्भुज है जिसमें D से AB पर शीर्षलम्ब AB को समद्विभाजित करता है। समचतुर्भुज के कोण ज्ञात कीजिए।

चित्र 8.30
हल:
ABCD एक समचतुर्भुज है जिसमें D से AB पर डाला गया शीर्ष लम्ब DE, AB को समद्विभाजित करता है अर्थात्
AE = EB …(1)
DB को मिलाइए।
चूँकि ∆DAB में आधार AB के मध्य-बिन्दु पर खींचा गया लम्बशीर्ष D से होकर जाता है।
⇒ AD = BD
AB = BC = CD = DA (समचतुर्भुज की भुजाएँ हैं)
⇒ AB = BC = CD = DA = BD (∵ DA = AD = BD)
⇒ ∆ABD एवं ∆BCD समबाहु त्रिभुज है।
⇒ ∠DAB = ∠ BCD = 60° कोण ∠ABC = ∠CDA = 180° – 60° = 120° (क्रमश: ∠DAB एवं ∠BCD के सम्पूरक हैं)
अतः समचतुर्भुज के अभीष्ट कोण ∠A = ∠C = 60° एवं ∠B = ∠D = 120°

प्रश्न 4.
D, E और F क्रमशः एक समबाहु त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य-बिन्दु mn हैं। दर्शाइए कि ∆DEF भी एक समबाहु त्रिभुज है।

चित्र 8.31
हल:
त्रिभुज ABC में AB = BC = CA तथा D, E और F क्रमशः
BC, CA और AB के मध्य-बिन्दु हैं।
चूँकि ∆ABC में E और F भुजाओं AB और AC के मध्य-बिन्दु हैं।
⇒ EF = \(\frac { 1 }{ 2 }\)BC …(1)
चूँकि ∆ABC में F और D भुजाओं AB और BC के मध्य-बिन्दु हैं।
⇒ FD = \(\frac { 1 }{ 2 }\)CA
चूँकि ∆ABC में D और E भुजाओं BC और CA के मध्य-बिन्दु हैं।
⇒ DE = \(\frac { 1 }{ 2 }\)AB …(3)
⇒ DE = EF = FD (बराबर के आधे बराबर होते हैं)
अतः त्रिभुज DEF की समबाहु त्रिभुज है। इति सिद्धम्

प्रश्न 5.
चतुर्भुज के कोई तीन प्रकार लिखिए, चित्र भी बनाइए। (2019)
हल:
चतुर्भुज के कोई तीन प्रकार

चित्र 8.32

MP Board Class 9th Maths Chapter 8 अति लघु उत्तरीय प्रश्न

प्रश्न 1.
एक समान्तर चतुर्भुज ABCD के विकर्ण AC और BD परस्पर O बिन्दु पर प्रतिच्छेद करते हैं। यदि OA = 3 cm और OD = 2 cm है, तो AC और BD की लम्बाई ज्ञात कीजिए। उत्तर:
AC = 2OA = 2 x 3 = 6 cm एवं BD = 2 x OD = 2 x 2 = 4 cm, क्योंकि समान्तर चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं।

प्रश्न 2.
“समान्तर चतुर्भुज के विकर्ण परस्पर लम्ब होते हैं।” क्या यह कथन सत्य है ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
कथन असत्य है, क्योंकि समान्तर चतुर्भुज के विकर्ण परस्पर किसी भी कोण पर समद्विभाजित करते हैं।

प्रश्न 3.
क्या कोण 110°, 80°, 70° और 95° किसी चतुर्भुज के कोण हो सकते हैं ? क्यों और क्यों नहीं ?
उत्तर:
नहीं हो सकते, क्योंकि कोणों का योग = 110° + 80° + 70° + 95° = 355° है, जबकि चतुर्भुज के चारों कोणों का योग 360° होता है।

प्रश्न 4.
चतुर्भुज ABCD में ∠A+ ∠D = 180° है। इस चतुर्भुज को कौन-सा विशेष नाम दिया जा सकता है ?
उत्तर:
समलम्ब चतुर्भुज, क्योंकि AB || CD है।

प्रश्न 5.
एक चतुर्भुज के सभी कोण बराबर हैं। इस चतुर्भुज को कौन-सा नाम दिया जा सकता है ?
उत्तर:
आयत, क्योंकि आयत का प्रत्येक कोण 90° का होता है।

प्रश्न 6.
एक आयत के विकर्ण परस्पर बराबर और लम्ब हैं। क्या यह कथन सत्य है ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
कथन असत्य है, क्योंकि आयत के विकर्णों का परस्पर लम्ब होना आवश्यक नहीं है।

प्रश्न 7.
क्या किसी चतुर्भुज के सभी कोण अधिक कोण हो सकते हैं ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
नहीं हो सकते, क्योंकि चतुर्भुज चारों अन्तः कोणों का योग 360° होता है।

प्रश्न 8.
∆ABC में AB = 5 cm, BC = 8 cm और CA = 7 cm है। यदि D और E क्रमशः AB और BC के मध्य-बिन्दु हैं, तो DE की लम्बाई निर्धारित कीजिए।
उत्तर:
DE = \(\frac { 1 }{ 2 }\) AC = \(\frac { 7 }{ 2 }\) = 3.5 cm, क्योंकि किसी त्रिभुज में दो भुजाओं के मध्य-बिन्दु को मिलाने
वाला रेखाखण्ड तीसरी के आधा होता है।

प्रश्न 9.
क्या किसी चतुर्भुज के सभी कोण न्यूनकोण हो सकते हैं ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
नहीं हो सकते, क्योंकि इसके अन्तः कोणों का योग चार समकोण से कम होगा जबकि यह चार समकोण होना चाहिए।

प्रश्न 10.
क्या किसी चतुर्भुज के सभी कोण समकोण हो सकते हैं ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
हो सकते हैं, क्योंकि इनका योग चार समकोण के बराबर है।

प्रश्न 11.
एक चतुर्भुज ABCD के विकर्ण परस्पर समद्विभाजित करते हैं। यदि ∠A= 35° है तो ∠B निर्धारित कीजिए।
उत्तर:
चूँकि चतुर्भुज एक समान्तर चतुर्भुज है। इसलिए ∠A + ∠B = 180° ⇒∠B = 180° – ∠A = 180° – 35° = 145°

प्रश्न 12.
एक चतुर्भुज ABCD के सम्मुख कोण बराबर हैं। यदि AB = 4 cm है, तो CD निर्धारित कीजिए।
उत्तर:
चतुर्भुज एक समान्तर चतुर्भुज है, इसलिए CD = AB = 4 cm.

प्रश्न 13.
चतुर्भुज के कोई चार प्रकार लिखिए। (2019)
उत्तर:
1. समान्तर चतुर्भुज,
2. समचतुर्भुज,
3. समलम्ब चतुर्भुज,
4. आयत।

प्रश्न 14.
यदि किसी चतुर्भुज के तीन कोण क्रमश: 90°, 120° व 80° हैं, तो चौथा कोण ज्ञात कीजिए। (2019)
हल:
मान लीजिए कि चौथा कोण x है, और चूँकि चतुर्भुज के चारों अन्तः कोणों का योग 360° होता हैं।
इसलिए, 90° + 120° + 80° + x° = 360°
⇒ 290° + x° = 360°
⇒ x° = 360° – 290° = 70°
अतः अभीष्ट कोण का मान = 70°.

प्रश्न 15.
किसी चतुर्भुज के तीन कोण 110°, 80° एवं 70° है, तो उसका चौथा कोण ज्ञात कीजिए। (2019)
हल:
निर्देशः उपर्युक्त प्रश्न की तरह हल करें।
उत्तर:
अभीष्ट कोण का मान = 100°

MP Board Class 9th Maths Chapter 8 वस्तुनिष्ठ प्रश्न

बहु-विकल्पीय प्रश्न

प्रश्न 1.
एक चतुर्भुज के तीन कोण 75°, 90° और 75° हैं। इसका चौथा कोण है :
(a) 90°
(b) 95°
(c) 105°
(d) 120°.
उत्तर:
(d) 120°

प्रश्न 2.
एक आयत का एक विकर्ण उसकी एक भुजा से 25° पर नत है। इसके विकर्णों के बीच न्यूनकोण
(a) 55°
(b) 50°
(c) 40°
(d) 25°
उत्तर:
(b) 50°

प्रश्न 3.
ABCD एक सम चतुर्भुज है जिसमें ∠ACB = 40° । तब ∠ADB है :
(a) 40°
(b) 45°
(c) 50°
(d) 60°
उत्तर:
(c) 50°

प्रश्न 4.
यदि चतुर्भुज ABCD के कोणों A, B, C और D का इसी क्रम में लेने पर अनुपात 3 : 7 : 6 : 4 है तो ABCD है एक:
(a) समचतुर्भुज
(b) समान्तर चतुर्भुज
(c) समलम्ब
(d) आयत।
उत्तर:
(c) समलम्ब

प्रश्न 5.
चतुर्भुज के चारों कोणों का योग होता है :
(a) 180°
(b) 90°
(c) 360°
(d) 720°.
उत्तर:
(c) 360°

प्रश्न 6.
यदि किसी चतुर्भुज की सम्मुख भुजाएँ समान हों, तो वह होगा :
(a) समलम्ब
(b) चक्रीय चतुर्भुज
(c) समान्तर चतुर्भुज
(d) आयत।
उत्तर:
(c) समान्तर चतुर्भुज

प्रश्न 7.
समान्तर चतुर्भुज ABCD में कोण बराबर होंगे :
(a) ∠A और B
(b) ∠B और ∠C
(c) ∠A और ∠C
(d) ∠C और ∠D.
उत्तर:
(c) ∠A और ∠C

प्रश्न 8.
एक चतुर्भुज के विकर्ण बराबर तथा परस्पर लम्ब हैं, तो वह चतुर्भुज होगा :
(a) आयत
(b) समान्तर चतुर्भुज
(c) वर्ग
(d) समचतुर्भुज।
उत्तर:
(c) वर्ग

प्रश्न 9.
किस आकृति के विकर्ण एक-दूसरे को समद्विभाजित नहीं करते :
(a) आयत
(b) समान्तर चतुर्भुज
(c) समलम्ब चतुर्भुज
(d) समचतुर्भुज।
उत्तर:
(c) समलम्ब चतुर्भुज

प्रश्न 10.
समचतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं :
(a) समकोण पर
(b) न्यूनकोण पर
(c) अधिक कोण पर
(d) इनमें से कोई नहीं।
उत्तर:
(a) समकोण पर

प्रश्न 11.
आयत का प्रत्येक कोण होता है :
(a) 90°
(b) 180°
(c) 360°
(d) 270°.
उत्तर:
(a) 90°

प्रश्न 12.
किसी चतुर्भुज के ऐसे दो कोण जिनकी कोई भुजा उभयनिष्ठ न हो, कहलाते हैं :
(a) सम्मुख कोण
(b) आसन्न कोण
(c) समकोण
(d) न्यूनकोण।
उत्तर:
(a) सम्मुख कोण

रिक्त स्थानों की पूर्ति

1. समान्तर चतुर्भुज के दोनों विकर्ण परस्पर ……. करते हैं।
2. आयत के विकर्ण बराबर होते हैं तथा एक-दूसरे को …………. करते हैं।
3. किसी वर्ग की भुजाओं के मध्य-बिन्दुओं को मिलाने से निर्मित चतुर्भुज ……. होगा।
4. यदि किसी समान्तर चतुर्भुज के विकर्ण परस्पर समान और लम्ब हों तो वह चतुर्भुज …….. होगा।
5. वह चतुर्भुज जिसके विकर्ण परस्पर समकोण पर समद्विभाजित करें ……….. होता है।
उत्तर:
1. समद्विभाजित,
2. समद्विभाजित,
3. वर्ग,
4. वर्ग,
5. समचतुर्भुज ।

जोड़ी मिलान

उत्तर:
1. → (c),
2. → (d),
3. → (e),
4. → (a),
5. → (b),
6. → (g),
7. → (f).

सत्य/असत्य कथन
1. चतुर्भुज के चारों कोणों का योग 180° होता है।
2. समान्तर चतुर्भुज के सम्मुख कोण बराबर होते हैं।
3. समलम्ब चतुर्भुज की सम्मुख भुजाएँ समान्तर होती हैं।
4. वर्ग के विकर्ण समान होते हैं तथा परस्पर समकोण पर समद्विभाजित करते हैं।
5. यदि किसी समान्तर चतुर्भुज के विकर्ण एक-दूसरे पर लम्ब और बराबर हों, तो वह आयत होता है।
उत्तर:
1. असत्य,
2. सत्य,
3. असत्य,
4. सत्य,
5. असत्य।

एक शब्द/वाक्य में उत्तर

1. चार रेखाखण्डों में निर्मित आकृति क्या कहलाती है?
2. यदि किसी चतुर्भुज की सम्मुख भुजाओं का एक युग्म बराबर और समान्तर हो तो वह चतुर्भुज क्या होगा?
3. किसी त्रिभुज की दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाली रेखा और तीसरी भुजा में क्या सम्बन्ध
4. किसी त्रिभुज की एक भुजा के मध्य-बिन्दु से दूसरी, भुजा के समान्तर खींची गई रेखा तीसरी भुजा को किस अनुपात में विभक्त करती है?
5. किसी चतुर्भुज में कितने शीर्ष होते हैं?
6. आयत का प्रत्येक कोण कितने अंश का होता है? (2019)
उत्तर:
1. चतुर्भुज,
2. समान्तर चतुर्भुज,
3. तीसरी भुजा के समान्तर और आधी,
4. 1 : 1,
5. चार,
6. 90°.

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 7 त्रिभुज Ex 7.3

प्रश्न 1.
∆ABC और ∆DBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि A और D भुजा BC के एक ही ओर स्थित हैं (देखिए संलग्न चित्र)। यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे तो दर्शाइए :
(i) ∆ABD ≅ ∆ACD.
(ii) ∆ABP ≅ ∆ACP
(iii) AP कोण A और कोण D दोनों को समद्विभाजित करता है।
(iv) AP रेखाखण्ड BC का लम्ब समद्विभाजक है।

चित्र 7.15
हल:
(i) ∆ABD और ∆ACD में,
चूँकि AB = AC (समद्विबाहु ∆ABC भी भुजाएँ हैं)
DB = DC (समद्विबाहु ∆DBC की भुजाएँ हैं।)
एवं AD = AD (उभयनिष्ठ है)
अतः ∆ABD ≅ ∆ACD. (SSS सर्वांगसमता प्रमेय) इति सिद्धम्

(ii) ∆ABP और ∆ACP में,
चूँकि AB = AC (समद्विबाहु ∆ABC भी भुजाएँ हैं)
∠BAP = ∠CAP (∆ABD ≅ ∆ACD के संगत कोण हैं)
एवं AP = AP (उभयनिष्ठ है)
अतः ∆ABP ≅ ∆ACP (SAS सर्वांगसमता प्रमेय) इति सिद्धम्

(iii) ∵ ∆ABD ≅ ∆ACD [भाग (i) में सिद्ध कर चुके हैं।]
⇒ ∠BAD = ∠CAD (CPCT)
इसलिए AP कोण A का समद्विभाजक है।
एवं ∠ADB = ∠ADC (CPCT)
एवं ∠BDP = ∠CDP (बराबर कोणों के सम्पूरक हैं)
इसलिए AP कोण D का समद्विभाजक है।
अतः AP कोण A और कोण D दोनों का समद्विभाजक हैं। इति सिद्धम्

(iv) ∵ ∆ABP ≅ ∆ACP [भाग (ii) में सिद्ध कर चुके हैं। ]
⇒ BP= CP (CPCT)
एवं ∠APB = ∠APC (CPCT)
लेकिन ∠APB + ∠APC = 180° (BC के बिन्दु P पर एक ही ओर बने कोण हैं)
इसलिए ∠APB = ∠APC = 90°
अतः AP रेखाखण्ड BC का लम्ब समद्विभाजक है। इति सिद्धम्

प्रश्न 2.
AD एक समद्विबाहु ∆ABC का एक शीर्ष लम्ब है जिसमें AB = AC है। दर्शाइए कि-
(i) AD रेखाखण्ड BC को समद्विभाजित करता है।
(ii) AD कोण A को समद्विभाजित करता है।

चित्र 1.16
हल:
(i) चूँकि ∠ADB = ∠ADC = 90° (∵ AD ⊥ BC)
इसलिए ∆ADB एवं ∆ADC समकोण त्रिभुज हैं।
अब समकोण ∆ADB और ∆ADC में,
चूँकि कर्ण AB = कर्ण AC (समद्विबाहु ∆ABC की भुजाएँ हैं)
एवं AD = AD (उभयनिष्ठ है)
⇒ ∆ADB ≅ ∆ADC (RHS सर्वांगसमता प्रमेय)
⇒ BD = CD (CPCT)
अतः AD रेखाखण्ड BC की समद्विभाजित करता है। इति सिद्धम्

(ii) चूँकि ∆ADB ≅ ∆ADC (सिद्ध कर चुके हैं)
∠BAD = ∠CAD (CPCT)
अत: AD कोण A को समद्विभाजित करता है। इति सिद्धम्

प्रश्न 3.
एक त्रिभुज ABC की दो भुजाएँ AB और BC तथा माध्यिका AM क्रमशः एक दूसरे त्रिभुज POR की भुजाओं PQ और OR तथा माध्यिका PN के बराबर है (देखिए संलग्न चित्र)। दर्शाइए कि-
(i) ∆ABM ≅ ∆PQN.
(ii) ∆ABC ≅ ∆PQR.

चित्र 1.17
हल:
त्रिभुज ABC और PQR में AB = PO, BC = QR एवं माध्यिका AM = PN (दिया है)
चूँकि BC = OR ⇒ \(\frac { 1 }{ 2 }\)BC = \(\frac { 1 }{ 2 }\)QR ⇒ BM = ON

(i) अब ∆ABM और ∆PON में,
चूँकि AB = PQ (दिया है)
BM = ON (सिद्ध कर चुके है)
AM = PN (दिया है)
अतः ∆ABM ≅ ∆PON. (SSS सर्वांगसमता प्रमेय) इति सिद्धम्

(ii) चूँकि ΔΑΒΜ ≅ ΔΡQΝ [भाग (i) में सिद्ध कर चुके हैं।]
⇒ ∠ABM = ∠PQN अर्थात्∠ABC = ∠PQR (CPCT)
अब ∆ABC और ∆PQR में,
चूँकि AB = PQ (दिया है)
∠ABC = ∠PQR (सिद्ध कर चुके हैं)
BC = QR (दिया है)
अतः ∆ABC ≅ ∆POR. इति सिद्धम्

प्रश्न 4.
BE और CF एक त्रिभुज ABC के दो बराबर शीर्ष लम्ब हैं। RHS सर्वांगसमता नियम का प्रयोग करके सिद्ध कीजिए कि ΔABC एक समद्विबाहु त्रिभुज है।

चित्र 1.18
हल:
दिया है : एक ∆ABC जिसमें BE एवं CF दो शीर्ष लम्ब हैं
तथा BE = CF,
समकोण ∆BFC एवं समकोण ∆CEB में (शीर्ष लम्ब BE ⊥ AC एवं CF ⊥ AB),
चूँकि BE = CF (दिया है)
एवं कर्ण BC = कर्ण BC (उभयनिष्ठ है)
⇒ ∆BFC ≅ ∆CEB (RHS सर्वांगसमता प्रमेय से)
⇒ ∠FBC = ∠ECB अर्थात् ∠ABC = ∠ACB. (CPCT)
AB = AC (बराबर कोणों की सम्मुख भुजाएँ हैं)
अत: AABC एक समद्विबाहु त्रिभुज है। इति सिद्धम्

प्रश्न 5.
ABC एक समद्विबाहु त्रिभुज है जिससे AB = AC है। AP ⊥ BC खींचकर दर्शाइए कि ∠B = ∠C है। (2019)
अथवा
सिद्ध कीजिए एक समद्विबाहु त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं। (2019)

चित्र 1.19
हल:
समद्विबाहु ∆ABC में AB = AC दिया गया है। AP ⊥ BC खींचा गया है।
अब समकोण त्रिभुज APB एवं समकोण ∆ APC
चूँकि कर्ण AB = कर्ण AC (दिया है)
एवं AP = AP (उभयनिष्ठ है)
⇒ ∆APB ≅ ∆APC (RHS सर्वांगसम प्रमेय)
⇒ ∠B = ∠C. (CPCT) इति सिद्धम्

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 7 त्रिभुज Ex 7.2

प्रश्न 1.
एक समद्विबाहु त्रिभुज ABC में जिसमें AB = AC है, ∠B और ∠C के समद्विभाजक परस्पर 0 बिन्दु पर प्रतिच्छेद करते हैं। A और O को जोड़िए। दर्शाइए कि-
(i) OB = OC.
(ii) AO, ∠A को समद्विभाजित करता है।

चित् 7.9
हल:
(i) चित्रानुसार (चित्र संलग्न है।)
चूँकि ∆ABC में, AB = AC (दिया है)
इसलिए ∠ABC = ∠ACB (समान भुजाओं के सम्मुख कोण हैं)
चूँकि OB एवं OC क्रमश: ∠ABC एवं ∠ACB के समद्विभाजक हैं। (दिया है)
इसलिए ∠OBC = ∠OCB (बराबर वस्तुओं के आधे बराबर होते हैं)
अतः OB = OC. (AOBC के बराबर कोणों की सम्मुख भुजाएँ हैं) इति सिद्धम्

(ii) अब ∆AOB और ∆AOC में,
चूँकि भुजा AB = भुजा AC (दिया है)
भुजा OB = भुजा OC (सिद्ध कर चुके हैं)
भुजा AO = भुजा A0 (उभयनिष्ठ है)
अतः ∆AOB ≅ ∆AOC (SSS सर्वांगसमता प्रमेय)
⇒ ∠BAO = ∠CAO (CPCT)
अत: AO, ∠A को समद्विभाजित करता है। इति सिद्धम्

प्रश्न 2.
∆ABC में AD भुजा BC का लम्ब समद्विभाजक है (देखिए संलग्न चित्र)। दर्शाइए कि ∆ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है।

चित् 7.10
हल:
∆ADB और ∆ADC में,
चूँकि BD = CD (दिया है : AD, BC का समद्विभाजक)
∠ADB = ∠ADC (दिया है : AD, BC पर लम्ब)
AD = AD (उभयनिष्ठ है)
⇒ ∆ADB ≅ ∆ADC (SAS सर्वांगसमता प्रमेय)
⇒ AB = AC (CPCT)
अत: ∆ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC. इति सिद्धम्

प्रश्न 3.
संलग्न चित्र में ABC एक समद्विबाहु त्रिभुज है जिसमें बराबर भुजाओं AC और AB पर क्रमशः शीर्ष लम्ब BE और CF खींचे गए हैं। दर्शाइए कि ये शीर्ष लम्ब बराबर है।

चित् 7.11
हल:
∆ABE और ∆ACF में,
चूँकि AB = AC (समद्विबाहु ∆ की । बराबर भुजाएँ दी गई हैं।)
∠BAE = ∠CAF (उभयनिष्ठ है)
⇒ ∠AEB = ∠AFC = 90° (:: BE ⊥ AC एवं CF ⊥ AB)
⇒ ∆ABE ≅ ∆ACF (AAS सर्वांगसमता प्रमेय)
⇒ BE = CF (CPCT)
अतः अभीष्ट शीर्ष लम्ब बराबर हैं। इति सिद्धम्

प्रश्न 4.
ABC एक त्रिभुज है जिसमें AC और AB पर खींचे गए शीर्ष लम्ब BE और CF समान हैं (देखिए संलग्न चित्र)।
दर्शाइए कि-
(i) ∆ABE ≅ ∆ACE
(ii) AB = AC अर्थात् ∆ABC एक समद्विबाहु त्रिभुज है।

चित् 7.12
हल:
(i) ∆ABE और ∆ACF में,
चूँकि ∠BAE = ∠CAF (उभयनिष्ठ है)
∠AEB = ∠AFC = 90° [∵ BE ⊥ AC और CF ⊥ AB (दिया है)]
एवं BE = CF (दिया है)
∆ABE ≅ ∆ACE (AAS सर्वांगसमता प्रमेय) इति सिद्धम्

(ii) ∆ABE ≅ ∆ACF [भाग (i) में सिद्ध कर चुके हैं।]
⇒ AB = AC (CPCT)
अतः त्रिभुज ABC एक समद्विबाहु त्रिभुज है। इति सिद्धम्

प्रश्न 5.
ABC और DBC समान आधार BC पर स्थित दो समद्विबाहु त्रिभुज है (देखिए संलग्न चित्र)। दर्शाइए कि-
∠ABD = ∠ACD. (2019)

चिन्न 7.13
हल:
∵ ∆ABC एक समद्विबाहु A है (दिया है)
⇒ ∠ABC = ∠ACB …(1) (समान BT भुजाओं के सम्मुख कोण हैं)
∵ ∆DBC एक समद्विबाहु त्रिभुज है (दिया है)
⇒ ∠DBC = ∠DCB …(2) (समान भुजाओं के सम्मुख कोण हैं)
⇒ ∠ABC + ∠DBC = ∠ACB + ∠DCB [समीकरण (1) एवं (2) से]
अतः ∠ABD = ∠ACD. (चित्रानुसार) इति सिद्धम्

प्रश्न 6.
ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है। भुजा BA बिन्दु D तक इस प्रकार बढ़ाई गई है कि AD = AB है (देखिए संलग्न चित्र)। दर्शाइए कि ∠BCD एक समकोण है।

चित्र 7.14
हल:
∆ABC में, AB = AC (दिया है)
⇒ ∠ABC = ∠ACB ….(1) (बराबर भुजाओं के सम्मुख कोण हैं)
चूँकि AB = AD एवं AB = AC (दिया है)
⇒ AD = AC (यूक्लिड अभिधारणा-I)
⇒ ∆ACD में, चूँकि AD = AC
⇒ ∠ADC = ∠ACD …(2) (बराबर भुजाओं के सम्मुख कोण है)
⇒ ∠ABC + ∠ADC = ∠ACB + ∠ACD [समी. (1) एवं (2) से]
⇒ ∠ABC + ∠ADC = ∠BCD (∵ ∠ACB + ∠ACD =∠BCD, चित्रानुसार)
लेकिन ∠ABC + ∠ADC + ∠BCD = 180° (त्रिभुज के अन्तः कोण है)
= ∠ABC + ∠ADC = ∠BCD = 90°
अतः अभीष्ट कोण ∠BCD = 90° इति सिद्धम्

प्रश्न 7.
ABC एक समकोण त्रिभुज है जिसमें ∠A = 90° और AB = AC है। ∠B और ∠C ज्ञात कीजिए।
हल:
दिया है AB = AC ⇒ ∠B = ∠C (बराबर भुजाओं के सम्मुख कोण हैं)
∵ ∠A + ∠B + ∠C = 180° (त्रिभुज के अन्तः कोण हैं)
⇒ 90° + x + x = 180° [माना ∠B = ∠C = x एवं ∠A = 90° (दिया है)]
⇒ 2x = 180° – 90° = 90°
⇒ x = 90°/2 = 45°
अतः अभीष्ट कोण ∠B = ∠C = 45°.

प्रश्न 8.
दर्शाइए किसी समबाहु त्रिभुज का प्रत्येक कोण 60° होता है।
हल:
चूँकि समबाहु त्रिभुज का प्रत्येक कोण एक-दूसरे के बराबर होता है। मान लीजिए इसका मान x° है।
इसलिए x + x + x = 180° (त्रिभुज के अन्तः कोण है)
⇒ 3x = 180° = x = 180°/3 = 60°
अतः समबाहु त्रिभुज का प्रत्येक कोण 60° होता है।

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 8 चतुर्भुज Ex 8.2

प्रश्न 1.
संलग्न चित्र में ABCD एक चतुर्भुज है जिसमें P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिन्दु हैं। AC उसका एक विकर्ण है। दर्शाइए कि
(i) SR || AC और SR = \(\frac { 1 }{ 2 }\) AC है। (2018)
(ii) PQ = RS है।
(iii) PORS एक समान्तर चतुर्भुज है।

चित्र 8.12
हल:
(i) ∆DAC में S और R क्रमशः DA और DC के मध्य-बिन्दु हैं।
अतः SR || AC और SR = \(\frac { 1 }{ 2 }\) AC.
(ii) ∆BCA में, P और Q क्रमश: AB और BC के मध्य-बिन्दु हैं।
⇒ PQ || AC और PO = \(\frac { 1 }{ 2 }\)AC .
लेकिन SR = \(\frac { 1 }{ 2 }\)AC अथवा RS = \(\frac { 1 }{ 2 }\)AC (सिद्ध कर चुके हैं)
अतः PQ = RS. इति सिद्धम्

(iii) PQ || AC एवं PQ = \(\frac { 1 }{ 2 }\)AC (सिद्ध कर चुके हैं)
RS || AC एवं RS = \(\frac { 1 }{ 2 }\) AC (सिद्ध कर चुके हैं)
PQ || RS एवं PQ = RS (एक ही वस्तु के बराबर और समान्तर आपस में बराबर और समान्तर होते हैं)
अतः PORS एक समान्तर चतुर्भुज है।

प्रश्न 2.
ABCD एक समचतुर्भुज है और P Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिन्दु हैं। दर्शाइए कि चतुर्भुज PQRS एक आयत है।

चित्र 8.13
हल:
दिया है: ABCD एक समचतुर्भुज है तथा P, O, R एवं S
क्रमशः AB, BC, CD एवं DA के मध्य-बिन्दु हैं।
PR एवं SQ को मिलाइए।
चूँकि AS || BQ एवं AS = BQ
(बराबर एवं समान्तर भुजाओं की आधी है)
⇒ ABQS एक समान्तर चतुर्भुज है ⇒ AB = SQ
चूँकि AP || DR एवं AP = DR (बराबर एवं समान्तर भुजाओं की आधी है)
⇒ APRD एक समान्तर चतुर्भुज है ⇒ AD = PR
लेकिन AB = AD ⇒ SQ = PR (समचतुर्भुज की भुजाएँ बराबर होती हैं)
अतः चतुर्भुज PORS एक आयत है। (विकर्ण SQ = PR) इति सिद्धम्

प्रश्न 3.
ABCD एक आयत है जिसमें P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिन्दु हैं। दर्शाइए चतुर्भुज PORS एक समचतुर्भुज है।

चित्र 8.14
हल:
ABCD एक आयत है जिसकी भुजाओं AB,BC, CD एवं DA के मध्य-बिन्दु क्रमशः P, Q, R और S हैं।
PQ और QS को मिलाइए। चूँकि P, Q, R, S आयत ABCD की संलग्न भुजाओं के मध्य-बिन्दु हैं।
⇒ PQRS एक समान्तर चतुर्भुज है।
चूँकि DR || AP एवं DR = AP (बराबर एवं समान्तर भुजाओं की आधी है)
⇒ DA ||RP|| CB
चूँकि AS || BQ एवं AS = BQ (बराबर एवं समान्तर भुजाओं की आधी है)
⇒ AB || SQ || DC
⇒ RP ⊥ SQ (∵ DA ⊥ AB)
अतः PQRS एक सम चतुर्भुज है। (विकर्ण परस्पर लम्बवत् हैं) इति सिद्धम्

प्रश्न 4.
ABCD एक समलम्ब चतुर्भुज है जिसमें AB || DC है। साथ ही BD एक विकर्ण है और E भुजा AD का मध्य-बिन्दु है। E से होकर एक रेखा AB के समान्तर खींची जाती है जो BC को F पर प्रतिच्छेद करती है (देखिए संलग्न चित्र)। दर्शाइए कि F भुजा BC का मध्य-बिन्दु है।

चित्र 8.15
हल:
ABCD एक समलम्ब चतुर्भुज है जिसमें AB || DC, DA के मध्य-बिन्दु E से AB के समान्तर रेखा खींची गई है जो BC को बिन्दु F पर प्रतिच्छेद करती है। BD समलम्ब चतुर्भुज का एक विकर्ण है। मान लीजिए रेखा EF, DB को बिन्दु G पर प्रतिच्छेद करती है।
चूँकि ∆DAB में DA के मध्य-बिन्दु E से EF || AB खींची गई है।
⇒ G भुजा DB का मध्य-बिन्दु होगा।
चूँकि AB || DC एवं AB | | EF (दिया है)
⇒ EF || DC तथा सिद्ध कर चुके है कि G भुजा DB का मध्य-बिन्दु है।
अतः F, भुजा BC का मध्य-बिन्दु होगा। इति सिद्धम्

प्रश्न 5.
संलग्न चित्र में एक समान्तर चतुर्भुज ARCD में E और F क्रमशः भुजाओं AB और CD के मध्य-बिन्दु हैं। दर्शाइए कि रेखाखण्ड AF और EC विकर्ण BD को समत्रिभाजित करते हैं।

चित्र 8.16
हल:
दिया है : ABCD एक समान्तर चतुर्भुज जिसमें E और F
क्रमशः भुजाओं AB और CD के मध्य-बिन्दु हैं। विकर्ण BD, AF एवं EC क्रमशः P और Q बिन्दु पर प्रतिच्छेद करते हैं।
रेखा l || AF एवं रेखा m || EC खींचिए।
चूँकि AB = CD एवं AB || CD के मध्य-बिन्दु क्रमशः E एवं F हैं।
⇒ AE = CF एवं AE || CF (बराबर एवं समान्तर रेखाओं के आधे है)
⇒ □AECF एक समान्तर चतुर्भुज है (समान्तर एवं बराबर रेखायुग्म AE एवं CF है)
⇒ AF || EC (समान्तर चतुर्भुज की सम्मुख भुजाएँ हैं)
⇒ l || AF || EC [चूँकि AF || EC एवं l || AF (रचना से)]
चूँकि l || AF || EC तिर्यक रेखाखण्ड DC से DF = FC अन्त:खण्ड काटते हैं।
⇒ l || AF || EC तिर्यक रेखाखण्ड DQ से DP = PQ अन्त:खण्ड काटेंगे,
अब AF || EC || m चूँकि AF || EC एवं EC || m (रचना से)]
चूँकि AF || EC || m रेखाखण्ड AB से AE = EB अन्त:खण्ड काटते हैं।
⇒ AF || EC || m रेखाखण्ड PB से PQ = QB रेखाखण्ड काटते हैं,
चूँकि DP = PQ एवं PQ = QB ⇒ DP = PQ = QB.
अतः रेखाखण्ड AF एवं EC विकर्ण BD को समत्रिभाजित करते हैं। इति सिद्धम्

प्रश्न 6.
दर्शाइए कि किसी चतुर्भुज की सम्मुख भुजाओं के मध्य-बिन्दुओं को मिलाने वाले रेखाखण्ड परस्पर । समद्विभाजित करते हैं।
हल:

चित्र 8.17
दिया है : ABCD एक चतुर्भुज जिसकी भुजाओं AB, BC, CD एवं DA के मध्य-बिन्दु क्रमशः P, Q, R और 5 हैं। PR और QS एक-दूसरे को बिन्दु O पर प्रतिच्छेद करते हैं।
PQ, QR, RS, SP एवं BD को मिलाइए।
अब ∆ABD में PS || BD एवं PS = \(\frac { 1 }{ 2 }\)BD (P और S क्रमशः AB और AD के मध्य-बिन्दु हैं)
एवं A CBD में QR || BD एवं QR = \(\frac { 1 }{ 2 }\)BD (Q और R क्रमशः BC और CD के मध्य-बिन्दु हैं)
⇒ PS || QR एवं PS = QR (PS एवं QR दोनों एक ही रेखाखण्ड BD के समान्तर और आधे हैं)
⇒ PQRS एक समान्तर चतुर्भुज है और PR एवं QS इसके विकर्ण हैं।
⇒ PQ = QR एवं QO = OS (समान्तर चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं)
अतः किसी चतुर्भुज की सम्मुख भुजाओं के मध्य-बिन्दुओं को मिलाने वाले रेखाखण्ड परस्पर समद्विभाजित करते हैं। इति सिद्धम्

प्रश्न 7.
ABC एक त्रिभुज है जिसका कोण C समकोण है। कर्ण AB के मध्य-बिन्दु M से होकर BC के समान्तर खींची गई रेखा AC को D पर प्रतिच्छेद करती है। दर्शाइए कि-
(i) D भुजा AC का मध्य-बिन्दु है।
(ii) MD ⊥ AC है।
(ii) CM = MA = \(\frac { 1 }{ 2 }\)AB है।

चित्र 8.18
हल:
ABC एक त्रिभुज दिया गया है जिसमें ∠C समकोण है तथा कर्ण AB के मध्य-बिन्दु M से MD || BC खींची गई है जो AC को बिन्दु D पर प्रतिच्छेद करती है।
(i) चूँकि ∆ABC में AB के मध्य-बिन्दु M से MD || BC खींची गई है।
⇒ MD रेखाखण्ड AC को बिन्दु D पर समद्विभाजित करेगी।
अत: D भुजा AC का मध्य-बिन्दु है। इति सिद्धम्

(ii) चूँकि MD || BC और BC ⊥AC (∠ACB समकोण दिया है)
अतः MD ⊥ AC. इति सिद्धम्

(iii) CM को मिलाइए।
चूँकि MD ⊥ AC एवं AD = DC
⇒ ∆AMC समद्विबाहु त्रिभुज है
⇒ CM = MA एवं MA = \(\frac { 1 }{ 2 }\)AB.
अतः CM = MA = \(\frac { 1 }{ 2 }\)AB. इति सिद्धम्

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 5 युक्लिड के ज्यामिति का परिचय Ex 5.2

प्रश्न 1.
आप यूक्लिड की पाँचवीं अभिधारणा को किस प्रकार लिखेंगे ताकि यह सरलता से समझी जा सके?
उत्तर:
यदि एक सीधी रेखा दो सीधी रेखाओं को प्रतिच्छेद करे और अपने एक ही ओर के दो अन्तः कोणों का योग 2 समकोण (180°) से कम है तो वे रेखाएँ प्रतिच्छेदी रेखाएँ होंगी, समान्तर नहीं।

प्रश्न 2.
क्या यूक्लिड की पाँचवीं अभिधारणा से समान्तर रेखाओं के अस्तित्व का औचित्य निर्धारित होता है ? स्पष्ट कीजिए।
उत्तर:

यदि कोई सरल रेखा l, दो सरल रेखाओं m एवं n पर पड़ती है इस प्रकार कि l के एक ओर के अन्तः कोणों का योग 2 समकोण (180°) हो तो वे रेखाएँ m एवं n इस ओर कभी भी नहीं मिलेंगी (यूक्लिड के पाँचवीं अभिगृहीत के अनुसार) एवं चूँकि दूसरी ओर के अन्त: कोणों का योग भी चित्र 5.12 दो समकोण (180°) होगा।
अतः ये इस तरफ भी नहीं मिलेंगी। अत: रेखाएँ m एवं n परस्पर समान्तर होंगी।

MP Board Class 9th Maths Solutions