MP Board Class 9th Maths Solutions Chapter 7 त्रिभुज Ex 7.3
प्रश्न 1.
∆ABC और ∆DBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि A और D भुजा BC के एक ही ओर स्थित हैं (देखिए संलग्न चित्र)। यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे तो दर्शाइए :
(i) ∆ABD ≅ ∆ACD.
(ii) ∆ABP ≅ ∆ACP
(iii) AP कोण A और कोण D दोनों को समद्विभाजित करता है।
(iv) AP रेखाखण्ड BC का लम्ब समद्विभाजक है।
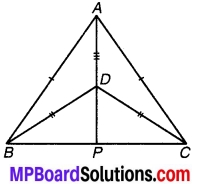
चित्र 7.15
हल:
(i) ∆ABD और ∆ACD में,
चूँकि AB = AC (समद्विबाहु ∆ABC भी भुजाएँ हैं)
DB = DC (समद्विबाहु ∆DBC की भुजाएँ हैं।)
एवं AD = AD (उभयनिष्ठ है)
अतः ∆ABD ≅ ∆ACD. (SSS सर्वांगसमता प्रमेय) इति सिद्धम्
(ii) ∆ABP और ∆ACP में,
चूँकि AB = AC (समद्विबाहु ∆ABC भी भुजाएँ हैं)
∠BAP = ∠CAP (∆ABD ≅ ∆ACD के संगत कोण हैं)
एवं AP = AP (उभयनिष्ठ है)
अतः ∆ABP ≅ ∆ACP (SAS सर्वांगसमता प्रमेय) इति सिद्धम्
(iii) ∵ ∆ABD ≅ ∆ACD [भाग (i) में सिद्ध कर चुके हैं।]
⇒ ∠BAD = ∠CAD (CPCT)
इसलिए AP कोण A का समद्विभाजक है।
एवं ∠ADB = ∠ADC (CPCT)
एवं ∠BDP = ∠CDP (बराबर कोणों के सम्पूरक हैं)
इसलिए AP कोण D का समद्विभाजक है।
अतः AP कोण A और कोण D दोनों का समद्विभाजक हैं। इति सिद्धम्
(iv) ∵ ∆ABP ≅ ∆ACP [भाग (ii) में सिद्ध कर चुके हैं। ]
⇒ BP= CP (CPCT)
एवं ∠APB = ∠APC (CPCT)
लेकिन ∠APB + ∠APC = 180° (BC के बिन्दु P पर एक ही ओर बने कोण हैं)
इसलिए ∠APB = ∠APC = 90°
अतः AP रेखाखण्ड BC का लम्ब समद्विभाजक है। इति सिद्धम्
![]()
प्रश्न 2.
AD एक समद्विबाहु ∆ABC का एक शीर्ष लम्ब है जिसमें AB = AC है। दर्शाइए कि-
(i) AD रेखाखण्ड BC को समद्विभाजित करता है।
(ii) AD कोण A को समद्विभाजित करता है।
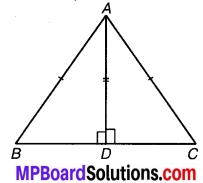
चित्र 1.16
हल:
(i) चूँकि ∠ADB = ∠ADC = 90° (∵ AD ⊥ BC)
इसलिए ∆ADB एवं ∆ADC समकोण त्रिभुज हैं।
अब समकोण ∆ADB और ∆ADC में,
चूँकि कर्ण AB = कर्ण AC (समद्विबाहु ∆ABC की भुजाएँ हैं)
एवं AD = AD (उभयनिष्ठ है)
⇒ ∆ADB ≅ ∆ADC (RHS सर्वांगसमता प्रमेय)
⇒ BD = CD (CPCT)
अतः AD रेखाखण्ड BC की समद्विभाजित करता है। इति सिद्धम्
(ii) चूँकि ∆ADB ≅ ∆ADC (सिद्ध कर चुके हैं)
∠BAD = ∠CAD (CPCT)
अत: AD कोण A को समद्विभाजित करता है। इति सिद्धम्
प्रश्न 3.
एक त्रिभुज ABC की दो भुजाएँ AB और BC तथा माध्यिका AM क्रमशः एक दूसरे त्रिभुज POR की भुजाओं PQ और OR तथा माध्यिका PN के बराबर है (देखिए संलग्न चित्र)। दर्शाइए कि-
(i) ∆ABM ≅ ∆PQN.
(ii) ∆ABC ≅ ∆PQR.
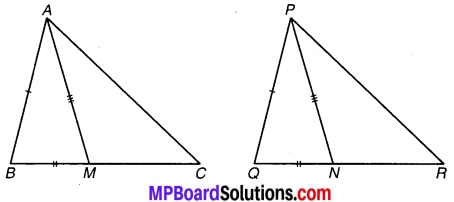
चित्र 1.17
हल:
त्रिभुज ABC और PQR में AB = PO, BC = QR एवं माध्यिका AM = PN (दिया है)
चूँकि BC = OR ⇒ \(\frac { 1 }{ 2 }\)BC = \(\frac { 1 }{ 2 }\)QR ⇒ BM = ON
(i) अब ∆ABM और ∆PON में,
चूँकि AB = PQ (दिया है)
BM = ON (सिद्ध कर चुके है)
AM = PN (दिया है)
अतः ∆ABM ≅ ∆PON. (SSS सर्वांगसमता प्रमेय) इति सिद्धम्
(ii) चूँकि ΔΑΒΜ ≅ ΔΡQΝ [भाग (i) में सिद्ध कर चुके हैं।]
⇒ ∠ABM = ∠PQN अर्थात्∠ABC = ∠PQR (CPCT)
अब ∆ABC और ∆PQR में,
चूँकि AB = PQ (दिया है)
∠ABC = ∠PQR (सिद्ध कर चुके हैं)
BC = QR (दिया है)
अतः ∆ABC ≅ ∆POR. इति सिद्धम्
प्रश्न 4.
BE और CF एक त्रिभुज ABC के दो बराबर शीर्ष लम्ब हैं। RHS सर्वांगसमता नियम का प्रयोग करके सिद्ध कीजिए कि ΔABC एक समद्विबाहु त्रिभुज है।
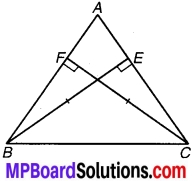
चित्र 1.18
हल:
दिया है : एक ∆ABC जिसमें BE एवं CF दो शीर्ष लम्ब हैं
तथा BE = CF,
समकोण ∆BFC एवं समकोण ∆CEB में (शीर्ष लम्ब BE ⊥ AC एवं CF ⊥ AB),
चूँकि BE = CF (दिया है)
एवं कर्ण BC = कर्ण BC (उभयनिष्ठ है)
⇒ ∆BFC ≅ ∆CEB (RHS सर्वांगसमता प्रमेय से)
⇒ ∠FBC = ∠ECB अर्थात् ∠ABC = ∠ACB. (CPCT)
AB = AC (बराबर कोणों की सम्मुख भुजाएँ हैं)
अत: AABC एक समद्विबाहु त्रिभुज है। इति सिद्धम्
![]()
प्रश्न 5.
ABC एक समद्विबाहु त्रिभुज है जिससे AB = AC है। AP ⊥ BC खींचकर दर्शाइए कि ∠B = ∠C है। (2019)
अथवा
सिद्ध कीजिए एक समद्विबाहु त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं। (2019)
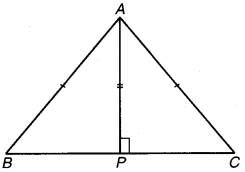
चित्र 1.19
हल:
समद्विबाहु ∆ABC में AB = AC दिया गया है। AP ⊥ BC खींचा गया है।
अब समकोण त्रिभुज APB एवं समकोण ∆ APC
चूँकि कर्ण AB = कर्ण AC (दिया है)
एवं AP = AP (उभयनिष्ठ है)
⇒ ∆APB ≅ ∆APC (RHS सर्वांगसम प्रमेय)
⇒ ∠B = ∠C. (CPCT) इति सिद्धम्