Prasanna

MP Board Class 8th Maths Solutions Chapter 16 संख्याओं के साथ खेलना Intext Questions

MP Board Class 8th Maths Chapter 16 पाठान्तर्गत प्रश्नोत्तर

पाठ्य-पुस्तक पृष्ठ संख्या # 260

प्रयास कीजिए (क्रमांक 16.1)

प्रश्न 1.
निम्नलिखित संख्याओं को व्यापक रूप में लिखिए –

1. 25
2. 73
3. 129
4. 302

हल:

1. 25 = 20 + 5 = 10 x 2 + 1 x 5
2. 73 = 70 + 3 = 10 x 7 + 1 x 3
3. 129 = 100 + 20 + 9 = 100 x 1 + 10 x 2 +1 x 9
4. 302 = 300 + 00 + 2 = 100 x 3 + 10 x 0 + 1 x 2

प्रश्न 2.
निम्नलिखित को सामान्य रूप में लिखिए –

1. 10 x 5 + 6
2. 100 x 7 + 10 x 1 + 8
3. 100a + 10c + b.

उत्तर:

1. 10 x 5 + 6 = 50 + 6 = 56
2. 100 x 7 + 10 x 1 + 8 = 700 + 10 + 8 = 718
3. 100a + 10c + b = acb

पाठ्य-पुस्तक पृष्ठ संख्या # 261

प्रयास कीजिए (क्रमांक 16.2)

प्रश्न 1.
जाँच कीजिए कि सुन्दरम ने निम्नलिखित संख्याएँ चुनी होतीं, तो परिणाम क्या प्राप्त होते –

1. 27
2. 39
3. 64
4. 17

उत्तर:

1. संख्या = 27
अंक पलटने पर संख्या = 72
दोनों संख्याओं को जोड़ने पर = 27 + 72 = 99
इस संख्या को 11 से भाग देने पर, 99 ÷ 11 = 9, शेषफल शून्य के साथ।
अतः भागफल = 9 = संख्या के अंकों का योग (∴ 2 + 7 = 9)

2. संख्या = 39
अंक पलटने पर संख्या = 93
दोनों संख्याओं का योग = 39 + 93 = 132
इस संख्या को 11 से भाग देने पर, 132 ∴ 11 = 12, शेषफल शून्य के साथ
अतः भागफल = 12 = संख्या के अंकों का योग
(∴ 3 + 9 = 12)

3. संख्या = 64
अंक पलटने पर संख्या = 46
दोनों संख्याओं का योग = 64 + 46 = 110
इस संख्या को 11 से भाग देने पर, 110 ÷ 11 = 10, शेषफल शून्य के साथ
अतः भागफल = 10 = संख्या के अंकों का योग
(∴ 6 + 4 = 10)

4. संख्या = 17
अंक पलटने पर संख्या = 71
दोनों संख्याओं का योग = 17 + 71 = 88
इस संख्या को 11 से भाग देने पर, 88 ÷ 11 = 8, शेषफल शून्य के साथ।
अतः भागफल = 8 = संख्या के अंकों का योग
(∴ 1 + 7 = 8)

प्रयास कीजिए (क्रमांक 16.3)

प्रश्न 1.
जाँच कीजिए कि यदि सुन्दरम ने उपर्युक्त के लिए निम्नलिखित संख्याएँ चुनी होतीं, तो क्या परिणाम प्राप्त होते –

1. 17
2. 21
3. 96
4. 37

हल:
1. सोची हुई संख्या = 17
अंक पलटने पर संख्या = 71
संख्याओं का अन्तर = 71 – 17 = 54
9 से विभाजन 54 ÷ 9 = 6, शेषफल शून्य के साथ
अतः भागफल = 8 = संख्या के अंकों का अन्तर
(∴ 7 – 1 = 6)

2. सोची हुई संख्या = 21
अंक पलटने पर संख्या = 12
संख्याओं का अन्तर = 21 – 12 = 9
9 से विभाजन 9 ÷ 9 = 1, शेषफल शून्य के साथ
अतः भागफल = 1 = संख्या के अंकों का अन्तर
(∴ 2 – 1 = 1)

3. सोची हुई संख्या = 96
अंक पलटने पर संख्या = 69
संख्याओं का अन्तर = 96 – 69 = 27
9 से विभाजन = 27 ÷ 9 = 3, शेषफल शून्य के साथ
अतः भागफल = 3 = संख्याओं के अंकों का अन्तर
(∴ 9 – 6 = 3)

4. सोची हुई संख्या = 37
अंक पलटने पर संख्या = 73
संख्याओं का अन्तर = 73 – 37 = 36
9 से विभाजन = 36 ÷ 9 = 4, शेषफल शून्य के साथ
अतः भागफल = 4 = संख्याओं के अंकों का अन्तर
(∴ 7 – 3 = 4)

पाठ्य-पुस्तक पृष्ठ संख्या # 262

प्रयास कीजिए (क्रमांक 16.4)

प्रश्न 1.
जाँच कीजिए कि यदि मीनाक्षी ने निम्नलिखित संख्याएँ चुनी होती, तो परिणाम क्या प्राप्त होता ? प्रत्येक स्थिति में, अन्त में प्राप्त हुए भागफल का एक रिकार्ड (record) रखिए।

1. 132
2. 469
3. 737
4. 901

हल:
1. संख्या = 132
अंक पलटने पर संख्या = 231
अन्तर = 231 – 132 = 99
99 से विभाजन = 99 ÷ 99 = 1, शेषफल शून्य के साथ।
अतः भागफल = 1 = संख्या के इकाई और सैकड़े के अंकों का अन्तर
(∴ 2 – 1 = 1)

2. संख्या = 469
अंक पलटने पर संख्या = 964
99 से विभाजन = 495 ÷ 99 = 5, शेषफल शून्य के साथ,
अतः भागफल = 5 = संख्या के इकाई और सैकड़े के अंकों का अन्तर
(∴ 9 – 4 = 5)

3. संख्या = 737
अंक पलटने पर संख्या = 737
अन्तर = 737 – 737 = 0
99 से विभाजन = 0 ÷ 99 = 0, शेषफल शून्य के साथ,
अतः भागफल = 0 = संख्या के इकाई और सैकड़े के अंकों का अन्तर
(∴ 7 – 7 = 0)

4. संख्या = 901
अंक पलटने पर संख्या = 109
अन्तर = 901 – 109 = 792
99 से विभाजन = 792 ÷ 99 = 8, शेषफल शून्य के साथ,
अत: भागफल = 8 = संख्या के इकाई और सैकड़े के अंकों का अन्तर
(∴ 9 – 1 = 8)

पाठ्य-पुस्तक पृष्ठ संख्या # 263

प्रयास कीजिए (क्रमांक 16.5)

प्रश्न 1.
जाँच कीजिए कि यदि सुन्दरम ने निम्नलिखित संख्याएँ सोची होती, तो परिणाम क्या प्राप्त होता –

1. 417
2. 632
3. 117
4. 937

हल:
1. संख्या = 417
4, 1, 7 से बनने वाली 3 अंकों की दो और संख्याएँ 741 और 174 है।
संख्याओं को जोड़ने पर

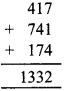
37 से विभाजन = 1332 ÷ 37 = 36, शेषफल शून्य के साथ

2. संख्या = 632
6, 3, 2 से बनने वाली 3 अंकों की दो अन्य संख्याएँ: 263, 326
संख्याओं के जोड़ने पर,

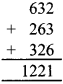
37 से विभाजन = 1221 ÷ 37 = 33, शेषफल शून्य के साथ।

3. संख्या = 117
1, 1, 7 से बनने वाली 3 अंकों की दो अन्य संख्याएँ: 711, 171
संख्याओं के जोड़ने पर,

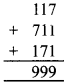
37 से विभाजन = 99937=27, शेषफल शून्य के साथ।

4. संख्या = 937
9, 3, 7 से बनने वाली 3 अंकों की दो अन्य संख्याएँ: 793, 379
संख्याओं को जोड़ने पर,

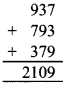
37 से विभाजन = 2109 + 37 = 57, शेषफल शून्य के साथ।

पाठ्य-पुस्तक पृष्ठ संख्या # 266

इन्हें कीजिए

प्रश्न 1.
दो अंकों की एक संख्या ab लिखिए तथा इसके अंकों को पलटने पर संख्या ba लिखिए। इसका योग ज्ञात कीजिए। मान लीजिए कि यह योग एक तीन अंकों की संख्या dad है।
अर्थात् ab + ba = dad
(10a + b) + (10b + a) = dad
11 (a + b) = dad
योग (a + b) संख्या 18 से अधिक नहीं हो सकता (क्यों ?)। क्या dad, 11 का एक गुणज है? क्या dad, 198 E से कम है ? 198 तक तीन अंकों की ऐसी संख्याएँ लिखिए, जो 11 की गुणज हैं। a और d के मान ज्ञात कीजिए।
हल:
माना कि दो अंकों की संख्या = ab है।
अंक पलटने पर संख्या = ba
इनका योग, 3 अंकों की संख्या = dad
अर्थात् ab + ba = dad
या (10a + b) + (10b + a) = dad
11 (a + b) = dad (a + b) का योग 18 से अधिक नहीं हो सकता, क्योंकि 2 अंकों की बड़ी से बड़ी संख्या = 99 है।
तथा 99 + 99 = 198
अतः संख्या dad, 11 से विभाज्य होगी।
अतः 11 से विभाज्य 198 तक 3- अंकों की संख्याएँ: 110, 121, 132, 143, 154, 165, 176, 187 और 198 हैं।
अतः dad = 121
या d = 1, a = 2

MP Board Class 8th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 14 प्रायोगिक ज्यामिती Ex 14.5

पाठ्य-पुस्तक पृष्ठ संख्या # 307-308

प्रश्न 1.
7.3 सेमी लम्बाई का एक रेखाखण्ड \(\overline { AB } \) खींचिए और उसकी सममित अक्ष ज्ञात कीजिए।
हल :
रचना के पद :
(1) एक रेखाखण्ड \(\overline { AB } \) = 7.3 सेमी खींचा।
(2) A को केन्द्र मानकर AB के आधे से अधिक त्रिज्या लेकर AB के दोनों ओर एक-एक चाप लगाते हैं।
(3) अब B को केन्द्र मानकर और AB के आधे से अधिक त्रिज्या लेकर AB के दोनों ओर दो चाप और लगाते हैं जो पहले वाले चापों को C और D पर काटते हैं।
(4) C को D से मिलाया। रेखा CD रेखाखण्ड \(\overline { AB } \) को M पर काटती है।

(5) बिन्दु M रेखाखण्ड \(\overline { AB } \) को समद्विभाजित करता है। इस प्रकार प्राप्त रेखाखण्ड सममित अक्ष है।

प्रश्न 2.
9.5 सेमी लम्बा एक रेखाखण्ड खींचिए और उसका लम्ब समद्विभाजक खींचिए।
हल :
रचना के पद :
(1) एक रेखाखण्ड AB = 9.5 सेमी खींचा।
(2) A को केन्द्र मानकर AB के आधे से अधिक दूरी की. त्रिज्या लेकर AB के दोनों ओर चाप लगाते हैं।

(3) अब B को केन्द्र मानकर इतनी ही त्रिज्या लेकर AB के दोनों ओर चाप लगाते हैं, जो पहले चापों को क्रमशः C और D पर काटते हैं।
(4) C को D से मिलाया।
रेखाखण्ड CD अभीष्ट लम्ब समद्विभाजक है।

प्रश्न 3.
एक रेखाखण्ड \(\overline { XY } \) का लम्ब समद्विभाजक खींचिए जिसकी लम्बाई 10.3 सेमी है।
(a) इस लम्ब समद्विभाजक पर कोई बिन्दु P लीजिए। जाँच कीजिए कि PX = PY है।
(b) यदि M रेखाखण्ड XY का मध्य-बिन्दु है, तो MX और XY के विषय में आप क्या कह सकते हैं ?
हल :
रचना के पद :
(1) रेखाखण्ड \(\overline { XY } \) = 10.3 सेमी खींचते हैं।
(2) X और Y को केन्द्र मानकर और XY के आधे से अधिक त्रिज्या लेकर दो चाप लगाते हैं, जो एक-दूसरे को A और B पर काटते हैं।

(3) A को B से मिलाया।
इस प्रकार AB ⊥ \(\overline { XY } \)
(4) \(\overline { AB } \) पर कोई बिन्दु P लेते हैं और PX तथा PY को जोड़ते हैं।
(a) मापने पर, \(\overline { PX } \) = \(\overline { PY } \)
(b) \(\overline { XY } \) का मध्य-बिन्दु M है। मापने पर,
\(\overline{X M}=\overline{M Y}=\frac{1}{2} \overline{X Y}\)

प्रश्न 4.
लम्बाई 12.8 सेमी वाला एक रेखाखण्ड खींचिए। रूलर और परकार की सहायता से इसके चार बराबर भाग कीजिए। मापन द्वारा अपनी रचना की जाँच कीजिए।
हल :
(1) रेखाखण्ड AB = 12.8 सेमी खींचा।
(2) AB का लम्ब समद्विभाजक ज्ञात किया जो AB को O पर काटता है।

(3) \(\overline { AO } \) का लम्ब समद्विभाजक खींचते हैं जो \(\overline { AB } \) को P पर काटता है।
(4) अब \(\overline { BO } \) का लम्ब समद्विभाजक खींचते हैं जो \(\overline { AB } \) को Q पर काटता है। (Q, \(\overline { OB } \) का मध्य-बिन्दु है।)
(5) रेखाखण्ड \(\overline { AB } \) बिन्दुओं P, O, Q द्वारा चार भागों में विभाजित हो जाता है।
मापने पर, \(\overline{A P}=\overline{P O}=\overline{O Q}=\overline{Q B}=3 \cdot 2\) सेमी

प्रश्न 5.
6.1 सेमी लम्बाई का एक रेखाखण्ड \(\overline { PQ } \) खींचिए फिर \(\overline { PQ } \) को व्यास मानकर एक वृत्त खींचिए।
हल :
रचना के पद :
(1) एक रेखाखण्ड \(\overline { PQ } \) = 6.1 सेमी खींचा।
(2) \(\overline { PQ } \) का लम्ब समद्विभाजक खींचा जो कि \(\overline { PQ } \) को O पर काटता है। (अर्थात् O, \(\overline { PQ } \) का मध्य-बिन्दु है।)

(3) O को केन्द्र मानकर और OP या OQ त्रिज्या लेकर P और Q से जाता हुआ एक वृत्त खींचा।।
वृत्त जिसका कि \(\overline { PQ } \) व्यास है, अभीष्ट वृत्त है।

प्रश्न 6.
केन्द्र C और त्रिज्या 3.4 सेमी लेकर एक वृत्त खींचिए। इसकी कोई जीवा \(\overline { AB } \) खींचिए। इस जीवा \(\overline { AB } \) का लम्ब समद्विभाजक खींचिए। जाँच कीजिए कि क्या यह वृत्त के केन्द्र C से होकर जाता है ?
हल :
रचना के पद:
(1) कागज पर कोई बिन्दु C लेते हैं।
(2) C को केन्द्र मानकर तथा 3.4 सेमी त्रिज्या लेकर एक वृत्त खींचते हैं।

(3) वृत्त की एक जीवा \(\overline { AB } \) खींचते हैं।
(4) वृत्त की जीवा का लम्ब समद्विभाजक PQ खींचते हैं।
हाँ, हम देखते हैं कि यह लम्ब समद्विभाजक वृत्त के केन्द्र से होकर जाता है।

प्रश्न 7.
प्रश्न 6.
की उस स्थिति के लिए दोबारा कीजिए जब \(\overline { AB } \) एक व्यास है।
हल :
रचना के पद :
(1) कागज पर कोई बिन्दु O लेते हैं।

(2) O को केन्द्र मानकर और 3.4 सेमी त्रिज्या लेकर एक वृत्त खींचते हैं।
(3) वृत्त का व्यास \(\overline { AB } \) खींचते हैं।
(4) \(\overline { AB } \) का लम्ब समद्विभाजक खींचते हैं। हम देखते हैं कि PQ, केन्द्र C से होकर जाता है और O व्यास \(\overline { AB } \) का मध्य-बिन्दु है।

प्रश्न 8.
4 सेमी त्रिज्या का एक वृत्त खींचिए। इसकी कोई दो जीवाएँ खींचिए। इन दोनों जीवाओं के लम्ब समद्विभाजक खींचिए। ये कहाँ मिलते हैं ?
हल :
रचना के पद :
(1) कागज पर कोई बिन्दु O अंकित करते हैं।
(2) O को केन्द्र मानकर और 4 सेमी त्रिज्या लेकर एक वृत्त खीचते हैं।

(3) वृत्त की दो जीवाएँ \(\overline { AB } \) और \(\overline { CD } \) खींचते हैं।
(4) जीवा \(\overline { AB } \) का लम्ब समद्विभाजक \(\overline { PQ } \) खींचते है।
(5) जीवा \(\overline { CD } \) का लम्ब समद्विभाजक \(\overline { RS } \) खींचते हैं।
ये दोनों लम्ब समद्विभाजक वृत्त के केन्द्र से होकर जाते हैं।

प्रश्न 9.
शीर्ष O वाला कोई कोण खींचिए। इसकी एक भुजा पर बिन्दु A और दूसरी भुजा पर एक अन्य बिन्दु B इस प्रकार लीजिए कि OA = OB है। \(\overline { OA } \) और \(\overline { OB } \) के लम्ब समद्विभाजक खींचिए। मान लीजिए ये Pपर प्रतिच्छेद करते हैं। क्या PA = PB है ?
हल :
रचना के पद :
(1) कोई कोण XOY बनाते हैं। इसका शीर्ष O है।
(2) \(\overline { OX } \) पर एक बिन्दु A तथा \(\overline { OY } \) पर एक अन्य बिन्दु B लेते हैं।
(3) \(\overline { OA } \) और \(\overline { OB } \) के लम्ब समद्विभाजक CD और EF खीचते हैं। माना कि ये P पर मिलते हैं।

(4) \(\overline { PA } \) और \(\overline { PB } \) को मिलाया
मापने पर, \(\overline{P A}=\overline{P B}\)

पाठ्य-पुस्तक पृष्ठ संख्या # 311

प्रयास कीजिए

प्रश्न 1.
पाठय-पुस्तक में दिए गए चरण 2 में, यदि हम त्रिज्या BC के आधे से कम लें, तो क्या कोण होगा?
उत्तर-
यदि हम BC के आधे से कम त्रिज्या लेंगे तो B तथा C को केन्द्र मानकर खींचे गए चाप आपस में नहीं काटेंगे। अतः कोण नहीं बनेगा।

पाठ्य-पुस्तक पृष्ठ संख्या # 312

प्रश्न 1.
ऊपर दर्शाए अनुसार 60° के कोण की रचना कीजिए। अब इस कोण को समद्विभाजित कीजिए। प्रत्येक कोण 30° का है। मापन द्वारा अपनी रचना की जाँच कीजिए।
हल :
रचना के पद :
(1) सर्वप्रथम एक किरण OA खींचते हैं।

(2) O को केन्द्र मानकर कोई भी उचित त्रिज्या लेकर एक चाप PS लगाते हैं, जो OA को P पर काटता है।
(3) P को केन्द्र मानकर इसी त्रिज्या से एक चाप लगाते हैं जो पहले चाप को Q पर काटता है।
(4) OQ को मिलाकर आगे बढ़ाते हैं और किरण OB प्राप्त करते हैं। तब ∠AOB = 60°
(5) P को केन्द्र मानकर और त्रिज्या > \(\frac { 1 }{ 2 }\) PQ लेकर, ∠AOB के अन्तः भाग में एक चाप लगाते हैं।
(6) Q को केन्द्र मानकर इसी त्रिज्या से (चरण 5) एक दूसरा चाप लगाते हैं जो पहले चाप को R पर काटता है।
(7) OR को मिलाते हुए C तक आगे बढ़ाते हैं।
तब ∠AOC = 30°

पाठ्य-पुस्तक पृष्ठ संख्या # 312

प्रयास कीजिए

प्रश्न 1.
15° के कोण की रचना आप किस प्रकार करेंगे?
हल :
रचना के पद :
(1) सर्वप्रथम 60° का ∠ABC बनाते हैं।
(2) ∠ABC को संमद्विभाजित करके 30° का कोण प्राप्त करते हैं। अर्थात् ∠ABD = 30°

(3) अब ∠ABD को इस प्रकार समद्विभाजित करते हैं कि \(\overline { BE } \) ∠ABD का समद्विभाजिक हो।
इस प्रकार ∠ABE = \(\frac { 1 }{ 2 }\) x 30° = 15°

पाठ्य-पुस्तक पृष्ठ संख्या # 313

प्रयास कीजिए

प्रश्न 1.
150° के कोण की रचना आप किस प्रकार करेंगे?
हल :
रचना के पद :
(1) सर्वप्रथम एक रेखा l खींचते हैं और इस पर कोई बिन्दु O लेते हैं।
(2) O को केन्द्र मानकर और उचित त्रिज्या लेकर एक चाप लगाते हैं, जो l को A पर काटता है।
(3) अब A को केन्द्र मानकर इसी त्रिज्या से एक चाप लगाते हैं जो पहले चाप को B पर काटता है।

(4) पुनः इसी त्रिज्या से B को केन्द्र मानकर दूसरा चाप लगाते हैं जो पहले चाप को C पर काटता है।
(5) एक बार पुनः इसी त्रिज्या से C को केन्द्र मानकर चाप लगाते हैं जो पहले चाप को D पर काटता है।
(6) अब ∠COD को समद्विभाजित करते हैं,
इस प्रकार ∠COE = ∠EOD = 30°
(7) चूँकि 150° = 120° + 30°
अतः ∠AOC + ∠COE = ∠AOE
अतः अभीष्ट ∠AOE = 150°

प्रयास कीजिए

प्रश्न 1.
45° के कोण की रचना आप किस प्रकार करेंगे?
हल :
रचना के पद:
(1) सर्वप्रथम 90° का ∠POQ बनाते हैं।
(2) ∠POQ का समद्विभाजक OR खींचते हैं।

इस प्रकार \(\frac { 1 }{ 2 }\)∠POQ = \(\frac { 1 }{ 2 }\) (90°) = 45°
अतः अभीष्ट ∠POR = 45°

MP Board Class 6th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 15 आलेखों से परिचय Ex 15.3

प्रश्न 1.
उपयुक्त पैमाने का प्रयोग करते हुए, निम्न तालिकाओं में दी गई राशियों के लिए आलेख बनाइए –
(a) सेबों का मूल्य

(b) कार द्वारा तय की गई दूरी

1. 7:30 बजे प्रातः व 8 बजे प्रातः के अन्तराल में कार द्वारा कितनी दूरी तय की गई?
2. कार के 100 km दूरी तय कर लेने पर समय क्या था?

(c) जमा धन पर वार्षिक ब्याज

1. क्या आलेख मूलबिन्दु से गुजरता है?
2. आलेख से ₹ 2,500 का वार्षिक ब्याज ज्ञात कीजिए।
3. ₹ 280 ब्याज प्राप्त करने के लिए कितना धन जमा करना होगा?

हल:
(a)

सर्वप्रथम ग्राफ पेपर पर X – अक्ष और Y – अक्ष निर्धारित करते हैं। X – अक्ष पर पैमाना 1 cm = 1 सेब तथा Y – अक्ष पैमाना 1 cm = ₹ 5 लेकर X – अक्ष पर सेबों की संख्या तथा Y – अक्ष पर सेबों का मूल्य अंकित किया।
अब दिये हुए बिन्दु क्रमशः (1, 5), (2, 10), (3, 15), । (4, 20) और (5, 25) अंकित किए।
अंकित किए गए इन बिन्दुओं को पैमाने की सहायता से मिलाया। इस प्रकार प्राप्त आलेख एक सरल रेखा है।

(b)

ग्राफ से:

1. 7.30 बजे प्रातः व 8 बजे प्रातः के अन्तराल में तय की गई दूरी = 120 km – 100 km = 20 km
2. कार द्वारा 100 km दूरी तय कर लेने पर समय 7:30 बजे प्रातः था।

(c)

ग्राफ से:

1. हाँ, आलेख मूल बिन्दु से गुजरता है।
2. आलेख से ₹ 2,500 का ब्याज = ₹ 200
3. ₹ 280 ब्याज प्राप्त करने के लिए ₹ 3,500 जमा करना होगा।

प्रश्न 2.
निम्न तालिकाओं के लिए आलेख खींचिए –
1.

क्या यह रैखिक आलेख है?

2.

क्या यह रैखिक आलेख है?
हल:
1.

हाँ, यह रैखिक आलेख है।

2.

नहीं, यह रैखिक आलेख नहीं है।

MP Board Class 8th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 14 प्रायोगिक ज्यामिती Ex 14.4

पाठ्य-पुस्तक पृष्ठ संख्या # 305

प्रश्न 1.
एक रेखाखण्ड \(\overline { AB } \) खींचिए। इस पर कोई बिन्दु M अंकित कीजिए। M से होकर \(\overline { AB } \) पर एक लम्ब रूलर और परकार द्वारा खींचिए।
हल :
रचना के पद :
(1) एक रेखाखण्ड \(\overline { AB } \) खींचा और इस पर कोई बिन्दु M अंकित किया।
(2) परकार के नुकीले सिरे को M पर रखकर और कोई सुविधाजनक त्रिज्या लेकर एक चाप लगाते हैं जो AB को P और Q पर काटता है।

(3) अब P और Q को केन्द्र मानकर और PM से अधिक त्रिज्या लेकर दो चाप इस प्रकार लगाते हैं कि वे परस्पर बिन्दु C पर काटते हैं।
C को M से मिलाया।
इस प्रकार CM ⊥ AB

प्रश्न 2.
एक रेखाखण्ड \(\overline { PQ } \) खींचिए। कोई बिन्दु R लीजिए जो PQ पर न हो। R से होकर PQ पर एक लम्ब खींचिए (रूलर और सेट स्क्वे यर द्वारा)।
हल :
रचना के पद :
(1) रेखाखण्ड \(\overline { PQ } \) खींचा और इसके बाहर कोई बिन्दु R लिया।
(2) एक सेट स्क्वे यर को \(\overline { PQ } \) पर इस प्रकार रखते हैं कि उसके समकोण का एक किनारा रेखाखण्ड के अनुदिश हो।

(3) अब सेट स्क्वेयर के समकोण के सम्मुख किनारे के अनुदिश एक रूलर को रखते हैं।
(4) रूलर को कसकर पकड़ते हैं और सेट स्क्वेयर को रूलर के अनुदिश तब तक सरकाते हैं जब तक कि R समकोण बनाने वाले दूसरे किनारे को स्पर्श न करने लगे।
(5) अब R को सेट स्क्वे यर के किनारे के अनुदिश M से मिलाते हुए रेखा खींचते हैं।
अब रेखा RM ⊥ PQ है।

प्रश्न 3.
एक रेखा l खींचिए और उस पर स्थित एक बिन्दु X से होकर, रेखा l पर एक लम्ब रेखाखण्ड \(\overline { XY } \) खींचिए।
अब Y से होकर \(\overline { XY } \) पर एक लम्ब रूलर और परकार द्वारा खींचिए।
हल :
रचना के पद :
(1) एक रेखा l खींचते हैं और इस पर एक बिन्दु X अंकित करते हैं।

(2) X को केन्द्र मानकर और उचित त्रिज्या लेकर एक चाप लगाते हैं जो l को P और Q पर काटता है।
(3) P और Q को केन्द्र मानकर और PX से अधिक त्रिज्या लेकर दो और चाप लगाते हैं, जो एक-दूसरे को M पर काटते हैं।
(4) X को M से मिलाते हुए Z तक बढाते हैं। XZ रेखा l पर अभीष्ट लम्ब है।
(5) अब XZ पर एक बिन्दु Y लेते हैं। Y को केन्द्र मानकर और उचित त्रिज्या लेकर एक चाप लगाते हैं जो XY को R और S पर काटता है।
(6) R और S को केन्द्र मानकर और YR से अधिक त्रिज्या लेकर दो और चाप लगाते हैं, जहाँ एक-दूसरे को N पर काटते हैं।
(7) Y को N से मिलाते हैं।
इस प्रकार YN ⊥ XY.

पाठ्य-पुस्तक पृष्ठ संख्या # 307

प्रयास कीजिए

प्रश्न 1.
रूलर और परकार की रचना के चरण 2 में, यदि हम त्रिज्या \(\overline { AB } \) के आधे से कम लें तो क्या होगा?
उत्तर-
चरण 2 में यदि हम त्रिज्या \(\overline { AB } \) के आधे से कम लें तो A और B को केन्द्र मानकर खींचे गए चाप आपस में नहीं काटेंगे और रचना सम्भव नहीं होगी।

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 14 प्रायोगिक ज्यामिती Ex 14.3

पाठ्य-पुस्तक पृष्ठ संख्या # 300

प्रश्न 1.
कोई रेखाखण्ड \(\overline { PQ } \) खींचिए। बिना मापे हुए \(\overline { PQ } \) के बराबर एक रेखाखण्ड की रचना कीजिए।
हल :
रचना के पदः
(i) एक रेखाखण्ड \(\overline { PQ } \) खींचा जिसकी लम्बाई ज्ञात नहीं है

(2) l एक रेखा खींची और इस पर एक बिन्दु R लिया।
(3) परकार को \(\overline { PQ } \) के बराबर खोलते हैं।
(4) अब परकार के फैलाव में बिना कोई परिवर्तन किए हुए उसके नुकीले सिरे को R पर रखते हैं।
(5) अब एक चाप लगाते हैं जो l को S पर काटता है। अतः \(\overline { RS } \) ही \(\overline { PQ } \) के बराबर अभीष्ट रेखाखण्ड है।

प्रश्न 2.
एक रेखाखण्ड \(\overline { AB } \) दिया हुआ है, जिसकी लम्बाई ज्ञात नहीं है। एक रेखाखण्ड \(\overline { PQ } \) की रचना कीजिए जिसकी लम्बाई \(\overline { AB } \) की लम्बाई की दो गुनी है।
हल :
रचना के पद:
(1) रेखाखण्ड \(\overline { AB } \) दिया हुआ है, जिसकी लम्बाई ज्ञात नहीं है।
(2) परकार के नुकीले सिरे को A पर रखकर परकार को B तक फैलाकर पेंसिल को B पर रखते हैं। परकार का यह फैलाव \(\overline { AB } \) की लम्बाई दर्शाता है।

(3) अब कोई रेखा l खींचते हैं और इस पर कोई बिन्दु P लेते हैं।
(4) परकार के फैलाव में बिना कोई परिवर्तन किए हुए, उसके नुकीले सिरे को P पर रखते हैं, और पेंसिल वाले सिरे से l पर एक चाप लगाते हैं जो रेखा l को Q पर काटता है।
(5) अब परकार के नुकीले सिरे को Q पर रखकर परकार के उसी फैलाव का एक दूसरा चाप लगाते हैं जो रेखा l को R पर काटता है।

अत: \(\overline { PR } \) अभीष्ट रेखाखण्ड है, जिसकी लम्बाई \(\overline { AB } \) की लम्बाई की दो गुनी है।
अर्थात् \(\overline { PR } \) = 2 \(\overline { AB } \)

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 14 प्रायोगिक ज्यामिती Ex 14.2

पाठ्य-पुस्तक पृष्ठ संख्या # 299

प्रश्न 1.
रूलर का प्रयोग करके 7.3 सेमी लम्बाई का एक रेखाखण्ड खींचिए।
हल :
रचना के पद:
(1) कागज पर एक बिन्दु A लेते हैं।
(2) अब पैमाने को सीधा रखकर उसका शून्य A पर रखते हैं।

(3) पेंसिल की सहायता से A से 7.3 सेमी की दूरी पर बिन्दु B पर निशान लगाते हैं।
(4) A को B से मिलाते हैं। इस प्रकार प्राप्त रेखाखण्ड AB वांछित रेखाखण्ड है।

प्रश्न 2.
रूलर और परकार का प्रयोग करते हुए 5.6 सेमी लम्बाई का एक रेखाखण्ड खींचिए।
हल :
रचना के पद :
(1) एक रेखा l खींचते हैं और इस पर एक बिन्दु P लेते हैं।

(2) परकार की नोंक को पैमाने के शून्य पर रखते हैं और परकार को इस प्रकार खोलते हैं कि पेंसिल पैमाने के 5.6 सेमी तक पहुँचे।
(3) परकार की नोंक को बिन्दु P पर रखते हैं।
(4) अब परकार में भरी दूरी से रेखा l पर एक चाप लगाते हैं, जो l को बिन्दु Q पर काटता है।
इस प्रकार रेखाखण्ड \(\overline { PQ } \) अभीष्ट रेखाखण्ड है।

प्रश्न 3.
7.8 सेमी लम्बाई का रेखाखण्ड \(\overline { AB } \) खींचिए। इसमें से \(\overline { AC } \) काटिए जिसकी लम्बाई 4.7 सेमी हो। BC को मापिए।
हल :
रचना के पदः

(1) 7.8 सेमी लम्बाई का एक रेखाखण्ड AB खींचा।
(2) यहाँ, \(\overline { AB } \) = 7.8 सेमी और \(\overline { AC } \) = 4.7 सेमी
अब परकार की सहायता से इस रेखाखण्ड पर बिन्दु C इस प्रकार काटते हैं कि AC = 4.7 सेमी।
(3) \(\overline { BC } \) को मापने पर, \(\overline { BC } \) = 3.1 सेमी।

प्रश्न 4.
3.9 सेमी लम्बाई का एक रेखाखण्ड \(\overline { AB } \) दिया हुआ है। एक रेखाखण्ड \(\overline { PQ } \) खींचिए जो रेखाखण्ड \(\overline { AB } \) का दो गुना हो। मापन से अपनी रचना की जाँच कीजिए।

(संकेत: \(\overline { PX } \) खींचिए ताकि \(\overline { PX } \) लम्बाई \(\overline { AB } \) की लम्बाई के बराबर हो। फिर \(\overline { XQ } \) काटिए ताकि \(\overline { XQ } \) की लम्बाई भी \(\overline { AB } \) की लम्बाई के बराबर हो। इस प्रकार \(\overline { PX } \) और \(\overline { XQ } \) की लम्बाई मिलकर \(\overline { AB } \) की लम्बाई का दो गुना हो जाएगी।)
हल :
रचना के पद :
(i) एक रेखा l खींचते हैं।
(ii) AB = 3.9 सेमी खींची।

(iii) रेखा l में से \(\overline { PX } \) = \(\overline { AB } \) = 3.9 सेमी काटा।
(iv) अब \(\overline { XQ } \) = \(\overline { AB } \) = 3.9 सेमी काटा।
अत: \(\overline { AB } \) की दो गुनी लम्बाई के लिए \(\overline { PX } \) और \(\overline { XQ } \) लम्बाई जोड़ते हैं।
जाँच : \(\overline { AB } \) + \(\overline { AB } \) = 3.9 सेमी + 3.9 सेमी
2 \(\overline { AB } \) = 7.8 सेमी = \(\overline { PQ } \)
अत: \(\overline { AB } \) का दो गुना = \(\overline { PQ } \)

प्रश्न 5.
7.3 सेमी लम्बाई का रेखाखण्ड \(\overline { AB } \) और 3.4 सेमी लम्बाई का रेखाखण्ड \(\overline { CD } \) दिया हुआ है। एक रेखाखण्ड \(\overline { XY } \) खींचिए ताकि \(\overline { XY } \) की लम्बाई \(\overline { AB } \) और \(\overline { CD } \) की लम्बाइयों के अन्तर के बराबर हो।
हल :
रचना के पद :
(1) सर्वप्रथम रेखाखण्ड \(\overline { AB } \) = 7.3 और \(\overline { CD } \) = 3.4 सेमी खींचते हैं।

(2) एक रेखा l खींचते हैं और इस पर कोई बिन्दु X लेते हैं।

(3) अब \(\overline { XR } \) इस प्रकार लेते हैं कि \(\overline { XR } \) की लम्बाई = \(\overline { AB } \) की लम्बाई = 7.3 सेमी

(4) अब \(\overline { RY } \) = \(\overline { CD } \) की लम्बाई (3.4 सेमी) इस प्रकार काटते हैं कि
\(\overline { XY } \) की लम्बाई = \(\overline { AB } \) की लम्बाई – \(\overline { CD } \) की लम्बाई
जाँच : मापने पर, हम प्राप्त करते हैं
\(\overline { XY } \) = 3.9 सेमी = 7.3 सेमी – 3.4 सेमी
= \(\overline { AB } \) – \(\overline { CD } \)
अतः \(\overline { XY } \) = \(\overline { AB } \) – \(\overline { CD } \)

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 14 प्रायोगिक ज्यामिती Ex 14.1

प्रश्न 1.
3.2 सेमी त्रिज्या का एक वृत्त खींचिए।
हल :
रचना के पद :
(1) कागज पर एक बिन्दु O लेते हैं।
(2) परकार को वांछित त्रिज्या 3.2 सेण्टीमीटर तक खोलते हैं।
(3) परकार की नोंक को स्थिर बिन्दु O पर रखते हैं तथा दूसरे पेंसिल वाले सिरे को घुमाते हैं। पेंसिल वाले सिर को घुमाने पर वांछित वृत्त प्राप्त होता है।

प्रश्न 2.
एक ही केन्द्र O लेकर 4 सेमी और 2.5 सेमी त्रिज्या वाले दो वृत्त खींचिए।
हल :
रचना के पद:
(1) कागज पर एक बिन्दु O लेते हैं।
(2) परकार को 2.5 सेमी तक खोलते हैं।
(3) परकार की नोंक को बिन्दु O पर रखकर पेंसिल वाले सिरे को घुमाकर वृत बनाते हैं। इस प्रकार प्राप्त वृत्त 2.5 सेमी त्रिज्या का वृत्त होगा।

(4) अब परकार को 4 सेमी के लिए खोलते हैं।
(5) परकार की नोंक को बिन्दु O पर रखकर पेंसिल वाले सिरे को घुमाते हैं। इस प्रकार प्राप्त वृत्त 4 सेमी त्रिज्या का वृत्त होगा।

प्रश्न 3.
एक वृत्त और उसके कोई दो व्यास खींचिए। यदि आप इन व्यासों के सिरों को जोड़े दें तो कौन-सी आकृति प्राप्त होती है ? यदि व्यास परस्पर लम्ब हों, तो कौन-सी आकृति प्राप्त होगी?
आप अपने उत्तर की जाँच किस प्रकार करेंगे ?
हल :
रचना के पदः
(1) O केन्द्र लेकर किसी भी त्रिज्या का एक वृत्त खींचा।
(2) दो व्यास AC और BD खींचे।
(3) AC और BD को मिलाकर चतुर्भुज ABCD बनाते हैं।
मापने पर, AB = CD और AD = BC
और ∠A = ∠B = ∠C = ∠D = 90°
अत: ABCD एक आयत है।

पुनः यदि व्यास AC और BD लम्बवत् हैं, तब
(1) AC और BD के सिरों को मिलाते हैं।
हम एक चतुर्भुज प्राप्त करते हैं।

मापने पर, हम प्राप्त करते हैं :
AB = BC = CD = DA
और ∠A = ∠B और ∠C = ∠D
अत: ABCD एक वर्ग है।

प्रश्न 4.
एक वृत्त खींचिए और बिन्दु A, B और C इस प्रकार अंकित कीजिए कि
(a) A वृत्त पर स्थित हो।
(b) B वृत्त के अभ्यंतर में स्थित हो।
(c) C वृत्त के बहिर्भाग में स्थित हो।
हल :

प्रश्न 5.
मान लीजिए A और B समान त्रिज्याओं वाले दो वृत्तों के केन्द्र हैं। इन्हें इस प्रकार खींचिए ताकि एक वृत्त दूसरे के केन्द्र से होकर जाए। इन्हें C और D पर प्रतिच्छेद करने दीजिए। जाँच कीजिए कि \(\overline { AB } \) और \(\overline { CD } \) परस्पर समकोण पर हैं।

उत्तर-
हाँ, रेखाखण्ड \(\overline { AB } \) और \(\overline { CD } \) परस्पर समकोण पर हैं।

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 14 प्रायोगिक ज्यामिती Intext Questions

पाठ्य-पुस्तक पृष्ठ संख्या # 297-298

सोचिए, चर्चा कीजिए और लिखिए

प्रश्न 1.
आप केन्द्र O लेकर, एक बिन्दु मान लीजिए P से कितने वृत्त खींचे सकते हैं?
उत्तर-
एक।

MP Board Class 6th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 15 आलेखों से परिचय Intext Questions

MP Board Class 8th Maths Chapter 15 पाठान्तर्गत प्रश्नोत्तर

पाठ्य-पुस्तक पृष्ठ संख्या # 253

सोचिए, चर्चा कीजिए और लिखिए

प्रश्न 1.
एक कार की पेट्रोल टंकी को भरने के लिए दी गई राशि खरीदे गए पेट्रोल की मात्रा (लीटर में) द्वारा निश्चित होती है। यहाँ पर कौन-सा चर स्वतन्त्र है? चर्चा कीजिए?
उत्तर:
क्योंकि पेट्रोल टंकी को भरने के लिए दी गई राशि पेट्रोल की मात्रा पर निर्भर करती है। अत: पेट्रोल की मात्रा स्वतन्त्र चर है।

पाठ्य-पुस्तक पृष्ठ संख्या # 254

प्रयास कीजिए (क्रमांक 15.1)

प्रश्न 1.
ऊपर के उदाहरण (उदाहरण 6) में, आलेख से ज्ञात कीजिए कि ₹ 800 में कितना पेट्रोल खरीदा जा सकता है?
उत्तर:
₹ 800 में 16 लीटर पेट्रोल खरीदा जा सकता है।

पाठ्य-पुस्तक पृष्ठ संख्या # 255

प्रयास कीजिए (क्रमांक 15.2)

प्रश्न 1.
क्या उदाहरण 7 एक समानुपात का उदाहरण है?
उत्तर:
हाँ, यह एक समानुपात का उदाहरण है।

MP Board Class 8th Maths Solutions

MP Board Class 6th Sanskrit Solutions Surbhi Chapter 20 श्रमस्य महत्वम्

MP Board Class 6th Sanskrit Chapter 20 अभ्यासः

प्रश्न 1.
एकपदेन उत्तरं लिखत (एक शब्द में उत्तर लिखो)
(क) सिक्खधर्मस्य प्रवर्तकः कः? (सिक्ख धर्म के प्रवर्तक कौन थे?)
उत्तर:
गुरुनानकदेवः

(ख) गुरुनानकदेवः कस्मिन् प्रान्ते अभवत्? (गुरुनानक देव किस प्रान्त में हुए?)
उत्तर:
पञ्जाब प्रान्ते

(ग) श्रमिकः काः समर्पितवान्? (श्रमिक ने क्या समर्पित किया?)
उत्तर:
रोटिकाः

(घ) धनिकः किम् अयच्छत्? (धनवान ने क्या प्रदान किया?)
उत्तर:
मिष्टान्नम्

(ङ) गुरुनानकः कस्य भोजनं स्वीकृतवान्? (गुरुनानक ने किसका भोजन स्वीकार किया?)
उत्तर:
श्रमिकस्य।।

प्रश्न 2.
एकवाक्येन उत्तरं लिखत (एक वाक्य में उत्तर लिखो)
(क) गुरुनानकः किमर्थं ग्रामम् अगच्छत्। (गुरुनानक किसलिए ग्राम को गये थे?)
उत्तर:
गुरुनानक: धर्मप्रचारार्थम् ग्रामम् अगच्छत्। (गुरुनानक धर्म के प्रचार के लिए ग्राम को गये।)

(ख) धनिकः किमर्थम् उत्तेजितः अभवत्? (धनिक किसलिए उत्तेजित हो गया?)
उत्तर:
धनिकस्य मिष्टान्नम् गुरुणा नानकेन अस्वीकृतः तेन सः धनिकः उत्तेजितः अभवत्। (धनिक का मिष्ठान्न गुरुनानक ने अस्वीकृत कर दिया। उससे वह धनवान उत्तेजित हो गया।)

(ग) गुरु धनिकं किम् उक्तवान्? (गुरू ने धनिक से क्या कहा?)
उत्तर:
गुरुः धनिकम् उक्तवान् यत् संसारे जात्या, धनेन च न कः अपि जन: उच्च: निम्नो वा। सर्वेजनाः समानाः। चरित्रेण एव श्रेष्ठता भवति। (गुरु ने धनवान से कहा कि संसार में जाति से और धन से कोई भी मनुष्य ऊँचा या नीचा नहीं होता है। सभी लोग समान होते हैं। चरित्र से श्रेष्ठता होती है।)

(घ) लक्ष्मी: शुद्धा कथं भवति? (लक्ष्मी शुद्ध किस तरह होती है?)
उत्तर:
श्रमेण अर्जिता लक्ष्मी: शुद्धा भवति। (परिश्रम से कमाई लक्ष्मी शुद्ध होती है।)

(ङ) मनुष्यस्य श्रेष्ठता केन भवति? (मनुष्य की श्रेष्ठता किससे होती है?)
उत्तर:
मनुष्यस्य श्रेष्ठता चरित्रेण भवति। (मनुष्य की श्रेष्ठता चरित्र से होती है।)

प्रश्न 3.
उचितशब्देन रिक्तस्थानं पूरयत (उचित शब्द से रिक्त स्थान को पूरा करो)
(क) “श्रम एव जयति” इति ध्येय …………. अस्ति। (वाक्यम्/वाक्यानि)
(ख) श्रमेण ……….. उन्नतिः भवति। (राष्ट्रस्य/राष्ट्रात्)
(ग) मम ………… सरसभोजनम् आनीतम्। (गृह/गृहात्)
(घ) एतत् …………. धनिकः सक्रोधम् अवदत्। (दृष्ट्वा /दृष्टम्)
(ङ) धनिकस्य भोजनं ……………… शुष्करोटिकाः स्वीकृतवान्। (त्यक्त्वा/त्यक्तुम्)
उत्तर:
(क) वाक्यम्
(ख) राष्ट्रस्य
(ग) गृहात्
(घ) दृष्ट्वा
(ङ) त्यक्त्वा।

प्रश्न 4.
उचितं मेलयत (उचित को मिलाओ)

उत्तर:
(क) → 3
(ख) → 4
(ग) → 1
(घ) → 2

प्रश्न 5.
क्त्वा प्रत्ययं योजयित्वा वाक्यनिर्माणं कुरुत (क्त्वा प्रत्यय जोड़कर वाक्य निर्माण करो)
(क) श्रमिकः गुरुं नमति, भोजनं यच्छति।
(ख) धनिकः गुरुं पश्यति, मिष्टान्नं यच्छति।
(ग) धनिकः गुरुवाक्यं शृणोति, सन्तुष्टः भवति।
(घ) धनिकः अभिमानं त्यजति, विनम्रः भवति।
उत्तर:
(क) श्रमिकः गुरुम नंत्वा भोजनं यच्छति।
(ख) धनिकः गुरुम् दृष्ट्वा मिष्टान्नं यच्छति।
(ग) धनिकः गुरुवाक्यं श्रुत्वा सन्तुष्टः भवति।
(घ) धनिकः अभिमानम् त्यक्त्वा विनम्रः भवति।

योग्यताविस्तारः

1. “श्रमस्य महत्वम्” विषयोपरि पञ्च वाक्यानि लिखत। (“श्रम के महत्व” विषय पर पाँच वाक्य लिखो)
उत्तर:
श्रमस्य महत्वम् :

• अपारे खलु संसारे सर्वे एव जनाः सुखमयं जीवनं कामयन्ते। इस अपार संसार में सभी लोग सुखमय जीवन की कामना करते हैं।
• जीवन सुखमयं विधातुं सुखं शान्तिश्च अपेक्षेते। जीवन को सुखमय बनाने के लिए सुख और शान्ति की अपेक्षा होती है।
• जीवनं पुरुषार्थेन एव चलति, अत: मानव पुरुषार्थी, उद्यमी श्रमशीलः च भवेत्। जीवन पुरुषार्थ से ही चलता है। अतः मनुष्य को पुरुषार्थी, उद्यमी और श्रमशील होना चाहिए।
• अकर्मणि कदापि प्रवृत्तिः न विधेया। अकर्म (निकम्मेपन में) प्रवृत्ति नहीं होनी चाहिए।
• उद्योगशीलः एव जनः सर्व दुःखानि विहाय सुखानि समृद्धिं च अनुभवति। उद्योगशील मनुष्य ही सभी दुःखों का त्याग करके सुख और समृद्धि का अनुभव करता है।
• संसारे परिश्रमस्य उद्योगस्य वा महत्वं सर्वैः स्वीकृतमस्ति। संसार में परिश्रम का अथवा उद्योग का महत्व सभी के द्वारा स्वीकारा गया है।

2. श्लोकं स्मरत (श्लोक को कण्ठाग्र करो)उद्यमः, साहस, धैर्य, बुद्धिः, शक्तिः, पराक्रमः। षडेते यत्र वर्तन्ते, तत्र देवः सहायकः॥

श्रमस्य महत्वम् हिन्दी अनुवाद

“श्रम एव जयति” इति अस्माकं ध्येयवाक्यम् अस्ति। श्रमेण राष्ट्रस्य उन्नतिः भवति। श्रमेण अर्जितं धनं श्रेष्ठं भवति। सिक्खधर्मस्यप्रवर्तकः गुरुनानकदेवः पञ्जाबप्रान्ते अभवत्। एकदा सः धर्मप्रचारार्थं एकं ग्रामम् अगच्छत्। तत्र एकः श्रमिकः गुरुं दृष्ट्वा स्वागतम् अकरोत् एवं च भोजनार्थं रोटिकाः समर्पयत्। एकः उच्चवर्गीयः धनिकः अपि गुरवे मिष्टान्नंअयच्छत्। नानकः किश्चित् विचार्य श्रमिकस्यरोटिकाः स्वीकृतवान्। एतत् दृष्ट्वा धनिकः सक्रोधम् अवदत्”महाराज! किमेतत् ? मम गृहात् आनीतं सरसभोजनं त्यक्त्वा भवान् श्रमिकस्य शुष्करोटिकाः स्वीकरोति। एतत् समीचीनं नास्ति। अहं प्रतिष्ठितः अस्मि। भवान् मम अपमानम् अकरोत्। किं मयि गुरुकृपा नास्ति? माम् अपि गौरवान्वितं करोतु।”

अनुवाद :
“परिश्रम ही विजय प्राप्त करता है।” यह हमारा ध्येय वाक्य है। परिश्रम से राष्ट्र की उन्नति होती है। श्रम से कमाया धन श्रेष्ठ होता है। सिक्ख पन्थ के प्रवर्तक गुरुनानक देव पंजाब प्रान्त में हुए थे। एक बार वे धर्म के प्रचार के लिए एक गाँव को गये। वहाँ एक श्रमिक (मजदूर) ने गुरु को देखकर स्वागत किया और भोजन के लिए रोटियाँ समर्पित कर दीं। एक उच्च वर्ग के धनवान ने भी गुरुजी को मिष्ठान (मीठे पकवान या मिठाइयाँ) दी। नानक ने कुछ विचार करके श्रमिक की रोटियों को स्वीकार कर लिया। इसे देखकर धनवान व्यक्ति क्रोधपूर्वक बोला-“महाराज! यह क्या है? मेरे घर से लाये गये सरस भोजन (स्वादिष्ट भोजन) को त्यागकर आपने श्रमिक की सूखी रोटियाँ स्वीकार की हैं। यह उचित नहीं है। मैं प्रतिष्ठावान् हूँ। आपने मेरा अपमान किया। क्या मुझ पर गुरु की कृपा नहीं है? मुझे भी गौरवान्वित कीजिए।”

गुरुनानकः क्षणं विचार्य मधुरवाण्या अवदत्-“संसारे जात्या, धनेन च न कोऽपि जन: उच्चः निम्नो वा। सर्वेजनाः समानाः। चरित्रेण एव श्रेष्ठता भवति। श्रमिकेण तु बहुश्रमेण धनं अर्जितम्। अतः तस्य भोजनं पवित्रम् अस्ति। अहं तस्य भोजनं स्वीकृतवान्। गुरुवाणीं श्रुत्वा प्रभावितः धनिकः अभिमानं त्यक्त्वा विनम्रः भूत्वा गुरुचरणयोः भूमौ अपतत्। उक्तं च “श्रमेण उपार्जिता लक्ष्मी: शुद्धा भवति।”

अनुवाद :
गुरुनानक क्षण भर विचार करके मधुर वाणी में बोले-“संसार में जाति से और धन से कोई भी व्यक्ति ऊँचा अथवा नीचा नहीं होता है। सभी लोग समान ही होते हैं। चरित्र से श्रेष्ठता होती है। श्रमिक ने बहुत परिश्रम से धन कमाया है। इसलिए उसका भोजन पवित्र है। मैंने उसका भोजन स्वीकार कर लिया। गुरु की वाणी को सुनकर प्रभावित हुआ धनवान अभिमान का त्याग करके विनम्र होकर गुरु के चरणों में जमीन पर गिर गया और कहा “परिश्रम से उपार्जित लक्ष्मी शुद्ध होती है।”

श्रमस्य महत्वम् शब्दार्थाः।

प्रवर्तक = चलाने वाले। विचार्य = विचार करके। श्रमिकः = मेहनत करने वाला, मजदूर। अयच्छत् = दिया। गौरवान्वितम् = धन्य।

MP Board Class 6th Sanskrit Solutions