Prasanna

MP Board Class 9th Maths Solutions Chapter 1 Number Systems Ex 1.4

Question 1.
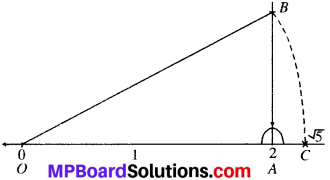
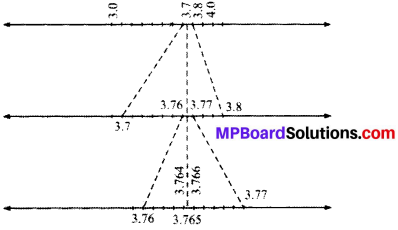
Visualise 3.765 on the number line, using successive magnification.
Solution:
Visualizing 3.765

Question 2.
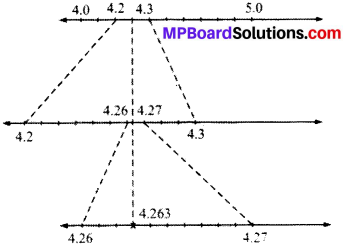
Visualise 4.26 on the number line, up to 4 decimal places.
Solution:
Visualising 4.26 = 4.2626
= 4.263

Rationalisation of the Denominator of an irrational number having two terms in the Denominator:
To rationalise the denominator of an irrational number having two terms in the denominator, multiply the numerator and denominator of the number by the conjugate of its denominator.

Example 1.
If a and b are rational numbers and \(\frac { 3+\sqrt { 7 } }{ 3-\sqrt { 7 } } \) = a + b√7 find value of a and b.
Solution:
We have \(\frac { 3+\sqrt { 7 } }{ 3-\sqrt { 7 } } \) = a + b√7
Multiply denominator and numerator by 3 + √7 on LHS, then we have

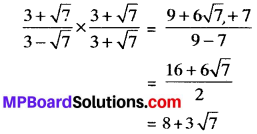
On comparing LHS and RHS, we get
a = 8, b = 3

Example 2.
Determine a and b if \(\frac { 5+\sqrt { 3 } }{ 7-4\sqrt { 3 } } \) = 94a + 3 √3b
Multiply numerator and denominator by 7 + 4√3 on LHS, then we have

On comparing LHS and RHS, we get
a = \(\frac{1}{2}\) and b = 9.

Example 3.
Determine a and 6 if \(\frac { 7+\sqrt { 5 } }{ 7-\sqrt { 5 } } \) – \(\frac { 7-\sqrt { 5 } }{ 7+\sqrt { 5 } } \) = a + 7√5b.
Solution:
We have

On comparing LHS and RHS, we get
a = 0 and b = \(\frac{1}{11}\).

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 1 Number Systems Ex 1.3

Write the following in decimal form and say what kind of decimal expansion each has:

1. \(\frac{36}{100}\)
2. \(\frac{1}{11}\)
3. 4\(\frac{1}{8}\)
4. \(\frac{3}{13}\)
5. \(\frac{2}{11}\)
6. \(\frac{329}{400}\)

Solution:
1. \(\frac{36}{100}\)
\(\frac{36}{100}\) = 0.36
The decimal expansion is terminating.

2. \(\frac{1}{11}\)

The decimal expansion is non-terminating repeating.

3. 4\(\frac{1}{8}\)

The decimal expansion is terminating.

4. \(\frac{3}{13}\)

The decimal expansion is non-terminating repeating.

5. \(\frac{2}{11}\)

The decimal expansion is non-terminating repeating.

6. \(\frac{329}{400}\)

The decimal expansion is terminating.

Question 2.
You know that \(\frac{1}{7}\) = \(\overline { 0.142857 } \). Can vou predict what the decimal expansions of \(\frac{2}{7}\), \(\frac{3}{7}\), \(\frac{4}{7}\), \(\frac{5}{7}\), \(\frac{6}{7}\) are, without actually doing the long division? If so, how?
[Hint: Study the remainders while finding the value of \(\frac{1}{7}\) carefully.]
Solution:
\(\frac{1}{7}\) = \(\overline { 0.142857 } \)

Question 3.
Expressthe following in the form \(\frac{p}{q}\), wherep and q are integers and q ≠ 0.

1. \(0 . \overline{6}\)
2. \(0 . \overline{oo1}\)

Solution:
1. \(0 . \overline{6}\)
Let x = \(0 . \overline{6}\) …(i)
10x = \(6 . \overline{6}\)
[Multiplying (i) by 10 on both sides] …(ii)
Subtracting (i) from (ii). we get
9x = 6
x = \(\frac{6}{9}\) = \(\frac{2}{3}\)
∴ \(6 . \overline{6}\) = \(\frac{2}{3}\)

2. \(0 . \overline{oo1}\)
1000x = \(1 . \overline{001}\)
[Multiplying (i) by 1000] …(ii)
Subtracting (i) from (ii), we get
999x = 1
x = \(\frac{1}{999}\)
∴ \(0 . \overline{001}\) = \(\frac{1}{999}\)

Question 4.
Express 0.99999….. in the form \(\frac{p}{q}\). Are you surprised by vour answer? With your teacher and classmates, discuss why the answer make sense.
Solution:
0.99999 = \(0 . \overline{9}\)
Let x = 0.9 …(i)
10x = \(9 . \overline{9}\)
[Multiplying (i) by 10] …(ii)
Subtracting (i) from (ii), we get
9x = 9
x = \(\frac{9}{9}\)
∴ \(9 . \overline{9}\) = 1

Question 5.
What can the maximum number of digits be in the repeating block of digits in the decimal expansion of \(\frac{1}{17}\)? Perform the division to check your answer.
Solution:
The maximum number of digits in the repeating block of digits in the decimal expansion \(\frac{1}{17}\) can be 16.
0. 05882352941176470588235294117647….

By Long Division, the number of digits in the repeating block of digits in the decimal expansion of = \(\frac{1}{17}\) = 16
∴ The answer is verified.

Question 6.
Look at several examples of rational numbers in the form \(\frac{p}{q}\) (q ≠ 0),where p and q are integers with no common factors other than 1 and having terminating decimal representation (expansions). Can you guess what property q must satisfy?
Solution:
Examples:

The property that q must satisfy is that the prime factorisation of q have only powers of 2 or powers of 5 or both.

Question 7.
Write three numbers whose decimal expansions are non – terminating non – recurring.
Solution:
0. 01001000100001……..,
0. 20200220002200002…….,
0. 003000300003

Question 8.
Find three different irrational numbers between the rational numbers \(\frac{5}{7}\) and \(\frac{9}{11}\).
Solution:
Irrational numbers between \(\frac{5}{7}\) and \(\frac{9}{11}\)
\(\frac{5}{7}\) = 0.71 and \(\frac{9}{11}\) = 0.81
Three irrational numbers between \(\frac{5}{7}\) and \(\frac{9}{11}\) are
0. 7201001000…
0. 7301001000…
0. 7401001000…

Question 9.
Classify the following numbers as rational or irrational:

1. \(\sqrt{23}\)
2. \(\sqrt{225}\)
3. 0. 3796
4. 7. 478478…
5. 1. 101001000100001…

Solution:

1. \(\sqrt{23}\) is an irrational number
2. \(\sqrt{225}\) = 15, a rational number
3. 0. 3796 is a rational number
4. 7. 478478….. is an irrational number
5. 1. 101001000100001… is an irrational number

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 1 Number Systems Ex 1.2

Question 1.
State whether the following statements are true or false. Justify your answers.

1. Every irrational number is a real number.
2. Every point on the number line is of the form √m , where m is a natural number.
3. Every real number is an irrational number.

Solutions:

1. True, because all irrational numbers come in the collection of real numbers.
2. False, because a negative number cannot be the square root of any natural number.
3. False, because the collection of real numbers contains not only irrational numbers but also rational numbers.

Question 2.
Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.
Solution:
No. For example, √4 = 2 is a rational number.

Question 3.
Show how √5 can be represented on the number line.
Solution:
Representing √5 on a number line as shown in fig. below.

1. Take OA = 2 units and draw perpendicular AB on A.
2. Cut AB = 1 unit and join OB.
3. By taking O as centre and OB as radius, draw an arc which inter-sect the number line at C.

Hence OC = √5
∴ Point C represents ^5 on the number line.
Proof:
OBD is a right angled A.
∴ OD² = OB² + BD²
OD² = (2)² + (1)² = 5
OD = √5

Representation of Real Numbers on Number Line

Real Numbers:
The rational and irrational numbers taken together are known as real numbers. Every real number Is either rational or irrational. Different operations on real numbers are shown below:
For example:

Example 1.
Add (3√2 + 5√3) and (√2 + √3).
Solution:
(3√2+ 5√5)+ (√2+ √3)
= 3√2 + 5√5 + √5 + √5 = (3√5+ √5)+ (5√5+ √5)
= 4√2 + 6√3
= 4√5 + 6√5

Example 2.
Add (√5 + 7√5) and (4√3 + 6√5).
Solution:
(√5 + 7√5) + (4√3 + 6√5)
= √3 + 7√5 + 4√3 + 6√5
= (√3 + 4√3) + (7√5 + 6√5)
= 5√3 + 13√5.

Example 3.
Simplify (3 + √2) (3 – √2).
Solution:
(3)² – (√2)²
(∴ a² – b² = (a + b) (a – b))
= 9 – 2
= 7.

Example 4.
Divide 16√6 by 4√2 .
Solution:
16√6 ÷ 4√2
\(\frac { 16\sqrt { 6 } }{ 4\sqrt { 2 } } \)
4√3.

Example 5.
Simplify the following:

Solution:
(i) \(\sqrt{45}\) – 3\(\sqrt{20}\) = 4\(\sqrt{5}\) = \(\sqrt{9×5}\) – 3\(\sqrt{4×5}\) + 4\(\sqrt{5}\)

Example 6.
Simplify by rationalising the denominator of \(\frac { 2+3\sqrt { 5 } }{ 2-3\sqrt { 5 } } \)
Solution:
We have 3 \(\frac { 2+3\sqrt { 5 } }{ 2-3\sqrt { 5 } } \), multiply numerator and denominator by 2 + 3√5, we have

MP Board Class 9th Maths Solutions

MP Board Class 6th Sanskrit व्याकरण-खण्डः

वर्ण-विचार

वर्णमाला के वर्णों का विभाजन

वर्ण दो प्रकार के होते हैं-स्वर तथा व्यंजन।

स्वर :
दो प्रकार के हैं-

1. ह्रस्व स्वर-अ, इ, उ, ऋ, ल।
2. दीर्घ स्वर-आ, ई, ऊ, ऋ, ए, ऐ, ओ, औ।

व्यंजन :
वर्णों को वर्ग के आधार पर निम्न प्रकार से विभाजित किया जा सकता है-

विसर्ग-उच्चारणस्य नियमाः

उच्चारण :
विसर्ग का स्थान पूर्ववर्ती अन्तिम वर्ण के स्थान के समान माना जाता है। अतः पूर्ववर्ती वर्ण अर्थात् विसर्ग के आश्रय वर्ण को ध्यान में रखते हुए सर्प शावक के श्वास के समान विसर्ग का उच्चारण करना चाहिए। इस विषय में उच्चारण के नियम कुछ विशेष हैं-

1. अकार/आकार तथा ऋकार/ऋकार के पश्चात् विसर्ग का उच्चारण हकार सदृश होता है।
2. इकार/ईकार के पश्चात् विसर्ग का उच्चारण हिकार सदृश होता है।
3. उकार/ऊकार के पश्चात् विसर्ग का उच्चारण हुकार सदृश होता है।
4. एकार के पश्चात् विसर्ग का उच्चारण हेकार सदृश होता है।
5. ओकार के पश्चात् विसर्ग का उच्चारण होकार सदृश होता।
6. ऐकार का शुद्ध उच्चारण ‘अइ’ के रूप में होता है अतः ऐकार का परवर्ती घटक इ हुआ इस कारण से ऐकार के बाद विसर्ग का उच्चारण हिकार सदृश होता है।
7. औकार का शुद्ध उच्चारण ‘अउ’ के रूप में होता है अतः औकार का परवर्ती घटक उ हुआ इस कारण से औकार के बाद विसर्ग का उच्चारण हुकार सदृश होता है। उदाहरणार्थ, सारण पी निम्नानुसार है-

सन्धिपरिचयः

वर्णयोः वर्णानां वा मेलनं सन्धिः। स्वरवर्णमेलनं स्वरसन्धिः। सन्धेः त्रयः प्रकाराः सन्ति। स्वरसन्धिः, व्यश्चनसन्धिः विसर्गसन्धिः च। स्वरसन्धेः बहवः प्रकाराः सन्ति। किन्तु अन केवलं दीर्घसन्धिं पठामः।

(दो वर्णों के मेल को संधि कहते हैं। स्वर वर्ण का मेल स्वर सन्धि होती है। सन्धि तीन प्रकार की होती हैं। स्वर, व्यञ्जन और विसर्ग। यहाँ केवल दीर्घ सन्धि पढ़ेंगे।)

दीर्घ सन्धिः -यदि अ, आ, इ, ई, उ, ऊ वर्णानां समक्षं समानाः स्वराः स्युः तदा द्वयोः स्थाने दीर्घः स्वरः भवति।

(यदि अ आ, इ, ई, उ, ऊ, वर्गों के सामने समान स्वर हों तो दोनों के स्थान पर दीर्घ स्वर हो जाता है।)

यथा-(जैसे-)
हिमाचलः = हिम + अचलः → अ + अ = आ
देहान्तः = देह + अन्तः → अ + अ = आ
हिमालयः = हिम + आलयः → अ + आ = आ
भोजनालयः = भोजन + आलयः → अ + आ = आ
विद्यार्थी = विद्या + अर्थी → आ + अ = आ
शिक्षार्थी = शिक्षा + अर्थी → आ + अ = आ
विद्यालयः = विद्या + आलयः → आ + आ = आ
महाशयः = महा + आशयः → आ + आ = आ
कवीन्द्रः = कवि + इन्द्रः → इ + इ = ई
गिरीशः = गिरि + ईशः → इ + ई = ई
महीन्द्रः = मही + इन्द्रः → ई + इ = ई
नदीशः = नदी + ईशः → ई + ई = ई
भानूदयः = भानु + उदयः → उ + उ + ऊ
भानूष्मा = भानु + ऊष्मा → उ + ऊ = ऊ
वधूत्सवः = वधू + उत्सवः → ऊ + उ = ऊ
वधूर्णावस्त्रम् = वधू + ऊर्णावस्त्रम् → ऊ + ऊ = ऊ

उपसर्गपरिचयः

यः शब्दांशः कस्यापि शब्दस्य धातोः वा पूर्वं प्रयुज्य तस्य अर्थे परिवर्तनं विशेषतां वा आनयति सः उपसर्गः। (जो शब्दांश किसी भी शब्द के या धातु से पहले प्रयुक्त होकर उसके अर्थ में परिवर्तन अथवा विशेषता ला देता है, वह उपसर्ग कहा जाता है।) उपसर्गाः निम्नलिखिताः सन्ति (उपसर्ग निम्नलिखित होते हैं)-

प्र, परा, अप, सम्, अनु, अव, निस्, निर्, दुस्, दुर, वि, आङ्, नि, अधि, अपि, अति, सु, उत्, अभि, प्रति, परि, उप, एते, उपसर्गाः।
यथा-
ह धातुः (हरणे), कृ धातु (करणे)
हरति = चुराता है।
प्रहरति = प्रहार करता है।
विहरति = घूमता है।
संहरति = संहार करता है।
करोति = करता है।
अनुकरोति = अनुकरण करता है।
प्रतिकरोति = प्रतिकार करता है।
संस्करोति = संस्कार करता है।

उपसर्गेण धात्वर्थो बलादन्यः प्रतीयते।
प्रहाराहारसंहारविहार परिहारवत्॥
[उपसर्ग के द्वारा धातु का अर्थ बलपूर्वक अन्य सा प्रतीत होता है, जैसे-प्रहार, आहार, संसार, विहार, परिहार।]

प्रत्ययपरिचयः

यः शब्दः धातोः शब्दस्य वा अन्ते प्रयुज्य विशेषार्थस्य विधानं करोति सः प्रत्ययः। प्रत्ययः द्विविधः-कृदन्तप्रत्ययः तद्धितप्रत्ययः च।
(जो शब्द धातु अथवा शब्द के अन्त में प्रयुक्त होकर विशेष अर्थ का विधान करता है, वह प्रत्यय होता है। प्रत्यय दो प्रकार के होते हैं-कृदन्त और तद्धित।)

कृदन्तप्रत्ययः यः प्रत्ययः धातोः अन्ते प्रयुज्यते सः कृदन्तप्रत्ययः।
(जो प्रत्यय धातु के अन्त में जोड़े जाते हैं वे कृदन्त प्रत्यय होते हैं।)

यथा-पठ् धातुः क्त्वा प्रत्ययः-पठित्वा।

तद्धितप्रत्ययः यः प्रत्ययः शब्दस्य अन्ते प्रयुज्यते सः तद्धितप्रत्ययः (जो प्रत्यय शब्द के अन्त में जोड़े जाते हैं वे तद्धित प्रत्यय होते हैं।)
यथा- भारत शब्दः घ (ईय) प्रत्ययः- भारतीयः।

अत्र केवलं वयं कृदन्तप्रत्ययं “क्त्वा” प्रत्ययं “तुमुन्” प्रत्ययं च पठामः।
(यहाँ केवल हम कृदन्त प्रत्यय क्त्वा प्रत्यय ‘तुमुन्’ प्रत्यय को पढ़ेंगे।)

क्त्वा प्रत्ययः “कर” या ‘करके’ इत्यर्थे क्त्वाप्रत्ययः भवति।

यथा-
हस् + क्त्वा = हसित्वा = हँसकर
चल् + क्त्वा = चलित्वा = चलकर
भू + क्त्वा = भूत्वा = होकर
गम् + क्त्वा = गत्वा = जाकर
दा + क्त्वा = दत्वा = देकर
पा + क्त्वा = पीत्वा = पीकर

तुमुन् प्रत्ययः “के लिए” इत्र्थे तुमुन् प्रत्ययः भवति।
यथा-
पठ् + तुमुन् = पठितुम् = पढ़ने के लिए
हस् + तुमुन् = हसितुम् = हँसने के लिए
दा + तुमुन् = दातुम् = देने के लिए
पा + तुमुन् = पातुम् = पीने के लिए
गम् + तुमुन् = गन्तुम् = जाने के लिए

अव्ययपरिचयः

यत् त्रिषु लिङ्गेषु, सर्वेषु वचनेषु सर्वासु विभक्तिषु च समानं भवति, तद् अव्ययं कथ्यते।
(जो तीनों ही लिङ्गों में, सभी वचनों में तथा सभी विभक्तियों में समान होता है, वह अव्यय कहा जाता है)

सदृशं त्रिषु लिङ्गेषु सर्वासु च विभक्तिषु।
वचनेषु च सर्वेषु यन्नव्येति तदव्ययम्॥

विभक्तिपरिचयः

व्यावहारिकसंस्कत शब्दावलिः
(व्यवहार में आने वाली संस्कृत शब्दावलि)

फलानि (फलों के नाम)-

आम्रम् = आम
सेवि = सेब
कदली = केला
जम्बुः = जामुन
दाडिमम् = अनार
बिल्वम् = बेल फल
कपित्थम् = कैथ का फल
द्राक्षा = अंगूर
बदरी = बेर

भोज्यपदार्थाः (भोज्य पदार्थ)-

रोटिका = रोटी
प्ररोटिका = पराँठा
पूरिका = पूरी
शाकम् = सब्जी
सूपः = दाल (पकी हुई)
ओदनम् = भात
अवलेहः = अचार, चटनी
शष्कुली = कचौड़ी, पूरी
संयावकः = हलवा
सुपिष्टकम् = बिस्किट
चाकलेहः = चॉकलेट (टॉफी)
दुग्धम् = दुध
लवणम् = नमक
रसगोलकम् = रसगुल्ला
मिष्टान्नम् = मिठाई
दधि = दही।

शाकानि (सब्जियों के नाम)-

आलुकम् = आलू
रक्ताङ्गः = टमाटर
कूष्माण्डः = कद्दू
मूलकम् = मूली
गृञ्जनम् = गाजर
भिण्डकः = भिण्डी
पालकी = पालक
वृन्ताकम् = भटा (बैंगन)
कारवेल्लः = करेला
मरीचिका = मिर्ची
अलाबुः = लौकी

पुष्पाणि (फलों के नाम)-

कमलम् = कमल
पाटलम् = गुलाब
कन्दुकः = गेंदा
चम्पकः = चम्पा
मालती = चमेली
मल्लिका = बेला
यूथिका = जूही

पाठ्यवस्तूनि (पाठ्य वस्तुएँ)-

पुस्तकम् = पुस्तक
लेखनी = कलम
उत्तरपुस्तिका = कॉपी
कर्गदम् = कागज
मसी = स्याही

दैनिकोपयोगीनि वस्तूनि

(दैनिक उपयोग की वस्तुएँ)-

स्नानफेनकम् = नहाने का साबुन
वस्त्रफेनकम् = कपड़े धोने का साबुन
दन्तेफेनकम् = टूथपेस्ट
क्षालनचूर्णम् = धोने का पावडर
व्यजनम् = पंखा
स्यूतः = थैला
छत्रम्। = छाता
कर्तरी = कैंची
तालकम् = ताला
अग्निपेटिका = माचिस
चुल्लिका = चूल्हा
वायुचुल्लिका = गैस चूल्हा
चायम् = चाय
जलम् = जल
भोजनम् = भोजन

परिजननामानि (परिवार के लोगों के नाम)-

पिता = पिता
माता = माता
पितामहः = दादा
पितामही = दादी
मातामहः = नाना
मामामही = नानी
भ्राता = भाई
भगिनी = बहन
अग्रजः = बड़ा भाई
अनुजः = छोटा भाई
अनुजा = छोटी बहन
अग्रजा = बड़ी बहन
मातुलः = मामा
मातुलानी = मामी
पितृव्यः = चाचा
पितव्या = चाची

शब्दरूपाणि

अकारान्तः पुल्लिङ्गः “बालक” शब्दः

एवमेव देवः, नरः, वृक्षः, ग्रामः, दीपः, गजः, इत्यादयः।
आकारान्तः स्त्रीलिङ्गः “लता” शब्दः

एवमेव माला, शाला, रमा, मापिका, सीता, स्थालिका इत्यादयः।

ईकारान्तः स्त्रीलिङ्गः “नदी” शब्दः

एवमेव लेखनी, नगरी, भगिनी, अङ्गुली, घटी, अङ्कनी इत्यादयः।

उकारान्तः स्त्रीलिङ्गः “धेनु” शब्दः

एवमेव रेणु, रज्जु इत्यादयः।
अकारान्तः नपुंसकलिङ्गः “फल” शब्दः

एवमेव ज्ञानम्, वनम् गृहम्, पुष्पम्, चित्रम्, पुस्तकम्, इत्यादयः।

इकारान्तः पुल्लिङ्गः “मुनि” शब्दः

एवमेव कविः, रविः, पतिः, हरिः इत्यादयः।

उकारान्तः पुल्लिङ्ग “गुरु” शब्दः

एवमेव भानुः, तरु, इत्यादयः।

सर्वनामशब्दरूपाणि

द्कारान्तः पुल्लिङ्ग “तद्” शब्दः

द्कारान्तः स्त्रीलिङ्गः “तद्” शब्दः

द्कारान्तः नपुंसकलिङ्गः “तद्” शब्दः

तृतीयातः सप्तमीपर्यन्तं पुल्लिङ्गवद् रूपाणि भवन्ति।

म्कारान्तः पुल्लिङ्गः “किम्” शब्दः

म्कारान्तः स्त्रीलिङ्ग “किम्” शब्दः

मकारान्तः नपुंसकलिङ्गः “किम्” शब्दः

तृतीयातः सप्तमीपर्यन्तं पुल्लिङ्गवद् रूपाणि भवन्ति

दकारान्तः त्रिलिङ्गकः “अस्मद” शब्दः

दकारान्तः त्रिलिङ्गकः “युष्मद” शब्दः

एक-संख्याबोधकशब्दः
(रूप केवल एकवचन में चलते हैं)

द्वि (दो)
(रूप केवल द्विवचन में चलते हैं)

त्रि (तीन)
(तीन से सभी संख्याओं के रूप केवल बहुवचन में ही चलते हैं)

चतुर् (चार)

पाँच से दस तक संख्याओं के रूप
(पाँच से संख्याओं में लिंग भेद नहीं होता है)

धातुरूपाणि

पठ् धातुः “लट् लकारः (वर्तमानकाले)

पठ् धातुः “लङ्” लकारः (भूतकाले)

पठ् धातुः “लृट् लकारः (भविष्यत्काले)

एवमेव वद्, लिख, गम् (गच्छ), क्रीड्, पा (पिब्) इत्यादयः।

‘कृ’ धातुः “लट् लकारः

“अस्” धातुः लट्लकारः

‘दा’ धातुः लट्लकारः

अनुवाद के नियम

संस्कृत में अनुवाद करने के लिए मुख्य रूप से हमें विभक्ति (कारक) वचन, लिङ्ग, पुरुष, शब्द और धातु का ज्ञान होना आवश्यक है। उदाहरण के लिए-प्रथम पुरुष के एकवचन के कर्ता के साथ धातु का प्रथम पुरुष एक वचन का रूप प्रयोगहोगा।
जैसे- वह जाता है-स: गच्छति।

प्रथम पुरुष :
वे दोनों जाते हैं-तौ गच्छतः।

के कर्ता :
वे सब जाते हैं-ते गच्छन्ति।

मध्यम पुरुष :
तुम जाते हो-त्वम् गच्छसि।

के कर्ता :
तुम दोनों जाते हो-युवाम् गच्छथः।
तुम सब जाते हो-यूयम् गच्छथ।

उत्तम पुरुष के :
मैं जाता हूँ-अहम् गच्छामि।

कर्ता :
हम दोनों जाते हैं-आवाम् गच्छावः।
हम सब जाते हैं-वयम् गच्छामः।

इस प्रकार शब्द और धातु के वचन व पुरुष समान होंगे। तीनों लिंग के शब्द रूप भिन्न होने पर भी धातु रूप एक ही प्रयोग किये जाते हैं। जैसे-

1. लड़की पढ़ती है-बालिका पठति।
2. लड़का पढ़ता है-बालकः पठति।
3. पत्र: गिरता है-पत्रम् पतति।

संस्कृत के व्याकरण के नियमों को हम इस प्रकार जानेंगे-

पुरुष या कर्ता :
कर्ता (पुरुष) तीन प्रकार के होते हैं-प्रथम या अन्य पुरुष, मध्यम पुरुष, उत्तम पुरुष।

प्रथम या अन्य पुरुष :
जिसके सम्बन्ध में कोई बात की जाए। जैसे-वे, सीता, लड़के, वह, वे दोनों, वे सब आदि।

मध्यम पुरुष :
जिससे बात की जाए। जैसे-तुम, तुम दोनों, तुम सब।

उत्तम पुरुष :
जो बात करता है। जैसे-मैं, हम दोनों, हम सब।

तीनों पुरुष तीन वचनों के साथ प्रयोग होते हैं। इनका प्रयोग धातु रूपों के साथ उसी क्रम से होता है। इनके रूप इस प्रकार से चलते हैं-

इसी प्रकार से धातु रूप भी चलते हैं। यथा पठ् धातु के रूप (वर्तमान काल) में क्रमशः तीनों पुरुष के साथ बनाने पर अनुवाद इस प्रकार बनेगा-

कारक चिह्न और विभक्ति

वर्ण परिचय

वर्ण दो प्रकार के हैं-स्वर और व्यंजन-
स्वर :
इन्हें किसी अन्य वर्ण के सहयोग के बिना उच्चारित किया जा सकता है। ये 13 हैं-
अ, आ, इ, ई, उ, ऊ, ऋ, ए, ऐ, ओ, औ, अं और अः।

व्यंजन :
व्यंजनों का उच्चारण करने के लिए स्वरों की सहायता की आवश्यकता होती है। व्यंजन 33 हैं-
क् ख् ग् घ् ङ् च्, छ् ज् झ् ञ् ट् ठ् ड् ढ् ण् त् थ् द् ध् न् प् फ् ब् भ् य् र् ल् व् श् ष् स्।

इनका उच्चारण करने के लिए प्रत्येक व्यंजन में ‘अ’ स्वर मिलाना पड़ता है; यथा-कमल लिखने के लिए-
क् + अ = क; म् + अ = म; ल् + अ = ल = कमल।
इसी प्रकार प्रत्येक व्यंजन में स्वर अ को मिलाकर पढ़ते हैं।

वर्ण समूह और उच्चारण स्थान :
वर्णों के उच्चारण स्थान के आधार पर उनका समूह होता है जो निम्नलिखित है-

वचन

संस्कृत में तीन वचन होते हैं-एकवचन, द्विवचन, बहुवचन।-
एकवचन :
इससे किसी एक व्यक्ति अथवा वस्तु का बोध होता है। जैसे-राम, सीता, गीता आदि।

द्विवचन :
इससे दो वस्तुओं आदि का बोध होता है। जैसे-दो बालक, दो पुस्तकें, दो फल आदि।

बहुवचन :
इससे दो से अधिक वस्तुओं, स्थान या व्यक्तियों – का बोध होता है। जैसे-लड़के, किताबें, स्त्रियाँ, बालिकाएँ आदि।

संस्कृत में अनुवाद बनाते समय प्रत्येक शब्द तथा धातु के साथ इन तीनों वचनों में से वाक्यानुसार किसी का भी प्रयोग होता है।

विभक्तियों का प्रयोग

चिन्ह के आधार पर वाक्य में उसी विभक्ति का प्रयोग होगा। यथा-

लिंग

संस्कृत में तीन लिंग होते हैं-पुल्लिग, स्त्रीलिंग और नपुंसकलिङ्ग।
पुल्लिग :
पुरुषवाचक शब्द पुल्लिग कहलाते हैं। जैसे-राम, मोहन, सोहन आदि।

स्त्रीलिंग :
स्त्रीवाचक शब्द स्त्रीलिंग कहलाते हैं। जैसे-सीता, गीता, लता, नदी, स्त्री आदि।

नपुंसकलिंग :
जिन शब्दों से किसी भौतिक वस्तु, फल आदि का बोध होता है। जैसे-फल, पुस्तक, कलम आदि।

परीक्षोपयोगी अनुवाद

MP Board Class 6th Sanskrit Solutions

MP Board Class 8th Maths Solutions Chapter 16 संख्याओं के साथ खेलना Ex 16.1

प्रश्न 1.
निम्नलिखित में से प्रत्येक में अक्षरों के मान ज्ञात कीजिए तथा सम्बद्ध चरणों के लिए कारण भी दीजिए –

हल:
1. इकाई स्तम्भ को जोड़ने पर अर्थात् A + 5 को जोड़ने पर हम इकाई का अंक 2 प्राप्त करते हैं।
अत: A = 7, (∴ A + 5 = 7 + 5 = 12)
अब दहाई स्तम्भ को जोड़ने पर
1 + 3 + 2 = B या B = 6
अतः अब पहेली इस प्रकार होगी –

∴ A = 7, B = 6

2. इकाई स्तम्भ से, A + 8 = 3
अर्थात् इकाई का अंक = 3 होना चाहिए।
अतः A = 5, (∴ A + 8 = 5 + 8 = 13)
अब दहाई स्तम्भ से, 1 + 4 + 9 = B या B = 14
∴ स्पष्ट है, B = 4 और C = 1 अब पहेली इस प्रकार होगी –

∴ A = 5, B = 4 तथा C = 1

3. क्योंकि इकाई का अंक A x A = A है।
∴ A = 1, A = 5 या A = 6
जबकि A = 1, तब,

अत: A ≠ 1
जबकि A = 5, तब,

अत: A ≠ 5
जबकि A = 6, तब,

अतः A = 6

4. दी हुई पहेली से,
B + 7 = A तथा A + 3 = 6
अतः सम्भावित मान
0 + 7 = 7 अर्थात् A = 7 परन्तु 7 + 3 ≠ 6
1 + 7 = 8 अर्थात् A = 8 परन्तु 8 + 3 ≠ 6
2 + 7 = 9 अर्थात् A = 9 परन्तु 9 + 3 ≠ 6
3 + 7 = 10 अर्थात् A = 0 परन्तु 1 + 0 + 3 ≠ 6
4 + 7 = 11 अर्थात् A = 1 परन्तु 1 + 1 + 3 ≠ 6
5 + 7 = 12 अर्थात् A = 2 और 1 + 2 + 3 = 6
B = 5 तथा A = 2
अब पहेली इस प्रकार है –

A = 2 और B = 5

5. ∴ इकाई स्तम्भ 3 x B = B, ∴ B = 0
अब पहेली इस प्रकार है –

अब, 3 x A = A, ∴ A = 5
अब, पहेली इस प्रकार है –

∴ A = 5, B = 0 और C = 16
6. ∴ इकाई स्तम्भ 5 x B = B अर्थात् B = 0 या 5
यदि B = 0, तब

अब, 5 x A = A या A = 0 या 5
परन्तु A0, A = 5 के लिए

∴ A = 5, B = 0 और C = 2
यदि B = 5, तब

अब, 5 x A + 2 = A ⇒ A = 2, ∴ 5 x 2 + 2 = 12
∴ इकाई का अंक = 2 = A
∴ B = 5 के लिए,

∴ A = 2, B = 5 और C = 1

7.

BBB के सम्भव मान: 111, 222, 333, आदि
∴ 111 ÷ 6 = 18 और शेषफल = 3 ∴ B ≠ 3
222 ÷ 6 = 37, शेषफल = 0, अतः भागफल 37 ≠ A2
333 ÷ 6 = 55, शेषफल = 3, अतः भागफल 55 ≠ A3
444 + 6 = 74, शेषफल = 4, अतः भागफल 74 ≠ A4
अतः A = 7 और B = 4

8. इकाई स्तम्भ से 1 + B = 0, इकाई स्तम्भ का अंक 0 है।
∴ B = 9 अब

परन्तु 90 – 19 = 71 अत: A1 = 71 या A = 7
अतः A = 7, B = 9

9. इकाई स्तम्भ से,
B + 1 = 8 अतः इकाई अंक 8 है।
B = 8 – 1 = 7
∴ B स्वयं एक अंक है, ∴ B = 7
अब

दहाई स्तम्भ से, A + 7 = 1
अतः A का इकाई अंक 1 होना चाहिए।
∴ A स्वयं एक अंक है। अत: A = 4
अब, पहेली

अतः A = 4, B = 7

10. दहाई के स्तम्भ से,
2 + A = 0
∴ संख्या का इकाई अंक 0 होना चाहिए।
∴ A = 8, तब

अब, 8 + B = 9, ∴ B = 9 – 8 = 1
अब,

∴ A = 8 और B = 1

पाठ्य-पुस्तक पृष्ठ संख्या # 268

प्रयास कीजिए (क्रमांक 16.6)

(पहला प्रश्न आपकी सहायता के लिए किया हुआ है।)
प्रश्न 1.
यदि विभाजन N ÷ 5 से शेषफल, 3 प्राप्त होता है, तो N की इकाई अंक क्या हो सकता है?
हल:
इकाई के अंक को 5 से भाग देने पर शेषफल 3 आना चाहिए। अतः इकाई का अंक 3 या 8 होगा।

प्रश्न 2.
यदि विभाजन N ÷ 5 से शेषफल 1 प्राप्त होता है, तो N का इकाई अंक क्या हो सकता है?
हल:
इकाई के अंक को 5 से भाग देने पर शेषफल 1 आना चाहिए।
अतः इकाई का अंक 1 या 6 होगा।

प्रश्न 3.
यदि विभाजन N 5 से शेषफल 4 प्राप्त होता है, तो N की इकाई का अंक क्या हो सकता है?
हल:
इकाई के अंक को 5 से भाग देने पर शेषफल 4 आना चाहिए।
अतः इकाई का अंक 4 या 9 होगा।

प्रयास कीजिए (क्रमांक 16.7)

(पहला प्रश्न आपकी सहायता के लिए किया हुआ है।)
प्रश्न 1.
यदि विभाजन N ÷ 2 से शेषफल 1 प्राप्त होता है, तो N की इकाई का अंक क्या हो सकता है?
हल:
N विषम है। इसलिए इसकी इकाई का अंक विषम होगा। अतः N की इकाई का अंक 1, 3, 5, 7 या 9 होगा।

प्रश्न 2.
यदि विभाजन N ÷ 2 से कोई शेष प्राप्त नहीं होता (अर्थात् शेषफल 0 है), तो N की इकाई का अंक क्या हो सकता है?
हल:
N सम होना चाहिए। इसलिए इसकी इकाई का अंक सम होगा। – अंत: N की इकाई का अंक 0, 2, 4, 6 या 8 होगा।

प्रश्न 3.
मान लीजिए कि विभाजन N ÷ 5 से शेषफल 4 और विभाजन N ÷ 2 से 1 प्राप्त होता है। N की इकाई का अंक क्या होना चाहिए?
हल:
क्योंकि N ÷ 5 से शेषफल 4 प्राप्त होता है। अत: N की इकाई का अंक 4 या 9 होगा।
N ÷ 2 से शेषफल 1 प्राप्त होता है। इसलिए इकाई का अंक विषम होना चाहिए।
अतः N की इकाई का अंक 1, 3, 5, 7 या 9 होगा। परन्तु यहाँ 9 दोनों स्थितियों को सन्तुष्ट करेगा।
अतः N की इकाई का अंक 9 होगा।

पाठ्य-पुस्तक पृष्ठ संख्या # 270

प्रयास कीजिए (क्रमांक 16.8)

प्रश्न 1.
निम्नलिखित संख्याओं की 9 से विभाज्यता की जाँच कीजिए –

1. 108
2. 616
3. 294
4. 432
5. 927

हल:
हम जानते हैं कि कोई संख्या 9 से विभाज्य होती है, यदि इसके अंकों का योग 9 से विभाज्य हो।

1. संख्या = 108
संख्या के अंकों का योग = 1 + 0 + 8 = 9, यह 9 से विभाज्य है।
इसलिए 108, 9 से विभाज्य है।

2. संख्या = 616
संख्या के अंकों का योग = 6 + 1 + 6 = 13, यह 9 से विभाज्य नहीं है।
इसलिए 616, 9 से विभाज्य नहीं है।

3. संख्या = 294
संख्या के अंकों का योग = 2 + 9 + 4 = 15, यह 9 से विभाज्य नहीं है।
इसलिए 294, 9 से विभाज्य नहीं है।

4. संख्या = 432
संख्या के अंकों का योग = 4 + 3 + 2 = 9, यह 9 से विभाज्य है।
इसलिए 432, 9 से विभाज्य है।

5. संख्या = 927
संख्या के अंकों का योग = 9 + 2 + 7 = 18, यह 9 से विभाज्य है।
इसलिए 927, 9 से विभाज्य है।

सोचिए, चचों कोजिए और लिखिए।

प्रश्न 1.
आप देख चुके हैं कि 450, 10 से विभाज्य है। यह 2 और 5 से भी विभाज्य है, जो 10 के गुणनखण्ड हैं। इसी प्रकार संख्या 135, 9 से विभाज्य है। यह 3 से भी विभाज्य है, जो 9 का एक गुणनखण्ड है।
क्या आप कह सकते हैं कि यदि कोई संख्या किसी संख्या m से विभाज्य हो, तो वह m के प्रत्येक गुणनखण्ड से भी विभाज्य होगी?
हल:
हाँ, यदि कोई संख्या m से विभाज्य हो, तो वह m के प्रत्येक गुणनखण्ड से भी विभाज्य होगी।

प्रश्न 2.
1. एक तीन अंकों की संख्या abc की 100 a + 10b + c के रूप में लिखिए। अब 100a + 10b + c = 99a + 11b + (a – b + c)
= 11 (9a + b) + (a – b + c)
यदि संख्या abc, 11 से विभाज्य है, तो आप (a-b+ c) के बारे में क्या कह सकते हैं ? क्या यह आवश्यक है कि (a+c-b), 11 से विभाज्य हो?

2. एक चार अंकों की संख्या abcd को इस प्रकार लिखिए –
1000a + 100b + 10c + d = (1001 a + 99b + 11c) -(a – b + c – d)
= 11 (91a + 9b + c) + [(b + d) – (a + c)]
यदि संख्या abcd, 11 से विभाज्य है, तो (b + d) – (a + c) के बारे में आप क्या कह सकते हैं?

3. उपर्युक्त (i) और (ii) से, क्या आप कह सकते हैं कि कोई संख्या 11 से विभाज्य होगी, यदि इसके विषम स्थानों के अंकों का योग और समस्थानों के अंकों के योग का अन्तर 11 से विभाज्य होगा?

हल:
1. हाँ, यह आवश्यक है कि (a + c – d), 11 से विभाज्य होगी।
2. यदि संख्या abcd, 11 से विभाज्य है, तब (b + d) – (a + c), 11 से विभाज्य होगी।
3. हाँ, हम कह सकते हैं कि यदि कोई संख्या 11 से विभाज्य होगी यदि इसके विषम स्थानों के अंकों का योग और समस्थानों के अंकों का योग का अन्तर 11 से विभाज्य हो।

पाठ्य-पुस्तक पृष्ठ संख्या # 271

प्रयास कीजिए (क्रमांक 16.9)

प्रश्न 1.
निम्नलिखित संख्याओं की 3 से विभाज्यता की जाँच कीजिए –

1. 108
2. 616
3. 294
4. 432
5. 927.

हल:
हम जानते हैं कि कोई संख्या 3 से विभाज्य होती है, यदि इसके अंकों का योग 3 से विभाज्य हो।
1. संख्या = 108
अंकों का योग = 1 + 0 + 8 = 9, यह 3 से विभाज्य है।
इसलिए 108,3 से विभाज्य है।

2. संख्या = 616
अंकों का योग = 6 + 1 + 6 = 13, यह 3 से विभाज्य नहीं है।
इसलिए 616, 3 से विभाज्य नहीं है।

3. संख्या = 294
अंकों का योग = 2 + 9 + 4 = 15, यह 3 से विभाज्य है।
इसलिए 294, 3 से विभाज्य है।

4. संख्या = 432
अंकों का योग = 4 + 3 + 2 = 9, यह 3 से विभाज्य है।
इसलिए 432, 3 से विभाज्य है।

5. संख्या = 927
अंकों का योग = 9 + 2 + 7 = 18, यह 3 से विभाज्य है।
इसलिए 927, 3 से विभाज्य है।

MP Board Class 8th Maths Solutions

MP Board Class 6th Sanskrit Solutions Surbhi विविधप्रश्नावलिः 3

प्रश्न 1.
प्रश्नानाम् उत्तराणि एकपदेन लिखत (प्रश्नों के उत्तर एक शब्द में लिखो)
(क) कस्मिन् मासे स्वतन्त्रतादिवसः भवति? (किस महीने में स्वतन्त्रता दिवस होता है?)
उत्तर:
अगस्तमासे

(ख) वस्तुनि केन शीतलानि भवन्ति? (वस्तुएँ किससे ठंडी होती हैं?)
उत्तर:
हिमशीतकेन

(ग) वयं कस्य सेवार्थं निरन्तरं चलिष्यामः? (हम किसकी सेवा के लिए निरन्तर चलते रहेंगे?)
उत्तर:
लोकसेवार्थं

(घ) धनिकः किम् अयच्छत्? (धनिक ने क्या दिया?)
उत्तर:
मिष्टान्नम्

(ङ) सिक्खधर्मस्य प्रवर्तकः कः? (सिक्ख धर्म के प्रवर्तक कौन थे?)
उत्तर:
गुरुनानकः

(च) कार्याणि केन सिध्यन्ति? (कार्य किससे सिद्ध होते हैं?)
उत्तर:
उद्यमेन

(छ) व्यापारिणां नूतनसंवत्सरः कदा आरभते? (व्यापारियों का नया वर्ष कब शुरू होता है?)
उत्तर:
कार्तिक प्रतिपदि शुक्लपक्षे।

प्रश्न 2.
प्रश्नानाम् उत्तराणि एकवाक्येन लिखत (प्रश्नों के उत्तर एक वाक्य में लिखो)
(क) प्रथमस्वतन्त्रतासङ्ग्रामः कदा अभवत्? (प्रथम स्वतन्त्रता संग्राम कब हुआ?)
उत्तर:
प्रथम स्वतन्त्रता संग्रामः ईसवीय वर्षे १८५७ तमे अभवत्। (प्रथम स्वतन्त्रता संग्राम सन् १८५७ ई. में हुआ था।)

(ख) दीपावल्यां लक्ष्मीः कदा पूज्यते? (दीपावली को लक्ष्मी कब पूजी जाती है?)
उत्तर:
दीपावल्यां लक्ष्मीः अमावस्यायां पूज्यते। (दीपावली पर लक्ष्मी की पूजा अमावस्या को होती है।)

(ग) विप्रम् अतिदरिद्रं ज्ञात्वा राजा किम् अपृच्छत्? (ब्राह्मण को अति दरिद्र जानकर राजा ने क्या पूछा?)
उत्तर:
विप्रम् अति दरिद्रं ज्ञात्वा राजा अपृच्छत् “विप्र! चर्मपात्रं किमर्थं हस्ते वहसि?” (ब्राह्मण को अति दरिद्र जानकर राजा ने पूछा, हे ब्राह्मण! चर्मपात्र को हाथ में किसलिए ढो रहे हो (लिए हुए हो)?

(घ) मनुष्यस्य श्रेष्ठता केन भवति? (मनुष्य की श्रेष्ठता किससे होती है?)
उत्तर:
मनुष्यस्य श्रेष्ठता चरित्रेण भवति। (मनुष्य की श्रेष्ठता चरित्र से होती है।)

(ङ) केन सर्वे जन्तवः तुष्यन्ति? (किसके कारण सभी प्राणी सन्तुष्ट हो जाते हैं?)
उत्तर:
प्रियवाक्यन प्रदानेन सर्वे जन्तवः तुष्यन्ति। (प्रिय वचन बोलने से सभी प्राणी सन्तुष्ट हो जाते हैं।)

(च) आवश्यकता केषां जननी अस्ति? (आवश्यकता किसकी जननी होती है?)
उत्तर:
“आवश्यकता आविष्काराणां जननी अस्ति”। (आवश्यकता आविष्कारों की जननी है।)

(छ) वयं कान् रक्षिष्यामः? (हम किनकी रक्षा करेंगे?)
उत्तर:
वयं सज्जनान् रक्षिष्यामः। (हम सज्जनों की रक्षा करेंगे।)

प्रश्न 3.
उचितशब्दैः रिक्तस्थानानि पूरयत (उचित शब्दों से रिक्त स्थानों को भरो)
(क) अधुना वयं………. गच्छामः। (ग्रहाय/गह)
(ख) आपणाः ग्राहकैः………… सन्ति। (परिपूर्णः/परिपूर्णाः)
(ग) ………… कार्याणि सिध्यन्ति। (उद्यमेन/उद्यमाय)
(घ) श्रमेण………… उन्नतिः भवति। (राष्ट्राय/राष्ट्रस्य)
(ङ) नाटकदर्शन………….. भवति। (दूरदर्शनेन/दूरदर्शनात्)
(च) नानकः धनिकस्य भोजनं………… शुष्करोटिकाः स्वीकृतवान्। (त्यक्त्वा/त्युक्तुम्)
(छ) शिक्षाक्षेत्रे………. महती भूमिका अस्ति। (सङ्गणकयन्त्रस्य/सङ्गणकयन्त्राय)
(ज) मम………… आनीतं भोजनम्। (गृहेण/गृहात्)
उत्तर:
(क) गृहं
(ख) परिपूर्णाः
(ग) उद्यमेन
(घ) राष्ट्रस्य
(ङ) दूरदर्शनेन
(च) त्यक्त्वा
(छ) सङ्गणकयन्त्रस्य
(ज) गृहात्।

प्रश्न 4.
निर्देशानुसारं परिवर्तनं कुरुत (निर्देश के अनुसार परिवर्तन करो)
(क) स्थास्यन्ति ………… (लट् लकारे)
(ख) गायन्ति …………. (लुट् लकारे)
(ग) शिक्षितः ………… (बहुवचने)
(घ) प्रदेशस्य ……….. (बहुवचने)
(ङ) भवति ………… (बहुवचने)
उत्तर:
(क) तिष्ठन्ति
(ख) गायिष्यन्ति
(ग) शिक्षिताः
(घ) प्रदेशानाम्
(ङ) भवन्ति।

प्रश्न 5.
अर्थानुसारं युग्मानि योजयत (अर्थ के अनुसार जोड़ों को जोड़ो)

उत्तर:
(क) → 3
(ख) → 1
(ग) → 2
(घ) → 5
(ङ) → 4
(च) → 7
(छ) → 6
(ज) → 10
(झ) → 8
(ञ) → 9

प्रश्न 6.
अन्वयपूर्ति कुरुत (अन्वय की पूर्ति करो)
(क) काकः ………… कृष्णः, कः भेदः………. , ……….. काले सम्प्राप्ते …………  काकः…………”पिकः।
(ख) वयम्………. विना सततं……….. करिष्यामः, ……….. चलिष्यामः, निरन्तरं ………..।
उत्तर:
(क) कृष्णः, पिकः, पिक काकयोः, वसन्त, काकः, पिकः।
(ख) आलस्यं, कार्याणि, अग्रे अग्रे, चलिष्यामः।

MP Board Class 6th Sanskrit Solutions

MP Board Class 6th Sanskrit Solutions Surbhi विविधप्रश्नावलिः 2

प्रश्न 1.
एकपदेन उत्तरं लिखत (एक शब्द में उत्तर लिखो)
(क) कः देशरक्षां करोति?
(ख) केभ्यः जयघोषः निःसरित?
(ग) मध्यप्रदेशस्य मध्यभागे का नदी प्रवहति?
(घ) दशरथस्य कति पुत्राः आसन्?
(ङ) जम्बूवृक्षः कुत्र आसीत्?
उत्तर:
(क) सैनिकः
(ख) भक्तजनमुखेभ्य
(ग) नर्मदा नदी
(घ) चत्वारः
(ङ) नद्याः तीरे।

प्रश्न 2.
एकवाक्येन उत्तरं लिखत (एक वाक्य में उत्तर लिखो)
(क) परोपकाराय के फलानि यच्छन्ति? (परोपकार के लिए कौन फल देते हैं?)
उत्तर:
परोपकाराय वृक्षाः फलानि यच्छन्ति। (परोपकार के लिए वृक्ष फल देते हैं।)

(ख) चन्द्रः कासां भूषणम् अस्ति? (चन्द्रमा किनका आभूषण है?)
उत्तर:
चन्द्रः ताराणां भूषणम् अस्ति। (चन्द्रमा तारों का आभूषण है।)

(ग) मध्यप्रदेशः कुत्र विराजते? (मध्यप्रदेश कहाँ विराजमान हैं?)
उत्तर:
मध्यप्रदेश: भारतदेशस्य मध्यभागे विराजते। (मध्यप्रदेश भारत देश के मध्य भाग में विराजमान है।)

(घ) आदिकविः कः अस्ति? (आदिकवि कौन हैं?)
उत्तर:
आदिकवि वाल्मीकिः अस्ति। (आदिकवि वाल्मीकि हैं।)

(ङ) कः उच्चैः गर्जति? (कौन ऊँचे स्वर में गरजता है?)
उत्तर:
सिंहः उच्चैः गर्जति। (शेर ऊँचे स्वर में गरजता है।)

प्रश्न 3.
रिक्तस्थानं पूरयत (रिक्त स्थान की पूर्ति करो)
(क) शास्त्रं ………… अस्ति। (पण्डिताः/पण्डिताय)
(ख) श्रीरामः …………पुत्रः। (दशरथस्य/दशरथेन)
(ग) भोपालनगरं मध्यप्रदेशस्य ………… अस्ति। (राजधानी/राजधानीम्)
(घ) सीतायाः विवाहः ……….. सह अभवत्। (रामस्य/रामेण)
(ङ) मयूरः अस्माकं ………… पक्षी अस्ति। (राष्ट्रियः/राष्ट्रीयम्)
(च) सिंह उच्चैः …………। (गर्जति/गर्जेत)
उत्तर:
(क) पण्डिताय
(ख) दशरथस्य
(ग) राजधानी
(घ) रामेण
(ङ) राष्ट्रियः
(च) गर्जति।

प्रश्न 4.
समीचीनं चिनुत (आम्/न) (उपयुक्त का चुनाव करो हाँ/न)
(क) अस्माभिः जलसंरक्षणं, वायुसंरक्षणं, भूसंरक्षणम् च अवश्यं करणीयम्।
(ख) स्वास्थ्यं ज्ञानाय परिश्रमाय न भवति।
(ग) प्राचीनकालात् आरभ्य उज्जयिनीक्षेत्रं संस्कृतविद्या केन्द्रमस्ति।
(घ) विद्या सर्वस्य भूषणं नास्ति।
(ङ) संस्कृतभाषा वेदानाम् उपनिषदां शास्त्राणांच भाषा वर्तते।
(च) नर्मदायाः दक्षितटे विन्ध्याचलः अस्ति।
(छ) मध्यप्रदेशस्य मध्ये नर्मदा नदी अस्य मेखला इव प्रवहति।
(ज) दशरथस्य आज्ञया रामः राज्यं त्यक्त्वा वनम् अगच्छत्।
(झ) लक्ष्मणेन रामः युद्धे घातितः।
उत्तर:
(क) आम्
(ख) न
(ग) आम्
(घ) न
(ङ) आम्
(च) न
(छ) आम्
(ज) आम्
(झ) न

प्रश्न 5.
अधोलिखितानि पदानि प्रयुज्यवाक्यानि लिखत(निम्नलिखित शब्दों का प्रयोग करके वाक्यों को लिखो)

उत्तर:
(क) सूर्यः लोकहिताय तपति।
(ख) नद्यः परोपकाराय वहन्ति।
(ग) मन्दिरात् घण्टानादः श्रूयते।
(घ) यात्रिकाः उज्जयिनीम् आगच्छन्ति ।

प्रश्न 6.
अक्षराणि प्रयुज्य पदचक्र पूरयत (अक्षरों का प्रयोग करके पदचक्र को पूरा करो)
ला, धु, भा, भा, स, षा

उत्तर:
(क) मधुरा भाषा
(ख) भारतभूषा
(ग) सरला भाषा।

प्रश्न 7.
अधोलिखितानि वाक्यानि यथाक्रमं लिखत (नीचे लिखे वाक्यों को क्रमानुसार लिखो)
(क) वने राक्षसराजः रावणः सीतां कपटेन अहरत्।
(ख) रामः सीता लक्ष्मणः च अयोध्याम् प्रत्यगच्छन्।
(ग) वानराः सागरे सेतुनिर्माणम् अकुर्वन।
(घ) रामेण रावणः युद्धे घातितः।
(ङ) विश्वामित्रः रामलक्ष्मणौ स्वाश्रमम् अनयत्।
उत्तर:
(1) ङ
(2) क
(3) ग
(4) घ
(5) ख

प्रश्न 8.
योजयत (जोड़ो)

उत्तर:
(क) → 3
(ख) → 1
(ग) → 4
(घ) → 2

प्रश्न 9.
रेखांकितपदानि लङ्लकारे परिवर्तयत (रेखांकित शब्दों को लङ् लकार में बदलो)-
एकः पिपासितः काकः अस्ति। सः जलं पातुम् इच्छति। ग्रीष्मकालः अस्ति, सः बहुत्र विहरति, पश्यति, किन्तु जलं न मिलति। काकः एकंघटं पश्यति, समीपं गच्छति। तस्मिन् घटे किञ्चित जलम् अस्ति। परितः पश्यति। जलं पातुंन पारयति। घटस्य पार्वे शिलाखण्डान् पश्यति। तान् घटे पातयति। जलम् उपर्युपरि आगच्छति। काकः जलम् पिबति। प्रसन्नः भवति। तत: गच्छति।
उत्तर:
एकः पिपासितः काकः आसीत्। सः जलं पातुं इच्छति। ग्रीष्मकालः अस्ति, स: बहुत्र विहरति, पश्यति, किन्तु जलं न अमिलत्। एकत्र एकं घटं अपश्यत्, समीपं अगच्छत्। तस्मिन् घटे किञ्चित जलम् आसीत्। परितः पश्यति। जलं पातुं न पारयति। घटस्य पार्वे शिलाखण्डान् पश्यति। तान् घटे अपातयत्। जलम् उपर्युपरि आगच्छत्। काकः जलम् अपिबत्। प्रसन्नः भवति। ततः अगच्छत्।

प्रश्न 10.
योगशब्दं चित्वा उचितस्थाने लिखत (उचित शब्द चुनकर उचित स्थान पर लिखें)
काकः, पिकः, गजः, व्याघ्रः, धेनुः, शशकः, मयूरः, सिंहः, अजाः, मार्जारः, सर्पः, अश्वः, हरिणः, भल्लूकः, वानरः, श्वानः, महिषी, चटका।

प्रश्न 11.
विभक्त्यनुसारं वाक्यानि लिखत (विभक्ति के अनुसार वाक्यों को लिखो)

उत्तर:

1. गीतायाः पितुः नाम सुरेशः। (षष्ठी विभक्ति)
2. भो गीते! अत्र आगच्छतु। (सम्बोधन)
3. माता गीतायै मोदकं ददाति। (चतुर्थी)
4. गीतां आह्वयतु। (द्वितीया)
5. गीतायाः पुस्तकं स्वीकरोतु। (पंचमी)
6. गीतया सह गीता गच्छति। (तृतीया)
7. गीता गच्छति। (प्रथमा)
8. गीतायाम् सद्गुणः सन्ति। (सप्तमी)

MP Board Class 6th Sanskrit Solutions

MP Board Class 6th Maths Solutions Chapter 14 प्रायोगिक ज्यामिती Ex 14.6

पाठ्य-पुस्तक पृष्ठ संख्या # 313

प्रश्न 1.
75° माप वाले कोण ∠POQ की रचना कीजिए।
हल :
रचना के पद :
(1) किरण OP’ खींचते हैं।
(2) ∠BOQ = 90° बनाते हैं जबकि ∠LOQ = 60° और ∠BOL = 30°

(3) ∠BOL का समद्विभाजक \(\overline { OP } \) खींचते हैं।
इस प्रकार ∠LOP = \(\frac { 1 }{ 2 }\) ∠BOL
या ∠LOP = \(\frac { 1 }{ 2 }\) (30°) = 15°
(4) ∵ 60° + 15 = 75°
अतः ∠QOL + ∠LOP = ∠POQ
∴∠POQ = 75°

प्रश्न 2.
147° माप वाले एक कोण की रचना कीजिए और उसका समद्विभाजक खींचिए।
हल :
रचना के पद :
(1) किरण \(\overrightarrow{O A}\) खीचते हैं।
(2) चाँदे की सहायता से ∠AOB = 147° बनाते हैं।

(3) O को केन्द्र मानकर और सुविधाजनक त्रिज्या लेकर एक चाप लगाते हैं जो भुजा \(\overrightarrow{O A}\) और \(\overrightarrow{O B}\) को क्रमशः Q तथा पर काटता है।
(4) P को केन्द्र मानकर और PQ के आधे से अधिक त्रिज्या लेकर एक चाप लगाते हैं।
(5) पुनः Q को केन्द्र मानकर और इसी त्रिज्या से दूसरा चाप लगाते हैं, जो पहले चाप को R पर काटता है।
(6) O और R को मिलाते हुए आगे बढ़ाते हैं।
इस प्रकार OR, ∠AOB का अभीष्ट समद्विभाजक है।

प्रश्न 3.
एक समकोण खींचिए और उसके समद्विभाजक की रचना कीजिए।
हल :
रचना के पद :
(1) सर्वप्रथम एक रेखा l खीचते हैं और इस पर कोई बिन्दु O लेते हैं।
(2) O को केन्द्र मानकर और सुविधाजनक त्रिज्या लेकर एक चाप लगाते हैं, जो l को A और B पर काटता है।

(3) अब A और B को केन्द्र मानकर और AB के आधे से अधिक त्रिज्या लेकर दो चाप लगाते हैं, जो परस्पर C पर काटते हैं।
(4) O और C को मिलाते हैं।
इस प्रकार ∠AOC = 90° प्राप्त होता है।
(5) A और D को केन्द्र मानकर और AD के आधे से अधिक त्रिज्या लेकर दो चाप लगाते हैं, जो परस्पर E पर काटते
(6) O और E को मिलाते हुए इसे आगे बढ़ाते हैं।
इस प्रकार \(\overrightarrow{O E}\) , ∠AOC का अभीष्ट समद्विभाजक है, अर्थात् \(\overrightarrow{O E}\) समकोण का समद्विभाजक है।

प्रश्न 4.
153° का एक कोण खींचिए और इसके चार बराबर भाग कीजिए।
हल :
रचना के पद:
(1) किरण \(\overrightarrow{ AB }\) खींची।

(2) A पर चाँदे की सहायता से ∠BAC = 153° बनाया।
(3) ∠BAC का समद्विभाजक \(\overrightarrow{ AD }\) खींचा।
(4) पुनः ∠DAC का समद्विभाजक \(\overrightarrow{ AE }\) खींचा।
(5) ∠BAD का समद्विभाजक \(\overrightarrow{ AF }\) खींचा।
इस प्रकार \(\overrightarrow{A E}, \overrightarrow{A D}\) और \(\overrightarrow{ AF }\) दिए हुए कोण ∠BAC को चार समान भागों में विभाजित करते हैं।

प्रश्न 5.
रूलर और परकार की सहायता से निम्न मापों के कोणों की रचना कीजिए :
(a) 60°
(b) 300
(c) 90°
(d) 120°
(e) 45°
(f) 135°
हल :
(a) रचना के पद :
(1) सर्वप्रथम किरण \(\overrightarrow{ OA }\) खींचते हैं।
(2) O को केन्द्र मानकर तथा उपयुक्त त्रिज्या लेकर एक चाप लगाया जो OA को P पर काटता है।

(3) P को केन्द्र मानकर तथा उसी त्रिज्या से चाप लगाया जो पहले चाप को R पर काटता है।
(4) O को R से मिलाया और B तक आगे बढ़ाया।
इस प्रकार ∠AOB = 60°

(b) (1) सर्वप्रथम किरण \(\overrightarrow{ OA }\) खीचते हैं।
(2) O को केन्द्र मानकर और उपयुक्त त्रिज्या लेकर एक चाप PS लगाया जो OA को P पर काटता है।
(3) P को केन्द्र मानकर उसी त्रिज्या से चाप लगाया जो पहले चाप को Q पर काटता है।
(4) O को Q से मिलाते हुए आगे B तक बढ़ाया।
इस प्रकार ∠AOB = 60°
(5) अब ∠AOB का समद्विभाजक \(\overrightarrow{ OC }\) ज्ञात किया।

इस प्रकार ∠AOC = \(\frac { 1 }{ 2 }\) ∠AOB
= \(\frac { 1 }{ 2 }\) x 60° = 30°
अतः अभीष्ट ∠AOC = 30°

(c) (1) सर्वप्रथम किरण \(\overrightarrow{ OA }\) खींचते हैं।
(2) O को केन्द्र मानकर और उपयुक्त त्रिज्या लेकर एक चाप लगाते हैं, जो OA को P पर काटता है।

(3) P को केन्द्र मानकर और उसी त्रिज्या से एक चाप लगाया जो पहले चाप को R पर काटता है।
(4) अब R को केन्द्र मानकर उसी त्रिज्या से दूसरा चाप लगाया जो पहले चाप को S पर काटता है।
(5) अब R और S को केन्द्र मानकर दो चाप लगाए जो परस्पर Q पर काटते हैं।
(6) O को Q से मिलाते हुए आगे बढ़ाया।
इस प्रकार अभीष्ट कोण ∠AOQ = 90°

(d) (1) सर्वप्रथम किरण OA खींचते हैं।
(2) O को केन्द्र मानकर और उपयुक्त त्रिज्या लेकर एक चाप लगाया जो OA को P पर काटता है।
(3) P को केन्द्र मानकर उसी त्रिज्या से एक चाप लगाया जो पहले चाप को R पर काटता है।

(4) R को केन्द्र मानकर उसी त्रिज्या से दूसरा चाप लगाते हैं जो पहले चाप को S पर काटता है।
(5) O को S से मिलाते हुए आगे B तक बढ़ाया।
इस प्रकार अभीष्ट ∠AOB = 120°

(e) (1) सर्वप्रथम ∠AOQ = 90° बनाते हैं।
(2) ∠AOQ का समद्विभाजक OR ज्ञात करते हैं।
इस प्रकार ∠AOR = 45°

(f) चूँकि 135° = 90° + 45°
अर्थात् 90° + \(\frac { 1 }{ 2 }\) (90°) = 135°
आकृति में, ∠BOD = 90°

∠BOD का समद्विभाजक OC ज्ञात करते हैं।
इस प्रकार ∠BOC = 45°
अतः ∠AOC = 135°

प्रश्न 6.
45° का कोण खींचिए और उसके समद्विभाजक कीजिए।
हल :
रचना के पद :
(1) सर्वप्रथम किरण \(\overrightarrow{ OA }\) खींचते हैं।
(2) ∠AOQ = 45° बनाते हैं।

(3) C को केन्द्र मानकर और CD के आधे से अधिक त्रिज्या लेकर एक चाप लगाते हैं।
(4) D को केन्द्र मानकर और उसी त्रिज्या से लेकर एक दूसरा चाप लगाते हैं जो पहले चाप को B पर काटता है।
(5) O को B से मिलाया और आगे बढ़ाया।
इस प्रकार \(\overrightarrow{ OB }\) , ∠AOQ को दो समान भागों में विभाजित करता है।
∠AOB = \(\frac { 1 }{ 2 }\) (45°) = 22\(\frac { 1 }{ 2 }\)°

प्रश्न 7.
135° का कोण खींचिए और उसे समद्विभाजित कीजिए।
हल :
रचना के पद :
(1) सर्वप्रथम रेखा AB खींचते हैं और इस पर कोई बिन्दु O लेते हैं।

(2) बिन्दु O पर ∠AOC = 135° बनाते हैं।
(3) ∠AOC का समद्विभाजक \(\overrightarrow{ OD }\) खींचते हैं।
इस प्रकार ∠AOD = \(\frac { 1 }{ 2 }\) (135°) = 67\(\frac { 1 }{ 2 }\)°

प्रश्न 8.
70° का कोण खींचिए। इस कोण के बराबर रूलर और परकार की सहायता से एक कोण बनाइए।
हल:

रचना के पद-
(1) रेखाखण्ड \(\overrightarrow{ OA }\) खींचा।
(2) बिन्दु O पर चाँद की सहायता से ∠AOB = 70° बनाया।
(3) अब किरण \(\overrightarrow{ PQ }\) खींचते हैं।
(4) O को केन्द्र मानकर और उपयुक्त त्रिज्या लेकर एक चाप लगाया जो \(\overrightarrow{ OA }\) और \(\overrightarrow{ OB }\) को क्रमशः E और F पर काटता है।
(5) P को केन्द्र मानकर और उसी त्रिज्या से एक दूसरा चाप लगाया जो \(\overrightarrow{ PQ }\) को R पर काटता है।
(6) R को केन्द्र मानकर और EF के बराबर त्रिज्या लेकर पहले चाप को S पर काटते हुए एक चाप लगाते हैं।
(7) P को 5 से मिलाते हुए आगे बढ़ाते हैं।
इस प्रकार ∠QPS = ∠AOB = 70°

प्रश्न 9.
40° का एक कोण खींचिए। इसके सम्पूरक के बराबर एक कोण बनाइए।
हल:

रचना के पद :
(1) चाँद की सहायता से ∠AOB = 40° बनाते हैं। इसका सम्पूरक कोण ∠COB है।
(2) एक किरण OL खींचते हैं।
(3) O को केन्द्र मानकर और उपयुक्त त्रिज्या लेकर एक चाप लगाते हैं जो \(\overrightarrow{ OC }\) और \(\overrightarrow{ OB }\) को क्रमश: E और F पर काटता है।
(4) P को केन्द्र मानकर और उसी त्रिज्या को लेकर एक चाप लगाते हैं जो \(\overrightarrow{ OP }\) को N पर काटता है।
(5) अब N को केन्द्र मानकर और EF त्रिज्या लेकर एक चाप लगाते हैं, जो पहले चाप को M पर काटता है।
(6) P को M से मिलाया और आगे बढ़ाया।
इस प्रकार ∠OPM = सम्पूरक ∠COB

MP Board Class 6th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 16 संख्याओं के साथ खेलना Ex 16.2

प्रश्न 1.
यदि 21y5, 9 का एक गुणज है, जहाँ y एक अंक है, तोy का मान क्या है?
हल:
क्योंकि 21y5, 9 का एक गुणज है।
इसलिए अंकों का योग = 2 + 1 + y + 5 = 8 + y, 9 का गुणज है।
∴ (8 + y), 0, 9, 18, 27 में से कोई एक संख्या होगी।
परन्तु y एक अंक है, इसलिए y + 8 = 9
या y = 9 – 8 = 1

प्रश्न 2.
यदि 3155, 9 का एक गुणज है, जहाँ : एक अंक है, तो का मान क्या है? आप देखेंगे कि इसके दो उत्तर हैं। ऐसा क्यों है?
हल:
क्योंकि 31z5, 9 का एक गुणज है।
इसलिए अंकों का योग = 3 + 1 + z + 5 = 9 + z, 9 का गुणज है।
∴ (9 + z), 0, 9, 18, 27 में से कोई एक संख्या होगी।
परन्तु z एक अंक है, इसलिए 9 + z = 9, 18, …
अर्थात् 9 + z = 9 या z = 0, 9 + z = 18 या z = 9
इसलिए, z = 0 और = 9
उत्तर यहाँ अंक 0 और 9 दोनों ही अंक क्रमशः संख्या 3105 तथा 3195 बनाते हैं, ये संख्याएँ 9 से विभाज्य हैं।

प्रश्न 3.
यदि 24x, 3 का एक गुणज है, जहाँ x एक अंक है, तोx का मान क्या है?
हल:
क्योंकि 24x, 3 का गुणज है, इसलिए इसके अंकों का योग 6 + x, 3 का एक गुणज है। अर्थात् 6 + x निम्नलिखित में से कोई एक संख्या होगी –
0, 3, 6, 9, 12, 15, 18, …..
परन्तु चूँकि x एक अंक है, इसलिए 6 + x = 6 या 6 + x = 9 या 6 + x = 12 या 6 + x = 15 हो सकता है। अतः x = 0 या 3 या 6 या 9 हो सकता है। इसलिए x का मान इन चारों विभिन्न मानों में से कोई एक हो सकता है।
इसलिए x = 0, 3, 6 या 9

प्रश्न 4.
31:5, 3 का एक गुणज है, जहाँ : एक अंक है, तो का मान क्या हो सकता है?
हल:
क्योंकि 3125, 3 का गुणज है, इसलिए इसके अंकों का योग 9 + z, 3 का एक गुणज है। अर्थात् 6 + x निम्नलिखित में से कोई एक संख्या होगी –
0, 3, 6, 9, 12, 15, 18,…
परन्तु चूँकि x एक अंक है, इसलिए 9 + z = 9 या 9 + z = 12 या 9+ z = 15 या 9 + z = 18 हो सकता है। अतः z = 0 या 3 या 6 या 9 हो सकता है। इसलिए z का मान इन चारों विभिन्न मानों में से कोई एक हो सकता है।
इसलिए 2 = 0, 3, 6 या 9

MP Board Class 8th Maths Solutions