MP Board Class 9th Maths Solutions Chapter 1 Number Systems Ex 1.4
Question 1.
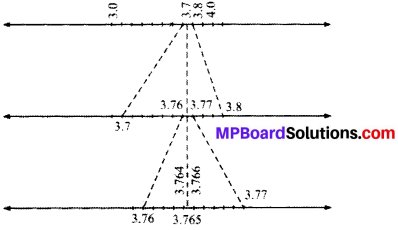
Visualise 3.765 on the number line, using successive magnification.
Solution:
Visualizing 3.765
Question 2.
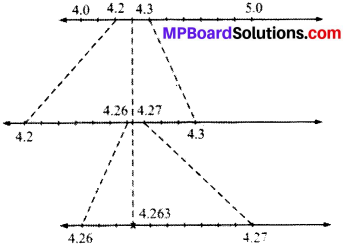
Visualise 4.26 on the number line, up to 4 decimal places.
Solution:
Visualising 4.26 = 4.2626
= 4.263
Rationalisation of the Denominator of an irrational number having two terms in the Denominator:
To rationalise the denominator of an irrational number having two terms in the denominator, multiply the numerator and denominator of the number by the conjugate of its denominator.
Example 1.
If a and b are rational numbers and \(\frac { 3+\sqrt { 7 } }{ 3-\sqrt { 7 } } \) = a + b√7 find value of a and b.
Solution:
We have \(\frac { 3+\sqrt { 7 } }{ 3-\sqrt { 7 } } \) = a + b√7
Multiply denominator and numerator by 3 + √7 on LHS, then we have
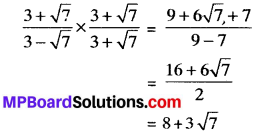
On comparing LHS and RHS, we get
a = 8, b = 3
Example 2.
Determine a and b if \(\frac { 5+\sqrt { 3 } }{ 7-4\sqrt { 3 } } \) = 94a + 3 √3b
Multiply numerator and denominator by 7 + 4√3 on LHS, then we have

On comparing LHS and RHS, we get
a = \(\frac{1}{2}\) and b = 9.
![]()
Example 3.
Determine a and 6 if \(\frac { 7+\sqrt { 5 } }{ 7-\sqrt { 5 } } \) – \(\frac { 7-\sqrt { 5 } }{ 7+\sqrt { 5 } } \) = a + 7√5b.
Solution:
We have

On comparing LHS and RHS, we get
a = 0 and b = \(\frac{1}{11}\).