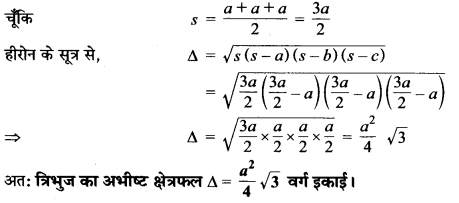Category: Class 9

MP Board Class 9th Science Solutions Chapter 8 गति

MP Board Class 9th Science Chapter 8 पाठ के अन्तर्गत के प्रश्नोत्तर

प्रश्न श्रृंखला-1 # पृष्ठ संख्या 110

प्रश्न 1.
एक वस्तु के द्वारा कुछ दूरी तय की गयी। क्या इसका विस्थापन शून्य हो सकता है? अगर हाँ, तो अपने उत्तर को उदाहरण के द्वारा समझाइए।
उत्तर:
हाँ, विस्थापन शून्य हो सकता है।
उदाहरण:
वृत्ताकार मार्ग पर गति करता हुआ कोई पिण्ड एक चक्कर लगाता है तो उसकी प्रारम्भिक एवं अन्तिम स्थिति एक ही है अतः विस्थापन शून्य है।

प्रश्न 2.
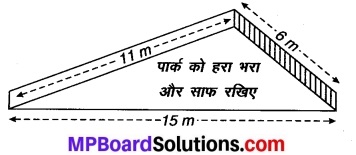
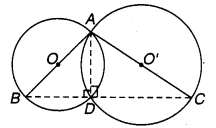
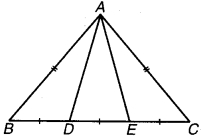
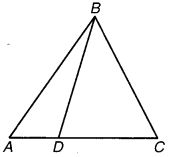
एक किसान 10 m की भुजा वाले एक वर्गाकार खेत की सीमा पर 40 s में चक्कर लगाता है। 2 मिनट 20 सेकण्ड के बाद किसान के विस्थापन का परिमाण क्या होगा?
हल:
1 चक्कर में लगा समय = 40 s (दिया है)
कुल समय 2 मिनट 20 से. = 120 + 20 = 140 s

अर्थात् यदि किसान चित्रानुसार A से गति प्रारम्भ करता है, तो C पर यात्रा समाप्त करेगा अर्थात् विस्थापन AC कर्ण होगा।
जिसका मान = वर्ग की भुजा x √2 = 10√2 मीटर = 14.14 मीटर
अतः अभीष्ट विस्थापन = 14.14 मीटर।

प्रश्न 3.
विस्थापन के लिए निम्न में कौन सही है –
(a) यह शून्य नहीं हो सकता।
(b) इसका परिमाण वस्तु के द्वारा तय की गई दूरी से अधिक है।
उत्तर:
उपर्युक्त कोई भी कथन सत्य नहीं है।

प्रश्न श्रृंखला-2 # पृष्ठ संख्या 112

प्रश्न 1.
चाल एवं वेग में अन्तर बताइए। (2018, 19)
उत्तर:
चाल और वेग में अन्तर:

प्रश्न 2.
किस अवस्था में किसी वस्तु के औसत वेग का परिमाण उसकी औसत चाल के बराबर होगा?
उत्तर:
जब वस्तु की गति एक निश्चित दिशा में सरल रेखीय होगी।

प्रश्न 3.
एक गाड़ी का ओडोमीटर क्या मापता है?
उत्तर:
गाड़ी द्वारा तय की गई दूरी।

प्रश्न 4.
जब वस्तु एकसमान गति में होती है तब इसका मार्ग कैसा दिखाई देता है?
उत्तर:
एक सरल रेखा।

प्रश्न 5.
एक प्रयोग के दौरान अन्तरिक्ष यान से एक सिग्नल को पृथ्वी पर पहुँचने में 5 मिनट का समय लगता है। पृथ्वी पर स्थित स्टेशन से इस अन्तरिक्ष यान की दूरी क्या है? (जबकि सिग्नल की चाल = प्रकाश की चाल = 3 x 108 m s^-1)
हल:
दिया है:
सिग्नल की चाल = प्रकाश की चाल = 3 x 10⁸ m s^-1
सिग्नल पहुँचने में लगा समय = 5 मिनट = 5 x 60 = 300 सेकण्ड
अन्तरिक्ष यान की दूरी = सिग्नल की चाल x समय
= 3 x 10⁸ x 300 = 9 x 10¹⁰ m = 9 x 10⁷ km
अतः अन्तरिक्ष यान की अभीष्ट दूरी = 9 x 10¹⁰ m अर्थात् 9 x 10⁷ km.

प्रश्न शृंखला-3 # पृष्ठ संख्या 114

प्रश्न 1.
आप किसी वस्तु के बारे में कब कहेंगे कि –
1. वह एकसमान त्वरण से गति में है।
2. वह असमान त्वरण से गति में है।
उत्तर:

1. जब वस्तु के वेग में परिवर्तन की दर समान हो।
2. जब वस्तु के वेग में परिवर्तन मीटर असमान हो।

प्रश्न 2.
एक बस की गति 5 s में 80 km h^-1 से घटकर 60 km h^-1 हो जाती है। बस का त्वरण ज्ञात कीजिए।
हल :
ज्ञात है:

समय t = 5 s.
चूँकि हम जानते हैं कि v = u + at

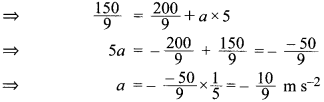
अत: अभीष्ट त्वरण \(=-\frac{10}{9} \mathrm{m} \mathrm{s}^{-2}\). (मंदन)

प्रश्न 3.
एक रेलगाड़ी स्टेशन से चलना प्रारम्भ करती है और एक समान त्वरण के साथ चलते हुए 10 मिनट में 40 km h^-1 की चाल प्राप्त करती है। इसका त्वरण ज्ञात कीजिए।
हल:
ज्ञात है:
रेलगाड़ी का प्रारम्भिक वेग u = 0 m s^-1
रेलगाड़ी का अन्तिम वेग y= 40 km/h
\(=40 \times \frac{5}{18}=\frac{100}{9} \mathrm{m} \mathrm{s}^{-1}\)
समय t = 10 मिनट = 10 x 6 = 600 s
चूँकि हम जानते हैं कि:
v = u + at

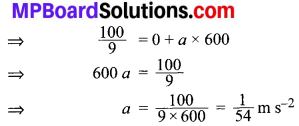
अतः अभीष्ट त्वरण \(=\frac{1}{54} \mathrm{m} \mathrm{s}^{-2}\).

प्रश्न शृंखला 4 # पृष्ठ संख्या 118

प्रश्न 1.
किसी वस्तु के एकसमान व असमान गति के लिए समय-दूरी ग्राफ की प्रकृति क्या होती है?
उत्तर:
किसी वस्तु के एकसमान गति के लिए समय-दूरी ग्राफ एक सरल रेखा होगी, जबकि असमान गति के लिए समय-दूरी ग्राफ एक वक्र होगा।

प्रश्न 2.
किसी वस्तु की गति के विषय में आप क्या कह सकते हैं जिसका दूरी-समय ग्राफ समय अक्ष के समानान्तर एक सरल रेखा है?
उत्तर:
वस्तु स्थिर है।

प्रश्न 3.
किसी वस्तु की गति के विषय में आप क्या कह सकते हैं जिसका चाल-समय ग्राफ समय अक्ष के समानान्तर एक सरल रेखा है?
उत्तर:
वस्तु समान वेग से गति कर रही है।

प्रश्न 4.
वेग-समय ग्राफ के नीचे के क्षेत्र से मापी गई राशि क्या होती है?
उत्तर:
चली गई दूरी।

प्रश्न शृंखला 5 # पृष्ठ संख्या 121

प्रश्न 1.
कोई बस विरामावस्था से चलना प्रारम्भ करती है तथा 2 मिनट तक 0.1 ms^-2 के एकसमान त्वरण से चलती है। परिकलन कीजिए –
(a) प्राप्त की गई चाल
(b) तय की गई दूरी।
हल:
ज्ञात है :
बस की प्रारम्भिक चाल u = 0 m s^-1 = 12 m s^-1.
बस का त्वरण a = 0.1 m s^-2
यात्रा का समय = 2 मिनट = 120 s
ज्ञात करना है:
(a) प्राप्त की गई चाल v = ?
(b) तय की गई दूरी s = ?
(a)
∵ v = u + at
v = 0 + 0.1 x 120
v = 12 m s^-1
अतः अभीष्ट चाल = 12 m s^-1

= 720 m
अत: अभीष्ट दूरी = 720 m.

प्रश्न 2.
कोई रेलगाड़ी 90 km h^-1 की चाल में चल रही है। ब्रेक लगाए जाने पर वह -0.5 m s^-2 का एकसमान त्वरण उत्पन्न करती है। रेलगाड़ी विरामावस्था में आने के पहले कितनी दूरी तय करेगी?
हल:
ज्ञात है:
रेलगाड़ी की प्रारभिक चाल u = 90 km h^-1
u = 90 x \(\frac{5}{18}\) = 25 m s^-1
रेलगाड़ी की अन्तिम चाल v = 0 ms^-1
त्वरण a = -0.5 m s^-2
ज्ञात करना है:
तय की गयी दूरी s = ?
∵ 2as = v² – u²
⇒ 2 (-0.5) s = (0)² – (25)²
⇒ – s = 0 – 625
⇒ s = 625 m
अतः तय की गई अभीष्ट दूरी = 625 m.

प्रश्न 3.
एक ट्रॉली एक आनत तल पर 2 m s^-2 के त्वरण से नीचे जा रही है। गति प्रारम्भ करने के 3 s के पश्चात् उसका वेग क्या होगा?
हल:
ज्ञात है:
त्वरण a = 2 m s^-2
प्रारम्भिक वेग u = 0 m s^-1
समय अन्तराल t = 3 s
ज्ञात करना है:
अन्तिम वेग v = ?
∵ v = u + at
⇒ v = 0 + 2 x 3
⇒ v = 0 + 6 = 6 m s^-1
अतः अभीष्ट अन्तिम वेग = 6 ms^-1.

प्रश्न 4.
एक रेसिंग कार का एकसमान त्वरण 4 ms^-2 है। गति आरम्भ करने के 10 s पश्चात् उसका वेग क्या होगा?
हल:
ज्ञात है:
त्वरण a = 4 m s^-2
प्रारम्भिक वेग u = 0 m s^-1
समयान्तराल t = 10 s
ज्ञात करना है:
अन्तिम वेग v = ?
⇒ v = u + at
⇒ v = 0 + 4 x 10
⇒ v = 0 + 40 = 40 m s^-1
अतः अभीष्ट अन्तिम वेग = 40 ms^-1.

प्रश्न 5.
किसी पत्थर को ऊर्ध्वाधर ऊपर की ओर 5 ms^-1 के वेग से फेंका जाता है। यदि गति के दौरान पत्थर का नीचे की ओर दिष्ट त्वरण 10 ms^-2 है, तो पत्थर के द्वारा कितनी ऊँचाई प्राप्त की गयी तथा उसे वहाँ पहुँचने में कितना समय लगा?
हल:
ज्ञात है:
पत्थर का प्रारम्भिक वेग = 5 m s^-1
नीचे की ओर दिष्ट त्वरण = -a = 10 ms^-2
⇒ a = – 10 m s^-2
पत्थर का अन्तिम वेग v = 0 m s^-1
ज्ञात करना है:
प्राप्त ऊँचाई s = ?
लगा समय t = ?
अतः प्राप्त अभीष्ट ऊँचाई = 1.25 m एवं पहुँचने में लगा समय = 0.5 s.
∵ 2as = v² – u²
⇒ 2 (-10) s = (0)² – (5)²
⇒ – 20 s = – 25
⇒ s = \(\frac{25}{20}\) = 1.25 m
एवं v = u + at
⇒ 0 = 5 + (- 10) t
⇒ 10 t = 5 ⇒ t = \(\frac{5}{10}\) = 0.55

MP Board Class 9th Science Chapter 8 पाठान्त अभ्यास के प्रश्नोत्तर

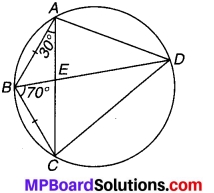
प्रश्न 1.
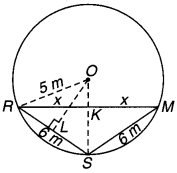
एक एथलीट वृत्तीय पथ, जिसका व्यास 200 m है, का एक चक्कर 40 s में लगाता है। 2 मिनट 20 सेकण्ड के बाद वह कितनी दूरी तय करेगा? और उसका विस्थापन क्या होगा?
हल:
ज्ञात है:
वृत्ताकार मार्ग का व्यास d = 200 m
एक चक्कर में लगा समय t₁ = 40 s
कुल समय = 2 min 20 s = 140 s
ज्ञात करना है:
दूरी = ?
विस्थापन = ?
एक चक्कर में चली दूरी = πd

चूँकि एथलीट \(3 \frac{1}{2}\) चक्कर लगाता है अतः उसकी अन्तिम स्थिति उसकी प्रारम्भिक स्थिति से वृत्ताकार मार्ग के व्यास के बराबर होगी।
इसलिए विस्थापन = व्यास की लम्बाई = 200 m
अतः अभीष्ट दूरी = 2200 m एवं अभीष्ट बिस्थापन = 200 m

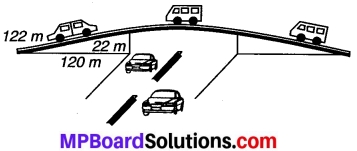
प्रश्न 2.
300 m सीधे रास्ते पर जोसेफ जागिंग करता हुआ 2 min 30 s में एक सिरे A से B पर पहुँचता है और घूमकर 1 min में 100 m पीछे बिन्दु C पर पहुँचता है। जोसेफ की औसत चाल और औसत वेग क्या होंगे?
(a) सिरे A से सिरे B तक, तथा
(b) सिरे A से सिरे C तक।
हुल:

(a)
सिरे A से सिरे B तक कुल चली गई दूरी s₁ = 300 m
A से B तक लगा कुल समय = 2 min 30 s = 120 + 30 = 150 s
सिरे A और B के बीच विस्थापन s = s₁ = 300 m

अत: अभीष्ट औसत चाल = 2 ms^-1 एवं अभीष्ट औसत वेग = 2 ms^-1.
(b)
सिरे A से C तक चली कुल दूरी = s₁ + S₂ = 300 + 100 = 400 m
A से C तक विस्थापन = s₁ – S₂ = 300 – 100 = 200 m
A से C तक यात्रा में लगा कुल समय = t₁ + t₂ = 2 min 30 s + 1 min
= 3 min 30 s = 180 + 30 = 210 s

अतः अभीष्ट औसत चाल = 1.9 m s^-1 एवं अभीष्ट औसत वेग = 0.952 m s^-1.

प्रश्न 3.
अब्दुल गाड़ी से स्कूल जाने के क्रम में औसत चाल को 20 km h-1 पाता है। उसी रास्ते से लौटने के समय वहाँ भीड़ कम है और औसत चाल 30 km h^-1 है। अब्दुल की इस पूरी यात्रा में उसकी औसत चाल क्या है?
हल:
मान लीजिए कि स्कूल की दूरी = x km

अत: अभीष्ट औसत चाल = 24 km h^-1

प्रश्न 4.
कोई मोटर बोट झील में विरामावस्था से सरल रेखीय पथ पर 3.0 m s^-2 के नियत त्वरण से 8.0 s तक चलती है। इस समय अन्तराल में मोटर बोट कितनी दूरी चलेगी?
हल:
ज्ञात है:
मोटर बोट की प्रारम्भिक चाल u = 0 ms^-1
त्वरण a = 3.0 m s^-2
समय अन्तराल t = 8.0 s
ज्ञात करना है:
चली गई दूरी s = ?
हम जानते हैं कि:
s = ut + \(\frac{1}{2}\) at
⇒ s = o x 8 + \(\frac{1}{2}\) (3.0) x (8.0)²
⇒ s = 0 + \(\frac{1}{2}\) x 3 x 64
⇒ s = 3 x 32 = 96 m
अतः चली गयी अभीष्ट दूरी = 96 m.

प्रश्न 5.
किसी गाड़ी का चालक 52 km h^-1 की गति से चल रही कार में ब्रेक लगाता है तथा कार विपरीत दिशा में एकसमान दर से त्वरित होती है। कार 5 5 में रुक जाती है। दूसरा चालक 30 km h^-1 की गति से चलती हुई दूसरी कार पर धीमे-धीमे ब्रेक लगाता है तथा 10 s में कार रुक जाती है। एक ही ग्राफ पेपर पर दोनों कारों के लिए चाल-समय ग्राफ आलेखित करें। ब्रेक लगाने के पश्चात् दोनों में से कौन-सी कार अधिक दूरी तक जायेगी ?
हल:
दोनों कारों का अभीष्ट चाल-समय ग्राफ –

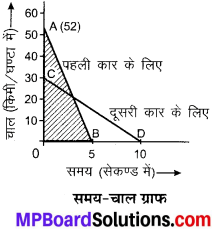
कार ‘A’ द्वारा चली गयी दूरी S_A = पहले त्रिभुज AOB का क्षेत्रफल

एवं कार ‘B’ द्वारा चली गयी दूरी S_B = दूसरे त्रिभुज COD का क्षेत्रफल
\(=\frac{1}{2} \times 30 \times \frac{5}{18} \times 10=\frac{375}{9} \mathrm{m}\)
अतः दूसरी कार अधिक दूरी तक जाएगी।

प्रश्न 6.
संलग्न चित्र में तीन वस्तुओं A, B और C का दूरी-समय ग्राफ प्रदर्शित है। ग्राफ का अध्ययन करके निम्न प्रश्नों के उत्तर दीजिए –
1. तीनों में से कौन सबसे तीव्र गति से गतिमान है?
2. क्या ये तीनों किसी भी समय सड़क के एक ही बिन्दु पर होंगे?
3. जिस समय B,A से गुजरती है उस समय तक C कितनी दूरी तय कर लेती है?
4. जिस समय B, C से गुजरती है उस समय तक यह कितनी दूरी तय कर लेती है?

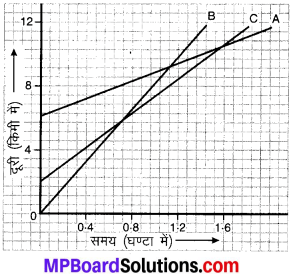
उत्तर:

1. तीनों में से सबसे तीव्र गति से B गतिमान है क्योंकि B के ग्राफ का ढाल (प्रवणता) अधिकतम है, अतः उसकी चाल अधिकतम है।
2. ये तीनों कभी भी एक समय पर सड़क के एक ही बिन्दु पर नहीं होंगे।
3. C द्वारा तय की गई दूरी = 8 – 2 = 6 km
4. B द्वारा तय की गई दूरी = 6 – 0 = 6 km.

प्रश्न 7.
20 m की ऊँचाई से एक गेंद को गिराया जाता है। यदि उसका वेग 10 ms^-2 के एकसमान त्वरण की दर से बढ़ता है, तो यह किस वेग से धरातल से टकराएगी तथा कितने समय पश्चात् वह धरातल से टकराएगी?
हल:
ज्ञात है:
गेंद का प्रारम्भिक वेग u = 0 m s^-1
ऊँचाई h = 20 m
त्वरण a = 10 m s^-2
ज्ञात करना है:
अन्तिम वेग v = ?
समयान्तराल t = ?
∵ v² = u² + 2as
⇒ v² = (0)² + 2 x 10 x 20
⇒ v² = 400 ⇒ v = √400 = 20 m s^-1
अब ∵ v = u + at
⇒ 20 = 0 + 10 x t
⇒ 10 t = 20 ⇒ t= \(\frac{20}{10}\) = 2 s
अत: गेंद धरातल से 20 ms^-1 के वेग से 2 s पश्चात् टकराएगी।

प्रश्न 8.
किसी कार का चाल-समय ग्राफ निम्न चित्र में दर्शाया गया है।
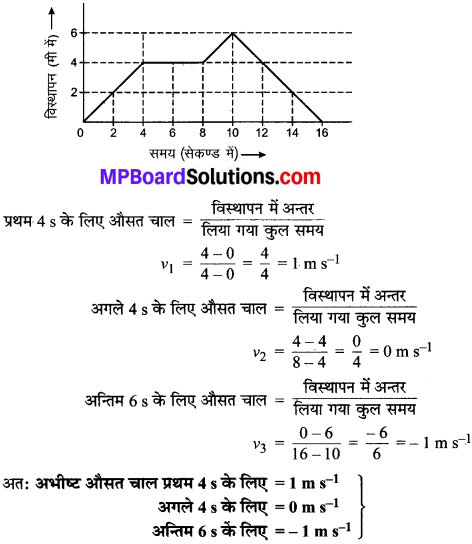
(a) पहले 4 s में कार कितनी दूरी तय करती है? इस अवधि में कार द्वारा तय की गई दूरी को ग्राफ में छायांकित क्षेत्र द्वारा दर्शाइए।

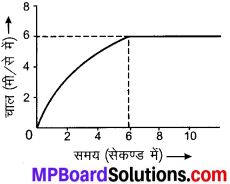
(b) ग्राफ का कौन-सा भाग कार की एकसमान गति को दर्शाता है?
उत्तर:
(a) प्रथम 4 s में तय की गई दूरी को छायांकित क्षेत्र द्वारा प्रदर्शन।

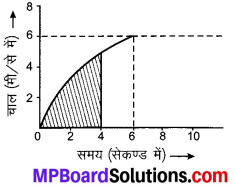
(b) ग्राफ का 6 5 से 10 s के बीच का भाग कार की एकसमान गति को दर्शाता है।

प्रश्न 9.
निम्नलिखित में से कौन-सी अवस्थाएँ सम्भव हैं तथा प्रत्येक के लिए एक उदाहरण दें –
(a) कोई वस्तु जिसका त्वरण नियत हो परन्तु वेग शून्य हो।
(b) कोई वस्तु किसी त्वरण से गति कर रही है लेकिन समान चाल से।
(c) कोई वस्तु किसी निश्चित दिशा में गति कर रही हो तथा त्वरण उसके लम्बवत् हो ?
उत्तर:
(a) यह अवस्था सम्भव है केवल स्वतन्त्रतापूर्वक गिरती वस्तु के प्रारम्भिक बिन्दु पर अथवा ऊर्ध्वाधर ऊपर की ओर फेंकी गयी वस्तु के अन्तिम बिन्दु पर जहाँ वस्तु का वेग शून्य तथा त्वरण गुरुत्वीय है।

(b) यह अवस्था सम्भव है जब कोई वस्तु वृत्ताकार मार्ग पर समान चाल से चल रही है जहाँ किसी भी बिन्दु पर त्वरण मार्ग के केन्द्र की ओर होगा।

(c) यह अवस्था केवल उस स्थिति में सम्भव है जब कोई वस्तु किसी दिशा में गति करना प्रारम्भ करती है तथा वृत्ताकार मार्ग पर चलती है उस समय उसका त्वरण उसकी गति की दिशा के लम्बवत् मार्ग के केन्द्र की ओर होगा।

प्रश्न 10.
एक कृत्रिम उपग्रह 42250 km त्रिज्या की वृत्ताकार कक्षा में घूम रहा है। यदि वह 24 घण्टे में पृथ्वी की परिक्रमा करता है तो उसकी चाल का परिकलन कीजिए।
हल:
ज्ञात है:
उपग्रह की कक्षा की त्रिज्या r = 42250 km
एक चक्कर में लगा समय t = 24 घण्टे
ज्ञात करना है:
चाल v = ?

अत: उपग्रह की अभीष्ट चाल = 11065.975 km h^-1
अर्थात् 3.074 km s^-1.

MP Board Class 9th Science Chapter 8 परीक्षोपयोगी अतिरिक्त प्रश्नोत्तर

MP Board Class 9th Science Chapter 8 वस्तुनिष्ठ प्रश्न

बहु-विकल्पीय प्रश्न

प्रश्न 1.
कोई कण त्रिज्या (r) के वृत्ताकार पथ में गमन कर रहा है। अर्धवृत्त पूरा करने के पश्चात् उसका विस्थापन होगा –
(a) शून्य
(b) πr
(c) 2r
(d) 2πr
उत्तर:
(c) 2r

प्रश्न 2.
एक पिण्ड वेग ‘u’ से ऊर्ध्वाधर ऊपर की ओर फेंका जाता है। इसके ऊपर उठने की अधिकतम ऊँचाई h होगी

उत्तर:
(b) \(\frac{u^{2}}{2 g}\)

प्रश्न 3.
किसी गतिमान पिण्ड के लिए विस्थापन तथा दूरी का आंकिक अनुपात क्या होता है?
(a) सदैव 1 से कम
(b) सदैव 1 के बराबर
(c) सदैव 1 से अधिक
(d) 1 के बराबर अथवा कम
उत्तर:
(d) 1 के बराबर अथवा कम

प्रश्न 4.
यदि किसी पिण्ड का विस्थापन, समय के वर्ग के अनुक्रमानुपाती है तो वह वस्तु गमन करती हैं –
(a) एकसमान वेग से
(b) एकसमान त्वरण से
(c) बढ़ते त्वरण से
(d) घटते त्वरण से
उत्तर:
(b) एकसमान त्वरण से

प्रश्न 5.
दिए गए v – t ग्राफ (संलग्न चित्र 8.7) से यह निष्कर्ष निकाल सकते हैं कि पिण्ड –

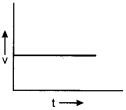
(a) एकसमान गति कर रहा है
(b) विराम अवस्था में है
(c) असमान गति कर रहा है
(d) एकसमान त्वरण से गति कर रहा है
उत्तर:
(a) एकसमान गति कर रहा है

प्रश्न 6.
मान लीजिए कोई लड़का 10 m s^-1 की नियत चाल से चल रहे ‘मेरीगोराडण्ड’ झूले पर सवारी करने का आनन्द ले रहा है। इससे ज्ञात होता है कि वह लड़का –
(a) विराम में है
(b) बिना त्वरण के गति कर रहा है
(c) त्वरित गति में है
(d) एकसमान वेग से गमन कर रहा है
उत्तर:
(c) त्वरित गति में है

प्रश्न 7.
v – t ग्राफ द्वारा घेरा गया क्षेत्रफल किसी भौतिक राशि को निरूपित करता है, जिसका मात्रक है –
(a) m²
(b) m
(c) m³
(d) m s^-1
उत्तर:
(c) m³

प्रश्न 8.
चार कार A, B, C तथा D किसी समतल सड़क पर गति कर रही हैं। इनके दूरी-समय ग्राफ संलग्न चित्र 8.8 में दर्शाये गए हैं। सही कथन चुनिए।

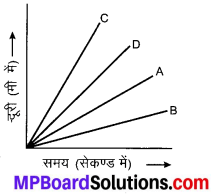
(a) कार A की चाल कार D से अधिक है
(b) कार B सबसे धीमी है
(c) कार D की चाल कार C से अधिक है
(d) कार C सबसे धीमी है।
उत्तर:
(b) कार B सबसे धीमी है

प्रश्न 9.
संलग्न चित्र का कौन-सा ग्राफ एकसमान गति का सही निरूपण करता है?

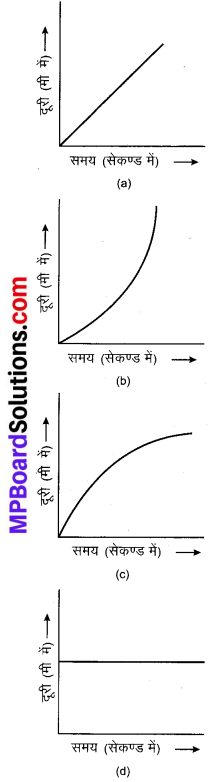
उत्तर:
(a)

प्रश्न 10.
वेग-समय ग्राफ की प्रवणता से प्राप्त होता है –
(a) दूरी
(b) विस्थापन
(c) त्वरण
(d) चाल
उत्तर:
(c) त्वरण

प्रश्न 11.
नीचे दिए गए प्रकरणों में से किसमें चली गई दूरी तथा विस्थापन के परिमाण समान होते हैं –
(a) यदि कार सीधी सड़क पर गमन कर रही है
(b) यदि कार वृत्ताकार पथ पर गमन कर रही है
(c) लोलक इधर-उधर गति कर रहा है
(d) पृथ्वी सूर्य की परिक्रमा कर रही है
उत्तर:
(a) यदि कार सीधी सड़क पर गमन कर रही है

प्रश्न 12.
वेग परिवर्तन की दर है – (2018)
(a) चाल
(b) त्वरण
(c) दाब
(d) बल
उत्तर:
(b) त्वरण

रिक्त स्थानों की पूर्ति

1. वेग परिवर्तन की दर …………….. कहलाती है।
2. विस्थापन की दर …………… कहलाती है।
3. वेग एक …………… राशि है।
4. विस्थापन एक …………… राशि है।
5. चाल एक ………….. राशि है।
6. दूरी एक …………….. राशि है।
7. यदि वस्तु की गति का पथ सरल रेखीय हो, तो ऐसी गति …………… कहलाती है।
8. त्वरण एक …………….. राशि है।
9. ऋणात्मक त्वरण …………….. कहलाता है।
10. वे भौतिक राशियाँ जिन्हें व्यक्त करने के लिए परिमाण एवं दिशा दोनों की आवश्यकता होती है, ……. कहलाती है।
11. वे भौतिक राशियाँ जिन्हें व्यक्त करने के लिए केवल परिमाण की आवश्यकता होती है, …………. कहलाती हैं।
उत्तर:

1. त्वरण
2. वेग
3. सदिश
4. सदिश
5. अदिश
6. अदिश
7. सरल रेखीय गति
8. सदिश
9. मंदन
10. सदिश
11. अदिश।

सही जोड़ी बनाना

उत्तर:

1. → (iii)
2. → (iv)
3. → (v)
4. → (vi)
5. → (i)
6. → (ii)

सत्य/असत्य कथन

1. प्रति सेकण्ड विस्थापन को चाल कहते हैं।
2. वेग परिवर्तन की दर त्वरण कहलाती है।
3. विस्थापन सदैव दूरी से अधिक होता है।
4. ऋणात्मक त्वरण को मंदन कहते हैं।
5. गतिमान वस्तु का वेग कभी भी शून्य नहीं हो सकता।
उत्तर:

1. असत्य
2. सत्य
3. असत्य
4. सत्य
5. असत्य।

एक शब्द/वाक्य में उत्तर

प्रश्न 1.
सरल आवर्त गति का उदाहरण दीजिए।
उत्तर:
लोलक की गति।

प्रश्न 2.
कोई पिण्ड एक वृत्ताकार मार्ग पर गति करता हुआ एक पूरा चक्कर लगाता है। उसका विस्थापन क्या होगा ?
उत्तर:
शून्य।

प्रश्न 3.
विस्थापन/समय अन्तराल व्यंजक किस भौतिक राशि को व्यक्त करते हैं?
उत्तर:
वेग।

प्रश्न 4.
वेग परिवर्तन की दर क्या कहलाती है?
उत्तर:
त्वरण।

प्रश्न 5.
प्रति सेकण्ड वेग में होने वाली कमी को क्या कहते हैं? (2019)
उत्तर:
मंदन।

MP Board Class 9th Science Chapter 8 अति लघु उत्तरीय प्रश्न

प्रश्न 1.
एकसमान गति से क्या समझते हो ? उदाहरण दीजिए।
उत्तर:
एकसमान गति:
“जब कोई वस्तु समान अन्तराल में समान दूरी तय करती है, तो उस वस्तु की गति को एकसमान गति कहते हैं।”
उदाहरण:
पृथ्वी के चारों ओर चन्द्रमा की गति।

प्रश्न 2.
असमान गति से क्या तात्पर्य है? उदाहरण दीजिए।
उत्तर:
असमान गति:
“जब कोई वस्तु समान समयान्तराल में असमान दूरी तय करती है तो उस वस्तु की गति को असमान गति कहते हैं।”
उदाहरण:
सड़क पर चलती कार की गति।

प्रश्न 3.
सरल रेखीय गति की परिभाषा दीजिए।
उत्तर:
सरल रेखीय गति:
“यदि किसी पिण्ड की गति का पथ एक सरल रेखा हो, तो उस पिण्ड की गति को सरल रेखीय गति कहते हैं।”

प्रश्न 4.
अदिश राशियों को परिभाषित कीजिए। उदाहरण भी दीजिए। (2019)
उत्तर:
अदिश राशियाँ:
“वे भौतिक राशियाँ जिनका व्यक्त करने के लिए केवल परिमाण की आवश्यकता होती है, दिशा की नहीं। अदिश राशियाँ कहलाती हैं।”
उदाहरण:
दूरी, चाल, घनत्व आदि।

प्रश्न 5.
सदिश राशियों को परिभाषित कीजिए। उदाहरण भी दीजिए। (2019)
उत्तर:
सदिश राशियाँ:
“वे भौतिक राशियाँ जिन्हें व्यक्त करने के लिए परिमाण के साथ-साथ दिशा की भी आवश्यकता होती है, सदिश राशियाँ कहलाती हैं।”
उदाहरण:
विस्थापन, वेग, त्वरण आदि।

प्रश्न 6.
चाल किसे कहते हैं? इसका मात्रक लिखिए।
उत्तर:
चाल:
“किसी वस्तु द्वारा इकाई समय अन्तराल में चली गई दूरी उस वस्तु की चाल कहलाती है।”

मात्रक:
मीटर प्रति सेकण्ड (m s^-1)

प्रश्न 7.
औसत चाल से क्या समझते हो?
उत्तर:
औसत चाल:
किसी समय अन्तराल में तय की गयी कुल दूरी और समय अन्तराल के अनुपात को औसत चाल कहते हैं।”

प्रश्न 8.
वेग की परिभाषा दीजिए तथा इसका मात्रक भी लिखिए।
उत्तर:
वेग-“समय के साथ विस्थापन की दर को वेग कहते हैं।”

मात्रक:
मीटर प्रति सेकण्ड (ms^-1)

प्रश्न 9.
असमान (परिवर्ती) वेग किसे कहते हैं?
उत्तर:
असमान (परिवर्ती) वेग:
“जब कोई गतिशील वस्तु बराबर समय-अन्तराल में बराबर दूरी तय करे लेकिन उसकी गति की दिशा बदल जाये अथवा बराबर समय अन्तराल में बराबर दूरी तय नहीं करे तो उस वस्तु का वेग असमान (परिवर्ती) वेग कहलाता है।”

प्रश्न 10.
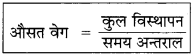
औसत वेग किसे कहते हैं?
उत्तर:
औसत वेग:
“किसी भी गतिशील वस्तु के कुल विस्थापन एवं समय-अन्तराल के अनुपात को औसत वेग कहते हैं।”

प्रश्न 11.
त्वरण किसे कहते हैं? इसका मात्रक लिखिए।
उत्तर:
त्वरण:
“वेग वृद्धि की समय के साथ दर को त्वरण कहते हैं।”

मात्रक:
मीटर प्रति सेकण्ड2 (m s^-2)

प्रश्न 12.
मंदन किसे कहते हैं? मंदन एवं त्वरण में क्या सम्बन्ध है?
उत्तर:
मंदन:
“किसी वस्तु के वेग में कमी एवं समय अन्तराल के अनुपात को मंदन कहते हैं।”

मंदन एवं त्वरण में सम्बन्ध:
ऋणात्मक त्वरण ही मंदन होता है।

प्रश्न 13.
वत्तीय गति किसे कहते हैं ? उदाहरण दीजिए।
उत्तर:
वृत्तीय गति:
“जब कोई गतिशील वस्तु किसी वृत्ताकार मार्ग पर गति करती है तो उस वस्तु की गति वृत्तीय गति कहलाती है।
उदाहरण:
वृत्ताकार मार्ग पर साइकिल चलाते सवार की गति।

प्रश्न 14.
एकसमान वृत्तीय गति किसे कहते हैं?
उत्तर:
एकसमान वृत्तीय गति:
“जब कोई वस्तु समान चाल से किसी वृत्ताकार मार्ग पर गति करती है तो उसकी गति को एकसमान वृत्ताकार गति कहते हैं।”

प्रश्न 15.
किसी गतिशील पिण्ड का दिए गए समय-अन्तराल में विस्थापन शून्य है। क्या इसके द्वारा चली गयी दूरी भी शून्य होगी? अपने उत्तर की पुष्टि कीजिए।
उत्तर:
नहीं।
वृत्ताकार मार्ग पर गतिमान कोई पिण्ड अपनी प्रारम्भिक स्थिति में लौट आता है तो उसका विस्थापन तो शून्य होता है लेकिन चली गयी दूरी शून्य नहीं है।

MP Board Class 9th Science Chapter 8 लघु उत्तरीय प्रश्न

प्रश्न 1.
गति के समीकरण किसी एकसमान वेग से गमन करते पिण्ड के लिए किस प्रकार परिवर्तित होते हैं?
हल:
∵ एकसमान वेग की स्थिति में त्वरण a = 0 m s^-2
∴ गति के समीकरण –
(1) v = u + at = u + 0 x t = v = u.
(2) s = ut + \(\frac{1}{2}\)at² = ut + \(\frac{1}{2}\) x 0 x t² = s = ut.
(3) v² = u² + 2as = u² + 2 x 0 x s = v = u.

प्रश्न 2.
कोई बालिका किसी सरल रेखीय पथ के अनुदिश चलकर पत्रपेटी में पत्र डालती है और वापस अपनी प्रारम्भिक स्थिति में लौट आती है। उसकी गति का दूरी-समय ग्राफ संलग्न चित्र में दर्शाया गया है। उसकी गति के लिए वर्ग-समय ग्राफ खींचिए।
हल:

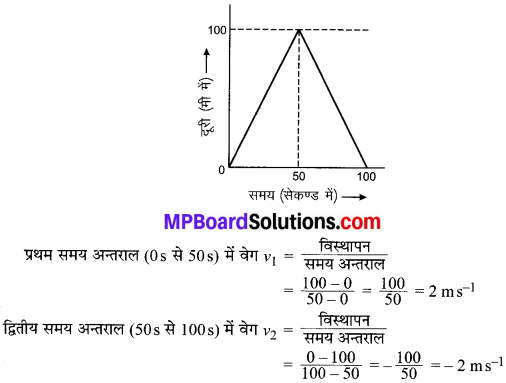
अतः अभीष्ट वेग-समय ग्राफ

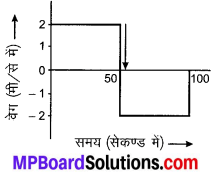
प्रश्न 3.
कोई कार विराम अवस्था से गति प्रारम्भ करके x – अक्ष के अनुदिश नियत त्वरण a’ = 5. m s^-2 से 85 तक गमन करती हैं। इसके पश्चात् यदि कार नियत वेग से गति करती रहती है, तो विराम से गति प्रारम्भ करने की पश्चात् 12 सेकण्ड में यह कितनी दूरी तय करेगी?
हल:
ज्ञात है:
प्रारम्भिक वेग u = 0 m s^-1
त्वरण a = 5 m s^-2
समय (त्वरित गति) t₁ = 8 s
अन्तिम समय t₂ = 12 s
प्रथम 8 सेकण्ड में चली दूरी
x₁ = ut₁ + \(\frac{1}{2}\)at₁²
= 0 x 8 + \(\frac{1}{2}\) x 5 x (8)²
= 160m
v₁ = u + at
= 0 + 5 x 8 = 40 m s^-1
8 s बाद कार एकसमान गति u = v₁ = 40 m s^-1 से गति करेगी।
अब अन्तिम 4 s (8वें सेकण्ड से 12वें सेकण्ड तक) में चली दूरी
x₂ = वेग x समय = 40 x (12 – 8)= 40 x 4= 160 m
कुल दूरी x = x₁ + x₂ = 160 m + 160 m = 320 m
अत: अभीष्ट दूरी = 320 m.

प्रश्न 4.
कोई मोटरसाइकिल सवार A से B तक 30 km h^-1 की एकसमान चाल से जाता है और 20 km h^-1 की चाल से वापस लौटता है। औसत चाल ज्ञात कीजिए।
हल:
ज्ञात है:
मोटरसाइकिल की जाते समय चाल = 30 km h^-1
एवं उसकी आते समय चाल = 20 km h^-1
माना A से B के बीच की दूरी x km है तो

अतः अभीष्ट औसत चाल = 24 km h^-1.

प्रश्न 5.
किसी साइकिल सवार की गति को वेग-समय ग्राफ (संलग्न चित्र) में दर्शाया गया है। इस गति का त्वरण, वेग तथा 15 5 में साइकिल सवार द्वारा तय की गई दूरी ज्ञात कीजिए।

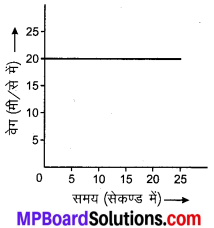
हल:
त्वरण:
चूँकि साइकिल 20 m s^-1 के एकसमान वेग से गतिमान है अर्थात् वेग में परिवर्तन नहीं है।
अतः त्वरण = 0 m s^-2
वेग:
ग्राफ के पाठांक के अनुसार वेग = 20 ms^-1 है अतः साइकिल का वेग = 20 m s^-1 प्रथम 15 s में साइकिल द्वारा तय की गयी दूरी संलग्न ग्राफ में छायांकित क्षेत्र से दिखाई गई है जिसका क्षेत्रफल = 20 x 15 = 300 m । इसलिए साइकिल द्वारा तय की गई दूरी = 300 m.

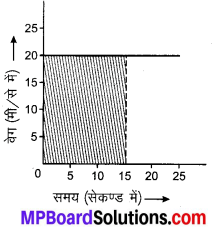
अतः अभीष्ट त्वरण = 0 m s^-2, वेग = 20 ms^-1 एवं तय की गई दूरी = 300 m.

प्रश्न 6.
उस पत्थर का वेग-समय ग्राफ खींचिए जो ऊर्ध्वाधर ऊपर फेंका जाता है और अधिकतम ऊँचाई पर पहुँचने के पश्चात् अधोमुखी वापस आ रहा है।
हल:
माना पत्थर प्रारम्भिक वेग से ऊपर की ओर ऊर्ध्वाधर फेंका जाता है जो गुरुत्वीय मंदन (ऋणात्मक गुरुत्वीय त्वरण) से गति करता है। अधिकतम ऊँचाई पर इसका वेग शून्य हो जाता है। पुनः यह गुरुत्वीय धनात्मक त्वरण से नीचे आता है। इसका समय-वेग अथवा वेग-समय ग्राफ संलग्न चित्र में दिखाया गया है।

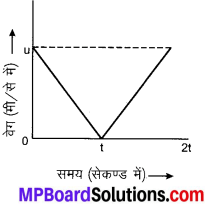
अतः अभीष्ट वेग-समय ग्राफ का उपर्युक्त चित्र है।

प्रश्न 7.
कोई पिण्ड 150 m की ऊँचाई से विश्राम से गिराया जाता है तथा उसी क्षण किसी अन्य पिण्ड को 100 m की ऊँचाई से विराम से गिराया जाता है। यदि दोनों प्रकरणों में त्वरण समान है तो 25 के पश्चात् इनकी ऊँचाई में क्या अन्तर है? समय में परिवर्तन के साथ इस ऊँचाई के अन्तर में क्या परिवर्तन होता है?
हल:
दोनों पिण्डों की प्रारम्भिक ऊँचाई में अन्तर = (150 m – 100 m) = 50 m
प्रथम पिण्ड द्वारा 2 s में चली गई दूरी
s₁ = 0 x 2 + \(\frac{1}{2}\) x g (2)² = 2g m
इस पिण्ड की ऊँचाई h₁ = (150 – 2g) m
दूसरे पिण्ड द्वारा 2 s में चली गई दूरी
s₂ = 0 x 2 + \(\frac{1}{2}\)g (2)₂ = 2gm [∴ u= 0 दिया है]
इस पिण्ड की ऊँचाई h₂ = (100 – 2g) m
इसलिए दोनों पिण्डों की ऊँचाइयों में अन्तर = (150 – 2g) – (100 – 2g) m
= 150 – 100 = 50 m = प्रारम्भिक ऊँचाई में अन्तर
अतः दोनों पिण्डों की (2s पश्चात्) ऊँचाइयों में अभीष्ट अन्तर = 50 m
समय परिवर्तन के साथ इस ऊँचाई के अन्तर में कोई परिवर्तन नहीं होगा।

प्रश्न 8.
5 x 10⁴ m s^-1 के वेग से गतिमान कोई इलेक्ट्रॉन एक समान विद्युत क्षेत्र में प्रवेश करके अपनी प्रारम्भिक गति की दिशा में 104 ms-2 का एकसमान त्वरण अर्जित करता है।
(i) वह समय परिकलित कीजिए जिसमें यह इलेक्ट्रॉन अपने प्रारम्भिक वेग का दो गुना वेग अर्जित करेगा।
(ii) इस समय में इलेक्ट्रॉन कितनी दूरी तय करेगा?
हल:
ज्ञात है:
इलेक्ट्रॉन का प्रारम्भिक वेग u = 5 x 10⁴ m s^-1
इसका अन्तिम वेग v = 2u = 10 x 10⁴ m s^-1
त्वरण a= 1 x 10⁴ m s^-2
ज्ञात करना है:
समय t = ?
तय दूरी x = ?
(i)
∵ v = u + at
⇒ 10 x 10⁴ = 5 x 10⁴ + 1 x 10⁴ t
⇒ 10⁴ t = 10 x 10⁴ – 5 x 10⁴ = 5 x 10⁴
t = 5 s.

(ii)
∵ x = ut + \(\frac{1}{2}\)at²
⇒ x = 5 x 10⁴ x 5 + \(\frac{1}{2}\) x 10⁴ x (5)²
= 25 x 10⁴ + \(\frac{25}{2}\) x 10⁴
= (25 + 12.5) x 10⁴ m
= 37.5 x 10⁴ m
अतः अभीष्ट समय = 5 s एवं अभीष्ट दूरी = 37.5 x 10⁴ m.

प्रश्न 9.
एकसमान त्वरण से गतिमान किसी पिण्ड द्वारा चौथे तथा पाँचवें सेकण्ड के अन्तराल के बीच दूरी के लिए सम्बन्ध व्युत्पन्न कीजिए।
हल:
मान लीजिए पिण्ड का प्रारम्भिक वेग u m s^-1 एवं एकसमान त्वरण a m s^-2 है तो
∵ s = ut + \(\frac{1}{2}\) at²
⇒ S₄ = u x 4+ \(\frac{1}{2}\)a (4)² = 4u + 8a
⇒ 5_s = u + 5 + \(\frac{1}{2}\)a (5)² = 5u + 12.5a
⇒ 5₅ – S₄ = u + 4.5 a = u + \(\frac{9}{2}\)a
अत: चौथे एवं पाँचवें सेकण्ड के अन्तराल में चली गई अभीष्ट दूरी = \(\left(u+\frac{9}{2} a\right)\)m.

प्रश्न 10.
दो गेंदें एक ही क्षण अपने-अपने क्रमशः प्रारम्भिक वेगों u₁ तथा u₂ से ऊपर की ओर ऊर्ध्वाधर दिशा में फेंकी जाती हैं। सिद्ध कीजिए कि इनके द्वारा तय की गई ऊँचाइयाँ u₁² : u₂² के अनुपात में होंगी। (यह मान लीजिए कि उपरिमुखी त्वरण – g तथा अधोमुखी त्वरण + g है।)
हल:
हम जानते हैं कि उपरिमुखी गति के लिए v² = u² – 2gh
परन्तु उच्चतम बिन्दु पर v = 0
इसलिए 0 = u² – 2gh

इससे सिद्ध होता है कि अभीष्ट गेंदों द्वारा तय की गई ऊँचाइयाँ u₁² : u₂² के अनुपात में होगी।

प्रश्न 11.
दूरी एवं विस्थापन में अन्तर लिखिए। (2018, 19)
उत्तर:
दूरी एवं विस्थापन में अन्तर:

MP Board Class 9th Science Chapter 8 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
ग्राफीय विधि से निम्न गति के समीकरणों की स्थापना कीजिए –

(1) v = u + at
(2) s = ut + \(\frac{1}{2}\)at²
(3) v² – u² = 2as.

हल:
मान लीजिए कि एकसमान त्वरण a से गतिमान किसी वस्तु का प्रारम्भिक वेग u एवं t सेकण्ड के समय अन्तराल के बाद अन्तिम वेग v है तथा इस समय अन्तराल में वस्तु द्वारा तय की गई दूरी s है तथा उसका वेग-समय ग्राफ संलग्न चित्र में दिया है।

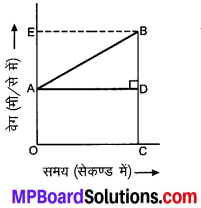
तो ग्राफ के अनुसार BC = v, OA = u तथा OC =t
तब BD = BC – DC = BC – OA = v – u
तथा AD = OC = t होगा।
चूँकि त्वरण = वेग-समय ग्राफ की प्रवणता = \(\frac{BD}{AD}\)
⇒ \(a=\frac{v-u}{t}\)
⇒ v – u = at
⇒ v = u + at …(1)
चूँकि वेग-समय ग्राफ में ग्राफ AB के नीचे घिरे क्षेत्र OABC द्वारा दूरी प्राप्त की जाती है।
इसलिए दूरी s = क्षेत्र. (OABC) = क्षेत्र. (आयत OADC) + क्षेत्र. (AABD)
= OC x OA+ \(\frac{1}{2}\)AD x BD
= t x u + \(\frac{1}{2}\) x t x (v – u)
⇒ s = ut + \(\frac{1}{2}\)(at) [∵ समीकरण (1) में v – u = at]
⇒ s = ut + \(\frac{1}{2}\)at² ….(2)
दूरी s = क्षेत्र. (समलम्ब चतुर्भुज OABC)

इस प्रकार गति के अभीष्ट समीकरणों –

1. v=u + at
2. s = ut + \(\frac{1}{2}\)at², एवं
3. 2as = v – u का ग्राफीय विधि से सत्यापन हुआ।

प्रश्न 2.
कोई पिण्ड विराम से गति प्रारम्भ करके पहले 2 5 में 20 m तथा अगले 45 में 160 m चलता है। प्रारम्भ से 7 s पश्चात् उसका वेग क्या होगा?
हल:
ज्ञात है:
प्रारम्भिक वेग u = 0
प्रथम t₁ = 2 s में दूरी s₁ = 20 m
अगले t₂ = 4 s में दूरी s₂ = 160 m
प्रारम्भ से समय t = 7.
s = ut + \(\frac{1}{2}\)at²
⇒ 20 = 0 x 2 + \(\frac{1}{2}\)a (2)²
⇒ 20 = 2a
⇒ a = \(\frac{20}{2}\) = 10^-2
2 s पश्चात् वेग v₁ है तो
v₁ = u + at
= 0 + 10 x 2 = 20 m s^-1
यह अगले 4 s के लिए प्रारम्भिक वेग / होगा। अब अगले 4 s में चली दूरी
S₂ = u’ t₂ + \(\frac{1}{2}\)a (t₂)
⇒ 160 = 20 x 4+ \(\frac{1}{2}\)a'(4)²
⇒ 160 = 80 + 8a’ ⇒ 8a’ = 160 – 80 = 80
a’ = \(\frac{80}{8}\) = 10 m s^-2
इस तरह हम देखते हैं कि त्वरण एकसमान है।
अब मान लीजिए 7 s पश्चात् वेग v है, तो
v =u+ at
v = 0 + 10 x 7 = 70 m s^-1
अतः 75 के पश्चात् अभीष्ट वेग = 70 m s^-1.

प्रश्न 3.
नीचे दिए गए आँकड़ों की सहायता से किसी गतिमान पिण्ड के लिए विस्थापन-समय ग्राफ खींचिए।

इस ग्राफ का उपयोग करके पहले 45 के लिए, अगले 4s के लिए तथा अन्तिम 6 s के लिए पिण्ड का औसत वेग ज्ञात कीजिए।
हल:
दिए हुए आँकड़ों के लिए विस्थापन-समय ग्राफ –

MP Board Class 9th Science Solutions

MP Board Class 9th Social Science Solutions Chapter 4 भारत : अपवाह तन्त्र

MP Board Class 9th Social Science Chapter 4 पाठान्त अभ्यास

MP Board Class 9th Social Science Chapter 4 वस्तुनिष्ठ प्रश्न

सही विकल्प चुनकर लिखिए

प्रश्न 1.
नदी अपने मार्ग के अन्त में निर्मित करती है (2009, 12)
(i) जल प्रताप
(ii) बाढ़ के मैदान
(iii) डेल्टा या एस्चुरी
(iv) गोखुर झील।
उत्तर:
(iii) डेल्टा या एस्चुरी

प्रश्न 2.
उत्तर भारत की नदियों की विशेषता नहीं हैं
(i) जल प्रतापों की संख्या कम है
(ii) यातायात हेतु उपयोग होता है
(iii) विसर्प नहीं मिलते हैं
(iv) जल की प्राप्ति हिम और वर्षा से होती है।
उत्तर:
(iii) विसर्प नहीं मिलते हैं

प्रश्न 3.
भारत एवं श्रीलंका के मध्य कौन-सी खाड़ी है?
(2009, 10)
(i) खम्भात की खाड़ी
(ii) कच्छ की खाड़ी
(iii) बंगाल की खाड़ी
(iv) मन्नार की खाड़ी।
उत्तर:
(iv) मन्नार की खाड़ी।

प्रश्न 4.
किस नदी को दक्षिण भारत की गंगा कहते हैं? (2009, 12, 15)
(i) नर्मदा नदी
(ii) कृष्णा नदी
(iii) कावेरी नदी,
(iv) गोदावरी नदी।
उत्तर:
(iv) गोदावरी नदी।

प्रश्न 5.
कृष्णा नदी किन राज्यों से प्रवाहित होती है? (2011)
(i) महाराष्ट्र, कर्नाटक, आन्ध्र प्रदेश
(ii) महाराष्ट्र, उड़ीसा, आन्ध्र प्रदेश
(iii) महाराष्ट्र, केरल, तमिलनाडु
(iv) मध्य प्रदेश, छत्तीसगढ़, उड़ीसा।
उत्तर:
(i) महाराष्ट्र, कर्नाटक, आन्ध्र प्रदेश

रिक्त स्थान पूर्ति

1. पाँच नदियों का प्रदेश …………. को कहा जाता है। (2008)
2. गंगा नदी ……….. नामक हिमानी से निकलती है।
3. नर्मदा नदी मध्य प्रदेश के ………. नामक स्थान से निकलती है।
4. हीराकुंड बाँध …………. पर बनाया गया है।
5. नागार्जुन सागर बाँध …………. नदी पर बना है।

उत्तर:

1. पंजाब
2. गंगोत्री
3. अमरकंटक पहाड़ी
4. महानदी
5. कृष्णा।

MP Board Class 9th Social Science Chapter 4 अति लघु उत्तरीय प्रश्न

प्रश्न 1.
अपवाह तन्त्र से क्या आशय है?
उत्तर:
अपवाह तन्त्र से आशय किसी क्षेत्र के नदी तन्त्र से है जो विभिन्न दिशाओं से बहकर आती है और मिलकर एक मुख्य नदी का निर्माण करती है।

प्रश्न 2.
नदी अपहरण से क्या तात्पर्य है?
उत्तर:
जब एक नदी दूसरी नदी के जल क्षेत्र को अपने में मिला लेती है तो उसे नदी अपहरण कहते हैं।

प्रश्न 3.
गंगा नदी की सहायक नदियों के नाम लिखिए। (2014, 17)
उत्तर:
गंगा नदी की सहायक नदियाँ हैं- यमुना, घाघरा, गण्डक और कोसी।

प्रश्न 4.
सिन्धु नदी की पाँच सहायक नदियाँ कौन-सी हैं?
उत्तर:
सिन्धु नदी की पाँच सहायक नदियाँ-झेलम, चिनाब, रावी, सतलज और व्यास हैं।

प्रश्न 5.
ब्रह्मपुत्र नदी को बांग्लादेश में किन-किन नामों से जाना जाता है?
उत्तर:
पद्मा और मेघना नाम से जाना जाता है।

प्रश्न 6.
भारत की पाँच प्रमुख झीलों के नाम लिखिए। (2014)
उत्तर:
भारत की पाँच प्रमुख झील हैं –

1. बुलर झील
2. लोनर झील
3. चिल्का झील
4. कोलेरू झील
5. पुलीकट झील।

प्रश्न 7.
अरब सागर में गिरने वाली दो नदियों के नाम लिखिए। (2018)
उत्तर:
नर्मदा और ताप्ती नदी।

प्रश्न 8.
पाँच नदियों का प्रदेश किसे कहा जाता है? (2018)
उत्तर:
पाँच नदियों का प्रदेश पंजाब को कहा जाता है।

MP Board Class 9th Social Science Chapter 4 लघु उत्तरीय प्रश्न

प्रश्न 1.
सिन्धु नदी तन्त्र को समझाइए।
उत्तर:
इस तन्त्र में सिन्धु और उसकी सहायक नदियों को शामिल किया जाता है। सिन्धु नदी की कुल लम्बाई लगभग 2900 किमी है। सिन्धु की पाँच सहायक नदियाँ झेलम, चिनाब, रावी, सतलज और व्यास हैं। इसमें जल प्रवाह की मात्रा वर्ष भर एक समान नहीं रहती है। उसके जल का उपयोग हम पंजाब, हरियाणा एवं राजस्थान के दक्षिण पश्चिम भागों में सिंचाई के लिये करते हैं।

प्रश्न 2.
उत्तर भारत की नदियों की प्रमुख विशेषताओं का वर्णन कीजिए।
उत्तर:
उत्तर भारत की नदियों की प्रमुख विशेषताएँ निम्नलिखित हैं –

1. इसमें जल प्रपातों की संख्या कम है।
2. इन नदियों का उपयोग यातायात के लिये किया जाता है।
3. ये नदियाँ गहरी घाटियों का निर्माण करती हैं।
4. इन नदियों के प्रवाह मार्ग में अनेक विसर्प हैं और प्रवाह धाराओं की दिशा भी बदलती रहती है।
5. इन नदियों में जल की प्राप्ति हिम और बर्फ से भी होती है।

प्रश्न 3.
नदियाँ अर्थव्यवस्था को कैसे प्रभावित करती हैं ? व्याख्या कीजिए।
उत्तर:
देश की अर्थव्यवस्था में नदियों का महत्त्वपूर्ण योगदान है। नदी द्वारा निर्मित मैदानों में कृषि होती है। ये स्वच्छ पेयजल की आपूर्ति करती हैं। पहले इनके किनारों पर ही गाँव और नगर स्थित होते थे। धार्मिक और सांस्कृतिक केन्द्र भी अधिकांशतः इनके तटों पर स्थित हैं। नदियों पर बाँध बनाकर सिंचाई के लिये पानी प्राप्त किया जाता है जिससे कृषि की जाती है। इसके अतिरिक्त विद्युत् उत्पादन भी किया जाता है।

प्रश्न 4.
भारत के समीपवर्ती समुद्रों की स्थिति लिखिए।
उत्तर:
भारत एक प्रायद्वीप है जो तीन तरफ से समुद्र से घिरा हुआ है। भारत के दक्षिण में हिन्द महासागर का विस्तार है। पश्चिमी तट के पश्चिम में अरब सागर एवं पूर्वी तट के पूर्व में बंगाल की खाड़ी है। अंडमान और निकोबार द्वीप समूह के पूर्व में अंडमान सागर है। भारत एवं श्रीलंका के मध्य मन्नार की खाड़ी स्थित है। गुजरात के तटवर्ती भाग में खम्भात और कच्छ की खाड़ियाँ हैं।

प्रश्न 5.
नदी प्रदूषण से क्या आशय है? नदियों को प्रदूषण से कैसे बचाया जा सकता है ?
उत्तर:
नदी प्रदूषण से आशय-हम एक ओर तो नदियों को पवित्र मानते हैं और दूसरी ओर इन्हें प्रदूषित करने का प्रयास करते हैं। उद्योगों का कचरा, घरों का गंदा जल, मरे हुए जानवरों को नदियों में प्रवाहित करते हैं। इससे प्रदूषण बढ़ता है। जलकुंभी के विस्तार ने भी नदियों को प्रदूषित किया है।

नदी प्रदूषण कम करने के उपाय –

1. प्रदूषण की समस्या के निराकरण के लिए सरकार द्वारा कानून बनाये गये हैं।
2. औद्योगिक कचरे को नदियों में प्रवाहित करने पर प्रतिबन्ध लगाया गया है।
3. सीवेज लाइनों के जल को परिष्कृत किया जाए।
4. सरकार द्वारा समय-समय पर नदियों की सफाई कराई जाए।
5. लोगों को नदी प्रदूषण की समस्या के प्रति जागरूक किया जाए।

MP Board Class 9th Social Science Chapter 4 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
उत्तर भारत के अपवाह तन्त्र का स्पष्ट वर्णन कीजिए।
उत्तर:
उत्तरी भारत के अपवाह तन्त्र में हिमालय पर्वत का महत्त्वपूर्ण स्थान है क्योंकि उत्तरी भारत की प्रमुख नदियाँ हिमालय पर्वत से ही निकलती हैं। इसलिए इन नदियों को हिमालय की नदियाँ भी कहते हैं। इस अपवाह तन्त्र की प्रमुख नदियाँ सिन्धु, गंगा और ब्रह्मपुत्र हैं।

(1) सिन्धु नदी तन्त्र :
सिन्धु नदी हिमालय पर्वत के पार कैलाश पर्वत के समीप से निकलकर आती है। इसकी कुल लम्बाई 2900 किमी है। यह तिब्बत के मानसरोवर के पास से निकलकर पश्चिम की ओर बहती हुई जम्मू और कश्मीर के लद्दाख जिले में 500 मीटर ऊँचा एक सुन्दर दर्शनीय गार्ज बनाती हुई बहती है। यहाँ से यह दक्षिण-पश्चिम में बहती हुई पाकिस्तान में प्रवेश कर अन्त में अरब सागर में मिल जाती है। सिन्धु की पाँच सहायक नदियाँ झेलम, चिनाब, रावी, सतलज और व्यास हैं। इसके जल का उपयोग हम पंजाब, हरियाणा एवं राजस्थान के दक्षिण पश्चिम भागों में सिंचाई के लिये करते हैं।

(2) गंगा नदी तन्त्र :
भारत के उत्तरी मैदान की प्रमुख नदी गंगा है। इसकी लम्बाई 2500 किमी. से अधिक है। यह गंगोत्री हिमनद से 4000 मीटर की ऊँचाई से निकलकर शिवालिक श्रेणियों को पार करके हरिद्वार के मैदान में प्रवेश करती है। इसकी सहायक नदियाँ यमुना, घाघरा, गंडक और कोसी प्रमुख हैं। ये नदियाँ उपजाऊ बाढ़ का मैदान बनाती हैं। इसमें नदी मोड़ तथा गोखुर झीलें पायी जाती हैं। अम्बाला के निकट जल विभाजक द्वारा गंगा एवं सिन्धु नदी के प्रवाह क्षेत्र का विभाजन होता है।

प्रायद्वीपीय भारत की कठोर भूमि से निकलने वाली चम्बल, केन, बेतवा, सोन और दामोदर नदियाँ भी गंगा प्रणाली का अंग हैं। इन पर बड़े-बड़े बाँधों का निर्माण किया गया है जिनसे जल विद्युत् बनाई जाती है और सिंचाई की जाती है। दक्षिण की ओर बहती हुई गंगा डेल्टा बनाते हुए बंगाल की खाड़ी में मिल जाती है। गंगा की मुख्य धारा बांग्लादेश में प्रवेश कर जाती है। ब्रह्मपुत्र नदी से मिलने के बाद यह मेघना कहलाती है।

(3) ब्रह्मपुत्र नदी तन्त्र :
ब्रह्मपुत्र नदी हिमालय के पार मानसरोवर झील के समीप से निकलकर आती है। हिमालय पर्वत के समानान्तर प्रवाहित होती हुई यह अरुणाचल प्रदेश में प्रवेश करती है। भारत में इसका प्रवाह 1400 किमी है। इसकी सहायक नदियाँ दिबांग, लोहित, धनश्री, कालांग आदि हैं। अधिक वर्षा के क्षेत्र बहने के कारण इसमें अवसाद अधिक होते हैं जिनके जमाव से प्रतिवर्ष बाढ़ आती है। नदियों का प्रवाह बदलता रहता है। नदी द्वीपों का भी निर्माण होता है। तिब्बत में इसे सांगपो, भारत में ब्रह्मपुत्र एवं बांग्लादेश में पद्मा और मेघना नाम से जाना जाता है। यह बहती हुई विशाल डेल्टा का निर्माण करती हुई बंगाल की खाड़ी में गिरती है।

प्रश्न 2.
उत्तर भारत एवं दक्षिण भारत की नदियों की तुलना कीजिए।
उत्तर:
उत्तरी तथा दक्षिणी भारत की नदियों की तुलना

प्रश्न 3.
नदियों का अर्थव्यवस्था में क्या महत्त्व है? समझाइए।
उत्तर:
नदियों का देश की अर्थव्यवस्था में निम्नलिखित महत्त्व है –

• पीने के जल की प्राप्ति :
  प्राचीनकाल में नदियों से ही पीने के लिए जल प्राप्त किया जाता था। आज भी अनेक गाँवों तथा नगरों में इस आधारभूत आवश्यकता की पूर्ति नदियों द्वारा की जाती है।
• सिंचाई सुविधा :
  भारत की नदियाँ सदावाहिनी हैं। अतः इनसे नहरें निकालकर सिंचाई की सुविधाएँ जुटाई जाती हैं। नहरें भारत में सिंचाई के महत्त्वपूर्ण साधन हैं जिनसे देश की 45% भूमि सींची जाती है।
• उपजाऊ मृदा का निर्माण :
  भारत की नदियाँ पर्वत से उपजाऊ मृदा बहाकर लाती हैं तथा इस मृदा को मैदानी भागों में बिछाकर उपजाऊ काँप मृदा का निर्माण करती हैं। यह उपजाऊ भूमि कृषि के लिए अत्यन्त उपयोगी होती है।
• जल-विद्युत् शक्ति का उत्पादन :
  उत्तर भारत की नदियों पर बाँध बनाकर तथा दक्षिण भारत की नदियों के प्राकृतिक प्रपातों पर जल विद्युत् बनायी जाती है। जल-विद्युत् ने उद्योग-धन्धों के विकास में बहुत सहयोग दिया है।
• बालू की प्राप्ति :
  नदियों के किनारों पर बालू पायी जाती है। इस बालू का प्रयोग भवन निर्माण व काँच उद्योग में किया जाता है।

MP Board Class 9th Social Science Chapter 4 अन्य परीक्षोपयोगी प्रश्न

MP Board Class 9th Social Science Chapter 4 वस्तुनिष्ठ प्रश्न

बहु-विकल्पीय प्रश्न

प्रश्न 1.
अपवाह तन्त्र शब्द से आशय किसी क्षेत्र के
(i) वायु तन्त्र से है
(ii) नदी तन्त्र से है
(iii) जल तन्त्र से है
(iv) पर्वत तन्त्र से है।
उत्तर:
(ii) नदी तन्त्र से है

प्रश्न 2.
नर्मदा नदी निकलती है
(i) सतपुड़ा से
(ii) अमरकंटक से
(iii) विन्ध्याचल से
(iv) हिमालय से।
उत्तर:
(ii) अमरकंटक से

प्रश्न 3.
गोदावरी नदी को भारत के किस क्षेत्र की गंगा कहते हैं?
(i) पूर्व
(ii) पश्चिम
(iii) उत्तर
(iv) दक्षिण।
उत्तर:
(iv) दक्षिण।

प्रश्न 4.
गंगा नदी की लम्बाई लगभग है
(i) 2500 किमी से अधिक
(ii) 4000 किमी से अधिक
(iii) 1500 किमी से अधिक
(iv) 5000 किमी से अधिक।
उत्तर:
(i) 2500 किमी से अधिक

प्रश्न 5.
अलमाटी और नागार्जुन सागर बाँध किस नदी पर बनाये गये हैं?
(i) कृष्णा
(ii) कावेरी
(iii) गोदावरी
(iv) नर्मदा।
उत्तर:
(i) कृष्णा

प्रश्न 6.
अरब सागर में गिरने वाली नदी है
(i) गंगा
(ii) नर्मदा
(iii) महानदी
(iv) ब्रह्मपुत्र।
उत्तर:
(ii) नर्मदा

प्रश्न 7.
सांभर झील किस राज्य में स्थित है?
(i) आन्ध्र प्रदेश
(ii) राजस्थान
(iii) उड़ीसा
(iv) तमिलनाडु।
उत्तर:
(ii) राजस्थान

रिक्त स्थान पूर्ति

1. चिल्का झील …………. राज्य में स्थित है। (2013, 17)
2. जलकुंभी के विस्तार ने भी नदियों को ……….. किया है।

उत्तर:

1. उड़ीसा
2. प्रदूषित।

सत्य/असत्य

प्रश्न 1.
हीराकुंड बाँध नर्मदा नदी पर बनाया गया है। (2009)
उत्तर:
असत्य

प्रश्न 2.
देश की अर्थव्यवस्था में नदियों का महत्त्वपूर्ण स्थान है। (2013)
उत्तर:
सत्य

प्रश्न 3.
वुलर झील जम्मू और कश्मीर राज्य में स्थित है। (2009)
उत्तर:
सत्य

प्रश्न 4.
भारत और श्रीलंका के बीच खम्भात की खाड़ी है। (2012)
उत्तर:
असत्य

प्रश्न 5.
सिन्धु नदी की कुल लम्बाई लगभग 2900 किमी है। (2012)
उत्तर:
सत्य

प्रश्न 6.
चिल्का झील बिहार में स्थित है। (2013)
उत्तर:
असत्य

सही जोड़ी मिलाइए

उत्तर:

1. → (ख)
2. → (घ)
3. → (क)
4. → (ङ)
5. → (ग)
6. → (च)।

एक शब्द/वाक्य में उत्तर

प्रश्न 1.
किस नदी को दक्षिण भारत की गंगा कहते हैं? (2017)
उत्तर:
गोदावरी नदी

प्रश्न 2.
नर्मदा नदी किस प्रदेश से निकलती है?
उत्तर:
मध्य प्रदेश

प्रश्न 3.
गंगा नदी एवं ब्रह्मपुत्र मिलने पर कहलाती है।
उत्तर:
मेघना

प्रश्न 4.
प्रायद्वीप नदियों की विशेषता है।
उत्तर:
मौसमी

प्रश्न 5.
तीनों ओर से समुद्र से घिरा क्षेत्र कहलाता है।
उत्तर:
प्रायद्वीप

प्रश्न 6.
सांगपो नदी को भारत में किस नाम से जाना जाता है? (2008)
उत्तर:
ब्रह्मपुत्र।

MP Board Class 9th Social Science Chapter 4 अति लघु उत्तरीय प्रश्न

प्रश्न 1.
भारतीय अपवाह तन्त्र के आधार पर भारतीय नदियों को कितने भागों में बाँटा जा सकता है?
उत्तर:
भारतीय अपवाह तन्त्र के आधार पर भारतीय नदियों को दो वर्गों में बाँटा जा सकता है

1. हिमालय की नदियाँ
2. प्रायद्वीपीय नदियाँ।

प्रश्न 2.
भ्रंश से क्या तात्पर्य है?
उत्तर:
आन्तरिक हलचलों के कारण भू-पृष्ठ पर पड़ी दरारें जिनके सहारे चट्टानें खिसक जाती हैं, भ्रंश कहलाते हैं।

प्रश्न 3.
नदी द्वारा लाए गये मलबे के निक्षेप से मैदानी क्षेत्र में बनी घुमावदार आकृति को क्या कहते हैं? (2009)
उत्तर:
विसर्प।

प्रश्न 4.
आन्तरिक अपवाह से क्या समझते हैं?
उत्तर:
आन्तरिक अपवाह एक ऐसा अपवाह तन्त्र होता है जिसमें नदियों का जल महासागरों में नहीं पहुँचता वरन् आन्तरिक समुद्रों या झीलों में गिरता है।

MP Board Class 9th Social Science Chapter 4 लघु उत्तरीय प्रश्न

प्रश्न 1.
क्या कारण है कि हिमालय से निकलने वाली नदियाँ सदावाहिनी होती हैं?
अथवा
उत्तर भारत की नदियों में वर्षभर पानी क्यों रहता है? (2015, 17)
उत्तर:
हिमालय पर्वत से निकलने वाली नदियों की मुख्य विशेषता है कि यह सदावाहिनी (वर्ष भर पानी रहता है) होती हैं। क्योंकि इस क्षेत्र की नदियों को वर्षा के जल के अतिरिक्त ऊँचे पर्वतों से हिम के पिघलने से जल की आपूर्ति होती रहती है।

प्रश्न 2.
ब्रह्मपुत्र नदी तन्त्र को समझाइए।
उत्तर:
कैलाश पर्वत एवं मानसरोवर झील के निकट इसका उद्गम है। हिमालय पर्वत के समानान्तर प्रवाहित होती हुई यह अरुणाचल में प्रवेश करती है। इसकी सहायक नदियाँ दिबांग, लोहित, धनश्री, कालांग आदि हैं। अधिक वर्षा के क्षेत्र में बहने के कारण इसमें अवसाद अधिक होते हैं, जिनके जमाव से इसमें प्रतिवर्ष बाढ़ आती है। यह बहती हुई विशाल डेल्टा का निर्माण करती हुई बंगाल की खाड़ी में गिरती है।

प्रश्न 3.
प्रायद्वीपीय भारत की नदियों की विशेषताएँ बताइए।
उत्तर:
प्रायद्वीपीय भारत की नदियों की विशेषताएँ हैं कि ये मौसमी हैं। शुष्क क्षेत्र में प्रवाहित होती हैं। इनकी लम्बाई भी हिमालय से निकलने वाली नदियों से कम है। ये गहरे जमाव के मैदान नहीं बनाती हैं। प्रायद्वीपीय भारत में मुख्य जल विभाजक का निर्माण पश्चिमी घाट द्वारा होता है जो पश्चिमी तट के निकट उत्तर से दक्षिण में स्थित है। प्रायद्वीपीय भाग की अधिकतर नदियाँ, जैसे-महानदी, गोदावरी, कृष्णा तथा कावेरी पूर्व की ओर बहते हुए बंगाल की खाड़ी में गिरती हैं। ये डेल्टा भी बनाती हैं।

प्रश्न 4.
लम्बी धारा होने के बावजूद तिब्बत के क्षेत्र में ब्रह्मपुत्र में कम गाद क्यों है?
उत्तर:
ब्रह्मपुत्र नदी कैलाश पर्वत एवं मानसरोवर झील के निकट से निकलती है। तिब्बत के पठार पर बहती हुई पूर्व में भारत में प्रवेश करती है। जिस स्थान से यह नदी निकलती है वह सदैव बर्फ से ढंका रहता है तथा तिब्बत का क्षेत्र एक पठारी भाग होने के कारण वहाँ पर अपरदन क्रिया नहीं के बराबर होती है। इसलिए ब्रह्मपुत्र नदी कम अवसाद लाती है।

प्रश्न 5.
नर्मदा अपवाह तन्त्र की मुख्य विशेषताएँ बताइए।
उत्तर:
इसकी मुख्य विशेषताएँ निम्न प्रकार हैं –

1. नर्मदा नदी का उद्गम मध्य प्रदेश में अमरकंटक पर्वत क्षेत्र है।
2. यह यहाँ से पश्चिम की ओर भू-भ्रंश घाटी में बहती हुई 1312 किमी का मार्ग तय करके अरब सागर में मिलती है।
3. अपने मुहाने पर यह कीप के आकार की गहरी घाटी में बहकर समुद्र में मिलती है।

MP Board Class 9th Social Science Chapter 4 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
प्रायद्वीपीय भारत की नदियों का वर्णन कीजिए।
अथवा
दक्षिण भारत में नदी-तन्त्र का स्पष्ट वर्णन कीजिए।
उत्तर:
दक्षिण भारत नदी तन्त्र में प्रमुख नदियाँ पश्चिमी घाट से निकलकर आती हैं तथा पूर्व की ओर बहती हैं और बंगाल की खाड़ी में मिल जाती हैं। इन नदियों में महानदी, गोदावरी, कृष्णा तथा कावेरी प्रमुख हैं। इसके अतिरिक्त पश्चिम की ओर बहने वाली दो नदियाँ नर्मदा तथा तापी अरब सागर में गिरती हैं।

• नर्मदा नदी :
  यह नदी मध्य प्रदेश में अमरकंटक पहाड़ी से निकलकर गहरी भ्रंश घाटी में 1312 किमी बहती हुई अरब सागर में गिरती है। इसका प्रवाह क्षेत्र मध्य प्रदेश और गुजरात में है। यह जबलपुर के निकट संगमरमर के शैलों में भेड़ाघाट पर धुंआधार जलप्रपात बनाती है।
• ताप्ती नदी :
  यह नदी मध्य प्रदेश में सतपुड़ा पर्वत श्रृंखलाओं में बैतूल जिले के मुल्ताई नामक स्थान से निकलती है। इसकी लम्बाई 724 किमी है। यह मध्य प्रदेश, महाराष्ट्र और गुजरात में बहती हुई खम्भात की खाड़ी में गिरती है।
• गोदावरी नदी :
  गोदावरी नदी नासिक के पास पश्चिमी घाट से निकलकर 1500 किमी उड़ीसा तथा आन्ध्र प्रदेश में बहती हुई बंगाल की खाड़ी में गिरती है। इसकी सहायक नदियाँ वर्धा, मांजरा, वेन गंगा तथा पेन गंगा हैं। बड़े आकार और विस्तार के कारण इसे दक्षिण की गंगा भी कहते हैं।
• महानदी नदी :
  इस नदी का उद्गम छत्तीसगढ़ की उच्च भूमि में सिहावा नामक स्थान से है। इसकी लम्बाई 858 किमी है। यह महाराष्ट्र, छत्तीसगढ़, झारखण्ड और उड़ीसा में बहती है। हीराकुड बाँध इसी नदी पर बनाया गया है।
• कृष्णा नदी :
  कृष्णा नदी महाराष्ट्र में महाबलेश्वर के पास से निकलती है। इसकी लम्बाई 1400 किमी है। कोयना, पचगंगा, मालप्रभा, घाटप्रभा, भीमा, मूसी और तुंगभद्रा इसकी सहायक नदियाँ हैं। अलमाटी और नागार्जुनसागर बाँध इसी नदी पर बनाये गये हैं।
• कावेरी नदी :
  इसका उद्गम कुर्ग की ब्रह्मगिरि पहाड़ी श्रृंखला से होता है। इसकी लम्बाई 760 किमी है। इसकी सहायक नदियाँ हेमावती, अमरावती, भवानी आदि हैं। शिवसमुद्रम् इसका प्रमुख प्रपात है। इस नदी से जल विद्युत् बनायी जाती है एवं सिंचाई की जाती है।

MP Board Class 9th Social Science Solutions

MP Board Class 9th Maths Solutions Chapter 12 हीरोन का सूत्र Ex 12.1

प्रश्न 1.
एक यातायात संकेत बोर्ड पर “आगे स्कूल है” लिखा है और यह भुजा a वाले एक समबाहु त्रिभुज के आकार का है। हीरोन के सूत्र का प्रयोग करके इस बोर्ड का क्षेत्रफल ज्ञात कीजिए। यदि संकेत बोर्ड का परिमाप 180 cm हो तो इसका क्षेत्रफल क्या होगा?
हल:

अब संकेत बोर्ड की परिमाप = 180 cm
⇒ बोर्ड की एक भुजा a = \(\frac { 180 }{ 3 }\) cm = 60 cm
संकेत बोर्ड का क्षेत्रफल ∆ = \(\frac{a^{2}}{4} \sqrt{3}=\frac{(60)^{2}}{4} \sqrt{3}=900 \sqrt{3}\) cm².
अतः संकेत बोर्ड का अभीष्ट क्षेत्रफल = 900√3 cm².

प्रश्न 2.
संलग्न चित्र में किसी फ्लाईओवर (Flyover) की त्रिभुजाकार दीवार को विज्ञापनों के लिए प्रयोग किया जाता है। दीवार की भुजाओं की लम्बाइयाँ 122 m, 22 m और 120 m हैं। इस विज्ञापन से प्रतिवर्ष ₹ 5,000 प्रति m² की प्राप्ति होती है। एक कम्पनी ने एक दीवार को विज्ञापन देने के लिए 3 महीने के लिए किराये
पर लिया। उसने कुल कितना किराया दिया ?

चित्र 12.5
हल:
दिया है : त्रिभुजाकार दीवार की भुजाएँ क्रमशः a = 122 m, b = 22 m और c = 120 m
\(s=\frac{a+b+c}{2}=\frac{122+22+120}{2}=\frac{264}{2}=132 \mathrm{m}\)
हीरोन के सूत्र से त्रिभुज का क्षेत्रफल

⇒ दीवार का क्षेत्रफल = 1320 m²
दीवार का कुल किराया = क्षेत्रफल – किराए की दर x समय
⇒ दीवार का कुल किराया = 1320 x 5000 x \(\frac { 3 }{ 12 }\) = ₹ 16,50,000
अतः कम्पनी द्वारा दिया गया अभीष्ट किराया₹ 16,50,000 है।

प्रश्न 3.
किसी पार्क में एक फिसलपट्टी (Slide) बनी हुई है। इसकी पार्वीय दीवारों (Side walls) में से एक दीवार पर किसी रंग से पेंट किया गया है और उस पर “पार्क को हरा-भरा और साफ रखिए” लिखा हुआ है (देखिए पार्क को हरा भरा संलग्न चित्र)। यदि इस दीवार और साफ रखिए की विमाएँ 15 m, 11 m, और 6 m हैं, तो रंग से पेंट हुए भाग का क्षेत्रफल ज्ञात कीजिए।

चित्र 12.6
हल:
मान लीजिए फिसलपट्टी की पार्वीय दीवारों की विमाएँ क्रमशः a = 15 m, b = 11 m एवं c = 6 m दी गई हैं।
तो s = \(\frac{a+b+c}{2}=\frac{15+11+6}{2}=\frac{32}{2}=16 \mathrm{m}\)
हीरोन के सूत्र से दीवार का क्षेत्रफल

अतः दीवार के पेंट किए हुए भाग का अभीष्ट क्षेत्रफल = 20√2 m².

प्रश्न 4.
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी दो भुजाएँ 18 cm और 10 cm हैं तथा उसका परिमाप 42 cm है।
हल:
मान लीजिए त्रिभुज की भुजाएँ क्रमशः a, b और c हैं
a = 18 cm, b = 10 cm, a + b + c = 42 cm (दिया है)
⇒ 18 + 10 + c = 42 ⇒ c = 42 – 28 = 14 cm
अब \(s=\frac{a+b+c}{2}=\frac{42}{2}=21 \mathrm{cm}\)
तथा हीरोन के सूत्र से त्रिभुज का क्षेत्रफल

अतः त्रिभुज का अभीष्ट क्षेत्रफल = 21√11 cm².

प्रश्न 5.
एक त्रिभुज की भुजाओं का अनुपात 12 : 17 : 25 है और उसका परिमाप 540 cm है। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
हल:
चूँकि त्रिभुज की भुजाएँ 12 : 17 : 25 के अनुपात में हैं तो मान लीजिए ये भुजाएँ 12 x, 17x और 25x हैं।
12x + 17x + 25x = 540 cm
⇒ 54x = 540 cm = x = 540/54 = 10
⇒ ∆ की भुजाएँ क्रमशः 120 cm, 170 cm और 250 cm

अतः त्रिभुज अभीष्ट क्षेत्रफल = 9000 cm².

प्रश्न 6.
एक समद्विबाहु त्रिभुज की परिमाप 30 cm है और उसकी बराबर भुजाएँ 12 cm की लम्बाई की हैं। उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
हल:
मान लीजिए कि त्रिभुज की बराबर भुजाएँ = a = b = 12 cm एवं परिमाप a + b + c = 30 cm.
तब c = 30 – 12 – 12 = 30 – 24 = 6 cm

अतः त्रिभुज अभीष्ट क्षेत्रफल = 9√15 cm².

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.1

प्रश्न 1.
1.5 m लम्बा, 1.25 m चौड़ा और 65 cm गहरा प्लास्टिक का एक डिब्बा बनाया जाता है। इसे ऊपर से खुला रखना है। प्लास्टिक शीट की मोटाई को नगण्य मानते हुए निर्धारित कीजिए कि
(i) डिब्बा बनाने के लिए आवश्यक प्लास्टिक शीट का क्षेत्रफल।
(ii) इस शीट का मूल्य, यदि 1 m² शीट का मूल्य Rs 20 है।
हल :
डिब्बा का आधार घनाभ है जिसका ऊपरी तल खुला है।
दिया है : डिब्बा की लम्बाई, l = 1.5 m, चौड़ाई b = 1.25 m और गहराई h = 65 cm = 0.65 m
(i) चूँकि डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल = 2 (2 + b) × h .
पार्श्व पृष्ठीय क्षेत्रफल = 2 (1.50 + 1.25) × 0.65
= 2 × 2.75 × 0.65
= 3:575 m²
एवं आधार का क्षेत्रफल = l × b = 1.50 × 1.25 = 1.875 m²
प्लास्टिक शीट का कुल क्षेत्रफल = 3.575 + 1.875 = 5.450 m²
अतः प्लास्टिक शीट का अभीष्ट क्षेत्रफल = 5.45 m².

(ii) प्लास्टिक शीट का मूल्य = दर × क्षेत्रफल
= 20 × 5.45
= Rs 109
अतः प्लास्टिक शीट का अभीष्ट मूल्य = Rs 109.

प्रश्न 2.
एक कमरे की लम्बाई, चौड़ाई और ऊँचाई क्रमशः 5 m, 4 m और 3 m है। Rs 7.50 प्रति m² की दर से इस कमरे की दीवारों और छत पर सफेदी कराने का व्यय ज्ञात कीजिए। (2019)
हल :
दिया है : कमरे की लम्बाई l = 5 m, चौड़ाई b = 4 m और ऊँचाई h = 3 m है।
कमरे की दीवारों का पार्श्व पृष्ठ = 2 (l + b) × h = 2 (5 + 4) × 3 = 54 m²
कमरे की छत का क्षेत्रफल = l × b = 5 × 4 = 20 m²
सफेदी के लिए कुल क्षेत्रफल = 54 + 20 = 74 m²
सफेदी कराने का व्यय = दर × क्षेत्रफल = 7.50 × 74 = Rs 555
अतः सफेदी कराने का अभीष्ट व्यय = Rs 555.

प्रश्न 3.
किसी आयताकार हॉल के फर्श का परिमाप 250 m है। यदि Rs 10 प्रति मीटर² की दर से चारों दीवारों पर पेंट कराने की लागत Rs 15,000 हो, तो इस हॉल की ऊँचाई ज्ञात कीजिए।
हल :
दिया है : हॉल के फर्श का परिमाप = 250 m, दीवारों पर पेंट की दर Rs 10 प्रति m² एवं पेंट कराने का व्यय Rs 15,000
मान लीजिए हॉल की ऊँचाई h मीटर है।
चूँकि दीवारों का क्षेत्रफल = फर्श की परिमाप × ऊँचाई
= 250 × h = 250 h m²
पेंट का व्यय = दर × क्षेत्रफल = 10 × 250 h = 15,000
\(h=\frac { 15,000 }{ 2,500 }=6m\)
अतः हॉल की अभीष्ट ऊँचाई = 6 m.

प्रश्न 4.
किसी डिब्बे में भरा हुआ पेंट 9.375 m² के क्षेत्रफल पर पेंट करने के लिए पर्याप्त है। इस डिब्बे के पेंट से 22.5 cm × 10 cm × 7.5 cm विमाओं वाली कितनी ईंटें पेंट की जा सकती
हैं ?
हल :
दिया है : एक ईंट की विमाएँ 22.5 cm × 10 cm × 7.5 cm तथा डिब्बे के रंग से पेंट हो सकने वाला क्षेत्रफल 9:375 m² अर्थात् 93750 cm².
एक ईंट का पृष्ठीय क्षेत्रफल = 2 (22.5 × 10 + 10 × 7.5 + 7.5 × 22.5) cm²
= 2 (225 + 75 + 168.75) = 937.5 cm²

अतः ईंटों की अभीष्ट संख्या = 100.

प्रश्न 5.
एक घनाकार डिब्बे का एक किनारा 10 cm लम्बाई का है तथा एक अन्य घनाभाकार डिब्बे की लम्बाई, चौड़ाईं तथा ऊँचाई क्रमशः 12.5 cm, 10 cm और 8 cm है।
(i) किस डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल अधिक है और कितना अधिक है ?
(ii) किस डिब्बे का कुल पृष्ठीय क्षेत्रफल कम है और कितना कम है ?
हल :
(i) पहले डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल = 4a² = 4 × 10² = 400 cm²
तथा दूसरे डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल = 2 (12.5 + 10) × 8 = 360 cm²
दोनों के पार्श्व पृष्ठीय क्षेत्रफलों का अन्तर = 400 – 360 = 40 cm²
अतः पहले डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल दूसरे से 40 cm² अधिक है।

(ii) पहले डिब्बे का कुल पृष्ठीय क्षेत्रफल = 6a² = 6 × 10² = 600 cm²
तथा द्वितीय डिब्बे का कुल पृष्ठीय क्षेत्रफल = 2[12.5 × 10 + 10 × 8 + 8 × 12.5]
= 2 (125 + 80 + 100)
= 2 × 305
= 610
दोनों के कुल पृष्ठीय क्षेत्रफल का अन्तर = 610 – 600 = 10 cm²
अतः पहले डिब्बे का कुल पृष्ठीय क्षेत्रफल दूसरे से 10 cm² कम है।

प्रश्न 6.
एक छोटा पौधा घर (green house) सम्पूर्ण रूप से शीशे की पट्टियों से (आधार भी सम्मिलित है) घर के अन्दर ही बनाया गया है और शीशे की पट्टियों को टेप द्वारा चिपका कर रोका गया है। यह पौधा घर 30 cm लम्बा, 25 cm चौड़ा 25 cm ऊँचा है।
(i) इसमें प्रयुक्त शीशे की पट्टियों का क्षेत्रफल क्या है ?
(ii) सभी 12 किनारों के लिए कितने टेप की आवश्यकता है ?
हल :
(i) शीशे की पट्टियों का क्षेत्रफल = 2 (30 × 25 + 25 × 25 + 25 × 30)
= 2 (750 + 625 + 750)
= 2 × 2125
= 4250 cm²
अतः शीशे की पट्टियों का कुल अभीष्ट क्षेत्रफल = 4250 cm².

(ii) टेप की कुल लम्बाई = सभी कोरों की लम्बाई का योग
= 4 (30 + 25 + 25)
= 4 × 80
= 320 cm
अतः टेप की कुल अभीष्ट लम्बाई = 320 cm.

प्रश्न 7.
शान्ति स्वीट स्टाल अपनी मिठाइयों को पैक करने के लिए गत्ते के डिब्बे बनाने का ऑर्डर दे रहा था। दो मापों के डिब्बों की आवश्यकता थी। बड़े डिब्बे की माप 25 cm × 20 cm × 5 cm और छोटे डिब्बे की माप 15 cm × 12 cm × 5 cm थी। सभी प्रकार की अतिव्यापकता (overlaps) के लिए कुल पृष्ठीय क्षेत्रफल के 5% के बराबर अतिरिक्त गत्ता लगेगा। यदि गत्ते की लागत Rs 4 प्रति 1000 cm² है, तो प्रत्येक प्रकार के 250 डिब्बे बनवाने की कितनी लागत आयेगी?
हल:
बड़े डिब्बे का पृष्ठीय क्षेत्रफल = 2 (25 × 20 + 20 × 5 + 5 × 25)
= 2 (500 + 100 + 125)
= 2 × 725
= 1450 cm²
250 डिब्बों के लिए गत्ते का कुल क्षेत्रफल = 1450 × \(\frac { 105 }{ 100 }\) × 250 = 380625 cm²
और छोटे डिब्बे का पृष्ठीय क्षेत्रफल = 2 (15 × 12 + 12 × 5 + 5 × 15)
= 2 (180 + 60 + 75)
= 2 × 315
= 630 cm²
250 डिब्बों के लिए गत्ते का कुल क्षेत्रफल = 630 × \(\frac { 105 }{ 100 }\) × 250 = 165375 cm²
गत्ते का कुल क्षेत्रफल = 380625 + 165375 = 546000 cm²
डिब्बे बनवाने का व्यय = 546000 × \(\frac { 4 }{ 1000 }\) = Rs 2184
अतः डिब्बे बनवाने का अभीष्ट व्यय = Rs 2,184.

प्रश्न 8.
परवीन अपनी कार खड़ी करने के लिए एक संदूक के प्रकार के ढाँचे जैसा एक अस्थाई स्थान तिरपाल की सहायता से बनाना चाहती है जो कार को चारों ओर से और ऊपर से ढक ले। (सामने वाला फलक लटका हुआ होगा जिसे घुमाकर ऊपर किया जा सकता है) यह मानते हुए कि सिलाई के समय लगा तिरपाल का अतिरिक्त कपड़ा नगण्य होगा, आधार विमाओं 4 m × 3 m और ऊँचाई 2.5 m वाले इस ढाँचे को बनाने के लिए कितने तिरपाल की आवश्यकता होगी?
हल:
ढाँचे का पार्श्व पृष्ठीय क्षेत्रफल = 2 (4 + 3) × 2.5 = 35 m²
ढाँचे की छत का क्षेत्रफल = 4 × 3 = 12 m²
तिरपाल का कुल क्षेत्रफल = 35 + 12 = 47 m²
अतः ढाँचे को बनाने के लिए आवश्यक अभीष्ट तिरपाल = 47 m².

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 10 वृत्त Ex 10.5

प्रश्न 1.
संलग्न चित्र में केन्द्र 0 वाले एक वृत्त पर तीन बिन्दु A, B और C इस प्रकार हैं कि ∠BOC = 30° तथा ∠AOB = 60° है। यदि चाप ABC के अतिरिक्त वृत्त पर D एक बिन्दु है, तो ∠ADC ज्ञात कीजिए। (2019)
हल:
चित्रानुसार,
∠AOC = ∠AOB + ∠BOC = 60° + 30° = 90°
(चूँकि ∠AOB = 60° एवं ∠BOC = 30° दिया है)

चित्र 10.17
चूंकि ∠ADC = \(\frac { 1 }{ 2 }\)∠AOC
(किसी चाप द्वारा शेष परिधि पर बना कोण उस चाप द्वारा केन्द्र पर बने कोण का आधा होता है)
⇒ ∠ADC = \(\frac { 1 }{ 2 }\) x 90° = 45°
अत: अभीष्ट कोण ∠ADC का मान = 45°.

प्रश्न 2.
किसी वृत्त की एक जीवा वृत्त की त्रिज्या के बराबर है। जीवा द्वारा लघु चाप के किसी बिन्दु पर अन्तरित कोण ज्ञात कीजिए तथा दीर्घ चाप के किसी बिन्दु पर भी अन्तरित कोण ज्ञात
कीजिए।
हल:

चित्र 10.18
दिया है : O केन्द्र वाले वृत्त में जीवा
AB = OA = OB (OA, OB वृत्त की त्रिज्याएँ हैं)
⇒ ∠AOB = 60° (समबाहु त्रिभुज का कोण है)
⇒ प्रतिवर्ती ∠AOB = 360° – 60° = 300° (एक बिन्दु पर बने कोणों का योग = 360°)
चूँकि किसी चाप द्वारा शेष परिधि पर बना कोण, केन्द्र पर बने कोण का आधा होता है।
⇒ लघु चाप में बना कोण ∠ACB = \(\frac { 1 }{ 2 }\) x प्रतिवर्ती ∠AOB
= \(\frac { 1 }{ 2 }\) x 300° = 150°
और दीर्घ चाप में बना कोण ∠ADB = \(\frac { 1 }{ 2 }\) x ∠AOB = \(\frac { 1 }{ 2 }\) x 60° = 30°
अत: लघु चाप के किसी बिन्दु पर बना अभीष्ट कोण = 150° एवं दीर्घ चाप के किसी बिन्दु पर बना अभीष्ट कोण = 30°.

प्रश्न 3.
संलग्न चित्र में ∠POR=100°, जहाँ P, Q तथा R केन्द्र O वाले एक वृत्त पर स्थित बिन्दु हैं। ∠OPR ज्ञात कीजिए।
हल:
चित्रानुसार, प्रतिवर्ती ∠POR = 2∠PQR
प्रतिवर्ती ∠POR = 2 x 100° = 200°
∠POR = 360° – 200° = 160° (एक बिन्दु पर बने कोणों का योग = 360°)
चूँकि OP = OR (वृत्त की त्रिज्याएँ हैं)
∠OPR = ∠ORP = x (मान लीजिए)

चित्र 10.14
(बराबर भुजाओं के सम्मुख कोण)
अब ∆OPR में चूँकि ∠POR + ∠OPR + ∠ORP = 180° (त्रिभुज के अन्तः कोणों का योग)
⇒ 160° + x + x = 180° ⇒ 2x = 20°
⇒ x = 10°
अत: ∠OPR का अभीष्ट मान = 10°.

प्रश्न 4.
संलग्न चित्र में ∠ABC = 69° और ∠ACB = 31° हो, तो AL ∠BDC ज्ञात कीजिए। (2018, 19)
हल:
चित्रानुसार, ∠ BAC + 690 + 31° = 180° (त्रिभुज के अन्तः कोणों को योग)

चित्र 10.15
⇒ ∠BAC = 180° – 100° = 80°
चूँकि ∠BDC = ∠BAC = 80° (एक ही वृत्तखण्ड के कोण हैं)
अतः ∠BDC का अभीष्ट मान = 80°.

प्रश्न 5.
संलग्न चित्र में एक वृत्त पर A, B, C और D चार बिन्दु है। AC और BD एक बिन्दु E पर इस प्रकार प्रतिच्छेद करते हैं। कि ∠ BEC = 130° तथा ∠ECD = 20° है। ∠BAC ज्ञात कीजिए।
हल:
चूँकि ∠ BEC, ∆CDE का बहिष्कोण है।
⇒ ∠BEC = ∠EDC + ∠DCE (बहिष्कोण = अन्तः कोणों का योग)
⇒ 130° = ∠EDC + 20° (कोणों के ज्ञात मान रखने पर)

चित्र 10.16
⇒ ∠BDC = ∠EDC
= 130° – 20° = 110° (∠BDC = ∠EDC एक ही कोण है)
चूँकि ∠BAC = ∠BDC = 110° (एक ही वृत्तखण्ड के कोण हैं तथा ∠BDC = 110°)
अतः ∠BAC का अभीष्ट मान = 110°.

प्रश्न 6.
ABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण एक बिन्दु E पर प्रतिच्छेद करते हैं। यदि ∠DBC = 70° और ∠BAC = 30° हो, तो ∠BCD ज्ञात कीजिए। पुनः यदि AB = BC हो, तो ∠ECD ज्ञात कीजिए।
हल:
चूँकि ∠BDC = ∠ BAC = 30° …(1) (एक ही वृत्त खण्ड के कोण हैं तथा ∠ BAC = 30°, दिया है)।
∆CBD में,
∵ ∠ BCD + ∠DBC + ∠BDC = 180° (∆ के अन्तः कोणों का योग है)
⇒ ∠BCD + 70° + 30° = 180° (कोणों में ज्ञात मान रखने पर)
⇒ ∠BCD = 180° – 100° = 80°
अब चूँकि ∆ABC में, AB = BC (दिया है)

चित्र 10.17
⇒ ∠BCA =∠BAC = 30° (बराबर-भुजाओं के सम्मुख कोण हैं तथा ∠BAC = 30° दिया है)
∠ECD = ∠BCD- ∠BCA (चित्रानुसार)
⇒ ∠ECD = 80° – 30° = 50° (ज्ञात कोणों के मान रखने पर)
अतः अभीष्ट कोण ∠BCD का मान = 80° एवं पुनश्च कोण ∠ECD का अभीष्ट मान = 50° है।

प्रश्न 7.
यदि एक चक्रीय चतुर्भुज के विकर्ण उसके शीर्षों से जाने वाले वृत्त के व्यास हों, तो सिद्ध कीजिए कि वह एक आयत है।
हल:
दिया है : ABCD एक चक्रीय चतुर्भुज जिसके विकर्ण AC एवं BD वृत्त के व्यास हैं। चूँकि वृत्त के व्यास परस्पर समद्विभाजित करते हैं तथा बराबर होते है।
इसलिए AC एवं BD परस्पर समद्विभाजित करेंगे।
चूँकि AC एवं BD चतुर्भुज ABCD के विकर्ण हैं तथा परस्पर समद्विभाजित करते हैं।
⇒ ABCD एक समान्तर चतुर्भुज होगा।

चित्र 10.18
चूँकि ABCD एक चक्रीय चतुर्भुज है।
⇒ ABCD एक आयत होगा। (समान्तर चक्रीय चतुर्भुज एक आयत होता है।)
अत: यदि एक चक्रीय चतुर्भुज के विकर्ण उसके शीर्षों में जाने वाले वृत्त के व्यास हों, तो वह एक आयत होगा। इति सिद्धम्

प्रश्न 8.
यदि किसी समलम्ब की असमान्तर भुजाएँ बराबर हों, तो सिद्ध कीजिए कि वह चक्रीय है।
हल:
दिया है: ABCD एक समलम्ब है जिसकी भुजा AB || DC एवं असमान्तर भुजाएँ AD = BC.
सिद्ध करना है: ABCD एक चक्रीय चतुर्भुज है।
रचना: C से CE || DA रेखाखण्ड खींचिए जो AB के E पर मिलता है।
⇒ AECD एक समान्तर चतुर्भुज है।
⇒ DA = CE(समान्तर चतुर्भुज की सम्मुख भुजाएँ हैं)
⇒ CE = CB [∵ DA = CB दिया है]
उपपत्ति: चूँकि AB || DC (दिया है) एवं CE || DA (रचना से)

चित्र 10.19
⇒ ∠CEB = ∠CBE (बराबर भुजाओं के सम्मुख कोण)
चूँकि DA || CE को तिर्यक रेखा AB बिन्दु A और E पर मिलती है।
⇒ ∠DAB = ∠CEB = ∠CBE (संगत कोण है तथा ∠CEB =∠CBE)
चूँकि AB || CD को तिर्यक रेखा (DA बिन्दु A और D पर मिलती है।)।
⇒ ∠ADC + ∠DAB = 180° (एक ही ओर के अन्तः कोणों का योग है)
⇒ ∠ADC + ∠ABC = 180° (∠DAB = CBE 3791C ∠DAB= ∠ABC)
अत: ABCD एक चक्रीय चतुर्भुज है। (सम्मुख कोण सम्पूरक हैं) इति सिद्धम्

प्रश्न 9.
दो वृत्त दो बिन्दुओं B और C पर प्रतिच्छेद करते हैं। B से जाने वाले दो रेखाखण्ड ABD और PBQ वृत्तों को A,D और P, Q पर क्रमशः प्रतिच्छेद करते हुए खींचे गये हैं (देखिए संलग्न चित्र)। सिद्ध कीजिए कि-
∠ACP =∠QCD है।
हल:

चित्र 10.20
ज्ञात है : दो बिन्दुओं B और C पर प्रतिच्छेद करते है हुए दो वृत्त B से जाने वाले दो रेखाखण्ड ABD और PBO वृत्तों को क्रमश: A, D और P, Q पर प्रतिच्छेद करते हुए खींचे गए हैं।
AC, PC, DC और QC को मिलाया गया है।
सिद्ध करना है: ∠ACP = ∠QCD
उपपत्ति: चूंकि LACP = ∠ABP …(1) (एक ही वृत्तखण्डACBP के कोण हैं)
चूँकि ∠OCD = ∠QBD …(2) (एक ही वृत्तखण्ड QCBD के कोण हैं)
चूँकि ∠ABP = ∠QBD ….(3) (प्रतिच्छेदी रेखाओं AD एवं PQ में बने सम्मुख कोण)
अतः ∠ACP = ∠QCD. [समीकरण (1), (2) एवं (3) से] इति सिद्धम्

प्रश्न 10.
यदि किसी त्रिभुज की दो भुजाओं को व्यास मानकर वृत्त खींचे जाएँ तो सिद्ध कीजिए कि इन वृत्तों का प्रतिच्छेद बिन्दु तीसरी भुजा पर स्थित है।
हल:

चित्र 10.21
ज्ञात है : एक ∆ABC जिसकी भुजाओं AB और AC को ।
व्यास मानकर दो वृत्त खींचे गये हैं जो परस्पर बिन्दु D पर प्रतिच्छेद करते हैं।
सिद्ध करना है : बिन्दु D भुजा BC पर स्थित है।
रचना : AD, BD एवं CD को मिलाइए।
उपपत्ति: ∵ ∠ADB = 90° …(1) (अर्द्ध वृत्त का कोण है)
⇒ ∠ADC = 90° ….(2) (अर्द्ध वृत्त का कोण है)
⇒ ∠ADB + ∠ADC = 90° + 90° = 180° [समीकरण (1) और (2) से]
⇒ ∠BDC = 90° + 90° = 180° [समीकरण (1) और (2) से]
⇒ BDC एक सरल रेखा है।
अतः बिन्दु D भुजा BC पर स्थित है। इति सिद्धम्

प्रश्न 11.
उभयनिष्ठ कर्ण AC वाले दो समकोण त्रिभुज ABC और ADC हैं। सिद्ध कीजिए कि ∠CAD = ∠CBD है।
हल:

चित्र 10.22
दिया है : AC उभयनिष्ठ कर्ण पर दो समकोण त्रिभुज ∆ABC एवं ∆ADC, BD को मिलाया।
सिद्ध करना है: ∠CAD = ∠CBD
उपपत्ति : ∠ABC = 90° एवं ∠ADC = 90°
(∆ABC एवं ∆ADC समकोण ∆ हैं)
⇒ ∠ABC + ∠ADC = 90° + 90° = 180°
⇒ चतुर्भुज ABCD एक चक्रीय चतुर्भुज है। (सम्पूरक कोणों का युग्म सम्पूरक है)
अतः ∠CAD = ∠CBD. (एक ही वृत्तखण्ड CBAD के कोण हैं) इति सिद्धम्

प्रश्न 12.
सिद्ध कीजिए कि चक्रीय समान्तर चतुर्भुज आयत होता है।
हल:
ज्ञात है : एक चक्रीय समान्तर चतुर्भुज ABCD.
सिद्ध करना है : ABCD एक आयत है।
उपपत्ति: ∠A = ∠C (समान्तर चतुर्भुज केसम्मुख कोण) …(1)
∵ ∠A + ∠C = 180° (चक्रीय चतुर्भुज के सम्मुख कोणों का योग)…(2)

चित्र 10.23
⇒ ∠A = ∠C = 90° [समीकरण (1) और (2) से]
अत: ABCD एक आयत है। (समान्तर चतुर्भुज जिसके कोण समकोण हों, आयत होता है)। इति सिद्धम्

MP Board Class 9th Maths Solutions

MP Board Class 9th Social Science Solutions Chapter 3 भारत : स्थिति एवं भौतिक विभाग

MP Board Class 9th Social Science Chapter 3 पाठान्त अभ्यास

MP Board Class 9th Social Science Chapter 3 वस्तुनिष्ठ प्रश्न

सही विकल्प चुनकर लिखिए

प्रश्न 1.
भारत का मानक समय निर्धारित होता है
(i) 72° पूर्व देशान्तर से
(ii) 80° 30′ पूर्व देशान्तर से
(iii) 82° 30′ पूर्व देशान्तर से
(iv) 85′ पूर्व देशान्तर से।
उत्तर:
(iii) 82° 30′ पूर्व देशान्तर से

प्रश्न 2.
भारत में कर्क रेखा किस राज्य से होकर नहीं गुजरती है? (2018)
(i) गुजरात
(ii) महाराष्ट्र
(iii) छत्तीसगढ़
(iv) मध्य प्रदेश।
उत्तर:
(ii) महाराष्ट्र

प्रश्न 3.
देश का सबसे बड़ा केन्द्र शासित क्षेत्र है
(i) अण्डमान निकोबार द्वीप समूह
(ii) दादरा और नागर हवेली
(iii) लक्षद्वीप,
(iv) पाण्डिचेरी।
उत्तर:
(i) अण्डमान निकोबार द्वीप समूह

प्रश्न 4.
भारतीय प्रायद्वीप पठार किस प्रकार की चट्टानों से बना है?
(i) परिवर्तित चट्टानों से,
(ii) अवसादी शैलों से
(iii) अत्यन्त प्राचीन चट्टानों से
(iv) उपर्युक्त में से कोई नहीं।
उत्तर:
(iii) अत्यन्त प्राचीन चट्टानों से

सत्य/असत्य

प्रश्न 1.
भारत के दक्षिण में हिंद महासागर है।
उत्तर:
सत्य

प्रश्न 2.
उत्तर पश्चिम राज्यों को सात बहनें कहा जाता है। (2018)
उत्तर:
असत्य

प्रश्न 3.
अंडमान निकोबार द्वीप समूह अरब सागर में स्थित है।
उत्तर:
असत्य।

MP Board Class 9th Social Science Chapter 3 अति लघु उत्तरीय प्रश्न

प्रश्न 1.
भारत को किन-किन नामों से जाना जाता है? (2014, 18)
उत्तर:
भारत को आर्यावर्त, हिन्दुस्तान और इण्डिया नाम से जाना जाता है।

प्रश्न 2.
भारत का क्षेत्रफल लिखिए।
उत्तर:
भारत का कुल क्षेत्रफल 32,87,263 वर्ग किमी है।

प्रश्न 3.
भारत में कितने राज्य और केन्द्र शासित प्रदेश हैं? (2010, 14, 16, 18)
उत्तर:
भारत में 29 राज्य तथा 7 केन्द्र शासित प्रदेश हैं।

प्रश्न 4.
भारत के दो द्वीपीय पड़ोसी देशों के नाम लिखिए।
उत्तर:
मालद्वीप और इण्डोनेशिया।

प्रश्न 5.
पूर्वी तट पर स्थित किन्हीं दो झीलों के नाम लिखिए। (2017)
उत्तर:
इस तट पर चिल्का, कोलेरू एवं पुलीकट झीलें हैं।

प्रश्न 6.
भारत के किन द्वीपों का निर्माण प्रवालों द्वारा हुआ है? (2016)
उत्तर:
प्रवाल (मुंगे) के निक्षेपों से बने इन द्वीपों को एटॉल कहा जाता है।

प्रश्न 7.
हिमालय पर्वतमाला के दो प्रमुख शिखरों के नाम लिखिए। (2013, 15)
उत्तर:
हिमालय पर्वतमाला के दो सर्वोच्च शिखर माउण्ट एवरेस्ट एवं कंचनजंघा हैं।

प्रश्न 8.
पश्चिम से पूर्व तक भारत का विस्तार कितना है?
उत्तर:
पूर्वी-पश्चिमी विस्तार 2,933 किलोमीटर है।

MP Board Class 9th Social Science Chapter 3 लघु उत्तरीय प्रश्न

प्रश्न 1.
भारत की भौगोलिक स्थिति का महत्त्व समझाइए। (2009)
उत्तर:
भारत विषुवतरेखा के उत्तर में 8°4′ उत्तरी अक्षांश से 37°6′ उत्तरी अक्षांश तक तथा 68°7′ पूर्वी देशान्तर से 97°25′ पूर्वी देशान्तर के मध्य स्थित है। इस प्रकार सम्पूर्ण भारतवर्ष उत्तरी गोलार्द्ध या पूर्वी गोलार्द्ध में स्थित है। इस आधार पर कहा जा सकता है कि पूर्वी गोलार्द्ध में भारत की स्थिति लगभग केन्द्रीय है। इसके निम्न महत्त्व हैं :

1. केन्द्रीय स्थिति के कारण भारत अन्तर्राष्ट्रीय जलमार्गों का केन्द्र है।
2. हिन्द महासागर के शीर्ष पर स्थित होने के कारण अफ्रीका और ऑस्ट्रेलिया महाद्वीपों से जुड़ा है।
3. भारत के तीन ओर समुद्री तटरेखा होने के कारण प्राकृतिक बन्दरगाहों की सुविधा है।
4. केन्द्रीय स्थिति के कारण भारत पूर्व से पश्चिम के अन्तर्राष्ट्रीय वायुमार्गों का संगम स्थल है। इस प्रकार अन्तर्राष्ट्रीय व्यापार की दृष्टि से भारत की भौगोलिक स्थिति अच्छी है।

प्रश्न 2.
भारत के उत्तर के विशाल मैदान का वर्णन कीजिए।
उत्तर:
उत्तर का विशाल मैदान :
भारत का उत्तरी मैदान हिमालय तथा प्रायद्वीपीय पठार से निकलने वाली नदियों द्वारा बहाकर लायी हुई मिट्टी से बना है। इसके निर्माण में सिन्धु नदी तन्त्र तथा गंगा-ब्रह्मपुत्र नदी तन्त्र का सर्वाधिक योगदान है। इसे गंगा और ब्रह्मपुत्र का मैदान भी कहते हैं। यह मैदान पूर्व से पश्चिम तक 3200 किमी लम्बा तथा पश्चिम में 500 किमी चौड़ा और पूर्व में 150 किमी चौड़ा है। यह लगभग एक सपाट मैदान है और इसके उच्चावच में बहुत कम अन्तर है। यहाँ की उपजाऊ मृदा, उपयुक्त जलवायु तथा पर्याप्त जल आपूर्ति कृषि कार्य के विकास में बहुत सहायक है। यह सघन जनसंख्या वाला क्षेत्र है। इसे तीन भाग में बाँट सकते हैं –

• पश्चिमी मैदान :
  इसका विस्तार पंजाब, हरियाणा और राजस्थान में है। इसका ढाल उत्तर-पूर्व से दक्षिण-पश्चिम की ओर है। इसका पश्चिमी भाग मरुस्थल है इसे थार मरुभूमि कहते हैं। लूनी यहाँ की प्रमुख नदी है। यमुना के पश्चिम में सतलज, व्यास और रावी नदियाँ बहती हैं।
• मध्यवर्ती मैदान :
  इसे गंगा का मैदान कहते हैं। इसका ढाल पश्चिम से पूर्व की ओर है। जिस क्षेत्र में बाढ़ का पानी प्रतिवर्ष पहुँचता है, उसे खादर और जहाँ नहीं पहुँचता है उसे बांगर कहते हैं। हिमालय से लगे भाग को तराई कहते हैं। यहाँ की मृदा जलोढ़ है।
• पर्वी मैदान :
  यह मैदान 650 किमी लम्बा एवं लगभग 100 किमी चौड़ा है। इसे ब्रह्मपुत्र का मैदान भी कहते हैं। इसका ढाल उत्तर-पूर्व से दक्षिण-पश्चिम की ओर है।

प्रश्न 3.
दक्कन के पठार का संक्षिप्त वर्णन कीजिए। (2009)
उत्तर:
दक्कन का पठार विशाल पठार का बहुत बड़ा भाग है। इसकी आकृति त्रिभुजाकार है। दक्कन पठार का निर्माण आग्नेय शैलों से हुआ है। इस पठार के उत्तरी भाग का ढाल उत्तर की ओर है। इस क्षेत्र की प्रमुख नदियों में चम्बल, सिन्धु, बेतवा, केन, सोन व दामोदर हैं, जो गंगा एवं गंगा की सहायक नदियों से मिल जाती हैं। पश्चिम की ओर बहने वाली नर्मदा व ताप्ती नदियाँ दरार घाटियों से होकर बहती हुई अरब सागर में जा मिलती हैं। दक्कन के पठार का ढाल पूर्व की ओर है। कावेरी-पेनार, कृष्णा, गोदावरी और महानदी इसके जल-निकास का काम करती हैं। ये सभी नदियाँ बंगाल की खाड़ी में मिलती हैं। पठार के उत्तर-पश्चिमी भाग में काली मृदा का विकास हुआ है। यह मृदा बहुत ही उपजाऊ तथा कपास की खेती के लिए उपयोगी है। भारत के पठारी भाग में खनिज सम्पदा के विशाल भण्डार हैं। इनमें कोयला, लोहा, अभ्रक, बॉक्साइट, ताँबा, मैंगनीज आदि प्रमुख हैं। इन खनिजों पर देश का आर्थिक व औद्योगिक विकास निर्भर करता है। दक्कन पठार की नदियाँ जल शक्ति के विकास में सहायक हुई हैं।

प्रश्न 4.
भारतवासियों के लिए हिमालय का क्या महत्त्व है? लिखिए। (2008, 09, 12, 13)
अथवा
“हिमालय भारत के लिए वरदान है।” सत्यापन कीजिए।
उत्तर:
हिमालय का महत्त्व –

1. हिमालय की स्थिति के कारण ही सम्पूर्ण भारत की जलवायु उष्ण कटिबन्धीय है।
2. हिमालय पर्वत श्रेणी के कारण भारत में स्पष्ट रूप से ऋतु-चक्र चलता है।
3. हिमालय पर्वत शीत ऋतु में उत्तर-पूर्व एशिया से आने वाली ठण्डी और शुष्क पवनों को रोककर भारत को अधिक ठण्डा और शुष्क होने से बचाता है।
4. ग्रीष्म ऋतु में दक्षिण-पश्चिम मानसून पवनों को रोककर भारतीय उपमहाद्वीप में वर्षा करने में सहायक होता है।
5. हिमालय पर्वतीय क्षेत्रों में चूने का पत्थर, बलुआ पत्थर, संगमरमर, जड़ी-बूटी एवं खनिज तेल के भण्डार पाये जाते हैं।

प्रश्न 5.
बांगर व खादर भूमि में अन्तर समझाइए। (2008, 09, 12)
उत्तर:
बांगर व खादर भूमि में अन्तर

प्रश्न 6.
पूर्वी तटीय मैदान का संक्षिप्त वर्णन कीजिए। (2009)
उत्तर:
पूर्वी तटीय मैदान-पूर्वी तटीय मैदान का विस्तार बंगाल की खाड़ी में गिरने वाली महानदी, गोदावरी, कृष्णा और कावेरी नदी के डेल्टा प्रदेश में है। यहाँ उपजाऊ काँप मिट्टी मिलती है। इस तट पर चिल्का, कोलेरु एवं पुलीकट झीलें हैं। उत्तरी भाग के तट को उत्तरी सरकार और दक्षिणी भाग को कोरोमण्डल तट कहते हैं।

MP Board Class 9th Social Science Chapter 3 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
भारत को कितने भौतिक विभागों में विभाजित किया जा सकता है? किसी एक का वर्णन कीजिए।
उत्तर:
भारत के भौतिक विभाग
भारत विभिन्न स्थलाकृतियों वाला एक विशाल राष्ट्र है। भारत में हर प्रकार की भू-आकृतियाँ पायी जाती हैं; जैसे-पर्वत, पठार, मैदान, नदी घाटी, मरुस्थल, द्वीप समूह। प्रकृति द्वारा प्रदत्त इन स्थलाकृतियों के आधार पर भारत को निम्न भौतिक विभागों में बाँटा गया है –

1. उत्तरीय पर्वतीय प्रदेश
2. उत्तर का विशाल मैदान
3. प्रायद्वीपीय पठार
4. तटीय प्रदेश
5. द्वीप समूह।

प्रायद्वीपीय पठार :
यह पठार प्राचीन गोंडवाना लैण्ड का अंग है जो कभी भी सागर तल में नहीं डूबा। उत्तरी मैदान के दक्षिण में एक त्रिभुजाकार रूप में तीन ओर समुद्र से घिरा हुआ दक्षिण का पठार फैला हुआ है। इस पठार का आधार उत्तर एवं शीर्ष दक्षिण में है। क्षेत्रफल की दृष्टि से प्रायद्वीपीय पठारी क्षेत्र देश का सबसे बड़ा भौतिक प्रदेश है। प्रायद्वीपीय पठार को दो उपभागों अर्थात् मध्यवर्ती उच्च भूमि तथा दक्कन के पठार में विभाजित किया जा सकता है।

प्रश्न 2.
भारत की स्थिति व विस्तार का वर्णन कीजिए।
अथवा
भारत के उत्तर में कौन-कौन से देश स्थित हैं? नाम बताइए। (2010) [संकेतः ‘विस्तार’ शीर्षक में देखें।
उत्तर:
भारत की स्थिति-भारत विषुवत्रेखा के उत्तर में 8°4′ उत्तरी अक्षांश से 37°6′ उत्तरी अक्षांश तक तथा 68°7′ पूर्वी देशान्तर से 97°25′ पूर्वी देशान्तर के मध्य स्थित है। इस प्रकार सम्पूर्ण भारतवर्ष उत्तरी गोलार्द्ध या पूर्वी गोलार्द्ध में स्थित है। कर्क रेखा 23° (उत्तरी अक्षांश) इसके मध्य से होकर गुजरती है और भारतवर्ष को दो भागों –

1. महाद्वीपीय भारत या उत्तरी भारत
2. उष्ण कटिबन्धीय भारत या दक्षिणी भारत में बाँटती है। इसी प्रकार 82° पूर्वी देशान्तर देश के मध्य से होकर गुजरती है।

विस्तार :
भारत का उत्तर-दक्षिण विस्तार 3214 किमी तथा पूर्व पश्चिम विस्तार 2933 किमी है। इसकी स्थलीय सीमा 15,200 किमी एवं कुल समुद्री सीमा 7,516.6 किमी है। इसका क्षेत्रफल 32,87,263 वर्ग किमी है। यह विश्व का सातवाँ बड़ा देश है। भारत के उत्तर-पश्चिम में पाकिस्तान, अफगानिस्तान, उत्तर में चीन, नेपाल एवं भूटान, पूर्व में बांग्लादेश, म्यांमार व दक्षिण में श्रीलंका है।

प्रश्न 3.
हिमालय पर्वतीय क्षेत्र का वर्णन कीजिए।
अथवा
आन्तरिक हिमालय पर टिप्पणी लिखिए। (2008) [संकेत-महान या आन्तरिक हिमालय शीर्षक देखें।]
उत्तर:
हिमालय की पर्वत श्रेणियाँ भारत के उत्तर में अर्द्ध चाप के आकार में उत्तर-पश्चिम, उत्तर तथा उत्तर-पूर्व की सीमा बनाती हैं। इनकी लम्बाई 2,400 किमी है। चौड़ाई 150 से 400 किमी है। विस्तार तथा ऊँचाई के आधार पर हिमालय को तीन भागों में बाँट सकते हैं –

(1) महान या आन्तरिक हिमालय :
यह हिमालय की सबसे ऊँची और सबसे लम्बी श्रेणी है। इसे प्रधान हिमालय और हिमाद्रि भी कहते हैं। इसकी औसत ऊँचाई 6000 मीटर है। यह अत्यन्त दुर्गम क्षेत्र है, किन्तु इसमें जोजिला, कराकोरम, शिपकी, नाथूला आदि कई दरें हैं जिनसे होकर इनको पार किया जा सकता है। इस क्षेत्र में हिमालय के कई ऊँचे शिखर मिलते हैं। मुख्य पर्वत शिखर माउण्ट एवरेस्ट, कंचनजंघा, धौलागिरी, नंगा पर्वत और नंदा देवी हैं।

(2) मध्य हिमालय या हिमालय :
यह महान हिमालय के दक्षिण में उसके लगभग समान्तर फैला हुआ है। इसकी ऊँचाई 3,700 मीटर से 4,500 मीटर के बीच है तथा औसत चौड़ाई 50 किलोमीटर है। सभी प्रमुख पर्वतीय नगर जैसे डलहौजी, धर्मशाला (हिमाचल प्रदेश), नैनीताल (उत्तराखण्ड), दार्जिलिंग (पश्चिमी बंगाल) इसी पर्वत श्रेणी पर हैं। कश्मीर की पीरपंजाल तथा हिमाचल प्रदेश की धौलाधार श्रेणी, मध्य हिमालय के ही भाग हैं। नेपाल की महाभारत श्रेणी भी इसी का भाग है। यहाँ चूने का पत्थर एवं स्लेट की चट्टानें मिलती हैं।

(3) शिवालिक हिमालय :
हिमालय की दक्षिणतम श्रेणी को बाहरी हिमालय या शिवालिक हिमालय कहते हैं। इनकी औसत ऊँचाई 900 से 1100 मी तथा चौड़ाई 10 से 50 किमी है। हिमालय के पश्चिमी अर्द्ध भाग में यह श्रेणी बहुत अधिक स्पष्ट है। यह पर्वत श्रेणी जलोढ़ अवसादों से बनी है। इनकी शैलें ठोस नहीं हैं। लघु हिमालय और शिवालिक श्रेणी के बीच अनेक घाटियाँ हैं जिन्हें पूर्व में ‘द्वार’ और पश्चिम में ‘दून’ कहा जाता है।

प्रश्न 4.
प्रायद्वीपीय पठार का वर्णन कीजिए। (2009)
उत्तर:
प्रायद्वीपीय पठार प्रायद्वीपीय पठार विशाल मैदान के दक्षिण में स्थित है। यह भारत का सबसे प्राचीन भू-भाग है। यह बंगाल की खाड़ी, अरब सागर और हिन्द महासागर द्वारा तीन ओर समुद्र से घिरा हुआ है, अतः इसे प्रायद्वीप कहा जाता है।

इसकी औसत ऊँचाई 600 से 900 मीटर है। यह त्रिभुजाकार क्षेत्र के रूप में विस्तृत है। इसका विस्तार अरावली पर्वत से राजमहल की पहाड़ियों तक तथा शीर्ष कन्याकुमारी की ओर है। इसका ढाल पश्चिम से पूर्व की ओर है। यह भूखण्ड गोण्डवाना लैण्ड का अंग है। क्षेत्रफल की दृष्टि से प्रायद्वीपीय पठारी क्षेत्र देश का सबसे बड़ा भौतिक प्रदेश है। प्रायद्वीपीय पठार को दो उपभागों अर्थात् मध्यवर्ती उच्च भूमि तथा दक्कन के पठार में विभाजित किया जा सकता है।

(1) मध्यवर्ती उच्चभूमि :
प्रायद्वीपीय भू-भाग के उत्तरी भाग को मध्यवर्ती उच्च भूमियाँ कहते हैं। यह भाग कठोर, आग्नेय तथा कायान्तरित शैलों का बना हुआ है। उत्तरी पश्चिम भाग अरावली पहाड़ियों द्वारा घिरा हुआ है, जो प्राचीन वलित पर्वत के अवशिष्ट हैं। मध्यवर्ती उच्च भूमि की दक्षिणी सीमा विध्यांचल पर्वतों तथा उनके पूर्वी विस्तार कैमूर पहाड़ियों से निर्धारित होती है। अमरावती तथा विध्यांचल पर्वतों के मध्य में मालवा – का पठार स्थित है। यहाँ पर बेतवा, पार्वती, काली सिन्ध, चम्बल और माही नदियाँ बहती हैं। इसके पूर्वी भाग को दक्षिण, उत्तर प्रदेश में बुन्देलखण्ड तथा बघेलखण्ड के नाम से पुकारते हैं। दक्षिण बिहार में इसे छोटा नागपुर पठार के नाम से जाना जाता है। दक्षिण की ओर से आने वाली यमुना और गंगा की सहायक नदियाँ इसका जल बहाकर ले जाती हैं। इस पठार में खनिज के असीम भण्डार हैं।

(2) दक्कन का पठार :
दक्कन का पठार विशाल पठार का बहुत बड़ा भाग है। इसकी आकृति त्रिभुजाकार है। दक्कन पठार का निर्माण आग्नेय शैलों से हुआ है। इस पठार के उत्तरी भाग का ढाल उत्तर की ओर है। इस क्षेत्र की प्रमुख नदियों में चम्बल, सिन्धु, बेतवा, केन, सोन व दामोदर हैं, जो गंगा एवं गंगा की सहायक नदियों से मिल जाती हैं। पश्चिम की ओर बहने वाली नर्मदा व ताप्ती नदियाँ दरार घाटियों से होकर बहती हुई अरब सागर में जा मिलती हैं। दक्कन के पठार का ढाल पूर्व की ओर है। कावेरी-पेनार, कृष्णा, गोदावरी और महानदी इसके जल-निकास का काम करती हैं। ये सभी नदियाँ बंगाल की खाड़ी में मिलती हैं।

पठार के उत्तर-पश्चिमी भाग में काली मृदा का विकास हुआ है। यह मृदा बहुत ही उपजाऊ तथा कपास की खेती के लिए उपयोगी है। भारत के पठारी भाग में खनिज सम्पदा के विशाल भण्डार हैं। इनमें कोयला, लोहा, अभ्रक, बॉक्साइट, ताँबा, मैंगनीज आदि प्रमुख हैं। इन खनिजों पर देश का आर्थिक व औद्योगिक विकास निर्भर करता है। दक्कन पठार की नदियाँ जल शक्ति के विकास में सहायक हुई हैं।

प्रायद्वीपीय पठार अत्यन्त प्राचीन चट्टानों से बना होने के कारण खनिज पदार्थों में धनी है। कर्नाटक में सोना, मध्य प्रदेश में हीरा, संगमरमर, चूने का पत्थर और मैंगनीज, आन्ध्र प्रदेश और पश्चिम बंगाल में कोयला तथा बिहार एवं ओडिशा में लोहा पाया जाता है। महाराष्ट्र काली मृदा के कारण कपास की खेती के लिए प्रसिद्ध है। दक्षिण-पश्चिमी प्रायद्वीप पठार मसाले, चाय व कॉफी उत्पादन के लिए जाना जाता है। यहाँ जल विद्युत् उत्पादन की भी सम्भावनाएँ हैं। इसी पठारी प्रदेश में ऊटकमण्ड, पंचमढ़ी, महाबलेश्वर आदि महत्त्वपूर्ण स्थान हैं।

प्रश्न 5.
टिप्पणी लिखिए-भारतीय तटवर्ती क्षेत्र, भारतीय द्वीप समूह।
उत्तर:
भारतीय तटवर्ती क्षेत्र-भारतभूमि सीमा लगभग 15,200 किमी है। मुख्य भूमि, लक्षद्वीप समूह और अण्डमान निकोबार द्वीप समूह के समुद्र-तट की कुल लम्बाई (कुल तट रेखा) 7516.6 किमी है। पूर्वी तट रेखा बंगाल की खाड़ी में गंगा डेल्टा से कुमारी अन्तरीप तक विस्तृत है। पूर्वी तट रेखा के उत्तरी भाग को उत्तरी सत्कार और दक्षिणी भाग को कारोमण्डल तट कहते हैं। पश्चिमी तट रेखा का विस्तार अरब सागर के किनारे है। इसके उत्तर में काठियावाड़ तथा मध्य में कोंकण तट और दक्षिण में मालाबार तट स्थित है। हमारे समुद्री पड़ोसी देश दक्षिण में श्रीलंका और मालद्वीप हैं। अण्डमान निकोबार द्वीप समूह के पूर्व में इण्डोनेशिया स्थित है।

भारतीय द्वीप समूह :
भारत के द्वीपीय समूहों-लक्षद्वीप तथा अण्डमान व निकोबार द्वीप समूह की उत्पत्ति अलग प्रकार से हुई है। केरल के तट के निकट अरब सागर में छोटे-छोटे द्वीपों का एक समूह है जिन्हें लक्षद्वीप समूह कहते हैं। ये सभी प्रवाल द्वीप हैं, अर्थात् इनकी रचना अल्पजीवी सूक्ष्म प्रवाल जीवों के सतत् और शान्त प्रयत्नों के द्वारा हुई है। ये प्रवाल जीव उथले एवं कोष्ण जल में ही भली-भाँति पनपते हैं। इनमें से अनेक द्वीपों की आकृति घोड़े की नाल या अँगूठी के समान है। इन्हें एटॉल या प्रवालद्वीपीय वलय कहते हैं। इनके विपरीत अण्डमान निकोबार द्वीप बड़े तथा संख्या में अधिक है। इनमें से कुछ की उत्पत्ति ज्वालामुखी उद्गार से हुई है। अण्डमान द्वीप एवं निकोबार द्वीप समूह में ज्ञात एवं अज्ञात कुल द्वीपों की संख्या लगभग 300 है। यह द्वीप समूह लगभग 8249 वर्ग किमी में फैले हैं। इन द्वीप समूहों का देश की सामरिक सुरक्षा की दृष्टि से महत्त्वपूर्ण स्थान है।

मानचित्र पठन
भारत के मानचित्र का अध्ययन कर निम्नांकित के विषय में लिखिए। –

प्रश्न 1.
भारत की उत्तरी सीमा का अक्षांशीय विस्तार।
उत्तर:
37°6′.

प्रश्न 2.
उन राज्यों के नाम जिनकी सीमाएँ चीन से मिलती हैं।
उत्तर:
जन्मू एवं कश्मीर, हिमाचल प्रदेश, उत्तराखण्ड, सिक्किम एवं अरुणाचल प्रदेश।

प्रश्न 3.
उन राज्यों के नाम जिनसे होकर कर्क रेखा गुजरती है।
उत्तर:
छत्तीसगढ़, मध्य प्रदेश, मिजोरम, त्रिपुरा, पश्चिम बंगाल, राजस्थान, झारखण्ड व गुजरात।

प्रश्न 4.
बंगाल की खाड़ी में गिरने वाली नदियों के नाम।
उत्तर:
गंगा, गोदावरी, महानदी, कृष्णा, कावेरी।

प्रश्न 5.
हिमालय में स्थित कोई तीन दरों के नाम।
उत्तर:
काराकोरम, नाथुला, बोमडिला।

MP Board Class 9th Social Science Chapter 3 अन्य परीक्षोपयोगी प्रश्न

MP Board Class 9th Social Science Chapter 3 वस्तुनिष्ठ प्रश्न

बहु-विकल्पीय प्रश्न

प्रश्न 1.
विश्व के क्षेत्रफल का कितना भू-भाग भारत में है?
(i) 1.25 प्रतिशत
(ii) 1.89 प्रतिशत
(iii) 2.42 प्रतिशत
(iv) 3.42 प्रतिशत।
उत्तर:
(iii) 2.42 प्रतिशत

प्रश्न 2.
पूर्वी मैदान को कहते हैं
(i) पश्चिमी मैदान
(ii) ब्रह्मपुत्र मैदान
(iii) मध्यवर्ती मैदान
(iv) उपर्युक्त में कोई नहीं।
उत्तर:
(ii) ब्रह्मपुत्र मैदान

प्रश्न 3.
भारत में कितने राज्य हैं? (2017)
(i) 15
(ii) 20
(iii) 29
(iv) 301
उत्तर:
(iii) 29

रिक्त स्थान पूर्ति

1. भारत उत्तरी गोलार्द्ध में एशिया महाद्वीप के ………… में स्थित है।
2. ………… भारत को लगभग दो बराबर भागों में बाँटती है। (2014)
3. क्षेत्रफल की दृष्टि से ………… सबसे बड़ा राज्य है।
4. भारत और श्रीलंका के बीच …………. खाड़ी है। (2008)
5. प्रवाल (मूंगे) के निक्षेपों से बने इन द्वीपों को …………. कहा जाता है।

उत्तर:

1. दक्षिणी भाग
2. कर्क रेखा
3. राजस्थान
4. मन्नार की
5. एटॉल।

सत्य/असत्य

प्रश्न 1.
भारत एवं श्रीलंका के मध्य मन्नार की खाड़ी स्थित है। (2008)
उत्तर:
सत्य

प्रश्न 2.
कर्क रेखा भारत को दो भागों में बाँटती है। (2008)
उत्तर:
सत्य

प्रश्न 3.
देश में तहसीलों की संख्या 6,38,588 है। (2015)
उत्तर:
असत्य

प्रश्न 4.
उत्तर-पश्चिम के सात राज्यों को “सात बहनें” कहा जाता है। (2017)
उत्तर:
असत्य

प्रश्न 5.
भारत के दक्षिण में हिन्द महासागर है। (2016)
उत्तर:
सत्य

प्रश्न 6.
क्षेत्रफल की दृष्टि से भारत विश्व का सातवाँ बड़ा देश है। (2017)
उत्तर:
सत्य

सही जोड़ी मिलाइए

उत्तर:

1. → (घ)
2. → (ङ)
3. → (ग)
4. → (ख)
5. → (क)

एक शब्द/वाक्य में उत्तर

प्रश्न 1.
भारत का क्षेत्रफल लिखिए। (2014, 16)
उत्तर:
32,87,263 वर्ग किमी

प्रश्न 2.
उत्तर-पूर्व के सात राज्यों को क्या कहा जाता है?
उत्तर:
सात बहनें

प्रश्न 3.
बाढ़ के मैदानों की नवीन जलोढक। (2015)
उत्तर:
खादर

प्रश्न 4.
भारत की स्थल सीमा कितनी है?
उत्तर:
15,200 किमी

प्रश्न 5.
भारतीय उपमहाद्वीप का सबसे प्राचीनतम भू-भाग कैना-सा है?
उत्तर:
विशाल प्रायद्वीप पठार

प्रश्न 6.
वे शैल जो मैग्मा के पृथ्वी के भीतर जम जाने से बनती है, क्या है?
उत्तर:
ग्रेनाइट

प्रश्न 7.
भारत एवं श्रीलंका के मध्य कौन-सी खाड़ी है? (2018)
उत्तर:
मन्नार की खाड़ी।

MP Board Class 9th Social Science Chapter 3 अति लघु उत्तरीय प्रश्न

प्रश्न 1.
भारत में सबसे बड़ा व सबसे छोटा जिला कौन-सा है?
उत्तर:
सबसे बड़ा जिला कच्छ (गुजरात) एवं सबसे छोटा जिला माहे (पुदुचेरी) है।

प्रश्न 2.
हिमाचल पर्वत की रचना लिखिए।
उत्तर:
हिमालय पर्वत, सिन्धु नदी से लेकर पूर्व में ब्रह्मपुत्र तक फैला है। इन दो सीमाओं के बीच इसकी आकृति, एक चाप के समान है। हिमालय की लम्बाई 2400 किमी है।

प्रश्न 3.
परिवर्तित सेल क्या हैं?
उत्तर:
पूर्व निर्मित आग्नेय या अवसादी शैलों पर अधिक दबाव या ताप के अवसाद का कारण भौतिक तथा रासायनिक परिवर्तन द्वारा बनी नई शैल।

प्रश्न 4.
उच्चावच किसे कहते हैं?
उत्तर:
धरातल या समुद्र की तलहटी पर प्राकृतिक रूपरेखा में पाए जाने वाले ऊँचाइयों के अन्तर को उच्चावच कहते हैं।

प्रश्न 5.
गोंडवाना लैण्ड क्या है? (2011, 15, 17)
उत्तर:
ये प्राचीन विशाल महाद्वीप पैंजिया का दक्षिणतम भाग है जिसमें आज के अफ्रीका, ऑस्ट्रेलिया तथा अंटार्कटिका शामिल हैं।

प्रश्न 6.
भारत की उन दो नदियों के नाम बताइए जो अपने मुहाने पर ज्वारनदमुख बनाती हैं ?
उत्तर:
नर्मदा और ताप्ती नदी।

MP Board Class 9th Social Science Chapter 3 लघु उत्तरीय प्रश्न

प्रश्न 1.
मध्यवर्ती मैदान हिमालय पर्वत का ‘उपहार’ क्यों कहा जाता है?
उत्तर:
मध्यवर्ती मैदान भारत के लगभग एक चौथाई क्षेत्रफल को घेरे हुए है। यहाँ भारत की लगभग 45 प्रतिशत जनसंख्या वास करती है। सिन्धु, सतलज, गंगा, ब्रह्मपुत्र नदियों द्वारा बहाकर लाई गई मृदा से बना होने और सिंचाई की सुविधा के कारण यह मैदान हिमालय पर्वत का ‘उपहार’ कहलाता है। उत्तरी मैदान कृषि की दृष्टि से महत्त्वपूर्ण है। यहाँ जनसंख्या बाहुल्य है। नहरों, सड़कों और रेलों का जाल बिछा है। यह मैदान सभ्यता की जन्मभूमि रहा है। अमृतसर, कुरुक्षेत्र, मथुरा, वृन्दावन, प्रयाग, काशी आदि तीर्थस्थल इसी मैदान में स्थित हैं।

प्रश्न 2.
पश्चिमी तटीय मैदान व पूर्वी तटीय मैदान में अन्तर स्पष्ट कीजिए। (2008)
उत्तर:
पश्चिमी तटीय मैदान व पूर्वी तटीय मैदान में अन्तर

MP Board Class 9th Social Science Chapter 3 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
टिप्पणी लिखिए
(1) उत्तर का पर्वतीय प्रदेश
(2) तटीय प्रदेश।
उत्तर:
(1) उत्तर का पर्वतीय प्रदेश :
भारत की उत्तरी सीमा पर वृहद् हिमालय विश्व की सबसे ऊँची व बनावट के दृष्टिकोण से नवीन वलित पर्वत श्रृंखला है। ये शृंखलाएँ पश्चिम-पूर्व दिशा में सिन्धु से लेकर ब्रह्मपुत्र तक फैली हैं। हिमालय 2400 किमी की लम्बाई में फैले एक धनुषाकार आकृति का निर्माण करता है। विस्तार एवं ऊँचाई के आधार पर हिमालय को तीन भागों में बाँट सकते हैं-

• महान या आन्तरिक हिमालय
• मध्य हिमालय, तथा
• शिवालिक श्रेणी।

(2) तटीय प्रदेश :
प्रायद्वीपीय पठार कच्छ से उड़ीसा तक तटीय मैदानों की एक सँकरी पट्टी से घिरा हुआ है। इस तटीय मैदान को इनकी बनावट में अन्तर के कारण इसे दो भागों में पश्चिमी तथा पूर्वी तटीय भागों में विभक्त किया जाता है। पश्चिमी तटीय मैदान अरब सागर के सहारे-सहारे गुजरात से केरल तक फैला हुआ है। यह मैदान सँकरे हैं, इन्हें उत्तरी भाग में कोंकण और गोवा के दक्षिण में मालाबार तटीय मैदान कहते हैं। पूर्वी तट-यह पश्चिमी तट की अपेक्षा अधिक चौड़े और समतल हैं। यहाँ उपजाऊ काँप मृदा मिलती है।

MP Board Class 9th Social Science Solutions

MP Board Class 9th Maths Solutions Chapter 15 प्रायिकता Ex 15.1

प्रश्न 1.
एक क्रिकेट मैच में, एक महिला बल्लेबाज खेली गई 30 गेंद में 6 बार चौका मारती है। चौका न मारने की प्रायिकता ज्ञात कीजिए। (2019)
हल :
चौका न मारने की घटना E = 30 – 6 = 24

अतः अभीष्ट प्रायिकता = \(\frac { 24 }{ 30 }\) अर्थात् \(\frac { 4 }{ 5 }\)

प्रश्न 2.
2 बच्चों वाले 1500 परिवारों का यदृच्छया चयन किया गया और निम्नलिखित आँकड़े लिख लिए गए हैं : (2019)

यदृच्छया चुने गए परिवार की प्रायिकता ज्ञात कीजिए जिसमें
(i) दो लड़कियाँ हों
(ii) एक लड़की हो
(iii) कोई लड़की न हो। साथ ही यह भी जाँच कीजिए कि इन प्रायिकताओं का योगफल 1 है या नहीं।
हल :
(i) चूँकि E1 = 475 एवं n = 1500
\(P\left(E_{1}\right)=\frac{E_{1}}{n}=\frac{475}{1500}=\frac{19}{60}\)
अत: दो लड़कियाँ होने की अभीष्ट प्रायिकता = \(\frac { 19 }{ 60 }\)

(ii) चूँकि E2 = 814 एवं n= 1500
\(P\left(E_{2}\right)=\frac{E_{2}}{n}=\frac{814}{1500}=\frac{407}{750}\)
अत: एक लड़की होने की अभीष्ट प्रायिकता = \(\frac { 407 }{ 750 }\).

(iii) चूँकि E3 = 211 एवं n = 1500
अतः एक भी लड़की न होने की अभीष्ट प्रायिकता = \(\frac { 211 }{ 1500 }\)
अब \(\frac{19}{60}+\frac{407}{750}+\frac{211}{1500}=\frac{475+814+211}{1500}=\frac{1500}{1500}=1\)
अतः प्रायिकताओं का योगफल 1 है।

प्रश्न 3.
नवीं कक्षा के 40 विद्यार्थियों से उनके जन्म का महीना बताने के लिए कहा गया। इस प्रकार प्राप्त आकड़ों से निम्नलिखित आलेख बनाया गया :

कक्षा के किसी एक विद्यार्थी का जन्म अगस्त में होने की प्रायिकता ज्ञात कीजिए।
हल :
दिया है : n = 40 एवं आलेखानुसार E = 6.
\(P(E)=\frac{E}{n}=\frac{6}{40}=\frac{3}{20}\)
अत: एक छात्र के अगस्त में जन्म लेने की अभीष्ट प्रायिकता = \(\frac { 3 }{ 20 }\).

प्रश्न 4.
तीन सिक्कों को एक साथ 200 बार उछाला गया तथा इनमें विभिन्न परिणामों की बारम्बारताएँ ये हैं :

यदि तीनों सिक्कों को पुनः एक साथ उछाला जाए, तो दो चित आने की प्रायिकता ज्ञात कीजिए।
हल :
चूँकि E = 72 एवं n = 200 (प्रश्नानुसार दिया है)
\(P(E)=\frac{E}{n}=\frac{72}{200}=\frac{9}{25}\)
अत: दो चित आने की अभीष्ट प्रायिकता = \(\frac { 9 }{ 25 }\)

प्रश्न 5.
एक कम्पनी ने यदृच्छया 2400 परिवार चुनकर एक घर की आय स्तर और वाहनों की संख्या के बीच सम्बन्ध स्थापित करने के लिए उनका सर्वेक्षण किया। एकत्रित किए गए आँकड़े नीचे सारणी में दिए गए हैं :

मान लीजिए एक परिवार चुना गया है। प्रायिकता ज्ञात कीजिए कि चुने गए परिवार :
(i) की आय Rs 10,000 से Rs 13,000 प्रतिमाह है और उसके पास ठीक-ठीक दो वाहन हैं।
(ii) की आय प्रतिमाह Rs 16,000 या इससे अधिक है और उसके पास ठीक एक वाहन है।
(iii) की आय Rs 7,000 प्रतिमाह से कम है और उसके पास कोई वाहन नहीं है।
(iv) की आय Rs 13,000 से Rs 16,000 प्रति माह है और उसके पास 2 से अधिक वाहन हैं।
(v) जिसके पास 1 से अधिक वाहन नहीं हैं।
हल :
(i) चूँकि n = 2,400 एवं E1 = 29 (दी गई सारणी से)
\(P\left(E_{1}\right)=\frac{E_{1}}{n}=\frac{29}{2,400}\)
अतः अभीष्ट प्रायकिता = \(\frac { 29 }{ 2400 }\)

(ii) चूँकि n = 2,400 एवं E2 = 579 (दी गई सारणी से)
\(P\left(E_{2}\right)=\frac{E_{2}}{n}=\frac{579}{2,400}=\frac{193}{800}\)
अतः अभीष्ट प्रायिकता = \(\frac { 579 }{ 2400 }\) अथात् \(\frac { 193 }{ 800 }\)

(iii) चूँकि n = 2400 एवं E3 = 10 (दी गई सारणी से)
\(P\left(E_{3}\right)=\frac{E_{3}}{n}=\frac{10}{2,400}=\frac{1}{240}\)
अतः अभीष्ट प्रायिकता = \(\frac { 1 }{ 240 }\)

(iv) चूँकि n = 2,400 एवं E4 = 25 (दी गई सारणी से)
\(P\left(E_{4}\right)=\frac{E_{4}}{n}=\frac{25}{2,400}=\frac{1}{96}\)

(v) चूँकि जिनके पास एक से अधिक वाहन नहीं हैं। उनके पास या तो 1 वाहन है अथवा एक भी वाहन नहीं अर्थात् शून्य है।
शून्य वाहन वाले परिवार = 10 + 0 + 1 + 2 + 1 = 14
एवं 1 वाहन वाले परिवार = 160 + 305 + 535 + 469 + 579 = 2,048
⇒ उन परिवारों की संख्या जिनके पास 1 से अधिक वाहन नहीं हैं = E5 = 2048 + 14 = 2,062
\(P\left(E_{5}\right)=\frac{E_{5}}{n}=\frac{2,062}{2,400}=\frac{1031}{1,200}\)
अतः अभीष्ट प्रायिकता = \(\frac { 1031 }{ 1200 }\)

प्रश्न 6.
100 अंक की गणित की परीक्षा में विद्यार्थियों ने निम्न प्रकार अंक प्राप्त किए :

(i) गणित की परीक्षा में एक विद्यार्थी द्वारा 20% से कम अंक प्राप्त करने की प्रायिकता ज्ञात कीजिए।
(ii) जब विद्यार्थी द्वारा 60 या इससे अधिक अंक प्राप्त करने की प्रायिकता ज्ञात कीजिए।
हल :
(i) चूँकि E1 = 7 एवं n = 90 (दी गई सारणी के अनुसार)
प्रायिकता \(P\left(E_{1}\right)=\frac{E_{1}}{n}=\frac{7}{90}\)
अत: अभीष्ट प्रायिकता = \(\frac { 7 }{ 90 }\)

(ii) चूँकि E2 = 15 + 8 = 23 एवं n = 90 (दी गई सारणी से)
प्रायिकता \(P\left(E_{2}\right)=\frac{E_{2}}{n}=\frac{23}{90}\)
अतः अभीष्ट प्रायिकता = \(\frac { 23 }{ 90 }\)

प्रश्न 7.
सांख्यिकी के बारे में विद्यार्थियों का मत जानने के लिए 200 विद्यार्थियों का सर्वेक्षण किया गया। प्राप्त आँकड़ों को नीचे दी गई सारणी में लिख लिया गया है : (2018, 19)

प्रायिकता ज्ञात कीजिए कि यदृच्छिक चुना गया एक विद्यार्थी :
(i) सांख्यिकी पसन्द करता है।
(ii) सांख्यिकी पसन्द नहीं करता है।
हल :
(i) चूँकि E1 = 135 एवं n = 200 (प्रश्नानुसार)
प्रायिकता = \(P\left(E_{1}\right)=\frac{E_{1}}{n}=\frac{135}{200}=\frac{27}{40}\)
अतः अभीष्ट प्रायिकता = \(\frac { 27 }{ 40 }\)

(ii) चूँकि E2 = 65 एवं n = 200 (प्रश्नानुसार)
प्रायिकता \(P\left(E_{2}\right)=\frac{E_{2}}{n}=\frac{65}{200}=\frac{13}{40}\)
अतः अभीष्ट प्रायिकता = \(\frac { 13 }{ 40 }\)

प्रश्न 8.
40 इन्जीनियरों की उनके आवास से कार्य (स्थल की (किलोमीटर में) दूरियाँ ये हैं :

इसकी आनुभविक प्रायिकता क्या होगी कि इन्जीनियर :
(i) अपने कार्य स्थल से 7 km से कम दूरी पर रहती है।
(ii) अपने कार्य स्थल से 7 km या इससे अधिक दूरी पर रहती है।
(iii) अपने कार्य स्थल से \(\frac { 1 }{ 2 }\) km या इससे कम दूरी पर रहती है।

हल :
(i) चूँकि E1 = 9 एवं n = 40 (सारणी के अनुसार)
प्रायिकता \(P\left(E_{1}\right)=\frac{E_{1}}{n}=\frac{9}{40}\)
अतः अभीष्ट प्रायिकता = \(\frac { 9 }{ 40 }\)

(ii) चूँकि E2 = 31 एवं n = 40 (सारणी के अनुसार)
प्रायिकता \(P\left(E_{2}\right)=\frac{E_{2}}{n}=\frac{31}{40}\)
अतः अभीष्ट प्रायिकता = \(\frac { 31 }{ 40 }\)

(iii) चूँकि E3 = 0 एवं n = 40 (सारणी के अनुसार)
प्रायिकता \(P\left(E_{3}\right)=\frac{E_{3}}{n}=\frac{0}{40}=0\)
अतः अभीष्ट प्रायिकता = 0.

प्रश्न 9.
अपने विद्यालय के गेट के सामने से एक समय अन्तराल में गुजरने वाले दो पहिया, तीन पहिया और चार पहिया वाहनों की बारम्बारता लिख लीजिए। आप द्वारा देखे गए वाहनों में से किसी एक वाहन का दो पहिया वाहन होने की प्रायिकता ज्ञात कीजिए।
हल :
(निर्देश : छात्र उक्त क्रियाकलाप स्वयं करें और अभीष्ट प्रायिकता का परिकलन करें।)

प्रश्न 10.
आप अपनी कक्षा के विद्यार्थियों से एक तीन अंकों वाली संख्या लिखने को कहिए। आप कक्षा से एक विद्यार्थी को यदृच्छया चुन लीजिए। इस बात की प्रायिकता क्या होगी कि उसके द्वारा लिखी गई संख्या 3 से भाज्य है ? याद रखिए कि कोई संख्या 3 से भाज्य होती है यदि उसके अंकों का योग 3 से भाज्य हो।
हल :
(निर्देश : छात्र इस क्रियाकलाप को स्वयं करें और अभीष्ट प्रायिकता का परिकलन करें।)

प्रश्न 11.
आटे की उन 11 थैलियों में जिन पर 5 kg अंकित है, वास्तव में आटे के निम्नलिखित भार (kg में) हैं:
4.97, 5.05, 5.08, 5.03, 5.00, 5.06, 5.08, 4.98, 5.04, 5.07, 5.00.
यदृच्छया चुनी गई एक थैली में 5 kg से अधिक आटा होने की प्रायिकता क्या होगी ?
हल :
चूँकि E = 5 kg से अधिक आटे वाले थैलियों की संख्या = 7 एवं कुल थैलियों की संख्या n = 11
प्रायिकता \(P(E)=\frac{E}{n}=\frac{7}{11}\)
अत: अभीष्ट प्रायिकता = \(\frac { 7 }{ 11 }\)

प्रश्न 12.
एक नगर की वायु में सल्फर डाइ-ऑक्साइड का सान्द्रण भाग प्रति मिलियन (ppm) में ज्ञात करने के लिए एक अध्ययन किया गया। 30 दिनों के प्राप्त आँकड़े ये हैं :

इनमें से किसी एक दिन अन्तराल (0.12 – 0.16) में सल्फर डाइ-ऑक्साइड के सान्द्रण होने की प्रायिकता ज्ञात कीजिए।
हल :
चूँकि वर्ग अन्तराल (0.12-0.16) में सल्फर डाइ-ऑक्साइड की दो सान्द्रताएँ 0.12 एवं 0.13 हैं।
इसलिए E = 2 एवं n = 30 (दिया है)
प्रायिकता \(P(E)=\frac{2}{30}=\frac{1}{15}\)
अतः अभीष्ट प्रायिकता = \(\frac { 1 }{ 15 }\).

प्रश्न 13.
आठवीं कक्षा के 30 विद्यार्थियों के रक्त समूह ये हैं :
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O
A, AB, O, A, A, O, O AB, B, A, O, B, A, B, O.
रक्त समूह से सम्बन्धित बारम्बारता बंटन सारणी बनाइए तथा हम सारणी की सहायता से इस कक्षा से यदृच्छया चुने गए एक विद्यार्थी का रक्त समूह AB होने की प्रायिकता ज्ञात कीजिए।
हल :

सारणी के अनुसार E = 3 एवं n = 30
प्रायिकता \(P(E)=\frac{E}{n}=\frac{3}{30}=\frac{1}{10}\)
अतः अभीष्ट प्रायिकता = \(\frac { 1 }{ 10 }\)

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 10 वृत्त Ex 10.4

प्रश्न 1.
5 cm और 3 cm की त्रिज्या वाले दो वृत्त दो बिन्दुओं पर प्रतिच्छेद करते हैं तथा उनके केन्द्रों के बीच की दूरी 4 cm है। उभयनिष्ठ जीवा की लम्बाई ज्ञात कीजिए।
हल:
दिए हुए वृत्त के केन्द्र क्रमशः O तथा O’ है जिनके बीच की दूरी OO’ = 4 cm है। वृत्त एक-दूसरे को P और Q दो बिन्दुओं पर प्रतिच्छेद करते है। वृत्तों की त्रिज्याएँ क्रमशः
OP = 5 cm तथा OP = 3 cm हैं।

चित्र 10.6
चूँकि (OO’)² + (O’P)² = (4)² + (3)² = 16 + 9 = 25 = (5)2 = (OP)²
अतः ∆OO’P एक समकोण त्रिभुज है। (पाइथागोरस का विलोम)
⇒ OO’ ⊥ O’P
चूँकि उभयनिष्ठ जीवा PQ छोटे वृत्त के केन्द्र O’ से जाती है, इसलिए PQ छोटे वृत्त का व्यास है।
⇒ PQ = 2 x O’P = 2 x 3 = 6 cm
अत: उभयनिष्ठ जीवा की अभीष्ट लम्बाई = 6 cm.

प्रश्न 2.
यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर परस्पर प्रतिच्छेद करें तो, सिद्ध कीजिए कि एक जीवा के खण्ड दूसरी जीवा के संगत खण्डों के बराबर है।
हल:
दिया है : O केन्द्र वाले एक वृत्त की दो जीवाएँ AB = CD परस्पर E बिन्दु पर प्रतिच्छेद करती हैं, तो सिद्ध करना है कि
AE = DE एवं CE = BE

चित्र 10.7
रचना : O से OM ⊥ AB तथा ON ⊥ CD खींचिए तथा OE को मिलाइए।
उपपत्ति : समकोण ∆OME एवं ∆ONE में,
चूँकि कर्ण OE = OE (उभयनिष्ठ है)
एवं OM = ON (बराबर जीवाएँ केन्द्र से बराबर दूरी पर होती है)
⇒ ΔΟΜΕ ≅ ΔΟΝΕ (RHS सर्वांगसमता प्रमेय)
⇒ ME = NE
चूँकि AB = CD, OM ⊥ AB एवं ON ⊥ CD
⇒ AM = DN एवं BM = CN
⇒ AM + ME = DN + NE [समीकरण (1) और (2) से]
⇒ AE = DE
एवं CN – EN = BM – EM [समीकरण (1) और (2) में]
⇒ CE = BE
अतः वृत्त की बराबर जीवाएँ वृत्त के अन्दर यदि प्रतिच्छेद करती हैं। तो उनके संगत खण्ड बराबर होते हैं। इति सिद्धम्

प्रश्न 3.
यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि प्रतिच्छेद बिन्दु को केन्द्र से मिलाने वाली रेखा जीवाओं से बराबर कोण बनाती है।
हल:

चित्र 10.8
ज्ञात है : O केन्द्र वाले एक वृत्त की दो जीवाएँ AB = CD वृत्त के अन्दर बिन्दु E पर परस्पर प्रतिच्छेद करती हैं। OE को मिलाया गया है।
सिद्ध करना है: ∠OEA = ∠OED
रचना : OM ⊥ AB एवं ON ⊥ CD खींचिए।
उपपत्ति : समकोण ΔOME एवं ΔONE में,
चूँकि कर्ण OE = कर्ण OE (उभयनिष्ठ है)
एवं OM = ON (बराबर जीवाएँ केन्द्र से बराबर दूरी पर होती हैं)
⇒ ΔΟΜΕ ≅ ΔΟΝΕ (RHS सर्वांगसमता प्रमेय)
⇒ ∠OEM = ∠OEN (CPCT)
अतः ∠OEA = ∠OED (चित्रानुसार) इति सिद्धम्

प्रश्न 4.
यदि एक रेखा दो संकेन्द्री वृत्तों (एक ही केन्द्र वाले वृत्त) को जिनका केन्द्र O है A, B, C और D पर प्रतिच्छेद करें, तो सिद्ध कीजिए कि AB = CD है (देखिए संलग्न चित्र)। (2019)
हल:

चित्र 10.9
दिया है : O केन्द्र वाले दो संकेन्द्री वृत्तों को रेखा AD बिन्दुओं A, B, C और D पर (चित्रानुसार) प्रतिच्छेद करती है तो सिद्ध करना है कि AB = CD
रचना : OM ⊥ AD खींचिए।
उपपत्ति : बाह्य वृत्त में चूँकि AD वृत्त की जीवा है तथा OM ⊥ AD
⇒ AM = DA …..(1) (केन्द्र से जीवा पर डाला लम्ब उसे समद्विभाजित करता है)
चूँकि अन्तः वृत्त की जीवा CB पर OM लम्ब है। (चित्रानुसार)
⇒ BM = CM …(2) (वृत्त के केन्द्र से जीवा पर डाला गया लम्ब उसे समद्विभाजित करता है)
⇒ AM – BM = DM – CM [समीकरण (1) और (2) से]
अतः AB = CD. (चित्रानुसार) इति सिद्धम्

प्रश्न 5.
एक पार्क में बने 5 m त्रिज्या वाले वृत्त पर खड़ी तीन लड़कियाँ रेशमा, सलमा एवं मनदीप खेल रही हैं। रेशमा एक गेंद को सलमा के पास, सलमा मनदीप के पास तथा मनदीप रेशमा के पास फेंकती है। यदि रेशमा तथा सलमा के बीच और सलमा तथा मनदीप के बीच की प्रत्येक दूरी 6 m हो, तो रेशमा और मनदीप की बीच की दूरी क्या है ?
हल:
मान लीजिए वृत्ताकार पार्क का केन्द्र O है। बिन्दु R, S और M पर क्रमशः रेशमा, सलमा और मनदीप हैं। वृत्त की त्रिज्या OR = 5 m, तथा RS = SM = 6 m दी गई है तो दूरी RM ज्ञात करना है।

चित्र 10.10

अत: रेशमा और मनदीप के बीच की दूरी RM = 2 x x = 2 x 4.8 = 9.6 m.

प्रश्न 6.
20 m त्रिज्या का एक गोल पार्क (वृत्ताकार) एक कॉलोनी में स्थित है। तीन लड़के अंकुर, सैय्यद, डेविड इसकी परिसीमा पर बराबर दूरी पर बैठे हैं और प्रत्येक के हाथ में एक खिलौना टेलीफोन आपस में बात करने के लिए है। प्रत्येक टेलीफोन की डोरी की लम्बाई ज्ञात कीजिए।

चित्र 10.11
हल:
दिया है : एक 20 m त्रिज्या का 0 केन्द्र वाला वृत्ताकार पार्क जिसकी परिसीमा पर अंकुर, सैय्यद और डेविड क्रमश: A, S और D बिन्दुओं पर इस प्रकार बैठे हैं कि AS = SD = DA =x मान लीजिए।
चूँकि समबाहु त्रिभुज की सभी माध्यिकाएँ बराबर होती हैं, वे सम्मुख भुजाओं को समकोण पर समद्विभाजित करती हैं तथा परस्पर एक बिन्दु पर 2 : 1 के अनुपात में प्रतिच्छेद करती है एवं यह बिन्दु उसके शीर्षों से समान दूरी पर होता है अर्थात् ASD से जाने वाले वृत्त का केन्द्र।
⇒ AO = SO = DO = 20 m (वृत्त की त्रिज्या दी है)
एवं OM = \(\frac { 1 }{ 2 }\)AO = \(\frac { 1 }{ 2 }\) x 20 = 10 m
⇒ AM = AO + OM = 20 + 10 = 30 m
समकोण ∆AMS में पाथागोरस प्रमेय से,
AS² = AM² + SM²

अतः प्रत्येक टेलीफोन की छोरी की अभीष्ट लम्बाई = 34.64 m.

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 10 वृत्त Ex 10.3

प्रश्न 1.
वृत्तों के कई जोड़े (युग्म) खींचिए। प्रत्येक जोड़े में कितने बिन्दु उभयनिष्ठ हैं ? उभयनिष्ठ बिन्दुओं की अधिकतम संख्या क्या होगी?
हल:
वृत्तों के अभीष्ट युग्म (जोड़े) :

चित्र 10.3
उभयनिष्ठ बिन्दुओं की संख्या-
(a) में शून्य,
(b) में एक,
(c) में दो,
(d) में एक,
(e) में शून्य।
अतः अधिकतम उभयनिष्ठ बिन्दुओं की संख्या = दो।

प्रश्न 2.
मान लीजिए आपको एक वृत्त दिया है। एक रचना इसके केन्द्र को ज्ञात करने के लिए दीजिए।
हल:

चित्र 10.4
एक वृत्त दिया है जिसका केन्द्र ज्ञात करना है।
रचना :
(i) वृत्त पर तीन बिन्दु P, Q और R लीजिए।
(ii) PQ एवं QR को मिलाइए।
(iii) PQ का लम्ब समद्विभाजक AB खींचिए।
(iv) OR का लम्ब समद्विभाजक CD खींचिए जो AB को बिन्दु O पर प्रतिच्छेद करता है। यही बिन्दु O वृत्त का अभीष्ट केन्द्र है।

प्रश्न 3.
यदि दो वृत्त परस्पर दो बिन्दुओं पर प्रतिच्छेद करें, तो सिद्ध कीजिए कि उनके केन्द्र उभयनिष्ठ जीवा के लम्ब समद्विभाजक पर स्थित हैं।
हल:

चित्र 10.5
दिया है : O और O’ केन्द्र वाले दो वृत्त एक-दूसरे को दो बिन्दुओं P और Q पर प्रतिच्छेद करते हैं। तो सिद्ध करना है कि उनके केन्द्र उभयनिष्ठ जीवा PQ के लम्ब समद्विभाजक पर स्थित हैं।
रचना : केन्द्र O और O’ को उभयनिष्ठ जीवा PQ के मध्य-बिन्दु R से मिलाइए।
उपपत्ति : चूँकि O केन्द्र वाले वृत्त में केन्द्र O को जीवा PQ के मध्य-बिन्दु R से मिलाया गया है।
⇒ OR ⊥ PO अर्थात् ∠ORP = 90° ….(1)
चूँकि O’ केन्द्र वाले वृत्त में केन्द्र O’ को जीवा PQ के मध्य बिन्दु R से मिलाया गया है।
⇒ OR ⊥ PO अर्थात् ∠O’RP = 90° …..(2)
⇒ ∠ORP + ∠O’RP = 180° [समीकरण (1) और (2) से]
⇒ ORO’ एक सरल रेखाखण्ड है जो जीवा PQ का लम्बार्द्धक है।
अतः यदि दो वृत्त परस्पर दो बिन्दुओं पर प्रतिच्छेद करें, तो उनके केन्द्र उभयनिष्ठ जीवा के लम्बार्द्धक पर स्थित हैं। इति सिद्धम्

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 7 त्रिभुज Additional Questions

MP Board Class 9th Maths Chapter 7 अतिरिक्त परीक्षोपयोगी प्रश्न

MP Board Class 9th Maths Chapter 7 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
ABCD एक चतुर्भुज है, जिसमें AB = BC और AD = CD। दर्शाइए कि BD दोनों कोणों ABC और ADC को समद्विभाजित करता है।
हल:

चित्र 7.34
दिया है : एक चतुर्भुज ABCD जिससे
AB = BC और AD = CD। BD चतुर्भुज ABCD का एक विकर्ण है।
अब ∆ABD और ∆CBD में,
चूँकि AB = BC (दिया है)
AD = CD (दिया है)
एवं BD = BD (उभयनिष्ठ है)
⇒ ∆ABD ≅ ∆CBD (SSS सर्वांगसमता प्रमेय)
⇒ ∠ABD ≅ ∠CBD एवं ∠ADB = ∠CDB (CPCT)
अत: BD दोनों कोण ∠ABC एवं ∠ADC को समद्विभाजित करता है। इति सिद्धम्

प्रश्न 2.
ABC एक समकोण त्रिभुज है जिससे AB = AC, CA का समद्विभाजक BC से D पर मिलता है। सिद्ध कीजिए कि BC = 2AD.
हल:

चित्र 7.34
दिया है: ABC एक समकोण त्रिभुज जिसमें AB = AC, ∠A समकोण है जिसका समद्विभाजक AD, BC को बिन्दु D पर मिलता है।
अब ∠CAD = ∠BAD = 45° (∵ ∠A समकोण है तथा AD इसका समद्विभाजक है) …(1)
∠ACB = ∠ABC = 45° ..(2) (∵AB = AC के सम्मुख चित्र 7.35 कोण हैं तथा ∠A = 90°)
∠CAD = ∠BAD= ∠ACB = ∠ABC = 45° ….(3) [समी. (1) एवं (2) से]
अब ∆ABD में, ∠BAD = ∠ABC [समीकरण (3) से]
BD = AD (समान कोणों की सम्मुख भुजाएँ हैं) …(4)
एवं ∆ACD में, ∠CAD = ∠ACB [समीकरण (3) से]
⇒ CD = AD (समान कोणों की सम्मुख भुजाएँ हैं) …(5)
⇒ BD + CD = AD + AD = 2AD [समीकरण (4) और (5) से]
अत: BC = 2AD. (∵ BD + CD = BC चित्रानुसार) इति सिद्धम्

प्रश्न 3.
ABC एक समद्विबाहु त्रिभुज है, जिससे AC = BC ⊥ AD और BE क्रमशः BC और AC पर शीर्ष लम्ब हैं। सिद्ध कीजिए कि AE = BD.
हल:

चित्र 7.36
दिया है : ABC एक समद्विबाहु त्रिभुज जिससे AC = BC एवं AD ⊥ BC तथा BE ⊥ AC
∠ADC = ∠BEC = 90° [∵ AD ⊥ BC एवं BE ⊥ AC (दिया है)]
अब ∆ADC और ∆BEC में,
चूँकि ∠ADC = ∠BEC [समीकरण (1) से]
∠C = ∠C (उभयनिष्ठ है)
एवं AC = BC (दिया है)
⇒ ∆ADC = ∆BEC (ADS सर्वांगसमता प्रमेय)
⇒ CD = CE अर्थात् EC = DC (CPCT) …(2)
लेकिन AC = BC (दिया है) …(3)
⇒ AC – EC = BC – DC [समीकरण (3) और (2) से]
अतः AE = BD. (चित्रानुसार AC – EC = AE एवं BC – DC = BD) इति सिद्धम्

प्रश्न 4.
एक त्रिभुज ABC में, D भुजा AC का मध्य-बिन्दु है, जहाँ BD = \(\frac { 1 }{ 2 }\)AC है। दर्शाइए कि ∠ABC एक समकोण है।
हल:
दिया है : ∆ABC में D, AC का मध्य-बिन्दु एवं BD = \(\frac { 1 }{ 2 }\)AC.
AD = CD = \(\frac { 1 }{ 2 }\)AC …(1)
(D, AC का मध्य-बिन्दु दिया है)
BD = \(\frac { 1 }{ 2 }\)AC (दिया है) …(2)

चित्र 7.37
⇒ AD = CD = BD [समी. (1) और (2) से] …(3)
∆ABD में, AD = BD [समीकरण (3) से]
⇒ ∠ABD = ∠BAD (बराबर भुजाओं के सम्मुख कोण हैं) …(4)
एवं ∆CBD में, CD = BD [समीकरण (3) से]
∠CBD = ∠BCD …(5) (बराबर भुजाओं के सम्मुख कोण हैं)
∠ABD+ ∠CBD = ∠BAD+ ∠BCD [समी. (4) और (5) से]
∠ABC = ∠BAC + ∠BCA (चित्रानुसार) लेकिन
∠ABC + ∠BAC + ∠BCA = 180° (त्रिभुज के अन्त: कोण)
∠ABC = ∠BAC + ∠BCA = 180°/2 = 90°
अतः ∠ABC एक समकोण है। इति सिद्धम्

प्रश्न 5.
ABCD एक चतुर्भुज इस प्रकार है कि विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता हैं। सिद्ध कीजिए कि
AB = AD और CB = CD है।
हल:

चित्र 7.38
दिया है : एक चतुर्भुज ABCD जिसमें विकर्ण AC कोण A और C का समद्विभाजक है अर्थात्
∠DAC = ∠BAC …(1)
और ∠DCA = ∠BCA …(2)
अब ∆ADC और ∆ABC में, चूँकि
∠DAC = ∠BAC [समी. (1) से]
∠DCA = ∠BCA [समी. (2) से]
एवं AC = AC (उभयनिष्ठ है)
⇒ ∆ADC ≅ ∆ABC (ASA सर्वांगसमता प्रमेय)
AB = AD और CB = CD. (CPCT) इति सिद्धम्

MP Board Class 9th Maths Chapter 7 लघु उत्तरीय प्रश्न

प्रश्न 1.
ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है तथा BD और CE इसकी दो मध्यिाकाएँ हैं। दर्शाइए कि BD = CE.
हल:

चित्र 7.39
दिया है : एक समद्विबाहु त्रिभुज ABC जिसमें AB = AC तथा BD एवं CE इसमें दो मध्यिकाएँ हैं, अर्थात्
AE = EB = \(\frac { 1 }{ 2 }\)AB TO AD = DC = \(\frac { 1 }{ 2 }\) AC
⇒ EB = DC
अब ∆EBC और ∆DBC में,
चूँकि EB = DC (सिद्ध कर चुके हैं)
∠EBC = ∠DCB (AB = AC के सम्मुख कोण हैं)
एवं BC = BC (उभयनिष्ठ है)
⇒ ∆EBC ≅ ∆DBC (SAS सर्वांगसमता प्रमेय)
अतः BD = CE. (CPCT) इति सिद्धम्

प्रश्न 2.
संलग्न चित्र में D और E त्रिभुज ABC की भुजा BC पर दो बिन्दु इस प्रकार स्थित हैं कि BD = CE और AD = AE है। तो दर्शाइए कि ∆ABD ≅ ∆ACE है।
हल:

चित्र 7.40
दिया है : ∆ABC की भुजा BC पर दो बिन्दु D एवं E इस प्रकार हैं कि BD = CE और AD = AE.
∠ADE = ∠AED
⇒ ∠ADB = ∠AEC. (बराबर कोण के सम्पूरक. कोण हैं)
अब ∆ADB और ∆AEC में,
चूँकि AD = AE (दिया है)
∠ADB = ∠AEC (सिद्ध कर चुके हैं)
एवं BD = EC
अतः ∆ABD ≅ ∆ACE. (SAS सर्वांगसमता प्रमेय) इति सिद्धम्

प्रश्न 3.
संलग्न चित्र में BA ⊥ AC और DE ⊥ DF इस प्रकार हैं कि BA = DE और BF = EC हैं। दशाईए कि ∆ABC ≅ ∆DEF.

हल:
चूँकि BF = EC (दिया है)
⇒ BF + FC = EC + FC (बराबर संख्याओं में समान संख्या का योग)
⇒ BC = FE (चित्रानुसार) .
∴ समकोण ∆ABC और समकोण ∆DEF में, कर्ण BC = FE (सिद्ध कर चुके हैं)
एवं BA = DE (दिया है)
अतः ∆ABC ≅ ∆DEE (RHS सर्वांगसमता प्रमेय) इति सिद्धम्

प्रश्न 4.
एक ∆PSR की भुजा SR पर एक बिन्दु 0 इस प्रकार स्थित है कि PQ = PR है। सिद्ध कीजिए कि- PS >PQ.

चित्र 7.42
हल:
त्रिभुज PSR में SR पर बिन्दु ए इस प्रकार दिया है कि PQ = PR
⇒ ∠PQR = ∠PRQ (बराबर भुजाओं के सम्मुख कोण हैं)
लेकिन ∠PQR > ∠PSQ (बहिष्कोण है)
⇒ ∠PRS > ∠PSR (∠PRS = ∠PRO = ∠PQR एवं ∠PSR = ∠PSQ)
⇒ PS > PQ. (बड़े कोण की सम्मुख भुजा है।)
अतः (PQ > PR) इति सिद्धम्

प्रश्न 5.
∆PQR की भुजा QR पर कोई बिन्दु स्थित है। दर्शाइए कि PQ + QR + RP> 2PS.

चित्र 7.43
हल:
प्रश्नानुसार (संलग्न चित्र से)
∆PQS में, PQ + QS > PS (दो भुजाओं का योग तीसरी से बड़ा होता है)…(1)
एवं ∆PSR में, RP + SR > PS (दो भुजाओं का योग तीसरी से बड़ा होता है) …(2)
⇒ PQ+ QS + RP + SR > PS + PS [समीकरण (1) और (2) से]
⇒ PQ + QS + SR + RP > 2PS
अतः PQ+ QR + RP > 2PS. (QS + SR = QR चित्रांनुसार) इति सिद्धम्

प्रश्न 6.
AB = AC वाले एक ∆ABC की भुजा AC पर कोई बिन्दु D स्थित है। दर्शाइए कि CD < BD है।
हल:

चित्र 7.44
∆ABC में, AB = AC तथा AC पर बिन्दु D है।
∠ABC = ∠ACB (AB = AC के सम्मुख कोण हैं)
लेकिन ∠DBC < ∠ABC (किसी संख्या का अंश संख्या से कम होता है)
= ∠DBC < ∠ACB (∵ ∠ABC = ∠ACB)
अतः CD < BD. (छोटे कोण के सामने की भुजा छोटी होती है) इति सिद्धम्

प्रश्न 7.
संलग्न चित्र में l || m है तथा m रेखाखण्ड AB का मध्य-बिन्दु है। दर्शाइए M किसी भी रेखाखण्ड CD का मध्य-बिन्दु है जिसके अन्तःबिन्दु क्रमशः l और m पर स्थित हों।

चित्र 7.45
हल:
l || m को तिर्यक रेखाखण्ड AB क्रमशः A और B पर मिलती है। ∠CAB = ∠ABD (एकान्तर कोण हैं) …(1)
l ||m को तिर्यक रेखाखण्ड CD क्रमश: C और D पर मिलती है। ∠ACD = ∠BDC (एकान्तर कोण है) …(2)
अब ∆AMC और ∆BMD में, चूँकि ∠CAM = ∠MBD [समी. (1) और ∠CAB = ∠CAM एवं ∠MBD = ∠ABD]
AM = BM (AB का मध्य-बिन्दु M दिया है)
एवं ∠ACM = ∠BDM [समी. (2) और ∠ACD = ∠ACM एवं ∠BDC = ∠BDM]
∆AMC ≅ ∆BMD (ASA सर्वांगसमता प्रमेय) CM = DM . (CPCT)
अत: M किसी भी रेखाखण्ड CD का भी मध्य-बिन्दु है। इति सिद्धम्

प्रश्न 8.
AB = AC वाले एक समद्विबाहु त्रिभुज के कोणों B और C के समद्विभाजक परस्पर O पर प्रतिच्छेद करते हैं। BO को एक बिन्दु M तक बढ़ाया गया है। सिद्ध कीजिए ∠MOC = ∠ABC है।
हल:

चित्र 7.46
ज्ञात है : AB = AC ⇒ ∠ABC = ∠ACB (बराबर भुजाओं के सम्मुख कोण हैं) चूँकि BO एवं CO क्रमश:
∠B एवं ∠C के समद्विभाजक है।
⇒ ∠OBC = \(\frac { 1 }{ 2 }\)ABC
एवं ∠OCB = \(\frac { 1 }{ 2 }\)∠ACB
⇒ ∠MOC = ∠OBC + ∠OCB (∠MOC, ∆OBC का बहिष्कोण है)
⇒ ∠MOC = \(\frac { 1 }{ 2 }\)∠ABC + \(\frac { 1 }{ 2 }\)∠ACB
अतः ∠MOC = ∠ABC. (∠ABC = ∠ACB सिद्ध कर चुके हैं) इति सिद्धम्

MP Board Class 9th Maths Chapter 7 अति लघु उत्तरीय प्रश्न

प्रश्न 1.
त्रिभुजों ABC और POR में ∠A = 20 और ∠B = ∠R हैं। ∆POR की कौन-सी भुजा ∆ABC की भुजा AB के बराबर होनी चाहिए कि दोनों त्रिभुज सर्वांगसम हों ? अपने उत्तर के लिए कारण दीजि
उत्तर:
QR, क्योंकि यह AB के संगत भुजा है। (ASA सर्वांगसमता)।

प्रश्न 2.
त्रिभुजों ABC और POR में ∠A = Q और ∠B = ∠R। POR की कौन-सी भुजा ∆ABC की BC भुजा के बराबर होनी चाहिए कि दोनों त्रिभुज सर्वांगसम हों ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
RP, क्योंकि यह BC के संगत भुजा है। (AAS सर्वांगसमता)

प्रश्न 3.
“यदि किसी त्रिभुज की दो भुजाओं और एक कोण दूसरे त्रिभुज की दो भुजाओं और एक कोण के बराबर हों, तो दोनों त्रिभुज अवश्य ही सर्वांगसम होने चाहिए।” क्या यह कथन सत्य है ? क्यों ?
उत्तर:
कथन असत्य है, क्योंकि भुजाओं के अंतर्गत कोण होना चाहिए।

प्रश्न 4.
“यदि किसी त्रिभुज के दो कोण एक भुजा, दूसरे त्रिभुज के दो कोण और एक भुजा के बराबर हों, तो दोनों त्रिभुज अवश्य ही सर्वांगसम होने चाहिए।” क्या यह कथन सत्य है ? क्यों ?
उत्तर:
कथन असत्य है, क्योंकि भुजाएँ संगत होनी चाहिए।

प्रश्न 5.
क्या भुजाओं की लम्बाइयों 4 सेमी, 3 सेमी और 7 सेमी लेकर किसी त्रिभुज की रचना की जा सकती है ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
त्रिभुज की रचना नहीं की जा सकती, क्योंकि यहाँ दो भुजाओं का योग तीसरी के बराबर है (यथा 4 + 3 = 7) जबकि यह बड़ा होना चाहिए।

प्रश्न 6.
∆ABC ≅ ∆RPQ दिया हुआ है। क्या यह कहना सत्य है कि BC = QR ? क्यों ?
उत्तर:
कथन सत्य नहीं है, क्योंकि भुजाएँ संगत होनी चाहिए।

प्रश्न 7.
यदि ∆POR ≅ ∆EDF है तो क्या यह कहना सत्य है कि PR = EF ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
कथन सत्य है, क्योंकि ये संगत भुजाएँ हैं।

प्रश्न 8.
∆POR में ∠P = 70° और ∠R = 30° है। उस त्रिभुज की कौन-सी भुजा सबसे लम्बी है ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
भुजा PR सबसे लम्बी है, क्योंकि ∠Q = 180° – 70° – 30° = 80° सबसे बड़ा है।

प्रश्न 9.
AD किसी त्रिभुज ABC की माध्यिका है। क्या यह कहना सत्य है कि AB + BC + CA > 2AD ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
कथन सत्य हैं, क्योंकि AB + BD > AD एवं AC + CD > AD.

प्रश्न 10.
M किसी त्रिभुज ABC की भुजा BC पर स्थित एक बिन्दु ऐसा है कि AM कोण BAC का समद्विभाजक है। क्या यह कहना सत्य है कि त्रिभुज का परिमाप 2AM से अधिक है ? अपने
उत्तर के लिए कारण दीजिए।
उत्तर:
कथन सत्य है, क्योंकि AB + BM > AM एवं AC + CM > AM.

प्रश्न 11.
क्या भुजाओं की लम्बाइयाँ 9 सेमी, 7 सेमी और 17 सेमी लेकर किसी त्रिभुज की रचना की जा सकती है ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
त्रिभुज की रचना नहीं की जा सकती, क्योंकि 9 + 7 < 17 जबकि दो भुजाओं का योग तीसरी से बड़ा होना चाहिए।

प्रश्न 12.
क्या भुजाओं की लम्बाइयों 8 सेमी, 7 सेमी और 4 सेमी लेकर किसी त्रिभुज की रचना की जा सकती है ? अपने उत्तर का कारण दीजिए।
उत्तर:
हाँ, रचना की जा सकती है। क्योंकि प्रत्येक स्थिति दो भुजाओं का योग तीसरी भुजा से बड़ा है।

MP Board Class 9th Maths Chapter 7 वस्तुनिष्ठ प्रश्न

बहु-विकल्पीय प्रश्न

प्रश्न 1.
निम्नलिखित में से कौन त्रिभुजों की सर्वांगसमता की एक कसौटी नहीं है :
(a) SAS
(b) ASA
(C) SSA
(d) SSS.
उत्तर:
(C) SSA

प्रश्न 2.
यदि AB = QR एवं BC = PR और CA = PQ है, तो :
(a) ∆ABC ≅ ∆PQR
(b) ∆CBA ≅ ∆PRQ
(c) ∆BAC ≅ ∆RPQ
(d) ∆PQR ≅ ∆BCA.
उत्तर:
(b) ∆CBA ≅ ∆PRQ

प्रश्न 3.
∆ABC में AB = AC और ∠B = 50° है तब ∠C बराबर है:
(a) 40°
(b) 50°
(c) 80°
(d) 130°.
उत्तर:
(b) 50°

प्रश्न 4.
∆ABC में BC = AB और ∠B = 80° तब ∠A बराबर है :
(a) 80°
(b) 40°
(c) 50°
(d) 100°.
उत्तर:
(c) 50°

प्रश्न 5.
∆POR में ∠R= ∠P तथा QR = 4 cm और PR = 5 cm है, तब PQ की लम्बाई है:
(a) 4 cm
(b) 5 cm
(c) 2 cm
(d) 2.5 cm.
उत्तर:
(a) 4 cm

प्रश्न 6.
D एक त्रिभुज ABC की भुजा BC पर एक बिन्दु इस प्रकार स्थित है कि AD कोण BAC को समद्विभाजित करता है। तब :
(a) BD = CD
(b) BA > BD
(c) BD > BA .
(d) CD > CA.
उत्तर:
(b) BA > BD

प्रश्न 7.
यह दिया है कि ∆ABC ≅ ∆FDE है तथा AB = 5 cm, ∠B = 40° एवं ∠A= 80° तब :
(a) DF = 5 cm, ∠F = 60°
(b) DF = 5 cm, ∠E = 60°
(c) DE = 5 cm, ∠F = 60°
(d) DE = 5 cm, ∠D = 40°.
उत्तर:
(b) DF = 5 cm, ∠E = 60°

प्रश्न 8.
एक त्रिभुज की दो भुजाओं की लम्बाइयाँ 5 cm और 1.5 cm है। इस त्रिभुज की तीसरी भुजा की लम्बाई निम्नलिखित नहीं हो सकती :
(a) 3.6 cm
(b) 4.1 cm
(c) 3.8 cm
(d) 3.4 cm.
उत्तर:
(d) 3.4 cm.

प्रश्न 9.
∆POR में यदि ∠P< ∠ R > ∠Q है, तो :
(a) QR > PR
(b) PQ > PR
(c) PQ < PR (d) QR > PR.
उत्तर:
(b) PQ > PR

प्रश्न 10.
∆ABC और ∆PQR में AB = AC, ∠C = ∠P और ∠B = 20 हैं। ये दोनों त्रिभुज हैं :
(a) समद्विबाहु परन्तु सर्वांगसम नहीं
(b) समद्विबाहु, सर्वांगसम
(c) सर्वांगसम परन्तु समद्विबाहु नहीं
(d) न तो सर्वांगसम और न हीं समद्विबाहु।
उत्तर:
(a) समद्विबाहु परन्तु सर्वांगसम नहीं

प्रश्न 11.
त्रिभुजों ABC और DEF में AB = FD तथा ∠A = ∠D है। दोनों त्रिभुज SAS अभिगृहीत से सर्वांगसम होंगे यदि :
(a) BC = EF
(b) AC = DE
(c) AC = EF
(d) BC = DE.
उत्तर:
(b) AC = DE

प्रश्न 12.
समान आकार एवं समान आकृति वाली आकृतियाँ होती हैं :
(a) बराबर
(b) समान
(c) सर्वांगसम
(d) समरूप।
उत्तर:
(c) सर्वांगसम

प्रश्न 13.
समकोण त्रिभुज में सबसे बड़ी भुजा होती है :
(a) लम्ब
(b) आधार
(c) कर्ण
(d) रेखा।
उत्तर:
(c) कर्ण

प्रश्न 14.
समबाहु त्रिभुज के प्रत्येक कोण का मान होता है : (2019)
(a) 90°
(b) 30°
(c) 60°
(d) 120°.
उत्तर:
(c) 60°

प्रश्न 15.
पाइथागोरस प्रमेय किस त्रिभुज के लिए प्रसिद्ध है :
(a) समबाहु त्रिभुज
(b) सर्वांगसम त्रिभुज
(c) समद्विबाहु त्रिभुज
(d) समकोण त्रिभुज।
उत्तर:
(d) समकोण त्रिभुज

रिक्त स्थानों की पूर्ति
1. समबाहु त्रिभुज का प्रत्येक कोण ……… होता है।
2. किसी त्रिभुज की दो भुजाओं का योग तीसरी भुजा से ……….. होता है।
3. समकोण त्रिभुज की सबसे बड़ी भुजा ………… होती है।
4. त्रिभुज के तीनों अन्तः कोणों का योग ………….. होता है।
5. समान आकार एवं समान आकृति वाली आकृतियाँ ……… होती हैं।
6. किसी त्रिभुज की दो भुजाएँ असमान हों तो, बड़ी भुजा के सामने का कोण ………. होता है।
7. किसी त्रिभुज की समान भुजाओं के सम्मुख कोण ………….. होते हैं।
8. किसी त्रिभुज में बड़े कोण के सामने की भुजा ………….. होती है।
उत्तर:
1. 60°,
2. बड़ा,
3. कर्ण,
4. 180°,
5. सर्वांगसम,
6. बड़ा,
7. बराबर,
8. बड़ी।

जोड़ी मिलान
स्तम्भ ‘A’                                                         स्तम्भ ‘B’
1. त्रिभुज जिसकी तीनों भुजाएँ समान हों     (a) अधिक कोण त्रिभुज
2. त्रिभुज जिसकी दो भुजाएँ समान हों        (b) न्यूनकोण त्रिभुज
3. त्रिभुज जिसका एक कोण 90° हो           (c) समबाहु त्रिभुज
4. त्रिभुज जिसका एक कोण अधिक कोण हो (d) केन्द्रक
5. त्रिभुज जिसका प्रत्येक कोण न्यूनकोण हो (e) समकोण त्रिभुज
6. माध्यिकाओं के संगमन बिन्दु को कहते हैं (2018) (f) समद्विबाहु त्रिभुज
उत्तर:
1. → (c),
2. → (1),
3. → (e),
4. → (a),
5. → (b),
6. → (d).

सत्य/असत्य कथन
1. समद्विबाहु त्रिभुज के तीनों कोण बराबर होते हैं। (2018)
2. किसी त्रिभुज के बड़े कोण के सामने की भुजा छोटी होती है।
3. किसी त्रिभुज की दो भुजाओं का योग, तीसरी भुजा से बड़ा होता है।
4. किसी रेखा के बाहर स्थित किसी बिन्दु से रेखा तक जितने रेखाखण्ड खींचे जा सकते हैं उनमें लम्ब सबसे छोटा होता है।
5. सभी वृत्त सर्वांगसम होते हैं।
6. यदि दो त्रिभुजों की संगत भुजाएँ बराबर हों, तो त्रिभुज बराबर हों, तो त्रिभुज सर्वांगसम होते हैं। (2019)
7. त्रिभुजों के तीनों कोणों का योग 180° होता है। (2019)
8. सर्वांगसम त्रिभुज में संगत भाग बराबर होते हैं। (2019)
उत्तर:
1. असत्य,
2. असत्य,
3. सत्य,
4. सत्य,
5. असत्य,
6. सत्य,
7. सत्य,
8. सत्य।

एक शब्द/वाक्य में उत्तर

1. किसी त्रिभुज में अधिकतम कितने समकोण हो सकते हैं ?
2. किसी त्रिभुज में अधिकतम कितने अधिक कोण हो सकते हैं ?
3. किसी त्रिभुज में कम-से-कम कितने न्यूनकोण हो सकते हैं ?
4. किसी त्रिभुज के बहिष्कोण और अन्तः कोणों में क्या सम्बन्ध होता है ?
5. समकोण समद्विबाहु त्रिभुज के प्रत्यके न्यूनकोण का मान कितना होता है ?
उत्तर:
1. एक,
2. एक,
3. दो,
4. त्रिभुज का बहिष्कोण सम्मुख अन्त:कोणों के योग के बराबर है अर्थात् प्रत्येक सम्मुख अन्तः कोण से बड़ा होता है,
5. 45° ।

MP Board Class 9th Maths Solutions