MP Board Class 9th Maths Solutions Chapter 10 वृत्त Ex 10.4

MP Board Class 9th Maths Solutions Chapter 10 वृत्त Ex 10.4

प्रश्न 1.
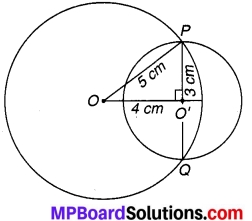
5 cm और 3 cm की त्रिज्या वाले दो वृत्त दो बिन्दुओं पर प्रतिच्छेद करते हैं तथा उनके केन्द्रों के बीच की दूरी 4 cm है। उभयनिष्ठ जीवा की लम्बाई ज्ञात कीजिए।
हल:
दिए हुए वृत्त के केन्द्र क्रमशः O तथा O’ है जिनके बीच की दूरी OO’ = 4 cm है। वृत्त एक-दूसरे को P और Q दो बिन्दुओं पर प्रतिच्छेद करते है। वृत्तों की त्रिज्याएँ क्रमशः
OP = 5 cm तथा OP = 3 cm हैं।

चित्र 10.6
चूँकि (OO’)² + (O’P)² = (4)² + (3)² = 16 + 9 = 25 = (5)2 = (OP)²
अतः ∆OO’P एक समकोण त्रिभुज है। (पाइथागोरस का विलोम)
⇒ OO’ ⊥ O’P
चूँकि उभयनिष्ठ जीवा PQ छोटे वृत्त के केन्द्र O’ से जाती है, इसलिए PQ छोटे वृत्त का व्यास है।
⇒ PQ = 2 x O’P = 2 x 3 = 6 cm
अत: उभयनिष्ठ जीवा की अभीष्ट लम्बाई = 6 cm.

प्रश्न 2.
यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर परस्पर प्रतिच्छेद करें तो, सिद्ध कीजिए कि एक जीवा के खण्ड दूसरी जीवा के संगत खण्डों के बराबर है।
हल:
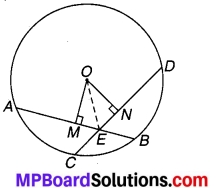
दिया है : O केन्द्र वाले एक वृत्त की दो जीवाएँ AB = CD परस्पर E बिन्दु पर प्रतिच्छेद करती हैं, तो सिद्ध करना है कि
AE = DE एवं CE = BE

चित्र 10.7
रचना : O से OM ⊥ AB तथा ON ⊥ CD खींचिए तथा OE को मिलाइए।
उपपत्ति : समकोण ∆OME एवं ∆ONE में,
चूँकि कर्ण OE = OE (उभयनिष्ठ है)
एवं OM = ON (बराबर जीवाएँ केन्द्र से बराबर दूरी पर होती है)
⇒ ΔΟΜΕ ≅ ΔΟΝΕ (RHS सर्वांगसमता प्रमेय)
⇒ ME = NE
चूँकि AB = CD, OM ⊥ AB एवं ON ⊥ CD
⇒ AM = DN एवं BM = CN
⇒ AM + ME = DN + NE [समीकरण (1) और (2) से]
⇒ AE = DE
एवं CN – EN = BM – EM [समीकरण (1) और (2) में]
⇒ CE = BE
अतः वृत्त की बराबर जीवाएँ वृत्त के अन्दर यदि प्रतिच्छेद करती हैं। तो उनके संगत खण्ड बराबर होते हैं। इति सिद्धम्

प्रश्न 3.
यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि प्रतिच्छेद बिन्दु को केन्द्र से मिलाने वाली रेखा जीवाओं से बराबर कोण बनाती है।
हल:

चित्र 10.8
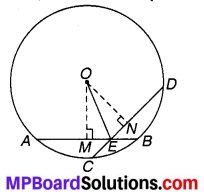
ज्ञात है : O केन्द्र वाले एक वृत्त की दो जीवाएँ AB = CD वृत्त के अन्दर बिन्दु E पर परस्पर प्रतिच्छेद करती हैं। OE को मिलाया गया है।
सिद्ध करना है: ∠OEA = ∠OED
रचना : OM ⊥ AB एवं ON ⊥ CD खींचिए।
उपपत्ति : समकोण ΔOME एवं ΔONE में,
चूँकि कर्ण OE = कर्ण OE (उभयनिष्ठ है)
एवं OM = ON (बराबर जीवाएँ केन्द्र से बराबर दूरी पर होती हैं)
⇒ ΔΟΜΕ ≅ ΔΟΝΕ (RHS सर्वांगसमता प्रमेय)
⇒ ∠OEM = ∠OEN (CPCT)
अतः ∠OEA = ∠OED (चित्रानुसार) इति सिद्धम्

प्रश्न 4.
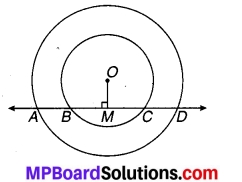
यदि एक रेखा दो संकेन्द्री वृत्तों (एक ही केन्द्र वाले वृत्त) को जिनका केन्द्र O है A, B, C और D पर प्रतिच्छेद करें, तो सिद्ध कीजिए कि AB = CD है (देखिए संलग्न चित्र)। (2019)
हल:

चित्र 10.9
दिया है : O केन्द्र वाले दो संकेन्द्री वृत्तों को रेखा AD बिन्दुओं A, B, C और D पर (चित्रानुसार) प्रतिच्छेद करती है तो सिद्ध करना है कि AB = CD
रचना : OM ⊥ AD खींचिए।
उपपत्ति : बाह्य वृत्त में चूँकि AD वृत्त की जीवा है तथा OM ⊥ AD
⇒ AM = DA …..(1) (केन्द्र से जीवा पर डाला लम्ब उसे समद्विभाजित करता है)
चूँकि अन्तः वृत्त की जीवा CB पर OM लम्ब है। (चित्रानुसार)
⇒ BM = CM …(2) (वृत्त के केन्द्र से जीवा पर डाला गया लम्ब उसे समद्विभाजित करता है)
⇒ AM – BM = DM – CM [समीकरण (1) और (2) से]
अतः AB = CD. (चित्रानुसार) इति सिद्धम्

प्रश्न 5.
एक पार्क में बने 5 m त्रिज्या वाले वृत्त पर खड़ी तीन लड़कियाँ रेशमा, सलमा एवं मनदीप खेल रही हैं। रेशमा एक गेंद को सलमा के पास, सलमा मनदीप के पास तथा मनदीप रेशमा के पास फेंकती है। यदि रेशमा तथा सलमा के बीच और सलमा तथा मनदीप के बीच की प्रत्येक दूरी 6 m हो, तो रेशमा और मनदीप की बीच की दूरी क्या है ?
हल:
मान लीजिए वृत्ताकार पार्क का केन्द्र O है। बिन्दु R, S और M पर क्रमशः रेशमा, सलमा और मनदीप हैं। वृत्त की त्रिज्या OR = 5 m, तथा RS = SM = 6 m दी गई है तो दूरी RM ज्ञात करना है।

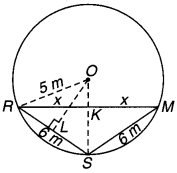
चित्र 10.10

अत: रेशमा और मनदीप के बीच की दूरी RM = 2 x x = 2 x 4.8 = 9.6 m.

प्रश्न 6.
20 m त्रिज्या का एक गोल पार्क (वृत्ताकार) एक कॉलोनी में स्थित है। तीन लड़के अंकुर, सैय्यद, डेविड इसकी परिसीमा पर बराबर दूरी पर बैठे हैं और प्रत्येक के हाथ में एक खिलौना टेलीफोन आपस में बात करने के लिए है। प्रत्येक टेलीफोन की डोरी की लम्बाई ज्ञात कीजिए।

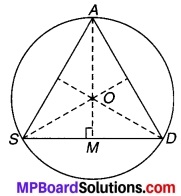
चित्र 10.11
हल:
दिया है : एक 20 m त्रिज्या का 0 केन्द्र वाला वृत्ताकार पार्क जिसकी परिसीमा पर अंकुर, सैय्यद और डेविड क्रमश: A, S और D बिन्दुओं पर इस प्रकार बैठे हैं कि AS = SD = DA =x मान लीजिए।
चूँकि समबाहु त्रिभुज की सभी माध्यिकाएँ बराबर होती हैं, वे सम्मुख भुजाओं को समकोण पर समद्विभाजित करती हैं तथा परस्पर एक बिन्दु पर 2 : 1 के अनुपात में प्रतिच्छेद करती है एवं यह बिन्दु उसके शीर्षों से समान दूरी पर होता है अर्थात् ASD से जाने वाले वृत्त का केन्द्र।
⇒ AO = SO = DO = 20 m (वृत्त की त्रिज्या दी है)
एवं OM = \(\frac { 1 }{ 2 }\)AO = \(\frac { 1 }{ 2 }\) x 20 = 10 m
⇒ AM = AO + OM = 20 + 10 = 30 m
समकोण ∆AMS में पाथागोरस प्रमेय से,
AS² = AM² + SM²

अतः प्रत्येक टेलीफोन की छोरी की अभीष्ट लम्बाई = 34.64 m.

MP Board Class 9th Maths Solutions