MP Board Class 9th Maths Solutions Chapter 7 त्रिभुज Additional Questions
MP Board Class 9th Maths Chapter 7 अतिरिक्त परीक्षोपयोगी प्रश्न
MP Board Class 9th Maths Chapter 7 दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
ABCD एक चतुर्भुज है, जिसमें AB = BC और AD = CD। दर्शाइए कि BD दोनों कोणों ABC और ADC को समद्विभाजित करता है।
हल:
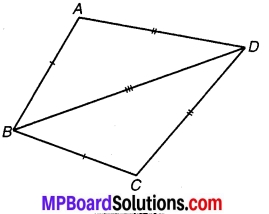
चित्र 7.34
दिया है : एक चतुर्भुज ABCD जिससे
AB = BC और AD = CD। BD चतुर्भुज ABCD का एक विकर्ण है।
अब ∆ABD और ∆CBD में,
चूँकि AB = BC (दिया है)
AD = CD (दिया है)
एवं BD = BD (उभयनिष्ठ है)
⇒ ∆ABD ≅ ∆CBD (SSS सर्वांगसमता प्रमेय)
⇒ ∠ABD ≅ ∠CBD एवं ∠ADB = ∠CDB (CPCT)
अत: BD दोनों कोण ∠ABC एवं ∠ADC को समद्विभाजित करता है। इति सिद्धम्
प्रश्न 2.
ABC एक समकोण त्रिभुज है जिससे AB = AC, CA का समद्विभाजक BC से D पर मिलता है। सिद्ध कीजिए कि BC = 2AD.
हल:
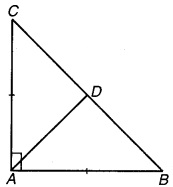
चित्र 7.34
दिया है: ABC एक समकोण त्रिभुज जिसमें AB = AC, ∠A समकोण है जिसका समद्विभाजक AD, BC को बिन्दु D पर मिलता है।
अब ∠CAD = ∠BAD = 45° (∵ ∠A समकोण है तथा AD इसका समद्विभाजक है) …(1)
∠ACB = ∠ABC = 45° ..(2) (∵AB = AC के सम्मुख चित्र 7.35 कोण हैं तथा ∠A = 90°)
∠CAD = ∠BAD= ∠ACB = ∠ABC = 45° ….(3) [समी. (1) एवं (2) से]
अब ∆ABD में, ∠BAD = ∠ABC [समीकरण (3) से]
BD = AD (समान कोणों की सम्मुख भुजाएँ हैं) …(4)
एवं ∆ACD में, ∠CAD = ∠ACB [समीकरण (3) से]
⇒ CD = AD (समान कोणों की सम्मुख भुजाएँ हैं) …(5)
⇒ BD + CD = AD + AD = 2AD [समीकरण (4) और (5) से]
अत: BC = 2AD. (∵ BD + CD = BC चित्रानुसार) इति सिद्धम्
प्रश्न 3.
ABC एक समद्विबाहु त्रिभुज है, जिससे AC = BC ⊥ AD और BE क्रमशः BC और AC पर शीर्ष लम्ब हैं। सिद्ध कीजिए कि AE = BD.
हल:
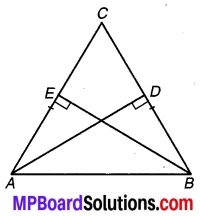
चित्र 7.36
दिया है : ABC एक समद्विबाहु त्रिभुज जिससे AC = BC एवं AD ⊥ BC तथा BE ⊥ AC
∠ADC = ∠BEC = 90° [∵ AD ⊥ BC एवं BE ⊥ AC (दिया है)]
अब ∆ADC और ∆BEC में,
चूँकि ∠ADC = ∠BEC [समीकरण (1) से]
∠C = ∠C (उभयनिष्ठ है)
एवं AC = BC (दिया है)
⇒ ∆ADC = ∆BEC (ADS सर्वांगसमता प्रमेय)
⇒ CD = CE अर्थात् EC = DC (CPCT) …(2)
लेकिन AC = BC (दिया है) …(3)
⇒ AC – EC = BC – DC [समीकरण (3) और (2) से]
अतः AE = BD. (चित्रानुसार AC – EC = AE एवं BC – DC = BD) इति सिद्धम्
![]()
प्रश्न 4.
एक त्रिभुज ABC में, D भुजा AC का मध्य-बिन्दु है, जहाँ BD = \(\frac { 1 }{ 2 }\)AC है। दर्शाइए कि ∠ABC एक समकोण है।
हल:
दिया है : ∆ABC में D, AC का मध्य-बिन्दु एवं BD = \(\frac { 1 }{ 2 }\)AC.
AD = CD = \(\frac { 1 }{ 2 }\)AC …(1)
(D, AC का मध्य-बिन्दु दिया है)
BD = \(\frac { 1 }{ 2 }\)AC (दिया है) …(2)
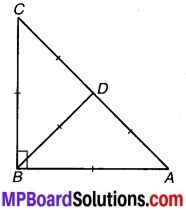
चित्र 7.37
⇒ AD = CD = BD [समी. (1) और (2) से] …(3)
∆ABD में, AD = BD [समीकरण (3) से]
⇒ ∠ABD = ∠BAD (बराबर भुजाओं के सम्मुख कोण हैं) …(4)
एवं ∆CBD में, CD = BD [समीकरण (3) से]
∠CBD = ∠BCD …(5) (बराबर भुजाओं के सम्मुख कोण हैं)
∠ABD+ ∠CBD = ∠BAD+ ∠BCD [समी. (4) और (5) से]
∠ABC = ∠BAC + ∠BCA (चित्रानुसार) लेकिन
∠ABC + ∠BAC + ∠BCA = 180° (त्रिभुज के अन्त: कोण)
∠ABC = ∠BAC + ∠BCA = 180°/2 = 90°
अतः ∠ABC एक समकोण है। इति सिद्धम्
प्रश्न 5.
ABCD एक चतुर्भुज इस प्रकार है कि विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता हैं। सिद्ध कीजिए कि
AB = AD और CB = CD है।
हल:
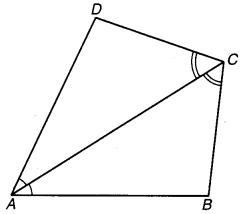
चित्र 7.38
दिया है : एक चतुर्भुज ABCD जिसमें विकर्ण AC कोण A और C का समद्विभाजक है अर्थात्
∠DAC = ∠BAC …(1)
और ∠DCA = ∠BCA …(2)
अब ∆ADC और ∆ABC में, चूँकि
∠DAC = ∠BAC [समी. (1) से]
∠DCA = ∠BCA [समी. (2) से]
एवं AC = AC (उभयनिष्ठ है)
⇒ ∆ADC ≅ ∆ABC (ASA सर्वांगसमता प्रमेय)
AB = AD और CB = CD. (CPCT) इति सिद्धम्
MP Board Class 9th Maths Chapter 7 लघु उत्तरीय प्रश्न
प्रश्न 1.
ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है तथा BD और CE इसकी दो मध्यिाकाएँ हैं। दर्शाइए कि BD = CE.
हल:
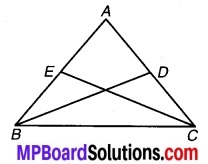
चित्र 7.39
दिया है : एक समद्विबाहु त्रिभुज ABC जिसमें AB = AC तथा BD एवं CE इसमें दो मध्यिकाएँ हैं, अर्थात्
AE = EB = \(\frac { 1 }{ 2 }\)AB TO AD = DC = \(\frac { 1 }{ 2 }\) AC
⇒ EB = DC
अब ∆EBC और ∆DBC में,
चूँकि EB = DC (सिद्ध कर चुके हैं)
∠EBC = ∠DCB (AB = AC के सम्मुख कोण हैं)
एवं BC = BC (उभयनिष्ठ है)
⇒ ∆EBC ≅ ∆DBC (SAS सर्वांगसमता प्रमेय)
अतः BD = CE. (CPCT) इति सिद्धम्
![]()
प्रश्न 2.
संलग्न चित्र में D और E त्रिभुज ABC की भुजा BC पर दो बिन्दु इस प्रकार स्थित हैं कि BD = CE और AD = AE है। तो दर्शाइए कि ∆ABD ≅ ∆ACE है।
हल:
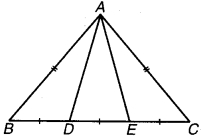
चित्र 7.40
दिया है : ∆ABC की भुजा BC पर दो बिन्दु D एवं E इस प्रकार हैं कि BD = CE और AD = AE.
∠ADE = ∠AED
⇒ ∠ADB = ∠AEC. (बराबर कोण के सम्पूरक. कोण हैं)
अब ∆ADB और ∆AEC में,
चूँकि AD = AE (दिया है)
∠ADB = ∠AEC (सिद्ध कर चुके हैं)
एवं BD = EC
अतः ∆ABD ≅ ∆ACE. (SAS सर्वांगसमता प्रमेय) इति सिद्धम्
प्रश्न 3.
संलग्न चित्र में BA ⊥ AC और DE ⊥ DF इस प्रकार हैं कि BA = DE और BF = EC हैं। दशाईए कि ∆ABC ≅ ∆DEF.
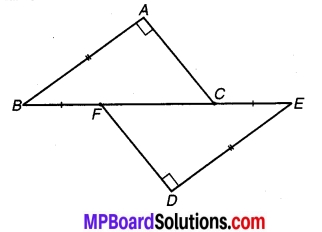
हल:
चूँकि BF = EC (दिया है)
⇒ BF + FC = EC + FC (बराबर संख्याओं में समान संख्या का योग)
⇒ BC = FE (चित्रानुसार) .
∴ समकोण ∆ABC और समकोण ∆DEF में, कर्ण BC = FE (सिद्ध कर चुके हैं)
एवं BA = DE (दिया है)
अतः ∆ABC ≅ ∆DEE (RHS सर्वांगसमता प्रमेय) इति सिद्धम्
प्रश्न 4.
एक ∆PSR की भुजा SR पर एक बिन्दु 0 इस प्रकार स्थित है कि PQ = PR है। सिद्ध कीजिए कि- PS >PQ.
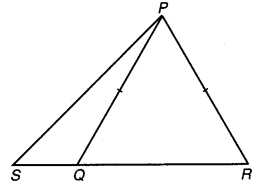
चित्र 7.42
हल:
त्रिभुज PSR में SR पर बिन्दु ए इस प्रकार दिया है कि PQ = PR
⇒ ∠PQR = ∠PRQ (बराबर भुजाओं के सम्मुख कोण हैं)
लेकिन ∠PQR > ∠PSQ (बहिष्कोण है)
⇒ ∠PRS > ∠PSR (∠PRS = ∠PRO = ∠PQR एवं ∠PSR = ∠PSQ)
⇒ PS > PQ. (बड़े कोण की सम्मुख भुजा है।)
अतः (PQ > PR) इति सिद्धम्
प्रश्न 5.
∆PQR की भुजा QR पर कोई बिन्दु स्थित है। दर्शाइए कि PQ + QR + RP> 2PS.
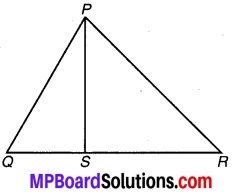
चित्र 7.43
हल:
प्रश्नानुसार (संलग्न चित्र से)
∆PQS में, PQ + QS > PS (दो भुजाओं का योग तीसरी से बड़ा होता है)…(1)
एवं ∆PSR में, RP + SR > PS (दो भुजाओं का योग तीसरी से बड़ा होता है) …(2)
⇒ PQ+ QS + RP + SR > PS + PS [समीकरण (1) और (2) से]
⇒ PQ + QS + SR + RP > 2PS
अतः PQ+ QR + RP > 2PS. (QS + SR = QR चित्रांनुसार) इति सिद्धम्
![]()
प्रश्न 6.
AB = AC वाले एक ∆ABC की भुजा AC पर कोई बिन्दु D स्थित है। दर्शाइए कि CD < BD है।
हल:
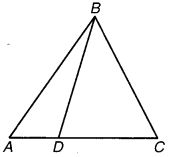
चित्र 7.44
∆ABC में, AB = AC तथा AC पर बिन्दु D है।
∠ABC = ∠ACB (AB = AC के सम्मुख कोण हैं)
लेकिन ∠DBC < ∠ABC (किसी संख्या का अंश संख्या से कम होता है)
= ∠DBC < ∠ACB (∵ ∠ABC = ∠ACB)
अतः CD < BD. (छोटे कोण के सामने की भुजा छोटी होती है) इति सिद्धम्
प्रश्न 7.
संलग्न चित्र में l || m है तथा m रेखाखण्ड AB का मध्य-बिन्दु है। दर्शाइए M किसी भी रेखाखण्ड CD का मध्य-बिन्दु है जिसके अन्तःबिन्दु क्रमशः l और m पर स्थित हों।
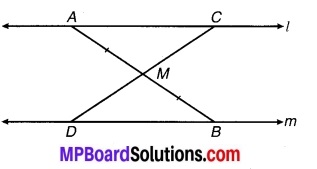
चित्र 7.45
हल:
l || m को तिर्यक रेखाखण्ड AB क्रमशः A और B पर मिलती है। ∠CAB = ∠ABD (एकान्तर कोण हैं) …(1)
l ||m को तिर्यक रेखाखण्ड CD क्रमश: C और D पर मिलती है। ∠ACD = ∠BDC (एकान्तर कोण है) …(2)
अब ∆AMC और ∆BMD में, चूँकि ∠CAM = ∠MBD [समी. (1) और ∠CAB = ∠CAM एवं ∠MBD = ∠ABD]
AM = BM (AB का मध्य-बिन्दु M दिया है)
एवं ∠ACM = ∠BDM [समी. (2) और ∠ACD = ∠ACM एवं ∠BDC = ∠BDM]
∆AMC ≅ ∆BMD (ASA सर्वांगसमता प्रमेय) CM = DM . (CPCT)
अत: M किसी भी रेखाखण्ड CD का भी मध्य-बिन्दु है। इति सिद्धम्
प्रश्न 8.
AB = AC वाले एक समद्विबाहु त्रिभुज के कोणों B और C के समद्विभाजक परस्पर O पर प्रतिच्छेद करते हैं। BO को एक बिन्दु M तक बढ़ाया गया है। सिद्ध कीजिए ∠MOC = ∠ABC है।
हल:
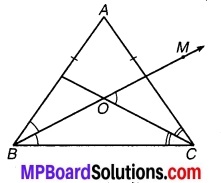
चित्र 7.46
ज्ञात है : AB = AC ⇒ ∠ABC = ∠ACB (बराबर भुजाओं के सम्मुख कोण हैं) चूँकि BO एवं CO क्रमश:
∠B एवं ∠C के समद्विभाजक है।
⇒ ∠OBC = \(\frac { 1 }{ 2 }\)ABC
एवं ∠OCB = \(\frac { 1 }{ 2 }\)∠ACB
⇒ ∠MOC = ∠OBC + ∠OCB (∠MOC, ∆OBC का बहिष्कोण है)
⇒ ∠MOC = \(\frac { 1 }{ 2 }\)∠ABC + \(\frac { 1 }{ 2 }\)∠ACB
अतः ∠MOC = ∠ABC. (∠ABC = ∠ACB सिद्ध कर चुके हैं) इति सिद्धम्
MP Board Class 9th Maths Chapter 7 अति लघु उत्तरीय प्रश्न
प्रश्न 1.
त्रिभुजों ABC और POR में ∠A = 20 और ∠B = ∠R हैं। ∆POR की कौन-सी भुजा ∆ABC की भुजा AB के बराबर होनी चाहिए कि दोनों त्रिभुज सर्वांगसम हों ? अपने उत्तर के लिए कारण दीजि
उत्तर:
QR, क्योंकि यह AB के संगत भुजा है। (ASA सर्वांगसमता)।
प्रश्न 2.
त्रिभुजों ABC और POR में ∠A = Q और ∠B = ∠R। POR की कौन-सी भुजा ∆ABC की BC भुजा के बराबर होनी चाहिए कि दोनों त्रिभुज सर्वांगसम हों ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
RP, क्योंकि यह BC के संगत भुजा है। (AAS सर्वांगसमता)
प्रश्न 3.
“यदि किसी त्रिभुज की दो भुजाओं और एक कोण दूसरे त्रिभुज की दो भुजाओं और एक कोण के बराबर हों, तो दोनों त्रिभुज अवश्य ही सर्वांगसम होने चाहिए।” क्या यह कथन सत्य है ? क्यों ?
उत्तर:
कथन असत्य है, क्योंकि भुजाओं के अंतर्गत कोण होना चाहिए।
प्रश्न 4.
“यदि किसी त्रिभुज के दो कोण एक भुजा, दूसरे त्रिभुज के दो कोण और एक भुजा के बराबर हों, तो दोनों त्रिभुज अवश्य ही सर्वांगसम होने चाहिए।” क्या यह कथन सत्य है ? क्यों ?
उत्तर:
कथन असत्य है, क्योंकि भुजाएँ संगत होनी चाहिए।
प्रश्न 5.
क्या भुजाओं की लम्बाइयों 4 सेमी, 3 सेमी और 7 सेमी लेकर किसी त्रिभुज की रचना की जा सकती है ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
त्रिभुज की रचना नहीं की जा सकती, क्योंकि यहाँ दो भुजाओं का योग तीसरी के बराबर है (यथा 4 + 3 = 7) जबकि यह बड़ा होना चाहिए।
प्रश्न 6.
∆ABC ≅ ∆RPQ दिया हुआ है। क्या यह कहना सत्य है कि BC = QR ? क्यों ?
उत्तर:
कथन सत्य नहीं है, क्योंकि भुजाएँ संगत होनी चाहिए।
![]()
प्रश्न 7.
यदि ∆POR ≅ ∆EDF है तो क्या यह कहना सत्य है कि PR = EF ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
कथन सत्य है, क्योंकि ये संगत भुजाएँ हैं।
प्रश्न 8.
∆POR में ∠P = 70° और ∠R = 30° है। उस त्रिभुज की कौन-सी भुजा सबसे लम्बी है ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
भुजा PR सबसे लम्बी है, क्योंकि ∠Q = 180° – 70° – 30° = 80° सबसे बड़ा है।
प्रश्न 9.
AD किसी त्रिभुज ABC की माध्यिका है। क्या यह कहना सत्य है कि AB + BC + CA > 2AD ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
कथन सत्य हैं, क्योंकि AB + BD > AD एवं AC + CD > AD.
प्रश्न 10.
M किसी त्रिभुज ABC की भुजा BC पर स्थित एक बिन्दु ऐसा है कि AM कोण BAC का समद्विभाजक है। क्या यह कहना सत्य है कि त्रिभुज का परिमाप 2AM से अधिक है ? अपने
उत्तर के लिए कारण दीजिए।
उत्तर:
कथन सत्य है, क्योंकि AB + BM > AM एवं AC + CM > AM.
प्रश्न 11.
क्या भुजाओं की लम्बाइयाँ 9 सेमी, 7 सेमी और 17 सेमी लेकर किसी त्रिभुज की रचना की जा सकती है ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
त्रिभुज की रचना नहीं की जा सकती, क्योंकि 9 + 7 < 17 जबकि दो भुजाओं का योग तीसरी से बड़ा होना चाहिए।
प्रश्न 12.
क्या भुजाओं की लम्बाइयों 8 सेमी, 7 सेमी और 4 सेमी लेकर किसी त्रिभुज की रचना की जा सकती है ? अपने उत्तर का कारण दीजिए।
उत्तर:
हाँ, रचना की जा सकती है। क्योंकि प्रत्येक स्थिति दो भुजाओं का योग तीसरी भुजा से बड़ा है।
MP Board Class 9th Maths Chapter 7 वस्तुनिष्ठ प्रश्न
बहु-विकल्पीय प्रश्न
प्रश्न 1.
निम्नलिखित में से कौन त्रिभुजों की सर्वांगसमता की एक कसौटी नहीं है :
(a) SAS
(b) ASA
(C) SSA
(d) SSS.
उत्तर:
(C) SSA
प्रश्न 2.
यदि AB = QR एवं BC = PR और CA = PQ है, तो :
(a) ∆ABC ≅ ∆PQR
(b) ∆CBA ≅ ∆PRQ
(c) ∆BAC ≅ ∆RPQ
(d) ∆PQR ≅ ∆BCA.
उत्तर:
(b) ∆CBA ≅ ∆PRQ
प्रश्न 3.
∆ABC में AB = AC और ∠B = 50° है तब ∠C बराबर है:
(a) 40°
(b) 50°
(c) 80°
(d) 130°.
उत्तर:
(b) 50°
प्रश्न 4.
∆ABC में BC = AB और ∠B = 80° तब ∠A बराबर है :
(a) 80°
(b) 40°
(c) 50°
(d) 100°.
उत्तर:
(c) 50°
प्रश्न 5.
∆POR में ∠R= ∠P तथा QR = 4 cm और PR = 5 cm है, तब PQ की लम्बाई है:
(a) 4 cm
(b) 5 cm
(c) 2 cm
(d) 2.5 cm.
उत्तर:
(a) 4 cm
प्रश्न 6.
D एक त्रिभुज ABC की भुजा BC पर एक बिन्दु इस प्रकार स्थित है कि AD कोण BAC को समद्विभाजित करता है। तब :
(a) BD = CD
(b) BA > BD
(c) BD > BA .
(d) CD > CA.
उत्तर:
(b) BA > BD
प्रश्न 7.
यह दिया है कि ∆ABC ≅ ∆FDE है तथा AB = 5 cm, ∠B = 40° एवं ∠A= 80° तब :
(a) DF = 5 cm, ∠F = 60°
(b) DF = 5 cm, ∠E = 60°
(c) DE = 5 cm, ∠F = 60°
(d) DE = 5 cm, ∠D = 40°.
उत्तर:
(b) DF = 5 cm, ∠E = 60°
![]()
प्रश्न 8.
एक त्रिभुज की दो भुजाओं की लम्बाइयाँ 5 cm और 1.5 cm है। इस त्रिभुज की तीसरी भुजा की लम्बाई निम्नलिखित नहीं हो सकती :
(a) 3.6 cm
(b) 4.1 cm
(c) 3.8 cm
(d) 3.4 cm.
उत्तर:
(d) 3.4 cm.
प्रश्न 9.
∆POR में यदि ∠P< ∠ R > ∠Q है, तो :
(a) QR > PR
(b) PQ > PR
(c) PQ < PR (d) QR > PR.
उत्तर:
(b) PQ > PR
प्रश्न 10.
∆ABC और ∆PQR में AB = AC, ∠C = ∠P और ∠B = 20 हैं। ये दोनों त्रिभुज हैं :
(a) समद्विबाहु परन्तु सर्वांगसम नहीं
(b) समद्विबाहु, सर्वांगसम
(c) सर्वांगसम परन्तु समद्विबाहु नहीं
(d) न तो सर्वांगसम और न हीं समद्विबाहु।
उत्तर:
(a) समद्विबाहु परन्तु सर्वांगसम नहीं
प्रश्न 11.
त्रिभुजों ABC और DEF में AB = FD तथा ∠A = ∠D है। दोनों त्रिभुज SAS अभिगृहीत से सर्वांगसम होंगे यदि :
(a) BC = EF
(b) AC = DE
(c) AC = EF
(d) BC = DE.
उत्तर:
(b) AC = DE
प्रश्न 12.
समान आकार एवं समान आकृति वाली आकृतियाँ होती हैं :
(a) बराबर
(b) समान
(c) सर्वांगसम
(d) समरूप।
उत्तर:
(c) सर्वांगसम
प्रश्न 13.
समकोण त्रिभुज में सबसे बड़ी भुजा होती है :
(a) लम्ब
(b) आधार
(c) कर्ण
(d) रेखा।
उत्तर:
(c) कर्ण
प्रश्न 14.
समबाहु त्रिभुज के प्रत्येक कोण का मान होता है : (2019)
(a) 90°
(b) 30°
(c) 60°
(d) 120°.
उत्तर:
(c) 60°
प्रश्न 15.
पाइथागोरस प्रमेय किस त्रिभुज के लिए प्रसिद्ध है :
(a) समबाहु त्रिभुज
(b) सर्वांगसम त्रिभुज
(c) समद्विबाहु त्रिभुज
(d) समकोण त्रिभुज।
उत्तर:
(d) समकोण त्रिभुज
![]()
रिक्त स्थानों की पूर्ति
1. समबाहु त्रिभुज का प्रत्येक कोण ……… होता है।
2. किसी त्रिभुज की दो भुजाओं का योग तीसरी भुजा से ……….. होता है।
3. समकोण त्रिभुज की सबसे बड़ी भुजा ………… होती है।
4. त्रिभुज के तीनों अन्तः कोणों का योग ………….. होता है।
5. समान आकार एवं समान आकृति वाली आकृतियाँ ……… होती हैं।
6. किसी त्रिभुज की दो भुजाएँ असमान हों तो, बड़ी भुजा के सामने का कोण ………. होता है।
7. किसी त्रिभुज की समान भुजाओं के सम्मुख कोण ………….. होते हैं।
8. किसी त्रिभुज में बड़े कोण के सामने की भुजा ………….. होती है।
उत्तर:
1. 60°,
2. बड़ा,
3. कर्ण,
4. 180°,
5. सर्वांगसम,
6. बड़ा,
7. बराबर,
8. बड़ी।
जोड़ी मिलान
स्तम्भ ‘A’ स्तम्भ ‘B’
1. त्रिभुज जिसकी तीनों भुजाएँ समान हों (a) अधिक कोण त्रिभुज
2. त्रिभुज जिसकी दो भुजाएँ समान हों (b) न्यूनकोण त्रिभुज
3. त्रिभुज जिसका एक कोण 90° हो (c) समबाहु त्रिभुज
4. त्रिभुज जिसका एक कोण अधिक कोण हो (d) केन्द्रक
5. त्रिभुज जिसका प्रत्येक कोण न्यूनकोण हो (e) समकोण त्रिभुज
6. माध्यिकाओं के संगमन बिन्दु को कहते हैं (2018) (f) समद्विबाहु त्रिभुज
उत्तर:
1. → (c),
2. → (1),
3. → (e),
4. → (a),
5. → (b),
6. → (d).
सत्य/असत्य कथन
1. समद्विबाहु त्रिभुज के तीनों कोण बराबर होते हैं। (2018)
2. किसी त्रिभुज के बड़े कोण के सामने की भुजा छोटी होती है।
3. किसी त्रिभुज की दो भुजाओं का योग, तीसरी भुजा से बड़ा होता है।
4. किसी रेखा के बाहर स्थित किसी बिन्दु से रेखा तक जितने रेखाखण्ड खींचे जा सकते हैं उनमें लम्ब सबसे छोटा होता है।
5. सभी वृत्त सर्वांगसम होते हैं।
6. यदि दो त्रिभुजों की संगत भुजाएँ बराबर हों, तो त्रिभुज बराबर हों, तो त्रिभुज सर्वांगसम होते हैं। (2019)
7. त्रिभुजों के तीनों कोणों का योग 180° होता है। (2019)
8. सर्वांगसम त्रिभुज में संगत भाग बराबर होते हैं। (2019)
उत्तर:
1. असत्य,
2. असत्य,
3. सत्य,
4. सत्य,
5. असत्य,
6. सत्य,
7. सत्य,
8. सत्य।
![]()
एक शब्द/वाक्य में उत्तर
1. किसी त्रिभुज में अधिकतम कितने समकोण हो सकते हैं ?
2. किसी त्रिभुज में अधिकतम कितने अधिक कोण हो सकते हैं ?
3. किसी त्रिभुज में कम-से-कम कितने न्यूनकोण हो सकते हैं ?
4. किसी त्रिभुज के बहिष्कोण और अन्तः कोणों में क्या सम्बन्ध होता है ?
5. समकोण समद्विबाहु त्रिभुज के प्रत्यके न्यूनकोण का मान कितना होता है ?
उत्तर:
1. एक,
2. एक,
3. दो,
4. त्रिभुज का बहिष्कोण सम्मुख अन्त:कोणों के योग के बराबर है अर्थात् प्रत्येक सम्मुख अन्तः कोण से बड़ा होता है,
5. 45° ।