Category: Class 12

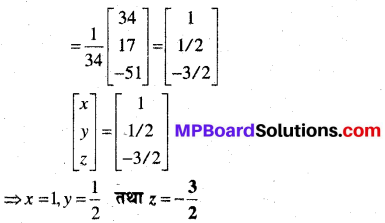
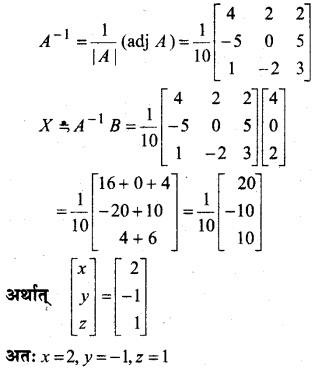
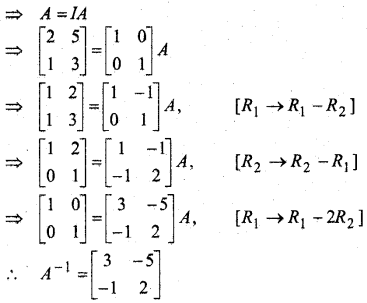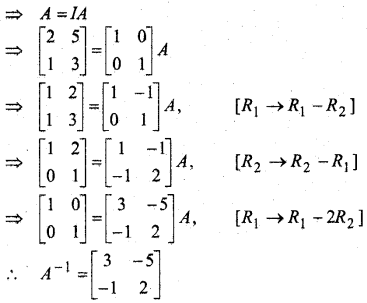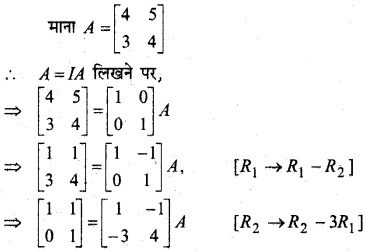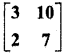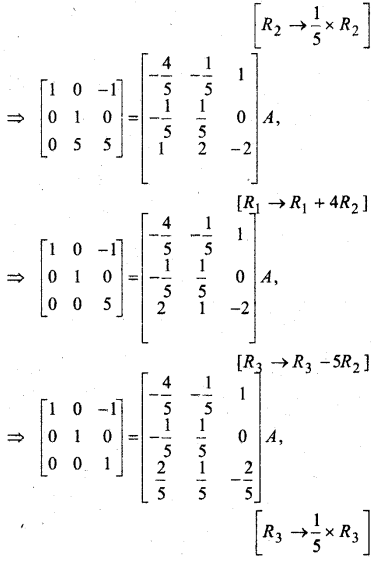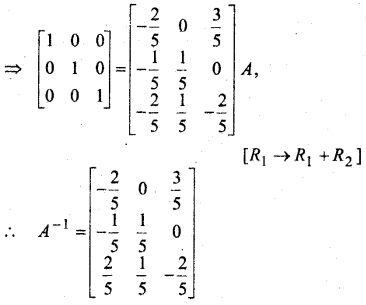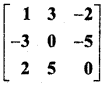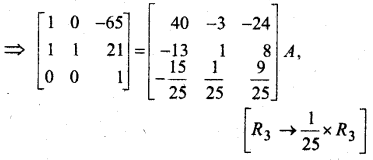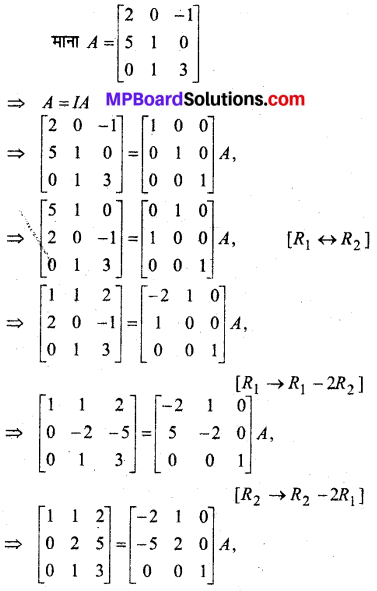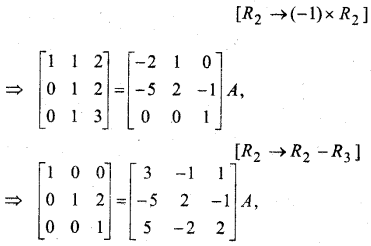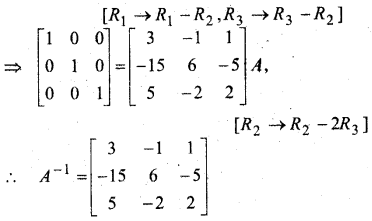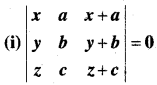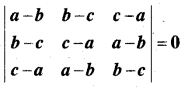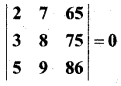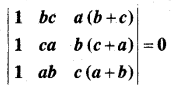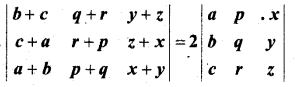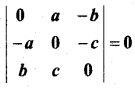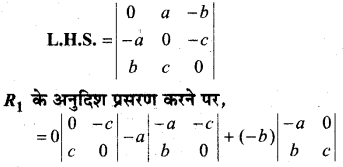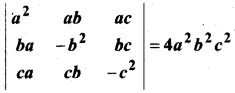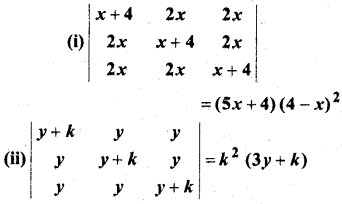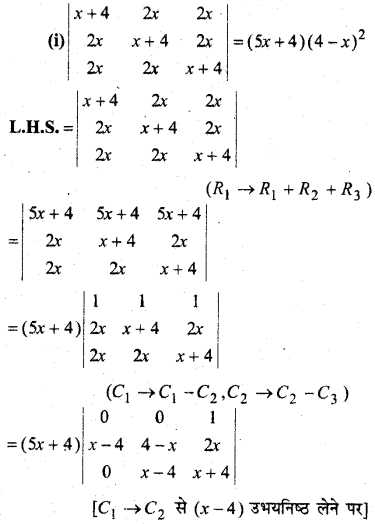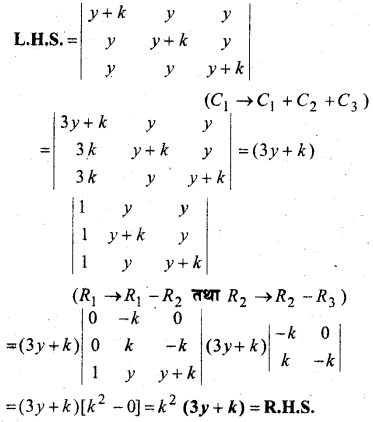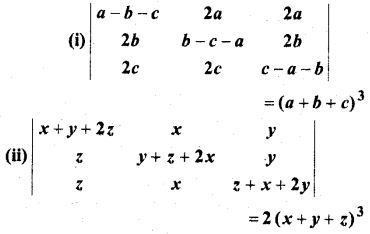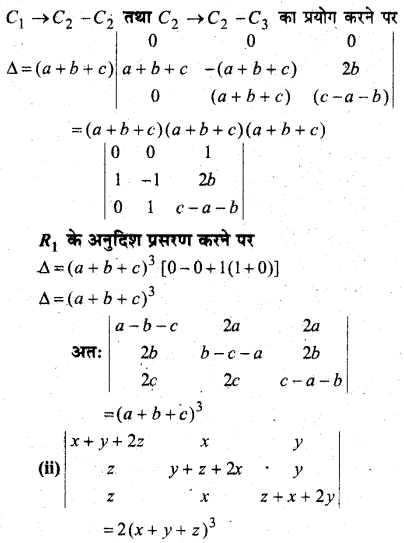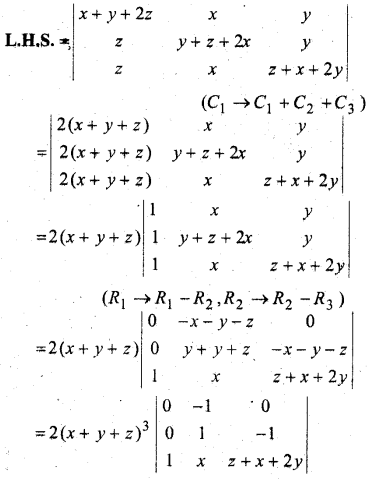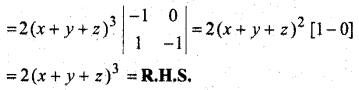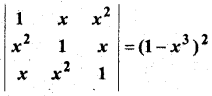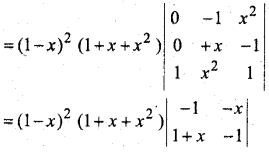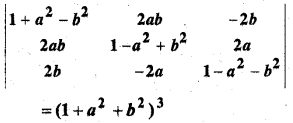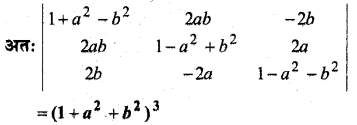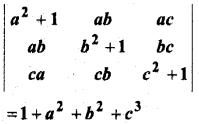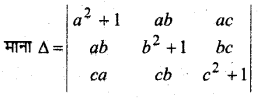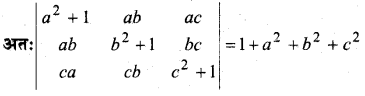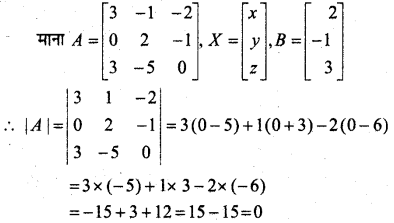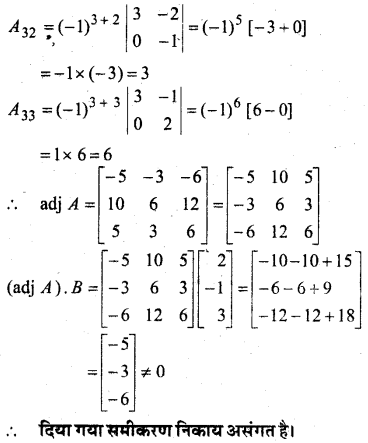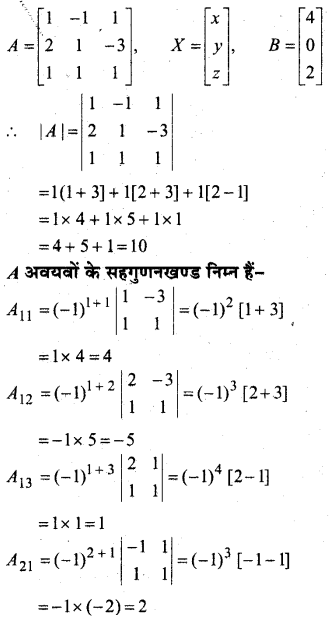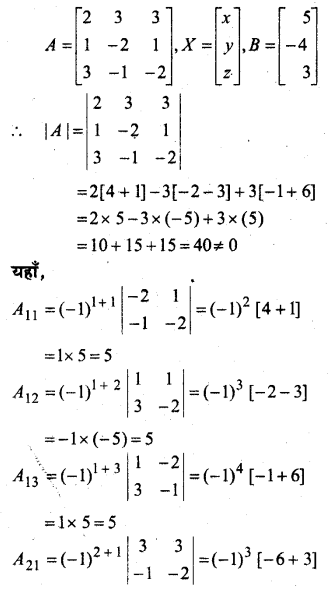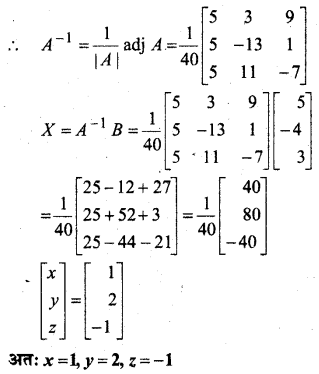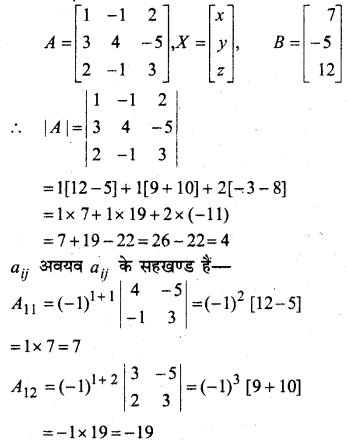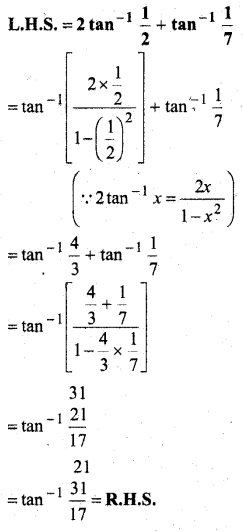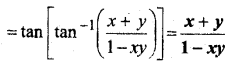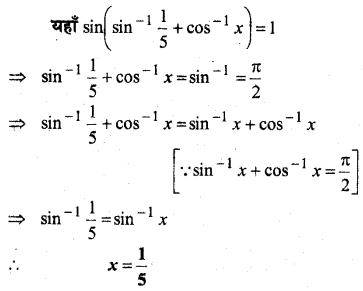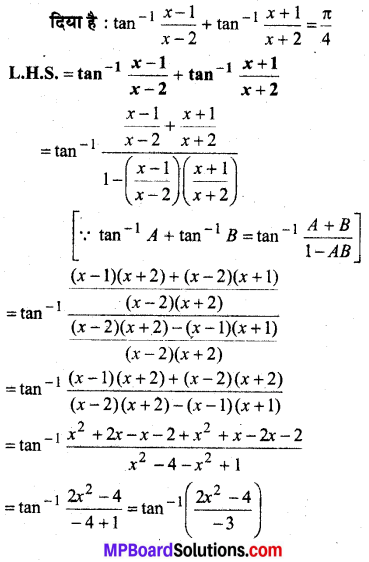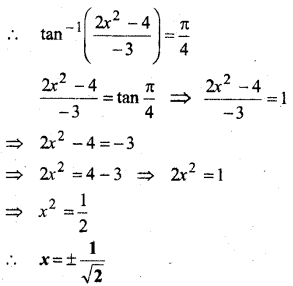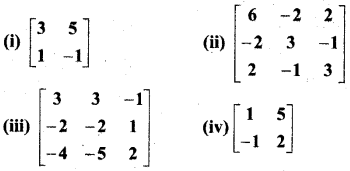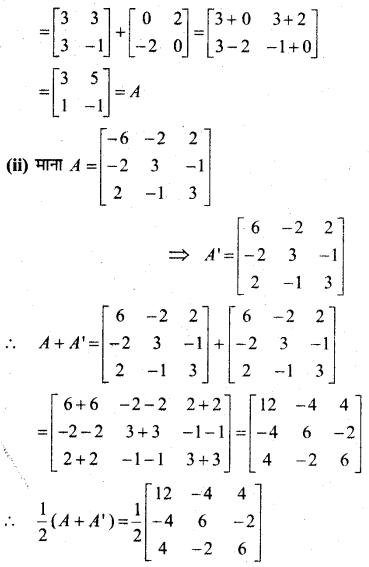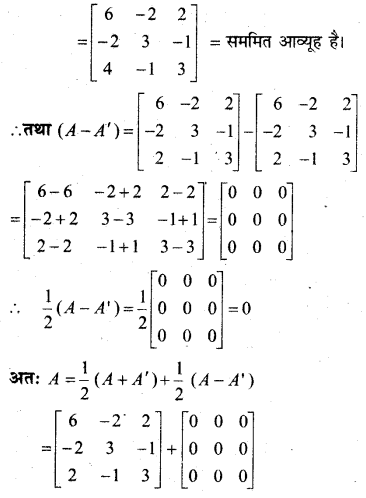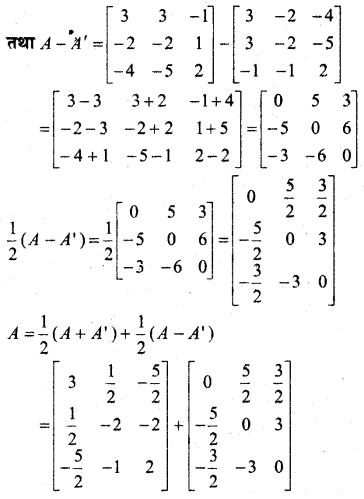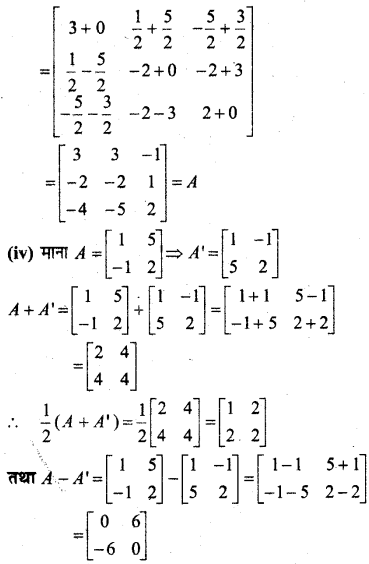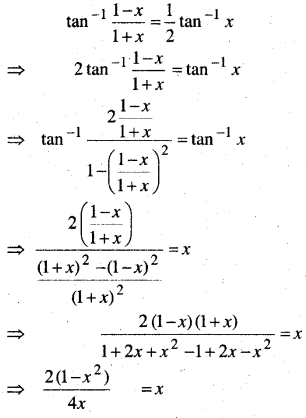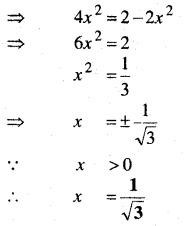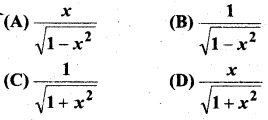In this article, we share MP Board Class 12th Maths Book Solutions Chapter 4 सारणिक विविध प्रश्नावली Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 4 सारणिक विविध प्रश्नावली

प्रश्न 1.
सिद्ध कीजिए कि सारणिक

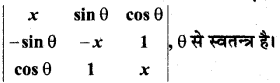
हल:

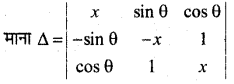
= x(-x² – 1) – sin θ (-xsin θ – cos θ) + cos θ(-sin θ + xcosθ)
= -x(x² + 1) + xsin²θ + sinθcos θ – sin θcos θ + xcos²θ
= -x(x² + 1) + x (sin²θ + cos²θ)
= -x(x² + 1) + x = -x[x² + 1 – 1] = -x³
जो कि θ से स्वतन्त्र है।

प्रश्न 2.
सारणिक का प्रसरण किए बिना सिद्ध कीजिए कि

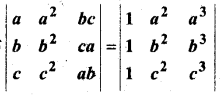
हल:

प्रश्न 3.

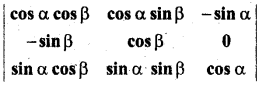
का नाम ज्ञात कीजिए
हल:

प्रश्न 4.
यदि a, b और c वास्तविक संख्याएँ हों और सारणिक

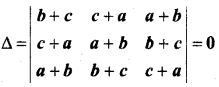
हो तो दर्शाइए कि या तो a + b + c = 0 या a = b = c है|
हल:


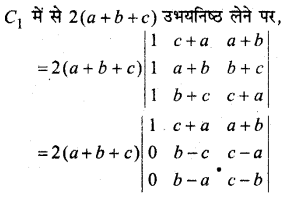
[R₂ → R₂ – R₁ तथा R₃ → R₃ – R₁]
= 2(a + b + c)[1{(b – c)(c – b) – (c – a)(b – a)} – (c + a){0 – 0} + (a + b){0 – 0}]
= 2(a + b + c)[-{(b – c)}² – (bc – ac – ab + a²)]
= 2(a + b + c)[-b² – c² + 2bc – bx + ac + ab – a²]
= 2(a + b + c)[-b² – c² + bc + ac + ab – a²]
= 2(a + b + c)[a² + b² + c² – ab – bc – ca]
= -(a + b + c)[2a² + 2b² + 2c² – 2ab -2bc – 2ca]
= -(a + b + c)[(a – b) + (b – c) + (c – a)²
अब ∆ = 0 ⇒ a + b + c = 0 या a = b = c

प्रश्न 5.
यदि a ≠ 0 हो तो समीकरण

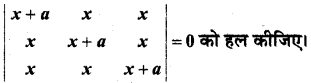
हल:

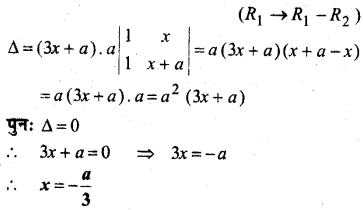
प्रश्न 6.
सिद्ध कीजिए कि

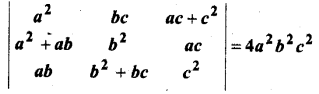
हल:


∆ = 2a²b²c[(a+ c)(1 – 0) – 1(a + b – b – c)]
= 2a²b²c[a + c – a + c] = 2a²b²c
2c = 4a²b²c²

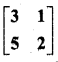
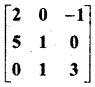
प्रश्न 7.
यदि A^-1 = \(\left[\begin{array}{ccc}{3} & {-1} & {1} \\ {-15} & {6} & {-5} \\ {5} & {-2} & {2}\end{array}\right]\) और B = \(\left[\begin{array}{ccc}{1} & {2} & {-2} \\ {-1} & {3} & {0} \\ {0} & {-2} & {1}\end{array}\right]\) हो तो (AB)^-1 का मान ज्ञात कीजिए।
हल:

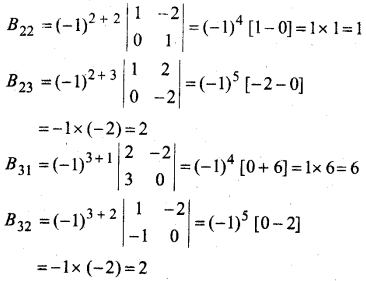
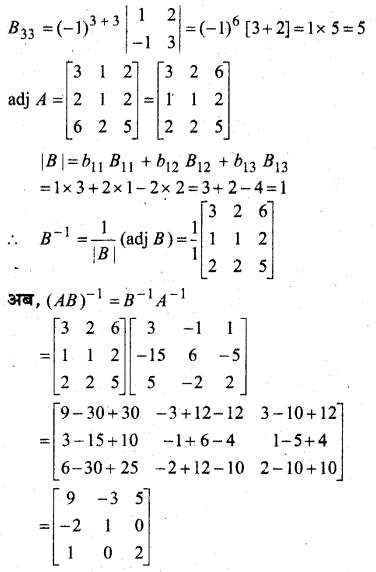
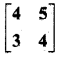
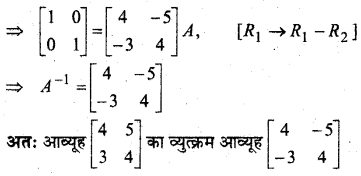
प्रश्न 8.
मान लीजिए कि A = \(\left[\begin{array}{ccc}{1} & {-2} & {1} \\ {-2} & {3} & {1} \\ {1} & {1} & {5}\end{array}\right]\) हो तो सत्यापित कीजिए कि
(i) [adj A]^-1 = adj (A^-1)
(ii) (A^-1)^-1 = A
हल:

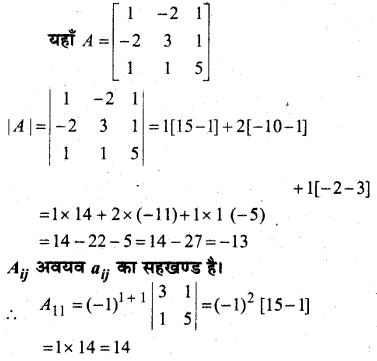
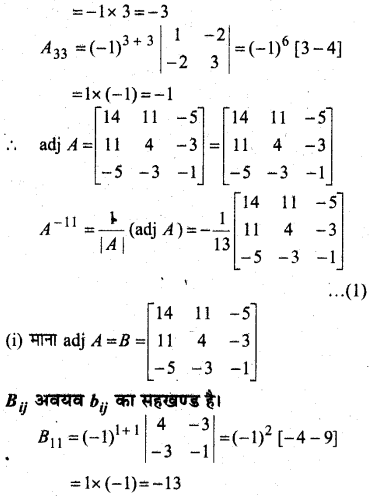
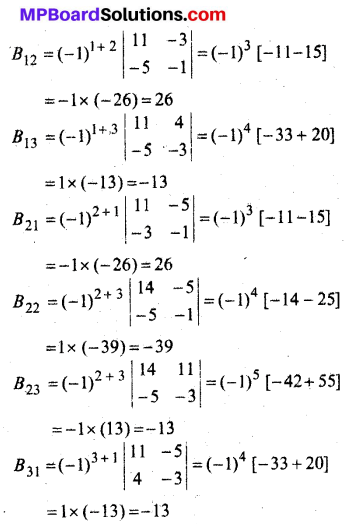
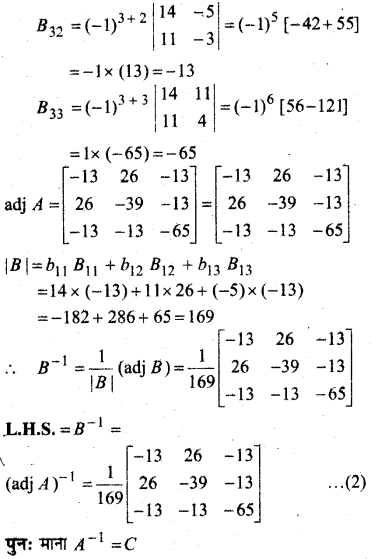
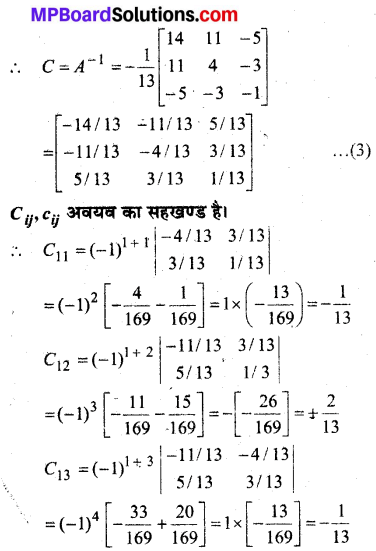
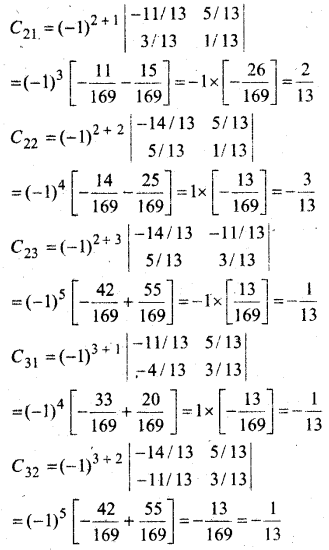
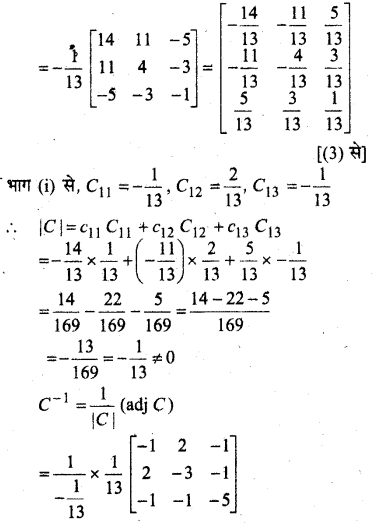
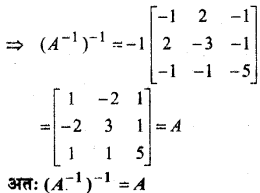
प्रश्न 9.

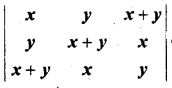
का मान ज्ञात कीजिए।
हल:

प्रश्न 10.

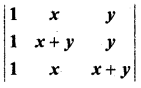
का मान ज्ञात कीजिए।
हल:

सारणिकों के गुणधर्मों का प्रयोग करके निम्नलिखित 11 से 15 तक प्रश्नों को सिद्ध कीजिए
प्रश्न 11.

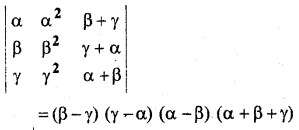
हल:

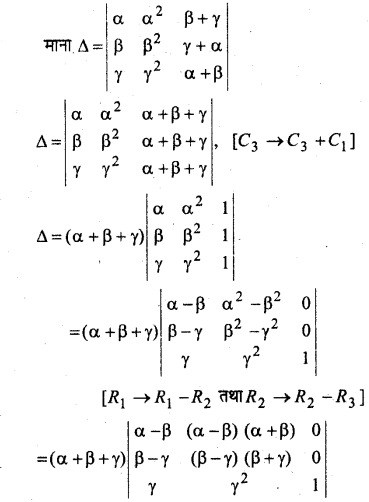
प्रश्न 12.

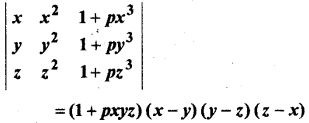
हल:

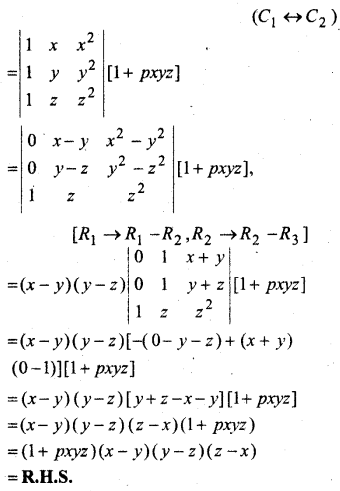
प्रश्न 13.

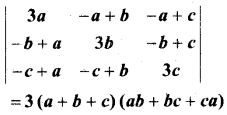
हल:

[R₁ → R₂ – R₁ तथा R₃ → R₃ – R₁]
= (a + b + c)[1{(2b + a)+ (2c + a) – (a – b)(a – c)}]
= (a + b + c)[4bc + 2ab + 2ac + a² – (a² – ac – ab + bc)]
= (a + b + c)[4bc + 2ab + 2ac + a² – a² + ac + ab – bc]
= (a + b + c)(3bc + 3ab + 3ac]
= 3 (a + b + c) (ab + bc + ca) = R.H.S.
अतः L.H.S. = R.H.S.

प्रश्न 14.

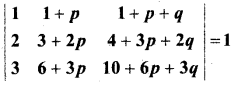
हल:

प्रश्न 15.

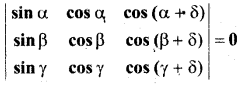
हल:

प्रश्न 16.
निम्नलिखित समीकरण को हल कीजिए

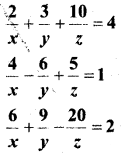
हल:

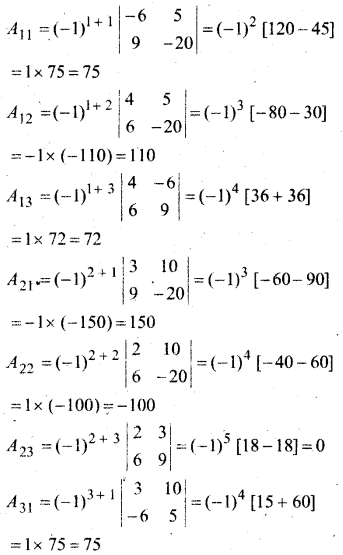
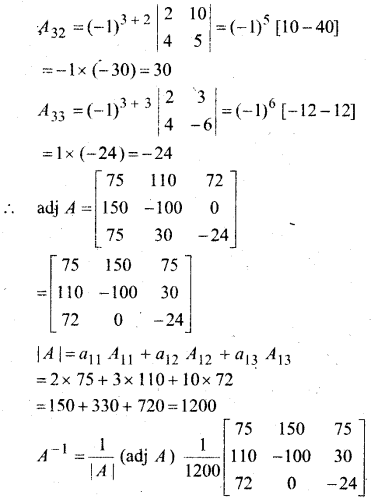
निम्नलिखित प्रश्नों 17 से 19 में सही उत्तर का चुनाव कीजिए।
प्रश्न 17.
यदि a, b, c समान्तर श्रेणी में हों तो सारणिक

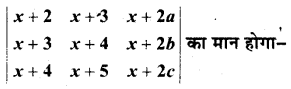
(A) 0
(B) 1
(C) x
(D) 2x
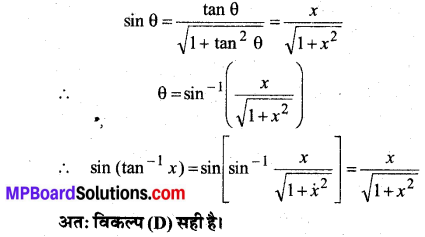
हल:

प्रश्न 18.
यदि x, y, z शून्येतर वास्तविक संख्याएँ हों तो आव्यूह A = \(\left[\begin{array}{lll}{\boldsymbol{x}} & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\boldsymbol{y}} & {\mathbf{0}} \\ {\boldsymbol{0}} & {\boldsymbol{0}} & {z}\end{array}\right]\) का व्युत्क्रम है-

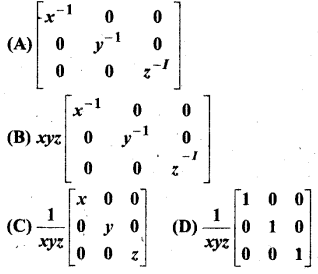
हल:

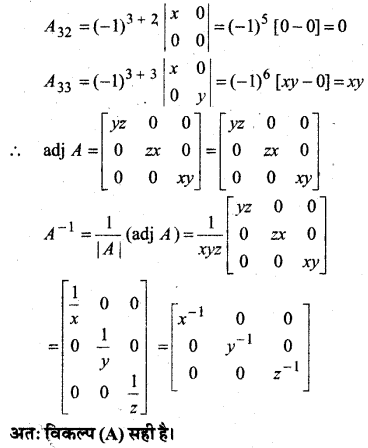
प्रश्न 19.
यदि A = \(\left[\begin{array}{ccc}{1} & {\sin \theta} & {1} \\ {-\sin \theta} & {1} & {\sin \theta} \\ {-1} & {-\sin \theta} & {1}\end{array}\right]\), जहाँ 0 ≤ θ ≤ 2 हो तो-
(A) det (A) = 0
(B) det (A) ϵ (2, ∞)
(C) det (A) ϵ (2, 4)
(D) det (A) ϵ [2, 4]
हल:

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 3 आव्यूह Ex 3.4 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 3 आव्यूह Ex 3.4

प्रश्न संख्या 1 से 17 तक के आव्यूहों के व्युत्क्रम, यदि उनका अस्तित्व है तो प्रारम्भिक रूपान्तरण के प्रयोग से ज्ञात कीजिए।
प्रश्न 1.

हल:

प्रश्न 2.

हल:

प्रश्न 3.

हल:

प्रश्न 4.

हल:

प्रश्न 5.

हल:

प्रश्न 6.

हल:

प्रश्न 7.

हल:

प्रश्न 8.

हल:

प्रश्न 9.

हल:

प्रश्न 10.
\(\left[\begin{array}{cc}{3} & {-1} \\ {-4} & {2}\end{array}\right]\)
हल:

प्रश्न 11.
\(\left[\begin{array}{ll}{2} & {-6} \\ {1} & {-2}\end{array}\right]\)
हल:

प्रश्न 12.
\(\left[\begin{array}{cc}{6} & {-3} \\ {-2} & {1}\end{array}\right]\)
हल:

पहली पंक्ति में दोनों अवयव शून्य हैं।
अत: A का व्युत्क्रम A^-1 का अस्तित्व नहीं है।

प्रश्न 13.
\(\left[\begin{array}{cc}{2} & {-3} \\ {-1} & {2}\end{array}\right]\)
हल:

प्रश्न 14.
\(\left[\begin{array}{ll}{2} & {1} \\ {4} & {2}\end{array}\right]\)
हल:

दूसरी पंक्ति में दोनों अवयव शून्य हैं।
अतः A के व्युत्क्रम का अस्तित्व नहीं है।

प्रश्न 15.
\(\left[\begin{array}{ccc}{2} & {-3} & {3} \\ {2} & {2} & {3} \\ {3} & {-2} & {2}\end{array}\right]\)
हल:

प्रश्न 16.

हल:

प्रश्न 17.

हल:

प्रश्न 18.
आव्यूह A तथा B एक-दूसरे के व्युत्क्रम होंगे केवल यदि
(A) AB = BA
(B) AB = BA = 0
(C) AB = 0, BA = I
(D) AB = BA = I
हल:
AB = BA = I, केवल इस स्थिति में A और B एक-दूसरे के व्युत्क्रम होंगे।
अतः विकल्प (D) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 4 सारणिक Ex 4.2 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 4 सारणिक Ex 4.2

बिना प्रसरण किए और सारणिकों के गुणधर्मों का प्रयोग करके निम्नलिखित प्रश्न 1 से 5 को सिद्ध कीजिए-
प्रश्न 1.

हल:

प्रश्न 2.

हल:

प्रश्न 3.

हल:

प्रश्न 4.

हल:

प्रश्न 5.

हल:

सारणिकों के गुणधर्मों का प्रयोग करके प्रश्न 6 से 14 तक को सिद्ध कीजिए-
प्रश्न 6.

हल:

= 0 – a(0 + bc) – b(-ac + 0)
= -abc + abc
= 0
= R.H.S.

प्रश्न 7.

हल:

प्रश्न 8.

हल:

प्रश्न 9.
\(\left|\begin{array}{lll}{x} & {x^{2}} & {y z} \\ {y} & {y^{2}} & {z x} \\ {z} & {z^{2}} & {x y}\end{array}\right|\) = (x – y) (y – z)(z – x) (xy + yz + zx)
हल:


= (x – y)(y – z)(z – x)[(z² – xy) – z(x + y + z)]
= (x – y)(y – z)(z – x)[z² – xy – xz – zy –z²]
= (x – y)(y – z)(z – x)[-(xy + yz + zx)]
= -(x – y)(y – z)(z – x)(xy + yz + zx)= R.H.S.

प्रश्न 10.

हल:

प्रश्न 11.

हल:

प्रश्न 12.

हल:


= (1 – x)² (1 + x + x²)[1 + x(1 + x)]
= (1 – x)² (1 + x + x² )[1 + x + x²]
= (1 – x)² (1 + x + x²)²
= [(1 – x)(1 + x + x²)]²
= (1 – x³)² = R.H.S.

प्रश्न 13.

हल:

प्रश्न 14.

हल:

R₁ के अनुदिश प्रसरण करने पर
∆ = (a² + 1)[(b² + 1)(c² + 1) – bc.cb] – ab [ab (c² + 1) – bc.ca] + ac[ab. cb – ac.b² + 1]
= (a² + 1)[b²c² + b² + c² + 1 – b²c²] – ab[abc² + ab – abc] + ac[ab²c – acb² – ac]
= (a² + 1)(b² + c² + 1) – ab (ab) – ac (ac)
=a²b² + a²c² + a² + b² + c² + 1 – a²b² – a²c²
= 1 + a² + b² + c²

प्रश्न संख्या 15 तथा 16 में सही उत्तर चुनिए।
प्रश्न 15.
यदि A एक 3 × 3 कोटि का वर्ग आव्यूह है तो |KA| का मान होगा-
(A) K|A|
(B) k²|A|
(C) k³|A|
(D) 3k|A|
हल:
|kA | को |A | के पद में व्यक्त करना

अतः विकल्प (C) सही है।

प्रश्न 16.
निम्नलिखित में से कौन-सा कथन सही है?
(A) सारणिक एक वर्ग आव्यूह है।
(B) सारणिक एक आव्यूह से सम्बद्ध एक संख्या है।
(C) सारणिक एक वर्ग आव्यूह से सम्बद्ध एक संख्या है।
(D) इनमें से कोई नहीं।
हल:
सारणिक एक वर्ग आव्यूह से सम्बद्ध एक संख्या है।
अतः विकल्प (C) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 4 सारणिक Ex 4.6 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 4 सारणिक Ex 4.6

निम्नलिखित प्रश्नों में 1 से 6 तक दी गई समीकरण निकायों का संगत अथवा असंगत के रूप में वर्गीकरण कीजिए।
प्रश्न 1.
x + 2y = 2
2x + 3y = 3
हल:
दिए गये समीकरण निकाय को हम इस प्रकार से लिख सकते हैं।
AX = B

प्रश्न 2.
2x – y = 5
x + y = 4
हल:
दिया गया समीकरण निकाय
2x – y = 5
x + y = 4

प्रश्न 3.
x + 3y = 5
2x + 6y = 8
हल:
दिए गए समीकरण निकाय को हम इस प्रकार से लिख सकते हैं।
AX = B

प्रश्न 4.
x + y + = 1
2x + 3y + 2z = 2
ax + ay + 2az =4
हल:
दिया गया समीकरण निकाय
x + y + z = 1
2x + 3y + 2z = 2
ax + ay + 2az = 4

= a[1(6 – 2) – 1(4 – 2) + 1(2 – 3)]
= a [1 × 4 – 1 × 2 + 1(-1)]
= a[4 – 2 – 1] = a × 1 = a ≠ 0
अतः दिया गया समीकरण निकाय संगत है।

प्रश्न 5.
3x – y – 2z = 2
2y – z = -1
3x – 5y = 3
हल:
3x – y – 2z = 2
2y – z = -1
3x – 5y = 3

प्रश्न 6.
5x – y + 4z = 5
2x + 3y + 5z = 2
5x – 2y + 6z = -1
हल:
दिए गए समीकरण निकाय को निम्न प्रकार से लिख सकते हैं
AX = B

= 5(18 + 10) + 1(12 – 25) + 4(-4 – 15)
= 140 – 13 – 76
= 51 ≠ 0
अतः समीकरण निकाय संगत है।

निम्नलिखित प्रश्न 7 से 14 तक प्रत्येक समीकरण निकाय को आव्यूह विधि से हल कीजिए।
प्रश्न 7.
5x + 2y = 4
7x + 3y = 5
हल:
दिया गया समीकरण निकाय
5x + 2y = 4
7x + 3y = 5

प्रश्न 8.
2x – y = -2
3x + 4y = 3
हल:
दी गई समीकरण निकाय
2x – y = -2
3x + 4y = 3
उपरोक्त समीकरणों को निम्न प्रकार से लिख सकते हैं-
AX = B

प्रश्न 9.
4x – 3y = 3
3x – 5y = 7
हल:
दिया गया समीकरण निकाय
4x – 3y = 3
3x – 5y = 7
समीकरण निकाय AX = B के रूप में लिखा जा सकता है, जहाँ

प्रश्न 10.
5x + 2y = 3
3x + 2y = 3
हल:
दिया गया समीकरण निकाय
5x + 2y = 3
3x + 2y = 5
समीकरण निकाय AX = B के रूप में लिखा जा सकता है, जहाँ

प्रश्न 11.
निम्नलिखित समीकरण निकाय को आव्यूह विधि से हल कीजिए
2x + y + z = 1
x – 2y -2z = 3/2
3y – 5z = 9
हल:
दी गई समीकरण निकाय को निम्न प्रकार से लिख सकते हैं-
AX = B

प्रश्न 12.
x – y + z = 4
2x + y – 3z = 0
x + y + z = 2
हल:
दिया गया समीकरण निकाय
x – y + z = 4
2x + y – 3z = 0
x + y + z = 2
समीकरण निकाय AX = B के रूप में लिखा जा सकता है, जहाँ,

प्रश्न 13.
2x + 3y + 3z = 5
x – 2y + 2 = -4
3x – y – 2z = 3
हल:
दिया गया समीकरण निकाय
2x + 3y + 3z = 5
x – 2y + z = -4
3x – y – 2z = 3
समीकरण निकाय को AX = B के रूप में लिखा जा सकता है, जहाँ

प्रश्न 14.
x – y + 2z = 7
3x + 4y – 5z = -5
2x – y + 3z = 12
हल:
दिया गया समीकरण निकाय
x – y + 2z = 7
3x + 4y – 5z = -5
2x – y + 3z = 12
समीकरण निकाय को AX = B के रूप में लिखा जा सकता है, जहाँ

प्रश्न 15.
यदि A = \(\left[\begin{array}{ccc}{2} & {-3} & {5} \\ {3} & {2} & {-4} \\ {1} & {1} & {-2}\end{array}\right]\) है तो A^-1 ज्ञात कीजिए। A^-1 का प्रयोग करके निम्नलिखित समीकरण निकाय को हल कीजिए।
2x – 3y + 5z = 11
3x + 2y – 4z = -5
x + y – 2z = -3
हल:

प्रश्न 16.
4 kg प्याज, 3 kg गेहूँ और 2 kg चावल का मूल्य Rs. 60 है। 2 kg प्याज, 4kg गेहूँ और 6 kg चावल का मूल्य Rs. 90 है। 6 kg प्याज, 2 kg गेहूँ और 3 kg चावल का मूल्य Rs. 70 है। आव्यूह विधि द्वारा प्रत्येक का मूल्य प्रति kg ज्ञात कीजिए।
हल:
माना प्याज, गेहूँ तथा चावल का मूल्य प्रति किग्रा क्रमश: x रु०, ५ रु० तथा 2 रु० है।
4 किग्रा प्याज 3 किया गेहूँ तथा 2 किग्रा चावल का मूल्य = 60 रुपये
∴ 4x + 3y + 2z = 60 …(1)
2 किग्रा प्याज, 4 किग्रा गेहूँ तथा 6 किग्रा चावल का मूल्य = 90 रु०
∴ 2x + 4y + 6z = 90 …(2)
6 किया प्याज, 2 किग्रा गेहूँ तथा 3 किग्रा चावल का मूल्य = 70 रु०
∴ 6x + 2y + 3z = 70 ….(3)
अब समीकरण निकाय
4x + 3y + 2z = 60
2x + 4y + 6z = 90
या x + 2y + 32 = 45
6x + 2y + 3z = 70
इसे AX = B के रूप में लिख सकते हैं, जबकि



अत: प्याज, गेहूँ तथा चावल का मूल्य प्रति किग्रा क्रमश: 5 रु०,8 रु०, तथा 8 रु० है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 2 प्रतिलोम त्रिकोणमितीय फलन Ex 2.1 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 2 प्रतिलोम त्रिकोणमितीय फलन Ex 2.1

निम्नलिखित के मुख्य मानों को ज्ञात कीजिए :
प्रश्न 1.
sin^-1\(\left(-\frac{1}{2}\right)\)
हल :
माना y = in^-1\(\left(-\frac{1}{2}\right)\)

प्रश्न 2.
cos^-1\(\frac{\sqrt{3}}{2}\)
हल :
माना y = cos^-1\(\frac{\sqrt{3}}{2}\)
⇒ cos y = \(\frac{\sqrt{3}}{2}\)
⇒ cos y = cos\(\frac{\pi}{6}\)
∵ cos^-1 की मुख्य शाखा का परिसर [0, π] होता है तथा cos \(\frac{\pi}{6}=\frac{\sqrt{3}}{2}\)
∴ cos\(\frac{\sqrt{3}}{2}\) का मुख्य मान \(\frac{\pi}{6}\) है।

प्रश्न 3.
cosec^-1(2)
हल :
माना y = cosec^-1 (2)
⇒ cosec y = 2
cosec y = cosec \(\frac{\pi}{6}\)
⇒ cosec^-1(cosec y) = \(\frac{\pi}{6}\)
y =\(\frac{\pi}{6}\)
अतः cosec^-1 (2) का मुख्य मान = \(\frac{\pi}{6}\)

प्रश्न 4.
tan^-1 (-\( \sqrt{{3}} \))
हल :
माना y = tan^-1(-\( \sqrt{{3}} \))
⇒ tan y = –\( \sqrt{{3}} \)
tan y = tan\(\left(-\frac{\pi}{3}\right)\)
∵ tan^-1 की मुख्य शाखा का परिसर \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\) और tan\(\tan \left(-\frac{\pi}{3}\right)=-\sqrt{3}\)
अत: tan^-1(-\( \sqrt{{3}} \))का मुख्य मान = \(\frac{-\pi}{3}\)

प्रश्न 5.
cos^-1\(\left(-\frac{1}{2}\right)\)
हल :
माना y = cos^-1\(\left(-\frac{1}{2}\right)\)

प्रश्न 6.
tan^-1(-1)
हल :
माना y = tan^-1(1)
⇒ tan y = -1
tany = tan\(\left(-\frac{\pi}{4}\right)\)
अत: tan^-1(-1) का मुख्य मान = \(-\frac{\pi}{4}\)

प्रश्न 7.
sec^-1\(\left(\frac{2}{\sqrt{3}}\right)\)
हल :
माना y = sec^-1\(\left(\frac{2}{\sqrt{3}}\right)\)

प्रश्न 8.
cot^-1\(\sqrt{3}\)
हल :
माना y = cot^-1\(\sqrt{3}\)
= cot y = (\(\sqrt{3}\)) = cot \(\frac{\pi}{6}\)
फलन cot^-1x का मुख्य मान शाखा का परिसर = (0, π) है। अतः cot^-1 (\(\sqrt{3}\)) = \(\frac{\pi}{6}\) है।

प्रश्न 9.
cos^-1\(\left(-\frac{1}{\sqrt{2}}\right)\)
हल :
माना y = cos^-1\(\left(-\frac{1}{\sqrt{2}}\right)\)

प्रश्न 10.
cosec^-1\(-\sqrt{2}\)
हल :
माना y = cosec^-1\(-\sqrt{2}\)
⇒ cosec y = –\(\sqrt{2}\) = -cosee \(\frac{\pi}{4}\) = cosee \(\left(-\frac{\pi}{4}\right)\)
फलन cosec^-1x का मुख्य मान शाखा का परिसर = \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\) – [0]
अतः cosec^-1(-\( \sqrt{{2}} \)) = –\(-\frac{\pi}{4}\) है।

प्रश्न 11.
निम्नलिखित के मान ज्ञात कीजिए
tan^-1(1) + cos^-1\(\left(-\frac{1}{2}\right)\) + sin^-1\(\left(-\frac{1}{2}\right)\)
हल :

प्रश्न 12.
cos^-1\(\left(\frac{1}{2}\right)\) + 2sin^-1\(\left(\frac{1}{2}\right)\)
हल :

प्रश्न 13.
यदि sin^-1 x = y तो

हल :

प्रश्न 14.
tan^-1\( \sqrt{{3}} \)– sec^-1(-2) का मान बराबर है-
(A) π
(B) \(-\frac{\pi}{3}\)
(C) \(\frac{\pi}{3}\)
(D) \(\frac{2 \pi}{3}\)
हल:
माना y = tan^-1\( \sqrt{{3}} \)– sec^-1(-2)

अतः विकल्प (B) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 2 प्रतिलोम त्रिकोणमितीय फलन Ex 2.2 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 2 प्रतिलोम त्रिकोणमितीय फलन Ex 2.2

निम्नलिखित को सिद्ध कीजिए-
प्रश्न 1.
3 sin^-1 x = sin^-1(3x – 4x³), x ϵ \(\left[-\frac{1}{2}, \frac{1}{2}\right]\)
हल:
माना sin^-1x = y
⇒ x = sin y
R.H.S. = sin^-1 (3x – 4x³)
= sin^-1(3 sin y – 4 sin³ y)
= sin^-1 (sin 3y)
(∵ sin 3y = 3 sin y – 4 sin³y)
= 3y (∵ sin^-1 sin x = x)
= 3 sin^-1 x
= L.H.S.
अत: 3 sin^-1x = sin^-1(3x – 4x³)

प्रश्न 2.
3 cos^-1 x = cos^-1 (4x³ – 3x), x ϵ \(\left[\frac{1}{2}, 1\right]\)
हल:
सिद्ध करना है
3cos^-1 x = cos^-1 (4x³ – 3x) …(1)
माना cos^-1 = y
⇒ x = cosy
∴ समी० (1) का RH.S.
=cos^-1(4x³ – 3x)
= cos^-1 (4cos³ y – 3cos y)
=cos^-1 (cos 3y)
= 3y
= 3cos^-1x (∵ cos^-1 x = y)
अत: 3cos^-1 = cos^-1 (4x³ – 3x)

प्रश्न 3.
tan^-1\(\frac{2}{11}\) + tan^-1\(\frac{7}{24}\) = tan^-1\(\frac{1}{2}\)
हल:
हम जानते हैं कि

प्रश्न 4.
2 tan^-1\(\frac{1}{2}\) + tan^-1\(\frac{1}{7}\) = tan^-1\(\frac{31}{17}\)
हल:
2 tan^-1\(\frac{1}{2}\) + tan^-1\(\frac{1}{7}\) = tan^-1\(\frac{31}{17}\)

निम्नलिखित फलनों को सरलतम रूप में लिखिए-
प्रश्न 5.
tan-1 \(\frac{\sqrt{1+x^{2}}-1}{x}\), x ≠ 0
हल:
माना x = tan θ ⇒ θ = tan^-1x

प्रश्न 6.
tan^-1\(\frac{1}{\sqrt{x^{2}-1}}\), |x| > 1.
हल:
माना x = secθ ⇒ θ = sec^-1x

प्रश्न 7.
tan^-1\((\sqrt{\frac{1-\cos x}{1+\cos x}})\), 0 < x < π
हल:

प्रश्न 8.
tan^-1\(\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right), \frac{-\pi}{4}<x<\frac{3 \pi}{4}\)
हल:

प्रश्न 9.
tan^-1\(\frac{x}{\sqrt{a^{2}-x^{2}}}\), |x| < a
हल:
माना x = a sin θ ⇒ \(\frac{x}{a}\) = sin θ

प्रश्न 10.

हल:
माना x = a tan θ ⇒ \(\frac{x}{a}\) = tan θ

निम्नलिखित में से प्रत्येक का मान ज्ञात कीजिए
प्रश्न 11.
tan^-1[2cos (2sin^-1\(\frac{1}{2}\))]
हल:

प्रश्न 12.
cot (tan^-1 a + cot^-1 a)
हल:
माना y = cot (tan^-1a + cot^-1a)
= cot\(\frac{\pi}{2}\) [∵ tan^-1a + cot^-1a = \(\frac{\pi}{2}\)]
= 0 [∵ cot \(\frac{\pi}{2}\) = 0]

प्रश्न 13.

|x| < 1, y > 0 तथा xy < 1
हल:
माना

प्रश्न 14.
यदि sin(sin^-1\(\frac{1}{5}\) + cos^-1x) = 1, तो x का मान ज्ञात कीजिए।
हल:

प्रश्न 15.
यदि tan^-1 \(\frac{x-1}{x-2}\) + tan^-1\(\frac{x+1}{x+2}=\frac{\pi}{4}\), तो x का मान ज्ञात कीजिए।
हल:

प्रश्न संख्या 16 से 18 में दिए गए प्रत्येक व्यंजक का मान ज्ञात कीजिए-
प्रश्न 16.
sin^-1 (sin\(\frac{2 \pi}{3}\))
हल:
माना y = sin^-1 (sin\(\frac{2 \pi}{3}\)), तब

प्रश्न 17.
tan^-1 (tan\(\frac{3 \pi}{4}\))
हल:
माना y = tan^-1 (tan\(\frac{3 \pi}{4}\))

प्रश्न 18.
tan (sin^-1\(\frac{3}{5}\) + cot^-1\(\frac{3}{2}\))
हल:
tan (sin^-1\(\frac{3}{5}\) + cot^-1\(\frac{3}{2}\))

प्रश्न 19.
cos^-1(cos \(\frac{7 \pi}{6}\)) का मान बराबर है-

हल:
cos^-1[cos \(\frac{7 \pi}{6}\)]
cos^-1 की मुख्य मान शाखा [0, π] है।

अत: विकल्प (B) सही है।

प्रश्न 20.
sin [\(\frac{\pi}{3}\) – sin^-1(\(-\frac{1}{2}\))] का मान है-

हल:

अत: विकल्प (D) सही है।

प्रश्न 21.
tan^-1\( \sqrt{{3}} \) – cot^-1 (-\( \sqrt{{3}} \)) का मान है
(A) π
(B) \(-\frac{\pi}{2}\)
(C) 0
(D) 2\( \sqrt{{3}} \)
हल:

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 3 आव्यूह Ex 3.3 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 3 आव्यूह Ex 3.3

प्रश्न 1.
निम्नलिखित आव्यूहों में से प्रत्येक का परिवर्त ज्ञात कीजिए-

हल:
यहाँ पंक्तियों को स्तम्भों में, स्तम्भों को पंक्तियों में बदलने पर,

प्रश्न 2.
यदि A = \(\left[\begin{array}{ccc}{-1} & {2} & {3} \\ {5} & {7} & {9} \\ {2} & {1} & {1}\end{array}\right]\) तथा B = \(\left[\begin{array}{ccc}{-4} & {1} & {-5} \\ {1} & {2} & {0} \\ {1} & {3} & {1}\end{array}\right]\) हैं तो सत्यापित कीजिए कि-
(i) (A + B)’ = A’ + B’
(ii) (A – B) = A’ – B’
हल:
यहाँ A = \(\left[\begin{array}{ccc}{-1} & {2} & {3} \\ {5} & {7} & {9} \\ {2} & {1} & {1}\end{array}\right]\), B = \(\left[\begin{array}{ccc}{-4} & {1} & {-5} \\ {1} & {2} & {0} \\ {1} & {3} & {1}\end{array}\right]\)


अतः (A – B)’ = A’ – B’

प्रश्न 3.
यदि A = \(\left[\begin{array}{rr}{3} & {4} \\ {-1} & {2} \\ {0} & {1}\end{array}\right]\) तथा B = \(\left[\begin{array}{rrr}{-1} & {2} & {1} \\ {1} & {2} & {3}\end{array}\right]\) हैं तो सत्यापित कीजिए कि-
(i) (A + B)’ = A’ + B’
(ii) (A – B)’ = A’ – B’
हल:

प्रश्न 4.
यदि A’ = \(\left[\begin{array}{rr}{-2} & {3} \\ {1} & {2}\end{array}\right]\) तथा B = \(\left[\begin{array}{rr}{-1} & {0} \\ {1} & {2}\end{array}\right]\) हैं तो (A + 2B)’ ज्ञात कीजिए।
हल:

प्रश्न 5.
A तथा B आव्यूहों के लिए सत्यापित कीजिए कि (AB)’ = B’A’, जहाँ

हल:

प्रश्न 6.
(i) यदि A = \(\left[\begin{array}{cc}{\cos \alpha} & {\sin \alpha} \\ {-\sin \alpha} & {\cos \alpha}\end{array}\right]\) हो तो सत्यापित कीजिए कि A’A = I
(ii) यदि B = \(\left[\begin{array}{cc}{\sin \alpha} & {\cos \alpha} \\ {-\cos \alpha} & {\sin \alpha}\end{array}\right]\) हो तो सत्यापित कीजिए कि A’A = I
हल:

प्रश्न 7.
(i) सिद्ध कीजिए कि आव्यूह A = \(\left[\begin{array}{ccc}{\mathbf{1}} & {-\mathbf{1}} & {\mathbf{5}} \\ {-\mathbf{1}} & {\mathbf{2}} & {\mathbf{1}} \\ {\mathbf{5}} & {\mathbf{1}} & {\mathbf{3}}\end{array}\right]\) एक सममित आव्यूह है।
(ii) सिद्ध कीजिए कि आव्यूह A = \(\left[\begin{array}{ccc}{\mathbf{0}} & {\mathbf{1}} & {-\mathbf{1}} \\ {-\mathbf{1}} & {\mathbf{0}} & {\mathbf{1}} \\ {\mathbf{1}} & {-\mathbf{1}} & {\mathbf{0}}\end{array}\right]\) एक विषम सममित आव्यूह है।
हल:

अतः आव्यूह A एक विषम सममित आव्यूह है।

प्रश्न 8.
आव्यूह A = \(\left[\begin{array}{ll}{1} & {5} \\ {6} & {7}\end{array}\right]\) के लिए सत्यापित कीजिए कि –
(i) (A + A’) एक समित आव्यूह है।
(ii) (A – A’) एक विषम सममित आव्यूह है।
हल:


अतः (A – A’) एक विषम सममित आव्यूह है।

प्रश्न 9.
यदि A = \(\left[\begin{array}{ccc}{\mathbf{0}} & {\boldsymbol{a}} & {\boldsymbol{b}} \\ {-\boldsymbol{a}} & {\boldsymbol{0}} & {\boldsymbol{c}} \\ {-\boldsymbol{b}} & {-\boldsymbol{c}} & {\boldsymbol{0}}\end{array}\right]\) तो \(\frac{1}{2}\)(A + A’) तथा \(\frac{1}{2}\)(A – A’) ज्ञात कीजिए।
हल:

प्रश्न 10.
निम्नलिखित आव्यूहों को एक सममित आव्यूह तथा एक विषम सममित आव्यूह के योगफल के रूप में व्यक्त कीजिए-

हल:

प्रश्न संख्या 11 तथा 12 में सही उत्तर चुनिए-
प्रश्न 11.
यदि A तथा B समान कोटि के सममित आव्यूह हैं तो AB – BA एक
(A) विषम सममित आव्यूह है
(B) सममित आव्यूह है
(C) शून्य आव्यूह है
(D) तत्समक आव्यूह है
हल:
A और B समान कोटि की सममित आव्यूह है।
∴ A = A, B’ = B
(AB – BA)’ = (AB)’ – (BA) = BA’ – A’B’
= BA – AB [∵ B’ = B, A’ = A]
= -(AB – BA)
⇒ AB – BA विषम सममित आव्यूह है।
अतः विकल्प (A) सही है।

प्रश्न 12.
यदि A = \(\left[\begin{array}{cc}{\cos \alpha} & {-\sin \alpha} \\ {\sin \alpha} & {\cos \alpha}\end{array}\right]\) तथा A’ + A = I, तो α का मान है-
(A) \(\frac{\pi}{6}\)
(B) \(\frac{\pi}{3}\)
(C) π
(D) \(\frac{3 \pi}{2}\)
हल:

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 1 संबंध एवं फलन विविध प्रश्नावली Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 1 संबंध एवं फलन विविध प्रश्नावली

प्रश्न 1.
मान लीजिए कि f: R → R, f(x) = 10x + 7 द्वारा परिभाषित फलन है। एक ऐसा फलन g: R → R ज्ञात कीजिए, जिसके लिए gof = fog = I_R हो।
हल:
यहाँ f: R → R इस प्रकार है कि f(x) = 10x + 7
माना y = 10x + 7

अतः f व्युत्क्रमणीय है, जो g : Y → X, g(y) = \(\frac{y – 7}{10}\) से परिभाषित है।

प्रश्न 2.
मान लीजिए कि f: W → W, f(n) = n – 1, यदि ॥ विषम है तथा f (n) = n + 1, यदि n सम है, द्वारा परिभाषित है। सिद्ध कीजिए कि f व्युत्क्रमणीय है। f का प्रतिलोम ज्ञात कीजिए। यहाँ के समस्त पूर्णांकों का समुच्चय
हल:
दिया है : f: W → W को

यदि n₁ विषम n₂ दोनों सम हों तो
f(n₁) = f(n₂) ⇒ n₁ – 1 = n₂ + 1
या n₁ – n₂ = 2, जो सम्भव नहीं है।
यदि n₁ और n₂ विषम हों तो
f(n₁)= f(n₂) ⇒ n₁ – 1 = n₂ – 1
⇒ n₁ = n₂
यदि n₁ और n₂ दोनों सम हों, तो
n₁ + 1 = n₂ + 1 ⇒ n₁ = n₂
अतः f एकैकी भी है।
सहप्रान्त में प्रत्येक अवयव 2r + 1, प्रान्त का 2 प्रतिबिम्ब है। इसी प्रकार कोई भी सम संख्या प्रान्त का 2r + 1 का प्रतिबिम्ब है।
इस प्रकार सहप्रान्त का प्रत्येक अवयव प्रान्त के किसी – न – किसी अवयव का प्रतिबिम्ब है।
∴ f आच्छादक तथा व्युत्क्रमणीय है।
अतः f ^{– 1}(y) = g(y) इस प्रकार है कि

अतः का प्रतिलोम स्वयं है।

प्रश्न 3.
यदि f : R → R जहाँ f(x) = x² – 3x + 2 द्वारा परिभाषित है तो fIf (x)] ज्ञात कीजिए।
हल:
यहाँ f: R → R, f(x) = x² – 3x + 2 द्वारा परिभाषित है।
∴ [f(x)] = f(x² – 3x + 2)
= (x² – 3x + 2)² – 3(x² – 3x + 2) + 2
= (x⁴ + 9x² + 4 – 6x³ – 12x + 4x²) + (- 3x² + 2x – 6) + 2
= x⁴ – 6x³ + 10x² – 3x

प्रश्न 4.
सिद्ध कीजिए कि
f: R → {x ϵ R: – 1 < x < 1} जहाँ f(x) = \(\frac{x}{1+|x|}\), x ϵ R द्वारा परिभाषित फलन एकैकी तथा आच्छादक है।
हल:
यहाँ f: R → {x ϵ R : – 1 < x < 1} तथा f(x)= \(\frac{x}{1+|x|}\) द्वारा परिभाषित है।
(a) माना x ≥ 0, |x| = x

उत्तर
⇒ x₁(1 + x₂) = x₂(1 + x₁)
या x₁ + x₁x₂ = x₂ + x₂x₁
जब x < 0 |x| = – x, f(x) = \(\frac{x}{1-x}\)
f(x₁) = f(x₂) ⇒ \(\frac{x_{1}}{1-x_{1}}=\frac{x_{2}}{1-x_{2}}\)
⇒ x₁ (1 – x₂) = x₂(1 – x₁)
⇒ x₁ – x₁x₂ = x₂ – x₂x₁
∴ x₁ = x₂
अतः f एकैकी है।

अतः दोनों ही अवस्था में सहप्रान्त का प्रत्येक अवयव प्रान्त के किसी – न – किसी अवयव का प्रतिबिम्ब है।
∴ f आच्छादक है।
अत: f एकैकी तथा आच्छादक है।

प्रश्न 5.
सिद्ध कीजिए कि f(x) = x³ द्वारा प्रदत्त फलन f: R → R एकैक (Injective) है।
हल:
यहाँ f: R → R, f(x) = x³ द्वारा परिभाषित है।
f(x₁) = f(x₂) ⇒ x₁³ x₂³
⇒ x₁ = x₁
अतः f एकैकी है।

प्रश्न 6.
दो फलनों f: N → Z तथा g : Z → Z के उदाहरण दीजिए जो इस प्रकार हों कि gof एकैक है परन्तु g एकैक नहीं है।
हल:
(i) यहाँ f: N → Z तथा g: Z → Z द्वारा परिभाषित है।
f(x) = – x, g(x) = |x| से,
g(x)= |x|, – 1, 1 दोनों का प्रतिबिम्ब 1 है। .
∴ g एकैक नहीं है।
परन्तु g[f(x)] =g (- x) = |-x| = |x|
x ϵ N, g[(fx)] = |x|x = x
अतः gof एकैकी है।

(ii) f(x) = -2x, g(x) = |2x|

प्रश्न 7.
दो फलनों f: N → N तथा g: N → N के उदाहरण दीजिए, जो इस प्रकार हों कि gof आच्छादक है किन्तु f आच्छादक नहीं है।
हल:
(i) यहाँ f : N → N तथा g : N → N

f(x) = y = x + 1
∴ x = y – 1
यदि y – 1, x = 0 जो कि प्राकृत संख्या नहीं है।
अतः f आच्छादक नहीं है।
यदि x > 1,
gof (x) = g[f(x)] =g (x + 1) = (x + 1) – 1 = x
अतः gof आच्छादक है।

प्रश्न 8.
एक अरिक्त समुच्चय X दिया हुआ है। P(X) जो कि के समस्त उपसमुच्चयों का समुच्चय है, पर विचार कीजिए। ‘निम्नलिखित तरह से P(X) में एक सम्बन्ध R परिभाषित कीजिए-
P(x) में उपसमुच्चयों, A, B के लिए ARB, यदि और केवल यदि A⊂B है। क्या R,P(X) में एक तुल्यता सम्बन्ध है? अपने उत्तर का औचित्य भी लिखिए।
हल:
(i) यहाँ A ⊂ A ⇒ R स्वतुल्य है। .
(ii) A ⊂ B, B ⊄ A ⇒ R सममित नहीं है।
(iii) A ⊂ B, B ⊂ C ⇒ A ⊂ C ⇒ R संक्रामक है।
अतः R तुल्यता सम्बन्ध नहीं है।

प्रश्न 9.
किसी प्रदत्त अरिक्त समुच्चय x के लिए एक द्विआधारी संक्रिया* : P(X) × P(X) → P(X) पर विचार कीजिए, जो A * B = A ∩ B, ∀ A, B ϵ P(X) द्वारा परिभाषित है, जहाँ P(X) समुच्चय x का घात समुच्चय (Power set) है। सिद्ध कीजिए कि इस संक्रिया का तत्समक अवयव X है तथा संक्रिया के लिए P(X) में केवल x व्युत्क्रमणीय अवयव है।
हल:
दिया है : P(X) × P(X) → P(X)
तथा A * B = A ∩ B
∴ X * A = X ∩ A = A, सभी A के लिए
इसी प्रकार A * X = A ∩ X = A.
∴X एक तत्समक अवयव है तथा व्युत्क्रमणीय अवयव है। माना I एक दूसरा तत्समक अवयव है।
∴ I ∩ A = A सभी A के लिए
तथा x ϵ X, I ∩ {x} = {x}
⇒ x ϵ I ⇒ x ⊂ I और I ⊂ x
∴ I = X

प्रश्न 10.
समुच्चय {1, 2, 3,…., n} से स्वयं तक के समस्त आच्छादक फलनों की संख्या ज्ञात कीजिए।
हल:
माना Y : 1 2 3….n
तथा X : 1 2 3…..n
समुच्चय – Y का प्रत्येक अवयव समुच्चय X में किसी – न – किसी अवयव का प्रतिबिम्ब है।
इस प्रकार x और Y के अवयवों में सम्बन्ध
n (n – 1)(n – 2)… 3 2 1 = n! तरीकों से हो सकता है।
अतः द्विआधारी संक्रियाओं की संख्या n! है।

प्रश्न 11.
मान लीजिए कि S = {a, b, c} तथा T = {1, 2, 3} है। S से T तक के निम्नलिखित फलनों F के लिए F^-1 ज्ञात कीजिए, यदि उसका अस्तित्व है :
(i) F = {(1, 3), (b, 2), (c, 1)}
(ii) F = {(a, 2), (b, 1), (c, 1)}
हल:
(i) यहाँ S = {a, b, c},T = {1, 2, 3}
तथा F = {(a, 3), (b, 2), (c, 1)}
F(a)= 3, F(b)= 2, F(c)=1
∴ F^-1(3)= a, F^-1 (2) = F^-1 (1) = c
∴ F^-1 = {(3, a),(2, b), (1, c)}
(ii) F = {(a, 2),(b, 1), (c, 1)}
फलन F में b तथा c का प्रतिबिम्ब 1 है।
∴ यह एकैकी नहीं है।
अत: यह फलन व्युत्क्रमणीय नहीं है।

प्रश्न 12.
a * b=|a – b| तथा a o b = a, ∀ a, b ϵ R द्वारा परिभाषित द्विआधारी संक्रियाओं* : R × R → R तथा 0: R × R → R पर विचार कीजिए। सिद्ध कीजिए कि * क्रमविनिमेय है परन्तु साहचर्य नहीं है, . साहचर्य है परन्तु क्रमविनिमेय नहीं है। पुनः सिद्ध कीजिए कि सभी a, b, c ϵ R के लिए a * (b o c) = (a * b) o (a * c) है। [यदि ऐसा होता है तो हम कहते हैं कि संक्रिया * संक्रिया o पर वितरित (Distributes) होती है। क्या o संक्रिया * पर वितरित होती है? अपने उत्तर का औचित्य भी बतलाइए।
हल:
दिया है : a * b = |a – b| और a o b = a
(i) (a) a * b = |a – b|, |b * a| = |b – a| = |a – b|
अतः यह क्रमविनिमेय संक्रिया है।
(b) a * b = |a – b|, b * c = |b – c|
⇒ a * c ≠ |a – c|
अत: यह साहचर्य संक्रिया नहीं है।

(ii) (a) a o b = a, b o a = b ⇒ a ≠ b
अतः o क्रमविनिमेय संक्रिया नहीं है।
a o b = a, b o c = b, a o c = a
अतः o एक साहचर्य संक्रिया है।

(iii) सिद्ध करना है :
a * (boc)= (a * b) 0 (b * c)
L.H.S. = a * (boc)= a * b = |a – b|
R.H.S. = (a * b) 0 (b * c)
= |a – b| o |b – c| = |a – b|
∴ L.H.S. = R..S.
अतः A * (boc)= (a * b) o (b * c)

(iv) क्या a o (b * c) और (a o b) * (a0c) बराबर है?
L.H.S. = a 0 * (b * c) = ao |b – c| = a
R.H.S. = (aob) * (aoc) = a * a = |a – a|= 0
∴ L.H.S. ≠ R.H.S.
अतः संक्रिया o संक्रिया * पर वितरण संक्रिया नहीं है।

प्रश्न 13.
किसी प्रदत्त अरिक्त समुच्चय x के लिए मान लीजिए कि * : P(X) × P(X) → P(X), जहाँ A * B = (A – B) ∪ (B – A), ∀A, B ϵ P(X) द्वारा परिभाषित है। सिद्ध कीजिए कि रिक्त समुच्चयक ϕ, संक्रिया * का तत्समक है तथा P(X) के समस्त अवयव A व्युत्क्रमणीय हैं, इस प्रकार कि A^-1 = A.
हल:
यहाँ * : P(X) × P(X) → P(X) जो इस प्रकार परिभाषित है।
A * B = (A – B) ∪ (B – A)
दिया है : A * B = (A – B) ∪ (B – A)
जब B = ϕ क रखने पर,
A * ϕ = (A – ϕ) ∪ (ϕ – A)
= A ∪ ϕ = A
ϕ * A = (ϕ – A) ∪ (A – ϕ) = ϕ ∪ A = A
⇒ A * ϕ = ϕ * A = A
अतः ϕ तत्समक अवयव है।

(ii) A * A = (A – A) ∪ (A – A) = ϕ
A * A = ϕ = A^-1 = A

प्रश्न 14.
निम्नलिखित प्रकार से समुच्चय {0, 1, 2, 3, 4, 5} में एक द्विआधारी संक्रिया * परिभाषित कीजिए।

सिद्ध कीजिए कि शून्य (0) इस संक्रिया का तत्समक है तथा समुच्चय का प्रत्येक अवयव a ≠ 0 व्युत्क्रमणीय है, इस प्रकार कि 6 – c, a का प्रतिलोम है।
हल:
यहाँ संक्रिया समुच्चय A = {0, 1, 2, 3, 4, 5} पर

(i) e तत्समक अवयव है, यदि a * e = e * a = a
अब, माना e = 0, a * e = a + 0 = a
e* a = 0 + a = a
∴ a * e = e * a = a
अतः O तत्समक अवयव है।

(ii) b अवयव a का व्युत्क्रम है, यदि a * b = b * a = e
a * (6 – a)= a + (6 – a) – 6 = a + 6 – a – 6 = 0
(6 – a) * a = (6 – a) + a – 6 = 0
∴ a * (6 – a) = (6 – a) * a = 0
अतः A के प्रत्येक अवयव a का 6 – a व्युत्क्रम है।

प्रश्न 15.
मान लीजिए कि A ={ – 1, 0, 1, 2}, B = { – 4, – 2, 0, 2} और f, g: A → B, क्रमशः f(x) = x² – x, x ϵ A तथा g(x) = 2x\(\left|x-\frac{1}{2}\right|\) – 1. x ϵ A द्वारा परिभाषित फलन हैं क्या है तथा g समान हैं? अपने उत्तर का औचित्य भी बताइए।
हल:
यहाँ, यदि A = { – 1, 0, 1, 2) B = { – 4, – 2, 0, 2}
और f, g . A → B फलन की f(x) = x² – x, x ϵ A और g(x)= \(\left|x-\frac{1}{2}\right|\) . 1, x ϵ A द्वारा परिभाषित है।

प्रश्न 16.
यदि A = {1, 2, 3} हो तो ऐसे सम्बन्ध जिनमें अवयव (1, 2) तथा (1, 3) हों और जो स्वतुल्य तथा सममित हैं किन्तु संक्रामक नहीं है, की संख्या है
(A) 1
(B) 2
(C) 3
(D) 4
हल:
यहाँ, A = {1, 2, 3}
वह सम्बन्ध जिसमें (1, 2) और (1, 3) हों तथा सम्बन्ध स्वतुल्य व सममित हो तथा संक्रामक न हो,
{(1, 2), (1, 3), (1, 1), (2, 2), (3, 3), (2, 1), (3, 1)}
∴ ऐसा एक ही सम्बन्ध है।
अतः विकल्प (A) सही है।

प्रश्न 17.
यदि A= {1, 2, 3} हो तो अवयव (1, 2) वाले तुल्यता सम्बन्धों की संख्या है
(A) 1
(B) 2
(C) 3
(D) 4
हल:
यहाँ, A = {1, 2, 3}
तुल्यता सम्बन्ध जिसमें (1, 2) सम्मिलित हो ऐसे 2 सम्बन्ध हो सकते हैं।
अतः विकल्प (B) सही है।

प्रश्न 18.
मान लीजिए कि f :R → R है तब निम्नलिखित प्रकार से परिभाषित चिह्न फलन (signum Function) है।

तथा g : R → R, g(x) = [x] द्वारा प्रदत्त महत्तम पूर्णांक फलन है, जहाँ [x], x से कम या x के बराबर पूर्णांक है तो क्या fog तथा gof, अन्तराल [0, 1] में सम्पाती (coincide) हैं?
हल:
यहाँ f: R → R, जो

तथा g: R → R जो g(x) = [x] से परिभाषित है।
∴ x ϵ [0, 0, f(x) = 1, g(x) = 0.
gof (x) = g [f(x)] = g(1) = 1
तथा fog(x) = f(0)= 0
इस प्रकार fog ≠ gof
अतः अन्तराल (0, 1) में fog तथा gof सम्पाती नहीं हैं।

प्रश्न 19.
समुच्चय {a, b} में द्विआधारी संक्रियाओं की संख्या है
(A) 10
(B) 16
(C) 20
(D) 8
हल:
यहाँ समुच्चय {a, b}
समुच्चय A में 2 अवयव हैं।
द्विआधारी संक्रियाओं की संख्या = 2⁴ = 16
अतः विकल्प (B) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 2 प्रतिलोम त्रिकोणमितीय फलन विविध प्रश्नावली Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 2 प्रतिलोम त्रिकोणमितीय फलन विविध प्रश्नावली

निम्नलिखित के मान ज्ञात कीजिए-
प्रश्न 1.
cos^-1(cos\(\frac{13 \pi}{6}\))
हल:
माना y = cos^-1(cos\(\frac{13 \pi}{6}\))
cos^-1 की मुख्य मान शाखा का परिसर [0, π] है।

प्रश्न 2.
tan^-1(tan\(\frac{7 \pi}{6}\))
हल:
माना y = tan^-1(tan\(\frac{7 \pi}{6}\))
tan^-1 की मुख्य मान शाखा का परिसर \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\) है।

प्रश्न 3.
सिद्ध कीजिए-
2 sin^-1\(\frac{3}{5}\) = tan^-1 \(\frac{24}{7}\)
हल:
2 sin^-1\(\frac{3}{5}\) = tan^-1 \(\frac{24}{7}\)

प्रश्न 4.
सिद्ध कीजिए
sin^-1\(\frac{8}{17}\) + sin^-1\(\frac{3}{5}\) = tan^-1\(\frac{77}{36}\)
हल:
यहाँ sin^-1\(\frac{8}{17}\) + sin^-1\(\frac{3}{5}\) = tan^-1\(\frac{77}{36}\)

प्रश्न 5.
सिद्ध कीजिए-
cos^-1\(\frac{4}{5}\) + cos^-1\(\frac{12}{13}\) = cos^-1\(\frac{33}{65}\)
हल:
cos^-1\(\frac{4}{5}\) + cos^-1\(\frac{12}{13}\) = cos^-1\(\frac{33}{65}\)

प्रश्न 6.
सिद्ध कीजिए-
cos^-1\(\frac{12}{13}\) + sin^-1\(\frac{3}{5}\) = sin^-1\(\frac{56}{65}\)
हल:
cos^-1\(\frac{12}{13}\) + sin^-1\(\frac{3}{5}\) = sin^-1\(\frac{56}{65}\)

प्रश्न 7.
सिद्ध कीजिए-
tan^-1\(\frac{63}{16}\) = sin^-1\(\frac{5}{13}\) + cos^-1\(\frac{3}{5}\)
हल:
R.H.S. = sin^-1\(\frac{5}{13}\) + cos^-1\(\frac{3}{5}\)

प्रश्न 8.
सिद्ध कीजिए-
tan^-1\(\frac{1}{5}\) + tan^-1\(\frac{1}{7}\) + tan^-1\(\frac{1}{3}\) + tan^-1\(\frac{1}{8}\) = \(\frac{\pi}{4}\)
हल:
L.H.S.
(tan^-1\(\frac{1}{5}\) + tan^-1\(\frac{1}{7}\)) + (tan^-1\(\frac{1}{3}\) + tan^-1\(\frac{1}{8}\))

सिद्ध कीजिए
प्रश्न 9.
tan^-1\( \sqrt{{x}} \) = \(\frac{1}{2} \) cos^-1\(\left(\frac{1-x}{1+x}\right)\), x ϵ [0, 1]
हल:
माना x = tan²θ ⇒ θ = tan^-1\( \sqrt{{x}} \)

प्रश्न 10.

हल:

प्रश्न 11.

हल:

प्रश्न 12.

हल:

निम्नलिखित समीकरणों को सरल कीजिए।
प्रश्न 13.
2 tan^-1(cosx) = tan^-1(2cosec x)
हल:
2 tan^-1(cosx) = tan^-1(2 cosecx)

प्रश्न 14.
tan^-1\(\frac{1-x}{1+x}=\frac{1}{2}\)tan^-1 x, (x > 0)
हल:

प्रश्न 15.
sin (tan^-1x), |x| < 1 बराबर होता है-

हल:
sin (tan^-1x)
माना tan^-1x = θ
x = tanθ

प्रश्न 16.
यदि sin^-1(1 – x) – 2 sin^-1 x = \(\frac{\pi}{2}\), तो x का मान बराबर है-
(A) 0, \(\frac{1}{2}\)
(B) 1, \(\frac{1}{2}\)
(C) 0
(D) \(\frac{1}{2}\)
हल:
sin^-1(1 – x) – 2sin^-1 x = \(\frac{\pi}{2}\)
हम जानते हैं, \(\frac{\pi}{2}\) = sin^-1(1 – x) + cos^-1(1 – x)
∴ sin^-1 (1 – x) – 2sin^-1 x = sin^-1 (1 – x) + cos^-1 (1 – x)
⇒ -2sin^-1 x = cos^-1 (1 – x) … (1)
माना sin^-1x = θ
∴ x = sin θ
∴ cos 2θ = 1 – 2sin² θ = 1 – 2x²
cos (-2θ) = 1 – 2x²
-2θ = cos^-1 (1 – 2x²)
-2sin^-1 x = cos^-1 (1 – 2x²) …(2)
समीकरण (1) व (2) से,
cos^-1(1 – 2x²) = cos^-1 (1 – x)
1 – 2x² = 1 – x
x² – 2x² = 0
x(1 – 2x²) = 0 = x = 0, x = \(\frac{1}{2}\)
x = \(\frac{1}{2}\) समीकरण को सन्तुष्ट नहीं करता है।
∴ x = 0
अतः विकल्प (C) सही है।

प्रश्न 17.
tan^-1\(\left(\frac{x}{y}\right)\) – tan^-1\(\frac{x-y}{x+y}\) का मान है-

हल:

In this article, we share MP Board Class 10th Maths Book Solutions Chapter 1 संबंध एवं फलन Ex 1.3 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 1 संबंध एवं फलन Ex 1.3

प्रश्न 1.
मान लीजिए कि f:{1, 3, 4} → {1, 2, 5} तथा g:{1, 2, 5} → {1, 3}, f = {(1, 2), (3, 5), (4, 1)} तथा g = {(1, 3), (2, 3), (5, 1)} द्वारा प्रदत्त है।g of ज्ञात कीजिए।
हल:
दिया है:
f = {(1, 2), (3, 5)(4, 1)}
तथा g = {(1, 3),(2, 3), (5, 1)}
∴ gof(1) = g (f (1))
= g(2)
= 3
gof(3) = g(f (3))
= g(5)
= 1
तथा g of(4) = g(f(4))
= g(1)
= 3
∴ gof = {(1, 3), (3, 1), (4, 3)}

प्रश्न 2.
मान लीजिए कि f,g तथा h, R से R तक दिए फलन हैं। सिद्ध कीजिए कि
(f + g)oh = foh + goh
(f.g)oh = (foh).(goh)
हल:
दिया है:
f: R → R, g: R → R, h: R → R
∴ (fog)oh(x) = (g + g)(h (x))
= g(h (x)) + g (h (x))
= (foh) (x) + (goh) (x)
= (foh + goh) (x)
∴ f(f + g) oh = foh + goh
पुनः (f.g) oh(x) = (f.g)(h (x))
= f (h (x)).g(h (x))
= (foh)x (goh) (x)
= [(goh) (goh)](x)
∴ (f.g)oh = (foh) (goh)

प्रश्न 3.
gof तथा fog ज्ञात कीजिए, यदि
(i) f(x) = |x| तथा g(x) = |5x – 2|
(ii) f(x) = 8x³ तथा g(x) = x^1/3
हल:
(i) ∵ f(x) = |x|
तथा g(x) = [5x – 2||
∴ gof(x) = g[f (x)]
= g[/x]
= |5 |x – 2|
तथा fog (x) = f|g(x)|
= f (|5x – 2|)
= |5x – 2|
= |5x – 2|

(ii) ∵ f(x) = 8x³
तथा g(x) = x^1/3
∴ gof(x) = g[f (x)]
= g(8x³)
= (8x³)^1/3
= 2x
तथा fog(x) = f[g(x)]
= f(x^1/3)
= 8(x^1/3)³
= 8x

प्रश्न 4.
यदि f(x) = \(\frac{(4 x+3)}{6 x – 4}\), x ≠ \(\frac{2}{3}\), तो सिद्ध कीजिए कि सभी x ≠ \(\frac{2}{3}\) के लिए f0f(x) = x है। का प्रतिलोम फलन क्या है?
हल:
दिया है :

⇒ y (6x – 4) = 4x + 3
⇒ 6xy – 4y = 4x + 3
⇒ 6xy – 4x = 4y + 3
⇒ 6xy – 4x = 4y + 3
⇒ x = \(\frac{4 y+3}{6 y-4}\)
⇒ g(y) = f^-1(y) = \(\frac{4 y+3}{6 y-4}\)
अतः f का प्रतिलोम f ही है।

प्रश्न 5.
कारण सहित बतलाइए कि क्या निम्नलिखित फलनों के प्रतिलोम हैं-
(i) f:{1, 2, 3, 4} → {10} जहाँ
f = {(1, 10), (2, 10), (3, 10), (4, 10)}
(ii) g : {5, 6, 7, 8} → {1, 2, 3, 4} जहाँ
g = {(5, 4), (6, 3), (7, 4),(8, 2}}
(iii) h: {2, 3, 4, 5} → {7, 9, 11, 13} जहाँ
h = {(2, 7), (3, 9), (4, 11), (5, 13)}
हल:
(i) दिया है : f :{1, 2, 3, 4} → {10) जहाँ
f = {(1, 10),(2, 10), (3, 10),(4, 10)}
∵ f(1) = 10, f(2) = 10, f(3) = 10, f(4) = 10
⇒ f(1) = f(2) = f(3) = f(4)
∴ f एकैक नहीं है।
अतः दिए गये फलन का प्रतिलोम नहीं है।

(ii) g = {5, 6,7, 8} → 1, 2, 3, 4) जहाँ
g = {(5, 4), (6, 3),(7, 4), (8, 2)}
∴ g (5) = 4 तथा g (7) = 4
∵ (5) = g (7) = 4
∴ एकैक नहीं है।
अतः दिये गये फलन का प्रतिलोम नहीं है।

(iii) h : {2, 3, 4, 5} → {7, 11, 13} जहाँ
h = {(2, 7),(3, 9),(4, 11), (5, 13)}
∴ h (2) = 7, h (3) = 9, h (4) = 11 तथा h (5) = 13
∴ h एकैक है
अतः दिए गए फलन (h) का प्रतिलोम है।

प्रश्न 6.
सिद्ध कीजिए कि f:[- 1, 1] → R, f(x) = \(\frac{x}{x+2}\), द्वारा प्रदत्त फलन एकैकी है। फलन f: [- 1, 1] → (f का परिसर), का प्रतिलोम फलन ज्ञात कीजिए।
हल:
यदि f(x₁) = f(x₂) तब,

प्रश्न 7.
f(x) = 4x + 3 द्वारा प्रदत्त फलन f : R → R पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्क्रमणीय है। का प्रतिलोम फलन ज्ञात कीजिए।
हल:
फलन f : R → R निम्न द्वारा परिभाषित है
f(x) = 4x + 3
यदि f(x₁) = f(x₂)
⇒ 4x₁ + 3 = 4x₂ + 3
⇒ x₁ = x₂
∴ f एकैक है।
तथा माना f(x) = y = 4x + 3
⇒ 4x = y – 3
⇒ x = \(\frac{y-3}{4}\) = g(y)
सहप्रान्त (Co – domain) प्रत्येक अवयव yE R का प्रान्त (do main) में पूर्व प्रतिबिम्ब (pre image) है।
∴ f आच्छादक (onto) है
अतः f एकैक और आच्छादक है।
अत: f व्युत्क्रमणीय है।
∴ f का प्रतिलोम फलन
f^-1 (y) = g(y)
= \(\frac{y-3}{4}\)

प्रश्न 8.
f(x) = x² + 4 द्वारा प्रदत्त फलन f : R → [4, ∞) पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्क्रमणीय है तथा f का प्रतिलोम f^-1, f^-1(y) = \(\sqrt{y-4}\), द्वारा प्राप्त होता है, जहाँ R सभी ऋणेत्तर वास्तविक संख्याओं का समुच्चय है।
हल:
यदि f (x₁) = f(x₂)
⇒ x₁² + 4 = x₁² + 4
⇒ x₁² = x₁² = x₁ = x₂
( ∵ x ϵ R₊
∴ x > 0)
∴ f एकैक है।
माना y = f(x) = x² + 4
= x² + 4 = y
x² = y – 4 = x = ±\(\sqrt{y-4}\)
लेकिन x धनात्मक है।
∴ x = \(\sqrt{y-4}\)
∴ f आच्छादक है।
अतः फलन f व्युत्क्रमणीय है।
∴ f का प्रतिलोम फलन
f^-1(y) = g(y)
= \(\sqrt{y-4}\) , y ≥ 4
∀ y ≥ 4, 8 (y) एक धनात्मक मान है।
अतः f का प्रतिलोम फलन = \(\sqrt{y-4}\)

प्रश्न 9.
f(x) = 9x² + 6x – 5 द्वारा प्रदत्त फलन f: R → [ – 5, ∞) पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्क्रमणीय है तथा f^-1 = \(\left(\frac{(\sqrt{y+6}-1)}{3}\right)\) है।
हल:
दिया है : f(x) = 9x² + 6x – 5 तथा f: R → [ – 5, ∞)
माना y = 9x² + 6x – 5
= (3x + 1)² – 6
⇒ y + 6 = (3x + 1)² ⇒ 3x + 1 = \(\sqrt{y+4}\)

प्रश्न 10.
मान लीजिए कि f: x → y व्युत्क्रमणीय फलन है। सिद्ध कीजिए कि f का प्रतिलोम फलन अद्वितीय (unique) है।
हल:
∵ यदि f एक व्युत्क्रमणीय है।
∴ gof (x) = I_x और fog (y) = I_y
⇒ f एकैक तथा आच्छादक है।
माना g₁ व g₂, f के दो प्रतिलोम फलन हैं।
∴ fog₁ (y) = I_y तथा g0g₂(y) = I_y
I_y दिए गये फलन f के लिए अद्वितीय है
∴ g₁(9) = g₂ (y) ⇒ f एकैक और आच्छादक है
अतः f का प्रतिलोम फलन अद्वितीय है।

प्रश्न 11.
f: {1, 2, 3} → {a, b, c}, f(1) = a, f(2) = b तथा f(3) = c द्वारा प्रदत्त फलन पर विचार कीजए। f^-1 ज्ञात कीजिए और सिद्ध कीजिए कि (f^-1)^-1 = f है।
हल:
दिया है :
f: {1, 2, 3} → a, b, d
तथा f(1) = a, f(2) = b, f (3) = c
माना x = {1, 2, 3} तथा y = {a, b, c}
इसलिए f: X → Y
∴ f^-1 : Y → X
= f^-1(a) = 1, f^-1(b) = 2, f^-1(c) = 3
इस फलन का प्रतिलोम फलन हम इस प्रकार से भी लिख सकते हैं
(f^-1)^-1 : x → y
⇒ (f^-1)^-1(1) = a, (f^-1)^-1
(2) = b, (f^-1)^-1(3) = c
इसलिए,
f: x → y
f(1) = a, f(2) = b, f(3) = c
अतः (f^-1)^-1 = f

प्रश्न 12.
मान लीजिए कि f:x → Y एक व्युत्क्रमणीय फलन है सिद्ध कीजिए कि f^-1 का प्रतिलोम f, है अर्थात् (f^-1)^-1 = f है।
हल:
f:x → Y एक व्युत्क्रमणीय फलन है।
∴ f एकैक तथा आच्छादक है।
⇒ g: y → x, जहाँ भी एकैक और आच्छादक है
∴ gof (x) = I_x तथा fog (y) = I_y
⇒ g = f
अतः f^-1 o(f^-1)^-1 = I
fo[f^-1 o(f^-1)^-1] = foI
⇒ (f of^-1) o(f^-1)^-1 = f
Io(f^-1)^-1 = f
⇒ (f^-1)^-1 = f

प्रश्न 13.
यदि f :R → R, f(x) = (3 – x³)^1/3, द्वारा प्रदत्त है तो fof(x) बराबर है.
(A) x^1/3
(B) x³
(C) x
(D) (3 – x³)
हल:
दिया है : f(x) = (3 – x³)^1/3 तथा f: R → R
∴ fof(x) = f[f(x)] = [[(3 – x²)^1/3]
= [3 – {(3 – x³ )^1/3}³}]^1/3
= [3 – (3 – x³)]^1/3 = x
अतः विकल्प (C) सही है।

प्रश्न 14.
मान लीजिए कि f(x) = \(\frac{4 x}{3 x+4}\) द्वारा परिभाषित एक फलन f: R – 1 – \(\left\{-\frac{4}{3}\right\}\) → R है। f का प्रतिलोम, अर्थात् प्रतिचित्र (Map) g : परिसर f → R – \(\left\{-\frac{4}{3}\right\}\), निम्नलिखित में से किसके द्वारा प्राप्त होगा-

हल:
दिया है : f(x) = \(\frac{4 x}{3 x+4}\) तथा f: R – \(\left\{-\frac{4}{3}\right\}\) → R
माना y = \(\frac{4 x}{3 x+4}\)
∴ y(3x + 4) = 4x या 3xy + 4y = 4x
⇒ x(3y – 4) + 4y = 0
⇒ x = \(\frac{4 y}{4-3 y}\) = g(y)
अतः विकल्प (B) सही है।