In this article, we share MP Board Class 10th Maths Book Solutions Chapter 1 संबंध एवं फलन Ex 1.3 Pdf, These solutions are solved by subject experts from the latest MP Board books.
MP Board Class 12th Maths Book Solutions Chapter 1 संबंध एवं फलन Ex 1.3
प्रश्न 1.
मान लीजिए कि f:{1, 3, 4} → {1, 2, 5} तथा g:{1, 2, 5} → {1, 3}, f = {(1, 2), (3, 5), (4, 1)} तथा g = {(1, 3), (2, 3), (5, 1)} द्वारा प्रदत्त है।g of ज्ञात कीजिए।
हल:
दिया है:
f = {(1, 2), (3, 5)(4, 1)}
तथा g = {(1, 3),(2, 3), (5, 1)}
∴ gof(1) = g (f (1))
= g(2)
= 3
gof(3) = g(f (3))
= g(5)
= 1
तथा g of(4) = g(f(4))
= g(1)
= 3
∴ gof = {(1, 3), (3, 1), (4, 3)}
प्रश्न 2.
मान लीजिए कि f,g तथा h, R से R तक दिए फलन हैं। सिद्ध कीजिए कि
(f + g)oh = foh + goh
(f.g)oh = (foh).(goh)
हल:
दिया है:
f: R → R, g: R → R, h: R → R
∴ (fog)oh(x) = (g + g)(h (x))
= g(h (x)) + g (h (x))
= (foh) (x) + (goh) (x)
= (foh + goh) (x)
∴ f(f + g) oh = foh + goh
पुनः (f.g) oh(x) = (f.g)(h (x))
= f (h (x)).g(h (x))
= (foh)x (goh) (x)
= [(goh) (goh)](x)
∴ (f.g)oh = (foh) (goh)
![]()
प्रश्न 3.
gof तथा fog ज्ञात कीजिए, यदि
(i) f(x) = |x| तथा g(x) = |5x – 2|
(ii) f(x) = 8x3 तथा g(x) = x1/3
हल:
(i) ∵ f(x) = |x|
तथा g(x) = [5x – 2||
∴ gof(x) = g[f (x)]
= g[/x]
= |5 |x – 2|
तथा fog (x) = f|g(x)|
= f (|5x – 2|)
= |5x – 2|
= |5x – 2|
(ii) ∵ f(x) = 8x3
तथा g(x) = x1/3
∴ gof(x) = g[f (x)]
= g(8x3)
= (8x3)1/3
= 2x
तथा fog(x) = f[g(x)]
= f(x1/3)
= 8(x1/3)3
= 8x
प्रश्न 4.
यदि f(x) = \(\frac{(4 x+3)}{6 x – 4}\), x ≠ \(\frac{2}{3}\), तो सिद्ध कीजिए कि सभी x ≠ \(\frac{2}{3}\) के लिए f0f(x) = x है। का प्रतिलोम फलन क्या है?
हल:
दिया है :

⇒ y (6x – 4) = 4x + 3
⇒ 6xy – 4y = 4x + 3
⇒ 6xy – 4x = 4y + 3
⇒ 6xy – 4x = 4y + 3
⇒ x = \(\frac{4 y+3}{6 y-4}\)
⇒ g(y) = f-1(y) = \(\frac{4 y+3}{6 y-4}\)
अतः f का प्रतिलोम f ही है।
प्रश्न 5.
कारण सहित बतलाइए कि क्या निम्नलिखित फलनों के प्रतिलोम हैं-
(i) f:{1, 2, 3, 4} → {10} जहाँ
f = {(1, 10), (2, 10), (3, 10), (4, 10)}
(ii) g : {5, 6, 7, 8} → {1, 2, 3, 4} जहाँ
g = {(5, 4), (6, 3), (7, 4),(8, 2}}
(iii) h: {2, 3, 4, 5} → {7, 9, 11, 13} जहाँ
h = {(2, 7), (3, 9), (4, 11), (5, 13)}
हल:
(i) दिया है : f :{1, 2, 3, 4} → {10) जहाँ
f = {(1, 10),(2, 10), (3, 10),(4, 10)}
∵ f(1) = 10, f(2) = 10, f(3) = 10, f(4) = 10
⇒ f(1) = f(2) = f(3) = f(4)
∴ f एकैक नहीं है।
अतः दिए गये फलन का प्रतिलोम नहीं है।
(ii) g = {5, 6,7, 8} → 1, 2, 3, 4) जहाँ
g = {(5, 4), (6, 3),(7, 4), (8, 2)}
∴ g (5) = 4 तथा g (7) = 4
∵ (5) = g (7) = 4
∴ एकैक नहीं है।
अतः दिये गये फलन का प्रतिलोम नहीं है।
(iii) h : {2, 3, 4, 5} → {7, 11, 13} जहाँ
h = {(2, 7),(3, 9),(4, 11), (5, 13)}
∴ h (2) = 7, h (3) = 9, h (4) = 11 तथा h (5) = 13
∴ h एकैक है
अतः दिए गए फलन (h) का प्रतिलोम है।
![]()
प्रश्न 6.
सिद्ध कीजिए कि f:[- 1, 1] → R, f(x) = \(\frac{x}{x+2}\), द्वारा प्रदत्त फलन एकैकी है। फलन f: [- 1, 1] → (f का परिसर), का प्रतिलोम फलन ज्ञात कीजिए।
हल:
यदि f(x1) = f(x2) तब,

प्रश्न 7.
f(x) = 4x + 3 द्वारा प्रदत्त फलन f : R → R पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्क्रमणीय है। का प्रतिलोम फलन ज्ञात कीजिए।
हल:
फलन f : R → R निम्न द्वारा परिभाषित है
f(x) = 4x + 3
यदि f(x1) = f(x2)
⇒ 4x1 + 3 = 4x2 + 3
⇒ x1 = x2
∴ f एकैक है।
तथा माना f(x) = y = 4x + 3
⇒ 4x = y – 3
⇒ x = \(\frac{y-3}{4}\) = g(y)
सहप्रान्त (Co – domain) प्रत्येक अवयव yE R का प्रान्त (do main) में पूर्व प्रतिबिम्ब (pre image) है।
∴ f आच्छादक (onto) है
अतः f एकैक और आच्छादक है।
अत: f व्युत्क्रमणीय है।
∴ f का प्रतिलोम फलन
f-1 (y) = g(y)
= \(\frac{y-3}{4}\)
प्रश्न 8.
f(x) = x2 + 4 द्वारा प्रदत्त फलन f : R → [4, ∞) पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्क्रमणीय है तथा f का प्रतिलोम f-1, f-1(y) = \(\sqrt{y-4}\), द्वारा प्राप्त होता है, जहाँ R सभी ऋणेत्तर वास्तविक संख्याओं का समुच्चय है।
हल:
यदि f (x1) = f(x2)
⇒ x12 + 4 = x12 + 4
⇒ x12 = x12 = x1 = x2
( ∵ x ϵ R+
∴ x > 0)
∴ f एकैक है।
माना y = f(x) = x2 + 4
= x2 + 4 = y
x2 = y – 4 = x = ±\(\sqrt{y-4}\)
लेकिन x धनात्मक है।
∴ x = \(\sqrt{y-4}\)
∴ f आच्छादक है।
अतः फलन f व्युत्क्रमणीय है।
∴ f का प्रतिलोम फलन
f-1(y) = g(y)
= \(\sqrt{y-4}\) , y ≥ 4
∀ y ≥ 4, 8 (y) एक धनात्मक मान है।
अतः f का प्रतिलोम फलन = \(\sqrt{y-4}\)
प्रश्न 9.
f(x) = 9x2 + 6x – 5 द्वारा प्रदत्त फलन f: R → [ – 5, ∞) पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्क्रमणीय है तथा f-1 = \(\left(\frac{(\sqrt{y+6}-1)}{3}\right)\) है।
हल:
दिया है : f(x) = 9x2 + 6x – 5 तथा f: R → [ – 5, ∞)
माना y = 9x2 + 6x – 5
= (3x + 1)2 – 6
⇒ y + 6 = (3x + 1)2 ⇒ 3x + 1 = \(\sqrt{y+4}\)

प्रश्न 10.
मान लीजिए कि f: x → y व्युत्क्रमणीय फलन है। सिद्ध कीजिए कि f का प्रतिलोम फलन अद्वितीय (unique) है।
हल:
∵ यदि f एक व्युत्क्रमणीय है।
∴ gof (x) = Ix और fog (y) = Iy
⇒ f एकैक तथा आच्छादक है।
माना g1 व g2, f के दो प्रतिलोम फलन हैं।
∴ fog1 (y) = Iy तथा g0g2(y) = Iy
Iy दिए गये फलन f के लिए अद्वितीय है
∴ g1(9) = g2 (y) ⇒ f एकैक और आच्छादक है
अतः f का प्रतिलोम फलन अद्वितीय है।
![]()
प्रश्न 11.
f: {1, 2, 3} → {a, b, c}, f(1) = a, f(2) = b तथा f(3) = c द्वारा प्रदत्त फलन पर विचार कीजए। f-1 ज्ञात कीजिए और सिद्ध कीजिए कि (f-1)-1 = f है।
हल:
दिया है :
f: {1, 2, 3} → a, b, d
तथा f(1) = a, f(2) = b, f (3) = c
माना x = {1, 2, 3} तथा y = {a, b, c}
इसलिए f: X → Y
∴ f-1 : Y → X
= f-1(a) = 1, f-1(b) = 2, f-1(c) = 3
इस फलन का प्रतिलोम फलन हम इस प्रकार से भी लिख सकते हैं
(f-1)-1 : x → y
⇒ (f-1)-1(1) = a, (f-1)-1
(2) = b, (f-1)-1(3) = c
इसलिए,
f: x → y
f(1) = a, f(2) = b, f(3) = c
अतः (f-1)-1 = f
प्रश्न 12.
मान लीजिए कि f:x → Y एक व्युत्क्रमणीय फलन है सिद्ध कीजिए कि f-1 का प्रतिलोम f, है अर्थात् (f-1)-1 = f है।
हल:
f:x → Y एक व्युत्क्रमणीय फलन है।
∴ f एकैक तथा आच्छादक है।
⇒ g: y → x, जहाँ भी एकैक और आच्छादक है
∴ gof (x) = Ix तथा fog (y) = Iy
⇒ g = f
अतः f-1 o(f-1)-1 = I
fo[f-1 o(f-1)-1] = foI
⇒ (f of-1) o(f-1)-1 = f
Io(f-1)-1 = f
⇒ (f-1)-1 = f
प्रश्न 13.
यदि f :R → R, f(x) = (3 – x3)1/3, द्वारा प्रदत्त है तो fof(x) बराबर है.
(A) x1/3
(B) x3
(C) x
(D) (3 – x3)
हल:
दिया है : f(x) = (3 – x3)1/3 तथा f: R → R
∴ fof(x) = f[f(x)] = [[(3 – x2)1/3]
= [3 – {(3 – x3 )1/3}3}]1/3
= [3 – (3 – x3)]1/3 = x
अतः विकल्प (C) सही है।
प्रश्न 14.
मान लीजिए कि f(x) = \(\frac{4 x}{3 x+4}\) द्वारा परिभाषित एक फलन f: R – 1 – \(\left\{-\frac{4}{3}\right\}\) → R है। f का प्रतिलोम, अर्थात् प्रतिचित्र (Map) g : परिसर f → R – \(\left\{-\frac{4}{3}\right\}\), निम्नलिखित में से किसके द्वारा प्राप्त होगा-
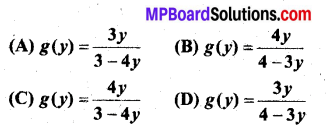
हल:
दिया है : f(x) = \(\frac{4 x}{3 x+4}\) तथा f: R – \(\left\{-\frac{4}{3}\right\}\) → R
माना y = \(\frac{4 x}{3 x+4}\)
∴ y(3x + 4) = 4x या 3xy + 4y = 4x
⇒ x(3y – 4) + 4y = 0
⇒ x = \(\frac{4 y}{4-3 y}\) = g(y)
अतः विकल्प (B) सही है।