In this article, we share MP Board Class 12th Maths Book Solutions Chapter 3 आव्यूह Ex 3.3 Pdf, These solutions are solved by subject experts from the latest MP Board books.
MP Board Class 12th Maths Book Solutions Chapter 3 आव्यूह Ex 3.3
प्रश्न 1.
निम्नलिखित आव्यूहों में से प्रत्येक का परिवर्त ज्ञात कीजिए-
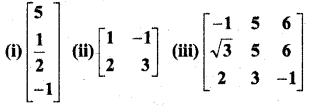
हल:
यहाँ पंक्तियों को स्तम्भों में, स्तम्भों को पंक्तियों में बदलने पर,

प्रश्न 2.
यदि A = \(\left[\begin{array}{ccc}{-1} & {2} & {3} \\ {5} & {7} & {9} \\ {2} & {1} & {1}\end{array}\right]\) तथा B = \(\left[\begin{array}{ccc}{-4} & {1} & {-5} \\ {1} & {2} & {0} \\ {1} & {3} & {1}\end{array}\right]\) हैं तो सत्यापित कीजिए कि-
(i) (A + B)’ = A’ + B’
(ii) (A – B) = A’ – B’
हल:
यहाँ A = \(\left[\begin{array}{ccc}{-1} & {2} & {3} \\ {5} & {7} & {9} \\ {2} & {1} & {1}\end{array}\right]\), B = \(\left[\begin{array}{ccc}{-4} & {1} & {-5} \\ {1} & {2} & {0} \\ {1} & {3} & {1}\end{array}\right]\)


अतः (A – B)’ = A’ – B’
प्रश्न 3.
यदि A = \(\left[\begin{array}{rr}{3} & {4} \\ {-1} & {2} \\ {0} & {1}\end{array}\right]\) तथा B = \(\left[\begin{array}{rrr}{-1} & {2} & {1} \\ {1} & {2} & {3}\end{array}\right]\) हैं तो सत्यापित कीजिए कि-
(i) (A + B)’ = A’ + B’
(ii) (A – B)’ = A’ – B’
हल:



प्रश्न 4.
यदि A’ = \(\left[\begin{array}{rr}{-2} & {3} \\ {1} & {2}\end{array}\right]\) तथा B = \(\left[\begin{array}{rr}{-1} & {0} \\ {1} & {2}\end{array}\right]\) हैं तो (A + 2B)’ ज्ञात कीजिए।
हल:

![]()
प्रश्न 5.
A तथा B आव्यूहों के लिए सत्यापित कीजिए कि (AB)’ = B’A’, जहाँ
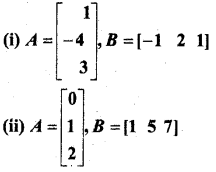
हल:
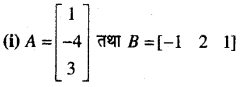
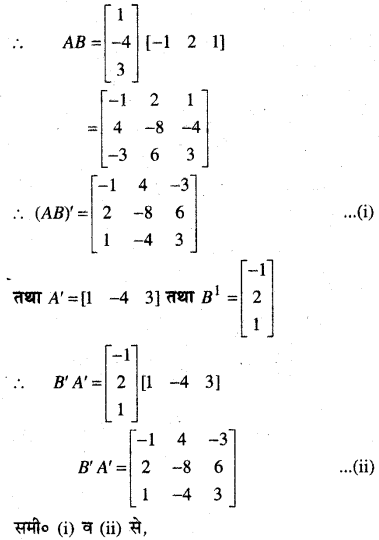

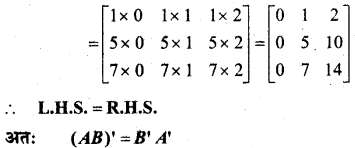
प्रश्न 6.
(i) यदि A = \(\left[\begin{array}{cc}{\cos \alpha} & {\sin \alpha} \\ {-\sin \alpha} & {\cos \alpha}\end{array}\right]\) हो तो सत्यापित कीजिए कि A’A = I
(ii) यदि B = \(\left[\begin{array}{cc}{\sin \alpha} & {\cos \alpha} \\ {-\cos \alpha} & {\sin \alpha}\end{array}\right]\) हो तो सत्यापित कीजिए कि A’A = I
हल:

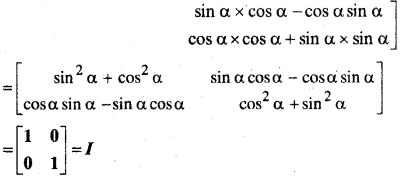
प्रश्न 7.
(i) सिद्ध कीजिए कि आव्यूह A = \(\left[\begin{array}{ccc}{\mathbf{1}} & {-\mathbf{1}} & {\mathbf{5}} \\ {-\mathbf{1}} & {\mathbf{2}} & {\mathbf{1}} \\ {\mathbf{5}} & {\mathbf{1}} & {\mathbf{3}}\end{array}\right]\) एक सममित आव्यूह है।
(ii) सिद्ध कीजिए कि आव्यूह A = \(\left[\begin{array}{ccc}{\mathbf{0}} & {\mathbf{1}} & {-\mathbf{1}} \\ {-\mathbf{1}} & {\mathbf{0}} & {\mathbf{1}} \\ {\mathbf{1}} & {-\mathbf{1}} & {\mathbf{0}}\end{array}\right]\) एक विषम सममित आव्यूह है।
हल:

अतः आव्यूह A एक विषम सममित आव्यूह है।
![]()
प्रश्न 8.
आव्यूह A = \(\left[\begin{array}{ll}{1} & {5} \\ {6} & {7}\end{array}\right]\) के लिए सत्यापित कीजिए कि –
(i) (A + A’) एक समित आव्यूह है।
(ii) (A – A’) एक विषम सममित आव्यूह है।
हल:
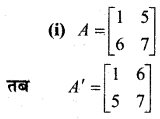

अतः (A – A’) एक विषम सममित आव्यूह है।
प्रश्न 9.
यदि A = \(\left[\begin{array}{ccc}{\mathbf{0}} & {\boldsymbol{a}} & {\boldsymbol{b}} \\ {-\boldsymbol{a}} & {\boldsymbol{0}} & {\boldsymbol{c}} \\ {-\boldsymbol{b}} & {-\boldsymbol{c}} & {\boldsymbol{0}}\end{array}\right]\) तो \(\frac{1}{2}\)(A + A’) तथा \(\frac{1}{2}\)(A – A’) ज्ञात कीजिए।
हल:

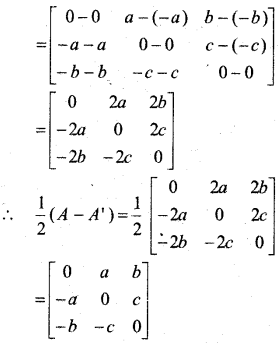
प्रश्न 10.
निम्नलिखित आव्यूहों को एक सममित आव्यूह तथा एक विषम सममित आव्यूह के योगफल के रूप में व्यक्त कीजिए-
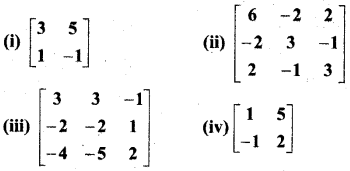
हल:

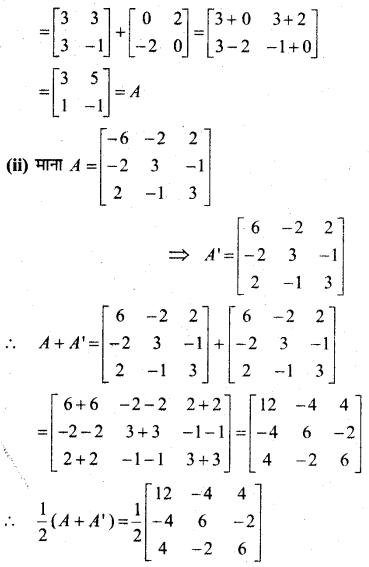
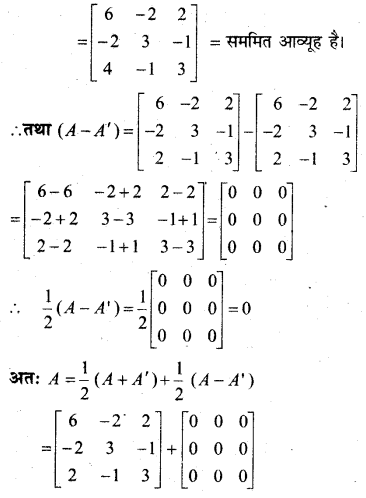

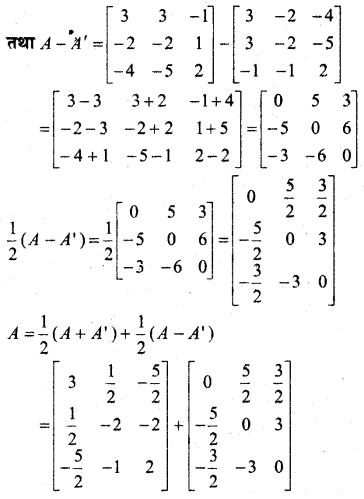
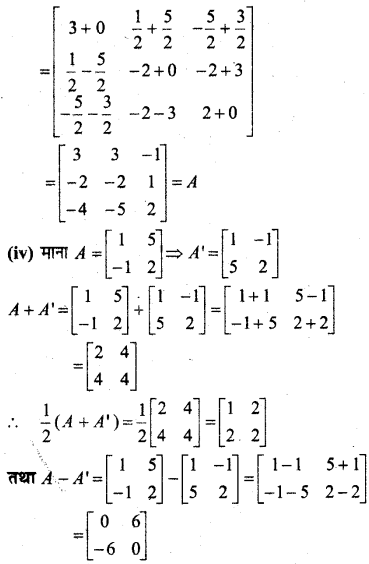

![]()
प्रश्न संख्या 11 तथा 12 में सही उत्तर चुनिए-
प्रश्न 11.
यदि A तथा B समान कोटि के सममित आव्यूह हैं तो AB – BA एक
(A) विषम सममित आव्यूह है
(B) सममित आव्यूह है
(C) शून्य आव्यूह है
(D) तत्समक आव्यूह है
हल:
A और B समान कोटि की सममित आव्यूह है।
∴ A = A, B’ = B
(AB – BA)’ = (AB)’ – (BA) = BA’ – A’B’
= BA – AB [∵ B’ = B, A’ = A]
= -(AB – BA)
⇒ AB – BA विषम सममित आव्यूह है।
अतः विकल्प (A) सही है।
प्रश्न 12.
यदि A = \(\left[\begin{array}{cc}{\cos \alpha} & {-\sin \alpha} \\ {\sin \alpha} & {\cos \alpha}\end{array}\right]\) तथा A’ + A = I, तो α का मान है-
(A) \(\frac{\pi}{6}\)
(B) \(\frac{\pi}{3}\)
(C) π
(D) \(\frac{3 \pi}{2}\)
हल:
