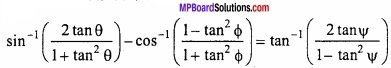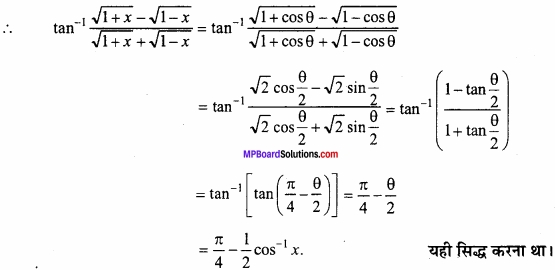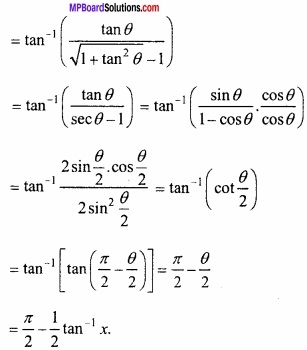Prasanna

MP Board Class 11th Hindi Swati Solutions पद्य Chapter 1 भक्ति

भक्ति अभ्यास

भक्ति अति लघु उत्तरीय प्रश्न

प्रश्न 1.
सही विकल्प चुनिए
(क) तुलसीदास के पद संकलित हैं (2009)
(अ) कवितावली में
(ब) गीतावली में
(स) विनय पत्रिका में
(द) रामचरितमानस में।
उत्तर:
(स) विनय पत्रिका में।

(ख) तुलसीदास के पदों में रस प्रधान है
(अ) शान्त
(ब) श्रृंगार
(स) वीर
(द) वात्सल्य।
उत्तर:
(अ) शान्त रस।

(ग) मीराबाई भक्त थीं (2009)
(अ) राम की
(ब) कृष्ण की
(स) शिव की
(द) विष्णु की।
उत्तर:
(ब) कृष्ण की।

प्रश्न 2.
तुलसीदास किसके चरण छोड़कर नहीं जाना चाहते? (2015, 17)
उत्तर:
तुलसीदास श्रीराम के चरण छोड़कर नहीं जाना चाहते।

प्रश्न 3.
तुलसीदास प्रण करके कहाँ बसना चाहते हैं?
उत्तर:
तुलसीदास प्रण करके श्रीराम के चरण कमलों में बसना चाहते हैं।

प्रश्न 4.
कृष्ण ने किसका घमण्ड चूर करने के लिये गोवर्धन पर्वत धारण किया था? (2016)
उत्तर:
कृष्ण ने इन्द्र का घमण्ड चूर करने के लिए गोवर्धन पर्वत को धारण किया था।

प्रश्न 5.
किसी रोगी की पीड़ा को सबसे अधिक कौन अनुभव कर सकता है?
उत्तर:
किसी रोगी की पीड़ा को सबसे अधिक श्रीराम ही अनुभव कर सकते हैं।

भक्ति लघु उत्तरीय प्रश्न

प्रश्न 1.
कवि के अनुसार राम के चरणों से किन-किनका उद्धार हुआ है?
उत्तर:
कवि के अनुसार राम के चरणों द्वारा पत्थर (अहिल्या), जटायु (पक्षी), मारीच (हिरण) आदि का उद्धार हुआ है।

प्रश्न 2.
‘करहलाज निजपन’ पंक्ति में निजपन’ से कवि का क्या आशय है?(2014)
उत्तर:
‘करहु लाज निजपन’ पंक्ति से कवि का अभिप्राय है कि मैं अपने इस मन के दोषपूर्ण एवं तुच्छ कार्यों का कहाँ तक वर्णन करूँ। आप तो अन्तर्यामी हैं अतः सेवक के मन की प्रत्येक अच्छी-बुरी बात को जानते हैं। मैं अपनी दोषयुक्त बातों को कहाँ तक बताऊँ?

प्रश्न 3.
मीरा ने अपने प्रियतम से मिलने में क्या कठिनाई बताई है? (2008)
उत्तर:
मीरा के प्रियतम श्रीकृष्ण की सेज गगन मण्डल में है, उस स्थान पर पहुँचना कठिन है। इसी कारण मीरा प्रियतम कृष्ण से मिलने में कठिनाई का अनुभव करती हैं।

प्रश्न 4.
मीरा के हृदय की पीड़ा को कौन-सा वैद्य दूर कर सकेगा? (2015)
उत्तर:
मीरा के हृदय की पीड़ा को दूर करने वाला एकमात्र वैद्य साँवला सलोना कृष्ण है।

भक्ति दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
तुलसीदास के अनुसार मानव मन की मूढ़ता क्या है? (2008, 13)
उत्तर:
तुलसीदास जी के अनुसार मानव मूर्ख है। वह प्रभु राम की भक्ति रूपी गंगा को त्यागकर विषय-वासना रूपी ओस के कणों से प्यास बुझाने की अभिलाषा रखता है। जिस प्रकार से धुएँ के समूह को देखकर प्यासा चातक उसे बादल समझकर अपनी प्यास बुझाना चाहता है, लेकिन उसको वहाँ से न तो शीतलता प्राप्त होती है और न ही उसकी प्यास बुझती है, लेकिन उसके नेत्रों को हानि अवश्य पहुँचती है। इसी प्रकार मनुष्य विषय-वासना में मग्न होकर आनन्द की प्राप्ति करना चाहता है, लेकिन उसको आनन्द के स्थान पर अशान्ति की प्राप्ति होती है। जिस प्रकार से मुर्ख बाज दर्पण में अपनी परछाईं को देखकर अन्य बाज समझकर उस पर झपटता है, लेकिन उसको आहार तो नहीं प्राप्त होता है परन्तु उसका मुख अवश्य क्षतिग्रस्त हो जाता है। इसी प्रकार मनुष्य भी मूर्खतावश सांसारिक विषय-वासनाओं में लिप्त रहना चाहता है। यदि मानव ईश्वर के प्रति सच्ची भक्ति करे तो निश्चय ही उसे सांसारिक कष्टों से मुक्ति मिल सकती है, क्योंकि प्रभु राम ही सब के कष्टों को दूर करके तारने वाले हैं।

प्रश्न 2.
तुलसीदास अपना भावी जीवन किस प्रकार बिताने का संकल्प लेते हैं? (2009, 10)
उत्तर:
तुलसीदास जी ने अपने भावी जीवन को श्रीराम की भक्ति में लगाने का संकल्प लिया है, क्योंकि उनका अनुभव है कि मानव जीवन की सार्थकता व मुक्ति का मार्ग राम भक्ति द्वारा ही सम्भव है। तुलसीदास जी का कथन है कि यह संसार मिथ्या है तथा संसार में अनुरक्त व्यक्ति कभी सफलता प्राप्त नहीं कर सकता है। अतः भगवान श्रीराम के चरणों में अपने मन को पूर्ण रूप से समर्पित करके ही जीवन को सफल बनाया जा सकता है।

जिस प्रकार मीरा ने कृष्ण को अपना आराध्य भाग था, उसी प्रकार तुलसीदास जी ने अपना भावी जीवन श्रीराम के चरणों में बिताने का संकल्प ले लिया।.

प्रश्न 3.
मीरा ने हरि के चरणों की कौन-कौन सी विशेषताएँ बताई हैं? (2009)
उत्तर:
मीरा ने हरि के चरणों की विशेषताओं का उल्लेख करते हुए बताया है कि जिन हरि के चरणों ने राजा बलि की दान स्वरूप प्रदान की हुई धरती को तीन पग में नाप लिया था, जिन चरणों का स्पर्श करके गौतम की पत्नी अहिल्या का उद्धार हो गया।

गोपलीला करने के लिये भगवान श्रीकृष्ण ने कालिया नाग का नाश कर भय मुक्त किया था। इन्द्र के अभिमान को नष्ट करने के लिए गोवर्धन पर्वत को अपनी कनिष्ठा उँगली पर धारण कर लिया था। ऐसे भगवान के चरण कमल ही मीरा दासी का उद्धार करने में सक्षम हैं।

प्रश्न 4.
निम्नलिखित पद्यांशों की सप्रसंग व्याख्या कीजिए
(क) ऐसी मूढ़ता या …………..आपने तन की।
(ख) अबलौं नसानी ………… कंचनहिं कसैहों।
(ग) बढ़त पल-पल …………पुनि डार।
(घ) गगन मंडल पै ………..की जिन लाई होय।
उत्तर:
(क) सन्दर्भ :
पूर्ववत्।

प्रसंग :
इस पद में भक्त तुलसीदास अपने अवगुणों को प्रभु के समक्ष प्रदर्शित करते हुए अवगुणों एवं अज्ञान से मुक्त होने की कामना व्यक्त करते हैं।

व्याख्या :
तुलसीदास जी कहते हैं कि मेरे इस मन की ऐसी मूर्खता है कि यह राम की भक्ति रूपी पवित्र गंगा को त्यागकर सांसारिक सुख रूपी ओस की इच्छा करता है। कहने का आशय है कि जिस भाँति कोई प्यासा चातक पक्षी धुएँ के समूह को देखकर उसे बादल समझ ले और जल पीने के लिए दौड़े परन्तु न उसमें शीतलता होती है न जल, अपितु नेत्रों की हानि होती है। इसी भाँति मेरा मन राम की भक्ति को त्यागकर सांसारिक विषयों में सुख समझकर उनकी ओर आकर्षित होता है।

तुलसीदास का कथन है कि मेरे मन की ऐसी स्थिति है कि जैसे फर्श में जड़े हुए काँच में कोई बाज पक्षी अपने शरीर की परछाईं को निहारे और उसे अन्य पक्षी अर्थात् अपना शिकार समझकर उस पक्षी पर भोजन के लिए झपटे। उसे यह ज्ञान नहीं है कि इस प्रकार फर्श पर टकराने से उसके मुँह की ही हानि होगी।

हे कृपालु प्रभु राम ! मैं अपने मन की कुचाल (वाचालता) का कहाँ तक वर्णन करूँ? आप तो मेरी गति को भली-भाँति समझते हैं। हे प्रभु! आप पतित पावन हैं। पतितों एवं दीन-दुःखियों की रक्षा करना आपका प्रण अथवा स्वभाव है, इसीलिए आप इस तुलसीदास के असहनीय कष्टों को हरकर अपने प्राण की लज्जा रखो।
उपर्युक्त पद्यांशों की सप्रसंग व्याख्या ‘सन्दर्भ-प्रसंग सहित पद्यांशों की व्याख्या’ भाग में देखिये।

(ख) सन्दर्भ :
पूर्ववत्।

प्रसंग :
प्रस्तुत पंक्तियों में तुलसीदास ने विगत जीवन के प्रति पश्चाताप का भाव व्यक्त किया है। अब उन्हें विवेक की प्राप्ति हो गई; अत: उन्होंने सुपथ पर चलने का दृढ़ निश्चय किया है।

व्याख्या :
हे नाथ! मेरी अब तक की आयु व्यर्थ में ही नष्ट हो गई, मैं उसका कोई भी सदुपयोग नहीं कर सका। लेकिन अब जो आयु शेष है, उसे मैं व्यर्थ में नष्ट न होने दूंगा, उसका सदुपयोग करूँगा। राम की कृपा से संसार रूपी रात्रि नष्ट हो गयी है, अब में जाग गया हूँ अर्थात् अब मैं इतना मूर्ख नहीं कि जागने के बाद पुनः सोने के लिये बिस्तर बिछा लूँ। मुझे अज्ञान और मोह के बन्धन का बोध हो गया है। अत: मैं इसकी वास्तविकता से परिचित हो गया हूँ। अब पुनः मैं सांसारिक माया में नहीं फसँगा।

मुझे तो राम नाम रूपी सुन्दर चिन्तामणि प्राप्त हो गई है जिसे मैं हृदयरूपी हाथ से खिसकने नहीं दूंगा और राम के सुन्दर श्याम रूप को कसौटी बनाकर उस पर अपने चित्त रूपी कंचन को करूँगा अर्थात् परीक्षा करूँगा कि मेरा मन राम के स्वरूप में लगता है अथवा नहीं। यदि लगता है तो वह शुद्ध स्वर्ण है और यदि नहीं लगता तो उसमें खोट निहित है।

अभी तक मेरा मन इन्द्रियों के वश में था। अतः इन्द्रियों ने मेरा खूब उपहास किया, लेकिन अब मैंने अपने मन को वश में कर लिया है, इसलिए इन्द्रियों को हँसने का अवसर अब नहीं दूंगा। मैं दृढ़ निश्चय करके अपने इस मन रूपी भ्रमर को राम के चरण कमलों में बसाऊँगा। मुझे पूर्ण विश्वास है कि मेरा मन अपनी चंचलता को त्यागकर राम के चरणों में लग जायेगा।

(ग) सन्दर्भ :
पूर्ववत्।

प्रसंग :
इस पद में मीराबाई ने मानव शरीर को पुण्य स्वरूप ठहराकर ईश्वर के प्रति समर्पित होने की प्रेरणा दी है।

व्याख्या :
मीराबाई कहती हैं कि मानव जीवन बार-बार नहीं मिलता है। जीव को पुण्य कर्मों के कारण ही मानव शरीर प्राप्त होता है। यह शरीर पल-पल एवं प्रतिक्षण क्षीण होता जा रहा है, अर्थात् मृत्यु की ओर बढ़ रहा है। जीवन का अन्त होने में तनिक भी विलम्ब नहीं होगा। जिस प्रकार वृक्ष से झड़े हुए पत्ते पुनः डाल पर नहीं लग सकते; तद्नुकूल मानव का अन्त होने पर यह निश्चय नहीं है कि उसे पुनः मानव शरीर प्राप्त होगा। संसार रूपी सागर में विषय-वासनाओं की अत्यन्त तीक्ष्ण धारा है। यदि मनुष्य सुरत अथवा प्रभु में अपना ध्यान लगाये तो शीघ्र ही संसार रूपी सागर से पार हो जायेगा अर्थात् सांसारिक विषय-वासनाओं से उसे छुटकारा मिल जायेगा।

साधु सन्त एवं महन्तों की मण्डली पुकार-पुकार कर कह रही है कि मानव जीवन चार दिनों का मेला है। अत: हे मानव! तू श्रीकृष्ण का आश्रय ग्रहण कर ले, इसी में तेरा हित है।

(घ) सन्दर्भ :
प्रस्तुत पद्यांश हमारी पाठ्य पुस्तक के पाठ ‘मीराबाई’ द्वारा रचित ‘पदावली’ शीर्षक से अवतरित है।

प्रसंग :
प्रस्तुत पद्यांश में मीराबाई की विरह जनित पीड़ा को बड़ा ही मार्मिक वर्णन है। मीराबाई का श्रीकृष्ण से मिलन नहीं हो पा रहा है। अतः उनको असहनीय पीड़ा हो रही है।

व्याख्या :
मीराबाई कहती हैं कि हे सखि! मैं तो श्रीकृष्ण के प्रेम में दीवानी हूँ। उनके प्रति मेरे प्रेम की पीड़ा को मेरे अतिरिक्त दूसरा नहीं जान सकता है। मेरी सेज (सूली) (शय्या) ऐसे दुर्गम स्थान (प्राण दण्ड देने के स्थल) पर है जहाँ मेरे समान सांसारिक प्राणी पहुँच ही नहीं सकता है। श्रीकृष्ण की शैया तो आकाश में है। अत: उनसे मिलना असम्भव है। व्यथा से व्यथित मानव ही व्यथा की पीड़ा का मूल्यांकन कर सकता है। घायल व्यक्ति की पीड़ा को घायल ही जान सकता है। मेरी वियोग की पीड़ा को केवल वही व्यक्ति जान सकता है जिसने वियोग जनित पीड़ा को भी कभी सहन किया हो।

जौहर की पीड़ा को जौहरी (स्वयं को अग्नि की गोद में समर्पित करने वाला) ही जान सकता है। वियोग की पीड़ा से मैं इतनी दुःखी हूँ कि वन-वन भटकती फिर रही हूँ। लेकिन मेरी इस पीड़ा को दूर करने वाला कोई वैद्य आज तक नहीं मिला। मेरे विरह की पीड़ा तो तभी समाप्त होगी, जब श्रीकृष्ण वैद्य के रूप में प्रस्तुत होकर इसका उपचार करें अर्थात् उनके दर्शन से ही मेरा दुःख दूर हो सकता है।

भक्ति काव्य सौन्दर्य

प्रश्न 1.
निम्नलिखित शब्दों के तत्सम रूप लिखिएनिसा, आस, पषान, चरन, सुचि, पुन्य, गरव, भौसागर।
उत्तर:
तत्सम रूप-निशा, आशा, पाषाण, चरण, शुचि, पुण्य, गर्व, भवसागर।

प्रश्न 2.
निम्नलिखित काव्य-पंक्तियों में अलंकार पहचान कर लिखिए
(अ) मन मधुकर पन कै तुलसी रघुपति पद कमल बसैहौं।
(ब) ज्यों गज काँच बिलोकि सेन जड़ छाँह आपने तन की।
(स) बढ़त पल पल घटत छिन छिन चलत न लागे बार।
(द) जौहरी की गति जौहरी जाने, की जिन जौहर होय।
(इ) स्याम रूप सुचि रूचिर कसौटी, चित कंचनहिं कसैहों।
उत्तर:
(अ) रूपक अलंकार
(ब) दृष्टान्त अलंकार
(स) पुनरुक्ति, अनुप्रास अलंकार
(द) पुनरुक्ति अलंकार
(इ) रूपक अलंकार।

प्रश्न 3.
मीरा के पदों में किन-किन बोली अथवा भाषाओं के शब्दों का प्रयोग हुआ है? संकलित अंश से छाँटकर लिखिए।
उत्तर:
मीरा के पदों में ब्रजभाषा के अतिरिक्त राजस्थानी, गुजराती एवं पंजाबी शब्दों का प्रयोग हुआ है।

उदाहरण के लिए राजस्थानी भाषा के शब्द देखें-दीवाणी, जाणे, सोणा, मिलणा, मिल्या।
ब्रजभाषा के उदाहरण- नहिं ऐसो जनम बारम्बार……….
मन रे परसि हरि के चरन……….
जिन चरन प्रभु परसि लीने तरी गौतम धरन………..

प्रश्न 4.
माधुर्य गुण में कोमलकान्त पदावली का प्रयोग किया जाता है। यह गुण प्रायः श्रृंगार, वात्सल्य और शान्त रस में होता है। संकलित अंश से उदाहरण देकर समझाइए।
उत्तर:
संकलित अंश के आधार पर रस के उदाहरण इस प्रकार हैं-श्रृंगार रस-शृंगार रस के दो भेद होते हैं-
(1) संयोग शृंगार,
(2) वियोग शृंगार। स्थायी भाव रति होता है।

वियोग श्रृंगार का उदाहरण :
हे री मैं तो प्रेम दिवाणी मेरा दरद न जाने कोय। उपर्युक्त पंक्ति में वियोग शृंगार है।
अन्य उदाहरण :
दरद की मारी वन-वन डोलूँ, वैद मिल्या नहिं कोय।
मीरा की प्रभु पीर मिटैगी, जब वैद सँवलिया होय।।

वात्सल्य रस :
सोभित कर नवनीत लिए।
मैया मैं तो चंद खिलौना लैहौं।
शान्त रस का स्थायी भाव निर्वेद है।.

उदाहरण देखें :
ऐसी मूढ़ता या मन की …………
…………. करहु लाज निज पन की।
अबलौं नसानी ………… पद कमल बसैहौं।

प्रश्न 5.
निम्नलिखित काव्य पंक्तियों में कौन-सा रस है? उसका स्थायी भाव लिखिए।
(अ) अबलौं नसानी, अब न नसैहों।
(ब) हेरी मैं तो प्रेम दिवाणी, मेरा दरद न जाने कोय।
उत्तर:
(अ) शान्त रस-स्थायी भाव निर्वेद।
(ब) वियोग शृंगार-स्थायी भाव रति।

प्रश्न 6.
“गगन मंडल पै सेज पिया की किस विध मिलणा होय।” पंक्ति में कौन-सी शब्द शक्ति है ?
उत्तर:
शब्द शक्ति लक्षणा है।

प्रश्न 7.
“ऐसी मूढ़ता या मन की परिहरि राम भक्ति सुर सरिता,
आस करत ओसकन की।”
में प्रयुक्त रस और उसका स्थायी भाव लिखिए।
उत्तर:
उपर्युक्त पंक्ति में शान्त रस है तथा स्थायी भाव निर्वेद है।

विनय के पद भाव सारांश

तुलसीदास अपने इष्टदेव श्रीराम से कहते हैं कि आपके चरणों का आश्रय छोड़कर अन्यत्र कहाँ जाऊँ? आप पतितों का उद्धार करने वाले तथा दीनों से अनुराग करने वाले हैं। देवता, राक्षस, मुनि, नाग तथा मनुष्य सभी माया के वशीभूत हैं। अग्रिम पद में अपने को मूर्ख ठहराया है जो राम भक्ति रूपी गंगाजी को त्यागकर ओस कणों से अपनी प्यास बुझाना चाहता है।

अब तुलसी संसार के माया जनित सम्बन्धों को मिथ्या ठहराकर उनके बन्धनों से मुक्त होकर, अपने जीवन को नष्ट नहीं करना चाहते हैं। वे अपने मन रूपी भौरे को श्रीराम के चरण कमलों में अर्पित करना चाहते हैं।

विनय के पद संदर्भ-प्रसंग सहित व्याख्या

[1] जाऊँ कहाँ तजि चरन तुम्हारे।
काको नाम पतित पावन जग, केहि अति दीन पियारे ।।1।।
कौने देव बराइ बिरद-हित, हठिहठि अधम उधारे।
खग, मृग, ब्याध, पषान, विटप जड़, जवन कवन सुर तारे ।।2।।
देव, दनुज, मुनि, नाग, मनुज, सब माया बिबस विचारे।
तिनके हाथ दास तुलसी प्रभु, कहा अपनपौ हारे ।।3।।

शब्दार्थ :
तजि = त्यागकर, छोड़कर; काको = किसका; पावन = पवित्र; जग = संसार; केहि = किसको; बराइ = चुन-चुन कर; बिरद = भक्ति; हठिहठि = हठपूर्वक; अधम = नीच, पापी; उधारे = उद्धार किया; खग = जटायु पक्षी; मृग = हिरण, मारीचि; ब्याध = बहेलिया; पषान = पत्थर, अहिल्या; विटप = वृक्ष; सुर = देवता; दनुज = राक्षस; मनुज = मनुष्य; बिबस = विवश, लाचार; तिनके = उनके।

सन्दर्भ :
प्रस्तुत पद्यांश हमारी पाठ्य पुस्तक के पाठ भक्ति’ के शीर्षक विनय के पद’ से अवतरित है। इसके रचयिता तुलसीदास हैं।

प्रसंग :
प्रस्तुत पद्य में तुलसीदास ने भगवान् राम के चरणों के प्रति अपनी अनन्य भक्ति का उल्लेख किया है।

व्याख्या :
तुलसीदास जी कहते हैं कि हे प्रभु ! मैं आपके चरणों को त्यागकर अन्यत्र कहाँ जाऊँ ? कहीं भी मुझे आश्रय दृष्टिगोचर नहीं होता। आपके समान पापियों को पवित्र करने वाला संसार में अन्य कोई नहीं है, निर्धनों से स्नेह करने वाला कोई दूसरा नहीं है। ऐसा कौन-सा देवता है जिसने हठपूर्वक अपने पतित भक्तों का उद्धार किया है। पक्षी, हिरन, बहेलिया, पत्थर, वृक्ष, जड़, देवता, राक्षस, ऋषि, नाग, मनुष्य सब माया के वशीभूत हैं। तुलसीदास जी कहते हैं कि ऐसे प्रभु राम के सामने मैं अपना सर्वस्व समर्पण करता हूँ।

काव्य सौन्दर्य :

1. हित, हठिहठि, पतित-पावन में अनुप्रास अलंकार है।
2. भाषा में तद्भव शब्दों का प्रयोग है, जैसे-पषान, बिबस, मनुज।
3. ब्रजभाषा का प्रयोग है।

[2] ऐसी मूढ़ता या मन की।
परिहरि राम भक्ति सुर सरिता आस करत ओसकन की।।1।।
धूम समूह निरखि जातक ज्यों, तृषित जानि मति घन की।
नहि तहँ शीतलता न बारि, पुनि हानि होत लोचन की ।।2।। (2012)
ज्यों गच काँच बिलोकि सेन जड़ छाँह आपने तन की।
टूटत अति आतुर अहार बस, छति बिसारि आनन की ।।3।।
कहँ लौ कहाँ कुचाल कृपानिधि, जानत हौं गति जन की।
तुलसीदास प्रभु हरहु दुसह दुखः, करहु लाज निज पन की ।।4।।

शब्दार्थ :
मूढ़ता = मूर्खता; परिहरि = त्यागकर, छोड़कर; ओसकन = ओस की बूंदें; धूम = धुआँ; निरखि = देखकर; सुर-सरिता = गंगा हो; तृषित = प्यास से व्याकुल; गच= भूमि, दीवार; वारि = जल; लोचन = नेत्र; काँच = दर्पण; बिलोकि = देखकर; सेन = बाज, श्येन; जड़ = मूर्ख; तन = शरीर; छति = क्षति, हानि; आनन = मुँह, चोंच; टूटत = झपटकर गिरता है; आतुर = दुःखी; कुचाल = कुचक्र; लाज = लज्जा; निज = अपना; पन = प्रण, प्रतिज्ञा।

सन्दर्भ :
पूर्ववत्।

प्रसंग :
इस पद में भक्त तुलसीदास अपने अवगुणों को प्रभु के समक्ष प्रदर्शित करते हुए अवगुणों एवं अज्ञान से मुक्त होने की कामना व्यक्त करते हैं।

व्याख्या :
तुलसीदास जी कहते हैं कि मेरे इस मन की ऐसी मूर्खता है कि यह राम की भक्ति रूपी पवित्र गंगा को त्यागकर सांसारिक सुख रूपी ओस की इच्छा करता है। कहने का आशय है कि जिस भाँति कोई प्यासा चातक पक्षी धुएँ के समूह को देखकर उसे बादल समझ ले और जल पीने के लिए दौड़े परन्तु न उसमें शीतलता होती है न जल, अपितु नेत्रों की हानि होती है। इसी भाँति मेरा मन राम की भक्ति को त्यागकर सांसारिक विषयों में सुख समझकर उनकी ओर आकर्षित होता है।

तुलसीदास का कथन है कि मेरे मन की ऐसी स्थिति है कि जैसे फर्श में जड़े हुए काँच में कोई बाज पक्षी अपने शरीर की परछाईं को निहारे और उसे अन्य पक्षी अर्थात् अपना शिकार समझकर उस पक्षी पर भोजन के लिए झपटे। उसे यह ज्ञान नहीं है कि इस प्रकार फर्श पर टकराने से उसके मुँह की ही हानि होगी।

हे कृपालु प्रभु राम ! मैं अपने मन की कुचाल (वाचालता) का कहाँ तक वर्णन करूँ? आप तो मेरी गति को भली-भाँति समझते हैं। हे प्रभु! आप पतित पावन हैं। पतितों एवं दीन-दुःखियों की रक्षा करना आपका प्रण अथवा स्वभाव है, इसीलिए आप इस तुलसीदास के असहनीय कष्टों को हरकर अपने प्राण की लज्जा रखो।

काव्य सौन्दर्य :

1. शान्त रस।
2. भक्त अपने अवगुणों को प्रभु के समक्ष व्यक्त कर अपनी दीनता का प्रदर्शन कर रहा है।
3. ब्रजभाषा तथा गेय मुक्तक शैली का प्रयोग है।
4. भ्रान्तिमान रूपक एवं उपमा अलंकार की छटा दर्शनीय है।

[3] अबलौं नसानी, अब न नसैहों।
राम कृपा भक निसा सिरानी, जागे पुनि न डसैहौं।।1।।
पायो नाम चारु चिन्तामनि, उर कर ते न खसैहौं।
स्यामरूप सुचि रुचिर कसौटी, चित कंचनहिं कसैहों।।2।।
परबस जानि हँस्यो इन इन्द्रिन, निज बसहै न हँसैहों।
मन मधुकर पन कै तुलसी रघुपति पद कमल बसैहौं।।3।। (2008, 09)

शब्दार्थ :
अबलौं = अब तक; नसानी = नष्ट की, बिगाड़ी; भव = संसार; निसा = रात्रि; सिरानी = शान्त हो गई, बीत गई; डसैहों = स्वयं को डसाऊँगा; उर = हृदय; चारु = सुन्दर; खसैहौं = गिराऊँगा; सुचि = पवित्र; चित = मन; कंचनहिं = सोने को; परबस = दूसरे के अधीन; पन कै= प्रण करके, प्रतिज्ञा करके बसैहौं = निवास करूँगा, बसाऊँगा; मन-मधुकर = मन रूपी भौंरा।

सन्दर्भ :
पूर्ववत्।

प्रसंग :
प्रस्तुत पंक्तियों में तुलसीदास ने विगत जीवन के प्रति पश्चाताप का भाव व्यक्त किया है। अब उन्हें विवेक की प्राप्ति हो गई; अत: उन्होंने सुपथ पर चलने का दृढ़ निश्चय किया है।

व्याख्या :
हे नाथ! मेरी अब तक की आयु व्यर्थ में ही नष्ट हो गई, मैं उसका कोई भी सदुपयोग नहीं कर सका। लेकिन अब जो आयु शेष है, उसे मैं व्यर्थ में नष्ट न होने दूंगा, उसका सदुपयोग करूँगा। राम की कृपा से संसार रूपी रात्रि नष्ट हो गयी है, अब में जाग गया हूँ अर्थात् अब मैं इतना मूर्ख नहीं कि जागने के बाद पुनः सोने के लिये बिस्तर बिछा लूँ। मुझे अज्ञान और मोह के बन्धन का बोध हो गया है। अत: मैं इसकी वास्तविकता से परिचित हो गया हूँ। अब पुनः मैं सांसारिक माया में नहीं फसँगा।

मुझे तो राम नाम रूपी सुन्दर चिन्तामणि प्राप्त हो गई है जिसे मैं हृदयरूपी हाथ से खिसकने नहीं दूंगा और राम के सुन्दर श्याम रूप को कसौटी बनाकर उस पर अपने चित्त रूपी कंचन को करूँगा अर्थात् परीक्षा करूँगा कि मेरा मन राम के स्वरूप में लगता है अथवा नहीं। यदि लगता है तो वह शुद्ध स्वर्ण है और यदि नहीं लगता तो उसमें खोट निहित है।

अभी तक मेरा मन इन्द्रियों के वश में था। अतः इन्द्रियों ने मेरा खूब उपहास किया, लेकिन अब मैंने अपने मन को वश में कर लिया है, इसलिए इन्द्रियों को हँसने का अवसर अब नहीं दूंगा। मैं दृढ़ निश्चय करके अपने इस मन रूपी भ्रमर को राम के चरण कमलों में बसाऊँगा। मुझे पूर्ण विश्वास है कि मेरा मन अपनी चंचलता को त्यागकर राम के चरणों में लग जायेगा।

काव्य सौन्दर्य :

1. यहाँ तुलसीदास जी ने मानव को अज्ञानता छोड़कर सुपथ पर चलने की प्रेरणा दी है।
2. शान्त रस का परिपाक है।
3. भाषा अलंकारिक गुणों से युक्त है। रूपक अलंकार है।
4. ब्रजभाषा का प्रयोग है।
5. पद्यांशों में प्रसाद गुण है।

पदावली भाव सारांश

मीरा ने अपनी पदावली में अपनी विरह जनित पीड़ा को व्यक्त किया है। उनका कथन है कि वह श्रीकृष्ण के विरह में अत्यन्त व्याकुल हैं। उनके प्रियतम की सेज आकाश मण्डल में शूली ऊपर है जहाँ पहुँचना अत्यन्त दुर्लभ है। वे यत्र-तत्र भटक रही हैं लेकिन उनकी विरह पीड़ा का शमन करने वाला कोई भी नहीं दिखाई देता। उनकी पीड़ा को तो श्रीकृष्ण ही मिटा सकते हैं।

मीरा मानव जीवन को अमूल्य ठहराती हुई कहती हैं कि संसार से पार होने के लिये प्रभु के चरणों का सहारा ही एकमात्र आश्रय है। इन्हीं चरणों ने अनेक पतितों तथा भक्तों का उद्धार किया है।

पदावली संदर्भ-प्रसंग सहित व्याख्या

[1] हेरी मैं तो प्रेम दिवाणी, मेरा दरद न जाणे कोय।
सूली ऊपर सेज हमारी, किस विधि सोणा होय।।
गगन मण्डल पै सेज पिया की, किस विध मिलणा होय।
घायल की गति घायल जानै, की जिन लाई होय।।
जौहरी की गति जौहरी जानै, की किन जौहर होय।
दरद की मारी वन वन डोलूँ, वैद मिल्या नहिं कोय।।
मीरा की प्रभु पीर मिटैगी, जब वैद सँवलिया होय।

शब्दार्थ :
दरद = पीड़ा; सेज = शैया; गगन = आकाश; पिया = प्रियतम; विध = विधि; जौहरी = जौहर करने वाला; वैद = वैद्य; वन-वन = जंगल-जंगल; डोलूँ = विचरण करूँ; प्रभु = ईश्वर; पीर = पीड़ा; मिटैगी = समाप्त होगी; सँवलिया = श्रीकृष्ण का उपनाम।

सन्दर्भ :
प्रस्तुत पद्यांश हमारी पाठ्य पुस्तक के पाठ ‘मीराबाई’ द्वारा रचित ‘पदावली’ शीर्षक से अवतरित है।

प्रसंग :
प्रस्तुत पद्यांश में मीराबाई की विरह जनित पीड़ा को बड़ा ही मार्मिक वर्णन है। मीराबाई का श्रीकृष्ण से मिलन नहीं हो पा रहा है। अतः उनको असहनीय पीड़ा हो रही है।

व्याख्या :
मीराबाई कहती हैं कि हे सखि! मैं तो श्रीकृष्ण के प्रेम में दीवानी हूँ। उनके प्रति मेरे प्रेम की पीड़ा को मेरे अतिरिक्त दूसरा नहीं जान सकता है। मेरी सेज (सूली) (शय्या) ऐसे दुर्गम स्थान (प्राण दण्ड देने के स्थल) पर है जहाँ मेरे समान सांसारिक प्राणी पहुँच ही नहीं सकता है। श्रीकृष्ण की शैया तो आकाश में है। अत: उनसे मिलना असम्भव है। व्यथा से व्यथित मानव ही व्यथा की पीड़ा का मूल्यांकन कर सकता है। घायल व्यक्ति की पीड़ा को घायल ही जान सकता है। मेरी वियोग की पीड़ा को केवल वही व्यक्ति जान सकता है जिसने वियोग जनित पीड़ा को भी कभी सहन किया हो।

जौहर की पीड़ा को जौहरी (स्वयं को अग्नि की गोद में समर्पित करने वाला) ही जान सकता है। वियोग की पीड़ा से मैं इतनी दुःखी हूँ कि वन-वन भटकती फिर रही हूँ। लेकिन मेरी इस पीड़ा को दूर करने वाला कोई वैद्य आज तक नहीं मिला। मेरे विरह की पीड़ा तो तभी समाप्त होगी, जब श्रीकृष्ण वैद्य के रूप में प्रस्तुत होकर इसका उपचार करें अर्थात् उनके दर्शन से ही मेरा दुःख दूर हो सकता है।

काव्य सौन्दर्य :

1. विरह की वेदना का मार्मिक चित्रण मुहावरों द्वारा किया गया है।
2. भाषा-राजस्थानी एवं ब्रजभाषा है।
3. रस-वियोग शृंगार।
4. अनुप्रास-दृष्टान्त, पुनरुक्तिप्रकाश है।
5. गुण-माधुर्य।
6. शब्द-शक्ति-लक्षणा एवं अभिधा है।’

[2] नहिं ऐसो जन्म बारम्बार।
क्या जानूँ कछु पुन्य प्रकटे, मानुसा अवतार।।
बढ़त पल पल घटत छिन छिन, चलत न लागे बार।
बिरछ के ज्यों पाँत टूटे, लागे नहिं पुनि डार।।
भौ सागर अति जोर कहिये, विषय ओखी धार।
सुरत का नर बाँधे बेंडा, बेगि उतरे पार।।
साधु सन्ता ते महन्ता, चलत करत पुकार।
‘दास मीरा’ लाल गिरिधर, जीवना दिन चार।। (2008)

शब्दार्थ :
बारम्बार = बार-बार; पुन्य = पुण्य; पल-पल = हर क्षण; घटत = कम होना, क्षीण होना; बिरछ = वृक्ष; पात = पत्ते; बार = देरी; पुनि = पुनः; डार = डाल; भौ सागर = भवसागर, संसार रूपी समुद्र; ओखी कठिन; सुरत = ध्यान लगाना, भगवान प्रेम; नर = मनुष्य; बेगि = शीघ्रता; बेंडा = आड़ा-तिरछा, कठिन; महन्ता – साधु मण्डली।

सन्दर्भ :
पूर्ववत्।

प्रसंग :
इस पद में मीराबाई ने मानव शरीर को पुण्य स्वरूप ठहराकर ईश्वर के प्रति समर्पित होने की प्रेरणा दी है।

व्याख्या :
मीराबाई कहती हैं कि मानव जीवन बार-बार नहीं मिलता है। जीव को पुण्य कर्मों के कारण ही मानव शरीर प्राप्त होता है। यह शरीर पल-पल एवं प्रतिक्षण क्षीण होता जा रहा है, अर्थात् मृत्यु की ओर बढ़ रहा है। जीवन का अन्त होने में तनिक भी विलम्ब नहीं होगा। जिस प्रकार वृक्ष से झड़े हुए पत्ते पुनः डाल पर नहीं लग सकते; तद्नुकूल मानव का अन्त होने पर यह निश्चय नहीं है कि उसे पुनः मानव शरीर प्राप्त होगा। संसार रूपी सागर में विषय-वासनाओं की अत्यन्त तीक्ष्ण धारा है। यदि मनुष्य सुरत अथवा प्रभु में अपना ध्यान लगाये तो शीघ्र ही संसार रूपी सागर से पार हो जायेगा अर्थात् सांसारिक विषय-वासनाओं से उसे छुटकारा मिल जायेगा।

साधु सन्त एवं महन्तों की मण्डली पुकार-पुकार कर कह रही है कि मानव जीवन चार दिनों का मेला है। अत: हे मानव! तू श्रीकृष्ण का आश्रय ग्रहण कर ले, इसी में तेरा हित है।

काव्य सौन्दर्य :

1. राजस्थानी एवं ब्रजभाषा का प्रयोग है।
2. उपमा, रूपक एवं पुनरुक्ति अलंकार हैं।
3. शब्द गुण माधुर्य से परिपूर्ण है।
4. शान्त-रस का प्रयोग है।
5. कवयित्री ने जीवन को क्षण-भंगुर बताया है।

[3] मन रे परसि हरि के चरन।
सुभग शीतल कमल कोमल, त्रिविध ज्वाला हरन।।
जे चरन प्रह्वाद परसे, इन्द्र पदवी धरन।
जिन चरन ध्रुव अटल कीन्हों, राखि अपने सरन।।
जिन चरन ब्रह्माण्ड भेट्यो, नख सिखौ श्री भरन।
जिन चरन प्रभु परसि लीने, तरी गौतम धरन।।
जिन चरन कालीहि नाश्यो, गोप लीला करन।
जिन चरन धारयो गोवर्धन, गरब मघवा हरन।।
‘दास मीरा’ लाल गिरधर, अगम तारन तरन।

शब्दार्थ :
परसि = स्पर्श, छूना; हरि = भगवान; चरण = चरन, पग; सुभग = सुन्दर; शीतल = ठण्डा; त्रिविध ज्वाला = तीन प्रकार के ताप दैहिक, दैविक, भौतिक; हरन = नष्ट करना; ध्रुव = एक तारा; सरन = शरण; भेट्यो = भेंट करना; नख सिखौ = सिर से पाँव तक; तरी = तारना, मुक्त करना; धरन = स्त्री, पत्नी; कालीहि = कालिया नाग का; नाश्यो = नष्ट करना; गोप = ग्वाल; धारयो = धारण करना; गरब : गर्व, घमण्ड, अभिमान; मघवा = इन्द्र; हरन = हर लेना, छीन लेना; अगम = कठिन, जहाँ पहुँचा न जा सके।

सन्दर्भ :
पूर्ववत्।

प्रसंग :
प्रस्तुत पद में मीरा उद्धार करने वाले प्रभु के चरणों में आश्रय लेने के लिए अपने मन को सम्बोधित करती हुई कह रही हैं।

व्याख्या :
मीराबाई कहती हैं, हे मन! तू भगवान श्रीकृष्ण के कमल के समान कोमल, सुन्दर एवं शीतल चरणों का स्पर्श कर। ईश्वर के चरणों का स्पर्श तीनों प्रकार के तापों की अग्नि को शान्त करने वाला है (तीन प्रकार के ताप दैहिक, दैविक एवं भौतिक)। जिन भगवान के चरण कमलों के द्वारा प्रह्लाद का उद्धार हुआ, इन्द्र के पद को धारण किया।

जिन चरणों ने अपना आश्रय लेने वाले ध्रुव को अटल एवं अमर पद प्रदान किया। भगवान के चरणों ने समस्त भू-मण्डल को माप लिया तथा सिर से लेकर पाँव तक जिन चरणों का स्पर्श करके गौतम की पत्नी अहिल्या का उद्धार हो गया। ग्वाल लीला करते समय जिन चरणों ने विषधर काली नाग का नाश किया, जिन चरणों ने इन्द्र का गर्व नष्ट करने के लिए गोवर्धन पर्वत को अपनी कनिष्ठा उँगली पर धारण किया। मीराबाई कहती हैं कि मैं तो श्रीकृष्ण की दासी हूँ जो कि कठिन से कठिन कार्य अथवा घोर पापों का भी उद्धार करने वाले हैं।

काव्य सौन्दर्य :

1. ब्रजभाषा है, पद गेय एवं लालित्यपूर्ण हैं।
2. अनुप्रास तथा उपमा अलंकार हैं।
3. गुण-माधुर्य।
4. शान्त रस है।

MP Board Class 11th Hindi Solutions

MP Board Class 11th Maths Important Questions Chapter 3 Trigonometric Functions

Trigonometric Functions Important Questions

Trigonometric Functions Objective Type Questions

(A) Choose the correct option :
Question 1.
The value of 1 + cosθ is :
(a) 2sin² θ
(b) \(\frac { { sin }^{ 2 }\theta }{ 2 }\)
(c) 2cos² θ
(d) cos² θ
Answer:
(c) 2cos² θ

Question 2.
The value of \(\frac { cos 11° + sin 11° }{ cos 11° – sin 11° }\) is :
(a) cot 56°
(b) cot 34°
(c) tan 34°
(d) tan 56°
Answer:
(d) tan 56°

Question 3.
The value of sin 18° is :

Answer:

Question 4.
The value of cos 1° cos 2° cos 3° ………… cos 179° is :
(a) 0
(b) 1
(c) – 1
(d) None of these
Answer:
(a) 0

Question 5.
The value of \(\frac { 3 π }{ 2 }\) radian in degree.
(a) 120°
(b) 170°
(c) 220°
(d) 270°
Answer:
(d) 270°

Question 6.
The value of cos² (60 + α) + cos² (60 – α) + cos² α = ……………
(a) 3
(b) \(\frac { 3 π }{ 2 }\)
(c) \(\frac { 1 }{ 2 }\)
(d) \(\frac { 3 }{ 4 }\)
Answer:
(b) \(\frac { 3 π }{ 2 }\)

Question 7.
Amplitude of the function f(x) = 2 sin x is :
(a) π
(b) 2π
(c) 1
(d) 2
Answer:
(d) 2

Question 8.
Period of the function f(x) = tan x is :
(a) π
(b) 2
(c) \(\frac { π }{ 2 }\)
(d) – π
Answer:
(a) π

Question 9.
Solution of the equation 4 sin²θ = 1 is :
(a) nπ ± \(\frac { π }{ 3 }\), n ∈ I
(b) 2nπ ± \(\frac { π }{ 3 }\), n ∈ I
(c) nπ ± \(\frac { π }{ 6 }\), n ∈ I
(d) 2nπ ± \(\frac { π }{ 6 }\), n ∈ I
Answer:
(c) nπ ± \(\frac { π }{ 6 }\), n ∈ I

Question 10.
Maximum value of 3cosθ + 4sinθ is :
(a) 3
(b) 4
(c) 5
(d) 7
Answer:
(c) 5

Question 11.
If tanθ = – \(\frac { 4 }{ 3 }\) , then the value of sinθ is :
(a) – \(\frac { 4 }{ 5 }\) but not \(\frac { 4 }{ 5 }\)
(b) \(\frac { 4 }{ 5 }\) but not \(\frac – { 4 }{ 5 }\)
(c) – \(\frac { 4 }{ 5 }\) or \(\frac { 4 }{ 5 }\)
(d) None of these
Answer:
(c) – \(\frac { 4 }{ 5 }\) or \(\frac { 4 }{ 5 }\)

Question 12.
The value of tan15° + cot15° is :
(a) 1
(b) 3
(c) 2
(d) 4
Answer:
(d) 4

Question 13.
The value of sin50° + sin70° + sin10° is :
(a) 0
(b) 1
(c) – 1
(d) None of these
Answer:
(a) 0

Question 14.
One value of θ which satisfy the equation cosθ +\/3sinθ = 2 is :
(a) \(\frac { π }{ 2 }\)
(b) \(\frac { π }{ 3 }\)
(c) \(\frac { 2π }{ 3 }\)
(d) \(\frac { π }{ 4 }\)
Answer:
(b) \(\frac { π }{ 3 }\)

Question 15.
The general value of θ satisfying the equation cosθ = , tanθ = 1is :
(a) 2nπ + \(\frac { 5π }{ 4 }\)
(b) 2nπ – \(\frac { 5π }{ 4 }\)
(c) 2nπ + \(\frac { π }{ 4 }\)
(d) 2nπ – \(\frac { π }{ 4 }\)
Answer:
(a) 2nπ + \(\frac { 5π }{ 4 }\)

(B) Match the following :

Answer:

1. (d)
2. (c)
3. (a)
4. (b)
5. (g)
6. (j)
7. (e)
8. (i)
9. (h)
10. (f)

(C) Fill in the blanks :

1. The value of cos 18° = ……………….
2. The value of sin 75° = ……………….
3. If tan A = \(\frac { 5 }{ 6 }\) and tan B = \(\frac { 1 }{ 3}\), then the value of A + B = ……………….
4. 2π radian is equal to ………………. right angle.
5. If sinθ + cosθ = 1, then the value of sinθ.cosθ = ……………….
6. The value of \(\frac { 3tanA-{ tan }^{ 3 }A }{ 1-3{ tan }^{ 2 }A }\) = ……………….
7. Solution of the equation cos2θ = cos²θ is ……………….
8. Amplitude of 3cosx is ……………….
9. The value of cot 22\(\frac { 1 }{ 2 }\)° is ……………….
10. If tan θ tan 2θ = 1, then the value of θ is ……………….
11. The value of sin(A + B).sin(A – B) = ……………….
12. The length of the arc of a circle of radian 6 cm substending an angle of 30° at the centre of the circle is ……………….

Answer:

1. \(\frac { \sqrt { 10+2\sqrt { 5 } } }{ 4 }\)
2. \(\frac { \sqrt { 3 } + 1 }{ 2\sqrt { 2 } }\)
3. 45°
4. 4
5. 0
6. tan 3A
7. nπ
8. 3
9. \(\sqrt {2}\) + 1
10. (n + \(\frac { 1 }{ 3}\))\(\frac { π }{ 3 }\)
11. sin²A – sin²B
12. πcm

(D) Write true / false :

1. The value of tan 105° is \(\frac { \sqrt { 3 } + 1 }{ 2\sqrt { 2 } }\)
2. The value of sin 3A is 4 sin³ A + 3sinA
3. The value of cos² A – sin²B is cos(A + B) cos (A – B)
4. The value of cos² 48°- sin² 12 is \(\frac { \sqrt { 5 } + 1 }{ 4 }\).
5. The value of cos² (\(\frac { π }{ 6 }\) + θ) + sin² (\(\frac { π }{ 6 }\) – θ) is 0.
6. If x is a real, then the equation sinθ = x + \(\frac { 1 }{ x }\) has unique solution.
7. Solution of tan² θ + cot² θ = 2 is 2nπ + \(\frac { π }{ 6 }\)
8. If f(x) = sin² x, then f(- x) = sin² x
9. The value of sin\(\frac { 5π }{ 12 }\).cos\(\frac { π }{ 12 }\) is \(\frac { \sqrt { 3 } – 2 }{ 4 }\).
10. If A + B = \(\frac { π }{ 3 }\) and cosA + cosB = 1, then cos(A – B) = – \(\frac { 1 }{ 3 }\).

Answer:

1. False
2. False
3. True
4. True
5. False
6. False
7. False
8. True
9. False
10. True

(E) Write answer in one word / sentence :

1. Find the solution of equation cos² θ – sin² θ – \(\frac { 1 }{ 4 }\) = 0
2. The value of tan 1° tan 2° tan 3° ……………. tan 18° is :
3. The value of sin(A + B) + sin(A – B) is :
4. If (1 + tan x) (1 + tan y) = 2, then find the value of (x + y):
5. The value of sin( \(\frac { π }{ 3 }\) + x) – sin(\(\frac { π }{ 4 }\) – x)

Answer:

1. θ = nπ + (-1)ⁿ\(\frac { π }{ 6 }\)
2. 1
3. 2sinA.cosB
4. \(\frac { π }{ 4 }\)
5. \(\sqrt { 2 }\) sinx

Trigonometric Functions Short Answer Type Questions

Question 1.
A wheel makes 360 revolutions in 1 min. then how many radians measure of an angle does it turn in 1 second? (NCERT)
Solution:
In 60 seconds number of revolutions of wheel = 360
∴ In 1 second number of revolutions of wheel = \(\frac { 360 }{ 60 }\)
∴ In one revolution angle made = 360° = 2π
∴ In 6 revolutions angle made = 2π x 6 = 12π radian

Question 2.
Find the degree measure of an angle substended at the centre of a circle of radius 100 cm by an arc of length 22 cm.
Solution:
We know that, θ = \(\frac { 1 }{ r }\), length of arc = l = 22 cm, radius = r = 100 cm, angle made at the centre = θ = ?
Applying formula θ = \(\frac { 1 }{ r }\)

Question 3.
In a circle of diameter 40 cm, the length of chord is 20 cm, then find the length of minor arc of the chord.
Solution:
Radius of circle = OA = OB = \(\frac { 40 }{ 2 }\) = 20 cm, AB = 20 cm

Hence OAB is an equilateral triangle.
∴ θ = \(\frac { 1 }{ r }\)
⇒ 60° = \(\frac { AB }{ 20 }\)
⇒ AB = 60° x 20 = 60 x \(\frac { π }{ 180 }\) x 20
= \(\frac { 20π }{ 3 }\) cm.

Question 4.
If in two circles, arc of the same length substend angles of 60° and 75° at the centre, then find the ratio of their radii. (NCERT)
Solution:

Question 5.
Find value : (i) sin75°, (ii) tan15°
Solution:

Question 6.
Prove that:
sin²\(\frac { π }{ 4 }\) + cos²\(\frac { π }{ 3 }\) = – \(\frac { 1 }{ 2 }\)
Solution:

Question 7.
Prove that:
cos 27°. tan 27°. tan 63°. cosec 63° = 1. (NCERT)
Solution:
L.H.S. = cos 27°. tan 27°.tan 63°. cosec 63°
= cos 27°. tan 27° tan(90° – 27°). cosec (90° – 27°)
= cos 27°. tan 27° cot 27°. sec 27°
= \(\frac { 1 }{ sec 27° }\).\(\frac { 1 }{ cot 27° }\)cot 27°. sec 27° sec 27° cot 27°
= 1 = R.H.S.

Question 8.
Find the general solution of the following equations :

1. sinθ = \(\frac { \sqrt { 3 } }{ 2 }\)
2. tanθ = 1
3. \(\sqrt { 3 }\) tanθ + 1 = 0.

Solution:
1. sinθ = \(\frac { \sqrt { 3 } }{ 2 }\)
⇒ sinθ = sin\(\frac { π }{ 3 }\)
∴ θ = nπ + ( – 1)ⁿ\(\frac { π }{ 3 }\) [ ∵ sinθ = sinα ⇒ θ = nπ + (- 1)ⁿα, where n ∈ I]

2. tanθ = 1
⇒ tanθ = tan\(\frac { π }{ 4 }\)
∴ θ = nπ + \(\frac { π }{ 4 }\) [ ∵tanθ = tanα ⇒ θ = nπ + α, where n ∈ I]

3. \(\sqrt { 3 }\) tanθ + 1 = 0.
⇒ tanθ = – \(\frac { 1 }{ \sqrt { 3 } }\) = – tan\(\frac { π }{ 6 }\)
⇒ tanθ = tan (π – \(\frac { π }{ 6 }\))
⇒ tanθ = tan\(\frac { 5π }{ 6 }\)
∴ θ = nπ + \(\frac { 5π }{ 4 }\) [ ∵tanθ = tanα ⇒ θ = nπ + α, where n ∈ I]

Question 9.
Solve the following equations :
(i) 4 sin² θ = 1
(ii) 3 tan² θ = 1.
Solution:

Question 10.
Find the principal value of x :
tan x = \(\sqrt { 3 }\)
Solution:
tan x =\(\sqrt { 3 }\)
tan x = tan\(\frac { π }{ 3 }\) = tan(π + \(\frac { π }{ 3}\))
⇒ tan x = tan\(\frac { π }{ 3 }\) = tan\(\frac { 4π }{ 3 }\)
⇒ x = \(\frac { π }{ 3 }\) or \(\frac { 4π }{ 3 }\)
Principal value of x = \(\frac { π }{ 3 }\)
∴ tan x = \(\sqrt { 3 }\) ⇒ tanx = tan\(\frac { π }{ 3 }\)
Hence, general solution of x = nπ + \(\frac { π }{ 3 }\), [ ∵tanθ = tanα ⇒ θ = nπ + α, where n ∈ I]

Question 11.
Find the principal value of x :
sec x = 2.
Solution:

Trigonometric Functions Long Answer Type Questions

Question 1.
Prove that:
\(\frac { sinx – siny }{ cosx + cosy }\) = tan\(\frac { x – y }{ 2 }\)
Solution:

Question 2.
Prove that:
\(\frac { sin3x + sinx }{ cos3x + cosx }\) = tan2x.
Solution:

Question 3.
Prove that:
\(\frac { sinx – sin3x }{ { sin }^{ 2 }x – { cos }^{ 2 }x }\) = 2 sinx.
Solution:

Question 4.
Prove that:
\(\frac { cos9x – cos5x }{ sin17x – sin3x }\) = – \(\frac { sin2x}{ cos10x }\)
Solution:

Question 5.
Prove that:
\(\frac { sin5x + sin3x }{ cos5x + cos3x }\) = tan4x.
Solution:

Question 6.
Prove that:
2sin²\(\frac { π }{ 6 }\) + cosec²\(\frac { 7π }{ 6 }\)cos²\(\frac { π }{ 3 }\) = \(\frac { 3 }{ 2 }\)
Solution:

Question 7.
Prove that:
cot²\(\frac { π }{ 6 }\) + cosec\(\frac { 5π }{ 6 }\) + 3tan²\(\frac { π }{ 6 }\) = 6
Solution:

Question 8.
Prove that:
2sin²\(\frac { 3π }{ 4 }\) + 2cos²\(\frac { π }{ 4 }\) + 2sec²\(\frac { π }{ 3 }\) = 10
Solution:

Question 9.
Prove that:
\(\frac { cos11° + sin11° }{ cos11° – sin11° }\) = tan56°
Solution:

Question 10.
Prove that:
tan 3A – tan 2A – tan A = tan 3A. tan 2A. tan A.
Solution:
tan3A – tan2A – tanA – tan3A.tan2A. tanA = 0
⇒ tan3A – tan2A – tanA (l + tan3A.tan2A) = 0
⇒ tan 3A – tan 2A = tan A (1 + tan 3 A. tan 2 A)
⇒ \(\frac { tan 3A – tan 2A}{ 1 + tan 2A.tan 3A }\)
⇒ tan(3A – 2 A) = tan A
⇒ tanA = tan A.

Question 11.
Prove that:
cos(\(\frac { π }{ 4 }\) + x) + cos(\(\frac { π }{ 4 }\) – x) = \(\sqrt {2}\)cosx
Solution:

Question 12.
Prove that:

Solution:

Question 13.
If α + β = \(\frac { π }{ 4 }\), then prove that :
(1 + tanα)(1 + tanβ) = 2.
Solution:
Given α + β = \(\frac { π }{ 4 }\)
tan(α + β) = tan \(\frac { π }{ 4 }\)

⇒ tan α + tan β = 1 – tanα.tan β
⇒ tan α + tan β.tanα.tan β = 1
⇒ tan α + tan β(1 + tanα) = 1
⇒ 1 + tan α + tan β(1 + tanα) = 1 + 1
⇒ ( 1 + tan α)(1 + tan β) = 2

Question 14.
Find the general solution of cos4x = cos 2x.
Solution:
Given equation :
cos4x = cos2x
⇒ cos4x – cos2x = 0
⇒ – 2sin\(\frac { 4x + 2x}{ 2 }\).sin\(\frac { 4x – 2x}{ 2 }\) = 0
⇒ – 2sin3x.sinx = 0
⇒ sinx.sin3x = 0
⇒ sin3x = 0 or sinx = 0
⇒ 3x = nπ or x = nπ
⇒ x = \(\frac { nπ}{ 3 }\) or x = nπ, where n∈I.

Question 15.
Solve the equation tan 2x = cot(x + \(\frac { π }{ 3 }\))
Solution:

Question 16.
Solve the equation sin 3θ = sin 2θ
Solution:
Given equation sin3θ = sin2θ
sin 3θ – sin 2θ = 0

Question 17.
Solve the equation tan2θ = tan\(\frac { 2 }{ θ }\)
Solution:
tan 2θ = tan\(\frac { 2 }{ θ }\)
⇒ 2θ = nπ + \(\frac { 2 }{ θ }\)
⇒ 2θ – \(\frac { 2 }{ θ }\) = nπ + \(\frac { 2 }{ θ }\)
⇒ 2θ – \(\frac { 2 }{ θ }\) = nπ
⇒ 2θ² – 2 = nπθ
⇒ 2θ² – nπθ – 2 = 0

Question 18.
Solve the equation tanθ.tan2θ = 1
Solution:

Question 19.
If sec x = \(\frac { 13 }{ 5 }\) and x is in fourth quadrant, then find the other five trigonometrical functions (NCERT)
Solution:
secx = \(\frac { 13 }{ 5 }\) ,
Given : x is in fourth quadrant,

Question 20.
If tan x = – \(\frac { 5 }{ 12 }\) and x is in second quadrant, then find the other five trigonometrical functions (NCERT)
Solution:
Given : tan x = – \(\frac { 5 }{ 12 }\) ,

∴ x is in second quadrant, ∵ secx is negative.

∵ x is in second quadrant, hence sinx is positive.
sinx = \(\frac { 5 }{ 13 }\)
cosecx = \(\frac { 1 }{ sin x }\) = \(\frac { 1 }{ 5/13 }\) = \(\frac { 13 }{ 5 }\)

Question 21.
Prove that:
cos 20°. cos 40°. cos 60°. cos 80°= \(\frac { 1 }{ 16 }\) .
Solution:
L.H.S. = cos 20° .cos 40°. cos 60°. cos 80°
= cos 20°.cos 40°.\(\frac { 1 }{ 2 }\). cos80°
= \(\frac { 1 }{ 4 }\)(2 cos 20°. cos 40°). cos 80°
= \(\frac { 1 }{ 4 }\)(cos 60° + cos 20°). cos 80°
= \(\frac { 1 }{ 4 }\) cos 60°. cos 80° + \(\frac { 1 }{ 4 }\) cos 20°. cos 80°
= \(\frac { 1 }{ 4 }\). \(\frac { 1 }{ 2}\). cos 80° + \(\frac { 1 }{ 8 }\)(2 cos 20°. cos 80°)
= \(\frac { 1 }{ 8 }\)cos 80° + \(\frac { 1 }{ 8 }\) (cos 100° + cos 60°)
= \(\frac { 1 }{ 8 }\)cos 80°+\(\frac { 1 }{ 8 }\)[cos(180° – 80°) + \(\frac { 1 }{ 2 }\)
= \(\frac { 1 }{ 8 }\)cos80° + \(\frac { 1 }{ 8 }\)(- cos80°) + \(\frac { 1 }{ 16 }\) [∵cos(180° – θ]= – cosθ]
= \(\frac { 1 }{ 8 }\)cos 80° – \(\frac { 1 }{ 8 }\)cos 80°+ \(\frac { 1 }{ 16 }\)
= \(\frac { 1 }{ 16 }\) = R.H.S.

Question 22.
Prove that:
sin 20°.sin40°.sin60°.sin80°=\(\frac { 3 }{ 16 }\).
Solution:

Question 23.
prove that:
(cosx + cosy)²+ (sinx – siny)² = 4cos²\(\frac { x + y }{ 2 }\)
Solution:

Question 24.
prove that:
(cosx – cosy)²+ (sinx – siny)² = 4sin²\(\frac { x – y }{ 2 }\)
Solution:
L.H.S. = (cosx – cosy)²+ (sinx – siny)²
= cos²x + cos²y – 2 cosxcosy + sin²x + sin²y – 2sinx siny
= cos²x + sin²x + cos²y + sin²y – 2[cosx cosy + sinx siny]
= 1 + 1 – 2cos(x – y) = 2 – 2cos(x – y)
= 2[1 – cos(x – y)] = 2 x 2sin²
= 4 sin²\(\frac { x – y }{ 2 }\) = R.H.S.

Question 25.
Prove that:
sinx + sin3x + sin5x + sin7x = 4 cosx cos2x sin4x.
Solution:
L.H.S. = sinx + sin3x + sin5x + sin 7x
= sin7x + sinx + sin5x + sin3x
= 2sin\(\frac { 7x + x }{ 2 }\).cos\(\frac { 7x – x }{ 2 }\) + 2sin\(\frac { 5x + 3x }{ 2 }\).cos\(\frac { 5x – 3x }{ 2 }\)
= 2sin4x.cos3x + 2sin4x.cosx
= 2sin4x[cos3x + cosx]
= 2sin4x[ 2 x cos\(\frac { 3x + x }{ 2 }\).cos\(\frac { 3x – x }{ 2 }\) ]
= 2sin4x[2cos2x.cosx]
= 4sin4x.cos2x.cosx
= R.H.S

Question 26.
Prove that:

Solution:

Question 27.
Solve the equation and find general solution of sec²2x = 1 – tan2x. (NCERT)
Solution:
The given equation is :
sec² 2x = 1 – tan 2x
⇒ 1 + tan²2x = 1 – tan 2x
⇒ tan² 2x = – tan2x
⇒ tan² 2x + tan2x = 0 ⇒ tan2x (tan2x + 1) = 0
⇒ tan2x = 0 tan2x(tan2x + 1) = 0 ⇒ 2x = nπ or tan2x = – 1

Question 28.
Solve the equation 2 cos² x + 3 sin x = 0
Solution:
2 cos² x + 3 sin x = 0
⇒ 2 (1 – sin²  x)+3 sinx = 0
⇒ 2 – 2sin² x+ 3 sinx = 0
⇒ 2 sin² x – 3 sinx – 2 = 0
⇒ 2 sin² x + sinx – 4sinx – 2 = 0
⇒ sinx(2 sinx + 1) – 2(2sinx + 1) = 0
⇒ (2sinx + 1)(sinx – 2) = 0
⇒ 2 sin x +1 = 0 or sinx – 2 = 0
⇒ 2 sin x = – 1 = 0 or sinx = 2
⇒ 2 sin x = – \(\frac { 1 }{ 2 }\)
⇒ sin x = sin(π + \(\frac { π }{ 6 }\)
⇒ sin x = sin\(\frac { 7π }{ 6 }\)
∴ x = nπ + (- 1)ⁿ\(\frac { 7π }{ 6 }\)

Question 29.
Solve the equation tan² θ + (1 – \(\sqrt { 3 }\)) tanθ = \(\sqrt { 3 }\)
Solution:
tan² θ + (1 – \(\sqrt { 3 }\)) tanθ = \(\sqrt { 3 }\)
⇒ tan² θ + (1 – \(\sqrt { 3 }\)) tanθ – \(\sqrt { 3 }\) = 0
⇒ tan² θ + tanθ – \(\sqrt { 3 }\) tanθ – \(\sqrt { 3 }\) = 0
⇒ tanθ(tanθ + 1) – \(\sqrt { 3 }\)(tanθ + 1) = 0
⇒ (tanθ + 1)(tan θ – \(\sqrt { 3 }\)) = 0
⇒ tanθ + 1 = 0 or tan θ – \(\sqrt { 3 }\) = 0
⇒ tanθ = – 1 or tan θ = \(\sqrt { 3 }\)
⇒ tanθ = tan \(\frac { – π }{ 4 }\) = tanθ = tan\(\sqrt { 3 }\)
⇒ tanθ = tan \(\frac { – π }{ 4 }\) = θ = nπ + \(\frac { π }{ 3 }\)
∴ θ = nπ – \(\frac { π }{ 4}\)

Question 30.
Solve the equation \(\sqrt { 2 }\) secθ + tanθ = 1.
Solution:

Question 31.
Find the general solution of the equation sinx + sin5x + sin5x = 0
Solution:

Question 32.
Prove that:
2cos\(\frac { π }{ 13 }\)cos\(\frac { 9π }{ 13 }\) + cos\(\frac { 3π }{ 13 }\) + cos\(\frac { 5π }{ 3 }\) = 0
Solution:

Question 33.
Prove that:

Solution:

MP Board Class 11th Maths Important Questions

MP Board Class 12th Maths Important Questions Chapter 2 प्रतिलोम त्रिकोणमितीय फलन

प्रतिलोम त्रिकोणमितीय फलन Important Questions

प्रतिलोम त्रिकोणमितीय फलन वस्तुनिष्ठ प्रश्न

प्रश्न 1.
सही विकल्प चुनकर लिखिए –

प्रश्न 1.
यदि sin^-1x – cos^-1 x = \(\frac { \pi }{ 6 } \) हो, तो x का मान ज्ञात कीजिए –
(a) \(\frac{1}{2}\)
(b) \(\frac { \sqrt { 3 } }{ 2 } \)
(c) – \(\frac{1}{2}\)
(d) इनमें से कोई नहीं।
उत्तर:
(a) \(\frac{1}{2}\)

प्रश्न 2.
यदि tan^-1 3 + tan^-1 x = tan^-1 8 हो, तो x का मान होगा –
(a) 5
(b) \(\frac{1}{5}\)
(c) \(\frac{5}{14}\)
(d) \(\frac{14}{5}\)
उत्तर:
(b) \(\frac{1}{5}\)

प्रश्न 3.
tan^-1 ( \(\frac{x}{y}\) ) – tan^-1 ( \(\frac { x-y }{ x+y } \) ) का मान है –
(a) \(\frac { \pi }{ 2 } \)
(b) \(\frac { \pi }{ 3 } \)
(c) \(\frac { \pi }{ 4 } \)
(d) \(\frac { -3\pi }{ 4 } \)
उत्तर:
(c) \(\frac { -3\pi }{ 4 } \)

प्रश्न 4.
2 tan^-1 {cosec (tan^-1 x) – tan (cot^-1 x)} का मान है –
(a) cot^-1 x
(b) cot^-1 \(\frac{1}{x}\)
(c) tan^-1 x
(d) tan^-1 \(\frac{1}{x}\)
उत्तर:
(c) tan^-1 x

प्रश्न 5.
tan {cos^-1 \(\frac { 1 }{ 5\sqrt { 2 } } \) – sin^-1 \(\frac { 4 }{ \sqrt { 17 } } \) } का मान होगा –
(a) \(\frac { \sqrt { 29 } }{ 3 } \)
(b) \(\frac{29}{3}\)
(c) \(\frac { \sqrt { 3 } }{ 29 } \)
(d) \(\frac{3}{29}\)
उत्तर:
(d) \(\frac{3}{29}\)

प्रश्न 2.
रिक्त स्थानों की पूर्ति कीजिए –

1. tan^-1 (1) + tan^-1 (2) + tan^-1 (3) = ………………………….
2. tan^-1 (2) – tan^-1 (1) = …………………………….
3. cot^-1 3 + cosec^-1 \(\sqrt{5}\)
4. sin(sin^-1 x + 2 cos^-1 x) = …………………………..
5. यदि sin^-1 ( \(\frac { 2a }{ 1+a^{ 2 } } \) ) + sin ( \(\frac { 2b }{ 1+b^{ 2 } } \) ) = 2 tan^-1 x, तो x = ………………………….
6. यदि tan^-1 ( \(\frac { 1-x }{ 1+x } \) ) = \(\frac{1}{2}\) tan^-1 x (जब x > 0), तो x =
7. tan^-1 ( \(\frac { a-b }{ 1+ab } \) ) + tan^-1 ( \(\frac { b-c }{ 1+bc } \) ) + tan^-1 c = ………………………..

उत्तर:

1. π
2. tan^-1 ( \(\frac{1}{3}\) )
3. \(\frac { \pi }{ 4 } \)
4. x
5. \(\frac { a+b }{ 1-ab } \)
6. \(\frac { 1 }{ \sqrt { 3 } } \)
7. tan^-1 (a)

प्रश्न 3.
निम्न कथनों में सत्य/असत्य बताइए –

1. tan^-1 x + tan^-1 y = tan^-1 \(\frac { x+y }{ 1-xy } \)
2. cos^-1(-x) = – cos^-1 x
3. sin^-1 (3x – 4x³) = sin^-1 \(\frac{x}{3}\)
4. cos^-1 ( \(\frac { 1-x^{ 2 } }{ 1+x^{ 2 } } \) ) = 2 tan^-1 x
5. sin^-1 x – sin^-1 y = sin^-1 [xy – \(\sqrt { 1-x^{ 2 } } \) \(\sqrt { 1-y^{ 2 } } \) ].

उत्तर:

1. सत्य
2. असत्य
3. असत्य
4. सत्य
5. असत्य।

प्रश्न 4.
सही जोड़ी बनाइये –

उत्तर:

1. (b)
2. (e)
3. (f)
4. (a)
5. (c)
6. (d)

प्रश्न 5.
एक शब्द/वाक्य में उत्तर दीजिए –

1. tan^-1\(\frac{1}{2}\) + tan^-1\(\frac{3}{2}\) का मान ज्ञात कीजिए।
2. tan^-1 \(\frac { x }{ \sqrt { 1-x^{ 2 } } } \) का मान ज्ञात कीजिए।
3. sin (2 sin^-1\(\frac{3}{5}\) ) का मान ज्ञात कीजिए।
4. समीकरण sin^-1 \(\frac{x}{5}\) + cosec^-1\(\frac{5}{4}\) = \(\frac { \pi }{ 2 } \) का मान ज्ञात कीजिए।
5. cos^-1 (cos \(\frac { 7\pi }{ 6 } \) ) का मुख्य मान लिखिए।
6. यदि cos^-1 ( \(\frac{1}{x}\) ) = θ हो, तो tan θ का मान लिखिए।

उत्तर:

1. tan^-1 8
2. sin^-1 x
3. \(\frac{24}{25}\)
4. x = 3
5. \(\frac { 5\pi }{ 6 } \)
6. \(\sqrt { x^{ 2 }-1 } \)

प्रतिलोम त्रिकोणमितीय फलन लाधु उतरिय प्रश्न

प्रश्न 1.
निम्नलिखित के मुख्य मान ज्ञात कीजिये – (CBSE 2014)

(i) tan^-1 [sin (- \(\frac { \pi }{ 2 } \) ) (CBSE 2014)

(ii) cot [ \(\frac { \pi }{ 2 } \) – 2 cot^-1 \(\sqrt{3}\) (CBSE 2014)

(iii) tan^-1 (-\(\sqrt{3}\) )

(iv) sec^-1 (-\(\frac{2}{3}\) \(\sqrt{3}\) ) (NCERT)

(v) cosec^-1 (2) (NCERT)

हल:
(i) tan^-1 [sin (- \(\frac { \pi }{ 2 } \) )
= tan^-1 [- sin \(\frac { \pi }{ 2 } \) ], [∵sin (- θ) = – sin θ]
= tan^-1 (-1), (∵ sin \(\frac { \pi }{ 2 } \) = 1)
= – tan^-1 (1), (∵ tan^-1 (-x) = – tan^-1 x)
= –\(\frac { \pi }{ 4 } \) (∵ tan^-1 (1) = \(\frac { \pi }{ 4 } \)
(ii) cot [ \(\frac { \pi }{ 2 } \) – 2cot^-1 \(\sqrt{3}\)

(iii) माना tan(-\(\sqrt{3}\)) = θ

(iv) sec^-1 \(\frac{-2}{3}\)\(\sqrt{3}\)) = θ

प्रश्न 2.
सिद्ध कीजिये –
(a) 2 cos^-1 \(\frac{4}{5}\) = cos^-1 \(\frac{7}{25}\)
(b) 2 sin^-1 \(\frac{3}{5}\) = sin^-1 \(\frac{24}{25}\)
(c) 2 sin^-1 \(\frac{5}{13}\) = sin^-1 \(\frac{120}{169}\)
हल:
(a) 2 cos^-1 \(\frac{4}{5}\) = cos^-1 \(\frac{7}{25}\)

(b) 2 sin^-1 \(\frac{3}{5}\) = sin^-1 \(\frac{24}{25}\)

(c) क्रमांक की 2(b) भाँती हल कीजिये।

प्रश्न 3.
मान ज्ञात कीजिये –
tan^-1 {2 cos (2 sin^-1 \(\frac{1}{2}\) )} (CBSE 2013, NCERT)
हल:
tan^-1 {2 cos (2 sin^-1 \(\frac{1}{2}\) )} = tan^-1 [2 cos (2 × \(\frac { \pi }{ 6 } \) ) ]
= tan^-1 [2 cos \(\frac { \pi }{ 3 } \) ] = tan^-1 [2 × \(\frac{1}{2}\) ]
= tan^-1 1
= \(\frac { \pi }{ 4 } \)

प्रश्न 4.
मान ज्ञात कीजिये –
sin [ \(\frac { \pi }{ 3 } \) – sin^-1 (- \(\frac{1}{2}\)) ] (CBSE 2008, 13)
हल:
sin [ \(\frac { \pi }{ 3 } \) – sin^-1 (- \(\frac{1}{2}\) ) ]
= sin [ \(\frac { \pi }{ 3 } \) + sin^-1 ( \(\frac{1}{2}\)) ], [∵sin^-1 (-x) = – sin^-1x]
= sin [ \(\frac { \pi }{ 3 } \) + \(\frac { \pi }{ 6 } \) ] = sin \(\frac { \pi }{ 2 } \) = 1

प्रश्न 5.
सिद्ध कीजिये –
2 tan^-1 \(\frac{1}{5}\) = tan^-1 \(\frac{5}{12}\)?
हल:
L.H.S = 2 tan^-1 \(\frac{1}{5}\)

प्रश्न 6.
मान ज्ञात कीजिये –
tan (2 tan^-1 \(\frac{1}{5}\) – \(\frac { \pi }{ 4 } \) )
हल:

प्रश्न 7.
सिद्ध कीजिये –
3 sin^-1 x = sin^-1 (3x – 4x³). (NCERT, CBSE 2018)
हल:
मानलो sin^-1 x = θ.
∴ x = sin θ
अब sin 3θ = 3 sinθ – 4sin³θ
= 3x – 4x³
∴ 3θ = sin^-1 (3x – 4x³)

यही सिद्ध करना था।

प्रश्न 8.
सिद्ध कीजिये –
3 cos^-1 x = cos^-1 (4x³ – 3x) (NCERT)
हल:
मानलो cos^-1 x = θ
∴ x = cos θ
अब cos 3θ = 4 cos³θ – 3 cos θ
= 4x³ – 3x
∴ 3θ = cos^-1 (4x³ – 3x)

यही सिद्ध करना था।

प्रश्न 9.
सिद्ध कीजिये –
(A) tan^-1 \(\frac{1}{2}\) + tan^-1 \(\frac{1}{3}\) = \(\frac { \pi }{ 4 } \)
(B) cos^-1\(\frac{12}{13}\) = tan^-1 \(\frac{5}{12}\)
(C) cos^-1\(\frac{3}{5}\) = sin^-1 \(\frac{4}{5}\)
हल:
(A) tan^-1 = \(\frac{1}{2}\) + tan^-1 \(\frac{1}{3}\) = \(\frac { \pi }{ 4 } \)
L.H.S = tan^-1 \(\frac{1}{2}\) + tan^-1 \(\frac{1}{3}\)

(B) cos^-1 \(\frac{12}{13}\) = tan^-1 \(\frac{5}{12}\)

समी. (1) तथा (2) L.H.S. = R.H.S. यही सिद्ध करना था।

(C) cos^-1 \(\frac{3}{5}\) = sin-1 \(\frac{4}{5}\)

समी. (1) तथा (2) L.H.S. = R.H.S. यही सिद्ध करना था।

प्रश्न 10.
सिद्ध कीजिये
(A) sec^-1 x + cosec^-1 x = \(\frac { \pi }{ 2 } \)
(B) sin^-1 x + cos^-1 x = \(\frac { \pi }{ 2 } \)
(C) tan^-1 x + cot^-1 x = \(\frac { \pi }{ 2 } \)
हल:
(A) sec^-1 x + cosec^-1 x = \(\frac { \pi }{ 2 } \)
माना sin^-1 x = θ ………………… (1)
⇒ x = sin θ
⇒ x = cos ( \(\frac { \pi }{ 2 } \) – θ) ………………………. (2)
समी. (1) तथा (2) को जोड़ने पर
sec^-1 x + cosec^-1 x = θ + \(\frac { \pi }{ 2 } \) – θ = \(\frac { \pi }{ 2 } \) यही सिद्ध करना था।

(B) sin^-1 x + cos^-1 x = \(\frac { \pi }{ 2 } \)
माना sin^-1 x = θ ………………….. (1)
⇒ x = sin θ
⇒ x = cos ( \(\frac { \pi }{ 2 } \) – θ)
⇒ cos^-1 x = \(\frac { \pi }{ 2 } \) – θ …………………………. (2)
समी. (1) तथा (2) को जोड़ने पर,
sin^-1 x + cos^-1 x = θ + \(\frac { \pi }{ 2 } \) – θ
⇒ sin^-1 x + cos^-1 x = \(\frac { \pi }{ 2 } \) यही सिद्ध करना था।

(C) tan^-1 x + cot^-1 x = \(\frac { \pi }{ 2 } \)
माना
⇒ tan^-1 x = θ …………………………… (1)
⇒ x = tan θ
⇒ x = cot ( \(\frac { \pi }{ 2 } \) – θ)
⇒ cot^-1 x = \(\frac { \pi }{ 2 } \) – θ ……………………… (2)

प्रश्न 11.
सिद्ध कीजिए कि
(A) tan^-1 5 – tan^-1 3 – tan^-1 \(\frac{1}{8}\)
(B) tan^-1 3 – tan^-1 2 = tan^-1 \(\frac{1}{7}\)
(C) tan^-1 7 – tan^-1 5 = tan^-1 \(\frac{1}{18}\)
हल:
(A) tan^-1 5 – tan^-1 3 = tan^-1 \(\frac{1}{8}\)
L.H.S = tan^-1 5 – tan^-1 3
= tan^-1 \(\frac { 5-3 }{ 1+5.3 } \) = tan^-1 \(\frac{2}{16}\) = tan^-1 \(\frac{1}{8}\)
= R.H.S. यही सिद्ध करना था।

(B) प्रश्न क्रमांक 11 (A) की भाँति हल कीजिये।

(C) प्रश्न क्रमांक 11 (A) की भाँति हल कीजिये।

प्रश्न 12.
सिद्ध कीजिये कि
(A) tan^-1 \(\frac{4}{7}\) – tan^-1 \(\frac{1}{5}\) = tan^-1 \(\frac{1}{3}\)
(B) tan^-1 \(\frac{1}{2}\) – tan^-1 \(\frac{2}{9}\) = tan^-1 \(\frac{1}{4}\)
(C) tan^-1 \(\frac{1}{7}\) + tan^-1 \(\frac{1}{8}\) = tan^-1 \(\frac{3}{11}\)
हल:
(A) tan^-1 \(\frac{4}{7}\) – tan^-1 \(\frac{1}{5}\) = tan^-1 \(\frac{1}{3}\)
L.H.S = tan^-1 \(\frac{4}{7}\) – tan^-1 \(\frac{1}{5}\)
= tan^-1 \(\frac { \frac { 4 }{ 7 } -\frac { 1 }{ 5 } }{ 1+\frac { 4 }{ 7 } .\frac { 1 }{ 5 } } \) = tan^-1 \(\frac{1}{3}\)
= tan^-1 \(\frac{13}{39}\) = tan^-1 \(\frac{1}{3}\)
= R.H.S यही सिद्ध करना था।

(B) प्रश्न क्रमांक 12 (A) की भाँति हल कीजिये।

(C) प्रश्न क्रमांक 12 (A) की भाँति हल कीजिये।

प्रश्न 13.
सिद्ध कीजिए कि
tan^-1 1 + tan^-1 2 + tan^-1 3 = π
हल: L.H.S. = tan^-1 1 + (tan^-1 2 + tan^-1 3)
= tan^-1 (1) + π + tan^-1 ( \(\frac { 2+3 }{ 1-2\times 3 } \) )
[∵ tan^-1 x + tan^-1 y = π + tan^-1 \(\frac { x+y }{ 1-xy } \), यदि x > 0, y > 0, xy > 1, यहाँ xy = 6 > 1]
= tan^-1 (1) + π + tan^-1 ( \(\frac{5}{5-6}\) )
= tan^-1 (1) + π + tan^-1 (-1)
= tan^-1 (1) + π – tan^-1 (1), [∵tan^-1(-x) = – tan^-1 x]
= π = R.H.S
∵ बाएँ पक्ष की राशियाँ धनात्मक कोण बनाती हैं, अतः बायाँ पक्ष शून्य नहीं हो सकता।
अत: बायाँ पक्ष = π = दायाँ पक्ष। यही सिद्ध करना था।

प्रश्न 14.
यदि tan^-1 ( \(\frac{1}{2}\) ) + tan^-1 ( \(\frac{1}{k}\) ) = \(\frac { \pi }{ 4 } \) हो, तो k का मान ज्ञात कीजिए।
हल: tan^-1 ( \(\frac{1}{2}\) ) + tan^-1 ( \(\frac{1}{k}\) ) = \(\frac { \pi }{ 4 } \)

⇒ \(\frac { k+2 }{ 2k-1 } \) = 1
⇒ k + 2 = 2k – 1
⇒ 2 + 1 = 2k – k
⇒ k = 3.

प्रश्न 15.
यदि tan^-1 ( \(\frac{3}{4}\) ) + tan^-1 ( \(\frac{1}{k}\) ) = \(\frac { \pi }{ 4 } \) हो, तो k का मान ज्ञात कीजिए।
हल:
प्रश्न क्रमांक 14 की भाँति हल कीजिये।
[उत्तर – k = 1.]

प्रश्न 16.
यदि tan^-1 ( \(\frac{4}{5}\) ) + tan^-1 ( \(\frac{1}{k}\) ) = \(\frac { \pi }{ 4 } \) हो, तो k का मान ज्ञात कीजिए।
हल:
प्रान क्रमांक 14 की भाँति हल कीजिये।
[उत्तर – k = 9.]

प्रश्न 17.
सिद्ध कीजिए कि
tan^-1 \(\sqrt{x}\) = \(\frac{1}{2}\) cos^-1 ( \(\frac { 1-x }{ 1+x } \) )
हल:
R.H.S. = \(\frac{1}{2}\) cos^-1 ( \(\frac { 1-x }{ 1+x } \) )
माना \(\sqrt{x}\) = tan θ
⇒ x = tan² θ
⇒ \(\frac { 1-x }{ 1+x } \) = \(\frac { 1-tan^{ 2 }\theta }{ 1+tan^{ 2 }\theta } \) = cos 2θ
∴ R.H.S = \(\frac{1}{2}\) cos^-1 (cos 2θ)
= \(\frac{1}{2}\) × 2θ = θ
= tan^-1 ( \(\sqrt{x}\) ), [∵ \(\sqrt{x}\) = tanθ ⇒ tan^-1 ( \(\sqrt{x}\) ) = θ]
= L.H.S. यही सिद्ध करना था।

प्रश्न 18.
सिद्ध कीजिए कि
sin (cos^-1x) = cos (sin^-1x)
हल:
L.H.S.= sin (cos^-1 x)
= sin [ \(\frac { \pi }{ 2 } \) – sin^-1 x], [∵sin^-1 x + cos^-1 x = \(\frac { \pi }{ 2 } \), cos^-1 x = \(\frac { \pi }{ 2 } \) – sin^-1 x] [∵ sin(90° – θ) = cos θ]
= cos (sin^-1 x),
= R.H.S यही सिद्ध करना था।

प्रश्न 19.
(A) सिद्ध कीजिए कि
tan^-1 ( \(\frac { b-c }{ 1+bc } \) ) + tan^-1 ( \(\frac { c-a }{ 1+ca } \) ) + tan^-1 a = tan^-1 b?
हल:
L.H.S = tan^-1 ( \(\frac { b-c }{ 1+bc } \) ) + tan^-1 ( \(\frac { c-a }{ 1+ca } \) ) + tan^-1 a
= tan^-1 b – tan^-1 c + tan^-1 c – tan^-1 a + tan^-1 a
= tan^-1 b = R.H.S. यही सिद्ध करना था।

(B) सिद्ध कीजिए कि
tan^-1 ( \(\frac { a-b }{ 1+ab } \) ) + tan^-1 ( \(\frac { b-c }{ 1+bc } \) ) + tan^-1 c = tan^-1 a?
हल:
L.H.S = tan^-1 ( \(\frac { a-b }{ 1+ab } \) ) + tan^-1 ( \(\frac { b-c }{ 1+bc } \) ) + tan^-1 c
= (tan^-1 a – tan^-1 b) + (tan^-1 b – tan^-1 c) + tan^-1 c
= tan^-1 a = R.H.S. यही सिद्ध करना था।

प्रश्न 20.
समीकरण हल कीजिए –
sin^-1 \(\frac { 2a }{ 1+a^{ 2 } } \) + sin^-1 \(\frac { 2b }{ 1+b^{ 2 } } \) = 2 tan^-1 x?
हल:
दिया गया समीकरण है:
sin^-1 \(\frac { 2a }{ 1+a^{ 2 } } \) + sin^-1 \(\frac { 2b }{ 1+b^{ 2 } } \) = 2 tan^-1 x
⇒ 2 tan^-1 a + 2 tan^-1 b = 2 tan^-1 x, [∵ sin^-1 \(\frac { 2x }{ 1+x^{ 2 } } \) = 2 tan^-1 x]
⇒ tan^-1 a + tan^-1 b = tan^-1 x
⇒ tan^-1 \(\frac { a-b }{ 1+ab } \) = tan^-1 x
x = \(\frac { a-b }{ 1+ab } \)

प्रश्न 21.
समीकरण हल कीजिए –
cos^-1 ( \(\frac { 1-a^{ 2 } }{ 1+a^{ 2 } } \) ) – cos^-1 ( \(\frac { 1-b^{ 2 } }{ 1+b^{ 2 } } \) ) = 2 tan^-1 x?
हल:
दिया गया समीकरण है:
cos^-1 ( \(\frac { 1-a^{ 2 } }{ 1+a^{ 2 } } \) ) – cos^-1 ( \(\frac { 1-b^{ 2 } }{ 1+b^{ 2 } } \) ) = 2 tan^-1 x
⇒ 2 tan^-1 a – 2 tan^-1 = 2 tan^-1 x
⇒ tan^-1 a – tan^-1 b = tan^-1 x
⇒ tan^-1 \(\frac { a-b }{ 1+ab } \) = tan^-1 x
∴ x = \(\frac { a-b }{ 1+ab } \)

प्रश्न 22.
(A) सिद्ध कीजिए –
2 tan^-1 \(\frac{1}{4}\) = tan^-1 \(\frac{8}{15}\)?
हल:
दिया है:
2 tan^-1 \(\frac{1}{4}\) = tan^-1 \(\frac{8}{15}\)
L.H.S = 2 tan^-1 \(\frac{1}{4}\)
= tan^-1 \(\frac { 2.1/4 }{ 1-(1/4)^{ 2 } } \) [∵ 2 tan^-1 x = tan^-1 \(\frac { 2x }{ 1-x^{ 2 } } \) ]
= tan^-1 \(\frac { 1/2 }{ 15/16 } \)
= tan^-1 \(\frac{8}{15}\) = R.H.S यही सिद्ध करना था।

(B) सिद्ध कीजिए –
2 tan^-1 ( \(\frac{1}{2}\) ) = tan^-1 ( \(\frac{4}{3}\) )
हल:
दिया है:
2 tan^-1 ( \(\frac{1}{2}\) ) = tan^-1 ( \(\frac{4}{3}\) )
L.H.S = 2 tan^-1 ( \(\frac{1}{2}\) )

यही सिद्ध करना था।

प्रश्न 23.
सरलतम रूप में लिखिए –
tan^-1 \(\sqrt { \frac { 1-cosx }{ 1+cosx } } \)?
हल:
दिया है:

प्रश्न 24.
सरलतम रूप में लिखिए –
cos^-1 \(\sqrt { \frac { 1 }{ 2 } (1+cosx) } \)?
हल:
दिया है:

प्रश्न 25.
यदि tan^-1 a + tan^-1 b + tan^-1 c = \(\frac { \pi }{ 2 } \) हो, तो सिद्ध कीजिए कि
ab + bc + ca = 1.
हल:
दिया है:
tan^-1 + tan^-1 b + tan^-1 c = \(\frac { \pi }{ 2 } \)
⇒ tan^-1a + tan^-1 b + tan^-1 c = tan^-1 a + cot^-1 a, [∵tan^-1 a + cot^-1 a = \(\frac { \pi }{ 2 } \) ]
⇒ tan^-1 b + tan^-1 c = cot^-1 a
⇒ tan^-1 ( \(\frac { b+c }{ 1-bc } \) ) = tan^-1 ( \(\frac{1}{a}\) )
⇒ \(\frac { b+c }{ 1-bc } \) = \(\frac{1}{a}\)
⇒ ab + ca = 1 – bc
⇒ ab + bc + ca = 1 यही सिद्ध करना था।

प्रश्न 26.
सिद्ध कीजिए –
यही सिद्ध करना था।
tan^-1 \(\frac{2}{11}\) + cot^-1 \(\frac{24}{7}\) = tan^-1 \(\frac{1}{2}\)?
हल:
L.H.S. = tan^-1 \(\frac{2}{11}\) + cot^-1 \(\frac{7}{24}\)
= tan^-1 \(\frac{2}{11}\) + tan^-1 \(\frac{7}{24}\)

= tan^-1 [ \(\frac{125}{250}\) ] = tan^-1 \(\frac{1}{2}\) = R.H.S. यही सिद्ध करना था।

प्रश्न 27.
सिद्ध कीजिए –
cos^-1 x = 2 cos^-1 \(\sqrt { \frac { 1+x }{ 2 } } \)
= 2 cos^-1 \(\sqrt { \frac { 1+cos\theta }{ 2 } } \), ( x = cos θ रखने पर)
= 2 cos^-1 \(\sqrt { \frac { 2cos^{ 2 }\frac { \theta }{ 2 } }{ 2 } } \) = 2. \(\frac { \theta }{ 2 } \)
= cos^-1 x = L.H.S. यही सिद्ध करना था।

प्रश्न 28.
सिद्ध कीजिए –
cos^-1 x = 2 tan^-1 \(\sqrt { \frac { 1-x }{ 1+x } } \)?
हल:
R.H.S = 2 tan^-1 \(\sqrt { \frac { 1-x }{ 1+x } } \)

= 2. \(\frac { \theta }{ 2 } \) = θ = cos^-1 x = L.H.S. यही सिद्ध करना था।

प्रश्न 29.
सिद्ध कीजिए कि
tan^-1 ( \(\frac{a}{b}\) ) – tan^-1 ( \(\frac { a-b }{ a+b } \) ) = \(\frac { \pi }{ 4 } \)?
हल:
L.H.S = tan^-1 ( \(\frac{a}{b}\) ) – tan^-1 ( \(\frac { a-b }{ a+b } \) )

= tan^-1 1
= \(\frac { \pi }{ 4 } \) = R.H.S. यही सिद्ध करना था।

प्रतिलोम त्रिकोणमितीय फलन दीर्घ उत्तरीय प्रश्न – I

प्रश्न 1.
(A) सिद्ध कीजिए कि
sin^-1 \(\frac { 1 }{ \sqrt { 5 } } \) + sin^-1 \(\frac { 1 }{ \sqrt { 10 } } \) = \(\frac { \pi }{ 4 } \)?
हल:
माना sin^-1 \(\frac { 1 }{ \sqrt { 5 } } \) = A, sin^-1 \(\frac { 1 }{ \sqrt { 10 } } \) = B
∴ A + B = \(\frac { \pi }{ 4 } \)
⇒ sin(A + B) = sin \(\frac { \pi }{ 4 } \)
⇒ sinA cosB + cosA sinB = \(\frac { 1 }{ \sqrt { 2 } } \)
L.H.S = sinA \(\sqrt { 1-sin^{ 2 }B } \) + \(\sqrt { 1-sin^{ 2 }A } \). sin B

(B) निम्न समीकरण को हल कीजिए:
sin^-1 x + sin^-1 (1 – x) = sin^-1 \(\sqrt { 1-x^{ 2 } } \)?
हल:
दिया गया समीकरण है:
sin^-1 x + sin^-1 (1 – x) = sin^-1 \(\sqrt { 1-x^{ 2 } } \)

वर्ग करने पर,
x² (2x – x²) = x² (1 – x²)
⇒ x² (2x – x² – 1 + x²) = 0
⇒ x² (2x – 1) = 0
अतः x = 0, \(\frac{1}{2}\).

प्रश्न 2.
(A) सिद्ध कीजिए कि tan^-1 \(\frac { x+1 }{ x } \) – tan^-1 \(\frac { 1 }{ 2x+1 } \) = \(\frac { \pi }{ 4 } \)?
(B) यदि tan^-1 x + tan^-1 y + tan^-1 z = \(\frac { \pi }{ 2 } \) हो, तो सिद्ध कीजिए xy + yz + zx = xyz.
(C) यदि tan^-1 x + tan^-1 y + tan^-1 z = \(\frac { \pi }{ 2 } \), हो, तो सिद्ध कीजिए xy + yz + zx = 1.
हल:
(A) tan^-1 \(\frac { x+1 }{ x } \) – tan^-1 \(\frac { 1 }{ 2x+1 } \) = \(\frac { \pi }{ 4 } \)

= R.H.S. यही सिद्ध करना था।
(B) tan^-1 x + tan^-1 z = π

⇒ x + y + z – xyz = 0 [∵ tan π = 0]
∴ x + y + z = xyz. यही सिद्ध करना था।
(C) प्रश्न क्रमांक 2 (B) की भाँति tan \(\frac { \pi }{ 2 } \) = ∞ = \(\frac{1}{0}\), रखकर विद्यार्थी स्वयं हल करें।

प्रश्न 3.
सरलतम रूप में लिखिए –
tan^-1 [ \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \) ]?
हल:
tan^-1 [ \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \) ]
माना x = tan θ

प्रश्न 4.
(A) सिद्ध कीजिए –
\(\frac{1}{2}\) sin^-1 x = cot^-1 \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \)?
हल:
R.H.S. = cot^-1 \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \)

(B) सिद्ध कीजिए –
\(\frac{1}{2}\) cot^-1 x = cot^-1 ( \(\sqrt { 1+x^{ 2 }+x } \) )?
हल:
\(\frac{1}{2}\) cot^-1 x = cot^-1 ( \(\sqrt { 1+x^{ 2 }+x } \) )
R.H.S. = cot^-1 ( \(\sqrt { 1+x^{ 2 }+x } \) )
माना x = cot θ

प्रश्न 5.
समीकरण को हल कीजिए –
tan^-1 (x + 1) + tan^-1 (x – 1) = tan^-1 ( \(\frac{6}{17}\) )?
हल:
दिया है:
tan^-1 (x + 1) + tan^-1 (x – 1) = tan^-1 ( \(\frac{6}{17}\) )?

⇒ 17x = 6 – 3x²
⇒ 3x² + 18 x – x – 6 = 0
⇒ 3x(x + 6) -1 (x + 6) = 0
⇒ (x + 6) (3x – 1) = 0
∴ x = – 6, x = \(\frac{1}{3}\)

प्रश्न 6.
सिद्ध कीजिए कि cos^-1 \(\frac{3}{5}\) + cos^-1 \(\frac{4}{5}\) = \(\frac { \pi }{ 2 } \)?
हल:
दिया है:
L.H.S = cos^-1 \(\frac{3}{5}\) + cos^-1 \(\frac{4}{5}\)

प्रश्न 7.
यदि cos^-1 x + cos^-1 y + cos^-1 z = π हो, तो सिद्ध कीजिए कि
x² + y² + z² + 2xyz = 1
हल:
दिया है:
cos^-1 x + cos^-1 y + cos^-1 z = π

दोनों पक्षों का वर्ग करने पर,
x²y² + z² + 2xyz = (1 – x²) (1 – y²)
⇒ x²y² + z² + 2xyz = 1 – y² – x² + x²y²
⇒ z² + 2xyz = 1 – y² – x²
⇒ x² + y² + z² + 2xyz = 1. यही सिद्ध करना था।

प्रश्न 8.
यदि sin^-1 \(\frac { 2a }{ 1+a^{ 2 } } \) – cos^-1 \(\frac { 1-b^{ 2 } }{ 1+b^{ 2 } } \) = tan^-1 \(\frac { 2x }{ 1-x^{ 2 } } \) हो, तो सिद्ध कीजिए कि x = \(\frac { a-b }{ 1+ab } \)?
हल:
यहाँ sin^-1 \(\frac { 2a }{ 1+a^{ 2 } } \) – cos^-1 \(\frac { 1-b^{ 2 } }{ 1+b^{ 2 } } \) = tan^-1 \(\frac { 2x }{ 1-x^{ 2 } } \) ………………………….. (1)
माना a = tan θ, b = tan ∅, x = tan Ψ
समी. (1) में इन मानों को रखने पर,

⇒ sin^-1 (sin 2θ) – cos^-1 (cos 2∅) = tan^-1 (tan 2Ψ)
⇒ 2θ – 2∅ = 2Ψ
⇒ θ – ∅ = Ψ
⇒ tan^-1 a – tan^-1 b = tan^-1 x
⇒ tan^-1 ( \(\frac { a-b }{ 1+ab } \) ) = tan^-1 x
⇒ x = \(\frac { a-b }{ 1+ab } \). यही सिद्ध करना था।

प्रश्न 9.
सिद्ध कीजिए कि
tan^-1 \(\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}}\) = \(\frac { \pi }{ 4 } \) – \(\frac{1}{2}\) cos¹ x
हल:
माना कि x = cos θ, तब θ = cos^-1 x

प्रश्न 10.
सरलतम रूप में लिखिये –
tan^-1 ( \(\frac { x }{ \sqrt { 1+x^{ 2 }-1 } } \) )?
हल:
tan^-1 ( \(\frac { x }{ \sqrt { 1+x^{ 2 }-1 } } \) ) में x = tan θ रखने पर,

प्रश्न 11.
सिद्ध कीजिए कि –
tan^-1 \(\sqrt{x}\) = \(\frac{1}{2}\) cos^-1 ( \(\frac { 1-x }{ 1+x } \) ) (NCERT)
हल:
R.H.S. = \(\frac{1}{2}\) cos^-1 ( \(\frac { 1-x }{ 1+x } \) )

माना \(\sqrt{x}\) = tan θ
तब, θ = tan^-1 \(\sqrt{x}\)
= \(\frac{1}{2}\) cos^-1 ( \(\frac { 1-tan^{ 2 }\theta }{ 1+tan^{ 2 }\theta } \) )
= \(\frac{1}{2}\) cos^-1 (cos 2θ), [∵ cos^-1 (cos x) = x]
= \(\frac{1}{2}\) × 2θ
= θ
= tan^-1 \(\sqrt{x}\), [समी. (1) से]
= L.H.S. यही सिद्ध करना था।

प्रश्न 12.
सिद्ध कीजिए कि –
tan^-1 \(\frac { 6x-8x^{ 3 } }{ 1-12x^{ 2 } } \) – tan^-1 \(\frac { 4x }{ 1-4x^{ 2 } } \) = tan^-1 2x, जहाँ |2x| < \(\frac { 1 }{ \sqrt { 3 } } \) (CBSE 2016)
हल:
L.H.S. = tan^-1 \(\frac { 6x-8x^{ 3 } }{ 1-12x^{ 2 } } \) – tan^-1 \(\frac { 4x }{ 1-4x^{ 2 } } \)
= tan^-1 \(\frac { 3(2x)-(2x)^{ 3 } }{ 1-3(2x)^{ 2 } } \) – tan^-1 \(\frac { 2\times 2x }{ 1-(2x)^{ 2 } } \)
माना 2x = tanθ
तब,
θ = tan^-1 2x

= 3θ – 2θ = θ
= tan^-1 2x [समी. (1) से]
= R.H.S. यही सिद्ध करना था।

प्रश्न 13.
सिद्ध कीजिए कि –
cos^-1 \(\frac{4}{5}\) + cos^-1 \(\frac{12}{13}\) = cos^-1 \(\frac{33}{65}\)?
हल:
L.H.S. = cos^-1 \(\frac{4}{5}\) + cos^-1 \(\frac{12}{13}\)

MP Board Class 12 Maths Important Questions

MP Board Class 12th Maths Important Questions Chapter 1 संबंध एवं फलन

संबंध एवं फलन Important Questions

संबंध एवं फलन वस्तुनिष्ठ प्रश्न

प्रश्न 1.
सही विकल्प चुनकर लिखिए –

प्रश्न 1.
मान लीजिए कि f (x) = 8x द्वारा परिभाषित फलन f : R → R फलन है –
(a) f एकैकी आच्छादक है
(b) f बहुएक आच्छादक है
(c) f एकैकी है परन्तु आच्छादक नहीं है
(d) f न तो एकैकी है और न आच्छादक है।
उत्तर:
(a) f एकैकी आच्छादक है

प्रश्न 2.
फलन f(x) = \(\frac { e^{ x^{ 2 } }-e^{ -x^{ 2 } } }{ e^{ x^{ 2 } }+e^{ -x^{ 2 } } } \) द्वारा परिभाषित फलन f : R → R है –
(a) f एकैकी है परन्तु आच्छादक नहीं है
(b) f एकैकी आच्छादक है
(c) f न तो एकैकी है और न आच्छादक है
(d) f बहुएक आच्छादक है।
उत्तर:
(a) f एकैकी है परन्तु आच्छादक नहीं है

प्रश्न 3.
यदि f : R → R, f(x) = (3 – x³)^1/3 द्वारा प्रदत्त है तो fof(x) बराबर हैं –
(a) x^1/3
(b) x³
(c) x
(d) (3 – x³)
उत्तर:
(c) x

प्रश्न 4.
a * b = a³ + b³ प्रकार से परिभाषित N में एक द्विआधारी संक्रिया * पर विचार कीजिए –
(a) * साहचर्य तथा क्रमविनिमेय दोनों है
(b) * क्रमविनिमेय है, किन्तु साहचर्य नहीं है
(c) * साहचर्य है, किन्तु क्रमविनिमेय नहीं है
(d) * न तो क्रमविनिमेय है और न साहचर्य है।
उत्तर:
(b) * क्रमविनिमेय है, किन्तु साहचर्य नहीं है

प्रश्न 5.
समुच्चय {a, b} में द्विआधारी संक्रियाओं की संख्या है –
(a) 10
(b) 16
(c) 20
(d) 8
उत्तर:
(b) 16

प्रश्न 2.
रिक्त स्थानों की पूर्ति कीजिए –

1. यदि A = {1, 2, 3} हो, तो अवयव (1, 2) वाले तुल्यता सम्बन्धों की संख्या ……………………………….. होगी।
2. यदि f : R → R जहाँ f(x) = 5x – 7, ∀x ∈ R तो f^-1(7) का मान ………………………….. होगा।
3. यदि f : R → R तथा f(x) = x² – 3x + 2 से परिभाषित है, तो f(f(x)) का मान …………………………….. होगा।
4. यदि f : R → R; f (x) = 2x + 5 द्वारा परिभाषित है तब f^-1(y) का मान …………………………….. होता है।
5. f(x) = x³ द्वारा प्रदत्त फलन f : R → R …………………………. है।

उत्तर:

1. 2
2. 0
3. x⁴ – 6x³ + 10x² – 3x
4. \(\frac{1}{2}\) (y-5)
5. एकैकी है।

प्रश्न 3.
निम्न कथनों में सत्य/असत्य बताइए –

1. माना कि समुच्चय A = {1, 2, 3} पर एक सम्बन्ध R= {(1, 3), (3, 1), (3, 3)} है। तब R सममित, संक्रामक है, किन्तु स्वतुल्य नहीं है।
2. यदि f : A → B एकैकी आच्छादक फलन हो, तो f का प्रतिलोम f^-1 अद्वितीय होता है।
3. फलनों का संजोयन क्रमविनिमेयी होता है।
4. प्रत्येक फलन व्युत्क्रमणीय होता है।
5. माना कि समुच्चय Q⁺ पर एक द्विआधारी संक्रिया ^*, a * b = \(\frac{ab}{3}\), ∀a, b ∈ Q⁺ से परिभाषित है, तब 4 * 6 का प्रतिलोम \(\frac{9}{8}\) है।

उत्तर:

1. असत्य
2. सत्य
3. असत्य
4. असत्य
5. सत्य।

प्रश्न 4.
एक शब्द/वाक्य में उत्तर दीजिए –

1. समुच्चय A = {a, b, c} पर तत्समक संबंध लिखिए।
2. फलन f(x) = \(\frac { \left| x-1 \right| }{ x-1 } \) का परिसर क्या है?
3. फलन f(x) = \(\sqrt { 25-x^{ 2 } } \) से परिभाषित वास्तविक फलन का प्रान्त लिखिए।
4. माना कि एक द्विआधारी संक्रिया *, a * b = 3a + 4b – 2 से परिभाषित है तब 4 * 5 ज्ञात कीजिए।
5. माना कि f.g: R → R क्रमशः f(x) = 2x +1 और g(x) = x² – 2, ∀x ∈ R से परिभाषित है। तब gof (x) ज्ञात कीजिए।

उत्तर:

1. {(a, a), (b, b), (c, c)}
2. {-1, 1}
3. [-5, 5]
4. 30
5. 4x² + 4x – 1.

संबंध एवं फलन दीर्घ उत्तरीय प्रश्न – I

प्रश्न 1.
सिद्ध कीजिए कि पूर्णांकों के समुच्चय z में R = { (a, b ) : संख्या 2, (a – b) को विभाजित करती है } द्वारा प्रदत्त संबंध एक तुल्यता संबंध है। (NCERT)
हल: समस्त a ∈ Z के लिए 2,(a – a) को विभाजित करेगा अर्थात् (a, a) ∈ R अत: R स्वतुल्य है।
माना (a,b) ∈ R ⇒ 2, (a – b) को विभाजित करता है
⇒ 2,- (b – a) को विभाजित करता है
(a,b) ∈ R ⇒ (b,a) ∈ R
अत: R, सममित है।
माना (a,b) ∈ R = 2,(a – b) को विभाजित करता है।
(b, c) ∈ R → 2,(b – c) को विभाजित करता है।
a – b तथा b – C, 2 से भाज्य है
a – b + b – c, भी 2 से भाज्य है
अर्थात् a – c भी 2 से भाज्य है
इसलिए (a,b) ∈ R, (b,c) ∈ R ⇒ (a,c) ∈ R
अत: R संक्रमक है। अतः R, स्वतुल्य, सममित तथा संक्रमक है अतः यह एक तुल्यता संबंध है। यही सिद्ध करना था।

प्रश्न 2.
मान लीजिए कि समुच्चय A = {1, 2, 3, 4, 5, 6, 7} में R = {(a, b): a तथा b दोनों ही या तो विषम है या सम है } द्वारा परिभाषित एक संबंध है। सिद्ध कीजिए कि R एक तुल्यता संबंध है। साथ ही सिद्ध कीजिए कि उपसमुच्चय {1, 3, 5, 7} के सभी अवयव एक-दूसरे से संबंधित हैं और उपसमुच्चय {2, 4, 6} के सभी अवयव एक-दूसरे से संबंधित हैं। परंतु उपसमुच्चय {1, 3, 5, 7} का कोई भी अवयव उपसमुच्चय {2, 4, 6} के किसी भी अवयव से संबंधित नहीं है। (NCERT)
हल: A का दिया गया कोई अवयव a या तो विषम है या सम है अतः (a, a) ∈ R अत: R स्वतुल्य है।
माना (a,b) ∈ R ⇒ a तथा b दोनों ही या तो विषम है या सम है।
⇒ b तथा a दोनों ही या तो विषम है या सम है।
(a,b) ∈ D (b, a) ∈ R
अत: R सममित है।
(a,b) ∈ R तथा (b, c) ∈ R ⇒ अवयव a, b, c सभी या तो विषम हैं या सम हैं।
(a,b) ∈ R तथा (b, c) ∈ R = (a,c) ∈ R
अत: R संक्रमक है।
यहाँ R, स्वतुल्य, सममित तथा संक्रमक है इसलिए R एक तुल्यता संबंध है। यही सिद्ध करना था।
पुनः {1, 3, 5, 7} के सभी अवयव एक – दूसरे से संबंधित हैं क्योंकि इस उपसमुच्चय के सभी अवयव विषम हैं।
इसी प्रकार {2, 4, 6} के सभी अवयव एक – दूसरे से संबंधित हैं क्योंकि ये सभी सम हैं साथ ही उपसमुच्चय {1, 3, 5, 7} का कोई भी अवयव {2, 4, 6} के किसी भी अवयव से संबंधित नहीं हो सकता क्योंकि {1, 3, 5, 7} के अवयव विषम हैं जबकि {2, 4, 6} के अवयव सम हैं।

प्रश्न 3.
माना कि N प्राकृत संख्याओं का समुच्चय है। यदि समुच्चय N × N में परिभाषित एक संबंध R ऐसा हो कि (a, b) R (c, d) यदि ad (b + c) = bc (a + d) तो सिद्ध कीजिए कि R एक तुल्यता संबंध है। (CBSE 2015)
हल: स्वतुल्यता: प्रत्येक (a, b) ∈ N × N के लिए
ab (b + a) = ba (a + b)
⇒ (a, b) R (a, b)
अत: R स्वतुल्य होगा।
सममितता: माना (a, b)(c, d) ∈ N × N
(a, b) R (c, d) ⇒ ab(b + c) = bc(a + d)
⇒ bc (a + d) = ab (b + c)
(a,b) R (c,d) ⇒ (c, d) R (a, b)
अत: R सममित होगा।
उत्तर संक्रमकता: माना (a, b) R (c, d ) तथा (c, d) R (e, f)
⇒ ad ( b + c) = bc (a + d)
तथा cf (d + e) = de (c + f)

⇒ af (b + e) = bc (a + f)
(a, b) R (c, d) तथा (c, d) R (e, f) ⇒ (a, b) R (e, f)
अत: R संक्रमक है।
R, स्वतुल्य, सममित तथा संक्रमक है अत: R एक तुल्यता संबंध है। यही सिद्ध करना था।

प्रश्न 4.
माना A = {1, 2, 3, 4, 5} तथा R = {(a,b): |a – b| 2 से विभाजित है} तो सिद्ध कीजिए कि R एक तुल्यता संबंध है तथा तुल्यता वर्ग भी बनाइए।
हल: A = { 1, 2, 3, 4, 5 }
R = { (a, b) : |a – b| 2 से विभाजित है }
R = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (1, 3), (1, 5), (2, 4), (3, 5), (3, 1) (5, 1), (4, 2),(5, 3)}
∀ a ∈ A (a,a) ∈ R
इसलिए R स्वतुल्य होगा।
क्योंकि (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) ∈ R
(a,b) ∈ R ⇒ (b,a) ∈ R
(1, 3), (1, 5), (2, 4), (3, 5), (3, 1), (5, 1), (4, 2), (5, 3) ∈ R
इसलिए R सममित है।
∀ (a, b) ∈ R,(b, c) ∈ R ⇒ (a, c) ∈ R
क्योंकि (1, 3)(3, 1) ∈ R = (1, 1) ∈ R
R संक्रमक है।
R, स्वतुल्य, सममित तथा संक्रमक है इसलिए R एक तुल्यता संबंध है।
यही सिद्ध करना था।
तुल्यता वर्ग
[1] = { a : a तथा 2 |a – 1| से विभाजित है}
[1] = {a : a ∈ A तथा a – 1 = 2 k}
[1] = {1, 3, 5}
[2] = { a : a तथा 2, |a – 2| से विभाजित है}
[2] = {a : a तथा a – 2 = 2k}
[2] = {2, 4}.

प्रश्न 5.
मान लीजिए कि समस्त n ∈ N के लिए।

द्वारा परिभाषित एक फलन f : N → N है। बताइए कि क्या फलन f एकैकी आच्छादक है। अपने उत्तर का औचित्य भी बताइए। (NCERT)
हल: f : N → N में,

यहाँ f (1) = f (2) ⇒ 1 ≠ 2
डोमेन के दो अवयव 1 और 2 का सह – डोमेन में एक ही प्रतिबिम्ब 1 है।
अत: f एकैकी फलन नहीं है।

स्थिति I.
जब n विषम हो
n = 2r + 1, r ∈ N
तब 4r + 1 ∈ N इस प्रकार विद्यमान है कि
f (4r + 1) = \(\frac { 4r+1+1 }{ 2 } \) = \(\frac { 4r+2 }{ 2 } \) = 2r + 1
स्पष्ट है सह – डोमेन के प्रत्येक अवयव का डोमेन में पूर्व प्रतिबिम्ब है इसलिए / आच्छादक फलन है।

स्थिति II.
माना n = 2r (सम संख्या)
तब 4r ∈ N इस प्रकार विद्यमान है कि
f(4r) = \(\frac{4r}{2}\) = 2r
स्पष्ट है सह – डोमेन के प्रत्येक अवयव का डोमेन में पूर्व प्रतिबिम्ब है इसलिए f आच्छादक फलन है।
अतः f एकैकी आच्छादक फलन नहीं है।

प्रश्न 6.
मान लीजिए कि A = R – {3} तथा B = R – {1} है। f(x) = \(\frac { x-2 }{ x-3 } \) द्वारा परिभाषित फलन f : A → B पर विचार कीजिए। क्या f एकैकी तथा आच्छादक है? अपने उत्तर का औचित्य भी बताइए। (NCERT)
हल:
f : A → B, f (x) = \(\frac { x-2 }{ x-3 } \), A = R – {3} तथा B = R – {1}
मान लीजिए x, y∈A इस प्रकार है कि
f (x) = f (y)
⇒ \(\frac { x-2 }{ x-3 } \) = \(\frac { y-2 }{ y-3 } \)
⇒ (x – 2) (y – 3) = (y – 2) (x – 3)
⇒ xy – 3x – 2y + 6 = xy – 3y – 2x + 6
⇒ -3x – 2y = -3y – 2x
⇒ 3x – 2x = 3y – 2y
⇒ x = y
यहाँ f (x) = f (y) ⇒ x = y
अतः f एकैकी फलन है।
f आच्छादक फलन होगा यदि x∈A इस प्रकार विद्यमान है कि f(x) = y
\(\frac { x-2 }{ x-3 } \) = y
⇒ x – 2 = y (x – 3)
⇒ x – 2 = xy – 3y
⇒ xy – x = 3y – 2
⇒ x = \(\frac { 3y-2 }{ y-1 } \)∈A
प्रत्येक y ∈ B के लिए x ∈ A
f (x) = f ( \(\frac { 3y-2 }{ y-1 } \) )

∵ f(x) = y
अतः f अचधक पालन है।
अतः f एकोकी अचधक पालन है।

प्रश्न 7.
सिद्ध कीजिए कि नीचे परिभाषित फलन f : N → N एकैकी तथा आच्छादक दोनों ही।

हल: माना f (x₁) = f (x₂)
यदि x, विषम तथा x, सम है, तब
x₁ + 1 = x₂ – 1
X₁ – x₂ = -2
जो कि असंभव है।
इस प्रकार x₁ के सम तथा x₂ के विषम होने की संभावना नहीं है।
इसलिए x₁ तथा x₂, दोनों ही या तो सम होंगे या विषम होंगे।
माना x₁, x₂ दोनों विषम हैं।
f (x₁) = f (x₂)
⇒ x₁ – 1 = x₂ – 1
⇒ x₁ = x₂
अतः f एकैकी है।
सहप्रांत N की कोई भी विषम संख्या 2r + 1 प्रांत N की संख्या 2r + 2 का प्रतिबिंब है और सहप्रांत N की कोई भी सम संख्या 27, N की संख्या 2r – 1 का प्रतिबिंब है।
अतः f आच्छादक है। यही सिद्ध करना था।

प्रश्न 8.
f (x) = 4x + 3 द्वारा प्रदत्त फलन f: R → R पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्क्रमणीय है। f का प्रतिलोम फलन भी ज्ञात कीजिए? (NCERT)
हल: f : R → R, f (x) = 4x + 3
फलन का डोमेन तथा सह – डोमेन R है।
माना x, y ∈ R इस प्रकार है कि
f (x) = f (y)
4x + 3 = 4y + 3
⇒ 4x = 4y
⇒ x = y
इस प्रकार f (x) = f (y)
⇒ x = y
अतः f एकैकी है।
माना कि सह – डोमेन R का कोई अवयव y है
y = f (x)
y = 4x + 3
⇒ 4x = y – 3
⇒ x = \(\frac { y-3 }{ 4 } \)
∴ f^-1(y) = \(\frac { y-3 }{ 4 } \) तथा f^-1(x) = \(\frac { x-3 }{ 4 } \)

प्रश्न 9.
मान लीजिए कि y = {n² : n ∈ N}⊂N है। फलन f : N → y, जहाँ f (n) = n² पर विचार कीजिए। सिद्ध कीजिए कि व्युत्क्रमणीय है। का प्रतिलोम भी ज्ञात कीजिए। (NCERT)
हल:
y = f(n) = n²
n = \(\sqrt{y}\)
इससे g (y) = \(\sqrt{x}\) द्वारा परिभाषित फलन g : y → N प्राप्त होता है।
gof (n) = g [f (n)]
= g [n²]
= \(\sqrt { n^{ 2 } } \) [g(n) = \(\sqrt{n}\), g(n²) = \(\sqrt { n^{ 2 } } \) = n]
(gof) n = n
तथा
(fog)y = f [g(y)]
= f[ \(\sqrt{y}\) ], [f(n) = n², f( \(\sqrt{y}\) ) = ( \(\sqrt{y}\) )² = y]
= y
स्पष्ट है कि gof = I_n तथा fog = I_y
अतः f व्युत्क्रमणीय है तथा f^-1 = g.
यही सिद्ध करना था।

प्रश्न 10.
यदि f : R → R तथा g : R → R फलन क्रमशः f (x) = cosx तथा g(x) = 3x² द्वारा परिभाषित है, तो gof और fog ज्ञात कीजिए। सिद्ध कीजिए कि gof ≠ fog? (NCERT)
हल: दिया है: f(x) = cosx
g (x) = 3x²
(gof) x = g [f (x)]
(gof) x = g [cost]
दिया है:
f (x) = cosx ……………………….. (1)
g (x) = 3x²
g (cosx) = 3 cos²x ……………………………. (2)
समी. (1) और (2) से,
(gof )x = 3cos²x
(fog) x = f [g(x)]
= f [3x²] ………………………………… (3)
दिया है:
g (x) = 3x²
f (x) = cosx
f [3x²] = cos3x²
समी. (3) और (4) से,
(fog) x = cos3x²
x = 0 के लिए
3cos²x ≠ cos3x²
अतः gof ≠ fog. यही सिद्ध करना था।

प्रश्न 11.
f: {1,2,3} → {a,b,c}, f(1) = a, f(2) = b, f(3) = c द्वारा प्रदत्त फलन f पर विचार कीजिए-ज्ञात कीजिए ओर सिद्ध कीजिए कि (f^-1)^-1 = f है। (NCERT)
हल: दिया गया है:
f: {1, 2,3} → { a, b, c}
f(1) = a, f (2) = b, f (3) = c
माना g : { a, b, c } → {1, 2, 3} में
g (a) = 1, g (b) = 2, g (c) = 3
(fog) a = f [g (a)]
= f [1] = a
(fog) b = f [g (b)]
= f (2) = b
(fog) c = f [g (c)]
= f (3) = c
तथा (gof) (1) = g [f (1)]
= g (a) = 1
(gof) (2) = g [f(2)]
= g (b) = 2
(gof) (3) = g [f (3)]
= g (c) = 3
अत: gof = I_x, तथा fog = I_y
जहाँ x = {1, 2, 3} तथा y = {a, b, c}
f का प्रतिलोम विद्यमान है तथा।
तथा f^-1 = g
∴ f^-1 {a, b, c} → {1, 2, 3} में,
f^-1 (a) = 1, f^-1(b) = 2, f^-1(c) = 3
अतः f^-1 का प्रतिलोम अथरिथ का प्रतिलोम जात करेंगे
माना h: {1, 2, 3} → {a, b, c}
h(1) = a, h(2) = b, h(3) = c
(goh) 1 = g[h(1)] = g(a) = 1
(goh) 2 = g[h(2)] = g(b) = 2
(goh) 3 = g[h(3)] = g(c) = 3
तथा (hog) a = h[g(a)] = h(1) = a
(hog) b = h [ g(b)] = h(2) = b
(hog) c = h[g(c)] = h(3) = c
अत: goh = I_x तथा hog = I_y
जहाँ x = {1, 2, 3} तथा y = {a, b, c}
g का प्रतिलोम विद्यमान है तथा g^-1 = h = (f^-1)^-1 = f
अत: h = f
∴ (f^-1)^-1 = f यही सिद्ध करना था।

प्रश्न 12.
सिद्ध कीजिए कि समस्त बहुभुजों के समुच्चय A में R = { (P₁, P₂ ) : P₁ तथा P₂ की भुजाओं की संख्या समान है।} प्रकार से परिभाषित संबंध R एक तुल्यता संबंध है। 3, 4 और 5 की भुजाओं वाले समकोण त्रिभुज से संबंधित समुच्चय A के सभी अवयवों का समुच्चय ज्ञात कीजिए। (NCERT)
हल: दिया है:
A = समस्त बहुभुजों का समुच्चय
R = {(P₁, P₂) : P₁, तथा P₂ की भुजाओं की संख्या समान है।
प्रत्येक बहुभुज P में भुजाओं की संख्या, बहुभुज P की भुजाओं की संख्या के बराबर है।
∴ (P, P) ∈ R, ∀P∈A
माना (P₁,P₂)∈R ⇒ बहुभुज P₁ तथा P₂ मे भुजाओं की संख्या समान हैं।
⇒ बहुभुज P₂ तथा बहुभुज P₁ में भुजाओं की संख्या समान हैं।
अत: R संक्रमक संबंध है।
R, स्वतुल्य, सममित तथा संक्रमक है।
अतः R एक तुल्यता संबंध है।
भुजाओं 3, 4 तथा 5 वाले समकोण त्रिभुज से वह बहुभुज संबंधित होगा जिसमें भुजाओं की संख्या तीन होगी। इसलिए भुजाओं 3, 4 तथा 5 वाले समकोण त्रिभुज से संबंधित बहुभुज त्रिभुज है। यही सिद्ध करना था।

प्रश्न 13.
यदि f(x) = \(\frac { 4x+3 }{ 6x-4 } \), x ≠ \(\frac{2}{3}\) हो, तो सिद्ध कीजिए कि सभी x ≠ \(\frac{2}{3}\) के लिए fof(x) = xहै। f का प्रतिलोम फलन क्या है? (NCERT)
हल:
f (x) = \(\frac { 4x+3 }{ 6x-4 } \)
fof (x) = f {f (x)}
f{ \(\frac { 4x+3 }{ 6x-4 } \) }

माना f का प्रतिलोम फलान f^-1(x) = y हैं।
तब f (y) = x
∴ \(\frac { 4y+3 }{ 6y-4 } \) = x
⇒ 4y + 3 = 6xy – 4x
⇒ 6xy – 4y = 3 + 4x
⇒ y (6x – 4) = 3 + 4x
⇒ y = \(\frac { 3+4x }{ 6x-4 } \)
⇒ f^-1 (x) = \(\frac { 3+4x }{ 6x-4 } \) = f(x)
∴ f^-1 = f.

प्रश्न 14.
सिद्ध कीजिए कि f : [-1, 1] → R, f (x) = \(\frac { x }{ x+2 } \) द्वारा प्रदत्त फलन एकैकी है। फलन f : [-1, 1] → (f का परिसर) का प्रतिलोम फलन ज्ञात कीजिए। (NCERT)
हल: f (x) = \(\frac { x }{ x+2 } \)
f : [-1, 1] → R
यहाँ, f (x) = f (y)
⇒ \(\frac { x }{ x+2 } \) = \(\frac { y }{ y+2 } \)
⇒ xy + 2x = xy + 2y
⇒ 2x = 2y
⇒ x = y यही सिद्ध करना था।
∴ f एकैकी है।
माना f^-1 (x) = y
∴ f (y) = x
⇒ \(\frac { y }{ y+2 } \) = x
⇒ y = xy + 2x
⇒ y (1 – x) = 2x
∴ y = \(\frac { 2x }{ 1-x } \)
⇒ f^-1(x) = \(\frac { 2x }{ 1-x } \)

प्रश्न 15.
यदि f (x) = \(\frac { x }{ 1+|x| } \), ∀ x ∈ R जहाँ -1 < x < 1, तो gof तथा fog ज्ञात कीजिए। दिखाइए कि fog = gof?
हल: दिया है,
f (x) = \(\frac { x }{ 1+|x| } \)
g (x) = \(\frac { x }{ 1-|x| } \)
∴ fog (x) = f {g(x)}
= f ( \(\frac { x }{ 1-|x| } \) )

= x ………………….. (2)
fog = gof
यही सिद्ध करना था।

प्रश्न 16.
तीन फलन f : N → N, g : N → N तथा h : N → R पर विचार कीजिए f (x) = 2x, g (y) = 3y + 4, तथा h (z) = sin z ∀ x, y तथा z ∈ N सिद्ध कीजिये की ho(gof)n = (hog)of? (NCERT)
हल:
ho(gof) x = h[gof(x)]
= h {g[f(x)}
= h (g (2x))
= h [3(2x) + 4]
= h [6x + 4]
= sin (6x + 4) ………………………… (1)
इसी प्रकार ((hog)of) x = (hog) f(x)
= (hog) 2x
= h (g (2x))
= h [3 (2x) + 4]
= h [6x + 4]
= sin (6x + 4)
समी, (1) और (2) से स्पस्ट है की
ho(gof) = (hog)of. यही सिद्ध करना था।

MP Board Class 12 Maths Important Questions

MP Board Class 11th Maths Important Questions Chapter 2 Relations and Functions

Relations and Functions Important Questions

Relations and Functions Objective Type Questions

(A) Choose the correct option :

Question 1.
If A = {2, 4, 5}, B = {7, 8, 9}, then n(A × B) =
(a) 6
(b) 9
(c) 3
(d) 0.
Answer:
(b) 9

Question 2.
If A = { 1, 2, 3, 4, 5} and 5 = {2, 3, 6, 7}, then the number of element in (A × B)∩(B × A) is:
(a) 4
(b) 5
(c) 10
(d) 20.
Answer:
(a) 4

Question 3.
If A and B are two non – empty sets, then:
(a) A × B = {(a, b) : a ∈ B, b ∈ A}
(b) A × B = {(a, b) : a ∈ A, b ∈ B}
(c) {(a, b) : (a, b) ∈ A, (a, b) ∈ B}
(d) None of these.
Answer:
(b) A × B = {(a, b) : a ∈ A, b ∈ B}

Question 4.
If f(x) = log \(\frac { 1+x }{ 1-x } \), then find f [ \(\frac { { 2x } }{ 1+{ x }^{ 2 } }\) ] =
(a) [f(x)]²
(b) [f(x)]³
(c) 2 f(x)
(d) 3 f(x).
Answer:
(c) 2 f(x)

Question 5.
Let A = {1,2} and B = {3,4}, then the number of relation from A to B will be:
(a) 2
(b) 4
(c) 8
(d) 16
Answer:
(d) 16

Question 6.
The range of the function f(x) = \(\sqrt { x-1 } \) is:
(a) [1, ∞)
(b) [0, ∞)
(c) (0, ∞)
(d) (1, ∞)
Answer:
(b) [0, ∞)

Question 7.
If f(x) = \(\frac { x^{ 2 }-1 }{ x^{ 2 }+1 } \), then f ( \(\frac{1}{x}\) ) is:
(a) f(x)
(b) – f(x)
(c) f(-x)
(d) \(\frac { 1 }{ f(x) } \)
Answer:
(b) – f(x)

Question 8.
Domain of the function f(x) = \(\frac { 1 }{ \sqrt { 2x-3 } } \) is:
(a) R – { \(\frac{3}{2}\) }
(b) ( \(\frac{3}{2}\), ∞)
(c) [ \(\frac{3}{2}\), ∞)
(d) None of these.
Answer:
(b) ( \(\frac{3}{2}\), ∞)

(B) Match the following :

Answer:

1. 1. (d)
   2. (a)
   3. (c)

1. (b)
2. (c)

(C) Fill in the blanks:

1. If A = {1, 2} and B = {3, 4, 5}, then the number of subsets of A × B is ………………………….
2. Range of the function f = {(2, 1), (3, 1), (4, 1), (5, 1)} is …………………………..
3. Range of the function f(x) = 11 – 7 sinx is …………………………..
4. If f(x) = x² and g(x) = x + 1, ∀ x ∈ R , then (f + g)x is …………………………
5. If f(x) = 1 – cosx, then the value of f ( \(\frac { \pi }{ 4 } \) ) …………………………….
6. Domain of the function f(x) = \(\frac { 1 }{ \sqrt { (1 – x)(x – 2) } } \) is ……………………………
7. If relation R = {(1, 3), (3, 3), (4, 5)} then the value of R^-1 is ……………………………

Answer:

1. 64
2. {1}
3. [4, 18]
4. x² + x + 1
5. 1 – \(\frac { 1 }{ \sqrt { 2 } } \)
6. (1, 2)
7. {(3, 1), (3, 3), (5, 4)}.

(D) Write true/false :

1. If A, B, C are three sets, then the value of A × (B∪C) is (A∪B) × (A∪C).
2. If A = {x : x² – 5x + 6 = o}, B = {2,4}, C = {4,5}, then A × (B∩C) = {(2, 4), (3, 4)}.
3. The relation R = {(2, 1), (3, 2), (4, 3), (5, 4)} is a function.
4. If a relation on Z is R = {(x, y) : x, y ∈ Z, x² + y² ≤ 4}, then domain of R is {0, ± 1, ± 2}.
5. Domain of the function f(x) = \(\sqrt { a^{ 2 }-x^{ 2 } } \), a > 0 is [0, a].

Answer:

1. False
2. True
3. True
4. True
5. False

(E) Write answer in one word/sentence:

1. If f(x) = x² and g(x) = x + 3, x ∈ R, then the value of (fog)(2).
2. Range of function f(x) = sin x.
3. If mapping f : R → R is defmd by f(x) = x² + 1 the value of f^-1 (26) is:
4. If A = {1, 2, 3} and B = {5, 7}, then the value of A×B is:
5. Domain of the function f(x) = \(\sqrt { 3-2x } \) is:
6. If function f(x) = \(\frac { { x }^{ 2 } }{ 1-{ x }^{ 2 } }\), then the value of f(sin θ) is :

Answer:

1. 25
2. [-1, 1]
3. {-5, 5}
4. {(1, 5), (1, 7), (2, 5), (2, 7), (3, 5), (3, 7)}
5. (-∞, \(\frac { 3 }{ 2 }\))
6. tan² θ

Straight Lines Very Short Answer Type Questions

Question 1.
If the set A has 3 elements and the set B = {3, 4, 5}, then find the number of elements in ( A x B). (NCERT)
Solution:
Given : n(A) = 3, B = {3, 4, 5}, n (B) = 3
∴ n (A x B) = n (A) x n (B) = 3 x 3
⇒ n (A x B) = 9.

Question 2.
If G = {7, 8} and H = {5, 4, 2}, then find G x H. (NCERT)
Solution:
G x H = { 7, 8} x {5, 4, 2}
G x H= { (7, 5), (7, 4), (7, 2), (8, 5), (8, 4), (8, 2)}.

Question 3.
If A x B = { (a, x), (a, y), (b, x), (b, y)} then find A and 5. (NCERT)
Solution:
Given:
A x B = {(a, x), (a, y), (6, x), (6, y)}
A = {a, b} and S = {x, y}.

Question 4.
If A = {1, 2} and B = {3, 4} then find A x B. (NCERT)
Solution:
A x B = { 1, 2} x {3, 4}
A x B = { ( 1, 3), (1, 4), (2, 3), (2, 4)}

Question 5.
The figure shows the relationship between the set P and Q. Write the relation : (NCERT)

1. In set builder form
2. In roster form
3. Find its domain
4. Find its range.

Solution:

1. Set builder form, R = {(x, y) : y = x – 2, x ∈ P and y ∈ Q}.
2. Roster form, R = {(5, 3), (6, 4), (7, 5)}
3. Domain = {5, 6, 7}
4. Range = {3, 4, 5}.

Question 6.
Let A = (1, 2, 3, 4, 6} and R be the relation on A defined by
{(a, b) : a, b ∈ A, b is exactly divisible by a } :

1. Write R in roster form,
2. Find the domain of R
3. Find the range of R. (NCERT)

Solution:
Given: A = {1, 2, 3, 4, 6}
1. R = {{a, b): a, be A, b is exactly divisible by a }
R= {(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (6, 6)}.

2. Domain = {1, 2, 3, 4, 6}.

3. Range = {1, 2, 3, 4, 6}.

Question 7.
Let A = {x, y, z} and B = {1, 2}. Find the number of relations from A to B. (NCERT)
Solution: A = {x, y, z}, B= {1, 2}
n(A) = 3, n(B) = 2
No. of relations from A to B = 2^mn = 23^3/2 = 2⁶
= 64.

Question 8.
A function f is defined by f (x) = 2x – 5, write down the following values : (NCERT)

1. f(0)
2. f(7)
3. f(-3).

Solution:
Given: f(x) = 2x – 5
1. Put x = 0,
f(0) = 2(0) – 5 = 0 – 5 = – 5.

2. Put x = 7,
f(7) = 2 x 7 – 5 = 14 – 5 = 9.

3. Put x = – 3,
f(- 3) = 2(- 3) – 5 = – 6 – 5 = – 11.

Question 9.
The function ‘t’ which maps temperature in degree celcius into temperature in degree fehrenheit, it is defined as t(c) = \(\frac { 9c }{ 5 }\) +32. Find the following : (NCERT)

1. t (0)
2. t (28)
3. t (- 10)
4. Find c, when t (c) = 212.

Solution:
Given :
t(c) = \(\frac { 9c }{ 5 }\) + 32
1. Put c = 0,
t(0) = \(\frac { 9 × 0 }{ 5 }\) + 32
⇒ t(0) = 32

2. Put c = 28,
t(28) = \(\frac { 9 × 28 }{ 5 }\) + 32 = \(\frac { 252}{ 5 }\) + \(\frac { 32}{ 1 }\)
⇒ t(28) = \(\frac { 252 + 160}{ 5 }\) = \(\frac { 412}{ 5 }\)

3. Put c = – 10,
t(- 10) = \(\frac { 9 x (- 10)}{ 5 }\) + 32
⇒ t(- 10) = – 18 + 32 = 14

4. Put t(c) = 212,
212 = \(\frac { 9c }{ 5 }\) + 32
⇒ \(\frac { 9c }{ 5 }\) = 212 – 32
⇒ \(\frac { 9c }{ 5 }\) = 180
⇒ c = \(\frac { 180 x 5 }{ 9 }\)

Question 10.
Find the domain and range of the function f(x) = |x|.
Solution:
f(x) = – |x|, f(x) < 0
Domain of f = R.
Range of f = {y : y ∈ R, y ≤ 0} = (- ∞, 0].

Straight Lines Short Answer Type Questions

Question 1.
Find the domain and range of the function f(x) = \(\sqrt { 9 – { x }^{ 2 } }\).
Solution:
Given : f(x) = \(\sqrt { 9 – { x }^{ 2 } }\)
Value of f(x) is real, if f(x) ≥ 0
9 – x² ≥ 0
⇒ – (x² – 9) ≥ 0
⇒ x² – 9 ≤ 0
⇒ (x + 3)(x – 3) ≤ 0
∴ Domain = [- 3, 3].

Question 2.
If f(x) = x², then find \(\frac { f(1.1) – f(1)}{ (1.1 – 1)}\)
Solution:
f(x) = x²
f(1.1) = (1.1)² = 1.21
f(1) = 1² = 1

Question 3.
Find domain of function f(x) = \(\frac { { x }^{ 2 } + 2x + 1 }{ { x }^{ 2 } – 8x + 12 }\)
Solution:
Given function is :

f(x) will be defined if,
x² – 8x + 12 ≠ 0
⇒ x² – 6x – 2x + 12 ≠ 0
⇒ x(x – 6) – 2(x – 6) ≠ 0
⇒ (x – 2)(x – 6) ≠ 0
x ≠ 2 and x ≠ 6
Domain of function = R – {2, 6}.

Question 4.
Let f : g → R → R be defined by f(x) = x + 1 and g(x) = 2x – 3 respectively, then find :

1. f + g
2. \(\frac { f }{ g }\)

Solution:
Given: f(x) = x + 1, g (x) = 2x – 3
1. (f + g)x = f(x) + g(x)
= x + 1 + 2x – 3
∴ (f + g)x = 3x – 2

2. \(\frac { f }{ g }\)(x) = \(\frac { f(x)}{ g(x) }\) = \(\frac { x +1 }{ 2x – 3}\)

Question 5.
If f(x) = x² – \(\frac { 1 }{ { x }^{ 2 } }\), then prove that:
f(x) + f\(\frac { 1 }{ x }\) = 0
Solution:

Question 6.
If f(x) = \(\frac { { x }^{ 2 } }{ 1-{ x }^{ 2 } }\), then prove that:
f(sinθ) = tan² θ.
Solution:

Question 7.
If f(x) = x³ + 3x + tanx, then prove that f(x) is an odd function.
Solution:
Given : f(x) = x³ + 3x + tanx
f(- x) = (- x)³ + 3(- x) + tan(- x)
= – x³ – 3x – tanx
= – (x³ + 3x + tanx)
= – f(x).
Hence, f(x) is an odd function.

Question 8.
If f(x) = x² + 2xsinx + 3, then prove that f(x) is an even function.
Solution:
Given: f(x) = x² + 2x sin x + 3
f(- x) = (- x)² + 2(- x) sin(- x) + 3
= x² + 2xsinx + 3, [∵ sin(- x) = – sinx]
= f(x).
Hence, f(x) is an even function

Question 9.
If f(x) = x², g(x) = x + 2, ∀ x ∈R, then find gof and fog. Is gof = fog.
Solution:
Given : f(x) = x², g(x) = x + 2
fog(x) = f[g(x)]
= f(x + 2) = (x+2)².
gof(x) = g[f(x)]
= g(x²) = x² + 2
Hence, fog(x) ≠ gof(x).

Question 10.
If f(x) = e^2x and g(x) = log \(\sqrt {x}\), x> 0, then find the value of fog(x) and gof(x).
Solution:

MP Board Class 11th Maths Important Questions

MP Board Class 11th Maths Important Questions Chapter 10 Straight Lines

Straight Lines Long Answer Type Questions

Question 1.
The slope of a line is double the slope of another line. If tangent of the angle between them is \(\frac {1}{3}\), then find the slope of the line.
Solution:
Let the angle between two lines be θ.

⇒ 1 + 2m² = 3m
⇒ 2m² – 3m + 1 = 0
⇒ 2m² – 2m – m + 1 = 0
⇒ 2m(m – 1) – 1 (m – 1) = 0
⇒ (m – 1)(2m – 1) = 0
⇒ m = 1,\(\frac {1}{2}\)

Question 2.
If three points (h, 0), (a, b) and (0, k) lies on same line, then prove that \(\frac {a}{h}\) + \(\frac {b}{k}\) = 1. (NCERT)
Solution:
Given points are A(h, 0), B(a, b) and C(0, k).

ab = (b – k)(a – h)
⇒ ab = ab – bh – ak + hk
⇒ bh + ak = hk
⇒ \(\frac {bh}{hk}\) \(\frac {ak}{hk}\) \(\frac {hk}{hk}\), (dividing both sides by hk)
⇒ \(\frac {a}{h}\) + \(\frac {b}{k}\) = 1.

Question 3.
Find the equation of the line passing through (- 3, 5) and perpendicular to the line through the points (2, 5) and (- 3, 6). (NCERT)
Solution:
Gradient of AB = m = \(\frac { { y }_{ 2 } – { y }_{ 1 } }{ { x }_{ 2 } – { x }_{ 1 } }\)
Where x₁ = 2 , y₁ = 5, x₂ = – 3, y₂ = 6
∴ m = \(\frac {6 – 5}{- 3 – 2}\) = \(\frac {1}{- 5}\)

Let the gradient of CD = m₁,
AB ⊥ CD
m x m₁ = – 1
⇒ \(\frac {-1}{5}\) x m₁ = – 1
⇒ m₁ = 5
Equation of line CD will be :
y – y₁ = m(x – x₁)
Here x₁ = – 3, y₁ = 5, m = 5 .
⇒ y – 5 = 5(x + 3)
⇒ y – 5 = 5x + 15
⇒ 5x – y + 20 = 0.

Question 4.
Find the equation of straight line passing through the point (2, 2) and cutting off intercepts the axes whose sum is 9. (NCERT)
Solution:
Let the required equation of line is :
\(\frac {x}{a}\) + \(\frac {y}{b}\) = 1 …. (1)
Given: a + b = 9 …. (2)
Line (1) passes through point (2, 2).
∴ \(\frac {2}{a}\) + \(\frac {2}{b}\) = 1
\(\frac {2a + 2b}{ab}\) = 1
2a + 2b = ab
Put b = 9 – a from equation (2), we get
2a + 2(9 – a) = a(9 – a)
⇒ 2a + 18 – 2a = 9a – a²
⇒ a² – 9a + 18 = 0
⇒ a² – 6a – 3a + 18 = 0
⇒ a (a – 6) – 3(a – 6) = 0
⇒ (a – 3)(a – 6) = 0
∴ a = 3 or a = 6
When a = 3, then b = 9 – a = 9 – 3 = 6
Hence the required equation is :
\(\frac {x}{3}\) + \(\frac {y}{6}\) = 1
⇒ 2x + y = 6.
When a = 6, then b = 9 – 6 = 3
Hence the required equation is :
\(\frac {x}{6}\) + \(\frac {y}{3}\) = 1
⇒ x + 2 y = 6.

Question 5.
Find the equation to that straight line which passes through the point (7,9) and such that the portion between the axes is divided by the point in the ratio 3 : 1.
Solution:
Let the required equation of the line is :
\(\frac {x}{a}\) + \(\frac {y}{b}\) = 1 …. (1)
Let the required line cuts the axes at points A (a, 0) and B(0, b),
and Point P intercept the line AB internally in ratio 3 : 1.

Putting values of a and b in eqn. (1), we get
\(\frac {x}{28}\) + \(\frac {y}{12}\) = 1
\(\frac {3x + 7y}{84}\) = 1
Hence required equation is 3x + 7y = 84.

Question 6.
Find the equation of the line which passes through the point (1, 2) and makes a right angled triangle with axes of area \(\frac {9}{2}\) sq units.
Solution:
Area of (∆AOB) = \(\frac {1}{2}\)a.b
⇒ \(\frac {9}{2}\) = \(\frac {1}{2}\)a.b
⇒ ab = 9

Let the equation of line \(\frac {x}{a}\) + \(\frac {y}{b}\) = 1 which passes through point (1, 2)
∴ \(\frac {1}{a}\) + \(\frac {2}{b}\) = 1
From equation (1), b = \(\frac {9}{a}\)
∴ \(\frac {1}{a}\) + \(\frac {2}{9}\) = 1
⇒ 9 + 2a² = 9a
⇒ 2a² – 9a + 9 = 0
⇒ 2a² – 3a – 6a + 9 = 0
⇒ a(2a – 3) – 3(2.a – 3) = 0
⇒ (2a – 3)(a – 3) = 0
∴ b = 6, 3
Equation of line \(\frac {x}{3/2}\) + \(\frac {y}{6}\) = 1
⇒ \(\frac {2x}{3}\) + \(\frac {y}{6}\) = 1
⇒ 12x + 3y = 18
⇒ 4x + y = 6
or \(\frac {x}{3}\) + \(\frac {y}{3}\) = 1
⇒ x + y = 3

Question 7.
If p is the length of perpendicular from the origin to the line whose intercepts on the axes are a and b, then prove that \(\frac { 1 }{ { p }^{ 2 } }\) = \(\frac { 1 }{ { a }^{ 2 } }\) + \(\frac { 1 }{ { b }^{ 2 } }\) (NCERT)
Solution:
Equation of given line be :
\(\frac {x}{a}\) + \(\frac {y}{b}\) = 1
⇒ bx + ay = ab
⇒ bx + ay – ab = 0 …. (1)
Let the form of required equation be :
xcosα + ysinβ – p = 0 …. (2)
Comparing equation (1) and (2),

Question 8.
Find the angle between the lines.
y = (2 – \(\sqrt {3}\))x + 6 and y = (2 + \(\sqrt {3}\))x – 8.
Solution:
y = (2 – \(\sqrt {3}\))x + 6 … (1)
m₁ = 2 – \(\sqrt {3}\)
Second line y = (2 + \(\sqrt {3}\))x – 8
m₂ = 2 + \(\sqrt {3}\)
Let θ be the angle between them,

Question 9.
If the perpendicular drawn from origin on line y = mx + c intersect the line at point (- 1, 2), then find the value of m and c. (NCERT)
Solution:
Let the equation of AB be :
y = mx + c … (1)
Gradient of eqn. (1) is m and OP is perpendicular to AB

Gradient of OP m₁ = \(\frac { { y }_{ 2 } – { y }_{ 1 } }{ { x }_{ 2 } – { x }_{ 1 } }\)
m₁ = \(\frac {2 – 0}{- 1 – 0}\) = – 2
∵ Op ⊥ AB
∴ m × m₁ = – 1
⇒ m(- 2) = – 1
⇒ m = \(\frac {1}{2}\)
put value of m in equation (1),
y = \(\frac {1}{2}\)x + c
Above equation passes through point (-1, 2), hence it will satisfy it.
2 = \(\frac {- 1}{2}\) + c
⇒ c = 2 + \(\frac {1}{2}\) = \(\frac {5}{2}\)
∴ m = \(\frac {1}{2}\), c = \(\frac {5}{2}\)

Question 10.
Find the coordinate of the foot of perpendicular from the point (- 1, 3) to the line 3x – 4y – 16 = 0.
Solution:
Equation of line CD is :
3x – 4y – 16 = 0  … (1)
Equation of line AB is perpendicular to equation (1),
4x + 3y + c = 0  … (2)

Equation (2) passes through point (- 1, 3).
∴ 4(- 1) + 3 x 3 + c = 0
– 4 + 9 + c = 0
c = – 5
Put c = – 5 in equation (2), we get 4x + 3y – 5 = 0
Now the intersection of lines (1) and (3) is the foot of perpendicular B
3x – 4y – 16 = 0
4x + 3y – 5 = 0
By cross multiplication method,

Question 11.
Find the equation of line parallel to y – axis and drawn through the point of intersection of line x – 7y + 5 = 0 and 3x + y = 0. (NCERT)
Solution:
Equation of given lines are :
x – 7y + 5 = 0 … (1)
3x + y = 0 … (2)
Equation of straight line passing through the intersection of equation (1) and (2) is :
x – 7y + 5 + λ(3x + y) = 0 … (3)

Put A = 7 in equation (3), we get
x – 7y + 5 + 7(3x + y) = 0
⇒ x – 7y + 5 + 21x + 7y = 0
⇒ 22x + 5 = 0.

Question 12.
Find the value of p so that the three lines 3x + y – 2 = 0, px + 2y – 3 = 0 and 2x – y – 3 = 0 may intersect at one point. (NCERT)
Solution:
Equation of given lines are :
3x + y – 2 = 0 … (1)
px + 2y – 3 = 0 … (2)
2x – y – 3 = 0 … (3)
From eqns. (1) and (3),
3x + y – 2 = 0
2x – y – 3 = 0
Solving by cross multiplication method,

Lines intersect at the one point, hence point (1, – 1) will satisfy equation (2). p(1) – 2 x 1 – 3 = 0
p = 5.

Question 13.
Find the equation of a line drawn perpendicular to the line \(\frac {x}{4}\) + \(\frac {y}{6}\) = 1 through the point where it meets the y – axis. (NCERT)
Solution:
Given equation is :
\(\frac {x}{4}\) + \(\frac {y}{6}\) = 1
Line (1) meets the F – axis at point (0, 6).
From eqn. (1), \(\frac {6x + 4y}{24}\) = 1
⇒ 6x + 4y = 24
⇒ 6x + 4y – 24 = 0 … (2)
Equation of line perpendicular to eqn. (2),
4x – 6y + c = 0 … (3)
Above equation passes through point (0, 6).
∴ 4 x 0 – 6 x 6 + c = 0
c = 36
Put value of c = 36 in equation (3),
4x – 6y + 36 = 0
2x – 3y + 18 = 0.

Question 14.
For what value of k the equation (k – 3) x (4 – k²)y + k² – 7k + 6 = 0 is :

1. Parallel to X – axis
2. Parallel to y – axis
3. Passes through origin.

Solution:
Equation of given line is :
(k – 3)x – (4 – k²)y + k² – 7k+6 = 0
(4 – k²)y = (k – 3)x + k² – 7k + 6
⇒ y = \(\frac { (k – 3)x }{ 4 – { k }^{ 2 } }\) + \(\frac { { k }^{ 2 } – 7k + 6 }{ 4 – { k }^{ 2 } }\)

1. Line parallel to X – axis :
∴ m = 0
⇒ \(\frac { k – 3 }{ 4 – { k }^{ 2 } }\)
⇒ k – 3 = 0
⇒ k = 3.

2. Line parallel to Y – axis :
∴ m = \(\frac {1}{0}\)
⇒ \(\frac { k – 3 }{ 4 – { k }^{ 2 } }\)
⇒ 4 – k² = 0
⇒ k²= 4
⇒ k = ± 2

3. Line passing through origin, if c = 0.
∴ \(\frac { { k }^{ 2 } – 7k + 6 }{ 4 – { k }^{ 2 } }\)
⇒ k² – 7k+6 = 0
⇒ k² – 6k – k+6 = 0
⇒ k(k – 6) – 1(k – 6) = 0
⇒ (k – 6)(k – 6) = 0
∴ k = 1, 6

Question 15.
The line passing through the points (h, 3) and (4,1) meets the line 7x – 9y – 19 = 0 at right angle. Find the value of h.
Solution:
Equation of given line is :
7x – 9y – 19 = 0
⇒ 9y = 7x – 19
⇒ y = \(\frac {7}{9}\)x – \(\frac {19}{9}\) … (1)
Gradient of eqn. (1) m₁ = \(\frac {7}{9}\)
Equation of line passing through points (h, 3) and (4, 1),
m₂ = \(\frac { { y }_{ 2 } – { y }_{ 1 } }{ { x }_{ 2 } – { x }_{ 1 } }\)
m₂ = \(\frac {1 – 3}{4 – h}\) = \(\frac {- 2}{4 – h}\)
∵ Lines are perpendicular.
∴m₁ x m₂= – 1
\(\frac {7(- 2)}{9(4 – h)}\) = – 1
⇒ – 14 = – 36 + 9h
⇒ 9h = 36 – 14
⇒ 9h = 22
∴ h =\(\frac {22}{9}\).

Question 16.
If the lengths of the perpendiculars drawn from origin on the straight lines xcosθ – y sinθ = kcos2θ and xsecθ + y cosec θ = k are p and q then prove that:
p² + 4q² = k²
Solution:
Equation of given lines :
xsecθ + ycosecθ = k … (1)
and x cosθ – y sinθ = k cos2θ … (2)
Length of perpendicular from origin on equation (1),

Adding equation (3) and (4),
4q² + p² = k² sin² 2θ +k² cos² 2θ
= k²(sin² 20 + cos²2θ)
⇒ p² + 4q² = k² .

Question 17.
Find the equation to the straight line passing through the intersection of lines 4x + 7y – 3 = 0 and 2x – 3y + 1 = 0 and makes an equal intercept on both the axes.
Solution:
Equation of given lines are :
4x + 7y – 3 = 0 … (1)
2x – 3y + 1 = 0 … (2)
Equation of straight line passing through intersection of lines (1) and (2),
4x + 7y – 3 + λ(2x – 3y + 1) = 0 … (3)
⇒ x(4 + 2 λ) + y(7 – 3 λ) – 3 + λ = 0
⇒ x(4 + 2 λ) + y(7 – 3 λ) = 3 – λ

Put λ = \(\frac {3}{5}\) in equation (3),
4x + 7y – 3 + \(\frac {3}{5}\)(2x – 3y + 1) = 0
⇒ 20x + 35y – 15 + 6x – 9y +3 = 0
⇒ 26x + 26y = 12
⇒ 13x + 13y = 6.
⇒ 13x + 13y – 6 = 0.

Question 18.
Find the distance of point (-1, 1) from the line 12 (x + 6) = 5 (y – 2). (NCERT)
Solution:
Equation of given line is :
12(x + 6) = 5(y – 2)
⇒ 12x + 72 = 5y – 10
⇒ 12x – 5y + 82 = 0
Length of perpendicular

Question 19.
Find the points on the X – axis, whose distance from the line \(\frac {x}{3}\) + \(\frac {y}{4}\) = 1 are 4 units. (NCERT)
Solution:
Equation of given line is :
\(\frac {x}{3}\) + \(\frac {y}{4}\) = 1
⇒ 4x + 3y = 12
⇒ 4x + 3y – 12 = 0
Let the point on X – axis is (h, 0).
Length of perpendicular drawn from point (h, 0) is 4.

Taking (+) sign,
4h = 20 + 12 = 32
⇒ h = 8
Taking (-) sign,
4h = – 20 + 12
⇒ 4h = – 8
⇒ h = – 2
Point on X – axis are ( – 2, 0) and (8, 0).

Question 20.
Find the distance between two parallel lines : 15x + 8y – 34 = 0 and 15x + 8y + 31 = 0.
Solution:
Equation of given lines are :
15x + 8y – 34 = 0
15x + 8y + 31 = 0
Put x = 0 in eqn. (1),
15(0) + 8y – 34 = 0
⇒ 8y = 34
y = \(\frac {34}{8}\) = \(\frac {17}{4}\)
Point (0, \(\frac {17}{4}\)) is on line (1),
Length of perpendicular from point (0, \(\frac {17}{4}\)) on equation (2),

= \(\frac {65}{17}\) units
Hence the distance between lines is \(\frac {65}{17}\) units

Question 21.
The length L (in centimeters) of a copper rod is a linear function of its Celsius temperature C. In an experiment. If L = 124.942 when C= 20 and L = 125.134 when C = 110. Express L in terms of C. (NCERT)
Solution:
Given : L = 124.942 when C = 20
L = 125.134 when C= 110
In coordinate form points (20, 124.942) and (110, 125.134) are two points.
Required equation of straight line :

Question 22.
The owner of a milk store finds that he can sell 980 L of milk each week at Rs. 14/L and 1220 L of milk each week at Rs. 16/L. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at Rs. 17 L? (NCERT)
Solution:
Let price and litre be denoted in ordered pair (x, y), two points are (14, 980) and (16,1220).
∴ Required equation of straight line will be :
y – y₁ = \(\frac { { y }_{ 2 } – { y }_{ 1 } }{ { x }_{ 2 } – { x }_{ 1 } }\)(x – x₁)
⇒ y – 980 = \(\frac {1220 – 980}{16 – 14}\)(x – 14)
⇒ y – 980 = \(\frac {240}{2}\)(x – 14)
⇒ y – 980 = 120 (x – 14)
⇒ y – 980 = 120 x – 120 x 14
⇒ y = 120 x – 1680 + 980
⇒ y = 120 x – 700
When x = 17, then
y = 120 x 17 – 700
⇒ y = 2040 – 700
⇒ y = 1340
Hence, he will sell weekly 1340 L milk at the rate of Rs. 17 L.

MP Board Class 11th Maths Important Questions

MP Board Class 11th Maths Important Questions Chapter 1 Sets

Sets Important Questions

Sets Objective Type Questions

(A) Choose the correct option:

Question 1.
A set is defind as:
(a) Collection of an object
(b) Collection of well defind object
(c) Nothing can be said
(d) None of these.
Answer:
(b) Collection of well defind object

Question 2.
If A = {1, 2, 3},B = {2, 3, 4} and U = {1, 2, 3, 4, 5, 6},then A’ ∩ B’ =
(a) {2, 3}
(b) {1, 5,6}
(c) {5, 6}
(d) {1, 4, 5, 6}.
Answer:
(c) {5, 6}

Question 3.
A and B are two sets, then A ∩ (A ∪ B) =
(a) A
(b) B
(c) ϕ
(d) None of these.
Answer:
(a) A

Question 4.
A set A = {x : x ∈ R, x² = 16 and 2x = 6} =
(a) ϕ
(b) {14,3,4}
(c) {3}
(d) {4}.
Answer:
(a) ϕ

Question 5.
For a non – empty set A:
(a) A∪A’ = A
(b) A∪A’ = A’
(c) A∪A’ = U
(d) A∪A’ = ϕ .
Answer:
(c) A∪A’ = U

Question 6.
If two non – empty sets A and B are not equal, then:
(a) A⊂A∩B
(b) B⊂A∩B
(c) A∩B⊂B
(d) A∩B⊂ϕ.
Answer:
(c) A∩B⊂B

Question 7.
A and B are two sets and n(A) = 70, n(B) = 60 and n(A∪B) = 110, then n(A∩B) =
(a) 240
(b) 50
(c) 40
(d) 20.
Answer:
(d) 20.

Question 8.
If A = {1,2,3,4,5}, then the number of proper subsets:
(a) 120
(b) 30
(c) 31
(d) 32.
Answer:
(d) 32.

Question 9.
If A, B and C are three sets, then A – (B∪C) is equal to:
(a) (B – A)∩C
(b) (A – B) ∪C
(c) (A – B) ∩(A – C)
(d) (A – B) ∪(A – C)
Answer:
(c) (A – B) ∩(A – C)

Question 10.
Let S = {1,2,3,4}. The total numbers of unordered pair of disjoint subsets of S is equal to:
(a) 25
(b) 34
(c) 42
(d) 41.
Answer:
(d) 41.

(B) Match the following:

Answer:

1. (e)
2. (c)
3. (a)
4. (b)
5. (f)
6. (d)

(C) Fill in the blanks:

1. If the elements of A mid B are 3 and 6, then minimum number of elements in A∪B is …………………………….
2. If X and Y are two sets such that n(X) = 17, n(Y) = 23 and n(X∪Y) = 38, then n(X∩Y) = …………………………
3. If sets A = {1, 2, 3, 4, 5, 6} and B = {2, 4, 6, 8}, then B – A = ……………………………..
4. A set which does not contain any element is called ………………………….
5. If set A has n elements, then the number of subsets of A are …………………………..
6. If A = {1, 2} and B = {3, 4}, then (A∪B)∩ϕ = ……………………………..

Answer:

1. 6
2. 2
3. {8}
4. Empty set
5. 2ⁿ
6. ϕ

(D) Write true/false:

1. If A ∩ B = B, then B ⊂ A.
2. If A = {1, 2, 3, 4} and B = {2, 3, 4, 5, 6}, then A ∆ B = {1, 5, 6}.
3. If n(A – B) = n(A) – n(A n B).
4. For a non – empty sets A is A∩A’- A’.
5. If A = {1, 2, 3, 4}, then n[P(A)] = 16.

Answer:

1. False
2. True
3. True
4. False
5. True.

Question (E)
Write answer in one word/sentence:

1. If A = {1, 2}, then write all the subsets of set A.
2. If A = {4, 5, 8, 12} and B = {1, 4, 6, 9}, then find the value of A – (B – A).
3. If n(U) = 700, n(A) = 200, n(B) = 300, and n(A∩B) = 100, then find the value of n(A’∩B’). ‘
4. Find the value of n[P{P{P(ϕ}}]
5. If A = {a, b, c, d}, then find all subsets of set A.
6. If U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, B = {2, 4, 6, 8} and C = {3, 4, 5, 6}, then find the value of (B – C)’.

Answer:

1. ϕ, {1}, {2}, {1,2}
2. {4, 5, 8, 12}
3. 300
4. 4
5. 16
6. {1, 3, 4, 5, 6, 7, 8, 9}.

Sets Very Short Answer Type Questions

Question 1.
Write the following sets in set builder form: (NCERT)

1. {3, 6, 9, 12}
2. {2, 4, 8, 16, 32}
3. {5, 25, 125, 625}
4. {2, 4, 6,},
5. {1, 4, 9, ………… 100}.

Solution:

1. A = {x : x is a natural number, multiple of 3 and x < 15}
2. B = {x : x = 2ⁿ, x∈N and n < 6}
3. C = {x : x = 5ⁿ, and x∈N and n ≤ 4}
4. D = {x : x is an even natural number}
5. E = {x : x = n², x ∈ N and n < 11}.

Question 2.
Write the following sets in roster form: (NCERT)

1. A = {x : x is an odd natural number}
2. B = {x : x is an integer – \(\frac{1}{2}\) < x < \(\frac{9}{2}\)
3. C = {x : x is an integer x² ≤ 4}
4. D = {x : x is a letter of a word LOYAL}
5. E = {x : x is a month of year which does not have 31 days}
6. F – {x : x is a consonant of English alphabet which comes before k}

Solution:

1. A = {1, 3, 5, 7, 9}
2. B = {0, 1, 2, 3, 4}
3. C = {-2, -1, 0, 1, 2}
4. D = {L, 0, Y, A}
5. E = {FEBRUARY, APRIL, JUNE, SEPTEMBER, NOVEMBER}
6. F = {b, c, d, f, g, h, j}.

Question 3.
From following find whether A = B. (NCERT)

1. A = {a, b, c, d}, B = {d, c, b, a}.
2. A = {4, 8, 12, 16}, B = {8,4, 16, 18}.
3. A = {2, 4, 6, 8, 10}, B = {x : x is a positive even integer x < 10}.
4. A = {x : x is a multiple of 10}, B = {10, 15, 20, 25, 30}.

Solution:
1. A = {a, b, c, d}, B = {d, c, b, a}
All the elements of set A is in set B
A = B.

2. A = {4, 8, 12, 16}, B = {8, 4, 16, 18}
All the elements of A is not in set B.
∴ A≠B.

3. Here A = {2, 4, 6, 8, 10} and B = { x : x is an even number and x ≤ 10}
B = {2, 4, 6, 8, 10}
i.e., The elements of set A and B are same.
∴ A = B

4. Here A = {x : x is a multiple of 10} = {10, 20, 30, 40}
and B = {10, 15, 20, 25, 30, …}
The elements of set A and B are not same.
∴ A≠B.

Question 4.
If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8} and D = {7, 8, 9, 10} then find the following: (NCERT)

1. A∪B
2. A∪C
3. B∪C
4. B∪D

Solution:

1. A ∪ B = {1, 2, 3, 4} ∪ {3, 4, 5, 6} = {1, 2, 3, 4, 5, 6}.
2. A ∪ C = {1, 2, 3, 4} ∪ {5, 6, 7, 8} = {1, 2, 3, 4, 5, 6, 7, 8}.
3. B ∪ C = {3, 4, 5, 6} ∪ {5, 6, 7, 8} = {3, 4, 5, 6, 7, 8}
4. B ∪ D = {3, 4, 5, 6} ∪ {7, 8, 9, 10} = {3, 4, 5, 6, 7, 8, 9, 10}

Question 5.
If A = {3, 5, 7, 9, 11}, B = {7, 9, 11, 13}, C= {11, 13, 15} and D = {15, 17} then, find the following:

1. A ∩ B
2. B ∩ C
3. A ∩ C
4. B ∩ D

Solution:

1. A ∩ B = {3, 5, 7, 9, 11} ∩ {7, 9, 11, 13} = {7, 9, 11}
2. B ∩ C = {7, 9, 11, 13} ∩ {11, 13, 15} = {11, 13}
3. A ∩ C = {3, 5, 7, 9, 11} ∩ {11, 13, 15} = {11}
4. B ∩ D = {7, 9, 11, 13} ∩ {15, 17} = ϕ

Question 6.
If A = {3, 6, 9, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20} then, find the following: (NCERT)

1. A – B
2. A – C
3. A – D
4. B – A
5. C – A
6. D – A
7. B – C
8. B – D
9. C – B
10. D – B
11. C – D
12. D – C?

Solution:
Let A and B are two sets and A – B is a set of those elements which one present in A and not in B.

1. A – B = {Those elements present in A and not in B}
= {3, 6, 9, 12, 15, 18, 21} – {4, 8, 12, 16, 20}
= {3, 6, 9, 15, 18, 21}.

2. A – C = {Those elements present in A and not in C}
= {3, 6, 9, 12, 15, 18, 21} – {2, 4, 6, 8, 10, 12, 14, 16}
= {3, 9, 15, 18, 21}.

3. A – D = {The elements which are in A but not in D}
= {3, 6, 9, 12, 15, 18, 21} – {5, 10, 15, 20}
= {3, 6, 9, 12, 18, 21}.

4. B – A = {The elements which are in B but not in A}
= {4, 8, 12, 16, 20} – {3, 6, 9, 12, 15, 18, 21}
= {4, 8, 16, 20}.

5. C – A = {The elements which are in C but not in A}
= {2, 4, 6, 8, 10, 12, 14, 16} – {3, 6, 9, 12, 15, 18, 21}
= {2, 4, 8, 10, 14, 16}.

6. D – A = {The elements which are in D but not in A}
= {5, 10, 15, 20} – {3, 6,9, 12, 15, 18, 21}
= {5, 10, 20}.

7. B – C = {The elements which are in B but not in C}
= {4, 8, 12, 16, 20} – {2, 4,6, 8, 10, 12, 14, 16}
= {20}.

8. B – D = {The elements which are in B but not in D}
= {4, 8, 12, 16, 20} – {5, 10, 15, 20}
= {4, 8, 12, 16}.

9. C – B = {The elements which are in C but not in B}
= {2, 4, 6, 8, 10, 12, 14, 16} – {4, 8, 12, 16, 20}
= {2, 6, 10, 14}.

10. D – B = {The elements which are in D but not in B}
= {5, 10, 15,20} – {4, 8, 12, 16, 20}
= {5, 10, 15}.

11. C – D = {The elements which are in C but not in D}
= {2, 4, 6, 8, 10, 12, 14, 16} – {5, 10, 15, 20}
= {2, 4, 6, 8, 12, 14, 16}.

12. D – C = {The elements which are in D but not in C}
= {5, 10, 15, 20} – {2, 4, 6, 8, 10, 12, 14, 16}
= {5, 15, 20}.

Question 7.
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {1, 2, 3, 4}, B = {2, 4, 6, 8} and C then find the following:

1. A’
2. B’
3. (A ∪ C)’
4. (A ∩ B)’
5. (A’)’
6. (B – C)’
7. (B – C)’

Solution:
1. A’= U – A
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 2, 3, 4}
⇒ A’= {5, 6, 7, 8, 9}.

2. B’ = U – B
⇒ {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2, 4, 6, 8}
⇒ B’ = {1, 3, 5, 7, 9}.

3. (A ∪ C) = {1, 2, 3, 4} ∪ {3, 4, 5, 6}
⇒ A ∪ C = {1, 2, 3, 4, 5, 6}
(A ∪ C)’= U – (A ∪ C)
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 2, 3, 4, 5, 6}
⇒ (A ∪ C)’ = {7, 8, 9}

4. A ∪ B = {1, 2, 3, 4} ∪ {2, 4, 6, 8} = {1, 2, 3, 4, 6, 8}
(A ∪ B)’ = ∪ – (A ∪ B)
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 2, 3, 4, 6, 8}
⇒ (A ∪ B)’ = {5, 7, 9}

5. (A’)’ = ∪ – A’
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {5, 6, 7, 8, 9}
⇒ (A’)’= {1, 2, 3, 4} = A

6. B – C = {2, 4, 6, 8} – {3, 4, 5, 6} = {2, 8}.
(B ∪ C)’ = U – (B – C)
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2, 8}
⇒ (B – C)’= {1, 3, 4, 5, 6, 7, 9}.

Sets Short Answer Type Questions

Question 1.
If X and Fare two sets, n(X) = 17, n(Y) = 23 and n(X ∪ F) = 38, then find n(X ∩ F)? (NCERT)
Solution:
We know that n(X ∪ Y) = n(X) + n(Y) – n(X∩Y)
Given: n(X) = 17, n(Y) = 23, n(X ∪ Y) = 38, n(X ∩ Y) = ?
∴ 38 = 17 + 23 – n(X ∩ Y)
⇒ 38 = 40 – n(X ∩ Y)
⇒ n(X ∩ Y) = 40 – 38
⇒ n(X ∩ Y) = 2.

Question 2.
If X and Y are two sets, such that X∪Y has 18 elements, X has 8 elements and F has 15 elements, then how many elements does X ∩ Y have? (NCERT)
Solution:
Given: n(X ∪ Y) = 18, n(X) = 8, n(Y) = 15.
Applying formula n(X ∪ Y) = n(X) + n(Y) – n(X ∩ Y)
18 = 8 + 15 – n(X ∩ Y)
⇒ n(X ∩ Y) = 23 – 18 = 5.

Question 3.
If S and Tare two sets, such that S has 21 elements, T has 32 elements and S∩T has 11 elements, how many elements does S∪T have? (NCERT)
Solution:
Given: n(S) = 21, n(T) = 32, n(S ∩ T) = 11, n(S ∪ T) = ?
∵ n(S ∪ T) = n(S) + n(T) – n(S ∩ T)
⇒ n(S ∪ T) = 21 + 32 – 11 = 42.

Question 4.
If X and Y are two sets such that X has 40 elements, X∪Y has 60 elements and X∩Y has 10 elements, then how many elements does Y have? (NCERT)
Solution:
Given: n(X) = 40, n(X ∪ Y) = 60, n(X ∩ Y) = 10, n(Y) = ?
Applying formula n(X ∪ Y) = n(X) + n(Y) – n{X ∩ Y)
⇒ 60 = 40 + n(Y) – 10
⇒ 60 = 30 + n(Y)
⇒ n(Y) = 30.

Question 5.
If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8} and D = {7, 8, 9, 10}, then find the following: (NCERT)

1. A ∪ B ∪ C
2. A ∪ B ∪ D
3. B ∪ C ∪ D.

Solution:
1. A ∪ B ∪ C = {1, 2, 3, 4} ∪ {3, 4, 5, 6} ∪ {5, 6, 7, 8}
= {1, 2, 3, 4, 5, 6} ∪ {5, 6, 7, 8}
= {1, 2, 3, 4, 5, 6, 7, 8}.

2. A ∪ B ∪ D = { 1, 2, 3, 4} ∪ {3, 4, 5, 6} ∪{7, 8, 9, 10}
= {1, 2, 3, 4, 5, 6} ∪ {7, 8, 9, 10}
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.

3. B ∪ C ∪ D = {3, 4, 5, 6} ∪ {5, 6, 7, 8} ∪ {7, 8, 9, 10}
= {3, 4, 5, 6} ∪ {5, 6, 7, 8, 9, 10}
= {3, 4, 5, 6, 7, 8, 9, 10}.

Sets Long Answer Type Questions

Question 1.
In a survey of 600 students in a school, 150 students were found to be taking tea and 225 taking coffee, 100 were taking both tea and coffee. Find how many students were taking neither tea nor coffee? (NCERT)
Solution:
Let C and T be the students taking coffee and tea.
Here, n(T) = 150, n(C) = 225, n(C ∩ T) = 100.
Applying formula n(C ∪ T) = n(T) + n(C) – n(C ∩ T)
n(C ∪ T) = 150 + 225 – 100 = 375 – 100
⇒ n(C ∪ T) = 275
Total number of students = 600 = n(U).
Number of students taking neither tea nor coffee = n(C ∪ T)’
n(C ∪ T)’ = n(U) – n(C ∪ T)
= 600 – 275 = 325.

Question 2.
In a group of 70 people, 37 likes coffee, 52 likes tea and each person likes at least one of these two drinks. Find the number of persons who likes both coffee and tea? (NCERT)
Solution:
Let C and T be the persons who likes coffee and tea.
Given: n(C) = 37, n(T) = 52, n(C ∪ T) = 70, n(C ∩ T) = ?
Applying formula n(C ∪ T) = n(C) + n(T) – n(C ∩ T)
⇒ 70 = 37 + 52 – n(C ∩ T)
⇒ 70 = 89 – n(C ∩ T)
⇒ n(C ∩ T) = 89 – 70
⇒ n(C ∩ T) = 19
∴ Number of people who likes both coffee and tea = 19.

Question 3.
In a group of 65 people, 40 likes cricket, 10 likes both cricket and tennis. How many like tennis only and not cricket? How many like tennis? (NCERT)
Solution:
Let C and T denotes the people who likes cricket and tennis respectively.
Given: n(C ∪ T) = 65, n(C) = 40, n(C ∩ T) = 10
We know that
n(C ∪ T) = n(C) + n(T) – (C ∩ T)
65 = 40 + n(T) – 10
⇒ n(T) = 65 – 30 = 35.
∴ Number of people who likes only tennis and not cricket
= n(T ∩ C)’ = n(T) – (C ∩ T)
= 35 – 10 = 25.

Question 4.
In a survey of 60 people, it was found that 25 people read newspaper H, 26 read newspaper T, 26 read newspaper I, 9 read both H and I. 11 read both H and T, 8 read both T and 1.3 read all three newspapers. Find

1. The number of people who read at least one of the newspapers.
2. The number of people who read exactly one newspaper. (NCERT)

Solution:
Given: n (H) = 25, n (T) = 26, n(I) = 26, n(H ∩ I) = 9, n(H ∩ T) = 11, n(T ∩ I) = 8, n(H ∩ T ∩ I) = 3

1. The number of people who reads at least one of the newspaper = n(H∪T∪I)
= n(H) + n(T) + n(I) – n(H ∩ T) – n(T ∩ I) – n(H ∩ I) + n(H ∩ T ∩ I)
= 25 + 26 + 26 – 11 – 8 – 9 + 3
= 77 – 28 + 3 = 80 – 28 = 52.

2. The number of people who reads exactly one newspaper.
= n(H) + n(T) + n(I) – 2n(H ∩ I) – 2n(H ∩ T) – 2n(T ∩ I) + 3n(H ∩ T ∩ I)
= 25 + 26 + 26 – 2 × 9 – 2 × 11 – 2 × 8 + 3 × 3 = 77 – 18 – 22 – 16 + 9
= 86 – 56 = 30.

Question 5.
In a survey it was found that 21 people liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked products B and C and 8 liked all the three products. Find how many liked product C only? (NCERT)
Solution:
Let A, B and C denotes the people liked the products A, B and C respectively.
Given: n(A) = 21, n(B) = 26, n(C) = 29, n(A ∩ B) = 14, n(C ∩ A) = 12, n(B ∩ C) = 14, n(A ∩ B ∩ C) = 8
n(only C) = n(C) – n(C ∩ A) – n(B ∩ C) + n(A ∩ B ∩ C)
= 29 – 12 – 14 + 8
= 37 – 26 = 11.

MP Board Class 11 Maths Important Questions

MP Board Class 12th Maths Important Questions Chapter 13 Probability

Probability Important Questions

Probability Objective Type Questions

Question 1.
Choose the correct answer:

Question 1.
A bag contains 5 brown and 4 white socks. A man drawn two socks from the bag. The probability that both are of the same colour is:
(a) \(\frac { 5 }{ 108 } \)
(b) \(\frac { 18 }{ 108 } \)
(c) \(\frac { 30 }{ 108 } \)
(d) \(\frac { 48 }{ 108 } \)
Answer:
(d) \(\frac { 48 }{ 108 } \)

Question 2.
A die is roiled three times. The probability of getting a larger number then the previous number each time is:
(a) \(\frac { 5 }{ 72 } \)
(b) \(\frac { 5 }{ 54 } \)
(c) \(\frac { 13 }{ 216 } \)
(d) \(\frac { 1 }{ 18 } \)
Answer:
(d) \(\frac { 1 }{ 18 } \)

Question 3.
It is given that the events A and B are such that P(A) = \(\frac{1}{4}\), P( \(\frac{A}{B}\) ) = \(\frac{1}{2}\) and P ( \(\frac{B}{A}\) ) = \(\frac{2}{3}\), then P(B) is:
(a) \(\frac{1}{3}\)
(b) \(\frac{2}{3}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{1}{6}\)
Answer:
(a) \(\frac{1}{3}\)

Question 4.
A coin is tossed 4 times. Probability of getting at least one head is:
(a) \(\frac{1}{16}\)
(b) \(\frac{2}{16}\)
(c) \(\frac{14}{16}\)
(d) \(\frac{15}{16}\)
Answer:
(d) \(\frac{15}{16}\)

Question 5.
The probability of A speaking a truth is \(\frac{4}{5}\) and that of B speaking a truth is \(\frac{3}{4}\) The probability that they will contradict each other in answering a fact is:
(a) \(\frac{3}{10}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{7}{20}\)
(d) \(\frac{2}{5}\)
Answer:
(c) \(\frac{7}{20}\)

Question 2.
Fill in the blanks:

1. P( \(\frac { A∪B }{ C } \) ) = P ( \(\frac{A}{C}\) ) + ……………………….
2. P(A∩B) = ………………….. or ………………………….
3. If A and B are two independent events then, P (A ∩ B) = ………………………………..
4. If A and B are two independent events then, P ( \(\frac{A}{B}\) ) = ……………………………….
5. If the probability of random variable X is P (X), then mean E (X) will be ……………………………..
6. If probability of random variable X is P(X), then variance Var (X) will be ……………………………

Answer:

1. P( \(\frac{B}{C}\) ) – P ( \(\frac { A∩B }{ C } \) )
2. P(B).P ( \(\frac{A}{B}\) ) or P(A) . P ( \(\frac{B}{A}\) )
3. P(A).P(B)
4. P(A), P(B) ≠ 0
5. ΣX.P(X)
6. ΣX².P(X) – [ΣX.P(X)]².

Question 3.
Write True/False:

1. If A and B are any two events, then P (A – B) = P(A) – P (A∩B).
2. If A and B are any two events, then P (A ∪ B) – P (A∩B) = P(A) + P(B).
3. P( \(\frac{A}{B}\) ) = \(\frac { P(A∩B) }{ P(A) } \).
4. If A and B are any two events of a sample space S and F is another event such that P(F) ≠ 0, then P ( \(\frac { P(A∪B) }{ P(F) } \) ) = P ( \(\frac{A}{F}\) ) + P ( \(\frac{B}{F}\) ) – P ( \(\frac { P(A∪B) }{ P(F) } \) )
5. For any two events A and B. P (A∪B) = P (A∩B ) + P ( \(\bar { A } \) ∩ B) + P (A ∩\(\bar { B } \) )

Answer:

1. True
2. False
3. False
4. True
5. True.

Question 4.
Write the answer in one word/sentence :

1. Find the probability that a leap year has 53 Friday.
2. A coin is tossed 4 times. Find the probability of getting at least one head.
3. It is given that the events A and B are such that P (A) = \(\frac{1}{4}\), P ( \(\frac{A}{B}\) ) = \(\frac{1}{2}\) and P ( \(\frac{B}{A}\) ) = \(\frac{2}{3}\), then find the value of P(B).
4. There are 5 letters and 5 addressed envelops. If the letters are placed at random what is the probability that exactly 3 letters are placed in right envelops?
5. A problem in mathematics is given to 3 students whose chance of solving it are \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\). What is the probability that the problem is solved?

Answer:

1. \(\frac{2}{7}\)
2. \(\frac{15}{16}\)
3. \(\frac{1}{3}\)
4. \(\frac{1}{12}\)
5. \(\frac{3}{4}\)

Probability Short Answer Type Questions

Question 1.
(A) Two dice are thrown simultaneously. Find the probability of getting a sum?
Solution:
When two dice are thrown simultaneously.
n(S) = 6² = 36.
Sample space of getting a sum 8 is
A = {(2, 6); (6, 2); (5, 3); (3, 5); (4, 4)}
∴ n(A) = 5
∴ Required probability
P(A) = \(\frac { n(A) }{ n(S) } \) = \(\frac{5}{36}\).

(B) Two cubical dice are thrown simultaneously. Find the probability of getting a sum of 9?
Solution:
Solve as Q.No. 1 (A)

(C) Two cubical dice are thrown simultaneously. Find the probability of getting a sum of 7?
Solve as Q.No. 1 (A)

Question 2.
The odds against happening of an event is 3 : 4? Find the probability of its failing?
Solution:
The odds against the happening of an event = 3 : 4
∵ Probability of its failing P ( \(\bar { A } \) ) = \(\frac { b }{ a+b } \)
⇒ P ( \(\bar { A } \) ) = \(\frac { 4 }{ 3+4 } \) = \(\frac { 4 }{ 7 } \).

Question 3.
A card is drawn from a pack of 52 cards. Find the probability that its face?
Solution:
Here, n(S) = 52
∵Cards having face = 4 knave + 4 queens + 4 kings
∴ n(A) = 4 + 4 + 4 = 12
Required probability P(A) = \(\frac { 12 }{ 52 } \) = \(\frac { 3 }{ 13 } \)

Question 4.
What is the probability that a leap year selected at random will contain 53 Sundays?
Solution:
A leap year consists of 366 days. It has 52 complete weeks and 2 days extra. The equally likely cases for the occurrence of these extra days are:

1. Monday and Tuesday,
2. Tuesday and Wednesday,
3. Wednesday and Thursday,
4. Thursday and Friday,
5. Friday and Saturday,
6. Saturday and Sunday,
7. Sunday and Monday.

Out of these 7 exclusive cases, the last two cases are favourable.
∴ n(S) = 7 and n(E) = 2
∴ The required probability = \(\frac { n(E) }{ n(S) } \) = \(\frac{2}{7}\).

Question 5.
The probability of the horse A of winning a race is \(\frac{1}{4}\) and the probability of the horse B winning the same race is \(\frac{1}{8}\)? What is the probability that one of the horse will win the race?
Solution:
Given, P(A) = Probability of winning the horse A = \(\frac{1}{4}\)
and P(B) = Probability of winning the horse B = \(\frac{1}{8}\)
Since, the events of winning the race by A and B are mutually exclusive, therefore
P(A∪B)= P(A) + P(B)
\(\frac{1}{4}\) + \(\frac{1}{8}\) = \(\frac{2+1}{8}\) = \(\frac{3}{8}\).

Question 6.
(A) A card is drawn from an ordinary pack of cards, find the probability of getting a king or a spade?
Solution:
Let the event A denotes the event of drawing a king and B of drawing a spade. Then we
n(S) = 52, n(A) = 4, n(B) = 13, n(A∩B) = 1
[Since there are 4 kings in pack of cards the cards of spade are 13 includes its king]
∴ P(A) = \(\frac { n(A) }{ n(S) } \) = \(\frac{4}{52}\), P(B) = \(\frac { n(B) }{ n(S) } \) = \(\frac{13}{52}\)
P(A∩B) = \(\frac{1}{52}\)
∴ P(A∪B)= P(A) + P(B) = P(A∩B )
= \(\frac{4}{52}\) + \(\frac{13}{52}\) – \(\frac{1}{52}\) = \(\frac{16}{52}\) = \(\frac{4}{13}\).

(B) A card is drawn from a pack of cards, find the probability that neither it is an ace nor a King?
Solution:
Total No. of King = 4, No. of ace = 4
And drawing one card from 8 cards = ⁸_C1
And drawing one card from 52 cards = ⁵²_C1
∴ P(A) = \(\frac { ^{ 8 }{ C_{ 1 } } }{ ^{ 52 }{ C_{ 1 } } } \)
∴ Probability of neither ace nor king = P( \(\bar { A } \) ) = 1 – P(A)
= 1 – \(\frac{2}{13}\) = \(\frac{11}{13}\)

Question 7.
(A) A dice is thrown once. Find the probability of getting even No. “or ” No. less than 5?
Solution:
When a dice is thrown once the sample space is
S = {1, 2, 3, 4, 5, 6}
n(S) = 6
E₁ = {2,4,6}, [∴ n(E₁) = 3]
E₁ = {1, 2, 3, 4}, [∴ n(E₂) = 4]
E₁∩E₂= {2, 4}, [∴ n(E₁ ∩E₂)
= \(\frac { n(E_{ 1 }) }{ n(S) } \) + \(\frac { n(E_{ 2 }) }{ n(S) } \) – \(\frac { n(E_{ 1 }\cap E_{ 2 }) }{ n(S) } \)
= \(\frac{3}{6}\) + \(\frac{4}{6}\) – \(\frac{2}{6}\) = \(\frac{7-2}{6}\) = \(\frac{5}{6}\).

(B) A pair of dice is thrown. Find the probability that the sum is not 9 or 11?
Solution:
Total number of ways in which 2 dice can be thrown = 6 × 6 = 36
n(S) = 36
Event of getting sum 9 = {(3, 6), (4, 5), (5, 4), (6, 3)}
Total No. = 4.
∴ Probability of getting sum 9 = \(\frac{4}{36}\) = \(\frac{1}{9}\)
Now event of getting sum 11 = {(5, 6), (6, 5)}
∴ Probability of getting sum 11 = \(\frac{2}{36}\) = \(\frac{1}{18}\)
Now probability of getting sum 9 or 11
P(A) = \(\frac{1}{9}\) + \(\frac{1}{18}\) = \(\frac{2+1}{18}\) = \(\frac{3}{18}\) = \(\frac{1}{6}\)
∴ probability of not getting sum 9 or 11
P( \(\bar { A } \) ) = 1 – P(A)
= 1 – \(\frac{1}{6}\) = \(\frac{6 – 1}{6}\) = \(\frac{5}{6}\).

Question 8.
If 3 coins are tossed simultaneously, then find the probability of getting at least one head?
Solution:
Here, n(S) = 2³ = 8
If \(\bar { A } \) A denotes not getting a head then A = {{T, T, T)}
∴ n( \(\bar { A } \) ) = 1
Probability of not getting a head P( \(\bar { A } \) ) = \(\frac { n(\bar { A) } }{ n(S) } \) = \(\frac{1}{8}\)
∴ Probability of getting at least one head P(A) = 1 – P( \(\bar { A } \) )
= 1 – \(\frac{1}{8}\) = \(\frac{7}{8}\)

Question 9.
A coin is tossed twice. Find the probability of getting head, both the times?
Solution:
Let the event of getting head in first throw be E₂ and the second throw be E₂.
∴ P(E₁) = \(\frac{1}{2}\) = P(E₂) = \(\frac{1}{2}\)
Both the events are independent
∴ P(E₁ ∩ E₂) = P(E₁) × P(E₂)
= \(\frac{1}{2}\) × \(\frac{1}{2}\)
∴ Probability of getting head both the times = P(E₁ ∩ E₂)
= \(\frac{1}{4}\)

Question 10.
In a given race, the odds in favour of three horses A, B and C are 1 : 2, 1 : 3 and 1 : 4. Find the chance that one of them will win the race?
Solution:
The probability of winning the horse, A = \(\frac { 1 }{ 1+2 } \) = \(\frac { 1 }{ 3 } \)
P(B) = The probability of winning the horse, B = \(\frac { 1 }{ 1+3 } \) = \(\frac { 1 }{ 4 } \)
P(C) = The probability of winning the horse, C = \(\frac { 1 }{ 1+4 } \) = \(\frac { 1 }{ 5 } \)
These events are mutually exclusive, therefore the probabilities of winning any one horses
= P(A) + P(B) + P(C)
= \(\frac{1}{3}\) + \(\frac{1}{4}\) + \(\frac{1}{5}\)
= \(\frac{20+15+12}{60}\) = \(\frac{47}{60}\)

Question 11.
A problem in mathematics is given to three students A, B and C whose chances of solving it are \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\) respectively. Find the probability that the problem will not be solved?
Solution:
The chances of A, B, C solving the problem are respectively
\(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\)
∴ The chances of A, B, C not solving the problem are respectively
1 – \(\frac{1}{2}\), 1 – \(\frac{1}{3}\), 1 – \(\frac{1}{4}\), i.e; \(\frac{1}{2}\), \(\frac{2}{3}\), \(\frac{3}{4}\)
∴ The probability that none of the students A, B, C is able to solve the probelm
= \(\frac{1}{2}\) × \(\frac{2}{3}\) × \(\frac{3}{4}\) = \(\frac{1}{4}\).

Probability Long Answer Type Questions – I

Question 1.
In Raipur 20% persons read English newspaper 40% persons read Hindi newspaper and 5% person read both. What percentage of persons are not read any newspaper?
Solution:
P(A) = The probability of reading English newspaper
= \(\frac{20}{100}\) = \(\frac{1}{5}\)
P(B) = The probability of reading Hindi newspaper
= \(\frac{40}{100}\) = \(\frac{2}{5}\)
P(A∩B) = The probability of reading both English and Hindi newpaper
= \(\frac{5}{100}\) = \(\frac{1}{20}\)
No. of persons not reading any newspaper

Question 2.
A speaks truth in 75% of the cases and B in 80% of the cases. In what percentage of cases are they likely to contradict each other in stating the same fact?
Or
Mohan speaks truth in 75% of cases. Sohan speaks truth in 80% of the cases. In what percentage of cases did the Mohan speaks truth and Sohan speaks lie (or when they contradict each other)?
Solution:
P(A) = Probability that A speaks the truth = \(\frac{75}{100}\) = \(\frac{3}{4}\)
and P(B) = Probability that B speaks the truth = \(\frac{80}{100}\) = \(\frac{4}{5}\)
∴ P( \(\bar { A } \) ) = Probability that A does not speak the truth = 1 – \(\frac{3}{4}\) = \(\frac{1}{4}\)
and P( \(\bar { A } \) ) = Probability that B does not speak the truth = 1 – \(\frac{4}{5}\) = \(\frac{1}{5}\)
It is clear that A and B will contradict each other if one of them speaks the truth and the other does not.
∴ P(A and B contradict) = P(A) P( \(\bar { B } \) ) + P( \(\bar { A } \) ) P(B)
= \(\frac{3}{4}\) × \(\frac{1}{5}\) + \(\frac{1}{4}\) × \(\frac{4}{5}\) = \(\frac{7}{20}\) = \(\frac{35}{100}\)
Hence, in 35% cases, A and B will contradict each other.

Question 3.
Prove that P(A) + P( \(\bar { A } \) ) = 1?
Solution:
In total a + b trails, if an events can happen in a ways and fails in b ways, when all of these ways being equally likely to occur, then the probability of happening of event A,
P(A) = \(\frac { a }{ a+b } \)
and probability of failing of event A,
P( \(\bar { A } \) ) = \(\frac { b }{ a+b } \)
Adding eqns. (1) and (2), we get
P(A) + P( \(\bar { A } \) ) = \(\frac { a }{ a+b } \) + \(\frac { b }{ a+b } \)
= \(\frac { a+b }{ a+b } \) = 1.
∴ P(A) + P( \(\bar { A } \) ) = 1. Proved.

Question 4.
If P(A) = \(\frac{1}{2}\), P(B) = \(\frac{1}{9}\) and P(A∩B) = \(\frac{1}{18}\), then find the value of following:

(i) P( \(\frac{A}{B}\) ),

(ii) P( \(\frac{B}{A}\) )

(iii) P(A∪B)

Solution:
Given: P(A) = \(\frac{1}{2}\), P(B) = \(\frac{1}{9}\) and P(A∩B) = \(\frac{1}{18}\)

Question 5.
A group of 10 children contains 6 boys and 4 girls. Three children are chosen at random from this group. Find the probability that this group chosen:

1. Does not contain any girl.
2. Contains at least one girl.

Solution:
Total number of children = 6B + 4G = 10
3 children out of total 10 may be chosen in ¹⁰_{C3 ways}

1. 3 boys out of 6 boys may be chosen in ⁶_C3 ways
∴ Required probability = \(\frac { ^{ 6 }C_{ 3 } }{ ^{ 10 }C_{ 3 } } \) = \(\frac{1}{6}\)

2. At least 1 girl may be taken as follows
2 boys + 1 girl, number of ways = ⁶_C2 × ⁴_C1
or 3 girls, number of ways = ⁴_{C3
Hence, the required probability}

Question 6.
4 cards are fallen down by one during the shuffling of the cards. Find the probability that one card is heart, the other is diamond, the third is spade and the fourth is a club?
Solution:
Number of cards = 52
The first can fall in 52 ways.
The favourable ways for the first card to be heart = 13
Probability = \(\frac{13}{52}\) = \(\frac{1}{4}\)
The number of remaining cards = 52 – 1 = 51
Another card can be fall in 51 ways.
The favourable ways for this card to be a spade = 13
Probability = \(\frac{13}{50}\)
Number of remaining cards = 50 – 1 = 49
∴ Probability = \(\frac{13}{49}\)
Therefore, by compound probability principle, required probability
= \(\frac{1}{4}\) × \(\frac{13}{51}\) × \(\frac{13}{50}\) × \(\frac{13}{49}\)

Question 7.
A problem of Maths is given to three students whose chances of solving it are \(\frac{1}{2}\), \(\frac{1}{3}\) and \(\frac{1}{4}\). What is the probability that the problem is solved by all?
Solution:
Let the probabilities of solving the question by the three students be P₁, P₂, P₃ respectively.
Then given that P₁ = \(\frac{1}{2}\), P₂ = \(\frac{1}{3}\), P₃ = \(\frac{1}{4}\)
∴ The probabilities of not solving the problem by them are
q₁ = 1 – p₁ = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
q₂ = 1 – p₂ = 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)
and q₃ = 1 – p₃ = 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\)
∴ Probability that all of the three students do not solve the problem
= q₁q₂q₃
= 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\).

Question 8.
A bag contains 6 red, 4 white and 5 blue balls. If balls are drawn one by one from bag and they are not replaced, then what is the probability of 1st red, 2nd white and 3rd blue?
Solution:
A bag contains 6 red (R), 4 white (W), 5 blue (B) balls.
Total No. of balls = 6 + 4 + 5 = 15
∴ Probability of 1st ball is red,
P(R) = \(\frac{6}{15}\)
Now total balls in the bag 15 – 1 = 14
∴ Probability of 2nd ball is white,
P(W) = \(\frac{4}{14}\)
Now the total No. of balls in bag 14 – 1 = 13
∴ Probability of 3rd ball is blue,
P(B) = \(\frac{5}{13}\)
Hence, required probability
= \(\frac{6}{15}\) × \(\frac{4}{14}\) × \(\frac{5}{13}\)
= \(\frac{2}{5}\) × \(\frac{2}{7}\) × \(\frac{5}{13}\) = \(\frac{4×1}{91}\) = \(\frac{4}{91}\)

Question 9.
A bag contains 6 red, 4 white and 6 blue balls. If balls are drawn one by one from bag without replacement, then what is the probability of drawing 1st ball red, 2nd ball white and 3rd ball blue?
Solution:
Solve as Q. No. 8.

Question 10.
Two cubical dice are thrown simultaneously. Find the probability that the first dice shows an even number or both the dice show the sum 9?
Solution:
Here (S) = 6 × 6 = 36
The events of getting an even number on the first dice is
E₁ = {(2, 1), (2,-2), (2, 3), (2,4), (2, 5), (2, 6), (4, 1), (4, 2), (4, 3), (4,4), (4, 5), (4, 6), (6, 1), (6, 2), (6, 3), (6,4), (6, 5), (6, 6)}
∴ n(E₁) = 18
The event of getting a total of 9 on the two dice is
E₂ = {(3,6), (4, 5), (5,4), (6, 3)}
∴ n(E₂) = 4 .
Also, E₁∩E₂
⇒ n(E₁∩E₂) = 2
∴ P(E₁) = \(\frac{18}{36}\), P(E₂) = \(\frac{4}{36}\) and P(E₁∩E₂) = \(\frac{2}{36}\)
∴ The required probability = P(E₁∪E₂)
= P(E₁) + P(E₂) – P(E₁∩E₂)
= \(\frac{18}{36}\) + \(\frac{4}{36}\) – \(\frac{2}{36}\) = \(\frac{20}{36}\) = \(\frac{5}{9}\)

Question 11.
Out of two bags one contains 3 black and 4 red balls and the second bag contains 8 black and 10 red balls. If one bag is chosen and a ball is drawn from it, then find the probability that is a red ball?
Solution:
I bag
3B + 4R = 7 balls total

II bag
8B + 10R = 18 balls total
(i) Selecting the I bag:
Probability that one bag is chosen (out of two bags) = \(\frac{1}{2}\)
1 red ball is drawn from I bag probability = \(\frac{4}{7}\)
Hence, the probability that the I bag is chosen as well as 1 red ball is drawn from it
(Compound event) P₁ = \(\frac{1}{2}\) × \(\frac{4}{7}\) = \(\frac{2}{7}\) ………………… (1)

(ii) If selecting II bag:
Probability that Il bag is chosen = \(\frac{1}{2}\)
I red ball is drawn from II bag probability = \(\frac{10}{18}\) = \(\frac{5}{9}\)
Hence, the probability that the II bag is chosen as well as 1 red ball is drawn from it
(Compound event) P₂ = \(\frac{1}{2}\) × \(\frac{5}{9}\) = \(\frac{5}{18}\) ……………………… (2)
The above two event are mutually exclusive.
Hence, only one event out of these two will happen.
Hence, the required probability P = P₁ + P₂
= \(\frac{2}{7}\) + \(\frac{5}{18}\)
= \(\frac{36+35}{126}\) = \(\frac{71}{126}\).

Question 12.
There are two bags, one contains 5 red and 7 white balls and second bag contains 3 red and 12 white balls. One ball is drawn from any of these bags at random? Find the probability that the ball is red?
Solution:
Solve same as Q. No. 11.

Question 13.
A bag contains 50 bolts and 150 nuts. Half of the bolts and nuts are rusted. If one item is taken out at random find out the probability that ¡ts rusted o is a bolt?
Solution:

Question 14.
A can hit a target 4 times in 5 shots; B, 3 times in 4 shots and C, 2 times 3 shoots at one time. Find the probability of at least two shots hit?
Solution:
Probability of A hitting the target = \(\frac{4}{5}\)
Probability of B hitting the target = \(\frac{3}{4}\)
Probability of C hitting the target = \(\frac{2}{3}\)
At least 2 can hit the target in the following ways:
(i) Probability that A, B,C all hit the target = \(\frac{4}{5}\) × \(\frac{3}{4}\) × \(\frac{2}{3}\) = \(\frac{2}{5}\)

(ii) Probability that B and C hit the target and not A
= ( 1 – \(\frac{4}{5}\) ) × \(\frac{3}{4}\) × \(\frac{2}{3}\) = \(\frac{1}{5}\) × \(\frac{3}{4}\) × \(\frac{2}{3}\) = \(\frac{1}{10}\)

(iii) Probability that C and A hit the target and not B
= \(\frac{4}{5}\) × (1 – \(\frac{3}{4}\) × \(\frac{2}{3}\) = \(\frac{4}{5}\) × \(\frac{1}{4}\) × \(\frac{2}{3}\)
= \(\frac{2}{15}\)

(iv) Probability that A and B hit the target but not C
= \(\frac{4}{5}\) × \(\frac{3}{4}\) × (1 – \(\frac{2}{3}\)) = \(\frac{4}{5}\) × \(\frac{3}{4}\) × \(\frac{1}{3}\) = \(\frac{1}{5}\)
Since, all these events are mutually exclusive,
∴ Required probability = \(\frac{2}{5}\) + \(\frac{1}{10}\) + \(\frac{2}{15}\) + \(\frac{1}{5}\) = \(\frac{5}{6}\)

Question 15.
In a class 30% students fail in physics, 25% fails in maths and 10% fails in both. If one student selects at random, then And the probability of:

(i) Fail in maths when fail in physics also,
(ii) Fail in physics when fail in maths also,
(iii) Fail in maths or physics.

Solution:
Probability of fail in physics is
P(A) = \(\frac{30}{100}\)
Probability of fail in maths is
P(B) = \(\frac{25}{100}\)
Probability of fail in physics and maths both is
P(A∩B) = \(\frac{10}{100}\)

Question 16.
Two bags A and B contain 8 green and 9 white balls and 5 green and 4 white balls respectively. One ball is drawn at random from one of the bags and it is found to be green. Find the probability that it is drawn from bag B? (NCERT)
Solution:
Let E₁ : Event of choosing bag A
∴ P(E₁) = \(\frac{1}{2}\) ………………………. (1)
E₂ = \(\frac{1}{2}\) ………………………… (2)
Again, let C: Event of drawing a green ball
∴ By defnition of conditional probability

The required probability (i.e; the probability of obtaining a ball from bag B when it is green.)

Question 17.
A company has two plants to manufacture bicycles. The first plant manufacture 60% of the bicycles and second plant 40%. Also 80% of the bicycles are rated standard quality at the first plant and 90% of standard quality at the second plant. A bicycle is picked up at random and found to be standard quality? Find the probability that it comes from the second plant? (CBSE 2003)
Solution:
Let E₁: The event of choosing a bicycle from first plant.
∴ P(E₁) = \(\frac{60}{100}\) ………………….. (1)
Let E₂: The event of choosing a bicycle from first plant.
P(E₂) = \(\frac{40}{100}\) ……………………….. (2)
Let E be event of choosing a bicycycle of standard quality, then
P ( \(\frac { E }{ E_{ 1 } } \) ) = Probability of choosing a bicycle of standard quality, given that it is produced by the first plant.
⇒ P ( \(\frac { E }{ E_{ 1 } } \) ) = \(\frac{80}{100}\), (given 80%)
P( \(\frac { E }{ E_{ 2 } } \) ) = Probability of choosing a bicycle of standard quality, given that it is produced by the second plant.
⇒ P( \(\frac { E }{ E_{ 2 } } \) ) = \(\frac{90}{100}\) (given 90%)
∴ The required probability (i.e., probability of choosing a bicycle from the second plant, given that it is of standard quality,

Question 18.
A company manufactures T.V., machine A, B and C manufatures 30%, 20% and 50% T.V. of the total production of their outputs 7%, 5% and 2% are defec¬tive T.V. respectively. A T.V. is selected at random from the production and is found to be defective?
Find the probability that defective T.V. which is manufactured by machine A? (CBSE 2015)
Solution:
Let the events T₁, T₂ and T₃ are the following:
Event T₁ : T.V. manufactured by machined A.
Event T₂ : T.V. manufactured by mechine B.
Event T₃: T.V. manufactured by machine C.
It is noted that these events are mutually exclusive.
Again, let E : The event of defective T.V.
Given, P(T₁) = 30% = \(\frac{30}{100}\) ………………….. (1)
P(T₂) = 20% = \(\frac{20}{100}\) ………………….. (2)
P(T₃) = 50% = \(\frac{50}{100}\) ………………….. (3)
Again P( \(\frac { E }{ T_{ 1 } } \) ) = The probability that T.V. is defective when it is manufactured by machine A.
⇒ P(\(\frac { E }{ T_{ 1 } } \) ) = 7% = \(\frac{7}{100}\)
P( \(\frac { E }{ T_{ 2 } } \) ) = The probability that T.V. is defective when it is manufactured by machine B.
⇒ P( \(\frac { E }{ T_{ 3 } } \) ) = 5% = \(\frac{5}{100}\)
Similarly,
P( \(\frac { E }{ T_{ 3 } } \) ) = The probability that T.V. is defective when it is manufactured by machine C.
⇒ P( \(\frac { E }{ T_{ 3 } } \) ) = 2% = \(\frac{2}{100}\)
Now, from Bayes’s theorem
P( \(\frac { T_{ 1 } }{ E } \) ) = The probability that T.V. is defective when it is manufactured by machine A.

Question 19.
The probability that Mohan does not speak the truth is \(\frac{1}{5}\) Mohan speaks the head when a coin is thrown, find the probability that really gettting head by the throw of a coin? (NCERT)
Solution:
Let A: The event of getting head.
P(A) = \(\frac{1}{2}\)
B: The event of not getting head.
∴ P(B) = 1 – P(B) = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
Again, Let E: The event that really getting head by the throw of a coin and Mohan speaks.
P( \(\frac{E}{B}\) ) = \(\frac{1}{5}\)
and P( \(\frac{E}{A}\) ) = 1 – \(\frac{1}{5}\) = \(\frac{4}{5}\)
Now, from Bayes’s thoerem
P( \(\frac{A}{E}\) ) = Probability that the report of the Mohan that head has occured is actually head.

Question 20.
Bag A contains 3 white and 4 red balls and bag B contains 5 white and 6 red balls. One ball is drawn at random from one of the bags and it is found to be red. Find the probability that it is drawn from bag B?
Solution:
Let E₁ = Event of choosing bag A.
E₂ = Event of choosing bag B.
P(E₁) = \(\frac{1}{2}\); P(E₂) = \(\frac{1}{2}\) ………………….. (1)
⇒ P(E₁) = P(E₂) = \(\frac{1}{2}\)
Again, let R = Event of drawing a red ball.
According to the question.
P( \(\frac { R }{ E_{ 1 } } \) ) = The probability that a red ball is drawn when it is selected from bag A.
⇒ P( \(\frac { R }{ E_{ 1 } } \) ) = \(\frac{4}{3+4}\) = \(\frac{4}{7}\) …………………. (2) [since bag A contains 3 white and 4 red balls]
P( \(\frac { R }{ E_{ 2 } } \) ) = \(\frac{6}{5+6}\) = \(\frac{6}{11}\) ……………….. (3) [since bag B contains 5 white and 6 red balls]
Now, from Bayes’s theorem,
P( \(\frac { E_{ 2 } }{ R } \) ) = The probability that a ball is drawn from bag B when it is red.

Question 21.
Three different bags A, B and C are given, each bag contains 2-2 books. Bag A contains both 2 mathematics books, bag B contains 2 chemistry books and bag C contains, one mathematics and one chemistry book. The student select one bag ran¬domly and from that bag he randomly take out one book. The book he has taken out is that of mathematics. Find the probability that the second book he draws out from that bag is also of mathematics or that he is selected bag A given? (NCERT)
Solution:
Let events E₁, E₂ and E₃ represents the selection of bag A, B and C respctively.
P(E₁) = P(E₂) = P(E₃) = \(\frac{1}{3}\) …………………….. (1)
D: The event of mathematics book happen
P( \(\frac { D }{ E_{ 1 } } \) ) = P(A mathematics book chosen from bag A)
= \(\frac{2}{2}\) = 1 ……………….. (2)
P( \(\frac { D }{ E_{ 2 } } \) ) = P(A mathematics book chosen from bag B)
= \(\frac{0}{2}\) = 0 ………………… (3)
[∵according to the questions, both chemistry books are in bag B]
P( \(\frac { D }{ E_{ 3 } } \) ) = P(A mathematics book chosen from bag C)
= \(\frac{1}{2}\)
Now, the required probability
P( \(\frac { E_{ 1 } }{ D } \) )
Now, by Bayes’ thoerem,
P( \(\frac { E_{ 1 } }{ D } \) )

Question 22.
By examining about a student that he is known to speak the truth 2 out of 5 times. He throws a die and reports that it is a six. Find the probability that it is actually a six?
Solution:
Let E: Event that the student reports that it is a six.
A : Event of getting a six on the upper face of die.
B : Event of not getting a six on the upper face of die.
∴ P(A) = \(\frac{1}{6}\) ………………….. (1)
P(B) = P(Not A) = P( \(\bar { A } \) )
⇒ P(B) = 1 – P(A) = 1 – \(\frac{1}{6}\)
⇒ P(B) = \(\frac{5}{6}\) ………………… (2)
P( \(\frac{E}{A}\) ) = Probability that the student reports that six occurs, when six has actually occured.
P ( \(\frac{E}{A}\) ) = Probability that the student speaks the truth
= \(\frac{2}{5}\) …………………… (3)
Now, P ( \(\frac{E}{B}\) ) = Probability that the student reports that six occurs, when six that has not actually occured.
P ( \(\frac{E}{B}\) ) = Probability that the student does not speak the truth.
P( \(\frac{E}{B}\) ) = 1 – \(\frac{2}{5}\) = \(\frac{3}{5}\)
Now, by Bayes’s thoerem
P( \(\frac{A}{E}\) ) = Probability of getting six, given that the student reports it to be six.

MP Board Class 12 Maths Important Questions

MP Board Class 11th Maths Important Questions Chapter 9 Sequences and Series Important Questions

Sequences and Series Important Questions 

Sequences and Series Objective Type Questions

(A) Choose the correct answer of the following:

Question 1.
The sum of the cube of first n positive integer is :
(a) \(\frac {n(n + 1)}{2}\)
(b) \(\frac {n(n + 1)(2n + 1)}{6}\)
(c) \(\frac {n(n + 1)(n + 2)}{6}\)
(d) {\(\frac {n(n + 1)}{2}\)}²
Answer:
(d) {\(\frac {n(n + 1)}{2}\)}²

Question 2.
The sum of n term of arithmetic progression is 2n + 3n², its second term will be :
(a) 10
(b) 12
(c) 16
(d) 11
Answer:
(c) 16

Question 3.
If arithmetic mean of a and b is \(\frac { { a }^{ n }+{ n }^{ n } }{ { a }^{ n – 1 }+{ b }^{ n – 1 } }\), then the value of n will be :
(a) 1
(b) 0
(c) – 1
(d) \(\frac {1}{2}\)
Answer:
(a) 1

Question 4.
Which term of the series 8, 4,0, ………….. is – 24 :
(a) 7^th
(b) 28^th
(c) 8^th
(d) 9^th
Answer:
(d) 9^th

Question 5.
If the first term of arithmetic progression be a and last term is l, then the sum of n terms will be :
(a) \(\frac {n}{2}\)[2a – (n – 1)d]
(b) \(\frac {n}{2}\)[2a + (n – 1)d]
(c) \(\frac {n}{2}\)(a + l)
(d ) \(\frac {n}{2}\)(a – l).
Answer:
(c) \(\frac {n}{2}\)(a + l)

Question 6.
The next term of the sequence 2\(\sqrt { 2 }\), \(\sqrt { 2 }\), 0, …………… is :
(a) – \(\sqrt { 3 }\)
(b) \(\frac { 1 }{ \sqrt { 2 } }\)
(c) – \(\sqrt { 2 }\)
(d) \(\sqrt { 2 }\)
Answer:
(c) – \(\sqrt { 2 }\)

Question 7.
If 2x, x + 8, 3x + 1 are in A.P, then value of x will be :
(a) 3
(b) 7
(c) 5
(d) 2
Answer:
(c) 5

Question 8.
The 15^th term from the end of the A.P. 2, 6,10, …………., 86 is :
(a) 30
(b) 32
(c) 46
(d) 48
Answer:
(a) 30

Question 9.
If first 15^th term of an A.P. is a, second term is b and n^th term is 2 a, then sum of the n terms is :
(a) \(\frac {ab}{2(b – a)}\)
(b) \(\frac {2ab}{3(b – a)}\)
(c) \(\frac {3ab}{2(b – a)}\)
(d) \(\frac {3ab}{(b – a)}\)
Answer:
(c) \(\frac {3ab}{2(b – a)}\)

Question 10.
In an A.P. S_n = 3n² + 5n and T_m = 164, then m equals to :
(a) 26
(b) 27
(c) 28
(d) None of these.
Answer:
(b) 27

Question 11.
A.M. of two number is 10 and GM. is 8, the numbers are
(a) a = 4, b = 16
(b) a = 2, b = 8
(c) a = 4, b = 9
(d) a = 2, b = 18.
Answer:
(a) a = 4, b = 16

Question 12.
The A.M. of two numbers is A and G M is G, then relation between them is :
(a) A < G (b) A = G (c) A > G
(d) None of these.
Answer:
(c) A > G

Question 13.
2^1/4.4^1/8.8^1/16 ……………. ∞ =
(a) 1
(b) 2
(c) 3/2
(d) 4
Answer:
(b) 2

Question 14.
If y = x – x² + x³ – x⁴ + ………. ∞, then value of x be (- 1 < x < 1) :
Answer:
(a) y + \(\frac {1}{y}\)
(b) \(\frac {y}{1 + y}\)
(c) y – \(\frac {1}{y}\)
(d) \(\frac {y}{1 – y}\)
Answer:
(d) \(\frac {y}{1 – y}\)

Question 15.
If the second, third and sixth terms of an A.P. are in GP, then the common ratio of the GP. is :
(a) 2
(b) 5
(c) 4
(d) 3
Answer:
(d) 3

Question 16.
Sum up to infinity of 1 + \(\frac {4}{5}\) + \(\frac { 7 }{ { 5 }^{ 2 } }\) + \(\frac { 10 }{ { 5 }^{ 2 } }\) + …………. :
(a) \(\frac {35}{16}\)
(b) \(\frac {37}{16}\)
(c) \(\frac {39}{16}\)
(d) 3
Answer:
(a) \(\frac {35}{16}\)

(B) Match the following :

Answer:

1. (d)
2. (f)
3. (a)
4. (g)
5. (b)
6. (j)
7. (c)
8. (i)
9. (e)
10. (h)

(C) Fill in the blanks :

1. – 7\(\sqrt { 3 }\) will be term of the series 5\(\sqrt { 3 }\), 3\(\sqrt { 3 }\), \(\sqrt { 3 }\), …………….
2. 116 is sum of the term of the series 25,22, 19 …………….
3. If sum of n terms of series is n² + 4n, then 15^th term of the series is …………….
4. 0 will be the term of the series 27, 24,21, 18 …………….
5. 729 will be the term of the series – \(\frac {1}{27}\), \(\frac {1}{9}\), – \(\frac {1}{3}\) …………….
6. The first term of GP. is a, common ratio r < 1 and its last term l, then its sum will be …………….
7. The ratio of the sum of first three term to the sum of first six term is 125 : 152, then common ratio will be …………….
8. First term 16 and fifth term \(\frac {1}{16}\), then its 4^th term will be …………….
9. Sum of n terms of the series x + 2x² + 4x³ + 8x⁴ + ……………. will be …………….
10. If a = 2, d = 2 and n = 50, then the last term of the series will be …………….

Answer:

1. 7
2. 12
3. 33
4. 10
5. 10
6. \(\frac {a – rl}{1 – r}\)
7. \(\frac {3}{5}\)
8. \(\frac {1}{4}\)
9. \(\frac { 1-({ 2x }^{ n })x }{ 1 – 2x }\)
10. 100

(D) Write true / false :

1. 1, 3, 5, 8, ………….. are inA.P.
2. n^th term of a G.P. is a + (n – 1 )d.
3. If 2x, x + 5 and x + 11 are in A.P., then value of x will be – 1.
4. Arithmetic mean of a and b is \(\sqrt { ab }\)
5. Sum of 9 terms of a sequence 24 + 20 + 16 + will be.
6. Four consicutive term of G.P. are \(\frac { a }{ { r }^{ 3 } }\) \(\frac {a}{r}\), ar, ar³.

Answer:

1. False
2. False
3. True
4. False
5. True
6. True.

(E) Write answer in one word / sentence :

1. If a, b, care inA.P., then find the value of ab + ac?
2. Arithmetic mean of (a + b)²and (a – b)² will be?
3. Sum of n arithmetic mean between x and 3x will be.
4. Find the sum of infinite terms of series : 9^1/3.9^1/3.9^1/27 ………….. up to ∞.
5. If a, b, c are in GP., then find the value \(\frac {1}{b}\) + \(\frac {1}{a – b}\) –\(\frac {1}{b – c}\)

Answer:

1. 2b²
2. a² + b²
3. 3nx
4. 3
5. 0

Sequences and Series Short Answer Type Questions

Question 1.
Which term of the sequence 27,24,21,18, …………. is zero? (NCERT)
Solution:
Here a = 27 and d= T₂ – T₁ = 24 – 27 = – 3.
Let the n^th term of series be 0.
∴ T_n = a + (n – 1)d
⇒ 0 = 27 + (n – 1)(- 3)
⇒ 3n – 3 = 27
⇒ 3n = 30
n = 10 or 10^th term.

Question 2.
The last term of the series 8,4,0, ……………. is – 24. Find the total number of terms. (NCERT)
Solution:
Given series 8,4, 0, … (1)
First term = a = 8 Common difference d = 4 – 8 = -4
d = 0 – 4 = – 4
∵ The common difference is same the series is in A.P.
last term l = – 24,
l = a + (n – 1)d,
= – 24 = 8 + (n – 1)(-4)
⇒ – 24 – 8 = (n – 1)(-4)
⇒ – 32 = (n – 1)(- 4)
⇒ (n – 1) = \(\frac {32}{4}\)
⇒ n – 1 = 8
⇒ n = 8 + 1
⇒ n = 9
∴ Number of terms n = 9

Question 3.
Seven times the 7^th term of a series is equal to eleven times of its 11th term. Find the 18^th term of the series. (NCERT)
Solution:
Let first term = a and common difference = d of A.P.
∴ 7^th term = a + 6d and 11^th term = a + 10 d.
∴ According to question,
7(a + 6d) = 11 + (a + 10d)
⇒ 7a + 42d = 11a + 110d
⇒ 7a – 11a = 110d – 42d
⇒ – 4a = 68 d
⇒ a = – 17d
Hence 18^th term = a + 17d
= – 17d + 17d [∵ a = – 17d]
= 0.

Question 4.
Prove that the sum of (m + n)^th term and (m – n)^th terms of an A.P. is twice of its m^th term.
Solution:
Let the first term = a and common difference = d.
T_n = a+(n – 1)d
T_{m + n}= a + (m + n – 1)d … (1)
T_{m – n} = a + (m – n – 1)d … (2)
T_m = a + (m – 1)d … (3)
T_m+n + T_m-n = a + (m + n – 1)d + a(m – n – 1)d
= 2a + (m + n – 1 + m – n – 1)d
= 2a + (2m – 2)d
= 2a + 2(m – 1)d
= 2[a+(m – 1)d]
T_m+n + T_m-n = 2T_m.

Question 5.
Insert three Arithmetic means between 3 and 19. (NCERT)
Solution:
Let three Arithmetic mean be A₁, A₂, A₃,
then 3, A₁, A₂, A₃, 19 are in A.P.
∴ 3 = a, 19 = T₅, let common difference = d
T₅ = a + 4d
T₅ = a + 4d
⇒ 19 = 3 + 4d
⇒ 16 = 4d
⇒ d = 4
Hence A₁ = 3 + 4 = 7, A₂ = 7 + 4 = 11, A₃ = 11 + 4 = 15.

Question 6.
If – 8, A₁, A₂ are in Arithmetic progression (A.P.), then find the value of A₁, A₂. (NCERT)
Solution:
– 8, A₁, A₂, 9 are in A.P.
∴ a = – 8, T₄ = 9, let common difference = d
T₄ = a + 3d
⇒ 9 = – 8 + 3 d
⇒ 3d = 11
⇒ d = \(\frac {17}{3}\)

Instruction :
Write the first five terms of each of the sequence and obtain the corresponding series.

Question 7.
(a) a₁ = 3, a_n = 3a_{n – 1} + 2, where n > 1. (NCERT)
Solution:
Given : a₁ = 3,
a₂ = 3a_{n – 1} + 2, where n > 1
a₂ = 3a_{2 – 1} + 2
⇒ a₂ = 3a₁ + 2
⇒ a₂ = 3 x 3 + 2 = 9 + 2 = 11
a₃ = 3a₁ + 2
= 3a₂ + 2
⇒ a₃ = 3(11)+ 2 = 33+ 2 = 35
a₄ = 3a_{4 – 1} + 2
= 3a₃ + 2
⇒ a₄ = 3(35) + 2 = 105 + 2 = 107
a₅ = 3a_{5 – 1} + 2
= 3a₄ + 2
= 3(107) + 2 = 321 + 2 = 323
Hence series is 3, 11, 35, 107, 323.

Question 7.
(b) a₁ = -1, a_n = \(\frac { { a }_{ n-1 } }{ n }\) where n ≥ 2.
Solution:

Question 8.
A person pays first instalment of Rs. 100 towards his loan. If he increases his instalment every month by Rs. 5, then what will be his 30^th instalment.
Solution:
Given : a = Rs. 100, d= Rs. 5, n = 30,
T_n = a + (n – 1)d
Amount of 30^th instalment
J₃₀ = 100 + (30 – 1) x 5
= 100 + 29 x 5 = 100 + 145
= Rs. 245.
Hence the 30^th instalment = Rs. 245.

Question 9.
Which term of the sequence \(\sqrt { 3 }\), 3, 3\(\sqrt { 3 }\) ……. is 729?
Solution:

Question 10.
How many terms are required in GP. 3,3²,3³ …………, so that their sum would be 120? (NCERT)
Solution:
Given : a = 3, r = \(\frac {9}{3}\) = 3, S_n = 120,
S_n = \(\frac { a({ r }^{ n }-1) }{ r-1 }\)
⇒ \(\frac { 3({ 3 }^{ n }-1) }{ 3-1 }\) = 120
⇒ 3ⁿ – 1 = \(\frac {120 × 2}{3}\)
⇒ 3ⁿ – 1 = 80
⇒ 3ⁿ = 81
⇒ 3ⁿ = 3⁴
⇒ n = 4

Question 11.
Show that ratio between sum of n terms and sum of (n +1)^th term to (2n)^th terms in a G.P. is \(\frac { 1 }{ { r }^{ n } }\)
Solution:
Let 1^st term of G.P. = a and common ratio = r
∴ n terms of GP. is a, ar, ar², ………….. , ar^{n – 1}
Let the sum to n terms be S₁
S₁ = \(\frac { a({ r }^{ n }-1) }{ r-1 }\)
GP. from (n + 1)^th term to (2n)^th term
arⁿ, ar^{n + 1}, …………. , ar^{2n – 1}
Let the sum of this G.P. up to n terms be S₂

Question 12.
If A.M. and GM. of roots of a quadratic equation are 8 and 5 respectively, then find the quadratic equation. (NCERT)
Solution:
Let the roots of equation be α and β
A.M. of roots = \(\frac {α + β}{2}\) = 8
⇒ α +β = 16
G.M. of roots = \(\sqrt {αβ }\) = 5
⇒ αβ = 25
If α, β are the roots of equation
then, x² – (α + β)x + αβ = 0
⇒ x² -16x + 25 = 0.

Question 13.
If the first and n^th term of GP. are a and b respectively and if p is the product of n terms, then prove that
p² = (ab)ⁿ. (NCERT)
Solution:
Let the common ratio of G.P. = r
Given: ar^{n – 1} = b, …(1)
then a.ar.ar²……. ar^{n – 1} = p
⇒ aⁿr^{1+2+3+……+(n – 1)} = p
⇒ aⁿr^{\(\frac {1}{2}\)(n – 1)n} = p
⇒ a²ⁿ.r^{(n – 1)n} = p²
⇒ p² = (a²r^{n – 1n}
⇒ p² = (a.ar^{n – 1})ⁿ
⇒ p² = (ab)ⁿ, [fromeqn. (1)]

Question 14.
If the 4^th term of a GP. is square of its second term and the 1^st term is -3, then find the 7^th term. (NCERT)
Solution:
Let a and r be the 1st term and common ratio of GP.
∴ T_n = ar^n-1
T₄ = ar^4-1 = ar³ … (1)
T₂ = ar^2-1 = ar … (2)
Given : T₄ = (T₂)²
⇒ ar³ = (ar)²
⇒ ar³ = a²r²
⇒ a = r = – 3 (given, a = -3)
T₇ = ar^7-1 = ar⁶
= (-3)(-3)⁶ = (-3)⁷
∴ T₇ = – 2187
Hence 7_th term of G.P. = – 2187.

Question 15.
Find the value of \(\sum _{ k=1 }^{ 11 }{ (2+{ 3 }^{ k }) }\).
Solution:

Sequences and Series Long Answer Type Questions

Question 1.
If m times of the m^th term of an A.P. is equal to n times the n^th term, then prove that (m + n)^th term of the series is zero.
Solution:
Let the 1^st term = a and common difference = d.
then t_m = a + (m – 1)d
t_n = a + (n – 1)d
Given: m[a + (n – 1)d] = n[a + (n – 1)d]
⇒ ma + m(m – 1 )d = na + n(n – 1 )d
⇒ (m² – m)d + (m – n)a = (n² – n)d
⇒ (m² – m – n² + n) d + (m – n)a = 0
⇒ [m² – n² – (m – n)] d + (m – n)a = 0
⇒ [(m – n)(m + n) – (m – n)] d+(m – n)a = 0
⇒ (m – n)[(m + n) – 1] d + (m – n)a = 0
⇒ a + (m + n – 1 )d = 0
⇒ t_m+n=0.

Question 2.
If the 6^th term of A.P. is 12 and 9^th term is 27, then find its r^th term.
Solution:
Let the 1^st term = a and common difference = d.
Given : t₆ = 12
⇒ a + 5d = 12 … (1)
t₉ = 27
⇒ a + 8d = 27 … (2)

Question 3.
If p^th term of an A.P. is \(\frac {1}{q}\) and q^th term is \(\frac {1}{p}\), then prove that (pq)^th
Solution:

Question 4.
If p^th term of an A.P. is \(\frac {1}{q}\) and q^th term is \(\frac {1}{p}\), then prove that (pq)^th terms is \(\frac {1}{2}\) (pq + 1), where p ≠ q.
Solution:

Question 5.
The sum of the series 25, 22, 19, ………….. of A.P. is 116, then find its last term. (NCERT)
Solution:
Given : a = 25, d = 22 – 25 = – 3, S_n = 116
S_n = \(\frac {n}{2}\) [2a + (n – 1)d]
⇒ 116 = \(\frac {n}{2}\)[2 x 25 + (n -1) x (-3)]
⇒ 232 = n[50 – 3n + 3]
⇒ 232 = n[53 – 3n]
⇒ 232 = 53n – 3n²
⇒ 3n² – 53n +232 = 0
⇒ 3n² – 24n – 29n + 232 = 0
⇒ 3n(n – 8) – 29(n – 8) = 0
⇒ (n – 8)(3n – 29) = 0
n = 8, or n = \(\frac {29}{3}\), (which is impossible)
∴ Last term l = a + (n – 1 )d
= 25 + (8 – 1) x (- 3)
⇒ l = 25 – 21 = 4.

Question 6.
If the A.M. of a and b is \(\frac { { a }^{ n }+{ b }^{ n } }{ { a }^{ n – 1 }+{ b }^{ n – 1 } }\), then find the value of it. (NCERT)
Solution:
A.M. of a and b = \(\frac {a+b}{2}\)
According to question,
\(\frac { { a }^{ n }+{ b }^{ n } }{ { a }^{ n – 1 }+{ b }^{ n – 1 } }\) = \(\frac {a+b}{2}\)
⇒ 2aⁿ + 2bⁿ = (a + b) (a^{n – 1} + b^{n – 1})
⇒ 2aⁿ +2bⁿ = aⁿ + bⁿ + ab^{n – 1} + ba^{n – 1}
⇒ aⁿ + bⁿ = ab^{n – 1} + ba^{n – 1}
⇒ aⁿ – ba^{n – 1} = ab^{n – 1} – bⁿ
⇒ a^{n – 1}(a – b) = b^{n – 1}(a – b)
⇒ a^{n – 1} = b^{n – 1}
⇒ \(\frac {a}{b}\)^{n – 1} = \(\frac {a}{b}\)⁰
⇒ n – 1 = 0
⇒ n = 1.

Question 7.
Between 1 and 31, m numbers have been inserted in such a way that the resulting sequence is an A.P. and the ratio of 7^th and (m – 1)^th mean is 5 : 9 then, find the value of m.
Solution:
Let A₁, A₂, A₃, ……… ,A_m are m A.M. respectively inserted between 1 and 31.
Then 1, A₁, A₂, A₃, ……… A_m 31 are in A.P. Here, 1^st term = 1 and (m + 2)^th term = 31 and let the common difference of sequence be d.

Question 8.
Show that the sum of (m + n)^th and (m – n)^th term of an A.P. is equal to twice the m^th term. (NCERT)
Solution:
Let the first term = a and common difference = d.
T_n = a + (n – 1)d
T_{m + n} =a +(m + n – 1)d … (1)
T_{m – n} = a + (m – n – 1)d … (2)
T_m = a + (m – 1)d … (3)
Adding equation (1) and (2),
T_{m + n} + T_{m – n} = a + (m + n – 1)d + a + (m – n – 1)d
= 2a + (m + n – 1 + m – n – 1)d
= 2a + (2m – 2 )d
= 2a + 2 (m – 1)d
= 2[a + (m – 1)d]
∴ T_{m + n} + T_{m – n} = 2T_m [From equation (3)]

Question 9.
If the sum of three numbers in A.P. is 24 and their product is 440, then find the numbers? (NCERT)
Solution:
Let the three numbers of A.P. are a – d, a, a + d.
Given : a – d + a + a + d = 24
3a = 24
⇒ a = 8
and (a – d) × a × (a + d) = 440
a(a² – d²) = 440
⇒ 8(64 – d²) = 440
⇒ 64 – d² = \(\frac {440}{8}\)
⇒ 64 – d² = 55
⇒ d² = 64 – 55
⇒ d² = 9
⇒ d = ± 3
When a = 8 and d = 3
Then, a – d = 8 – 3 = 5, a = 8, a + d= 8 + 3 = 11
When a = 8 and d = – 3
Then, a – d = 8 + 3 = 11, a = 8, a + d = 8 – 3 = 5
Hence required numbers are 5, 8, 11 or 11, 8, 5.

Question 10.
If the sum of n, 2n and 3n terms in A.P. are S₁ S₂ and S₃, then show that S₃ = 3(S₂ – S₁).
Solution:

Question 11.
Find the sum of all natural numbers lying between 200 and 400, which are divisible by 7. (NCERT)
Solution:
Numbers divisible by 7 are 203, 210, 217, …………. , 399
Here a = 203, d = 210 – 203 = 7, l = 399
l = a + (n – 1)d
399 = 203 + (n – 1) x 7
⇒ 399 – 203 = (n – 1) x 7
⇒ (n – 1)7 = 196
⇒ (n – 1) = \(\frac {196}{7}\)
⇒ (n – 1) = 28
∴ n = 29.
Hence required sum, S₂₉ = \(\frac {n}{2}\)[a+l]
⇒ S₂₉ = \(\frac {29}{2}\)[203 + 399]
⇒ S₂₉ = \(\frac {29}{2}\)[602] = \(\frac {17458}{2}\) = 8729.

Question 12.
If the 5^th, 8^th and 11^th terms of a GP. are p, q and s respectively, then show
that q² = ps. (NCERT)
Solution:
Let the 1st term of GP. = a and common ratio = r.
Then, T_n = ar^{n – 1}
T₅ = ar^{5 – 1} =p
⇒ ar⁴ = P … (1)
T₈ = ar^8-1 = q
⇒ ar⁷ = q … (2)
T₁₁ = ar^{11 – 1} = s
⇒ ar¹⁰ = s
ps = ar⁴.ar¹⁰, [from equation (1) And (3)]
⇒ ps = a²r¹⁴
⇒ ps = (ar⁷)²
⇒ ps = q², [from equation (2)]
∴ q² = ps.

Question 13.
If the first term of G.P. a = 729 and 7^th term is 64, then find S₇. (NCERT)
Solution:

Question 14.
If the 4^th terms of a GP is square of its 2^nd term and first term is – 3, then find its 7^th (NCERT)
Solution:
Let the 1st term of GP. = a and common ratio = r.
Then, T_n = ar^{n – 1}
T₄ = ar^{4 – 1} = ar³ … (1)
T₂ = ar^2-1 = ar … (2)
Given : T₄ = T₂²
ar³ = (ar)₂
ar³ = a²r²
⇒ ar³ = a²r²
⇒ a = r = – 3 (given a = – 3)
T₇ = ar^{7 – 1} = ar⁶
= (-3)(-3)⁶ = (-3)⁷
∴ T₇ = – 2187
Hence, 7^thterm of G. P. = – 2187.

Question 15.
Find the sum of the sequence 8,88,888,8888 ……….. up to n terms. (NCERT)
Solution:
Let the sum of the n terms be S

Question 16.
Find the sunt of the numbers 7,77,777, 7777 up to n terms. (NCERT)
Solution:
Let the sum of n terms is S.

Question 17.
If the A.M. and GM. between two positive numbers a and b are 10 and 8 respectively, then find the numbers. (NCERT)
Solution:
A.M. A = \(\frac {a+b}{2}\)
a + b = 20 … (1)
G.M. G = \(\sqrt {ab}\)
ab = 64 … (2)
(a – b)² = (a + b)² – 4ab
= (20)² – 4 × 64, [From equation (2)]
= 400 – 256
(a – b)² = 144 = (12)² … (3)

Put a = 16 in equation (1), we get,
16 + b = 20
∴ b = 4
Numbers are 16 and 4.
When a – b = – 12, then
a + b = 20
a – b = – 12
On adding 2a = 8
⇒ a = 4
Put a = 4 in equation (1), we get,
4 + 6 = 20
∴ b = 16
Numbers are 4 and 16.
Hence numbers a and b are 4, 16 or 16,4.

Question 18.
The sum of two numbers is 6 times their geometric mean, show that the . numbers are in the ratio (3 + 2\(\sqrt {2}\)) ; (3 – 2\(\sqrt {2}\)). (NCERT)
Solution:
Let the numbers are a and 6.
Given: a + b = 6 \(\sqrt {ab}\)
\(\frac { a+b }{ 2\sqrt { ab } }\) = \(\frac {3}{1}\)
⇒ a + b = 3K …. (1)
and 2 \(\sqrt {ab}\) = K ⇒ 4ab = K²
(a – b)² = (a + b)² – 4ab
= (3K)² – (K)²
= 9K² – K² = 8K²
⇒ a – b = 2\(\sqrt {2}\)K …. (2)

Sequences and Series Very Long Answer Type Questions

Question 1.
If the ratio of the sum of n terms of two A.P. is 5n + 4 : 9n + 6, then find the ratio of their 18^th term.
Solution:
Let the two A.P. are :
a, a + d, a + 2d, ………….
and A, A + D, A +2D …………..

Question 2.
The ratio of the sum of m and n terms of an A.P. is m² : n². Show that the ratio of and u* term is (2m – 1) : (2n – 1). (NCERT)
Solution:
Let the A.P. are a, a + d, a + 2d, ……………
∴ m^th term of A.P. Tm = a + (m – 1)d
n^th term of A.P. Tn= a + (n – 1)d

Question 3.
If the sum of first three terms of a G.P. is \(\frac {39}{10}\) and their product is 1, then find the common ratio and the terms. (NCERT)
Solution:
Let the three terms of G.P. are \(\frac {a}{r}\), a, ar.
Given: \(\frac {a}{r}\) × a × ar = 1
⇒ a³ = 1 ⇒ a = 1
and \(\frac {a}{r}\) + a + ar = \(\frac {39}{10}\)
⇒ a(\(\frac {a}{r}\) + r + 1) = \(\frac {39}{10}\)
⇒ 1 x \(\frac { 1+{ r }^{ 2 }+r }{ r }\) = \(\frac {39}{10}\)
⇒ 10r² + 10r + 10 = 39r
⇒ 10r² – 29r + 10 = 0
⇒ 10r² – 25r – 4r + 10 = 0
⇒ 5r(2r – 5) – 2(2r – 5) = 0
⇒ (5r – 2)(2r – 5) = 0
∴ r = \(\frac {2}{5}\) and r = \(\frac {5}{2}\)
When a = 1 and r = \(\frac {2}{5}\)

Question 4.
Find four numbers forming a G.P. in which the third term is greater than the lint term by 9 and the second term is greater than 4^th term by 18. (NCERT)
Solution:
Let the four terms of G.P. be a, ar, ar²,ar³.
Given: T₃ = T₁ + 9
⇒ T₃ = T₁ + 9
⇒ T₃ = a + 9
⇒ ar² = a + 9 …. (1)
According to question,
T₂ = T₄ + 18
⇒ ar = a³ + 18
⇒ ar – ar³ = 18 …. (2)

Put r = – 2 in equation (1), we get
a(- 2)² – a = 9
⇒ 4a – a = 9
⇒ 3a = 9
⇒ a = 3
∴ Numbers are 3, 3(- 2), 3(- 2)², 3(-2)³, ……………..
3, – 6, 12, – 24, ………………

Question 5.
If S be the sum of it terms of a GP., P be the product and R be the sum of reciprocal of n terms, then prove that
P²Rⁿ = Sⁿ. (NCERT)
Solution:
Let n terms of GP. be a, ar, ar², …………… ar^{n – 1}.
According to the question,

Question 6.
If x = 1 + a + a² + ………….∞ (\(\left| a \right|\)<1)
y = 1 + b + b² + …………….∞ (\(\left| b \right|\)<1)
then prove that
1 + ab + a²b² + …………….∞ = \(\frac {xy}{x + y – 1}\)
Solution:

Question 7.
The sum of infinite terms of a Geometric Progression is 15 and sum of the square of its terms is 45. Find the Geometric Progression. (NCERT)
Solution:
Let a be the first term and r be the common ratio.
∵ \(\left| r \right|\)<1,
Then, \(\frac {a}{1 – r}\) = 1.5 …. (1)
Squaring the terms of GP. the new G.P. is
a², a² r², a² r⁴, a² r⁶, ……….
Sum of infinity of G.P. = \(\frac { { a }^{ 2 } }{ { 1 – r }^{ 2 } }\).
\(\frac { { a }^{ 2 } }{ { 1 – r }^{ 2 } }\) = 45, (given) … (2)
Squaring both sides of equation (1) and the result is divided by equation (2),
\(\frac { { a }^{ 2 } }{ { 1 – r }^{ 2 } }\)² × \(\frac { 1-{ r }^{ 2 } }{ { a }^{ 2 } }\) = \(\frac {15×15}{45}\)
⇒ \(\frac {1 + r}{1 – r}\) = 5
⇒ 1 + r = 5 – 5r
⇒ 6r = 4
⇒ r = \(\frac {2}{3}\)
Put r =\(\frac {2}{3}\) in equation (1), we get

Hence required progression is 5, 5 × \(\frac {2}{3}\), 5 × (\(\frac {2}{3}\))², …………….
Hence 5, \(\frac {10}{3}\), \(\frac {20}{9}\), ………………

Question 8.
A farmer buys a used tractor of Rs. 12,000. He pays Rs. 6,000 cash and agrees to pay the balance in annual instalment of Rs. 500 plus 12% interest on theunpaid amount How much the tractor cost him?
Solution:
Cost of tractor = Rs. 12, 000, down payment = Rs. 6,000
Balance amount = 12,000 – 6,000 = Rs. 6,000

Actual cost of tractor = 12,000 + 4,680 = Rs. 16,680. Ans.

Question 9.
Shamshad Ali buys a scooter for Rs. 22,000. He pays Rs. 4,000 cash and agrees to pay the balance in annual instalment of Rs. 1,000 plus 10% interest on the unpaid amount How much will scooter cost him? (NCERT)
Solution:
Cost of scooter = Rs. 22,000, Cash down payment = Rs. 4,000.
Remaining amount = 22,000 – 4,000 = Rs. 18,000

Actual cost = 22,000 + 17,100 = Rs. 39,100.
Total amount paid for scooter = Rs. 39,100.

Question 10.
A person writes a letter to four of his friends. He asks each one of them, to copy the letter and mail to four different persons with instructions that they move the chain similarly. Assuming that the chain is not broken and that is costs 50 paisa to mail one letter. Find the amount on postage when 8^th set of letter is mailed. (NCERT)
Solution:
First person sends 4 letters.
2^nd step, he sends 4 x 4= 16 letters
3^rd step, he sends 4 x 4 x 4 = 64 letters
Hence 4, 16, 64, 256, …………… is a Geometric series.
Here a = 4, r = \(\frac {16}{4}\) = 4
S_n = \(\frac { { a(r }^{ n } – 1) }{ r – 1 }\) [∵r>1]
∴ Total number of letters till 8^th set = S₈ = \(\frac { { 4(r }^{ 4 } – 1) }{ 4 – 1 }\)
= \(\frac {4}{3}\) (65536 – 1) = \(\frac {4}{3}\) x 65535
Cost for one letter = Rs. 0.50
∴ Hence total cost = \(\frac {4}{3}\) x 65535 x 0.50 = Rs. 43690.

Question 11.
150 workers were engaged to finish a job in a certain number of days, 4 workers dropped out on second day, 4 more workers dropped out on third day and so on. It took 8 more days to finish the work. Find the number of days in which the work was completed. (NCERT)
Solution:
150, 146, 142, 138, …………, it is a Geometric series.
Let the number of days required complete the work be n.

If the workers not dropped then the work would have complited in (n – 8) days with 150 workers working on each day.
Hence the total workers worked for n days = 150 (n – 8)
= 150n – 1200 ….. (2)
From equation (1) and (2),
150n – 1200 = 152n – 2n₂
2n₂ + 150n – 152n – 1200 = 0
2n₂ – 2n – 1200 = 0
n₂ – n – 600 =0
n₂ – 25n + 24n – 600 = 0
n(n – 25) + 24(n – 25) = 0
(n – 25)(n + 24) = 0
n =25 and n = – 24 (not possible)
∴ Work is completed in 25 days.

MP Board Class 11th Maths Important Questions

MP Board Class 12th Physics Important Questions Chapter 15 Communication Systems

Communication Systems Important Questions 

Communication Systems Objective Type Questions

Question 1.
Choose the correct answer of the following:

Question 1.
The elements of communication system are :
(a) One transmitter
(b) Only receiver
(c) Only communication channel
(d) All of the above.
Answer:
(d) All of the above.

Question 2.
Sound wave are not directly transmitted after converting them into electric signals because:
(a) They propagates with speed of sound
(b) Their frequency does not remain constant
(c) For their transmission very high antenna is needed
(d) Their energy is very high.
Answer:
(c) For their transmission very high antenna is needed

Question 3.
The super imposing of audio waves with carrier wave is called :
(a) Transmission
(b) Reception
(c) Modulation
(d) Defection.
Answer:
(c) Modulation

Question 4.
The frequency range used for T.V. transmission is :
(a) 30 – 300 MHz
(b) 30 – 300 GHz
(c) 30 – 300 KHz
(d) 30 – 300 Hz.
Answer:
(a) 30 – 300 MHz

Question 5.
The periodic time of communication satellite is :
(a) 1 year
(b) 1 day
(c) 12 hours
(d) 12 minutes.
Answer:
(b) 1 day

Question 6.
T. V. signals are reflacted by :
(a) Mesosphere
(b) Ionosphere
(c) Troposphere
(d) None of these.
Answer:
(d) None of these.

Question 7.
The short wave band of radio waves are transmitted through :
(a) Sky wave propagation
(b) Ground wave propagation
(c) Artificial satellite
(d) Direct sending from transmitter to receiver.
Answer:
(a) Sky wave propagation

Question 8.
T.V. network uses :
(a) Microwaves
(b) Radio waves of very high frequency
(c) Gamma rays
(d) X – ray.
Answer:
(b) Radio waves of very high frequency

Question 9.
The waves used in telecommunication are :
(a) Infrared rays
(b) UV – rays
(c) Microwaves
(d) Cosmic rays.
Answer:
(c) Microwaves

Question 2.
Fill in the blanks :

1. …………….. is that signal which varies periodically with time.
2. Digital signal is represented by two binary number …………….. and……………..
3. The range of audio signals is ……………..
4. The frequency of carrier waves is of order of ……………..
5. The order of frequency of radio waves which can be transmitted by total internal reflection through ionosphere is ……………..
6. The band width of AM waves is ……………..
7. The T.V. transmission was invented by……………..
8. WWW means ……………..
9. …………….. is a device with the help of which the location of any place can be obtained.

Answer:

1. Analog signals
2. 0 and 1
3. 20 Hz to 20000 Hz
4. MHz
5. 30 – 300 MHz
6. Frequency of modulating wave
7. J. L. Baird
8. World Wide Web
9. GPS.

Question 3.
Match the columns:
I.

Answer:

1. (e)
2. (d)
3. (b)
4. (c)
5. (a)

II.

Answer:

1. (e)
2. (c)
3. (d)
4. (b)
5. (a)

Question 4.
Write the answer in one word/sentence:

1. Write any two light sources which are used in optical communication?
2. On what principle does the optical fibre work?
3. Who invented the T, V. transmission?
4. What is FAX?
5. What is meant by channel width? Write channel width of AM and FM radio station.
6. What is demodulation or detection?

Answer:

1. Light emitting diode (LED) and Diode LASER
2. Total internal reflection
3. J. L. Baird
4. The electronic reproduction of a document at a distant place is known as facsimile telegraphy or FAX
5. Channel width is that frequency range in which signals can be transmitted from a station. The channel width of AM is 10
6. kHz and of FM is 150 kHz
7. The process of extracting the audio signal from the modulated wave is known as demodulation or detection.

Communication Systems Very Short Answer Type Questions

Question 1.
What is principle of semiconductor LASER?
Answer:
In these LASER Gallium Arsenide (Ga – As) is used. This LASER the ability to produce LASER rays in the range 0.75 to 0.9 um.

Question 2.
Why is a parallel wire line not suitable for microwave transmission?
Answer:
In microwave transmission, half the operating wavelength approaches the separation between the two parallel wire lines. Therefore energy loss in the form of radiation becomes maximum.

Question 3.
What do you understand by channel and channel noise?
Answer:
The frequency range prescribed for a given transmission is called channel. The unwanted signals present by known or unknown reason in the transmitted signal is called noise.

Question 4.
What is importance of modulation index?
Answer:
The modulation index determines the strength and quality of the transmitted signal. If the modulation index is small the amount of variation in the carrier amplitude will be small.

Question 5.
Write full form of LED and LASER.
Answer:
Full form of LED is “Light Emitting Diode”. Full form of LASER is “Light Amplification by Stimulated Emission of Radiations”.

Question 6.
Which device is used to transmit the T.V. signals up to long distances?
Answer:
Communication satellites are used to transmit the T.V. signals up to long distances.

Question 7.
What is a communication system?
Answer:
Communication system is that system through which the signals are transmitted from one place and required at the other place.

Question 8.
What are message signals?
Answer:
A message signal is a single valued function of time that conveys the information. The electrical analog of information or basic message is called message signal. These are obtained by suitable transducers.

Question 9.
What are analog signals?
Answer:
An analog signal is continuous single value which at any instant lies within the range of a maximum and minimum value.

Question 10.
What is a digital signal?
Answer:
Digital signal is a discontinuous signal value which appears in steps in predetermined levels rather than having the continuous change.

Question 11.
What is noise?
Answer:
Noise refers to the unwanted signals that tends to disturb the transmission and processing of message signals in a communication system.

Question 12.
What is modulation?
Answer:
Modulation is a process in which the signal of low frequency (audio signals) are superimposed over a signal of high frequency (carrier signal).

Question 13.
What is FAX?
Answer:
Fax is a type of communication in which an electronic copy of a document is sent to a distance place.

Question 14.
Which type of signal is used in communication through computer?
Answer:
Digital Signal.

Question 15.
Write basic difference between the light emitted by LED and LASER.
Answer:
The light emitted by LASER is completely coherent and monochromatic while the light emitted by the LED is not coherent.

Question 16.
What is bandwidth? What is bandwidth of audio signals?
Answer:
The frequency range of a signal is called its bandwidth. The bandwidth audio signals is 20 Hz to 20 KHz.

Communication Systems Short Answer Type Questions

Question 1.
Write name of two system used for pulse modulation.
Answer:

1. PAM : Pulse Amplitude Modulation.
2. PCM : Pulse Code Modulation.

Question 2.
Write name of two systems which are used to convert the digital data into analog data.
Answer:

1. Amplitude Shift Keying (ASK)
2. Phase Shift Keying (PSK).

Question 3.
FM signals are less sensitive as compared to AM signals. Why?
Answer:
In FM transmission the information (message) in the carrier waves is in the form ofvariation (change) in frequency. In the AM the noise get amplitude modulated. Hence the amplitude carrier wave varies. That is why the FM signals are less sensitive as compared to AM signals.

Question 4.
Write limitations of frequency modulation.
Answer:

1. Area of reception for FM is much smaller.
2. About 10 times wider channel is required by FM.
3. FM receivers and transmitters are very complex and costly.

Question 5.
Write the meaning of LASER and two uses.
Answer:
Meaning of LASER:
Light Amplification by stimulated Emission of Radiations.

Uses:

1. Communication and
2. The medical field to determine vary long distances.

Question 6.
Write any two uses of optical communication.
Answer:

1. It is free from noise.
2. Its bandwidth is large, so number of channels can be transmitted simultaneously.

Question 7.
What is Light Emitting Diode?
Answer:
It is forward biased P – N junction which emits the light. It converts electrical energy into light energy.

Question 8.
What is optical fibre? On what principle does it work?
Answer:
An optical fibre is a device with the help of which the optical signals can be transmitted over through a zig-zag path without loss of energy. It is based on principle of total internal reflection.

Question 9.
What is meant by population inversion and optical pumping?
Answer:
Population inversion:
The process by which the number of atoms are increased . in the excited state as compared to ground state by stimulated absorption, is called population inversion.

Optical pumping:
The process by which population inversion is obtained, is called optical pumping.

Question 10.
Give two characteristics of LASER rays.
Answer:

1. LASER rays are monochromatic.
2. These are highly coherent.

Question 11.
What are the elements of communication system? Explain with the help of block diagram and also describe the different kinds of communication system.
Or
What is communication system? What are its main parts? Explain with block diagram.
Answer:
Communication system is that system through which the signals are transmitted from one place and received at the other place.

Elements of communication system : Following are the elements of a communication system:

1. Transmitter : Its function is to transmit the information after modifying it, to a form suitable for transmission.
Block diagram of transmitter :

2. Communication channel : The free space through which the electromagnetic waves sent by the transmitter, reach the receiver is called communication channel. It may be a coupled wire, coaxial cable or radio wave.

3. Receiver : Its function is to receive information.
Block diagram of receiver:

Question 12.
What is noise? Why digital communication is popular? What are A/D and D/A converter?
Answer:
Noise : Noise is unwanted disturbance or foreign element interfering with the desired information or signal. Noise can come up in any part of the communnication system but it has its worst effect when the signal is weakest.

The digital communication is popular nowaday because of the following characteristics :

1. Its quality is good.
2. Digital signals are in the form of pulses, they can produce easily by using logic gates.
3. These signals do not get distorted by noise.
4. These signals can be stored as digital data.
5. In this transmission many information can be transmitted using one channel.

A/D and D/A converter:
The electric circuit which can convert the analog signal to digital signal is called A/D converter. The electric circuit which can convert the digital signal into analog signal is called D/A converter.

Question 13.
Write difference between Analog and Digital signals.
Answer:
Difference between Analog and Digital signals :

Analog signal:

• In this signal value of current or voltage changes continuously with time.
• It is a continuous function of time.
• A simple analog signal is represented by a sine wave.
• The signal obtained by converting a speech, music or intensity of reflected light are analog signals.

Digital signal:

• In these signals the current or voltage has only two descrete levels 0 and 1.
• It is discontinuous function of time.
• Digital signal is represented in the form of pulses.
• The letters of a book, output of digital computers or the information obtained from a FAX are digital signals.

Communication Systems Long Answer Type Questions

Question 1.
Explain need of modulation and define the term modulation.
Or
What is modulation? Why it is needed for the transmission of signals?
Answer:
Modulation:
Modulation is a process in which the signal of low frequency (audio signals) superimposed over a signal of high frequency (carrier signal). Such that same properties of carrier wave like amplitude, frequency or phase varies in accordance with the instantaneous value of audio signals.

Need of Modulation:
Modulation is necessary for a low frequency signal when it is to be sent to a distant place so that the information may not die out in the way itself as well as for the proper identification of a signal and to keep the height of antenna small also.

For the transmission of electromagnetic waves the length of antenna should be of order of wavelength of the transmitted waves. Since, λ= \(\frac {c}{ ν}\) therefore the required length of antenna for the audible range should be equal to \(\frac { 3\times { 10 }^{ 8 } }{ 20,000 }\) = 1.5 x 10⁴m to \(\frac { 3\times { 10 }^{ 8 } }{ 20 }\) = 1.5 x 10⁷

This length of antenna is not possible in practical. Now if the waves of 300kHz or more than it are to be transmitted then the required length of antenna will be \(\frac { 3\times { 10 }^{ 8 } }{ 3,00,000 }\) = 100 m or less than it. The antenna of this size can be constructed easily. Hence to transmit the audio signals they are superimposed with the radio waves of frequency of order of Mega Hertz. These waves are called carrier waves and this process is called modulation.

Question 2.
How many types of modulation are there? Explain each types of modula-tion.
Answer:
The equation of carrier wave is given as :
e_c = E_c. cos (ω_ct + θ)
Where e_c is instantaneous value of carrier signal. E_c is amplitude of carrier wave, ω_c is angular frequency and θ is phase angle. Thus, there are three types of modulation corresponding to E_c, m_c and θ.

1. Amplitude modulation:
When an audio frequency (modulating) signal is superimposed that the amplitude of modulated wave is linear function of instantaneous value of modulating signal, then this type of modulation is called as amplitude modulation.

2. Frequency modulation:
Frequency modulation is that modulation in which the frequency of carrier wave varies in accordance with the instantaneous value of modulating signal. In this modulation the amplitude and phase of modulating signal are equal to that of carrier wave.

3. Phase Modulation:
In the phase modulation, the modulating waves are super imposed with carrier waves such that the phase of the modulated wave is the linear function of the amplitude of the modulating wave but the frequency and amplitude of the modulated signal remains same as the frequency and amplitude of the carrier wave.

Question 3.
What are limitations of amplitude modulation?
Answer:
The limitations (disadvantages) of amplitude modulation are as follows :

1. Efficiency of Amplitude modulation is smaller:
In AM modulation the message signals are contained in side bands, but not contained in the carrier wave. It is found that in amplitude modulation only one third power is contained inside bands, remaining power is contained in carrier wave. Hence efficiency decreases.

2. Amplitude modulation is more likely to suffer from noise.

3. In Amplitude modulation the fidelity of reception is less:
The range of audio signal is 20 Hz to 20 kHz. Hence the bandwidth must be 40 kHz. But the disturbance created by the nearby radio station should be taken into account and hence the bandwidth is kept only of about 20 kHz.

4. Its transmission range is low. Due to less power it is not possible to transmit the signals up to long distance. Inspite of these limitations the AM is mostly used for the transmission of audio signals.

Question 4.
Write advantages and disadvantages of frequency modulation.
Answer:
Advantages:

1. Frequency modulation is inherently and practically free from the effects of noise.
2. In frequency modulation, noise can further be decreased by increasing the deviation 8.
3. FM receiver can further be improved with the help of limiters to remove amplitude changes, if any which controls the noise level.
4. In FM it is possible to operate many independent transmitters on same frequency without interference.

Disadvantages:

1. A bout 10 times wider channel is required by FM.
2. Area of reception for FM is much smaller.
3. FM receivers and transmitters are very complicated and costly.

Question 5.
Explain the data transmission and retreival with the help of block diagram.
Answer:
The important use of data transmission and retrieval is in the microprocessor and computers. All the informations and signals which are to be transmitted are converted into digital signals by coding, which are then modulated with the carrier signals and are sent to far distant places. These signals are received by receivers. These received signals are amplified and demodulated in their original form. The block diagram of this process is shown in fig.

Question 6.
What is FAX machine? Draw its block diagram and explain its working.
Answer:

1. FAX : The electronic reproduction of a document at a distant place is known as facsimile telegraphy or Fax. To send the document through FAX following functions are performed.

• Optical scanning
• Conversion of data for transmission and reception.
• Printing a copy of images of the original document at the receiving end.

The block diagram of working of FAX is shown in fig.

Question 7.
Write notes on ‘MODEM’.
Or
What is MODEM? Write its working and uses.
Answer:
The block diagram of a modem is shown ahead : A modem is basically a modulator and a demodulator circuit.

Working:
At the transmitting end i.e., at section A, a modem change the digital data (obtained from source) into analogue form in audio frequency range.

So, it is easily modulated and transmitted by communication network through telephone lines and transmitter and sent to receiver for section B. At the receiving end i.e., at sermon B, the modem converts the analogue signal to digital signal.

Uses : It is used for short distance communication by connecting one computer to another through telephone lines.

Kinds of MODEM : MODEM are of two types.

• Internal MODEM : These are internally attached in the computer.
• External MODEM : These are connected externally with the computer.

Question 8.
Describe the following in short:

1. E – mail
2. Internet
3. World Wide Web
4. Celular phone
5. Pager.

Answer:
1. E – mail:
Its full form is electronic mail the message produced by using word processing, programs are transmitted over the world wide network called internet and they get stored in a computer called mail server. Any person connected to the internet can contact mail server. Any person connected to the internet can contact the mail server to check whether it is holding mail for him.

2. Internet:
Internet is a world wide network which connects the millions of computers which are linked together for data transmission. It is a global system of inter connected computer networks.

3. World Wide Web:
Its abreviation is WWW. It was invented by Tim Berners Lee in 1989 – 91 which is highly enlarged encylopedia which is accessible to every one for knowledge.

4. Celular Phone:
It is basically mini wireless phones for exchanging messages as well as for mobile telephonic conversation.

5. Pager:
It is a wireless device which records the messages in writing.

Question 9.
What is line communication? Explain.
Answer:
In a communication system the communication channel is a medium which provides the physicals path between transmitter and receiver. There are two types of communication medium:

1. Guided medium:
This medium connects transmitter and receiver in the case of point to point communication, double line cable, coaxial cable and optical fibre are the examples of guided medium.

2. Unguided medium:
This medium connects one transmitter and many receivers. Sky wave communication is an example of this medium. Its band frequency rays from few thousand kHz to few GHZ.

In the sky wave communication there is no point to point connection between transmitter and antenna. But in some communication applications the point to point connection is needed for example in telephone and telegraph the transmitter and receiver are connected by wire lines. It is called as line communication.

Question 10.
What is Global Positioning System (G.P.S.)? Write its applications.
Answer:
It is a space based satellite navigation system that provides users with accurate information on position time wherein the world even through the local streets and in all weather conditions.

To use GP.S. system of a satellite the user must have a GP.S. device fitted with transmitter and receiver for sending and receiving radio wave signal.

Applications of G.P.S

1. Navigation on land, water and air.
2. Keeping standard time all over the world.
3. Used in unmanned automatic vehicles movement and mobile telephony.
4. In desiging map of a location.

Communication Systems Numericals Questions

Question 1.
When there is 50% modulation the transmitter emits the 20 kW power calculate the power of carrier wave.
Solution:
Given : m_a = 50% = \(\frac {50}{100}\) = P_t = 20 kW = 20,000 W
Formula:

Question 2.
When a modulating of 500 Hz is given to a frequency modulation generator then it produces a frequency deviation of 2.25 kHz. Calculate modulation depth.
Solution:
Given : δ_max = 2.25 kHz = 2250 Hz, f_m = 500 Hz

Question 3.
The maximum and minimum amplitude of a amplitude modulated wave are 16 mV and 4 mV. What is the depth of modulation?
Solution:
Given : E_max = 16mV, E_min = 4mV
Formula:

Question 4.
A 20 kHz modulating signal is modulated with a carrier wave of 4 MHz. What will be the upper side band and lower side band? What will be the channel width?
Solution:
Given: f_m = 20 kHz, f_c = 4 MHz =4,000 kHz
f_USB = f_c + f_m = 4000 + 20 = 4020 kHz.
f_LSB = f_c – f_m= 4000 – 20 = 3980 kHz.
Channel width = f_USB – f_LSB
= 4020 – 3980 = 40 kHz.

Question 5.
Find out the modulation index of a frequency modulated wave whose modulating frequency is 2 kHz and maximum frequency deviation is 10 kHz.
Solution:
Given : f_m = 2 kHz and δ_max = 10 kHz
Formula : m_f = \(\frac { { \delta }_{ max } }{ { f }_{ m } }\)
m_f = \(\frac {10}{2}\) = 5

MP Board Class 12th Physics Important Questions