MP Board Class 12th Maths Important Questions Chapter 2 प्रतिलोम त्रिकोणमितीय फलन

MP Board Class 12th Maths Important Questions Chapter 2 प्रतिलोम त्रिकोणमितीय फलन

प्रतिलोम त्रिकोणमितीय फलन Important Questions

प्रतिलोम त्रिकोणमितीय फलन वस्तुनिष्ठ प्रश्न

प्रश्न 1.
सही विकल्प चुनकर लिखिए –

प्रश्न 1.
यदि sin^-1x – cos^-1 x = \(\frac { \pi }{ 6 } \) हो, तो x का मान ज्ञात कीजिए –
(a) \(\frac{1}{2}\)
(b) \(\frac { \sqrt { 3 } }{ 2 } \)
(c) – \(\frac{1}{2}\)
(d) इनमें से कोई नहीं।
उत्तर:
(a) \(\frac{1}{2}\)

प्रश्न 2.
यदि tan^-1 3 + tan^-1 x = tan^-1 8 हो, तो x का मान होगा –
(a) 5
(b) \(\frac{1}{5}\)
(c) \(\frac{5}{14}\)
(d) \(\frac{14}{5}\)
उत्तर:
(b) \(\frac{1}{5}\)

प्रश्न 3.
tan^-1 ( \(\frac{x}{y}\) ) – tan^-1 ( \(\frac { x-y }{ x+y } \) ) का मान है –
(a) \(\frac { \pi }{ 2 } \)
(b) \(\frac { \pi }{ 3 } \)
(c) \(\frac { \pi }{ 4 } \)
(d) \(\frac { -3\pi }{ 4 } \)
उत्तर:
(c) \(\frac { -3\pi }{ 4 } \)

प्रश्न 4.
2 tan^-1 {cosec (tan^-1 x) – tan (cot^-1 x)} का मान है –
(a) cot^-1 x
(b) cot^-1 \(\frac{1}{x}\)
(c) tan^-1 x
(d) tan^-1 \(\frac{1}{x}\)
उत्तर:
(c) tan^-1 x

प्रश्न 5.
tan {cos^-1 \(\frac { 1 }{ 5\sqrt { 2 } } \) – sin^-1 \(\frac { 4 }{ \sqrt { 17 } } \) } का मान होगा –
(a) \(\frac { \sqrt { 29 } }{ 3 } \)
(b) \(\frac{29}{3}\)
(c) \(\frac { \sqrt { 3 } }{ 29 } \)
(d) \(\frac{3}{29}\)
उत्तर:
(d) \(\frac{3}{29}\)

प्रश्न 2.
रिक्त स्थानों की पूर्ति कीजिए –

1. tan^-1 (1) + tan^-1 (2) + tan^-1 (3) = ………………………….
2. tan^-1 (2) – tan^-1 (1) = …………………………….
3. cot^-1 3 + cosec^-1 \(\sqrt{5}\)
4. sin(sin^-1 x + 2 cos^-1 x) = …………………………..
5. यदि sin^-1 ( \(\frac { 2a }{ 1+a^{ 2 } } \) ) + sin ( \(\frac { 2b }{ 1+b^{ 2 } } \) ) = 2 tan^-1 x, तो x = ………………………….
6. यदि tan^-1 ( \(\frac { 1-x }{ 1+x } \) ) = \(\frac{1}{2}\) tan^-1 x (जब x > 0), तो x =
7. tan^-1 ( \(\frac { a-b }{ 1+ab } \) ) + tan^-1 ( \(\frac { b-c }{ 1+bc } \) ) + tan^-1 c = ………………………..

उत्तर:

1. π
2. tan^-1 ( \(\frac{1}{3}\) )
3. \(\frac { \pi }{ 4 } \)
4. x
5. \(\frac { a+b }{ 1-ab } \)
6. \(\frac { 1 }{ \sqrt { 3 } } \)
7. tan^-1 (a)

प्रश्न 3.
निम्न कथनों में सत्य/असत्य बताइए –

1. tan^-1 x + tan^-1 y = tan^-1 \(\frac { x+y }{ 1-xy } \)
2. cos^-1(-x) = – cos^-1 x
3. sin^-1 (3x – 4x³) = sin^-1 \(\frac{x}{3}\)
4. cos^-1 ( \(\frac { 1-x^{ 2 } }{ 1+x^{ 2 } } \) ) = 2 tan^-1 x
5. sin^-1 x – sin^-1 y = sin^-1 [xy – \(\sqrt { 1-x^{ 2 } } \) \(\sqrt { 1-y^{ 2 } } \) ].

उत्तर:

1. सत्य
2. असत्य
3. असत्य
4. सत्य
5. असत्य।

प्रश्न 4.
सही जोड़ी बनाइये –

उत्तर:

1. (b)
2. (e)
3. (f)
4. (a)
5. (c)
6. (d)

प्रश्न 5.
एक शब्द/वाक्य में उत्तर दीजिए –

1. tan^-1\(\frac{1}{2}\) + tan^-1\(\frac{3}{2}\) का मान ज्ञात कीजिए।
2. tan^-1 \(\frac { x }{ \sqrt { 1-x^{ 2 } } } \) का मान ज्ञात कीजिए।
3. sin (2 sin^-1\(\frac{3}{5}\) ) का मान ज्ञात कीजिए।
4. समीकरण sin^-1 \(\frac{x}{5}\) + cosec^-1\(\frac{5}{4}\) = \(\frac { \pi }{ 2 } \) का मान ज्ञात कीजिए।
5. cos^-1 (cos \(\frac { 7\pi }{ 6 } \) ) का मुख्य मान लिखिए।
6. यदि cos^-1 ( \(\frac{1}{x}\) ) = θ हो, तो tan θ का मान लिखिए।

उत्तर:

1. tan^-1 8
2. sin^-1 x
3. \(\frac{24}{25}\)
4. x = 3
5. \(\frac { 5\pi }{ 6 } \)
6. \(\sqrt { x^{ 2 }-1 } \)

प्रतिलोम त्रिकोणमितीय फलन लाधु उतरिय प्रश्न

प्रश्न 1.
निम्नलिखित के मुख्य मान ज्ञात कीजिये – (CBSE 2014)

(i) tan^-1 [sin (- \(\frac { \pi }{ 2 } \) ) (CBSE 2014)

(ii) cot [ \(\frac { \pi }{ 2 } \) – 2 cot^-1 \(\sqrt{3}\) (CBSE 2014)

(iii) tan^-1 (-\(\sqrt{3}\) )

(iv) sec^-1 (-\(\frac{2}{3}\) \(\sqrt{3}\) ) (NCERT)

(v) cosec^-1 (2) (NCERT)

हल:
(i) tan^-1 [sin (- \(\frac { \pi }{ 2 } \) )
= tan^-1 [- sin \(\frac { \pi }{ 2 } \) ], [∵sin (- θ) = – sin θ]
= tan^-1 (-1), (∵ sin \(\frac { \pi }{ 2 } \) = 1)
= – tan^-1 (1), (∵ tan^-1 (-x) = – tan^-1 x)
= –\(\frac { \pi }{ 4 } \) (∵ tan^-1 (1) = \(\frac { \pi }{ 4 } \)
(ii) cot [ \(\frac { \pi }{ 2 } \) – 2cot^-1 \(\sqrt{3}\)

(iii) माना tan(-\(\sqrt{3}\)) = θ

(iv) sec^-1 \(\frac{-2}{3}\)\(\sqrt{3}\)) = θ

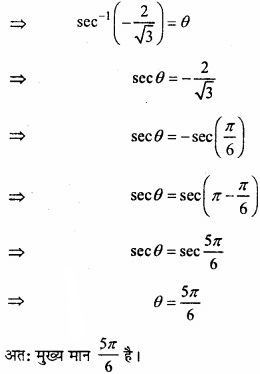
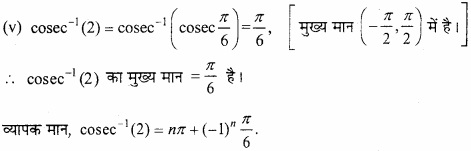
प्रश्न 2.
सिद्ध कीजिये –
(a) 2 cos^-1 \(\frac{4}{5}\) = cos^-1 \(\frac{7}{25}\)
(b) 2 sin^-1 \(\frac{3}{5}\) = sin^-1 \(\frac{24}{25}\)
(c) 2 sin^-1 \(\frac{5}{13}\) = sin^-1 \(\frac{120}{169}\)
हल:
(a) 2 cos^-1 \(\frac{4}{5}\) = cos^-1 \(\frac{7}{25}\)

(b) 2 sin^-1 \(\frac{3}{5}\) = sin^-1 \(\frac{24}{25}\)

(c) क्रमांक की 2(b) भाँती हल कीजिये।

प्रश्न 3.
मान ज्ञात कीजिये –
tan^-1 {2 cos (2 sin^-1 \(\frac{1}{2}\) )} (CBSE 2013, NCERT)
हल:
tan^-1 {2 cos (2 sin^-1 \(\frac{1}{2}\) )} = tan^-1 [2 cos (2 × \(\frac { \pi }{ 6 } \) ) ]
= tan^-1 [2 cos \(\frac { \pi }{ 3 } \) ] = tan^-1 [2 × \(\frac{1}{2}\) ]
= tan^-1 1
= \(\frac { \pi }{ 4 } \)

प्रश्न 4.
मान ज्ञात कीजिये –
sin [ \(\frac { \pi }{ 3 } \) – sin^-1 (- \(\frac{1}{2}\)) ] (CBSE 2008, 13)
हल:
sin [ \(\frac { \pi }{ 3 } \) – sin^-1 (- \(\frac{1}{2}\) ) ]
= sin [ \(\frac { \pi }{ 3 } \) + sin^-1 ( \(\frac{1}{2}\)) ], [∵sin^-1 (-x) = – sin^-1x]
= sin [ \(\frac { \pi }{ 3 } \) + \(\frac { \pi }{ 6 } \) ] = sin \(\frac { \pi }{ 2 } \) = 1

प्रश्न 5.
सिद्ध कीजिये –
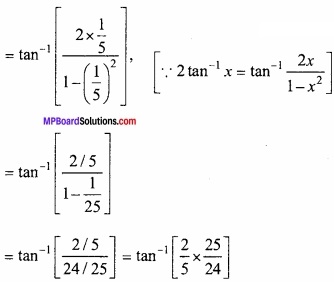
2 tan^-1 \(\frac{1}{5}\) = tan^-1 \(\frac{5}{12}\)?
हल:
L.H.S = 2 tan^-1 \(\frac{1}{5}\)

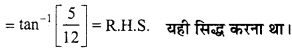
प्रश्न 6.
मान ज्ञात कीजिये –
tan (2 tan^-1 \(\frac{1}{5}\) – \(\frac { \pi }{ 4 } \) )
हल:

प्रश्न 7.
सिद्ध कीजिये –
3 sin^-1 x = sin^-1 (3x – 4x³). (NCERT, CBSE 2018)
हल:
मानलो sin^-1 x = θ.
∴ x = sin θ
अब sin 3θ = 3 sinθ – 4sin³θ
= 3x – 4x³
∴ 3θ = sin^-1 (3x – 4x³)

यही सिद्ध करना था।

प्रश्न 8.
सिद्ध कीजिये –
3 cos^-1 x = cos^-1 (4x³ – 3x) (NCERT)
हल:
मानलो cos^-1 x = θ
∴ x = cos θ
अब cos 3θ = 4 cos³θ – 3 cos θ
= 4x³ – 3x
∴ 3θ = cos^-1 (4x³ – 3x)

यही सिद्ध करना था।

प्रश्न 9.
सिद्ध कीजिये –
(A) tan^-1 \(\frac{1}{2}\) + tan^-1 \(\frac{1}{3}\) = \(\frac { \pi }{ 4 } \)
(B) cos^-1\(\frac{12}{13}\) = tan^-1 \(\frac{5}{12}\)
(C) cos^-1\(\frac{3}{5}\) = sin^-1 \(\frac{4}{5}\)
हल:
(A) tan^-1 = \(\frac{1}{2}\) + tan^-1 \(\frac{1}{3}\) = \(\frac { \pi }{ 4 } \)
L.H.S = tan^-1 \(\frac{1}{2}\) + tan^-1 \(\frac{1}{3}\)

(B) cos^-1 \(\frac{12}{13}\) = tan^-1 \(\frac{5}{12}\)

समी. (1) तथा (2) L.H.S. = R.H.S. यही सिद्ध करना था।

(C) cos^-1 \(\frac{3}{5}\) = sin-1 \(\frac{4}{5}\)

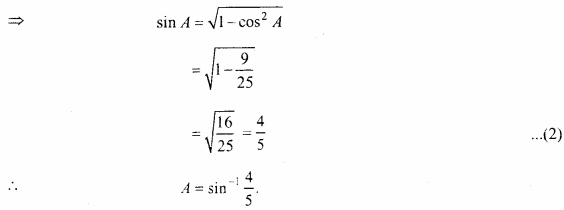
समी. (1) तथा (2) L.H.S. = R.H.S. यही सिद्ध करना था।

प्रश्न 10.
सिद्ध कीजिये
(A) sec^-1 x + cosec^-1 x = \(\frac { \pi }{ 2 } \)
(B) sin^-1 x + cos^-1 x = \(\frac { \pi }{ 2 } \)
(C) tan^-1 x + cot^-1 x = \(\frac { \pi }{ 2 } \)
हल:
(A) sec^-1 x + cosec^-1 x = \(\frac { \pi }{ 2 } \)
माना sin^-1 x = θ ………………… (1)
⇒ x = sin θ
⇒ x = cos ( \(\frac { \pi }{ 2 } \) – θ) ………………………. (2)
समी. (1) तथा (2) को जोड़ने पर
sec^-1 x + cosec^-1 x = θ + \(\frac { \pi }{ 2 } \) – θ = \(\frac { \pi }{ 2 } \) यही सिद्ध करना था।

(B) sin^-1 x + cos^-1 x = \(\frac { \pi }{ 2 } \)
माना sin^-1 x = θ ………………….. (1)
⇒ x = sin θ
⇒ x = cos ( \(\frac { \pi }{ 2 } \) – θ)
⇒ cos^-1 x = \(\frac { \pi }{ 2 } \) – θ …………………………. (2)
समी. (1) तथा (2) को जोड़ने पर,
sin^-1 x + cos^-1 x = θ + \(\frac { \pi }{ 2 } \) – θ
⇒ sin^-1 x + cos^-1 x = \(\frac { \pi }{ 2 } \) यही सिद्ध करना था।

(C) tan^-1 x + cot^-1 x = \(\frac { \pi }{ 2 } \)
माना
⇒ tan^-1 x = θ …………………………… (1)
⇒ x = tan θ
⇒ x = cot ( \(\frac { \pi }{ 2 } \) – θ)
⇒ cot^-1 x = \(\frac { \pi }{ 2 } \) – θ ……………………… (2)

प्रश्न 11.
सिद्ध कीजिए कि
(A) tan^-1 5 – tan^-1 3 – tan^-1 \(\frac{1}{8}\)
(B) tan^-1 3 – tan^-1 2 = tan^-1 \(\frac{1}{7}\)
(C) tan^-1 7 – tan^-1 5 = tan^-1 \(\frac{1}{18}\)
हल:
(A) tan^-1 5 – tan^-1 3 = tan^-1 \(\frac{1}{8}\)
L.H.S = tan^-1 5 – tan^-1 3
= tan^-1 \(\frac { 5-3 }{ 1+5.3 } \) = tan^-1 \(\frac{2}{16}\) = tan^-1 \(\frac{1}{8}\)
= R.H.S. यही सिद्ध करना था।

(B) प्रश्न क्रमांक 11 (A) की भाँति हल कीजिये।

(C) प्रश्न क्रमांक 11 (A) की भाँति हल कीजिये।

प्रश्न 12.
सिद्ध कीजिये कि
(A) tan^-1 \(\frac{4}{7}\) – tan^-1 \(\frac{1}{5}\) = tan^-1 \(\frac{1}{3}\)
(B) tan^-1 \(\frac{1}{2}\) – tan^-1 \(\frac{2}{9}\) = tan^-1 \(\frac{1}{4}\)
(C) tan^-1 \(\frac{1}{7}\) + tan^-1 \(\frac{1}{8}\) = tan^-1 \(\frac{3}{11}\)
हल:
(A) tan^-1 \(\frac{4}{7}\) – tan^-1 \(\frac{1}{5}\) = tan^-1 \(\frac{1}{3}\)
L.H.S = tan^-1 \(\frac{4}{7}\) – tan^-1 \(\frac{1}{5}\)
= tan^-1 \(\frac { \frac { 4 }{ 7 } -\frac { 1 }{ 5 } }{ 1+\frac { 4 }{ 7 } .\frac { 1 }{ 5 } } \) = tan^-1 \(\frac{1}{3}\)
= tan^-1 \(\frac{13}{39}\) = tan^-1 \(\frac{1}{3}\)
= R.H.S यही सिद्ध करना था।

(B) प्रश्न क्रमांक 12 (A) की भाँति हल कीजिये।

(C) प्रश्न क्रमांक 12 (A) की भाँति हल कीजिये।

प्रश्न 13.
सिद्ध कीजिए कि
tan^-1 1 + tan^-1 2 + tan^-1 3 = π
हल: L.H.S. = tan^-1 1 + (tan^-1 2 + tan^-1 3)
= tan^-1 (1) + π + tan^-1 ( \(\frac { 2+3 }{ 1-2\times 3 } \) )
[∵ tan^-1 x + tan^-1 y = π + tan^-1 \(\frac { x+y }{ 1-xy } \), यदि x > 0, y > 0, xy > 1, यहाँ xy = 6 > 1]
= tan^-1 (1) + π + tan^-1 ( \(\frac{5}{5-6}\) )
= tan^-1 (1) + π + tan^-1 (-1)
= tan^-1 (1) + π – tan^-1 (1), [∵tan^-1(-x) = – tan^-1 x]
= π = R.H.S
∵ बाएँ पक्ष की राशियाँ धनात्मक कोण बनाती हैं, अतः बायाँ पक्ष शून्य नहीं हो सकता।
अत: बायाँ पक्ष = π = दायाँ पक्ष। यही सिद्ध करना था।

प्रश्न 14.
यदि tan^-1 ( \(\frac{1}{2}\) ) + tan^-1 ( \(\frac{1}{k}\) ) = \(\frac { \pi }{ 4 } \) हो, तो k का मान ज्ञात कीजिए।
हल: tan^-1 ( \(\frac{1}{2}\) ) + tan^-1 ( \(\frac{1}{k}\) ) = \(\frac { \pi }{ 4 } \)

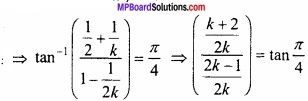
⇒ \(\frac { k+2 }{ 2k-1 } \) = 1
⇒ k + 2 = 2k – 1
⇒ 2 + 1 = 2k – k
⇒ k = 3.

प्रश्न 15.
यदि tan^-1 ( \(\frac{3}{4}\) ) + tan^-1 ( \(\frac{1}{k}\) ) = \(\frac { \pi }{ 4 } \) हो, तो k का मान ज्ञात कीजिए।
हल:
प्रश्न क्रमांक 14 की भाँति हल कीजिये।
[उत्तर – k = 1.]

प्रश्न 16.
यदि tan^-1 ( \(\frac{4}{5}\) ) + tan^-1 ( \(\frac{1}{k}\) ) = \(\frac { \pi }{ 4 } \) हो, तो k का मान ज्ञात कीजिए।
हल:
प्रान क्रमांक 14 की भाँति हल कीजिये।
[उत्तर – k = 9.]

प्रश्न 17.
सिद्ध कीजिए कि
tan^-1 \(\sqrt{x}\) = \(\frac{1}{2}\) cos^-1 ( \(\frac { 1-x }{ 1+x } \) )
हल:
R.H.S. = \(\frac{1}{2}\) cos^-1 ( \(\frac { 1-x }{ 1+x } \) )
माना \(\sqrt{x}\) = tan θ
⇒ x = tan² θ
⇒ \(\frac { 1-x }{ 1+x } \) = \(\frac { 1-tan^{ 2 }\theta }{ 1+tan^{ 2 }\theta } \) = cos 2θ
∴ R.H.S = \(\frac{1}{2}\) cos^-1 (cos 2θ)
= \(\frac{1}{2}\) × 2θ = θ
= tan^-1 ( \(\sqrt{x}\) ), [∵ \(\sqrt{x}\) = tanθ ⇒ tan^-1 ( \(\sqrt{x}\) ) = θ]
= L.H.S. यही सिद्ध करना था।

प्रश्न 18.
सिद्ध कीजिए कि
sin (cos^-1x) = cos (sin^-1x)
हल:
L.H.S.= sin (cos^-1 x)
= sin [ \(\frac { \pi }{ 2 } \) – sin^-1 x], [∵sin^-1 x + cos^-1 x = \(\frac { \pi }{ 2 } \), cos^-1 x = \(\frac { \pi }{ 2 } \) – sin^-1 x] [∵ sin(90° – θ) = cos θ]
= cos (sin^-1 x),
= R.H.S यही सिद्ध करना था।

प्रश्न 19.
(A) सिद्ध कीजिए कि
tan^-1 ( \(\frac { b-c }{ 1+bc } \) ) + tan^-1 ( \(\frac { c-a }{ 1+ca } \) ) + tan^-1 a = tan^-1 b?
हल:
L.H.S = tan^-1 ( \(\frac { b-c }{ 1+bc } \) ) + tan^-1 ( \(\frac { c-a }{ 1+ca } \) ) + tan^-1 a
= tan^-1 b – tan^-1 c + tan^-1 c – tan^-1 a + tan^-1 a
= tan^-1 b = R.H.S. यही सिद्ध करना था।

(B) सिद्ध कीजिए कि
tan^-1 ( \(\frac { a-b }{ 1+ab } \) ) + tan^-1 ( \(\frac { b-c }{ 1+bc } \) ) + tan^-1 c = tan^-1 a?
हल:
L.H.S = tan^-1 ( \(\frac { a-b }{ 1+ab } \) ) + tan^-1 ( \(\frac { b-c }{ 1+bc } \) ) + tan^-1 c
= (tan^-1 a – tan^-1 b) + (tan^-1 b – tan^-1 c) + tan^-1 c
= tan^-1 a = R.H.S. यही सिद्ध करना था।

प्रश्न 20.
समीकरण हल कीजिए –
sin^-1 \(\frac { 2a }{ 1+a^{ 2 } } \) + sin^-1 \(\frac { 2b }{ 1+b^{ 2 } } \) = 2 tan^-1 x?
हल:
दिया गया समीकरण है:
sin^-1 \(\frac { 2a }{ 1+a^{ 2 } } \) + sin^-1 \(\frac { 2b }{ 1+b^{ 2 } } \) = 2 tan^-1 x
⇒ 2 tan^-1 a + 2 tan^-1 b = 2 tan^-1 x, [∵ sin^-1 \(\frac { 2x }{ 1+x^{ 2 } } \) = 2 tan^-1 x]
⇒ tan^-1 a + tan^-1 b = tan^-1 x
⇒ tan^-1 \(\frac { a-b }{ 1+ab } \) = tan^-1 x
x = \(\frac { a-b }{ 1+ab } \)

प्रश्न 21.
समीकरण हल कीजिए –
cos^-1 ( \(\frac { 1-a^{ 2 } }{ 1+a^{ 2 } } \) ) – cos^-1 ( \(\frac { 1-b^{ 2 } }{ 1+b^{ 2 } } \) ) = 2 tan^-1 x?
हल:
दिया गया समीकरण है:
cos^-1 ( \(\frac { 1-a^{ 2 } }{ 1+a^{ 2 } } \) ) – cos^-1 ( \(\frac { 1-b^{ 2 } }{ 1+b^{ 2 } } \) ) = 2 tan^-1 x
⇒ 2 tan^-1 a – 2 tan^-1 = 2 tan^-1 x
⇒ tan^-1 a – tan^-1 b = tan^-1 x
⇒ tan^-1 \(\frac { a-b }{ 1+ab } \) = tan^-1 x
∴ x = \(\frac { a-b }{ 1+ab } \)

प्रश्न 22.
(A) सिद्ध कीजिए –
2 tan^-1 \(\frac{1}{4}\) = tan^-1 \(\frac{8}{15}\)?
हल:
दिया है:
2 tan^-1 \(\frac{1}{4}\) = tan^-1 \(\frac{8}{15}\)
L.H.S = 2 tan^-1 \(\frac{1}{4}\)
= tan^-1 \(\frac { 2.1/4 }{ 1-(1/4)^{ 2 } } \) [∵ 2 tan^-1 x = tan^-1 \(\frac { 2x }{ 1-x^{ 2 } } \) ]
= tan^-1 \(\frac { 1/2 }{ 15/16 } \)
= tan^-1 \(\frac{8}{15}\) = R.H.S यही सिद्ध करना था।

(B) सिद्ध कीजिए –
2 tan^-1 ( \(\frac{1}{2}\) ) = tan^-1 ( \(\frac{4}{3}\) )
हल:
दिया है:
2 tan^-1 ( \(\frac{1}{2}\) ) = tan^-1 ( \(\frac{4}{3}\) )
L.H.S = 2 tan^-1 ( \(\frac{1}{2}\) )

यही सिद्ध करना था।

प्रश्न 23.
सरलतम रूप में लिखिए –
tan^-1 \(\sqrt { \frac { 1-cosx }{ 1+cosx } } \)?
हल:
दिया है:

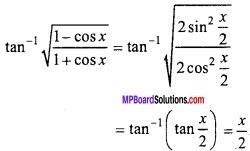
प्रश्न 24.
सरलतम रूप में लिखिए –
cos^-1 \(\sqrt { \frac { 1 }{ 2 } (1+cosx) } \)?
हल:
दिया है:

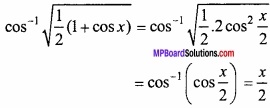
प्रश्न 25.
यदि tan^-1 a + tan^-1 b + tan^-1 c = \(\frac { \pi }{ 2 } \) हो, तो सिद्ध कीजिए कि
ab + bc + ca = 1.
हल:
दिया है:
tan^-1 + tan^-1 b + tan^-1 c = \(\frac { \pi }{ 2 } \)
⇒ tan^-1a + tan^-1 b + tan^-1 c = tan^-1 a + cot^-1 a, [∵tan^-1 a + cot^-1 a = \(\frac { \pi }{ 2 } \) ]
⇒ tan^-1 b + tan^-1 c = cot^-1 a
⇒ tan^-1 ( \(\frac { b+c }{ 1-bc } \) ) = tan^-1 ( \(\frac{1}{a}\) )
⇒ \(\frac { b+c }{ 1-bc } \) = \(\frac{1}{a}\)
⇒ ab + ca = 1 – bc
⇒ ab + bc + ca = 1 यही सिद्ध करना था।

प्रश्न 26.
सिद्ध कीजिए –
यही सिद्ध करना था।
tan^-1 \(\frac{2}{11}\) + cot^-1 \(\frac{24}{7}\) = tan^-1 \(\frac{1}{2}\)?
हल:
L.H.S. = tan^-1 \(\frac{2}{11}\) + cot^-1 \(\frac{7}{24}\)
= tan^-1 \(\frac{2}{11}\) + tan^-1 \(\frac{7}{24}\)

= tan^-1 [ \(\frac{125}{250}\) ] = tan^-1 \(\frac{1}{2}\) = R.H.S. यही सिद्ध करना था।

प्रश्न 27.
सिद्ध कीजिए –
cos^-1 x = 2 cos^-1 \(\sqrt { \frac { 1+x }{ 2 } } \)
= 2 cos^-1 \(\sqrt { \frac { 1+cos\theta }{ 2 } } \), ( x = cos θ रखने पर)
= 2 cos^-1 \(\sqrt { \frac { 2cos^{ 2 }\frac { \theta }{ 2 } }{ 2 } } \) = 2. \(\frac { \theta }{ 2 } \)
= cos^-1 x = L.H.S. यही सिद्ध करना था।

प्रश्न 28.
सिद्ध कीजिए –
cos^-1 x = 2 tan^-1 \(\sqrt { \frac { 1-x }{ 1+x } } \)?
हल:
R.H.S = 2 tan^-1 \(\sqrt { \frac { 1-x }{ 1+x } } \)

= 2. \(\frac { \theta }{ 2 } \) = θ = cos^-1 x = L.H.S. यही सिद्ध करना था।

प्रश्न 29.
सिद्ध कीजिए कि
tan^-1 ( \(\frac{a}{b}\) ) – tan^-1 ( \(\frac { a-b }{ a+b } \) ) = \(\frac { \pi }{ 4 } \)?
हल:
L.H.S = tan^-1 ( \(\frac{a}{b}\) ) – tan^-1 ( \(\frac { a-b }{ a+b } \) )

= tan^-1 1
= \(\frac { \pi }{ 4 } \) = R.H.S. यही सिद्ध करना था।

प्रतिलोम त्रिकोणमितीय फलन दीर्घ उत्तरीय प्रश्न – I

प्रश्न 1.
(A) सिद्ध कीजिए कि
sin^-1 \(\frac { 1 }{ \sqrt { 5 } } \) + sin^-1 \(\frac { 1 }{ \sqrt { 10 } } \) = \(\frac { \pi }{ 4 } \)?
हल:
माना sin^-1 \(\frac { 1 }{ \sqrt { 5 } } \) = A, sin^-1 \(\frac { 1 }{ \sqrt { 10 } } \) = B
∴ A + B = \(\frac { \pi }{ 4 } \)
⇒ sin(A + B) = sin \(\frac { \pi }{ 4 } \)
⇒ sinA cosB + cosA sinB = \(\frac { 1 }{ \sqrt { 2 } } \)
L.H.S = sinA \(\sqrt { 1-sin^{ 2 }B } \) + \(\sqrt { 1-sin^{ 2 }A } \). sin B

(B) निम्न समीकरण को हल कीजिए:
sin^-1 x + sin^-1 (1 – x) = sin^-1 \(\sqrt { 1-x^{ 2 } } \)?
हल:
दिया गया समीकरण है:
sin^-1 x + sin^-1 (1 – x) = sin^-1 \(\sqrt { 1-x^{ 2 } } \)

वर्ग करने पर,
x² (2x – x²) = x² (1 – x²)
⇒ x² (2x – x² – 1 + x²) = 0
⇒ x² (2x – 1) = 0
अतः x = 0, \(\frac{1}{2}\).

प्रश्न 2.
(A) सिद्ध कीजिए कि tan^-1 \(\frac { x+1 }{ x } \) – tan^-1 \(\frac { 1 }{ 2x+1 } \) = \(\frac { \pi }{ 4 } \)?
(B) यदि tan^-1 x + tan^-1 y + tan^-1 z = \(\frac { \pi }{ 2 } \) हो, तो सिद्ध कीजिए xy + yz + zx = xyz.
(C) यदि tan^-1 x + tan^-1 y + tan^-1 z = \(\frac { \pi }{ 2 } \), हो, तो सिद्ध कीजिए xy + yz + zx = 1.
हल:
(A) tan^-1 \(\frac { x+1 }{ x } \) – tan^-1 \(\frac { 1 }{ 2x+1 } \) = \(\frac { \pi }{ 4 } \)

= R.H.S. यही सिद्ध करना था।
(B) tan^-1 x + tan^-1 z = π

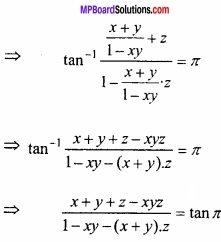
⇒ x + y + z – xyz = 0 [∵ tan π = 0]
∴ x + y + z = xyz. यही सिद्ध करना था।
(C) प्रश्न क्रमांक 2 (B) की भाँति tan \(\frac { \pi }{ 2 } \) = ∞ = \(\frac{1}{0}\), रखकर विद्यार्थी स्वयं हल करें।

प्रश्न 3.
सरलतम रूप में लिखिए –
tan^-1 [ \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \) ]?
हल:
tan^-1 [ \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \) ]
माना x = tan θ

प्रश्न 4.
(A) सिद्ध कीजिए –
\(\frac{1}{2}\) sin^-1 x = cot^-1 \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \)?
हल:
R.H.S. = cot^-1 \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \)

(B) सिद्ध कीजिए –
\(\frac{1}{2}\) cot^-1 x = cot^-1 ( \(\sqrt { 1+x^{ 2 }+x } \) )?
हल:
\(\frac{1}{2}\) cot^-1 x = cot^-1 ( \(\sqrt { 1+x^{ 2 }+x } \) )
R.H.S. = cot^-1 ( \(\sqrt { 1+x^{ 2 }+x } \) )
माना x = cot θ

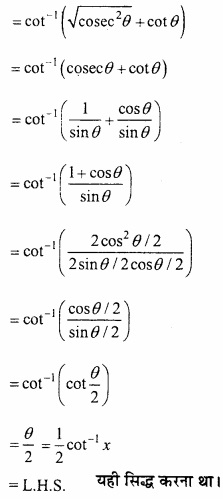
प्रश्न 5.
समीकरण को हल कीजिए –
tan^-1 (x + 1) + tan^-1 (x – 1) = tan^-1 ( \(\frac{6}{17}\) )?
हल:
दिया है:
tan^-1 (x + 1) + tan^-1 (x – 1) = tan^-1 ( \(\frac{6}{17}\) )?

⇒ 17x = 6 – 3x²
⇒ 3x² + 18 x – x – 6 = 0
⇒ 3x(x + 6) -1 (x + 6) = 0
⇒ (x + 6) (3x – 1) = 0
∴ x = – 6, x = \(\frac{1}{3}\)

प्रश्न 6.
सिद्ध कीजिए कि cos^-1 \(\frac{3}{5}\) + cos^-1 \(\frac{4}{5}\) = \(\frac { \pi }{ 2 } \)?
हल:
दिया है:
L.H.S = cos^-1 \(\frac{3}{5}\) + cos^-1 \(\frac{4}{5}\)

प्रश्न 7.
यदि cos^-1 x + cos^-1 y + cos^-1 z = π हो, तो सिद्ध कीजिए कि
x² + y² + z² + 2xyz = 1
हल:
दिया है:
cos^-1 x + cos^-1 y + cos^-1 z = π

दोनों पक्षों का वर्ग करने पर,
x²y² + z² + 2xyz = (1 – x²) (1 – y²)
⇒ x²y² + z² + 2xyz = 1 – y² – x² + x²y²
⇒ z² + 2xyz = 1 – y² – x²
⇒ x² + y² + z² + 2xyz = 1. यही सिद्ध करना था।

प्रश्न 8.
यदि sin^-1 \(\frac { 2a }{ 1+a^{ 2 } } \) – cos^-1 \(\frac { 1-b^{ 2 } }{ 1+b^{ 2 } } \) = tan^-1 \(\frac { 2x }{ 1-x^{ 2 } } \) हो, तो सिद्ध कीजिए कि x = \(\frac { a-b }{ 1+ab } \)?
हल:
यहाँ sin^-1 \(\frac { 2a }{ 1+a^{ 2 } } \) – cos^-1 \(\frac { 1-b^{ 2 } }{ 1+b^{ 2 } } \) = tan^-1 \(\frac { 2x }{ 1-x^{ 2 } } \) ………………………….. (1)
माना a = tan θ, b = tan ∅, x = tan Ψ
समी. (1) में इन मानों को रखने पर,

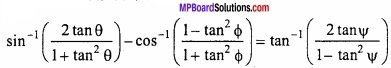
⇒ sin^-1 (sin 2θ) – cos^-1 (cos 2∅) = tan^-1 (tan 2Ψ)
⇒ 2θ – 2∅ = 2Ψ
⇒ θ – ∅ = Ψ
⇒ tan^-1 a – tan^-1 b = tan^-1 x
⇒ tan^-1 ( \(\frac { a-b }{ 1+ab } \) ) = tan^-1 x
⇒ x = \(\frac { a-b }{ 1+ab } \). यही सिद्ध करना था।

प्रश्न 9.
सिद्ध कीजिए कि
tan^-1 \(\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}}\) = \(\frac { \pi }{ 4 } \) – \(\frac{1}{2}\) cos¹ x
हल:
माना कि x = cos θ, तब θ = cos^-1 x

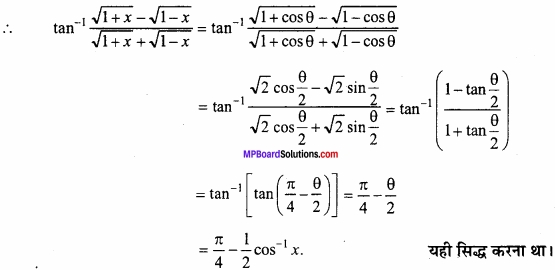
प्रश्न 10.
सरलतम रूप में लिखिये –
tan^-1 ( \(\frac { x }{ \sqrt { 1+x^{ 2 }-1 } } \) )?
हल:
tan^-1 ( \(\frac { x }{ \sqrt { 1+x^{ 2 }-1 } } \) ) में x = tan θ रखने पर,

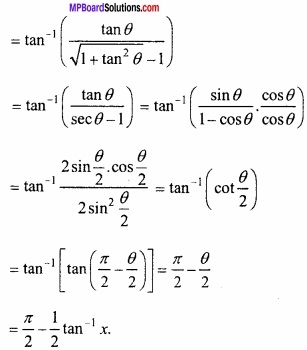
प्रश्न 11.
सिद्ध कीजिए कि –
tan^-1 \(\sqrt{x}\) = \(\frac{1}{2}\) cos^-1 ( \(\frac { 1-x }{ 1+x } \) ) (NCERT)
हल:
R.H.S. = \(\frac{1}{2}\) cos^-1 ( \(\frac { 1-x }{ 1+x } \) )

माना \(\sqrt{x}\) = tan θ
तब, θ = tan^-1 \(\sqrt{x}\)
= \(\frac{1}{2}\) cos^-1 ( \(\frac { 1-tan^{ 2 }\theta }{ 1+tan^{ 2 }\theta } \) )
= \(\frac{1}{2}\) cos^-1 (cos 2θ), [∵ cos^-1 (cos x) = x]
= \(\frac{1}{2}\) × 2θ
= θ
= tan^-1 \(\sqrt{x}\), [समी. (1) से]
= L.H.S. यही सिद्ध करना था।

प्रश्न 12.
सिद्ध कीजिए कि –
tan^-1 \(\frac { 6x-8x^{ 3 } }{ 1-12x^{ 2 } } \) – tan^-1 \(\frac { 4x }{ 1-4x^{ 2 } } \) = tan^-1 2x, जहाँ |2x| < \(\frac { 1 }{ \sqrt { 3 } } \) (CBSE 2016)
हल:
L.H.S. = tan^-1 \(\frac { 6x-8x^{ 3 } }{ 1-12x^{ 2 } } \) – tan^-1 \(\frac { 4x }{ 1-4x^{ 2 } } \)
= tan^-1 \(\frac { 3(2x)-(2x)^{ 3 } }{ 1-3(2x)^{ 2 } } \) – tan^-1 \(\frac { 2\times 2x }{ 1-(2x)^{ 2 } } \)
माना 2x = tanθ
तब,
θ = tan^-1 2x

= 3θ – 2θ = θ
= tan^-1 2x [समी. (1) से]
= R.H.S. यही सिद्ध करना था।

प्रश्न 13.
सिद्ध कीजिए कि –
cos^-1 \(\frac{4}{5}\) + cos^-1 \(\frac{12}{13}\) = cos^-1 \(\frac{33}{65}\)?
हल:
L.H.S. = cos^-1 \(\frac{4}{5}\) + cos^-1 \(\frac{12}{13}\)

MP Board Class 12 Maths Important Questions