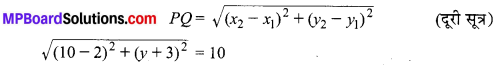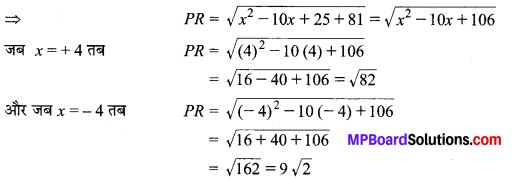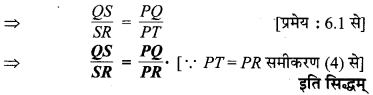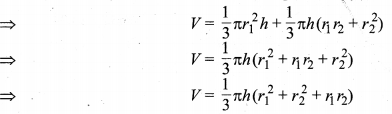Prasanna

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 5 समान्तर श्रेढ़ियाँ Ex 5.2 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 5 समान्तर श्रेढ़ियाँ Ex 5.2

प्रश्न 1.
निम्नलिखित सारणी में रिक्त स्थानों को भरिए, जहाँ A.P. का प्रथम पद a, सार्वान्तर d और n वाँ पद a_n है :
हल:

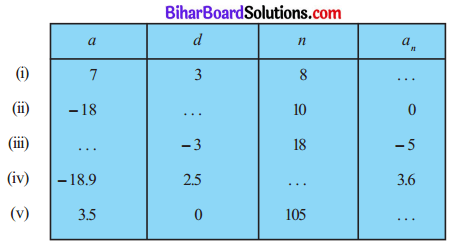
हल:
(i) ∵ a_n = a + (n – 1) × d
⇒ a_n = 7 + (8 – 1) × 3
⇒ a_n = 7 + 7 × 3
⇒ a_n = 7 + 21 = 28

(ii) ∵ a_n = a + (n – 1) × d
⇒ 0 = – 18 + (10 – 1) × d
⇒ 0 = – 18 + 9d
⇒ 9d = 18
⇒ d = \(\frac { 18 }{ 9 } \) = 2.

(iii) ∵ a_n = a + (n – 1) × d
⇒ -5 = a + (18 – 1) (-3)
⇒ -5 = a+ 17(-3)
⇒ -5 = a – 51
⇒ a = 51 – 5 = 46.

(iv) ∵ a_n = a + (n – 1) × d
⇒ 3.6 = 18.9 + (n – 1) × 25
⇒ 3.6 = – 18.9 + 2.5n – 2.5
⇒ 2.5n = 18.9 + 3.6 + 2.5
⇒ 2.5 n = 25.0
⇒ n = \(\frac { 25 }{ 2.5 } \) = 10

(v) ∵ a_n = a + (n – 1) × d
⇒ a_n = 35 + (105 – 1) × 0
⇒ a_n = 35 + 104 × 0
⇒ a_n = 3.5
अतः अत: a_n = 3.5

प्रश्न 2.
निम्नलिखित में सही उत्तर चुनिए और उसका औचित्य दीजिए:
(i) AP: 19,7, 4 ….. 30 वाँ पद है :
(a) 97
(b) 77
(c) -77
(d) -87

(ii) AP -3, –\(\frac { 1 }{ 2 } \), 2, …….. का 11 वाँ पद है:
(a) 28
(b) 22
(c) -38
(d) -48 \(\frac { 1 }{ 2 } \)
हल:
(i) सही उत्तर (C) -77 है, क्योंकि a = 10, d = -3, n = 30
एवं a_n = a + (n – 1)d ⇒ a₃₀ = 10 + (30 – 1) (-3)
⇒ a₃₀ = 10 – 29 × 3 ⇒ 10 – 87 = -77

(ii) सही उत्तर (B) 22 है, क्योंकि a = -3, d = 2\(\frac { 1 }{ 2 } \), n = 11
एवं a_n = a + (n – 1)d ⇒ a_n = -3 + (11 – 1) (2.5)
⇒ a₁₁ = -3 + 10 × 2.5 = -3 + 25 = 22

प्रश्न 3.
निम्नलिखित सामान्तर श्रेढ़ियों में रिक्त स्थानों (boxes) के पदों को ज्ञात कीजिए।
(i) 2, [], 26
(ii) [], 13, [], 3
(iii) 5, [], [], 9\(\frac { 1 }{ 2 } \)
(iv) -4, [], [], [], [], 6
(v) [], 38, [], [], [],-22
हल:
(i) प्रश्नानुसार, a = 2, a₃ = 26 एवं n = 3.
चूंकि an = a + (n – 1) (d)
⇒ 26 = 2 + (3 – 1)d
⇒ 26 = 2 + 2d ⇒ 2d = 26 – 2 = 24 ⇒ d = \(\frac { 24 }{ 2 } \) = 12
अतः रिक्त स्थान a₂ = a + d = 2 + 12 = 14
अत: अभीष्ट रिक्त स्थान (box) में पद 14 होगा।

(ii) प्रश्नानुसार, a₂ = 13 एवं a₄ = 3
⇒ 13 = a + (2 – 1)d ⇒ a + d = 13 ….(1)
एवं 3 = a+ (4 – 1)d ⇒ a + 3d = 3 …..(2)
⇒ 2d = 3 – 13 = – 10 ⇒ d = –\(\frac { 10 }{ 2 } \) = -5
[समी. (2) – समी. (1) से]
d = -5 का मान समीकरण (1) में रखने पर,
a – 5 = 13 ⇒ a = 13 + 5 = 18
एवं a₃ = a + (3 – 1) (-5) = 18 + 2(-5) = 18 – 10 = 8
अतः अभीष्ट रिक्त स्थान में पद क्रमशः 18 एवं 8 होंगे।

(iii) प्रश्नानुसार, a = 5 एवं a₄ = 9 \(\frac { 1 }{ 2 } \)
⇒ 9\(\frac { 1 }{ 2 } \) = 5 + (4 – 1) (d) ⇒ 9\(\frac { 1 }{ 2 } \) = 5 + 3d
⇒ 3d = 9 \(\frac { 1 }{ 2 } \) – 5 = 4 \(\frac { 1 }{ 2 } \) ⇒ d = \(\frac { 1 }{ 3 } \) × 4\(\frac { 1 }{ 2 } \) = 1\(\frac { 1 }{ 2 } \)
⇒ a2 = 5 + 1 \(\frac { 1 }{ 2 } \) = 6\(\frac { 1 }{ 2 } \)
एवं a3 = 5 + 2 × 1 \(\frac { 1 }{ 2 } \) = 5 + 3 = 8
अत: अभीष्ट रिक्त स्थानों के अभीष्ट पद क्रमशः 6\(\frac { 1 }{ 2 } \) एवं 8 हैं।

(iv) प्रश्नानुसार, a = – 4 एवं a₆ = 6
⇒ 6 = -4 + (6 – 1)d = 6 = -4 + 5d
⇒ 5d = 6 + 4 = 10 ⇒ d = \(\frac { 10 }{ 5 } \) = 2
अब a₂ = -4 + 2 = -2
a₃ = -4 + 2 × 2 = -4 + 4 = 0
a₄ = -4 + 3 × 2 = -4 + 6 = 2
a₅ = -4 + 4 × 2 = -4 + 8 = 4
अतः अभीष्ट पद क्रमशः – 2,0,2 एवं 4 हैं।

(v) प्रश्नानुसार, a₂ = 38 एवं a₆ = -22
⇒ 38 = a + d ⇒ a + d = 38 ….(i)
एवं -22 = a + 5d ⇒ a + 5d = – 22 ….(ii)
⇒ 4d = -60 [समीकरण (2)- समीकरण (1) से]
⇒ d = – \(\frac { 60 }{ 4 } \) = -15
d =-15 का मान समीकरण (1) में रखने पर,
a + (-15) = 38 ⇒ a = 38 + 15 = 53
अब a₃ = 53 + 2 × (-15) = 53 – 30 = 23
a₄ = 53 + 3 × (-15) = 53 – 45 = 8
a₅ = 53 + 4 × (-15) = 53 – 60 = -7
a₆ = 53 + 5 × (- 15) = 53 – 75 = – 22
अत: अभीष्ट रिक्त स्थान में पद क्रमशः 53, 23, 8, -7 होंगे।

प्रश्न 4.
AP : 3, 8, 13, 18, ……….. का कौन-सा पद 78 है?
हल:
प्रश्नानुसार, a = 3,d = 8 – 3 = 5, a_n = 78
एवं a_n = a + (n – 1) × d
⇒ 78 = 3 + (n – 1) × 5 = 3 + 5n – 5
⇒ 5n = 78 + 5 – 3 = 80
⇒ n = \(\frac { 80 }{ 5 } \) = 16
अत: अभीष्ट 16वाँ पद 78 है।

प्रश्न 5.
निम्नलिखित समान्तर श्रेढ़ियों में से प्रत्येक श्रेणी में कितने पद हैं?
(i) 7, 13, 19, ………. 205
(ii) 18, 15\(\frac { 1 }{ 2 } \),13, …..(-47)
हल:
(i) चूँकि A.P : 7, 13, 19, ……. 205 (दी गयी है।)
प्रश्नानुसार, a = 7,d = 13 – 7 = 6 एवं a_n = 205
चँकि a_n = a + (n – 1) (d)
⇒ 205 = 7 + (n – 1) (6)
⇒ 205 = 7 + 6n – 6
⇒ 6n = 205 + 6 – 7 = 204
⇒ n = \(\frac { 204 }{ 6 } \) = 34
अतः श्रेणी में अभीष्ट 34 पद हैं।

(ii) चूँकि AP : 18, 15\(\frac { 1 }{ 2 } \), 13, ….., (-47) (दी गयी है)
प्रश्नानुसार, a = 18, d = 15, – 18 = -2\(\frac { 1 }{ 2 } \), एवं a_n = -47
चूँकि a_n = a + (n – 1) (d)
⇒ -47 = 18 + (n – 1) (-2\(\frac { 1 }{ 2 } \))
⇒ – 47 = 18 – 2\(\frac { 1 }{ 2 } \)n + 2\(\frac { 1 }{ 2 } \)
⇒ \(\frac { 5 }{ 2 } \)n = 47 + 18 + 2\(\frac { 1 }{ 2 } \) = 67\(\frac { 1 }{ 2 } \) = \(\frac { 135 }{ 2 } \)
⇒ n = \(\frac { 135 }{ 2 } \) × \(\frac { 2 }{ 5 } \) = 27
अतः श्रेणी में अभीष्ट 27 पद हैं।

प्रश्न 6.
क्या AP. 11,8, 5, 2 ……… का एक पद — 150 है? क्यों?
हल:
प्रश्नानुसार, a = 11, d = 8 – 11 = -3, a_n = – 150.
चूँकि a_n = a + (n – 1) (d)
⇒ – 150 = 11 + (n – 1) (- 3) = 11 – 3n + 3
⇒ 3n = 150 + 11 + 3 = 164
⇒ n = \(\frac { 164 }{ 3 } \) = 54 \(\frac { 2 }{ 3 } \) जो एक पूर्णांक नहीं है।
अत: दत्त AP का कोई भी पद -150 नहीं होगा।

प्रश्न 7.
उस AP का 31वाँ पद ज्ञात कीजिए जिसका 11वाँ पद 38 है और 16वाँ पद 73 है। (2019)
हल:
प्रश्नानुसार, n₁₁ = 38 एवं n₁₆ = 73.
⇒ 38 = a + 10d ⇒ a + 10d = 38 …..(1)
एवं 73 = a + 15d ⇒ a + 15d = 73 …..(2)
⇒ 5d = 35 [समीकरण (2) – समीकरण (1) से]
⇒ d = \(\frac { 35 }{ 5 } \) = 7
अब d = 7 का मान समीकरण (1) में रखने पर,
a + 10 × 7 = 38 ⇒ a = 38 – 70 = – 32
अब a₃₁ = a + 30d = – 32 + 30 × 7
⇒ a₃₁ = -32 + 210 = 178
अंतः अभीष्ट 31वाँ पद = 178 है।

प्रश्न 8.
एक AP में 50 पद है, जिसका तीसरा पद 12 है और अन्तिम पद 106 है। इसका 29वाँ पद ज्ञात कीजिए।
हल:
प्रश्नानुसार, n = 50, a₃ = 12 एवं a₅₀ = 106.
चूँकि a_n = a + (n – 1)d
⇒ 106 = a + 49d ⇒ a + 49d = 106 …..(1)
एवं 12 = a + 2d ⇒ a + 2d = 12 …..(2)
⇒ 47d = 94 [समीकरण (2) – समीकरण (1) से
⇒ d = \(\frac { 94 }{ 47 } \) = 2
d = 2 का मान समीकरण (2) में रखने पर,
a + 2 × 2 = 12 ⇒ a = 12 – 4 = 8
अब n₂₉ = 8 + 28 × 2 = 8 + 56 = 64
अतः अभीष्ट 29वाँ पद = 64 है।

प्रश्न 9.
यदि किसी AP के तीसरे और नौवें पद क्रमशः 4 और – 8 हैं, तो इसका कौन-सा पद शून्य होगा?
हल:
प्रश्नानुसार, a₃ = 4 एवं a₉ = – 8 है।
⇒ a₃ = a + 2d = 4 …..(1)
एवं a₉ = a + 8d = – 8 …..(2)
⇒ 6d = -12 [समीकरण (2)- समीकरण (1) से]
⇒ d = –\(\frac { 12 }{ 6 } \) = -2
d = – 2 का मान समीकरण (1) में रखने पर
चूँकि a + 2(-2) = 4 ⇒ a = 4 + 4 = 8.
अब a_n = a + (n – 1)d
⇒ 0 = 8 + (n – 1)(-2) ⇒ 0 = 8 – 2n + 2
⇒ 2n = 8 + 2 = 10 ⇒ n = \(\frac { 10 }{ 2 } \) = 5
अतः अभीष्ट पाँचवाँ पद शून्य होगा।

प्रश्न 10.
किसी AP का 17वाँ पद उसके 10वें पद से 7 अधिक है। इसका सार्वान्तर ज्ञात कीजिए।
हल:
प्रश्नानुसार, (a + 16d) – (a + 9d) = 7
⇒ 16d – 9d = 7 ⇒ 7d = 7 ⇒ d = \(\frac { 7 }{ 7 } \) = 1
अतः d का अभीष्ट मान = 1 है।

प्रश्न 11.
AP3 , 15, 27, 39, …………. का कौन-सा पद उसके 54वें पद से 132 अधिक होगा?
हल:
प्रश्नानुसार, a = 3, d = 15 – 3 = 12 एवं a_n – a₅₄ = 132
⇒ [3 + (n – 1) (12)] – [3 + (54 – 1) (12)] = 132
⇒ (3 + 12n – 12) – (3 + 53 × 12) = 132
⇒ 12n – 12 – 636 = 132
⇒ 12n = 132 + 12 + 636 = 780
⇒ n = \(\frac { 780 }{ 12 } \) = 65
अतः अभीष्ट 65वाँ पद होगा।

प्रश्न 12.
दो समान्तर श्रेढ़ियों का सार्वान्तर समान है। यदि इनके 100वें पदों का अन्तर 100 है, तो इनके 1000 वें पदों का अन्तर क्या होगा?
हल:
प्रश्नानुसार, दो समान्तर श्रेढ़ियाँ क्रमशः a, a + d, a + 2d, …………., a + (n – 1)d
एवं b, b + d, b + 2d, …………, b + (n – 1)d
एवं [a+ (100 – 1)d] – [b + (100 – 1)d] = 100
⇒ (a + 99d) – (b + 99a) = 100
⇒ a – b = 100 ….(1)
अब [a + (1000 – 1)d] – [b+ (1000 – 1)d]
= (a + 999d) – (b + 999d)
= a – b = 100 [समीकरण (1) से]
अतः हजारवें पदों का अभीष्ट अन्तर = 100 होगा।

प्रश्न 13.
तीन अंकों वाली कितनी संख्याएँ 7 से विभाज्य हैं।
हल:
7 से विभाज्य तीन अंकों वाली संख्याओं की सूची है।
105, 112, 119, ……………., 994
जहाँ, a = 105, d = 112 – 105 = 7 एवं a_n = 994
चूँकि an = a + (n – 1)d
⇒ 994 = 105+ (n – 1) × 7
⇒ 994 = 105 + 7n – 7
⇒ 7n = 994 + 7 – 105
⇒ 7n = 1001 – 105 = 896
⇒ n = \(\frac { 896 }{ 7 } \) = 128
अतः 7 से विभाज्य तीन अंकों वाली कुल अभीष्ट संख्याएँ 128 हैं।

प्रश्न 14.
10 और 250 के बीच में 4 के कितने गुणज हैं?
हल:
10 और 250 के बीच 4 के गुणजों की सूची है :
12, 16, 20, 24, …………, 248
जहाँ, a = 12,d = 16 – 12 = 4 एवं a_n = 248
चूँकि a_n = a + (n – 1)d
⇒ 248 = 12 + (n – 1) (4)
⇒ 248 = 12 + 4n – 4 = 4n + 8
⇒ 4n = 248 – 8 = 240
⇒ n = \(\frac { 240 }{ 4 } \) = 60
अत: 10 और 250 के बीच 4 के गुणजों की अभीष्ट संख्या 60 है।

प्रश्न 15.
n के किस मान के लिए दोनों समान्तर श्रेढ़ियों 63, 65,67,………….. और 3, 10, 17,……… के nवें पद बराबर होंगे?
हल:
चूँकि प्रथम AP का a = 63 एवं d = 65 – 63 = 2, एवं द्वितीय A.P. का a’ = 3 एवं d’ = 10 – 3 = 7 है, तो प्रश्नानुसार,
63 + (n – 1) (2) = 3 + (n – 1) (7)
63 + 2n – 2 = 3 + 7n – 7
⇒ 61 + 2n = 7n -4
⇒ 7n – 2n = 61 + 4
⇒ 5n = 65 ⇒ n= \(\frac { 65 }{ 5 } \) = 13
अतः n के अभीष्ट मान 13 के लिए दोनों श्रेढ़ियों के nवें पद बराबर होंगे।

प्रश्न 16.
वह AP ज्ञात कीजिए जिसकी तीसरा पद 16 है और 7वाँ पद 5वें पद से 12 अधिक है।
हल:
मान लीजिए कि AP का प्रथम पद a तथा सार्वान्तर d है, तो
प्रश्नानुसार, a₃ = 16 ⇒ a + 2d = 16 ….(i)
एवं a₇ – a₅ = 12 ⇒ (a + 6d) – (a + 4d) = 12
⇒ 2d = 12 ⇒ d = \(\frac { 12 }{ 2 } \) = 6 …..(2)
d का मान समीकरण (2) से समीकरण (1) में रखने पर,
a + 2 × 6 = 16 ⇒ a + 12 = 16 ⇒ a = 16 – 12 = 4
अतः अभीष्ट AP = 4, 10, 16, 22, ……… है।

प्रश्न 17.
AP 3,8, 13, ……………, 253 में अन्तिम पद से 20वाँ पद ज्ञात कीजिए।
हल:
AP को घटते क्रम में लिखने पर,
253, 248, 243, ………… 13, 8, 3.
जहाँ a = 253 एवं d = (248 – 253) = -5
⇒ a₂₀ = 253 + (20 – 1) (-5)
= 253 + 19 (-5) = 253 – 95
= 158
अतः दत्त AP के अन्तिम पद से अभीष्ट 20वाँ पद = 158 है।

प्रश्न 18.
किसी AP के चौथे और 8वें पदों का योग 24 है तथा 6वें और 10वें पदों का योग 44 है। इस AP के प्रथम तीन पद ज्ञात कीजिए।
हल:
मान लीजिए a, a + d, a + 2d, a + 3d, ……., समान्तर श्रेढ़ी में हैं, तब प्रश्नानुसार,
∵ a₄ + a₈ = 24
⇒ (a + 3d) + (a + 7a) = 24
⇒ 2a + 10d = 24 ⇒ a + 5d = 12 ……(1)
एवं a₆ + a₁₀ = 44
⇒ (a + 5a) + (a + 9d) = 44
⇒ 2a + 14d = 44 ⇒ a + 7d = 22 …..(2)
⇒ 2d = 10 [समीकरण (2) – (1) से]
⇒ d = \(\frac { 10 }{ 2 } \) = 5
d का मान समीकरण (1) में रखने पर,
a + 5 × 5 = 12 ⇒ a + 25 = 12 ⇒ a = 12 – 25 = – 13
⇒ a2 = a + d = -13 + 5 = -8
एवं a = a + 2d = – 13 + 5 × 2 = – 13 + 10 = -3
अतः दी हुई समान्तर श्रेढ़ी के अभीष्ट प्रथम तीन पद क्रमश: -13, -8 एवं -3 हैं।

प्रश्न 19.
सुब्बाराव ने 1995 में ₹ 5,000 के मासिक वेतन पर कार्य प्रारम्भ किया ओर प्रत्येक वर्ष ₹200 की वेतन वृद्धि प्राप्त की। किस वर्ष में उसका वेतन ₹ 7000 हो गया?
हल:
सुब्बाराव के प्रतिवर्ष के वेतन की सूची एक AP का निर्माण करेगी, जिसमें a = ₹ 5,000, d = ₹ 200 एवं an = ₹ 7,000 होगा।
इसलिए प्रश्नानुसार,
a_n = a + (n – 1)d
⇒ 7000 = 5000 + (n – 1) × 200
⇒ 7000 = 5000 + 200n – 200
⇒ 7000 = 4800 + 200n
⇒ 200n = 7000 – 4800 = 2200
⇒ n = \(\frac { 2200 }{ 200 } \) = 11
अत: सुब्बाराव का अभीष्ट वेतन 11वें वर्ष में होगा।

प्रश्न 20.
रामकली ने किसी वर्ष के प्रथम सप्ताह में ₹5 की बचत की और फिर अपनी साप्ताहिक बचत में ₹ 1.75 बढ़ाती गयी। यदि वें सप्ताह में उसकी बचत ₹ 20.75 हो जाती है, तो n ज्ञात
कीजिए।
हल:
रामकली के साप्ताहिक बचत की सूची एक AP का निर्माण करती है जिसमें a = ₹5 एवं d = ₹ 1.75 तथा a_n = ₹ 20.75, तो प्रश्नानुसार,
a_n = a + (n – 1)d
⇒ 20.75 = 5 + (n – 1) (1.75)
⇒ 20.75 = 5 + 1.75n – 1.75
⇒ 1.75n = 20.75 + 1.75 – 5
⇒ 1.75n = 22.50 – 5 = 17.50
⇒ n = \(\frac { 17.50 }{ 1.75 } \) = 10
अतः n का अभीष्ट मान = 10 है।

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 4 द्विघात समीकरण Ex 4.2 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 4 द्विघात समीकरण Ex 4.2

प्रश्न 1.
गुणनखण्ड विधि से निम्न द्विघात समीकरणों के मूल ज्ञात कीजिए:
(i) x² – 3x – 10 = 0
(ii) 2x² + x – 6 = 0
(iii) \(\sqrt { 2 }\) x² + 7x + 5\(\sqrt { 2 }\) = 0
(iv) 2x² – x + \(\frac { 1 }{ 8 } \) = 0
(v) 100x² – 20x + 1 = 0
हल:
(i) x² – 3x – 10 = 0
⇒ x – 5x + 2x – 10 = 0
⇒ x (x – 5) + 2 (x – 5) = 0
⇒ (x – 5) (x + 2) = 0
या तो x – 5 = 0 ⇒ x = 5
अथवा x + 2 = 0 ⇒ x = -2
अत: दत्त समीकरण के अभीष्ट मूल 5 एवं -2 हैं।

(ii) 2x² + x – 6 = 0
⇒ 2x² + 4x – 3x – 6 = 0
⇒ 2x (x + 2)- 3 (x + 2) = 0
⇒ (x + 2) (2x – 3) = 0
या तो x + 2 = 0 ⇒ x = -2
अथवा 2x – 3 = 0 ⇒ x = \(\frac { 3 }{ 2 } \)
अतः दत्त समीकरण के अभीष्ट मूल – 2 एवं \(\frac { 3 }{ 2 } \) हैं।

(iii) \(\sqrt { 2 }\) x² + 2x + 5 \(\sqrt { 2 }\) = 0
⇒ \(\sqrt { 2 }\) x² + 5x + 2x + 5\(\sqrt { 2 }\) = 0
⇒ x(\(\sqrt { 2 }\)x + 5) + \(\sqrt { 2 }\) (\(\sqrt { 2 }\)x + 5) = 0
⇒ (\(\sqrt { 2 }\) x + 5) (x + \(\sqrt { 2 }\)) = 0
या तो \(\sqrt { 2 }\) x + 5 = 0 ⇒ x = \(-\frac{5}{\sqrt{2}}\)
अथवा x + \(\sqrt { 2 }\) = 0 ⇒ x = – \(\sqrt { 2 }\)
अतः दत्त समीकरण के अभीष्ट मूल \(\frac{-5}{\sqrt{2}}\) एवं –\(\sqrt { 2 }\)

(iv) 2×2 – x + \(\frac { 1 }{ 8 } \) = 0
⇒ 16x² – 4x – 4x + 1 = 0
⇒ 16x² – 4x – 4x + 1 = 0
⇒ 4x(4x – 1) -1 (4x – 1) = 0
⇒ (4x – 1) (4x – 1) = 0
⇒ (4x – 1)² = 0
⇒ 4x – 1 = 0
⇒ x = \(\frac { 1 }{ 4 } \)
अत: दत्त समीकरण के अभीष्ट मूल \(\frac { 1 }{ 4 } \) एवं \(\frac { 1 }{ 4 } \) हैं।

(v) 100x² – 20x + 1 = 0
⇒ 100x² – 10x – 10x + 1 = 0
⇒ 10x (10x – 1)- 1 (10x – 1) = 0
⇒ (10x – 1) (10x – 1) = 0
⇒ (10x – 1)² = 0
⇒ 10x – 1 = 0
⇒ x = \(\frac { 1 }{ 10 } \)
अतः दत्त समीकरण के अभीष्ट मूल \(\frac { 1 }{ 10 } \) एवं \(\frac { 1 }{ 10 } \) हैं।

प्रश्न 2.
(i) जॉन और जीवन्ती दोनों के पास कुल 45 कंचे हैं। दोनों पाँच-पाँच कंचे खो देते हैं और अब उनके पास कंचों की संख्या का गुणनफल 124 है। बताइए आरम्भ में उनके पास कितने-कितने कंचे थे?
(ii) एक कुटीर उद्योग एक दिन में कुछ खिलौने निर्मित करता है। प्रत्येक खिलौने का मूल्य (₹ में) 55 में से एक दिन में निर्माण किए गए खिलौनों की संख्या को घटाने से प्राप्त संख्या के बराबर है। किसी एक दिन कुल निर्माण लागत ₹ 750 थी। उस दिन निर्माण किए गए खिलौने की संख्या ज्ञात कीजिए।
हल:
(i) मान लीजिए जॉन के पास प्रारम्भ में x कंचे थे तो जीवन्ती के पास प्रारम्भिक कंचों की संख्या = 45 – x
पाँच-पाँच कंचे खोने के बाद दोनों के पास शेष बचे कंचों की संख्या क्रमशः (x – 5) एवं (40 – X) हुई।
अब प्रश्नानुसार, (x – 5) (40 – x) = 124
⇒ 40x – x² – 200 + 5x = 124
⇒ x² – 45x + 324 = 0
⇒ x² – 9x – 36x + 324 = 0
⇒ x (x – 9) – 36 (x – 9) = 0
⇒ (x – 9) (x – 36) = 0
या तो x – 9 = 0 ⇒ x = 9
अथवा x – 36 = 0 ⇒x = 36
चूँकि 9 और 36 का योग 45 और गुणनफल 324 है।
अतः उनके पास अभीष्ट 9 और 36 कंचे थे।

(ii) मान लीजिए किसी दिन निर्मित खिलौनों की संख्या : है। इसलिए प्रश्नानुसार प्रत्येक खिलौने का मूल्य = ₹ (55 – x)
खिलौनों का कुल मूल्य x (55 – x) = 750
⇒ 55x – x² = 750
⇒ x² – 55x + 750 = 0
⇒ x² – 25x – 30x + 750 = 0
⇒ x (x – 25) – 30 (x – 25) = 0
⇒ (x – 25) (x – 30) = 0
या तो x – 25 = 0 ⇒ x = 25
अथवा x – 30 = 0 ⇒ x = 30
अतः उस दिन निर्मित खिलौनों की संख्या या तो 25 अथवा 30 है।

प्रश्न 3.
ऐसी दो संख्याएँ ज्ञात कीजिए जिनका योग 27 और गुणनफल 182 हो।
हल:
मान लीजिए एक संख्या x है, तो दूसरी संख्या 27 – x होगी [चूँकि योग 27 दिया है]
अब प्रश्नानुसार, x (27 – x) = 182
⇒ 27x – x² = 182
⇒ x² – 27x + 182 = 0
⇒ x² – 13x – 14x + 182 = 0
⇒ x (x – 13) – 14 (x – 13) = 0
⇒ (x – 13) (x – 14) = 0
या तो x – 13 = 0 ⇒ x = 13
अथवा x – 14 = 0 ⇒ x = 14
चूँकि 13 और 14 का योग 27 और गुणनफल 182 है।
अतः अभीष्ट संख्याएँ 13 एवं 14 हैं।

प्रश्न 4.
दो क्रमागत धनात्मक पूर्णांक ज्ञात कीजिए जिनके वर्गों का योग 365 है।
हल:
मान लीजिए दो क्रमागत धनात्मक पूर्णांक x एवं x + 1 हैं, तो प्रश्नानुसार,
(x + 1)² + (x)² = 365
⇒ x² + 2x + 1 + x² = 365
⇒ 2x² + 2x – 364 = 0
⇒ x² + x – 182 = 0
⇒ x² + 14x – 13x – 182 = 0
⇒ x (x + 14) – 13 (x + 14) = 0
⇒ (x + 14) (x – 13) = 0
या तो x + 14 = 0 ⇒ x = – 14 (जो धनात्मक नहीं हैं)
अथवा x – 13 = 0 ⇒ x = 13
अतः अभीष्ट धनात्मक पूर्णांक 13 एवं 14 हैं।

प्रश्न 5.
एक समकोण त्रिभुज की ऊँचाई उसके आधार से 7 cm कम है। यदि कर्ण 13 cm का हो, तो अन्य दो भुजाएँ ज्ञात कीजिए।
हल:
मान लीजिए समकोण त्रिभुज का आधार x cm है, तो त्रिभुज की ऊँचाई = (x – 7) cm (प्रश्नानुसार)
चूँकि (आधार)² + (ऊँचाई)² = (कर्ण)² (पाइथागोरस प्रमेय से)
⇒ (x)² + (x – 7)² = (13)² (∵ कर्ण = 17 cm दिया है)
⇒ x² + x² – 14x + 49 = 169
⇒ 2x² – 14x – 120 = 0
⇒ x² – 7x – 60 = 0
⇒ x² – 12x + 5x – 60 = 0
⇒ x(x – 12) + 5 (x – 12) = 0
⇒ (x – 12) (x + 5) = 0
या तो x + 5 = 0 ⇒ x = -5 (जो असम्भव है)
अथवा x – 12 = 0 ⇒ x = 12 cm
⇒ ऊँचाई = x = 12 – 7 = 5 cm
अतः समकोण त्रिभुज का आधार = 12 cm तथा ऊँचाई = 5 cm है।

प्रश्न 6.
एक कुटीर उद्योग एक दिन में कुछ बर्तनों का निर्माण करता है। एक विशेष दिन यह देखा गया कि प्रत्येक नग की निर्माण लागत (₹ में) उस दिन के निर्माण किए गए बर्तनों की संख्या के दुगने से 3 अधिक थी। यदि उस दिन की कुल निर्माण लागत ₹ 90 थी, तो निर्मित बर्तनों की संख्या और प्रत्येक नग की लागत ज्ञात कीजिए।
हल:
माना विशेष दिन निर्मित बर्तनों की संख्या x है, तो प्रत्येक बर्तन की लागत = (2x + 3) प्रश्नानुसार
अब कुल लागत = लागत दर × बर्तनों की संख्या
⇒ (2x + 3) × x = 90
⇒ 2x² + 3x = 90
⇒ 2x² + 3x – 90 = 0
⇒ 2x² + 15x – 12x – 90 = 0
⇒ x (2x + 15) – 6(2x + 15) = 0
⇒ (2x + 15) (x – 6) = 0
या तो 2x + 15 = 0 ⇒ x = \(\frac { -15 }{ 2 } \) (जो असम्भव है)
अथवा x – 6 = 0 ⇒ x = 6
प्रति बर्तन लागत = 2x + 3 = 2 × 6 + 3
= 12 + 3 = 15
अत: निर्मित बर्तनों की अभीष्ट संख्या = 6 तथा प्रत्येक बर्तन की लागत = ₹ 15 है।

In this article, we share MP Board Class 10th Maths Book Solutions Chapter 1 वास्तविक संख्याएँ Ex 1.1 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 10th Maths Solutions Chapter 1 वास्तविक संख्याएँ Ex 1.1

प्रश्न 1.
निम्नलिखित संख्याओं का HCF ज्ञात करने के लिए यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग कीजिए :
(i) 135 और 225
(ii) 196 और 38220
(iii) 867 और 255
हल :
(i) चरण – 1 : यहाँ 225 > 135 है, इसलिए हम 225 और 135 पर यूक्लिड प्रमेयिका का प्रयोग करने पर प्राप्त करते हैं :
225 = 135 × 1 + 90
चरण – 2 : चूँकि शेषफल 90 + 0 है, इसलिए हम 135 और 90 पर यूक्लिड प्रमेयिका का प्रयोग करने पर प्राप्त करते हैं :
135 = 90 × 1 + 45
चरण – 3 : चूँकि शेषफल 45 + 0 है, इसलिए हम नए भाजक 90 एवं नए शेषफल 45 पर यूक्लिड प्रमेयिका का प्रयोग करने पर प्राप्त करते हैं :
90 = 45 × 2 + 0
चूँकि यहाँ शेषफल 0 (शून्य) आया है और नया भाजक 45 है। अत: अभीष्ट HCF (135, 225) = 45
(ii) चरण – 1 : यहाँ 38220 > 196 है, इसलिए हम 38220 और 196 पर यूक्लिड प्रमेयिका का प्रयोग करने पर प्राप्त करते हैं :
38220 = 196 × 195 + 0
चूँकि यहाँ शेषफल 0 (शून्य) आया है और नया भाजक 196 है। अतः अभीष्ट HCF (196, 38220) = 196
(iii) चरण – 1 : यहाँ 867 > 255 है, इसलिए हम 867 और 255 पर यूक्लिड प्रमेयिका का प्रयोग करने पर प्राप्त करते हैं :
867 = 255 × 3 + 102
चरण – 2 : चूँकि शेषफल 102 ≠ 0, इसलिए हम 255 और 102 पर यूक्लिड प्रमेयिका का प्रयोग करके प्राप्त करते हैं :
255 = 102 × 2 + 51
चरण-3 : चूँकि शेषफल 51 ≠ 0, इसलिए हम नए भाजक 102 एवं नए शेषफल 51 पर यूक्लिड प्रमेयिका का प्रयोग करके प्राप्त करते हैं :
102 = 51 × 2 + 0
चूँकि यहाँ शेषफल 0 (शून्य) आया है और नया भाजक 51 है। अत: HCF (867, 255) = 51

प्रश्न 2.
दर्शाइए कि कोई धनात्मक विषम पूर्णांक 6q + 1 या 6q + 3 या 6q + 5 के रूप का होता है।
हल :
हम एक धनात्मक विषम पूर्णांक a लेकर प्रश्न को हल करना प्रारम्भ करते हैं। इसके लिए हम a और b = 6 में विभाजन एल्गोरिथ्म का प्रयोग करते हैं।
चूँकि 0 < r < 6 है, इसलिए सम्भावित शेषफल 0, 1, 2, 3, 4 और 5 होंगे।
अर्थात् a संख्याओं 6q, 6q + 1, 6q + 2, 6q + 3, 6q + 4 और 6q + 5 के रूप का हो सकता है।
चूँकि a एक विषम संख्या है। अत: यह 6q, 6q + 2 एवं 6q + 4 के रूप का नहीं हो सकता क्योंकि ये संख्याएँ 2 से विभाज्य हैं अर्थात् सम संख्याएँ हैं।
अतः कोई भी धनात्मक विषम पूर्णांक 6q + 1 या 6q + 3 या 6q + 5 के रूप का होता है। इति सिद्धम्

प्रश्न 3.
किसी परेड में 616 सदस्यों वाली एक सेना (आर्मी) की टुकड़ी को 32 सदस्यों वाले एक आर्मी बैण्ड के पीछे कार्य करना है। दोनों समूहों को समान संख्या वाले स्तम्भों में मार्च करना है। उन स्तम्भों की अधिकतम संख्या क्या है, जिसमें वे मार्च कर सकते हैं?
हल :
इसे क्रमबद्ध रूप से हल करने के लिए हम HCF (616, 32) ज्ञात करते हैं। इसे ज्ञात करने के लिए
हम यूक्लिड एल्गोरिथ्म का प्रयोग करके प्राप्त करते हैं :
616 = 32 × 19 + 8
32 = 8 × 4 + 0
⇒ HCF (616,32) का मान = 8
अतः, स्तम्भों की अभीष्ट अधिकतम संख्या = 8.

प्रश्न 4.
यूक्लिड विभाजन प्रमेयिका का प्रयोग करके दर्शाइए कि किसी धनात्मक पूर्णांक का वर्ग, किसी पूर्णांक m के लिए 3m या 3m +1 के रूप का होता है।
हल :
मान लीजिए x कोई धनात्मक पूर्णांक है, तब यह 3q, 3q + 1 या 3q + 2 के रूप में लिखा जा सकता है, जहाँ q एक धनात्मक पूर्णांक है।
अब (3q)² = 9q² = 3 (3q²) = 3m, जहाँ m = 3q² एक धनात्मक पूर्णांक है।
(3q+ 1)² = 9q² + 6q + 1
= 3q (3q + 2) + 1
= 3m + 1, जहाँ m =q (3q + 2) एक धनात्मक पूर्णांक है।
(3q + 2)² = 9q² + 12q + 4 = 9q² + 12q + 3 + 1
= 3 (3q² + 4q + 1) + 1 = 3 (3q + 1) (q + 1) + 1
= 3m + 1 जहाँ m = (+ 1) (3q + 1) एक धनात्मक पूर्णांक है।
अतः, किसी धनात्मक पूर्णांक का वर्ग किसी पूर्णांक m के लिए 3m या 3m + 1 के रूप का होता है। इति सिद्धम्

प्रश्न 5.
यूक्लिड विभाजन प्रमेयिका का प्रयोग करके दर्शाइए कि किसी धनात्मक पूर्णाक का घन 9m, 9m + 1 या 9m + 8 के रूप का होता है।
हल :
मान लीजिए x कोई धनात्मक पूर्णांक है, तब यह 34, 3q + 1 या 3q + 2 के रूप में लिखा जा सकता है, जहाँ q एक धनात्मक पूर्णांक है।
अब (34)³ = 27q³ = 9 (3q³) = 9m, जहाँ m = 3q³ एक धनात्मक पूर्णांक है।
(3q + 1)³ = 27q³ + 27q² + 9q + 1
= 9q (3q² + 3q + 1) + 1
= 9m + 1, जहाँ m = q (3q² + 3q + 1) एक धनात्मक पूर्णांक है।
(3q + 2)³ = 27q³ + 54q² + 36q + 8
= 9q (3q² + 6q + 4) + 8
= 9m + 8, जहाँ m = q (3q² + 6q + 4) एक धनात्मक पूर्णांक है।
अतः, किसी धनात्मक पूर्णांक का घन 9m, 9m + 1 या 9m + 8 के रूप का होता है। इति सिद्धम्

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 5 समान्तर श्रेढ़ियाँ Ex 5.4 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 5 समान्तर श्रेढ़ियाँ Ex 5.4

प्रश्न 1.
AP: 121, 117, 113 ………… का कौन-सा पद सबसे पहला ऋणात्मक पद होगा?
हल:
यहाँ AP का a = 121, d = 117 – 121 = -4
a_n < 0 प्रथम ऋणात्मक पद
चूँकि a_n = a + (n – 1) d < 0
⇒ 121 + (n – 1) (-4) < 0
⇒ 121 – 4n + 4 < 0
⇒ 125 – 4n < 0
⇒ 4n > 125
⇒ n > \(\frac { 125 }{ 4 } \) ⇒ n > 31 \(\frac { 1 }{ 4 } \)
अत: अभीष्ट 32वाँ पद प्रथम ऋणात्मक होगा।

प्रश्न 2.
किसी AP के तीसरे और सातवें पदों का योग 6 है और उनका गुणनफल 8 है। इस AP के प्रथम 16 पदों का योग ज्ञात कीजिए।
हल:
∵ a₃ + a₇ = (a + 2d) + (a + 6d) = 6 (दिया है)
⇒ 2a + 8d = 6 ⇒ a + 4d = 3 …….(1)
एवं a₃.a₇ = (a + 2d).(a + 6d) = 8 (दिया है।)
⇒ a² + 6ad + 2ad + 12d² = 8
⇒ a² + 8ad + 12d² = 8 ……(2)
समीकरण (1) से a = (3 – 4d) का मान समीकरण (2) में रखने पर,
(3 – 4d)² + 8(3 – 4d) (d) + 12d² = 8
⇒ 9 – 24d + 16d² + 24d – 32d² + 12d² = 8
⇒ 28d² – 32d² + 24d – 24d = 8 – 9
⇒ -4d² = -1 ⇒ 4d² = 1
⇒ d² = \(\frac { 1 }{ 4 } \) ⇒ d = ± \(\sqrt{\frac{1}{4}}\) = ±\(\frac { 1 }{ 2 } \)
d = + \(\frac { 1 }{ 2 } \) समीकरण (1) में रखने पर,
a + 4 (\(\frac { 1 }{ 2 } \)) = 3 ⇒ a = 3 – 2 = 1
एवं d = – \(\frac { 1 }{ 2 } \) समीकरण (1) में रखने पर,

अतः प्रथम 16 पदों का अभीष्ट योग 76 अथवा 20 है।

प्रश्न 3.
एक सीढ़ी के क्रमागत डण्डे परस्पर 25 cm की दूरी पर हैं। (देखिए संलग्न आकृति 5.4) डण्डों की लम्बाई एक समान रूप से घटती जाती है तथा सबसे निचले डण्डे की लम्बाई 45 cm है और सबसे ऊपर वाले डण्डे की लम्बाई 25 cm है। यदि ऊपरी और निचले डण्डे के बीच की दूरी 2\(\frac { 1 }{ 2 } \) m है, तो डण्डों को बनाने के लिए लकड़ी की कितनी लम्बाई 25 cm की आवश्यकता होगी?
हल:

आकृति 5.4

चूँकि डण्डों की संख्या = \(\frac { 250 }{ 25 } \) + 1 = 10 + 1 = 11
डण्डों की लम्बाई ऊपर से नीचे क्रमशः
25 cm, (25 + d) cm, (25 + 2d) cm, ………. = 45 cm.
जो AP का निर्माण करती है?
जहाँ a = 25 cm, a_n = 45 cm एवं n = 11
∴ S_n = \(\frac { n }{ 2 } \) [a + a_n]
= \(\frac { 11 }{ 2 } \) [25 + 45] = \(\frac { 11 }{ 2 } \) × 70
= 11 × 35
= 385 cm अर्थात् 3.85 m
अतः लकड़ी की कुल अभीष्ट लम्बाई = 385 cm अर्थात् 3.85 m है।

प्रश्न 4.
एक पंक्ति के मकानों को क्रमागत रूप से 1 से 49 तक अंकित किया गया है। दर्शाइए कि x.का एक ऐसा मान है कि x से अंकित मकान से पहले के मकानों की संख्याओं का योग उसके बाद वाले मकानों की संख्याओं के योग के बराबर है। x का मान ज्ञात कीजिए।
हल:
मकानों के क्रमांक क्रमशः 1, 2, 3, 4, ………….., 49 हैं जो एक AP का निर्माण करते हैं।
जहाँ a = 1 एवं d = 2 – 1 = 1 एवं n = 49.
प्रश्नानुसार, चूँकि S_x-1 = S₄₉ – S_x

अतः x का अभीष्ट मान = 35 है।

प्रश्न 5.
एक फुटबॉल के मैदान में एक छोटा चबूतरा है, जिसमें 15 सीढ़ियाँ बनी हुई हैं। इन सीढ़ियों में से प्रत्येक की लम्बाई 50 m है और वह ठोस कंक्रीट (Concrete) की बनी है। प्रत्येक सीढ़ी में \(\frac { 1 }{ 4 } \) m की चढ़ाई है और \(\frac { 1 }{ 2 } \) m का फैलाव (चौड़ाई) है। (देखिए संलगन आकृति 5.5) इस चबूतरे को बनाने में लगी कुल कंक्रीट का आयतन परिकलित कीजिए।

हल:
पहली सीढ़ी का आयतन = \(\frac { 1 }{ 4 } \) × \(\frac { 1 }{ 2 } \) × 50 = \(\frac { 25 }{ 4 } \) m³
दूसरी सीढ़ी का आयतन = \(\frac { 1 }{ 4 } \) × 1 × 50 = \(\frac { 50 }{ 4 } \) m³
तीसरी सीढ़ी का आयतन = \(\frac { 1 }{ 4 } \) × \(\frac { 3 }{ 2 } \) × 50 = \(\frac { 75 }{ 4 } \) m³
…………………………….
…………………………….
अतः सीढ़ियों के आयतन क्रमशः (ऊपर से नीचे की ओर). \(\frac { 25 }{ 4 } \) m³, \(\frac { 50 }{ 4 } \) m³, \(\frac { 75 }{ 4 } \) m³, ……………..15 पद एक AP का निर्माण करते हैं,

अतः कंक्रीट का अभीष्ट आयतन 750 m³ होगा।

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 7 निर्देशांक ज्यामिति Ex 7.1 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 7 निर्देशांक ज्यामिति Ex 7.1

प्रश्न 1.
बिन्दुओं के निम्नलिखित युग्मों के बीच दूरियाँ ज्ञात कीजिए :
(i) (2, 3), (4, 1) (2019)
(ii) (-5, 7), (-1,3)
(iii) (a, b), (-a-b)
हल :
(i) मान लीजिए कि बिन्दु युग्म P (2, 3) एवं Q (4, 1) हैं।

अतः बिन्दु के युग्म के बीच की अभीष्ट दूरी = 2√2 मात्रक है।

(ii) मान लीजिए बिन्दु युग्म P (-5, 7) और Q (-1, 3) हैं।

अतः बिन्दुओं के युग्म के बीच की अभीष्ट दूरी = 4√2 मात्रक है।

(iii) मान लीजिए बिन्दु युग्म P (a, b) एवं Q(-a, -b) हैं।

अतः बिन्दुओं के युग्म के बीच की अभीष्ट दूरी \(2 \sqrt{a^{2}+b^{2}}\) मात्रक है।

प्रश्न 2.
बिन्दुओं (0,0) और (36, 15) के बीच की दूरी ज्ञात कीजिए। क्या आप अब अनुच्छेद 7.2 में दिए दोनों शहरों A और B के बीच की दूरी ज्ञात कर सकते हैं?
हल :
मान लीजिए P (0, 0) और Q (36, 15) दो बिन्दु हैं।

हाँ हम उन दोनों शहरों A और B के बीच की दूरी ज्ञात कर सकते हैं। चूँकि शहरों के निर्देशांक A (0,0), B (36, 15), इसलिए दोनों शहरों के बीच की दूरी = 39 km
अतः दिए गए बिन्दुओं के बीच की दूरी 39 मात्रक एवं दोनों शहरों A और B के बीच की दूरी 39 km है।

प्रश्न 3.
निर्धारित कीजिए कि क्या बिन्दु (1, 5), (2, 3) और (-2, – 11) संरेखी हैं।
हल :
मान लीजिए दिए हुए बिन्दु P (1,5), Q (2,3) और R (-2, -11) हैं।

अतः दिए हुए बिन्दु सरेख नहीं हैं।

प्रश्न 4.
जाँच कीजिए कि क्या बिन्दु (5, -2), (6, 4) और (7,- 2) एक समद्विबाहु त्रिभुज के शीर्ष हैं।
हल :
मान लीजिए A (5, -2), B (6, 4) एवं C (7,-2) हैं।।

अतः दिए हुए बिन्दु एक समाद्विबाहु त्रिभुज के शीर्ष हैं।
इति सिद्धम्

प्रश्न 5.
किसी कक्षा में चार मित्र बिन्दुओं A, B, C और D पर बैठे हुए हैं (जैसा कि संलग्न आकृति 7.1 में दर्शाया गया है)। चम्पा और चमेली कक्षा के अन्दर जाती हैं और कुछ मिनट तक देखने के बाद, चम्पा चमेली से पूछती है कि “क्या तुम नहीं सोचती हो कि ABCD एक वर्ग है?” चमेली इससे सहमत नहीं है। दूरी सूत्र का प्रयोग करके बताइए कि इसमें कौन सही है ?

हल :
संलग्न आकृति के अवलोकन से (ग्राफ द्वारा) A (3, 4), B (6, 7), C (9, 4) एवं D (6, 1).
चूँकि दूरी सूत्र

AB = BC = CD = DA = √18 …..(1)
⇒ ABCD एक समचतुर्भुज हैं। (चारों भुजाएँ बराबर)

⇒ विकर्ण AC = विकर्ण BD
चूँकि समान विकर्ण वाला समचतुर्भज वर्ग होता है।
अत: ABCD एक वर्ग है। इसलिए चम्पा सही है।

प्रश्न 6.
निम्नलिखित बिन्दुओं द्वारा बनने वाले चतुर्भुज का प्रकार (यदि कोई है तो) बताइए तथा अपने उत्तर के लिए कारण भी दीजिए :
(i) (-1,- 2,), (1,0), (-1, 2), (-3,0)
(ii) (-3, 5), (3, 1), (0, 3), (-1, -4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
हल :
(i) चूँकि A (-1, – 2), B (1,0), C (-1, 2) एवं D (-3, 0) मान लीजिए

भुजाएँ AB = BC = CD = DA = √8
एव विकर्ण AC = BD = √16 = 4
अतः दिए हुए बिन्दुओं द्वारा बनने वाला चतुर्भुज एक वर्ग है क्योंकि दूसरी चारों भुजाएँ तथा विकर्ण बराबर हैं।

(ii) मान लीजिए A (-3, 5), B (3, 1), C (0, 3), एवं D (-1, -4)
चूँकि दूरी सूत्र

चूँकि ∆ABC में BC + AC = √13 + √13 = 2 √13 = AB
अतः दिए हुए बिन्दुओं से कोई भी चतुर्भुज नहीं बनेगा।

(iii) मान लीजिए : A (4, 5), B (7,6), C (4, 3) एवं D (1, 2)
चूँकि दूरी सूत्र


चतुर्भुज की सम्मुख भुजाएँ बराबर हैं। (समान्तर चतुर्भुज के प्रगुण)
अतः दिए हुए बिन्दुओं से बना चतुर्भुज एक समान्तर चतुर्भुज होगा।

प्रश्न 7.
x-अक्ष पर वह बिन्दु ज्ञात कीजिए.जो (2,-5) और (-2, 9) से समदूरस्थ है।
हल :
मान लीजिए x-अक्ष पर स्थित बिन्दु P (x, 0) है तथा दिए हुए बिन्दु Q (2,-5) एवं R (-2, 9) हैं।
तब प्रश्नानुसार : PQ = PR दिया है

(2 – x)² + (-5)² = (-2 – x)² + (9)² [दोनों ओर वर्ग करने पर]
4 – 4x + x² + 25 = 4 + 4x + x² + 81
4x + 4x = 4 + 25 – 4 – 81
8x = -56
x = \(\frac { -56 }{ 8 }\) = -7
अत: x-अक्ष पर स्थित अभीष्ट बिन्दु के निर्देशांक (-7,0) हैं।

प्रश्न 8.
y का वह मान ज्ञात कीजिए जिसके लिए बिन्दु P (2, – 3) और Q (10, 9) के बीच की दूरी 10 मात्रक है।
हल :
चूँकि

⇒ (8)² + (y + 3)² = 100 (दोनों ओर वर्ग करने पर)
⇒ 64 + y² + 6y + 9 = 100
⇒ y² + 6y + 73 – 100 = 0
⇒ y² + 6y – 27 = 0
⇒ y² + 9y – 3y – 27 = 0
⇒ y (y + 9) – 3 (y + 9) = 0
⇒ (y + 9) (y – 3) = 0
या तो y + 9 = 0 ⇒ y = -9
अथवा y – 3 = 0 ⇒ y = +3
अतः y के अभीष्ट मान – 9 अथवा + 3 है।

प्रश्न 9.
यदि Q (0, 1) बिन्दु P (5, – 3) और R (x, 6) से समदूरस्थ है, तो x के मान ज्ञात कीजिए। दूरियाँ QR एवं PR भी ज्ञात कीजिए।
हल :
∵प्रश्नानुसार QP = QR


अतः x का अभीष्ट मान ±4, QR = √41 एवं PR = √82 अथवा 9√2 है।

प्रश्न 10.
x और y में एक ऐसा सम्बन्ध ज्ञात कीजिए कि बिन्दु (x,y) बिन्दुओं (3, 6) और (-3, 4) से समदूरस्थ हो।
हल :
मान लीजिए P (x, y), Q (3, 6) एवं R (-3, 4) है तो प्रश्नानुसार PQ = PR

⇒ (x – 3)² + (y – 6)² = (x + 3)² + (y – 4)² (दोनों ओर वर्ग करने पर)
⇒ x² – 6x + 9 + y² – 12y + 36 = x² + 6x + 9 + y² – 8y + 16
⇒ 6x + 6x + 12y – 8y + 25 – 45 = 0
⇒ 12x + 4y – 20 = 0
⇒ 3x + y – 5 = 0
अतः x एवं y का अभीष्ट सम्बन्ध है : 3x + y – 5 = 0 है।

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 6 त्रिभुज Ex 6.6 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 6 त्रिभुज Ex 6.6

प्रश्न 1.
संलग्नआकृति 6.48 में PS कोण QPR कासमद्विभाजकहै। सिद्ध कीजिए \(\frac{Q S}{S R}=\frac{P Q}{P T}\) है।
हल :

ज्ञात है : ∆PQR में शीर्ष कोण ∠QPR का समद्विभाजक PS, आधार QR को S बिन्दु पर प्रतिच्छेद करता है।
रचना : QP को आगे बढ़ाया। बिन्दु R से TR || PS रेखाखण्ड खींचा जो QP को बिन्दु T पर प्रतिच्छेद करता है (देखिए आकृति 6.49)।
चूँकि PS || TR को QT तिर्यक रेखा प्रतिच्छेद करती है।
⇒ ∠QPS = ∠PTR …(1)
चूँकि PS || TR को तिर्यक रेखा PR प्रतिच्छेद करती है।
⇒ ∠SPR = ∠PRT …(2)
[एकान्तर कोण हैं।]
⇒ ∠QPS = ∠SPR …(3)
⇒ [PS, ∠QPR का समद्विभाजक दिया है]
⇒ ∠PTR = ∠PRT [समीकरण (1), (2) एवं (3) से]
⇒ PT = PR …(4) [समान कोणों की सम्मुख भुजाएँ हैं|
अब ∆QRT में, PS || TR

प्रश्न 2.
संलग्न आकृति 6.50 में D त्रिभुज ABC के कर्ण AC पर स्थित एक बिन्दु है जबकि BD ⊥ AC तथा DM ⊥ BC और DN ⊥ AB. सिद्ध कीजिए कि :
(i) DM² = DN.MC
(ii) DN² = DM.AN.
हल :

चूँकि DMBN एक आयत है
[∠M = ∠B = ∠N = 90° दिया है]
⇒ DM = BN एवं DN = MB
(i) ∵ समकोण ∆BDC के समकोण वाले शीर्ष D से DM ⊥ CB खींचा गया है।
⇒ ∆DMC ~ ∆BMD [प्रमेय : 6.7 से]
⇒ \(\frac{D M}{M B}=\frac{M C}{D M}\) [समरूप त्रिभुजों के प्रगुण]
⇒ DM² = MB.MC
⇒ DM² = DN.MC [∵ DN = MB समीकरण (1) से]
इति सिद्धम्

(ii) समकोण ∆ADB से समकोण वाले शीर्ष D से DN I AB खींचा गया है।
⇒ ∆DNB ~ ∆AND [प्रमेय : 6.7 से]
⇒ \(\frac{D N}{A N}=\frac{B N}{D N}\) [समरूप त्रिभुजों के प्रगुण से]
⇒ DN² = BN. AN
⇒ DN² = DM.AN. [∵ BN = DM समीकरण (1) से]
इति सिद्धम्

प्रश्न 3.
संलग्न आकृति 6.51 में ABC एक त्रिभुज है, जिसमें ∠ABC > 90° है तथा AD ⊥ CB है। सिद्ध कीजिए कि AC² = AB² + BC² + 2 BC.BD है।
हल :

ज्ञात है : एक अधिक कोण ∆ABC, जिसका कोण B अधिक कोण है तथा AD ⊥ CB.
∵ समकोण ∆ADB में, ∠ADB में समकोण है
⇒ AD² + DB² = AB² …(1) [पाइथागोरस प्रमेय से]
∵ समकोण ∆ADC में, ∠ADC समकोण है
⇒ AC² = AD² + DC² [पाइथागोरस प्रमेय से]
⇒ AC² = AD² + (DB + BC)²
⇒ AC² = AD² + DB² + BC² + 2DB.BC …..(2)
⇒ AC² = AB² + BC² + 2DB.BC. [समीकरण (1) एवं (2) से)
इति सिद्धम्

प्रश्न 4.
संलग्न आकृति 6.52 में ABC एक त्रिभुज है जिसमें ∠ABC < 90° तथा AD ⊥ BC है। सिद्ध कीजिए कि AC² = AB² BC² – 2BC.BD है।
हल :

ज्ञात है : एक न्यूनकोण ∆ABC, जिसका कोण B न्यूनकोण है तथा AD ⊥ BC.
∵ समकोण ∆ADB में, ∠ADB समकोण है
⇒ AD² + BD² = AB² …(1) [पाइथागोरस प्रमेय से]
∵ समकोण ∆ADC में, ∠ADC समकोण है
⇒ AC² = AD² + DC² [पाइथागोरस प्रमेय से]
⇒ AC² = AD² + (BC – BD)²
⇒ AC² = AD² + BC² + BD² – 2BC. BD
⇒ AC² = AD² + BD² + BC² – 2BC.BD …(2)
⇒ AC² = AB² + BC² – 2BC.BD. [समीकरण (1) और (2) से]
इति सिद्धम्

प्रश्न 5.
संलग्न आकृति 6.53 में AD ∆ABC की माध्यिका है तथा AM ⊥ BC है। सिद्ध कीजिए कि:
(i) AC² = AD² + BC.DM + \(\left(\frac{B C}{2}\right)^{2}\)
(ii) AB² = AD² – BC.DM + \(\left(\frac{B C}{2}\right)^{2}\)
(iii) AC² + AB² = 2AD² + \(\frac { 1 }{ 2 }\) BC²
हल :

(i) ∵ समकोण ∆AMD में, ∠AMD समकोण है
⇒ AM² + MD² = AD² …(1) [पाइथागोरस प्रमेय से]
∵ समकोण ∆AMC में, ∠AMC समकोण है
⇒ AC² = AM² + MC² [पाइथागोरस प्रमेय से]
⇒ AC² = AM² + (MD + DC)²
⇒ AC² = AM² + MD² + DC² + 2MD.DC
⇒ AC² = AMD + MD² + \(\left(\frac{B C}{2}\right)^{2}\) + BC.DM …(2)
[DC = \(\frac { BC }{ 2 }\) , BC = 2 DC]
⇒ AC² = AD² + \(\left(\frac{B C}{2}\right)^{2}\) + BC.DM [समीकरण (1) और (2)]
⇒ AC² = AD² + BC.DM + \(\left(\frac{B C}{2}\right)^{2}\)
इति सिद्धम्

(ii) ∵ समकोण ∆AMD में, ∠ADM समकोण है
⇒ AM² + MD² = AD² …(1)[पाइथागोरस प्रमेय से]
∵ समकोण ∆AMB में ∠AMB समकोण है
⇒ AB² = AM² + BM² [पाइथागोरस प्रमेय से]
⇒ AB² = AM² + (BD – MD)²
⇒ AB² = AM² + BD² + MD² – 2BD.MD.
⇒ AB² = AM² + MD² – 2BD.DM + BD²
⇒ AB² = AM² + MD² – BC.DM + \(\left(\frac{B C}{2}\right)^{2}\) ….( 2 )
[2BD = BC ⇒ BD = \(\frac { BC }{ 2 }\) ]
⇒ AB² = AD² – BC.DM + \(\left(\frac{B C}{2}\right)^{2}\)
इति सिद्धम्

(iii) अधिककोण ∆ADC में,
चूँकि AC² = AD² + BC.DM + \(\left(\frac{B C}{2}\right)^{2}\) …..(1)
[भाग (i) में सिद्ध कर चुके हैं।]
एवं न्यूनकोण त्रिभुज ADB में,
चूँकि AB² = AD² – BC.DM + \(\left(\frac{B C}{2}\right)^{2}\) …(2)
[भाग (ii) में सिद्ध कर चुके हैं।
⇒ AC² + AB² = 2AD² + 2 \(\left(\frac{B C}{2}\right)^{2}\) [समीकरण (1) एवं (2) से]
⇒ AC² + AB² = 2AD² + 2 \(\frac{B C^{2}}{4}\)
⇒ AC² + AB² = 2AD² + \(\frac { 1 }{ 2 }\) BC²
इति सिद्धम्

प्रश्न 6.
सिद्ध कीजिए कि एक समान्तर चतुर्भुज के विकर्णों के वर्गों का योग उसकी भुजाओं के वर्गों के योग के बराबर होता है।
हल :

मान लीजिए ABCD एक समान्तर चतुर्भुज है। A से AE ⊥ BC एवं D से DF ⊥ BC खींचिए। ABCD के विकर्ण AC और BD हैं। यहाँ AEFD एक आयत है।
समकोण ∆AEB और ∆DFC में,
∵कर्ण AB = कर्ण DC
[समान्तर चतुर्भुज की सम्मुख भुजाएँ]
∵भुजा AE = भुजा DF [आयत की सम्मुख भुजाएँ हैं]
⇒ ∆AEB ≅ ∆DFC [RHS सर्वांगसमता]
⇒ BE = CF …(1) [CPCT]
अधिककोण ∆DCB में ∠DCB अधिककोण है
⇒BD² = BC² + CD² + 2BC.CF .(2)[अधिककोण उपप्रमेय से]
∵न्यूनकोण ∆ABC में ∠ABC न्यूनकोण है
⇒AC² = AB² + BC² – 2 BE.BC [न्यूनकोण उपप्रमेय से]
⇒AC² = AB² + DA² – 2 BC.CF …(3)
[∵ BE = CF समीकरण (1) तथा BC = AD समान्तर ABCD की सम्मुख भुजाएँ हैं।]
⇒AC² + BD² = AB² + DA² + BC² + CD²
[समीकरण (2) + समीकरण (3) से]
⇒AC² + BD² = AB² + BC² + CD² + DA²
अतः किसी समान्तर चतुर्भुज में उसके विकर्णों के वर्गों का योग उसकी भुजाओं के वर्गों के योग के बराबर होता है।
इति सिद्धम्

प्रश्न 7.
संलग्न आकृति 6.55 में एक वृत्त की दो जीवाएँ AB और CD , परस्पर बिन्दु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि:
(i) ∆APC ~ ∆DPB
(ii) AP.PB = CP.DP.
हल :

(i) ∆APC और ∆DPB में,
∠ACP = ∠DBP [एक ही वृत्तखण्ड के कोण हैं]
∠CAP = ∠BDP [एक ही वृत्तखण्ड के कोण हैं]
∠APC = ∠DPB [शीर्षाभिमुख कोण हैं
∆APC ~ ∆DPB. [AAA समरूपता]
इति सिद्धम्

(ii) :.. ∆APC ~ ∆DPB. [भाग (i) में सिद्ध कर चुके हैं।]
\(\frac{A P}{D P}=\frac{C P}{B P}\) [समरूप त्रिभुजों के प्रगुण से]
AP.PB = CP.DP.
इति सिद्धम्

प्रश्न 8.
संलग्न आकृति 6.56 में एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिन्दु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि:
(i) ∆PAC ~ ∆PDB
(ii) PA.PB = PC.PD
हल :

∵∠PCA + ∠ACD = 180° …(1) रैखिक युग्म है|
∵∠ACD + ∠ABD = 180° ….(2) [चक्रीय चतुर्भुज के सम्मुख कोण]
⇒ ∠PCA = ∠ABD [समीकरण (1) एवं (2) से]
⇒ ∠PCA = ∠PBD …(3) [चित्रानुसार उभयनिष्ठ हैं]

(i) अब APAC एवं APDB में,
∵ ∠PCA = ∠PBD [समीकरण (3) से]
∵ ∠APC = ∠BPD [चित्रानुसार उभयनिष्ठ हैं|
⇒∆PAC ~ ∆PDB. [AA समरूपता]
इति सिद्धम्

(iii) ∵ ∆PAC ~ ∆PDB [भाग (i) में सिद्ध कर चुके हैं।]
⇒ \(\frac{P A}{P D}=\frac{P C}{P B}\) [समरूप त्रिभुजों के प्रगुण]
⇒ PA.PB = PC.PD.
इति सिद्धम्

प्रश्न 9.
संलग्न आकृति 6.57 में त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार है कि \(\frac{B D}{C D}=\frac{A B}{A C}\) है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।
हल :

दिया है : AABC की भुजा BC पर बिन्दु D इस प्रकार कि
\(\frac{B D}{C D}=\frac{A B}{A C}\) …(1)
रचना : AD को बढ़ाइए। CE || AD रेखा खींचिए जो AD को बिन्दु E पर प्रतिच्छेद करती है।
अब ∆ABD और ∆ECD में,

∠ABD = ∠ECD
[AB || CE एवं BD तिर्यक रेखा है।]
∠ADB = ∠EDC [शीर्षाभिमुख कोण है]
∆ABD ~ ∆ECD [AA समरूपता]
\(\frac{B D}{C D}=\frac{A B}{E C}\) …(2)
[समरूप त्रिभुजों के प्रगुण]
\(\frac{A B}{A C}=\frac{A B}{E C}\)
[समीकरण (1) एवं (2) से]
⇒ AC = EC
⇒ ∠CAD = ∠CED …(3) [बराबर भुजाओं के सम्मुख कोण]
लेकिन ∠BAD = ∠CED …(4) [समरूप ∆ABD एवं ∆ECD के संगत कोण हैं|
∴ ∠BAD = ∠CAD [समीकरण (3) एवं (4) से]
अतः AD कोण BAC का समद्विभाजक है।
इति सिद्धम्

प्रश्न 10.
नाजिया एक नदी की धारा में मछलियाँ पकड़ रही है। इसकी मछली पकड़ने वाली छड़ का सिरा पानी की सतह से 1.8 m ऊपर है तथा डोरी के निचले सिरे से लगा काँटा पानी की सतह पर इस प्रकार स्थित है कि उसकी नाजिया से दूरी 3.6 m है और छड़ के सिरे के ठीक नीचे पानी के सतह पर स्थित बिन्दु से उसकी दूरी 2.4 m है। यह मानते हुए कि उसकी डोरी (उसकी छड़ के सिरे से काँटे तक) तनी हुई है, उसने कितनी डोरी बाहर निकाली हुई है। (देखिए संलग्न आकृति) यदि वह डोरी को 5 cm/s की दर से अन्दर खींचे, तो 12 सेकण्ड के बाद नाजिया की काँटे
से क्षैतिज दूरी कितनी होगी?

हल :

मान लीजिए कि नाजिया की प्रारम्भिक स्थिति P पर छड़ का सिरा Q पर, काँटे की स्थिति R पर तथा Q से PR पर डाले गये लम्ब के पाद की स्थिति M पर है (आकृति 6.60) । तब प्रश्नानुसार,
PR = 3.6, QM = 1.8 m एवं RM = 2.4 m
PM = PR – RM = 3.6 – 2.4 = 1.2 m
मान लीजिए कि डोरी की वर्तमान लम्बाई = l m तो समकोण ∆QMR में, ∠QMR समकोण है
QR² = RM² + QM² [पाइथागोरस प्रमेय से]
l² = (2.4)² + (1.8)²
= 5.76 + 3.24
= 9.00
l = √9 = 3 m
5 cm/s की चाल से 12 s में डोरी की लम्बाई में कमी
= 12 x 5
= 60 cm
= 0.6 m
डोरी की नई लम्बाई QS = 3.00 – 0.60
= 2.40 m
अब समकोण ∆QMS में, ∠QMS समकोण है
(SM)² = (QS)² – (QM)² [पाइथागोरस प्रमेय से]
(SM)² = (2.4)² – (1.8)²
= 5.76 – 3.24
= 2.52
SM = √2.52
= 1.59 m
नाजिया की काँटे से नवीन दूरी = SP = SM + MP
= 1.59 + 1.2
= 2.79 m
अतः नाजिया की काँटे से अभीष्ट दूरी = 2.79 m है।

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 10 वृत्त Ex 10.1 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 10 वृत्त Ex 10.1

प्रश्न 1.
एक वृत्त की कितनी स्पर्श रेखाएँ हो सकती हैं?
हल :
अपरिमित रूप से अनेक।

प्रश्न 2.
रिक्त स्थानों की पूर्ति कीजिए :

1. किसी वृत्त की स्पर्श रेखा उसे ……. बिन्दुओं पर प्रतिच्छेद करती है।
2. वृत्त को दो बिन्दुओं पर प्रतिच्छेद करने वाली रेखा को ………………….. कहते हैं।
3. एक वृत्त की ………………….. समान्तर स्पर्श रेखाएँ हो सकती है।
4. वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिन्दु को …………………. कहते हैं।

हल :

1. केवल एक,
2. छेदक रेखा,
3. दो,
4. स्पर्श बिन्दु।

प्रश्न 3.
5 सेमी त्रिज्या वाले वृत्त के बिन्दु P पर स्पर्श रेखा PQ केन्द्र O से जाने वाली एक रेखा से बिन्दु Q पर इस प्रकार मिलती है कि OQ = 12 सेमी। PQ ए की लम्बाई हैं :
(A) 12 सेमी
(B) 13 सेमी
(C) 8.5 सेमी
(D) √119 सेमी।
हल :
(D) √119 सेमी।

प्रश्न 4.
एक वृत्त खींचिए और एक दी गई रेखा के समान्तर दो ऐसी रेखाएँ खींचिए कि उनमें से एक स्पर्श रेखा हो तथा दूसरी छेदक रेखा हो।
हल :

(1) किसी बिन्दु O को केन्द्र लेकर किसी त्रिज्या में एक वृत्त खींचा।
(2) वृत्त के केन्द्र O से OP ⊥ AB. (जहाँ AB एक दी गई रेखा है) खींचा जो वृत्त को बिन्दु R पर प्रतिच्छेद करता है।
(3) R से होकर CD ⊥ OP एक रेखा खींची। यही जो CD || AB एक अभीष्ट स्पर्श रेखा है।
(4) वृत्त के अन्दर OP के किसी बिन्दु Q से होकर EF ⊥ OP एक रेखा खींची जो वृत्त को क्रमशः G और H बिन्दुओं पर प्रतिच्छेद करती है।
अतः रेखा EF वृत्त की अभीष्ट छेदक रेखा तथा CD अभीष्ट स्पर्श रेखा है जो दी गई रेखा AB के समान्तर है।

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 10 वृत्त Ex 10.2 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 10 वृत्त Ex 10.2

(निर्देश : प्रश्न संख्या 1, 2 एवं 3 में सही विकल्प चुनिए एवं उचित कारण लिखिए।)

प्रश्न 1.
एक बिन्दु Q से एक वृत्त पर स्पर्श रेखा की लम्बाई 24 cm तथा Q की केन्द्र से दूरी 25 cm है, तो वृत्त की त्रिज्या है :
(A) 7 cm
(B) 12 cm
(C) 15 cm
(D) 245 cm.
हल :

अभीष्ट सही विकल्प (A) 7 cm है, क्योंकि आकृति 10.2 देखिए, जहाँ OQ = 25 cm एवं QT = 24 cm
त्रिज्या OT

(A) 7 cm

प्रश्न 2.
संलग्न आकृति 10.3 में यदि TP, TQ केन्द्र O वाले किसी वृत्त पर दो स्पर्श रेखाएँ इस प्रकार हैं कि ∠POQ = 110°, तो ∠PTQ हैं:
(A) 60°
(B) 70°
(C) 80°
(D) 90°
हल :

अभीष्ट सही विकल्प (B) 70° है, क्योंकि ∠P = 90°,
∠Q = 90°, ∠O = 110°
तब
∠PTQ = 360° – 90° – 90° – 110°
= 360° – 290° = 70°.

प्रश्न 3.
यदि एक बिन्दु P से O केन्द्र वाले किसी वृत्त पर PA, PB स्पर्श रेखाएँ परस्पर 80° के कोण पर झुकी हैं तो ∠POA बराबर है :
(A) 50°
(B) 60°
(C) 70°
(D) 80°
हल :

अभीष्ट सही विकल्प (A) 50° है, क्योंकि (देखिए आकृति 10.4) ∠APB = 80° (दिया है)
चूँकि केन्द्र को बाह्य बिन्दु से मिलाने वाली रेखा स्पर्श रेखाओं के मध्य कोण को समद्विभाजित करती है।
⇒∠OPA = \(\frac { 1 }{ 2 }\) x 80° = 40°
चूँकि OA ⊥ AP = ∠OAP = 90°
चूँकि ∠POA = 180° – ∠OAP – ∠OPA
= 180° – 90° – 40°
⇒∠POA = 180° – 130° = 50°.

प्रश्न 4.
सिद्ध कीजिए कि किसी वृत्त के किसी व्यास के सिरों पर खींची गयी स्पर्श-रेखाएँ समान्तर होती हैं। (2019)
हल :

माना लीजिए PQ एक O केन्द्र वाले वृत्त का व्यास है जिसके सिरों पर P और Q पर स्पर्श रेखाएँ क्रमशः AB एवं CD खींची गयी हैं।
चूँकि OP ⊥ AB [प्रमेय : 10.1]
∠OPB = 90° …(1)
चूँकि OQ ⊥ CD [प्रमेय : 10.1]
∠OQC = 90°
∠OPB + ∠OQC = 90° (एकान्तर कोण)
AB || CD
अतः, किसी वृत्त के किसी व्यास के सिरों पर खींची गयी स्पर्श रेखाएँ परस्पर समान्तर होती हैं।
इति सिद्धम्

प्रश्न 5.
सिद्ध कीजिए कि स्पर्श बिन्दु से स्पर्श रेखा पर खींचा गया लम्ब वृत्त के केन्द्र से होकर जाता हैं।
हल :

दिया है : एक वृत्त जिसका केन्द्र O है तथा इसकी एक स्पर्श
रेखा AB वृत्त को स्पर्श बिन्दु P पर स्पर्श करती है।
QP ⊥ AB खींचा गया है।
सिद्ध करना है : PQ वृत्त के केन्द्र O से होकर जाता है। मान लीजिए कि PQ वृत्त के केन्द्र O से होकर नहीं जाता तो त्रिज्या OP को मिलाइए।
चूँकि OP ⊥ AB [प्रमेय 10.1 से]
लेकिन QP ⊥ AB दिया हुआ है]
चूँकि किसी रेखा के किसी बिन्दु पर एक ही ओर दो लम्ब नहीं हो सकते, इसलिए OP एवं QP संपाती हैं।
अतः, स्पर्श बिन्दु से स्पर्श रेखा पर खींचा गया लम्ब वृत्त के केन्द्र से होकर जाता है।
इति सिद्धम्

प्रश्न 6.
एक बिन्दु A से जो एक वृत्त के केन्द्र से 5 cm की दूरी पर है, वृत्त पर बिन्दु A से खींची स्पर्श रेखा की लम्बाई 4 cm है। वृत्त की त्रिज्या ज्ञात कीजिए।
हल :

O केन्द्र वाले वृत्त के बाहर A कोई बिन्दु है। OA को मिलाया गया है तथा A से वृत्त पर एक स्पर्श रेखा AP खींची गयी है। OP को मिलाया गया है।
यहाँ OA = 5 cm एवं AP = 4 cm दिए हैं। यहाँ
∠OPA = 90° अब समकोण ∆OPA में,
OP = \(\sqrt{(O A)^{2}-(A P)^{2}}\)
पाइथागोरस प्रमेय से,

= 3 cm
अतः, अभीष्ट त्रिज्या की लम्बाई 3 cm है।

प्रश्न 7.
दो संकेन्द्रीय वृत्तों की त्रिज्याएँ 5 cm तथा 3 cm हैं। बड़े वृत्त की उस जीवा की लम्बाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती हो।
हल :

O केन्द्र वाले दो संकेन्द्री वृत्त दिए हैं जिनकी त्रिज्याएँ क्रमशः OQ = 5 cm एवं OM = 3 cm हैं, जहाँ PQ बड़ी त्रिज्या वाले वृत्त की जीवा है तथा छोटी त्रिज्या वाले वृत्त की स्पर्श बिन्दु M पर स्पर्श रेखा है।
OM ⊥ PQ = ∠OMQ = 90°.
[प्रमेय : 10.1]
P अब समकोण ∆OMQ में पाइथागोरस प्रमेय से,

= 4 cm
चूँकि PQ = 2MQ = 2 x 4 = 8 cm
[केन्द्र से जीवा पर डाला गया लम्ब जीवा को समद्विभाजित करता है।]
अतः, अभीष्ट जीवा की लम्बाई 8 cm है।

प्रश्न 8.
एक वृत्त के परिमत एक चतुर्भुज ABCD खींचा गया है। (देखिए संलग्न आकृति : 10.9)। सिद्ध कीजिए कि: AB + CD = AD + BC.
हल :

एक दिए हुए वृत्त के परिगत एक चतुर्भुज ABCD दिया है, के जो वृत्त को क्रमशः P, Q, R एवं S बिन्दुओं पर (चित्रानुसार) स्पर्श करता है।
चूँकि A से वृत्त पर दो स्पर्श रेखाएँ AS एवं AP हैं।
⇒ AP = AS …(1) [प्रमेय : 10.2 से]
चूँकि B से वृत्त पर दो स्पर्श रेखाएँ BP एवं BQ हैं :
⇒ BP = BQ …(2) [प्रमेय 10.2 से]
चूँकि C से वृत्त पर दो स्पर्श रेखाएँ CR एवं CQ हैं।
⇒ CR = CQ …(3) [प्रमेय 10.2 से]
चूँकि D से वृत्त पर दो स्पर्श रेखाएँ DS एवं DR है।
⇒ DR = DS …(4) [प्रमेय 10.2 से]
⇒ AP + BP + CR + DR = AS + DS + BQ + CQ
[समीकरण (1) + (2) + (3) + (4) से]
⇒ AB + CD = AD + BC. [चित्रानुसार]
इति सिद्धम्

प्रश्न 9.
संलग्न आकृति 10.10 से XY तथा X’Y’ O केन्द्र वाले किसी वृत्त पर दो समान्तर स्पर्श रेखाएँ हैं और स्पर्श बिन्दु C पर स्पर्श रेखा AB, XY को A तथा X’Y’ को B पर प्रतिच्छेद करती है। सिद्ध कीजिए कि: ∠AOB = 90 है।
हल :

चित्रानुसार स्पर्श रेखाएँ XY ||X’Y’ दिया है। रेखाखण्ड AB बिन्दु C पर स्पर्श रेखा है जो XY || X’Y’ को क्रमशः बिन्दु A एवं B पर प्रतिच्छेद कर रहा है।
चूँकि XY || X’Y’ को तिर्यक रेखा AB प्रतिच्छेद करती है।
∠XAB + ∠X’BA = 180° …(1) [एक ही ओर के अन्तः कोण है।]
चूँकि बाह्य बिन्दु A से दो स्पर्श रेखाएँ AX एवं AB हैं तथा AO द्वारा बाह्य बिन्दु को केन्द्र से मिलाया गया है।
∠OAB = \(\frac { 1 }{ 2 }\)∠XAB …(2)
चूँकि बाह्य बिन्दु B से दो स्पर्श रेखाएँ BX’ एवं BA हैं तथा BO द्वारा बाह्य बिन्दु को केन्द्र से मिलाया गया है।
∠OBA = \(\frac { 1 }{ 2 }\)∠X’BA …(3)
∠OAB + ∠OBA = \(\frac { 1 }{ 2 }\)∠X AB + \(\frac { 1 }{ 2 }\)∠X’BA …(4)
[समीकरण (2) + (3) से]
∠OAB + ∠OBA = \(\frac { 1 }{ 2 }\)(∠XAB + ∠X’BA) = \(\frac { 1 }{ 2 }\) x 180° = 90° …(5)
∵ ∠AOB + ∠OAB + ∠ORA = 180° …(6) [∆AOB के अन्त:कोण है]
∠AOB + 90° = 180° [समीकरण (5) एवं (6) से]
∠AOB = 180° – 90° = 90°
इति सिद्धम्

प्रश्न 10.
सिद्ध कीजिए कि किसी बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण स्पर्श बन्दुओं को मिलाने वाले रेखाखण्ड द्वारा केन्द्र पर अन्तरित कोण का सम्पूरक होता है।
हल :

मान लीजिए O केन्द्र वाले वृत्त के बाहर स्थित बिन्दु P से वृत्त पर दो स्पर्श रेखाएँ PQ एवं PR खींची गयी हैं। QR को मिलाया गया है तथा QR वृत्त के केन्द्र पर ∠QOR बनाती है। रचना : OP को मिलाइए (देखिए आकृति : 10.11)
समकोण ∆OQP में, ∠OOP = 90° (समकोण है)
⇒∠QOP + ∠QPO = 90° …(1)
समकोण ∆ORP में, ∠ORP = 90° (समकोण)
⇒∠ROP + ∠RPO = 90° ….(2)
⇒∠QOP + ∠ROP + ∠QPO + ∠RPO = 90° + 90° = 180°
[समीकरण (1) + (2) से ]
⇒∠OOR + ∠QPR = 180°
(सम्पूरक कोण हैं)
अतः बाह्य बिन्द से किसी वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण स्पर्श बिन्दुओं को मिलाने वाले रेखाखण्ड द्वारा केन्द्र पर अन्तरित कोण का सम्पूरक होता है। इति सिद्धम्

प्रश्न 11.
सिद्ध कीजिए कि किसी वृत्त के परिगत समान्तर चतुर्भुज समचतुर्भुज होता है।
हल :

मान लीजिए ABCD एक समानान्तर चतुर्भुज किसी O केन्द्र वाले वृत्त के परिगत दिया हुआ है। इसकी भुजाएँ AB, BC, CD एवं DA क्रमशः वृत्त को बिन्दुओं P, Q, R एवं S पर स्पर्श करती हैं OA, OB, OC एवं OD को मिलाया (देखिए आकृति 10.12)। चूँकि वृत्त के बाह्य बिन्दु A से वृत्त पर खींची गयी स्पर्श रेखाएँ AB एवं AD हैं तथा A को केन्द्र O से मिलाने वाली रेखा AO है
∠BAO = ∠DAO = \(\frac { 1 }{ 2 }\)∠BAD …(1)
चूँकि वृत्त के बाह्य बिन्दु B से वृत्त पर खींची गयी स्पर्श रेखाएँ BA एवं BC हैं तथा B को केन्द्र O से मिलाने वाली रेखा BO हैं।
∠ABO = ∠CBO = \(\frac { 1 }{ 2 }\)∠ABC ….(2)
∠BAO + ∠ABO = \(\frac { 1 }{ 2 }\)∠BAD + \(\frac { 1 }{ 2 }\)∠ABC …(3) [समीकरण (1) + (2) से]
लेकिन ∠BAD + ∠ABC = 180° …(4) [समान्तर चतुर्भुज के आसन्न कोण हैं]
∠BAO + ∠ABO = \(\frac { 1 }{ 2 }\)(∠BAD + ∠ABC) = \(\frac { 1 }{ 2 }\) x 180° = 90° …(5)
[समीकरण (3) एवं समीकरण (4) से]
∆ABO में, ∠BAO + ∠ABO + ∠AOB = 180° …(6) [त्रिभुज ABO के अन्त:कोण है]
∠AOB = 90° [समीकरण (6) – समीकरण (5) से]
इसी प्रकार सिद्ध कर सकते हैं कि
∠BOC = 90°, ∠COD = 90° एवं ∠DOA = 90°
∠AOB + ∠BOC = 180° एवं ∠AOB + ∠AOD = 180° जो रैखिक युग्म है।
AC एवं BD सरल रेखाएँ हैं।
चूँकि AC एवं BD समान्तर चतुर्भुज के विकर्ण हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
अतः ABCD एक समचतुर्भुज है।
इति सिद्धम्

प्रश्न 12.
4 cm त्रिज्या वाले एक वृत्त के परिमत एक त्रिभुज ABC इस प्रकार खींचा गया है कि रेखाखण्ड BD और DC (जिनमें स्पर्श बिन्दु D द्वारा BC विभाजित है) की लम्बाईयाँ क्रमशः 8 cm और 6 cm हैं। (देखिए आकृति 10.13) भुजाएँ AB और AC ज्ञात कीजिए।
हल :

मान लीजिए कि O केन्द्र वाले एवं 4 cm त्रिज्या वाले वृत्त के परिगत एक त्रिभुज ABC है जिसकी भुजाएँ BC, CA एवं AB वृत्त के क्रमश: D, E एवं F बिन्दुओं पर स्पर्श करती है। CD = 6 cm एवं DB = 8 cm है, OD, OE एवं OF तथा OA, OB एवं OC को मिलाइए। चूँकि OD = OE = OF = 4 cm …(1) (वृत्त की त्रिज्याएँ हैं)
CE = CD = 6 cm एवं BD = BF = 8 cm ; AE = AF = x cm (मान लीजिए)
अब AB = AF + BF = (x + 8) cm, AC = AE + CE = (x + 6) cm
एवं BC = BD + DC = 8 + 6 = 14 cm

ar (∆OBC) = \(\frac { 1 }{ 2 }\) × BC × OD
= \(\frac { 1 }{ 2 }\) × 14 × 4
= 28 cm²
ar (∆OCA) = \(\frac { 1 }{ 2 }\) × CA × OE
= \(\frac { 1 }{ 2 }\) × (x + 6) × 4
= (2x + 12) cm²
एवं ar (∆OAB) = \(\frac { 1 }{ 2 }\) × AB × OF
= \(\frac { 1 }{ 2 }\) × (x + 8) × 4
= (2x + 16) cm²
ar (∆ABC) = ar (OBC) + ar (OCA) + ar (OAB)
ar (∆ABC) = 28 cm² + (2x + 12) cm² + (2x + 16) cm²
ar (∆ABC) = (4x + 56) cm² …(1)
\(s=\frac{A B+B C+C A}{2}=\frac{(x+8)+14+(x+6)}{2}\)
= (x + 14) cm
अब हीरो के सूत्र से,

⇒ (x + 14)² = 3x² + 42x
⇒ x² + 28x + 196 = 3x² + 42x
⇒ 2x² + 14x – 196 = 0
⇒ x² + 7x – 98 = 0
⇒ x² + 14x – 7x – 98 = 0
⇒ x (x + 14) – 7 (x + 14) = 0
⇒ (x + 14) (x – 7) = 0
या तो x + 14 = 0 तब x = – 14
(दूरियाँ ऋणात्मक नहीं होती, अत: यह असम्भव है।
अथवा x – 7 = 0 ⇒ x = 7
⇒ AB = x + 8 = 7 + 8 = 15 cm
एवं AC = x + 6 = 7 + 6 = 13 cm
अतः, त्रिभुज की भुजाओं AB एवं AC के अभीष्ट मान क्रमश: 15 cm एवं 13 cm हैं।

प्रश्न 13.
सिद्ध कीजिए कि वृत्त के परिगत बनी चतुर्भुज की आमने-सामने की भुजाएँ केन्द्र पर सम्पूरक कोण अन्तरित करती हैं।
हल :

मान लीजिए कि O केन्द्र वाले वृत्त के परिगत बना चतुर्भुज ABCD है। OA, OB, OC एवं OD को मिलाया गया है। (देखिए आकृति 10.15)
चतुर्भुज ABCD की भुजाएँ वृत्त को P, Q, R एवं S पर स्पर्श करती हैं। चूँकि बाह्य बिन्दु D से वृत्त पर खींची गयी स्पर्श रेखाखण्ड DA एवं DC हैं तथा DO बिन्दु D को केन्द्र O से मिलाने वाली रेखा है।
चूँकि DO, ∠ADC की समद्विभाजक है।
∠CDO = ∠ADO = \(\frac { 1 }{ 2 }\) ∠D …..(1)
इसी प्रकार ∠DAO = ∠BAO = \(\frac { 1 }{ 2 }\)∠A ….(2)
∠ABO = ∠CBO = \(\frac { 1 }{ 2 }\) ∠B …(3)
∠BCO = ∠DCO = \(\frac { 1 }{ 2 }\) ∠C …..(4)
चूँकि ∠A + ∠B + ∠C + ∠D = 360° [चतुर्भुज के अन्त:कोण हैं]
⇒\(\frac { 1 }{ 2 }\)∠A + \(\frac { 1 }{ 2 }\)∠B + \(\frac { 1 }{ 2 }\)∠C + \(\frac { 1 }{ 2 }\)∠D = 180° ….(5)
∵∠DOC + ∠CDO + ∠DCO = 180° …(6)[ADOC के अन्त:कोण है]
⇒∠DOC + \(\frac { 1 }{ 2 }\) ∠D + \(\frac { 1 }{ 2 }\) ∠C = 180° …(7)
[समीकरण (1) एवं (4) से मान रखने पर]
∵∠AOB + ∠ABO + ∠BAO = 180° …(8)[AAOB के अन्त:कोण हैं]
⇒∠AOB + \(\frac { 1 }{ 2 }\) ∠B + \(\frac { 1 }{ 2 }\) ∠A = 180° …(9)
[समीकरण (2) एवं (3) से मान रखने पर]
⇒∠DOC + ∠AOB + \(\frac { 1 }{ 2 }\) ∠A + \(\frac { 1 }{ 2 }\) ∠B + \(\frac { 1 }{ 2 }\) ∠C + \(\frac { 1 }{ 2 }\) ∠D = 360° …(10)
[समीकरण (7) + (9) से]
⇒∠DOC + ∠AOB = 180°[समीकरण (10)- समीकरण (5) से]
अतः, वृत्त के परिगत बने चतुर्भुज की आमने-सामने की भुजाएँ केन्द्र पर सम्पूरक कोण अन्तरित करती हैं।
इति सिद्धम्

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 11 रचनाएँ Additional Questions Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 11 रचनाएँ Additional Questions

MP Board Class 10th Maths Chapter 11 अतिरिक्त परीक्षोपयोगी प्रश्न

MP Board Class 10th Maths Chapter 11 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
एक त्रिभुज ABC की रचना कीजिए जिसमें AB = 6 cm, ∠A = 30° तथा ∠B = 60° हो। एक अन्य त्रिभुज AB’C’ की रचना कीजिए जो कि त्रिभुज ABC के समरूप हो तथा जिसका आधार AB’ = 8 cm हो।
हल :

रचना के पद :

1. एक किरण AP खींचिए।
2. किरण AP से AB = 6 cm का रेखाखण्ड काटिए।
3. बिन्दु A पर ∠QAP = 30° का कोण बनाते हुए किरण AQ खींचिए।
4. बिन्दु B पर ∠ABR = 60° का कोण बनाते हुए किरण BR खींचिए जो किरण AQ को बिन्दु C पर प्रतिच्छेद करती है। यही अभीष्ट ∆ABC है।
5. किरण AP से AB’ = 8 cm का रेखाखण्ड काटिए।
6. B’ पर ∠AB’S = 60° का कोण बनाते हुए एक किरण B’S खींचिए जो किरण AQ को बिन्दु C’ पर प्रतिच्छेद करती है। यही ∆AB’C’ अभीष्ट त्रिभुज है।

प्रश्न 2.
एक त्रिभुज ABC की रचना कीजिए जिसमें भुजा BC = 7 cm, ∠B = 45°, ∠A = 105° हों। तब एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ ∆ABC की भुजाओं की \(\frac { 3 }{ 4 }\) गुनी हों।
हल :

एक त्रिभुज ABC की रचना करनी है जिसमें भुजा BC = 7 cm, ∠B = 45° एवं ∠A = 105°; अतः ∠C = 180° – (45° + 105°) = 30° एक अन्य समरूप A की रचना भी करनी है जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac { 3 }{ 4 }\) गुनी हैं।
रचना के पद :

1. BC = 7 cm का एक रेखाखण्ड खींचिए।
2. B पर ∠CBY = 45° का कोण बनाते हुए एक किरण BY खींचिए।
3. C पर ∠BCZ = 30° का कोण बनाते हुए एक किरण CZ खींचिए जो किरण BY को बिन्दु A पर प्रतिच्छेद करती है। यही अभीष्ट त्रिभुज ABC है।
4. रेखाखण्ड BC से BC’ = \(\frac { 3 }{ 4 }\) BC काटिए।
5. C’ से CT || CA एक किरण खींचिए जो किरण BY को बिन्दु A’ पर काटती है। यही ∆A’BC’ अभीष्ट त्रिभुज है।

प्रश्न 3.
4 cm त्रिज्या का एक वृत्त खींचिए। उस वृत्त पर दो स्पर्श रेखाएँ खींचिए जिनके बीच का कोण 60° का हो।
हल :

एक वृत्त (O, 4 cm) की रचना करके इस पर दो स्पर्श रेखाएँ PR एवं QR इस प्रकार खींचनी हैं कि ∠PRQ = 60°
चूँकि ∠XOP = ∠XOQ
= 90° – 30°
= 60°
रचना के पद :

1. एक किरण OX खींचिए।
2. O को केन्द्र लेकर 4 सेमी त्रिज्या का एक वृत्त खींचिए।
3. OX के साथ ∠XOY = 60° का कोण बनाते हुए किरण OY तथा ∠XOZ = 60° का कोण बनाते हुए किरण OZ खींचिए जो वृत्त को क्रमश: P एवं Q बिन्दुओं पर प्रतिच्छेद करती हैं।
4. बिन्दु P पर ∠OPT = 90° का कोण बनाते हुए किरण PT खींचिए जो किरण OX को बिन्दु R पर प्रतिच्छेद करती है।
5. QR को मिलाइए। यही PR एवं QR अभीष्ट स्पर्श रेखाएँ हैं।

प्रश्न 4.
एक समचतुर्भुज ABCD दिया है जिसमें AB = 4 cm एवं ∠ABC = 60°. इस समचतुर्भुज को दो त्रिभुजों ABC एवं ADC में विभाजित कीजिए। त्रिभुज ABC के समरूप त्रिभुज AB’C की संरचना कीजिए जिसका स्केल गुणक \(\frac { 2 }{ 3 }\) है। CD के समान्तर एक रेखाखण्ड C’D’ खींचिए जहाँ D’ रेखाखण्ड AD पर प्रतिच्छेद करता है। क्या AB’C’D’ एक समचतुर्भुज है।
हल :

1. एक किरण AX खींचिए।
2. AX किरण से AB = 4 cm की त्रिज्या का एक चाप खींचिए जो किरण AX को बिन्दु B पर काटता है।
3. बिन्दु B पर ∠ABY = 60° का कोण बनाते हुए किरण BY खींचिए।
4. किरण BY से BC = 4 cm की त्रिज्या का एक चाप खींचिए, जो BY को बिन्दु C पर प्रतिच्छेद करता है।
5. बिन्दु A एवं C को केन्द्र लेकर 4 cm त्रिज्या के चाप खीचिएा जो परस्पर बिन्दु D पर प्रतिच्छेद करते हैं।
6. बिन्दु D को बिन्दु A एवं C से मिलाइए।
7. AC को मिलाइए। इस प्रकार दिए हुए समचतुर्भुज ABCD दो त्रिभुजों ABC एवं ADC में विभाजित हो जाता है।
8. AB के बिन्दु B’ पर AB’ : AB = 2 : 3 अर्थात् AB’ : B’B = 2 : 1 के अनुपात में विभाजित कीजिए।
9. B’ से B’C’ || BC रेखाखण्ड खींचिए जो AC को C’ पर प्रतिच्छेद करता है। यही AB’C’ अभीष्ट समरूप त्रिभुज है।
10. अब C’D’ || CD रेखाखण्ड खींचिए जो AD को बिन्दु D’ पर प्रतिच्छेद करता है।

हाँ ₹AB’C’D’ एक समचतुर्भुज है, क्योंक AB’ = B’C’ = CD’ = D’A = \(\frac { 2 }{ 3 }\)
\(\frac{A B^{\prime}}{A B}=\frac{B^{\prime} C^{\prime}}{B C}=\frac{C^{\prime} D^{\prime}}{C D}=\frac{D^{\prime} A}{D A}=\frac{2}{3}\)
AB = BC = CD = DA . [समचतुर्भुज की भुजाएँ]
AB’ = B’C’ = C’D’ = D’A.

प्रश्न 5.
एक समान्तर चतुर्भुज ABCD की रचना कीजिए जिसमें BC = 5 cm, AB = 3 cm एवं ∠ABC = 60°। इसको विकर्ण BD द्वारा ∆BCD एवं ∆ABD में विभाजित कीजिए। ∆BDC के समरूप ∆BD’C’ की रचना स्केल गुणक \(\frac { 4 }{ 3 }\) के साथ कीजिए। DA के समान्तर एक रेखाखण्ड D’A’ खींचिए, जहाँ A’ भुजा BA को बढ़ाने पर उस पर स्थित हो। क्या A’BC’D’ एक समान्तर चतुर्भुज है?
हल :

1. एक किरण BP खींचिए।
2. किरण BP में से BC = 5 cm का रेखाखण्ड काटिए।
3. B पर CBQ = 60° का कोण बनाते हुए एक किरण BQ खींचिए।
4. BQ में से BA = 3 cm का रेखाखण्ड काटिए।
5. बिन्दु A से 5 cm एवं बिन्दु C से 3 cm की त्रिज्याएँ लेकर चाप कीजिए जो परस्पर बिन्दु D पर प्रतिच्छेद करते हैं। AD एवं CD को मिलाइए। किरण BDR खींचिए।
   यही ABCD अभीष्ट समान्तर चतुर्भुज एवं ∆BCD तथा ∆BAD उसके दो विभाजन हैं।
6. किरण BP में से BC’ : BC = 4 : 3 में रेखाखण्ड काटिए।
7. C’D’ || CD रेखाखण्ड खींचिए जो किरण BR को बिन्दु D’ पर प्रतिच्छेद करता है।
   यही ∆BC’D’, ∆BCD के समरूप है अभीष्ट त्रिभुज है।।
8. D’A’ || DA खींचिए जो किरण BQ को बिन्दु A’ पर प्रतिच्छेद करती है।
   हाँ ₹A’BC’D’ एक समान्तर चतुर्भुज है क्योंक A’B || D’C’ एवं A’D’ || BC’.

प्रश्न 6.
3 cm एवं 5 cm त्रिज्याओं के दो संकेन्द्रीय वृत्त खींचिए। बाह्य वृत्त पर कोई बिन्दु लेकर अन्तः वृत्त पर उससे दो स्पर्श रेखाएँ खींचिए। एक स्पर्श रेखा की लम्बाई का मापन कीजिए तथा वास्तविक गणना द्वारा उसकी पुष्टि कीजिए।
हल :

रचना के चरण :

1. O को केन्द्र लेकर क्रमश: 3 cm एवं 5 cm की त्रिज्याएँ लेकर दो संकेन्द्री वृत्त खींचिए।
2. बाह्य वृत्त पर कोई बिन्दु P लीजिए और PO को मिलाइए।
3. PO का मध्य-बिन्दु S ज्ञात कीजिए।
4. S को केन्द्र लेकर SO की दूरी के बराबर त्रिज्या लेकर एक वृत्त खींचिए जो अन्त:वृत्त को Q एवं R बिन्दुओं पर प्रतिच्छेद करता है।
5. PR एवं PQ को मिलाइए। यही PR एवं PQ अभीष्ट स्पर्श रेखाएँ हैं।
6. PQ को मापिए। इसका मान मापने पर = 4 cm आता है।
7. OQ को मिलाइए। ∠OQP समकोण है। [अर्द्धवृत्त का कोण]

अब समकोण ∆OQP में पाइथागोरस प्रमेय से,
PQ = \(\sqrt{O P^{2}-O Q^{2}}=\sqrt{(5)^{2}-(3)^{2}}=\sqrt{25-9}=\sqrt{16}\)
= 4 cm
[जहाँ OP = 5 एवं OQ = 3 त्रिज्याएँ दी हैं।]
अतः स्पर्श रेखा PQ की अभीष्ट लम्बाई = 4 cm है जिसकी वास्तविक गणना द्वारा पुष्टि होती हैं।

प्रश्न 7.
एक ∆ABC की रचना कीजिए जिसमें AB = 5 cm, BC = 6 cm एवं ∠ABC = 60° ∆ABC के समरूप स्केल गुणक \(\frac { 5 }{ 7 }\) के साथ एक अन्य त्रिभुज की रचना कीजिए।
हल :

1. एक किरण BX खींचिए तथा BC = 6 cm का रेखाखण्ड काटिए।
2. बिन्दु B पर ∠CBY = 60° का कोण बनाते हुए एक किरण BY खींचिए।
3. किरण BY में से BA = 5 cm का रेखाखण्ड काटिए जो किरण BY को बिन्दु A पर प्रतिच्छेद करता है।
4. AC को मिलाइए।
   यही ∆ABC अभीष्ट त्रिभुज है।
5. BC को BC’ : BC = 5 : 7 अर्थात BC’ : C’C = 5 : 2 के अनुपात में विभाजित कीजिए।
6. C’ से C’A’ || CA रेखाखण्ड खींचिए जो BY को बिन्दु A’ पर प्रतिच्छेद करता है।
   यही ∆A’BC’ ~ ∆ABC अभीष्ट त्रिभुज है जिसका स्केल गुणक \(\frac { 5 }{ 7 }\) है।

प्रश्न 8.
एक त्रिभुज ABC की रचना कीजिए जिसमें AB = 4 cm, BC = 6 cm एवं AC = 9 cm. ∆ABC के समरूप स्केल गुणक \(\frac { 3 }{ 2 }\) के साथ एक त्रिभुज की रचना कीजिए। अपनी रचना की पुष्टि कीजिए। क्या दोनों त्रिभुज सर्वांगसम हैं जबकि तीनों कोण एवं दो भुजाएँ दोनों त्रिभुजों में बराबर हैं।
हल :

1. एक किरण BX खींचिए।
2. किरण BX में से एक रेखाखण्ड BC = 6 cm काटिए।
3. B को केन्द्र लेकर AB = 4 cm एवं C को केन्द्र लेकर AC = 9 cm की त्रिज्याओं से चाप खींचिए जो एक-दूसरे को बिन्दु A पर प्रतिच्छेद करते हैं।
4. BA को मिलाइए और Y तक बढ़ाइए तथा C को मिलाइए।
5. BX किरण से एक रेखाखण्ड CC’ = \(\frac { 1 }{ 2 }\) BC काटिए ताकि BC : CC’ = 2 : 1 अर्थात् BC’ : BC = 3 : 2 हो जाए।
6. C’ से C’A’ || CA खींचिए जो किरण BY को बिन्दु A’ पर प्रतिच्छेद करती है।

यही ∆A’BC ~ ∆ABC है जिसका स्केल गुणक में \(\frac { 3 }{ 2 }\) है पुष्टि ∆A’CC’ में AC || A’C’ तथा BC’/BC = \(\frac { 3 }{ 2 }\) है।
∆A’BC’ ~ ∆ABC एवं स्केल गुणक 3/2 है। \(\Delta A^{\prime} B C \neq \Delta A B C\) क्योंकि संगत भुजाए बराबर नहीं बल्कि 3 : 2 के समानुपाती हैं।

प्रश्न 9.
एक समकोण ∆ABC की रचना कीजिए जिसमें BC = 12 cm, AB = 5 cm एवं ∠B = 90°.इस त्रिभुज के समरूप अन्य त्रिभुज की रचना कीजिए जिसका स्केल गुणक \(\frac { 2 }{ 3 }\) हो। क्या नया त्रिभुज भी समकोण त्रिभुज है?
हल :

1. एक किरण BX खींचिए।
2. किरण BX से रेखाखण्ड BC = 12 cm काटिए।
3. बिन्दु B पर ∠CBY = 90° का कोण बनाते हुए एक किरण BY खींचिए।
4. किरण BY से AB = 5 cm का रेखाखण्ड काटिए।
5. AC को मिलाइए।
6. किरण BX से रेखाखण्ड BC’ = \(\frac { 2 }{ 3 }\) BC काटिए।
7. C’ से A’C’ || AC खींचिए।
   यही ∆A’BC’ ~ ∆ABC है जिसका स्केल गुणक \(\frac { 2 }{ 3 }\) है तथा ∠A’BC’ भी समकोण हैं।

प्रश्न 10.
एक त्रिभुज ABC की रचना कीजिए जिसमें BC = 6 cm, CA = 5 cm एवं AB = 4 cm। इसके समरूप एक अन्य त्रिभुज की रचना कीजिए जिसका स्केल गुणक \(\frac { 5 }{ 3 }\) है।
हल :

1. एक किरण BX खींचिए।
2. किरण BX में से BC = 6 cm का रेखाखण्ड काटिए।
3. B को केन्द्र लेकर AB = 4 cm एवं C को केन्द्र लेकर AC = 5 cm की त्रिज्या लेकर चाप खींचिए जो परस्पर बिन्दु A पर प्रतिच्छेद करते हैं।
4. CA को मिलाइए तथा BA की मिलाते हुए किरण BY खींचिए।
5. किरण BX में से BC’ = \(\frac { 5 }{ 3 }\)BC रेखाखण्ड काटिए।
6. बिन्दु C’ से A’C’ || AC खींचिए जो किरण BY को बिन्दु A’ पर प्रतिच्छेद करती है।
   यही ∆A’BC’ ~ ∆ABC अभीष्ट त्रिभुज है जिसका स्केल गुणक \(\frac { 5 }{ 3 }\) है।

MP Board Class 10th Maths Chapter 11 लघु उत्तरीय प्रश्न

प्रश्न 1.
7 cm लम्बाई का एक रेखाखण्ड खींचिए। इस पर एक बिन्दु P इस प्रकार ज्ञात कीजिए कि यह रेखाखण्ड को 3 : 5 के अनुपात में विभाजित करता हो।
हल :

1. एक रेखाखण्ड BC = 7 cm खींचिए।
2. बिन्दु B पर नीचे की ओर न्यूनकोण ∠CBX = θ बनाते हुए किरण BX खींचिए।
3. बिन्दु C पर ऊपर की ओर ∠BCY = θ बनाते हुए किरण CY खींचिए।
4. किरण BX से BB1 = B1B2 = B2B3 रेखाखण्ड काटिए तथा किरण CY से BB1 = CC1 = C1C2 = C2C3 = C3C4 = C4C5 काटिए।
5. B3 को C5 से मिलाइए जो BC को बिन्दु P पर प्रतिच्छेद करता है।
   यही अभीष्ट बिन्दु P है जो रेखाखण्ड को 3:5 के अनुपात में विभाजित करता है।

प्रश्न 2.
4 cm त्रिज्या वाले एक वृत्त पर उसके केन्द्र से 6 cm की दूरी पर स्थित बिन्दु से स्पर्श रेखाएँ खींचिए।
हल :

1. रेखाखण्ड OP = 6 cm खींचिए।
2. O को केन्द्र लेकर OM = 4 cm की त्रिज्या से एक वृत्त खींचिए जो OP को बिन्दु M पर प्रतिच्छेद करता है।
3. OP को बिन्दु N पर समद्विभाजित कीजिए।
4. N को केन्द्र लेकर ON के बराबर दूरी की त्रिज्या से एक वृत्त खींचिए जो पूर्व वृत्त को बिन्दु Q एवं R पर प्रतिच्छेद करता है।
5. PQ एवं PR को मिलाइए। यही PQ एवं PR अभीष्ट स्पर्श रेखाएँ हैं।

MP Board Class 10th Maths Chapter 11 अति लघु उत्तरीय प्रश्न

निम्न में सत्य/असत्य कथन लिखिए तथा अपने उत्तर का कारण भी दीजिए।

प्रश्न 1.
एक रेखाखण्ड को ज्यामितीय विधि से दो रेखाखण्डों में (2 + √3) : (2 – √3) के अनुपात में विभाजित किया जा सकता है।
हल :
कथन असत्य है, क्योंकि (2 + √3) : (2 – √3) को सरल करने पर (7 + 4√3):1 प्राप्त होता है है जिसमें 1 तो धनात्मक पूर्णांक है लेकिन (7 + 4√3) धनात्मक पूर्णांक नहीं है।

प्रश्न 2.
ज्यामितीय विधि से यह सम्भव है कि किसी रेखाखण्ड को \(\sqrt{3} : \frac{1}{\sqrt{3}}\) के अनुपात में विभाजित किया जा सकता है।
हल :
कथन सत्य है, क्योंकि \(\sqrt{3} : \frac{1}{\sqrt{3}}\) अनुपात को सरल करने पर 3 : 1 का अनुपात होता है, जहाँ 3 एवं 1 दोनों धनपूर्णांक हैं।

प्रश्न 3.
एक ∆ABC के समरूप एक अन्य त्रिभुज में जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac { 7 }{ 3 }\) हों, BC के बिन्दु B पर A के विपरीत नीचे की ओर एक न्यूनकोण बनाते किरण BX खींचिए BX पर BC के सापेक्ष बिन्दु B1, B2, ….., B7 बराबर-बराबर दूरी अंकित कीजिए। B3 को C से मिलाइए तब एक रेखाखण्ड B6C’ || B3C खींचिए जहाँ C’BC को बढ़ाने पर उसको मिलता है। अन्त में रेखाखण्ड A’C’ || AC खींचिए।
हल :
कथन असत्य है, क्योंकि B7C’ || B3C खींचनी है।

प्रश्न 4.
3.5 cm त्रिज्या के एक वृत्त के केन्द्र से 3 cm की दूरी पर स्थित बिन्दु से वृत्त पर दो स्पर्श रेखाएँ खींची जा सकती हैं।
हल :
कथन असत्य है, क्योंकि बिन्दु वृत्त के अन्दर है जिससे वृत्त पर कोई भी स्पर्श रेखा नहीं खींची जा सकती।

प्रश्न 5.
किसी वृत्त पर परस्पर 170° पर झुकी दो स्पर्श रेखाएँ खींची जा सकती हैं।
हल :
कथन सत्य है, क्योंकि उनका झुकाव 180° से कम है।

MP Board Class 10th Maths Chapter 11 वस्तुनिष्ठ प्रश्न

MP Board Class 10th Maths Chapter 11 बहु-विकल्पीय प्रश्न

प्रश्न 1.
एक रेखाखण्ड AB को 5 : 7 के अनुपात में विभाजित करने के लिए पहले किरण AX इस प्रकार खींची जाती है कि ∠BAX एक न्यूनकोण हो तथा बराबर दूरियों पर AX बिन्दु अंकित किए गए इस प्रकार कि इन बिन्दुओं की न्यूनतम संख्या होगी :
(a) 8
(b) 10
(c) 11
(d) 12.
उत्तर:
(d) 12.

प्रश्न 2.
एक रेखाखण्ड AB को 4 : 7 के अनुपात में विभाजित करने के लिए सबसे पहले ∠BAX एक न्यूनकोण बनाते हुए किरण AX खींचिए। फिर AX पर बराबर-बराबर दूरियों पर बिन्दु A₁, A₂, A₃, …… अंकित किए। बिन्दु B को मिलाया जायेगा :
(a) A₁₂
(b) A₁₁
(c) A₁₀
(d) A₉
उत्तर:
(b) A₁₁

प्रश्न 3.
एक रेखाखण्ड AB को 5 : 6 के अनुपात में विभाजित करने के लिए न्यूनकोण ∠BAX बनाते हुए किरण AX खींची एवं दूसरी किरण BY || AX खींची और AX एवं BY किरणों पर बराबर-बराबर दूरियों पर A₁, A₂, A₃, …… एवं B₁, B₂, B₃, …… क्रमशः अंकित किए तब मिलाए गए बिन्दु हैं :
(a) A₅ एवं B₆
(b) A₆ एवं B₅
(c) A₄ एवं B₄
(d) A₅ एवं B₄
उत्तर:
(a) A₅ एवं B₆

प्रश्न 4.
एक त्रिभुज ∆ABC के समरूप त्रिभुज जिसकी भुजाएँ क्रमशः ∆ABC की संगत भुजाओं की \(\frac { 3 }{ 7 }\) हों, की रचना करने के लिए न्यूनकोण ∠CBX इस प्रकार बनाते हुए किरण BX खींचिए कि X बिन्दु BC के सापेक्ष AB के विपरीत दिशा में हो। तब किरण BX पर बराबर-बराबर दूरियों पर क्रमशः बिन्दु B₁, B₂, B₃, …… अंकित किए और अगला चरण निम्न बिन्दुओं को जोड़ेगा :
(a) B₁₀ से C
(b) B₃ से C
(c) B₇ से C
(d) B₄ से C.
उत्तर:
(c) B₇ से C

प्रश्न 5.
∆ABC के समरूप ऐसे त्रिभुज की रचना करने के लिए जिसकी भुजाएँ क्रमशः ∆ABC की संगत भुजाओं की \(\frac { 8 }{ 5 }\) हो एक किरण BX इस प्रकार खींचिए कि ∠CBX.एक न्यूनकोण हो तथा X बिन्दु BC के सापेक्ष AB के विपरीत दिशा में स्थित हो तब किरण BX पर बराबर-बराबर दूरियों पर बिन्दु अंकित कीजिए। इन बिन्दुओं की न्यूनतम संख्या होगी :
(a) 5
(b) 8
(c) 13
(d) 3.
उत्तर:
(b) 8

प्रश्न 6.
एक वृत्त पर किसी बाह्य बिन्दु से दो स्पर्श रेखाएँ इस प्रकार खींचने के लिए कि उनके बीच कोण 60° हो। यह आवश्यक है कि उन दो त्रिज्याओं के अन्त्य बिन्दुओं पर स्पर्श रेखाएँ खींची जाएँ जिनके बीच का कोण है :
(a) 135°
(b) 90°
(c) 60°
(d) 12°.
उत्तर:
(d) 12°.

प्रश्न 7.
किसी रेखाखण्ड AB को p:q के अनुपात में (जहाँ p एवं q धनात्मक पूर्णांक हैं) विभाजित करने के लिए एक न्यूनकोण ∠BAX बनाते हुए एक किरण AX खींचिए तब किरण AX पर बराबर-बराबर दूरियों पर बिन्दु इस प्रकार अंकित करने होंगे कि उन बिन्दुओं की न्यूनतम संख्या m होगी:
(a) m > p + q
(b) m = p + q
(c) m = p + q – 1
(d) m = pq.
उत्तर:
(b) m = p + q

प्रश्न 8.
किसी वृत्त पर दो स्पर्श रेखाएँ जो परस्पर 35° पर झुकी हों, खींचने के लिए यह आश्यक है कि उन त्रिज्याओं के अन्त्य बिन्दुओं पर स्पर्श रेखाएँ खींची जाए जिनके बीच का कोण हो :
(a) 105°
(b) 70°
(c) 140°
(d) 145°.
उत्तर:
(d) 145°.

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.5 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.5

ज्ञातव्य – यह प्रश्नावली परीक्षा की दृष्टि से नहीं है।

प्रश्न 1.
व्यास 3 mm वाले ताँबे के एक तार को 12 cm लम्बे और 10 cm व्यास वाले एक बेलन पर इस प्रकार लपेटा जाता है कि वह बेलन के वक्रपृष्ठ को पूर्णतया ढक लेता है। तार की लम्बाई और द्रव्यमान ज्ञात कीजिए, यह मानते हुए कि ताँबे का घनत्व 8.88 g प्रति cm³ है।
हल :
मान लीजिए बेलन की ऊँचाई h = 12 cm एवं व्यास D = 10 cm तथा तार का व्यास d = 2r = 3 mm = 0.3 cm ⇒ r = 0.15 cm
चूँकि बेलन का वक्रपृष्ठ = πDh = 3.14 x 10 x 12 cm²
S_c = 376.8 cm²
मान लीजिए तार की लम्बाई l है, जो बेलन को पूर्णतया ढक लेती है।

अतः, तार की अभीष्ट लम्बाई = 1256 cm है।
चूँकि तार का आयतन = πr²l
⇒ V = 3.14 x (0.15)² x 1256
ताँबे का आयतन V = 88.74 cm³
ताँबे का घनत्व = 8.88 g/cm³ (दिया है)
चूँकि तार का द्रव्यमान = तार का आयतन x ताँबे का घनत्व
⇒ M = 88.74 x 8.88
= 788 g (लगभग)
अतः, ताँबे का अभीष्ट द्रव्यमान = 788 g (लगभग) है।

प्रश्न 2.
एक समकोण त्रिभुज जिसकी भुजाएँ 3 cm और 4 cm हैं (कर्ण के अतिरिक्त) को उसके कर्ण के परितः घुमाया जाता है। इस प्रकार प्राप्त द्वि शंकु (double cone) के आयतन एवं पृष्ठीय क्षेत्रफल ज्ञात कीजिए (π का मान जो भी उपयुक्त लगे प्रयोग कीजिए)।
हल :

मान लीजिए कि ∆ABC एक समकोण ∆ है जिसमें AB = 4cm एवं BC = 3 cm दिए हैं तथा ∆ABC को कर्ण AC के परितः घुमाया गया है जिसमें दो शंकु प्राप्त होते हैं।
मान लीजिए AO = h cm
(देखिए संलग्न आकृति)
समकोण ∆ABC में, \(A C=\sqrt{A B^{2}+B C^{2}}\)
(पाइथागोरस प्रमेय से)
\(A C=\sqrt{(4)^{2}+(3)^{2}}=\sqrt{16+9}\)
= √25
= 5 cm
चूँकि AO = h माना गया है। OC = (5 – h) cm
चूँकि ₹ABCB’ के ∠ABC + ∠AB’C = 180°
⇒ चतुर्भुज ABCB’ एक चक्रीय चतुर्भुज है, जिसकी जीवा AC, जीवा BB’ का लम्ब समद्विभाजक हैं।
[ ∆AB’B एक समद्विबाहु ∆ है तथा AC शीर्ष लम्ब है।]
OB’ = OB = r (मान लीजिए)
OB’ x OB = AO x OC
⇒ r² = h x (5 – h) ….(1)
समकोण ∆AOB में पाइथागोरस प्रमेय से,
OB² = AB² – AO²
r² = (4)² – (h)² ….(2)
एवं समकोण ∆BOC में पाइथागोरस प्रमेय से,
OB² = BC² – OC²
r² = (3)² – (5 – h)² …(3)
⇒ (3)² – (5 – h)² = (4)² – (h)²
[समीकरण (2) एवं (3) से]
⇒ 9 – (25 – 10h + h²) = 16 – h²
⇒ 9 – 25 + 10h – h² = 16 – h²
⇒ 10h = 16 + 25 – 9 = 32
⇒ h = \(\frac { 32 }{ 10 }\) = 3.2 cm
⇒ h² = (4)² – (3.2)²
= 16 – 10.24
= 5.76 ….(4)
⇒ r = √5.76
= 2.4 cm
चूँकि द्विशंकु का आयतन

एवं द्विशंकु का पृष्ठीय क्षेत्रफल = πrl₁ + πrl₂
S_w = πr(l₁ + l₂) = \(\frac { 22 }{ 7 }\) x 2.4 x (4 + 3)
= \(\frac { 22 }{ 7 }\) x 2.4 x 7
= 52.8 cm²
अतः, द्विशंकु का अभीष्ट आयतन = 30.17 cm³
एवं उसका अभीष्ट पृष्ठीय क्षेत्रफल = 52.8 cm² है।

प्रश्न 3.
एक टंकी जिसका आन्तरिक मापन 150 cm x 120 cm x 110 cm है, में 129600 cm³ पानी है। इस पानी में कुछ छिद्रों वाली ईंटें तब तक डाली जाती हैं जब तक कि टंकी पूरी ऊपर तक न भर जाये। प्रत्येक ईंट अपने आयतन का \(\frac { 1 }{ 17 }\) पानी सोख लेती है। यदि प्रत्येक ईंट की माप 22.5 cm x 7.5 cm x 6.5 cm है, तो टंकी में कुल कितनी ईंटें डाली जा सकती हैं ताकि उसमें से पानी बाहर न बहे।
हल :
मान लीजिए कि टंकी में n ईंटें डाली जा सकती है। टंकी में पानी का आयतन = 129600 cm²
टंकी का आयतन V = 150 x 120 x 110
= 19,80,000 cm³.
n ईंटों का आयतन = n x 22.5 x 7.5 x 6.5.
= 1096.875 n cm³.
n ईंटों द्वारा सोखे गए पानी का आयतन = \(=\frac{1096 \cdot 875 n}{17} \mathrm{cm}^{3}\)
= 64.522 n cm³.
प्रश्नानुसार, टंकी का आयतन = ईंटों का आयतन + जल का आयतन – ईंटों द्वारा गए जल का आयतन
1980000 = 1096.875 n+ 129600 – 64.522 n
1096.875 n – 64.522 n = 1980000 – 129600
1032.353 n = 1850400
\(n=\frac{1850400}{1032 \cdot 353}=1792 \cdot 41\)
= 1792
ईंटें। अतः, ईंटों की अभीष्ट संख्या = 1792 है।

प्रश्न 4.
किसी महीने के 15 दिनों में एक नदी की घाटी में 10 cm वर्षा हुई। यदि इस घाटी का क्षेत्रफल 7280 km² है, तो दर्शाइए कि कुल वर्षा लगभग तीन नदियों के सामान्य पानी के योग के समतुल्य थी जबकि प्रत्येक नदी 1072 km लम्बी, 75 m चौड़ी और 3 m गहरी है।
हल :
मान लीजिए कि वर्षा के जल के तल की ऊँचाई x = 10 cm = \(\frac{10}{1,00,000}\) km एवं घाटी का क्षेत्रफल A = 7280 km². नदी की लम्बाई l = 1072 km, चौड़ाई b = 75 m = 0.075 km
एवं ऊँचाई (गहराई) h = 3 m = 0.003 km
तथा नदियों की संख्या n = 3.
वर्षा के जल का आयतन V₁ = \(A \times x=\frac{7280 \times 10}{1,00,000}\)
V₁ = 0.72800 km³
तीनों नदियों का आयतन = n × l × b × h
V₂ = 3 × 1072 × 0.075 × 0.003
V₂ = 0.7236 km³.
अतः, वर्षा के जल का आयतन लगभग तीनों नदियों के जल के आयतन के योग के बराबर है।

प्रश्न 5.
टीन की बनी एक तेल की कुप्पी 10 cm लम्बे बेलन में एक शंकु के छिन्नक को जोड़ने से बनी है। यदि इसकी कुल ऊँचाई 22 cm है, बेलनाकार भाग का व्यास 8 cm और कुप्पी के ऊपरी सिरे का व्यास 18 cm है, तो इसके बनने में लगी टीन की चादर का क्षेत्रफल ज्ञात कीजिए (देखिए संलग्न आकृति)।
हल :

मानलीजिए एकटीन की बनी तेल की कुप्पी h₁ = 10cm लम्बे एक बेलन जिसका व्यास d₁ = 2r₁ = 8 cm ⇒ r₁ = \(\frac { 8 }{ 2 }\) cm = 4 cm है पर एक शंकु छिन्नक जिसका ऊपरी व्यास d₂ = 2r₂ = 18 cm
r2 = \(\frac { 18 }{ 2 }\) = 9 cm से मिलकर बनी है। कुप्पी की कुल ऊँचाई h = 22 cm है, तो शंकु-छिन्नक की ऊँचाई h₂ = h – h₁ = 22 – 10 = 12 cm है। सुविधा हेतु कुप्पी के शंकु-छिन्नक को संलग्न चित्र में दिखाया गया है।

मान लीजिए शंकु-छिन्नक की तिर्यक ऊँचाई l cm है। आकृति के अनुसार, समकोण ∆PQR में ∠PQR = 90°, PQ = h2 = 12 cm एवं RQ = \(\frac{18-8}{2}=\frac{10}{2}=5 \mathrm{cm}\)
अब समकोण ∆POR में पाइथागोरस प्रमेय से,

अब कुप्पी का कुल वक्र पृष्ठीय क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल + शंकु छिन्नक का वक्र पृष्ठीय क्षेत्रफल
S_c = 2πr₁h₁ + πl(r₁ + r₂)
= 2 × π × 4 × 10 + π × 13 (4 + 9)
= 80π + 169π
= 249π
= 249 × \(\frac { 22 }{ 7 }\)
= \(\frac{5478}{7}=782 \frac{4}{7} \mathrm{cm}^{2}\)
अतः, कुप्पी को बनाने के लिए आवश्यक टीन का अभीष्ट क्षेत्रफल = \(782 \frac{4}{7} \mathrm{cm}^{2}\) है।

प्रश्न 6.
शंकु के एक छिन्नक के लिए पूर्व स्पष्ट किए गए संकेतों का प्रयोग करते हुए, वक्र पृष्ठीय क्षेत्रफल और सम्पूर्ण पृष्ठीय क्षेत्रफल के उन सूत्रों को सिद्ध कीजिए जो अनुच्छेद 13.5 में दिए गए हैं, जो कि निम्न प्रकार हैं
(i) शंकु के छिन्नक का वक्र पृष्ठीय क्षेत्रफल S_c = π(r₁ + r₂)l जहाँ \(l=\sqrt{h^{2}+\left(r_{1}-r_{2}\right)^{2}}\)
(ii) शंकु के छिन्नक का सम्पूर्ण पृष्ठीय क्षेत्रफल
S_W = π(r₁ + r₂)l + πr₁² + πr₂² जहाँ \(l=\sqrt{h^{2}+\left(r_{1}-r_{2}\right)^{2}}\)
हल :

(i) मान लीजिए शंकु-छिन्नक के दोनों वृत्ताकार सिरों की त्रिज्याएँ क्रमश: NR = r₁ एवं MP = r₂ मात्रक तथा उनके बीच की दूरी (शंकु-छिन्नक की ऊँचाई)
= h मात्रक है = MN
P से RN पर PQ ⊥ RN डालिए। अब MNQP
एक आयत है। जिसमें PQ = MN = h मात्रक एवं QN = PM = r₂ मात्रक है।
RQ = RN – QN
= (r₁ – r₂) मात्रक
मान लीजिए PR = छिन्नक की तिर्यक ऊँचाई
= l मात्रक
समकोण ∆PQR में पाइथागोरस प्रमेय से,
PR² = PQ² + RQ²
l² = h² + (r1 – ri)
\(l=\sqrt{h^{2}+\left(r_{1}-r_{2}\right)^{2}}\)

यदि हम छिन्नक के वक्र पृष्ठ को एक खड़ी रेखाखण्ड के द्वारा काटकर खोल दें तो हमको एक समलम्ब चतुर्भुज प्राप्त होगा जिसमें दोनों समान्तर रेखाओं के मान क्रमश: AB = a = 2πr₁ तथा CD = b = 2πr₂ होंगे तथा बीच की दूरी = l मात्रक (देखिए संलग्न आकृति) हम जानते हैं कि समलम्ब चतुर्भुज का क्षेत्रफल \(=\frac{l(a+b)}{2}\)
\(S_{c}=l\left(\frac{2 \pi r_{1}+2 \pi r_{2}}{2}\right)\)
S_c = πl(r₁ + r₂)

(ii) जहाँ \(l=\sqrt{h^{2}+\left(r_{1}-r_{2}\right)^{2}}\)
एवं सम्पूर्ण पृष्ठ का क्षेत्रफल = वक्र पृष्ठीय क्षेत्रफल + दोनों वृत्ताकार सिरों का क्षेत्रफल
S_w = S_c + πr₁² + πr₂²
S_w = πl(r₁ + r₂) + πr₁² + π₂²
\(l=\sqrt{h^{2}+\left(r_{1}-r_{2}\right)^{2}}\)
इति सिद्धम्

प्रश्न 7.
शंकु के एक छिन्नक के लिए पूर्व स्पष्ट किए संकेतों का प्रयोग करते हुए, आयतन का वह सूत्र सिद्ध कीजिए, जो अनुच्छेद 13.5 में दिया गया है, जो निम्न प्रकार है : आयतन \(\boldsymbol{V}=\frac{1}{3} \pi h\left(r_{1}^{2}+r_{2}^{2}+r_{1} r_{2}\right)\)
हल :

मान लीजिए शंकु छिन्नक के वृत्ताकार फलकों की त्रिज्याएँ क्रमशः r₁ एवं r₂ है जहाँ r₁ > r₂ एवं उसकी ऊँचाई (दोनों फलकों के बीच की दूरी) = h मात्रक है। उस शंक को पूरा कीजिए जिसका यह छिन्नक भाग है।
मान लीजिए शंकु की ऊर्ध्वाधर काट PQR हैं तथा ST|| QR है एवं छोटे शंकु का शीर्ष लम्ब PM =x मात्रक है, तो बड़े शंकु का शीर्ष लम्ब PN = PM + MN
= (x + h) मात्रक
समकोण ∆PNQ में SM || QN है।
∆PMS ~ ∆PNQ

छिन्नक का आयतन = बड़े शंकु का आयतन – छोटे शंकु का आयतन

[समीकरण (1) सेx का मान (2) में रखने पर]

इति सिद्धम्