In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 10 वृत्त Ex 10.2 Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 10 वृत्त Ex 10.2
(निर्देश : प्रश्न संख्या 1, 2 एवं 3 में सही विकल्प चुनिए एवं उचित कारण लिखिए।)
प्रश्न 1.
एक बिन्दु Q से एक वृत्त पर स्पर्श रेखा की लम्बाई 24 cm तथा Q की केन्द्र से दूरी 25 cm है, तो वृत्त की त्रिज्या है :
(A) 7 cm
(B) 12 cm
(C) 15 cm
(D) 245 cm.
हल :
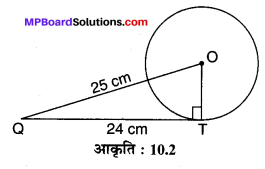
अभीष्ट सही विकल्प (A) 7 cm है, क्योंकि आकृति 10.2 देखिए, जहाँ OQ = 25 cm एवं QT = 24 cm
त्रिज्या OT
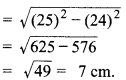
(A) 7 cm
प्रश्न 2.
संलग्न आकृति 10.3 में यदि TP, TQ केन्द्र O वाले किसी वृत्त पर दो स्पर्श रेखाएँ इस प्रकार हैं कि ∠POQ = 110°, तो ∠PTQ हैं:
(A) 60°
(B) 70°
(C) 80°
(D) 90°
हल :
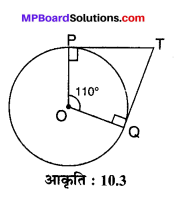
अभीष्ट सही विकल्प (B) 70° है, क्योंकि ∠P = 90°,
∠Q = 90°, ∠O = 110°
तब
∠PTQ = 360° – 90° – 90° – 110°
= 360° – 290° = 70°.
प्रश्न 3.
यदि एक बिन्दु P से O केन्द्र वाले किसी वृत्त पर PA, PB स्पर्श रेखाएँ परस्पर 80° के कोण पर झुकी हैं तो ∠POA बराबर है :
(A) 50°
(B) 60°
(C) 70°
(D) 80°
हल :
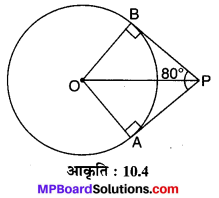
अभीष्ट सही विकल्प (A) 50° है, क्योंकि (देखिए आकृति 10.4) ∠APB = 80° (दिया है)
चूँकि केन्द्र को बाह्य बिन्दु से मिलाने वाली रेखा स्पर्श रेखाओं के मध्य कोण को समद्विभाजित करती है।
⇒∠OPA = \(\frac { 1 }{ 2 }\) x 80° = 40°
चूँकि OA ⊥ AP = ∠OAP = 90°
चूँकि ∠POA = 180° – ∠OAP – ∠OPA
= 180° – 90° – 40°
⇒∠POA = 180° – 130° = 50°.
प्रश्न 4.
सिद्ध कीजिए कि किसी वृत्त के किसी व्यास के सिरों पर खींची गयी स्पर्श-रेखाएँ समान्तर होती हैं। (2019)
हल :
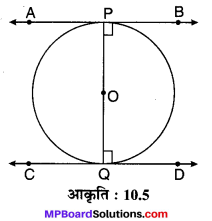
माना लीजिए PQ एक O केन्द्र वाले वृत्त का व्यास है जिसके सिरों पर P और Q पर स्पर्श रेखाएँ क्रमशः AB एवं CD खींची गयी हैं।
चूँकि OP ⊥ AB [प्रमेय : 10.1]
∠OPB = 90° …(1)
चूँकि OQ ⊥ CD [प्रमेय : 10.1]
∠OQC = 90°
∠OPB + ∠OQC = 90° (एकान्तर कोण)
AB || CD
अतः, किसी वृत्त के किसी व्यास के सिरों पर खींची गयी स्पर्श रेखाएँ परस्पर समान्तर होती हैं।
इति सिद्धम्
![]()
प्रश्न 5.
सिद्ध कीजिए कि स्पर्श बिन्दु से स्पर्श रेखा पर खींचा गया लम्ब वृत्त के केन्द्र से होकर जाता हैं।
हल :
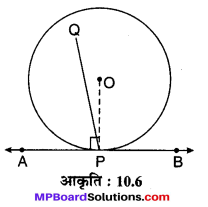
दिया है : एक वृत्त जिसका केन्द्र O है तथा इसकी एक स्पर्श
रेखा AB वृत्त को स्पर्श बिन्दु P पर स्पर्श करती है।
QP ⊥ AB खींचा गया है।
सिद्ध करना है : PQ वृत्त के केन्द्र O से होकर जाता है। मान लीजिए कि PQ वृत्त के केन्द्र O से होकर नहीं जाता तो त्रिज्या OP को मिलाइए।
चूँकि OP ⊥ AB [प्रमेय 10.1 से]
लेकिन QP ⊥ AB दिया हुआ है]
चूँकि किसी रेखा के किसी बिन्दु पर एक ही ओर दो लम्ब नहीं हो सकते, इसलिए OP एवं QP संपाती हैं।
अतः, स्पर्श बिन्दु से स्पर्श रेखा पर खींचा गया लम्ब वृत्त के केन्द्र से होकर जाता है।
इति सिद्धम्
प्रश्न 6.
एक बिन्दु A से जो एक वृत्त के केन्द्र से 5 cm की दूरी पर है, वृत्त पर बिन्दु A से खींची स्पर्श रेखा की लम्बाई 4 cm है। वृत्त की त्रिज्या ज्ञात कीजिए।
हल :
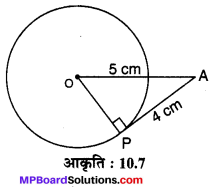
O केन्द्र वाले वृत्त के बाहर A कोई बिन्दु है। OA को मिलाया गया है तथा A से वृत्त पर एक स्पर्श रेखा AP खींची गयी है। OP को मिलाया गया है।
यहाँ OA = 5 cm एवं AP = 4 cm दिए हैं। यहाँ
∠OPA = 90° अब समकोण ∆OPA में,
OP = \(\sqrt{(O A)^{2}-(A P)^{2}}\)
पाइथागोरस प्रमेय से,
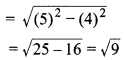
= 3 cm
अतः, अभीष्ट त्रिज्या की लम्बाई 3 cm है।
प्रश्न 7.
दो संकेन्द्रीय वृत्तों की त्रिज्याएँ 5 cm तथा 3 cm हैं। बड़े वृत्त की उस जीवा की लम्बाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती हो।
हल :
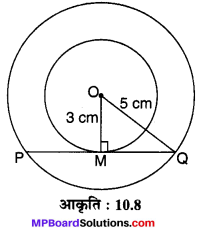
O केन्द्र वाले दो संकेन्द्री वृत्त दिए हैं जिनकी त्रिज्याएँ क्रमशः OQ = 5 cm एवं OM = 3 cm हैं, जहाँ PQ बड़ी त्रिज्या वाले वृत्त की जीवा है तथा छोटी त्रिज्या वाले वृत्त की स्पर्श बिन्दु M पर स्पर्श रेखा है।
OM ⊥ PQ = ∠OMQ = 90°.
[प्रमेय : 10.1]
P अब समकोण ∆OMQ में पाइथागोरस प्रमेय से,
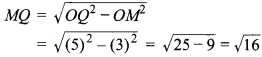
= 4 cm
चूँकि PQ = 2MQ = 2 x 4 = 8 cm
[केन्द्र से जीवा पर डाला गया लम्ब जीवा को समद्विभाजित करता है।]
अतः, अभीष्ट जीवा की लम्बाई 8 cm है।
प्रश्न 8.
एक वृत्त के परिमत एक चतुर्भुज ABCD खींचा गया है। (देखिए संलग्न आकृति : 10.9)। सिद्ध कीजिए कि: AB + CD = AD + BC.
हल :
एक दिए हुए वृत्त के परिगत एक चतुर्भुज ABCD दिया है, के जो वृत्त को क्रमशः P, Q, R एवं S बिन्दुओं पर (चित्रानुसार) स्पर्श करता है।
चूँकि A से वृत्त पर दो स्पर्श रेखाएँ AS एवं AP हैं।
⇒ AP = AS …(1) [प्रमेय : 10.2 से]
चूँकि B से वृत्त पर दो स्पर्श रेखाएँ BP एवं BQ हैं :
⇒ BP = BQ …(2) [प्रमेय 10.2 से]
चूँकि C से वृत्त पर दो स्पर्श रेखाएँ CR एवं CQ हैं।
⇒ CR = CQ …(3) [प्रमेय 10.2 से]
चूँकि D से वृत्त पर दो स्पर्श रेखाएँ DS एवं DR है।
⇒ DR = DS …(4) [प्रमेय 10.2 से]
⇒ AP + BP + CR + DR = AS + DS + BQ + CQ
[समीकरण (1) + (2) + (3) + (4) से]
⇒ AB + CD = AD + BC. [चित्रानुसार]
इति सिद्धम्
![]()
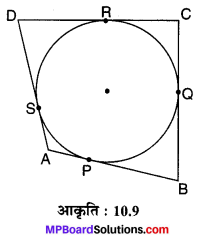
प्रश्न 9.
संलग्न आकृति 10.10 से XY तथा X’Y’ O केन्द्र वाले किसी वृत्त पर दो समान्तर स्पर्श रेखाएँ हैं और स्पर्श बिन्दु C पर स्पर्श रेखा AB, XY को A तथा X’Y’ को B पर प्रतिच्छेद करती है। सिद्ध कीजिए कि: ∠AOB = 90 है।
हल :
चित्रानुसार स्पर्श रेखाएँ XY ||X’Y’ दिया है। रेखाखण्ड AB बिन्दु C पर स्पर्श रेखा है जो XY || X’Y’ को क्रमशः बिन्दु A एवं B पर प्रतिच्छेद कर रहा है।
चूँकि XY || X’Y’ को तिर्यक रेखा AB प्रतिच्छेद करती है।
∠XAB + ∠X’BA = 180° …(1) [एक ही ओर के अन्तः कोण है।]
चूँकि बाह्य बिन्दु A से दो स्पर्श रेखाएँ AX एवं AB हैं तथा AO द्वारा बाह्य बिन्दु को केन्द्र से मिलाया गया है।
∠OAB = \(\frac { 1 }{ 2 }\)∠XAB …(2)
चूँकि बाह्य बिन्दु B से दो स्पर्श रेखाएँ BX’ एवं BA हैं तथा BO द्वारा बाह्य बिन्दु को केन्द्र से मिलाया गया है।
∠OBA = \(\frac { 1 }{ 2 }\)∠X’BA …(3)
∠OAB + ∠OBA = \(\frac { 1 }{ 2 }\)∠X AB + \(\frac { 1 }{ 2 }\)∠X’BA …(4)
[समीकरण (2) + (3) से]
∠OAB + ∠OBA = \(\frac { 1 }{ 2 }\)(∠XAB + ∠X’BA) = \(\frac { 1 }{ 2 }\) x 180° = 90° …(5)
∵ ∠AOB + ∠OAB + ∠ORA = 180° …(6) [∆AOB के अन्त:कोण है]
∠AOB + 90° = 180° [समीकरण (5) एवं (6) से]
∠AOB = 180° – 90° = 90°
इति सिद्धम्
प्रश्न 10.
सिद्ध कीजिए कि किसी बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण स्पर्श बन्दुओं को मिलाने वाले रेखाखण्ड द्वारा केन्द्र पर अन्तरित कोण का सम्पूरक होता है।
हल :
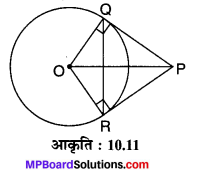
मान लीजिए O केन्द्र वाले वृत्त के बाहर स्थित बिन्दु P से वृत्त पर दो स्पर्श रेखाएँ PQ एवं PR खींची गयी हैं। QR को मिलाया गया है तथा QR वृत्त के केन्द्र पर ∠QOR बनाती है। रचना : OP को मिलाइए (देखिए आकृति : 10.11)
समकोण ∆OQP में, ∠OOP = 90° (समकोण है)
⇒∠QOP + ∠QPO = 90° …(1)
समकोण ∆ORP में, ∠ORP = 90° (समकोण)
⇒∠ROP + ∠RPO = 90° ….(2)
⇒∠QOP + ∠ROP + ∠QPO + ∠RPO = 90° + 90° = 180°
[समीकरण (1) + (2) से ]
⇒∠OOR + ∠QPR = 180°
(सम्पूरक कोण हैं)
अतः बाह्य बिन्द से किसी वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण स्पर्श बिन्दुओं को मिलाने वाले रेखाखण्ड द्वारा केन्द्र पर अन्तरित कोण का सम्पूरक होता है। इति सिद्धम्
प्रश्न 11.
सिद्ध कीजिए कि किसी वृत्त के परिगत समान्तर चतुर्भुज समचतुर्भुज होता है।
हल :
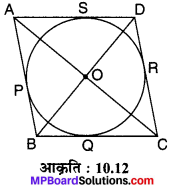
मान लीजिए ABCD एक समानान्तर चतुर्भुज किसी O केन्द्र वाले वृत्त के परिगत दिया हुआ है। इसकी भुजाएँ AB, BC, CD एवं DA क्रमशः वृत्त को बिन्दुओं P, Q, R एवं S पर स्पर्श करती हैं OA, OB, OC एवं OD को मिलाया (देखिए आकृति 10.12)। चूँकि वृत्त के बाह्य बिन्दु A से वृत्त पर खींची गयी स्पर्श रेखाएँ AB एवं AD हैं तथा A को केन्द्र O से मिलाने वाली रेखा AO है
∠BAO = ∠DAO = \(\frac { 1 }{ 2 }\)∠BAD …(1)
चूँकि वृत्त के बाह्य बिन्दु B से वृत्त पर खींची गयी स्पर्श रेखाएँ BA एवं BC हैं तथा B को केन्द्र O से मिलाने वाली रेखा BO हैं।
∠ABO = ∠CBO = \(\frac { 1 }{ 2 }\)∠ABC ….(2)
∠BAO + ∠ABO = \(\frac { 1 }{ 2 }\)∠BAD + \(\frac { 1 }{ 2 }\)∠ABC …(3) [समीकरण (1) + (2) से]
लेकिन ∠BAD + ∠ABC = 180° …(4) [समान्तर चतुर्भुज के आसन्न कोण हैं]
∠BAO + ∠ABO = \(\frac { 1 }{ 2 }\)(∠BAD + ∠ABC) = \(\frac { 1 }{ 2 }\) x 180° = 90° …(5)
[समीकरण (3) एवं समीकरण (4) से]
∆ABO में, ∠BAO + ∠ABO + ∠AOB = 180° …(6) [त्रिभुज ABO के अन्त:कोण है]
∠AOB = 90° [समीकरण (6) – समीकरण (5) से]
इसी प्रकार सिद्ध कर सकते हैं कि
∠BOC = 90°, ∠COD = 90° एवं ∠DOA = 90°
∠AOB + ∠BOC = 180° एवं ∠AOB + ∠AOD = 180° जो रैखिक युग्म है।
AC एवं BD सरल रेखाएँ हैं।
चूँकि AC एवं BD समान्तर चतुर्भुज के विकर्ण हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
अतः ABCD एक समचतुर्भुज है।
इति सिद्धम्
प्रश्न 12.
4 cm त्रिज्या वाले एक वृत्त के परिमत एक त्रिभुज ABC इस प्रकार खींचा गया है कि रेखाखण्ड BD और DC (जिनमें स्पर्श बिन्दु D द्वारा BC विभाजित है) की लम्बाईयाँ क्रमशः 8 cm और 6 cm हैं। (देखिए आकृति 10.13) भुजाएँ AB और AC ज्ञात कीजिए।
हल :
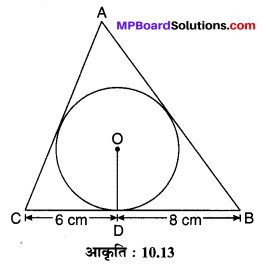
मान लीजिए कि O केन्द्र वाले एवं 4 cm त्रिज्या वाले वृत्त के परिगत एक त्रिभुज ABC है जिसकी भुजाएँ BC, CA एवं AB वृत्त के क्रमश: D, E एवं F बिन्दुओं पर स्पर्श करती है। CD = 6 cm एवं DB = 8 cm है, OD, OE एवं OF तथा OA, OB एवं OC को मिलाइए। चूँकि OD = OE = OF = 4 cm …(1) (वृत्त की त्रिज्याएँ हैं)
CE = CD = 6 cm एवं BD = BF = 8 cm ; AE = AF = x cm (मान लीजिए)
अब AB = AF + BF = (x + 8) cm, AC = AE + CE = (x + 6) cm
एवं BC = BD + DC = 8 + 6 = 14 cm
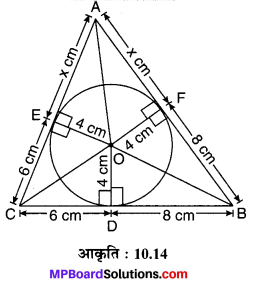
ar (∆OBC) = \(\frac { 1 }{ 2 }\) × BC × OD
= \(\frac { 1 }{ 2 }\) × 14 × 4
= 28 cm²
ar (∆OCA) = \(\frac { 1 }{ 2 }\) × CA × OE
= \(\frac { 1 }{ 2 }\) × (x + 6) × 4
= (2x + 12) cm²
एवं ar (∆OAB) = \(\frac { 1 }{ 2 }\) × AB × OF
= \(\frac { 1 }{ 2 }\) × (x + 8) × 4
= (2x + 16) cm²
ar (∆ABC) = ar (OBC) + ar (OCA) + ar (OAB)
ar (∆ABC) = 28 cm² + (2x + 12) cm² + (2x + 16) cm²
ar (∆ABC) = (4x + 56) cm² …(1)
\(s=\frac{A B+B C+C A}{2}=\frac{(x+8)+14+(x+6)}{2}\)
= (x + 14) cm
अब हीरो के सूत्र से,
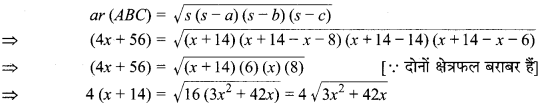
⇒ (x + 14)² = 3x² + 42x
⇒ x² + 28x + 196 = 3x² + 42x
⇒ 2x² + 14x – 196 = 0
⇒ x² + 7x – 98 = 0
⇒ x² + 14x – 7x – 98 = 0
⇒ x (x + 14) – 7 (x + 14) = 0
⇒ (x + 14) (x – 7) = 0
या तो x + 14 = 0 तब x = – 14
(दूरियाँ ऋणात्मक नहीं होती, अत: यह असम्भव है।
अथवा x – 7 = 0 ⇒ x = 7
⇒ AB = x + 8 = 7 + 8 = 15 cm
एवं AC = x + 6 = 7 + 6 = 13 cm
अतः, त्रिभुज की भुजाओं AB एवं AC के अभीष्ट मान क्रमश: 15 cm एवं 13 cm हैं।
![]()
प्रश्न 13.
सिद्ध कीजिए कि वृत्त के परिगत बनी चतुर्भुज की आमने-सामने की भुजाएँ केन्द्र पर सम्पूरक कोण अन्तरित करती हैं।
हल :
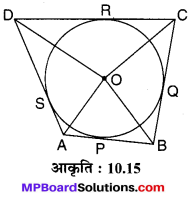
मान लीजिए कि O केन्द्र वाले वृत्त के परिगत बना चतुर्भुज ABCD है। OA, OB, OC एवं OD को मिलाया गया है। (देखिए आकृति 10.15)
चतुर्भुज ABCD की भुजाएँ वृत्त को P, Q, R एवं S पर स्पर्श करती हैं। चूँकि बाह्य बिन्दु D से वृत्त पर खींची गयी स्पर्श रेखाखण्ड DA एवं DC हैं तथा DO बिन्दु D को केन्द्र O से मिलाने वाली रेखा है।
चूँकि DO, ∠ADC की समद्विभाजक है।
∠CDO = ∠ADO = \(\frac { 1 }{ 2 }\) ∠D …..(1)
इसी प्रकार ∠DAO = ∠BAO = \(\frac { 1 }{ 2 }\)∠A ….(2)
∠ABO = ∠CBO = \(\frac { 1 }{ 2 }\) ∠B …(3)
∠BCO = ∠DCO = \(\frac { 1 }{ 2 }\) ∠C …..(4)
चूँकि ∠A + ∠B + ∠C + ∠D = 360° [चतुर्भुज के अन्त:कोण हैं]
⇒\(\frac { 1 }{ 2 }\)∠A + \(\frac { 1 }{ 2 }\)∠B + \(\frac { 1 }{ 2 }\)∠C + \(\frac { 1 }{ 2 }\)∠D = 180° ….(5)
∵∠DOC + ∠CDO + ∠DCO = 180° …(6)[ADOC के अन्त:कोण है]
⇒∠DOC + \(\frac { 1 }{ 2 }\) ∠D + \(\frac { 1 }{ 2 }\) ∠C = 180° …(7)
[समीकरण (1) एवं (4) से मान रखने पर]
∵∠AOB + ∠ABO + ∠BAO = 180° …(8)[AAOB के अन्त:कोण हैं]
⇒∠AOB + \(\frac { 1 }{ 2 }\) ∠B + \(\frac { 1 }{ 2 }\) ∠A = 180° …(9)
[समीकरण (2) एवं (3) से मान रखने पर]
⇒∠DOC + ∠AOB + \(\frac { 1 }{ 2 }\) ∠A + \(\frac { 1 }{ 2 }\) ∠B + \(\frac { 1 }{ 2 }\) ∠C + \(\frac { 1 }{ 2 }\) ∠D = 360° …(10)
[समीकरण (7) + (9) से]
⇒∠DOC + ∠AOB = 180°[समीकरण (10)- समीकरण (5) से]
अतः, वृत्त के परिगत बने चतुर्भुज की आमने-सामने की भुजाएँ केन्द्र पर सम्पूरक कोण अन्तरित करती हैं।
इति सिद्धम्