In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 6 त्रिभुज Ex 6.6 Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 6 त्रिभुज Ex 6.6
प्रश्न 1.
संलग्नआकृति 6.48 में PS कोण QPR कासमद्विभाजकहै। सिद्ध कीजिए \(\frac{Q S}{S R}=\frac{P Q}{P T}\) है।
हल :
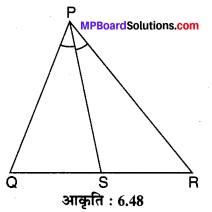
ज्ञात है : ∆PQR में शीर्ष कोण ∠QPR का समद्विभाजक PS, आधार QR को S बिन्दु पर प्रतिच्छेद करता है।
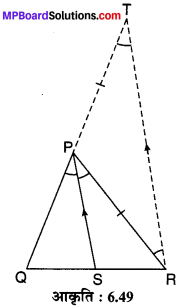
रचना : QP को आगे बढ़ाया। बिन्दु R से TR || PS रेखाखण्ड खींचा जो QP को बिन्दु T पर प्रतिच्छेद करता है (देखिए आकृति 6.49)।
चूँकि PS || TR को QT तिर्यक रेखा प्रतिच्छेद करती है।
⇒ ∠QPS = ∠PTR …(1)
चूँकि PS || TR को तिर्यक रेखा PR प्रतिच्छेद करती है।
⇒ ∠SPR = ∠PRT …(2)
[एकान्तर कोण हैं।]
⇒ ∠QPS = ∠SPR …(3)
⇒ [PS, ∠QPR का समद्विभाजक दिया है]
⇒ ∠PTR = ∠PRT [समीकरण (1), (2) एवं (3) से]
⇒ PT = PR …(4) [समान कोणों की सम्मुख भुजाएँ हैं|
अब ∆QRT में, PS || TR
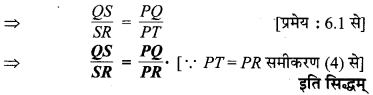
प्रश्न 2.
संलग्न आकृति 6.50 में D त्रिभुज ABC के कर्ण AC पर स्थित एक बिन्दु है जबकि BD ⊥ AC तथा DM ⊥ BC और DN ⊥ AB. सिद्ध कीजिए कि :
(i) DM² = DN.MC
(ii) DN² = DM.AN.
हल :
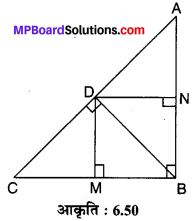
चूँकि DMBN एक आयत है
[∠M = ∠B = ∠N = 90° दिया है]
⇒ DM = BN एवं DN = MB
(i) ∵ समकोण ∆BDC के समकोण वाले शीर्ष D से DM ⊥ CB खींचा गया है।
⇒ ∆DMC ~ ∆BMD [प्रमेय : 6.7 से]
⇒ \(\frac{D M}{M B}=\frac{M C}{D M}\) [समरूप त्रिभुजों के प्रगुण]
⇒ DM² = MB.MC
⇒ DM² = DN.MC [∵ DN = MB समीकरण (1) से]
इति सिद्धम्
(ii) समकोण ∆ADB से समकोण वाले शीर्ष D से DN I AB खींचा गया है।
⇒ ∆DNB ~ ∆AND [प्रमेय : 6.7 से]
⇒ \(\frac{D N}{A N}=\frac{B N}{D N}\) [समरूप त्रिभुजों के प्रगुण से]
⇒ DN² = BN. AN
⇒ DN² = DM.AN. [∵ BN = DM समीकरण (1) से]
इति सिद्धम्
प्रश्न 3.
संलग्न आकृति 6.51 में ABC एक त्रिभुज है, जिसमें ∠ABC > 90° है तथा AD ⊥ CB है। सिद्ध कीजिए कि AC² = AB² + BC² + 2 BC.BD है।
हल :
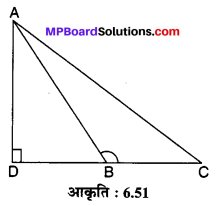
ज्ञात है : एक अधिक कोण ∆ABC, जिसका कोण B अधिक कोण है तथा AD ⊥ CB.
∵ समकोण ∆ADB में, ∠ADB में समकोण है
⇒ AD² + DB² = AB² …(1) [पाइथागोरस प्रमेय से]
∵ समकोण ∆ADC में, ∠ADC समकोण है
⇒ AC² = AD² + DC² [पाइथागोरस प्रमेय से]
⇒ AC² = AD² + (DB + BC)²
⇒ AC² = AD² + DB² + BC² + 2DB.BC …..(2)
⇒ AC² = AB² + BC² + 2DB.BC. [समीकरण (1) एवं (2) से)
इति सिद्धम्
प्रश्न 4.
संलग्न आकृति 6.52 में ABC एक त्रिभुज है जिसमें ∠ABC < 90° तथा AD ⊥ BC है। सिद्ध कीजिए कि AC² = AB² BC² – 2BC.BD है।
हल :
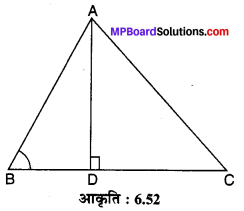
ज्ञात है : एक न्यूनकोण ∆ABC, जिसका कोण B न्यूनकोण है तथा AD ⊥ BC.
∵ समकोण ∆ADB में, ∠ADB समकोण है
⇒ AD² + BD² = AB² …(1) [पाइथागोरस प्रमेय से]
∵ समकोण ∆ADC में, ∠ADC समकोण है
⇒ AC² = AD² + DC² [पाइथागोरस प्रमेय से]
⇒ AC² = AD² + (BC – BD)²
⇒ AC² = AD² + BC² + BD² – 2BC. BD
⇒ AC² = AD² + BD² + BC² – 2BC.BD …(2)
⇒ AC² = AB² + BC² – 2BC.BD. [समीकरण (1) और (2) से]
इति सिद्धम्
![]()
प्रश्न 5.
संलग्न आकृति 6.53 में AD ∆ABC की माध्यिका है तथा AM ⊥ BC है। सिद्ध कीजिए कि:
(i) AC² = AD² + BC.DM + \(\left(\frac{B C}{2}\right)^{2}\)
(ii) AB² = AD² – BC.DM + \(\left(\frac{B C}{2}\right)^{2}\)
(iii) AC² + AB² = 2AD² + \(\frac { 1 }{ 2 }\) BC²
हल :
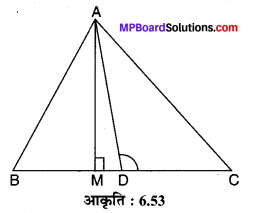
(i) ∵ समकोण ∆AMD में, ∠AMD समकोण है
⇒ AM² + MD² = AD² …(1) [पाइथागोरस प्रमेय से]
∵ समकोण ∆AMC में, ∠AMC समकोण है
⇒ AC² = AM² + MC² [पाइथागोरस प्रमेय से]
⇒ AC² = AM² + (MD + DC)²
⇒ AC² = AM² + MD² + DC² + 2MD.DC
⇒ AC² = AMD + MD² + \(\left(\frac{B C}{2}\right)^{2}\) + BC.DM …(2)
[DC = \(\frac { BC }{ 2 }\) , BC = 2 DC]
⇒ AC² = AD² + \(\left(\frac{B C}{2}\right)^{2}\) + BC.DM [समीकरण (1) और (2)]
⇒ AC² = AD² + BC.DM + \(\left(\frac{B C}{2}\right)^{2}\)
इति सिद्धम्
(ii) ∵ समकोण ∆AMD में, ∠ADM समकोण है
⇒ AM² + MD² = AD² …(1)[पाइथागोरस प्रमेय से]
∵ समकोण ∆AMB में ∠AMB समकोण है
⇒ AB² = AM² + BM² [पाइथागोरस प्रमेय से]
⇒ AB² = AM² + (BD – MD)²
⇒ AB² = AM² + BD² + MD² – 2BD.MD.
⇒ AB² = AM² + MD² – 2BD.DM + BD²
⇒ AB² = AM² + MD² – BC.DM + \(\left(\frac{B C}{2}\right)^{2}\) ….( 2 )
[2BD = BC ⇒ BD = \(\frac { BC }{ 2 }\) ]
⇒ AB² = AD² – BC.DM + \(\left(\frac{B C}{2}\right)^{2}\)
इति सिद्धम्
(iii) अधिककोण ∆ADC में,
चूँकि AC² = AD² + BC.DM + \(\left(\frac{B C}{2}\right)^{2}\) …..(1)
[भाग (i) में सिद्ध कर चुके हैं।]
एवं न्यूनकोण त्रिभुज ADB में,
चूँकि AB² = AD² – BC.DM + \(\left(\frac{B C}{2}\right)^{2}\) …(2)
[भाग (ii) में सिद्ध कर चुके हैं।
⇒ AC² + AB² = 2AD² + 2 \(\left(\frac{B C}{2}\right)^{2}\) [समीकरण (1) एवं (2) से]
⇒ AC² + AB² = 2AD² + 2 \(\frac{B C^{2}}{4}\)
⇒ AC² + AB² = 2AD² + \(\frac { 1 }{ 2 }\) BC²
इति सिद्धम्
प्रश्न 6.
सिद्ध कीजिए कि एक समान्तर चतुर्भुज के विकर्णों के वर्गों का योग उसकी भुजाओं के वर्गों के योग के बराबर होता है।
हल :
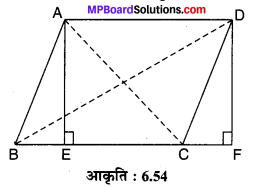
मान लीजिए ABCD एक समान्तर चतुर्भुज है। A से AE ⊥ BC एवं D से DF ⊥ BC खींचिए। ABCD के विकर्ण AC और BD हैं। यहाँ AEFD एक आयत है।
समकोण ∆AEB और ∆DFC में,
∵कर्ण AB = कर्ण DC
[समान्तर चतुर्भुज की सम्मुख भुजाएँ]
∵भुजा AE = भुजा DF [आयत की सम्मुख भुजाएँ हैं]
⇒ ∆AEB ≅ ∆DFC [RHS सर्वांगसमता]
⇒ BE = CF …(1) [CPCT]
अधिककोण ∆DCB में ∠DCB अधिककोण है
⇒BD² = BC² + CD² + 2BC.CF .(2)[अधिककोण उपप्रमेय से]
∵न्यूनकोण ∆ABC में ∠ABC न्यूनकोण है
⇒AC² = AB² + BC² – 2 BE.BC [न्यूनकोण उपप्रमेय से]
⇒AC² = AB² + DA² – 2 BC.CF …(3)
[∵ BE = CF समीकरण (1) तथा BC = AD समान्तर ABCD की सम्मुख भुजाएँ हैं।]
⇒AC² + BD² = AB² + DA² + BC² + CD²
[समीकरण (2) + समीकरण (3) से]
⇒AC² + BD² = AB² + BC² + CD² + DA²
अतः किसी समान्तर चतुर्भुज में उसके विकर्णों के वर्गों का योग उसकी भुजाओं के वर्गों के योग के बराबर होता है।
इति सिद्धम्
प्रश्न 7.
संलग्न आकृति 6.55 में एक वृत्त की दो जीवाएँ AB और CD , परस्पर बिन्दु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि:
(i) ∆APC ~ ∆DPB
(ii) AP.PB = CP.DP.
हल :
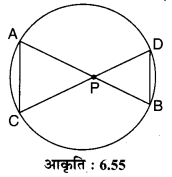
(i) ∆APC और ∆DPB में,
∠ACP = ∠DBP [एक ही वृत्तखण्ड के कोण हैं]
∠CAP = ∠BDP [एक ही वृत्तखण्ड के कोण हैं]
∠APC = ∠DPB [शीर्षाभिमुख कोण हैं
∆APC ~ ∆DPB. [AAA समरूपता]
इति सिद्धम्
(ii) :.. ∆APC ~ ∆DPB. [भाग (i) में सिद्ध कर चुके हैं।]
\(\frac{A P}{D P}=\frac{C P}{B P}\) [समरूप त्रिभुजों के प्रगुण से]
AP.PB = CP.DP.
इति सिद्धम्
प्रश्न 8.
संलग्न आकृति 6.56 में एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिन्दु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि:
(i) ∆PAC ~ ∆PDB
(ii) PA.PB = PC.PD
हल :
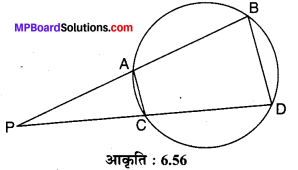
∵∠PCA + ∠ACD = 180° …(1) रैखिक युग्म है|
∵∠ACD + ∠ABD = 180° ….(2) [चक्रीय चतुर्भुज के सम्मुख कोण]
⇒ ∠PCA = ∠ABD [समीकरण (1) एवं (2) से]
⇒ ∠PCA = ∠PBD …(3) [चित्रानुसार उभयनिष्ठ हैं]
(i) अब APAC एवं APDB में,
∵ ∠PCA = ∠PBD [समीकरण (3) से]
∵ ∠APC = ∠BPD [चित्रानुसार उभयनिष्ठ हैं|
⇒∆PAC ~ ∆PDB. [AA समरूपता]
इति सिद्धम्
(iii) ∵ ∆PAC ~ ∆PDB [भाग (i) में सिद्ध कर चुके हैं।]
⇒ \(\frac{P A}{P D}=\frac{P C}{P B}\) [समरूप त्रिभुजों के प्रगुण]
⇒ PA.PB = PC.PD.
इति सिद्धम्
![]()
प्रश्न 9.
संलग्न आकृति 6.57 में त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार है कि \(\frac{B D}{C D}=\frac{A B}{A C}\) है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।
हल :
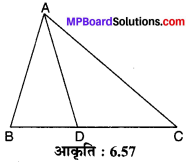
दिया है : AABC की भुजा BC पर बिन्दु D इस प्रकार कि
\(\frac{B D}{C D}=\frac{A B}{A C}\) …(1)
रचना : AD को बढ़ाइए। CE || AD रेखा खींचिए जो AD को बिन्दु E पर प्रतिच्छेद करती है।
अब ∆ABD और ∆ECD में,
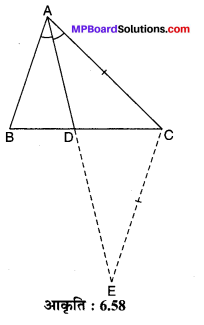
∠ABD = ∠ECD
[AB || CE एवं BD तिर्यक रेखा है।]
∠ADB = ∠EDC [शीर्षाभिमुख कोण है]
∆ABD ~ ∆ECD [AA समरूपता]
\(\frac{B D}{C D}=\frac{A B}{E C}\) …(2)
[समरूप त्रिभुजों के प्रगुण]
\(\frac{A B}{A C}=\frac{A B}{E C}\)
[समीकरण (1) एवं (2) से]
⇒ AC = EC
⇒ ∠CAD = ∠CED …(3) [बराबर भुजाओं के सम्मुख कोण]
लेकिन ∠BAD = ∠CED …(4) [समरूप ∆ABD एवं ∆ECD के संगत कोण हैं|
∴ ∠BAD = ∠CAD [समीकरण (3) एवं (4) से]
अतः AD कोण BAC का समद्विभाजक है।
इति सिद्धम्
प्रश्न 10.
नाजिया एक नदी की धारा में मछलियाँ पकड़ रही है। इसकी मछली पकड़ने वाली छड़ का सिरा पानी की सतह से 1.8 m ऊपर है तथा डोरी के निचले सिरे से लगा काँटा पानी की सतह पर इस प्रकार स्थित है कि उसकी नाजिया से दूरी 3.6 m है और छड़ के सिरे के ठीक नीचे पानी के सतह पर स्थित बिन्दु से उसकी दूरी 2.4 m है। यह मानते हुए कि उसकी डोरी (उसकी छड़ के सिरे से काँटे तक) तनी हुई है, उसने कितनी डोरी बाहर निकाली हुई है। (देखिए संलग्न आकृति) यदि वह डोरी को 5 cm/s की दर से अन्दर खींचे, तो 12 सेकण्ड के बाद नाजिया की काँटे
से क्षैतिज दूरी कितनी होगी?
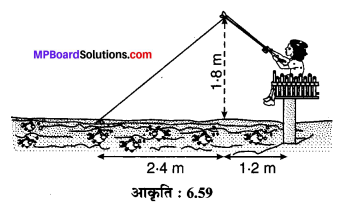
हल :
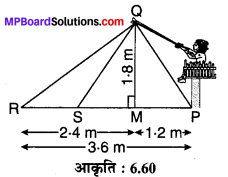
मान लीजिए कि नाजिया की प्रारम्भिक स्थिति P पर छड़ का सिरा Q पर, काँटे की स्थिति R पर तथा Q से PR पर डाले गये लम्ब के पाद की स्थिति M पर है (आकृति 6.60) । तब प्रश्नानुसार,
PR = 3.6, QM = 1.8 m एवं RM = 2.4 m
PM = PR – RM = 3.6 – 2.4 = 1.2 m
मान लीजिए कि डोरी की वर्तमान लम्बाई = l m तो समकोण ∆QMR में, ∠QMR समकोण है
QR² = RM² + QM² [पाइथागोरस प्रमेय से]
l² = (2.4)² + (1.8)²
= 5.76 + 3.24
= 9.00
l = √9 = 3 m
5 cm/s की चाल से 12 s में डोरी की लम्बाई में कमी
= 12 x 5
= 60 cm
= 0.6 m
डोरी की नई लम्बाई QS = 3.00 – 0.60
= 2.40 m
अब समकोण ∆QMS में, ∠QMS समकोण है
(SM)² = (QS)² – (QM)² [पाइथागोरस प्रमेय से]
(SM)² = (2.4)² – (1.8)²
= 5.76 – 3.24
= 2.52
SM = √2.52
= 1.59 m
नाजिया की काँटे से नवीन दूरी = SP = SM + MP
= 1.59 + 1.2
= 2.79 m
अतः नाजिया की काँटे से अभीष्ट दूरी = 2.79 m है।