MP Board Class 10th Maths Solutions Chapter 11 रचनाएँ Additional Questions

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 11 रचनाएँ Additional Questions Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 11 रचनाएँ Additional Questions

MP Board Class 10th Maths Chapter 11 अतिरिक्त परीक्षोपयोगी प्रश्न

MP Board Class 10th Maths Chapter 11 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
एक त्रिभुज ABC की रचना कीजिए जिसमें AB = 6 cm, ∠A = 30° तथा ∠B = 60° हो। एक अन्य त्रिभुज AB’C’ की रचना कीजिए जो कि त्रिभुज ABC के समरूप हो तथा जिसका आधार AB’ = 8 cm हो।
हल :

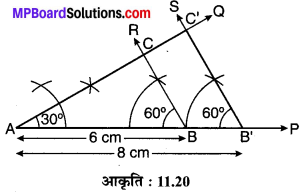
रचना के पद :

1. एक किरण AP खींचिए।
2. किरण AP से AB = 6 cm का रेखाखण्ड काटिए।
3. बिन्दु A पर ∠QAP = 30° का कोण बनाते हुए किरण AQ खींचिए।
4. बिन्दु B पर ∠ABR = 60° का कोण बनाते हुए किरण BR खींचिए जो किरण AQ को बिन्दु C पर प्रतिच्छेद करती है। यही अभीष्ट ∆ABC है।
5. किरण AP से AB’ = 8 cm का रेखाखण्ड काटिए।
6. B’ पर ∠AB’S = 60° का कोण बनाते हुए एक किरण B’S खींचिए जो किरण AQ को बिन्दु C’ पर प्रतिच्छेद करती है। यही ∆AB’C’ अभीष्ट त्रिभुज है।

प्रश्न 2.
एक त्रिभुज ABC की रचना कीजिए जिसमें भुजा BC = 7 cm, ∠B = 45°, ∠A = 105° हों। तब एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ ∆ABC की भुजाओं की \(\frac { 3 }{ 4 }\) गुनी हों।
हल :

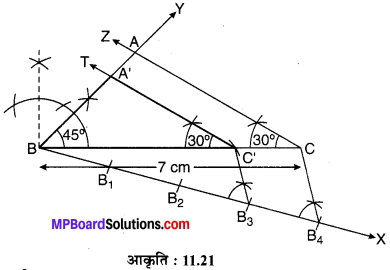
एक त्रिभुज ABC की रचना करनी है जिसमें भुजा BC = 7 cm, ∠B = 45° एवं ∠A = 105°; अतः ∠C = 180° – (45° + 105°) = 30° एक अन्य समरूप A की रचना भी करनी है जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac { 3 }{ 4 }\) गुनी हैं।
रचना के पद :

1. BC = 7 cm का एक रेखाखण्ड खींचिए।
2. B पर ∠CBY = 45° का कोण बनाते हुए एक किरण BY खींचिए।
3. C पर ∠BCZ = 30° का कोण बनाते हुए एक किरण CZ खींचिए जो किरण BY को बिन्दु A पर प्रतिच्छेद करती है। यही अभीष्ट त्रिभुज ABC है।
4. रेखाखण्ड BC से BC’ = \(\frac { 3 }{ 4 }\) BC काटिए।
5. C’ से CT || CA एक किरण खींचिए जो किरण BY को बिन्दु A’ पर काटती है। यही ∆A’BC’ अभीष्ट त्रिभुज है।

प्रश्न 3.
4 cm त्रिज्या का एक वृत्त खींचिए। उस वृत्त पर दो स्पर्श रेखाएँ खींचिए जिनके बीच का कोण 60° का हो।
हल :

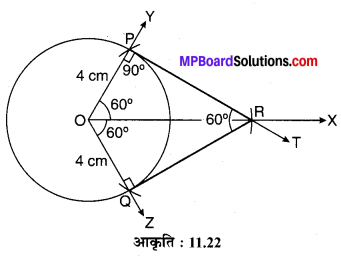
एक वृत्त (O, 4 cm) की रचना करके इस पर दो स्पर्श रेखाएँ PR एवं QR इस प्रकार खींचनी हैं कि ∠PRQ = 60°
चूँकि ∠XOP = ∠XOQ
= 90° – 30°
= 60°
रचना के पद :

1. एक किरण OX खींचिए।
2. O को केन्द्र लेकर 4 सेमी त्रिज्या का एक वृत्त खींचिए।
3. OX के साथ ∠XOY = 60° का कोण बनाते हुए किरण OY तथा ∠XOZ = 60° का कोण बनाते हुए किरण OZ खींचिए जो वृत्त को क्रमश: P एवं Q बिन्दुओं पर प्रतिच्छेद करती हैं।
4. बिन्दु P पर ∠OPT = 90° का कोण बनाते हुए किरण PT खींचिए जो किरण OX को बिन्दु R पर प्रतिच्छेद करती है।
5. QR को मिलाइए। यही PR एवं QR अभीष्ट स्पर्श रेखाएँ हैं।

प्रश्न 4.
एक समचतुर्भुज ABCD दिया है जिसमें AB = 4 cm एवं ∠ABC = 60°. इस समचतुर्भुज को दो त्रिभुजों ABC एवं ADC में विभाजित कीजिए। त्रिभुज ABC के समरूप त्रिभुज AB’C की संरचना कीजिए जिसका स्केल गुणक \(\frac { 2 }{ 3 }\) है। CD के समान्तर एक रेखाखण्ड C’D’ खींचिए जहाँ D’ रेखाखण्ड AD पर प्रतिच्छेद करता है। क्या AB’C’D’ एक समचतुर्भुज है।
हल :

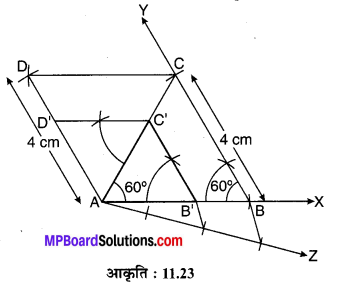
1. एक किरण AX खींचिए।
2. AX किरण से AB = 4 cm की त्रिज्या का एक चाप खींचिए जो किरण AX को बिन्दु B पर काटता है।
3. बिन्दु B पर ∠ABY = 60° का कोण बनाते हुए किरण BY खींचिए।
4. किरण BY से BC = 4 cm की त्रिज्या का एक चाप खींचिए, जो BY को बिन्दु C पर प्रतिच्छेद करता है।
5. बिन्दु A एवं C को केन्द्र लेकर 4 cm त्रिज्या के चाप खीचिएा जो परस्पर बिन्दु D पर प्रतिच्छेद करते हैं।
6. बिन्दु D को बिन्दु A एवं C से मिलाइए।
7. AC को मिलाइए। इस प्रकार दिए हुए समचतुर्भुज ABCD दो त्रिभुजों ABC एवं ADC में विभाजित हो जाता है।
8. AB के बिन्दु B’ पर AB’ : AB = 2 : 3 अर्थात् AB’ : B’B = 2 : 1 के अनुपात में विभाजित कीजिए।
9. B’ से B’C’ || BC रेखाखण्ड खींचिए जो AC को C’ पर प्रतिच्छेद करता है। यही AB’C’ अभीष्ट समरूप त्रिभुज है।
10. अब C’D’ || CD रेखाखण्ड खींचिए जो AD को बिन्दु D’ पर प्रतिच्छेद करता है।

हाँ ₹AB’C’D’ एक समचतुर्भुज है, क्योंक AB’ = B’C’ = CD’ = D’A = \(\frac { 2 }{ 3 }\)
\(\frac{A B^{\prime}}{A B}=\frac{B^{\prime} C^{\prime}}{B C}=\frac{C^{\prime} D^{\prime}}{C D}=\frac{D^{\prime} A}{D A}=\frac{2}{3}\)
AB = BC = CD = DA . [समचतुर्भुज की भुजाएँ]
AB’ = B’C’ = C’D’ = D’A.

प्रश्न 5.
एक समान्तर चतुर्भुज ABCD की रचना कीजिए जिसमें BC = 5 cm, AB = 3 cm एवं ∠ABC = 60°। इसको विकर्ण BD द्वारा ∆BCD एवं ∆ABD में विभाजित कीजिए। ∆BDC के समरूप ∆BD’C’ की रचना स्केल गुणक \(\frac { 4 }{ 3 }\) के साथ कीजिए। DA के समान्तर एक रेखाखण्ड D’A’ खींचिए, जहाँ A’ भुजा BA को बढ़ाने पर उस पर स्थित हो। क्या A’BC’D’ एक समान्तर चतुर्भुज है?
हल :

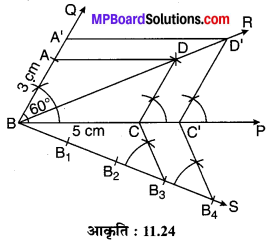
1. एक किरण BP खींचिए।
2. किरण BP में से BC = 5 cm का रेखाखण्ड काटिए।
3. B पर CBQ = 60° का कोण बनाते हुए एक किरण BQ खींचिए।
4. BQ में से BA = 3 cm का रेखाखण्ड काटिए।
5. बिन्दु A से 5 cm एवं बिन्दु C से 3 cm की त्रिज्याएँ लेकर चाप कीजिए जो परस्पर बिन्दु D पर प्रतिच्छेद करते हैं। AD एवं CD को मिलाइए। किरण BDR खींचिए।
   यही ABCD अभीष्ट समान्तर चतुर्भुज एवं ∆BCD तथा ∆BAD उसके दो विभाजन हैं।
6. किरण BP में से BC’ : BC = 4 : 3 में रेखाखण्ड काटिए।
7. C’D’ || CD रेखाखण्ड खींचिए जो किरण BR को बिन्दु D’ पर प्रतिच्छेद करता है।
   यही ∆BC’D’, ∆BCD के समरूप है अभीष्ट त्रिभुज है।।
8. D’A’ || DA खींचिए जो किरण BQ को बिन्दु A’ पर प्रतिच्छेद करती है।
   हाँ ₹A’BC’D’ एक समान्तर चतुर्भुज है क्योंक A’B || D’C’ एवं A’D’ || BC’.

प्रश्न 6.
3 cm एवं 5 cm त्रिज्याओं के दो संकेन्द्रीय वृत्त खींचिए। बाह्य वृत्त पर कोई बिन्दु लेकर अन्तः वृत्त पर उससे दो स्पर्श रेखाएँ खींचिए। एक स्पर्श रेखा की लम्बाई का मापन कीजिए तथा वास्तविक गणना द्वारा उसकी पुष्टि कीजिए।
हल :

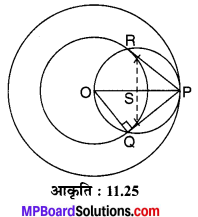
रचना के चरण :

1. O को केन्द्र लेकर क्रमश: 3 cm एवं 5 cm की त्रिज्याएँ लेकर दो संकेन्द्री वृत्त खींचिए।
2. बाह्य वृत्त पर कोई बिन्दु P लीजिए और PO को मिलाइए।
3. PO का मध्य-बिन्दु S ज्ञात कीजिए।
4. S को केन्द्र लेकर SO की दूरी के बराबर त्रिज्या लेकर एक वृत्त खींचिए जो अन्त:वृत्त को Q एवं R बिन्दुओं पर प्रतिच्छेद करता है।
5. PR एवं PQ को मिलाइए। यही PR एवं PQ अभीष्ट स्पर्श रेखाएँ हैं।
6. PQ को मापिए। इसका मान मापने पर = 4 cm आता है।
7. OQ को मिलाइए। ∠OQP समकोण है। [अर्द्धवृत्त का कोण]

अब समकोण ∆OQP में पाइथागोरस प्रमेय से,
PQ = \(\sqrt{O P^{2}-O Q^{2}}=\sqrt{(5)^{2}-(3)^{2}}=\sqrt{25-9}=\sqrt{16}\)
= 4 cm
[जहाँ OP = 5 एवं OQ = 3 त्रिज्याएँ दी हैं।]
अतः स्पर्श रेखा PQ की अभीष्ट लम्बाई = 4 cm है जिसकी वास्तविक गणना द्वारा पुष्टि होती हैं।

प्रश्न 7.
एक ∆ABC की रचना कीजिए जिसमें AB = 5 cm, BC = 6 cm एवं ∠ABC = 60° ∆ABC के समरूप स्केल गुणक \(\frac { 5 }{ 7 }\) के साथ एक अन्य त्रिभुज की रचना कीजिए।
हल :

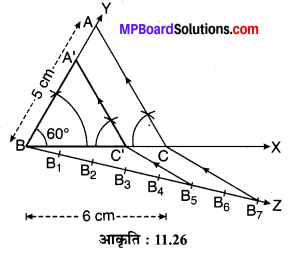
1. एक किरण BX खींचिए तथा BC = 6 cm का रेखाखण्ड काटिए।
2. बिन्दु B पर ∠CBY = 60° का कोण बनाते हुए एक किरण BY खींचिए।
3. किरण BY में से BA = 5 cm का रेखाखण्ड काटिए जो किरण BY को बिन्दु A पर प्रतिच्छेद करता है।
4. AC को मिलाइए।
   यही ∆ABC अभीष्ट त्रिभुज है।
5. BC को BC’ : BC = 5 : 7 अर्थात BC’ : C’C = 5 : 2 के अनुपात में विभाजित कीजिए।
6. C’ से C’A’ || CA रेखाखण्ड खींचिए जो BY को बिन्दु A’ पर प्रतिच्छेद करता है।
   यही ∆A’BC’ ~ ∆ABC अभीष्ट त्रिभुज है जिसका स्केल गुणक \(\frac { 5 }{ 7 }\) है।

प्रश्न 8.
एक त्रिभुज ABC की रचना कीजिए जिसमें AB = 4 cm, BC = 6 cm एवं AC = 9 cm. ∆ABC के समरूप स्केल गुणक \(\frac { 3 }{ 2 }\) के साथ एक त्रिभुज की रचना कीजिए। अपनी रचना की पुष्टि कीजिए। क्या दोनों त्रिभुज सर्वांगसम हैं जबकि तीनों कोण एवं दो भुजाएँ दोनों त्रिभुजों में बराबर हैं।
हल :

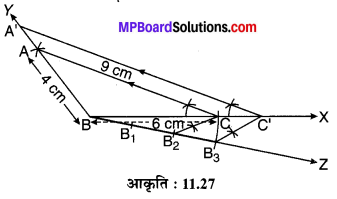
1. एक किरण BX खींचिए।
2. किरण BX में से एक रेखाखण्ड BC = 6 cm काटिए।
3. B को केन्द्र लेकर AB = 4 cm एवं C को केन्द्र लेकर AC = 9 cm की त्रिज्याओं से चाप खींचिए जो एक-दूसरे को बिन्दु A पर प्रतिच्छेद करते हैं।
4. BA को मिलाइए और Y तक बढ़ाइए तथा C को मिलाइए।
5. BX किरण से एक रेखाखण्ड CC’ = \(\frac { 1 }{ 2 }\) BC काटिए ताकि BC : CC’ = 2 : 1 अर्थात् BC’ : BC = 3 : 2 हो जाए।
6. C’ से C’A’ || CA खींचिए जो किरण BY को बिन्दु A’ पर प्रतिच्छेद करती है।

यही ∆A’BC ~ ∆ABC है जिसका स्केल गुणक में \(\frac { 3 }{ 2 }\) है पुष्टि ∆A’CC’ में AC || A’C’ तथा BC’/BC = \(\frac { 3 }{ 2 }\) है।
∆A’BC’ ~ ∆ABC एवं स्केल गुणक 3/2 है। \(\Delta A^{\prime} B C \neq \Delta A B C\) क्योंकि संगत भुजाए बराबर नहीं बल्कि 3 : 2 के समानुपाती हैं।

प्रश्न 9.
एक समकोण ∆ABC की रचना कीजिए जिसमें BC = 12 cm, AB = 5 cm एवं ∠B = 90°.इस त्रिभुज के समरूप अन्य त्रिभुज की रचना कीजिए जिसका स्केल गुणक \(\frac { 2 }{ 3 }\) हो। क्या नया त्रिभुज भी समकोण त्रिभुज है?
हल :

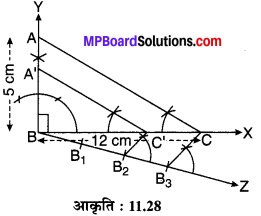
1. एक किरण BX खींचिए।
2. किरण BX से रेखाखण्ड BC = 12 cm काटिए।
3. बिन्दु B पर ∠CBY = 90° का कोण बनाते हुए एक किरण BY खींचिए।
4. किरण BY से AB = 5 cm का रेखाखण्ड काटिए।
5. AC को मिलाइए।
6. किरण BX से रेखाखण्ड BC’ = \(\frac { 2 }{ 3 }\) BC काटिए।
7. C’ से A’C’ || AC खींचिए।
   यही ∆A’BC’ ~ ∆ABC है जिसका स्केल गुणक \(\frac { 2 }{ 3 }\) है तथा ∠A’BC’ भी समकोण हैं।

प्रश्न 10.
एक त्रिभुज ABC की रचना कीजिए जिसमें BC = 6 cm, CA = 5 cm एवं AB = 4 cm। इसके समरूप एक अन्य त्रिभुज की रचना कीजिए जिसका स्केल गुणक \(\frac { 5 }{ 3 }\) है।
हल :

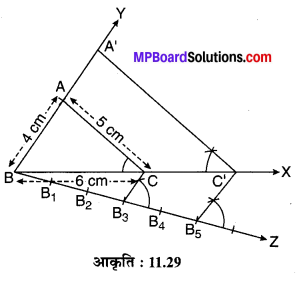
1. एक किरण BX खींचिए।
2. किरण BX में से BC = 6 cm का रेखाखण्ड काटिए।
3. B को केन्द्र लेकर AB = 4 cm एवं C को केन्द्र लेकर AC = 5 cm की त्रिज्या लेकर चाप खींचिए जो परस्पर बिन्दु A पर प्रतिच्छेद करते हैं।
4. CA को मिलाइए तथा BA की मिलाते हुए किरण BY खींचिए।
5. किरण BX में से BC’ = \(\frac { 5 }{ 3 }\)BC रेखाखण्ड काटिए।
6. बिन्दु C’ से A’C’ || AC खींचिए जो किरण BY को बिन्दु A’ पर प्रतिच्छेद करती है।
   यही ∆A’BC’ ~ ∆ABC अभीष्ट त्रिभुज है जिसका स्केल गुणक \(\frac { 5 }{ 3 }\) है।

MP Board Class 10th Maths Chapter 11 लघु उत्तरीय प्रश्न

प्रश्न 1.
7 cm लम्बाई का एक रेखाखण्ड खींचिए। इस पर एक बिन्दु P इस प्रकार ज्ञात कीजिए कि यह रेखाखण्ड को 3 : 5 के अनुपात में विभाजित करता हो।
हल :

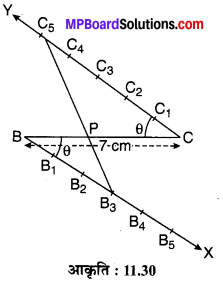
1. एक रेखाखण्ड BC = 7 cm खींचिए।
2. बिन्दु B पर नीचे की ओर न्यूनकोण ∠CBX = θ बनाते हुए किरण BX खींचिए।
3. बिन्दु C पर ऊपर की ओर ∠BCY = θ बनाते हुए किरण CY खींचिए।
4. किरण BX से BB1 = B1B2 = B2B3 रेखाखण्ड काटिए तथा किरण CY से BB1 = CC1 = C1C2 = C2C3 = C3C4 = C4C5 काटिए।
5. B3 को C5 से मिलाइए जो BC को बिन्दु P पर प्रतिच्छेद करता है।
   यही अभीष्ट बिन्दु P है जो रेखाखण्ड को 3:5 के अनुपात में विभाजित करता है।

प्रश्न 2.
4 cm त्रिज्या वाले एक वृत्त पर उसके केन्द्र से 6 cm की दूरी पर स्थित बिन्दु से स्पर्श रेखाएँ खींचिए।
हल :

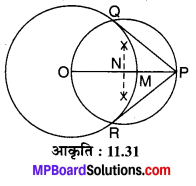
1. रेखाखण्ड OP = 6 cm खींचिए।
2. O को केन्द्र लेकर OM = 4 cm की त्रिज्या से एक वृत्त खींचिए जो OP को बिन्दु M पर प्रतिच्छेद करता है।
3. OP को बिन्दु N पर समद्विभाजित कीजिए।
4. N को केन्द्र लेकर ON के बराबर दूरी की त्रिज्या से एक वृत्त खींचिए जो पूर्व वृत्त को बिन्दु Q एवं R पर प्रतिच्छेद करता है।
5. PQ एवं PR को मिलाइए। यही PQ एवं PR अभीष्ट स्पर्श रेखाएँ हैं।

MP Board Class 10th Maths Chapter 11 अति लघु उत्तरीय प्रश्न

निम्न में सत्य/असत्य कथन लिखिए तथा अपने उत्तर का कारण भी दीजिए।

प्रश्न 1.
एक रेखाखण्ड को ज्यामितीय विधि से दो रेखाखण्डों में (2 + √3) : (2 – √3) के अनुपात में विभाजित किया जा सकता है।
हल :
कथन असत्य है, क्योंकि (2 + √3) : (2 – √3) को सरल करने पर (7 + 4√3):1 प्राप्त होता है है जिसमें 1 तो धनात्मक पूर्णांक है लेकिन (7 + 4√3) धनात्मक पूर्णांक नहीं है।

प्रश्न 2.
ज्यामितीय विधि से यह सम्भव है कि किसी रेखाखण्ड को \(\sqrt{3} : \frac{1}{\sqrt{3}}\) के अनुपात में विभाजित किया जा सकता है।
हल :
कथन सत्य है, क्योंकि \(\sqrt{3} : \frac{1}{\sqrt{3}}\) अनुपात को सरल करने पर 3 : 1 का अनुपात होता है, जहाँ 3 एवं 1 दोनों धनपूर्णांक हैं।

प्रश्न 3.
एक ∆ABC के समरूप एक अन्य त्रिभुज में जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac { 7 }{ 3 }\) हों, BC के बिन्दु B पर A के विपरीत नीचे की ओर एक न्यूनकोण बनाते किरण BX खींचिए BX पर BC के सापेक्ष बिन्दु B1, B2, ….., B7 बराबर-बराबर दूरी अंकित कीजिए। B3 को C से मिलाइए तब एक रेखाखण्ड B6C’ || B3C खींचिए जहाँ C’BC को बढ़ाने पर उसको मिलता है। अन्त में रेखाखण्ड A’C’ || AC खींचिए।
हल :
कथन असत्य है, क्योंकि B7C’ || B3C खींचनी है।

प्रश्न 4.
3.5 cm त्रिज्या के एक वृत्त के केन्द्र से 3 cm की दूरी पर स्थित बिन्दु से वृत्त पर दो स्पर्श रेखाएँ खींची जा सकती हैं।
हल :
कथन असत्य है, क्योंकि बिन्दु वृत्त के अन्दर है जिससे वृत्त पर कोई भी स्पर्श रेखा नहीं खींची जा सकती।

प्रश्न 5.
किसी वृत्त पर परस्पर 170° पर झुकी दो स्पर्श रेखाएँ खींची जा सकती हैं।
हल :
कथन सत्य है, क्योंकि उनका झुकाव 180° से कम है।

MP Board Class 10th Maths Chapter 11 वस्तुनिष्ठ प्रश्न

MP Board Class 10th Maths Chapter 11 बहु-विकल्पीय प्रश्न

प्रश्न 1.
एक रेखाखण्ड AB को 5 : 7 के अनुपात में विभाजित करने के लिए पहले किरण AX इस प्रकार खींची जाती है कि ∠BAX एक न्यूनकोण हो तथा बराबर दूरियों पर AX बिन्दु अंकित किए गए इस प्रकार कि इन बिन्दुओं की न्यूनतम संख्या होगी :
(a) 8
(b) 10
(c) 11
(d) 12.
उत्तर:
(d) 12.

प्रश्न 2.
एक रेखाखण्ड AB को 4 : 7 के अनुपात में विभाजित करने के लिए सबसे पहले ∠BAX एक न्यूनकोण बनाते हुए किरण AX खींचिए। फिर AX पर बराबर-बराबर दूरियों पर बिन्दु A₁, A₂, A₃, …… अंकित किए। बिन्दु B को मिलाया जायेगा :
(a) A₁₂
(b) A₁₁
(c) A₁₀
(d) A₉
उत्तर:
(b) A₁₁

प्रश्न 3.
एक रेखाखण्ड AB को 5 : 6 के अनुपात में विभाजित करने के लिए न्यूनकोण ∠BAX बनाते हुए किरण AX खींची एवं दूसरी किरण BY || AX खींची और AX एवं BY किरणों पर बराबर-बराबर दूरियों पर A₁, A₂, A₃, …… एवं B₁, B₂, B₃, …… क्रमशः अंकित किए तब मिलाए गए बिन्दु हैं :
(a) A₅ एवं B₆
(b) A₆ एवं B₅
(c) A₄ एवं B₄
(d) A₅ एवं B₄
उत्तर:
(a) A₅ एवं B₆

प्रश्न 4.
एक त्रिभुज ∆ABC के समरूप त्रिभुज जिसकी भुजाएँ क्रमशः ∆ABC की संगत भुजाओं की \(\frac { 3 }{ 7 }\) हों, की रचना करने के लिए न्यूनकोण ∠CBX इस प्रकार बनाते हुए किरण BX खींचिए कि X बिन्दु BC के सापेक्ष AB के विपरीत दिशा में हो। तब किरण BX पर बराबर-बराबर दूरियों पर क्रमशः बिन्दु B₁, B₂, B₃, …… अंकित किए और अगला चरण निम्न बिन्दुओं को जोड़ेगा :
(a) B₁₀ से C
(b) B₃ से C
(c) B₇ से C
(d) B₄ से C.
उत्तर:
(c) B₇ से C

प्रश्न 5.
∆ABC के समरूप ऐसे त्रिभुज की रचना करने के लिए जिसकी भुजाएँ क्रमशः ∆ABC की संगत भुजाओं की \(\frac { 8 }{ 5 }\) हो एक किरण BX इस प्रकार खींचिए कि ∠CBX.एक न्यूनकोण हो तथा X बिन्दु BC के सापेक्ष AB के विपरीत दिशा में स्थित हो तब किरण BX पर बराबर-बराबर दूरियों पर बिन्दु अंकित कीजिए। इन बिन्दुओं की न्यूनतम संख्या होगी :
(a) 5
(b) 8
(c) 13
(d) 3.
उत्तर:
(b) 8

प्रश्न 6.
एक वृत्त पर किसी बाह्य बिन्दु से दो स्पर्श रेखाएँ इस प्रकार खींचने के लिए कि उनके बीच कोण 60° हो। यह आवश्यक है कि उन दो त्रिज्याओं के अन्त्य बिन्दुओं पर स्पर्श रेखाएँ खींची जाएँ जिनके बीच का कोण है :
(a) 135°
(b) 90°
(c) 60°
(d) 12°.
उत्तर:
(d) 12°.

प्रश्न 7.
किसी रेखाखण्ड AB को p:q के अनुपात में (जहाँ p एवं q धनात्मक पूर्णांक हैं) विभाजित करने के लिए एक न्यूनकोण ∠BAX बनाते हुए एक किरण AX खींचिए तब किरण AX पर बराबर-बराबर दूरियों पर बिन्दु इस प्रकार अंकित करने होंगे कि उन बिन्दुओं की न्यूनतम संख्या m होगी:
(a) m > p + q
(b) m = p + q
(c) m = p + q – 1
(d) m = pq.
उत्तर:
(b) m = p + q

प्रश्न 8.
किसी वृत्त पर दो स्पर्श रेखाएँ जो परस्पर 35° पर झुकी हों, खींचने के लिए यह आश्यक है कि उन त्रिज्याओं के अन्त्य बिन्दुओं पर स्पर्श रेखाएँ खींची जाए जिनके बीच का कोण हो :
(a) 105°
(b) 70°
(c) 140°
(d) 145°.
उत्तर:
(d) 145°.