Prasanna

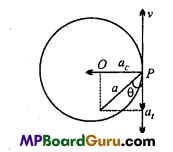
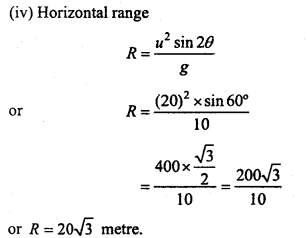
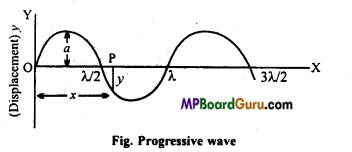
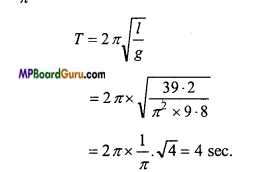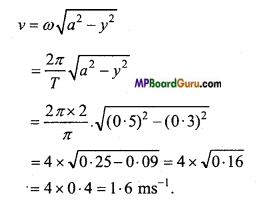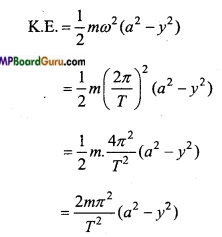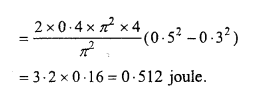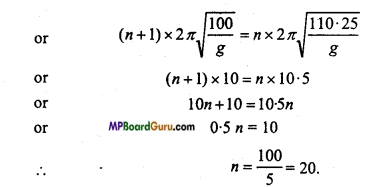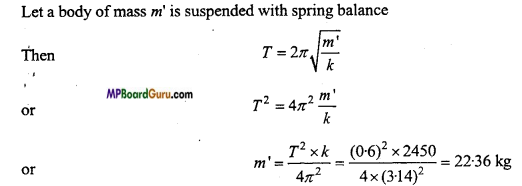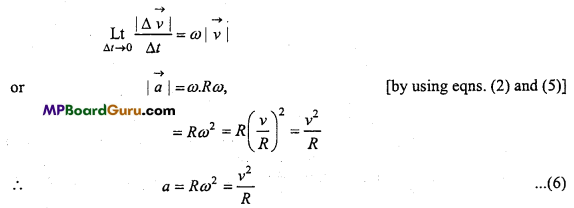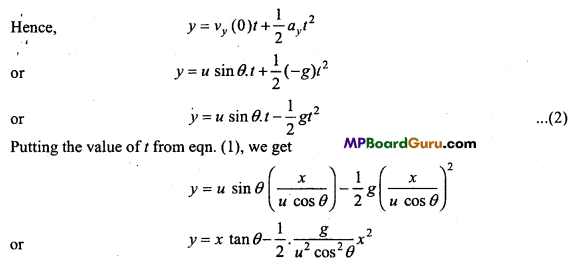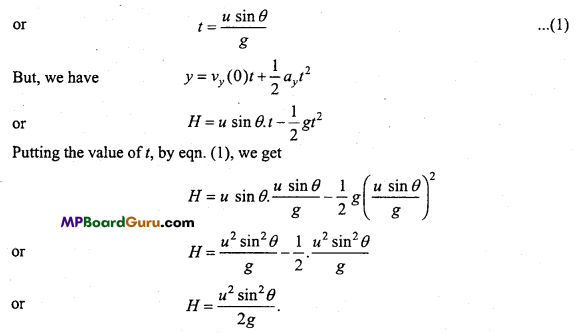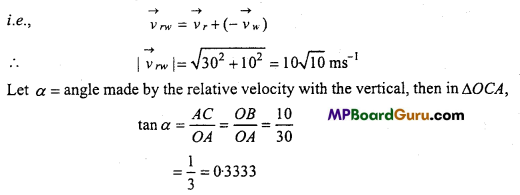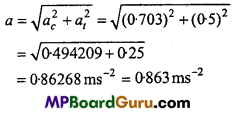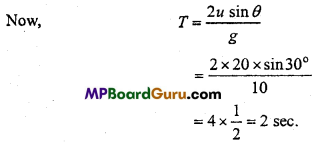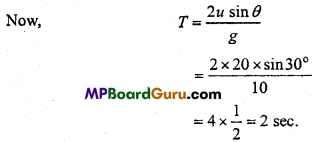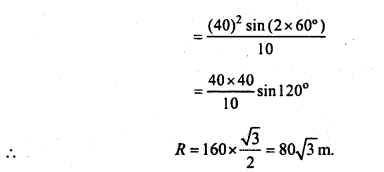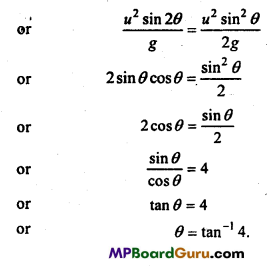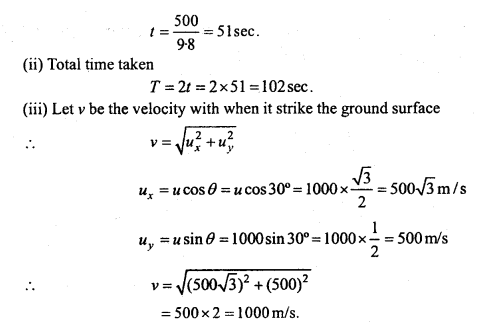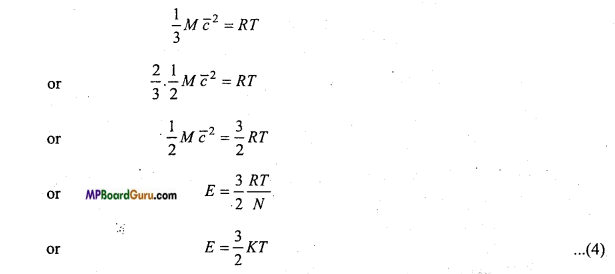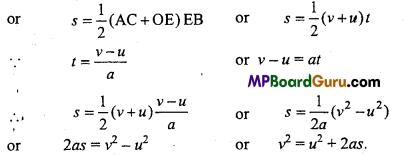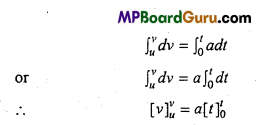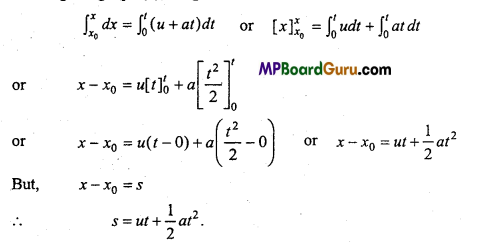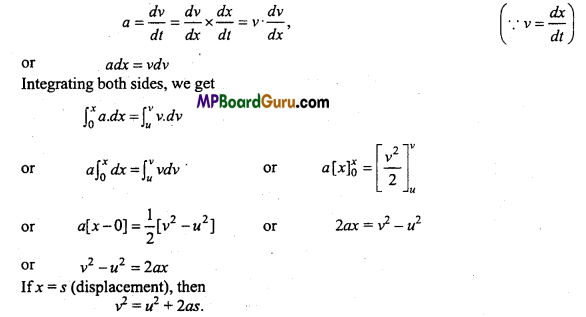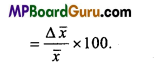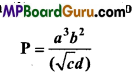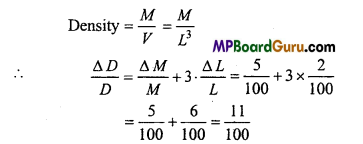Students get through the MP Board Class 11th Physics Important Questions Chapter 5 Laws of Motion which are most likely to be asked in the exam.

MP Board Class 11th Physics Important Questions Chapter 5 Laws of Motion

Laws of Motion Class 11 Important Questions Very Short Answer Type

Question 1.
What is inertia? What are its types?
Answer:
The property of the bodies by virtue of which the bodies are unable to change their state of rest or motion, is called inertia.
Inertia is of two types :

1. Inertia of rest and
2. Inertia of motion.
   • Inertia of rest: If a body is at rest it will remain at rest until and unless an external force is applied on it. This property of the body is called inertia of rest.
   • Inertia of motion : If a body is in motion it will continue its motion until and unless an external force is applied. This property of the body is called inertia of motion.

Question 2.
How the inertia of a body depends upon the mass of a body?
Answer:
Inertia of a body is directly proportional to its mass.

Question 3.
What is force ? What are its effects ?
Answer:
Force: The force is an external agent which produces or tends to produce change in the state of rest, motion, shape or size of a body.
Effect of force :

• Change in state of motion.
• Change in state of rest.
• Change in shape or size.

Question 4.
What will be the magnitude of the resultant force acting upon a body which is in uniform motion?
Answer:
Force upon the body will be zero because, when velocity remains constant, the acceleration of the body is zero.

Question 5.
What do you mean by momentum?
Answer:
The product of mass and velocity of a body is called its momentum.
Momentum = Mass × Velocity.

Question 6.
Write the laws of inertia.
Answer:
Newton’s first law of motion : If a body is at rest, it will remain at rest and if it is in motion, it will continue its motion, until and unless an external force is acted upon it.

Question 7.
Define 1 newton of force.
Answer:
The force required to produce an acceleration of 1 ms^-2 on a body of mass 1 kg, is called 1 newton.

Question 8.
What is impulse?
Answer:
When a greater force is applied for small interval of time on a body, then the product of force and time interval is called impulse.
Impulse shows the effect of force, i. e.,
I = Ft.

Question 9.
A cricket player moves his hand backward while he catches the ball. Why?
Answer:
Impulse of a force is given by FΔt = ΔI
∴ F = \(\frac{\Delta I}{\Delta t}\)
As Δt increases, force F decreases. Therefore, while taking the catch, the time interval Δt increases when he withdraws his hands, thus F decreases and player is not injured.

Question 10.
How do the man walk on earth?
Answer:
The man presses the earth in the backward direction, as a result, by Newton’s third law, the earth applies an equal and opposite force in the forward direction. It is due to reaction force, the person moves in the forward direction.

Question 11.
When a gun is fired it gives backwards jerk. Why?
Answer:
When the bullet is fired from the gun, the bullet moves with high velocity and due to its reaction, a force acts on the gun in opposite direction and hence, it gives jerk.

Question 12.
Jumping on the hard floor is hurtful but not on the sand. Why?
Answer:
When a man jumps on a hard floor, the legs come to rest immediately, therefore value of Δt is very less, which increase the force and hence, the jumping becomes hurtful than on the sand.

Question 13.
Shock absorber are used in vehicles. Why?
Answer:
Shock absorber increases At. At the time of jerks, the force F decreases. Thus, the driver of vehicle receives less jerks.

Question 14.
What is Newton’s third law of motion?
Answer:
According to Newton’s third law of motion, “Every action has equal and opposite reaction.”
\(\vec{F}_{21}=-\vec{F}_{12}\)

Question 15.
Action and reaction are equal and opposite, do they cancel each other. Why?
Answer:
Action and reaction do not cancel each other because both act on different bodies.

Question 16.
What are concurrent forces? What is the condition of their equilibrium ?
Answer:
When the lines of action of two or more forces pass through a point, then the forces are called concurrent forces.
Let \(\vec{F}_{1}, \vec{F}_{2}, \vec{F}_{3}, \ldots, \vec{F}_{n}\) forces are acting on a point, then the condition of equilibrium is
\(\vec{F}_{1}+\vec{F}_{2}+\vec{F}_{3}+\ldots+\vec{F}_{n}=0\)

Question 17.
What is absolute unit of force?
Answer:
1 Newton = 1 kg × 1 m/s²
and 1 Dyne = 1 g × 1 cm/s².

Question 18.
Which is the fundamental laws of motion and why?
Answer:
Newton’s second law is the fundamental laws of motion because first law and third laws can be derived from it.

Question 19.
What has been specified by Newton first law of motion?
Answer:
Newton first law defines force and inertia.

Question 20.
A passenger sitting in a bus at rest pushes it from within will it move. Why?
Answer:
No, internal forces are unable to produce motion in a system.

Question 21.
According to Newton’s third laws of motion, every force is accompanied by an equal and opposite force called reaction, then how can a movement take place?
Answer:
As the action and reaction never act on the same body, so the motion is possible.

Question 22.
A stone when thrown on a glass window smashes the window pane to pieces. But a bullet fired from a gun passes through it making a hole, why?
Answer:
This is due to inertia at rest.

Question 23.
Explain why jet planes cannot move in air free space but rockets can move?
Answer:
Jet plane uses atmospheric oxygen for their fuel but rockets carry their own fuel and don’t depend on atmospheric oxygen.

Question 24.
What are the absolute unit of force ? Write its definition?
Answer:
Newton is the absolute unit of force in S.I. unit.
1 Newton = 1 kg × 1 m/s²
The force requird to produce an acceleration of 1 m/s² in a body of mass 1 kg is called one Newton.
In C.G.S unit the absolute unit is dyne, 1 dyne = 1 g × 1 cm/s²
It is defined as the force required to produce an acceleration of 1 cm/s² in a body of mass 1 gram
1 Newton = 1 kg × 1 m/s²
= 1000 g × 100 cm/s²
= 10⁵ g-cm/s²
or 1 Newton = 10⁵ dyne
This is the relation between Newton and dyne.

Question 25.
A body is moving with uniform velocity. Does force is neccessary to maintain constant velocity?
Answer:
No, according to the first law of motion velocity reamains constant in the presence of force.

Question 26.
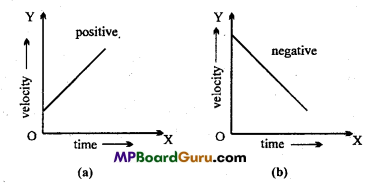
A constant force is acting upon a body. Among velocity, acceleration and kinetic energy, which quantity remain conserved and which will change ?
Answer:
Acceleration will remain conserved.
Since acceleration = \(\frac{\text { Constant force }}{\text { Constant mass }}\)
Velocity and kinetic energy will get changed.

Question 27.
What is friction force ? What is its nature?
Answer:
When there is a relative motion between two surfaces in contact, then an opposing forces acts between the surfaces, is called friction force.
Its nature is that it always opposes the motion.

Question 28.
Ball bearings are used to reduce friction. Why?
Answer:
The rolling friction is lesser than that of sliding friction, therefore ball bearing are used to reduce friction.

Question 29.
How many types of friction are there ?
Answer:
Friction are of two types :

1. Static friction,
2. Kinetic friction.

Question 30.
Write advantages of friction.
Answer:

• We can walk on ground due to friction.
• We can stop vehicle by applying brakes due to friction.
• We get fire due to friction.
• We can chew food due to friction.

Question 31.
Write disadvantages of friction.
Answer:

• Machinary parts get damaged due to friction.
• Efficiency of machine decreases.
• Some part of energy given to machine get lost in form of heat.

Question 32.
How can we reduce friction?
Answer:

• By polishing,
• Ball bearing,
• By greasing.

Question 33.
A body of mass m is rotated in the circular paths of radii r₁ and r₂ with the velocities ν₁ and ν₂. If r₁, > r₂, then which will be greater ν₁ or ν₂, supposing that same centripetal force is required for the motion.
Answer:
As the centripetal forces are equal

Question 34.
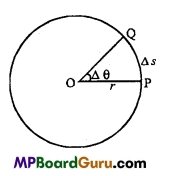
A body is moving in a circular path with uniform speed. If its frequency is n and radius of path is r, then write the formula of centripetal acceleration in terms of r and n.
Answer:
Centripetal acceleration = rω² = r(2πn)²
= 4π²n²r.

Question 35.
Define centripetal force.
Answer:
When a body moves in a circular path, a force acts towards the centre of the path, which revolves the body, is called centripetal force.
Centripetal foree = mνω=mω²r = \(\frac{m v^{2}}{r}\)

Question 36.
Derive the dimension formula of centripetal force by its formula.
Answer:
Centnpetal force = \(\frac{m v^{2}}{r}\)
=\(\frac{[\mathrm{M}]\left[\mathrm{LT}^{-1}\right]^{2}}{[\mathrm{~L}]}\)
= \(\frac{[M]\left[L^{2} T^{-2}\right]}{[L]}=\)
= [MLT^-2].

Question 37.
If the velocity and radius of circular path, both are doubled, then what will be the change in centripetal force?
Answer:
Centripetal force = \(\frac{m v^{2}}{r}\)
When the radius and velocity are doubled, then
centripetal force = \(\frac{m(2 v)^{2}}{2 r}=\frac{4 m v^{2}}{2 r}=\frac{2 m v^{2}}{r}\)
Hence, the centripetal force will be doubled.

Question 38.
Milk is stirred, to separate the cream. Why?
Answer:
The cream particles are lighter than milk particles. Therefore, cream particles need lesser centripetal force to move in circular path. When the milk is stirred both type of the particles receive same centripetal force, hence the cream particles move in the circular paths of lesser radii than that of milk particles. Thus cream particles are separated.

Question 39.
Why the roads are banked at the turnings?
Or
The outer rails are raised at the turnings. Why?
Answer:
The reasons are :

• It prevents the vehicle from skidding.
• The speed of vehicle should be greater at the turnings.
• Least damage to the tyres by friction.

Question 40.
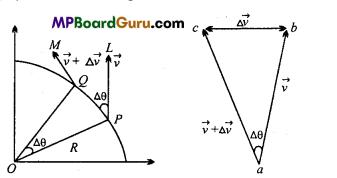
A particle is moving with uniform speed in a circular path. What is the nature of its acceleration?
Answer:
The acceleration acts towards the centre, perpendicular to the direction of velocity.

Question 41.
The circular roads on the hills are banked out sider. Why?
Answer:
The roads are banked outside to prevent the vehicle from skidding, the speed can be more and the tyres are less damaged by friction.

Question 42.
The wings of an aeroplane lean inwards while taking turn. Why?
Answer:
The wings of an aeroplane lean inwards to provide necessary centripetal force to moves in a circular path.

Question 43.
It is easy to rotate a stone with smaller string than longer string. Why?
Answer:
The necessary centripetal force to rotate in a circular path is provided by the tension of the string. For smaller string, less centripetal force is required to rotate, which can be provided easily by applying less force.

Question 44.
A man sitting in a moving bus dashes against the window, when the bus takes turn. How does the man explain this accident and how another man standing outside the bus will explain?
Answer:
A man sitting in the bus will think that the reaction force of centripetal force, acted on him. While the person standing outside will think that the man dashes against the window due to inertia of motion.

Laws of Motion Class 11 Important Questions Short Answer Type

Question 1.
State Newton’s laws of motion.
Answer:
First Law : A body can’t change its state of rest or of uniform motion along a straight line unless an external force acts on it.
Second Law : The rate of change of momentum is directly proportional to the impressed force and directed towards the direction of force.
Third Law : For every action there is equal and opposite reaction.
\(\vec{F}_{21}=-\vec{F}_{12}\)

Question 2.
What is law of conservation of momentum? Prove it.
Answer:
Law of conservation of momentum: In the absence of external force the linear momentum of a system remains always constant.
Proof: Let a force \(\vec{F}\) is applied on a system for time interval dt, so that its momentum changes by dp.
∴ By Newton’s second law, F = \(\underline{d p}\)
If the system is in equilibrium, then the sum of all the forces acting on it will be zero,
F = 0
∴ \(\frac{d p}{d t}\)= 0
or p = constant, (by differential calculus, that \(\frac{d}{d t}\) const. = 0)
Thus, in the absence of external force the linear momentum of a system is always conserved.

Question 3.
Define momentum. If two bodies are moving with equal velocities, then the momentum of the heavier body will be more than that of lighter body.
Answer:
Momentum is the product of mass and velocity of a body :
(i) If the masses of a heavier body and a lighter body are M and m respectively and if they are moving with equal velocities ν, then
Momentum of the heavier body
P₁ = Mν … (1)
and the momentum of the lighter body
p₂ = mν … (2)
On dividing the eqn. (1) by eqn. (2), we have
\(\frac{p_{1}}{p_{2}}=\frac{M v}{m v}\)
or \(\frac{p_{1}}{p_{2}}=\frac{M}{m}\) ….(3)
But M > m
∴ P₁ > p₂
Clearly, if two bodies are moving with equal velocities, then the momentum of the heavier body will be more than that of the lighter body.

Question 4.
If two bodies are having same momentum, then velocity of lighter body will be more than velocity of heavier body.
Answer:
Let the mass of heavier body be M and lighter body be m. Momentian of both bodies be p. Let’s their velocities be ν₁ and ν₂
Then, Momentum of heavier body = Mν₁
and Momentum of lighter body = mν₂
Since Momentum of both bodies are same.
Mν₁ = mν₂
or
\(\frac{v_{2}}{v_{1}}=\frac{M}{m}\)
Since M > m ∴ ν_{2 >} ν₁ i.e., velocity of lighter body is more than that of velocity of heavier body.

Question 5.
Write Newton’s second law of motion and prove that force = mass x acceleration.
Answer:
Newton’s second law of motion : The rate of change of momentum is directly proportional to the force applied and directed towards the direction of force.
Let the initial velocity of a body of mass m is u.
∴ Initial momentum \(\overrightarrow{p_{1}}=m \vec{u}\)
If force \(\vec{F}\) is applied for time Δt, so that its velocity becomes \(\vec{v}\).

∴ Final momentum, \(\vec{p}_{2}=\overrightarrow{m v}\)
∴ Change in momentum, Δp = \(\overrightarrow{p_{2}}-\overrightarrow{p_{1}}\)
or
or Δp = \(\vec{m} \vec{v}-\overrightarrow{m u}\)
= \(m(\vec{v}-\vec{u})=m \Delta \vec{v}\)
Where, Δ \(\vec{v}\) is change in velocity.
∴ Rate of change of momentum = \(\frac{m \Delta \vec{v}}{\Delta t}\)
But Acceleration, \(\vec{a}=\frac{\Delta \vec{v}}{\Delta t}\)
∴ Rate of change of momentum = \(\vec{m} a\)
∴ By Newton’s law,\(\vec{F} \propto \overrightarrow{m a}\)
or \(\vec{F}=k \overrightarrow{m a}\)
Where, k is constant.

Question 6.
Derive Newton’s first law from Newton’s second law.
Answer:
According to second laws of Newton’s
\(\vec{F}=m \vec{a}\)
If \(\vec{F}\) = 0
Then, \(\vec{a}\) = 0
i.e., if any force is not acting upon a body then acceleration of it will be zero i.e., if a body is at rest, it will be at rest or if it is in motion it will be in motion unless an external force acts upon it. This is Newton’s first law.

Question 7.
What do you understand by impulse? Prove that impulse of the force is equal to change in momentum.
Answer:
Impulse : When a greater force is applied for small interval of time on a body, then the product of force and time interval is called impulse.
Impulse shows the effect of force, i. e.,
I = Ft.
Relation between impulse and change in momentum : Suppose a force acting on a body of mass m for an interval Δt, produces a change in velocity Δν. Then according to Newton’s second law of motion.

or F.Δt = F.Δp
Hence, Impulse of the force = Change in momentum. Proved.

Question 8.
Prove that it is easier to pull a roller than to push.
Answer:
Let force F is applied on a roller. Force F can be resolved into two components.

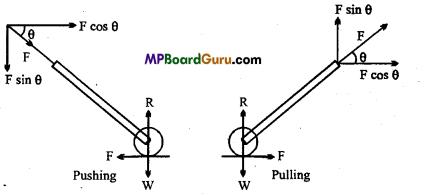
• Horizontal component F cos θ and
• Vertical component Fsinθ.

At the time of pushing the roller, the components Fsin 8 increases the weight of the roller. While when roller is pulled the component Fsin 8 decreases the weight of the roller.

Question 9.
Find out recoiling velocity of gun.
Answer:
Let the mass of the gun be Mand of the bullet is m moving with a velocity of ν₁ and the recoil velocity of gun will be ν₂ Before firing the momentum of gun and bullet will be zero and after firing the total momentum will be
Mν₂ + mν₁
According to laws of conservation of linear momentum
Total linear momentum after firing = Total linear momentum before firing
Mν₂ + mν₁ = 0
or Mν₂ = 0 – mν₁
or Recoil velocity of gun ν₂ = – \(\frac{m v_{1}}{M}\)
Negative sign shows that gun moves backward when the bullet is fired.
Since m<<M
∴ ν₂ < ν₁ i-e-> Recoil velocity of gun is lesser than velocity of bullet.

Question 10.
State the principle of equilibrium of concurrent forces.
Answer:
“If a number of forces act at the same point, they are called concurrent forces.”
Consider that a body is under the action of a number of forces. Suppose that the body is in equilibrium under the action of these forces, i.e., the body remains in its state of rest or of uniform motion along a straight line, when acted upon these forces.
“The condition that the body may be in equilibrium or the number of forces acting on the body may be in equilibrium is that these forces should produce zero resultant force.”

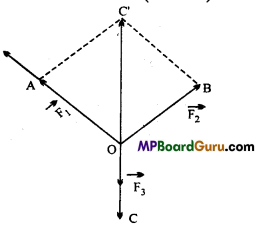
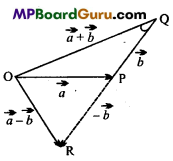
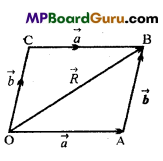
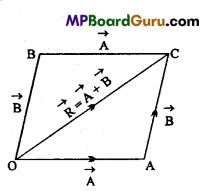
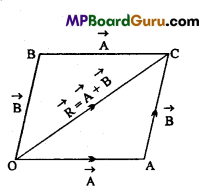
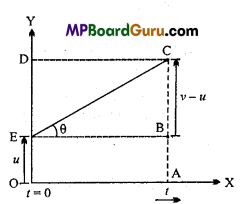
Consider three concurrent forces \(\vec{F}_{1}, \vec{F}_{2}\) and \(\vec{F}_{3}\)acting at the point ‘O’ (see Fig.).
In order to find the resultant of \(\vec{F}_{1}, \vec{F}_{2}\) and \(\vec{F}_{3}\), we first find the resultant of \(\vec{F}_{1}\) and \(\vec{F}_{2}\) by completing the parallelogram OAC’B. The diagonal OC’ of the parallelogram OAC ‘B gives
\(\vec{F}_{1}+\vec{F}_{2}\) i.e., the resultant of \(\vec{F}_{1}\) and \(\vec{F}_{2}\) . If F\(\vec{F}_{3}\) (represented by OC) as equal and opposite to
\(\vec{F}_{1}+\vec{F}_{2}\) (represented by \(\overrightarrow{o \vec{C}})\) then resultant of force \(\vec{F}_{1}\), \(\vec{F}_{2}\) and \(\vec{F}_{3}\) acting at point O will be zero. Therefore, for \(\vec{F}_{1}\),\(\vec{F}_{2}\) and \(\vec{F}_{3}\) to be in equilibrium, \(O \vec{C}=O \vec{C}^{\prime}\)
or \(\vec{F}_{3}=-\left(\vec{F}_{1}+\vec{F}_{2}\right)\)
or F\(\vec{F}_{1}\)+\(\vec{F}_{2}\)+\(\vec{F}_{3}\) = 0
The condition for equilibrium of three concurrent forces is triangle law
of addition of vectors. Suppose that the forces \(\vec{F}_{1}\),F\(\vec{F}_{2}\) and \(\vec{F}_{3}\) are such that they can be represented by the three sides \(\overrightarrow{A B}, \overrightarrow{B C}\) and \(\overrightarrow{C A}\) of the triangle ABC taken in same order, i.e., \(\overrightarrow{A B}=\vec{F}_{1}, \overrightarrow{B C}=\vec{F}_{2}\) and \(\overrightarrow{C A}=\vec{F}_{3}\) According to the triangle law of addition of vectors,
\(\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C} \text { or } \overrightarrow{A B}+\overrightarrow{B C}-\overrightarrow{A C}\) = 0
Now the vectors AC and CA are equal in magnitude but opposite in direction.
or \(\overrightarrow{A C}=-\overrightarrow{C A}\)
Hence, the eqn. (2) becomes .
\(\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C A}=0 \text { or } \vec{F}_{1}+\vec{F}_{2}+\vec{F}_{3}\) = 0
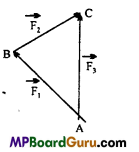
Therefore, the resultant of three concurrent forces will be zero and hence they will be in equilibrium, if they can be represented completely by the three sides of a triangle taken in same order.
In general, the concurrent forces, \(\vec{F}_{1}, \vec{F}_{2}, \vec{F}_{3} \quad \ldots . . \vec{F}_{n}\) Fn be in equilibrium, if their
resultant is zero, i.e.,
\(\vec{F}_{1}+\vec{F}_{2}+\vec{F}_{3}+\ldots .+\vec{F}_{n}\) = 0 …(3)
In case, a number of forces act at a point, then they will be in equilibrium, if they can be represented completely by the sides of a closed polygon taken in order.

Question 11.
State law of conservation of momentum and derive third law of motion with the help of this law.
Answer:
Law of conservation of momentum : Law of conservation of momentum: In the absence of external force the linear momentum of a system remains always constant.
Proof: Let a force \(\vec{F}\) is applied on a system for time interval dt, so that its momentum changes by dp.
∴ By Newton’s second law, F = \(\frac{d p}{d t}\)
If the system is in equilibrium, then the sum of all the forces acting on it will be zero,
F = 0
∴ \(\frac{d p}{d t}\)= 0
or p = constant, (by differential calculus, that \(\frac{d}{d t}\) const. = 0)
Thus, in the absence of external force the linear momentum of a system is always conserved.

Let the initial momentum of two bodies A and B are \(\vec{p}_{1}\) and \(\vec{p}_{2}\), respectively interact.
Body B applies force on A is \(\overrightarrow{F_{12}}\) and body A applies force \(\overrightarrow{F_{21}}\) on body B.
Due to interaction the change in momentum are Δ \(\vec{p}_{1}\) and Δ \(\vec{p}_{2}\)
∴ By the law of conservation of momentum,

Hence, force applied on A by B is equal and opposite to that of 5 by A. This is Newton’s third law of motion.

Question 12.
Write the laws of friction.
Answer:
Limiting friction :
When a force is applied to a body to move on a surface or another body, the position at which the body is about to move on, is called the limiting equilibrium and the friction force acting is called limiting friction.

Laws of limiting friction :

• Friction force always opposes the motion of the body. Its direction is always opposite to the direction of motion.
• The limiting friction depends upon the nature of the two surfaces.
• The limiting friction does not depend upon the area of contact or shape of the two surfaces if normal reaction is constant.
• The magnitude of limiting friction fs is directly proportional to the normal reaction.

i.e., f_s ∝ R
or f_s = µ_sR
Where, µ_s is a constant called the coefficient of static friction.
µ_s = \(\frac{f_{s}}{R}\)

Question 13.
Write difference between Sliding friction and Rolling friction.
Answer:
Difference between Sliding friction and Rolling friction:

Question 14.
Define angle of friction and angle of repose prove that they are equal to each other.
Answer:
Angle of Friction : The angle between the resultant of limiting friction and the normal reaction is called angle of friction.
μ_s = tan λ …(1)

Angle of Repose : When a body is in limiting equilibrium on an inclined plane, then the inclination of the plane with the horizontal is called angle of repose.
μ_s = tan θ …(2)
From eqns. (1) and (2),
tan λ = tan θ
λ = θ
i.e., angle of friction is equal to angle of repose. Proved.

Question 15.
Explain the types of friction.
Answer:
Frictions is of two types :
1. Static friction :
When a body tends to move on a surface but does not move, then the friction force acting between the surface is called static friction. The maximum value is called limiting friction.

2. Dynamic friction :
When a body moves on the surface, the friction force acting between the surface is called dynamic friction.
Dynamic friction is of two types :
(i) Sliding friction
(ii) Rolling friction.

(i) Sliding friction:
When a body slide over on another body, the friction force acting between the surfaces of contact is called sliding friction.
(ii) Rolling friction :
When a body roll over on another body, the friction force between the body and surface is called rolling friction.

Question 16.
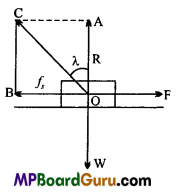
What is angle of friction? Prove that the tangent of angle of friction is equal to the coefficient of friction.
Answer:
Angle of friction : The angle between the resultant of limiting friction and the normal reaction is called angle of friction.
Let a body is in the position of limiting friction on a surface.
Now, complete the parallelogram OACB.
∴ OC will represent the resultant of R and f_s.
∴ Angle of friction ∠AOC = λ
Now, in right angle Δ OAC.
tan λ = \(\frac{A C}{O A}=\frac{O B}{O A}=\frac{f_{s}}{R}\)
But \(\frac{f_{s}}{R}\) = μ_s
∴ μ_s = tan λ

Question 17.
What is angle of repose? Prove that the tangent of angle of repose is equal to coefficient of friction.
Answer:

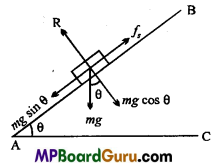
Angle of Repose: When a body is in limiting equilibrium, on an inclined plane, then the inclination of the plane with the horizon is called angle of repose.
Let a body is in limiting equilibrium on an inclined R plane, its mass is m and angle of inclination is θ.
Now, the forces acting on the body are :

• mg acting vertically downward.
• Normal reaction R.
• Limiting forces f_s, along the plane upward.

Now, resolving the weight mg, we get
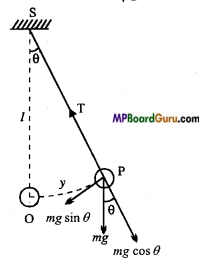
R = mg cos θ and
f_s = mg sin θ
Dividing eqn. (2) by eqn. (1), we get
\(\frac{f_{s}}{R}=\frac{m g \sin \theta}{m g \cos \theta}\) = tan θ
But, \(\frac{f_{s}}{R}\) = μ_s
μ_s = tan θ

Question 18.
Write the advantages and disadvantages of friction.
Answer:
Advantages of friction :

• We can walk on earth with the help of friction. Good grip and working with the hand as holding pen, writing over paper, etc., are possible due to friction.
• Speed of the vehicle increases due to friction.
• The brakes work on the friction.
• Burning of matchsticks.
• Belts are used in the machines to transfer the force.
• Nails can be fixed on the wall or wood. Also, knots of ropes are due to friction force.

Disadvantages of friction :

• The efficiency of the machines are reduced.
• Large amount of energy is wasted in the form of heat energy.
• It causes wear and tear in the machines.

Laws of Motion Class 11 Important Questions Long Answer Type

Question 1.
Explain laws of conservation of linear momentum. Prove that in absence of enternal forces, linear momentum of a moving particles is constant.
Answer:
According to the laws of conservation of linear momentum, in an isolated system the vector sum of the linear momentum of all the bodies of the system is conserved and is not affected due to their mutual action and reaction.

(1) For a system of one particle : According to Newton’s second law,
Force acting upon a particle = Rate of change in momentum
i.e., \(\vec{F}=\frac{\Delta \vec{p}}{\Delta t}\)
If force acting upon the particle is zero i.e., \(\vec{F}\) = 0,
Then, \(\frac{\Delta p}{\Delta t}\) = 0
or
\(\Delta \vec{p}\) = 0
or
\(\vec{p}\) = Costant
i.e., in absence of external force, total momentum p is constant.

(2) For two particle system : Consider a two particle system in which a particle
execute F₂ force on another particle and second particle execute F₁ force on first particle. If change in momentum of both particles are ΔP₁ and ΔP₂, then according to Newton’s second
law,
Force = Rate of change in momentum
∴ Force on first particle \(\vec{F}_{1}=\frac{\Delta \overrightarrow{p_{1}}}{\Delta t}\)
and Force on second particle \(\vec{F}_{2}=\frac{\Delta p_{2}}{\Delta t}\)
But according to Newton’s third law

Question 2.
Derive the expressions for the maximum speed in circular motion for safe
driving when
(i) Friction force Is zero and
(ii) Road is plane,
(iii) Road is banked.
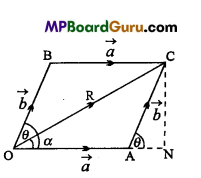
Answer:
Let a car of mass m is moving on a banked road in the circular path of radius r₁ as shown in the figure. Then the forces acting on the car will be:

• Weight mg of car acting downwards.
• R, normal reaction at the angle θ with the vertical.
• \(\frac{m v^{2}}{r}\), the centnpetal force radially inwards.
• ,F, the friction force between tyre and road.

Now, reaction R can be resolved into two components

• R cosθ along the vertical and
• R sinθ along the horizontal.

Also, F can be resolved into two components:

• F cosθ, along the horizontal and
• F sinθ, along the vertical.

Hence, we have
R cosθ = mg + F sinθ ….(1)
R sinθ + F cosθ = \(\frac{m v^{2}}{r}\) ….(2)

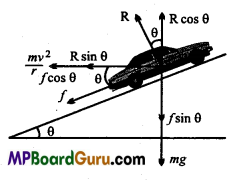
and F= μR …(3)
Where, μ is coefficient of kinetic friction.
Now, from eqn. (1),
mg=R cosθ – F sinθ ….(4)
Dividing eqn. (2) by eqn. (4), we get

Laws of Motion Class 11 Important Numerical Questions

Question 1.
Give the magnitude and direction of the net force acting on:
(a) A drop of rain falling down with a constant speed
(b) A cork of mass lOg floating on water
(c) A kite skillfully held stationary in the sky
(d) A car moving with a constant velocity of 30 km/h on a rough road
(e) A high speed electron in space far from all gravitating (material) objects and
free of electric and magnetic fields.
Solution:
(a) Net force acting on the drop of rain falling down with a constant speed will be zero. Weight of drop will be balanced by upthrust of air and viscous force.

(b) Net force acting on the cork will be zero, as its weight is balanced by the upthrust (i.e. weight of the water displaced).

(c) As the kite is held stationary, net force on the kite is zero. The force exerted on kite is balanced by its weight and tension in the string.

(d) Force is being applied to overcome the force of friction between the road and tyres. But as velocity of the car is constant, its acceleration a = 0 and hence net force = ma = 0.

(e) Net force on the high speed electron will be zero, since no gravitational/magnetic field is acting on it.

Question 2.
A constant retarding force of 50N is applied to a body of mass 20kg moving initially with a speed of 15ms^-1. How long does it take to stop?
Solution:
Given :F = -50N (-ve sign shows that it is retarding force)
m = 20kg, u = 15m/s, ν = 0, t = ?
∴ F = ma
∴ -50 = 20 × a
-50 „ c . 2
⇒ a = \(\frac{-50}{20}\) = -2.5m/s²
From ν = u +at
0 = 15-2.5t
∴ t = \(\frac{15}{2 \cdot 5}\) = 6 sec.

Question 3.
A body of mass 5.0kg is acted upon by two perpendicular forces 8N and 6N. Give the magnitude and direction of the acceleration of the body.
Solution:

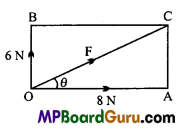
Given : m 5kg, a = ?
Resultant of 8N and 6N will be
F = \(\sqrt{(8)^{2}+(6)^{2}} \mathrm{~N}\)
or F = \(\sqrt{64+36}\) = \(\sqrt{100}\)N
or, F = 10N
If the resultant force makes angle 9 with 8N force, then
tanθ = \(\frac{6}{8}\) = 0.75
∴ θ = tan^-1 (0.75) = 37°
This is the direction of resultant force and hence the direction of acceleration of the
body.
Using F = ma
10 = 5 × a
⇒ a = \(\frac{10}{5}\) = 2m/s ²

Question 4.
A force produces an acceleration of 10 ms 2 on a trolley of mass 5 kg. Calculate the force.
Solution:
Given : m = 5 kg, a = 10 ms².
Now, F = ma
= 5 × 10= 50 N.

Question 5.
A shell of mass 0.02 kg is fired from a gun of mass 100 kg with a velocity of 80 ms^-1. Calculate the recoil velocity of the gun.
Solution:
Given : M = 100kg, m = 0.02kg, ν = 80ms^-1.
If the velocity of recoil is V, then
MV + mν = 0
or
V = \(-\frac{m v}{M}\)
∴ V = \(-\frac{0 \cdot 02 \times 80}{100}\) = 0.016ms^-1

Question 6.
Two balls of masses 40 kg and 20 kg are moving with velocities 10 ms^-1 and 50 ms^-1 respectively towards each other. They collide and embedded. What will be the velocity of the system?
Solution:
Given : m₁ = 40 kg,m₂ – 20 kg, ν₁ 10 ms ^-1, ν₂ = 50 ms^-1
Let the velocity of the system after collision = ν
∴By the law of conservation of momentum,

Hence, 10ms^-1 towards 20 kg mass.

Question 7.
A bullet of mass 10 gram moving with a velocity of 250m/s get embedded 2.5cm inside a wall. Find out the force exerted by the wall on bullet.
Solution:
Given : u = 250m/s, v =0,s = 2.5cm = 2.5 × 10^-2 m,m = 10 gm= 0.01 kg From v²=u²+2as
0 = (250)² + 2a × 2.5 × 10^-2
or
a = \(\frac{-(250 \times 250)}{2 \cdot 5 \times 10^{-2} \times 2}\)
= -1.25 × 10⁶m/s²
∴ Force exerted by wall on bullet
F = m.a = 0.01 × ( – 1.25 × 10⁶) = -1.25 × 10⁴ N.

Question 8.
A force of 10 N acts upon a body of mass 5 kg for 5 second Calculate :
(i) Impulse,
(ii) Change in momentum,
(iii) Change in velocity,
(iv) Acceleration.
Solution:
Given : m = 5 kg, F = 10 N, Δt = 5 sec
(i) Impulse = F.Δt
= 10 × 5 = 50 N-s.

(ii) Change in momentum = Impulse
= 50 kg m/s.

(iii) Change m velocity = \(\frac{\text { Change in momentum }}{\text { Mass of object }}\)
= \(\frac{50}{5}\) = 10 m/s.

(iv) Acceleration a = \(\frac{F}{m}\)
or a = \(\frac{10}{5}\) = 2m/s²

Question 9.
A driver can stop a car by applying a brake in 4 sec. If the car were running with a speed of 36 km/hr. Calculate the retarding force on the car, if the mass of the car is 400 kg and the mass of the driver is 65 kg.
Solution:
Given : ν (0) = 36 km/hr.
= \(\frac{36000 \mathrm{~m}}{60 \times 60 \mathrm{~s}}\) = 10m/s
ν (t) = 0, t = 4 s, m = 400 + 65 = 465 kg.
Using formula ν (t) = ν (0) + at, we have
0= 10 + a × 4
or 4a = -10
∴ a = –\(\frac{10}{4}\) -2.5m/s²
From formula F=ma
= 465 × (-2.5) = – 1162.5 N
∴ Retarding force = 1162.5 N.

Question 10.
In a rocket, the fuel is burning at the rate of 01 kg × s^-1. The velocity of gas ejecting is 2 kms^-1. Calculate the thrust on the rocket.
Solution:
Given:
ν = 2 km × s^-1 = 2 × 10³ ms^-1.
∴ \(\frac{\Delta m}{\Delta t}\) = 0.1 kg × s^-1
Now, change in momentum per second = \(\frac{\Delta m}{\Delta t}\)× ν
= 0.1 × 2 × 10³
=200kg ms^-2
∴ Force on gas = Rate of change of momentum.
= 200 N
But, Thrust on rocket = Force on gas
= 200 N.

Question 11.
A body moving in uniform motion is stopped by applying force of 2000 N in \(\frac{1}{4}\) seconds. Find out initial momentum of the body?
Solution:
Given : F = 2000 N, Δt = \(\frac{1}{4}\) sec = 0.25 sec
Change in momentum Δp = F. Δt
Let p₁ and p₂ be initial and final momentum.
Then, Δp = p₁ -p₂ = p₁ – 0 = p₁
∴ P₁ = F.Δt
= 2000 × \(\frac{1}{4}\) = 500 N-s.

Question 12.
Two circular bodies of mass 40 kg and 10 kg are moving with a velocity of 5 m/s and 20 m/s. Their direction is face to face. When they collide with each other forms a system. Find the velocity of the system.
Solution:
Given: m₁=40 kg, m₂= 10 kg, ν₁= 5 m/s, ν₂= -20 m/s, (since direction on is opposite) If ν is the velocity of the system, then

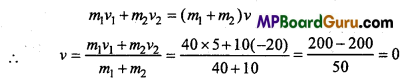
or ν = 0
i.e., the system will get stoped.

Question 13.
A bomb of mass 25 kg moving with a velocity of 10 m/s get bombaded into two piece of masses 15 kg and 10 kg. If the velocity of big piece is zero then find the velocity of small piece.
Solution:
Given : M = 25 kg, ν = 10 m/s,
Initial momentum of the bomb = Mν = 25 × 10
= 250 kg m/s.
After bombarding m₁ = 15 kg, m₂= 10 kg, ν₁= 0, ν₂ = ?
Total momentum =15 × 0 + 10 × ν₂
According to laws of conservation of momentum
10ν₂ = 250
or
ν₂ = \(\frac{250}{10}\)= 25m/s

Question 14.
A force of 72 N acting upon a body at an angle of 60° from the horizontal of mass 9 kg. Find out the acceleration of it in horizontal direction.
Solution:
Given :F= 72 N, θ=60°, m = 9 kg .
Component of force in horizontal direction F_H=F cosθ
or F_H = 72 × cos60° = 72 × \(\frac{1}{2}\) = 36 N
∴ Acceleration in horizontal direction a = \(\frac{F_{\mathrm{H}}}{m}=\frac{36}{9}\)
= 4/ms²

Question 15.
A body of mass 0.25 kg moving with a velocity of 12 m/s is stopped by applying a force of 0.6 N. In how much time the body will stop and what will be the impulse?
Solution:
u = 12 m/s, m = 0.25kg, F = 0.6 N
Let the time be t in which the body get stopped.
From a= \(-\frac{F}{m}\),weget
a = \(\frac{-0 \cdot 6}{0 \cdot 25}\) = \(\frac{-12}{5}\) m/s
Again from ν = u + at, we get
0 = 12 – \(\frac{12}{5}\)t
or \(\frac{12}{5}\)t = 12
or t = 5sec
and Impulse = F × Δt
0.6 × 5 =3N-s

Question 16.
A 10 gram bullet is shot from a 5 kg gun with a velocity of 400 m/s. What is the speed of recoil of the gun ?
Solution:
Given : m₁ = 10g = 10^-2kg, m₂= 5kg, ν₁ 400m/s, ν₂ = ?
From m₁ν₁= m₂ν₂, we get
ν₂ = \(-\frac{m_{1} v_{1}}{m_{2}}\)
or ν₂ = \(\frac{-10^{-2} \times 400}{5}\)
or ν₂ = -0.8 m/s .

Question 17.
A man of mass 70 kg stands on a weighing machine in a lift, which is moving:
(a) Upwards with a uniform speed of 10m/s.
(b) Downwards with a uniform acceleration of 5m/s².
(c) Upwards with a uniform acceleration of 5m/s².
What would be the readings on the scale in each case?
(d) What would be the reading if the lift mechanism failed and it hurtled down freely under gravity
Solution:
Given : m = 70kg; g = 10m/s²
(a) Lift is moving upwards with uniform speed, its acceleration = 0
∴ R = mg = 70 × 10 = 700N.
∴ Reading of the scale = \(\frac{700}{10^{\circ}}\) = 70 kg

(b) Lift is moving downwards with uniform acceleration a = 5m/s²
∴ mg – R = F
⇒ ma = mg – R
⇒ R=m(g – a) = 70 × (10 – 5)
R = 350N.
∴ Reading of the scale = \(\frac{350}{10}\) = 35

(c) Lift is moving upwards with uniform acceleration a = 5m/s², then
R – mg = F
⇒ R = ma + mg, [∴F = ma]
⇒ R = m(g + a) = 70 × (10 + 5)
or R = 1050N
∴ Reading of the scale = \(\frac{1050}{10}\)
= 105kg

(d) When the lift falls freely under gravity, then a = g
Using, R = m(g – a)
R = 70(g – g) = 0.
Thus the reading on the scale is zero, this is the state of weightlessness.

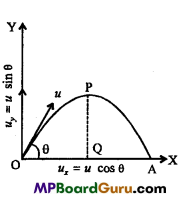
Question 18.
Two masses 8kg and 12kg are connected at the two ends of a light inextensible string that passes over a frictionless pulley as shown in figure. Find the acceleration of the masses and the tension in the string, when the masses are released.
Solution:
Let a be the acceleration of the bodies and T be the tension in the string. Then, equation of motion for mass m₁
T – m₁g = m₁a …(1)
For mass m₂
m₂g – T = m₂a …(2)
On adding eqns.(1)and(2), and putting the value of m₁ =8 kg,m₂= 12kg and g 10ms^-2

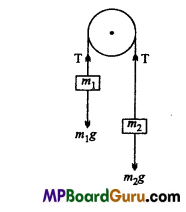
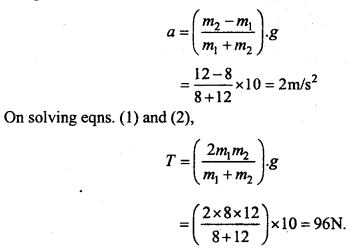
Question 19.
When a force of 50 kg weight applied on a sledge of mass 500 kg then it tends to move. Find out the coefficient of friction between it.
Solution:
Given, f_s = F =50 kg – wt =50 × g – N, R = 500g – N
From μ_s = \(\frac{f_{s}}{\mathrm{R}}\) we get
μ_s = \(\frac{50 \mathrm{~g}-\mathrm{N}}{500 \mathrm{~g}-\mathrm{N}}\) = 0.1

Question 20.
A mass of 2 kg is placed on a rough inclined plane of angle 30°. If coefficient of friction is 0.7 then find out the resultant friction force, acting on the block.
Solution:
Given, m = 2 kg, θ = 30°, μ_s = 0.7
From μ_s = \(\frac{f_{s}}{\mathrm{R}}\) we get
f_s = μ_s.R
or
f_s = μ_s.mg cosθ
or f_s = 0.7 × 2 × 9.8 ×cos30°
= 0.7 × 2 × 9.8 ×\(\frac{\sqrt{3}}{2}\)
= 6.86 × 1.732
= 11.88N

Question 21.
A block of 1 kg is resting on the plane of a truck. If the coefficient of friction between them is 0-6 and the acceleration of the truck is 10m/s2. Find out the friction force acting on the block.
Solution:
Given : = μ_s = 0.6,a = 10m/s²,m₁ = 1kg
∴ Frictional force acting upon the block = μ_s.m₁g – m₁a
= 0.6 × 1 × 9.8-1 × 10
= 5.88 – 10
= -4.12 N.

Question 22.
A man of mass 100 kg is slipping from an electric pole. If the frictional force is 480 N, then find out the acceleration of the mass. Given g = 9.8 m/s²
Solution:
Given, m = 100kg, frictional force F = 480 N, g = 9-8 m/s² Let the acceleration of the mass be a.
∴ From second laws of motion
ma = mg – F
or a = g – \(\frac{F}{m}\)
or a = 9.8 – \(\frac{480}{100}\)
or a = 9.8 – 4.8
or a =5 m/s².

Question 23.
A horizontal force of 1.2 kg-wt. is applied on a 3 kg block, which rest on a horizontal surface. If the coefficient of friction is 0.2, find the acceleration produced in the block.
Solution:
Given, m – 3 kg, μ = 0.2,F = 1.2 kg-wt. = 1.2 × 9.8 N.
Let the acceleration of the block be a.
μ = \(\frac{f_{k}}{m g}\) we get
f_k = μ.mg = 0.2 × 3 × 9.8 = 5.88 N
Again from f= F – f_k, we get
f =1.2 × 9.8 – 5.88 N
or f =11.76 – 5.88 = 5.88 N
∴ Acceleration a = \(\frac{f}{m}=\frac{5 \cdot 88}{3}\) = 1.96m/s²

Question 24.
A car is moving with a velocity of 20 m/s on a plane road. If the coefficient of friction between tyre and road is 0.4. Find out the distance after which the car will get stopped, (g = 10 m/s²)
Solution:
Given, u = 20 m/s, μ = 0.4,g = 10 m/s²
Let the retardation of the car be a and its mass be m.
From μ = \(\frac{\mathrm{F}}{R}\) we get
μ = \(\frac{m \cdot a}{m \cdot g}=\frac{a}{g}\)
or a = μ.g = 0.4 × 10 = 4m/s²
Let the car get stopped after travelling s distance.
∴ From v² = u² – 2as, we get
0 = u² – 2as
or s = \(\frac{u^{2}}{2 a}=\frac{20^{2}}{2 \times 4}\)
= 50m

Question 25.
A body of mass 4 kg ¡s tied with a string and rotated in a circular path of diameter 8 m. If the body Is moving with uniform peed of 600 m per minute, calculate the centripetal acceleration and centripetal force.
Solution:
Given:m = 4kg,r=\(\frac{8}{2}\) = 4m,ν = 600m × min^-1
= \(\frac{600}{60}\) ms ^-1
= 10 ms ^-1 
∴ Centripetal acceleration = \(\frac{v^{2}}{r}=\frac{10 \times 10}{4}\) =25ms^-1
and Centripetal force = \(\frac{m v^{2}}{r}\) = 4 × 25 = 100 N

Question 26.
The mass of scooter and driver moving with a speed of 36 km x h-1 is 150 kg, suddenly the scooter takes a turn at the radius of 30 m. What will be the horizontal force to make it possible?
Solution:
Given : r=30m,m = 150 kg and ν = 36km x h^-1
ν = \(\frac{36 \times 1000}{60 \times 60}\) = 10ms^-1
∴ Horizontal force = \(\frac{m v^{2}}{r}\)
= \(\frac{150 \times 10^{2}}{30}=\frac{150 \times 100}{30}\) = 500 N

Question 27.
A car of mass 1600 kg moving In a circular horizontal road of radius 20 m, with a speed 12.5 ms^-1. What should be the friction force between car and road, so that the car does not skid?
Solution:
Given: m = 1600 kg ,r =20 m , ν = 12.5 ms^-1.
Now, friction force, F = \(ms-1\)
∴  F = \(\frac{1600 \times(12 \cdot 5)^{2}}{20}\) = 1.25 x 10⁴ N
Again F = µrg
or µ = \(\frac{F}{r g}\)
= \(\frac{1 \cdot 25 \times 10^{4}}{20 \times 9 \cdot 8}\) = 63.78

Question 28.
A boy ties a stone of mass 0.5 kg at one end of 40 cm string and whirled it in a vertical circle. The speed of the stone at the lowest point of the circle is 3m/s. Find the tension at this point.
Solution:
Given : mass m = 0.5 kg, length of string r = 40 cm = 0.4m, velocity at lowest point V_L= 3m/s.
Tension at lowermost point T_L = mg + \(\frac{m V_{L}^{2}}{r}\)
= 0.5 × 10 + \(\frac{0 \cdot 5 \times 3 \times 3}{0 \cdot 4}\)
= 5 + \(\frac{45}{4}\) = 5 + 11.25 = 16.25N.

Question 29.
What will be the maximum speed of a car in a circular path of radius 30 m, if the coefficient of friction between tyre and road is 0.4
Solution:
Given : r = 30 μ= 0.4
Now, ν = \(\sqrt{\mu r g}\)
= \(\sqrt{0 \cdot 4 \times 30 \times 9 \cdot 8}\)= 10.84 ms^-1.

Question 30.
A particle completes 7 revolutions in 100 seconds while moving with a uniform speed in a circular groove of 12 cm radius. Calculate its angular speed, linear speed and centripetal acceleration.
Solution:
7 revolutions are completed in 100 second.
1 revolution is completed in time-period T = \(\frac{100}{7}\) sec:
Radius = -12 cm.
Angular speed ω = \(\frac{2 \pi}{T}=\frac{2 \times \pi \times 7}{100}=\frac{2 \times 22 \times 7}{10 \times 70}=\frac{44}{100}\)
Linear speed v = = ωr = 0.44 × 12 = 5.28 cm/sec.
Centripetal acceleration a= (ω²r = \(\frac{44}{100}\) ×\(\frac{44}{100}\) × 12 = 2.32 cm/s².

Question 31.
A string of 1 m can resist a force of 100 N. One end of this string is tied with a stone of mass 1 kg and whirled in horizontal plane. Calculate the maximum linear speed, so that string does not break.
Solution:
Given : centripetal force = 100 N, m = 1 kg and r = 1 m.
Now, centripetal force, F = \(\frac{m v^{2}}{r}\)
or 100 =\(\frac{1 \times v^{2}}{1}\)
or ν² = 100
∴ ν = \(\sqrt{100}\) = 10ms^-1

Laws of Motion Class 11 Important Questions Objective Type

1. Multiple- choice questions:

Question 1.
The first law of motion is also known as :
(a) Momentum
(b) Laws of inertia
(c) Action-reaction
(d) None of these.
Answer:
(b) Laws of inertia

Question 2.
The measure of inertia is its :
(a) Mass
(b) Velocity
(c) Both
(d) None of these.
Answer:
(a) Mass

Question 3.
If net force in a body is zero, then its acceleration :
(a) Will increase
(b) Will decrease
(c) Will be zero
(d) None of these.
Answer:
(c) Will be zero

Question 4.
One Newton is equal to :
(a) kg × metre × time
(b) kg × \(\frac{\text { metre }}{\text { second }}\)
(c) metre × second
(d) kg × second
Answer:
(b) kg × \(\frac{\text { metre }}{\text { second }}\)

Question 5.
If constant force is acting upon a body, then which will be among uniform :
(a) Velocity
(b) Acceleration
(e) Momentum
(d) Kinetic energy.
Answer:
(b) Acceleration

Question 6.
Rocket propulsion is based on :
(a) First laws of motion
(b) Laws of conservation of momentum
(c) Second laws of motion
(d) None of these.
Answer:
(b) Laws of conservation of momentum

Question 7.
Limiting friction depends upon :
(a) Area of the surface
(b) Size of the surface
(c) Nature of surface
(d) Normal Reaction.
Answer:
(c) Nature of surface

Question 8.
Weight of a person in a lift will be maximum, when lift moves :
(a) Upward
(b) Downward
(c) Independently
(d) None of these.
Answer:
(a) Upward

Question 9.
From which laws of Newton’s, the other two laws can be deduced :
(a) Newton’s first law
(b) Newton’s second laws
(c) Newton’s third law
(d) None of these.
Answer:
(b) Newton’s second laws

Question 10.
If a lift is falling independently, the weight of the person of 100 kg will be:
(a) 880 joule
(b) 980 Newton
(c) 980 kg
(d) Zero.
Answer:
(d) Zero.

Question 11.
Formula for coefficient of static friction is: .
(a) f_s × R
(b) R | f_s
(c) μ_s = f_s ×R
(d) μ_s = f_s
Answer:
(c) μ_s = f_s ×R

Question 12.
Relation between angle of friction and angle of repose is :
(a) tanθ + tanλ
(b) tanθ = tanλ
(c) tanθ × tanλ
(d) tanθ ÷ tanλ
Answer:
(b) tanθ = tanλ

Question 13.
On applying a force on a trolley of 5 kg, acceleration produced is 10 m/s2, then the applied force will be :
(a) 100 Newton
(b) 50 Newton
(c) 25 Newton
(d) 20 Newton.
Answer:
(b) 50 Newton

Question 14.
A body of 1 kilogram falls freely on the surface of the ground, on touching ground the force applied by it is :
(a) 1 kilogram
(b) 1 kilogram-weight
(c) 2 kilogram
(d) 2 kilogram-weight.
Answer:
(b) 1 kilogram-weight

Question 15.
When a force of 10 Newton acts upon a body of mass 5 kg for 5 second, then its impulse will be:
(a) 25 Newton × second
(b) 20 Newton × second
(c) 15 Newton × second
(d) 50 Newton × second.
Answer:
(d) 50 Newton × second.

2. Fill in the blanks:

1. One newton = ………………… dyne.
Answer:
10⁵

2. Force = Mass × ………………..
Answer:
Acceleration

3. First laws of motion is called as ………………
Answer:
Inertia

4. Rate of change in momentum is directly proportional to ………………….
Answer:
Force

5. For every action there is equal and opposite …………………
Answer:
Reaction

6. SI unit of force is …………………
Answer:
Newton

7. Rocket propulsion is based on …………………. principle.
Answer:
Conservation of momentum

8. C.G.S. unit of force is ………………….
Answer:
Dyne

9. 1 kilogram-weight = ………………….. Newton.
Answer:
9.8

10. All the frames of reference in which Newtons laws hold true are called …………………….
Answer:
Inertial frames

11. The force which does not act on the body but due to acceleration of frame of reference, appears to act on body is called ………………..
Answer:
Fictitious force

12. Kinetic friction is always less than ………………….
Answer:
Static limiting friction

13. The ratio of limiting static friction and normal reaction is called ………………….
Answer:
Coefficient of limiting friction

14. Frictional force is independent of ………………..
Answer:
Area of contact

15. Newton’s laws of motion doesn’t apply for …………………. frame.
Answer:
Non-inertial

3. Match the following:
I

Answer:
1. (b) Impulse
2. (e) Third laws of motion.
3. (d) Force opposing motion
4. (a) Congruent force
5. (c) Ball bearing

II

Answer:
1. (c) Inertia of motion
2. (e) Inertia at rest.
3. (d) Conservation of momentum
4. (a) To reduce impulse
5. (b) Action-reaction

4. Write true or false:

1. Newton’s first law is laws of inertia.
Answer:
True

2. Change in momentum is not directly proportional to applied force.
Answer:
False

3. For every action there is equal and opposite reaction.
Answer:
True

4. When a bullet penetrate inside a wood, its velocity remain conserved.
Answer:
False

5. When the lift moves upward, weight of the person inside it, get decreased.
Answer:
False

6. If the body is not in rest the net force acting upon it cannot be zero.
Answer:
False

7. Bus moving in circular path is the example of non-inertial frame of reference.
Answer:
True

8. The body remains at rest when an external force acts upon it.
Answer:
True

9. Walking in sand is difficult.
Answer:
True

10. Weight of free falling body is not zero.
Answer:
False

11. Momentum will be zero when brakes is applied on vehicle in motion.
Answer:
True

12. Force is neccesary to maintain the body in motion with constant velocity.
Answer:
False

13. It is easior to walk in smooth surface.
Answer:
False

14. When a cork float on the surface of water, the net force acting is zero.
Answer:
True

15. The earth extract gravitational force on moon.
Answer:
True

16. Momentum remain conserved for a body thrown upward.
Answer:
False

5. Answer in one word:

1. Many forces act on a body can it stay in the state of rest.
Answer:
Yes, if the resultant of all forces become zero.

2. Is the net force on a cork floating on water surface zero.
Answer:
Yes.

3. Give an example of fictitious force.
Answer:
Centrifugal force.

4. Which force is strongest and which force is weakest in nature?
Answer:
Strongest force: Strong nuclear force. Weakest force: Gravitational force.

5. A bullet strikes a wooden block and gets embedded into it. What remains conserved, momentum or kinetic energy.
Answer:
Momentum.

MP Board Class 11th Physics Important Questions Chapter 14 Oscillations

Oscillations Class 11 Important Questions Very Short Answer Type

Question 1.
Define simple harmonic motion with example.
Answer:
When a body moves to and fro about a point in a straight line such that its acceleration is always directly proportional to the displacement and directed towards the mean position, then its motion is called simple harmonic motion.
Example: Motion of a body suspended by a spring, motion of simple pendulum.

Question 2.
What is oscillatory motion?
Answer:
When a body moves periodically to and fro or back and forth about a definite point, then its motion is called oscillatory motion.
Motion of simple pendulum, vibration of tuning fork etc. are the examples of oscillatory motion.

Question 3.
For what type of motion of a body acceleration is directly proportional to displacement?
Answer:
It is simple harmonic motion.

Question 4.
When the velocity and acceleration will be maximum in S.H.M.?
Answer:
The velocity is maximum at the mean position and acceleration is maximum at the extreme position.

Question 5.
Write the formula for kinetic energy and potential energy for a body executing S.H. M.?
Answer:
Kinetic Energy = \(\frac{1}{2} m \omega^{2}\left(a^{2}-y^{2}\right)\)
Potential Energy = \(\frac{1}{2} m \omega^{2} y^{2}\)
Where m – particle of mass,
ω – angular frequency,
a – amplitude and
y = displace-ment of the particle form its mean position.

Question 6.
At which position kinetic energy and potential energy is zero for a body executing S.H.M.?
Answer:
At maximum displacement position (y = ±a) kinetic energy is zero and at mean position (y = 0) potential energy is zero.

Question 7.
Define simple pendulum.
Answer:
When a heavy point mass is suspended by a weightless, inextensible and perfectly flexible string by a rigid support, then it is called simple pendulum.

Question 8.
Which of the following relationships between acceleration ‘a’ and the dis-placement x: of a particle involve simple harmonic motion ? (NCERT)
(a) a = 0.7x,
(b) a = 200x²,
(c) a = -10x²
(d) a = 100x³.
Answer:
In a S.H.M. the relation between acceleration and displacement is
a=-ω²x
(a) a = 0.7 x
Comparing with eqn. (1),
-ω² = 0.7
or’
ω = \(\sqrt{-0 \cdot 7}\)
∵ Value of a is not real therefore the motion is not S.H.M.

(b) a = -200x²
This motion is not a S.H.M.

(c) a = -10x
Comparing-with eqn. (1),
ω² =10
or
ω = \(\sqrt{10}\)
∵ ω has a real value therefore, the relation shows a S.H.M.

(d) a = 100 x³
This motion is not a S.H.M.

Question 9.
The length of a spring is increased, how the time-period be affected?
Answer:
The time-period will increase.

Question 10.
On which conservation law S.H.M. is based?
Answer:
S.H.M. is based on law of conservation of energy.

Question 11.
What is second pendulum? What is its length?
Answer:
The pendulum whose periodic time is two seconds is known as second pendulum. The length of second pendulum is about 100 cm.

Question 12.
Write the characteristics of S.H.M.
Answer:
Characteristics of S.H.M.:

• The motion is periodic.
• The particle moves to and fro about a point in a straight line.
• The acceleration is directly proportional to the displacement.
• The direction of acceleration is always towards the mean position.

Question 13.
Define time-period, frequency and amplitude.
Answer:
Time period: The time taken by an oscillating body to complete one oscillation is called time-period.
Frequency: The number of vibrations or oscillations in one second is called frequency.
Amplitude: The maximum displacement of a particle about its mean position is called amplitude. It is denoted by a or A.

Question 14.
What is the relation between S.H.M. and Circular motion?
Answer:
When any particle is performing uniform motion on the circumference of a circle, then the perpendicular dropped on the diameter of the circle from any point of rotation execute S.H.M. along the diameter of circle.

Question 15.
Define spring constant and write its S.I. unit and dimensional formula.
Answer:
Spring constant: The force required to elongate or compress a spring through unit length is called spring constant.
Unit: SI unit of spring constant is Nm1.
Dimensional formula : Dimensional formula is [ML°T^-2].

Question 16.
Write the formula for the time-period of a body suspended by a spring.
Answer:
Where, T= Time-period, m = Mass suspended and k = Force constant.

Question 17.
What is meant by the effective length of a simple pendulum?
Answer:
The length of pendulum from the point of suspension to the centre of bob is called effective length.

Question 18.
Why the length of simple pendulum is measured up to the centre of the bob?
Answer:
The centre of gravity point of spherical bob lies at its centre. The concept of heavy point mass is assumed that the weight of the body acts at the C.G. point. Therefore the effective length is measured up to centre of the bob.

Question 19.
How time period of a simple pendulum change with effective length of a simple pendulum.
Answer:
We know \(T=2 \pi \sqrt{\frac{l}{g}}\)
or
T ∝ \(\sqrt{l}\)
When effective length is increased, time period also get increased.

Question 20.
Can the pendulum clock be used in a satellite?
Answer:
No, because g = 0 inside satellite, therefore T = ∞.
So, in place of pendulum clock, spring clock can be used inside it.

Question 21.
The pendulum clock cannot be used in artificial satellite. Why?
Answer:
In an artificial satellite, the bodies are in the state of weightlessness. Hence, g becomes zero. Thus, the time-period becomes infinite.Therefore, it cannot be used in the satellite.

Question 22.
A boy is swinging, sitting on a swing. If another boy sits beside him, what will happen to its time-period?
Answer:
The time period is independent of mass, hence there will be no effect.

Question 23.
A boy is swinging, standing on a swing. If he sits on it, what happen to the time-period?
Answer:
When the boy will sit on the swing, his C.G. point will shift downwards. Hence, the effective length will increase therefore the time-period will also increase.

Question 24.
What is the reason that the frequency of oscillation clocks depend on the rise and fall of mercury level in the thermometer?
Answer:
If the mercury level increases, it shows that temperature has increased and the decreases in mercury level shows a decrease in temperature. Due to increase in temperature, the length of pendulum increases and \(T \propto \sqrt{l}\) so time period also increases. Hence clock runs slow, i.e., the frequency of oscillation decreases. But with decrease in temperature, length decreases and so time-period decreases. Hence clock runs fast i.e., frequency of oscillation increases.

Question 25.
The pendulum clock becomes fast when it is taken to pole from equator. Why?
Answer:
We have, T = \(2 \pi \sqrt{\frac{l}{g}}\)
If l is constant ,then T ∝ \(\frac{1}{\sqrt{g}}\)
Hence, time-period is inversely proportional to the square root of acceleration due to gravity. At poles the value of g is greatest, hence the time-period will decrease at poles, hence the clock will be fast.

Question 26.
Why pendulum clock does not show time at satellite?
Answer:
At satellite g = 0, therefore, i.e., time period of pendulum become infinity, therefore it does not show time of satellite.

Question 27.
What is damped oscillation?
Answer:
When the amplitude of an oscillating body decrease gradually by some external opposing force, then its oscillation is called damped oscillation.

Question 28.
Define forced vibration.
Answer:
When an oscillating body oscillates under the influence of some external force, then it oscillates with the frequency of external force, then its oscillation is called forced vibration.

Question 29.
What do you mean by forced oscillation?
Answer:
When the body oscillate under the influence of an external periodic force, with a constant amplitude and a frequency equal to the periodic force, the oscillation of the body is called forced oscillation.

Question 30.
Define resonance.
Answer:
When a body vibrates under the influence of a periodic force and its frequency becomes equal to that of periodic force then the amplitude of the body increases. This phenomenon is known as resonance.

Question 31.
Why marching troops are asked to break their steps while crossing the bridge?
Answer:
The footsteps of marching troops produces a periodic force on the bridge. If the frequency of foot-steps becomes equal to the natural frequency of bridge, the amplitude of bridge will increase and hence the bridge may break.

Question 32.
What is the effect of forced oscillation on amplitude and frequency?
Answer:
Due to forced oscillation amplitude of oscillating body go on reducing and frequency become less than the natural frequency.

Question 33.
When forced oscillation become resonance oscillation?
Answer:
When the natural frequency of the body becomes equal to the frequency due to periodic force then forced oscillation is converted into resonance oscillation.

Question 34.
A simple pendulum is suspended in a lift, whose time-period is T. What will aeration ‘a’ (i) upward, (ii) downward.
Answer:
(i) When the lift accelerate with acceleration ‘a’ upward then the time-period will decrease
( T = \(2 \pi \sqrt{\frac{l}{g+a}}\))
(ii) On acceleration with acceleration ‘a’ downward then its timeperiod will increase
( T = \(2 \pi \sqrt{\frac{l}{g-a}}\) )

Question 35.
What will be the time-period of effective length infinity?
Answer:
84.6 minute.

Question 36.
What will be the time period of pendulum at the centre of earth? Why?
Answer:
At the centre of earth the time-period of pendulum will be infinity as ‘g’ is zero at the centre.

Question 37.
A spring of spring constant k is cut into three equal pieces. What will be the time period of each?
Answer:
The spring constant of each piece will be 3k.

Oscillations Class 11 Important Questions Short Answer Type 

Question 1.
The bob of simple pendulum is a ball filled with water, if a small hole is made at the bottom of the ball, how will its time period change as water is drains out of it?
Answer:
When the ball is completely filled with water, its centre of gravity be at its geometric centre. So, it will oscillate with definite time period. But as the water drains out of it through the hole, the centre of gravity is displaced gradually downward. Hence the effective length also increases gradually. Therefore the time period of the pendulum also increases gradually. But when whole of the water is removed then its centre of gravity again shifted to its geometric centre and its time-period become same as was in initial position.

Question 2.
What is simple harmonic motion. Write its four characteristics.
Answer:
When a body moves to and fro about a point in a straight line such that its acceleration is always directly proportional to the displacement and directed towards the mean position, then its motion is called simple harmonic motion.
Example: Motion of a body suspended by a spring, motion of simple pendulum.
Characteristics of S.H.M.:

• The motion is periodic.
• The particle moves to and fro about a point in a straight line.
• The acceleration is directly proportional to the displacement.
• The direction of acceleration is always towards the mean position.

Question 3.
Write the relation between acceleration and displacement of a particle ex-ecuting1 S.H.M. Also deduce expression for time-period from it?
Answer:
Acceleration of the particle with displacement y is α = -ω²y
Where ω is angular velocity of particle here (-) sign indicate the direction of accel-eration only.
Hence, ω² = \(\frac{\alpha}{y}\) = \(\frac{\text { Acceleration }}{\text { Displacement }}\)
or
ω = \(\sqrt{\frac{\alpha}{y}}\)
But T =\(\frac{2 \pi}{\omega}=\frac{2 \pi}{\sqrt{\frac{\alpha}{y}}}=2 \pi \sqrt{\frac{y}{\alpha}}\)
T = \(2 \pi \sqrt{\frac{\text { Displacement }}{\text { Acceleration }}}\)

Question 4.
Write the expression for displacement, velocity and acceleration of a particle executing S.H.M. and say :
(i) When the velocity of the particle will be maximum and zero.
(ii) When the acceleration of the particle will be maximum and zero.
Answer:
Displacement y = a sin ωt
Velocity ν = ω \(\sqrt{a^{2}-y^{2}}\)
Acceleration a = – ω²y
Where a is amplitude and ω is angular acceleration.

(i) Velocity is maximum at mean position (y = 0)
νmax = ω.a
Velocity is zero at maximum displacement position ν = 0 , when y = ±a.

(ii) Acceleration is maximum when displacement is maximum (y = ±a)
α = ± ω² a, when y = ±a
Acceleration is zero at mean position α = 0, when y = 0.

Question 5.
What is meant by simple pendulum? When the bob is displaced from its mean position it starts oscillations. Why?
Answer:
If a heavy point mass be suspended by a weightless, perfectly flexible and inextensible string from a rigid support and an arrangement is made for its frictionless oscillations, then this arrangement is called simple pendulum. As shown in fig. when bob is displaced from its mean position A to a position B, then the bob raised up to height ‘h\ so that its potential energy increases.
Now, if the bob is released, then its centre of gravity falls down to obtain the stable equilibrium and when it reaches to the mean position its potential energy is converted into kinetic energy. At points, it will not stay, but due to inertia moves forward and hence the bob starts to execute simple harmonic motion to and fro about its mean position.

Question 6.
Write down the formula of time-period of simple pendulum and state the factors on which it does depend.
Answer:
The time-period of simple pendulum is given by :
T = 2π \(\sqrt{\frac{l}{g}}\)
From the above formula, it is clear that the time period of simple pendulum depends on its effective length ‘l’ and acceleration due to gravity ‘g’.
(i) Dependence on length f: The time period of simple pendulum is directly proportional to the square root of effective length of pendulum, i.e., T α \(\sqrt{l}\)
Example: When a boy swinging on a swing stand up suddenly, then his centre of gravity rises up and so the effective length of the swing reduces which results an increase in time period.
(ii) Dependence on acceleration due to gravity ‘g’: The time-period T of simple pendulum is inversely proportional to the square root of acceleration due to gravity at that place i.e., T α \(\frac{1}{\sqrt{g}}\)
Example: When a pendulum is taken up to hills or down in a mine get slow because time-period T increases due to decrease in the value of ‘g’.

Question 7.
Write down the laws of simple pendulum. Give practical application of each law.
Answer:
The laws of simple pendulum and their practical applications are given below :
(i) Law of length: If the value of ‘g’ remains constant, then the time period of simple pendulum is directly proportional to the square root of effecti ve length of simple pendulum.
i-e., T α \(\sqrt{l}\)
This law is used to repair the pendulum clocks when they get slow or becomes fast while taken up to hills or down in a mine.

(ii) Law of acceleration due to gravity : If the effective length of simple pendulum remains constant, then the time period T of the simple pendulum is inversely proportional to the acceleration due to gravity, i.e., T α \(\frac{1}{\sqrt{g}}\)
Due to this reason the pendulum clock get slow while taken up to hills or down in mines.

(iii) Law of mass: The time period of simple pendulum does not depend upon the mass of bob or that of thread.
Hence, either bob is heavy or lighter, if the value of 7’ and ‘g’ are constant, then there is no effect in its time-period. .

(iv) Law of isochronism: If the amplitude of oscillations of simple pendulum are very small, then the time-period of pendulum does not depend upon the amplitude of oscillations.
Because of this, the angular displacement of the bob is kept small in the experiment of simple pendulum.

Question 8.
Establish the relation between time-period and frequency.
Answer:
Let the time-period of a particle is T and its frequency is υ.
∴ The particle complete one vibration in T sec.
Hence, in 1 sec the number of vibration, υ = \(\frac{1}{T}\)
or
υT = 1.

Question 9.
Derive an expression for the displacement of a particle executing S.H.M.
Or
Find an expression for the displacement of S.H.M.
Answer:
Let XYX’Y’ is a circle whose centre is O and radius a. A particle is moving with uniform angular speed ω on the circle.
Let at time t = 0, the particle is at X and in time t, it is at P. A perpendicular PN is drawn on YOY’ from P and N is foot of the perpendicular.

The particle takes t second to subtend an ∠POX = θ.
∴ ω = \(\frac{\theta}{t}\)
or
θ = ωt
Let the displacement ON = y
∴ In ∆ NPO, sin NPO = \(\frac{O N}{O P}\)
But, ∠NPO = ∠POX = θ = ωt
∴ sin ωt = \(\frac{y}{a}\)
or
y = a sin ωt
This is the required equation for the displacement of S.H.M.

Question 10.
Derive the expression for the velocity of a particle executing S.H.M.
Or
Derive an expression for velocity of a particle executing S.H.M. When is the velocity maximum and minimum?
Answer:
Expression for velocity: Let XYX’Y’ is a circle of centre O and radius a. A particle is moving on the circle with angular velocity ω.
Let at t = 0, the particle is at X and after t sec, it is at P.
Let at point P, the velocity of the particle is ν along the tangent at P.

Now, velocity v is resolved into two parts :
(i) ν sin θ, parallel to PN and
(ii) ν cos θ, perpendicular to PN.
Since,ν cos θ is parallel to the direction of motion of foot of the perpendicular N.
∴ Velocity of N, υ = ν cosθ
υ = ν cos ωt.
or
υ = ν \(\sqrt{1-\sin ^{2} \omega t}\)
( ∴ sin² ωt + cos² = 1)

This is the required expression.
Case 1. Ify = 0, then from eqn. (1), we get
ν =ω \(\sqrt{a^{2}-0}\) = ωa
∴ Velocity will be maximum at mean position.

Case 2. If y = a, then from eqn. (1), we get
ν =ω \(\sqrt{a^{2}-a^{2}}=\) = 0
∴ Velocity will be minimum at the extreme position.

Question 11.
Derive the expression for the acceleration of a particle executing S.H.M. Find where the acceleration is maximum and minimum.
Answer:
We have by displacement equation,
y = a sin(ωt + Φ) …(1)
If the acceleration is α, then we have


This is the required expression.
Case 1. If y = 0, then by eqn. (3),
α =0
i.e., at the mean position the acceleration will be zero i.e., minimum.

Case 2. If y = a, then by eqn. (3),
α = – ω²a
i.e., at extreme position the acceleration is maximum.

Question 12.
Derive the expression for the time>period and frequency of a particle ex-ecuting S.H.M.
Answer:
Now, we have the magnitude of acceleration is given by

Again, we know that frequency,
υ = \(\frac{1}{T}\)
∴ υ = \(\frac{1}{2 \pi} \sqrt{\frac{\text { Acceleration }}{\text { Displacement }}}\)

Question 13.
Mass m is suspended by an ideal spring. It oscillates up and down. If the force constant of spring Is k, then prove that the time-period,
T =2 π \(\sqrt{\frac{m}{k}}\)
or
A mass is suspended by a spring. It Is pulled downwards and then left. Prove that it executes S.H.M. Find the expression for time-period.
Answer:
Let a spring is suspended by a rigid support and mass ni is suspended at its lower end.
It is displaced downwards at a distance y and left.
The restoring force F = -ky …( 1)
Where, k is force constant.

Also, by Newton’s second law of motion,
F=mα …………. (2)
Where, α is acceleration.
∴ From eqns. (1)and (2), we get
mα =-ky ……….. (3)
or
α =\(-\frac{k}{m}\) .y

Also, we have, for S.H.M.
α = – ω² y ……..(4)
Since, the L.H.S. of eqns. (3) and (4) are equal, hence the R.H.S. must be equal.

Question 14.
Derive the expression for K.E. and P.E. of a particle executing S.H.M. and also prove that total energy of a particle remains constant.
Answer:
K.E. of the particle : We know that velocity of a particle executing S.H.M. is given by,
ν = ω\( \sqrt{a^{2}-y^{2}} \)
K.E.= \( \frac{1}{2}\)mv²
=\( \frac{1}{2}\) m{ ω\( \sqrt{a^{2}-y^{2}} \)²
=\( \frac{1}{2}\)mω²(a²-y²) …(1)

P.E. of the particle: Now, the acceleration of a particle executing S.H.M. is given by α = -ω²y
Also, by Newton’s second law of motion,
Force = Mass x Acceleration
∴ F = mα
or
F = -mω²y
Now initially the displacement was zero and force was zero. The force was gradually increases and hence the displacement also increases to y.

∴Mean force =\(\frac{0+F}{2} \) = mω²y
∵ Work W= Mean force x Displacement
∴ W = \(\frac{1}{2} \) mω²y ×y
or
W = \(\frac{1}{2} \) mω²y²

By equns.(1) and (2), we get
K.E +P.E = \(\frac{1}{2} \) mω² (a²-y²)+ \(\frac{1}{2} \) mω² y²
or
E = \(\frac{1}{2} \) mω²a² –\(\frac{1}{2}\)mω²y² +\(\frac{1}{2}\)mω²y²
or
E = \(\frac{1}{2}\)mω²a²
As ω and a are constant, therefore the total energy remains constant.

Question 15.
What is second’s pendulum? Calculate its effective length.
Answer:
Second’s pendulum: A simple pendulum whose time-period is 2 seconds, is called second’s pendulum.

Oscillations Class 11 Important Questions Long Answer Type

Question 1.
Deduce the expression for time-period of simple pendulum T = 2π \(\sqrt{\frac{l}{g}} \)
Answer:
Motion of a simple pendulum: Suppose that m is the mass of the bob and l is the effective length of a simple pendulum. S is a point of suspension and O is mean position of the bob. Suppose at any instant during oscillation, the bob is in the position P. Then displacement OP = y and ∠ OSP = θ. In this position of the bob, two forces act upon it:
(i) Tension T is the thread, in the direction PS upward along the thread and

(ii) The weight of the bob, mg, vertically downward. The weight mg can be resolved into two components :
(a) mg cos θ, in the direction SP downward along the thread.
(b) mg sin θ, perpendicular to the thread SP.
The component mg cos θ balances the tension Tin the thread. The component mg sin θ tends to bring the bob back to its mean position. This is known as restorting force on the bob. Thus, the restorting force acting on the bob is given as F= -mg sinθ

Where negative sign shows that the direction of force is opposite to the direction which displacement increases, i.e., towards the mean position O.
1f the angular displacement of the bob be small, then sin θ = 0 (for example, if θ = 5⁰, then sin θ= 0.0872 and θ=0.0873 radian). Thus,
F= -mgθ
But,
θ= \( \frac{\mathrm{Arc}}{\mathrm{Radius}} \) = \( \frac{O P}{S P} \) = \( \frac{y}{l} \)
F= -mg.\( \frac{y}{l} \) …….. (1)

If α be the acceleration produced in the bob due to restoring force, then by Newton’s law of motion
F = mα ……. (2)
From eqns. (1) and (2), we get
mα = -mg \( \frac{y}{l} \)
or
α= –\( \frac{g}{l} \).y …(3)

At a given place g is constant and for a given pendulum lis constant.
Therefore,
α ∞ -y …….. (4)
Thus, the acceleration of the bob is directly proportional to its displacement. Hence, for small amplitude the motion of a simple pendulum is simple harmonic motion. Its periodic time is

Oscillations Class 11 Important Numerical Questions

Question 1.
The time-period of a particle executing S.H.M. is 2 sec. Calculate the time after t =0, that its amplitude be half of the displacement.
Solution:
Given: T= 2 sec and y = \(\frac{a}{2}\)
∵ y = a sin ωt
Where ω =\( \frac{2 \pi}{T} \)
∴ y = a sin \( \frac{2 \pi}{T} \) t ⇒ \( \frac{a}{2}= \) = a sin \( \frac{2 \pi}{T} \) t

Question 2.
The length of a simple pendulum ¡s 39.2 / π² metre. If g = 9.8 ms^-2, then calculate the time-period of simple pendulum.
Solution:
Given:l = \( \frac{39 \cdot 2}{\pi^{2}} \), g = 9.8 ms^-2
Formula:

Question 3.
The mass of a particle executing S.H.M. is 0.4 kg and amplitude and time period are 0.5 m and π/ 2 respectively. Calculate the velocity and ICE. of particle at a displacement 0.3 m.
Solution :
Given:m = 0.4kg , a = 0.5 m, T= π/2 sec, y = 0.3 m.
Npw we have

Again,

Question 4.
A simple pendulum execute 60 oscillation per minute. Find its effective length ? (g = 981 cm/ s²)
Solution:
Given: Time-period T = \( \frac{\text { Time }}{\text { No.of oscillations }} \) = \frac{1 \mathrm{~min}}{60} = 1 sec

Question 5.
The value of acceleration due to gravity on a planet is \( \frac{1}{4} \) th of that of earth.
If the time-period of simple pendulum on earth is 2 sec, then find the time-period on the planet.
Solution:
g₂= \( \frac{1}{4}\) g₁

Question 6.
What will be the time.period of a simple pendulum of length \( \frac{9 \cdot 8}{\pi^{2}} \) m? Name such pendulum.
Solution:
Given: l= \( \frac{9 \cdot 8}{\pi^{2}} \)m g = 9.8 ms^-2
Formula:
T =2π \( \sqrt{\frac{l}{g}} \)

Question 7.
Two pendulum of length 100 cm and 110*25 cm start oscillating at same time. After how much oscillation again they will oscillate at same time.
Solution:
Let the time-period of the 100 cm pendulum be T₁
T₁ = 2 π\( \sqrt{\frac{100}{g}} \)
and if T₂is the time-period for 110.25 cm pendulum, then
T₂ = 2 π\( \sqrt{\frac{110 \cdot 25}{g}} \)
T₁ <T₂
∴ Both the pendulum to oscillate at same time if the big pendulum perform n oscillaion and small pendulum, perform (n + 1) oscillation.
i.e.,(n+1)T₁ = nT ₂

i.e., Big pendulum after 20 oscillation or small pendulum after 21 oscillation will start oscillating together.

Question 8.
Find the length of second pendulum at (i) Surface of earth (g = 9-8 m/s2), (ii) Surface of moon (g = 1.65 m/s2).
Solution:
Time-period for second pendulum is T= 2 sec.
∴From T = 2 π\( \sqrt{\frac{l}{g}} \)
(i) Length at earth surface
2 = 2π² \( \sqrt {\frac{l}{9.8}} \)
or
l = π² \( \ {\frac{l}{9.8}} \)
or
π².l = 9.8
or
l =\( \frac{9 \cdot 8}{(\pi)^{2}} \) = \( \frac{9 \cdot 8}{(3 \cdot 14)^{2}} \) = 0.99m
(ii) Length of moon
l = \( \frac{1 \cdot 65}{\pi^{2}} \)
or
l = \( \frac{1 \cdot 65}{(3 \cdot 14)^{2}} \) = 0.167 m.

Question 9.
A mass of 98 kg suspended in a spring is oscillating whose spring constant is 200 N/m. Find its time-period.
Solution:
We know,
T = 2π\( \sqrt{\frac{m}{k}} \)
or
T = 2 ×3.14 \( \sqrt{\frac{98}{200}} \)
T= 4-396 second.

Question 10.
The total energy of a particle executing S.H.M. is E. What will be the K.E. and P.E. of particle at the displacement half of the amplitude?
Solution:
We know that total energy is
E = \( \frac{1}{2} \) mω² a²
Also, K.E = \( \frac{1}{2} \) mω²( a² – y ²)

Now, at y = \( a / 2 \),
K.E = \( \frac{1}{2} \) mω²\( \left(a^{2}-\frac{a^{2}}{4}\right) \)
= \( \frac{1}{2} \) mω² . \( \frac{3 a^{2}}{4} \)
= \( \frac{3}{8} \) mω²a² = \( \frac{3}{4} \) E.

Again, P.E = \( \frac{1}{2} \) mω² y ²
Now, at y = \( a / 2 \),
P.E = \( \frac{1}{2} \) mω² \( \frac{a^{2}}{4} \)
P.E = \( \frac{1}{8} \) mω² a² = \( \frac{1}{4} \) E.

Question 11.
The amplitude of a particle executing S.H.M. is 0*01 m and frequency is 60 Hz. What will be the maximum acceleration of the particle?
Solution:
Given : a = 0.01m, υ = 60 Hz Now, maximum acceleration is given by
α = ω² a
= (2π υ ) ²a
= 4π²υ ²a
= 4×3.14 ×3.14×60×60×0.01
= 1419.78ms^-2

Question 12.
At a place a body travels 125 m in 5 sec during the free fall under gravity. What will be the time period of a simple pendulum of length 2-5 m at that place?
Solution:
Given : S= 125 m, υ = 0, t = 5 sec.
Now, s = ut + \( \frac{1}{2} \) gt²
or
125 = 0 +\( \frac{1}{2} \)g×25
or
g = 10 ms^-2

Again,
= 2π\( \sqrt{\frac{l}{g}} \)
= 2π \( \sqrt{\frac{2.5}{10}} \)
= 2π ×0.5 = π sec.

Question 13.
A spring balance has a scale that reads from 0 to 50 kg. The length of the scale is 20 cm. A body suspended from this balance, when displaced and released, oscillates with a period of 0-6 s. What is the weight of the body ? (NCERT)
Solution:
Given :m = 50 kg, y = 20 cm = 0.2 m, T- 0.6 s
From F=ky
∴ mg = ky
or
K = \( \frac{\mathrm{mg}}{\mathrm{y}} \) = [ latex] \frac{50 \times 9 \cdot 8}{0 \cdot 2} [/latex] = 2450Nm^-1

Weight of the body
W = m’g
= 22.36×9.8 = 219.17 N
≈ 219N.

Question 14.
A spring having spring constant 1200 Nm’ is mounted on a horizontal table as shown in fig. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled side ways to a distance of 2.0 cm and released. (NCERT)
Determine
(j) The frequency of oscillations.
(ii) Maximum acceleration of the mass and
(iii) The maximum speed of the mass.

Solution:
Given:k=1200Nm^-1,m= 3kg, amplitude a =2 cm =2 × 10²m
(i) Frequency υ =\( \frac{1}{2 \pi} \) \( \sqrt{\frac{k}{m}} \) = \( \frac{1}{2 \times 3 \cdot 14} \sqrt{\frac{1200}{3}} \)
= \( \frac{1}{6 \cdot 28} \) ×\( \sqrt{400}\) = \( \) \frac{20}{6 \cdot 28}
= 3.18 s^-1 ≈3.2 ^-1

(ii) α = -ω ² y
∴α _max = ω ²a = \( \frac{k}{m} \) .a = \( \frac{1200}{3} \) ×2 ×10^-2
= 8.0 ms ^-2

(iii) ∴ν _max=ωa= \( \sqrt{\frac{k}{m}} \) ×a =\( \sqrt{\frac{1200}{3}} \) ×2 ×10^-2
= 20 × 2 × 10^-2 = 0.4 ms ^-1

Oscillations Class 11 Important Questions Objective Type

1. Multiple- choice questions:

Question 1.
Which of the following equation does not represent simple harmonic, motion:
(a) x = asin(ωt+δ)
(b) x = bcos(ωt+Φ)
(c) x = atan(ωt + Φ)
(d) x = asin(ωt cosωt.
Answer:
(c) x=atan(ωt + Φ)

Question 2.
Time-period and amplitude of a particle executing simple harmonic motion is Tand a. The minimum time taken to reach distance will be:
(a) T
(b) \(\frac{T}{4}\)
(c) \(\frac{T}{8}\)
(d) \(\frac{T}{16}\)
Answer:
(c) \(\frac{T}{8}\)

Question 3.
Time-period and amplitude of a particle executing simple harmonic motion is T and a. Its maximum velocity is :
(a) \(\frac{4 a}{T}\)
(b) \(\frac{4 a}{T}\)
(c ) \(2 \pi \sqrt{\frac{a}{T}}\)
(d) \(\frac{2 \pi a}{T}\)
Answer:
(d) \(\frac{2 \pi a}{T}\)

Question 4.
Acceleration in S.H.M. is :
(a) Maximum at amplitude position
(b) Maximum at mean position
(c) Remain constant
(d) None of these.
Answer:
(a) Maximum at amplitude position

Question 5.
The ratio of acceleration to displacement of a particle executing S.H.M. is measurement of:
(a) Spring constant
(b) Angular acceleration
(c) (Angular acceleration)²
(d) Restoring force.
Answer:
(c) (Angular acceleration)²

Question 6.
When displacement is half of amplitude, then ratio of potential energy to the total energy is:
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{4}\)
(c) 1
(d) \(\frac{1}{8}\)
Answer:
(b) \(\frac{1}{4}\)

Question 7.
What remain constant in S.H.M.:
(a) Restoring force
(b) Kinetic energy
(c) Potential energy
(d) Time-period.
Answer:
(d) Time-period.

Question 8.
Graph between ‘f and ‘F obtained as :
(a) Hyperbola
(b) Parabola
(c) Straight line
(d) None of these.
Answer:
(b) Parabola

Question 9.
The time-period of a seconds pendulum is :
(a) 1 second
(b) 2 second
(c) 3 second
(d) 4 second.
Answer:
(b) 2 second

Question 10.
Resonance is example of:
(a) Tuning fork
(b) Forced oscillation
(c) Free oscillation
(d) Damped oscillation.
Answer:
(b) Forced oscillation

2. Fill in the blanks:

1. A periodic motion of constant amplitude and same frequency is called ………… .
Answer:
Simple harmonic motion

2. In simple harmonic motion its total energy is ………. .
Answer:
Constant

3. The restoring force setup per unit extension in the spring is called ………… .
Answer:
Spring constant (Force constant)

4. When a body oscillates on both sides of its mean position in a straight line, then this bind of motion is called ………… .
Answer:
Simple harmonic motion

5. The maximum displacement of a body in oscillatory motion is called ………… .
Answer:
Amplitude

6. In the presence of damping forces, the amplitude of oscillations of a body ………… .
Answer:
Decreases

7. The time-period of second pendulum is ………… second.
Answer:
Two

8. The periodic time of simple pendulum does not depends upon
Answer:
Mass.

3. Match the following:
I.

Answer:
1. (c) At mean position
2. (d) At maximum displacement
3. (b) Remain constant
4. (e) Directly proportional to displacement.
5.  (a) 2π\( \sqrt{\frac{\text { Displacement }}{\text { Acceleration }}} \).

II.

Answer:
1. (c) Periodic motion
2. (a) Forced oscillation
3. (e) S.H.M.
4. (b) Conservation of energy and momentum
5. ((d) Main frequency.

4. Write true or false:

1. Every S.H.M. is a periodic motion.
Answer:
True

2. Every periodic motion is S.H.M.
Answer:
False

3. In S.H.M. total energy is directly proportional to square of amplitude.
Answer:
True

4. Acceleration is always zero for a particle executing S.H.M.
Answer:
False

5. Time-period of simple pendulum is directly proportion to square root of its length.
Answer:
True

6. Time-period of simple pendulum is inversely proportional to the square root of acceleration due to gravity.
Answer:
True

7. Time-period of simple pendulum depends on mass, material and size of the pendulum.
Answer:
False

8. In S.H.M., velocity is maximum when acceleration is minimum.
Answer:
True

9. The motion of moon around the earth is S.H.M.
Answer:
False

10. Time-period of hard spring is less than soft spring.
Answer:
True

11. Time-period of a simple pendulum cannot be one day.
Answer:
True

MP Board Class 11th Physics Important Questions

Students get through the MP Board Class 11th Physics Important Questions Chapter 4 Motion in a Plane which are most likely to be asked in the exam.

MP Board Class 11th Physics Important Questions Chapter 4 Motion in a Plane

Motion in a Plane Class 11 Important Questions Very Short Answer Type

Question 1.
State for each of the following physical quantities, if it is a scalar or a vector : Volume, mass, speed, acceleration, density, number of moles, velocity, angular
frequency, displacement, angular velocity.
Answer:
Scalar quantities : Volume, mass, speed, density, number of moles, angular frequency.
Vector quantities : Acceleration, velocity, displacement, angular velocity.

Question 2.
Pick out the only vector quantity in the following list:
Temperature, pressure, impulse, time, power, total path, length, energy, gravitational potential, coefficient of friction, charge.
Answer:
Impulse. As impulse = force × time = change in momentum . As force and momentum are vector quantities, so it is a vector.

Question 3.
What do you mean by magnitude of a vector quantity?
Answer:
The positive value of the modulus of a vector quantity is called magnitude of
vector quantity. It is represented by \(|\vec{a}|\)

Question 4.
Whether addition of two vectors depends upon the order of placement of the vectors.
Answer:
No, according to the commutative law of vector addition \(\vec{a}+\vec{b}\) = \(\vec{b}+\vec{a}\).

Question 5.
Can two vectors of different dimension can be added?
Answer:
No, we can add two vectors of same dimension.

Question 6.
How can a vector and scalar be added?
Answer:
A vector and a scalar cannot be added.

Question 7.
How can three vectors be added so that its resultant is zero?
Answer:
If three vectors can be represented completely by the three sides of a triangle taken in the same order, then their resultant is zero.

Question 8.
What do you mean by unit vector and zero vector?
Answer:
If the magnitude of a vector is one then it is called as unit vector and if its
magnitude is zero and direction is uncertain is called zero vector, unit vector
\(\hat{a}=\frac{\vec{a}}{|\vec{a}|}\)

Question 9.
What do you mean by resolution of a vector?
Answer:
When a vector is divided into two or more components such that their addition is the same vector then it is called resolution of vector.

Question 10.
Can the magnitude of component of vector more than its original vector?
Answer:
No, it cannot be.

Question 11.
Can a vector be multiplied with a scalar? Illustrate with example.
Answer:
Yes, \(\vec{F}=m \cdot \vec{a}\)

Question 12.
When the scalar product of two vectors is maximum?
Answer:
When both the vectors are parallel, then angle between them is 0° or 180°. Then scalar product will be maximum.

Question 13.
Area of a surface is vector or scalar quantity?
Answer:
It is vector quantity because its direction is perpendicular to its surface.

Question 14.
Which type of quantity is modulus of a vector?
Answer:
Modulus of a vector is scalar quantity.

Question 15.
What do you mean by displacement vector?
Answer:
Displacement vector is those vector which specify that how much and in which direction an object has displaced in time intervel t₁ and t₂.

Question 16.
What do you mean by equal vectors?
Answer:
Two vectors whose magnitude and directions are same are called equal vectors.

Question 17.
Write the triangle law of vector addition.
Answer:
Triangle law of vector addition : If two vectors are represented by the adjacent sides of a triangle in a definite order. Then the
resultant will be given by the third side taken in the opposite manner.
i.e., \(\vec{R}=\overrightarrow{O A}+\overrightarrow{A B}\)

Question 18.
Can a vector of IS dyne be added in a vector of 10 Newton?
Answer:
Yes, it can be added because dimensions of both physical quantities are same.

Question 19.
Why displacement vector and velocity vector cannot be added?
Answer:
They cannot be added because their dimensions are different.

Question 20.
What will happen if a vector is extended in its parallel direction?
Answer:
No changes will occur in vector.

Question 21.
When the addition of two vectors are maximum and minimum?
Answer:
When both the vectors are parallel the addition is maximum and when they are opposite their addition is minimum.

Question 22.
Can the resultant of two different vectors be zero?
Answer:
No, because the minimum magnitude of \(\vec{A}+\vec{B}\) is A – B.

Question 23.
Whether addition of vectors depends on order they placed?
Answer:
No.

Question 24.
If P and Q are two vector quantities then PQ will be which quantity?
Answer:
It is a scalar quantity.

Question 25.
When vector product of two vectors is maximum?
Answer:
When two vectors are perpendicular to each other, then their vector product is maximum.

Question 26.
If a component of a vector is zero and other component of same vector is non-zero, can the magnitude of that vector be zero?
Answer:
No.

Question 27.
If the angle between two vectors are changed keeping magnitude to be same; then what will be the effect on resultant vector?
Answer:
Magnitude and direction of resultant vector will get changed.

Question 28.
When addition and subtraction of two vectors are equal?
Answer:
When the magnitude of both vectors are same and mutually perpendicular to each other then addition and subtraction of two vectors will be equal.

Question 29.
If \(\vec{A} \cdot \vec{C}=\vec{B} \cdot \vec{C}\) whether \(\vec{A}\) and \(\overrightarrow{\boldsymbol{B}}\) will be always equal?
Answer:
No.

Question 30.
What is projectile motion? When does the trajectory is parabola?
Answer:
When a body is projected at an angle other than vertical, the body moves under gravity and falls at different points on the earth. The path traced out by the body is called trajectory and its motion is called projectile.
Example : Motion of cannon ball, the object released from an aeroplane flying horizontally. Trajectory is parabola when air of friction is negligible.

Question 31.
At what angle the horizontal range is maximum?
Answer:
When θ = 45°, = R _max = \(\frac{u^{2}}{g}\)

Question 32.
From top of a tower two bullets are shot with different velocities in horizontal direction. Which one will reach on the ground first?
Answer:
Both bullets will reach the ground at the same time because initial velocity in vertical direction is same for them.

Motion in a Plane Class 11 Important Questions Short Answer Type

Question 1.
Establish the following vector inequalities geometrically or otherwise :
(a) \(|a+b| \leq|a|+|b|\)
(b) \(|\boldsymbol{a}+\boldsymbol{b}| \geq\|\boldsymbol{a}|-| \boldsymbol{b}\|\).
When does the equality sign above apply?
Answer:
Let the two vectors \(\vec{a}\) and \(\vec{b}\) be represented by the sides OP and PQ of the ΔOPQ taken in the same order, then their resultant is represented by the side OQ of the triangle such that
OQ = a + b as shown in fig.
Thus, OP = a,PQ = b
∴ \(|O P|=|a|,|P Q|=|b|\)
and \(|O Q|=|a+b|\)
(a) \(|a+b| \leq|a|+|b|\)

Proof:
We know from the property of a triangle that its one side is always less than the sum of the lengths of its two other sides.
Now in Δ OPQ,
OQ<OP+PQ
or \(|a+b|<|a|+|b|\) …(1)
If the two vectors a and b are acting along the same straight line i.e., are collinear and in the same direction, then
θ (angle between them) = 0
∴ \(|a+b|=\sqrt{a^{2}+b^{2}+2 a b \cos \theta}=\sqrt{(a+b)^{2}}\)
= a + b = \(|a|+|b|\) ..(2)
From eqns. (1) and (2), we get
\(|a+b| \leq|a|+|b|\)
The equality sign applies if a and b are collinear and act in same direction.
(b) \(\text { (b) }|a+b| \geq \| a|-| b||\)

Proof:
One side is more than the difference of two other sides i.e., in ΔOPQ in fig.
OQ >\(|O P-P Q|\)
The modulus of (OP – PQ) has been taken because L.H.S. is + ve and R.H.S. may be – ve if OP < PQ.
or \(|a+b|>\| a|-| b||\) ….(3)
If a and b are acting along the same straight line in the opposite direction, then
\(|a+b|>\| a|-| b||\)
From eqns. (3) and (4), we get
\(|a+b| \geq \| a|-| b||\)
Equality sign holds for as stated in eqn. (4).

Question 2.
Explain scalar product of two vectors?
Answer:
Let the angle between two vectors \(\vec{A}\) and \(\vec{B}\) is θ
∴ Scalar product of \(\vec{A}\) and \(\vec{B}\) will be
\(\vec{A} \cdot \vec{B}\) = AB cosθ

Example:
Let a force\(\vec{F}\) is acting on a particle and is displaced through \(\vec{r}\) at an angle θ then
\(\vec{F} \cdot \vec{r}\) = Frcosθ
Now, \(\vec{A} \cdot \vec{B}\) = AB cosθ
Hence, \(\vec{A} \cdot \vec{B}\) = 0 if either \(|\vec{A}|\) = 0 or \(|\vec{B}|\)= 0 or θ= 90°.

Question 3.
What type of quantity is work?
Answer:
Since work = Force × Displacement
i.e., W = \(\vec{F} \cdot \vec{d}\)
Since scalar product of two vectors are scalar, therefore work is a scalar quantity.

Question 4.
What type of quantity is kinetic energy?
Answer:
K.E =\(\frac{1}{2}\)mv² = \(\frac{1}{2}\)m \((\vec{v} \cdot \vec{v})\)
Since, \(\vec{v} \cdot \vec{v}\) will be a scalar quantity, so kinetic energy will be a scalar quantity.

Question 5.
Prove that addition of vectors obeys commutative law.
Or
State and prove the commutative law of vector addition.
Answer:
Consider two vectors \(\vec{a}\) and \(\vec{b}\) which are in the same plane \(\overrightarrow{O A}=\vec{a}\) and \(\overrightarrow{A B}=\vec{b}\).
Join \(\overrightarrow{O B}\).
By triangle law of addition,
\(\vec{a}+\vec{b}=\overrightarrow{O A}+\overrightarrow{A B}=\overrightarrow{O B}\) …(1)
Complete the parallelogram OABC. In a parallelogram, op¬posite sides are parallel and equal. Hence,
\(\overrightarrow{A B}=\overrightarrow{O C}=\vec{b} \text { and } \overrightarrow{O A}=\overrightarrow{C B}=\vec{a}\)
By triangle law of addition,
\(\vec{b}+\vec{a}=\overrightarrow{O C}+\overrightarrow{C B}=\overrightarrow{O B}\) …..(2)
From eqns. (1) and (2), \(\vec{a}+\vec{b}=\vec{b}+\vec{a}\)
Hence, the addition of vectors obey commutative law.

Question 6.
Show that addition of vectors obey the associative law.
Answer:
In a plane choose origin O and construct

Question 7.
Explain the law of parallelogram of vector’s addition.
Answer:
If the two vectors acting at a point are represented in magnitude and direction by the adjacent sides of a parallelogram, then their resultant vector is represented in magnitude and direction by the diagonal passing through their common origin.
If two vectors \(\vec{A}\) and \(\vec{B}\) are represented by two adjacent sides of a parallelogram OACB, the diagonal OC represents the resultant of these two vectors.
In parallelogram OACB,
OB= AC
∴ \(\overrightarrow{O B}=\overrightarrow{A C}=\vec{B}\)
In ? OAC, as per triangle law of vector addition,
\(\overrightarrow{O C}=\overrightarrow{O A}+\overrightarrow{A C}\)
∴ \(\vec{R}=\vec{A}+\vec{B}\)

Question 8.
Write the expression of position vector, velocity vector and acceleration vector for a particle moving in a plane.
Answer:

Question 9.
What is the effect of air on the time of flight and range of projectile?
Answer:
Time of flight and range will be decreased.

Question 10.
A food packet is released from an aeroplane flying horizontally. What will be the path of packet:
(i) Seen from the plane and
(ii) Seen from the earth?
Answer:
(i) In a straight line vertically downward.
(ii) Parabolic.

Question 11.
An aeroplane is moving horizontally with uniform velocity. A bomb is dropped from the plane. What will be the position of plane, when the bomb strikes the ground?
Answer:
When the friction of medium is zero, the plane will be just above the point where the bomb strike the ground.
When the friction is not zero, the plane will be little ahead above the point where the bomb will strike the ground.

Question 12.
What will be the change in centripetal force when speed of an object and radius of path are doubled in circular motion.
Answer:
Centripetal force F = \(\frac{m v^{2}}{r}\)
When v₁ = 2v and r₁ = 2r
Then, F₁ = \(\frac{m v_{1}^{2}}{r_{1}}\)
or F₁ = \(\frac{m(2 v)^{2}}{2 r}=\frac{4 m v^{2}}{2 r}\)
or F₁ = \(\frac{2 m v^{2}}{r}\)
or F₁= 2F is centripetal force will get doubled.

Question 13.
What do you mean by uniform circular motion? Give two examples.
Answer:
When a body moves in a circular path with constant speed, then its motion is called uniform circular motion.
Example: Motion of the tip of the blade of a fan, motion of the earth around the sun is nearly a uniform circular motion.

Question 14.
What do you mean by angular displacement?
Answer:
The angle suspended by the particle on the circular path in given time interval is called an angular displacement of the particle its unit is radian.

Question 15.
If the velocity of projectile motion is doubled then what will be the effect on its horizontal range?
Answer:
since R = \(\frac{u^{2} \sin ^{2} \theta}{g}\)
i.e., R ∝ u²
When velocity of projectile motion is doubled then its horizontal range get four times increased.

Question 16.
What do you understand by time-period and frequency?
Answer:
Time-period is defined as the time taken by an object to complete one rotation. Its unit is second. If the angular velocity of an object is a> and angle suspended at the centre during one complete rotation is 2π, then
Time-period T = \(\frac{2 \pi}{\omega}\)
or ω = \(\frac{2 \pi}{T}\)
Frequency is defined as the number of rotations completed by the body in one second. Its unit is hertz.
If time-period is T, then frequency n = \(\frac{1}{T}\)
or n = \(\frac{1}{2 \pi / \omega}=\frac{\omega}{2 \pi}\)
or ω = 2πn

Question 17.
Define linear velocity and angular velocity of a particle in circular motion. Establish the relation between them.
Answer:
Angular velocity :
The rate of change of angle subtended by a body moving in a circular path, at the centre of the path per second is called angular velocity of the body.
Linear velocity :
The distance travelled by the particle on the circular path in one second is called linear velocity.
Its SI unit is ms^-1.

Relation between linear velocity and angular velocity:
Let a particle is moving in a circular path of radius r and centre O. Its linear velocity is v and angular velocity is ω
If in small time Δt, the particle travels distance Δs on the circle,
∴ ∠POQ = Δθ
Hence’ ω = \(\frac{\Delta \theta}{\Delta t}\) ….(1)
and ν = \(\frac{\Delta s}{\Delta t}\) ….(2)
But, Angle = \(\frac{\text { Arc }}{\text { Radius }}\)
∴ Δθ = \(\frac{\Delta s}{r}\)
∴ From eqn. (1), we get
ω = \(\frac{\Delta s}{r \Delta t}\)
or \(\frac{\Delta s}{\Delta t}\) = ωr
∴ ν = ωr

Hence, Linear velocity = Angular velocity × Radius.

Question 18.
Define centripetal acceleration and derive its expression. Also deduce its direction.
Answer:
Centripetal acceleration :
It is defined as the acceleration which always acts towards the centre along the radius of the circular path.
“Centripetal” comes from a Greek term which means “centre seeking”.
Expression for centripetal acceleration:
Let a body be moving with constant angular velocity? and constant speed? in a circular path of radius R and centre O.

Let the body be at points P and Q at time t and t + Δt respectively.
Also let Δθ= ∠POQ be the angular displacement in a small time interval Δt, thus
ω = \(\frac{\Delta \theta}{\Delta t}\) = or Δθ = ωΔt …(1)
If ν and \(\vec{v}+\Delta \vec{v}\)be the velocity vectors of the body at points P and Q acting along PL and QM respectively. As the body is moving with uniform speed, so lengths PL and PM are equal i.e., PL = PM. The change in velocity \(\Delta \vec{v}\) from P to Q is due to the change in the direction of velocity vector.
Hence magnitude of acceleration of the body is given by

From point’a’draw \(\overrightarrow{a b}\) parallel and equal to \(\overrightarrow{P L}\) and \(\overrightarrow{a c}\) parallel and equal to \(\overrightarrow{Q M}\),
thus
\(\overrightarrow{a b}=\vec{v}, \overrightarrow{a c}=\vec{v}+\Delta \vec{v}\)
∴ \(\overrightarrow{b c}=\Delta \vec{v}\)
Clearly the angle between \(\overrightarrow{a b}\) and \(\overrightarrow{a c}\) is Δθ . As Δt is quite small so a and c lie very close to each other, thus be can be taken to be an arc of \(\widehat{b c}\) a circle of radius
ab = \(|\vec{v}|\)

Also when Δt → 0, then L.H.S. of eqn. (4) represents acceleration. Thus eqn. (4) can be written as

Eqn. (6) gives the magnitude of the acceleration produced in the body.
Direction of acceleration :
Acceleration always acts in the direction of Δν which acts from b to c. When Δt is decreased, Δθ also decreases. If Δt → 0, then Δθ → 0, so Δν tends to be perpendicular in ab. As ab || PL, so Δν tends to act perpendicular to PL i.e., along PO is along the radius towards the centre of circular path.
Since ν and R are always constant, so magnitude of centripetal acceleration is also constant. But the direction changes pointing always towards the centre. So centripetal acceleration is not a constant vector.

Motion in a Plane Class 11 Important Questions Long Answer Type

Question 1.
State parallelogram law of vector addition of two vectors and derive an expression for their resultant vector.
Ans. Parallelogram law of vector addition : If the two vectors acting at a point are represented in magnitude and direction by the adjacent sides of a parallelogram, then their resultant vector is represented in magnitude and direction by the diagonal passing through their common origin.
If two vectors \(\vec{A}\) and \(\vec{B}\) are represented by two adjacent sides of a parallelogram OACB, the diagonal OC represents the resultant of these two vectors.
In parallelogram OACB,
OB= AC
∴ \(\overrightarrow{O B}=\overrightarrow{A C}=\vec{B}\)
In Δ OAC, as per triangle law of vector addition,
\(\overrightarrow{O C}=\overrightarrow{O A}+\overrightarrow{A C}\)
∴ \(\vec{R}=\vec{A}+\vec{B}\)

Two vectors \(\vec{a}\) and \(\vec{b}\) are completely represented by the two sides OA and OB of a parallelogram respectively as shown in fig.

The angle between two vectors \(\vec{a}\) and \(\vec{b}\) is θ. The diagonal
OC of the paralellogram gives the resultant \(\vec{R}\),
Such that \(\vec{R}\) = \(\vec{R}=\vec{a}+\vec{b}\)
The resultant \(\vec{R}\) makes a angle with direction of \(\vec{a}\) From point C draw a perpendicular CN on extended OA.
In ΔANC,
sinθ = \(\frac{C N}{A C}\) ⇒ CN= AC sinθ
⇒ CN = b sinθ ….(1)
Also, cosθ = \(\frac{A N}{A C}\)
⇒ AN = AC cosθ = b cosθ ….(2)
∴ ON = OA + AN =a+b cosθ ….(3)
In ΔONC, OC² = ON² + CN²
⇒ R² = (a +b cosθ)² +(bsin?)²
or R² = a² +b² cos² θ+2abcosθ+b² sin²θ
or R² = a² +b²(sin²θ+ cos² θ) + 2abcosθ
or R² = a² +b² +2abcosθ
or R = \(\sqrt{a^{2}+b^{2}+2 a b \cos \theta}\) …(4)
The above eqn. (4) is the required expression.
Direction of R is given by
tanα = \(\frac{b \sin \theta}{a+b \cos \theta}\) or a = tan^-1\(\left(\frac{b \sin \theta}{a+b \cos \theta}\right)\)

Question 2.
What do you mean by two-dimensional motion? Establish the relation between displacement, velocity and acceleration.
Answer:
TWo-dimensional motion: When a body moves in a plane, its motion is called two-dimensional motion.
Example: Motion in circular path, motion of the bullet fired from the gun.
Let a body is moving with uniform acceleration \(\vec{a}\). At time t = 0 its velocity is \(\vec{?}\) (0) and at t sec velocity is ν(t). 1f the position vectors are \(\vec{r}\) (0) and \(\vec{r}\) (t) respectively.

Question 3.
What do you understand by projectile motion? Prove that the path of projectile is parabolic.
Answer:
Projectile motion :
When a body is projected at an angle other than vertical, the body moves under gravity and falls at different points on the earth. The path traced out by the body is called trajectory and its motion is called projectile.
Example : Motion of cannon ball, the object released from an aeroplane flying horizontally. Trajectory is parabola when air of friction is negligible.

Let a body is projected with velocity u, at an angleθ with the horizontal. Thus, we have two components of u.
i.e., Horizontal component along X-axis = u cosθ
and Vertical component along T-axis = u sinθ
∵ The horizontal velocity is free from gravitational acceleration,
∴ u_x = v_x(0) = u cosθ and a_x = 0
If x (t) is the position of the particle of any instant of time, then the displacement will be x(t) – λ(0),
But, λ(0) = 0
∴ x(t) – λ(0) = λ(t) = x
Hence, x = v_x(0)t + \(\frac{1}{2}\) a_xt²
or x = u cosθ t
or t = \(\frac{x}{u \cos \theta}\) …(1)
Now, for the vertical component,
v_y = u sinθ and a_y = -g, (∵ the particle moves in upward direction) If y(t) is the position of the particle at any instant of time, then the displacement will be y(t) -y(0)
But, y(0) = 0
∴ y(t) – y(0)=y(t) = y

or y = x tanθ –\(\frac{g}{2 u^{2} \cos ^{2} \theta} x^{2}\) …(3)
Since, u, g and θ are constant, therefore the eqn. (3) is in the form of
y = ax – bx²
Where, a = tanθ and b = \(\frac{g}{2 u^{2} \cos ^{2} \theta}\)
Which is the equation of a parabola. Since, it is a quadratic equation in x. Proved.

Question 4.
Derive the expression for time of flight, horizontal range and maximum height attain for a projectile motion.
Answer:
Expression for time of flight: Let a body is projected with initial velocity u at an angle θ with the horizontal.
∴ The components of u are:
(i) Horizontal component, u_x = u cosθ and
(ii) Vertical component, u_y = u Sinθ
The time taken by the projectile to travel from point O to A, is called its time of flight.
Now, initial velocity along Y-axis is
u_y=ν_y(0)=u sinθ
Now,at highest point
ν_y(t) = 0 and a_y = -g
If the time taken by the projectile from O to P is t, then
ν_y(t)= ν_y(0)+at
or
0=u sinθ-gt
or t = \(\frac{u \sin \theta}{g}\)
But Time of flight, T = 2t
∴ T = \(\frac{2 u \sin \theta}{g}\)

Horizontal Range:
The horizontal distance travelled in the time of flight is called range.
Now, Range=OA=R
∴ R = Horizontal velocity × Time of flight
or R= u cosθ × \(\frac{2 u \sin \theta}{g}\)
or R= \(\frac{u^{2} \cdot 2 \sin \theta \cos \theta}{g}\)
∴ R = \(\frac{u^{2} \sin 2 \theta}{g}\) (∵ 2sinθ cosθ = sin2θ)

For maximum range, sin2θ = 1
or sin2θ= sin9o°
or 2θ = 90°
∴ θ =45°
For maximum range the angle of projection should be 45°.
∴ R_max = \(\frac{u^{2}}{g} .\)

Maximum height attain: Now, we have two resolved parts of initial velocity u, i,e.,
(i) Horizontal component u_x = u cosθ and
(ii) Vertical component u_y = u Sinθ.
Suppose, the maximum height of projectile is Hand it takes r sec. to reach the highest point.
Now, for vertical motion,
ν_y(0) = u sinθ and a_y = -g
At highest point, ν_y(t) = 0
:. By the equation, ν_y(t)=ν_y(0)+a_yt
or 0 = u sinθ – gt

Motion in a Plane Class 11 Important Numerical Questions

Question 1.
Find modulus and unit vector of the vector
\(\vec{a}=\hat{i}-2 \hat{j}+\hat{k}\)
Solution:

Question 2.
If \(\vec{a}=\hat{i}+3 \hat{j}-4 \hat{k}\) and \(\vec{b}=2 \hat{i}-3 \hat{j}+4 \hat{k}\) then find out \(\vec{a}+\vec{b}\),
\(\vec{a} \cdot \vec{b}\) and \(\vec{a} \times \vec{b}\)
Solution:

Question 3.
If\(|\vec{a}+\vec{b}|=|\vec{a}-\vec{b}|\), then prove that \(\text { a }\) and \(\text { b }\) are mutually perpendicular to each other.
Solution:

Question 4.
When the resultant of two equal vectors will be A.
Solution:
R² = A² + B² + 2ABcosθ
When \(\vec{B}=\vec{A}\), then
R² = A² + A² + 2A.Acosθ
= 2A² +2A²cosθ
If costθ = – \(\frac{1}{2}\) = cos 120°
Then R² = A²
i.e., R = A
i.e., θ = 120°.

Question 5.
Prove that \(3 \hat{i}+2 \hat{j}-\hat{k}\) and \(2 \hat{i}-2 \hat{j}+2 \hat{k}\) are perpendicular to each other.
Solution:

Question 6.
If A = \(\vec{A}=2 \hat{i}+2 \hat{j}+p \hat{k}\) and \(\vec{B}=2 \hat{i}-\hat{j}+\hat{k}\)are perpendicular, then find the value of p.
Solution:
Given : \(\vec{A}\) and \(\vec{B}\) are perpendicular
∴ \(\vec{A} \cdot \vec{B}\) = 0
or \((2 \hat{i}+2 \hat{j}+p \hat{k}) \cdot(2 \hat{i}-\hat{j}+\hat{k})\) = 0
∴ 2.2 + 2.(-1) + p.(1) = 0
or 4 -2 + p = 0
or P = -2.

Question 7.
Rain is falling vertically with a speed of 30 ms *. A woman rides a bicycle
with a speed of 10 ms 1 in the north to south direction. What is the direction in which she should hold her umbrella?

Solution:
Let the rain be falling vertically downward with the speed of 30 ms^-1 along OA. The woman is moving along OS with a speed of 10 ms^-1.
To protect herself from rain, the woman should hold her umbrella in the direction of relative velocity of the rain with respect to the woman i.e., ν_rw. To determine the ν_rw the woman must be brought to rest by imposing an equal and opposite velocity of the observer both on woman as well as on the rain. Rain thus has two velocities :
(i) Its own velocity of 30 ms ^-1 along \(\overrightarrow{O A}\)
(ii) Imposed velocity of 10 ms^-1 along \(\overrightarrow{O B}\)
The relative velocity is the resultant of these two velocities.

tan α = tan18°26′
α = 18° 26′
So woman should hold umbrella at an angle of 18°26′ with the vertical towards south.

Question 8.
A cyclist is riding with a speed of 27 kmh^-1. As he approaches a circular turn on the road of radius 80 m, he applies brakes and reduces his speed at the constant rate of 0.5 ms^-1 every second. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn?
Answer:

Speed of cyclist ν = 27kmh^-1
= 27 x \(\frac{5}{18}\) ms^-1
= \(\frac{15}{2}\) ms^-1
Radius of circular turn, r = 80 m
Here the cyclist will be acted upon by two accelerations a_c and a_t Centripetal acceleration (a_c) is given by

Let P be the point at which the cyclist applies brakes, then the tangential acceleration a_t, (which will be negative) will act opposite to velocity of cyclist and is given by
a_t = \(\frac{\text { Change in velocity }}{\text { Time }}=\frac{0 \cdot 5}{1}\) ms^-2
= 0.5 ms^-2
As both a_c and a_t, act along the radius of circle and tangent to the circle respectively, so ac and a, are mutually perpendicular, thus the magnitude of the net acceleration ‘a’
(i.e., resultant acceleration) is given by

Direction of a: Let θ be the angle made by the net acceleration with the velocity of cyclist, then
tanθ \(\frac{a_{c}}{a_{t}}\) = \(\frac{0.703}{0.5}\)
= 1.406
or tanθ = tan54°33′
θ = 54° 33′ = 54-44°.

Question 9.
A ball is projected at an angle of 30° with a velocity of 20 ms^-1. Find the time of flight.
Solution:
u = 20 ms^-1, θ= 30°.

Question 10.
A cricketor can throw a ball to a maximum horizontal distance of 100 m. How much high above the ground can the cricketor throw the same ball?
Solution:
Given:
R = 100 m
From the formula R = \(\frac{u^{2}}{g}\), we get g
100 = \(\frac{u^{2}}{g}\)
and H = \(\frac{u^{2}}{2 g}=\frac{R}{2}=\frac{100}{2}\) = 50m

Question 11.
A ball is projected at an angle of 60° with a velocity of 40 ms^-1. What will be the maximum height and range?
Solution:

Question 12.
A body is projected at an angle of 15° and its range is 50 m. If it is projected at an angle of 45°, then find the range.
Solution:

Question 13.
A particle is executing 3 revolutions per second in a circular path of radius 15 cm. Find out angular velocity and linear velocity.
Solution:
Given r = 15 cm, frequency n = 3 revolutions per second
From ω = 2πn, we get
ω = 2 × π × 3 = 6π radian/sec.
Again, from ν = rω, we get
ν = 15 × 6π = 90πcm/sec.

Question 14.
In a projectile motion of the horizontal range and maximum height attain of an object is same, then find out the angle of projection of the object.
Solution:
Given, R = H

Question 15.
The coordinate of a particle moving in a plane at any time f is given by JC =
ct2 and y = bt² Determine the velocity of the particle.
Solution:

Question 16.
For any projectile motion the horizontal range is four times of maximum height attain. Find out the angle of projection.
Solution:
Given R = 4 H

Question 17.
A bullet is fired with a velocity of 1,000 m/s from a rifle at an angle of 30° w.r.t horizontal, find out:
(i) Time taken to reach highest point from the rifle.
(ii) Total time of flight
(iii) What will be the velocity of bullet when it strike ground surface?
(iv) At what height the buUet will raise ?
(v) At what distance from the rifle the bullet will strike the ground surface?
Solution:

Question 18.
A football player kicks the football with a velocity of 20 m/s making an angle of 30° from the horizontal. Find out
(i) Time of flight
(ii) Maximum height attain by the football
(iii) Velocity of the football and its direction after striking the ground.
(iv) Horizontal range, (given g = 10 m/s²).
Solution:

Question 19.
An aeroplane is flying at a height of 1960 m with a velocity of 600 km/hr. When it is just above a point A on the earth, a packet is dropped, which falls at point B. Calculate AB.
Solution:
u = 600 km/hr =600 × \(\frac{5}{18}\) m/s
= \(\frac{500}{3}\) m/s
For motion of a packet in downward direction,
y = \(\frac{1}{2}\) gt²
or 1960 =\(\frac{1}{2}\) × 9.8 × t²
or t² =400t = 20 sec.
∴ AB = ut = \(\frac{500}{3}\) × 20
Horizontal distance covered by packet i.e.,AB
AB = ut = \(\frac{500}{3}\) × 20
= 3333.3m
= 3.33km.

Motion in a Plane Class 11 Important Questions Objective Type

1. Multiple- choice questions:

Question 1.
1. Torque is a :
(a) Vector quantity
(b) Scalar quantity
(c) Both
(d) None of these
Answer:
(b) Scalar quantity

Question 2.
If \(\vec{A}=2 \hat{i}+4 \hat{j}\)and \(\vec{B}=2 \hat{i}-5 \hat{j}\), then \(\vec{A}+\vec{B}\) will be :
(a) \(5 \hat{i}-\hat{j}\)
(b) \(3 \hat{i}-\hat{j}\)
(c) \(4 \hat{i}-\hat{j}\)
(d) \(3 \hat{i}-3 \hat{j}\)
Answer:
(c) \(4 \hat{i}-\hat{j}\)

Question 3.
Unit vector in direction of vector \(\vec{A}\) will be :
(a) \(\hat{\mathrm{A}}=\frac{A}{\vec{A}}\)
(b) \(\hat{\mathrm{A}}=\frac{\vec{A}}{A}\)
(c) \(\text { (c) } \hat{\mathrm{A}}=A \cdot \vec{A}\)
(d) \(\text { (d) } \hat{\mathrm{A}}=A+\vec{A}\)
Answer:
(b) \(\hat{\mathrm{A}}=\frac{\vec{A}}{A}\)

Question 4.
Angle between velocity and acceleration of maximum height of a projectile is :
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Answer:
(d) 90°

Question 5.
Path of a projectile is :
(a) Circular
(b) Straight line
(c) Parabolic
(d) Uncertain.
Answer:
(c) Parabolic

Question 6.
For maximum range of a projectile, the angle must be :
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Answer:
(b) 45°

Question 7.
Time of flight of a projectile is tx and time taken to reach maximum height is t2, then the relation between them will be :
(a) t₁ =2t₂
(b) t₂ =2t₁
(c) t₂ =3t₁
(d) t ₁=t₂
Answer:
(a) t₁ =2t₂

Question 8.
If the velocity of projectile is doubled, then its range will be :
(a) Same
(b) Become double
(c) Become half
(d) Become four times.
Answer:
(b) Become double

Question 9.
At maximum height of projectile, velocity is :
(a) Zero
(b) Minimum
(c) Equal to initial velocity
(d) None of these.
Answer:
(b) Minimum

Question 10.
Rate of change of angular velocity is called :
(a) Angular displacement
(b) Angular speed
(c) Angular acceleration
(d) Angular momentum.
Answer:
(c) Angular acceleration

2. Fill in the blanks:

1. Angular momentum is a ………………….quantity.
Answer:
Vector

2. Magnitude of a vector \(2 \hat{i}-\hat{j}\) is …………………….
Answer:
√5

3. If an object is thrown horizontally from a height, then its path is ………………..
Answer:
Parabolic

4. At maximum height of a projectile motion, velocity of an object is ………………..
Answer:
Minimum

5. The maximum horizontal distance covered by a projectile in its time of flight is called ………………………
Answer:
Horizontal range

6. ……………………….. is constant in uniform circular motion.
Answer:
Speed

7. At maximum height the direction of acceleration in projectile motion is ………………….
Answer:
Vertically downwards

8. In uniform circular motion there is ……………………. changes in angular momentum of a particle.
Answer:
Zero

9. Angle between velocity and acceleration in uniform circular motion is …………………..
Answer:
90°

10. SI unit of angular momentum is …………………
Answer:
Radian/second

3. Match the following:

I.

Answer:
1. (c) \(\frac{u^{2} \sin 2 \theta}{2 g}\)
2. (d) \(\frac{2 u \sin \theta}{g}\)
3. (e) \(\frac{u^{2} \sin 2 \theta}{g}\)
4. (a) u cosθ
5. (b) u sinθ

II.

Answer:
1. (c) Changes
2. (e) Toward centre
3. (b) ν = rω
4. (a) Tangential
5. (d) Constant

 4. Write true or false:

1. If \(\vec{A} \cdot \vec{B}\) = AB, then angle between \(\vec{A}\) and \(\vec{B}\) is zero.
Answer:
True

2. If a unit vector is added or subtracted from a given vector, we always obtain given vector.
Answer:
True

3. A scalar quantity can be added with vector quantity.
Answer:
False

4. Resultant of three coplaner vector can be zero.
Answer:
True

5. Path of motion is a straight line in two-dimensional motion moving with uniform velocity.
Answer:
True

6. Acceleration is constant in projectile motion.
Answer:
True

7. Horizontal velocity is constant in projectile motion.
Answer:
True

8. If an object is dropped from running train, then its path will be parabolic.
Answer:
True

9. Kinetic energy is zero at maximum height of a projectile motion.
Answer:
False

10. In a given time interval, the ratio of change in velocity to the time-interval gives average acceleration.
Answer:
True

5. Answer in one word:

1. A projectile is thrown upwards. At the topmost point, the acceleration is in which direction.
Answer:
Vertically downwards

2. When an object is projected from earth surface, then which quantity remains constant?
Answer:
Horizontal component of velocity

3. Twp bullets are fired horizontally with different velocities from the same height. Which bullet would reach the earth’s surface earlier.
Answer:
Both bullets reach the earth’s surface in the same time

4. A particle is moving in a circular path. What is angle between its velocity and acceleration?
Answer:
90°

5. A particle has uniform circular motion. What is the change in its angular velocity after one half cycle.
Answer:
No change in angular velocity

Students get through the MP Board Class 11th Physics Important Questions Chapter 13 Kinetic Theory  which are most likely to be asked in the exam.

MP Board Class 11th Physics Important Questions Chapter 13 Kinetic Theory

Kinetic Theory Class 11 Important Questions Very Short Answer Type

Question 1.
State Boyle’s law.
Answer:
According to Boyle’s law “At constant temperature the volume of a given mass of a gas inversely proportional to its pressure, i.e.,
V∝\( \frac{1}{\mathrm{P}} \)
or
V=K.\( \frac{1}{\mathrm{P}} \)
or
PV = K (constant).

Question 2.
Write the condition at which Boyle’s law function.
Answer:
Boyle’s law function at low pressure and high temperature.

Question 3.
Write down Charle’s law.
Answer:
According to Charle’s law “ The volume of given mass of a gas at constant pressure increases by \( \frac{1}{273} \) of its volume at 0°C, for each 1°C rise in temperature.

Question 4.
Prove that with help of Charle’s law that at -273°C, volume of a gas is zero.
Answer:
According to Charle’s law.
V = V₀( 1 + \( \frac{1}{273} \) t)
At t =-273° C
or
V = V₀(1+ \( \frac{-273}{273} \) )
or
V = V₀ (1-1) = 0
i.e., at -273°C volume of a gas is zero.

Question 5.
What are ideal gases?
Answer:
The gases which obey Boyle’s law and Charle’s law completely are called ideal gases.

Question 6.
State Avogadro’s law.
Answer:
According to Avogadro’s law, “Equal volume of all the gases under similar con-ditions of temperature and pressure contain the same number of molecules.”

Question 7.
Write down Dalton’s law of partial pressure.
Answer:
Dalton’s law of partial pressure states that the total pressure exerted by a mixture of gases which do not interact in any way is equal to the sum of their individual pressures.

Question 8.
What is Grahm’ law of diffusion?
Answer:
According to Grahm’s law of diffusion, “The rate of diffusion of a gas is directly proportional to the square root of its density.”

Question 9.
What is meant by absolute scale of temperature?
Answer:
The scientist Kelvin had developed a temperature scale by considering – 273°C as zero of the scale. This scale is called absolute scale of temperature. The value of its each division is 1°C. It is also called as Kelvin scale.

Question 10.
What do you mean by absolute zero?
Answer:
The absolute zero is that temperature at which the volume of a gas becomes zero.

Question 11.
If a gas is suddenly compressed, then its temperature increased. Why?
Answer:
The temperature of a gas is directly proportional to its mean kinetic energy. When a gas is suddenly compressed, then the mean kinetic energy of gas is increased. Therefore, the temperature of gas is increased suddenly.

Question 12.
What is Boltzmann constant? Write its value.
Answer:
The ratio of universal gas constant (R) and Avogadro’s number (N) is known as Boltzmann’s constant
K= \( \frac{\mathrm{R}}{\mathrm{N}} \)
Its value is 1.38 x 10^-23 joule/kelvin.

Question 13.
Write down relation between universal gas constant and specific gas constant.
Answer:
The relation between universal gas constant and specific gas constant is given below:
Specific gas constant r = \( \frac{\text { Universal gas constant }(\mathrm{R})}{\text { Molecular weight of } operatorname{gas}(\mathrm{M})} \) .

Question 14.
Write the ideal gas equation.
Answer:
PV = nRT.

Question 15.
Find out dimensional formula for R.
Answer:
From PV = RT
R = \( \frac{\mathrm{PV}}{\mathrm{T}} \)
or
[R] = \( \frac{\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]\left[\mathrm{L}^{3}\right]}{[\theta]} \)
= \( \left[\mathrm{ML}^{2} \mathrm{~T}^{-2} \theta^{-1}\right] \) .

Question 16.
At equal temperature (T) and pressure (P), two gases of same volume (V) are mixed together. If the temperature and volume of the mixure is T and V, then what will be its pressure?
Answer:
According to Dalton’s law of partial pressure it will be 2P.

Question 17.
At NTP, 1cm³ H₂ and 1cm³ O₂ are given. In which gas number of molecules will be more and why?
Answer:
According to Avogadro’s law number of molecules of 1 cm³ H₂ and 1 cm³ O₂ will be equal.

Question 18.
Oxygen and hydrogen gases are filled in a porous pot in equal amount, which one will diffuse soon?
Answer:
By the kinetic theory of gas,
ν rms ∝\( \frac{1}{\sqrt{\mathrm{M}}} \)
Since M_H < M₀ hence ν_H > ν₀
Thus, the hydrogen will diffuse soon.

Kinetic Theory Class 11 Important Questions Short Answer Type 

Question 1.
What is gas equation? Establish it.
Or
For a gas equation prove that PV = RT.
Or
Establish ideal gas equation.
Answer:
Let the initial pressure of one gram mole of a gas of molecular weight M is P₁ its volume is V₁ and absolute temperature is T₁. After a thermodynamic process the pressure of gas become P₂, volume and temperature becomes V₂ and T₂ respectively. The change occurs in the state of gas can be considered to be a combination of two processes.
(i) Keeping the temperature T₁ of gas constant, its pressure is varied from P₁ to P₂, so that as shown in fig. the volume of gas becomes V’. Hence, as per Boyle’s law :
P ₁V₁ = P₂V’ …(1)

(ii) Keeping the pressure P2 constant, the temperature of gas is varied from T₁ to T₂ so that its volume changes from V’ to V₂ as shown in fig. then according to Charle’s law :

\( \frac{\mathrm{V}^{\prime}}{\mathrm{T}_{\mathrm{l}}} \) = \( \frac{\mathrm{V}_{2}}{\mathrm{~T}_{2}} \)
or
\( V’ = \frac{\mathrm{V}_{2} \mathrm{~T}_{1}}{\mathrm{~T}_{2}} \) ………. (2)
Substituting the value V’ from eqn. (2) in eqn.(1)
P₁V ₁ = \( \frac{\mathrm{P}_{2} \mathrm{~V}_{2} \mathrm{~T}_{1}}{\mathrm{~T}_{2}} \)
or
P₁V ₁ = \( \frac{P_{2} V_{2}}{T_{2}} \)
\( \frac{\mathrm{PV}}{\mathrm{T}} \) = Constant …….. (3)
The value of this constant is same (= 8.314 joule per mole-kelvin) for 1 mole of all the gases. It is denoted by R. Hence,
\( \frac{\mathrm{PV}}{\mathrm{T}} \) = R
or
PV = RT …(4)
Where, R is called universal gas constant. Eqn. (4) is called gas equation for one mole of gas.

Question 2.
Write down postulates of kinetic theory of gases.
Answer:
The postulates of kinetic theory of gas are given below :

• Every gas is composed of minute particles called molecules.
• The size of these molecules is negligible as compared to their intermolecular dis¬tance. t
• The molecules of gas are spherical uniform in all aspects rigid and perfectly elastic.
• The molecules are always in state of random motion and move in all possible direction with all possible velocities.
• Due to their continuous motion, these molecules collide with each other and also with the walls of container during their random motion. Due to these collision, there is no change in density of gas, i.e., the number of molecules per unit volume of the gas remains unchanged.
• After collision the direction of velocity of molecules changes. The collision is instantaneous, i.e., the time taken in collision is negligible as compared with the time taken between two consecutive collisions.
• The collisions are perfectly elastic, i.e., kinetic energy of molecules remains con-served.
• Between the two successive collisions a molecule travels in a straight line with uniform velocity. The distance covered by a molecule between two consecutive collisions is called ‘Free path’, The average distance travelled by a molecule between successive collisions is called mean-free-path.
• The molecules of gas collide with the walls of container and hence they exert the force on the walls. The force acting per unit area on the wall is called pressure of gas.
• The mass of molecules of gas is negligible and velocity is high. Therefore, there is no effect of gravity on the motion of molecules.

Question 3.
Prove that: P = \( \frac{1}{3} \) ρc^-2
Answer:
We know P = \( \frac{1}{3} \) \( \frac{m N c^{2}}{V} \)
Here mN = M
∴ P = \( \frac{1}{3} \) \( \frac{M \bar{c}^{2}}{V} \)
But \( \frac{M}{V} \) = ρ (density)
∴ P = \( \frac{1}{3} \) ρc^-2

Question 4.
On the basis of kinetic theory of gases, prove that p = \( \frac{2}{3} \) E where symbols have their meanings,
Answer:
According to kinetic theory of gases, the pressure exerted by the gas is gi ven by
P = \( \frac{m N \bar{c}^{2}}{3 V} \) ………….. (1)

Where, N is the number of molecules, c ^-2 mean square velocity and V is volume. Let m be the mass of one molecule, then the mass of gas be mN
∴Density of gas ρ = \(\frac{m N}{V}\) …………. (2)
From eqns. (1) and (2),
P = \( \frac{1}{3} \) ρc^-2
= \( \frac{2}{3} \) .\( \frac{1}{2} \) ρc^-2 = \( \frac{2}{3} \) E
Where, E is kinetic energy of per unit volume of gas.

Question 5.
Explain kinetic energy of a gas on the basis of kinetic theory of gases.
Or
Prove that : P = \( \frac{2}{3} \) E
Answer:
Kinetic energy of gas: Let the mass of one molecule of gas is m and number of molecules is N. Hence, the mass of gas will be mN.
∴Density of gas ρ = \(\frac{m N}{V}\) …………. (1)
According to Kinetic theory of gas the pressure exerted by gas is
P= \( \frac{m N \bar{c}^{2}}{3 V} \) ……………. (2)
From equns. (1) and (2)
P = \( \frac{1}{3} \) ρc^-2 = \( \frac{2}{3} \) . \( \frac{1}{3} \) ρc^-2
P= \( \frac{2}{3} \) E …….. (3)

Where, E is kinetic energy of a gas per unit volume. From eqn. (3),
or
E = \( \frac{3}{2} \) P
or
P = \( \frac{2}{3} \) E.

Question 6.
On the basis of kinetic theory of gases prove that the mean kinetic energy of molecules of gas is directly proportional to the absolute temperature of gas.
Or
Prove that the mean kinetic energy of gas is E = \( \frac{3}{2} \) KT.
Answer:
According to kinetic theory of gases, the pressure exerted by the gas is given by :
P = \( \frac{m N \bar{c}^{2}}{3 V} \)

Where, m is mass of one molecule of gas, N is the number of molecules in the volume V,c^-2 is mean square velocity of gas and V is volume. In the above equation if V is volume of one mole of gas, then N be the Avogadro’s number, mN be the gram molecular weight (M) hence from the above equation :
PV=\( \frac{1}{3} \)mNc^-2
= \( \frac{1}{3} \)Mc^-2 …(1)

But by the gas equation,
PV = RT ……………. (2)
From eqns. (1) and (2), we get
\( \frac{1}{3} \)Mc^-2 =RT
or
c^-2 = \( \frac{3 R T}{M} \) …… (3)
From eqn. (3), it is clear that c^-2 ∝T
Thus, the absolute temperature of a gas is directly proportional to the mean square velocity of the molecules of a gas.
Again from eqn. (3),

Where, K =\( \frac{R}{N} \) is called Boltzmann’s constant. Its value is 1.38 × 10^-23 joule per kelvin. This is formula of mean kinetic energy of molecules. From this equation, it is clear that
E∝T.

Question 7.
Explain absolute zero on basis of kinetic theory of gas.
Answer:
We know E =\( \frac{3}{2} \) KT
, If T=0, then E = 0.
Therefore, absolute zero temperature is that temperature at which average kinetic energy of the gaseous molecules is zero.

Question 8.
Prove that\( \overline{\boldsymbol{c}} \) =\( \sqrt{\frac{3 K T}{M}} \) where K is Boltzmann’s constant, T is absolute temperature and M is mass of one molecule of gas.
Answer:
According to kinetic theory of gases,
\( \overline{\boldsymbol{c}} \) = \( \sqrt{\frac{3 R T}{M}} \) =\( \sqrt{\frac{3 R T}{mN}} \), [∵M= mn]
= \( \sqrt{\frac{3 K T}{m}} \), [∵ K = \( \frac{R}{N} \) ]
or
\( \overline{\boldsymbol{c}} \) ∝ \( \sqrt{T} \)
i.e., r.m.s. value of velocity of gaseous molecule is directly proportional to square root of absolute temperature.

Question 9.
If the number of molecules in a box is halved, then what will be the effect on its pressure?
Answer:
According to kinetic theory of gas, the pressure of gas :
P= \(\frac{1}{3} \frac{m N \bar{c}^{2}}{V}\)
If the number of molecules is halved ,then the pressure of gas :
P’=\(\frac{1}{3} \frac{m}{V} \frac{N}{2} \bar{c}^{2}\)
P’ = \( \frac{1}{2}\left[\frac{m N \bar{c}^{2}}{3 V}\right]\)
or
\(\frac{P^{\prime}}{P}\) = \(\frac{1}{2}\)
or
P’ = \(\frac{1}{2}\)P
Thus, the pressure will Also be halved.

Question 10.
Derive Boyle’s law on basis of kinetic theory of gases.
Answer:
Derivation of Boyle’s law: According to kinetic theory of gases the pressure exerted by gas is :
P = \(\frac{1}{3}\) \( \frac{m N \bar{c}^{2}}{V} \)
or
PV = \( \frac{1}{3} \) \( m N \bar{c}^{2} \)
= \( \frac{1}{3} \) . \( m N \bar{c}^{2} \)
= \( \frac{2}{3} \).N .\(\frac{1}{2} \) \( m \bar{c}^{2}\)
= \( \frac{2}{3} \) NE, [ ∵ E = \( \frac{1}{2} \) \( m \bar{c}^{2}\)]
= \( \frac{2}{3} \) NKT, (∵E = KT ) …….. (1)
If the mass and absolute temperature of gas are constant,then
= \( \frac{2}{3} \) NKT be also constant
∵ PV = constant
This is Boyle’s law.

Question 11.
Derive Ctiarie’s law on basis of kinetic theory of gases.
Answer:
Derivation of Charle’s law : According to kinetic theory of gases, the pressurue exertd by gas is
P = \( \frac{1}{3} \) \( \frac{m N \bar{c}^{2}}{V} \) …….. (1)
or
PV = \( \frac{1}{3}\) \( m N \bar{c}^{2} \)
or
PV = \( \frac{1}{3} \) \( M \bar{c}^{2} \) ……… (2)

Where, M = mN is mass of gas which remains constant .
If the pressure of gas remains constant,then from the above equation.
V= \( \frac{M}{3 P} \bar{c}^{2} \)
or
V ∝\( \bar{c}^{2} \)
or
Since, \( \bar{c}^{2} \) ∝T therefore
V ∝T
This is Charle’s law.

Question 12.
Derive Dalton’s law of partial pressure on basis of kinetic theory of gases.
Answer:
Dalton’s law of partial pressure: According to Dalton’s law of partial pressure, the total pressure exerted by a mixture of gases which do not interact in any way is equal to the sum of their individual pressure.
Let us consider about a vessel of volume V₁ having number of gases mixed together.
Let the gases one, two, three ………….contain N₁ molecules of mass muN₂ molecules of mass
m₂, N₃ molecules of mass m₃ ……………respectively. Let their root mean square velocities are
\( \bar{c}_{1}, \bar{c}_{2}, \bar{c}_{3}\)…………… respectively.

Then the pressure due to first gas
P₁ = \( \frac{1}{3} \) m₁N₁c^-2
Similarly, the pressure due to second, third,………….gases are

If all the gases are mixed at same temperature, then mean kinetic energy óf the molcules of each gas will be the same i.e.,


This is Delton’s law of partial pressure.

Question 13.
A vessel is filled up with mixture of two different gases. Explain with reason :
(i) Is Average kinetic energy per unit molecule are same?
(ii) Is root-mean-square value of velocity are same?
(iii) Is pressure same?
Answer:
(i) Yes, as E = \(\frac{3}{2} \)KT, it depends on absolute temperature only.

(ii) No, because \( \bar{c} \) = \( \sqrt{\frac{3 R T}{M}} \) and it depends on molecular weight M and temperature T.

(iii) Nothing cannot be said about pressure as mass is not known.

Question 14.
Write the law of equipartition of energy.
Answer:
According to this law, for any dynamical system in thermal equilibrium, the total energy distributed equally amongst all the degree of freedom, and the energy associated
with each molecule per degree of freedom is\( \frac{1}{2} \) KT, where K is Boltzmann’s constant and T is temperature of the system.

Question 15.
Explain degree of freedom.
Answer:
The number of degrees of freedom of a dynamical system is defined as the total number of coordinates or independent quantities required to describe completely the position and configuration of the system.
For Example:
(i) When a particle moves along a straight line, say along X-axis, its position can be specified by its displacement along the X-axis. Therefore, such a particle has one-translational degree of freedom.

(ii) If the particle is moving in a plane, its position at any instant can be determined by knowing the displacements of the particle along the X-axis and Y-axis. Therefore it has two- translational degrees of freedom.

(iii) If the particle is moving in space, its position at any instant can be determined by knowing the displacement of the particle along X-axis, Y-axis and Z-axis. Therefore, such a particle has three-translational degrees of freedom.
For example, a bob of an oscillating simple pendulum has one degree of freedom, an insect moving on a horizontal floor has two degrees of freedom and a buzzing bee has three degrees of freedom.

Question 16.
Find out ratio of specific heats for monoatomic gas.
Answer:
For monoatomic gas like He or Ar, whose degree of freedom is 3 but according to law of equipartition of energy.
Energy =3 × \( \frac{1}{2} \) KT = \( \frac{3}{2} \)kT
But energy associated with one mole of gas
U =\( \frac{3}{2} \) nkT
Where n is number of gas molecule for 1 mole of gas.
But Boltzmann’s constant k = \( \frac{R}{n} \)
or
nk = R
Putting value in eqn. (1), we get
U = \( \frac{3}{2} \)RT
But C_v = \( \frac{d U}{d T} \) = \( \frac{d}{d T} \) \( \left(\frac{3}{2} R T\right) \)
or
C_v =\( \frac{3}{2} \) R

Question 17.
Find out ratio of specific heat for diatomic gas.
Answer:
For diatomic gas like Hydrogen, Oxygen etc. degree of freedom is 5.
Therefore energy associated with one mole of gas is
U = \(\frac{5}{2} \)nkT
or
U= \(\frac{5}{2} \)RT
But, nk =R

since C_v = \( \frac{d U}{d T} \) = \( \frac{d}{d T} \) \( \left(\frac{5}{2} R T\right) \) =\(\frac{5}{2} \) R
∴ From C_p – C_v = R
C_p = R +C_v
or
C_p = R +\(\frac{5}{2} \) R = \(\frac{7}{2} \) R
∴ γ = \( \frac{C_{P}}{C_{V}} \) = \( \frac{\frac{7}{2} R}{\frac{5}{2} R} \) = \(/frac{7}{5} \) = 1.40

Question 18.
Find out ratio of specific heat for triatomic gas.
Answer:
For triatomic gas like C02, H2S degree of freedom is 6. Energy associated with one mole of gas is
U =\(\frac{6}{2} \)nKT
or
U = \(\frac{6}{2} \)RT = 3RT

But Cv=\( \frac{d U}{d T} \) = \( \frac{d}{d T} \) (3RT) = 3R
∴ From C_p-C_v = R
C_p =R + C_v =R + 3 R = 4R
∴ γ = \( \frac{C_{P}}{C_{V}} \) = \( \frac{4_{R}}{3_{R}} \) = \(\frac{4}{3} \) = 1.33

Kinetic Theory Class 11 Important Questions Long Answer Type

Question 1.
Establish formula for pressure of a gas on the basis of kinetic theory of gases.
Answer:
When a gas is filled in a closed vessel, then molecules of gas are in state of continuous random motion. They collide with one another and also with the walls of con-tainer. Due to these collisions, the molecules of gas exert the force on the walls of the vessel. The force acting per unit area of the walls is called pressure of gas.
Let us consider a hollow cubical vessel of sides of length ‘l’ as depicted in fig. An ideal gas is filled in it. Let the mass of one molecule is m. Consider a molecule of gas moving with velocity C. The components of velocity C along X, Y and Z direction are, u, v and w respectively.
∴ C² = u²+ v² + w² ……….. (1)
Let us consider about two faces A and B, perpendicular to the direction of X-axis.

If the molecule P collides with the face A with velocity u. It will returned with a velocity -u after collision.
∴ Linear momentum of molecule before collision = mu Linear momentum of molecule after collision = – mu.
∴ Change in linear momentum due to collision = mu – (-mu) = 2mu
The molecule rebounded from A collides with the opposite face B, rebounds and again strikes with face A. Thus, the total distance travelled by the molecule will be 2l.

∴ Time taken by the molecule in travelling the distance 2l be
= \( \frac{2_{l}}{{u}} \), [ ∵ T ime = \( \frac{\text { Distance }}{\text { Velocity }} \) ]
Thus, after covering the distance 21 i.e., after every interval \( \frac{2l}{u} \) , the molecule P will
again strike with the face A.
Number of collision with face A per second be = \( \frac{u}{2 l} \)
The momentum transferred by molecule to the face A per second i.e., rate of change ofmomentum
= 2mu ×\( \frac{u}{2 l} \) = \( \frac{m u^{2}}{l} \)

But according to Newton’s second law of motion, the rate of change of momentum is equal to the force exerted on that face.
∴The force exerted by molecule at face Abe = \( \frac{m u^{2}}{l} \)
∴ Pressure exerted by the molecule on the face A be
= \( \frac{\mathrm{mu}^{2}}{\mathrm{l}} \) = \( \frac{n u^{2}}{l^{3}} \)

Let N be the number of molecules in gas and their velocity components along X direction are u₁, u₂, u₃, un respectively, then pressure exerted by these molecules on the face A

Where, V = l³ = Volume of vessel i.e., volume of gas.
Similarly, the pressure exerted by N molecule along Y-axis and Z-axis be
P_y = \( \frac{m}{V} \) \( \left[v_{1}^{2}+v_{2}^{2}+v_{3}^{2}+\ldots \ldots+v_{n}^{2}\right] \) ……… (3)
P_z = \( \frac{m}{V} \) \( \left[w_{1}^{2}+w_{2}^{2}+w_{3}^{2}+\ldots \ldots+w_{n}^{2}\right] \) ………… (4)
But a gas exerts the same pressure in all directions i.e., P_x=P_y=P_z=P (say)
∴ P = \( \frac{P_{x}+P_{y}+P_{z}}{3} \) …………….. (5)
Hence, from eqns. (2), (3), (4) and (5),
P = \( \frac{P_{x}+P_{y}+P_{z}}{3} \)

Let \( \bar{c} \) = \( \sqrt{\frac{c_{1}^{2}+c_{2}^{2}+\ldots . .+c_{n}^{2}}{N}} \) where \( \bar{c} \) is root mean square velocity , then
N\( \bar{c}^{2}\) = \( c_{1}^{2}+c_{2}^{2}+\ldots \ldots+c_{n}^{2} \) ………….. (7)

From eqns. (6) and (7),
P = \( \frac{m}{3 V} \)N\( \bar{c}^{2}\)
or
P = \( \frac{m N \bar{c}^{2}}{3 V} \)
This is expression of pressure exerted by gas.

Kinetic Theory  Class 11 Important Numerical Questions

Question 1.
Up to what temperature should an ideal gas initially at 27°C be heated so that its volume becomes doubled at constant pressure?
Solution:
Given:T₁ = 27°C = 273+27 = 300K
V₁ = V,V₂ = 2V
∴ According to Charle’s law,
\( \frac{V_{1}}{T_{1}} \) = \( \frac{V_{2}}{T_{2}} \)
or
T₂ = \( \frac{V_{2}}{V_{1}} \) T₁= \(\frac{2 V}{V} \) × 300
= 600 K
= 600 – 273 = 327°C

Question 2.
A gas is filled in a vessel at 127°C at 4 atm. pressure. If the temperature of gas increased up to 527°C, then what would be the pressure of gas?
Answer:
T₁ = 127°C = 127+273 = 400K
T₂ = 527°C = 527 + 273 = 800 K
P₁ = 4 atm. pressure
∴ By the pressure law,

\( \frac{P_{1}}{P_{2}} \) = \( \frac{T_{1}}{T_{2}} \)
or
P₂ = P₁ \( \frac{T_{2}}{T_{1}} \) = 4 × \( \frac{800}{400} \) = 8
= 8 atm.pressure

Question 3.
Number of molecule per cubic centimetre ¡n a space is five and temperature is 3 K. What will be the pressure, there? (R 1.38 × 10^-23 joule/m/K)
solution:
PV = nRT
P = \( \frac{n R T}{V} \)
Given: V = 1 cm³ = 10 ^-6, R = 1.38 ×10^-23 J/m /K, n =5 , T = 3K
∴ P = \( \frac{5 \times 1 \cdot 38 \times 10^{-23} \times 3}{1} \) = 2.07 ×10^-22N/m²

Question 4.
Temperature of any gas is -68°C. By what temperature it must be heated so that
(i) kinetic energy between the molecules become double
(ii) value of velocity of molecule become double.
Solution :
(i) From E = \(\frac{3}{2} \)KT,
E ∝ T
or
\( \frac{E_{1}}{E_{2}} \) = \( \frac{T_{1}}{T_{2}} \)
Given: E ₂ = 2E₁,=T₁ = 273-68 = 205 K
∴ \( \frac{E_{1}}{2 E_{1}} \) = \( \frac{205}{T_{2}} \)
or
T ₂ = 205 ×2 = 410K = 410 – 273° =137°C

(ii) From C^-2 = \( \frac{3 R T}{\gamma} \) we get
\( \bar{c}^{2}\) ∝ \( \sqrt{T} \)
or
\(\frac{\bar{c}_{1}}{\bar{c}_{2}}\) = \( \sqrt{\frac{T_{1}}{T_{2}}} \)
Given: \(\bar{c}_{2}\) = 2\( \bar{c}_{1} \) ,T ₁ = 205K
∴ \( \frac{\bar{c}_{1}}{\bar{2c}_{1}} \) = \( \sqrt{\frac{205}{T_{2}}} \)
or
\( \frac{1}{4} \) =\( \frac{205}{T_{2}} \)
or
T ₂ = 205 × 4 = 820
or
T ₂ = 820 – 273 = 574°C

Question 5.
At 30°C temperature, mixture of Helium and Hydrogen gas is filled in a vessel. Find out the ratio of r.m.s. value of velocity of the molecule at this temperature.
Solution:
From C^-2 = \( \frac{3 R T}{M} \)
\( \bar{c} \) = \( \frac{1}{\sqrt{M}} \)
or
\( \frac{\bar{c}_{1}}{\bar{c}_{2}} \) = \( \sqrt{\frac{M_{2}}{M_{1}}} \)

Given, molecular weight of Helium M₁ = 4
and Molecular weight of Hydrogen M₂ =2
∴ \( \frac{\bar{c}_{1}}{\bar{c}_{2}} \) = \( \sqrt{\frac{2}{4}} \) = \( \frac{1}{\sqrt{2}} \) = 1:\( \sqrt{2} \)
or
\( \bar{c}_{1} \): \( \bar{c}_{2} \) = 1:\( \sqrt{2} \)

Question 6.
If the absolute temperature of gas is done four times then by how much times their r.m.s. velocity of molecule increases? Also by how much times their kinetic energy and pressure also increases?
Solution: From \( \bar{c} \) = \( \frac{3 R T}{M} \) , where R and M are constant
∴ \(\bar{c} \) ∝ \( \sqrt{T}\)
or
\( \frac{\bar{c}_{1}}{\bar{c}_{2}} \) = \( \sqrt{\frac{T_{1}}{T_{2}}} \)
or
\( \frac{\bar{c}_{1}}{\bar{c}_{2}} \) = \( \sqrt{\frac{T_{1}}{4 T_{1}}} \) = \( \sqrt{\frac{1}{4}} \) = \( \frac{1}{2} \)
or
\( \bar{c}_{2} \) = 2 \( \bar{c}_{1} \)
i.e., r.m.s velocity will increase by two Times

From formula E = \( \frac{3}{2} \) KT
E ∝ T or \( \frac{E_{1}}{E_{2}} \) = \( \frac{T_{1}}{T_{2}} \)
Putting T₂ = 4T₁
\( \frac{E_{1}}{E_{2}} \) = \( \frac{T_{1}}{4 T_{1}} \) = \( \frac{1}{4} \)
or
E₂ = 4E ₁
\( \frac{P_{1}}{P_{2}} \) = \( \frac{T_{\mathrm{l}}}{4 T_{1}} \) = \( \frac{1}{4} \)
or
P₂ = 4P₁
∴ Pressure will become four Times.

Question 7.
If the temperature of a gas increased from 77°C to 227°C, then what will be the ratio of kinetic energy of then molecules?
Solution:
Given:T₁ = (273+ 77)K = 350K and T₂ = (273 + 227)K = 500K.
From formula E ∝ T
\( \frac{E_{1}}{E_{2}} \) = \( \frac{T_{1}}{T_{2}} \) = \( \frac{350}{500}\) = \( \frac{7}{10} \)
E₁: E ₂ = 7 : 10

Question 8.
Volume of vessel is two times the volume of vessel B and same gas is filled in both vessels. If the temperature and pressure of the vessel A is double w.r.t. vessel B, then what will be the ratio of molecules of the gas of vessel A and B?
Solution:
From PV = nRT

Question 9.
The velocities of four molecules of a gas are 2, 4, 6 and 8 km/sec.
Calculate : (i) Average velocity, (ii) root-mean-square velocity.
Solution:
Given : c₁ = 2 km/sec, c₂ = 4 km/ sec, c₃ = 6 km/sec and c4 = 8 km/sec.
(i) Average velocity:
c = \( \frac{c_{1}+c_{2}+c_{3}+c_{4}}{4} \)
= \( \frac{2+4+6+8}{4} \) = 5 km/sec

(ii) Root-mean-square velocity:

Question 10.
Estimate the fraction of molecular volume to the actual volume occupied by oxygen gas at N.T.P. Take the diameter of oxygen molecule to be roughly 3Å. (NCERT)
Solution:
Given, diameter of one molecule of oxygen = 3 Å
∴ Radius r = \( \frac{3}{2} \) = 1.5 Å = 1.5 × 10 ^-10m
∴ Volume of one molecule of oxygen = \( \frac{4}{3} \) πr³
= \( \frac{4}{3} \) ×3.14 (1.5 × 10 ^-10)³
= 14.13 × 10 ^-30 m³
∴ Volume of 1 mole of oxygen = 6.02 × 10 ²³ × 14.13 ×^-30
= 85.06 × 10 ^-7 m³

The volume of 1 mole of oxygen at STP = 22.4 litre
= 22.4 × 10^-3m³
∴ Fraction of the molecular volume of the actual volume = \( \frac{85 \cdot 06 \times 10^{-7}}{22 \cdot 4 \times 10^{-3}} \)
= 3.797 × 10 ^-4
= 3.8 ×10^-4 ≈ 4 × 10^-4

Question 11.
Molar volume is the volume occupied by 1 mole of any ideal gas at standard temperature and pressure (STP: 1 atm pressure, 0°C). Show that it is 22.4 litre. (NCERT)
Solution:
At S.T.P., T = 0°C = 0 + 273 =273K
Pressure P = 1 atm = 1-013 x 10⁵Nm^-2 ; R = 8.3 J mol^-1‘K^-1 By gas equation
∴ By gas equation for 1 mole PV =RT
V = \( \frac{R T}{P} \) = \( \frac{8 \cdot 3 \times 273}{1 \cdot 013 \times 10^{5}} \)
= 2236.82 ×10 ^-5
= 22.3682 ×10 ^-3 m ³
= 22.4 ×10 ^-3m ³ = 22.4 litre.

Question 12.
An air bubble of volume l-0cm3 rises from the bottom of a lake 40m deep at a temperature of 12°C. To what volume does it grow when it reaches the surface which is at a temperature of 35°C? (NCERT)
Solution:
Given, Initial volume of bubble
V₁ = 10cm³ = 1.0 × 10^-6m³
Initial temperature T₁ = 273 +12 = 285 K
Initial pressure on bubble P₁ = Atmospheric pressure + Pressure of 40 m high water column
= 1.013×10⁵+hdg
= 1.013×10⁵ + 40×10³ × 9.8
= 4.933 × 10⁵ Pa

Final pressure on bubble P₂ = 1 atm = 1.013 ×10⁵ Pa
Fina temperature T₂ = 273+ 35=308 K
From the equation \( \frac{P_{V_{1}}}{T_{1}} \) = \( \frac{P_{2} V_{2}}{T_{2}} \)
or
V₂ = \( \frac{P_{V_{1}}}{T_{1}} \) ×\( \frac{T_{2}}{P_{2}} \) = \( \frac{4 \cdot 933 \times 10^{5} \times 1 \cdot 0 \times 10^{-6} \times 308}{285 \times 1 \cdot 013 \times 10^{5}} \)
= 5.26 ×10^-6 m³ ≈ 5.3 × 10^-6 m³

Question 13.
At what temperature is the root-mean-square speed of an atom is an argon gas cylinder equal to the r.m.s. speed of a helium gas atom at – 20°C? (Atomic mass of Ar = 39.9 u, of He = 4.0 u). (NCERT)
Solution:
Given, atomic mass of He M₁=4.0u
Atomic mass of Ar M₂ =39.3u
Temperature of He gas T ₁ = -20+273 = 253K

Kinetic Theory  Class 11 Important Questions Objective Type

1. Multiple- choice questions:

Question 1.
There are N molecules in a vessel, if the number of molecules are doubled then the pressure of gas will be :
(a) Double
(b) Remain same
(c) Become four times
(d) Become one fourth.
Answer:
(a) Double

Question 2.
Motion of gaseous molecule at absolute zero temperature :
(a) Become less
(b) Increases
(c) Become zero
(d) None of these.
Answer:
(c) Become zero

Question 3.
At -273°C, molecules of gas moves with :
(a) Maximum velocity
(b) Minimum velocity
(c) Zero velocity
(d) None of these.
Answer:
(c) Zero velocity

Question 4.
Reason for deviating from gaseous law of ideal gas at less temperature is :
(a) Maximum collision become inelastic
(b) Volume of molecules cannot be negligible
(c) Force acting between molecules become less
(d) Molecular velocity become less.
Answer:
(b) Volume of molecules cannot be negligible

Question 5.
Root-mean-square velocity of ideal gas molecules at constant temperature :
(a) Remain same
(b) Inversely proportional to square root of molecular weight
(c) Proportional to square root of molecular weight
(d) Inversely proportional to molecular weight.
Answer:
(b) Inversely proportional to square root of molecular weight

Question 6.
Graph between PV and P of a gas which obey Boyle’s law will be :
(a) Hyperbola
(b) Parallel line with PV axis
(c) Parallel line with P axis
(d) None of these.
Answer:
(c) Parallel line with P axis

Question 7.
False statement regarding kinetic theory of gas is :
(a) Collision between two molecules are perfectly elastic
(b) Kinetic energy between molecules is proportional to absolute temperature
(c) Absolute temperature of gas is inversely proportional to root-mean-square velocity.
(d) At absolute temperature average kinetic energy of molecules is zero.
Answer:
(c) Absolute temperature of gas is inversely proportional to root-mean-square velocity.

Question 8.
Reason for pressure exerted by gaseous molecules on the wall of vessel is :
(a) Losses its own kinetic energy
(b) Get stick with the walls of vessel
(c) Due to collision with wall of vessel its momentum get change
(d) Get accelerated toward wall.
Answer:
(c) Due to collision with wall of vessel its momentum get change

Question 9.
There is no atmosphere in moon, because :
(a) It is closer to earth
(b) It revolve around the earth
(c) It obtain light from sun
(d) Escape velocity is less than root-mean-square velocity.
Answer:
(d) Escape velocity is less than root-mean-square velocity.

Question 10.
The temperature of an ideal gas is raised from 27°C to 927°C the root-mean-square velocity of its molecules will become :
(a) Two times
(b) Half
(c) Four times
(d) One fourth.
Answer:
(a) Two times

Question 11.
Every gas behaves as ideal gas at:
(a) Low pressure and high temperature
(b) High pressure and low temperature
(c) At equal pressure and temperature
(d) High pressure and high temperature.
Answer:
(a) Low pressure and high temperature

Question 12.
Unit of universal gas constant is :
(a) joule/mole-kelvin
(b) mole/joule-kelvin
(c) joule-mole-kelvin
(d) kelvin/joule/mole.
Answer:
(a) joule/mole-kelvin

Question 13.
If the temperature of gas remain constant and pressure become half then the volume will get.
(a) Half
(b) Double
(c) Unchanged
(d) Four times.
Answer:
(b) Double

Question 14.
In gas equation PV = RT, V is volume of:
(a) Gas
(b)1 gram gas
(c) 1 litre gas
(d) 1 mole gas.
Answer:
(d) 1 mole gas.

Question 15.
Pressure of gas filled in closed vessel is due to :
(a) Large number of molecules
(b) Attraction between wall and molecules
(c) Collision of molecules with wall
(d) None of these.
Answer:
(c) Collision of molecules with wall

Question 16.
The average kinetic energy associated with each degree of freedom is :
(a) \( \frac{3}{2} \) KT
(b) KT
(c) \( \frac{1}{2} \) KT
(d) \( \frac{3}{2} \) RT.
Answer:
(c) \( \frac{1}{2} \) KT

Question 17.
The mean kinetic energy of the molecule of gas depends upon :
(a) Nature of gas
(b) Absolute temperature
(c) Volume of gas
(d) None of these.
Answer:
(b) Absolute temperature

Question 18.
Root-mean-square velocity of gas is :
(a) Directly proportional to its specific molecular weight
(b) Directly proportional to its square of molecular weight
(c) Directly proportional to its molar weight
(d) Directly proportional to its absolute temperature.
Answer:
(c) Directly proportional to its molar weight

Question 19.
Magnitude of R for 1 gram mole of gas is :
(a) 8.31 erg
(b) 8.31 MKS unit
(c) 4.2 joule
(d) 4.2 calorie.
Answer:
(b) 8.31 MKS unit

Question 20.
If the r.nus. velocity of a gas is doubled, then its pressure will:
(a) Increase
(b) Decrease
(c) Remain same
(d) None of these.
Answer:
(a) Increase

2. Fill in the blanks:

1. Momentum applied per unit area on the wall of a vessel by the molecule of gas is equal to ………………………. .
Answer:
Pressure

2. At absolute temperature ………………………. of gas becomes zero.
Answer:
Kinetic energy

3. For a diatomic gas, the degree of freedom is ………………………. .
Answer:
Five

4. Kinetic energy associated with each degree of freedom is ………………………. .
Answer:
\( \frac{1}{2} \)KT

5. The value of 0°C on the kelvin scale is ………………………. .
Answer:
273 K.

3. Match the following:

 Answer:
1. (e) \( \frac{1}{3} \) \( \frac{m N}{V} \)c^-2
2. (d) ∝ c^-2
3. (a) ∝ T
4. (b) 3
5. (c) 5.

Students get through the MP Board Class 11th Physics Important Questions Chapter 14 Oscillations  which are most likely to be asked in the exam.

MP Board Class 11th Physics Important Questions Chapter 14 Oscillations

Oscillations Class 11 Important Questions Very Short Answer Type

Question 1.
Define simple harmonic motion with example.
Answer:
When a body moves to and fro about a point in a straight line such that its acceleration is always directly proportional to the displacement and directed towards the mean position, then its motion is called simple harmonic motion.
Example: Motion of a body suspended by a spring, motion of simple pendulum.

Question 2.
What is oscillatory motion?
Answer:
When a body moves periodically to and fro or back and forth about a definite point, then its motion is called oscillatory motion.
Motion of simple pendulum, vibration of tuning fork etc. are the examples of oscillatory motion.

Question 3.
For what type of motion of a body acceleration is directly proportional to displacement?
Answer:
It is simple harmonic motion.

Question 4.
When the velocity and acceleration will be maximum in S.H.M.?
Answer:
The velocity is maximum at the mean position and acceleration is maximum at the extreme position.

Question 5.
Write the formula for kinetic energy and potential energy for a body executing S.H. M.?
Answer:
Kinetic Energy = \(\frac{1}{2} m \omega^{2}\left(a^{2}-y^{2}\right)\)
Potential Energy = \(\frac{1}{2} m \omega^{2} y^{2}\)
Where m – particle of mass,
ω – angular frequency,
a – amplitude and
y = displace-ment of the particle form its mean position.

Question 6.
At which position kinetic energy and potential energy is zero for a body executing S.H.M.?
Answer:
At maximum displacement position (y = ±a) kinetic energy is zero and at mean position (y = 0) potential energy is zero.

Question 7.
Define simple pendulum.
Answer:
When a heavy point mass is suspended by a weightless, inextensible and perfectly flexible string by a rigid support, then it is called simple pendulum.

Question 8.
Which of the following relationships between acceleration ‘a’ and the dis-placement x: of a particle involve simple harmonic motion ? (NCERT)
(a) a = 0.7x,
(b) a = 200x²,
(c) a = -10x²
(d) a = 100x³.
Answer:
In a S.H.M. the relation between acceleration and displacement is
a=-ω²x
(a) a = 0.7 x
Comparing with eqn. (1),
-ω² = 0.7
or’
ω = \(\sqrt{-0 \cdot 7}\)
∵ Value of a is not real therefore the motion is not S.H.M.

(b) a = -200x²
This motion is not a S.H.M.

(c) a = -10x
Comparing-with eqn. (1),
ω² =10
or
ω = \(\sqrt{10}\)
∵ ω has a real value therefore, the relation shows a S.H.M.

(d) a = 100 x³
This motion is not a S.H.M.

Question 9.
The length of a spring is increased, how the time-period be affected?
Answer:
The time-period will increase.

Question 10.
On which conservation law S.H.M. is based?
Answer:
S.H.M. is based on law of conservation of energy.

Question 11.
What is second pendulum? What is its length?
Answer:
The pendulum whose periodic time is two seconds is known as second pendulum. The length of second pendulum is about 100 cm.

Question 12.
Write the characteristics of S.H.M.
Answer:
Characteristics of S.H.M.:

• The motion is periodic.
• The particle moves to and fro about a point in a straight line.
• The acceleration is directly proportional to the displacement.
• The direction of acceleration is always towards the mean position.

Question 13.
Define time-period, frequency and amplitude.
Answer:
Time period: The time taken by an oscillating body to complete one oscillation is called time-period.
Frequency: The number of vibrations or oscillations in one second is called frequency.
Amplitude: The maximum displacement of a particle about its mean position is called amplitude. It is denoted by a or A.

Question 14.
What is the relation between S.H.M. and Circular motion?
Answer:
When any particle is performing uniform motion on the circumference of a circle, then the perpendicular dropped on the diameter of the circle from any point of rotation execute S.H.M. along the diameter of circle.

Question 15.
Define spring constant and write its S.I. unit and dimensional formula.
Answer:
Spring constant: The force required to elongate or compress a spring through unit length is called spring constant.
Unit: SI unit of spring constant is Nm1.
Dimensional formula : Dimensional formula is [ML°T^-2].

Question 16.
Write the formula for the time-period of a body suspended by a spring.
Answer:
Where, T= Time-period, m = Mass suspended and k = Force constant.

Question 17.
What is meant by the effective length of a simple pendulum?
Answer:
The length of pendulum from the point of suspension to the centre of bob is called effective length.

Question 18.
Why the length of simple pendulum is measured up to the centre of the bob?
Answer:
The centre of gravity point of spherical bob lies at its centre. The concept of heavy point mass is assumed that the weight of the body acts at the C.G. point. Therefore the effective length is measured up to centre of the bob.

Question 19.
How time period of a simple pendulum change with effective length of a simple pendulum.
Answer:
We know \(T=2 \pi \sqrt{\frac{l}{g}}\)
or
T ∝ \(\sqrt{l}\)
When effective length is increased, time period also get increased.

Question 20.
Can the pendulum clock be used in a satellite?
Answer:
No, because g = 0 inside satellite, therefore T = ∞.
So, in place of pendulum clock, spring clock can be used inside it.

Question 21.
The pendulum clock cannot be used in artificial satellite. Why?
Answer:
In an artificial satellite, the bodies are in the state of weightlessness. Hence, g becomes zero. Thus, the time-period becomes infinite.Therefore, it cannot be used in the satellite.

Question 22.
A boy is swinging, sitting on a swing. If another boy sits beside him, what will happen to its time-period?
Answer:
The time period is independent of mass, hence there will be no effect.

Question 23.
A boy is swinging, standing on a swing. If he sits on it, what happen to the time-period?
Answer:
When the boy will sit on the swing, his C.G. point will shift downwards. Hence, the effective length will increase therefore the time-period will also increase.

Question 24.
What is the reason that the frequency of oscillation clocks depend on the rise and fall of mercury level in the thermometer?
Answer:
If the mercury level increases, it shows that temperature has increased and the decreases in mercury level shows a decrease in temperature. Due to increase in temperature, the length of pendulum increases and \(T \propto \sqrt{l}\) so time period also increases. Hence clock runs slow, i.e., the frequency of oscillation decreases. But with decrease in temperature, length decreases and so time-period decreases. Hence clock runs fast i.e., frequency of oscillation increases.

Question 25.
The pendulum clock becomes fast when it is taken to pole from equator. Why?
Answer:
We have, T = \(2 \pi \sqrt{\frac{l}{g}}\)
If l is constant ,then T ∝ \(\frac{1}{\sqrt{g}}\)
Hence, time-period is inversely proportional to the square root of acceleration due to gravity. At poles the value of g is greatest, hence the time-period will decrease at poles, hence the clock will be fast.

Question 26.
Why pendulum clock does not show time at satellite?
Answer:
At satellite g = 0, therefore, i.e., time period of pendulum become infinity, therefore it does not show time of satellite.

Question 27.
What is damped oscillation?
Answer:
When the amplitude of an oscillating body decrease gradually by some external opposing force, then its oscillation is called damped oscillation.

Question 28.
Define forced vibration.
Answer:
When an oscillating body oscillates under the influence of some external force, then it oscillates with the frequency of external force, then its oscillation is called forced vibration.

Question 29.
What do you mean by forced oscillation?
Answer:
When the body oscillate under the influence of an external periodic force, with a constant amplitude and a frequency equal to the periodic force, the oscillation of the body is called forced oscillation.

Question 30.
Define resonance.
Answer:
When a body vibrates under the influence of a periodic force and its frequency becomes equal to that of periodic force then the amplitude of the body increases. This phenomenon is known as resonance.

Question 31.
Why marching troops are asked to break their steps while crossing the bridge?
Answer:
The footsteps of marching troops produces a periodic force on the bridge. If the frequency of foot-steps becomes equal to the natural frequency of bridge, the amplitude of bridge will increase and hence the bridge may break.

Question 32.
What is the effect of forced oscillation on amplitude and frequency?
Answer:
Due to forced oscillation amplitude of oscillating body go on reducing and frequency become less than the natural frequency.

Question 33.
When forced oscillation become resonance oscillation?
Answer:
When the natural frequency of the body becomes equal to the frequency due to periodic force then forced oscillation is converted into resonance oscillation.

Question 34.
A simple pendulum is suspended in a lift, whose time-period is T. What will aeration ‘a’ (i) upward, (ii) downward.
Answer:
(i) When the lift accelerate with acceleration ‘a’ upward then the time-period will decrease
( T = \(2 \pi \sqrt{\frac{l}{g+a}}\))
(ii) On acceleration with acceleration ‘a’ downward then its timeperiod will increase
( T = \(2 \pi \sqrt{\frac{l}{g-a}}\) )

Question 35.
What will be the time-period of effective length infinity?
Answer:
84.6 minute.

Question 36.
What will be the time period of pendulum at the centre of earth? Why?
Answer:
At the centre of earth the time-period of pendulum will be infinity as ‘g’ is zero at the centre.

Question 37.
A spring of spring constant k is cut into three equal pieces. What will be the time period of each?
Answer:
The spring constant of each piece will be 3k.

Oscillations Class 11 Important Questions Short Answer Type 

Question 1.
The bob of simple pendulum is a ball filled with water, if a small hole is made at the bottom of the ball, how will its time period change as water is drains out of it?
Answer:
When the ball is completely filled with water, its centre of gravity be at its geometric centre. So, it will oscillate with definite time period. But as the water drains out of it through the hole, the centre of gravity is displaced gradually downward. Hence the effective length also increases gradually. Therefore the time period of the pendulum also increases gradually. But when whole of the water is removed then its centre of gravity again shifted to its geometric centre and its time-period become same as was in initial position.

Question 2.
What is simple harmonic motion. Write its four characteristics.
Answer:
When a body moves to and fro about a point in a straight line such that its acceleration is always directly proportional to the displacement and directed towards the mean position, then its motion is called simple harmonic motion.
Example: Motion of a body suspended by a spring, motion of simple pendulum.
Characteristics of S.H.M.:

• The motion is periodic.
• The particle moves to and fro about a point in a straight line.
• The acceleration is directly proportional to the displacement.
• The direction of acceleration is always towards the mean position.

Question 3.
Write the relation between acceleration and displacement of a particle ex-ecuting1 S.H.M. Also deduce expression for time-period from it?
Answer:
Acceleration of the particle with displacement y is α = -ω²y
Where ω is angular velocity of particle here (-) sign indicate the direction of accel-eration only.
Hence, ω² = \(\frac{\alpha}{y}\) = \(\frac{\text { Acceleration }}{\text { Displacement }}\)
or
ω = \(\sqrt{\frac{\alpha}{y}}\)
But T =\(\frac{2 \pi}{\omega}=\frac{2 \pi}{\sqrt{\frac{\alpha}{y}}}=2 \pi \sqrt{\frac{y}{\alpha}}\)
T = \(2 \pi \sqrt{\frac{\text { Displacement }}{\text { Acceleration }}}\)

Question 4.
Write the expression for displacement, velocity and acceleration of a particle executing S.H.M. and say :
(i) When the velocity of the particle will be maximum and zero.
(ii) When the acceleration of the particle will be maximum and zero.
Answer:
Displacement y = a sin ωt
Velocity ν = ω \(\sqrt{a^{2}-y^{2}}\)
Acceleration a = – ω²y
Where a is amplitude and ω is angular acceleration.

(i) Velocity is maximum at mean position (y = 0)
νmax = ω.a
Velocity is zero at maximum displacement position ν = 0 , when y = ±a.

(ii) Acceleration is maximum when displacement is maximum (y = ±a)
α = ± ω² a, when y = ±a
Acceleration is zero at mean position α = 0, when y = 0.

Question 5.
What is meant by simple pendulum? When the bob is displaced from its mean position it starts oscillations. Why?
Answer:
If a heavy point mass be suspended by a weightless, perfectly flexible and inextensible string from a rigid support and an arrangement is made for its frictionless oscillations, then this arrangement is called simple pendulum. As shown in fig. when bob is displaced from its mean position A to a position B, then the bob raised up to height ‘h\ so that its potential energy increases.

Now, if the bob is released, then its centre of gravity falls down to obtain the stable equilibrium and when it reaches to the mean position its potential energy is converted into kinetic energy. At points, it will not stay, but due to inertia moves forward and hence the bob starts to execute simple harmonic motion to and fro about its mean position.

Question 6.
Write down the formula of time-period of simple pendulum and state the factors on which it does depend.
Answer:
The time-period of simple pendulum is given by :
T = 2π \(\sqrt{\frac{l}{g}}\)
From the above formula, it is clear that the time period of simple pendulum depends on its effective length ‘l’ and acceleration due to gravity ‘g’.
(i) Dependence on length f: The time period of simple pendulum is directly proportional to the square root of effective length of pendulum, i.e., T α \(\sqrt{l}\)
Example: When a boy swinging on a swing stand up suddenly, then his centre of gravity rises up and so the effective length of the swing reduces which results an increase in time period.

(ii) Dependence on acceleration due to gravity ‘g’: The time-period T of simple pendulum is inversely proportional to the square root of acceleration due to gravity at that place i.e., T α \(\frac{1}{\sqrt{g}}\)
Example: When a pendulum is taken up to hills or down in a mine get slow because time-period T increases due to decrease in the value of ‘g’.

Question 7.
Write down the laws of simple pendulum. Give practical application of each law.
Answer:
The laws of simple pendulum and their practical applications are given below :
(i) Law of length: If the value of ‘g’ remains constant, then the time period of simple pendulum is directly proportional to the square root of effecti ve length of simple pendulum.
i-e., T α \(\sqrt{l}\)
This law is used to repair the pendulum clocks when they get slow or becomes fast while taken up to hills or down in a mine.

(ii) Law of acceleration due to gravity : If the effective length of simple pendulum remains constant, then the time period T of the simple pendulum is inversely proportional to the acceleration due to gravity, i.e., T α \(\frac{1}{\sqrt{g}}\)
Due to this reason the pendulum clock get slow while taken up to hills or down in mines.

(iii) Law of mass: The time period of simple pendulum does not depend upon the mass of bob or that of thread.
Hence, either bob is heavy or lighter, if the value of 7’ and ‘g’ are constant, then there is no effect in its time-period. .

(iv) Law of isochronism: If the amplitude of oscillations of simple pendulum are very small, then the time-period of pendulum does not depend upon the amplitude of oscillations.
Because of this, the angular displacement of the bob is kept small in the experiment of simple pendulum.

Question 8.
Establish the relation between time-period and frequency.
Answer:
Let the time-period of a particle is T and its frequency is υ.
∴ The particle complete one vibration in T sec.
Hence, in 1 sec the number of vibration, υ = \(\frac{1}{T}\)
or
υT = 1.

Question 9.
Derive an expression for the displacement of a particle executing S.H.M.
Or
Find an expression for the displacement of S.H.M.
Answer:
Let XYX’Y’ is a circle whose centre is O and radius a. A particle is moving with uniform angular speed ω on the circle.
Let at time t = 0, the particle is at X and in time t, it is at P. A perpendicular PN is drawn on YOY’ from P and N is foot of the perpendicular.

The particle takes t second to subtend an ∠POX = θ.
∴ ω = \(\frac{\theta}{t}\)
or
θ = ωt
Let the displacement ON = y
∴ In ∆ NPO, sin NPO = \(\frac{O N}{O P}\)
But, ∠NPO = ∠POX = θ = ωt
∴ sin ωt = \(\frac{y}{a}\)
or
y = a sin ωt
This is the required equation for the displacement of S.H.M.

Question 10.
Derive the expression for the velocity of a particle executing S.H.M.
Or
Derive an expression for velocity of a particle executing S.H.M. When is the velocity maximum and minimum?
Answer:
Expression for velocity: Let XYX’Y’ is a circle of centre O and radius a. A particle is moving on the circle with angular velocity ω.
Let at t = 0, the particle is at X and after t sec, it is at P.
Let at point P, the velocity of the particle is ν along the tangent at P.

Now, velocity v is resolved into two parts :
(i) ν sin θ, parallel to PN and
(ii) ν cos θ, perpendicular to PN.
Since,ν cos θ is parallel to the direction of motion of foot of the perpendicular N.
∴ Velocity of N, υ = ν cosθ
υ = ν cos ωt.
or
υ = ν \(\sqrt{1-\sin ^{2} \omega t}\)
( ∴ sin² ωt + cos² = 1)

This is the required expression.

Case 1. Ify = 0, then from eqn. (1), we get
ν =ω \(\sqrt{a^{2}-0}\) = ωa
∴ Velocity will be maximum at mean position.
Case 2. If y = a, then from eqn. (1), we get
ν =ω \(\sqrt{a^{2}-a^{2}}=\) = 0
∴ Velocity will be minimum at the extreme position.

Question 11.
Derive the expression for the acceleration of a particle executing S.H.M. Find where the acceleration is maximum and minimum.
Answer:
We have by displacement equation,
y = a sin(ωt + Φ) …(1)
If the acceleration is α, then we have


This is the required expression.
Case 1. If y = 0, then by eqn. (3),
α =0
i.e., at the mean position the acceleration will be zero i.e., minimum.
Case 2. If y = a, then by eqn. (3),
α = – ω²a
i.e., at extreme position the acceleration is maximum.

Question 12.
Derive the expression for the time>period and frequency of a particle ex-ecuting S.H.M.
Answer:
Now, we have the magnitude of acceleration is given by

Again, we know that frequency,
υ = \(\frac{1}{T}\)
∴ υ = \(\frac{1}{2 \pi} \sqrt{\frac{\text { Acceleration }}{\text { Displacement }}}\)

Question 13.
Mass m is suspended by an ideal spring. It oscillates up and down. If the force constant of spring Is k, then prove that the time-period,
T =2 π \(\sqrt{\frac{m}{k}}\)
or
A mass is suspended by a spring. It Is pulled downwards and then left. Prove that it executes S.H.M. Find the expression for time-period.
Answer:
Let a spring is suspended by a rigid support and mass ni is suspended at its lower end.
It is displaced downwards at a distance y and left.
The restoring force F = -ky …( 1)
Where, k is force constant.
Also, by Newton’s second law of motion,
F=mα …………. (2)
Where, α is acceleration.
∴ From eqns. (1)and (2), we get
mα =-ky ……….. (3)
or
α =\(-\frac{k}{m}\) .y
Also, we have, for S.H.M.
α = – ω² y ……..(4)
Since, the L.H.S. of eqns. (3) and (4) are equal, hence the R.H.S. must be equal.

Question 14.
Derive the expression for K.E. and P.E. of a particle executing S.H.M. and also prove that total energy of a particle remains constant.
Answer:
K.E. of the particle : We know that velocity of a particle executing S.H.M. is given by,
ν = ω\( \sqrt{a^{2}-y^{2}} \)

K.E.= \( \frac{1}{2}\)mv²
=\( \frac{1}{2}\) m{ ω\( \sqrt{a^{2}-y^{2}} \)²
=\( \frac{1}{2}\)mω²(a²-y²) …(1)
P.E. of the particle: Now, the acceleration of a particle executing S.H.M. is given by α = -ω²y

Also, by Newton’s second law of motion,
Force = Mass x Acceleration
∴ F = mα
or
F = -mω²y
Now initially the displacement was zero and force was zero. The force was gradually increases and hence the displacement also increases to y.

∴Mean force =\(\frac{0+F}{2} \) = mω²y
∵ Work W= Mean force x Displacement
∴ W = \(\frac{1}{2} \) mω²y ×y
or
W = \(\frac{1}{2} \) mω²y²

By equns.(1) and (2), we get
K.E +P.E = \(\frac{1}{2} \) mω² (a²-y²)+ \(\frac{1}{2} \) mω² y²
or
E = \(\frac{1}{2} \) mω²a² –\(\frac{1}{2}\)mω²y² +\(\frac{1}{2}\)mω²y²
or
E = \(\frac{1}{2}\)mω²a²
As ω and a are constant, therefore the total energy remains constant.

Question 15.
What is second’s pendulum? Calculate its effective length.
Answer:
Second’s pendulum: A simple pendulum whose time-period is 2 seconds, is called second’s pendulum.

Oscillations Class 11 Important Questions Long Answer Type

Question 1.
Deduce the expression for time-period of simple pendulum T = 2π \(\sqrt{\frac{l}{g}} \)
Answer:
Motion of a simple pendulum: Suppose that m is the mass of the bob and l is the effective length of a simple pendulum. S is a point of suspension and O is mean position of the bob. Suppose at any instant during oscillation, the bob is in the position P. Then displacement OP = y and ∠ OSP = θ. In this position of the bob, two forces act upon it:
(i) Tension T is the thread, in the direction PS upward along the thread and

(ii) The weight of the bob, mg, vertically downward. The weight mg can be resolved into two components :
(a) mg cos θ, in the direction SP downward along the thread.
(b) mg sin θ, perpendicular to the thread SP.
The component mg cos θ balances the tension Tin the thread. The component mg sin θ tends to bring the bob back to its mean position. This is known as restorting force on the bob. Thus, the restorting force acting on the bob is given as F= -mg sinθ

Where negative sign shows that the direction of force is opposite to the direction which displacement increases, i.e., towards the mean position O.
1f the angular displacement of the bob be small, then sin θ = 0 (for example, if θ = 5⁰, then sin θ= 0.0872 and θ=0.0873 radian). Thus,
F= -mgθ
But,
θ= \( \frac{\mathrm{Arc}}{\mathrm{Radius}} \) = \( \frac{O P}{S P} \) = \( \frac{y}{l} \)
F= -mg.\( \frac{y}{l} \) …….. (1)

If α be the acceleration produced in the bob due to restoring force, then by Newton’s law of motion
F = mα ……. (2)
From eqns. (1) and (2), we get
mα = -mg \( \frac{y}{l} \)
or
α= –\( \frac{g}{l} \).y …(3)

At a given place g is constant and for a given pendulum is constant.
Therefore,
α ∞ -y …….. (4)
Thus, the acceleration of the bob is directly proportional to its displacement. Hence, for small amplitude, the motion of a simple pendulum is simple harmonic motion. Its periodic time is

Oscillations Class 11 Important Numerical Questions

Question 1.
The time-period of a particle executing S.H.M. is 2 sec. Calculate the time after t =0, that its amplitude behalf of the displacement.
Solution:
Given: T= 2 sec and y = \(\frac{a}{2}\)
∵ y = a sin ωt
Where ω =\( \frac{2 \pi}{T} \)
∴ y = a sin \( \frac{2 \pi}{T} \) t ⇒ \( \frac{a}{2}= \) = a sin \( \frac{2 \pi}{T} \) t

Question 2.
The length of a simple pendulum ¡s 39.2 / π² metre. If g = 9.8 ms^-2, then calculate the time-period of simple pendulum.
Solution:
Given:l = \( \frac{39 \cdot 2}{\pi^{2}} \), g = 9.8 ms^-2
Formula:

Question 3.
The mass of a particle executing S.H.M. is 0.4 kg and amplitude and time period are 0.5 m and π/ 2 respectively. Calculate the velocity and ICE. of particle at a displacement 0.3 m.
Solution :
Given:m = 0.4kg , a = 0.5 m, T= π/2 sec, y = 0.3 m.
Npw we have

Again,

Question 4.
A simple pendulum execute 60 oscillation per minute. Find its effective length ? (g = 981 cm/ s²)
Solution:
Given: Time-period T = \( \frac{\text { Time }}{\text { No.of oscillations }} \) = \frac{1 \mathrm{~min}}{60} = 1 sec

Question 5.
The value of acceleration due to gravity on a planet is \( \frac{1}{4} \) th of that of earth.
If the time-period of simple pendulum on earth is 2 sec, then find the time-period on the planet.
Solution:
g₂= \( \frac{1}{4}\) g₁

Question 6.
What will be the time.period of a simple pendulum of length \( \frac{9 \cdot 8}{\pi^{2}} \) m? Name such pendulum.
Solution:
Given: l= \( \frac{9 \cdot 8}{\pi^{2}} \)m g = 9.8 ms^-2
Formula:
T =2π \( \sqrt{\frac{l}{g}} \)

Question 7.
Two pendulum of length 100 cm and 110*25 cm start oscillating at same time. After how much oscillation again they will oscillate at same time.
Solution:
Let the time-period of the 100 cm pendulum be T₁
T₁ = 2 π\( \sqrt{\frac{100}{g}} \)

and if T₂is the time-period for 110.25 cm pendulum, then
T₂ = 2 π\( \sqrt{\frac{110 \cdot 25}{g}} \)
T₁ <T₂
∴ Both the pendulum to oscillate at same time if the big pendulum perform n oscillaion and small pendulum, perform (n + 1) oscillation.
i.e.,(n+1)T₁ = nT ₂

i.e., Big pendulum after 20 oscillation or small pendulum after 21 oscillation will start oscillating together.

Question 8.
Find the length of second pendulum at (i) Surface of earth (g = 9-8 m/s2), (ii) Surface of moon (g = 1.65 m/s2).
Solution:
Time-period for second pendulum is T= 2 sec.
∴From T = 2 π\( \sqrt{\frac{l}{g}} \)

(i) Length at earth surface
2 = 2π² \( \sqrt {\frac{l}{9.8}} \)
or
l = π² \( \ {\frac{l}{9.8}} \)
or
π².l = 9.8
or
l =\( \frac{9 \cdot 8}{(\pi)^{2}} \) = \( \frac{9 \cdot 8}{(3 \cdot 14)^{2}} \) = 0.99m

(ii) Length of moon
l = \( \frac{1 \cdot 65}{\pi^{2}} \)
or
l = \( \frac{1 \cdot 65}{(3 \cdot 14)^{2}} \) = 0.167 m.

Question 9.
A mass of 98 kg suspended in a spring is oscillating whose spring constant is 200 N/m. Find its time-period.
Solution:
We know,
T = 2π\( \sqrt{\frac{m}{k}} \)
or
T = 2 ×3.14 \( \sqrt{\frac{98}{200}} \)
T= 4-396 second.

Question 10.
The total energy of a particle executing S.H.M. is E. What will be the K.E. and P.E. of particle at the displacement half of the amplitude?
Solution:
We know that total energy is
E = \( \frac{1}{2} \) mω² a²
Also, K.E = \( \frac{1}{2} \) mω²( a² – y ²)

Now, at y = \( a / 2 \),
K.E = \( \frac{1}{2} \) mω²\( \left(a^{2}-\frac{a^{2}}{4}\right) \)
= \( \frac{1}{2} \) mω² . \( \frac{3 a^{2}}{4} \)
= \( \frac{3}{8} \) mω²a² = \( \frac{3}{4} \) E.

Again, P.E = \( \frac{1}{2} \) mω² y ²
Now, at y = \( a / 2 \),
P.E = \( \frac{1}{2} \) mω² \( \frac{a^{2}}{4} \)
P.E = \( \frac{1}{8} \) mω² a² = \( \frac{1}{4} \) E.

Question 11.
The amplitude of a particle executing S.H.M. is 0*01 m and frequency is 60 Hz. What will be the maximum acceleration of the particle?
Solution:
Given : a = 0.01m, υ = 60 Hz Now, maximum acceleration is given by
α = ω² a
= (2π υ ) ²a
= 4π²υ ²a
= 4×3.14 ×3.14×60×60×0.01
= 1419.78ms^-2

Question 12.
At a place a body travels 125 m in 5 sec during the free fall under gravity. What will be the time period of a simple pendulum of length 2-5 m at that place?
Solution:
Given : S= 125 m, υ = 0, t = 5 sec.
Now, s = ut + \( \frac{1}{2} \) gt²
or
125 = 0 +\( \frac{1}{2} \)g×25
or
g = 10 ms^-2
Again,
= 2π\( \sqrt{\frac{l}{g}} \)
= 2π \( \sqrt{\frac{2.5}{10}} \)
= 2π ×0.5 = π sec.

Question 13.
A spring balance has a scale that reads from 0 to 50 kg. The length of the scale is 20 cm. A body suspended from this balance, when displaced and released, oscillates with a period of 0-6 s. What is the weight of the body ? (NCERT)
Solution:
Given :m = 50 kg, y = 20 cm = 0.2 m, T- 0.6 s
From F=ky
∴ mg = ky
or
K = \( \frac{\mathrm{mg}}{\mathrm{y}} \) = [ latex] \frac{50 \times 9 \cdot 8}{0 \cdot 2} [/latex] = 2450Nm^-1

Weight of the body
W = m’g
= 22.36×9.8 = 219.17 N
≈ 219N.

Question 14.
A spring having spring constant 1200 Nm’ is mounted on a horizontal table as shown in fig. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled side ways to a distance of 2.0 cm and released. (NCERT)
Determine
(j) The frequency of oscillations.
(ii) Maximum acceleration of the mass and
(iii) The maximum speed of the mass.

Solution:
Given:k=1200Nm^-1,m= 3kg, amplitude a =2 cm =2 × 10²m
(i) Frequency υ =\( \frac{1}{2 \pi} \) \( \sqrt{\frac{k}{m}} \) = \( \frac{1}{2 \times 3 \cdot 14} \sqrt{\frac{1200}{3}} \)
= \( \frac{1}{6 \cdot 28} \) ×\( \sqrt{400}\) = \( \) \frac{20}{6 \cdot 28}
= 3.18 s^-1 ≈3.2 ^-1

(ii) α = -ω ² y
∴α _max = ω ²a = \( \frac{k}{m} \) .a = \( \frac{1200}{3} \) ×2 ×10^-2
= 8.0 ms ^-2

(iii) ∴ν _max=ωa= \( \sqrt{\frac{k}{m}} \) ×a =\( \sqrt{\frac{1200}{3}} \) ×2 ×10^-2
= 20 × 2 × 10^-2 = 0.4 ms ^-1

Oscillations Class 11 Important Questions Objective Type

1. Multiple- choice questions:

Question 1.
Which of the following equation does not represent simple harmonic, motion:
(a) x = asin(ωt+δ)
(b) x = bcos(ωt+Φ)
(c) x = atan(ωt + Φ)
(d) x = asin(ωt cosωt.
Answer:
(c) x=atan(ωt + Φ)

Question 2.
Time-period and amplitude of a particle executing simple harmonic motion is Tand a. The minimum time taken to reach distance will be:
(a) T
(b) \(\frac{T}{4}\)
(c) \(\frac{T}{8}\)
(d) \(\frac{T}{16}\)
Answer:
(c) \(\frac{T}{8}\)

Question 3.
Time-period and amplitude of a particle executing simple harmonic motion is T and a. Its maximum velocity is :
(a) \(\frac{4 a}{T}\)
(b) \(\frac{4 a}{T}\)
(c ) \(2 \pi \sqrt{\frac{a}{T}}\)
(d) \(\frac{2 \pi a}{T}\)
Answer:
(d) \(\frac{2 \pi a}{T}\)

Question 4.
Acceleration in S.H.M. is :
(a) Maximum at amplitude position
(b) Maximum at mean position
(c) Remain constant
(d) None of these.
Answer:
(a) Maximum at amplitude position

Question 5.
The ratio of acceleration to displacement of a particle executing S.H.M. is measurement of:
(a) Spring constant
(b) Angular acceleration
(c) (Angular acceleration)²
(d) Restoring force.
Answer:
(c) (Angular acceleration)²

Question 6.
When displacement is half of amplitude, then ratio of potential energy to the total energy is:
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{4}\)
(c) 1
(d) \(\frac{1}{8}\)
Answer:
(b) \(\frac{1}{4}\)

Question 7.
What remain constant in S.H.M.:
(a) Restoring force
(b) Kinetic energy
(c) Potential energy
(d) Time-period.
Answer:
(d) Time-period.

Question 8.
Graph between ‘f and ‘F obtained as :
(a) Hyperbola
(b) Parabola
(c) Straight line
(d) None of these.
Answer:
(b) Parabola

Question 9.
The time-period of a seconds pendulum is :
(a) 1 second
(b) 2 second
(c) 3 second
(d) 4 second.
Answer:
(b) 2 second

Question 10.
Resonance is example of:
(a) Tuning fork
(b) Forced oscillation
(c) Free oscillation
(d) Damped oscillation.
Answer:
(b) Forced oscillation

2. Fill in the blanks:

1. A periodic motion of constant amplitude and same frequency is called ………… .
Answer:
Simple harmonic motion

2. In simple harmonic motion its total energy is ………. .
Answer:
Constant

3. The restoring force setup per unit extension in the spring is called ………… .
Answer:
Spring constant (Force constant)

4. When a body oscillates on both sides of its mean position in a straight line, then this bind of motion is called ………… .
Answer:
Simple harmonic motion

5. The maximum displacement of a body in oscillatory motion is called ………… .
Answer:
Amplitude

6. In the presence of damping forces, the amplitude of oscillations of a body ………… .
Answer:
Decreases

7. The time-period of second pendulum is ………… second.
Answer:
Two

8. The periodic time of simple pendulum does not depends upon
Answer:
Mass.

3. Match the following:
I.

Answer:
1. (c) At mean position
2. (d) At maximum displacement
3. (b) Remain constant
4. (e) Directly proportional to displacement.
5.  (a) 2π\( \sqrt{\frac{\text { Displacement }}{\text { Acceleration }}} \).

II.

Answer:
1. (c) Periodic motion
2. (a) Forced oscillation
3. (e) S.H.M.
4. (b) Conservation of energy and momentum
5. ((d) Main frequency.

4. Write true or false:

1. Every S.H.M. is a periodic motion.
Answer:
True

2. Every periodic motion is S.H.M.
Answer:
False

3. In S.H.M. total energy is directly proportional to square of amplitude.
Answer:
True

4. Acceleration is always zero for a particle executing S.H.M.
Answer:
False

5. Time-period of simple pendulum is directly proportion to square root of its length.
Answer:
True

6. Time-period of simple pendulum is inversely proportional to the square root of acceleration due to gravity.
Answer:
True

7. Time-period of simple pendulum depends on mass, material and size of the pendulum.
Answer:
False

8. In S.H.M., velocity is maximum when acceleration is minimum.
Answer:
True

9. The motion of moon around the earth is S.H.M.
Answer:
False

10. Time-period of hard spring is less than soft spring.
Answer:
True

11. Time-period of a simple pendulum cannot be one day.
Answer:
True

Students get through the MP Board Class 11th Physics Important Questions Chapter 3 Motion in a Straight Line which are most likely to be asked in the exam.

MP Board Class 11th Physics Important Questions Chapter 3 Motion in a Straight Line

Motion in a Straight Line Class 11 Important Questions Very Short Answer Type

Question 1.
When do an object of definite size is considered as a point object, in motion?
Answer:
When the distance travelled by the object is very large in comparison to the size of object.

Question 2.
What is one-dimensional motion? Give three examples.
Answer:
When an object moves in a straight line, then its motion is called one-dimensional motion.
Examples :

• A body falling under gravity.
• Train running on straight rails.
• A man moving on a straight road.

Question 3.
Define displacement and distance.
Answer:
Displacement : The change in position in a particular direction is called displacement.
Distance : The length of a path covered by a particle in a given time interval is called its distance.

Question 4.
Direction of motion of an object is determined by velocity or acceleration.
Answer:
Velocity.

Question 5.
Define velocity. Write its SI unit.
Answer:
Displacement per unit time of a moving body is called its velocity.
Or
In a particular direction, the distance travelled in unit time is called velocity.
Formula: Velocity = \(\frac{\text { Displacement }}{\text { Time }}\) Time
The SI unit of velocity is m/s. It is a vector quantity.

Question 6.
Define speed. Is it a scalar or vector quantity?
Answer:
The rate of change of position of a moving body is called its speed.
Or
The distance travelled in unit time by a moving body is called its speed. It is a scalar quantity.
speed = \(\frac{\text { Distance }}{\text { Time }}\)

Question 7.
What do you understand by relative velocity?
Answer:
Relative velocity : The relative velocity of a body w.r.t. another body is the rate of change of position of that body relative to another body.
Let the velocity of bodies A and B are v₁ and v₂ respectively, then
Velocity of B w.r.t. A = v₂ – v₁
and Velocity of A w.r.t. B= v₁ – v₂.

Question 8.
Define acceleration and write its SI unit.
Answer:
Acceleration is defined as rate of change in velocity. Its SI unit is metre/second².

Question 9.
If the velocity of a body is constant, then what will be its acceleration?
Answer:
Zero.

Question 10.
What will be the displacement of a bullet fired vertically upward when it returns to its original point?
Answer:
Displacement of bullet will be zero.

Question 11.
Explain with reason, can a moving body have acceleration when :
(1) It is moving with uniform speed.
Answer:
Yes, because when speed is uniform its direction may be changed.

(2) It is moving with uniform velocity.
Answer:
No, as acceleration is defined as change in velocity.

Question 12.
Can a moving particle has constant speed but variable velocity?
Answer:
Yes, in uniform circular motion.

Question 13.
Can a body moving with constant speed has acceleration?
Answer:
Yes, in uniform circular motion.

Question 14.
Can uniform acceleration change the direction of velocity?
Answer:
Yes, when a body thrown vertically upwards, at its highest point the direction of velocity changes, while the direction of g is always acting downwards.

Question 15.
Can the speed be zero in one-dimensional motion and acceleration be not zero?
Answer:
Yes, at the highest point, when the body is thrown vertically upwards.

Question 16
What does the area enclosed between the velocity-time curve and time axis show?
Answer:
Distance travelled by the body.

Question 17.
(i) Draw velocity-time graph of a body moving uniformly in a straight line,
(ii) Draw position-time graph of a body moving uniformly in a straight line.
Answer:

Question 18.
Draw the graphs of positive and negative accelerated motion of velocity-time graph.
Answer:

Question 19.
What does the slope represent in position-time graph?
Answer:
The slope of a position-time graph represents velocity of an object.

Question 20.
Which quantity is represented by the area under the velocity-time graphs?
Answer:
It represents displacement of an object.

Motion in a Straight Line Class 11 Important Questions Short Answer Type

Question 1.
Differentiate displacement and distance.
Answer:
Difference between displacement and distance :

Question 2.
Differentiate velocity and speed.
Answer:
Difference between velocity and speed :

Question 3.
Define uniform motion and uniform velocity.
Answer:
Uniform motion :
When a body travels equal distance in equal interval of time, in the same direction, then its motion is called uniform motion.
Uniform velocity :
When the displacement of a moving body is equal in equal interval of time, then its velocity is called uniform velocity.

Question 4.
In which of the following examples of motion can the body be considered approximately a point object:
(a) A railway carriage moving without jerks between two stations.
(b) A monkey sitting on the top of a man cycling smoothly on a circular track.
(c) A spinning cricket ball that turns sharply on hitting the ground.
(d) A tumbling beaker that has slipped off the edge of a table?
Answer:
In (a) and (b), we can consider the body approximately as a point object because the motion of the object involves changes of position by distance much greater than its size.

Question 5.
A player throws a ball upwards with an initial speed of 29 m/s :
(a) What is the direction of acceleration during the upward motion of the ball?
(b) What are the velocity and acceleration of the ball at the highest point of its motion?
(c)Choose the x = 0 m and t₀ = 0 s to be the location and time of the ball at its highest point, vertically downward direction to the positive direction of X-axis, and give the signs of position, velocity and acceleration of the ball during its upward and downward motion.
(d) To what height does the ball rise and after how long does the ball return to the player’s hand? (Take g = 9.8 ms^-2 and neglect air resistance)
Answer:
(a) Since the ball is moving under the effect of gravity, the direction of acceleration due to gravity is always vertically downwards.

(b) When the ball is at the highest point of its motion, its velocity becomes zero and the acceleration is equal to the acceleration due to gravity = 9.8 ms^-2in vertically downward direction.

(c) When the highest point is chosen as the location for x = 0 and t = 0 and vertically downward direction to be the positive direction of X-axis.
During upward motion : Sign of position is negative, sign of velocity negative and the sign of acceleration positive i.e., v < 0, a > 0.
During downward motion : Sign of position is positive, sign of velocity is positive and the sign of acceleration is also positive i.e:, v > 0, a > 0.

(d) Let, t = Time taken by the ball to reach the highest point.
H = Height of the highest point from the ground.
Taking vertically upward motion of the ball.
∴ Initial velocity, u =-29.4 ms^-1, a =g = 9-8 ms^-2,
Final velocity v = 0, s = H = ?, t =?
Using the relation, v²-u² = 2as, we get
0² – (29.4)² = 2 × 9.8 H
or H = \(\frac{-29 \cdot 4 \times 29 \cdot 4}{2 \times 9 \cdot 8}\) = -44.1 m
Where -ve sign shows that the distance is covered in upward direction. Using equations v=u + at, we get
0 = -29.4 + 9.8 × t
t = \(\frac{29 \cdot 4}{9 \cdot 8}\) = 3s
i.e., Time of ascent = 3s.
Also we know that when the object moves under the effect of gravity alone, the time of ascent is always equal to the time of descent.
∴ Total time after which the ball returns to the player’s hand = 2t = 2 × 3 = 6s.

Question 6.
Derive graphically the first equation of motion.
Answer:
Velocity-time graph for an uniformly accelerated motion is shown in the figure. It is clear from the graph that at t = 0 the initial velocity of a particle is u and after t sec the final velocity is v.
From ΔEBC

∴ Slope of the curve = Acceleration
or a = \(\frac{v-u}{t}\)
or at = v-u or v=u + at.

Question 7.
What is relative velocity? Derive the expression for it.
Answer:
The relative velocity with respect to a body at rest or in motion is defined the rate of change of position of a body with respect to another body.
Let A and B are two bodies moving with velocities v₁and v₂ and at time t their position coordinate are x₁(t) and x₂(t) respectively.
x₁(t) = x₁1(0) + v₁t …(1)
∴ x₂(t) = x₂(0) + v₂t …(2)
Where x₁(0) and x₂ (0) are position coordinates at t = 0.
Subtracting eqn. (1) from eqn. (2),
∴ x₂(t) – x₁(t) = x₂(0) – x₁(0) + (v₂ -v₁)t …(3)
In the eqn. (3), x₂(t)- x₁(t) represents the position of B w.r.t. A at time t.
∴ x₂(0) – x₁(0) represents the relative position or distance of B w.r.t. A,
Putting t = 0 in eqn. (3) then the relative displacement in 1 sec. will be v₂-v₁
∴ Relative velocity of B w.r.t. A = v₂-v₁
∴ By eqn. (3),

Question 8.
Derive graphically the second equation of motion.
Answer:
From the given graph displacement of an object = Area under the curve OACE
or
s = Area of rectangle OABE + Area of ∆EBC
or
s = OA × AB + \(\frac{1}{2}\)EB × BC
or
s = ut+\(\frac{1}{2}\)t(v – u)
v – u=at
s = ut + \(\frac{1}{2}\)t ×at
s = ut + \(\frac{1}{2}\)at ²

Question 9.
Derive graphically the third equation of motion.
Answer:
From the above v-t graph
Displacement of an object = Area of trapezium OACE

Motion in a Straight Line Class 11 Important Questions Long Answer Type

Question 1.
Derive the equation of motion by Integration method.
Answer:
First equation of motion : v = u + at :Let at any instant t, the velocity of a particle is v.
∴ Acceleration, a = \(\frac{d v}{d t}\)
or dv = adt …(1)
Let at t = 0, v = u
∴ Integrating eqn. (1), we get

∴ v-u = a(t- 0)
or v – u- at or v = u + at.
Second equation of motion : Let a particle is moving with velocity u along X-axis and at any instant t, its displacement is x.
∴ v = \(\frac{d x}{d t}\)
or
dx = vdt
Also, we know that,
v = u + at
∴ dx = (u + at)dt ….(1)
Now, at t = 0, x = x₀
∴ Integrating eqn. (1), we get

Third equation of motion :
Accordrng to definition of acceleration

Question 2.
Derive graphically the second and third equation of motion.
Answer:
From the given graph displacement of an object = Area under the curve OACE
or
s = Area of rectangle OABE + Area of ∆EBC
or
s = OA × AB + \(\frac{1}{2}\)EB × BC
or
s = ut+\(\frac{1}{2}\)t(v – u)
v – u=at
s = ut + \(\frac{1}{2}\)t ×at
s = ut + \(\frac{1}{2}\)at ²

From the above v-t graph
Displacement of an object = Area of trapezium OACE

Motion in a Straight Line Class 11 Important Numerical Questions

Question 1.
A car travels from a city A to city B with a speed of 40 km/h and returns back to city A, with the speed of 50 km/h. What is the average speed of car? What will be its average velocity?
Solution:
Let the distance between A and B is x.

Question 2.
A body obtain a velocity of 10m/s in 3 second from rest. Find its acceleration.
Solution:
Given, u = 0, v = 10m/s and t = 3sec.
From Ist equation of motion,
v = u + at
a = \(\frac{v-u}{t}\)
Putting the values in above equation, we get
a = \(\frac{10-0}{3}\) = \(\frac{10}{3}\) m/s²
or
a = 3.33 m/s²

Question 3.
A body describes 45 m in 8^th second with uniform acceleration from rest. Find its acceleration.
Solution:
Given :u-0,t=8s,s = 45m

Question 4.
A car moving with a velocity of 36 km/h. When brakes are applied it stop after 10m. Calculate acceleration and time taken to stop.
Solution:

Question 5.
A body describe 15m in sixth second and 23m in tenth second. Find initial velocity and acceleration of the body.
Solution:

or 2u+19a=46
Solving eqns. (1) and (2),…..(2)
u = 4 m/s and a = 2m/s²

Question 6.
Two trains are running parallely in two tracks in the same direction with a speed of 10 m/s and 15 m/s. Find relative velocity.
Solution:
Given, V₁ = 10 m/s, v₂ = 15 m/s
Relative velocity = v₂ – v₁
= 15-10 = 5 m/s.

Question 7.
A car is running on a straight road with a velocity of 126 km/hr. It stops after travelling a distance of 200 m. Find the retardation of the car. How much time does it take to stop?
Solution:
Given, initial velocity u = 126km/h
= 126 × \(\frac{5}{18}\) = 35m/s.
Distance curved s = 200 m
Final velocity v = 0.
Using third equation of motion,
v² = u² + 2as
or 0 = 35 × 35 + 2 × a × 200
a = \(-\frac{35 \times 35}{2 \times 200}\) = 3.06m/s²
Using first equation of motion,
v = u + at
or 0=35 – 3.06t
or t= \(\frac{35}{3 \cdot 06}\)
=11.43sec.

Question 8.
A car travels first \(\frac{1}{3}\) part of total distance at a speed of 10km/hr, second\(\frac{1}{3}\) part at 20km/hr and last \(\frac{1}{3}\) part at 60 km/hr. Find out average speed of the car.
Solution:
Let the distance travelled by car = x km
Given, v₁ = 10 km/hr, v₂ = 20km/hr, v₃ 60 km/hr

Question 9.
A ball is thrown vertically upward reaches the roof of a house 100m in height. At same instant a second ball is dropped downward from the roof of the house will zero initial velocity. At what height both the ball will cross each other?
Solution:
Given, h = 100m
Let, both the ball cross each other at a distance of x m after t sec.
For vertically upward motion,
u = ? v = 0 a = -g and h = 100 m
v² = u² +2as, we get
0 = u² – 2 × g × 100
or u² = 200g = 200 × 9.8 = 1960
or
for vertically downward motion, .
u = 0, a = g, s = (100 -x)
From s = ut + \(\frac{1}{2}\)at², weget
100 – x = 0 +\(\frac{1}{2}\) × 9.8 × t² =4.9t²
or 100 – x = 4.9 t²
When the ball is thrown upward, distance covered by it
s = ut + \(\frac{1}{2}\) at² ….

or x = 100 – 25 = 75m

Question 10.
A jet plane is moving with a velocity of 500km/hr. Velocity of gas ejecting out with respect to jet plane is 1500 km/hr. find out the velocity of gas ejecting out w.r.t. a man standing on ground surface.
Solution:
Velocity of gas ejecting out from the jet plane w.r.t. man standing on ground surface
= v_g-v_j =1500-500
= 1000 km/hr.

Question 11.
A woman starts from her home at 9-00 am., walks with a speed of 5 kmh^-1 on a straight road up to her Office 2-5 km away, stays at the office up to 5-00 p.m. and returns home by an auto with a speed of 25 kmh^-1. Choose suitable scales and plot the x – t graph of her motion.
Solution:
x -t graph of the motion of woman is shown in fig. V₁ = speed of woman while walking at 5kmh^-1.
x = Distance covered by her = 2-5 km If t¹ = time taken to reach office, then it can be calculated by using
x₁ = v₁t₁
or t₁ = \(\frac{x}{v_{1}}\)
∴ t₁ = \(\frac{2 \cdot 5}{5}\) = \(\frac{1}{2}\) h = 30 minutes

If O is regraded as origin for both time and distance, then at t = 9.00 am., x = 0 at t = 9.30 am., x = 2.5 km and she reaches in her office. So OA represents x – t graph of the motion, when the woman walks from her home to office.
When she stays at her office from 9.30 a.m to 5.00 p.m., then she is stationary and hence her stay is represented by the straight line AB in the graph.
On return, speed of auto, v₂ = 25 km/h
∴ If t₂ = time taken by her i.e., by auto from office to her home, then
t₂ \(\frac{x}{v_{2}}\) = \(\frac{2 \cdot 5}{25}\) = \(\frac{1}{10}\) = 6minutes
Thus, she reaches back to her home at 5.06 p.m.
Her motion on the return journey in shown by BC part of the graph.
Scale chosen :
Time on X-axis, 1 division = 1 hour.
Distance on Y-axis, 1 division = 0.5 km.

Question 12.
A body travels half of its total path in the last second of its fall from rest. Find the time and height of its fall.
Solution:
Let the body falls from a height h and takes time t to fall.
From Second equation of motion, fall from/I to B is given by

Motion in a Straight Line Class 11 Important Questions Objective Type

1. Multiple- choice questions:

Question 1.
If the velocity of an object is doubled then among the following which will be doubled:
(a) Acceleration
(b) Kinetic energy
(c) Momentum
(d) Weight.
Answer:
(c) Momentum

Question 2.
An object dropped from peak of a tower takes 2 second to cross half its height. The height of the tower will be : (If g = 9-8 m/s²)
(a) 9.8m
(b) 19.6m
(c) 20m
(d) 39.2m.
Answer:
(d) 39.2m.

Question 3.
Ratio of instantaneous velocity and instantaneous speed is ……………….
(a) Less than 1
(b) More than 1
(c) Zero (d) Equal to 1.
(d) Equal to 1.
Answer:
(d) Equal to 1.

Question 4.
If acceleration-time graphs, the area represents :
(a) Displacement
(b) Velocity
(c) Change in velocity
(d) Distance covered.
Answer:
(c) Change in velocity

Question 5.
An object is falling freely under the gravitation. The ratio of the distance covered by it in first, second and third seconds will be :
(a) 1 : 3 : 5
(b) 1 : 2 : 3
(c) 1 : 4 : 9
(d) 1 : 5: 6.
Answer:
(a) 1 : 3 : 5

Question 6.
The motion of a particle of a gas are :
(a) One-dimensional
(b) Two-dimensional
(c) Three-dimensional
(d) Vertically upward and downward.
Answer:
(c) Three-dimensional

Question 7.
Which of the following quantity may be zero for any particle in motion :
(a) Displacement
(b) Distance
(c) Speed
(d) None of these.
Answer:
(a) Displacement

Question 8.
If a player throws a ball vertically upward with initial velocity 29 m/s. The velocity of the ball at its peak of motion will be :
(a) 29 m/s
(b) -29 m/s
(c) Zero
(d) None of these.
Answer:
(c) Zero

Question 9.
A car covers half a distance between two points with a speed of 40 km/hr and next half with a speed of 60 km/hr. The average speed will be :
(a) 40 km/hr
(b) 48 km/hr
(c) 50 km/hr
(d) 60 km/hr.
Answer:
(b) 48 km/hr

Question 10.
The position vector of a particle is represented by the equation x = (3t³ + 7t²+14t + 8)m, the acceleration of the particle at t = 1 sec will be :
(a) 10 m/s²
(b) 32 m/s²
(c) 23 m/s²
(d) 16 m/s².
Answer:
(b) 32 m/s²

2. Fill in the blanks:

1. A device used to measure instantaneous velocity is called ………………
Answer:
Speedometer

2. The motion of the Billiard ball is …………….. motion.
Answer:
Two-dimensional

3. The change in position of a body with respect to time is called ………………….
Answer:
Motion

4. When a body moves in a straight line, then its motion is ……………………
Answer:
One-dimensional

5. The distance travelled by a body in a definite direction is called ………………….
Answer:
Displacement

6. The rate of change of position of a body in motion is called its ………………..
Answer:
Velocity

3. Match the following:

 4. Write true or false:

1. From a velocity-time graph, the distance travelled can be measured.
Answer:
True

2. In two dimensional motion, the path of uniform velocity is a straight line.
Answer:
True

3. The displacement can be zero, negative as well as positive.
Answer:
True

4. The unit of acceleration in SI system is not metre/sec².
Answer:
False

5. Displacement is a vector quantity.
Answer:
True

6. The slope of velocity time graph represents acceleration.
Answer:
True

5. Answer in one word:

1. A body is moving with constant velocity. What is the value of its acceleration?
Answer:
Zero

2. What does the slope of position-time graph give?
Answer:
Velocity

3. What does the slope of velocity-time graph give?
Answer:
Acceleration

4. Who had derived the equations of motion?
Answer:
Gallileo,

5. What is the value of acceleration due to gravity on earth’s surface?
Answer:
9.81 m/s²

Students get through the MP Board Class 11th Physics Important Questions Chapter 2 Units and Measurements which are most likely to be asked in the exam.

MP Board Class 11th Physics Important Questions Chapter 2 Units and Measurements

Units and Measurements Class 11 Important Questions Very Short Answer Type

Question 1.
What do you mean by measurement?
Answer:
In physics, the measurement means comparison of the given physical quantity with standard quantity of same nature.

Question 2.
What are the different type of measurement?
Answer:
The different type of measurement are :

1. F.P.S. (Foot Pound Second)
2. C.G.S. (Centimetre Gram Second)
3. M.K.S. (Metre Kilogram Second).

Question 3.
Define unit.
Answer:
The standard value of any physical quantity is known as its unit.

Question 4.
What are fundamental physical quantities?
Answer:
The physical quantities which do not depend upon other quantities are called fundamental.
Example: Mass, Length, Time etc.

Question 5.
What are derived physical quantities?
Answer:
The physical quantities which are derived from fundamental quantities are called derived quantities e.g.,
Volume = length × breadth × height = (length)³
Similarly Force, Momentum, Pressure, Power etc. are derived quantities.

Question 6.
Define metre.
Answer:
The distance travelled by light ray in \(\frac{1}{29,97,92,458}\) seconds in vaccum is called metre.

Question 7.
What are the different units to measure astronomical distance?
Answer:

• Light year: Distance travelled by light rays in one year in vacuum is called one light year.
  1 light year = 3 × 10⁸ × 365 × 24 × 60 × 60 metre = 9.46 × 10¹⁵ m.
• Parsec : It is the unit to measure the distance of stars from the earth.
  1 Parsec = 3.26 light year= 3.08 × 10¹³ km.
• Astronomical unit: Average distance between sun and earth is called astronomical units. It is denoted by A.U.
  1A.U.= 1.496 × 10¹¹metre.

Question 8.
What do you mean by one kilogram?
Answer:
The mass of platinum-iridium cylinder, kept at International Bureau of weights and measure at severes near Paris in France is defined as one kilogram.

Question 9.
Define one second.
Answer:
One second is the time-interval in which Cs – 133 atom execute 9 19 26 31 770 vibrations.

Question 10.
Define the dimensions of a physical quantity with example.
Answer:
The suitable powers, by which a derived unit is expressed in terms of fundamental units are called dimensions of that physical quantity.
Examples :
(i) Area = Length × Breadth
= [L] × [L] = [L]² = [M⁰L²T⁰].

(ii) Velocity = \(\frac{\text { Distance }}{\text { Time }}\)
= \(\begin{array}{l}
{[\mathrm{L}]} \\
\hline[\mathrm{T}]
\end{array}\) = [LT^-1] = [M⁰LT^-1
Thus, dimension of area in length is 2 and that of velocity are, in length 1 and time -1.

Question 11.
What is dimensional equation? Explain with examples.
Answer:
The equation which represents the relation of a derived unit with the fundamental units is called dimensional equation. In mechanics dimensional equation is represented as
[X] = [M^aL^bT^c]
Examples : Velocity = [M⁰LT^-1 ]
and Force = [MLT^-2].

Question 12.
Which of the three physical quantities have the dimensional formula [ML^-1T^-2]?
Answer:
Pressure, Stress and Young’s modulus.
∵ [ML^-1T^-2]=\(\frac{\left[\mathrm{MLT}^{-2}\right]}{\left[\mathrm{L}^{2}\right]}\) = \(\frac{\text { Force }}{\text { Area }}\)
[L2] Area

Question 13.
What are dimensionless quantities? Give three examples.
Answer:
The quantities which are having no dimension are called dimensionless quantities e.g., relative density, strain, relative humidity.

Question 14.
What is significant figure? What is the significant figure in 7.000 × 10³ m?
Answer:
Significant figure :
The number of digits used to express accurately the measured value of the physical quantity is called the significant figures.
The significant figure of 7.000 × 10³ m is 3.

Question 15.
How many significant figures are in the following :
(i) 6.320 joule,
(ii) 0.2370 gm,
(iii) 0.007 kg,
(iv) 2.64 × 10^-5m.
Answer:
(i)  4,
(ii) 4,
(iii) 1,
(iv) 3.

Question 16.
Candela is unit of which physical quantity?
Answer:
Candela is unit of Luminious intensity.

Question 17.
What do you mean by Armstrong unit?
Answer:
It is the unit to measure micro distance 1 Å = 10^-10 metre.

Question 18.
What are the merits of SI system?
Answer:
The main features of SI system are :

• It is a coherent system of units.
• In this system a physical quantity has only one unit, e.g., the unit of energy is joule, whether it is mechanical energy, heat energy or electrical energy.
• It is a decimal system. Smallest and biggest quantities are expressed in the power of 10. e.g.,
  1 kilometre = 10³ m; 1 mm = 10^-3m etc.
• It is closely related to C.G.S. and M.K.S. system.
• All the derived units in this system are accepted on international level.

 Units and Measurements Class 11 Important Questions Short Answer Type

Question 1.
Which of the following is the most precise device for measuring length :
(a) A vernier callipers with 20 divisions on the sliding scale.
(b) A screw gauge of pitch 1mm and 100 divisions on the circular scale.
(c) An optical instrument that can measure length to within a wavelength of light.
Answer:
The most precise device is that whose least count is minimum.
Now, (a) Least count of vernier callipers = 1 MSD – 1 VSD
= 1MSD – \(-\frac{19}{20}\) MSD = \(\frac{1}{20}\) MSD
= \(\frac{1}{20}\) mm =\(\frac{1}{200}\) cm
= 0.005 cm
(b) Least count of screw guage
= 0.001cm
(c) Wavelength of light, λ ≈ 10 ^-5 cm = 0.00001 cm
∴ Least count of optical instrument = 0.00001 cm Thus, clearly the optical instrument is the most precise.

Question 2.
What are the uses of dimensional analysis?
Answer:
Uses :

• To find the unit of a physical quantity.
• To change one system of units into another system.
• To check the correctness of a physical relation.
• To establish relation between different physical quantities.

Question 3.
Distinguish between fundamental units and derived units.
Answer:
Difference between fundamental and derived units :

Question 4.
Answer the following:
(a) You are given a thread and a metre scale. How will you estimate the diametre of the thread?
(b) A screw gauge has a pitch of 1.0 mm and 200 divisions on the circular scale. Do you think it is possible to increase the accuracy of the screw gauge arbitrarily by increasing the number of divisions on the circular scale?
Answer:
(a) The diameter of a thread is so small that is cannot be measured using a metre scale. We wind the thread on in close turns on a pencil or a cylindrical glass rod so that the turns touch one another and are tight. Count the number of turns (n) and find the average length (l) of the coiled thread using the metre scale. Divide this average length by the number of turns to get the diameter i.e.,
Diameter = \(\frac{\text { Average length }}{\text { Number of turns }}\) = \(\frac{l}{n}\)

(b) Yes, the accuracy of the gauge increases by increasing the number of divisions of the circular scale because the least count is given by :
Least count = \(\frac{\text { Pitch }}{\text { No. of divisions on the circular scale }}\)
So, theoretically speaking, least count decreases on increasing the number of divisions on the circular scale.

Question 5.
Let us choose such a unit accordance to which velocity of light be one unit. On the basis of this new unit, what will be the distance between Sun and Earth if light takes 8 minute and 20 second to reach earth?
Answer:
Velocity of light = 1 (as per new unit)
Time taken by light to reach earth surface = (60 × 8 + 20) = 500 sec.
∴ Distance between Sun and Earth = Velocity of Light × Time
= 1 × 500 = 500 Unit of length.

Question 6.
Check the correctness of formula, v² = u² +2las by dimensional method.
Answer:
v²=u²+las
Now, dimensions ofu and v = [LT^-1], dimensions of a =[LT^-2]
Dimensions of s = [L]
and 2 is dimensionless
∴ [LT^-1]² =[LT^-1]²+[LT^-2L]
or [ L²T^-2 ] = [ L²T^-2] + [ L²T^-2]
Since, the dimensions of each term is same, hence the formula is true.

Question 7.
What do you mean by principle of homogeneity of dimensions?
Answer:
According to this principle the dimensions of all terms on both the sides of a dimensional equation are same.

Units and Measurements Class 11 Important Questions Long Answer Type

Question 1.
The velocity of sound waves in a medium depends upon the coefficient of elasticity of the medium (E) and its density (d). Establish the formula for the velocity of wave by dimensional method.
Answer:
Let the velocity of sound in the air depends upon the coefficient of elasticity and density of medium, then
v ∝ E^ad^b
or v = k ,E^ad^b ……..(1)
Where v = velocity of sound, E = coefficient of elasticity, d – density and a and b are numbers and k is dimensionless constant.
Now, the dimensional formulae of quantities are :
v=[LT^-1]
E = [ML^-1T^-2]
d = [ML^-3]
By eqn. (1) we get
or [LT^-1] =[ML^-1T^-2]^a[ML^-3]^b
or [LT^-1] =[M^aL^-a’T^-2aM^bL^-3b]
or [LT^-1] =[M^a+b + L^-a-3bT^-2a]
Now,by the principle of homogeneity, the dimension of both the sides will be equal.
a + b = 0 …(2)
∴ -a-3b=1 …(3)
-2a = -1 …(4)
Hence, a=\(\frac{1}{2}\)
Putting the value of a in eqn. (1), we get
\(\frac{1}{2}\)+ b = 0
or
b = – \(\frac{1}{2}\)

Putting the values of a and b in eqn. (1), we get
v = k.E^1/2d-d^-1/2
or

This is the required relation.

Question 2.
How much dyne is in one Newton?
Answer:
Dimensional formula for force is [MLT^-2].
Here, a=1,b=1 and c = -2

Putting the value, we get
n₂= n₁[10³] [10² ] [1]
or
n₂ = n₁ × 10n⁵
If n₁ = 1 dyne
Then n₂ = 1 Newton
∴ 1 Newton = 10⁵ dyne.

Question 3.
According to van der Wall relation between pressure P, volume V and temperature T is given by

Where a and b are constant. Find the dimensions of a and b.
Answer:
According to homogineity of dimensional equation, a
Dimension of \(\frac{a}{V^{2}}\)= Dimension of P.
∴ Dimension of a = Dimension of P ×(Dimension of V)²
= [M¹L^-1T^-2][L³]²
∴ Dimension of a =[M¹L⁵T^-2] and Dimension of b = Dimension of V = [L³]
or Dimension of b = [M⁰L³T⁰].

Question 4.
Find the fundamental unit of force and work using dimensional equation.
Answer:
(1) Force = Mass × Acceleration

(2) Work Force Displacement
= Mass x Acceleration x Displacement

∴ Dimensional formula of work = [ML²T^-2]
SI unit = kg-metre²/sec²
C.G.S. unit = g-cm²/sec².

Question 5.
What are the limitations of dimensional equations?
Explain the limitations of dimensional analysis.
Answer:
Limitations :

• The dimensional formulae of only those quantities can be ob- :d which can be expressed in terms of fundamental quantities.
• It is not applicable to trigonometrical, exponential or logarithmic functions.
• The value of constants cannot be determined by this system.
• If an equation has a constant having dimensions e.g., G, Then relation cannot be blished.

Question 6.
The periodic time of a simple pendulum T, depends upon its effective length (l) acceleration due to gravity (g). Derive the formula for time-period by dimensional
Or
Find out an expression for periodic time of a simple pendulum using dimensional sis.
Answer:
Let the formula for periodic time (T) be,
T ∝ l^a g^b
T = K. l^a g^b
Putting the dimensions of periodic time (7), effective length (l) and acceleration due to gravity in eqn. (1).
[M⁰L⁰T] = [L]^a x [LT^-2]^b .
or
[M⁰L⁰T] = [M⁰L^a+bT^2b]
By the principle of homogeneity, comparing the powers of length and time, we get
a + b = 0 …(2)
and – 2b = 1
⇒ b = – \(\frac{1}{2}\)
Putting in eqn. (2), we get
a- \(\frac{1}{2}\) = 0
∴ a = \(\frac{1}{2}\)
Putting the values of a and b in eqn. (1), we get
T = kl^1/2g^-1/2
or

This is the required formula.

Question 7.
What are the different type of errors in measurement? Explain.
Answer:
Random error :
If an observer measures a physical quantity and each time he finds different readings, then such an error is called random error.
Example : Suppose the diameter of a wire is determined by a screw gauge and each time the reading is different because the wire is not uniform.
To remove this error, so many readings are taken and then mean is calculated.
If a physical quantity is measured n times and its readings are a₁,a₂, a₃ …..a_n

Absolute error :
The difference between the observed value and actual value of a physical quantity is called absolute error. It is always positive.
The absolute error of a quantity x is denoted by | Δx |
Let the observed values of a physical quantity are x₁,x₂, x₃ …..x_nand the average value is x.

Relative error :
The ratio of absolute error and actual value is called relative error.
∴ Relative error = \(\frac{\text { Average absolute error }}{\text { Actual value }}\)
= \(\frac{\text { Actual value }-\text { Measured value }}{\text { Actual value }}\)
or

Percentage error: When the relative error is expressed in percentage, then it is called percentage error.
∴ Percentage error = \(\frac{\text { Average absolute error }}{\text { Actual value }}\) ×100

Question 8.
What do you understand by significant figure ? How do you find significant figure of a quantity?
Answer:
The number of digits used to express accurately, the measured value of a physical quantity is called significant figure.

Counting of significant figures :

• By changing the decimal point, the number of significant figures does not change.
  For example; 1.234, 12.34 and 123.4 the number of significant figure is 4.
• All the zeros between two non-zero numbers are significant.
  For example; Significant figures in 3100-05 is 6.
• The zeros before the first non-zero digit are ignored while all the zeros to the right are counted.
  For example; Significant figure in 0 007 is 1 and that of 6-320 is 4,
• The zeros in a whole number at the end are not counted.
  For example; Significant figure in 6320 is 3 and in 13200 is 3.
• The significant figure does not change with the change of units i.e.,
  0.0432m = 4.32 cm, both have the significant figure 3.
• When a number is expressed in the power of 10, then the power is not counted, i.e., 10.52 × 10⁵ has significant figure 4.

Units and Measurements Class 11 Important Numerical Questions

Question 1.
Convert 0.53 Å into metre.
Solution:
We know that, 1Å = 10^-10 m
0.53 Å = 0.53 ×10^-10m
= 5.3 ×10^-11m

Question 2.
A student measures the thickness of a human hair by looking at it through
a microscope of magnification 100. He makes 20 observations and finds that the average width of the hair in the field of view of the microscope is 35mm. What is theestimate on the thickness of hair?
Solution:
Estimate on the thickness of hair is given by:

Question 3.
State the number of significant figures in the following :
(a) 0.007m²,
(b) 2.64 × 10²⁴kg,
(c) 0.2370 g cm^-3,
(d) 6.320 J,
(e) 6.032 Nm^-2,
(f) 0.0006032 m².
Answer:
The number of significant figures is as given below :
(a) 1,
(b) 3,
(c) 4,
(d) 4,
(e) 4,
(f) 4.

Question 4.
The length, breadth and thickness of a rectangular sheet of metal are 4.234m, l-005m and 2.01cm respectively. Give the area and volume of the sheet to correct significant figures.
Solution:
Here, Length, l = 4.234m
Breadth, b = 1.005m
Thickness, h = 2.01cm = 0 0201m
Area of the sheet = 2(lb + bh + hl)
= 2(4.234 × 1.005 + 1.005 × 0.0201 + 0.0201 × 4.234)
= 8.7209468m²
As the least number of significant figures in thickness is 3,
∴ Area = 8.72m²
Volume = l × b × h
= 4.234 × 1.005 × 0.0201m³
= 0-0855m³

Question 5.
A physical quantity P is related to four observables a, b, c and d as follows :

The percentage errors of measurement in a, b, c and d are 1%, 3%, 4% and 2% respectively. What is the percentage error in the quantity P ? If the value of P calcu-lated using the above relation turns out to be 3.763, to what value should you round off the result?
Solution:

The calculation of error clearly shows that the number of significant figures is 2, so the result of P may be rounded off to two significant digits i.e.,
P = 3.763 = 3.8.

Question 6.
The percentage errors in the measurement of length and mass are 2% and 5% respectively. What will be the percentage error in the measurement of density of a cube?
Solution:

Maximum % error in the measurement of density will be 11%.

Question 7.
Given that the period T of oscillation of a gas bubble from an explosion under water depends on P, d and E, where the symbols are pressure, density and total energy of explosion. Find dimensionally a relation for T.
Solution:
Let T∝P^ad^bE^c
or T =kPsup>ad^bE^c, (where His a dimensionless constant) …(1)
Writing dimensional formula of each physical quantity on both sides of eqn. (1), we
[M⁰L⁰T¹] = [ML^-1T^-2 ]^a [ML^-3 ]^b [ML²T^-2 ]^c
= [M^a+b+c][L^-a-3b+2c][T^-2a-2c]
Comparing power of,
M, 0 = a + b + c ……(2)
L, 0 = – a – 3b + 2c ……(3)
T, 1 = -2a – 2c
or a + c = –\(\frac{1}{2}\)
∴ From eqns. (2) and (4), we get
b = – (a + c)
= \(-\left(-\frac{1}{2}\right)\) = \(-\left(\frac{1}{2}\right)\)
Putting the value of b in eqn. (3),
– a + 2c = 3b
=> -a + 2c =3 x \(\frac{1}{2}\)= \(\frac{3}{2}\)
Adding eqns. (4) and (5),

Question 8.
An object of mass ‘m’ is executing simple harmonic motion suspended at one end of a spring. If its spring constant is K and time-period is T, then prove with the help of dimensional method that equation T=2π\(\frac{m}{\mathbf{K}}\) incorrect. Also find its correct
equation.
Solution:
Given, T = 2π\(\frac{m}{\mathbf{K}}\)
Writing dimensional formula of the above equation
[T] = \(\frac{[\mathrm{M}]}{\left[\mathrm{MT}^{-2}\right]}\) = [T²]
Since, the dimension of T on both sides are not same, therefore the given equation is incorrect.
Let us assume that time-period T, a^th power of mass (m) and b^th power of spring constant (K), then
T∝m^aK^b
or T = K.m^aK^b
Let K = 2π
∴ T = 2πm^aK^b
or [T] = 2π[M]^a [MT^-2]^b
= [M] ^(a+b)[T]^-2b
Comparing both sides, we get
a + b = 0
and -2b = 1
or b = –\(\frac{1}{2}\)
∴ a+ \(-\left(-\frac{1}{2}\right)\)=0
or
a = \(\frac{1}{2}\)
Putting the values of a and b in the above equation,
T = 2πm\(\frac{1}{2}\). K-\(\frac{1}{2}\)

This is the correct form of the equation.

Question 9.
Equation of a particle of velocity (v) and time (t) is given by v = A + Bt +\(\frac{C}{D+t}\) find out the dimension of A, B, C and D.
Solution:
Each form of R.H.S. must have dimension of v.
∴ Dimensional formula of A = Dimensional formula of velocity
v = [LT^-1].
Dimensional formula of B.t = Dimensional formula of v = [LT^-1]
∴ Dimensional formula of B =\(\frac{\left[\mathrm{LT}^{-1}\right]}{[\mathrm{T}]}\) [LT^-2]
∴Dimensional formula off D = Dimensional formula off t = [T].
Dimensional formula of\(\frac{C}{D+t}\) = Dimensional formula of v= [LT^-1]
and Dimensional formula of C = [LT^-1] x [Dimensions of D + t] – [L¹].

Question 10.
Assuming energy E, length L and time T as the fundamental unit, what would be dimensions of mass ? If energy E is being replaced by force F then what would be the dimensions of mass ?
Solution:

∴ Dimensions of mass will be = [E¹L^-2T²].
Replacing energy E by force F, we get
Force F = Mass x Acceleration

Question 11.
If m and c represent mass and velocity, then find with the help of dimensional method the quantity mc² is equivalent to which form?
Solution:
Dimensions of mc² – Dimensions of mass x (Dimensions of velocity)²
= M[LT^-1]²
= [M¹L²T^-2 ] = Dimensions of energy.

Question 12.
The centripetal force acting on a particle revolving in a circular path depends upon velocity of the particle v and radius of circle (r). Using dimensional method establish the formula for the centripetal acceleration (a).
Solution:
According to given question
a ∝ v^a r^b
or a = kv^a r^b …(1)
Writing the dimensional formula for the quantities
[M⁰LT^-2] = [M⁰LT⁰]^b
=[M⁰L^a+bT^-a]
Comparing the powers of M, L and T both sides,
a + b= 1 …(2)
and – a = -2 or a = 2
Putting the value of a in eqn. (2), we get
2 + b=1
or b = 1 – 2 = – 1
Hence, from eqn. (1), we get
a = k.v² r^-1 or a = \(\frac{k v^{2}}{r}\)
If k= 1, then a= \(\frac{v^{2}}{r}\)

Question 13.
Diameter of a sphere is 2.348 cm. Find out volume and surface area of it up to required significant number.
Solution:
Given,
2R = 2.348 cm
∴ R= 1.174 cm
Volume of sphere V =\(\frac{4}{3}\)πR³ = \(\frac{4}{3}\) × 3.14 ×(1.174)³
or
V = 6.774 cm³
and Surface area of sphere S = 4πR²
=4 × 3.14 × (1.174)²
= 17.311 = 17.31cm².

Motion in a Straight Line Class 11 Important Questions Objective Type

1. Multiple- choice questions:

Question 1.
Light year is unit of:
(a) Time
(b) Distance
(c) Speed
(d) Intensity of light.
Answer:
(b) Distance

Question 2.
Fermi is unit of:
(a) Energy
(b) Momentum
(c) Impulse
(d) Length.
Answer:
(d) Length.

Question 3.
The dimensional formula of gravitational constant is :
(a) [ML²T^-2]
(b) [M^-1L³T^-2]
(c) [M^-1L²T^-3]
(d) [ML³T²]
Answer:
(b) [M^-1L³T^-2]

Question 4.
Choose a pair of physical quantities having the same dimensional formula:
(a) Pressure and stress
(b) Stress and strain .
(c) Pressure and force
(d) Power and force.
Answer:
(a) Pressure and stress

Question 5.
Units of energy is :
(a) watt
(b) joule
(c) Electron volt
(d) Calorie.
Answer:
(a) watt

Question 6.
Relation between v and t, velocity of sound and time is
v = at+\(\frac{b}{t+c}\) dimensional formula for a, b and c will be:
(a) [L²], [T], [LT^-2]
(b) [LT^-2], [L], [T]
(c) [LT⁺²], [LT], [L]
(d) [L], [LT], [T²].
Answer:
(b) [LT^-2], [L], [T]

Question 7.
Order of 4-12 × 10⁵ is :
(a) 4
(b) 6
(c) 5
(d) None of these.
Answer:
(b) 6

Question 8.
Which among the following have significant number four :
(a) 0.630
(b) 0.0024
(c) 6.023
(d) 0.004.
Answer:
(c) 6.023

Question 9.
Which among the following is not a fundamental unit:
(a) Metre
(b) Ampere
(c) Kelvin
(d) Litre.
Answer:
(a) Metre

Question 10.
Which among the following physical quantities do not have the dimensional
formula [ML^-1T^-2 ] :
(a) Youngs modulus
(b) Stress
(c) Strain
(d) Pressure.
Answer:
(c) Strain

Question 11.
Light year is equal to :
(a) 9.46 × 10¹⁰ km
(b) 9.46 × 10¹² km
(c) 9.46 × 10¹² metre
(d) 9.46 × 10^-12 km.
Answer:
(b) 9.46 × 10¹² km

Question 12.
If the length of a simple pendulum is increased, then its percentage increase in its time-period will be:
(a) 0.5%
(b) 2.0%
(c) 1%
(d) 4%.
Answer:
(b) 2.0%

2. Fill in the blanks:

1. The volume of cube of side 1cm is equal to ……………….. m³.
Answer:
10^-6

2. A vehicle moving with speed of 18 km/hr covers ……………….. m in 1 second.
Answer:
5

3. 3.0 m/s² = ………………….. km/h².
Answer:
3.9 × 10^-4

4. Number of significant figure in 2.64 × 10²⁴ kg is ………………….
Answer:
3

5. Number of fundamental unit in SI system is …………………..
Answer:
7

6. 1 micron = ………………… metre.
Answer:
10^-6

7. 1Å = …………………….. metre.
Answer:
10^-10

8. The error due to observer measurement is called ………………..
Answer:
Individual error

9. 1 newton = ……………………. dyne.
Answer:
10⁵

10. Dimensional formula of charge is ……………………
Answer:
[AT]

3. Match the following:
I.

Answer:
1. (c) [M⁰LT⁰]
2. (e) [M⁰L⁰T^-1].
3. (b) Dimensional of planck constant
4. (a) Dimension of momentum
5. (d) [ML²T^-2]

II.

Answer:
1. (c) Pressure
2. (e) Force.
3. (d) Candela
4. (b) Newton × second
5. (a) Light year

4. Write true or false:

1. Dimensional formula for heat and work are same.
Answer:
True

2. The equation v = u + at, can be derived from dimensional method.
Answer:
False

3. Dimensional formula of impulse and momentum are different.
Answer:
False

4. Dimensional formula for pressure, coefficient of Young modulus and stress are [ML^-1T^-2].
Answer:
True

5. Candela is units of Luminious intensity.
Answer:
True

6. Significant figure changes with change in its units of a physical quantity.
Answer:
False

7. It is not necessary that the physical quantity will be the same, if their dimensional formula and units are same.
Answer:
True

8. The value of constant can be determined by dimensional method.
Answer:
False

9. On knowing one dimensions of a physical quantity, its unit can be determined.
Answer:
True

10. The physical quantity is more significant which have more significant figure.
Answer:
True

Students get through the MP Board Class 11th Physics Important Questions Chapter 15 Waves which are most likely to be asked in the exam.

MP Board Class 11th Physics Important Questions Chapter 15 Waves

Waves Class 11 Important Questions Very Short Answer Type

Question 1.
What do you mean by wave motion?
Answer:
It is a method of energy transformation in which the disturbance produced in the medium propagates without the flow of medium.

Question 2.
What is progressive wave. Write the formula for displacement of it?
Answer:
When disturbance is created continuously in a medium, then the particle of medium vibrates to and fro about their mean position without leaving their place. The distur¬bance move forward. The wave thus produced are called progressive wave.
Its displacement equation is :
\(y=a \sin \frac{2 \pi}{\lambda}(v t-x)\)

Question 3.
Write the principle of superposition of waves.
Answer:
When any number of waves meet simultaneously at a point in a medium, the net displacement at a given time is the algebraic sum of the displacement due to each wave at that time.

Question 4.
Write the name of the phenomenon obtained due to superposition of waves.
Answer:
Interference,

• Beats,
• Stationary waves.

Question 5.
What are stationary waves?
Answer:
When two identical waves of equal frequency travel along the same line but in opposite direction superimpose, then the resultant wave thus formed is called stationary waves.

Question 6.
How many types of stationary waves are there? Write one example of them.
Answer:
There are two types of stationary wave :

1. Transverse wave,
2. Longitudinal wave.

1.Transverse wave: If during the propagation of mechanical wave in a medium, the particles of the medium vibrate about their mean position in a direction perpendicular to the direction of wave propagation then the wave is called transverse wave

2. Longitudinal wave: If during the propagation of mechanical wave in a medium, the particles of the medium vibrate about their mean position along the direction of wave propagation then this type of wave is called longitudinal wave.

Question 7.
What are beats?
Answer:
When two waves with slight difference in frequencies travel in a medium simul¬taneously in the same direction then as a result of their superposition, the intensity of sound at any point increase and decreases alternately. This successive rise and fall in the intensity of sound is called beats.

Question 8.
What are the conditions of beats?
Answer:

• Both the waves should travel along the same straight line, in the same medium, with same velocity.
• These should be slight difference in their frequencies.
• The amplitudes of both the waves should be nearly equal.

Question 9.
If two tunning fork of frequency n₁ and n₂ are hammered together. Then how many beats will be obtained per second?
Answer:
Per second number of beat = n₁~ n₂.

Question 10.
Write three applications of beats?
Answer:

• Determination of frequency of a tuning fork.
• Matching the frequency of sound instruments.
• To enquire about poisonous gas in the mines.

Question 11.
On which factors the velocity of transverse wave produced in stretched string depends on?
Answer:

• Tension of string,
• Mass per unit length of string.

Question 12.
Write the formula for frequency of a stretched string
Answer:
\(n=\frac{1}{2 l} \sqrt{\frac{T}{m}}\)
Where, l = Length of stretched string, T = Time-period, m = Mass per unit length of string.

Question 13.
Explain beats period and frequency of beats.
Answer:
One rise and one fall of sound form one beat. The time interval between two consecutive intense sounds is called ‘beat period’.
The number of times the intensity of sound rises and falls in one second is called ‘beat frequency’.
Let the frequencies are υ₁ and υ₂
Beat frequency = \(v_{1}-v_{2}\)
and Beat period = \(\frac{1}{v_{1}-v_{2}}\)

Question 14.
What is Doppler’s effect?
Answer:
When, there is a relative motion between a sound source and a listener, then the change in the frequency of the source appears to the listener. This effect is called Doppler’s effect.

Question 15.
What are the limitations of Doppler’s effect?
Answer:
Limitations :

• The effect expresses the apparent change in the frequency, not the intensity of sound. ,
• The velocity of source or listener should not be greater than the velocity of sound.

Question 16.
What is difference between the Doppler’s effect on sound and in light waves?
Answer:
Doppler’s effect on sound waves depends upon the relative velocity and velocity of source and listener. While in light waves Doppler’s effect depends upon the relative velocity only.

Question 17.
Explain one application of Doppler’s effect.
Answer:
To estimate the speeds of aeroplanes or submarine: When radio waves transmitted from the Radar, come back after reflection from aeroplane, then their wavelength is changed. If an aeroplane is approaching then its wavelength decreases or frequency increases and if the aeroplane receding from the station, the wavelength increases. Thus, by the change of wavelength or frequency, the speed of aeroplane can be calculated.

Question 18.
What do you mean by organ pipe?
Answer:
The pipe in which sound is produced by vibrating the molecules of air or gas-filled in it.

Question 19.
The open organ pipe produces more melody sound than dosed organ pipe. Why?
Answer:
In open organ pipe the harmonics produced are odd and even both while in closed organ pipe only odd harmonics are produced, therefore harmonics produced by open organ pipe are melody.

Question 20.
A sound-producing whistle is whirled fast in a horizontal circle. What change in the frequency will be observed by an observer standing (i) at the centre of the circle, (ii) outside of the circle?
Answer:

• Since, the whistle is always constant distance from the observer, hence no change in frequency will be observed.
• For the observer standing outside the circle, the whistle will approach and move away from him in every half rotation. Hence, the frequency will be observed increasing and decreasing.

Question 21.
Why a flute has several holes in it?
Answer:
A flute is an open organ pipe, melodious sound of different frequencies can be produced by changing the length of air column by putting fingers on the holes.

Question 22.
Why sound travels faster in moist air than in dry air?
Answer:
Presence of water vapour decreases the density of air. Since velocity of sound is inversely proportional to the density. Hence, sound travels faster in moist air than in dry air.

Question 23.
Why the sound heard is more in carbon dioxide than in air?
Answer:
Velocity of sound in a gas is inversely proportional to the square root of the density of gas. Since carbon dioxide is lighter than air. Thus, velocity of sound is greater in carbon dioxide. Hence, sound heard is more in carbon dioxide than in air.

Question 24.
Sound travels faster on a hot day than on a cold day. Why?
Answer:
Velocity of sound is directly proportional to the square root of temperature. Therefore, sound travels faster on a hot day than on a cold day.

Question 25.
Why are transverse waves not produced in gases?
Answer:
Because the gases are not rigid.

Question 26.
Which property is common to all types of mechanical waves?
Answer:
When the waves propagate through a medium, the particles of a medium do not advance along with waves.

Question 27.
What will be the effect on the speed of sound waves in a gas if the absolute temperature of gas is increased to 4 times of its previous value?
Answer:
According to the formula \(v \propto \sqrt{T}\), speed of sound waves will be doubled.

Question 28.
The speed of sound in air is 330m/s. What will be the effect on the speed of sound waves if pressure is doubled, keeping the temperature constant?
Answer:
No effect, because speed of sound does not depend upon pressure.

Question 29.
Solids can support both longitudinal and transverse waves, but only longitudinal waves can propagate in gases? (NCERT)
Answer:
For the propagation of transverse waves through a medium, the medium should posses rigidity. Gases do not have property of rigidity, so the transverse waves cannot propagate through them. Due to rigidity of solids both, transverse as well as longitudinal wave can propagate through them.

Question 30.
The shape of pulse gets distorted during propagation in a dispersive medium. (NCERT)
Answer:
A sound pulse is a combination of waves of different wavelengths. In a dispersive medium, the waves of different wavelengths travel with different speeds in different directions i.e., with different velocities. So the shape of the pulse gets distorted i.e., a plane wavefront in a non-dispersive medium does not remain a plane wavefront in a dispersive medium.

Question 31.
A sitar, a tambour, and a harmonium all the three are made in unison at the same frequency, even then their voice can be recognised separately. Why is it so?
Answer:
Because the sounds of different qualities are produced by them.

Waves Class 11 Important Questions Short Answer Type 

Question 1.
What are progressive waves? Derive its equation.
Answer:
When the disturbance produced from the body executing simple harmonic motion propagates in the medium, then the particles of medium vibrates to and fro about their mean position and the disturbance advances in the medium. The waves thus produced are called progressive waves.

Consider a harmonic wave propagat- g O ing in a medium along the positive direction of x-axis as shown in fig. The speed ofpropagation of wave is v. Its source is at origin ‘O’. As the source is executing
S.H.M., then the displacement of the particle situated at ‘O’ at any instant ‘f be \(y=a \sin \omega t\) ………(1)
Where, ‘a’ is amplitude of vibration and ‘ co ‘ is angular frequency. Now, \(\omega=2 \pi v=\frac{2 \pi}{T}\)

Where, u is frequency and T is time-period. Since the speed of wave is v hence the disturbance will reach the point ‘P’ at a distance V from the origin ‘O’ in \(\frac{x}{v}\) sec. Thus, at any instant ‘f the displacement of the particle situated at P will be \(y=a \sin \omega\left(t-\frac{x}{v}\right)\) …….(2)

The particle of medium situated at ‘P’ will begin to vibrate after \(\frac{x}{v}\) sec. from the particle situated at ‘O’. Thus, in time ‘t’ the displacement of particle at P will be the same as that the particle at O, before \(\frac{x}{v}\) sec.Therefore, instead of ‘t’ in the eqn. (1) we should write \(\left(t-\frac{x}{v}\right)\) Eqn. (2) shows a progressive wave which is propagating along positive direction of X- axis with velocity v. If a progressive wave is travelling along negative direction of A-axis, then its equation will be :
\(y=a \sin \omega\left(t+\frac{x}{v}\right)\) …………. (3)
As ω = 2πυ
∴ From eqn.(2)
\(y=a \sin 2 \pi v\left(t-\frac{x}{v}\right)\) ……………. (4)
But ν = υλ

\(v=\frac{v}{\lambda}\)
∴ \(y=a \sin 2 \pi \frac{v}{\lambda}\left(t-\frac{x}{v}\right)\)
or
\(y=a \sin \frac{2 \pi}{\lambda}(v t-x)\)
This is the equation of a progressive wave.

Question 2.
Explain Newton’s formula for velocity of sound in air.
Answer:
From purely theoretical considerations, Newton gave an empirical relation to calculate the velocity of sound in a gas.
\(v=\sqrt{\frac{B}{\rho}}\) …………. (1)
Where B is bulk modulus and P is density of the gas.

Sound travels through a gas in the form of compressions and rarefactions. Newton assumed that the changes in pressure and volume of a gas, when sound waves are propagated through it, are isothermal. The amount of heat produced during compression is lost to the surroundings and similarly, the amount of heat lost during rarefaction is gained from the surroundings, so as to keep the temperature constant. Using

coefficient of isothermal elasticity, i.e., Bi in Eqn. (1), Newton’s formula becomes: …(2)
\(v=\sqrt{\frac{B_{i}}{\rho}}\)
Calculation of B_i:
Consider a certain mass of the gas.
Let P = initial pressure of the gas, V= initial volume of the gas. Under isothermal conditions PV= constant
Differentiating both sides, we get
PdV + VdP = 0
PdV = -VdP
\(P=-\frac{V d P}{d V}=-\frac{d P}{\frac{d V}{V}}=B_{i}\) (by definition)
Substituting this value in eqn. (2), we obtain
\(v=\sqrt{\frac{P}{\rho}}\)

Question 3.
Write the characteristics of progressive waves.
Answer:
Characteristics of progressive wave are as follows :

• A harmonic (progressive) wave is a disturbance which travels through a medium with a definite velocity, without change in shape.
• Energy is transferred along the direction of propagation of wave, but there is no net transport of the material of the medium.
• The velocity of an oscillating particle is different on different states of oscillation, being maximum at the mean position and momentarily zero at the extreme positions. The velocity of propagation of the wave is however, constant, depending on the nature of the medium.
• At any instant, the phase of the oscillation varies from particle to particle, because each particle starts oscillating a little later than the previous particle.
• For particles separated by an integral multiple of wavelength λ, the displacement, velocity and acceleration of the particle have the same values at any instant.

Question 4.
Write characteristics of stationary waves.
Answer:
Characteristics of stationary waves :

• These waves do not advance in the medium but remain steady at its place. This is why these waves are called stationary waves.
• No energy is transferred by these waves because the flow of energy at any point of the medium in one direction due to incident wave is the same as the flow of energy at that point in opposite direction due to reflected wave.
• To produce these waves, the presence of bounded medium is necessary because the wave travelling in such a medium, after being reflected from the boundary, produce an identical wave moving in opposite direction. As a result of superposition of incident and reflected wave, the stationary wave is produced.
  The stationary waves cannot be produced in vacuum or in unlimited medium.
• In the waves, certain points in the medium are always at rest, i.e., their displacement remain zero. These points are called nodes. These points are situated at equal distances. In case of longitudinal stationary waves, change in pressure and in density is maximum at nodes as compared to other points.
• The displacement of the point in between two consecutive nodes is maximum as compared to other points. These points are called antinodes. In longitudinal stationary waves, there is no change in pressure and in density at antinodes.
• The distance between two consecutive nodes or between two consecutive antinodes is λ / 2. The distance between a node and its neighbouring antinode is λ / 4.
• Except at nodes, all the particles of the medium vibrates but the amplitude of vibration of the particles are different. The amplitude of the vibration is zero at the nodes and maximum at the antinodes.
• All the particles between two consecutive nodes vibrate in the same phase, i.e., they reach simultaneously through their equilibrium positions.
• At any instant, the particles of both the sides of a node are in mutually opposite phases but the particles of both the sides of an antinode are in the same phase.
• All the particles of medium pass through their mean positions simultaneously twice in each period.

Question 5.
Give difference between progressive waves and stationary waves.
Answer:
Comparison of Progressive and Stationary waves

Question 6.
What are beats? What are the necessary conditions to obtain beats?
Answer:
Beats: When two waves with slight difference in frequencies travel in a medium simultaneously in the same direction then as a result of their superposition, the intensity of sound at any point increase and decreases alternately. This successive rise and fall in the intensity of sound is called beats.

Conditions:

• Both the waves should travel along the same straight line, in the same medium, with same velocity.
• These should be slight difference in their frequencies.
• The amplitudes of both the waves should be nearly equal.

Question 7.
Derive Newton’s formula for velocity of sound. Point our error in Newton’s formula and hence discuss Laplace correction.
Answer:
Newton assumed that sound travels through air under isothermal conditions and for elastic medium velocity of longitudinal waves,
\(v=\sqrt{\frac{E}{\rho}}\)
∴ PV = constant under isothermal condition.
On differentiating, PdV+ VdP = 0
or
PdV = -VdP
\(P=\frac{-d P}{d V / V}=\frac{\text { stress }}{\text { strain }}=E\)
∴ \(v=\sqrt{\frac{P}{\rho}}\) [from eqn. (1)]
This is Newton’s formula for the velocity of sound in air, which given 280 m/s whereas actual value is 332 m/s.
Laplace correction : Laplace suggested that sound waves travel under adiabatic conditions because:
(i) When sound waves travels in air, changes in volume and pressure takes place rapidly.
(ii) ( Air is a bad conductor of heat. Thus, PVγ = constant
On differentiation Pd(Vγ) + VγdP = 0
or
PγVγ-1 dV + VγdP = 0
or
\(\gamma P=\frac{-V d P}{d V}=\frac{-d P}{d V / V}\)

Hence, according to Laplace, the velocity of sound is \(v=\sqrt{\frac{\gamma P}{\rho}}\) (for air, γ =1.4)
∴ \(v=\sqrt{1 \cdot 4} \times 280=331 \cdot 3 \mathrm{~m} / \mathrm{s}\)

Question 8.
Derive the equation of stationary waves when it is reflected by rigid boundary.
Answer:
When a progressive wave is reflected by a rigid surface, then phase difference of n is produced.
Let the wave is travelling in +ve direction along the Y-axis,
Equation of wave will be
\(y_{1}=a \sin \frac{2 \pi}{\lambda}(v t-x)\) ……….. (1)
Where, a = Amplitude, y =Velocity and λ Wavelength.

When this wave is reflected back, then it will travel along -ve direction of X-axis. ……….. (2)
\(y_{2}=-a \sin \frac{2 \pi}{\lambda}(v t+x)\)
Let the two waves superimpose and stationary wave is formed.
∴By the principle of superposition.
y = y₁ + y₂
or

This is the required equation.

Question 9.
Derive the equation of stationary wave, when reflected by free boundry.
Answer:
Let the incident wave is
\(y_{1}=a \sin \frac{2 \pi}{\lambda}(v t-x)\)
∴ Reflected wave, as the phase does not change
\(y_{2}=a \sin \frac{2 \pi}{\lambda}(v t+x)\)
∴ By the principle of superposition,

Question 10.
Explain beats period and frequency of beats.
Answer:
One rise and one fall of sound form one beat. The time interval between two consecutive intense sounds is called ‘beat period’.
The number of times the intensity of sound rises and falls in one second is called ‘beat frequency’.
Let the frequencies are υ1 and υ2
∴ Beat frequency = υ1 – υ2
and Beat period = \(\frac{1}{v_{1}-v_{2}}\).

Question 11.
Differentiate interference and beats.
Answer:
Distinction between Interference and Beats :

Question 12.
Use the formula \(v=\sqrt{\frac{\gamma P}{\rho}}\)
to explain why the speed of sound in air:
(a) Is independent of pressure,
(b) Increases with temperature,
(c) Increases with humidity.
Answer:
Given : \(v=\sqrt{\frac{\gamma P}{\rho}}\)
By gas equation PV = RT
or
\(P=\frac{R T}{V}\)
∴ \(v=\sqrt{\frac{\gamma R T}{V \cdot \rho}}\)
But V, p = M (molecular weight of gas)
\(v=\sqrt{\frac{\gamma R T}{M}}\)
(a) In the eqn. (1) P does not appear so the speed is independent of pressure at constant temperature.

(b) If y, R and M are constant, then,
\(v \propto \sqrt{T}\)
i.e., the velocity (speed) of sound is directly proportional to the square root of absolute temperature.
∴ With increase in temperature the speed of sound increases.

(c) From the formula \(v=\sqrt{\frac{\gamma P}{\rho}}\) , it is clear that
\(v \propto \frac{1}{\sqrt{\rho}}\)
The density of humid air is less than that of dry air therefore with increase in humidity the speed of sound increases.

Question 13.
What are harmonics? Which harmonics can be produced in a stretched string?
Answer:
The harmonics are those tones, whose frequency is integral multiple of that of fundamental tone. The harmonics whose frequencies are even multiple of that of fundamental tone, are called even harmonics and the harmonics whose frequencies are odd multiple of that of fundamental tone are called odd harmonics.

In a stretched string even and odd both harmonics can be produced. In Fig. the first, second and third harmonics are shown.

Question 14.
How do you determine the frequency of a tuning fork with the help of beats?
Answer:
Determine frequencies of a tuning fork: Suppose that we have to determine the frequency of a tuning fork. For this purpose, we take such a fork of known frequency
υ₂ whose frequency υ₂ differ slightly from unknown frequency υ₁. Now, both the tuning forks are sounded together and the beats are heard. Let the number of beats heard per second be x. Then,
υ₁ = υ₂ +x or υx = υ₂-x

To find which value is correct out of two values, a little wax is attached to the prong of the tuning fork of unknown frequency υ₁.
Again, the two forks are sounded together and beats are heard.
If number of beats per second increase, then the frequency of the first tuning fork will be (υ₂ – ×) because according to
(υ₁ – υ₂) = ×, × increases as υ₁ decreases.
If number of beats per second decreases, then the frequency of the first tuning fork will be (υ₂ + x) because according to
(υ₁ – υ₂) = -x, x decreases as υ₁ decreases.

Question 15.
Prove that the frequency of fundamental frequency of open organ pipe is double of the fundamental frequency of closed organ pipe of same length.
Or
If the frequency of fundamental tone of an open organ pipe is «, and that of closed organ pipe is n₂, then prove that n₁ = 2n₂.
Answer:
Let the length of organ pipe is l. For the fundamental frequency of open organ pipe.

\(l=\frac{\lambda_{1}}{2}\)
Where, λ1 is the wavelength
λ1 = 2l
If the fundmental frequency is n₁,then

Waves Class 11 Important Questions Long Answer Type

Question 1.
Prove that beats obtained by two sound sources per second is equal to the differences of frequencies of the sound source.
Answer:
When two sources of sound of nearly equal frequencies are sounded together, the amplitude of resultant wave due to superposition of waves at a point is in space. Some¬times the amplitude is maximum and sometimes, it is minimum.

As intensity is directly proportional to the square of amplitude, the intensity also varies periodically with time from maximum to minimum and to maximum again. Let two waves be,
\(y_{1}=a \sin 2 \pi v_{1} t\) and \(y_{2}=a \sin 2 \pi v_{2} t \) are superimposed. On superposition, we get a resultant wave as,
y = y₁+y₂

Question 2.
Prove that even and odd harmonics are produced by a stretched string.
Answer:
When a stretched string is plucked, then transverse waves are produced. The wave reflected from both- the ends and produced stationary waves.
∴The wave is reflected from the rigid end, hence the equation of stationazy wave will be
\(y=-2 a \sin \frac{2 \pi x}{\lambda} \cdot \cos \frac{2 \pi v t}{\lambda}\) ……………… (1)

Let one end of string is at x = 0 and another at x =l. where l is the length of string.
Now, at x = 0, from eqn. (1), we get
\(y=-2 a \sin 0^{\circ} \cdot \cos \left(\frac{2 \pi v t}{\lambda}\right)\)
or
y=0
Again, at x = l, from eqn. (1),
\(y=-2 a \sin \frac{2 \pi l}{\lambda} \cos \frac{2 \pi v t}{\lambda}\)
Now, at x =l, y = 0

Now, the mode of vibration will be obtained by putting k = 1, 2, 3,….
First mode of vibration: If k = 1 and the wavelength of stationary wave is λ₁, then from eqn. (2),
λ₁ = 2l
\(l=\frac{\lambda_{1}}{2}\)
Hence, the string vibrates in one segment. Now, if the velocity is and frequency n₁, then
\(n_{1}=\frac{v}{\lambda_{1}}=\frac{v}{2 l}\) ………… (3)

This frequency is called fundamental frequency or first harmonics.

Second mode of vibratioñ : If k =2 and wavelength ‘λ₂, then from eqn. (2),
λ₂ = l
Also, if the frequency is n₂,then
\(n_{2}=\frac{v}{\lambda_{2}}\)
or
\(n_{2}=\frac{v}{l}=\frac{2 v}{2 l}=2 n_{1}\)

Question 3.
Prove that in a dosed organ pipe odd harmonics are produced.
Or
In a closed organ pipe, describe the mode of vibrations and prove that:
(i) The frequency of fundamental note is inversely proportional to the length of the organ pipe.
(ii) Only odd harmonics are produced.
Answer:
Organ pipe is a long cylindrical tube of uniform diameter and made of wood or metal. Sound is produced by this pipe as a result of vibrations in air column inside this. If one end of this tube is closed then it is called closed organ pipe and if both ends are open then it is called open organ pipe.

When we place a source of sound near the open end of a closed organ pipe, a wave travels towards the closed end. This wave, after being reflected by the closed end, returns. A stationary longitudinal wave is produced inside the closed organ pipe as a result of superposition of incident wave and reflected wave. An antinode is always formed at the open end because the air particles are free to vibrate there. A node is always formed at the closed end because at the closed end the air particles are not free to vibrate.

Suppose that the closed end of the closed organ pipe is at x = 0 and open end at x = L, where L is the length of the organ pipe.
\(y=-2 a \sin \frac{2 \pi x}{\lambda} \cdot \cos \frac{2 \pi v t}{\lambda}\)
Case (i): At x = 0, we have y = o
Thus, the wave function vanishes at x = 0.

Case (ii) : At x = L, we have
\(y=-2 a \sin \frac{2 \pi L}{\lambda} \cdot \cos \frac{2 \pi v t}{\lambda}\)
At x =L, the displacement y has its maximum value ,y will be maximum when \(\sin \frac{2 \pi L}{\lambda}\) maximum i.e,

Where, k = 0, 1,2, 3,4,….
\(\lambda=\frac{4 L}{(2 k+1)}\)
Here, k = 0, 1, 2,… correspond to first, second, third,…. mode of vibration.

First mode of vibration: If λ₁ be the wavelength of the wave produced in air column corresponding k = 0, then from eqn. (2), we have
λ₁ = 4L
If n₁ be the frequency of the wave set up, then
\(n_{1}=\frac{v}{\lambda_{1}}=\frac{v}{4 L}\)

It is the tone of minimum frequency which produces in closed end organ pipe. It is called fundamental tone or first harmonic.
Also,
\(n_{1} \propto \frac{1}{L}\)
i.e., Fundamental frequency is inversely proportional to the length of the organ pipe.

Second mode of vibration :
If λ₂ be the wavelength of the wave set up in air column corresponding to k = 1, then from eqn. (2), we have
\(\lambda_{2}=\frac{4 L}{3}\)
If n₂ be the frequency of the wave set up, then

Thus, in this case, the frequency of the tone produced is three times the frequency of fundamental tone. It is called third harmonic or first overtone.

Third mode of vibration : If k = 2 and corresponding wavelength is λ₃, then from eqn. (2), we get
\(\lambda_{3}=\frac{4 L}{5}\)
If n₃ be the frequency of the wave set up, then
\(n_{3}=\frac{v}{\lambda_{3}}=\frac{v}{4 L / 5}=5 \cdot \frac{v}{4 L}\)
or
n₃ = 5n₁
Hence, the fifth harmonics of second overtone is five times of fundamental frequency.
Hence, the harmonics are n₁, 3n₁ 5n₁,….
Thus, odd harmonics are produced.

Question 4.
Prove that in open organ pipe both odd and even harmonics are produced. Ans. When a source of sound is kept at one end of an open organ pipe, the compressions and rarefactions are set up in the pipe. At the open ends antinodes are formed, hence rarefactions will be produced at the open ends and it returns in the form of compression. Thus, incident wave and reflected wave superimpose and stationary wave is formed.
Since, the reflection is, from free boundary,
\(y=2 a \cos \frac{2 \pi x}{\lambda} \cdot \sin \frac{2 \pi v t}{\lambda}\)

Now, the one end of organ pipe is at x = 0 and another end is at x = l.
Putting x = 0, we get
\(y=2 a \cos 0 \cdot \sin \frac{2 \pi v t}{\lambda}=2 a \sin \frac{2 \pi v t}{\lambda}\)
Again, putting x = l, we get
\(y=2 a \cos \frac{2 \pi l}{\lambda} \cdot \sin \frac{2 \pi v t}{\lambda}\)
For y is maximum,
\(\left|\cos \frac{2 \pi l}{\lambda}\right|=1 t\)
or
\(\frac{2 \pi l}{\lambda}=k \pi \) …………. (2)
Where,k= 1,2,3………

First mode of vibration: If k = I and wavelength is λ₁, then from eqn. (2), we get
λ₁ = 2l
Also
\(n_{1}=\frac{v}{\lambda_{1}}=\frac{v}{2 l} \)

n₁ s the least frequency called fundamental frequency or first harmonics.

Second mode of vibration : 1f k = 2 and corresponding wavelength is λ₂.
then
\(\lambda_{2}=\frac{2 l}{2}=l \)
∴ Frequency ,n₂= \(\frac{v}{\lambda_{2}}=\frac{v}{l}=\frac{2 v}{2 l}\)
n₂ = 2n₁
Hence, second harmonic is obtained at double of fundamental frequency.

Third mode of vibration: If k = 3 and corresponding wavelength is λ₃ and frequency n₃, then

Hence, third harmonic is 3 times of fundamental frequency.
Thus, the harmonics are both odd and even multiple of fundamental frequency.

Question 5.
Derive the expression for the apparent frequency, when the source of sound is moving towards a stationary listener.
Answer:
Suppose S is a source moving towards a stationary listener O. Let υ be the real frequency of the source and υ is the velocity of sound wave. Now, the first wave emitted by the source covers a distance υ in 1 sec. If the source is stationary then these υ waves will be
spread in the distance υ. Thus, the length of one wave i.e., the wavelength will be \(\lambda=\frac{u}{v}\)

Now, suppose the sound-source S is moving with velocity us towards the observer. Then the source covers a distance us in one second towards the listener. Therefore, the v waves emitted by the source in 1 second will spread in a distance (υ-υ_s) only. Thus, the wavelength will be shortened. Let the changed wavelength be λ’.
Then, \(\lambda^{\prime}=\frac{u-u_{s}}{v}\) ………….(1)

Thus, the listener will receive waves of wavelength λ’. Hence, the frequency of sound will appear to him changed. If the apparent frequency be υ’, then
\(v^{\prime}=\frac{u}{\lambda^{\prime}}\) (∴ Velocity of sound υ is steady )
Substituting the value of λ’ in eqn. (1), we have
\(\dot{v^{\prime}}=\frac{u}{\left(u-u_{s}\right) / v}\)
or
\(v^{\prime}=\left(\frac{u}{u-u_{s}}\right) v\) …………. (2)
As (υ-υ_s)< υ,therefore υ’ > υ i.e., the apparent frequency is greater than the real frequency.

If the source S is going away from the listener O, then the wavelength will be in-creased and its value will be given by
\(v^{\prime}=\left(\frac{u}{u+u_{s}}\right) v\)

As (υ + υ_s) > υ_s, therefore, υ‘ < υ i.e., the apparent frequency is less than the real frequency.

Question 6.
Derive the expression for the apparent frequency, when the listener is moving toward stationary source.
Answer:
Suppose, S is a sound source of frequency u and u is the velocity of sound. Again suppose that O is a listener who is coming towards the source with the velocity υ₀. If the listener were stationary then he would have received u waves in 1 second. Therefore, the real wavelength is given by
λ = \(\frac{u}{v}\)

But, the listener himself is moving towards the source with a velocity υ₀ that is, he covers a distance υ₀ toward the source in 1 second. Hence the listener, in addition to υ waves, also receives υ₀/ λ waves contained in the distance υ₀. Therefore, the total waves received by the listener in 1 second i.e., the apparent frequency of the sound is

As (υ+ υ₀) > u, hence υ‘ > υ i.e., apparent frequency will be greater than the actual frequency.

Question 7.
Derive the expression for the apparent frequency heared by a listener, when the source and listener both are moving in the same direction.
Answer:
Let the source and listener are moving with the velocities υ_s and υ₀ respectively in the same direction as shown in the figure.
If the source is moving only.
∴ The frequency heard by the listener will be \(n_{1}=\left(\frac{u}{u-u_{s}}\right) n\)
But, listener is moving away from the source

∴ Apparent frequency, \(n^{\prime}=\left(\frac{u-u_{o}}{u}\right) n_{1}\)

Putting the value of n₁, we get
\(n^{\prime}=\left(\frac{u-u_{o}}{u}\right) \times \frac{u}{u-u_{s}} \cdot n\)
or
\(n^{\prime}=\left(\frac{u-u_{o}}{u-u_{s}}\right) n\)
This is the required expression.

Waves Class 11 Important Numerical Questions

Question 1.
The speed of a wave ¡n a medium is 960m/s. If 3600 waves are passing through a point in the medium in 1 minute, then calculate the wavelength.
Solution:
Given: Speed of wave ν = 960 m/s
Frequency of wave n = \(\frac{3600}{60}\) =60/ second
Wavelength λ = \(\frac{v}{n}=\frac{960}{60}\)
or
λ = 16m.

Question 2.
The speed of sound in air at 14°C is 340 m/s. What is the speed of sound in air at 157.5°C when pressure becomes two times of its initial value.
Solution:
The change in pressure has no effect on speed of sound.
Given: t₁= 14°C,ν₁= 340m/s,t₂ = 1575°C,ν₂ =?

Question 3.
The distance between two consecutive nodes of a stationary wave is 25 cm. If the velocity ¡s 300 mc’, then calculate the frequency.
Solution:
Given: λ /2=25cm
or
λ =50cm = 50 ×\(10^{-2}\)
or
ν = 300 ms^-1
ν = nλ
or
300 = n ×50 ×\(10^{-2}\)
or
\(n=\frac{300}{50 \times 10^{-2}}=6 \times 10^{2}\) = Hz

Question 4.
The frequency of a whistle is 256 Hz. It is moving towards a stationary listener with a velocity of \(\frac{v}{3}\) , where v is the velocity of sound waves, then calculate the apparent frequency.
Solution :
Given : n = 256 Hz, \(v_{s}=\frac{v}{3}\)

Question 5.
An observer is moving towards a stationary source of frequency n. The frequency heard by the observer is 2n. If the velocity of sound is 332 ms^-1, then find the velocity of observer.
Solution:
Given : n’ = 2n, ν = 332 ms^-1.

Question 6.
The frequencies of two sources are 512 Hz and 516 Hz. Find the time inter-val between two consecutive beats.
Solution:
Given : n₁ =512 Hz, n₂ =516 Hz.
∴ Beat period = \(\frac{1}{n_{2}-n_{1}}\)
\(=\frac{1}{516-512}=\frac{1}{4}=0 \cdot 25 \mathrm{sec}\).

Question 7.
Two sound waves of wavelength 1 metre and 1.01 metre produce 40 beats in 10 seconds in a gas. Find the speed of sound in gas.
Solution:
Beats per second \(=\frac{40}{10}=4\)
If ν is the velocity of sound in gas, then
Frequency of first wave υ₁ = \(\frac{v}{1}\)
Frequency of second wave υ₂ \(\frac{v}{1.01}\)

Question 8.
Two tuning forks produce 6 beats when they are sounded together. The frequency of one tuning fork is 288 Hz. Now, the second tuning fork is loaded by little wax, then the beats are not heard. Find the frequency of another tuning fork.
Solution:
Let the frequency of second tuning fork is n.
∴ n = 288 + 6 or 288 – 6
or
n = 294 or 282 Hz
Since, second fork is loaded hence its frequency will decrease.
Since, no beat is heard.
Hence, the frequency of second tuning fork = 294 Hz.

Question 9.
Two sources of sound of equal frequencies are kept at a distance 100 m apart. A listener is moving between the sources and hears 4 beats. If the distance between the sources becomes 400 m, what will be the beats heard ?
Answer:
Spl. The frequency of beats depends upon the frequencies of the sources, not the distance. Hence, 4 beats will be heard.

Question 10.
Frequency of open end organ pipe is 256 Hz. What will be the frequency of same length closed end organ pipe ?
Solution:
Frequency of l length open end organ pipe
\(n=\frac{v}{2 l}\)
Frequency of closed ended organ pipe
\(n^{\prime}=\frac{v}{4 l}\)
or
\(\frac{n}{n^{\prime}}=\frac{v / 2 l}{v / 4 l}=\frac{2}{1}\)
Given, n = 256
∴ \(\frac{256}{n^{\prime}}=\frac{2}{1}\)
or
\(n^{\prime}=\frac{256}{2}=128 \mathrm{~Hz}\).

Question 11.
A string of mass 2-50 kg is under a tension of 200 N. The length of the stretched string is 20-0m. If the transverse jerk is struck at one end of the string, how long does the disturbance take to reach the other end ? (NCERT)
Solution:
Given : M= 2.50 kg, l = 20m, T= 200N
Mass per unit length m = \(\frac{M}{l}=\frac{2 \cdot 5}{20}\) = 0.125kg/m
∴ \(v=\sqrt{\frac{T}{m}}\)
or
\(v=\sqrt{\frac{200}{0 \cdot 125}}=\sqrt{1600}\) = 40 m/sec.
Time taken by distance (jerk) be
\(t=\frac{l}{v}\)
or
(∴ Velocity = \(\frac{\text { displacement }}{\text { time }}\) )
\(t=\frac{20}{40}\) = 0.5 sec.

Question 12.
A stone dropped from the top of a tower of height 300 m high splashes into the water of a pond near the base of the tower. When is the spHsh heard at the top given that the speed of sound in air is 340 ms^-1? (g = 9.8 ms 2) (NCERT)
Solution:
Given : Height of tower h = 300 m Speed of sound v = 340 ms^-1, initial velocity of stone u = 0 Let the time taken by stone to base of tower is t₁ Then by equation of motion
\(h=u t+\frac{1}{2} g t^{2}\)
300 = \(0 \times t_{1}+\frac{1}{2} \times 9 \cdot 8 t_{1}^{2}\)
or
\(4 \cdot 9 t_{1}^{2}=300\)
or
\(t_{1}=\sqrt{\frac{300}{4 \cdot 9}}=\) = 7.82 sec.

If the time taken to reach the sound up to top of tower is t₂, then \(t_{2}=\frac{h}{v}=\frac{300}{340}\) = 0.885
∴ Total time t = t₁+t₂.
= 7.82+0.885=8.705 = 8.7 sec .

Question 13.
A bat emits ultrasonic sound of frequency 1,000 kHz in air. 1f the sound meets a water surface. What is the wavelength of (a) the reflected sound (b) the transmiffed sound? Speed of sound in air is 340 ms^-1 and in water 1486 ms. (NCERT)
Solution:
Given :
n = 1,000 kHz =I000x10³Hz =10⁶Hz
Speed of sound in air ν_a = 340ms^-1 and that in water νw = 1486ms^-1 
(a) Reflected sound propagate in air

(b) Transmitted sound propagate in water

Waves Class 11 Important Questions Objective Type

1. Multiple- choice questions:

Question 1.
Sound of which frequency can be heard by human beings :
(a) 5 vib /sec
(b) 500 vib /sec
(c) 27000 vib / sec
(d) 50, 000 vib /sec.
Answer:
(b) 500 vib /sec

Question 2.
Astronaut cannot hear sound of his partner in moon, because :
(a) Frequency produced is more than audible frequency
(b) No medium is there for propagation of sound
(c) Temperature at night is very low
(d) There are lots of reason in moon.
Answer:
(b) No medium is there for propagation of sound

Question 3.
Two sources of frequency f₁ and f₂ will have beat frequency :
(a) \(\text { (a) } \sqrt{f_{2}}-\sqrt{f_{1}}\)
(b) f₁-f₂
(C) \(2\left(f_{1}-f_{2}\right)\)
(d) \(\sqrt{\left(f_{1}^{2}-f_{2}^{2}\right)}\)
Answer:
(b) f₁-f₂

Question 4.
The law relating sound between source and observer is :
(a) Doppler’s law
(b) Huygens law
(c) Newton’s law
(d) Galilean’s law.
Answer:
(a) Doppler’s law

Question 5.
The effect of beats due to two waves is because of:
(a) Refraction
(b) Reflection
(c) Dispersion
(d) Interference.
Answer:
(d) Interference.

Question 6.
As a utensil is filled with water, its frequency :
(a) Increases
(b) Decreases
(c) Remains same
(d) None of the above.
Answer:
(a) Increases

Question 7.
Waves transport from one end to another :
(a) Energy
(b) Amplitude
(c) Wavelength
(d) Matter.
Answer:
(a) Energy

Question 8.
Energy is not carried by :
(a) Transverse progressive waves
(b) Longitudinal progressive waves
(c) Stationary waves
(d) Electromagnetic waves.
Answer:
(c) Stationary waves

Question 9.
Velocity of sound in air is 350 m/s, frequency in open organ pipe of 50 cm length is:
(a) 175 Hz
(b) 350 Hz
(c) 700 Hz
(d) 50 Hz.
Answer:
(b) 350 Hz

Question 10.
y = 0.15 sin 5x cos 3001 represent an equation of stationary wave. Its wavelength will be :
(a) Zero
(b) 1.25m
(c) 2.512 m
(d) None of these.
Answer:
(b) 1.25m

2. Fill in the blanks:

1. The velocity of sound at 0°C is …………….. .
Answer:
332 m/s

2. …………….. waves require a physical medium for their propagation.
Answer:
Mechanical