MP Board Class 11th Physics Important Questions Chapter 3 Motion in a Straight Line

Students get through the MP Board Class 11th Physics Important Questions Chapter 3 Motion in a Straight Line which are most likely to be asked in the exam.

MP Board Class 11th Physics Important Questions Chapter 3 Motion in a Straight Line

Motion in a Straight Line Class 11 Important Questions Very Short Answer Type

Question 1.
When do an object of definite size is considered as a point object, in motion?
Answer:
When the distance travelled by the object is very large in comparison to the size of object.

Question 2.
What is one-dimensional motion? Give three examples.
Answer:
When an object moves in a straight line, then its motion is called one-dimensional motion.
Examples :

• A body falling under gravity.
• Train running on straight rails.
• A man moving on a straight road.

Question 3.
Define displacement and distance.
Answer:
Displacement : The change in position in a particular direction is called displacement.
Distance : The length of a path covered by a particle in a given time interval is called its distance.

Question 4.
Direction of motion of an object is determined by velocity or acceleration.
Answer:
Velocity.

Question 5.
Define velocity. Write its SI unit.
Answer:
Displacement per unit time of a moving body is called its velocity.
Or
In a particular direction, the distance travelled in unit time is called velocity.
Formula: Velocity = \(\frac{\text { Displacement }}{\text { Time }}\) Time
The SI unit of velocity is m/s. It is a vector quantity.

Question 6.
Define speed. Is it a scalar or vector quantity?
Answer:
The rate of change of position of a moving body is called its speed.
Or
The distance travelled in unit time by a moving body is called its speed. It is a scalar quantity.
speed = \(\frac{\text { Distance }}{\text { Time }}\)

Question 7.
What do you understand by relative velocity?
Answer:
Relative velocity : The relative velocity of a body w.r.t. another body is the rate of change of position of that body relative to another body.
Let the velocity of bodies A and B are v₁ and v₂ respectively, then
Velocity of B w.r.t. A = v₂ – v₁
and Velocity of A w.r.t. B= v₁ – v₂.

Question 8.
Define acceleration and write its SI unit.
Answer:
Acceleration is defined as rate of change in velocity. Its SI unit is metre/second².

Question 9.
If the velocity of a body is constant, then what will be its acceleration?
Answer:
Zero.

Question 10.
What will be the displacement of a bullet fired vertically upward when it returns to its original point?
Answer:
Displacement of bullet will be zero.

Question 11.
Explain with reason, can a moving body have acceleration when :
(1) It is moving with uniform speed.
Answer:
Yes, because when speed is uniform its direction may be changed.

(2) It is moving with uniform velocity.
Answer:
No, as acceleration is defined as change in velocity.

Question 12.
Can a moving particle has constant speed but variable velocity?
Answer:
Yes, in uniform circular motion.

Question 13.
Can a body moving with constant speed has acceleration?
Answer:
Yes, in uniform circular motion.

Question 14.
Can uniform acceleration change the direction of velocity?
Answer:
Yes, when a body thrown vertically upwards, at its highest point the direction of velocity changes, while the direction of g is always acting downwards.

Question 15.
Can the speed be zero in one-dimensional motion and acceleration be not zero?
Answer:
Yes, at the highest point, when the body is thrown vertically upwards.

Question 16
What does the area enclosed between the velocity-time curve and time axis show?
Answer:
Distance travelled by the body.

Question 17.
(i) Draw velocity-time graph of a body moving uniformly in a straight line,
(ii) Draw position-time graph of a body moving uniformly in a straight line.
Answer:

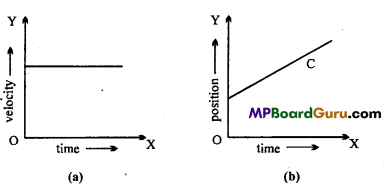
Question 18.
Draw the graphs of positive and negative accelerated motion of velocity-time graph.
Answer:

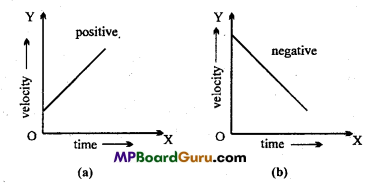
Question 19.
What does the slope represent in position-time graph?
Answer:
The slope of a position-time graph represents velocity of an object.

Question 20.
Which quantity is represented by the area under the velocity-time graphs?
Answer:
It represents displacement of an object.

Motion in a Straight Line Class 11 Important Questions Short Answer Type

Question 1.
Differentiate displacement and distance.
Answer:
Difference between displacement and distance :

Displacement	Distance
1. The difference of position coordinates in a given time-interval is called displacement.	The length of the path in a given time interval is called distance.
2. It is a vector quantity.	It is a scalar quantity.
3. Displacement may be positive, negative or zero.	It is always positive.
4. It does not depend upon the nature of the path.	It depends upon the nature of the path.

Question 2.
Differentiate velocity and speed.
Answer:
Difference between velocity and speed :

Velocity	Speed
1. The distance travelled in unit time in a particular direction, by a moving body is called its velocity.	The distance travelled in unit time by a moving body is called its speed.
2. It is a vector quantity.	It is a scalar quantity.
3. Velocity may be positive, negative or zero.	Speed is always positive.

Question 3.
Define uniform motion and uniform velocity.
Answer:
Uniform motion :
When a body travels equal distance in equal interval of time, in the same direction, then its motion is called uniform motion.
Uniform velocity :
When the displacement of a moving body is equal in equal interval of time, then its velocity is called uniform velocity.

Question 4.
In which of the following examples of motion can the body be considered approximately a point object:
(a) A railway carriage moving without jerks between two stations.
(b) A monkey sitting on the top of a man cycling smoothly on a circular track.
(c) A spinning cricket ball that turns sharply on hitting the ground.
(d) A tumbling beaker that has slipped off the edge of a table?
Answer:
In (a) and (b), we can consider the body approximately as a point object because the motion of the object involves changes of position by distance much greater than its size.

Question 5.
A player throws a ball upwards with an initial speed of 29 m/s :
(a) What is the direction of acceleration during the upward motion of the ball?
(b) What are the velocity and acceleration of the ball at the highest point of its motion?
(c)Choose the x = 0 m and t₀ = 0 s to be the location and time of the ball at its highest point, vertically downward direction to the positive direction of X-axis, and give the signs of position, velocity and acceleration of the ball during its upward and downward motion.
(d) To what height does the ball rise and after how long does the ball return to the player’s hand? (Take g = 9.8 ms^-2 and neglect air resistance)
Answer:
(a) Since the ball is moving under the effect of gravity, the direction of acceleration due to gravity is always vertically downwards.

(b) When the ball is at the highest point of its motion, its velocity becomes zero and the acceleration is equal to the acceleration due to gravity = 9.8 ms^-2in vertically downward direction.

(c) When the highest point is chosen as the location for x = 0 and t = 0 and vertically downward direction to be the positive direction of X-axis.
During upward motion : Sign of position is negative, sign of velocity negative and the sign of acceleration positive i.e., v < 0, a > 0.
During downward motion : Sign of position is positive, sign of velocity is positive and the sign of acceleration is also positive i.e:, v > 0, a > 0.

(d) Let, t = Time taken by the ball to reach the highest point.
H = Height of the highest point from the ground.
Taking vertically upward motion of the ball.
∴ Initial velocity, u =-29.4 ms^-1, a =g = 9-8 ms^-2,
Final velocity v = 0, s = H = ?, t =?
Using the relation, v²-u² = 2as, we get
0² – (29.4)² = 2 × 9.8 H
or H = \(\frac{-29 \cdot 4 \times 29 \cdot 4}{2 \times 9 \cdot 8}\) = -44.1 m
Where -ve sign shows that the distance is covered in upward direction. Using equations v=u + at, we get
0 = -29.4 + 9.8 × t
t = \(\frac{29 \cdot 4}{9 \cdot 8}\) = 3s
i.e., Time of ascent = 3s.
Also we know that when the object moves under the effect of gravity alone, the time of ascent is always equal to the time of descent.
∴ Total time after which the ball returns to the player’s hand = 2t = 2 × 3 = 6s.

Question 6.
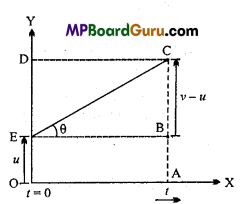
Derive graphically the first equation of motion.
Answer:
Velocity-time graph for an uniformly accelerated motion is shown in the figure. It is clear from the graph that at t = 0 the initial velocity of a particle is u and after t sec the final velocity is v.
From ΔEBC

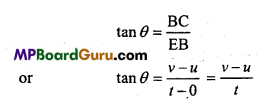
∴ Slope of the curve = Acceleration
or a = \(\frac{v-u}{t}\)
or at = v-u or v=u + at.

Question 7.
What is relative velocity? Derive the expression for it.
Answer:
The relative velocity with respect to a body at rest or in motion is defined the rate of change of position of a body with respect to another body.
Let A and B are two bodies moving with velocities v₁and v₂ and at time t their position coordinate are x₁(t) and x₂(t) respectively.
x₁(t) = x₁1(0) + v₁t …(1)
∴ x₂(t) = x₂(0) + v₂t …(2)
Where x₁(0) and x₂ (0) are position coordinates at t = 0.
Subtracting eqn. (1) from eqn. (2),
∴ x₂(t) – x₁(t) = x₂(0) – x₁(0) + (v₂ -v₁)t …(3)
In the eqn. (3), x₂(t)- x₁(t) represents the position of B w.r.t. A at time t.
∴ x₂(0) – x₁(0) represents the relative position or distance of B w.r.t. A,
Putting t = 0 in eqn. (3) then the relative displacement in 1 sec. will be v₂-v₁
∴ Relative velocity of B w.r.t. A = v₂-v₁
∴ By eqn. (3),

Question 8.
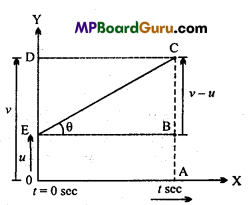
Derive graphically the second equation of motion.
Answer:
From the given graph displacement of an object = Area under the curve OACE
or
s = Area of rectangle OABE + Area of ∆EBC
or
s = OA × AB + \(\frac{1}{2}\)EB × BC
or
s = ut+\(\frac{1}{2}\)t(v – u)
v – u=at
s = ut + \(\frac{1}{2}\)t ×at
s = ut + \(\frac{1}{2}\)at ²

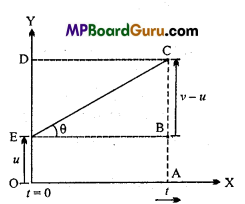
Question 9.
Derive graphically the third equation of motion.
Answer:
From the above v-t graph
Displacement of an object = Area of trapezium OACE

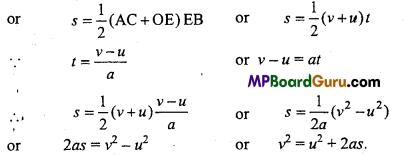
Motion in a Straight Line Class 11 Important Questions Long Answer Type

Question 1.
Derive the equation of motion by Integration method.
Answer:
First equation of motion : v = u + at :Let at any instant t, the velocity of a particle is v.
∴ Acceleration, a = \(\frac{d v}{d t}\)
or dv = adt …(1)
Let at t = 0, v = u
∴ Integrating eqn. (1), we get

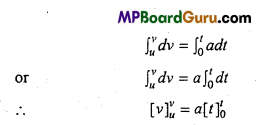
∴ v-u = a(t- 0)
or v – u- at or v = u + at.
Second equation of motion : Let a particle is moving with velocity u along X-axis and at any instant t, its displacement is x.
∴ v = \(\frac{d x}{d t}\)
or
dx = vdt
Also, we know that,
v = u + at
∴ dx = (u + at)dt ….(1)
Now, at t = 0, x = x₀
∴ Integrating eqn. (1), we get

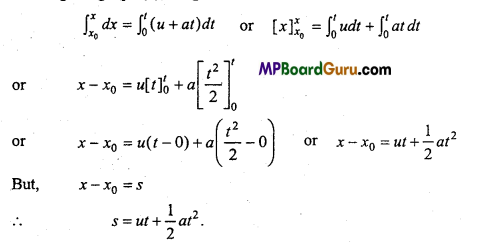
Third equation of motion :
Accordrng to definition of acceleration

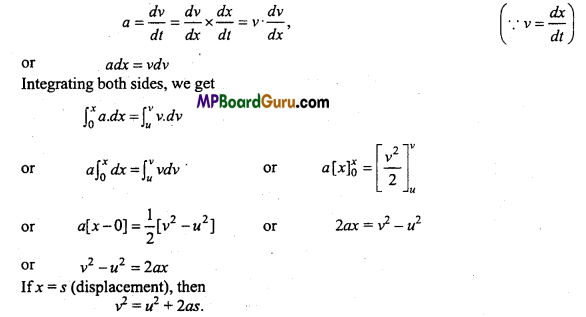
Question 2.
Derive graphically the second and third equation of motion.
Answer:
From the given graph displacement of an object = Area under the curve OACE
or
s = Area of rectangle OABE + Area of ∆EBC
or
s = OA × AB + \(\frac{1}{2}\)EB × BC
or
s = ut+\(\frac{1}{2}\)t(v – u)
v – u=at
s = ut + \(\frac{1}{2}\)t ×at
s = ut + \(\frac{1}{2}\)at ²

From the above v-t graph
Displacement of an object = Area of trapezium OACE

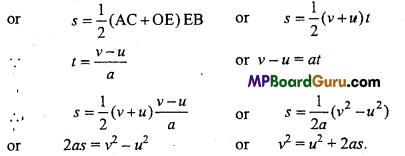
Motion in a Straight Line Class 11 Important Numerical Questions

Question 1.
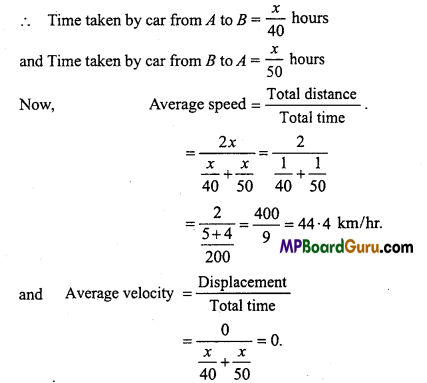
A car travels from a city A to city B with a speed of 40 km/h and returns back to city A, with the speed of 50 km/h. What is the average speed of car? What will be its average velocity?
Solution:
Let the distance between A and B is x.

Question 2.
A body obtain a velocity of 10m/s in 3 second from rest. Find its acceleration.
Solution:
Given, u = 0, v = 10m/s and t = 3sec.
From Ist equation of motion,
v = u + at
a = \(\frac{v-u}{t}\)
Putting the values in above equation, we get
a = \(\frac{10-0}{3}\) = \(\frac{10}{3}\) m/s²
or
a = 3.33 m/s²

Question 3.
A body describes 45 m in 8^th second with uniform acceleration from rest. Find its acceleration.
Solution:
Given :u-0,t=8s,s = 45m

Question 4.
A car moving with a velocity of 36 km/h. When brakes are applied it stop after 10m. Calculate acceleration and time taken to stop.
Solution:

Question 5.
A body describe 15m in sixth second and 23m in tenth second. Find initial velocity and acceleration of the body.
Solution:

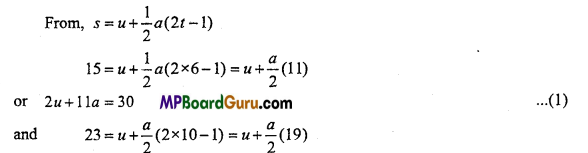
or 2u+19a=46
Solving eqns. (1) and (2),…..(2)
u = 4 m/s and a = 2m/s²

Question 6.
Two trains are running parallely in two tracks in the same direction with a speed of 10 m/s and 15 m/s. Find relative velocity.
Solution:
Given, V₁ = 10 m/s, v₂ = 15 m/s
Relative velocity = v₂ – v₁
= 15-10 = 5 m/s.

Question 7.
A car is running on a straight road with a velocity of 126 km/hr. It stops after travelling a distance of 200 m. Find the retardation of the car. How much time does it take to stop?
Solution:
Given, initial velocity u = 126km/h
= 126 × \(\frac{5}{18}\) = 35m/s.
Distance curved s = 200 m
Final velocity v = 0.
Using third equation of motion,
v² = u² + 2as
or 0 = 35 × 35 + 2 × a × 200
a = \(-\frac{35 \times 35}{2 \times 200}\) = 3.06m/s²
Using first equation of motion,
v = u + at
or 0=35 – 3.06t
or t= \(\frac{35}{3 \cdot 06}\)
=11.43sec.

Question 8.
A car travels first \(\frac{1}{3}\) part of total distance at a speed of 10km/hr, second\(\frac{1}{3}\) part at 20km/hr and last \(\frac{1}{3}\) part at 60 km/hr. Find out average speed of the car.
Solution:
Let the distance travelled by car = x km
Given, v₁ = 10 km/hr, v₂ = 20km/hr, v₃ 60 km/hr

Question 9.
A ball is thrown vertically upward reaches the roof of a house 100m in height. At same instant a second ball is dropped downward from the roof of the house will zero initial velocity. At what height both the ball will cross each other?
Solution:
Given, h = 100m
Let, both the ball cross each other at a distance of x m after t sec.
For vertically upward motion,
u = ? v = 0 a = -g and h = 100 m
v² = u² +2as, we get
0 = u² – 2 × g × 100
or u² = 200g = 200 × 9.8 = 1960
or
for vertically downward motion, .
u = 0, a = g, s = (100 -x)
From s = ut + \(\frac{1}{2}\)at², weget
100 – x = 0 +\(\frac{1}{2}\) × 9.8 × t² =4.9t²
or 100 – x = 4.9 t²
When the ball is thrown upward, distance covered by it
s = ut + \(\frac{1}{2}\) at² ….

or x = 100 – 25 = 75m

Question 10.
A jet plane is moving with a velocity of 500km/hr. Velocity of gas ejecting out with respect to jet plane is 1500 km/hr. find out the velocity of gas ejecting out w.r.t. a man standing on ground surface.
Solution:
Velocity of gas ejecting out from the jet plane w.r.t. man standing on ground surface
= v_g-v_j =1500-500
= 1000 km/hr.

Question 11.
A woman starts from her home at 9-00 am., walks with a speed of 5 kmh^-1 on a straight road up to her Office 2-5 km away, stays at the office up to 5-00 p.m. and returns home by an auto with a speed of 25 kmh^-1. Choose suitable scales and plot the x – t graph of her motion.
Solution:
x -t graph of the motion of woman is shown in fig. V₁ = speed of woman while walking at 5kmh^-1.
x = Distance covered by her = 2-5 km If t¹ = time taken to reach office, then it can be calculated by using
x₁ = v₁t₁
or t₁ = \(\frac{x}{v_{1}}\)
∴ t₁ = \(\frac{2 \cdot 5}{5}\) = \(\frac{1}{2}\) h = 30 minutes

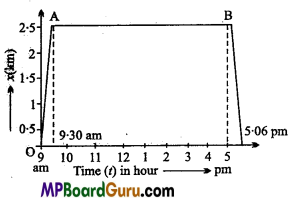
If O is regraded as origin for both time and distance, then at t = 9.00 am., x = 0 at t = 9.30 am., x = 2.5 km and she reaches in her office. So OA represents x – t graph of the motion, when the woman walks from her home to office.
When she stays at her office from 9.30 a.m to 5.00 p.m., then she is stationary and hence her stay is represented by the straight line AB in the graph.
On return, speed of auto, v₂ = 25 km/h
∴ If t₂ = time taken by her i.e., by auto from office to her home, then
t₂ \(\frac{x}{v_{2}}\) = \(\frac{2 \cdot 5}{25}\) = \(\frac{1}{10}\) = 6minutes
Thus, she reaches back to her home at 5.06 p.m.
Her motion on the return journey in shown by BC part of the graph.
Scale chosen :
Time on X-axis, 1 division = 1 hour.
Distance on Y-axis, 1 division = 0.5 km.

Question 12.
A body travels half of its total path in the last second of its fall from rest. Find the time and height of its fall.
Solution:
Let the body falls from a height h and takes time t to fall.
From Second equation of motion, fall from/I to B is given by

Motion in a Straight Line Class 11 Important Questions Objective Type

1. Multiple- choice questions:

Question 1.
If the velocity of an object is doubled then among the following which will be doubled:
(a) Acceleration
(b) Kinetic energy
(c) Momentum
(d) Weight.
Answer:
(c) Momentum

Question 2.
An object dropped from peak of a tower takes 2 second to cross half its height. The height of the tower will be : (If g = 9-8 m/s²)
(a) 9.8m
(b) 19.6m
(c) 20m
(d) 39.2m.
Answer:
(d) 39.2m.

Question 3.
Ratio of instantaneous velocity and instantaneous speed is ……………….
(a) Less than 1
(b) More than 1
(c) Zero (d) Equal to 1.
(d) Equal to 1.
Answer:
(d) Equal to 1.

Question 4.
If acceleration-time graphs, the area represents :
(a) Displacement
(b) Velocity
(c) Change in velocity
(d) Distance covered.
Answer:
(c) Change in velocity

Question 5.
An object is falling freely under the gravitation. The ratio of the distance covered by it in first, second and third seconds will be :
(a) 1 : 3 : 5
(b) 1 : 2 : 3
(c) 1 : 4 : 9
(d) 1 : 5: 6.
Answer:
(a) 1 : 3 : 5

Question 6.
The motion of a particle of a gas are :
(a) One-dimensional
(b) Two-dimensional
(c) Three-dimensional
(d) Vertically upward and downward.
Answer:
(c) Three-dimensional

Question 7.
Which of the following quantity may be zero for any particle in motion :
(a) Displacement
(b) Distance
(c) Speed
(d) None of these.
Answer:
(a) Displacement

Question 8.
If a player throws a ball vertically upward with initial velocity 29 m/s. The velocity of the ball at its peak of motion will be :
(a) 29 m/s
(b) -29 m/s
(c) Zero
(d) None of these.
Answer:
(c) Zero

Question 9.
A car covers half a distance between two points with a speed of 40 km/hr and next half with a speed of 60 km/hr. The average speed will be :
(a) 40 km/hr
(b) 48 km/hr
(c) 50 km/hr
(d) 60 km/hr.
Answer:
(b) 48 km/hr

Question 10.
The position vector of a particle is represented by the equation x = (3t³ + 7t²+14t + 8)m, the acceleration of the particle at t = 1 sec will be :
(a) 10 m/s²
(b) 32 m/s²
(c) 23 m/s²
(d) 16 m/s².
Answer:
(b) 32 m/s²

2. Fill in the blanks:

1. A device used to measure instantaneous velocity is called ………………
Answer:
Speedometer

2. The motion of the Billiard ball is …………….. motion.
Answer:
Two-dimensional

3. The change in position of a body with respect to time is called ………………….
Answer:
Motion

4. When a body moves in a straight line, then its motion is ……………………
Answer:
One-dimensional

5. The distance travelled by a body in a definite direction is called ………………….
Answer:
Displacement

6. The rate of change of position of a body in motion is called its ………………..
Answer:
Velocity

3. Match the following:

Column ‘A’	Column ‘B’
1. First equation of motion	(a) s = ut+\(\frac{1}{2}\)at2
2. Second equation of motion	(b) v = u + at
3. Third equation of motion	(c) \(\frac{\text { Change in velocity }}{\text { Time interval }}\)
4. Average acceleration	(d) u + \(\frac{1}{2}\)a(2t – 1)
5. Distance travelled in tth second	(e) v2= u2 +2as.

 4. Write true or false:

1. From a velocity-time graph, the distance travelled can be measured.
Answer:
True

2. In two dimensional motion, the path of uniform velocity is a straight line.
Answer:
True

3. The displacement can be zero, negative as well as positive.
Answer:
True

4. The unit of acceleration in SI system is not metre/sec².
Answer:
False

5. Displacement is a vector quantity.
Answer:
True

6. The slope of velocity time graph represents acceleration.
Answer:
True

5. Answer in one word:

1. A body is moving with constant velocity. What is the value of its acceleration?
Answer:
Zero

2. What does the slope of position-time graph give?
Answer:
Velocity

3. What does the slope of velocity-time graph give?
Answer:
Acceleration

4. Who had derived the equations of motion?
Answer:
Gallileo,

5. What is the value of acceleration due to gravity on earth’s surface?
Answer:
9.81 m/s²