MP Board Class 11th Physics Important Questions Chapter 2 Units and Measurements

Students get through the MP Board Class 11th Physics Important Questions Chapter 2 Units and Measurements which are most likely to be asked in the exam.

MP Board Class 11th Physics Important Questions Chapter 2 Units and Measurements

Units and Measurements Class 11 Important Questions Very Short Answer Type

Question 1.
What do you mean by measurement?
Answer:
In physics, the measurement means comparison of the given physical quantity with standard quantity of same nature.

Question 2.
What are the different type of measurement?
Answer:
The different type of measurement are :

1. F.P.S. (Foot Pound Second)
2. C.G.S. (Centimetre Gram Second)
3. M.K.S. (Metre Kilogram Second).

Question 3.
Define unit.
Answer:
The standard value of any physical quantity is known as its unit.

Question 4.
What are fundamental physical quantities?
Answer:
The physical quantities which do not depend upon other quantities are called fundamental.
Example: Mass, Length, Time etc.

Question 5.
What are derived physical quantities?
Answer:
The physical quantities which are derived from fundamental quantities are called derived quantities e.g.,
Volume = length × breadth × height = (length)³
Similarly Force, Momentum, Pressure, Power etc. are derived quantities.

Question 6.
Define metre.
Answer:
The distance travelled by light ray in \(\frac{1}{29,97,92,458}\) seconds in vaccum is called metre.

Question 7.
What are the different units to measure astronomical distance?
Answer:

• Light year: Distance travelled by light rays in one year in vacuum is called one light year.
  1 light year = 3 × 10⁸ × 365 × 24 × 60 × 60 metre = 9.46 × 10¹⁵ m.
• Parsec : It is the unit to measure the distance of stars from the earth.
  1 Parsec = 3.26 light year= 3.08 × 10¹³ km.
• Astronomical unit: Average distance between sun and earth is called astronomical units. It is denoted by A.U.
  1A.U.= 1.496 × 10¹¹metre.

Question 8.
What do you mean by one kilogram?
Answer:
The mass of platinum-iridium cylinder, kept at International Bureau of weights and measure at severes near Paris in France is defined as one kilogram.

Question 9.
Define one second.
Answer:
One second is the time-interval in which Cs – 133 atom execute 9 19 26 31 770 vibrations.

Question 10.
Define the dimensions of a physical quantity with example.
Answer:
The suitable powers, by which a derived unit is expressed in terms of fundamental units are called dimensions of that physical quantity.
Examples :
(i) Area = Length × Breadth
= [L] × [L] = [L]² = [M⁰L²T⁰].

(ii) Velocity = \(\frac{\text { Distance }}{\text { Time }}\)
= \(\begin{array}{l}
{[\mathrm{L}]} \\
\hline[\mathrm{T}]
\end{array}\) = [LT^-1] = [M⁰LT^-1
Thus, dimension of area in length is 2 and that of velocity are, in length 1 and time -1.

Question 11.
What is dimensional equation? Explain with examples.
Answer:
The equation which represents the relation of a derived unit with the fundamental units is called dimensional equation. In mechanics dimensional equation is represented as
[X] = [M^aL^bT^c]
Examples : Velocity = [M⁰LT^-1 ]
and Force = [MLT^-2].

Question 12.
Which of the three physical quantities have the dimensional formula [ML^-1T^-2]?
Answer:
Pressure, Stress and Young’s modulus.
∵ [ML^-1T^-2]=\(\frac{\left[\mathrm{MLT}^{-2}\right]}{\left[\mathrm{L}^{2}\right]}\) = \(\frac{\text { Force }}{\text { Area }}\)
[L2] Area

Question 13.
What are dimensionless quantities? Give three examples.
Answer:
The quantities which are having no dimension are called dimensionless quantities e.g., relative density, strain, relative humidity.

Question 14.
What is significant figure? What is the significant figure in 7.000 × 10³ m?
Answer:
Significant figure :
The number of digits used to express accurately the measured value of the physical quantity is called the significant figures.
The significant figure of 7.000 × 10³ m is 3.

Question 15.
How many significant figures are in the following :
(i) 6.320 joule,
(ii) 0.2370 gm,
(iii) 0.007 kg,
(iv) 2.64 × 10^-5m.
Answer:
(i)  4,
(ii) 4,
(iii) 1,
(iv) 3.

Question 16.
Candela is unit of which physical quantity?
Answer:
Candela is unit of Luminious intensity.

Question 17.
What do you mean by Armstrong unit?
Answer:
It is the unit to measure micro distance 1 Å = 10^-10 metre.

Question 18.
What are the merits of SI system?
Answer:
The main features of SI system are :

• It is a coherent system of units.
• In this system a physical quantity has only one unit, e.g., the unit of energy is joule, whether it is mechanical energy, heat energy or electrical energy.
• It is a decimal system. Smallest and biggest quantities are expressed in the power of 10. e.g.,
  1 kilometre = 10³ m; 1 mm = 10^-3m etc.
• It is closely related to C.G.S. and M.K.S. system.
• All the derived units in this system are accepted on international level.

 Units and Measurements Class 11 Important Questions Short Answer Type

Question 1.
Which of the following is the most precise device for measuring length :
(a) A vernier callipers with 20 divisions on the sliding scale.
(b) A screw gauge of pitch 1mm and 100 divisions on the circular scale.
(c) An optical instrument that can measure length to within a wavelength of light.
Answer:
The most precise device is that whose least count is minimum.
Now, (a) Least count of vernier callipers = 1 MSD – 1 VSD
= 1MSD – \(-\frac{19}{20}\) MSD = \(\frac{1}{20}\) MSD
= \(\frac{1}{20}\) mm =\(\frac{1}{200}\) cm
= 0.005 cm
(b) Least count of screw guage
= 0.001cm
(c) Wavelength of light, λ ≈ 10 ^-5 cm = 0.00001 cm
∴ Least count of optical instrument = 0.00001 cm Thus, clearly the optical instrument is the most precise.

Question 2.
What are the uses of dimensional analysis?
Answer:
Uses :

• To find the unit of a physical quantity.
• To change one system of units into another system.
• To check the correctness of a physical relation.
• To establish relation between different physical quantities.

Question 3.
Distinguish between fundamental units and derived units.
Answer:
Difference between fundamental and derived units :

Fundamental units	Derived units
1. The units of fundamental quantities are called fundamental units.	The units of derived quantities are called derived units.
2. These units are independent.	These units depend upon fundamental units.
3. There are seven fundamental units and two supplementary units in SI system.	These units are not limited in number.

Question 4.
Answer the following:
(a) You are given a thread and a metre scale. How will you estimate the diametre of the thread?
(b) A screw gauge has a pitch of 1.0 mm and 200 divisions on the circular scale. Do you think it is possible to increase the accuracy of the screw gauge arbitrarily by increasing the number of divisions on the circular scale?
Answer:
(a) The diameter of a thread is so small that is cannot be measured using a metre scale. We wind the thread on in close turns on a pencil or a cylindrical glass rod so that the turns touch one another and are tight. Count the number of turns (n) and find the average length (l) of the coiled thread using the metre scale. Divide this average length by the number of turns to get the diameter i.e.,
Diameter = \(\frac{\text { Average length }}{\text { Number of turns }}\) = \(\frac{l}{n}\)

(b) Yes, the accuracy of the gauge increases by increasing the number of divisions of the circular scale because the least count is given by :
Least count = \(\frac{\text { Pitch }}{\text { No. of divisions on the circular scale }}\)
So, theoretically speaking, least count decreases on increasing the number of divisions on the circular scale.

Question 5.
Let us choose such a unit accordance to which velocity of light be one unit. On the basis of this new unit, what will be the distance between Sun and Earth if light takes 8 minute and 20 second to reach earth?
Answer:
Velocity of light = 1 (as per new unit)
Time taken by light to reach earth surface = (60 × 8 + 20) = 500 sec.
∴ Distance between Sun and Earth = Velocity of Light × Time
= 1 × 500 = 500 Unit of length.

Question 6.
Check the correctness of formula, v² = u² +2las by dimensional method.
Answer:
v²=u²+las
Now, dimensions ofu and v = [LT^-1], dimensions of a =[LT^-2]
Dimensions of s = [L]
and 2 is dimensionless
∴ [LT^-1]² =[LT^-1]²+[LT^-2L]
or [ L²T^-2 ] = [ L²T^-2] + [ L²T^-2]
Since, the dimensions of each term is same, hence the formula is true.

Question 7.
What do you mean by principle of homogeneity of dimensions?
Answer:
According to this principle the dimensions of all terms on both the sides of a dimensional equation are same.

Units and Measurements Class 11 Important Questions Long Answer Type

Question 1.
The velocity of sound waves in a medium depends upon the coefficient of elasticity of the medium (E) and its density (d). Establish the formula for the velocity of wave by dimensional method.
Answer:
Let the velocity of sound in the air depends upon the coefficient of elasticity and density of medium, then
v ∝ E^ad^b
or v = k ,E^ad^b ……..(1)
Where v = velocity of sound, E = coefficient of elasticity, d – density and a and b are numbers and k is dimensionless constant.
Now, the dimensional formulae of quantities are :
v=[LT^-1]
E = [ML^-1T^-2]
d = [ML^-3]
By eqn. (1) we get
or [LT^-1] =[ML^-1T^-2]^a[ML^-3]^b
or [LT^-1] =[M^aL^-a’T^-2aM^bL^-3b]
or [LT^-1] =[M^a+b + L^-a-3bT^-2a]
Now,by the principle of homogeneity, the dimension of both the sides will be equal.
a + b = 0 …(2)
∴ -a-3b=1 …(3)
-2a = -1 …(4)
Hence, a=\(\frac{1}{2}\)
Putting the value of a in eqn. (1), we get
\(\frac{1}{2}\)+ b = 0
or
b = – \(\frac{1}{2}\)

Putting the values of a and b in eqn. (1), we get
v = k.E^1/2d-d^-1/2
or

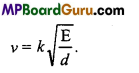
This is the required relation.

Question 2.
How much dyne is in one Newton?
Answer:
Dimensional formula for force is [MLT^-2].
Here, a=1,b=1 and c = -2

Putting the value, we get
n₂= n₁[10³] [10² ] [1]
or
n₂ = n₁ × 10n⁵
If n₁ = 1 dyne
Then n₂ = 1 Newton
∴ 1 Newton = 10⁵ dyne.

Question 3.
According to van der Wall relation between pressure P, volume V and temperature T is given by

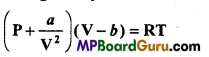
Where a and b are constant. Find the dimensions of a and b.
Answer:
According to homogineity of dimensional equation, a
Dimension of \(\frac{a}{V^{2}}\)= Dimension of P.
∴ Dimension of a = Dimension of P ×(Dimension of V)²
= [M¹L^-1T^-2][L³]²
∴ Dimension of a =[M¹L⁵T^-2] and Dimension of b = Dimension of V = [L³]
or Dimension of b = [M⁰L³T⁰].

Question 4.
Find the fundamental unit of force and work using dimensional equation.
Answer:
(1) Force = Mass × Acceleration

(2) Work Force Displacement
= Mass x Acceleration x Displacement

∴ Dimensional formula of work = [ML²T^-2]
SI unit = kg-metre²/sec²
C.G.S. unit = g-cm²/sec².

Question 5.
What are the limitations of dimensional equations?
Explain the limitations of dimensional analysis.
Answer:
Limitations :

• The dimensional formulae of only those quantities can be ob- :d which can be expressed in terms of fundamental quantities.
• It is not applicable to trigonometrical, exponential or logarithmic functions.
• The value of constants cannot be determined by this system.
• If an equation has a constant having dimensions e.g., G, Then relation cannot be blished.

Question 6.
The periodic time of a simple pendulum T, depends upon its effective length (l) acceleration due to gravity (g). Derive the formula for time-period by dimensional
Or
Find out an expression for periodic time of a simple pendulum using dimensional sis.
Answer:
Let the formula for periodic time (T) be,
T ∝ l^a g^b
T = K. l^a g^b
Putting the dimensions of periodic time (7), effective length (l) and acceleration due to gravity in eqn. (1).
[M⁰L⁰T] = [L]^a x [LT^-2]^b .
or
[M⁰L⁰T] = [M⁰L^a+bT^2b]
By the principle of homogeneity, comparing the powers of length and time, we get
a + b = 0 …(2)
and – 2b = 1
⇒ b = – \(\frac{1}{2}\)
Putting in eqn. (2), we get
a- \(\frac{1}{2}\) = 0
∴ a = \(\frac{1}{2}\)
Putting the values of a and b in eqn. (1), we get
T = kl^1/2g^-1/2
or

This is the required formula.

Question 7.
What are the different type of errors in measurement? Explain.
Answer:
Random error :
If an observer measures a physical quantity and each time he finds different readings, then such an error is called random error.
Example : Suppose the diameter of a wire is determined by a screw gauge and each time the reading is different because the wire is not uniform.
To remove this error, so many readings are taken and then mean is calculated.
If a physical quantity is measured n times and its readings are a₁,a₂, a₃ …..a_n

Absolute error :
The difference between the observed value and actual value of a physical quantity is called absolute error. It is always positive.
The absolute error of a quantity x is denoted by | Δx |
Let the observed values of a physical quantity are x₁,x₂, x₃ …..x_nand the average value is x.

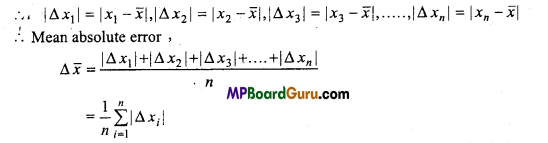
Relative error :
The ratio of absolute error and actual value is called relative error.
∴ Relative error = \(\frac{\text { Average absolute error }}{\text { Actual value }}\)
= \(\frac{\text { Actual value }-\text { Measured value }}{\text { Actual value }}\)
or

Percentage error: When the relative error is expressed in percentage, then it is called percentage error.
∴ Percentage error = \(\frac{\text { Average absolute error }}{\text { Actual value }}\) ×100

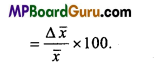
Question 8.
What do you understand by significant figure ? How do you find significant figure of a quantity?
Answer:
The number of digits used to express accurately, the measured value of a physical quantity is called significant figure.

Counting of significant figures :

• By changing the decimal point, the number of significant figures does not change.
  For example; 1.234, 12.34 and 123.4 the number of significant figure is 4.
• All the zeros between two non-zero numbers are significant.
  For example; Significant figures in 3100-05 is 6.
• The zeros before the first non-zero digit are ignored while all the zeros to the right are counted.
  For example; Significant figure in 0 007 is 1 and that of 6-320 is 4,
• The zeros in a whole number at the end are not counted.
  For example; Significant figure in 6320 is 3 and in 13200 is 3.
• The significant figure does not change with the change of units i.e.,
  0.0432m = 4.32 cm, both have the significant figure 3.
• When a number is expressed in the power of 10, then the power is not counted, i.e., 10.52 × 10⁵ has significant figure 4.

Units and Measurements Class 11 Important Numerical Questions

Question 1.
Convert 0.53 Å into metre.
Solution:
We know that, 1Å = 10^-10 m
0.53 Å = 0.53 ×10^-10m
= 5.3 ×10^-11m

Question 2.
A student measures the thickness of a human hair by looking at it through
a microscope of magnification 100. He makes 20 observations and finds that the average width of the hair in the field of view of the microscope is 35mm. What is theestimate on the thickness of hair?
Solution:
Estimate on the thickness of hair is given by:

Question 3.
State the number of significant figures in the following :
(a) 0.007m²,
(b) 2.64 × 10²⁴kg,
(c) 0.2370 g cm^-3,
(d) 6.320 J,
(e) 6.032 Nm^-2,
(f) 0.0006032 m².
Answer:
The number of significant figures is as given below :
(a) 1,
(b) 3,
(c) 4,
(d) 4,
(e) 4,
(f) 4.

Question 4.
The length, breadth and thickness of a rectangular sheet of metal are 4.234m, l-005m and 2.01cm respectively. Give the area and volume of the sheet to correct significant figures.
Solution:
Here, Length, l = 4.234m
Breadth, b = 1.005m
Thickness, h = 2.01cm = 0 0201m
Area of the sheet = 2(lb + bh + hl)
= 2(4.234 × 1.005 + 1.005 × 0.0201 + 0.0201 × 4.234)
= 8.7209468m²
As the least number of significant figures in thickness is 3,
∴ Area = 8.72m²
Volume = l × b × h
= 4.234 × 1.005 × 0.0201m³
= 0-0855m³

Question 5.
A physical quantity P is related to four observables a, b, c and d as follows :

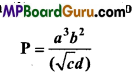
The percentage errors of measurement in a, b, c and d are 1%, 3%, 4% and 2% respectively. What is the percentage error in the quantity P ? If the value of P calcu-lated using the above relation turns out to be 3.763, to what value should you round off the result?
Solution:

The calculation of error clearly shows that the number of significant figures is 2, so the result of P may be rounded off to two significant digits i.e.,
P = 3.763 = 3.8.

Question 6.
The percentage errors in the measurement of length and mass are 2% and 5% respectively. What will be the percentage error in the measurement of density of a cube?
Solution:

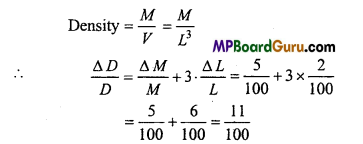
Maximum % error in the measurement of density will be 11%.

Question 7.
Given that the period T of oscillation of a gas bubble from an explosion under water depends on P, d and E, where the symbols are pressure, density and total energy of explosion. Find dimensionally a relation for T.
Solution:
Let T∝P^ad^bE^c
or T =kPsup>ad^bE^c, (where His a dimensionless constant) …(1)
Writing dimensional formula of each physical quantity on both sides of eqn. (1), we
[M⁰L⁰T¹] = [ML^-1T^-2 ]^a [ML^-3 ]^b [ML²T^-2 ]^c
= [M^a+b+c][L^-a-3b+2c][T^-2a-2c]
Comparing power of,
M, 0 = a + b + c ……(2)
L, 0 = – a – 3b + 2c ……(3)
T, 1 = -2a – 2c
or a + c = –\(\frac{1}{2}\)
∴ From eqns. (2) and (4), we get
b = – (a + c)
= \(-\left(-\frac{1}{2}\right)\) = \(-\left(\frac{1}{2}\right)\)
Putting the value of b in eqn. (3),
– a + 2c = 3b
=> -a + 2c =3 x \(\frac{1}{2}\)= \(\frac{3}{2}\)
Adding eqns. (4) and (5),

Question 8.
An object of mass ‘m’ is executing simple harmonic motion suspended at one end of a spring. If its spring constant is K and time-period is T, then prove with the help of dimensional method that equation T=2π\(\frac{m}{\mathbf{K}}\) incorrect. Also find its correct
equation.
Solution:
Given, T = 2π\(\frac{m}{\mathbf{K}}\)
Writing dimensional formula of the above equation
[T] = \(\frac{[\mathrm{M}]}{\left[\mathrm{MT}^{-2}\right]}\) = [T²]
Since, the dimension of T on both sides are not same, therefore the given equation is incorrect.
Let us assume that time-period T, a^th power of mass (m) and b^th power of spring constant (K), then
T∝m^aK^b
or T = K.m^aK^b
Let K = 2π
∴ T = 2πm^aK^b
or [T] = 2π[M]^a [MT^-2]^b
= [M] ^(a+b)[T]^-2b
Comparing both sides, we get
a + b = 0
and -2b = 1
or b = –\(\frac{1}{2}\)
∴ a+ \(-\left(-\frac{1}{2}\right)\)=0
or
a = \(\frac{1}{2}\)
Putting the values of a and b in the above equation,
T = 2πm\(\frac{1}{2}\). K-\(\frac{1}{2}\)

This is the correct form of the equation.

Question 9.
Equation of a particle of velocity (v) and time (t) is given by v = A + Bt +\(\frac{C}{D+t}\) find out the dimension of A, B, C and D.
Solution:
Each form of R.H.S. must have dimension of v.
∴ Dimensional formula of A = Dimensional formula of velocity
v = [LT^-1].
Dimensional formula of B.t = Dimensional formula of v = [LT^-1]
∴ Dimensional formula of B =\(\frac{\left[\mathrm{LT}^{-1}\right]}{[\mathrm{T}]}\) [LT^-2]
∴Dimensional formula off D = Dimensional formula off t = [T].
Dimensional formula of\(\frac{C}{D+t}\) = Dimensional formula of v= [LT^-1]
and Dimensional formula of C = [LT^-1] x [Dimensions of D + t] – [L¹].

Question 10.
Assuming energy E, length L and time T as the fundamental unit, what would be dimensions of mass ? If energy E is being replaced by force F then what would be the dimensions of mass ?
Solution:

∴ Dimensions of mass will be = [E¹L^-2T²].
Replacing energy E by force F, we get
Force F = Mass x Acceleration

Question 11.
If m and c represent mass and velocity, then find with the help of dimensional method the quantity mc² is equivalent to which form?
Solution:
Dimensions of mc² – Dimensions of mass x (Dimensions of velocity)²
= M[LT^-1]²
= [M¹L²T^-2 ] = Dimensions of energy.

Question 12.
The centripetal force acting on a particle revolving in a circular path depends upon velocity of the particle v and radius of circle (r). Using dimensional method establish the formula for the centripetal acceleration (a).
Solution:
According to given question
a ∝ v^a r^b
or a = kv^a r^b …(1)
Writing the dimensional formula for the quantities
[M⁰LT^-2] = [M⁰LT⁰]^b
=[M⁰L^a+bT^-a]
Comparing the powers of M, L and T both sides,
a + b= 1 …(2)
and – a = -2 or a = 2
Putting the value of a in eqn. (2), we get
2 + b=1
or b = 1 – 2 = – 1
Hence, from eqn. (1), we get
a = k.v² r^-1 or a = \(\frac{k v^{2}}{r}\)
If k= 1, then a= \(\frac{v^{2}}{r}\)

Question 13.
Diameter of a sphere is 2.348 cm. Find out volume and surface area of it up to required significant number.
Solution:
Given,
2R = 2.348 cm
∴ R= 1.174 cm
Volume of sphere V =\(\frac{4}{3}\)πR³ = \(\frac{4}{3}\) × 3.14 ×(1.174)³
or
V = 6.774 cm³
and Surface area of sphere S = 4πR²
=4 × 3.14 × (1.174)²
= 17.311 = 17.31cm².

Motion in a Straight Line Class 11 Important Questions Objective Type

1. Multiple- choice questions:

Question 1.
Light year is unit of:
(a) Time
(b) Distance
(c) Speed
(d) Intensity of light.
Answer:
(b) Distance

Question 2.
Fermi is unit of:
(a) Energy
(b) Momentum
(c) Impulse
(d) Length.
Answer:
(d) Length.

Question 3.
The dimensional formula of gravitational constant is :
(a) [ML²T^-2]
(b) [M^-1L³T^-2]
(c) [M^-1L²T^-3]
(d) [ML³T²]
Answer:
(b) [M^-1L³T^-2]

Question 4.
Choose a pair of physical quantities having the same dimensional formula:
(a) Pressure and stress
(b) Stress and strain .
(c) Pressure and force
(d) Power and force.
Answer:
(a) Pressure and stress

Question 5.
Units of energy is :
(a) watt
(b) joule
(c) Electron volt
(d) Calorie.
Answer:
(a) watt

Question 6.
Relation between v and t, velocity of sound and time is
v = at+\(\frac{b}{t+c}\) dimensional formula for a, b and c will be:
(a) [L²], [T], [LT^-2]
(b) [LT^-2], [L], [T]
(c) [LT⁺²], [LT], [L]
(d) [L], [LT], [T²].
Answer:
(b) [LT^-2], [L], [T]

Question 7.
Order of 4-12 × 10⁵ is :
(a) 4
(b) 6
(c) 5
(d) None of these.
Answer:
(b) 6

Question 8.
Which among the following have significant number four :
(a) 0.630
(b) 0.0024
(c) 6.023
(d) 0.004.
Answer:
(c) 6.023

Question 9.
Which among the following is not a fundamental unit:
(a) Metre
(b) Ampere
(c) Kelvin
(d) Litre.
Answer:
(a) Metre

Question 10.
Which among the following physical quantities do not have the dimensional
formula [ML^-1T^-2 ] :
(a) Youngs modulus
(b) Stress
(c) Strain
(d) Pressure.
Answer:
(c) Strain

Question 11.
Light year is equal to :
(a) 9.46 × 10¹⁰ km
(b) 9.46 × 10¹² km
(c) 9.46 × 10¹² metre
(d) 9.46 × 10^-12 km.
Answer:
(b) 9.46 × 10¹² km

Question 12.
If the length of a simple pendulum is increased, then its percentage increase in its time-period will be:
(a) 0.5%
(b) 2.0%
(c) 1%
(d) 4%.
Answer:
(b) 2.0%

2. Fill in the blanks:

1. The volume of cube of side 1cm is equal to ……………….. m³.
Answer:
10^-6

2. A vehicle moving with speed of 18 km/hr covers ……………….. m in 1 second.
Answer:
5

3. 3.0 m/s² = ………………….. km/h².
Answer:
3.9 × 10^-4

4. Number of significant figure in 2.64 × 10²⁴ kg is ………………….
Answer:
3

5. Number of fundamental unit in SI system is …………………..
Answer:
7

6. 1 micron = ………………… metre.
Answer:
10^-6

7. 1Å = …………………….. metre.
Answer:
10^-10

8. The error due to observer measurement is called ………………..
Answer:
Individual error

9. 1 newton = ……………………. dyne.
Answer:
10⁵

10. Dimensional formula of charge is ……………………
Answer:
[AT]

3. Match the following:
I.

Column ‘A’	Column ‘B’
1. Dimensional formula of light year	(a) Dimension of momentum
2. Dimensional formula of frequency	(b) Dimensional of planck constant
3. Dimensional formula of angular ‘ momentum will be equal to	(c) [M0LT0]
4. Dimensional formula of impulse	(d) [ML2T-2]
5. Dimensional formula of work	(e) [M0L0T-1].

Answer:
1. (c) [M⁰LT⁰]
2. (e) [M⁰L⁰T^-1].
3. (b) Dimensional of planck constant
4. (a) Dimension of momentum
5. (d) [ML²T^-2]

II.

Column ‘A’	Column ‘B’
1. [ML-1T-2] is dimensional formula of	(a) Light year
2. Newton-metre2 is unit of	(b) Newton × second
3. Unit of luminious intensity is	(c) Pressure
4. Unit of momentum is	(d) Candela
5. Unit of long distance is	(e) Force.

Answer:
1. (c) Pressure
2. (e) Force.
3. (d) Candela
4. (b) Newton × second
5. (a) Light year

4. Write true or false:

1. Dimensional formula for heat and work are same.
Answer:
True

2. The equation v = u + at, can be derived from dimensional method.
Answer:
False

3. Dimensional formula of impulse and momentum are different.
Answer:
False

4. Dimensional formula for pressure, coefficient of Young modulus and stress are [ML^-1T^-2].
Answer:
True

5. Candela is units of Luminious intensity.
Answer:
True

6. Significant figure changes with change in its units of a physical quantity.
Answer:
False

7. It is not necessary that the physical quantity will be the same, if their dimensional formula and units are same.
Answer:
True

8. The value of constant can be determined by dimensional method.
Answer:
False

9. On knowing one dimensions of a physical quantity, its unit can be determined.
Answer:
True

10. The physical quantity is more significant which have more significant figure.
Answer:
True