MP Board Class 11th Physics Important Questions Chapter 15 Waves

Students get through the MP Board Class 11th Physics Important Questions Chapter 15 Waves which are most likely to be asked in the exam.

MP Board Class 11th Physics Important Questions Chapter 15 Waves

Waves Class 11 Important Questions Very Short Answer Type

Question 1.
What do you mean by wave motion?
Answer:
It is a method of energy transformation in which the disturbance produced in the medium propagates without the flow of medium.

Question 2.
What is progressive wave. Write the formula for displacement of it?
Answer:
When disturbance is created continuously in a medium, then the particle of medium vibrates to and fro about their mean position without leaving their place. The distur¬bance move forward. The wave thus produced are called progressive wave.
Its displacement equation is :
\(y=a \sin \frac{2 \pi}{\lambda}(v t-x)\)

Question 3.
Write the principle of superposition of waves.
Answer:
When any number of waves meet simultaneously at a point in a medium, the net displacement at a given time is the algebraic sum of the displacement due to each wave at that time.

Question 4.
Write the name of the phenomenon obtained due to superposition of waves.
Answer:
Interference,

• Beats,
• Stationary waves.

Question 5.
What are stationary waves?
Answer:
When two identical waves of equal frequency travel along the same line but in opposite direction superimpose, then the resultant wave thus formed is called stationary waves.

Question 6.
How many types of stationary waves are there? Write one example of them.
Answer:
There are two types of stationary wave :

1. Transverse wave,
2. Longitudinal wave.

1.Transverse wave: If during the propagation of mechanical wave in a medium, the particles of the medium vibrate about their mean position in a direction perpendicular to the direction of wave propagation then the wave is called transverse wave

2. Longitudinal wave: If during the propagation of mechanical wave in a medium, the particles of the medium vibrate about their mean position along the direction of wave propagation then this type of wave is called longitudinal wave.

Question 7.
What are beats?
Answer:
When two waves with slight difference in frequencies travel in a medium simul¬taneously in the same direction then as a result of their superposition, the intensity of sound at any point increase and decreases alternately. This successive rise and fall in the intensity of sound is called beats.

Question 8.
What are the conditions of beats?
Answer:

• Both the waves should travel along the same straight line, in the same medium, with same velocity.
• These should be slight difference in their frequencies.
• The amplitudes of both the waves should be nearly equal.

Question 9.
If two tunning fork of frequency n₁ and n₂ are hammered together. Then how many beats will be obtained per second?
Answer:
Per second number of beat = n₁~ n₂.

Question 10.
Write three applications of beats?
Answer:

• Determination of frequency of a tuning fork.
• Matching the frequency of sound instruments.
• To enquire about poisonous gas in the mines.

Question 11.
On which factors the velocity of transverse wave produced in stretched string depends on?
Answer:

• Tension of string,
• Mass per unit length of string.

Question 12.
Write the formula for frequency of a stretched string
Answer:
\(n=\frac{1}{2 l} \sqrt{\frac{T}{m}}\)
Where, l = Length of stretched string, T = Time-period, m = Mass per unit length of string.

Question 13.
Explain beats period and frequency of beats.
Answer:
One rise and one fall of sound form one beat. The time interval between two consecutive intense sounds is called ‘beat period’.
The number of times the intensity of sound rises and falls in one second is called ‘beat frequency’.
Let the frequencies are υ₁ and υ₂
Beat frequency = \(v_{1}-v_{2}\)
and Beat period = \(\frac{1}{v_{1}-v_{2}}\)

Question 14.
What is Doppler’s effect?
Answer:
When, there is a relative motion between a sound source and a listener, then the change in the frequency of the source appears to the listener. This effect is called Doppler’s effect.

Question 15.
What are the limitations of Doppler’s effect?
Answer:
Limitations :

• The effect expresses the apparent change in the frequency, not the intensity of sound. ,
• The velocity of source or listener should not be greater than the velocity of sound.

Question 16.
What is difference between the Doppler’s effect on sound and in light waves?
Answer:
Doppler’s effect on sound waves depends upon the relative velocity and velocity of source and listener. While in light waves Doppler’s effect depends upon the relative velocity only.

Question 17.
Explain one application of Doppler’s effect.
Answer:
To estimate the speeds of aeroplanes or submarine: When radio waves transmitted from the Radar, come back after reflection from aeroplane, then their wavelength is changed. If an aeroplane is approaching then its wavelength decreases or frequency increases and if the aeroplane receding from the station, the wavelength increases. Thus, by the change of wavelength or frequency, the speed of aeroplane can be calculated.

Question 18.
What do you mean by organ pipe?
Answer:
The pipe in which sound is produced by vibrating the molecules of air or gas-filled in it.

Question 19.
The open organ pipe produces more melody sound than dosed organ pipe. Why?
Answer:
In open organ pipe the harmonics produced are odd and even both while in closed organ pipe only odd harmonics are produced, therefore harmonics produced by open organ pipe are melody.

Question 20.
A sound-producing whistle is whirled fast in a horizontal circle. What change in the frequency will be observed by an observer standing (i) at the centre of the circle, (ii) outside of the circle?
Answer:

• Since, the whistle is always constant distance from the observer, hence no change in frequency will be observed.
• For the observer standing outside the circle, the whistle will approach and move away from him in every half rotation. Hence, the frequency will be observed increasing and decreasing.

Question 21.
Why a flute has several holes in it?
Answer:
A flute is an open organ pipe, melodious sound of different frequencies can be produced by changing the length of air column by putting fingers on the holes.

Question 22.
Why sound travels faster in moist air than in dry air?
Answer:
Presence of water vapour decreases the density of air. Since velocity of sound is inversely proportional to the density. Hence, sound travels faster in moist air than in dry air.

Question 23.
Why the sound heard is more in carbon dioxide than in air?
Answer:
Velocity of sound in a gas is inversely proportional to the square root of the density of gas. Since carbon dioxide is lighter than air. Thus, velocity of sound is greater in carbon dioxide. Hence, sound heard is more in carbon dioxide than in air.

Question 24.
Sound travels faster on a hot day than on a cold day. Why?
Answer:
Velocity of sound is directly proportional to the square root of temperature. Therefore, sound travels faster on a hot day than on a cold day.

Question 25.
Why are transverse waves not produced in gases?
Answer:
Because the gases are not rigid.

Question 26.
Which property is common to all types of mechanical waves?
Answer:
When the waves propagate through a medium, the particles of a medium do not advance along with waves.

Question 27.
What will be the effect on the speed of sound waves in a gas if the absolute temperature of gas is increased to 4 times of its previous value?
Answer:
According to the formula \(v \propto \sqrt{T}\), speed of sound waves will be doubled.

Question 28.
The speed of sound in air is 330m/s. What will be the effect on the speed of sound waves if pressure is doubled, keeping the temperature constant?
Answer:
No effect, because speed of sound does not depend upon pressure.

Question 29.
Solids can support both longitudinal and transverse waves, but only longitudinal waves can propagate in gases? (NCERT)
Answer:
For the propagation of transverse waves through a medium, the medium should posses rigidity. Gases do not have property of rigidity, so the transverse waves cannot propagate through them. Due to rigidity of solids both, transverse as well as longitudinal wave can propagate through them.

Question 30.
The shape of pulse gets distorted during propagation in a dispersive medium. (NCERT)
Answer:
A sound pulse is a combination of waves of different wavelengths. In a dispersive medium, the waves of different wavelengths travel with different speeds in different directions i.e., with different velocities. So the shape of the pulse gets distorted i.e., a plane wavefront in a non-dispersive medium does not remain a plane wavefront in a dispersive medium.

Question 31.
A sitar, a tambour, and a harmonium all the three are made in unison at the same frequency, even then their voice can be recognised separately. Why is it so?
Answer:
Because the sounds of different qualities are produced by them.

Waves Class 11 Important Questions Short Answer Type 

Question 1.
What are progressive waves? Derive its equation.
Answer:
When the disturbance produced from the body executing simple harmonic motion propagates in the medium, then the particles of medium vibrates to and fro about their mean position and the disturbance advances in the medium. The waves thus produced are called progressive waves.

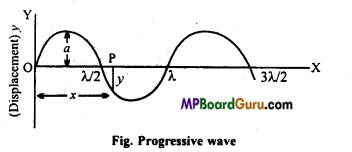
Consider a harmonic wave propagat- g O ing in a medium along the positive direction of x-axis as shown in fig. The speed ofpropagation of wave is v. Its source is at origin ‘O’. As the source is executing
S.H.M., then the displacement of the particle situated at ‘O’ at any instant ‘f be \(y=a \sin \omega t\) ………(1)
Where, ‘a’ is amplitude of vibration and ‘ co ‘ is angular frequency. Now, \(\omega=2 \pi v=\frac{2 \pi}{T}\)

Where, u is frequency and T is time-period. Since the speed of wave is v hence the disturbance will reach the point ‘P’ at a distance V from the origin ‘O’ in \(\frac{x}{v}\) sec. Thus, at any instant ‘f the displacement of the particle situated at P will be \(y=a \sin \omega\left(t-\frac{x}{v}\right)\) …….(2)

The particle of medium situated at ‘P’ will begin to vibrate after \(\frac{x}{v}\) sec. from the particle situated at ‘O’. Thus, in time ‘t’ the displacement of particle at P will be the same as that the particle at O, before \(\frac{x}{v}\) sec.Therefore, instead of ‘t’ in the eqn. (1) we should write \(\left(t-\frac{x}{v}\right)\) Eqn. (2) shows a progressive wave which is propagating along positive direction of X- axis with velocity v. If a progressive wave is travelling along negative direction of A-axis, then its equation will be :
\(y=a \sin \omega\left(t+\frac{x}{v}\right)\) …………. (3)
As ω = 2πυ
∴ From eqn.(2)
\(y=a \sin 2 \pi v\left(t-\frac{x}{v}\right)\) ……………. (4)
But ν = υλ

\(v=\frac{v}{\lambda}\)
∴ \(y=a \sin 2 \pi \frac{v}{\lambda}\left(t-\frac{x}{v}\right)\)
or
\(y=a \sin \frac{2 \pi}{\lambda}(v t-x)\)
This is the equation of a progressive wave.

Question 2.
Explain Newton’s formula for velocity of sound in air.
Answer:
From purely theoretical considerations, Newton gave an empirical relation to calculate the velocity of sound in a gas.
\(v=\sqrt{\frac{B}{\rho}}\) …………. (1)
Where B is bulk modulus and P is density of the gas.

Sound travels through a gas in the form of compressions and rarefactions. Newton assumed that the changes in pressure and volume of a gas, when sound waves are propagated through it, are isothermal. The amount of heat produced during compression is lost to the surroundings and similarly, the amount of heat lost during rarefaction is gained from the surroundings, so as to keep the temperature constant. Using

coefficient of isothermal elasticity, i.e., Bi in Eqn. (1), Newton’s formula becomes: …(2)
\(v=\sqrt{\frac{B_{i}}{\rho}}\)
Calculation of B_i:
Consider a certain mass of the gas.
Let P = initial pressure of the gas, V= initial volume of the gas. Under isothermal conditions PV= constant
Differentiating both sides, we get
PdV + VdP = 0
PdV = -VdP
\(P=-\frac{V d P}{d V}=-\frac{d P}{\frac{d V}{V}}=B_{i}\) (by definition)
Substituting this value in eqn. (2), we obtain
\(v=\sqrt{\frac{P}{\rho}}\)

Question 3.
Write the characteristics of progressive waves.
Answer:
Characteristics of progressive wave are as follows :

• A harmonic (progressive) wave is a disturbance which travels through a medium with a definite velocity, without change in shape.
• Energy is transferred along the direction of propagation of wave, but there is no net transport of the material of the medium.
• The velocity of an oscillating particle is different on different states of oscillation, being maximum at the mean position and momentarily zero at the extreme positions. The velocity of propagation of the wave is however, constant, depending on the nature of the medium.
• At any instant, the phase of the oscillation varies from particle to particle, because each particle starts oscillating a little later than the previous particle.
• For particles separated by an integral multiple of wavelength λ, the displacement, velocity and acceleration of the particle have the same values at any instant.

Question 4.
Write characteristics of stationary waves.
Answer:
Characteristics of stationary waves :

• These waves do not advance in the medium but remain steady at its place. This is why these waves are called stationary waves.
• No energy is transferred by these waves because the flow of energy at any point of the medium in one direction due to incident wave is the same as the flow of energy at that point in opposite direction due to reflected wave.
• To produce these waves, the presence of bounded medium is necessary because the wave travelling in such a medium, after being reflected from the boundary, produce an identical wave moving in opposite direction. As a result of superposition of incident and reflected wave, the stationary wave is produced.
  The stationary waves cannot be produced in vacuum or in unlimited medium.
• In the waves, certain points in the medium are always at rest, i.e., their displacement remain zero. These points are called nodes. These points are situated at equal distances. In case of longitudinal stationary waves, change in pressure and in density is maximum at nodes as compared to other points.
• The displacement of the point in between two consecutive nodes is maximum as compared to other points. These points are called antinodes. In longitudinal stationary waves, there is no change in pressure and in density at antinodes.
• The distance between two consecutive nodes or between two consecutive antinodes is λ / 2. The distance between a node and its neighbouring antinode is λ / 4.
• Except at nodes, all the particles of the medium vibrates but the amplitude of vibration of the particles are different. The amplitude of the vibration is zero at the nodes and maximum at the antinodes.
• All the particles between two consecutive nodes vibrate in the same phase, i.e., they reach simultaneously through their equilibrium positions.
• At any instant, the particles of both the sides of a node are in mutually opposite phases but the particles of both the sides of an antinode are in the same phase.
• All the particles of medium pass through their mean positions simultaneously twice in each period.

Question 5.
Give difference between progressive waves and stationary waves.
Answer:
Comparison of Progressive and Stationary waves

Progressive waves	Stationary waves
1. These waves advance in a medium with a definite velocity.	1. These waves remain stationary between two boundaries in the medium.
2. Crests and troughs in transverse progressive waves and centre of compression and rarefaction in longitudinal progressive waves occur alternately and advance with a definite velocity.	2. Crests and troughs in transverse stationary waves and centres of compression and rarefaction in longitudinal stationary waves occur alternately at definite places and do not advance. These waves transmit energy in the medium.
3. These waves transmit energy in the medium.	3. These waves do not transmit energy in the medium.
4. In these waves, all the particles of the medium vibrate about their mean positions and the amplitude of vibration is the same for all of them.	4. In these waves, all the particles of the medium do not vibrate and amplitude of vibration also is not the same for all particles. The amplitude is zero at the nodes and maximum at the antinodes.
5. In these waves, at no instant all the particles of the medium pass through their mean positions simultaneously.	5. In these waves, all the particles of the medium pass through their mean positions simultaneously twice in each time period.

Question 6.
What are beats? What are the necessary conditions to obtain beats?
Answer:
Beats: When two waves with slight difference in frequencies travel in a medium simultaneously in the same direction then as a result of their superposition, the intensity of sound at any point increase and decreases alternately. This successive rise and fall in the intensity of sound is called beats.

Conditions:

• Both the waves should travel along the same straight line, in the same medium, with same velocity.
• These should be slight difference in their frequencies.
• The amplitudes of both the waves should be nearly equal.

Question 7.
Derive Newton’s formula for velocity of sound. Point our error in Newton’s formula and hence discuss Laplace correction.
Answer:
Newton assumed that sound travels through air under isothermal conditions and for elastic medium velocity of longitudinal waves,
\(v=\sqrt{\frac{E}{\rho}}\)
∴ PV = constant under isothermal condition.
On differentiating, PdV+ VdP = 0
or
PdV = -VdP
\(P=\frac{-d P}{d V / V}=\frac{\text { stress }}{\text { strain }}=E\)
∴ \(v=\sqrt{\frac{P}{\rho}}\) [from eqn. (1)]
This is Newton’s formula for the velocity of sound in air, which given 280 m/s whereas actual value is 332 m/s.
Laplace correction : Laplace suggested that sound waves travel under adiabatic conditions because:
(i) When sound waves travels in air, changes in volume and pressure takes place rapidly.
(ii) ( Air is a bad conductor of heat. Thus, PVγ = constant
On differentiation Pd(Vγ) + VγdP = 0
or
PγVγ-1 dV + VγdP = 0
or
\(\gamma P=\frac{-V d P}{d V}=\frac{-d P}{d V / V}\)

Hence, according to Laplace, the velocity of sound is \(v=\sqrt{\frac{\gamma P}{\rho}}\) (for air, γ =1.4)
∴ \(v=\sqrt{1 \cdot 4} \times 280=331 \cdot 3 \mathrm{~m} / \mathrm{s}\)

Question 8.
Derive the equation of stationary waves when it is reflected by rigid boundary.
Answer:
When a progressive wave is reflected by a rigid surface, then phase difference of n is produced.
Let the wave is travelling in +ve direction along the Y-axis,
Equation of wave will be
\(y_{1}=a \sin \frac{2 \pi}{\lambda}(v t-x)\) ……….. (1)
Where, a = Amplitude, y =Velocity and λ Wavelength.

When this wave is reflected back, then it will travel along -ve direction of X-axis. ……….. (2)
\(y_{2}=-a \sin \frac{2 \pi}{\lambda}(v t+x)\)
Let the two waves superimpose and stationary wave is formed.
∴By the principle of superposition.
y = y₁ + y₂
or

This is the required equation.

Question 9.
Derive the equation of stationary wave, when reflected by free boundry.
Answer:
Let the incident wave is
\(y_{1}=a \sin \frac{2 \pi}{\lambda}(v t-x)\)
∴ Reflected wave, as the phase does not change
\(y_{2}=a \sin \frac{2 \pi}{\lambda}(v t+x)\)
∴ By the principle of superposition,

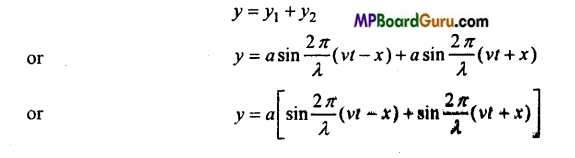
Question 10.
Explain beats period and frequency of beats.
Answer:
One rise and one fall of sound form one beat. The time interval between two consecutive intense sounds is called ‘beat period’.
The number of times the intensity of sound rises and falls in one second is called ‘beat frequency’.
Let the frequencies are υ1 and υ2
∴ Beat frequency = υ1 – υ2
and Beat period = \(\frac{1}{v_{1}-v_{2}}\).

Question 11.
Differentiate interference and beats.
Answer:
Distinction between Interference and Beats :

Interference	Beats
1. In this phenomenon, the frequencies of two sound waves are exactly the same.	1. In this phenomenon, the frequencies of two sound waves differ slightly.
2. At any point of the medium, the phase difference between two waves remains constant.	2. At any point of the medium, the phase difference between two waves varies with time.
3. The amplitude of the resultant wave remains constant at every point of the medium.	3. The amplitude of resultant wave varies with time at each point of the medium.
4. Though the intensity of sound is different at different points of the medium yet the intensity of sound does not vary with time at any point of the medium.	4. The intensity of sound decreases and increases alternately with times at any point of the medium.

Question 12.
Use the formula \(v=\sqrt{\frac{\gamma P}{\rho}}\)
to explain why the speed of sound in air:
(a) Is independent of pressure,
(b) Increases with temperature,
(c) Increases with humidity.
Answer:
Given : \(v=\sqrt{\frac{\gamma P}{\rho}}\)
By gas equation PV = RT
or
\(P=\frac{R T}{V}\)
∴ \(v=\sqrt{\frac{\gamma R T}{V \cdot \rho}}\)
But V, p = M (molecular weight of gas)
\(v=\sqrt{\frac{\gamma R T}{M}}\)
(a) In the eqn. (1) P does not appear so the speed is independent of pressure at constant temperature.

(b) If y, R and M are constant, then,
\(v \propto \sqrt{T}\)
i.e., the velocity (speed) of sound is directly proportional to the square root of absolute temperature.
∴ With increase in temperature the speed of sound increases.

(c) From the formula \(v=\sqrt{\frac{\gamma P}{\rho}}\) , it is clear that
\(v \propto \frac{1}{\sqrt{\rho}}\)
The density of humid air is less than that of dry air therefore with increase in humidity the speed of sound increases.

Question 13.
What are harmonics? Which harmonics can be produced in a stretched string?
Answer:
The harmonics are those tones, whose frequency is integral multiple of that of fundamental tone. The harmonics whose frequencies are even multiple of that of fundamental tone, are called even harmonics and the harmonics whose frequencies are odd multiple of that of fundamental tone are called odd harmonics.

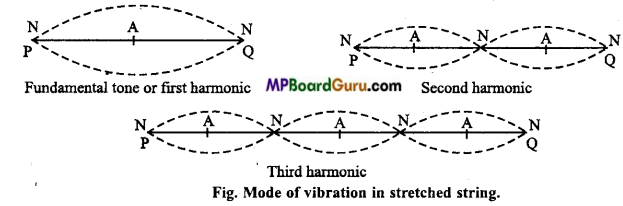
In a stretched string even and odd both harmonics can be produced. In Fig. the first, second and third harmonics are shown.

Question 14.
How do you determine the frequency of a tuning fork with the help of beats?
Answer:
Determine frequencies of a tuning fork: Suppose that we have to determine the frequency of a tuning fork. For this purpose, we take such a fork of known frequency
υ₂ whose frequency υ₂ differ slightly from unknown frequency υ₁. Now, both the tuning forks are sounded together and the beats are heard. Let the number of beats heard per second be x. Then,
υ₁ = υ₂ +x or υx = υ₂-x

To find which value is correct out of two values, a little wax is attached to the prong of the tuning fork of unknown frequency υ₁.
Again, the two forks are sounded together and beats are heard.
If number of beats per second increase, then the frequency of the first tuning fork will be (υ₂ – ×) because according to
(υ₁ – υ₂) = ×, × increases as υ₁ decreases.
If number of beats per second decreases, then the frequency of the first tuning fork will be (υ₂ + x) because according to
(υ₁ – υ₂) = -x, x decreases as υ₁ decreases.

Question 15.
Prove that the frequency of fundamental frequency of open organ pipe is double of the fundamental frequency of closed organ pipe of same length.
Or
If the frequency of fundamental tone of an open organ pipe is «, and that of closed organ pipe is n₂, then prove that n₁ = 2n₂.
Answer:
Let the length of organ pipe is l. For the fundamental frequency of open organ pipe.

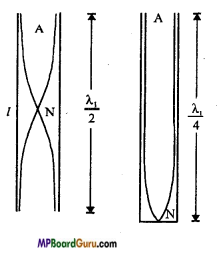
\(l=\frac{\lambda_{1}}{2}\)
Where, λ1 is the wavelength
λ1 = 2l
If the fundmental frequency is n₁,then

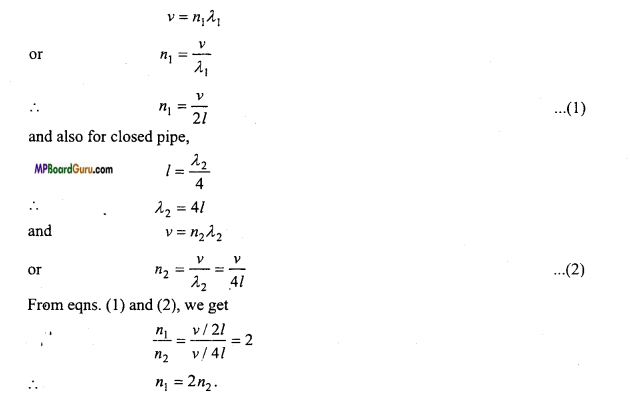
Waves Class 11 Important Questions Long Answer Type

Question 1.
Prove that beats obtained by two sound sources per second is equal to the differences of frequencies of the sound source.
Answer:
When two sources of sound of nearly equal frequencies are sounded together, the amplitude of resultant wave due to superposition of waves at a point is in space. Some¬times the amplitude is maximum and sometimes, it is minimum.

As intensity is directly proportional to the square of amplitude, the intensity also varies periodically with time from maximum to minimum and to maximum again. Let two waves be,
\(y_{1}=a \sin 2 \pi v_{1} t\) and \(y_{2}=a \sin 2 \pi v_{2} t \) are superimposed. On superposition, we get a resultant wave as,
y = y₁+y₂

Question 2.
Prove that even and odd harmonics are produced by a stretched string.
Answer:
When a stretched string is plucked, then transverse waves are produced. The wave reflected from both- the ends and produced stationary waves.
∴The wave is reflected from the rigid end, hence the equation of stationazy wave will be
\(y=-2 a \sin \frac{2 \pi x}{\lambda} \cdot \cos \frac{2 \pi v t}{\lambda}\) ……………… (1)

Let one end of string is at x = 0 and another at x =l. where l is the length of string.
Now, at x = 0, from eqn. (1), we get
\(y=-2 a \sin 0^{\circ} \cdot \cos \left(\frac{2 \pi v t}{\lambda}\right)\)
or
y=0
Again, at x = l, from eqn. (1),
\(y=-2 a \sin \frac{2 \pi l}{\lambda} \cos \frac{2 \pi v t}{\lambda}\)
Now, at x =l, y = 0

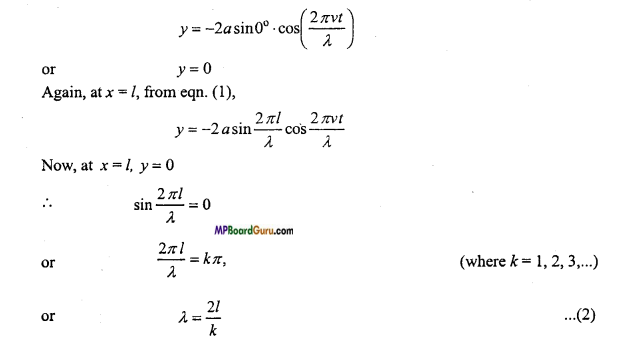
Now, the mode of vibration will be obtained by putting k = 1, 2, 3,….
First mode of vibration: If k = 1 and the wavelength of stationary wave is λ₁, then from eqn. (2),
λ₁ = 2l
\(l=\frac{\lambda_{1}}{2}\)
Hence, the string vibrates in one segment. Now, if the velocity is and frequency n₁, then
\(n_{1}=\frac{v}{\lambda_{1}}=\frac{v}{2 l}\) ………… (3)

This frequency is called fundamental frequency or first harmonics.

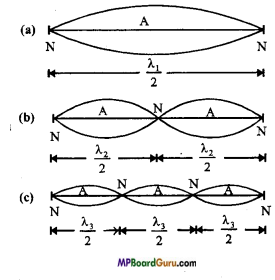
Second mode of vibratioñ : If k =2 and wavelength ‘λ₂, then from eqn. (2),
λ₂ = l
Also, if the frequency is n₂,then
\(n_{2}=\frac{v}{\lambda_{2}}\)
or
\(n_{2}=\frac{v}{l}=\frac{2 v}{2 l}=2 n_{1}\)

Question 3.
Prove that in a dosed organ pipe odd harmonics are produced.
Or
In a closed organ pipe, describe the mode of vibrations and prove that:
(i) The frequency of fundamental note is inversely proportional to the length of the organ pipe.
(ii) Only odd harmonics are produced.
Answer:
Organ pipe is a long cylindrical tube of uniform diameter and made of wood or metal. Sound is produced by this pipe as a result of vibrations in air column inside this. If one end of this tube is closed then it is called closed organ pipe and if both ends are open then it is called open organ pipe.

When we place a source of sound near the open end of a closed organ pipe, a wave travels towards the closed end. This wave, after being reflected by the closed end, returns. A stationary longitudinal wave is produced inside the closed organ pipe as a result of superposition of incident wave and reflected wave. An antinode is always formed at the open end because the air particles are free to vibrate there. A node is always formed at the closed end because at the closed end the air particles are not free to vibrate.

Suppose that the closed end of the closed organ pipe is at x = 0 and open end at x = L, where L is the length of the organ pipe.
\(y=-2 a \sin \frac{2 \pi x}{\lambda} \cdot \cos \frac{2 \pi v t}{\lambda}\)
Case (i): At x = 0, we have y = o
Thus, the wave function vanishes at x = 0.

Case (ii) : At x = L, we have
\(y=-2 a \sin \frac{2 \pi L}{\lambda} \cdot \cos \frac{2 \pi v t}{\lambda}\)
At x =L, the displacement y has its maximum value ,y will be maximum when \(\sin \frac{2 \pi L}{\lambda}\) maximum i.e,

Where, k = 0, 1,2, 3,4,….
\(\lambda=\frac{4 L}{(2 k+1)}\)
Here, k = 0, 1, 2,… correspond to first, second, third,…. mode of vibration.

First mode of vibration: If λ₁ be the wavelength of the wave produced in air column corresponding k = 0, then from eqn. (2), we have
λ₁ = 4L
If n₁ be the frequency of the wave set up, then
\(n_{1}=\frac{v}{\lambda_{1}}=\frac{v}{4 L}\)

It is the tone of minimum frequency which produces in closed end organ pipe. It is called fundamental tone or first harmonic.
Also,
\(n_{1} \propto \frac{1}{L}\)
i.e., Fundamental frequency is inversely proportional to the length of the organ pipe.

Second mode of vibration :
If λ₂ be the wavelength of the wave set up in air column corresponding to k = 1, then from eqn. (2), we have
\(\lambda_{2}=\frac{4 L}{3}\)
If n₂ be the frequency of the wave set up, then

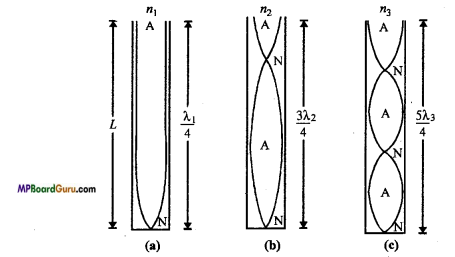
Thus, in this case, the frequency of the tone produced is three times the frequency of fundamental tone. It is called third harmonic or first overtone.

Third mode of vibration : If k = 2 and corresponding wavelength is λ₃, then from eqn. (2), we get
\(\lambda_{3}=\frac{4 L}{5}\)
If n₃ be the frequency of the wave set up, then
\(n_{3}=\frac{v}{\lambda_{3}}=\frac{v}{4 L / 5}=5 \cdot \frac{v}{4 L}\)
or
n₃ = 5n₁
Hence, the fifth harmonics of second overtone is five times of fundamental frequency.
Hence, the harmonics are n₁, 3n₁ 5n₁,….
Thus, odd harmonics are produced.

Question 4.
Prove that in open organ pipe both odd and even harmonics are produced. Ans. When a source of sound is kept at one end of an open organ pipe, the compressions and rarefactions are set up in the pipe. At the open ends antinodes are formed, hence rarefactions will be produced at the open ends and it returns in the form of compression. Thus, incident wave and reflected wave superimpose and stationary wave is formed.
Since, the reflection is, from free boundary,
\(y=2 a \cos \frac{2 \pi x}{\lambda} \cdot \sin \frac{2 \pi v t}{\lambda}\)

Now, the one end of organ pipe is at x = 0 and another end is at x = l.
Putting x = 0, we get
\(y=2 a \cos 0 \cdot \sin \frac{2 \pi v t}{\lambda}=2 a \sin \frac{2 \pi v t}{\lambda}\)
Again, putting x = l, we get
\(y=2 a \cos \frac{2 \pi l}{\lambda} \cdot \sin \frac{2 \pi v t}{\lambda}\)
For y is maximum,
\(\left|\cos \frac{2 \pi l}{\lambda}\right|=1 t\)
or
\(\frac{2 \pi l}{\lambda}=k \pi \) …………. (2)
Where,k= 1,2,3………

First mode of vibration: If k = I and wavelength is λ₁, then from eqn. (2), we get
λ₁ = 2l
Also
\(n_{1}=\frac{v}{\lambda_{1}}=\frac{v}{2 l} \)

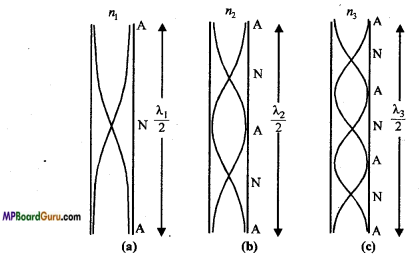
n₁ s the least frequency called fundamental frequency or first harmonics.

Second mode of vibration : 1f k = 2 and corresponding wavelength is λ₂.
then
\(\lambda_{2}=\frac{2 l}{2}=l \)
∴ Frequency ,n₂= \(\frac{v}{\lambda_{2}}=\frac{v}{l}=\frac{2 v}{2 l}\)
n₂ = 2n₁
Hence, second harmonic is obtained at double of fundamental frequency.

Third mode of vibration: If k = 3 and corresponding wavelength is λ₃ and frequency n₃, then

Hence, third harmonic is 3 times of fundamental frequency.
Thus, the harmonics are both odd and even multiple of fundamental frequency.

Question 5.
Derive the expression for the apparent frequency, when the source of sound is moving towards a stationary listener.
Answer:
Suppose S is a source moving towards a stationary listener O. Let υ be the real frequency of the source and υ is the velocity of sound wave. Now, the first wave emitted by the source covers a distance υ in 1 sec. If the source is stationary then these υ waves will be
spread in the distance υ. Thus, the length of one wave i.e., the wavelength will be \(\lambda=\frac{u}{v}\)

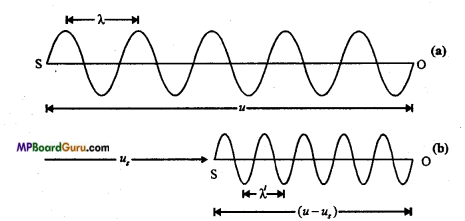
Now, suppose the sound-source S is moving with velocity us towards the observer. Then the source covers a distance us in one second towards the listener. Therefore, the v waves emitted by the source in 1 second will spread in a distance (υ-υ_s) only. Thus, the wavelength will be shortened. Let the changed wavelength be λ’.
Then, \(\lambda^{\prime}=\frac{u-u_{s}}{v}\) ………….(1)

Thus, the listener will receive waves of wavelength λ’. Hence, the frequency of sound will appear to him changed. If the apparent frequency be υ’, then
\(v^{\prime}=\frac{u}{\lambda^{\prime}}\) (∴ Velocity of sound υ is steady )
Substituting the value of λ’ in eqn. (1), we have
\(\dot{v^{\prime}}=\frac{u}{\left(u-u_{s}\right) / v}\)
or
\(v^{\prime}=\left(\frac{u}{u-u_{s}}\right) v\) …………. (2)
As (υ-υ_s)< υ,therefore υ’ > υ i.e., the apparent frequency is greater than the real frequency.

If the source S is going away from the listener O, then the wavelength will be in-creased and its value will be given by
\(v^{\prime}=\left(\frac{u}{u+u_{s}}\right) v\)

As (υ + υ_s) > υ_s, therefore, υ‘ < υ i.e., the apparent frequency is less than the real frequency.

Question 6.
Derive the expression for the apparent frequency, when the listener is moving toward stationary source.
Answer:
Suppose, S is a sound source of frequency u and u is the velocity of sound. Again suppose that O is a listener who is coming towards the source with the velocity υ₀. If the listener were stationary then he would have received u waves in 1 second. Therefore, the real wavelength is given by
λ = \(\frac{u}{v}\)

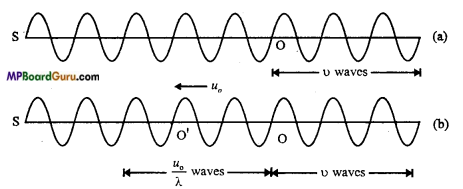
But, the listener himself is moving towards the source with a velocity υ₀ that is, he covers a distance υ₀ toward the source in 1 second. Hence the listener, in addition to υ waves, also receives υ₀/ λ waves contained in the distance υ₀. Therefore, the total waves received by the listener in 1 second i.e., the apparent frequency of the sound is

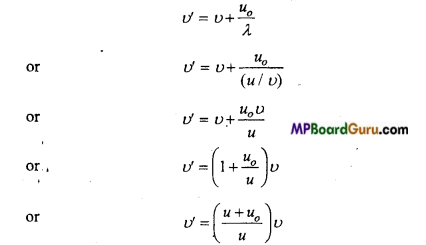
As (υ+ υ₀) > u, hence υ‘ > υ i.e., apparent frequency will be greater than the actual frequency.

Question 7.
Derive the expression for the apparent frequency heared by a listener, when the source and listener both are moving in the same direction.
Answer:
Let the source and listener are moving with the velocities υ_s and υ₀ respectively in the same direction as shown in the figure.
If the source is moving only.
∴ The frequency heard by the listener will be \(n_{1}=\left(\frac{u}{u-u_{s}}\right) n\)
But, listener is moving away from the source

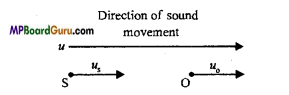
∴ Apparent frequency, \(n^{\prime}=\left(\frac{u-u_{o}}{u}\right) n_{1}\)

Putting the value of n₁, we get
\(n^{\prime}=\left(\frac{u-u_{o}}{u}\right) \times \frac{u}{u-u_{s}} \cdot n\)
or
\(n^{\prime}=\left(\frac{u-u_{o}}{u-u_{s}}\right) n\)
This is the required expression.

Waves Class 11 Important Numerical Questions

Question 1.
The speed of a wave ¡n a medium is 960m/s. If 3600 waves are passing through a point in the medium in 1 minute, then calculate the wavelength.
Solution:
Given: Speed of wave ν = 960 m/s
Frequency of wave n = \(\frac{3600}{60}\) =60/ second
Wavelength λ = \(\frac{v}{n}=\frac{960}{60}\)
or
λ = 16m.

Question 2.
The speed of sound in air at 14°C is 340 m/s. What is the speed of sound in air at 157.5°C when pressure becomes two times of its initial value.
Solution:
The change in pressure has no effect on speed of sound.
Given: t₁= 14°C,ν₁= 340m/s,t₂ = 1575°C,ν₂ =?

Question 3.
The distance between two consecutive nodes of a stationary wave is 25 cm. If the velocity ¡s 300 mc’, then calculate the frequency.
Solution:
Given: λ /2=25cm
or
λ =50cm = 50 ×\(10^{-2}\)
or
ν = 300 ms^-1
ν = nλ
or
300 = n ×50 ×\(10^{-2}\)
or
\(n=\frac{300}{50 \times 10^{-2}}=6 \times 10^{2}\) = Hz

Question 4.
The frequency of a whistle is 256 Hz. It is moving towards a stationary listener with a velocity of \(\frac{v}{3}\) , where v is the velocity of sound waves, then calculate the apparent frequency.
Solution :
Given : n = 256 Hz, \(v_{s}=\frac{v}{3}\)

Question 5.
An observer is moving towards a stationary source of frequency n. The frequency heard by the observer is 2n. If the velocity of sound is 332 ms^-1, then find the velocity of observer.
Solution:
Given : n’ = 2n, ν = 332 ms^-1.

Question 6.
The frequencies of two sources are 512 Hz and 516 Hz. Find the time inter-val between two consecutive beats.
Solution:
Given : n₁ =512 Hz, n₂ =516 Hz.
∴ Beat period = \(\frac{1}{n_{2}-n_{1}}\)
\(=\frac{1}{516-512}=\frac{1}{4}=0 \cdot 25 \mathrm{sec}\).

Question 7.
Two sound waves of wavelength 1 metre and 1.01 metre produce 40 beats in 10 seconds in a gas. Find the speed of sound in gas.
Solution:
Beats per second \(=\frac{40}{10}=4\)
If ν is the velocity of sound in gas, then
Frequency of first wave υ₁ = \(\frac{v}{1}\)
Frequency of second wave υ₂ \(\frac{v}{1.01}\)

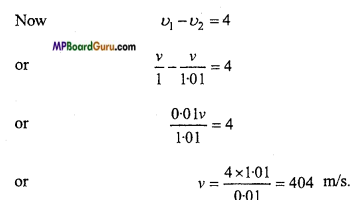
Question 8.
Two tuning forks produce 6 beats when they are sounded together. The frequency of one tuning fork is 288 Hz. Now, the second tuning fork is loaded by little wax, then the beats are not heard. Find the frequency of another tuning fork.
Solution:
Let the frequency of second tuning fork is n.
∴ n = 288 + 6 or 288 – 6
or
n = 294 or 282 Hz
Since, second fork is loaded hence its frequency will decrease.
Since, no beat is heard.
Hence, the frequency of second tuning fork = 294 Hz.

Question 9.
Two sources of sound of equal frequencies are kept at a distance 100 m apart. A listener is moving between the sources and hears 4 beats. If the distance between the sources becomes 400 m, what will be the beats heard ?
Answer:
Spl. The frequency of beats depends upon the frequencies of the sources, not the distance. Hence, 4 beats will be heard.

Question 10.
Frequency of open end organ pipe is 256 Hz. What will be the frequency of same length closed end organ pipe ?
Solution:
Frequency of l length open end organ pipe
\(n=\frac{v}{2 l}\)
Frequency of closed ended organ pipe
\(n^{\prime}=\frac{v}{4 l}\)
or
\(\frac{n}{n^{\prime}}=\frac{v / 2 l}{v / 4 l}=\frac{2}{1}\)
Given, n = 256
∴ \(\frac{256}{n^{\prime}}=\frac{2}{1}\)
or
\(n^{\prime}=\frac{256}{2}=128 \mathrm{~Hz}\).

Question 11.
A string of mass 2-50 kg is under a tension of 200 N. The length of the stretched string is 20-0m. If the transverse jerk is struck at one end of the string, how long does the disturbance take to reach the other end ? (NCERT)
Solution:
Given : M= 2.50 kg, l = 20m, T= 200N
Mass per unit length m = \(\frac{M}{l}=\frac{2 \cdot 5}{20}\) = 0.125kg/m
∴ \(v=\sqrt{\frac{T}{m}}\)
or
\(v=\sqrt{\frac{200}{0 \cdot 125}}=\sqrt{1600}\) = 40 m/sec.
Time taken by distance (jerk) be
\(t=\frac{l}{v}\)
or
(∴ Velocity = \(\frac{\text { displacement }}{\text { time }}\) )
\(t=\frac{20}{40}\) = 0.5 sec.

Question 12.
A stone dropped from the top of a tower of height 300 m high splashes into the water of a pond near the base of the tower. When is the spHsh heard at the top given that the speed of sound in air is 340 ms^-1? (g = 9.8 ms 2) (NCERT)
Solution:
Given : Height of tower h = 300 m Speed of sound v = 340 ms^-1, initial velocity of stone u = 0 Let the time taken by stone to base of tower is t₁ Then by equation of motion
\(h=u t+\frac{1}{2} g t^{2}\)
300 = \(0 \times t_{1}+\frac{1}{2} \times 9 \cdot 8 t_{1}^{2}\)
or
\(4 \cdot 9 t_{1}^{2}=300\)
or
\(t_{1}=\sqrt{\frac{300}{4 \cdot 9}}=\) = 7.82 sec.

If the time taken to reach the sound up to top of tower is t₂, then \(t_{2}=\frac{h}{v}=\frac{300}{340}\) = 0.885
∴ Total time t = t₁+t₂.
= 7.82+0.885=8.705 = 8.7 sec .

Question 13.
A bat emits ultrasonic sound of frequency 1,000 kHz in air. 1f the sound meets a water surface. What is the wavelength of (a) the reflected sound (b) the transmiffed sound? Speed of sound in air is 340 ms^-1 and in water 1486 ms. (NCERT)
Solution:
Given :
n = 1,000 kHz =I000x10³Hz =10⁶Hz
Speed of sound in air ν_a = 340ms^-1 and that in water νw = 1486ms^-1 
(a) Reflected sound propagate in air

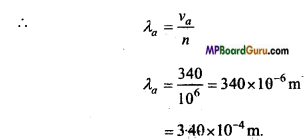
(b) Transmitted sound propagate in water

 

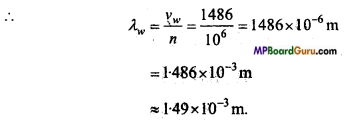
Waves Class 11 Important Questions Objective Type

1. Multiple- choice questions:

Question 1.
Sound of which frequency can be heard by human beings :
(a) 5 vib /sec
(b) 500 vib /sec
(c) 27000 vib / sec
(d) 50, 000 vib /sec.
Answer:
(b) 500 vib /sec

Question 2.
Astronaut cannot hear sound of his partner in moon, because :
(a) Frequency produced is more than audible frequency
(b) No medium is there for propagation of sound
(c) Temperature at night is very low
(d) There are lots of reason in moon.
Answer:
(b) No medium is there for propagation of sound

Question 3.
Two sources of frequency f₁ and f₂ will have beat frequency :
(a) \(\text { (a) } \sqrt{f_{2}}-\sqrt{f_{1}}\)
(b) f₁-f₂
(C) \(2\left(f_{1}-f_{2}\right)\)
(d) \(\sqrt{\left(f_{1}^{2}-f_{2}^{2}\right)}\)
Answer:
(b) f₁-f₂

Question 4.
The law relating sound between source and observer is :
(a) Doppler’s law
(b) Huygens law
(c) Newton’s law
(d) Galilean’s law.
Answer:
(a) Doppler’s law

Question 5.
The effect of beats due to two waves is because of:
(a) Refraction
(b) Reflection
(c) Dispersion
(d) Interference.
Answer:
(d) Interference.

Question 6.
As a utensil is filled with water, its frequency :
(a) Increases
(b) Decreases
(c) Remains same
(d) None of the above.
Answer:
(a) Increases

Question 7.
Waves transport from one end to another :
(a) Energy
(b) Amplitude
(c) Wavelength
(d) Matter.
Answer:
(a) Energy

Question 8.
Energy is not carried by :
(a) Transverse progressive waves
(b) Longitudinal progressive waves
(c) Stationary waves
(d) Electromagnetic waves.
Answer:
(c) Stationary waves

Question 9.
Velocity of sound in air is 350 m/s, frequency in open organ pipe of 50 cm length is:
(a) 175 Hz
(b) 350 Hz
(c) 700 Hz
(d) 50 Hz.
Answer:
(b) 350 Hz

Question 10.
y = 0.15 sin 5x cos 3001 represent an equation of stationary wave. Its wavelength will be :
(a) Zero
(b) 1.25m
(c) 2.512 m
(d) None of these.
Answer:
(b) 1.25m

2. Fill in the blanks:

1. The velocity of sound at 0°C is …………….. .
Answer:
332 m/s

2. …………….. waves require a physical medium for their propagation.
Answer:
Mechanical

3. …………….. waves do not require any medium for their propagation.
Answer:
Electromagnetic

4. In transverse waves, the distance between any two consecutive crest or trough is called …………….. .
Answer:
Wavelength

5. After one …………….. the phase of a particle is same as in the initial moment.
Answer:
Time period

6. Sound waves cannot propagate through …………….. .
Answer:
Vacuum.

.

3. Match the following:

Column ‘A’	Column ‘B’
1. Speed of waves	(a) \(\sqrt{\frac{\gamma P}{D}}\)
2.Speed of sound in gas	(b) \(\frac{2 \pi}{\lambda}\) × path difference
3. Phase of difference	(c) Sound navigation and Ranging
4. Principle of super position	(d) Frequency × Wavelength
5. SONAR	(e)\(\vec{y}=\overrightarrow{y_{1}}+\overrightarrow{y_{2}}+\ldots+\overrightarrow{y_{n}}\)

Answer:
1. (d) Frequency × Wavelength
2. (a) \(\sqrt{\frac{\gamma P}{D}}\)
3. (b) \(\frac{2 \pi}{\lambda}\) × path difference,
4.  (e)\(\vec{y}=\overrightarrow{y_{1}}+\overrightarrow{y_{2}}+\ldots+\overrightarrow{y_{n}}\)
5.  (c) Sound navigation and Ranging

4. Write true or false:

1. When two sound sources travelling perpendicularly. Doppler effect will implement.
Answer:
False

2. Propagation of mechanical wave in medium is possible due to elasticity and inertia.
Answer:
True

3. Propagation of wave in air is a isothermal changes.
Answer:
False

4. If the velocity of listener is more than velocity of sound then Doppler’s effect will not implement.
Answer:
True

5. Velocity of sound in moisture is less than velocity of sound in air.
Answer:
False

6. A person is standing at a point and a car is coming toward him blowing horn. The frequency of horn will be less than original frequency.
Answer:
False

7. Stationary wave does not carry energy.
Answer:
True

8. Beats is produced when frequency of two sound source are same.
Answer:
True

9. In a resonance air column, always transverse non- progressive wave is produced.
Answer:
False

10. Expansion of universe is observed by Doppler’s effect. ‘
Answer:
True