MP Board Class 11th Physics Important Questions Chapter 13 Kinetic Theory 

Students get through the MP Board Class 11th Physics Important Questions Chapter 13 Kinetic Theory  which are most likely to be asked in the exam.

MP Board Class 11th Physics Important Questions Chapter 13 Kinetic Theory

Kinetic Theory Class 11 Important Questions Very Short Answer Type

Question 1.
State Boyle’s law.
Answer:
According to Boyle’s law “At constant temperature the volume of a given mass of a gas inversely proportional to its pressure, i.e.,
V∝\( \frac{1}{\mathrm{P}} \)
or
V=K.\( \frac{1}{\mathrm{P}} \)
or
PV = K (constant).

Question 2.
Write the condition at which Boyle’s law function.
Answer:
Boyle’s law function at low pressure and high temperature.

Question 3.
Write down Charle’s law.
Answer:
According to Charle’s law “ The volume of given mass of a gas at constant pressure increases by \( \frac{1}{273} \) of its volume at 0°C, for each 1°C rise in temperature.

Question 4.
Prove that with help of Charle’s law that at -273°C, volume of a gas is zero.
Answer:
According to Charle’s law.
V = V₀( 1 + \( \frac{1}{273} \) t)
At t =-273° C
or
V = V₀(1+ \( \frac{-273}{273} \) )
or
V = V₀ (1-1) = 0
i.e., at -273°C volume of a gas is zero.

Question 5.
What are ideal gases?
Answer:
The gases which obey Boyle’s law and Charle’s law completely are called ideal gases.

Question 6.
State Avogadro’s law.
Answer:
According to Avogadro’s law, “Equal volume of all the gases under similar con-ditions of temperature and pressure contain the same number of molecules.”

Question 7.
Write down Dalton’s law of partial pressure.
Answer:
Dalton’s law of partial pressure states that the total pressure exerted by a mixture of gases which do not interact in any way is equal to the sum of their individual pressures.

Question 8.
What is Grahm’ law of diffusion?
Answer:
According to Grahm’s law of diffusion, “The rate of diffusion of a gas is directly proportional to the square root of its density.”

Question 9.
What is meant by absolute scale of temperature?
Answer:
The scientist Kelvin had developed a temperature scale by considering – 273°C as zero of the scale. This scale is called absolute scale of temperature. The value of its each division is 1°C. It is also called as Kelvin scale.

Question 10.
What do you mean by absolute zero?
Answer:
The absolute zero is that temperature at which the volume of a gas becomes zero.

Question 11.
If a gas is suddenly compressed, then its temperature increased. Why?
Answer:
The temperature of a gas is directly proportional to its mean kinetic energy. When a gas is suddenly compressed, then the mean kinetic energy of gas is increased. Therefore, the temperature of gas is increased suddenly.

Question 12.
What is Boltzmann constant? Write its value.
Answer:
The ratio of universal gas constant (R) and Avogadro’s number (N) is known as Boltzmann’s constant
K= \( \frac{\mathrm{R}}{\mathrm{N}} \)
Its value is 1.38 x 10^-23 joule/kelvin.

Question 13.
Write down relation between universal gas constant and specific gas constant.
Answer:
The relation between universal gas constant and specific gas constant is given below:
Specific gas constant r = \( \frac{\text { Universal gas constant }(\mathrm{R})}{\text { Molecular weight of } operatorname{gas}(\mathrm{M})} \) .

Question 14.
Write the ideal gas equation.
Answer:
PV = nRT.

Question 15.
Find out dimensional formula for R.
Answer:
From PV = RT
R = \( \frac{\mathrm{PV}}{\mathrm{T}} \)
or
[R] = \( \frac{\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]\left[\mathrm{L}^{3}\right]}{[\theta]} \)
= \( \left[\mathrm{ML}^{2} \mathrm{~T}^{-2} \theta^{-1}\right] \) .

Question 16.
At equal temperature (T) and pressure (P), two gases of same volume (V) are mixed together. If the temperature and volume of the mixure is T and V, then what will be its pressure?
Answer:
According to Dalton’s law of partial pressure it will be 2P.

Question 17.
At NTP, 1cm³ H₂ and 1cm³ O₂ are given. In which gas number of molecules will be more and why?
Answer:
According to Avogadro’s law number of molecules of 1 cm³ H₂ and 1 cm³ O₂ will be equal.

Question 18.
Oxygen and hydrogen gases are filled in a porous pot in equal amount, which one will diffuse soon?
Answer:
By the kinetic theory of gas,
ν rms ∝\( \frac{1}{\sqrt{\mathrm{M}}} \)
Since M_H < M₀ hence ν_H > ν₀
Thus, the hydrogen will diffuse soon.

Kinetic Theory Class 11 Important Questions Short Answer Type 

Question 1.
What is gas equation? Establish it.
Or
For a gas equation prove that PV = RT.
Or
Establish ideal gas equation.
Answer:
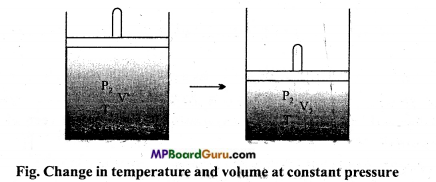
Let the initial pressure of one gram mole of a gas of molecular weight M is P₁ its volume is V₁ and absolute temperature is T₁. After a thermodynamic process the pressure of gas become P₂, volume and temperature becomes V₂ and T₂ respectively. The change occurs in the state of gas can be considered to be a combination of two processes.
(i) Keeping the temperature T₁ of gas constant, its pressure is varied from P₁ to P₂, so that as shown in fig. the volume of gas becomes V’. Hence, as per Boyle’s law :
P ₁V₁ = P₂V’ …(1)

(ii) Keeping the pressure P2 constant, the temperature of gas is varied from T₁ to T₂ so that its volume changes from V’ to V₂ as shown in fig. then according to Charle’s law :

\( \frac{\mathrm{V}^{\prime}}{\mathrm{T}_{\mathrm{l}}} \) = \( \frac{\mathrm{V}_{2}}{\mathrm{~T}_{2}} \)
or
\( V’ = \frac{\mathrm{V}_{2} \mathrm{~T}_{1}}{\mathrm{~T}_{2}} \) ………. (2)
Substituting the value V’ from eqn. (2) in eqn.(1)
P₁V ₁ = \( \frac{\mathrm{P}_{2} \mathrm{~V}_{2} \mathrm{~T}_{1}}{\mathrm{~T}_{2}} \)
or
P₁V ₁ = \( \frac{P_{2} V_{2}}{T_{2}} \)
\( \frac{\mathrm{PV}}{\mathrm{T}} \) = Constant …….. (3)
The value of this constant is same (= 8.314 joule per mole-kelvin) for 1 mole of all the gases. It is denoted by R. Hence,
\( \frac{\mathrm{PV}}{\mathrm{T}} \) = R
or
PV = RT …(4)
Where, R is called universal gas constant. Eqn. (4) is called gas equation for one mole of gas.

Question 2.
Write down postulates of kinetic theory of gases.
Answer:
The postulates of kinetic theory of gas are given below :

• Every gas is composed of minute particles called molecules.
• The size of these molecules is negligible as compared to their intermolecular dis¬tance. t
• The molecules of gas are spherical uniform in all aspects rigid and perfectly elastic.
• The molecules are always in state of random motion and move in all possible direction with all possible velocities.
• Due to their continuous motion, these molecules collide with each other and also with the walls of container during their random motion. Due to these collision, there is no change in density of gas, i.e., the number of molecules per unit volume of the gas remains unchanged.
• After collision the direction of velocity of molecules changes. The collision is instantaneous, i.e., the time taken in collision is negligible as compared with the time taken between two consecutive collisions.
• The collisions are perfectly elastic, i.e., kinetic energy of molecules remains con-served.
• Between the two successive collisions a molecule travels in a straight line with uniform velocity. The distance covered by a molecule between two consecutive collisions is called ‘Free path’, The average distance travelled by a molecule between successive collisions is called mean-free-path.
• The molecules of gas collide with the walls of container and hence they exert the force on the walls. The force acting per unit area on the wall is called pressure of gas.
• The mass of molecules of gas is negligible and velocity is high. Therefore, there is no effect of gravity on the motion of molecules.

Question 3.
Prove that: P = \( \frac{1}{3} \) ρc^-2
Answer:
We know P = \( \frac{1}{3} \) \( \frac{m N c^{2}}{V} \)
Here mN = M
∴ P = \( \frac{1}{3} \) \( \frac{M \bar{c}^{2}}{V} \)
But \( \frac{M}{V} \) = ρ (density)
∴ P = \( \frac{1}{3} \) ρc^-2

Question 4.
On the basis of kinetic theory of gases, prove that p = \( \frac{2}{3} \) E where symbols have their meanings,
Answer:
According to kinetic theory of gases, the pressure exerted by the gas is gi ven by
P = \( \frac{m N \bar{c}^{2}}{3 V} \) ………….. (1)

Where, N is the number of molecules, c ^-2 mean square velocity and V is volume. Let m be the mass of one molecule, then the mass of gas be mN
∴Density of gas ρ = \(\frac{m N}{V}\) …………. (2)
From eqns. (1) and (2),
P = \( \frac{1}{3} \) ρc^-2
= \( \frac{2}{3} \) .\( \frac{1}{2} \) ρc^-2 = \( \frac{2}{3} \) E
Where, E is kinetic energy of per unit volume of gas.

Question 5.
Explain kinetic energy of a gas on the basis of kinetic theory of gases.
Or
Prove that : P = \( \frac{2}{3} \) E
Answer:
Kinetic energy of gas: Let the mass of one molecule of gas is m and number of molecules is N. Hence, the mass of gas will be mN.
∴Density of gas ρ = \(\frac{m N}{V}\) …………. (1)
According to Kinetic theory of gas the pressure exerted by gas is
P= \( \frac{m N \bar{c}^{2}}{3 V} \) ……………. (2)
From equns. (1) and (2)
P = \( \frac{1}{3} \) ρc^-2 = \( \frac{2}{3} \) . \( \frac{1}{3} \) ρc^-2
P= \( \frac{2}{3} \) E …….. (3)

Where, E is kinetic energy of a gas per unit volume. From eqn. (3),
or
E = \( \frac{3}{2} \) P
or
P = \( \frac{2}{3} \) E.

Question 6.
On the basis of kinetic theory of gases prove that the mean kinetic energy of molecules of gas is directly proportional to the absolute temperature of gas.
Or
Prove that the mean kinetic energy of gas is E = \( \frac{3}{2} \) KT.
Answer:
According to kinetic theory of gases, the pressure exerted by the gas is given by :
P = \( \frac{m N \bar{c}^{2}}{3 V} \)

Where, m is mass of one molecule of gas, N is the number of molecules in the volume V,c^-2 is mean square velocity of gas and V is volume. In the above equation if V is volume of one mole of gas, then N be the Avogadro’s number, mN be the gram molecular weight (M) hence from the above equation :
PV=\( \frac{1}{3} \)mNc^-2
= \( \frac{1}{3} \)Mc^-2 …(1)

But by the gas equation,
PV = RT ……………. (2)
From eqns. (1) and (2), we get
\( \frac{1}{3} \)Mc^-2 =RT
or
c^-2 = \( \frac{3 R T}{M} \) …… (3)
From eqn. (3), it is clear that c^-2 ∝T
Thus, the absolute temperature of a gas is directly proportional to the mean square velocity of the molecules of a gas.
Again from eqn. (3),

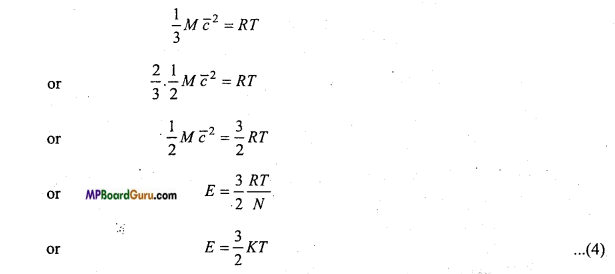
Where, K =\( \frac{R}{N} \) is called Boltzmann’s constant. Its value is 1.38 × 10^-23 joule per kelvin. This is formula of mean kinetic energy of molecules. From this equation, it is clear that
E∝T.

Question 7.
Explain absolute zero on basis of kinetic theory of gas.
Answer:
We know E =\( \frac{3}{2} \) KT
, If T=0, then E = 0.
Therefore, absolute zero temperature is that temperature at which average kinetic energy of the gaseous molecules is zero.

Question 8.
Prove that\( \overline{\boldsymbol{c}} \) =\( \sqrt{\frac{3 K T}{M}} \) where K is Boltzmann’s constant, T is absolute temperature and M is mass of one molecule of gas.
Answer:
According to kinetic theory of gases,
\( \overline{\boldsymbol{c}} \) = \( \sqrt{\frac{3 R T}{M}} \) =\( \sqrt{\frac{3 R T}{mN}} \), [∵M= mn]
= \( \sqrt{\frac{3 K T}{m}} \), [∵ K = \( \frac{R}{N} \) ]
or
\( \overline{\boldsymbol{c}} \) ∝ \( \sqrt{T} \)
i.e., r.m.s. value of velocity of gaseous molecule is directly proportional to square root of absolute temperature.

Question 9.
If the number of molecules in a box is halved, then what will be the effect on its pressure?
Answer:
According to kinetic theory of gas, the pressure of gas :
P= \(\frac{1}{3} \frac{m N \bar{c}^{2}}{V}\)
If the number of molecules is halved ,then the pressure of gas :
P’=\(\frac{1}{3} \frac{m}{V} \frac{N}{2} \bar{c}^{2}\)
P’ = \( \frac{1}{2}\left[\frac{m N \bar{c}^{2}}{3 V}\right]\)
or
\(\frac{P^{\prime}}{P}\) = \(\frac{1}{2}\)
or
P’ = \(\frac{1}{2}\)P
Thus, the pressure will Also be halved.

Question 10.
Derive Boyle’s law on basis of kinetic theory of gases.
Answer:
Derivation of Boyle’s law: According to kinetic theory of gases the pressure exerted by gas is :
P = \(\frac{1}{3}\) \( \frac{m N \bar{c}^{2}}{V} \)
or
PV = \( \frac{1}{3} \) \( m N \bar{c}^{2} \)
= \( \frac{1}{3} \) . \( m N \bar{c}^{2} \)
= \( \frac{2}{3} \).N .\(\frac{1}{2} \) \( m \bar{c}^{2}\)
= \( \frac{2}{3} \) NE, [ ∵ E = \( \frac{1}{2} \) \( m \bar{c}^{2}\)]
= \( \frac{2}{3} \) NKT, (∵E = KT ) …….. (1)
If the mass and absolute temperature of gas are constant,then
= \( \frac{2}{3} \) NKT be also constant
∵ PV = constant
This is Boyle’s law.

Question 11.
Derive Ctiarie’s law on basis of kinetic theory of gases.
Answer:
Derivation of Charle’s law : According to kinetic theory of gases, the pressurue exertd by gas is
P = \( \frac{1}{3} \) \( \frac{m N \bar{c}^{2}}{V} \) …….. (1)
or
PV = \( \frac{1}{3}\) \( m N \bar{c}^{2} \)
or
PV = \( \frac{1}{3} \) \( M \bar{c}^{2} \) ……… (2)

Where, M = mN is mass of gas which remains constant .
If the pressure of gas remains constant,then from the above equation.
V= \( \frac{M}{3 P} \bar{c}^{2} \)
or
V ∝\( \bar{c}^{2} \)
or
Since, \( \bar{c}^{2} \) ∝T therefore
V ∝T
This is Charle’s law.

Question 12.
Derive Dalton’s law of partial pressure on basis of kinetic theory of gases.
Answer:
Dalton’s law of partial pressure: According to Dalton’s law of partial pressure, the total pressure exerted by a mixture of gases which do not interact in any way is equal to the sum of their individual pressure.
Let us consider about a vessel of volume V₁ having number of gases mixed together.
Let the gases one, two, three ………….contain N₁ molecules of mass muN₂ molecules of mass
m₂, N₃ molecules of mass m₃ ……………respectively. Let their root mean square velocities are
\( \bar{c}_{1}, \bar{c}_{2}, \bar{c}_{3}\)…………… respectively.

Then the pressure due to first gas
P₁ = \( \frac{1}{3} \) m₁N₁c^-2
Similarly, the pressure due to second, third,………….gases are

If all the gases are mixed at same temperature, then mean kinetic energy óf the molcules of each gas will be the same i.e.,


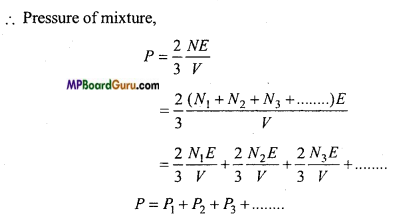
This is Delton’s law of partial pressure.

Question 13.
A vessel is filled up with mixture of two different gases. Explain with reason :
(i) Is Average kinetic energy per unit molecule are same?
(ii) Is root-mean-square value of velocity are same?
(iii) Is pressure same?
Answer:
(i) Yes, as E = \(\frac{3}{2} \)KT, it depends on absolute temperature only.

(ii) No, because \( \bar{c} \) = \( \sqrt{\frac{3 R T}{M}} \) and it depends on molecular weight M and temperature T.

(iii) Nothing cannot be said about pressure as mass is not known.

Question 14.
Write the law of equipartition of energy.
Answer:
According to this law, for any dynamical system in thermal equilibrium, the total energy distributed equally amongst all the degree of freedom, and the energy associated
with each molecule per degree of freedom is\( \frac{1}{2} \) KT, where K is Boltzmann’s constant and T is temperature of the system.

Question 15.
Explain degree of freedom.
Answer:
The number of degrees of freedom of a dynamical system is defined as the total number of coordinates or independent quantities required to describe completely the position and configuration of the system.
For Example:
(i) When a particle moves along a straight line, say along X-axis, its position can be specified by its displacement along the X-axis. Therefore, such a particle has one-translational degree of freedom.

(ii) If the particle is moving in a plane, its position at any instant can be determined by knowing the displacements of the particle along the X-axis and Y-axis. Therefore it has two- translational degrees of freedom.

(iii) If the particle is moving in space, its position at any instant can be determined by knowing the displacement of the particle along X-axis, Y-axis and Z-axis. Therefore, such a particle has three-translational degrees of freedom.
For example, a bob of an oscillating simple pendulum has one degree of freedom, an insect moving on a horizontal floor has two degrees of freedom and a buzzing bee has three degrees of freedom.

Question 16.
Find out ratio of specific heats for monoatomic gas.
Answer:
For monoatomic gas like He or Ar, whose degree of freedom is 3 but according to law of equipartition of energy.
Energy =3 × \( \frac{1}{2} \) KT = \( \frac{3}{2} \)kT
But energy associated with one mole of gas
U =\( \frac{3}{2} \) nkT
Where n is number of gas molecule for 1 mole of gas.
But Boltzmann’s constant k = \( \frac{R}{n} \)
or
nk = R
Putting value in eqn. (1), we get
U = \( \frac{3}{2} \)RT
But C_v = \( \frac{d U}{d T} \) = \( \frac{d}{d T} \) \( \left(\frac{3}{2} R T\right) \)
or
C_v =\( \frac{3}{2} \) R

Question 17.
Find out ratio of specific heat for diatomic gas.
Answer:
For diatomic gas like Hydrogen, Oxygen etc. degree of freedom is 5.
Therefore energy associated with one mole of gas is
U = \(\frac{5}{2} \)nkT
or
U= \(\frac{5}{2} \)RT
But, nk =R

since C_v = \( \frac{d U}{d T} \) = \( \frac{d}{d T} \) \( \left(\frac{5}{2} R T\right) \) =\(\frac{5}{2} \) R
∴ From C_p – C_v = R
C_p = R +C_v
or
C_p = R +\(\frac{5}{2} \) R = \(\frac{7}{2} \) R
∴ γ = \( \frac{C_{P}}{C_{V}} \) = \( \frac{\frac{7}{2} R}{\frac{5}{2} R} \) = \(/frac{7}{5} \) = 1.40

Question 18.
Find out ratio of specific heat for triatomic gas.
Answer:
For triatomic gas like C02, H2S degree of freedom is 6. Energy associated with one mole of gas is
U =\(\frac{6}{2} \)nKT
or
U = \(\frac{6}{2} \)RT = 3RT

But Cv=\( \frac{d U}{d T} \) = \( \frac{d}{d T} \) (3RT) = 3R
∴ From C_p-C_v = R
C_p =R + C_v =R + 3 R = 4R
∴ γ = \( \frac{C_{P}}{C_{V}} \) = \( \frac{4_{R}}{3_{R}} \) = \(\frac{4}{3} \) = 1.33

Kinetic Theory Class 11 Important Questions Long Answer Type

Question 1.
Establish formula for pressure of a gas on the basis of kinetic theory of gases.
Answer:
When a gas is filled in a closed vessel, then molecules of gas are in state of continuous random motion. They collide with one another and also with the walls of con-tainer. Due to these collisions, the molecules of gas exert the force on the walls of the vessel. The force acting per unit area of the walls is called pressure of gas.
Let us consider a hollow cubical vessel of sides of length ‘l’ as depicted in fig. An ideal gas is filled in it. Let the mass of one molecule is m. Consider a molecule of gas moving with velocity C. The components of velocity C along X, Y and Z direction are, u, v and w respectively.
∴ C² = u²+ v² + w² ……….. (1)
Let us consider about two faces A and B, perpendicular to the direction of X-axis.

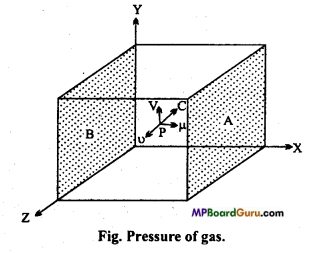
If the molecule P collides with the face A with velocity u. It will returned with a velocity -u after collision.
∴ Linear momentum of molecule before collision = mu Linear momentum of molecule after collision = – mu.
∴ Change in linear momentum due to collision = mu – (-mu) = 2mu
The molecule rebounded from A collides with the opposite face B, rebounds and again strikes with face A. Thus, the total distance travelled by the molecule will be 2l.

∴ Time taken by the molecule in travelling the distance 2l be
= \( \frac{2_{l}}{{u}} \), [ ∵ T ime = \( \frac{\text { Distance }}{\text { Velocity }} \) ]
Thus, after covering the distance 21 i.e., after every interval \( \frac{2l}{u} \) , the molecule P will
again strike with the face A.
Number of collision with face A per second be = \( \frac{u}{2 l} \)
The momentum transferred by molecule to the face A per second i.e., rate of change ofmomentum
= 2mu ×\( \frac{u}{2 l} \) = \( \frac{m u^{2}}{l} \)

But according to Newton’s second law of motion, the rate of change of momentum is equal to the force exerted on that face.
∴The force exerted by molecule at face Abe = \( \frac{m u^{2}}{l} \)
∴ Pressure exerted by the molecule on the face A be
= \( \frac{\mathrm{mu}^{2}}{\mathrm{l}} \) = \( \frac{n u^{2}}{l^{3}} \)

Let N be the number of molecules in gas and their velocity components along X direction are u₁, u₂, u₃, un respectively, then pressure exerted by these molecules on the face A

Where, V = l³ = Volume of vessel i.e., volume of gas.
Similarly, the pressure exerted by N molecule along Y-axis and Z-axis be
P_y = \( \frac{m}{V} \) \( \left[v_{1}^{2}+v_{2}^{2}+v_{3}^{2}+\ldots \ldots+v_{n}^{2}\right] \) ……… (3)
P_z = \( \frac{m}{V} \) \( \left[w_{1}^{2}+w_{2}^{2}+w_{3}^{2}+\ldots \ldots+w_{n}^{2}\right] \) ………… (4)
But a gas exerts the same pressure in all directions i.e., P_x=P_y=P_z=P (say)
∴ P = \( \frac{P_{x}+P_{y}+P_{z}}{3} \) …………….. (5)
Hence, from eqns. (2), (3), (4) and (5),
P = \( \frac{P_{x}+P_{y}+P_{z}}{3} \)

Let \( \bar{c} \) = \( \sqrt{\frac{c_{1}^{2}+c_{2}^{2}+\ldots . .+c_{n}^{2}}{N}} \) where \( \bar{c} \) is root mean square velocity , then
N\( \bar{c}^{2}\) = \( c_{1}^{2}+c_{2}^{2}+\ldots \ldots+c_{n}^{2} \) ………….. (7)

From eqns. (6) and (7),
P = \( \frac{m}{3 V} \)N\( \bar{c}^{2}\)
or
P = \( \frac{m N \bar{c}^{2}}{3 V} \)
This is expression of pressure exerted by gas.

Kinetic Theory  Class 11 Important Numerical Questions

Question 1.
Up to what temperature should an ideal gas initially at 27°C be heated so that its volume becomes doubled at constant pressure?
Solution:
Given:T₁ = 27°C = 273+27 = 300K
V₁ = V,V₂ = 2V
∴ According to Charle’s law,
\( \frac{V_{1}}{T_{1}} \) = \( \frac{V_{2}}{T_{2}} \)
or
T₂ = \( \frac{V_{2}}{V_{1}} \) T₁= \(\frac{2 V}{V} \) × 300
= 600 K
= 600 – 273 = 327°C

Question 2.
A gas is filled in a vessel at 127°C at 4 atm. pressure. If the temperature of gas increased up to 527°C, then what would be the pressure of gas?
Answer:
T₁ = 127°C = 127+273 = 400K
T₂ = 527°C = 527 + 273 = 800 K
P₁ = 4 atm. pressure
∴ By the pressure law,

\( \frac{P_{1}}{P_{2}} \) = \( \frac{T_{1}}{T_{2}} \)
or
P₂ = P₁ \( \frac{T_{2}}{T_{1}} \) = 4 × \( \frac{800}{400} \) = 8
= 8 atm.pressure

Question 3.
Number of molecule per cubic centimetre ¡n a space is five and temperature is 3 K. What will be the pressure, there? (R 1.38 × 10^-23 joule/m/K)
solution:
PV = nRT
P = \( \frac{n R T}{V} \)
Given: V = 1 cm³ = 10 ^-6, R = 1.38 ×10^-23 J/m /K, n =5 , T = 3K
∴ P = \( \frac{5 \times 1 \cdot 38 \times 10^{-23} \times 3}{1} \) = 2.07 ×10^-22N/m²

Question 4.
Temperature of any gas is -68°C. By what temperature it must be heated so that
(i) kinetic energy between the molecules become double
(ii) value of velocity of molecule become double.
Solution :
(i) From E = \(\frac{3}{2} \)KT,
E ∝ T
or
\( \frac{E_{1}}{E_{2}} \) = \( \frac{T_{1}}{T_{2}} \)
Given: E ₂ = 2E₁,=T₁ = 273-68 = 205 K
∴ \( \frac{E_{1}}{2 E_{1}} \) = \( \frac{205}{T_{2}} \)
or
T ₂ = 205 ×2 = 410K = 410 – 273° =137°C

(ii) From C^-2 = \( \frac{3 R T}{\gamma} \) we get
\( \bar{c}^{2}\) ∝ \( \sqrt{T} \)
or
\(\frac{\bar{c}_{1}}{\bar{c}_{2}}\) = \( \sqrt{\frac{T_{1}}{T_{2}}} \)
Given: \(\bar{c}_{2}\) = 2\( \bar{c}_{1} \) ,T ₁ = 205K
∴ \( \frac{\bar{c}_{1}}{\bar{2c}_{1}} \) = \( \sqrt{\frac{205}{T_{2}}} \)
or
\( \frac{1}{4} \) =\( \frac{205}{T_{2}} \)
or
T ₂ = 205 × 4 = 820
or
T ₂ = 820 – 273 = 574°C

Question 5.
At 30°C temperature, mixture of Helium and Hydrogen gas is filled in a vessel. Find out the ratio of r.m.s. value of velocity of the molecule at this temperature.
Solution:
From C^-2 = \( \frac{3 R T}{M} \)
\( \bar{c} \) = \( \frac{1}{\sqrt{M}} \)
or
\( \frac{\bar{c}_{1}}{\bar{c}_{2}} \) = \( \sqrt{\frac{M_{2}}{M_{1}}} \)

Given, molecular weight of Helium M₁ = 4
and Molecular weight of Hydrogen M₂ =2
∴ \( \frac{\bar{c}_{1}}{\bar{c}_{2}} \) = \( \sqrt{\frac{2}{4}} \) = \( \frac{1}{\sqrt{2}} \) = 1:\( \sqrt{2} \)
or
\( \bar{c}_{1} \): \( \bar{c}_{2} \) = 1:\( \sqrt{2} \)

Question 6.
If the absolute temperature of gas is done four times then by how much times their r.m.s. velocity of molecule increases? Also by how much times their kinetic energy and pressure also increases?
Solution: From \( \bar{c} \) = \( \frac{3 R T}{M} \) , where R and M are constant
∴ \(\bar{c} \) ∝ \( \sqrt{T}\)
or
\( \frac{\bar{c}_{1}}{\bar{c}_{2}} \) = \( \sqrt{\frac{T_{1}}{T_{2}}} \)
or
\( \frac{\bar{c}_{1}}{\bar{c}_{2}} \) = \( \sqrt{\frac{T_{1}}{4 T_{1}}} \) = \( \sqrt{\frac{1}{4}} \) = \( \frac{1}{2} \)
or
\( \bar{c}_{2} \) = 2 \( \bar{c}_{1} \)
i.e., r.m.s velocity will increase by two Times

From formula E = \( \frac{3}{2} \) KT
E ∝ T or \( \frac{E_{1}}{E_{2}} \) = \( \frac{T_{1}}{T_{2}} \)
Putting T₂ = 4T₁
\( \frac{E_{1}}{E_{2}} \) = \( \frac{T_{1}}{4 T_{1}} \) = \( \frac{1}{4} \)
or
E₂ = 4E ₁
\( \frac{P_{1}}{P_{2}} \) = \( \frac{T_{\mathrm{l}}}{4 T_{1}} \) = \( \frac{1}{4} \)
or
P₂ = 4P₁
∴ Pressure will become four Times.

Question 7.
If the temperature of a gas increased from 77°C to 227°C, then what will be the ratio of kinetic energy of then molecules?
Solution:
Given:T₁ = (273+ 77)K = 350K and T₂ = (273 + 227)K = 500K.
From formula E ∝ T
\( \frac{E_{1}}{E_{2}} \) = \( \frac{T_{1}}{T_{2}} \) = \( \frac{350}{500}\) = \( \frac{7}{10} \)
E₁: E ₂ = 7 : 10

Question 8.
Volume of vessel is two times the volume of vessel B and same gas is filled in both vessels. If the temperature and pressure of the vessel A is double w.r.t. vessel B, then what will be the ratio of molecules of the gas of vessel A and B?
Solution:
From PV = nRT

Question 9.
The velocities of four molecules of a gas are 2, 4, 6 and 8 km/sec.
Calculate : (i) Average velocity, (ii) root-mean-square velocity.
Solution:
Given : c₁ = 2 km/sec, c₂ = 4 km/ sec, c₃ = 6 km/sec and c4 = 8 km/sec.
(i) Average velocity:
c = \( \frac{c_{1}+c_{2}+c_{3}+c_{4}}{4} \)
= \( \frac{2+4+6+8}{4} \) = 5 km/sec

(ii) Root-mean-square velocity:

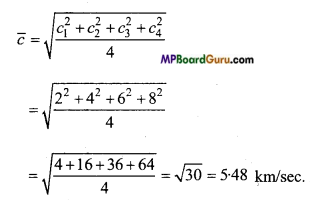
Question 10.
Estimate the fraction of molecular volume to the actual volume occupied by oxygen gas at N.T.P. Take the diameter of oxygen molecule to be roughly 3Å. (NCERT)
Solution:
Given, diameter of one molecule of oxygen = 3 Å
∴ Radius r = \( \frac{3}{2} \) = 1.5 Å = 1.5 × 10 ^-10m
∴ Volume of one molecule of oxygen = \( \frac{4}{3} \) πr³
= \( \frac{4}{3} \) ×3.14 (1.5 × 10 ^-10)³
= 14.13 × 10 ^-30 m³
∴ Volume of 1 mole of oxygen = 6.02 × 10 ²³ × 14.13 ×^-30
= 85.06 × 10 ^-7 m³

The volume of 1 mole of oxygen at STP = 22.4 litre
= 22.4 × 10^-3m³
∴ Fraction of the molecular volume of the actual volume = \( \frac{85 \cdot 06 \times 10^{-7}}{22 \cdot 4 \times 10^{-3}} \)
= 3.797 × 10 ^-4
= 3.8 ×10^-4 ≈ 4 × 10^-4

Question 11.
Molar volume is the volume occupied by 1 mole of any ideal gas at standard temperature and pressure (STP: 1 atm pressure, 0°C). Show that it is 22.4 litre. (NCERT)
Solution:
At S.T.P., T = 0°C = 0 + 273 =273K
Pressure P = 1 atm = 1-013 x 10⁵Nm^-2 ; R = 8.3 J mol^-1‘K^-1 By gas equation
∴ By gas equation for 1 mole PV =RT
V = \( \frac{R T}{P} \) = \( \frac{8 \cdot 3 \times 273}{1 \cdot 013 \times 10^{5}} \)
= 2236.82 ×10 ^-5
= 22.3682 ×10 ^-3 m ³
= 22.4 ×10 ^-3m ³ = 22.4 litre.

Question 12.
An air bubble of volume l-0cm3 rises from the bottom of a lake 40m deep at a temperature of 12°C. To what volume does it grow when it reaches the surface which is at a temperature of 35°C? (NCERT)
Solution:
Given, Initial volume of bubble
V₁ = 10cm³ = 1.0 × 10^-6m³
Initial temperature T₁ = 273 +12 = 285 K
Initial pressure on bubble P₁ = Atmospheric pressure + Pressure of 40 m high water column
= 1.013×10⁵+hdg
= 1.013×10⁵ + 40×10³ × 9.8
= 4.933 × 10⁵ Pa

Final pressure on bubble P₂ = 1 atm = 1.013 ×10⁵ Pa
Fina temperature T₂ = 273+ 35=308 K
From the equation \( \frac{P_{V_{1}}}{T_{1}} \) = \( \frac{P_{2} V_{2}}{T_{2}} \)
or
V₂ = \( \frac{P_{V_{1}}}{T_{1}} \) ×\( \frac{T_{2}}{P_{2}} \) = \( \frac{4 \cdot 933 \times 10^{5} \times 1 \cdot 0 \times 10^{-6} \times 308}{285 \times 1 \cdot 013 \times 10^{5}} \)
= 5.26 ×10^-6 m³ ≈ 5.3 × 10^-6 m³

Question 13.
At what temperature is the root-mean-square speed of an atom is an argon gas cylinder equal to the r.m.s. speed of a helium gas atom at – 20°C? (Atomic mass of Ar = 39.9 u, of He = 4.0 u). (NCERT)
Solution:
Given, atomic mass of He M₁=4.0u
Atomic mass of Ar M₂ =39.3u
Temperature of He gas T ₁ = -20+273 = 253K

Kinetic Theory  Class 11 Important Questions Objective Type

1. Multiple- choice questions:

Question 1.
There are N molecules in a vessel, if the number of molecules are doubled then the pressure of gas will be :
(a) Double
(b) Remain same
(c) Become four times
(d) Become one fourth.
Answer:
(a) Double

Question 2.
Motion of gaseous molecule at absolute zero temperature :
(a) Become less
(b) Increases
(c) Become zero
(d) None of these.
Answer:
(c) Become zero

Question 3.
At -273°C, molecules of gas moves with :
(a) Maximum velocity
(b) Minimum velocity
(c) Zero velocity
(d) None of these.
Answer:
(c) Zero velocity

Question 4.
Reason for deviating from gaseous law of ideal gas at less temperature is :
(a) Maximum collision become inelastic
(b) Volume of molecules cannot be negligible
(c) Force acting between molecules become less
(d) Molecular velocity become less.
Answer:
(b) Volume of molecules cannot be negligible

Question 5.
Root-mean-square velocity of ideal gas molecules at constant temperature :
(a) Remain same
(b) Inversely proportional to square root of molecular weight
(c) Proportional to square root of molecular weight
(d) Inversely proportional to molecular weight.
Answer:
(b) Inversely proportional to square root of molecular weight

Question 6.
Graph between PV and P of a gas which obey Boyle’s law will be :
(a) Hyperbola
(b) Parallel line with PV axis
(c) Parallel line with P axis
(d) None of these.
Answer:
(c) Parallel line with P axis

Question 7.
False statement regarding kinetic theory of gas is :
(a) Collision between two molecules are perfectly elastic
(b) Kinetic energy between molecules is proportional to absolute temperature
(c) Absolute temperature of gas is inversely proportional to root-mean-square velocity.
(d) At absolute temperature average kinetic energy of molecules is zero.
Answer:
(c) Absolute temperature of gas is inversely proportional to root-mean-square velocity.

Question 8.
Reason for pressure exerted by gaseous molecules on the wall of vessel is :
(a) Losses its own kinetic energy
(b) Get stick with the walls of vessel
(c) Due to collision with wall of vessel its momentum get change
(d) Get accelerated toward wall.
Answer:
(c) Due to collision with wall of vessel its momentum get change

Question 9.
There is no atmosphere in moon, because :
(a) It is closer to earth
(b) It revolve around the earth
(c) It obtain light from sun
(d) Escape velocity is less than root-mean-square velocity.
Answer:
(d) Escape velocity is less than root-mean-square velocity.

Question 10.
The temperature of an ideal gas is raised from 27°C to 927°C the root-mean-square velocity of its molecules will become :
(a) Two times
(b) Half
(c) Four times
(d) One fourth.
Answer:
(a) Two times

Question 11.
Every gas behaves as ideal gas at:
(a) Low pressure and high temperature
(b) High pressure and low temperature
(c) At equal pressure and temperature
(d) High pressure and high temperature.
Answer:
(a) Low pressure and high temperature

Question 12.
Unit of universal gas constant is :
(a) joule/mole-kelvin
(b) mole/joule-kelvin
(c) joule-mole-kelvin
(d) kelvin/joule/mole.
Answer:
(a) joule/mole-kelvin

Question 13.
If the temperature of gas remain constant and pressure become half then the volume will get.
(a) Half
(b) Double
(c) Unchanged
(d) Four times.
Answer:
(b) Double

Question 14.
In gas equation PV = RT, V is volume of:
(a) Gas
(b)1 gram gas
(c) 1 litre gas
(d) 1 mole gas.
Answer:
(d) 1 mole gas.

Question 15.
Pressure of gas filled in closed vessel is due to :
(a) Large number of molecules
(b) Attraction between wall and molecules
(c) Collision of molecules with wall
(d) None of these.
Answer:
(c) Collision of molecules with wall

Question 16.
The average kinetic energy associated with each degree of freedom is :
(a) \( \frac{3}{2} \) KT
(b) KT
(c) \( \frac{1}{2} \) KT
(d) \( \frac{3}{2} \) RT.
Answer:
(c) \( \frac{1}{2} \) KT

Question 17.
The mean kinetic energy of the molecule of gas depends upon :
(a) Nature of gas
(b) Absolute temperature
(c) Volume of gas
(d) None of these.
Answer:
(b) Absolute temperature

Question 18.
Root-mean-square velocity of gas is :
(a) Directly proportional to its specific molecular weight
(b) Directly proportional to its square of molecular weight
(c) Directly proportional to its molar weight
(d) Directly proportional to its absolute temperature.
Answer:
(c) Directly proportional to its molar weight

Question 19.
Magnitude of R for 1 gram mole of gas is :
(a) 8.31 erg
(b) 8.31 MKS unit
(c) 4.2 joule
(d) 4.2 calorie.
Answer:
(b) 8.31 MKS unit

Question 20.
If the r.nus. velocity of a gas is doubled, then its pressure will:
(a) Increase
(b) Decrease
(c) Remain same
(d) None of these.
Answer:
(a) Increase

2. Fill in the blanks:

1. Momentum applied per unit area on the wall of a vessel by the molecule of gas is equal to ………………………. .
Answer:
Pressure

2. At absolute temperature ………………………. of gas becomes zero.
Answer:
Kinetic energy

3. For a diatomic gas, the degree of freedom is ………………………. .
Answer:
Five

4. Kinetic energy associated with each degree of freedom is ………………………. .
Answer:
\( \frac{1}{2} \)KT

5. The value of 0°C on the kelvin scale is ………………………. .
Answer:
273 K.

3. Match the following:

Column ‘A’	Column ‘B’
1. Pressure of gas P	(a) ∝ T
2. Absolute temperature of gas T	(b) 3
3. Average kinetic energy E	(c) 5
4. Degree of freedom of monoatomic gas	(d) ∝ c-2
5. Degree of freedom of diatomic gas	(e) \( \frac{1}{3} \) \( \frac{m N}{V} \)c-2

 Answer:
1. (e) \( \frac{1}{3} \) \( \frac{m N}{V} \)c^-2
2. (d) ∝ c^-2
3. (a) ∝ T
4. (b) 3
5. (c) 5.