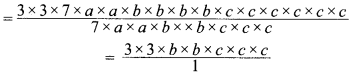Prasanna

MP Board Class 6th Maths Solutions Chapter 12 अनुपात और समानुपात Ex 12.1

पाठ्य-पुस्तक पृष्ठ संख्या # 271-272

प्रश्न 1.
एक कक्षा में 20 लड़कियाँ और 15 लड़के हैं। अनुपात ज्ञात कीजिए :
(a) लड़कियों की संख्या का लड़कों की संख्या से
(b) लड़कियों की संख्या का कुल विद्यार्थियों की संख्या से।
हल :
लड़कियों की संख्या = 20,
लड़कों की संख्या = 15
∴ कुल विद्यार्थियों की संख्या = 20 + 15 = 35
(a)∴अभीष्ट अनुपात

(b) अभीष्ट अनुपात

प्रश्न 2.
30 विद्यार्थियों की कक्षा में 6 फुटबॉल, 12 क्रिकेट और बाकी टेनिस पसंद करते हैं। अनुपात ज्ञात कीजिए :
(a) फुटबॉल पसंद करने वालों की संख्या का टेनिस पसंद करने वालों की संख्या से
(b) क्रिकेट प्रेमियों का कुल विद्यार्थियों की संख्या से।
हल :
कक्षा में कुल विद्यार्थियों की संख्या = 30
फुटबॉल पसंद करने वाले विद्यार्थियों की संख्या = 6
क्रिकेट पसंद करने वाले विद्यार्थियों की संख्या = 12
∴टेनिस पसंद करने वाले विद्यार्थी = 30 – (6 + 12)
= 30 – 18
= 12
(a) अभीष्ट अनुपात

(b) अभाष्ट अनुपात

प्रश्न 3.
पाठ्य-पुस्तक में दी गई आकृति को देखकर अनुपात निकालिए:
(a) आयत के अन्दर के सभी त्रिभुजों की संख्या का वृत्तों की संख्या से।
(b) आयत के अन्दर के सभी वर्गों की संख्या का सभी आकृतियों से।
(c) आयत के अन्दर के सभी वृत्तों का सभी आकृतियों से।
हल :
(a) आयत में त्रिभुजों की संख्या = 3,
वृत्तों की संख्या = 2
∴अभीष्ट अनुपात

(b) वर्गों की संख्या = 2,
सभी आकृतियों की संख्या = 7
∴अभीष्ट अनुपात

(c) वृत्तों की संख्या = 2,
सभी आकृतियों की संख्या = 7
∴अभीष्ट अनुपात

प्रश्न 4.
हामिद और अख्तर ने एक घण्टे में क्रमश: 9 किमी और 12 किमी की दूरी तय की। हामिद और अख्तर की चालों का अनुपात ज्ञात कीजिए।
हल :
हामिद की चाल = 9 किमी/घण्टा
अख्तर की चाल = 12 किमी/घण्टा
∴अभीष्ट अनपात

प्रश्न 5.
रिक्त स्थानों को भरिए

(क्या ये तुल्य अनुपात हैं?)
हल :

हाँ, ये तुल्य अनुपात हैं।

प्रश्न 6.
निम्न में से प्रत्येक का अनुपात ज्ञात कीजिए :
(a) 81 का 108 से
(b) 98 का 63 से
(c) 33 किमी का 121 किमी से
(d) 30 मिनट का 45 मिनट से।
हल :
(a) अनुपात = \(\frac{81}{108}=\frac{3}{4}\) या 3 : 4
(b) अनुपात = \(\frac{98}{63}=\frac{14}{9}\) या 14 : 9
(c) अनुपात = \(\frac{33}{121}=\frac{3}{11}\) या 3 : 11
(d) अनुपात = \(\frac{30}{45}=\frac{2}{3}\) या 2 : 3

प्रश्न 7.
निम्न में से प्रत्येक का अनुपात ज्ञात कीजिए :
(a) 30 मिनट का 1.5 घण्टे
(b) 40 सेमी का 1.5 मी.
(c) 55 पैसे का Rs 1
(d) 500 मिली का 2 लीटर।
हल :
(a) अनुपात

(b) अनुपात

(c) अनुपात

(d) अनुपात

प्रश्न 8.
एक वर्ष में सीमा Rs 1,50,000 कमाती है और Rs 50,000 की बचत करती है। प्रत्येक का अनुपात ज्ञात कीजिए।
(a) सीमा की आय और उसकी बचत का।
(b) सीमा द्वारा की गई बचत और उसके द्वारा किए गये व्यय का।
हल :
सीमा की आय = Rs 1,50,000
सीमा द्वारा बचत = Rs 50,000
सीमा द्वारा व्यय = Rs 1,50,000 – Rs 50,000
= Rs 1,00,000
(a) अभीष्ट अनुपात

(b) अभीष्ट अनुपात

प्रश्न 9.
एक विद्यालय में 3,300 विद्यार्थी और 102 शिक्षक हैं। शिक्षकों की संख्या का विद्यार्थियों की संख्या से अनुपात ज्ञात कीजिए।
हल :
शिक्षकों की संख्या = 102
विद्यार्थियों की संख्या = 3300
अभीष्ट अनुपात

प्रश्न 10.
एक कॉलेज में 4320 विद्यार्थियों में से 2300 लड़कियाँ हैं। अनुपात निकालिए :
(a) लड़कियों की संख्या और कुल विद्यार्थियों की संख्या का
(b) लड़कों की संख्या और लड़कियों की संख्या का
(c) लड़कों की संख्या और कुल विद्यार्थी की संख्या का।
हल :
कुल विद्यार्थियों की संख्या = 4320
लड़कियों की संख्या = 2300
∴ लड़कों की संख्या = 4320 – 2300 = 2020
(a)∴ अभीष्ट अनुपात

(b)∴ अभीष्ट अनुपात

(c)∴ अभीष्ट अनुपात

या 101 : 216

प्रश्न 11.
एक विद्यालय के 1800 विद्यार्थियों में से 750 ने बास्केट बॉल, 800 ने क्रिकेट और शेष ने टेबल टेनिस खेलना पसन्द किया है। यदि एक छात्र केवल एक खेल चुने तो अनुपात ज्ञात कीजिए :
(a) बास्केट बॉल खेलने वालों और टेबल टेनिस खेलने वालों का।
(b) क्रिकेट खेलने वालों और बास्केट बॉल खेलने वालों का।
(c) बास्केट बॉल खेलने वालों और कुल विद्यार्थियों का।
हल:
कुल विद्यार्थी = 1800
बास्केट बॉल खेलने वाले विद्यार्थी = 750
क्रिकेट खेलने वाले विद्यार्थी = 800
टेबल टेनिस खेलने वाले विद्यार्थी = 1800 – (750 + 800)
= 250
(a)∴ अभीष्ट अनुपात

(b)∴अभीष्ट अनुपात

(c)∴अभीष्ट अनपात

प्रश्न 12.
एक दर्जन पेन का मूल्य Rs 180 है और 8 बॉल पेन का मूल्य Rs 56 है। पेन के मूल्य का बॉल पेन के मूल्य से अनुपात ज्ञात कीजिए।
हल :
∵12 पेन का मूल्य = Rs 180
∴1 पेन का मूल्य = Rs \(\frac { 180 }{ 12 }\) = Rs 15
∵8 बॉल पेन का मूल्य = Rs 56
∴1 बॉल पेन का मूल्य = \(\frac { 56 }{ 8 }\) = Rs 7
∴अभीष्ट अनपात

प्रश्न 13.
कथन को देखें : एक हॉल की चौड़ाई और लम्बाई का अनुपात 2 : 5 है। निम्न सारणी को पूरा कीजिए जो कि हॉल की कुछ सम्भव चौड़ाई व लम्बाई दिखाती है:

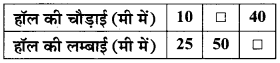
हल :

प्रश्न 14.
शीला और संगीता के बीच 20 पेनों को 3 : 2 में बाँटिए।
हल :
अनुपाती योग = 3 + 2 = 5
कुल पेन = 20
शीला का भाग = \(\frac { 3 }{ 5 }\) x 20 = 12 पेन
संगीता का भाग = \(\frac { 2 }{ 5 }\) x 20 = 8 पेन

प्रश्न 15.
एक माता अपनी बेटी श्रेया और भूमिका में Rs 36 को उनकी आयु के अनुपात में बाँटना चाहती है। यदि श्रेया की आयु 15 वर्ष और भूमिका की आयु 12 वर्ष हो, तो श्रेया और भूमिका को कितना-कितना मिलेगा ?
हल :
श्रेया की आयु : भूमिका की आयु
= 15 : 12
= 5 : 4
∵माता Rs 36 को श्रेया और भूमिका को उनकी आयु के अनुपात में बाँटना चाहती है।
∴Rs 36 को 5 : 4 में बाँटना है।
अतः अनुपाती योग = 5 + 4 = 9
∴श्रेया का भाग = \(\frac { 5 }{ 9 }\) x Rs 36 = Rs 20
और भूमिका का भाग = \(\frac { 4 }{ 9 }\) x Rs 36 = Rs 16

प्रश्न 16.
पिता की वर्तमान आयु 42 वर्ष और उसके पुत्र की आयु 14 वर्ष है। अनुपात ज्ञात कीजिए :
(a) पिता की वर्तमान आयु का पुत्र की वर्तमान आयु से।
(b) पिता की आयु का पुत्र की आयु से, जब पुत्र 12 वर्ष का था।
(c) 10 वर्ष बाद भी पिता की आयु का 10 वर्ष बाद की पुत्र की आयु से
(d) पिता की आयु का पुत्र की आयु से जब पिता 30 वर्ष का था।
हल :
(a) पिता की वर्तमान आयु = 42 वर्ष,
पुत्र की वर्तमान आयु = 14 वर्ष
∴अभीष्ट अनुपात

(b) 2 वर्ष पूर्व पुत्र 12 वर्ष का था
2 वर्ष पूर्व पिता की आयु = 42 वर्ष – 2 वर्ष = 40 वर्ष
∴अभीष्ट अनुपात

(c) 10 वर्ष बाद पिता की आयु = 42 वर्ष + 10 वर्ष = 52 वर्ष 10 वर्ष बाद पुत्र की आयु = 14 वर्ष + 10 वर्ष = 24 वर्ष
∴अभीष्ट अनुपात

(d)∴ 42 वर्ष – 30 वर्ष = 12 वर्ष
12 वर्ष पूर्व पिता की आयु = 30 वर्ष
और 12 वर्ष पूर्व पुत्र की आयु = 14 वर्ष – 12 वर्ष
= 2 वर्ष
∴अभीष्ट अनुपात

पाठ्य-पुस्तक पृष्ठ संख्या # 275

प्रयास कीजिए

प्रश्न 1.
जाँच कीजिए कि दिए गए अनुपात समान हैं अर्थात् वे समानुपात में हैं। यदि हाँ, तो उन्हें सही ढंग से लिखिए।
1. 1 : 5 और 3 : 15
2. 2 : 9 और 18 : 81
3. 15 : 45 और 5 : 25
4. 4 : 12 और 9 : 27
5. Rs 10 का Rs 15 और 4 का 6 से।
हल :
1. 1 : 5 = \(\frac { 1 }{ 5 }\)
और 3 : 15 = \(\frac{3}{15}=\frac{1}{5}\)
∴1 : 5 और 3 : 15 समानुपात में हैं।
अतः सही रूप है-1 : 5 :: 3 : 15

2. 2 : 9 = \(\frac { 2 }{ 9 }\)
और 18 : 81 = \(\frac{18}{81}=\frac{2}{9}\)
∴2 : 9 और 18 : 81 समानुपात में हैं।
अतः सही रूप है-2 : 9 : : 18 : 81

3. 15 : 45 = \(\frac{15}{45}=\frac{1}{3}\)
और 5 : 25 = \(\frac{5}{25}=\frac{1}{5}\)
\(\frac{1}{3} \neq \frac{1}{5}\)
∴15 : 45 और 5 : 25 समानुपात में नहीं हैं।

4. 4 : 12 = \(\frac{4}{12}=\frac{1}{3}\)
और 9 : 27 = \(\frac{9}{27}=\frac{1}{3}\)
∴4 : 12 और 9 : 27 समानुपात में हैं।
अतः सही रूप है-4 : 12 : : 9 : 27

5. Rs 10 : Rs 15 = \(\frac{10}{15}=\frac{2}{3}\)
और 4 : 6 = \(\frac{4}{6}=\frac{2}{3}\)
∴Rs 10 : Rs 15 = 4 : 6
या Rs 10 ; Rs 15, 4 और 6 समानुपात में हैं।
अतः सही रूप है- Rs 10 : Rs 15 :: 4 : 6

MP Board Class 6th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 14 गुणनखंडन Ex 14.3

प्रश्न 1.

(i) 28x⁴ ÷ 56x
(ii) – 36y³ ÷ 9y²
(iii) 66pq²r³ ÷ 11qr²
(iv) 34x³y³z³ ÷ 51xy²z³
(v) 12a⁸b⁸ ÷ (- 6a⁶b⁴)

हल:

प्रश्न 2.
दिए हुए बहुपद को दिए हुए एकपदी से भाग दीजिए –

(i) (5x² – 6x) ÷ 3x
(ii) (3y² – 4y⁶ + 5y⁴) ÷ y⁴
(ii) 8 (x³y²z² + x²y³z² + x²y²z³) ÷ 4x²y²z²
(iv) (x³ + 2x² + 3x) ÷ 2x
(v) (p³q⁶ – p⁶q³) ÷ p³q³

हल:

प्रश्न 3.
निम्नलिखित विभाजन कीजिए –

(i) (10x – 25) ÷ 5
(ii) (10x – 25) ÷ (2x – 5)
(iii) 10y (6y + 21) ÷ 5 (2y + 7)
(iv) 9x²y² (3z – 24) ÷ 27xy (z – 8)
(v) 96abc (3a – 12) (5b – 30) ÷ 144(a – 4) (b – 6)

हल:

प्रश्न 4.
निर्देशानुसार भाग दीजिए –

(i) 5 (2x + 1) (3x+5) ÷ (2x + 1)
(ii) 26xy (x + 5) (y – 4) ÷ 13x (y – 4)
(iii) 52pqr (p + q) (q + r) (r + p) ÷ 104 pq (q + r) (r + p)
(iv) 20 (y + 4) (y² + 5y + 3) ÷ 5 (y + 4)
(v) x (x + 1) (x + 2) (x + 3) ÷ x (x + 1)

हल:

प्रश्न 5.
व्यंजक के गुणनखण्ड कीजिए और निर्देशानुसार भाग दीजिए –

1. (y² + 7y + 10) ÷ (y + 5)
2. (m² – 14m – 32) ÷ (m + 2)
3. (5p² – 25p + 20) ÷ (p – 1)
4. 4yz (z² + 6z – 16) ÷ 2y (z + 8)
5. 5pq (p² – q²) ÷ 2p (p + q)
6. 12xy (9x² – 16y²) ÷ 4xy (3x + 4y)
7. 39y³ (50y² – 98) ÷ 26y² (5y + 7)

हल:
1. यहाँ, y² + 7y + 10 = y² + 2y + 5y + 10
= y (y + 2) + 5 (y + 2)
= (y + 2) (y + 5)
(y² + 7y + 10) ÷ (y + 5) = \(\frac{(y+2)(y+5)}{(y+5)}\)
= (y + 2)

2. यहाँ, m² – 14m – 32 = m² + 2m – 16m – 32
= m (m + 2) – 16 (m + 2)
= (m + 2) (m – 16)
(m² – 14m – 32) ÷ (m + 2) = \(\frac{(m+2)(m-16)}{(m+2)}\)
= (m – 16)

3. यहाँ, 5p² – 25p + 20 = 5 (p² – 5p + 4)
=5 (p² p – 4p + 4)
= 5 [p(p – 1) – 4(p – 1)]
= 5 (p – 1) (p – 4)
(5p² – 25p + 20) ÷ (p – 1) = \(\frac{5(p+2)(p-4)}{(p-1)}\)
= 5 (p – 24)

4. यहाँ, 4yz (z² + 6z – 16) = 4yz (z² + 8 – z2 – 16)
= 4yz [z (z + 8) – 2 (z + 8)]
= 4yz (z + 8) (z – 2)
4yz (z2 + 6z – 16) ÷ 2y (z + 8) = \(\frac{4yz (z+8)(z-2)}{2y(z-2)}\)
= 2z (z – 2)

5. यहाँ, 5pq (p² – q²) = 5pq (p + q) (p – q)
5pq (p² – q²) ÷ 2p (p + q) = \(\frac{5pq(p+q)(p-q)}{2p(p+q)}\)
= \(\frac{5}{2}\)q(p – q)

6. यहाँ, 12xy (9x² – 16y²) = 12xy (3x + 4y) (3x – 4y)
12xy (9x² – 16y²) ÷ 4xy (3x + 4y) = \(\frac{12xy(3x+4y)(3x-4y)}{4xy(3x+4y)}\)
= 3 (3x – 4y)

7. यहाँ, 39y³ (50y² – 98) = 39y³ x 2 (25y² – 49)
= 78y² (5y + 7) (5y – 7)
39y³ (50y² – 98) ÷ 26y² (y+7) = \(\frac { 78y^{ 3 }(5y+7)(5y-7) }{ 26y^{ 2 }(y+7) } \)
= 3y (5y – 7)

पाठ्य-पुस्तक पृष्ठ संख्या # 236-237

क्या आप त्रुटि ज्ञात कर सकते हैं?

कार्य (Task) 1.
एक समीकरण को हल करते समय, . सरिता निम्न प्रकार से हल करती हैं –
3x + x + 5x = 72
अतः x = 72
और इसलिए x = \(\frac{72}{8}\) = 9.
उसने कहाँ त्रुटि की है ? सही उत्तर ज्ञात कीजिए।
हल:
यहाँ, सरिता ने दूसरे पद x के गुणांक 1 को योग में सम्मिलित नहीं किया है।
3x + x + 5x = 72
अतः 9x = 72
और इसलिए x = \(\frac{72}{9}\) = 8

कार्य (Task) 2.
अप्पू ने यह किया x = – 3, 5x = 5 – 3 = 2
क्या उसकी प्रक्रिया सही है? यदि नहीं तो इसे सही कीजिए।
हल:
अप्पू की यह प्रक्रिया सही नहीं है।
x = – 3, 5x = 5 x (- 3) = – 15

कार्य (Task) 3.
नम्रता और सलमा ने बीजीय व्यंजकों का गुणा निम्नलिखित प्रकार से किया –

क्या नम्रता और सलमा द्वारा किए गए गुणन सही हैं? कारण सहित अपने उत्तर दीजिए।
हल:
नम्रता द्वारा किए गुणन सही नहीं हैं। लेकिन सलमा द्वारा किए गए गुणन सही हैं।

(a) नम्रता ने कोष्ठक में बन्द व्यंजकों में उसके बाहर लिखे अचर 3 से प्रत्येक पद में गुणा नहीं किया है जबकि सलमा ने कोष्ठक में बन्द दोनों पदों को 3 से गुणा किया है।
(b) नम्रता ने 2x का वर्ग सही नहीं किया है।
(c) नम्रता ने गुणा करते समय मध्य पद को छोड़ दिया है।
(d) व (e) में नम्रता ने सूत्रों का प्रयोग सही नहीं किया है।

कार्य (Task) 4.
जोसफ ने एक विभाजन इस प्रकार किया: \(\frac{a+5}{5}\) = a + 1
उसके मित्र गिरीश ने यह विभाजन इस प्रकार किया:
उसके अन्य मित्र सुमन ने इसे इस प्रकार किया:
किसने विभाजन सही किया? किसने विभाजन गलत विधि से किया? और क्यों?
हल:
सुमन ने विभाजन सही किया। जोसफ और गिरीश ने विभाजन गलत विधि से किया। जोसफ और गिरीश ने द्विपदी को एकपदी से भाग देते समय अंश के प्रत्येक पद a और 5 को हर 5 से सही प्रकार से भाग नहीं दिया।

MP Board Class 8th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 12 अनुपात और समानुपात Intext Questions

पाठ्य-पुस्तक पृष्ठ संख्या # 265

प्रयास कीजिए

प्रश्न 1.
एक कक्षा में 20 लड़के और 40 लड़कियाँ हैं। लड़कों की संख्या का, लड़कियों की संख्या से क्या अनुपात होगा?
हल :
लड़कों की संख्या = 20,
लड़कियों की संख्या = 40
लड़कों की संख्या का लड़कियों की संख्या के साथ अनुपात

प्रश्न 2.
रवि एक घण्टे में 6 किमी चलता है जबकि रोशन 1 घण्टे में 4 किमी चलता है। रवि द्वारा तय की गई दूरी से रोशन द्वारा तय की गई दूरी का अनुपात ज्ञात कीजिए।
हल :
रवि द्वारा चली गई दूरी = 6 किमी
रोशन द्वारा चली गई दूरी = 4 किमी
रवि द्वारा चली गई दूरी का रोशन द्वारा चली गई दूसरी से अनुपात

पाठ्य-पुस्तक पृष्ठ संख्या # 267

प्रयास कीजिए

प्रश्न 1.
सौरभ घर से स्कूल पहुँचने में 15 मिनट लेता है और सचिन एक घण्टा लेता है। सौरभ द्वारा लिए गए समय और सचिन द्वारा लिए गए समय का अनुपात ज्ञात करो।
हल :
सौरभ द्वारा लिया गया समय = 15 मिनट
सचिन द्वारा लिया गया समय = 1 घण्टा = 60 मिनट
∴सौरभ तथा सचिन द्वारा लिए गये समय का अनुपात

प्रश्न 2.
एक टॉफी का मूल्य 50 पैसे है और एक चॉकलेट का मूल्य Rs 10। टॉफी के मूल्य का चॉकलेट के मूल्य से अनुपात ज्ञात कीजिए।
हल :
टॉफी का मूल्य = 50 पैसे,
चॉकलेट का मूल्य = Rs 10 = 1000 पैसे
∴अभीष्ट अनुपात

प्रश्न 3.
एक स्कूल में एक वर्ष में 73 छुट्टियाँ बनती हैं। छुट्टियों का वर्ष के कुलं दिनों के साथ अनुपात ज्ञात कीजिए।
हल :
छुट्टियों की संख्या = 73 दिन
एक साल में दिनों की संख्या = 365 दिन
∴ अभीष्ट अनपात

पाठ्य-पुस्तक पृष्ठ संख्या # 268

कुछ और उदाहरण

प्रश्न 1.
Rs 1250 को अमित और मिलन में 2 : 3 के अनुपात में बाँटिए।
हल :
अनुपातीय राशियों का योग = 2 + 3 = 5
कुल राशि = Rs 1250
∴ अमित का भाग = 1250 x \(\frac { 2 }{ 5 }\) = Rs 500
और मिलन का भाग = 1250 x \(\frac { 3 }{ 5 }\) = Rs 750

प्रश्न 2.
दो संख्याओं का अनुपात 4 : 5 है। यदि संख्याओं का योग 135 है, तो संख्याएँ ज्ञात कीजिए।
हल :
अनुपातीय राशियों का योग = 4 + 5 = 9
संख्याओं का योग = 135
∴पहली संख्या = \(\frac { 4 }{ 9 }\) x 135 = 60
और दूसरी संख्या = \(\frac { 5 }{ 9 }\) x 135 = 75

प्रश्न 3.
Rs 5,000 के लाभ को राम और श्याम के बीच 3 : 7 के अनुपात में बाँटिए।
हल :
अनुपातीय राशियों का योग = 3 + 7 = 10
∴राम का भाग = \(\frac { 3 }{ 10 }\) x 5,000
= Rs 1,500
और श्याम का भाग = \(\frac { 7 }{ 10 }\) x 5,000 = Rs 3500

पाठ्य-पुस्तक पृष्ठ संख्या # 268-269

प्रयास कीजिए

प्रश्न 1.
अपने बैग में रखी कॉपियों की संख्या का पुस्तकों की संख्या से अनुपात ज्ञात कीजिए।
हल :
मानाकि बैग में रखी कॉपियों की संख्या = 10 तथा
पुस्तकों की संख्या = 5

प्रश्न 2.
अपनी कक्षा की कुल डैस्कों और कुर्सियों की संख्या का अनुपात ज्ञात कीजिए।
हल :
माना कि कक्षा में डैस्कों की संख्या = 35 तथा
कुर्सियों की संख्या = 45
∴अभीष्ट अनुपात

प्रश्न 3.
अपनी कक्षा में उन छात्रों की संख्या ज्ञात कीजिए जिनकी आयु 12 वर्ष से ऊपर है। अब 12 वर्ष से ऊपर आयु वाले छात्रों की संख्या का कक्षा के बाकी छात्रों की संख्या के साथ अनुपात ज्ञात कीजिए।
हल :
माना कि कक्षा में छात्रों की कुल संख्या 48 है।
12 वर्ष से ऊपर आयु के छात्रों की संख्या = 16
शेष छात्रों की संख्या = 48 – 16 = 32
∴अभीष्ट अनुपात

प्रश्न 4.
अपनी कक्षा के दरवाजों की संख्या का खिड़कियों की संख्या से अनुपात निकालिए।
हल :
माना कि कक्षा के दरवाजों की संख्या = 2
और खिड़कियों की संख्या = 6
अभीष्ट अनुपात

प्रश्न 5.
एक आयत बनाइए। उसकी लम्बाई का चौड़ाई से अनुपात निकालिए।
हल :
माना कि आयत की लम्बाई = 5 सेमी तथा चौड़ाई = 2.5 सेमी
अभीष्ट अनपात

MP Board Class 6th Maths Solutions

MP Board Class 6th Sanskrit Solutions Surbhi Chapter 15 स्वतन्त्रतादिवसः

MP Board Class 6th Sanskrit Chapter 15 अभ्यासः

प्रश्न 1.
एकपदेन उत्तरं लिखत (एक शब्द में उत्तर लिखो)
(क) कस्मिन् मासे स्वतन्त्रतादिवसः भवति? (किस महीने में स्वतन्त्रता दिवस होता है?)
उत्तर:
अगस्तमासे

(ख) विद्यालये कः ध्वजोत्तोलनं करिष्यति? (विद्यालय में ध्वजारोहण कौन करेगा?)
उत्तर:
प्रधानाध्यापकः

(ग) सुरेशमीनाक्षीकाशीनाथैश्च सह कस्य अभ्यासः करणीयः? (सुरेश, मीनाक्षी, काशीनाथ के साथ किसका अभ्यास करना है?)
उत्तर:
समूहगीतस्य

(घ) भगतसिंहादयः कस्यै प्राणार्पणम् अकुर्वन्? (भगतसिंह आदि ने किसके लिए प्राण अर्पित कर दिए?)
उत्तर:
स्वतन्त्रतायै।

प्रश्न 2.
एकवाक्येन उत्तरं लिखत (एक वाक्य में उत्तर लिखो)
(क) प्रथमस्वतन्त्रतासंग्रामः कदा अभवत्? (पहला स्वतन्त्रता संग्राम कब हुआ?)
उत्तर:
प्रथम स्वतन्त्रता संग्रामः ईसवीय वर्षे १८५७ तमे अभवत्। (प्रथम स्वतन्त्रता संग्राम सन् १८५७ ई. में हुआ था।)

(ख) छात्राः पङ्क्तिबद्धाः कुत्र स्थास्यन्ति? (छात्र पंक्तिबद्ध होकर कहाँ खड़े होंगे?)
उत्तर:
छात्राः पंक्तिबद्धाः ध्वजस्थलस्य समीपे स्थास्यन्ति। (छात्र पंक्तिबद्ध हो, ध्वजस्थल के पास खड़े लागे।)

(ग) के विद्यालये विशेषसज्जां कुर्वन्ति? (विद्यालय में विशेष सजावट कौन करते हैं?)
उत्तर:
वरिष्ठाः छात्राः विद्यालये विशेषसज्जां कुर्वन्ति? (वरिष्ठ छात्र विद्यालय में विशेष सज्जा करते हैं।)

(घ) भारतीयाः कस्यै निरन्तरं प्रयासम् अकुर्वन्? (भारतीयों ने किसके लिए निरन्तर प्रयास किये थे?)
उत्तर:
भारतीयाः स्वतन्त्रतायै निरन्तरं प्रयासम् अकुर्वन् (भारतीयों ने स्वतन्त्रता के लिए निरन्तर प्रयास किये।)

प्रश्न 3.
प्रश्नवाचक शब्दान् प्रयुज्य प्रश्ननिर्माणं कुरुत (प्रश्नवाचक शब्दों का प्रयोग करके प्रश्न निर्माण करो)-
(किम्, के, कस्य, कदा)
(क) छात्राः प्रातः सप्तवादने विद्यालयम् आगमिष्यन्ति।
(ख) ‘क्रान्तिकारीणां कार्यम्’ इति नागेशस्य भाषणस्य विषयः।
(ग) सर्वे समवेतस्वरेण ‘जनगणमन’ इति राष्ट्रगानं गास्यन्ति।
(घ) वरदा संस्कृतमाध्यमेन भाषणं करिष्यति।
उत्तर:
(क) छात्राः प्रातः कदा विद्यालये आगमिष्यन्ति?
(ख) ‘क्रान्तिकारीणां कार्यम्’ इति कस्य भाषणस्यं विषयः?
(ग) के समवेतस्वरेण ‘जनगणमन’ इति राष्ट्रगानं गास्यन्ति?
(घ) वरदा संस्कृतमाध्यमेन किम् करिष्यति?

प्रश्न 4.
निर्देशानुसारं लकारपरिवर्तनं कुरुत (निर्देशानुसार लकार में परिवर्तन करो)
(क) करिष्यन्ति – लङ्लकारे
(ख) स्थास्यन्ति – लट्लकारे
(ग) भविष्यन्ति – लङ्लकारे
(घ) करिष्यन्ति – लट्लकारे
उत्तर:
(क) अकुर्वन्
(ख) तिष्ठन्ति
(ग) अभवन्
(घ) कुर्वन्ति।

प्रश्न 5.
कोष्ठकात् उचितशब्दान् चित्वा रिक्तस्थानानि पूरयत (कोष्ठक से उचित शब्दों को चुनकर रिक्त स्थानों को भरो)
(क) श्व: ……….. पञ्चदशदिनाङ्क भविष्यति। (अगस्तमासं/अगस्तमासस्य)
(ख) ………. छात्राः विशेषसज्जां कुर्वन्ति। (अष्टमकक्षायाः/अष्टमकक्षया)
(ग) इदानीं वयं ………… गच्छामः।, (गृह/गृहस्य)
(घ) भोः ………… (मनधीर/मनधीरः)
उत्तर:
(क) अगस्तमासस्य
(ख) अष्टमकक्षाया
(ग) गृहं
(घ) मनधीर।

प्रश्न 6.
उचितक्रमेण वाक्यानां पुनर्लेखनं कुरुत (उचित क्रम से वाक्यों को पुनः लिखो)
(क) ध्वजस्थलस्य समीपे छात्राः पङ्क्तिबद्धाः स्थास्यन्ति।
(ख) प्रातः सप्तवादने छात्राः विद्यालयम् आगमिष्यन्ति।
(ग) प्रधानाध्यापकः ध्वजोत्तोलनं करिष्यति।
(घ) छात्राः विद्यालये विशेषसज्जां कुर्वन्ति।
(ङ) स्वतन्त्रतादिवसस्य उत्सवः भविष्यति।
उत्तर:
(ङ) स्वतन्त्रतादिवसस्य उत्सवः भविष्यति।
(घ) छात्राः विद्यालये विशेषसज्जां कुर्वन्ति।
(ख) प्रातः सप्तवादने छात्राः विद्यालयम् आगमिष्यन्ति।
(क) ध्वजस्थलस्य समीपे छात्राः पङ्क्तिबद्धाः स्थास्यन्ति।
(ग) प्रधानाध्यापकः ध्वजोत्तोलनं करिष्यति।

योग्यताविस्तारः

शब्दचयनं कृत्वा राष्ट्रध्वजस्य वर्णनं कुरुत (शब्द चुनकर राष्ट्रध्वज का वर्णन करो)
(क) राष्ट्रध्वजे (त्रयः/चत्वारः) वर्णाः सन्ति।
(ख) ध्वजस्य प्रथमपट्टिकायां (हरितः/केसरः) वर्णः वर्तते।
(ग) ध्वजस्य मध्यमपट्टिकायां (कुङ्कमः/श्वेतः) वर्णः वर्तते।
(घ) ध्वजस्य अध:पट्टिकायां (श्वेतः/हरितः) वर्णः वर्तते।
(ङ) ध्वजस्य मध्यपट्टिकायां (सुदर्शनचक्र/अशोकचक्र:) वर्तते।
उत्तर:
(क) राष्ट्र ध्वजे त्रयः वर्णाः सन्ति।
(ख) ध्वजस्य प्रथमपट्टिकायां केसर: वर्ण: वर्तते।
(ग) ध्वजस्य मध्यमपट्टिकायां श्वेतः वर्ण: वर्तते।
(घ) ध्वजस्य अध:पट्टिकायां हरितः वर्ण: वर्तते।
(ङ) ध्वजस्य मध्यपट्टिकायां अशोकचक्रः वर्तते।

स्वतन्त्रतादिवसः हिन्दी अनुवाद

(केचन छात्राः विद्यालयस्य प्राङ्गणे तिष्ठन्ति चर्चा कुर्वन्ति च)

सुरेशः :
भो महेश! पश्य! अष्टमकक्षायाः छात्राः किं कुर्वन्ति?

महेशः :
श्वः अगस्तमासस्य पञ्चदशदिनाङ्कः। अस्माकं स्वतन्त्रादिवसस्य समारोहः भविष्यति। अतः वरिष्ठाः छात्राः विद्यालये विशेषसज्जां कुर्वन्ति।

सुधीरः :
अहं पठितवान् यत् १८५७ तमे वर्षे प्रथमस्वतन्त्रतासंग्रामः अभवत्। ततः भारतीयाः स्वतन्त्रतायै निरन्तरं प्रयासम् अकुर्वन्। ते भीषणकष्टानि असहन्त।।

मनधीरः :
सत्यम्! अनन्तरम् एव १९४७ तमे वर्षे अगस्तमासस्य पञ्चदशदिनाङ्के तेषां प्रयत्नाः सफलाः जाताः। तस्य स्मृत्यर्थम् एव प्रतिवर्ष स्वतन्त्रतादिवसस्य उत्सवः भवति।

वरदा :
पश्य! सुरेश पश्य! अवन्तिका, मीनाक्षी काशीनाथ चः अत्रैव आगच्छन्ति। (सर्वे तत्र आगछन्ति)

मीनाक्षी :
अहो शोभनम्! श्वः समारोहे किं किं भविष्यति?

अनवाद :
(कुछ छात्र विद्यालय के प्राङ्गण में खड़े हुए हैं और चर्चों करते हैं।)

सुरेश :
हे महेश! देखो! आठवीं कक्षा के छात्र क्या करते हैं?

महेश :
कल (आने वाला) अगस्त महीने की पन्द्रहवीं तारीख है। हमारे स्वतन्त्रता दिवस का समारोह (उत्सव) होगा। इसलिए वरिष्ठ छात्र विद्यालय में विशेष सजावट (तैयारी) करते हैं।

सुधीर :
मैंने पढ़ा था कि सन् १८५७ ई. में प्रथम स्वतन्त्रता संग्राम हुआ था। उसके बाद भारतीयों ने स्वतन्त्रता के लिए निरन्तर प्रयास किये। उन्होंने भयंकर कष्टों को सहन किया।

मनधीर :
सत्य है (ठीक है)! बाद में ही सन् १९४७ ई. में अगस्त महीने की पन्द्रहवीं तारीख को उनके प्रयत्न सफल हो गये। उनको स्मरण बनाये रखने के लिए ही प्रत्येक वर्ष स्वतन्त्रता दिवस का उत्सव होता है।

वरदा :
देखो! सुरेश देखो! अवन्तिका, मीनाक्षी और काशीनाथ यहाँ ही आ रहे हैं। (सभी वहाँ आ रहे है)

मीनाक्षी :
अहा! यह कितना सुन्दर है। कल समारोह में क्या-क्या होगा?

सुरेशः :
सर्वे छात्रा: गणवेशे प्रातः सप्तवादने विद्यालयम् आगमिष्यन्ति। ध्वजस्थलस्य समीपे पङ्क्तिबद्धाः स्थास्यन्ति।

सोमदत्त: :
सर्वे शिक्षकाः कर्मचारिणः अपि स्थास्यन्ति। अनन्तरम् अस्माकं प्रधानाध्यापकः ध्वजोत्तोलनं करिष्यति। तत्पश्चात् सर्वे समवेतस्वरेण ‘जनगणमन’ इति राष्ट्रगानं गास्यन्ति। पश्चात् प्रधानाध्यापकमहोदयः उद्बोधनं करिष्यति।

माधवी :
तदनन्तरं छात्रसभायां केचन छात्रा: गीतानि गास्यन्ति केचन च भाषणानि करिष्यन्ति। मिष्ठान्नवितरणेन कार्यक्रमस्य समापनं भविष्यति।

वरदा :
अहं संस्कृतमाध्यमेन तिलकस्य, महात्मागान्धि महोदयस्य, नेहरुमहोदयस्य, सुभाषचन्द्रस्य च महत्कार्यविषये भाषणं करिष्यामि।

नागेश: :
चन्द्रशेखर

आजादः :
अशफाकउल्लाह

खानः :
भगतसिंहादयः स्वतन्त्रतायै प्राणार्पणम् अकुर्वन्। भाषणस्य मम विषयः ‘क्रान्तिकारीणां कार्यम्’ इति अस्ति।

मनधीरः :
शोभनो हि स्वतन्त्रतादिवसः। इदानीं वयं गृहं गच्छामः। मया अपि सुरेशमीनाक्षीकाशीनाथैश्च सह समूहगीतस्य अभ्यासः करणीयः।
“ध्वजो धूयतां भारतीयस्य लोके।”

अनवाद :
सुरेश :
सभी छात्र गणवेश में प्रातः सात बजे विद्यालय में आ जायेंगे। ध्वजस्थल के पास पंक्तिबद्ध खड़े हो जायेंगे।

सोमदत्त :
सभी शिक्षक और कर्मचारी भी खड़े होंगे। इसके बाद हमारे प्रधानाध्यापक ध्वजारोहण करेंगे। उसके बाद, सभी एक स्वर से ‘जनगणमन’ इस राष्ट्रगान को गायेंगे। बाद में, प्रधानाध्यापक महोदय उद्बोधन करेंगे।

माधवी :
उसके बाद छात्रसभा में कुछ छात्र गीत गायेंगे और कुछ भाषण करेंगे। मिष्ठान्न वितरण के साथ ही कार्यक्रम का समापन हो जायेगा।

वरदा :
मैं संस्कृत भाषा के माध्यम से तिलक, महात्मा गांधी महोदय के, नेहरू महोदय के तथा सुभाषचन्द्र के महान कार्यों के विषय में भाषण करूँगी।

नागेश :
चन्द्रशेखर आजादः, अशफाक उल्लाह खान, भगतसिंह आदि ने स्वतन्त्रता के लिए प्राण न्योछावर कर दिए। मेरे भाषण का विषय है ‘क्रान्तिकारियों के कार्य’।

मनधीर :
स्वतन्त्रता दिवस (अति) शोभनीय है। अब हम सब घर चलते हैं। मुझे भी सुरेश, मीनाक्षी और काशीनाथ के साथ समूह गान का अभ्यास करना चाहिए। “भारतीय लोक में ध्वज ऊँचा ही लहराता रहे।”

स्वतन्त्रतादिवसः शब्दार्थाः

प्राङ्गणे = प्राङ्गण में। तिष्ठन्ति = खड़े हैं। श्वः = आने वाला कल। विशेषसज्जां = विशेष सजावट। प्रथमस्वतन्त्रतासङ्ग्रामः = आजादी की पहली लड़ाई। निरन्तरम् = लगातार। भीषण कष्टानि = अत्यधिक कष्टों को। असहन्त = सहन किया। स्मृत्यर्थम् = स्मरण के लिये। धारयित्वा = पहनकर। ध्वज. स्थलस्य = झण्डा फहराने के स्थान के। स्थास्यन्ति = खड़े रहेंगे। ध्वजोत्तोलनं = झण्डा फहराना। समवेतस्वरेण = एक स्वर में। प्राणार्पणम् = बलिदान। अनन्तरम् = उसके बाद। गास्यन्ति = गाएँगे। धूयतां = फहराएँगे। गो

MP Board Class 6th Sanskrit Solutions

MP Board Class 6th Maths Solutions Chapter 11 बीजगणित Ex 11.5

पाठ्य-पुस्तक पृष्ठ संख्या # 260-262

प्रश्न 1.
बताइए कि निम्नलिखित में से कौन-से कथन समीकरण (चर संख्याओं के) हैं ? सकारण उत्तर दीजिए। समीकरण में सम्बद्ध चर भी लिखिए।
(a) 17 = x + 17
(b) (t – 7) > 5
(c) \(\frac { 4 }{ 2 }=2\)
(d) 7 × 3 – 13 = 8
(e) 5 × 4 – 8 = 2x
(f) x – 2 = 0
(g) 2m < 30
(h) 2n + 1 = 11
(i) 7 = 11 × 5 – 12 × 4
(j) 7 = 11 × 2 + p
(k) 20 = 5y
(l) \(\frac { 3q }{ 2 }\) < 5
(m) z + 12 > 24
(n) 20 – (10 – 5) = 3 × 5
(o) 7 – x = 5
उत्तर-
(a) चर x में समीकरण है।
(b) यह समीकरण नहीं है, क्योंकि इसमें = का चिह्न नहीं है।
(c) यह समीकरण नहीं है, क्योंकि इसमें चर नहीं है।
(d) यह समीकरण नहीं है, क्योंकि इसमें चर नहीं है।
(e) यह चर x में समीकरण है।
(f) यह चर x में समीकरण है।
(g) यह समीकरण नहीं है, क्योंकि इसमें = का चिह्न नहीं है।
(h) यह चर n में समीकरण है।
(i) यह समीकरण नहीं है, क्योंकि इसमें चर नहीं है।
(j) चह चर p में समीकरण है।
(k) चह चर y में समीकरण है।
(l) यह समीकरण नहीं है, क्योंकि इसमें = का चिह्न नहीं है।
(m) यह समीकरण नहीं है, क्योंकि इसमें = का चिह्न नहीं है।
(n) यह समीकरण नहीं है, क्योंकि इसमें चर नहीं है।
(o) यह चर x में समीकरण है।

प्रश्न 2.
सारणी के तीसरे स्तम्भ में प्रविष्टियों को पूरा कीजिए
हल :

प्रश्न 3.
प्रत्येक समीकरण के सम्मुख कोष्ठकों में दिए मानों में से समीकरण का हल चुनिए। दर्शाइए कि अन्य मान समीकरण को सन्तुष्ट नहीं करते हैं।
(a) 5m = 60 (10, 5, 12, 15)
(b) n + 12 = 20 (12, 8, 20, 0)
(c) p – 5 = 5 (0, 10, 5, -5)
(d) \(\frac { q }{ 2 }=7\) (7, 2, 10, 14)
(e) r – 4 = 0 (4, -4, 8, 0)
(f) x + 4 = 2 (-2, 0, 2, 4)
हल :
(a) m = 10 के लिए,
L.H.S. = 5 x 10 = 50
और R.H.S. = 60
∵L.H.S. ≠ R.H.S.
∴m = 10 समीकरण को सन्तुष्ट नहीं करता है।
m = 5 के लिए, L.H.S. = 5 x 5 = 25
और R.H.S. = 60
∵L.H.S. ≠ R.H.S.
∴m = 5 समीकरण को सन्तुष्ट नहीं करता है।
m = 12 के लिए,
L.H.S. = 5 x 12 = 60
और R.H.S. = 60
∵L.H.S. = R.H.S.
∴m = 12 समीकरण का हल है।
m = 15 के लिए,
L.H.S. = 5 x 15 = 75
और R.H.S. = 60
∵L.H.S. ≠ R.H.S.
∴m = 15 समीकरण को सन्तुष्ट नहीं करता है।

(b) n = 12 के लिए,
L.H.S. = 12 + 12 = 24
और R.H.S. = 20
∵L.H.S. ≠ R.H.S.
∴n = 12 समीकरण को सन्तुष्ट नहीं करता है।
n = 8 के लिए, L.H.S. = 8 + 12 = 20
और R.H.S. = 20
∵L.H.S. = R.H.S.
∴n = 8 समीकरण का हल है।
n = 20 के लिए,
L.H.S. = 20 + 12 = 32
और R.H.S. =20
∵L.H.S. ≠ R.H.S.
∴n = 20, समीकरण को सन्तुष्ट नहीं करता है।
n = 0 के लिए,
L.H.S. = 0 + 12 = 12
और R.H.S.= 20
∵L.H.S. ≠ R.H.S.
∴n = 0 समीकरण को सन्तुष्ट नहीं करता है।

(c) p = 0 के लिए,
L.H.S. = 0 – 5 = -5
और R.H.S. = 5
∵L.H.S. ≠ R.H.S.
∴p = 0 समीकरण को सन्तुष्ट नहीं करता है।
p = 10 के लिए,
L.H.S. = 10 – 5 = 5
और R.H.S. = 5
∵L.H.S. = R.H.S.
∴p = 10 समीकरण का हल है।
p = 5 के लिए, L.H.S. = 5 – 5 = 0
और R.H.S. = 5
∵L.H.S. ≠ R.H.S.
∴p = 5, समीकरण को सन्तुष्ट नहीं करता है।
p = -5 के लिए,
L.H.S. = – 5 – 5 = -10
और R.H.S. = 5
∵L.H.S. ≠ R.H.S.
∴p = – 5 समीकरण को सन्तुष्ट नहीं करता है।

(d) q = 7 के लिए,
L.H.S. = \(\frac { 7 }{ 2 }\)
और R.H.S. = 7
∵L.H.S. ≠ R.H.S.
∴q = 7 समीकरण को सन्तुष्ट नहीं करता है।
q = 2 के लिए,
L.H.S. = \(\frac { 2 }{ 2 }\) = 1
और R.H.S. = 7
∵L.H.S. ≠ R.H.S.
∴q = 2 समीकरण को सन्तुष्ट नहीं करता है।
q = 10 के लिए,
L.H.S. = \(\frac { 10 }{ 2 }\) = 5
और R.H.S. = 7
∵L.H.S. ≠ R.H.S.
∴q = 10 समीकरण को सन्तुष्ट नहीं करता है।
q = 14 के लिए,
L.H.S. = \(\frac { 14 }{ 2 }\) = 7
और R.H.S. = 7
∵L.H.S. = R.H.S.
∴q = 14 समीकरण का हल है।

(e) r = 4 के लिए,
L.H.S. = 4 – 4 = 0
और R.H.S. = 0
∵L.H.S. = R.H.S.
∴r = 4 समीकरण का हल है।
r = -4 के लिए,
L.H.S. = -4 – 4 = -8
और R.H.S. = 0
∵L.H.S. ≠ R.H.S.
∴r = -4 समीकरण को सन्तुष्ट नहीं करता है।
r = 8 के लिए,
L.H.S. = 8 – 4 = 4
और R.H.S. = 0
∵L.H.S. ≠ R.H.S.
∴r = 8 समीकरण को सन्तुष्ट नहीं करता है।
r = 0 के लिए,
L.H.S. = 0 – 4 = – 4
और R.H.S. = 0
∵L.H.S. ≠ R.H.S.
∴r = 0 समीकरण को सन्तुष्ट नहीं करता है।

(f) x = – 2 के लिए,
L.H.S. = – 2 + 4 = 2
और R.H.S. = 2
∵L.H.S. = R.H.S.
∴x = – 2 समीकरण का हल है।
x = 0 के लिए,
L.H.S. = 0 + 4 = 4
और R.H.S. =2
∵L.H.S. ≠ R.H.S.
∴x = 0 समीकरण को सन्तुष्ट नहीं करता है।
x = 2 के लिए,
L.H.S. = 2 + 4 = 6
और R.H.S. = 2
∵L.H.S. ≠ R.H.S.
∴x = 2 समीकरण को सन्तुष्ट नहीं करता है।
x = 4 के लिए,
L.H.S. = 4 + 4 = 8
और R.H.S. = 2
∵L.H.S. ≠ R.H.S.
∴x = 4 समीकरण को सन्तुष्ट नहीं करता है।

प्रश्न 4.
(a) नीचे दी हुई सारणी को पूरा कीजिए और इस सारणी को देखकर ही समीकरण m + 10 = 16 का हल ज्ञात कीजिए।

(b) नीचे दी सारणी को पूरा कीजिए और इस सारणी को देखकर ही समीकरण 5t = 35 का हल ज्ञात कीजिए।

(c) सारणी को पूरा कीजिए और समीकरण \(\frac { z }{ 3 }\) = 4 का हल ज्ञात कीजिए

(d) सारणी को पूरा कीजिए और समीकरण m – 7 = 3 का हल ज्ञात कीजिए

हल :
(a) सारणी को पूरा करने पर

सारणी से स्पष्ट है कि m = 6 समीकरण m + 10 = 16 को सन्तुष्ट करता है। अतः m = 6 समीकरण का हल है।

(b) सारणी को पूरा करने पर,

सारणी से स्पष्ट है कि t = 7 समीकरण 5t = 35 को सन्तुष्ट करता है। अत: t = 7 समीकरण का हल है।

(c) सारणी को पूरा करने पर,

सारणी से स्पष्ट है कि z = 12 समीकरण \(\frac { z }{ 3 }\) = 4 को सन्तुष्ट करता है।
अतः z = 12 समीकरण का हल है।

(d) सारणी को पूरा करने पर,

सारणी से स्पष्ट है कि m = 10 समीकरण m – 7 = 3 को सन्तुष्ट करता है।
अतः m = 10 समीकरण का हल है।

प्रश्न 5.
निम्नलिखित पहेलियों को हल कीजिए। आप ऐसी पहेलियाँ स्वयं भी बना सकते हैं। मैं कौन हूँ?
(i) एक वर्ग के अनुदिश जाइए।
प्रत्येक कोने को तीन बार
गिनकर और उससे अधिक नहीं,
मुझमें जोड़िए और
ठीक चौंतीस प्राप्त कीजिए।

(ii) सप्ताह के प्रत्येक दिन के लिए,
मेरे से ऊपर गिनिए।
यदि आपने कोई गलती नहीं की है,
तो आप तेईस प्राप्त करेंगे।
(iii) मैं एक विशिष्ट संख्या हूँ।
मुझमें से एक छः निकालिए।
और क्रिकेट की एक टीम बनाइए।

(iv) बताइए, मैं कौन हूँ।
मैं एक सुन्दर संकेत दे रही हूँ
आप मुझे वापस पाएँगे।
यदि मुझे बाईस में से निकालेंगे।
हल :
(i) माना कि मैं ‘x’ हूँ।
वर्ग के चार कोने हैं। तीन बार प्रत्येक कोने को गिनने पर हम प्राप्त करते हैं,
3 × 4 = 12
अब प्रश्नानुसार, x + 12 = 34
या x + 12 – 12 = 34 – 12
या x + 0 = 22
⇒ x = 22
अतः मैं 22 हूँ।

(ii) माना कि मैं x हूँ।
प्रश्नानुसार, x + 7 = 23
या x + 7 – 7 = 23 – 7
x + 0 = 16
⇒ x = 16

(iii) माना कि विशिष्ट संख्या x है।
प्रश्नानुसार, x – 6 = 11
या x – 6 + 6 = 11 + 6
या x + 0 = 17
⇒ x = 17
अतः विशिष्ट संख्या 17 है

(iv) माना कि मैं x हूँ।
प्रश्नानुसार, 22 – x = x
या 22 – x + x = x + x
या 22 + 0 = 2x
या 2x = 22
⇒ \(x=\frac { 22 }{ 2 }\) = 11
अतः मैं 11 हूँ।

MP Board Class 6th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 14 गुणनखंडन Ex 14.2

प्रश्न 1.
निम्नलिखित व्यंजकों के गुणनखण्ड कीजिए –

1. a² + 8a + 16
2. p² – 10p + 25
3. 25m² + 30m + 9
4. 49y² + 84yz + 36z²
5. 4x² – 8x + 4
6. 121b² – 88bc + 16c²
7. (l + m)² – 4lm
8. a⁴ + 2a²b² + b⁴

हल:
1. a² + 8a + 16 = (a)² + 2 x a x 4 + (4)²
[∴ a² + 2ab + b² = (a + b)²]
= (a + 4)²

2. p² – 10p + 25 = (p)² – 2 x p x 5 + (5)²
[∴ a² – 2ab + b² = (a – b)]
= (p – 5)²

3. 25m² + 30m + 9 = (5m)² + 2 x 5m x 3 + (3)²
= (5m + 3)²

4. 49y² + 84yz + 36z²
= (7y)² + 2 x 7y x 6z + (6z)²
= (7y + 6z)²

5. 4x² – 8x + 4 = (2x)² – 2 x 4x × 2 + (2)²
= (2x – 2)²

6. 121b² – 88bc + 16c²
= (11b)² – 2 x 11b x 4c + (4c)²
= (11b – 4c)

7. (l + m)² – 4lm = l² + 2lm + m² – 4lm
= l² – 2lm + m²
= (l)² – 2 x 1 x m + (m)² = (1 – m)

8. a⁴ + 2a²b² + b⁴ = (a²)² + 2 x a² x b² + (a)²
= (a + b)²

प्रश्न 2.
गुणनखण्ड कीजिए –

1. 4p² – 9q²
2. 63a² – 112b²
3. 49x² – 36
4. 16x⁵ – 144x³
5. (l + m)² – (l – m)
6. 9x²y² – 16
7. (x² – 2xy +y²) – z²
8. 25a² – 4b² + 28bc – 49c²

हल:
1. 4p² – 9q²
a² – b² = (a – b) (a + b)
4p² – 9q² = (2p)² – (3q)²
= (2p – 3q) (2p + 3q)

2. 63a² – 112b² = 7 (9a² – 16b²)
= 7 {(3a)² – (4b)²}
= 7 (3a – 4b) (3a + 4b)

3. 49x² – 36 = (7x)² – (6)²
= (7x – 6) (7x + 6)

4. 16x⁵ – 144x³ = 16x³ (x² – 9)
= 16x³ (x² – 3²)
= 16x³ (x – 3) (x + 3)

5. (l + m)² – (l – m) = [(l + m) – (l – m)][(l + m) – (l – m)]
= (l + m – 1 + m) (l + m + l – m)
= 2m x 2l = 4lm

6. 9x²y² – 16 = (3xy)² – (4)²
= (3xy – 4) (3xy + 4)

7. x² – 2xy + y² – z² = (x – y)² – z²
= [(x – y) – z] [(x – y) + z]
= (x – y – z) (x – y + z)

8. 25a² – 4b² + 28bc – 49c²
= 25a² – (4b² – 28bc + 49c²)
= 25a² – [(2b)² – 2 x 26 x 7c + (7c)²]
= (5a)² – (2b – 7c)²
= [5a – (2b – 7c)] [5a + (2b – 7c)]
= (5a – 25 + 7c) (5a + 2b – 7c)

प्रश्न 3.
निम्नलिखित व्यंजकों के गुणनखण्ड कीजिए –

1. ax² + bx
2. 7p² + 21q²
3. 2x² + 2xy² + 2xz²
4. am² + bm² + bn² + an²
5. (lm + 1) + m + 1
6. y (y + z) + 9 (y + z)
7. 5y² – 20y – 8z + 2yz
8. 10ab + 4a + 5b + 2
9. 6xy – 4y + 6 – 9x.

हल:
1. ax² + bx = x (ax + b)

2. 7p² + 21q² = 7 (p² + 3q²)

3. 2x² + 2xy² + 2xz² = 2x (x² + y² + z²)

4. amv + bm² + bn² + an²
= (am² + bm²) + (bn² + an²)
= m² (a + b) + n² (b+ a)
= (a + b) (m² + n²)

5. (lm + 1) + m + 1 = 1(m + 1) + 1 (m + 1)
= (m + 1) (1 + 1)

6. y (y + z) + 9 (y + z) = (y + z) (y + 9)

7. 5y² – 20y – 8z + 2yz
= (5y² – 20y) + (2yz – 8z)
= 5y (y – 4) + 2z (y – 4).
= (y – 4) (5y + 2z)

8. 10ab + 4a + 56+2
= (10ab + 5b) + (4a + 2)
= 5b (2a + 1) + 2 (2a + 1)
= (2a + 1) (5b + 2)

9. 6xy – 4y + 6 – 9x
= (6xy – 4y) – (9x – 6)
= 2y (3x – 2) – 3 (3x – 2)
= (3x – 2) (2y – 3)

प्रश्न 4.
गुणनखण्ड कीजिए –

1. a⁴ – b⁴
2. p⁴ – 81
3. x⁴ (y + z)⁴
4. x⁴ – (x – z)⁴
5. a² – 2a²b² + b⁴

हल:
1. a⁴ – b⁴ = (a²)² – (b²)²
= (a² + b²) (a² – b²)
= (a² + b²) (a + b) (a – b)

2. p⁴ – 81 = (p²)² – (9)²
= (p² + 9) (p² – 9)
= (p² + 9) (p + 3) (p – 3)

3. x⁴ – (y + z)⁴ = (x²)² – [(y + 2)²]²
= [x² – (y + z)²] [x² + (y + z)²]
= [x – (y + z)] [x + (y + z)] [x² + (y + z)²]
= (x – y – z) (x + y + z) [x² + (y + z)²]

4. x⁴ – (x – z)⁴ = (x²)² – [(x – z)²]²
= [x² – (x – z)²] [x² + (x – z)]
= [x – (x – z)] [x + (x – z)] [x² + (x² – 2x² + z²)] = (x – x + z) (x + x – z)(2x² – 2xz + z²)
= z(2x – z) (2x² – 2xz + z²)

5. a⁴ – 2a²b² + b² = (a²)² – 2 x a² x b² + (b²)²
= [a² – b²]²
= [(a – b) (a + b)]²
= (a – b)² (a + b)²

प्रश्न 5.
निम्नलिखित व्यंजकों के गुणनखण्ड कीजिए –

1. p² + 6p + 8
2. q² – 10q + 21
3. p² + 6p – 16

हल:
1. P² + 6p + 8 = p² + (4 + 2) p + 8
(∴8 = 4 x 2)
= p² + 4p + 2p +8
= p (p + 4) + 2 (p + 4)
= (p + 4) (p + 2)

2. q² – 10q + 21 = q² – (7 + 3) q + 21
(∴ 21 = 3 x 7)
=q² – 7q – 3q + 21
= q(q – 7) – 3 (q – 7)
= q (q – 7) (q – 3)
= (q – 3) (q – 7)

3. p² + 6p – 16 = p² + (8 – 2)p – 16
(∴ 16 = 8 x 2)
= p² + 8p – 2p – 16
= p (p + 8) – 2 (p + 8)
= (p + 8) (p – 2)

पाठ्य-पुस्तक पृष्ठ संख्या # 234

प्रयास कीजिए (क्रमांक 14.2)

प्रश्न 1.
भाग दीजिए –

1. 24xy²3z³ को 6yz² से
2. 63a²b⁴c⁶ को 7a²b²c³ से।

हल:
1. 24xy²z³ + 6yz²

= 4xyz

2. 63a²b⁴c⁶ ÷ 7a²b²c³

= 9b²c³

MP Board Class 8th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 11 बीजगणित Ex 11.4

पाठ्य-पुस्तक पृष्ठ संख्या # 255-256

प्रश्न 1.
निम्नलिखित प्रश्नों के उत्तर दीजिए :
(a) सरिता की वर्तमान आयु y वर्ष लीजिए।
(i) आज से 5 वर्ष बाद उसकी आयु क्या होगी ?
(ii) 3 वर्ष पहले उसकी आयु क्या थी?
(iii) सरिता के दादाजी की आयु उसकी आयु की 6 गुनी है। उसके दादाजी की क्या आयु है ?
(iv) उसकी दादीजी दादाजी से 2 वर्ष छोटी है। दादीजी की आयु क्या है ?
(v) सरिता के पिता की आयु सरिता की आयु के तीन गुने से 5 वर्ष अधिक है। उसके पिता की आयु क्या है ?

(b) एक आयताकार हॉल की लम्बाई उसकी चौड़ाई के तिगुने से 4 मीटर कम है। यदि चौड़ाई b मीटर है, तो लम्बाई क्या है ?
(c) एक आयताकार बक्स की चौड़ाई h सेमी है। इसकी लम्बाई, ऊँचाई की 5 गुनी है और चौड़ाई लम्बाई से 10 सेमी कम है। बक्स की लम्बाई और चौड़ाई को ऊँचाई के पदों में व्यक्त कीजिए।
(d) मीना, बीना और लीना पहाड़ी की चोटी पर पहुँचने के लिए सीढ़ियाँ चढ़ रही हैं। मीना सीढ़ी s पर है। बीना मीना से 8 सीढ़ियाँ आगे है और लीना मीना से 7 सीढ़ियाँ पीछे है। बीना और लीना कहाँ पर हैं ? चोटी पर पहुँचने के लिए कुल सीढ़ियाँ मीना द्वारा चढ़ी गई सीढ़ियों की संख्या के चार गुने से 10 कम हैं। सीढ़ियों की कुल संख्या को s के पदों में व्यक्त कीजिए।
(e) एक बस v किमी प्रति घण्टा की चाल से चल रही है। यह दासपुर से बीसपुर जा रही है। बस के 5 घण्टे चलने के बाद भी बीसपुर 20 किमी दूर रह जाता है। दासपुर से बीसपुर की दूरी क्या है ? इसे v का प्रयोग करते हुए व्यक्त कीजिए।
उत्तर-
(a) (i) सरिता की वर्तमान आयु = y वर्ष
5 वर्ष बाद उसकी आयु = y + 5 वर्ष
(ii) 3 वर्ष पहले उसकी आयु = y – 3 वर्ष
(iii) दादाजी की आयु = 6 x सरिता की वर्तमान आयु
= 6y वर्ष
(iv) दादीजी की आयु = दादाजी की आयु – 2
= 6y – 2 वर्ष
(v) सरिता के पिता की आयु = 3 x सरिता की आयु + 5 वर्ष
= 3y + 5 वर्ष

(b) ∵ हॉल की चौड़ाई = b मीटर
लम्बाई = 3 x चौड़ाई – 4 मीटर
= 3b – 4 मीटर

(c) माना कि बक्स की ऊँचाई = h सेमी
∴ बक्स की लम्बाई = 5 x चौड़ाई = 5h सेमी
और बक्स की चौड़ाई = (लम्बाई – 10) सेमी
= (5h – 10) सेमी

(d) ∵ मीना सीढ़ी s पर है।
∴ बीना की स्थिति = s + 8 सीढ़ियाँ
और लीना की स्थिति = s – 7 सीढ़ियाँ
∴ चोटी पर पहुँचने के लिए कुल सीढ़ियाँ
= 4 x मीना द्वारा चढ़ी गई सीढ़ियों की संख्या – 10
= 4 x s – 10
= 4s – 10 सीढ़ियाँ

(e) बस की चाल = v किमी/घण्टा
5 घण्टे में चली गई दूरी = 5 x v किमी
= 5v किमी
∴ बीसपुर की दूरी = 5v + 20 किमी
अतः दासपुर से बीसपुर की दूरी = 5v + 20 किमी

प्रश्न 2.
व्यंजकों के प्रयोग से बने निम्न कथनों को साधारण भाषा के कथनों में बदलिए :
(उदाहरणार्थ, एक क्रिकेट मैच में सलीम ने r रन बनाए और नलिन ने (r + 15) रन बनाए। साधारण भाषा में, नलिन ने सलीम से 15 अधिक बनाए हैं।)
(a) एक अभ्यास पुस्तिका का मूल्य Rs p है। एक पुस्तक का मूल्य Rs 3p है।
(b) टोनी ने मेज पर q कंचे रखे। उसके पास डिब्बे में 8q कंचे हैं।
(c) हमारी कक्षा में n विद्यार्थी हैं। स्कूल में 20n विद्यार्थी हैं।
(d) जग्गू की आयु z वर्ष है। उसके चाचा की आयु 4z वर्ष है और उसकी चाची की आयु (4z – 3) वर्ष है।
(e) बिन्दुओं (dots) की एक व्यवस्था में r पंक्तियाँ हैं। प्रत्येक पंक्ति में 5 बिन्दु हैं।
उत्तर-
(a) पुस्तक का मूल्य अभ्यास-पुस्तिका के मूल्य का तीन गुना है।
(b) टोनी के डिब्बे में मेज पर रखे कंचों के 8 गुने कंचे हैं।
(c) स्कूल के विद्यार्थियों की कुल संख्या हमारी कक्षा के विद्यार्थियों की बीस गुनी है।
(d) जग्गू के चाचा की आयु जग्गू की आयु की 4 गुनी है और जग्गू की चाची की आयु उसके चाचा से 3 वर्ष कम है।
(e) बिन्दुओं की संख्या पंक्तियों की संख्या की 5 गुनी है।

प्रश्न 3.
(a) मुन्नू की आयु x वर्ष दी हुई है। क्या आप अनुमान लगा सकते हैं कि (x – 2) क्या दर्शाएगा?
(संकेत : मुन्नू के छोटे भाई के बारे में सोचिए।) क्या आप अनुमान लगा सकते हैं कि (x + 4) क्या दर्शाएगा और 3x + 7 क्या दर्शाएगा?
(b) सारा की वर्तमान आयु y वर्ष दी हुई है। उसकी भविष्य की आयु और पिछली आयु के बारे में सोचिए। निम्नलिखित व्यंजक क्या सूचित करते हैं?
y + 7, y – 3, y + \(4\frac { 1 }{ 2 }\), y – \(2\frac { 1 }{ 2 }\)
(c) दिया हुआ है कि एक कक्षा के n विद्यार्थी फुटबॉल खेलना पसन्द करते हैं। 2n क्या दर्शाएगा? \(\frac { n }{ 2 }\) क्या दर्शा सकता है ? (संकेत : फुटबॉल के अतिरिक्त अन्य खेलों के बारे में सोचिए।)
उत्तर-
(a) (i) x – 2 सम्भवतः उसके छोटे भाई या बहन की आयु दर्शाएगा?
(ii) (x + 4) उसके बड़े भाई की आयु दर्शाएगा।
(iii) (3x + 7) उसकी माँ की आयु दर्शाएगा।
मुन्नू की माँ की आयु उसकी आयु के तीन गुने से 7 वर्ष अधिक है।

(b) (i) व्यंजक (y + 7)7 वर्ष बाद सारा की आयु दर्शाता है। व्यंजक (y – 3), 3 वर्ष पूर्व सारा की आयु दर्शाता है।
(ii) व्यंजक (y + \(4\frac { 1 }{ 2 }\)), \(4\frac { 1 }{ 2 }\) वर्ष पश्चात् सारा की उम्र दर्शाता है।
(iii) व्यंजक (y – \(2\frac { 1 }{ 2 }\)), \(2\frac { 1 }{ 2 }\) वर्ष पूर्व सारा की आयु दर्शाता है।

(c) चूँकि n विद्यार्थी फुटबॉल खेलना पसन्द करते हैं।
(i) ∴ 2n (फुटबॉल खिलाड़ियों के दो गुने) हॉकी खेलने वाले विद्यार्थियों की संख्या दर्शाएगा।
(ii) व्यंजक \(\frac { n }{ 2 }\) (फुटबॉल खिलाड़ियों के आधे) टेनिस खेलने वाले विद्यार्थियों की संख्या दर्शाएगा।

पाठ्य-पुस्तक पृष्ठ संख्या # 258

प्रश्न 1.
समीकरण के कुछ उदाहरण नीचे दिए जा रहे हैं। (कुछ समीकरणों में सम्बद्ध चर भी दिए गए हैं।)
वांछित रिक्त स्थानों को भरिए :
हल :

1. x + 10 = 30 (चर x)
2. p – 3 = 7 (चर p)
3. 3n = 21 (चर n)
4. \(\frac { t }{ 5 }\) = 4 (चर t)
5. 2l + 3 = 7 (चर l)
6. 2m – 3 = 5 (चर m)

पाठ्य-पुस्तक पृष्ठ संख्या # 259

प्रश्न 1.
अब निम्नलिखित सारणी की प्रविष्टियों को पूरा कीजिए और स्पष्ट कीजिए कि आपके उत्तर हाँ/नहीं क्यों हैं ?
हल :

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 11 बीजगणित Ex 11.3

पाठ्य-पुस्तक पृष्ठ संख्या # 253-254

प्रश्न 1.
आप तीन संख्या 5, 7 और 8 से संख्याओं वाले (चर नहीं) जितने व्यंजक बना सकते हैं बनाइए। एक संख्या एक से अधिक बार प्रयोग नहीं की जानी चाहिए। केवल योग, व्यवकलन (घटाना) और गुणन का ही प्रयोग करें। (संकेत : तीन सम्भावित व्यंजक 5 + (8 – 7), 5 – (8 – 7) और 5 x 8 + 7 हैं। अन्य व्यंजक बनाइए।)
हल :
अन्य सम्भावित व्यंजक
(i) 5 + (7 + 8)
(ii) 7 x 5 + 8
(iii) (8 – 5) x 7
(iv) (7 – 5) x 8
(v) (5 x 7) – 8
(vi) (8 – 7) + 5
(vii) 8 – 5 + 7
(viii) (8 x 7) + 5

प्रश्न 2.
निम्नलिखित में से कौन-से व्यंजक केवल संख्याओं वाले व्यंजक ही हैं ?
(a) y + 3
(b) 7 × 20 – 8
(c) 5 (21 – 7) + 7 × 2
(d) 5
(e) 3x
(f) 5 – 5n
(g) 7 × 20 – 5 × 10 – 45 + P
उत्तर-
व्यंजक (c) और (d) में कोई चर नहीं है।
अतः व्यंजक (c) और (d) केवल संख्याओं वाले व्यंजक है।

प्रश्न 3.
निम्न व्यंजकों को बनाने में प्रयुक्त संक्रियाओं (योग, व्यवकलन, गुणन, विभाजन) को पहचानिए (छाँटिए) और बताइए कि ये व्यंजक किस प्रकार बनाए गए हैं ?
(a) z + 1, z – 1, y + 17, y – 17
(b) 17y, \(\frac { y }{ 17 }\), 5z
(c) 2y + 17, 2y – 17
(d) 7m, – 7m + 3, – 7m – 3.
हल:

प्रश्न 4.
निम्नलिखित स्थितियों के लिए व्यंजक दीजिए:
(a) p में 7 जोड़ना
(b) p में से 7 घटाना
(c) p को 7 से गुणा करना
(d) p को 7 से भाग देना
(e) – m में से 7 घटाना
(f) – p को 5 से गुणा करना
(g) – p को 5 से भाग देना
(h) p को – 5 से गुणा करना
उत्तर-
व्यंजक
(a) p + 7
(b) p – 7
(c) 7p
(d) \(\frac { p }{ 7 }\)
(e) – m – 7
(f) 5 (-p) = – 5p
(g) \(\frac { -p }{ 5 }\)
(h) – 5p

प्रश्न 5.
निम्नलिखित स्थितियों के लिए व्यंजक दीजिए:
(a) 2m में 11 जोड़ना
(b) 2m में से 11 घटाना
(c) y के 5 गुने में 3 जोड़ना
(d) y के 5 गुने में से 3 घटाना
(e) y का – 8 से गुणा
(f) y को – 8 से गुणा करके परिणाम में 5 जोड़ना
(g) y को 5 से गुणा करके परिणाम को 16 में से घटाना
(h) y को -5 से गुणा करके परिणाम को 16 में जोड़ना
उत्तर-
व्यंजक
(a) 2m + 11
(b) 2m – 11
(c) (5 × y) + 3 = 5y + 3
(d) (5 × y) – 3 = 5y – 3.
(e) y × (-8) = – 8y
(f) y × (-8) + 5 = – 8y + 5
(g) 16 – (5 × y) = 16 – 5y
(h) 16 + [y × (-5)] = 16 +(-5y) = – 5y + 16

प्रश्न 6.
(a) t और 4 का प्रयोग करके व्यंजक बनाइए। एक से अधिक संख्या संक्रिया का प्रयोग न करें। प्रत्येक व्यंजक में t अवश्य होना चाहिए।
(b) y, 2 और 7 का प्रयोग करके व्यंजक बनाइए। प्रत्येक व्यंजक में y अवश्य होना चाहिए। केवल दो संख्या संक्रियाओं का प्रयोग करें। ये भिन्न-भिन्न होनी चाहिए।
हल :
(a) t और 4 से बनने वाले व्यंजक t + 4, t – 4, 4t, \(\frac { t }{ 4 }\), 4 – t, \(\frac { 4 }{ t }\)

(b) 1, 2 और 7 से बनने वाले व्यंजक
2y + 7, 2y – 7, 7y + 2, 7y – 2, \(\frac { y }{ 2 }\) + 7, \(\frac { y }{ 7 }\) – 2, ………

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 11 बीजगणित Ex 11.2

पाठ्य-पुस्तक पृष्ठ संख्या # 250-251

प्रश्न 1.
एक समबाहु त्रिभुज की भुजा को l से दर्शाया गया है। इस समबाहु त्रिभुज के परिमाप को l का प्रयोग करते हुए व्यक्त कीजिए।
हल :
∵समबाहु त्रिभुज की भुजा = l
∴इसका परिमाप = l + l + l = 3l

प्रश्न 2.
एक समषड्भुज (Regular hexagon) की एक भुजा को l से व्यक्त किया गया है (पाठ्य-पुस्तक में दी गई आकृति।) l का प्रयोग करते हुए इस षड्भुज के परिमाप को व्यक्त कीजिए। (संकेत : एक समषड्भुज की सभी 6 भुजाएँ बराबर होती हैं और सभी कोण बराबर होते हैं।)
हल :
∵ समषड्भुज की सभी भुजाएँ बराबर हैं।
और समषड्भुज की प्रत्येक भुजा = l
∴ इसका परिमाप = l + l + l + l + l + l
= 61

प्रश्न 3.
घन (cube) एक त्रिविमीय (three dimensional) आकृति होती है जैसा कि पाठ्य-पुस्तक में दी गई आकृति में दिखाया गया है। इसके 6 फलक होते हैं और ये सभी सर्वसम (identical) वर्ग होते हैं। घन के एक किनारे की लम्बाई l से दी जाती है। घन के किनारों की कुल लम्बाई के लिए एक सूत्र ज्ञात कीजिए।
हल :
घन के 6 सर्वसम फलक हैं। घन के 12 किनारे हैं।
प्रत्येक किनारे की लम्बाई l समान है।
∴ घन के किनारों की कुल लम्बाई = 12 x l
= 12l

प्रश्न 4.
वृत्त का एक व्यास वह रेखाखण्ड है जो वृत्त पर स्थित दो बिन्दुओं को जोड़ता है और उसके केन्द्र से होकर जाता है। पाठ्य-पुस्तक में दी गई आकृति में AB वृत्त का व्यास है और C उसका केन्द्र है। वृत्त के व्यास (d) को उसकी त्रिज्या (r) के पदों में व्यक्त कीजिए।
हल :
वृत्त की त्रिज्या = r तथा व्यास = d
चूँकि वृत्त का व्यास त्रिज्या का दो गुना होता है।
∴व्यास = 2 x त्रिज्या
या d = 2 x r या d = 2r

प्रश्न 5.
तीन संख्याओं 14, 27 और 13 के योग पर विचार कीजिए। हम यह योग दो प्रकार से ज्ञात कर सकते हैं:
(a) हम पहले 14 और 27 को जोड़कर 41 प्राप्त कर सकते हैं और फिर 41 में 13 जोड़कर 54 प्राप्त कर सकते हैं। या
(b) हम पहले 27 और 13 को जोड़कर 40 प्राप्त कर सकते हैं और फिर उसे 14 में जोड़कर कुल योग 54 प्राप्त कर सकते हैं। इस प्रकार, (14 + 27) + 13 = 14 + (27 + 13) हुआ।
ऐसा किन्हीं भी तीन संख्याओं के लिए किया जा सकता है। यह गुण संख्याओं के योग का साहचर्य (associative) गुण कहलाता है। इस गुण को जिसे हम पूर्ण संख्याओं के अध्याय में पढ़ चुके हैं, चर a, b और c का प्रयोग करते हुए, एक व्यापक रूप में व्यक्त कीजिए।
हल :
माना कि तीन संख्याएँ a, b और c हैं।
∴योग के साहचर्य नियम के अनुसार, हम a, b और c को । निरूपित कर सकते हैं
(a + b) + c = a + (b + c)

MP Board Class 6th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 14 गुणनखंडन Ex 14.1

प्रश्न 1.
दिए हुए पदों में सार्वगुणनखण्ड ज्ञात कीजिए –

1. 12x, 36
2. 2y, 22xy
3. 14pq, 28p²q²
4. 2x, 3x², 4
5. 6abc, 24ab², 12ab
6. 16x³, – 4x², 32x
7. 10pq, 20qr, 30rp
8. 3x²y³, 10x³y², 6x²y²z.

हल:
1. 12x = 12 × x
36 = 12 x 3
∴ सार्व गुणनखण्ड = 12

2. 2y = 2 x y
22xy = 2 x 11 × x × y
∴ सार्व गुणनखण्ड = 2 x y = 2y

3. 14pq = 2 x 7 x p x q
28 p²q² = 2 x 2 x 7 x p x p x q x q
∴ सार्व गुणनखण्ड = 2 x 7 x p x q = 14pq

4. 2x = 2 × x × 1
3x² = 3 × x × x × 1
4 = 2 x 2 x 1
∴ सार्व गुणनखण्ड = 1

5. 6abc = 2 x 3 x 4 x 6 x c
24ab² =2 x 2 x 2 x 3 x a x b x b
12a²b = 2 x 2 x 3 x a x a x b
∴ सार्व गुणनखण्ड = 2 x 3 x a x b = 6ab

6. 16x³ = 2 × 2 × 2 × 2 × x × x × x
4x² = (-1) × 2 × 2 × x × x
32x = 2 × 2 × 2 × 2 × 2 × x
∴ सार्व गुणनखण्ड = 2 × 2 × x = 4x

7. 10pq = 2 x 5 x p x q
20qr = 2 x 2 x 5 x q x r
30pr = 2 x 3 x 5 x p x r
∴ सार्व गुणनखण्ड = 2 x 5 = 10

8. 3x²y³ = 3 × x × x × y × y × y
10x³y² = 2 × 5 × x × x × x × y × y
6x²y²z = 2 × 3 × x × x × y × y × z
∴ सार्व गुणनखण्ड = x × x × y × y = xy²

प्रश्न 2.
निम्नलिखित व्यंजकों के गुणनखण्ड कीजिए –

1. 7x – 42
2. 6p – 12q
3. 7a² + 14a
4. -16z + 20z³
5. 20l²m + 30alm
6. 5x²y – 15xy²
7. 10a² – 15b² + 20c²
8. -4a + 4ab – 4ac
9. x²y + z + xy²z + xyz² (तीनों पदों को मिलाने पर)
10. ax²y + bxy² + cxyz

हल:
1. 7x – 42 = 7 × x – 2 × 3 × 7
= 7(x – 2 x 3)
= 7 (x – 6)

2. 6p – 12q = 2 x 3 x p – 2 x 2 x 3 x q
= 2 x 3 (p – 2 x q)
= 6 (p – 24)

3. 7a² + 14a = 7 x a x a + 2 x 7 x a
= 7 x a x (a + 2)
= 7a (a + 2)

4. – 16z + 20z³
= -2 x 2 x 2 x 2 x z + 2 x 2 x 5 x z x z x z
= 2 x 2 x z x (- 2 x 2 + 5 x z x z)
= 4z (- 4 + 57²)

5. 20l²m + 30alm
= 2 x 2 x 5 x 1 x 1 x m + 2 x 3 x 5 x a x l x m
= 2 x 5 x 1 x m (2 x 1 + 3 x a)
= 10lm (21+ 3a)

6. 5x²y – 15xy²
= 5 × x × x × y – 3 × 5 × x × y × y
= 5 × x × y × (x – 3 × y)
= 5xy (x – 3y)

7. 10a² – 15b² + 20c²
= 2 x 5 x a x a – 3 x 5 x b x b + 2 x 2 x 5 x c x c
= 5 (2 x a x a – 3 x b x b + 2 x 2 x c x c)²
=5 (2a² – 3b² – 4c)

8. -4a² + 4ab – 4ac
= – 2 x 2 x a x a + 2 x 2 x a x b – 2 x 2 x a x c
= 2 x 2 x a x (- a + b – c)
= 4a (- a + b – c)

9. xyz + xyz + xyz²
= x × x × y × z + x × y × y × z + x × y × z × z
= x × y × z (x + y + z)
=xyz (x + y + z)

10. ax²y + bxy² + cxyz
= a × x × x × y + b × x × y × y + c × x × y × z
= x × y × (a × x + b × y + c × z)
= xy (ax + by + cz)

प्रश्न 3.
गुणनखण्ड कीजिए –

1. x + xy + 8x + 8y
2. 15xy – 6x + 5y – 2
3. ax + bx – ay – by
4. 15pq + 15 + 9q + 25p
5. z – 7 + 7xy – xyz

हल:
1. x² + xy + 8x + 8y = (x² + xy) + (8x + 8y)
= x (x + y) + 8 (x + y)
= (x + y) (x + 8)

2. 15xy – 6x + 5y – 2 = (15xy – 6x) + (5y – 2)
= 3x (5y – 2) + 1 (5y – 2)
= (5y – 2) (3x + 1)

3. ax + bx – ay – by = (ax + bx) – (ay + by)
= x (a + b) – y (a + b)
= (a + b) (x – y)

4. 15pq + 15 + 9q + 25p = (15pq + 9q) + (25p + 15)
(पुनः समूहन करने पर)
= 3q (5p + 3) + 5 (5p + 3)
= (5p + 3) (3q + 5)

5. z – 7 + 7xy – xyz = z – 7 – xyz + 7xy
(पुनः समूहन करने पर)
= 1 (z – 7) – xy (z – 7)
= (z – 7) (1 – xy)

MP Board Class 8th Maths Solutions