MP Board Class 6th Maths Solutions Chapter 11 बीजगणित Ex 11.5
पाठ्य-पुस्तक पृष्ठ संख्या # 260-262
प्रश्न 1.
बताइए कि निम्नलिखित में से कौन-से कथन समीकरण (चर संख्याओं के) हैं ? सकारण उत्तर दीजिए। समीकरण में सम्बद्ध चर भी लिखिए।
(a) 17 = x + 17
(b) (t – 7) > 5
(c) \(\frac { 4 }{ 2 }=2\)
(d) 7 × 3 – 13 = 8
(e) 5 × 4 – 8 = 2x
(f) x – 2 = 0
(g) 2m < 30
(h) 2n + 1 = 11
(i) 7 = 11 × 5 – 12 × 4
(j) 7 = 11 × 2 + p
(k) 20 = 5y
(l) \(\frac { 3q }{ 2 }\) < 5
(m) z + 12 > 24
(n) 20 – (10 – 5) = 3 × 5
(o) 7 – x = 5
उत्तर-
(a) चर x में समीकरण है।
(b) यह समीकरण नहीं है, क्योंकि इसमें = का चिह्न नहीं है।
(c) यह समीकरण नहीं है, क्योंकि इसमें चर नहीं है।
(d) यह समीकरण नहीं है, क्योंकि इसमें चर नहीं है।
(e) यह चर x में समीकरण है।
(f) यह चर x में समीकरण है।
(g) यह समीकरण नहीं है, क्योंकि इसमें = का चिह्न नहीं है।
(h) यह चर n में समीकरण है।
(i) यह समीकरण नहीं है, क्योंकि इसमें चर नहीं है।
(j) चह चर p में समीकरण है।
(k) चह चर y में समीकरण है।
(l) यह समीकरण नहीं है, क्योंकि इसमें = का चिह्न नहीं है।
(m) यह समीकरण नहीं है, क्योंकि इसमें = का चिह्न नहीं है।
(n) यह समीकरण नहीं है, क्योंकि इसमें चर नहीं है।
(o) यह चर x में समीकरण है।
प्रश्न 2.
सारणी के तीसरे स्तम्भ में प्रविष्टियों को पूरा कीजिए
हल :

![]()
प्रश्न 3.
प्रत्येक समीकरण के सम्मुख कोष्ठकों में दिए मानों में से समीकरण का हल चुनिए। दर्शाइए कि अन्य मान समीकरण को सन्तुष्ट नहीं करते हैं।
(a) 5m = 60 (10, 5, 12, 15)
(b) n + 12 = 20 (12, 8, 20, 0)
(c) p – 5 = 5 (0, 10, 5, -5)
(d) \(\frac { q }{ 2 }=7\) (7, 2, 10, 14)
(e) r – 4 = 0 (4, -4, 8, 0)
(f) x + 4 = 2 (-2, 0, 2, 4)
हल :
(a) m = 10 के लिए,
L.H.S. = 5 x 10 = 50
और R.H.S. = 60
∵L.H.S. ≠ R.H.S.
∴m = 10 समीकरण को सन्तुष्ट नहीं करता है।
m = 5 के लिए, L.H.S. = 5 x 5 = 25
और R.H.S. = 60
∵L.H.S. ≠ R.H.S.
∴m = 5 समीकरण को सन्तुष्ट नहीं करता है।
m = 12 के लिए,
L.H.S. = 5 x 12 = 60
और R.H.S. = 60
∵L.H.S. = R.H.S.
∴m = 12 समीकरण का हल है।
m = 15 के लिए,
L.H.S. = 5 x 15 = 75
और R.H.S. = 60
∵L.H.S. ≠ R.H.S.
∴m = 15 समीकरण को सन्तुष्ट नहीं करता है।
(b) n = 12 के लिए,
L.H.S. = 12 + 12 = 24
और R.H.S. = 20
∵L.H.S. ≠ R.H.S.
∴n = 12 समीकरण को सन्तुष्ट नहीं करता है।
n = 8 के लिए, L.H.S. = 8 + 12 = 20
और R.H.S. = 20
∵L.H.S. = R.H.S.
∴n = 8 समीकरण का हल है।
n = 20 के लिए,
L.H.S. = 20 + 12 = 32
और R.H.S. =20
∵L.H.S. ≠ R.H.S.
∴n = 20, समीकरण को सन्तुष्ट नहीं करता है।
n = 0 के लिए,
L.H.S. = 0 + 12 = 12
और R.H.S.= 20
∵L.H.S. ≠ R.H.S.
∴n = 0 समीकरण को सन्तुष्ट नहीं करता है।
(c) p = 0 के लिए,
L.H.S. = 0 – 5 = -5
और R.H.S. = 5
∵L.H.S. ≠ R.H.S.
∴p = 0 समीकरण को सन्तुष्ट नहीं करता है।
p = 10 के लिए,
L.H.S. = 10 – 5 = 5
और R.H.S. = 5
∵L.H.S. = R.H.S.
∴p = 10 समीकरण का हल है।
p = 5 के लिए, L.H.S. = 5 – 5 = 0
और R.H.S. = 5
∵L.H.S. ≠ R.H.S.
∴p = 5, समीकरण को सन्तुष्ट नहीं करता है।
p = -5 के लिए,
L.H.S. = – 5 – 5 = -10
और R.H.S. = 5
∵L.H.S. ≠ R.H.S.
∴p = – 5 समीकरण को सन्तुष्ट नहीं करता है।
![]()
(d) q = 7 के लिए,
L.H.S. = \(\frac { 7 }{ 2 }\)
और R.H.S. = 7
∵L.H.S. ≠ R.H.S.
∴q = 7 समीकरण को सन्तुष्ट नहीं करता है।
q = 2 के लिए,
L.H.S. = \(\frac { 2 }{ 2 }\) = 1
और R.H.S. = 7
∵L.H.S. ≠ R.H.S.
∴q = 2 समीकरण को सन्तुष्ट नहीं करता है।
q = 10 के लिए,
L.H.S. = \(\frac { 10 }{ 2 }\) = 5
और R.H.S. = 7
∵L.H.S. ≠ R.H.S.
∴q = 10 समीकरण को सन्तुष्ट नहीं करता है।
q = 14 के लिए,
L.H.S. = \(\frac { 14 }{ 2 }\) = 7
और R.H.S. = 7
∵L.H.S. = R.H.S.
∴q = 14 समीकरण का हल है।
(e) r = 4 के लिए,
L.H.S. = 4 – 4 = 0
और R.H.S. = 0
∵L.H.S. = R.H.S.
∴r = 4 समीकरण का हल है।
r = -4 के लिए,
L.H.S. = -4 – 4 = -8
और R.H.S. = 0
∵L.H.S. ≠ R.H.S.
∴r = -4 समीकरण को सन्तुष्ट नहीं करता है।
r = 8 के लिए,
L.H.S. = 8 – 4 = 4
और R.H.S. = 0
∵L.H.S. ≠ R.H.S.
∴r = 8 समीकरण को सन्तुष्ट नहीं करता है।
r = 0 के लिए,
L.H.S. = 0 – 4 = – 4
और R.H.S. = 0
∵L.H.S. ≠ R.H.S.
∴r = 0 समीकरण को सन्तुष्ट नहीं करता है।
(f) x = – 2 के लिए,
L.H.S. = – 2 + 4 = 2
और R.H.S. = 2
∵L.H.S. = R.H.S.
∴x = – 2 समीकरण का हल है।
x = 0 के लिए,
L.H.S. = 0 + 4 = 4
और R.H.S. =2
∵L.H.S. ≠ R.H.S.
∴x = 0 समीकरण को सन्तुष्ट नहीं करता है।
x = 2 के लिए,
L.H.S. = 2 + 4 = 6
और R.H.S. = 2
∵L.H.S. ≠ R.H.S.
∴x = 2 समीकरण को सन्तुष्ट नहीं करता है।
x = 4 के लिए,
L.H.S. = 4 + 4 = 8
और R.H.S. = 2
∵L.H.S. ≠ R.H.S.
∴x = 4 समीकरण को सन्तुष्ट नहीं करता है।
प्रश्न 4.
(a) नीचे दी हुई सारणी को पूरा कीजिए और इस सारणी को देखकर ही समीकरण m + 10 = 16 का हल ज्ञात कीजिए।

(b) नीचे दी सारणी को पूरा कीजिए और इस सारणी को देखकर ही समीकरण 5t = 35 का हल ज्ञात कीजिए।

(c) सारणी को पूरा कीजिए और समीकरण \(\frac { z }{ 3 }\) = 4 का हल ज्ञात कीजिए

(d) सारणी को पूरा कीजिए और समीकरण m – 7 = 3 का हल ज्ञात कीजिए

हल :
(a) सारणी को पूरा करने पर

सारणी से स्पष्ट है कि m = 6 समीकरण m + 10 = 16 को सन्तुष्ट करता है। अतः m = 6 समीकरण का हल है।
![]()
(b) सारणी को पूरा करने पर,
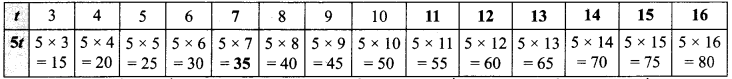
सारणी से स्पष्ट है कि t = 7 समीकरण 5t = 35 को सन्तुष्ट करता है। अत: t = 7 समीकरण का हल है।
(c) सारणी को पूरा करने पर,

सारणी से स्पष्ट है कि z = 12 समीकरण \(\frac { z }{ 3 }\) = 4 को सन्तुष्ट करता है।
अतः z = 12 समीकरण का हल है।
(d) सारणी को पूरा करने पर,
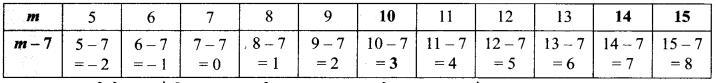
सारणी से स्पष्ट है कि m = 10 समीकरण m – 7 = 3 को सन्तुष्ट करता है।
अतः m = 10 समीकरण का हल है।
प्रश्न 5.
निम्नलिखित पहेलियों को हल कीजिए। आप ऐसी पहेलियाँ स्वयं भी बना सकते हैं। मैं कौन हूँ?
(i) एक वर्ग के अनुदिश जाइए।
प्रत्येक कोने को तीन बार
गिनकर और उससे अधिक नहीं,
मुझमें जोड़िए और
ठीक चौंतीस प्राप्त कीजिए।
(ii) सप्ताह के प्रत्येक दिन के लिए,
मेरे से ऊपर गिनिए।
यदि आपने कोई गलती नहीं की है,
तो आप तेईस प्राप्त करेंगे।
(iii) मैं एक विशिष्ट संख्या हूँ।
मुझमें से एक छः निकालिए।
और क्रिकेट की एक टीम बनाइए।
(iv) बताइए, मैं कौन हूँ।
मैं एक सुन्दर संकेत दे रही हूँ
आप मुझे वापस पाएँगे।
यदि मुझे बाईस में से निकालेंगे।
हल :
(i) माना कि मैं ‘x’ हूँ।
वर्ग के चार कोने हैं। तीन बार प्रत्येक कोने को गिनने पर हम प्राप्त करते हैं,
3 × 4 = 12
अब प्रश्नानुसार, x + 12 = 34
या x + 12 – 12 = 34 – 12
या x + 0 = 22
⇒ x = 22
अतः मैं 22 हूँ।
(ii) माना कि मैं x हूँ।
प्रश्नानुसार, x + 7 = 23
या x + 7 – 7 = 23 – 7
x + 0 = 16
⇒ x = 16
![]()
(iii) माना कि विशिष्ट संख्या x है।
प्रश्नानुसार, x – 6 = 11
या x – 6 + 6 = 11 + 6
या x + 0 = 17
⇒ x = 17
अतः विशिष्ट संख्या 17 है
(iv) माना कि मैं x हूँ।
प्रश्नानुसार, 22 – x = x
या 22 – x + x = x + x
या 22 + 0 = 2x
या 2x = 22
⇒ \(x=\frac { 22 }{ 2 }\) = 11
अतः मैं 11 हूँ।