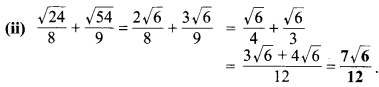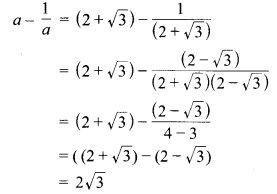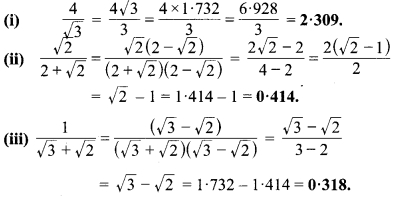Category: Class 9

MP Board Class 9th Social Science Solutions Chapter 3 भारत : स्थिति एवं भौतिक विभाग

MP Board Class 9th Social Science Chapter 3 पाठान्त अभ्यास

MP Board Class 9th Social Science Chapter 3 वस्तुनिष्ठ प्रश्न

सही विकल्प चुनकर लिखिए

प्रश्न 1.
भारत का मानक समय निर्धारित होता है
(i) 72° पूर्व देशान्तर से
(ii) 80° 30′ पूर्व देशान्तर से
(iii) 82° 30′ पूर्व देशान्तर से
(iv) 85′ पूर्व देशान्तर से।
उत्तर:
(iii) 82° 30′ पूर्व देशान्तर से

प्रश्न 2.
भारत में कर्क रेखा किस राज्य से होकर नहीं गुजरती है? (2018)
(i) गुजरात
(ii) महाराष्ट्र
(iii) छत्तीसगढ़
(iv) मध्य प्रदेश।
उत्तर:
(ii) महाराष्ट्र

प्रश्न 3.
देश का सबसे बड़ा केन्द्र शासित क्षेत्र है
(i) अण्डमान निकोबार द्वीप समूह
(ii) दादरा और नागर हवेली
(iii) लक्षद्वीप,
(iv) पाण्डिचेरी।
उत्तर:
(i) अण्डमान निकोबार द्वीप समूह

प्रश्न 4.
भारतीय प्रायद्वीप पठार किस प्रकार की चट्टानों से बना है?
(i) परिवर्तित चट्टानों से,
(ii) अवसादी शैलों से
(iii) अत्यन्त प्राचीन चट्टानों से
(iv) उपर्युक्त में से कोई नहीं।
उत्तर:
(iii) अत्यन्त प्राचीन चट्टानों से

सत्य/असत्य

प्रश्न 1.
भारत के दक्षिण में हिंद महासागर है।
उत्तर:
सत्य

प्रश्न 2.
उत्तर पश्चिम राज्यों को सात बहनें कहा जाता है। (2018)
उत्तर:
असत्य

प्रश्न 3.
अंडमान निकोबार द्वीप समूह अरब सागर में स्थित है।
उत्तर:
असत्य।

MP Board Class 9th Social Science Chapter 3 अति लघु उत्तरीय प्रश्न

प्रश्न 1.
भारत को किन-किन नामों से जाना जाता है? (2014, 18)
उत्तर:
भारत को आर्यावर्त, हिन्दुस्तान और इण्डिया नाम से जाना जाता है।

प्रश्न 2.
भारत का क्षेत्रफल लिखिए।
उत्तर:
भारत का कुल क्षेत्रफल 32,87,263 वर्ग किमी है।

प्रश्न 3.
भारत में कितने राज्य और केन्द्र शासित प्रदेश हैं? (2010, 14, 16, 18)
उत्तर:
भारत में 29 राज्य तथा 7 केन्द्र शासित प्रदेश हैं।

प्रश्न 4.
भारत के दो द्वीपीय पड़ोसी देशों के नाम लिखिए।
उत्तर:
मालद्वीप और इण्डोनेशिया।

प्रश्न 5.
पूर्वी तट पर स्थित किन्हीं दो झीलों के नाम लिखिए। (2017)
उत्तर:
इस तट पर चिल्का, कोलेरू एवं पुलीकट झीलें हैं।

प्रश्न 6.
भारत के किन द्वीपों का निर्माण प्रवालों द्वारा हुआ है? (2016)
उत्तर:
प्रवाल (मुंगे) के निक्षेपों से बने इन द्वीपों को एटॉल कहा जाता है।

प्रश्न 7.
हिमालय पर्वतमाला के दो प्रमुख शिखरों के नाम लिखिए। (2013, 15)
उत्तर:
हिमालय पर्वतमाला के दो सर्वोच्च शिखर माउण्ट एवरेस्ट एवं कंचनजंघा हैं।

प्रश्न 8.
पश्चिम से पूर्व तक भारत का विस्तार कितना है?
उत्तर:
पूर्वी-पश्चिमी विस्तार 2,933 किलोमीटर है।

MP Board Class 9th Social Science Chapter 3 लघु उत्तरीय प्रश्न

प्रश्न 1.
भारत की भौगोलिक स्थिति का महत्त्व समझाइए। (2009)
उत्तर:
भारत विषुवतरेखा के उत्तर में 8°4′ उत्तरी अक्षांश से 37°6′ उत्तरी अक्षांश तक तथा 68°7′ पूर्वी देशान्तर से 97°25′ पूर्वी देशान्तर के मध्य स्थित है। इस प्रकार सम्पूर्ण भारतवर्ष उत्तरी गोलार्द्ध या पूर्वी गोलार्द्ध में स्थित है। इस आधार पर कहा जा सकता है कि पूर्वी गोलार्द्ध में भारत की स्थिति लगभग केन्द्रीय है। इसके निम्न महत्त्व हैं :

1. केन्द्रीय स्थिति के कारण भारत अन्तर्राष्ट्रीय जलमार्गों का केन्द्र है।
2. हिन्द महासागर के शीर्ष पर स्थित होने के कारण अफ्रीका और ऑस्ट्रेलिया महाद्वीपों से जुड़ा है।
3. भारत के तीन ओर समुद्री तटरेखा होने के कारण प्राकृतिक बन्दरगाहों की सुविधा है।
4. केन्द्रीय स्थिति के कारण भारत पूर्व से पश्चिम के अन्तर्राष्ट्रीय वायुमार्गों का संगम स्थल है। इस प्रकार अन्तर्राष्ट्रीय व्यापार की दृष्टि से भारत की भौगोलिक स्थिति अच्छी है।

प्रश्न 2.
भारत के उत्तर के विशाल मैदान का वर्णन कीजिए।
उत्तर:
उत्तर का विशाल मैदान :
भारत का उत्तरी मैदान हिमालय तथा प्रायद्वीपीय पठार से निकलने वाली नदियों द्वारा बहाकर लायी हुई मिट्टी से बना है। इसके निर्माण में सिन्धु नदी तन्त्र तथा गंगा-ब्रह्मपुत्र नदी तन्त्र का सर्वाधिक योगदान है। इसे गंगा और ब्रह्मपुत्र का मैदान भी कहते हैं। यह मैदान पूर्व से पश्चिम तक 3200 किमी लम्बा तथा पश्चिम में 500 किमी चौड़ा और पूर्व में 150 किमी चौड़ा है। यह लगभग एक सपाट मैदान है और इसके उच्चावच में बहुत कम अन्तर है। यहाँ की उपजाऊ मृदा, उपयुक्त जलवायु तथा पर्याप्त जल आपूर्ति कृषि कार्य के विकास में बहुत सहायक है। यह सघन जनसंख्या वाला क्षेत्र है। इसे तीन भाग में बाँट सकते हैं –

• पश्चिमी मैदान :
  इसका विस्तार पंजाब, हरियाणा और राजस्थान में है। इसका ढाल उत्तर-पूर्व से दक्षिण-पश्चिम की ओर है। इसका पश्चिमी भाग मरुस्थल है इसे थार मरुभूमि कहते हैं। लूनी यहाँ की प्रमुख नदी है। यमुना के पश्चिम में सतलज, व्यास और रावी नदियाँ बहती हैं।
• मध्यवर्ती मैदान :
  इसे गंगा का मैदान कहते हैं। इसका ढाल पश्चिम से पूर्व की ओर है। जिस क्षेत्र में बाढ़ का पानी प्रतिवर्ष पहुँचता है, उसे खादर और जहाँ नहीं पहुँचता है उसे बांगर कहते हैं। हिमालय से लगे भाग को तराई कहते हैं। यहाँ की मृदा जलोढ़ है।
• पर्वी मैदान :
  यह मैदान 650 किमी लम्बा एवं लगभग 100 किमी चौड़ा है। इसे ब्रह्मपुत्र का मैदान भी कहते हैं। इसका ढाल उत्तर-पूर्व से दक्षिण-पश्चिम की ओर है।

प्रश्न 3.
दक्कन के पठार का संक्षिप्त वर्णन कीजिए। (2009)
उत्तर:
दक्कन का पठार विशाल पठार का बहुत बड़ा भाग है। इसकी आकृति त्रिभुजाकार है। दक्कन पठार का निर्माण आग्नेय शैलों से हुआ है। इस पठार के उत्तरी भाग का ढाल उत्तर की ओर है। इस क्षेत्र की प्रमुख नदियों में चम्बल, सिन्धु, बेतवा, केन, सोन व दामोदर हैं, जो गंगा एवं गंगा की सहायक नदियों से मिल जाती हैं। पश्चिम की ओर बहने वाली नर्मदा व ताप्ती नदियाँ दरार घाटियों से होकर बहती हुई अरब सागर में जा मिलती हैं। दक्कन के पठार का ढाल पूर्व की ओर है। कावेरी-पेनार, कृष्णा, गोदावरी और महानदी इसके जल-निकास का काम करती हैं। ये सभी नदियाँ बंगाल की खाड़ी में मिलती हैं। पठार के उत्तर-पश्चिमी भाग में काली मृदा का विकास हुआ है। यह मृदा बहुत ही उपजाऊ तथा कपास की खेती के लिए उपयोगी है। भारत के पठारी भाग में खनिज सम्पदा के विशाल भण्डार हैं। इनमें कोयला, लोहा, अभ्रक, बॉक्साइट, ताँबा, मैंगनीज आदि प्रमुख हैं। इन खनिजों पर देश का आर्थिक व औद्योगिक विकास निर्भर करता है। दक्कन पठार की नदियाँ जल शक्ति के विकास में सहायक हुई हैं।

प्रश्न 4.
भारतवासियों के लिए हिमालय का क्या महत्त्व है? लिखिए। (2008, 09, 12, 13)
अथवा
“हिमालय भारत के लिए वरदान है।” सत्यापन कीजिए।
उत्तर:
हिमालय का महत्त्व –

1. हिमालय की स्थिति के कारण ही सम्पूर्ण भारत की जलवायु उष्ण कटिबन्धीय है।
2. हिमालय पर्वत श्रेणी के कारण भारत में स्पष्ट रूप से ऋतु-चक्र चलता है।
3. हिमालय पर्वत शीत ऋतु में उत्तर-पूर्व एशिया से आने वाली ठण्डी और शुष्क पवनों को रोककर भारत को अधिक ठण्डा और शुष्क होने से बचाता है।
4. ग्रीष्म ऋतु में दक्षिण-पश्चिम मानसून पवनों को रोककर भारतीय उपमहाद्वीप में वर्षा करने में सहायक होता है।
5. हिमालय पर्वतीय क्षेत्रों में चूने का पत्थर, बलुआ पत्थर, संगमरमर, जड़ी-बूटी एवं खनिज तेल के भण्डार पाये जाते हैं।

प्रश्न 5.
बांगर व खादर भूमि में अन्तर समझाइए। (2008, 09, 12)
उत्तर:
बांगर व खादर भूमि में अन्तर

प्रश्न 6.
पूर्वी तटीय मैदान का संक्षिप्त वर्णन कीजिए। (2009)
उत्तर:
पूर्वी तटीय मैदान-पूर्वी तटीय मैदान का विस्तार बंगाल की खाड़ी में गिरने वाली महानदी, गोदावरी, कृष्णा और कावेरी नदी के डेल्टा प्रदेश में है। यहाँ उपजाऊ काँप मिट्टी मिलती है। इस तट पर चिल्का, कोलेरु एवं पुलीकट झीलें हैं। उत्तरी भाग के तट को उत्तरी सरकार और दक्षिणी भाग को कोरोमण्डल तट कहते हैं।

MP Board Class 9th Social Science Chapter 3 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
भारत को कितने भौतिक विभागों में विभाजित किया जा सकता है? किसी एक का वर्णन कीजिए।
उत्तर:
भारत के भौतिक विभाग
भारत विभिन्न स्थलाकृतियों वाला एक विशाल राष्ट्र है। भारत में हर प्रकार की भू-आकृतियाँ पायी जाती हैं; जैसे-पर्वत, पठार, मैदान, नदी घाटी, मरुस्थल, द्वीप समूह। प्रकृति द्वारा प्रदत्त इन स्थलाकृतियों के आधार पर भारत को निम्न भौतिक विभागों में बाँटा गया है –

1. उत्तरीय पर्वतीय प्रदेश
2. उत्तर का विशाल मैदान
3. प्रायद्वीपीय पठार
4. तटीय प्रदेश
5. द्वीप समूह।

प्रायद्वीपीय पठार :
यह पठार प्राचीन गोंडवाना लैण्ड का अंग है जो कभी भी सागर तल में नहीं डूबा। उत्तरी मैदान के दक्षिण में एक त्रिभुजाकार रूप में तीन ओर समुद्र से घिरा हुआ दक्षिण का पठार फैला हुआ है। इस पठार का आधार उत्तर एवं शीर्ष दक्षिण में है। क्षेत्रफल की दृष्टि से प्रायद्वीपीय पठारी क्षेत्र देश का सबसे बड़ा भौतिक प्रदेश है। प्रायद्वीपीय पठार को दो उपभागों अर्थात् मध्यवर्ती उच्च भूमि तथा दक्कन के पठार में विभाजित किया जा सकता है।

प्रश्न 2.
भारत की स्थिति व विस्तार का वर्णन कीजिए।
अथवा
भारत के उत्तर में कौन-कौन से देश स्थित हैं? नाम बताइए। (2010) [संकेतः ‘विस्तार’ शीर्षक में देखें।
उत्तर:
भारत की स्थिति-भारत विषुवत्रेखा के उत्तर में 8°4′ उत्तरी अक्षांश से 37°6′ उत्तरी अक्षांश तक तथा 68°7′ पूर्वी देशान्तर से 97°25′ पूर्वी देशान्तर के मध्य स्थित है। इस प्रकार सम्पूर्ण भारतवर्ष उत्तरी गोलार्द्ध या पूर्वी गोलार्द्ध में स्थित है। कर्क रेखा 23° (उत्तरी अक्षांश) इसके मध्य से होकर गुजरती है और भारतवर्ष को दो भागों –

1. महाद्वीपीय भारत या उत्तरी भारत
2. उष्ण कटिबन्धीय भारत या दक्षिणी भारत में बाँटती है। इसी प्रकार 82° पूर्वी देशान्तर देश के मध्य से होकर गुजरती है।

विस्तार :
भारत का उत्तर-दक्षिण विस्तार 3214 किमी तथा पूर्व पश्चिम विस्तार 2933 किमी है। इसकी स्थलीय सीमा 15,200 किमी एवं कुल समुद्री सीमा 7,516.6 किमी है। इसका क्षेत्रफल 32,87,263 वर्ग किमी है। यह विश्व का सातवाँ बड़ा देश है। भारत के उत्तर-पश्चिम में पाकिस्तान, अफगानिस्तान, उत्तर में चीन, नेपाल एवं भूटान, पूर्व में बांग्लादेश, म्यांमार व दक्षिण में श्रीलंका है।

प्रश्न 3.
हिमालय पर्वतीय क्षेत्र का वर्णन कीजिए।
अथवा
आन्तरिक हिमालय पर टिप्पणी लिखिए। (2008) [संकेत-महान या आन्तरिक हिमालय शीर्षक देखें।]
उत्तर:
हिमालय की पर्वत श्रेणियाँ भारत के उत्तर में अर्द्ध चाप के आकार में उत्तर-पश्चिम, उत्तर तथा उत्तर-पूर्व की सीमा बनाती हैं। इनकी लम्बाई 2,400 किमी है। चौड़ाई 150 से 400 किमी है। विस्तार तथा ऊँचाई के आधार पर हिमालय को तीन भागों में बाँट सकते हैं –

(1) महान या आन्तरिक हिमालय :
यह हिमालय की सबसे ऊँची और सबसे लम्बी श्रेणी है। इसे प्रधान हिमालय और हिमाद्रि भी कहते हैं। इसकी औसत ऊँचाई 6000 मीटर है। यह अत्यन्त दुर्गम क्षेत्र है, किन्तु इसमें जोजिला, कराकोरम, शिपकी, नाथूला आदि कई दरें हैं जिनसे होकर इनको पार किया जा सकता है। इस क्षेत्र में हिमालय के कई ऊँचे शिखर मिलते हैं। मुख्य पर्वत शिखर माउण्ट एवरेस्ट, कंचनजंघा, धौलागिरी, नंगा पर्वत और नंदा देवी हैं।

(2) मध्य हिमालय या हिमालय :
यह महान हिमालय के दक्षिण में उसके लगभग समान्तर फैला हुआ है। इसकी ऊँचाई 3,700 मीटर से 4,500 मीटर के बीच है तथा औसत चौड़ाई 50 किलोमीटर है। सभी प्रमुख पर्वतीय नगर जैसे डलहौजी, धर्मशाला (हिमाचल प्रदेश), नैनीताल (उत्तराखण्ड), दार्जिलिंग (पश्चिमी बंगाल) इसी पर्वत श्रेणी पर हैं। कश्मीर की पीरपंजाल तथा हिमाचल प्रदेश की धौलाधार श्रेणी, मध्य हिमालय के ही भाग हैं। नेपाल की महाभारत श्रेणी भी इसी का भाग है। यहाँ चूने का पत्थर एवं स्लेट की चट्टानें मिलती हैं।

(3) शिवालिक हिमालय :
हिमालय की दक्षिणतम श्रेणी को बाहरी हिमालय या शिवालिक हिमालय कहते हैं। इनकी औसत ऊँचाई 900 से 1100 मी तथा चौड़ाई 10 से 50 किमी है। हिमालय के पश्चिमी अर्द्ध भाग में यह श्रेणी बहुत अधिक स्पष्ट है। यह पर्वत श्रेणी जलोढ़ अवसादों से बनी है। इनकी शैलें ठोस नहीं हैं। लघु हिमालय और शिवालिक श्रेणी के बीच अनेक घाटियाँ हैं जिन्हें पूर्व में ‘द्वार’ और पश्चिम में ‘दून’ कहा जाता है।

प्रश्न 4.
प्रायद्वीपीय पठार का वर्णन कीजिए। (2009)
उत्तर:
प्रायद्वीपीय पठार प्रायद्वीपीय पठार विशाल मैदान के दक्षिण में स्थित है। यह भारत का सबसे प्राचीन भू-भाग है। यह बंगाल की खाड़ी, अरब सागर और हिन्द महासागर द्वारा तीन ओर समुद्र से घिरा हुआ है, अतः इसे प्रायद्वीप कहा जाता है।

इसकी औसत ऊँचाई 600 से 900 मीटर है। यह त्रिभुजाकार क्षेत्र के रूप में विस्तृत है। इसका विस्तार अरावली पर्वत से राजमहल की पहाड़ियों तक तथा शीर्ष कन्याकुमारी की ओर है। इसका ढाल पश्चिम से पूर्व की ओर है। यह भूखण्ड गोण्डवाना लैण्ड का अंग है। क्षेत्रफल की दृष्टि से प्रायद्वीपीय पठारी क्षेत्र देश का सबसे बड़ा भौतिक प्रदेश है। प्रायद्वीपीय पठार को दो उपभागों अर्थात् मध्यवर्ती उच्च भूमि तथा दक्कन के पठार में विभाजित किया जा सकता है।

(1) मध्यवर्ती उच्चभूमि :
प्रायद्वीपीय भू-भाग के उत्तरी भाग को मध्यवर्ती उच्च भूमियाँ कहते हैं। यह भाग कठोर, आग्नेय तथा कायान्तरित शैलों का बना हुआ है। उत्तरी पश्चिम भाग अरावली पहाड़ियों द्वारा घिरा हुआ है, जो प्राचीन वलित पर्वत के अवशिष्ट हैं। मध्यवर्ती उच्च भूमि की दक्षिणी सीमा विध्यांचल पर्वतों तथा उनके पूर्वी विस्तार कैमूर पहाड़ियों से निर्धारित होती है। अमरावती तथा विध्यांचल पर्वतों के मध्य में मालवा – का पठार स्थित है। यहाँ पर बेतवा, पार्वती, काली सिन्ध, चम्बल और माही नदियाँ बहती हैं। इसके पूर्वी भाग को दक्षिण, उत्तर प्रदेश में बुन्देलखण्ड तथा बघेलखण्ड के नाम से पुकारते हैं। दक्षिण बिहार में इसे छोटा नागपुर पठार के नाम से जाना जाता है। दक्षिण की ओर से आने वाली यमुना और गंगा की सहायक नदियाँ इसका जल बहाकर ले जाती हैं। इस पठार में खनिज के असीम भण्डार हैं।

(2) दक्कन का पठार :
दक्कन का पठार विशाल पठार का बहुत बड़ा भाग है। इसकी आकृति त्रिभुजाकार है। दक्कन पठार का निर्माण आग्नेय शैलों से हुआ है। इस पठार के उत्तरी भाग का ढाल उत्तर की ओर है। इस क्षेत्र की प्रमुख नदियों में चम्बल, सिन्धु, बेतवा, केन, सोन व दामोदर हैं, जो गंगा एवं गंगा की सहायक नदियों से मिल जाती हैं। पश्चिम की ओर बहने वाली नर्मदा व ताप्ती नदियाँ दरार घाटियों से होकर बहती हुई अरब सागर में जा मिलती हैं। दक्कन के पठार का ढाल पूर्व की ओर है। कावेरी-पेनार, कृष्णा, गोदावरी और महानदी इसके जल-निकास का काम करती हैं। ये सभी नदियाँ बंगाल की खाड़ी में मिलती हैं।

पठार के उत्तर-पश्चिमी भाग में काली मृदा का विकास हुआ है। यह मृदा बहुत ही उपजाऊ तथा कपास की खेती के लिए उपयोगी है। भारत के पठारी भाग में खनिज सम्पदा के विशाल भण्डार हैं। इनमें कोयला, लोहा, अभ्रक, बॉक्साइट, ताँबा, मैंगनीज आदि प्रमुख हैं। इन खनिजों पर देश का आर्थिक व औद्योगिक विकास निर्भर करता है। दक्कन पठार की नदियाँ जल शक्ति के विकास में सहायक हुई हैं।

प्रायद्वीपीय पठार अत्यन्त प्राचीन चट्टानों से बना होने के कारण खनिज पदार्थों में धनी है। कर्नाटक में सोना, मध्य प्रदेश में हीरा, संगमरमर, चूने का पत्थर और मैंगनीज, आन्ध्र प्रदेश और पश्चिम बंगाल में कोयला तथा बिहार एवं ओडिशा में लोहा पाया जाता है। महाराष्ट्र काली मृदा के कारण कपास की खेती के लिए प्रसिद्ध है। दक्षिण-पश्चिमी प्रायद्वीप पठार मसाले, चाय व कॉफी उत्पादन के लिए जाना जाता है। यहाँ जल विद्युत् उत्पादन की भी सम्भावनाएँ हैं। इसी पठारी प्रदेश में ऊटकमण्ड, पंचमढ़ी, महाबलेश्वर आदि महत्त्वपूर्ण स्थान हैं।

प्रश्न 5.
टिप्पणी लिखिए-भारतीय तटवर्ती क्षेत्र, भारतीय द्वीप समूह।
उत्तर:
भारतीय तटवर्ती क्षेत्र-भारतभूमि सीमा लगभग 15,200 किमी है। मुख्य भूमि, लक्षद्वीप समूह और अण्डमान निकोबार द्वीप समूह के समुद्र-तट की कुल लम्बाई (कुल तट रेखा) 7516.6 किमी है। पूर्वी तट रेखा बंगाल की खाड़ी में गंगा डेल्टा से कुमारी अन्तरीप तक विस्तृत है। पूर्वी तट रेखा के उत्तरी भाग को उत्तरी सत्कार और दक्षिणी भाग को कारोमण्डल तट कहते हैं। पश्चिमी तट रेखा का विस्तार अरब सागर के किनारे है। इसके उत्तर में काठियावाड़ तथा मध्य में कोंकण तट और दक्षिण में मालाबार तट स्थित है। हमारे समुद्री पड़ोसी देश दक्षिण में श्रीलंका और मालद्वीप हैं। अण्डमान निकोबार द्वीप समूह के पूर्व में इण्डोनेशिया स्थित है।

भारतीय द्वीप समूह :
भारत के द्वीपीय समूहों-लक्षद्वीप तथा अण्डमान व निकोबार द्वीप समूह की उत्पत्ति अलग प्रकार से हुई है। केरल के तट के निकट अरब सागर में छोटे-छोटे द्वीपों का एक समूह है जिन्हें लक्षद्वीप समूह कहते हैं। ये सभी प्रवाल द्वीप हैं, अर्थात् इनकी रचना अल्पजीवी सूक्ष्म प्रवाल जीवों के सतत् और शान्त प्रयत्नों के द्वारा हुई है। ये प्रवाल जीव उथले एवं कोष्ण जल में ही भली-भाँति पनपते हैं। इनमें से अनेक द्वीपों की आकृति घोड़े की नाल या अँगूठी के समान है। इन्हें एटॉल या प्रवालद्वीपीय वलय कहते हैं। इनके विपरीत अण्डमान निकोबार द्वीप बड़े तथा संख्या में अधिक है। इनमें से कुछ की उत्पत्ति ज्वालामुखी उद्गार से हुई है। अण्डमान द्वीप एवं निकोबार द्वीप समूह में ज्ञात एवं अज्ञात कुल द्वीपों की संख्या लगभग 300 है। यह द्वीप समूह लगभग 8249 वर्ग किमी में फैले हैं। इन द्वीप समूहों का देश की सामरिक सुरक्षा की दृष्टि से महत्त्वपूर्ण स्थान है।

मानचित्र पठन
भारत के मानचित्र का अध्ययन कर निम्नांकित के विषय में लिखिए। –

प्रश्न 1.
भारत की उत्तरी सीमा का अक्षांशीय विस्तार।
उत्तर:
37°6′.

प्रश्न 2.
उन राज्यों के नाम जिनकी सीमाएँ चीन से मिलती हैं।
उत्तर:
जन्मू एवं कश्मीर, हिमाचल प्रदेश, उत्तराखण्ड, सिक्किम एवं अरुणाचल प्रदेश।

प्रश्न 3.
उन राज्यों के नाम जिनसे होकर कर्क रेखा गुजरती है।
उत्तर:
छत्तीसगढ़, मध्य प्रदेश, मिजोरम, त्रिपुरा, पश्चिम बंगाल, राजस्थान, झारखण्ड व गुजरात।

प्रश्न 4.
बंगाल की खाड़ी में गिरने वाली नदियों के नाम।
उत्तर:
गंगा, गोदावरी, महानदी, कृष्णा, कावेरी।

प्रश्न 5.
हिमालय में स्थित कोई तीन दरों के नाम।
उत्तर:
काराकोरम, नाथुला, बोमडिला।

MP Board Class 9th Social Science Chapter 3 अन्य परीक्षोपयोगी प्रश्न

MP Board Class 9th Social Science Chapter 3 वस्तुनिष्ठ प्रश्न

बहु-विकल्पीय प्रश्न

प्रश्न 1.
विश्व के क्षेत्रफल का कितना भू-भाग भारत में है?
(i) 1.25 प्रतिशत
(ii) 1.89 प्रतिशत
(iii) 2.42 प्रतिशत
(iv) 3.42 प्रतिशत।
उत्तर:
(iii) 2.42 प्रतिशत

प्रश्न 2.
पूर्वी मैदान को कहते हैं
(i) पश्चिमी मैदान
(ii) ब्रह्मपुत्र मैदान
(iii) मध्यवर्ती मैदान
(iv) उपर्युक्त में कोई नहीं।
उत्तर:
(ii) ब्रह्मपुत्र मैदान

प्रश्न 3.
भारत में कितने राज्य हैं? (2017)
(i) 15
(ii) 20
(iii) 29
(iv) 301
उत्तर:
(iii) 29

रिक्त स्थान पूर्ति

1. भारत उत्तरी गोलार्द्ध में एशिया महाद्वीप के ………… में स्थित है।
2. ………… भारत को लगभग दो बराबर भागों में बाँटती है। (2014)
3. क्षेत्रफल की दृष्टि से ………… सबसे बड़ा राज्य है।
4. भारत और श्रीलंका के बीच …………. खाड़ी है। (2008)
5. प्रवाल (मूंगे) के निक्षेपों से बने इन द्वीपों को …………. कहा जाता है।

उत्तर:

1. दक्षिणी भाग
2. कर्क रेखा
3. राजस्थान
4. मन्नार की
5. एटॉल।

सत्य/असत्य

प्रश्न 1.
भारत एवं श्रीलंका के मध्य मन्नार की खाड़ी स्थित है। (2008)
उत्तर:
सत्य

प्रश्न 2.
कर्क रेखा भारत को दो भागों में बाँटती है। (2008)
उत्तर:
सत्य

प्रश्न 3.
देश में तहसीलों की संख्या 6,38,588 है। (2015)
उत्तर:
असत्य

प्रश्न 4.
उत्तर-पश्चिम के सात राज्यों को “सात बहनें” कहा जाता है। (2017)
उत्तर:
असत्य

प्रश्न 5.
भारत के दक्षिण में हिन्द महासागर है। (2016)
उत्तर:
सत्य

प्रश्न 6.
क्षेत्रफल की दृष्टि से भारत विश्व का सातवाँ बड़ा देश है। (2017)
उत्तर:
सत्य

सही जोड़ी मिलाइए

उत्तर:

1. → (घ)
2. → (ङ)
3. → (ग)
4. → (ख)
5. → (क)

एक शब्द/वाक्य में उत्तर

प्रश्न 1.
भारत का क्षेत्रफल लिखिए। (2014, 16)
उत्तर:
32,87,263 वर्ग किमी

प्रश्न 2.
उत्तर-पूर्व के सात राज्यों को क्या कहा जाता है?
उत्तर:
सात बहनें

प्रश्न 3.
बाढ़ के मैदानों की नवीन जलोढक। (2015)
उत्तर:
खादर

प्रश्न 4.
भारत की स्थल सीमा कितनी है?
उत्तर:
15,200 किमी

प्रश्न 5.
भारतीय उपमहाद्वीप का सबसे प्राचीनतम भू-भाग कैना-सा है?
उत्तर:
विशाल प्रायद्वीप पठार

प्रश्न 6.
वे शैल जो मैग्मा के पृथ्वी के भीतर जम जाने से बनती है, क्या है?
उत्तर:
ग्रेनाइट

प्रश्न 7.
भारत एवं श्रीलंका के मध्य कौन-सी खाड़ी है? (2018)
उत्तर:
मन्नार की खाड़ी।

MP Board Class 9th Social Science Chapter 3 अति लघु उत्तरीय प्रश्न

प्रश्न 1.
भारत में सबसे बड़ा व सबसे छोटा जिला कौन-सा है?
उत्तर:
सबसे बड़ा जिला कच्छ (गुजरात) एवं सबसे छोटा जिला माहे (पुदुचेरी) है।

प्रश्न 2.
हिमाचल पर्वत की रचना लिखिए।
उत्तर:
हिमालय पर्वत, सिन्धु नदी से लेकर पूर्व में ब्रह्मपुत्र तक फैला है। इन दो सीमाओं के बीच इसकी आकृति, एक चाप के समान है। हिमालय की लम्बाई 2400 किमी है।

प्रश्न 3.
परिवर्तित सेल क्या हैं?
उत्तर:
पूर्व निर्मित आग्नेय या अवसादी शैलों पर अधिक दबाव या ताप के अवसाद का कारण भौतिक तथा रासायनिक परिवर्तन द्वारा बनी नई शैल।

प्रश्न 4.
उच्चावच किसे कहते हैं?
उत्तर:
धरातल या समुद्र की तलहटी पर प्राकृतिक रूपरेखा में पाए जाने वाले ऊँचाइयों के अन्तर को उच्चावच कहते हैं।

प्रश्न 5.
गोंडवाना लैण्ड क्या है? (2011, 15, 17)
उत्तर:
ये प्राचीन विशाल महाद्वीप पैंजिया का दक्षिणतम भाग है जिसमें आज के अफ्रीका, ऑस्ट्रेलिया तथा अंटार्कटिका शामिल हैं।

प्रश्न 6.
भारत की उन दो नदियों के नाम बताइए जो अपने मुहाने पर ज्वारनदमुख बनाती हैं ?
उत्तर:
नर्मदा और ताप्ती नदी।

MP Board Class 9th Social Science Chapter 3 लघु उत्तरीय प्रश्न

प्रश्न 1.
मध्यवर्ती मैदान हिमालय पर्वत का ‘उपहार’ क्यों कहा जाता है?
उत्तर:
मध्यवर्ती मैदान भारत के लगभग एक चौथाई क्षेत्रफल को घेरे हुए है। यहाँ भारत की लगभग 45 प्रतिशत जनसंख्या वास करती है। सिन्धु, सतलज, गंगा, ब्रह्मपुत्र नदियों द्वारा बहाकर लाई गई मृदा से बना होने और सिंचाई की सुविधा के कारण यह मैदान हिमालय पर्वत का ‘उपहार’ कहलाता है। उत्तरी मैदान कृषि की दृष्टि से महत्त्वपूर्ण है। यहाँ जनसंख्या बाहुल्य है। नहरों, सड़कों और रेलों का जाल बिछा है। यह मैदान सभ्यता की जन्मभूमि रहा है। अमृतसर, कुरुक्षेत्र, मथुरा, वृन्दावन, प्रयाग, काशी आदि तीर्थस्थल इसी मैदान में स्थित हैं।

प्रश्न 2.
पश्चिमी तटीय मैदान व पूर्वी तटीय मैदान में अन्तर स्पष्ट कीजिए। (2008)
उत्तर:
पश्चिमी तटीय मैदान व पूर्वी तटीय मैदान में अन्तर

MP Board Class 9th Social Science Chapter 3 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
टिप्पणी लिखिए
(1) उत्तर का पर्वतीय प्रदेश
(2) तटीय प्रदेश।
उत्तर:
(1) उत्तर का पर्वतीय प्रदेश :
भारत की उत्तरी सीमा पर वृहद् हिमालय विश्व की सबसे ऊँची व बनावट के दृष्टिकोण से नवीन वलित पर्वत श्रृंखला है। ये शृंखलाएँ पश्चिम-पूर्व दिशा में सिन्धु से लेकर ब्रह्मपुत्र तक फैली हैं। हिमालय 2400 किमी की लम्बाई में फैले एक धनुषाकार आकृति का निर्माण करता है। विस्तार एवं ऊँचाई के आधार पर हिमालय को तीन भागों में बाँट सकते हैं-

• महान या आन्तरिक हिमालय
• मध्य हिमालय, तथा
• शिवालिक श्रेणी।

(2) तटीय प्रदेश :
प्रायद्वीपीय पठार कच्छ से उड़ीसा तक तटीय मैदानों की एक सँकरी पट्टी से घिरा हुआ है। इस तटीय मैदान को इनकी बनावट में अन्तर के कारण इसे दो भागों में पश्चिमी तथा पूर्वी तटीय भागों में विभक्त किया जाता है। पश्चिमी तटीय मैदान अरब सागर के सहारे-सहारे गुजरात से केरल तक फैला हुआ है। यह मैदान सँकरे हैं, इन्हें उत्तरी भाग में कोंकण और गोवा के दक्षिण में मालाबार तटीय मैदान कहते हैं। पूर्वी तट-यह पश्चिमी तट की अपेक्षा अधिक चौड़े और समतल हैं। यहाँ उपजाऊ काँप मृदा मिलती है।

MP Board Class 9th Social Science Solutions

MP Board Class 9th Maths Solutions Chapter 15 प्रायिकता Ex 15.1

प्रश्न 1.
एक क्रिकेट मैच में, एक महिला बल्लेबाज खेली गई 30 गेंद में 6 बार चौका मारती है। चौका न मारने की प्रायिकता ज्ञात कीजिए। (2019)
हल :
चौका न मारने की घटना E = 30 – 6 = 24

अतः अभीष्ट प्रायिकता = \(\frac { 24 }{ 30 }\) अर्थात् \(\frac { 4 }{ 5 }\)

प्रश्न 2.
2 बच्चों वाले 1500 परिवारों का यदृच्छया चयन किया गया और निम्नलिखित आँकड़े लिख लिए गए हैं : (2019)

यदृच्छया चुने गए परिवार की प्रायिकता ज्ञात कीजिए जिसमें
(i) दो लड़कियाँ हों
(ii) एक लड़की हो
(iii) कोई लड़की न हो। साथ ही यह भी जाँच कीजिए कि इन प्रायिकताओं का योगफल 1 है या नहीं।
हल :
(i) चूँकि E1 = 475 एवं n = 1500
\(P\left(E_{1}\right)=\frac{E_{1}}{n}=\frac{475}{1500}=\frac{19}{60}\)
अत: दो लड़कियाँ होने की अभीष्ट प्रायिकता = \(\frac { 19 }{ 60 }\)

(ii) चूँकि E2 = 814 एवं n= 1500
\(P\left(E_{2}\right)=\frac{E_{2}}{n}=\frac{814}{1500}=\frac{407}{750}\)
अत: एक लड़की होने की अभीष्ट प्रायिकता = \(\frac { 407 }{ 750 }\).

(iii) चूँकि E3 = 211 एवं n = 1500
अतः एक भी लड़की न होने की अभीष्ट प्रायिकता = \(\frac { 211 }{ 1500 }\)
अब \(\frac{19}{60}+\frac{407}{750}+\frac{211}{1500}=\frac{475+814+211}{1500}=\frac{1500}{1500}=1\)
अतः प्रायिकताओं का योगफल 1 है।

प्रश्न 3.
नवीं कक्षा के 40 विद्यार्थियों से उनके जन्म का महीना बताने के लिए कहा गया। इस प्रकार प्राप्त आकड़ों से निम्नलिखित आलेख बनाया गया :

कक्षा के किसी एक विद्यार्थी का जन्म अगस्त में होने की प्रायिकता ज्ञात कीजिए।
हल :
दिया है : n = 40 एवं आलेखानुसार E = 6.
\(P(E)=\frac{E}{n}=\frac{6}{40}=\frac{3}{20}\)
अत: एक छात्र के अगस्त में जन्म लेने की अभीष्ट प्रायिकता = \(\frac { 3 }{ 20 }\).

प्रश्न 4.
तीन सिक्कों को एक साथ 200 बार उछाला गया तथा इनमें विभिन्न परिणामों की बारम्बारताएँ ये हैं :

यदि तीनों सिक्कों को पुनः एक साथ उछाला जाए, तो दो चित आने की प्रायिकता ज्ञात कीजिए।
हल :
चूँकि E = 72 एवं n = 200 (प्रश्नानुसार दिया है)
\(P(E)=\frac{E}{n}=\frac{72}{200}=\frac{9}{25}\)
अत: दो चित आने की अभीष्ट प्रायिकता = \(\frac { 9 }{ 25 }\)

प्रश्न 5.
एक कम्पनी ने यदृच्छया 2400 परिवार चुनकर एक घर की आय स्तर और वाहनों की संख्या के बीच सम्बन्ध स्थापित करने के लिए उनका सर्वेक्षण किया। एकत्रित किए गए आँकड़े नीचे सारणी में दिए गए हैं :

मान लीजिए एक परिवार चुना गया है। प्रायिकता ज्ञात कीजिए कि चुने गए परिवार :
(i) की आय Rs 10,000 से Rs 13,000 प्रतिमाह है और उसके पास ठीक-ठीक दो वाहन हैं।
(ii) की आय प्रतिमाह Rs 16,000 या इससे अधिक है और उसके पास ठीक एक वाहन है।
(iii) की आय Rs 7,000 प्रतिमाह से कम है और उसके पास कोई वाहन नहीं है।
(iv) की आय Rs 13,000 से Rs 16,000 प्रति माह है और उसके पास 2 से अधिक वाहन हैं।
(v) जिसके पास 1 से अधिक वाहन नहीं हैं।
हल :
(i) चूँकि n = 2,400 एवं E1 = 29 (दी गई सारणी से)
\(P\left(E_{1}\right)=\frac{E_{1}}{n}=\frac{29}{2,400}\)
अतः अभीष्ट प्रायकिता = \(\frac { 29 }{ 2400 }\)

(ii) चूँकि n = 2,400 एवं E2 = 579 (दी गई सारणी से)
\(P\left(E_{2}\right)=\frac{E_{2}}{n}=\frac{579}{2,400}=\frac{193}{800}\)
अतः अभीष्ट प्रायिकता = \(\frac { 579 }{ 2400 }\) अथात् \(\frac { 193 }{ 800 }\)

(iii) चूँकि n = 2400 एवं E3 = 10 (दी गई सारणी से)
\(P\left(E_{3}\right)=\frac{E_{3}}{n}=\frac{10}{2,400}=\frac{1}{240}\)
अतः अभीष्ट प्रायिकता = \(\frac { 1 }{ 240 }\)

(iv) चूँकि n = 2,400 एवं E4 = 25 (दी गई सारणी से)
\(P\left(E_{4}\right)=\frac{E_{4}}{n}=\frac{25}{2,400}=\frac{1}{96}\)

(v) चूँकि जिनके पास एक से अधिक वाहन नहीं हैं। उनके पास या तो 1 वाहन है अथवा एक भी वाहन नहीं अर्थात् शून्य है।
शून्य वाहन वाले परिवार = 10 + 0 + 1 + 2 + 1 = 14
एवं 1 वाहन वाले परिवार = 160 + 305 + 535 + 469 + 579 = 2,048
⇒ उन परिवारों की संख्या जिनके पास 1 से अधिक वाहन नहीं हैं = E5 = 2048 + 14 = 2,062
\(P\left(E_{5}\right)=\frac{E_{5}}{n}=\frac{2,062}{2,400}=\frac{1031}{1,200}\)
अतः अभीष्ट प्रायिकता = \(\frac { 1031 }{ 1200 }\)

प्रश्न 6.
100 अंक की गणित की परीक्षा में विद्यार्थियों ने निम्न प्रकार अंक प्राप्त किए :

(i) गणित की परीक्षा में एक विद्यार्थी द्वारा 20% से कम अंक प्राप्त करने की प्रायिकता ज्ञात कीजिए।
(ii) जब विद्यार्थी द्वारा 60 या इससे अधिक अंक प्राप्त करने की प्रायिकता ज्ञात कीजिए।
हल :
(i) चूँकि E1 = 7 एवं n = 90 (दी गई सारणी के अनुसार)
प्रायिकता \(P\left(E_{1}\right)=\frac{E_{1}}{n}=\frac{7}{90}\)
अत: अभीष्ट प्रायिकता = \(\frac { 7 }{ 90 }\)

(ii) चूँकि E2 = 15 + 8 = 23 एवं n = 90 (दी गई सारणी से)
प्रायिकता \(P\left(E_{2}\right)=\frac{E_{2}}{n}=\frac{23}{90}\)
अतः अभीष्ट प्रायिकता = \(\frac { 23 }{ 90 }\)

प्रश्न 7.
सांख्यिकी के बारे में विद्यार्थियों का मत जानने के लिए 200 विद्यार्थियों का सर्वेक्षण किया गया। प्राप्त आँकड़ों को नीचे दी गई सारणी में लिख लिया गया है : (2018, 19)

प्रायिकता ज्ञात कीजिए कि यदृच्छिक चुना गया एक विद्यार्थी :
(i) सांख्यिकी पसन्द करता है।
(ii) सांख्यिकी पसन्द नहीं करता है।
हल :
(i) चूँकि E1 = 135 एवं n = 200 (प्रश्नानुसार)
प्रायिकता = \(P\left(E_{1}\right)=\frac{E_{1}}{n}=\frac{135}{200}=\frac{27}{40}\)
अतः अभीष्ट प्रायिकता = \(\frac { 27 }{ 40 }\)

(ii) चूँकि E2 = 65 एवं n = 200 (प्रश्नानुसार)
प्रायिकता \(P\left(E_{2}\right)=\frac{E_{2}}{n}=\frac{65}{200}=\frac{13}{40}\)
अतः अभीष्ट प्रायिकता = \(\frac { 13 }{ 40 }\)

प्रश्न 8.
40 इन्जीनियरों की उनके आवास से कार्य (स्थल की (किलोमीटर में) दूरियाँ ये हैं :

इसकी आनुभविक प्रायिकता क्या होगी कि इन्जीनियर :
(i) अपने कार्य स्थल से 7 km से कम दूरी पर रहती है।
(ii) अपने कार्य स्थल से 7 km या इससे अधिक दूरी पर रहती है।
(iii) अपने कार्य स्थल से \(\frac { 1 }{ 2 }\) km या इससे कम दूरी पर रहती है।

हल :
(i) चूँकि E1 = 9 एवं n = 40 (सारणी के अनुसार)
प्रायिकता \(P\left(E_{1}\right)=\frac{E_{1}}{n}=\frac{9}{40}\)
अतः अभीष्ट प्रायिकता = \(\frac { 9 }{ 40 }\)

(ii) चूँकि E2 = 31 एवं n = 40 (सारणी के अनुसार)
प्रायिकता \(P\left(E_{2}\right)=\frac{E_{2}}{n}=\frac{31}{40}\)
अतः अभीष्ट प्रायिकता = \(\frac { 31 }{ 40 }\)

(iii) चूँकि E3 = 0 एवं n = 40 (सारणी के अनुसार)
प्रायिकता \(P\left(E_{3}\right)=\frac{E_{3}}{n}=\frac{0}{40}=0\)
अतः अभीष्ट प्रायिकता = 0.

प्रश्न 9.
अपने विद्यालय के गेट के सामने से एक समय अन्तराल में गुजरने वाले दो पहिया, तीन पहिया और चार पहिया वाहनों की बारम्बारता लिख लीजिए। आप द्वारा देखे गए वाहनों में से किसी एक वाहन का दो पहिया वाहन होने की प्रायिकता ज्ञात कीजिए।
हल :
(निर्देश : छात्र उक्त क्रियाकलाप स्वयं करें और अभीष्ट प्रायिकता का परिकलन करें।)

प्रश्न 10.
आप अपनी कक्षा के विद्यार्थियों से एक तीन अंकों वाली संख्या लिखने को कहिए। आप कक्षा से एक विद्यार्थी को यदृच्छया चुन लीजिए। इस बात की प्रायिकता क्या होगी कि उसके द्वारा लिखी गई संख्या 3 से भाज्य है ? याद रखिए कि कोई संख्या 3 से भाज्य होती है यदि उसके अंकों का योग 3 से भाज्य हो।
हल :
(निर्देश : छात्र इस क्रियाकलाप को स्वयं करें और अभीष्ट प्रायिकता का परिकलन करें।)

प्रश्न 11.
आटे की उन 11 थैलियों में जिन पर 5 kg अंकित है, वास्तव में आटे के निम्नलिखित भार (kg में) हैं:
4.97, 5.05, 5.08, 5.03, 5.00, 5.06, 5.08, 4.98, 5.04, 5.07, 5.00.
यदृच्छया चुनी गई एक थैली में 5 kg से अधिक आटा होने की प्रायिकता क्या होगी ?
हल :
चूँकि E = 5 kg से अधिक आटे वाले थैलियों की संख्या = 7 एवं कुल थैलियों की संख्या n = 11
प्रायिकता \(P(E)=\frac{E}{n}=\frac{7}{11}\)
अत: अभीष्ट प्रायिकता = \(\frac { 7 }{ 11 }\)

प्रश्न 12.
एक नगर की वायु में सल्फर डाइ-ऑक्साइड का सान्द्रण भाग प्रति मिलियन (ppm) में ज्ञात करने के लिए एक अध्ययन किया गया। 30 दिनों के प्राप्त आँकड़े ये हैं :

इनमें से किसी एक दिन अन्तराल (0.12 – 0.16) में सल्फर डाइ-ऑक्साइड के सान्द्रण होने की प्रायिकता ज्ञात कीजिए।
हल :
चूँकि वर्ग अन्तराल (0.12-0.16) में सल्फर डाइ-ऑक्साइड की दो सान्द्रताएँ 0.12 एवं 0.13 हैं।
इसलिए E = 2 एवं n = 30 (दिया है)
प्रायिकता \(P(E)=\frac{2}{30}=\frac{1}{15}\)
अतः अभीष्ट प्रायिकता = \(\frac { 1 }{ 15 }\).

प्रश्न 13.
आठवीं कक्षा के 30 विद्यार्थियों के रक्त समूह ये हैं :
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O
A, AB, O, A, A, O, O AB, B, A, O, B, A, B, O.
रक्त समूह से सम्बन्धित बारम्बारता बंटन सारणी बनाइए तथा हम सारणी की सहायता से इस कक्षा से यदृच्छया चुने गए एक विद्यार्थी का रक्त समूह AB होने की प्रायिकता ज्ञात कीजिए।
हल :

सारणी के अनुसार E = 3 एवं n = 30
प्रायिकता \(P(E)=\frac{E}{n}=\frac{3}{30}=\frac{1}{10}\)
अतः अभीष्ट प्रायिकता = \(\frac { 1 }{ 10 }\)

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 10 वृत्त Ex 10.4

प्रश्न 1.
5 cm और 3 cm की त्रिज्या वाले दो वृत्त दो बिन्दुओं पर प्रतिच्छेद करते हैं तथा उनके केन्द्रों के बीच की दूरी 4 cm है। उभयनिष्ठ जीवा की लम्बाई ज्ञात कीजिए।
हल:
दिए हुए वृत्त के केन्द्र क्रमशः O तथा O’ है जिनके बीच की दूरी OO’ = 4 cm है। वृत्त एक-दूसरे को P और Q दो बिन्दुओं पर प्रतिच्छेद करते है। वृत्तों की त्रिज्याएँ क्रमशः
OP = 5 cm तथा OP = 3 cm हैं।

चित्र 10.6
चूँकि (OO’)² + (O’P)² = (4)² + (3)² = 16 + 9 = 25 = (5)2 = (OP)²
अतः ∆OO’P एक समकोण त्रिभुज है। (पाइथागोरस का विलोम)
⇒ OO’ ⊥ O’P
चूँकि उभयनिष्ठ जीवा PQ छोटे वृत्त के केन्द्र O’ से जाती है, इसलिए PQ छोटे वृत्त का व्यास है।
⇒ PQ = 2 x O’P = 2 x 3 = 6 cm
अत: उभयनिष्ठ जीवा की अभीष्ट लम्बाई = 6 cm.

प्रश्न 2.
यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर परस्पर प्रतिच्छेद करें तो, सिद्ध कीजिए कि एक जीवा के खण्ड दूसरी जीवा के संगत खण्डों के बराबर है।
हल:
दिया है : O केन्द्र वाले एक वृत्त की दो जीवाएँ AB = CD परस्पर E बिन्दु पर प्रतिच्छेद करती हैं, तो सिद्ध करना है कि
AE = DE एवं CE = BE

चित्र 10.7
रचना : O से OM ⊥ AB तथा ON ⊥ CD खींचिए तथा OE को मिलाइए।
उपपत्ति : समकोण ∆OME एवं ∆ONE में,
चूँकि कर्ण OE = OE (उभयनिष्ठ है)
एवं OM = ON (बराबर जीवाएँ केन्द्र से बराबर दूरी पर होती है)
⇒ ΔΟΜΕ ≅ ΔΟΝΕ (RHS सर्वांगसमता प्रमेय)
⇒ ME = NE
चूँकि AB = CD, OM ⊥ AB एवं ON ⊥ CD
⇒ AM = DN एवं BM = CN
⇒ AM + ME = DN + NE [समीकरण (1) और (2) से]
⇒ AE = DE
एवं CN – EN = BM – EM [समीकरण (1) और (2) में]
⇒ CE = BE
अतः वृत्त की बराबर जीवाएँ वृत्त के अन्दर यदि प्रतिच्छेद करती हैं। तो उनके संगत खण्ड बराबर होते हैं। इति सिद्धम्

प्रश्न 3.
यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि प्रतिच्छेद बिन्दु को केन्द्र से मिलाने वाली रेखा जीवाओं से बराबर कोण बनाती है।
हल:

चित्र 10.8
ज्ञात है : O केन्द्र वाले एक वृत्त की दो जीवाएँ AB = CD वृत्त के अन्दर बिन्दु E पर परस्पर प्रतिच्छेद करती हैं। OE को मिलाया गया है।
सिद्ध करना है: ∠OEA = ∠OED
रचना : OM ⊥ AB एवं ON ⊥ CD खींचिए।
उपपत्ति : समकोण ΔOME एवं ΔONE में,
चूँकि कर्ण OE = कर्ण OE (उभयनिष्ठ है)
एवं OM = ON (बराबर जीवाएँ केन्द्र से बराबर दूरी पर होती हैं)
⇒ ΔΟΜΕ ≅ ΔΟΝΕ (RHS सर्वांगसमता प्रमेय)
⇒ ∠OEM = ∠OEN (CPCT)
अतः ∠OEA = ∠OED (चित्रानुसार) इति सिद्धम्

प्रश्न 4.
यदि एक रेखा दो संकेन्द्री वृत्तों (एक ही केन्द्र वाले वृत्त) को जिनका केन्द्र O है A, B, C और D पर प्रतिच्छेद करें, तो सिद्ध कीजिए कि AB = CD है (देखिए संलग्न चित्र)। (2019)
हल:

चित्र 10.9
दिया है : O केन्द्र वाले दो संकेन्द्री वृत्तों को रेखा AD बिन्दुओं A, B, C और D पर (चित्रानुसार) प्रतिच्छेद करती है तो सिद्ध करना है कि AB = CD
रचना : OM ⊥ AD खींचिए।
उपपत्ति : बाह्य वृत्त में चूँकि AD वृत्त की जीवा है तथा OM ⊥ AD
⇒ AM = DA …..(1) (केन्द्र से जीवा पर डाला लम्ब उसे समद्विभाजित करता है)
चूँकि अन्तः वृत्त की जीवा CB पर OM लम्ब है। (चित्रानुसार)
⇒ BM = CM …(2) (वृत्त के केन्द्र से जीवा पर डाला गया लम्ब उसे समद्विभाजित करता है)
⇒ AM – BM = DM – CM [समीकरण (1) और (2) से]
अतः AB = CD. (चित्रानुसार) इति सिद्धम्

प्रश्न 5.
एक पार्क में बने 5 m त्रिज्या वाले वृत्त पर खड़ी तीन लड़कियाँ रेशमा, सलमा एवं मनदीप खेल रही हैं। रेशमा एक गेंद को सलमा के पास, सलमा मनदीप के पास तथा मनदीप रेशमा के पास फेंकती है। यदि रेशमा तथा सलमा के बीच और सलमा तथा मनदीप के बीच की प्रत्येक दूरी 6 m हो, तो रेशमा और मनदीप की बीच की दूरी क्या है ?
हल:
मान लीजिए वृत्ताकार पार्क का केन्द्र O है। बिन्दु R, S और M पर क्रमशः रेशमा, सलमा और मनदीप हैं। वृत्त की त्रिज्या OR = 5 m, तथा RS = SM = 6 m दी गई है तो दूरी RM ज्ञात करना है।

चित्र 10.10

अत: रेशमा और मनदीप के बीच की दूरी RM = 2 x x = 2 x 4.8 = 9.6 m.

प्रश्न 6.
20 m त्रिज्या का एक गोल पार्क (वृत्ताकार) एक कॉलोनी में स्थित है। तीन लड़के अंकुर, सैय्यद, डेविड इसकी परिसीमा पर बराबर दूरी पर बैठे हैं और प्रत्येक के हाथ में एक खिलौना टेलीफोन आपस में बात करने के लिए है। प्रत्येक टेलीफोन की डोरी की लम्बाई ज्ञात कीजिए।

चित्र 10.11
हल:
दिया है : एक 20 m त्रिज्या का 0 केन्द्र वाला वृत्ताकार पार्क जिसकी परिसीमा पर अंकुर, सैय्यद और डेविड क्रमश: A, S और D बिन्दुओं पर इस प्रकार बैठे हैं कि AS = SD = DA =x मान लीजिए।
चूँकि समबाहु त्रिभुज की सभी माध्यिकाएँ बराबर होती हैं, वे सम्मुख भुजाओं को समकोण पर समद्विभाजित करती हैं तथा परस्पर एक बिन्दु पर 2 : 1 के अनुपात में प्रतिच्छेद करती है एवं यह बिन्दु उसके शीर्षों से समान दूरी पर होता है अर्थात् ASD से जाने वाले वृत्त का केन्द्र।
⇒ AO = SO = DO = 20 m (वृत्त की त्रिज्या दी है)
एवं OM = \(\frac { 1 }{ 2 }\)AO = \(\frac { 1 }{ 2 }\) x 20 = 10 m
⇒ AM = AO + OM = 20 + 10 = 30 m
समकोण ∆AMS में पाथागोरस प्रमेय से,
AS² = AM² + SM²

अतः प्रत्येक टेलीफोन की छोरी की अभीष्ट लम्बाई = 34.64 m.

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 10 वृत्त Ex 10.3

प्रश्न 1.
वृत्तों के कई जोड़े (युग्म) खींचिए। प्रत्येक जोड़े में कितने बिन्दु उभयनिष्ठ हैं ? उभयनिष्ठ बिन्दुओं की अधिकतम संख्या क्या होगी?
हल:
वृत्तों के अभीष्ट युग्म (जोड़े) :

चित्र 10.3
उभयनिष्ठ बिन्दुओं की संख्या-
(a) में शून्य,
(b) में एक,
(c) में दो,
(d) में एक,
(e) में शून्य।
अतः अधिकतम उभयनिष्ठ बिन्दुओं की संख्या = दो।

प्रश्न 2.
मान लीजिए आपको एक वृत्त दिया है। एक रचना इसके केन्द्र को ज्ञात करने के लिए दीजिए।
हल:

चित्र 10.4
एक वृत्त दिया है जिसका केन्द्र ज्ञात करना है।
रचना :
(i) वृत्त पर तीन बिन्दु P, Q और R लीजिए।
(ii) PQ एवं QR को मिलाइए।
(iii) PQ का लम्ब समद्विभाजक AB खींचिए।
(iv) OR का लम्ब समद्विभाजक CD खींचिए जो AB को बिन्दु O पर प्रतिच्छेद करता है। यही बिन्दु O वृत्त का अभीष्ट केन्द्र है।

प्रश्न 3.
यदि दो वृत्त परस्पर दो बिन्दुओं पर प्रतिच्छेद करें, तो सिद्ध कीजिए कि उनके केन्द्र उभयनिष्ठ जीवा के लम्ब समद्विभाजक पर स्थित हैं।
हल:

चित्र 10.5
दिया है : O और O’ केन्द्र वाले दो वृत्त एक-दूसरे को दो बिन्दुओं P और Q पर प्रतिच्छेद करते हैं। तो सिद्ध करना है कि उनके केन्द्र उभयनिष्ठ जीवा PQ के लम्ब समद्विभाजक पर स्थित हैं।
रचना : केन्द्र O और O’ को उभयनिष्ठ जीवा PQ के मध्य-बिन्दु R से मिलाइए।
उपपत्ति : चूँकि O केन्द्र वाले वृत्त में केन्द्र O को जीवा PQ के मध्य-बिन्दु R से मिलाया गया है।
⇒ OR ⊥ PO अर्थात् ∠ORP = 90° ….(1)
चूँकि O’ केन्द्र वाले वृत्त में केन्द्र O’ को जीवा PQ के मध्य बिन्दु R से मिलाया गया है।
⇒ OR ⊥ PO अर्थात् ∠O’RP = 90° …..(2)
⇒ ∠ORP + ∠O’RP = 180° [समीकरण (1) और (2) से]
⇒ ORO’ एक सरल रेखाखण्ड है जो जीवा PQ का लम्बार्द्धक है।
अतः यदि दो वृत्त परस्पर दो बिन्दुओं पर प्रतिच्छेद करें, तो उनके केन्द्र उभयनिष्ठ जीवा के लम्बार्द्धक पर स्थित हैं। इति सिद्धम्

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 7 त्रिभुज Additional Questions

MP Board Class 9th Maths Chapter 7 अतिरिक्त परीक्षोपयोगी प्रश्न

MP Board Class 9th Maths Chapter 7 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
ABCD एक चतुर्भुज है, जिसमें AB = BC और AD = CD। दर्शाइए कि BD दोनों कोणों ABC और ADC को समद्विभाजित करता है।
हल:

चित्र 7.34
दिया है : एक चतुर्भुज ABCD जिससे
AB = BC और AD = CD। BD चतुर्भुज ABCD का एक विकर्ण है।
अब ∆ABD और ∆CBD में,
चूँकि AB = BC (दिया है)
AD = CD (दिया है)
एवं BD = BD (उभयनिष्ठ है)
⇒ ∆ABD ≅ ∆CBD (SSS सर्वांगसमता प्रमेय)
⇒ ∠ABD ≅ ∠CBD एवं ∠ADB = ∠CDB (CPCT)
अत: BD दोनों कोण ∠ABC एवं ∠ADC को समद्विभाजित करता है। इति सिद्धम्

प्रश्न 2.
ABC एक समकोण त्रिभुज है जिससे AB = AC, CA का समद्विभाजक BC से D पर मिलता है। सिद्ध कीजिए कि BC = 2AD.
हल:

चित्र 7.34
दिया है: ABC एक समकोण त्रिभुज जिसमें AB = AC, ∠A समकोण है जिसका समद्विभाजक AD, BC को बिन्दु D पर मिलता है।
अब ∠CAD = ∠BAD = 45° (∵ ∠A समकोण है तथा AD इसका समद्विभाजक है) …(1)
∠ACB = ∠ABC = 45° ..(2) (∵AB = AC के सम्मुख चित्र 7.35 कोण हैं तथा ∠A = 90°)
∠CAD = ∠BAD= ∠ACB = ∠ABC = 45° ….(3) [समी. (1) एवं (2) से]
अब ∆ABD में, ∠BAD = ∠ABC [समीकरण (3) से]
BD = AD (समान कोणों की सम्मुख भुजाएँ हैं) …(4)
एवं ∆ACD में, ∠CAD = ∠ACB [समीकरण (3) से]
⇒ CD = AD (समान कोणों की सम्मुख भुजाएँ हैं) …(5)
⇒ BD + CD = AD + AD = 2AD [समीकरण (4) और (5) से]
अत: BC = 2AD. (∵ BD + CD = BC चित्रानुसार) इति सिद्धम्

प्रश्न 3.
ABC एक समद्विबाहु त्रिभुज है, जिससे AC = BC ⊥ AD और BE क्रमशः BC और AC पर शीर्ष लम्ब हैं। सिद्ध कीजिए कि AE = BD.
हल:

चित्र 7.36
दिया है : ABC एक समद्विबाहु त्रिभुज जिससे AC = BC एवं AD ⊥ BC तथा BE ⊥ AC
∠ADC = ∠BEC = 90° [∵ AD ⊥ BC एवं BE ⊥ AC (दिया है)]
अब ∆ADC और ∆BEC में,
चूँकि ∠ADC = ∠BEC [समीकरण (1) से]
∠C = ∠C (उभयनिष्ठ है)
एवं AC = BC (दिया है)
⇒ ∆ADC = ∆BEC (ADS सर्वांगसमता प्रमेय)
⇒ CD = CE अर्थात् EC = DC (CPCT) …(2)
लेकिन AC = BC (दिया है) …(3)
⇒ AC – EC = BC – DC [समीकरण (3) और (2) से]
अतः AE = BD. (चित्रानुसार AC – EC = AE एवं BC – DC = BD) इति सिद्धम्

प्रश्न 4.
एक त्रिभुज ABC में, D भुजा AC का मध्य-बिन्दु है, जहाँ BD = \(\frac { 1 }{ 2 }\)AC है। दर्शाइए कि ∠ABC एक समकोण है।
हल:
दिया है : ∆ABC में D, AC का मध्य-बिन्दु एवं BD = \(\frac { 1 }{ 2 }\)AC.
AD = CD = \(\frac { 1 }{ 2 }\)AC …(1)
(D, AC का मध्य-बिन्दु दिया है)
BD = \(\frac { 1 }{ 2 }\)AC (दिया है) …(2)

चित्र 7.37
⇒ AD = CD = BD [समी. (1) और (2) से] …(3)
∆ABD में, AD = BD [समीकरण (3) से]
⇒ ∠ABD = ∠BAD (बराबर भुजाओं के सम्मुख कोण हैं) …(4)
एवं ∆CBD में, CD = BD [समीकरण (3) से]
∠CBD = ∠BCD …(5) (बराबर भुजाओं के सम्मुख कोण हैं)
∠ABD+ ∠CBD = ∠BAD+ ∠BCD [समी. (4) और (5) से]
∠ABC = ∠BAC + ∠BCA (चित्रानुसार) लेकिन
∠ABC + ∠BAC + ∠BCA = 180° (त्रिभुज के अन्त: कोण)
∠ABC = ∠BAC + ∠BCA = 180°/2 = 90°
अतः ∠ABC एक समकोण है। इति सिद्धम्

प्रश्न 5.
ABCD एक चतुर्भुज इस प्रकार है कि विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता हैं। सिद्ध कीजिए कि
AB = AD और CB = CD है।
हल:

चित्र 7.38
दिया है : एक चतुर्भुज ABCD जिसमें विकर्ण AC कोण A और C का समद्विभाजक है अर्थात्
∠DAC = ∠BAC …(1)
और ∠DCA = ∠BCA …(2)
अब ∆ADC और ∆ABC में, चूँकि
∠DAC = ∠BAC [समी. (1) से]
∠DCA = ∠BCA [समी. (2) से]
एवं AC = AC (उभयनिष्ठ है)
⇒ ∆ADC ≅ ∆ABC (ASA सर्वांगसमता प्रमेय)
AB = AD और CB = CD. (CPCT) इति सिद्धम्

MP Board Class 9th Maths Chapter 7 लघु उत्तरीय प्रश्न

प्रश्न 1.
ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है तथा BD और CE इसकी दो मध्यिाकाएँ हैं। दर्शाइए कि BD = CE.
हल:

चित्र 7.39
दिया है : एक समद्विबाहु त्रिभुज ABC जिसमें AB = AC तथा BD एवं CE इसमें दो मध्यिकाएँ हैं, अर्थात्
AE = EB = \(\frac { 1 }{ 2 }\)AB TO AD = DC = \(\frac { 1 }{ 2 }\) AC
⇒ EB = DC
अब ∆EBC और ∆DBC में,
चूँकि EB = DC (सिद्ध कर चुके हैं)
∠EBC = ∠DCB (AB = AC के सम्मुख कोण हैं)
एवं BC = BC (उभयनिष्ठ है)
⇒ ∆EBC ≅ ∆DBC (SAS सर्वांगसमता प्रमेय)
अतः BD = CE. (CPCT) इति सिद्धम्

प्रश्न 2.
संलग्न चित्र में D और E त्रिभुज ABC की भुजा BC पर दो बिन्दु इस प्रकार स्थित हैं कि BD = CE और AD = AE है। तो दर्शाइए कि ∆ABD ≅ ∆ACE है।
हल:

चित्र 7.40
दिया है : ∆ABC की भुजा BC पर दो बिन्दु D एवं E इस प्रकार हैं कि BD = CE और AD = AE.
∠ADE = ∠AED
⇒ ∠ADB = ∠AEC. (बराबर कोण के सम्पूरक. कोण हैं)
अब ∆ADB और ∆AEC में,
चूँकि AD = AE (दिया है)
∠ADB = ∠AEC (सिद्ध कर चुके हैं)
एवं BD = EC
अतः ∆ABD ≅ ∆ACE. (SAS सर्वांगसमता प्रमेय) इति सिद्धम्

प्रश्न 3.
संलग्न चित्र में BA ⊥ AC और DE ⊥ DF इस प्रकार हैं कि BA = DE और BF = EC हैं। दशाईए कि ∆ABC ≅ ∆DEF.

हल:
चूँकि BF = EC (दिया है)
⇒ BF + FC = EC + FC (बराबर संख्याओं में समान संख्या का योग)
⇒ BC = FE (चित्रानुसार) .
∴ समकोण ∆ABC और समकोण ∆DEF में, कर्ण BC = FE (सिद्ध कर चुके हैं)
एवं BA = DE (दिया है)
अतः ∆ABC ≅ ∆DEE (RHS सर्वांगसमता प्रमेय) इति सिद्धम्

प्रश्न 4.
एक ∆PSR की भुजा SR पर एक बिन्दु 0 इस प्रकार स्थित है कि PQ = PR है। सिद्ध कीजिए कि- PS >PQ.

चित्र 7.42
हल:
त्रिभुज PSR में SR पर बिन्दु ए इस प्रकार दिया है कि PQ = PR
⇒ ∠PQR = ∠PRQ (बराबर भुजाओं के सम्मुख कोण हैं)
लेकिन ∠PQR > ∠PSQ (बहिष्कोण है)
⇒ ∠PRS > ∠PSR (∠PRS = ∠PRO = ∠PQR एवं ∠PSR = ∠PSQ)
⇒ PS > PQ. (बड़े कोण की सम्मुख भुजा है।)
अतः (PQ > PR) इति सिद्धम्

प्रश्न 5.
∆PQR की भुजा QR पर कोई बिन्दु स्थित है। दर्शाइए कि PQ + QR + RP> 2PS.

चित्र 7.43
हल:
प्रश्नानुसार (संलग्न चित्र से)
∆PQS में, PQ + QS > PS (दो भुजाओं का योग तीसरी से बड़ा होता है)…(1)
एवं ∆PSR में, RP + SR > PS (दो भुजाओं का योग तीसरी से बड़ा होता है) …(2)
⇒ PQ+ QS + RP + SR > PS + PS [समीकरण (1) और (2) से]
⇒ PQ + QS + SR + RP > 2PS
अतः PQ+ QR + RP > 2PS. (QS + SR = QR चित्रांनुसार) इति सिद्धम्

प्रश्न 6.
AB = AC वाले एक ∆ABC की भुजा AC पर कोई बिन्दु D स्थित है। दर्शाइए कि CD < BD है।
हल:

चित्र 7.44
∆ABC में, AB = AC तथा AC पर बिन्दु D है।
∠ABC = ∠ACB (AB = AC के सम्मुख कोण हैं)
लेकिन ∠DBC < ∠ABC (किसी संख्या का अंश संख्या से कम होता है)
= ∠DBC < ∠ACB (∵ ∠ABC = ∠ACB)
अतः CD < BD. (छोटे कोण के सामने की भुजा छोटी होती है) इति सिद्धम्

प्रश्न 7.
संलग्न चित्र में l || m है तथा m रेखाखण्ड AB का मध्य-बिन्दु है। दर्शाइए M किसी भी रेखाखण्ड CD का मध्य-बिन्दु है जिसके अन्तःबिन्दु क्रमशः l और m पर स्थित हों।

चित्र 7.45
हल:
l || m को तिर्यक रेखाखण्ड AB क्रमशः A और B पर मिलती है। ∠CAB = ∠ABD (एकान्तर कोण हैं) …(1)
l ||m को तिर्यक रेखाखण्ड CD क्रमश: C और D पर मिलती है। ∠ACD = ∠BDC (एकान्तर कोण है) …(2)
अब ∆AMC और ∆BMD में, चूँकि ∠CAM = ∠MBD [समी. (1) और ∠CAB = ∠CAM एवं ∠MBD = ∠ABD]
AM = BM (AB का मध्य-बिन्दु M दिया है)
एवं ∠ACM = ∠BDM [समी. (2) और ∠ACD = ∠ACM एवं ∠BDC = ∠BDM]
∆AMC ≅ ∆BMD (ASA सर्वांगसमता प्रमेय) CM = DM . (CPCT)
अत: M किसी भी रेखाखण्ड CD का भी मध्य-बिन्दु है। इति सिद्धम्

प्रश्न 8.
AB = AC वाले एक समद्विबाहु त्रिभुज के कोणों B और C के समद्विभाजक परस्पर O पर प्रतिच्छेद करते हैं। BO को एक बिन्दु M तक बढ़ाया गया है। सिद्ध कीजिए ∠MOC = ∠ABC है।
हल:

चित्र 7.46
ज्ञात है : AB = AC ⇒ ∠ABC = ∠ACB (बराबर भुजाओं के सम्मुख कोण हैं) चूँकि BO एवं CO क्रमश:
∠B एवं ∠C के समद्विभाजक है।
⇒ ∠OBC = \(\frac { 1 }{ 2 }\)ABC
एवं ∠OCB = \(\frac { 1 }{ 2 }\)∠ACB
⇒ ∠MOC = ∠OBC + ∠OCB (∠MOC, ∆OBC का बहिष्कोण है)
⇒ ∠MOC = \(\frac { 1 }{ 2 }\)∠ABC + \(\frac { 1 }{ 2 }\)∠ACB
अतः ∠MOC = ∠ABC. (∠ABC = ∠ACB सिद्ध कर चुके हैं) इति सिद्धम्

MP Board Class 9th Maths Chapter 7 अति लघु उत्तरीय प्रश्न

प्रश्न 1.
त्रिभुजों ABC और POR में ∠A = 20 और ∠B = ∠R हैं। ∆POR की कौन-सी भुजा ∆ABC की भुजा AB के बराबर होनी चाहिए कि दोनों त्रिभुज सर्वांगसम हों ? अपने उत्तर के लिए कारण दीजि
उत्तर:
QR, क्योंकि यह AB के संगत भुजा है। (ASA सर्वांगसमता)।

प्रश्न 2.
त्रिभुजों ABC और POR में ∠A = Q और ∠B = ∠R। POR की कौन-सी भुजा ∆ABC की BC भुजा के बराबर होनी चाहिए कि दोनों त्रिभुज सर्वांगसम हों ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
RP, क्योंकि यह BC के संगत भुजा है। (AAS सर्वांगसमता)

प्रश्न 3.
“यदि किसी त्रिभुज की दो भुजाओं और एक कोण दूसरे त्रिभुज की दो भुजाओं और एक कोण के बराबर हों, तो दोनों त्रिभुज अवश्य ही सर्वांगसम होने चाहिए।” क्या यह कथन सत्य है ? क्यों ?
उत्तर:
कथन असत्य है, क्योंकि भुजाओं के अंतर्गत कोण होना चाहिए।

प्रश्न 4.
“यदि किसी त्रिभुज के दो कोण एक भुजा, दूसरे त्रिभुज के दो कोण और एक भुजा के बराबर हों, तो दोनों त्रिभुज अवश्य ही सर्वांगसम होने चाहिए।” क्या यह कथन सत्य है ? क्यों ?
उत्तर:
कथन असत्य है, क्योंकि भुजाएँ संगत होनी चाहिए।

प्रश्न 5.
क्या भुजाओं की लम्बाइयों 4 सेमी, 3 सेमी और 7 सेमी लेकर किसी त्रिभुज की रचना की जा सकती है ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
त्रिभुज की रचना नहीं की जा सकती, क्योंकि यहाँ दो भुजाओं का योग तीसरी के बराबर है (यथा 4 + 3 = 7) जबकि यह बड़ा होना चाहिए।

प्रश्न 6.
∆ABC ≅ ∆RPQ दिया हुआ है। क्या यह कहना सत्य है कि BC = QR ? क्यों ?
उत्तर:
कथन सत्य नहीं है, क्योंकि भुजाएँ संगत होनी चाहिए।

प्रश्न 7.
यदि ∆POR ≅ ∆EDF है तो क्या यह कहना सत्य है कि PR = EF ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
कथन सत्य है, क्योंकि ये संगत भुजाएँ हैं।

प्रश्न 8.
∆POR में ∠P = 70° और ∠R = 30° है। उस त्रिभुज की कौन-सी भुजा सबसे लम्बी है ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
भुजा PR सबसे लम्बी है, क्योंकि ∠Q = 180° – 70° – 30° = 80° सबसे बड़ा है।

प्रश्न 9.
AD किसी त्रिभुज ABC की माध्यिका है। क्या यह कहना सत्य है कि AB + BC + CA > 2AD ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
कथन सत्य हैं, क्योंकि AB + BD > AD एवं AC + CD > AD.

प्रश्न 10.
M किसी त्रिभुज ABC की भुजा BC पर स्थित एक बिन्दु ऐसा है कि AM कोण BAC का समद्विभाजक है। क्या यह कहना सत्य है कि त्रिभुज का परिमाप 2AM से अधिक है ? अपने
उत्तर के लिए कारण दीजिए।
उत्तर:
कथन सत्य है, क्योंकि AB + BM > AM एवं AC + CM > AM.

प्रश्न 11.
क्या भुजाओं की लम्बाइयाँ 9 सेमी, 7 सेमी और 17 सेमी लेकर किसी त्रिभुज की रचना की जा सकती है ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
त्रिभुज की रचना नहीं की जा सकती, क्योंकि 9 + 7 < 17 जबकि दो भुजाओं का योग तीसरी से बड़ा होना चाहिए।

प्रश्न 12.
क्या भुजाओं की लम्बाइयों 8 सेमी, 7 सेमी और 4 सेमी लेकर किसी त्रिभुज की रचना की जा सकती है ? अपने उत्तर का कारण दीजिए।
उत्तर:
हाँ, रचना की जा सकती है। क्योंकि प्रत्येक स्थिति दो भुजाओं का योग तीसरी भुजा से बड़ा है।

MP Board Class 9th Maths Chapter 7 वस्तुनिष्ठ प्रश्न

बहु-विकल्पीय प्रश्न

प्रश्न 1.
निम्नलिखित में से कौन त्रिभुजों की सर्वांगसमता की एक कसौटी नहीं है :
(a) SAS
(b) ASA
(C) SSA
(d) SSS.
उत्तर:
(C) SSA

प्रश्न 2.
यदि AB = QR एवं BC = PR और CA = PQ है, तो :
(a) ∆ABC ≅ ∆PQR
(b) ∆CBA ≅ ∆PRQ
(c) ∆BAC ≅ ∆RPQ
(d) ∆PQR ≅ ∆BCA.
उत्तर:
(b) ∆CBA ≅ ∆PRQ

प्रश्न 3.
∆ABC में AB = AC और ∠B = 50° है तब ∠C बराबर है:
(a) 40°
(b) 50°
(c) 80°
(d) 130°.
उत्तर:
(b) 50°

प्रश्न 4.
∆ABC में BC = AB और ∠B = 80° तब ∠A बराबर है :
(a) 80°
(b) 40°
(c) 50°
(d) 100°.
उत्तर:
(c) 50°

प्रश्न 5.
∆POR में ∠R= ∠P तथा QR = 4 cm और PR = 5 cm है, तब PQ की लम्बाई है:
(a) 4 cm
(b) 5 cm
(c) 2 cm
(d) 2.5 cm.
उत्तर:
(a) 4 cm

प्रश्न 6.
D एक त्रिभुज ABC की भुजा BC पर एक बिन्दु इस प्रकार स्थित है कि AD कोण BAC को समद्विभाजित करता है। तब :
(a) BD = CD
(b) BA > BD
(c) BD > BA .
(d) CD > CA.
उत्तर:
(b) BA > BD

प्रश्न 7.
यह दिया है कि ∆ABC ≅ ∆FDE है तथा AB = 5 cm, ∠B = 40° एवं ∠A= 80° तब :
(a) DF = 5 cm, ∠F = 60°
(b) DF = 5 cm, ∠E = 60°
(c) DE = 5 cm, ∠F = 60°
(d) DE = 5 cm, ∠D = 40°.
उत्तर:
(b) DF = 5 cm, ∠E = 60°

प्रश्न 8.
एक त्रिभुज की दो भुजाओं की लम्बाइयाँ 5 cm और 1.5 cm है। इस त्रिभुज की तीसरी भुजा की लम्बाई निम्नलिखित नहीं हो सकती :
(a) 3.6 cm
(b) 4.1 cm
(c) 3.8 cm
(d) 3.4 cm.
उत्तर:
(d) 3.4 cm.

प्रश्न 9.
∆POR में यदि ∠P< ∠ R > ∠Q है, तो :
(a) QR > PR
(b) PQ > PR
(c) PQ < PR (d) QR > PR.
उत्तर:
(b) PQ > PR

प्रश्न 10.
∆ABC और ∆PQR में AB = AC, ∠C = ∠P और ∠B = 20 हैं। ये दोनों त्रिभुज हैं :
(a) समद्विबाहु परन्तु सर्वांगसम नहीं
(b) समद्विबाहु, सर्वांगसम
(c) सर्वांगसम परन्तु समद्विबाहु नहीं
(d) न तो सर्वांगसम और न हीं समद्विबाहु।
उत्तर:
(a) समद्विबाहु परन्तु सर्वांगसम नहीं

प्रश्न 11.
त्रिभुजों ABC और DEF में AB = FD तथा ∠A = ∠D है। दोनों त्रिभुज SAS अभिगृहीत से सर्वांगसम होंगे यदि :
(a) BC = EF
(b) AC = DE
(c) AC = EF
(d) BC = DE.
उत्तर:
(b) AC = DE

प्रश्न 12.
समान आकार एवं समान आकृति वाली आकृतियाँ होती हैं :
(a) बराबर
(b) समान
(c) सर्वांगसम
(d) समरूप।
उत्तर:
(c) सर्वांगसम

प्रश्न 13.
समकोण त्रिभुज में सबसे बड़ी भुजा होती है :
(a) लम्ब
(b) आधार
(c) कर्ण
(d) रेखा।
उत्तर:
(c) कर्ण

प्रश्न 14.
समबाहु त्रिभुज के प्रत्येक कोण का मान होता है : (2019)
(a) 90°
(b) 30°
(c) 60°
(d) 120°.
उत्तर:
(c) 60°

प्रश्न 15.
पाइथागोरस प्रमेय किस त्रिभुज के लिए प्रसिद्ध है :
(a) समबाहु त्रिभुज
(b) सर्वांगसम त्रिभुज
(c) समद्विबाहु त्रिभुज
(d) समकोण त्रिभुज।
उत्तर:
(d) समकोण त्रिभुज

रिक्त स्थानों की पूर्ति
1. समबाहु त्रिभुज का प्रत्येक कोण ……… होता है।
2. किसी त्रिभुज की दो भुजाओं का योग तीसरी भुजा से ……….. होता है।
3. समकोण त्रिभुज की सबसे बड़ी भुजा ………… होती है।
4. त्रिभुज के तीनों अन्तः कोणों का योग ………….. होता है।
5. समान आकार एवं समान आकृति वाली आकृतियाँ ……… होती हैं।
6. किसी त्रिभुज की दो भुजाएँ असमान हों तो, बड़ी भुजा के सामने का कोण ………. होता है।
7. किसी त्रिभुज की समान भुजाओं के सम्मुख कोण ………….. होते हैं।
8. किसी त्रिभुज में बड़े कोण के सामने की भुजा ………….. होती है।
उत्तर:
1. 60°,
2. बड़ा,
3. कर्ण,
4. 180°,
5. सर्वांगसम,
6. बड़ा,
7. बराबर,
8. बड़ी।

जोड़ी मिलान
स्तम्भ ‘A’                                                         स्तम्भ ‘B’
1. त्रिभुज जिसकी तीनों भुजाएँ समान हों     (a) अधिक कोण त्रिभुज
2. त्रिभुज जिसकी दो भुजाएँ समान हों        (b) न्यूनकोण त्रिभुज
3. त्रिभुज जिसका एक कोण 90° हो           (c) समबाहु त्रिभुज
4. त्रिभुज जिसका एक कोण अधिक कोण हो (d) केन्द्रक
5. त्रिभुज जिसका प्रत्येक कोण न्यूनकोण हो (e) समकोण त्रिभुज
6. माध्यिकाओं के संगमन बिन्दु को कहते हैं (2018) (f) समद्विबाहु त्रिभुज
उत्तर:
1. → (c),
2. → (1),
3. → (e),
4. → (a),
5. → (b),
6. → (d).

सत्य/असत्य कथन
1. समद्विबाहु त्रिभुज के तीनों कोण बराबर होते हैं। (2018)
2. किसी त्रिभुज के बड़े कोण के सामने की भुजा छोटी होती है।
3. किसी त्रिभुज की दो भुजाओं का योग, तीसरी भुजा से बड़ा होता है।
4. किसी रेखा के बाहर स्थित किसी बिन्दु से रेखा तक जितने रेखाखण्ड खींचे जा सकते हैं उनमें लम्ब सबसे छोटा होता है।
5. सभी वृत्त सर्वांगसम होते हैं।
6. यदि दो त्रिभुजों की संगत भुजाएँ बराबर हों, तो त्रिभुज बराबर हों, तो त्रिभुज सर्वांगसम होते हैं। (2019)
7. त्रिभुजों के तीनों कोणों का योग 180° होता है। (2019)
8. सर्वांगसम त्रिभुज में संगत भाग बराबर होते हैं। (2019)
उत्तर:
1. असत्य,
2. असत्य,
3. सत्य,
4. सत्य,
5. असत्य,
6. सत्य,
7. सत्य,
8. सत्य।

एक शब्द/वाक्य में उत्तर

1. किसी त्रिभुज में अधिकतम कितने समकोण हो सकते हैं ?
2. किसी त्रिभुज में अधिकतम कितने अधिक कोण हो सकते हैं ?
3. किसी त्रिभुज में कम-से-कम कितने न्यूनकोण हो सकते हैं ?
4. किसी त्रिभुज के बहिष्कोण और अन्तः कोणों में क्या सम्बन्ध होता है ?
5. समकोण समद्विबाहु त्रिभुज के प्रत्यके न्यूनकोण का मान कितना होता है ?
उत्तर:
1. एक,
2. एक,
3. दो,
4. त्रिभुज का बहिष्कोण सम्मुख अन्त:कोणों के योग के बराबर है अर्थात् प्रत्येक सम्मुख अन्तः कोण से बड़ा होता है,
5. 45° ।

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 6 रेखाएँ और कोण Additional Questions

MP Board Class 9th Maths Chapter 6 अतिरिक्त परीक्षोपयोगी प्रश्न

MP Board Class 9th Maths Chapter 6 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
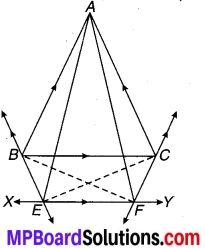
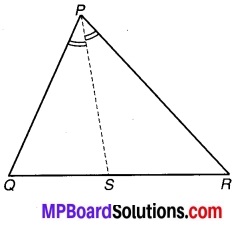
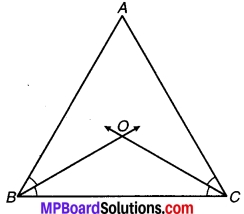
एक त्रिभुज ABC के कोण B और C के समद्विभाजक परस्पर बिन्दु 0 पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि-
∠BOC = 90° + \(\frac { 1 }{ 2 }\) ∠A.

हल:
दिया है :
∆ABC जिसके ∠B एवं ∠C के समद्विभाजक BO एवं CO परस्पर बिन्दु O पर प्रतिच्छेद करते हैं तो सिद्ध करना है कि-
∠BOC = 90° + \(\frac { 1 }{ 2 }\) ∠A.
उपपत्ति : त्रिभुज ABC में,
∵∠A + ∠ABC + ∠ACB = 180° (त्रिभुज का कोण योग गुण)
= \(\frac { 1 }{ 2 }\)∠A + \(\frac { 1 }{ 2 }\)∠ABC + \(\frac { 1 }{ 2 }\) ∠ACB = \(\frac { 1 }{ 2 }\) x 180° = 90°
⇒ \(\frac { 1 }{ 2 }\) ∠A + ∠OBC + ∠OCB = 90° (क्योंकि BO एवं CO क्रमशः ∠B एवं ∠C के समद्विभाजक हैं)
⇒ ∠OBC + ∠OCB = 90° \(\frac { 1 }{ 2 }\) ∠A ….(1)
लेकिन ∠BOC + ∠OBC + ∠OCB = 180° (त्रिभुज का कोण योग गुण)
⇒ ∠OBC + ∠OCB = 180° – ∠BOC …(2)
⇒ 90° – \(\frac { 1 }{ 2 }\) ∠A = 180° – ∠BOC [समीकरण (1) एवं (2) से]
⇒ ∠BOC = 180° – 90° + \(\frac { 1 }{ 2 }\) ∠A
अतः ∠BOC = 90° + 1 इति सिद्धम्

प्रश्न 2.
यदि दो रेखाएँ प्रतिच्छेद करती है तो सिद्ध कीजिए कि शीर्षाभिमुख कोण बराबर होते हैं।
हल:
मान लीजिए दो रेखाएँ AB एवं CD परस्पर O बिन्दु पर प्रतिच्छेद करती हैं तो सिद्ध करना है कि-
∠AOC = ∠BOD एवं ∠BOC = ∠AOD
उपपत्ति: ∵ ∠AOC + ∠COB = 180° (∵ रेखा AB के बिन्दु O पर एक ही ओर बने कोण हैं।)

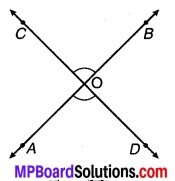
चित्र 6.37
∵ ∠COB + ∠BOD = 180° …(2) (∵ रेखा CD के बिन्दु 0 पर एक ही ओर बने कोण हैं।)
⇒ ∠AOC + ∠COB = ∠COB + ∠BOD [समीकरण (1) एवं (2) से]
⇒ ∠AOC = ∠BOD (∠COB उभयनिष्ठ है)
इसी प्रकार सिद्ध कर सकते हैं कि ∠BOC = ∠AOD.
अतः यदि दो रेखाएँ परस्पर प्रतिच्छेद करती हैं तो शीर्षाभिमुख कोण बराबर होते हैं। इति सिद्धम्

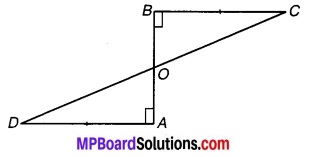
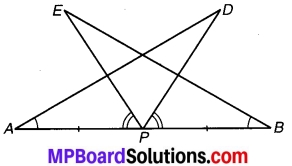
प्रश्न 3.
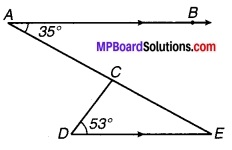
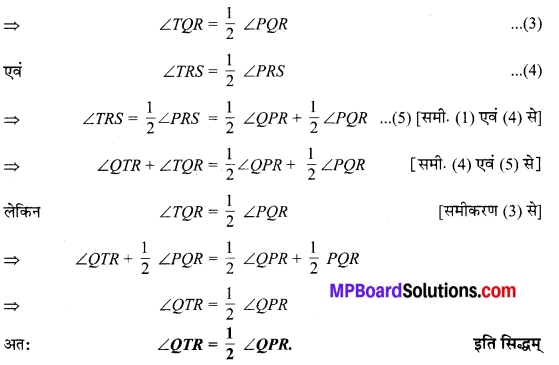
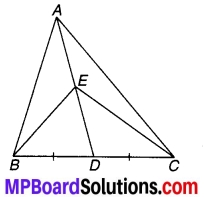
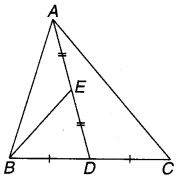
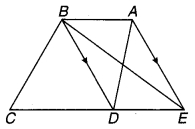
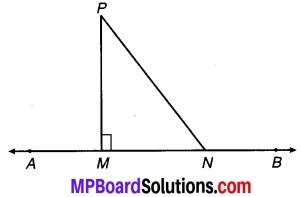
∆ABC के अन्तःकोण ∠B और बहिष्कोण ∠ACD के समद्विभाजक बिन्दु T पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि ∠BTC = \(\frac { 1 }{ 2 }\)∠BAC.
हल:
ज्ञात है : ∆ABC के अन्त:कोण ∠B एवं बहिष्कोण ∠ACD के समद्विभाजक बिन्दु T पर प्रतिच्छेद करते हैं।
सिद्ध करना है: ∠BTC = \(\frac { 1 }{ 2 }\)∠BAC.
उपपत्ति : ∵ ∆ABC का बहिष्कोण ∠ACD

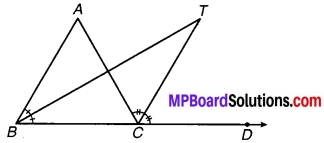
चित्र 6.38
⇒ ∠ACD = ∠BAC + ∠ABC
⇒ \(\frac { 1 }{ 2 }\)∠ACD = \(\frac { 1 }{ 2 }\)∠BAC + \(\frac { 1 }{ 2 }\) ∠ABC
⇒ ∠TCD = \(\frac { 1 }{ 2 }\)∠BAC + ∠TBC …(1)
(चूँकि BT एवं CT क्रमशः ∠ABC एवं ∠ACD के समद्विभाजक हैं।)
∵ ∆TBC का बहिष्कोण ∠TCD है। ∠TCD = ∠TBC + ∠BTC …(2)
⇒ ∠TBC + ∠BTC = \(\frac { 1 }{ 2 }\) ∠BAC + ∠TBC [समीकरण (1) एवं (2) से]
अतः ∠BTC = \(\frac { 1 }{ 2 }\) ∠BAC. इति सिद्धम्

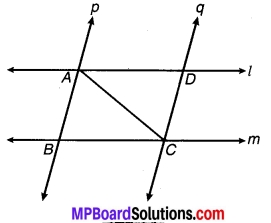
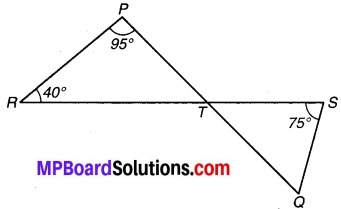
प्रश्न 4.
एक तिर्यक रेखा दो समान्तर रेखाओं को प्रतिच्छेद करती है। सिद्ध कीजिए कि इस प्रकार बने संगत कोणों के युग्म के समद्विभाजक समान्तर होते हैं।
हल:
ज्ञात है : एक तिर्यक रेखा l, दो समानान्तर रेखाओं m एवं n को क्रमशः A एवं B बिन्दुओं पर प्रतिच्छेद करती हैं, संगत कोण ∠lAm एवं ∠ABn के समद्विभाजक क्रमश: Ap एवं Bq हैं तो सिद्ध करना है कि Ap || Bq.

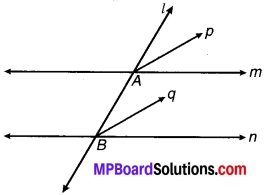
चित्र 6.39
उपपत्ति : चूँकि p एवं q क्रमशः कोण ∠lAm एवं ∠ABn के समद्विभाजक हैं।
⇒ ∠lAp = ∠pAm
एवं ∠ABq = ∠qBn
⇒ ∠lAp = \(\frac { 1 }{ 2 }\)∠lam एवं ∠ABq = \(\frac { 1 }{ 2 }\)∠ABn …(1)
चूँकि m|| n को तिर्यक रेखा l प्रतिच्छेद करती है
⇒ ∠lAm = ∠ABn ….(2)
⇒ ∠lAp = ∠ABq [समीकरण (1) एवं (2) से]
लेकिन ∠lAp एवं ∠ABq संमत कोण हैं।
अतः Ap || Bq. इति सिद्धम्

MP Board Class 9th Maths Chapter 6 लघु उत्तरीय प्रश्न

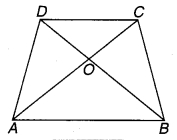
प्रश्न 1.
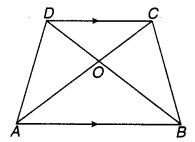
संलग्न चित्र में OD कोण ∠AOC का समद्विभाजक है, OE कोण ∠BOC का समद्विभाजक है तथा OD 1 OE। दर्शाइए कि AOB संरेख हैं।

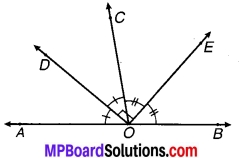
चित्र 6.40
हल:
चूँकि OD कोण AOC एवं OE कोण BOC के समद्विभाजक हैं।
⇒ ∠AOD = ∠DOC
एवं ∠BOE = ∠EOC.
⇒ ∠AOD + ∠BOE = ∠DOC + ∠EOC = ∠DOE = 90° [चूँकि OD ⊥ OE (दिया है)]
= ∠AOD + ∠BOE + ∠DOC + ∠EOC = 180°
चूँकि बिन्दु O पर किरण OA एवं OB के एक ही ओर बने कोण का योग 180° है।
इसलिए OA एवं OB एक सरल रेखा में हैं।
अतः AOB संरेख हैं। इति सिद्धम्

प्रश्न 2.
संलग्न चित्र में ∠1 = 60° और ∠6 = 120° हैं। दर्शाइए m और n समान्तर है।

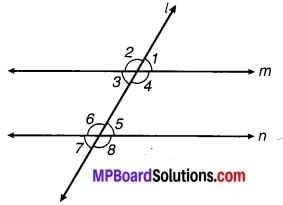
चित्र 6.41
हल:
∠1 + ∠4 = 180° (∵ एक रेखा के एक बिन्दु पर एक ओर बने कोण हैं)
⇒ ∠4 = 180° – ∠1 .
= 180° + 60°= 120°
⇒ ∠6 = 24 = 120° [क्योंकि ∠6 = 120° (दिया गया है)]
लेकिन ये एकान्तर कोण है।
अतः m || n. इति सिद्धम् ।

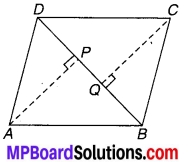
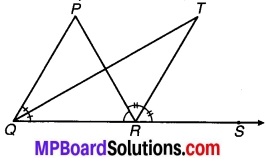
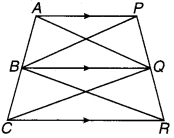
प्रश्न 3.
संलग्न चित्र में AP और BQ उन दो एकान्तर अन्तःकोणों के समद्विभाजक हैं जो समान्तर रेखाओं l और m के तिर्यक रेखा t द्वारा प्रतिच्छेद से बनते हैं। दर्शाइए कि AP || BQ.

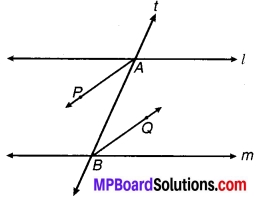
चित्र 6.42
हल:
चूँकि l || m को तिर्यक रेखा t बिन्दु A और B पर प्रतिच्छेद करती है। (दिया है)
⇒ ∠lAB = ∠ABm (एकान्तर कोण हैं) …(1)
चूँकि AP एवं BQ क्रमशः ∠lAB एवं ABm के समद्विभाजक हैं (दिया है)
⇒ ∠PAB = \(\frac { 1 }{ 2 }\)∠lAB एवं ∠ABQ = \(\frac { 1 }{ 2 }\)∠ABm …(2)
⇒ ∠PAB = ∠ABQ [समीकरण (1) एवं (2) से]
लेकिन ये एकान्तर कोण हैं
अतः AP || BQ. इति सिद्धम्

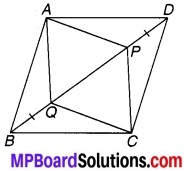
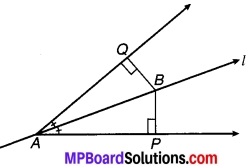
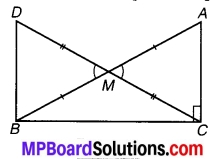
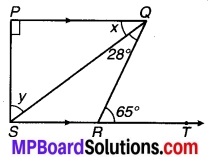
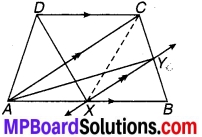
प्रश्न 4.
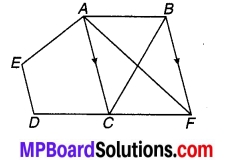
संलग्न चित्र में DE || QR तथा AP और BP क्रमशः कोण ∠EAB और ∠RBA की समद्विभाजक हैं। ∠APB ज्ञात कीजिए।

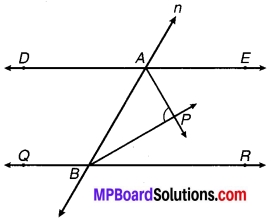
चित्र 6.43
हल:
चूँकि DE || QR को तिर्यक रेखा n क्रमशः बिन्दु A एवं B पर प्रतिच्छेद करती हैं।
⇒ ∠EAB + ∠ABR = 180° …(1) (एक ही ओर के अन्तः कोण हैं)
चूँकि AP एवं BP क्रमशः कोण EAB एवं ABR के समद्विभाजक हैं।
⇒ ∠PAB = \(\frac { 1 }{ 2 }\)∠EAB एवं ∠PBA = \(\frac { 1 }{ 2 }\)∠ABR
⇒ ∠PAB + ∠PBA = \(\frac { 1 }{ 2 }\) (∠EAB + ∠ABR) ….(2)
⇒ ∠PAB + ∠PBA = 90° [समीकरण (1) एवं (2) से] …(3)
⇒ ∠PAB + ∠PBA + ∠APB = 180° [त्रिभुज के अन्तःकोण हैं] …(4)
⇒ 90° + ∠APB = 180° [समीकरण (3) एवं (4) से)]
⇒∠APB = 180° – 90° = 90°
अतः ∠APB का अभीष्ट मान = 90°.

प्रश्न 5.
किसी त्रिभुज के कोणों का अनुपात 2 : 3 : 4 है। त्रिभुज के तीनों कोण ज्ञात कीजिए।
हल:
कोणों के अनुपात का योग = 2 + 3 + 4 = 9, कोणों के मानों का योग = 180° (हम जानते हैं)

अतः त्रिभुज के तीनों कोणों से अभीष्ट मान क्रमशः 40°, 60° एवं 80° हैं।

MP Board Class 9th Maths Chapter 6 अति लघु उत्तरीय प्रश्न

प्रश्न 1.
संलग्न चित्र में x + y के किस मान के लिए ABC एक रेखा होगी ? अपने उत्तर का औचित्य दीजिए।

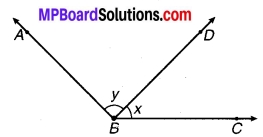
चित्र 6.44
उत्तर:
x + y = 180°, क्योंकि ABC को एक रेखा होने के लिए दोनों कोणों का योग 180° होना चाहिए।

प्रश्न 2.
क्या किसी त्रिभुज के सभी कोण 60° से कम हो सकते हैं ? अपने उत्तर के लिए कारण दीजिए। (2019)
उत्तर:
नहीं हो सकते, क्योंकि त्रिभुजों के तीनों कोणों का योग 180° होता है। उक्त स्थिति में कोणों का योग 180° से कम होगा।

प्रश्न 3.
क्या किसी त्रिभुज के दो अधिककोण हो सकते हैं ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
नहीं हो सकते, क्योंकि उक्त स्थिति में त्रिभुज के तीनों कोणों का योग 180° से अधिक होगा जबकि त्रिभुज के तीनों कोणों का योग 180° होता है।

प्रश्न 4.
कोणों 45°, 64° और 72° वाले कितने त्रिभुज खींचे जा सकते हैं ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
कोई भी त्रिभुज नहीं खींचा जा सकता, क्योंकि उक्त स्थिति में तीनों कोणों का योग 45° + 64° + 72° = 181° हो जाता है जो 180° से अधिक है।

प्रश्न 5.
कोणों 53°, 64° और 63° वाले कितने त्रिभुज खींचे जा सकते हैं ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
अपरिमित रूप से अनेक त्रिभुज खींचे जा सकते हैं, क्योंकि प्रत्येक दशा में कोणों का योग 53° + 64° + 63° = 180 होता है।

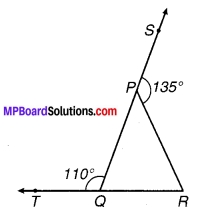
प्रश्न 6.
संलग्न चित्र में x का मान ज्ञात कीजिए जिसके लिए l और m समान्तर होंगे।

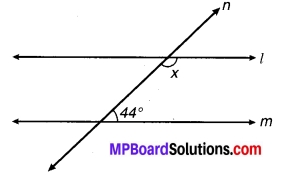
चित्र 6.45
हल:
x + 44° = 180°
⇒ x = 180° – 44° = 136°
अतः x का अभीष्ट मान = 136°.

प्रश्न 7.
दो आसन्न कोण बराबर है। क्या यह आवश्यक है कि वे दोनों कोण समकोण हों ? अपने
उत्तर:
का औचित्य दीजिए। उत्तर- कोई आवश्यक नहीं, क्योंकि यह तभी सम्भव है जब ये रेखायुग्म बनाएँ।

प्रश्न 8.
यदि दो प्रतिच्छेदी रेखाओं से बना एक कोण समकोण है, तो अन्य तीनों कोणों के बारे में आप क्या कह सकते हैं ? अपने उत्तर का कारण दीजिए।
उत्तर:
अन्य तीनों कोण भी समकोण होंगे, रैखिक युग्म अभिगृहीत के कारण।

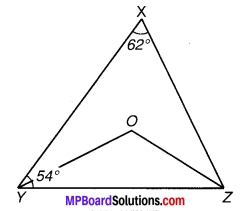
प्रश्न 9.
निम्न चित्र में कौन-सी दो रेखाएँ समान्तर हैं और क्यों?

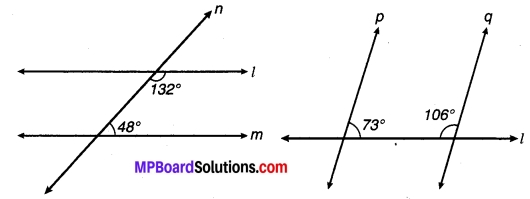
चित्र 6.46
उत्तर:
रेखाएँ l || m क्योंकि एक ही ओर के अन्तः कोणों का योग = 132° + 48° = 180°
रेखाएँ p एवं q समान्तर नहीं है, क्योंकि एक ही ओर के अन्तः कोणों का योग = 73° + 106° = 179° + 180°

प्रश्न 10.
दो रेखाएँ l और m एक ही रेखा n पर लम्ब हैं। क्या l और m परस्पर लम्ब हैं ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
नहीं, क्योंकि ये समान्तर हैं।

MP Board Class 9th Maths Chapter 6 वस्तुनिष्ठ प्रश्न

बहु-विकल्पीय प्रश्न

प्रश्न 1.
यदि किसी त्रिभुज का एक कोण अन्य दो कोणों के योग के बराबर हो, तो वह त्रिभुज है एक :
(a) समद्विबाहु त्रिभुज
(b) अधिक कोण त्रिभुज
(c) समबाहु त्रिभुज
(d) समकोण त्रिभुज।
उत्तर:
(d) समकोण त्रिभुज

प्रश्न 2.
एक त्रिभुज का एक बहिष्कोण 105° है तथा उसके दोनों अन्तः विपरीत कोण बराबर हैं। इनमें से प्रत्येक बराबर कोण है :
(a) 37 \(\frac { 1 }{ 2 }\) °
(b) 27 \(\frac { 1 }{ 2 }\)°
(c) 72 \(\frac { 1 }{ 2 }\) °
(d) 75°.
उत्तर:
(b) 27 \(\frac { 1 }{ 2 }\)°

प्रश्न 3.
किसी त्रिभुज के कोणों का अनुपात 5 : 3 : 7 है। वह त्रिभुज है एक :
(a) न्यूनकोण त्रिभुज
(b) अधिक कोण त्रिभुज
(c) समकोण त्रिभुज
(d) समद्विबाहु त्रिभुज।
उत्तर:
(a) न्यूनकोण त्रिभुज

प्रश्न 4.
किसी त्रिभुज का एक कोण 130° है तो अन्य दोनों कोणों के समद्विभाजकों के बीच कोण हो सकता है:
(a) 50°
(b) 65°
(c) 145°
(d) 155°
उत्तर:
(d) 155°

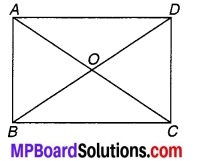
प्रश्न 5.
संलग्न चित्र में POQ एक रेखा है। x का मान है :

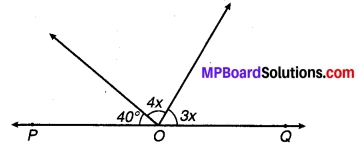
चित्र 6.47
(a) 20°
(b) 25°
(c) 30°
(d) 35°.
उत्तर:
(a) 20°

प्रश्न 6.
एक त्रिभुज के कोण 2 : 4 : 3 के अनुपात में हैं। त्रिभुज का सबसे छोटा कोण है :
(a) 60°
(b) 40°
(c) 80°
(d) 20°.
उत्तर:
(b) 40°

रिक्त स्थानों की पूर्ति
1. सरल रेखा का वह भाग जिसके दो अन्त बिन्दु हों, ………… कहलाता है।
2. यदि तीन या अधिक बिन्दु एक ही सरल रेखा में हों, तो वे बिन्दु ……. कहलाते हैं।
3. सरल रेखा का वह भाग जिसका एक बिन्दु हो ……… कहलाता है।
4. जब दो किरण एक ही अन्त बिन्दु से आरम्भ होती हैं तो एक ………. बनता है।
5. कोण बनाने वाली दोनों किरणें ………. कहलाती हैं।
6. यदि दो आसन्न कोणों का योग ……… हो, तब वे रैखिक युग्म बनाते हैं। (2019)
उत्तर:
1. रेखाखण्ड,
2. सरेख बिन्दु,
3. किरण,
4. कोण,
5. उस कोण की भुजाएँ,
6. 180°.

जोड़ी मिलान

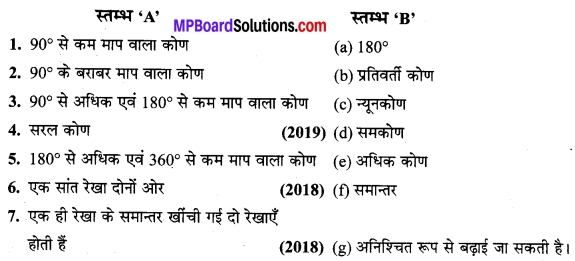
उत्तर:
1. → (c),
2. → (d),
3. → (e),
4. → (a),
5. → (b),
6. → (g),
7. → (1).

सत्य/असत्य कथन
1. कोटि पूरक कोणों का योग 180° होता है।
2. किसी त्रिभुज में कम-से-कम दो न्यूनकोण होते हैं।
3. सम्पूरक कोणों का योग 90° होता है।
4. किसी त्रिभुज में दो समकोण नहीं हो सकते।
5. जब दो असमान्तर रेखाओं को एक तिर्यक रेखा प्रतिच्छेद करे तो एकान्तर कोण बराबर होते हैं।
उत्तर:
1. असत्य,
2. सत्य,
3. असत्य,
4. सत्य,
5. असत्य।

एक शब्द/वाक्य में उत्तर
1. त्रिभुजों के तीनों अन्तः कोणों का योग कितना होता है?
2. समबाहु त्रिभुज के प्रत्येक कोण का माप क्या होता है?
3. दो समान्तर रेखाओं को एक तिर्यक रेखा प्रतिच्छेद करे तो एक ही ओर के दो अन्त: कोणों का योग कितना होता है?
4. दो रेखाएँ प्रतिच्छेद करती हैं तो शीर्षाभिमुख कोणों में क्या सम्बन्ध होता है? 5. समकोण समद्विबाहु त्रिभुज के न्यूनकोण का माप क्या होगा?
उत्तर:
1. 180°,
2. 60°,
3. 180°,
4. बराबर होते हैं,
5. 45°.

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 5 युक्लिड के ज्यामिति का परिचय Additional Questions

MP Board Class 9th Maths Chapter 5 अतिरिक्त परीक्षोपयोगी प्रश्न

MP Board Class 9th Maths Chapter 5 दीर्घ उत्तरीय प्रश्न

प्रश्न 1. निम्नलिखित कथन को पढ़िए :
“एक समबाहु त्रिभुज तीन रेखाखण्डों से बना एक बहुभुज है जिनमें से दो रेखाखण्ड तीसरे रेखाखण्ड के बराबर हैं तथा इसका प्रत्येक कोण 60° का है।” इस परिभाषा में उन पदों को परिभाषित कीजिए जिन्हें आप आवश्यक समझते हैं। क्या इसमें कोई अपरिभाषित पद है ? क्या आप इसका औचित्य दे सकते हैं कि एक समबाहु त्रिभुज के सभी कोण और सभी भुजाएँ बराबर होती हैं। उत्तर:
परिभाषित किए जाने वाले पद :
बहुभुज : तीन या तीन से अधिक रेखाखण्डों से बनी एक सरल बन्द आकृति।
रेखाखण्ड : रेखा का वह भाग जिसके दो अन्त-बिन्दु हों।
रेखा : अपरिभाषित पद।
बिन्दु : अपरिभाषित पद।
कोण : उभयनिष्ठ शीर्ष वाली दो किरणों से बनी आकृति।
किरण : रेखा का वह भाग जिसका एक अन्त-बिन्दु हो।
त्रिभुज : तीन रेखाखण्डों से निर्मित एक सरल बन्द आकृति।
अपरिभाषित पद : रेखा एवं बिन्दु।। त्रिभुज का प्रत्येक कोण का माप 60° है (दिया है)
अतः समबाहु त्रिभुज के सभी कोण बराबर हैं। दो रेखाखण्ड तीसरे रेखाखण्ड के बराबर है (दिया है)।
अतः समबाहु त्रिभुज की तीनों भुजाएँ बराबर होंगी। (यूक्लिड की प्रथम अभिगृहीत से “वे वस्तुएँ जो एक ही वस्तु के बराबर हों, परस्पर बराबर होती हैं।”)

MP Board Class 9th Maths Chapter 5 लघु उत्तरीय प्रश्न

प्रश्न 1.
दो सेल्समेनों ने अगस्त महीने में बराबर बिक्री की। सितम्बर में प्रत्येक सेल्समेन अपनी बिक्री अगस्त के महीने की बिक्री की दो गुनी कर लेता है। दोनों की सितम्बर की बिक्रियों की तुलना
कीजिए।
उत्तर:
चूँकि अगस्त में दोनों सेल्समेनों की बिक्री बराबर है। सितम्बर में दोनों की बिक्री अगस्त की बिक्री की दो गुनी है।
अत: दोनों की सितम्बर की बिक्री भी बराबर होगी, क्योंकि बराबर का दो गुना बराबर होता है। (अभिगृहीत-6 के अनसार।)

प्रश्न 2.
यह ज्ञात है कि x + y = 10 और x = है। दर्शाइए कि x + y = 10 है।
हल:
चूंकि y = y (अभिगृहीत – 4 से)
एवं x = z (दिया है)
⇒ x + y = z + y
(अभिगृहीत – 2 से)
एवं x + y = 10 (दिया है)
अतः z + y = 10. (अभिगृहीत-1 से) इति सिद्धम्

प्रश्न 3.
संलग्न चित्र को देखिए। दर्शाइए :
AH > AB + BC + CD है।

हल :
चित्रानुसार,
AB+ BC + CD, AH का एक भाग है
अतः AH > AB + BC + CD. (अभिगृहीत – 5)
अर्थात् पूर्ण अपने भाग से बड़ा होता है।

प्रश्न 4.
संलग्न चित्र में AB = BC एवं BX = BY दर्शाइए कि AX = CY है।
हल:

∵AB = BC (दिया है)
∵ BX = BY (दिया है)
AB – BX = BC – BY (अभिगृहीत – 3)
लेकिन AB – BX = AX
एवं BC – BY = CY (चित्रानुसार)
अतः Ax = CY.  इति सिद्धम्

प्रश्न 5.
संलग्न चित्र में AC = DC और CB = CE है। दर्शाइए कि AB = DE है।

हल:
AC = DC (दिया है)
एवं CB = CE (दिया है)
AC + CB = DC + CE (अभिगृहीत – 2)
लेकिन AC + CB = AB
एवं DC + CE = DE (चित्रानुसार)
अतः AB = DE. इति सिद्धम्

MP Board Class 9th Maths Chapter 5 अति लघु उत्तरीय प्रश्न

निम्न कथन सत्य हैं या असत्य लिखिए। अपने उत्तर का औचित्य दीजिए :

प्रश्न 1.
यूक्लिडीय ज्यामिति केवल वक्र पृष्ठों के लिए ही मान्य है।
उत्तर:
असत्य कथन। यह केवल तल में बनी आकृतियों के लिए ही मान्य है।

प्रश्न 2.
ठोसों की परिसीमाएँ वक्र होती हैं।
उत्तर:
असत्य कथन। ठोसों की परिसीमाएँ पृष्ठ होते हैं।

प्रश्न 3.
एक पृष्ठ के किनारे वक्र होते हैं।
उत्तर:
असत्य कथन। पृष्ठों के किनारे रेखाएँ होती हैं।

प्रश्न 4.
वस्तुएँ जो एक ही वस्तु की दो गुनी हों बराबर होती हैं।
उत्तर:
सत्य कथन। यह यूक्लिड का एक अभिगृहीत है।

प्रश्न 5.
यदि एक राशि B एक अन्य राशि A का एक भाग है, तो A को B और एक अन्य राशि C के रूप में लिखा जा सकता है।
उत्तर:
सत्य कथन। यूक्लिड के एक अभिगृहीत के कारण।

प्रश्न 6.
वे कथन जिन्हें सिद्ध किया जा सकता है, अभिगृहीत कहलाते हैं।
उत्तर:
असत्य कथन। सिद्ध किए गए कथन प्रमेय कहलाते हैं।

प्रश्न 7.
कथन प्रत्यके रेखा l और उस पर न स्थित प्रत्येक बिन्दु P के लिए एक अद्वितीय रेखा का अस्तित्व है जो P से होकर जाती है और l के समान्तर है, प्लेफेयर अभिगृहीत कहलाता है।
उत्तर:
सत्य कथन। यह यूक्लिड की पाँचवीं अभिधारणा का एक रूपान्तरण है।

प्रश्न 8.
दो भिन्न प्रतिच्छेदी रेखाएँ एक ही रेखा के समान्तर नहीं हो सकती।
उत्तर:
सत्य कथन। यह यूक्लिड की पाँचवीं अभिधारणा का एक रूपान्तरण है।

प्रश्न 9.
यूक्लिड की पाँचवीं अभिधारणा को अन्य अभिधारणाओं और अभिगृहीतों का प्रयोग करते हुए सिद्ध करने के प्रयासों के फलस्वरूप अन्य अनेक ज्यामितियों की खोज हुई।
उत्तर:
सत्य कथन। ये ज्यामितियाँ यूक्लिडीय ज्यामिति से भिन्न है।

MP Board Class 9th Maths Chapter 5 वस्तुनिष्ठ प्रश्न

बहु-विकल्पीय प्रश्न

प्रश्न 1.
प्राचीन भारत में, आयतों, त्रिभुजों और समलम्बों से समायोजित आकारों की वेदियाँ निम्नलिखित में प्रयोग होती थीं:
(a) सार्वजनिक पूजास्थल
(b) घरेलू पूजास्थल
(c) A और B दोनों
(d) इनमें से कोई नहीं।
उत्तर:
(a) सार्वजनिक पूजास्थल

प्रश्न 2.
प्राचीन भारत में घरेलू पूजा कार्य में प्रयोग की जाने वाली वेदियों के आकार होते थे :
(a) वर्ग और वृत्त
(b) त्रिभुज और आयत
(c) समलम्ब और पिरामिड
(d) आयत और वर्ग।
उत्तर:
(a) वर्ग और वृत्त

प्रश्न 3.
अथर्ववेद में दिए गए ‘श्री यन्त्र’ में एक-दूसरे के साथ जुड़े अन्तर्निहित समद्विबाहु त्रिभुजों की संख्या है:
(a) सात
(b) आठ
(c) नौ
(d) ग्यारह।
उत्तर:
(c) नौ

प्रश्न 4.
यूनानियों ने निम्नलिखित पर बल दिया :
(a) आगमन, तर्कण
(b) निगमन, तर्कण
(c) A और B
(d) ज्यामिति का व्यावहारिक प्रयोग।
उत्तर:
(b) निगमन, तर्कण

प्रश्न 5.
यूक्लिड निम्नलिखित देश का वासी था :
(a) बेबीलोनिया
(b) मिस्र
(c) यूनान
(d) भारत।
उत्तर:
(c) यूनान

प्रश्न 6.
थेल्स निम्नलिखित देश का वासी था :
(a) बेबीलोनिया
(b) मिस्र
(c) यूनान
(d) रोम।
उत्तर:
(c) यूनान

प्रश्न 7.
पाइथागोरस एक विद्यार्थी था :
(a) थेल्स का
(b) यूक्लिड का
(c) (a) और (b) दोनों का
(d) आर्कमिडीज का।
उत्तर:
(a) थेल्स का

प्रश्न 8.
निम्नलिखित में से किसकी उपपत्ति की आवश्यकता है :
(a) प्रमेय
(b) अभिगृहीत
(c) परिभाषा
(d) अभिधारणा।
उत्तर:
(a) प्रमेय

प्रश्न 9.
यूक्लिड के कथन सभी समकोण एक दूसरे के बराबर होते हैं निम्न के रूप में दिया गया है :
(a) अभिगृहीत
(b) परिभाषा
(c) अभिधारणा
(d) उपपत्ति।
उत्तर:
(c) अभिधारणा

प्रश्न 10.
“रेखाएँ समान्तर होती हैं, यदि वे प्रतिच्छेद नहीं करतीं” का कथन निम्न रूप में दिया गया है:
(a) अभिगृहीत
(b) परिभाषा
(c) अभिधारणा
(d) उपपत्ति।
उत्तर:
(b) परिभाषा

रिक्त स्थानों की पूर्ति

1. पिरामिड का आधार …….. होता है।
2. पिरामिड के पार्श्व फलक ……… होते हैं।
3. कोणों की परिसीमाएँ ……….. होती हैं।
4. पृष्ठों की परिसीमाएँ …….होती हैं।
5. सिन्धु घाटी की सभ्यता में निर्माण हेतु प्रयुक्त ईंटों की विमाओं में ……… का अनुपात था।
6. ………….. अपने भाग से बड़ा होता है। (2019)
उत्तर:
1. कोई भी बहुभुज,
2. त्रिभुजाकार,
3. पृष्ठ,
4. वक्र,
5. 4 : 2 : 1,
6. पूर्ण।

जोड़ी मिलान
स्तम्भ ‘A’                                               स्तम्भ ‘B’
1. एक ठोस की विमाओं की संख्या          (a) 13
2. एक पृष्ठ की विमाओं की संख्या           (b) 465
3. एक बिन्दु की विमाओं की संख्या         (c) 3
4. एलीमेण्ट्स में अध्यायों की संख्या        (d) 2
5. एलीमेण्ट्स में साध्यों की संख्या           (e) 0
उत्तर:
1. → (c),
2. → (d),
3. → (e),
4. → (a),
5. → (b).

सत्य/असत्य कथन

1. पिरामिड एक ठोस है जिसका आधार सदैव एक समबाहु त्रिभुज होता है।
2. ज्यामिति में हम बिन्दु, रेखा और तल को अपरिभाषित पद मानते हैं।
3. यूक्लिड की चौथी अभिगृहीत “प्रत्येक वस्तु स्वयं के बराबर होती है।”
4. यूक्लिड की ज्यामिति केवल तल में स्थित आकृतियों के लिए मान्य है।
5. बराबर वस्तुओं में समान वस्तु जोड़ने पर योग बराबर नहीं होता।
उत्तर:
1. असत्य,
2. सत्य,
3. सत्य,
4. सत्य,
5. असत्य।

एक शब्द/वाक्य में उत्तर

1. एक बिन्दु से होकर कितनी सरल रेखाएँ खींची जा सकती हैं? (2019)
2. दो बिन्दुओं के बीच कितनी सरल रेखाएँ खींची जा सकती हैं?
3. “पूर्ण अपने भाग से बड़ा होता है” कौन-सी अभिगृहीत है?
4. “सभी समकोण एक-दूसरे के बराबर होते हैं” कौन-सी अभिधारणा है?
5. जो वस्तुएँ एक ही वस्तु के बराबर हों उनमें क्या सम्बन्ध होता है?
6. यूक्लिड की एक अवधारणा लिखिए। (2019)
उत्तर:
1. असंख्य,
2. एक,
3. पाँचवीं अभिगृहीत,
4. चौथी अभिधारणा,
5. बराबर होती हैं,
6. एक बिन्दु से एक अन्य बिन्दु तक एक सीधी रेखा खींची जा सकती है।

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 2 बहुपद Additional Questions

MP Board Class 9th Maths Chapter 2 अतिरिक्त परीक्षोपयोगी प्रश्न

MP Board Class 9th Maths Chapter 2 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
यदि बहुपदों az³ + 4z³ + 3z – 4 और z³ – 4z + a को z – 3 से भाग देने पर प्रत्येक दशा में समान शेषफल प्राप्त होता है, तो a का मान ज्ञात कीजिए।
हल:
मान लीजिए p(E) = az³ + 4z³ + 3z – 4
तथा q(a) = z³ – 4z + a
∵ z – 3 दिए गए बहुपदों का भाजक है जिसका शून्यक 2 -3 = 0 ⇒ z = 3 है
तो शेषफल p(3) = a(3)³ + 4(3)² + 3(3) – 4 = 27a + 36 + 9 – 4 = 27a + 41
एवं शेषफल q(3) = (3)³ – 4(3) + a = 27 – 12 + a = a + 15
चूँकि शेषफल p(3) = शेषफल q(3) (दिया हुआ है)
⇒ 27a + 41 = a + 15
⇒ 27a – a = 15 – 41
⇒ 26a = – 26
⇒ a = – 1
अतः a का अभीष्ट मान = -1.

प्रश्न 2.
यदि x – 2 और x – \(\frac { 1 }{ 2 }\) दोनों ही px² + 5x +r के गुणनखण्ड हैं, तो दर्शाइए कि p = r है।
हल:
मान लीजिए कि बहुपद q(x) = px² + 5x +r (दिया है)
चूँकि x – 2 दिए हुए बहुपद q(x) का एक गुणनखण्ड है।
इसलिए x – 2 = 0 अर्थात् x = 2 इसका एक शून्यक होगा।
⇒ q(2) = p(2)³ + 5(2) + r = 0 =
⇒ 4p + 10 + r = 0  …(i)
चूँकि x – \(\frac { 1 }{ 2 }\)  दिए हुए बहुपद q(x) का एक गुणनखण्ड है इसलिए x – \(\frac { 1 }{ 2 }\) = 0 अर्थात् x = \(\frac { 1 }{ 2 }\) इसका एक शून्यक होगा।
⇒\(q\left(\frac{1}{2}\right)=p\left(\frac{1}{2}\right)^{2}+5\left(\frac{1}{2}\right)+r=0\)
⇒  1/4 p + 5/2  + r = 0
⇒  p+ 10 + 4r = 0 ….(ii)
⇒ 3p – 3r = 0  समी. (1) – समी. (2) से]
⇒ 3p  = 3r
⇒ p = r

प्रश्न 3.
बिना वास्तविक विभाजन के सिद्ध कीजिए कि x² – 3x + 2 से 2x⁴ – 5x³ + 2x² – x + 2 विभाज्य है।
हल :
x² – 3x + 2  = x² – x – 2x + 2
=x (x – 1)- 2 (x – 1)
= (x – 1) (x – 2)
अतः (x – 1) एवं (x – 2) दोनों बहुपद x² – 3x + 2 के शून्यक हैं।
माना दिया हुआ बहुपद p(x) = 2x⁴ – 5x³ + 2x² – x + 2 है
p(1) = 2(1)⁴ – 5(1)³ + 2(1)² – (1) + 2
p(1) = 2 – 5 + 2 – 1 + 2 = 6 – 6 = 0 है
इसलिए दिया हुआ बहुपद (x – 1) से विभाज्य है।
अब  p(2) = 2(2)⁴ – 5(2)³ + 2(2)² – (2) +2
= 2(16) – 5(8) + 2(4) –  2 + 2
= 32 – 40 + 8 – 2 + 2 = 42 – 42 = 0 है
इसलिए दिया हुआ बहुपद (x – 2) से भी विभाज्य है।
अर्थात् दिया हुआ बहुपद (x – 1) (x – 2) अर्थात् (x²  – 3x + 2) से विभाज्य है;
अतः (x² – 3x + 2) से बहुपद (2x⁴ – 5x² + 2x² + 2) विभाज्य है। इति सिद्धम्

प्रश्न 4.
3x² + x – 1 को x + 1 से भाग दीजिए एवं भागफल, शेषफल लिखिए। (2019)
हल:

अतः अभीष्ट भागफल = 3x – 2 एवं शेषफल = 1.

MP Board Class 9th Maths Chapter 2 लघु उत्तरीय प्रश्न

प्रश्न 1.
निम्नलिखित बहुपदों को एक पद वाले, दो पद वाले, इत्यादि बहुपदों में वर्गीकृत कीजिए :
(i) x² + x + 1,
(ii) y³ – 5y,
(iii) xy + yz + zx,
(iv) x² – 2xy + y² + 1.
उत्तर:
(i) त्रिपद,
(ii) द्विपद,
(iii) त्रिपद,
(iv) चतुर्पद।

प्रश्न 2.
निम्नलिखित बहुपदों में से प्रत्येक की घात निर्धारित कीजिए :
(i) 2x – 1,
(ii) -10,
(iii) x³ – 9x + 3x⁵,
(iv) y³ (1 – y⁴).
उत्तर:
(i) घात = 1,
(ii) घात = 0,
(iii) घात = 5.
(iv) घात = 7.

प्रश्न 3.
बहुपद \( \frac{x^{3}+2 x+1}{5}-\frac{7}{2} x^{2}-x^{6}\) के लिए, लिखिए :
(i) बहुपद की घात
(ii) x³ का गुणांक
(iii) x⁶ का गुणांक
(iv) अचर पद।
उत्तर:
(i) घात = 6,
(ii) x³ का गुणांक = \(\frac { 1 }{ 5 }\)
(iii) x⁶ का गुणांक = – 1,
(iv) अचर पद = \(\frac { 1 }{ 5 }\)

प्रश्न 4.
निम्नलिखित में से प्रत्येक में x का गुणांक लिखिए :
(i) \(\frac{\pi}{6} x+x^{2}+1\)
(ii) 2x – 5
(ii) (x – 1) (3x – 4)
(iv) (2x – 5) (2x² – 3x + 1).
उत्तर:
(i) x² का अभीष्ट गुणांक = 1
(ii) x² का अभीष्ट गुणांक = 0 (शून्य)
(iii) (x – 1) (3x – 4) = 3x² – 7x + 4 में x² का अभीष्ट गुणांक = 3
(iv) (2x – 5) (2x² – 3x + 1) = 2x (2x² – 3x + 1) – 5 (2x² – 3x + 1)
= 4x³ – 6x² + 2x – 10x² + 15x -5
= 4x³ – 16x² + 17x – 5 में x² का गुणांक = – 16

प्रश्न 5.
निम्नलिखित को एक अचर रैखिक, द्विघात और त्रिघात बहुपदों के रूप में वर्गीकृत कीजिए:
(i) 2 – x² +x³
(ii) 3x³
(iii) 5t – √7
(iv) 4 – 5y²
(v) 3
(vi) 2 + x
(vii) y³ – y
(viii) 1 + x + x²
(ix) t²
(x) √2x – 1.
उत्तर:
(i) त्रिघात,
(ii) त्रिघात,
(iii) रैखिक,
(iv) द्विघात,
(v) अचर,
(vi) रैखिक,
(vii) त्रिघात,
(viii) द्विघात,
(ix) द्विघात,
(x) रैखिक।

प्रश्न 6.
एक ऐसे बहुपद का उदाहरण दीजिए, जो :
(i) घात 1 का एकपदी है।
(ii) घात 20 का द्विपदी है।
(iii) घात 2 का एक त्रिपदी है।
उत्तर:
(i) ax, जहाँ a अचर है।
(ii) ar²⁰ + b, जहाँ a एवं b अचर हैं।
(iii) ar² + bx + c, जहाँ a, b एवं c अचर हैं।

प्रश्न 7.
निम्नलिखित के लिए p(0), p(1) और p(-2) ज्ञात कीजिए :
(i) p(x) = 10x – 4x² – 3
(ii) p(y) = (y + 2) (y – 2).
हल:
(i) ∵ p(x) = 10x – 4x² – 3
⇒ p(0) = 10(0) – 4(0)² – 3 = 0 – 0 – 3 = – 3
तथा p(1) = 10(1) – 4(1)² – 3 = 10 – 4 – 3 = 10 – 7 = +3
एवं  p(-2) = 10(-2) – 4(-2)² – 3 = – 20 – 16 – 3 = – 39
अतः अभीष्ट मान p(0) = – 3, p(1) = + 3 एवं p(-2) = – 39.

(ii) ∵ p(y) = (y + 2) (y² – 2) = y² – 4
⇒ p(0) = (0)² – 4 = 0-4 =-4
तथा p(1) = (1)² – 4 = 1 – 4 = – 3
एवं p(-2) = (-2)² – 4 = 4 – 4 = 0
अतः अभीष्ट मान p(0) = -4, p(1) = – 3 एवं p(-2) = 0.

प्रश्न 8.
जाँच कीजिए कि निम्नलिखित कथन सत्य हैं या असत्य :
(i) – 3 बहुपद x – 3 का एक शून्यक है।
(ii) -1/3 बहुपद 3x + 1 का एक शून्यक है।
(iii) -4/5 बहुपद 4 – 5y का एक शून्यक है।
(iv) 0 और 2 बहुपद t² – 2t के शून्यक हैं।
(v) -3 बहुपद y² + y – 6 का एक शून्यक है।
उत्तर:
(i) असत्य है, क्योंकि (-3) – 3 = – 6 ≠ 0
(ii) सत्य है, क्योंकि 3 (-\(\frac { 1 }{ 3 }\)) + 1 =- 1 + 1 = 0
(iii) असत्य है, क्योंकि 4 – 5(-\(\frac { 4 }{ 5 }\)) = 4 + 4 = 8 ≠ 0
(iv) सत्य है, क्योंकि (0)² – 2(0) = 0 – 0 = 0 एवं (2)² – 2(2) = 4 – 4 = 0.
(v) सत्य है, क्योंकि (-3)² + (-3)- 6 = 9 – 3 – 6 = 9 – 9 = 0

प्रश्न 9.
निम्नलिखित में से प्रत्येक में बहुपद के शून्यक ज्ञात कीजिए : (2019)
(i) p(x) = x – 4
(ii) g(x) = 3 – 6x
(iii) q(x) = 2x – 7
(iv) h(y) = 2y.
हल:
(i) ∵ p(x) =x-4 = 0 ⇒ x = 4, अत: अभीष्ट शून्यक = 4.
(ii) g(x) = 3 – 6x = 0 ⇒ 6x = 3 ⇒  x= \(\frac { 3 }{ 6 }\)  = \(\frac { 1 }{ 2 }\) =, अतः अभीष्ट शून्यक =  \(\frac { 1 }{ 2 }\)
(ii) q(x) = 2x – 7 = 0 ⇒ 2x = 7 ⇒  x = \(\frac { 7 }{ 2 }\), अतः अभीष्ट शून्यक = \(\frac { 7 }{ 2 }\)
(iv) h(y) = 2y = 0 ⇒ y = \(\frac { 0 }{ 2 }\) = 0, अतः अभीष्ट शून्यक = 0.

प्रश्न 10.
शेषफल प्रमेय से शेषफल ज्ञात कीजिए, जब p(x) को q(x) से भाग दिया जाता है, जहाँ
(i) p(x) = x³ – 2x² – 4x – 1, q(x) = x + 1
(ii) p(x) =x³ – 3x² + 4x + 50, q(x) = x – 3
(iii) p(x) = 4x³ – 12x² + 14x – 3, q(x) = 2x -1
(iv) p(x) = x³  – 6x² + 2x – 4, q(x) = 1 – \(\frac { 3 }{ 2 }\)x.
हल:
(i) चूँकि भाजक q(x) = x + 1 = 0 का शून्यक x = – 1 है
p(x) = x³ – 2x² – 4x – 1,
⇒ शेषफल  p(- 1) = (-1)³ – 2(-1)² – 4(-1)-1 (शेषफल प्रमेय से)
= (-1) – 2 (1) + 4 – 1
= -1 – 2 + 4 – 1 = 4 – 4 = 0
अतः अभीष्ट शेषफल = 0.

(ii) चूँकि भाजक q(x) =  x – 3 = 0 का शून्यक x = 3 है
और p(x) = x³ – 3x² + 4x + 50
⇒ शेषफल p(3) = (3)³ – 3(3)² + 4(3) + 50
= 27 – 27 + 12 + 50 = 62
अतः अभीष्ट शेषफल = 62.

(iii) चूँकि भाजक q(x) = 2x – 1 = 0 का शून्यक x = \(\frac { 1 }{ 2 }\) , है और
p(x) = 4x³ – 12x² + 14x – 3

(iv) चूँकि भाजक q(x) = 1 – \(\frac { 3 }{ 2 }\)x = 0 का शून्यक = 2/3 है
और p(x) = x³ – 6x² + 2x -4
⇒ शेषफल p (2/3) = (2/3)³ – 6 (2/3)² + 2 (2/3) – 4

अतः अभीष्ट शेषफल = -136/27.

प्रश्न 11.
जाँच कीजिए कि p(x), q(x) का एक गुणज है या नहीं :
(i) p(x) = x³ – 4x² + 4x – 3 ; q(x) = x – 2 है
(ii) p(x) = 2x³ – 11x² – 4x + 5 ; q(x) = 2x + 1 है
_(iii) p(x)= x³ – x + 1 ; q(x) = 2 – 3x है
हल:
(i) p(x), q(x) का एक गुणज होगा यदि q(x), p(x) को पूर्णतया विभाजित करेगा अर्थात् शेषफल शून्य होगा अन्यथा नहीं।
अब q(x) = x – 2 = 0 ⇒ x = 2, q(x) का एक शून्यक है।
एवं p(x) = x³ – 4x² + 4x – 3
⇒ शेषफल p(2) = (2)³ – 5(2)² + 4(2) – 3
= 8 – 20 + 8 – 3
= 16 – 23 = -7 ≠ 0
अतः p(x), q(x) का गुणज नहीं है।

(ii) p(x), q(x) का एक गुणज होगा यदि q(x), p(x) को पूर्णतया विभाजित करेगा अर्थात् शेषफल शून्य होगा अन्यथा नहीं।
अब q(x) = 2x + 1 = 0 = x = -1/2, 4(x) का एक शून्यक है।
एवं p(x) = 2x³ – 11x² – 4x + 5

अतः p(x), q(x) का गुणज नहीं है।

(iii) p(x), q(x) का गुणज होगा यदि q(x), p(x) को पूर्णतया विभाजित करेगा अर्थात् शेषफल शून्य होगा अन्यथा नहीं।
अब q(x) = 2 – 3x = 0 ⇒ x = 2/3, q(x) का एक शून्यक है
एवं p(x) = x³ – x + 1

अतः p(x), q(x) का गुणज नहीं है।

प्रश्न 12.
दर्शाइए कि:
(i) x + 3 बहुपद 69 + 11x – x +3 का एक गुणनखण्ड है।
(ii) 2x – 3 बहुपद x + 2x³ – 9x² + 12 का एक गुणनखण्ड है।
(iii) q(x), p(x) का एक गुणनखण्ड है जहाँ q(x) =  \( \frac{x}{3}-\frac{1}{4} \) एवं p(x) = 8x³ – 6x ² – 4x + 3.
हल:
(i) चूँकि x + 3 का शून्यक – 3 है
p(x) = 69 + 11x – x2 +x – शेषफल
p(-3) = 69 + 11(-3)-(-3)² + (-3)³
= 69 – 33 – 9 – 27 = 69 – 69 = 0
अतः (x + 3) बहुपद 69 + 11x – x² + x³ का एक गुणनखण्ड है।

(ii) चूँकि 2x -3 का शून्यक 3/2 है
p(x) = x + 2x³ – 9x² + 12
शेषफल  p (3/2) = (3/2) + 2 (3/2)³ – 9 (3/2)² + 12
= 3/2 + 2 (27/8) – 9 (9/4) + 12

अत: 2x – 3 बहुपद x + 2x³ – 9x² + 12 का एक गुणनखण्ड है।

(iii) चूँकि q(x) = \( \frac{x}{3}-\frac{1}{4} \)  ⇒ x – 3/4 का शून्यक 3/4 है
एवं  p(x) = 8x³ – 6x²– 4x + 3.
शेषफल p (3/4) = 8 (3/4)³ – 6 (3/4)² – 4 (3/4) + 3.

अतः q(x), p(x) का एक गुणनखण्ड है।

प्रश्न 13.
m के किस मान के लिए x³ – 2mx² + 16 द्विपद x + 2 से विभाज्य है ?
हल:
चूँकि बहुपद x³ – 2mx² + 16 द्विपद x + 2 से विभाज्य है
अतः शेषफल शून्य होगा। द्विपद x + 2 का शून्यक x + 2 = 0 ⇒ x = -2
एवं बहुपद p(x) = x³ – 2mx² + 16
⇒ शेषफल p(-2) = (-2)³ – 2 m (-2) + 16 = 0
⇒ – 8 – 8 m + 16 = 0
⇒ 8m = 8 = m = 8/8 = 1
अतः m का अभीष्ट मान = 1.

प्रश्न 14.
m का मान ज्ञात कीजिए जबकि 2x – 1 बहुपद 8x⁴ + 4x³ – 16x² + 10x + m का गुणनखण्ड है।
हल:
चूँकि 2x – 1 बहुपद p(x) = 8x⁴  + 4x³ – 16x² + 10x + m का एक गुणनखण्ड है और 2x – 1
का शून्यक 2x – 1 = 0 ⇒ x = 1/2 है।
इसलिए शेषफल p (1/2) = 8 (1/2)⁴ + 4 (1/2)³ – 16(1/2)² + 10 (1/2) + m = 0

अतः m का अभीष्ट मान = – 2.

प्रश्न 15.
गुणनखण्ड कीजिए :
(i) x² + 9x + 18
(ii) 6x² + 7x – 3
(ii) 2x² – 7x – 15
(iv) 84 – 2r – 2r².
हल:
(i) x²+ 9x + 18 = x² + (3 + 6) x + 18
= x² + 3x + 6x + 18
= x (x + 3)+6 (x + 3)
= (x + 3) (x + 6)
अतः अभीष्ट गुणनखण्ड = (x + 3) (x + 6).

(ii) 6x² + 7x -3 = 6x² + (9 – 2)x – 3
= 6x² + 9x – 2x -3
= 3x (2x + 3) – 1 (2x + 3)
= (2x + 3) (3x – 1)
अतः अभीष्ट गुणखण्ड = (2x + 3) (3x -1).

(iii) 2x² – 7x – 15 = 2x² – (10 -3)x – 15
= 2x² – 10x + 3x – 15
= 2x (x – 5) + 3 ( x- 5)
= (x – 5)(2x + 3)
अतः अभीष्ट गुणखण्ड = (x – 5) (2x + 3).

(iv) 84 – 2r – 2r² = 2 [42 -r – r²]
= 2 [42 – (7 – 6) – r²]
= 2 [42 – 7r + 6r – r²]
= 2 [7 (6 – r) + r (6 – r)]
= 2 (6 – 1) (7+r)
अतः अभीष्ट गुणखण्ड = 2 (6 – 1) (7 + r).

प्रश्न 16.
गुणनखण्ड कीजिए :
(i) 2x³ – 3x² -17x + 30
(ii) x³ – 6x² + 11x – 6
(iii) x³ + x² – 4x – 4
(iv) 3x³ – x² – 3x + 1.
हल:
(i) मान लीजिए – p(x) = 2x³ – 3x² – 17x + 30
अब चूँकि p(2) = 2 (2)³ – 3 (2)² – 17 (2) + 30
= 16 – 12 -34 + 30
= 46 – 46 = 0 है
अतः x = 2 अर्थात् x – 2, p(x) का एक गुणनखण्ड है

अब 2x³ – 3x² – 17x + 30 = 2x³ – 4x² + x² – 2x – 15x + 30
= 2x² (x – 2) + x (x -2) – 15 (x – 2)
= (x – 2) [2x² + x – 15]
= (x – 2)[2x³ + (6 – 5)x – 15]
= (x – 2) [2x² + 6x – 5x – 15]
= (x – 2)[2x (x + 3) – 5 (x + 3)]
= (x – 2) (x + 3) (2x – 5)
अतः अभीष्ट गुणखण्ड = (x – 2) (x + 3) (2x – 5).

(ii) मान लीजिए p(x) = x³ – 6x² + 11x – 6
अब चूंकि p(1) = (1)³ – 6 (1)² + 11 (1) – 6
= 1 – 6 + 11 – 6 = 12 – 12 = 0 है
अतः x – 1 बहुपद p(x) का एक गुणखण्ड है।
अब x³ – 6x² + 11x – 6 = x³ – x² – 5x² + 5x + 6x – 6
= x² (x – 1) – 5x (x – 1)+ 6 (x – 1)
= (x – 1) [x² – 5x + 6]
= (x – 1) [x² – (2 + 3)x  + 6]
= (x – 1) [x² – 2x – 3x + 6]
= (x- 1) [x(x – 2)-  3 (x – 2)]
= (x – 1) (x – 2) (x – 3)
अतः अभीष्ट गुणखण्ड = (x – 1) ( x- 2) (x – 3).

(iii) मान लीजिए p(x) = x³ + x²– 4x – 4
= x² (x + 1) – 4 (x + 1)
= (x + 1) [x² – 4]
= (x + 1) [(x) – (2)]
= (x + 1) (x – 2) (x + 2)
अतः अभीष्ट गुणनखण्ड = (x – 2) (x + 1) (x + 2).

(iv) मान लीजिए p(x) = 3x³ – x² – 3x + 1
= x² (3x – 1)- 1 (3x – 1)
= (3x – 1) [x² – 1] = (3x – 1) [(x) – (1)]
= (3x- 1) (x – 1) (x + 1)
अतः अभीष्ट गुणखण्ड = (3x – 1) (x – 1) (x + 1).

प्रश्न 17.
उपयुक्त सर्वसमिका का उपयोग करते हुए निम्नलिखित के मान निकालिए :
(i) 103³
(ii) 101 x 102
(iii) 999².
हल:
(i) ∵ सर्वसमिका : (a + b)³ = a³ + 3a²b + 3ab² + b3
⇒ (100 + 3)³ = (100)³ + 3 (100)² (3) + 3 (100) (3)² + (3)³ (a = 100 एवं b = 3 रखने पर)
⇒ (103)³ = 1000000 + 90000 + 2700 + 27
= 1092727
अतः अभीष्ट मान = 1092727.

(ii) (101) x (102) = (100 + 1) x (100 + 2)
सर्वसमिका : (x +.a) (x + b) = x² + (a + b)x + ab.
अब x = 100, a = 1 एवं b = 2 लेने पर,
(100 + 1) (100 + 2) = (100)² + (1 + 2) x 100 + 1 x 2
(101) x (102) = 10000 + 300 + 2 = 10302
अतः अभीष्ट मान = 10302.

(iii) (999)² = (1000 – 1)²
सर्वसमिका : (a – b)² = a² – 2ab + b²
अब a = 1000 एवं b = 1 लेने पर,
(1000 – 1)² = (1000)² – 2 (1000) (1) + (1)²
= 1000000 – 2000 + 1
= 1000001 – 2000 = 998001
अतः अभीष्ट मान = 998001.

प्रश्न 18.
निम्नलिखित के गुणनखण्ड कीजिए :
(i) 4x² + 20x + 25
(ii) 9y² – 66yz + 12z²
हल:
(i) 4x² + 20x + 25 = (2x)² + 2 (2x) (5) + (5)²
= (2x + 5)²  [∵ a² + 2ab + b² = (a + b)² सर्वसमिका]
अतः अभीष्ट गुणनखण्ड = (2x + 5)².

(ii) 9y² – 66yz + 121z² = (3y)²  – 2 (3y) (112) + (112)² .
= (3y – 112)² (∵ सर्वसमिका a² – 2ab + b²  = (a – b)]
अतः अभीष्ट गुणनखण्ड = (3y – 11z)².

प्रश्न 19.
(4a – b + 2c)² का प्रसार लिखिए।
हल:
∵  सर्वसमिका : (x + y + z)² = x² + y² + z² + 2xy +2yz + 2zx
यहाँ x = 4a, y = – b एवं z = 2c लेने पर,
⇒ (4a – b + 2c)² = (4a)² + (- b)² + (2c)² + 2 (4a) (- b) + 2 (- b) (2c) + 2(2c) (4a)
= 16a² + b² + 4c² – 8ab – 4bc + 16ca
अतः अभीष्ट प्रसार = 16a² + b² + 4c² – 8ab – 4bc + 16ca.

प्रश्न 20.
सर्वसमिका का प्रयोग कर (2x + y + z)² का प्रसार कीजिए। (2019)
हल:
4x²  + 2 + 2 + 4xy + 2yz + 4zx

प्रश्न 21.
यदि a + b + c= 9 और ab + bc + ca = 26 है, तो a² + b² + c² का मान ज्ञात कीजिए।
हल:
∵ (a + b + c)²= (a² + b² + c²) + 2 (ab + bc + ca) (सर्वसमिका)
⇒ (9)² = (a² + b² + c²) + 2 (26)
[∵  (a + b + c) = 9 एवं (ab + bc + ca) = 26 दिया है]
⇒ 81 = a² + b² + c² + 52
⇒ a² + b² + c² = 81 – 52 = 29
अतः  a² + b² + c² का अभीष्ट मान = 29.

प्रश्न 22.
(3a – 2b)³ का प्रसार कीजिए।
हल:
सर्वसमिका : (x – y)³ = x³ – 3x²y + 3xy² – y³
अब x = 3a एवं y = 2b रखने पर प्राप्त होता है :
(3a – 2b)³ = (3a)³ – 3(3a)² (2b) + 3(3a)(2b)² – (2b)³
= 27a³ – 54a²b + 36ab² – 8b³
अतः अभीष्ट प्रसार = 27a³ – 54a²b + 36ab² – 8b³.

प्रश्न 23.
गुणनखण्ड कीजिए : 1+ 64x³.
हल:
1+ 64x³ = (1)³ + (4x)³
= (1 + 4x) [(1) ²– (1) (4x) + (4x)²]
[∵  सर्वसमिका a³ + b³ = (a + b) (a² – ab + b²) से]
= (1 + 4x) (1 – 4x + 16x²)
अतः अभीष्ट गुणनखण्ड = (1 + 4x) (1 – 4x + 16x²).

प्रश्न 24.
गुणनखण्ड कीजिए : a³ – 8b³ – 64c³ – 24abc.
हल:
a³ – 8b³ – 64c3 – 24abc
= (a)³ + (-2b)³ + (-4c)³ – 3(a) (-2b) (-4c)
= (a – 2b -4c) [(a)² + (-2b)² + (-4c)² – (a) (-2b)- (-2b) (-4c)- (-4c) (a)]
[∵ सर्वसमिका : x³ + y³ + z³ – 3xyz = (x + y + z) (x² + y² + 2 – xy – yz – zx)]
= (a – 2b – 4c) (a + 4b² + 16c² + 2ab – 8bc + 4ca)
अतः अभीष्ट गुणनखण्ड = (a – 2b – 4c) (a² + 4b² + 16c² + 2ab – 8bc + 4ca).

MP Board Class 9th Maths Chapter 2 अति लघु उत्तरीय प्रश्न

प्रश्न 1.
निम्नलिखित में से कौन से व्यंजक बहुपद हैं ? अपने उत्तर का औचित्य दीजिए :
(i) 8
(ii) √3x² – 2x
(iii) 1 – √5x
(iv)
(v)
(vi) \(\frac{1}{x+1}\)
(vii) \(\frac{1}{7} a^{3}-\frac{2}{\sqrt{3}} a^{2}+4 a-7\)
(viii) \(\frac{1}{2x}\).
उत्तर:
(i) 8 में चर का घातांक शून्य है जो एक पूर्ण संख्या है, अत: बहुपद है।
(ii) √3x² – 2x में चर की प्रत्येक घात पूर्ण संख्या है, इसलिए बहुपद है।
(ii) 1 – √5x  में चर की घात 1/2 है जो पूर्ण संख्या नहीं है, इसलिए बहुपद नहीं है।
(iv)   अर्थात् \(\frac{1}{5}\)x² + 5x + 7 में चर की प्रत्येक घात पूर्ण संख्या है, अत: यह बहुपद है।
(v)   में चर का घातांक – 1 है जो पूर्ण संख्या नहीं है, इसलिए यह बहुपद नहीं है।
(vi) \(\frac{1}{x+1}\) में चर की घात पूर्ण संख्या नहीं है, अत: यह बहुपद नहीं है।
(vi) \(\frac{1}{7} a^{3}-\frac{2}{\sqrt{3}} a^{2}+4 a-7\)  में चर की प्रत्येक घात पूर्ण संख्या है, अत: यह बहुपद है।
(viii) \(\frac{1}{2x}\) अर्थात् \(\frac{1}{2}\)x^-1 में चर की घात – 1 है जो पूर्ण संख्या नहीं है। अत: यह बहुपद नहीं है।

प्रश्न 2.
क्या निम्नलिखित कथन सत्य हैं या असत्य, लिखिए। अपने उत्तर का औचित्य दीजिए।
(i) एक द्विपद के अधिकतम दो पद हो सकते हैं।
(ii) प्रत्येक बहुपद एक द्विपद है।
(iii) एक द्विपद की घात 5 हो सकती है।
(iv) एक बहुपद का शून्यक सदैव 0 होता है।
(v) एक बहुपद के एक से अधिक शून्यक नहीं हो सकते हैं।
(vi) घात 5 वाले दो बहुपदों के योग की घात सदैव 5 होती है।
(vii) \(\frac{1}{\sqrt{5}} x^{1 / 2}+1\)  एक बहुपद है।
(vii) \( \frac{6 \sqrt{x}+x^{3 / 2}}{\sqrt{x}}\)  , x ≠ 0 एक बहुपद है।
उत्तर:
(i) असत्य है, क्योंकि द्विपद में ठीक दो पद होते हैं।
(ii) असत्य है, क्योंकि किसी बहपद में कितने भी पद हो सकते हैं।
(iii) सत्य है, क्योंकि द्विपद की कितनी भी घात हो सकती है।
(iv) असत्य है, क्योंकि बहुपद का शून्यक कोई भी वास्तविक संख्या हो सकती है।
(v) असत्य है, क्योंकि एक बहुपद के कितने भी शून्यक हो सकते हैं।
(vi) असत्य है, क्योंकि x + 3 एवं – x⁵ + x + 5 का योग x + 8 है जिसकी घात 5 है।
(vii) असत्य है, क्योंकि चर की घात 1/2 है जो पूर्ण संख्या नहीं है।
(viii) सत्य है, क्योंकि \( \frac{6 \sqrt{x}+x^{3 / 2}}{\sqrt{x}}\) = 6 + x है जिसमें चर की घात पूर्ण संख्या है।

MP Board Class 9th Maths Chapter 1 वस्तुनिष्ठ प्रश्न

बहु-विकल्पीय प्रश्न

प्रश्न 1.
निम्नलिखित में से कौन एक बहुपद है :

उत्तर:
(c)

प्रश्न 2.
√2 निम्नलिखित घात का एक बहुपद है :
(a) 2
(b) 0
(c) 1
(d)  \(\frac { 1 }{ 2 }\)
उत्तर:
(b) 0

प्रश्न 3.
बहुपद 4x⁴ + 0x³ + 0x⁵ + 5x + 7 की घात है :
(a) 4
(b) 5
(c) 3
(d) 7
उत्तर:
(a) 4

प्रश्न 4.
शून्य बहुपद की घात है :
(a) 0
(b) 1
(c) कोई भी प्राकृत संख्या
(d) परिभाषित नहीं।
उत्तर:
(d) परिभाषित नहीं

प्रश्न 5.
यदि p(x) = x² – 2√2 x + 1 है, तो p (2√2) बराबर है :
(a) 0
(b) 1
(c) 4√2
(d) 8√2 + 1.
उत्तर:
(b) 1

प्रश्न 6.
जब x = -1 है, तो बहुपद 5x – 4x² + 3 का मान है :
(a) -6
(b) 6
(c) 2
(d) -2.
उत्तर:
(a) -6

प्रश्न 7.
यदि p(x) = x + 3 है, तो p(x) + p(-x) बराबर है :
(a) 3
(b) 2x
(c) 0
(d) 6.
उत्तर:
(d) 6.

प्रश्न 8.
शून्य बहुपद का शून्यक है :
(a) 0
(b) 1
(c) कोई वास्तविक संख्या
(d) परिभाषित नहीं।
उत्तर:
(c) कोई वास्तविक संख्या

प्रश्न 9.
बहुपद p(x) = 2x + 5 का शून्यक है :
(a) – 2/5
(b) -5/2
(c) 2/5
(d) 5/2.
उत्तर:
(b) -5/2

प्रश्न 10.
बहुपद 2x² + 7x – 4 के शून्यकों में से एक है :
(a) 2
(b) 1/2
(c) -1/2
(d) -2.
उत्तर:
(b) 1/2

प्रश्न 11.
यदि x⁵¹ + 51 को x + 1 से भाग दिया जाय तो शेषफल है :
(a) 0
(b) 1
(c) 490
(d) 50.
उत्तर:
(d) 50.

प्रश्न 12.
यदि x + 1 बहुपद 2x² + kx का एक गुणखण्ड है, तो k मान है :
(a) -3
(b) 4
(c) 2
(d) -2.
उत्तर:
(c) 2

प्रश्न 13.
x +1 निम्नलिखित बहुपद का एक गुणनखण्ड है :
(a) x³ + x² – x + 1
(b) x³ + x² + x +1
(c) x⁴ + x³ +  x² +1
(d) x⁴ + 3x³ + 3x² + x + 1.
उत्तर:
(b) x³ + x² + x +1

प्रश्न 14.
(25x² – 1) + (1 + 5x)² के गुणनखण्डों में से एक है :
(a) 5 +x
(b) 5 – x
(c) 5x – 1
(d) 10x.
उत्तर:
(d) 10x.

प्रश्न 15.
249² – 248² का मान है :
(a) 12
(b) 477
(c) 487
(d) 497.
उत्तर:
(d) 497.

प्रश्न 16.
4x² + 8x + 3 का गुणनखण्ड है :
(a) (x + 1) (x + 3)
(b) (2x + 1) (2x + 3)
(c) (2x + 2) (2x + 5)
(d) (2x – 1) (2x – 3).
उत्तर:
(b) (2x + 1) (2x + 3)

प्रश्न 17.
निम्नलिखित में से कौन (x + y) – (x + y) का एक गुणनखण्ड है :
(a) x² + y² + 2xy
(b) x² + y² –  xy .
(c) xy²
(d) 3xy.
उत्तर:
(d) 3xy

प्रश्न 18.
(x + 3)³ के प्रसार में x का गुणांक है :
(a) 1
(b) 9
(c) 18
(d) 27.
उत्तर:
(d) 27

प्रश्न 19.
यदि \( \frac{x}{y}+\frac{y}{x}=-1(x, y \neq 0)\)  है, तो x³ – y³ का मान है :
(a) 1
(b) -1
(c) 0
(d) 1/2
उत्तर:
(c) 0

प्रश्न 20.
यदि 49x² – b = (7x + \(\frac { 1 }{ 2 }\)) (7x –\(\frac { 1 }{ 2 }\)) है, तो 6 का मान है :
(a) 0
(b) \(\frac { 1 }\sqrt{ 2 }\)
(c) 1/4
(d) \(\frac { 1 }{ 2 }\).
उत्तर:
(c) 1/4

प्रश्न 21.
यदि a + b + c = 0 है, तो a³ + b³ + c³ बराबर है:
(a)0
(b) abc
(c) 3abc
(d) 2abc.
उत्तर:
(c) 3abc

प्रश्न 22.
यदि सभी x के लिए 2 + kx + 6 = (x + 2) (x + 3) हैं, तो k का मान है :
(a) 1
(b) -1
(c) 5
(d) 3
उत्तर:
(c) 5

प्रश्न 23.
बहुपद 5x – 4x² + 3 का मान जब x = 2 हो, तो है :
(a) 10
(b) -3
(c) 12
(d) 3.
उत्तर:
(b) -3

प्रश्न 24.
बहुपद x² + x – 6 का एक गुणनखण्ड (x – 2) है, तो दूसरा गुणनखण्ड होगा :
(a) (x + 3)
(b) (x + 2)
(c) (x – 3)
(d) (x – 2).
उत्तर:
(a) (x + 3)

प्रश्न 25.
बहुपद x² – 11x + 10 का एक गुणनखण्ड (x – 1) है, तो दूसरा गुणनखण्ड होगा :
(a) (x + 10)
(b) (x – 10)
(c) (x – 11)
(d) (x + 11).
उत्तर:
(b) (x – 10)

प्रश्न 26.
बहुपद x² – 10x – 24 का एक गुणनखण्ड (x + 2) है, तो दूसरा गुणनखण्ड होगा :
(a) (x + 12)
(b) (x – 12)
(c) (x + 8)
(d) (x – 8).
उत्तर:
(b) (x – 12)

प्रश्न 27.
एक घात वाले बहुपद को कहते हैं : (2018)
(a) द्विघात
(b) त्रिघात
(c) द्विपद
(d) रैखिक।
उत्तर:
(d) रैखिक

प्रश्न 28.
p(x) = x + x² + 2 कितने पदीय होगा :
(a) एक पदी
(b) द्विपदी
(c) त्रिपदी
(d) इनमें से कोई नहीं।
उत्तर:
(c) त्रिपदी

प्रश्न 29.
बहुपद 9x⁷ – 4x⁶ +x + 9 की घात है :
(a) 9
(b) 7
(c) 4
(d) 6.
उत्तर:
(b) 7

प्रश्न 30.
बहुपद 1 +3y है :
(a) रेखीय
(b) द्विघाती
(c) त्रिघाती
(d) चतुर्घाती।
उत्तर:
(a) रेखीय

प्रश्न 31.
बहुपद 2 – x + x³ में x का गुणांक है :
(a) 1
(b) 2
(c) 0
(d) -1.
उत्तर:
(d) -1.

प्रश्न 32.
बहुपद 4x² + 5x +7 की घात है : (2019)
(a) 2
(b) 3
(c) 7
(d) 5.
उत्तर:
(a) 2

प्रश्न 33.
रेखीय बहुपद है : (2019)
(a) 3x + 5
(b) 4x + 5x
(c) 4x² + 6x + 7
(d) x² + 15.
उत्तर:
(a) 3x + 5

प्रश्न 34.
बहुपद p(x) = 3x – 2 का शून्यक है : (2019)
(a) -2/3
(b) 2/3
(c) 3/2
(d) 0.
उत्तर:
(b) 2/3

रिक्त स्थानों की पूर्ति

1. x² – y² का गुणनखण्ड ………. है।
2. बहुपद में सबसे बड़े घात वाले घातांक को बहुपद का ……….. कहते हैं।
3. एक बीजीय व्यंजक जिसमें चर के घातों में अनेक पद हो, तो ………….. कहलाता है।
4. बहुपद में चर की घात सदैव ……… होती है।
5. अशून्य अचर पद की घात सदैव ………….. होती है।
6. रेखीय बहुपद में चर की अधिकतम घात ……….. होती है। (2019)
7. 3x³ में x का गुणांक ………. है। (2018)
8. बहुपद x³ – x² + 1 में x² का गुणांक ……….. है। (2019)
उत्तर;
1. (x + y) (x -y),
2. घात,
3. बहुपद,
4. पूर्ण संख्या,
5. शून्य,
6. एक,
7. तीन,
8. – 1.

जोड़ी मिलान

स्तम्भ ‘A’  स्तम्भ ‘B’

1. x³ + y³ (2019)  (a)-1
2. x³ – y³   (2019) (b) 2
3. बहुपद x + 1 का शून्यक (2019) (c) (x + y) (x² – xy + y²)
4. बहुपद x² + x + 5 की घात (2019) (d) (x -y) (x² +xy + y²) .
उत्तर:
1.→(c), 2.→(d), 3.→(a), 4.→(b).

सत्य/असत्य कथन
1. बहुपद 7 एक एकपदी व्यंजक है।
2. शून्य बहुपद की घात शून्य होती है।
3. x⁵ – x⁴ + 3 की घात 5 है।
4. अशून्य अचर पद की घात परिभाषित नहीं है।
5. बहुपद 7x³ एक त्रिघात बहुपद है।
6. 3x² + 5 एक रेखीय बहुपद है।
7. ल. स. x म. स. = बहुपदों का गुणनफल। (2018)
8. बहुपद x² + 2x + 3 एक द्विपदी बहुपद है। (2019)
9. 7x² + 3x + 5 में x² का गुणांक 5 है। (2019)
उत्तर:
1. सत्य,
2. असत्य,
3. सत्य,
4. असत्य,
5. सत्य,
6. असत्य,
7. सत्य,
8. असत्य,
9. असत्य।

एक शब्द/वाक्य में उत्तर

1. ऐसा बहुपद क्या कहलाता है जिसके सभी गुणांक शून्य हैं।
2. ऐसा बहुपद क्या कहलाता है जिसमें केवल एक पद हो ?
3. केवल दो पदों वाला बहुपद क्या कहलाता है ?
4. केवल तीन पदों वाला बहुपद क्या कहलाता है ?
5. एक घात वाले बहुपद को क्या कहते हैं ?
6. बहुपद 2 – y² – y³ + 2y⁸ की धात लिखिए।
उत्तर:
1. शून्य बहुपद,
2. एक पदीय बहुपद,
3. द्विपद,
4. त्रिपद,
5. रेखीय बहुपद,
6. 8 (आठ)।

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 1 संख्या पद्धति Additional Questions

MP Board Class 9th Maths Chapter 1 अतिरिक्त परीक्षोपयोगी प्रश्न

MP Board Class 9th Maths Chapter 1 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
0.6 + \(0.\overline { 7 }\) + \(0.4\overline { 7 }\) को p/q के रूप में व्यक्त कीजिए; जहाँ p और q पूर्णांक हैं तथा q ≠ 0 है।
हल:
0.6 = \(\frac { 6 }{ 10 }\) = \(\frac { 3 }{ 5 }\)
मान लीजिए x = \(0.\overline { 7 }\) = 0.777 ….
⇒ 10x = 7.777…. = 7 + 0.777 = 7 + x.
⇒ 9x = 7 ⇒ x = \(\frac { 7 }{ 9 }\)

मान लीजिए y = \(0.4\overline { 7 }\) = 0.4777….
⇒ 10y = 4.7777….. = 4.3 + 0.4777…… = 4.3 + y

अतः दी हुई राशि का अभीष्ट p/q रूप = \(\frac { 167 }{ 90 }\) .

प्रश्न 2.
सरल कीजिए:

हल:

अतः दिए हुए अपरिमेय व्यंजक का अभीष्ट सरल मान = 1.

प्रश्न 3.
यदि √2 = 1.414, √ 3= 1.732 हो, तो  का मान ज्ञात कीजिए।
हल:


अतः दिए हुए अपरिमेय व्यंजक का अभीष्ट मान = 2.063.

प्रश्न 4.
सरल कीजिए : \( (256)^{-\left(4^{-3 / 2}\right)}\)
हल:

अतः अभीष्ट सरल मान = 1/2.

प्रश्न 5.
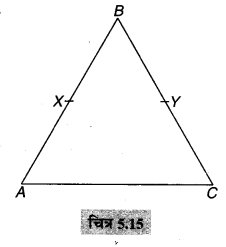
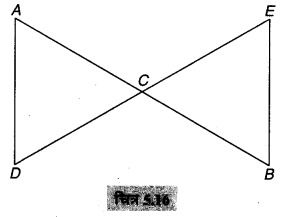
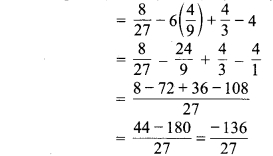
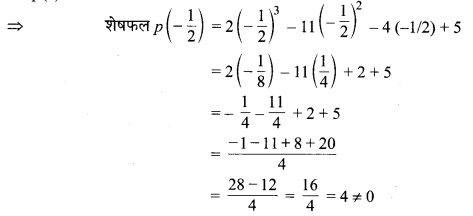
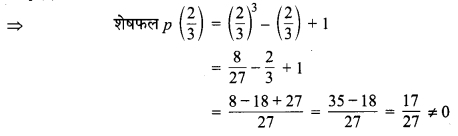
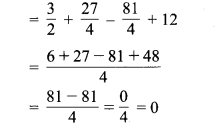
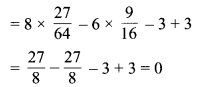
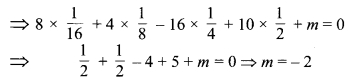
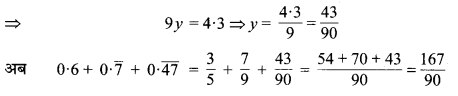
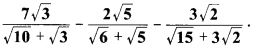
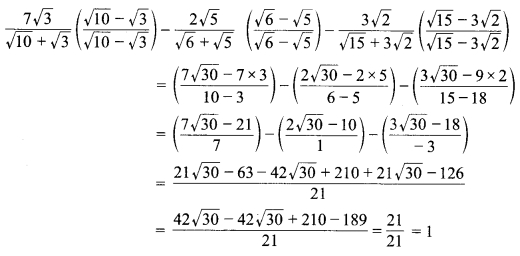
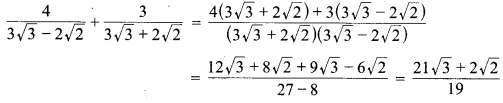
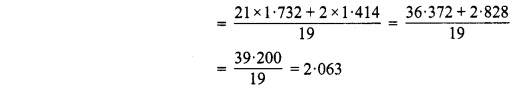
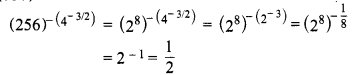
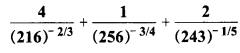का मान ज्ञात कीजिए।
हल:

= 4(216)^2/3 + (256)^3/4 + 2(243)^1/5
= 4(6³)^2/3+ (2⁸)^3/4 + 2(3⁵)^1/5
= 4 x 6² + 2⁶ + 2 x 3
= 4 x 36 + 64 + 6
= 144 + 64 + 6 = 214
अत: अभीष्ट मान = 214.

MP Board Class 9th Maths Chapter 1 लघु उत्तरीय प्रश्न

प्रश्न 1.
ज्ञात कीजिए कि कौन-से चर x, y, z और u परिमेय संख्याएँ निरूपित करते हैं तथा कौन-से चर अपरिमेय संख्याएँ निरूपित करते हैं :
(i) x² = 5
(ii) y² = 9
(iii) z² = 0.04
(iv) u² = \(\frac { 17 }{ 4 }\).
हल:
(i) x² = 5 ⇒ x = √5 अपरिमेय संख्या
(ii) y² = 9 = y = √9 = 3 परिमेय संख्या
(iii) z² = 0.04 ⇒ y² = (0.2)² = y = 0.2 परिमेय संख्या
(iv) u² = \(\frac { 17 }{ 4 }\) ⇒ u = \(\sqrt [ 17 ]{ 4 }\) = \(\sqrt [ 17 ]{ 2 }\)
अतः y एवं z परिमेय संख्याएँ हैं तथा x एवं u अपरिमेय संख्याएँ हैं।

प्रश्न 2.
निम्नलिखित के बीच तीन परिमेय संख्याएँ ज्ञात कीजिए :
(i) -1 और -2
(ii) 0.1 और 0.11
(iii) \(\frac { 5 }{ 7 }\) और \(\frac { 6 }{ 7 }\)
(iv) \(\frac { 1 }{ 4 }\) और \(\frac { 1 }{ 5 }\).
हल:
(i) – 1 और – 2 को \(\frac { 4 }{ 4 }\) से गुणा करके लिखने पर,

अतः अभीष्ट परिमेय संख्याएँ हैं : – 5/4, – 6/4 एवं – 7/4.

(ii) 0.1 और 0.11 को = से गुणा करके लिखने पर,

अत: अभीष्ट परिमेय संख्याएँ हैं : \(\frac { 0.41 }{ 4 }\), \(\frac { 0.42 }{ 4 }\) एवं \(\frac { 0.43 }{ 4 }\).

(iii) \(\frac { 5 }{ 7 }\) और \(\frac { 6 }{ 7 }\) को \(\frac { 4 }{ 4 }\) से गुणा करके लिखने पर,

अत: अभीष्ट परिमेय संख्याएँ हैं : \(\frac { 21 }{ 28 }\),\(\frac { 22 }{ 28 }\) एवं \(\frac { 23 }{ 28 }\).

(iv) \(\frac { 1 }{ 4 }\) और \(\frac { 1 }{ 5 }\) को \(\frac { 4 }{ 4 }\) से गुणा करके लिखने पर,

अत: अभीष्ट परिमेय संख्याएँ हैं : \(\frac { 4 }{ 17 }\), \(\frac { 4 }{ 18 }\) एवं \(\frac { 4 }{ 19 }\)

प्रश्न 3.
\(\frac { 5 }{ 7 }\) और \(\frac { 6 }{ 7 }\) के बीच दो परिमेय संख्याएँ लिखिए। (2019)
हल:
\(\frac { 16 }{ 21 }\) एवं \(\frac { 17 }{ 21 }\)

प्रश्न 4.
निम्नलिखित के बीच एक परिमेय संख्या और एक अपरिमेय संख्या प्रविष्ट कीजिए :
(i) 2 और 3
(ii) 0 और 0.1
(iii) \(\frac { 1 }{ 3 }\) और \(\frac { 1 }{ 2 }\)
(iv) \(\frac { -2 }{ 5 }\) और \(\frac { 1 }{ 2 }\)
(v) 0.15 और 0.16
(vi) √2 और √3
(vii) 2.357 और 3.121
(viii) 0.0001 और 0.001
(ix) 3.623623 और 0.484848
(x) 6.375289 और 6.375738.
उत्तर:
(i) 2 और 3 के बीच परिमेय संख्या = 2.5 एवं अपरिमेय संख्या = √6
(ii) 0 और 0.1 के बीच परिमेय संख्या = 0.05 एवं अपरिमेय संख्या = 0.010010001…
(iii) \(\frac { 1 }{ 3 }\) और \(\frac { 1 }{ 2 }\) के बीच परिमेय संख्या = \(\frac { 2 }{ 5 }\) = एवं अपरिमेय संख्या = \(\frac { 1 }{ \sqrt { 5 } }\)
(iv) –\(\frac { 2 }{ 5 }\) और \(\frac { 1 }{ 2 }\) के बीच परिमेय संख्या = \(\frac { 1 }{ 4 }\) = एवं अपरिमेय संख्या = \(\frac { 1 }{ \sqrt { 5 } }\)
(v) 0.15 और 0.16 के बीच परिमेय संख्या = 0.155 एवं अपरिमेय संख्या = 0.15050050005 ….
(vi) √2 एवं √3 के बीच परिमेय संख्या = 1.5 एवं अपरिमेय संख्या = 1.505005000…..
(vii) 2.357 एवं 3.121 के बीच परिमेय संख्या = 2.5 एवं अपरिमेय संख्या = 3.010010001….
(viii) 0.0001 और 0:001 के बीच परिमेय संख्या = 0.0005 एवं अपरिमेय संख्या = 0.0083030030003……..
(ix) 3.623623 और 0.484848 के बीच परिमेय संख्या = 2 एवं अपरिमेय संख्या = 2.01001000100001……..
(x) 6.375289 और 6.375738 के बीच परिमेय संख्या = 6.3755 एवं अपरिमेय संख्या = 6.37530300300030000 …

प्रश्न 5.
संख्या रेखा पर (i) √5, (ii) √10 , (iii) √13 और (iv) √17 को निरूपित कीजिए।
हल:
(i) संख्या रेखा पर √5 का निरूपण :

(ii) संख्या रेखा पर √10 का निरूपण :

(iii) संख्या रेखा पर √13 का निरूपण :

(iv) संख्या रेखा पर √17 का निरूपण :

अतः अभीष्ट मान संख्या रेखा पर बिन्दु C से निरूपित हैं।

प्रश्न 6.
संख्या रेखा पर निम्नलिखित संख्याओं को ज्यामितीय रूप से निरूपित कीजिए :
(i) \(\sqrt { 4.5 }\)
(ii) \(\sqrt { 5.6 }\)
(iii) \(\sqrt { 8.1 }\)
(iv) \(\sqrt { 2.3 }\)
हल:
(i) \(\sqrt { 4.5 }\) का संख्या रेखा पर ज्यामितीय निरूपण :

अत: संख्या रेखा पर अभीष्ट बिन्दु E = \(\sqrt { 4.5 }\) निरूपित हैं।

(ii) \(\sqrt { 5.6 }\) का संख्या रेखा पर ज्यामितीय निरूपण :

चित्र 1.10 अतः संख्या रेखा पर अभीष्ट बिन्दु E = \(\sqrt { 5.6 }\) निरूपित है।

(iii) \(\sqrt { 8.1 }\) का संख्या रेखा पर ज्यामितीय निरूपण :

अतः संख्या रेखा पर अभीष्ट बिन्दु E = \(\sqrt { 8.1 }\) निरूपित है।

(iv) \(\sqrt { 2.3 }\) का संख्या रेखा पर ज्यामितीय निरूपण करना :

अतः संख्या रेखा पर अभीष्ट बिन्दु E = \(\sqrt { 2.3 }\) निरूपित है।

प्रश्न 7.
निम्नलिखित को p/q के रूप में व्यक्त कीजिए; जहाँ p और q पूर्णांक हैं तथा q ≠ 0 है :
(i) 0.2
(ii) \(0.\overline { 8 }\) अथवा 0.888…. (2019)
(iii) \(5.\overline { 2 }\),
(iv) \(0.\overline { 001 }\),
(v) 0.2555….
(vi) \(0.1\overline { 34 }\)
(vii) 0.00323232 ….
(viii) 0-404040 ….
(ix) \(0.12\overline { 3 }\).
हल:
(i) 0.2 = \(\frac { 2 }{ 10 }\) = \(\frac { 1 }{ 5 }\) .
(ii) 0.888 …. = x (मान लीजिए)
⇒ 10x = 8.888…..= 8 + 0.888….. = 8 + x.
⇒ 9x = 8 ⇒ x = \(\frac { 8 }{ 9 }\)

(iii) \(5.\overline { 2 }\) = 5.222….. = x (मान लीजिए)
⇒ 10x = 52.222…. = = 47 + 5.222 . . . . = 47 + x
⇒ 9x = 47 ⇒ x = \(\frac { 47 }{ 9 }\).

(iv) 0.001 = 0.001001001 …. =x (मान लीजिए)
⇒ 1000x = 1:001001001…. = 1+ 0.001001001 = 1 + x
⇒ 999x = 1 ⇒ x = \(\frac { 1 }{ 999 }\)

(v) 0.2555 …. = x (मान लीजिए)
⇒ 10x = 2.555 ….. = 2.3 + 0.2555 …. = 2.3 +x
⇒ 9x = 2.3 ⇒ n = 2.3 = \(\frac { 23 }{ 90 }\).

(vi) \(0.1\overline { 34 }\) = 0.1343434 …. =x (मान लीजिए)।
⇒ 100x = 13.434343…. = 13.3 + 0.1343434…. = 13:3 + x
⇒ 99x = 13.3 ⇒ x = \(\frac { 13.3 }{ 99 }\) = \(\frac { 133 }{ 990 }\).

(vii) 0.00323232 …. = x (मान लीजिए)
⇒ 100x = 0. 323232 .. . = 0.32 + 0.003232 …. = 0.32 + x
⇒ 99x = 032 ⇒ x = \(\frac { 0.32 }{ 99 }\) = \(\frac { 32 }{ 9900 }\) = \(\frac { 8 }{ 2475 }\)

(viii) 0.404040….. = x (मान लीजिए)
⇒ 100x = 40.404040….40 + 0.404040 …. = 40 +x
⇒ 99x = 40 ⇒ x = \(\frac { 40 }{ 99 }\)

(ix) \(0.12\overline { 3 }\) = 0.12333 …. = x (मान लीजिए)
⇒ 10x = 1.2333…. = 1.11 + 0.12333 . . . . = 1.11 + x
⇒ 9x = 1.11 ⇒ x = \(\frac { 1.11 }{ 9 }\) = \(\frac { 111 }{ 900 }\).

प्रश्न 8.
दर्शाइए कि 0.142857142857….= \(\frac { 1 }{ 7 }\) है।
हल:
मान लीजिए x = 0.142857142857 ….
⇒ 1000000x = 142857.142857142857…..
= 142857 + 0.142857142857 . . . . .
= 142857 + x
⇒ 999999x = 142857
⇒ x = \(\frac { 142857 }{ 999999 }\) = \(\frac { 1 }{ 7 }\)
⇒ 0.142857142857 ….. = \(\frac { 1 }{ 7 }\)

प्रश्न 9.
निम्नलिखित को सरल कीजिए :
(i) \(\sqrt { 45 }\) – 3\(\sqrt { 20 }\) + 4√5
(ii) \(\frac{\sqrt{24}}{8}+\frac{\sqrt{54}}{9}\)
(ii) 4√12 x 7√6
(iv) 4√28 ÷ 3√7.
हल:
(i) \(\sqrt { 45 }\) – 3\(\sqrt { 20 }\) + 4√5 = 3√5 – 6√5 + 4√5
= 7√5 – 6√5 = 5

(iii) 4√12 x 7√6 = 28√72 = 28 x 6√2 = 168√2.
(iv) 4√28 – 3√7 = 8√7 + 3√7 = 8√3.

प्रश्न 10.
यदि a = 2 + √3 है, तो a – \(\frac { 1 }{a }\) का मान ज्ञात कीजिए।
हल:

अत: a – \(\frac { 1 }{a }\) का अभीष्ट मान = 2√3.

प्रश्न 11.
निम्नलिखित में से प्रत्येक में हर का परिमेयीकरण कीजिए और फिर √2 = 1:414, √3 = 1.732 और √5 = 2:236 लेते हुए, तीन दशमलव अंक तक प्रत्येक का मान ज्ञात कीजिए:

हल:

MP Board Class 9th Maths Chapter 1 अति लघु उत्तरीय प्रश्न

प्रश्न 1.
मान लीजिए कि x और y क्रमशः परिमेय और अपरिमेय संख्याएँ हैं। क्या x + y आवश्यक रूप से एक अपरिमेय संख्या है ? अपने उत्तर की पुष्टि के लिए एक उदाहरण दीजिए।
उत्तर:
हाँ।
उदाहरण: मान लीजिए x = 2 एवं y = √2
x + y = 2 + 1.41421356237…….. = 3.41421356237
जो असांत एवं अनावर्ती है अत: x + y एक अपरिमेय संख्या है।

प्रश्न 2.
मान लीजिए x एक परिमेय संख्या है और । एक अपरिमेय संख्या है। क्या xy आवश्यक रूप से एक अपरिमेय संख्या है ? एक उदाहरण द्वारा अपने उत्तर का औचित्य दीजिए।
उत्तर:
नहीं।
उदाहरण : मान लीजिए x = 0 एवं y = √2 तब x.y = 0 x √2 = 0 एक परिमेय संख्या है
अत: यह आवश्यक नहीं कि xy एक अपरिमेय संख्या ही हो।

प्रश्न 3.
बताइए निम्नलिखित कथन सत्य हैं या असत्य। अपने उत्तर का औचित्य दीजिए :
(i) √2√3 एक परिमेय संख्या है।
(ii) किन्हीं दो पूर्णांकों के बीच अपरिमित रूप से अनेक पूर्णांक हैं।
(iii) 15 और 18 के बीच में परिमेय संख्याओं की संख्या परिमित है।
(iv) कुछ संख्याएँ ऐसी हैं जिन्हें p/q, q ≠ 0 के रूप में नहीं लिखा जा सकता; जहाँ p और q दोनों पूर्णांक हैं।
(v) एक अपरिमेय संख्या का वर्ग सदैव एक परिमेय संख्या होती है।
(vi) [/latex]\frac{\sqrt{12}}{\sqrt{3}}[/latex], \(\frac { p }{ q }\) ≠ 0 के रूप में लिखी है, इसलिए यह एक परिमेय संख्या है।
(vii) [/latex]\frac{\sqrt{15}}{\sqrt{3}}[/latex], \(\frac { p }{ q }\), q ≠ 0 के रूप में लिखी है, इसलिए यह एक परिमेय संख्या है।
(viii) एक संख्या x ऐसी है कि x² अपरिमेय है और x⁴ परिमेय है। उदाहरण की सहायता से अपने उत्तर का औचित्य दीजिए।
उत्तर:
(i) असत्य है, क्योंकि p अर्थात् √2 पूर्णांक नहीं है।
(ii) असत्य है, क्योंकि 2 और 3 के बीच एक भी पूर्णांक नहीं है।
(iii) असत्य है, क्योंकि 15 और 18 के बीच अपरिमित परिमेय संख्याएँ हैं।
(iv) सत्य है, क्योंकि [/latex]\frac{\sqrt{2}}{\sqrt{3}}[/latex] में √2 एवं √3 पूर्णांक नहीं हैं, इसलिए इसे p/q, q ≠ 0 के रूप में नहीं लिख सकते जहाँ p एवं q पूर्णांक हों।
(v) असत्य है, क्योंकि \(((\sqrt[3]{5})^{2}=\sqrt[3]{25}\) जो अपरिमेय संख्या है।
(vi) सत्य है, क्योंकि \(\frac{\sqrt{12}}{\sqrt{3}}=\sqrt{4}=2\) एक परिमेय संख्या है, किन्तु इसलिए नहीं कि p/q के रूप में लिखी है, अपितु इसलिए कि इसको सरलतम रूप में के रूप में लिखा जा सकता है।
(vii) असत्य है, क्योंकि \(\frac{\sqrt{15}}{\sqrt{3}}=\sqrt{5}\) है जो एक अपरिमेय संख्या है।
(vii) सत्य है, क्योंकि x = [/latex]\frac{\sqrt{4}}{\sqrt{3}}[/latex] तो x² = ( [/latex]\frac{\sqrt{4}}{\sqrt{3}}[/latex])² = √3 एक अपरिमेय संख्या है, जबकि x⁴ = ( [/latex]\frac{\sqrt{4}}{\sqrt{3}}[/latex])⁴ = 3 एक परिमेय संख्या है।

प्रश्न 4.
औचित्य देते हुए निम्नलिखित को परिमेय या अपरिमेय संख्याओं के रूप में वर्गीकृत कीजिए:
(i) \(\sqrt { 196 }\)
(ii) 3\(\sqrt { 18 }\) ,
(iii) \(\sqrt { \frac { 9 }{ 27 } }\)
(iv) \(\frac{\sqrt{28}}{\sqrt{343}}\)
(v) – \(\sqrt { 0.4 }\),
(vi) \(\frac{\sqrt{12}}{\sqrt{75}}\),
(vi) 0.5918,
(viii) (1 + √5) – (4 + √5),
(ix) 10.124124….
(x) 1.010010001….
उत्तर:
(i) \(\sqrt { 196 }\) = 14 एक परिमेय संख्या है।
(ii) 3\(\sqrt { 18 }\) = 9√2 अपरिमेय है, क्योंकि यह परिमेय संख्या 9 एवं अपरिमेय संख्या √2 का गुणनफल है।
(iii) \(\sqrt { \frac { 9 }{ 27 } }\) = \({ \frac { 1 } { √3 } }\) अपरिमेय है, क्योंकि यह परिमेय संख्या 1 एवं अपरिमेय संख्या √3 का भागफल है।
(vi) परिमेय \(\frac{\sqrt{28}}{\sqrt{343}}=\frac{2 \sqrt{7}}{7 \sqrt{7}}=\frac{2}{7}\) संख्या है, क्योंकि यह दो परिमेय संख्याओं 2 एवं 7 का भागफल है।
(v) अपरिमेय संख्या है क्योंकि \(-\sqrt{0 \cdot 4}=\frac{-2}{\sqrt{10}}\) जो एक परिमेय संख्या – 2 एवं एक अपरिमेय संख्या √10 का भागफल है।
(vi) \(\frac{\sqrt{12}}{\sqrt{75}}=\frac{2 \sqrt{3}}{5 \sqrt{3}}=\frac{2}{5}\) एक परिमेय संख्या है क्योंकि यह दो परिमेय संख्याओं 2 एवं 5 का भागफल है।
(vii) 0.5918 परिमेय संख्या है, क्योंकि दशमलव प्रसार सांत है।
(viii) (1 + √5) – (4 + √5) = 1 + √5 – 4 – √5 = – 3 एक परिमेय संख्या है।
(ix) 10.124124 ….. एक परिमेय संख्या है क्योंकि दशमलव प्रसार असांत आवर्ती है।
(x) 1.010010001 …. एक अपरिमेय संख्या है क्योंकि दशमलव प्रसार असांत अनावर्ती है।

प्रश्न 5.
क्या ऐसी दो अपरिमेय संख्याएँ हैं जिनका योग एवं गुणनफल दोनों ही परिमेय संख्याएँ हैं। अपने उत्तर का औचित्य दीजिए।
उत्तर:
हाँ, (2 + √3) एवं (2 – √3) ऐसी संख्याएँ हैं
जिनका योग = (2 + √3) + (2 – √3) = 2 + √3 + 2 – √3 = 4 परिमेय है
तथा जिनका गुणनफल = (2 + √3)(2 – √3) = 4 – 3 = 1 परिमेय संख्या है।

प्रश्न 6.
सरल कीजिए : (5 + √7) x (5 – √7). (2019)
हल:
(5 + √7) x (5 – √7) = (5)² – (√7)² = 25 – 7 = 18
अतः अभीष्ट मान = 18.

MP Board Class 9th Maths Chapter 1 बहु-विकल्पीय प्रश्न

प्रश्न 1.
प्रत्येक परिमेय संख्या है:
(a) एक प्राकृत संख्या
(b) एक पूर्णांक
(c) एक वास्तविक संख्या
(d) एक पूर्णांक संख्या।
उत्तर:
(c) एक वास्तविक संख्या

प्रश्न 2.
दो परिमेय संख्याओं के बीच में:
(a) कोई परिमेय संख्या नहीं होती
(b) ठीक एक परिमेय संख्या होती है
(c) अपरिमित रूप से अनेक परिमेय संख्याएँ होती हैं
(d) केवल परिमेय संख्याएँ होती हैं तथा कोई अपरिमेय संख्या नहीं होती।
उत्तर:
(c) अपरिमित रूप से अनेक परिमेय संख्याएँ होती हैं

प्रश्न 3.
एक परिमेय संख्या का दशमलव निरूपण नहीं हो सकता :
(a) सांत
(b) असांत
(c) असांत आवर्ती
(d) असांत अनावर्ती।
उत्तर:
(d) असांत अनावर्ती

प्रश्न 4.
किन्हीं दो अपरिमेय संख्याओं का गुणनफल होता है:
(a) सदैव एक अपरिमेय संख्या मारमय सख्या
(b) सदैव एक परिमेय संख्या
(c) सदैव एक पूर्णांक
(d) कभी परिमेय संख्या कभी अपरिमेय संख्या।
उत्तर:
(d) कभी परिमेय संख्या कभी अपरिमेय संख्या

प्रश्न 5.
संख्या √2 का दशमलव प्रसार है :
(a) एक परिमित दशमलव
(b) 1:41421
(c) असांत आवर्ती
(d) असांत अनावर्ती।
उत्तर:
(d) असांत अनावर्ती

प्रश्न 6.
निम्नलिखित में से कौन-सी एक अपरिमेय संख्या है :

उत्तर:
(c)

प्रश्न 7.
निम्नलिखित में से कौन-सी एक अपरिमेय संख्या है :
(a) 0.14
(b) \(0.4\overline { 16 }\)
(c) \(0.\overline { 1416 }\)
(d) 0.4014001400014….
उत्तर:
(d) 0.4014001400014….

प्रश्न 8.
√2 और √3 के बीच एक परिमेय संख्या है :

उत्तर:
(c)

प्रश्न 9.
p/q के रूप में 1.999… का मान, जहाँ p और q पूर्णांक हैं तथा q ≠ 0 होगा :
(a) \(\frac { 19 }{ 18 }\)
(b) \(\frac { 1999 }{ 1000 }\)
(c) 2
(d) \(\frac { 1 }{ 9 }\)
उत्तर:
(c) 2

प्रश्न 10.
2√3 + √3 बराबर है :
(a) 2√6
(b) 6
(c) 3√5
(d) 4√6.
उत्तर:
(c) 3√5

प्रश्न 11.
√10 x √15 बराबर है :
(a) 6√5
(b) 5√6
(c) √25
(d) 10√5.
उत्तर:
(b) 5√6

प्रश्न 12.
\(\frac{1}{\sqrt{7}-2}\) के परिमेयीकरण करने पर प्राप्त संख्या है :

उत्तर:
(a)

प्रश्न 13.
\(\frac{1}{\sqrt{9}-\sqrt{8}}\) बराबर है :

उत्तर:
(d)

प्रश्न 14.
\(\frac{7}{3 \sqrt{3}-2 \sqrt{2}}\) के हर का परिमेयीकरण करने पर हमें प्राप्त हर है :
(a) 13
(b) 19
(c) 5
(d) 35
उत्तर:
(b) 19

प्रश्न 15.
\(\frac{\sqrt{32}+\sqrt{48}}{\sqrt{8}+\sqrt{12}}\) का मान बराबर है :
(a) √2
(b) 2
(c) 4
(d) 8
उत्तर:
(b) 2

प्रश्न 16.
यदि √2 = 1.4142 है, तो \(\sqrt{\frac{\sqrt{2}-1}{\sqrt{2}+1}}\) बराबर है :
(a) 2.4142
(b) 5.8282
(c) 0.4142
(d) 0.1718.
उत्तर:
(c) 0.4142

प्रश्न 17.
\(\sqrt[4]{\sqrt[3]{2^{2}}}\) बराबर है :
(a) 2^-1/6
(b) 2^-6
(c) 2^1/6
(d) 2⁶
उत्तर:
(c) 2^1/6

प्रश्न 18.
गुणनफल 12 x 4/2 x 12/32 बराबर है :
(a) √2
(b) 2
(c) \(\sqrt[2]{2}\)
(d) 1
उत्तर:
(b) 2

प्रश्न 19.
\(\sqrt[4]{(81)^{-2}}\) का मान है :
(a) \(\frac { 1 }{ 9 }\)
(b) \(\frac { 1 }{ 3 }\)
(c) 9
(d) \(\frac { 1 }{ 81 }\)
उत्तर:
(a) \(\frac { 1 }{ 9 }\)

प्रश्न 20.
(256)^0.16 x (256)^0.09 का मान है:
(a) 4
(b) 16
(c) 64
(d) 256.25
उत्तर:
(a) 4

प्रश्न 21.
निम्नलिखित में से कौन x के बराबर है :

उत्तर:
(c)

प्रश्न 22.
निम्नलिखित से कौन [(5/6)^1/5]^-1/6 के बराबर नहीं है :

उत्तर:
(a)

प्रश्न 23.
किसी वास्तविक संख्या का निरपेक्ष मान सदैव होता है : (2018)
(a) प्राकृत संख्या
(b) परिमेय संख्या
(c) ऋण संख्या
(d) धन संख्या।
उत्तर:
(d) धन संख्या

प्रश्न 24.
निम्न में से कौन-सी परिमेय संख्या नहीं है: (2019)
(a) \(\sqrt { 23 }\)
(b) \(\sqrt { 225 }\)
(c) \(\sqrt { 249 }\)
(d) \(5.\overline { 328 }\)
उत्तर:
(a) \(\sqrt { 23 }\)

प्रश्न 25.
निम्नलिखित में कौन-सी अपरिमेय संख्या है : (2019)
(a) 0.23
(b) 0:2023002300023 ……..
(c) \(0.23\overline { 25 }\)
(d) \(0.\overline { 2325 }\)
उत्तर:
(b) 0:2023002300023 ……..

प्रश्न 26.
a^m x aⁿ का मान होगा : (2019)
(a) a^m+n
(b) a^mn
(c) a^m-n
(d) a^m/n
उत्तर:
(a) a^m+n

रिक्त स्थानों की पूर्ति

1. सभी प्राकृत संख्याएँ एवं शून्य मिलकर ………कहलाती हैं।
2. जो संख्याएँ p/q, q ≠ 0 के रूप में व्यक्त की जा सकती हैं, जहाँ p, q पूर्णांक है, ………. कहलाती हैं।
3. जो संख्याएँ p/q, q ≠ 0 के रूप में व्यक्त नहीं की जा सकती; जहाँ p, q पूर्णांक हैं ……….. कहलाती हैं।
4. दो परिमेय संख्याओं के मध्य ……….. परिमेय संख्याएँ होती हैं। (2019)
5. दो अपरिमेय संख्याओं के मध्य ………. अपरिमेय संख्याएँ होती हैं।
6. 3√5 का करणी घात ………. है। (2018)
7. सबसे छोटी प्राकृत संख्या ……….. है। (2019)
उत्तर:
1. पूर्णांक संख्याएँ,
2. परिमेय संख्याएँ,
3. अपरिमेय संख्याएँ,
4. अनन्तत: अनेक,
5. अनन्ततः अनेक,
6. पाँच (5),
7. 1 (एक)।

जोड़ी मिलान
स्तम्भ ‘A’                                                            स्तम्भ ‘B’
1. सांत दशमलव प्रसार                              (a) वास्तविक संख्याएँ
2. अनवसानी अनावर्ती दशमलव प्रसार         (b) पूर्ण संख्याएँ
3. 8^-1/3 (2019)                                       (c) परिमेय संख्या
4. सभी परिमेय एवं अपरिमेय संख्याएँ           (d) अपरिमेय संख्या
5. शून्य एवं प्राकृत संख्याएँ मिलकर              (e) 1/2
उत्तर:
1.→(c), 2.→(d), 3.→(e), 4.→(a), 5.→(b).

सत्य/असत्य कथन

1. दो परिमेय संख्याओं का योग सदैव परिमेय होता है।
2. दो अपरिमेय संख्याओं का योग सदैव अपरिमेय होता है
3. प्रत्येक पूर्णांक परिमेय संख्या होती है।
4. प्रत्येक वास्तविक संख्या परिमेय संख्या होती है।
5. प्रत्येक अपरिमेय संख्या वास्तविक संख्या होती है।
6. \(\frac { 32 }{ 48 }\), \(\frac { 2 }{ 3 }\) के तुल्य परिमेय संख्या है। (2019)
7. √2 एक परिमेय संख्या है। (2019)
उत्तर:
1. सत्य,
2. असत्य
3. सत्य,
4. असत्य,
5. सत्य,
6. सत्य,
7. असत्य।

एक शब्द/वाक्य में उत्तर

1. a^m x aⁿ का सरलतम रूप क्या होगा?
2. a^m x bⁿ को सरल रूप में लिखिए।
3. a^m ÷ aⁿ का सरल रूप लिखिए।
4. a° का मान कितना होता है ?
5. a^-m को धनात्मक घातांक में लिखिए।
6. √3 का मान लिखिए। (2019)
उत्तर:
1. a^m+n,
2. (ab)ⁿ,
3. a^m-n,
4. 1,
5. (1/a)^m ,
6. 1.732……. .

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 8 चतुर्भुज Ex 8.1

प्रश्न 1.
एक चतुर्भुज के कोण 3 : 5 : 9 : 13 के अनुपात में हैं। इस चतुर्भुज के सभी कोण ज्ञात कीजिए। (2018, 19)
हल:
चूँकि चतुर्भुज के चारों कोणों का अनुपात = 3 : 5 : 9 : 13 (दिया है)
मान लीजिए उसके कोण क्रमश: 3x, 5x, 9x एवं 13x हैं तो 3x + 5x + 9x + 13x = 360° (चतुर्भुज के कोणों का योग 360° होगा।)
⇒ 30x = 360°
⇒ x = 360°/30 = 12
इसलिए प्रथम कोण = 3 x x = 3 x 12 = 36°
द्वितीय कोण = 5 x x = 5 x 12 = 60°
तृतीय कोण = 9 x x = 9 x 12 = 108°
चतुर्थ कोण = 13 x x = 13 x 12 = 156°
अतः कोणों का अभीष्ट मान क्रमशः 36°, 60°, 108° एवं 156° हैं।

प्रश्न 2.
यदि एक समान्तर चतुर्भुज के विकर्ण बराबर हों तो दर्शाइए कि वह एक आयत है। (2019)

चित्र 8.1
हल:
समान्तर चतुर्भुज ABCD के विकर्ण AC = DB (दिया है)
∆ABC एवं ∆DCB में,
चूँकि AB = DC (समान्तर चतुर्भुज की सम्मुख भुजाएँ हैं)
AC = DB (दिया है)
एवं BC = BC (उभयनिष्ठ है)
∆ABC ≅ ∆DCB (SSS सर्वांगसमता प्रमेय)
∠ABC = ∠DCB (CPCT)
लेकिन ∠ABC + ∠DCB = 180° (AB || DC, BC तिर्यक के एक ओर के अन्तः कोण हैं)
⇒ ∠ABC = ∠DCB = 90°
लेकिन ∠A = ∠C तथा ∠B = ∠D (समान्तर – के सम्मुख कोण)
⇒ ∠A =∠B = ∠C = ∠D = 90° (समकोण)
अत: ABCD एक आयत है। इति सिद्धम्

प्रश्न 3.
दर्शाइए कि यदि एक चतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करें तो वह एक समचतुर्भुज होता है।

हल:
दिया है: एक चतुर्भुज जिसके विकर्ण AC और BD परस्पर समकोण पर समद्विभाजित करते हैं, अर्थात्
AO = CO एवं BO = DO …..(1)
और ∠AOB = ∠ BOC = ∠COD = ∠DOA = 90° …(2)
∆AOB और ∆AOD में,
चूँकि BO = DO [समीकरण (1) से]
∠AOB = ∠DOA [समीकरण (2) से]
एवं AO = AO (उभयनिष्ठ है)
⇒ ∆AOB ≅ ∆AOD (SAS सर्वांगसमता प्रमेय)
⇒ AB = AD (CPCT)
अब ∆AOD और ∆COB में,
चूँकि AO = CO [समीकरण (1) से]
⇒ ∆AOD ≅ ∆COB [समीकरण (2) से]
एवं DO = BO [समीकरण (1) से]
⇒ ∆AOD ≅ ∆COB (SAS प्रमेय से)
⇒ AD = BC (CPCT)
एवं ∠ADO = ∠CBO (CPCT)
AD || BC (एकान्तर कोण ∠ADO = ∠CBO)
इसलिए ABCD एक समान्तर चतुर्भुज है। (क्योंकि रेखा युग्म AD, BC बराबर और समान्तर हैं)
AB = BC = CD = DA (∵ AB = CD, DA = BC एवं AB = DA)
अतः ABCD एक सम चतुर्भुज है। इति सिद्धम्

प्रश्न 4.
दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
हल:

चित्र 8.3
दिया है : एक वर्ग ABCD जिसके विकर्ण AC एवं BD परस्पर O बिन्दु पर प्रतिच्छेद करते हैं।
अब ∆ABC एवं ∆DCB में,
चूँकि AB = DC (वर्ग की भुजाएँ हैं)।
∠ABC = ∆DCB = 90° (वर्ग के कोण हैं)
एवं BC = BC (उभयनिष्ठ है)
⇒ ∆ABC ≅ ∆DCB (SAS सर्वांगसमता प्रमेय)
⇒ AC = BD (CPCT)
अतः वर्ग के विकर्ण बराबर होते हैं।
इति सिद्धम् चूँकि वर्ग एक समान्तर चतुर्भुज है, इसलिए उसके विकर्ण AC एवं BD परस्पर O बिन्दु पर समद्विभाजित करेंगे।
अर्थात् AO = CO एवं BO = DO …(1)
अब, ∆ABO और ∆ADO में, AB = AD (वर्ग की भुजाएँ हैं)
BO = DO [समीकरण (1) से]
एवं AO = AO (उभयनिष्ठ है)
⇒ ∆ABO ≅ ∆ADO (SSS सर्वांगसमता प्रमेय)
⇒ ∠AOB = ∠AOD (CPCT)
लेकिन ∠AOB + ∠AOD = 180° (रेखाखण्ड BD बिन्दु 0 पर एक ही ओर बने कोण हैं)
⇒∠AOB = ∠AOD = 90°
अतः वर्ग के विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं। इति सिद्धम्

प्रश्न 5.
दर्शाइए कि यदि एक चतुर्भुज के विकर्ण बराबर हों और परस्पर लम्बवत् समद्विभाजित करें तो वह एक वर्ग होगा।

चित्र 8.4
हल:
दिया है : ABCD चतुर्भुज के विकर्ण AC और BD परस्पर बिन्दु O पर लम्ब समद्विभाजित करते हैं तथा परस्पर बराबर हैं अर्थात्
AO = CO, BO = DO,
∠AOB = ∠ BOC = ∠COD = ∠DOA = 90°
एवं विकर्ण AC = BD
अब ∆AOD और ∆COB में,
चूँकि AO = CO (दिया है)
∠DOA = ∠BOC = 90° (दिया है)
एवं DO = BO (दिया है)
⇒ ∆AOD ≅ ∆COB (SAS सर्वांगसमता प्रमेय)
⇒ AD = BC (CPCT)
⇒ ∠ADO = ∠OBC (CPCT)
⇒ AD || BC (∠ADO एवं ∠OBC एकान्तर कोण हैं)
⇒ □ABCD एक समान्तर चतुर्भुज है। (चूँकि AD = BC एवं AD || BC)
AB = CD एवं BC = DA (सम्मुख भुजाएँ हैं) …(1)
अब ∆AOB और ∆AOD में,
चूँकि BO = DO (दिया है)
∠AOB = ∠AOD = 90° (दिया है)
एवं AO = AO (उभयनिष्ठ है)
⇒ ∆AOB ≅ ∆AOD (CPCT) (SAS सर्वांगसमता प्रमेय)
⇒ AB = DA …(2)
⇒ AB = BC = CD = DA [समीकरण (1) एवं (2) से]
इसलिए ABCD एक समचतुर्भुज है।
अब ∆ABC एवं ∆DCB में,
चूँकि AB = DC (समान्तर चतुर्भुज की सम्मुख भुजाएँ हैं)
AC = DB (दिया है)
एवं BC = BC (उभयनिष्ठ है)
∆ABC ≅ ∆DCB (SSS सर्वांगसमता प्रमेय)
∠ABC = ∠DCB (CPCT)
∠ABC = ∠CDA
एवं ∠DAB = ∠ BCD (समान्तर □ के सम्मुख कोण हैं)
∠ABC = ∠BCD = ∠CDA = ∠ DAB
लेकिन ∠ABC + ∠BCD + ∠CDA + ∠DAB = 360° (चतुर्भुज के अन्तः कोण)
= ∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
अत: ABCD एक वर्ग है। (परिभाषा से) इति सिद्धम्

प्रश्न 6.
संलग्न चित्र में समान्तर चतुर्भुज ABCD का विकर्ण AC कोण A को समद्विभाजित करता है। दर्शाइए कि
(i) यह LC को भी समद्विभाजित करता है।
(ii) ABCD एक समचतुर्भुज है।

चित्र 8.4
हल:
ABCD एक समान्तर चतुर्भुज दिया है जिसका विकर्ण AC ∠A का समद्विभाजक है अर्थात्
∠DAC = ∠ BAC …(1)
एवं DC || AB एवं AD || BC (समान्तर – की सम्मुख भुजाएँ हैं)

(i) चूँकि DC || AB को तिर्यक रेखा AC प्रतिच्छेद करती है।
⇒ ∠DCA = ∠BAC (एकान्तर कोण है।) …(2)
चूँकि AD || BC को AC तिर्यक रेखा प्रतिच्छेद करती है
⇒ ∠DAC = ∠ BCA (एकान्तर कोण है) …(3)
⇒ ∠DCA = ∠BCA [समीकरण (1), (2) एवं (3) से]
अतः विकर्ण AC कोण LC को भी समद्विभाजित करता है। । इति सिद्धम्

(ii) ∆DAC में, ∠DAC = ∠DCA (∠A = ∠C के अर्द्धक हैं)
⇒ DA = CD (बराबर कोणों की सम्मुख भुजाएँ हैं)…(4)
चूँकि AB = CD एवं DA = BC (समान्तर □ की सम्मुख भुजाएँ हैं) …(5)
⇒ AB = BC = CD = DA [समीकरण (4) और (5) से]
अतः चतुर्भुज ABCD एक समचतुर्भुज है। इति सिद्धम्

प्रश्न 7.
ABCD एक समचतुर्भुज है। दर्शाइए कि विकर्ण AC कोणों A और C दोनों को समद्विभाजित करता है तथा विकर्ण BD कोणों B और D दोनों को समद्विभाजित करता है।
हल:

चित्र 8.6
दिया है : ABCD एक समचतुर्भुज जिसमें AC एवं BD विकर्ण एक-दूसरे को बिन्दु 0 पर समकोण पर समद्विभाजित करते हैं,
AB = BC = CD = DA …(1)
AO = OC, BO = OD …(2)
∆AOB और ∆AOD में,
चूँकि AB = AD [समीकरण (1) से।]
BO = OD [समीकरण (2) से]
एवं AO = AO (उभयनिष्ठ है)
⇒ ∆AOB ≅ ∆AOD (SSS सर्वांगसमता प्रमेय)
⇒ ∠BAO = ∠DAO (CPCT)
∆COB और ∆COD में,
चूँकि CB = CD [समीकरण (1) से]
BO = OD [समीकरण (2) से]
एवं CO = CO (उभयनिष्ठ है)
⇒ ∆COB ≅ ∆COD (SSS सर्वांगसमता प्रमेय)
⇒ ∠BCO = ∠ DCO (CPCT)
अत: AC विकर्ण ∠A और LC दोनों को समद्विभाजित करता है। इति सिद्धम्
अब ∆BOA और ∆BOC में,
चूँकि BA = BC [समीकरण (1) से]
AO = OC [समीकरण (2) से]
एवं BO = BO (उभयनिष्ठ है)
⇒ ∆BOA ≅ ∆BOC (SSS सर्वांगसमता प्रमेय)
⇒ ∠ABO = ∠CBO. (CPCT)
∆DOA और ∆DOC में,
चूँकि DA = DC [समीकरण (1) से]
AO = OC [समीकरण (2) से ]
एवं DO = DO (उभयनिष्ठ है)
⇒ ∆DOA = ∆DOC (SSS सर्वांगसमता प्रमेय)
⇒ ∠ADO = ∠CDO (CPCT)
अतः विकर्ण BD, LB और CD दोनों को समद्विभाजित करता है। इति सिद्धम्

प्रश्न 8.
ABCD एक आयत है जिसके विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता है। दर्शाइए कि-
(i) ABCD एक वर्ग है।
(ii) विकर्ण BD दोनों कोणों B और D को समद्विभाजित करता है।

चित्र 8.7
हल:
(i) ABCD एक आयत है जिसका विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता है।
अब ∆ABC एवं ∆ADC में,
चूँकि ∠BAC = ∠DAC (∠A के आधे हैं)
AC = AC (उभयनिष्ठ है)
एवं ∠ACB = ∠ACD (∠C के आधे हैं)
⇒ ∆ABC ≅ ∆ADC (ASA सर्वांगसमता प्रमेय)
⇒ AB = AD (CPCT) …(1)
AB = CD एवं AD = BC ( आयत की सम्मुख भुजाएँ हैं)…(2)
AB = BC = CD = DA [समीकरण (1) और (2) से]
अत: ABCD एक वर्ग है। (आयत जिसकी भुजाएँ बराबर हों वर्ग होता है।) इति सिद्धम्

(ii) मान लीजिए कि विकर्ण AC एवं BD परस्पर O बिन्दु पर प्रतिच्छेद करते हैं।
∆AOB और ∆COB में,
चूँकि AB = BC (वर्ग की भुजाएँ हैं)
चूँकि AO = CO (वर्ग के विकर्ण परस्पर समद्विभाजित करते हैं)
चूँकि BO = BO (उभयनिष्ठ है)
⇒ ∆AOB ≅ ∆COB (SSS सर्वांगसमता प्रमेय)
⇒ ∠ABO = ∠CBO (CPCT)
अब ∆AOD और ∆COD में,
चूँकि AD = CD (वर्ग की भुजाएँ हैं)
AO = CO (वर्ग के विकर्ण परस्पर समद्विभाजित करते हैं)
चूँकि DO = DO (उभयनिष्ठ है)
⇒ ∆AOD ≅ ∆COD (SSS सर्वांगसमता प्रमेय)
⇒ ∠ADO ≅ ∠CDO (CPCT)
अतः विकर्ण BD दोनों कोणों B और D को समद्विभाजित करता है। इति सिद्धम्

प्रश्न 9.
समान्तर चतुर्भुज ABCD के विकर्ण BD पर दो बिन्दु P और Q इस प्रकार स्थित है कि DP = BQ है (देखिए संलग्न चित्र)। दर्शाइए कि-
(i) ∆APD ≅ ∆CQB
(ii) AP= CQ
(iii) ∆AQB ≅ ∆CPD
(iv) AQ = CP
(v) APCQ एक समान्तर चतुर्भुज है।

चित्र 8.8
हल:
(i) ∆APD और ∆COB में,
चूँकि AD = CB (समान्तर – की सम्मुख भुजाएँ हैं)
DP = BQ (दिया है)
एवं ∠ADP = ∠CBQ (एकान्तर कोण हैं)
अतः ∆APD ≅ ∆CQB. (SAS सर्वांगसमता प्रमेय) इति सिद्धम्

(ii) चूँकि ∆APD ≅ ∆CQB (सिद्ध कर चुके हैं)
अतः AP = CQ. (CPCT) इति सिद्धम्

(iii) ∆AQB और ∆CPD में,
AB = CD (समान्तर □ की सम्मुख भुजाएँ हैं)
BQ = PD (दिया है)
∠ABQ = ∠ CDP (एकान्तर कोण है)
अतः ∆AQB ≅ ∆CPD. (SAS सर्वांगसमता प्रमेय) इति सिद्धम्

(iv) चूंकि ∆AQB ≅ ∆CPD (सिद्ध कर चुके हैं)
अतः AQ = CP. (CPCT) इति सिद्धम्

(v) चूँकि AP = CQ [भाग (ii) में सिद्ध कर चुके हैं।]
चूँकि AQ = CP [भाग (iv) में सिद्ध कर चुके हैं।]
अतः चतुर्भुज ∆PCQ एक समान्तर चतुर्भुज है। (चूँकि सम्मुख भुजाएँ समान हैं) इति सिद्धम्

प्रश्न 10.
ABCD एक समान्तर चतुर्भुज है तथा AP और CQ शीर्ष A और C से विकर्ण BD पर क्रमशः डाले गए लम्ब हैं देखिए संलग्न चित्र। दर्शाइए कि-
(i) ∆APB ≅ ∆COD
(ii) AP = CP.

चित्र 8.9
हल:
(i) ∆APB और ∆COD में,
चूँकि DC = AB (समान्तर □ की सम्मुख भुजाएँ हैं)
∠CDQ = ∠ABP (एकान्तर कोण है)
∠APB = ∠CQD = 90° (AP ⊥ DB एवं CQ ⊥ DB)
अतः ∆APB ≅ ∆CQD. (SAA सर्वांगसमता प्रमेय) इति सिद्धम्

(ii) चूँकि ∆APB ≅ ∆COD (सिद्ध कर चुके हैं)
अतः AP = CQ. (CPCT) इति सिद्धम्

प्रश्न 11.
∆ABC और ∆DEF में, AB = DE, AB || DE, BC = EF और BC || EF है। शीर्ष A, B और C को क्रमशः शीर्ष D, E और F से जोड़ा जाता है (देखिए संलग्न चित्र)। दर्शाइए कि –

चित्र 8.10
(i) चतुर्भुज ABED एक समान्तर चतुर्भुज है।
(ii) चतुर्भुज BEFC एक समान्तर चतुर्भुज है।
(iii) AD || CF और AD = CE
(iv) चतुर्भुज ACFD एक समान्तर चतुर्भुज है।
(v) AC = DF है।
(vi) ∆ABC ≅ ∆DEF है।
हल:
(i) चूंकि AB = DE एवं AB || DE (दिया है)
अत: ABED एक समान्तर चतुर्भुज है। इति सिद्धम्

(ii) चूँकि BC = EF एवं BC || EF (दिया है)
अतः BEFC एक समान्तर चतुर्भुज है। इति सिद्धम्

(iii) चूँकि AD = BE एवं AD || BE (समान्तर □ABED की सम्मुख भुजाएँ हैं) …(1)
CF = BE एवं CF || BE (समान्तर □ BEFC की सम्मुख भुजाएँ हैं)…(2)
अत: AD = CF एवं AD || CE [समीकरण (1) एवं (2) से] । इति सिद्धम्

(iv) चूँकि AD = CF एवं AD || CF (सिद्ध कर चुके हैं)
अत: ACFD एक समान्तर चतुर्भुज है। इति सिद्धम्

(v) चूँकि चतुर्भुज ACFD एक समान्तर चतुर्भुज है (सिद्ध कर चुके हैं)
अत: AC = DE (समान्तर चतुर्भुज की सम्मुख भुजा हैं) इति सिद्धम्

(vi) ∆ABC और ∆DEF में,
चूँकि AB = DE (समान्तर □ABED की सम्मुख भुजाएँ हैं)
AC = DF (समान्तर □ACFD की सम्मुख भुजाएँ हैं)
BC = EF (समान्तर □CBEF की सम्मुख भुजाएँ हैं)
अत: ∆ABC ≅ ∆DEE (SSS सर्वांगसम प्रमेय) इति सिद्धम्

प्रश्न 12.
संलग्न आकृति में ABCD एक समलम्ब है जिसमें AB || DC और AD = BC है। दर्शाइए कि
(i) ∠A = ∠B.
(ii) ∠C = ∠D.
(iii) ∆ABC ≅ ∆BAD.
(iv) विकर्ण AC = विकर्ण BD है।

चित्र 8.11
हल:
दिया है : ABCD एक समलम्ब चतुर्भुज जिसमें AB || DC और AD = BC है। विकर्ण AC और BD को मिलाया गया है।
रचना : AB को आगे बढ़ाइए और C से होकर CE || DA खींचिए जो AB को E पर प्रतिच्छेद करती है।

(i) AD = BC (दिया है) तथा AD = EC (रचना से)
⇒ BC = EC (एक वस्तु के बराबर वस्तुएँ बराबर होती हैं)
⇒ ∠CBE = ∠CEB (त्रिभुज की बराबर भुजाओं के सम्मुख कोण हैं)
चूँकि ∠ABC + ∠ CBE = 180° (रेखा AE के बिन्दु B पर एक ओर बने कोण है)…(1)
चूँकि AD || EC को AE तिर्यक रेखा मिलती है।
⇒ ∠DAE + ∠CEB = 180° (एक ही ओर के अन्तः कोण हैं)
⇒ ∠DAE + ∠CBE = 180° (∵ ∠CEB = ∠CBE) …(2)
∠DAE = ∠ABC [समीकरण (1) और (2) से]
∠A = ∠B. इति सिद्धम्

(ii) चूँकि ∠A + ∠D = 180° (AB || DC, AD तिर्यक रेखा है) …(3)
∠B + ∠C = 180° (AB || DC, BC तिर्यक रेखा है) …(4)
∠A + ∠D = ∠B + ∠C [समीकरण (3) और (4) से]
अतः ∠C = ∠D. (क्योंकि ∠A = ∠B सिद्ध कर चुके हैं) इति सिद्धम्

(iii) ∆ABC और ∆BAD में,
चूँकि BC = AD (दिया है)
∠B = ∠A (सिद्ध कर चुके हैं)
एवं AB = AB (उभयनिष्ठ है)
अतः ∆ABC ≅ ∆BAD. (SAS सर्वांगसमता नियम) इति सिद्धम्

(iv) चूँकि AABC ≅ A BAD (सिद्ध कर चुके हैं)
अतः विकर्ण AC = विकर्ण BD है। (CPCT) इति सिद्धम्

MP Board Class 9th Maths Solutions