Category: Class 7

MP Board Class 7th Science Solutions Chapter 17 वन: हमारी जीवन रेखा

MP Board Class 7th Science Chapter 17 पाठान्त अभ्यास के प्रश्नोत्तर

प्रश्न 1.
समझाइए कि वन में रहने वाले जन्तु किस प्रकार वनों की वृद्धि करने और पुनर्जनन में सहायक होते हैं?
उत्तर:
वन में रहने वाले जन्तुओं द्वारा किए गए गोबर के ढेर पर शाकों और झाड़ियों के नवोद्भिद अंकुरित हो जाते हैं।इनको उगने के लिए पोषक तत्त्व भी गोबर से प्राप्त हो जाते हैं। ये जन्तु कुछ पादपों के बीजों को प्रकीर्णित कर देते हैं। ये बीज नये पादपों को जन्म देते हैं। पादपों की अधिक किस्में शाकाहारी जन्तुओं को भोजन और आवास के लिए अधिक अवसर प्रदान करते हैं। शाकाहारियों की अधिक संख्या माँसभक्षियों के लिए भोजन बनते हैं। इस प्रकार जन्तु वनों की वृद्धि करने और पुनर्जनन में सहायक हैं।

प्रश्न 2.
समझाइए कि वन, बाढ़ की रोकथाम कैसे करते हैं?
उत्तर:
वन वर्षा जल के प्राकृतिक अवशोषक का काम करते हैं और उसे अवस्रावित होने देते हैं। वृक्षों तथा पौधों के मूल मृदा को एक साथ बाँधे रखते हैं। मृदा भू-तल पर गिरने वाले वर्षा जल को अवशोषित करके पृथ्वी के अन्दर भेज देती है। इस प्रकार वन बाढ़ों की रोकथाम करने में सहायक होते हैं।

प्रश्न 3.
अपघटक किन्हें कहते हैं? इनमें से किन्हीं दो के नाम बताइए। ये वन में क्या करते हैं?
उत्तर:
पादपों और जन्तुओं के मृत शरीर को ह्यूमस में परिवर्तित करने वाले सूक्ष्म जीव, अपघटक कहलाते हैं।
अपघटक: मशरूम, मिलीपीड़ों।
सूक्ष्मजीव मृत पादपों और जन्तु ऊतकों को खाते हैं और उन्हें एक गहरे रंग के पदार्थ ह्यूमस में बदल देते हैं। ह्यूमस मृदा को उर्वर बनाता है और पादपों को पोषण प्रदान करता है।

प्रश्न 4.
वायुमण्डल में ऑक्सीजन और कार्बन डाइऑक्साइड के बीच सन्तुलन को बनाए रखने में वनों की भूमिका को समझाइए।
उत्तर:
सभी हरे पेड़-पौधे दिन में सूर्य के प्रकाश की उपस्थिति में प्रकाश संश्लेषण की क्रिया करते हैं, जिसमें ये कार्बन डाइऑक्साइड लेते हैं तथा आक्सीजन छोड़ते हैं जिससे वायुमण्डल में ऑक्सीजन तथा कार्बन डाइऑक्साइड का सन्तुलन बना रहता है।

प्रश्न 5.
समझाइए कि वनों में कुछ भी व्यर्थ क्यों नहीं होता है?
उत्तर:
वनों के कारण खनिज पदार्थ एवं अन्य उपयोगी पदार्थों की मात्रा का सन्तुलन बना रहता है तथा विभिन्न पदार्थों का चक्रीकरण होता रहता है। मृदा में ह्यूमस की उपस्थिति से मृत पादपों और जन्तुओं के पोषक तत्त्व मृदा में निर्मुक्त होते रहते हैं। वहाँ से इन पोषक तत्त्वों को सजीव पादपों की मूलों द्वारा अवशोषित कर लिया जाता है। इन पोषक तत्त्वों का चक्र चलता रहता है जिससे वन में कुछ भी व्यर्थ नहीं जाता है।

प्रश्न 6.
ऐसे पाँच उत्पादों के नाम बताइए, जिन्हें हम वनों से प्राप्त करते हैं।
उत्तर:
वनों से प्राप्त होने वाले उत्पाद-लाख, गोंद, चन्दन, कपूर, जैव ईधन आदि।

प्रश्न 7.
रिक्त स्थानों की पूर्ति कीजिए –

1. कीट, तितलियाँ, मधुमक्खियाँ और पक्षी, पुष्पीय पादपों की ………. में सहायता करते हैं।
2. वन परिशुद्ध करते हैं ……… और ……… को।
3. शाक वन में …………. परत बनाते हैं।
4. वन में क्षयमान पत्तियाँ और जन्तुओं की लीद ……….को समृद्ध करते हैं।

उत्तर:

1. वृद्धि।
2. जलवायु, वायु।
3. सबसे नीचे की।
4. मृदा।

प्रश्न 8.
हमें अपने से दूर स्थित वनों से सम्बन्धित परिस्थितियों और मुद्दों के विषय में चिंतित होने की क्यों आवश्यकता है?
उत्तर:
हमें वनों से सम्बन्धित परिस्थितियों और मुद्दों के विषय में चिंतित होने की आवश्यकता इसलिए है कि यदि वन नष्ट हो जाएँगे तो मनुष्य के जीवन की कल्पना नहीं की जो सकती क्योंकि –

1. वनों के न होने से वन्य जीवों को आवास एवं भोजन उपलब्ध नहीं होगा जिससे वे नष्ट हो जायेंगे। इसके परिणामस्वरूप मनुष्य को वनों से उपलब्ध होने वाले उपयोगी औषधीय पादप, काष्ठ और अनेक उपयोगी पदार्थ प्राप्त नहीं हो सकेंगे।
2. वन हमें ऑक्सीजन प्रदान करते हैं और मृदा को सुरक्षित रखते हैं। वातावरण में ऑक्सीजन की कमी से कार्बन डाइऑक्साइड की मात्रा बढ़ जाएगी। वन वायुमण्डल में ऑक्सीजन तथा कार्बन डाइऑक्साइड का सन्तुलन बनाए रखते हैं।
   वर्षा नहीं होगी। इससे भू-जल स्तर गिरता चला जाएगा और वर्षा के अभाव में अकाल पड़ जाएगा।
3. पौधे प्रकाश संश्लेषण की क्रिया में भोजन का निर्माण करते हैं, इस भोजन पर सभी जीव प्रत्यक्ष या अप्रत्यक्ष रूप से निर्भर रहते हैं। अतः मनुष्य को भोजन नहीं मिल पाएगा।
4. वातावरण का तापमान बढ़ता जाएगा, क्योंकि पौधे वातावरणीय तापमान को बढ़ने से रोकते हैं। एक निश्चित तापमान के बाद जीवन असम्भव है।

प्रश्न 9.
समझाइए कि वनों में विभिन्न प्रकार के जन्तुओं और पादपों के होने की आवश्यकता क्यों है?
उत्तर:
वनों में विभिन्न प्रकार के जन्तुओं और पादपों का होना इसलिए आवश्यक है, क्योंकि –

1. जन्तुओं और पादपों से हमें अनेक महत्त्वपूर्ण वस्तुएँ प्राप्त होती हैं, जैसे- लाख, गोंद, सुगन्धित पदार्थ, शहद, औषधियाँ, पशु-चारा, जैव ईधन, ऊन, फर तथा भोज्य पदार्थ इत्यादि।
2. पादप भोजन का निर्माण करते हैं। सभी जन्तु चाहे वे शाकाहारी हों अथवा माँसाहारी अन्ततः भोजन के लिए पादपों पर ही निर्भर होते हैं। जो जीव पादपों से भोजन लेते हैं, उन्हें अन्य जन्तुओं द्वारा भोजन के रूप में लिया जाता है। इस प्रकार यह क्रम चलता रहता है।
   पादप → कीट → मेंढक → सर्प → उकाब (गरुड़)
3. जन्तुओं और पादपों से प्राकृतिक सन्तुलन बना रहता है।

प्रश्न 10.
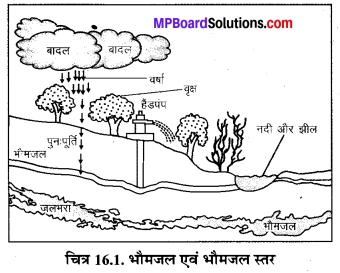
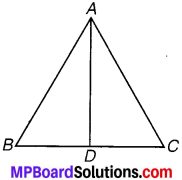
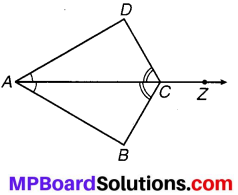
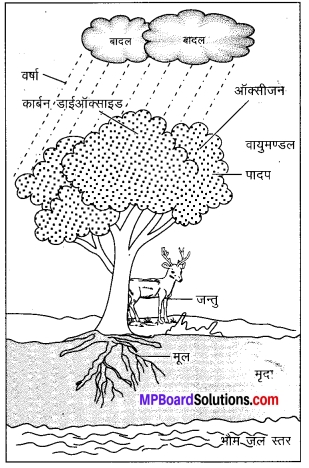
संलग्न चित्र में चित्रकार, चित्र को नामांकित करना और तीरों द्वारा दिशा दिखाना भूल गया है। तीरों पर दिशा को दिखाइए और चित्र को निम्नलिखित नामों द्वारा नामांकित करिए –
बादल, वर्णा, वायुमंडल, कार्बन डाइऑक्साइड, ऑक्सीजन, पादप, जन्तु, मृदा, अपघटक, मूल, भौमजल स्तर।
उत्तर:

प्रश्न 11.
निम्नलिखित में से कौन-सा वन उत्पाद नहीं है?

1. गोंद।
2. प्लाईवुड।
3. सील करने का लाख।
4. कैरोसीन।

उत्तर:
कैरोसीन।

प्रश्न 12.
निम्नलिखित में से कौन-सा वक्तव्य सही नहीं है?

1. वन, मृदा को अपरदन से बचाते हैं।
2. वन में पादप और जन्तु एक दूसरे पर निर्भर नहीं होते हैं।
3. वन जलावायु और चल चक्र को प्रभावित करते हैं।
4. मृदा, वनों की वृद्धि और पुनर्जनन में सहायक होती है।

उत्तर:
वन में पादप और जन्तु एक-दूसरे पर निर्भर नहीं होते हैं।

प्रश्न 13.
सूक्ष्मजीवों द्वारा मृत पादपों पर क्रिया करने से बनने वाले एक उत्पाद का नाम है –

1. बालू।
2. मशरूम।
3. ह्यूमस।
4. काष्ठ।

उत्तर:
ह्यूमस।

MP Board Class 7th Science Solutions

MP Board Class 7th Science Solutions Chapter 16 जल: एक बहुमूल्य संसाधन

MP Board Class 7th Science Chapter 16 पाठान्त अभ्यास के प्रश्नोत्तर

प्रश्न 1.
निम्नलिखित वक्तव्य ‘सत्य’ हैं अथवा ‘असत्य’

1. भौमजल विश्वभर की नदियों और झीलों में पाये जाने वाले जल से कहीं अधिक है।
2. जल की कमी की समस्या का सामना केवल ग्रामीण क्षेत्रों के निवासी करते हैं।
3. नदियों का जल खेतों में सिंचाई का एकमात्र स्रोत है।
4. वर्षा जल का चरम स्रोत है।

उत्तर:

1. सत्य।
2. असत्य।
3. असत्य।
4. सत्य।

प्रश्न 2.
समझाइए कि भौमजल की पुनःपूर्ति किस प्रकार होती है?
उत्तर:
भौमजल स्तर की पुन:पूर्ति वर्षा जल के द्वारा की जाती है। वर्षा के रूप में गिरने वाला अधिकांश जल नदियों तथा झरनों के द्वारा समुद्र में पहुँच जाता है। वर्षा का कुछ जल वाष्प बनकर उड़ जाता है तथा कुछ जल भूमि द्वारा सोख लिया जाता है। इस प्रकार भूमि द्वारा सोखा हुआ वर्षा जल भौमजल स्तर की पुनः पूर्ति करता है।

प्रश्न 3.
किसी गली में पचास घर हैं जिनके लिए दस नलकूप (ट्यूब वैल) लगाए गए हैं। भौमजल स्तर पर इसका दीर्घावधि प्रभाव क्या होगा?
उत्तर:
पचास घरों के लिए दस नलकूपों की संख्या अपेक्षाकृत अधिक है। इससे पानी अपव्यय अधिक होगा और दीर्घावधि में प्राकृतिक प्रक्रमों द्वारा पुन:पूर्ति न होने पर भौमजल स्तर नीचे गिर जाएगा।

प्रश्न 4.
मान लीजिए आपको किसी बगीचे का रखरखाव करने की जिम्मेदारी दी जाती है। आप जल का सदुपयोग करने के लिए क्या कदम उठाएँगे?
उत्तर:
जल का सदुपयोग निम्न प्रकार किया जा सकता है –

1. अगर बगीचे में कहीं पानी का दुरुपयोग हो रहा है तो इसे रोककर अपव्यय कम करेंगे।
2. पेड़-पौधों को कम व्यास के पाइपों द्वारा पानी देंगे, जिससे कि उनकी जड़ों तक जल पहुँच सके। इससे आवश्यकतानुसार ही पानी का उपयोग होगा।
3. पेड़-पौधों के लिए आवश्यक जल की आपूर्ति सुनियोजित ढंग से करेंगे।
4. वर्षा के पानी का अधिकतम उपयोग करेंगे।

प्रश्न 5.
भौमजल स्तर के नीचे गिरने के लिए उत्तरदायी कारकों को समझाइए।
उत्तर:
भौमजल स्तर के नीचे गिरने के लिए उत्तरदायी कारक:
(1) जनसंख्या वृद्धि:
जनसंख्या बढ़ने से भवनों, दुकानों, कार्यालयों और सड़कों के निर्माण में वृद्धि हो जाती है। इससे खुले क्षेत्रों में कमी आ जाती है। इसके कारण वर्षा जल के अवस्रवण की दर कम हो जाती है। निर्माण कार्य के लिए भी अधिक मात्रा में जल की आवश्यकता होती है। जनसंख्या वृद्धि से पानी का उपयोग भी बढ़ जाता है।

(2) बढ़ते हुए उद्योग:
उद्योगों की संख्या निरन्तर बढ़ती जा रही है। अधिकांश उद्योगों द्वारा उपयोग किये जाने वाला जल भूमि से निकाला जा रहा है। इससे जल स्तर नीचे गिर रहा है।

(3) कृषि गतिविधियाँ:
कृषि में जल अत्यन्त आवश्यक है। खेतों की सिंचाई के लिए वर्षा जल के अतिरिक्त अन्य स्रोतों से जल का उपयोग किया जाता है। अनियमित वर्षा के कारण भी जल की उपलब्धता में कमी आयी है। जनसंख्या के बढ़ते दबाव के कारण कृषि के लिए भौमजल का उपयोग दिन-प्रतिदिन बढ़ता जा रहा है। इसके परिणामस्वरूप भौमजल स्तर निरन्तर गिर रहा है।

प्रश्न 6.
रिक्त स्थानों की उचित शब्द भरकर पूर्ति कीजिए।

1. भौमजल प्राप्त करने के लिए … तथा ….. का उपयोग होता है।
2. जल की तीन अवस्थाएँ ….., ……, और ….. हैं।
3. भूमि की जल धारण करने वाली परत ………. कहलाती है।
4. भूमि में जल के अवस्रवण के प्रक्रम को ……… कहते हैं।

उत्तर:

1. नलकूप, हैण्डपम्प।
2. ठोस, द्रव, गैस।
3. भौमजल स्तर।
4. जल चक्र।

प्रश्न 7.
निम्नलिखित में से कौन-सा कारक जल की कमी के लिए उत्तरदायी नहीं है?

1. औद्योगीकरण में वृद्धि।
2. बढ़ती जनसंख्या।
3. अत्यधिक वर्षा।
4. जल संसाधनों का कुप्रबन्धन।

उत्तर:
अत्यधिक वर्षा।

प्रश्न 8.
सही विकल्प का चयन कीजिए –

1. विश्व की सभी झीलों और नदियों में कुल मात्रा नियत (स्थिर) रहती है।
2. भूमिगत जल की कुल मात्रा नियत रहती है।
3. विश्व के समुद्रों और महासागरों में जल की कुल मात्रा नियत है।
4. विश्व में जल की कुल मात्रा नियत है।

उत्तर:
विश्व में जल की कुल मात्रा नियत है।

प्रश्न 9.
भौमजल और भौमजल स्तर को दिखाते हुए एक चित्र बनाइए। उसे चिह्नित कीजिए।
उत्तर:
भौमजल एवं भौमजल स्तर।

MP Board Class 7th Science Solutions

MP Board Class 7th Maths Solutions Chapter 7 त्रिभुजों की सर्वांगसमता Ex 7.2

प्रश्न 1.
निम्न में आप कौन-से सर्वांगसम प्रतिबन्धों का प्रयोग करेंगे ?
(a) दिया है : AC = DF AB = DE, BC = EF

इसलिए, ∆ABC ≅ ∆DEF
(b) दिया है : ZX = RP RQ = ZY
∠PRQ = ∠XZY
इसलिए, ∆PQR = ∆XYZ
(c) दिया है: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
इसलिए, ∆LMN ≅ ∆GFH
(d) दिया है: EB = DB
AE = BC
∠A = ∠C
इसलिए, ∆ABE ≅ ∆CDB
उत्तर:
(a) S.S.S. सर्वांगसमता प्रतिबन्ध द्वारा,
∆ABC ≅ ∆DEE
(b) S.A.S. सर्वांगसमता प्रतिबन्ध द्वारा,
∆PQR ≅ ∆XYZ.
(c) A.S.A. सर्वांगसमता प्रतिबन्ध द्वारा,
∆LMN ≅ ∆GFH.
(d) R.H.S. सर्वांगसमता प्रतिबन्ध द्वारा,
∆ABE ≅ ∆CDB.

प्रश्न 2.
आप ∆ART ≅ ∆PEN दर्शाना चाहते हैं।
(a) यदि आप S.S.S. सर्वांगसमता प्रतिबन्ध का प्रयोग करें तो आपको दर्शाने की आवश्यकता है:
(i) AR =
(ii) RT =
(iii) AT =
(b) यदि यह दिया गया है कि ∠T = ∠N और आपको S.A.S. प्रतिबन्ध का प्रयोग करना है, तो आपको आवश्यकता होगी:
(i) RT = और (ii) PN =

(c) यदि यह दिया गया है कि AT = PN और आपको A.S.A. प्रतिबन्ध का प्रयोग करना है, तो आपको आवश्यकता होगी:
(i) ? =
(ii) ? =
हल:
(a) ∆ART ≅ ∆PEN को S.S.S. सर्वांगसमता प्रतिबन्ध द्वारा दर्शाने के लिए दर्शाना होगा –
(i) AR = PE
(ii) RT = EN
(iii) AT = PN
(b) ∴ ∠T = ∠N
∴ (i) RT = EN
(ii) PN = AT
(c) यदि AT = PN और A.S.A. सर्वांगसमता के लिए आवश्यकता होगी –
(i) ∠RAT = ∠EPN
(ii) ∠ATR = ∠PNE

प्रश्न 3.
आपको ∆AMP ≅ ∆AMQ दर्शाना है। निम्न चरणों में, रिक्त कारणों को भरिए:

उत्तर:
(i) दिया है
(ii) दिया है
(iii) उभयनिष्ठ
(iv) S.A.S. सर्वांगसमता प्रतिबन्ध।

प्रश्न 4.
∆ABC में ∠L = 30°, ∠B = 40° और ∠C = 110°, ∆PQR में, ∠P = 30° ∠Q = 40° और ∠R = 110°. एक विद्यार्थी कहता है कि A.A.A. सर्वांगसमता प्रतिबन्ध से ∆ABC ≅ ∆PQR है।
क्या यह कथन सत्य है ? क्यों या क्यों नहीं ?
हल:
यहाँ ∆MBC के तीनों कोण ∆PQR के तीनों कोणों के बराबर हैं। तो यह आवश्यक नहीं कि त्रिभुज सर्वांगसम हों क्योंकि यदि ∆ABC में, भुजा BC = 3.0-सेमी तथा ∆POR में, भुजा QR = 4.0 सेमी हो, तो इस दशा में त्रिभुज के संगत कोण तो बराबर हैं परन्तु यह सर्वांगसम नहीं हैं। क्योंकि BC ≠ QR अतः विद्यार्थी की A.A.A. सर्वांगसमता का प्रतिबन्ध तर्कसंगत नहीं है।

प्रश्न 5.
संलग्न आकृति में दो त्रिभुज ART तथा OWN सर्वांगसम हैं जिनके संगत भागों को अंकित किया गया है। हम लिख सकते हैं ∆RAT = ?

हल:
हम लिख सकते हैं ∆RAT ≅ ∆WON
(∴ O ↔ A, N ↔ T, W ↔ R)

प्रश्न 6.
कथनों को पूरा कीजिए –

∆BCA ≅ ? ∆QRS ≅ ?
उत्तर:
∆BCA ≅ ∆ABTA, ∆QRS = ∆TPQ

प्रश्न 7.
एक वर्गांकित शीट पर, बराबर क्षेत्रफलों वाले दो त्रिभुजों को इस प्रकार बनाइए कि
(i) त्रिभुज सर्वांगसम हों
(ii) त्रिभुज सर्वांगसम न हों। आप उनके परिमाप के बारे में क्या कह सकते हैं?
हल:

(i) चित्र 7.19 (1) में,
∆ ABC का क्षेत्रफल = ∆EDC का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × 3 × 4 = 6 cm²
∆ ABC का परिमाप = 3 + 4 + 5 = 12 cm
∆ EDE का परिमाप = 3 + 4 + 5 = 12 cm
∆ ABC का परिमाप = ∆EDC का परिमाप,
अतः चित्र 7.19 में, ∆ABC ≅ ∆EDC है।
(ii) चित्र 7.19 (ii) में,
∆ PQR का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × PQ × PR
= \(\frac { 1 }{ 2 } \) × 3 × 4 = 6 cm²
तथा ∆ PSR का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × ST × PR
\(\frac { 1 }{ 2 } \) × 3 × 4 = 6 cm²

∴ ∆ POR का क्षेत्रफल = ∆ PSR का क्षेत्रफल
अब, ∆ PQR का परिमाप = 3 + 4 + 5 = 12 cm
तथा ∆ PRS का परिमाप = 4 + 35 + 4 = 11’5 cm
∆ POR का परिमाप ≠ ∆PRS का परिमाप
अत: चित्र 7.19 (ii) में ∆POR व ∆PRS सर्वांगसम नहीं हैं क्योंकि इनके क्षेत्रफल तो समान हैं परन्तु परिमाप समान नहीं

प्रश्न 8.
संलग्न आकृति में एक सर्वांगसम भागों का एक अतिरिक्त युग्म बताइए जिससे ∆ABC और ∆PQR सर्वांगसम हो जाएँ। आपने किस प्रतिबन्ध का प्रयोग किया ?

हल:
यहाँ, ∆ABC ≅ ∆PQR
∴ ∠B = ∠Q IR ∠C = ∠R
∴ सर्वांगसम भागों का अतिरिक्त युग्म –
BC = QR
उत्तर हमने यहाँ A.S.A. सर्वांगसम प्रतिबन्ध का प्रयोग किया है।

प्रश्न 9.
चर्चा कीजिए, क्यों?
∆ABC ≅ ∆FED.

हल:
∠B = ∠E = 90°,
∠A = ∠F (दिया हुआ है)
∴ ∠C = ∠D (तीसरा कोण)
BC = DE (दिया हुआ है)
अत: ASA सर्वांगसम प्रतिबन्ध से ∆ ABC ≅ ∆ FED परिणाम प्राप्त होगा।

पाठ्य-पुस्तक पृष्ठ संख्या # 163

ज्ञानवर्धक क्रियाकलाप

प्रश्न 1.
अलग-अलग माप के वर्गों के कट-आउट सोचिए। अध्यारोपण विधि का प्रयोग वर्गों की सर्वांगसमता के लिए प्रतिबन्ध ज्ञात करने के लिए कीजिए। कैसे “सर्वांगसम भागों” की संकल्पना सर्वांगसम के अंतर्गत उपयोग होती है ? क्या यहाँ संगत भुजाएँ हैं ? क्या यहाँ संगत विकर्ण हैं ?
हल:
हम जानते हैं कि समतल आकृतियाँ सर्वांगसम होती हैं। जब आकृतियों के आकार समान होते हैं तो वे एक-दूसरे की ठीक-ठीक पूरा ढक लेती हैं। सभी वर्ग समान आकृति के होते हैं लेकिन वर्ग का आकार उनकी भुजाओं की लम्बाई पर निर्भर करता है।

ABCD व PQRS दो वर्ग हैं। वर्ग ABCD के कट-आउट को वर्ग PQRS के ऊपर इस प्रकार रखते हैं कि शीर्ष A, वर्ग PQRS के शीर्ष P पर और भुजा AB भुजा PQ पर आए।

स्पष्ट है कि ABCD वर्ग PQRS को पूर्णतया ढक लेता है।

यदि AB = PQ तो दो वर्ग सर्वागसम होंगे यदि उनकी भुजाओं की लम्बाइयाँ समान हों।

अत: वर्ग ABCD ≅ वर्ग PORS यदि AB = PQ

हम एक वर्ग की किसी भी भुजा को दूसरे वर्ग की किसी भुजा के संगत ले सकते हैं। दूसरी संगत भुजाओं के युग्म इसी प्रकार बदल जाएँगे। यह बात विकर्णों के लिए भी सत्य है।

प्रश्न 2.
यदि आप वृत्त लेते हैं तो क्या होता है ? दो वृत्तों की सर्वांगसमता के लिए प्रतिबन्ध क्या है ? क्या, आप फिर अध्यारोपण विधि का प्रयोग कर सकते हैं ? पता लगाइए।
हल:
सभी वृत्तों की समान आकृति होती है और वृत्त का आकार वृत्त की त्रिज्या पर निर्भर करता है। यहाँ दो वृत्त C₁ व C₂ हैं। इनमें से किसी एक वृत्त का कट-आउट (माना वृत्त C₂ का) वृत्त C₁ पर रखते हैं। वृत्त C₂ वृत्त C₁ को पूरी तरह ठीक-ठीक ढल लेता है। यदि दोनों वृत्तों की त्रिज्याएँ समान होंगी तो दोनों वृत्त सर्वांगसम होंगे।

वृत्त C₁ वृत्त C₂ जबकि C₁ वृत्त की त्रिज्या = C₂ वृत्त की त्रिज्या।

प्रश्न 3.
इस संकल्पना को बढ़ाकर तल की दूसरी आकृतियाँ जैसे समषद्भुज इत्यादि के लिए प्रयत्न कीजिए।
हल:
हम जानते हैं कि समतल आकृतियाँ सर्वांगसम होती हैं यदि वे एक-दूसरे को पूर्णतया ढक लेती हैं। सभी समषट्भुज समान आकृति के होते हैं और इनका आकार समषट्भुज की भुजा की लम्बाई पर निर्भर करता है। दो समषट्भुज ABCDEF व PQRSTU लेते हैं। इनके कट-आउट लेते हैं जिनमें से प्रत्येक की सभी भुजाएँ समान हों।

अब PQRSTU के कट-आउट को ABCDEF पर इस प्रकार रखते हैं कि PQRSTU का बिन्दु P बिन्दु A पर आए तथा भुजा PQ भुजा AB पर आए। यदि PQ = AB तो समषट्भुज PQRSTU, समषट्भुज ABCDEF को पूर्णतया ठीक-ठीक ढक लेता है। अत: दो समषट्भुज सर्वांगसम होते हैं यदि इनकी भुजाओं की लम्बाई समान हो।

अत: समषट्भुज ABCDEF = समषट्भुज PQRSTU.

प्रश्न 4.
एक त्रिभुज की दो सर्वांगसम प्रतिलिपियाँ लीजिए। कागज को मोड़कर पता लगाइए कि क्या उनके शीर्ष लम्ब बराबर हैं ? क्या उनकी माध्यिकाएँ समान हैं ? आप उनके परिमाप तथा क्षेत्रफल के बारे में क्या कह सकते हैं ?
हल:
माना ∆ABC ≅ ∆DEF
कागज को मोड़कर प्रत्येक त्रिभुज के शीर्ष बनाए। हम देखते हैं कि
AL = DP BM = EQ और CN = FR
अर्थात् संगत शीर्ष लम्ब समान हैं।

इसी प्रकार हम देख सकते हैं कि सर्वांगसम त्रिभुजों में संगत माध्यिकाएँ समान होती हैं और इनके परिमाप व क्षेत्रफल समान होते हैं।

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 7 त्रिभुजों की सर्वांगसमता Ex 7.1

प्रश्न 1.
निम्न कथनों को पूरा कीजिए :
(a) दो रेखाखण्ड सर्वांगसम होते हैं यदि …….. ।
(b) दो सर्वांगसम कोणों में से एक की माप 70° है, दूसरे कोण की माप …….. है।
(c) जब हम ∠A = ∠B लिखते हैं, हमारा वास्तव में अर्थ होता है ……… ।
उत्तर:
(a) इनकी लम्बाइयाँ समान हों।
(b)70°
(c) m ∠A = m∠B

प्रश्न 2.
वास्तविक जीवन से सम्बन्धित सर्वांगसम आकारों के कोई दो उदाहरण दीजिए।
उत्तर:
उदाहरण – समान मान के दो नोट, एक ही ताले की दो चाबियाँ।

प्रश्न 3.
यदि सुमेलन ABC ↔ FED के अंतर्गत ∆ARC ≅ ∆FED तो त्रिभुजों के सभी संगत सर्वांगसम भागों को लिखिए।
उत्तर:
∆ABC तथा ∆FED के संगत सर्वांगसम भाग

प्रश्न 4.
यदि ∆DEF ≅ ∆BCA हो, तो ∆BCA के उन भागों को लिखिए जो निम्न के संगत हों :
(i) ∠E
(ii) \(\overline{E F}\)
(iii) ∠F
(iv) \(\overline{D F}\)
उत्तर:
∵ ∆DEF ≅ ∆BCA
∴ (i) ∠E ↔∠C
(ii) \(\overline{E F}\) ↔ \(\overline{C A}\)
(iii) ∠F ↔ ∠A
(iv) \(\overline{D F}\) ↔ \(\overline{B A}\)

पाठ्य-पुस्तक पृष्ठ संख्या # 152-153

प्रयास कीजिए

प्रश्न 1.
संलग्न आकृति में त्रिभुजों की भुजाओं की लम्बाइयाँ दर्शाई गई हैं। S.S.S. सर्वांगसमता के प्रतिबन्ध का प्रयोग करके बताइए कि कौन-कौन से त्रिभुज-युग्म सर्वांगसम हैं। सर्वांगसमता की स्थिति में उत्तर को सांकेतिक रूप में लिखिए।

हल:
(i) ∆ABC और ∆POR में,
AB = 1.5 cm, PQ = 1.5 cm, ∴ AB = PQ
BC = 2.5 cm, QR = 2.5 cm, ∴ BC = QR
AC = 2-2 cm, PR = 2-2 cm, ∴ AC = PR
चूँकि ∆ABC की तीन भुजाएँ ∆PQR की तीन भुजाओं के बराबर हैं। अत: दोनों त्रिभुज सर्वांगसम हैं। (S.S.S. सर्वांगसमता)
साथ ही, A ↔ P, B ↔ Q और C ↔ R
∴ ∆ABC ≅ ∆PQR

(ii) ∆DEF और ∆LMN में,
DE = 3.2 cm, MN = 3-2 cm, ∴ DE = MN
DF = 3.5 cm, LN = 3.5cm, ∴ DF = LN
EF = 3 cm, LM = 3 cm, ∴ EF = LM
चूँकि ∆DEF की तीन भुजाएँ ∆LMN की तीन भुजाओं के बराबर हैं। अत: दोनों त्रिभुज सर्वांगसम हैं। (S.S.S. सर्वांगसमता)
साथ ही, D ↔ N, E ↔ M, और F ↔ L
∴ ∆DEF ≅ ∆NML

(iii) ∆ABC और ∆POR में,
AC = 5 cm, PR = 5 cm, ∴ AC = PR
BC = 4 cm, PQ = 4 cm, ∴ BC = PQ
AB = 2 cm, QR = 2.5 cm, ∴ BC ≠ PQ
चूँकि, AB ≠ QR, अत: ∆ABC और ∆PQR सर्वांगसम नहीं हैं।

(iv) ∆ABD और ∆ADC में,
AB = 3.5 cm, AC = 3.5 cm, ∴ AB = AC
BD = 2.5 cm, CD = 2.5 cm, ∴ BD = CD
AD = AD (उभयनिष्ठ है)
चूँकि ∆ABD की तीन भुजाएँ ∆ADC की तीन भुजाओं के बराबर हैं। अत: दोनों त्रिभुज सर्वांगसम हैं (S.S.S सर्वांगसमता)।
साथ ही, A ↔ A, B ↔ C और D ↔ D
∆ABD ≅ ∆ACD

प्रश्न 2.
संलग्न आकृति में AB = AC और D, \(\overline{B C}\) का मध्य-बिन्दु है।
(i) ∆ADB और ∆ADC में बराबर भागों के तीन युग्म बताइए।
(ii) क्या ∆ADB ≅ ∆ADC है ? कारण दीजिए।
(iii) क्या ∠B = ∠C है? क्यों?

हल:
यहाँ, AB = AC और D, \(\overline{B C}\) का मध्य बिन्दु है
अर्थात् BD = DC
(i) ∆ABD तथा ∆ADC से, बराबर भागों के तीन युग्म
AB = AC (दिया हुआ है)
AD = AD (उमयनिष्ठ है)
BD = DC (∵ D,CB का मध्य बिन्दु है)

(ii) ∆ABD की तीन भुजाएँ ∆ADC की तीन भुजाओं के बराबर हैं।
अतः सर्वांगसमता के S.S.S प्रतिबन्ध से,
∆ABD और ∆ADC सर्वांगसम हैं
और A ↔ A, B ↔ C, D ↔ D
∴ ∆ADB ≅ ∆ADC.

(iii) ∵ ∆ABC ≅ ∆ADC
∴ उनके संगत भाग बराबर हैं।
अर्थात् B ↔ C या ∠B = ∠C.

प्रश्न 3.
संलग्न आकृति में AC = BD और AD = BC हैं। निम्नलिखित कथनों में कौन-सा कथन सत्य है ?
(i) ∆ABC ≅ ∆ABD
(ii) ∆ABC ≅ ∆BAD

हल:
यहाँ AC = BD और AD = BC
(i) ∆ABC तथा ∆ABD में,
AB = AB (सही है)
BC = BD (सही नहीं है)
CA = DA (सही नहीं हैं)
अत: हम ∆ABC = ∆ABD नहीं लिख सकते।

(ii) ∆ABC तथा ∆BAD में,
AB = AB (उभयनिष्ठ)
BC = AD (दिया है)
CA = BD (दिया हैं)
यहाँ S.S.S. सर्वांगसमता है।
अत: ≅ABC ≅ ∆BAD लिख सकते हैं।
अतः
(i) ∴ ∆ABC ≅ ∆ABD असत्य है।
(ii) ∆ABC ≅ ∆BAD सत्य है।

सोचिए, चर्चा कीजिए एवं लिखिए

प्रश्न 1.
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है।
∆ABC की एक अक्स प्रतिलिपि लीजिए और इसे भी ∆ABC का नाम दीजिए।
(i) ABC और ∆ACB में बराबर भागों के तीन युग्म बताइए।
(ii) क्या ∆ABC ≅ ∆ACB है ? क्यों अथवा क्यों नहीं ?
(iii) क्या ∠B = ∠C है? क्यों अथवा क्यों नहीं ?

हल:
∆ABC एक समद्विबाहु त्रिभुज है
जिसमें AB = AC, BC = CB तथा AC = AB.

(i) अब ∆ABC और ∆ACB में, बराबर भागों के तीन
युग्म – BC = BC (उभयनिष्ठ है)
AB = AC (दिया हुआ है)
AC = AB (रचना से)

(ii) हाँ, ∆ABC = ∆ACB.
क्योंकि ∆ABC की तीनों भुजाएँ ∆ACB की तीनों भुजाओं के बराबर हैं और A ↔ A, B ↔ C,C ↔ B.

(iii) हाँ, ∠B = ∠C ∴ B ↔ C

पाठ्य-पुस्तक पृष्ठ संख्या # 156 – 157

इन्हें कीजिए

प्रश्न 1.
∆DEF की भुजाओं \(\overline{D E}\) और \(\overline{E F}\) का अंतर्गत कोण कौन-सा है?
उत्तर:
∆DEF में, भुजाओं \(\overline{D E}\) और \(\overline{E F}\) के अंतर्गत कोण, ∠DEF है।

प्रश्न 2.
S.A.S. सर्वांगसमता प्रतिबन्ध का उपयोग करके आप ∆POR ≅ ∆FED स्थापित करना चाहते हैं। यह दिया गया है कि PQ = FE और RP = DF है। सर्वांगसमता को स्थापित करने के लिए अन्य किस तथ्य या सूचना की आवश्यकता होगी?
हल:
∆PQR ≅ ∆FED (सर्वांगसमता के प्रतिबन्ध S.A.S. के अनुसार)
PQ = FE और RP = DF (दिया है)
अन्य तथ्य और सूचना :
चूँकि S.A.S. प्रतिबन्ध के अन्तर्गत भुजाओं PQ और RP तथा FE और DF के बीच बने कोण भी बराबर होना चाहिए।
∴ ∠P = ∠F

प्रश्न 3.
संलग्न आकृति में त्रिभुजों के युग्मों में कुछ भागों की माप अंकित की गई है। S.A.S. सर्वांगसमता प्रतिबन्ध का उपयोग करके, इनमें वे युग्म छाँटिए जो सर्वांगसम हैं। सर्वांगसम त्रिभुजों की स्थिति में उन्हें सांकेतिक रूप में भी लिखिए।

हल:
(i) ∆ABC और ∆DEF में,
यहाँ, AB = DE = 2.5 cm
AC = DF = 2.8 cm
∠A = 80°,∠D = 70°
∴ ∠A ≠ ∠D
∴ ∆ABC और ∆DEF सर्वांगसम नहीं है।

(ii) ∆ABC और ∆POR में,
यहाँ AC = PR = 2.5 cm
BC = PQ = 3 cm
∠C = ∠P = 35°
∴ ∆ABC की दो भुजाएँ और उनके अंतर्गत कोण ∆POR की दो संगत भुजाओं और उनके अंतर्गत कोण के बराबर हैं।
अतः दोनों त्रिभुज सर्वांगसमता के S.A.S प्रतिबन्ध के आधार पर सर्वांगसम हैं।
साथ ही C ↔ P A ↔ R और B ↔ Q
∴ ∆ABC ≅ ∆RQP

(iii) ∆DEF तथा ∆PQR में,
यहाँ, EF = QR = 3 cm
DF = PQ = 3.5 cm
भुजाओं के अंतर्गत कोण ∠F = ∠Q = 40°
∴ ∆DEF की दो भुजाएँ और उनके अन्तर्गत कोण ∆PQR की दो संगत भुजाओं और उनके अन्तर्गत कोण के बराबर हैं।

अतः दोनों त्रिभुज सर्वांगसमता के S.A.S. प्रतिबन्ध के आधार पर सवांगसम हैं।
साथ ही, F ↔ Q.D ↔ P और E ↔ R
∴ ∆DEF ≅ ∆PRQ

(iv) ∆PQR और ∆RSP में,
PQ = R = 3.5 cm
PR = PR (उभयनिष्ठ है)
अंतर्गत कोण ∠QPR = ∠PRS = 30°
अत: ∆PQR की दो भुजाएँ और उनके अन्तर्गत कोण ∆RSP की दो संगत भुजाओं और उनके अन्तर्गत बीच के कोण के बराबर हैं।
अतः दोनों त्रिभुज सर्वांगसमता के प्रतिबन्ध S.A.S. के आधार पर सर्वांगसम हैं
साथ ही, P ↔ R, Q ↔ S
∴ ∆PQR ≅ ∆RSP

प्रश्न 4.
संलग्न आकृति में \(\overline{A B}\) और \(\overline{C D}\) एक दूसरे को O पर समद्विभाजित करते हैं।
(i) दोनों त्रिभुज AOC और BOD में बराबर भागों के तीन युग्मों को बताइए।
(ii) निम्न कथनों में से कौन-सा कथन सत्य है?
(a) ∆AOC ≅ ∆DOB
(b) ∆AOC ≅ ∆BOD

हल:
∵ \(\overline{A B}\) और \(\overline{C D}\) एक दूसरे को O पर समद्विभाजित करते हैं।
∴ AO = BO और CO = DO
साथ ही ऊर्ध्वाधर सम्मुख ∠AOC = ∠BOD
(i) ∆MOC तथा ∆BOD में, बराबर भागों के तीन युग्म –
AO = BO और CO = DO
∠AOC = ∠BOD

(ii) उपर्युक्त सम्बन्धों के आधार पर ∆AOC की दो भुजाएँ और उनके अन्तर्गत कोण ∆BOD की दो संगत भुजाओं और उनके अन्तर्गत कोण के बराबर हैं।
अत: सर्वांगसमता के गुण S.A.S. के आधार पर दोनों त्रिभुज सर्वांगसम हैं।
साथ ही,O ↔ O,A ↔ B, और C ↔ D
∴ ∆AOC ≅ ∆BOD
(a) कथन ∆AOC ≅ ∆DOB असत्य है।
(b) कथन ∆AOC ≅ ∆BOD सत्य है।

पाठ्य-पुस्तक पृष्ठ संख्या # 158

इन्हें कीजिए

प्रश्न 1.
∆MNP में कोणों M तथा N के अंतर्गत भुजा क्या है ?
उत्तर:
∆MNP में कोणों M तथा N के अंतर्गत भुजा MN है।

प्रश्न 2.
A.S.A. सर्वांगसमता प्रतिबन्ध का उपयोग करके आप ∆DEF ≅ ∆MNP स्थापित करना चाहते हैं। आपको दिया गया है कि ∠D = ∠M और ∠F = ∠P। इस सर्वांगसमता को स्थापित करने के लिए और कौन-कौन से तथ्य की आवश्यकता है ? (खाका आकृति बनाकर कोशिश कीजिए।)
हल:
∆DEF ≅ ∆MNP स्थापित करने के लिए A.S.A. सर्वांगसमता के प्रतिबन्ध के लिए हमें आवश्यकता होगी-भुजाएँ जिनसे ∠D और ∠F बनते हैं तथा समान भुजाएँ जिनसे ∠M और ∠P बनते हैं।
अर्थात् हमें आवश्यकता होगी \(\overline{D F}\) = \(\overline{M P}\)

प्रश्न 3.
संलग्न आकृति में, त्रिभुज के कुछ भागों की माप अंकित की गई है। A.S.A. सर्वांगसमता प्रतिबन्ध का उपयोग करके बताइए कौन-से त्रिभुजों के युग्म सर्वांगसम हैं। सर्वांगसमता की स्थिति में, उत्तर को सांकेतिक रूप में लिखिए।

हल:
(i) ∆ABC और ∆DEF में,
AB = EF = 3.5 cm,
∠A = ∠F = 40°
और ∠B = ∠E = 60°.
∴ A.S.A. सर्वांगसमता प्रतिबन्ध से ये दो त्रिभुज सर्वांगसम हैं। साथ ही, A ↔ F,B ↔ E और C ↔ D
∴ ∆ABC ≅ ∆FED

(ii) ∆POR और ∆DEF में,
∆POR में, ∠P = 180° – (90° + 50°) = 40°
इसी प्रकार ∆DEF में, ∠F = 180° – (90° + 50°) = 40°
अब, PR = 3.3 cm, EF = 3.5 cm ∴ PR ≠ EF
∠R = ∠E = 50° और ∠P = ∠F = 40° ∴ ∠P = ∠F
∴ A.S.A. सर्वांगसमता प्रतिबन्ध से त्रिभुज सर्वांगसम नहीं है।

(iii) ∆PQR और ∆LMN में,
RQ = LN = 6 cm, ∠R = ∠L = 60° और ∠Q = ∠N = 30° ∴ A.S.A. सर्वांगसमता प्रतिबन्ध से ये दो त्रिभुज सर्वांगसम हैं
साथ ही, R ↔ L, Q ↔ N और P ↔ M
∴ ∆PQR ≅ ∆MNL

(iv) ∆ABC और ∆ABD में,
AB = AB (उभयनिष्ठ हैं),
∠BAC = ∠DBA = 30°
∠BAD = 45° + 30° = 75°
∠ABC = ∠45° + 30° = 75°
∴ A.S.A. सर्वांगसमता प्रतिबन्ध से ये दो त्रिभुज सर्वांगसम हैं।
साथ ही, A ↔ B, D ↔ C
∴ ∆ABC ≅ ∆BAD.

प्रश्न 4.
दो त्रिभुजों के कुछ भागों की निम्न माप दी गई है। A.S.A. सर्वांगसमता प्रतिबन्ध का उपयोग करके जाँचिए कि क्या ये दो त्रिभुज सर्वांगसम हैं या नहीं। सर्वांगसमता की स्थिति में उत्तर को सांकेतिक रूप में भी लिखिए।
∆DEF ∆PQR
(i) ∠D = 60°, ∠F = 80°, ∠Q = 60°, ∠R = 80°,
DF = 5 cm QR = 5 cm
(ii) ∠D = 60°, ∠F = 80°, ∠Q = 60°, ∠R = 80°,
DF = 6 cm, P = 6 cm
(iii) ∠E = 80°, ∠F = 30°, ∠P = 80°, PQ = 5 cm
EF = 5 cm, ∠R = 30°
हल:
(i) ∆DEF और ∆PQR में,
∠D = ∠Q = 60°, ∠F = ∠R = 80°
अन्तर्गत भुजा DF = अन्तर्गत भुजा QR = 5 cm
A.S.A. सर्वांगसमता प्रतिबन्ध से ये दो त्रिभुज सर्वांगसम हैं।
साथ ही, D ↔ Q. F ↔ R. और E ↔ P
∴ ∆DEF = ∆QPR

(ii) यहाँ ∆DEF तक ∆PQR में समान कोणों के बीच की भुजाएँ DF व QR समान नहीं हैं।
∴ दिए गये त्रिभुज सर्वांगसम नहीं हैं।

(iii) यहाँ ∆DEF तक ∆PQR में समान कोणों के बीच की भुजाएँ EF व PR समान नहीं हैं।
∴ दिए गये त्रिभुज सर्वांगसम नहीं हैं।

प्रश्न 5.
संलग्न आकृति में किरण AZ, ∠DAB तथा ∠DCB को समद्विभाजित करती है।

(i) त्रिभुज BAC और DAC में बराबर भागों के तीन युग्म बताइए।
(ii) क्या ∆BACE ≅ ∆DAC है ? कारण दीजिए।
(iii) क्या AB = AD है ? अपने उत्तर का उचित कारण दीजिए।
(iv) क्या CD = CB है? कारण दीजिए।
हल:
(i) ∵ AC, ∠DAB और ∠DCB का समद्विभाजक है।
∠DAC = ∠BAC
और ∠DCA = ∠BCA
अब, ∆BAC और ∆DAC में, बराबर भागों के युग्म हैं –
AC = AC (उभयनिष्ठ)
∠DAC = ∠BAC (AC समद्विभाजक है)
∠DCA = ∠BCA (AC समद्विभाजक है)

(ii) उपर्युक्त सम्बन्धों से, ये दो त्रिभुज सर्वांगसम हैं (A.S.A. सर्वांगसमता)
साथ ही, A ↔ A, C ↔ C और D ↔ B
∴ ∆BAC ≅ ∆DAC

(iii) ∴ ∆BAC ≅ ∆DAC
∴ संगत भाग बराबर हैं।
अर्थात् AB = AD

(iv) ∴ C ↔ C और A ↔ A तथा AC = AC
अर्थात् ∆BAC ≅ ∆DAC
∴ संगत भाग बराबर हैं,
अर्थात् CD = CB

पाठ्य-पुस्तक पृष्ठ संख्या # 160-161

इन्हें कीजिए

प्रश्न 1.
संलग्न आकृति में त्रिभुजों के कुछ भागों की माप दी गई है। R.H.S. सर्वांगसमता प्रतिबन्ध का उपयोग करके बताइए कि कौन-कौन से त्रिभुज युग्म सर्वांगसम हैं। सर्वांगसम त्रिभुजों की स्थिति में उन्हें सांकेतिक रूप में लिखिए।

हल:
(i) समकोण ∆PQR तथा समकोण ∆DEF में,
कर्ण PR = कर्ण DF = 6 cm
भुजा PQ = 3 cm ≠ भुजा DE = 2.5 cm
∴ ∆POR और ∆DEF सर्वांगसम नहीं हैं।

(ii) समकोण ∆ABC और समकोण ∆ABD में, कर्ण AB = कर्ण BA = 3.5 cm (उभयनिष्ठ) भुजा AC = भुजा BD = 2 cm तथा ∠C = ∠D = 90°
∴ समकोण त्रिभुजों की R.H.S. सर्वांगसमता के गुण के अनुसार त्रिभुज सर्वांगसम हैं।
साथ ही, A ↔ B, B ↔ A, C ↔ D
∴ ∆ABD ≅ ∆BAC

(iii) समकोण ∆ABC और समकोण ∆ADC में,
कर्ण AC = कर्ण AC (उभयनिष्ठ)
भुजा AD = भुजा AB = 3.6 cm
तथा ∠B = ∠D = 90°
∴ समकोण त्रिभुजों की R.H.S. सर्वांगसमता के गुण के अनुसार त्रिभुज सर्वांगसम हैं।
साथ ही, A ↔ A,C ↔ C,B ↔ D
∆ABC ≅ ∆ADC

(iv) समकोण ∆PQS और समकोण ∆PRS में,
कर्ण PQ = कर्ण PR = 3 cm
भुजा PS = भुजा PS (उभयनिष्ठ)
तथा ∠PSQ तथा ∠PSR = 90°
∴ समकोण त्रिभुजों की R.H.S. सर्वांगसमता के गुण के अनुसार त्रिभुज सर्वांगसम हैं।
साथ ही P ↔ P, S ↔ S, Q ↔ R
∆PQS ≅ ∆PRS.

प्रश्न 2.
R.H.S. सर्वांगसमता प्रतिबन्ध से ∆ABC ≅ ∆RPO स्थापित करना है। यदि यह दिया गया हो कि ∠B = ∠P = 90° और AB = RP है, तो अन्य किस और सूचना की आवश्यकता है ?
हल:
R.H.S. सर्वांगसमता प्रतिबन्ध द्वारा ∠ABC ≅ ∠RPO स्थापित करने के लिए हमें कर्ण AC = कर्ण RQ को समान करने की आवश्यकता होगी।

प्रश्न 3.
संलग्न आकृति में, BD और CE, ∆ABC के शीर्षलम्ब हैं और BD = CE.

(i) ∆CBD और ∆BCE में, बराबर भागों के तीन युग्म बताइए।
(ii) क्या ∠CBD ≅ ∠BCE है ? क्यों अथवा क्यों नहीं ?
(iii) क्या ∆DCB = ∆EBC है ? क्यों या क्यों नहीं?
हल:
(i) ∆CBD और ∆BCE में बराबर भागों के तीन युग्म –
कर्ण BC = कर्ण BC (उभयनिष्ठ)
भुजा BD = भुजा CE
∠BEC = ∠BDC = प्रत्येक 90°

(ii)∴∠D = ∠E, CB = BC तथा BD = CE
अत: RHS सर्वांगसमता से
हाँ, ∆CBD ≅ ∆BCE,

(iii)∴ ∆CBD ≅ ∆BCE
∴ उनके संगत भाग बराबर हैं।
अब, हाँ, ∠DCB = ∠EBC

प्रश्न 4.
∆ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC और AD इसका शीर्ष लम्ब है।
(i) ∆ADB और ∆ADC में, बराबर भागों के-तीन युग्म बताइए।
(ii) क्या ∆ADB ≅ ∆ADC है ? क्यों अथवा क्यों नहीं ?
(iii) क्या ∠B = ∠C है ? क्यों या क्यों नहीं ?
(iv) क्या BD = CD है? क्यों या क्यों नहीं?

हल:
(i) ∆ADB और ∆ADC में, बराबर भागों के तीन युग्म हैं –
AD = AD (उभयनिष्ठ)
कर्ण AB = कर्ण AC
∠ADB = ∠ADC (प्रत्येक 90°)

(ii) ∴ AB = AC, AD = AD, D ↔ D
अब, हाँ, ∆ADB ≅ ∆ADC

(iii) हाँ, ∠B = ∠C
∴ ∆ADB ≅ ∆ADC
∴ संगत भाग समान हैं, ∴ ∠B = ∠C

(iv) साथ ही, हाँ, \(\overline{B D}\) = \(\overline{C D}\)
∆ADB ≅ ∆ADC, ∴ संगत भाग समान हैं
∴ \(\overline{B D}\) = \(\overline{C D}\)

MP Board Class 7th Maths Solutions

MP Board Class 7th Science Solutions Chapter 14 विद्युत धारा और इसके प्रभाव

MP Board Class 7th Science Chapter 14 पाठान्त अभ्यास के प्रश्नोत्तर

प्रश्न 1.
विद्युत् परिपथ में निम्नलिखित अवयवों को निरूपित करने वाले प्रतीक अपनी नोटबुक पर खींचिए: संयोजक तार, स्विच ‘ऑफ’ की स्थिति में, विद्युत् बल्ब, विद्युत् सेल, स्विच ‘ऑन’ की स्थिति में तथा बैटरी।
उत्तर:

प्रश्न 2.
संलग्न चित्र में दर्शाए गए विद्युत् परिपथ को निरूपित करने के लिए परिपथ आरेख खींचिए।

उत्तर:

प्रश्न 3.
संलग्न चित्र में चार सेल दिखाए गए हैं। रेखाएँ खींचकर यह निर्दिष्ट कीजिए कि चार सेलों के टर्मिनलों को तारों द्वारा संयोजित करके आप बैटरी कैसे बनाएँगे?

उत्तर:

प्रश्न 4.
संलग्न चित्र में दर्शाए गए परिपथ में बल्ब दीप्त नहीं हो पा रहा है। क्या आप इसका कारण पता लगा सकते हैं? परिपथ में आवश्यक परिवर्तन करके बल्ब को प्रदीप्त कीजिए।

उत्तर:

प्रश्न 5.
विद्युत् धारा के किन्हीं दो प्रभावों के नाम लिखिए।
उत्तर:
विद्युत् धारा के प्रभाव:

1. विद्युत् धारा का चुम्बकीय प्रभाव।
2. विद्युत् धारा का तापीय प्रभाव।।

प्रश्न 6.
जब किसी तार से धारा प्रवाहित करने के लिए स्विच को ‘ऑन’ करते हैं, तो तार के निकट रखी चुम्बकीय सुई अपनी उत्तर-दक्षिण स्थिति से विक्षेपित हो जाती है। स्पष्ट कीजिए।
उत्तर:
जैसे ही तार में धारा प्रवाहित करने के लिए स्विच को ऑन’ करते हैं, तो तार के आसपास चुम्बकीय क्षेत्र उत्पन्न हो जाता है, जिससे तार के निकट रखी चुम्बकीय सुई उत्तर-दक्षिण दिशा में विक्षेपित हो जाती है, क्योंकि स्वतन्त्रतापूर्वक लटका हुआ चुम्बक सदैव उत्तर-दक्षिण दिशा में ठहरता है।

प्रश्न 7.
यदि संलग्न चित्र में दर्शाए गए विद्युत् परिपथ में स्विच को ‘ऑफ’ किया जाए, तो क्या चुम्बकीय सुई विक्षेप दर्शाएगी?

उत्तर:
दिये गये विद्युत् परिपथ में स्विच को ‘ऑफ’ करने पर चुम्बकीय सुई विक्षेप नहीं दर्शाएगी।

प्रश्न 8.
रिक्त स्थानों की पूर्ति कीजिए:

1. विद्युत् सेल के प्रतीक में लम्बी रेखा, उसके ……… टर्मिनल को निरूपित करती है।
2. दो या अधिक विद्युत् सेलों के संयोजन को ……. कहते हैं।
3. जब किसी विद्युत् हीटर के स्विच को ‘ऑन’ करते है, तो इसका ……. रक्त तप्त (लाल) हो जाता है।
4. विद्युत धारा के तापीय प्रभाव पर आधारित सुरक्षा युक्ति का …… कहते हैं।

उत्तर:

1. धन।
2. बैटरी।
3. ऐलीमेंट।
4. विद्युत् फ्यूज।

प्रश्न 9.
निम्नलिखित कथनों पर सत्य अथवा असत्य अंकित कीजिए –

1. दो सेलों की बैटरी बनाने के लिए एक सेल के ऋण टर्मिनल को दूसरे सेल के ऋण टर्मिनल से संयोजित कहते हैं। (सत्य/असत्य)
2. जब किसी फ्यूज में से किसी निश्चित सीमा से अधिक विद्युत् धारा प्रवहित होती है, तो वह पिघलकर टूट जाता है। (सत्य/असत्य)
3. विद्युत् चुम्बक, चुम्बकीय पदार्थों को आकर्षित नहीं करता। (सत्य/असत्य)
4. विद्युत् घंटी में विद्युत चुम्बक होता है। (सत्य/असत्य)

उत्तर:

1. असत्य।
2. सत्य।
3. असत्य।
4. सत्य।

प्रश्न 10.
क्या विद्युत् चुम्बक का उपयोग किसी कचरे के ढेर से प्लास्टिक को पृथक् करने के लिए किया जा सकता है? स्पष्ट कीजिए।
उत्तर:
विद्युत् चुम्बक का उपयोग किसी कचरे के ढेर से प्लास्टिक को पृथक् करने में नहीं किया जा सकता है क्योंकि प्लास्टिक चुम्बकीय पदार्थ नहीं है।

प्रश्न 11.
मान लीजिए कि कोई विद्युत् मिस्त्री आपके घर के विद्युत् परिपथ में कोई मरम्मत कर रहा है। वह ताँबे के एक तार को फ्यूज के रूप में उपयोग करना चाहता है। क्या आप उससे सहमत होंगे? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
फ्यूज एक सुरक्षा युक्ति है। ये ऐसे पदार्थों के बनाये जाते हैं जो अधिक धारा प्रवाहित होने पर शीघ्र पिघल जाएँ। ताँबे का तार विद्युत् का अच्छा सुचालक है वह अधिक विद्युत् धारा को अपने अन्दर से प्रवाहित होने देता है। अतः यह शीघ्र नहीं पिघल पायेगा। अतः ताँबे के तार के फ्यूज के लिए हमें सहमत नहीं होना चाहिए।

प्रश्न 12.
जुबैदा ने चित्र 14.9 में दर्शाए अनुसार एक सेल होल्डर बनाया तथा इसे एक स्विच और एक बल्ब से जोड़कर कोई विद्युत् परिपथ बनाया। जब उसने स्विच को ‘ऑन’ की स्थिति में किया, तो बल्ब दीप्त नहीं हुआ। परिपथ में संभावित दोष को पहचानने में जुबैदा की सहायता कीजिए।

उत्तर:
जुबैदा ने दोनों सेलों के ऋण (समान) टर्मिनलों को जोड़ दिया है। उसे दूसरे सेल का धन टर्मिनल पहले सेल के ऋण टर्मिनल से जोड़ना चाहिए।

प्रश्न 13.
संलग्न चित्र में दर्शाए गये विद्युत् परिपथ में:

1. जब स्विच ऑफ’ की स्थिति में है, तो क्या कोई भी बल्ब दीप्त होगा?
2. जब स्विच को ‘ऑन’ की स्थिति में लाते हैं, तो बल्बों A, B तथा C के दीप्त होने का क्रम क्या होगा?

उत्तर:

1. स्विच ‘ऑफ’ की स्थिति में कोई भी बल्ब दीप्त नहीं होगा।
2. जब स्विच को ऑन की स्थिति में लाते हैं, तो बल्बों के दीप्त होने का क्रम क्रमश: C, B, A होगा।

MP Board Class 7th Science Solutions

MP Board Class 7th Maths Solutions Chapter 6 त्रिभुज और उसके गुण Ex 6.5

प्रश्न 1.
PQR एक त्रिभुज है जिसका P एक समकोण है। यदि PQ = 10 cm तथा PR = 24 cm तब QR ज्ञात कीजिए।
हल:
समकोण त्रिभुज PQR में पाइथागोरस प्रमेय का प्रयोग करने पर,
QR² = PQ² + PR²
OR² = (10)² + (24)²

या QR² = 100 + 576 = 676
या QR² = (26)²
∴ QR = 26 cm

प्रश्न 2.
ABC एक त्रिभुज है जिसका ∠C एक समकोण है। यदि AB = 25 cm तथा AC = 7 cm तब BC ज्ञात कीजिए।
हल:
समकोण त्रिभुज ABC में पाइथागोरस प्रमेय का प्रयोग करने पर,

AC² + BC² = AB²
(7)² + x² = (25)²
या 49 + x² = 625
या x² = 625 – 49 = 576
या x² = 242 ⇒ x = 24
∴ BC = 24 cm

प्रश्न 3.
दीवार के सहारे उसके पैर कुछ दूरी पर टिका कर 15 m लम्बी एक सीढ़ी भूमि से 12 m ऊँचाई पर स्थित खिड़की तक पहुँच जाती है। दीवार से सीढ़ी के पैर की दूरी ज्ञात कीजिए।
हल:
माना कि सीढ़ी के पैर दीवार से am की दूरी पर हैं।

∴ पाइथागोरस प्रमेय से,
a² + 122 = 152
या a² + 144 = 225
या a² = 225 – 144 = 81
शस a² = (9)² ⇒ a = 9m
अत: सीढ़ी के पैर की दीवार से अभीष्ट दूरी = 9 m

प्रश्न 4.
निम्नलिखित में भुजाओं के कौन-से समूह एक समकोण त्रिभुज बना सकते हैं?
(i) 2.5 cm, 6-5 cm,6cm
(ii) 2 cm, 2 cm, 5 cm
(iii) 1.5 cm, 2 cm, 2.5 cm
हल:
(i) माना, त्रिभुज की भुजाएँ x = 2.5 cm, y = 6.5 cm, z = 6 cm हैं।
यहाँ, सबसे बड़ी भुजा की लम्बाई y = 6.5 cm
अब, x² + z² = (2.5)² + (6)² = 6.25 + 36
= 42.25
तथा, y² = (6.5)² = 42.25,
∵ x² + z² = y²
अतः दी गई भुजाएँ समकोण त्रिभुज बना सकती हैं और भुजा 6.5 cm के सामने का कोण समकोण होगा।

(ii) माना त्रिभुज की भुजाएँ x = 2 cm, y = 2 cm, z = 5 cm है।
यहाँ, सबसे बड़ी भुजा की लम्बाई z = 5 cm है।
अब, x² + y² = (2)² + (2)²
= 4 + 4 = 8
तथा z² = (5)² = 25
अत: अत: दी गई भुजाएँ समकोण त्रिभुज नहीं बना सकती हैं।

(iii) माना, त्रिभुज की भुजाएँ x = 1.5 cm, y = 2 cm और z = 2.5 cm हैं।
यहाँ, सबसे बड़ी भुजा की लम्बाई z = 2.5 cm है।
अब, x² + y² = (1.5)² + (2)² = 2.25 + 4.00
= 6.25
तथा z² = (2.5)² = 6.25,
∵ x² + y² = z²
अतः दी गई भुजाएँ समकोण त्रिभुज बना सकती हैं और भुजा 2.5cm के सामने का कोण समकोण होगा।

प्रश्न 5.
एक पेड़ भूमि से 5m की ऊँचाई पर टूट गया है और उसका ऊपरी सिरा भूमि को उसके आधार से 12 m की दूरी पर छूता है। पेड़ की पूरी ऊँचाई ज्ञात कीजिए।
हल:
माना कि पेड़ BD बिन्दु C से टूटा है,
इस प्रकार, CD = CA

अब पाइथागोरस प्रमेय से, ∆ABC में,
AB² + BC² = AC²
12² + 5² = AC²
या 144 + 25 = AC²
या AC² = 169 = 13²
या AC = 13 m
अब, पेड़ की ऊँचाई = BD = BC + CD
= BC + AC (∵AC = CD)
= 5 m + 13 m = 18 m
अतः पेड़ की अभीष्ट लम्बाई = 18 m

प्रश्न 6.
त्रिभुज PQR में कोण Q = 25° तथा कोण R = 25° है। अग्रलिखित में कौन-सा कथन सत्य है ?

(i) PQ² + QR = RP
(ii) PQ² + RP² = QR²
(iii) RP² + QR² = PQ²
हल:
∆PQR में,
∠P + ∠Q + ∠R = 180°
∠P + 25° + 65° = 180°
या ∠P + 90° = 180°
या ∠P = 180° – 90° = 90°
अत: ∆PQR समकोण त्रिभुज है, जिसका कोण P समकोण है।
अब, कर्ण = कोण P के सामने की भुजा = QR पाइथागोरस प्रमेय द्वारा
QR² = PQ² + PR²
अतः सम्बन्ध (ii) PQ² + RP² = QR² सत्य है।

प्रश्न 7.
एक आयत की लम्बाई 40 cm है तथा उसका एक विकर्ण 41 cm है। इसका परिमाप ज्ञात कीजिए।
हल:
आयत की लम्बाई = 40 cm, विकर्ण = 41 cm
माना कि आयत की चौड़ाई = x cm

समकोण त्रिभुज BAD से,
AB² + AD² = BD²
40² + AD² = 41²
या AD² = 41² – 40² = 1681 – 1600
= 81 = 9²
∴ चौड़ाई x = 9 cm
अब परिमाप = 2 (लम्बाई + चौड़ाई)
= 2 (40 + 9) = 2 × 49 = 98 cm
अत: आयत का परिमाप = 98 cm

प्रश्न 8.
एक समचतुर्भुज के विकर्ण 16 cm तथा 30 cm हैं। इसका परिमाप ज्ञात कीजिए।
हल:
माना कि ABCD एक समचतुर्भुज है, जिसमें AC = 30 cm और BD = 16 cm.

हम जानते हैं कि समचतुर्भुज के विकर्ण एक-दूसरे को समकोण पर काटते हैं। (यहाँ ये O पर काटते हैं।)
∠AOB = 90°

अब समकोण ∆AOB में,
AB² = 40 + BO²
= 15² + 8²
= 225 + 64 = 289
या AB² = 17² ⇒ AB = 17
∴ समचतुर्भुज का परिमाप = 4 × AB = 4 × 17 cm
= 68 cm

पाठ्य-पुस्तक पृष्ठ संख्या # 143

सोचिए, चर्चा कीजिए एवं लिखिए

प्रश्न 1.
त्रिभुज PQR का कोण P एक समकोण है। इसकी सबसे लम्बी भुजा कौन-सी है?
हल:
∵ शीर्ष P पर कोण 90° बनता है।
∴ समकोण बनाने वाली भुजाएँ PQ और PR हैं।
∴ कर्ण = QR
अत: त्रिभुज की सबसे लम्बी भुजा QR है।

प्रश्न 2.
त्रिभुज ARC का कोण B एक समकोण है। इसकी सबसे लम्बी भुजा कौन-सी है ?
हल:
शीर्ष B पर कोण 90° बनता है।
∴ ∆ABC की समकोण बनाने वाली भुजाएँ AB और BC हैं।
∴ कर्ण = AC
अतः त्रिभुज की सबसे लम्बी भुजा AC है।

प्रश्न 3.
किसी समकोण त्रिभुज में सबसे लम्बी भुजा कौन-सी होती है ?
हल:
समकोण त्रिभुज में सबसे लम्बी भुजा कर्ण होती है।

प्रश्न 4.
किसी आयत में विकर्ण पर बने वर्ग का क्षेत्रफल उसकी लम्बाई तथा चौड़ाई पर बने वर्गों के क्षेत्रफल के योग के बराबर होता है। यह बौधायन का प्रमेय है। इसकी पाइथागोरस गुण से तुलना कीजिए।
हल:
पाइथागोरस प्रमेय के अनुसार, “समकोण त्रिभुज में कर्ण का वर्ग शेष दो भुजाओं के वर्गों के योग के बराबर होता है।” बौधायन ने सुलभ सूत्र में कहा है कि “आयत के कर्ण द्वारा बनाया गया क्षेत्रफल उसकी दोनों भुजाओं के द्वारा बनाये गये क्षेत्रफल के बराबर होता है।”

अब, माना कि आयत की लम्बाई और चौड़ाई क्रमशः a और b है तथा इसका विकर्ण c है। इसलिए विकर्ण पर बने वर्ग का क्षेत्रफल = c × c = c² तथा आयत की भुजाओं पर बने वर्गों के क्षेत्रफल a² और b² हैं।
∴ c² = a² + b² (बौधायन सुलभ सूत्र)
अतः स्पष्ट है कि पूर्व में बौधायन कथन ही वर्तमान में पाइथागोरस प्रमेय है।

MP Board Class 7th Maths Solutions

MP Board Class 7th Science Solutions Chapter 13 गति एवं समय

MP Board Class 7th Science Chapter 13 पाठान्त अभ्यास के प्रश्नोत्तर

प्रश्न 1.
निम्नलिखित गतियों का वर्गीकरण सरल रेखा के अनुदिश, वर्तुल तथा दोलन गति में कीजिए –
(क) दौड़ते समय आपके हाथों की गति।
(ख) सीधी सड़क पर गाड़ी को खींचते घोड़े की गति।
(ग) ‘मैरी गो राउण्ड’ झूले में बच्चे की गति।
(घ) ‘सी-सॉ’ झूले पर बच्चे की गति।
(च) विद्युत घण्टी के हथोड़े की गति।
(छ) सीधे पुल पर रेलगाड़ी की गति।
उत्तर:
सरल रेखा के अनुदिश गति।
(ख)सीधी सड़क पर गाड़ी को खींचते घोड़े की गति।
(छ) सीधे पुल पर रेलगाड़ी की गति।

वर्तुल गति:
(ग) ‘मैरी गो राउण्ड’ झूले में बच्चे की गति।

दोलन गति:
(क) दौड़ते समय आपके हाथों की गति।
(घ) ‘सी-सॉ’ झूले पर बच्चे की गति।
(च) विद्युत घण्टी के हथोड़े की गति।

प्रश्न 2.
निम्नलिखित में कौन-सा कथन सही नहीं है?

1. समय का मूल मात्रक सेकण्ड है।
2. प्रत्येक वस्तु नियत चाल से गति करती है।
3. दो शहरों के बीच की दूरियाँ किलोमीटर में मापी जाती हैं।
4. किसी दिए गए लोलक का आवर्तकाल नियत नहीं होता।
5. रेलगाड़ी की चाल m/h में व्यक्त की जाती है।

उत्तर:

1. सत्य।
2. असत्य।
3. सत्य।
4. सत्य।
5. असत्य।

प्रश्न 3.
कोई सरल लोलक 20 दोलन पूरे करने में 32 sec लेता है। लोलक का आवर्तकाल क्या है?
हल:

प्रश्न 4.
दो स्टेशनों के बीच की दूरी 240 km है। कोई रेलगाड़ी इस दूरी को तय करने में 4 घण्टे लेती है। रेलगाड़ी की चाल परिकलित कीजिए।
हल:

प्रश्न 5.
किसी कार के पथगामी का 08:30 AM पर पाठ्यांक 57321.0 km है। यदि 08.50 AM पर पथगामी का पाठ्यांक परिवर्तित होकर 57336.0 km हो जाता है, तो कार द्वारा चली गई दूरी कितनी है? कार की चाल km/min में परिकलित कीजिए। इस चाल को km/h में भी व्यक्त कीजिए।
हल:

प्रश्न 6.
सलमा अपने घर से साइकिल पर विद्यालय पहुँचने में 15 मिनट लेती है। यदि साइकिल की चाल 2 m/s है, तो घर से विद्यालय की दूरी परिकलित कीजिए।
हल:

प्रश्न 7.
निम्नलिखित स्थितियों में गति के दूरी-समय ग्राफ की आकृति दर्शाइए:

1. नियत चाल से गति करती कार।
2. सड़क के किनारे खड़ी कोई कार।

उत्तर:
1. नियत चाल से गति करती कार:

2. सड़क के किनारे खड़ी कोई कार:

प्रश्न 8.
निम्नलिखित में कौन-सा सम्बन्ध सही है?

उत्तर:

प्रश्न 9.
चाल का मूल मात्रक है –

1. km/min
2. m/min
3. km/h
4. m/s

उत्तर:
m/s

प्रश्न 10.
कोई कार 40 km/h की चाल से 15 मिनट चलती है, इसके पश्चात् वह 60 km/h की चाल से 15 मिनट चलती है। कार द्वारा तय की गई कुल दूरी होगी –

1. 100 km
2. 25 km
3. 15 km
4. 10 km

उत्तर:
25 km

प्रश्न 11.
मान लीजिए संलग्न चित्र में दर्शाए गए फोटोग्राफ 10 सेकण्ड के अंतराल पर खींचे गए। यदि इन फोटोग्राफ में 100 मीटर की दूरी को 1 cm द्वारा दर्शाया गया है, तो तीव्रतम कार की चाल परिकलित कीजिए।
हल:

प्रश्न 12.
संलग्न चित्र में दो वाहनों, A तथा B की गति के दूरी-समय ग्राफ दर्शाए गए हैं। इनमें से कौन-सा वाहन अपेक्षाकृत तीव्र गति से चल रहा है?

उत्तर:
चित्र में दूरी – समय ग्राफ का ढाल वाहन A के लिए, वाहन B की अपेक्षा अधिक है। अत: वाहन A, वाहन B की अपेक्षाकृत तीव्र गति से चल रहा है।

प्रश्न 13.
निम्नलिखित दूरी-ग्राफों में से कौन उस ट्रक की गति को दर्शाता है, जिसमें उसकी चाल नियत नहीं है?

उत्तर:
(iii) में ट्रक की चाल नियत नहीं है।

MP Board Class 7th Science Solutions

MP Board Class 7th Maths Solutions Chapter 6 त्रिभुज और उसके गुण Ex 6.4

प्रश्न 1.
निम्न दी गई भुजाओं की मापों से क्या कोई त्रिभुज सम्भव है ?
(i) 2 cm, 3 cm, 5 cm
(ii) 3 cm, 6 cm,7cm
(iii) 6cm, 3 cm, 2 cm.
हल:
(i) ∵ 2 cm + 3 cm = 5 cm और तीसरी भुजा = 5cm
∴ दो भुजाओं की लम्बाइयों का योग = तीसरी भुजाओं की लम्बाई, जो कि असम्भव है।
अतः भुजाओं की इन मापों से त्रिभुज सम्भव नहीं है।

(ii) ∵ 3cm + 6 cm = 9 cm
और 9cm > 7 cm
6cm + 7 cm = 13 cm
और 13 cm > 3 cm
7 cm + 3 cm = 10 cm
और 10 cm > 6cm
अत: भुजाओं की इन मापों से त्रिभुज सम्भव है।

(iii) ∵ 6cm + 3 cm = 9 cm
और 9cm > 2 cm
3 cm + 2 cm = 5 cm
और 5 cm ≠ 6cm
2 cm + 6 cm = 8 cm
और 8 cm > 5 cm
अतः भुजाओं की इन मापों से त्रिभुज सम्भव नहीं है।

प्रश्न 2.
त्रिभुज PQR के अभ्यंतर में कोई बिन्दु O लीजिए। क्या यह सही है कि –

(i) OP + OQ > PQ?
(ii) OQ + OR > QR?
(iii) OR + OP > RP?
हल:
∆POR में OP, OQ तथा OR को मिलाया। अत: त्रिभुज के गुण से,
(i) हाँ, OP + OQ > PQ
(ii) हाँ, OQ – OR > QR

(iii) हाँ, OR + OP > RP.

प्रश्न 3.
त्रिभुज ABC की एक माध्यिका AM है। बताइये कि क्या AB + BC + CA > 2 AM?

(संकेत : ∆ABM तथा ∆AMC की भुजाओं पर विचार कीजिए।)
हल:
चूँकि त्रिभुज की दो भुजाओं की लम्बाइयों का योग तीसरी भुजा की लम्बाई से अधिक होता है।
∴ ∆ABM में, AB + BM > AM …..(i)
इसी प्रकार ∆AMC में, CA + CM > AM …(2)
(1) और (2) को जोड़ने पर,
(AB + BM) + (CA + CM) > AM + AM
या AB – (BM + CM) + CA > 2 AM
अत: AB + BC + CA > 2 AM (∵ BM + MC = BC)

प्रश्न 4.
ABCD एक चतुर्भुज है। क्या AB + BC + CD + DA > AC + BD?

हल:
∵ त्रिभुज की दो भुजाओं की लम्बाइयों का योग तीसरा भुजा की लम्बाई से अधिक होता है।
∴ ∆ABC में, AB + BC > AC …..(1)
∴ ∆ACD में, CD + DA > AC …..(2)
∆ABD में, AB + DA > BD ….(3)
तथा ∆BCD में, BC + CD > BD ….(4)
समीकरण (1), (2), (3) व (4) को जोड़ने पर,
2(AB + BC + CD + DA) > 2(AC + BD)
या AB + BC + CD + DA > AC + BD इति सिद्धम्

प्रश्न 5.
ABCD एक चतुर्भुज है। क्या AB + BC + CD + DA < 2 (AC + BD)?
हल:
∵ किसी त्रिभुज की दो भुजाओं की लम्बाइयों का योग तीसरी भुजा की लम्बाई से अधिक होता है।

∴ ∆OAB में, OA + OB > AB …..(1)
∆OBC में, OB + OC > BC …..(2)
∆OCD में, OC + OD > CD …..(3)
∆OAD में, OA + OD > AD …(4)
(1), (2), (3) व (4) को जोड़ने पर,
2(OA + OB + OC + OD) > (AB + BC + CD + DA)
या AB + BC + CD + DA < 2 (OA + OB + OC + OD)
या AB + BC + CD + DA < 2 [(OA + OC)+ (OB + OD)]
या AB + BC + CD + DA < 2 (AC + BD) इति सिद्धम्

प्रश्न 6.
एक त्रिभुज की दो भुजाओं की माप 12 cm तथा 15 cm है। इसकी तीसरी भुजा की माप किन दो मापों के बीच होनी चाहिए?
हल:
चूँकि हम जानते हैं कि किसी त्रिभुज की दो भुजाओं की लम्बाइयों का योग तीसरी भुजा की लम्बाई से अधिक होता है।
∴ 12 cm + 15 cm > तीसरी भुजा
अर्थात् 27 > तीसरी भुजा
या तीसरी भुजा < 27 cm.
साथ ही किन्हीं दो भुजाओं की लम्बाइयों का अन्तर तीसरी भुजा की लम्बाई से कम होता है।
∴ 15 cm – 12 cm < तीसरी भुजा या
या 3 cm < तीसरी भुजा अतः
या 3 cm < तीसरी भुजा < 27 cm.
अतः तीसरी भुजा की लम्बाई 3 cm और 27 cm के बीच में होनी चाहिए।

पाठ्य-पुस्तक पृष्ठ संख्या # 139

सोचिए, चर्चा कीजिए एवं लिखिए

प्रश्न 1.
किसी त्रिभुज में क्या उसके किन्हीं दो कोणों का योग तीसरे कोण से सदैव अधिक होता है ?
हल:
किसी त्रिभुज में उसके किन्हीं दो कोणों का योग सदैव तीसरे कोण से अधिक नहीं होता है।

पाठ्य-पुस्तक पृष्ठ संख्या # 141-142

प्रयास कीजिए

प्रश्न 1.
निम्न आकृतियों में अज्ञात लम्बाई x ज्ञात कीजिए –

हल:
(i) दी हुई आकृति समकोण त्रिभुज है, जिसमें सबसे लम्बी भुजा कर्ण है।
∴ x² = 3² + 4² (पाइथागोरस प्रमेय से)
या x² = 9 + 16
या x² = 25 = 52
∴ x = 5

(ii) दी हुई आकृति समकोण त्रिभुज है।
∴ x² = 6² + 8² (पाइथागोरस प्रमेय से)
या x² = 36 + 64
या x² = 100 = 102
∴ x = 10

(iii) दी हुई आकृति समकोण त्रिभुज है।
∴ x² = 15² + 8² (पाइथागोरस प्रमेय से)
या x² = 225 + 64
या x² = 289 = 17²
∴ x = 17 cm

(iv) दी हुई आकृति समकोण त्रिभुज है।
∴ x² = 24² + 7²
या x² = 576 + 49
या x² = 625 = 252
∴ x = 25

(v) समकोण त्रिभुज (1) में,
y² + 12² = 372
या y² + 144 = 1369
या y² = 1369 – 144 = 1225
या y² = 35² ⇒ y = 35

समकोण त्रिभुज (2) में,
(x – 7)² + 12² = 37²
या (x – y)² + 144 = 1369
या (x – 35)² = 1369 – 144 = 1225
या (x – 35)² = 35²
या x – 35 = 35
x = 35 + 35 = 70

(vi) चित्र से, x² + 3² = 12²
या x² = 12² – 3² = 144 – 9
या x² = 135
⇒ x = \(\sqrt { 135 }\)

पाठ्य-पुस्तक पृष्ठ संख्या # 142

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 6 त्रिभुज और उसके गुण Ex 6.3

प्रश्न 1.
निम्नांकित आकृतियों में अज्ञात x का मान ज्ञात कीजिए –

हल:
∵ त्रिभुज के तीनों अन्त:कोणों का योग 180° (दो समकोण) के बराबर होता है। अतः
(i) x+ 50° + 60° = 180°
या x + 110° = 180°
या x = 180° – 110° = 700
अतः x का अभीष्ट मान = 70°

(ii) x + 90° + 30° = 180°
या x + 120° = 180°
या x = 180° – 120° = 60°
अतः का अभीष्ट मान = 60°

(iii) x + 30° + 110° = 180°
या x + 140° = 180°
या x = 180° – 140° = 40°
अत: x का अभीष्ट मान = 40°

(iv) x + x + 50 = 180°
या 2x + 50° = 180°
या 2x = 180° – 50° = 130°
या x = \(\frac { 180 }{ 3 } \) = 60°
अतः x का अभीष्ट मान = 65°

(v) x + x + x = 180°
या 3x = 180°
या x = \(\frac { 180 }{ 3 } \) = 60°
अतः x का अभीष्ट मान = 60°

(vi) x + 2x + 90° = 180°
या 3x = 180° – 90° = 90°
या x = \(\frac { 90 }{ 3 } \) = 30°
अतः x का अभीष्ट मान = 30°

प्रश्न 2.
निम्नांकित आकृतियों में अज्ञात x और y का मान ज्ञात कीजिए –

हल:
(i) ∵ कोण y और 120° रैखिक युग्म बनाते हैं।
∴ y + 120° = 180°
या y = 180° – 120° = 60°
(∵ त्रिभुज के तीनों अन्तः कोणों का योग = 180°)
अब x + y + 50° = 180°
या x + 60° + 50° = 180°
या x + 110° = 180°
या x = 180° – 110° = 70°
अतः x = 70° और y = 60°

(ii) ∵ कोण y और 80° ऊर्ध्वाधर सम्मुख कोण हैं,
∴ y = 80°
∵ त्रिभुज के तीनों अन्त:कोणों का योग 180° होता है।
∴ x + y + 50° = 180°
या x + 80° + 50° = 180°
या x + 130° = 180°
या x = 180° – 130° = 50°
अत: x = 50° और y = 80°

(iii) ∵ त्रिभुज के तीनों अन्तः कोणों का योग = 180°
∴ 50° + 60° + y = 180°
या 110° + y = 180°
या y = 180° – 110° = 70°
पुनः कोण x और y रैखिक युग्म बनाते हैं
∴ x + y = 180°
या x + 70° = 180°
या x = 180° – 70° = 110°
अतः x = 110° और y = 70°

(iv) ∵ कोण x और 60° ऊर्ध्वाधर सम्मुख कोण हैं।
∴ x = 60°
अब, ∵ त्रिभुज के तीनों अन्त:कोणों का योग 180° होता है।
∴ x + 1 + 30° = 180°
या 60 + 1 + 30° = 180°
या y + 90° = 180°
या y = 180° – 90° = 90°
अतः x = 60° और y = 90°

(v) ∵ कोण । और 90° ऊर्ध्वाधर सम्मुख कोण हैं,
∴ y = 90°
अब, ∵ त्रिभुज के तीनों अन्त:कोणों का योग = 180°
∴ x + x + y = 180°
या 2x + 90° = 180°
या 2x = 180° – 90°
= 90°
⇒ x = \(\frac { 90 }{ 2 } \) =45°
अतः x = 45° और y = 90°

(vi) त्रिभुज का एक अन्त:कोण y है। शेष दो कोण ऊर्ध्वाधर सम्मुख कोण x के बराबर हैं।
∴ x + x + y = 180°
या 2x + y = 180°
या 2x + x = 180° (∵ ∠x = ∠y)
या 3x = 180°
या x = \(\frac { 180 }{ 3 } \) = 60°
अतः x = 60° और y = 60°

पाठ्य-पुस्तक पृष्ठ संख्या # 184

प्रयास कीजिए

प्रश्न 1.
एक त्रिभुज के दो कोण 30° तथा 80° हैं। इस त्रिभुज का तीसरा कोण ज्ञात कीजिए।
हल:
माना कि तीसरा कोण x है,
∵ त्रिभुज के तीनों अन्त:कोणों का योग = 180°
∴ 30° + 80° + x = 180°
या 110° + x = 180°
या x = 180° – 110° = 70°
अतः त्रिभुज का तीसरा कोण = 70°

प्रश्न 2.
किसी त्रिभुज का एक कोण 80° तथा शेष दोनों कोण बराबर हैं। बराबर कोणों में प्रत्येक कोण की माप ज्ञात कीजिए।
हल:
माना कि बराबर कोणों में प्रत्येक कोण x है।
∵ त्रिभुज के तीनों अन्तः कोणों का योग 180° होता है।
∴ x + x + 80° = 180°
या 2x + 80° = 180°
या 2x = 180° – 80° = 100°
या x = \(\frac { 100 }{ 2 } \) = 50°
अत: बराबर कोणों में प्रत्येक कोण = 50°

प्रश्न 3.
किन्हीं त्रिभुज के तीनों कोणों में 1 : 2 : 1 का अनुपात है। त्रिभुज के तीनों कोण ज्ञात कीजिए। त्रिभुज का दोनों प्रकार से वर्गीकरण भी कीजिए।
हल:
माना कि त्रिभुज के कोण x, 2x व x हैं।
∴ x + 2x + x = 180°
या 4x = 180°
या x = \(\frac { 180 }{ 4 } \) = 45°
त्रिभुज के कोण x = 45° तथा 2x = 2 × 45° = 90°
अत: त्रिभुज के कोण 45°, 90° और 45° हैं।
अतः त्रिभुज समकोण त्रिभुज है तथा यह समद्विबाहु त्रिभुज भी है।

सोचिए, चर्चा कीजिए एवं लिखिए

प्रश्न 1.
क्या कोई ऐसा त्रिभुज सम्भव है जिसके दो कोण समकोण हों ?
हल:
नहीं, ऐसा त्रिभुज सम्भव नहीं हैं जिसके दो कोण समकोण हों क्योंकि त्रिभुज के तीनों अन्तः कोणों का योग 180° होता है।

प्रश्न 2.
क्या कोई ऐसा त्रिभुज सम्भव नहीं है जिसमें दो | कोण अधिक कोण हों ?
हल:
नहीं, ऐसा त्रिभुज सम्भव नहीं है, जिसमें दो कोण अधिक कोण हों। यहाँ इस स्थिति में त्रिभुज के तीनों कोणों का योग दो समकोण से अधिक हो जाएगा।

प्रश्न 3.
क्या कोई ऐसा त्रिभुज सम्भव है जिसमें दो – कोण न्यून कोण हों ?
हल:
हाँ, ऐसा त्रिभुज सम्भव है जिसमें दो न्यून कोण हों।

प्रश्न 4.
क्या कोई ऐसा त्रिभुज सम्भव है जिसमें तीनों कोण 60° से अधिक हों ?
हल:
नहीं, ऐसा त्रिभुज सम्भव नहीं है जिसमें सभी तीनों कोण 60° से अधिक हों। इस स्थिति में त्रिभुज के तीनों कोणों का योग 180° से अधिक हो जाएगा, लेकिन यह 180° के बराबर होना चाहिए।

प्रश्न 5.
क्या कोई ऐसा त्रिभुज सम्भव है जिसमें तीनों कोण 60° के हो ?
हल:
हाँ, ऐसा त्रिभुज सम्भव है जिसमें तीनों कोण 60° के हों।

प्रश्न 6.
क्या कोई ऐसा त्रिभुज सम्भव है। जिसमें तीनों कोण 60° से कम हों ?
हल:
नहीं, ऐसा त्रिभुज सम्भव नहीं है जिसमें तीनों कोण 60° से कम हों। ऐसी स्थिति में त्रिभुज के तीनों कोणों का योग 180° से कम होगा जबकि यह 180° होना चाहिए।

पाठ्य-पुस्तक पृष्ठ संख्या # 135-136

प्रयास कीजिए

प्रश्न 1.
प्रत्येक आकृति में कोण x का मान ज्ञात कीजिए –

हल:
(i) आकृति समद्विबाहु त्रिभुज है जिसमें दो भुजाएँ समान हैं और समान भुजाओं के सामने के कोण समान होते हैं।
∴ अभीष्ट कोण x = 40°

(ii) आकृति समकोण समद्विबाहु त्रिभुज है, जिसकी दो भुजाएँ समान हैं और समान भुजाओं के सामने के कोण समान होते हैं।
अतः दूसरी समान भुजा के सामने का कोण 45° है।
चूँकि हम जानते हैं कि त्रिभुज के तीनों कोणों का योग 180° होता है। अतः
x + 45° + 45° = 180°
या x + 90° = 180°
या x = 180° – 90° = 90°
∴ अभीष्ट कोण x = 90°

(iii) आकृति में त्रिभुज की दो भुजाएँ समान हैं और समान भुजाओं के सामने के कोण समान होते हैं,
∴ अभीष्ट कोण x = 50°

(iv) आकृति में त्रिभुज की दो भुजाएँ समान हैं और समान भुजाओं के सामने के कोण समान होते हैं।
∴ आधार का दूसरा कोण = x.
अब, त्रिभुज के तीनों कोणों का योग = 180°
∴ x + x + 100° = 180°
या 2x + 100° = 180°
या 2x = 180° – 100°
= 80°
∴ अभीष्ट कोण x = \(\frac { 80 }{ 2 } \) = 40°

(v) आकृति में दो भुजाएँ समान हैं तथा एक कोण समकोण है और समान भुजाओं के सामने के कोण समान होते हैं।
∴ दूसरा कोण = x
∵ त्रिभुज के तीनों अन्त: कोणों का योग = 180°
∴ x + x + 90° = 180°
या 2x = 180° – 90° = 90°
∴ अभीष्ट कोण x = \(\frac { 90 }{ 2 } \) = 45°

(vi) आकृति में त्रिभुज की दो भुजाएँ समान हैं और त्रिभुज में समान भुजाओं के सामने के कोण समान होते हैं।
∴ दूसरा कोण भी x होगा।
∵ त्रिभुज के तीनों कोणों का योग = 180°
∴ x + x + 40° = 180°
या 2x + 40° = 180°
या 2x = 180° – 40° = 140°
∴ अभीष्ट कोण x = \(\frac { 140 }{ 2 } \) = 70°

(vii) आकृति में त्रिभुज की दो भुजाएँ समान हैं और त्रिभुज में समान भुजाओं के सामने के कोण समान होते हैं।
∴ दूसरा आधार का कोण = x
∵ दूसरा आधार कोण x और 120° रैखिक युग्म बनाते हैं।
∴ x + 120° = 180°
∴ अभीष्ट कोण x = 180° – 120°
= 60°

(viii) आकृति में त्रिभुज की दो भुजाएँ समान हैं और त्रिभुज में समान भुजाओं के सामने के कोण समान होते हैं।
∴ दूसरा आधार का कोण = x
चूँकि सम्मुख अत: कोणों का योग = बाह्य कोण
∴ x + x = 110°
या 2x = 110°
∴ अभीष्ट कोण x = \(\frac { 110 }{ 2 } \) = 55°

(ix) आकृति में त्रिभुज की दो भुजाएँ समान हैं और त्रिभुज में समान भुजाओं के सामने के कोण समान होते हैं।
∴ दूसरा आधार का कोण = x
साथ ही, ऊर्ध्वाधर सम्मुख कोण x और 30° बराबर हैं।
∴ अभीष्ट कोण x = 30°

प्रश्न 2.
प्रत्येक आकृति में x तथा y के मान ज्ञात कीजिए –

हल:
(i) आकृति में त्रिभुज की दो भुजाएँ समान हैं।
∴ समान भुजाओं के सामने के कोण समान हैं।
चूँकि एक आधार का कोण = y
∴ दूसरा आधार का कोण = y
अब, दूसरा आधार कोण y और 120° रैखिक युग्म बनाते हैं।
∴ y + 120° = 180°
या y = 180° – 120° = 60°
अब, त्रिभुज के तीनों अन्तः कोणों का योग = 180°
∴ x + y + y = 180°
या x + 2y = 180°
या x + 2 × 60° = 180°
या x = 180° – 120° = 60
अतः, x = 60° और y = 60°

(ii) आकृति में त्रिभुज की दो भुजाएँ समान हैं।
∴ समान भुजाओं के सामने के कोण समान हैं।
∵ समान कोणों में एक कोण x है, अतः दूसरा कोण = x साथ ही, त्रिभुज समकोण त्रिभुज है
∴ तीसरा कोण = 90°
अब, त्रिभुज के तीनों अन्त:कोणों का योग = 180°
∴ x + x + 90° = 180°
या 2x + 90° = 180°
या 2x = 180° – 90° = 90°
या x = \(\frac { 90 }{ 2 } \) = 45°
अब, दूसरा कोण x और रैखिक युग्म बनाते हैं।
∴ x + y = 180°
या 45° + y = 180°
∴ y = 180° – 45° = 135°
अतः x = 45° और y = 135°

(iii) आकृति में त्रिभुज की दो भुजाएँ समान हैं।
∴ समान भुजाओं के सामने के कोण समान हैं।
समान कोण में एक कोण x है।
अतः दूसरा आधार कोण = x
त्रिभुज का तीसरा कोण = ऊर्ध्वाधर सम्मुख कोण
= 92°
अब, त्रिभुज के तीनों अन्त:कोणों का योग = 180°
∴ x + x + 92° = 180°
या 2x + 92° = 180°
या 2x = 180° – 92° = 88°
या x = \(\frac { 88 }{ 2 } \) = 44°
अब, दूसरा आधार कोण x और y रैखिक युग्म बनाते हैं।
∴ x + y = 180°
या 44° + y = 180°
या y = 180° – 44° = 136°
अतः x = 44° और y = 136°

पाठ्य-पुस्तक पृष्ठ संख्या # 137

प्रश्न 1.
अपनी अभ्यास-पुस्तिका में कोई तीन त्रिभुज, जैसे – ∆ABC, ∆PQR और ∆XYZ बनाइए। अपने पैमाने की सहायता से इन त्रिभुजों की भुजाओं को मापकर, एक तालिका के रूप में निम्न प्रकार से लिखिए
हल:


पाठ्य-पुस्तक पृष्ठ संख्या # 138-139

MP Board Class 7th Maths Solutions

MP Board Class 7th Science Solutions Chapter 11 जंतुओं और पादप में परिवहन

MP Board Class 7th Science Chapter 11 पाठान्त अभ्यास के प्रश्नोत्तर

प्रश्न 1.
कॉलम A में दी गई संरचनाओं का कॉलम B में दिए गए प्रक्रमों से मिलान कीजिए –

उत्तर:
(क) → (ii)
(ख) → (iv)
(ग) → (i)
(घ) → (iii)

प्रश्न 2.
रिक्त स्थानों की पूर्ति कीजिए –

1. हृदय से रक्त का शरीर के सभी अंगों में परिवहन के …. द्वारा होता है।
2. हीमोग्लोबिन …… कोशिकाओं में पाया जाता है।
3. धमनियाँ और शिराएँ ………. के जाल द्वारा जुड़ी रहती हैं।
4. हृदय का लयबद्ध विस्तार और संकुचन ……….. कहलाता है।
5. मानव शरीर के प्रमुख उत्सर्जित उत्पाद ……………. है।
6. पसीने में जल और ………. होता है।
7. वृक्क अपशिष्ट पदार्थों को द्रव रूप में बाहर निकालते हैं, जिसे हम …………. कहते हैं।
8. वृक्षों में बहुत अधिक ऊँचाइयों तक जल पहुँचाने के कार्य में द्वारा ……….. उत्पन्न चूषण अभिकर्षण बल सहायता करता है।

उत्तर:

1. धमनियों।
2. लाल रक्त।
3. कोशिकाओं।
4. हृदय स्पंदन।
5. मूत्र।
6. लवण।
7. यूरिया।
8. वाष्पोत्सर्जन।

प्रश्न 3.
सही विकल्प का चयन करिए :
(क) पादपों में जल का परिवहन होता है –

1. जाइलम के द्वारा।
2. फ्लोएम के द्वारा
3. रन्ध्रों के द्वारा।
4. मूल रोमों के द्वारा।

(ख) मूलों द्वारा जल के अवशोषण की दर को बढ़ाया जा सकता है, उन्हें –

1. छाया में रखकर।
2. मंद प्रकाश में रखकर।
3. पंखे के नीचे रखकर।
4. पॉलीथीन की थैली में रखकर।

उत्तर:
(क) जाइलम के द्वारा।

(ख) मन्द प्रकाश में रखकर।

प्रश्न 4.
पादपों अथवा जन्तुओं में पदार्थों का परिवहन क्यों आवश्यक है? समझाइए।
उत्तर:
पादप तथा जन्तुओं में परिवहन द्वारा रक्त के माध्यम से भोजन, जल, ऑक्सीजन एवं अन्य महत्वपूर्ण उपयोगी पदार्थों को शरीर के विभिन्न भागों में पहुँचाया जाता है जिससे मनुष्य जैविक क्रियाएँ करता है। परिवहन द्वारा उन अंगों में उत्पन्न हानिकारक पदार्थों जैसे- कार्बन डाइऑक्साइड, पसीना, मूत्र आदि को शरीर से बाहर निकाला जाता है। अतः पादपों और जन्तुओं में पदार्थों का परिवहन आवश्यक है।

प्रश्न 5.
क्या होगा यदि रक्त में पट्टिकाणु नहीं होंगे?
उत्तर:
पट्टिकाणु चोट लगने पर थक्का जमाने में सहायक हैं। रक्त में यदि पट्टिकाणु नहीं होंगे तो चोट लगने पर थक्का नहीं जमेगा। थक्का न जमने से शरीर से अधिक रक्त बह जायेगा जिससे व्यक्ति की मृत्यु भी हो सकती है।

प्रश्न 6.
रन्ध्र क्या हैं? रन्धों के दो कार्य बताइए।
उत्तर:
पादप की पत्तियों में गैसों के विनिमय के लिए सूक्ष्म छिद्र होते हैं, जो रन्ध्र कहलाते हैं।

रन्ध्रों के कार्य:
पादपों में उपस्थित अतिरिक्त जल, वाष्प बनकर उड़ता रहता है।
रन्ध्रों से पत्तियों ऑक्सीजन एवं कार्बन डाइऑक्साइड का आदान-प्रदान करती हैं।

प्रश्न 7.
क्या वाष्पोत्सर्जन पादपों में कोई उपयोगी कार्य करता है?
उत्तर:
वाष्पोत्सर्जन से चूषण अभिकर्षण बल उत्पन्न होता है जिसके कारण मूलों द्वारा अवशोषित जल तने और पत्तियों तक पहुँचता है। यह पादपों का ठण्डा भी रखता है।

प्रश्न 8.
रक्त के घटकों के नाम बताइए।
उत्तर:
रक्त के घटक: प्लाज्मा, लाल रक्त कोशिकाएँ (RBC), श्वेत रक्त कोशिकाएँ (WBC), तथा पट्टिकाणु (प्लैटलेट्स) हैं।

प्रश्न 9.
शरीर के सभी अंगों को रक्त की आवश्यकता क्यों होती है?
उत्तर:

1. रक्त ऑक्सीजन, भोजन, हार्मोन्स एवं अन्य:आवश्यक पदार्थों को शरीर के विभिन्न भागों में ले जाता है।
2. कार्बन डाइऑक्साइड तथा अन्य उत्सर्जी पदार्थों को शरीर के विभिन्न भागों से लाकर फेफड़ों एवं अन्य उत्सर्जी अंगों की सहायता से निष्कासित करता है।
3. उपापचय में बने विषैले एवं हानिकारक पदार्थों को हानिरहित बनाने के लिए यकृत में भेजता है।

इस प्रकार सभी अंगों को रक्त की आवश्यकता होती है।

प्रश्न 10.
रक्त लाल रंग का क्यों दिखाई देता है?
उत्तर:
रक्त में लाल रंग का वर्णक होता है जिसे हीमोग्लोबिन कहते हैं। हीमोग्लोबिन की उपस्थिति के कारण ही रक्त का रंग लाल होता है।

प्रश्न 11.
हृदय के कार्य बताइए।
उत्तर:
हृदय के कार्य:

1. हृदय शरीर के समस्त अंगों एवं कोशिकाओं में शुद्ध रक्त प्रवाहित करता है।
2. अशुद्ध रक्त को अंगों से एकत्रित करके फेफड़ों, वृक्क एवं यकृत में शुद्ध होने के लिए प्रवाहित करता है।
3. हृदय रक्त के माध्यम से सभी कोशिकाओं को जल एवं अन्य उपयोगी पदार्थों का संवहन करता है।

प्रश्न 12.
शरीर द्वारा अपशिष्ट पदार्थों को उत्सर्जित करना क्यों आवश्यक है?
उत्तर:
शरीर में जैविक क्रियाओं के अन्तर्गत कुछ हानिकारक पदार्थों का निर्माण होता है। इनका शरीर से बाहर निकलना अत्यन्त आवश्यक है अन्यथा शरीर में विष उत्पन्न हो जाएगा जिससे मृत्यु हो सकती है।

प्रश्न 13.
मानव का उत्सर्जन तन्त्र का चित्र बनाइए और उसके विभिन्न भागों को नामांकित कीजिए।
उत्तर:
मानव का उत्सर्जन तन्त्र:

MP Board Class 7th Science Solutions