MP Board Class 7th Maths Solutions Chapter 7 त्रिभुजों की सर्वांगसमता Ex 7.1
प्रश्न 1.
निम्न कथनों को पूरा कीजिए :
(a) दो रेखाखण्ड सर्वांगसम होते हैं यदि …….. ।
(b) दो सर्वांगसम कोणों में से एक की माप 70° है, दूसरे कोण की माप …….. है।
(c) जब हम ∠A = ∠B लिखते हैं, हमारा वास्तव में अर्थ होता है ……… ।
उत्तर:
(a) इनकी लम्बाइयाँ समान हों।
(b)70°
(c) m ∠A = m∠B
प्रश्न 2.
वास्तविक जीवन से सम्बन्धित सर्वांगसम आकारों के कोई दो उदाहरण दीजिए।
उत्तर:
उदाहरण – समान मान के दो नोट, एक ही ताले की दो चाबियाँ।
प्रश्न 3.
यदि सुमेलन ABC ↔ FED के अंतर्गत ∆ARC ≅ ∆FED तो त्रिभुजों के सभी संगत सर्वांगसम भागों को लिखिए।
उत्तर:
∆ABC तथा ∆FED के संगत सर्वांगसम भाग
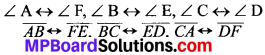
![]()
प्रश्न 4.
यदि ∆DEF ≅ ∆BCA हो, तो ∆BCA के उन भागों को लिखिए जो निम्न के संगत हों :
(i) ∠E
(ii) \(\overline{E F}\)
(iii) ∠F
(iv) \(\overline{D F}\)
उत्तर:
∵ ∆DEF ≅ ∆BCA
∴ (i) ∠E ↔∠C
(ii) \(\overline{E F}\) ↔ \(\overline{C A}\)
(iii) ∠F ↔ ∠A
(iv) \(\overline{D F}\) ↔ \(\overline{B A}\)
पाठ्य-पुस्तक पृष्ठ संख्या # 152-153
प्रयास कीजिए
प्रश्न 1.
संलग्न आकृति में त्रिभुजों की भुजाओं की लम्बाइयाँ दर्शाई गई हैं। S.S.S. सर्वांगसमता के प्रतिबन्ध का प्रयोग करके बताइए कि कौन-कौन से त्रिभुज-युग्म सर्वांगसम हैं। सर्वांगसमता की स्थिति में उत्तर को सांकेतिक रूप में लिखिए।
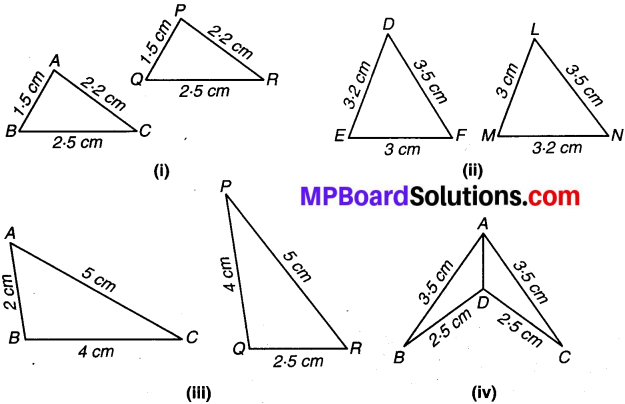
हल:
(i) ∆ABC और ∆POR में,
AB = 1.5 cm, PQ = 1.5 cm, ∴ AB = PQ
BC = 2.5 cm, QR = 2.5 cm, ∴ BC = QR
AC = 2-2 cm, PR = 2-2 cm, ∴ AC = PR
चूँकि ∆ABC की तीन भुजाएँ ∆PQR की तीन भुजाओं के बराबर हैं। अत: दोनों त्रिभुज सर्वांगसम हैं। (S.S.S. सर्वांगसमता)
साथ ही, A ↔ P, B ↔ Q और C ↔ R
∴ ∆ABC ≅ ∆PQR
(ii) ∆DEF और ∆LMN में,
DE = 3.2 cm, MN = 3-2 cm, ∴ DE = MN
DF = 3.5 cm, LN = 3.5cm, ∴ DF = LN
EF = 3 cm, LM = 3 cm, ∴ EF = LM
चूँकि ∆DEF की तीन भुजाएँ ∆LMN की तीन भुजाओं के बराबर हैं। अत: दोनों त्रिभुज सर्वांगसम हैं। (S.S.S. सर्वांगसमता)
साथ ही, D ↔ N, E ↔ M, और F ↔ L
∴ ∆DEF ≅ ∆NML
(iii) ∆ABC और ∆POR में,
AC = 5 cm, PR = 5 cm, ∴ AC = PR
BC = 4 cm, PQ = 4 cm, ∴ BC = PQ
AB = 2 cm, QR = 2.5 cm, ∴ BC ≠ PQ
चूँकि, AB ≠ QR, अत: ∆ABC और ∆PQR सर्वांगसम नहीं हैं।
(iv) ∆ABD और ∆ADC में,
AB = 3.5 cm, AC = 3.5 cm, ∴ AB = AC
BD = 2.5 cm, CD = 2.5 cm, ∴ BD = CD
AD = AD (उभयनिष्ठ है)
चूँकि ∆ABD की तीन भुजाएँ ∆ADC की तीन भुजाओं के बराबर हैं। अत: दोनों त्रिभुज सर्वांगसम हैं (S.S.S सर्वांगसमता)।
साथ ही, A ↔ A, B ↔ C और D ↔ D
∆ABD ≅ ∆ACD
प्रश्न 2.
संलग्न आकृति में AB = AC और D, \(\overline{B C}\) का मध्य-बिन्दु है।
(i) ∆ADB और ∆ADC में बराबर भागों के तीन युग्म बताइए।
(ii) क्या ∆ADB ≅ ∆ADC है ? कारण दीजिए।
(iii) क्या ∠B = ∠C है? क्यों?
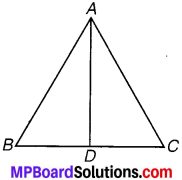
हल:
यहाँ, AB = AC और D, \(\overline{B C}\) का मध्य बिन्दु है
अर्थात् BD = DC
(i) ∆ABD तथा ∆ADC से, बराबर भागों के तीन युग्म
AB = AC (दिया हुआ है)
AD = AD (उमयनिष्ठ है)
BD = DC (∵ D,CB का मध्य बिन्दु है)
(ii) ∆ABD की तीन भुजाएँ ∆ADC की तीन भुजाओं के बराबर हैं।
अतः सर्वांगसमता के S.S.S प्रतिबन्ध से,
∆ABD और ∆ADC सर्वांगसम हैं
और A ↔ A, B ↔ C, D ↔ D
∴ ∆ADB ≅ ∆ADC.
(iii) ∵ ∆ABC ≅ ∆ADC
∴ उनके संगत भाग बराबर हैं।
अर्थात् B ↔ C या ∠B = ∠C.
प्रश्न 3.
संलग्न आकृति में AC = BD और AD = BC हैं। निम्नलिखित कथनों में कौन-सा कथन सत्य है ?
(i) ∆ABC ≅ ∆ABD
(ii) ∆ABC ≅ ∆BAD
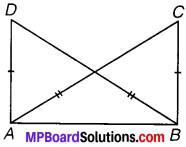
हल:
यहाँ AC = BD और AD = BC
(i) ∆ABC तथा ∆ABD में,
AB = AB (सही है)
BC = BD (सही नहीं है)
CA = DA (सही नहीं हैं)
अत: हम ∆ABC = ∆ABD नहीं लिख सकते।
(ii) ∆ABC तथा ∆BAD में,
AB = AB (उभयनिष्ठ)
BC = AD (दिया है)
CA = BD (दिया हैं)
यहाँ S.S.S. सर्वांगसमता है।
अत: ≅ABC ≅ ∆BAD लिख सकते हैं।
अतः
(i) ∴ ∆ABC ≅ ∆ABD असत्य है।
(ii) ∆ABC ≅ ∆BAD सत्य है।
![]()
सोचिए, चर्चा कीजिए एवं लिखिए
प्रश्न 1.
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है।
∆ABC की एक अक्स प्रतिलिपि लीजिए और इसे भी ∆ABC का नाम दीजिए।
(i) ABC और ∆ACB में बराबर भागों के तीन युग्म बताइए।
(ii) क्या ∆ABC ≅ ∆ACB है ? क्यों अथवा क्यों नहीं ?
(iii) क्या ∠B = ∠C है? क्यों अथवा क्यों नहीं ?
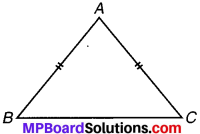
हल:
∆ABC एक समद्विबाहु त्रिभुज है
जिसमें AB = AC, BC = CB तथा AC = AB.
(i) अब ∆ABC और ∆ACB में, बराबर भागों के तीन
युग्म – BC = BC (उभयनिष्ठ है)
AB = AC (दिया हुआ है)
AC = AB (रचना से)
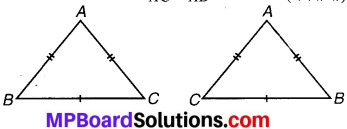
(ii) हाँ, ∆ABC = ∆ACB.
क्योंकि ∆ABC की तीनों भुजाएँ ∆ACB की तीनों भुजाओं के बराबर हैं और A ↔ A, B ↔ C,C ↔ B.
(iii) हाँ, ∠B = ∠C ∴ B ↔ C
![]()
पाठ्य-पुस्तक पृष्ठ संख्या # 156 – 157
इन्हें कीजिए
प्रश्न 1.
∆DEF की भुजाओं \(\overline{D E}\) और \(\overline{E F}\) का अंतर्गत कोण कौन-सा है?
उत्तर:
∆DEF में, भुजाओं \(\overline{D E}\) और \(\overline{E F}\) के अंतर्गत कोण, ∠DEF है।
प्रश्न 2.
S.A.S. सर्वांगसमता प्रतिबन्ध का उपयोग करके आप ∆POR ≅ ∆FED स्थापित करना चाहते हैं। यह दिया गया है कि PQ = FE और RP = DF है। सर्वांगसमता को स्थापित करने के लिए अन्य किस तथ्य या सूचना की आवश्यकता होगी?
हल:
∆PQR ≅ ∆FED (सर्वांगसमता के प्रतिबन्ध S.A.S. के अनुसार)
PQ = FE और RP = DF (दिया है)
अन्य तथ्य और सूचना :
चूँकि S.A.S. प्रतिबन्ध के अन्तर्गत भुजाओं PQ और RP तथा FE और DF के बीच बने कोण भी बराबर होना चाहिए।
∴ ∠P = ∠F
प्रश्न 3.
संलग्न आकृति में त्रिभुजों के युग्मों में कुछ भागों की माप अंकित की गई है। S.A.S. सर्वांगसमता प्रतिबन्ध का उपयोग करके, इनमें वे युग्म छाँटिए जो सर्वांगसम हैं। सर्वांगसम त्रिभुजों की स्थिति में उन्हें सांकेतिक रूप में भी लिखिए।
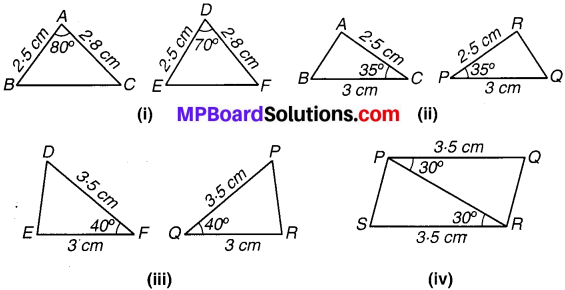
हल:
(i) ∆ABC और ∆DEF में,
यहाँ, AB = DE = 2.5 cm
AC = DF = 2.8 cm
∠A = 80°,∠D = 70°
∴ ∠A ≠ ∠D
∴ ∆ABC और ∆DEF सर्वांगसम नहीं है।
(ii) ∆ABC और ∆POR में,
यहाँ AC = PR = 2.5 cm
BC = PQ = 3 cm
∠C = ∠P = 35°
∴ ∆ABC की दो भुजाएँ और उनके अंतर्गत कोण ∆POR की दो संगत भुजाओं और उनके अंतर्गत कोण के बराबर हैं।
अतः दोनों त्रिभुज सर्वांगसमता के S.A.S प्रतिबन्ध के आधार पर सर्वांगसम हैं।
साथ ही C ↔ P A ↔ R और B ↔ Q
∴ ∆ABC ≅ ∆RQP
(iii) ∆DEF तथा ∆PQR में,
यहाँ, EF = QR = 3 cm
DF = PQ = 3.5 cm
भुजाओं के अंतर्गत कोण ∠F = ∠Q = 40°
∴ ∆DEF की दो भुजाएँ और उनके अन्तर्गत कोण ∆PQR की दो संगत भुजाओं और उनके अन्तर्गत कोण के बराबर हैं।
अतः दोनों त्रिभुज सर्वांगसमता के S.A.S. प्रतिबन्ध के आधार पर सवांगसम हैं।
साथ ही, F ↔ Q.D ↔ P और E ↔ R
∴ ∆DEF ≅ ∆PRQ
(iv) ∆PQR और ∆RSP में,
PQ = R = 3.5 cm
PR = PR (उभयनिष्ठ है)
अंतर्गत कोण ∠QPR = ∠PRS = 30°
अत: ∆PQR की दो भुजाएँ और उनके अन्तर्गत कोण ∆RSP की दो संगत भुजाओं और उनके अन्तर्गत बीच के कोण के बराबर हैं।
अतः दोनों त्रिभुज सर्वांगसमता के प्रतिबन्ध S.A.S. के आधार पर सर्वांगसम हैं
साथ ही, P ↔ R, Q ↔ S
∴ ∆PQR ≅ ∆RSP
प्रश्न 4.
संलग्न आकृति में \(\overline{A B}\) और \(\overline{C D}\) एक दूसरे को O पर समद्विभाजित करते हैं।
(i) दोनों त्रिभुज AOC और BOD में बराबर भागों के तीन युग्मों को बताइए।
(ii) निम्न कथनों में से कौन-सा कथन सत्य है?
(a) ∆AOC ≅ ∆DOB
(b) ∆AOC ≅ ∆BOD
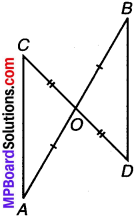
हल:
∵ \(\overline{A B}\) और \(\overline{C D}\) एक दूसरे को O पर समद्विभाजित करते हैं।
∴ AO = BO और CO = DO
साथ ही ऊर्ध्वाधर सम्मुख ∠AOC = ∠BOD
(i) ∆MOC तथा ∆BOD में, बराबर भागों के तीन युग्म –
AO = BO और CO = DO
∠AOC = ∠BOD
(ii) उपर्युक्त सम्बन्धों के आधार पर ∆AOC की दो भुजाएँ और उनके अन्तर्गत कोण ∆BOD की दो संगत भुजाओं और उनके अन्तर्गत कोण के बराबर हैं।
अत: सर्वांगसमता के गुण S.A.S. के आधार पर दोनों त्रिभुज सर्वांगसम हैं।
साथ ही,O ↔ O,A ↔ B, और C ↔ D
∴ ∆AOC ≅ ∆BOD
(a) कथन ∆AOC ≅ ∆DOB असत्य है।
(b) कथन ∆AOC ≅ ∆BOD सत्य है।
पाठ्य-पुस्तक पृष्ठ संख्या # 158
इन्हें कीजिए
प्रश्न 1.
∆MNP में कोणों M तथा N के अंतर्गत भुजा क्या है ?
उत्तर:
∆MNP में कोणों M तथा N के अंतर्गत भुजा MN है।
प्रश्न 2.
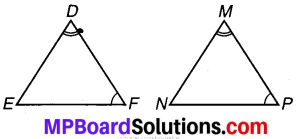
A.S.A. सर्वांगसमता प्रतिबन्ध का उपयोग करके आप ∆DEF ≅ ∆MNP स्थापित करना चाहते हैं। आपको दिया गया है कि ∠D = ∠M और ∠F = ∠P। इस सर्वांगसमता को स्थापित करने के लिए और कौन-कौन से तथ्य की आवश्यकता है ? (खाका आकृति बनाकर कोशिश कीजिए।)
हल:
∆DEF ≅ ∆MNP स्थापित करने के लिए A.S.A. सर्वांगसमता के प्रतिबन्ध के लिए हमें आवश्यकता होगी-भुजाएँ जिनसे ∠D और ∠F बनते हैं तथा समान भुजाएँ जिनसे ∠M और ∠P बनते हैं।
अर्थात् हमें आवश्यकता होगी \(\overline{D F}\) = \(\overline{M P}\)
प्रश्न 3.
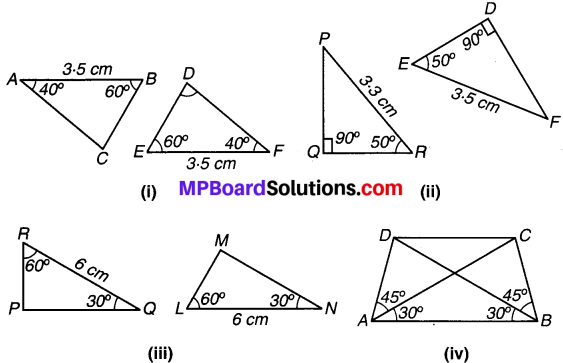
संलग्न आकृति में, त्रिभुज के कुछ भागों की माप अंकित की गई है। A.S.A. सर्वांगसमता प्रतिबन्ध का उपयोग करके बताइए कौन-से त्रिभुजों के युग्म सर्वांगसम हैं। सर्वांगसमता की स्थिति में, उत्तर को सांकेतिक रूप में लिखिए।
हल:
(i) ∆ABC और ∆DEF में,
AB = EF = 3.5 cm,
∠A = ∠F = 40°
और ∠B = ∠E = 60°.
∴ A.S.A. सर्वांगसमता प्रतिबन्ध से ये दो त्रिभुज सर्वांगसम हैं। साथ ही, A ↔ F,B ↔ E और C ↔ D
∴ ∆ABC ≅ ∆FED
(ii) ∆POR और ∆DEF में,
∆POR में, ∠P = 180° – (90° + 50°) = 40°
इसी प्रकार ∆DEF में, ∠F = 180° – (90° + 50°) = 40°
अब, PR = 3.3 cm, EF = 3.5 cm ∴ PR ≠ EF
∠R = ∠E = 50° और ∠P = ∠F = 40° ∴ ∠P = ∠F
∴ A.S.A. सर्वांगसमता प्रतिबन्ध से त्रिभुज सर्वांगसम नहीं है।
(iii) ∆PQR और ∆LMN में,
RQ = LN = 6 cm, ∠R = ∠L = 60° और ∠Q = ∠N = 30° ∴ A.S.A. सर्वांगसमता प्रतिबन्ध से ये दो त्रिभुज सर्वांगसम हैं
साथ ही, R ↔ L, Q ↔ N और P ↔ M
∴ ∆PQR ≅ ∆MNL
(iv) ∆ABC और ∆ABD में,
AB = AB (उभयनिष्ठ हैं),
∠BAC = ∠DBA = 30°
∠BAD = 45° + 30° = 75°
∠ABC = ∠45° + 30° = 75°
∴ A.S.A. सर्वांगसमता प्रतिबन्ध से ये दो त्रिभुज सर्वांगसम हैं।
साथ ही, A ↔ B, D ↔ C
∴ ∆ABC ≅ ∆BAD.
प्रश्न 4.
दो त्रिभुजों के कुछ भागों की निम्न माप दी गई है। A.S.A. सर्वांगसमता प्रतिबन्ध का उपयोग करके जाँचिए कि क्या ये दो त्रिभुज सर्वांगसम हैं या नहीं। सर्वांगसमता की स्थिति में उत्तर को सांकेतिक रूप में भी लिखिए।
∆DEF ∆PQR
(i) ∠D = 60°, ∠F = 80°, ∠Q = 60°, ∠R = 80°,
DF = 5 cm QR = 5 cm
(ii) ∠D = 60°, ∠F = 80°, ∠Q = 60°, ∠R = 80°,
DF = 6 cm, P = 6 cm
(iii) ∠E = 80°, ∠F = 30°, ∠P = 80°, PQ = 5 cm
EF = 5 cm, ∠R = 30°
हल:
(i) ∆DEF और ∆PQR में,
∠D = ∠Q = 60°, ∠F = ∠R = 80°
अन्तर्गत भुजा DF = अन्तर्गत भुजा QR = 5 cm
A.S.A. सर्वांगसमता प्रतिबन्ध से ये दो त्रिभुज सर्वांगसम हैं।
साथ ही, D ↔ Q. F ↔ R. और E ↔ P
∴ ∆DEF = ∆QPR
(ii) यहाँ ∆DEF तक ∆PQR में समान कोणों के बीच की भुजाएँ DF व QR समान नहीं हैं।
∴ दिए गये त्रिभुज सर्वांगसम नहीं हैं।
(iii) यहाँ ∆DEF तक ∆PQR में समान कोणों के बीच की भुजाएँ EF व PR समान नहीं हैं।
∴ दिए गये त्रिभुज सर्वांगसम नहीं हैं।
![]()
प्रश्न 5.
संलग्न आकृति में किरण AZ, ∠DAB तथा ∠DCB को समद्विभाजित करती है।
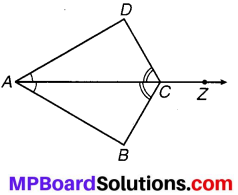
(i) त्रिभुज BAC और DAC में बराबर भागों के तीन युग्म बताइए।
(ii) क्या ∆BACE ≅ ∆DAC है ? कारण दीजिए।
(iii) क्या AB = AD है ? अपने उत्तर का उचित कारण दीजिए।
(iv) क्या CD = CB है? कारण दीजिए।
हल:
(i) ∵ AC, ∠DAB और ∠DCB का समद्विभाजक है।
∠DAC = ∠BAC
और ∠DCA = ∠BCA
अब, ∆BAC और ∆DAC में, बराबर भागों के युग्म हैं –
AC = AC (उभयनिष्ठ)
∠DAC = ∠BAC (AC समद्विभाजक है)
∠DCA = ∠BCA (AC समद्विभाजक है)
(ii) उपर्युक्त सम्बन्धों से, ये दो त्रिभुज सर्वांगसम हैं (A.S.A. सर्वांगसमता)
साथ ही, A ↔ A, C ↔ C और D ↔ B
∴ ∆BAC ≅ ∆DAC
(iii) ∴ ∆BAC ≅ ∆DAC
∴ संगत भाग बराबर हैं।
अर्थात् AB = AD
(iv) ∴ C ↔ C और A ↔ A तथा AC = AC
अर्थात् ∆BAC ≅ ∆DAC
∴ संगत भाग बराबर हैं,
अर्थात् CD = CB
![]()
पाठ्य-पुस्तक पृष्ठ संख्या # 160-161
इन्हें कीजिए
प्रश्न 1.
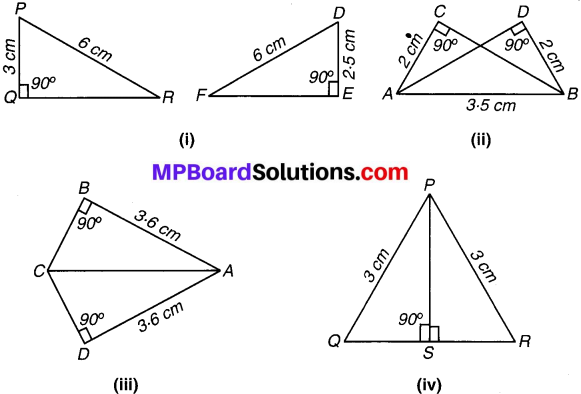
संलग्न आकृति में त्रिभुजों के कुछ भागों की माप दी गई है। R.H.S. सर्वांगसमता प्रतिबन्ध का उपयोग करके बताइए कि कौन-कौन से त्रिभुज युग्म सर्वांगसम हैं। सर्वांगसम त्रिभुजों की स्थिति में उन्हें सांकेतिक रूप में लिखिए।
हल:
(i) समकोण ∆PQR तथा समकोण ∆DEF में,
कर्ण PR = कर्ण DF = 6 cm
भुजा PQ = 3 cm ≠ भुजा DE = 2.5 cm
∴ ∆POR और ∆DEF सर्वांगसम नहीं हैं।
(ii) समकोण ∆ABC और समकोण ∆ABD में, कर्ण AB = कर्ण BA = 3.5 cm (उभयनिष्ठ) भुजा AC = भुजा BD = 2 cm तथा ∠C = ∠D = 90°
∴ समकोण त्रिभुजों की R.H.S. सर्वांगसमता के गुण के अनुसार त्रिभुज सर्वांगसम हैं।
साथ ही, A ↔ B, B ↔ A, C ↔ D
∴ ∆ABD ≅ ∆BAC
(iii) समकोण ∆ABC और समकोण ∆ADC में,
कर्ण AC = कर्ण AC (उभयनिष्ठ)
भुजा AD = भुजा AB = 3.6 cm
तथा ∠B = ∠D = 90°
∴ समकोण त्रिभुजों की R.H.S. सर्वांगसमता के गुण के अनुसार त्रिभुज सर्वांगसम हैं।
साथ ही, A ↔ A,C ↔ C,B ↔ D
∆ABC ≅ ∆ADC
(iv) समकोण ∆PQS और समकोण ∆PRS में,
कर्ण PQ = कर्ण PR = 3 cm
भुजा PS = भुजा PS (उभयनिष्ठ)
तथा ∠PSQ तथा ∠PSR = 90°
∴ समकोण त्रिभुजों की R.H.S. सर्वांगसमता के गुण के अनुसार त्रिभुज सर्वांगसम हैं।
साथ ही P ↔ P, S ↔ S, Q ↔ R
∆PQS ≅ ∆PRS.
प्रश्न 2.
R.H.S. सर्वांगसमता प्रतिबन्ध से ∆ABC ≅ ∆RPO स्थापित करना है। यदि यह दिया गया हो कि ∠B = ∠P = 90° और AB = RP है, तो अन्य किस और सूचना की आवश्यकता है ?
हल:
R.H.S. सर्वांगसमता प्रतिबन्ध द्वारा ∠ABC ≅ ∠RPO स्थापित करने के लिए हमें कर्ण AC = कर्ण RQ को समान करने की आवश्यकता होगी।
प्रश्न 3.
संलग्न आकृति में, BD और CE, ∆ABC के शीर्षलम्ब हैं और BD = CE.
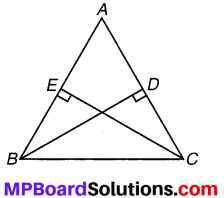
(i) ∆CBD और ∆BCE में, बराबर भागों के तीन युग्म बताइए।
(ii) क्या ∠CBD ≅ ∠BCE है ? क्यों अथवा क्यों नहीं ?
(iii) क्या ∆DCB = ∆EBC है ? क्यों या क्यों नहीं?
हल:
(i) ∆CBD और ∆BCE में बराबर भागों के तीन युग्म –
कर्ण BC = कर्ण BC (उभयनिष्ठ)
भुजा BD = भुजा CE
∠BEC = ∠BDC = प्रत्येक 90°
(ii)∴∠D = ∠E, CB = BC तथा BD = CE
अत: RHS सर्वांगसमता से
हाँ, ∆CBD ≅ ∆BCE,
(iii)∴ ∆CBD ≅ ∆BCE
∴ उनके संगत भाग बराबर हैं।
अब, हाँ, ∠DCB = ∠EBC
प्रश्न 4.
∆ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC और AD इसका शीर्ष लम्ब है।
(i) ∆ADB और ∆ADC में, बराबर भागों के-तीन युग्म बताइए।
(ii) क्या ∆ADB ≅ ∆ADC है ? क्यों अथवा क्यों नहीं ?
(iii) क्या ∠B = ∠C है ? क्यों या क्यों नहीं ?
(iv) क्या BD = CD है? क्यों या क्यों नहीं?
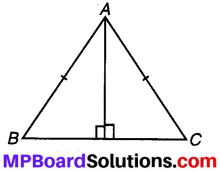
हल:
(i) ∆ADB और ∆ADC में, बराबर भागों के तीन युग्म हैं –
AD = AD (उभयनिष्ठ)
कर्ण AB = कर्ण AC
∠ADB = ∠ADC (प्रत्येक 90°)
(ii) ∴ AB = AC, AD = AD, D ↔ D
अब, हाँ, ∆ADB ≅ ∆ADC
(iii) हाँ, ∠B = ∠C
∴ ∆ADB ≅ ∆ADC
∴ संगत भाग समान हैं, ∴ ∠B = ∠C
(iv) साथ ही, हाँ, \(\overline{B D}\) = \(\overline{C D}\)
∆ADB ≅ ∆ADC, ∴ संगत भाग समान हैं
∴ \(\overline{B D}\) = \(\overline{C D}\)