MP Board Class 7th Maths Solutions Chapter 6 त्रिभुज और उसके गुण Ex 6.4
प्रश्न 1.
निम्न दी गई भुजाओं की मापों से क्या कोई त्रिभुज सम्भव है ?
(i) 2 cm, 3 cm, 5 cm
(ii) 3 cm, 6 cm,7cm
(iii) 6cm, 3 cm, 2 cm.
हल:
(i) ∵ 2 cm + 3 cm = 5 cm और तीसरी भुजा = 5cm
∴ दो भुजाओं की लम्बाइयों का योग = तीसरी भुजाओं की लम्बाई, जो कि असम्भव है।
अतः भुजाओं की इन मापों से त्रिभुज सम्भव नहीं है।
(ii) ∵ 3cm + 6 cm = 9 cm
और 9cm > 7 cm
6cm + 7 cm = 13 cm
और 13 cm > 3 cm
7 cm + 3 cm = 10 cm
और 10 cm > 6cm
अत: भुजाओं की इन मापों से त्रिभुज सम्भव है।
(iii) ∵ 6cm + 3 cm = 9 cm
और 9cm > 2 cm
3 cm + 2 cm = 5 cm
और 5 cm ≠ 6cm
2 cm + 6 cm = 8 cm
और 8 cm > 5 cm
अतः भुजाओं की इन मापों से त्रिभुज सम्भव नहीं है।
प्रश्न 2.
त्रिभुज PQR के अभ्यंतर में कोई बिन्दु O लीजिए। क्या यह सही है कि –
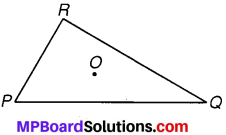
(i) OP + OQ > PQ?
(ii) OQ + OR > QR?
(iii) OR + OP > RP?
हल:
∆POR में OP, OQ तथा OR को मिलाया। अत: त्रिभुज के गुण से,
(i) हाँ, OP + OQ > PQ
(ii) हाँ, OQ – OR > QR
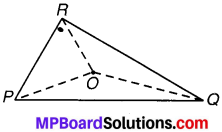
(iii) हाँ, OR + OP > RP.
प्रश्न 3.
त्रिभुज ABC की एक माध्यिका AM है। बताइये कि क्या AB + BC + CA > 2 AM?
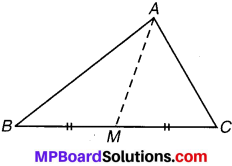
(संकेत : ∆ABM तथा ∆AMC की भुजाओं पर विचार कीजिए।)
हल:
चूँकि त्रिभुज की दो भुजाओं की लम्बाइयों का योग तीसरी भुजा की लम्बाई से अधिक होता है।
∴ ∆ABM में, AB + BM > AM …..(i)
इसी प्रकार ∆AMC में, CA + CM > AM …(2)
(1) और (2) को जोड़ने पर,
(AB + BM) + (CA + CM) > AM + AM
या AB – (BM + CM) + CA > 2 AM
अत: AB + BC + CA > 2 AM (∵ BM + MC = BC)
![]()
प्रश्न 4.
ABCD एक चतुर्भुज है। क्या AB + BC + CD + DA > AC + BD?
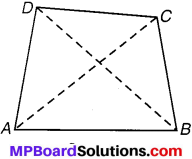
हल:
∵ त्रिभुज की दो भुजाओं की लम्बाइयों का योग तीसरा भुजा की लम्बाई से अधिक होता है।
∴ ∆ABC में, AB + BC > AC …..(1)
∴ ∆ACD में, CD + DA > AC …..(2)
∆ABD में, AB + DA > BD ….(3)
तथा ∆BCD में, BC + CD > BD ….(4)
समीकरण (1), (2), (3) व (4) को जोड़ने पर,
2(AB + BC + CD + DA) > 2(AC + BD)
या AB + BC + CD + DA > AC + BD इति सिद्धम्
प्रश्न 5.
ABCD एक चतुर्भुज है। क्या AB + BC + CD + DA < 2 (AC + BD)?
हल:
∵ किसी त्रिभुज की दो भुजाओं की लम्बाइयों का योग तीसरी भुजा की लम्बाई से अधिक होता है।
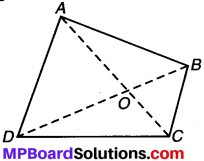
∴ ∆OAB में, OA + OB > AB …..(1)
∆OBC में, OB + OC > BC …..(2)
∆OCD में, OC + OD > CD …..(3)
∆OAD में, OA + OD > AD …(4)
(1), (2), (3) व (4) को जोड़ने पर,
2(OA + OB + OC + OD) > (AB + BC + CD + DA)
या AB + BC + CD + DA < 2 (OA + OB + OC + OD)
या AB + BC + CD + DA < 2 [(OA + OC)+ (OB + OD)]
या AB + BC + CD + DA < 2 (AC + BD) इति सिद्धम्
![]()
प्रश्न 6.
एक त्रिभुज की दो भुजाओं की माप 12 cm तथा 15 cm है। इसकी तीसरी भुजा की माप किन दो मापों के बीच होनी चाहिए?
हल:
चूँकि हम जानते हैं कि किसी त्रिभुज की दो भुजाओं की लम्बाइयों का योग तीसरी भुजा की लम्बाई से अधिक होता है।
∴ 12 cm + 15 cm > तीसरी भुजा
अर्थात् 27 > तीसरी भुजा
या तीसरी भुजा < 27 cm.
साथ ही किन्हीं दो भुजाओं की लम्बाइयों का अन्तर तीसरी भुजा की लम्बाई से कम होता है।
∴ 15 cm – 12 cm < तीसरी भुजा या
या 3 cm < तीसरी भुजा अतः
या 3 cm < तीसरी भुजा < 27 cm.
अतः तीसरी भुजा की लम्बाई 3 cm और 27 cm के बीच में होनी चाहिए।
![]()
पाठ्य-पुस्तक पृष्ठ संख्या # 139
सोचिए, चर्चा कीजिए एवं लिखिए
प्रश्न 1.
किसी त्रिभुज में क्या उसके किन्हीं दो कोणों का योग तीसरे कोण से सदैव अधिक होता है ?
हल:
किसी त्रिभुज में उसके किन्हीं दो कोणों का योग सदैव तीसरे कोण से अधिक नहीं होता है।
पाठ्य-पुस्तक पृष्ठ संख्या # 141-142
प्रयास कीजिए
प्रश्न 1.
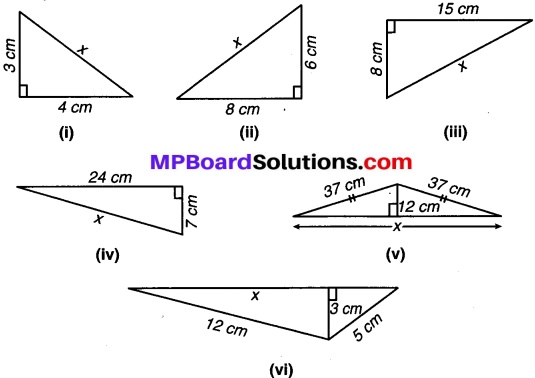
निम्न आकृतियों में अज्ञात लम्बाई x ज्ञात कीजिए –
हल:
(i) दी हुई आकृति समकोण त्रिभुज है, जिसमें सबसे लम्बी भुजा कर्ण है।
∴ x2 = 32 + 42 (पाइथागोरस प्रमेय से)
या x2 = 9 + 16
या x2 = 25 = 52
∴ x = 5
(ii) दी हुई आकृति समकोण त्रिभुज है।
∴ x2 = 62 + 82 (पाइथागोरस प्रमेय से)
या x2 = 36 + 64
या x2 = 100 = 102
∴ x = 10
(iii) दी हुई आकृति समकोण त्रिभुज है।
∴ x2 = 152 + 82 (पाइथागोरस प्रमेय से)
या x2 = 225 + 64
या x2 = 289 = 172
∴ x = 17 cm
(iv) दी हुई आकृति समकोण त्रिभुज है।
∴ x2 = 242 + 72
या x2 = 576 + 49
या x2 = 625 = 252
∴ x = 25
(v) समकोण त्रिभुज (1) में,
y2 + 122 = 372
या y2 + 144 = 1369
या y2 = 1369 – 144 = 1225
या y2 = 352 ⇒ y = 35
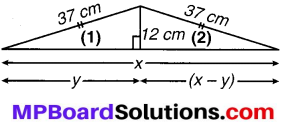
समकोण त्रिभुज (2) में,
(x – 7)2 + 122 = 372
या (x – y)2 + 144 = 1369
या (x – 35)2 = 1369 – 144 = 1225
या (x – 35)2 = 352
या x – 35 = 35
x = 35 + 35 = 70
(vi) चित्र से, x2 + 32 = 122
या x2 = 122 – 32 = 144 – 9
या x2 = 135
⇒ x = \(\sqrt { 135 }\)
पाठ्य-पुस्तक पृष्ठ संख्या # 142