Prasanna

MP Board Class 12th Maths Important Questions Chapter 2 प्रतिलोम त्रिकोणमितीय फलन

प्रतिलोम त्रिकोणमितीय फलन Important Questions

प्रतिलोम त्रिकोणमितीय फलन वस्तुनिष्ठ प्रश्न

प्रश्न 1.
सही विकल्प चुनकर लिखिए –

प्रश्न 1.
यदि sin^-1x – cos^-1 x = \(\frac { \pi }{ 6 } \) हो, तो x का मान ज्ञात कीजिए –
(a) \(\frac{1}{2}\)
(b) \(\frac { \sqrt { 3 } }{ 2 } \)
(c) – \(\frac{1}{2}\)
(d) इनमें से कोई नहीं।
उत्तर:
(a) \(\frac{1}{2}\)

प्रश्न 2.
यदि tan^-1 3 + tan^-1 x = tan^-1 8 हो, तो x का मान होगा –
(a) 5
(b) \(\frac{1}{5}\)
(c) \(\frac{5}{14}\)
(d) \(\frac{14}{5}\)
उत्तर:
(b) \(\frac{1}{5}\)

प्रश्न 3.
tan^-1 ( \(\frac{x}{y}\) ) – tan^-1 ( \(\frac { x-y }{ x+y } \) ) का मान है –
(a) \(\frac { \pi }{ 2 } \)
(b) \(\frac { \pi }{ 3 } \)
(c) \(\frac { \pi }{ 4 } \)
(d) \(\frac { -3\pi }{ 4 } \)
उत्तर:
(c) \(\frac { -3\pi }{ 4 } \)

प्रश्न 4.
2 tan^-1 {cosec (tan^-1 x) – tan (cot^-1 x)} का मान है –
(a) cot^-1 x
(b) cot^-1 \(\frac{1}{x}\)
(c) tan^-1 x
(d) tan^-1 \(\frac{1}{x}\)
उत्तर:
(c) tan^-1 x

प्रश्न 5.
tan {cos^-1 \(\frac { 1 }{ 5\sqrt { 2 } } \) – sin^-1 \(\frac { 4 }{ \sqrt { 17 } } \) } का मान होगा –
(a) \(\frac { \sqrt { 29 } }{ 3 } \)
(b) \(\frac{29}{3}\)
(c) \(\frac { \sqrt { 3 } }{ 29 } \)
(d) \(\frac{3}{29}\)
उत्तर:
(d) \(\frac{3}{29}\)

प्रश्न 2.
रिक्त स्थानों की पूर्ति कीजिए –

1. tan^-1 (1) + tan^-1 (2) + tan^-1 (3) = ………………………….
2. tan^-1 (2) – tan^-1 (1) = …………………………….
3. cot^-1 3 + cosec^-1 \(\sqrt{5}\)
4. sin(sin^-1 x + 2 cos^-1 x) = …………………………..
5. यदि sin^-1 ( \(\frac { 2a }{ 1+a^{ 2 } } \) ) + sin ( \(\frac { 2b }{ 1+b^{ 2 } } \) ) = 2 tan^-1 x, तो x = ………………………….
6. यदि tan^-1 ( \(\frac { 1-x }{ 1+x } \) ) = \(\frac{1}{2}\) tan^-1 x (जब x > 0), तो x =
7. tan^-1 ( \(\frac { a-b }{ 1+ab } \) ) + tan^-1 ( \(\frac { b-c }{ 1+bc } \) ) + tan^-1 c = ………………………..

उत्तर:

1. π
2. tan^-1 ( \(\frac{1}{3}\) )
3. \(\frac { \pi }{ 4 } \)
4. x
5. \(\frac { a+b }{ 1-ab } \)
6. \(\frac { 1 }{ \sqrt { 3 } } \)
7. tan^-1 (a)

प्रश्न 3.
निम्न कथनों में सत्य/असत्य बताइए –

1. tan^-1 x + tan^-1 y = tan^-1 \(\frac { x+y }{ 1-xy } \)
2. cos^-1(-x) = – cos^-1 x
3. sin^-1 (3x – 4x³) = sin^-1 \(\frac{x}{3}\)
4. cos^-1 ( \(\frac { 1-x^{ 2 } }{ 1+x^{ 2 } } \) ) = 2 tan^-1 x
5. sin^-1 x – sin^-1 y = sin^-1 [xy – \(\sqrt { 1-x^{ 2 } } \) \(\sqrt { 1-y^{ 2 } } \) ].

उत्तर:

1. सत्य
2. असत्य
3. असत्य
4. सत्य
5. असत्य।

प्रश्न 4.
सही जोड़ी बनाइये –

उत्तर:

1. (b)
2. (e)
3. (f)
4. (a)
5. (c)
6. (d)

प्रश्न 5.
एक शब्द/वाक्य में उत्तर दीजिए –

1. tan^-1\(\frac{1}{2}\) + tan^-1\(\frac{3}{2}\) का मान ज्ञात कीजिए।
2. tan^-1 \(\frac { x }{ \sqrt { 1-x^{ 2 } } } \) का मान ज्ञात कीजिए।
3. sin (2 sin^-1\(\frac{3}{5}\) ) का मान ज्ञात कीजिए।
4. समीकरण sin^-1 \(\frac{x}{5}\) + cosec^-1\(\frac{5}{4}\) = \(\frac { \pi }{ 2 } \) का मान ज्ञात कीजिए।
5. cos^-1 (cos \(\frac { 7\pi }{ 6 } \) ) का मुख्य मान लिखिए।
6. यदि cos^-1 ( \(\frac{1}{x}\) ) = θ हो, तो tan θ का मान लिखिए।

उत्तर:

1. tan^-1 8
2. sin^-1 x
3. \(\frac{24}{25}\)
4. x = 3
5. \(\frac { 5\pi }{ 6 } \)
6. \(\sqrt { x^{ 2 }-1 } \)

प्रतिलोम त्रिकोणमितीय फलन लाधु उतरिय प्रश्न

प्रश्न 1.
निम्नलिखित के मुख्य मान ज्ञात कीजिये – (CBSE 2014)

(i) tan^-1 [sin (- \(\frac { \pi }{ 2 } \) ) (CBSE 2014)

(ii) cot [ \(\frac { \pi }{ 2 } \) – 2 cot^-1 \(\sqrt{3}\) (CBSE 2014)

(iii) tan^-1 (-\(\sqrt{3}\) )

(iv) sec^-1 (-\(\frac{2}{3}\) \(\sqrt{3}\) ) (NCERT)

(v) cosec^-1 (2) (NCERT)

हल:
(i) tan^-1 [sin (- \(\frac { \pi }{ 2 } \) )
= tan^-1 [- sin \(\frac { \pi }{ 2 } \) ], [∵sin (- θ) = – sin θ]
= tan^-1 (-1), (∵ sin \(\frac { \pi }{ 2 } \) = 1)
= – tan^-1 (1), (∵ tan^-1 (-x) = – tan^-1 x)
= –\(\frac { \pi }{ 4 } \) (∵ tan^-1 (1) = \(\frac { \pi }{ 4 } \)
(ii) cot [ \(\frac { \pi }{ 2 } \) – 2cot^-1 \(\sqrt{3}\)

(iii) माना tan(-\(\sqrt{3}\)) = θ

(iv) sec^-1 \(\frac{-2}{3}\)\(\sqrt{3}\)) = θ

प्रश्न 2.
सिद्ध कीजिये –
(a) 2 cos^-1 \(\frac{4}{5}\) = cos^-1 \(\frac{7}{25}\)
(b) 2 sin^-1 \(\frac{3}{5}\) = sin^-1 \(\frac{24}{25}\)
(c) 2 sin^-1 \(\frac{5}{13}\) = sin^-1 \(\frac{120}{169}\)
हल:
(a) 2 cos^-1 \(\frac{4}{5}\) = cos^-1 \(\frac{7}{25}\)

(b) 2 sin^-1 \(\frac{3}{5}\) = sin^-1 \(\frac{24}{25}\)

(c) क्रमांक की 2(b) भाँती हल कीजिये।

प्रश्न 3.
मान ज्ञात कीजिये –
tan^-1 {2 cos (2 sin^-1 \(\frac{1}{2}\) )} (CBSE 2013, NCERT)
हल:
tan^-1 {2 cos (2 sin^-1 \(\frac{1}{2}\) )} = tan^-1 [2 cos (2 × \(\frac { \pi }{ 6 } \) ) ]
= tan^-1 [2 cos \(\frac { \pi }{ 3 } \) ] = tan^-1 [2 × \(\frac{1}{2}\) ]
= tan^-1 1
= \(\frac { \pi }{ 4 } \)

प्रश्न 4.
मान ज्ञात कीजिये –
sin [ \(\frac { \pi }{ 3 } \) – sin^-1 (- \(\frac{1}{2}\)) ] (CBSE 2008, 13)
हल:
sin [ \(\frac { \pi }{ 3 } \) – sin^-1 (- \(\frac{1}{2}\) ) ]
= sin [ \(\frac { \pi }{ 3 } \) + sin^-1 ( \(\frac{1}{2}\)) ], [∵sin^-1 (-x) = – sin^-1x]
= sin [ \(\frac { \pi }{ 3 } \) + \(\frac { \pi }{ 6 } \) ] = sin \(\frac { \pi }{ 2 } \) = 1

प्रश्न 5.
सिद्ध कीजिये –
2 tan^-1 \(\frac{1}{5}\) = tan^-1 \(\frac{5}{12}\)?
हल:
L.H.S = 2 tan^-1 \(\frac{1}{5}\)

प्रश्न 6.
मान ज्ञात कीजिये –
tan (2 tan^-1 \(\frac{1}{5}\) – \(\frac { \pi }{ 4 } \) )
हल:

प्रश्न 7.
सिद्ध कीजिये –
3 sin^-1 x = sin^-1 (3x – 4x³). (NCERT, CBSE 2018)
हल:
मानलो sin^-1 x = θ.
∴ x = sin θ
अब sin 3θ = 3 sinθ – 4sin³θ
= 3x – 4x³
∴ 3θ = sin^-1 (3x – 4x³)

यही सिद्ध करना था।

प्रश्न 8.
सिद्ध कीजिये –
3 cos^-1 x = cos^-1 (4x³ – 3x) (NCERT)
हल:
मानलो cos^-1 x = θ
∴ x = cos θ
अब cos 3θ = 4 cos³θ – 3 cos θ
= 4x³ – 3x
∴ 3θ = cos^-1 (4x³ – 3x)

यही सिद्ध करना था।

प्रश्न 9.
सिद्ध कीजिये –
(A) tan^-1 \(\frac{1}{2}\) + tan^-1 \(\frac{1}{3}\) = \(\frac { \pi }{ 4 } \)
(B) cos^-1\(\frac{12}{13}\) = tan^-1 \(\frac{5}{12}\)
(C) cos^-1\(\frac{3}{5}\) = sin^-1 \(\frac{4}{5}\)
हल:
(A) tan^-1 = \(\frac{1}{2}\) + tan^-1 \(\frac{1}{3}\) = \(\frac { \pi }{ 4 } \)
L.H.S = tan^-1 \(\frac{1}{2}\) + tan^-1 \(\frac{1}{3}\)

(B) cos^-1 \(\frac{12}{13}\) = tan^-1 \(\frac{5}{12}\)

समी. (1) तथा (2) L.H.S. = R.H.S. यही सिद्ध करना था।

(C) cos^-1 \(\frac{3}{5}\) = sin-1 \(\frac{4}{5}\)

समी. (1) तथा (2) L.H.S. = R.H.S. यही सिद्ध करना था।

प्रश्न 10.
सिद्ध कीजिये
(A) sec^-1 x + cosec^-1 x = \(\frac { \pi }{ 2 } \)
(B) sin^-1 x + cos^-1 x = \(\frac { \pi }{ 2 } \)
(C) tan^-1 x + cot^-1 x = \(\frac { \pi }{ 2 } \)
हल:
(A) sec^-1 x + cosec^-1 x = \(\frac { \pi }{ 2 } \)
माना sin^-1 x = θ ………………… (1)
⇒ x = sin θ
⇒ x = cos ( \(\frac { \pi }{ 2 } \) – θ) ………………………. (2)
समी. (1) तथा (2) को जोड़ने पर
sec^-1 x + cosec^-1 x = θ + \(\frac { \pi }{ 2 } \) – θ = \(\frac { \pi }{ 2 } \) यही सिद्ध करना था।

(B) sin^-1 x + cos^-1 x = \(\frac { \pi }{ 2 } \)
माना sin^-1 x = θ ………………….. (1)
⇒ x = sin θ
⇒ x = cos ( \(\frac { \pi }{ 2 } \) – θ)
⇒ cos^-1 x = \(\frac { \pi }{ 2 } \) – θ …………………………. (2)
समी. (1) तथा (2) को जोड़ने पर,
sin^-1 x + cos^-1 x = θ + \(\frac { \pi }{ 2 } \) – θ
⇒ sin^-1 x + cos^-1 x = \(\frac { \pi }{ 2 } \) यही सिद्ध करना था।

(C) tan^-1 x + cot^-1 x = \(\frac { \pi }{ 2 } \)
माना
⇒ tan^-1 x = θ …………………………… (1)
⇒ x = tan θ
⇒ x = cot ( \(\frac { \pi }{ 2 } \) – θ)
⇒ cot^-1 x = \(\frac { \pi }{ 2 } \) – θ ……………………… (2)

प्रश्न 11.
सिद्ध कीजिए कि
(A) tan^-1 5 – tan^-1 3 – tan^-1 \(\frac{1}{8}\)
(B) tan^-1 3 – tan^-1 2 = tan^-1 \(\frac{1}{7}\)
(C) tan^-1 7 – tan^-1 5 = tan^-1 \(\frac{1}{18}\)
हल:
(A) tan^-1 5 – tan^-1 3 = tan^-1 \(\frac{1}{8}\)
L.H.S = tan^-1 5 – tan^-1 3
= tan^-1 \(\frac { 5-3 }{ 1+5.3 } \) = tan^-1 \(\frac{2}{16}\) = tan^-1 \(\frac{1}{8}\)
= R.H.S. यही सिद्ध करना था।

(B) प्रश्न क्रमांक 11 (A) की भाँति हल कीजिये।

(C) प्रश्न क्रमांक 11 (A) की भाँति हल कीजिये।

प्रश्न 12.
सिद्ध कीजिये कि
(A) tan^-1 \(\frac{4}{7}\) – tan^-1 \(\frac{1}{5}\) = tan^-1 \(\frac{1}{3}\)
(B) tan^-1 \(\frac{1}{2}\) – tan^-1 \(\frac{2}{9}\) = tan^-1 \(\frac{1}{4}\)
(C) tan^-1 \(\frac{1}{7}\) + tan^-1 \(\frac{1}{8}\) = tan^-1 \(\frac{3}{11}\)
हल:
(A) tan^-1 \(\frac{4}{7}\) – tan^-1 \(\frac{1}{5}\) = tan^-1 \(\frac{1}{3}\)
L.H.S = tan^-1 \(\frac{4}{7}\) – tan^-1 \(\frac{1}{5}\)
= tan^-1 \(\frac { \frac { 4 }{ 7 } -\frac { 1 }{ 5 } }{ 1+\frac { 4 }{ 7 } .\frac { 1 }{ 5 } } \) = tan^-1 \(\frac{1}{3}\)
= tan^-1 \(\frac{13}{39}\) = tan^-1 \(\frac{1}{3}\)
= R.H.S यही सिद्ध करना था।

(B) प्रश्न क्रमांक 12 (A) की भाँति हल कीजिये।

(C) प्रश्न क्रमांक 12 (A) की भाँति हल कीजिये।

प्रश्न 13.
सिद्ध कीजिए कि
tan^-1 1 + tan^-1 2 + tan^-1 3 = π
हल: L.H.S. = tan^-1 1 + (tan^-1 2 + tan^-1 3)
= tan^-1 (1) + π + tan^-1 ( \(\frac { 2+3 }{ 1-2\times 3 } \) )
[∵ tan^-1 x + tan^-1 y = π + tan^-1 \(\frac { x+y }{ 1-xy } \), यदि x > 0, y > 0, xy > 1, यहाँ xy = 6 > 1]
= tan^-1 (1) + π + tan^-1 ( \(\frac{5}{5-6}\) )
= tan^-1 (1) + π + tan^-1 (-1)
= tan^-1 (1) + π – tan^-1 (1), [∵tan^-1(-x) = – tan^-1 x]
= π = R.H.S
∵ बाएँ पक्ष की राशियाँ धनात्मक कोण बनाती हैं, अतः बायाँ पक्ष शून्य नहीं हो सकता।
अत: बायाँ पक्ष = π = दायाँ पक्ष। यही सिद्ध करना था।

प्रश्न 14.
यदि tan^-1 ( \(\frac{1}{2}\) ) + tan^-1 ( \(\frac{1}{k}\) ) = \(\frac { \pi }{ 4 } \) हो, तो k का मान ज्ञात कीजिए।
हल: tan^-1 ( \(\frac{1}{2}\) ) + tan^-1 ( \(\frac{1}{k}\) ) = \(\frac { \pi }{ 4 } \)

⇒ \(\frac { k+2 }{ 2k-1 } \) = 1
⇒ k + 2 = 2k – 1
⇒ 2 + 1 = 2k – k
⇒ k = 3.

प्रश्न 15.
यदि tan^-1 ( \(\frac{3}{4}\) ) + tan^-1 ( \(\frac{1}{k}\) ) = \(\frac { \pi }{ 4 } \) हो, तो k का मान ज्ञात कीजिए।
हल:
प्रश्न क्रमांक 14 की भाँति हल कीजिये।
[उत्तर – k = 1.]

प्रश्न 16.
यदि tan^-1 ( \(\frac{4}{5}\) ) + tan^-1 ( \(\frac{1}{k}\) ) = \(\frac { \pi }{ 4 } \) हो, तो k का मान ज्ञात कीजिए।
हल:
प्रान क्रमांक 14 की भाँति हल कीजिये।
[उत्तर – k = 9.]

प्रश्न 17.
सिद्ध कीजिए कि
tan^-1 \(\sqrt{x}\) = \(\frac{1}{2}\) cos^-1 ( \(\frac { 1-x }{ 1+x } \) )
हल:
R.H.S. = \(\frac{1}{2}\) cos^-1 ( \(\frac { 1-x }{ 1+x } \) )
माना \(\sqrt{x}\) = tan θ
⇒ x = tan² θ
⇒ \(\frac { 1-x }{ 1+x } \) = \(\frac { 1-tan^{ 2 }\theta }{ 1+tan^{ 2 }\theta } \) = cos 2θ
∴ R.H.S = \(\frac{1}{2}\) cos^-1 (cos 2θ)
= \(\frac{1}{2}\) × 2θ = θ
= tan^-1 ( \(\sqrt{x}\) ), [∵ \(\sqrt{x}\) = tanθ ⇒ tan^-1 ( \(\sqrt{x}\) ) = θ]
= L.H.S. यही सिद्ध करना था।

प्रश्न 18.
सिद्ध कीजिए कि
sin (cos^-1x) = cos (sin^-1x)
हल:
L.H.S.= sin (cos^-1 x)
= sin [ \(\frac { \pi }{ 2 } \) – sin^-1 x], [∵sin^-1 x + cos^-1 x = \(\frac { \pi }{ 2 } \), cos^-1 x = \(\frac { \pi }{ 2 } \) – sin^-1 x] [∵ sin(90° – θ) = cos θ]
= cos (sin^-1 x),
= R.H.S यही सिद्ध करना था।

प्रश्न 19.
(A) सिद्ध कीजिए कि
tan^-1 ( \(\frac { b-c }{ 1+bc } \) ) + tan^-1 ( \(\frac { c-a }{ 1+ca } \) ) + tan^-1 a = tan^-1 b?
हल:
L.H.S = tan^-1 ( \(\frac { b-c }{ 1+bc } \) ) + tan^-1 ( \(\frac { c-a }{ 1+ca } \) ) + tan^-1 a
= tan^-1 b – tan^-1 c + tan^-1 c – tan^-1 a + tan^-1 a
= tan^-1 b = R.H.S. यही सिद्ध करना था।

(B) सिद्ध कीजिए कि
tan^-1 ( \(\frac { a-b }{ 1+ab } \) ) + tan^-1 ( \(\frac { b-c }{ 1+bc } \) ) + tan^-1 c = tan^-1 a?
हल:
L.H.S = tan^-1 ( \(\frac { a-b }{ 1+ab } \) ) + tan^-1 ( \(\frac { b-c }{ 1+bc } \) ) + tan^-1 c
= (tan^-1 a – tan^-1 b) + (tan^-1 b – tan^-1 c) + tan^-1 c
= tan^-1 a = R.H.S. यही सिद्ध करना था।

प्रश्न 20.
समीकरण हल कीजिए –
sin^-1 \(\frac { 2a }{ 1+a^{ 2 } } \) + sin^-1 \(\frac { 2b }{ 1+b^{ 2 } } \) = 2 tan^-1 x?
हल:
दिया गया समीकरण है:
sin^-1 \(\frac { 2a }{ 1+a^{ 2 } } \) + sin^-1 \(\frac { 2b }{ 1+b^{ 2 } } \) = 2 tan^-1 x
⇒ 2 tan^-1 a + 2 tan^-1 b = 2 tan^-1 x, [∵ sin^-1 \(\frac { 2x }{ 1+x^{ 2 } } \) = 2 tan^-1 x]
⇒ tan^-1 a + tan^-1 b = tan^-1 x
⇒ tan^-1 \(\frac { a-b }{ 1+ab } \) = tan^-1 x
x = \(\frac { a-b }{ 1+ab } \)

प्रश्न 21.
समीकरण हल कीजिए –
cos^-1 ( \(\frac { 1-a^{ 2 } }{ 1+a^{ 2 } } \) ) – cos^-1 ( \(\frac { 1-b^{ 2 } }{ 1+b^{ 2 } } \) ) = 2 tan^-1 x?
हल:
दिया गया समीकरण है:
cos^-1 ( \(\frac { 1-a^{ 2 } }{ 1+a^{ 2 } } \) ) – cos^-1 ( \(\frac { 1-b^{ 2 } }{ 1+b^{ 2 } } \) ) = 2 tan^-1 x
⇒ 2 tan^-1 a – 2 tan^-1 = 2 tan^-1 x
⇒ tan^-1 a – tan^-1 b = tan^-1 x
⇒ tan^-1 \(\frac { a-b }{ 1+ab } \) = tan^-1 x
∴ x = \(\frac { a-b }{ 1+ab } \)

प्रश्न 22.
(A) सिद्ध कीजिए –
2 tan^-1 \(\frac{1}{4}\) = tan^-1 \(\frac{8}{15}\)?
हल:
दिया है:
2 tan^-1 \(\frac{1}{4}\) = tan^-1 \(\frac{8}{15}\)
L.H.S = 2 tan^-1 \(\frac{1}{4}\)
= tan^-1 \(\frac { 2.1/4 }{ 1-(1/4)^{ 2 } } \) [∵ 2 tan^-1 x = tan^-1 \(\frac { 2x }{ 1-x^{ 2 } } \) ]
= tan^-1 \(\frac { 1/2 }{ 15/16 } \)
= tan^-1 \(\frac{8}{15}\) = R.H.S यही सिद्ध करना था।

(B) सिद्ध कीजिए –
2 tan^-1 ( \(\frac{1}{2}\) ) = tan^-1 ( \(\frac{4}{3}\) )
हल:
दिया है:
2 tan^-1 ( \(\frac{1}{2}\) ) = tan^-1 ( \(\frac{4}{3}\) )
L.H.S = 2 tan^-1 ( \(\frac{1}{2}\) )

यही सिद्ध करना था।

प्रश्न 23.
सरलतम रूप में लिखिए –
tan^-1 \(\sqrt { \frac { 1-cosx }{ 1+cosx } } \)?
हल:
दिया है:

प्रश्न 24.
सरलतम रूप में लिखिए –
cos^-1 \(\sqrt { \frac { 1 }{ 2 } (1+cosx) } \)?
हल:
दिया है:

प्रश्न 25.
यदि tan^-1 a + tan^-1 b + tan^-1 c = \(\frac { \pi }{ 2 } \) हो, तो सिद्ध कीजिए कि
ab + bc + ca = 1.
हल:
दिया है:
tan^-1 + tan^-1 b + tan^-1 c = \(\frac { \pi }{ 2 } \)
⇒ tan^-1a + tan^-1 b + tan^-1 c = tan^-1 a + cot^-1 a, [∵tan^-1 a + cot^-1 a = \(\frac { \pi }{ 2 } \) ]
⇒ tan^-1 b + tan^-1 c = cot^-1 a
⇒ tan^-1 ( \(\frac { b+c }{ 1-bc } \) ) = tan^-1 ( \(\frac{1}{a}\) )
⇒ \(\frac { b+c }{ 1-bc } \) = \(\frac{1}{a}\)
⇒ ab + ca = 1 – bc
⇒ ab + bc + ca = 1 यही सिद्ध करना था।

प्रश्न 26.
सिद्ध कीजिए –
यही सिद्ध करना था।
tan^-1 \(\frac{2}{11}\) + cot^-1 \(\frac{24}{7}\) = tan^-1 \(\frac{1}{2}\)?
हल:
L.H.S. = tan^-1 \(\frac{2}{11}\) + cot^-1 \(\frac{7}{24}\)
= tan^-1 \(\frac{2}{11}\) + tan^-1 \(\frac{7}{24}\)

= tan^-1 [ \(\frac{125}{250}\) ] = tan^-1 \(\frac{1}{2}\) = R.H.S. यही सिद्ध करना था।

प्रश्न 27.
सिद्ध कीजिए –
cos^-1 x = 2 cos^-1 \(\sqrt { \frac { 1+x }{ 2 } } \)
= 2 cos^-1 \(\sqrt { \frac { 1+cos\theta }{ 2 } } \), ( x = cos θ रखने पर)
= 2 cos^-1 \(\sqrt { \frac { 2cos^{ 2 }\frac { \theta }{ 2 } }{ 2 } } \) = 2. \(\frac { \theta }{ 2 } \)
= cos^-1 x = L.H.S. यही सिद्ध करना था।

प्रश्न 28.
सिद्ध कीजिए –
cos^-1 x = 2 tan^-1 \(\sqrt { \frac { 1-x }{ 1+x } } \)?
हल:
R.H.S = 2 tan^-1 \(\sqrt { \frac { 1-x }{ 1+x } } \)

= 2. \(\frac { \theta }{ 2 } \) = θ = cos^-1 x = L.H.S. यही सिद्ध करना था।

प्रश्न 29.
सिद्ध कीजिए कि
tan^-1 ( \(\frac{a}{b}\) ) – tan^-1 ( \(\frac { a-b }{ a+b } \) ) = \(\frac { \pi }{ 4 } \)?
हल:
L.H.S = tan^-1 ( \(\frac{a}{b}\) ) – tan^-1 ( \(\frac { a-b }{ a+b } \) )

= tan^-1 1
= \(\frac { \pi }{ 4 } \) = R.H.S. यही सिद्ध करना था।

प्रतिलोम त्रिकोणमितीय फलन दीर्घ उत्तरीय प्रश्न – I

प्रश्न 1.
(A) सिद्ध कीजिए कि
sin^-1 \(\frac { 1 }{ \sqrt { 5 } } \) + sin^-1 \(\frac { 1 }{ \sqrt { 10 } } \) = \(\frac { \pi }{ 4 } \)?
हल:
माना sin^-1 \(\frac { 1 }{ \sqrt { 5 } } \) = A, sin^-1 \(\frac { 1 }{ \sqrt { 10 } } \) = B
∴ A + B = \(\frac { \pi }{ 4 } \)
⇒ sin(A + B) = sin \(\frac { \pi }{ 4 } \)
⇒ sinA cosB + cosA sinB = \(\frac { 1 }{ \sqrt { 2 } } \)
L.H.S = sinA \(\sqrt { 1-sin^{ 2 }B } \) + \(\sqrt { 1-sin^{ 2 }A } \). sin B

(B) निम्न समीकरण को हल कीजिए:
sin^-1 x + sin^-1 (1 – x) = sin^-1 \(\sqrt { 1-x^{ 2 } } \)?
हल:
दिया गया समीकरण है:
sin^-1 x + sin^-1 (1 – x) = sin^-1 \(\sqrt { 1-x^{ 2 } } \)

वर्ग करने पर,
x² (2x – x²) = x² (1 – x²)
⇒ x² (2x – x² – 1 + x²) = 0
⇒ x² (2x – 1) = 0
अतः x = 0, \(\frac{1}{2}\).

प्रश्न 2.
(A) सिद्ध कीजिए कि tan^-1 \(\frac { x+1 }{ x } \) – tan^-1 \(\frac { 1 }{ 2x+1 } \) = \(\frac { \pi }{ 4 } \)?
(B) यदि tan^-1 x + tan^-1 y + tan^-1 z = \(\frac { \pi }{ 2 } \) हो, तो सिद्ध कीजिए xy + yz + zx = xyz.
(C) यदि tan^-1 x + tan^-1 y + tan^-1 z = \(\frac { \pi }{ 2 } \), हो, तो सिद्ध कीजिए xy + yz + zx = 1.
हल:
(A) tan^-1 \(\frac { x+1 }{ x } \) – tan^-1 \(\frac { 1 }{ 2x+1 } \) = \(\frac { \pi }{ 4 } \)

= R.H.S. यही सिद्ध करना था।
(B) tan^-1 x + tan^-1 z = π

⇒ x + y + z – xyz = 0 [∵ tan π = 0]
∴ x + y + z = xyz. यही सिद्ध करना था।
(C) प्रश्न क्रमांक 2 (B) की भाँति tan \(\frac { \pi }{ 2 } \) = ∞ = \(\frac{1}{0}\), रखकर विद्यार्थी स्वयं हल करें।

प्रश्न 3.
सरलतम रूप में लिखिए –
tan^-1 [ \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \) ]?
हल:
tan^-1 [ \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \) ]
माना x = tan θ

प्रश्न 4.
(A) सिद्ध कीजिए –
\(\frac{1}{2}\) sin^-1 x = cot^-1 \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \)?
हल:
R.H.S. = cot^-1 \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \)

(B) सिद्ध कीजिए –
\(\frac{1}{2}\) cot^-1 x = cot^-1 ( \(\sqrt { 1+x^{ 2 }+x } \) )?
हल:
\(\frac{1}{2}\) cot^-1 x = cot^-1 ( \(\sqrt { 1+x^{ 2 }+x } \) )
R.H.S. = cot^-1 ( \(\sqrt { 1+x^{ 2 }+x } \) )
माना x = cot θ

प्रश्न 5.
समीकरण को हल कीजिए –
tan^-1 (x + 1) + tan^-1 (x – 1) = tan^-1 ( \(\frac{6}{17}\) )?
हल:
दिया है:
tan^-1 (x + 1) + tan^-1 (x – 1) = tan^-1 ( \(\frac{6}{17}\) )?

⇒ 17x = 6 – 3x²
⇒ 3x² + 18 x – x – 6 = 0
⇒ 3x(x + 6) -1 (x + 6) = 0
⇒ (x + 6) (3x – 1) = 0
∴ x = – 6, x = \(\frac{1}{3}\)

प्रश्न 6.
सिद्ध कीजिए कि cos^-1 \(\frac{3}{5}\) + cos^-1 \(\frac{4}{5}\) = \(\frac { \pi }{ 2 } \)?
हल:
दिया है:
L.H.S = cos^-1 \(\frac{3}{5}\) + cos^-1 \(\frac{4}{5}\)

प्रश्न 7.
यदि cos^-1 x + cos^-1 y + cos^-1 z = π हो, तो सिद्ध कीजिए कि
x² + y² + z² + 2xyz = 1
हल:
दिया है:
cos^-1 x + cos^-1 y + cos^-1 z = π

दोनों पक्षों का वर्ग करने पर,
x²y² + z² + 2xyz = (1 – x²) (1 – y²)
⇒ x²y² + z² + 2xyz = 1 – y² – x² + x²y²
⇒ z² + 2xyz = 1 – y² – x²
⇒ x² + y² + z² + 2xyz = 1. यही सिद्ध करना था।

प्रश्न 8.
यदि sin^-1 \(\frac { 2a }{ 1+a^{ 2 } } \) – cos^-1 \(\frac { 1-b^{ 2 } }{ 1+b^{ 2 } } \) = tan^-1 \(\frac { 2x }{ 1-x^{ 2 } } \) हो, तो सिद्ध कीजिए कि x = \(\frac { a-b }{ 1+ab } \)?
हल:
यहाँ sin^-1 \(\frac { 2a }{ 1+a^{ 2 } } \) – cos^-1 \(\frac { 1-b^{ 2 } }{ 1+b^{ 2 } } \) = tan^-1 \(\frac { 2x }{ 1-x^{ 2 } } \) ………………………….. (1)
माना a = tan θ, b = tan ∅, x = tan Ψ
समी. (1) में इन मानों को रखने पर,

⇒ sin^-1 (sin 2θ) – cos^-1 (cos 2∅) = tan^-1 (tan 2Ψ)
⇒ 2θ – 2∅ = 2Ψ
⇒ θ – ∅ = Ψ
⇒ tan^-1 a – tan^-1 b = tan^-1 x
⇒ tan^-1 ( \(\frac { a-b }{ 1+ab } \) ) = tan^-1 x
⇒ x = \(\frac { a-b }{ 1+ab } \). यही सिद्ध करना था।

प्रश्न 9.
सिद्ध कीजिए कि
tan^-1 \(\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}}\) = \(\frac { \pi }{ 4 } \) – \(\frac{1}{2}\) cos¹ x
हल:
माना कि x = cos θ, तब θ = cos^-1 x

प्रश्न 10.
सरलतम रूप में लिखिये –
tan^-1 ( \(\frac { x }{ \sqrt { 1+x^{ 2 }-1 } } \) )?
हल:
tan^-1 ( \(\frac { x }{ \sqrt { 1+x^{ 2 }-1 } } \) ) में x = tan θ रखने पर,

प्रश्न 11.
सिद्ध कीजिए कि –
tan^-1 \(\sqrt{x}\) = \(\frac{1}{2}\) cos^-1 ( \(\frac { 1-x }{ 1+x } \) ) (NCERT)
हल:
R.H.S. = \(\frac{1}{2}\) cos^-1 ( \(\frac { 1-x }{ 1+x } \) )

माना \(\sqrt{x}\) = tan θ
तब, θ = tan^-1 \(\sqrt{x}\)
= \(\frac{1}{2}\) cos^-1 ( \(\frac { 1-tan^{ 2 }\theta }{ 1+tan^{ 2 }\theta } \) )
= \(\frac{1}{2}\) cos^-1 (cos 2θ), [∵ cos^-1 (cos x) = x]
= \(\frac{1}{2}\) × 2θ
= θ
= tan^-1 \(\sqrt{x}\), [समी. (1) से]
= L.H.S. यही सिद्ध करना था।

प्रश्न 12.
सिद्ध कीजिए कि –
tan^-1 \(\frac { 6x-8x^{ 3 } }{ 1-12x^{ 2 } } \) – tan^-1 \(\frac { 4x }{ 1-4x^{ 2 } } \) = tan^-1 2x, जहाँ |2x| < \(\frac { 1 }{ \sqrt { 3 } } \) (CBSE 2016)
हल:
L.H.S. = tan^-1 \(\frac { 6x-8x^{ 3 } }{ 1-12x^{ 2 } } \) – tan^-1 \(\frac { 4x }{ 1-4x^{ 2 } } \)
= tan^-1 \(\frac { 3(2x)-(2x)^{ 3 } }{ 1-3(2x)^{ 2 } } \) – tan^-1 \(\frac { 2\times 2x }{ 1-(2x)^{ 2 } } \)
माना 2x = tanθ
तब,
θ = tan^-1 2x

= 3θ – 2θ = θ
= tan^-1 2x [समी. (1) से]
= R.H.S. यही सिद्ध करना था।

प्रश्न 13.
सिद्ध कीजिए कि –
cos^-1 \(\frac{4}{5}\) + cos^-1 \(\frac{12}{13}\) = cos^-1 \(\frac{33}{65}\)?
हल:
L.H.S. = cos^-1 \(\frac{4}{5}\) + cos^-1 \(\frac{12}{13}\)

MP Board Class 12 Maths Important Questions

MP Board Class 12th Maths Important Questions Chapter 1 संबंध एवं फलन

संबंध एवं फलन Important Questions

संबंध एवं फलन वस्तुनिष्ठ प्रश्न

प्रश्न 1.
सही विकल्प चुनकर लिखिए –

प्रश्न 1.
मान लीजिए कि f (x) = 8x द्वारा परिभाषित फलन f : R → R फलन है –
(a) f एकैकी आच्छादक है
(b) f बहुएक आच्छादक है
(c) f एकैकी है परन्तु आच्छादक नहीं है
(d) f न तो एकैकी है और न आच्छादक है।
उत्तर:
(a) f एकैकी आच्छादक है

प्रश्न 2.
फलन f(x) = \(\frac { e^{ x^{ 2 } }-e^{ -x^{ 2 } } }{ e^{ x^{ 2 } }+e^{ -x^{ 2 } } } \) द्वारा परिभाषित फलन f : R → R है –
(a) f एकैकी है परन्तु आच्छादक नहीं है
(b) f एकैकी आच्छादक है
(c) f न तो एकैकी है और न आच्छादक है
(d) f बहुएक आच्छादक है।
उत्तर:
(a) f एकैकी है परन्तु आच्छादक नहीं है

प्रश्न 3.
यदि f : R → R, f(x) = (3 – x³)^1/3 द्वारा प्रदत्त है तो fof(x) बराबर हैं –
(a) x^1/3
(b) x³
(c) x
(d) (3 – x³)
उत्तर:
(c) x

प्रश्न 4.
a * b = a³ + b³ प्रकार से परिभाषित N में एक द्विआधारी संक्रिया * पर विचार कीजिए –
(a) * साहचर्य तथा क्रमविनिमेय दोनों है
(b) * क्रमविनिमेय है, किन्तु साहचर्य नहीं है
(c) * साहचर्य है, किन्तु क्रमविनिमेय नहीं है
(d) * न तो क्रमविनिमेय है और न साहचर्य है।
उत्तर:
(b) * क्रमविनिमेय है, किन्तु साहचर्य नहीं है

प्रश्न 5.
समुच्चय {a, b} में द्विआधारी संक्रियाओं की संख्या है –
(a) 10
(b) 16
(c) 20
(d) 8
उत्तर:
(b) 16

प्रश्न 2.
रिक्त स्थानों की पूर्ति कीजिए –

1. यदि A = {1, 2, 3} हो, तो अवयव (1, 2) वाले तुल्यता सम्बन्धों की संख्या ……………………………….. होगी।
2. यदि f : R → R जहाँ f(x) = 5x – 7, ∀x ∈ R तो f^-1(7) का मान ………………………….. होगा।
3. यदि f : R → R तथा f(x) = x² – 3x + 2 से परिभाषित है, तो f(f(x)) का मान …………………………….. होगा।
4. यदि f : R → R; f (x) = 2x + 5 द्वारा परिभाषित है तब f^-1(y) का मान …………………………….. होता है।
5. f(x) = x³ द्वारा प्रदत्त फलन f : R → R …………………………. है।

उत्तर:

1. 2
2. 0
3. x⁴ – 6x³ + 10x² – 3x
4. \(\frac{1}{2}\) (y-5)
5. एकैकी है।

प्रश्न 3.
निम्न कथनों में सत्य/असत्य बताइए –

1. माना कि समुच्चय A = {1, 2, 3} पर एक सम्बन्ध R= {(1, 3), (3, 1), (3, 3)} है। तब R सममित, संक्रामक है, किन्तु स्वतुल्य नहीं है।
2. यदि f : A → B एकैकी आच्छादक फलन हो, तो f का प्रतिलोम f^-1 अद्वितीय होता है।
3. फलनों का संजोयन क्रमविनिमेयी होता है।
4. प्रत्येक फलन व्युत्क्रमणीय होता है।
5. माना कि समुच्चय Q⁺ पर एक द्विआधारी संक्रिया ^*, a * b = \(\frac{ab}{3}\), ∀a, b ∈ Q⁺ से परिभाषित है, तब 4 * 6 का प्रतिलोम \(\frac{9}{8}\) है।

उत्तर:

1. असत्य
2. सत्य
3. असत्य
4. असत्य
5. सत्य।

प्रश्न 4.
एक शब्द/वाक्य में उत्तर दीजिए –

1. समुच्चय A = {a, b, c} पर तत्समक संबंध लिखिए।
2. फलन f(x) = \(\frac { \left| x-1 \right| }{ x-1 } \) का परिसर क्या है?
3. फलन f(x) = \(\sqrt { 25-x^{ 2 } } \) से परिभाषित वास्तविक फलन का प्रान्त लिखिए।
4. माना कि एक द्विआधारी संक्रिया *, a * b = 3a + 4b – 2 से परिभाषित है तब 4 * 5 ज्ञात कीजिए।
5. माना कि f.g: R → R क्रमशः f(x) = 2x +1 और g(x) = x² – 2, ∀x ∈ R से परिभाषित है। तब gof (x) ज्ञात कीजिए।

उत्तर:

1. {(a, a), (b, b), (c, c)}
2. {-1, 1}
3. [-5, 5]
4. 30
5. 4x² + 4x – 1.

संबंध एवं फलन दीर्घ उत्तरीय प्रश्न – I

प्रश्न 1.
सिद्ध कीजिए कि पूर्णांकों के समुच्चय z में R = { (a, b ) : संख्या 2, (a – b) को विभाजित करती है } द्वारा प्रदत्त संबंध एक तुल्यता संबंध है। (NCERT)
हल: समस्त a ∈ Z के लिए 2,(a – a) को विभाजित करेगा अर्थात् (a, a) ∈ R अत: R स्वतुल्य है।
माना (a,b) ∈ R ⇒ 2, (a – b) को विभाजित करता है
⇒ 2,- (b – a) को विभाजित करता है
(a,b) ∈ R ⇒ (b,a) ∈ R
अत: R, सममित है।
माना (a,b) ∈ R = 2,(a – b) को विभाजित करता है।
(b, c) ∈ R → 2,(b – c) को विभाजित करता है।
a – b तथा b – C, 2 से भाज्य है
a – b + b – c, भी 2 से भाज्य है
अर्थात् a – c भी 2 से भाज्य है
इसलिए (a,b) ∈ R, (b,c) ∈ R ⇒ (a,c) ∈ R
अत: R संक्रमक है। अतः R, स्वतुल्य, सममित तथा संक्रमक है अतः यह एक तुल्यता संबंध है। यही सिद्ध करना था।

प्रश्न 2.
मान लीजिए कि समुच्चय A = {1, 2, 3, 4, 5, 6, 7} में R = {(a, b): a तथा b दोनों ही या तो विषम है या सम है } द्वारा परिभाषित एक संबंध है। सिद्ध कीजिए कि R एक तुल्यता संबंध है। साथ ही सिद्ध कीजिए कि उपसमुच्चय {1, 3, 5, 7} के सभी अवयव एक-दूसरे से संबंधित हैं और उपसमुच्चय {2, 4, 6} के सभी अवयव एक-दूसरे से संबंधित हैं। परंतु उपसमुच्चय {1, 3, 5, 7} का कोई भी अवयव उपसमुच्चय {2, 4, 6} के किसी भी अवयव से संबंधित नहीं है। (NCERT)
हल: A का दिया गया कोई अवयव a या तो विषम है या सम है अतः (a, a) ∈ R अत: R स्वतुल्य है।
माना (a,b) ∈ R ⇒ a तथा b दोनों ही या तो विषम है या सम है।
⇒ b तथा a दोनों ही या तो विषम है या सम है।
(a,b) ∈ D (b, a) ∈ R
अत: R सममित है।
(a,b) ∈ R तथा (b, c) ∈ R ⇒ अवयव a, b, c सभी या तो विषम हैं या सम हैं।
(a,b) ∈ R तथा (b, c) ∈ R = (a,c) ∈ R
अत: R संक्रमक है।
यहाँ R, स्वतुल्य, सममित तथा संक्रमक है इसलिए R एक तुल्यता संबंध है। यही सिद्ध करना था।
पुनः {1, 3, 5, 7} के सभी अवयव एक – दूसरे से संबंधित हैं क्योंकि इस उपसमुच्चय के सभी अवयव विषम हैं।
इसी प्रकार {2, 4, 6} के सभी अवयव एक – दूसरे से संबंधित हैं क्योंकि ये सभी सम हैं साथ ही उपसमुच्चय {1, 3, 5, 7} का कोई भी अवयव {2, 4, 6} के किसी भी अवयव से संबंधित नहीं हो सकता क्योंकि {1, 3, 5, 7} के अवयव विषम हैं जबकि {2, 4, 6} के अवयव सम हैं।

प्रश्न 3.
माना कि N प्राकृत संख्याओं का समुच्चय है। यदि समुच्चय N × N में परिभाषित एक संबंध R ऐसा हो कि (a, b) R (c, d) यदि ad (b + c) = bc (a + d) तो सिद्ध कीजिए कि R एक तुल्यता संबंध है। (CBSE 2015)
हल: स्वतुल्यता: प्रत्येक (a, b) ∈ N × N के लिए
ab (b + a) = ba (a + b)
⇒ (a, b) R (a, b)
अत: R स्वतुल्य होगा।
सममितता: माना (a, b)(c, d) ∈ N × N
(a, b) R (c, d) ⇒ ab(b + c) = bc(a + d)
⇒ bc (a + d) = ab (b + c)
(a,b) R (c,d) ⇒ (c, d) R (a, b)
अत: R सममित होगा।
उत्तर संक्रमकता: माना (a, b) R (c, d ) तथा (c, d) R (e, f)
⇒ ad ( b + c) = bc (a + d)
तथा cf (d + e) = de (c + f)

⇒ af (b + e) = bc (a + f)
(a, b) R (c, d) तथा (c, d) R (e, f) ⇒ (a, b) R (e, f)
अत: R संक्रमक है।
R, स्वतुल्य, सममित तथा संक्रमक है अत: R एक तुल्यता संबंध है। यही सिद्ध करना था।

प्रश्न 4.
माना A = {1, 2, 3, 4, 5} तथा R = {(a,b): |a – b| 2 से विभाजित है} तो सिद्ध कीजिए कि R एक तुल्यता संबंध है तथा तुल्यता वर्ग भी बनाइए।
हल: A = { 1, 2, 3, 4, 5 }
R = { (a, b) : |a – b| 2 से विभाजित है }
R = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (1, 3), (1, 5), (2, 4), (3, 5), (3, 1) (5, 1), (4, 2),(5, 3)}
∀ a ∈ A (a,a) ∈ R
इसलिए R स्वतुल्य होगा।
क्योंकि (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) ∈ R
(a,b) ∈ R ⇒ (b,a) ∈ R
(1, 3), (1, 5), (2, 4), (3, 5), (3, 1), (5, 1), (4, 2), (5, 3) ∈ R
इसलिए R सममित है।
∀ (a, b) ∈ R,(b, c) ∈ R ⇒ (a, c) ∈ R
क्योंकि (1, 3)(3, 1) ∈ R = (1, 1) ∈ R
R संक्रमक है।
R, स्वतुल्य, सममित तथा संक्रमक है इसलिए R एक तुल्यता संबंध है।
यही सिद्ध करना था।
तुल्यता वर्ग
[1] = { a : a तथा 2 |a – 1| से विभाजित है}
[1] = {a : a ∈ A तथा a – 1 = 2 k}
[1] = {1, 3, 5}
[2] = { a : a तथा 2, |a – 2| से विभाजित है}
[2] = {a : a तथा a – 2 = 2k}
[2] = {2, 4}.

प्रश्न 5.
मान लीजिए कि समस्त n ∈ N के लिए।

द्वारा परिभाषित एक फलन f : N → N है। बताइए कि क्या फलन f एकैकी आच्छादक है। अपने उत्तर का औचित्य भी बताइए। (NCERT)
हल: f : N → N में,

यहाँ f (1) = f (2) ⇒ 1 ≠ 2
डोमेन के दो अवयव 1 और 2 का सह – डोमेन में एक ही प्रतिबिम्ब 1 है।
अत: f एकैकी फलन नहीं है।

स्थिति I.
जब n विषम हो
n = 2r + 1, r ∈ N
तब 4r + 1 ∈ N इस प्रकार विद्यमान है कि
f (4r + 1) = \(\frac { 4r+1+1 }{ 2 } \) = \(\frac { 4r+2 }{ 2 } \) = 2r + 1
स्पष्ट है सह – डोमेन के प्रत्येक अवयव का डोमेन में पूर्व प्रतिबिम्ब है इसलिए / आच्छादक फलन है।

स्थिति II.
माना n = 2r (सम संख्या)
तब 4r ∈ N इस प्रकार विद्यमान है कि
f(4r) = \(\frac{4r}{2}\) = 2r
स्पष्ट है सह – डोमेन के प्रत्येक अवयव का डोमेन में पूर्व प्रतिबिम्ब है इसलिए f आच्छादक फलन है।
अतः f एकैकी आच्छादक फलन नहीं है।

प्रश्न 6.
मान लीजिए कि A = R – {3} तथा B = R – {1} है। f(x) = \(\frac { x-2 }{ x-3 } \) द्वारा परिभाषित फलन f : A → B पर विचार कीजिए। क्या f एकैकी तथा आच्छादक है? अपने उत्तर का औचित्य भी बताइए। (NCERT)
हल:
f : A → B, f (x) = \(\frac { x-2 }{ x-3 } \), A = R – {3} तथा B = R – {1}
मान लीजिए x, y∈A इस प्रकार है कि
f (x) = f (y)
⇒ \(\frac { x-2 }{ x-3 } \) = \(\frac { y-2 }{ y-3 } \)
⇒ (x – 2) (y – 3) = (y – 2) (x – 3)
⇒ xy – 3x – 2y + 6 = xy – 3y – 2x + 6
⇒ -3x – 2y = -3y – 2x
⇒ 3x – 2x = 3y – 2y
⇒ x = y
यहाँ f (x) = f (y) ⇒ x = y
अतः f एकैकी फलन है।
f आच्छादक फलन होगा यदि x∈A इस प्रकार विद्यमान है कि f(x) = y
\(\frac { x-2 }{ x-3 } \) = y
⇒ x – 2 = y (x – 3)
⇒ x – 2 = xy – 3y
⇒ xy – x = 3y – 2
⇒ x = \(\frac { 3y-2 }{ y-1 } \)∈A
प्रत्येक y ∈ B के लिए x ∈ A
f (x) = f ( \(\frac { 3y-2 }{ y-1 } \) )

∵ f(x) = y
अतः f अचधक पालन है।
अतः f एकोकी अचधक पालन है।

प्रश्न 7.
सिद्ध कीजिए कि नीचे परिभाषित फलन f : N → N एकैकी तथा आच्छादक दोनों ही।

हल: माना f (x₁) = f (x₂)
यदि x, विषम तथा x, सम है, तब
x₁ + 1 = x₂ – 1
X₁ – x₂ = -2
जो कि असंभव है।
इस प्रकार x₁ के सम तथा x₂ के विषम होने की संभावना नहीं है।
इसलिए x₁ तथा x₂, दोनों ही या तो सम होंगे या विषम होंगे।
माना x₁, x₂ दोनों विषम हैं।
f (x₁) = f (x₂)
⇒ x₁ – 1 = x₂ – 1
⇒ x₁ = x₂
अतः f एकैकी है।
सहप्रांत N की कोई भी विषम संख्या 2r + 1 प्रांत N की संख्या 2r + 2 का प्रतिबिंब है और सहप्रांत N की कोई भी सम संख्या 27, N की संख्या 2r – 1 का प्रतिबिंब है।
अतः f आच्छादक है। यही सिद्ध करना था।

प्रश्न 8.
f (x) = 4x + 3 द्वारा प्रदत्त फलन f: R → R पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्क्रमणीय है। f का प्रतिलोम फलन भी ज्ञात कीजिए? (NCERT)
हल: f : R → R, f (x) = 4x + 3
फलन का डोमेन तथा सह – डोमेन R है।
माना x, y ∈ R इस प्रकार है कि
f (x) = f (y)
4x + 3 = 4y + 3
⇒ 4x = 4y
⇒ x = y
इस प्रकार f (x) = f (y)
⇒ x = y
अतः f एकैकी है।
माना कि सह – डोमेन R का कोई अवयव y है
y = f (x)
y = 4x + 3
⇒ 4x = y – 3
⇒ x = \(\frac { y-3 }{ 4 } \)
∴ f^-1(y) = \(\frac { y-3 }{ 4 } \) तथा f^-1(x) = \(\frac { x-3 }{ 4 } \)

प्रश्न 9.
मान लीजिए कि y = {n² : n ∈ N}⊂N है। फलन f : N → y, जहाँ f (n) = n² पर विचार कीजिए। सिद्ध कीजिए कि व्युत्क्रमणीय है। का प्रतिलोम भी ज्ञात कीजिए। (NCERT)
हल:
y = f(n) = n²
n = \(\sqrt{y}\)
इससे g (y) = \(\sqrt{x}\) द्वारा परिभाषित फलन g : y → N प्राप्त होता है।
gof (n) = g [f (n)]
= g [n²]
= \(\sqrt { n^{ 2 } } \) [g(n) = \(\sqrt{n}\), g(n²) = \(\sqrt { n^{ 2 } } \) = n]
(gof) n = n
तथा
(fog)y = f [g(y)]
= f[ \(\sqrt{y}\) ], [f(n) = n², f( \(\sqrt{y}\) ) = ( \(\sqrt{y}\) )² = y]
= y
स्पष्ट है कि gof = I_n तथा fog = I_y
अतः f व्युत्क्रमणीय है तथा f^-1 = g.
यही सिद्ध करना था।

प्रश्न 10.
यदि f : R → R तथा g : R → R फलन क्रमशः f (x) = cosx तथा g(x) = 3x² द्वारा परिभाषित है, तो gof और fog ज्ञात कीजिए। सिद्ध कीजिए कि gof ≠ fog? (NCERT)
हल: दिया है: f(x) = cosx
g (x) = 3x²
(gof) x = g [f (x)]
(gof) x = g [cost]
दिया है:
f (x) = cosx ……………………….. (1)
g (x) = 3x²
g (cosx) = 3 cos²x ……………………………. (2)
समी. (1) और (2) से,
(gof )x = 3cos²x
(fog) x = f [g(x)]
= f [3x²] ………………………………… (3)
दिया है:
g (x) = 3x²
f (x) = cosx
f [3x²] = cos3x²
समी. (3) और (4) से,
(fog) x = cos3x²
x = 0 के लिए
3cos²x ≠ cos3x²
अतः gof ≠ fog. यही सिद्ध करना था।

प्रश्न 11.
f: {1,2,3} → {a,b,c}, f(1) = a, f(2) = b, f(3) = c द्वारा प्रदत्त फलन f पर विचार कीजिए-ज्ञात कीजिए ओर सिद्ध कीजिए कि (f^-1)^-1 = f है। (NCERT)
हल: दिया गया है:
f: {1, 2,3} → { a, b, c}
f(1) = a, f (2) = b, f (3) = c
माना g : { a, b, c } → {1, 2, 3} में
g (a) = 1, g (b) = 2, g (c) = 3
(fog) a = f [g (a)]
= f [1] = a
(fog) b = f [g (b)]
= f (2) = b
(fog) c = f [g (c)]
= f (3) = c
तथा (gof) (1) = g [f (1)]
= g (a) = 1
(gof) (2) = g [f(2)]
= g (b) = 2
(gof) (3) = g [f (3)]
= g (c) = 3
अत: gof = I_x, तथा fog = I_y
जहाँ x = {1, 2, 3} तथा y = {a, b, c}
f का प्रतिलोम विद्यमान है तथा।
तथा f^-1 = g
∴ f^-1 {a, b, c} → {1, 2, 3} में,
f^-1 (a) = 1, f^-1(b) = 2, f^-1(c) = 3
अतः f^-1 का प्रतिलोम अथरिथ का प्रतिलोम जात करेंगे
माना h: {1, 2, 3} → {a, b, c}
h(1) = a, h(2) = b, h(3) = c
(goh) 1 = g[h(1)] = g(a) = 1
(goh) 2 = g[h(2)] = g(b) = 2
(goh) 3 = g[h(3)] = g(c) = 3
तथा (hog) a = h[g(a)] = h(1) = a
(hog) b = h [ g(b)] = h(2) = b
(hog) c = h[g(c)] = h(3) = c
अत: goh = I_x तथा hog = I_y
जहाँ x = {1, 2, 3} तथा y = {a, b, c}
g का प्रतिलोम विद्यमान है तथा g^-1 = h = (f^-1)^-1 = f
अत: h = f
∴ (f^-1)^-1 = f यही सिद्ध करना था।

प्रश्न 12.
सिद्ध कीजिए कि समस्त बहुभुजों के समुच्चय A में R = { (P₁, P₂ ) : P₁ तथा P₂ की भुजाओं की संख्या समान है।} प्रकार से परिभाषित संबंध R एक तुल्यता संबंध है। 3, 4 और 5 की भुजाओं वाले समकोण त्रिभुज से संबंधित समुच्चय A के सभी अवयवों का समुच्चय ज्ञात कीजिए। (NCERT)
हल: दिया है:
A = समस्त बहुभुजों का समुच्चय
R = {(P₁, P₂) : P₁, तथा P₂ की भुजाओं की संख्या समान है।
प्रत्येक बहुभुज P में भुजाओं की संख्या, बहुभुज P की भुजाओं की संख्या के बराबर है।
∴ (P, P) ∈ R, ∀P∈A
माना (P₁,P₂)∈R ⇒ बहुभुज P₁ तथा P₂ मे भुजाओं की संख्या समान हैं।
⇒ बहुभुज P₂ तथा बहुभुज P₁ में भुजाओं की संख्या समान हैं।
अत: R संक्रमक संबंध है।
R, स्वतुल्य, सममित तथा संक्रमक है।
अतः R एक तुल्यता संबंध है।
भुजाओं 3, 4 तथा 5 वाले समकोण त्रिभुज से वह बहुभुज संबंधित होगा जिसमें भुजाओं की संख्या तीन होगी। इसलिए भुजाओं 3, 4 तथा 5 वाले समकोण त्रिभुज से संबंधित बहुभुज त्रिभुज है। यही सिद्ध करना था।

प्रश्न 13.
यदि f(x) = \(\frac { 4x+3 }{ 6x-4 } \), x ≠ \(\frac{2}{3}\) हो, तो सिद्ध कीजिए कि सभी x ≠ \(\frac{2}{3}\) के लिए fof(x) = xहै। f का प्रतिलोम फलन क्या है? (NCERT)
हल:
f (x) = \(\frac { 4x+3 }{ 6x-4 } \)
fof (x) = f {f (x)}
f{ \(\frac { 4x+3 }{ 6x-4 } \) }

माना f का प्रतिलोम फलान f^-1(x) = y हैं।
तब f (y) = x
∴ \(\frac { 4y+3 }{ 6y-4 } \) = x
⇒ 4y + 3 = 6xy – 4x
⇒ 6xy – 4y = 3 + 4x
⇒ y (6x – 4) = 3 + 4x
⇒ y = \(\frac { 3+4x }{ 6x-4 } \)
⇒ f^-1 (x) = \(\frac { 3+4x }{ 6x-4 } \) = f(x)
∴ f^-1 = f.

प्रश्न 14.
सिद्ध कीजिए कि f : [-1, 1] → R, f (x) = \(\frac { x }{ x+2 } \) द्वारा प्रदत्त फलन एकैकी है। फलन f : [-1, 1] → (f का परिसर) का प्रतिलोम फलन ज्ञात कीजिए। (NCERT)
हल: f (x) = \(\frac { x }{ x+2 } \)
f : [-1, 1] → R
यहाँ, f (x) = f (y)
⇒ \(\frac { x }{ x+2 } \) = \(\frac { y }{ y+2 } \)
⇒ xy + 2x = xy + 2y
⇒ 2x = 2y
⇒ x = y यही सिद्ध करना था।
∴ f एकैकी है।
माना f^-1 (x) = y
∴ f (y) = x
⇒ \(\frac { y }{ y+2 } \) = x
⇒ y = xy + 2x
⇒ y (1 – x) = 2x
∴ y = \(\frac { 2x }{ 1-x } \)
⇒ f^-1(x) = \(\frac { 2x }{ 1-x } \)

प्रश्न 15.
यदि f (x) = \(\frac { x }{ 1+|x| } \), ∀ x ∈ R जहाँ -1 < x < 1, तो gof तथा fog ज्ञात कीजिए। दिखाइए कि fog = gof?
हल: दिया है,
f (x) = \(\frac { x }{ 1+|x| } \)
g (x) = \(\frac { x }{ 1-|x| } \)
∴ fog (x) = f {g(x)}
= f ( \(\frac { x }{ 1-|x| } \) )

= x ………………….. (2)
fog = gof
यही सिद्ध करना था।

प्रश्न 16.
तीन फलन f : N → N, g : N → N तथा h : N → R पर विचार कीजिए f (x) = 2x, g (y) = 3y + 4, तथा h (z) = sin z ∀ x, y तथा z ∈ N सिद्ध कीजिये की ho(gof)n = (hog)of? (NCERT)
हल:
ho(gof) x = h[gof(x)]
= h {g[f(x)}
= h (g (2x))
= h [3(2x) + 4]
= h [6x + 4]
= sin (6x + 4) ………………………… (1)
इसी प्रकार ((hog)of) x = (hog) f(x)
= (hog) 2x
= h (g (2x))
= h [3 (2x) + 4]
= h [6x + 4]
= sin (6x + 4)
समी, (1) और (2) से स्पस्ट है की
ho(gof) = (hog)of. यही सिद्ध करना था।

MP Board Class 12 Maths Important Questions

MP Board Class 11th Maths Important Questions Chapter 2 Relations and Functions

Relations and Functions Important Questions

Relations and Functions Objective Type Questions

(A) Choose the correct option :

Question 1.
If A = {2, 4, 5}, B = {7, 8, 9}, then n(A × B) =
(a) 6
(b) 9
(c) 3
(d) 0.
Answer:
(b) 9

Question 2.
If A = { 1, 2, 3, 4, 5} and 5 = {2, 3, 6, 7}, then the number of element in (A × B)∩(B × A) is:
(a) 4
(b) 5
(c) 10
(d) 20.
Answer:
(a) 4

Question 3.
If A and B are two non – empty sets, then:
(a) A × B = {(a, b) : a ∈ B, b ∈ A}
(b) A × B = {(a, b) : a ∈ A, b ∈ B}
(c) {(a, b) : (a, b) ∈ A, (a, b) ∈ B}
(d) None of these.
Answer:
(b) A × B = {(a, b) : a ∈ A, b ∈ B}

Question 4.
If f(x) = log \(\frac { 1+x }{ 1-x } \), then find f [ \(\frac { { 2x } }{ 1+{ x }^{ 2 } }\) ] =
(a) [f(x)]²
(b) [f(x)]³
(c) 2 f(x)
(d) 3 f(x).
Answer:
(c) 2 f(x)

Question 5.
Let A = {1,2} and B = {3,4}, then the number of relation from A to B will be:
(a) 2
(b) 4
(c) 8
(d) 16
Answer:
(d) 16

Question 6.
The range of the function f(x) = \(\sqrt { x-1 } \) is:
(a) [1, ∞)
(b) [0, ∞)
(c) (0, ∞)
(d) (1, ∞)
Answer:
(b) [0, ∞)

Question 7.
If f(x) = \(\frac { x^{ 2 }-1 }{ x^{ 2 }+1 } \), then f ( \(\frac{1}{x}\) ) is:
(a) f(x)
(b) – f(x)
(c) f(-x)
(d) \(\frac { 1 }{ f(x) } \)
Answer:
(b) – f(x)

Question 8.
Domain of the function f(x) = \(\frac { 1 }{ \sqrt { 2x-3 } } \) is:
(a) R – { \(\frac{3}{2}\) }
(b) ( \(\frac{3}{2}\), ∞)
(c) [ \(\frac{3}{2}\), ∞)
(d) None of these.
Answer:
(b) ( \(\frac{3}{2}\), ∞)

(B) Match the following :

Answer:

1. 1. (d)
   2. (a)
   3. (c)

1. (b)
2. (c)

(C) Fill in the blanks:

1. If A = {1, 2} and B = {3, 4, 5}, then the number of subsets of A × B is ………………………….
2. Range of the function f = {(2, 1), (3, 1), (4, 1), (5, 1)} is …………………………..
3. Range of the function f(x) = 11 – 7 sinx is …………………………..
4. If f(x) = x² and g(x) = x + 1, ∀ x ∈ R , then (f + g)x is …………………………
5. If f(x) = 1 – cosx, then the value of f ( \(\frac { \pi }{ 4 } \) ) …………………………….
6. Domain of the function f(x) = \(\frac { 1 }{ \sqrt { (1 – x)(x – 2) } } \) is ……………………………
7. If relation R = {(1, 3), (3, 3), (4, 5)} then the value of R^-1 is ……………………………

Answer:

1. 64
2. {1}
3. [4, 18]
4. x² + x + 1
5. 1 – \(\frac { 1 }{ \sqrt { 2 } } \)
6. (1, 2)
7. {(3, 1), (3, 3), (5, 4)}.

(D) Write true/false :

1. If A, B, C are three sets, then the value of A × (B∪C) is (A∪B) × (A∪C).
2. If A = {x : x² – 5x + 6 = o}, B = {2,4}, C = {4,5}, then A × (B∩C) = {(2, 4), (3, 4)}.
3. The relation R = {(2, 1), (3, 2), (4, 3), (5, 4)} is a function.
4. If a relation on Z is R = {(x, y) : x, y ∈ Z, x² + y² ≤ 4}, then domain of R is {0, ± 1, ± 2}.
5. Domain of the function f(x) = \(\sqrt { a^{ 2 }-x^{ 2 } } \), a > 0 is [0, a].

Answer:

1. False
2. True
3. True
4. True
5. False

(E) Write answer in one word/sentence:

1. If f(x) = x² and g(x) = x + 3, x ∈ R, then the value of (fog)(2).
2. Range of function f(x) = sin x.
3. If mapping f : R → R is defmd by f(x) = x² + 1 the value of f^-1 (26) is:
4. If A = {1, 2, 3} and B = {5, 7}, then the value of A×B is:
5. Domain of the function f(x) = \(\sqrt { 3-2x } \) is:
6. If function f(x) = \(\frac { { x }^{ 2 } }{ 1-{ x }^{ 2 } }\), then the value of f(sin θ) is :

Answer:

1. 25
2. [-1, 1]
3. {-5, 5}
4. {(1, 5), (1, 7), (2, 5), (2, 7), (3, 5), (3, 7)}
5. (-∞, \(\frac { 3 }{ 2 }\))
6. tan² θ

Straight Lines Very Short Answer Type Questions

Question 1.
If the set A has 3 elements and the set B = {3, 4, 5}, then find the number of elements in ( A x B). (NCERT)
Solution:
Given : n(A) = 3, B = {3, 4, 5}, n (B) = 3
∴ n (A x B) = n (A) x n (B) = 3 x 3
⇒ n (A x B) = 9.

Question 2.
If G = {7, 8} and H = {5, 4, 2}, then find G x H. (NCERT)
Solution:
G x H = { 7, 8} x {5, 4, 2}
G x H= { (7, 5), (7, 4), (7, 2), (8, 5), (8, 4), (8, 2)}.

Question 3.
If A x B = { (a, x), (a, y), (b, x), (b, y)} then find A and 5. (NCERT)
Solution:
Given:
A x B = {(a, x), (a, y), (6, x), (6, y)}
A = {a, b} and S = {x, y}.

Question 4.
If A = {1, 2} and B = {3, 4} then find A x B. (NCERT)
Solution:
A x B = { 1, 2} x {3, 4}
A x B = { ( 1, 3), (1, 4), (2, 3), (2, 4)}

Question 5.
The figure shows the relationship between the set P and Q. Write the relation : (NCERT)

1. In set builder form
2. In roster form
3. Find its domain
4. Find its range.

Solution:

1. Set builder form, R = {(x, y) : y = x – 2, x ∈ P and y ∈ Q}.
2. Roster form, R = {(5, 3), (6, 4), (7, 5)}
3. Domain = {5, 6, 7}
4. Range = {3, 4, 5}.

Question 6.
Let A = (1, 2, 3, 4, 6} and R be the relation on A defined by
{(a, b) : a, b ∈ A, b is exactly divisible by a } :

1. Write R in roster form,
2. Find the domain of R
3. Find the range of R. (NCERT)

Solution:
Given: A = {1, 2, 3, 4, 6}
1. R = {{a, b): a, be A, b is exactly divisible by a }
R= {(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (6, 6)}.

2. Domain = {1, 2, 3, 4, 6}.

3. Range = {1, 2, 3, 4, 6}.

Question 7.
Let A = {x, y, z} and B = {1, 2}. Find the number of relations from A to B. (NCERT)
Solution: A = {x, y, z}, B= {1, 2}
n(A) = 3, n(B) = 2
No. of relations from A to B = 2^mn = 23^3/2 = 2⁶
= 64.

Question 8.
A function f is defined by f (x) = 2x – 5, write down the following values : (NCERT)

1. f(0)
2. f(7)
3. f(-3).

Solution:
Given: f(x) = 2x – 5
1. Put x = 0,
f(0) = 2(0) – 5 = 0 – 5 = – 5.

2. Put x = 7,
f(7) = 2 x 7 – 5 = 14 – 5 = 9.

3. Put x = – 3,
f(- 3) = 2(- 3) – 5 = – 6 – 5 = – 11.

Question 9.
The function ‘t’ which maps temperature in degree celcius into temperature in degree fehrenheit, it is defined as t(c) = \(\frac { 9c }{ 5 }\) +32. Find the following : (NCERT)

1. t (0)
2. t (28)
3. t (- 10)
4. Find c, when t (c) = 212.

Solution:
Given :
t(c) = \(\frac { 9c }{ 5 }\) + 32
1. Put c = 0,
t(0) = \(\frac { 9 × 0 }{ 5 }\) + 32
⇒ t(0) = 32

2. Put c = 28,
t(28) = \(\frac { 9 × 28 }{ 5 }\) + 32 = \(\frac { 252}{ 5 }\) + \(\frac { 32}{ 1 }\)
⇒ t(28) = \(\frac { 252 + 160}{ 5 }\) = \(\frac { 412}{ 5 }\)

3. Put c = – 10,
t(- 10) = \(\frac { 9 x (- 10)}{ 5 }\) + 32
⇒ t(- 10) = – 18 + 32 = 14

4. Put t(c) = 212,
212 = \(\frac { 9c }{ 5 }\) + 32
⇒ \(\frac { 9c }{ 5 }\) = 212 – 32
⇒ \(\frac { 9c }{ 5 }\) = 180
⇒ c = \(\frac { 180 x 5 }{ 9 }\)

Question 10.
Find the domain and range of the function f(x) = |x|.
Solution:
f(x) = – |x|, f(x) < 0
Domain of f = R.
Range of f = {y : y ∈ R, y ≤ 0} = (- ∞, 0].

Straight Lines Short Answer Type Questions

Question 1.
Find the domain and range of the function f(x) = \(\sqrt { 9 – { x }^{ 2 } }\).
Solution:
Given : f(x) = \(\sqrt { 9 – { x }^{ 2 } }\)
Value of f(x) is real, if f(x) ≥ 0
9 – x² ≥ 0
⇒ – (x² – 9) ≥ 0
⇒ x² – 9 ≤ 0
⇒ (x + 3)(x – 3) ≤ 0
∴ Domain = [- 3, 3].

Question 2.
If f(x) = x², then find \(\frac { f(1.1) – f(1)}{ (1.1 – 1)}\)
Solution:
f(x) = x²
f(1.1) = (1.1)² = 1.21
f(1) = 1² = 1

Question 3.
Find domain of function f(x) = \(\frac { { x }^{ 2 } + 2x + 1 }{ { x }^{ 2 } – 8x + 12 }\)
Solution:
Given function is :

f(x) will be defined if,
x² – 8x + 12 ≠ 0
⇒ x² – 6x – 2x + 12 ≠ 0
⇒ x(x – 6) – 2(x – 6) ≠ 0
⇒ (x – 2)(x – 6) ≠ 0
x ≠ 2 and x ≠ 6
Domain of function = R – {2, 6}.

Question 4.
Let f : g → R → R be defined by f(x) = x + 1 and g(x) = 2x – 3 respectively, then find :

1. f + g
2. \(\frac { f }{ g }\)

Solution:
Given: f(x) = x + 1, g (x) = 2x – 3
1. (f + g)x = f(x) + g(x)
= x + 1 + 2x – 3
∴ (f + g)x = 3x – 2

2. \(\frac { f }{ g }\)(x) = \(\frac { f(x)}{ g(x) }\) = \(\frac { x +1 }{ 2x – 3}\)

Question 5.
If f(x) = x² – \(\frac { 1 }{ { x }^{ 2 } }\), then prove that:
f(x) + f\(\frac { 1 }{ x }\) = 0
Solution:

Question 6.
If f(x) = \(\frac { { x }^{ 2 } }{ 1-{ x }^{ 2 } }\), then prove that:
f(sinθ) = tan² θ.
Solution:

Question 7.
If f(x) = x³ + 3x + tanx, then prove that f(x) is an odd function.
Solution:
Given : f(x) = x³ + 3x + tanx
f(- x) = (- x)³ + 3(- x) + tan(- x)
= – x³ – 3x – tanx
= – (x³ + 3x + tanx)
= – f(x).
Hence, f(x) is an odd function.

Question 8.
If f(x) = x² + 2xsinx + 3, then prove that f(x) is an even function.
Solution:
Given: f(x) = x² + 2x sin x + 3
f(- x) = (- x)² + 2(- x) sin(- x) + 3
= x² + 2xsinx + 3, [∵ sin(- x) = – sinx]
= f(x).
Hence, f(x) is an even function

Question 9.
If f(x) = x², g(x) = x + 2, ∀ x ∈R, then find gof and fog. Is gof = fog.
Solution:
Given : f(x) = x², g(x) = x + 2
fog(x) = f[g(x)]
= f(x + 2) = (x+2)².
gof(x) = g[f(x)]
= g(x²) = x² + 2
Hence, fog(x) ≠ gof(x).

Question 10.
If f(x) = e^2x and g(x) = log \(\sqrt {x}\), x> 0, then find the value of fog(x) and gof(x).
Solution:

MP Board Class 11th Maths Important Questions

MP Board Class 11th Maths Important Questions Chapter 10 Straight Lines

Straight Lines Long Answer Type Questions

Question 1.
The slope of a line is double the slope of another line. If tangent of the angle between them is \(\frac {1}{3}\), then find the slope of the line.
Solution:
Let the angle between two lines be θ.

⇒ 1 + 2m² = 3m
⇒ 2m² – 3m + 1 = 0
⇒ 2m² – 2m – m + 1 = 0
⇒ 2m(m – 1) – 1 (m – 1) = 0
⇒ (m – 1)(2m – 1) = 0
⇒ m = 1,\(\frac {1}{2}\)

Question 2.
If three points (h, 0), (a, b) and (0, k) lies on same line, then prove that \(\frac {a}{h}\) + \(\frac {b}{k}\) = 1. (NCERT)
Solution:
Given points are A(h, 0), B(a, b) and C(0, k).

ab = (b – k)(a – h)
⇒ ab = ab – bh – ak + hk
⇒ bh + ak = hk
⇒ \(\frac {bh}{hk}\) \(\frac {ak}{hk}\) \(\frac {hk}{hk}\), (dividing both sides by hk)
⇒ \(\frac {a}{h}\) + \(\frac {b}{k}\) = 1.

Question 3.
Find the equation of the line passing through (- 3, 5) and perpendicular to the line through the points (2, 5) and (- 3, 6). (NCERT)
Solution:
Gradient of AB = m = \(\frac { { y }_{ 2 } – { y }_{ 1 } }{ { x }_{ 2 } – { x }_{ 1 } }\)
Where x₁ = 2 , y₁ = 5, x₂ = – 3, y₂ = 6
∴ m = \(\frac {6 – 5}{- 3 – 2}\) = \(\frac {1}{- 5}\)

Let the gradient of CD = m₁,
AB ⊥ CD
m x m₁ = – 1
⇒ \(\frac {-1}{5}\) x m₁ = – 1
⇒ m₁ = 5
Equation of line CD will be :
y – y₁ = m(x – x₁)
Here x₁ = – 3, y₁ = 5, m = 5 .
⇒ y – 5 = 5(x + 3)
⇒ y – 5 = 5x + 15
⇒ 5x – y + 20 = 0.

Question 4.
Find the equation of straight line passing through the point (2, 2) and cutting off intercepts the axes whose sum is 9. (NCERT)
Solution:
Let the required equation of line is :
\(\frac {x}{a}\) + \(\frac {y}{b}\) = 1 …. (1)
Given: a + b = 9 …. (2)
Line (1) passes through point (2, 2).
∴ \(\frac {2}{a}\) + \(\frac {2}{b}\) = 1
\(\frac {2a + 2b}{ab}\) = 1
2a + 2b = ab
Put b = 9 – a from equation (2), we get
2a + 2(9 – a) = a(9 – a)
⇒ 2a + 18 – 2a = 9a – a²
⇒ a² – 9a + 18 = 0
⇒ a² – 6a – 3a + 18 = 0
⇒ a (a – 6) – 3(a – 6) = 0
⇒ (a – 3)(a – 6) = 0
∴ a = 3 or a = 6
When a = 3, then b = 9 – a = 9 – 3 = 6
Hence the required equation is :
\(\frac {x}{3}\) + \(\frac {y}{6}\) = 1
⇒ 2x + y = 6.
When a = 6, then b = 9 – 6 = 3
Hence the required equation is :
\(\frac {x}{6}\) + \(\frac {y}{3}\) = 1
⇒ x + 2 y = 6.

Question 5.
Find the equation to that straight line which passes through the point (7,9) and such that the portion between the axes is divided by the point in the ratio 3 : 1.
Solution:
Let the required equation of the line is :
\(\frac {x}{a}\) + \(\frac {y}{b}\) = 1 …. (1)
Let the required line cuts the axes at points A (a, 0) and B(0, b),
and Point P intercept the line AB internally in ratio 3 : 1.

Putting values of a and b in eqn. (1), we get
\(\frac {x}{28}\) + \(\frac {y}{12}\) = 1
\(\frac {3x + 7y}{84}\) = 1
Hence required equation is 3x + 7y = 84.

Question 6.
Find the equation of the line which passes through the point (1, 2) and makes a right angled triangle with axes of area \(\frac {9}{2}\) sq units.
Solution:
Area of (∆AOB) = \(\frac {1}{2}\)a.b
⇒ \(\frac {9}{2}\) = \(\frac {1}{2}\)a.b
⇒ ab = 9

Let the equation of line \(\frac {x}{a}\) + \(\frac {y}{b}\) = 1 which passes through point (1, 2)
∴ \(\frac {1}{a}\) + \(\frac {2}{b}\) = 1
From equation (1), b = \(\frac {9}{a}\)
∴ \(\frac {1}{a}\) + \(\frac {2}{9}\) = 1
⇒ 9 + 2a² = 9a
⇒ 2a² – 9a + 9 = 0
⇒ 2a² – 3a – 6a + 9 = 0
⇒ a(2a – 3) – 3(2.a – 3) = 0
⇒ (2a – 3)(a – 3) = 0
∴ b = 6, 3
Equation of line \(\frac {x}{3/2}\) + \(\frac {y}{6}\) = 1
⇒ \(\frac {2x}{3}\) + \(\frac {y}{6}\) = 1
⇒ 12x + 3y = 18
⇒ 4x + y = 6
or \(\frac {x}{3}\) + \(\frac {y}{3}\) = 1
⇒ x + y = 3

Question 7.
If p is the length of perpendicular from the origin to the line whose intercepts on the axes are a and b, then prove that \(\frac { 1 }{ { p }^{ 2 } }\) = \(\frac { 1 }{ { a }^{ 2 } }\) + \(\frac { 1 }{ { b }^{ 2 } }\) (NCERT)
Solution:
Equation of given line be :
\(\frac {x}{a}\) + \(\frac {y}{b}\) = 1
⇒ bx + ay = ab
⇒ bx + ay – ab = 0 …. (1)
Let the form of required equation be :
xcosα + ysinβ – p = 0 …. (2)
Comparing equation (1) and (2),

Question 8.
Find the angle between the lines.
y = (2 – \(\sqrt {3}\))x + 6 and y = (2 + \(\sqrt {3}\))x – 8.
Solution:
y = (2 – \(\sqrt {3}\))x + 6 … (1)
m₁ = 2 – \(\sqrt {3}\)
Second line y = (2 + \(\sqrt {3}\))x – 8
m₂ = 2 + \(\sqrt {3}\)
Let θ be the angle between them,

Question 9.
If the perpendicular drawn from origin on line y = mx + c intersect the line at point (- 1, 2), then find the value of m and c. (NCERT)
Solution:
Let the equation of AB be :
y = mx + c … (1)
Gradient of eqn. (1) is m and OP is perpendicular to AB

Gradient of OP m₁ = \(\frac { { y }_{ 2 } – { y }_{ 1 } }{ { x }_{ 2 } – { x }_{ 1 } }\)
m₁ = \(\frac {2 – 0}{- 1 – 0}\) = – 2
∵ Op ⊥ AB
∴ m × m₁ = – 1
⇒ m(- 2) = – 1
⇒ m = \(\frac {1}{2}\)
put value of m in equation (1),
y = \(\frac {1}{2}\)x + c
Above equation passes through point (-1, 2), hence it will satisfy it.
2 = \(\frac {- 1}{2}\) + c
⇒ c = 2 + \(\frac {1}{2}\) = \(\frac {5}{2}\)
∴ m = \(\frac {1}{2}\), c = \(\frac {5}{2}\)

Question 10.
Find the coordinate of the foot of perpendicular from the point (- 1, 3) to the line 3x – 4y – 16 = 0.
Solution:
Equation of line CD is :
3x – 4y – 16 = 0  … (1)
Equation of line AB is perpendicular to equation (1),
4x + 3y + c = 0  … (2)

Equation (2) passes through point (- 1, 3).
∴ 4(- 1) + 3 x 3 + c = 0
– 4 + 9 + c = 0
c = – 5
Put c = – 5 in equation (2), we get 4x + 3y – 5 = 0
Now the intersection of lines (1) and (3) is the foot of perpendicular B
3x – 4y – 16 = 0
4x + 3y – 5 = 0
By cross multiplication method,

Question 11.
Find the equation of line parallel to y – axis and drawn through the point of intersection of line x – 7y + 5 = 0 and 3x + y = 0. (NCERT)
Solution:
Equation of given lines are :
x – 7y + 5 = 0 … (1)
3x + y = 0 … (2)
Equation of straight line passing through the intersection of equation (1) and (2) is :
x – 7y + 5 + λ(3x + y) = 0 … (3)

Put A = 7 in equation (3), we get
x – 7y + 5 + 7(3x + y) = 0
⇒ x – 7y + 5 + 21x + 7y = 0
⇒ 22x + 5 = 0.

Question 12.
Find the value of p so that the three lines 3x + y – 2 = 0, px + 2y – 3 = 0 and 2x – y – 3 = 0 may intersect at one point. (NCERT)
Solution:
Equation of given lines are :
3x + y – 2 = 0 … (1)
px + 2y – 3 = 0 … (2)
2x – y – 3 = 0 … (3)
From eqns. (1) and (3),
3x + y – 2 = 0
2x – y – 3 = 0
Solving by cross multiplication method,

Lines intersect at the one point, hence point (1, – 1) will satisfy equation (2). p(1) – 2 x 1 – 3 = 0
p = 5.

Question 13.
Find the equation of a line drawn perpendicular to the line \(\frac {x}{4}\) + \(\frac {y}{6}\) = 1 through the point where it meets the y – axis. (NCERT)
Solution:
Given equation is :
\(\frac {x}{4}\) + \(\frac {y}{6}\) = 1
Line (1) meets the F – axis at point (0, 6).
From eqn. (1), \(\frac {6x + 4y}{24}\) = 1
⇒ 6x + 4y = 24
⇒ 6x + 4y – 24 = 0 … (2)
Equation of line perpendicular to eqn. (2),
4x – 6y + c = 0 … (3)
Above equation passes through point (0, 6).
∴ 4 x 0 – 6 x 6 + c = 0
c = 36
Put value of c = 36 in equation (3),
4x – 6y + 36 = 0
2x – 3y + 18 = 0.

Question 14.
For what value of k the equation (k – 3) x (4 – k²)y + k² – 7k + 6 = 0 is :

1. Parallel to X – axis
2. Parallel to y – axis
3. Passes through origin.

Solution:
Equation of given line is :
(k – 3)x – (4 – k²)y + k² – 7k+6 = 0
(4 – k²)y = (k – 3)x + k² – 7k + 6
⇒ y = \(\frac { (k – 3)x }{ 4 – { k }^{ 2 } }\) + \(\frac { { k }^{ 2 } – 7k + 6 }{ 4 – { k }^{ 2 } }\)

1. Line parallel to X – axis :
∴ m = 0
⇒ \(\frac { k – 3 }{ 4 – { k }^{ 2 } }\)
⇒ k – 3 = 0
⇒ k = 3.

2. Line parallel to Y – axis :
∴ m = \(\frac {1}{0}\)
⇒ \(\frac { k – 3 }{ 4 – { k }^{ 2 } }\)
⇒ 4 – k² = 0
⇒ k²= 4
⇒ k = ± 2

3. Line passing through origin, if c = 0.
∴ \(\frac { { k }^{ 2 } – 7k + 6 }{ 4 – { k }^{ 2 } }\)
⇒ k² – 7k+6 = 0
⇒ k² – 6k – k+6 = 0
⇒ k(k – 6) – 1(k – 6) = 0
⇒ (k – 6)(k – 6) = 0
∴ k = 1, 6

Question 15.
The line passing through the points (h, 3) and (4,1) meets the line 7x – 9y – 19 = 0 at right angle. Find the value of h.
Solution:
Equation of given line is :
7x – 9y – 19 = 0
⇒ 9y = 7x – 19
⇒ y = \(\frac {7}{9}\)x – \(\frac {19}{9}\) … (1)
Gradient of eqn. (1) m₁ = \(\frac {7}{9}\)
Equation of line passing through points (h, 3) and (4, 1),
m₂ = \(\frac { { y }_{ 2 } – { y }_{ 1 } }{ { x }_{ 2 } – { x }_{ 1 } }\)
m₂ = \(\frac {1 – 3}{4 – h}\) = \(\frac {- 2}{4 – h}\)
∵ Lines are perpendicular.
∴m₁ x m₂= – 1
\(\frac {7(- 2)}{9(4 – h)}\) = – 1
⇒ – 14 = – 36 + 9h
⇒ 9h = 36 – 14
⇒ 9h = 22
∴ h =\(\frac {22}{9}\).

Question 16.
If the lengths of the perpendiculars drawn from origin on the straight lines xcosθ – y sinθ = kcos2θ and xsecθ + y cosec θ = k are p and q then prove that:
p² + 4q² = k²
Solution:
Equation of given lines :
xsecθ + ycosecθ = k … (1)
and x cosθ – y sinθ = k cos2θ … (2)
Length of perpendicular from origin on equation (1),

Adding equation (3) and (4),
4q² + p² = k² sin² 2θ +k² cos² 2θ
= k²(sin² 20 + cos²2θ)
⇒ p² + 4q² = k² .

Question 17.
Find the equation to the straight line passing through the intersection of lines 4x + 7y – 3 = 0 and 2x – 3y + 1 = 0 and makes an equal intercept on both the axes.
Solution:
Equation of given lines are :
4x + 7y – 3 = 0 … (1)
2x – 3y + 1 = 0 … (2)
Equation of straight line passing through intersection of lines (1) and (2),
4x + 7y – 3 + λ(2x – 3y + 1) = 0 … (3)
⇒ x(4 + 2 λ) + y(7 – 3 λ) – 3 + λ = 0
⇒ x(4 + 2 λ) + y(7 – 3 λ) = 3 – λ

Put λ = \(\frac {3}{5}\) in equation (3),
4x + 7y – 3 + \(\frac {3}{5}\)(2x – 3y + 1) = 0
⇒ 20x + 35y – 15 + 6x – 9y +3 = 0
⇒ 26x + 26y = 12
⇒ 13x + 13y = 6.
⇒ 13x + 13y – 6 = 0.

Question 18.
Find the distance of point (-1, 1) from the line 12 (x + 6) = 5 (y – 2). (NCERT)
Solution:
Equation of given line is :
12(x + 6) = 5(y – 2)
⇒ 12x + 72 = 5y – 10
⇒ 12x – 5y + 82 = 0
Length of perpendicular

Question 19.
Find the points on the X – axis, whose distance from the line \(\frac {x}{3}\) + \(\frac {y}{4}\) = 1 are 4 units. (NCERT)
Solution:
Equation of given line is :
\(\frac {x}{3}\) + \(\frac {y}{4}\) = 1
⇒ 4x + 3y = 12
⇒ 4x + 3y – 12 = 0
Let the point on X – axis is (h, 0).
Length of perpendicular drawn from point (h, 0) is 4.

Taking (+) sign,
4h = 20 + 12 = 32
⇒ h = 8
Taking (-) sign,
4h = – 20 + 12
⇒ 4h = – 8
⇒ h = – 2
Point on X – axis are ( – 2, 0) and (8, 0).

Question 20.
Find the distance between two parallel lines : 15x + 8y – 34 = 0 and 15x + 8y + 31 = 0.
Solution:
Equation of given lines are :
15x + 8y – 34 = 0
15x + 8y + 31 = 0
Put x = 0 in eqn. (1),
15(0) + 8y – 34 = 0
⇒ 8y = 34
y = \(\frac {34}{8}\) = \(\frac {17}{4}\)
Point (0, \(\frac {17}{4}\)) is on line (1),
Length of perpendicular from point (0, \(\frac {17}{4}\)) on equation (2),

= \(\frac {65}{17}\) units
Hence the distance between lines is \(\frac {65}{17}\) units

Question 21.
The length L (in centimeters) of a copper rod is a linear function of its Celsius temperature C. In an experiment. If L = 124.942 when C= 20 and L = 125.134 when C = 110. Express L in terms of C. (NCERT)
Solution:
Given : L = 124.942 when C = 20
L = 125.134 when C= 110
In coordinate form points (20, 124.942) and (110, 125.134) are two points.
Required equation of straight line :

Question 22.
The owner of a milk store finds that he can sell 980 L of milk each week at Rs. 14/L and 1220 L of milk each week at Rs. 16/L. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at Rs. 17 L? (NCERT)
Solution:
Let price and litre be denoted in ordered pair (x, y), two points are (14, 980) and (16,1220).
∴ Required equation of straight line will be :
y – y₁ = \(\frac { { y }_{ 2 } – { y }_{ 1 } }{ { x }_{ 2 } – { x }_{ 1 } }\)(x – x₁)
⇒ y – 980 = \(\frac {1220 – 980}{16 – 14}\)(x – 14)
⇒ y – 980 = \(\frac {240}{2}\)(x – 14)
⇒ y – 980 = 120 (x – 14)
⇒ y – 980 = 120 x – 120 x 14
⇒ y = 120 x – 1680 + 980
⇒ y = 120 x – 700
When x = 17, then
y = 120 x 17 – 700
⇒ y = 2040 – 700
⇒ y = 1340
Hence, he will sell weekly 1340 L milk at the rate of Rs. 17 L.

MP Board Class 11th Maths Important Questions

MP Board Class 11th Maths Important Questions Chapter 1 Sets

Sets Important Questions

Sets Objective Type Questions

(A) Choose the correct option:

Question 1.
A set is defind as:
(a) Collection of an object
(b) Collection of well defind object
(c) Nothing can be said
(d) None of these.
Answer:
(b) Collection of well defind object

Question 2.
If A = {1, 2, 3},B = {2, 3, 4} and U = {1, 2, 3, 4, 5, 6},then A’ ∩ B’ =
(a) {2, 3}
(b) {1, 5,6}
(c) {5, 6}
(d) {1, 4, 5, 6}.
Answer:
(c) {5, 6}

Question 3.
A and B are two sets, then A ∩ (A ∪ B) =
(a) A
(b) B
(c) ϕ
(d) None of these.
Answer:
(a) A

Question 4.
A set A = {x : x ∈ R, x² = 16 and 2x = 6} =
(a) ϕ
(b) {14,3,4}
(c) {3}
(d) {4}.
Answer:
(a) ϕ

Question 5.
For a non – empty set A:
(a) A∪A’ = A
(b) A∪A’ = A’
(c) A∪A’ = U
(d) A∪A’ = ϕ .
Answer:
(c) A∪A’ = U

Question 6.
If two non – empty sets A and B are not equal, then:
(a) A⊂A∩B
(b) B⊂A∩B
(c) A∩B⊂B
(d) A∩B⊂ϕ.
Answer:
(c) A∩B⊂B

Question 7.
A and B are two sets and n(A) = 70, n(B) = 60 and n(A∪B) = 110, then n(A∩B) =
(a) 240
(b) 50
(c) 40
(d) 20.
Answer:
(d) 20.

Question 8.
If A = {1,2,3,4,5}, then the number of proper subsets:
(a) 120
(b) 30
(c) 31
(d) 32.
Answer:
(d) 32.

Question 9.
If A, B and C are three sets, then A – (B∪C) is equal to:
(a) (B – A)∩C
(b) (A – B) ∪C
(c) (A – B) ∩(A – C)
(d) (A – B) ∪(A – C)
Answer:
(c) (A – B) ∩(A – C)

Question 10.
Let S = {1,2,3,4}. The total numbers of unordered pair of disjoint subsets of S is equal to:
(a) 25
(b) 34
(c) 42
(d) 41.
Answer:
(d) 41.

(B) Match the following:

Answer:

1. (e)
2. (c)
3. (a)
4. (b)
5. (f)
6. (d)

(C) Fill in the blanks:

1. If the elements of A mid B are 3 and 6, then minimum number of elements in A∪B is …………………………….
2. If X and Y are two sets such that n(X) = 17, n(Y) = 23 and n(X∪Y) = 38, then n(X∩Y) = …………………………
3. If sets A = {1, 2, 3, 4, 5, 6} and B = {2, 4, 6, 8}, then B – A = ……………………………..
4. A set which does not contain any element is called ………………………….
5. If set A has n elements, then the number of subsets of A are …………………………..
6. If A = {1, 2} and B = {3, 4}, then (A∪B)∩ϕ = ……………………………..

Answer:

1. 6
2. 2
3. {8}
4. Empty set
5. 2ⁿ
6. ϕ

(D) Write true/false:

1. If A ∩ B = B, then B ⊂ A.
2. If A = {1, 2, 3, 4} and B = {2, 3, 4, 5, 6}, then A ∆ B = {1, 5, 6}.
3. If n(A – B) = n(A) – n(A n B).
4. For a non – empty sets A is A∩A’- A’.
5. If A = {1, 2, 3, 4}, then n[P(A)] = 16.

Answer:

1. False
2. True
3. True
4. False
5. True.

Question (E)
Write answer in one word/sentence:

1. If A = {1, 2}, then write all the subsets of set A.
2. If A = {4, 5, 8, 12} and B = {1, 4, 6, 9}, then find the value of A – (B – A).
3. If n(U) = 700, n(A) = 200, n(B) = 300, and n(A∩B) = 100, then find the value of n(A’∩B’). ‘
4. Find the value of n[P{P{P(ϕ}}]
5. If A = {a, b, c, d}, then find all subsets of set A.
6. If U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, B = {2, 4, 6, 8} and C = {3, 4, 5, 6}, then find the value of (B – C)’.

Answer:

1. ϕ, {1}, {2}, {1,2}
2. {4, 5, 8, 12}
3. 300
4. 4
5. 16
6. {1, 3, 4, 5, 6, 7, 8, 9}.

Sets Very Short Answer Type Questions

Question 1.
Write the following sets in set builder form: (NCERT)

1. {3, 6, 9, 12}
2. {2, 4, 8, 16, 32}
3. {5, 25, 125, 625}
4. {2, 4, 6,},
5. {1, 4, 9, ………… 100}.

Solution:

1. A = {x : x is a natural number, multiple of 3 and x < 15}
2. B = {x : x = 2ⁿ, x∈N and n < 6}
3. C = {x : x = 5ⁿ, and x∈N and n ≤ 4}
4. D = {x : x is an even natural number}
5. E = {x : x = n², x ∈ N and n < 11}.

Question 2.
Write the following sets in roster form: (NCERT)

1. A = {x : x is an odd natural number}
2. B = {x : x is an integer – \(\frac{1}{2}\) < x < \(\frac{9}{2}\)
3. C = {x : x is an integer x² ≤ 4}
4. D = {x : x is a letter of a word LOYAL}
5. E = {x : x is a month of year which does not have 31 days}
6. F – {x : x is a consonant of English alphabet which comes before k}

Solution:

1. A = {1, 3, 5, 7, 9}
2. B = {0, 1, 2, 3, 4}
3. C = {-2, -1, 0, 1, 2}
4. D = {L, 0, Y, A}
5. E = {FEBRUARY, APRIL, JUNE, SEPTEMBER, NOVEMBER}
6. F = {b, c, d, f, g, h, j}.

Question 3.
From following find whether A = B. (NCERT)

1. A = {a, b, c, d}, B = {d, c, b, a}.
2. A = {4, 8, 12, 16}, B = {8,4, 16, 18}.
3. A = {2, 4, 6, 8, 10}, B = {x : x is a positive even integer x < 10}.
4. A = {x : x is a multiple of 10}, B = {10, 15, 20, 25, 30}.

Solution:
1. A = {a, b, c, d}, B = {d, c, b, a}
All the elements of set A is in set B
A = B.

2. A = {4, 8, 12, 16}, B = {8, 4, 16, 18}
All the elements of A is not in set B.
∴ A≠B.

3. Here A = {2, 4, 6, 8, 10} and B = { x : x is an even number and x ≤ 10}
B = {2, 4, 6, 8, 10}
i.e., The elements of set A and B are same.
∴ A = B

4. Here A = {x : x is a multiple of 10} = {10, 20, 30, 40}
and B = {10, 15, 20, 25, 30, …}
The elements of set A and B are not same.
∴ A≠B.

Question 4.
If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8} and D = {7, 8, 9, 10} then find the following: (NCERT)

1. A∪B
2. A∪C
3. B∪C
4. B∪D

Solution:

1. A ∪ B = {1, 2, 3, 4} ∪ {3, 4, 5, 6} = {1, 2, 3, 4, 5, 6}.
2. A ∪ C = {1, 2, 3, 4} ∪ {5, 6, 7, 8} = {1, 2, 3, 4, 5, 6, 7, 8}.
3. B ∪ C = {3, 4, 5, 6} ∪ {5, 6, 7, 8} = {3, 4, 5, 6, 7, 8}
4. B ∪ D = {3, 4, 5, 6} ∪ {7, 8, 9, 10} = {3, 4, 5, 6, 7, 8, 9, 10}

Question 5.
If A = {3, 5, 7, 9, 11}, B = {7, 9, 11, 13}, C= {11, 13, 15} and D = {15, 17} then, find the following:

1. A ∩ B
2. B ∩ C
3. A ∩ C
4. B ∩ D

Solution:

1. A ∩ B = {3, 5, 7, 9, 11} ∩ {7, 9, 11, 13} = {7, 9, 11}
2. B ∩ C = {7, 9, 11, 13} ∩ {11, 13, 15} = {11, 13}
3. A ∩ C = {3, 5, 7, 9, 11} ∩ {11, 13, 15} = {11}
4. B ∩ D = {7, 9, 11, 13} ∩ {15, 17} = ϕ

Question 6.
If A = {3, 6, 9, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20} then, find the following: (NCERT)

1. A – B
2. A – C
3. A – D
4. B – A
5. C – A
6. D – A
7. B – C
8. B – D
9. C – B
10. D – B
11. C – D
12. D – C?

Solution:
Let A and B are two sets and A – B is a set of those elements which one present in A and not in B.

1. A – B = {Those elements present in A and not in B}
= {3, 6, 9, 12, 15, 18, 21} – {4, 8, 12, 16, 20}
= {3, 6, 9, 15, 18, 21}.

2. A – C = {Those elements present in A and not in C}
= {3, 6, 9, 12, 15, 18, 21} – {2, 4, 6, 8, 10, 12, 14, 16}
= {3, 9, 15, 18, 21}.

3. A – D = {The elements which are in A but not in D}
= {3, 6, 9, 12, 15, 18, 21} – {5, 10, 15, 20}
= {3, 6, 9, 12, 18, 21}.

4. B – A = {The elements which are in B but not in A}
= {4, 8, 12, 16, 20} – {3, 6, 9, 12, 15, 18, 21}
= {4, 8, 16, 20}.

5. C – A = {The elements which are in C but not in A}
= {2, 4, 6, 8, 10, 12, 14, 16} – {3, 6, 9, 12, 15, 18, 21}
= {2, 4, 8, 10, 14, 16}.

6. D – A = {The elements which are in D but not in A}
= {5, 10, 15, 20} – {3, 6,9, 12, 15, 18, 21}
= {5, 10, 20}.

7. B – C = {The elements which are in B but not in C}
= {4, 8, 12, 16, 20} – {2, 4,6, 8, 10, 12, 14, 16}
= {20}.

8. B – D = {The elements which are in B but not in D}
= {4, 8, 12, 16, 20} – {5, 10, 15, 20}
= {4, 8, 12, 16}.

9. C – B = {The elements which are in C but not in B}
= {2, 4, 6, 8, 10, 12, 14, 16} – {4, 8, 12, 16, 20}
= {2, 6, 10, 14}.

10. D – B = {The elements which are in D but not in B}
= {5, 10, 15,20} – {4, 8, 12, 16, 20}
= {5, 10, 15}.

11. C – D = {The elements which are in C but not in D}
= {2, 4, 6, 8, 10, 12, 14, 16} – {5, 10, 15, 20}
= {2, 4, 6, 8, 12, 14, 16}.

12. D – C = {The elements which are in D but not in C}
= {5, 10, 15, 20} – {2, 4, 6, 8, 10, 12, 14, 16}
= {5, 15, 20}.

Question 7.
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {1, 2, 3, 4}, B = {2, 4, 6, 8} and C then find the following:

1. A’
2. B’
3. (A ∪ C)’
4. (A ∩ B)’
5. (A’)’
6. (B – C)’
7. (B – C)’

Solution:
1. A’= U – A
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 2, 3, 4}
⇒ A’= {5, 6, 7, 8, 9}.

2. B’ = U – B
⇒ {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2, 4, 6, 8}
⇒ B’ = {1, 3, 5, 7, 9}.

3. (A ∪ C) = {1, 2, 3, 4} ∪ {3, 4, 5, 6}
⇒ A ∪ C = {1, 2, 3, 4, 5, 6}
(A ∪ C)’= U – (A ∪ C)
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 2, 3, 4, 5, 6}
⇒ (A ∪ C)’ = {7, 8, 9}

4. A ∪ B = {1, 2, 3, 4} ∪ {2, 4, 6, 8} = {1, 2, 3, 4, 6, 8}
(A ∪ B)’ = ∪ – (A ∪ B)
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 2, 3, 4, 6, 8}
⇒ (A ∪ B)’ = {5, 7, 9}

5. (A’)’ = ∪ – A’
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {5, 6, 7, 8, 9}
⇒ (A’)’= {1, 2, 3, 4} = A

6. B – C = {2, 4, 6, 8} – {3, 4, 5, 6} = {2, 8}.
(B ∪ C)’ = U – (B – C)
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2, 8}
⇒ (B – C)’= {1, 3, 4, 5, 6, 7, 9}.

Sets Short Answer Type Questions

Question 1.
If X and Fare two sets, n(X) = 17, n(Y) = 23 and n(X ∪ F) = 38, then find n(X ∩ F)? (NCERT)
Solution:
We know that n(X ∪ Y) = n(X) + n(Y) – n(X∩Y)
Given: n(X) = 17, n(Y) = 23, n(X ∪ Y) = 38, n(X ∩ Y) = ?
∴ 38 = 17 + 23 – n(X ∩ Y)
⇒ 38 = 40 – n(X ∩ Y)
⇒ n(X ∩ Y) = 40 – 38
⇒ n(X ∩ Y) = 2.

Question 2.
If X and Y are two sets, such that X∪Y has 18 elements, X has 8 elements and F has 15 elements, then how many elements does X ∩ Y have? (NCERT)
Solution:
Given: n(X ∪ Y) = 18, n(X) = 8, n(Y) = 15.
Applying formula n(X ∪ Y) = n(X) + n(Y) – n(X ∩ Y)
18 = 8 + 15 – n(X ∩ Y)
⇒ n(X ∩ Y) = 23 – 18 = 5.

Question 3.
If S and Tare two sets, such that S has 21 elements, T has 32 elements and S∩T has 11 elements, how many elements does S∪T have? (NCERT)
Solution:
Given: n(S) = 21, n(T) = 32, n(S ∩ T) = 11, n(S ∪ T) = ?
∵ n(S ∪ T) = n(S) + n(T) – n(S ∩ T)
⇒ n(S ∪ T) = 21 + 32 – 11 = 42.

Question 4.
If X and Y are two sets such that X has 40 elements, X∪Y has 60 elements and X∩Y has 10 elements, then how many elements does Y have? (NCERT)
Solution:
Given: n(X) = 40, n(X ∪ Y) = 60, n(X ∩ Y) = 10, n(Y) = ?
Applying formula n(X ∪ Y) = n(X) + n(Y) – n{X ∩ Y)
⇒ 60 = 40 + n(Y) – 10
⇒ 60 = 30 + n(Y)
⇒ n(Y) = 30.

Question 5.
If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8} and D = {7, 8, 9, 10}, then find the following: (NCERT)

1. A ∪ B ∪ C
2. A ∪ B ∪ D
3. B ∪ C ∪ D.

Solution:
1. A ∪ B ∪ C = {1, 2, 3, 4} ∪ {3, 4, 5, 6} ∪ {5, 6, 7, 8}
= {1, 2, 3, 4, 5, 6} ∪ {5, 6, 7, 8}
= {1, 2, 3, 4, 5, 6, 7, 8}.

2. A ∪ B ∪ D = { 1, 2, 3, 4} ∪ {3, 4, 5, 6} ∪{7, 8, 9, 10}
= {1, 2, 3, 4, 5, 6} ∪ {7, 8, 9, 10}
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.

3. B ∪ C ∪ D = {3, 4, 5, 6} ∪ {5, 6, 7, 8} ∪ {7, 8, 9, 10}
= {3, 4, 5, 6} ∪ {5, 6, 7, 8, 9, 10}
= {3, 4, 5, 6, 7, 8, 9, 10}.

Sets Long Answer Type Questions

Question 1.
In a survey of 600 students in a school, 150 students were found to be taking tea and 225 taking coffee, 100 were taking both tea and coffee. Find how many students were taking neither tea nor coffee? (NCERT)
Solution:
Let C and T be the students taking coffee and tea.
Here, n(T) = 150, n(C) = 225, n(C ∩ T) = 100.
Applying formula n(C ∪ T) = n(T) + n(C) – n(C ∩ T)
n(C ∪ T) = 150 + 225 – 100 = 375 – 100
⇒ n(C ∪ T) = 275
Total number of students = 600 = n(U).
Number of students taking neither tea nor coffee = n(C ∪ T)’
n(C ∪ T)’ = n(U) – n(C ∪ T)
= 600 – 275 = 325.

Question 2.
In a group of 70 people, 37 likes coffee, 52 likes tea and each person likes at least one of these two drinks. Find the number of persons who likes both coffee and tea? (NCERT)
Solution:
Let C and T be the persons who likes coffee and tea.
Given: n(C) = 37, n(T) = 52, n(C ∪ T) = 70, n(C ∩ T) = ?
Applying formula n(C ∪ T) = n(C) + n(T) – n(C ∩ T)
⇒ 70 = 37 + 52 – n(C ∩ T)
⇒ 70 = 89 – n(C ∩ T)
⇒ n(C ∩ T) = 89 – 70
⇒ n(C ∩ T) = 19
∴ Number of people who likes both coffee and tea = 19.

Question 3.
In a group of 65 people, 40 likes cricket, 10 likes both cricket and tennis. How many like tennis only and not cricket? How many like tennis? (NCERT)
Solution:
Let C and T denotes the people who likes cricket and tennis respectively.
Given: n(C ∪ T) = 65, n(C) = 40, n(C ∩ T) = 10
We know that
n(C ∪ T) = n(C) + n(T) – (C ∩ T)
65 = 40 + n(T) – 10
⇒ n(T) = 65 – 30 = 35.
∴ Number of people who likes only tennis and not cricket
= n(T ∩ C)’ = n(T) – (C ∩ T)
= 35 – 10 = 25.

Question 4.
In a survey of 60 people, it was found that 25 people read newspaper H, 26 read newspaper T, 26 read newspaper I, 9 read both H and I. 11 read both H and T, 8 read both T and 1.3 read all three newspapers. Find

1. The number of people who read at least one of the newspapers.
2. The number of people who read exactly one newspaper. (NCERT)

Solution:
Given: n (H) = 25, n (T) = 26, n(I) = 26, n(H ∩ I) = 9, n(H ∩ T) = 11, n(T ∩ I) = 8, n(H ∩ T ∩ I) = 3

1. The number of people who reads at least one of the newspaper = n(H∪T∪I)
= n(H) + n(T) + n(I) – n(H ∩ T) – n(T ∩ I) – n(H ∩ I) + n(H ∩ T ∩ I)
= 25 + 26 + 26 – 11 – 8 – 9 + 3
= 77 – 28 + 3 = 80 – 28 = 52.

2. The number of people who reads exactly one newspaper.
= n(H) + n(T) + n(I) – 2n(H ∩ I) – 2n(H ∩ T) – 2n(T ∩ I) + 3n(H ∩ T ∩ I)
= 25 + 26 + 26 – 2 × 9 – 2 × 11 – 2 × 8 + 3 × 3 = 77 – 18 – 22 – 16 + 9
= 86 – 56 = 30.

Question 5.
In a survey it was found that 21 people liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked products B and C and 8 liked all the three products. Find how many liked product C only? (NCERT)
Solution:
Let A, B and C denotes the people liked the products A, B and C respectively.
Given: n(A) = 21, n(B) = 26, n(C) = 29, n(A ∩ B) = 14, n(C ∩ A) = 12, n(B ∩ C) = 14, n(A ∩ B ∩ C) = 8
n(only C) = n(C) – n(C ∩ A) – n(B ∩ C) + n(A ∩ B ∩ C)
= 29 – 12 – 14 + 8
= 37 – 26 = 11.

MP Board Class 11 Maths Important Questions

MP Board Class 12th Maths Important Questions Chapter 13 Probability

Probability Important Questions

Probability Objective Type Questions

Question 1.
Choose the correct answer:

Question 1.
A bag contains 5 brown and 4 white socks. A man drawn two socks from the bag. The probability that both are of the same colour is:
(a) \(\frac { 5 }{ 108 } \)
(b) \(\frac { 18 }{ 108 } \)
(c) \(\frac { 30 }{ 108 } \)
(d) \(\frac { 48 }{ 108 } \)
Answer:
(d) \(\frac { 48 }{ 108 } \)

Question 2.
A die is roiled three times. The probability of getting a larger number then the previous number each time is:
(a) \(\frac { 5 }{ 72 } \)
(b) \(\frac { 5 }{ 54 } \)
(c) \(\frac { 13 }{ 216 } \)
(d) \(\frac { 1 }{ 18 } \)
Answer:
(d) \(\frac { 1 }{ 18 } \)

Question 3.
It is given that the events A and B are such that P(A) = \(\frac{1}{4}\), P( \(\frac{A}{B}\) ) = \(\frac{1}{2}\) and P ( \(\frac{B}{A}\) ) = \(\frac{2}{3}\), then P(B) is:
(a) \(\frac{1}{3}\)
(b) \(\frac{2}{3}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{1}{6}\)
Answer:
(a) \(\frac{1}{3}\)

Question 4.
A coin is tossed 4 times. Probability of getting at least one head is:
(a) \(\frac{1}{16}\)
(b) \(\frac{2}{16}\)
(c) \(\frac{14}{16}\)
(d) \(\frac{15}{16}\)
Answer:
(d) \(\frac{15}{16}\)

Question 5.
The probability of A speaking a truth is \(\frac{4}{5}\) and that of B speaking a truth is \(\frac{3}{4}\) The probability that they will contradict each other in answering a fact is:
(a) \(\frac{3}{10}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{7}{20}\)
(d) \(\frac{2}{5}\)
Answer:
(c) \(\frac{7}{20}\)

Question 2.
Fill in the blanks:

1. P( \(\frac { A∪B }{ C } \) ) = P ( \(\frac{A}{C}\) ) + ……………………….
2. P(A∩B) = ………………….. or ………………………….
3. If A and B are two independent events then, P (A ∩ B) = ………………………………..
4. If A and B are two independent events then, P ( \(\frac{A}{B}\) ) = ……………………………….
5. If the probability of random variable X is P (X), then mean E (X) will be ……………………………..
6. If probability of random variable X is P(X), then variance Var (X) will be ……………………………

Answer:

1. P( \(\frac{B}{C}\) ) – P ( \(\frac { A∩B }{ C } \) )
2. P(B).P ( \(\frac{A}{B}\) ) or P(A) . P ( \(\frac{B}{A}\) )
3. P(A).P(B)
4. P(A), P(B) ≠ 0
5. ΣX.P(X)
6. ΣX².P(X) – [ΣX.P(X)]².

Question 3.
Write True/False:

1. If A and B are any two events, then P (A – B) = P(A) – P (A∩B).
2. If A and B are any two events, then P (A ∪ B) – P (A∩B) = P(A) + P(B).
3. P( \(\frac{A}{B}\) ) = \(\frac { P(A∩B) }{ P(A) } \).
4. If A and B are any two events of a sample space S and F is another event such that P(F) ≠ 0, then P ( \(\frac { P(A∪B) }{ P(F) } \) ) = P ( \(\frac{A}{F}\) ) + P ( \(\frac{B}{F}\) ) – P ( \(\frac { P(A∪B) }{ P(F) } \) )
5. For any two events A and B. P (A∪B) = P (A∩B ) + P ( \(\bar { A } \) ∩ B) + P (A ∩\(\bar { B } \) )

Answer:

1. True
2. False
3. False
4. True
5. True.

Question 4.
Write the answer in one word/sentence :

1. Find the probability that a leap year has 53 Friday.
2. A coin is tossed 4 times. Find the probability of getting at least one head.
3. It is given that the events A and B are such that P (A) = \(\frac{1}{4}\), P ( \(\frac{A}{B}\) ) = \(\frac{1}{2}\) and P ( \(\frac{B}{A}\) ) = \(\frac{2}{3}\), then find the value of P(B).
4. There are 5 letters and 5 addressed envelops. If the letters are placed at random what is the probability that exactly 3 letters are placed in right envelops?
5. A problem in mathematics is given to 3 students whose chance of solving it are \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\). What is the probability that the problem is solved?

Answer:

1. \(\frac{2}{7}\)
2. \(\frac{15}{16}\)
3. \(\frac{1}{3}\)
4. \(\frac{1}{12}\)
5. \(\frac{3}{4}\)

Probability Short Answer Type Questions

Question 1.
(A) Two dice are thrown simultaneously. Find the probability of getting a sum?
Solution:
When two dice are thrown simultaneously.
n(S) = 6² = 36.
Sample space of getting a sum 8 is
A = {(2, 6); (6, 2); (5, 3); (3, 5); (4, 4)}
∴ n(A) = 5
∴ Required probability
P(A) = \(\frac { n(A) }{ n(S) } \) = \(\frac{5}{36}\).

(B) Two cubical dice are thrown simultaneously. Find the probability of getting a sum of 9?
Solution:
Solve as Q.No. 1 (A)

(C) Two cubical dice are thrown simultaneously. Find the probability of getting a sum of 7?
Solve as Q.No. 1 (A)

Question 2.
The odds against happening of an event is 3 : 4? Find the probability of its failing?
Solution:
The odds against the happening of an event = 3 : 4
∵ Probability of its failing P ( \(\bar { A } \) ) = \(\frac { b }{ a+b } \)
⇒ P ( \(\bar { A } \) ) = \(\frac { 4 }{ 3+4 } \) = \(\frac { 4 }{ 7 } \).

Question 3.
A card is drawn from a pack of 52 cards. Find the probability that its face?
Solution:
Here, n(S) = 52
∵Cards having face = 4 knave + 4 queens + 4 kings
∴ n(A) = 4 + 4 + 4 = 12
Required probability P(A) = \(\frac { 12 }{ 52 } \) = \(\frac { 3 }{ 13 } \)

Question 4.
What is the probability that a leap year selected at random will contain 53 Sundays?
Solution:
A leap year consists of 366 days. It has 52 complete weeks and 2 days extra. The equally likely cases for the occurrence of these extra days are:

1. Monday and Tuesday,
2. Tuesday and Wednesday,
3. Wednesday and Thursday,
4. Thursday and Friday,
5. Friday and Saturday,
6. Saturday and Sunday,
7. Sunday and Monday.

Out of these 7 exclusive cases, the last two cases are favourable.
∴ n(S) = 7 and n(E) = 2
∴ The required probability = \(\frac { n(E) }{ n(S) } \) = \(\frac{2}{7}\).

Question 5.
The probability of the horse A of winning a race is \(\frac{1}{4}\) and the probability of the horse B winning the same race is \(\frac{1}{8}\)? What is the probability that one of the horse will win the race?
Solution:
Given, P(A) = Probability of winning the horse A = \(\frac{1}{4}\)
and P(B) = Probability of winning the horse B = \(\frac{1}{8}\)
Since, the events of winning the race by A and B are mutually exclusive, therefore
P(A∪B)= P(A) + P(B)
\(\frac{1}{4}\) + \(\frac{1}{8}\) = \(\frac{2+1}{8}\) = \(\frac{3}{8}\).

Question 6.
(A) A card is drawn from an ordinary pack of cards, find the probability of getting a king or a spade?
Solution:
Let the event A denotes the event of drawing a king and B of drawing a spade. Then we
n(S) = 52, n(A) = 4, n(B) = 13, n(A∩B) = 1
[Since there are 4 kings in pack of cards the cards of spade are 13 includes its king]
∴ P(A) = \(\frac { n(A) }{ n(S) } \) = \(\frac{4}{52}\), P(B) = \(\frac { n(B) }{ n(S) } \) = \(\frac{13}{52}\)
P(A∩B) = \(\frac{1}{52}\)
∴ P(A∪B)= P(A) + P(B) = P(A∩B )
= \(\frac{4}{52}\) + \(\frac{13}{52}\) – \(\frac{1}{52}\) = \(\frac{16}{52}\) = \(\frac{4}{13}\).

(B) A card is drawn from a pack of cards, find the probability that neither it is an ace nor a King?
Solution:
Total No. of King = 4, No. of ace = 4
And drawing one card from 8 cards = ⁸_C1
And drawing one card from 52 cards = ⁵²_C1
∴ P(A) = \(\frac { ^{ 8 }{ C_{ 1 } } }{ ^{ 52 }{ C_{ 1 } } } \)
∴ Probability of neither ace nor king = P( \(\bar { A } \) ) = 1 – P(A)
= 1 – \(\frac{2}{13}\) = \(\frac{11}{13}\)

Question 7.
(A) A dice is thrown once. Find the probability of getting even No. “or ” No. less than 5?
Solution:
When a dice is thrown once the sample space is
S = {1, 2, 3, 4, 5, 6}
n(S) = 6
E₁ = {2,4,6}, [∴ n(E₁) = 3]
E₁ = {1, 2, 3, 4}, [∴ n(E₂) = 4]
E₁∩E₂= {2, 4}, [∴ n(E₁ ∩E₂)
= \(\frac { n(E_{ 1 }) }{ n(S) } \) + \(\frac { n(E_{ 2 }) }{ n(S) } \) – \(\frac { n(E_{ 1 }\cap E_{ 2 }) }{ n(S) } \)
= \(\frac{3}{6}\) + \(\frac{4}{6}\) – \(\frac{2}{6}\) = \(\frac{7-2}{6}\) = \(\frac{5}{6}\).

(B) A pair of dice is thrown. Find the probability that the sum is not 9 or 11?
Solution:
Total number of ways in which 2 dice can be thrown = 6 × 6 = 36
n(S) = 36
Event of getting sum 9 = {(3, 6), (4, 5), (5, 4), (6, 3)}
Total No. = 4.
∴ Probability of getting sum 9 = \(\frac{4}{36}\) = \(\frac{1}{9}\)
Now event of getting sum 11 = {(5, 6), (6, 5)}
∴ Probability of getting sum 11 = \(\frac{2}{36}\) = \(\frac{1}{18}\)
Now probability of getting sum 9 or 11
P(A) = \(\frac{1}{9}\) + \(\frac{1}{18}\) = \(\frac{2+1}{18}\) = \(\frac{3}{18}\) = \(\frac{1}{6}\)
∴ probability of not getting sum 9 or 11
P( \(\bar { A } \) ) = 1 – P(A)
= 1 – \(\frac{1}{6}\) = \(\frac{6 – 1}{6}\) = \(\frac{5}{6}\).

Question 8.
If 3 coins are tossed simultaneously, then find the probability of getting at least one head?
Solution:
Here, n(S) = 2³ = 8
If \(\bar { A } \) A denotes not getting a head then A = {{T, T, T)}
∴ n( \(\bar { A } \) ) = 1
Probability of not getting a head P( \(\bar { A } \) ) = \(\frac { n(\bar { A) } }{ n(S) } \) = \(\frac{1}{8}\)
∴ Probability of getting at least one head P(A) = 1 – P( \(\bar { A } \) )
= 1 – \(\frac{1}{8}\) = \(\frac{7}{8}\)

Question 9.
A coin is tossed twice. Find the probability of getting head, both the times?
Solution:
Let the event of getting head in first throw be E₂ and the second throw be E₂.
∴ P(E₁) = \(\frac{1}{2}\) = P(E₂) = \(\frac{1}{2}\)
Both the events are independent
∴ P(E₁ ∩ E₂) = P(E₁) × P(E₂)
= \(\frac{1}{2}\) × \(\frac{1}{2}\)
∴ Probability of getting head both the times = P(E₁ ∩ E₂)
= \(\frac{1}{4}\)

Question 10.
In a given race, the odds in favour of three horses A, B and C are 1 : 2, 1 : 3 and 1 : 4. Find the chance that one of them will win the race?
Solution:
The probability of winning the horse, A = \(\frac { 1 }{ 1+2 } \) = \(\frac { 1 }{ 3 } \)
P(B) = The probability of winning the horse, B = \(\frac { 1 }{ 1+3 } \) = \(\frac { 1 }{ 4 } \)
P(C) = The probability of winning the horse, C = \(\frac { 1 }{ 1+4 } \) = \(\frac { 1 }{ 5 } \)
These events are mutually exclusive, therefore the probabilities of winning any one horses
= P(A) + P(B) + P(C)
= \(\frac{1}{3}\) + \(\frac{1}{4}\) + \(\frac{1}{5}\)
= \(\frac{20+15+12}{60}\) = \(\frac{47}{60}\)

Question 11.
A problem in mathematics is given to three students A, B and C whose chances of solving it are \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\) respectively. Find the probability that the problem will not be solved?
Solution:
The chances of A, B, C solving the problem are respectively
\(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\)
∴ The chances of A, B, C not solving the problem are respectively
1 – \(\frac{1}{2}\), 1 – \(\frac{1}{3}\), 1 – \(\frac{1}{4}\), i.e; \(\frac{1}{2}\), \(\frac{2}{3}\), \(\frac{3}{4}\)
∴ The probability that none of the students A, B, C is able to solve the probelm
= \(\frac{1}{2}\) × \(\frac{2}{3}\) × \(\frac{3}{4}\) = \(\frac{1}{4}\).

Probability Long Answer Type Questions – I

Question 1.
In Raipur 20% persons read English newspaper 40% persons read Hindi newspaper and 5% person read both. What percentage of persons are not read any newspaper?
Solution:
P(A) = The probability of reading English newspaper
= \(\frac{20}{100}\) = \(\frac{1}{5}\)
P(B) = The probability of reading Hindi newspaper
= \(\frac{40}{100}\) = \(\frac{2}{5}\)
P(A∩B) = The probability of reading both English and Hindi newpaper
= \(\frac{5}{100}\) = \(\frac{1}{20}\)
No. of persons not reading any newspaper

Question 2.
A speaks truth in 75% of the cases and B in 80% of the cases. In what percentage of cases are they likely to contradict each other in stating the same fact?
Or
Mohan speaks truth in 75% of cases. Sohan speaks truth in 80% of the cases. In what percentage of cases did the Mohan speaks truth and Sohan speaks lie (or when they contradict each other)?
Solution:
P(A) = Probability that A speaks the truth = \(\frac{75}{100}\) = \(\frac{3}{4}\)
and P(B) = Probability that B speaks the truth = \(\frac{80}{100}\) = \(\frac{4}{5}\)
∴ P( \(\bar { A } \) ) = Probability that A does not speak the truth = 1 – \(\frac{3}{4}\) = \(\frac{1}{4}\)
and P( \(\bar { A } \) ) = Probability that B does not speak the truth = 1 – \(\frac{4}{5}\) = \(\frac{1}{5}\)
It is clear that A and B will contradict each other if one of them speaks the truth and the other does not.
∴ P(A and B contradict) = P(A) P( \(\bar { B } \) ) + P( \(\bar { A } \) ) P(B)
= \(\frac{3}{4}\) × \(\frac{1}{5}\) + \(\frac{1}{4}\) × \(\frac{4}{5}\) = \(\frac{7}{20}\) = \(\frac{35}{100}\)
Hence, in 35% cases, A and B will contradict each other.

Question 3.
Prove that P(A) + P( \(\bar { A } \) ) = 1?
Solution:
In total a + b trails, if an events can happen in a ways and fails in b ways, when all of these ways being equally likely to occur, then the probability of happening of event A,
P(A) = \(\frac { a }{ a+b } \)
and probability of failing of event A,
P( \(\bar { A } \) ) = \(\frac { b }{ a+b } \)
Adding eqns. (1) and (2), we get
P(A) + P( \(\bar { A } \) ) = \(\frac { a }{ a+b } \) + \(\frac { b }{ a+b } \)
= \(\frac { a+b }{ a+b } \) = 1.
∴ P(A) + P( \(\bar { A } \) ) = 1. Proved.

Question 4.
If P(A) = \(\frac{1}{2}\), P(B) = \(\frac{1}{9}\) and P(A∩B) = \(\frac{1}{18}\), then find the value of following:

(i) P( \(\frac{A}{B}\) ),

(ii) P( \(\frac{B}{A}\) )

(iii) P(A∪B)

Solution:
Given: P(A) = \(\frac{1}{2}\), P(B) = \(\frac{1}{9}\) and P(A∩B) = \(\frac{1}{18}\)

Question 5.
A group of 10 children contains 6 boys and 4 girls. Three children are chosen at random from this group. Find the probability that this group chosen:

1. Does not contain any girl.
2. Contains at least one girl.

Solution:
Total number of children = 6B + 4G = 10
3 children out of total 10 may be chosen in ¹⁰_{C3 ways}

1. 3 boys out of 6 boys may be chosen in ⁶_C3 ways
∴ Required probability = \(\frac { ^{ 6 }C_{ 3 } }{ ^{ 10 }C_{ 3 } } \) = \(\frac{1}{6}\)

2. At least 1 girl may be taken as follows
2 boys + 1 girl, number of ways = ⁶_C2 × ⁴_C1
or 3 girls, number of ways = ⁴_{C3
Hence, the required probability}

Question 6.
4 cards are fallen down by one during the shuffling of the cards. Find the probability that one card is heart, the other is diamond, the third is spade and the fourth is a club?
Solution:
Number of cards = 52
The first can fall in 52 ways.
The favourable ways for the first card to be heart = 13
Probability = \(\frac{13}{52}\) = \(\frac{1}{4}\)
The number of remaining cards = 52 – 1 = 51
Another card can be fall in 51 ways.
The favourable ways for this card to be a spade = 13
Probability = \(\frac{13}{50}\)
Number of remaining cards = 50 – 1 = 49
∴ Probability = \(\frac{13}{49}\)
Therefore, by compound probability principle, required probability
= \(\frac{1}{4}\) × \(\frac{13}{51}\) × \(\frac{13}{50}\) × \(\frac{13}{49}\)

Question 7.
A problem of Maths is given to three students whose chances of solving it are \(\frac{1}{2}\), \(\frac{1}{3}\) and \(\frac{1}{4}\). What is the probability that the problem is solved by all?
Solution:
Let the probabilities of solving the question by the three students be P₁, P₂, P₃ respectively.
Then given that P₁ = \(\frac{1}{2}\), P₂ = \(\frac{1}{3}\), P₃ = \(\frac{1}{4}\)
∴ The probabilities of not solving the problem by them are
q₁ = 1 – p₁ = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
q₂ = 1 – p₂ = 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)
and q₃ = 1 – p₃ = 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\)
∴ Probability that all of the three students do not solve the problem
= q₁q₂q₃
= 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\).

Question 8.
A bag contains 6 red, 4 white and 5 blue balls. If balls are drawn one by one from bag and they are not replaced, then what is the probability of 1st red, 2nd white and 3rd blue?
Solution:
A bag contains 6 red (R), 4 white (W), 5 blue (B) balls.
Total No. of balls = 6 + 4 + 5 = 15
∴ Probability of 1st ball is red,
P(R) = \(\frac{6}{15}\)
Now total balls in the bag 15 – 1 = 14
∴ Probability of 2nd ball is white,
P(W) = \(\frac{4}{14}\)
Now the total No. of balls in bag 14 – 1 = 13
∴ Probability of 3rd ball is blue,
P(B) = \(\frac{5}{13}\)
Hence, required probability
= \(\frac{6}{15}\) × \(\frac{4}{14}\) × \(\frac{5}{13}\)
= \(\frac{2}{5}\) × \(\frac{2}{7}\) × \(\frac{5}{13}\) = \(\frac{4×1}{91}\) = \(\frac{4}{91}\)

Question 9.
A bag contains 6 red, 4 white and 6 blue balls. If balls are drawn one by one from bag without replacement, then what is the probability of drawing 1st ball red, 2nd ball white and 3rd ball blue?
Solution:
Solve as Q. No. 8.

Question 10.
Two cubical dice are thrown simultaneously. Find the probability that the first dice shows an even number or both the dice show the sum 9?
Solution:
Here (S) = 6 × 6 = 36
The events of getting an even number on the first dice is
E₁ = {(2, 1), (2,-2), (2, 3), (2,4), (2, 5), (2, 6), (4, 1), (4, 2), (4, 3), (4,4), (4, 5), (4, 6), (6, 1), (6, 2), (6, 3), (6,4), (6, 5), (6, 6)}
∴ n(E₁) = 18
The event of getting a total of 9 on the two dice is
E₂ = {(3,6), (4, 5), (5,4), (6, 3)}
∴ n(E₂) = 4 .
Also, E₁∩E₂
⇒ n(E₁∩E₂) = 2
∴ P(E₁) = \(\frac{18}{36}\), P(E₂) = \(\frac{4}{36}\) and P(E₁∩E₂) = \(\frac{2}{36}\)
∴ The required probability = P(E₁∪E₂)
= P(E₁) + P(E₂) – P(E₁∩E₂)
= \(\frac{18}{36}\) + \(\frac{4}{36}\) – \(\frac{2}{36}\) = \(\frac{20}{36}\) = \(\frac{5}{9}\)

Question 11.
Out of two bags one contains 3 black and 4 red balls and the second bag contains 8 black and 10 red balls. If one bag is chosen and a ball is drawn from it, then find the probability that is a red ball?
Solution:
I bag
3B + 4R = 7 balls total

II bag
8B + 10R = 18 balls total
(i) Selecting the I bag:
Probability that one bag is chosen (out of two bags) = \(\frac{1}{2}\)
1 red ball is drawn from I bag probability = \(\frac{4}{7}\)
Hence, the probability that the I bag is chosen as well as 1 red ball is drawn from it
(Compound event) P₁ = \(\frac{1}{2}\) × \(\frac{4}{7}\) = \(\frac{2}{7}\) ………………… (1)

(ii) If selecting II bag:
Probability that Il bag is chosen = \(\frac{1}{2}\)
I red ball is drawn from II bag probability = \(\frac{10}{18}\) = \(\frac{5}{9}\)
Hence, the probability that the II bag is chosen as well as 1 red ball is drawn from it
(Compound event) P₂ = \(\frac{1}{2}\) × \(\frac{5}{9}\) = \(\frac{5}{18}\) ……………………… (2)
The above two event are mutually exclusive.
Hence, only one event out of these two will happen.
Hence, the required probability P = P₁ + P₂
= \(\frac{2}{7}\) + \(\frac{5}{18}\)
= \(\frac{36+35}{126}\) = \(\frac{71}{126}\).

Question 12.
There are two bags, one contains 5 red and 7 white balls and second bag contains 3 red and 12 white balls. One ball is drawn from any of these bags at random? Find the probability that the ball is red?
Solution:
Solve same as Q. No. 11.

Question 13.
A bag contains 50 bolts and 150 nuts. Half of the bolts and nuts are rusted. If one item is taken out at random find out the probability that ¡ts rusted o is a bolt?
Solution:

Question 14.
A can hit a target 4 times in 5 shots; B, 3 times in 4 shots and C, 2 times 3 shoots at one time. Find the probability of at least two shots hit?
Solution:
Probability of A hitting the target = \(\frac{4}{5}\)
Probability of B hitting the target = \(\frac{3}{4}\)
Probability of C hitting the target = \(\frac{2}{3}\)
At least 2 can hit the target in the following ways:
(i) Probability that A, B,C all hit the target = \(\frac{4}{5}\) × \(\frac{3}{4}\) × \(\frac{2}{3}\) = \(\frac{2}{5}\)

(ii) Probability that B and C hit the target and not A
= ( 1 – \(\frac{4}{5}\) ) × \(\frac{3}{4}\) × \(\frac{2}{3}\) = \(\frac{1}{5}\) × \(\frac{3}{4}\) × \(\frac{2}{3}\) = \(\frac{1}{10}\)

(iii) Probability that C and A hit the target and not B
= \(\frac{4}{5}\) × (1 – \(\frac{3}{4}\) × \(\frac{2}{3}\) = \(\frac{4}{5}\) × \(\frac{1}{4}\) × \(\frac{2}{3}\)
= \(\frac{2}{15}\)

(iv) Probability that A and B hit the target but not C
= \(\frac{4}{5}\) × \(\frac{3}{4}\) × (1 – \(\frac{2}{3}\)) = \(\frac{4}{5}\) × \(\frac{3}{4}\) × \(\frac{1}{3}\) = \(\frac{1}{5}\)
Since, all these events are mutually exclusive,
∴ Required probability = \(\frac{2}{5}\) + \(\frac{1}{10}\) + \(\frac{2}{15}\) + \(\frac{1}{5}\) = \(\frac{5}{6}\)

Question 15.
In a class 30% students fail in physics, 25% fails in maths and 10% fails in both. If one student selects at random, then And the probability of:

(i) Fail in maths when fail in physics also,
(ii) Fail in physics when fail in maths also,
(iii) Fail in maths or physics.

Solution:
Probability of fail in physics is
P(A) = \(\frac{30}{100}\)
Probability of fail in maths is
P(B) = \(\frac{25}{100}\)
Probability of fail in physics and maths both is
P(A∩B) = \(\frac{10}{100}\)

Question 16.
Two bags A and B contain 8 green and 9 white balls and 5 green and 4 white balls respectively. One ball is drawn at random from one of the bags and it is found to be green. Find the probability that it is drawn from bag B? (NCERT)
Solution:
Let E₁ : Event of choosing bag A
∴ P(E₁) = \(\frac{1}{2}\) ………………………. (1)
E₂ = \(\frac{1}{2}\) ………………………… (2)
Again, let C: Event of drawing a green ball
∴ By defnition of conditional probability

The required probability (i.e; the probability of obtaining a ball from bag B when it is green.)

Question 17.
A company has two plants to manufacture bicycles. The first plant manufacture 60% of the bicycles and second plant 40%. Also 80% of the bicycles are rated standard quality at the first plant and 90% of standard quality at the second plant. A bicycle is picked up at random and found to be standard quality? Find the probability that it comes from the second plant? (CBSE 2003)
Solution:
Let E₁: The event of choosing a bicycle from first plant.
∴ P(E₁) = \(\frac{60}{100}\) ………………….. (1)
Let E₂: The event of choosing a bicycle from first plant.
P(E₂) = \(\frac{40}{100}\) ……………………….. (2)
Let E be event of choosing a bicycycle of standard quality, then
P ( \(\frac { E }{ E_{ 1 } } \) ) = Probability of choosing a bicycle of standard quality, given that it is produced by the first plant.
⇒ P ( \(\frac { E }{ E_{ 1 } } \) ) = \(\frac{80}{100}\), (given 80%)
P( \(\frac { E }{ E_{ 2 } } \) ) = Probability of choosing a bicycle of standard quality, given that it is produced by the second plant.
⇒ P( \(\frac { E }{ E_{ 2 } } \) ) = \(\frac{90}{100}\) (given 90%)
∴ The required probability (i.e., probability of choosing a bicycle from the second plant, given that it is of standard quality,

Question 18.
A company manufactures T.V., machine A, B and C manufatures 30%, 20% and 50% T.V. of the total production of their outputs 7%, 5% and 2% are defec¬tive T.V. respectively. A T.V. is selected at random from the production and is found to be defective?
Find the probability that defective T.V. which is manufactured by machine A? (CBSE 2015)
Solution:
Let the events T₁, T₂ and T₃ are the following:
Event T₁ : T.V. manufactured by machined A.
Event T₂ : T.V. manufactured by mechine B.
Event T₃: T.V. manufactured by machine C.
It is noted that these events are mutually exclusive.
Again, let E : The event of defective T.V.
Given, P(T₁) = 30% = \(\frac{30}{100}\) ………………….. (1)
P(T₂) = 20% = \(\frac{20}{100}\) ………………….. (2)
P(T₃) = 50% = \(\frac{50}{100}\) ………………….. (3)
Again P( \(\frac { E }{ T_{ 1 } } \) ) = The probability that T.V. is defective when it is manufactured by machine A.
⇒ P(\(\frac { E }{ T_{ 1 } } \) ) = 7% = \(\frac{7}{100}\)
P( \(\frac { E }{ T_{ 2 } } \) ) = The probability that T.V. is defective when it is manufactured by machine B.
⇒ P( \(\frac { E }{ T_{ 3 } } \) ) = 5% = \(\frac{5}{100}\)
Similarly,
P( \(\frac { E }{ T_{ 3 } } \) ) = The probability that T.V. is defective when it is manufactured by machine C.
⇒ P( \(\frac { E }{ T_{ 3 } } \) ) = 2% = \(\frac{2}{100}\)
Now, from Bayes’s theorem
P( \(\frac { T_{ 1 } }{ E } \) ) = The probability that T.V. is defective when it is manufactured by machine A.

Question 19.
The probability that Mohan does not speak the truth is \(\frac{1}{5}\) Mohan speaks the head when a coin is thrown, find the probability that really gettting head by the throw of a coin? (NCERT)
Solution:
Let A: The event of getting head.
P(A) = \(\frac{1}{2}\)
B: The event of not getting head.
∴ P(B) = 1 – P(B) = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
Again, Let E: The event that really getting head by the throw of a coin and Mohan speaks.
P( \(\frac{E}{B}\) ) = \(\frac{1}{5}\)
and P( \(\frac{E}{A}\) ) = 1 – \(\frac{1}{5}\) = \(\frac{4}{5}\)
Now, from Bayes’s thoerem
P( \(\frac{A}{E}\) ) = Probability that the report of the Mohan that head has occured is actually head.

Question 20.
Bag A contains 3 white and 4 red balls and bag B contains 5 white and 6 red balls. One ball is drawn at random from one of the bags and it is found to be red. Find the probability that it is drawn from bag B?
Solution:
Let E₁ = Event of choosing bag A.
E₂ = Event of choosing bag B.
P(E₁) = \(\frac{1}{2}\); P(E₂) = \(\frac{1}{2}\) ………………….. (1)
⇒ P(E₁) = P(E₂) = \(\frac{1}{2}\)
Again, let R = Event of drawing a red ball.
According to the question.
P( \(\frac { R }{ E_{ 1 } } \) ) = The probability that a red ball is drawn when it is selected from bag A.
⇒ P( \(\frac { R }{ E_{ 1 } } \) ) = \(\frac{4}{3+4}\) = \(\frac{4}{7}\) …………………. (2) [since bag A contains 3 white and 4 red balls]
P( \(\frac { R }{ E_{ 2 } } \) ) = \(\frac{6}{5+6}\) = \(\frac{6}{11}\) ……………….. (3) [since bag B contains 5 white and 6 red balls]
Now, from Bayes’s theorem,
P( \(\frac { E_{ 2 } }{ R } \) ) = The probability that a ball is drawn from bag B when it is red.

Question 21.
Three different bags A, B and C are given, each bag contains 2-2 books. Bag A contains both 2 mathematics books, bag B contains 2 chemistry books and bag C contains, one mathematics and one chemistry book. The student select one bag ran¬domly and from that bag he randomly take out one book. The book he has taken out is that of mathematics. Find the probability that the second book he draws out from that bag is also of mathematics or that he is selected bag A given? (NCERT)
Solution:
Let events E₁, E₂ and E₃ represents the selection of bag A, B and C respctively.
P(E₁) = P(E₂) = P(E₃) = \(\frac{1}{3}\) …………………….. (1)
D: The event of mathematics book happen
P( \(\frac { D }{ E_{ 1 } } \) ) = P(A mathematics book chosen from bag A)
= \(\frac{2}{2}\) = 1 ……………….. (2)
P( \(\frac { D }{ E_{ 2 } } \) ) = P(A mathematics book chosen from bag B)
= \(\frac{0}{2}\) = 0 ………………… (3)
[∵according to the questions, both chemistry books are in bag B]
P( \(\frac { D }{ E_{ 3 } } \) ) = P(A mathematics book chosen from bag C)
= \(\frac{1}{2}\)
Now, the required probability
P( \(\frac { E_{ 1 } }{ D } \) )
Now, by Bayes’ thoerem,
P( \(\frac { E_{ 1 } }{ D } \) )

Question 22.
By examining about a student that he is known to speak the truth 2 out of 5 times. He throws a die and reports that it is a six. Find the probability that it is actually a six?
Solution:
Let E: Event that the student reports that it is a six.
A : Event of getting a six on the upper face of die.
B : Event of not getting a six on the upper face of die.
∴ P(A) = \(\frac{1}{6}\) ………………….. (1)
P(B) = P(Not A) = P( \(\bar { A } \) )
⇒ P(B) = 1 – P(A) = 1 – \(\frac{1}{6}\)
⇒ P(B) = \(\frac{5}{6}\) ………………… (2)
P( \(\frac{E}{A}\) ) = Probability that the student reports that six occurs, when six has actually occured.
P ( \(\frac{E}{A}\) ) = Probability that the student speaks the truth
= \(\frac{2}{5}\) …………………… (3)
Now, P ( \(\frac{E}{B}\) ) = Probability that the student reports that six occurs, when six that has not actually occured.
P ( \(\frac{E}{B}\) ) = Probability that the student does not speak the truth.
P( \(\frac{E}{B}\) ) = 1 – \(\frac{2}{5}\) = \(\frac{3}{5}\)
Now, by Bayes’s thoerem
P( \(\frac{A}{E}\) ) = Probability of getting six, given that the student reports it to be six.

MP Board Class 12 Maths Important Questions

MP Board Class 11th Maths Important Questions Chapter 9 Sequences and Series Important Questions

Sequences and Series Important Questions 

Sequences and Series Objective Type Questions

(A) Choose the correct answer of the following:

Question 1.
The sum of the cube of first n positive integer is :
(a) \(\frac {n(n + 1)}{2}\)
(b) \(\frac {n(n + 1)(2n + 1)}{6}\)
(c) \(\frac {n(n + 1)(n + 2)}{6}\)
(d) {\(\frac {n(n + 1)}{2}\)}²
Answer:
(d) {\(\frac {n(n + 1)}{2}\)}²

Question 2.
The sum of n term of arithmetic progression is 2n + 3n², its second term will be :
(a) 10
(b) 12
(c) 16
(d) 11
Answer:
(c) 16

Question 3.
If arithmetic mean of a and b is \(\frac { { a }^{ n }+{ n }^{ n } }{ { a }^{ n – 1 }+{ b }^{ n – 1 } }\), then the value of n will be :
(a) 1
(b) 0
(c) – 1
(d) \(\frac {1}{2}\)
Answer:
(a) 1

Question 4.
Which term of the series 8, 4,0, ………….. is – 24 :
(a) 7^th
(b) 28^th
(c) 8^th
(d) 9^th
Answer:
(d) 9^th

Question 5.
If the first term of arithmetic progression be a and last term is l, then the sum of n terms will be :
(a) \(\frac {n}{2}\)[2a – (n – 1)d]
(b) \(\frac {n}{2}\)[2a + (n – 1)d]
(c) \(\frac {n}{2}\)(a + l)
(d ) \(\frac {n}{2}\)(a – l).
Answer:
(c) \(\frac {n}{2}\)(a + l)

Question 6.
The next term of the sequence 2\(\sqrt { 2 }\), \(\sqrt { 2 }\), 0, …………… is :
(a) – \(\sqrt { 3 }\)
(b) \(\frac { 1 }{ \sqrt { 2 } }\)
(c) – \(\sqrt { 2 }\)
(d) \(\sqrt { 2 }\)
Answer:
(c) – \(\sqrt { 2 }\)

Question 7.
If 2x, x + 8, 3x + 1 are in A.P, then value of x will be :
(a) 3
(b) 7
(c) 5
(d) 2
Answer:
(c) 5

Question 8.
The 15^th term from the end of the A.P. 2, 6,10, …………., 86 is :
(a) 30
(b) 32
(c) 46
(d) 48
Answer:
(a) 30

Question 9.
If first 15^th term of an A.P. is a, second term is b and n^th term is 2 a, then sum of the n terms is :
(a) \(\frac {ab}{2(b – a)}\)
(b) \(\frac {2ab}{3(b – a)}\)
(c) \(\frac {3ab}{2(b – a)}\)
(d) \(\frac {3ab}{(b – a)}\)
Answer:
(c) \(\frac {3ab}{2(b – a)}\)

Question 10.
In an A.P. S_n = 3n² + 5n and T_m = 164, then m equals to :
(a) 26
(b) 27
(c) 28
(d) None of these.
Answer:
(b) 27

Question 11.
A.M. of two number is 10 and GM. is 8, the numbers are
(a) a = 4, b = 16
(b) a = 2, b = 8
(c) a = 4, b = 9
(d) a = 2, b = 18.
Answer:
(a) a = 4, b = 16

Question 12.
The A.M. of two numbers is A and G M is G, then relation between them is :
(a) A < G (b) A = G (c) A > G
(d) None of these.
Answer:
(c) A > G

Question 13.
2^1/4.4^1/8.8^1/16 ……………. ∞ =
(a) 1
(b) 2
(c) 3/2
(d) 4
Answer:
(b) 2

Question 14.
If y = x – x² + x³ – x⁴ + ………. ∞, then value of x be (- 1 < x < 1) :
Answer:
(a) y + \(\frac {1}{y}\)
(b) \(\frac {y}{1 + y}\)
(c) y – \(\frac {1}{y}\)
(d) \(\frac {y}{1 – y}\)
Answer:
(d) \(\frac {y}{1 – y}\)

Question 15.
If the second, third and sixth terms of an A.P. are in GP, then the common ratio of the GP. is :
(a) 2
(b) 5
(c) 4
(d) 3
Answer:
(d) 3

Question 16.
Sum up to infinity of 1 + \(\frac {4}{5}\) + \(\frac { 7 }{ { 5 }^{ 2 } }\) + \(\frac { 10 }{ { 5 }^{ 2 } }\) + …………. :
(a) \(\frac {35}{16}\)
(b) \(\frac {37}{16}\)
(c) \(\frac {39}{16}\)
(d) 3
Answer:
(a) \(\frac {35}{16}\)

(B) Match the following :

Answer:

1. (d)
2. (f)
3. (a)
4. (g)
5. (b)
6. (j)
7. (c)
8. (i)
9. (e)
10. (h)

(C) Fill in the blanks :

1. – 7\(\sqrt { 3 }\) will be term of the series 5\(\sqrt { 3 }\), 3\(\sqrt { 3 }\), \(\sqrt { 3 }\), …………….
2. 116 is sum of the term of the series 25,22, 19 …………….
3. If sum of n terms of series is n² + 4n, then 15^th term of the series is …………….
4. 0 will be the term of the series 27, 24,21, 18 …………….
5. 729 will be the term of the series – \(\frac {1}{27}\), \(\frac {1}{9}\), – \(\frac {1}{3}\) …………….
6. The first term of GP. is a, common ratio r < 1 and its last term l, then its sum will be …………….
7. The ratio of the sum of first three term to the sum of first six term is 125 : 152, then common ratio will be …………….
8. First term 16 and fifth term \(\frac {1}{16}\), then its 4^th term will be …………….
9. Sum of n terms of the series x + 2x² + 4x³ + 8x⁴ + ……………. will be …………….
10. If a = 2, d = 2 and n = 50, then the last term of the series will be …………….

Answer:

1. 7
2. 12
3. 33
4. 10
5. 10
6. \(\frac {a – rl}{1 – r}\)
7. \(\frac {3}{5}\)
8. \(\frac {1}{4}\)
9. \(\frac { 1-({ 2x }^{ n })x }{ 1 – 2x }\)
10. 100

(D) Write true / false :

1. 1, 3, 5, 8, ………….. are inA.P.
2. n^th term of a G.P. is a + (n – 1 )d.
3. If 2x, x + 5 and x + 11 are in A.P., then value of x will be – 1.
4. Arithmetic mean of a and b is \(\sqrt { ab }\)
5. Sum of 9 terms of a sequence 24 + 20 + 16 + will be.
6. Four consicutive term of G.P. are \(\frac { a }{ { r }^{ 3 } }\) \(\frac {a}{r}\), ar, ar³.

Answer:

1. False
2. False
3. True
4. False
5. True
6. True.

(E) Write answer in one word / sentence :

1. If a, b, care inA.P., then find the value of ab + ac?
2. Arithmetic mean of (a + b)²and (a – b)² will be?
3. Sum of n arithmetic mean between x and 3x will be.
4. Find the sum of infinite terms of series : 9^1/3.9^1/3.9^1/27 ………….. up to ∞.
5. If a, b, c are in GP., then find the value \(\frac {1}{b}\) + \(\frac {1}{a – b}\) –\(\frac {1}{b – c}\)

Answer:

1. 2b²
2. a² + b²
3. 3nx
4. 3
5. 0

Sequences and Series Short Answer Type Questions

Question 1.
Which term of the sequence 27,24,21,18, …………. is zero? (NCERT)
Solution:
Here a = 27 and d= T₂ – T₁ = 24 – 27 = – 3.
Let the n^th term of series be 0.
∴ T_n = a + (n – 1)d
⇒ 0 = 27 + (n – 1)(- 3)
⇒ 3n – 3 = 27
⇒ 3n = 30
n = 10 or 10^th term.

Question 2.
The last term of the series 8,4,0, ……………. is – 24. Find the total number of terms. (NCERT)
Solution:
Given series 8,4, 0, … (1)
First term = a = 8 Common difference d = 4 – 8 = -4
d = 0 – 4 = – 4
∵ The common difference is same the series is in A.P.
last term l = – 24,
l = a + (n – 1)d,
= – 24 = 8 + (n – 1)(-4)
⇒ – 24 – 8 = (n – 1)(-4)
⇒ – 32 = (n – 1)(- 4)
⇒ (n – 1) = \(\frac {32}{4}\)
⇒ n – 1 = 8
⇒ n = 8 + 1
⇒ n = 9
∴ Number of terms n = 9

Question 3.
Seven times the 7^th term of a series is equal to eleven times of its 11th term. Find the 18^th term of the series. (NCERT)
Solution:
Let first term = a and common difference = d of A.P.
∴ 7^th term = a + 6d and 11^th term = a + 10 d.
∴ According to question,
7(a + 6d) = 11 + (a + 10d)
⇒ 7a + 42d = 11a + 110d
⇒ 7a – 11a = 110d – 42d
⇒ – 4a = 68 d
⇒ a = – 17d
Hence 18^th term = a + 17d
= – 17d + 17d [∵ a = – 17d]
= 0.

Question 4.
Prove that the sum of (m + n)^th term and (m – n)^th terms of an A.P. is twice of its m^th term.
Solution:
Let the first term = a and common difference = d.
T_n = a+(n – 1)d
T_{m + n}= a + (m + n – 1)d … (1)
T_{m – n} = a + (m – n – 1)d … (2)
T_m = a + (m – 1)d … (3)
T_m+n + T_m-n = a + (m + n – 1)d + a(m – n – 1)d
= 2a + (m + n – 1 + m – n – 1)d
= 2a + (2m – 2)d
= 2a + 2(m – 1)d
= 2[a+(m – 1)d]
T_m+n + T_m-n = 2T_m.

Question 5.
Insert three Arithmetic means between 3 and 19. (NCERT)
Solution:
Let three Arithmetic mean be A₁, A₂, A₃,
then 3, A₁, A₂, A₃, 19 are in A.P.
∴ 3 = a, 19 = T₅, let common difference = d
T₅ = a + 4d
T₅ = a + 4d
⇒ 19 = 3 + 4d
⇒ 16 = 4d
⇒ d = 4
Hence A₁ = 3 + 4 = 7, A₂ = 7 + 4 = 11, A₃ = 11 + 4 = 15.

Question 6.
If – 8, A₁, A₂ are in Arithmetic progression (A.P.), then find the value of A₁, A₂. (NCERT)
Solution:
– 8, A₁, A₂, 9 are in A.P.
∴ a = – 8, T₄ = 9, let common difference = d
T₄ = a + 3d
⇒ 9 = – 8 + 3 d
⇒ 3d = 11
⇒ d = \(\frac {17}{3}\)

Instruction :
Write the first five terms of each of the sequence and obtain the corresponding series.

Question 7.
(a) a₁ = 3, a_n = 3a_{n – 1} + 2, where n > 1. (NCERT)
Solution:
Given : a₁ = 3,
a₂ = 3a_{n – 1} + 2, where n > 1
a₂ = 3a_{2 – 1} + 2
⇒ a₂ = 3a₁ + 2
⇒ a₂ = 3 x 3 + 2 = 9 + 2 = 11
a₃ = 3a₁ + 2
= 3a₂ + 2
⇒ a₃ = 3(11)+ 2 = 33+ 2 = 35
a₄ = 3a_{4 – 1} + 2
= 3a₃ + 2
⇒ a₄ = 3(35) + 2 = 105 + 2 = 107
a₅ = 3a_{5 – 1} + 2
= 3a₄ + 2
= 3(107) + 2 = 321 + 2 = 323
Hence series is 3, 11, 35, 107, 323.

Question 7.
(b) a₁ = -1, a_n = \(\frac { { a }_{ n-1 } }{ n }\) where n ≥ 2.
Solution:

Question 8.
A person pays first instalment of Rs. 100 towards his loan. If he increases his instalment every month by Rs. 5, then what will be his 30^th instalment.
Solution:
Given : a = Rs. 100, d= Rs. 5, n = 30,
T_n = a + (n – 1)d
Amount of 30^th instalment
J₃₀ = 100 + (30 – 1) x 5
= 100 + 29 x 5 = 100 + 145
= Rs. 245.
Hence the 30^th instalment = Rs. 245.

Question 9.
Which term of the sequence \(\sqrt { 3 }\), 3, 3\(\sqrt { 3 }\) ……. is 729?
Solution:

Question 10.
How many terms are required in GP. 3,3²,3³ …………, so that their sum would be 120? (NCERT)
Solution:
Given : a = 3, r = \(\frac {9}{3}\) = 3, S_n = 120,
S_n = \(\frac { a({ r }^{ n }-1) }{ r-1 }\)
⇒ \(\frac { 3({ 3 }^{ n }-1) }{ 3-1 }\) = 120
⇒ 3ⁿ – 1 = \(\frac {120 × 2}{3}\)
⇒ 3ⁿ – 1 = 80
⇒ 3ⁿ = 81
⇒ 3ⁿ = 3⁴
⇒ n = 4

Question 11.
Show that ratio between sum of n terms and sum of (n +1)^th term to (2n)^th terms in a G.P. is \(\frac { 1 }{ { r }^{ n } }\)
Solution:
Let 1^st term of G.P. = a and common ratio = r
∴ n terms of GP. is a, ar, ar², ………….. , ar^{n – 1}
Let the sum to n terms be S₁
S₁ = \(\frac { a({ r }^{ n }-1) }{ r-1 }\)
GP. from (n + 1)^th term to (2n)^th term
arⁿ, ar^{n + 1}, …………. , ar^{2n – 1}
Let the sum of this G.P. up to n terms be S₂

Question 12.
If A.M. and GM. of roots of a quadratic equation are 8 and 5 respectively, then find the quadratic equation. (NCERT)
Solution:
Let the roots of equation be α and β
A.M. of roots = \(\frac {α + β}{2}\) = 8
⇒ α +β = 16
G.M. of roots = \(\sqrt {αβ }\) = 5
⇒ αβ = 25
If α, β are the roots of equation
then, x² – (α + β)x + αβ = 0
⇒ x² -16x + 25 = 0.

Question 13.
If the first and n^th term of GP. are a and b respectively and if p is the product of n terms, then prove that
p² = (ab)ⁿ. (NCERT)
Solution:
Let the common ratio of G.P. = r
Given: ar^{n – 1} = b, …(1)
then a.ar.ar²……. ar^{n – 1} = p
⇒ aⁿr^{1+2+3+……+(n – 1)} = p
⇒ aⁿr^{\(\frac {1}{2}\)(n – 1)n} = p
⇒ a²ⁿ.r^{(n – 1)n} = p²
⇒ p² = (a²r^{n – 1n}
⇒ p² = (a.ar^{n – 1})ⁿ
⇒ p² = (ab)ⁿ, [fromeqn. (1)]

Question 14.
If the 4^th term of a GP. is square of its second term and the 1^st term is -3, then find the 7^th term. (NCERT)
Solution:
Let a and r be the 1st term and common ratio of GP.
∴ T_n = ar^n-1
T₄ = ar^4-1 = ar³ … (1)
T₂ = ar^2-1 = ar … (2)
Given : T₄ = (T₂)²
⇒ ar³ = (ar)²
⇒ ar³ = a²r²
⇒ a = r = – 3 (given, a = -3)
T₇ = ar^7-1 = ar⁶
= (-3)(-3)⁶ = (-3)⁷
∴ T₇ = – 2187
Hence 7_th term of G.P. = – 2187.

Question 15.
Find the value of \(\sum _{ k=1 }^{ 11 }{ (2+{ 3 }^{ k }) }\).
Solution:

Sequences and Series Long Answer Type Questions

Question 1.
If m times of the m^th term of an A.P. is equal to n times the n^th term, then prove that (m + n)^th term of the series is zero.
Solution:
Let the 1^st term = a and common difference = d.
then t_m = a + (m – 1)d
t_n = a + (n – 1)d
Given: m[a + (n – 1)d] = n[a + (n – 1)d]
⇒ ma + m(m – 1 )d = na + n(n – 1 )d
⇒ (m² – m)d + (m – n)a = (n² – n)d
⇒ (m² – m – n² + n) d + (m – n)a = 0
⇒ [m² – n² – (m – n)] d + (m – n)a = 0
⇒ [(m – n)(m + n) – (m – n)] d+(m – n)a = 0
⇒ (m – n)[(m + n) – 1] d + (m – n)a = 0
⇒ a + (m + n – 1 )d = 0
⇒ t_m+n=0.

Question 2.
If the 6^th term of A.P. is 12 and 9^th term is 27, then find its r^th term.
Solution:
Let the 1^st term = a and common difference = d.
Given : t₆ = 12
⇒ a + 5d = 12 … (1)
t₉ = 27
⇒ a + 8d = 27 … (2)

Question 3.
If p^th term of an A.P. is \(\frac {1}{q}\) and q^th term is \(\frac {1}{p}\), then prove that (pq)^th
Solution:

Question 4.
If p^th term of an A.P. is \(\frac {1}{q}\) and q^th term is \(\frac {1}{p}\), then prove that (pq)^th terms is \(\frac {1}{2}\) (pq + 1), where p ≠ q.
Solution:

Question 5.
The sum of the series 25, 22, 19, ………….. of A.P. is 116, then find its last term. (NCERT)
Solution:
Given : a = 25, d = 22 – 25 = – 3, S_n = 116
S_n = \(\frac {n}{2}\) [2a + (n – 1)d]
⇒ 116 = \(\frac {n}{2}\)[2 x 25 + (n -1) x (-3)]
⇒ 232 = n[50 – 3n + 3]
⇒ 232 = n[53 – 3n]
⇒ 232 = 53n – 3n²
⇒ 3n² – 53n +232 = 0
⇒ 3n² – 24n – 29n + 232 = 0
⇒ 3n(n – 8) – 29(n – 8) = 0
⇒ (n – 8)(3n – 29) = 0
n = 8, or n = \(\frac {29}{3}\), (which is impossible)
∴ Last term l = a + (n – 1 )d
= 25 + (8 – 1) x (- 3)
⇒ l = 25 – 21 = 4.

Question 6.
If the A.M. of a and b is \(\frac { { a }^{ n }+{ b }^{ n } }{ { a }^{ n – 1 }+{ b }^{ n – 1 } }\), then find the value of it. (NCERT)
Solution:
A.M. of a and b = \(\frac {a+b}{2}\)
According to question,
\(\frac { { a }^{ n }+{ b }^{ n } }{ { a }^{ n – 1 }+{ b }^{ n – 1 } }\) = \(\frac {a+b}{2}\)
⇒ 2aⁿ + 2bⁿ = (a + b) (a^{n – 1} + b^{n – 1})
⇒ 2aⁿ +2bⁿ = aⁿ + bⁿ + ab^{n – 1} + ba^{n – 1}
⇒ aⁿ + bⁿ = ab^{n – 1} + ba^{n – 1}
⇒ aⁿ – ba^{n – 1} = ab^{n – 1} – bⁿ
⇒ a^{n – 1}(a – b) = b^{n – 1}(a – b)
⇒ a^{n – 1} = b^{n – 1}
⇒ \(\frac {a}{b}\)^{n – 1} = \(\frac {a}{b}\)⁰
⇒ n – 1 = 0
⇒ n = 1.

Question 7.
Between 1 and 31, m numbers have been inserted in such a way that the resulting sequence is an A.P. and the ratio of 7^th and (m – 1)^th mean is 5 : 9 then, find the value of m.
Solution:
Let A₁, A₂, A₃, ……… ,A_m are m A.M. respectively inserted between 1 and 31.
Then 1, A₁, A₂, A₃, ……… A_m 31 are in A.P. Here, 1^st term = 1 and (m + 2)^th term = 31 and let the common difference of sequence be d.

Question 8.
Show that the sum of (m + n)^th and (m – n)^th term of an A.P. is equal to twice the m^th term. (NCERT)
Solution:
Let the first term = a and common difference = d.
T_n = a + (n – 1)d
T_{m + n} =a +(m + n – 1)d … (1)
T_{m – n} = a + (m – n – 1)d … (2)
T_m = a + (m – 1)d … (3)
Adding equation (1) and (2),
T_{m + n} + T_{m – n} = a + (m + n – 1)d + a + (m – n – 1)d
= 2a + (m + n – 1 + m – n – 1)d
= 2a + (2m – 2 )d
= 2a + 2 (m – 1)d
= 2[a + (m – 1)d]
∴ T_{m + n} + T_{m – n} = 2T_m [From equation (3)]

Question 9.
If the sum of three numbers in A.P. is 24 and their product is 440, then find the numbers? (NCERT)
Solution:
Let the three numbers of A.P. are a – d, a, a + d.
Given : a – d + a + a + d = 24
3a = 24
⇒ a = 8
and (a – d) × a × (a + d) = 440
a(a² – d²) = 440
⇒ 8(64 – d²) = 440
⇒ 64 – d² = \(\frac {440}{8}\)
⇒ 64 – d² = 55
⇒ d² = 64 – 55
⇒ d² = 9
⇒ d = ± 3
When a = 8 and d = 3
Then, a – d = 8 – 3 = 5, a = 8, a + d= 8 + 3 = 11
When a = 8 and d = – 3
Then, a – d = 8 + 3 = 11, a = 8, a + d = 8 – 3 = 5
Hence required numbers are 5, 8, 11 or 11, 8, 5.

Question 10.
If the sum of n, 2n and 3n terms in A.P. are S₁ S₂ and S₃, then show that S₃ = 3(S₂ – S₁).
Solution:

Question 11.
Find the sum of all natural numbers lying between 200 and 400, which are divisible by 7. (NCERT)
Solution:
Numbers divisible by 7 are 203, 210, 217, …………. , 399
Here a = 203, d = 210 – 203 = 7, l = 399
l = a + (n – 1)d
399 = 203 + (n – 1) x 7
⇒ 399 – 203 = (n – 1) x 7
⇒ (n – 1)7 = 196
⇒ (n – 1) = \(\frac {196}{7}\)
⇒ (n – 1) = 28
∴ n = 29.
Hence required sum, S₂₉ = \(\frac {n}{2}\)[a+l]
⇒ S₂₉ = \(\frac {29}{2}\)[203 + 399]
⇒ S₂₉ = \(\frac {29}{2}\)[602] = \(\frac {17458}{2}\) = 8729.

Question 12.
If the 5^th, 8^th and 11^th terms of a GP. are p, q and s respectively, then show
that q² = ps. (NCERT)
Solution:
Let the 1st term of GP. = a and common ratio = r.
Then, T_n = ar^{n – 1}
T₅ = ar^{5 – 1} =p
⇒ ar⁴ = P … (1)
T₈ = ar^8-1 = q
⇒ ar⁷ = q … (2)
T₁₁ = ar^{11 – 1} = s
⇒ ar¹⁰ = s
ps = ar⁴.ar¹⁰, [from equation (1) And (3)]
⇒ ps = a²r¹⁴
⇒ ps = (ar⁷)²
⇒ ps = q², [from equation (2)]
∴ q² = ps.

Question 13.
If the first term of G.P. a = 729 and 7^th term is 64, then find S₇. (NCERT)
Solution:

Question 14.
If the 4^th terms of a GP is square of its 2^nd term and first term is – 3, then find its 7^th (NCERT)
Solution:
Let the 1st term of GP. = a and common ratio = r.
Then, T_n = ar^{n – 1}
T₄ = ar^{4 – 1} = ar³ … (1)
T₂ = ar^2-1 = ar … (2)
Given : T₄ = T₂²
ar³ = (ar)₂
ar³ = a²r²
⇒ ar³ = a²r²
⇒ a = r = – 3 (given a = – 3)
T₇ = ar^{7 – 1} = ar⁶
= (-3)(-3)⁶ = (-3)⁷
∴ T₇ = – 2187
Hence, 7^thterm of G. P. = – 2187.

Question 15.
Find the sum of the sequence 8,88,888,8888 ……….. up to n terms. (NCERT)
Solution:
Let the sum of the n terms be S

Question 16.
Find the sunt of the numbers 7,77,777, 7777 up to n terms. (NCERT)
Solution:
Let the sum of n terms is S.

Question 17.
If the A.M. and GM. between two positive numbers a and b are 10 and 8 respectively, then find the numbers. (NCERT)
Solution:
A.M. A = \(\frac {a+b}{2}\)
a + b = 20 … (1)
G.M. G = \(\sqrt {ab}\)
ab = 64 … (2)
(a – b)² = (a + b)² – 4ab
= (20)² – 4 × 64, [From equation (2)]
= 400 – 256
(a – b)² = 144 = (12)² … (3)

Put a = 16 in equation (1), we get,
16 + b = 20
∴ b = 4
Numbers are 16 and 4.
When a – b = – 12, then
a + b = 20
a – b = – 12
On adding 2a = 8
⇒ a = 4
Put a = 4 in equation (1), we get,
4 + 6 = 20
∴ b = 16
Numbers are 4 and 16.
Hence numbers a and b are 4, 16 or 16,4.

Question 18.
The sum of two numbers is 6 times their geometric mean, show that the . numbers are in the ratio (3 + 2\(\sqrt {2}\)) ; (3 – 2\(\sqrt {2}\)). (NCERT)
Solution:
Let the numbers are a and 6.
Given: a + b = 6 \(\sqrt {ab}\)
\(\frac { a+b }{ 2\sqrt { ab } }\) = \(\frac {3}{1}\)
⇒ a + b = 3K …. (1)
and 2 \(\sqrt {ab}\) = K ⇒ 4ab = K²
(a – b)² = (a + b)² – 4ab
= (3K)² – (K)²
= 9K² – K² = 8K²
⇒ a – b = 2\(\sqrt {2}\)K …. (2)

Sequences and Series Very Long Answer Type Questions

Question 1.
If the ratio of the sum of n terms of two A.P. is 5n + 4 : 9n + 6, then find the ratio of their 18^th term.
Solution:
Let the two A.P. are :
a, a + d, a + 2d, ………….
and A, A + D, A +2D …………..

Question 2.
The ratio of the sum of m and n terms of an A.P. is m² : n². Show that the ratio of and u* term is (2m – 1) : (2n – 1). (NCERT)
Solution:
Let the A.P. are a, a + d, a + 2d, ……………
∴ m^th term of A.P. Tm = a + (m – 1)d
n^th term of A.P. Tn= a + (n – 1)d

Question 3.
If the sum of first three terms of a G.P. is \(\frac {39}{10}\) and their product is 1, then find the common ratio and the terms. (NCERT)
Solution:
Let the three terms of G.P. are \(\frac {a}{r}\), a, ar.
Given: \(\frac {a}{r}\) × a × ar = 1
⇒ a³ = 1 ⇒ a = 1
and \(\frac {a}{r}\) + a + ar = \(\frac {39}{10}\)
⇒ a(\(\frac {a}{r}\) + r + 1) = \(\frac {39}{10}\)
⇒ 1 x \(\frac { 1+{ r }^{ 2 }+r }{ r }\) = \(\frac {39}{10}\)
⇒ 10r² + 10r + 10 = 39r
⇒ 10r² – 29r + 10 = 0
⇒ 10r² – 25r – 4r + 10 = 0
⇒ 5r(2r – 5) – 2(2r – 5) = 0
⇒ (5r – 2)(2r – 5) = 0
∴ r = \(\frac {2}{5}\) and r = \(\frac {5}{2}\)
When a = 1 and r = \(\frac {2}{5}\)

Question 4.
Find four numbers forming a G.P. in which the third term is greater than the lint term by 9 and the second term is greater than 4^th term by 18. (NCERT)
Solution:
Let the four terms of G.P. be a, ar, ar²,ar³.
Given: T₃ = T₁ + 9
⇒ T₃ = T₁ + 9
⇒ T₃ = a + 9
⇒ ar² = a + 9 …. (1)
According to question,
T₂ = T₄ + 18
⇒ ar = a³ + 18
⇒ ar – ar³ = 18 …. (2)

Put r = – 2 in equation (1), we get
a(- 2)² – a = 9
⇒ 4a – a = 9
⇒ 3a = 9
⇒ a = 3
∴ Numbers are 3, 3(- 2), 3(- 2)², 3(-2)³, ……………..
3, – 6, 12, – 24, ………………

Question 5.
If S be the sum of it terms of a GP., P be the product and R be the sum of reciprocal of n terms, then prove that
P²Rⁿ = Sⁿ. (NCERT)
Solution:
Let n terms of GP. be a, ar, ar², …………… ar^{n – 1}.
According to the question,

Question 6.
If x = 1 + a + a² + ………….∞ (\(\left| a \right|\)<1)
y = 1 + b + b² + …………….∞ (\(\left| b \right|\)<1)
then prove that
1 + ab + a²b² + …………….∞ = \(\frac {xy}{x + y – 1}\)
Solution:

Question 7.
The sum of infinite terms of a Geometric Progression is 15 and sum of the square of its terms is 45. Find the Geometric Progression. (NCERT)
Solution:
Let a be the first term and r be the common ratio.
∵ \(\left| r \right|\)<1,
Then, \(\frac {a}{1 – r}\) = 1.5 …. (1)
Squaring the terms of GP. the new G.P. is
a², a² r², a² r⁴, a² r⁶, ……….
Sum of infinity of G.P. = \(\frac { { a }^{ 2 } }{ { 1 – r }^{ 2 } }\).
\(\frac { { a }^{ 2 } }{ { 1 – r }^{ 2 } }\) = 45, (given) … (2)
Squaring both sides of equation (1) and the result is divided by equation (2),
\(\frac { { a }^{ 2 } }{ { 1 – r }^{ 2 } }\)² × \(\frac { 1-{ r }^{ 2 } }{ { a }^{ 2 } }\) = \(\frac {15×15}{45}\)
⇒ \(\frac {1 + r}{1 – r}\) = 5
⇒ 1 + r = 5 – 5r
⇒ 6r = 4
⇒ r = \(\frac {2}{3}\)
Put r =\(\frac {2}{3}\) in equation (1), we get

Hence required progression is 5, 5 × \(\frac {2}{3}\), 5 × (\(\frac {2}{3}\))², …………….
Hence 5, \(\frac {10}{3}\), \(\frac {20}{9}\), ………………

Question 8.
A farmer buys a used tractor of Rs. 12,000. He pays Rs. 6,000 cash and agrees to pay the balance in annual instalment of Rs. 500 plus 12% interest on theunpaid amount How much the tractor cost him?
Solution:
Cost of tractor = Rs. 12, 000, down payment = Rs. 6,000
Balance amount = 12,000 – 6,000 = Rs. 6,000

Actual cost of tractor = 12,000 + 4,680 = Rs. 16,680. Ans.

Question 9.
Shamshad Ali buys a scooter for Rs. 22,000. He pays Rs. 4,000 cash and agrees to pay the balance in annual instalment of Rs. 1,000 plus 10% interest on the unpaid amount How much will scooter cost him? (NCERT)
Solution:
Cost of scooter = Rs. 22,000, Cash down payment = Rs. 4,000.
Remaining amount = 22,000 – 4,000 = Rs. 18,000

Actual cost = 22,000 + 17,100 = Rs. 39,100.
Total amount paid for scooter = Rs. 39,100.

Question 10.
A person writes a letter to four of his friends. He asks each one of them, to copy the letter and mail to four different persons with instructions that they move the chain similarly. Assuming that the chain is not broken and that is costs 50 paisa to mail one letter. Find the amount on postage when 8^th set of letter is mailed. (NCERT)
Solution:
First person sends 4 letters.
2^nd step, he sends 4 x 4= 16 letters
3^rd step, he sends 4 x 4 x 4 = 64 letters
Hence 4, 16, 64, 256, …………… is a Geometric series.
Here a = 4, r = \(\frac {16}{4}\) = 4
S_n = \(\frac { { a(r }^{ n } – 1) }{ r – 1 }\) [∵r>1]
∴ Total number of letters till 8^th set = S₈ = \(\frac { { 4(r }^{ 4 } – 1) }{ 4 – 1 }\)
= \(\frac {4}{3}\) (65536 – 1) = \(\frac {4}{3}\) x 65535
Cost for one letter = Rs. 0.50
∴ Hence total cost = \(\frac {4}{3}\) x 65535 x 0.50 = Rs. 43690.

Question 11.
150 workers were engaged to finish a job in a certain number of days, 4 workers dropped out on second day, 4 more workers dropped out on third day and so on. It took 8 more days to finish the work. Find the number of days in which the work was completed. (NCERT)
Solution:
150, 146, 142, 138, …………, it is a Geometric series.
Let the number of days required complete the work be n.

If the workers not dropped then the work would have complited in (n – 8) days with 150 workers working on each day.
Hence the total workers worked for n days = 150 (n – 8)
= 150n – 1200 ….. (2)
From equation (1) and (2),
150n – 1200 = 152n – 2n₂
2n₂ + 150n – 152n – 1200 = 0
2n₂ – 2n – 1200 = 0
n₂ – n – 600 =0
n₂ – 25n + 24n – 600 = 0
n(n – 25) + 24(n – 25) = 0
(n – 25)(n + 24) = 0
n =25 and n = – 24 (not possible)
∴ Work is completed in 25 days.

MP Board Class 11th Maths Important Questions

MP Board Class 12th Physics Important Questions Chapter 15 Communication Systems

Communication Systems Important Questions 

Communication Systems Objective Type Questions

Question 1.
Choose the correct answer of the following:

Question 1.
The elements of communication system are :
(a) One transmitter
(b) Only receiver
(c) Only communication channel
(d) All of the above.
Answer:
(d) All of the above.

Question 2.
Sound wave are not directly transmitted after converting them into electric signals because:
(a) They propagates with speed of sound
(b) Their frequency does not remain constant
(c) For their transmission very high antenna is needed
(d) Their energy is very high.
Answer:
(c) For their transmission very high antenna is needed

Question 3.
The super imposing of audio waves with carrier wave is called :
(a) Transmission
(b) Reception
(c) Modulation
(d) Defection.
Answer:
(c) Modulation

Question 4.
The frequency range used for T.V. transmission is :
(a) 30 – 300 MHz
(b) 30 – 300 GHz
(c) 30 – 300 KHz
(d) 30 – 300 Hz.
Answer:
(a) 30 – 300 MHz

Question 5.
The periodic time of communication satellite is :
(a) 1 year
(b) 1 day
(c) 12 hours
(d) 12 minutes.
Answer:
(b) 1 day

Question 6.
T. V. signals are reflacted by :
(a) Mesosphere
(b) Ionosphere
(c) Troposphere
(d) None of these.
Answer:
(d) None of these.

Question 7.
The short wave band of radio waves are transmitted through :
(a) Sky wave propagation
(b) Ground wave propagation
(c) Artificial satellite
(d) Direct sending from transmitter to receiver.
Answer:
(a) Sky wave propagation

Question 8.
T.V. network uses :
(a) Microwaves
(b) Radio waves of very high frequency
(c) Gamma rays
(d) X – ray.
Answer:
(b) Radio waves of very high frequency

Question 9.
The waves used in telecommunication are :
(a) Infrared rays
(b) UV – rays
(c) Microwaves
(d) Cosmic rays.
Answer:
(c) Microwaves

Question 2.
Fill in the blanks :

1. …………….. is that signal which varies periodically with time.
2. Digital signal is represented by two binary number …………….. and……………..
3. The range of audio signals is ……………..
4. The frequency of carrier waves is of order of ……………..
5. The order of frequency of radio waves which can be transmitted by total internal reflection through ionosphere is ……………..
6. The band width of AM waves is ……………..
7. The T.V. transmission was invented by……………..
8. WWW means ……………..
9. …………….. is a device with the help of which the location of any place can be obtained.

Answer:

1. Analog signals
2. 0 and 1
3. 20 Hz to 20000 Hz
4. MHz
5. 30 – 300 MHz
6. Frequency of modulating wave
7. J. L. Baird
8. World Wide Web
9. GPS.

Question 3.
Match the columns:
I.

Answer:

1. (e)
2. (d)
3. (b)
4. (c)
5. (a)

II.

Answer:

1. (e)
2. (c)
3. (d)
4. (b)
5. (a)

Question 4.
Write the answer in one word/sentence:

1. Write any two light sources which are used in optical communication?
2. On what principle does the optical fibre work?
3. Who invented the T, V. transmission?
4. What is FAX?
5. What is meant by channel width? Write channel width of AM and FM radio station.
6. What is demodulation or detection?

Answer:

1. Light emitting diode (LED) and Diode LASER
2. Total internal reflection
3. J. L. Baird
4. The electronic reproduction of a document at a distant place is known as facsimile telegraphy or FAX
5. Channel width is that frequency range in which signals can be transmitted from a station. The channel width of AM is 10
6. kHz and of FM is 150 kHz
7. The process of extracting the audio signal from the modulated wave is known as demodulation or detection.

Communication Systems Very Short Answer Type Questions

Question 1.
What is principle of semiconductor LASER?
Answer:
In these LASER Gallium Arsenide (Ga – As) is used. This LASER the ability to produce LASER rays in the range 0.75 to 0.9 um.

Question 2.
Why is a parallel wire line not suitable for microwave transmission?
Answer:
In microwave transmission, half the operating wavelength approaches the separation between the two parallel wire lines. Therefore energy loss in the form of radiation becomes maximum.

Question 3.
What do you understand by channel and channel noise?
Answer:
The frequency range prescribed for a given transmission is called channel. The unwanted signals present by known or unknown reason in the transmitted signal is called noise.

Question 4.
What is importance of modulation index?
Answer:
The modulation index determines the strength and quality of the transmitted signal. If the modulation index is small the amount of variation in the carrier amplitude will be small.

Question 5.
Write full form of LED and LASER.
Answer:
Full form of LED is “Light Emitting Diode”. Full form of LASER is “Light Amplification by Stimulated Emission of Radiations”.

Question 6.
Which device is used to transmit the T.V. signals up to long distances?
Answer:
Communication satellites are used to transmit the T.V. signals up to long distances.

Question 7.
What is a communication system?
Answer:
Communication system is that system through which the signals are transmitted from one place and required at the other place.

Question 8.
What are message signals?
Answer:
A message signal is a single valued function of time that conveys the information. The electrical analog of information or basic message is called message signal. These are obtained by suitable transducers.

Question 9.
What are analog signals?
Answer:
An analog signal is continuous single value which at any instant lies within the range of a maximum and minimum value.

Question 10.
What is a digital signal?
Answer:
Digital signal is a discontinuous signal value which appears in steps in predetermined levels rather than having the continuous change.

Question 11.
What is noise?
Answer:
Noise refers to the unwanted signals that tends to disturb the transmission and processing of message signals in a communication system.

Question 12.
What is modulation?
Answer:
Modulation is a process in which the signal of low frequency (audio signals) are superimposed over a signal of high frequency (carrier signal).

Question 13.
What is FAX?
Answer:
Fax is a type of communication in which an electronic copy of a document is sent to a distance place.

Question 14.
Which type of signal is used in communication through computer?
Answer:
Digital Signal.

Question 15.
Write basic difference between the light emitted by LED and LASER.
Answer:
The light emitted by LASER is completely coherent and monochromatic while the light emitted by the LED is not coherent.

Question 16.
What is bandwidth? What is bandwidth of audio signals?
Answer:
The frequency range of a signal is called its bandwidth. The bandwidth audio signals is 20 Hz to 20 KHz.

Communication Systems Short Answer Type Questions

Question 1.
Write name of two system used for pulse modulation.
Answer:

1. PAM : Pulse Amplitude Modulation.
2. PCM : Pulse Code Modulation.

Question 2.
Write name of two systems which are used to convert the digital data into analog data.
Answer:

1. Amplitude Shift Keying (ASK)
2. Phase Shift Keying (PSK).

Question 3.
FM signals are less sensitive as compared to AM signals. Why?
Answer:
In FM transmission the information (message) in the carrier waves is in the form ofvariation (change) in frequency. In the AM the noise get amplitude modulated. Hence the amplitude carrier wave varies. That is why the FM signals are less sensitive as compared to AM signals.

Question 4.
Write limitations of frequency modulation.
Answer:

1. Area of reception for FM is much smaller.
2. About 10 times wider channel is required by FM.
3. FM receivers and transmitters are very complex and costly.

Question 5.
Write the meaning of LASER and two uses.
Answer:
Meaning of LASER:
Light Amplification by stimulated Emission of Radiations.

Uses:

1. Communication and
2. The medical field to determine vary long distances.

Question 6.
Write any two uses of optical communication.
Answer:

1. It is free from noise.
2. Its bandwidth is large, so number of channels can be transmitted simultaneously.

Question 7.
What is Light Emitting Diode?
Answer:
It is forward biased P – N junction which emits the light. It converts electrical energy into light energy.

Question 8.
What is optical fibre? On what principle does it work?
Answer:
An optical fibre is a device with the help of which the optical signals can be transmitted over through a zig-zag path without loss of energy. It is based on principle of total internal reflection.

Question 9.
What is meant by population inversion and optical pumping?
Answer:
Population inversion:
The process by which the number of atoms are increased . in the excited state as compared to ground state by stimulated absorption, is called population inversion.

Optical pumping:
The process by which population inversion is obtained, is called optical pumping.

Question 10.
Give two characteristics of LASER rays.
Answer:

1. LASER rays are monochromatic.
2. These are highly coherent.

Question 11.
What are the elements of communication system? Explain with the help of block diagram and also describe the different kinds of communication system.
Or
What is communication system? What are its main parts? Explain with block diagram.
Answer:
Communication system is that system through which the signals are transmitted from one place and received at the other place.

Elements of communication system : Following are the elements of a communication system:

1. Transmitter : Its function is to transmit the information after modifying it, to a form suitable for transmission.
Block diagram of transmitter :

2. Communication channel : The free space through which the electromagnetic waves sent by the transmitter, reach the receiver is called communication channel. It may be a coupled wire, coaxial cable or radio wave.

3. Receiver : Its function is to receive information.
Block diagram of receiver:

Question 12.
What is noise? Why digital communication is popular? What are A/D and D/A converter?
Answer:
Noise : Noise is unwanted disturbance or foreign element interfering with the desired information or signal. Noise can come up in any part of the communnication system but it has its worst effect when the signal is weakest.

The digital communication is popular nowaday because of the following characteristics :

1. Its quality is good.
2. Digital signals are in the form of pulses, they can produce easily by using logic gates.
3. These signals do not get distorted by noise.
4. These signals can be stored as digital data.
5. In this transmission many information can be transmitted using one channel.

A/D and D/A converter:
The electric circuit which can convert the analog signal to digital signal is called A/D converter. The electric circuit which can convert the digital signal into analog signal is called D/A converter.

Question 13.
Write difference between Analog and Digital signals.
Answer:
Difference between Analog and Digital signals :

Analog signal:

• In this signal value of current or voltage changes continuously with time.
• It is a continuous function of time.
• A simple analog signal is represented by a sine wave.
• The signal obtained by converting a speech, music or intensity of reflected light are analog signals.

Digital signal:

• In these signals the current or voltage has only two descrete levels 0 and 1.
• It is discontinuous function of time.
• Digital signal is represented in the form of pulses.
• The letters of a book, output of digital computers or the information obtained from a FAX are digital signals.

Communication Systems Long Answer Type Questions

Question 1.
Explain need of modulation and define the term modulation.
Or
What is modulation? Why it is needed for the transmission of signals?
Answer:
Modulation:
Modulation is a process in which the signal of low frequency (audio signals) superimposed over a signal of high frequency (carrier signal). Such that same properties of carrier wave like amplitude, frequency or phase varies in accordance with the instantaneous value of audio signals.

Need of Modulation:
Modulation is necessary for a low frequency signal when it is to be sent to a distant place so that the information may not die out in the way itself as well as for the proper identification of a signal and to keep the height of antenna small also.

For the transmission of electromagnetic waves the length of antenna should be of order of wavelength of the transmitted waves. Since, λ= \(\frac {c}{ ν}\) therefore the required length of antenna for the audible range should be equal to \(\frac { 3\times { 10 }^{ 8 } }{ 20,000 }\) = 1.5 x 10⁴m to \(\frac { 3\times { 10 }^{ 8 } }{ 20 }\) = 1.5 x 10⁷

This length of antenna is not possible in practical. Now if the waves of 300kHz or more than it are to be transmitted then the required length of antenna will be \(\frac { 3\times { 10 }^{ 8 } }{ 3,00,000 }\) = 100 m or less than it. The antenna of this size can be constructed easily. Hence to transmit the audio signals they are superimposed with the radio waves of frequency of order of Mega Hertz. These waves are called carrier waves and this process is called modulation.

Question 2.
How many types of modulation are there? Explain each types of modula-tion.
Answer:
The equation of carrier wave is given as :
e_c = E_c. cos (ω_ct + θ)
Where e_c is instantaneous value of carrier signal. E_c is amplitude of carrier wave, ω_c is angular frequency and θ is phase angle. Thus, there are three types of modulation corresponding to E_c, m_c and θ.

1. Amplitude modulation:
When an audio frequency (modulating) signal is superimposed that the amplitude of modulated wave is linear function of instantaneous value of modulating signal, then this type of modulation is called as amplitude modulation.

2. Frequency modulation:
Frequency modulation is that modulation in which the frequency of carrier wave varies in accordance with the instantaneous value of modulating signal. In this modulation the amplitude and phase of modulating signal are equal to that of carrier wave.

3. Phase Modulation:
In the phase modulation, the modulating waves are super imposed with carrier waves such that the phase of the modulated wave is the linear function of the amplitude of the modulating wave but the frequency and amplitude of the modulated signal remains same as the frequency and amplitude of the carrier wave.

Question 3.
What are limitations of amplitude modulation?
Answer:
The limitations (disadvantages) of amplitude modulation are as follows :

1. Efficiency of Amplitude modulation is smaller:
In AM modulation the message signals are contained in side bands, but not contained in the carrier wave. It is found that in amplitude modulation only one third power is contained inside bands, remaining power is contained in carrier wave. Hence efficiency decreases.

2. Amplitude modulation is more likely to suffer from noise.

3. In Amplitude modulation the fidelity of reception is less:
The range of audio signal is 20 Hz to 20 kHz. Hence the bandwidth must be 40 kHz. But the disturbance created by the nearby radio station should be taken into account and hence the bandwidth is kept only of about 20 kHz.

4. Its transmission range is low. Due to less power it is not possible to transmit the signals up to long distance. Inspite of these limitations the AM is mostly used for the transmission of audio signals.

Question 4.
Write advantages and disadvantages of frequency modulation.
Answer:
Advantages:

1. Frequency modulation is inherently and practically free from the effects of noise.
2. In frequency modulation, noise can further be decreased by increasing the deviation 8.
3. FM receiver can further be improved with the help of limiters to remove amplitude changes, if any which controls the noise level.
4. In FM it is possible to operate many independent transmitters on same frequency without interference.

Disadvantages:

1. A bout 10 times wider channel is required by FM.
2. Area of reception for FM is much smaller.
3. FM receivers and transmitters are very complicated and costly.

Question 5.
Explain the data transmission and retreival with the help of block diagram.
Answer:
The important use of data transmission and retrieval is in the microprocessor and computers. All the informations and signals which are to be transmitted are converted into digital signals by coding, which are then modulated with the carrier signals and are sent to far distant places. These signals are received by receivers. These received signals are amplified and demodulated in their original form. The block diagram of this process is shown in fig.

Question 6.
What is FAX machine? Draw its block diagram and explain its working.
Answer:

1. FAX : The electronic reproduction of a document at a distant place is known as facsimile telegraphy or Fax. To send the document through FAX following functions are performed.

• Optical scanning
• Conversion of data for transmission and reception.
• Printing a copy of images of the original document at the receiving end.

The block diagram of working of FAX is shown in fig.

Question 7.
Write notes on ‘MODEM’.
Or
What is MODEM? Write its working and uses.
Answer:
The block diagram of a modem is shown ahead : A modem is basically a modulator and a demodulator circuit.

Working:
At the transmitting end i.e., at section A, a modem change the digital data (obtained from source) into analogue form in audio frequency range.

So, it is easily modulated and transmitted by communication network through telephone lines and transmitter and sent to receiver for section B. At the receiving end i.e., at sermon B, the modem converts the analogue signal to digital signal.

Uses : It is used for short distance communication by connecting one computer to another through telephone lines.

Kinds of MODEM : MODEM are of two types.

• Internal MODEM : These are internally attached in the computer.
• External MODEM : These are connected externally with the computer.

Question 8.
Describe the following in short:

1. E – mail
2. Internet
3. World Wide Web
4. Celular phone
5. Pager.

Answer:
1. E – mail:
Its full form is electronic mail the message produced by using word processing, programs are transmitted over the world wide network called internet and they get stored in a computer called mail server. Any person connected to the internet can contact mail server. Any person connected to the internet can contact the mail server to check whether it is holding mail for him.

2. Internet:
Internet is a world wide network which connects the millions of computers which are linked together for data transmission. It is a global system of inter connected computer networks.

3. World Wide Web:
Its abreviation is WWW. It was invented by Tim Berners Lee in 1989 – 91 which is highly enlarged encylopedia which is accessible to every one for knowledge.

4. Celular Phone:
It is basically mini wireless phones for exchanging messages as well as for mobile telephonic conversation.

5. Pager:
It is a wireless device which records the messages in writing.

Question 9.
What is line communication? Explain.
Answer:
In a communication system the communication channel is a medium which provides the physicals path between transmitter and receiver. There are two types of communication medium:

1. Guided medium:
This medium connects transmitter and receiver in the case of point to point communication, double line cable, coaxial cable and optical fibre are the examples of guided medium.

2. Unguided medium:
This medium connects one transmitter and many receivers. Sky wave communication is an example of this medium. Its band frequency rays from few thousand kHz to few GHZ.

In the sky wave communication there is no point to point connection between transmitter and antenna. But in some communication applications the point to point connection is needed for example in telephone and telegraph the transmitter and receiver are connected by wire lines. It is called as line communication.

Question 10.
What is Global Positioning System (G.P.S.)? Write its applications.
Answer:
It is a space based satellite navigation system that provides users with accurate information on position time wherein the world even through the local streets and in all weather conditions.

To use GP.S. system of a satellite the user must have a GP.S. device fitted with transmitter and receiver for sending and receiving radio wave signal.

Applications of G.P.S

1. Navigation on land, water and air.
2. Keeping standard time all over the world.
3. Used in unmanned automatic vehicles movement and mobile telephony.
4. In desiging map of a location.

Communication Systems Numericals Questions

Question 1.
When there is 50% modulation the transmitter emits the 20 kW power calculate the power of carrier wave.
Solution:
Given : m_a = 50% = \(\frac {50}{100}\) = P_t = 20 kW = 20,000 W
Formula:

Question 2.
When a modulating of 500 Hz is given to a frequency modulation generator then it produces a frequency deviation of 2.25 kHz. Calculate modulation depth.
Solution:
Given : δ_max = 2.25 kHz = 2250 Hz, f_m = 500 Hz

Question 3.
The maximum and minimum amplitude of a amplitude modulated wave are 16 mV and 4 mV. What is the depth of modulation?
Solution:
Given : E_max = 16mV, E_min = 4mV
Formula:

Question 4.
A 20 kHz modulating signal is modulated with a carrier wave of 4 MHz. What will be the upper side band and lower side band? What will be the channel width?
Solution:
Given: f_m = 20 kHz, f_c = 4 MHz =4,000 kHz
f_USB = f_c + f_m = 4000 + 20 = 4020 kHz.
f_LSB = f_c – f_m= 4000 – 20 = 3980 kHz.
Channel width = f_USB – f_LSB
= 4020 – 3980 = 40 kHz.

Question 5.
Find out the modulation index of a frequency modulated wave whose modulating frequency is 2 kHz and maximum frequency deviation is 10 kHz.
Solution:
Given : f_m = 2 kHz and δ_max = 10 kHz
Formula : m_f = \(\frac { { \delta }_{ max } }{ { f }_{ m } }\)
m_f = \(\frac {10}{2}\) = 5

MP Board Class 12th Physics Important Questions

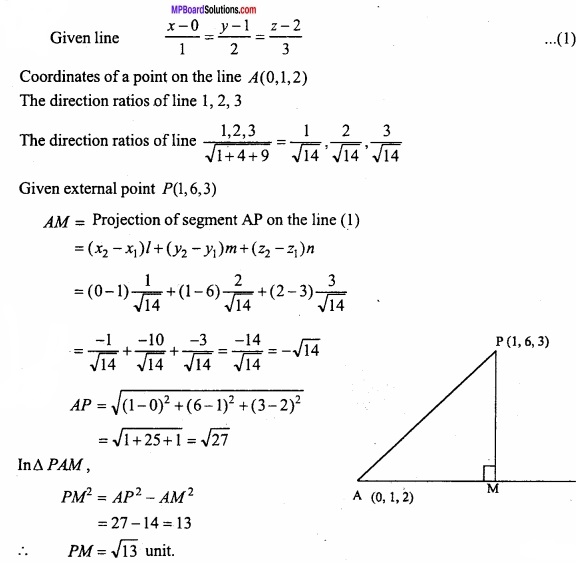
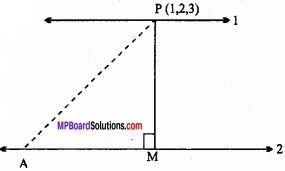
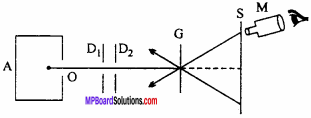
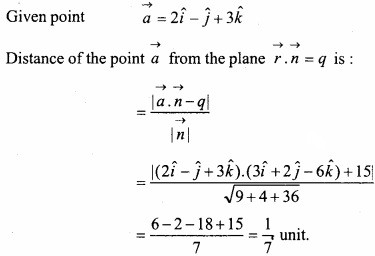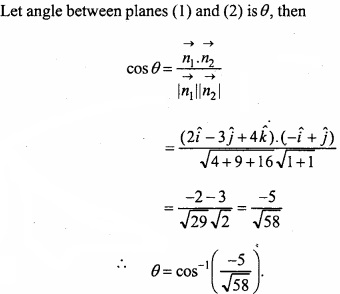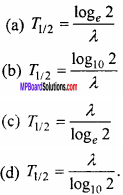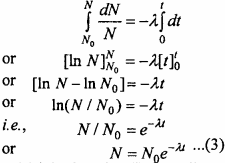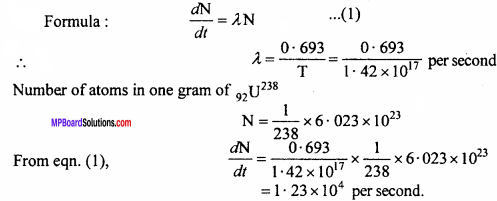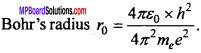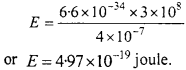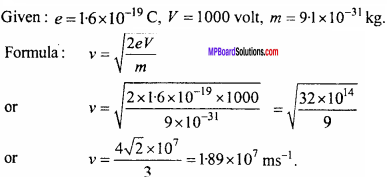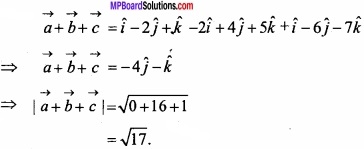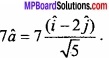MP Board Class 12th Maths Important Questions Chapter 12 Linear Programming

Linear Programming Important Questions

Linear Programming Objective Type Questions

Question 1.
Choose the correct answer:

Question 1.
At which point the value of 3x + 2y is maximum under the constraints x + y ≤ 2, x ≥ 0, y ≥ 0:
(a) (0,0)
(b) (1.5, 1.5)
(c) (2, 0)
(d) (0,2).
Answer:
(c) (2, 0)

Question 2.
Variables of the objective function of linear programming problem are:
(a) negative
(b) zero or negative
(c) zero
(d) zero or positive.
Answer:
(d) zero or positive

Question 3.
Consider the inequalities x₁ + x₂ ≤ 3, 2x₁ + 5x₂ ≥ 10, x₁ ≥ 0, x₂ ≥ 0, which of the following points like in a feasible region:
(a) (2, 1)
(b) (4, 2)
(c) (2, 2)
(d) (1, 2).
Answer:
(d) (1, 2)

Question 4.
In linear constraints the maximum value of objective function will be:
(a) at centre of feasible region
(b) at (0,0)
(c) at one of the vertices of the feasible region
(d) at the vertex which is situated at maximum distance from (0,0).
Answer:
(c) at one of the vertices of the feasible region

Question 5.
Under constraints x – 2y ≤ 6, x + 2y ≥ 0, x ≤ 6 maximum value of P = 3x + 4y is:
(a) 16
(b) 17
(c) 18
(d) 19.
Answer:
(c) 18

Question 2.
Fill in the blanks:

1. The function whose maximum and minimum value is to be found subject to given linear constraints is called …………………………..
2. The maximum or minimum value of objective function is called …………………………..
3. The graph of x ≥ 0 is situated in the …………………… quadrant.
4. The process of doing certain specified step in a given order is called …………………………….
5. The common region determined by all constraints including the non – negative constraints x ≥ 0, y ≥ 0 of a linear programming problem is called the ……………………. for the problem.

Answer:

1. Objective function
2. Optimum value
3. First
4. Programming
5. Feasible region.

Question 3.
Match the Column:

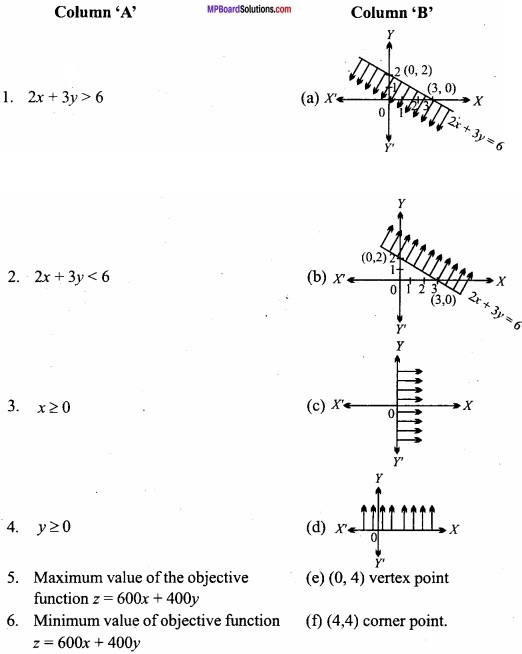
Answer:

1. (b)
2. (a)
3. (d)
4. (c)
5. (f)
6. (e).

Question 4.
Write True/False:

1. If the variable x is such that its value lies between two fixed point a and b, then {x: a < x < b} is called closed interval.
2. The function whose maximum or minimum value is to be found is called objective function.
3. The set of values of the variables satisfying all constraints is called feasible solution of the problem.
4. If the feasible region is void, then the problem has bounded solution.
5. Graph of two or more than two equation is called linear inequation system.

Answer:

1. False
2. True
3. True
4. False
5. False.

Question 5.
Write the answer in one word/sentence:

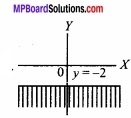
1. Represent y ≤ – 2 graphically?
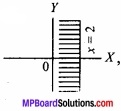
2. Represent 2x – 4 ≤ 0 graphically?
3. The graph of inequation x ≥ 0 and y ≥ 0 will be situated in which quadrant?
4. What word is used for the maximum or minimum value of the objective function?
5. P = 5x + 3y is an objective function. The coordinate of the vertices of feasible region are (3, 0), (12, 0), (0, 6). Write minimum value of objective function?

Answer:

1.
2.
3. First
4. Optimum value
5.15.

Linear Programming Long Answer Type Question – I

Question 1.
Find the maximum value of the function P = 2x + 3 y when the constraints are:
x ≥ 0, y ≥ 0,x + 2y ≤ 10; 2x + y ≤ 14?
Solution:
Because of the constraints x ≥ 0 and y ≥ 0, the graph of other linear inequation should be found on first quadrant only.

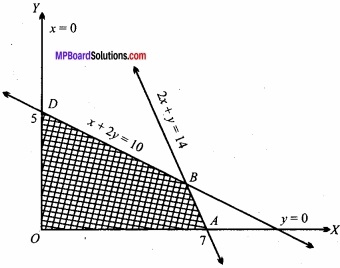
For x + 2y = 10, the table for values of x and y are given below:

For testing point (0, 0) the inequation x + 2y ≤ 10 therefore the region is towards origin 0 + 2 × 0 ≤ 10.
For 2x + y = 14 the table for the values of x and y are given below:

For origin (0, 0), 2x + y ≤ 14 is true because 2(0) + 0 ≤ 14. Therefore the region is towards the origin.
The required graph is the common region of the inequations shown by shaded portion OABD of the above graph whose vertices OABD the values of objective function P=2x + 3y is shown in the following table:

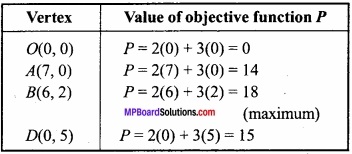
∴ The maximum value of P is 18 which is on point B (6, 2) for which x = 6, y = 2.

Question 2.
Find the minimum value of function P = x + y subject to constraints 3x + 2y ≥ 12, x + 3y ≥ 11, x ≥ 0, y ≥ 0?
Solution:
Because x ≥ 0, y ≥ 0 the graph of other constraints lies on first quadrant. They are
3x + 2y ≥ 12 ………………….. (1)
x + 3y ≥ 11 …………………… (2)

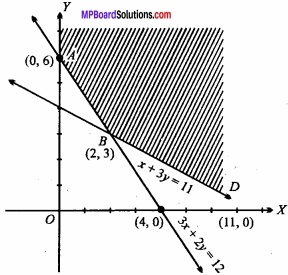
(i) For 3x + 2y = 12 the table for the values of x andy are given below:

(ii) For x + 3y = 11 the table for the values of x and y are given below:

The testing point (0, 0) does not satisfy both the inequations because
3 (0) +2 (0) ≥ 12 which is false
0 + 3(0) ≥ 11 which is false
Therefore the possible region in an open region whose vertices are A, B, D. The calculation of objective function according to the fundamental extreme point theorem is as below:

Therefore, minimum value of P is 5 when x = 2,y = 3.

Question 3.
Show graphically the fixed region by the inequations given below:
x ≥ 0, y ≥ 0, 2x + 5y ≤ 16, 2x + y ≤ 8?
and find the value of* andy for which the function P = 5x+ 4y has maximum value?
Solution:
2x + 5y ≤ 16 ……………………. (1)
and 2x + y ≤ 8 …………………………. (2)
\(\frac { 2x }{ 16 } \) + \(\frac { 5y }{ 16 } \) ≤ 1, [from inequation (1)]
⇒ \(\frac{x}{4}\) + \(\frac { y }{ \frac { 16 }{ 5 } } \) ≤ 1 ………………….. (3)
Similarly, \(\frac { 2x }{ 8 } \) + \(\frac { y }{ 8 } \) ≤ 1 [from inequation (2)]
⇒ \(\frac{x}{4}\) + \(\frac{y}{8}\) ≤ 1 ……………………….. (4)
The region x ≥ 0 and y ≥ 0 representing graphically the inequations (3) and (4),

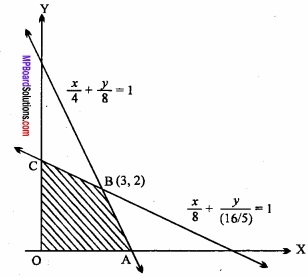
Lines \(\frac{x}{4}\) + \(\frac{y}{8}\) = 1
and \(\frac{x}{4}\) + \(\frac { y }{ \frac { 16 }{ 5 } } \) = 1
Intersects each other at the point B(4, 2). Hence OABC is the region bounded by the lines, where the coordinates of the points O, A, B, C are 0 (0, 0), A (4, 0), B (3, 2), C (0, \(\frac{16}{5}\) ) respectively
On the vertices the value of P = 5x + 4y will be following:

From the above table the maximum, value of P is 23 on the point B (3, 2).
Hence the value is maximum at x = 3 and y = 2.

Question 4.
If a young man rides his motorcycle at 25 km per hour, he has to spend Rs. 2 per km on petrol, if he rides it in a faster speed of 40 km per hour, the petrol cost increases to Rs. 5 per km. He has Rs. 100 to spend on petrol and wishes to find what is maximum distance he can travel within one hour. Express this as a linear program¬ming problem and then solve it?
Solution:
Let the distance travelled at 25 km/hour = x km.
And distance travelled at 40 km/hour = y km.
We wish to maximize z = x + y subject to the constraints
2x + 5y ≤ 100 …………………….. (1)
\(\frac{x}{25}\) + \(\frac{y}{40}\) ≤ 1
Now let us solve the linear programme in the following way:
As x ≥ 0 and y ≥ 0 we shall shade the solution set of the other inequalities in the first quadrant.

For, eqn. (1),
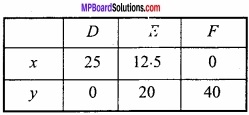
2x + 5y = 100
x = \(\frac{100 – 5y}{2}\)
Now the test point O (0, 0) makes the inequation (1) true so we shade the half plane containing (0, 0).
For eqn.(2), \(\frac{x}{25}\) + \(\frac{y}{40}\) ≤ 1
or 8x + 5y ≤ 200
⇒ 8x + 5y = 200
⇒ x = \(\frac{200-5y}{8}\)
Again the test point (0, 0) makes the inequality (2) true so we shade the half plane containing (0, 0).

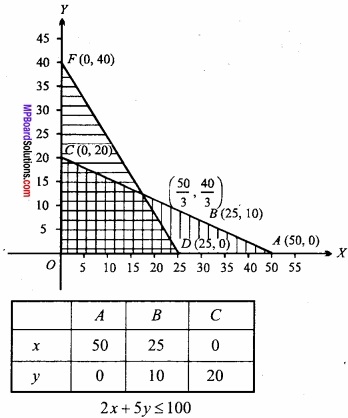
The vertices of feasible region are
0(0,0), D (25, 0), G ( \(\frac{50}{3}\), \(\frac{40}{3}\) ) , C (0, 20)
Let us caluculate z = x + y at these points.
At D (25, 0) z = 25 + 0 = 25
At G ( \(\frac{50}{3}\), \(\frac{40}{3}\) ) z = \(\frac{50}{3}\) + \(\frac{40}{3}\) = 30
At C (0, 20) z = 0 + 20 = 20
Hence, Maximum z = 30 km at ( \(\frac{50}{3}\), \(\frac{40}{3}\) ).

Question 5.
A manufacturer plants to install some new machines in his workshop. Type A machine costs Rs. 800 and occupies 3 square metre of floor space. Type B machine costs Rs. 1600 and occupies 1 \(\frac{1}{2}\) square metres of space. He can spend Rs. 20,000 altogether and the space available is 30 sq. metres. Type A turns out 10 components per hour where as type B 15 per hour. Trade restrictions compel him to have at least 3 machines of type A and 4 machines of type B?
What is the maximum number of machines he can install? Which arrangement gives him the maximum output?
Solution:
Let us assume that he buys x machines of type A and y machines of type B. Taking on account the costs of the machines and the total money available 800x + 1600y ≤ 20,000
or x + 2y ≤ 25 ………………. (1)
Again using the conditions of the space available and the space required for the machines
3x + \(\frac{3}{2}\) y ≤ 30
2x + y ≤ 20 …………………….. (2)
Also using the trade restrictions on having two types of machines
x ≥ 3 ……………………….. (3)
y ≥ 4 ……………………. (4)
The number of machines he buys will be x + y and the total output (10x + 15y) per hour.
Let N = x+y ……………………. (5)
and O = 10x + 15y ……………………… (6)
Now our problem is to maximize (5) and (6) subject to constraints (1) to (4).
The shaded region is the feasible region. The comers of the feasible region are the points (3, 4), (8, 4), (5, 10) and (3, 11).
At the point (3, 4)
N = 3+ 4 = 7,O = 30+ 60 = 90
At the point (8,4)
N = 8+ 4 = 12, O = 80 + 60 = 140
At the point (5, 10)
N = 5 + 10 = 15, O = 50 + 150 = 200
At the point (3, 11)
N = 3 + 11 = 14, O = 30 + 165 = 195

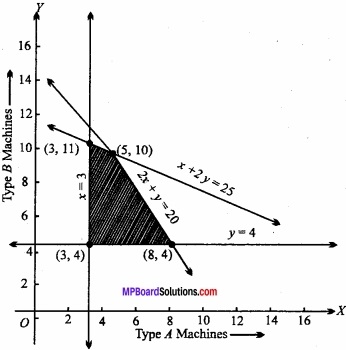
The maximum number of machines he can buy is 15. Also maximum output can be obtained by using 5 machines of type A and 10 machines of type B.

Question 6.
A soft drinks firm has two bottling plants one located at P and other at Q? Each plant produces three different soft drinks A, B and C? The capacities of two plants in number of bottles per day are as follows:

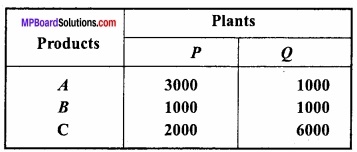
A market survey indicates that during the month of April there will be a demand for 24,000 bottles of A, 16,000 bottles of B and 48,000 bottles of C. The operating cost per day of running plants P and Q are respectively Rs. 6,000 and Rs. 4,000. Find graphi-cally how many days should the firm run each plant in April so that the production cost is minimized?
Solution:
Suppose that firm runs plant P for x days and plant Q for y days in April so the total operating cost of two plants is given by:
z = 6000x + 4000y (objective function)
As P plant produces 3000 bottles and Q plant produces 1000 bottles of drink A per day, so total production of drink A in the supposed period is
(3000x + 1000y) bottles
But there will be a demand for 24,000 bottles of this drink so the restriction 3000x + 1000y ≥ 24000 i.e., 3x + y ≥ 24
Similarly for the other two drink we have the constraints 1000x + 1000y ≥ 16000 i.e., x + y ≥ 16
2000 x + 6000 y ≥ 48000 i.e., x + 3y ≥ 24
Moreover x and y are non – negative. So x ≥ 0, y ≥ 0.
Mathematically, the given problem now reduces to minimize
z = 6000 x – 4000 y (objective function)
Subject to the conditions

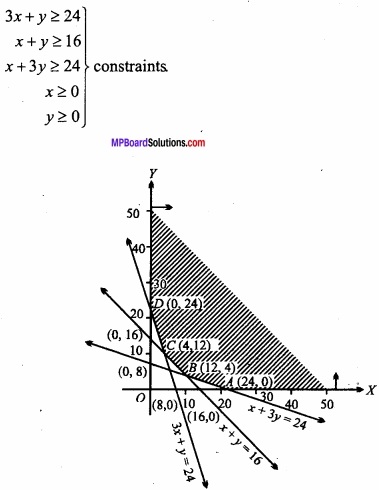
The graph of the system or inequations can be easily obtained arid is as shown in figure, As (x ≥ 0 and y ≥ 0 the graph has been drawn in the first quadrant only). The points in the region which is common shaded area unbounded above constitutes the graph of the system of inequations.
Now the minimum value of the cost function z = 6000 x + 4000 y
As at one of the points A (24, 0), B (12,4), C (4, 12) and D (0, 24).

Hence P is minimum at x = 4 and y = 12. Therefore for minimum cost the firm P should run for 4 days and Q for 12 days.
Minimum cost will be Rs. 72,000.

Question 7.
A and B are the two tailor A earns Rs. 150 per day and B earns Rs. 200 per day? A can stich 6 shirts and 4 pants per day and B can stich 10 shirts and 4 pants per day? Formulate the above as a linear programming problem (L.P.P.) for minimizing the cost of at least 60 shirts and 32 pants? (CBSE 2005)
Solution:
Let, tailor works x days and tailor B works y day.
Hence, invest function is
Z = 150x + 200y
According to the function, tailor A, stich 6 shirts and B stich 10 shirts, for minimizing the cost of at least 60 shirts.
6x + 10 ≤ 60
and tailor A stich, 4 pants and B stich 4 pants, for minimizing the cost of at least 32 pants.
4x + 4y ≤ 32
and x ≥ 0, y ≥ 0
Similarly,
For minimizing invest function Z = 150x + 200y subject to the following contraints
6x + 10y ≤ 60
4x + 4y ≤ 32.
Note: For drawing the graph of constraints 6x + 10y ≤ 60, we will draw the graph of 6x + 1o y = 60.
\(\frac{6x}{60}\) + \(\frac{10y}{60}\) = 1
\(\frac{x}{10}\) + \(\frac{y}{6}\) = 1 ……………….. (1)
Line (1) cuts the intercepts 10 and 6 respectively with the coordinates axes.
i.e., By joining the points P(10,0) and Q( 0,6) get the graph of line 6x +10y = 60 easily.
Similarly draw the graph of 4x + 4y = 32
⇒ \(\frac{4x}{32}\) + \(\frac{4y}{32}\) = 1
⇒ \(\frac{x}{8}\) + \(\frac{y}{8}\) = 1 …………………….. (2)

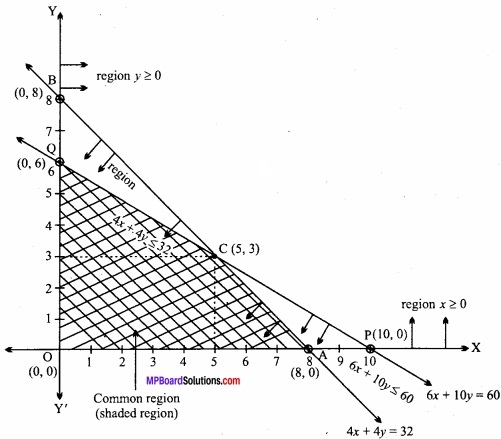
Line (2) cuts the intercepts 8, 8 with the coordinates respectively i.e., graph of line 4x + 4y = 32 can be find by joining the points A(8, 0) and B(0, 8).
(i) x ≥ 0, all points above and on the X – axis in the solution set.
(ii) y ≥ 0, all points above and on the Y – axis in the solution set.
(iii) Taking testing point O (0, 0) for finding the solution set of 6x + 10y ≤ 60 we have, 6 × 0 + 10 × 0 < 60
⇒ 0 < 60 , which is true.
Hence all points on the line 6x + 10y = 60 including all points near to the origin is the solution set of 6x +10y ≤ 60.
(iv) Similarly, solution set of 4x + 4y ≤ 32 towards to the origin and each point on the line 4x + 4y = 32.
Hence, the common region of x ≥ 0, y ≥ 0, 6x + 10y ≤ 60 and 4x + 4y ≤ 32 shown in above graph by shaded region.
i.e., the required region is OACQ whose corner points are O (0, 0), A (8, 0), C (5, 3) and Q (0, 6).

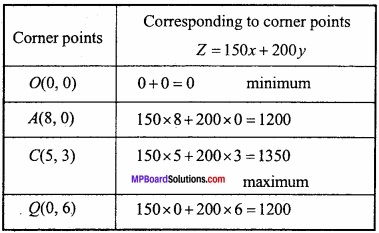
Minimum value of invest Z = 150x + 200y is 0 and maximum invest cost of Rs. 1350 is corresponding to point (5, 3).

MP Board Class 12 Maths Important Questions

MP Board Class 12th Physics Important Questions Chapter 14 Semiconductor Electronics: Materials, Devices and Simple Circuits

Semiconductor Electronics: Materials, Devices and Simple Circuits Important Questions 

Semiconductor Electronics: Materials, Devices and Simple Circuits Objective Type Questions

Question 1.
Choose the correct answer of the following:

Question 1.
The forbidden energy gap in Germanium crystal is :
(a) 1.2 x 10^-19J
(b) 1.76 x 10^-19J
(c) 1.6 x 10^-19J
(d) Zero
Answer:
(a) 1.2 x 10^-19J

Question 2.
The valency of impurity dopped in a pure germanium crystal to make it P – type semiconductor is:
(a) 3
(b) 4
(c) 5
(d) 6
Answer:
(a) 3

Question 3.
The deplection layer of P – N junction has :
(a) Electrons
(b) Protons
(c) Mobile ions
(d) Immobile ions
Answer:
(d) Immobile ions

Question 4.
The width of deplection layer in P-N junction diode is
(a) 10^-3 m
(b) 10^-4 m
(c) 10^-5 m
(d) 10^-6 m
Answer:
(d) 10^-6 m

Question 5.
Zener diode is used as :
(a) Amplifier
(b) Rectifier
(c) Oscillator
(d) Voltage regulation
Answer:
(d) Voltage regulation

Question 6.
Light emitting diode is formed by :
(a) Silicon
(b) Germanium
(c) Carbon
(d) Ga – As
Answer:
(d) Ga – As

Question 7.
Which of the following is a photo voltaic device :
(a) Photo cell
(b) LED
(c) Zener diode
(d) Solar cell
Answer:
(d) Solar cell

Question 8.
When N – P – N transistor is used as amplifier then :
(a) Electrons goes from base to collector
(b) Holes goes from emitter to base
(c) Holes goes from collector to base
(d) Holes goes from base to emitter.
Answer:
(a) Electrons goes from base to collector

Question 9.
The relation between current gain in CB mode (α) and current gain (β) in CE mode is:
(a) β = α + 1
(b) β = \(\frac {α}{1 – α}\)
(c) β = \(\frac {α}{1 + α}\)
(d) β = 1 – α.
Answer:
(b) β = \(\frac {α}{1 – α}\)

Question 10.
In CE amplifier the phase difference between input and output signals is :
(a) 0°
(b) 90°
(c) 180°
(d) 270°.
Answer:
(c) 180°

Question 11.
Oscillator is an amplifier with :
(a) Positive feed back
(b) Negative feed back
(c) No feed back
(d) High current gain.
Answer:
(a) Positive feed back

Question 12.
The boolean expression for NAND gate is :
(a) A + B = Y
(b) A – B = Y
(c) A = Y
(d) AB = Y.
Answer:
(d) AB = Y.

Question 2.
Match the Column :

Answer:

1. (c)
2. (e)
3. (d)
4. (b)
5. (a)

Question 3.
Fill in the blanks :

1. Zenar diode is used as ……………..
2. The ratio of change in output voltage to change in the input Voltage is called ……………..
3. Power gain = (Current gain)² x ……………..
4. With increase in temperature of a semiconductor its conductivity ……………..
5. In an intrinsic semiconducter the forbidden energy gap is of order of ……………..
6. Main function of a tank circuit is to produced ……………..
7. In a NAND gate there is a …………….. gate along with AND gate.
8. NOT gate is also called as ……………..
9. The boolean expression of AND gate is ……………..
10. If Y = \(\overline {A+B}\) then gate is ……………..
11. Photo diode is used as ……………..
12. Light emitting diode is used in …………..

Answer:

1. Voltage regulation
2. Voltage gain
3. Resistance gain
4. Increases
5. 1 eV
6. Oscillations
7. NOT
8. Inverter
9. Y = A.B
10. NOR
11. To defect light
12. Light emission.

Question 4.
Write the answer in one word/sentence :

1. How does the energy gap in the intrinsic semiconductor varies on introducing a penta valent impurity in it?
2. Whose drift velocity is greater holes or electrons.
3. On increasing the reverse bias in P – N junction diode how does the width of depletion layer vary?
4. In which bias the resistance of P – N junction diode is very high?
5. What is use of zener diode?
6. A transistor is used as an amplifier in common emitter mode rather than in common base mode why?

Answer:

1. The energy gap decreases
2. The drift velocity of electrons is greater than that of holes
3. The width of depletion layer increases
4. Reverse bias.
5. It is used as voltage regulator
6. Because in common emitter amplifier the voltage gain and power gain is more.

Semiconductor Electronics: Materials, Devices and Simple Circuits Very Short Answer Type Questions

Question 1.
What are semiconductors? Write down names of any two semiconductors.
Answer:
The substances which have electrical conductivity between conductors and insulators are called semiconductors.
Examples:
Germanium, silicon.

Question 2.
How does the conductivity of semiconductors affected on heating the semi – conductors?
Answer:
When a semiconductors is heated then the covalent bond get broken and the valence electrons becomes free. With increase in temperature the number of free electrons increases. Hence the conductivity of semiconductor increases.

Question 3.
Choose the conductor, insulator and semiconductors in the following : Germanium, Tungsten, Air, Silver, Silicon, Carbon.
Answer:

1. Conductor : Tungsten, Silver.
2. Insulator : Air
3. Semiconductor : Germanium, Carbon, Silicon.

Question 4.
Write difference between the charge occurs in the resistivity of metals and intrinsic semiconductor with temperature.
Answer:
With increase in the temperature the resistivity of metals increases while that of intrinsic semiconductor decreases.

Question 5.
Draw the symbol of P – N junction diode.
Answer:

Question 6.
How can a pure semiconductor be converted into a P – type semiconductor?
Answer:
When a trivalent impurity such as indium, boron etc are introduced into pure semiconductor then P – type semiconductor is formed.

Question 7.
How can a pure semiconductor be converted into a N – type semiconductor?
Answer:
When a pentavalent impurity such as antimeny, arsenic phosphorus etc. are introduced into pure semiconductor then N – type semiconductor is formed.

Question 8.
What is the ratio of number of holes to number of electrons in an intrinsic semiconductor?
Answer:
1 : 1.

Question 9.
Write the name of majority charge carriers in P – type and N – type semiconductors.
Answer:
In P – type semiconductor majority charge carriers are holes and in , N – type semiconductor majority charge carriers are electrons.

Question 10.
What is LED?
Answer:
It is Abbreviation of ‘Light Emitting Diode’. It is a P – N junction which, when used in reverse bias, emits the light.

Question 11.
In a transistor emitter is always forward biased and collector is reverse biased, why?
Answer:
The charge carriers (electrons or holes) are moved only when the emitter is forward biased while collector will occupy them only when it is reverse biased. So that there is a unidirectional flow of current.

Question 12.
What are universal gate?
Answer:
NOR gate and NAND gate are called as universal gate, because by the combination of these gates, other logic gates can be obtained.

Question 13.
What is dopping? Why it is necessary?
Answer:
The process of introducing the impurities in a pure semiconductor is called dopping. To form N – type and P – type semiconductors dopping is necessary.

Semiconductor Electronics: Materials, Devices and Simple Circuits Short Answer Type Questions

Question 1.
What do you understand by intrinsic and extrinsic semiconductors?
Answer:
Intrinsic semiconductors:
Pure semiconductors are called intrinsic semiconductors example germanium and silicon. The number of electrons and holes are equal in it.

Extrinsic semiconductors:
The semiconductors containing impurities of pentavalent or trivalent substances are called extrinsic semiconductors. The electron density is not equal to hole density.

Question 2.
Semiconductors are used to form the transistor. Why?
Answer:
Transistor are made by N – type and P – type semiconductors where the charge carriers are electrons and holes. Thus, the function of transistor is based on the control over the motion of electrons and holes. This control is not possible in conductors and insulators. Therefore only semiconductors are used to make transistors.

Question 3.
Explain the meaning of word “Transistor”.
Answer:
Transistor is a short form of transformation of resistance. The low resistance of forward biased junction is transformed to high resistance of reverse biased junction. Therefore it is called as transistor.

Question 4.
Why the base is designed thin in comparison to emitter and collector in a transistor?
Answer:
A thin and lightly doped base region will contain a smaller number of majority charge carriers. This will reduce the recombination rate of electrons and holes when major-ity charge carriers move from emitter to collector.

Question 5.
Draw symbols of P – N – P and N – P – N transistors.
Answer:
P – N – P Transistor N – P – N Transistor

Question 6.
What is difference between transformer and transistor?
Answer:
The transformer changes alternating voltage but the power remains same. Amplifier increases power of alternating voltage.

Question 7.
Draw symbol of NAND and NOR gate.
Answer:

Question 8.
What is Universal gate? Why they are called so?
Answer:
NOR and NAND gates are called as universal gates because by the combination of these gates other gates can be formed.

Question 9.
How will you obtain NOT gate from NAND gate? Draw logic symbol and write truth table.
Answer:
When the two input signal of NAND gate are joined together then the output signal obtained is equivalent to that of NOT gate.
Symbol :

Truth table:

Question 10.
How will you obtain AND gate from NOR gate?
Answer:
To obtain AND gate from NOR gate:
If the output of two NOT gate obtained by NOR gates are used as two inputs of a NOR gate then the resultants output be same as the output of AND gate.
Symbol:

Truth table:

Question 11.
How will you obtain OR gate from NAND gate?
Answer:
If the two outputs of NOT gates obtained by NAND gates are used as inputs of a NAND gate then the final output be same as the output of OR gate.
Symbol:

Truth table:

Question 12.
What is dopping? Why it is necessary?
Answer:
The process of introducing the impurities in a pure semiconductor is called dopping. To form N – type and P – type semiconductors dopping is necessary.

Question 13.
Identify the following symbol, write its boolean expression and write the truth table:

Answer:
It is a NAND gate.
Boolean expression : y = \(\overline { A.B } \quad\)
Truth table:

Question 14.
Explain the following terms with reference to a P – N junction :

1. Uncovered charge
2. Depletion layer
3. Potential barrier.

Answer:

1. Uncovered charge : The positive immobile ions present on the N – region and negative immobile ions present in P – region near the junction are called uncovered charge.

2. Depletion layer : The layer on either side of P – N junction which does not contain any charge carrier (neither positive charge carrier nor negative charge carrier) is called depletion layer.

3. Potential barrier : The potential difference developed across the depletion layer is called the potential barrier.

Question 15.
What is P – N diode? Explain the formation of depletion layer in it.
Answer:
When P – type semiconductor is joined with N – type semiconductor by some special techniques as etching or sandwitching, then the junction formed is called P – N diode. It works similar to that of diode valve. Hence, it is called P – N junction diode. When P – N junction diode is made, then free electrons present in N – type get diffused across the boundary into P – type and few number of holes diffuse into N – type from P – type. Thus, a thin film (less than 10^-3 cm) at the junction becomes free from holes and electrons. This thin film is called depletion layer.

Question 16.
What is zener diode? Explain it.
Answer:
Zener diode is P – N junction diode which is fabricated for a definite breakdown voltage. The value of breakdown voltage depend upon the doping density of P – and ,V – type semiconductor. The breakdown voltage depends upon the concentration of doping, in a highly dopped P – N junction, the depletion layer is very thin so that the value of zener voltage becomes very small.

For a definite breakdowm voltage zener diode ner diode is constructed by a special doping in such a way that it doesn’t get damaged even it working at breakdown voltage at reverse bias.

Symbol:
The symbol of zener diode is shown in adjacent fig.

Principle:
In the reverse biased zener diode, on applying breakdown voltage it allows easy flow of current. But inspite of flow of current the P – N junction do not get de – stroyed. When the applied voltage becomes less than breakdown voltage it again becomes a normal P – N junction diode.

Use:
It is used as voltage regulator.

Question 17.
What is a Solar cell?
Or
How a junction diode can be used as a solar cell?
Answer:
Solar cell:
It is a P – N junction diode which converts the solar energy into electrical energy. It works on the principle of photoelectric effect.

When the solar light fall on the P – N junction then an e.m.f. is produced across its ends. This e.m.f. is called as photoelectric e.m.f. Hence a P – N junction acts as source of e.m.f. This is called solar cell.

Working:
When light photons reach the junction they excite electrons from the valence band to conduction band leaving behind equal number of holes in the valence band. The electron hole pairs generated in the deplection region move in opposite directions due to the barrier field. Photo generated electrons move towards N – region and holes towards P – region.

The collection of these charge carriers make P – region positive electrode and N – region a negative electrode. Hence photovoltage is set up across the junction. When a load resistance R is connected in the external circuit, a photo current I flows through it.

Question 18.
Explain the working of N – P – N transistor with labelled diagram.
Answer:
The adjacent fig. shows the N – P – N transistor in CE mode.

The emitter is at negative potential w.r.t. the base and collector. The electron of emitter region are repelled by the negative terminal of the battery V_BE and move towards the base region, as the base region is very thin most of the electrons cross this region and enter to the collector region. Only 2% to 5% of electrons combine with the holes present in base region, therefore I_b the base current flows. The electrons entering into collector region are attracted very fast by the positive terminal of battery V_CE and collector current I_c flows through the external circuit.
If the emitter current is Ie then by Kirchhoff’s law
I_e = I_b + I_c

Semiconductor Electronics: Materials, Devices and Simple Circuits Long Answer Type Questions

Question 1.
Explain P – type semiconductors in terms of energy band.
Answer:
When a trivalent impurity (Such as Boron, Aluminium etc.) is introduced (dopped) in a pure Ge crystal then a P – type semiconductor is formed.

In a P – type semiconductor each acceptor impurity atom process a hole. This hole is fulfilled by an electron of nearest Ge – Ge band. To remove the electron from covalent band and to bring it to the hole very small amount of energy (about 0.01 – 0.05 eV) is required. Hence the acceptor energy level is slightly above the top of valence band. At room temperature the electrons of valence band get excited and reach to the acceptor level. Therefore same number of holes are created in valence band. Thus in P- type semiconductor the number of holes in valence band is much greater than the number of electron in conduction band.

Question 2.
What do you understand by N – type and P – type semiconductors? Give differences between them.
Or
Differentiate between the P – type and N – type semiconductors.
Answer:
N – type : When pure germanium is introduced by small amount of a pentavalent atoms as antimony, arsenic, etc. then N – type semiconductors are formed.

P – type : When pure germanium is introduced by small amount of a trivalent atoms as indium, boron, etc. then P – type semiconductors are formed.

Difference between N – type and P – type semiconductors :
N – type:

• N – type of semiconductors are formed by the impurities of pentavalent elements.
• Electrons are the charge carriers.
• Number of electrons in conduction band is greater than the number of holes in valence band.
• Fermi level is towards conduction band.

P – type:

• P – type of semiconductors are formed by the impurities of trivalent elements.
• Holes are the charge carriers.
• Number of holes in valence band is greater than the number of electrons in conduction band.
• Fermi level is towards valence band.

Question 3.
Explain working of P – N – P transistor in CE mode.
Answer:
Working of P – N – P transistor :
The figure shows the common emitter circuit. The emitter is at positive potential w.r.t. the potential of base and collector. The holes coming from the emitter are only 2% to 5% which combine in the base region thus low current is flown in emitter circuit and other holes are attracted by the negative terminal of the battery V_ce.

As soon as the hole reaches to the end, the electron from the negative terminal of the battery V_ce neutralizes it and at the same time, a covalent band breaks at emitter region. Thus, an electron enters the positive terminal of the battery V_be and the same process is repeated. Thus, the current flows through P – N – P transistor by holes and outside it in external circuit by electrons. If the emitter current be I_e. Then, I_e = I_b + I_c.

Question 4.
Explain with a circuit diagram, how common emitter P – N – P transistor is used as amplifier?
Or
Explain the working of P – N – P transistor as amplifier in CE mode with a circuit diagram.
Answer:
In concerning circuit use of transistor as an amplifier is shown :
Where, S → Input signal, R → Load resistance, V_c → Collector voltage. In this circuit, emitter is kept at positive potential relative to the base and collector. Input signal is applied between base and emitter. Load resistance R is added to the collector circuit.

As a result collector becomes more negative and output signal becomes negative. In next half cycle of input signal, potential of base becomes more negative relative to emitter and I_c increases, therefore value of collector voltage V_c decreases or it becomes negative which gives positive output signal.

In this way, opposite signals are obtained in different half cycles of input signal. So, it is clear that there is phase difference of 180° between the input and output signals.

Question 5.
Explain the working of N-P-N transistor as amplifier in CE mode under following points :

1. Circuit diagram
2. Working
3. Voltage gain.

Answer:
1. Circuit diagram :

2. Working:
The emitter terminal is common to both the input and output circuit. While the input circuit is forward – biased, the output circuit is reverse – biased.

When no a.c. signal (input) is supplied to the input, the collector current I_c flows through load resistance (R) will produce a voltage drop I_c R across R. Hence, the net output voltage is
V_c =V_ce – I_c R … (1)

Suppose the signal to be amplified is now fed the input circuit. During the positive half cycle of input, the forward bias of base – emitter increases. So, emitter and collector current increases. Hence, from equation (1), V_c decreases. But V_c is joined to high potential, so high potential value decreases. So, amplified signal becomes negative. This explains the amplification of positive half cycle.

During the negative half cycle of input, forward bias decreases both emitter and collector current decreases, hence V_c increases by equation (1). So, the output becomes more positive. Clearly, the output signal is 180° out of phase from the input signal.

3. Voltage gain:
The ratio of change in output voltage to the change in input voltage is called voltage gain. It is denoted by Av.

Question 6.
What is NAND gate? Write its symbol, truth table and boolean expression.
Answer:
When a NOT gate is connected at the output of AND gate then the logic gate formed is known as NAND gate.
Symbol:

Truth Table:

Boolean expression : \(\overline { A.B } \quad\) = Y.

Question 7.
Explain NOT gate under the following heads :

1. Symbol
2. Relation between input and output
3. Equivalent circuit.

Answer:
1. Symbol:

2. Relation between input and output : Y = \(\overline { A}\), where Y is output and A is input.

3. Equivalent circuit:

Question 8.
What is rectification? Explain half – wave rectification by diode on the basis of following points:

1. Labelled diagram of circuit
2. Working

Or
Describe the use of P – N junction diode as half wave rectifier under the following heads:

1. Labelled circuit diagram
2. Working
3. Graph for time variation of input and output potential.

Answer:
Rectification:
The phenomenon of conversion of a.c. to d.c. is known as rectification.

1. Labelled diagram:
a.c. → Input a.c. voltage, T → Step – up transformer, PN → Junction diode, R → Load.

2. Working:
When an a.c. voltage is applied to the primary coil of transformer, then an a.c. voltage is induced in the secondary coil of transformer. Let in half cycle, A is at positive potential w.r.t. that of B. Then P – N junction diode is in forward – biased. Thus, the current flows through it and conventional cunrent flows through R, from C to D.

In the next half cycle, A is at negative potential w.r.t. B. The junction diode is in reverse – biased and no current flows through R. The same phenomenon is repeated in the next cycle. Therefore, only half cycle of the input a.c. wave is converted into d.c. This process is called half – wave rectification.

Question 9.
What is rectification? Drawing the electrical circuit show a P – N diode can be used as full wave rectifier.
or
Describe the use of P – N junction diode as a full wave rectifier under the following heads:

1. Labelled circuit diagram
2. Working
3. Wave form of output signals.

Or
What is a rectifier? Draw circuit diagram to explain the use of P – N junction diode as full wave rectifier.
Answer:
The process of converting the alternating current into direct current is called rectification and the circuit used for the purpose of rectification is called rectifier circuit.

1. Labelled diagram :
T → Step – up transformer, D₁ D₂ → Diodes, R → Load.

2. Working function:
When a.c. voltage is applied on primary coil of step – up transformer T, a.c. voltage induces in secondary coils. In first half cycle, A is at positive and B is at negative potential with respect to E. Therefore, diode D₁ becomes forward – biased and current flows in load resistance R from C to D. This time point B is at lower potential relative to E, therefore D₂ is at reverse biased.

In second half cycle, A is at negative and B is at positive potential relative to E. D₁ gets reverse – biased and stops working where D₂ is at forward – biased and allows current to flow from C to D. In this way in both the half cycles, current flows through the load resistance and diode behaves as full-wave rectifier.

Question 10.
Draw a labelled circuit to explain the use of P – N – P transistor in CE mode as an amplifier. Obtain expression for current gain, voltage gain and power gain.
Answer:
See Long Answer Type Question No. 4 for circuit diagram and working.

1. Current gain : The ratio of change in collector current to change in base current is called current gain. It is denoted by β.

2. Voltage gain: The ratio of change in output voltage ∆V_CE to change in input voltage ∆V_BE is called voltage gain A_V.

3. Power gain : The ratio of change in output power to change in input power is called power gain.

Question 11.
What is oscillator? Explain the function of transistor as an oscillator.
Or
What is an oscillator? Draw necessary circuit diagram to show the use of transistor as an oscillator.
Or
What is an oscillator? Explain use of transistor as oscillator under following points:

1. Labelled circuit diagram
2. Working.

Answer:
Oscillator : Oscillator is a device which can produce high frequency oscillations.

Use of transistor as an oscillator : A circuit is given in which a transistor is used in common emitter configuration.

Theory:
By proper coupling a tank circuit (L₁ – C₁ circuit) and feedback circuit a transistor oscillator can be made. A tank circuit is joined between the collector and key K. C₁ is a variable capacitor with the help of which any desired frequency can be obtained in tank circuit. An inductor L₁ is added between the base and emitter. Inductor L is coupled properly with inductor L₁.

Working function:
When key K is pressed electric oscillation starts in tank circuit. As L is coupled with L₁, e.m.f. is produced in inductor L due to induction of which value changes in magnitude and direction. In this way increase in base potential causes increase in collector current which helps oscillation in tank circuit. As a result, tank circuit L₁ – C₁ oscillates with constant amplitude. Energy wasted is recovered from the battery.
Frequency of oscillation, ν = \(\frac { 1 }{ 2\pi \sqrt { { L }_{ 1 }{ C }_{ 1 } } }\)
Where, L₁ = Induction of inductor L,C₁ = Capacity of capacitor C.

Semiconductor Electronics: Materials, Devices and Simple Circuits Numerical Questions

Question 1.
In a P – N junction, width of depletion layer is 10^-6 m and potential barrier is 0.7 Volt. Calculate the barrier electric field.
Solution:
Given : d = 10^-6 m, V = 0.7 volt
Formula: E = \(\frac {V}{d}\)
∴E = \(\frac { 0.7 }{ { 10 }^{ -6 } }\), or E = 7 x 10⁵ volt/metre.

Question 2.
In a P – N junction diode if the potential is changed by 0.12 volt then cunrent changes by 1.5 mA. Find out dynamic resistance of diode.
Solution:
Given : ∆V = 0.12 volt, ∆ I = 1.5 mA = 1.5 x 10^-3A
Formula : r_d = \(\frac {∆V}{∆d}\)
or r_d = \(\frac { 0.12 }{ 1.5\times { 10 }^{ -3 } }\)
= \(\frac {0.12}{1.5}\) x 10³ = 80 ohm.

Question 3.
The current gain of a transistor in CB mode is 0.987. What will be its current gain in CE mode?
Solution:
Given : α = 0.987
Formula : β = \(\frac {α}{1 – α}\)
β = \(\frac {0.987}{1 – 0.987}\) = 75.93.

MP Board Class 12th Physics Important Questions