MP Board Class 12th Maths Important Questions Chapter 10 Vector Algebra

MP Board Class 12th Maths Important Questions Chapter 10 Vector Algebra

Vector Algebra Important Questions

Vector Algebra Objective Type Questions

Question 1.
Choose the correct answer:

Question 1.
Unit vector parallel to the resultant vector of vectors 2\(\hat { i } \) + 4\(\hat { j } \) – 5\(\hat { k } \) and \(\hat { i } \) + 2\(\hat { j } \) + 3\(\hat { k } \) is:
(a) – \(\hat { i } \) – \(\hat { j } \) + 8\(\hat { k } \)
(b) \(\frac { 3\hat { i } +6\hat { j } -2\hat { k } \quad }{ 7 } \)
(c) \(\frac { -\hat { i } -+8\hat { k } \quad }{ \sqrt { 69 } } \)
(d) \(\frac { -\hat { i } +2\hat { j } -8\hat { k } \quad }{ \sqrt { 69 } } \)

Question 2.
If \(\vec { O } \)A = a, \(\vec { O } \)B = b and C is a point on AB such that \(\vec { A } \)C = 3AB, then \(\vec { O } \)C is equal to:
(a) 3\(\vec { a } \) – 2\(\vec { b } \)
(b) 3\(\vec { b } \) – 2\(\vec { a } \)
(c) 3\(\vec { a } \) – \(\vec { b } \)
(d) 3\(\vec { b } \) – \(\vec { a } \)

Question 3.
If \(\vec { a } \) and \(\vec { b } \) are two vectors such that |\(\vec { a } \)| = 2, |\(\vec { b } \)| = 1 and \(\vec { a } \).\(\vec { b } \) = \(\sqrt { 3 } \), then the angle between them is:
(a) \(\frac { \pi }{ 2 } \)
(b) \(\frac { \pi }{ 4 } \)
(c) \(\frac { \pi }{ 6 } \)
(d) \(\frac { \pi }{ 7 } \)

Question 4.
Area of parallelogram whose adjacent sides are \(\hat { i } \) – 2\(\hat { j } \) + 3\(\hat { k } \) and 2\(\hat { i } \) + \(\hat { j } \) – 4\(\hat { k } \) is:
(a) 3\(\sqrt{6}\)
(b) 4\(\sqrt{6}\)
(c) 5\(\sqrt{6}\)
(d) 6\(\sqrt{6}\)

Question 5.
If \(\vec { a } \) = \(\vec { b } \) + \(\vec { c } \), then \(\vec { a } \).( \(\vec { b } \) × \(\vec { c } \) ) is equal to:
(a) 2\(\vec { a } \). ( \(\vec { b } \) + \(\vec { c } \) )
(b) 0
(c) \(\vec { b } \) = ( \(\vec { a } \) + \(\vec { c } \) )
(d) None of these

Question 2.
Fill in the blanks:

1. Sum or difference of two vectors is always a ………………………….
2. Addition of vectors obeys ………………………….
3. ( \(\vec { a } \) + \(\vec { b } \) ) + \(\vec { c } \) = \(\vec { a } \) + …………………………..
4. Addition of two vectors can be obtained from ……………………………..
5. Position vector of point (1,2, 3) w.r.t. the origin will be ……………………………..
6. If \(\vec { a } \) and \(\vec { b } \) are parllel then \(\vec { a } \) × \(\vec { b } \) = …………………………..
7. If \(\vec { a } \) and \(\vec { b } \) are parallel then \(\vec { a } \) × \(\vec { a } \) = ………………………..
8. The unit vector in the direction of vector \(\vec { a } \) will be ……………………………
9. The projection of \(\vec { b } \) along the direction of \(\vec { a } \) will be ……………………………..
10. If the vectors 2\(\hat { i } \) – \(\hat { j } \) + \(\hat { k } \) 3\(\hat { i } \) + p\(\hat { j } \) + 5\(\hat { k } \) are coplanar then value of p will be …………………………….
11. A force 2\(\hat { i } \) + \(\hat { j } \) + \(\hat { k } \), acts at a point A whose position vector 2\(\hat { i } \) – \(\hat { j } \) The moment of the force with respect to the origin will be ………………………………..
12. The area of the parallelogram will be …………………………. whose diagonals are 3\(\hat { i } \) + \(\hat { j } \) – 2\(\hat { k } \) and \(\hat { i } \) – 3\(\hat { j } \) + 4\(\hat { k } \).

Answer:

1. New vector
2. Commutative and associative law
3. ( \(\vec { b } \) + \(\vec { c } \) )
4. Traingle law of vector addition
5. \(\hat { i } \) + 2\(\hat { j } \) + 3\(\hat { k } \)
6. collinear
7. \(\vec { O } \)
8. \(\frac { \vec { a } }{ |\vec { a } | } \)
9. \(\frac { \vec { a } .\vec { b } }{ |\vec { a } | } \)
10. -4
11. \(\hat { i } \) + 2\(\hat { j } \) + 4\(\hat { k } \)
12. 5\(\sqrt { 3 } \) sq. unit.

Question 3.
Write True/False:

1. The sum of the vectors determined by the sides of a triangle taken in order is zero.
2. If \(\vec { a } \) and \(\vec { b } \) are two non collinear vectors, then |\(\vec { a } \) + \(\vec { b } \)| ≥ |\(\vec { a } \) + \(\vec { b } \)|
3. A vector whose initial and terminal points are coincident is called unit vector.
4. If the position vector of the points P and Q are \(\hat { i } \) + 3\(\hat { j } \) – 7\(\hat { k } \) and 5\(\hat { i } \) – 2\(\hat { j } \) + 4\(\hat { k } \) respectively, then the value of |\(\vec { P } \)Q| is 9\(\sqrt { 2 } \).
5. If |\(\vec { a } \) + \(\vec { a } \)|=|\(\vec { a } \) – \(\vec { b } \)|, then \(\vec { a } \) × \(\vec { b } \) = \(\vec { 0 } \).
6. The value of \(\vec { a } \).( \(\vec { a } \) × \(\vec { b } \) ) is zero.
7. If the vectors \(\hat { i } \) – λ\(\hat { j } \) + \(\hat { k } \) and \(\hat { i } \) – \(\hat { j } \) + 5\(\hat { k } \) are mutually perpendicular, then the value of λ is 6.

Answer:

1. True
2. False
3. False
4. True
5. False
6. True
7. False.

Question 4.
Write the answer is one word/sentence:

1. If \(\vec { a } \), \(\vec { b } \), \(\vec { c } \) are the position vectors of the vectors of the ∆ABC, then write the formula for area of ∆ABC.
2. If \(\vec { a } \) = \(\hat { i } \) – 2\(\hat { j } \) + 3\(\hat { k } \),\(\vec { b } \) = 2\(\hat { i } \) + \(\hat { j } \) – \(\hat { k } \) and \(\vec { c } \) = \(\hat { j } \) + \(\hat { k } \), then find the value of [ \(\vec { a } \) \(\vec { b } \) \(\vec { c } \) ]
3. Find the angle between two vector 3\(\hat { i } \) – 2\(\hat { j } \) + 4\(\hat { k } \) and \(\hat { i } \) – \(\hat { j } \) + 5\(\hat { k } \).
4. Find the value of \(\hat { i } \) × ( \(\hat { j } \) + 3\(\hat { k } \) ) + \(\hat { j } \) × ( \(\hat { k } \) + \(\hat { i } \) ) + \(\hat { k } \) × ( \(\hat { i } \) + \(\hat { j } \) )
5. Find the projection of \(\vec { a } \) in the direction of \(\vec { b } \).
6. If \(\vec { a } \) and \(\vec { b } \) are mutually perpendicular vector then find, the value ( \(\vec { a } \) + \(\vec { b } \) ) ²

Answer:

1. \(\frac{1}{2}\) |\(\vec { a } \) × \(\vec { b } \) + \(\vec { b } \) × \(\vec { c } \) + \(\vec { c } \) × \(\vec { a } \)|
2. 12
3. cos^-1 \(\frac { 25 }{ \sqrt { 783 } } \)
4. 0
5. \(\frac { \vec { a } .\vec { b } }{ |\vec { b } | } \)
6. |\(\vec { a } \)|² + |\(\vec { b } \)|²

Question 4.
Match the Column:

Answer:

1. (d)
2. (e)
3. (a)
4. (b)
5. (c)
6. (g)
7. (f).

Vector Algebra Very Short Answer Type Questions

Question 1.
Given vectors \(\vec { a } \) = \(\hat { i } \) – 2\(\hat { j } \) + \(\hat { k } \), \(\vec { b } \) = – 2\(\hat { i } \) + 4\(\hat { j } \) + 5\(\hat { k } \) and \(\vec { c } \) = \(\hat { i } \) – 6\(\hat { j } \) – 7\(\hat { k } \). Then find the value of |\(\vec { a } \) + \(\vec { b } \) + \(\vec { c } \)|? (NCERT, CBSE 2012)
Solution:

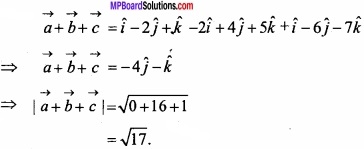
Question 2.
Find the unit vector in the direction of sum of the vectors \(\vec { a } \) = 2\(\hat { i } \) – \(\hat { j } \) + 2\(\hat { k } \) and \(\vec { b } \) = – \(\hat { i } \) + \(\hat { j } \) + 3\(\hat { k } \)?
Solution:

Question 3.
Find the vector in the direction of vector \(\vec { a } \) = \(\hat { i } \) – 2\(\hat { j } \) which has magnitude 7 units? (NCERT)
Solution:
\(\vec { a } \) = \(\hat { i } \) – 2\(\hat { j } \)
Unit vector in the direction of given vector a is:

The vector having magnitude be equal to 7:

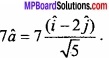
Question 4.
Prove that the vectors 2\(\hat { i } \) – 3\(\hat { j } \) + 4\(\hat { k } \) and -4\(\hat { i } \) + 6\(\hat { j } \) – 8\(\hat { k } \) are collinear? (NCERT)
Solution:

Hence vector \(\vec { a } \), \(\vec { b } \) are collinear. Proved.

Question 5.
Find direction cosine of the vector \(\hat { i } \) + 2\(\hat { j } \) + 3\(\hat { k } \)? (NCERT)
Solution:

Question 6.
If \(\vec { a } \) = 2 \(\hat { i } \) – 3 \(\hat { j } \) + \(\hat { k } \) and \(\vec { a } \) = \(\hat { i } \) + \(\hat { j } \) – 2\(\hat { k } \), then find \(\vec { a } \) – \(\vec { b } \)?
Solution:

Question 7.
If \(\vec { a } \) = \(\hat { i } \) + \(\hat { j } \) + 2\(\hat { k } \) and \(\vec { b } \) = 3\(\hat { i } \) + 2\(\hat { j } \) – \(\hat { k } \), then find |2\(\vec { a } \) – \(\vec { b } \)|?
Solution:

Question 8.
If the vector \(\vec { a } \) = 2\(\hat { i } \) + \(\hat { j } \) + \(\hat { k } \) and \(\vec { b } \) = \(\hat { i } \) – 4\(\hat { j } \) + λ\(\hat { k } \) are perpendicular then find the value of λ?
Solution:
The given vectors are perpendicular
Hence \(\vec { a } \) . \(\vec { b } \) = 0
(2\(\hat { i } \) + \(\hat { j } \) + \(\hat { k } \) ). ( \(\hat { i } \) – 4\(\hat { j } \) + λ\(\hat { k } \) ) = 0
⇒ 2 – 4 + λ = 0
⇒ λ = 2.

Question 9.
(A) Prove that the vectors 2\(\hat { i } \) – \(\hat { j } \) + \(\hat { k } \) and –\(\hat { i } \) + 3\(\hat { j } \) + 5\(\hat { k } \) are perpendicular to each other?
Solution:

L.H.S = – 2 – 3 + 5
= 0 = R.H.S. Proved

(B) Prove that vector 3\(\hat { i } \) – 2\(\hat { j } \) + \(\hat { k } \) and 2\(\hat { i } \) + \(\hat { j } \) – 4\(\hat { k } \) are perpendicular?
Solution:
Solve as Q.No. 9(A)

Question 10.
If \(\vec { a } \) = 4\(\hat { i } \) – \(\hat { j } \) + \(\hat { k } \) and \(\vec { b } \) p\(\hat { i } \) + 2\(\hat { j } \) + 3\(\hat { k } \) are perpendicular. Find the value of p?
Solution:
\(\vec { a } \) = 4\(\hat { i } \) – \(\hat { j } \) + \(\hat { k } \) and \(\vec { b } \) p\(\hat { i } \) + 2\(\hat { j } \) + 3\(\hat { k } \)
\(\vec { a } \) and \(\vec { b } \) are perpendicular
\(\vec { a } \).\(\vec { b } \) = 0
∴ 4p – 2 + 3 = 0
⇒ 4p = -1
⇑ p = – \(\frac{1}{4}\)

Question 11.
(A) Find the angle between the vectors (2\(\hat { i } \) + 3\(\hat { j } \) – 4\(\hat { k } \) ) and (3\(\hat { i } \) + 2\(\hat { j } \) + 3\(\hat { k } \) )?
Solution:
Let \(\vec { a } \) = 2\(\hat { i } \) + 3\(\hat { j } \) – 4\(\hat { k } \), \(\vec { b } \) = 3\(\hat { i } \) + 2\(\hat { j } \) + 3\(\hat { k } \)
Let θ be the angle between them

(B) Find the angle between vectors \(\vec { a } \) = 2\(\hat { i } \) – 2\(\hat { j } \) – \(\hat { k } \) and \(\vec { b } \) = 6\(\hat { i } \) – 3\(\hat { j } \) + 2\(\hat { k } \)?
Solution:
Solve as Q.No. 11(A)

(C) If \(\vec { a } \) = 2\(\hat { i } \) – \(\hat { j } \) + \(\hat { k } \) and \(\vec { b } \) = 3\(\hat { i } \) – 4\(\hat { j } \) – 4\(\hat { k } \), then find their dot product and angle between them?
Solution:

If θ be the angle between them

Question 12.
If |\(\bar { |a| } \) = 10, \(\bar { |b| } \) = 2 and \(\bar { a } \). \(\bar { b } \) = 2 and \(\bar { a } \). \(\bar { b } \) = 12, then find the value of |\(\bar { a } \) × \(\bar { b } \)?
Solution:

Question 13.
If \(\vec { a } \) = \(\hat { i } \) + \(\hat { j } \) + \(\hat { k } \) and \(\vec { b } \) = \(\hat { i } \) – \(\hat { j } \) – \(\hat { k } \), then find \(\vec { a } \) × \(\vec { b } \)?
Solution:

Question 14.
A force \(\vec { F } \) = 4\(\hat { i } \) – 3\(\hat { j } \) + 2\(\hat { k } \) is acting along the direction \(\vec { d } \) = – \(\hat { i } \) – 3\(\hat { j } \) + 5\(\hat { k } \)? Find the work done by the force?
Solution:
\(\vec { d } \) = – \(\hat { i } \) – 3\(\hat { j } \) + 5\(\hat { k } \), \(\vec { F } \) = 4\(\hat { i } \) – 3\(\hat { j } \) + 2\(\hat { k } \) (given)
∴ Work done by force
W = \(\vec { F } \). \(\vec { d } \)
= (4\(\hat { i } \) – 3\(\hat { j } \) + 2\(\hat { k } \) ). (-\(\hat { i } \) – 3\(\hat { j } \) + 5\(\hat { k } \) )
= -4 + 9 + 10 = 15 unit.

Question 15.
If |\(\vec { a } \) + \(\vec { b } \)| = |\(\vec { a } \) – \(\vec { b } \)|, then prove that \(\vec { a } \) and \(\vec { b } \) are perpendicular?
Solution:

Since dot product is zero. So vectors \(\vec { a } \) and \(\vec { b } \) are perpendiculars. Proved.

Question 16.
If \(\vec { a } \) and \(\vec { b } \) are two vectors such that |\(\vec { a } \)| = 2, |\(\vec { b } \)| = 3 and \(\vec { a } \). \(\vec { a } \) = 3, then find angle between \(\vec { a } \) and \(\vec { b } \)?
Solution:
Solve as Q.No. 17

Question 17.
If |\(\vec { a } \)| = 4, |\(\vec { b } \)| = 4 and \(\vec { a } \). \(\vec { b } \) = 6, then find the angle between \(\vec { a } \) and \(\vec { b } \)?
Solution:

Question 18.
If \(\vec { a } \) and \(\vec { b } \) are two two vectors such that |\(\vec { a } \)| = 2, |\(\vec { b } \)| = 7 and \(\vec { a } \) ×
\(\vec { b } \) = 3\(\hat { i } \) + 2\(\hat { j } \) + 6\(\hat { k } \), then find the angle between \(\vec { a } \) and \(\vec { b } \)?
Solution:
Let θ be the angle between \(\vec { a } \) and \(\vec { b } \)

Question 19.
Find cosine angle between vectors 2\(\hat { i } \) – 3\(\hat { j } \) + \(\hat { k } \) and \(\hat { i } \) + \(\hat { j } \) – 2\(\hat { k } \)?
Solution:

Question 20.
Find the area of the parallelogram whose two adjacent sides are represented by the vectors \(\vec { a } \) = 2\(\hat { i } \) – 3\(\hat { j } \) + \(\hat { k } \), \(\vec { b } \) = \(\hat { i } \) – \(\hat { j } \) + 2\(\hat { k } \) and \(\vec { c } \) = 2\(\hat { i } \) + \(\hat { j } \) – \(\hat { k } \)?
Solution:


= 2(1 – 2) + 3(-1-4) + 1(1 + 2)
= -2 – 15 + 3
= -14 cubic unit

Question 21.
Prove that:
\(\hat { i } \).( \(\hat { j } \) × \(\hat { k } \) + ( \(\hat { i } \) × \(\hat { k } \)). \(\hat { j } \) = 0?
Solution:

Question 22.
If vectors \(\vec { a } \) and \(\vec { b } \) are perpendicular then prove that |\(\vec { a } \) + \(\vec { b } \)|² = |\(\vec { a } \)|² + |\(\vec { b } \)|²?
Solution:
We know that
|\(\vec { a } \) + \(\vec { b } \)|² = |\(\vec { a } \)|² + |\(\vec { b } \)|²
Vector \(\vec { a } \) and \(\vec { b } \) are perpendicular, then
\(\vec { a } \). \(\vec { b } \) = 0
⇒ |\(\vec { a } \) + \(\vec { a } \)|² + |\(\vec { a } \)|² + |\(\vec { b } \)|². Proved.

Question 23.
Prove that:
\(\vec { a } \) × ( \(\vec { b } \) + \(\vec { c } \) ) + \(\vec { b } \) × ( \(\vec { c } \) + \(\vec { a } \) ) + \(\vec { c } \) × ( \(\vec { a } \) + \(\vec { b } \) ) = \(\vec { 0 } \)?
Solution:

Question 24.
Find the work done by the force \(\vec { F } \) = 2\(\hat { i } \) – \(\hat { j } \) + \(\hat { k } \) in the direction \(\vec { d } \) = 3\(\hat { i } \) + 2\(\hat { j } \) + 5\(\hat { k } \)?
Solution:
W = \(\vec { F } \). \(\vec { d } \)
= (2\(\hat { i } \) – \(\hat { j } \) + \(\hat { k } \) ). (3\(\hat { i } \) + 2\(\hat { j } \) + 3\(\hat { k } \) )
= 6 – 2 + 3 = 7 unit.

Question 25.
If modulus of two vectors \(\vec { a } \) and \(\vec { a } \) are equal and angle between them is 60° and their dot product is \(\frac{9}{2}\) find their modulus? (CBSE 2018)
Solution:

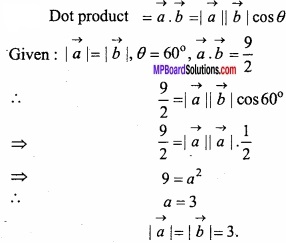
Question 26.
Find the area of the parallelogram whose adjacent sides are given by vectors \(\vec { a } \) = 2\(\hat { i } \) – \(\hat { j } \) + \(\hat { k } \) and \(\vec { b } \) = 3\(\hat { i } \) + 4\(\hat { j } \) – \(\hat { k } \)?
Solution:

Question 27.
If \(\vec { a } \) = 4\(\hat { i } \) + \(\hat { j } \) + \(\hat { k } \), \(\vec { b } \) = \(\hat { i } \) – 2\(\hat { k } \) then find the value of |2\(\vec { b } \) × \(\vec { a } \)|?
Solution:

Question 28.
If \(\vec { a } \) = 4\(\hat { i } \) + 3\(\hat { j } \) + 3\(\hat { k } \) and \(\vec { b } \) = 3\(\hat { i } \) + 2\(\hat { k } \) then, find the value of |\(\vec { b } \) × 2\(\vec { a } \)|?
Solution:

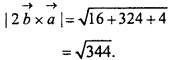
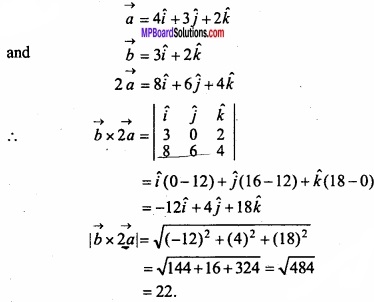
Question 29.
If \(\vec { a } \) = 2\(\hat { i } \) + \(\hat { j } \) + 2\(\hat { k } \) and \(\vec { b } \) = 5\(\hat { i } \) – 3\(\hat { j } \) + \(\hat { k } \), then find the magnitude of vector \(\vec { b } \) in the direction of \(\vec { a } \)?
Solution:

Question 30.
If \(\vec { a } \) = \(\hat { i } \) + 3\(\hat { j } \) – 2\(\hat { k } \), \(\vec { b } \) = – \(\hat { j } \) + 3\(\hat { k } \) then find the value |\(\vec { a } \) × \(\vec { b } \)|?
Solution:

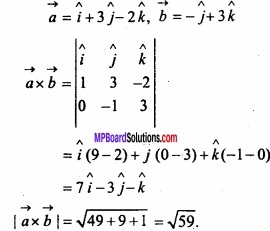
Vector Algebra Short Answer Type Questions

Question 1.
Prove that: A(-2\(\hat { i } \) + 3\(\hat { j } \) + 5\(\hat { k } \) ), B( \(\hat { i } \) + 2\(\hat { j } \) + 3\(\hat { k } \) ) and C(7\(\hat { i } \) + 0\(\hat { j } \) – \(\hat { k } \) ) are coplanar? (NCERT)
Solution:
Let O be the origin then position vector of A, B and C is

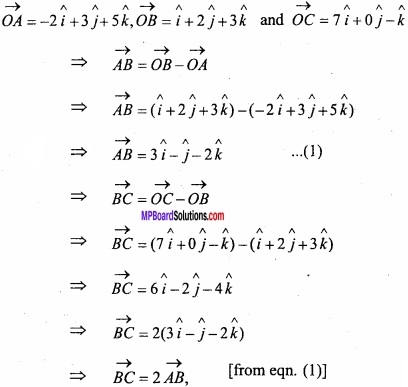
Hence vector \(\vec { A } \)B and \(\vec { B } \)C are parallel but \(\vec { A } \)B and \(\vec { B } \)C has common point B. Hence points A, B and C are coplanar.

Question 2.
If position vectors of points A, B, C and D are 2\(\hat { i } \) + 4\(\hat { k } \), 5\(\hat { i } \) + 3\(\sqrt { 3 } \) \(\hat { j } \) + 4\(\hat { k } \), -2\(\sqrt { 3 } \) \(\hat { j } \) + \(\hat { k } \) then prove that:
CD||AB and CD = \(\frac{2}{3}\) \(\vec { A } \)B?
Solution:
Let O be the origin

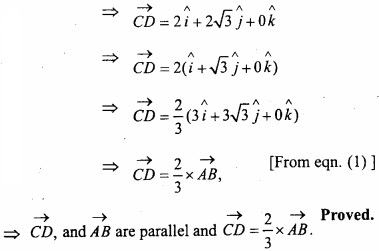
Question 3.
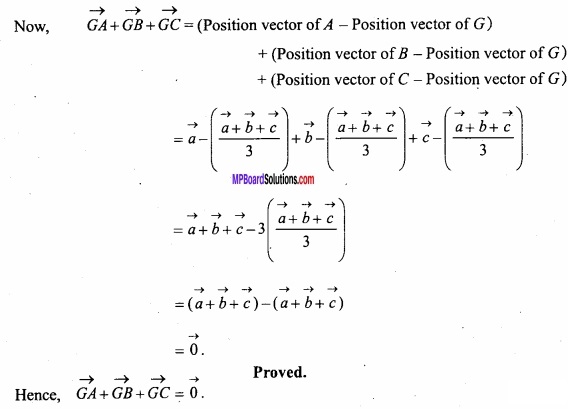
If G is centroid of ∆ABC, then prove that:
\(\vec { G } \)A + \(\vec { G } \)B + \(\vec { G } \)C = \(\vec { 0 } \)?
Solution:
Let vectors of vertices A,B and C of ∆ABC are \(\vec { a } \), \(\vec { b } \) and \(\vec { c } \) respectively.
∴ Position vector of centroid G = \(\frac { \vec { a } +\vec { b } +\vec { c } }{ 3 } \)

Question 4.
Using vectors prove that the medians of traiangle are concurrent?
Solution:
Let medium of ∆ABC are AD, BE and CF.
Let \(\vec { a } \), \(\vec { b } \) and \(\vec { c } \) be the positive vector of points A, B and C respectively.

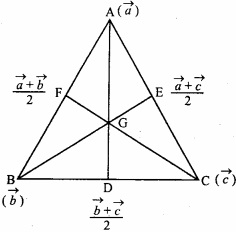
Now position vector of a point dividing the median AD in the ratio 2 : 1 is

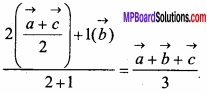
Position vector of a point which divides median BE in the ratio of 2 : 1 is

Position vector of a point which divides median BE in the ratio of 2 : 1 is

Hence, medians of triangle meets at point G it means concurrent whose position vector is \(\frac { \vec { a } +\vec { b } +\vec { c } }{ 3 } \). Point G is centroid of traingle.

Question 5.
A vector \(\vec { O } \)P, makes angle 45° with OX and 60° with OY. Find the angle made by \(\vec { O } \)P with OZ?
Solution:
Let angle made by vector \(\vec { O } \)P with axes OX, OY and OZ are α, β, γ respectively. then
α = 45°,
β = 60°
∴ l = cos α = cos 45° = \(\frac { 1 }{ \sqrt { 2 } } \)
m = cos β = cos 60° = \(\frac{1}{2}\)
and n = cos γ
We know that
l² + m² + n² = 1

Question 6.
Find the vector \(\vec { a } \) which makes an angle with X – axis, F – axis and Z – axis respectively are \(\frac { \pi }{ 4 } \), \(\frac { \pi }{ 2 } \) and angle θ and its magnitude is 5\(\sqrt { 2 } \)?
Solution:
Given:
α = \(\frac { \pi }{ 4 } \),
β = \(\frac { \pi }{ 2 } \), γ = θ
∴l = cos \(\frac { \pi }{ 4 } \) = \(\frac { 1 }{ \sqrt { 2 } } \), m = cos \(\frac { \pi }{ 2 } \) = 0, n = cos θ.
We know that


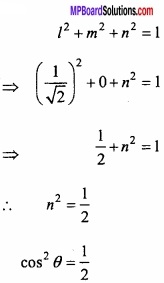
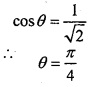
Direction cosine of vector \(\frac { 1 }{ \sqrt { 2 } } \), 0 , \(\frac { 1 }{ \sqrt { 2 } } \)

Question 7.
Prove that:
( \(\vec { a } \) × \(\vec { b } \) )² = a²b² – ( \(\vec { a } \).\(\vec { b } \) )²?
Solution:
L.H.S = ( ( \(\vec { a } \) × \(\vec { b } \) )² = ( \(\vec { a } \) × \(\vec { b } \) ).( \(\vec { a } \) ×  \(\vec { b } \) )
= (ab sin θ\(\hat { n } \) ). (ab sin θ \(\hat { n } \) ) = a² b² sin²θ,
= a² b² (1 – cos²θ)
= a² b² – a² b²cos²θ
= a² b² – (ab cos θ)²
= a² b² – ( \(\vec { a } \). \(\vec { b } \) )² = R.H.S Proved.

Question 8.
If \(\vec { a } \) = 2\(\hat { i } \) – 3\(\hat { j } \) + \(\hat { k } \), \(\vec { b } \) = \(\hat { i } \) – \(\hat { j } \) + 2\(\hat { k } \) and \(\vec { c } \) = 2\(\hat { i } \) + \(\hat { j } \) – \(\hat { k } \) then find the value of \(\vec { a } \) × ( \(\vec { b } \) × \(\vec { c } \) )?
Solution:

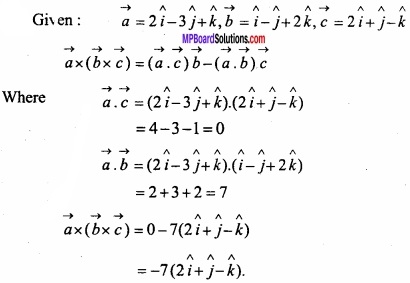
Question 9.
Find the volume of parallel cuboid whose vectors of three faces are denoted by: \(\hat { i } \) + \(\hat { j } \) + \(\hat { k } \), \(\hat { i } \) – \(\hat { j } \) + \(\hat { k } \), \(\hat { i } \) + \(\hat { j } \) – \(\hat { k } \)?
Solution:

Question 10.
If \(\vec { a } \) = 2\(\hat { i } \) – 3\(\hat { j } \) + \(\hat { k } \), \(\vec { b } \) = \(\hat { i } \) – \(\hat { j } \) + 2\(\hat { k } \) and \(\vec { c } \) = 2\(\hat { i } \) + \(\hat { j } \) – \(\hat { k } \) then find the value of [ \(\vec { a } \) \(\vec { b } \) \(\vec { c } \) ]
Solution:

Question 11.
If \(\vec { a } \) = 3\(\hat { i } \) – \(\hat { j } \) + 2\(\hat { k } \), \(\vec { b } \) = 2\(\hat { i } \) + \(\hat { j } \) – \(\hat { k } \) and \(\vec { c } \) = \(\hat { i } \) – 2\(\hat { j } \) + 2\(\hat { k } \) then, find the value of \(\vec { a } \), \(\vec { b } \), \(\vec { c } \)?
Solution:
Solve like Q.No.10.

Question 12.
If \(\vec { a } \) = \(\hat { i } \) – 2\(\hat { j } \) + 3\(\hat { k } \), \(\vec { b } \) = – \(\hat { i } \) + 3 \(\hat { j } \) – 4 \(\hat { k } \) and \(\vec { c } \) = \(\hat { i } \) – 3\(\hat { j } \) + 5\(\hat { k } \) then prove that \(\vec { a } \), \(\vec { b } \), \(\vec { c } \) are coplanar?
Solution:
If \(\vec { a } \), \(\vec { b } \), \(\vec { c } \) are coplanar then

Question 13.
Prove that 2\(\hat { i } \) – \(\hat { j } \) + \(\hat { k } \), \(\hat { i } \) + 2\(\hat { j } \) – 3\(\hat { k } \) and 3\(\hat { i } \) – 4\(\hat { j } \) + 5k are coplanar?
Solution:
Let \(\vec { a } \) = 2\(\hat { i } \) – \(\hat { j } \) + \(\hat { k } \), \(\hat { i } \) + 2\(\hat { j } \) – 3\(\hat { k } \) and 3\(\hat { i } \) – 4\(\hat { j } \) + 5\(\hat { k } \)

Question 14.
(A) Find the value of λ for which the vectors λ\(\hat { i } \) + 3\(\hat { j } \) + 2\(\hat { k } \), 2\(\hat { i } \) + 2\(\hat { j } \) + 3\(\hat { k } \) and 2\(\hat { i } \) + 3\(\hat { j } \) + 4\(\hat { k } \) are coplanar?
Solution:
Let \(\vec { a } \) = λ\(\hat { i } \) + 3\(\hat { j } \) + 2\(\hat { k } \), \(\vec { b } \) = 2\(\hat { i } \) + 2\(\hat { j } \) + 3\(\hat { k } \) and 2\(\hat { i } \) + 3\(\hat { j } \) + 4\(\hat { k } \) are coplanar?
Solution:
Let \(\vec { a } \) = λ\(\hat { i } \) + 3\(\hat { j } \) + 2\(\hat { k } \), \(\vec { b } \) = 2\(\hat { i } \) + 2\(\hat { j } \) + 3\(\hat { k } \), \(\vec { c } \) = 2\(\hat { i } \) + 3\(\hat { j } \) + 4\(\hat { k } \)
Given vector are coplanar if
[ \(\vec { a } \) \(\vec { b } \) \(\vec { c } \) ] = 0
\(\left|\begin{array}{lll}
{\lambda} & {3} & {2} \\
{2} & {2} & {3} \\
{2} & {3} & {4}
\end{array}\right|\) = 0
⇒ λ(8 – 9) -2(12 – 6+ 2 (9 – 4) = 0
⇒ -λ – 12 + 10 = 0
⇒ λ = -2.

(B) Find the value of λ for which given vectors are coplanar
\(\hat { i } \) – \(\hat { j } \) + \(\hat { k } \), 2\(\hat { i } \) + \(\hat { j } \) – \(\hat { k } \), λ\(\hat { i } \) – \(\hat { j } \) + λ\(\hat { k } \)
Solution:
Solve like Q.No. 14 (A)
Answer:
λ = 1

(C) Find the value of λ for which the given vectors are coplanar 2\(\hat { i } \) – \(\hat { j } \) + \(\hat { k } \), \(\hat { i } \) + 2\(\hat { j } \) – 3\(\hat { k } \) and 3\(\hat { i } \) + λ\(\hat { j } \) + 5\(\hat { k } \)?
Solution:
Solve like Q.No. 14 (A)
Answer:
λ = – \(\frac{18}{5}\)

Question 15.
If the angle between two unit vectors \(\vec { a } \) and \(\vec { b } \) is θ then prove that:
cos \(\frac { \theta }{ 2 } \) = \(\frac{1}{2}\) |\(\bar { a } \) + \(\bar { b } \)| is θ then prove that:
sin \(\frac { \theta }{ 2 } \) = \(\frac{1}{2}\) |\(\bar { a } \) – \(\bar { b } \)|
Solution:

Question 16.
The angle between two vectors \(\vec { a } \) and \(\vec { b } \) is θ then prove that:
sin \(\frac { \theta }{ 2 } \) = \(\frac{1}{2}\) |\(\bar { a } \) – \(\bar { b } \)|
Solution:
sin \(\frac { \theta }{ 2 } \) = \(\frac{1}{2}\) |\(\bar { a } \) – \(\bar { b } \)|

Question 17.
In any traiangle prove that ABC?
(A) ac cos B – bc cos A = a² – b²?
(B) 2(bc cos A + ca cos B + ab cos C) = a² + b² + c²?
Solution:

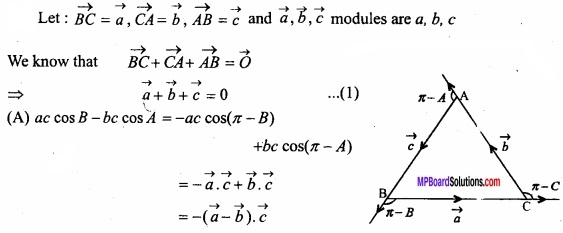
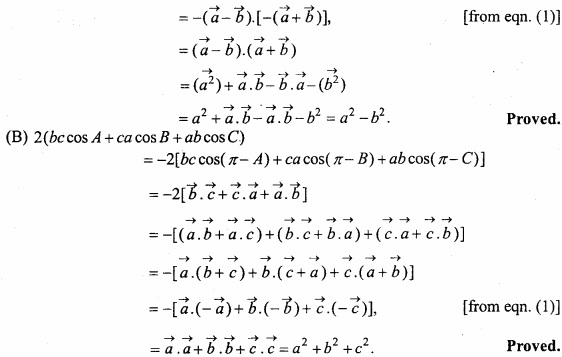
Question 18.
In ∆ABC prove by vector method c = acosB + bcosA?
Solution:
In ∆ABC

⇒ c² = ac cos B + bc cos A
⇒ c² = c(a cos B + b cos A)
⇒ c = a cos B + b cos A. Proved.

Question 19.
In ∆ABC prove by vector method
b² = a² + c² – 2ac cos B?
Solution:
In ∆ABC we know that

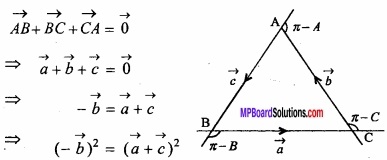
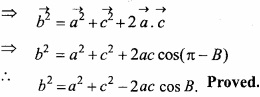
Question 20.
In ∆ABC Prove the following:
(A) a² = b² + c² – 2bc cos A?
(B) c² = a² + b² – 2ab cos C?
Solution:
Solve like Q.No. 19

Question 21.
(A) Find the unit vector normal to the vector \(\vec { a } \) = 2\(\hat { i } \) + 2\(\hat { j } \) + \(\hat { k } \) and \(\vec { b } \)
= 4\(\hat { i } \) + 4\(\hat { j } \) – 7\(\hat { k } \)?
Solution:

(B) Find the unit vector normal to the vectors \(\vec { a } \) = \(\hat { i } \) – \(\hat { j } \) + \(\hat { k } \) and \(\vec { b } \) =
\(\hat { i } \) + 2\(\hat { j } \) – \(\hat { k } \)?
Solution:
Solve like Q.No. 21 (A)

(C) Find the unit vector normal to the vectors \(\vec { a } \) = 3\(\hat { i } \) + \(\hat { j } \) – 2\(\hat { k } \) and \(\vec { b } \) = 2\(\hat { i } \) + 3\(\hat { j } \) – \(\hat { k } \)?
Solution:
Solve like Q.No. (A)
Answer:

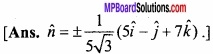
Question 22.
Find the unit vector normal to the vectors \(\vec { a } \) = 2\(\hat { i } \) – \(\hat { j } \) + \(\hat { k } \) and \(\vec { b } \) = 3\(\hat { i } \) – 4\(\hat { j } \) – \(\hat { k } \)?
Solution:
Solve like Q.No. 21 (A)
Answer:

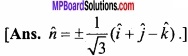
Question 23.
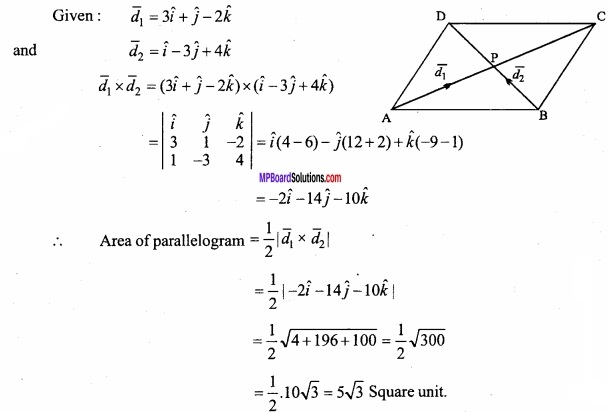
Find the area of parallelogram whose digonals are 3\(\hat { i } \) + \(\hat { j } \) – 2\(\hat { k } \) and \(\hat { i } \) – 3\(\hat { j } \) + 4\(\hat { k } \)?
Solution:
ABCD is parallelogram whose diagonals are \(\vec { A } \)C = \(\vec { d } \)₁ and \(\vec { B } \)D = \(\vec { d } \)₂

Question 24.
By vector method prove that the square of the hypotenuse of a right angle triangle is equal to the sum of the square of the other two sides?
Solution:
Let OAB be a right angled triangle at O. Taking O as the origin. Let the position vector of \(\vec { a } \) and \(\vec { b } \) be a and b respectively then \(\vec { O } \)A = \(\vec { a } \) and \(\vec { O } \)B = \(\vec { b } \) and ∠BOA = 90°.
∴\(\vec { a } \). \(\vec { b } \) = 0

Question 25.
Find the moment of force 5\(\hat { i } \) + \(\hat { k } \) passing through the point 9\(\hat { i } \) – \(\hat { j } \) + 2\(\hat { k } \) about the point 3\(\hat { i } \) + 2\(\hat { j } \) + \(\hat { k } \)?
Solution:

Moment of the force \(\vec { F } \) about the point O = \(\vec { r } \) × \(\vec { F } \)

Question 26.
(A) Prove that:

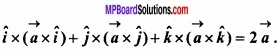
Solution:

(B) Prove that:

Question 27.
Prove that:

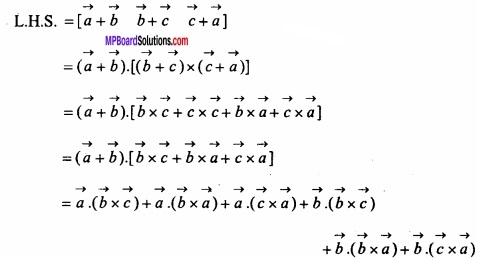
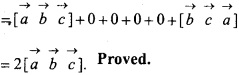
Question 28.
Two forces are represented by vectors \(\vec { p } \) = 4\(\hat { i } \) + \(\hat { j } \) – 3\(\hat { k } \) and \(\vec { Q } \) = 3\(\hat { i } \) + \(\hat { j } \) – \(\hat { k } \) displace a particle from points (1,2,3) to point2? (5,4,1)? Find the work done by the forces?
Solution:

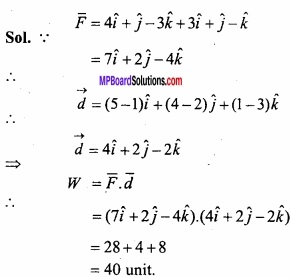
Question 29.
Two forces 4\(\hat { i } \) + 3\(\hat { j } \) and 3\(\hat { i } \) + 2\(\hat { j } \) are acting on a particle, Due to the forces the particle is displaced from the point \(\hat { i } \) + 2\(\hat { j } \) to the point 5\(\hat { i } \) + 4\(\hat { j } \)? Find the work done by the forces?
Solution:

Question 30.
Alorce of 6 units along the direction of vector 2\(\hat { i } \) – 2\(\hat { j } \) + \(\hat { k } \) acts on a partical? The partical is displaced from point \(\hat { i } \) + 2\(\hat { j } \) + 3\(\hat { k } \) to 5\(\hat { i } \) + 3\(\hat { j } \) + 7\(\hat { k } \). Find the work done by the force?
Solution:
Unit vector parllel to vector 2\(\hat { i } \) – 2\(\hat { j } \) + \(\hat { k } \)

Question 31.
Prove that |\(\vec { a } \) – \(\vec { b } \) \(\vec { b } \) – \(\vec { c } \) \(\vec { c } \) – \(\vec { a } \)| = 0?
Solution:
We know

MP Board Class 12 Maths Important Questions