MP Board Class 9th Maths Solutions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Ex 9.2
प्रश्न 1.
संलग्न चित्र में ABCD एक समान्तर चतुर्भुज है। AE ⊥ DC और CF ⊥ AD है। यदि AB = 16 cm, AE = 8 cm और CF = 10 cm हो, तो AD ज्ञात कीजिए। (2019)
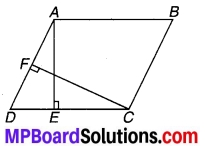
चित्र 9.2
हल:
चूँकि समान्तर चतुर्भुज ABCD का क्षेत्रफल = आधार x शीर्षलम्ब
⇒ AD x CF = DC x AE (क्रमशः AD और DC को आधार लेकर)
⇒ AD x CF = AB x AE (∵AB = DC समान्तर चतुर्भुज की सम्मुख भुजाएँ हैं)
⇒ AD x 10 = 16 x 8 = 128
⇒ AD = \(\frac { 128 }{ 10 }\) = 12.8 cm
अत: AD का अभीष्ट मान = 12.8 cm.
प्रश्न 2.
यदि E, F, G और H क्रमशः समान्तर चतुर्भुज ABCD की भुजाओं के मध्य-बिन्दु हैं तो दर्शाइए कि-
ar (EFGH) = \(\frac { 1 }{ 2 }\) ar (ABCD).
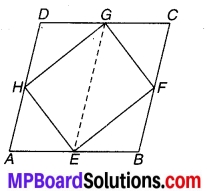
चित्र 9.3
हल:
□ EFGH, समान्तर चतुर्भुज ABCD की भुजाओं AB, BC, CD और DA के मध्य-बिन्दुओं E, F, G और H को क्रमशः मिलाने से बना है।
EG को मिलाइए।
अब आधार EG पर EG || AD के मध्य समान्तर चतुर्भुज DAEG और ∆HEG स्थित हैं
⇒ ar (HEG) = \(\frac { 1 }{ 2 }\)ar (DAEG) …..(1)
एवं आधार EG पर EG || BC के मध्य समान्तर चतुर्भुज CBEG एवं ∆FEG स्थित हैं
⇒ ar (FEG) = \(\frac { 1 }{ 2 }\) ar (CBEG) …(2)
⇒ ar (HEG) + ar (FEG) = \(\frac { 1 }{ 2 }\)ar (DAEG) + \(\frac { 1 }{ 2 }\)ar (CBEG)
अतः ar (EFGH) = \(\frac { 1 }{ 2 }\)ar (ABCD). (fearger) इति सिद्धम्
![]()
प्रश्न 3.
P और Q क्रमशः समान्तर चतुर्भुज ABCD की भुजाओं DC और AD पर स्थित बिन्दु हैं। दर्शाइए कि-
ar (APB) = ar (BQC). (2019)
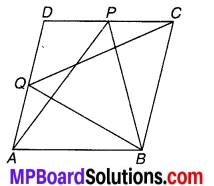
चित्र 9.4
हल:
चूँकि एक ही आधार AB पर AB || DC के मध्य ∆APB और समान्तर चतुर्भुज ABCD स्थित है।
⇒ ar (APB) = \(\frac { 1 }{ 2 }\)ar (ABCD) …(1) ,
चूँकि एक ही आधार BC और BC || AD के बीच ∆BOC और समान्तर चतुर्भुज ABCD स्थित हैं।
⇒ ar (BQC) = \(\frac { 1 }{ 2 }\)ar (ABCD)
अतः ar (APB) = ar (BQC). [समीकरण (1) और (2) से] इति सिद्धम्
प्रश्न 4.
संलग्न चित्र में P समान्तर चतुर्भुज ABCD के अभ्यन्तर में स्थित कोई बिन्दु है। दर्शाइए कि-
(i) ar (APB) + ar (PCD) = \(\frac { 1 }{ 2 }\)ar (ABCD).
(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD).
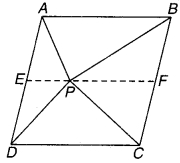
चित्र 9.5
हल:
दिया है : ABCD एक समान्तर चतुर्भुज जिसके अभ्यन्तर P कोई दिया हुआ बिन्दु है। PA, PB, PC एवं PD को मिलाया।
बिन्दु P से होकर EPF || AB रेखा खींचिए।
यहाँ EF || AB || DC (AB || DC समान्तर चतुर्भुज की सम्मुख भुजाएँ हैं)
(i) चूँकि उभयनिष्ठ आधार EF पर EF || AB के मध्य समान्तर चतुर्भुज AEFB और ∆APB स्थित हैं।
⇒ ar (APB) = \(\frac { 1 }{ 2 }\)ar (AEFB) …(1)
एवं उभयनिष्ठ आधार DC पर DC || EF के मध्य समान्तर चतुर्भुज EDCF एवं ∆PCD स्थित है।
⇒ ar (PCD) = \(\frac { 1 }{ 2 }\) ar (EDCF) …(2)
⇒ ar (APB) + ar (PCD) = \(\frac { 1 }{ 2 }\) ar (AEFB) + \(\frac { 1 }{ 2 }\) ar (EDCF) [समीकरण (1) एवं (2) से]
अतः ar (APB) + ar (PCD) = \(\frac { 1 }{ 2 }\) ar (ABCD). (AEFB + EDCF = ABCD) इति सिद्धम्
(ii) चूँकि ar (APB) + ar (PCD) = \(\frac { 1 }{ 2 }\) ar (ABCD) [भाग (i) से सिद्ध कर चुके हैं] …(3)
और ar (APB) + ar (PCD) + ar (APD) + ar (PBC) = ar (ABCD) (चित्रानुसार) …(4)
⇒ ar (APD) + ar (PBC) = \(\frac { 1 }{ 2 }\)ar (ABCD) [समीकरण (3) और (4) से] …(5)
अतः ar (APB) + ar (PCD) = ar (APD) + ar (PBC). समी. (4) और (5) में] इति सिद्धम्
![]()
प्रश्न 5.
संलग्न चित्र में PORS और ABRS समान्तर चतुर्भुज हैं तथा x भुजा BR पर स्थित कोई बिन्दु है। दर्शाइए कि-
(i) ar (PQRS) = ar (ABRS).
(ii) ar (AXS) = \(\frac { 1 }{ 2 }\) ar (PQRS).
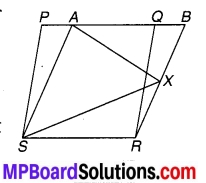
चित्र 9.6
हल:
(i) चूँकि उभयनिष्ठ आधार SR पर SR || PB के मध्य समान्तर चतुर्भुज ABRS एवं PQRS स्थित हैं।
अतः ar (PQRS) = ar (ABRS). इति सिद्धम्
(ii) चूँकि उभयनिष्ठ आधार AS पर AS | | BR के मध्य एक समान्तर चतुर्भुज ABRS एवं एक ∆AXS स्थित हैं
⇒ ar (AXS) = \(\frac { 1 }{ 2 }\) ar (ABRS)
अतः ar (AXS) = \(\frac { 1 }{ 2 }\) ar (PQRS). [∵ ar (PQRS) = ar (ABRS)] इति सिद्धम्
प्रश्न 6.
एक किसान के पास समान्तर चतुर्भुज PQRS के रूप का एक खेत था। उसने RS पर स्थित कोई बिन्दु A लिया और उसे P और Q से मिला दिया। खेत कितने भागों में विभाजित हो गया है ? इन भागों के आकार क्या हैं ? वह किसान खेत में गेहूँ और दालें बराबर-बराबर भागों में अलग-अलग बोना चाहता है। वह ऐसा कैसे करे ?
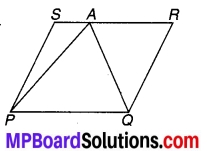
चित्र 9.6
उत्तर:
किसान का खेत PQRS समान्तर चतुर्भुज के आकार का है जिसकी भुजा RS पर स्थित बिन्दु A को P और Q से मिला दिया गया है।
- खेत तीन भागों में विभक्त हो गया है।
- तीनों भाग त्रिभुजाकार हैं।
- वह किसान गेहूँ APQ भाग में तथा शेष APS एवं AQR में दालें बोए अथवा APQ में दालें तथा APS एवं AOR में गेहूँ बोए।