MP Board Class 9th Maths Solutions Chapter 9 Areas of Parallelograms and Triangles Ex 9.2

MP Board Class 9th Maths Solutions Chapter 9 Areas of Parallelograms and Triangles Ex 9.2

Question 1.
In fig. given below, ABCD is a parallelogram, AE ⊥ DCand CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.

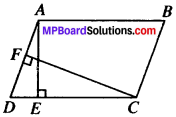
Solution:
ar (ABCD) = AE x DC ….(i)
ar (ABCD) = AD x CF ….(ii)
From (i) and (ii), we get
AE x DC = AD x CF
⇒ AE x AB = AD x CF (∵ AB = DC)

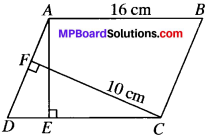
8 x 16 = AD x 10
\(\frac{8×16}{10}\) = AD
\(\frac{128}{10}\) = AD
AD = 12.8 cm.

Question 2.
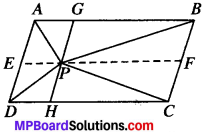
If E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar (EFGH) \(\frac{1}{2}\) = ar (ABCD)
Solution:
Given
ABCD is a ∥^gm E, F, G, H, are the mid-points of AB, BC, CD and DA respectively.

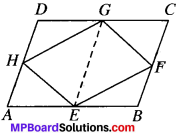
To prove:
ar (EFGH) = \(\frac{1}{2}\) ar (ABCD)
Construction: Join GE.
Proof:
ABCD is a ∥gm
∴ AB ∥ DC and AB = DC
⇒ \(\frac{1}{2}\)AB ∥ \(\frac{1}{2}\)DC and \(\frac{1}{2}\) AB = \(\frac{1}{2}\) DC
AE ∥ DG and AE = DG
∴ AEGD is a parallelogram.
Similarly BCGE is also a parallelogram.
∥gm AEGD and AEGH both lie on the same base EG and are between the same parallels AD and EG.
ar (EGH) = \(\frac{1}{2}\) ar {AEGD) …(1)
Similarly ar {GEF) = \(\frac{1}{2}\) ar {BCGE) …(2)
Adding (1) and (2), we get
ar (EGH) + ar (GEF) = ar (AEGD) + \(\frac{1}{2}\) ar {BCGE)
ar (EFGH) ar {EFGH) = \(\frac{1}{2}\) [ar (AEGD) + ar (BCGE)]

Question 3.
P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
Solution:
Given:
ABCD is a ∥^gm
To prove:
ar (APB) = ar (BQC)..
Proof:
∆APB and ∥^gm ABCD lie on the same base BC and are between the same parallels AB and DC.

ar(APB) = \(\frac{1}{2}\) ar (ABCD)
∆BQC and ∥^gm ABCD lie on the same base BC and are between the same parallels BC and AD.
ar (BQC) = \(\frac{1}{2}\) ar (ABCD) …(2)
From (1) and (2), we get
ar (APB) = ar (BQC)

Question 4.
In Fig. given below, P is a point in the interior of a parallelogram ABCD, Show that

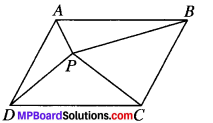
1. ar (APB) + ar (PCD) = \(\frac{1}{2}\) ar (ABCD)
2. ar (APD) + ar (PBC) = ar (APB) + ar (PCD)

[Hint: Thorough P, draw a line parallel to AB.]
Solution:
Given:
P is any point in the interior of ∥^gm ABCD.
To prove:

1. ar (APB) + ar (PCD) \(\frac{1}{2}\) ar (ABCD)
2. ar (APD) + ar (PBC) ar (APB) + ar (PCD)

1. Construction:
Draw a line EF passing through point P parallel to AB.
Proof:
AB ∥EF (By construction) …(1)
AB ∥ DC (∵ ABCD is a ∥gm) …(2)
EF ∥ DC [From (1) and (2)]

In quadrilateral ABFE, AB ∥ EF and AE ∥ BF (∵ AD ∥ BC)
∴ ABFE is a ∥gm
∆ APB and ∥gm ABEF lie on same base base AB and are between the same parallels AB and EF.
ar (APB) = \(\frac{1}{2}\) ar (ABFE) …. (A)
Similarly, ar (PCD) = \(\frac{1}{2}\) ar (DCFE) …(B)
Adding (A) and (B), we get
ar (APB) + ar (PCD) = \(\frac{1}{2}\) ar (ABFE) + \(\frac{1}{2}\) (DCFE)
= \(\frac{1}{2}\) [ar (ABFE) + ar (DCFE)]
= \(\frac{1}{2}\) ar (ABCD) …(3)

2. Construction:
Draw a line GH passing through point P parallel to AD.
Proof:
AD ∥ GH (by construction) …(4)
AD ∥ BC (∵ ABCD is a ∥^gm) …(5)
GH ∥ BC [From (4) and (5)]
In quadrilateral ADHG,
AD ∥ GH (by construction)
and AG ∥ DH (∵ AB\\DC)
∴ ADHG is a parallelogram.
∆APD and ∥gm ADHG lie on the same base AD and lie betweeiwthe same parallels AD and GH.
ar(APD) = \(\frac{1}{2}\) ar (ADHG) …(6)
Similarly, ar (BCP) = \(\frac{1}{2}\) ar (BCHG) …(7)
Adding (6) and (7), we get
ar (APD) + ar (BCP) = \(\frac{1}{2}\) ar (ADHG) + \(\frac{1}{2}\) ar (BCHG)
= \(\frac{1}{2}\) ar (ADHG) + ar (BCHG)
= \(\frac{1}{2}\) [ar (ADHG) + ar (BCHG)]
= \(\frac{1}{2}\) ar (ABCD) …(8)
From (3) and (8), we get
ar (APB) + ar (PCD) = ar (APD) + ar (BCP)

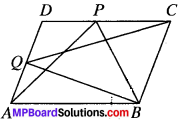
Question 5.
In Fig. given below PQRS and ABRS are parallelograms and X is any point on side BR. Show that

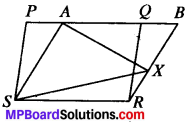
1. ar (PQRS) = ar (ABRS)
2. ar (AZS) = \(\frac{1}{2}\) ar (PQRS)

Solution:
Given
PQRS and ABRS are H801 and X is any point on side BR.
To prove:

1. ar (PQRS) = ar (ABRS)
2. ar (AXS) \(\frac{1}{2}\) ar (PQRS)

Proof:
1. ∥^gm PQRS and ABRS lie on the same base SR and are on the same parallels SR and PB.
∴ ar (PQRS) = ar (ABRS) …(i)

2. D AXS and ∥^gm ABRS lie on the same base AS and are on the same parallels AS and BR.
ar (∆ AXS) = \(\frac{1}{2}\) ar (ABRS) …(ii)

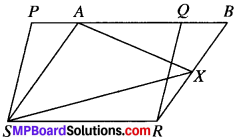
From (i) and (ii), we get
ar (AXS) = \(\frac{1}{2}\) ar (PQRS)

Question 6.
A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts the fields is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?
Solution:
The field will be divided in three parts. The shapes of three parts are triangles.
Given:
PQRS is a ∥^gm
To prove:
ar (APQ) = ar (APS) + ar (AQR)
Construction:
Draw a line AB ∥ SP.
Proof:
∆APQ and ∥^gm PQRS are on the same base PQ and are between the same parallels PQ and SR.

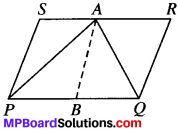
ar (PQRS) = \(\frac{1}{2}\) ar (PQRS)
⇒ 2ar (APQ) = ar (PQRS)
2ar (APQ) = ar (APS) + ar (APQ) + ar (AQR)
2ar (APQ) – ar (APQ) = ar (APQ) ar (AQR)
ar (APQ) = ar (APS) + ar (AQR)

MP Board Class 9th Maths Solutions