MP Board Class 9th Maths Solutions Chapter 8 Quadrilaterals Ex 8.2

MP Board Class 9th Maths Solutions Chapter 8 Quadrilaterals Ex 8.2

Question 1.
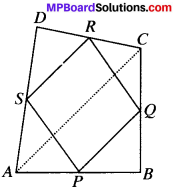
ABCD is quadrilateral in which P, Q, R and S are mid-point^jf the sides AB, BC, CD and DA (see Fig.). AC is a diagonal. Show that:

1. SR ∥ AC and SR = \(\frac{1}{2}\) AC
2. PQ = SR
3. PQRS is a parallelogram.

Solution:
Given
ABCD is in which P, Q, R and S are the mid-points of sides AB,BC, CD and DA.
To prove.

1. SR ∥ AC and SR= \(\frac{1}{2}\) AC
2. PQ = SR
3. PQRS is a parallelogram.

Proof:
In ∆ABC. P is the mid point of AB and Q is the midpoint of BC.
∴ PQ ∥ AC and PQ = \(\frac{1}{2}\) AC (by MPT)…(1)
In ∆ADC, S is the mid-point of AD and R is the mid – point of DC.
SR ∥ AC and SR = \(\frac{1}{2}\) AC (by MPT)…(2)

1. SR ∥ AC and SR = \(\frac{1}{2}\) AC (proved)
2. PQ ∥ AC and SR = \(\frac{1}{2}\) AC
∴ PQ = SR
3. From (1) and (2), we get
PQ ∥ SR and PQ = SR
∴ PQRS is a parallelogram

Question 2.
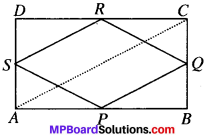
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral P&RS is a rectangle.
Solution:
Given
ABCD is rhombus and P, Q and R and S are the mid-points of sides AB, BC, CD and DA.
To prove
PQRS is a rectangle.
Construction:
Join AC and BD).

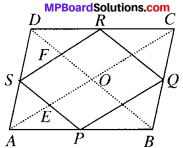
Proof:
In ∆ABC, P is the midpoint of AB and Q is the midpoint of BC.
∴ PQ ∥AC (By MPT) …(1)
In ∆ADC, S is the midpoint of AD and R is the midpoint of DC.
SR ∥ AC (By MPT) …(2)
From (1) and (2), we get
PQ ∥ SR …(3)
In ∆ABD, P is the midpoint of AB and S is the midpoint of AD.
PS ∥ BD …(4)
In ABCD, Q is the midpoint of BC and R is the midpoint of CD
∴ QR ∥ BD (ByMPT) …(5)
From (4) and (5), we get
PS ∥ QR …(6)
In quadrilateral PQRS, PQ ∥ SR and PS ∥ QR
∴ PQRS is a parallelogram.
In quadrilateral OESF
SF ∥ EO (∴ SR ∥ AO …(7)
SE ∥ FO (∴ SP ∥ BD) …(8)
SEOF is a parallelogram.
We know that, that in a parallelogram opposite angles are equal.
∴ ∠ESF = ∠EOF= 90°
(∴ In a rhombus, diagonals intersect each other at right angles)
Hence, PQRS is a rectangle.

Question 3.
ABCD is a rectangle and P,Q,R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
Given
ABCD is a rectangle P,Q,R and S are the mid-points of AB, BC, CD and DA.
To prove.
PQRS is a rhombus.
Proof:
In ∆ABC, P is the midpoint of AB and Q is the midpoint of BC.

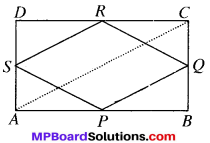
PQ ∥ AC and PQ = \(\frac{1}{2}\) AC (By MPT) ….(1)
In ∆ADC, S is the midpoint of AD and R is the midpoint of DC.
∴ SR ∥ AC and SR = \(\frac{1}{2}\) AC (By MPT)…(2)
From (1) and (2),we get
PQ ∥ SB and PQ = SR
PQRS is a parallelogram
AD = BC (∴ ABCD is a rectangle)
⇒ \(\frac{1}{2}\) AD = \(\frac{1}{2}\) BC
AS = BQ
In ∆PAS and ∆PBQ, AS = BQ (proved)
AP = BP P is the mid-point of AB
∠A = ∠B (each 90°)
and so PS = PQ (ByCPCT)
In a ∥^gm, if adjacent sides are equal, then it a rhombus.
∴ PQRS is a rhombus.

Question 4.
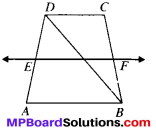
ABCD is a trapezium in which AB ∥ DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC and F (see Fig. below). Show that F is the mid-point of BC.

Solution:
Given
AB ∥ DC, DE = AE and EF ∥ AS.
To prove
F is the mid-point of BC
Proof:
AB ∥ DC (given) …(1)
AB ∥ EF (given) …(2)

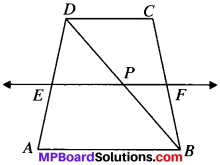
From (1) and (2) we get,
DC ∥ EF
In ∆ABD, E is the mid – point of AD
EP ∥ AB (∴ EF∥AB)
∴ P is the mid – point of BD (By CMPT)
In ∆BCD, P is the midpoint of BD.
PF ∥ DC (∴ EF ∥ DC)
F is the midpoint of BC (By CMPT).

Question 5.
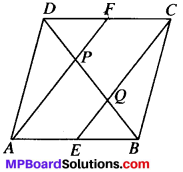
In a parallelogram ABCD, E and F are the mid-point of sides AB and CD respectively (See Fig.). Show that the line segments AD and EC trisect the diagonal BD.

Solution:
Given
ABCD is a ∥^gm, E and F are the mid-point of AB and CD.
To prove:
BQ = PQ = DP
Proof:
AB ∥ DC and AB = DC (∴ ABCD is a ∥gm)
⇒ \(\frac{1}{2}\) ∥ AB \(\frac{1}{2}\) DC and \(\frac{1}{2}\) AB = \(\frac{1}{2}\)DC
⇒ AE ∥ FC and AE = FC (∴ \(\frac{1}{2}\) AB = AE and \(\frac{1}{2}\) DC = FC)
AECF is a parallelogram (∴ AECF is a ∥^gm)
In ∆ABP, E is the mid – point of AB,
EQ ∥AP (∴ AECF is a ∥<sup<gm)

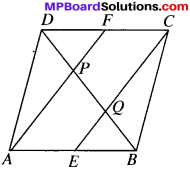
∴ Q is the midpoint of BP (∴ by CMPT) …(1)
BQ = PQ
In ∆DQC, F is the midpoint of DC
EF ∥ CQ AECF is a ∥<sup<gm)
P is the midpoint of DQ
i.e., DP = PQ
From (1) and (2), we get BQ = PQ = DP.

Question 6.
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
Solution:
Given
ABCD is a in which P, Q.R and S are the mid-points of AB, BC, CD and DA respectively.
To prove
PR and SQ bisect each other.
Construction:
Join AC. Join PQ, QR, RS and SP.

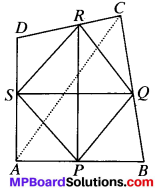
Proof:
In ∆ABC, P is the midpoint of AB and Q is the midpointof BC.
PQ ∥ AC and PQ = \(\frac{1}{2}\) AC (By MPT) …..(1)
In ∆ADC, S is the midpoint of AD and R is the midpoint of DC.
SR ∥ AC and SR = \(\frac{1}{2}\) AC (by MPT) …(2)
Form (1) and (2), we get
PQ ∥ SR and PQ = SR
∴ PQRS is a parallelogram in which PR and SQ are diagonals^ and so PR and SQ bisect each other (In a ∥^gm, diagnaols bisect each other)

Question 7.
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that

1. D is the mid – point of AC
2. MD ⊥ AC
3. CM = MA = \(\frac{1}{2}\) AB.

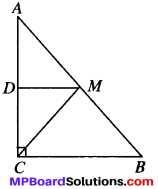
Solution:
Given
ABC is a right ∆. ∠C = 90°
AM = BM and MD ∥ BC.
To prove:

1. D is the mid-point of AC, i.e., AD – CD
2. MD ⊥ AC
3. CM = MA = \(\frac{1}{2}\) AB

Proof:
1. In ∆ACB, M is the mid-point of AB and MD ∥ BC
∴ D is the mid – point of AC (By CMPT)
i.e., AD = CD

2. MD ∥ BC and AC is the transversal
∴ ∠ADM = ∠ACB (CA’s)
⇒ ∠ADM = 90° (∠ACB = 90°)
∴ MD ⊥ AC

3. In ∆ADM and ∆CDM,
AD = CD (proved)
∠ADM = ∠CDM (each 90°)
[∴ ∠ADM + ∠CDM = 180° (LPA’s); 90° + ∠CDM= 180°; ∠CDM = 90°]
MD = MD (common)
∴ ∆ADM = ∆CDM (By SAS)
and so MA = MC (By cpct) …(1)
MA = \(\frac{1}{2}\) AB (Given) …(2)
Form (1) and (2), we get MA = MC = \(\frac{1}{2}\) AB.

MP Board Class 9th Maths Solutions