MP Board Class 9th Maths Solutions Chapter 7 Triangles Ex 7.1
Question 1.
In quadrilateral ABCD, AC = AD and AB bisects ∠A (see below). Show that ∆ABC = ∆ABD. What can you say about BC and BD?
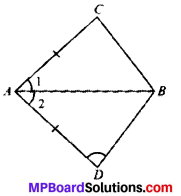
Solution:
Given AC = AD
AB is the bisector of ∠A
i. e., ∠1 = ∠2
To prove: ∆ABC = ∆ABD
Proof:
In ∆ABC and ∆ABD
∠1 = ∠2 (given)
AC = AD (given)
AB = AB (common)
∆ABC ≅ ∆ABD (by SAS)
![]()
Question 2.
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (see below). Prove that
- ∆ABD = ∆BAC
- BD = AC
- ∠ABD = ∠BAC
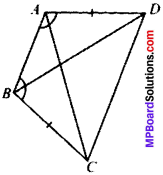
Solution:
Given AD = BC
∠DAB = ∠CBA
To prove:
- ∆ABD ≅ ∆BAC
- BD = AC
- ∠ABD = ∠BAC
Proof:
1. In ∆ABD and ∆BAC
AD = BC (Given)
∠DAB = ∠CBA (given)
AB = BA (common)
∆ABD = ∆BAC (by SAS)
and so 2. BD = AC (by CPCT)
and so 3. ∠ABD – ∠BAC (by CPCT)
Question 3.
AD and BC are equal perpendiculars to a line segment AB (see below). Show that CD bisects AB.
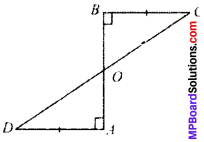
Solution:
Given: ∠B = ∠A (each 90°)
AD = BC
To prove: OA = OB
Proof:
In ∆OBC and ∆OAD
∠B = ∠A (each 90°)
BC = AD (given)
∠BOC = ∠AOD (V.O.A’s)
∆OBC = ∆OAD (by SAS)
and so OA = OB (by CPCT)
Question 4.
l and m are two parallel lines intersected by another pair of parallel lines p and q (see below). Show that ∆ABC = ∆CDM.
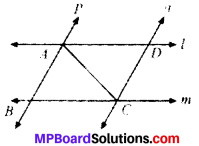
Solution:
Given: l ∥ m and p ∥ q
To prove:
∆ABC = ∆CDA
Proof:
In quadrilateral ABCD
AB ∥ DC and BC ∥ AD
∴ ABCD is a parallelogram
and so AB = DC [Opposite sides]
BC = AD
In ∆ABC and ∆CDA
AB = CD (proved)
BC = DA (proved)
AC = CA (proved)
∆ABC = ∆CDA (by SSS)
![]()
Question 5.
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see below). Show that
- ∆APB = ∆AQB
- BP = BQ or B is equidistant from the arms of ∠A.
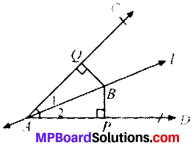
Solution:
Given
∠1 = ∠2
BQ ⊥ AC
and BP ⊥ AD
To prove:
- ∆APB ≅ ∆AQB
- BP = BQ
Proof:
In ∆APB and ∆AQB
∠2 = ∠1 (given)
∠P = ∠Q (each 90°)
AB = AB (common)
∆APB ≅ ∆AQB (byAAS)
BP = BQ (by CPCT)
Question 6.
In Fig. given below, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
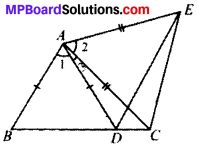
Solution:
Given
AC = AE
AB = AD
∠BAD = ∠EAC i.e., ∠1 = ∠2
To prove: BC = DE
Proof:
In ∆ABC and ∆ADE
AB = AD (given)
AC = AE (given)
∠1 = ∠2 (given)
Adding ∠3 on both sides
∠1 + ∠3 = ∠2 + ∠3
∠BAC = ∠DAE
∆ABC = ∆ADE , (by SAS)
and so BC = DE (by CPCT)
![]()
Question 7.
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see below). Show that
- ∆DAP ≅ ∆EBP
- AD = BE
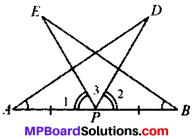
Solution:
Given:
AP = BP
∠BAD = ∠ABE
∠EPA = ∠DPB
∠1 = ∠2
To prove:
- ∆DAP ≅ ∆EBP
- AD = BE
Proof:
∠1 = ∠2 (given)
Adding ∠3 on both sides
∠1 + ∠3 = ∠2 + ∠3
∠APD = ∠BPE
In ∆DAP and ∆EBP
∠APD = ∠BPE (proved)
AP = BP (given)
∠PAD = ∠PBE (given)
∆DAP ≅ ∆EBP (by ASA)
and so AD = BE (by CPCT)
Question 8.
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see below). Show that:
- ∆AMC = ∆BMD
- ∠DBC is a right angle.
- ∆DBC = ∆ACB
- CM = \(\frac{1}{2}\) AB
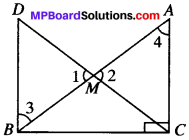
Solution:
∠C = 90°
AM = BM
DM = CM
To prove:
- ∆AMC ≅ ∆BMD
- ∆DBC = 90°
- ∆DBC ≅ ∆ACB
- CM = \(\frac{1}{2}\) AB
Proof:
1. ∆AMC and ∆BMD
AM = BM (given)
MC = MD (given)
∠1 = ∠2 (V.O.A’s)
∆AMC = ∆BMD (by SAS)
and so AC = DB and ∠4 and ∠3 (by CPCT)
2. ∠4 = ∠3 (proved) [AIA’s]
∴ DB ∥ AC
AC ∥ BD and BC is the transversal
∠C + ∠B = 180° (C.I.A’s)
∠B = 180° – 90° = 90°
3. In DBC and ∆ACB
DB = AC (proved)
∠B = ∠C (each 90°)
BC = CB (common)
∆DBC = ∆ACB (by SAS)
and so DC = AB (by CPCT)
4. DC =AB (proved)
\(\frac{1}{2}\)DC = \(\frac{1}{2}\)AB
CM = \(\frac{1}{2}\)AB.
![]()
Theorem 7.3
AAS (Angle-Angle-Side) Congruence Theorem:
If any two angles and a non-included side of one triangle are equal to the corresponding angles and side of another triangle, then the two triangles are congruent.
Given:
In ∆s ABC and DEF, we have
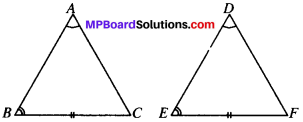
∠A = ∠D
∠B = ∠E
and BC = EF
To prove:
∆ABC = ∆DEF
Proof:
Since the sum of the angles of a triangle is 180°. We have
∠A + ∠B + ∠C = ∠D + ∠E + ∠F
Since ∠A = ∠D and ∠B – ∠E (Given)
∠C = ∠F …..(i)
Now, in ∆ABC and ∆DEF, we have
∠B = ∠E (Given)
∠C = ∠F [From, (i)]
and BC = EF (Given)
∴ ∆ABC ≅ ∆DEF [ASA Cong. Theorem]