MP Board Class 9th Maths Solutions Chapter 2 Polynomials Ex 2.3
Question 1.
Find the remainder when x3 + 3x3 + 3x + 1 is divided by
- x + 1
- x – \(\frac{1}{2}\)
- x
- x + π
- 5 + 2x.
Solution:
Let p(x) = x3 + 3x2 + 3x + 1
1. x + 1
x + 1 = 0
x = – 1
Remainder
= p(- 1)= (- 1)3 + 3 (- 1)2 + 3 (-1) +1
= – 1 + 3 – 3 + 1 = 0.
2. x – \(\frac{1}{2}\) = 0
x =π
When p(x) is divided by ( x – \(\frac{1}{2}\)) the remainder is P(\(\frac{1}{2}\))
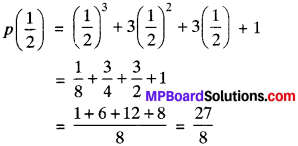
3. x = 0
When p(x) is divided by x, the remainder is p(0).
p(0) = (0) + 3(0)2 + 3(0) + 1
= 0 + 0 + 0 + 1 = 1
4. x + π = 0
x = – π
When p(x) is divided by (x + π), the remainder is p(- π) p(- K) = (- π)3 + 3 (- π)2 + 3 (- π) + 1
= – π3 + 3π2 – 3π + 1
5. 5 + 2x = 0 x = \(\frac{-5}{2}\)
When p(x) is divided by (5 + 2x), the remainder is p(\(\frac{-5}{2}\))

Question 2.
Find the remainder when x3 – ax2 + 6x – a is divided by x – a.
Solution:
Let p(x) = x2 – ax2 + 6x – 1
x – a = 0
x = a
Remainder = (a)3 – a(a)2 + 6(a) – a
= a2 – a2 + 6a – a
= 5a.
![]()
Question 3.
Check whether 7 + 3x is a factor of 3x3 + 7x.
Solution:
p(x) = 3x3 + 7x
7 + 3X = 0
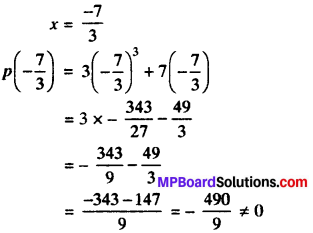
(7 + 3x) is not a factor of p(x).
Factorization of Polynomials:
Factor Theorem:
Let p{x) be any polynomial of degree equal to or greater than 1 and ‘a’ be any real number such that –
- If p(a) = 0, then (x – a) is a factor of p(x)
- If (x – a) is a factor then p(a) = 0
Proof:
Let p(x) be a polynomial of degree ≥ 1 and be a real number.
1. If p(a) = 0, then (x – a) is a factor of p(x)
Suppose q(x) be the quotient when p(x) is divided by (x – a). By remainder theorem, remainder = p(a).
P(x) = (x – a) x q(x) + p(a)
p(x) = (x – a) x q(x) (∴ p(a) = 0, given)
= (x – a) is a factor of p(x).
2. If (x – a) is a factor then p(a) = 0
=> p(x) when divided by (x – a) gives remainder = 0 …(i)
But by remainder theorem
When p(x) is divided by (x – a), remainder = p(a) …(ii)
From (i) and (ii), we get
p(a) = 0 Proved.