MP Board Class 9th Maths Solutions Chapter 2 बहुपद Ex 2.2
प्रश्न 1.
निम्नलिखित पर बहुपद 5x – 4x2 + 3 के मान ज्ञात कीजिए :
(i) x = 0
(ii) x = -1
(iii) x = 2.
हल:
∵ p(x) = 5x – 4x2 + 3
(i) ⇒ p (0) = 5(0) – 4(0) + 3 = 0 – 0 + 3 = 3.
(ii) ⇒ p (- 1) = 5(-1) – 4(-1)2 + 3 = – 5 – 4 + 3 = – 9 + 3 = -6.
(iii) ⇒ p(2) = 5(2) – 4(2)2 + 3 = 10 – 16 + 3 = 13 – 16 = – 3.
![]()
प्रश्न 2.
निम्नलिखित बहुपदों में से प्रत्येक बहुपद के लिए p(0), p(1) और p(2) ज्ञात कीजिए :
(i) P(y) = y2 – y + 1
(ii) p(t) = 2 + t + 2t2 – t3
(iii) P(x) = x3
(iv) p(x) = (x – 1) (x + 1).
हल:
(i) ∵ p(y) = y2 – y + 1
⇒ p(0) = (0)2 – (0) + 1 = 0 – 0 + 1 = 1
तथा p(1) = (1)2 – (1) + 1 = 1 – 1 + 1 = 1
एवं p(2) = (2)2 – (2) + 1 = 4 – 2 + 1 = 5 – 2 = 3
अत: p(0) = 1, p(1) = 1 एवं p(2) = 3 अभीष्ट मान हैं।
(ii) ∵ p(t) = 2 + t + 2t2 – t3
⇒ p(0) = 2 + 0 + 2(0)2 – (0)3 = 2 + 0 + 0 – 0 = 2
तथा p(1) = 2 + 1 + 2(1)2 – (1)3= 2 + 1 + 2 – 1 = 4
एवं p(2) = 2 + 2 + 2 (2)2 – (2)3 = 2 + 2 + 8 – 8 = 4
अतः p(0) = 2, p(1)= 4 एवं p(2) = 4 अभीष्ट मान हैं।
(iii) ∵ p(x) = x3
⇒ p(0) = (0)3 = 0
तथा p(1) = (1)3 = 1
एवं p(2) = (2)3 = 8
अतः p(0) = 0, p(1)= 1 एवं p(2) = 8 अभीष्ट मान हैं।
(iv) ∵ p(x) = (x – 1) (x + 1)
⇒ p(0) = (0 – 1) (0 + 1) = (-1) (+ 1) = -1
तथा p(1) = (1 – 1) (1 + 1) = (0) (2) = 0
p(2) = (2 – 1) (2 + 1) = (1) (3) = 3
अतः p(0) = – 1, p(1) = 0 एवं p(2) = 3 अभीष्ट मान हैं।
प्रश्न 3.
सत्यापित कीजिए कि दिखाए गए मान निम्नलिखित स्थितियों में संगत बहुपदों के शून्यक हैं :
(i) p(x) = 3x + 1 ; x = –\(\frac { 1 }{ 3 }\)
(ii) p(x) = 5x – π ; x = \(\frac { 4 }{ 5 }\)
(iii) p(x) = x2 – 1 ; x = 1,-1
(iv) p(x) = (x + 1) (x – 2) ; x = -1, 2
(v) p(x) = x2 ; x = 0
(vi) p(x) = lx + m ; x = -m/l
(vii) p(x) = 3x2 – 1 ; x = \( -\frac{1}{\sqrt{3}}, \frac{2}{\sqrt{3}}\)
(viii) p(x) = 2x + 1; x = \(\frac { 1 }{ 2 }\)
हल:
(i) p(x) = 3x + 1
⇒ p(- 1/3) = 3 (- 1/3) + 1 = – 1 + 1 = 0
अतः –\(\frac { 1 }{ 3 }\) दिए व्यंजक का शून्यक है।
(ii) p(x) = 5x – π
⇒ p(\(\frac { 4 }{ 5 }\))= 5 x \(\frac { 4 }{ 5 }\) – π = 4 – π ≠ 0
अतः \(\frac { 4 }{ 5 }\) दिए व्यंजक का शून्यक नहीं है।
(iii) p(x) = x2 – 1
⇒ p(+ 1) = (1)2 – 1 = 1 – 1 = 0
अत: 1 एवं – 1 दिए व्यंजक के शून्यक हैं।
(iv) p(x) = (x + 1) (x -2)
⇒ p(- 1) = (-1 + 1) (-1-3) = (0) (-4) = 0
एवं p(2) = (2 + 1) (2 – 2) = (3) (0) = 0
अतः -1 एवं 2 दिए व्यंजक के शून्यक हैं।
(v) p(x) = x2
⇒ p (0) = (0) = 0
अतः 0 (शून्य) दिए व्यंजक का शून्यक है।
(vi) p(x) = lx + m
⇒ \( p\left(-\frac{m}{l}\right)=l\left(-\frac{m}{l}\right)+m=-m+m=0\)
अतः- ” दिए व्यंजक का शून्यक है।
(vii) p(x) = 3x2 – 1
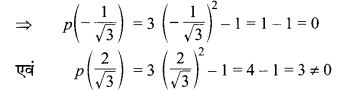
अत: –\( \frac{1}{\sqrt{3}}\) तो दिए व्यंजक का शून्यक है लेकिन \( \frac{2}{\sqrt{3}}\) शून्यक नहीं है।
(viii) p(x) = 2x + 1
⇒ p(\(\frac { 1 }{ 2 }\)) = 2 (\(\frac { 1 }{ 2 }\)) + 1 = 1 + 1 = 2 + 0
अतः \(\frac { 1 }{ 2 }\) दिए व्यंजक का शून्यक नहीं है।
![]()
प्रश्न 4.
निम्नलिखित स्थितियों में से प्रत्येक स्थिति में बहुपद का शून्यक ज्ञात कीजिए :
(i) p(x) = x + 5
(ii) p(x) = x – 5
(iii) p(x) = 2x + 5
(iv) p(x) = 3x – 2
(v) p(x) = 3x
(vi) p(x) = ax; a ≠ 0
(vii) p(x) = cx + d; c ≠ 0, c, d वास्तविक संख्याएँ हैं।
हल:
(i) माना p(x) = x + 5 = 0 (शून्यक ज्ञात करने के लिए
⇒ x = -5
अतः -5 दिए हुए व्यंजक का अभीष्ट शून्यक है।
(ii) माना p(x) = x – 5 = 0 (शून्यक ज्ञात करने के लिए)
⇒ x = 5
अत: 5 दिए व्यंजक का अभीष्ट शून्यक है।
(iii) माना p(x) = 2x + 5 = 0 (शून्यक ज्ञात करने के लिए)
⇒ 2x = -5 ⇒ x = –\(\frac { 5 }{ 2 }\)
अतः – दिए व्यंजक का अभीष्ट शून्यक है।
(iv) माना p(x) = 3x – 2 = 0 (शून्यक ज्ञात करने के लिए)
⇒ 3x = 2 ⇒ x = \(\frac { 2 }{ 3 }\)
अतः \(\frac { 2 }{ 3 }\) दिए हुए व्यंजक का अभीष्ट शून्यक है।
(v) माना p(x) = 3x = 0 (शून्यक ज्ञात करने के लिए)
⇒ x = \(\frac { 0 }{ 3 }\) = 0
अत: 0 (शून्य) दिए हुए व्यंजक का अभीष्ट शून्यक है।
(vi) माना p(x) = ax = 0 (शून्यक ज्ञात करने के लिए)
⇒ x = \(\frac { 0 }{ a }\) = 0 (चूँकि a ≠ 0)
अतः 0 (शून्य) दिए हुए व्यंजक का अभीष्ट शून्यक है।
(vii) माना p(x) = cx + d= 0 (शून्यक ज्ञात करने के लिए)
⇒ cx = -d ⇒ x = –\(\frac { d }{ c }\) ; यहाँ c ≠ 0
अतः –\(\frac { d }{ c }\) (जहाँ c ≠ 0, c, d वास्तविक संख्याएँ हैं) दिए व्यंजक का अभीष्ट शून्यक है।