MP Board Class 9th Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.2
(जब तक अन्यथा न कहा जाए तब तक \(\pi=\frac{22}{7}\) लीजिए।)
प्रश्न 1.
ऊँचाई 14 cm वाले एक लम्बवृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल 88 cm³ है। बेलन के आधार का व्यास ज्ञात कीजिए। (2018, 19)
हल :
चूँकि वृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल Sc = 2πrh
⇒ \(2 \times \frac{22}{7} \times r \times 14=88\)
⇒ \(r=\frac{88 \times 7}{2 \times 22 \times 14}\)
= 1 cm
∴ व्यास = 2r = 2 x 1 = 2 cm
अत: बेलन का अभीष्ट व्यास = 2 cm.
प्रश्न 2.
एकधातु की चादर से 1 m ऊँची और 140 cm व्यास के आधार वाली एक बन्द बेलनाकार टंकी बनाई जानी है। इस कार्य के लिए कितने वर्ग मीटर चादर की आवश्यकता होगी? (2019)
हल :
बेलनाकार टंकी की ऊँचाई h = 1 m = 100 cm, आधार का व्यास d = 140 cm
त्रिज्या r = \(\frac { 140 }{ 2 }\) = 70 cm .
∴ टंकी का सम्पूर्ण पृष्ठ = 2πr (r + h) = 2 x \(\frac { 22 }{ 7 }\) x 70 (70 + 100)
= 440 x 170
= 74800 cm²
= 7.48 m²
अतः चादर का अभीष्ट क्षेत्रफल = 7.48 m².
प्रश्न 3.
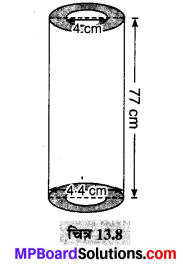
धातु का एक पाइप 77 cm लम्बा है। इसके एक अनुप्रस्थ काट का आन्तरिक व्यास 4 cm है और बाहरी व्यास 4.4 cm है (देखिए संलग्न चित्र)। ज्ञात कीजिए:
(i) आन्तरिक वक्र पृष्ठीय क्षेत्रफल।
(ii) बाहरी वक्र पृष्ठीय क्षेत्रफल।
(iii) कुल पृष्ठीय क्षेत्रफल।
हल :
दिया है : धातु के पाइप (खोखले बेलन) की लम्बाई (ऊँचाई) h = 77 cm
अनुप्रस्थ काट (वृत्ताकार छल्ला) का बाह्य व्यास d1 = 4.4 cm ⇒ r1 = 2.2 cm एवं आन्तरिक व्यास d2 = 4 cm ⇒ r2 = 2 cm
(i) आन्तरिक वक्र पृष्ठीय क्षेत्रफल = πd2h
= \(\frac{22}{7} \times 4 \times 77\)
= 22 x 44
= 968 cm² …(1)
अतः अभीष्ट आन्तरिक वक्र पृष्ठीय क्षेत्रफल = 968 cm².
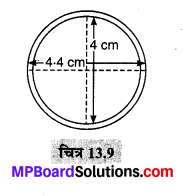
(ii) बाह्य वक्र पृष्ठीय क्षेत्रफल = πd1h
= \(\frac{22}{7} \times 4.4 \times 77\)
= 22 x 4.4 x 11
= 1064.8 cm² ….(2)
अत: अभीष्ट बाह्य वक्र पृष्ठीय क्षेत्रफल = 1064.8 cm².
(iii) पाइप के दोनों सिरों का क्षेत्रफल = \(2 \pi\left(r_{1}^{2}-r_{2}^{2}\right)=2 \times \frac{22}{7}\left[(2 \cdot 2)^{2}-(2)^{2}\right]\)
= \(2 \times \frac{22}{7}(4 \cdot 84-4)\)
= \(2 \times \frac{22}{7} \times 0.84\)
= 44 x 0.12
= 5.28 cm² …(3)
पाइप का कुल पृष्ठीय क्षेत्रफल = 968 + 1064.8 + 5.28 . [(1) + (2) + (3) से]
= 2038.08 cm²
अतः पाइप का अभीष्ट कुल पृष्ठीय क्षेत्रफल = 2038.08 cm².
![]()
प्रश्न 4.
एक रोलर (roller) का व्यास 84 cm है और लम्बाई 120 cm है। एक खेल के मैदान को एक बार समतल करने के लिए 500 चक्कर लगाने पड़ते हैं। खेल के मैदान का मीटर में क्षेत्रफल
ज्ञात कीजिए।
हल :
रोलर का व्यास d = 84 cm तथा लम्बाई h = 120 cm
चूँकि बेलन का पार्श्व पृष्ठीय क्षेत्रफल = πdh = \(\frac { 22 }{ 7 }\) x 84 x 120 cm²
= 22 x 12 x 120
= 31680 cm²
500 चक्कर में कुल क्षेत्रफल = 500 x 31680 cm²
= \(\frac{500 \times 31680}{10000} \mathrm{m}^{2}\)
= 1584 m²
अतः खेल के मैदान का अभीष्ट क्षेत्रफल = 1584 m².
प्रश्न 5.
किसी बेलनाकार स्तम्भ का व्यास 50 cm है और ऊँचाई 3.5 m है। Rs 12.50 प्रति m² की दर से इस स्तम्भ के वक्र पृष्ठ पर पेंट कराने का व्यय ज्ञात कीजिए।
हल :
दिया है : बेलनाकार स्तम्भ का व्यास, d = 50 cm = 0.5 m
ऊँचाई h = 3.5 m, और पेंट कराने की दर = Rs 12.50 प्रति m²
स्तम्भ का वक्र पृष्ठ = πdh = \(\frac { 22 }{ 7 }\) x 0.5 x 3.5 = 5.50 m²
पेंट कराने का व्यय = दर x क्षेत्रफल = 12.50 x 5.50 = Rs 68.75
अत: पेंट कराने का अभीष्ट व्यय = Rs 68.75.
प्रश्न 6.
एक लम्ब वृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल 4.4 m² है। यदि बेलन के आधार की त्रिज्या 0.7 m है तो उसकी ऊँचाई ज्ञात कीजिए।
हल :
दिया है : बेलन का वक्र पृष्ठीय क्षेत्रफल Sc = 4.4 m² एवं आधार की त्रिज्या r = 0.7 m
चूँकि बेलन का वक्र पृष्ठ Sc = 2πrh
⇒ \(2 \times \frac{22}{7} \times 0.7 \times h=4 \cdot 4\)
⇒ \(h=\frac{4 \cdot 4 \times 7}{2 \times 22 \times 0.7}=1 \mathrm{m}\)
अतः बेलन की अभीष्ट ऊँचाई = 1 m.
![]()
प्रश्न 7.
किसी वृत्ताकार कुएँ का आन्तरिक व्यास 3.5 m है और यह 10 m गहरा है। ज्ञात कीजिए :
(i) आन्तरिक वक्र पृष्ठीय क्षेत्रफल।
(ii) Rs 40 प्रति m² की दर से इसके वक्र पृष्ठ पर प्लास्टर कराने का व्यय।
हल :
कुएँ का आन्तरिक व्यास d = 3.5 m तथा गहराई h = 10 m दिया हुआ है तथा पेंट कराने की दर Rs 40 प्रति m² है।
(i) चूँकि कुएँ का आन्तरिक वक्र पृष्ठीय क्षेत्रफल = \(\pi d \times h=\frac{22}{7} \times 3.5 \times 10\) = 110 m²
अतः कुएँ का अभीष्ट आन्तरिक वक्र पृष्ठीय क्षेत्रफल = 110 m².
(ii) प्लास्टर कराने का व्यय = दर x क्षेत्रफल = 40 x 110 = Rs 4,400
अतः वक्र पृष्ठ पर प्लास्टर कराने का अभीष्ट व्यय = Rs 4,400.
प्रश्न 8.
गर्म पानी द्वारा गर्म रखने वाले एक संयन्त्र में 28 m लम्बाई और 5 cm व्यास वाला एक बेलनाकार पाइप है। इस संयन्त्र में गर्मी देने वाला कुल कितना पृष्ठ है?
हल :
पाइप की लम्बाई h = 28 m एवं व्यास d = 5 cm = 0.05 m
पाइप का वक्र पृष्ठ = \(\pi d h=\frac{22}{7} \times 0.05 \times 28\) = 4.4 m²
अतः संयन्त्र का गर्मी देने वाला अभीष्ट पृष्ठ = 4.4 m².
प्रश्न 9.
ज्ञात कीजिए:
(i) एक बेलनाकार पेट्रोल की बंद टंकी का पार्श्व तल या वक्र पृष्ठीय क्षेत्रफल जिसका व्यास 4.2 m और ऊँचाई 4.5 m है।
(ii) टंकी को बनाने में कुल कितना इस्पात (steel) लगा होगा, यदि कुल इस्पात का \(\frac { 1 }{ 12 }\) भाग बनाने में नष्ट हो जाता है।
हल :
दिया है : बेलनाकार पेट्रोल की टंकी का व्यास d = 4.2 m, ऊँचाई h = 4.5 m और टंकी बनाने में कुल इस्पात का \(\frac { 1 }{ 12 }\) भाग नष्ट होता है अर्थात् \(\frac { 11 }{ 12 }\) भाग प्रयुक्त होता है।
(i) पार्श्व पृष्ठ = \(\pi d h=\frac{22}{7} \times 4 \cdot 2 \times 4 \cdot 5\) = 59.4 m²
अतः टंकी का अभीष्ट पार्श्व तल = 59.4 m².
(ii) टंकी का कुल पृष्ठ = \(2 \pi r(h+r)=2 \times \frac{22}{7} \times 2 \cdot 1(4 \cdot 5+2 \cdot 1)\)
= 2 x 22 x 0.3 x 6.6 m² [d = 4.2 ⇒ r = 2.1]
चूँकि इस्पात का \(\frac { 1 }{ 12 }\) भाग नष्ट हो जाता है अतः \(\frac { 11 }{ 12 }\) भाग प्रयुक्त होता है।
मान लीजिए इस्पात का कुल क्षेत्रफल = x m² है, तो
\(\frac{11}{12} x=2 \times 22 \times 0 \cdot 3 \times 6 \cdot 6\)
\(x=\frac{2 \times 22 \times 0.3 \times 6.6 \times 12}{11}\)
∴ x = 1.2 x 6.6 x 12 = 95.04 m²
अतः इस्पात का अभीष्ट कुल क्षेत्रफल = 95.04 m².
![]()
प्रश्न 10.
संलग्न चित्र में आप एक लैंपशेड का फ्रेम देख रहे हैं। इसे एक सजावटी कपड़े से ढका जाना है। इस फ्रेम के आधार का व्यास 20 cm है और ऊँचाई 30 cm है। फ्रेम के ऊपर और नीचे मोड़ने के लिए दोनों ओर 2.5 cm अतिरिक्त कपड़ा भी छोड़ा जाना है। ज्ञात कीजिए कि लैंपशेड को ढकने के लिए कुल कितने कपड़े की आवश्यकता होगी?
हल :
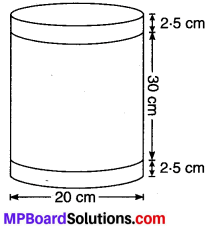
दिया है : फ्रेम के आधार का व्यास d = 20 cm
एवं ऊँचाई = 30 cm लेकिन दोनों सिरों पर (2.5 cm + 2.5 cm) = 5.0 cm कपड़ा छोड़ा जाना है,
अतः प्रभावी ऊँचाई h = 30 + 5 = 35 cm
कपड़े का क्षेत्रफल = पार्श्व पृष्ठ का प्रभावी क्षेत्रफल
\(=\pi d \times h=\frac{22}{7} \times 20 \times 35=2200 \mathrm{cm}^{2}\)
अतः अभीष्ट कपड़े की आवश्यकता = 2200 cm².
प्रश्न 11.
किसी विद्यालय के विद्यार्थियों से एक आधार वाले बेलनाकार कलमदानों को गत्ते से बनाने और सजाने की प्रतियोगिता में भाग लेने के लिए कहा गया। प्रत्येक कलमदान को 3 cm त्रिज्या और 10.5 cm ऊँचाई का होना था। विद्यालय को इसके लिए प्रतिभागियों को गत्ता देना था। यदि इसमें 35 प्रतिभागी थे तो विद्यालय को कितना गत्ता खरीदना पड़ा होगा?
हल :
दिया है : कलमदान के आधार की त्रिज्या, r = 3 cm और ऊँचाई = 10.5 cm तथा कलमदानों की संख्या 35 है।
कलमदान का पार्श्व पृष्ठीय क्षेत्रफल = 2πrh = 2π x 3 x 10.5 = 63.0 π cm²
आधार का क्षेत्रफल = πr² = π x 3² = 9π cm²
एक कलमदान में प्रयुक्त कुल गत्ता = 63π + 9π = 72π cm²
35 कलमदानों में प्रयुक्त कुल गत्ता = 35 x 72π = 35 x 72 x \(\frac { 22 }{ 7 }\) cm²
= 7920 cm²
अत: गत्ते का अभीष्ट क्षेत्रफल = 7920 cm².