MP Board Class 9th Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.1
Question 1.
A plastic box 1.5 m long, 1.25 m wide and 65 cm deep is to be made. It is to be open at the top. Ignoring the thickness of the plastic sheet, determine:
- The area of the sheet required for making the box.
- The cost of sheet for it, if a sheet measuring 1m2 costs ₹ 20.
Solution:
Given
l = 1.5 m = 150 cm
b = 1.25 m = 125 cm
h = 65 cm
1. Total area of plastic sheet required = LSA + Area of base
= 2h(l + b) + l x b
= 2 x 65 (150 + 125) + 150 x 125
= 130 (275) + 18750
= 35750 + 18750
= 54500 cm2
= 5.45 m2
2. Cost of sheet = area of plastic sheet x rate = 5.45 x 20
= 109.00
= ₹ 109.
![]()
Question 2.
The length, breadth and height of a room are 5 m, 4 m and 3 m respectively. Find the cost of white washing the walls of the room and the ceiling at the rate of ₹ 7.50 per m2.
Solution:
Given
l = 5m
b = 4m
h = 3 m
Area of the room to be white washed = LSA + Area of ceiling
= 2h(l + b) + l x b
= 2 x 3 (5 + 4) + 5 x 4
= 6(9) + 20
= 54 + 20 = 74 m2
Cost of painting = 7.50 x 74 m2
= ₹ 555
Question 3.
The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of ₹ 10 per m2 is ₹ 15000, find the height of the hall.
Solution:
Given
P = 250 m
Rate of painting = ₹ 10/ m2
Cost of painting = ₹ 15000
Area of walls to be painted = \(\frac{15000}{10}\) = 1500 m2
Perimeter = 2 (l + b) = 250
∴ l + b = 250/2 = 125m
Area of walls = LSA = 2h (l + b) = 1500
= h (l + b) = \(\frac{1500}{10}\) = 750 m2 …..(i)
Putting the value of (l + b) in (i), we get
h(125) = 750
h = \(\frac{750}{125}\) = 6 m.
Question 4.
The paint in a certain container is sufficient to paint an area equal to 9315 m2. How many bricks of dimensions 22.5 cm x 10 cm x 7.5 cm can be painted out of this container?
Solution:
Given
l = 22.5 cm
h = 7.5 cm = 0.075 m
b = 10 cm = 0.1 m
Area to be painted = 9.375 m2 = 93750 cm2
Area of one brick = 2(lb + bh + hl)
= 2(22.5 x 10 + 10 x 7.5 + 7.5 x 22.5)
= 2(225 + 75 + 168.75)
= 2 x 468.75
= 937.5 cm2
No. of bricks which can be painted = \(\frac{93750}{937.5}\) = 100
![]()
Question 5.
A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high.
- Which box has the greater lateral surface area and by how much?
- Which box has the smaller total surface area and by how much? Sol.
Solution:
1. LSA of cubical box = 4a2
= 4 x 10 x 10 = 400 cm2
LSA of cuboidal box = 2h (l + b)
= 2 x 8 (12.5 x 10)
= 16 x 22.5
= 360 cm2
LSA of cubical box is more than cuboidal box by 40 cm2.
2. TSA of cubical box = 6a2 = 6 x 10 x 10
= 600 cm2
TSA of cuboidal box = 2 (lb + bh + hl)
= 2(12.5 x 10 + 10 x 8 + 12.5 x 8)
= 2(125 + 80 + 100)
= 2 x 305 = 610 cm2.
∴ TSA of cuboidal box is more than cubical box by 10 cm2.
Question 6.
A small indoor green house (herbarium) is made entirely of glass panes (including base) held together with tape. It is 30 cm long, 25 cm wide and 25 cm high.
- What is the area of the glass?
- How much of tape is needed for all the 12 edges?
Solution:
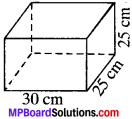
Given
l = 30 cm
b = 25 cm and
h = 25 cm
Area of glass required = 2(30 x 25 + 25 x 25 x 30)
= 2(750 + 625 + 750)
= 2 x 2125 = 4250 cm2
Length of tape required = 4(l + b + h)
= 4(30 + 25 + 25)
= 4 x 80 = 320 cm
![]()
Question 7.
Shanti Sweets Stall was placing an order for making cardboard boxes for packing their sweets. Two sizes of boxes were required. The bigger of dimensions 25 cm x 20 cm x 5 cm and the smaller of dimensions 15 cm x 12 cm x 5 cm. For all the overlaps, 5% of the total surface area is required extra. If the cost of the cardboard is ₹ 4 for 1000 cm2, find the cost of cardboard required for supplying 250 boxes of each kind.
Solution:
Big Box :
l = 25 cm
b = 20 cm
h = 5 cm
Small Box:
l = 15 cm
b = 12 cm
h = 5 cm
Number of boxes required = 250
Rate = ₹ 4 per 1000 cm2
TSA of bigger box = 2 (25 x 20 + 20 x 5 + 5 x 25)
= 2(500 + 100 + 125)
= 2 x 725 = 1450 cm2
TSA of smaller box = 2 (15 x 12 +12 x 5 + 5 x 15)
= 2 (180 + 60 + 75)
= 2 x 315 = 630 cm2
Area of cardboard required one bigger = TSA + 5% of TSA
= 1450 + \(\frac{5}{100}\) x 1450
= 1522.5 cm2
Area of cardboard required for 250 boxes of bigger size = 250 x 1522.5
= 380625 cm2
Area of cardboard required for one small box = 630 + \(\frac{5}{100}\) x 630
= 661.5 cm2
Total area of cardboard required for 250 boxes of smaller size = 250 x 661.5
= 165375 cm2
Total area = (165375 + 380625) cm2
= 546000 cm2
Total cost of each kind of cardboard = \(\frac{4}{1000}\) x 546000
= ₹ 2184/-
Question 8.
Parveen wanted to make a temporary shelter for her car, by making a box – like structure with tarpaulin that covers all the four sides and the top of the car (with the front face as a flap which can be rollpd up). Assuming that the stitching margins are very small, and therefore negligible, how much tarpaulin would be required to make the shelter of height 2.5 m, with base dimensions 4 m x 3 m?
Solution:
Given
l = 4m
b = 3 m and
h = 2.5 m
Area of the tarpaulin required = 2h(l + b) + l x b
= 2 x 2.5(4 + 3) + 4 x 3
= 5 x 7 + 12
= 35 + 12= 47m