MP Board Class 9th Maths Solutions Chapter 12 हीरोन का सूत्र Ex 12.2
प्रश्न 1.
एक पार्क चतुर्भुज ABCD के आकार का है जिसमें ∠C = 90°, AB = 9 m, BC = 12 m, CD = 5 m और AD = 8 m है। इस पार्क का कितना क्षेत्रफल है ?
हल:
दिए हुए पार्क का आकार संलग्न चित्र में प्रदिर्शित है जिसमें
∠C = 90°, AB = 9 m, BC = 12 m, CD = 5 m और AD = 8 m है।
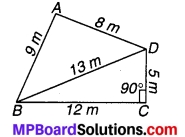
चित्र 12.7

पार्क का कुल क्षेत्रफल = ar (ABD) + ar (BCD)
= 6 √35 + 30 = 6 x 5.916 + 30 [समी. (1) + (2) से]
⇒ ar (ABCD) = 35.496 + 30 = 65-496 ≈ 65.5 m2 (लगभग)
अतः पार्क का अभीष्ट क्षेत्रफल = 65.5 m2.(लगभग)
प्रश्न 2.
एक चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए जिसमें AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm और AC = 5 cm है।
हल:
चतुर्भुज ABCD का आकार संलग्न चतुर्भुज में दिखाया गया है
जिसमें AB = 3 cm, BC = 4 cm, CD = 4 cm, AD = 5 cm और AC = 5 cm है।
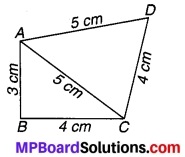
चित्र 12.8
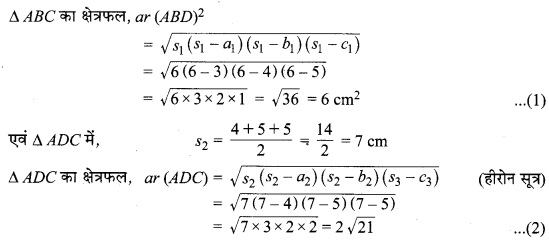
ar (ABCD) = ar (ABD) + ar (ADC)
= 6 + 2√21
= 6 + 9.165
= 15.165 cm2
= 15.2 cm2 (लगभग)
अतः चतुर्भुज ABCD का अभीष्ट क्षेत्रफल = 15.2 cm2.(लगभग)।
प्रश्न 3.
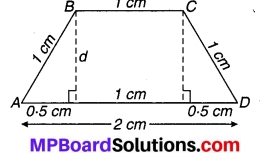
राधा ने एक रंगीन कागज से एक हवाई जहाज का चित्र बनाया जैसा संलग्न चित्र में दिखाया गया है। प्रयोग किए गए कागज का कुल क्षेत्रफल ज्ञात कीजिए।
हल:
चित्र कुल 5 भागों में बँटा हुआ है।
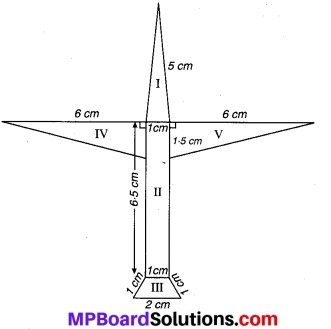
चित्र 12.9
I भाग एक समद्विबाहु त्रिभुजाकार है जिसकी भुजाएँ 5 cm, 5 cm. 1 cm।
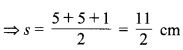

II भाग एक आयत है जिसकी भुजाएँ 6-5 cm एवं 1 cm हैं।
⇒ ar (II) = 6.5 x 1 = 6.5 cm2 …(2)
III भाग एक समलम्ब चतुर्भुज है जिसकी समान्तर भुजाएँ 1 cm और 2 cm है तथा असमान्तर भुजाएँ 1 cm और 1 cm हैं। मान लीजिए दोनों समान्तर भुजाओं के बीच की दूरी में है तो के अनुसार
चित्र 12.10
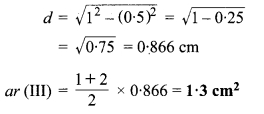
IV एवं V भाग दो समान विमाओं के समकोण त्रिभुज हैं जिनकी समकोण बनाने वाली भुजाएँ 6 cm एवं 1.5 cm हैं।
⇒ ar (IV & V) = 2 x \(\frac { 1 }{ 2 }\) x 6 x 1.5
= 9.0 cm2 ….(4)
ar (हवाई जहाज) = ar (I) + ar (II) + ar (III) + ar (IV &V)
⇒ ar (हवाई जहाज) = 2.5 + 6.5 + 1.3 + 9.0 = 19.3 cm2 (लगभग)
अतः प्रयोग किए गए रंगीन कागज का अभीष्ट क्षेत्रफल = 19.3 cm2.(लगभग)
प्रश्न 4.
एक त्रिभुज और एक समान्तर चतुर्भुज का एक ही आधार है और क्षेत्रफल भी एक ही है। यदि त्रिभुज की भुजाएँ 26 cm, 28 cm और 30 cm हैं तथा समान्तर चतुर्भुज 28 cm के आधार पर स्थित है तो उसकी संगत ऊँचाई ज्ञात कीजिए।
हल:
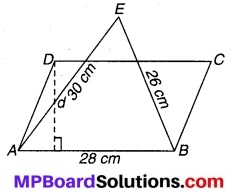
चित्र 12.9
ज्ञात है : एक ही आधार AB = 28 cm पर एक समान्तर AL
चतुर्भुज ABCD एवं त्रिभुज EAB स्थित हैं जिसमें
AE = 30 cm एवं BE = 26 cm है।
ar (EAB) = ar (ABCD)
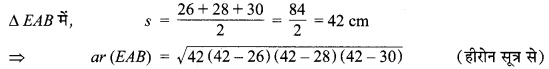
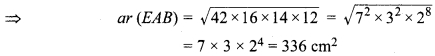
मान लीजिए समान्तर चतुर्भुज की संगत ऊँचाई = d cm है।
चूँकि ar (ABCD) = ar (EAB) (दिया है)
28 x d = 336
d = \(\frac { 336 }{ 28 }\) = 12 cm
अतः समान्तर चतुर्भुज की अभीष्ट संगत ऊँचाई = 12 cm.
प्रश्न 5.
एक समचतुर्भुजाकार घास के खेत में 18 गायों के चरने के लिए घास है। यदि इस समचतुर्भुज की प्रत्येक भुजा 30 m है और बड़ा विकर्ण 48 m है, तो प्रत्येक गाय को चरने के लिए इस घास के खेत का कितना क्षेत्रफल प्राप्त होगा? (2018)
हल:
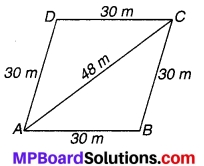
चित्र 12.12
ज्ञात है : एक सम चतुर्भुजाकार घास का मैदान ABCD जिसकी भुजा AB = BC = CD = DA = 30 m एवं दीर्घ विकर्ण AC = 48 m, जैसा कि चित्र में दिखाया गया है। विकर्ण AC समचतुर्भुज ABCD को बराबर के क्षेत्रफल वाले ar (ABC) = ar (DAC) में विभक्त करता है।
अब ∆ABC की भुजाएँ क्रमशः 30 m, 30 m, एवं 48 m हैं।
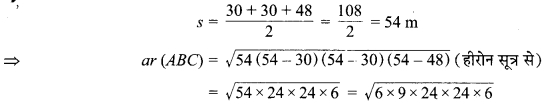
= 24 x 6 x 3 = 432 m2
चूँकि ar (ABCD) = 2 x ar (ABC)
= 2 x 432 = 864 m2
एक गाय के लिए उपलब्ध क्षेत्रफल = 800 = 48 m2
अतः एक गाय के चरने के लिए उपलब्ध घास के खेत का अभीष्ट क्षेत्रफल = 48 m2.
प्रश्न 6.
दो विभिन्न रंगों के कपड़ों के 10 त्रिभुजाकार टुकड़ों को सीकर एक छाता बनाया गया है (देखिए संलग्न चित्र)। प्रत्येक टुकड़े की माप 20 cm, 50 cm और . 50 cm है। छाते में प्रत्येक रंग का कितना कपड़ा लगा है ?
हल:
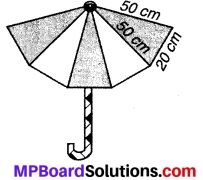
चित्र 12.13
ज्ञात है : 10 त्रिभुजाकार समान क्षेत्रफल वाले दो रंग के कपड़े के टुकड़े जिनकी विमाएँ प्रत्येक 20 cm, 50 cm और 50
cm हैं तथा प्रत्येक रंग के 5 टुकड़े हैं।
एक त्रिभुजाकार टुकड़े के लिए,
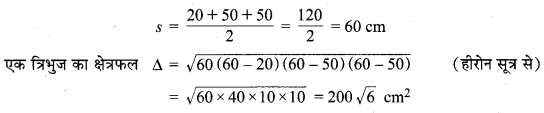
⇒ प्रत्येक रंग के 5 टुकड़ों का क्षेत्रफल = 5 x 200√6 cm2
= 1000√6 cm2
अतः प्रत्येक रंग के कपड़े का अभीष्ट क्षेत्रफल = 1000√6 cm2.
प्रश्न 7.
एक पतंग तीन भिन्न-भिन्न शेडों (Shades) के कागजों से बनी है। इन्हें संलग्न चित्र में I, II और III से दर्शाया गया है। पतंग का ऊपरी भाग 32 cm विकर्ण का एक वर्ग है और निचला भाग 6 cm, 6 cm और 8 cm भुजाओं का एक समद्विबाहु त्रिभुज है। ज्ञात कीजिए कि प्रत्येक शेड का कितना कागज प्रयुक्त किया गया है।
हल:
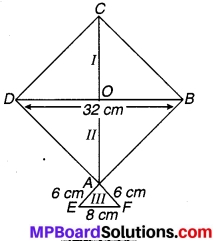
चित्र 12.14
ज्ञात है : एक पतंग जिसमें ABCD एक वर्ग है जिसके विकर्ण DB = CA = 32 cm तथा AEF एक समद्विबाहु त्रिभुज जिसमें AE = AF = 6 cm एवं EF = 8 cm है। मान लीजिए विकर्ण DB एवं CA बिन्दु 0 पर परस्पर लम्ब समद्विभाजक हैं। (वर्ग के प्रगुण के अनुसार)
यह पतंग तीन अलग-अलग रंग के भागों
I∆CDB, II ∆DAB और III ∆ AEF में विभाजित है।
ar (∆CDB) = ar (∆DAB) (वर्ग का विकर्ण वर्ग को समद्विभाजित करता है)
भाग I-अब ∆ CDB में आधार DB = 32 cm एवं शीर्षलम्ब
CO = \(\frac { 1 }{ 2 }\) = CA = \(\frac { 1 }{ 2 }\) = x 32 = 16 cm है।
ar (CDB) = \(\frac { 1 }{ 2 }\) x 32 x 16 = 256 cm2
भाग II-चूँकि ar (DAB) = ar (CDB) (बराबर त्रिभुज हैं)
= 256 cm2 (∵ ar (CDB) = 256 cm2 ज्ञात कर चुके हैं)
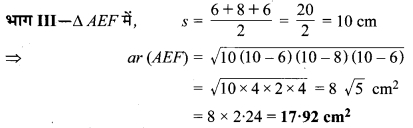
अतः I भाग का अभीष्ट क्षेत्रफल = II भाग का अभीष्ट क्षेत्रफल = 256 cm2 एवं III भाग का अभीष्ट क्षेत्रफल = 17.92 cm2.
प्रश्न 8.
फर्श पर एक फूलों का डिजायन 16 त्रिभुजाकार टाइलों से बनाया गया है जिनमें से प्रत्येक की भुजाएँ 9 cm, 28 cm और 35 cm हैं (देखिए संलग्न चित्र)।. इन टाइलों को 50 पैसे प्रति cm की दर से पॉलिश कराने का व्यय ज्ञात कीजिए।
हल:
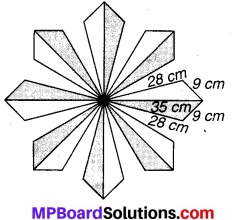
चित्र 12.15
दिया है : संलग्न चित्र में 16 त्रिभुजाकार टाइलों से बना डिजायन, प्रत्येक की भुजाएँ 9 cm, 28 cm और 35 cm हैं।
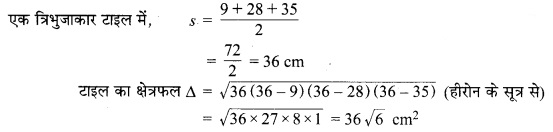
⇒ 16 टाइलों का क्षेत्रफल = 16∆ = 16 x 36√6 cm2
चूँकि टाइलों पर पॉलिश का व्यय = दर x क्षेत्रफल
⇒ कुल व्यय = ₹ 70 x 16 x 36√6
= ₹ 705.60
अत: टाइलों पर पॉलिश का अभीष्ट व्यय = ₹ 705.60.
प्रश्न 9.
एक खेत एक समलम्ब के आकार का है जिसकी समान्तर भुजाएँ 25 m और 10 m है। इसकी असमान्तर भुजाएँ 14 m और 13 m हैं। इस खेत का क्षेत्रफल ज्ञात कीजिए।
हल:
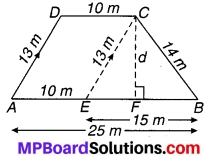
चित्र 12.16
ज्ञात है : एक समलम्ब के आकार का खेत जिसमें AB|| DC,
AB = 25 m, DC = 10 m, BC = 14 m एवं DA = 13 m है।
CE || DA एवं CF ⊥ AB खींचिए।
चूँकि AECD एक समान्तर चतुर्भुज है [DC || AB (दिया है) और CE || DA (रचना से)]
⇒ CE = DA = 13 cm (समान्तर चतुर्भुज की सम्मुख भुजाएँ हैं)
चूंकि EB = AB – AE = AB – DC (AE = DC समान्तर चतुर्भुज की सम्मुख भुजाएँ)
⇒ EB = 25 – 10 = 15 m
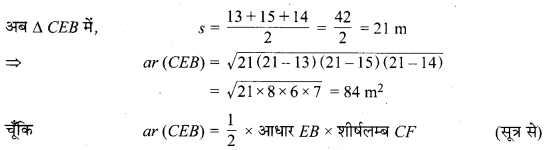
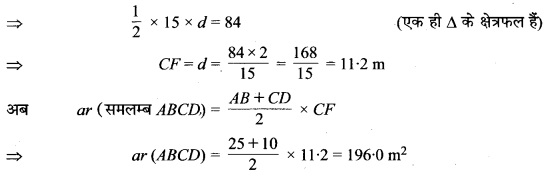
अत: समलम्ब खेत का का अभीष्ट क्षेत्रफल = 196.0 m2
MP Board Class 9th Maths Solutions