MP Board Class 8th Maths Solutions Chapter 13 सीधा और प्रतिलोम समानुपात Ex 13.1
प्रश्न 1.
एक रेलवे स्टेशन के निकट कार पार्किंग शुल्क इस प्रकार है –
- 4 घण्टों तक – ₹ 60
- 8 घण्टों तक – ₹ 100
- 12 घण्टों तक – ₹ 140
- 24 घण्टों तक – ₹180
जाँच कीजिए कि क्या कार पार्किंग शुल्क पार्किंग समय के प्रत्यक्ष अनुपात में है?
हल:
∴ \(\frac{4}{60}\) ≠ \(\frac{8}{100}\) ≠ \(\frac{12}{140}\) ≠ \(\frac{24}{180}\)
∴ कार पार्किंग शुल्क पार्किंग समय के प्रत्यक्ष अनुपात में नहीं है।
![]()
प्रश्न 2.
एक पेंट के मूल मिश्रण (base) के 8 भागों में लाल रंग के पदार्थ का 1 भाग मिलाकर मिश्रण तैयार किया जाता है। निम्नलिखित सारणी में, मूल मिश्रण के वे भाग ज्ञात कीजिए जिन्हें मिलाए जाने की आवश्यकता है –
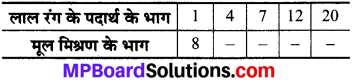
हल:
यहाँ, माना कि लाल रंग के पदार्थ का भाग x, मूल मिश्रण के ” भाग में मिलाया जाता है, तथा x और y प्रत्यक्ष अनुपात में हैं।
अतः x और y का अनुपात अचर रहेगा।
तब \(\frac{x}{y}\) = \(\frac{1}{8}\)
अतः अभीष्ट अनुपात = \(\frac{4}{32}\), \(\frac{7}{56}\), \(\frac{12}{96}\), \(\frac{20}{160}\)
सारणी में रखने पर,

प्रश्न 3.
प्रश्न 2. में यदि लाल रंग पदार्थ के 1 भाग के लिए 75 mL मूल मिश्रण की आवश्यकता है, तो मूल मिश्रण के 1800 mL में हमें कितना लाल रंग का पदार्थ मिलाना चाहिए?
हल:
माना कि 1800 mL में x भाग लाल रंग का पदार्थ मिलाना चाहिए।
सारणी में रखने पर,
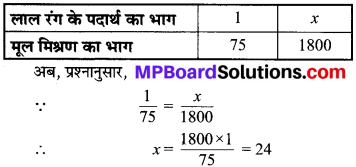
अतः मूल मिश्रण में हमें 24 भाग लाल रंग का पदार्थ मिलाना चाहिए।
प्रश्न 4.
किसी सॉफ्ट ड्रिंक फैक्ट्री में एक मशीन 840 बोतलें 6 घण्टे में भरती है। वह मशीन पाँच घण्टे में कितनी बोतलें भरेगी?
हल:
माना कि 5 घण्टे में x बोतलें भरी जा सकती हैं। तब सारणी के रूप में रखने पर,

अतः मशीन 5 घण्टे में 700 बोतलें भरेगी।
प्रश्न 5.
एक बैक्टीरिया या जीवाणु के फोटोग्राफ (चित्र) को 50,000 गुना आवर्धित करने पर उसकी लम्बाई 5 cm हो जाती है, जैसा कि संलग्न चित्र में दिखाया गया है। इस बैक्टीरिया की वास्तविक लम्बाई क्या है ? यदि फोटोग्राफ को केवल 20,000 गुना आवर्धित किया जाए, तो उसकी आवर्धित लम्बाई क्या होगी?
हल:
बैक्टीरिया की आवर्धित लम्बाई = 50,000 गुना
बैक्टीरिया की लम्बाई = 5 cm

अतः बैक्टीरिया की वास्तविक लम्बाई = 10-4 cm
यहाँ, फोटोग्राफ की लम्बाई तथा आवर्धित लम्बाई अनुक्रमानुपाती हैं।
माना कि आवर्धित लम्बाई x cm है
सारणी के रूप में लिखने पर,
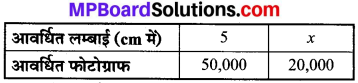
यहाँ आवर्धित लम्बाई तथा आवर्धित फोटोग्राफ परस्पर अनुक्रमानुपाती हैं।
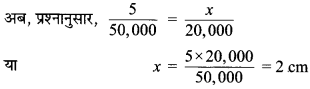
अतः आवर्धित लम्बाई = 2 cm
![]()
प्रश्न 6.
एक जहाज के मॉडल में उसका मस्तूल (mast) 9 cm ऊँचा है, जबकि वास्तविक जहाज का मस्तूल 12 m ऊँचा है। यदि जहाज की लम्बाई 28 m है तो उसके मॉडल की लम्बाई कितनी है?
हल:
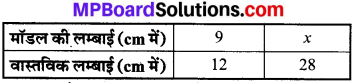
स्पष्ट है, मॉडल की लम्बाई और वास्तविक लम्बाई परस्पर – अनुक्रमानुपाती हैं।
\(\frac{9}{12}\) = \(\frac{x}{28}\)
x = \(\frac{9×28}{12}\) = 21
अतः जहाज के मॉडल की लम्बाई = 21 cm
प्रश्न 7.
मान लीजिए 2 kg चीनी में 9x 10 क्रिस्टल हैं। निम्नलिखित चीनी में कितने क्रिस्टल होंगे?
- 5 kg
- 1.2 kg.
हल:
माना कि 5 kg चीनी और 1.2 kg चीनी में क्रमशः x और y क्रिस्टल हैं। इन्हें सारणी रूप में लिखने पर,

स्पष्ट है कि यहाँ क्रिस्टल की संख्या और चीनी की मात्रा परस्पर अनुक्रमानुपाती हैं।
1.
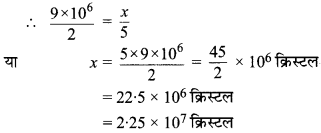
अतः 5 kg चीनी में 2.25 x 107 क्रिस्टल होंगे।
2.
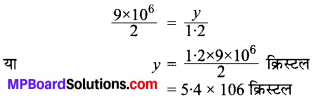
अतः 1.2 kg चीनी में 5.4 x 106 क्रिस्टल होंगे।
प्रश्न 8.
रश्मि के पास एक सड़क का मानचित्र है, जिसके पैमाने में 1 cm की दूरी 18 km निरूपित करती है। वह उस सड़क पर अपनी गाड़ी से 72 km की दूरी तय करती है। उसके द्वारा तय की गई दूरी मानचित्र में क्या होगी?
हल:
यहाँ, 1 cm की दूरी = 18 km.
माना कि रश्मि के द्वारा तय की गई दूरी मानचित्र में x cm है, तब दी हुई सूचना को सारणी के रूप में निरूपित करने पर,

यहाँ, मानचित्र में दूरी तथा वास्तविक दूरी परस्पर अनुक्रमानुपाती हैं।
\(\frac{1}{18}\) = \(\frac{x}{72}\)
या x = \(\frac{1×72}{18}\) cm = 4 cm
अतः मानचित्र में दूरी = 4 cm
प्रश्न 9.
एक 5 m 60 cm ऊँचे ऊर्ध्वाधर खम्भे की छाया की लम्बाई 3 m 20 cm है। उसी समय पर ज्ञात कीजिए –
- 10 m 50 cm ऊँचे एक अन्य खम्भे की छाया की लम्बाई।
- उस खम्भे की ऊँचाई जिसकी छाया की लम्बाई 5 m है।
हल:
1. माना कि x m उस खम्भे की लम्बाई है जिसकी छाया की लम्बाई 10 m 50 cm है। y m उस खम्भे की ऊँचाई है जिसकी छाया 5 m है।
इन्हें सारणी के रूप निरूपित करने पर,

यहाँ, यह स्पष्ट है कि खम्भे की ऊँचाई और छाया परस्पर अनुक्रमानुपाती हैं।
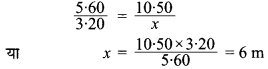
अतः छाया की लम्बाई = 6 m
2.

अतः खम्भे की ऊँचाई = 8 m 75 cm
प्रश्न 10.
माल से लदा हुआ एक ट्रक 25 मिनट में 14 km चलता है। यदि चाल वही रहे, तो वह 5 घण्टे में कितनी दूरी तय कर पाएगा?
हल:
माना कि ट्रक 5 घण्टे में x km दूरी तय करता है। तब इन्हें सारणी के रूप में निरूपित करने पर,
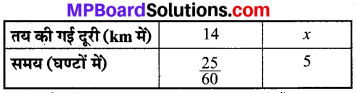
यहाँ, दूरी तथा समय परस्पर अनुक्रमानुपाती हैं।
\(\frac{14}{25/60}\) = \(\frac{x}{5}\)
या x = \(\frac{5x14x60}{25}\) = 168 km
अतः ट्रक द्वारा 5 घण्टे में तय की गई दूरी = 168 km
पाठ्य-पुस्तक पृष्ठ संख्या # 216-217
![]()
इन्हें कीजिए (क्रमांक 13.3)
प्रश्न 1.
एक वर्गांकित कागज पर भिन्न-भिन्न भुजाओं के पाँच वर्ग खींचिए। निम्नलिखित सूचना को एक सारणी के रूप में लिखिए –
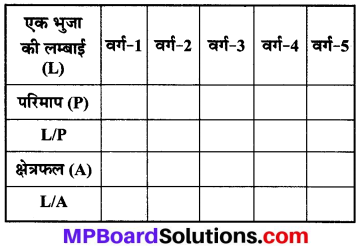
ज्ञात कीजिए कि क्या भुजा की लम्बाई –
- वर्ग के परिपाम के अनुक्रमानुपाती है।
- वर्ग के क्षेत्रफल के अनुक्रमानुपाती है।
हल:

सूचना को सारणी के रूप में निरूपित करने पर,
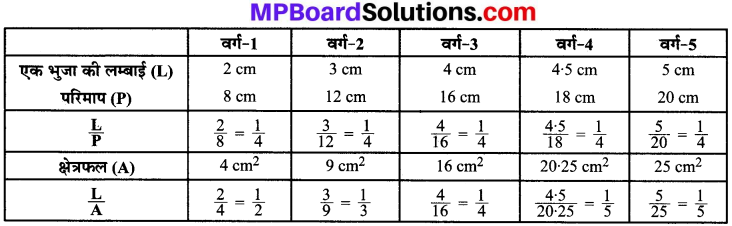
यहाँ स्पष्ट है कि,
- वर्ग की भुजा की लम्बाई वर्ग के परिमाप के अनुक्रमानुपाती है।
- वर्ग की भुजा की लम्बाई वर्ग के क्षेत्रफल के अनुक्रमानुपाती नहीं है।
प्रश्न 2.
पाँच व्यक्तियों के लिए हलवा बनाने के लिए, निम्नलिखित सामग्री की आवश्यकता होती है: सूजी/रवा = 250 g, चीनी = 300 g, घी = 200 g, पानी = 200 g. समानुपात की अवधारणा का प्रयोग करते हुए, अपनी कक्षा के लिए हलवा बनाने के लिए इन सामग्रियों की मात्राओं में होने वाले परिवर्तनों का आकलन (estimate) कीजिए।
हल:
माना कि कक्षा में विद्यार्थियों की संख्या = 20 है।
स्पष्ट है कि यहाँ अनुक्रमानुपाती की स्थिति है।
अत: वांछित सामग्री \(\frac{20}{5}\) = 4 गुना होगी –
अर्थात् सूजी/रवा = 250 x 4g = 1000 g = 1 kg
चीनी = 300 x 4g = 1200 g = 1.200kg
घी = 200 x 4g = 800 g
पानी = 200 x 4g = 800 g.
प्रश्न 3.
एक पैमाने का चुनाव करते हुए, अपनी कक्षा के कमरे का मानचित्र खींचिए, जिसमें खिड़कियाँ, दरवाजे, ब्लैकबोर्ड इत्यादि दर्शाए गए हों (एक उदाहरण यहाँ दिया है।
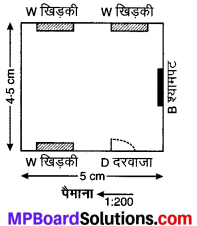
हल: माना की पैमाना 1 : 40 है, तब
मानचित्र इस प्रकार है –
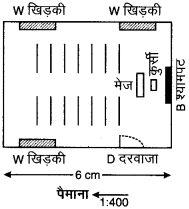
सोचिए, चर्चा कीजिए और लिखिए (क्रमांक 13.2)
प्रश्न 1.
सीधा समानुपात (विचरण) की अब तक हल की गई समस्याओं में से कुछ को लीजिए। क्या आप सोचते हैं कि इन समस्याओं को इकाई की विधि या ऐकिक विधि (unitary method) से हल किया जा सकता है?
हल:
हाँ, इन समस्याओं को ऐकिक विधि से हल किया जा सकता है।
हम यहाँ प्रश्नावली 13.1 से प्रश्न 4 एवं प्रश्न 10 को हल करते हैं –
प्रश्न 4 का हल:
∴ 6 घण्टे में भरी जाने वाली बोतलें = 840
∴ 1 घण्टे में भरी जाने वाली बोतलें = \(\frac{840}{6}\)
∴ 5 घण्टे में भरी जाने वाली बोतलें = \(\frac{840×5}{6}\)
= 140 x 5 = 700 बोतलें।
प्रश्न 10 का हल:
25 मिनट = \(\frac{25}{60}\) घण्टे
∴ \(\frac{25}{60}\) घण्टे में तय की गई दूरी = 14 km
∴ 1 घण्टे में तय की गई दूरी = \(\frac{14}{25/60}\) km
∴ 5 घण्टे में तय की गई दूरी = \(\frac{14x60x5}{25}\) km
= 168 km
![]()
पाठ्य-पुस्तक पृष्ठ संख्या # 219
इन्हें कीजिए (क्रमांक 13.4)
प्रश्न 1.
एक वर्गांकित कागज लीजिए और उस पर 48 काउंटरों (counters) को पंक्तियों की विभिन्न संख्याओं में नीचे दर्शाए अनुसार व्यवस्थित कीजिए –
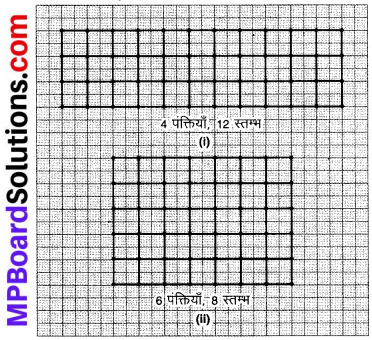
आप क्या देखते हैं? जब R में वृद्धि होती है, तो C में कमी होती है।
- क्या R1 : R2 = C2 : C1 है?
- क्या R3 : R4 = C4 : C3
- क्या R और C परस्पर व्युत्क्रमानुपाती है?
इस क्रियाकलाप को 36 काउंटरों के साथ प्रयास कीजिए।
हल:
C1 → 24
C2 → 16
C5 → 6
हम यहाँ देखते हैं कि R में वृद्धि होती है तो C में कमी होती
1. R1 : R2 = 2 : 3 और
C2 : C1 = 16 : 24 = 2 : 3
R1 : R2 = C2 : C1
2. R3 : R4 = 4 : 6 = 2 : 3 और
C4 : C3 = 8 : 12 = 2 : 3
R3 : R4 = C4 : C3
3. हाँ, R और C परस्पर व्युत्क्रमानुपाती हैं। उत्तर अब, 36 काउण्टरों के साथ क्रियाकलाप।
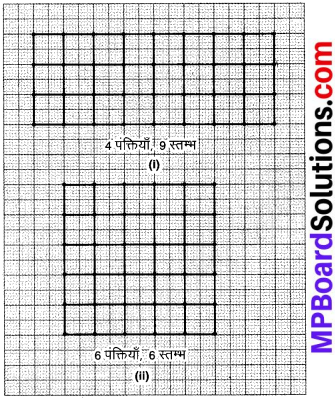
सूचना को सारणी के रूप में लिखने पर, हम प्राप्त करते हैं –
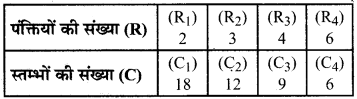
हम देखते हैं कि R में वृद्धि होती है, तो C में कमी होती हैं।
1. R1 : R2 = 2 : 3 और C2 : C1 = 12 : 18 = 2 : 3
R1 : R2 = C2 : C1
2. R3 : R4 = 4 : 6 = 2 : 3 और C4 : C3 = 6 : 9 = 2 : 3
R3 : R4 = C4 : C3
3. हाँ, R और C परस्पर व्युत्क्रमानुपाती हैं।
![]()
प्रयास कीजिए (क्रमांक 14.2)
प्रश्न 1.
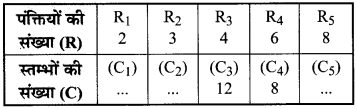
निम्नलिखित सारणियों को देखिए तथा ज्ञात कीजिए कि कौन-कौन से चरों (यहाँ x और y) के युग्म परस्पर प्रतिलोम समानुपात में हैं –
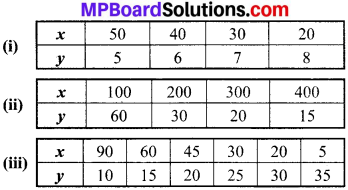
हल:
(i) हम देखते हैं कि
x × y = 50 x 5 ≠ 40 x 6 ≠ 30 x 7 ≠ 20 x 8
अतः x और y परस्पर प्रतिलोम समानुपात में नहीं हैं।
(ii) हम देखते हैं कि
x × y = 100 x 6 = 200 x 30 = 300 x 20
= 400 x 15 = अचर
अतः x और y परस्पर प्रतिलोम समानुपात में हैं।
(iii) हम देखते हैं कि
x × y = 90 x 10 = 60 x 15 = 45 x 20 ≠ 30 x 25 ≠ 20 x 30 ≠ 5 x 35
अतःx और , परस्पर प्रतिलोम समानुपात में नहीं हैं।