MP Board Class 7th Maths Solutions Chapter 8 राशियों की तुलना Ex 8.2
प्रश्न 1.
दी गई भिन्न संख्याओं को प्रतिशत में बदलो :
(a) \(\frac { 1 }{ 8 } \)
(b) \(\frac { 5 }{ 4 } \)
(c) \(\frac { 3 }{ 40 } \)
(d) \(\frac { 2 }{ 7 } \)
हल:
(a) \(\frac { 1 }{ 8 } \) = \(\frac { 1 }{ 8 } \) × \(\frac { 100 }{ 100 } \) = \(\frac { 100 }{ 8 } \) % = \(\frac { 25 }{ 2 } \) % = 12.5%
(b) \(\frac { 5 }{ 4 } \) = \(\frac { 5 }{ 4 } \) × \(\frac { 100 }{ 100 } \) = \(\frac{5 \times 100}{4}\)% = 125%
(c) \(\frac { 3 }{ 40 } \) = \(\frac { 3 }{ 40 } \) × \(\frac { 100 }{ 100 } \) = \(\frac{3 \times 100}{40}\)% = 7.5%
(d) \(\frac { 2 }{ 7 } \) = \(\frac { 2 }{ 7 } \) × \(\frac { 100 }{ 100 } \) = \(\frac { 200 }{ 7 } \)% = 28\(\frac { 4 }{ 7 } \)%
प्रश्न 2.
दी गई दशमलव भिन्नों को प्रतिशत में बदलो:
(a) 0.65
(b) 2.1
(c) 0.02
(d) 12.35
हल:
(a) 0.65 = \(\frac { 65 }{ 100 } \) = \(\frac { 65 }{ 100 } \) × 100% = 65%
(b) 2.1 = \(\frac { 21 }{ 10 } \) = \(\frac { 21 }{ 10 } \) × 100% = 210%
(c) 0.02 = \(\frac { 2 }{ 100 } \) = \(\frac { 2 }{ 100 } \) × 100% = 2%
(d) 12.35 = \(\frac { 1235 }{ 100 } \) = \(\frac { 1235 }{ 100 } \) × 100% = 1235%
![]()
प्रश्न 3.
अनुमान लगाइए कि आकृति का कितना भाग रंग दिया गया है और इस प्रकार ज्ञात कीजिए कि कितने प्रतिशत रंगीन है।
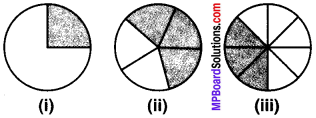
हल:
(i) ∵ रंगीन भाग = \(\frac { 1 }{ 4 } \)
∴ रंगे भाग का प्रतिशत = \(\frac { 1 }{ 4 } \) × 100% = 25%
अतः रंगीन भाग 25% है।
(ii) ∵ रंगीन भाग = \(\frac { 3 }{ 5 } \)
∴ रंगे भाग का प्रतिशत = \(\frac { 3 }{ 5 } \) × 100% = 60%
अतः रंगीन भाग 60% है।
(iii) यहाँ 8 में से 3 भाग रंगीन हैं।
∴ रंगीन भाग = \(\frac { 3 }{ 8 } \)
∴ रंगे भाग का प्रतिशत = \(\frac { 3 }{ 8 } \) × 100% = \(\frac { 75 }{ 2 } \) %
= 37.5%
अत: रंगीन भाग 37.5% है।
प्रश्न 4.
ज्ञात कीजिए:
(a) 250 का 15%
(b) 1 घण्टे का 1%
(c) 2500 का 20%
(d) 1 किग्रा का 75%
हल:
(a) 250 का 15% = \(\frac { 15 }{ 100 } \) × 250
= \(\frac { 75 }{ 2 } \) = 37.5%
(b) 1 घण्टे का 1% = \(\frac { 1 }{ 100 } \) × 1 घण्टे
= \(\frac { 1 }{ 100 } \) × 60 मिनट
= \(\frac { 3 }{ 5 } \) मिनट
= \(\frac { 3 }{ 5 } \) × 60 सेकण्ड
= 36 सेकण्ड
(c) 2500 का 20% = \(\frac { 20 }{ 100 } \) × 2500 = 500
(d) 1 किग्रा का 75% = \(\frac { 75 }{ 100 } \) × 1 किग्रा
= 0.75 किग्रा
= 0.75 × 1000 ग्राम = 750 ग्राम
![]()
प्रश्न 5.
सम्पूर्ण राशि ज्ञात कीजिए, यदि
(a) इसका 5%, 600 है।
(b) इसका 12%, 1080 है।
(c) इसका 40%,500 km है।
(d) इसका 70%, 14 मिनट है।
(e) इसका 8%, 40 लीटर है।
हल:
(a) माना कि सम्पूर्ण राशि x है।
∴ x का 5% = 600
या \(\frac { 5 }{ 100 } \) × x = 600
या x = \(\frac{600 \times 100}{5}\) = 12000
अत: अभीष्ट राशि 12000 है।
(b) मानाकि सम्पूर्ण राशि x है।
∴ x का 12% = 1080
या \(\frac { 12 }{ 100 } \) × x = 1080
या x = \(\frac{1080 \times 100}{12}\) = 9000
अतः अभीष्ट राशि 9000 है।
(c) मानाकि सम्पूर्ण राशि x है।
∴ x का 40% = 500 km
या \(\frac { 40 }{ 100 } \) × x = 500 km
या x = \(\frac{500 \times 100}{40}\) km = 1250 km
अतः अभीष्ट राशि 1250 km है।
(d) मानाकि सम्पूर्ण राशि x है।
∴ x का 70% = 14 मिनट या \(\frac { 70 }{ 100 } \) × x = 14 मिनट
या x = \(\frac{14 \times 100}{70}\) मिनट = 20 मिनट
अतः अभीष्ट राशि 20 मिनट है।
(e) मानाकि सम्पूर्ण राशि x है।
∴ x का 8% = 40 लीटर
या \(\frac { 8 }{ 100 } \) × x = 40 लीटर
या x = \(\frac{40 \times 100}{8}\) लीटर = 500 लीटर
अतः अभीष्ट राशि 500 लीटर है।
प्रश्न 6.
दिए गए प्रतिशतों को साधारण व दशमलव भिन्नों में बदलो और अपने उत्तर को सरलतम रूप में लिखो :
(a) 25%
(b) 150%
(c) 20%
(d) 5%
हल:
(a) साधारण भिन्न – 25% = \(\frac { 25 }{ 100 } \) = \(\frac { 1 }{ 4 } \)
दशमलव भिन्न = \(\frac { 1 }{ 4 } \) = 0.25
(b) साधारण भिन्न – 150% = \(\frac { 150% }{ 100 } \) = \(\frac { 3 }{ 2 } \)
दशमलव भिन्न – \(\frac { 3 }{ 2 } \) = 1.5
(c) साधारण भिन्न – 20% = \(\frac { 20 }{ 100 } \) = \(\frac { 1 }{ 5 } \)
दशमलव भिन्न- \(\frac { 1 }{ 5 } \) = 0.20
(d) साधारण भिन्न – 5% = \(\frac { 5 }{ 100 } \) = \(\frac { 1 }{ 20 } \)
दशमलव भिन्न – \(\frac { 1 }{ 20 } \) = 0.05
प्रश्न 7.
एक नगर में 30% महिलाएं, 40% पुरुष तथा शेष बच्चे हैं। बच्चों का प्रतिशत कितना है ?
हल:
∴ महिलाएँ = 30% तथा पुरुष = 40%
∴ बच्चों का प्रतिशत = 100% – (30% + 40%)
= 100% – 70% = 30%
प्रश्न 8.
किसी क्षेत्र के 15,000 मतदाताओं में से 60% ने मतदान में भाग लिया। ज्ञात कीजिए कि कितने प्रतिशत ने मतदान में भाग नहीं लिया। क्या अब ज्ञात कर सकते हैं कि वास्तव में कितने मतदाताओं ने मतदान नहीं किया ?
हल:
कुल मतदाता = 15,000
मतदान करने वाले मतदाताओं का प्रतिशत = 60%
∴ मतदान न करने वाले मतदाताओं का प्रतिशत
= 100% – 60% = 40%
मतदान न करने वाले मतदाताओं की संख्या
= 15000 का 40%
= \(\frac { 40 }{ 100 } \) × 15000 = 6000
अत: 6000 मतदाताओं ने मतदान नहीं किया।
![]()
प्रश्न 9.
मीता अपने वेतन में से ₹ 4000 बचाती है। यदि यह उसके वेतन का 10% है, तब उसका वेतन कितना है ?
हल:
माना कि उसका वेतन ₹ है।
उसकी बचत = वेतन का 10%
∴ x का 10% = ₹4000
या \(\frac { 10 }{ 100 } \) × x = ₹4000
या x = ₹ \(\frac{4000 \times 100}{10}\) = ₹40000
अत: उसका वेतन ₹40000 है।
प्रश्न 10.
एक स्थानीय क्रिकेट टीम ने, एक सत्र (Season) में 20 मैच खेले। इनमें से उस टीम ने 25% मैच जीते। जीते गए मैचों की संख्या कितनी थी ?
हल:
कुल खेले गये मैचों की संख्या = 20
टीम द्वारा जीते गए मैच = 25%
∴ जीते गए मैचों की संख्या = 20 का 25%
= \(\frac { 25 }{ 100 } \) × 20 = 5
अत: टीम ने 5 मैच जीते।
पाठ्य-पुस्तक पृष्ठ संख्या # 179
प्रयास कीजिए
प्रश्न 1.
15 मिठाइयों को मनु तथा सोनू में इस प्रकार बाँटिए कि उन्हें कुल का क्रमशः 20% तथा 80% मिले।
हल:
कुल मिठाइयों की संख्या = 15
मनु का हिस्सा = 15 का 20%
= \(\frac { 20 }{ 100 } \) × 15
= 3 मिठाइयाँ
सोनू का हिस्सा = 15 का 80%
= \(\frac { 80 }{ 100 } \) × 15
= 12 मिठाइयाँ
प्रश्न 2.
यदि किसी त्रिभुज के कोणों में अनुपात 2:3:4 है तब उसके प्रत्येक कोण की माप क्या होगी?
हल:
∵ त्रिभुज के तीनों अन्त:कोणों का योग = 180°
त्रिभुज के कोणों का अनुपात = 2:3:4
अनुपात का योग = 2 + 3 + 4 = 9

अतः अभीष्ट कोण 40°, 60° और 80° हैं।
![]()
पाठ्य-पुस्तक पृष्ठ संख्या # 180
प्रयास कीजिए
प्रश्न 1.
बढ़ने या घटने का प्रतिशत ज्ञात कीजिए :
(i) कमीज का मूल्य ₹ 80 से घटकर 60 हो गया।
(ii) किसी परीक्षा में प्राप्तांक बढ़कर 20 से 30 हो गए।
हल:
(i) कमीज का वास्तविक मूल्य = ₹ 80
कमीज का नया मूल्य = ₹60
कमीज के मूल्य में कमी = ₹80 – ₹60 = ₹20

(ii) मूल प्राप्तांक = 20
नये प्राप्तांक = 30
प्राप्तांक में वृद्धि = 30 – 20 = 10

प्रश्न 2.
मेरी माताजी कहती हैं कि उनके बचपन, के समय पैट्रोल की दर ₹ 1 प्रति लीटर थी और आजकल यह ₹52 प्रति लीटर है। पैट्रोल की दर में कितने प्रतिशत की वृद्धि हुई ?
हल:
पैट्रोल का पहले का मूल्य = ₹ 1 प्रति लीटर
पैट्रोल का नया मूल्य = ₹52 प्रति लीटर
पैट्रोल के मूल्य में वृद्धि =₹52 – ₹ 1 = ₹51

![]()
पाठ्य-पुस्तक पृष्ठ संख्या # 183
प्रयास कीजिए
प्रश्न 1.
एक दुकानदार ने एक कुर्सी ₹ 375 में खरीदी तथा ₹ 400 में बेच दी। उसका लाभ प्रतिशत ज्ञात कीजिए।
हल:
कुर्सी का क्रय मूल्य = ₹ 375
कुर्सी का विक्रय मूल्य = ₹ 400
∴ विक्रय मूल्य > क्रय मूल्य
∴ लाभ = ₹400 – ₹375 = ₹25

प्रश्न 2.
एक वस्तु ₹50 में क्रय की गई तथा 12 प्रतिशत लाभ पर बेच दी गई। उसका विक्रय मूल्य ज्ञात कीजिए।
हल:
वस्तु का क्रय मूल्य = ₹50, लाभ = 12%
∴ ₹50 पर लाभ = ₹50 का 12%
= \(\frac { 12 }{ 100 } \) × ₹50 = ₹6
अत: वस्तु का विक्रय मूल्य = ₹50 + ₹6 = ₹56
प्रश्न 3.
एक वस्तु ₹ 250 में बेचने पर 5 प्रतिशत लाभ प्राप्त हुआ। उसका क्रय मूल्य क्या था?
हल:
वस्तु का विक्रय मूल्य = ₹250, लाभ = 5%
माना कि क्रय मूल्य x रूपया है।
लाभ = x का 5%
= \(\frac { 5 }{ 100 } \) × x = ₹ \(\frac { x }{ 20 } \)
∴ विक्रय मूल्य = क्रय मूल्य + लाभ
∴ ₹ 250 = ₹x + ₹\(\frac { x }{ 20 } \)
या ₹250 = ₹ \(\frac { 21x }{ 20 } \)
या x = ₹ \(\frac{250 \times 20}{21}\) = ₹ 238 \(\frac { 2 }{ 21 } \)
अत: वस्तु का क्रय मूल्य = ₹ 238 \(\frac { 2 }{ 21 } \)
प्रश्न 4.
एक वस्तु 5 प्रतिशत हानि उठाकर ₹ 540 में बेची गई। उसका क्रय मूल्य क्या था ?
हल:
वस्तु का विक्रय मूल्य = ₹ 540, हानि = 5%
माना कि वस्तु का क्रय मूल्य = ₹ x
हानि = ₹ x का 5% = \(\frac { 5 }{ 100 } \) × x = ₹ \(\frac { x }{ 20 } \)
∴ विक्रय मूल्य = क्रय मूल्य – हानि
∴ ₹540 = ₹x – ₹\(\frac { x }{ 20 } \) = ₹ \(\frac { 19 }{ 20 } \)x
या x = ₹ \(\frac{540 \times 20}{19}\) = ₹ 568 \(\frac { 8 }{ 19 } \)
अत: वस्तु का क्रय मूल्य = 568 \(\frac { 8 }{ 19 } \)
![]()
पाठ्य-पुस्तक पृष्ठ संख्या # 185
प्रयास कीजिए
प्रश्न 1.
₹ 10000, 5 प्रतिशत वार्षिक दर से जमा किए जाते हैं। एक वर्ष बाद कितना ब्याज प्राप्त होगा?
हल:
मूलधन (P) = ₹10000, दर R = 5%,
समय (T) = 1 वर्ष
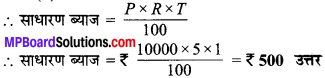
प्रश्न 2.
₹ 3500, 7 प्रतिशत वार्षिक दर से उधार दिए जाते हैं। दो वर्ष बाद कितना साधारण ब्याज देय होगा?
हल:
मूलधन (P) = ₹ 3500, दर (R) = 7%, समय (T) = 2 वर्ष
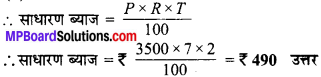
प्रश्न 3.
₹ 6,050, 6.5 प्रतिशत वार्षिक दर से उधार लिए जाते हैं। 3 वर्ष बाद कितना ब्याज तथा कितना मिश्रधन देय होगा?
हल:
मूलधन (P) = ₹ 6050, दर (R) = 6.5%, समय (T) = 3 वर्ष

∴ मिश्रधन = मूलधन + ब्याज
∴ मिश्रधन = ₹6050 + ₹ 1179.75
= ₹7229.75
प्रश्न 4.
₹ 7000, 3.5 प्रतिशत वार्षिक दर से दो वर्ष के लिए उधार लिए जाते हैं। दो वर्ष बाद कितना मिश्रधन देय होगा?
हल:
मूलधन (P) = ₹ 7000, दर (R) = 3.5%, समय (T) = 2 वर्ष

∴ मिश्रधन = मूलधन + ब्याज
∴ मिश्रधन = ₹7,000 + ₹490
= ₹7,490
![]()
पाठ्य-पुस्तक पृष्ठ संख्या # 186
प्रयास कीजिए
प्रश्न 1.
आपके बैंक खाते में ₹ 2,400 जमा हैं तथा ब्याज की दर 5 प्रतिशत वार्षिक है। कितने वर्षों बाद ब्याज की राशि ₹ 240 होगी?
हल:
यहाँ, मूलधन (P) = ₹ 2,400, दर (R) = 5%, ब्याज (S.I.) = ₹240, समय (T) = ?
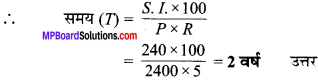
प्रश्न 2.
किसी धन का 5 प्रतिशत वार्षिक दर से 3 वर्ष का ब्याज ₹ 450 होता है। वह धन ज्ञात कीजिए।
हल:
यहाँ, दर (R) = 5%, समय (T) = 3 वर्ष, साधारण ब्याज (S.I.) = ₹ 450, मूलधन (P) = ?
