MP Board Class 7th Maths Solutions Chapter 12 बीजीय व्यंजक Ex 12.4
प्रश्न 1.
बराबर लम्बाई के रेखाखण्डों से बनाए गए अंकों के पैटर्न को देखिए। आप रेखाखण्डों से बने हुए इस प्रकार के अंकों को इलेक्ट्रॉनिक घड़ियों या कैलकुलेटरों पर देख सकते हैं।
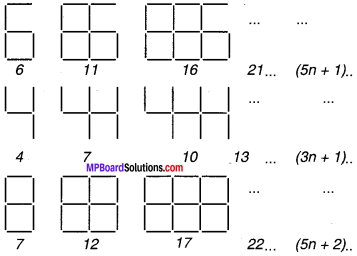
यदि बनाए गए अंकों की संख्या n ली जाए, तो उसके लिए आवश्यक रेखाखण्डों की n संख्या दर्शाने वाला बीजीय व्यंजक पैटर्न के दाईं ओर लिखा गया है। 6,4,8 के प्रकार के 5, 10, 100 अंकों को बनाने के लिए कितने रेखाखण्डों की आवश्यकता होगी?
हल:
(i) ∵ 6 की तरह n अंकों को बनाने में लगे रेखाखण्डों की संख्या
= (5n + 1)
∴ 5 अंकों की संख्या के लिए रेखाखण्डों की संख्या
= 5 × 5 + 1 = 25 + 1 = 26
10 अंकों की संख्या के लिए रेखाखण्डों की संख्या
= 5 × 10 + 1 = 50 + 1 = 51
100 अंकों की संख्या के लिए रेखाखण्डों की संख्या
= 5 × 100 + 1 = 500 + 1 = 501
(ii) ∵ 4 की तरह n अंकों को बनाने के लिए रेखाखण्डों की संख्या = (3n + 1)
∴ 5, 10, 100 अंकों को बनाने के लिए रेखाखण्डों की संख्या क्रमशः
3 × 5 + 1 = 15 + 1 = 16
3 × 10 + 1 = 30 + 1 = 31
3 × 100 + 1 = 300 + 1 = 301
(iii) 8 की तरह n अंकों को बनाने में लगे रेखाखण्डों की संख्या = (5n + 2)
∴ 5, 10, 100 को बनाने में लगे रेखाखण्डों की संख्या क्रमशः
5 × 5 + 2 = 25 + 2 = 27
5 × 10 + 2 = 50 + 2 = 52
5 × 100 + 2 = 500 + 2 = 502
![]()
प्रश्न 2.
संख्या पैटों की निम्नलिखित सारणी को पूरा करने के लिए, दिए हुए बीजीय व्यंजकों का प्रयोग कीजिए:
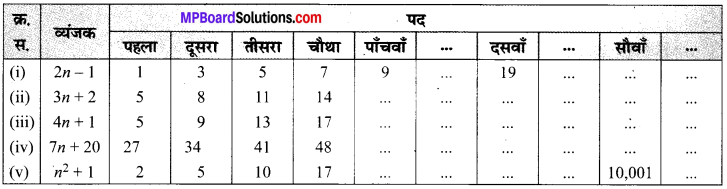
हल:
(i) व्यंजक (2n – 1) के लिए
100 वाँ पद = 2 × 100 – 1 = 200 – 1 = 199
(ii) व्यंजक (3n + 2) के लिए
5 वाँ पद = 3 × 5 + 2 = 15 + 2 = 17
10 वाँ पद = 3 × 10 + 2 = 30 + 2 = 32
100 वाँ पद = 3 × 100 + 2 = 300 + 2 = 302
(iii) व्यंजक (4n + 1) के लिए
5 वाँ पद = 4 × 5 + 1 = 20 + 1 = 21
10 वाँ पद = 4 × 10 + 1 = 40 + 1 = 41
100 वाँ पद = 4 × 100 + 1 = 400 + 1 = 401
(iv) व्यंजक 7n + 20 के लिए
5 वाँ पद = 7 × 5 + 20 = 35 + 20 = 55
10 वाँ पद = 7 × 10 + 20 = 70 + 20 = 90
100 वाँ पद = 7 × 100 + 20 = 700 + 20 = 720
(v) व्यंजक n2 + 1 के लिए
5 वाँ पद = (5)2 + 1 = 25 + 1 = 26
10 वाँ पद = (10)2 + 1 = 100 + 1 = 101